Caccioppoli-type estimates and $\mathcal {H}$-matrix approximations to inverses for FEM-BEM couplings

Abstract

We consider three different methods for the coupling of the finite element method and the boundary element method, the Bielak–MacCamy coupling, the symmetric coupling, and the Johnson–Nédélec coupling. For each coupling, we provide discrete interior regularity estimates. As a consequence, we are able to prove the existence of exponentially convergent $\mathcal {H}$-matrix approximants to the inverse matrices corresponding to the lowest order Galerkin discretizations of the couplings.

1 Introduction

Transmission problems are usually posed on unbounded domains, where a (possibly nonlinear) equation is given on some bounded domain, and another linear equation is posed on the complement of the bounded domain. While the interior problem can be treated numerically by the finite element method (FEM), the unbounded nature of the exterior problem makes requires a different approach. A suitable method to treat unbounded problems is provided by the boundary element method (BEM), where the differential equation in the unbounded domain is reformulated via an integral equation posed just on the boundary. In order to combine both methods for transmission problems, additional conditions on the interface have to be imposed, and the precise choice of these conditions leads to different couplings of the FEM and the BEM. We study three different FEM-BEM couplings, the Bielak–MacCamy coupling [9], Costabel’s symmetric coupling [13, 15], and the Johnson–Nédélec coupling [27]. Well-posedness and unique solvability of these formulation have been studied in, e.g., [1, 32, 35], where a main observation is that the coupled formulations are equivalent to an elliptic problem.

Elliptic problems typically feature interior regularity known as Caccioppoli estimates, where stronger norms can be estimated by weaker norms on larger domains. In this paper, we provide such Caccioppoli-type estimates for the discretized problem. More precisely, we obtain simultaneous interior regularity estimates for the finite element solution as well as for the single- and double-layer potential of the boundary element solution (cf. Theorems 2.4–2.6). Discrete Caccioppoli-type estimates for the FEM and the BEM separately can be found in our previous works [2, 18,19,20]. While the techniques for the FEM and the BEM part are similar therein, some essential modifications have to be made to treat the coupling terms on the boundary.

Caccioppoli-type estimates are at the heart of the proof that the inverses of stiffness matrices can be approximated by blockwise low-rank matrices. In this context, [8] was the first to construct local, separable approximations of the Green’s function of elliptic boundary value problems that converge at an exponential rate in the number of terms. The technique relies on iterating local approximations and using a Caccioppoli inequality on the continuous level. A projection then transfers this approximation to the discrete level and results in exponentially convergent blockwise low-rank approximations to the stiffness matrix up to the projection error. These results were further generalized in [3, 5, 10]. [16] extended this technique from elliptic PDEs to pseudodifferential operators. Fully discrete Caccioppoli inequalities, as developed here, allow one to avoid the final projection step and yield exponential convergence in the block rank. This approach was first developed for FEM-discretizations of elliptic PDEs in [18] and extended to BEM-matrices in [19, 20] and the fractional Laplacian in [28]. Here, we show also for the inverse of the FEM-BEM coupling matrix that it can be approximated at an exponential rate in the block rank by blockwise low-rank matrices. We adopt the specific setting of ${\mathcal H}$-matrices introduced in [23]. In comparison with other compression methods, $\mathcal {H}$-matrices have the advantage that they come with an additional approximate arithmetic that allows for addition, multiplication, inversion or LU-decompositions in the $\mathcal {H}$-matrix format; for more details, we refer to [21, 22, 24].

The paper is structured as follows: in Sect. 2, we present our model problem and state the main results of the article, the discrete Caccioppoli-type interior regularity estimates for each coupling, and the existence of exponentially convergent $\mathcal {H}$-matrix approximants to the inverse matrices corresponding to the FEM-BEM discretizations of the couplings. Section 3 provides an abstract framework for the proof of low-rank approximability to inverse matrices using Caccioppoli-type estimates, which can be applied for other problems as well. Section 4 is concerned with the proofs of the Caccioppoli-type estimates. Section 5 verifies the assumptions of the abstract framework of Sect. 3 for the three considered FEM-BEM couplings and consequently shows the approximation results for the inverse stiffness matrices. Finally, Sect. 6 provides some numerical examples.

2 Main results

On a Lipschitz domain $\varOmega \subset \mathbb {R}^d$, $d=2$, 3 with polygonal (for $d = 2$) or polyhedral (for $d = 3$) boundary $\varGamma := \partial \varOmega$, we study the transmission problem

$$\begin{aligned} -{\text {*}}{div}( \mathbf {C}\cdot \nabla u)&=f \qquad \qquad \qquad \text {in} \,\,\varOmega , \end{aligned}$$

(2.1a)

$$\begin{aligned} -\varDelta u ^ {{\text {*}}{ext}}&= 0\qquad \qquad \qquad \text {in} \,\,\,\varOmega ^ {\text {{ext}}}, \end{aligned}$$

(2.1b)

$$\begin{aligned} u-u ^ {{\text {*}}{ext}}&= u_0 \qquad \qquad \qquad \text {on} \,\, \varGamma , \end{aligned}$$

(2.1c)

$$\begin{aligned} \left( \mathbf {C} \nabla u - \nabla u ^ {{\text {*}}{ext}}\right) \cdot \nu&= \varphi _0 \qquad \qquad \qquad \text {on} \,\, \varGamma , \end{aligned}$$

(2.1d)

$$\begin{aligned} u ^ {{\text {*}}{ext}}&= {\left\{ \begin{array}{ll} \mathcal {O} ( \left| x \right| ^ {-1}) &{} \hbox { as}\, |x| \rightarrow \infty \, \hbox {if}\, d = 3\\ b \log |x| + \mathcal {O} ( \left| x \right| ^ {-1}) &{} \text{ for } b \in \mathbb {R} \text{ as } |x| \rightarrow \infty \text{ if } d = 2\text{. } \end{array}\right. }&\end{aligned}$$

(2.1e)

Here, $\varOmega ^\mathrm{ext}:= \mathbb {R}^d {\setminus }{\overline{\varOmega }}$ denotes the exterior of $\varOmega$, and $\nu$ denotes the outward normal vector. For the data, we assume $f \in L^2(\varOmega )$, $u_0 \in H^{1/2}(\varGamma )$, $\varphi _0 \in H^{-1/2}(\varGamma )$, and $\mathbf {C} \in L^{\infty }(\varOmega ;\mathbb {R}^d)$ to be pointwise symmetric and positive definite, i.e., there is a constant $C_\mathrm{ell}>0$ such that

(2.2)

For $d = 2$, we assume ${\text {diam}} \varOmega < 1$ for the single-layer operator V introduced below to be elliptic.

Remark 2.1

The radiation condition (2.1e) is such that the representation form $u^\mathrm{ext} = - \widetilde{V}\varphi + \widetilde{K}u^\mathrm{ext}$ holds in $\varOmega ^\mathrm{ext}$ with $\varphi = \nabla u^\mathrm{ext} \cdot \nu$ (see, e.g., [33, Chap. 3.1]). For $d =2$, the compatibility condition $\langle f,1\rangle _{L^2(\varOmega )} + \langle \varphi _0,1\rangle _{L^2(\varGamma )} = 0$ ensures $b = 0$ in (2.1e). See also [30, Thm. 8.9] for more on the radiation condition.

With the Green’s function for the Laplacian $G(x) = -\frac{1}{2\pi } \log \left| x \right|$ for $d=2$ and $G(x) = \frac{1}{4\pi }\frac{1}{\left| x \right| }$ for $d=3$, we introduce the single-layer boundary integral operator $V \in L(H^{-1/2}(\varGamma ),H^{1/2}(\varGamma ))$ by

$$\begin{aligned} V\phi (x) := \int _{\varGamma } G(x-y)\phi (y)ds_y, \quad x \in \varGamma . \end{aligned}$$

The double-layer operator $K \in L(H^{1/2}(\varGamma ),H^{1/2}(\varGamma ))$ has the form

$$\begin{aligned} K\phi (x) := \int _{\varGamma } (\partial _{\nu (y)}G(x-y))\phi (y)ds_y, \quad x \in \varGamma , \end{aligned}$$

where $\partial _{\nu (y)}$ denotes the normal derivative at the point y. The adjoint of K is denoted by $K'$. Finally, the hyper-singular operator $W\in L(H^{1/2}(\varGamma ),H^{-1/2}(\varGamma ))$ is given by

$$\begin{aligned} W\phi (x) := -\partial _{\nu (x)}\int _{\varGamma } (\partial _{\nu (y)}G(x-y))\phi (y)ds_y, \quad x \in \varGamma . \end{aligned}$$

The single-layer operator V is elliptic for $d=3$ and for $d=2$ provided ${\text {*}}{diam}(\varOmega ) < 1$. The hyper-singular operator W is semi-elliptic with a kernel of dimension being the number of components of connectedness of $\varGamma$. In addition to the boundary integral operators, we need the volume potentials $\widetilde{V}$ and $\widetilde{K}$ defined by

$$\begin{aligned} \widetilde{V} \phi ( x)&:= \int _{\varGamma }G( x-y) \phi ( y) d s _y, \quad x \in \mathbb {R}^d \backslash \varGamma ,\\ \widetilde{K} \phi ( x)&:= \int _{\varGamma } \partial _{{\nu } ( y) }G( x-y) \phi ( y) d s_y, \quad x \in \mathbb {R}^d \backslash \varGamma . \end{aligned}$$

Moreover, by $\gamma _0^\mathrm{int}$ we denote the interior trace operator (see [33, Thm. 2.6.8]) for $\varOmega$. In the following, in order to keep notation compact, we do not write trace operators, when it is clear that they are used, e.g., we write Wu for $u \in H^1(\varOmega )$ instead of $W(\gamma _0^\mathrm{int} u)$ or omit them, when we are using scalar products on $\varGamma$.

In this paper, we study discretizations of weak solutions of the model problem reformulated via three different FEM-BEM couplings: the Bielak–MacCamy coupling, Costabel’s symmetric coupling, and the Johnson–Nédélec coupling. All these couplings lead to a variational formulation of finding $(u,\varphi ) \in H^1(\varOmega ) \times H^{-1/2}(\varGamma ) =: \mathbf {X}$ such that

$$\begin{aligned} a(u,\varphi ;\psi ,\zeta ) = g(\psi ,\zeta ) \quad \forall (\psi ,\zeta ) \in \mathbf {X}, \end{aligned}$$

(2.3)

where $a: \mathbf {X}\times \mathbf {X} \rightarrow \mathbb {R}$ is a bilinear form and $g: \mathbf {X} \rightarrow \mathbb {R}$ is a continuous linear functional.

For the discretization, we assume that $\varOmega$ is triangulated by a quasi-uniform mesh ${\mathcal T}_h=\{T_1,\dots ,T_{{\widehat{n}}}\}$ of mesh width $h := \max _{T_j\in \mathcal {T}_h}\mathrm{diam}(T_j)$. The elements $T_j \in \mathcal {T}_h$ are open triangles ($d=2$) or tetrahedra ($d=3$). Additionally, we assume that the mesh $\mathcal {T}_h$ is regular in the sense of Ciarlet and $\gamma$-shape regular in the sense that we have $\mathrm{diam}(T_j) \le \gamma \,|T_j|^{1/d}$ for all $T_j\in \mathcal {T}_h$, where $|T_j|$ denotes the Lebesgue measure of $T_j$. By $\mathcal {K}_h:=\{K_1,\dots ,K_ {\widehat{m}}\}$, we denote the restriction of ${\mathcal T}_h$ to the boundary $\varGamma$, which is a regular and shape-regular triangulation of the boundary.

For simplicity, we consider lowest order Galerkin discretizations in $S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$, where

$$\begin{aligned} S^{1,1}({\mathcal T}_h)&:= \{u \in C({\overline{\varOmega }})\, :\, u|_T \in P_1(T) \quad \forall T \in \mathcal {T}_h \}, \\ S^{0,0}(\mathcal {K}_h)&:= \{u \in L^2(\varGamma )\, :\, u|_K \in P_0(K) \quad \forall K \in \mathcal {K}_h \}, \end{aligned}$$

with $P_p(T)$ denoting the space of polynomials of degree (at most) p on an element T of the triangulation. We let ${\mathcal B}_h:= \{\xi _j\, :\, j = 1,\dots , n\}$ be the basis of $S^{1,1}({\mathcal T}_h)$ consisting of the standard nodal hat functions, and we let ${\mathcal W}_h:= \{\chi _j\, :\, j = 1,\dots , m\}$ be the basis of $S^{0,0}({\mathcal K}_h)$ that consists of the characteristic functions of the surface elements. These bases feature the following norm equivalences:

$$\begin{aligned}&c_1h^{d/2}\left\| \mathbf {x} \right\| _2 \le \left\| \varPhi \mathbf {x} \right\| _{L^2(\varOmega )} \le c_2 h^{d/2}\left\| \mathbf {x} \right\| _2 \quad \quad \;\; \forall \, \mathbf {x} \in \mathbb {R}^n, \end{aligned}$$

(2.4a)

$$\begin{aligned}&c_3h^{(d-1)/2}\left\| \mathbf {y} \right\| _2 \le \left\| \varPsi \mathbf {y} \right\| _{L^2(\varGamma )} \le c_4 h^{(d-1)/2}\left\| \mathbf {y} \right\| _2 \quad \forall \, \mathbf {y} \in \mathbb {R}^m \end{aligned}$$

(2.4b)

for the isomorphisms $\varPhi :\mathbb {R}^n\rightarrow S^{1,1}({\mathcal T}_h)$, $\mathbf {x} \mapsto \sum _{j=1}^n\mathbf {x}_j\xi _j$ and $\varPsi :\mathbb {R}^m\rightarrow S^{0,0}({\mathcal K}_h)$, $\mathbf {y} \mapsto \sum _{j=1}^m\mathbf {y}_j\chi _j$.

Remark 2.2

We note that differently scaled bases can be employed as well, which would just change the powers of h on the right-hand sides in the main result, Theorem 2.13.

Finally, we need the notion of concentric boxes.

Definition 2.3

(Concentric boxes) A cube (for $d = 3$) or a square (for $d = 2$) will be called a box. Two boxes $B_R$ and $B_{R^\prime }$ of side length R and ${R^\prime }$ are said to be concentric if they have the same barycenter and $B_R$ can be obtained by a stretching of $B_{R^\prime }$ by the factor $R/R^\prime$ taking their common barycenter as the origin.

Before we can state our first main results, the interior regularity estimates, we specify the norm we are working with, an h-weighted norm equivalent to the $H^1$-norm. For a box $B_R$ with side length R, an open set $\omega \subset \mathbb {R}^d$, and $v \in H^1(B_R\cap \omega )$, we introduce

$$\begin{aligned} \left| \! \left| \! \left| v \right| \! \right| \! \right| ^2 _{h, R, \omega } := h^2\left\| \nabla v \right\| ^2_{L^2(B_{R}\cap \omega )} + \left\| v \right\| ^2_{L^2(B_{R}\cap \omega )}. \end{aligned}$$

(2.5)

For the case $\omega = \mathbb {R}^d$, we abbreviate $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{h,R,\mathbb {R}^d} =: \left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{h,R}$ and for the case $\omega = \mathbb {R}^d\backslash \varGamma$ we write $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{h,R,\mathbb {R}^d\backslash \varGamma } =: \left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{h,R,\varGamma ^c}$ and understand the norms over $B_R\backslash \varGamma$ as a sum of integrals over $B_R\cap \varOmega$ and $B_R\cap \varOmega ^\mathrm{ext}$. Moreover, for triples $(u,v,w) \in H^1(B_R\cap \varOmega ) \times H^1(B_R)\times H^1(B_R\backslash \varGamma )$, we set

$$\begin{aligned} \left| \! \left| \! \left| (u,v,w) \right| \! \right| \! \right| _{h,R}^2 := \left| \! \left| \! \left| u \right| \! \right| \! \right| _{h,R,\varOmega }^2+\left| \! \left| \! \left| v \right| \! \right| \! \right| _{h,R}^2+\left| \! \left| \! \left| w \right| \! \right| \! \right| _{h,R,\varGamma ^c}^2. \end{aligned}$$

(2.6)

We mention that u will be the interior solution, v be chosen as a single-layer potential and w as a double-layer potential (which jumps across $\varGamma$), which explains the different requirements for the set $\omega$.

2.1 The Bielak–MacCamy coupling

The Bielak–MacCamy coupling is derived by making a single-layer ansatz for the exterior solution, i.e., $u^\mathrm{ext} = \widetilde{V}\varphi$ in $\varOmega ^\mathrm{ext}$ with an unknown density $\varphi \in H^{-1/2}(\varGamma )$. For more details, we refer to [9]. This approach leads to the bilinear form

(2.7a)

(2.7b)

Replacing $H^1 (\varOmega ) \times H^{-{1}/{2}}(\varGamma )$ by the finite dimensional subspace $S^{1,1}(\mathcal {T}_h) \times S^{0,0}( \mathcal {\mathcal {K}}_h)$, we arrive at the Galerkin discretization of (2.7) of finding $( u _h , \varphi _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$ such that

(2.8a)

(2.8b)

If the ellipticity constant of $\mathbf {C}$ satisfies $C_\mathrm{ell} > 1/4$, then [1, Thm. 9] shows that the Bielak–MacCamy coupling is equivalent to an elliptic problem with the use of a (theoretical) implicit stabilization. Therefore, (2.8) is uniquely solvable.

The following theorem is one of the main results of our paper. It states that for the interior finite element solution and the single-layer potential of the boundary element solution, a Caccioppoli type estimate holds, i.e., the stronger $H^1$-seminorm can be estimated by a weaker h-weighted $H^1$-norm on a larger domain.

Theorem 2.4

Assume that $C_\mathrm{ell} > 1/4$ in (2.2). Let $\varepsilon \in (0,1)$ and $R \in (0,2{\text {*}}{diam}(\varOmega ))$ be such that $\frac{h}{R} < \frac{\varepsilon }{16}$, and let $B_R$ and $B_{(1+\varepsilon )R}$ be two concentric boxes. Assume that the data is localized away from $B_{(1+\varepsilon )R}$, i.e., $({\text {*}}{supp} f \cup {\text {*}}{supp} \varphi _0 \cup {\text {*}}{supp} u_0) \cap B_{(1+\varepsilon )R} = \emptyset$. Then, there exists a constant C depending only on $\varOmega$, d, ${{\mathbf {C}}}$, and the $\gamma$-shape regularity of the quasi-uniform triangulation $\mathcal {T}_h$ such that for the solution $(u_h,\varphi _h)$ of (2.8) we have

$$\begin{aligned} \left\| \nabla u_h \right\| _ {L^2(B_{R}\cap \varOmega )} +\left\| \nabla \widetilde{V} \varphi _h \right\| _ {L^2(B_{R})}&\le \frac{C}{\varepsilon R} \left( \left| \! \left| \! \left| u_h \right| \! \right| \! \right| _{h,( 1+\varepsilon ) R, \varOmega } + \left| \! \left| \! \left| \widetilde{V}\varphi _h \right| \! \right| \! \right| _{h,(1+\varepsilon ) R} \right) , \end{aligned}$$

where the norms on the right-hand side are defined in (2.5).

With the bases $\mathcal {B}_h$ of $S^{1,1}(\mathcal {T}_h)$ and $\mathcal {W}_h$ of $S^{0,0}(\mathcal {K}_h)$, the Galerkin discretization (2.8) leads to a block matrix $\mathbf {A}_\mathrm{bmc} \in \mathbb {R}^ {(n+m) \times ( n+m)}$

$$\begin{aligned} \mathbf {A}_\mathrm{bmc}:= \begin{pmatrix} \mathbf {A}&{}\quad \frac{1}{2}\mathbf {M}^T-\mathbf {K}^T\\ \mathbf {M}&{}\quad \;\;\; {-}\mathbf {V} \end{pmatrix}, \end{aligned}$$

(2.9)

where $\mathbf {A} \in \mathbb {R} ^ {n\times n}$ is given by , $\mathbf {M} \in \mathbb {R} ^ {m\times n}$ by , $\mathbf {K} \in \mathbb {R} ^ {m\times n}$ by , and $\mathbf {V} \in \mathbb {R} ^ {m\times m}$ by . As mentioned in the introduction, we omitted the trace operators, i.e., in $\mathbf {M}$ and $\mathbf {K}$, $\xi _i$ is understood as $\gamma _0^\mathrm{int} \xi _i$.

2.2 Costabel’s symmetric coupling

The coupling is based on the representation formula $u^\mathrm{ext} = - \widetilde{V}\varphi + \widetilde{K}u^\mathrm{ext}$ in $\varOmega ^\mathrm{ext}$ with $\varphi = \nabla u^\mathrm{ext} \cdot \nu$ (see, e.g., [33, Chap. 3.1]). Coupling the interior and exterior solution in a symmetric way (which uses all four boundary integral operators) results in Costabel’s symmetric coupling, introduced in [15, 25]. Here, the bilinear form and right-hand side are given by

(2.10a)

(2.10b)

The Galerkin discretization leads to the problem of finding $(u_h , \varphi _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$ such that

(2.11a)

(2.11b)

for all $(\psi _h,\zeta _h) \in S^{1,1}(\mathcal {T}_h)\times S^{0,0}(\mathcal {K}_h)$.

With similar arguments as for the Bielak–MacCamy coupling, [1] proves unique solvability for the symmetric coupling for any $C_\mathrm{ell}>0$.

The following theorem is similar to Theorem 2.4 and provides a simultaneous Caccioppoli-type estimate for the interior solution as well as for the single-layer potential of the boundary solution and the double-layer potential of the trace of the interior solution. Here, the double-layer potential appears in addition since all boundary integral operators, especially the hyper-singular operator, arise in the coupling.

Theorem 2.5

Let $\varepsilon \in (0,1)$ and $R \in (0,2{\text {*}}{diam}(\varOmega ))$ be such that $\frac{h}{R} < \frac{\varepsilon }{32}$, and let $B_R$ and $B_{(1+\varepsilon )R}$ be two concentric boxes. Assume that the data is localized away from $B_{(1+\varepsilon )R}$, i.e., $({\text {*}}{supp} f \cup {\text {*}}{supp}v_0 \cup {\text {*}}{supp} w_0) \cap B_{(1+\varepsilon )R} = \emptyset$. Then, there exists a constant C depending only on $\varOmega$, d, ${{\mathbf {C}}}$ and the $\gamma$-shape regularity of the quasi-uniform triangulation $\mathcal {T}_h$ such that for the solution $(u_h,\varphi _h)$ of (2.11) we have

$$\begin{aligned}&\left\| \nabla u_h \right\| _ {L^2(B_{R}\cap \varOmega )} + \left\| \nabla \widetilde{V} \varphi _h \right\| _ {L^2(B_{R})} + \left\| \nabla \widetilde{K}u_h \right\| _ {L^2(B_{R}\backslash \varGamma )}\nonumber \\&~~~~~~~~~~~\qquad \qquad \qquad \quad \le \frac{C}{\varepsilon R} \left| \! \left| \! \left| (u_h,{\widetilde{V}} \phi _h,{\widetilde{K}} u_h) \right| \! \right| \! \right| _{h,(1+\varepsilon ) R}, \end{aligned}$$

(2.12)

where the norm on the right-hand side is defined in (2.6).

With the bases $\mathcal {B}_h$ of $S^{1,1}(\mathcal {T}_h)$ and $\mathcal {W}_h$ of $S^{0,0}(\mathcal {K}_h)$, the Galerkin discretization (2.11) leads to a block matrix $\mathbf {A}_\mathrm{sym} \in \mathbb {R}^ {(n+m) \times ( n+m)}$

$$\begin{aligned} \mathbf {A}_\mathrm{sym}:= \begin{pmatrix} \mathbf {A}+\mathbf {W}&{}\ \mathbf {K}^T-\frac{1}{2}\mathbf {M}^T\\ \frac{1}{2}\mathbf {M}-\mathbf {K}&{}\ \mathbf {V} \end{pmatrix}, \end{aligned}$$

(2.13)

where $\mathbf {A}$, $\mathbf {M}$, $\mathbf {K}$ are defined in (2.9), and $\mathbf {W} \in \mathbb {R}^{n\times n}$ is given by . As mentioned in the introduction, we omitted the trace operators. Thus, the matrix $\mathbf {W}$ is assembled with respect to the traces of basis functions in the volume $\varOmega$.

2.3 The Johnson–Nédélec coupling

The Johnson–Nédélec coupling, introduced in [27] again uses the representation formula for the exterior solution, but differs from the symmetric coupling in the way how the interior and exterior solutions are coupled on the boundary. Instead of all four boundary integral operators, only the single-layer and the double-layer operator are needed. The bilinear form for the Johnson–Nédélec coupling is given by

(2.14a)

(2.14b)

The Galerkin discretization in $S^{1,1}(\mathcal {T}_h) \times S^{0,0}( \mathcal {\mathcal {K}}_h)$ leads to the problem of finding $(u_h,\varphi _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}( \mathcal {\mathcal {K}}_h)$ such that, for all $\psi _h \in S^{1,1}(\mathcal {T}_h)$ and $\zeta _h \in S^{0,0}( \mathcal {\mathcal {K}}_h).$

(2.15a)

(2.15b)

As in the case of the Bielak–MacCamy coupling, the Johnson–Nédélec coupling has a unique solution provided $C_\mathrm{ell}>1/4$, see [1].

The following theorem gives the result analogous to Theorems 2.4 and 2.5 for the Johnson–Nédélec coupling. Similarly to the symmetric coupling, we simultaneously control a stronger norm of the interior solution and both layer potentials by a weaker norm on a larger domain.

Theorem 2.6

Assume that $C_\mathrm{ell} > 1/4$ in (2.2). Let $\varepsilon \in (0,1)$ and $R \in (0,2{\text {*}}{diam}(\varOmega ))$ be such that $\frac{h}{R} < \frac{\varepsilon }{32}$, and let $B_R$ and $B_{(1+\varepsilon )R}$ be two concentric boxes. Assume that the data is localized away from $B_{(1+\varepsilon )R}$, i.e., $({\text {*}}{supp} f\cup {\text {*}}{supp} \varphi _0 \cup {\text {*}}{supp} w_0) \cap B_{(1+\varepsilon )R} = \emptyset$. Then, there exists a constant C depending only on $\varOmega$, d, ${{\mathbf {C}}}$ and the $\gamma$-shape regularity of the quasi-uniform triangulation $\mathcal {T}_h$ such that for the solution $(u_h,\varphi _h)$ of (2.11) we have

$$\begin{aligned}&\left\| \nabla u_h \right\| _ {L^2(B_{R}\cap \varOmega )} + \left\| \nabla \widetilde{V} \varphi _h \right\| _ {L^2(B_{R})} + \left\| \nabla \widetilde{K}u_h \right\| _ {L^2(B_{R}\backslash \varGamma )}\nonumber \\&~~~~~~~~~\qquad \qquad \qquad \qquad \le C \frac{R}{(\varepsilon R)^2} \left| \! \left| \! \left| (u_h, \widetilde{V}\varphi _h, \widetilde{K}u_h ) \right| \! \right| \! \right| _{h,( 1+\varepsilon ) R}, \end{aligned}$$

(2.16)

where the norm on the right-hand side is defined in (2.6).

With the bases $\mathcal {B}_h$ of $S^{1,1}(\mathcal {T}_h)$ and $\mathcal {W}_h$ of $S^{0,0}(\mathcal {K}_h)$, the Galerkin discretization (2.15) leads to a matrix $\mathbf {A}_\mathrm{jn} \in \mathbb {R}^ {(n+m) \times ( n+m)}$

$$\begin{aligned} \mathbf {A}_\mathrm{jn}:= \begin{pmatrix} \mathbf {A} &{}\ -\mathbf {M}^T\\ \frac{1}{2}\mathbf {M}-\mathbf {K}&{}\ \mathbf {V} \end{pmatrix}, \end{aligned}$$

(2.17)

where $\mathbf {A}$, $\mathbf {M}$, $\mathbf {K}$, $\mathbf {V}$ are defined in (2.9).

2.4 $\mathcal {H}$-Matrix approximation of inverses

As a consequence of the Caccioppoli-type inequalities, we are able to prove the existence of $\mathcal {H}$-matrix approximants to the inverses of the stiffness matrices corresponding to the discretized FEM-BEM couplings.

We briefly introduce the matrix compression format of $\mathcal {H}$-matrices. For more detailed information, we refer to [6, 11, 23, 24]. The main idea of $\mathcal {H}$-matrices is to store certain far field blocks of the matrix efficiently as a low-rank matrix. In order to choose blocks that are suitable for compression, we need to introduce the concept of admissibility.

Definition 2.7

(Bounding boxes and $\eta$-admissibility) A cluster $\tau$ is a subset of the index set $\mathcal {I}=\{1,2,...,n+m\}$. For a cluster $\tau \subset \mathcal {I}$, a set $B_{R_\tau } \subseteq \mathbb {R}^d$ is called a bounding box if $B_{R_\tau }$ is an axis-parallel hyper cube with side length $R_\tau$ and $\cup _ {i \in \tau } {\text {*}}{supp} \xi _i \subseteq B_{R_\tau }$ as well as $\cup _ {i \in \tau } {\text {*}}{supp} \chi _i \subseteq B_{R_\tau }$.

For $\eta >0$, a pair of clusters $(\tau , \sigma )$ with $\tau , \sigma \subset \mathcal {I}$ is called $\eta$-admissible, if there exist bounding boxes $B_{R_\tau }$ and $B_{R_\sigma }$ such that

$$\begin{aligned} \max \{{\text {*}}{diam}(B_{R_\tau }), {\text {*}}{diam}(B_{R_\sigma })\} \le \eta \, {\text {*}}{dist} (B_{R_\tau },B_{R_\sigma }). \end{aligned}$$

Remark 2.8

Definition 2.7 clusters the degrees of freedom associated with the triangulation ${\mathcal T}_h$ of $\varOmega$ and the triangulation ${\mathcal K}_h$ of $\varGamma$ simultaneously.

The symmetry of the matrix $\mathbf {A}_\mathrm{sym}$ of the symmetric coupling also allows one to use the weaker admissibility condition $\min \{{\text {*}}{diam}(B_{R_\tau }), {\text {*}}{diam}(B_{R_\sigma })\} \le \eta \, {\text {*}}{dist} (B_{R_\tau },B_{R_\sigma })$.

The block-partition of $\mathcal {H}$-matrices is based on so-called cluster trees.

Definition 2.9

(Cluster tree) A cluster tree with leaf size $n_\mathrm{leaf} \in \mathbb {N}$ is a binary tree $\mathbb {T}_{\mathcal {I}}$ with root $\mathcal {I}$ such that each cluster $\tau \in \mathbb {T}_{\mathcal {I}}$ is either a leaf of the tree and satisfies $\left| \tau \right| \le n_\mathrm{leaf}$, or there exist disjoint subsets $\tau '$, $\tau '' \in \mathbb {T}_{\mathcal {I}}$ of $\tau$, so-called sons, with $\tau = \tau ' \cup \tau ''$. We denote the set of sons of $\tau$ by $\mathcal { S}(\tau ) := \left\{ \tau ' , \tau '' \right\} .$ Here and below, $\left| \tau \right|$ denotes the cardinality of the finite set $\tau$. The level function $\mathrm{level}: \mathbb {T}_{\mathcal {I}} \rightarrow \mathbb {N}_0$ is inductively defined by $\mathrm{level}(\mathcal {I}) = 0$ and $\mathrm{level}(\tau ') := \mathrm{level}(\tau ) + 1$ for $\tau '$ a son of $\tau$. The depth of a cluster tree is $\mathrm{depth}(\mathbb {T}_{\mathcal {I}}) := \max _{\tau \in \mathbb {T}_{\mathcal {I}}}\mathrm{level}(\tau )$.

Definition 2.10

(Block cluster tree, sparsity constant and partition) Let $\mathbb {T}_ \mathcal {I}$ be a cluster tree with root $\mathcal { I}$ and $\eta > 0$ be a fixed admissibility parameter. The block cluster tree $\mathbb {T}_{\mathcal {I} \times \mathcal {I}}$ is a tree constructed recursively from the root $\mathcal {I} \times \mathcal {I}$ such that for each block $\tau \times \sigma \in \mathbb {T}_{\mathcal {I} \times \mathcal {I}}$ with $\tau ,\, \sigma \in \mathbb {T}_\mathcal {I}$, the set of sons of $\tau \times \sigma$ is defined as

$$\begin{aligned} \mathcal {S} (\tau \times \sigma ):= \left\{ \begin{array}{ll} \emptyset &{} \quad \hbox {if } \tau \times \sigma \hbox { is}\, \eta \hbox {-admissible or}\, \mathcal {S} (\tau )= \emptyset \hbox { or }\mathcal {S} (\sigma )= \emptyset , \\ \mathcal {S} (\tau ) \times \mathcal {S} (\sigma ) &{} \quad \text{ else }. \end{array} \right. \end{aligned}$$

The sparsity constant $C_\mathrm{sp}$ of a block cluster tree, see, e.g., [22, 26], is given as

$$\begin{aligned} C_\mathrm{sp} := \max \left\{ \begin{array}{l}\max _{\tau \in \mathbb {T}_{\mathcal {I}}} \left| \{\sigma \in \mathbb {T}_{\mathcal {I}} \, : \, \tau \times \sigma \in \mathbb {T}_{\mathcal {I} \times \mathcal {I}}\} \right| ,\\ \max _{\sigma \in \mathbb {T}_{\mathcal {I}}}\left| \{\tau \in \mathbb {T}_{\mathcal {I}} \, : \, \tau \times \sigma \in \mathbb {T}_{\mathcal {I} \times \mathcal {I}}\} \right| \end{array}\right\} . \end{aligned}$$

(2.18)

The leaves of the block cluster tree induce a partition P of the set $\mathcal {I} \times \mathcal {I}$. For such a partition P and a fixed admissibility parameter $\eta > 0$, we define the far field and the near field as

$$\begin{aligned} P_\mathrm{far} := \{(\tau ,\sigma ) \in P \; : \; (\tau ,\sigma ) \; \text {is} \,\eta \hbox {-admissible}\}, \quad P_\mathrm{near} := P{\setminus } P_\mathrm{far}. \end{aligned}$$

(2.19)

Remark 2.11

For our purposes, a precise and efficient construction of a partition is not of interest; it suffice to have a given partition and decomposition into near field and far field at hand. As such, we call a partition satisfying the conditions of Definitions 2.10 a partition of $\mathcal {I} \times \mathcal {I}$ that is based on a cluster tree $\mathbb {T}_{\mathcal {I}}$.

Definition 2.12

($\mathcal {H}$-matrices) Let P be a partition of $\mathcal {I} \times \mathcal {I}$ that is based on a cluster tree $\mathbb {T}_{\mathcal {I}}$ and $\eta >0$. A matrix $\mathbf {A} \in \mathbb {R} ^ {(n+m)\times (n\times m)}$ is an $\mathcal {H}$-matrix with blockwise rank r, if for every $\eta$-admissible cluster pair $(\tau , \sigma ) \in P_\mathrm{far}$, we have a low-rank factorization

$$\begin{aligned} \mathbf {A}|_{\tau \times \sigma }=\mathbf {X}_{\tau \sigma } \mathbf {Y}^ T_{\tau \sigma }, \end{aligned}$$

where $\mathbf {X}_{\tau \sigma } \in \mathbb {R} ^ {|\tau |\times r}$ and $\mathbf {Y}_{\tau \sigma } \in \mathbb {R} ^ {|\sigma |\times r }$.

Due to the low-rank structure on far-field blocks, the memory requirement to store an $\mathcal {H}$ matrix is given by $\mathcal {O}(C_\mathrm{sp}{\text {*}}{depth}(\mathbb {T}_{\mathcal {I}})r(n+m))$. Provided $C_\mathrm{sp}$ is bounded and the cluster tree is balanced, i.e., ${\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) = \mathcal {O}(\log (n+m))$, which can be ensured by suitable clustering methods (e.g. geometric clustering [24]), we get a storage complexity of $\mathcal {O}(r(n+m)\log (n+m))$.

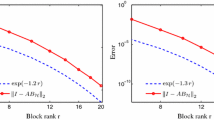
The following theorem shows that the inverse matrices $\mathbf {A}_\mathrm{bmc}^{-1}$, $\mathbf {A}_\mathrm{sym}^{-1}$, and $\mathbf {A}_\mathrm{jn}^{-1}$ corresponding to the three mentioned FEM-BEM couplings can be approximated in the $\mathcal {H}$-matrix format, and the error converges exponentially in the maximal block rank employed.

Theorem 2.13

For a fixed admissibility parameter $\eta >0$, let P be a partition of $\mathcal {I} \times \mathcal {I}$ that is based on the cluster tree $\mathbb {T}_{\mathcal {I}}$. Then, there exists an $\mathcal {H}$-matrix $\mathbf {B}_{\mathcal {H}}$ with maximal blockwise rank r such that

$$\begin{aligned} \left\| \mathbf {A}_\mathrm{bmc}^{-1} -\mathbf {B}_{\mathcal {H}} \right\| _2 \le C_\mathrm{apx} C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) h^{-(2+d)} e^{-br^{1/(2d+1)}} \end{aligned}$$

for the Bielak–MacCamy coupling. In the same way, there exists a blockwise rank-r $\mathcal {H}$-matrix $\mathbf {B}_{\mathcal {H}}$ such that

$$\begin{aligned} \left\| \mathbf {A}_\mathrm{sym}^{-1} -\mathbf {B}_{\mathcal {H}} \right\| _2 \le C_\mathrm{apx} C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) h^{-(2+d)} e^{-br^{1/(3d+1)}} \end{aligned}$$

for the symmetric coupling and

$$\begin{aligned} \left\| \mathbf {A}_\mathrm{jn}^{-1} -\mathbf {B}_{\mathcal {H}} \right\| _2 \le C_\mathrm{apx} C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) h^{-(2+d)} e^{-br^{1/(6d+1)}} \end{aligned}$$

for the Johnson–Nédélec coupling. Here, $\left\| \cdot \right\| _2$ denotes the spectral norm and the constants $C_\mathrm{apx}>0$ and $b>0$ depend only on $\varOmega$, d, ${{\mathbf {C}}}$, $\eta$, and the $\gamma$-shape regularity of the quasi-uniform triangulations $\mathcal {T}_h$ and $\mathcal {K}_h$.

Remark 2.14

The previous approximation result can also be formulated in norms other than the spectral norm, e.g., the Frobenius norm $\left\| \mathbf {\cdot } \right\| _F$ that is commonly used in the $\mathcal {H}$-matrix literature. Using the norm equivalence $\left\| \mathbf {A} \right\| _2 \le \left\| \mathbf {A} \right\| _F \le \sqrt{N}\left\| \mathbf {A} \right\| _2$ for arbitrary $\mathbf {A} \in \mathbb {R}^{N\times N}$ shows that this simply produces a different (algebraic) prefactor to the exponentials in Theorem 2.13.

3 An abstract setting for $\mathcal {H}$-matrix approximation to inverse matrices

Analyzing the procedure in [2, 18, 19] shows structural similarities in the derivation of ${\mathcal H}$-matrix approximations based on low-dimensional spaces of functions: A single-step approximation is obtained by using a Scott–Zhang operator on a coarse grid. Iterating this argument is made possible by a Caccioppoli-inequality, resulting in a multi-step approximation. The key ingredients of the argument are collected in properties (A1)–(A3) below. We mainly follow [2].

3.1 Abstract setting: from matrices to functions

We start by reformulating the matrix approximation problem as a question of approximating certain functions from low dimensional spaces. Let $\mathbf {X}$ be a Hilbert space of functions. We consider variational problems of the form: find $\mathbf {u} \in \mathbf {X}$ such that

for given $a(\cdot ,\cdot ): \mathbf {X}\times \mathbf {X} \rightarrow \mathbb {R}$, $\varvec{f} \in \mathbf {X}'$. Here, the bold symbols may denote vectors, e.g., $\mathbf {u}= (u,\varphi )$ in (2.3) for $\mathbf {X}= H^1(\varOmega )\times H^{-1/2}(\varGamma )$, and denotes the appropriate duality bracket.

For fixed k, $\ell \in \mathbb {N}$ (given by the formulation of the problem), we define $\mathbf {L}^2 := L^2(\varOmega )^k\times L^2(\varGamma )^\ell$.

Definition 3.1

Let $\mathbf {X}_N \subset \mathbf {X}$ be a finite dimensional subspace of dimension N that is also a subspace $\mathbf {X}_N \subset \mathbf {L}^2$. Then, the linear mapping $\mathcal {S}_N : \mathbf {X}' \rightarrow \mathbf {X}_N$ is called the discrete solution operator, if for every $\varvec{f} \in \mathbf {X}'$, there exists a unique function $\mathcal {S}_N \varvec{f} \in \mathbf {X}_N$ satisfying

(3.1)

Let $\{\varvec{\phi }_1,\dots ,\varvec{\phi }_N\} \subseteq \mathbf {X}_N$ be a basis of $\mathbf {X}_N$. We denote the Galerkin matrix $\mathbf {A} \in \mathbb {R}^{N \times N}$ by

$$\begin{aligned} \mathbf {A} =\left( a(\varvec{\phi }_j,\varvec{\phi }_i)\right) _ {i,j=1} ^N. \end{aligned}$$

(3.2)

The translation of the problem of approximating matrix blocks of $\mathbf {A}^{-1}$ to the problem of approximating certain functions from low dimensional spaces essentially depends on the following crucial property (A1), the existence of a local dual basis.

• (A1) There exist dual functions $\{\varvec{\lambda }_1,\dots ,\varvec{\lambda }_N\} \subset \mathbf {L}^2$ satisfying

  

  for all $i,j \in \{1,\dots ,N\}$ and $\mathbf {x} \in \mathbb {R}^N$. Moreover, we require the $\varvec{\lambda }_i$ to have local support in the sense that $\#\{j \;:\; {\text {*}}{supp}(\varvec{\lambda }_i)\cap {\text {*}}{supp}(\varvec{\lambda }_j)\ne \emptyset \} \lesssim 1$ for all $i \in \{1,\dots ,N\}$.

We denote the coordinate mappings corresponding to the basis and the dual basis by

$$\begin{aligned} \varPhi : \left\{ \begin{array}{ccc} \mathbb {R}^N &{} \longrightarrow &{} \mathbf {X}_N \\ \mathbf {x} &{} \longmapsto &{} \sum _{j=1}^N \mathbf {x}_j \varvec{\phi }_j \end{array} \right. ,\quad \varLambda : \left\{ \begin{array}{ccc} \mathbb {R}^N &{} \longrightarrow &{} \mathbf {L}^2 \\ \mathbf {x} &{} \longmapsto &{} \sum _{j=1}^N \mathbf {x}_j \varvec{\lambda }_j \end{array} \right. . \end{aligned}$$

The Hilbert space transpose of $\varLambda$ is denoted by $\varLambda ^T$. Moreover, for $\tau \subset \{1,\dots ,N\}$, we define the sets $D_j(\tau ) := \cup _{i \in \tau } {\text {*}}{supp} \varvec{\lambda }_{i,j}$, where $\varvec{\lambda }_{i,j}$ is the j-th component of $\varvec{\lambda }_{i}$, and write $\mathbf {L}^2(\tau ):= \prod _{j=1}^{k+\ell }L^2(D_j(\tau ))$.

In the following lemma, we derive a representation formula for $\mathbf {A} ^ {-1}$ based on three linear operators $\varLambda ^T,\, \mathcal {S}_N$ and $\varLambda$.

Lemma 3.2

([2, Lemma 3.10], [2, Lemma 3.11]) The restriction of $\varLambda ^T$ to $\mathbf {X}_ N$ is the inverse mapping $\varPhi ^{-1}$. More precisely, for all $\mathbf {x}, \mathbf {y} \in \mathbb {R}^N$ and $\mathbf {v} \in \mathbf {X}_N$, we have

The mappings $\varLambda$ and $\varLambda ^T$ preserve locality, i.e, for $\tau \subset \{1,\dots ,N\}$ and $\mathbf {x} \in \mathbb {R}^N$ with $\{i:\mathbf {x}_i \ne 0\} \subset \tau$, we have ${\text {*}}{supp}(\varLambda \mathbf {x}) \subset \prod _j D_j(\tau )$. For $\mathbf {v} \in \mathbf {L}^2$, we have

$$\begin{aligned} \left\| \varLambda ^T \mathbf {v} \right\| _{\ell ^2(\tau )} \le \left\| \varLambda \right\| \left\| \mathbf {v} \right\| _{\mathbf {L}^2(\tau )}. \end{aligned}$$

Moreover, there holds the representation formula

$$\begin{aligned} \mathbf {A} ^ {-1} \mathbf {x}= \varLambda ^T \mathcal {S}_N \varLambda \mathbf {x} \qquad \forall \mathbf {x} \in \mathbb {R}^N. \end{aligned}$$

Proof

For sake of completeness, we provide the derivation of the representation formula from [2, Lemma 3.11]. Using that $\varLambda ^T = \varPhi ^{-1}|_{\mathbf {X}_N}$ and the definition of the discrete solution operator, we compute

for arbitrary $\mathbf {y} \in \mathbb {R}^N$. $\square$

This lemma is the crucial step in the proof of the following lemma.

Lemma 3.3

Let $\mathbf {A}$ be the Galerkin matrix, $\varLambda$ be the coordinate mapping for the dual basis, and $\mathcal {S}_N$ be the discrete solution operator. Let $\tau \times \sigma \subset \{1,\dots ,N\}\times \{1, \dots , N\}$ be an admissible block and $\mathbf {W}_r \subseteq \mathbf {L}^2$ be a finite dimensional space. Then, there exist matrices $\mathbf {X}_{\tau \sigma } \in \mathbb {R}^{\left| \tau \right| \times r},\mathbf {Y}_{\tau \sigma } \in \mathbb {R}^{\left| \sigma \right| \times r}$ of rank $r \le \dim \mathbf {W}_r$ satisfying

$$\begin{aligned} \left\| \mathbf {A}^{-1}|_{\tau \times \sigma } -\mathbf {X}_{\tau \sigma }\mathbf {Y}_{\tau \sigma }^T \right\| _2 \le \left\| \varLambda \right\| ^2 \sup _{\begin{array}{c} \varvec{f} \in \mathbf {L}^2:\\ {\text {*}}{supp}(\varvec{f}) \subset \prod _j D_j(\sigma ) \end{array}} \frac{\inf _{\mathbf {w} \in \mathbf {W}_r}\left\| \mathcal {S}_N \varvec{f} -\mathbf {w} \right\| _{\mathbf {L}^2(\tau )}}{\left\| \varvec{f} \right\| _{\mathbf {L}^2}}, \end{aligned}$$

where $\left\| \cdot \right\| _2$ denotes the spectral norm.

Proof

We use the representation formula from Lemma 3.2. With the given space $\mathbf {W}_r$, we define $\mathbf {X}_{\tau \sigma } \in \mathbb {R}^{\left| \tau \right| \times r}$ columnwise as vectors from an orthonormal basis of the space $\widehat{\mathbf {W}}:=(\varLambda ^T \mathbf {W}_r)|_\tau$. Then, the product $\mathbf {X}_{\tau \sigma } \mathbf {X}_{\tau \sigma }^T$ is the orthogonal projection onto $\widehat{\mathbf {W}}$. Defining $\mathbf {Y}_{\tau \sigma } := (\mathbf {A}^{-1}|_{\tau \times \sigma })^T \mathbf {X}_{\tau \sigma }$, we can compute for all $\mathbf {x} \in \mathbb {R}^N$ with $\{i\;:\;\mathbf {x}_i \ne 0\} \subset \sigma$

$$\begin{aligned} \left\| (\mathbf {A}^{-1}|_{\tau \times \sigma } -\mathbf {X}_{\tau \sigma }\mathbf {Y}_{\tau \sigma }^T)\mathbf {x}|_\sigma \right\| _{\ell ^2(\tau )}&= \left\| (\mathbf {I}-\mathbf {X}_{\tau \sigma }\mathbf {X}_{\tau \sigma }^T)(\mathbf {A}^{-1}\mathbf {x})|_\sigma \right\| _{\ell ^2(\tau )}\\&= \inf _{\widehat{\mathbf {w}}\in \widehat{\mathbf {W}}} \left\| (\mathbf {A}^{-1}\mathbf {x})|_\sigma -\widehat{\mathbf {w}} \right\| _{\ell ^2(\tau )} \\&{\mathop {=}\limits ^{\mathrm{Lemma}~3.2}} \inf _{\mathbf {w}\in \mathbf {W}_r} \left\| \varLambda ^T(\mathcal {S}_N\varLambda \mathbf {x}-\mathbf {w}) \right\| _{\ell ^2(\tau )}\\&\le \left\| \varLambda \right\| \inf _{\mathbf {w}\in \mathbf {W}_r} \left\| \mathcal {S}_N\varLambda \mathbf {x}-\mathbf {w} \right\| _{\mathbf {L}^2(\tau )}. \end{aligned}$$

Dividing both sides by $\left\| \mathbf {x} \right\| _2$, substituting $\varvec{f} :=\varLambda \mathbf {x}$ and using that the mapping $\varLambda$ preserves supports, we get the desired result.$\square$

Finally, the question of approximating the whole matrix $\mathbf {A}^{-1}$ can be reduced to the question of blockwise approximation. For arbitrary matrices $\mathbf {M} \in \mathbb {R}^{N\times N}$ and an arbitrary block partition P of $\{1,\dots ,N\} \times \{1,\dots ,N\}$ this follows from

$$\begin{aligned} \left\| \mathbf {M} \right\| _2 \le N^2\max \{\left\| \mathbf {M}|_{\tau \times \sigma } \right\| _2 : (\tau ,\sigma ) \in P\}. \end{aligned}$$

If the block partition P is based on a cluster tree $\mathbb {T}_{\mathcal {I}}$, the more refined estimate

$$\begin{aligned} \left\| \mathbf {M} \right\| _2 \le C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}})\max \{\left\| \mathbf {M}|_{\tau \times \sigma } \right\| _2 : (\tau ,\sigma ) \in P\} \end{aligned}$$

(3.3)

holds, see [22, 24, Lemma 6.32], [11].

In Sect. 5, we give explicit definitions of the dual basis for the FEM-BEM coupling model problem.

3.2 Abstract setting: low dimensional approximation

We present a general framework that only uses a Caccioppoli type estimate for the construction of exponentially convergent low dimensional approximations.

Let $M \in \mathbb {N}$ be fixed. For $R >0$ let $\mathcal {B}_R:=\lbrace B_i \rbrace _{i=1} ^M$ be a collection of boxes, i.e., $B_i \in \{B_R\cap \varOmega ,B_R,B_R\backslash \varGamma \}$ for all $i=1,\dots ,M$, where $B_R$ denotes a box of side length R. The choice, which of the three sets is taken for each index i, is determined by the application and fixed.

We write $\mathcal {B}\subset \mathcal {B}' := \lbrace B_i' \rbrace _{i=1} ^M$ meaning that $B_i \subset B_i'$ for all $i=1,\dots ,M$. For a parameter $\delta > 0$, we call $\mathcal {B}_R^\delta := \{B_i^\delta \}_{i=1}^M$ a collection of $\delta$-enlarged boxes of $\mathcal {B}_R$, if it satisfies

$$\begin{aligned} B_i^\delta \in \{B_{R+2\delta }\cap \varOmega ,B_{R+2\delta },B_{R+2\delta }\backslash \varGamma \} \;\; \forall i=1,\dots ,M, \quad \text { and } \quad \mathcal {B}^\delta _R \supset \mathcal {B}_R, \end{aligned}$$

where $B_R$ and $B_{R+2\delta }$ are concentric boxes. Defining ${\text {*}}{diam}(\mathcal {B}_R) := \max \{{\text {diam}}(B_i), i=1,\dots ,M\},$ we get

$$\begin{aligned} {\text {*}}{diam}(\mathcal {B}_R^\delta )\le {\text {*}}{diam}(\mathcal {B}_R) + 2\sqrt{d}\delta . \end{aligned}$$

(3.4)

In order to simplify notation, we drop the subscript R and write $\mathcal {B}:= \mathcal {B}_R$ in the following abstract setting.

We use the notation $\mathbf {H}^1(\mathcal {B})$ to abbreviate the product space $\mathbf {H}^1(\mathcal {B}) = \prod _{i=1}^M H^1(B_i)$, and write $\left\| \mathbf {v} \right\| _{\mathbf {H}^1(\mathcal {B})}^2:= \sum _{i=1}^M \left\| \mathbf {v}_i \right\| _{H^1(B_i)}^2$ for the product norm.

Remark 3.4

For the application of the present paper, we chose boxes (or suitable subsets of those) for the sets $B_i$. We also mention that different constructions can be employed as demonstrated in [2], where a construction for non-uniform grids is presented and where the metric is not the Euclidean one but one that is based on the underlying finite element mesh.

In the following, we fix some assumptions on the collections $\mathcal {B}$ of interest and the norm $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}}$ on $\mathcal {B}$ we derive our approximation result in. In essence, we want a norm weaker than the classical $H^1$-norm that has the correct scaling (e.g., an $L^2$-type norm).

• (A2) Assumptions on the approximation norm $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}}$: For each $\mathcal {B}$, the Hilbertian norm $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}}$ is a norm on $\mathbf {H}^1(\mathcal {B})$ and such that for any $\delta >0$ and enlarged boxes $\mathcal {B}^\delta$ and $H>0$ there is a discrete space $\mathbf {V}_{H,\mathcal {B}^\delta } \subset \mathbf {H}^1(\mathcal {B}^\delta )$ of dimension $\dim \mathbf {V}_{H,\mathcal {B}^\delta } \le C_\mathrm{dim} ({\text {*}}{diam}(\mathcal {B}^\delta )/H)^{Md}$ and a linear operator $Q_H : \mathbf {H}^1(\mathcal {B}^\delta ) \rightarrow \mathbf {V}_{H,\mathcal {B}^\delta }$ such that

  $$\begin{aligned} \left| \! \left| \! \left| \mathbf {v}-Q_H \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}} \le C_\mathrm{Qap}H (\left\| \nabla \mathbf {v} \right\| _{L^2(\mathcal {B}^\delta )}+\delta ^{-1}\left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^\delta }) \end{aligned}$$

  with constants $C_\mathrm{dim}$, $C_\mathrm{Qap}>0$ that do not depend on $\mathcal {B}$, $\mathcal {B}^\delta$, $\delta$, and N.

Finally, we require a Caccioppoli type estimate with respect to the norm from (A2).

• (A3) Caccioppoli type estimate: For each $\mathcal {B}$, $\delta >0$ and collection $\mathcal {B}^\delta$ of $\delta$-enlarged boxes with $\delta \ge C_\mathrm{Set}(N)$ with a fixed constant $C_\mathrm{Set}(N)>0$ that may depend on N, there is a subspace $\mathcal {H}_h(\mathcal {B}^\delta )\subset \mathbf {H}^1(\mathcal {B}^\delta )$ such that for all $\mathbf {v} \in \mathcal {H}_h(\mathcal {B}^\delta )$ the inequality

  $$\begin{aligned} \left\| \nabla {\mathbf {v}}\right\| _ {L^2(\mathcal {B}) } \le C_\mathrm{Cac}\frac{{\text {*}}{diam}(\mathcal {B})^{\alpha -1}}{\delta ^{\alpha }} \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^\delta } \end{aligned}$$

  (3.5)

  holds. Here, the constants $C_\mathrm{Cac}>0$ and $\alpha \ge 1$ do not depend on $\mathcal {B},\mathcal {B}^\delta$, $\delta$, and N. We additionally assume the spaces $\mathcal {H}_h(\mathcal {B}^\delta )$ to be finite dimensional and nested, i.e., $\mathcal {H}_h(\mathcal {B}') \subset \mathcal {H}_h(\mathcal {B})$ for $\mathcal {B}\subset \mathcal {B}'$.

By $\varPi _{h,\mathcal {B}}$, we denote the orthogonal projection $\varPi _{h,\mathcal {B}}: \mathbf {H}^1(\mathcal {B}) \rightarrow \mathcal {H}_h(\mathcal {B})$ onto that space with respect to the norm $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}}$, which is well-defined since $\mathcal {H}_h(\mathcal {B})$ is closed by assumption.

Lemma 3.5

(Single-step approximation) Let $2{\text {*}}{diam}(\varOmega ) \ge \delta \ge 2C_\mathrm{Set}(N)$ with the constant $C_\mathrm{Set}(N)$ from (A3), $\mathcal {B}$ be a given collections of boxes and $\mathcal {B}\subset \mathcal {B}^{\delta /2}\subset \mathcal {B}^\delta$ be enlarged boxes of $\mathcal {B}$. Let $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}^\delta }$ be a norm on $\mathbf {H}^1(\mathcal {B}^\delta )$ such that (A2) holds for the sets $\mathcal {B}\subset \mathcal {B}^{\delta /2}$. Let $\mathbf {v} \in \mathcal {H}_h(\mathcal {B}^\delta )$ meaning that (A3) holds with the collection $\mathcal {B}$ replaced by $\mathcal {B}^{\delta /2}$ therein. Then, there exists a space $\mathbf {W}_1$ of dimension $\dim \mathbf {W} _1 \le C_\mathrm{ssa} \left( \frac{{\text {*}}{diam}(\mathcal {B}^\delta )}{\delta }\right) ^ {\alpha Md}$ such that

$$\begin{aligned} \inf _{\mathbf {w}\in \mathbf {W}_1}\left| \! \left| \! \left| \mathbf {v}- \mathbf {w} \right| \! \right| \! \right| _{\mathcal {B}} \le \frac{1}{2} \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^\delta }. \end{aligned}$$

Proof

We set $\mathbf {W}_1 := \varPi _{h,\mathcal {B}}Q_H \mathcal {H}_h(\mathcal {B}^\delta ) \subset \mathbf {V}_{H,\mathcal {B}^\delta }$. Since $\mathbf {v} \in \mathcal {H}_h(\mathcal {B}^\delta )$, we obtain from (A2) and (A3) that

$$\begin{aligned} \left| \! \left| \! \left| \mathbf {v}- \varPi _{h,\mathcal {B}}Q_H \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}}&= \left| \! \left| \! \left| \varPi _{h,\mathcal {B}}(\mathbf {v}- Q_H \mathbf {v}) \right| \! \right| \! \right| _{\mathcal {B}}\nonumber \\&\le \left| \! \left| \! \left| \mathbf {v}- Q_H \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}} \le C_\mathrm{Qap}H( \left\| \nabla \mathbf {v} \right\| _{L^2(\mathcal {B}^{\delta /2})} + 2\delta ^{-1}\left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^{\delta /2}}) \nonumber \\&\le C_1 C_\mathrm{Qap}C_\mathrm{Cac}\frac{{\text {*}}{diam}(\mathcal {B}^{\delta /2})^{\alpha -1}}{\delta ^\alpha } H \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^\delta } \end{aligned}$$

(3.6)

with a constant $C_1$ depending only on $\varOmega$ since $\alpha \ge 1$ and $\delta \le 2 {\text {*}}{diam}(\varOmega )$. With the choice $H = \frac{\delta ^\alpha }{2C_1C_\mathrm{Qap}C_\mathrm{Cac}{\text {*}}{diam}(\mathcal {B}^\delta )^{\alpha -1}}$, we get the asserted error bound. Since $\mathbf {W}_1 \subset \mathbf {V}_{H,\mathcal {B}^\delta }$ and by choice of H, we have

$$\begin{aligned} \dim \mathbf {W}_1&\le C_\mathrm{dim} \left( \frac{{\text {*}}{diam}(\mathcal {B}^\delta )}{H}\right) ^ {Md} \le C_\mathrm{dim} \left( 2C_1 C_\mathrm{Qap}C_\mathrm{Cac} \frac{{\text {*}}{diam}(\mathcal {B}^\delta )^\alpha }{\delta ^\alpha } \right) ^ {Md}\\&=: C_\mathrm{ssa} \left( \frac{{\text {*}}{diam}(\mathcal {B}^\delta )}{\delta } \right) ^ {\alpha Md} , \end{aligned}$$

which concludes the proof.$\square$

Iterating the single-step approximation on concentric boxes leads to exponential convergence.

Lemma 3.6

(Multi-step approximation) Let $L \in \mathbb {N}$ and $\delta \ge 2 C_\mathrm{Set}(N)$ with the constant $C_\mathrm{Set}(N)$ from (A3). Let $\mathcal {B}$ be a collection of boxes and $\mathcal {B}^{\delta L} \supset \mathcal {B}$ a collection of $\delta L$-enlarged boxes. Then, there exists a space $\mathbf {W}_L \subseteq \mathcal {H}_h({\mathcal {B}^{\delta L}})$ such that for all $\mathbf {v}\in \mathcal {H}_h(\mathcal {B}^{\delta L})$ we have

$$\begin{aligned} \inf _{\mathbf {w}\in \mathbf {W}_L }\left| \! \left| \! \left| \mathbf {v}- \mathbf {w} \right| \! \right| \! \right| _{ \mathcal {B}} \le 2 ^ {-L } \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^{\delta L}}, \end{aligned}$$

and, with $C^\prime _\mathrm{dim}:= 2 \sqrt{d} C_\mathrm{ssa}$,

$$\begin{aligned} \dim \mathbf {W} _L \le C^\prime _ \mathrm{dim}\Big (L+ \frac{{\text {*}}{diam}(\mathcal {B})}{\delta }\Big )^{\alpha Md+1}. \end{aligned}$$

Proof

The assumptions on $\mathcal {B}$ and $\mathcal {B}^{\delta L}$ allow for the construction of a sequence of nested enlarged boxes $\mathcal {B}\subseteq \mathcal {B}^\delta \subseteq \mathcal {B}^{2\delta } \subseteq \ldots \subseteq \mathcal {B}^{\delta L}$ satisfying ${\text {*}}{diam}(\mathcal {B}^{\ell \delta }) \le {\text {*}}{diam}(\mathcal {B}) + C\ell \delta$.

We iterate the approximation result of Lemma 3.5 on the sets $\mathcal {B}^{\delta \ell }$, $\ell = L,\ldots ,1$. For $\ell =L$, Lemma 3.5 applied with the sets $\mathcal {B}^{(L-1)\delta } \subset \mathcal {B}^{\delta L}$ provides a subspace $\mathbf {V}_1 \subset \mathcal {H}_h(\mathcal {B}^{\delta L})$ with $\dim \mathbf {V}_1 \le C_\mathrm{ssa} \Big (\frac{{\text {*}}{diam}(\mathcal {B}^{\delta L })}{\delta } \Big )^{\alpha Md}$ such that

$$\begin{aligned} \inf _{\widehat{\mathbf {v}}_1 \in \mathbf {V}_1} \left| \! \left| \! \left| \mathbf {v}-\widehat{\mathbf {v}}_1 \right| \! \right| \! \right| _{\mathcal {B}^{(L-1)\delta } } \le 2 ^ {-1} \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^{\delta L}}. \end{aligned}$$

(3.7)

For $\widehat{\mathbf {v}}_1 \in \mathbf {V}_1$, we have $(\mathbf {v}- \widehat{\mathbf {v}}_1)\in \mathcal {H}_h(\mathcal {B}^{(L-1)\delta })$, so we can use Lemma 3.5 again with the sets $\mathcal {B}^{(L-2)\delta } \subset \mathcal {B}^{(L-1)\delta }$, and get a subspace $\mathbf {V}_2$ of $\mathcal {H}_h(\mathcal {B}^{(L-2)\delta })$ with $\dim \mathbf {V}_2 \le C_\mathrm{ssa} \big (\frac{{\text {*}}{diam}(\mathcal {B}^{(L-1)\delta })}{\delta }\big )^{\alpha Md}$. This implies

$$\begin{aligned} \inf _{\widehat{\mathbf {v}}_2 \in \mathbf {V}_2} \inf _{\widehat{\mathbf {v}}_1 \in \mathbf {V}_1} \left| \! \left| \! \left| (\mathbf {v}- \widehat{\mathbf {v}}_1) -\widehat{\mathbf {v}}_2 \right| \! \right| \! \right| _{\mathcal {B}^{(L-2)\delta } } \le 2^{-1} \inf _{\widehat{\mathbf {v}}_1 \in \mathbf {V}_1} \left| \! \left| \! \left| \mathbf {v}- \widehat{\mathbf {v}}_1 \right| \! \right| \! \right| _{\mathcal {B}^{(L-1)\delta } } \le 2 ^ {-2} \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}^{\delta L}}. \end{aligned}$$

(3.8)

Continuing this process $L -2$ times leads to the subspace $\mathbf {W}_L := \bigoplus \limits _{\ell =1} ^L \mathbf {V}_\ell$ of $\mathcal {H}_h({\mathcal {B}^{\delta L}})$ with dimension

$$\begin{aligned} \dim \mathbf {W}_L&\le C_\mathrm{ssa} \sum _{\ell =1}^{L}\Big (\frac{{\text {*}}{diam}(\mathcal {B}^{\delta \ell })}{\delta } \Big )^{\alpha Md} \le C_\mathrm{ssa} \sum _{\ell =1}^{L}\Big (\frac{{\text {*}}{diam}(\mathcal {B})}{\delta }+ \ell 2 \sqrt{d} \Big )^{\alpha Md}\\&\le C _ \mathrm{ssa} 2\sqrt{d} \Big ( L+ \frac{{\text {*}}{diam}(\mathcal {B})}{\delta } \Big )^{\alpha Md+1}, \end{aligned}$$

which finishes the proof.$\square$

4 The Caccioppoli-type inequalities

In this section, we provide the proofs of the interior regularity estimates of Theorems 2.4–2.6. The techniques employed are fairly similar to [18, 19], where Caccioppoli-type estimates for FEM and BEM are proven. Nonetheless, in the case of the FEM-BEM couplings, the additional terms in the bilinear forms arising from the coupling on the boundary need to be treated carefully.

4.1 Preliminary estimates

In the following, we collect some well-known facts about the volume potential operators $\widetilde{V}$, ${\widetilde{K}}$ and the boundary integral operators $V,K,K',W$ as well as some super-approximation estimates and inverse type inequalities for the volume potentials. We assume that $\varGamma$ is Lipschitz.

For details concerning the following mapping properties, we refer to [33, Chap. 3] and [34, Chap. 6].

• With the interior trace operator $\gamma _0^\mathrm{int}$ (for $\varOmega$) and exterior trace operator $\gamma _0^\mathrm{ext}$ (for $\mathbb {R}^d\backslash {\overline{\varOmega }}$), we have

  $$\begin{aligned}&\gamma _0^\mathrm{int} \widetilde{V}\varphi = V\varphi = \gamma _0^\mathrm{ext} \widetilde{V}\varphi , \nonumber \\&\gamma _0^\mathrm{int} \widetilde{K}u = (-1/2 + K)u \qquad \text {and} \qquad \gamma _0^\mathrm{ext} \widetilde{K}u = (1/2 + K) u, \end{aligned}$$

  (4.1)

  which implies the jump conditions across $\varGamma$

  $$\begin{aligned}{}[\gamma _0 \widetilde{V}\varphi ] := \gamma _0^\mathrm{ext} \widetilde{V}\varphi -\gamma _0^\mathrm{int} \widetilde{V}\varphi = 0, \qquad [\gamma _0 \widetilde{K}u] = u. \end{aligned}$$

  (4.2)

• Similarly, with the interior $\gamma _1^\mathrm{int} u := \gamma _0^\mathrm{int}\nabla u \cdot \nu$ and exterior conormal derivative $\gamma _1^\mathrm{ext} u := \gamma _0^\mathrm{ext}\nabla u \cdot \nu$ ($\nu$ is the outward normal vector of $\varOmega$), we have

  $$\begin{aligned}&\gamma _1^\mathrm{int} \widetilde{V}\varphi = (1/2+K')\varphi \qquad \text {and} \qquad \gamma _1^\mathrm{ext} \widetilde{V}\varphi = (-1/2 + K')\varphi , \nonumber \\&\gamma _1^\mathrm{int} \widetilde{K}u = -Wu = \gamma _1^\mathrm{ext} \widetilde{K}u, \end{aligned}$$

  (4.3)

  and consequently the jump conditions

  $$\begin{aligned}{}[\gamma _1 \widetilde{V}\varphi ] := \gamma _1^\mathrm{ext} \widetilde{V}\varphi -\gamma _1^\mathrm{int} \widetilde{V}\varphi = -\varphi , \quad [\gamma _1 \widetilde{K}u] = 0. \end{aligned}$$

  (4.4)

• The potentials $\widetilde{V} \varphi$ and $\widetilde{K}u$ are harmonic in $\mathbb {R}^d \backslash \varGamma$ and are bounded operators (see [33, Chap. 3.1.2])

  $$\begin{aligned}&{\widetilde{V}} : H^{-1/2+s}(\varGamma ) \rightarrow H_\mathrm{loc}^{1+s}(\mathbb {R}^d),\nonumber \\&{\widetilde{K}} : H^{1/2+s}(\varGamma ) \rightarrow H_\mathrm{loc}^{1+s}(\mathbb {R}^d\backslash \varGamma ), \quad \left| s \right| \le 1/2. \end{aligned}$$

  (4.5)

• For $|s| \le 1/2$ we have the boundedness for the boundary integral operators (see [14])

  $$\begin{aligned}&V : H^{-1/2+s}(\varGamma ) \rightarrow H^{1/2+s}(\varGamma ), \quad K : H^{1/2+s}(\varGamma ) \rightarrow H^{1/2+s}(\varGamma ),\nonumber \\&W : H^{1/2+s}(\varGamma ) \rightarrow H^{-1/2+s}(\varGamma ). \end{aligned}$$

  (4.6)

In the following, we use the notation $\lesssim$ to abbreviate $\le$ up to a constant $C>0$ which depends only on $\varOmega$, the dimension d, the coefficient $\mathbf {C}$ in the model problem, and the $\gamma$-shape regularity of $\mathcal {T}_h$. Moreover, we use $\simeq$ to indicate that both estimates $\lesssim$ and $\gtrsim$ hold.

We continue with a classical approximation result, so-called super-approximation, see, e.g., [31, 37].

Lemma 4.1

Let $I_h^{\varGamma }:L^2(\varGamma ) \rightarrow S^{0,0}(\mathcal {K}_h)$ be the $L^2(\varGamma )$-orthogonal projection. Then, there is $C > 0$ depending only on the $\gamma$-shape regularity of the triangulation and $\varGamma$ such that for any discrete function $\psi _h \in S^{0,0}(\mathcal {K}_h)$ and any $\eta \in W^{1,\infty }(\varGamma )$

$$\begin{aligned} \left\| \eta \psi _h - I_h^{\varGamma }(\eta \psi _h) \right\| _{H^{-1/2}(\varGamma )} \le C h^{3/2} \left\| \nabla \eta \right\| _{L^{\infty }(\varGamma )}\left\| \psi _h \right\| _{L^2(\varGamma \cap {\text {*}}{supp}(\eta ))}. \end{aligned}$$

(4.7)

Proof

The main observation is that, on each element $K \in \mathcal {K}_h$, we have $\nabla \psi _h|_K \equiv 0$. Therefore, a standard approximation result provides

$$\begin{aligned} \left\| \eta \psi _h - I_h^{\varGamma }(\eta \psi _h) \right\| _{L^2(K)} \lesssim h \left\| \nabla (\eta \psi _h) \right\| _{L^2(K)} \lesssim h \left\| \nabla (\eta )\psi _h \right\| _{L^2(K)}. \end{aligned}$$

(4.8)

Using the orthogonality and approximation properties of the $L^2$-projection, we have

Together with (4.8), this completes the proof.$\square$

Similarly, there also holds a super-approximation result for the nodal interpolation operator.

Lemma 4.2

Let $I_h^{\varOmega } : C({\overline{\varOmega }}) \rightarrow S^{1,1}(\mathcal {T}_h)$ be the nodal interpolation operator. Then, there is $C > 0$ depending only on the $\gamma$-shape regularity of the triangulation and $\varOmega$ such that for any discrete function $v_h \in S^{1,1}(\mathcal {T}_h)$ and any $\eta \in W^{1,\infty }(\varOmega )$

$$\begin{aligned}&\left\| \eta v_h - I _h^{\varOmega }(\eta v_h) \right\| _{H^k(\varOmega )}\nonumber \\&\quad \le C h^{2-k} \left( \left\| \nabla \eta \right\| _{L^\infty (\varOmega )} \left\| \nabla v_h \right\| _{L^2({\text {*}}{supp}(\eta ))} + \left\| D^2 \eta \right\| _{L^\infty (\varOmega )} \left\| v_h \right\| _{L^2({\text {*}}{supp}(\eta ))} \right) \end{aligned}$$

(4.9)

for $k=0,1$, where $H^{0}(\varOmega ):= L^2(\varOmega )$.

Proof

On each element $T \in \mathcal {T}_h$, we have $D^2 v_h|_T \equiv 0$. Therefore, the standard approximation result for nodal interpolation gives

$$\begin{aligned} \left\| \eta v_h - I _h^{\varOmega }(\eta v_h) \right\| _{H^k(T)}&\lesssim h^{2-k} \left| \eta v_h \right| _{H^2(T)}\nonumber \\&\lesssim h^{2-k} \left( {\left\| (D ^2 \eta ) v_h \right\| _{L^2(T)} + \left\| \nabla \eta \cdot \nabla v_h \right\| _{L^2(T)}}\right) , \end{aligned}$$

and summation over all elements concludes the proof.$\square$

In the proof of the Caccioppoli type inequality, we need the following inverse inequalities from [19, Lemma 3.8] and [20, Lemma 3.6].

Lemma 4.3

([19, Lemma 3.8], [20, Lemma 3.6]) Let $B_R \subset B_{R'}$ be concentric boxes with ${\text {*}}{dist}(B_R,\partial B_{R'}) \ge 4h$. Then, for every $\psi _h \in S^{0,0}(\mathcal {K}_h)$ and every $v_h \in S^{1,1}(\mathcal {T}_h)$, we have

$$\begin{aligned}&\left\| \psi _h \right\| _{L^2(B_R\cap \varGamma )} \lesssim h^{-1/2}\left\| \nabla \widetilde{V}\psi _h \right\| _{L^2(B_{R'})}, \end{aligned}$$

(4.10)

$$\begin{aligned}&\left\| \gamma _1 \widetilde{K}v _h \right\| _{L^{2}(B_R\cap \varGamma )} \lesssim h^{-1/2}\left( \left\| \nabla \widetilde{K}v _h \right\| _{L^{2}(B_{R'})} +\frac{1}{{\text {*}}{dist}(B_R,\partial B_{R'})}\left\| \widetilde{K}v_h \right\| _{L^{2}(B_{R'})} \right) . \end{aligned}$$

(4.11)

Combining Lemma 4.1 with Lemma 4.3 (assuming ${\text {*}}{supp}\eta \subset B_R$), we obtain estimates of the form

$$\begin{aligned} \left\| \eta \psi _h - I_h^{\varGamma }(\eta \psi _h) \right\| _{H^{-1/2}(\varGamma )} \lesssim h \left\| \nabla \eta \right\| _{L^{\infty }(\varGamma )}\left\| \nabla \widetilde{V}\psi _h \right\| _{L^2(B_{R'})}. \end{aligned}$$

(4.12)

Remark 4.4

An inspection of the proof of (4.10) [20, Lemma 3.6] shows that the main observation is that $\widetilde{K}v_h$ is harmonic. The remaining arguments therein only use mapping properties and jump conditions for the potential ${\widetilde{K}}$ and can directly be modified such that the same result holds for the single-layer potential as well, i.e., for every $\psi _h \in S^{0,0}(\mathcal {K}_h)$, we have

$$\begin{aligned} \left\| \gamma _1 \widetilde{V}\psi _h \right\| _{L^{2}(B_R\cap \varGamma )} \lesssim h^{-1/2}\left( \left\| \nabla \widetilde{V}\psi _h \right\| _{L^{2}(B_{R'})} +\frac{1}{{\text {*}}{dist}(B_R,\partial B_{R'})}\left\| \widetilde{V}\psi _h \right\| _{L^{2}(B_{R'})} \right) . \end{aligned}$$

(4.13)

4.2 The Bielak–MacCamy coupling

With the help of a localized ellipticity result, the discrete variational formulation, and super-approximation, we are able to prove Theorem 2.4.

Proof

(Proof of Theorem 2.4) In order to reduce unnecessary notation, we write $(u,\varphi )$ for the Galerkin solution $(u_h,\varphi _h)$. The assumption on the support of the data implies the local orthogonality

$$\begin{aligned} a_\mathrm{bmc}(u,\varphi ;\psi _h,\zeta _h)&= 0 \quad \forall (\psi _h,\zeta _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)\nonumber \\ {}&~~~\quad \text {with}\quad {\text {*}}{supp}\psi _h, {\text {*}}{supp}\zeta _h \subset B_{(1+\varepsilon )R}. \end{aligned}$$

(4.14)

Let $\eta \in C_0^\infty (\mathbb {R}^d)$ be a cut-off function with $\text {supp}\, \eta \subseteq B_{(1+\delta /4)R}$, $\eta \equiv 1$ on $B_R$, $0 \le \eta \le 1$, and $\left\| D^j \eta \right\| _{L^\infty (B_{(1+\delta )R})} \lesssim \frac{1}{(\delta R)^j}$ for $j=1,2$. Here, $0<\delta \le \varepsilon$ is such that $\frac{h}{R} \le \frac{\delta }{8}$. We note that this choice of $\delta$ implies that $\bigcup \{K \in \mathcal {K}_h \, : \, {\text {*}}{supp}\eta \cap K \ne \emptyset \} \subset B_{(1+\delta /2)R}$. In the final step of the proof, we will choose two different values for $\delta$ ($\le \varepsilon$) depending on $\varepsilon$ - one of them, $\delta =\frac{\varepsilon }{2}$, explains the assumption made on $\varepsilon$ in the theorem.

Step 1: We provide a “localized” ellipticity estimate, i.e., we prove an inequality of the form

$$\begin{aligned}&\left\| \nabla (\eta u ) \right\| _{L^2(\varOmega )}^2 + \left\| \nabla (\eta \widetilde{V} \varphi ) \right\| _{L^2(\mathbb {R}^d)}^2\\&~~~~~~~~~~~~~~~~~~~\,\,\quad \lesssim a_\mathrm{bmc}(u,\varphi ;\eta ^2 u,\eta ^2\varphi ) \quad + \quad \text {terms in weaker norms}. \end{aligned}$$

See (4.25) for the precise form. Since the ellipticity constant $C_\mathrm{ell}$ of $\mathbf {C}$ satisfies $C_\mathrm{ell}>1/4$, we may choose a $\rho >0$ such that $1/4< \rho /2 < C_\mathrm{ell}$. This implies $C_{\rho }:=\min \{1-\frac{1}{2\rho },C_\mathrm{ell}-\frac{\rho }{2}\} > 0$, and we start with

$$\begin{aligned}&\left( C_\mathrm{ell}-\frac{\rho }{2}\right) \left\| \nabla (\eta u ) \right\| _{L^2(\varOmega )}^2 + \left( 1-\frac{1}{2\rho }\right) \left\| \nabla (\eta \widetilde{V} \varphi ) \right\| _{L^2(\mathbb {R}^d)}^2\nonumber \\&~~~~~~~~~~~~\quad \quad \quad \le C_\mathrm{ell}\left\| \nabla (\eta u) \right\| _{L^2(\varOmega )}^2+ \left\| \nabla (\eta \widetilde{V}\varphi ) \right\| _{L^2(\mathbb {R}^d)}^2 \nonumber \\&~~~~~~~~~~~~\quad \quad \quad -\, \frac{1}{2\rho }\left\| \nabla (\eta \widetilde{V}\varphi ) \right\| _{L^2(\varOmega )}^2 - \frac{\rho }{2}\left\| \nabla (\eta u) \right\| _{L^2(\varOmega )}^2. \end{aligned}$$

(4.15)

Young’s inequality implies

(4.16)

Inserting (4.16) into (4.15) leads to

(4.17)

An elementary calculation shows

(4.18)

Since the single-layer potential is harmonic in $\varOmega$, integration by parts (in $\varOmega$) and $\gamma _1^\mathrm{int}{\widetilde{V}} = 1/2+K'$ lead to

(4.19)

Similarly, with integration by parts (in $\varOmega$ and $\varOmega ^\mathrm{ext}$) and the jump condition of the single-layer potential we obtain

(4.20)

Moreover, the symmetry and positive definiteness of $\mathbf {C}$ implies

(4.21)

Plugging (4.18)–(4.21) into (4.17), we infer

(4.22)

Young’s inequality and $\left\| \nabla \eta \right\| _{L^{\infty }(\mathbb {R}^d)}\lesssim \frac{1}{\delta R}$ imply

(4.23)

as well as

(4.24)

Absorbing the gradient terms in (4.23)–(4.24) into the left-hand side of (4.22), we arrive at

$$\begin{aligned}&\left\| \nabla (\eta u) \right\| _{L^2(\varOmega )}^2+ \left\| \nabla (\eta \widetilde{V}\varphi ) \right\| _{L^2(\mathbb {R}^d)}^2 \nonumber \\&\lesssim a_\mathrm{bmc}(u,\varphi ;\eta ^2u,\eta ^2\varphi )+\, \frac{1}{(\delta R)^2} \left\| \widetilde{V}\varphi \right\| _{L^2(B_{(1+\delta )R})}^2\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \,\, + \frac{1}{(\delta R)^2} \left\| u\right\| _{L^2(B_{(1+\delta )R}\cap \varOmega )}^2. \end{aligned}$$

(4.25)

Step 2: We apply the local orthogonality of $(u,\varphi )$ to piecewise polynomials and use approximation properties.

Let $I_h^{\varOmega }: C({\overline{\varOmega }}) \rightarrow S^{1,1}(\mathcal {T}_h)$ be the nodal interpolation operator and $I_h^{\varGamma }$ the $L^2(\varGamma )$-orthogonal projection mapping onto $S^{0,0}(\mathcal {K}_h)$. Then, the orthogonality (4.14) leads to

(4.26)

We mention that the volume term $T_1$ and the boundary term $T_3$ involving V were already treated in [18, 19]. However, for the sake of completeness, we also provide the estimates in the following. For $T_1$ in (4.26), the assumptions on the cut-off function $\eta$, the super-approximation properties of $I_h^{\varOmega }$ from Lemma 4.2, Young’s inequality, and $\frac{h}{\delta R} \le 1$ lead to

(4.27)

For the term $T_3$, we mention that the assumption $8h\le \delta R$ implies that ${\text {*}}{supp}I_h^{\varGamma }(\eta ^2 \varphi ) \subseteq B_{(1+\delta /2)R}.$ In the following, we employ a second cut-off function $\widetilde{\eta }$ with $0 \le \widetilde{\eta } \le 1$, $\widetilde{\eta } \equiv 1$ on $B_{(1+\delta /2)R}\supseteq {\text {*}}{supp} (\eta ^2 \varphi - I_h^{\varGamma }(\eta ^2 \varphi ))$, ${\text {*}}{supp} \widetilde{\eta } \subseteq \overline{B_{(1+\delta )R}}$ and $\left\| \nabla \widetilde{\eta } \right\| _{L^\infty (B_{(1+\delta )R})} \lesssim \frac{1}{\delta R}$. The trace inequality together with the super-approximation properties of $I_h^{\varGamma }$, expressed in (4.12), lead to

(4.28)

With the same arguments, we obtain an estimate for $T_4$:

(4.29)

It remains to treat the coupling term $T_2$ involving the adjoint double-layer operator in (4.26). With the support property ${\text {*}}{supp}(I_h^{\varOmega }(\eta ^2 u) - \eta ^2 u) \subset B_{(1+\delta /2)R}$, which follows from $8h \le \delta R$, and $(1/2-K')\varphi = -\gamma _1^\mathrm{ext} \widetilde{V}\varphi$, we obtain

(4.30)

The multiplicative trace inequality for $\varOmega$, see, e.g., [12], the super-approximation property of $I_h^{\varOmega }$ from Lemma 4.2, and $\frac{h}{\delta R} \lesssim 1$ lead to

$$\begin{aligned} \left\| I_h^{\varOmega }(\eta ^2 u) - \eta ^2 u \right\| _{L^{2}(\varGamma )}&\lesssim \left\| I_h^{\varOmega }(\eta ^2 u) - \eta ^2 u \right\| _{L^2(\varOmega )}\nonumber \\&\quad +\, \left\| I_h^{\varOmega }(\eta ^2 u) - \eta ^2 u \right\| ^{1/2}_{L^{2}(\varOmega )} \left\| \nabla ( I_h^{\varOmega }(\eta ^2 u) - \eta ^2 u) \right\| ^{1/2}_{L^{2}(\varOmega )}\nonumber \\&\lesssim \left( \frac{h^2}{(\delta R)^2} \left\| u \right\| _{L^2(B_{(1+\delta )R}\cap \varOmega )}+\frac{h^2}{\delta R} \left\| \nabla u \right\| _{L^2(B_{(1+\delta )R}\cap \varOmega )}\right) \nonumber \\&\quad +\, \left( \frac{h }{\delta R} \left\| u \right\| ^{1/2}_{L^2(B_{(1+\delta )R}\cap \varOmega )}+\frac{h}{(\delta R)^{1/2}} \left\| \nabla u \right\| ^{1/2}_{L^2(B_{(1+\delta )R}\cap \varOmega )}\right) \nonumber \\&\qquad \left( \frac{h ^{1/2}}{\delta R} \left\| u \right\| ^{1/2}_{L^2(B_{(1+\delta )R}\cap \varOmega )}+\frac{h ^{1/2}}{(\delta R)^{1/2}} \left\| \nabla u \right\| ^{1/2}_{L^2(B_{(1+\delta )R}\cap \varOmega )}\right) \nonumber \\&\lesssim \frac{h^{3/2}}{\delta R} \left\| \nabla u \right\| _{L^2(B_{(1+ \delta )R}\cap \varOmega )} + \frac{h^{3/2}}{(\delta R)^2} \left\| u \right\| _{L^2(B_{(1+\delta )R}\cap \varOmega )}. \end{aligned}$$

(4.31)

We use estimate (4.13) and (4.31) in (4.30), which implies

(4.32)

Finally, inserting (4.28), (4.29), (4.27), and (4.32) into (4.26) and further into (4.25) implies

$$\begin{aligned} \left\| \nabla u \right\| _{L^2(B_R\cap \varOmega )}^2 + \left\| \nabla \widetilde{V}\varphi \right\| _{L^2(B_R)}^2&\le \left\| \nabla (\eta u) \right\| _{L^2(\varOmega )}^2 +\left\| \nabla (\eta \widetilde{V}\varphi ) \right\| _{L^2( \mathbb {R}^d)}^2\nonumber \\&\lesssim \frac{h}{\delta R} \left( \left\| \nabla u \right\| ^2_{L^2(B_{(1+\delta )R}\cap \varOmega )}+ \left\| \nabla \widetilde{V}\varphi \right\| ^2_{L^{2}(B_{(1+\delta )R})} \right) \nonumber \\&\quad + \,\frac{1}{(\delta R)^2} \left( \left\| u \right\| ^2_{L^2(B_{(1+\delta )R}\cap \varOmega )} +\left\| \widetilde{V}\varphi \right\| ^2_ {L^2(B_{(1+\delta )R})} \right) . \end{aligned}$$

(4.33)

Step 3: We iterate (4.33) to improve the powers of h for the gradient terms to finally obtain the result of Theorem 2.4.

We set $\delta = \frac{\varepsilon }{2}$, and use (4.33) again for the gradient terms on the right-hand side with the boxes $B_{\widetilde{R}}$ and $B_{(1+\widetilde{\delta })\widetilde{R}}$, where $\widetilde{\delta } = \frac{\varepsilon }{\varepsilon +2}$ and $\widetilde{R} = (1+\varepsilon /2)R$. We note that $16h\le \varepsilon R$ implies $8h\le \widetilde{\delta } \widetilde{R}$, so we may apply (4.33). Since $(1+\widetilde{\delta })(1+\frac{\varepsilon }{2}) = 1+\varepsilon$, we get

$$\begin{aligned} \left\| \nabla u \right\| _{L^2(B_R\cap \varOmega )}^2&+ \left\| \nabla \widetilde{V}\varphi \right\| _{L^2(B_R)}^2 \lesssim \frac{h^2}{ (\varepsilon R)^2 }\left( \left\| \nabla u \right\| ^2_{L^{2}(B_{(1+\varepsilon )R}\cap \varOmega )}+ \left\| \nabla \widetilde{V}\varphi \right\| ^2_{L^{2}(B_{(1+\varepsilon )R})} \right) \nonumber \\&+ \,\left( \frac{h}{(\varepsilon R )^3 }+ \frac{1}{(\varepsilon R )^2 }\right) \left( \left\| u \right\| ^2_ {L^2(B_{(1+\varepsilon )R}\cap \varOmega )} +\left\| \widetilde{V}\varphi \right\| ^2_ {L^2(B_{(1+\varepsilon )R})}\right) , \end{aligned}$$

(4.34)

and with $\frac{h}{\varepsilon R} <1$, we conclude the proof.$\square$

4.3 The symmetric coupling

In this section, we provide the proof of Theorem 2.5. While some parts of the proof are similar to the proof of Theorem 2.4 and are therefore shortened, there are some differences as well, namely, that it does not suffice to study the single-layer potential. Indeed, one has to add a term containing the double-layer potential to the Caccioppoli inequality in order to get a localized ellipticity estimate.

Proof

(Proof of Theorem 2.5) Again, we write $(u,\varphi )$ for the Galerkin solution $(u_h,\varphi _h)$. The assumption on the support of the data implies the local orthogonality

$$\begin{aligned} a_\mathrm{sym}(u,\varphi ;\psi _h,\zeta _h)&= 0 \quad \forall (\psi _h,\zeta _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)\nonumber \\&\quad \,\,\, \text {with}\quad {\text {*}}{supp}\psi _h, {\text {*}}{supp}\zeta _h \subset B_{(1+\varepsilon )R}. \end{aligned}$$

(4.35)

As in the proof of Theorem 2.4 let $\eta \in C_0^\infty (\mathbb {R}^d)$ be a cut-off function with $\text {supp}\, \eta \subseteq B_{( 1+\delta /4) R}$, $\eta \equiv 1$ on $B_R$, $0 \le \eta \le 1$, and $\left\| D^j \eta \right\| _{L^\infty (B_{(1+\delta )R})} \lesssim \frac{1}{\delta R}$ for $j=1,2$. Here, $0<\delta \le \varepsilon$ satisfies $\frac{h}{R}\le \frac{\delta }{16}$ and will be chosen in the last step of the proof.

Step 1: We start with a localized ellipticity estimate. More precisely, we show

$$\begin{aligned}&\left\| \nabla (\eta u) \right\| ^2_{L^2(\varOmega )} +\left\| \nabla (\eta \widetilde{V} \varphi ) \right\| ^2_{L^2(\mathbb {R}^d) } +\left\| \nabla (\eta \widetilde{K} u) \right\| ^2_{L^2(\mathbb {R}^d{\setminus }\varGamma )}\\&~~~~~~~~~~~~~~~~~~~~\quad \quad \quad \le a_\mathrm{sym}(u, \varphi ; \eta ^2 u , \eta ^2 \varphi )+ \mathrm{terms \, in \, weaker \, norms}. \end{aligned}$$

See (4.40) for the precise statement. From (4.21) and the Cauchy-Schwarz inequality we get

(4.36)

A direct calculation reveals that . Inserting this and (4.20) in (4.36) yields

(4.37)

Integration by parts together with the jump conditions (4.2), (4.4) for the double-layer potential gives

(4.38)

With a calculation analogous to (4.18) (in fact, replace u therein with $\widetilde{K} u$), we get

where the omitted terms (cf. (4.18))

$$\begin{aligned} \text {l.o.t.} = \langle (\nabla \eta ) \widetilde{V} \varphi , \nabla (\eta {\widetilde{K}} u)\rangle _{L^2(\mathbb {R}^d{\setminus }\varGamma )} - \langle \nabla \widetilde{V} \varphi ,\eta (\nabla \eta ) {\widetilde{K}} u\rangle _{L^2(\mathbb {R}^d{\setminus }\varGamma )} \end{aligned}$$

can be estimated in weaker norms (i.e., $\Vert \widetilde{V}\varphi \Vert _{L^2(B_{(1+\delta /2)R})}$, $\Vert {\widetilde{K}} u\Vert _{L^2(B_{(1+\delta /2)R}{\setminus } \varGamma )}$) or lead to terms that are absorbed in the left-hand side as in the proof of Theorem 2.4 (see (4.23), (4.24)). With integration by parts on $\varOmega$ and $\varOmega ^\mathrm{ext}$, we get

(4.39)

Putting everything together and using $\left\| \nabla \eta \right\| _{L^{\infty }(B_{(1+\delta )R})} \lesssim \frac{1}{\delta R}$, we obtain

$$\begin{aligned}&\nonumber \left\| \nabla (\eta u) \right\| ^2_{L^2(\varOmega )} +\left\| \nabla (\eta \widetilde{V} \varphi ) \right\| ^2_{L^2(\mathbb {R}^d) } +\left\| \nabla (\eta \widetilde{K} u) \right\| ^2_{L^2(\mathbb {R}^d{\setminus }\varGamma )}\\&\quad \qquad \lesssim a_\mathrm{sym}(u, \varphi , \eta ^2 u , \eta ^2 \varphi ) + \frac{1}{(\delta R)^2} \left\| u \right\| _{L^2(B_{(1+\delta )R}\cap \varOmega )}^2\nonumber \\&\qquad \quad + \,\frac{1}{(\delta R)^2} \left\| \widetilde{V}\varphi \right\| _{L^2(B_{(1+\delta )R})}^2 + \frac{1}{(\delta R)^2} \left\| \widetilde{K}u \right\| _{L^2(B_{(1+\delta )R}{\setminus }\varGamma )}^2. \end{aligned}$$

(4.40)

Step 2: We apply the local orthogonality as well as approximation results.

With the $L^2(\varGamma )$-orthogonal projection $I_h^{\varGamma }$ and the nodal interpolation operator $I_h^{\varOmega }$, the orthogonality (4.35) implies

(4.41)

The terms $T_1$, $T_3$, $T_4$ can be estimated with (4.27), (4.32), and (4.28) respectively as in the case for the Bielak–MacCamy coupling. We also mention that the term $T_2$ involving the hyper-singular integral operator W was treated in [20]. For our purpose, a simplified version of the proof is sufficient, which is presented in the following.

For the term $T_2$, we mention that the assumption $16h\le \delta R$ implies that ${\text {*}}{supp}I_h^{\varGamma }(\eta ^2 \varphi ) \subseteq B_{(1+\delta /2)R}.$ We employ equation (4.10) from Lemma 4.3 for ${\widetilde{K}} u$ and the boxes $B_{(1+\delta /2)R}$ and $B_{(1+\delta )R}$ satisfying ${\text {*}}{dist}(B_{(1+\delta /2)R}, \partial B_{(1+\delta )R}) = \frac{\delta }{4} \ge 4h$ due to the assumptions on $\delta$. Together with $Wu= - \gamma _1^\mathrm{int} \widetilde{ K} u$, (cf. (4.31)), and the Young inequality this implies

We finish the proof by estimating $T_5$. To that end, we need another cut-off function $\widetilde{\eta } \in S^{1,1}(\mathcal {T}_h )$ with $0 \le \widetilde{\eta } \le 1$, $\widetilde{\eta } \equiv 1$ on $B_{(1+\delta /2)R}\supseteq \text {supp} \left( I_h ^ \varGamma ( \eta ^2 \varphi ) - \eta ^2 \varphi \right)$, $\text {supp}\,\widetilde{\eta } \subseteq B_{(1+ \delta )R}$ and $\left\| \nabla \widetilde{\eta } \right\| _{L^\infty (B_{( 1+\delta ) R} ) } \lesssim \frac{1}{\delta R}$. Since $( 1/2-K)u= - \gamma _0^\mathrm{int} \widetilde{ K} u$, we get with a trace inequality and the approximation properties expressed in (4.12) that

(4.42)

Putting everything together in (4.41) and further in (4.40) finally yields

$$\begin{aligned}&\nonumber \left\| \nabla u \right\| ^2_{L^2(B_R\cap \varOmega )} +\left\| \nabla \widetilde{V}\varphi \right\| ^2_{L^2(B_R)} + \left\| \nabla \widetilde{K}u \right\| ^2_{L^2(B_R{\setminus }\varGamma )} \\&\quad \lesssim \frac{h}{\delta R} \left( \left\| \nabla u \right\| ^2_{L^2(B_{(1+\delta )R}\cap \varOmega )} +\left\| \nabla \widetilde{K}u \right\| ^2_{L^2(B_{(1+\delta )R}{\setminus }\varGamma )} + \left\| \nabla \widetilde{V}\varphi \right\| ^2_{L^2(B_{(1+\delta )R})} \right) \nonumber \\&\qquad +\, \frac{1}{(\delta R)^2} \left( \left\| u \right\| ^2_ {L^2(B_{(1+\delta )R}\cap \varOmega )} + \left\| \widetilde{V}\varphi \right\| ^2_ {L^2(B_{(1+\delta )R})} +\left\| \nabla \widetilde{K}u \right\| ^2_{L^2(B_{(1+\delta )R}{\setminus }\varGamma )} \right) . \end{aligned}$$

(4.43)

Step 3: By reapplying (4.43) to the gradient terms with $\delta = \frac{ \varepsilon }{2}$ and suitable boxes, we get the desired result exactly as in step 3 of the proof of Theorem 2.4.$\square$

4.4 The Johnson–Nédélec coupling

In this section, we prove the Caccioppoli-type inequality from Theorem 2.6 for the Johnson–Nédélec coupling. Most of the appearing terms have already been treated in the previous sections. The main difference is that the double-layer potential appears naturally due to the boundary coupling terms, but the local orthogonality is not suited to provide an approximation for it, since the hypersingular operator does not appear in the bilinear form. A remedy for this problem is to localize the double-layer potential by splitting it into a local near-field and a non-local, but smooth far-field. This techniques follows [17], where a similar localization using commutators is employed.

Lemma 4.5

Let $\delta \in (0,1)$ and $R \in (0,2{\text {*}}{diam}(\varOmega ))$ and let $B_R$ and $B_{(1+\delta )R}$ be two concentric boxes. Let $\eta \in C_0^\infty (\mathbb {R}^d)$ be a cut-off function with $\text {supp}\, \eta \subseteq B_{( 1+\delta /2) R}$, $\eta \equiv 1$ on $B_{( 1+\delta /4) R}$, $0 \le \eta \le 1$, and $\left\| D^j\eta \right\| _{L^\infty (B_{(1+\delta )R})} \lesssim \frac{1}{(\delta R)^j}$ for $j=1,2$. Then, for $u \in H^1(\varOmega )$, we have

$$\begin{aligned} \left\| \nabla \widetilde{K}u \right\| _{L^2(B_R{\setminus }\varGamma )}&\lesssim \sqrt{1+1/\delta }\left\| \eta u \right\| _{H^1(\varOmega )} + \frac{1}{\delta R}\left\| u \right\| _{L^2(B_{(1+\delta /4)R}\cap \varOmega )}\nonumber \\&\quad +\, \frac{1}{\delta R}\left\| \widetilde{K}u \right\| _{L^2(B_{(1+\delta /4)R}{\setminus }\varGamma )}. \end{aligned}$$

(4.44)

Proof

We start with a localized splitting for the double-layer potential. More precisely, with a second cut-off function $\widehat{\eta }$ satisfying $\widehat{\eta } \equiv 1$ on $B_R$, ${\text {supp}}\, {\widehat{\eta }} \subseteq B_{( 1+\delta /4) R}$, and $\left\| \nabla {\widehat{\eta }} \right\| _{L^\infty (B_{(1+\delta )R})} \lesssim \frac{1}{\delta R}$, we write

$$\begin{aligned} {\widehat{\eta }} \widetilde{K}u = {\widehat{\eta }}\widetilde{K}(\eta u) + {\widehat{\eta }}\widetilde{K}(1-\eta )u =: v_\mathrm{near} + v_\mathrm{far}. \end{aligned}$$

First, we estimate the near-field $v_\mathrm{near} := {\widehat{\eta }}\widetilde{K}(\eta u)$. The mapping properties of the double-layer potential, (4.5), together with the fact that ${\text {supp}} \nabla {\widehat{\eta }} \subset B_{(1+\delta /4)R}{\setminus } B_R$ and the trace inequality provide

$$\begin{aligned} \left\| \nabla v_\mathrm{near} \right\| _{L^2(B_R{\setminus }\varGamma )}&\lesssim \left\| \eta u \right\| _{H^{1/2}(\varGamma )} +\frac{1}{\delta R}\Vert \widetilde{K} (\eta u)\Vert _{L^2(B_{(1+\delta /4)R}{\setminus } B_R) }\\&\lesssim \left\| \eta u \right\| _{H^1(\varOmega )} + \frac{1}{\delta R} \Vert \widetilde{K} (\eta u)\Vert _{L^2(B_{(1+\delta /4)R}{\setminus } B_R)}. \end{aligned}$$

Since ${\widehat{\eta }} (1-\eta ) \equiv 0$, the far field $v_\mathrm{far}$ is smooth. Integration by parts using $\varDelta \widetilde{K}((1-\eta ) u) = 0$, as well as $[\gamma _1 \widetilde{K}u] = 0$ and ${\widehat{\eta }} (1-\eta )\equiv 0$ (therefore no boundary terms appear), leads to

Here, we used that ${\text {*}}{supp}(\nabla {\widehat{\eta }})\subset B_{(1+\delta /4)R}\backslash B_{R}$. For the last term, we apply [19, Lemma 3.7,(ii)], which states that

$$\begin{aligned}&\left\| \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R}\backslash B_{R})}\\&\quad \lesssim \sqrt{\delta R}\left( \frac{1}{\sqrt{(1+\delta )R}} \left\| \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R} {\setminus } \varGamma )} + \sqrt{(1+\delta )R}\left\| \nabla \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R}{\setminus }\varGamma )}\right) . \end{aligned}$$

[19, Lemma 3.7,(i)] provides the estimate

$$\begin{aligned} \left\| \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R})} \lesssim \sqrt{ R}\left\| \gamma _0 ^{\text {int}}\widetilde{K}(\eta u) \right\| _{L^2(\varGamma )} + R\left\| \nabla \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R}{\setminus }\varGamma )}. \end{aligned}$$

The combination of these two estimates and the fact that $\gamma _0^\mathrm{int} \widetilde{K}u = (-1/2 + K)u$ gives us

$$\begin{aligned} \left\| \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R}\backslash B_{R})}&\lesssim \sqrt{\delta R}\left\| (1/2-K)(\eta u) \right\| _{L^2(\varGamma )}\\&\quad +\, \sqrt{\delta R}\sqrt{(1+\delta )R}\left\| \nabla \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R}{\setminus }\varGamma )}. \end{aligned}$$

With the mapping properties of K, $\widetilde{K}$ from (4.5), (4.6) and the multiplicative trace inequality this implies

$$\begin{aligned}&\frac{1}{\delta R}\left\| \widetilde{K}(\eta u) \right\| _{L^2(B_{(1+\delta /4)R}\backslash B_{R})} \lesssim \frac{1}{\sqrt{\delta R}}\left\| \eta u \right\| _{L^2(\varGamma )} + \sqrt{1+1/\delta }\left\| \eta u \right\| _{H^1(\varOmega )} \\&\qquad \quad \quad \quad \lesssim \frac{1}{\sqrt{\delta R}}\left\| \eta u \right\| _{L^2(\varOmega )} + \frac{1}{\sqrt{\delta R}}\left\| \eta u \right\| ^{1/2}_{L^2(\varOmega )}\left\| \nabla (\eta u) \right\| ^{1/2}_{L^2(\varOmega )}\\&\qquad \quad \quad \quad \quad + \,\sqrt{1+1/\delta }\left\| \eta u \right\| _{H^1(\varOmega )}\\&\qquad \quad \quad \quad \lesssim \frac{1}{\delta R}\left\| \eta u \right\| _{L^2(\varOmega )} + \left\| \nabla (\eta u) \right\| _{L^2(\varOmega )}+ \sqrt{1+1/\delta }\left\| \eta u \right\| _{H^1(\varOmega )}. \end{aligned}$$

Putting the estimates for the near-field and the far-field together, we obtain

$$\begin{aligned} \left\| \nabla \widetilde{K}u \right\| _{L^2(B_R{\setminus }\varGamma )}&\le \left\| \nabla v_\mathrm{near} \right\| _{L^2(B_R{\setminus }\varGamma )} + \left\| \nabla v_\mathrm{far} \right\| _{L^2(B_R{\setminus }\varGamma )}\nonumber \\&\lesssim \sqrt{1+1/\delta }\left\| \eta u \right\| _{H^1(\varOmega )} + \frac{1}{\delta R}\left\| u \right\| _{L^2(B_{(1+\delta /4)R}\cap \varOmega )}\\&\quad +\, \frac{1}{\delta R}\left\| \widetilde{K}u \right\| _{L^2(B_{(1+\delta /4)R}{\setminus }\varGamma )}, \end{aligned}$$

which finishes the proof.$\square$

Proof

(Proof of Theorem 2.6) Once again, we write $(u,\varphi )$ for the Galerkin solution $(u_h,\varphi _h)$. The assumption on the support of the data implies the local orthogonality

$$\begin{aligned} a_\mathrm{jn}(u,\varphi ;\psi _h,\zeta _h)&= 0 \quad \forall (\psi _h,\zeta _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)\nonumber \\&~~~~\quad \text {with}\quad {\text {*}}{supp}\psi _h, {\text {*}}{supp}\zeta _h \subset B_{(1+\varepsilon )R}. \end{aligned}$$

(4.45)

Let $\eta \in C_0^\infty (\mathbb {R}^d)$ be a cut-off function with $\text {supp}\, \eta \subseteq B_{( 1+\delta /2) R}$, $\eta \equiv 1$ on $B_{( 1+\delta /4) R}$, $0 \le \eta \le 1$, and $\left\| D^j\eta \right\| _{L^\infty (B_{(1+\delta )R})} \lesssim \frac{1}{(\delta R)^j}$ for $j=1,2$. Here, $0<\delta \le \varepsilon$ is given such that $\frac{h}{R}\le \frac{\delta }{16}$. We note that the condition $\eta \equiv 1$ on $B_{( 1+\delta /4) R}$ is additionally imposed in order to satisfy estimate (4.44), as the localization of the double-layer operator is additionally needed in comparison with the other couplings.

Step 1: We provide a localized ellipticity estimate, i.e., we prove

$$\begin{aligned}&\left\| \nabla (\eta u) \right\| ^2_{L^2(\varOmega )} +\left\| \nabla (\eta \widetilde{V} \varphi ) \right\| ^2_{L^2(\mathbb {R}^d) } +\left\| \nabla \widetilde{K} u \right\| ^2_{L^2(B_R{\setminus }\varGamma )}\\&~~~~~~~~~~~~~~~~~\quad \quad \quad \lesssim a_\mathrm{jn}(u, \varphi ; \eta ^2 u , \eta ^2 \varphi )+ {\text {terms in weaker norms}}. \end{aligned}$$

See (4.50 for the precise form). We start with (4.44) to obtain

$$\begin{aligned}&\left\| \nabla (\eta u ) \right\| ^2_{L^2(\varOmega ) } +\left\| \nabla ( \eta \widetilde{V} \varphi ) \right\| ^2_{L^2(\mathbb {R}^d) } +\left\| \nabla \widetilde{K} u \right\| _ {L^2( B_R {\setminus }\varGamma ) }^2 \nonumber \\ \nonumber&\quad \lesssim (1+1/\delta )\left( \left\| \nabla (\eta u ) \right\| ^2_{L^2(\varOmega )} +\left\| \nabla ( \eta \widetilde{V} \varphi ) \right\| ^2_{L^2(\mathbb {R}^d) } \right) + \frac{(1+1/\delta )}{(\delta R)^2}\left\| u \right\| _{L^2(B_{(1+\delta )R}\cap \varOmega )}^2\nonumber \\&\qquad +\, \frac{1}{(\delta R)^2}\left\| \widetilde{K}u \right\| _{L^2(B_{(1+\delta )R}{\setminus }\varGamma )}^2. \end{aligned}$$

(4.46)

The last two terms are already in weaker norms, and for the first two terms, we apply (4.17). Since we assumed $C_\mathrm{ell}>1/4$ for unique solvability, we choose a $\rho >0$ such that $1/4< \rho /2 < C_\mathrm{ell}$ and set $C_{\rho }:=\min \{1-\frac{1}{2\rho },C_\mathrm{ell}-\frac{\rho }{2}\} > 0$. Then, (4.17) implies

(4.47)

The first three terms can be expanded as in Theorem 2.4, where (4.18) leads to

(4.48)

where the omitted terms (cf. (4.18))

$$\begin{aligned} \text {l.o.t.} = \langle (\nabla \eta ) \widetilde{V} \varphi , \nabla (\eta u)\rangle _{L^2(\varOmega )} - \langle \nabla \widetilde{V} \varphi ,\eta (\nabla \eta ) u\rangle _{L^2(\varOmega )} \end{aligned}$$

can be estimated in weaker norms (i.e., $\Vert \widetilde{V}\varphi \Vert _{L^2(B_{(1+\delta /2)R}\cap \varOmega )}$, $\Vert u\Vert _{L^2(B_{(1+\delta /2)R}\cap \varOmega )}$) or lead to terms that are absorbed in the left-hand side as in the proof of Theorem 2.4 [see (4.23), (4.24)]. Equations (4.39) and (4.19) give

(4.49)

Therefore, we only have to estimate the last term in (4.47). We write in the same way as in (4.48)

where again, the omitted terms

$$\begin{aligned} \text {l.o.t.} = 2 \langle (\nabla (\eta \widetilde{V} \varphi ), (\nabla \eta ) \widetilde{K} u\rangle _{L^2(\mathbb {R}^d{\setminus }\varGamma )} - 2 \langle (\nabla \eta ) \widetilde{V} \varphi , \nabla (\eta \widetilde{K} u)\rangle _{L^2(\mathbb {R}^d{\setminus }\varGamma )} \end{aligned}$$

can be estimated in weaker norms (i.e., by $\Vert \widetilde{K} u\Vert _{L^2(B_{(1+\delta /2)R}{\setminus }\varGamma )}$ and $\Vert \widetilde{V} \varphi \Vert _{L^2(B_{(1+\delta /2)R}}$) or absorbed in the left-hand side. Integration by parts on $\mathbb {R}^d\backslash {\overline{\varOmega }}$ and $\varOmega$ together with $\varDelta \widetilde{K}u = 0$ and $[\gamma _1 \widetilde{K}u] = 0 = [\eta ^2\widetilde{V} \varphi ]$ implies

Putting everything together into (4.47) and in turn into (4.46), we obtain

$$\begin{aligned}&\nonumber \left\| \nabla (\eta u ) \right\| ^2_{L^2(\varOmega ) } +\left\| \nabla ( \eta \widetilde{V} \varphi ) \right\| ^2_{L^2(\mathbb {R}^d) } +\left\| \nabla (\eta \widetilde{K} u ) \right\| _ {L^2( \mathbb {R}^d {\setminus } \varGamma ) }^2 \\&\quad \lesssim (1+1/\delta )\, a_\mathrm{jn}(u, \varphi ; \eta ^2 u , \eta ^2 \varphi ) +\frac{(1+1/\delta )}{(\delta R)^2} \left\| \widetilde{K}u\right\| ^2_{L ^ 2( B_{ ( 1+\delta )R } {\setminus }\varGamma ) } \nonumber \\&\qquad +\,\frac{(1+1/\delta )}{(\delta R)^2}\left\| u \right\| ^2 _{L^2( B_{ ( 1+\delta )R }\cap \varOmega )} + \frac{(1+1/\delta )}{(\delta R)^2} \left\| \widetilde{V} \varphi \right\| _{L^2(B_{(1+\delta )R})}^2. \end{aligned}$$

(4.50)

Step 2: We apply the local orthogonality of $(u,\varphi )$ to piecewise polynomials and use approximation properties. Let $I_h^{\varOmega }: C({\overline{\varOmega }}) \rightarrow S^{1,1}(\mathcal {T}_h)$ be the nodal interpolation operator and $I_h^{\varGamma }$ the $L^2(\varGamma )$-orthogonal projection mapping onto $S^{0,0}(\mathcal {K}_h)$. Then, the orthogonality (4.45) leads to

(4.51)

The terms $T_1$, $T_2$ have already been estimated in the proof of Theorem 2.4, inequalities (4.27), (4.28), and $T_4$ was treated in (4.42) in the proof of Theorem 2.5.

It remains to estimate $T_3$. With $\text {supp}\left( \eta ^2 u - I_h ^ \varOmega ( \eta ^2 u) \right) \subset B_{(1+\delta /2)R}$ due to $16h\le \delta R$, we get

Lemma 4.3 provides

$$\begin{aligned} \left\| \varphi \right\| _{{L^2}( B_{(1+\delta /2)R}) }&\lesssim h ^{-1/2} \left\| \nabla \widetilde{V}\varphi \right\| _{L^2( B_{ ( 1+\delta )R })}. \end{aligned}$$

Therefore, with (4.31), we obtain

(4.52)

Putting the estimates of $T_1$, $T_2$, $T_3$, $T_4$ together and using $\delta \lesssim 1$ leads to

$$\begin{aligned}&\left\| \nabla u \right\| _{L^2(B_R\cap \varOmega )}^2 + \left\| \nabla \widetilde{V} \varphi \right\| _{L^2(B_R)}^2 +\left\| \nabla \widetilde{K} u \right\| _ {L^2(B_R {\setminus } \varGamma )}^2 \nonumber \\&\quad \lesssim \frac{h}{ \delta ^2 R}\left( \left\| \nabla u \right\| ^2_{L^2 ( B_{(1+ \delta )R } \cap \varOmega ) } +\left\| \nabla \widetilde{V} \varphi \right\| ^2_{L^2 ( B_{(1+ \delta )R } ) }+\left\| \nabla \widetilde{K} u \right\| ^2_{L^2 ( B_{(1+ \delta )R } {\setminus }\varGamma ) }\right) \nonumber \\&\qquad + \,\frac{1}{\delta ^3 R^2} \left( \left\| u \right\| ^2_{L^2 ( B_{(1+ \delta )R } \cap \varOmega ) } +\left\| \widetilde{V} \varphi \right\| ^2_{L^2 ( B_{(1+ \delta )R } ) } +\left\| \widetilde{K} u \right\| ^2_{L^2 ( B_{(1+ \delta )R } {\setminus } \varGamma ) }\right) . \end{aligned}$$

(4.53)

Step 3: Reapplying (4.53) to the gradient terms with $\delta = \frac{ \varepsilon }{2}$ and suitable boxes, we get the desired result exactly as in step 3 of the proof of Theorem 2.4. $\square$

5 $\mathcal {H}$-Matrix approximation to inverses: application of the abstract framework for the FEM-BEM couplings

In this section, we prove the existence of exponentially convergent $\mathcal {H}$-matrix approximants to the inverses of the stiffness matrices of the FEM-BEM couplings, as stated in Theorem 2.13. For this purpose, we ascertain the validity of the assumptions (A1)–(A3) from Sect. 3 for the FEM-BEM couplings.

5.1 The local dual basis

In the setting of Sect. 3.1, we have $\mathbf {X}= H^1(\varOmega ) \times H^{-1/2}(\varGamma )$. In order to suitably represent the data $f,u_0,\varphi _0$ in (2.1), we understand the discrete space $S^{1,1}(\mathcal {T}_h) \simeq S^{1,1}_0(\mathcal {T}_h) \times S^{1,1}(\mathcal {K}_h) \subset L^2(\varOmega )\times L^2(\varGamma )$, where $S^{1,1}_0(\mathcal {T}_h) := S^{1,1}(\mathcal {T}_h) \cap H^1_0(\varOmega )$. Having identified $S^{1,1}(\mathcal {T}_h)$ with $S^{1,1}_0(\mathcal {T}_h) \times S^{1,1}(\mathcal {K}_h)$, we view the full FEM-BEM coupling problem as one approximating in $S^{1,1}_0(\mathcal {T}_h) \times S^{1,1}(\mathcal {K}_h) \times S^{0,0}(\mathcal {K}_h)$. That is, we set $k=1$ and $\ell =2$, and consider $\mathbf {L}^2 = L^2(\varOmega ) \times L^2(\varGamma )\times L^2(\varGamma )$ for all three FEM-BEM couplings. The discrete space $\mathbf {X}_N =S^{1,1}_0(\mathcal {T}_h) \times S^{1,1}(\mathcal {K}_h) \times S^{0,0}(\mathcal {K}_h) \subset \mathbf {L}^2$ has dimension $N = n_1+n_2+m$, where $n_1 = {\text {*}}{dim}(S^{1,1}_0(\mathcal {T}_h))$, $n_2 = {\text {*}}{dim}(S^{1,1}(\mathcal {K}_h))$ ($n_1+n_2 = n$) and $m = {\text {*}}{dim}(S^{0,0}(\mathcal {K}_h))$. It remains to show (A1).

The dual functions $\varvec{\lambda }_i$ are constructed by use of $L^2$-dual bases for $S^{1,1}(\mathcal {T}_h)$ and $S^{0,0}(\mathcal {K}_h)$. [2, Sect. 3.3] gives an explicit construction of a suitable dual basis $\{\lambda _i^\varOmega \,:\, i=1,\dots ,n_1\}$ for $S^{1,1}_0(\mathcal {T}_h)$. This is done elementwise in a discontinuous fashion, i.e., $\lambda _i^\varOmega \in S^{1,0}(\mathcal {T}_h) \subset L^2(\varOmega )$, where each $\lambda _i^\varOmega$ is non-zero only on one element of $\mathcal {T}_h$ (in the patch of the hat function $\xi _i$), and the function on this element is given by the push-forward of a dual shape function on the reference element. Moreover, the local stability estimate

$$\begin{aligned} \Big \Vert \sum _{j=1}^{n_1} \mathbf {x}_j \lambda _j^\varOmega \Big \Vert _{L^2(\varOmega )}\le h^{-d/2} \left\| \mathbf {x} \right\| _2 \end{aligned}$$

(5.1)

holds for all $\mathbf {x}\in \mathbb {R}^{n_1}$, and we have ${\text {supp}} \lambda _i^\varOmega \subset {\text {supp}} \xi _i$. We note that the zero boundary condition is irrelevant for the construction. The same can be done for the boundary degrees of freedom, i.e., there exists a dual basis $\{\lambda _i^\varGamma \,:\, i=1,\dots ,n_2\}$ with the analogous stability and support properties.

For the boundary degrees of freedom in $S^{0,0}(\mathcal {K}_h)$, the dual mappings are given by $\mu _i^\varGamma := \chi _i/\left\| \chi _i \right\| _{L^2(\varOmega )}^2$, i.e., the dual basis coincides—up to scaling—with the given basis $\{\chi _i\,:\, i=1,\dots , m\}$ of $S^{0,0}(\mathcal {K}_h)$. With (2.4b), this gives

$$\begin{aligned} \Big \Vert \sum _{j=1}^m \mathbf {y}_j \mu _j^\varGamma \Big \Vert _{L^2(\varOmega )}\le h^{-(d-1)/2} \left\| \mathbf {y} \right\| _2 \end{aligned}$$

(5.2)

for all $\mathbf {y} \in \mathbb {R}^m$.

The dual basis is defined as $\varvec{\lambda }_i := (\lambda ^{\varOmega }_i,0,0)$ for $i = 1,\dots ,n_1$, $\varvec{\lambda }_{i+n_1} := (0,\lambda ^{\varGamma }_i,0)$ for $i = 1,\dots ,n_2$, and $\varvec{\lambda }_{i+n} := (0,0,\mu ^{\varGamma }_i)$ for $i = 1,\dots ,m$. The estimates (5.1), (5.2) together with the analogous one for the $\lambda _i^\varGamma$ show (A1).

5.2 Low dimensional approximation

The sets $\mathcal {B}$, $\mathcal {B}^\delta$ and the norm $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}}$: We take $M=3$ and choose collections $\mathcal {B}= \mathcal {B}_R := \{B_R\cap \varOmega ,B_R,B_R\backslash \varGamma \}$, where $B_R$ is a box of side length R. For $\ell \in \mathbb {N}$, the enlarged sets $\mathcal {B}^{\delta \ell }$ then have the form

$$\begin{aligned} \mathcal {B}^{\delta \ell } = \mathcal {B}_R^{\delta \ell } := \{B_{R+2\delta \ell }\cap \varOmega ,B_{R+2\delta \ell },B_{R+2\delta \ell }\backslash \varGamma \} \quad \end{aligned}$$

(5.3)

with the concentric boxes $B_{R+2\delta \ell }$ of side length $R+2\delta \ell$.

For $\mathbf {v} = (u,v,w)$, we use the norm from (2.6)

$$\begin{aligned} \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}}:= \left| \! \left| \! \left| (u,v,w) \right| \! \right| \! \right| _{h,R} \end{aligned}$$

in (A2). For the Bielak–MacCamy coupling, taking $M=2$ and choosing collections $\mathcal {B}_R := \{B_R\cap \varOmega ,B_R\}$ would suffice, however, in order to keep the notation short, we can use $M=3$ for this coupling as well by setting the third component to zero, i.e., $\mathbf {v} =(u,v,0)$.

The operator $Q_H$ and (A2): For the operator $Q_H$, we use a combination of localization and Scott–Zhang interpolation, introduced in [36], on a coarse grid. Since the double-layer potential is discontinuous across $\varGamma$, we need to employ a piecewise Scott–Zhang operator. Let $\mathcal {R}_H$ be a quasi-uniform (infinite) triangulation of $\mathbb {R} ^d$ (into open simplices $R \in {\mathcal R}_H$) with mesh width H that conforms to $\varOmega$, i.e., every $R \in {\mathcal {R}_H}$ satisfies either $R \subset \varOmega$ or $R\subset \varOmega ^\mathrm{ext}$ and the restrictions ${\mathcal R}_H|_{\varOmega }$ and ${\mathcal R}_H|_{\varOmega ^\mathrm{ext}}$ are $\gamma$-shape regular, regular triangulations of $\varOmega$ and $\varOmega ^\mathrm{ext}$ of mesh size H, respectively.

With the Scott–Zhang projections $I_H^\mathrm{int}$, $I_H^\mathrm{ext}$ for the grids $\mathcal {R}_H|_{\varOmega }$ and $\mathcal {R}_H|_{{\varOmega }^c}$, we define the operator $I_H^\mathrm{pw}:H^1(\mathbb {R}^d{\setminus } \varGamma ) \rightarrow S^{1,1}_\mathrm{pw}(\mathcal {R}_H):= \{v: v|_\varOmega \in S^{1,1}({\mathcal R}_H|_{\varOmega })$ and $v|_{\varOmega ^\mathrm{ext}} \in S^{1,1}({\mathcal R}_H|_{\varOmega ^\mathrm{ext}})\}$ in a piecewise fashion by

$$\begin{aligned} I_H^\mathrm{pw} v = \left\{ \begin{array}{l} I_H^\mathrm{int} v \quad \text {on } \varOmega , \\ I_H^\mathrm{ext} v \quad \text {on } \varOmega ^\mathrm{ext}. \end{array} \right. \end{aligned}$$

(5.4)

We denote the patch of an element $R \in \mathcal {R} _H$ by

$$\begin{aligned} \omega _R^{\varOmega }&:= {\text {interior}} \left( \bigcup \left\{ \overline{R^\prime }\,:\, R^\prime \in \mathcal {R}_H|_{\varOmega } \quad \text {s.t.}\quad \overline{R} \cap \overline{R^ \prime } \ne \emptyset \right\} \right) , \\ \omega _R^{\varOmega ^\mathrm{ext}}&:= {\text {interior}} \left( \bigcup \left\{ \overline{R^\prime } \,:\, R^\prime \in \mathcal {R}_H|_{\varOmega ^\mathrm{ext}} \quad \text {s.t.} \quad \overline{R} \cap \overline{R^ \prime } \ne \emptyset \right\} \right) . \end{aligned}$$

The Scott–Zhang projection reproduces piecewise affine functions and has the following local approximation property for piecewise $H^s$ functions:

$$\begin{aligned} \left\| v - I_H^\mathrm{pw} v\right\| ^2_{H ^ t( R) } \le C H ^ {2 (s-t) } {\left\{ \begin{array}{ll} \left| v \right| ^2_{H^{s}(\omega _R^\varOmega )} &{}\hbox { if}\ R \subset \varOmega \\ \left| v \right| ^2_{H^{s}(\omega _R^{\varOmega ^\mathrm{ext}})} &{}\hbox { if}\ R \subset \varOmega ^\mathrm{ext}\end{array}\right. } \end{aligned}$$

(5.5)

with $t, s \in \{0,1\}, \quad 0 \le t \le s\le 1$, and a constant C depending only on the shape-regularity of $\mathcal {R}_H$ and d.

Let $\eta \in C^ \infty _0 ( B _{R+2\delta } )$ be a cut-off function satisfying ${\text {supp}} \,\eta \subset B_{R+\delta }, \, \eta \equiv 1$ on $B_R$ and $\left\| \nabla \eta \right\| _{L^\infty (\mathbb {R}^d)}\lesssim \frac{1}{\delta }$. We define the operator

$$\begin{aligned} Q_H\mathbf {v} := (I_H^\mathrm{int}(\eta \mathbf {v}_1), I_H(\eta \mathbf {v}_2), I_H^\mathrm{pw}(\eta \mathbf {v}_3)), \end{aligned}$$

(5.6)

where $I_H$ denotes the classical Scott–Zhang operator for the mesh $\mathcal {R}_H$. We have

$$\begin{aligned} \left| \! \left| \! \left| \mathbf {v}- Q_H\mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}}^2 = \left\| \mathbf {v}_1- I_H^\mathrm{int}(\eta \mathbf {v}_1) \right\| _{h,R,\varOmega }^2 + \left\| \mathbf {v}_2- I_H(\eta \mathbf {v}_2) \right\| _{h,R}^2 + \left\| \mathbf {v}_3- I_H^\mathrm{pw}(\eta \mathbf {v}_3) \right\| _{h,R,\varGamma ^c}^2. \end{aligned}$$

Each term on the right-hand side can be estimated with the same arguments. We only work out the details for the second component. Assuming $h\le H$, and using approximation properties and stability of the Scott–Zhang projection, we get

$$\begin{aligned} \left\| \mathbf {v}_2- I_H(\eta \mathbf {v}_2) \right\| _{h,R}^2&= \left\| \eta \mathbf {v}_2- I_H(\eta \mathbf {v}_2) \right\| _{h,R}^2 \\&= h^2 \left\| \nabla (\eta \mathbf {v}_2- I_H(\eta \mathbf {v}_2)) \right\| _{L^2(B_R)}^2 + \left\| \eta \mathbf {v}_2- I_H(\eta \mathbf {v}_2) \right\| _{L^2(B_R)}^2 \\&\lesssim (h^2+H^2) \left\| \nabla (\eta \mathbf {v}_2) \right\| ^2_{L^2(\mathbb {R}^d)}\\&\lesssim H^2\left( \left\| \nabla \mathbf {v}_2 \right\| _{L^2(B_{R+2\delta })}^2 + \delta ^{-1}\left\| \mathbf {v}_2 \right\| _{L^2(B_{R+2\delta })}^2 \right) , \end{aligned}$$

which shows (A2) for the discrete space $V_{H,\mathcal {B}^\delta } = S^{1,1}(\mathcal {R}_H)|_{B_{R+2\delta }\cap \varOmega } \times S^{1,1}(\mathcal {R}_H)|_{B_{R+2\delta }} \times S^{1,1}_\mathrm{pw}(\mathcal {R}_H)|_{B_{R+2\delta }}$ of dimension $\dim V_{H,\mathcal {B}^\delta } \le C \left( \frac{{\text {*}}{diam}(B_{R+2\delta })}{H}\right) ^{Md}$.

The Caccioppoli inequalities and (A3): Theorems 2.4–2.6 provide the Caccioppoli type estimates asserted in (A3) with $\delta = \varepsilon R/2$. For the Bielak–MacCamy coupling, we have $\alpha =1$ and $C_\mathrm{Set} =8h$, for the symmetric coupling $\alpha =1$ and $C_\mathrm{Set} =16h$. For the Johnson–Nédélec coupling, we have to take $\alpha =2$ and $C_\mathrm{Set} =16h$. For $\mathcal {B}_R = \{B_R\cap \varOmega ,B_R,B_R\backslash \varGamma \}$, the spaces $\mathcal {H}_h(\mathcal {B}_R)$ can be characterized by

$$\begin{aligned} \mathcal {H}_h(\mathcal {B}_R)&:= \{(v,\widetilde{V}\phi ,\widetilde{K}v) \in H^1(B_R\cap \varOmega )\times H^1(B_R) \times H^1(B_R\backslash \varGamma ): \\&~~~~~~~~ \, \, \exists {\widetilde{v}} \in S^{1,1}(\mathcal {T}_h), {\widetilde{\phi }} \in S^{0,0}(\mathcal {K}_h):\\&~~~~~~~~\quad {\widetilde{v}}|_{B_R \cap \varOmega } =v|_{B_R \cap \varOmega }, \quad \widetilde{V} {\widetilde{\phi }} |_{B_R} =\widetilde{V}\phi |_{ B_R}, \\&~~~~~~~~ \quad \widetilde{K} {\widetilde{v}}|_{B_R\backslash \varGamma } =\widetilde{K} v|_{ B_R\backslash \varGamma }, a(v,\phi ;\psi _h,\zeta _h) = 0 \\&~~~~~~~~\quad \forall (\psi _h,\zeta _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h), \, {\text {*}}{supp} \psi _h,\zeta _h \subset B_R \}, \end{aligned}$$

where the bilinear form $a(\cdot ,\cdot )$ is either $a_\mathrm{sym}$ or $a_\mathrm{jn}$. For the Bielak–MacCamy coupling, it suffices to require

$$\begin{aligned} \mathcal {H}_h(\mathcal {B}_R) :=&\{(v,\widetilde{V}\phi ,0) \in H^1(B_R\cap \varOmega )\times H^1(B_R) \times H^1(B_R\backslash \varGamma ){:}\\ {}&\,\, \exists {\widetilde{v}} \in S^{1,1}(\mathcal {T}_h), {\widetilde{\phi }} \in S^{0,0}(\mathcal {K}_h){:}\\&\,\, {\widetilde{v}}|_{B_R \cap \varOmega } =v|_{B_R \cap \varOmega }, \quad \widetilde{V} {\widetilde{\phi }} |_{B_R} =\widetilde{V}\phi |_{ B_R}, \quad a_\mathrm{bmc}(v,\phi ;\psi _h,\zeta _h) = 0 \\&\quad \forall (\psi _h,\zeta _h) \in S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h), \, {\text {*}}{supp} \psi _h,\zeta _h \subset B_R \}. \end{aligned}$$

With these definitions, the closedness and nestedness of the spaces $\mathcal {H}_h(\mathcal {B}_R)$ clearly holds.

5.3 Proof of Theorem 2.13

As a consequence of the above discussions, the abstract framework of the previous sections can be applied and it remains to put everything together.

The following propositions constructs the finite dimensional space required from Lemma 3.3, from which the Galerkin solution can be approximated exponentially well.

Proposition 5.1

(Low dimensional approximation for the symmetric coupling) Let $(\tau , \sigma )$ be a cluster pair with bounding boxes $B_{R_\tau }$ and $B_{R_\sigma }$ that satisfy for given $\eta > 0$

$$\begin{aligned} \eta {\text {*}}{dist}(B_{R_\tau },B_{R_\sigma }) \ge {\text {*}}{diam}(B_{R_\tau }). \end{aligned}$$

Then, for each $L \in \mathbb {N}$, there exists a space $\widehat{\mathbf {W}}_L \subset S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$ with dimension $\dim \widehat{\mathbf {W}}_L \le C_\mathrm{low} L ^{3d+1}$ such that for arbitrary right-hand sides $f \in L^2 (\varOmega )$, $v_0 \in L^2(\varGamma )$, and $w_0 \in {L^2(\varGamma )}$ with $\big ({\text {*}}{supp} f \cup {\text {*}}{supp}v_0 \cup {\text {*}}{supp}w_0\bigr ) \subset B_{R_\sigma },$ the corresponding Galerkin solution $(u_h,\varphi _h)$ of (2.11) satisfies

$$\begin{aligned}&\min \limits _{\left( \widetilde{u}, \widetilde{\varphi }\right) \in \widehat{\mathbf {W}}_L} \left( \left\| u_h- \widetilde{u}\right\| _{L^2 (B_{R_\tau } \cap \varOmega )}+ \left\| \varphi _h- \widetilde{\varphi }\right\| _{L^{2} (B_{R_\tau }\cap \varGamma )}\right) \\&~~~\quad ~~~~\quad \quad \le C_\mathrm{{box}}h^{-2}2^{-L}\left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| v_0 \right\| _ {L^{2} (\varGamma )} +\left\| w_0 \right\| _ {L^{2} (\varGamma )} \right) . \end{aligned}$$

The constants $C_\mathrm{low}$, $C_\mathrm{box}$ depend only on $\varOmega$, d, ${{\mathbf {C}}}$, $\eta$, and the $\gamma$-shape regularity of the quasi-uniform triangulation $\mathcal {T}_h$ and $\mathcal {K}_h$.

Proof

For given $L \in \mathbb {N}$, we choose $\delta := \frac{R_{\tau }}{2\eta L}$. Then, we have

$$\begin{aligned} {\text {*}}{dist}(B_{R_\tau +2\delta L},B_ {R_\sigma }) \ge {\text {*}}{dist} (B_ {R_\tau },B_ {R_\sigma })- L \delta \sqrt{d} \ge \sqrt{d} R_\tau \Big (\frac{1}{\eta }-\frac{1}{2\eta }\Big ) >0. \end{aligned}$$

With $\mathcal {B}_{R_\tau } = \{B_{R_\tau }\cap \varOmega ,B_{R_\tau },B_{R_\tau }\backslash \varGamma \}$ and $\mathcal {B}^{\delta L}_{R_\tau } = \{B_{R_\tau +2\delta L}\cap \varOmega ,B_{R_\tau +2\delta L},B_{R_\tau +2\delta L}\backslash \varGamma \}$ from (5.3), the assumption on the support of the data therefore implies the local orthogonality imposed in the space $\mathcal {H}_h(\mathcal {B}^{\delta L}_{R_\tau })$. In order to define the space $\widehat{\mathbf {W}}_L$, we distinguish two cases.

Case $\delta > 2C_\mathrm{Set}$: Then, Lemma 3.6 applied with the sets $\mathcal {B}_{R_\tau }^\delta$ and $\mathcal {B}_{R_\tau }^{\delta L}$ provides a space $\mathbf {W}_L$ of dimension

$$\begin{aligned} \dim \mathbf {W} _L \le C _ \mathrm{dim}\Big (L-1+ \frac{{\text {*}}{diam}(\mathcal {B}_{R_\tau }^\delta )}{\delta }\Big )^{3d+1} \lesssim \Big (L+ \frac{\sqrt{d}R_\tau 2\eta L}{R_\tau }\Big )^{3d+1} \lesssim L^{3d+1} \end{aligned}$$

with the approximation properties for $\mathbf {v} = (u_h,\widetilde{V}\varphi _h,\widetilde{K}u_h)$

$$\begin{aligned} \inf _{\mathbf {w}\in \mathbf {W}_L }\left| \! \left| \! \left| \mathbf {v}- \mathbf {w} \right| \! \right| \! \right| _{ \mathcal {B}_{R_\tau }^\delta } \le 2 ^ {-(L-1) } \left| \! \left| \! \left| \mathbf {v} \right| \! \right| \! \right| _{\mathcal {B}_{R_\tau }^{\delta L}}. \end{aligned}$$

(5.7)

Therefore, it remains to estimate the norm $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right| _{\mathcal {B}}$ from above and below.

With $h\lesssim 1$, the mapping properties of $\widetilde{V}$ and $\widetilde{K}$ from (4.5), and the trace inequality we estimate

$$\begin{aligned} \nonumber \left| \! \left| \! \left| (u_h,\widetilde{V}\varphi _h,\widetilde{K}u_h) \right| \! \right| \! \right| _{\mathcal {B}^{\delta L}_{R_\tau }}&\lesssim \left\| u_h \right\| _ {H^1 (\varOmega )}+ \left\| \widetilde{V}\varphi _h \right\| _{H ^1(B_{(1+1/(2\eta ))R_\tau })} + \left\| \widetilde{K}u_h \right\| _{H ^1(B_{(1+1/(2\eta ))R_\tau }\backslash \varGamma )} \\&\lesssim \left\| u_h \right\| _ {H^1 (\varOmega )}+ \left\| \varphi _h\right\| _{H^{-1/2}(\varGamma )}. \end{aligned}$$

(5.8)

The stabilized form is elliptic by [1]. Moreover, [1, Theorem 18] proves that the Galerkin solution $(u_h,\varphi _h)$ also solves . Therefore, we have

(5.9)

The stabilization term can be estimated with the mapping properties of V and K from (4.6) and the trace inequality by

Inserting this in (5.9), using the trace inequality and an inverse estimate we further estimate

$$\begin{aligned} \nonumber \left\| \varphi _h\right\| ^2_{H^{-1/2}(\varGamma )}+\left\| u_h \right\| ^2_{H^1(\varOmega )}&\lesssim \left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| v_0 \right\| _ {H^{-1/2} (\varGamma )}\right) \left\| u_h \right\| _{H^1(\varOmega )}\\&\nonumber \quad +\,\left\| w_0 \right\| _ {L^{2} (\varGamma )} \left( \left\| \varphi _h \right\| _{L^{2}(\varGamma )}+\left\| u_h \right\| _{H^1(\varOmega )} +\left\| \varphi _h \right\| _{H^{-1/2}(\varGamma )}\right) \\ {}&\nonumber \le \left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| v_0 \right\| _ {H^{-1/2} (\varGamma )}\right) \left\| u_h \right\| _{H^1(\varOmega )} \\&\quad +\,h^{-1/2}\left\| w_0 \right\| _{L^2(\varGamma )}\left( \left\| u_h \right\| _{H^1(\varOmega )} +\left\| \varphi _h \right\| _{H^{-1/2}(\varGamma )}\right) . \end{aligned}$$

With Young’s inequality and inserting this in (5.8), we obtain the upper bound

$$\begin{aligned} \left| \! \left| \! \left| (u_h,\widetilde{V}\varphi _h,\widetilde{K}u_h) \right| \! \right| \! \right| _{\mathcal {B}_{R_\tau }^{\delta L}}&\lesssim \left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| v_0 \right\| _ {L^2(\varGamma )} +h ^{-1/2}\left\| w_0 \right\| _ {L^2(\varGamma )}\right) . \end{aligned}$$

(5.10)

The jump conditions of the single-layer potential and Lemma 4.3 provide for arbitrary $\widetilde{\varphi } \in S^{0,0}(\mathcal {K}_h)$

$$\begin{aligned} \left\| \varphi _h -\widetilde{\varphi } \right\| _{L^2 (B_{R_\tau } \cap \varGamma ) }&= \left\| [\gamma _1 \widetilde{V}\varphi _h ] -[\gamma _1 \widetilde{V} \widetilde{\varphi }] \right\| _{L^2 (B_{R_\tau } \cap \varGamma ) }\nonumber \\&\lesssim h^{-1/2}\left\| \nabla ( \widetilde{V}\varphi _h-\widetilde{V}\widetilde{\varphi }) \right\| _{L^2(B_{R+2\delta })} \nonumber \\&\lesssim h^{-3/2}\left| \! \left| \! \left| \widetilde{V}\varphi _h- \widetilde{V}\widetilde{\varphi } \right| \! \right| \! \right| _{h,R+2\delta }. \end{aligned}$$

(5.11)

Finally, we define $\widehat{\mathbf {W}}_L := \{(\widetilde{u},[\gamma _1 \widetilde{v}])\,:\, (\widetilde{u},\widetilde{v},\widetilde{w})\in \mathbf {W}_L\}$. Then, the dimension of $\widehat{\mathbf {W}}_L$ is bounded by ${\text {dim}}\widehat{\mathbf {W}}_L \le C L^{3d+1}$, and the error estimate follows from (5.7) since

$$\begin{aligned}&\nonumber \inf \limits _{(\widetilde{u},\widetilde{\varphi }) \in \widehat{\mathbf {W}}_L} \left( \left\| u_h- \widetilde{u}\right\| _{L^2 (B_{R_\tau }\cap \varOmega )} +\left\| \varphi _h -\widetilde{\varphi } \right\| _{L^2 (B_{R_\tau } \cap \varGamma ) } \right) \\&~~~~~~~~~\quad \quad \lesssim h^{-3/2}\inf \limits _{\mathbf {w} \in \mathbf {W}_L} \left| \! \left| \! \left| (u_h,\widetilde{V}\varphi _h,\widetilde{K}u_h)-\mathbf {w} \right| \! \right| \! \right| _{\mathcal {B}_{R_\tau }^{\delta }} \\&\nonumber ~~~~~~~~~\quad \quad \lesssim h^{-3/2} 2 ^{-L} \left| \! \left| \! \left| (u_h,\widetilde{V}\varphi _h,\widetilde{K}u_h) \right| \! \right| \! \right| _{\mathcal {B}_{R_\tau }^{\delta L}}. \end{aligned}$$

Applying estimate (5.10) finishes the proof for the case $\delta \ge 2 C_\mathrm{set}.$

Case $\delta \le 2 C_\mathrm{set} = 32h$: Here, we use the space $\widehat{\mathbf {W}}_L:= S^{1,1}(\mathcal {T}_h)|_{B_{R_\tau }} \times S^{0,0}(\mathcal {K}_h)|_{B_{R_\tau }}$. Since $(u_h,\varphi _h)|_{B_{R_\tau }} \in \widehat{\mathbf {W}}_L$, the error estimate holds trivially. For the dimension of $\widehat{\mathbf {W}}_L$, we obtain

$$\begin{aligned} {\text {dim}} \widehat{\mathbf {W}}_L \le C \left( \frac{{\text {*}}{diam}(B_{R_\tau })}{h}\right) ^{2d} \le C \left( \frac{32\sqrt{d} R_\tau }{\delta }\right) ^{2d} \le C \left( 2C_\mathrm{set}\sqrt{d}2\eta L\right) ^{2d} \lesssim L^{2d}, \end{aligned}$$

which finishes the proof.$\square$

Proposition 5.2

(Low dimensional approximation for the Bielak–MacCamy coupling) Let $(\tau , \sigma )$ be a cluster pair with bounding boxes $B_{R_\tau }$ and $B_{R_\sigma }$ that satisfy for given $\eta > 0$

$$\begin{aligned} \eta {\text {*}}{dist}(B_{R_\tau },B_{R_\sigma }) \ge {\text {*}}{diam}(B_{R_\tau }). \end{aligned}$$

Then, for each $L \in \mathbb {N}$, there exists a space $\widehat{\mathbf {W}}_L \subset S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$ with dimension $\dim \widehat{\mathbf {W}}_L \le C_\mathrm{low} L ^{2d+1}$ such that for arbitrary right-hand sides $f \in L^2 (\varOmega )$, $\varphi _0 \in L^2(\varGamma )$, and $u_0 \in {L^2(\varGamma )}$ with $\big ({\text {*}}{supp} f \cup {\text {*}}{supp}\varphi _0 \cup {\text {*}}{supp}u_0\bigr ) \subset B_{R_\sigma },$ the corresponding Galerkin solution $(u_h,\varphi _h)$ of (2.8) satisfies

$$\begin{aligned}&\min \limits _{\left( \widetilde{u}, \widetilde{\varphi }\right) \in \widehat{\mathbf {W}}_L} \left( \left\| u_h- \widetilde{u}\right\| _{L^2 (B_{R_\tau } \cap \varOmega )}+ \left\| \varphi _h- \widetilde{\varphi }\right\| _{L^{2} (B_{R_\tau }\cap \varGamma )}\right) \\&\quad \quad \quad ~~~~~~~\le C_\mathrm{{box}}h^{-2}2^{-L}\left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| \varphi _0 \right\| _ {L^{2} (\varGamma )} +\left\| u_0 \right\| _ {L^{2} (\varGamma )} \right) . \end{aligned}$$

The constants $C_\mathrm{low}$, $C_\mathrm{box}$ depend only on $\varOmega$, d, ${{\mathbf {C}}}$, $\eta$, and the $\gamma$-shape regularity of the quasi-uniform triangulation $\mathcal {T}_h$ and $\mathcal {K}_h$.

Proof

The proof is essentially identical to the proof of Proposition 5.1. We stress that the bound of the dimension $\dim \widehat{\mathbf {W}}_L \le C_\mathrm{low} L ^{2d+1}$ is better, since no approximation for the double-layer potential is needed, i.e., we can choose $M=2$ in the abstract setting.$\square$

Proposition 5.3

(Low dimensional approximation for the Johnson-Nédélec coupling) Let $(\tau , \sigma )$ be a cluster pair with bounding boxes $B_{R_\tau }$ and $B_{R_\sigma }$ that satisfy for given $\eta > 0$

$$\begin{aligned} \eta {\text {*}}{dist}(B_{R_\tau },B_{R_\sigma }) \ge {\text {*}}{diam}(B_{R_\tau }). \end{aligned}$$

Then, for each $L \in \mathbb {N}$, there exists a space $\widehat{\mathbf {W}}_L \subset S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$ with dimension $\dim \widehat{\mathbf {W}}_L \le C_\mathrm{low} L ^{6d+1}$, such that for arbitrary right-hand sides $f \in L^2 (\varOmega )$, $\varphi _0 \in L^2(\varGamma )$, and $w_0 \in {L^2(\varGamma )}$ with $\big ({\text {*}}{supp} f \cup {\text {*}}{supp}\varphi _0 \cup {\text {*}}{supp}w_0\bigr ) \subset B_{R_\sigma },$ the corresponding Galerkin solution $(u_h,\varphi _h)$ of (2.15) satisfies

$$\begin{aligned}&\min \limits _{\left( \widetilde{u}, \widetilde{\varphi }\right) \in \widehat{\mathbf {W}}_L} \left( \left\| u_h- \widetilde{u}\right\| _{L^2 (B_{R_\tau } \cap \varOmega )}+ \left\| \varphi _h- \widetilde{\varphi }\right\| _{L^{2} (B_{R_\tau }\cap \varGamma )}\right) \\&\quad \quad \quad \le C_\mathrm{{box}}h^{-2}2^{-L}\left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| \varphi _0 \right\| _ {L^{2} (\varGamma )} +\left\| w_0 \right\| _ {L^{2} (\varGamma )} \right) . \end{aligned}$$

The constants $C_\mathrm{low}$, $C_\mathrm{box}$ depend only on $\varOmega$, d, ${{\mathbf {C}}}$, $\eta$, and the $\gamma$-shape regularity of the quasi-uniform triangulation $\mathcal {T}_h$ and $\mathcal {K}_h$.

Proof

The proof is essentially identical to the proof of Proposition 5.1. We stress that the bound of the dimension $\dim \widehat{\mathbf {W}}_L \le C_\mathrm{low} L ^{6d+1}$ is worse than for the other couplings, since in the abstract setting, we have to choose $M=3$ and $\alpha =2$, and the bound follows from Lemma 3.6.$\square$

Finally, we can prove the existence of $\mathcal {H}$-matrix approximants to the inverse FEM-BEM stiffness matrix.

Proof

(Proof of Theorem 2.13) We start with the symmetric coupling.We mention that the symmetry of the system matrix together with the requirement $\eta {\text {*}}{dist}(B_{R_\tau },B_{R_\sigma }) \ge {\text {*}}{diam}(B_{R_\tau })$ of Proposition 5.1 does also allow one to use the weaker admissibility condition mentioned in Remark 2.8. As $\mathcal {H}$ matrices are low rank only on admissible blocks, we set $\mathbf {B_\mathcal {H}}|_{\tau \times \sigma }= \mathbf {A_\mathrm{sym}^{-1}}|_ {\tau \times \sigma }$ for non-admissible cluster pairs and consider an arbitrary admissible cluster pair $(\tau ,\sigma )$ in the following.

With a given rank bound r, we take $L := \lfloor (r/C_\mathrm{low})^{1/(3d+1)} \rfloor$. With this choice, we apply Proposition 5.1, which provides a space $\widehat{\mathbf {W}}_L \subset S^{1,1}(\mathcal {T}_h) \times S^{0,0}(\mathcal {K}_h)$ and use this space in Lemma 3.3, which produces matrices $\mathbf {X}_{\tau \sigma },\mathbf {Y}_{\tau \sigma }$ of maximal rank $\dim \widehat{\mathbf {W}}_L$, which is by choice of L bounded by

$$\begin{aligned} \dim \widehat{\mathbf {W}}_L = C_\mathrm{low}L^{3d+1} \le r. \end{aligned}$$

Proposition 5.1 can be rewritten in terms of the discrete solution operator of the framework of Sect. 3.1. Let $\varvec{f} = (f,v_0,w_0) \in \mathbf {L}^2$ be arbitrary with ${\text {*}}{supp}(\varvec{f}) \subset \prod _j D_j(\sigma )$. Then, the locality of the dual functions implies $\big ({\text {*}}{supp} f \cup {\text {*}}{supp}v_0 \cup {\text {*}}{supp}w_0\big ) \subset B_{R_\sigma }$, and we obtain

$$\begin{aligned} \inf _{\mathbf {w} \in \widehat{\mathbf {W}}_L}\left\| \mathcal {S}_N \varvec{f} -\mathbf {w} \right\| _{\mathbf {L}^2(\tau )}&\le \inf \limits _{\left( \widetilde{u}, \widetilde{\varphi }\right) \in \widehat{\mathbf {W}}_L} \left( \left\| u_h- \widetilde{u}\right\| _{L^2 (B_{R_\tau } \cap \varOmega )}+ \left\| \varphi _h- \widetilde{\varphi }\right\| _{L^{2} (B_{R_\tau }\cap \varGamma )}\right) \\&\lesssim h^{-2}2^{-L}\left( \left\| f\right\| _ {L^2 (\varOmega )} +\left\| v_0 \right\| _ {L^{2} (\varGamma )} +\left\| w_0 \right\| _ {L^{2} (\varGamma )} \right) \\&\lesssim h^{-2}2^{-L} \left\| \varvec{f} \right\| _{\mathbf {L}^2}. \end{aligned}$$

Defining $\mathbf {B}_\mathcal {H}|_{\tau \times \sigma } := \mathbf {X}_{\tau \sigma } \mathbf {Y}_{\tau \sigma }^T$, the estimates (3.3) and $\left\| \varLambda \right\| \lesssim h^{-d/2}$ together with Lemma 3.3 then give the error bound

$$\begin{aligned}&\left\| \mathbf {A}_\mathrm{sym}^{-1}-\mathbf {B}_\mathcal {H} \right\| _2 \le C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) \max \left\{ \left\| \left( \mathbf {A}^{-1}-\mathbf {B}_\mathcal {H}\right) \Big |_{\tau \times \sigma } \right\| _2 : (\tau ,\sigma ) \in P\right\} \\&\quad \le C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) \left\| \varLambda \right\| ^2 \max _{ (\tau ,\sigma ) \in P_\mathrm{far}} \sup _{\begin{array}{c} \varvec{f} \in \mathbf {L}^2:\\ {\text {*}}{supp}(\varvec{f}) \subset \prod _j D_j(\sigma ) \end{array}} \frac{\inf _{\mathbf {w} \in \widehat{\mathbf {W}}_L}\left\| \mathcal {S}_N \varvec{f} -\mathbf {w} \right\| _{\mathbf {L}^2(\tau )}}{\left\| \varvec{f} \right\| _{\mathbf {L}^2}} \\&\quad \lesssim C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) h^{-(d+2)} 2^{-L} \\&\quad \le C_\mathrm{apx}C_\mathrm{sp} {\text {*}}{depth}(\mathbb {T}_{\mathcal {I}}) h^{-(d+2)} \exp (-b r^{1/(3d+1)}). \end{aligned}$$

This finishes the proof for the symmetric coupling.

The approximations to $\mathbf {A}^{-1}_\mathrm{bmc}$ and $\mathbf {A}^{-1}_\mathrm{jn}$ are constructed in exactly the same fashion. The different exponentials appear due to the different dimensions of the low-dimensional space $\widehat{\mathbf {W}}_L$ in Propositions 5.2 and 5.3.$\square$

6 Numerical results

In this section, we provide a numerical example that supports the theoretical results from Theorem 2.13, i.e, we compute an exponentially convergent $\mathcal {H}$-matrix approximant to an inverse FEM-BEM coupling matrix.

If one is only interested in solving a linear system with one (or few) different right-hand sides, rather than computing the inverse—and maybe even its low-rank approximation—it is more beneficial to use an iterative solver. The $\mathcal {H}$-matrix approximability of the inverse naturally allows for black-box preconditioning of the linear system. [5] constructed LU-decompositions in the $\mathcal {H}$-matrix format for FEM matrices by approximating certain Schur-complements under the assumption that the inverse can be approximated with arbitrary accuracy. Theorem 2.13 provides such an approximation result and the techniques of [5, 18,19,20] can also be employed to prove the existence of $\mathcal {H}$-LU-decompositions for the whole FEM-BEM matrices for each coupling provided the Schur complements of all quadratic principal subblocks of the system matrix exist. With certain stabilizations, see [1], this can be ensured.

We choose the 3d-unit cube $\varOmega = (0,1)^3$ as our geometry, and we set $\mathbf {C} = \mathbf {I}$. In the following, we only consider the Johnson-Nédélec coupling, the other couplings can be treated in exactly the same way.

In order to guarantee positive definiteness, we study the stabilized system (see [1, Theorem 15] for the assertion of positive definiteness)

$$\begin{aligned} \left( \begin{pmatrix} \mathbf {A} &{}\quad -\mathbf {M}^T \\ \frac{1}{2}\mathbf {M} - \mathbf {K} &{}\quad \mathbf {V} \end{pmatrix}+ \mathbf {s}\mathbf {s}^T\right) \begin{pmatrix} \mathbf {x} \\ \varvec{\phi } \end{pmatrix} = \begin{pmatrix} \mathbf {f} \\ \mathbf {g} \end{pmatrix}, \end{aligned}$$

(6.1)

where the stabilization $\mathbf {s}\in \mathbb {R}^{N+M}$ is given by for $i \in \{1,\dots , N\}$ and for $i \in \{N+1,\dots , M\}$.

We stress that [1] shows that solving the stabilized (elliptic) system is equivalent to solving the non-stabilized system (with a modified right-hand side). By $\mathbf {A}^{\mathrm {st}}:= \mathbf {A} + \mathbf {b}\mathbf {b}^T$, we denote the stabilization of $\mathbf {A}$, where $\mathbf {b}$ contains the degrees of freedom of $\mathbf {s}$ corresponding to the FEM part.

Fig. 1

$\mathcal {H}$-matrix approximation to inverse of FEM-BEM matrix. Left: error vs. block rank r; right: memory requirement vs. block rank r; top: $N= 6959$ (FEM-dofs), $M=3888$ (BEM-dofs); bottom: $N=10648$, $M=5292$

All computations are done using the C-library HLiB, [7], where we employed a geometric clustering algorithm with admissibility parameter $\eta = 2$ and a leaf size of 25.

6.1 Approximation to the inverse matrix

The $\mathcal {H}$-matrices are computed by using a very accurate blockwise low-rank approximation to

$$\begin{aligned} \mathbf {B} := \begin{pmatrix} \mathbf {A} &{}\qquad -\mathbf {M}^T \\ \frac{1}{2}\mathbf {M} - \mathbf {K} &{}\qquad \mathbf {V} \end{pmatrix} + \mathbf {s}\mathbf {s}^T. \end{aligned}$$

(6.2)

Then, using $\mathcal {H}$-matrix arithmetic and blockwise projection to rank r, the $\mathcal {H}$-matrix inverse is computed with a blockwise algorithm using the $\mathcal {H}$-arithmetic from [22]. In order to not compute the inverse of a dense matrix, we use the upper bound

$$\begin{aligned} \left\| \mathbf {B}^{-1}- \mathbf {B}_{\mathcal {H}} \right\| _2 \le \left\| \mathbf {B}^{-1} \right\| _2 \left\| \mathbf {I}- \mathbf {B}\mathbf {B}_{\mathcal {H}} \right\| _2 \end{aligned}$$

as our error measure.

We also compute a second approximate inverse by use of the $\mathcal {H}$-LU decomposition, which can be computed using a blockwise algorithm from [4, 29]. To measure the error without computing ${{\mathbf {B}}}^{-1}$, we compute $\left\| \mathbf {I}- \mathbf {B}(\mathbf {L}_{\mathcal {H}}\mathbf {U}_{\mathcal {H}})^{-1} \right\| _2$.

Figure 1 shows convergence of the upper bounds of the error and the growth of the storage requirements with respect to the block-rank r for two different problem sizes. We observe exponential convergence and linear growth in storage for the approximate inverse using $\mathcal {H}$-arithmetics and the approximate inverse using the $\mathcal {H}$-LU decomposition, where the $\mathcal {H}$-LU decomposition performs significantly better. The observed exponential convergence is even better than the asserted bound from Theorem 2.13.