Abstract
We study the problem of finding the nearest \(\varOmega \)-stable matrix to a certain matrix A, i.e., the nearest matrix with all its eigenvalues in a prescribed closed set \(\varOmega \). Distances are measured in the Frobenius norm. An important special case is finding the nearest Hurwitz or Schur stable matrix, which has applications in systems theory. We describe a reformulation of the task as an optimization problem on the Riemannian manifold of orthogonal (or unitary) matrices. The problem can then be solved using standard methods from the theory of Riemannian optimization. The resulting algorithm is remarkably fast on small-scale and medium-scale matrices, and returns directly a Schur factorization of the minimizer, sidestepping the numerical difficulties associated with eigenvalues with high multiplicity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\varOmega \) be a non-empty closed subset of \(\mathbb {C}\), and define
the set of \(n \times n\) matrices (with entries in either \(\mathbb {F}=\mathbb {C}\) or \(\mathbb {F}=\mathbb {R}\)) whose eigenvalues all belong to \(\varOmega \). (Here \(\varLambda (X)\) denotes the spectrum of the square matrix X.)
Given \(A \in \mathbb {F}^{n \times n}\), we consider the problem of finding a matrix \(B \in S(\varOmega , n, \mathbb {F})\) nearest to A, as well as the distance from A to B. This is known as the nearest \(\varOmega \)-stable matrix problem. More formally, the problem is to find
together with the value of the minimum. The norm considered here is the Frobenius norm \({\Vert }{M}{\Vert }_F := (\sum _{i,j=1}^n {|}{M_{ij}}{|}^2)^{1/2}=\sqrt{{{\,\mathrm{tr}\,}}(M^*M)}\).
Important examples of nearest \(\varOmega \)-stable matrix problems include:
-
the nearest Hurwitz stable matrix problemFootnote 1 (\(\varOmega = \varOmega _H := \{ z \in \mathbb {C}: \mathfrak {R}z \le 0 \}\)), which arises in control theory [11, Section 7.6]. Here, \(\mathfrak {R}z\) denotes the real part of \(z\in \mathbb {C}\). Hurwitz stability is related to asymptotical stability of the dynamical system \(\dot{x} = Ax\); in some cases, numerical or modelling errors produce an unstable system in lieu of a stable one, and it is desirable to find a way to ‘correct’ it to a stable one without modifying its entries too much.
-
the nearest Schur stable matrix problem (\(\varOmega = \varOmega _S := \{ z \in \mathbb {C}: |z| \le 1 \}\)), which is the direct analogue of the Hurwitz stable matrix problem that arises when, instead of a continuous-time, one has a discrete-time dynamical system \(x_{k+1} = Ax_k\) [11].
-
the problem of finding nearest matrix with all real eigenvalues (\(\varOmega = \mathbb {R}\)), which was posed (possibly more as a mathematical curiosity than for an engineering-driven application) as an open question in some internet mathematical communities [2, 12].
Moreover, in the literature interest has been given also to more exotic choices. For instance, in [9] this problem is considered for the case where \(\varOmega \) is a region generated by the intersection of lines and circles.
Another common related (but different!) problem is that of finding the nearest \(\varOmega \)-unstable matrix, i.e., given a matrix A with all its eigenvalues in the interior of a closed set \(\varOmega \), finding the nearest matrix with at least one eigenvalue outside the interior of \(\varOmega \), together with its distance from A. For \(\varOmega =\varOmega _H\) (resp. \(\varOmega = \varOmega _S\)), this minimal distance (known as stability radius) is related to the pseudospectral abscissa (resp. pseudospectral radius), respectively, and has been studied extensively; see for instance [4, 6, 7, 20, 21, 23, 26, 30, 31, 35, 36]. Other variants and extensions have been studied recently as well [13,14,15, 22, 37].
Nearest \(\varOmega \)-stable matrix problems are notoriously hard. Unlike various other matrix nearness problems [25], and to our knowledge, there is no closed-form solution based on an eigenvalue or Schur decomposition. At least for the choices of \(\varOmega \) illustrated above, the feasible region \(S(\varOmega , n, \mathbb {F})\) is nonconvex. As a result, currently existing algorithms cannot guarantee that a global minimizer is found, and are often caught in local minima. In the most popular case of the nearest Hurwitz stable matrix problem, many approaches have been proposed, including the following.
-
Orbandexivry, Nesterov and Van Dooren [38] use a method based on successive projections on convex approximations of the feasible region \(S(\varOmega , n, \mathbb {F})\).
-
Curtis, Mitchell and Overton [10], improving on a previous method by Lewis and Overton [33], use a BFGS method for non-smooth problems, applying it directly to the largest real part among all eigenvalues.
-
Choudhary, Gillis and Sharma [9, 16] use a reformulation using dissipative Hamiltonian systems, paired with various optimization methods, including semidefinite programming.
In this paper, we consider the problem for a completely general \(\varOmega \) and we describe a novel approach: we parametrize X with its complex Schur factorization \(X=UTU^*\), and observe that, if U is fixed, then there is an easy solution to the simplified problem in the variable T only. As a remarkable consequence, we demonstrate that finding an \(\varOmega \)-stable matrix nearest to A is equivalent to minimizing a certain function (depending both on \(\varOmega \) and on A) over the matrix Riemannian manifold of unitary matrices U(n). A version of the method employing only real arithmetic (and minimizing over the manifold of orthogonal matrices O(n)) can be developed with some additional considerations.
This reformulation of the problem is still difficult. Indeed, local minima of the original problem are also mapped to local minima of the equivalent Riemannian optimization problem. As a result, we cannot guarantee a global optimum either. However, there are several advantages coming from the new point of view:
-
1.
The approach is completely general, and unlike some previously known algorithms it works for any closed set \(\varOmega \);
-
2.
It can exploit the robust existing machinery of general algorithms for optimization over Riemannian manifolds [1, 5];
-
3.
In the most popular practical case of Hurwitz stability, numerical experiments show that our algorithm performs significantly better than state-of-the-art existing algorithms, both in terms of speed and in terms of accuracy, measured as the distance of the (possibly not global) minimum found from the matrix A;
-
4.
Our algorithm first finds an optimal unitary/orthogonal matrix Q, then performs (implicitly) a unitary/orthogonal similarity \(A \mapsto Q^*A Q\), and finally projects in a simple way onto \(S(\varOmega , n, \mathbb {F})\): the simplicity of this procedure ensures backward stability of the computation of B.
-
5.
The algorithm produces as an output directly a Schur decomposition \(B = QTQ^*\) (or a close analogue) of the minimizer. This decomposition is useful in applications, and is a ‘certificate’ of stability. Chances are that the problem of computing the Schur decomposition a posteriori given B is a highly ill-conditioned one, since in many cases the minimizer B has multiple eigenvalues with high multiplicity. Hence, it is convenient to have this decomposition directly available.
The paper is structured as follows. After some preliminaries concerning the distance from closed subsets of \(\mathbb {R}^N\) (Sect. 2), in Sect. 3 we describe the theory underlying our method for complex matrices, while in Sect. 4 we set up the slightly more involved theoretical background for real matrices. Section 5 deals with the \(2\times 2\) case of the problem: we compute a closed-form solution for the cases \(\varOmega _H\) and \(\varOmega _S\). Section 6 describes the details of how to compute the gradient of the objective function in our reformulation of the problem, which is key for devising a practical algorithm. In Sect. 7, we describe the results of some numerical experiments, comparing (with rather promising outcome) with existing methods. We finally draw some conclusions in Sect. 8.
The code that we used for our numerical experiments is made publicly available from the repository https://github.com/fph/nearest-omega-stable.
2 Squared distance from closed sets
Let \(\varOmega \subseteq \mathbb {C}\) be a non-empty closed set, and define
Note that \(p_\varOmega \) is not always uniquely defined: for instance, take \(\varOmega = \{0,2\} \subset \mathbb {C}\) and let z be any point with \(\mathfrak {R}z = 1\). In many practical cases the minimum is always achieved in a unique point (for instance, when \(\varOmega \) is convex), but in general there may be a non-empty set of points z for which the minimizer is non-unique, known as medial axis of \(\varOmega \).
The same definitions can be formulated for \(\mathbb {R}^N\), and indeed the definitions on \(\mathbb {C}\) are just a special case of the following ones, thanks to the isomorphism \(\mathbb {C} \simeq \mathbb {R}^2\). Let now \(\varOmega \subseteq \mathbb {R}^N\) be a non-empty closed set, and define
The following result proves differentiability of the squared distance function \(d_\varOmega ^2\): it is stated in [8, Proposition 4.1] for a compact \(\varOmega \subseteq \mathbb {R}^N\), but it is not difficult to see that it holds also for unbounded closed sets, since it is a local property.
Theorem 2.1
The squared distance function \(d_\varOmega ^2(z)\) is continuous on \(\mathbb {R}^N\) (or \(\mathbb {C}\)), and almost everywhere differentiable. Indeed, it is differentiable on the complement of the medial axis of \(\varOmega \). Its gradient is \(\nabla _z d_\varOmega ^2(z) = 2(z-p_\varOmega (z))\).
In this paper, we will mostly be concerned in cases in which the set \(\varOmega \) is convex, so the medial axis is empty, but most of the framework still works even in more general cases. When the medial axis is not empty, we henceforth tacitly assume that, for all z belonging to the medial axis, \(p_\varOmega (z)\) has been fixed by picking one of the possible minimizers (if necessary, via the axiom of choice).
3 Reformulating the problem: the complex case
We start with a lemma that shows how to solve (2) with the additional restriction that X is upper triangular.
Lemma 3.1
Let \(\hat{A}\in \mathbb {C}^{n\times n}\) be given. Then, a solution of
is given by
Proof
We have
Clearly, \(\textcircled {1}\) is constant, the minimum of \(\textcircled {2}\) under the constraint that \(T_{ii} \in \varOmega \) is achieved when \(T_{ii} = p_{\varOmega }(\hat{A}_{ii})\), and the minimum of \(\textcircled {3}\) is achieved when \(T_{ij}=\hat{A}_{ij}\). \(\square \)
In particular, it holds that
with \(\mathcal {L}(\hat{A}) = \hat{A} - \mathcal {T}(\hat{A})\). One can see that the matrix \(\mathcal {L}(\hat{A})\) is lower triangular, and has entries
Note that the matrices \(\mathcal {T}(\hat{A})\) and \(\mathcal {L}(\hat{A})\) are uniquely defined if and only if \(p_\varOmega (\hat{A}_{ii})\) is unique for each i. However, the quantity \({\Vert }{\mathcal {L}(\hat{A})}{\Vert }_F^2\), which is the optimum of (4), is always uniquely determined, since \({|}{\hat{A}_{ii} - p_\varOmega (\hat{A}_{ii})}{|}^2 = d_\varOmega ^2(\hat{A}_{ii})\) is uniquely determined.
Thanks to Lemma 3.1, we can convert the nearest \(\varOmega \)-stable matrix problem (2) into an optimization problem over the manifold of unitary matrices
Indeed, Theorem 3.2 below shows the equivalence of (2) and (7).
Theorem 3.2
-
1.
The optimization problems (2) and (7) have the same minimum value.
-
2.
If U is a local (resp. global) minimizer for (7), then \(B = UTU^*\), where \(T = \mathcal {T}(U^*AU)\), is a local (resp. global) minimizer for (2).
-
3.
If B is a local (resp. global) minimizer for (2), and \(B=UTU^*\) is a Schur decomposition, then U is a local (resp. global) minimizer for (7) and \(T = \mathcal {T}(U^*AU)\).
Proof
Taking a Schur form of the optimization matrix variable \(X=UTU^*\), we have
where the last step holds because of Lemma 3.1. All the statements follow from this equivalence. \(\square \)
In addition, we can restrict the optimization problem (7) to the special unitary group SU(n). Indeed, given \(U \in U(n)\), defining \(D=\mathrm {diag}(1,\dots ,1,\det (U))\), we have \(UD^* \in SU(n)\) and
4 Reformulating the problem: the real case
The version of our result for \(\mathbb {F}=\mathbb {R}\) is somewhat more involved. We can identify two separate cases, one being a faithful analogue of the complex case and the other involving some further analysis.
4.1 \(\varOmega \subseteq \pmb {\mathbb {R}}\)
The simpler version of the real case is when \(\varOmega \) is a subset of the reals. This allows one to solve, for instance, the problem of the nearest matrix with real eigenvalues, \(\varOmega =\mathbb {R}\).
In this case, matrices \(X \in S(\varOmega ,n,\mathbb {R})\) have a real Schur form in which the factor T is upper triangular (as opposed to quasi-triangular with possible \(2\times 2\) blocks). In this case, mutatis mutandis, all the arguments in Sect. 3 still hold. Specifically, it suffices to replace \(\mathbb {C}\) with \(\mathbb {R}\), U(n) with O(n), SU(n) with SO(n) (observe in passing that SO(n) is connected while O(n) is not) and there is nothing more to say.
4.2 \(\varOmega \not \subseteq \pmb {\mathbb {R}}\)
In the more general case, matrices \(X \in S(\varOmega ,n,\mathbb {R})\) may have complex eigenvalues, so their real Schur form will have a quasi-triangular T. Since the zero pattern of T is not uniquely determined, we need to modify slightly the approach of Sect. 3 to be able to define a suitable objective function f(Q). We solve this issue by imposing a specific zero pattern for T.
Definition 4.1
A real matrix \(T \in \mathbb {R}^{n \times n}\) is said to be in modified real Schur form if it is block upper triangular with all \(2 \times 2\) blocks on the diagonal, except (if and only if n is odd) for a unique \(1 \times 1\) block at the right bottom.
A modified real Schur decomposition of a matrix \(M \in \mathbb {R}^{n \times n}\) is \(M=Q T Q^\top \) where \(Q \in \mathbb {R}^{n \times n}\) is orthogonal and T is in modified real Schur form.
Since one can reorder blocks in the real Schur decomposition [29, Theorem 2.3.4], in particular one can obtain a real Schur decomposition in which all non-trivial \(2\times 2\) diagonal blocks are on top. Thus, the existence of modified real Schur decompositions is an immediate corollary of the existence of real Schur decompositions. Further modified Schur decompositions, having more non-trivial \(2 \times 2\) blocks than the special ones described above, can be obtained by applying Givens rotations to appropriate \(2\times 2\) triangular blocks of classical real Schur forms.
Example 4.2
The matrix
is in modified real Schur form. Note that in this example the top \(2 \times 2\) block on the diagonal is associated with two real eigenvalues, a case which would not be allowed in the classical real Schur form.
More formally, we partition \(\{1,2,\dots ,n\}\) into
With this notation, T is in modified real Schur form if \(T_{IJ}=0\) for any two elements \(I,J \in \mathfrak {I}\) of the partition such that \(I>J\) (in the natural order).
Furthermore, to solve the real analogue of problem (4), we will use a projection \(p_{S(\varOmega , 2, \mathbb {R})}\), i.e., a function that maps any matrix A to a minimizer of the distance from A among all \(2 \times 2\) real matrices with eigenvalues in \(\varOmega \). Note that this is just a special case of (3), with the (closed) set \(S(\varOmega ,n,\mathbb {R})\) in place of \(\varOmega \), since \(\mathbb {R}^{2\times 2} \simeq \mathbb {R}^4\).
We can now state Lemma 4.3 and Theorem 4.4, the real analogues of Lemma 3.1 and Theorem 3.2. We omit their proofs, which are very similar to the complex case.
Lemma 4.3
Let \(\hat{A} \in \mathbb {R}^{n\times n}\) be given. Then, a solution of
is given by
where \(I,J \in \mathfrak {I}\) (as in (8)).
Analogously, we can define the block lower triangular matrix \(\mathcal {L}(\hat{A}) = \hat{A}-\mathcal {T}(\hat{A})\), with blocks
so that the optimum of (9) is \({\Vert }{\mathcal {L}(\hat{A})}{\Vert }_F^2\).
Similarly to the complex case, we can recast any (real) nearest \(\varOmega \)-stable matrix problem as the optimization problem over the manifold of orthogonal matrices
where the function \(\mathcal {L}\) is defined by either (6) (if \(\varOmega \subseteq \mathbb {R}\)) or (11) (otherwise).
Theorem 4.4
-
1.
The optimization problems (2) and (12) have the same minimum value.
-
2.
If Q is a local (resp. global) minimizer for (12), then \(B = QTQ^\top \), where \(T = \mathcal {T}(Q^\top AQ)\), is a local (resp. global) minimizer for (2).
-
3.
If B is a local (resp. global) minimizer for (2), and \(B=QTQ^\top \) is a (modified) Schur decomposition, then Q is a local (resp. global) minimizer for (12) and \(T = \mathcal {T}(Q^\top AQ)\).
Moreover, it is clear that once again we can restrict the optimization problem to \(Q \in SO(n)\). This concludes the theoretical overview needed to reformulate (complex or real) nearest \(\varOmega \)-stable matrix problems as minimization over (unitary or orthogonal) matrix manifolds.
To solve (7) or (12) in practice for a given closed set \(\varOmega \), we need an implementation of the projection \(p_\varOmega \). In addition, for real problems with \(\varOmega \not \subseteq \mathbb {R}\), we also need an implementation of \(p_{S(\varOmega ,2,\mathbb {R})}\) for \(2\times 2\) matrices, which is not obvious. In the next section, we discuss how to develop such an implementation in the important cases \(\varOmega = \varOmega _H\) (nearest Hurwitz stable matrix) and \(\varOmega = \varOmega _S\) (nearest Schur stable matrix).
5 Computing real \(2\times 2\) nearest stable matrices
We start with a few auxiliary results that will be useful in this section. Given \(\alpha \in \mathbb {R}\), we set
Lemma 5.1
Let \(A\in \mathbb {R}^{2\times 2}\). Then, there exists \(\alpha \in [0,\pi /2)\) such that \(\hat{A} = U(\alpha )A U(\alpha )^\top \) has \(\hat{A}_{1,1}=\hat{A}_{2,2} = \frac{1}{2} {{\,\mathrm{tr}\,}}(A)\).
Proof
Let \(f(\alpha ) = \hat{A}_{1,1}-\hat{A}_{2,2}\). If \(A_{1,1}=A_{2,2}\) we can take \(\alpha =0\). Otherwise, note that \(f(0) = A_{1,1}-A_{2,2}\) and \(f(\pi /2) = A_{2,2}-A_{1,1}\) have opposite signs. Hence, by continuity, there is \(\alpha \in (0,\pi /2)\) such that \(f(\alpha )=0\). Since A and \(\hat{A}\) are similar, they have the same trace, and hence \({{\,\mathrm{tr}\,}}(A) = {{\,\mathrm{tr}\,}}(\hat{A}) = 2\hat{A}_{1,1}\). \(\square \)
We say that a non-empty closed set \(\mathcal {S} \subseteq \mathbb {R}^{2\times 2}\) is rotation-invariant if \(X\in \mathcal {S}\) implies \(U(\alpha )XU(\alpha )^\top \in \mathcal {S}\) for all \(\alpha \in \mathbb {R}\).
Lemma 5.2
Let \(\mathcal {S} \subseteq \mathbb {R}^{2 \times 2}\) be rotation-invariant, and let B be a local minimizer of
for some \(A\in \mathbb {R}^{2\times 2}\) satisfying \(A_{1,1}=A_{2,2}\). Then:
-
1.
If \(A_{2,1} \ne -A_{1,2}\), then \(B_{1,1}=B_{2,2}\).
-
2.
If \(A_{2,1} = -A_{1,2}\), then there exists \(\alpha \in [0,\pi /2)\) such that \(B = U(\alpha )\hat{B}U(\alpha )^\top \), where \(\hat{B}\) is another local minimizer with the same objective value and \(\hat{B}_{1,1} = \hat{B}_{2,2}\).
Proof
1. Let \(f(\alpha ) = {\Vert }{A - U(\alpha )B U(\alpha )^\top }{\Vert }_F^2\). A direct computation shows that
Note that \(U(\alpha )B U(\alpha )^\top \in \mathcal {S}\) for each \(\alpha \). Hence, under our assumptions f has a local minimum for \(\alpha =0\). Thus the right-hand side must vanish, and this implies \(B_{1,1}=B_{2,2}\).
2. A, \(U(\alpha )\) and \(U(\alpha )^\top \) are matrices of the form  for some \(a,b \in \mathbb {R}\). Hence, they all commute with each other; in particular, for each \(X\in \mathcal {S}\),
for some \(a,b \in \mathbb {R}\). Hence, they all commute with each other; in particular, for each \(X\in \mathcal {S}\),
This computation shows that if B is a local minimizer, then all matrices of the form \(U(\alpha )^\top B U(\alpha )\) are local minimizers with the same objective value. By Lemma 5.1, we can choose \(\alpha \) so that \(U(\alpha )^\top BU(\alpha ) = \hat{B}\) has \(\hat{B}_{1,1} = \hat{B}_{2,2}\). \(\square \)
We say that a non-empty closed set \(\mathcal {S} \subseteq \mathbb {R}^{2\times 2}\) is doubly rotation-invariant if \(X\in \mathcal {S}\) implies \(U(\alpha )XU(\beta )^\top \in \mathcal {S}\) for any \(\alpha ,\beta \in \mathbb {R}\).
Lemma 5.3
Let \(\mathcal {S} \subseteq \mathbb {R}^{2 \times 2}\) be doubly rotation-invariant, and let B be a local minimizer of
for some diagonal \(A = {\text {diag}}(\sigma _1,\sigma _2) \in \mathbb {R}^{2 \times 2}\) with \(\sigma _1 > 0\) and \(\sigma _1 \ge \sigma _2 \ge 0\). Then:
-
1.
If \(\sigma _1 \ne \sigma _2\), then B is diagonal with \(B_{11}-B_{22} \ge 0\) and \(B_{11}+B_{22}\ge 0\).
-
2.
If \(\sigma _1 = \sigma _2\), then there is \(\alpha \in [0,\pi /2)\) such that \(B = U(\alpha )\hat{B}U(\alpha )^\top \), where \(\hat{B}\) is another local minimizer with the same objective value and \(\hat{B}_{1,2}=\hat{B}_{2,1}=0\).
Proof
1. We set \(f(\alpha ,\beta ) = {\Vert }{A - U(\alpha +\beta )B U(\alpha -\beta )^\top }{\Vert }_F^2\). Since \(U(\alpha +\beta )B U(\alpha -\beta )^\top \in \mathcal {S}\) for all \(\alpha ,\beta \in \mathbb {R}\), f must have a local minimum for \(\alpha =\beta =0\). A direct computation shows that
Under our assumptions, \(\sigma _1+\sigma _2 > 0\) and \(\sigma _1-\sigma _2 > 0\), hence \(B_{21}=B_{12}=0\), \(B_{11}-B_{22} \ge 0\) and \(B_{11}+B_{22}\ge 0\).
2. The matrix A is in the form  , so (13) holds and shows that \({\Vert }{A-B}{\Vert }_{F} = {\Vert }{A-U(\alpha )BU(\alpha )^\top }{\Vert }_{F}\) for each \(\alpha \). If \(\sigma _1=\sigma _2 \ne 0\) then \(\sigma _1+\sigma _2\ne 0\), and (14b) again shows that \(B_{21}=B_{12}\). A direct computation shows then that \(\hat{B} = U(\alpha )^\top BU(\alpha )\) has \(\hat{B}_{12}=\hat{B}_{21}\) for each choice of \(\alpha \). For \(\alpha =0\) we have \(\hat{B}_{12}=B_{12}\), while for \(\alpha =\pi /2\) we have \(\hat{B}_{12}=-B_{12}\). Hence by continuity there is \(\alpha \in [0,\pi /2)\) such that \(\hat{B}_{21}=\hat{B}_{12}=0\). \(\square \)
, so (13) holds and shows that \({\Vert }{A-B}{\Vert }_{F} = {\Vert }{A-U(\alpha )BU(\alpha )^\top }{\Vert }_{F}\) for each \(\alpha \). If \(\sigma _1=\sigma _2 \ne 0\) then \(\sigma _1+\sigma _2\ne 0\), and (14b) again shows that \(B_{21}=B_{12}\). A direct computation shows then that \(\hat{B} = U(\alpha )^\top BU(\alpha )\) has \(\hat{B}_{12}=\hat{B}_{21}\) for each choice of \(\alpha \). For \(\alpha =0\) we have \(\hat{B}_{12}=B_{12}\), while for \(\alpha =\pi /2\) we have \(\hat{B}_{12}=-B_{12}\). Hence by continuity there is \(\alpha \in [0,\pi /2)\) such that \(\hat{B}_{21}=\hat{B}_{12}=0\). \(\square \)
The following result is a simple variant of the Routh–Hurwitz stability criterion (see e.g. [28, Sec. 26.2]).
Lemma 5.4
Both roots of the polynomial \(p(\lambda ) = a\lambda ^2 + b\lambda + c\), with \(a \ne 0\) lie in the closed left half-plane \(\varOmega _H\) if and only if a, b, c are either all non-negative or all non-positive.
Note that we can extend the result so that it holds also when \(a=0\) by considering \(\infty \) as a root belonging to \(\varOmega _H\).
Proof
We may assume (after a division) that \(a=1\). If \(p(\lambda )\) has two complex conjugate roots \(\alpha \pm i \beta \), then stability is equivalent to \(b = -2 \alpha \ge 0\), whereas \(c=\alpha ^2 + \beta ^2 \ge 0\) is vacuously true. If instead p has two real roots \(\lambda _1\) and \(\lambda _2\), then \(\lambda _1 \le 0\) and \(\lambda _2 \le 0\) if and only if
\(\square \)
5.1 Hurwitz stability
By applying Lemma 5.4 to the characteristic polynomial of \(X \in \mathbb {R}^{2\times 2}\), it follows immediately that the set of \(2 \times 2\) real Hurwitz stable matrices \(S(\varOmega _H, 2, \mathbb {R})\) is \(\mathcal {S}_t \cap \mathcal {S}_d\), where
Observe that the frontiers of \(\mathcal {S}_t\) and \(\mathcal {S}_d\) are, respectively, the sets of traceless and singular matrices
To visualize the geometry of \(S(\varOmega _H, 2, \mathbb {R})\), we can assume up to a change of basis that \(A_{11} = A_{22}\); indeed, the orthogonal change of basis in Lemma 5.1 preserves eigenvalues and Frobenius distance. Under this assumption, since \(S(\varOmega _H,2,\mathbb {R})\) is rotation-invariant, Lemma 5.2 shows that (even when there are multiple minimizers) we can always choose a nearest Hurwitz stable matrix B with \(B_{11} = B_{22}\). Hence it makes sense to visualize \(S(\varOmega _H, 2, \mathbb {R}) \cap \{A \in \mathbb {R}^{2\times 2} :A_{11}=A_{22}\}\) as a volume parametrized by the three coordinates \(A_{11},A_{12},A_{21}\). We show a few images of this set in Fig. 1.
Some images of the set of Hurwitz stable matrices \(S(\varOmega _H, 2, \mathbb {R})\) (in cyan), intersecated with the hyperplane \(A_{11}=A_{22}\) and the cube \(-2 \le A_{ij} \le 2\). The left picture is a 3D view of the set; the center and right one are two 2D sections with \(A_{21}=1\) and \(A_{11}=A_{22}=-1\), respectively
One can distinguish, in the 3D image on the left of Fig. 1, two straight faces (corresponding to the linear condition \({{\,\mathrm{tr}\,}}(A) = 0\)) and two curved ones (corresponding to the nonlinear condition \(\det (A) = 0\)). The ‘cross’ formed by the two edges \(A_{11}=A_{22}=A_{21}=0\) and \(A_{11}=A_{22}=A_{12}=0\) corresponds to matrices with two zero eigenvalues.
The following result can be used to find explicitly a nearest Hurwitz stable matrix to A.
Lemma 5.5
Let \(A\in \mathbb {R}^{2\times 2}\) have a singular value decomposition  , and \(G\in SO(2)\) be a matrix such that \(\hat{A}=G^\top AG\) satisfies \(\hat{A}_{11}=\hat{A}_{22}\) (G exists by Lemma 5.1).
, and \(G\in SO(2)\) be a matrix such that \(\hat{A}=G^\top AG\) satisfies \(\hat{A}_{11}=\hat{A}_{22}\) (G exists by Lemma 5.1).
Then, the set
with
and
contains a Hurwitz stable matrix nearest to A.
Proof
We assume that A is not Hurwitz stable, otherwise the result is trivial, and let B be a Hurwitz stable matrix nearest to A. One of the following three cases must hold (depending on which of the two constraints \(\det (X) \ge 0\) and \({{\,\mathrm{tr}\,}}(X) \le 0\) are active):
-
1.
\(B \in \partial \mathcal {S}_t\), \(B \not \in \partial \mathcal {S}_d\);
-
2.
\(B \in \partial \mathcal {S}_d\), \(B \not \in \partial \mathcal {S}_t\), ;
-
3.
\(B \in \partial \mathcal {S}_t \cap \partial \mathcal {S}_d\).
Indeed, any Hurwitz stable matrix B nearest to A must belong to the boundary of the set. This implies that either \(\det (B)=0\), or \({{\,\mathrm{tr}\,}}(B)=0\), or both. We treat the three cases separately.
-
1.
\(B \in \partial \mathcal {S}_t\), \(B \not \in \partial \mathcal {S}_d\). Then, B must be a local minimizer of \({\Vert }{A-X}{\Vert }_F^2\) in \(\partial \mathcal {S}_t\). The only such minimizer is \(A - \frac{1}{2} {{\,\mathrm{tr}\,}}(A) I\): this is easy to see by parametrizing
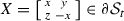 and studying the resulting function, which is strictly convex trivariate quadratic.
and studying the resulting function, which is strictly convex trivariate quadratic. -
2.
\(B \in \partial \mathcal {S}_d\), \(B \not \in \partial \mathcal {S}_t\). As in the previous case, note that B must be a local minimizer of \({\Vert }{A-X}{\Vert }_F^2\) in \(\partial \mathcal {S}_d\). In addition, \(\partial \mathcal {S}_d\) is doubly rotation-invariant, and we may assume \(\sigma _1\ne 0\) since otherwise \(A=0\), which is Hurwitz stable. We divide further into two subcases.
-
(a)
\(\sigma _1 > \sigma _2\). We have
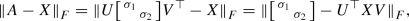
hence, for a local minimizer \(B \in \partial \mathcal {S}_d\), the matrix \(C = U^\top BV\) is a local minimizer of
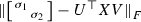 in \(U^\top (\partial \mathcal {S}_d) V = \partial \mathcal {S}_d\). In particular, Lemma 5.3 shows that $$\begin{aligned} U^\top BV = \begin{bmatrix} \tau _1 \\ &{} \tau _2 \end{bmatrix}, \quad \tau _1, \tau _2 \in \mathbb {R}. \end{aligned}$$
in \(U^\top (\partial \mathcal {S}_d) V = \partial \mathcal {S}_d\). In particular, Lemma 5.3 shows that $$\begin{aligned} U^\top BV = \begin{bmatrix} \tau _1 \\ &{} \tau _2 \end{bmatrix}, \quad \tau _1, \tau _2 \in \mathbb {R}. \end{aligned}$$For this matrix to be in \(\partial \mathcal {S}_d\), we must have \(\tau _1\tau _2=0\). Hence, we have a point \((\tau _1,\tau _2)\in \mathbb {R}^2\) on one of the two coordinate axes \(\tau _1=0\) or \(\tau _2=0\) which minimizes locally the distance from the point \((\sigma _1,\sigma _2)\) among all points on the axes. An easy geometric argument shows that the only such minimizers are \((\tau _1,\tau _2) = (0,\sigma _2)\) and \((\tau _1,\tau _2) = (\sigma _1,0)\), and only the latter satisfies the condition \(\tau _1-\tau _2\ge 0\) coming from Lemma 5.3. Hence
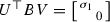 , i.e., \(B=B_0\).
, i.e., \(B=B_0\). -
(b)
\(\sigma _1 = \sigma _2\). We argue as in the previous case, but now from Lemma 5.3 it follows only that
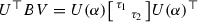 , where
, where 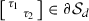 is another local minimizer of
is another local minimizer of  . By the same argument as in the previous case, this minimizer must be
. By the same argument as in the previous case, this minimizer must be 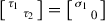 . Hence
. Hence 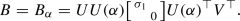
for some \(\alpha \in [0,\pi /2)\). The matrices \(B_\alpha \) all have the same distance from A, but it may be the case that only some of them are Hurwitz stableFootnote 2. In the case when \(B_0\) is Hurwitz stable, \(B_0\) is another Hurwitz stable matrix nearest to A, and we have proved the thesis. In the case when \(B = B_\alpha \in \partial \mathcal {S}_d\) is Hurwitz stable but \(B_0 \in \partial \mathcal {S}_d\) is not, by continuity there is a smallest value \(\hat{\alpha }\) for which \(B_\alpha \) is Hurwitz stable, and \(B_{\hat{\alpha }}\) must belong to \(\partial \mathcal {S}_t\). In particular, \(B_{\hat{\alpha }}\) is another Hurwitz stable matrix nearest to A in \(\partial \mathcal {S}_t \cap \partial \mathcal {S}_d\), and by case 3 below \(B_{\hat{\alpha }} \in \{B_+, B_-\}\).
-
(a)
-
3.
\(B \in \partial \mathcal {S}_t \cap \partial \mathcal {S}_d\). Note that \(\partial \mathcal {S}_t \cap \partial \mathcal {S}_d\) is the set of matrices with a double zero eigenvalue, and it is rotation-invariant. We have
$$\begin{aligned} {\Vert }{A-X}{\Vert }_F = {\Vert }{G^\top AG - G^\top XG}{\Vert }_F = {\Vert }{\hat{A} - G^\top XG}{\Vert }_F, \end{aligned}$$hence B is a global minimizer of \({\Vert }{A-X}{\Vert }_F\) in \(\partial \mathcal {S}_t \cap \partial \mathcal {S}_d\) if and only if \(C = G^\top BG\) is a global minimizer of \({\Vert }{\hat{A} - C}{\Vert }_F\) in \(G^\top (\partial \mathcal {S}_t \cap \partial \mathcal {S}_d)G = \partial \mathcal {S}_t \cap \partial \mathcal {S}_d\). By Lemma 5.2, we may assume (up to replacing C with another global minimizer) that \(C_{1,1}=C_{2,2}\), and since \({{\,\mathrm{tr}\,}}{C}=0\) it must be the case that \(C_{1,1}=C_{2,2}=0\). Then, \(\det C=0\) implies that either \(C_{21}=0\) or \(C_{12}=0\). To minimize \({\Vert }{\hat{A}-C}{\Vert }_F\) under these constraints, the only remaining nonzero entry must be equal to the corresponding entry of \(\hat{A}\). Hence \(B = B_+\) or \(B= B_-\).
\(\square \)
Lemma 5.5 yields an explicit algorithm to find a projection \(p_{S(\varOmega _H,2,\mathbb {R})}(A)\): we compute the five matrices in the set (15), and among those of them that are Hurwitz stable we choose one which is nearest to A. (Note that at least \(B_+\) and \(B_-\) are always Hurwitz stable, so this algorithm always returns a matrix.)
Example 5.6
Let \(A = \begin{bmatrix} 1 &{} 2\\ 1 &{} 1 \end{bmatrix}\). Then,
-
A is not Hurwitz stable since it has an eigenvalue \(1+\sqrt{2} > 0\).
-
\(A - \frac{1}{2} {{\,\mathrm{tr}\,}}(A) I_2 = \begin{bmatrix} 0 &{} 2\\ 1 &{} 0 \end{bmatrix}\) is not Hurwitz stable either since it has an eigenvalue \(\sqrt{2} > 0\).
-
\(B_0 \approx \begin{bmatrix} 1.17 &{} 1.89\\ 0.72 &{} 1.17 \end{bmatrix}\), and this matrix is not Hurwitz stable either since it has a positive eigenvalue \(\approx 2.34\).
-
\(G=I\), \(B_+ = \begin{bmatrix} 0 &{} 2\\ 0 &{} 0 \end{bmatrix}\), and \(B_- = \begin{bmatrix} 0 &{} 0\\ 1 &{} 0 \end{bmatrix}\).
So the set (15) contains only two Hurwitz stable matrices, \(B_+\) and \(B_-\). We have \({\Vert }{A-B_+}{\Vert }_F = \sqrt{3}\) and \({\Vert }{A-B_-}{\Vert }_F = \sqrt{6}\). The smallest of these two values is achieved by \(B_+\), hence by Lemma 5.5 the matrix \(B_+\) is a Hurwitz stable matrix nearest to A, and we can set \(p_{S(\varOmega _H,2,\mathbb {R})}(A) = B_+\). Going through the proof of Lemma 5.5, we can also show that this projection is unique. Note that, by continuity, for any matrix in a sufficiently small neighborhood of A the same inequalities will hold, and hence we will fall under the same case. In particular, the set of matrices A for which \(p_{S(\varOmega _H,2,\mathbb {R})}(A)\) has a double zero eigenvalue is not negligible.
Remark 5.7
After the present paper appeared as a preprint, a follow-up work has appeared in which the authors find a different formula for the minimizer that does not require comparing several candidates [32].
5.2 Schur stability
We can obtain analogous results for Schur stability.
Lemma 5.8
We have \(S(\varOmega _S,2,\mathbb {R}) = \mathcal {S}_{-} \cap \mathcal {S}_0 \cap \mathcal {S}_{+}\), where
Proof
Let \(t = {{\,\mathrm{tr}\,}}X\) and \(d = \det X\) for brevity. The matrix X is Schur stable if and only if its characteristic polynomial \(p(\lambda ) = \lambda ^2 - t\lambda + d\) has both roots inside the closed unit disk. This is equivalent to imposing that its Cayley transform [27],
has both roots inside the (closed) left half-plane. (Note that this result extends to the case when \(\lambda =1\) is a root, corresponding to \(\mu =\infty \), which is by convention to be considered in the closed left half-plane.) By Lemma 5.4, this holds if and only if the coefficients \(1-t+d, 2(1-d), 1+t+d\) are all non-negative or all non-positive. We shall show that these three coefficients cannot all be non-positive at the same time: indeed, if the three relations \(1-t+d \le 0, 1-d\le 0\) and \(1+t+d\le 0\) hold, then one gets
which is impossible. Hence Schur stability is equivalent to the three coefficients being non-negative, which are the conditions (5.8). \(\square \)
We note in passing that \(X \in \mathcal {S}_+ \cap \mathcal {S}_-\) implies in turn that \(-1 -\det (X) \le 1+ \det (X) \Leftrightarrow \det (X) \ge -1\). Exactly like for Hurwitz stable matrices, one can assume (up to an orthogonal similarity) that A has \(A_{11}=A_{22}\), and in this case Lemma 5.2 ensures that there is a nearest Schur stable matrix B with \(B_{11}=B_{22}\). Hence it makes sense to visualize in 3D space the set \(S(\varOmega _S, 2, \mathbb {R}) \cap \{A \in \mathbb {R}^{2\times 2} :A_{11}=A_{22}\}\). A few images of this set are shown in Fig. 2.
Some images of the set of Schur stable matrices \(S(\varOmega _S, 2, \mathbb {R})\) (in cyan), intersecated with the hyperplane \(A_{11}=A_{22}\) and the cube \(-2 \le A_{ij} \le 2\). The left picture is a 3D view of the set; the center and right one are two 2D sections with \(A_{21}=1\) and \(A_{11}=A_{22}=0\), respectively
Note the cross visible in the front of the figure, formed by the matrices with \(A_{11}=A_{22}=-1\) and either \(A_{12}=0\) or \(A_{21}=0\); these matrices all have a double eigenvalue \(-1\). There is an analogous cross in the back of the figure with \(A_{11}=A_{22}=1\). In addition, on the top-left and bottom-right side of the 3D figure there are two sharp edges which correspond to the matrices with \(A_{11}=A_{22}=0\) and \(A_{21}A_{12}=1\). These edges are formed by the intersection of the two smooth surfaces \(\mathcal {S}_+\) and \(\mathcal {S}_-\), and are formed by points where two constraints are active simultaneously. Observe that there are no corresponding sharp edges in the other two quadrants, since only one constraint is active for the matrices with \(A_{11}=A_{22}=0\) and \(A_{21}A_{12}=-1\).
To formulate the analogue of Lemma 5.5 for Schur stable matrices, we first define \(\mathcal {M}(\sigma _1,\sigma _2)\) to be the set of critical points \((\tau _1,\tau _2)\in \mathbb {R}^2\) of the function
subject to \(\tau _1 \tau _2=1\). Geometrically, these are the critical points of the distance between a given point \((\sigma _1, \sigma _2)\in \mathbb {R}^2\) and the hyperbola \(\tau _1 \tau _2 = 1\). The solutions to this problem can be computed exactly for any given pair \((\sigma _1,\sigma _2)\), since solving
amounts to computing the roots of a degree-4 polynomial. In particular, the set \(\mathcal {M}(\sigma _1,\sigma _2)\) has at most four elements for any choice of \((\sigma _1,\sigma _2)\).
With this definition, we can state the following lemma.
Lemma 5.9
Let \(A\in \mathbb {R}^{2\times 2}\), and \(G\in SO(2)\) be a matrix such that \(\hat{A}=G^\top AG\) satisfies \(\hat{A}_{11}=\hat{A}_{22}\) (G exists by Lemma 5.1). Suppose moreover that A has SVD \(A = U_0 \begin{bmatrix} \sigma _{0,1}\\ &{} \sigma _{0,2} \end{bmatrix}V_0^\top \) and that \(A \mp I\) have SVDs \(A \mp I = U_{\pm } \begin{bmatrix} \sigma _{\pm ,1}\\ &{} \sigma _{\pm ,2} \end{bmatrix} V_{\pm }^\top \). Then, the set
where
and
contains a Schur stable matrix nearest to A.
Note that the set in (18) contains at most 15 elements.
Proof
The proof of this result is similar to the one of Lemma 5.5 but more involved. For this reason, the arguments that are analogous to those already discussed for Lemma 5.5 will only be sketched.
We assume that A is not Schur stable, otherwise the result is trivial, and let B be a Schur stable matrix nearest to A. Any Schur stable matrix B nearest to A must belong to the boundary of the set \(\mathcal {S}_{-} \cap \mathcal {S}_0 \cap \mathcal {S}_{+}\). Observe that \(\partial \mathcal {S}_0\) is the set of matrices with determinant 1, while \(\partial \mathcal {S}_{\pm }\) is the set of matrices with an eigenvalue \(\pm 1\). In particular, the set \(\partial \mathcal {S}_{-} \cap \partial \mathcal {S}_{0} \cap \partial \mathcal {S}_{+}\) where all three constraints are active is empty, since a \(2\times 2\) matrix with both 1 and \(-1\) as eigenvalues cannot have determinant 1. Hence, one of the following cases must hold (corresponding to all possible remaining combinations of active constraints):
-
1.
\(B \in \partial \mathcal {S}_0\), \(B \not \in \partial \mathcal {S}_{+}\), \(B \not \in \partial \mathcal {S}_{-}\);
-
2.
\(B \in \partial \mathcal {S}_{+}\), \(B \not \in \partial \mathcal {S}_{0}\), \(B \not \in \partial \mathcal {S}_{-}\);
-
3.
\(B \in \partial \mathcal {S}_{-}\), \(B \not \in \partial \mathcal {S}_{0}\), \(B \not \in \partial \mathcal {S}_{+}\);
-
4.
\(B \in \partial \mathcal {S}_0 \cap \partial \mathcal {S}_{+}\), \(B \not \in \partial \mathcal {S}_{-}\);
-
5.
\(B \in \partial \mathcal {S}_0 \cap \partial \mathcal {S}_{-}\), \(B \not \in \partial \mathcal {S}_{+}\);
-
6.
\(B \in \partial \mathcal {S}_{+} \cap \partial \mathcal {S}_{-}\), \(B \not \in \partial \mathcal {S}_{0}\);
We treat the six cases separately.
-
1.
\(B \in \partial \mathcal {S}_0\), \(B \not \in \partial \mathcal {S}_{+}\), \(B \not \in \partial \mathcal {S}_{-}\). Then, B is a local minimizer of \({\Vert }{A-X}{\Vert }_F\) in the doubly rotation-invariant set \(\partial \mathcal {S}_0\), and \(C = U_0^\top B V_0\) is a local minimizer of
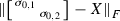 in \(\partial \mathcal {S}_0\).
in \(\partial \mathcal {S}_0\).If \(\sigma _{0,1}\ne \sigma _{0,2}\), then C is diagonal by Lemma 5.3, and for
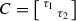 (with \(\tau _1\tau _2 = \det C = 1\)) to be a local minimizer we must have \((\tau _1,\tau _2) \in \mathcal {M}(\sigma _{0,1},\sigma _{0,2})\). Hence, \(B \in \mathcal {B}_0\).
(with \(\tau _1\tau _2 = \det C = 1\)) to be a local minimizer we must have \((\tau _1,\tau _2) \in \mathcal {M}(\sigma _{0,1},\sigma _{0,2})\). Hence, \(B \in \mathcal {B}_0\).If \(\sigma _{0,1} = \sigma _{0,2}\) instead, then
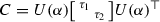 and
and 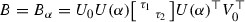 for some \(\alpha \in [0,\pi /2)\). If \(B_0\) is stable, then \(B_0\in \mathcal {B}_0\) is another nearest Schur stable matrix to A, and we are done. If \(B_0\) is not stable, then there is a minimum \(\alpha \) such that \(B_\alpha \) is stable, and this is another nearest Schur stable matrix to A in which one more constraint is active; hence it falls in one of the cases 4–6.
for some \(\alpha \in [0,\pi /2)\). If \(B_0\) is stable, then \(B_0\in \mathcal {B}_0\) is another nearest Schur stable matrix to A, and we are done. If \(B_0\) is not stable, then there is a minimum \(\alpha \) such that \(B_\alpha \) is stable, and this is another nearest Schur stable matrix to A in which one more constraint is active; hence it falls in one of the cases 4–6. -
2.
\(B \in \partial \mathcal {S}_{+}\), \(B \not \in \partial \mathcal {S}_{0}\), \(B \not \in \partial \mathcal {S}_{-}\). Then,
$$\begin{aligned} {\Vert }{A-X}{\Vert }_F = {\Vert }{(U_{+}^\top (A - I)V_{+} - U_{+}^\top (X - I)V_{+}}{\Vert }_F, \end{aligned}$$hence B is a local minimizer of \({\Vert }{A-X}{\Vert }_F\) in \(\partial \mathcal {S}_+\) if and only if \(C = U_{+}^\top (X - I)V_{+}\) is a local minimizer of \({\Vert }{(U_{+}^\top (A - I)V_{+} - X}{\Vert }_F\) in \(\partial \mathcal {S}_d\) (the set of singular \(2 \times 2\) real matrices): indeed, X has an eigenvalue 1 if and only if \(U_+^\top (X-I)V_+\) has determinant zero. Arguing as in Case 2 of Lemma 5.5, either
 and hence \(B = B_+\), or we can find a minimizer with the same objective value in one of the cases 4–6.
and hence \(B = B_+\), or we can find a minimizer with the same objective value in one of the cases 4–6. -
3.
\(B \in \partial \mathcal {S}_{-}\), \(B \not \in \partial \mathcal {S}_{0}\), \(B \not \in \partial \mathcal {S}_{+}\). We argue as in Case 2, swapping all plus and minus signs.
-
4.
\(B \in \partial \mathcal {S}_0 \cap \partial \mathcal {S}_{+}\), \(B \not \in \partial \mathcal {S}_{-}\). Note that \(\partial \mathcal {S}_0 \cap \partial \mathcal {S}_{+}\) is the (rotation-invariant) set of matrices with a double eigenvalue \(+1\) (since they must have an eigenvalue equal to \(+1\) and determinant 1). B is a minimizer if and only if \(C= G^\top BG\) is a minimizer of \({\Vert }{{\hat{A}} - X}{\Vert }_F\) in \(\partial \mathcal {S}_0 \cap \partial \mathcal {S}_{+}\), and by Lemma 5.2 we can assume \(C_{1,1}=C_{2,2}=\frac{1}{2} {{\,\mathrm{tr}\,}}(C) = \frac{1}{2} {{\,\mathrm{tr}\,}}(B) = +1\). Since \(\det C = 1\), at least one among \(C_{1,2}\) and \(C_{2,1}\) is zero, and to minimize the distance from \(\hat{A}\) the other must be equal to the corresponding element of \(\hat{A}\). Thus we get \(B \in \mathcal {B}_{+}\).
-
5.
\(B \in \partial \mathcal {S}_0 \cap \partial \mathcal {S}_{-}\), \(B \not \in \partial \mathcal {S}_{+}\). We argue as in Case 2, swapping all plus and minus signs.
-
6.
\(B \in \partial \mathcal {S}_{+} \cap \partial \mathcal {S}_{-}\), \(B \not \in \partial \mathcal {S}_{0}\). Note that \(\partial \mathcal {S}_{+} \cap \partial \mathcal {S}_{-}\) is the (rotation-invariant) set of matrices with eigenvalues 1 and \(-1\). Arguing as in Case 4,
$$\begin{aligned} G^\top BG = C = \begin{bmatrix} 0 &{} \tau _1\\ \tau _2 &{} 0 \end{bmatrix}, \quad \tau _1\tau _2 = 1, \end{aligned}$$as C must have \(C_{1,1}=C_{2,2}=\frac{1}{2} {{\,\mathrm{tr}\,}}C=0\) and \(\det C = -1\). Moreover, to minimize \({\Vert }{\hat{A}-C}{\Vert }_F\) we must have \((\tau _1,\tau _2) \in \mathcal {M}(\hat{A}_{1,2},\hat{A}_{2,1})\), and \(B \in \mathcal {B}_{*}\).
\(\square \)
6 The gradient of the objective function
To apply most optimization algorithms, one needs the gradient of the objective function; we compute it in this section. We start from the real case, which is simpler.
6.1 Computing the gradient: real case
We assume in this section that \(\mathbb {F}= \mathbb {R}\); we wish to compute the gradient of the function \(f(Q) = {\Vert }{\mathcal {L}(Q^\top AQ)}{\Vert }_F^2\), where the function \(\mathcal {L}(\cdot )\) is given by either (6) or (11).
In the set-up of optimization on matrix manifolds, the most appropriate version of the gradient to consider is the so-called Riemannian gradient [1, Section 3.6]. In the case of an embedded manifold (which includes our case, since O(n) is embedded in \(\mathbb {R}^{n\times n} \simeq \mathbb {R}^{n^2}\)) the Riemannian gradient \({{\,\mathrm{grad}\,}}f\) is simply the projection on the tangent space \(T_Q O(n)\) of the Euclidean gradient of f: i.e., its gradient \(\nabla _Q f\) when f is considered as a function in the ambient space \(\mathbb {R}^{n\times n} \rightarrow \mathbb {R}\).
Thus we start by computing the Euclidean gradient \(\nabla _Q f\). The function \(f = g \circ h\) is the composition of \(g(X) = {\Vert }{\mathcal {L}(X)}{\Vert }_F^2\) and \(h(Q) = Q^\top AQ\). Here and in the following, for ease of notation, we set \(L := \mathcal {L}(Q^\top AQ)\), together with \(T := \mathcal {T}(Q^\top AQ)\) and \(\hat{A}=Q^\top AQ = L+T\). The gradient of g is
this follows from the fact that when \(i \ne j\) the gradient of \(L_{ij}^2\) is \(2L_{ij}\), and by Theorem 2.1 the gradient of \(L_{ii}^2 = {|}{X_{ii} - p_\varOmega (X_{ii})}{|}^2\) is \(2(X_{ii} - p_\varOmega (X_{ii}))\).
When one uses the block version (11) of the function \(\mathcal {L}(\cdot )\), the same result holds blockwise: the gradient of \({\Vert }{L_{II}}{\Vert }_F^2 = {\Vert }{X_{II} - p_{S(\varOmega ,2,\mathbb {R})}(X_{II})}{\Vert }_F^2\) is \(2(X_{II} - p_{S(\varOmega ,2,\mathbb {R})}(X_{II}))\) even when \(X_{II}\) is a \(2\times 2\) block. This follows again from Theorem 2.1, applied to the closed set \(S(\varOmega ,2,\mathbb {R}) \subset \mathbb {R}^{2\times 2} \simeq \mathbb {R}^4\).
The Fréchet derivative of h(Q) is \(D_h[Q](H) = H^\top AQ + Q^\top AH\); hence, using vectorization and Kronecker products [28, Section 11.4] its Jacobian is
where the permutation matrix \(\varPi =\varPi ^\top \) is often called the vec-permutation matrix [3] or the perfect shuffle matrix, and it is defined as the \(n^2\times n^2\) matrix such that \(\varPi {\text {vec}}(X) = {\text {vec}} (X^\top ) \) for all X.
By the chain rule,
and hence, transposing everything,
We now need to project \(\nabla _Q f = 2(AQ L^\top + A^\top Q L)\) on the tangent space \(T_Q O(n)\) to get the Riemannian gradient. One has (see [1, Example 3.5.3] or more generally [3, Lemma 3.2])
In particular, we can write the projection of a matrix M onto \(T_Q O(n)\) by using the skew-symmetric part operator \({{\,\mathrm{skew}\,}}(G) = \frac{1}{2} (G-G^\top )\) as
Thus, recalling \(\hat{A}=Q^\top AQ=L+T\),
The matrix \(TL^\top - L^\top T\) is a strictly upper triangular matrix with entries
Remark 6.1
Observe that the gradient vanishes if and only if \(TL^\top = L^\top T\). It follows from the definitions of T and L that \(Q T Q^\top = B\) and \(Q L Q^\top = A-B\), hence changing basis this condition becomes \(B(A-B)^\top = (A-B)^\top B\).
6.2 Computing the gradient: complex case
The computation of the gradient in the complex case is similar, but technically more involved. To work only with real differentiation, following (with a slightly different notation) [3, Section 2.1], we define a complex version of the vectorization operator to map \(\mathbb {C}^{n\times n}\) into \(\mathbb {R}^{2n^2}\)
Here \(\mathfrak {R}X\) and \(\mathfrak {I}X\) denote the real and imaginary parts (defined componentwise) of the matrix X.
Similarly, we define a complex version of the Kronecker product \(\otimes _c\), to obtain a complex version of the identity \({{\,\mathrm{vec}\,}}(AXB) = B^\top \otimes A {{\,\mathrm{vec}\,}}(X)\).
Note that \((B^* \otimes _c A)^\top = (B \otimes _c A^*)\).
Finally, let \(\varPi _c\in \mathbb {R}^{2n^2\times 2n^2} = {\text {diag}}(\varPi , -\varPi )\) be the permutation matrix (with \(\varPi _c = \varPi _c^\top \)) such that \(\varPi _c {\text {cvec}}(X) = {\text {cvec}}(X^*)\). We now have all the complex vectorization machinery available to perform a direct analogue of the computation in the previous section. Again, for ease of notation we define \(\hat{A} = U^* AU=L+T\), with \(L = \mathcal {L}(\hat{A})\) and \(T = \mathcal {T}(\hat{A})\).
The gradient of \(g(X) = {\Vert }{\mathcal {L}(X)}{\Vert }_F^2\) is \(\nabla _X g = 2 \mathcal {L}(X)\). The Jacobian of \(h(U) = U^*AU\) is
Hence
The tangent space to the manifold of unitary matrices is, by a special case of [3, Lemma 3.2],
and the associated projection is
Thus
The diagonal entries of \(TL^* - L^*T\) are equal to \(T_{ii}\overline{L_{ii}} - \overline{L_{ii}}T_{ii} =0\), hence that matrix is again strictly upper triangular. Its nonzero entries are given by
Remark 6.2
By an argument analogous to that in Remark 6.1, \({{\,\mathrm{grad}\,}}f(U)\) vanishes if and only if \(B(A-B)^* = (A-B)^*B\).
7 Numerical experiments
We used the solver trustregions from the Matlab package Manopt [5] (version 6.0) for optimization on matrix manifolds. The solver is a quasi-Newton trust-region method; a suitable approximation of the Hessian is produced automatically by Manopt using finite differences.
For problems with \(\mathbb {F}=\mathbb {R}\), we specified the manifold O(n), the cost function \(f(Q) = {\Vert }{\mathcal {L}(Q^\top AQ)}{\Vert }_F^2\) (with \(\mathcal {L}(\cdot )\) as in (11)) and the Riemannian gradient \({\text {grad}} f(Q) = 2Q {\text {skew}}(TL^\top -L^\top T)\). For problems with \(\mathbb {F}=\mathbb {C}\), we specified the manifold U(n), the cost function \(f(Q) = {\Vert }{\mathcal {L}(Q^\top AQ)}{\Vert }_F^2\) (with \(\mathcal {L}(\cdot )\) as in (6)) and the Riemannian gradient \({\text {grad}} f(U) = 2U {\text {skew}}(TL^* -L^* T)\).
All the experiments were performed on an Intel i7-4790K CPU 4.00 GHz with 32 Gib of RAM, running Matlab R2018b (Lapack 3.7.0 and MKL 2018.0.1) on a Linux system. Our implementation of the algorithm for the three cases \(\varOmega \in \{\varOmega _H, \varOmega _S, \mathbb {R}\}\) is available for download at https://github.com/fph/nearest-omega-stable.
Remark 7.1
It is somewhat surprising that our algorithm does not make use of an eigensolver (Matlab’s eig, schur, eigs or similar), even though the original problem (2) is intrinsically about eigenvalues. Indeed, the minimization procedure itself is as an eigensolver in a certain sense: it computes a Schur form by trying to minimize the strictly subdiagonal part of \(Q^\top AQ\), not much unlike Jacobi’s method for eigenvalues ( [17], see also [34] for more references). Indeed, when run with \(\varOmega = \mathbb {C}\), the method essentially becomes a Jacobi-like method to compute the Schur form.
7.1 Experiments from Gillis and Sharma
We took matrices with dimension \(n\in \{10,20,50,100\}\) of six different types as follows.
Type | Description |
|---|---|
1 | \(A_{ij}= {\left\{ \begin{array}{ll} 1 &{} j-i = -1,\\ -0.1 &{} (i,j)=(1,n),\\ 0 &{} \text {otherwise.} \end{array}\right. }\) |
2 | \(A_{ij}= {\left\{ \begin{array}{ll} -1 &{} j-i =-1,\\ -1 &{} j-i \in {0,1,2,3},\\ 0 &{} \text {otherwise.} \end{array}\right. }\) (Matlab’s gallery(’grcar’, n)). |
3 | Random with independent entries in N(0, 1) (Matlab’s randn(n)). |
4 | Random with independent entries in U([0, 1]) (Matlab’s rand(n)). |
5 | Complex random with independent entries in N(0, 1) (Matlab’s randn(n) + 1i*randn(n)). |
6 | Complex random with independent entries in U([0, 1]) (Matlab’s rand(n) + 1i*rand(n)). |
Types 1–4 were used, with the same dimensions, in the paper by Gillis and Sharma [16]. We added types 5–6 to test the complex version of our algorithm as well as the real one.
For each matrix, we computed the nearest Hurwitz stable matrix (\(\varOmega = \varOmega _H\)) with \(\mathbb {F}=\mathbb {R}\) for matrices of types 1–4 , and \(\mathbb {F}=\mathbb {C}\) for matrices of types 5–6. We compared our results with the algorithms BCD, Grad, FGM from [16], the algorithm SuccConv from [38], and a BFGS algorithm based on GRANSO [10] (which is an improvement of HANSO [33]). The new algorithm presented here is dubbed Orth. The implementations of all competitors are by their respective authors and are taken from Nicolas Gillis’ website https://sites.google.com/site/nicolasgillis/code. We highlight the fact that we are comparing methods that rely on different formulations of the problem (based on different parametrizations of the feasible set); we are not simply plugging in a different general-purpose optimization algorithm.
The convergence plots in Figs. 3, 4, 5, 6 show that the new algorithm converges in vastly quicker time scales on matrices of small size. In addition, in all but one case the local minimizers produced by the new algorithm are of better quality, i.e., they have a smaller objective function \({\Vert }{A-B}{\Vert }_F\) than the ones of the competitors. This can be seen in the plots by comparing the lower horizontal level reached by each line.
We report in Fig. 7 the results of another experiment taken from [16], which aims to produce a performance profile. The result confirms that in the vast majority of the cases the local minima found by the new algorithm have a lower objective function.
Performance profile of the values of \({\Vert }{A-X}{\Vert }_F\) obtained by the algorithms on 100 random \(10\times 10\) matrices (equal split of rand and randn). For each algorithm, given a ratio \(r \ge 1\) (horizontal axis), the plot shows the fraction of test problems whose computed distance from stability is at most r times larger than the best value amongst those computed by all the algorithms. This kind of plot is described for instance in [24, Section 22.4]
7.2 Multiple eigenvalues
Inspecting the minimizers produced by the various methods, we observed that in many cases the new algorithm produces matrices with multiple eigenvalues (especially multiple zero eigenvalues), while other methods settle for worse minimizers with eigenvalues of lower multiplicities (particularly BCD and Grad). An illustrative example is in Fig. 8. We observe that, as illustrated by Example 5.6, the instances where the global minimum has multiple eigenvalues are not expected to be rare for this problem. This observation provides a qualitative insight to explain why our approach appears to be so highly competitive.
Location of the eigenvalues eig(B) for the local minimizers produced by the methods on a sample random \(6\times 6\) matrix A. The new method Orth produces a local minimizer with a zero eigenvalue of multiplicity 4 and a negative real eigenvalue of multiplicity 2. Methods FGM, SuccConv, and BFGS produce a different local minimizer (with worse objective function) with a double zero eigenvalue. BCD and Grad produce two (even worse) local minimizers with only one zero eigenvalue and the others having magnitude \(\gtrapprox 10^{-2}\)
7.3 Comparison with the method by Guglielmi and Lubich
Due to the lack of available code, we could not compare directly our method with the algorithm in [19], which is arguably one of the best competitors. We report some remarks about it based on published figures.
-
On the matrix gallery(’grcar’, 5), the new method computes in 0.1 seconds a different minimizer than the one reported in [19]; both have very close objective values: \({\Vert }{A-B}{\Vert }_F=2.3097\) reported in [19] vs. 2.309628 found by the new method. We suspect that this minimal difference could simply be due to different stopping criteria.
-
On gallery(’grcar’, 10), the new method computes in 0.3 seconds a minimizer with \({\Vert }{A-B}{\Vert }_F = 3.2834\): this time, undoubtedly a better value than those reported in [19].
-
On gallery(’grcar’, 30), the new method computes in 3.5 seconds a minimizer with \({\Vert }{A-B}{\Vert }_F = 5.66\), which again improves on the outcomes reported in [19]. The computed minimizer has all its eigenvalues on the imaginary axis: a complex conjugate pair with multiplicity 14 each, and a complex conjugate pair with multiplicity 1 each. In contrast, in [18], Guglielmi reports a minimizer with \({\Vert }{A-B}{\Vert }_F = 6.57\) and seemingly all distinct eigenvalues all on the imaginary axis, found in 143 seconds (on a different machine, so times cannot be compared directly: still, their very different orders of magnitude suggest that the new algorithm is competitive also in terms of speed).
-
Guglielmi and Lubich [19] report experiments with matrices of size 800, 1000, and 1090. Currently, our method cannot handle those sizes, since the optimization method used stagnates: after an initial improvement it fails to reduce the objective function further, oscillating between various values with nonzero gradient and showing convergence issues in the tCG algorithm used as an inner solver used in the trustregions algorithm. It is an interesting task for future research to study how to improve our algorithm so that it can deal with larger matrices; see Sect. 8.
-
Another advantage of the algorithm in [19] is the ability to deal with many different additional constraints in the form of matrix structure (e.g. sparsity, Toeplitz structure). The new algorithm cannot handle those, and it seems challenging to include them since they do not interact well with the conjugation \(Q^\top AQ\) that is a crucial step in our procedure.
7.4 Experiments on Schur stability
We ran analogous experiments for the case of Schur stability, using (in the case \(\mathbb {F}=\mathbb {R}\)) Lemma 5.9 to solve the \(2\times 2\) case. Our terms of comparison were the algorithm FGM from [13] and SuccConv from [38], again with the code from https://sites.google.com/site/nicolasgillis/code. The algorithms were run with various choices of initial values as suggested in [13]. We refer the reader to that paper for a more detailed description of the other competitors.
Matrices of type 2–6 are the same that were used in Sect. 7.1; type 1 would not make much sense here, since those matrices are already Schur stable for each n, so we replaced it with the following, which is a case considered also in [13].
Type | Description |
|---|---|
1 | all entries equal to 2 (Matlab’s 2*ones(n)). |
The results in Figs. 9, 10, 11, 12 confirm the superiority of the new method in this case, too, both in terms of computational time and quality of the minimizers.
In addition, we consider some of the special cases discussed in [13] and [22]. For the matrix
we obtain the same minimizer as [13] and [22] (this is proved to be a global minimizer in [22]). For the matrix  we recover one of the two global minimizers given by
we recover one of the two global minimizers given by  and its transpose (this is not surprising, because our method based on Lemma 5.9 is guaranteed to compute a global minimizer for the real \(2\times 2\) case). For the matrix 2*ones(3,3), our method computes the solution
and its transpose (this is not surprising, because our method based on Lemma 5.9 is guaranteed to compute a global minimizer for the real \(2\times 2\) case). For the matrix 2*ones(3,3), our method computes the solution
with a triple eigenvalue 1 and \({\Vert }{A-B_1}{\Vert }_F^2\) which is almost exactly 15 (up to an error of order \(10^{-15}\)). This matrix is orthogonally similar to
which has \({\Vert }{A-B_2}{\Vert }_F^2=15\) and is very likely a global optimum. A suboptimal solution with entries similar to those of \(B_1\) and \({\Vert }{A-B_3}{\Vert }^2 \approx 15.02\) is returned in [13]. For the \(5\times 5\) matrix appearing in [22, Section 4.4], we obtain a local minimizer B with \({\Vert }{A - B}{\Vert }^2_F \approx 0.5595\), beating the best value 0.5709 reported in [13].
7.5 Nearest matrix with real eigenvalues
For a final set of experiments, we have implemented the version of the algorithm that computes the nearest matrix with real eigenvalues. As discussed in Sect. 4, in this case we do not need to use the quasi-Schur form, and we can simply take \(\mathcal {T}(\hat{A}) = {\text {triu}}(\hat{A})\), the upper triangular part of \(\hat{A}=Q^\top A Q\). Then \(\mathcal {L}(\hat{A})= \hat{A} - \mathcal {T}(\hat{A})\) is defined accordingly, and we can use the objective function \(f(Q) = {\Vert }{\mathcal {L}(Q^\top A Q)}{\Vert }_F^2\) and the gradient computed in Sect. 6. We tested the algorithm on the examples discussed in [2]. On the matrix
the candidates suggested in [2] are:
-
the matrix obtained from the eigendecomposition \(A = VDV^{-1}\) as \(B_1 = V (\mathfrak {R}D) V^{-1}\), which has distance \({\Vert }{A-B_1}{\Vert }_F = 1.5811\);
-
the matrix
$$\begin{aligned} B_2 = \begin{bmatrix} 0.9 &{} 0 &{} 0 \\ -2 &{} -0.1 &{} 0\\ 0 &{} 0 &{} 0 \end{bmatrix}, \end{aligned}$$which has distance \({\Vert }{A-B_2}{\Vert }_F = 1.4213\) (this matrix actually is not even a local minimizer);
-
the matrix obtained from the real Schur factorization \(A= QTQ^\top \) as \(B_3 = Q{\text {triu}}(T)Q^\top \), which has distance \({\Vert }{A-B_3}{\Vert }_F = 0.5\).
Our method computes in about 0.1 seconds a minimizer
with a triple eigenvalue at 1/3 and slightly lower distance \({\Vert }{A-B_4}{\Vert }_F = 0.4946\). So in this example the matrix produced via the truncated real Schur form is very close to being optimal.
Another example considered in [2] is the matrix
we tested this problem setting, for concreteness, \(a=10\). The user Christian Remling suggested [2] the minimizer (having two double eigenvalues at \(\pm 1\))
which achieves \({\Vert }{A-B_1}{\Vert }_F = 0.4\), beating the minimizer constructed with the Schur form, which has \({\Vert }{A-B_2}{\Vert }_F = \sqrt{2}\). Our method computes in less than 1 second the minimizer
with a quadruple eigenvalue at 0 and \({\Vert }{A-B_3}{\Vert } = 0.2181\).
These results confirm that none of the strategies suggested in [2] are optimal, and suggest that minimizers with high-multiplicity eigenvalues are to be expected for this problem as well.
7.6 The complex case and a conjecture
An interesting observation is that in all the (limited) examples that we tried, for a real \(A\in \mathbb {R}^{n\times n}\) we observed that the solution of
was also a solution of the corresponding problem where X is allowed to vary over the larger set of complex matrices, i.e.,
It does not seem obvious to prove that this must be the case, since the set \(S(\varOmega _H,n,\mathbb {C})\) is non-convex, and in particular there are examples of matrices such that \(X\in \mathbb {C}^{n\times n}\) is Hurwitz stable, but \(\mathfrak {R}X\) is not. We formulate it as a conjecture.
Conjecture 1
For any \(A\in \mathbb {R}^{n\times n}\), the problem (22) has a real solution B.
To support this conjecture, we prove a weaker result.
Theorem 7.2
Let \(B \in \mathbb {R}^{n\times n}\) be a solution of (21), i.e., a real nearest Hurwitz stable matrix to a given \(A\in \mathbb {R}^{n\times n}\). Then, B has a complex Schur decomposition \(UTU^*\) where \(T = \mathcal {T}(U^*AU)\), and U is a stationary point of (7).
Proof
In this proof, we need to relate the quantities computed in Sects. 6.1 and 6.2; we use a subscript \(\mathbb {R}\) or \(\mathbb {C}\) to tell them apart, so for instance the formula in the theorem becomes \(T_{\mathbb {C}} = \mathcal {T}_{\mathbb {C}}(U^*AU)\).
We start by proving that \(T_{\mathbb {C}} = \mathcal {T}_{\mathbb {C}}(U^*AU)\) in the \(2\times 2\) case. We assume that A is not already Hurwitz stable (otherwise the result is trivial), and divide into two subcases.
-
B has real eigenvalues. Then, one can take a real modified Schur decomposition \(B = QT_{\mathbb {R}} Q^\top \) in which Q is real and \(T_{\mathbb {R}}\) is truly upper triangular and not a \(2\times 2\) block. By Theorem 4.4, \(T_{\mathbb {R}}=\mathcal {T}_{\mathbb {R}}(Q^\top A Q)\) and Q is a minimizer of (12), hence \({{\,\mathrm{grad}\,}}f_{\mathbb {R}}(Q) = 0\). Since \(B=QT_{\mathbb {R}} Q^\top \) is also a complex Schur form, we can take \(Q=U\) and hence \(T_{\mathbb {C}} = T_{\mathbb {R}} = \mathcal {T}_{\mathbb {C}}(U^*AU)\).
-
B has two complex conjugate eigenvalues \(\alpha \pm i\beta \). Then, looking at Lemma 5.5 and its proof, we see that we must fall in case 1, because in all the other cases B has real eigenvalues. Hence \(\alpha = 0\) and \({{\,\mathrm{tr}\,}}(A) > 0\). In addition, \(B =A - \frac{1}{2} {{\,\mathrm{tr}\,}}(A) I_2\). So A and B have the same eigenvectors, and (taking an arbitrary complex Schur decomposition \(B = UT_{\mathbb {C}}U^*\)) the matrix \(U^*AU = \frac{1}{2} {{\,\mathrm{tr}\,}}(A) I+T_{\mathbb {C}}\) is upper triangular. Thus it is easy to see that \(T_{\mathbb {C}} = \mathcal {T}_{\mathbb {C}}(U^*AU)\).
We now show that \(T_{\mathbb {C}} = \mathcal {T}_{\mathbb {C}}(U^*AU)\) holds also for larger matrices \(A \in \mathbb {R}^{n\times n}\). Let \(B = QT_{\mathbb {R}}Q^\top \) be a modified real Schur decomposition. Note that to obtain a complex Schur decomposition it is sufficient to reduce the \(2\times 2\) diagonal blocks to upper triangular form with an unitary block diagonal matrix D, thus obtaining a decomposition with \(T_{\mathbb {C}} = D^*T_{\mathbb {R}}D\) and \(U = QD\). Since B is a real minimizer, \(T_{\mathbb {R}} = \mathcal {T}_{\mathbb {R}}(Q^*AQ)\).
From these equalities it follows that \( D T_{\mathbb {C}} D^* =\mathcal {T}_{\mathbb {R}}(DU^*AUD^*)\). We can use this equality to prove that \(T_{\mathbb {C}} = \mathcal {T}_{\mathbb {C}}(U^*AU)\). Let us split \(T_{\mathbb {C}}\) into blocks according to the partition \(\mathfrak {I}\) as in (8). The maps \(\mathcal {T}_{\mathbb {R}}\) and \(\mathcal {T}_{\mathbb {C}}\) leave unchanged the blocks in the strictly upper triangular part, hence for \(I < J\) we have
thus \((T_{\mathbb {C}})_{IJ} = (\mathcal {T}_{\mathbb {C}}(U^*AU))_{IJ} = (U^*AU)_{IJ}\). On diagonal blocks, \((T_{\mathbb {R}})_{II}\) is a distance minimizer, hence by the \(2\times 2\) version of this result that we have just proved
It remains to prove that \({{\,\mathrm{grad}\,}}f_{\mathbb {C}}(U)=0\). This follows by combining Remarks 6.1 and 6.2: if \(B\in \mathbb {R}^{n\times n}\) is a minimizer on the reals, then \({{\,\mathrm{grad}\,}}f_{\mathbb {R}}(Q)=0\) by Theorem 4.4 and \(B(A-B)^\top = (A-B)^\top B\); both A and B are real matrices, so \(B(A-B)^* = (A-B)^* B\) also holds, and \({{\,\mathrm{grad}\,}}f_{\mathbb {C}}(U)\) vanishes. \(\square \)
8 Conclusions
In this paper, we introduced a method to solve the nearest \(\varOmega \)-stable matrix problem, based on a completely novel approach rather than improving on those known in the literature. The algorithm has remarkably good numerical results on matrices of sufficiently small size (up to \(n\approx 100\)), both in terms of computational time compared to its competitors, and of quality of the local minima found.
We attribute a good part of the success of this method to the fact that it computes eigenvalues only indirectly; thus, it is able to avoid the inaccuracies associated with multiple eigenvalues. Indeed, it is well-known that computing eigenvalues with high multiplicity is an ill-conditioned problem: if a matrix has an eigenvalue \(\lambda \) of multiplicity k, a perturbation of size \(\varepsilon \) will, generically, produce a matrix with k simple eigenvalues at distance \(\mathcal {O}(\varepsilon ^{1/k})\) from \(\lambda \) (see, for instance, [39, Chapter 2]). The method can, in principle, be generalized to similar problems by defining appropriate Schur-like decompositions; for instance, to the problem of finding matrices with at least a given number k of eigenvalues inside a certain set \(\varOmega \).
In our future research, we plan to study extensions such as the one mentioned above, and to investigate further the behaviour of the method on larger matrices. Hopefully, convergence on larger matrices can be obtained by adjusting parameters in the optimization method, deriving preconditioners that approximate the Hessian of the objective function \(f(Q) = {\Vert }{\mathcal {L}(Q^\top AQ)}{\Vert }_F^2\), or including some techniques borrowed from traditional eigensolvers.
Data Availability Statement
Not applicable.
Notes
In the control theory literature, a matrix satisfying our definition of Hurwitz stability is often referred to as Hurwitz semistable, whereas the adjective stable is reserved for matrices in the interior of \(S(\varOmega _H, n, \mathbb {F})\), i.e., matrices whose eigenvalues have strictly negative real part. However, open sets cannot possibly contain a nearest matrix to a given matrix A. Thus, given the context of this paper, we prefer for simplicity to simply define stable matrices as the matrices whose eigenvalues have nonpositive real part. Similar comments apply to other choices of \(\varOmega \).
If \(U,V \in SO(2)\) are rotation matrices, then \(U(\alpha )\) commutes with U and V and hence \(B_\alpha =U(\alpha )B_0U(\alpha )^\top \), so that the eigenvalues of \(B_\alpha \) do not depend on \(\alpha \). However, generally U and V may have determinant \(-1\).
References
Absil, P.-A., Mahony, R., Sepulchre, R.: Optimization Algorithms on Matrix Manifolds. Princeton University Press, Princeton, NJ (2008)
Andrea F. et al. Finding the nearest matrix with real eigenvalues. https://mathoverflow.net/questions/273669/finding-the-nearest-matrix-with-real-eigenvalues. Post on the Q&A site Mathoverflow (2017)
Arslan, B., Noferini, V., Tisseur, F.: The structured condition number of a differentiable map between matrix manifolds, with applications. SIAM J. Matrix Anal. Appl. 40(2), 774–799 (2019)
Benner, P., Mitchell, T.: Extended and improved criss-cross algorithms for computing the spectral value set abscissa and radius. SIAM J. Matrix Anal. Appl. 40(4), 1325–1352 (2019)
Boumal, N., Mishra, B., Absil, P.-A., Sepulchre, R.: Manopt, a matlab toolbox for optimization on manifolds. J. Mach. Learn. Res. 15, 1455–1459 (2014)
Burke, J.V., Lewis, A.S., Overton, M.L.: Optimization and pseudospectra, with applications to robust stability. SIAM J. Matrix Anal. Appl. 25(1), 80–104 (2003)
Byers, R.: A bisection method for measuring the distance of a stable matrix to the unstable matrices. SIAM J. Sci. Stat. Comput. 9(5), 875–881 (1988)
Chazal, F., Cohen-Steiner, D., Lieutier, A., Mérigot, Q., Thibert, B.: Inference of curvature using tubular neighborhoods. In: L. Najman and P. Romon, editors, Lecture Notes in Mathematics, volume 2184 of Modern Approaches to Discrete Curvature, pp. 133–158. Springer (2017)
Choudhary, N., Gillis, N., Sharma, P.: On approximating the nearest \({\varOmega }\)-stable matrix. Preprint available at arxiv:1901.03069
Curtis, F.E., Mitchell, T., Overton, M.L.: A BFGS-SQP method for nonsmooth, nonconvex, constrained optimization and its evaluation using relative minimization profiles. Optim. Methods Softw. 32(1), 148–181 (2017)
Datta, B.N.: Numerical Methods for Linear Control Systems. Elsevier Academic Press, San Diego, CA (2004)
Gary, B., et al.: Finding the nearest matrix with real eigenvalues. https://groups.google.com/d/topic/comp.soft-sys.matlab/mwk1yXTuFWc/discussion, 2010. Discussion on the newsgroup comp.soft.sys.matlab
Gillis, N., Karow, M., Sharma, P.: Approximating the nearest stable discrete-time system. Linear Algebra Appl. 573, 37–53 (2019)
Gillis, N., Karow, M., Sharma, P.: A note on approximating the nearest stable discrete-time descriptor systems with fixed rank. Appl. Numer. Math. 148, 131–139 (2020)
Gillis, N., Mehrmann, V., Sharma, P.: Computing the nearest stable matrix pairs. Numerical Lin. Alg. Appl. 25(5) (2018)
Gillis, N., Sharma, P.: On computing the distance to stability for matrices using linear dissipative hamiltonian systems. Automatica 85, 113–121 (2017)
Greenstadt, J.: A method for finding roots of arbitrary matrices. Math. Tables Aids Comput. 9, 47–52 (1955)
Guglielmi, N.: Matrix stabilization using differential equations. http://www1.mat.uniroma1.it/ricerca/convegni/2017/numoc2017/TALKS/guglielmi_numoc17.pdf, (2017). NUMOC-2017 conference talk
Guglielmi, N., Lubich, C.: Matrix stabilization using differential equations. SIAM J. Numer. Anal. 55(6), 3097–3119 (2017)
Guglielmi, N., Manetta, M.: Approximating real stability radii. IMA J. Numer. Anal. 35, 1402–1425 (2015)
Guglielmi, N., Overton, M.L.: Fast algorithms for the approximation of the pseudospectral abscissa and pseudospectral radius of a matrix. SIAM J. Matrix Anal. Appl. 32(4), 1166–1192 (2011)
Guglielmi, N., Protasov, V.Y.: On the closest stable/unstable nonnegative matrix and related stability radii. SIAM J. Matrix Anal. Appl. 39(4), 1642–1669 (2018)
He, C., Watson, G.A.: An algorithm for computing the distance to instability. SIAM J. Matrix Anal. Appl. 20(1), 101–116 (1999)
Higham, D.J., Higham, N.J.: MATLAB guide. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, second edition (2005)
Higham, N.J.: Matrix nearness problems and applications. In: Applications of Matrix Theory, pp. 1–27. Oxford University Press (1989)
Hinrichsen, D., Pritchard, A.J.: Stability radii of linear systems. Syst. Control Lett. 7(1), 1–10 (1986)
Hinrichsen, D., Pritchard, A.J.: Mathematical Systems Theory I: Modelling, State Space Analysis, Stability and Robustness, vol. 48. Springer Science & Business Media, Berlin (2011)
Hogben, L.: editor. Handbook of Linear Algebra. Discrete Mathematics and its Applications (Boca Raton). CRC Press, Boca Raton, FL, second edition (2014)
Horn, R.A., Johnson, C.R.: Matrix Analysis, second edition edn. Cambridge University Press, Cambridge (2013)
Kostić, V.R., Miȩdlar, A., Stolwijk, J.J.: On matrix nearness problems: distance to delocalization. SIAM J. Matrix Anal. Appl. 36(2), 435–460 (2015)
Kressner, D., Vandereycken, B.: Subspace methods for computing the pseudospectral abscissa and the stability radius. SIAM J. Matrix Anal. Appl. 35(1), 292–313 (2014)
Kuo, Y.-C., Cheng, H.-C., Syu, J.-Y., Shieh, S.-F.: On the nearest stable \(2\times 2\) matrix, dedicated to Prof. Sze-Bi Hsu in appreciation of his inspiring ideas. Discrete & Continu. Dyn. Syst. B, 22 (2020)
Lewis, A. S., Overton, M. L.: Nonsmooth optimization via BFGS. http://www.cs.nyu.edu/overton/papers/pdffiles/bfgs%5FinexactLS.pdf (2009)
Mehl, C.: On asymptotic convergence of nonsymmetric Jacobi algorithms. SIAM J. Matrix Anal. Appl. 30(1), 291–311 (2008)
Mengi, E.: Large-scale and global maximization of the distance to instability. SIAM J. Matrix Anal. Appl. 39(4), 1776–1809 (2018)
Mengi, E., Overton, M.L.: Algorithms for the computation of the pseudospectral radius and the numerical radius of a matrix. IMA J. Numer. Anal. 25(4), 648–669 (2005)
Nesterov, Y., Protasov, V.Y.: Computing Closest Stable Nonnegative Matrix. SIAM J. Matrix Anal. Appl. 41(1), 1–28 (2020)
Orbandexivry, F.-X., Nesterov, Y., Van Dooren, P.: Nearest stable system using successive convex approximations. Automatica 49(5), 1195–1203 (2013)
Wilkinson, J. H.: The algebraic eigenvalue problem. Monographs on Numerical Analysis. The Clarendon Press, Oxford University Press, New York. Oxford Science Publications (1988)
Acknowledgements
We are grateful to two anonymous reviewers for their insightful comments.
Funding
Open access funding provided by Aalto University. VN acknowledges partial support by the Visiting Fellows Programme of the University of Pisa and support by an Academy of Finland grant (Suomen Akatemian päätös 331240). FP acknowledges partial support by INdAM/GNCS and by a PRA (Progetto di Ricerca d’Ateneo) of the University of Pisa.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Not applicable.
Code availability
The code for the paper is freely available at https://github.com/fph/nearest-omega-stable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Noferini, V., Poloni, F. Nearest \(\varOmega \)-stable matrix via Riemannian optimization. Numer. Math. 148, 817–851 (2021). https://doi.org/10.1007/s00211-021-01217-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01217-4





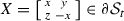 and studying the resulting function, which is strictly convex trivariate quadratic.
and studying the resulting function, which is strictly convex trivariate quadratic.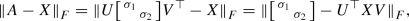
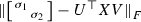 in
in 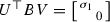 , i.e.,
, i.e., 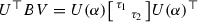 , where
, where 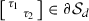 is another local minimizer of
is another local minimizer of  . By the same argument as in the previous case, this minimizer must be
. By the same argument as in the previous case, this minimizer must be 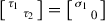 . Hence
. Hence 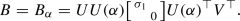

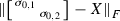 in
in 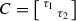 (with
(with 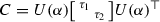 and
and 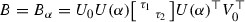 for some
for some  and hence
and hence 








