Abstract
The Bergman projection \(P_\alpha \), induced by a standard radial weight, is bounded and onto from \(L^\infty \) to the Bloch space \(\mathcal {B}\). However, \(P_\alpha : L^\infty \rightarrow \mathcal {B}\) is not a projection. This fact can be emended via the boundedness of the operator \(P_\alpha :\textrm{BMO}_2(\Delta )\rightarrow \mathcal {B}\), where \(\textrm{BMO}_2(\Delta )\) is the space of functions of bounded mean oscillation in the Bergman metric. We consider the Bergman projection \(P_\omega \) and the space \(\textrm{BMO}_{\omega ,p}(\Delta )\) of functions of bounded mean oscillation induced by \(1<p<\infty \) and a radial weight \(\omega \in \mathcal {M}\). Here \(\mathcal {M}\) is a wide class of radial weights defined by means of moments of the weight, and it contains the standard and the exponential-type weights. We describe the weights such that \(P_\omega :\textrm{BMO}_{\omega ,p}(\Delta )\rightarrow \mathcal {B}\) is bounded. They coincide with the weights for which \(P_\omega : L^\infty \rightarrow \mathcal {B}\) is bounded and onto. This result seems to be new even for the standard radial weights when \(p\ne 2\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
It is well-known that the Bergman projection \(P_\alpha \), induced by the standard weight \((\alpha +1)(1-|z|^2)^\alpha \), is bounded and onto from \(L^\infty \) to the Bloch space \(\mathcal {B}\) [6, Section 5.1]. This is a very useful result with a large variety of applications in the operator theory on spaces of analytic functions on \(\mathbb {D}\). However, the operator \(P_\alpha :L^\infty \rightarrow \mathcal {B}\) is in fact not a projection because of the strict inclusion \(H^\infty \subsetneq \mathcal {B}\). This downside can be emended by replacing \(L^\infty \) by the space \(\textrm{BMO}_2(\Delta )\) of functions of bounded mean oscillation in the Bergman metric [6, Section 8.1]. It is known that the analytic functions in \(\textrm{BMO}_2(\Delta )\) constitute the Bloch space \(\mathcal {B}\) [6, Theorem 8.7], and it is a folklore result that \(P_\alpha :\textrm{BMO}_2(\Delta )\rightarrow \mathcal {B}\) is bounded. Professor Kehe Zhu kindly offered us the following proof:
If \(f\in \textrm{BMO}_2(\Delta )\), then the big Hankel operators \(H^{\alpha }_f(g)=(I-P_\alpha )(fg)\) and \(H^{\alpha }_{\overline{f}}(g)=(I-P_\alpha )(\overline{f}g)\) are both bounded on the Bergman space \(A^2_\alpha \) by [6, Section 8.1], and therefore so are the little Hankels \(h^\alpha _f(g)=\overline{P_\alpha }(fg)\) and \(h^\alpha _{\overline{f}}(g)=\overline{P_\alpha }(\overline{f}g)\). Now that \(h^\alpha _{\overline{f}}=h^\alpha _{\overline{P_\alpha (f)}}\), and the little Hankel operator \(h^{\alpha }_{\overline{\varphi }}\), induced by an analytic symbol \(\varphi \), is bounded on \(A^2_\alpha \) if and only if \(\varphi \in \mathcal {B}\) by [6, Section 8.7], it follows that \(P_\alpha (f)\in \mathcal {B}\), whenever \(f\in \textrm{BMO}_2(\Delta )\). Since this argument preserves the information on the norms, it follows that \(P_\alpha :\textrm{BMO}_2(\Delta )\rightarrow \mathcal {B}\) is bounded.
In this paper we are interested in understanding the nature of a space X of complex-valued functions such that \(X\cap \mathcal {H}(\mathbb {D})=\mathcal {B}\), and radial weights \(\omega \) for which the Bergman projection \(P_\omega :X\rightarrow \mathcal {B}\) is bounded. Here, as usual, \(\mathcal {H}(\mathbb {D})\) stands for the space of analytic functions in the unit disc \(\mathbb {D}=\{z\in \mathbb {C}:|z|<1\}\). We proceed towards the statements via necessary notation.
For a non-negative function \(\omega \in L^1([0,1))\), its extension to \(\mathbb {D}\), defined by \(\omega (z)=\omega (|z|)\) for all \(z\in \mathbb {D}\), is called a radial weight. For \(0<p<\infty \) and such an \(\omega \), the Lebesgue space \(L^p_\omega \) consists of complex-valued measurable functions f on \(\mathbb {D}\) such that
where \(dA(z)=\frac{dx\,dy}{\pi }\) is the normalized Lebesgue area measure on \(\mathbb {D}\). The corresponding weighted Bergman space is \(A^p_\omega =L^p_\omega \cap \mathcal {H}(\mathbb {D})\). Throughout this paper we assume \(\widehat{\omega }(z)=\int _{|z|}^1\omega (s)\,ds>0\) for all \(z\in \mathbb {D}\), for otherwise \(A^p_\omega =\mathcal {H}(\mathbb {D})\). For a radial weight \(\omega \), the orthogonal Bergman projection \(P_\omega \) from \(L^2_\omega \) to \(A^2_\omega \) is
where \(B^\omega _{z}\) are the reproducing kernels of the Hilbert space \(A^2_\omega \). It has been recently shown in [5, Theorems 1-2-3] that the Bergman projection \(P_\omega \), induced by a radial weight \(\omega \), is bounded from \(L^\infty \) to the Bloch space \(\mathcal {B}\) if and only if  , while the Bloch space is continuously embedded into \(P_\omega (L^\infty )\) if and only if \(\omega \in \mathcal {M}\). Therefore, \(P_\omega : L^\infty \rightarrow \mathcal {B}\) is bounded and onto if and only
, while the Bloch space is continuously embedded into \(P_\omega (L^\infty )\) if and only if \(\omega \in \mathcal {M}\). Therefore, \(P_\omega : L^\infty \rightarrow \mathcal {B}\) is bounded and onto if and only  . Recall that a radial weight \(\omega \) belongs to the class
. Recall that a radial weight \(\omega \) belongs to the class  if there exists a constant \(C=C(\omega )>1\) such that \(\widehat{\omega }(r)\le C\widehat{\omega }(\frac{1+r}{2})\) for all \(0\le r<1\), while \(\omega \in \mathcal {M}\) if \(\omega _{x}\ge C\omega _{Kx}\), for all \(x\ge 1\), for some \(C=C(\omega )>1\) and \(K=K(\omega )>1\). Here and from now on \(\omega _x=\int _0^1r^x\omega (r)\,dr\), for all \(x\ge 0\).
if there exists a constant \(C=C(\omega )>1\) such that \(\widehat{\omega }(r)\le C\widehat{\omega }(\frac{1+r}{2})\) for all \(0\le r<1\), while \(\omega \in \mathcal {M}\) if \(\omega _{x}\ge C\omega _{Kx}\), for all \(x\ge 1\), for some \(C=C(\omega )>1\) and \(K=K(\omega )>1\). Here and from now on \(\omega _x=\int _0^1r^x\omega (r)\,dr\), for all \(x\ge 0\).
Let \(\beta (z,\zeta )\) denote the hyperbolic distance between the points z and \(\zeta \) in \(\mathbb {D}\), and let \(\Delta (z,r)\) stand for the hyperbolic disc of center \(z\in \mathbb {D}\) and radius \(0<r<\infty \). Further, let \(\omega \) be a radial weight and \(0<r<\infty \) such that \(\omega \left( \Delta (z,r)\right) >0\) for all \(z\in \mathbb {D}\). Then, for \(f\in L^p_{\omega }\) with \(1\le p<\infty \), write
where
The space \(\textrm{BMO}(\Delta )_{\omega ,p,r}\) consists of \(f\in L^p_{\omega }\) such that
It is known by [4, Theorem 11] that for each \(\omega \in \mathcal {D}\) there exists \(r_0=r_0(\omega )>0\) such that
We call this space \(\textrm{BMO}(\Delta )_{\omega ,p}\) whenever (1.1) holds, and assume that the norm is always calculated with respect to a fixed \(r\ge r_0\). However, in contrast to the class \(\mathcal {D}\), for each prefixed \(r>0\), the quantity \(\omega (\Delta (z,r))\) may equal to zero for some z arbitrarily close to the boundary if  , by Proposition 3 below. Therefore the space \(\textrm{BMO}(\Delta )_{\omega ,p,r}\) is not necessarily well-defined if
, by Proposition 3 below. Therefore the space \(\textrm{BMO}(\Delta )_{\omega ,p,r}\) is not necessarily well-defined if  , and consequently, we consider the class \(\mathcal {D}\) in the main results of this paper.
, and consequently, we consider the class \(\mathcal {D}\) in the main results of this paper.
It is clear that the space \(\textrm{BMO}(\Delta )_{\omega ,p}\) depends on \(\omega \in \mathcal {D}\), but for \(\omega \in \mathcal {Inv}\), straightforward calculations show that for each \(r_1,r_2\in (0,\infty )\), we have \(\textrm{BMO}(\Delta )_{\omega ,p,r_1}=\textrm{BMO}(\Delta )_{\nu ,p,r_2}\) where \(\nu (z)\equiv 1\). Therefore we call this space \(\textrm{BMO}(\Delta )_{p}\). Recall that \(\omega \) is invariant, denoted by \(\omega \in \mathcal {Inv}\), if for some (equivalently for all) \(r\in (0,\infty )\) there exists a constant \(C=C(r)\ge 1\) such that such that \(C^{-1}\omega (\zeta )\le \omega (z)\le C\omega (\zeta )\) for all \(\zeta \in \Delta (z,r)\). That is, an invariant weight is essentially constant in each hyperbolically bounded region. The class \(\mathcal {R}\) of regular weights, which is a large subclass of smooth weights in \(\mathcal {D}\), satisfies \(\mathcal {R}\subset \mathcal {Inv}\cap \mathcal {D}\) by [1, Section 1.3]. The space \(\textrm{BMO}(\Delta )_{\omega ,p}\) certainly depends on p as is seen by considering the function \(f(z)=|z|^{-\frac{2}{p}}\) which satisfies \(f\in \textrm{BMO}(\Delta )_q\setminus \textrm{BMO}(\Delta )_p\) for \(q<p\).
We recall one last thing before stating the main result of this paper. Namely, an analytic function f belongs to \(\mathcal {B}\) if and only if it is Lipschitz continuous in the hyperpolic metric [6, Theorem 5.5]. Therefore \(\mathcal {B}\subset \textrm{BMO}(\Delta )_{\omega ,p,r}\) for each \(1\le p<\infty \), \(0<r<\infty \) and a radial weight \(\omega \) such that \(\omega \left( \Delta (z,r)\right) >0\) for all \(z\in \mathbb {D}\).
Theorem 1
Let \(1<p<\infty \) and \(\omega \in \mathcal {M}\). Then the following statements are equivalent:
-
(i)
There exists \(r_0=r_0(\omega )\in (0,\infty )\) such that \(\textrm{BMO}(\Delta )_{\omega ,p,r}\) does not depend on r, provided \(r\ge r_0\). Moreover, \(P_\omega :\textrm{BMO}(\Delta )_{\omega ,p}\rightarrow \mathcal {B}\) is bounded;
-
(ii)
\(P_\omega :L^\infty \rightarrow \mathcal {B}\) is bounded;
-
(iii)
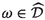 .
.
As far as we know, the statement in Theorem 1 is new even for the standard weights when \(p\ne 2\). The class \(\mathcal {M}\) is a wide class of radial weights containing the standard radial weights as well as exponential-type weights [1, Chapter 1]. It is also worth observing that weights in \(\mathcal {M}\) may admit a substantial oscillating behavior. In fact, a careful inspection of the proof of [5, Proposition 14] reveals the existence of a weight \(\omega \in \mathcal {M}\) such that \(\textrm{BMO}(\Delta )_{\omega ,p,r}\) is not well-defined for any \(r>0\) and \(1<p<\infty \), and therefore we cannot get rid of the first statement in the case (i) in Theorem 1. However, each weight \(\omega \) in the class  has the property that \(\omega (\Delta (z,r))>0\) for all \(z\in \mathbb {D}\) and for all r sufficiently large depending on \(\omega \). The class
has the property that \(\omega (\Delta (z,r))>0\) for all \(z\in \mathbb {D}\) and for all r sufficiently large depending on \(\omega \). The class  consists of radial weights \(\omega \) for which there exist constants \(K=K(\omega )>1\) and \(C=C(\omega )>1\) such that \(\widehat{\omega }(r)\ge C\widehat{\omega }\left( 1-\frac{1-r}{K}\right) \) for all \(0\le r<1\). Recall that
consists of radial weights \(\omega \) for which there exist constants \(K=K(\omega )>1\) and \(C=C(\omega )>1\) such that \(\widehat{\omega }(r)\ge C\widehat{\omega }\left( 1-\frac{1-r}{K}\right) \) for all \(0\le r<1\). Recall that  but
but  by [5, Proof of Theorem 3 and Proposition 14].
by [5, Proof of Theorem 3 and Proposition 14].
As for the proof of Theorem 1, the equivalence between (ii) and (iii) is already known by [5, Theorem 3], so our contribution here consists of showing that (iii) implies (i). Our approach to this implication does not involve the Hankel operators, is direct and based on the decomposition \(\textrm{BMO}(\Delta )_{\omega ,p}= \textrm{BA}(\Delta )_{\omega ,p}+\textrm{BO}(\Delta )\), provided in [4, Theorem 11(ii)]. For continuous \(f:\mathbb {D}\rightarrow \mathbb {C}\) and \(0<r<\infty \), we define
and let \(\textrm{BO}(\Delta )\) denote the space of those f such that
It is known that the definition of \(\textrm{BO}(\Delta )\) is independent of the choice of r by [6, Lemma 8.1]. Further, if \(\omega \) is a radial weight such that \(\omega \left( \Delta (z,r)\right) >0\) for all \(z\in \mathbb {D}\), then, for \(0<p<\infty \), the space \(\textrm{BA}(\Delta )_{\omega ,p,r}\) consists of \(f\in L^p_{\omega }\) such that
If \(\omega \in \mathcal {D}\), then the space \(\textrm{BA}(\Delta )_{\omega ,p,r}\) depends on p and \(\omega \) but, by [4, Lemma 10], there exists an \(r_0=r_0(\omega )\in (0,\infty )\) such that it is independent of r as long as \(r\ge r_0\), so we write \(\textrm{BA}(\Delta )_{\omega ,p}\) for short. With these definitions and observations the decomposition \(\textrm{BMO}(\Delta )_{\omega ,p}=\textrm{BA}(\Delta )_{\omega ,p}+\textrm{BO}(\Delta )\) gets explained.
The rest of the paper consists of the proof of Theorem 1. But before getting to that, we finish the section with couple of words about the notation used. The letter \(C=C(\cdot )\) will denote an absolute constant whose value depends on the parameters indicated in the parenthesis, and may change from one occurrence to another. We will use the notation \(a\lesssim b\) if there exists a constant \(C=C(\cdot )>0\) such that \(a\le Cb\), and \(a\gtrsim b\) is understood in an analogous manner. In particular, if \(a\lesssim b\) and \(a\gtrsim b\), then we write \(a\asymp b\) and say that a and b are comparable.
2 Preliminary results on radial weights
We begin with a known characterization of weights in  , proved in [2, Lemma 2.1].
, proved in [2, Lemma 2.1].
Lemma A
Let \(\omega \) be a radial weight. Then,  if and only if there exist \(C=C(\omega )>0\) and \(\beta =\beta (\omega )>0\) such that
if and only if there exist \(C=C(\omega )>0\) and \(\beta =\beta (\omega )>0\) such that
The following simple lemma is useful for our purposes. It reveals that \(\mathcal {D}\) is closed under multiplication by a suitably small negative power of the hat of another weight in  .
.
Lemma 2
Let \(\omega \in \mathcal {D}\) and  . Then there exists \(\gamma _0=\gamma _0(\omega ,\nu )>0\) such that, for each \(\gamma \in (0,\gamma _0]\), we have \((\widehat{\nu })^{-\gamma }\omega \in \mathcal {D}\), and
. Then there exists \(\gamma _0=\gamma _0(\omega ,\nu )>0\) such that, for each \(\gamma \in (0,\gamma _0]\), we have \((\widehat{\nu })^{-\gamma }\omega \in \mathcal {D}\), and
Proof
By [5, (2.27)],  if and only if there exist constants \(C=C(\omega )>0\) and \(\alpha _0=\alpha _0(\omega )>0\) such that
if and only if there exist constants \(C=C(\omega )>0\) and \(\alpha _0=\alpha _0(\omega )>0\) such that
for all \(\alpha \in (0,\alpha _0]\). Let \(\gamma =\gamma (\omega ,\nu )\in (0,\alpha _0/\beta )\), where \(\beta =\beta (\nu )>0\) is that of Lemma A. Then
Two integrations by parts together with (2.2) and Lemma A yield
Therefore (2.1) is satisfied, and standard arguments show that \((\widehat{\nu })^{-\gamma }\omega \in \mathcal {D}\).
We finish the section by showing that the space \(\textrm{BMO}(\Delta )_{\omega ,p,r}\) is not necessarily well-defined for all \(r\in (0,1)\) if  . This serves us as a justification for the initial hypotheses on \(\omega \) in our study.
. This serves us as a justification for the initial hypotheses on \(\omega \) in our study.
Proposition 3
Let \(\psi :[0,1)\rightarrow [(\log 3)/4,\infty )\) be arbitrary. Then there exist an  and a sequence \(\{r_n\}_{n=1}^\infty \) of points on (0, 1) depending on \(\psi \) only such that \(\lim _{n\rightarrow \infty }r_n=1\) and \(\omega _{\psi }(\Delta (r_n,\psi (r_{n-1}))=0\) for all \(n\in \mathbb {N}\).
and a sequence \(\{r_n\}_{n=1}^\infty \) of points on (0, 1) depending on \(\psi \) only such that \(\lim _{n\rightarrow \infty }r_n=1\) and \(\omega _{\psi }(\Delta (r_n,\psi (r_{n-1}))=0\) for all \(n\in \mathbb {N}\).
Proof
Let us consider the increasing sequence \(\{t_n\}_{n=1}^\infty \in [0,1)\) defined inductively by the identities \(t_1=0\) and \(\beta (t_n,t_{n+1})=2\psi (t_{n})\) for all \(n\in \mathbb {N}\). Since the range of \(\psi \) is \([(\log 3)/4,\infty )\), we have
Therefore \( t_{n+1} \ge \frac{1+t_n}{2}, \) and consequently, \(\lim _{n\rightarrow \infty }t_n=1\). Then, for \(n\ge 2\), the annulus \(\{z\in \mathbb {D}:t_n\le |z|\le t_{n+1}\}\) contains \(\Delta (s_n,\psi (s_{n-1}))\), where \(s_n\) is the hyperbolic midpoint of \((t_n,t_{n+1})\). Define \(\omega =\sum _{n=1}^\infty a_n\chi _{\{z:t_{2n}\le |z|\le t_{2n+1}\}}\), where \(\{a_n\}_{n=1}^\infty \) are chosen such that \(a_n(t_{2n+1}-t_{2n})=2^{-n}\) for all \(n\in \mathbb {N}\). Then \(\widehat{\omega }(t_{2n})=\sum _{j=n}^\infty 2^{-j}=2^{1-n}\) for all \(n\in \mathbb {N}\), and it follows that  because \(\beta \left( r,\frac{1+r}{2}\right) \asymp 1\) for all \(0\le r<1\), and \(\beta (t_{2n},t_{2(n+1)})=2(\psi (t_{2n})+\psi (t_{2n+1}))\rightarrow \infty \), as \(n\rightarrow \infty \). Further, by setting \(r_n=s_{2n+1}\), we have \(\omega (\Delta (r_n,\psi (r_{n-1})))=0\) for all \(n\in \mathbb {N}\). This also implies that \(\omega \not \in \mathcal {D}\).
because \(\beta \left( r,\frac{1+r}{2}\right) \asymp 1\) for all \(0\le r<1\), and \(\beta (t_{2n},t_{2(n+1)})=2(\psi (t_{2n})+\psi (t_{2n+1}))\rightarrow \infty \), as \(n\rightarrow \infty \). Further, by setting \(r_n=s_{2n+1}\), we have \(\omega (\Delta (r_n,\psi (r_{n-1})))=0\) for all \(n\in \mathbb {N}\). This also implies that \(\omega \not \in \mathcal {D}\).
3 Proof of Theorem 1
The statements (ii) and (iii) are equivalent by [5, Theorem 1], and the fact that (i) implies (ii) is an immediate consequence of the continuous embedding \(L^\infty \subset \textrm{BMO}(\Delta )_{\omega ,p}\). Assume now (iii), that is, \(\omega \in \mathcal {D}\). In the proof we will use the fact that \(f\in \textrm{BMO}_{\omega ,p}(\Delta )\) if and only if it can be decomposed as \(f=f_1+f_2\), where \(f_1\in \textrm{BA}(\Delta )_{\omega ,p}\) and \(f_2\in \textrm{BO}(\Delta )\) such that \(\Vert f_1\Vert _{\textrm{BA}(\Delta )_{\omega ,p}}+\Vert f_2\Vert _{\textrm{BO}(\Delta )}\lesssim \Vert f\Vert _{\textrm{BMO}(\Delta )_{\omega ,p}}\). This statement follows from [4, Theorem 11(ii)] and its proof. Consequently, it is enough to prove that \(P_\omega : \textrm{BA}(\Delta )_{\omega ,p}\rightarrow \mathcal {B}\) and \(P_\omega : \textrm{BO}(\Delta ) \rightarrow \mathcal {B}\) are bounded operators.
We first show that \(P_\omega : \textrm{BA}(\Delta )_{\omega ,p}\rightarrow \mathcal {B}\) is bounded. To do this, choose \(0<r_0<\infty \) such that \(\textrm{BA}(\Delta )_{\omega ,p,r}=\textrm{BA}(\Delta )_{\omega ,p}\) is independent of r as long as \(r\ge r_0\). Further, let \(f_1\in \textrm{BA}(\Delta )_{\omega ,p}\) and \(r\ge r_0\), and let \(\{a_k\}_{k=1}^\infty \) be an r-lattice. Then Hölder’s inequality and the definition of \(\textrm{BA}(\Delta )_{\omega ,p}\) yield
from which the subharmonicity and standard estimates give
Next, for each \(a\in \mathbb {D}\setminus \{0\}\), consider the interval \(I_a=\left\{ e^{i\theta }:|\arg (a e^{-i\theta })|\le \frac{(1-|a|)}{2}\right\} \), and let \(S(a)=\{z\in \mathbb {D}: |z|\ge |a|,\, e^{it}\in I_a\}\) denote the Carleson square induced by a. Then Fubini’s theorem yields
where \(R'=R'(r)\in (0,\infty )\) and \(b=b(a,r)\in \mathbb {D}\) satisfies \(\arg b=\arg a\) and \(1-|b|\asymp 1-|a|\) for all \(a\in \mathbb {D}\setminus \overline{D(0,R')}\). Since  by the hypothesis, we have \(\omega (S(b))\lesssim \omega (S(a))\) by Lemma A. Therefore (3.1) and [2] [Theorem 3.3] imply
by the hypothesis, we have \(\omega (S(b))\lesssim \omega (S(a))\) by Lemma A. Therefore (3.1) and [2] [Theorem 3.3] imply
Since [3, Theorem 1] yields
we deduce that \(P_\omega : \textrm{BA}(\Delta )_{\omega ,p}\rightarrow \mathcal {B}\) is bounded.
It remains to show that \({P_\omega : \textrm{BO}(\Delta ) \rightarrow \mathcal {B}}\) is bounded. Let \(f_2\in \textrm{BO}(\Delta )\). First, observe that an application of Lemma 2 yields
Further, since \(1=\langle 1,B^\omega _z\rangle _{A^2_\omega }\) and \(0=\langle 1,(B^\omega _z)'\rangle _{A^2_\omega }\), we have
By Lemma 2 there exists \(\varepsilon _0=\varepsilon _0(\omega )>0\) such that for each \(\varepsilon \in (0,\varepsilon _0]\), we have \(\omega _{[-\varepsilon ]}=(1-|z|)^{-\varepsilon }\omega (z)\in \mathcal {D}\) and \(\widehat{\omega _{[-\varepsilon ]}}\asymp \widehat{\omega }_{[-\varepsilon ]}\) on \(\mathbb {D}\). Take \(0<\varepsilon <\min \left\{ \frac{1}{2+\beta },\frac{\varepsilon _0}{1+\varepsilon _0}\right\} \), where \(\beta \) is that from Lemma A. Since \(f_2\in \textrm{BO}(\Delta )\), we have
Therefore Hölder’s inequality yields
where
and
By Lemma 2, [3, Theorem 1], Lemma A and our choice of \(\varepsilon \), we have
Let us now bound \(I_1(z)\). To do this we first observe that
By [3, Theorem 1] we have
Further, we have \(n(\omega _{2n+1}-\omega _{2n+3})=n\int _{0}^1\,s^{2n+1}(1-s^2)\omega (s)\,ds\lesssim \omega _{2n+1}\) for all \(n\in \mathbb {N}\) by [5, (1.3)]. Therefore another application of [3, Theorem 1] gives
and it follows that
This estimate, (3.2) and (3.3) yield
Consequently, \(P_\omega : \textrm{BO}(\Delta ) \rightarrow \mathcal {B}\) is bounded. This finishes the proof of the theorem.
Data availability
This manuscript has no associate data
References
Peláez, J.A., Rättyä, J.: Weighted Bergman spaces induced by rapidly increasing weights. Mem. Am. Math. Soc. 227(1066), 1–127 (2014)
Peláez, J.A.: Small weighted Bergman spaces. Proceedings of the Summer School in Complex and Harmonic Analysis, and Related Topics, Mekrijrärvi (2014)
Peláez, J.A., Rättyä, J.: Two weight inequality for Bergman projection. J. Math. Pures Appl. 105, 102–130 (2016)
Peláez, J.A., Perälä, A., Rättyä, J.: Hankel operators induced by radial Bekollé–Bonami weights on Bergman spaces. Math. Z. 296(1–2), 211–238 (2020)
Peláez, J.A., Rättyä, J.: Bergman projection induced by radial weight. Adv. Math. 391, 107950 (2021)
Zhu, K.: Operator Theory in Function Spaces, Mathematical Surveys and Monographs, vol. 138, 2nd edn. American Mathematical Society, Providence (2007)
Funding
Funding for open access publishing: Universidad de Málaga/CBUA.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are indebted to Kehe Zhu for explaining how the special case \(p=2\) works in the setting of the standard weighted Bergman spaces. The authors would also like to thank Antti Perälä for enlightening conversations on the topic. Moreover, the authors are very grateful for the anonymous referee for his/her insightful comments and suggestions. The proof presented in this paper is an adaptation of the guideline provided by the referee for the case of standard radial weights. Our original proof was based on Hankel operators and was certainly more technical and laborious compared to the reader friendly reasoning presented in this final version.
The research was supported in part by La Junta de Andalucía, project FQM210, and Vilho, Yrjö ja Kalle Väisälä foundation of Finnish Academy of Science and Letters.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peláez, J.Á., Rättyä, J. Bergman projection and BMO in hyperbolic metric: improvement of classical result. Math. Z. 305, 19 (2023). https://doi.org/10.1007/s00209-023-03343-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00209-023-03343-1
Keywords
- Bergman projection
- Bergman metric
- Bergman space
- Bloch space
- Doubling weight
- Hankel operator
- Mean oscillation



 .
.