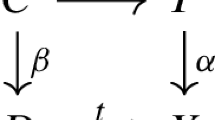Spaces of positive scalar curvature metrics on totally nonspin manifolds with spin boundary

Abstract

In this article we study the space of positive scalar curvature metrics on totally nonspin manifolds with spin boundary. We prove that for such manifolds of certain dimensions, those spaces are not connected and have nontrivial fundamental group. Furthermore we show that a well-known propagation technique for detection results on spaces of positive scalar curvature metrics on spin manifolds ceases to work in the totally nonspin case.

1 Introduction

For a closed smooth manifold M we denote by ${\mathcal {R}}^+(M)$ the space of all Riemannian metrics of positive scalar curvature (psc-metrics) equipped with the $C^\infty$-topology. In recent years, there has been a lot of research activity around such spaces of metrics with lower curvature bounds, see e.g. [3, 6, 11, 12, 14, 18]. It has been shown that in the presence of a spin structure, ${\mathcal {R}}^+(M)$ has a lot of interesting topological features like nontrivial homotopy or homology groups.

In this article, we deviate from this setup in two ways: First, we consider compact manifolds M with non-empty boundary $\partial M$ and we require the metrics in ${\mathcal {R}}^+(M)$ to be cylindrical in a neighbourhood of the boundary (see Sect. 2.1 for a precise definition). Second, we want $\partial M$ to be ${\textrm{Spin}}$, whereas M shall be totally nonspin, i.e. its universal cover $\widetilde{M}$ does not admit a spin structure. Employing this discrepancy, we show that index-theoretic secondary obstructions on the boundary can be used to distinguish components and elements in the fundamental group of ${\mathcal {R}}^+(M)$.

We also observe that a well-known propagation technique for positive scalar curvature metrics on spin manifolds ceases to work in the totally nonspin case. More precisely we show that there exist non-isotopic psc-metrics on the disc which become isotopic after extending them arbitrarily to a totally nonspin manifold.

Throughout this article we will assume that M and $\partial M$ admit psc-metrics.

1.1 Spaces of metrics on manifolds with boundary

Consider the map

$$\begin{aligned} \textrm{res}:{\mathcal {R}}^+(M)\rightarrow {\mathcal {R}}^+(\partial M) \end{aligned}$$

given by restricting a psc-metric to the boundary which is a Serre-fibration by [9, Theorem 1.1]. For $h\in {\mathcal {R}}^+(\partial M)$ we define ${\mathcal {R}}^+(M)_h:= \textrm{res}^{-1}(h)$. One powerful tool for studying the space of psc-metrics on a spin manifold N is the index-difference first introduced by Hitchin in [20]. After fixing a base-point $g\in {\mathcal {R}}^+(N)_h$, it induces a map

$$\begin{aligned} \textrm{inddiff}_g:\pi _k({\mathcal {R}}^+(N)_h)\rightarrow {\textrm{KO}}^{-\dim (N)-k-1}({\textrm{pt}}). \end{aligned}$$

This map is often non-trivial (see for example [3, Theorem A]) and our first main result is the following.

Theorem A

Let M be a compact, oriented, totally nonspin manifold of dimension $\dim M=d\ge 8$ with non-empty spin boundary $\partial M$.

• (i) If $d\equiv 0,1(8)$ and $\partial M$ is ${\textrm{Spin}}\times B\pi _1(\partial M)$-nullbordant¹, there exists an $h\in {\mathcal {R}}^+(\partial M)$ such that ${\mathcal {R}}^+(M)_h$ is non-empty and the following composition is surjective

  $$\begin{aligned} \pi _1({\mathcal {R}}^+(M))\overset{\textrm{res}}{\longrightarrow }\pi _1({\mathcal {R}}^+(\partial M)) \overset{\textrm{inddiff}_h}{\longrightarrow }{\textrm{KO}}^{-d-1}({\textrm{pt}})\cong {\mathbb {Z}}/2. \end{aligned}$$

• (ii) For any $h\in {\mathcal {R}}^+(\partial M)$ such that ${\mathcal {R}}^+(M)_h$ is non-empty, the following composition is surjective:

  $$\begin{aligned} \pi _0({\mathcal {R}}^+(M))\overset{\textrm{res}}{\longrightarrow }\pi _0({\mathcal {R}}^+(\partial M)) \overset{\textrm{inddiff}_h}{\longrightarrow }{\textrm{KO}}^{-d}({\textrm{pt}}). \end{aligned}$$

Remark 1.1

• (i) The most prominent examples of totally nonspin manifolds are even-dimensional complex projective spaces. For $D^{4k}\subset {{\mathbb {C}}{\mathbb {P}}}^{{2k}}$ an embedded open disk, Theorem A implies

  $$\begin{aligned}&\pi _1({\mathcal {R}}^+({{\mathbb {C}}{\mathbb {P}}}^{{4n}}\setminus D^{8n}))\not =1\quad \ \ \, \text { for}\ n\ge 1\\ |&\pi _0({\mathcal {R}}^+({{\mathbb {C}}{\mathbb {P}}}^{{2n}}\setminus D^{4n}))| = \infty \quad \text { for}\ n\ge 2. \end{aligned}$$

• (ii) Theorem A remains true, if we consider spaces of metrics with for example mean convex or minimal boundary instead of requiring product form near the boundary. By [1, Corollary 40] the space of psc-metrics on M which satisfy one of these boundary conditions and whose restriction to the boundary is again of positive scalar curvature, is homotopy equivalent to ${\mathcal {R}}^+(M)$.

Remark 1.2

(State of the art) To the best of the author’s knowledge, Theorem A is the first detection result concerning higher homotopy groups of the space of psc-metrics on a nonspin manifold. Furthermore, it is also the first such result about ${\mathcal {R}}^+(M)$ for manifolds with boundary, where the manifold and its boundary are allowed to have isomorphic fundamental groups and can even be simply connected.

In the case where M is nonspin, but its universal cover is ${\textrm{Spin}}$, there are cases where ${\mathcal {R}}^+(M)$ is not connected or has even infinitely many path components, see [2, 7, 8, 15, 16, 23, 25]. For totally nonspin manifolds, Kastenholz–Reinhold give an example of a closed, totally nonspin manifold of dimension 6 whose space of psc-metrics has infinitely many components in [21].

In [1, Theorem 44], Bär–Hanke give examples of spin manifolds M with boundary where ${\mathcal {R}}^+(M)$ has a non-vanishing homotopy group. In their examples however, M has infinite fundamental group and the induced map $\pi _1(\partial M)\rightarrow \pi _1(M)$ is not an isomorphism.

1.2 Gluing in psc-metrics on disks

Let N be a closed d-dimensional spin manifold. One nice feature of the index-difference map is the following “propagation principle”: let $D\subset N$ be an embedded disk and let h be a psc-metric on $S^{d-1}$ such that ${\mathcal {R}}^+(N{\setminus } \textrm{int}(D))_{h}\not =\emptyset \not ={\mathcal {R}}^+(D^d)_{h}$. The additivity theorem for the index-difference [3, Proposition 3.18] implies that

$$\begin{aligned} \textrm{inddiff}_{g_0}([g_1]) = \textrm{inddiff}_{g_0\cup g}([g_1\cup g]), \end{aligned}$$

for any $g\in {\mathcal {R}}^+(N{\setminus } \textrm{int}(D))_{h}$ and any $g_0,g_1\in {\mathcal {R}}^+(D^d)_{h}$. Therefore, non-isotopic psc-metrics on the disc which are detected by the index-difference remain non-isotopic after being extended arbitrarily to another spin manifold, implying one can propagate detection results. The following result states that in the totally nonspin case, this is no longer possible.

Theorem B

Let $d\equiv 0,1(8)$, $d\ge 8$ and let M be a closed, oriented d-dimensional, totally nonspin manifold with $D\subset M$ an embedded disc. Let $h\in {\mathcal {R}}^+(S^{d-1})$ such that ${\mathcal {R}}^+(M\setminus \textrm{int}(D))_{h}\not =\emptyset \not ={\mathcal {R}}^+(D^d)_{h}$ and let $g\in {\mathcal {R}}^+(M\setminus \textrm{int}(D))_{h}$ be arbitrary. Then there exist metrics $g_0, g_1\in {\mathcal {R}}^+(D^d)_{h}$ with $\textrm{inddiff}_{g_0}(g_1)\not =0\in {\textrm{KO}}^{-d-1}({\textrm{pt}})\cong {\mathbb {Z}}/2$, such that $g_0\cup g$ and $g_1\cup g$ are isotopic.

Remark 1.3

• (i) As mentioned above, Theorem B does not hold in the spin case. Even further, we have the following result (cf. [11, Theorem E]): if N is closed, 2-connected and of dimension $d\ge 6$, there exists a right-stable metric $g_{\textrm{rst}}\in {\mathcal {R}}^+(N{\setminus } \textrm{int}(D))_h$ for some boundary metric $h\in {\mathcal {R}}^+(S^{d-1})$. By definition of right-stability, the gluing map

  $$\begin{aligned} \mu _{g_{\textrm{rst}}}:{\mathcal {R}}^+(D^d)_{h} \longrightarrow {\mathcal {R}}^+(N),\ g \mapsto g_{\textrm{rst}}\cup g \end{aligned}$$

  is a weak homotopy equivalence, in particular bijective on components. If M is as above and $h\in {\mathcal {R}}^+(S^{d-1})$ extends to a psc-metric on both $D^d$ and $M\setminus \textrm{int}(D)$, then Theorem B implies that no metric in ${\mathcal {R}}^+(M\setminus \textrm{int}(D))_h$ is right-stable.

• (ii) Theorem B also holds if one replaces D by any closed, codimension 0 submanifold $W\subset M$ which admits a spin structure. This follows easily from the above-mentioned additivity theorem for the index-difference by considering a disc inside W.

In dimensions $d\equiv 3(4)$, we have ${\textrm{KO}}^{-d-1}\cong {\mathbb {Z}}$. Since the map $\textrm{inddiff}$ is surjective on components by [3, Theorem D], there is an infinite family $(g_n)_{n\in {\mathbb {N}}}\subset {\mathcal {R}}^+(D^d)_{h_\circ }$ of pairwise non-isotopic psc-metrics. An elementary argument shows that these metrics become concordant² after extending them arbitrarily to a totally nonspin manifold. We present this proof in Sect. 4.

2 Preliminaries

2.1 Spaces of metrics of positive scalar curvature on a manifold with boundary

For a closed manifold M let ${\mathcal {R}}^+(M)$ denote the space of all metrics of positive scalar curvature. If M has non-empty boundary $\partial M$ let $c:[0,1]\times \partial M \hookrightarrow M$ be a collar embedding such that $c(\{0\}\times \partial M)= \partial M\subset M$ and $c|_{\{0\}\times \partial M}$ is the canonical projection. We define ${\mathcal {R}}^+(M)$ to consist of all metrics g on M such that there exists a psc-metric h on $\partial M$ and an $\epsilon >0$ with

$$\begin{aligned} c^*g|_{[0,\epsilon ] \times \partial M} = \textrm{dt}^2 + h, \end{aligned}$$

i.e. we require metrics on M to be cylindrical in a neighbourhood of the boundary. One nice feature about having cylindrical boundary is that the restriction map

$$\begin{aligned} \textrm{res}:{\mathcal {R}}^+(M)\longrightarrow {\mathcal {R}}(\partial M) \end{aligned}$$

actually lands in the subspace ${\mathcal {R}}^+(\partial M)$ of psc-metrics. For $h\in {\mathcal {R}}^+(\partial M)$ we define ${\mathcal {R}}^+(M)_h:= \textrm{res}^{-1}(h)$. By [9, Theorem 1.6] the map $\textrm{res}$ is a Serre-fibration and hence for $h\in {\mathcal {R}}^+(\partial M)$ and $g\in {\mathcal {R}}^+(M)_h$ we have a long exact sequence of homotopy groups

$$\begin{aligned} \dots \rightarrow \pi _k({\mathcal {R}}^+(M),g)\rightarrow \pi _k({\mathcal {R}}^+(\partial M),h) \overset{\partial }{\rightarrow }\pi _{k-1}({\mathcal {R}}^+(M)_h,g)\rightarrow \dots \end{aligned}$$

(1)

To prove Theorem A (i) we need to get a more explicit description of the boundary map in this exact sequence. For our purposes it suffices to identify the boundary map on the image of the orbit of pullback-action of the topological group³$\textrm{Diff}_\partial (M)$ of self-diffeomorphisms of M. Let $(f_t)_{t\in [0,1]^k}$ be a continuous family of diffeomorphisms of $\partial M$ such that $f_t=\textrm{id}$ for t near $\partial [0,1]^k$. For $s\in [0,1]^{k-1}$ we define $F_s:M\rightarrow M$ by

$$\begin{aligned} F_s(x) = {\left\{ \begin{array}{ll} x &{} \text { if } x\not \in \textrm{im}c\\ c(r, f_{s,(1-r)}(y)) &{}\text { if } x=c(r,y) \end{array}\right. } \end{aligned}$$

(2)

Note that by our assumption on the family $(f_t)$ we have $F_s=\textrm{id}$ for s near $\partial [0,1]^{k-1}$ and $c(r, f_{s,r}(y)) = c(r,y)$ for r near 0 or 1. Therefore, $F_s$ is a smooth diffeomorphism and restricts to the identity in a neighbourhood of the boundary.

Lemma 2.1

Let $h\in {\mathcal {R}}^+(\partial M)$ and $g\in {\mathcal {R}}^+(M)_h$ be base points. Then

$$\begin{aligned} \partial \bigr ((f_t^*h)_{t\in [0,1]^k}\bigr )=(F_s^*g)_{s\in [0,1]^{k-1}}. \end{aligned}$$

Proof

Consider the following lifting problem:

where $J^{k-1}:= [0,1]^{k-1}\times \{0\})\cup (\partial [0,1]^{k-1}\times [0,1])$ and $\alpha (t) = f_t^*h$. Since the boundary map in (1) is determined by $\partial (\alpha ) = \beta |_{[0,1]^{k-1}\times \{1\}}$, we need to specify a lift $\beta$. Note that in our case $J^{k-1}\subset \partial [0,1]^k$ maps to the base point metric g. We define a family $\tilde{F}_{s,\ell }$ of diffeomorphisms of M for $s\in [0,1]^{k-1}$ and $\ell \in [0,1]$ as follows:

$$\begin{aligned} \tilde{F}_{s,\ell }(x):={\left\{ \begin{array}{ll} x &{}\text { if } x\not \in \textrm{im}~ c\\ c(r, f_{s,(1-r)\ell }(y)) &{}\text { if } x=c(r,y) \end{array}\right. }. \end{aligned}$$

This satisfies:

• $\tilde{F}_{s,\ell } = \textrm{id}$ for $(s,\ell )\in J^{k-1}$.

• $\tilde{F}_{s,\ell }(c(0,y)) = c(0, f_{s,\ell }(y)) = f_{s,\ell }(y)$.

• $\tilde{F}_{s,1}(c(r,y)) = c(r,f_{s,(1-r)}(y))$.

In particular, one possible choice of $\beta$ is given by $\tilde{F}_{s,\ell }^*g$ and the proof is finished by the observation that $\tilde{F}_{s,1} = F_s$ for $F_s$ the diffeomorphism defined in (2). $\square$

2.2 Recollection of existence results for positive scalar curvature

Before we get to positive scalar curvature, let us recall tangential structures. Let $B{\textrm{O}}(n)$ denote the classifying space for rank n-vector bundles. Extending an orthonormal matrix by 1 in the lower right corner induces a stabilisation map $B{\textrm{O}}(n)\rightarrow B{\textrm{O}}(n+1)$. A tangential structure is defined to be a fibration $\theta :B\rightarrow B{\textrm{O}}(n)$. Given a tangential structure $\theta$ a $\theta$-structure on a $\textrm{rank}\,n$-vector bundle $V\rightarrow X$ is a bundle map $\hat{\ell }:V\rightarrow \theta ^*U_n$ for $U_n\rightarrow B{\textrm{O}}(n)$ the universal rank n vector bundle. A (stabilised) $\theta$-structure on a manifold M of dimension $d\le n$ is a $\theta$-structure on $TM\oplus \underline{{\mathbb {R}}}^{n-d}$ and a (stabilised) $\theta$-manifold is a manifold together with a $\theta$-structure. For $d<n$ we denote the cobordism group of closed $\theta$-manifolds by $\Omega _d^\theta$.⁴

Example 2.2

Consider the fibrations $\theta _{{\textrm{Spin}},\pi }:B{\textrm{Spin}}(n)\times B\pi \rightarrow B{\textrm{O}}(n)$ and $\theta _{{\textrm{SO}},\pi }:B{\textrm{SO}}(n)\times B\pi \rightarrow B{\textrm{O}}(n)$. The corresponding cobordism groups are simply the singular cobordism groups $\Omega _d^{\textrm{Spin}}(B\pi ) =\Omega _d^{\theta _{{\textrm{Spin}},\pi }}$ and $\Omega _d(B\pi ) =\Omega _d^{\theta _{{\textrm{SO}},\pi }}$. If $M_0$ and $M_1$ represent the same class in $\Omega _d^{\textrm{Spin}}(B\pi )$ (resp. $\Omega _n^{\theta _{{\textrm{SO}},\pi }}$), we will say that $M_0$ and $M_1$ are ${\textrm{Spin}}\times B\pi$-cobordant (resp. ${\textrm{SO}}\times B\pi$-cobordant). In the special case that $M_0=\emptyset$, we say $M_1$ is ${\textrm{Spin}}\times B\pi$-nullbordant (resp. ${\textrm{SO}}\times B\pi$-nullbordant).

Recall the following useful lemma, stating that doubles are $\theta$-cobordant to cylinders.

Lemma 2.3

[13, Proposition 3.25] Let $W^d:M_0 \leadsto M_1$ be a $\theta$-cobordism. Then there exists a $\theta$-structure on $W^{\textrm{op}}:M_1\leadsto M_0$ such that $W\cup W^{\textrm{op}}$ is $\theta$-cobordant to $M_0\times [0,1]$ relative to $M_0\times \{0,1\}$.

For positive scalar curvature questions, the relevant tangential structure one needs to consider is usually the tangential 2-type of the underlying manifold.

Definition 2.4

Let M be a connected manifold of dimension $d<n$ and let $\tau :M\rightarrow B{\textrm{O}}(n)$ be the stabilised classifying map of the tangent bundle. For $k\ge 1$ we define the stabilised tangential k-type of M as the k-th stage of the Moore–Postnikov tower for the map $\tau$.

Example 2.5

• (i) If M is ${\textrm{Spin}}$ and $n>d$, the stabilised tangential 2-type of M is given by $B{\textrm{Spin}}(n)\times B\pi _1(M)$.

• (ii) If $n>d$ and M is orientable, totally nonspin, the stabilised tangential 2-type of M is given by $B{\textrm{SO}}(n)\times B\pi _1(M)$.

The reason, why the tangential 2-type shows up in the study of positive scalar curvature metrics, originates from the famous Gromov–Lawson–Schoen–Yau surgery theorem [17, 24]. It states that the existence of a psc-metric is invariant under surgeries of codimension at least 3 on the underlying manifold. We have the following, cobordism-theoretic translation of the surgery theorem.

Lemma 2.6

[17, Theorem A], [9, Theorem 1.5] Let M be ${\textrm{Spin}}$ (resp. totally nonspin) and ${\textrm{Spin}}\times B\pi _1(M)$-cobordant (resp. ${\textrm{SO}}\times B\pi _1(M)$-cobordant) to some manifold N of positive scalar curvature. Then M admits positive scalar curvature. If N and M have equal boundary and the cobordism is constant on the boundary the same result holds and the metrics on M and N can be chosen to restrict to the same metric on the boundary.

The version for manifolds with boundary can be derived from [9, Theorem 1.6 and proof of Theorem 1.5]. We also need an existence result for psc-metrics on cobordisms. First, let us recall the notion of right-stable metrics. Let $W:M_0\leadsto M_1$ be a manifold with boundary $\partial W=M_0\amalg M_1$ and $h_i\in {\mathcal {R}}^+(M_i)$. Then a metric $g\in {\mathcal {R}}^+(W)_{h_0,h_1}$ is called right-stable if for every cobordism $V:M_1\leadsto M_2$, the map

$$\begin{aligned} \mu _g:{\mathcal {R}}^+(V)_{h_1,h_2}\rightarrow {\mathcal {R}}^+(W\cup V)_{h_0,h_2}, \ \ G\mapsto g\cup G \end{aligned}$$

is a weak homotopy equivalence. On the $\pi _0$-level, this implies that every psc-metric on M is homotopic to one which restricts to g on W. Ebert–Randal–Williams have proven the following result.

Theorem 2.7

[11, Theorem E] If $\dim W\ge 6$ and $M_1\hookrightarrow W$ is 2-connected, then for any $h_0\in {\mathcal {R}}^+(M_0)$, there exists an $h_1\in {\mathcal {R}}^+(M_1)$ and a right-stable metric $g\in {\mathcal {R}}^+(W)_{h_0,h_1}$.

Remark 2.8

• (i) There is no restriction on $M_0$ except for admitting positive scalar curvature. In particular, if $M_0$ is empty, Theorem 2.7 implies the existence of right-stable metrics on nullcobordisms if $\partial W\hookrightarrow W$ is 2-connected. Therefore, we have the following implication: If $W\subset M$ is a closed, codimension 0 submanifold such that $\partial W\hookrightarrow W$ is 2-connected, then there exists a psc-metric $g\in {\mathcal {R}}^+(W)_h$ such that the gluing map

  $$\begin{aligned} \mu _g:{\mathcal {R}}^+(M\setminus \textrm{int}(W))_{h}\rightarrow {\mathcal {R}}^+(M), \ \ G\mapsto g\cup G \end{aligned}$$

  is a weak homotopy equivalence.

• (ii) A parametrised version of the surgery theorem has been proven by Chernysh [4] (see also [9, 22]). In its general form, it states that for $k\ge 3$ the metric $g_N + g_\textrm{tor}$ is a right-stable metric on $N\times D^k$, $g_\textrm{tor}$ a torpedo metric⁵ and $g_N$ any metric on N such that $g_N+g_\textrm{tor}$ has positive scalar curvature. In particular, the torpedo metric on $D^k$ itself is right-stable. Theorem 2.7 can be seen as an improved parametrised surgery theorem.

2.3 The action of $\textrm{Diff}(M)$ on ${\mathcal {R}}^+(M)$

To prove Theorem A (i) and Theorem B, we use a rigidity result for the pullback-action $\textrm{Diff}(M)\curvearrowright {\mathcal {R}}^+(M)$. Let us recall the definition of the structured mapping class group.

Definition 2.9

For $(M,\hat{l})$ be a stabilised $\theta$-manifold, the $\theta$-mapping class group denoted by $\Gamma ^\theta (M,\hat{l})$ is given by

$$\begin{aligned} \Gamma ^\theta (M,\hat{l}):=\left\{ (f,L):\begin{array}{l} f:M\overset{\cong }{\longrightarrow }M\text { is a diffeomorphism}\\ L\text { is a homotopy of bundle maps } \hat{l}\circ df\leadsto \hat{l} \end{array}\right\} \Big /\sim \end{aligned}$$

where the equivalence relation is given by homotopies of f and L.

There is a forgetful homomorphism

$$\begin{aligned} \Phi :\Gamma ^\theta (M, \hat{l})\rightarrow \pi _0(\textrm{Diff}(M)) \end{aligned}$$

(3)

to the ordinary mapping class group, which in general is neither surjective nor injective. By composing $\Phi$ with the pullback action, we get an action $\Gamma ^\theta (M,\hat{l})\curvearrowright \pi _0({\mathcal {R}}^+(M))$. Furthermore, there is a homomorphism $T:\Gamma ^\theta (M,\hat{l})\rightarrow \Omega _{d+1}^\theta$ mapping (f, L) to the mapping torus $T_f$ with a $\theta$-structure determined by L. We have the following rigidity result about this pullback action.

Theorem 2.10

[13, Corollary 3.32] If $\theta$ is the stabilised tangential 2-type of a closed manifold M of dimension at least 6, then the action $\Gamma ^\theta (M,\hat{l})\curvearrowright \pi _0({\mathcal {R}}^+(M))$ factors through $\Omega _{d+1}^\theta$ via the mapping torus construction. In particular, if $T_f$ is $\theta$-cobordant to a mapping torus of the identity, then $f^*g$ is homotopic to g for all $g\in {\mathcal {R}}^+(M)$.

Note that a mapping torus of the identity need not be $\theta$-nullbordant, even though the underlying manifold $T_{\textrm{id}}$ is simply given by $M\times S^1$: An example is already given by $S^1$ which is a mapping torus of $\textrm{id}:\{{\textrm{pt}}\}\rightarrow \{{\textrm{pt}}\}$ but admits a spin structure which is not spin nullbordant. We need the following version of Theorem 2.10 for manifolds with boundary.

Corollary 2.11

Let M and $\theta$ be as above and let $N\subset M$ be a closed, codimension 0 submanifold such that the inclusion $\partial N\hookrightarrow N$ is 2-connected. Let $(f,L)\in \Gamma ^\theta (M, \hat{l})$ such that $f|_N=\textrm{id}$. Then there exists an $h\in {\mathcal {R}}^+(\partial N)$ with the following property: If $T_{f}$ is $\theta$-cobordant to a mapping torus of the identity, then $(f|_{M\setminus N})^*g$ is homotopic to g for all $g\in {\mathcal {R}}^+(M\setminus N)_{h}$.

Proof

By Theorem 2.7 the assumption on N implies that there exists an $h\in {\mathcal {R}}^+(\partial N)$ and a right-stable metric $g_\textrm{rst}\in {\mathcal {R}}^+(N)_h$. The map ${\mathcal {R}}^+(M{\setminus } N)_{h}\hookrightarrow {\mathcal {R}}^+(M)$ given by gluing in $g_\textrm{rst}$ is hence a homotopy equivalence. Since $f|_{N}=\textrm{id}$, we have the following commutative diagram

where the horizontal maps are equal homotopy equivalences. Therefore $f^*$ is homotopic to the identity if and only if $(f|_{M{\setminus } N})^*$ is homotopic to the identity. The rest follows from Theorem 2.10. $\square$

We also need a detection result due to Hitchin [20] which has later been generalised by Crowley–Schick [5] and Crowley–Schick–Steimle [6].

Theorem 2.12

[20, Theorem 4.7], [5, Corollary 1.2], [6, Corollary 1.9] Let N be a compact spin manifold of dimension $d\ge 6$, $h\in {\mathcal {R}}^+(\partial N)$ and $g\in {\mathcal {R}}^+(N)_h$. Let furthermore $k\ge 0$ such that $d+k+1\equiv 1,2(8)$. Then the composition

$$\begin{aligned} \pi _k(\textrm{Diff}_\partial (D^d))\rightarrow \pi _k(\textrm{Diff}_\partial (N)) \rightarrow \pi _k({\mathcal {R}}^+(N)_h)\rightarrow {\textrm{KO}}_{d+k+1}\cong {\mathbb {Z}}/2 \end{aligned}$$

is split surjective. Here, the first map is given by extending a diffeomorphism on an embedded disk by the identity, second map is induced by the orbit map $f\mapsto f^*g$ and the last map is the index-difference.

Remark 2.13

Even though this result is only stated for closed manifolds in the papers [5, 6, 20], a version for manifolds with boundary is easily deduced.

Next, we will give an explicit model for the homomorphisms

$$\begin{aligned} \lambda _{k,d}:\pi _k(\textrm{Diff}_\partial (D^d))\rightarrow \pi _{k-1} \textrm{Diff}_\partial (D^{d+1}) \end{aligned}$$

inducing the Gromoll-Filtration of homotopy spheres: For $n\ge 1$ we fix once and for all $c_n:= \frac{1}{2\sqrt{n}}$ and note that $[0,c_n]^d\subset D^d$ for every $n\ge d$. Let $f_\sigma :[0,1]^k\rightarrow \textrm{Diff}_\partial (D^d)$ represent an element $\sigma \in \pi _k(\textrm{Diff}_\partial (D^d))$. After possibly applying a suitable compressing homotopy, we may assume that $f_\sigma (t)(x) = x$ for (t, x) outside of $[0,c_{d+1}]^k\times [0,c_{d+1}]^d$, i.e. $f_\sigma$ is supported on the cube $[0,c_{d+1}]^{d+k}$. For $s\in [0,c_{d+1}]^{k-1}$, $x\in [0,c_{d+1}]^d$ and $l\in [0,c_{d+1}]$ we define

$$\begin{aligned} F_\sigma (s)(x,\ell ):= \bigl (\ell ,f_\sigma (s,\ell )(x)\bigr ). \end{aligned}$$

By our assumption on $f_\sigma$ we see that $F_\sigma (s) = \textrm{id}$ on $\partial ([0,c_{d+1}]^{d+1})$ and by our choice of $c_{d+1}$ we can hence extend this by the identity to a map $F_\sigma :[0,1]^{k-1}\rightarrow \textrm{Diff}_\partial (D^{d+1})$ which is a representative $\lambda _{k,d}(\sigma )$.

For an element $\sigma \in \pi _k(\textrm{Diff}_\partial (D^d))$ the successive composition of the maps $\lambda _{m,d+m}$ for $0\le m\le k$ yields an element $[f_\sigma ]\in \pi _0(\textrm{Diff}_\partial (D^{d+k}))$ which defines a homotopy sphere $\Sigma$ by clutching along $f_\sigma$. The composition in Theorem 2.12 is equal to mapping $\sigma$ to the $\alpha$-invariant of $\Sigma$. We call homotopy spheres with non-vanishing $\alpha$-invariant Hitchin spheres.

Lemma 2.14

Let $M^d$ be a manifold with boundary $\partial M$ and let $h\in {\mathcal {R}}^+(\partial M)$ and $g\in {\mathcal {R}}^+(M)_h$. Then there exist embeddings $D^{d-1}\hookrightarrow \partial M$ and $D^{d}\hookrightarrow M$ such that the following diagram commutes

where the horizontal maps $\rho$ are given by extending by the identity outside of the embedded disks and acting via pullback.

Proof

Let $\sigma \in \pi _k(\textrm{Diff}_\partial (D^{d-1}))$ and let $f_\sigma$ be a representative, for which we again may assume that $f_\sigma (t)(x) = x$ for $(t,x)\not \in [0,c_{d}]^k\times [0,c_{d}]^{d-1}$ (see above for the definition of $c_d$). Let $D^{d-1}\subset \partial X$ be some embedded disk and let $f_\sigma$ be extended by the identity to $\partial X$. By Lemma 2.1 the composition $\partial \circ \rho$ is given by pullback along the following family of diffeomorphisms

$$\begin{aligned} F(s)(x) = {\left\{ \begin{array}{ll} x &{} \text { if } x\not \in \textrm{im}~c\\ c(r, f_\sigma (s,(1-r))(y)) &{}\text { if } x=c(r,y) \end{array}\right. } \end{aligned}$$

(4)

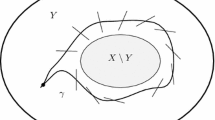
where $c:[0,1]\times \partial X\hookrightarrow X$ is the collar embedding. Applying a compressing and shifting homotopy, we may assume that $F(s)(c(r,y)) = c(r, f_\sigma (s,(c_d-r))(y))$. By our assumption on $f_\sigma$, F is concentrated in an embedded cube $[0,c_d]^d\subset S^{d-1}\times [0,1]$. We choose an embedded disk $\iota _D:D^d\subset \partial X\times [0,1]$ that extends the inclusion of $[0,c_d]^{d}\subset \partial X\times [0,1]$. This is depicted in Fig. 1.

Fig. 1

The collar $\partial X\times [0,1]$ of X

For $s\in [0,1]^{k-1}$ and $(y,\ell )\in D^{d}$, a representative of $-\lambda _{k,d-1} (\sigma ) = \lambda _{k,d-1}(-\sigma )$ is given by

$$\begin{aligned} F_{-\sigma }(s)(y,\ell )&= (\ell ,f_{-\sigma }(s,\ell )(y))\\&= (\ell ,f_\sigma (s,c_d-\ell )(y)) \end{aligned}$$

since $f_\sigma$ was supported on $[0,c_d]^{k}\times [0,c_d]^{d-1}$. After applying an appropriate shifting and rescaling homotopy that stretches the embedded cube to the collar, we see that $\iota _D\circ (-\lambda _{k,d-1})(\sigma )$ is represented by F in (4) which proves the lemma. $\square$

Let us close this section with the following well known proposition which is the key observation enabling us to employ Theorem 2.10 and Corollary 2.11.

Proposition 2.15

Every homotopy sphere is oriented nullbordant.

Proof

Oriented bordism is classified by Pontryagin- and Stiefel–Whitney numbers. For a homotopy sphere all characteristic classes have to vanish except for possibly the top ones. However, the top Pontryagin number is a nonzero multiple of the signature and the top Stiefel–Whitney number is the mod 2 reduction of the Euler characteristic. Both of these vanish for homotopy spheres. $\square$

3 Proofs of the main results

The proofs for Theorem B and the first half of Theorem A (i) both rely on the following lemma.

Lemma 3.1

Let $d\ge 6$ and let $f_\Sigma :(D^d,\partial D^d) \rightarrow (D^d, \partial D^d)$ be a diffeomorphism as in Theorem 2.12 and let $M^d$ be a compact, oriented, totally nonspin-manifold with spin boundary $\partial M$ which is ${\textrm{Spin}}\times B\pi _1(\partial M)$-nullbordant or empty. Let furthermore $D\subset M$ be an embedded disk away from the boundary and let $f:= f_\Sigma \cup \textrm{id}$. Then, there exists an $h\in {\mathcal {R}}^+(\partial M)$ such that for all $g\in {\mathcal {R}}^+(M)_h$, the metric $f^*g$ is homotopic to g.

Remark 3.2

If $\partial M=\emptyset$, then the conclusion of the lemma holds for all $g\in {\mathcal {R}}^+(M)$.

Proof

By the assumption on $\partial M$, there is a nullbordism W of $\partial M$ such that the inclusion $\partial M\hookrightarrow W$ is 2-connected. This ensures that we are in a situation where Theorem 2.10 (if $\partial M=\emptyset$) and Corollary 2.11 (if $\partial M\not =\emptyset$) are applicable.

If M is orientable with fundamental group $\pi$ then its stabilised tangential 2-type is given by the projection $B{\textrm{SO}}(d+1)\times B\pi \rightarrow B{\textrm{SO}}(d+1)\rightarrow B{\textrm{O}}(d+1)$. A $\theta$-structure in this case is a bundle map $TM\rightarrow \theta ^*U_{d+1} \cong \theta _{SO}^*U_{d+1} \times B\pi$ for $\theta _{SO}:B{\textrm{SO}}(d+1)\rightarrow B{\textrm{O}}(d+1)$ and hence, it is equivalently described by an orientation and a map $\gamma :M\rightarrow B\pi$. Therefore, an element in $\Gamma ^\theta (M,\gamma )$ is given by a pair (f, L) of an orientation preserving diffeomorphism f and a homotopy L of the maps $\gamma$ and $\gamma \circ f$.

Note that the diffeomorphism $f_\Sigma$ is supported in the disk $D\subset M$ and hence fixes all points $p\in M{\setminus } D$. Furthermore, the induced map $f_*:\pi _1(M,p)\rightarrow \pi _1(M,p)$ is the identity since any loop is homotopic to one, which does not intersect D. Therefore, the maps $\gamma$ and $\gamma \circ f$ induce equal maps on fundamental groups. The space $B\pi =K(G,1)$ is an Eilenberg–Maclane space and maps from CW-complexes into Eilenberg–Maclane spaces are determined uniquely up to homotopy by the induced map on $\pi _1$ (see e.g. [19, Proposition 1B.9]). Therefore, we deduce that the maps $\gamma$ and $\gamma \circ f$ are homotopic. This implies that f is in the image of the forgetful map $\Phi :\Gamma ^\theta (M,\gamma )\rightarrow \pi _0\textrm{Diff}(M)$ from (3). The mapping torus of f is ${\textrm{SO}}\times B\pi _1(M)$-cobordant to $[M\times S^1\amalg \Sigma , \beta ]$ in $\Omega _{d+1}(B\pi )$, where $\Sigma$ is the Hitchin sphere associated to $f_\Sigma$ and $\beta$ is constant on $\Sigma$. By Proposition 2.15, this is ${\textrm{SO}}\times B\pi _1(M)$-cobordant to a mapping torus of the identity. We conclude from Theorem 2.10 and Corollary 2.11 that there exists a boundary metric $h\in {\mathcal {R}}^+(\partial M)$ such that $f^*:{\mathcal {R}}^+(M)_h\rightarrow {\mathcal {R}}^+(M)_h$ is homotopic to the identity and in particular $f^*g\sim g$. $\square$

Proof of Theorem B

Let $g\in {\mathcal {R}}^+(M{\setminus } \textrm{int}(D))_{h}$ and $g_0\in {\mathcal {R}}^+(D^d)_{h}$ be arbitrary. By Theorem 2.12 there exists a diffeomorphism $f_\Sigma :(D^d, \partial D^d)\rightarrow (D^d, \partial D^d)$ such that $\textrm{inddiff}_{g_0}(f_\Sigma ^*g_0) \not =0$ and hence $g_1:= f_\Sigma ^*g_0$ is not homotopic to $g_0$. By Lemma 3.1 we have

$$\begin{aligned} g_1\cup g = (f_\Sigma ^*g_0)\cup g = (f_\Sigma \cup \textrm{id}) (g_0\cup g) \overset{3.1}{\sim }g_0\cup g \end{aligned}$$

which concludes the proof. $\square$

Proof of Theorem A (i)

Let $D^{d-1}\subset \partial M$ be an embedded disk and let h be as in Lemma 3.1. By Theorem 2.12 there exists a family $(f^D_t)_{t\in S^1}$ of self-diffeomorphisms of $(D^{d-1},\partial D^{d-1})$ such that for $f_t:= f_t^D\cup \textrm{id}$ we have $\textrm{inddiff}_h([f_t^*h])\not =0$ and hence $[f_t^*h]\not =0\in \pi _1({\mathcal {R}}^+(\partial M), h)$. Consider the long exact sequence of homotopy groups associated to the fibration $\textrm{res}:{\mathcal {R}}^+(M)\rightarrow {\mathcal {R}}^+(\partial M)$:

$$\begin{aligned} \dots \longrightarrow \pi _1({\mathcal {R}}^+(M))\overset{\textrm{res}}{\longrightarrow }\pi _1 ({\mathcal {R}}^+(\partial M))&\overset{\partial }{\longrightarrow }\pi _{0} ({\mathcal {R}}^+(M)_{h_\circ })\longrightarrow \dots \\ {[}f_t^*h]\qquad&\mapsto \qquad \partial [(f_t)^*g] \end{aligned}$$

Now, Lemma 2.14 states that $\partial ([f_t^*h])$ is given by $F^*g$ for F is an extension of $-\lambda _{1,d-1}(f_t)$ by the identity. Therefore, F is a diffeomorphism which clutches a Hitchin-sphere and Lemma 3.1 implies that $F^*g$ and g are homotopic. Hence $[f_t^*h]$ has to be in the image of the restriction map $\pi _1({\mathcal {R}}^+(M))\rightarrow \pi _1({\mathcal {R}}^+(\partial M))$. $\square$

Remark 3.3

It is not possible to use the rigidity result on the pullback action obtained in [10, Theorem E], as it requires the inclusion $\partial M\hookrightarrow M$ to be 2-connected. Our proof crucially relies on M and $\partial M$ having different tangential 2-types.

Proof of Theorem A (ii)

Let $x\in {\textrm{KO}}^{-d}({\textrm{pt}})$, $h\in {\mathcal {R}}^+(\partial M)$ and $g\in {\mathcal {R}}^+(M)_h$. Since the $\alpha$-invariant $\Omega _d^{\textrm{Spin}}\rightarrow {\textrm{KO}}^{-d}({\textrm{pt}})$ is surjective, there exists a closed spin manifold X with $\alpha (X) = x$ and we may without loss of generality assume that X is 2-connected. By Theorem 2.7 we conclude that there exists a (right-stable) metric $g_x\in {\mathcal {R}}^+((\partial M\times [0,1])\#X)_{h,h_x}$ for some boundary metric $h_x\in {\mathcal {R}}^+(\partial M)$. Note that $\textrm{inddiff}_h([h_x]) = -x$ which follows from the definition of $\textrm{inddiff}$ and the spin bordism invariance of the index of the spin Dirac operator. Gluing $g_x$ onto g, we obtain a psc-metric on $M\# X$ that restricts to $h_x$ on the boundary. Now, X is oriented cobordant to a closed, oriented, totally nonspin manifold $X^\textrm{or}$, for example $X^\textrm{or}$ can be chosen to be $X\#({{\mathbb {C}}{\mathbb {P}}}^{{2}}\times S^{d-4})$. Note that $X^\textrm{or}$ which admits a metric of positive scalar curvature by [17, Corollary C]. Hence there is a psc-metric on $M\#X\#(X^\textrm{or})^{\textrm{op}}$ restricting to $h_x$ on the boundary by Lemma 2.6. But $M\#X\#(X^\textrm{or})^{\textrm{op}}$ is totally nonspin and ${\textrm{SO}}\times B\pi _1(M)$-cobordant to M relative to the boundary. Therefore, there is a psc-metric $g_{M,x}$ on M restricting to $h_x$ on the boundary which finishes the proof. $\square$

4 Concordance classes of psc-metrics

Having proven Theorem B, it is natural to ask if all psc-metric on the disc become isotopic after extending them to a totally nonspin manifold. It is well-known that for $d\ge 7$, $d\equiv 3(4)$ there is an infinite family $(g_n)_{n\in {\mathbb {N}}}\subset {\mathcal {R}}^+(D^d)_{h_\circ }$ of pairwise non-isotopic and even non-concordant metrics.⁶ Such a family can be constructed as follows:

Let $\beta$ be a $(d+1)$-dimensional, 2-connected (spin) manifold, with $\alpha (\beta )=1\in {\textrm{KO}}^{-d-1}({\textrm{pt}})\cong {\mathbb {Z}}$. Let $\beta _n:=\beta ^{\#n}$ denote the n-fold connected sum of $\beta$ with itself and let $W_n:= S^{d}\times [0,1]\#\beta _n$. Since $W_n$ is 2-connected, it admits a metric $G_n'$ of positive scalar curvature, which is of product type in a neighbourhood of the boundary and restricts to the metric $g_\textrm{tor}\cup g_\textrm{tor}^{\textrm{op}}$ on the lefthand boundary by Theorem 2.7. Furthermore, we may assume that the metric $G_n'$ restricted to the cylinder over the lower hemisphere $D_{-}^d\subset D_{-}^d\cup D^d_+ = S^d$ is given by the cylinder over a torpedo-metric by Chernysh’s parametrised surgery theorem (cf. Remark 2.8 (ii)). Restricting to the complement of $\textrm{int}(D_{-}^d)\times [0,1]$ yields a psc-metric $G_n$ on $W_n\setminus (\textrm{int}(D_{-}^d)\times [0,1])$. The metric $G_n$ restricted to the boundary is given as follows: On the left-hand part of the boundary it is a torpedo-metric $g_\textrm{tor}$, on the bottom part of the boundary it is equal to $h_\circ +\textrm{dt}^2$ for $h_\circ$ the round metric and on the right-hand boundary it restricts to some metrics $g_n$, see Fig. 2.

Fig. 2

The manifold $W_n\setminus (D_{-}^d\times [0,1])$ with the psc-metric $G_n$

Again, by the spin bordism invariance of the index, we have $\textrm{inddiff}_{g_\textrm{tor}}(g_n) = \alpha (\beta _n) = n$, hence the metrics $(g_n)_{n\in {\mathbb {N}}}$ are pairwise not concordant. We arrive at the following first instance of the question mentioned above.

Question 4.1

Do the metrics $(g_n)_{n\in {\mathbb {N}}}$ become isotopic after extending them arbitrarily to a totally nonspin manifold?

Note that the proof of Theorem B relies crucially on the observation that Hitchin spheres are oriented nullbordant (see Proposition 2.15) which then enables the use of Theorem 2.10 and Corollary 2.11. The manifold $\beta$ however is not oriented nullbordant, since the $\alpha$-invariant of a spin manifold in these dimensions is equal to a multiple of its $\hat{{\mathcal {A}}}$-genus, which is a Pontryagin number, hence it is not possible to use these rigidity results.⁷ However, when working with concordance classes instead, we have the following result pointing towards an affirmative answer of Question 4.1.

Theorem 4.2

Let M be a d-dimensional, closed, oriented, totally nonspin manifold with $D\subset M$ an embedded disk and let $g\in {\mathcal {R}}^+(M\setminus \textrm{int}(D))_{h_\circ }$. Then the metrics $g_j\cup g$ and $g_i\cup g$ are concordant for all $i,j\in {\mathbb {N}}$.

Proof

Now let $W_n$, $G_n$ and $g_n$ be as above. We define

$$\begin{aligned} W_{M,n}:= \Bigl (W_n\setminus \bigl (\textrm{int}(D_{-}^d) \times [0,1]\bigr )\Bigr )\cup _{S^{d-1}\times [0,1]} \Bigl (\bigl (M\setminus \textrm{int}(D)\bigr )\times [0,1]\Bigr ) \end{aligned}$$

and let $G_{M,n}:= G_n\cup g+dt^2$ and $g_{M,n}:= g_n\cup g$. We will show that $g_{M,n}$ is concordant to $g_M:= g_{M,0}$. Note that $\beta _n$ is oriented cobordant to a simply connected, oriented, (totally) nonspin manifold $\beta _n^\textrm{or}$, for example take $\beta _n^\textrm{or}:=\beta _n\#({{\mathbb {C}}{\mathbb {P}}}^{{2}}\times S^{d-4})$. By [17, Corollary C], $\beta _n^\textrm{or}$ admits a psc-metric and by Lemma 2.6, there is a psc-metric on $W_{M,n}^\textrm{or}:= M\times [0,1]\#\beta _n^\textrm{or}$, which restricts to $g_M$ on both boundary components. Since $W_{M,n}$ is ${\textrm{SO}}\times B\pi _1(M)$-cobordant to $W_{M,n}^\textrm{or}$ relative to the boundary and the stabilised tangential 2-type of $W_{M,n}$ is given by ${\textrm{SO}}\times B\pi _1(M)$, Lemma 2.6 further implies that $W_{M,n}$ also admits a psc-metric G restricting to $g_M$ on both boundary components. By gluing the metric $G^{{\textrm{op}}}$ obtained by flipping G onto $G_{M,n}$, we obtain a psc-metric on $W:=\overline{W_{M,n}^{\textrm{op}}}\cup W_{M,n}$ restricting to $g_M$ and $g_{M,n}$ on the respective boundary components. But W is the double of $W_{M,n}$ and hence ${\textrm{SO}}\times B\pi _1(M)$-cobordant to $M\times [0,1]$ relative to the boundary and again by Lemma 2.6, there is a concordance between $g_M$ and $g_{M,n}$. $\square$

Remark 4.3

• (i) As mentioned above, isotopic psc-metrics are concordant. The converse to this is a wide open conjecture. An affirmative solution to that conjecture would imply that Theorem 4.2 also holds for isotopy classes and hence yields an affirmative answer to Question 4.1.

• (ii) To the best of the author’s knowledge, all known components of ${\mathcal {R}}^+(D^d)_{h_\circ }$ contain one of the metrics from Theorem B or Theorem 4.2. One might be tempted to believe that all psc-metrics on $D^d$ restricting to the round metric on the boundary become concordant or even isotopic after gluing them into a totally nonspin manifold. Theorem B and Theorem 4.2 could be seen as evidence to support this believe.