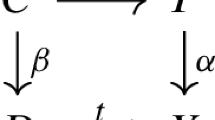The action of the mapping class group on metrics of positive scalar curvature

Abstract

We present a rigidity theorem for the action of the mapping class group $\pi _0({\mathrm{Diff}}(M))$ on the space $\mathcal {R}^+(M)$ of metrics of positive scalar curvature for high dimensional manifolds M. This result is applicable to a great number of cases, for example to simply connected 6-manifolds and high dimensional spheres. Our proof is fairly direct, using results from parametrised Morse theory, the 2-index theorem and computations on certain metrics on the sphere. We also give a non-triviality criterion and a classification of the action for simply connected 7-dimensional ${\mathrm{Spin}}$-manifolds.

1 Introduction

1.1 Statement of the results

For a closed manifold M of dimension $(d-1)$ let $\mathcal {R}^+(M)$ denote the space of all Riemannian metrics of positive scalar curvature on M. The diffeomorphism group ${\mathrm{Diff}}(M)$ of M acts on the space $\mathcal {R}^+(M)$ by pullback and this action defines a group homomorphism

$$\begin{aligned}\Theta :\Gamma (M)\,{:}{=}\,\pi _0({\mathrm{Diff}}(M))\longrightarrow \pi _0(\mathrm{h}\mathbf {Aut}(\mathcal {R}^+(M)))\end{aligned}$$

from the mapping class group of M to the group of homotopy classes of homotopy self-equivalences of $\mathcal {R}^+(M)$. Our main result is that the image of this map is often very small. To state this precisely without too many technicalities, we confine ourselves to the special case where M is simply connected and ${\mathrm{Spin}}$ in this introduction, but remark that we prove results for all manifolds of dimension at least 6.

Let $\ell$ be a ${\mathrm{Spin}}$-structure on M and recall that a ${\mathrm{Spin}}$-diffeomorphism of $(M,\ell )$ is a pair $(f,{\hat{f}})$ consisting of an orientation preserving diffeomorphism $f:M\rightarrow M$ and an isomorphism ${\hat{f}}:f^*\ell \rightarrow \ell$ of ${\mathrm{Spin}}$-structures. We denote by ${\mathrm{Diff}}^{\mathrm{Spin}}(M,\ell )$ the group of all ${\mathrm{Spin}}$-diffeomorphisms and by $\Gamma ^{\mathrm{Spin}}(M,\ell )\,{:}{=}\,\pi _0({\mathrm{Diff}}^{\mathrm{Spin}}(M,\ell ))$ the ${\mathrm{Spin}}$-mapping class group of $(M,\ell )$. For a diffeomorphism f of M denote the mapping torus by $T_f\,{:}{=}\,M\times [0,1]/(x,0)\sim (f(x),1)$. If $(f,{\hat{f}})$ is a ${\mathrm{Spin}}$-diffeomorphism, $T_f$ inherits a ${\mathrm{Spin}}$-structure. This construction defines a group homomorphism

$$\begin{aligned}T:\Gamma ^{\mathrm{Spin}}(M,\ell )\longrightarrow \Omega _d^{\mathrm{Spin}}\end{aligned}$$

to the cobordism group of closed d-dimensional ${\mathrm{Spin}}$-manifolds. Our main result is the following.

Theorem A

If $(M,\ell )$ is a simply connected ${\mathrm{Spin}}$-manifold of dimension $d-1\ge 6$, there exists a group homomorphism

$$\begin{aligned}\mathcal {S}\mathcal {E}:\Omega _d^{{\mathrm{Spin}}}\longrightarrow \pi _0(\mathrm{h}\mathbf {Aut}(\mathcal {R}^+(M))),\end{aligned}$$

such that the following diagram, where F is the forgetful map, commutes

Note that Theorem A is true but vacuous for $\mathcal {R}^+(M)=\emptyset$. Since $\Omega _7^{\mathrm{Spin}}=0$ (cf. [29, Théorème II.16, p. 49]), $f^*:\mathcal {R}^+(M)\rightarrow \mathcal {R}^+(M)$ is homotopic to the identity for every ${\mathrm{Spin}}$-diffeomorphism $(f,{\hat{f}})$ of a simply connected, 6-dimensional ${\mathrm{Spin}}$-manifold M. Using computations in characteristic classes we get the following.

Theorem B

Let M be a simply connected, stably parallelizable manifold of dimension $d-1\ge 6$, equipped with a ${\mathrm{Spin}}$-structure. Let $(f,{\hat{f}})$ be a ${\mathrm{Spin}}$-diffeomorphism. Then the map

$$\begin{aligned}f^*:\mathcal {R}^+(M) \longrightarrow \mathcal {R}^+(M)\end{aligned}$$

is homotopic to the identity unless $d\equiv 1,2\; (\bmod \; 8)$. In the latter case, $(f^2)^*$ is homotopic to the identity.

Remark

Any orientation-preserving diffeomorphism f of M can be lifted to a ${\mathrm{Spin}}$-diffeomorphism if M is simply connected. Therefore $f^*:\mathcal {R}^+(M)\rightarrow \mathcal {R}^+(M)$ is homotopic to the identity for each orientation preserving diffeomorphism of M if $d\not \equiv 1,2\;(\bmod \; 8)$. This conclusion does not hold for orientation-reversing diffeomorphisms (for example it is false if $f:S^7\rightarrow S^7$ is an orthogonal matrix of determinant $-1$).

For more examples we refer to [10, Chapter 4.1]. Using Theorem A one can also use computational results on $\pi _0(\mathcal {R}^+(M))$ and $\pi _0({\mathrm{Diff}}_{x_0}(M))$ (for example [3] and [14]) to find elements in $\pi _0$ and $\pi _1$ of the observer moduli space of psc-metrics for certain manifolds. In the situation of Theorem A, assume that $f^*g$ is homotopic to g for one $g\in \mathcal {R}^+(M)$. Then the mapping torus admits a psc metric and hence $\alpha (T_f)=0$. This has an interesting consequence for manifolds of dimension 7. Recall that the map $\Omega _8^{\mathrm{Spin}}\overset{\cong }{\longrightarrow }\mathbb {Z}\oplus \mathbb {Z}$, $[W]\mapsto (\mathrm{sign}(W),\alpha (W))$ is an isomorphism. Since the signature of a mapping torus always vanishes we deduce

Corollary C

Let M be a simply connected ${\mathrm{Spin}}$-manifold of dimension 7 and let f be a ${\mathrm{Spin}}$-diffeomorphism. If there exists a metric $g\in \mathcal {R}^+(M)$ such that $f^*g$ lies in the same path component as g, then the map $f^*:\mathcal {R}^+(M)\rightarrow \mathcal {R}^+(M)$ is homotopic to the identity.

Proposition D

Let $d\ge 7$, let $f:S^{d-1}\rightarrow S^{d-1}$ be a ${\mathrm{Spin}}$-diffeomorphism and let $g_\circ$ denote the round metric. If $f^*g_\circ$ and $g_\circ$ lie in the same path component, then $f^*$ is homotopic to the identity.

Remark

The first result concerning the action of the mapping class group on the space of positive scalar curvature metrics was given by Hitchin [18], where he constructed a map $\mathrm{inddiff}:\pi _0(\mathcal {R}^+(M^{d-1}))\times \pi _0(\mathcal {R}^+(M^{d-1}))\longrightarrow KO^{-d}(\mathrm{pt})$ and used the Atiyah–Singer index theorem to show that $\mathrm{inddiff}(g,f^*g) = \alpha (T_f)$. Hence, the $\alpha$-invariant of the mapping torus of f is an obstruction to f acting trivially on $\pi _0(\mathcal {R}^+(M))$. For $S^{d-1}$ with $d\ge 9$ and $d\equiv 1,2\;(\bmod \;8)$ there exist diffeomorphisms f with $\alpha (T_f)\ne 0$ which implies that $\mathcal {R}^+(S^{d-1})$ is not connected in these dimensions. Theorem A shows that these are the only dimensions where simply connected, stably parallelizable manifolds admit such a diffeomorphism.

Remark

In [3] a factorisation result similar to Theorem A is proven. It is shown that for certain manifolds the image of $\pi _0({\mathrm{Diff}}_\partial (M^{2n}))\rightarrow \pi _0(\mathrm{h}\mathbf {Aut}\mathcal {R}^+(M)))$ is abelian, where ${\mathrm{Diff}}_\partial$ denotes those diffeomorphisms that fix a neighbourhood of the boundary point-wise. Using an obstruction theoretic argument they conclude that this map factors through $\pi _1(MT{\mathrm{Spin}}(2n))$. This has been upgraded in [8] and [9] to hold for a bigger class of manifolds. Theorem A directly implies abelianess of the image and improves the named results since the map $\pi _1(MT{\mathrm{Spin}}(d-1))\rightarrow \Omega _d^{\mathrm{Spin}}$ has nontrivial kernel.

1.2 Outline of the proof

Theorem A follows from a more general, cobordism theoretic result which we will develop in this outline. The main geometric ingredient is a parametrised version of the famous Gromov–Lawson–Schoen–Yau surgery theorem due to Chernysh. Let $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M$ be an embedding and let $\mathcal {R}^+(M,\varphi )\,{:}{=}\,\{g\in \mathcal {R}^+(M)|\varphi ^*g=g_\circ +g_{\mathrm{tor}}\}$ be the space of those metrics that have a fixed standard form on the image of $\varphi$. Here $g_\circ$ denotes the round metric on $S^{k-1}$ and $g_{tor}$ is a torpedo metric on $D^{d-k}$, i.e.an ${\mathrm{O}}(d-k)$-invariant metric of positive scalar curvature that restricts to the round metric on the boundary.

Theorem 1.1

([4, Theorem 1.1], [32, Main Theorem]) If $d-k\ge 3$, the inclusion $\mathcal {R}^+(M,\varphi )\hookrightarrow \mathcal {R}^+(M)$ is a weak equivalence.

As a consequence we obtain a map

$$\begin{aligned}\mathcal {S}_\varphi :\mathcal {R}^+(M)\dashrightarrow \mathcal {R}^+(M,\varphi ) \overset{\cong }{\longrightarrow }\mathcal {R}^+(M_\varphi ,\varphi ^{\mathrm{op}})\hookrightarrow \mathcal {R}^+(M_\varphi ),\end{aligned}$$

where the first map is the homotopy inverse to the inclusion and the second one is given by cutting out $\varphi _*(g_\circ + g_{\mathrm{tor}})$ and pasting in $\varphi ^{\mathrm{op}}_*(g_{\mathrm{tor}} + g_\circ )$. Here, $\varphi ^\mathrm{op}:D^{k}\times S^{d-k-1}\hookrightarrow M_\varphi$ denotes the surgery embedding complementary to $\varphi$. Next we want to define the map $\mathcal {S}$ for general cobordisms. In this paper, a cobordism between $(d-1)$-dimensional manifolds $M_0$ and $M_1$ is a triple $(W,\psi _0,\psi _1)$ consisting of a d-dimensional manifold W whose boundary has a decomposition $\partial W =\partial _0W\amalg \partial _1W$ and diffeomorphisms $\psi _i:\partial _iW\rightarrow M_i$ for $i=0,1$. We will only consider ${\mathrm{Spin}}$-structures on cobordisms in the final step of the proof. An admissible handle decomposition H of $(W,\psi _0,\psi _1)$ is a collection of manifolds $N_1,\dots , N_{n}$, embeddings $\varphi _i:S^{k_i-1}\times D^{d-k_i}\hookrightarrow N_{i}$ with $d-k_i\ge 3$ for $i=1,\dots ,n$ and diffeomorphisms $f_0:\partial _0W\overset{\cong }{\longrightarrow }N_1$, $f_n:(N_n)_{\varphi _n}\overset{\cong }{\longrightarrow }\partial _1 W$ and $f_i:(N_{i})_{\varphi _{i}}\overset{\cong }{\longrightarrow }N_{i+1}$ for $i=1,\dots , n-1$ such that there exists a diffeomorphism ${\mathrm{rel }} \partial W$

$$\begin{aligned}W\cong \partial _0W\times [0,1]\cup _{f_0}{} \mathbf{tr} \,(\varphi _1) \cup _{f_1}{} \mathbf{tr} \,(\varphi _2)\cup _{f_2}\dots \cup _{f_{n-1}} \mathbf{tr} \,(\varphi _{n})\cup _{f_{n}}\partial _1W\times [0,1]\end{aligned}$$

and $(W,\psi _0,\psi _1)$ is called an admissible cobordism if it admits an admissible handle decomposition. By the theory of handle cancellation developed by Smale [27] (see also [21, 30]), a cobordism is admissible if the inclusion $\psi _1^{-1}:M_1\hookrightarrow W$ is 2-connected. For a cobordism W with an admissible handle decomposition H we define the surgery map $\mathcal {S}_{W,H}:\mathcal {R}^+(M_0)\rightarrow \mathcal {R}^+(M_1)$ by

$$\begin{aligned}\mathcal {S}_{W,H}\,{:}{=}\,(\psi _1)_*\circ (f_n)_*\circ \mathcal {S}_{\varphi _{n}}\circ \dots \circ (f_1)_*\circ \mathcal {S}_{\varphi _1}\circ (f_0)_*\circ (\psi _0)^*.\end{aligned}$$

Lemma E

Let $d\ge 7$. Then the homotopy class of $\mathcal {S}_{W,H}$ is independent of the choice of admissible handle decomposition H. We will write $\mathcal {S}_W\,{:}{=}\,\mathcal {S}_{W,H}$. If the inclusion $\psi _0^{-1}:M_0\hookrightarrow W$ is 2-connected as well, $\mathcal {S}_W$ is a weak homotopy equivalence.

Remark

In [33], Walsh constructed a psc metric $g_H$ on (W, H) that restricts to a given metric $g_0$ on $\partial _0W$. He shows that the homotopy class of $g_H$ is independent of H. Using boundary identifications $\psi _i$ this gives a well defined map $\mathcal {S}_W:\pi _0(\mathcal {R}^+(M_0))\rightarrow \pi _0(\mathcal {R}^+(M_1))$. We adapt the proof from [33] so that we obtain a well-defined homotopy class of a map of spaces inducing Walsh’s map on $\pi _0$.

To prove this one uses Cerf theory to show that different handle decompositions are related by a finite sequence of elementary moves. The parametrized handle exchange theorem of Igusa [20] ensures that these moves keep the handle decomposition admissible. Igusa’s theorem is the point where $d\ge 7$ is used. Next we show surgery invariance of $\mathcal {S}_W$.

Lemma F

Let $d\ge 7$, let $M_0$, $M_1$ be two $(d-1)$-manifolds, let W be an admissible cobordism and let $\Phi :S^{k-1}\times D^{d-k+1}\hookrightarrow \mathrm{Int }\ W$ be an embedding with $3\le k\le d-3$. Then $\mathcal {S}_W \sim \mathcal {S}_{W_\Phi }$.

Now we are able to derive the general cobordism theoretic result. Let ${\hat{\Omega _d^{\mathrm{Spin}}}}$ denote the following category: objects are given by closed, simply connected, $(d-1)$-dimensional ${\mathrm{Spin}}$-manifolds M and morphisms from $M_0$ to $M_1$ are given by cobordism classes of compact d-dimensional ${\mathrm{Spin}}$-cobordisms $(W,\psi _0,\psi _1)$. Note that every such cobordism class contains an admissible cobordism and two admissible cobordisms in the same class are related by a sequence of surgeries satisfying the index constraints from the previous Lemma.

Theorem G

Let $d\ge 7$. Then there exists a functor $\mathcal {S}:{\hat{\Omega _d^{\mathrm{Spin}}\longrightarrow }} \mathrm{hTop}$ into the homotopy category of spaces with the following properties:

• (1) On objects, $\mathcal {S}$ is given by $\mathcal {S}(M)=\mathcal {R}^+(M)$,

• (2) if $f:M_1\rightarrow M_0$ is a diffeomorphism, then $\mathcal {S}(M_0\times [0,1],\mathrm{id},f^{-1}) = f^*$,

• (3) if $\alpha \in {\hat{\Omega _d^{\mathrm{Spin}}}}(M_0,M_1)$ is represented by $(\mathbf{tr} \,(\varphi ), \mathrm{id},\mathrm{id})$ for $\mathbf{tr} \,(\varphi )$ the trace of a surgery datum $\varphi$ with codimension at least 3, then $\mathcal {S}(\alpha ) = \mathcal {S}_\varphi$.

Furthermore, $\mathcal {S}$ is uniquely determined by these properties, up to natural isomorphism.

This immediately implies Theorem A: For a closed ${\mathrm{Spin}}$-manifold V let $\mathcal {S}\mathcal {E}(V)\,{:}{=}\, \mathcal {S}(M\times [0,1]\amalg V,\mathrm{id},\mathrm{id})$ and since $(M\times [0,1]\amalg T_f,\mathrm{id},\mathrm{id})$ is ${\mathrm{Spin}}$-cobordant to $(M\times [0,1],\mathrm{id},f^{-1})$ the given diagram commutes.

Structure of the paper. Section 2 contains the geometric arguments required for proving the main results. After preliminaries on Riemannian metrics and handle decompositions we analyse how two admissible handle decompositions are related. We show that passing from one to another does not alter the homotopy class of $\mathcal {S}$ in 2.6 leading to the proof of Lemma E (Lemma 2.25). We then give a direct geometric argument that shows the surgery invariance of the homotopy class of $\mathcal {S}$ in 2.7 which proves Lemma F (Lemma 2.30). There are no assumptions on the existence of ${\mathrm{Spin}}$-structures and connectivity until here. In Section 3 we introduce tangential structures and prove the general version of Theorem G (Theorem 3.6). Afterwards we define the (structured) mapping class group as well as the (structured) cobordism group and we relate these to the general version of the category ${\hat{\Omega _d^{\mathrm{Spin}}}}$ described above. As an application we prove Theorem B in 3.5. In 3.6 we take a closer look at the 7-dimensional case which leads to the proof of Corollary C.

2 Handle decompositions and the surgery map

2.1 Spaces of Riemannian metrics

For a closed manifold M we denote by $\mathcal {R}(M)$ the contractible space of all Riemannian metrics on M equipped with the (weak) Whitney $C^\infty$-topology. The subspace of metrics whose scalar curvature is strictly positive will be denoted by $\mathcal {R}^+(M)$.

Definition 2.1

Let M and N be compact manifolds of dimension $d-1\ge 0$ and let $\varphi :N\hookrightarrow M$ be an embedding. For a metric g on N, we define

$$\begin{aligned}\mathcal {R}^+(M,\varphi ;g):=\{h\in \mathcal {R}^+(M):\varphi ^*h=g\}.\end{aligned}$$

For $N=\coprod _{i=1}^nS^{k_i-1}\times D^{d-k_i}$ and $g=\coprod _{i=1}^ng^{k_i-1}_\circ +g^{d-k_i}_{\mathrm{tor}}$ we write $\mathcal {R}^+(M,\varphi ):=\mathcal {R}^+(M, \varphi ;g)$. Here, $g^{k_i-1}_\circ$ denotes the round metric and $g^{d-k_i}_{\mathrm{tor}}$ a torpedo metric¹. If there is no chance of confusion, we will omit the dimension of these metrics.

There is the following generalization of the famous Gromov–Lawson–Schoen–Yau surgery theorem (cf. [12, 28]) which is originally due to Chernysh [4] and has been first published by Walsh [32]. A detailed exposition of Chernysh’s proof can be found in [7]. Let M be a $(d-1)$-manifold and for $i=1,\dots , n$ let $N_i$ be closed manifolds of dimension $(k_i-1)$. Let $d-k_i\ge 3$ for all i and let $g_{N_i}$ be metrics on $N_i$ such that $\mathbf{scal }(g_{N_i} + g_{\mathrm{tor}})>0$. Let $N:=\coprod _{i=1}^nN_i\times D^{d-k_i}$, $g:=\coprod _{i=1}^ng_{N_i} + g_{\mathrm{tor}}$ and let $\varphi :N\hookrightarrow M$ be an embedding.

Theorem 2.2

[Parametrized Surgery Theorem [4, Theorem 1.1], [32, Main Theorem]] The map

$$\begin{aligned}\mathcal {R}^+(M,\varphi ; g)\hookrightarrow \mathcal {R}^+(M)\end{aligned}$$

is a weak homotopy equivalence. In particular, if $M_1$ is obtained from $M_0$ by performing surgery along $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M_0$ of index $k \le d-3$ then there exists a zig-zag of maps

$$\begin{aligned}\mathcal {R}^+(M_0)\overset{\simeq }{\hookleftarrow }\mathcal {R}^+(M_0,\varphi ) \overset{\cong }{\longrightarrow }\mathcal {R}^+(M_1,\varphi ^{\mathrm{op}})\hookrightarrow \mathcal {R}^+(M_1).\end{aligned}$$

If furthermore $k\ge 3$, the rightmost map in this composition is also a weak equivalence and we obtain a zig-zag of weak equivalences from $\mathcal {R}^+(M_0)$ to $\mathcal {R}^+(M_1)$.

Remark 2.3

The space $\mathcal {R}^+(M)$ is homotopy equivalent to a CW-complex (see [25, Theorem 13]). By Whitehead’s theorem, a weak homotopy equivalence of CW-complexes is an actual homotopy equivalence. Therefore we may assume that weak homotopy equivalences of $\mathcal {R}^+(M)$ have actual homotopy-inverses.

2.2 Handle decompositions of cobordisms

In this section we discuss handle decompositions of a cobordism W. First, we give a model for attaching a handle. We adapt the one given in [26, Construction 8.1] which is convenient.

Construction 2.4

Let $\epsilon \in (0,\frac{1}{4})$ be fixed and let $k\in \{0,\dots ,d\}$. We fix once and for all an ${\mathrm{O}}(k)\times {\mathrm{O}}(d-k)$-invariant submanifold

$$\begin{aligned}T_k\subset [0,1]\times D^k\times D^{d-k}\end{aligned}$$

with the following properties (see Fig. 1 for a visualization)

• (1) $(s,0,0)\in T_k$ if and only if $s=\frac{1}{2}$.

• (2) The projection $T_k\overset{pr}{\longrightarrow }[0,1]$ is a Morse function and $(\frac{1}{2},0,0)$ is the only critical point of this Morse function. Its index is k.

• (3) We have the following equalities for intersections

  $$\begin{aligned} T_k\cap ([0,\epsilon )\times S^{k-1}\times D^{d-k})&= [0,\epsilon )\times S^{k-1}\times D^{d-k}\\ T_k\cap ((1-\epsilon ,1]\times D^{k}\times S^{d-k-1})&= (1-\epsilon ,1]\times D^{k}\times S^{d-k-1}\\ T_k\cap ([0,1]\times S^{k-1}\times S^{d-k-1})&= [0,1]\times S^{k-1}\times S^{d-k-1} \end{aligned}$$

• (4) The boundary of $T_k$ is given by

  $$\begin{aligned}\partial T_k \!=\! (\{0\}\times S^{k-1}\times D^{d-k})\cup (\{1\}\!\times \! D^{k}\times S^{d-k-1})\cup ([0,1]\!\times \! S^{k-1}\!\times \! S^{d-k-1}).\end{aligned}$$

We call $T_k$ the standard trace of a k-surgery.

Fig. 1

A standard trace

Definition 2.5

Let M be a manifold and let $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M$ be an embedding. We call such an embedding a k-surgery datum in M and we define the trace of $\varphi$ to be

$$\begin{aligned} \mathbf{tr} \,(\varphi )\,{:}{=}\,\Bigl ([0,1]\times (M{\setminus } {\mathrm{im}}\varphi )\Bigr ) \cup _{\mathrm{id}_{[0,1]}\times \varphi } T_k.\end{aligned}$$

There is a Morse function $h_\varphi :\mathbf{tr} \,(\varphi )\rightarrow [0,1]$ with precisely one critical point with value $\frac{1}{2}$ and index k. We define $M_\varphi :=h_\varphi ^{-1}(1) \cong (M{\setminus }{\mathrm{im}}\varphi ) \cup (D^k\times S^{d-k-1})$.

For a surgery datum $\varphi$ in M there is an obvious reversed surgery datum $\varphi ^{\mathrm{op}}:S^{d-k-1}\times D^k\hookrightarrow M_\varphi$ and there is a canonical diffeomorphism $(M_\varphi )_{\varphi ^{\mathrm{op}}}\cong M$. We define the attaching sphere of $\varphi$ to be $\varphi (S^{k-1}\times \{0\})\subset M$ and the belt sphere of $\varphi$ as $\varphi ^{\mathrm{op}}(\{0\}\times S^{d-k-1})\subset M_\varphi$.

Definition 2.6

• (1) Let $(W,\psi _0,\psi _1):M_0\leadsto M_1$ be a cobordism and let $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M_1$ be an embedding. We define the manifold W with a k-handle attached along $\varphi$ to be $(W\cup _{\psi _1} \mathbf{tr} \,(\varphi ),\psi _0,\mathrm{id})$.

• (2) A handle decomposition of $(W,\psi _0,\psi _1):M_0\leadsto M_1$ is a collection of manifolds $N_1,\dots , N_{n}$, embeddings $\varphi _i:S^{k_i-1}\times D^{d-k_i}\hookrightarrow N_{i}$ for $i=1,\dots ,n$ and diffeomorphisms $f_0:\partial _0W\overset{\cong }{\longrightarrow }N_1$, $f_n:(N_n)_{\varphi _n}\overset{\cong }{\longrightarrow }\partial _1W$ and $f_i:(N_{i})_{\varphi _{i}}\overset{\cong }{\longrightarrow }N_{i+1}$ for $i=1,\dots , n-1$ such that there exists a diffeomorphism $\mathrm{rel}\ \partial W$

  $$\begin{aligned}W\cong \partial _0W\!\times \![0,1]\cup _{f_0}{} \mathbf{tr} \,(\varphi _1) \cup _{f_1}{} \mathbf{tr} \,(\varphi _2)\cup _{f_2}\dots \cup _{f_{n-1}} \mathbf{tr} \,(\varphi _{n})\cup _{f_{n}}\partial _1W\!\times \![0,1].\end{aligned}$$

  We call $f_i$ the identifying diffeomorphisms and $\varphi _i$ the surgery data.

Remark 2.7

For a diffeomorphism $f:M_0\overset{\cong }{\longrightarrow }M_1$ and a surgery datum $\varphi$ in $M_0$ there exists a canonical induced diffeomorphism $F:\mathbf{tr} \,\varphi \rightarrow \mathbf{tr} \,(f\circ \varphi )$ that restricts to f on the incoming boundary and to a diffeomorphism $f_\varphi :(M_0)_\varphi \rightarrow (M_1)_{f\circ \varphi }$ such that $f_\varphi$ is equal to f on $M_0{\setminus }{\mathrm{im}}\varphi$ and $f_\varphi \circ \varphi ^{\mathrm{op}} = (f\circ \varphi )^{\mathrm{op}}$ on the outgoing boundary.

In order to compare different handle decompositions of a manifold, we need to describe a model for handle cancellation. Let $W:M_0\leadsto M_1$ be a cobordism which has a handle decomposition with two handles²: Let $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M_0$ and $\varphi ':S^k\times D^{d-k-1}\hookrightarrow (M_0)_\varphi$ be two surgery data such that the belt sphere of $\varphi$ and the attaching sphere of $\varphi '$ intersect transversely in a single point. By [34, Theorem 5.4.3] there exists an embedding of a disk $D^{d-1}\cong D\subset M_0$ such that ${\mathrm{im}}\varphi \subset D$ and ${\mathrm{im}}\varphi '\subset D_{\varphi }$. Therefore it suffices to have a closer look at handle cancellation on the sphere. Let $M_0 = D\cup D' = S^{d-1}$ where $D'$ is another disk. Let $a\in S^{d-k-1}$ and $b\in S^k$ such that $\varphi ^\mathrm{op}(0,a)=\varphi '(b,0)$ is the unique intersection point. Since the belt sphere of $\varphi$ and the attaching sphere of $\varphi '$ intersect transversally here, there is a disc $S^{k}_+\subset S^k$ such that $\varphi '(S^{k}_+\times \{0\})=\varphi ^{op}(D^k\times \{a\})$ after possibly changing the coordinates of D. Let $S^k_-\,{:}{=}\,\overline{S^k{\setminus } S^k_+}$. Then $\varphi '(S^k_-\times \{0\})\subset M{\setminus }{\mathrm{im}}\varphi$ (see Fig. 2).

Fig. 2

.

Because of transversality we may isotopy $\varphi '$ such that $\varphi '(S^k_-\times D^{d-k-1})\subset M{\setminus }{\mathrm{im}}\varphi$. Then $\varphi (S^{k-1}\times D^{d-k})\cup \varphi '(S^k_-\times D^{d-k-1})\cong D^{d-1}$ (cf. [34, Lemma 5.4.2.]) and also $A\,{:}{=}\,\overline{S^{d-1}{\setminus } \bigr (\varphi (S^{k-1}\times D^{d-k})\cup \varphi '(S^k_-\times D^{d-k-1})\bigr )}\cong D^{d-1}$. By choosing an identification $A\cong D^k\times D^{d-k-1}$ we have $\varphi '(S^k_-\times D^{d-k-1})\cup A \cong S^k\times D^{d-k-1}$. We see that

$$\begin{aligned}S^{d-1} = \bigr (\varphi (S^{k-1}\times D^{d-k})\cup \underbrace{\varphi '(S^k_-\times D^{d-k-1})\bigr )\cup A}_{\cong S^k\times D^{d-k-1}}\end{aligned}$$

and hence we can change coordinates on $S^{d-1}$ by changing the embedding $D^{d-1}\hookrightarrow M$ such that $\varphi$ is the embedding of the first factor of the solid torus decomposition

$$\begin{aligned}a^k:S^{d-1} \overset{\cong }{\longrightarrow }(S^{k-1}\times D^{d-k})\cup (D^k\times S^{d-k-1}),\end{aligned}$$

i.e.$a_k\circ \varphi = \iota _{(S^{k-1}\times D^{d-k})}$. We get an induced map

$$\begin{aligned}a^k_\varphi :S^{d-1}_\varphi \overset{\cong }{\longrightarrow }(D^k\times S^{d-k-1})\cup (D^k\times S^{d-k-1}),\end{aligned}$$

where we identify $(D^k\times S^{d-k-1})\cup (D^k\times S^{d-k-1}) = S^k\times S^{d-k-1} = (S^k\times D^{d-k-1})\cup (S^k\times D^{d-k-1})$. Because of transversality we may change $\varphi '$ by an isotopy so that $(a^k_\varphi )\circ \varphi '$ is equal to the inclusion of the first factor in $S^k\times D^{d-k-1}\cup S^k\times D^{d-k-1}$. Then

$$\begin{aligned}(a^k_\varphi )_{\varphi '}:(S^{d-1}_\varphi )_{\varphi '} \overset{\cong }{\longrightarrow }D^{k+1}\times S^{d-k-2}\cup S^k\times D^{d-k-1}\end{aligned}$$

This is a solid torus decomposition of $(S^{d-1}_\varphi )_{\varphi '}$. We get a diffeomorphism $H_k:S^{d-1}\times [0,2]\overset{\cong }{\longrightarrow }\mathbf{tr} \,(\varphi )\cup \mathbf{tr} \,(\varphi ')$ which fixes the strip $D'\times [0,2]\subset (S^{d-1})\times [0,2]$ and the lower boundary point-wise. We may also assume that $H_k$ restricts on the upper boundary to a diffeomorphism $\eta _k:S^{d-1}\overset{\cong }{\longrightarrow }(S^{d-1}_\varphi )_{\varphi '}$ which translates $(a^k_\varphi )_{\varphi '}$ into the solid torus decomposition $a^{k+1}$, i.e.$\bigl ((a^k_{\varphi })_{\varphi '}\circ \eta _k\bigr ) = a^{k+1}$. For every $k\in \{0,\dots , d\}$ we fix the diffeomorphisms $H_k$ (and hence $\eta _k$) once and for all. The following proposition is well known and can be proven by analyzing paths of generalized Morse functions using Cerf theory (see [15, Theorem 3.4] or [10, Proposition 1.5.7]).

Proposition 2.8

Let $d\ge 7$. Then any two handle decompositions of W only differ by a finite sequence of the following moves:

• (1) An identifying diffeomorphism is replaced by an isotopic one.

• (2) A surgery datum is replaced by an isotopic one.

• (3) A k-surgery datum is precomposed with an element $A\in {\mathrm{O}}(k)\times {\mathrm{O}}(d-k)$.

• (4) The order of two surgery data with disjoint images is changed.

• (5) Let $\varphi$ and $\varphi '$ be k- and $(k+1)$-surgery data such that the belt sphere of $\varphi$ and the attaching sphere of $\varphi '$ intersect transversally in a single point. Then the two handles are replaced by the identifying diffeomorphism $\mathrm{id}\ \#\ \eta _k$.

2.3 Hatcher–Igusa’s 2-index theorem

Since Theorem 2.2 has restrictions on the indices of surgery data, we need to consider handle decompositions with index constraints. Let $(W^d,\psi _0,\psi _1):M_0\leadsto M_1$ be a cobordism.

Definition 2.9

$(W,\psi _0,\psi _1)$ is called admissible if $\psi _1^{-1}:M_1\hookrightarrow W$ is 2-connected. An admissible handle decomposition is a handle decomposition where all surgery data $\varphi _i:S^{k_i-1}\times D^{d-k_i}\hookrightarrow N_{i}$ satisfy $k_i\le d-3$.

Remark 2.10

It follows from the proof of the h-cobordism theorem due to Smale [27] (see also [21, 30]) that every admissible cobordism admits an admissible handle decomposition.

Next we want to analyze different admissible handle decompositions. Recall that a birth-death-singularity of a smooth function $f:W^d\rightarrow \mathbb {R}$ is a point $p\in W$ for which there exist coordinates $(x_1,\dots ,x_d)$ around p such that

$$\begin{aligned}f(x) = f(p) + x_1^3 - \sum _{i=2}^\lambda x_i^2 + \sum _{i=\lambda +1}^d x_i^2\end{aligned}$$

near p. In this case we call $(\lambda -1)$ the index of f at p. A smooth function $f:W\rightarrow \mathbb {R}$ that has only non-degenerate and birth-death-singularities is called a generalized Morse function.

Definition 2.11

We define $\mathcal {H}(W)$ to be the space of generalized Morse functions on W with the $C^\infty$-topology. For $i\le j\in \{0,\dots ,d\}$ we denote by $\mathcal {H}_{i,j}(W)$ the space of generalized Morse functions such that non-degenerate critical points have index in $\{i,\dots , j\}$ and birth-death-singularities have index in $\{i,\dots ,j-1\}$.

Theorem 2.12

Let $d\ge 7$ and let $M_1\hookrightarrow W$ be 2-connected. Then the space $\mathcal {H}_{0,d-3}(W)$ is path-connected. If furthermore $M_0\hookrightarrow W$ is 2-connected as well, the space $\mathcal {H}_{3,d-3}(W)$ is path-connected, too. In particular, there exists a Morse-function without critical values of index $\{d-2,d-1,d\}$ or $\{0,1,2,d-2,d-1,d\}$ respectively.

This follows from the parametrized handle exchange theorem. It was first proven by Hatcher [16] “in a short and elegant paper which ignores most technical details” [20, p. 5]. A complete and rigorous proof has been given by Igusa in [20]. Note that there is an index shift: Igusa considers $n+1$-dimensional cobordisms, whereas our cobordisms are d-dimensional.

Parametrized Handle Exchange Theorem ([20, p. 211, Theorem 1.1]) Let $i,j,k\in \mathbb {N}$ and assume that

• (1) $(W,M_0)$ is i-connected,

• (2) $j\ge i+2$,

• (3) $i\le d-k-2-\min (j-1,k-1)$,

• (4) $i\le d-k-4.$

Then the inclusion $\mathcal {H}_{i+1,j}(W)\hookrightarrow \mathcal {H}_{i,j}(W)$ is k-connected. There is a dual version of this: Assume that

• (1) $(W,M_1)$ is $d-j$-connected,

• (2) $j\ge i+2$,

• (3) $d-j\le d-k-2-\min (j-1,k-1)$,

• (4) $d-j\le d-k-4.$

Then the inclusion $\mathcal {H}_{i,j-1}(W)\hookrightarrow \mathcal {H}_{i,j}(W)$ is k-connected.

Proof of Theorem 2.12

Consider the chain of maps

$$\begin{aligned} \mathcal {H}_{3,d-3}(W)&\rightarrow \mathcal {H}_{2,d-3}(W)\rightarrow \mathcal {H}_{1,d-3}(W)\rightarrow \mathcal {H}_{0,d-3}(W)\rightarrow \\&\rightarrow \mathcal {H}_{0,d-2}(W)\rightarrow \mathcal {H}_{0,d-1}(W)\rightarrow \mathcal {H}(W) \end{aligned}$$

If $M_1\hookrightarrow W$ is 2-connected and $d\ge 7$, the last three maps are 1-connected. If $M_0\hookrightarrow W$ is 2-connected, the first three maps are 1-connected as well. The theorem follows as $\mathcal {H}(W)$ is connected.

Remark 2.13

There is a small mistake in [33, Proof of Theorem 3.1], where he only requires $d\ge 6$. But the map $\mathcal {H}_{0,d-2}(W)\hookrightarrow \mathcal {H}(W)$ is only 0-connected, i.e.$\pi _0$-surjective but not necessarily $\pi _0$-injective under this assumption. Therefore it does not follow, that $\mathcal {H}_{0,d-2}(W)$ is path-connected as claimed in loc. cit.. However, if $d\ge 7$ the map is not only $\pi _0$-injective but also 1-connected which is more than needed.

The following result can again be proven by analyzing paths of generalized Morse functions with index constraints: Any two admissible handle decompositions arise from a Morse function having only critical points of index $\le d-3$. By Theorem 2.12 there exists a path of generalized Morse functions also having only critical points of index $\le d-3$ and birth-death-points of index $\le d-4$. The rest of the proof is analogous to the one of Proposition 2.8 (again, see [15, Theorem 3.4] or [10, Proposition 1.5.7 and Proposition 1.6.4]).

Proposition 2.14

[10, 1.6.4] Let $W:M_0\leadsto M_1$ be an admissible cobordism of dimension $d\ge 7$. Then any two admissible handle decompositions of W only differ by a finite sequence of the 5 moves from Proposition 2.8 with the following difference:

• 5’. Let $k\le d-4$ and let $\varphi$ and $\varphi '$ be k- and $(k+1)$-surgery data such that the belt sphere of $\varphi$ and the attaching sphere of $\varphi '$ intersect transversally in a single point. Then the two handles are replaced by the identifying diffeomorphism $\mathrm{id}\ \#\ \eta _k$.

2.4 The surgery datum category

We recall the following method to construct a category. For details see [24, pp. 48].

Definition 2.15

A graph is a tuple $(O,A,\partial _0,\partial _1)$, where O and A are sets called the object set and the arrow set and $\partial _0,\partial _1$ are maps $A\rightrightarrows O$. We say that two arrows $f,g\in A$ are composable if $\partial _0g = \partial _1f$.

Definition 2.16

Let $G=(O,A,\partial _0,\partial _1)$ be a graph. We define the category $\mathcal {C}(G)$ to have elements of O as objects and morphisms of $\mathcal {C}(G)$ are (possibly empty) strings of composable morphisms of A. We call $\mathcal {C}(G)$ the free category generated by G.

Proposition 2.17

[[24, p. 51, Proposition 1]] Let $\mathcal {C}$ be a small category and let R be a binary relation, i.e.a map that assigns to each pair (a, b) of objects a subset of $\mathbf{mor} _{\mathcal {C}}({a,b})^2$. Then, there exists a category $\mathcal {C}/R$ with object set $\mathbf{obj} _\mathcal {C}$ and a functor $Q:\mathcal {C}\rightarrow \mathcal {C}/R$ (which is the identity on objects) such that

• (1) If $(f,f')\in R(a,b)$ then $Qf=Qf'$.

• (2) If $H:\mathcal {C}\rightarrow \mathcal {D}$ is a functor such that $(f,f')\in R(a,b)$ implies $Hf=Hf'$, then there exists a unique functor $H':\mathcal {C}/R\rightarrow \mathcal {D}$ such that $H'\circ Q = H$.

Let ${\mathcal {B}{\mathrm{ord}}}_d$ denote the category with objects $(d-1)$-manifolds and morphisms given by diffeomorphism classes of cobordisms $(W,\psi _0,\psi _1)$. The main goal of this chapter is to give a presentation of ${\mathcal {B}{\mathrm{ord}}}_d$, i.e. a graph G, a relation R and an equivalence of categories $\mathcal {C}(G)/R\overset{\cong }{\longrightarrow }{\mathcal {B}{\mathrm{ord}}}_d$. Let us first construct the graph G. Objects in O are the objects of ${\mathcal {B}{\mathrm{ord}}}_d$ and arrows will be given by diffeomorphisms and elementary cobordisms:

• (1) For a diffeomorphism $f:M_0\rightarrow M_1$ we get an arrow $I_f\in A$ from $M_0$ to $M_1$.

• (2) For a surgery datum $\varphi$ in M we get an arrow $S_\varphi \in A$ from M to $M_\varphi$.

Next, we need to construct the relation R on $\mathcal {C}(G)$. Recall that for a diffeomorphism $f:M\rightarrow M'$ and a surgery datum $\varphi$ in M there exists a canonical induced diffeomorphism $f_\varphi :M_\varphi \rightarrow M'_{f\circ \varphi }$. Also, if $\varphi$ and $\varphi '$ are two surgery embeddings into M with disjoint images, there are obvious induced surgery data $\varphi '_\varphi$ and $\varphi _{\varphi '}$ on $M_\varphi$ and $(M_{\varphi })_{\varphi '_\varphi } = (M_{\varphi '})_{\varphi _{\varphi '}}$. We define R to be the relation on morphism sets of $\mathcal {C}(G)$ generated by the following:

• (1) $I_{\mathrm{id}} = \mathrm{id}$.

• (2) If $f:M_0\overset{\cong }{\longrightarrow }M_1$ and $g:M_1\overset{\cong }{\longrightarrow }M_2$ are diffeomorphisms, then $I_g \circ I_f = I_{g\circ f}$.

• (3) Let $f:M_0\overset{\cong }{\longrightarrow }M_1$ and let $\varphi$ be a surgery embedding into $M_0$. Then $S_{f\circ \varphi }\circ I_f = I_{f_\varphi } \circ S_{\varphi }$.

• (4) If $f,f':M\overset{\cong }{\longrightarrow }M'$ are isotopic, then $I_f=I_{f'}$.

• (5) If $A\in O(k)\times O(d-k)$, then $S_\varphi = S_{\varphi \circ A}$.

• (6) If $\varphi ,\varphi '$ are two surgery embeddings into M with disjoint images, then $S_{\varphi _{\varphi '}}\circ S_{\varphi '} = S_{\varphi '_\varphi }\circ S_\varphi$.

• (7) Let $\varphi$ be a k-surgery datum in M and $\varphi '$ a $(k+1)$-surgery datum in $M_\varphi$ such that the belt sphere of $\varphi$ and the attaching sphere of $\varphi '$ intersect transversely in a single point. Then $S_{\varphi '}\circ S_\varphi = I_{\mathrm{id}\ \#\ \eta _k}$, where $\eta _k$ is the diffeomorphism described Sect. 2.2, below Remark 2.7.

Remark 2.18

For isotopic surgery embeddings $\varphi$ and $\varphi '$ we get a diffeotopy H of M such that $H_0=id$ and $H_1\circ \varphi = \varphi '$ by the isotopy extension theorem. Then

$$\begin{aligned}S_{\varphi '} = S_{H_1\circ \varphi } \circ I_{H_0} = S_{H_1\circ \varphi } \circ I_{H_1} = I_{(H_1)_\varphi }\circ S_{\varphi }.\end{aligned}$$

Definition 2.19

We define the surgery datum category $\mathcal {X}_d$ to be $\mathcal {C}(G)/R$ and $Q:\mathcal {C}(G)\rightarrow \mathcal {X}_d$ shall denote the projection functor.

2.5 A presentation of the cobordism category

In this section we prove that the surgery datum gives a presentation of the category ${\mathcal {B}{\mathrm{ord}}}_d$. This is the main result of this chapter.

Theorem 2.20

Let $P:\mathcal {C}(G)\rightarrow {\mathcal {B}{\mathrm{ord}}}_d$ denote the functor which is the identity on objects and is given on morphisms by

• (1) For $f:M_0\rightarrow M_1$, $I_f$ is mapped to $(M_0\times [0,1],\mathrm{id},f)\cong (M_1\times [0,1],f^{-1},\mathrm{id})$

• (2) For a surgery datum $\varphi$ in M, $S_\varphi$ is mapped to $(\mathbf{tr} \,(\varphi ),\mathrm{id},\mathrm{id})$.

Then P descends to a functor $\mathcal {P}:\mathcal {X}_d\rightarrow {\mathcal {B}{\mathrm{ord}}}_d$ which is an equivalence of categories.

Proof

First we check well-definedness. By Proposition 2.17 it suffices to show that P respects the relations of $\mathcal {X}_d$.

• (1) $(M_0\times [0,1],\mathrm{id},\mathrm{id})$ is the identity.

• (2) $\begin{aligned} (M_1\times [0,1],\mathrm{id},f)&\circ (M_0\times [0,1],\mathrm{id},g)\! \,{:}{=}\,\! (M_0\times [0,1]\cup _g M_1\times [0,1],\mathrm{id},f)\\&\overset{\cong }{\longrightarrow }(M_0\times [0,2],\mathrm{id},f\circ g) \end{aligned}$ and the diffeomorphism is given by the identity on ${M_0\times [0,1]}$ and by the map $(p,t)\mapsto (g^{-1}(p),t+1)$ for $(p,t)\in M_1\times [0,1]$.

• (3) Let $\varphi$ be a surgery embedding into $M_0$ and let $f:M_0\overset{\cong }{\longrightarrow }M_1$ be a diffeomorphism.

  $$\begin{aligned} P(I_{f_\varphi }\circ S_\varphi )&= (\mathbf{tr} \,(\varphi )\cup (M_0)_\varphi \times [0,1],\mathrm{id}, f_\varphi )\\ P(S_{f\circ \varphi }\circ I_f)&= ([0,1]\times M_0\cup _{f}{} \mathbf{tr} \,(f\circ \varphi ),\mathrm{id},\mathrm{id}) \end{aligned}$$

  We will show that both of these are diffeomorphic to $X\,{:}{=}\,(M_0\times [0,1]\cup \mathbf{tr} \,\varphi \cup _{f_\varphi }(M_1)_{f\circ \varphi }\times [0,1],\mathrm{id},\mathrm{id})$. The diffeomorphism $X\overset{\cong }{\longrightarrow }P(I_{f_\varphi }\circ S_\varphi )$ is given by shrinking $M_0\times [0,1]\cup \mathbf{tr} \,\varphi$ to $\mathbf{tr} \,\varphi$ and by $f_\varphi \times \mathrm{id}$ on $(M_0)_{\varphi }\times [0,1]$. Recall that there is a canonical diffeomorphism $F:\mathbf{tr} \,\varphi \overset{\cong }{\longrightarrow }\mathbf{tr} \,(f\circ \varphi )$. The diffeomorphism $X\overset{\cong }{\longrightarrow }P(S_{f\circ \varphi }\circ I_f)$ is given by the identity on $M_0\times [0,1]$, F on $\mathbf{tr} \,(\varphi )$ and by shrinking the collar of $(M_1)_{f\circ \varphi }$.

• (4) Let $f_t:M_0\overset{\cong }{\longrightarrow }M_1$ be a diffeotopy. Then we get a diffeomorphism $F:([0,1]\times M_0,\mathrm{id},f_0)\overset{\cong }{\longrightarrow }([0,1]\times M_0,\mathrm{id},f_1)$ given by $F(t,x) = f_t^{-1}\circ f_0(x)$.

• (5) For every $A\in {\mathrm{O}}(k)\times {\mathrm{O}}(d-k)$, $\varphi \circ A$ is just a reparametrization of $\varphi$ and hence this does not change $\mathbf{tr} \,(\varphi )$ since the standard model was chosen to be ${\mathrm{O}}(k)\times {\mathrm{O}}(d-k)$-invariant (cf. Construction 2.4).

• (6) Let $\varphi ,\varphi '$ be surgery embeddings into M with disjoint images and let $U, U'$ be disjoint neighborhoods of ${\mathrm{im}}\varphi , {\mathrm{im}}\varphi '$ in M. Let $F:[0,2]\times M\overset{\cong }{\longrightarrow }[0,2]\times M$ be a diffeomorphism such that

  • (a) $F|_{[0,\frac{\epsilon }{2})\times M\cup (2-\frac{\epsilon }{2},2]\times M} =\mathrm{id}$

  • (b) $F(t,x) = (t+1,x)$ for $1-\epsilon _1>t>\epsilon _1$ and $x\in U$

  • (c) $F(t,x) = (t-1,x)$ for $2-\epsilon _{1}>t>1+\epsilon _1$ and $x\in U'$

  Then, F induces a diffeomorphism ${\overline{F}}:\mathbf{tr} \,(\varphi )\cup \mathbf{tr} \,(\varphi '_\varphi )\cong \mathbf{tr} \,(\varphi ')\cup \mathbf{tr} \,(\varphi _{\varphi '})$ which is the identity on a collar of the boundary.

• (7) This is precisely the situation discussed below Remark 2.7.

Therefore there is an essentially surjective functor $\mathcal {P}:\mathcal {X}_d\rightarrow {\mathcal {B}{\mathrm{ord}}}_d$. Every cobordism admits a handle decomposition and hence this functor is full. It is faithful by Proposition 2.8: Any two preimages of a cobordism W under $\mathcal {P}$ only differ by a finite sequence of the seven relations of $\mathcal {X}_d$. $\square$

Definition 2.21

Let $a,b\in \{-1,0,1,\dots \}$. We define:

• (1) We define ${\mathcal {B}{\mathrm{ord}}}_d^{a,b}\subset {\mathcal {B}{\mathrm{ord}}}_d$ to be the wide³ subcategory defined by the following: $\mathbf{mor} _{{\mathcal {B}{\mathrm{ord}}}^{a.b}_d}({M_0,M_1})$ contains those morphisms $(W,\psi _0,\psi _1)$ where $\psi _0^{-1}:M_0\hookrightarrow W$ is a-connected and $\psi _1^{-1}:M_1{\hookrightarrow } W$ is b-connected. Here $(-1)$-connected shall be the empty condition.

• (2) $G^{a,b}$ to be the graph with the same object set as G and morphisms as follows: For $f:M_0\overset{\cong }{\longrightarrow }M_1$ we have $I_f\in A$ connecting $M_0$ and $M_1$ and for every surgery embedding $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M$ with $k\in [a+1,d-b-1]$ we have $S_\varphi \in A$ connecting M and $M_\varphi$. Analogously to Definition 2.19, we define $\mathcal {X}_d^{a,b}\,{:}{=}\,\mathcal {C}(G^{a,b})/R$.

Note that ${\mathcal {B}{\mathrm{ord}}}_d^{a,b}$ is a category by the Blakers-Massey excision theorem [5, Theorem 6.4.1].

Theorem 2.22

For $d\ge 7$, the induced functor $\mathcal {P}^{-1,2}:\mathcal {X}_d^{-1,2} \rightarrow {\mathcal {B}{\mathrm{ord}}}_d^{-1,2}$ is an equivalence of categories.

Proof

The proof goes along the same lines as the proof of Theorem 2.20. For fullness we note that if the inclusions $\psi _1^{-1}:M_1\hookrightarrow W$ is 2-connected respectively, there exists a Morse function with all indices $\le d-3$ by Theorem 2.12. Faithfulness follows from Proposition 2.14. $\square$

2.6 Definition of the surgery map

Let $\mathrm{hTop}$ denote the homotopy category of spaces, i.e.the category with spaces as objects and homotopy classes of maps as morphisms.

Definition 2.23

We define a functor

$$\begin{aligned}{\overline{\mathcal {S}}}:\mathcal {C}(G^{-1,2})\longrightarrow \mathrm{hTop}\end{aligned}$$

by the following:

• (1) ${\overline{\mathcal {S}}}(M) = \mathcal {R}^+(M)$.

• (2) For a diffeomorphism $f:M_0\overset{\cong }{\longrightarrow }M_1$ the morphism $I_f$ is mapped to $[g\mapsto f_*g]$, where $f_*\,{:}{=}\,(f^{-1})^*$.

• (3) For $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M$ with $k\le d-3$,

  $$\begin{aligned}S_\varphi \mapsto [\mathcal {R}^+(M)\dashrightarrow \mathcal {R}^+(M,\varphi ) \overset{\cong }{\longrightarrow }\mathcal {R}^+(M_\varphi ,\varphi ^{\mathrm{op}})\hookrightarrow \mathcal {R}^+(M_\varphi )],\end{aligned}$$

  where the first map in this chain is the homotopy inverse to the inclusion (cf. Theorem 2.2) and the second one works as follows: For a metric ${\tilde{g}}$ on $M{\setminus }{\mathrm{im}}\varphi$, the metric ${\tilde{g}} \cup \varphi _*(g^{k-1}_\circ + g^{d-k}_{\mathrm{tor}})$ is mapped to ${\tilde{g}} \cup (\varphi ^{\mathrm{op}})_*(g^k_{\mathrm{tor}} + g^{d-k-1}_\circ )$.

We will abbreviate ${\overline{\mathcal {S}}}_f\,{:}{=}\,{\overline{\mathcal {S}}}(I_f)$ and ${\overline{\mathcal {S}}}_\varphi \,{:}{=}\,{\overline{\mathcal {S}}}(S_\varphi )$.

Remark 2.24

We have ${\overline{\mathcal {S}}}(\mathbf{mor} _{\mathcal {C}(G^{2,2})}({M_0,M_1}))\subset \mathrm{h}\mathbf {Iso}(\mathcal {R}^+(M_0),\mathcal {R}^+(M_1))$, i.e. ${\overline{\mathcal {S}}}$ maps morphisms in ${\mathcal {C}(G^{2,2})}$ to (the homotopy classes of) homotopy equivalences. This follows from the Parametrized Surgery Theorem (cf. Theorem 2.2).

Lemma 2.25

${\overline{\mathcal {S}}}$ induces a well-defined functor $\mathcal {X}_d^{-1,2}\longrightarrow \mathrm{hTop}$.

Proof

For $d\le 2$ the statement and the proof of this theorem is trivial since $\mathbf{mor} _{\mathcal {X}^{-1,2}_d}$ is generated by diffeomorphisms and it suffices to note that isotopic diffeomorphisms induce homotopic maps. Therefore we may assume $d\ge 3$ throughout this proof. Furthermore, we will use dashed arrows for maps that contain inverses of weak homotopy equivalences (cf. Remark 2.3).

We need to show that the relations R from Definition 2.19 do not change the homotopy class of ${\overline{\mathcal {S}}}(\alpha )$ for $\alpha \in \mathbf{mor} _{\mathcal {X}_d^{-1,2}}({M_0,M_1})$. This is obvious for relations 1, 2 and 4. For relation 5 this is easy as well, because $g_\circ + g_{\mathrm{tor}}$ is $O(k)\times O(d-k)$-invariant. Also, $S_{f\circ \varphi }\circ I_f$ and $I_{f_\varphi }\circ S_\varphi$ give homotopic maps because of the following homotopy-commutative diagram.

For relation 6 let $\varphi ,\varphi '$ be two surgery embeddings into M with disjoint images. Then there are inclusions $\mathcal {R}^+(M,\varphi )\hookleftarrow \mathcal {R}^+(M,\varphi \amalg \varphi ')\hookrightarrow \mathcal {R}^+(M,\varphi ')$ and performing both surgeries at the same time is the same as performing them one after another. The most difficult part of this proof is to show that handle cancellation does not alter the homotopy class of ${\overline{\mathcal {S}}}(\alpha )$. If $d=3$ the only surgery data in $\mathbf{mor} _{\mathcal {X}_d^{-1,2}}$ are of the form $S^{-1}\times D^{3}\hookrightarrow M$. Hence there cannot be cancelling surgeries and we may assume that $d\ge 4$ from now on. The proof now consists of two steps: We first reduce to the statement that cancelling surgeries do not change the path component of the round metric in $\mathcal {R}^+(S^{d-1})$ which afterwards is proven by an elementary computation using [31, Lemma 1.9]. Let $\varphi$, $\varphi '$ be surgery data in M as in relation 7 and let $f\,{:}{=}\,\mathrm{id}_M\ \#\ \eta _k$ where $\eta _k:S^{d-1}\overset{\cong }{\longrightarrow }(S^{d-1}_\varphi )_{\varphi '}$ is the fixed diffeomorphism from Section 2.2. Note that in this case we have $k\le d-4$ and $d\ge 4$. There exists an embedding of a disk $D^{d-1}\cong D\subset M$ such that ${\mathrm{im}}\varphi \subset D$ and ${\mathrm{im}}\varphi '\subset D_\varphi$. It suffices to show that the composition

is homotopic to the inclusion $\iota$: By the Theorem 2.2, the inclusion map $\iota$ is a weak homotopy equivalence since $d\ge 4$ and hence ${\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_{\varphi }$ is homotopic to $f_*$.

Let $g\in \mathcal {R}^+(D,\varphi )_{g_\circ }$ be a metric in the component of $g_{\mathrm{tor}}\in \mathcal {R}^+(D)_{g_\circ }$ which exists by Theorem 2.2. Consider the following diagram:

The composition of the top maps is given by gluing in g and the composition of the lower maps is given by gluing in $g_{\mathrm{tor}}$. These two metrics are homotopic relative to the boundary and hence this diagram commutes up to homotopy. The bottom map and the right-hand vertical map are weak equivalences by Theorem 2.2 because $d\ge 4$ and $k\le d-4$. Hence, the inclusion map $\mathcal {R}^+(M,D;g)\hookrightarrow \mathcal {R}^+(M,\varphi )$ is a weak equivalence as well. Let $g_\varphi$ be the metric obtained from g by cutting out $\varphi _*(g_\circ ^{k-1} + g^{d-k}_{\mathrm{tor}})$ and gluing in $\varphi ^{\mathrm{op}}_*(g_{\mathrm{tor}}^{k} + g_\circ ^{d-k-1})$. The following diagram where the horizontal maps are given by replacing g with $g_\varphi$ commutes on the nose with the non-dashed arrows and up to homotopy with the dashed arrow:

It again follows that the right-hand vertical map and the right-hand diagonal map are weak equivalences. Note that the composition of the bottom horizontal maps is precisely the map ${\overline{\mathcal {S}}}_\varphi$. Now let $\tilde{g}\in \mathcal {R}^+(D_\varphi ,\varphi ')_{g_\circ }$ be a metric in the component of $g_\varphi \in \mathcal {R}^+(D_\varphi )_{g_\circ }$. We get the following diagram

which is homotopy-commutative as ${\tilde{g}}$ and $g_\varphi$ are homotopic. The righthand vertical map is a weak equivalence because $d-k-1\ge 3$ and we deduce that $\mathcal {R}^+(M_\varphi ,D_\varphi ; \tilde{g})\hookrightarrow \mathcal {R}^+(M_\varphi , \varphi ')$ is a weak equivalence as well. Let ${\tilde{g}}_{\varphi '}$ be the metric obtained from $\tilde{g}$ by cutting out $\varphi '_*(g_\circ ^{k} + g^{d-k-1}_{\mathrm{tor}})$ and gluing in $\varphi '^{\mathrm{op}}{}_*(g_{\mathrm{tor}}^{k+1} + g_\circ ^{d-k-2})$. We get the analogous homotopy-commutative diagram:

This accumulates to the following diagram where all arrows are weak equivalences:

Here, the map (1) is given by cutting out $g_\varphi$ and gluing in ${\tilde{g}}$. Since these are homotopic relative to the boundary, the inside triangle and hence the entire diagram commutes up to homotopy. Therefore, the composition $f^*\circ {\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_\varphi \circ \iota$ is homotopic to the inclusion if and only if the top row composition in this diagram is. In contrast to $f^*\circ {\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_\varphi \circ \iota$ this composition only consists of actual maps which are given as follows: For $h\in \mathcal {R}^+(M{\setminus } D)_{g_\circ }$ we have

We will denote the path component of a psc-metric g on M by $[g]\in \pi _0(\mathcal {R}^+(M))$. By the above argument it suffices to show that $[f^*\tilde{g}_{\varphi '}]=[g_{\mathrm{tor}}]\in \pi _0(\mathcal {R}^+(D)_{g_\circ })$. This is implied by Lemma 2.26 as follows: We can assume that $D\subset S^{d-1}$ is a hemisphere and we have $f^*\circ {\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_{\varphi }([g_{\mathrm{tor}}\cup g_{\mathrm{tor}}])\sim [g_{\mathrm{tor}}\cup f^*{\tilde{g}}_{\varphi '}]$ by the above argument for $M=S^{d-1}$ and $h=g_{\mathrm{tor}}$. After possibly changing the coordinates of the disk D we may assume the following: If $a^k:S^{d-1}\overset{\cong }{\longrightarrow }(S^{k-1}\times D^{d-k})\cup (D^k\times S^{d-k-1})$ is the solid torus decomposition then $a^{k}\circ \varphi$ is given by the inclusion of the first factor and $a^k_\varphi \circ \varphi ':S^{k}\times D^{d-k-1}\hookrightarrow (S^{k}\times D^{d-k-1})\cup (S^{k}\times D^{d-k-1})$ is also given by the inclusion of the first factor (cf. Sect. 2.2). In this case we have $f=\eta _k$. The metric $[g_{\mathrm{tor}}\cup g_{\mathrm{tor}}]$ is homotopic to the round metric by [31, Lemma 1.9] and we have

$$\begin{aligned}{}[g_{\mathrm{tor}}\cup f^*{\tilde{g}}_{\varphi '}]&\sim \eta _k^*\circ {\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_{\varphi } ([g_{\mathrm{tor}}\cup g_{\mathrm{tor}}])\\ {}&\sim \eta _k^*\circ {\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_{\varphi } ([g_\circ ]) \overset{\text {{Lemma}~2.26}}{\sim }[g_\circ ] \sim [g_{\mathrm{tor}}\cup g_{\mathrm{tor}}]. \end{aligned}$$

Also $g_1\,{:}{=}\,g_{\mathrm{tor}}\cup f^*{\tilde{g}}_{\varphi '}$ and $g_2\,{:}{=}\,g_{\mathrm{tor}}\cup g_{\mathrm{tor}}$ are both in the image of the inclusion map $\mathcal {R}^+(D)_{g_\circ }\hookrightarrow \mathcal {R}^+(S^{d-1})$ which is a weak equivalence and since $[g_1]=[g_2]$ it follows that $[g_{\mathrm{tor}}]=[f^*\tilde{g}_{\varphi '}]\in \pi _0(\mathcal {R}^+(D)_{g_{\circ }})$. $\square$

Lemma 2.26

Let $g_\circ \in \mathcal {R}^+(S^{d-1})$ be the round metric and let $a^k:S^{d-1}\overset{\cong }{\longrightarrow }(S^{k-1}\times D^{d-k})\cup (D^{k}\times S^{d-k-1})$ be the solid torus decomposition. Let $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow S^{d-1}$ and let $\varphi ':S^{k}\times D^{d-k-1}\hookrightarrow S^{d-1}_\varphi$ be surgery data such that $a^k\circ \varphi$ and $a^k_\varphi \circ \varphi '$ are both given by the inclusion of the respective first factor. Then ${\overline{\mathcal {S}}}_{\varphi '}\circ {\overline{\mathcal {S}}}_{\varphi } ([g_\circ ]) \sim {\overline{\mathcal {S}}}_{\eta _k}([g_\circ ]) = (\eta _k)_*[g_\circ ]$.

Proof

Let $g^k_{\mathrm{mtor}}\,{:}{=}\,(g_\circ ^{k-1} + g_{\mathrm{tor}}^{d-k})\cup (g_{\mathrm{tor}}^k + g_\circ ^{d-k-1})$ denote the mixed torpedo metric on$(S^{k-1}\times D^{d-k})\cup (D^{k}\times S^{d-k-1})$. By [31, Lemma 1.9]) we have $(a^k){}^*g_{\mathrm{mtor}}^k\sim g_\circ$ and hence

$$\begin{aligned} {\overline{\mathcal {S}}}_\varphi (g_\circ )&\sim {\overline{\mathcal {S}}}_\varphi \bigl ((a^k){}^*g^k_{\mathrm{mtor}}\bigr ) = {\overline{\mathcal {S}}}_\varphi ({\overline{\mathcal {S}}}_{(a^k)^{-1}}(g^k_{\mathrm{mtor}}))\\&\sim {\overline{\mathcal {S}}}_{(a_\varphi ^k{})^{-1}}{\overline{\mathcal {S}}}_{a^k{}\circ \varphi }(g^k_{\mathrm{mtor}}) = (a_\varphi ^k)^*{\overline{\mathcal {S}}}_{a^k{}\circ \varphi }(g^k_{\mathrm{mtor}}) \end{aligned}$$

Now $a^k\circ \varphi$ is given by the inclusion and hence

$$\begin{aligned}{\overline{\mathcal {S}}}_{a^k\circ \varphi }(g^k_{\mathrm{mtor}})\sim (g_{\mathrm{tor}}+g_\circ )\cup (g_{\mathrm{tor}} + g_\circ ) \sim g_\circ + g_\circ \sim \underbrace{(g_{\circ }+g_{\mathrm{tor}})\cup (g_{\circ } + g_{\mathrm{tor}})}_{={\overline{g}}}\end{aligned}$$

on $(D^k\times S^{d-k-1})\cup (D^k\times S^{d-k-1}) = S^k\times S^{d-k-1} = (S^k\times D^{d-k-1})\cup (S^k\times D^{d-k-1})$. We can now compute

$$\begin{aligned} {\overline{\mathcal {S}}}_{\varphi '}{\overline{\mathcal {S}}}_\varphi (g_\circ )&\sim (a_\varphi ^k{})_{\varphi '}{}^*\ \underbrace{{\overline{\mathcal {S}}}_{(a^k_\varphi )\circ \varphi '}\Bigl ((g_{\circ }+g_{\mathrm{tor}})\cup (g_{\circ } + g_{\mathrm{tor}})\Bigr )}_{=(g_{\mathrm{tor}}+g_{\circ })\cup (g_{\circ } + g_{\mathrm{tor}}) = g^{k+1}_{\mathrm{mtor}}}\\&\sim (a^k_\varphi )_{\varphi '}{}^*\ g^{k+1}_{\mathrm{mtor}} \end{aligned}$$

We have to show that $(a^k_\varphi )_{\varphi '}{}^*\ g^{k+1}_{\mathrm{mtor}}\sim \eta _k{}_*g_\circ$ which is equivalent to

$$\begin{aligned}\eta _k^*\left( (a^k_\varphi )_{\varphi '}{}\right) ^*\ g^{k+1}_{\mathrm{mtor}}\sim g_\circ \end{aligned}$$

But $\eta _k$ was chosen such that $\bigl ((a^k_\varphi )_{\varphi '}\circ \eta _k\bigr )=a^{k+1}$ and therefore

$$\begin{aligned} \eta _k^*(a^k_\varphi )_{\varphi '}{}^*g^{k+1}_{\mathrm{mtor}}&=(a^{k+1})^*g^{k+1}_{\mathrm{mtor}} \sim g_\circ . \end{aligned}$$

$\square$

We get the following Corollary which follows immediately from Lemma 2.25 and Theorem 2.22.

Corollary 2.27

Let $d\ge 7$. Then there is a unique functor⁴

$$\begin{aligned}{\overline{\mathcal {S}}}:{\mathcal {B}{\mathrm{ord}}}_d^{-1,2}\longrightarrow \mathrm{hTop}\end{aligned}$$

which satisfies:

• 1. ${\overline{\mathcal {S}}}(M) = \mathcal {R}^+(M)$

• 2. ${\overline{\mathcal {S}}}_{(M\times I, \mathrm{id},f)} = f_*$

• 3. ${\overline{\mathcal {S}}}_{(\mathbf{tr} \,\varphi ,\mathrm{id},\mathrm{id})}(g) = {\overline{\mathcal {S}}}_\varphi$.

Corollary 2.28

Let $W = (W,\psi _0,\psi _1):M_0\leadsto M_1$ be an admissible cobordism. Then there is a well defined homotopy class of a map ${\overline{\mathcal {S}}}_W:\mathcal {R}^+(M_0)\rightarrow \mathcal {R}^+(M_1)$. If $W^{\mathrm{op}}\,{:}{=}\,(W^{\mathrm{op}},\psi _1,\psi _0)$ is also admissible, i.e. $\psi _0^{-1}:M_0\hookrightarrow W$ is also 2-connected, then ${\overline{\mathcal {S}}}_{W}$ is a homotopy equivalence and a homotopy-inverse is given by $\mathcal {S}_{W^\mathrm{op}}$.

Remark 2.29

The constructions from the proof of [31, Theorem 3.1] show the following: If $W = (W,\mathrm{id},\mathrm{id}):M_0\leadsto M_1$ is an admissible cobordism, $g_0\in \mathcal {R}^+(M_0)$ and $g_1\in \mathcal {R}^+(M_1)$ are metrics such that ${\overline{\mathcal {S}}}_W([g_0])\sim [g_1]$, then there exists a metric $G\in \mathcal {R}^+(W)_{g_0, g_1}$.

2.7 Surgery invariance of ${\overline{\mathcal {S}}}$

In this section we prove the following Lemma.

Lemma 2.30

Let $d\ge 7$ and let $M_0$, $M_1$ be two $(d-1)$-manifolds, let $W=[W,\mathrm{id},\mathrm{id}]\in \mathbf{mor} _{{\mathcal {B}{\mathrm{ord}}}_d^{-1,2}}({M_0,M_1})$ and let $\Phi :S^{k-1}\times D^{d-k+1}\hookrightarrow \mathrm{Int }\ W$ be an embedding with $3\le k\le d-3$. Then ${\overline{\mathcal {S}}}_W \sim {\overline{\mathcal {S}}}_{W_\Phi }$.

Proof

First we note that for $3\le k\le d-3$, $W_\Phi$ is again an admissible cobordism: Let $W^\circ \,{:}{=}\,W{\setminus } {\mathrm{im}}\Phi$. Then $W^\circ \hookrightarrow W$ is $(d-k)$-connected and $W^\circ \hookrightarrow W_\Phi$ is $(k-1)$-connected. We have the following diagram:

Since $3\le k \le d- 3$, the inclusions $M_1\hookrightarrow W^\circ$ and $M_1\hookrightarrow W_\Phi$ are 2-connected and hence $W_\Phi$ is admissible.

We first prove Lemma 2.30 in the case that $k\ne 3$. Let $c:M_1\times [1-\epsilon ,1]\hookrightarrow W$ be a collar which does not intersect ${\mathrm{im}}\Phi$ and let $\gamma :[0,1]\times D^{d-1}\hookrightarrow W$ be an embedded, thickened path connecting $M_1\times \{1-\epsilon \}$ and ${\mathrm{im}}\Phi$. Let

$$\begin{aligned} W_1&\,{:}{=}\,{\mathrm{im}} c\ \#_\partial \ {\mathrm{im}}\Phi \,{:}{=}\,{\mathrm{im}} c\cup {\mathrm{im}}\gamma \cup {\mathrm{im}}\Phi \\ W_1'&\,{:}{=}\,{\mathrm{im}} c\ \#_\partial \ {\mathrm{im}}\Phi ^{\mathrm{op}}\\ W_0&\,{:}{=}\,W{\setminus } W_1. \end{aligned}$$

We choose $\gamma$, so that the boundaries of all of these are smooth. Then $W_1\simeq M_1\vee S^{k-1}$, $W_1' \simeq M_1\vee S^{d-k}$, $W_0\cup W_1 = W$ and $W_0\cup W_1' = W_\Phi$. Since $M_1\hookrightarrow W$ and $M_1\hookrightarrow W_\Phi$ are 2-connected and $4\le k\le d-3$, the maps $M_1\vee S^{k-1}\simeq W_1\hookrightarrow W$ and $M_1\vee S^{d-k}\simeq W'\hookrightarrow W_\Phi$ are 2-connected as well.

Fig. 3

Surgery on the cobordism W

Fig. 4

Gluing $W_1^{\mathrm{op}}$ to $W_1'$

Note that $W_1$ and $W_1'$ have the same boundary $M_1'$ given by

$$\begin{aligned} \partial W_1 = M_1\amalg \underbrace{(M_1\ \#\ \partial ({\mathrm{im}}\Phi ))}_{=M_1'\cong M_1\# (S^{k-1}\times S^{d-k})} = M_1\amalg (M_1\ \#\ \partial ({\mathrm{im}}\Phi ^{\mathrm{op}} )) = \partial W_1'.\end{aligned}$$

Next, we show that $W_0$, $W_1$, $W_1'$ and $W_1^{\mathrm{op}}$ are again admissible. Because of $W_1\simeq M_1\vee S^{k-1}$ and $W_1'\simeq M_1\vee S^{d-k}$ we get

• $(W_1,M_1)$ is $(k-2)$-connected.

• $(W_1,M_1')$ is $(d-k)$-connected.

• $(W_1',M_1)$ is $(d-k-1)$-connected.

So, for $4\le k\le d-3$ all of these are at least 2-connected and hence $W_1$, $W_1'$ and $W_1^{\mathrm{op}}$ are admissible⁵. For $W_0$ we note that W is homotopy equivalent to $W_0$ with a $(d-k+1)$-cell attached along $\Phi (\{1\}\times S^{d-k})$:

$$\begin{aligned} W_0\cup D^{d-k+1}&= \bigl (W{\setminus } ({\mathrm{im}}\Phi \cup {\mathrm{im}}\gamma )\bigr )\cup D^{d-k+1}\\&=W{\setminus } (\underbrace{{\mathrm{im}}\Phi {\setminus } D^{d-k+1}}_{\simeq D^{d}}\cup \ {\mathrm{im}}\gamma )\simeq W. \end{aligned}$$

Therefore $W_0\hookrightarrow W$ is $(d-k)$-connected and we have the following diagram.

and hence $M_1'\hookrightarrow W_0$ is 2-connected, too.

So we get a decompositions into admissible cobordisms $W=W_0\cup W_1$ and $W_\Phi = W_0\cup W_1'$ which implies ${\overline{\mathcal {S}}}_W = {\overline{\mathcal {S}}}_{W_1} \circ {\overline{\mathcal {S}}}_{W_0}$ and ${\overline{\mathcal {S}}}_{W_\Phi } = {\overline{\mathcal {S}}}_{W_1'} \circ {\overline{\mathcal {S}}}_{W_0}$. In the homotopy category $\mathrm{hTop}$ we have

$$\begin{aligned} {\overline{\mathcal {S}}}_{W_\Phi }&= {\overline{\mathcal {S}}}_{W_1'}\circ \underbrace{{\overline{\mathcal {S}}}_{W_1\cup W_1^{\mathrm{op}}}}_{=\mathrm{id}} \circ {\overline{\mathcal {S}}}_{W_0}\\&= {\overline{\mathcal {S}}}_{W_1'}\circ {\overline{\mathcal {S}}}_{W_1^{\mathrm{op}}} \circ {\overline{\mathcal {S}}}_{W_1} \circ {\overline{\mathcal {S}}}_{W_0} = {\overline{\mathcal {S}}}_{W_1^{\mathrm{op}}\cup W_1'} \circ {\overline{\mathcal {S}}}_{W}, \end{aligned}$$

where $W_1^{\mathrm{op}}\cup W_1'$ denotes the manifold obtained by gluing the outgoing boundary of $W_1^\mathrm{op}$ to the incoming boundary of $W_1'$ along $\mathrm{id}_{M_1'}$. It suffices to show that $W_1^{\mathrm{op}}\cup W_1'$ is diffeomorphic to $M_1\times I$ relative to the boundary since ${\overline{\mathcal {S}}}_W$ only depends on the diffeomorphism type of W (see Lemma 2.25 and Corollary 2.27). We have (see Fig. 4)

$$\begin{aligned} W_1^{\mathrm{op}}\cup W_1' ={}&\left( (M_1\times [0,\epsilon ])\ \#_\partial \ S^{k-1}\times D^{d-k+1}\right) \\&\underset{M_1'}{\cup }\left( D^{k}\times S^{d-k}\ \#_\partial \ (M_1\times [1-\epsilon ,1])\right) \\ \cong {}&M_1\times [0,2\epsilon ]\ \#\ \underbrace{\left( (S^{k-1}\times D^{d-k+1})\underset{S^{k-1}\times S^{d-k}}{\cup }(D^{k}\times S^{d-k})\right) }_{\cong S^d}\\ \cong {}&M_1\times [0,1]. \end{aligned}$$

and these diffeomorphisms are supported on a small neighbourhood of $M_1'$ and hence relative to the boundary. This finishes the proof for the case $k\ne 3$.

For the case $k=3$ we need a different argument, because $W_1$ might not be admissible in this case. Consider the map

$$\begin{aligned}{\mathrm{Emb}}(S^2\times D^{d-3}, M_1) \longrightarrow {\mathrm{Emb}}(S^2\times D^{d-2}, M_1\times [0,2])\end{aligned}$$

which is given by $\varphi \mapsto \Phi$ with $\Phi (x,(y,t))=(\varphi (x,y),t)$ for $x\in S^2$ and $(y,t)\in D^{d-2}\subset D^{d-3}\times [0,1]$. We also have a map ${\mathrm{Emb}}(S^2\times D^{d-2}, M_1\times [0,2])\hookrightarrow {\mathrm{Emb}}(S^2\times D^{d-2}, W)$ given by shrinking the interval and composing with the inclusion of the collar. We will use the following Lemma.

Lemma 2.31

In the present situation, the maps ${\mathrm{Emb}}(S^2\times D^{d-3}, M_1) \longrightarrow {\mathrm{Emb}}(S^2\times D^{d-2}, M_1\times [0,2])$ and ${\mathrm{Emb}}(S^2\times D^{d-2}, M_1\times [0,2])\hookrightarrow {\mathrm{Emb}}(S^2\times D^{d-2}, W)$ are both 0-connected.

By this Lemma we may isotope the embedding $\Phi :S^2\times D^{d-2}\hookrightarrow W$ so that its image is contained in the collar of the boundary $M_1$. So we may assume that $W=M_1\times [0,2]$. We abbreviate $M\,{:}{=}\,M_1$. Again by the above lemma, we can isotope $\Phi$ such that $\Phi (S^2\times D^{d-3}\times \{0\})\subset M\times \{1\}$, i.e.$\Phi$ is a thickening of $\varphi \,{:}{=}\,\Phi |_{S^2\times D^{d-3}\times \{0\}}$. Let us now give the diffeomorphism

$$\begin{aligned}\underbrace{(M\times [0,\tfrac{1}{2}]\underset{\varphi }{\cup }D^3\times D^{d-3})}_{\cong \mathbf{tr} \,\varphi } \cup \underbrace{(M\times [\tfrac{1}{2},1]\underset{\varphi }{\cup }D^3\times D^{d-3})}_{\cong (\mathbf{tr} \,\varphi )^{\mathrm{op}}}\overset{\alpha }{\longrightarrow }\underbrace{(M\times I){\setminus }{\mathrm{im}}\Phi \cup D^3\times S^{d-3}}_{\cong (M\times I)_\Phi }.\end{aligned}$$

On $(M{\setminus }{\mathrm{im}}\varphi )\times I$ the diffeomorphism $\alpha$ shall be given by the identity. Next we take diffeomorphisms

$$\begin{aligned} \alpha _1&:{\mathrm{im}}\varphi \times \left[ 0,\frac{1}{2}\right] \overset{\cong }{\longrightarrow }\left( {\mathrm{im}}\varphi \times \left[ 0,\frac{1}{2}\right] \right) {\setminus }\left( {\mathrm{im}}\Phi \cap \left[ 0,\frac{1}{2}\right] \right) \\ \alpha _2&:{\mathrm{im}}\varphi \times \left[ \frac{1}{2},1\right] \overset{\cong }{\longrightarrow }\left( {\mathrm{im}}\varphi \times \left[ \frac{1}{2},1\right] \right) {\setminus }\left( {\mathrm{im}}\Phi \cap \left[ \frac{1}{2},1\right] \right) . \end{aligned}$$

On the $D^3\times D^{d-3}$-parts it is given by the inclusion of the lower or upper hemisphere $D^{3}\times S^{d-3}_\pm \subset D^{3}\times S^{d-3}$. The entire diffeomorphism is visualized in Fig. 5. Therefore we have ${\overline{\mathcal {S}}}_{(M\times I)_\Phi }\sim {\overline{\mathcal {S}}}_\mathbf{tr \,\varphi ^{\mathrm{op}}}\circ {\overline{\mathcal {S}}}_\mathbf{tr \,\varphi }\sim \mathrm{id}\sim {\overline{\mathcal {S}}}_{M\times I}$ and the proof is finished modulo Lemma 2.31. $\square$

Fig. 5

The diffeomorphism $\alpha$

Proof of Lemma 2.31

We have the following diagram

where ${\mathrm{Mon}}$ denotes the space of bundle monomorphisms. Note that the bottom-most vertical maps are homeomorphisms because $S^2$ is stably parallelizable and the middle ones are homotopy equivalences by the Smale-Hirsch immersion theorem (cf. [2, Section 3.9]). The map (1) is 0-connected because of the Whitney embedding (cf. [17, pp. 26]) and the maps (5) and (6) are $\pi _0$-bijections again by the Whitney-embedding theorem. It remains to show that (2) and (3) are 0-connected. Then the map (4) is 0-connected, too. For (2) consider the following diagram of fibrations.

Since $d-4\ge 3$, the map (2) is 0-connected. The map (3) fits into a similar diagram:

Since $M_1\hookrightarrow W$ is 2-connected, the bottom-most map is 0-connected and hence so is the map (3). $\square$

3 Tangential structures and proof of main result

3.1 Tangential structures

In order to get rid of the connectivity assumptions of the category ${\mathcal {B}{\mathrm{ord}}}_d^{-1,2}$, we need tangential structures. For $d\ge 0$ let $B{\mathrm{O}}(d+1)$ be the classifying space of the $(d+1)$-dimensional orthogonal group and let $U_{d+1}$ be the universal vector bundle over $B{\mathrm{O}}(d+1)$. Let $\theta :B\rightarrow B{\mathrm{O}}(d+1)$ be a fibration. We call $\theta$ a tangential structure.

Definition 3.1

A $\theta$-structure on a real $\hbox {rank}{d+1}$-vector bundle $V\rightarrow X$ is a bundle map ${\hat{l}}:V\rightarrow \theta ^*U_{d+1}$. A $\theta$-structure on a manifold $W^{{d+1}}$ is a $\theta$-structure on TW and a $\theta$-manifold is a pair $(W,{\hat{l}})$ consisting of a manifold W and a $\theta$-structure ${\hat{l}}$ on W. For $0\le k\le d$ a stabilized $\theta$-structure on $M^k$ is a $\theta$-structure on $TM\oplus {{\underline{\mathbb {R}}}}^{{d+1}-k}$.

An important source of tangential structures are covers of $B{\mathrm{O}}({d+1})$. For example we have $B{\mathrm{SO}}({d+1})\rightarrow B{\mathrm{O}}({d+1})$ or $B{\mathrm{Spin}}({d+1})\rightarrow B{\mathrm{O}}({d+1})$ or more generally $B{\mathrm{O}}({d+1})\langle k\rangle \rightarrow B{\mathrm{O}}({d+1})$, where $B{\mathrm{O}}({d+1})\langle k\rangle$ denotes the k-connected cover of $B{\mathrm{O}}({d+1})$. Other sources of tangential structures are Moore-Postnikov towers:

Definition 3.2

Let $M^{d-1}$ be a connected manifold, let $l:M\rightarrow B{\mathrm{O}}({d+1})$ be the classifying map of the stabilized tangent bundle and let ${\hat{l}}:TM\oplus {{\underline{\mathbb {R}}}}^2\rightarrow U_{d+1}$ be a bundle map covering l. The n-th stage of the Moore-Postnikov tower for the map l is called the stabilized tangential n-type of M.

Example 3.3

• (1) The stabilized tangential 2-type of a connected ${\mathrm{Spin}}$-manifold M of dimension at least 3 is $B{\mathrm{Spin}}({d+1})\times B\pi _1(M)$.

• (2) The stabilized tangential 2-type of a simply connected, non-spinnable manifold M of dimension at least 3 is $B{\mathrm{SO}}({d+1})$.

Recall the following lemma which is frequently used when working with surgery results concerning positive scalar curvature.

Lemma 3.4

[[23, Proposition 4], [19, Proposition, Appendix B], [10, Lemma B.4]] Let $\theta :B\rightarrow B{\mathrm{O}}(d+1)$ be a tangential structure, with B of type $F_n$. Let $W^m:M_0\leadsto M_1$ be a $\theta$-cobordism and let $M_1\rightarrow B$ be n-connected. If $n\le \frac{m}{2}-1$, there exists a $\theta$-cobordism $W':M_0\leadsto M_1$ such that $(W',M_1)$ is n-connected. If furthermore $M_0\rightarrow B$ is also n-connected, there exists a $\theta$-cobordism $W':M_0\leadsto M_1$ such that $(W',M_i)$ is n-connected for $i=0,1$. Furthermore $W'$ is $\theta$-cobordant to W relative to the boundary.

3.2 Proof of the main result

We will now prove the general version of Theorem G which is the main result of this article.

Definition 3.5

We define $\Omega _{d,2}$ to be the category given by the following:

Objects are given by tuples $(M,B,\theta ,{\hat{l}})$ where

• M is a closed $(d-1)$-dimensional manifold.

• $\theta :B\rightarrow B{\mathrm{O}}(d+1)$ is a 2-coconnected tangential structure.

• ${\hat{l}}$ is a stabilized $\theta$-structure such that the underlying map $l:M\rightarrow B$ is 2-connected.

Morphisms $(M_0,B_0,\theta _0,{\hat{l}}_0)$ to $(M_1,B_1,\theta _1,{\hat{l}}_1)$ are given by equivalence classes of tuples $(W,\psi _0,\psi _1,{\hat{\ell }}, h)$ where

• $h:B_0\rightarrow B_1$ is a map over $B{\mathrm{O}}(d+1)$. This gives an induced map

  $$\begin{aligned}{\hat{h}}:\theta _0^*U_{d+1}\rightarrow \theta _1^*U_{d+1}.\end{aligned}$$

• $(W,\psi _0,\psi _1)$ is a cobordism from $M_0$ to $M_1$.

• ${\hat{\ell }}$ is a stabilized $\theta _1$-structure on W.

• ${\hat{\ell }}|_{\partial _0W}= {\hat{h}}\circ {\hat{l}}_0\circ \mathrm{d}\psi _0$ und ${\hat{\ell }}|_{\partial _1W}=-{\hat{l}}_1\circ \mathrm{d}\psi _1$, where $-{\hat{l}}_1$ denotes the bundle map given by

  $$\begin{aligned}{\hat{l}}_1\circ \left( \mathrm{id}\oplus \left( \begin{matrix} -1 &{} \\ &{} 1 \end{matrix}\right) \right) :TM_1\oplus {{\underline{\mathbb {R}}}}^2 \rightarrow TM_1\oplus {{\underline{\mathbb {R}}}}^2\rightarrow \theta _1^*U_{d+1}\end{aligned}$$

• $(W,\psi _0,\psi _1,{\hat{\ell }}, h)\sim (W',\psi _0',\psi _1',{\hat{\ell }}', h')$ if $h=h'$ and there exists a $(d+1)$-dimensional $\theta _1$-manifold $(X,\ell _X)$ with corners such that there exists a partition of $\partial X=\bigcup _{i=0,3} \partial _iX$ together with diffeomorphisms

  $$\begin{aligned} \partial _0X&\overset{\cong }{\longrightarrow }M_0\times I&\partial _2X&\overset{\cong }{\longrightarrow }M_1\times I\\ \partial _1X&\overset{\cong }{\longrightarrow }W&\partial _3X&\overset{\cong }{\longrightarrow }W' \end{aligned}$$

  such that $\theta$-structures and diffeomorphisms fit together (see Fig. 7).

Composition is given by gluing cobordisms along the common boundary:

$$\begin{aligned}&(W',\psi _0',\psi _1',\hat{\ell }', h')\circ (W,\psi _0,\psi _1,\hat{\ell }, h)\\&\quad = (W\cup _{(\psi _0')^{-1}\circ \psi _1} W', \psi _0,\psi _1',\hat{\ell }\cup _{(\psi _0')^{-1}\circ \psi _1}\hat{\ell }',h'\circ h). \end{aligned}$$

Fig. 6

A representative of a morphism in $\Omega _{d,2}$

Fig. 7

The relation in the category $\Omega _{d,2}$

Theorem 3.6

Let $d\ge 7$. There is a functor

$$\begin{aligned}\mathcal {S}:\Omega _{d,2}\longrightarrow \mathrm{hTop}\end{aligned}$$

with the following properties:

• (1) On objects, $\mathcal {S}$ is given by $\mathcal {S}(M,B,\theta ,{\hat{l}})=\mathcal {R}^+(M)$.

• (2) If $\alpha \in \Omega _{d,2}\bigl ((M_0,B_0,\theta _0,{\hat{l}}_0),(M_1,B_1,\theta _1,{\hat{l}}_1)\bigr )$ is represented by a cobordism whose underlying manifold is given by $(M_0\times [0,1], \mathrm{id}, f^{-1})$ for a diffeomorphism $f:M_1\rightarrow M_0$, then $\mathcal {S}(\alpha ) = f^*$.

• (3) If $\alpha \in \Omega _{d,2}\bigl ((M_0,B_0,\theta _0,{\hat{l}}_0),(M_1,B_1,\theta _1,{\hat{l}}_1)\bigr )$ is represented by a cobordism whose underlying manifold is given by the trace $(\mathbf{tr} \,(\varphi ),\mathrm{id},\mathrm{id})$ of a surgery datum $\varphi :S^{k-1}\times D^{d-k}\hookrightarrow M_0$ with $d-k\ge 3$, then $\mathcal {S}(\alpha ) = {\overline{\mathcal {S}}}_\varphi$ (cf. Definition 2.23).

Furthermore, $\mathcal {S}$ is uniquely determined by these properties, up to natural isomorphism.

Proof

Let $V\,{:}{=}\,(V,\psi _0,\psi _1,\ell _V):(M_0, {\hat{h}}\circ {\hat{l}}_0)\leadsto (M_1,{\hat{l}}_1)$ be a $\theta _1$-cobordism. By Lemma 3.4, there exists an admissible $\theta _1$-cobordism $V':M_0\leadsto M_1$ in the same cobordism class. We define $\mathcal {S}_V\,{:}{=}\,{\overline{\mathcal {S}}}_{V'}$. By definition of ${\overline{\mathcal {S}}}$ it is clear that this fulfils the desired properties and is compatible with composition. It remains to show that this is well-defined. Let $X:V_0\leadsto V_1$ be a $\theta _1$-cobordism relative to $\partial V_0 = \partial V_1$ and let $X_i:V_i\leadsto V_i'$ be relative $\theta _1$-cobordisms such that $(V_i',M_1)$ is admissible for $i=0,1$. We get a relative $\theta _1$-cobordism ${\widetilde{X}}\,{:}{=}\,X_0^{\mathrm{op}}\cup X\cup X_1:V_0' \leadsto V_0 \leadsto V_1\leadsto V_1'$. Again, by Lemma 3.4, we may assume that $({\widetilde{X}},V_i')$ is 2-connected. So, $V_1'$ is obtained from $V_0'$ by a sequence of surgeries of index $k\in \{3,\dots ,d-2\}$. One can order these surgeries, so that one first performs the 3-surgeries, the 4-surgeries next and so on up to the $d-3$-surgeries. By Lemma 2.30 all of these do not change the homotopy class of ${\overline{\mathcal {S}}}$ and we may assume that $V_1'$ is obtained from $V_0'$ by a finite sequence of $d-2$-surgeries. Reversing these surgeries we deduce that $V_0'$ is obtained from $V_1'$ by a finite sequence of 3-surgeries and by Lemma 2.30 the map ${\overline{\mathcal {S}}}_{V_0'}$ is homotopic to ${\overline{\mathcal {S}}}_{V_1'}$. Hence $\mathcal {S}$ is well-defined. $\square$

Remark 3.7

Note that if $M_0$ and $M_1$ have the same tangential 2-type, there exists an admissible cobordism $V'$ in the same cobordism class as V such that $(V')^\mathrm{op}$ is admissible as well. Then $\mathcal {S}_{(V')^\mathrm{op}}$ is a homotopy-inverse for $\mathcal {S}_V$.

Remark 3.8

As mentioned in Remark 2.29 (see also [31]), Walsh constructed a psc-metric G on an admissible self-cobordism $W:M\leadsto M$ extending a given psc-metric $g_0$ on the incoming boundary using the same construction used here. He showed that the homotopy class of G restricted to the outgoing boundary does not depend on the handle presentation [33, Theorem 1.3]. Therefore he obtained a map $f_W\in \mathrm{Aut}(\pi _0(\mathcal {R}^+(M)))$ given by $[g_0]\mapsto [G|_{M\times \{1\}}]$. By separating the cobordism part of the picture (Section 2.2 to Section 2.5) from the scalar curvature part of the picture (Section 2.6 and Section 2.7) we upgraded this to give an actual homotopy class of a map $\mathcal {S}_W\in \pi _0(\mathrm{h}\mathbf {Aut}(\mathcal {R}^+(M)))$ inducing Walsh’s map on $\pi _0(\mathcal {R}^+(M))$. The second improvement lies in the cobordism-invariance of $\mathcal {S}$ which drastically enlarges its kernel and enables us to define $\mathcal {S}_W$ for any $\theta$-cobordism W.

Before we start deriving the general version of Theorem A, let us list two interesting facts about the surgery map. The first one is proven by an argument similar to the reduction step in the proof of Lemma 2.25 and uses the notion of left-/right-stable metrics (cf. [8]).

Let $M_0$ be a manifold and let $M_0^{(2)}$ consist of all 0-, 1- and 2-handles of $M_0$. We write $Q_0\,{:}{=}\,M_0{\setminus } M_0^{(2)}$ and $N\,{:}{=}\,\partial (M_0{\setminus } M_0^{(2)})$. We get a decomposition of $M_0$ into two cobordisms $\emptyset \overset{M_0^{(2)}}{\leadsto }N\overset{Q_0}{\leadsto }\emptyset$. A metric $g\in \mathcal {R}^+(M_0^{(2)})_h$ is called right-stable if for every cobordism $V:N\leadsto N'$ the map $\mu (g,\_):\mathcal {R}^+(V)_{h,h'}\rightarrow \mathcal {R}^+(M_0^{(2)}\cup V)_{h'}$ which glues in g is a weak homotopy equivalence. Analogously a metric $g\in \mathcal {R}^+(Q_0)_h$ is called left-stable if for every cobordism $V:N'\leadsto N$ the map $\mu (\_,g):\mathcal {R}^+(V)_{h',h}\rightarrow \mathcal {R}^+(V\cup Q_0)_{h'}$ which glues in g is a weak homotopy equivalence.

Proposition 3.9

Let $M_0$ be such that there exists a metric $g=g_{\mathrm{rst}}\cup g_{\mathrm{lst}}\in \mathcal {R}^+(M_0)$ which is the union of a right-stable metric $g_{\mathrm{rst}}\in \mathcal {R}^+(M_0^{(2)})_h$ and a left-stable metric $g_{\mathrm{lst}}\in \mathcal {R}^+(Q_0)_h$. Let $W = (W,\mathrm{id},\mathrm{id}), W'=(W',\mathrm{id},\mathrm{id}):M_0\leadsto M_1$ be admissible cobordisms with $\mathcal {S}_W(g) \sim \mathcal {S}_{W'}(g)$. Then $\mathcal {S}_W$ is homotopic to $\mathcal {S}_{W'}$.

Proof of Proposition 3.9

Since W and $W'$ are admissible, they consist of handles glued along surgery data with codimension at least 3. By transversality we may assume that all handles are attached in the interior of $Q_0$. Hence we can decompose $M_1$ into $M_0^{(2)}\cup Q_1$ and W (resp $W'$) into $M_0^{(2)}\times [0,1]$ and a relative cobordism $V:Q_0\leadsto Q_1$ (resp. $V'$). Let $g_{\mathrm{lst}}^V$ and $g_{\mathrm{lst}}^{V'}$ represent the resulting path components of $\mathcal {S}_V(g_{\mathrm{lst}})$ and $\mathcal {S}_V'(g_{\mathrm{lst}})$. Since $g_\mathrm{lst}$ is left-stable $\mu (\_,g_\mathrm{lst})$ is a weak equivalence and $\mathcal {S}_W=\mu (\_,g_\mathrm{lst})^{-1}\circ \mu (\_,g_\mathrm{lst}^V)$ and $\mathcal {S}_{W'}=\mu (\_,g_\mathrm{lst})^{-1}\circ \mu (\_,g_\mathrm{lst}^{V'})$. By assumption $g_{\mathrm{rst}}\cup g^{V}_{\mathrm{lst}}$ is homotopic to $g_{\mathrm{rst}}\cup g^{V'}_{\mathrm{lst}}$ and because $g_\mathrm{rst}$ is right-stable, $g^{V}_{\mathrm{lst}}$ is homotopic to $g^{V'}_{\mathrm{lst}}$. Therefore $\mu (\_,g^{V}_{\mathrm{lst}})\sim \mu (\_,g^{V'}_{\mathrm{lst}})$ and hence $\mathcal {S}_W\sim \mathcal {S}_{W'}$.

Remark 3.10

This theorem applies for example if $M_0$ is the double $dM_0^{(2)}=M_0^{(2)} \cup (M_0^{(2)})^\mathrm{op}$ of $M_0^{(2)}$ and the metric g is given by $g_{\mathrm{rst}}\cup g_\mathrm{rst}^\mathrm{op}$ which covers the case $M_0=S^{d-1}$ and $g=g_\circ$.

The second fact states that the surgery map induces a well defined map on concordance classes of psc-metrics which will be used in forthcoming work [11]. Let us first recall the notion of concordance of psc-metrics.

Definition 3.11

Let $g_0,g_1\in \mathcal {R}^+(M)$. We say $g_0$ and $g_1$ are concordant if $\mathcal {R}^+(M\times [0,1])_{g_0,g_1}\ne \emptyset$. This defines an equivalence relation and we denote the set of concordance classes of $\mathcal {R}^+(M)$ by ${\tilde{\pi }}_0(\mathcal {R}^+(M))$.

Proposition 3.12

$\mathcal {S}$ induces a well defined map on concordance classes.

Proof

Let $M_0, M_1$ be as in Theorem 3.6, $g,g'\in \mathcal {R}^+(M_0)$ be concordant metrics via $G\in \mathcal {R}^+(M_0\times [0,1])_{g,g'}$ and let $[W]\in \Omega _d^{\theta _1}(M_0,M_1)$. Without loss of generality we may assume that W is admissible. The map $\mathcal {S}_W$ induces a map on components and since isotopy of psc-metrics implies concordance of psc-metrics, there are unique concordance classes $[\mathcal {S}_W[g]]$ and $[\mathcal {S}_W[g']]$ represented by h and $h'$ respectively. It remains to show that h and $h'$ are concordant. By [31, Theorem 3.1] (cf. Remark 2.29) there exist metrics $H\in \mathcal {R}^+(W)_{g,h}$ and $H'\in \mathcal {R}^+(W)_{g',h'}$. This gives the psc-metric $H'^{\mathrm{op}}\cup G\cup H\in \mathcal {R}^+(W^{op}\cup M_0\times [0,1]\cup W)_{h',h}$. By Proposition 3.25, $W^{\mathrm{op}}\cup M_0\times [0,1]\cup W$ is $\theta _1$-cobordant to $M_1\times [0,1]$ relative to the boundary and by the surgery theorem there exists a psc-metric ${\tilde{H}}\in \mathcal {R}^+(M_1\times [0,1])_{h',h}$. $\square$

Remark 3.13

Let $W:M_0\leadsto M_1$ be an admissible cobordism. A similar argument shows that on concordance classes we have

$$\begin{aligned} = [h] \iff \exists G\in \mathcal {R}^+(W)_{g,h}\end{aligned}$$

3.3 The Structured Mapping Class Group

In this section we will give the definitions and present two models for the structured mapping class group of a manifold. For the next two sections let $\theta :B\rightarrow B{\mathrm{O}}(d+1)$ be a fixed tangential structure.

Definition 3.14

For a smooth manifold $M^{d-1}$ we denote by ${\mathrm{Diff}}(M)$ the topological group of diffeomorphisms of M with the (weak) $C^\infty$-topology. If M is oriented we denote the subgroup of orientation preserving diffeomorphisms of M by ${\mathrm{Diff}}^+(M)$. The (unoriented) mapping class group $\Gamma (M)$ is defined to be $\pi _0({\mathrm{Diff}}(M))$ and the oriented mapping class group $\Gamma ^+(M)$ is defined as $\pi _0({\mathrm{Diff}}^+(M))$.

Definition 3.15

Let $M^{d-1}$ be a smooth oriented manifold. We define

$$\begin{aligned} E{\mathrm{Diff}}^\theta (M)&\,{:}{=}\,E{\mathrm{Diff}}(M)\times \mathrm{Bun}(TM\oplus {\underline{\mathbb {R}}}^2,\theta ^*U_{d+1})\\ B{\mathrm{Diff}}^\theta (M)&\,{:}{=}\,E{\mathrm{Diff}}^\theta (M)/{\mathrm{Diff}}(M) = E{\mathrm{Diff}}(M)\underset{{\mathrm{Diff}}(M)}{\times }\mathrm{Bun}(TM\oplus {\underline{\mathbb {R}}}^2,\theta ^*U_{d+1}), \end{aligned}$$

where we use the model $E{\mathrm{Diff}}(M)\,{:}{=}\,\{j:M\hookrightarrow \mathbb {R}^{\infty -1}\}$ which is the (contractible) space of embeddings and $\mathrm{Bun}(\_,\_)$ denotes the space of bundle maps. More concretely,

$$\begin{aligned}B{\mathrm{Diff}}^\theta (M)= \{(N, {\hat{l}}):N\subset \mathbb {R}^{\infty -1},\ N\cong M\text { and } {\hat{l}}\in \mathrm{Bun}(TN\oplus {\underline{\mathbb {R}}}^2,\theta ^*U_{d+1})\}.\end{aligned}$$

Given an embedding $j:M\hookrightarrow \mathbb {R}^{\infty -1}$ and a (stabilized) $\theta$-structure ${\hat{l}}$ on M, we get a base-point $(j(M),{\hat{l}})\in B{\mathrm{Diff}}^\theta (M)$. We also define the universal M-bundle with $\theta$-structure $U_{M,\theta }$ by

$$\begin{aligned}U_{M,\theta }\,{:}{=}\,E{\mathrm{Diff}}^\theta (M)\underset{{\mathrm{Diff}}(M)}{\times }M \longrightarrow B{\mathrm{Diff}}^\theta (M).\end{aligned}$$

Remark 3.16

For $\theta _{B{\mathrm{SO}}}:B{\mathrm{SO}}({d+1})\rightarrow B{\mathrm{O}}({d+1})$ we abbreviate $B{\mathrm{Diff}}^{\theta _{B{\mathrm{SO}}}}(M)$ by $B{\mathrm{Diff}}^+(M)$. Note that with our convention $E{\mathrm{Diff}}^+(M)$ is not contractible but homotopy equivalent to $\mathrm{Bun}(TM\oplus {{\underline{\mathbb {R}}}}^2, \theta _{B{\mathrm{SO}}}^*U_{d+1})$ which has two contractible components provided that M is connected (cf. [10, p. 6]). However, if M is connected and admits an orientation reversing diffeomorphism, $B{\mathrm{Diff}}^+(M)$ is still a model for the classifying space of ${\mathrm{Diff}}^+(M)$-principal bundles.

Definition 3.17

Let M be a smooth submanifold of $\mathbb {R}^{\infty -1}$ and let ${\hat{l}}$ be a stabilized $\theta$-structure on M. The $\theta$-structured mapping class group $\Gamma ^\theta (M, {\hat{l}})$ is defined by

$$\begin{aligned}\Gamma ^{\theta }(M, {\hat{l}}):=\pi _1(B{\mathrm{Diff}}^\theta (M),(M, {\hat{l}})).\end{aligned}$$

For $\gamma :S^1\rightarrow B{\mathrm{Diff}}^\theta (M)$ we define the structured mapping torus $M_\gamma :=\gamma ^*U_{M,\theta }$.

Remark 3.18

The mapping torus $M_\gamma$ has a $\theta$-structure on the vertical tangent bundle. Since the tangent bundle of the circle is trivial, this gives a $\theta$-structure on $M_\gamma$.

Since the case of $B=B{\mathrm{Spin}}({d+1})$ is of great interest in the present paper we will have a closer look at it. Let us recall the more traditional description of ${\mathrm{Spin}}$-structures (cf. [6, Chapter 3]): A ${\mathrm{Spin}}$-structure $\sigma$ on a manifold M is a pair $(P,\alpha )$ consisting of a ${\mathrm{Spin}}(d+1)$-principal bundle P and an isomorphism $\alpha :P\times _{{\mathrm{Spin}}({d+1})} \mathbb {R}^{d+1}\overset{\cong }{\longrightarrow }TM\oplus {{\underline{\mathbb {R}}}}^2$. An isomorphism of ${\mathrm{Spin}}$-structures $\sigma _0=(P_0,\alpha _0)$ and $\sigma _1=(P_1,\alpha _1)$ is an isomorphism $\beta :P_0\overset{\cong }{\longrightarrow }P_1$ of ${\mathrm{Spin}}({d+1})$-principal bundles over $\mathrm{id}_M$ such that $\alpha _1\circ (\beta \times _{{\mathrm{Spin}}({d+1})}\mathrm{id}_{\mathbb {R}^{d+1}})=\alpha _0$. If $f:M\rightarrow M$ is an orientation preserving diffeomorphism and $\sigma =(P,\alpha )$ is a ${\mathrm{Spin}}$-structure on M, we define $f^*\sigma \,{:}{=}\,(f^*P, (df)^{-1}\circ f^*\alpha )$.

Now, let $\sigma _0, \sigma _1$ be two ${\mathrm{Spin}}$-structures of M. A ${\mathrm{Spin}}$-diffeomorphsim $(M,\sigma _0)\overset{\cong }{\longrightarrow }(M,\sigma _1)$ is a pair $(f,{\hat{f}})$ consisting of an orientation preserving diffeomorphism $f:M\overset{\cong }{\longrightarrow }M$ and an isomorphism ${\hat{f}}$ of ${\mathrm{Spin}}$-structures $\sigma _0$ and $f^*\sigma _1$ (cf. [6, Definition 3.3.3]). We denote by ${\mathrm{Diff}}^{\mathrm{Spin}}((M,\sigma _0),(M,\sigma _1))$ the space of ${\mathrm{Spin}}$-diffeomorphisms $(M,\sigma _0)\overset{\cong }{\longrightarrow }(M,\sigma _1)$. This gives rise to the groupoid ${\mathrm{Diff}}^{\mathrm{Spin}}(M)$ which has ${\mathrm{Spin}}$-structures on M as objects and morphisms spaces are given by ${\mathrm{Diff}}^{\mathrm{Spin}}((M,\sigma _0),(M,\sigma _1))$. For a ${\mathrm{Spin}}$-structure $\sigma$ on M, we define

$$\begin{aligned}{\mathrm{Diff}}^{\mathrm{Spin}}(M,\sigma )\,{:}{=}\,{\mathrm{Diff}}^{\mathrm{Spin}}((M,\sigma ),(M,\sigma )).\end{aligned}$$

Proposition 3.19

Let M be a simply connected ${\mathrm{Spin}}$-manifold. Then the forgetful homomorphism ${\mathrm{Diff}}^{\mathrm{Spin}}(M,\sigma ) \rightarrow {\mathrm{Diff}}^+(M)$ is surjective and its kernel has two elements.

Proof

Since M is simply connected, the ${\mathrm{Spin}}$-structure $\sigma$ of an oriented manifold is unique up to isomorphism. So for every orientation preserving diffeomorphism $f:M\overset{\cong }{\longrightarrow }M$, there is an isomorphism $\sigma \overset{\cong }{\longrightarrow }f^*\sigma$, hence the map is surjective. The rest follows from [6, Lemma 3.3.6]. $\square$

If $\theta$ is an arbitrary tangential structure we also have a different model for $\Gamma ^\theta (M,{\hat{l}})$.

Definition 3.20

For a $\theta$-structure ${\hat{l}}$ on $M^{d-1}$ we define

$$\begin{aligned}B^\theta (M,{\hat{l}})\,{:}{=}\,\left\{ (f,L):\begin{array}{l}f:M\overset{\cong }{\longrightarrow }M\text { is a diffeomorphism}\\ L\text { is a homotopy of bundle maps } {\hat{l}}\circ df\leadsto {\hat{l}} \end{array}\right\} \Big /\sim \end{aligned}$$

where the equivalence relation is given by homotopies of f and L.

Proposition 3.21

[10, Proposition 1.2.11] There is a group isomorphism $\Gamma ^\theta (M,{\hat{l}})\overset{\cong }{\longrightarrow }B^\theta (M,{\hat{l}})$.

Example 3.22

Since we usually will be interested in the case where $\theta$ is the (stabilized) tangential 2-type of a high-dimensional manifold M, let us consider the case $B=B{\mathrm{Spin}}({d+1})\times BG$. The map $\theta :B{\mathrm{Spin}}({d+1})\times BG\rightarrow B{\mathrm{O}}({d+1})$ factors through the 3-connected cover $\theta _{\mathrm{Spin}}:B{\mathrm{Spin}}({d+1})\rightarrow B{\mathrm{O}}({d+1})$ and we get

$$\begin{aligned}\mathrm{Bun}(TM\oplus {{\underline{\mathbb {R}}}}^2,\theta ^*U_{d+1}) = \mathrm{Bun}(TM\oplus {{\underline{\mathbb {R}}}}^2,\theta _{\mathrm{Spin}}^*U_{d+1})\times {\mathrm{Map}}(M,BG).\end{aligned}$$

So, a $\theta$-structure ${\hat{l}}$ on M is given by a ${\mathrm{Spin}}$-structure $\sigma$ on M and a map $M\rightarrow BG$. Let $\psi \,{:}{=}\,[f,L]\in B^\theta (M,{\hat{l}})$. Then f is an orientation preserving diffeomorphism of M and L is the homotopy class of a path connecting the bundle maps ${\hat{l}}_{\mathrm{Spin}},{\hat{l}}_{\mathrm{Spin}}\circ df:TM\oplus {{\underline{\mathbb {R}}}}^2 \rightarrow \theta _{\mathrm{Spin}}^*U_{d+1}$ together with the homotopy class of a path connecting the maps $\alpha$ and $\alpha \circ f:M\rightarrow BG$. If $G=\pi _1(M,x)$ for some base-point $x\in M$, this means that the induced map $f_*:\pi _1(M,x)\rightarrow \pi _1(M,f(x))$ is given by conjugation by a path $\gamma :[0,1]\rightarrow M$ with $\gamma (0)=x$ and $\gamma (1)=f(x)$. We say that f acts on the fundamental group by an inner automorphism in this case.

3.4 Cobordism sets

Before we can derive the general version of Theorem A we need to take a closer look at the morphism sets of $\Omega _{d,2}$. Recall that we fixed a tangential structure $\theta :B\rightarrow B{\mathrm{O}}(d+1)$.

Definition 3.23

Let $M_0^{d-1},M_1^{d-1}$ be compact manifolds with (stabilized) $\theta$-structures ${\hat{l}}_0,{\hat{l}}_1$. We define the cobordism set of manifolds with $\theta$-structure and fixed boundary by

$$\begin{aligned}\Omega ^\theta _d\bigl ((M_0,{\hat{l}}_0),(M_1,{\hat{l}}_1)\bigr ):=\bigr \{(W,\psi _0,\psi _1,{\hat{\ell }})\bigl \}/\sim .\end{aligned}$$

Here, W is a d-manifold with boundary $\partial W =\partial _0W\ \coprod \partial _1W$, ${\hat{\ell \in }} \mathrm{Bun}(TW\oplus {{\underline{\mathbb {R}}}},\theta ^*U_{d+1})$ is a bundle map and $\psi _i:\partial _iW\rightarrow M_i$, $i=0,1$ are diffeomorphisms such that $(-1)^i{\hat{l}}_i\circ \mathrm{d}\psi _i = {\hat{\ell }}|_{\partial _iW}$. We call $M_0$ the incoming boundary and $M_1$ the outgoing boundary (see Fig. 6 in Definition 3.5). The equivalence relation is given by the cobordism relation: We say that $(W,\psi _0,\psi _1,\ell )$ and $(W',\psi _0',\psi _1',\ell ')$ are cobordant if there exists a $(d+1)$-dimensional $\theta$-manifold $(X,\ell _X)$ with corners such that there exists a partition of $\partial X=\bigcup _{i=0,3} \partial _iX$ together with diffeomorphisms

$$\begin{aligned} M_0\times I&\cong \partial _0 X&M_1\times I&\cong \partial _3X\\ W&\cong \partial _2X&W'&\cong \partial _1X \end{aligned}$$

such that $\theta$-structures and identifying diffeomorphisms fit together (see Fig. 7 in Definition 3.5).

Remark 3.24

• (1) Since $\theta$ is a fibration we do not need to consider homotopies $(-1)^i{\hat{l}}_i\circ \mathrm{df} \sim {\hat{\ell }}|_{\partial _iW}$ but we can arrange the $\theta$-structures to actually agree.

• (2) $\Omega _d^\theta ((M,{\hat{l}}),(M,{\hat{l}}))$ becomes a monoid via concatenation of cobordisms and identifying them along the boundary diffeomorphisms, i.e.

  $$\begin{aligned}(W',\psi _0',\psi _1',\ell ') \cdot (W,\psi _0,\psi _1,\ell ) := (W\cup _{\psi _0'\circ \psi _1^{-1}} W', \psi _0,\psi _1', \ell \cup _{{\hat{\psi }}'_0\circ {\hat{\psi }}_1^{-1}}\ell ').\end{aligned}$$

  This monoid is actually an abelian group (cf. Corollary 3.28).

• (3) Note that one has a map $\Omega _d^\theta ((M,{\hat{l}}),(M,{\hat{l}}))\rightarrow \Omega _d^\theta (\emptyset ,\emptyset )=\Omega _d^\theta$ given by identifying the equal boundaries of a cobordism $W:M\leadsto M$. This map turns out to be an isomorphism of groups (cf. Corollary 3.28 and the remark below it).

Proposition 3.25

Let $W^d:M_0 \leadsto M_1$ be $\theta$-cobordism. Then there exists a $\theta$-structure on $W^\mathrm{op}:M_1\leadsto M_0$ such that $W\cup W^\mathrm{op}\sim M_0\times [0,1]\ \mathrm{rel}\ M_0\times \{0,1\}$. In particular, if $W:\emptyset \leadsto M$ is a $\theta$-nullbordism, the double $dW\,{:}{=}\,W\cup W^\mathrm{op}$ is nullbordant and $W^\mathrm{op}\amalg W$ is cobordant to the cylinder on M.

Fig. 8

Introducing corners to obtain the desired cobordism

Proof

Consider the manifold with corners $W\times I$. We introduce new corners as in Fig. 8. Next, we construct the $\theta$-structures⁶. Let $\ell _W:TW\oplus {{\underline{\mathbb {R}}}}\rightarrow \theta ^*U_{d+1}$ be the $\theta$-structure on W. Since $W\hookrightarrow W\times [0,1]$ is a homotopy equivalence there is a unique extension up to homotopy

where the vertical map sends $v\in {{\underline{\mathbb {R}}}}_{>0}$ to the inwards pointing vector. This gives a $\theta$-structure on $W\times I$ and by restriction a $\theta$-structure on $W^{\mathrm{op}}$. $\square$

Now we can prove another useful tool.

Proposition 3.26

The action of $\Omega _d^\theta$ on $\Omega _d^\theta \bigl ((M_0,{\hat{l}}_0),(M_1,{\hat{l}}_1)\bigr )$ given by disjoint union is free and transitive.

Proof

Since disjoint union is associative up to cobordism and disjoint union with the emptyset is the identity this really defines a group action. In the case that $\Omega _d^\theta \bigl ((M_0,l_0),(M_1,l_1)\bigr )=\emptyset$ the statement is trivial. So let

$$\begin{aligned}(L,\psi _0^L,\psi _1^L,\ell _L):(M_0,{\hat{l}}_0)\leadsto (M_1,{\hat{l}}_1)\end{aligned}$$

be a cobordism. Let $\Phi _L:\Omega _d^\theta \longrightarrow \Omega _d^\theta \bigr ((M_0,l_0),(M_1,l_1)\bigl )$ be given by $\Phi _L(V) = V\amalg L$. Also let

$$\begin{aligned}{\tilde{\Phi }}_L:\Omega _d^\theta \bigr ((M_0,l_0),(M_1,l_1)\bigl )\longrightarrow \Omega _d^\theta \end{aligned}$$

be defined given by gluing in the cobordism $(L^{\mathrm{op}},\psi _1^L,\psi _0^L,\ell _L^{\mathrm{op}})$ along the boundary as follows: We concatenate with $L^\mathrm{op}$ and then identify the equal boundaries:

$$\begin{aligned}\Omega _d^\theta \bigr ((M_0,l_0),(M_1,l_1)\bigl ) \overset{\cup L^\mathrm{op}}{\longrightarrow }\Omega _d^\theta \bigr ((M_0,l_0),(M_0,l_0)\bigl )\longrightarrow \Omega _d^\theta \end{aligned}$$

We will prove the Proposition by showing that $\Phi$ and $\tilde{\Phi }$ are mutually inverse bijections. By Proposition 3.25 we have

$$\begin{aligned}{\tilde{\Phi }}(\Phi ([V])) = {\tilde{\Phi }}([V\amalg L]) = [V\amalg (L\cup L^{\mathrm{op}})] = [V].\end{aligned}$$

It remains to show that ${\tilde{\Phi }}_L(W)\amalg L = (W\cup L^{\mathrm{op}}) \amalg L$ is cobordant to W. First we note that $(W,\psi _0,\psi _1)$ is diffeomorphic to $(M_0\times I\cup _{\psi _0}W\cup _{\psi _1^{-1}}M_1\times I,\mathrm{id},\mathrm{id})$ and so it suffices to consider the case that all boundary identifications are given by the identity. We now decompose $(W\cup L^{\mathrm{op}})\amalg L$ as follows:

$$\begin{aligned} V_0&\,{:}{=}\,M_0\times [0,\epsilon ]\cup M_1\times [1-\epsilon ,1]&V_1&\,{:}{=}\,L\\ V_2&\,{:}{=}\,L^{\mathrm{op}}&V_3&\,{:}{=}\,W \end{aligned}$$

Note that

$$\begin{aligned} \partial V_0&= (M_0\times \{0\})\amalg \underbrace{(M_0\times \{\epsilon \})\amalg (M_1\times \{1-\epsilon \})}_{=\partial _+V_0} \amalg (M_1\times \{1\})\\ \partial V_1&= M_0\amalg M_1 = \partial V_2 = \partial V_3 \end{aligned}$$

By identifying $\partial _+ V_0$ and $\partial V_2$ with $\partial V_1$ and $\partial V_3$ in different ways we obtain

$$\begin{aligned} V_0\cup V_1&= L&V_2\cup V_3&= L^\mathrm{op}\cup W\\ V_0\cup V_3&= W&V_2\cup V_3&= L^\mathrm{op}\cup L=dL \end{aligned}$$

We will now construct the cobordism $X:(V_0\cup V_1)\amalg (V_2\cup V_3)\leadsto (V_0\cup V_3)\amalg (V_2\cup V_1)$. We construct this by taking $V_i\times I$ for every $i=0,1,2,3$, introducing corners at the boundary (and at $\partial _+V)$ respectively) as shown in Fig. 9.

We then glue together these manifolds as follows: We identify

• $\partial V_0\times \{t\} \text { with } \partial V_1\times \{t\} \text { and } \partial V_2\times \{t\} \text { with } \partial V_3\times \{t\} \text { for } t\in [0,\frac{1}{2}]$

• $\partial V_0\times \{t\} \text { with } \partial V_3\times \{t\} \text { and } \partial V_1\times \{t\} \text { with } \partial V_2\times \{t\} \text { for } t\in [\frac{1}{2},1]$.

This is shown in Fig. 10. The $\theta$-structures are given by $\hat{\ell }_{V_i}\oplus \mathrm{id}_{{{\underline{\mathbb {R}}}}}$ (the arrows in Fig. 10 indicate the incoming and outgoing boundary of X). $\square$

Fig. 9

Introducing corners at the boundary of $V_i\times [0,1]$

Fig. 10

The cobordism $X:(V_0\cup V_1)\amalg (V_2\cup V_3)\leadsto (V_0\cup V_3)\amalg (V_2\cup V_1)$

Remark 3.27

Proposition 3.26 can also be proven using structured cobordism categories. The presented proof however is much more direct.

Corollary 3.28

Let (M, l) be a $(d-1)$-dimensional $\theta$-manifold. Then the map

$$\begin{aligned}\Phi :\Omega ^\theta _d\overset{\cong }{\longrightarrow }\Omega ^{\theta }_d\bigr ((M,{\hat{l}}),(M,{\hat{l}})\bigr )\end{aligned}$$

given by $(V,{\hat{\ell }})\mapsto (M\times [0,1]\amalg V,\mathrm{id},\mathrm{id},({\hat{l}}\oplus \mathrm{id}_{{{\underline{\mathbb {R}}}}})\amalg {\hat{\ell }})$ is an isomorphism of groups. In particular, $\Omega ^{\theta }_d\bigr ((M,{\hat{l}}),(M,{\hat{l}})\bigr )$ is an abelian group.

Proof

It is a group homomorphism because

$$\begin{aligned} \Phi (V\amalg W)&= M\times [0,1]\ \amalg \ V\amalg W\\ {}&=(M\times [0,1]\ \amalg \ V)\cup (M\times [1,2]\ \amalg \ W) = \Phi (V)\cup \Phi (W). \end{aligned}$$

The rest follows from Proposition 3.26. $\square$

Remark 3.29

The inverse is given by mapping $(W,\psi _0,\psi _1)$ to the manifold obtained by gluing $\partial _1W$ to $\partial _0W$ along the diffeomorphism $\psi _0^{-1}\circ \psi _1$.

Corollary 3.30

The map $\Gamma ^\theta (M,{\hat{l}})\rightarrow \Omega _d^{\theta }$ given by $[\gamma ]\mapsto [M_\gamma ]$ is a homomorphism.

Proof

Let $\gamma :[0,1]\rightarrow B{\mathrm{Diff}}^\theta (M)$ be a path from $(M,{\hat{l}})$ to itself. We define the mapping cylinder map by $A:\Gamma ^\theta (M,{\hat{l}})\rightarrow \Omega _d^{\theta }(M,M), \gamma \mapsto (\gamma ^*U_{M,\theta },\mathrm{id},\mathrm{id})$. Since the bundle classified by $\gamma _0*\gamma _1$ is the same as the union of the bundles classified by $\gamma _i$, this satisfies

$$\begin{aligned} A(\gamma _0*\gamma _1)&= ((\gamma _0*\gamma _1)^*U_{M,\theta },\mathrm{id},\mathrm{id})\\&= (\gamma _0^*U_{M,\theta } \cup \gamma _1^*U_{M,\theta },\mathrm{id},\mathrm{id})\\&= (\gamma _0^*U_{M,\theta },\mathrm{id},\mathrm{id})\cup (\gamma _1^*U_{M,\theta },\mathrm{id},\mathrm{id}) = A(\gamma _0)\cup A(\gamma _1). \end{aligned}$$

Since the isomorphism $\Omega _d^{\theta }(M,M)\rightarrow \Omega _d^\theta$ is given by gluing the boundary, we have $M_\gamma = {\tilde{\Phi }}(\gamma ^*U_{M,\theta })$ and hence

$$\begin{aligned} M_{\gamma _0*\gamma _1}&= {\tilde{\Phi }}(A(\gamma _0*\gamma _1))={\tilde{\Phi }}(A(\gamma _0)\cup A(\gamma _1)) \\&\overset{3.28}{=} {\tilde{\Phi }}(A(\gamma _0))\amalg {\tilde{\Phi }}(A(\gamma _1)) = M_{\gamma _0}\amalg M_{\gamma _1}. \end{aligned}$$

$\square$

Remark 3.31

Using the model $B^\theta (M,{\hat{l}})$ for the mapping class group, we see that the map $A:B^\theta (M,{\hat{l}})\rightarrow \Omega _d^{\theta }(M,M)$ is given by $\psi \mapsto (M\times [0,1],\mathrm{id},\psi ^{-1})$ for P . Note that since $\Omega _d^\theta (M,M)$ is commutative, $\psi \mapsto (M\times [0,1],\mathrm{id},\psi )$ is a homomorphism as well.

3.5 The action of the mapping class group

We will now give the general statement of Theorem A. For a space X let $\mathrm{h}\mathbf {Aut}(X)$ denote the group-like⁷H-space of weak homotopy equivalences of X.

Corollary 3.32

Let $d\ge 7$, let M be a $(d-1)$-dimensional manifold and let $\theta :B\rightarrow B{\mathrm{O}}(d+1)$ be the stabilized tangential 2-type of M where ${\hat{l}}:TM\oplus {{\underline{\mathbb {R}}}}^2\rightarrow \theta ^*U_{d+1}$ is a $\theta$-structure. Then there exists a group homomorphism

$$\begin{aligned}\mathcal {S}\mathcal {E}:\Omega _d^{\theta }\longrightarrow \pi _0(\mathrm{h}\mathbf {Aut}(\mathcal {R}^+(M))),\end{aligned}$$

such that the following diagram, where F is the forgetful map and T is the mapping torus map, commutes

Proof

We define $\mathcal {S}\mathcal {E}(W)\,{:}{=}\,\mathcal {S}_{M\times [0,1]\amalg W,\mathrm{id},\mathrm{id}}$. Then $\mathcal {S}\mathcal {E}$ is a group homomorphism by Corollary 3.28 and because $\mathcal {S}$ is compatible with composition. By Theorem 3.6 the above diagram is commutative since $[M\times I\ \amalg \ T_\psi ,\mathrm{id},\mathrm{id}] = [M\times I,\mathrm{id},\psi ^{-1}]$ (cf. Corollary 3.30 and Remark 3.31). $\square$

Proof of Theorem B

Since M is simply connected and stably parallelizable, the tangential 2-type of M is given by $B{\mathrm{Spin}}(d+1)$. Let $f:M\rightarrow M$ be a ${\mathrm{Spin}}$-diffeomorphism. By Corollary 3.32 we need to show that the class $[T_f]\in \Omega _d^{\mathrm{Spin}}$ vanishes. The kernel of the forgetful homomorphism $\Omega ^{\mathrm{Spin}}_d\rightarrow \Omega ^{{\mathrm{SO}}}_d$ is a finite dimensional $\mathbb {F}_2$-vector space and concentrated in degrees congruent $\equiv 1,2(8)$ (cf. [1]). By [22, Proposition 13] mapping tori of stably parallelizable manifolds are orientedly nullbordant. This finishes the proof.

There are more examples to which Corollary 3.32 is applicable which can be found in [10, Section 4.1].

Proof of Proposition D

By Proposition 3.19 we may assume that f is a ${\mathrm{Spin}}$-diffeomorphism. Let $W:S^{d-1}\rightarrow S^{d-1}$ be an admissible cobordism ${\mathrm{Spin}}$-cobordant to $S^{d-1}\times [0,1]\amalg T_f$. Then $f^*\sim \mathcal {S}\mathcal {E}_{T_f}\sim \mathcal {S}_W$ and by Proposition 3.9 and Remark 3.10 this is homotopic to the identity if $\mathcal {S}_W(g_\circ )$ is homotopic to $g_\circ$.

3.6 The action for simply connected ${\mathrm{Spin}}$ 7-manifolds

We have the following result for 7-manifolds which implies Corollary C.

Corollary 3.33

Let $M^7$ be a simply connected ${\mathrm{Spin}}$-manifold and let $f:M\overset{\cong }{\longrightarrow }M$ be a ${\mathrm{Spin}}$-diffeomorphism. Then the following are equivalent:

• (1) ${\hat{{\mathscr {A}}}}(T_f)=0$.

• (2) $T_f$ is ${\mathrm{Spin}}$-nullbordant.

• (3) $f^*$ is homotopic to the identity.

• (4) $f^*g\sim g$ for every $g\in \mathcal {R}^+(M)$.

• (5) There exists a metric $g\in \mathcal {R}^+(M)$ such that $f^*g\sim g$.

Proof

The implications $3.\Rightarrow 4.$ and $4.\Rightarrow 5.$ are obvious and the implication $2.\Rightarrow 3$ follows from Corollary 3.32. For $1.\Rightarrow 2.$ we note that

$$\begin{aligned}\Omega ^{{\mathrm{Spin}}}_8\cong \mathbb {Z}\oplus \mathbb {Z} \cong \langle [{\mathbb {H}\mathbb {P}}^2],[\beta ]\rangle ,\end{aligned}$$

where $\beta$ denotes the Bott manifold with ${\hat{{\mathscr {A}}}}(\beta )=1$ and $\mathrm{sign}(\beta )=0$. Furthermore, $\mathrm{sign}({\mathbb {H}\mathbb {P}}^2)\ne 0$ and ${\hat{{\mathscr {A}}}}({\mathbb {H}\mathbb {P}}^2)=0$. Since for $T_f$ both these invariants vanish, it has to be ${\mathrm{Spin}}$-nullbordant. Finally $5.\Rightarrow 1.$ is proven as follows: Let $g_t$ be an isotopy between $f^*g$ and g. Since isotopy of psc-metrics implies concordance of psc-metrics, there exists a psc-metric G on $M\times [0,1]$ restricting to $f^*g$ and g. Then G induces a psc-metric on $T_f$ as one can identify the metrics on the boundary along $f^*$ and hence $\hat{\mathscr {A}}(T_f)=0$. $\square$

Remark 3.34

Since M is simply connected the forgetful map ${\mathrm{Diff}}^{{\mathrm{Spin}}}(M)\rightarrow {\mathrm{Diff}}^+(M)$ is surjective. Hence the above Corollary classifies the action of $\Gamma ^+(M)$ on $\mathcal {R}^+(M)$ for every simply connected 7-dimensional ${\mathrm{Spin}}$-manifold.

Note that the implications $2.\Rightarrow 3.\Rightarrow 4.\Rightarrow 5.\Rightarrow 1.$ don’t require the restriction to dimension 7. For simply connected, 7-dimensional ${\mathrm{Spin}}$-manifolds, we get a further factorization of the action map:

This factorization is sharp in the sense that $\ker \eta =\ker {\hat{{\mathscr {A}}\circ }} T$ by Corollary 3.33.

Proposition 3.35

Let M be a $(d-1)$-dimensional, simply connected ${\mathrm{Spin}}$-manifold and let $W^d$ be a closed ${\mathrm{Spin}}$-manifold with $\alpha (W)\ne 0$. Then $\mathcal {S}\mathcal {E}_W(g)\not \sim g$ for every psc-metric g on M.

Proof

By Lemma 3.4 we can perform (${\mathrm{Spin}}$-)surgery on the interior of $M\times [0,1]\amalg W$ to get an admissible cobordism $V:M\leadsto M$. If there exists a psc-metric $g_0\in \mathcal {R}^+(M)$ such that $\mathcal {S}\mathcal {E}_W(g_0)\sim g_0$, there exists a psc-metric G on V that restricts to $g_0$ on both boundaries by Remark 2.29. We obtain a psc-metric on the manifold $V'$ given by gluing the boundaries of V together along the identity. So, $\alpha (V')=0$ by the Lichnerowicz-formula and since $\alpha$ is ${\mathrm{Spin}}$-cobordism invariant we get

$$\begin{aligned} 0&=\alpha (V')=\alpha ((M\times S^1)\amalg W) = \alpha (W). \end{aligned}$$

$\square$

This shows that vanishing of the $\alpha$-invariant of W is a necessary condition for $\mathcal {S}\mathcal {E}(W)$ to be homotopic to the identity. We close with the following question.

Question 3.36

Let M be simply connected and ${\mathrm{Spin}}$. Is vanishing of the $\alpha$-invariant of W a sufficient condition for $\mathcal {S}\mathcal {E}(W)$ to be homotopic to the identity on $\mathcal {R}^+(M)$?

If the answer to Question 3.36 were yes, we would get the following diagram.