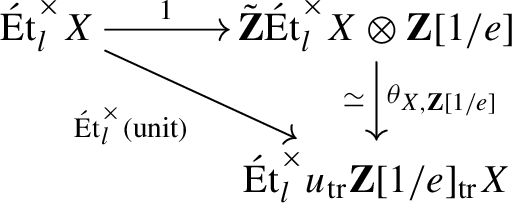The étale symmetric Künneth theorem

Abstract

Let k be an algebraically closed field, $l\ne {{\,\textrm{char}\,}}k$ a prime number, and X a quasi-projective scheme over k. We show that the étale homotopy type of the dth symmetric power of X is $\textbf{Z}/l$-homologically equivalent to the dth strict symmetric power of the étale homotopy type of X. We deduce that the $\textbf{Z}/l$-local étale homotopy type of a motivic Eilenberg–Mac Lane space is an ordinary Eilenberg–Mac Lane space.

1 Introduction

In the first part of this paper we show that the étale homotopy type of the dth symmetric power of a quasi-projective scheme X over a separably closed field k is $\textbf{Z}/l$-homologically equivalent to the dth symmetric power of the étale homotopy type of X, where $l\ne {{\,\textrm{char}\,}}k$ is any prime. Symbolically,

where $\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}$ is the étale homotopy type, $\textrm{S}^d$ is the dth symmetric power (more precisely the strict symmetric power), and $L_{\textbf{Z}/l}$ is $\textbf{Z}/l$-localization á la Bousfield–Kan. The étale homotopy type $\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}X$ of a scheme X is a pro-space originally defined by Artin and Mazur [1] and later refined by Friedlander [11]. It is characterized by the property that the (nonabelian) étale cohomology of X with constant coefficients coincides with the cohomology of $\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}X$.

The formula (⁎) is related to a theorem of Deligne about the étale cohomology of symmetric powers [2, XVII, Théorème 5.5.21], but there are three significant differences:

• (1) Deligne’s theorem is about cohomology with proper support, and so does not say anything about the cohomology of non-proper schemes.

• (2) We give an equivalence at the level of homotopy types, whereas Deligne only gives an equivalence at the level of cochains.

• (3) Deligne’s theorem works over an arbitrary quasi-compact quasi-separated base and with arbitrary Noetherian torsion coefficients; for our result the base must be a separably closed field whose characteristic is prime to the torsion of the coefficients.

While there may be a relative version of (⁎) over a base, the localization away from the residual characteristics cannot be avoided when dealing with non-proper schemes.

In his proof, after reducing to the case where the base is a field k, Deligne employs Witt vectors to further reduce to the case where k has characteristic zero (concluding with a transcendental argument). In this step it is crucial that X be proper over k. Our arguments are thus necessarily quite different. We use the existence a schematic topology, finer than the étale topology but cohomologically equivalent to it, for which the quotient map $X^d\rightarrow \textrm{S}^d X$ is a covering; this is the qfh topology used extensively by Voevodsky in his work on triangulated categories of motives.

Combining (⁎) with the motivic Dold–Thom theorem, we show that if k is algebraically closed and A is an abelian group on which the characteristic exponent of k acts invertibly, then the $\textbf{Z}/l$-local étale homotopy type of a motivic Eilenberg–Mac Lane space K(A(q), p) is the $\textbf{Z}/l$-localization of an ordinary Eilenberg–Mac Lane space K(A, p).

1.1 Conventions

Throughout this paper, we use the language of $\infty$-categories developed in [24] and [23]. Although our main results can be stated in more classical language, their proofs use the flexibility of higher category theory in an essential way. We warn the reader that this is the default language in this paper, so for example the word “colimit” always means “homotopy colimit”, “unique” means “unique up to a contractible space of choices”, etc. We will use the following notation:

• $\mathcal S$ is the $\infty$-category of small $\infty$-groupoids, which we also call spaces;

• $\mathcal {S}\textrm{et}_\Delta$ is the category of simplicial sets;

• $\mathcal T\textrm{op}_\infty$ is the $\infty$-category of $\infty$-topoi and geometric morphisms [24, §6.3];

• $\mathcal C_{\le n}$ is the subcategory of n-truncated objects in an $\infty$-category $\mathcal C$;

• $\mathcal C^\omega$ is the subcategory of compact objects in an $\infty$-category $\mathcal C$ with filtered colimits;

• ${\textrm{h}}\mathcal C$ is the homotopy 1-category of an $\infty$-category $\mathcal C$;

• $\mathcal X^\wedge$ is the hypercompletion of an $\infty$-topos $\mathcal X$ [24, §6.5.2].

1.2 Historical note

The first draft of this paper was written in 2011 as a step towards the computation of the motivic Steenrod algebra in positive characteristic. Afterwards I realized that the technology of étale homotopy types could be avoided completely using the Bloch–Kato conjecture, which was the approach taken in [16]. Since I had no other application in mind I did not attempt to turn this draft into a publishable paper. More recently however, the main result of this paper was used by Zargar [31] to compute the weight 0 homotopy groups of the motivic sphere spectrum in positive characteristic. Given this new application, it seemed important that this paper be published after all. I want to thank Chuck Weibel for encouraging me to finally take this paper out of its draft state.

2 Homotopy types of schemes

Let $\tau$ be a pretopology on the category of schemes (in the sense of [2, II, Définition 1.3]). If X is a scheme, the small $\tau$-site of X is the full subcategory of ${\mathcal S}\textrm{ch}_X$ spanned by the members of the $\tau$-coverings of X and equipped with the Grothendieck topology induced by $\tau$ (we assume that this is an essentially small category). We denote by $X_\tau$ the $\infty$-topos of sheaves of spaces on the small $\tau$-site of X. The assignment $X\mapsto X_\tau$ is functorial: a morphism of schemes $f:X\rightarrow Y$ induces a geometric morphism of $\infty$-topoi $f_*:X_\tau \rightarrow Y_\tau$ given by $f_*(\mathcal F)(U)=\mathcal F(U\times _YX)$.

Recall that the functor $\mathcal S\rightarrow \mathcal T\textrm{op}_\infty$ associating to an $\infty$-groupoid its classifying $\infty$-topos admits a pro-left adjoint $\Pi _\infty :\mathcal T\textrm{op}_\infty \rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)$ associating to any $\infty$-topos its shape (see [24, §7.1.6] or [15]). The $\tau$-homotopy type $\Pi _\infty ^\tau X$ of a scheme X is the shape of the $\infty$-topos $X_\tau$:

$$\begin{aligned} \Pi _\infty ^\tau X=\Pi _\infty (X_\tau ). \end{aligned}$$

This construction defines a functor $\Pi _\infty ^\tau :{\mathcal S}\textrm{ch}\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)$.

Let $\mathcal X$ be an $\infty$-topos and let $c:\mathcal S\rightarrow \mathcal X$ be the constant sheaf functor. By definition of the shape, we have ${{\,\textrm{Map}\,}}_{\mathcal X}(*,cK)\simeq {{\,\textrm{Map}\,}}_{{{\,\textrm{Pro}\,}}(\mathcal S)}(\Pi _\infty \mathcal X, K)$ for every $K\in \mathcal S$. In particular, the cohomology of $\mathcal X$ with coefficients in an abelian group can be computed as the continuous cohomology of the pro-space $\Pi _\infty \mathcal X$. If $\mathcal X$ is locally connected (i.e., if for every $X\in \mathcal X$ the pro-set $\pi _0\Pi _\infty (\mathcal X_{/X})$ is constant), we have more generally that the category ${{\,\textrm{Fun}\,}}(\Pi _\infty \mathcal X,\mathcal {S}\textrm{et})$ of discrete local systems on $\Pi _\infty \mathcal X$ is equivalent to the category of locally constant sheaves of sets on $\mathcal X$ [15, Theorem 3.13], and, if $\mathcal A$ is such a sheaf of abelian groups, then $H^*(\mathcal X,\mathcal A)$ coincides with the continuous cohomology of the pro-space $\Pi _\infty \mathcal X$ with coefficients in the corresponding local system [15, Proposition 2.15].

Remark 1.1

In the definition of $\Pi _\infty ^\tau X$, we could have used any $\tau$-site of X-schemes containing the small one. For if $X_{\tau }'$ is the resulting $\infty$-topos of sheaves, the canonical geometric morphism $X_\tau \rightarrow X_{\tau }'$ is obviously a shape equivalence. It follows that the functor $\Pi _\infty ^\tau$ depends only on the Grothendieck topology induced by $\tau$.

Remark 1.2

For schemes over a fixed base scheme S, we can define in the same way a relative version of the $\tau$-homotopy type functor taking values in the $\infty$-category ${{\,\textrm{Pro}\,}}(S_\tau )$.

Remark 1.3

Let $X_\tau ^\wedge$ be the hypercompletion of $X_\tau$. By the generalized Verdier hypercovering theorem [9, Theorem7.6(b)] $\Pi _\infty (X_\tau ^\wedge )$ is corepresented by the simplicially enriched diagram $\Pi _0:\textrm{HC}_\tau (X)\rightarrow \mathcal {S}\textrm{et}_\Delta$ where $\textrm{HC}_\tau (X)$ is the cofiltered simplicial category of $\tau$-hypercovers of X and $\Pi _0(U_\bullet )$ is the simplicial set that has in degree n the colimit of the presheaf $U_n$. See [15, §5] for details.

Remark 1.4

When $\tau ={{\acute{\textrm{e}}}\textrm{t}}$ is the étale pretopology and X is locally Noetherian, $\Pi _\infty (X_{{\acute{\textrm{e}}}\textrm{t}}^\wedge )$ is corepresented by the étale topological type defined by Friedlander [11, §4]. This follows easily from Remark 1.3.

Lemma 1.5

Let U be a diagram in the small $\tau$-site of a scheme X whose colimit in $X_\tau$ is X. Then $\Pi _\infty ^\tau X$ is the colimit of the diagram of pro-spaces $\Pi _\infty ^\tau U$.

Proof

By [24, Proposition 6.3.5.14], the $\infty$-topos $X_\tau$ is the colimit in $\mathcal T\textrm{op}_\infty$ of the diagram of $\infty$-topoi $U_\tau$. Since $\Pi _\infty :\mathcal T\textrm{op}_\infty \rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)$ is left adjoint, it preserves this colimit. $\square$

Remark 1.6

Similarly, if $U_\bullet \rightarrow X$ is a representable $\tau$-hypercover of X, then it is a colimit diagram in $X_\tau ^\wedge$, so that $\Pi _\infty (X_\tau ^\wedge )$ is the colimit of the simplicial pro-space $\Pi _\infty ((U_\bullet )_\tau ^\wedge )$. The trivial proof of this fact can be compared with the rather technical proof of [18, Theorem 3.4],, which is the special case $\tau ={{\acute{\textrm{e}}}\textrm{t}}$. This is a good example of the usefulness of the topos-theoretic definition of the shape.

3 Strict symmetric powers in $\infty$-categories

If X is a CW complex, its dth symmetric power $\textrm{S}^dX$ is the set of orbits of the action of the symmetric group $\Sigma _d$ on $X^d$, endowed with the quotient topology. Even though the action of $\Sigma _d$ on $X^d$ is not free, it is well known that the homotopy type of $\textrm{S}^d X$ is an invariant of the homotopy type of X. More generally, if G is a group acting on a CW complex X, the orbit space X/G can be written as the homotopy colimit

$$\begin{aligned} X/G\simeq \mathop {\textrm{hocolim}}\limits _{H\in \mathcal O(G)^\textrm{op}}X^H, \end{aligned}$$

(2.1)

where $\mathcal O(G)$ is the orbit category of G (whose objects are the subgroups of G and whose morphisms are the G-equivariant maps between the corresponding quotients) and $X^H$ is the subspace of H-fixed points [10, Chapter 4, Lemma A.3],. In the case of the symmetric group $\Sigma _d$ acting on $X^d$, if H is a subgroup of $\Sigma _d$, then $(X^d)^H\simeq X^{o(H)}$ where o(H) is the set of orbits of the action of H on $\{1,\dotsc ,d\}$ and where the factor of $X^{o(H)}$ indexed by an orbit $\{i_1,\dotsc , i_r\}$ is sent diagonally into the corresponding r factors of $X^d$. The formula (2.1) becomes

$$\begin{aligned} \textrm{S}^d X\simeq \mathop {\textrm{hocolim}}\limits _{H\in \mathcal O(\Sigma _d)^\textrm{op}}X^{o(H)}. \end{aligned}$$

This shows that $\textrm{S}^d$ preserves homotopy equivalences between CW complexes. In particular, it induces a functor $\textrm{S}^d$ from the $\infty$-category of spaces to itself.

This motivates the following definition:

Definition 2.2

Let $\mathcal C$ be an $\infty$-category with colimits and finite products and $d\ge 0$ an integer. The dth strict symmetric power of $X\in \mathcal C$ is

$$\begin{aligned} \textrm{S}^d X = \mathop {\textrm{colim}}\limits _{H\in \mathcal O(\Sigma _d)^\textrm{op}}X^{o(H)}. \end{aligned}$$

We will relate strict symmetric powers to the notion of strictly commutative monoid in Sect. 7. Note that $\textrm{S}^0X$ is a final object of $\mathcal C$ and that $\textrm{S}^1 X\simeq X$. For example, in an $\infty$-category of sheaves of spaces on a site, $\textrm{S}^d$ is computed by applying $\textrm{S}^d$ objectwise and sheafifying the result, and in a 1-category it is the usual symmetric power, namely the coequalizer of the action groupoid $\Sigma _d\times X^d\rightrightarrows X^d$. We note that any functor that preserves colimits and finite products commutes with $\textrm{S}^d$.

Remark 2.3

If the product in $\mathcal C$ preserves sifted colimits in each variable (for example, if $\mathcal C$ is cartesian closed or projectively generated), it follows from [24, Lemma 5.5.8.11] that the functor $\textrm{S}^d:\mathcal C\rightarrow \mathcal C$ preserves sifted colimits. In particular, $\textrm{S}^d:\mathcal S\rightarrow \mathcal S$ is the left Kan extension of the functor $\textrm{S}^d:\mathcal F\textrm{in}\rightarrow \mathcal F\textrm{in}$, where $\mathcal F\textrm{in}$ is the category of finite sets.

Remark 2.4

More generally, one has a strict symmetric power $\textrm{S}^\varphi X$ for any group homomorphism $\varphi :G\rightarrow \Sigma _d$:

$$\begin{aligned} \textrm{S}^\varphi X = \mathop {\textrm{colim}}\limits _{H\in \mathcal O(G)^\textrm{op}}X^{o(H)}. \end{aligned}$$

Lemma 2.5

Let $\mathcal X$ be an $\infty$-topos. Then the inclusion $\mathcal X_{\le 0}\hookrightarrow \mathcal X$ of the subcategory of discrete objects preserves strict symmetric powers.

Proof

This is true if $\mathcal X=\mathcal S$ since symmetric powers preserve discrete CW complexes, hence if $\mathcal X$ is a presheaf $\infty$-topos. It remains to observe that if $a:\mathcal X\rightarrow \mathcal Y$ is a left exact localization and the result is true in $\mathcal X$, then it is true in $\mathcal Y$: this follows from the fact that a preserves 0-truncated objects [24, Proposition 5.5.6.16]. $\square$

4 Homological localizations of pro-spaces

Let ${{\,\textrm{Pro}\,}}(\mathcal S)$ denote the $\infty$-category of pro-spaces. Recall that this is the $\infty$-category freely generated by $\mathcal S$ under cofiltered limits and that it is equivalent to the full subcategory of ${{\,\textrm{Fun}\,}}(\mathcal S,\mathcal S)^\textrm{op}$ spanned by accessible left exact functors [22, Proposition 3.1.6]. Any such functor is equivalent to $Y\mapsto \mathop {\textrm{colim}}\limits _{i\in I}{{\,\textrm{Map}\,}}(X_i,Y)$ for some small cofiltered diagram $X:I\rightarrow \mathcal S$. Moreover, combining [24, Proposition 5.3.1.16] and the proof of [2, Proposition 8.1.6], we can always find such a corepresentation where I is a cofiltered poset such that, for each $i\in I$, there are only finitely many j with $i\le j$; such a poset is called cofinite.

In [19], Isaksen constructs a proper model structure on the category ${{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$ of pro-simplicial sets, called the strict model structure, with the following properties:

• a pro-simplicial set X is fibrant if and only if it is isomorphic to a diagram $(X_s)_{s\in I}$ such that I is a cofinite cofiltered poset and $X_s\rightarrow \lim _{s<t}X_t$ is a Kan fibration for all $s\in I$;

• the inclusion $\mathcal {S}\textrm{et}_\Delta \hookrightarrow {{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$ is a left Quillen functor;

• it is a simplicial model structure with simplicial mapping sets defined by

  $$\begin{aligned}{{\,\textrm{Map}\,}}_\Delta (X,Y)={{\,\textrm{Hom}\,}}(X\times \Delta ^\bullet ,Y).\end{aligned}$$

Denote by ${{\,\textrm{Pro}\,}}'(\mathcal S)$ the $\infty$-category associated to this model category, and by $c:\mathcal S\rightarrow {{\,\textrm{Pro}\,}}'(\mathcal S)$ the left derived functor of the inclusion $\mathcal {S}\textrm{et}_\Delta \hookrightarrow {{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$. Since ${{\,\textrm{Pro}\,}}'(\mathcal S)$ admits cofiltered limits, there is a unique functor $\varphi :{{\,\textrm{Pro}\,}}(\mathcal S)\rightarrow {{\,\textrm{Pro}\,}}'(\mathcal S)$ that preserves cofiltered limits and such that $\varphi \circ j\simeq c$, where $j:\mathcal S\hookrightarrow {{\,\textrm{Pro}\,}}(\mathcal S)$ is the Yoneda embedding.

Lemma 3.1

$\varphi :{{\,\textrm{Pro}\,}}(\mathcal S)\rightarrow {{\,\textrm{Pro}\,}}'(\mathcal S)$ is an equivalence of $\infty$-categories.

Proof

Let $X\in {{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$ be fibrant. Then X is isomorphic to a diagram $(X_s)$ indexed by a cofinite cofiltered poset and such that $X_s\rightarrow \lim _{s<t}X_t$ is a Kan fibration for all s, and so, for all $Z\in {{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$, ${{\,\textrm{Map}\,}}_\Delta (Z,X_s)\rightarrow \lim _{s<t}{{\,\textrm{Map}\,}}_\Delta (Z,X_t)$ is a Kan fibration. It follows that the limit ${{\,\textrm{Map}\,}}_\Delta (Z,X)\simeq \lim _s{{\,\textrm{Map}\,}}_\Delta (Z,X_s)$ in $\mathcal {S}\textrm{et}_\Delta$ is in fact a limit in $\mathcal S$, so that $X\simeq \lim _s c(X_s)$ in ${{\,\textrm{Pro}\,}}'(\mathcal S)$. This shows that $\varphi$ is essentially surjective.

Let $X\in {{\,\textrm{Pro}\,}}(\mathcal S)$ and choose a corepresentation $X:I\rightarrow \mathcal S$ where I is a cofinite cofiltered poset. Using the model structure on $\mathcal {S}\textrm{et}_\Delta$, X can be strictified to a diagram $X':I\rightarrow \mathcal {S}\textrm{et}_\Delta$ such that $X'_s\rightarrow \lim _{s<t} X'_t$ is a Kan fibration for all $s\in I$. By the first part of the proof, we then have $X'\simeq \lim _s c(X'_s)$ in ${{\,\textrm{Pro}\,}}'(\mathcal S)$, whence $\varphi X\simeq X'$. Given also $Y\in {{\,\textrm{Pro}\,}}(\mathcal S)$, we have

$$\begin{aligned} {{\,\textrm{Map}\,}}(X',Y')\simeq \lim _t{{\,\textrm{Map}\,}}(X',cY'_t)\simeq \mathop {\textrm{holim}}\limits _t{{\,\textrm{Map}\,}}_\Delta (X',Y'_t)\simeq \lim _t\mathop {\textrm{colim}}\limits _s{{\,\textrm{Map}\,}}(X'_s,Y'_t), \end{aligned}$$

where in the last step we used that filtered colimits of simplicial sets are always colimits in $\mathcal S$. This shows that $\varphi$ is fully faithful. $\square$

Let $\mathcal S_{<\infty }\subset \mathcal S$ be the $\infty$-category of truncated spaces. A pro-truncated space is a pro-object in $\mathcal S_{<\infty }$. It is clear that the full embedding ${{\,\textrm{Pro}\,}}(\mathcal S_{<\infty })\hookrightarrow {{\,\textrm{Pro}\,}}(\mathcal S)$ admits a left adjoint

$$\begin{aligned} \tau _{<\infty }:{{\,\textrm{Pro}\,}}(\mathcal S)\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S_{<\infty }) \end{aligned}$$

that preserves cofiltered limits and sends a constant pro-space to its Postnikov tower; it also preserves finite products since truncations do. The $\tau _{<\infty }$-equivalences in ${{\,\textrm{Pro}\,}}(\mathcal S_*^{\ge 1})$ are precisely those maps that become $\natural$-isomorphisms in ${{\,\textrm{Pro}\,}}({\textrm{h}}\mathcal S_*^{\ge 1})$ in the sense of Artin and Mazur [1, Definition 4.2].

Remark 3.2

The model structure on ${{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$ defined in [17] is the left Bousfield localization of the strict model structure at the class of $\tau _{<\infty }$-equivalences. It is therefore a model for the $\infty$-category ${{\,\textrm{Pro}\,}}(\mathcal S_{<\infty })$ of pro-truncated spaces.

Let R be a commutative ring. A morphism $f:X\rightarrow Y$ in ${{\,\textrm{Pro}\,}}(\mathcal S)$ is called an R-homological equivalence (resp. an R-cohomological equivalence) if it induces an equivalence of homology pro-groups $H_*(X,R)\simeq H_*(Y,R)$ (resp. an equivalence of cohomology groups $H^*(Y,R)\simeq H^*(X,R)$). By [20, Proposition 5.5], f is an R-homological equivalence if and only if it induces isomorphisms in cohomology with coefficients in arbitrary R-modules. A pro-space X is called R-local if it is local with respect to the class of R-homological equivalences, i.e., if for every R-homological equivalence $Y\rightarrow Z$ the induced map ${{\,\textrm{Map}\,}}(Z,X)\rightarrow {{\,\textrm{Map}\,}}(Y,X)$ is an equivalence in $\mathcal S$. A pro-space is called R-profinite¹ if it is local with respect to the class of R-cohomological equivalences. We denote by ${{\,\textrm{Pro}\,}}(\mathcal S)_R$ (resp. ${{\,\textrm{Pro}\,}}(\mathcal S)^R$) the $\infty$-category of R-local (resp. R-profinite) pro-spaces.

The characterization of R-homological equivalences in terms of cohomology shows that any $\tau _{<\infty }$-equivalence is an R-homological equivalence. We thus have a chain of full embeddings

$$\begin{aligned} {{\,\textrm{Pro}\,}}(\mathcal S)^R\subset {{\,\textrm{Pro}\,}}(\mathcal S)_R\subset {{\,\textrm{Pro}\,}}(\mathcal S_{<\infty })\subset {{\,\textrm{Pro}\,}}(\mathcal S). \end{aligned}$$

Proposition 3.3

The inclusions ${{\,\textrm{Pro}\,}}(\mathcal S)_R\subset {{\,\textrm{Pro}\,}}(\mathcal S)$ and ${{\,\textrm{Pro}\,}}(\mathcal S)^R\subset {{\,\textrm{Pro}\,}}(\mathcal S)$ admit left adjoints $L_R$ and $L^R$. Moreover, $L_R$ preserves finite products.

Proof

The existence of the localization functors $L_R$ and $L^R$ follows from Lemma 3.1 and the existence of the corresponding left Bousfield localizations of the strict model structure on ${{\,\textrm{Pro}\,}}(\mathcal {S}\textrm{et}_\Delta )$ [20, Theorems 6.3 and 6.7]. We also give a self-contained proof in Proposition 3.7 below. For the last statement, we must show that the canonical map

$$\begin{aligned} L_R(X\times Y) \rightarrow L_R(X) \times L_R(Y) \end{aligned}$$

is an equivalence for all $X,Y\in {{\,\textrm{Pro}\,}}(\mathcal S)$. Since both sides are R-local, it suffices to show that this map an R-homological equivalence. By definition of $L_R$, the canonical map $C_*(X,R)\rightarrow C_*(L_RX,R)$ induces an isomorphism on homology pro-groups. Since $C_*(-,R):\mathcal S\rightarrow \mathcal D(R)_{\ge 0}$ is a symmetric monoidal functor, we have a natural equivalence

$$\begin{aligned} C_*(X\times Y,R) \simeq C_*(X,R) \otimes _R C_*(Y,R) \end{aligned}$$

in the $\infty$-category ${{\,\textrm{Pro}\,}}(\mathcal D(R)_{\ge 0})$. Since $C_*(X,R)\rightarrow C_*(L_R(X),R)$ is a pro-homology isomorphism by definition of $L_R$, it remains to show that the tensor product in ${{\,\textrm{Pro}\,}}(\mathcal D(R)_{\ge 0})$ preserves pro-homology isomorphisms. A morphism in ${{\,\textrm{Pro}\,}}(\mathcal D(R)_{\ge 0})$ is a pro-homology isomorphism if and only if it induces an equivalence on n-truncations for all n, so the claim follows from the fact that the canonical map $M\otimes _RN \rightarrow \tau _{\le n}M\otimes _R \tau _{\le n} N$ is a $\tau _{\le n}$-equivalence for all $M,N\in \mathcal D(R)_{\ge 0}$. $\square$

The fact that $L_R$ preserves finite products is very useful and we will use it often. It implies in particular that $L_R$ preserves commutative monoids and commutes with the formation of strict symmetric powers. Here is another consequence:

Corollary 3.4

Finite products distribute over finite colimits in ${{\,\textrm{Pro}\,}}(\mathcal S)_R$.

Proof

Finite colimits are universal in ${{\,\textrm{Pro}\,}}(\mathcal S)$, i.e., are preserved by any base change (since pushouts and pullbacks can be computed levelwise). The result follows using that $L_R$ preserves finite products. $\square$

Remark 3.5

Let $\mathcal X$ be an $\infty$-topos and let $\mathcal X^\wedge$ be its hypercompletion. The geometric morphism $\mathcal X^\wedge \rightarrow \mathcal X$ induces an equivalence of pro-truncated shapes (since truncated objects are hypercomplete [24, Lemma 6.5.2.9]), and a fortiori also of R-local and R-profinite shapes for any commutative ring R.

Remark 3.6

Let l be a prime number. The Bockstein long exact sequences show that any $\textbf{Z}/l$-cohomological equivalence is also a $\textbf{Z}/l^n$-cohomological equivalence for all $n\ge 1$. In particular, if $\mathcal X$ is an $\infty$-topos, its $\textbf{Z}/l$-profinite shape $L^{\textbf{Z}/l}\Pi _\infty \mathcal X$ remembers the cohomology of $\mathcal X$ with l-adic coefficients.

As shown in [20, Proposition 7.3], if R is solid (e.g., $R=\textbf{Z}/n$ for some integer n) and $X\in \mathcal S$ is connected, then $L_RX$ is the pro-truncation of the Bousfield-Kan R-tower of X [3, I, §4]. It follows that the limit of the pro-space $L_R X$ is the Bousfield-Kan R-completion $R_\infty X$.

The existence of the localization functors $L_R$ and $L^R$ is a special case of a more general result which we now formulate. If $\mathcal C$ is any locally small $\infty$-category, ${{\,\textrm{Pro}\,}}(\mathcal C)^\textrm{op}$ is the full subcategory of ${{\,\textrm{Fun}\,}}(\mathcal C,\mathcal S)$ spanned by small filtered colimits of corepresentable functors [24, Remark 5.3.5.9]. If $\mathcal K$ is any collection of objects of $\mathcal C$, a morphism $X\rightarrow Y$ in ${{\,\textrm{Pro}\,}}(\mathcal C)$ is called a $\mathcal K$-equivalence if it induces equivalences ${{\,\textrm{Map}\,}}(Y,K)\simeq {{\,\textrm{Map}\,}}(X,K)$ for every $K\in \mathcal K$, and an object $Z\in {{\,\textrm{Pro}\,}}(\mathcal C)$ is called $\mathcal K$-local if every $\mathcal K$-equivalence $X\rightarrow Y$ induces an equivalence ${{\,\textrm{Map}\,}}(Y,Z)\simeq {{\,\textrm{Map}\,}}(X,Z)$. Note that $\mathcal K$-equivalences are preserved by cofiltered limits, since $\mathcal K\subset \mathcal C$ and the objects of $\mathcal C$ are cocompact in ${{\,\textrm{Pro}\,}}(\mathcal C)$. We denote by

$$\begin{aligned} {{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}\subset {{\,\textrm{Pro}\,}}(\mathcal C) \end{aligned}$$

the full subcategory of $\mathcal K$-local objects.

Proposition 3.7

Let $\mathcal C$ be a presentable $\infty$-category and $\mathcal K$ a collection of objects of $\mathcal C$. Suppose that $\mathcal K$ is the essential image of an accessible functor. Then the inclusion ${{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}\subset {{\,\textrm{Pro}\,}}(\mathcal C)$ admits a left adjoint. Moreover, ${{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}={{\,\textrm{Pro}\,}}(\widehat{\mathcal K})$ where $\widehat{\mathcal K}\subset \mathcal C$ is the closure of $\mathcal K$ under finite limits.

Proof

With no assumptions on $\mathcal K$, there is an obvious inclusion ${{\,\textrm{Pro}\,}}(\widehat{\mathcal K})\subset {{\,\textrm{Pro}\,}}(\mathcal S)_{\mathcal K}$. If $\mathcal K$ is small, then every functor $\widehat{\mathcal K}\rightarrow \mathcal S$ is a small colimit of corepresentables, so the inclusion ${{\,\textrm{Pro}\,}}(\widehat{\mathcal K})\subset {{\,\textrm{Pro}\,}}(\mathcal C)$ has a left adjoint L given by restricting a functor $\mathcal C\rightarrow \mathcal S$ to $\widehat{\mathcal K}$. If $X\in {{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}$, then the canonical map $X\rightarrow LX$ is a $\mathcal K$-equivalence between $\mathcal K$-local objects, hence it is an equivalence. This proves the proposition when $\mathcal K$ is small.

The proof of the general case follows [20, Proposition6.10]. For any $X\in {{\,\textrm{Pro}\,}}(\mathcal C)$, we must construct a $\mathcal K$-equivalence $X\rightarrow Y$ where Y is $\mathcal K$-local. Suppose that $\mathcal K$ is the essential image of a functor $\varphi :\mathcal L\rightarrow \mathcal C$ that preserves $\kappa$-filtered colimits, where $\mathcal C$ and $\mathcal L$ are $\kappa$-accessible. For $\lambda \gg \kappa$, let $\mathcal K^\lambda =\varphi (\mathcal L^\lambda )$ where $\mathcal L^\lambda \subset \mathcal L$ is the subcategory of $\lambda$-compact objects. Choose $\lambda _0\gg \kappa$ such that X is a cofiltered limit of $\lambda _0$-compact objects of $\mathcal C$, and let $X\rightarrow Y_0$ be the $\mathcal K^{\lambda _0}$-localization of X. Inductively, choose $\lambda _n\gg \lambda _{n-1}$ such that $Y_{n-1}$ is a cofiltered limit of $\lambda _{n}$-compact objects, and let $X\rightarrow Y_n$ be the $\mathcal K^{\lambda _n}$-localization of X. Finally, let $Y=\lim _n Y_n$. Then Y is $\mathcal K$-local, and it remains to show that the induced map $X\rightarrow Y$ is a $\mathcal K$-equivalence.

Let $K\in \mathcal K$ be the image of $L\in \mathcal L$. For any $n\ge 0$, let $\mathcal L_n$ be the $\lambda _n$-filtered $\infty$-category $(\mathcal L^{\lambda _n})_{/L}$. Since $\varphi$ preserves $\lambda _n$-filtered colimits, K is the colimit of $\varphi |\mathcal L_n$ for any n. The conclusion now follows by evaluating the colimit

$$\begin{aligned} \mathop {\textrm{colim}}\limits _{m,n}\mathop {\textrm{colim}}\limits _{A\in \mathcal L_n}{{\,\textrm{Map}\,}}(Y_m, \varphi (A)) \end{aligned}$$

in two ways. Setting $m=n$, we have

$$\begin{aligned} \mathop {\textrm{colim}}\limits _n \mathop {\textrm{colim}}\limits _{A\in \mathcal L_n}{{\,\textrm{Map}\,}}(Y_n, \varphi (A)) \simeq \mathop {\textrm{colim}}\limits _n \mathop {\textrm{colim}}\limits _{A\in \mathcal L_n}{{\,\textrm{Map}\,}}(X, \varphi (A))\simeq {{\,\textrm{Map}\,}}(X,K), \end{aligned}$$

since $X\rightarrow Y_n$ is a $\mathcal K^{\lambda _n}$-equivalence and X is a cofiltered limit of $\lambda _n$-compact objects for any n. Setting $m=n-1$, we have

$$\begin{aligned} \mathop {\textrm{colim}}\limits _n\mathop {\textrm{colim}}\limits _{A\in \mathcal L_n}{{\,\textrm{Map}\,}}(Y_{n-1},\varphi (A)) \simeq \mathop {\textrm{colim}}\limits _n {{\,\textrm{Map}\,}}(Y_{n-1},K) \simeq {{\,\textrm{Map}\,}}(Y,K), \end{aligned}$$

since $Y_{n-1}$ is a cofiltered limit of $\lambda _n$-compact objects. This concludes the proof of the existence of the left adjoint. By construction, Y is in fact $\mathcal K^\lambda$-local for any large enough $\lambda \gg \kappa$, so we have also proved that

$$\begin{aligned} {{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}=\bigcup _{\lambda \gg \kappa }{{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K^\lambda }. \end{aligned}$$

This implies that ${{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}\subset {{\,\textrm{Pro}\,}}(\widehat{\mathcal K})$, since we already know it when $\mathcal K$ is small. $\square$

Proposition 3.7 applies in particular whenever $\mathcal K$ is small. For example, if $\mathcal K$ is the collection of Eilenberg–Mac Lane spaces K(R, n) with $n\ge 0$, then ${{\,\textrm{Pro}\,}}(\mathcal S)_{\mathcal K}={{\,\textrm{Pro}\,}}(\mathcal S)^R$. Proposition 3.7 also applies with $\mathcal K$ the collection of Eilenberg–Mac Lane spaces K(M, n) for M any R-module and $n\ge 0$, this being the image of a filtered-colimit-preserving functor from a countable disjoint union of copies of the category of R-modules. In this case, ${{\,\textrm{Pro}\,}}(\mathcal S)_{\mathcal K}={{\,\textrm{Pro}\,}}(\mathcal S)_R$.

Remark 3.8

If l is a prime number, the spaces that can be obtained from the Eilenberg–Mac Lane spaces $K(\textbf{Z}/l,n)$ using finite limits are precisely the truncated spaces with finite $\pi _0$ and whose homotopy groups are finite l-groups. Hence, ${{\,\textrm{Pro}\,}}(\mathcal S)^{\textbf{Z}/l}$ coincides with the $\infty$-category of l-profinite spaces studied in [22, §3].

Lemma 3.9

Let $\mathcal C$ be a presentable $\infty$-category, let $(\mathcal K_\alpha )_\alpha$ be a small filtered diagram of collections of objects of $\mathcal C$ satisfying the assumption of Proposition 3.7, and let $\mathcal K=\bigcup _\alpha \mathcal K_\alpha$. Then the localization functors induce an equivalence

$$\begin{aligned} {{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K} \simeq \lim _\alpha {{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K_\alpha }. \end{aligned}$$

Proof

Note that $\mathcal K$ also satisfies the assumption of Proposition 3.7, so that ${{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K}={{\,\textrm{Pro}\,}}(\widehat{\mathcal K})$. Since $\widehat{\mathcal K}=\mathop {\textrm{colim}}\limits _\alpha \widehat{\mathcal K}{}_\alpha$, we have an equivalence

$$\begin{aligned} {{\,\textrm{Fun}\,}}(\widehat{\mathcal K},\mathcal S)\simeq \lim _\alpha {{\,\textrm{Fun}\,}}(\widehat{\mathcal K}{}_\alpha ,\mathcal S), \end{aligned}$$

which implies that the functor ${{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K} \rightarrow \lim _\alpha {{\,\textrm{Pro}\,}}(\mathcal C)_{\mathcal K_\alpha }$ is fully faithful. It remains to show that a functor $F:\widehat{\mathcal K}\rightarrow \mathcal S$ is a small filtered colimit of corepresentables if each of its restrictions $F|\widehat{\mathcal K}{}_\alpha$ is. This is true since $F\simeq \mathop {\textrm{colim}}\limits _\alpha F_\alpha$ where $F_\alpha$ is the left Kan extension of $F|\widehat{\mathcal K}{}_\alpha$ to $\widehat{\mathcal K}$. $\square$

For $n\ge 0$, we define ${{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_R$ to be the subcategory of $\mathcal K$-local objects in ${{\,\textrm{Pro}\,}}(\mathcal S)$ where $\mathcal K$ is the collection of Eilenberg–Mac Lane spaces K(M, i) with M an R-module and $0\le i\le n$. Since $\mathcal K$ consists of n-truncated R-local objects, we have²

$$\begin{aligned} {{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_R \subset {{\,\textrm{Pro}\,}}(\mathcal S_{\le n})\cap {{\,\textrm{Pro}\,}}(\mathcal S)_R. \end{aligned}$$

By Proposition 3.7, the inclusion ${{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_R\subset {{\,\textrm{Pro}\,}}(\mathcal S)$ admits a left adjoint $L_{R,\le n}$. We define ${{\,\textrm{Pro}\,}}(\mathcal S_{\le n})^R$ and the localization functor $L^R_{\le n}$ similarly (using only the R-module R). By Lemma 3.9, the localization functors $L_{R,\le n}$ induce an equivalence

$$\begin{aligned} {{\,\textrm{Pro}\,}}(\mathcal S)_R \simeq \lim _n {{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_R \end{aligned}$$

(3.10)

and similarly for ${{\,\textrm{Pro}\,}}(\mathcal S)^R$.

The following proposition shows that the localizations $L_R$ and $L^R$ agree in many cases of interest, partially answering [20, Question 11.2].

Proposition 3.11

Let F be a prime field and let X be a pro-space whose F-homology pro-groups are pro-finite-dimensional vector spaces. Then $L_FX$ is F-profinite. In other words, the canonical map $L_FX\rightarrow L^FX$ is an equivalence.

Proof

First we claim that any F-profinite pro-space with profinite $\pi _0$ satisfies the given condition on X. Such a pro-space is a cofiltered limit of spaces with finite $\pi _0$ that are obtained from K(F, n)’s using finite limits. By [3, Proposition 5.3], each connected component of such a space is obtained from the point by a finite sequence of principal fibrations with fibers K(F, n) with $n\ge 1$. Using Eilenberg–Moore [22, Corollary 1.1.10], it thus suffices to show that $H^m(K(F,n),F)$ is finite-dimensional for every $m\ge 0$ and $n\ge 1$, which is a well-known computation. Thus, both X and $L^FX$ have pro-finite-dimensional F-homology pro-groups. It follows that the canonical map $X\rightarrow L^FX$ induces an isomorphism on F-cohomology ind-groups, whence on F-homology pro-groups. $\square$

Remark 3.12

It is clear that the class of pro-spaces X satisfying the hypothesis of Proposition 3.11 is preserved by $L_F$, retracts, finite products, and finite colimits (it suffices to verify the latter for pushouts).

Proposition 3.13

Let F be a prime field and let X be a pro-space whose F-homology pro-groups in degrees $\le n$ are pro-finite-dimensional vector spaces. Then the canonical map $L_{F,\le n}X\rightarrow L^F_{\le n}X$ is an equivalence. Furthermore, $L_{F,\le n}$ preserves finite products of such pro-spaces.

Proof

As in the proof of Proposition 3.11, $L^F_{\le n}X$ has pro-finite-dimensional F-homology pro-groups, hence the canonical map $X\rightarrow L^F_{\le n}X$ induces an isomorphism on F-cohomology ind-groups in degrees $\le n$. Since these groups are finite-dimensional F-vector spaces, this remains true for cohomology with coefficients in any F-vector space, which implies the first statement. For the second statement, we must show that the canonical map

$$\begin{aligned} X\times Y \rightarrow L_{\le n}^FX \times L_{\le n}^F Y \end{aligned}$$

induces an isomorphism on F-cohomology in degrees $\le n$. Since F is a field, we have an isomorphism of graded pro-vector spaces $H_*(X\times Y,F)\simeq H_*(X,F)\otimes _F H_*(Y,F)$, which are pro-finite-dimensional in degrees $\le n$. Dualizing and taking the colimit, we find that

$$\begin{aligned} H^m(X\times Y, F) \simeq \bigoplus _{r+s=m}H^r(X,F) \otimes H^s(Y,F) \end{aligned}$$

for any $m\le n$. The same formula applies to $L_{\le n}^FX$ and $L_{\le n}^FY$. By definition of $L_{\le n}^F$, we have $H^m(X,F)\simeq H^m(L_{\le n}^FX,F)$ for all $m\le n$ and similarly for Y, so we are done. $\square$

5 The h and qfh topologies

Let X be a Noetherian scheme. An h covering of X is a finite family $\{U_i\rightarrow X\}$ of morphisms of finite type such that the induced morphism $\coprod _i U_i\rightarrow X$ is universally submersive (a morphism of schemes $f:Y\rightarrow X$ is submersive if it is surjective and if the underlying topological space of X has the quotient topology). If in addition each $U_i\rightarrow X$ is quasi-finite, it is a qfh covering. These notions of coverings define pretopologies on Noetherian schemes which we denote by h and qfh, respectively. The h and qfh topologies are both finer than the fppf topology, and they are not subcanonical.

Proposition 4.1

Let X be a Noetherian scheme.

• (1) The canonical map $\Pi _\infty ^{\textrm{qfh}}X\rightarrow \Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}X$ induces an isomorphism in cohomology with any local system of abelian coefficients. In particular, for any commutative ring R,

  $$\begin{aligned} L_{R}\Pi _\infty ^{\textrm{qfh}}X\simeq L_{R}\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}X. \end{aligned}$$

• (2) If X is excellent, the canonical map $\Pi _\infty ^{\textrm{h}}X\rightarrow \Pi _\infty ^{\textrm{qfh}}X$ induces an isomorphism in cohomology with any local system of torsion abelian coefficients. In particular, for any torsion commutative ring R,

  $$\begin{aligned} L_{R}\Pi _\infty ^{\textrm{h}}X\simeq L_{R}\Pi _\infty ^{\textrm{qfh}}X. \end{aligned}$$

Proof

Recall that the cohomology of $\Pi _\infty \mathcal X$ with coefficients in a local system coincides with the cohomology of $\mathcal X$ with coefficients in the associated locally constant sheaf (see Sect. 1). The first statements are thus translations of [29, Theorem 3.4.4] and [29, Theorem 3.4.5], respectively (the excellence of X is a standing assumption in loc. cit., but it is not used in the proof of (1); see also [28, §10] for self-contained proofs). The statements about the R-local shapes follow immediately, since $L_R$ inverts morphisms that induce isomorphisms in cohomology with coefficients in any R-module (see Sect. 3). $\square$

Remark 4.2

Voevodsky’s proof also shows that $H^1_{{\acute{\textrm{e}}}\textrm{t}}(X,G)\simeq H^1_{\textrm{qfh}}(X,G)$ for any locally constant étale sheaf of groups G. It follows from [17, Proposition 18.4] (and Remark 3.2) that $\Pi _\infty ^{\textrm{qfh}}X\rightarrow \Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}X$ is in fact a $\tau _{<\infty }$-equivalence.

For $\mathcal C$ a small $\infty$-category, we denote by $r:\mathcal C\hookrightarrow {{\,\textrm{PSh}\,}}(\mathcal C)$ the Yoneda embedding, and if $\tau$ is a topology on $\mathcal C$, we denote by $r_\tau =a_\tau r$ the $\tau$-sheafified Yoneda embedding.

Lemma 4.3

Let S be a Noetherian scheme and let $\tau \in \{{\textrm{h}},{\textrm{qfh}},{{\acute{\textrm{e}}}\textrm{t}}\}$. Then, for any $n\ge 0$, the image of the Yoneda functor $r_\tau :{\mathcal S}\textrm{ch}_S^{\textrm{ft}}\rightarrow {{\,\textrm{Shv}\,}}_\tau (\mathcal {\mathcal S}\textrm{ch}_S^{\textrm{ft}})_{\le n}$ consists of compact objects.

Proof

The category ${\mathcal S}\textrm{ch}_S^{\textrm{ft}}$ has finite limits and the topology $\tau$ is finitary, and so the $\infty$-topos ${{\,\textrm{Shv}\,}}_\tau ({\mathcal S}\textrm{ch}_S^{\textrm{ft}})$ is locally coherent and coherent. The result now follows from [22, Corollary 2.3.10(1)]. $\square$

The advantage of the qfh topology over the étale topology is that it can often cover singular schemes by smooth schemes. Let us make this explicit in the case of quotients of smooth schemes by finite group actions. We first recall the classical existence result for such quotients.

A groupoid scheme $X_\bullet$ is a simplicial scheme such that, for every scheme Y, ${{\,\textrm{Hom}\,}}(Y,X_\bullet )$ is a groupoid. If P is any property of morphisms of schemes that is stable under base change, we say that $X_\bullet$ has property P if every face map in $X_\bullet$ has property P (of course, it suffices that $d_0:X_1\rightarrow X_0$ have property P).

Lemma 4.4

Let S be a scheme and let $X_\bullet$ be a finite and locally free groupoid scheme over S. Suppose that for any $x\in X_0$, $d_1(d_0^{-1}(x))$ is contained in an affine open subset of $X_0$ (for example, $X_0$ is quasi-projective over S). Then $X_\bullet$ has a colimiting cone $p:X_\bullet \rightarrow Y$ in the category of S-schemes. Moreover,

• (1) p is integral and surjective, and in particular universally submersive;

• (2) the canonical morphism $X_\bullet \rightarrow {{\,\textrm{cosk}\,}}_0(p)$ is degreewise surjective;

• (3) if S is locally Noetherian and $X_0$ is of finite type over S, then Y is of finite type over S.

Proof

The claim in parentheses follows from [13, Corollaire 4.5.4] and the definition of quasi-projective morphism [13, Définition 5.3.1]. An integral and surjective morphism is universally submersive because integral morphisms are closed [13, Proposition 6.1.10]. The existence of p which is integral and surjective and (2) are proved in [7, III, §2, 3.2] or [8, V, Théorème 4.1]. Part (3) is proved in [8, V,Lemme 6.1(ii)]. $\square$

Proposition 4.5

Let S be a Noetherian scheme and $X_\bullet$ a groupoid scheme of finite type over S as in Lemma 4.4 with colimit Y. Then $r_{\textrm{qfh}}X_\bullet \rightarrow r_{\textrm{qfh}}Y$ is a colimiting cone in ${{\,\textrm{Shv}\,}}_{\textrm{qfh}}({\mathcal S}\textrm{ch}_S^{\textrm{ft}})$.

Proof

By Lemma 4.4, the colimiting cone $X_\bullet \rightarrow Y$ is a qfh hypercover, and it is 2-coskeletal since $X_\bullet$ is a groupoid scheme. Hence, if $\mathcal F$ is a qfh sheaf, we have $\mathcal F(Y)\simeq \lim \mathcal F(X_\bullet )$ by [24, Lemma 6.5.3.9]. $\square$

Corollary 4.6

Let S be a Noetherian scheme and X a quasi-projective S-scheme. Then the Yoneda functor $r_{\textrm{qfh}}:{\mathcal S}\textrm{ch}_S^{\textrm{ft}}\rightarrow {{\,\textrm{Shv}\,}}_{\textrm{qfh}}({\mathcal S}\textrm{ch}_S^{\textrm{ft}})$ preserves strict symmetric powers of X, i.e., it sends the schematic symmetric power $\textrm{S}^dX$ to the sheafy symmetric power $\textrm{S}^dr_{\textrm{qfh}}X$.

Proof

Since the strict symmetric power is the usual symmetric power in a 1-category, we have $r_{\textrm{qfh}}\textrm{S}^d X\simeq \textrm{S}^dr_{\textrm{qfh}}X$ in ${{\,\textrm{Shv}\,}}_{\textrm{qfh}}({\mathcal S}\textrm{ch}_S^{\textrm{ft}})_{\le 0}$ by Proposition 4.5, whence in ${{\,\textrm{Shv}\,}}_{\textrm{qfh}}({\mathcal S}\textrm{ch}_S^{\textrm{ft}})$ by Lemma 2.5. $\square$

Proposition 4.7

Let k be a perfect field and $i:\mathcal C\hookrightarrow {\mathcal S}\textrm{ch}_k^{\textrm{ft}}$ the inclusion of a full subcategory such that every smooth k-scheme is Zariski-locally in $\mathcal C$. Let $i^*:{{\,\textrm{PSh}\,}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})\rightarrow {{\,\textrm{PSh}\,}}(\mathcal C)$ be the restriction functor and let $i_!$ be its left adjoint. For every $\mathcal F\in {{\,\textrm{PSh}\,}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})$, the counit morphism $i_!i^*\mathcal F \rightarrow \mathcal F$ is an $a_{\textrm{h}}^\wedge$-equivalence.

Proof

By a well-known theorem of de Jong [5, Theorem 4.1], every scheme of finite type over a perfect field k is h-locally smooth, hence is h-locally in $\mathcal C$. It follows that there is an induced h topology on $\mathcal C$ whose covering sieves are the restrictions of h-covering sieves in ${\mathcal S}\textrm{ch}_k^{\textrm{ft}}$, or equivalently those sieves that generate an h-covering sieve in ${\mathcal S}\textrm{ch}_k^{\textrm{ft}}$. By the comparison lemma [2, III, Théorème 4.1], the restriction functor $i^*$ and its right adjoint $i_*$ restrict to an equivalence between the subcategories of h sheaves of sets, hence between the $\infty$-categories of hypercomplete h sheaves (since they are the hypercompletions of the associated 1-localic $\infty$-topoi). $\square$

6 The Étale homotopy type of symmetric powers

Proposition 5.1

Let k be a separably closed field, $l\ne {{\,\textrm{char}\,}}k$ a prime number, and X and Y schemes of finite type over k. Let $\tau \in \{{\textrm{h}},{\textrm{qfh}},{{\acute{\textrm{e}}}\textrm{t}}\}$. Then

$$\begin{aligned} L_{\textbf{Z}/l}\Pi _\infty ^\tau (X\times _kY)\simeq L_{\textbf{Z}/l}\Pi _\infty ^\tau X\times L_{\textbf{Z}/l}\Pi _\infty ^\tau Y. \end{aligned}$$

Proof

By Proposition 4.1, it suffices to prove the lemma for $\tau ={{\acute{\textrm{e}}}\textrm{t}}$. Since $L_{\textbf{Z}/l}$ preserves finite products and $X_{{\acute{\textrm{e}}}\textrm{t}}$ and $X_{{\acute{\textrm{e}}}\textrm{t}}^\wedge$ have the same $\textbf{Z}/l$-local shape (see Remark 3.5), it suffices to show that the canonical map

$$\begin{aligned} \Pi _\infty (X\times _kY)_{{\acute{\textrm{e}}}\textrm{t}}^\wedge \rightarrow \Pi _\infty X_{{\acute{\textrm{e}}}\textrm{t}}^\wedge \times \Pi _\infty Y_{{\acute{\textrm{e}}}\textrm{t}}^\wedge \end{aligned}$$

(5.2)

is a $\textbf{Z}/l$-homological equivalence or, equivalently, that it induces an isomorphism in cohomology with coefficients in any $\textbf{Z}/l$-module M. Both sides of (5.2) are corepresented by cofiltered diagrams of simplicial sets having finitely many simplices in each degree (by Remark 1.3 and the fact that any étale hypercovering of a Noetherian scheme is refined by one that is degreewise Noetherian). If K is any such pro-space, $C_*(K,\textbf{Z}/l)$ is a cofiltered diagram of degreewise finite chain complexes of vector spaces. On the one hand, this implies

$$\begin{aligned} C^*(K,M)\simeq C^*(K,\textbf{Z}/l)\otimes M, \end{aligned}$$

so we may assume that $M=\textbf{Z}/l$. On the other hand, it implies that the Küneth map

$$\begin{aligned} H^*(\Pi _\infty X_{{\acute{\textrm{e}}}\textrm{t}}^\wedge ,\textbf{Z}/l)\otimes H^*(\Pi _\infty Y_{{\acute{\textrm{e}}}\textrm{t}}^\wedge ,\textbf{Z}/l)\rightarrow H^*(\Pi _\infty X_{{\acute{\textrm{e}}}\textrm{t}}^\wedge \times \Pi _\infty Y_{{\acute{\textrm{e}}}\textrm{t}}^\wedge ,\textbf{Z}/l) \end{aligned}$$

is an isomorphism. The composition of this isomorphism with the map induced by (5.2) in cohomology is the canonical map

$$\begin{aligned} H^*_{{\acute{\textrm{e}}}\textrm{t}}(X,\textbf{Z}/l)\otimes H^*_{{\acute{\textrm{e}}}\textrm{t}}(Y,\textbf{Z}/l)\rightarrow H^*_{{\acute{\textrm{e}}}\textrm{t}}(X\times _kY,\textbf{Z}/l), \end{aligned}$$

which is also an isomorphism by [6, Th. finitude, Corollaire 1.11]. $\square$

Remark 5.3

Let X be a Noetherian scheme and let $\tau \in \{{\textrm{h}},{\textrm{qfh}},{{\acute{\textrm{e}}}\textrm{t}}\}$. We observed in the proof of Proposition 5.1 that the pro-space $\Pi _\infty (X_\tau ^\wedge )$ is the limit of a cofiltered diagram of spaces whose integral homology groups are finitely generated. It follows from Proposition 3.11 that $L_F\Pi _\infty ^\tau X$ is F-profinite for any prime field F, which answers [20, Question 11.3] quite generally.

Now let $\tau$ and $\sigma$ be pretopologies on ${\mathcal S}\textrm{ch}_S$ with $\tau$ finer than $\sigma$, and let $\mathcal C$ be a small full subcategory of ${\mathcal S}\textrm{ch}_S$ closed under $\sigma$-coverings (but not necessarily under $\tau$-coverings). Then the functor $\Pi _\infty ^\tau :\mathcal C\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)$ takes values in a cocomplete $\infty$-category and is a $\sigma$-cosheaf according to Lemma 1.5, so it lifts uniquely to a left adjoint functor

Remark 5.4

If $\mathcal C$ is such that $\mathcal C_{/X}$ contains the small $\tau$-site of X for any $X\in \mathcal C$, then $\overline{\Pi }{}_\infty ^\tau$ is simply the composition

where for $\mathcal X$ an $\infty$-topos the inclusion $\mathcal X\hookrightarrow \mathcal T\textrm{op}_\infty$ is $X\mapsto \mathcal X_{/X}$. Indeed, this composition preserves colimits (by [24, Proposition 6.3.5.14]), and it restricts to $\Pi _\infty ^\tau$ on $\mathcal C$ (cf. Remark 1.1). However, the reader should be warned that we will use $\overline{\Pi }{}_\infty ^\tau$ in situations where this hypothesis on $\mathcal C$ is not satisfied.

Remark 5.5

The extension $\overline{\Pi }{}_\infty ^\tau$ involves taking infinite colimits in ${{\,\textrm{Pro}\,}}(\mathcal S)$, which are somewhat ill-behaved (they are not universal, for example). As we will see in Sect. 9, it is sometimes advantageous to consider a variant of $\overline{\Pi }{}_\infty ^\tau$ taking values in ind-pro-spaces.

Theorem 5.6

Let k be a separably closed field, $l\ne {{\,\textrm{char}\,}}k$ a prime number, and X a quasi-projective scheme over k. Let $\tau \in \{{\textrm{h}},{\textrm{qfh}},{{\acute{\textrm{e}}}\textrm{t}}\}$. Then for any $d\ge 0$ there is a canonical equivalence

$$\begin{aligned} L_{\textbf{Z}/l}\Pi _\infty ^\tau (\textrm{S}^dX)\simeq L_{\textbf{Z}/l} \textrm{S}^d\Pi _\infty ^\tau (X). \end{aligned}$$

Proof

Let $\mathcal C$ be the category of quasi-projective schemes over k. By Corollary 4.6, the representable sheaf functor $r_{\textrm{qfh}}:\mathcal C\rightarrow {{\,\textrm{Shv}\,}}_{\textrm{qfh}}(\mathcal C)$ preserves strict symmetric powers. Using Proposition 5.1 and the fact that $L_{\textbf{Z}/l}\overline{\Pi }{}_\infty ^{\textrm{qfh}}$ preserves colimits, we deduce that $L_{\textbf{Z}/l}\Pi _\infty ^{\textrm{qfh}}$ preserves strict symmetric powers on $\mathcal C$. For $\tau \in \{{\textrm{h}},{\textrm{qfh}},{{\acute{\textrm{e}}}\textrm{t}}\}$, we get

$$\begin{aligned} L_{\textbf{Z}/l}\Pi _\infty ^\tau (\textrm{S}^dX)\simeq L_{\textbf{Z}/l}\Pi _\infty ^{\textrm{qfh}}(\textrm{S}^d X)\simeq \textrm{S}^d L_{\textbf{Z}/l}\Pi _\infty ^{\textrm{qfh}}(X)\simeq \textrm{S}^d L_{\textbf{Z}/l}\Pi _\infty ^\tau (X), \end{aligned}$$

the first and last equivalences being from Proposition 4.1. The functor $L_{\textbf{Z}/l}$ itself also preserves finite products (Proposition 3.3) and hence strict symmetric powers, so we are done. $\square$

Remark 5.7

It is possible to define a natural map

$$\begin{aligned} \Pi _\infty ((\textrm{S}^d X)_\tau ^\wedge )\rightarrow \textrm{S}^d\Pi _\infty (X_\tau ^\wedge ) \end{aligned}$$

in ${{\,\textrm{Pro}\,}}(\mathcal S)$ inducing the equivalence of Theorem 5.6. It suffices to make the square

commute. Using the model for the $\tau$-homotopy type discussed in Remark 1.3 and the commutativity of the functor of connected components with symmetric powers, the task to accomplish is the following: associate to any $\tau$-hypercover $U_\bullet \rightarrow X$ a $\tau$-hypercover $V_\bullet \rightarrow \textrm{S}^d X$ refining $\textrm{S}^dU_\bullet \rightarrow \textrm{S}^d X$ and such that $V_\bullet \times _{\textrm{S}^d X}X^d\rightarrow X^d$ refines $U_\bullet ^d\rightarrow X^d$, in a simplicially enriched functorial way (i.e., we must define a simplicial functor $\textrm{HC}_\tau (X)\rightarrow \textrm{HC}_\tau (\textrm{S}^d X)$ and the refinements must be natural). If $\tau ={\textrm{h}}$ or $\tau ={\textrm{qfh}}$, $\textrm{S}^dU_\bullet \rightarrow \textrm{S}^d X$ is itself a $\tau$-hypercover and we are done, but things get more complicated for $\tau ={{\acute{\textrm{e}}}\textrm{t}}$ as symmetric powers of étale maps are not étale anymore.

We refer to [21, §4.5] and [27, §3] for more details on the following ideas. Given a finite group G and quasi-projective G-schemes U and X, a map $f:U\rightarrow X$ is G-equivariant if and only if it admits descent data for the action groupoid of G on X. The map f is fixed-point reflecting if it admits descent data for the Čech groupoid of the quotient map $X\rightarrow X/G$ (this condition can be expressed more explicitly using the fact that $G\times X\rightarrow X\times _{X/G}X$ is faithfully flat: f is fixed-point reflecting if and only if it is G-equivariant and induces a fiberwise isomorphism between the stabilizer schemes). Since étale morphisms descend effectively along universally open surjective morphisms [26, Theorem 5.19], such as $X\rightarrow X/G$, the condition that f reflects fixed points is equivalent to the induced map $U/G\rightarrow X/G$ being étale and the square

being cartesian. If f is G-equivariant, there exists a largest G-equivariant open subset ${{\,\textrm{fpr}\,}}(f)\subset U$ on which f is fixed-point reflecting. Moreover, if $f:U\rightarrow X$ is an étale cover, the restriction of $f^d$ to ${{\,\textrm{fpr}\,}}(f^d)$ is still surjective. Now given an étale hypercover $U_\bullet \rightarrow X$, we can define an étale hypercover $V_\bullet \rightarrow \textrm{S}^d X$ refining $\textrm{S}^d U_\bullet \rightarrow \textrm{S}^d X$ as follows. Let $W_0\subset U_0^d$ be the locus where $U_0^d\rightarrow X^d$ reflects fixed points. If $W_\bullet$ has been defined up to level $n-1$, define $W_n$ by the cartesian square

in which the vertical maps are $\Sigma _d$-equivariant fixed-point reflecting étale covers (because fixed-point reflecting morphisms are stable under base change). Finally, let $V_n=W_n/\Sigma _d$. It is then easy to prove that $V_\bullet \rightarrow \textrm{S}^d X$ is an étale hypercover with the desired functoriality.

Using the commutativity of ((5.8)), one can also show that the map induced by $\Pi _\infty ((\textrm{S}^d X)_{{\acute{\textrm{e}}}\textrm{t}}^\wedge )\rightarrow \textrm{S}^d\Pi _\infty (X_{{\acute{\textrm{e}}}\textrm{t}}^\wedge )$ in cohomology with coefficients in a $\textbf{Z}/l$-module coincides with the symmetric Künneth map defined in [2, XVII, (5.5.17.2)]. Thus, for X proper, it is possible to deduce Theorem 5.6 from [2, XVII, Théorème 5.5.21].

7 $\textbf{A}^1$-localization

Let S be a quasi-compact quasi-separated scheme and $\mathcal C$ a full subcategory of ${\mathcal S}\textrm{ch}_S$ such that

• (1) objects of $\mathcal C$ are of finite presentation over S;

• (2) $S\in \mathcal C$ and $\textbf{A}^1_S\in \mathcal C$;

• (3) if $X\in \mathcal C$ and $U\rightarrow X$ is étale, separated, and of finite presentation, then $U\in \mathcal C$;

• (4) $\mathcal C$ is closed under finite products and finite coproducts.

Following [30, §0], we call such a category $\mathcal C$ admissible. Note that every smooth S-scheme admits an open covering by schemes in $\mathcal C$. Let ${{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)$ denote the $\infty$-topos of sheaves of spaces on $\mathcal C$ for the Nisnevich topology, and let ${{\,\textrm{Shv}\,}}_{{\textrm{Nis}}}(\mathcal C)_{\textbf{A}^1}\subset {{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)$ be the full subcategory of $\textbf{A}^1$-invariant Nisnevich sheaves. We shall denote by

$$\begin{aligned} L_{{\textrm{Nis}},\textbf{A}^1}:{{\,\textrm{PSh}\,}}(\mathcal C)\rightarrow {{\,\textrm{Shv}\,}}_{{\textrm{Nis}}}(\mathcal C)_{\textbf{A}^1} \end{aligned}$$

the left adjoint to the inclusion.

From now on we fix a prime number l different from the residual characteristics of S. In Sect. 1, we defined the functor

$$\begin{aligned} \Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}:\mathcal C\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S), \end{aligned}$$

and we observed in Sect. 5 that it lifts to a left adjoint functor

$$\begin{aligned} \overline{\Pi }{}_\infty ^{{\acute{\textrm{e}}}\textrm{t}}:{{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S). \end{aligned}$$

By [14, VII, Corollaire 1.2], the composition

sends any morphism $\textbf{A}^1\times X\rightarrow X$ in $\mathcal C$ to an equivalence and therefore factors through the $\textbf{A}^1$-localization functor $L_{{\textrm{Nis}},\textbf{A}^1}$. That is, there is a commutative square of left adjoint functors

The functor ${{\acute{\textrm{E}}}\textrm{t}}_l$ is called the $\textbf{Z}/l$-local étale homotopy type functor. Note that if S is Noetherian (resp. Noetherian and excellent), we could also use $\overline{\Pi }{}_\infty ^{\textrm{qfh}}$ (resp. $\overline{\Pi }{}_\infty ^{\textrm{h}}$) instead of $\overline{\Pi }{}_\infty ^{{\acute{\textrm{e}}}\textrm{t}}$ in the above diagram, according to Proposition 4.1.

Remark 6.1

The $\textbf{Z}/l$-profinite completion $L^{\textbf{Z}/l}{{\acute{\textrm{E}}}\textrm{t}}_l$ is the $\infty$-categorical incarnation of the étale realization functor defined by Isaksen in [18] as a left Quillen functor, but our results do not require this stronger completion. Note that ${{\acute{\textrm{E}}}\textrm{t}}_l X$ is already $\textbf{Z}/l$-profinite if S is Noetherian and $X\in ({{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1})^\omega$, by Remarks 5.3 and 3.12.

We now assume that $S={{\,\textrm{Spec}\,}}k$ where k is a separably closed field.

Lemma 6.2

The restriction of ${{\acute{\textrm{E}}}\textrm{t}}_l$ to the subcategory of compact objects $({{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1})^\omega$ preserves finite products.

Proof

By Proposition 5.1, the functor $L_{\textbf{Z}/l}\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}$ preserves finite products on $\mathcal C$. Since the functor $L_{{\textrm{Nis}},\textbf{A}^1} r:\mathcal C\rightarrow {{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1}$ also preserves finite products, the restriction of ${{\acute{\textrm{E}}}\textrm{t}}_l$ to the image of $\mathcal C$ preserves finite products. Finally, since $({{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1})^\omega$ is the closure of the image of $\mathcal C$ under finite colimits and retracts, the result follows from Corollary 3.4. $\square$

Let $p\ge q\ge 0$. We define the $\textbf{Z}/l$-local mixed spheres $S^{p,q}_l\in {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l,*}$ by

$$\begin{aligned} S^{1,0}_l=L_{\textbf{Z}/l}S^1=K(\textbf{Z}_l,1),\quad S^{1,1}_l=K(T_l\mu ,1),\quad S^{p,q}_l=(S^{1,0}_l)^{\wedge p-q}\wedge (S^{1,1}_l)^{\wedge q}, \end{aligned}$$

where $\mu$ is the group of roots of unity in k and $T_l\mu =\lim _n \mu _{l^n}$ is its l-adic Tate module. Here we regard $\textbf{Z}_l$ and $T_l\mu$ as pro-groups. Of course, $S^{p,q}_l\simeq L_{\textbf{Z}/l}S^p$, but if $q>0$ this equivalence depends on infinitely many noncanonical choices ( viz., an isomorphism $\textbf{Z}_l\simeq T_l\mu$). By Proposition 3.11, $S^{p,q}_l$ is $\textbf{Z}/l$-profinite.

Note that the functor $\acute{\textrm{E}}t_{l}$ preserves pointed objects, since $\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}({{\,\textrm{Spec}\,}}k)\simeq *$.

Proposition 6.3

Let $p\ge q\ge 0$. Then $\acute{\textrm{E}}t_{l}S^{p,q}\simeq S^{p,q}_l$.

Proof

This is obvious if $q=0$. By Lemma 6.2, it remains to treat the case $p=q=1$. The étale $\mu _{l^n}$-torsor $l^n:\textbf{G}_m\rightarrow \textbf{G}_m$ is classified by a morphism $\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}\textbf{G}_m\rightarrow K(\mu _{l^n},1)$. In the limit over $n\ge 0$, we obtain a morphism of pro-spaces $\varphi :\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}\textbf{G}_m \rightarrow K(T_l\mu ,1)$. We claim that $\varphi$ is a $\textbf{Z}/l$-homological equivalence, i.e., it induces an isomorphism in cohomology with coefficients in any $\textbf{Z}/l$-module M. By [14, VII, Proposition 1.3(i)(c)], we have

$$\begin{aligned} H^i_{{\acute{\textrm{e}}}\textrm{t}}(\textbf{G}_m,M)={\left\{ \begin{array}{ll} M &{} \text {if } i=0, \\ {{\,\textrm{Hom}\,}}(\mu _l,M) &{} \text {if} i=1, \\ 0 &{} \text {if }i\ge 2.\end{array}\right. } \end{aligned}$$

In fact, this computation shows that the morphism $\Pi _\infty ^{{\acute{\textrm{e}}}\textrm{t}}\textbf{G}_m\rightarrow K(\mu _l,1)$ induces an isomorphism on $H^i(-,M)$ for $i\le 1$. The same is true for the projection $K(T_l\mu ,1)\rightarrow K(\mu _l,1)$, hence also for $\varphi$. Since both the source and the target of $\varphi$ have vanishing cohomology in degrees $\ge 2$, this completes the proof. $\square$

8 Group completion and strictly commutative monoids

Let $\mathcal C$ be an $\infty$-category with finite products. Recall from [23, §2.4.2] that a commutative monoid in $\mathcal C$ is a functor $M:\mathcal F\textrm{in}_*\rightarrow \mathcal C$ such that for all $n\ge 0$ the canonical map $M(\langle n\rangle )\rightarrow M(\langle 1\rangle )^n$ is an equivalence. We let $\textrm{CMon}(\mathcal C)$ denote the full subcategory of ${{\,\textrm{Fun}\,}}(\mathcal F\textrm{in}_*,\mathcal C)$ spanned by the commutative monoids.

A commutative monoid M in $\mathcal C$ has an underlying simplicial object, namely its restriction along the functor ${{\,\textrm{Cut}\,}}:\Delta ^\textrm{op}\rightarrow \mathcal F\textrm{in}_*$ sending [n] to the finite set of cuts of [n] pointed at the trivial cut, which can be identified with $\langle n\rangle$. The commutative monoid M is called grouplike if its underlying simplicial object is a groupoid object in the sense of [24, Definition 6.1.2.7]. This is equivalent to requiring both shearing maps $M\times M\rightarrow M\times M$ to be equivalences. We denote by $\textrm{CMon}^\textrm{gp}(\mathcal C)\subset \textrm{CMon}(\mathcal C)$ the full subcategory of grouplike objects.

If $f:\mathcal C\rightarrow \mathcal D$ preserves finite products (and $\mathcal C$ and $\mathcal D$ admit finite products), then it induces a functor $\textrm{CMon}(\mathcal C)\rightarrow \textrm{CMon}(\mathcal D)$ by postcomposition; this functor clearly preserves grouplike objects and hence restricts to a functor $\textrm{CMon}^\textrm{gp}(\mathcal C)\rightarrow \textrm{CMon}^\textrm{gp}(\mathcal D)$. We will continue to use f to denote either induced functor.

Lemma 7.1

Suppose that $f:\mathcal C\rightarrow \mathcal D$ preserves finite products and has a right adjoint g. Then the functors $\textrm{CMon}(\mathcal C)\rightarrow \textrm{CMon}(\mathcal D)$ and $\textrm{CMon}^\textrm{gp}(\mathcal C)\rightarrow \textrm{CMon}^\textrm{gp}(\mathcal D)$ induced by f are left adjoint to the corresponding functors induced by g.

Proof

The functors f and g induce adjoint functors between $\infty$-categories of $\mathcal F\textrm{in}_*$-diagrams, and it remains to observe that they both preserve the full subcategory of (grouplike) commutative monoids. $\square$

Definition 7.2

An $\infty$-category $\mathcal C$ is distributive if it is presentable and if finite products in $\mathcal C$ distribute over colimits. A functor $f:\mathcal C\rightarrow \mathcal D$ between distributive $\infty$-categories is distributive if it preserves colimits and finite products.

For example, for any $\infty$-topos $\mathcal X$, the truncation functors $\tau _{\le n}:\mathcal X\rightarrow \mathcal X_{\le n}$ are distributive, and for any admissible category $\mathcal C\subset {\mathcal S}\textrm{ch}_S$ and any topology $\tau$ on $\mathcal C$, the localization functor $L_{\tau ,\textbf{A}^1}:{{\,\textrm{PSh}\,}}(\mathcal C)\rightarrow {{\,\textrm{Shv}\,}}_\tau (\mathcal C)_{\textbf{A}^1}$ is distributive.

If $\mathcal C$ is distributive, then the $\infty$-category $\textrm{CMon}(\mathcal C)$ is presentable by [23, Corollary 3.2.3.5], and the subcategory $\textrm{CMon}^\textrm{gp}(\mathcal C)$ is strongly reflective since it is accessible (by [24, Proposition 6.1.2.9] and [24, Proposition 5.4.6.6]) and is clearly closed under limits and sifted colimits. That is, there exists a group completion functor

$$\begin{aligned} \textrm{CMon}(\mathcal C)\rightarrow \textrm{CMon}^\textrm{gp}(\mathcal C), \quad M\mapsto M^\textrm{gp}, \end{aligned}$$

which exhibits $\textrm{CMon}^\textrm{gp}(\mathcal C)$ as an accessible localization of $\textrm{CMon}(\mathcal C)$.³

Lemma 7.3

Let $f:\mathcal C\rightarrow \mathcal D$ be a distributive functor and let $M\in \textrm{CMon}(\mathcal C)$. Then $f(M^\textrm{gp})\simeq f(M)^\textrm{gp}$.

Proof

By Lemma 7.1, the square

has a commutative right adjoint and hence is commutative. $\square$

Remark 7.4

If $\mathcal X$ is an $\infty$-topos, group completion of commutative monoids in $\mathcal X$ preserves 0-truncated objects. As in the proof of Lemma 2.5, it suffices to prove this for $\mathcal X=\mathcal S$, where it follows from the McDuff-Segal group completion theorem (see [25] for a modern proof of the latter).

We can define a generalized “free $\textbf{Z}$-module” functor in any distributive $\infty$-category as follows. Let $\textrm{FFree}{}_\textbf{N}$ (resp. $\textrm{FFree}{}_\textbf{Z}$) be the full subcategory of $\textrm{CMon}(\mathcal {S}\textrm{et})$ spanned by $(\textbf{N}^n,+)$ (resp. by $(\textbf{Z}^n,+)$) for $n\ge 0$. If $\mathcal C$ is an $\infty$-category with finite products, we shall denote by

$$\begin{aligned} \textrm{Mod}{}_\textbf{N}(\mathcal C)\subset {{\,\textrm{Fun}\,}}(\textrm{FFree}{}_\textbf{N}^\textrm{op},\mathcal C)\quad \text {and}\quad \textrm{Mod}{}_\textbf{Z}(\mathcal C)\subset {{\,\textrm{Fun}\,}}(\textrm{FFree}{}_\textbf{Z}^\textrm{op},\mathcal C) \end{aligned}$$

the full subcategories of finite-product-preserving functors. The objects of $\textrm{Mod}{}_\textbf{N}(\mathcal C)$ are called strictly commutative monoids in $\mathcal C$. Since $\textrm{FFree}{}_\textbf{N}$ is semiadditive [23, Definition 6.1.6.13], the $\infty$-category $\textrm{Mod}{}_\textbf{N}(\mathcal C)$ is also semiadditive [12, Corollary 2.4] and the forgetful functor

$$\begin{aligned} \textrm{Mod}{}_\textbf{N}(\mathcal C)\rightarrow \mathcal C, \quad M\mapsto M(\textbf{N}), \end{aligned}$$

factors uniquely through the $\infty$-category $\textrm{CMon}(\mathcal C)$ [12, Corollary 2.5(iii)]. Similarly, as $\textrm{FFree}{}_\textbf{Z}$ is additive, the $\infty$-category $\textrm{Mod}{}_\textbf{Z}(\mathcal C)$ is additive and the forgetful functor $\textrm{Mod}{}_\textbf{Z}(\mathcal C)\rightarrow \mathcal C$ factors uniquely through $\textrm{CMon}^\textrm{gp}(\mathcal C)$.

Assume now that $\mathcal C$ is distributive. The forgetful functors $\textrm{Mod}{}_\textbf{N}(\mathcal C)\rightarrow \mathcal C$ and $\textrm{Mod}{}_\textbf{Z}(\mathcal C) \rightarrow \mathcal C$ then preserve limits and sifted colimits, hence admit left adjoints

$$\begin{aligned} \textbf{N}:\mathcal C\rightarrow \textrm{Mod}{}_\textbf{N}(\mathcal C)\quad \text {and}\quad \textbf{Z}:\mathcal C\rightarrow \textrm{Mod}{}_\textbf{Z}(\mathcal C). \end{aligned}$$

Since the $\infty$-categories $\textrm{Mod}{}_\textbf{N}(\mathcal C)$ and $\textrm{Mod}{}_\textbf{Z}(\mathcal C)$ are pointed, we also have reduced versions ${\tilde{\textbf{N}}} X$ and ${\tilde{\textbf{Z}}} X$ when X is a pointed object of $\mathcal C$. More precisely, ${\tilde{\textbf{N}}}$ is the unique colimit-preserving extension of $\textbf{N}$ to $\mathcal C_*$, and similarly for ${\tilde{\textbf{Z}}}$.

Lemma 7.5

If $\mathcal C$ is an $\infty$-category with finite products, the square

is cartesian. If $\mathcal C$ is distributive, the top functor $\textrm{Mod}{}_\textbf{Z}(\mathcal C) \rightarrow \textrm{Mod}{}_\textbf{N}(\mathcal C)$ admits a left adjoint such that the following square commutes:

In particular, ${\tilde{\textbf{Z}}} X\simeq ({\tilde{\textbf{N}}} X)^\textrm{gp}$ for any $X\in \mathcal C_*$.

Proof

Since $\textrm{FFree}{}_\textbf{N}$ is semiadditive and $\textrm{FFree}{}_\textbf{Z}$ is additive, the forgetful functors $\textrm{CMon}^\textrm{gp}(\mathcal C)\rightarrow \textrm{CMon}(\mathcal C)\rightarrow \mathcal C$ induce equivalences

$$\begin{aligned} \textrm{Mod}{}_\textbf{N}(\mathcal C)&\simeq \textrm{Mod}{}_\textbf{N}(\textrm{CMon}(\mathcal C)), \\ \textrm{Mod}{}_\textbf{Z}(\mathcal C)&\simeq \textrm{Mod}{}_\textbf{Z}(\textrm{CMon}^\textrm{gp}(\mathcal C)). \end{aligned}$$

The key point is that the $\infty$-category $\textrm{FFree}{}_\textbf{Z}$ is obtained from $\textrm{FFree}{}_\textbf{N}$ be group-completing the mapping spaces, so that $\textrm{FFree}{}_\textbf{N}\rightarrow \textrm{FFree}{}_\textbf{Z}$ is the universal finite-product-preserving functor to an additive $\infty$-category. Therefore, the forgetful functor

$$\begin{aligned} \textrm{Mod}{}_\textbf{Z}(\mathcal C) \rightarrow \textrm{Mod}{}_\textbf{N}(\mathcal C) \end{aligned}$$

can be identified with the functor

$$\begin{aligned} \textrm{Mod}{}_\textbf{Z}(\textrm{CMon}^\textrm{gp}(\mathcal C))\simeq \textrm{Mod}{}_\textbf{N}(\textrm{CMon}^\textrm{gp}(\mathcal C)) \rightarrow \textrm{Mod}{}_\textbf{N}(\textrm{CMon}(\mathcal C)). \end{aligned}$$

This description immediately implies the claims: the first claim follows since a finite-product-preserving functor $M:\textrm{FFree}{}_\textbf{N}^\textrm{op}\rightarrow \textrm{CMon}(\mathcal C)$ lands in $\textrm{CMon}^\textrm{gp}(\mathcal C)$ if and only if $M(\textbf{N})$ is grouplike, and the second claims follows since group completion preserves finite products. $\square$

We can describe free strictly commutative monoids more concretely using strict symmetric powers (see Sect. 2):

Lemma 7.6

Let $\mathcal C$ be a distributive $\infty$-category. Then the composite functor

$$\begin{aligned} \mathcal C \xrightarrow {\textbf{N}} \textrm{Mod}{}_\textbf{N}(\mathcal C) \xrightarrow {\textrm{forget}} \mathcal C \end{aligned}$$

is given by $\displaystyle X\mapsto \coprod _{d\ge 0}\textrm{S}^d X$.

Proof

It suffices to check this for the universal X, which lives in the distributive $\infty$-category ${{\,\textrm{Fun}\,}}(\mathcal F\textrm{in},\mathcal S)$. We may thus assume $\mathcal C=\mathcal S$. In that case, the forgetful functor $\textrm{Mod}{}_\textbf{N}(\mathcal S)\rightarrow \mathcal S$ is modeled by the right Quillen functor $\textrm{Mod}{}_\textbf{N}(\mathcal {S}\textrm{et}_\Delta ) \rightarrow \mathcal {S}\textrm{et}_\Delta$ [24, Proposition 5.5.9.1], whose left adjoint is given by the desired formula. Since the functor $\textrm{S}^d$ on $\mathcal S$ can be computed using symmetric powers of CW complexes, this completes the proof. $\square$

Remark 7.7

Lemma 7.6 shows that the endofunctor $X\mapsto \coprod _{d\ge 0}\textrm{S}^d X$ of any distributive $\infty$-category has a canonical structure of monad. Its multiplication involves a canonical equivalence $\textrm{S}^d(X\amalg Y) \simeq \coprod _{e+f=d}\textrm{S}^eX\times \textrm{S}^fY$ and a canonical map $\textrm{S}^d\textrm{S}^e X \rightarrow \textrm{S}^{de} X$.

If $\mathcal C$ is presentable and $\mathcal A$ is a small $\infty$-category with finite products, we have

$$\begin{aligned} {{\,\textrm{Fun}\,}}^\times (\mathcal A,\mathcal C) \simeq \mathcal C\otimes {{\,\textrm{Fun}\,}}^\times (\mathcal A,\mathcal S) \end{aligned}$$

where $\otimes$ denotes the tensor product of presentable $\infty$-categories (this follows immediately from [23, Proposition 4.8.1.17]). Hence, the presentable $\infty$-category $\textrm{Mod}{}_\textbf{Z}(\mathcal C)$ of grouplike strictly commutative monoids in $\mathcal C$ is a module over $\textrm{Mod}{}_\textbf{Z}(\mathcal S)$, which is the $\infty$-category of connective $H\textbf{Z}$-modules. For $X\in \textrm{Mod}{}_\textbf{Z}(\mathcal C)$ and A a connective $H\textbf{Z}$-module, we will write $X\otimes A$ for the result of the action of A on X. Note that the construction $X\mapsto X\otimes A$ is preserved by any colimit-preserving functor $f:\mathcal C\rightarrow \mathcal D$.

In particular, if $\mathcal C$ is distributive and $X\in \mathcal C$, one can form the strictly commutative monoid $\textbf{ZX}\otimes A$ for any connective $H\textbf{Z}$-module A, which can be described more concretely as follows. Any connective $H\textbf{Z}$-module A can be obtained from $\textbf{Z}$ in the following steps:

• (1) take finite products of copies of $\textbf{Z}$ to get finitely generated free $\textbf{Z}$-modules;

• (2) take filtered colimits of finitely generated free $\textbf{Z}$-modules to get arbitrary flat $\textbf{Z}$-modules;

• (3) take colimits of simplicial diagrams of free $\textbf{Z}$-modules to get arbitrary connective $H\textbf{Z}$-modules [24, Lemma 5.5.8.13].

Since the forgetful functor $\textrm{Mod}{}_\textbf{Z}(\mathcal C)\rightarrow \mathcal C$ preserves finite products and sifted colimits, the object $\textbf{ZX}\otimes A$ in $\mathcal C$ can be obtained from $\textbf{ZX}$ using the same steps.

In the distributive $\infty$-category $\mathcal S$, $\textbf{ZX}\otimes A$ has its “usual” meaning. For instance, if A is an abelian group, then ${\tilde{\textbf{Z}}} S^p\otimes A$ is an Eilenberg–Mac Lane space K(A, p).

9 Sheaves with transfers

Let S be a Noetherian scheme, $\mathcal C\subset {\mathcal S}\textrm{ch}_S$ an admissible category consisting of separated S-schemes, and R a commutative ring. We denote by $\mathcal C\textrm{or}(\mathcal C,R)$ the additive category whose objects are those of $\mathcal C$ and whose morphisms are the finite correspondences with coefficients in R [4, §9],⁴ We denote by ${{\,\textrm{PSh}\,}}^*(\mathcal C)$ the $\infty$-category of pointed presheaves on $\mathcal C$, by

$$\begin{aligned} {{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R) = {{\,\textrm{Fun}\,}}^\times (\mathcal C\textrm{or}(\mathcal C,R)^\textrm{op}, \mathcal S) \end{aligned}$$

the $\infty$-category of presheaves with R-transfers, and by

$$\begin{aligned}R_\textrm{tr}: {{\,\textrm{PSh}\,}}^*(\mathcal C)\rightleftarrows {{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R):u_\textrm{tr}\end{aligned}$$

the free-forgetful adjunction. The functor $u_\textrm{tr}$ preserves limits and sifted colimits and factors through the $\infty$-category $\textrm{CMon}^\textrm{gp}({{\,\textrm{PSh}\,}}(\mathcal C))$; in fact, it factors through the $\infty$-category of grouplike strictly commutative monoids, using the finite-product-preserving functor

$$\begin{aligned} \textrm{FFree}{}_\textbf{Z}\rightarrow \mathcal C\textrm{or}(\mathcal C,R), \quad \textbf{Z}^n \mapsto S^{\amalg n}. \end{aligned}$$

Since finite products and finite coproducts coincide in semiadditive $\infty$-categories, the functor

$$\begin{aligned}u_\textrm{tr}:{{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R)\rightarrow \textrm{Mod}{}_\textbf{Z}({{\,\textrm{PSh}\,}}(\mathcal C))\end{aligned}$$

preserves all colimits.

For $\tau$ a topology on $\mathcal C$, we denote by ${{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)$ the $\infty$-category of $\tau$-sheaves with R-transfers on $\mathcal C$, and by ${{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)_{\textbf{A}^1}$ the $\infty$-category of homotopy invariant $\tau$-sheaves with R-transfers on $\mathcal C$; these are defined by the cartesian squares

By [24, Proposition 5.5.4.15], the $\infty$-categories ${{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)$ and ${{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)_{\textbf{A}^1}$ are presentable and there exist localization functors

$$\begin{aligned} a_\tau ^\textrm{tr}:{{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R)\rightarrow {{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R),\\ L_{\tau ,\textbf{A}^1}^\textrm{tr}:{{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R) \rightarrow {{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)_{\textbf{A}^1}. \end{aligned}$$

Furthermore, by [24, Proposition 5.4.6.6], the forgetful functors $u_\textrm{tr}$ in the above diagram are accessible. Since they preserve limits, they admit left adjoint functors, which we will denote by $R_\textrm{tr}$ (it will always be clear from the context which category $R_\textrm{tr}$ is defined on).

We say that a topology $\tau$ on $\mathcal C$ is compatible with R-transfers if for any presheaf with R-transfers $\mathcal F$ on $\mathcal C$, the canonical map

$$\begin{aligned} a_\tau u_\textrm{tr}\mathcal F\rightarrow u_\textrm{tr}a_\tau ^\textrm{tr}\mathcal F \end{aligned}$$

is an equivalence. The following lemma shows that $\tau$ is compatible with transfers if and only if it is weakly compatible with transfers in the sense of [4, Definition 9.3.2]. For example, it follows from [4, Proposition 9.3.3] that the Nisnevich and étale topologies are compatible with any transfers on any admissible category.

Lemma 8.1

A topology $\tau$ on $\mathcal C$ is compatible with R-transfers if and only if, for every $\tau$-covering sieve $U\hookrightarrow X$, the morphism

$$\begin{aligned} a_\tau u_\textrm{tr}R_\textrm{tr}(U_+) \rightarrow a_\tau u_\textrm{tr}R_\textrm{tr}(X_+) \end{aligned}$$

is an equivalence in ${{\,\textrm{Shv}\,}}_\tau ^*(\mathcal C)$.

Proof

If $\tau$ is compatible with transfers, then for any $\mathcal F\in {{\,\textrm{PSh}\,}}^*(\mathcal C)$,

$$\begin{aligned} a_\tau u_\textrm{tr}R_\textrm{tr}\mathcal F\simeq u_\textrm{tr}a_\tau ^\textrm{tr}R_\textrm{tr}\mathcal F\simeq u_\textrm{tr}R_\textrm{tr}a_\tau \mathcal F. \end{aligned}$$

Since $a_\tau (U_+)\simeq a_\tau (X_+)$, this proves the “only if” direction.

Conversely, define

$$\begin{aligned} E=\{R_\textrm{tr}U_+\rightarrow R_\textrm{tr}X_+\,\vert \,U\hookrightarrow X\text { is a} \tau -\text {covering sieve}\} \end{aligned}$$

so that ${{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)\subset {{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R)$ is the subcategory of E-local objects, and suppose that the functor $a_\tau u_\textrm{tr}$ sends elements of E to equivalences. Let ${\bar{E}}$ be the strong saturation of E, i.e., the smallest class of morphisms containing E, satisfying the 2-out-of-3 property, and closed under colimits in ${{\,\textrm{Fun}\,}}(\Delta ^1,{{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R))$. By [24, Proposition 5.5.4.15(4) and Proposition 5.2.7.12], the localization functor $a_\tau ^\textrm{tr}:{{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R)\rightarrow {{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)$ is the universal functor sending elements of ${\bar{E}}$ to equivalences. We claim that $a_\tau u_\textrm{tr}$ sends morphisms in ${\bar{E}}$ to equivalences. It will suffice to show that the class of morphisms f such that $a_\tau u_\textrm{tr}(f)$ is an equivalence is closed under the 2-out-of-3 property (which is obvious) and colimits. The functor $u_\textrm{tr}:{{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R)\rightarrow {{\,\textrm{PSh}\,}}^*(\mathcal C,R)$ does not preserve colimits, but it preserves sifted colimits and transforms finite coproducts into finite products. Since $a_\tau$ is left exact and any colimit can be built out of finite coproducts and sifted colimits, this proves the claim. Thus, there exists a functor $f:{{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)\rightarrow {{\,\textrm{Shv}\,}}_\tau ^*(\mathcal C)$ making the diagram

commute. Since the horizontal compositions are the identity, $f\simeq u_\textrm{tr}$ and $a_\tau u_\textrm{tr}\simeq u_\textrm{tr}a_\tau ^\textrm{tr}$. $\square$

Lemma 8.2

Suppose that $\tau$ is compatible with R-transfers. Then the square

commutes.

Proof

Consider the diagram

It will suffice to show that a functor f exists as indicated. Define

$$\begin{aligned} E_\tau&= \{R_\textrm{tr}U_+\rightarrow R_\textrm{tr}X_+\,\vert \,U\hookrightarrow X\text { is a} \tau -\text {covering sieve in} \mathcal C\},\\ E_{\textbf{A}^1}&= \{R_\textrm{tr}(X\times \textbf{A}^1)_+\rightarrow R_\textrm{tr}X_+\,\vert \,X\in \mathcal C\}, \end{aligned}$$

so that ${{\,\textrm{Shv}\,}}_\tau ^\textrm{tr}(\mathcal C,R)_{\textbf{A}^1}\subset {{\,\textrm{PSh}\,}}^\textrm{tr}(\mathcal C,R)$ is the full subcategory of $(E_\tau \cup E_{\textbf{A}^1})$-local objects. The functor $L_{\tau ,\textbf{A}^1}u_\textrm{tr}$ carries morphisms in $E_\tau$ and $E_{\textbf{A}^1}$ to equivalences: for $E_\tau$, this is because $\tau$ is compatible with R-transfers and for $E_{\textbf{A}^1}$ it is because $u_\textrm{tr}R_\textrm{tr}(X\times \textbf{A}^1)_+\rightarrow u_\textrm{tr}R_\textrm{tr}X_+$ is an $\textbf{A}^1$-homotopy equivalence (see the last part of the proof of [30, Theorem 1.7]). By [24, Proposition 5.5.4.20], there exists a functor f making the above diagram commutes. $\square$

Corollary 8.3

Suppose that $\tau$ is compatible with R-transfers. Then the forgetful functor $u_\textrm{tr}:{{\,\textrm{Shv}\,}}^\textrm{tr}_\tau (\mathcal C,R)_{\textbf{A}^1}\rightarrow \textrm{Mod}{}_\textbf{Z}({{\,\textrm{Shv}\,}}_\tau (\mathcal C)_{\textbf{A}^1})$ preserves colimits.

Proof

This follows immediately from Lemma 8.2. $\square$

The $\infty$-category ${{\,\textrm{Shv}\,}}_{\tau }^\textrm{tr}(\mathcal C,R)_{\textbf{A}^1}$ is tensored over connective HR-modules. For $p\ge q\ge 0$ and A a connective HR-module, the motivic Eilenberg–Mac Lane space

$$\begin{aligned} K(A(q),p)_{\mathcal C}\in {{\,\textrm{Shv}\,}}_{\textrm{Nis}}^*(\mathcal C)_{\textbf{A}^1} \end{aligned}$$

is defined by

$$\begin{aligned} K(A(q),p)_{\mathcal C}=u_\textrm{tr}(R_\textrm{tr}S^{p,q}\otimes A), \end{aligned}$$

where $S^{p,q}\in {{\,\textrm{Shv}\,}}_{\textrm{Nis}}^*(\mathcal C)_{\textbf{A}^1}$ is the motivic p-sphere of weight q. Although this construction depends on the coefficient ring R in general, it does not if either the schemes in $\mathcal C$ are regular or if the positive residual characteristics of S are invertible in R [4, Remark 9.1.3(3)]; the latter will always be the case in what follows.

10 The Étale homotopy type of motivic Eilenberg–Mac Lane spaces

Let k be a separably closed field, $l\ne {{\,\textrm{char}\,}}k$ a prime number, and $\mathcal C\subset {\mathcal S}\textrm{ch}_k$ an admissible category. One defect of the $\textbf{Z}/l$-local étale homotopy type functor $\acute{\textrm{E}}t_{l}:{{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1}\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}$ is that it does not preserve finite products and hence does not preserve commutative monoids. We have seen in Lemma 6.2 that $\acute{\textrm{E}}t_{l}$ preserves finite products between compact motivic spaces, but motivic Eilenberg–Mac Lane spaces are certainly not compact. We will fix this problem by constructing a factorization

$$\begin{aligned} {{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1}\xrightarrow {\acute{\textrm{E}}t_{l}^{\times }} \mathcal E\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l} \end{aligned}$$

of $\acute{\textrm{E}}t_{l}$ such that $\acute{\textrm{E}}t_{l}^{\times }$ is distributive and $\mathcal E$ is a “close approximation” of ${{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}$ by a distributive $\infty$-category (see Definition 7.2). For our applications, we will also need $\acute{\textrm{E}}t_{l}^{\times }$ to factor through ${{\,\textrm{Shv}\,}}_{\textrm{h}}^\wedge ({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\textbf{A}^1}$. The fact that the latter $\infty$-category may not be compactly generated explains some of the complexity of the following construction.

Construction 9.1

Let $i:\mathcal C\hookrightarrow {\mathcal S}\textrm{ch}_k^{\textrm{ft}}$ be the inclusion and let $i_!:{{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)\rightarrow {{\,\textrm{Shv}\,}}_{\textrm{Nis}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})$ be its colimit-preserving extension. Since $\mathcal C$ is admissible and in particular closed under finite products, the functor $i_!$ is distributive. Note that we have a commuting triangle

where $\overline{\Pi }{}_\infty ^{\textrm{h}}$ was defined in Sect. 5, and that the functor $\overline{\Pi }{}_\infty ^{\textrm{h}}$ on the right is simply $\Pi _\infty$, in the sense of Remark 5.4. For any $\infty$-topos $\mathcal X$, we have a commutative square

where the horizontal maps are given by truncation and $\Pi _n=\tau _{\le n}\circ \Pi _\infty$. We can therefore factor the $\textbf{Z}/l$-local shape functor $L_{\textbf{Z}/l}\Pi _\infty :\mathcal X\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}$ as

$$\begin{aligned} \mathcal X\rightarrow \mathcal X^\wedge \xrightarrow {\tau _{\le *}}\lim _n\mathcal X_{\le n}\rightarrow \lim _n{{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_{\textbf{Z}/l}\simeq {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}, \end{aligned}$$

where the last equivalence is (3.10). Since truncations preserve colimits and finite products, the functor $\tau _{\le *}$ is distributive. Applying this procedure to the $\infty$-topos $\mathcal X={{\,\textrm{Shv}\,}}_{\textrm{h}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})$, we obtain a factorization of $L_{\textbf{Z}/l}\overline{\Pi }{}_\infty ^{\textrm{h}}$ as

$$\begin{aligned} {{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)\xrightarrow {a_{\textrm{h}}^\wedge i_!}{{\,\textrm{Shv}\,}}_{\textrm{h}}^\wedge ({\mathcal S}\textrm{ch}_k^{\textrm{ft}})\xrightarrow {\tau _{\le *}}\lim _n{{\,\textrm{Shv}\,}}_{\textrm{h}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n}\rightarrow \lim _n{{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_{\textbf{Z}/l}\simeq {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}. \end{aligned}$$

Let ${{\,\textrm{Pro}\,}}'(\mathcal S)$ be the smallest full subcategory of ${{\,\textrm{Pro}\,}}(\mathcal S)$ containing $\Pi _\infty ^{\textrm{h}}X$ for every k-scheme of finite type X and closed under finite products, finite colimits, and retracts. We similarly define the $\infty$-categories ${{\,\textrm{Pro}\,}}'(\mathcal S)_{\textbf{Z}/l}$, ${{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})$, and ${{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l}$ to be generated by the respective localizations of $\Pi _\infty ^{\textrm{h}}X$. Recall that the localization functors $L_{\textbf{Z}/l}$ and $\tau _{\le n}$ preserve finite products (Proposition 3.3). By Remarks 5.3 and 3.12, the pro-spaces in ${{\,\textrm{Pro}\,}}'(\mathcal S)$ satisfy the assumption of Proposition 3.13, so that the localization functor $L_{\textbf{Z}/l,\le n}:{{\,\textrm{Pro}\,}}'(\mathcal S)\rightarrow {{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l}$ also preserves finite products. It follows that finite products distribute over finite colimits in each of these $\infty$-categories, so that their ind-completions are distributive.

Consider the colimit-preserving functor

$$\begin{aligned} L_{\textbf{Z}/l,\le n}\overline{\Pi }{}_\infty ^{\textrm{h}}:{{\,\textrm{Shv}\,}}_{{\textrm{h}}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n}\rightarrow {{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_{\textbf{Z}/l}. \end{aligned}$$

By Lemma 4.3, the $\infty$-category ${{\,\textrm{Shv}\,}}_{\textrm{h}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n}$ is compactly generated by representables, so that $({{\,\textrm{Shv}\,}}_{{\textrm{h}}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n})^\omega$ is generated by representables under finite colimits and retracts. Hence, this functor restricts to a functor

$$\begin{aligned} L_{\textbf{Z}/l,\le n}\overline{\Pi }{}_\infty ^{\textrm{h}}:({{\,\textrm{Shv}\,}}_{{\textrm{h}}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n})^\omega \rightarrow {{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l} \end{aligned}$$

that preserves finite colimits. It also preserves finite products by Proposition 5.1, so that the induced functor on ind-completions

$$\begin{aligned} {{\,\textrm{Shv}\,}}_{\textrm{h}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n}\rightarrow {{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l}) \end{aligned}$$

is distributive. Thus, the composition

$$\begin{aligned} {{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)\xrightarrow {\tau _{\le *}a_{\textrm{h}}^\wedge i_!}\lim _n{{\,\textrm{Shv}\,}}_{\textrm{h}}({\mathcal S}\textrm{ch}_k^{\textrm{ft}})_{\le n}\rightarrow \lim _n{{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l}) \end{aligned}$$

is distributive, and it inverts $X\times \textbf{A}^1\rightarrow X$ for every $X\in \mathcal C$ since $L_{\textbf{Z}/l}\Pi _\infty ^{\textrm{h}}$ does, so it induces a distributive functor

$$\begin{aligned} {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }:{{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1}\rightarrow \lim _n{{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l}). \end{aligned}$$

By construction, ${{\acute{\textrm{E}}}\textrm{t}}_l$ is the composition of ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }$ and the colimit functor

$$\begin{aligned} \lim _n{{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l})\rightarrow \lim _n{{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_{\textbf{Z}/l}\simeq {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}. \end{aligned}$$

$\square$

The next theorem is our étale version of [30, Proposition3.41]. We point out that the category $\mathcal C$ in the statement below need not be closed under symmetric powers, so the theorem applies directly with $\mathcal C$ the category of smooth separated k-schemes with no need for resolutions of singularities.

Theorem 9.2

Let k be an algebraically closed field of characteristic exponent e, $l\ne e$ a prime number, and $\mathcal C\subset {\mathcal S}\textrm{ch}_k$ an admissible subcategory consisting of semi-normal separated schemes. Then for any pointed object X in ${{\,\textrm{Shv}\,}}_{{\textrm{Nis}}}(\mathcal C)_{\textbf{A}^1}$ and any connective $H\textbf{Z}[1/e]$-module A, there is an equivalence

$$\begin{aligned} \theta _{X,A}:{\tilde{\textbf{Z}}}{\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }X\otimes A \simeq {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }u_\textrm{tr}(\textbf{Z}_\textrm{tr}X\otimes A) \end{aligned}$$

of grouplike strictly commutative monoids in $\lim _n{{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l})$, natural in X and A, with the following properties:

• (1) the triangle

  

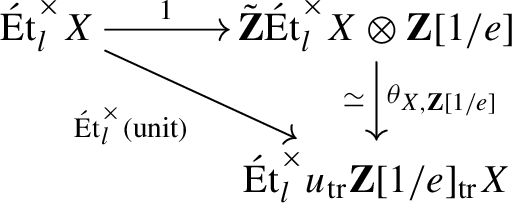
  is commutative;

• (2) given X, Y, A, and B, the square

  

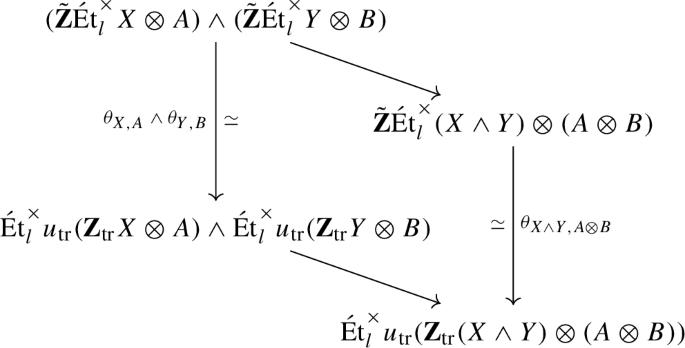
  is commutative.

Proof

Any k-scheme of finite type is Zariski-locally quasi-projective, so we can assume that the schemes in $\mathcal C$ are quasi-projective without changing the categories and functors involved. As X varies, the source and target of $\theta _{X,A}$ are functors taking values in strictly commutative monoids in $\lim _n{{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l})$, and as such they preserve colimits: for the left-hand side this is clear and for the right-hand side it follows from Corollary 8.3. In particular, these functors are left Kan extended from their restriction to $\mathcal C$. To show the existence of $\theta _{X,A}$, it will therefore suffice to define $\theta _{X,A}$ for X representable, i.e., $X=L_{{\textrm{Nis}},\textbf{A}^1}r(Z)_+$ for some $Z\in \mathcal C$, and this construction should be natural in Z and A. Furthermore, since $u_\textrm{tr}$ is $H\textbf{Z}$-linear and ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }$ is distributive, we have

$$\begin{aligned} {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }u_\textrm{tr}(\textbf{Z}_\textrm{tr}X\otimes A) \simeq {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }u_\textrm{tr}(\textbf{Z}_\textrm{tr}X)\otimes A \end{aligned}$$

so we can assume $A=\textbf{Z}[1/e]$. Let $i:\mathcal C\hookrightarrow {\mathcal S}\textrm{ch}_k^{\textrm{ft}}$ be the inclusion. By the motivic Dold-Thom theorem [30, Theorem3.7] (see also [28, Theorem 6.8]), there is an equivalence

$$\begin{aligned} u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}Z_+\simeq a_{\textrm{Nis}}((\coprod _{d\ge 0}i^*r(\textrm{S}^dZ))^\textrm{gp}[1/e]) \end{aligned}$$

of pointed presheaves on $\mathcal C$, natural in Z. Note that the validity of this formula does not depend on the scheme $\textrm{S}^dZ$ belonging to $\mathcal C$. By Lemma 8.2 and the distributivity of $L_{{\textrm{Nis}},\textbf{A}^1}$, we obtain equivalences

$$\begin{aligned} u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}X\simeq L_{{\textrm{Nis}},\textbf{A}^1}\left( \left( \coprod _{d\ge 0}i^*r(\textrm{S}^dZ)\right) ^\textrm{gp}[1/e]\right) \simeq \left( \coprod _{d\ge 0}L_{{\textrm{Nis}},\textbf{A}^1} i^*r(\textrm{S}^dZ)\right) ^\textrm{gp}[1/e] \end{aligned}$$

in ${{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\textbf{A}^1}$. Since ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }$ preserves group completions of commutative monoids (Lemma 7.3) and colimits,

$$\begin{aligned} {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}X\simeq \left( \coprod _{d\ge 0}{\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }L_{{\textrm{Nis}},\textbf{A}^1} i^* r(\textrm{S}^dZ)\right) ^\textrm{gp}[1/e]. \end{aligned}$$

On the other hand, by Lemmas 7.5 and 7.6 and since ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }L_{{\textrm{Nis}},\textbf{A}^1}$ commutes with $\textrm{S}^d$,

$$\begin{aligned} {\tilde{\textbf{Z}}}{\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }X\otimes \textbf{Z}[1/e]\simeq \left( \coprod _{d\ge 0}{\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }L_{{\textrm{Nis}},\textbf{A}^1}\textrm{S}^dr_{\textrm{Nis}}(Z)\right) ^\textrm{gp}[1/e]. \end{aligned}$$

We then define $\theta _{X,\textbf{Z}[1/e]}:{\tilde{\textbf{Z}}}{\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }X\otimes \textbf{Z}[1/e]\rightarrow {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}X$ to be the map induced by the obvious canonical map

$$\begin{aligned} \varphi :\textrm{S}^d r_{\textrm{Nis}}(Z)\rightarrow i^* r(\textrm{S}^dZ) \end{aligned}$$

in ${{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)_{\le 0}$. To show that $\theta _{X,\textbf{Z}[1/e]}$ is an equivalence, it suffices to show that ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }L_{{\textrm{Nis}},\textbf{A}^1}(\varphi )$ is an equivalence. By definition of ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }$, the functor ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }L_{{\textrm{Nis}},\textbf{A}^1}$ factors through $a_{{\textrm{h}}}^\wedge i_!:{{\,\textrm{Shv}\,}}_{\textrm{Nis}}(\mathcal C)\rightarrow {{\,\textrm{Shv}\,}}_{\textrm{h}}^\wedge ({\mathcal S}\textrm{ch}_k^{\textrm{ft}})$, so it suffices to show that $a_{{\textrm{h}}}^\wedge i_!(\varphi )$ is an equivalence. This follows from Corollary 4.6 and Proposition 4.7 (since k is perfect and every smooth k-scheme is Zariski-locally in $\mathcal C$).

The strategy to prove (1) and (2) is the following: we first reduce as above to the representable case, where the statements follow from properties of the motivic Dold–Thom equivalence. For (1), we may assume that X is represented by $Z\in \mathcal C$. Then the adjunction map $X\rightarrow u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}X$ corresponds, through the Dold–Thom equivalence, to the map

$$\begin{aligned} Z_+\simeq \textrm{S}^0Z\amalg \textrm{S}^1Z\hookrightarrow \coprod _{d\ge 0}\textrm{S}^dZ\rightarrow \left( \coprod _{d\ge 0}\textrm{S}^dZ\right) ^\textrm{gp}[1/e], \end{aligned}$$

which proves the result. For (2), we may assume that X and Y are represented by Z and W and that $A=B=\textbf{Z}[1/e]$. Moreover, we can replace ${\tilde{\textbf{Z}}}$ with ${\tilde{\textbf{N}}}$. It then suffices to note that the pairing

$$\begin{aligned} u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}X\wedge u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}Y\rightarrow u_\textrm{tr}\textbf{Z}[1/e]_\textrm{tr}(X\wedge Y) \end{aligned}$$

arising from the monoidal structure of $\textbf{Z}[1/e]_\textrm{tr}$ is induced, via the Dold-Thom equivalence, by the obvious maps $\textrm{S}^a Z\times \textrm{S}^b W\rightarrow \textrm{S}^{ab}(Z\times W)$. $\square$

For A a connective $H\textbf{Z}$-module, let $A_l$ be the pro-$H\textbf{Z}$-module $\lim _n A/l^n$. Note that $A_l\simeq A$ if A admits an $H\textbf{Z}/l^n$-module structure for some $n\ge 1$.

Lemma 9.3

Let A be a connective $H\textbf{Z}$-module and $p\ge 1$. Then

$$\begin{aligned} L_{\textbf{Z}/l}K(A,p) \simeq \tau _{<\infty }K(A_l,p). \end{aligned}$$

Proof

We can assume A truncated, as both sides preserve the limit of the Postnikov tower of A. Then A is a finite product of $H\textbf{Z}$-modules of the form B[i] with B discrete and $i\ge 0$. Since $K(B[i],p)\simeq K(B,p+i)$ and since both sides preserve finite products (see Proposition 3.3), we can assume A discrete. By the principal fibration lemma [3, III,3.6], we can reduce to the case $p=1$ and A free abelian. In this case we have $\pi _nL_{\textbf{Z}/l}K(A,1)=0$ for $n\ge 2$ [3, IV,Lemma 4.4] and $\pi _1L_{\textbf{Z}/l}K(A,1)\simeq A_l$ by the proof of [3, IV, Lemma 2.4]. $\square$

Given $q\in \textbf{Z}$, we let $A_l(q)=A_l\otimes _{\textbf{Z}_l}T_l\mu ^{\otimes q}$ (which is noncanonically isomorphic to $A_l$). For example, $\textbf{Z}/l^n(q)\simeq \mu _{l^n}^{\otimes q}$.

Theorem 9.4

Let k be an algebraically closed field of characteristic exponent e, $l\ne e$ a prime number, and $\mathcal C\subset {\mathcal S}\textrm{ch}_k$ an admissible subcategory consisting of semi-normal separated schemes. For any connective $H\textbf{Z}[1/e]$-module A and any integers p, q with $p\ge 1$ and $p\ge q\ge 0$, there is a canonical equivalence

$$\begin{aligned} {{{\acute{\textrm{E}}}\textrm{t}}}_l K(A(q),p)_{\mathcal C}\simeq \tau _{<\infty }K(A_l(q),p) \end{aligned}$$

of pointed objects in ${{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l}$, natural in A, and ${{\acute{\textrm{E}}}\textrm{t}}_l$ preserves smash products between such spaces. Furthermore, under these equivalences,

• (1) ${{\acute{\textrm{E}}}\textrm{t}}_l$ sends the canonical map

  $$\begin{aligned}S^{p,q}\rightarrow K(\textbf{Z}[1/e](q),p)_{\mathcal C}\end{aligned}$$

  to the canonical map

  $$\begin{aligned}S^{p,q}_l\rightarrow K(\textbf{Z}_l(q),p);\end{aligned}$$

• (2) ${{\acute{\textrm{E}}}\textrm{t}}_l$ sends the canonical map

  $$\begin{aligned}K(A(q),p)_{\mathcal C}\wedge K(B(s),r)_{\mathcal C}\rightarrow K((A\otimes B)(q+s),p+r)_{\mathcal C}\end{aligned}$$

  to the canonical map

  $$\begin{aligned}\tau _{<\infty }K(A_l(q),p)\wedge \tau _{<\infty }K(B_l(s),r)\rightarrow \tau _{<\infty }K((A\otimes B)_l(q+s),p+r).\end{aligned}$$

Proof

By Theorem 9.2, we have

$$\begin{aligned} {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }K(A(q),p)_{\mathcal C}\simeq {\tilde{\textbf{Z}}}{\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }S^{p,q}\otimes A. \end{aligned}$$

By Proposition 6.3 and the definition of ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }$ (see Construction 9.1), we have

$$\begin{aligned} {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }S^{p,q} \simeq L_{\textbf{Z}/l,\le *} S^{p,q}_l, \end{aligned}$$

where $S^{p,q}_l\in {{\,\textrm{Pro}\,}}'(\mathcal S)_{\textbf{Z}/l}$ is considered as a constant ind-$\textbf{Z}/l$-local pro-space. Thus,

$$\begin{aligned} {\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }K(A(q),p)_{\mathcal C}\simeq {\tilde{\textbf{Z}}} L_{\textbf{Z}/l,\le *} S^{p,q}_l\otimes A. \end{aligned}$$

Now we apply the colimit functor

$$\begin{aligned} c:\lim _n{{\,\textrm{Ind}\,}}({{\,\textrm{Pro}\,}}'(\mathcal S_{\le n})_{\textbf{Z}/l})\rightarrow \lim _n{{\,\textrm{Pro}\,}}(\mathcal S_{\le n})_{\textbf{Z}/l}\simeq {{\,\textrm{Pro}\,}}(\mathcal S)_{\textbf{Z}/l} \end{aligned}$$

to both sides. The left-hand side becomes ${{\acute{\textrm{E}}}\textrm{t}}_l K(A(q),p)_{\mathcal C}$, by definition of ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }$. We are thus reduced to proving that

$$\begin{aligned} c({\tilde{\textbf{Z}}} L_{\textbf{Z}/l,\le *}S^{p,q}_l\otimes A) \simeq \tau _{<\infty } K(A_l(q),p). \end{aligned}$$

(9.5)

For this, we consider the following commutative diagram:

Note that $L_{\textbf{Z}/l,\le *}S^{p,0}_l$ is the image of $S^p$ by the top row of this diagram. The functor $j^\textrm{ind}$ is clearly distributive and $L^\textrm{ind}$ is distributive by Proposition 3.13. We therefore have equivalences

$$\begin{aligned} c({\tilde{\textbf{Z}}} L_{\textbf{Z}/l,\le *}S^{p,0}_l\otimes A) \simeq c ({\tilde{\textbf{Z}}} (L^\textrm{ind}j^\textrm{ind}iS^{p})\otimes A)\simeq c L^\textrm{ind}j^\textrm{ind}({\tilde{\textbf{Z}}} iS^p\otimes A) \simeq L_{\textbf{Z}/l} jK(A,p), \end{aligned}$$

which concludes the case $q=0$ by Lemma 9.3. It also concludes the general case if one is willing to choose an isomorphism $\textbf{Z}_l\simeq T_l\mu$. However, the twisting for $q>0$ makes the equivalence (9.5) independent of such a choice, as a consequence of the following observation: if $\alpha$ is an automorphism of $\textbf{Z}_l$, then the automorphism $\textrm{id}^{\wedge (p-q)}\wedge \alpha ^{\wedge q}$ of $S^{p,0}_l$ induces $\alpha ^{\otimes q}$ on the top homology pro-group $\textbf{Z}_l$. A similar argument shows that ${{\acute{\textrm{E}}}\textrm{t}}_l(X\wedge Y)\simeq {{\acute{\textrm{E}}}\textrm{t}}_l(X)\wedge {{\acute{\textrm{E}}}\textrm{t}}_l(Y)$ whenever ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }X$ and ${\acute{\textrm{E}}\textrm{t}}_{ l }^{\times }Y$ belong to the essential image of $L^\textrm{ind}j^\textrm{ind}$. The remaining statements are easily deduced from properties (1) and (2) in Theorem 9.2. $\square$

In conclusion, let us emphasize the two most important special cases of Theorem 9.4:

Corollary 9.6

Let k be an algebraically closed field of characteristic exponent e, $l\ne e$ a prime number, and $\mathcal C\subset {\mathcal S}\textrm{ch}_k$ an admissible subcategory consisting of semi-normal separated schemes.

• (1) For any $\textbf{Z}[1/e]\subset \Lambda \subset \textbf{Z}_{(l)}$, there is a canonical equivalence

  $$\begin{aligned} {{\acute{\textrm{E}}}\textrm{t}}_l K(\Lambda (q),p)_{\mathcal C} \simeq K(T_l\mu ^{\otimes q}, p), \end{aligned}$$

  where $T_l\mu ^{\otimes q}$ is the l-adic Tate module of $\mu ^{\otimes q}$ viewed as a pro-group.

• (2) For any $n\ge 1$, there is a canonical equivalence

  $$\begin{aligned} {{\acute{\textrm{E}}}\textrm{t}}_l K(\textbf{Z}/l^n(q),p)_{\mathcal C} \simeq K(\mu _{l^n}^{\otimes q}, p). \end{aligned}$$

  In particular, ${{\acute{\textrm{E}}}\textrm{t}}_l K(\textbf{Z}/l^n(q),p)_{\mathcal C}$ is a constant pro-space.

In both cases, the $\textbf{Z}/l$-local étale homotopy type is already $\textbf{Z}/l$-profinite.