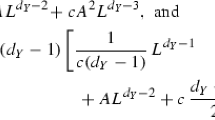Abstract
We prove an effective restriction theorem for stable vector bundles E on a smooth projective variety: \(E|_D\) is (semi)stable for all irreducible divisors \(D \in |kH|\) for all k greater than an explicit constant. As an application, we show that Mercat’s conjecture in any rank greater than 2 fails for curves lying on K3 surfaces. Our technique is to use wall-crossing with respect to (weak) Bridgeland stability conditions which we also use to reprove Camere’s result on slope stability of the tangent bundle of \({\mathbb {P}}^n\) restricted to a K3 surface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inspired by the construction of Bridgeland stability conditions on K3 surfaces [7] Bayer et al. [5, 6] studied weak stability conditions on any smooth complex projective variety. In this paper, we use wall-crossing with respect to these weak stability conditions to prove an effective restriction theorem that expresses sufficient conditions on a slope-stable reflexive sheaf such that its restriction to a hypersurface remains stable. Restriction theorems provide us with the possibility of studying higher dimensional varieties via the geometry of their subvarieties. That is why they have been long-studied via different approaches; see [16, Chapter 7] for a survey.
Let X be a smooth complex projective variety of dimension \(n \ge 2\) with an ample divisor H. For a \(\mu \)-stable coherent sheaf E of positive rank on X, we define
and \(\delta (E) {:}{=}\min \left\{ \mu ^{\min }(E) - \mu (E),\, \mu (E) -\mu ^{\max }(E) \right\} \).
Theorem 1.1
Let E be a \(\mu \)-stable reflexive sheaf on X of rank \({\text {rk}}> 0\). The restricted sheaf \(E|_D\) for any irreducible divisorFootnote 1\(D \in |k H|\) is \(\mu \)-semistable on D if
Moreover, \(E|_D\) is \(\mu \)-stable on D if the inequalities in (3) are both strict.
The \(\mu \)-slope of a coherent sheaf and the notion of \(\mu \)-(semi)stability are defined in Section 2. Note that if \(k \ge 2\delta (E)\), the conditions in (3) are equivalent to
When \({\text {rk}}> 1\), we always have \(\delta (E) \ge \frac{1}{H^n{\text {rk}}({\text {rk}}-1)} \). If we substitute this lower bound, we obtain one of Langer’s restriction theorems [19], see Corollary 4.4 and Remark 4.5 for more details.
1.1 Clifford indices
The Clifford index Cliff(C) of a smooth curve C is the second important invariant of C after the genus g, which carries the information of special line bundles on C. Lange and Newstead [22] proposed a generalisation of Cliff(C) to higher rank Clifford index Cliff\(_r(C)\) which depends on rank r-semistable vector bundles on C.
Take a vector bundle E of rank r and degree d on C. The Clifford index of E is defined as Cliff\((E) = \frac{1}{r}(d-2(h^0(E)-r))\). We say E contributes to the rank r-Clifford index of C if E is \(\mu \)-semistable with degree \(d \le r(g-1)\) and \(h^0(C,E) \ge 2r\). Then the rank r - Clifford index of C is defined as the quantity
Note that Cliff\(_1(C) = \text {Cliff}(C)\) is the classical Clifford index of C. In terms of these new invariants, Mercat’s conjecture [24] can be expressed as
which says higher rank Clifford indices are equal to the rank one Clifford index.
Curves over K3 surfaces have played an important role in the Brill-Noether theory of vector bundles on curves. In [4], the conjecture \(\mathbf{M_2}(C)\) was proved for any smooth curve \(C \in |H|\) on a K3 surface S when \(\text {Pic}(S) = \mathbb {Z}.H\). Using this, \(\mathbf{M_2}(C)\) was shown for generic curves of every genus. However, the restriction of Lazarsfeld-Mukai bundles on S to the curve C (see Section 5 for a definition) have led to counterexamples to \(\mathbf{M_3}(C)\) [12] and \(\mathbf{M_4}(C)\) [1]. As a consequence of Theorem 1.2, we generalise these results to higher ranks and show \(\mathbf{M_r}(C)\) fails for \(r \ge 3\) and any smooth curve \(C \in |H|\).
Theorem 1.2
Let (S, H) be a smooth polarised K3 surface such that
e.g. \({\text {Pic}}(S) = \mathbb {Z}.H\). Take a \(\mu \)-stable vector bundle E on S with Chern character \({\text {ch}}(E) = (r, H, {\text {ch}}_2)\) such that \(r \ge 2\) and \({\text {ch}}_2 \ge 0\). Then for any smooth curve \(C \in |H|\) of genus g, the restricted bundle \(E|_C\) contributes to the rank r-Clifford index of C. If \(r \ge 4\), or, \(r=3\) and \(g -{\text {ch}}_2 < 4+ \frac{3}{2}\lfloor \frac{g-1}{2} \rfloor \), then
In particular, \(\mathbf{M_r}(C)\) does not hold if either (i) \(r \ge 4\) and \(g \ge r^2\), or (ii) \(r=3\) and \(g=7, 9\) or \(g \ge 11\).
1.2 Slope stability of the restriction of tangent bundle of \(\mathbb {P}^n\) to a K3 surface.
Let S be a smooth projective K3 surface and let L be an ample line bundle generated by its global sections on S. Then there is a well-defined morphism
In the final part of the paper, we apply wall-crossing with respect to Bridgeland stability conditions on K3 surfaces to reprove Camere’s result on slope-stability of \(\phi _L^{*}T_{\mathbb {P}^n}\). The restriction of the Euler exact sequence to the K3 surface S and tensoring with \(L^*\) gives the short exact sequence
Theorem 1.3
[8, Theorem 1] Let S be a smooth projective K3 surface over \(\mathbb {C}\), and let L be a globally generated ample line bundle on S. Then the kernel \(M_L\) of the evaluation map on the global sections of L
is \(\mu \)-stable with respect to L.
1.3 Method of the proof of Theorem 1.1
There is an abelian subcategory \(\mathcal {A} \subset {\mathcal {D}}(X)\) of the bounded derived category of coherent sheaves on X which includes E and \(E(-k H)[1]\) for \(k \in \mathbb {N}\). Thus for any irreducible divisor \(D \in |k H|\), the restricted sheaf \(E|_D\) lies in an exact sequence
in \(\mathcal {A}\). The slope-stability of the reflexive sheaf E implies that there is a weak stability condition \(\sigma \) on \({\mathcal {A}}\) such that both E and \(E(-k H)[1]\) are stable with respect to \(\sigma \). If k is large enough, we may apply wall-crossing techniques to show that we can deform the weak stability condition \(\sigma \), while keeping E and \(E(-k H)[1]\) stable, to reach a weak stability condition \(\sigma '\) where E and \(E(-k H)[1]\) have the same slope (phase). Thus their extension \(E|_D\) is \(\sigma '\)-semistable of the same slope. Then a general argument immediately implies that \(E|_D\) is slope-stable.
The main advantage of this method is the possibility to strengthen effective restriction theorems for special sheaves E as soon as we have more control over the position of the walls for E and \(E(-kH)[1]\); see for instance Proposition 4.6.
1.4 Related work
Theorem 1.1 appeared in an earlier version of this paper [9], where it was stated for K3 surfaces only. However the proof works for any variety, as the current version of the paper makes explicit. The result has now found applications in [18, 21] to construct Bridgeland stability conditions on Calabi–Yau threefolds, and in [17] to investigate the stability of the restriction of stable vector bundles on a surface to any integral curve, not necessarily multiples of H.
In joint work with Li [11], we employed the techniques in the current paper and [10] to compute rank \(\ge 2\) Clifford indices of curves over K3 surfaces.
2 Two-dimensional slice of weak stability conditions
In this section, we recall the notion of (weak) Bridgeland stability conditions on the bounded derived category of coherent sheaves. The main references are [5, 6].
Let X be a projective scheme over \(\mathbb {C}\) and let H be the class of an ample divisor on X. Recall that the Hilbert polynomial P(E, m) of a coherent sheaf E is defined via the Euler characteristic \(m \mapsto \chi (E \otimes \mathcal {O}_X(mH))\). It can be uniquely written as
with integral coefficients \(\alpha _i(E)\) for \(i=0, \dots , \dim E\) where \(\dim E\) is the dimension of the support of E [16]. If E is a coherent sheaf of dimension \(d = \dim X\), we define the rank and degree of E as
Then for any coherent sheaf E, the slope is defined as
Definition 2.1
A coherent sheaf E of dimension \(d = \dim (X)\) is \(\mu \)-(semi)stable if for all non-trivial quotient sheaves \(E \twoheadrightarrow F\) we have \(\mu (E) < (\le ) \ \mu (F)\).
From now on, we assume X is a smooth projective complex variety of dimension \(n \ge 2\). For any coherent sheaf E on X, the Hirzebruch-Riemann-Roch formula shows that \(\deg (E) = {\text {ch}}_1(E).H^{n-1}\).
We denote the bounded derived category of coherent sheaves on X by \(\mathcal {D}(X)\) and its Grothendieck group by K(X). For any \(b \in \mathbb {R}\), consider the full abelian subcategory of complexes
Here \(\mu ^{\pm }(E)\) for a coherent sheaf E is the maximum (minimum) slope in the Harder-Narasimhan filtration of E with respect to \(\mu \)-stability. By [7, Lemma 6.1], \({\text {Coh}}^b(X)\) is the heart of a bounded t-structure on \({\mathcal {D}}(X)\).
For any \(w > \frac{b^2}{2}\), we define the function \(Z_{b,w} :K(X) \rightarrow \mathbb {C}\) such that for any \(E \in K(X)\),
Each \(E\in {\text {Coh}}^b(X)\) satisfies Im\([Z_{b,w}(E)] \ge 0\), and if Im\([Z_{b,w}(E)] = 0\), then Re\([Z_{b,w}(E)] \le 0\) [5, Proposition 12.2].Footnote 2 Thus for objects in \({\text {Coh}}^b(X)\), we have the slope function
Definition 2.2
Fix \(w>\frac{b^2}{2}\). We say \(E\in {\mathcal {D}}(X)\) is \(\nu _{b,w}\)-(semi)stable if and only if
-
\(E[k]\in {\text {Coh}}^b(X)\) for some \(k\in {\mathbb {Z}}\), and
-
\(\nu _{b,w}(F)\, < (\le )\,\nu _{b,w}\big (E[k]/F\big )\) for all non-trivial subobjects \(F\hookrightarrow E[k]\) in \({\text {Coh}}^b(X)\).
Note that \(\nu _{b,w}\)-stability defines a Harder-Narasimhan (HN) filtration on \({\text {Coh}}^b(X)\), and so a weak stability condition on \({\mathcal {D}}(X)\) [5, Proposition 12.2].
In Fig. 1 we plot the (b, w)-plane simultaneously with the image of the projection map

The pair (b, w) for our weak stability condition \(\nu _{b,w}\) is in the shaded open subset
Also, the image \(\Pi (E)\) of \(\nu _{b,w}\)-semistable objects E with \({\text {ch}}_0(E)\ne 0\) is always outside U due to the classical Bogomolov-Gieseker-type inequality for the H-discriminant,
proved for \(\nu _{b,w}\)-semistable objects E in [5, Theorem 3.5]. The slope \(\nu _{b,w}(E)\) of E is the gradient of the line connecting (b, w) to \(\Pi (E)\), see [23, Section 1.3] for more details.
Objects of \({\mathcal {D}}(X)\) give the space of weak stability conditions a wall and chamber structure, explained in [13, Proposition 4.1] for instance.
Proposition 2.3
(Wall and chamber structure) Fix an object \(E \in \mathcal {D}(X)\) such that the vector \(\left( {\text {ch}}_0(E), {\text {ch}}_1(E).H^2, {\text {ch}}_2(E).H\right) \) is non-zero. There exists a set of lines \(\{\ell _i\}_{i \in I}\) in \(\mathbb {R}^2\) such that the segments \(\ell _i\cap U\) (called “walls”) are locally finite and satisfy (Fig. 2)
-
(a)
If \({\text {ch}}_0(E)\ne 0\) then all lines \(\ell _i\) pass through \(\Pi (E)\).
-
(b)
If \({\text {ch}}_0(E)=0\) then all lines \(\ell _i\) are parallel of slope \(\frac{{\text {ch}}_2(E).H^{n-2}}{{\text {ch}}_1(E).H^{n-1}}\).
-
(c)
The \(\nu _{b,w}\)-(semi)stability of E is unchanged as (b, w) varies within any connected component (called a “chamber") of \(U \setminus \bigcup _{i \in I}\ell _i\).
-
(d)
For any wall \(\ell _i\cap U\) there is \(k_i \in \mathbb {Z}\) and a map \(f:E[k_i] \rightarrow F\) in \({\mathcal {D}}(X)\) such that
-
for any \((b,w) \in \ell _i \cap U\), the objects \(E[k_i],\,F\) lie in the heart \({\text {Coh}}^b(X)\),
-
\(E[k_i]\) is \(\nu _{b,w}\)-semistable with \(\nu _{b,w}(E)=\nu _{b,w}(F)=\,\mathrm {slope}\,(\ell _i)\) constant on the wall \(\ell _i \cap U\), and
-
f is a surjection \(E[k_i] \twoheadrightarrow F\) in \({\text {Coh}}^b(X)\) which strictly destabilises \(E[k_i]\) for (b, w) in one of the two chambers adjacent to the wall \(\ell _i\).
\(\square \)
3 Large volume limit
As before X is a smooth projective complex variety of dimension \(n \ge 2\) and H is an ample divisor on X. In this section, we first prove the following general statement which holds for any coherent sheaf.
Theorem 3.1
Given a coherent sheaf E of rank bigger than one, there is no wall for E crossing the vertical line \(b = b_0\) at a point inside U whenever
Proof
Suppose for a contradiction that there is a wall \(\ell \) for E which intersects the vertical line \(b=b_0\). Since E is \(\nu _{b,w}\)-semistable for \((b,w) \in \ell \cap U\), we have \(\Delta (E) \ge 0\) (12). If \(\Delta (E) = 0\), then [5, Corollary 3.10] implies that there is no wall for E in U crossing the vertical line \(b=b_0\) for \(b_0 < \mu (E)\), so we may assume \(\Delta (E) > 0\). Hence \(\Pi (E)\) lies outside \(\overline{U} = U \cup \partial U\). Let
and let \(p_0\) be the intersection point of \(\ell \) with the vertical line \(b=b_0\). The line segment connecting the point \(\Pi (E)\) (which is outside \(\overline{U}\)) to \(p_0\) (which lies inside U and has lower first coordinate, i.e. \(b_0 < \frac{c}{r}\)) intersects the boundary \(\partial U\) at a point \(p_1= (b_1, w_1)\), so
We know the mentioned line segment is part of the line \(\ell \) which intersects \(\partial U\) at another point \(p_2 =(b_2, w_2)\) with \(b_2< b_0 < b_1\), see Fig. 3.
Let \(\delta _i {:}{=}\frac{c}{r} - b_i\) for \(i=1, 2\). The inequality (13) gives
which implies \(0< \delta _1 = \frac{c}{r} -b_1 < \frac{H^n}{r(r-H^n)}\). One can easily check
Thus we get
Step 1. First assume \(r \ge 3H^n\) or \(\Delta (E) \ge 3\). Recall that \(r = H^n{\text {ch}}_0(E)\) and E is of rank bigger than or equal to 2, i.e. \({\text {ch}}_0(E) \ge 2\). Thus
and (15) gives
Hence there is \(k \in \mathbb {Z}\) such that

so the wall \(\ell \) intersects the vertical line \(b= b^*\) at a point \((b^*, w^*)\) inside U. Let
be a destabilising sequence for E which makes it unstable in one side of the wall \(\ell \) with
At any \((b,w) \in \ell \cap U\), we have \(\nu _{b,w}(E) = \nu _{b,w}(E_i)\) for \(i=1,2\), so
We consider two different cases:
Case i. First assume
for \((b,w) \in U\) above the wall \(\ell \), i.e. our destabilising sequence destabilises E below \(\ell \). Then \(r_1 \ne 0\) and
Suppose \(b_2< b < b_1\), then (18) implies \(r_1 > 0\) as the denominators are positive by (17). Thus (18) implies
The limit of (17) when \(b \rightarrow b_1^{-}\) implies that \(0 \le c_1 - r_1 b_1\).
Combining this with (19) gives
We claim
Then by (20) we get
which is not possible by our assumption (14).
To prove the claim, first assume \(0< r_1 < r\). We have
The numerator in the right fraction is a positive integral multiple of \(H^n\) and
Hence
so the claim (21) follows from (22). If \(r \le r_1\), inequality (17) at \(b= b^*\) gives \(c_1-b^*r_1 >0\), thus
We know \(b^*r = \frac{H^n}{r-H^n}{ k{\text {ch}}_0(E)}\) and \(b^*r_1 = \frac{H^n}{r-H^n}{ k{\text {ch}}_0(E_1)}\), so they are both integral multiples of \(\frac{H^n}{r-H^n} = \frac{1}{{\text {ch}}_0(E) -1}\). Since \(c, c_1 \in \mathbb {Z}\), we get
Applying (17) at \((b^*, w^*)\) gives \(c-b^*r - (c_1-b^*r_1) >0\), thus (23) implies our claim (21).
Case ii. Suppose our destabilising sequence makes E unstable above the wall \(\ell \), then
for \((b,w) \in U\) above \(\ell \). Hence \(r_2 \ne 0\) and
If \(b_2<b <b_1\), (17) implies \(r_2 >0\) and so
Then limit of (17) when \(b \rightarrow b_1^-\) implies that
Hence applying the same argument as in (22) and (23) reach a contradiction.
Step 2. Finally, we show that if \(r=2H^n\) and \(\Delta (E) = 1\), or 2, there is no wall for E in U, so the claim follows. Suppose there is a wall with the destabilising sequence (16). The same argument as in [5, Corollary 3.10] gives
If \(\Delta (E) =1\), then \(\Delta (E_i) =0\) for \(i=1, 2\), so
which is not possible. Similarly, if \(\Delta (E) = 2\), one of the following cases happens:
-
(a)
\(\Delta (E_i) = 0\) for \(i=1, 2\). Since \(H^n|r_i\), we get \(H^n|c_i^2\), but
$$\begin{aligned} 1 = \frac{\Delta (E)}{2} = c_1c_2 - (r_1h_2 +r_2h_1) \end{aligned}$$implies that \(\gcd (H^n, c_i) = 1\), a contradiction.
-
(b)
\(\Delta (E_1) = 1\) and \(\Delta (E_2) = 0\), then
$$\begin{aligned} 1 = \Delta (E)- \Delta (E_1) = 2c_1c_2 -2(r_1h_2 +r_2h_1) \end{aligned}$$which is not again possible. Similar argument applies to the case \(\Delta (E_1) = 0\) and \(\Delta (E_2) = 1\).
-
(c)
\(\Delta (E_i) =1\) for \(i=1, 2\), then \(\gcd (H^n, c_i^2) =1\) for \(i=1, 2\), but
$$\begin{aligned} 0 = \Delta (E) - \Delta (E_1) -\Delta (E_2) = 2c_1c_2 - 2(r_1h_2 +r_2h_1) \end{aligned}$$which implies \(H^n | c_1c_2\), a contradiction.
\(\square \)
By combing the ideas in the proof of Theorem 3.1 and the notion of safe area introduced in [14], we get the following.
Proposition 3.2
Take a \(\mu \)-stable coherent sheaf E of positive rank, and let \(\ell \) be a line passing through \(\Pi (E)\) which intersects \(\partial U\) at two points with b-values \(b_2 <b_1 \le \mu (E)\) satisfying
where \(\mu ^{\max }(E)\) is defined as in (1). Then E is \(\nu _{b,w}\)-stable for any \((b,w) \in \ell \cap U\).
Proof
A similar argument as in [7, Proposition 14.2] or [5, Lemma 2.7] implies that E is \(\nu _{b,w}\)-stable when \(b< \mu (E)\) and \(w \gg 0\).
If \(\Delta (E) = 0\), then [5, Corollary 3.10] implies that there is no wall for E on the left hand side of \(b= \mu (E)\), so the claim follows. Thus we may assume \(\Delta (E) > 0\), i.e. \(\Pi (E)\) lies outside \(\overline{U} = U \cup \partial U\). Then there is a unique line through \(\Pi (E)\) which is tangent to \(\partial U\) at a point to the left of \(\Pi (E)\). If we move this line upwards while making it pass through \(\Pi (E)\), its intersection point with \(\partial U\) move further apart until we find a unique \(\ell _E\) for which the b-values \(b_2^* < b_1^*\) of the two points of \(\ell _E \cap \partial U\) satisfy
We show there is no wall for E above the line \(\ell _E\) to the left of \(\Pi (E)\). Since the line \(\ell \) in the Proposition lies above \(\ell _E\), the claim follows.
Suppose for a contradiction there is a wall \(\tilde{\ell }\) for E which lies above \(\ell _E\) to the left of \(\Pi (E)\) and intersects \(\partial U\) at two points with b-values \(\tilde{b}_2< \tilde{b}_1\) satisfying
Let \(E_1 \hookrightarrow E \twoheadrightarrow E_2\) be a destabilising sequence for E which makes it unstable below \(\tilde{\ell }\). We first show that both \(E_1\) and \(E_2\) are coherent sheaves. Taking cohomology from the destabilising sequence gives the long exact sequence of coherent sheaves
This immediately gives \(E_1\) is a sheaf. Suppose \({\mathcal {H}}^{-1}(E_2)\) is of rank \(r' \ne 0\). As we move \(b \uparrow \tilde{b}_1\) or \(b \downarrow \tilde{b}_2\) along \(\tilde{\ell }\), \(E_1\) and \(E_2\) remain in the heart \({\text {Coh}}^b(X)\) by Proposition 2.3. This implies
Combining this with (26) gives
Therefore \(\mu (E) -b_1^* > \frac{1}{{\text {ch}}_0(E)} (b_1^* -b_2^*)\) which is not possible by (25), so \(r' =0\). We know \({\mathcal {H}}^{-1}(E_2)\) is a torsion-free sheaf by the definition (8) of \({\text {Coh}}^b(X)\), thus it is zero and \(E_2\) is a sheaf. Hence \(E_1\) is a subsheaf of E. The wall \(\tilde{\ell }\) intersects the vertical line \(b = b_1^*\) at a point \((b^*, w)\) inside U where \(E_1\) and E have the same \(\nu _{b^*_1, w}\)-slope, see Fig. 4. Thus
which implies
The second inequality comes from \(\mu \)-stability of E. Note that the quotient sheaf \(E_2\) cannot be supported in co-dimension at least 2, otherwise its \(\nu _{b,w}\)-slope is \(+\infty \) and it cannot destabilise E, so \(\mu (E_1) \ne \mu (E)\). Therefore
which is not possible by (25). \(\square \)
The next step is to analyse points \((b,w) \in U\) where the shift of a slope-stable reflexive sheaf is stable. The following Lemma is well-known, we add it for completeness.
Lemma 3.3
Let E be a \(\mu \)-stable reflexive sheaf of positive rank. Then E[1] is \(\nu _{b_0,w}\)-stable for \(b_0=\mu (E)\) and all \(w > \frac{b_0^2}{2}\).
Proof
By definition \(E[1] \in {\text {Coh}}^{b_0}(X)\) and Im\([Z_{b_0, w}(E)] = 0\). Therefore E[1] is \(\nu _{b_0, w}\)-semistable of slope \(+ \infty \). Suppose E[1] is strictly \(\nu _{b_0,w}\)-semistable, so there is a short exact sequence in \({\text {Coh}}^{b_0}(X)\)
such that \(\nu _{b_0, w}(E_1) = \nu _{b_0, w}(E_2) = +\infty \).
Case i. First assume \({\mathcal {H}}^{-1}(E_1) = 0\), then
If \({\text {ch}}_0({\mathcal {H}}^{0}(E_1)) \ne 0\), we get \(\mu ({\mathcal {H}}^0(E_1)) =b_0\) which is not possible by the definition (8) of \({\text {Coh}}^{b_0}(X)\). Therefore, \(E_1\) is a sheaf supported in co-dimension at least 2. Taking cohomology from (27) gives the short exact sequence of coherent sheaves
Since E is a reflexive sheaf, [15, Proposition 1.1] implies that E lies in the short exact sequence
where G is a locally free sheaf and \(G'\) is torsion-free. Since \({\mathcal {H}}^0(E_1)\) is supported in co-dimension at least 2, we have
This implies Ext\(^1({\mathcal {H}}^0(E_1), E) = 0\), thus (29) gives \({\mathcal {H}}^{-1}(E_2) \cong E \oplus {\mathcal {H}}^0(E_1)\) which is not possible because \({\mathcal {H}}^{-1}(E_2)\) is torsion-free.
Case ii. If \({\mathcal {H}}^{-1}(E_1) \ne 0\), the exact sequence \({\mathcal {H}}^{-1}(E_1)[1] \hookrightarrow E_1 \twoheadrightarrow {\mathcal {H}}^0(E_1)\)
in \({\text {Coh}}^{b_0}(X)\) implies that \({\mathcal {H}}^{-1}(E_1)[1]\) is a subobject of E[1] of \(\nu _{b_0, w}\)-slope \(+\infty \); so there is a short exact sequence
in \({\text {Coh}}^{b_0}(X)\) where \(E_2'\) lies in the exact sequence \({\mathcal {H}}^0(E_1) \hookrightarrow E_2' \twoheadrightarrow E_2\) in \({\text {Coh}}^{b_0}(X)\). Note that \(E_2' \ne 0\) otherwise \(E_2 \cong {\mathcal {H}}^0(E_1)[1]\) which is not possible because \({\mathcal {H}}^0(E_1)[1] \notin {\text {Coh}}^{b_0}(X)\).
Taking cohomology from (30) gives a short exact sequence of coherent sheaves
thus \({\mathcal {H}}^0(E_2') = 0\). The torsion-free sheaves E, \({\mathcal {H}}^{-1}(E_1)\) and \({\mathcal {H}}^{-1}(E_2')\) satisfy
Thus they all have the same \(\mu \)-slope which is not possible by \(\mu \)-stability of E. \(\square \)
By applying a similar argument to the proof of Proposition 3.2, we get the following.
Proposition 3.4
Take a \(\mu \)-stable reflexive sheaf E of positive rank, and let \(\ell \) be a line passing through \(\Pi (E)\) which intersects \(\partial U\) at two points with b-values \(b_2 <b_1 \) such that
where \(\mu ^{\min }(E)\) is defined as in (2). Then E[1] is \(\nu _{b,w}\)-stable for any \((b,w) \in \ell \cap U\).
Proof
Lemma 3.3 implies E[1] is \(\nu _{b_0, w}\)-stable for \(b_0 = \mu (E)\). Thus the structure of walls described in Proposition 2.3 implies that E[1] is \(\nu _{b, w}\)-stable where \(\mu (E)<b\) and \(w \gg 0\).
If \(\Delta (E) = 0\), there is no wall for E[1] in U by [5, Corollary 3.11(a)], so the claim follows. Hence we may assume \(\Delta (E) > 0\). There is a unique line \(\ell _{E[1]}\) passing through \(\Pi (E)\) such that the b-values \(b_2^*< b_1^*\) of the two points of \(\ell _{E[1]} \cap \partial U\) satisfy
To prove the claim we only need to show there is no wall for E[1] above the line \(\ell _{E[1]}\) to the right of \(\Pi (E)\), see Fig. 5. Suppose there is such a wall \(\tilde{\ell }\) above \(\ell _{E[1]}\) whose intersection point with \(\partial U\) has b-values \(\tilde{b}_2 < \tilde{b}_1\) satisfying \(\tilde{b}_2 < b_2^*\) and \(b_1^* < \tilde{b}_1\). Let \(E_1 \hookrightarrow E[1] \twoheadrightarrow E_2\) be a destabilising sequence which makes E[1] unstable below \(\tilde{\ell }\). Taking cohomology from the destabilising sequence gives the long exact sequence of coherent sheaves
We first show that \({\mathcal {H}}^{0}(E_1)\) is of rank zero. Suppose it is of rank \(r' \ne 0\), then
which is not possible by (31). Thus \({\mathcal {H}}^{0}(E_1)\) is of rank zero and the exact sequence (32) gives
Since \(\tilde{\ell }\) crosses the vertical line \(b=b_2^*\) at a point inside U, we gain
Combining this with (33) gives
which is not again possible by (31). \(\square \)
Proposition 3.2 and 3.4 can be directly shown using [25, Theorem 1.3 and 1.4]. However, we gave here independent proof. We finish this section by mentioning another way to control the position of walls.
Lemma 3.5
Take an object \(E \in {\text {Coh}}^{b_0}(X)\) which is \(\nu _{b_0,w_0}\)-semistable for some \(w_0 > \frac{b_0^2}{2}\). If
then E is \(\nu _{b_0,w}\)-stable for all \(w > \frac{b_0^2}{2}\).
Proof
Assume otherwise, so when we move along the vertical line \(b=b_0\), E gets strictly \(\nu _{b_0, w}\)-semistable for some \(w > \frac{b_0^2}{2}\).
There is an exact sequence \(E_1 \hookrightarrow E \twoheadrightarrow E_2\) in \({\text {Coh}}^{b_0}(X)\) such that \(\nu _{b_0, w}(E_i) = \nu _{b_0, w}(E) < +\infty \), thus Im\([Z_{b_0, w}(E_i)] \ne 0\) for \(i=1,2\). Since
we gain Im\([Z_{b_0, w}(E_i)] < \text {Im}[Z_{b_0, w} (E)]\) which is not possible by our assumption. \(\square \)
4 Slope stability of the restricted sheaf
In this section, we prove our main result Theorem 1.1 which provides sufficient conditions to the slope stability of the restriction of a slope stable reflexive sheaf to a hypersurface. Firstly, we examine \(\mu \)-stability of a sheaf supported on a hypersurface via the Chern character of its push-forward.
Lemma 4.1
Take an irreducible divisor \(D \in |k H |\) with the embedding \(i :D \hookrightarrow X\). A coherent sheaf F on D is
\(\mu \)-(semi)stable if for any quotient sheaf \(F \twoheadrightarrow F'\), we have
Proof
For any coherent sheaf Q on D, by adjuction, we get
Since X is a smooth projective variety, Hirzebruch-Riemann-Roch Formula gives
Thus
and
Since Q is supported on an irreducible divisor \(D \in |k H|\), \({\text {ch}}_1(i_*Q)\) is a multiple of H, so
Therefore, if \(\alpha _{n-1}(i_*Q) \ne 0\), the slope of Q is
Hence, for a quotient sheaf \(F \twoheadrightarrow F'\) on D, we have \(\mu (F) < (\le )\ \mu (F')\) if and only if (34) holds.
\(\square \)
The next proposition describes how we can use the 2-dimensional slice U of weak stability conditions to prove the \(\mu \)-stability of the restricted sheaf.
Proposition 4.2
Let E be a reflexive sheaf on X such that for a point \((b,w) \in U\), E and \(E(-kH)[1]\) are \(\nu _{b,w}\)-semistable objects in \({\text {Coh}}^b(X)\) with
Then the restricted sheaf \(E|_{D}\) for any irreducible divisor \(D \in |k H|\) is \(\mu \)-semistable on D if it has no quotient sheaf \(E|_D \twoheadrightarrow F\) whose point \(Z_{b,w}(F)\) lies inside the triangle \(\triangle opp'\) or on its sides except \(\overline{op'}\) where \(p = Z_{b,w}(E)\) and \(p' = Z_{b,w}(E|_D)\).
Proof
Consider the short exact sequence of coherent sheaves \({\mathcal {O}}_X(-kH) \hookrightarrow {\mathcal {O}}_X \twoheadrightarrow \iota _*{\mathcal {O}}_D\). Taking the derived tensor product \((- \otimes ^{L} E)\) gives the exact triangle
in \({\mathcal {D}}(X)\). By the projection formula \(i_*{\mathcal {O}}_D \otimes ^{L} E \simeq i_*(Li^*E)\). Taking cohomology from the above exact triangle together with the assumption that E is torsion-free implies that \({\mathcal {H}}^{-1}(i_*(Li^*E)) = 0\) and so \(i_*{\mathcal {O}}_D \otimes ^{L} E = E|_D\).
Since E and \(E(-kH)[1]\) are in the heart \({\text {Coh}}^b(X)\), the exact triangle
implies that \(E|_D \in {\text {Coh}}^b(X)\). Let \(F^{+} \hookrightarrow E|_D\) be the subobject of \(E|_D\) of maximum \(\nu _{b,w}\)-slope in the HN filtration of \(E|_D\). If \(\nu _{b,w}(F^{+}) > \nu _{b,w}(E(-k)[1])\), then (35) implies
which is not possible by the exact sequence (36), thus the maximum slope \(\nu ^{\max }_{b,w}(E|_D)\) in the HN filtration of \(E|_D\) satisfies
A similar argument also implies
where \(\nu ^{\min }_{b,w}(E|_D)\) is the minimum \(\nu _{b,w}\)-slope in the HN filtration of \(E|_D\).
Suppose \(E|_D\) is not \(\mu \)-semistable on D. Then there is a sequence of coherent sheaves
such that \(\mu (F)< \mu (E|_D) < \mu (F')\). By definition of the heart \({\text {Coh}}^b(X)\), any torsion sheaf Q is in the heart and its \(\nu _{b,w}\)-slope is equal to \(\frac{{\text {ch}}_2(Q).H^{n-2}}{{\text {ch}}_1(Q)H^{n-1}}\) if \({\text {ch}}_1(Q)H^{n-1} \ne 0\), otherwise it is \(+\infty \). Thus (39) is an exact sequence in \({\text {Coh}}^b(X)\) and by Lemma 4.1,
This implies \(Z_{b,w}(F)\) lies to the right of \(\overline{op'}\), see Fig. 6. Moreover, we have
Combining this with (37) and (38) shows that
The first inequality implies \(Z_{b,w}(F)\) cannot be to the right of \(\overline{op}\), and the second one shows \(Z_{b,w}(F)\) cannot be above \(\overline{p'p}\). Note that the slope of the line segment \(\overline{p'p}\) corresponds to \(\nu _{b,w}(E(-kH)[1])\). Hence \(Z_{b,w}(F)\) lies inside \(\triangle opp'\) or on the line segments \(\overline{op}\) or \(\overline{pp'}\). \(\square \)
Proposition 4.2 in particular, implies the following result.
Corollary 4.3
Let E be a slope-stable reflexive sheaf such that E and \(E(-k H) [1]\) are \(\nu _{b,w}\)-stable of the same slope, then \(E|_{D}\) is \(\mu \)-stable for any irreducible divisor \(D \in |kH|\).
Proof
By Proposition 4.2\(E|_D\) is \(\mu \)-semistable. Suppose it is strictly \(\mu \)-semistable and \(E|_D \twoheadrightarrow F\) is a proper quotient sheaf with \(\mu (E|_D) = \mu (F)\). We know F is also a quotient object of \(E|_D\) in \({\text {Coh}}^{b}(X)\) with the same \(\nu _{b, w}\)-slope as \(E|_D\). Thus \(E|_D\) is strictly \(\nu _{b, w}\)-semistable.
Since E is \(\nu _{b, w}\)-stable, the composition \(E \hookrightarrow E|_D \twoheadrightarrow F\) in \({\text {Coh}}^{b}(X)\) must either be zero or injective. It cannot be zero because this would give a surjection \(E(-k H)[1] \twoheadrightarrow F\) in \({\text {Coh}}^{b}(X)\), contradicting the \(\nu _{b, w}\)-stability of \(E(-k H)[1]\). Thus it is injective, then its cokernel C in \({\text {Coh}}^{b}(X)\) lies in a commutative diagram

Since E and F are \(\nu _{b, w}\)-semistable of the same slope, C is also \(\nu _{b, w}\)-semistable. Hence the right hand surjection again contradicts the \(\nu _{b,w}\)-stability of \(E(-k H)[1]\).
\(\square \)
Proof of Theorem 1.1
Take a \(\mu \)-stable reflexive sheaf E on X of rank \({\text {rk}}= {\text {ch}}_0(E) > 0\). If \({\text {rk}}=1\), the claim is trivial, so we may assume \({\text {rk}}\ge 2\). Let \(\ell \) be the line passing through \(\Pi (E)\) and \(\Pi (E(-kH))\) for \(k >0\), and let \(r = H^n{\text {ch}}_0(E)\). If
then \(\ell \) intersects the boundary \(\partial U\) at two points with b-values \(b_2 <b_1\) where
By Proposition 3.2 and 3.4, E and \(E(-k H)[1]\) are \(\nu _{b,w}\)-stable for any \((b,w) \in \ell \cap U\) if the following three conditions are satisfied:
-
(a)
\(\frac{r}{H^n}(b_2 - \mu (E(-k H)))= \frac{r}{H^n}(\mu (E) -b_1)< b_1-b_2 = 2\sqrt{\frac{k^2}{4} - \frac{\Delta (E)}{r^2}}\)
-
(b)
\( \mu (E) -b_1 < \delta (E)\)
-
(c)
\(b_2 -\mu (E(-k H)) < \delta (E)\)
where \(\delta (E) = \min \left\{ \mu ^{\min }(E(-kH))-\mu (E(-kH)) ,\ \mu (E) -\mu ^{\max }(E) \right\} \).
The condition (a) is equivalent to
and thus to
This holds if and only if
Note that (42) and so condition (a) implies (41). Also (b) and (c) are equivalent to
which holds if and only if
If we have strict inequalities in (3), using \(\widetilde{\Delta }(E) = \frac{\Delta (E)}{(H^n {\text {rk}})^2} = \frac{\Delta (E)}{r^2}\), one can see (43) and (45), and so conditions (a), (b) and (c) hold. Thus E and \(E(-kH)[1]\) are \(\nu _{b,w}\)-stable of the same slope for \((b,w) \in \ell \cap U\), so \(E|_D\) is \(\mu \)-stable by Corollary 4.3.
Now suppose we have equality in (a), (b), or (c) which means equality in one of the inequalities in (3). The above computation shows that still (41) holds, so \(\ell \cap U \ne \emptyset \). Then the structure of walls and Proposition 3.2 and 3.4 imply that E and \(E(-kH)[1]\) are \(\nu _{b,w}\)-semistable for \((b,w) \in \ell \cap U\). Hence \(E|_D\) is \(\mu \)-semistable on D by Proposition 4.2 (Fig. 7). \(\square \)
As a consequence of Theorem 1.1, we obtain a variant of Langer’s restriction Theorem [19, Theorem 5.2].
Corollary 4.4
Let E be a \(\mu \)-stable reflexive sheaf of rank \({\text {rk}}>1\). The restricted sheaf \(E|_D\) for any irreducible divisor \(D \in |kH|\) is \(\mu \)-stable if
Proof
We always have
Thus (46) implies
Therefore (44) and so the second inequality in (3) is satisfied. If \({\text {rk}}\ge 3\) or \(\Delta (E) \ge 3\), then
Thus the first inequality in (3) holds as well, so the claim follows from Theorem 1.1.
If \({\text {rk}}=2\) and \(0 \le \Delta (E) \le 2\), then the assumption (46) implies that (41) holds. Thus there are points \((b_0,w_0) \in U\) where E and \(E(-kH)[1]\) are in \({\text {Coh}}^{b_0}(X)\) and have the same \(\nu _{b_0,w_0}\)-slope. Moreover, the same argument as in Step 2 in the proof of Theorem 3.1 implies that there are no walls for E and \(E(-kH)[1]\) in U. Thus E and \(E(-kH)[1]\) are \(\nu _{b_0, w_0}\)-stable and so the claim follows from Corollary 4.3. \(\square \)
Remark 4.5
[19, Theorem 5.2] covers more general cases than Corollary 4.4, it allows X to be a smooth projective variety over an arbitrary algebraically closed field, and assumes E to be a \(\mu \)-stable torsion free sheaf with respect to some nef divisors.
In some special cases, we have more control over the position of the walls for E and \(E(-kH)[1]\), so we gain stronger effective restriction results. For instance, suppose (X, H) is a smooth polarised complex projective variety of dimension \(n \ge 2\) such that
Let E be a \(\mu \)-stable reflexive sheaf with \(\gcd \left( H^n{\text {ch}}_0(E) , {\text {ch}}_1(E)H^{n-1}\right) =H^n\). We define
Proposition 4.6
Let E be a \(\mu \)-stable reflexive sheaf as above with rank \({\text {rk}}> 1\). The restricted sheaf \(E|_D\) for any irreducible divisor \(D \in |kH|\) is \(\mu \)-(semi)stable on D if
where \(\delta = \frac{1}{{\text {rk}}} \times \min \{\frac{1}{m(E)^+} , \frac{1}{m(E)^-}\}\). In particular, \(E|_D\) is \(\mu \)-(semi)stable if
Proof
First of all, since \(\delta \le \frac{1}{2}\), (48) is equivalent to
As in the proof of Theorem 1.1, let \(\ell \) be the line passing through \(\Pi (E)\) and \(\Pi (E(-kH))\). First assume the inequality in (48) is strict, so
Thus (41) holds and so \(\ell \cap U \ne \emptyset \). Let \(b_2 <b_1\) be the values of b at the intersections points of \(\ell \) with \(\partial U\). Hence (50) with applying the same argument as in the proof of Theorem 1.1 implies
Therefore the line \(\ell \) intersects the vertical lines \(b = \mu (E) -\frac{1}{{\text {rk}}m(E)^-}\) and \(b = \mu (E(-kH)) +\frac{1}{{\text {rk}}m(E)^+}\) at points inside U. So by Lemma 3.5, E and \(E(-kH)[1]\) are \(\nu _{b,w}\)-stable for any \((b,w) \in \ell \cap U\) and the claim follows from Corollary 4.3. If we have equality in (48) which means equality in (51) or (52), we obtain the claim by applying Proposition 4.2 at the point \((b,w) \in U\) just slightly above \(\ell \).
Finally, by definition of \(m(E)^{\pm }\), we know \(\delta \ge \frac{1}{{\text {rk}}({\text {rk}}-1)}\). Thus (50) implies \(E|_D\) for \(D \in |kH|\) is \(\mu \)-(semi)stable if
which is equivalent to (49). \(\square \)
5 Clifford indices of curves over K3 surfaces
In this section, we assume (S, H) is a smooth polarized K3 surface over \(\mathbb {C}\) such that
Let \(\iota :C \hookrightarrow S\) be any smooth curve in the linear system |H| of genus g. It is proved in [20] and [3, Theorem 1.1] that there exists a globally generated degree d line bundle A on C with r global sections if and only if
Take such a line bundle A on C. Then the kernel of the evaluation of sections of \(\iota _*A\)
is a vector bundle of rank r. The Lazarsfeld-Mukai bundle \(E_{C,A}\) associated to the pair (C, A) is the dual of \(F_{C,A}\) and it is of character
The bundle \(E_{C,A}\) has been appeared, for example, in Lazarsfeld’s proof of Brill-Noether Petri Theorem [20], in the Mukai’s classification of prime Fano manifolds of coindex 3, or in Voisin’s proof of Green’s canonical syzygy conjecture [26]; see [2] for a survey of applications.
The \(\mu \)-slope of any destabilising subsheaf of \(F_{C,A}\) must be less than zero because of the exact sequence (54), thus \(F_{C,A}\) and so \(E_{C,A}\) are \(\mu \)-stable. Hence (53) implies that for any \({\text {ch}}_2 \in \mathbb {Z}\) with
there is a stable vector bundle \(E_{C,A}\) of Chern character \(v = (r, H, {\text {ch}}_2)\) for any curve \(C \in |H|\).
The restriction of Lazarsfeld-Mukai bundle \(E_{C,A}\) to curves on the K3 surface S has led to counterexamples to \(\mathbf{M_3}(C)\) [12] and \(\mathbf{M_4}(C)\) [1]. By applying Theorem 1.1, we extend these results to higher ranks.
Proof of Theorem 1.2
By Proposition 4.6, inequality (49), we know \(E|_C\) is \(\mu \)-semistable if
which clearly holds when \({\text {ch}}_2 \ge 0\). Since E is \(\mu \)-stable of positive slope, hom\((E, {\mathcal {O}}_X) = 0\), thus
Hence if \(r \ge 2\) and \({\text {ch}}_2 \ge 0\), the restricted bundle \(E|_C\) is \(\mu \)-semistable with
The last inequality follows from hom\(({\mathcal {O}}_S, E(-H)) = 0\). So \(E|_C\) contributes to the rank r-Clifford index of C.
By (53), we obtain \({\text {Cliff}}(C) = \left\lfloor \frac{g-1}{2} \right\rfloor \). Moreover,
and the right hand side is clearly less than \(\left\lfloor \frac{g-1}{2} \right\rfloor \) when (i) \(r \ge 4\), or (ii) \(r=3\) and
If \(r \ge 4\) and \(g \ge r^2\), then by (55), there is a stable vector bundle E on S with Chern character \((r, H, {\text {ch}}_2)\) such that \({\text {ch}}_2 \ge 0\). The above argument implies \(E|_C\) contributes to the rank r-Clifford index of C and
thus \(\mathbf{M_r}(C)\) fails. If \(r=3\), then by (55) there is a stable vector bundle E of class \((3, H, {\text {ch}}_2)\) when \({\text {ch}}_2 = \lfloor \frac{g}{3} \rfloor -3\). Then (56) implies \({\text {Cliff}}(E|_C)\) is less than the expected number if
which holds for \(g=7, 9\) and \(g \ge 11\) as claimed. \(\square \)
6 Slope-stability of the restriction of tangent bundle of \(\mathbb {P}^n\)
Let S be a smooth projective K3 surface and let L be an ample line bundle generated by its global sections. The kernel of the evaluation of sections of L is denoted by \(M_L\) (6). In this section, we prove \(M_{L}\) is \(\mu \)-stable with respect to L.
Let \(L =kH\) where H is a primitive ample line bundle on S. Similar to Section 2, we define \(\nu _{b,w}\)-stability and the projection \(\Pi \) (10) with respect to the polarisation H. On K3 surfaces, we can slightly enlarge the 2-dimensional slice of stability conditions U due to a stronger Bogomolov-type inequality. Recall that an object \(E \in \mathcal {D}(S)\) is called spherical if \(\text {Hom}_{\mathcal {D}(S)}(E,E[i]) = \mathbb {C}\) for \(i=0,2\) and it is zero otherwise.
Lemma 6.1
For any point \((b,w) \in \mathbb {R}^2\) with \(w > \frac{b^2}{2} - \frac{1}{H^2}\), the pair \(\left( {\text {Coh}}^b(X), Z_{b,w}\right) \) is a Bridgeland stability condition on S if for any spherical bundle E on S with \(\mu (E) =b\), we have \(\frac{{\text {ch}}_2(E)}{H^2{\text {ch}}_0(E)} < w\).
Proof
As it is shown in the proof of [7, Lemma 6.2], we only need to check that for any slope-stable vector bundle E on S with Im\([Z_{b,w}(E)] = 0\), we have Re\([Z_{b,w}(E)] > 0\). We know Hom\((E, E) = \text {Hom}(E, E[2]) = \mathbb {C}\), thus Riemann-Roch theorem gives
which implies \(-\chi (E, E) \ge -2\). If E is not spherical, i.e. \(-\chi (E, E) \ge 0\), then Hodge index theorem gives
Hence if \(\mu (E) = b\), we get
because \(w > \frac{b^2}{2} - \frac{1}{H^2}\) by our assumption. Thus we only need to check positivity of the real part for spherical bundles as mentioned. \(\square \)
The next step is to control the position of the projection of spherical bundles. Since \(h^0(L) = \chi ({\mathcal {O}}_X, L) = \frac{L^2}{2} +2\), we get
Define
Lemma 6.2
If \(k = L.H/H^2 > 1\), there is no spherical bundle E on S such that its projection \(\Pi (E)\) lies in the area V, see Fig. 8.
Proof
Suppose for a contradiction that there is such an spherical bundle E of class \({\text {ch}}(E) = ({\text {ch}}_0, {\text {ch}}_1, {\text {ch}}_2)\).
Since \(\chi (E, E) = 2\), the Hodge index theorem gives
Thus \(\Pi (E)\) cannot be in the area U above \(w = \frac{b^2}{2}\), so
which implies
Here the last equality comes from \(L = kH\). Thus we get \({\text {ch}}_0 \le \frac{L^2}{2}+1\).
The second inequality of (59) gives \(-1 < \frac{{\text {ch}}_2}{{\text {ch}}_0}\) which gives \(-{\text {ch}}_0 +1 \le {\text {ch}}_2\) as \({\text {ch}}_2 \in \mathbb {Z}\). Combining this with (58) gives
If \({\text {ch}}_0 > 1\), the left hand side is minimum when \({\text {ch}}_0\) is the maximum value \(\frac{L^2}{2} +1\), so we must have
which is not possible by (59). Thus \({\text {ch}}_0 =1\), so (59) gives
which is not again possible for \(k> 1\). \(\square \)
Therefore, by Lemma 6.1, the pair \(\big ({\text {Coh}}^b(X), Z_{b,w} \big )\) is a Bridgeland stability condition on \(\mathcal {D}^b(X)\) for any \((b,w) \in V\) if \(k >1\).
Proof of Theorem 1.3
The line bundle L is in the heart \({\text {Coh}}^b(X)\) for \(b<k = \frac{L.H}{H^2}\). Since \(\Delta (L) = 0\), it is \(\nu _{b,w}\)-stable for any \((b,w) \in U\) [5, Corollary 3.11(a)]. Similarly, \({\mathcal {O}}_X[1] \in {\text {Coh}}^b(X)\) for \(b \ge 0\) and it is \(\nu _{b,w}\)-stable for any \((b,w) \in U\). Let \(\ell \) be the line passing through \(\Pi (L)\) and \(\Pi ({\mathcal {O}}_X)\). Then L and \({\mathcal {O}}_X[1]\) are \(\nu _{b_0, w_0}\)-stable of the same slope for any \((b_0,w_0) \in \ell \cap U\). Thus the short exact sequence
in \({\text {Coh}}^{b_0}(X)\) implies that \(M_L[1]\) is also \(\nu _{b_0, w_0}\)-semistable.
We claim \(M_L[1]\) is \(\nu _{b_0, w^+}\)-stable where \(w_0 < w^+ \ll w_0 +1\). Otherwise, the structure of locally finite set of walls described in Proposition 2.3 shows that there is a destabilising sequence
such that the \(E_i\) have the same \(\nu _{b_0, w_0}\)-slope as \(M_L[1]\) and they make \(M_L[1]\) unstable above \(\ell \), i.e.
for any \(w > w_0\). Hence, rank of \(E_1\) is negative. We know \(\nu _{b_0, w_0}\)-stable factors of \(E_1\) and \(E_2\) are the Jordan-H\(\ddot{\text {o}}\)lder factors of \(M_L[1]\). Since L and \(h^0(L)\)-copies of \({\mathcal {O}}_X[1]\) are the \(\nu _{b_0, w_0}\)-Jordan-H\(\ddot{\text {o}}\)lder factors of \(M_L[1]\), we gain the stable factors of \(E_1\) are either
-
(a)
L and m-copies of \({\mathcal {O}}_X[1]\), or
-
(b)
\(m'\)-copies of \({\mathcal {O}}_X[1]\).
In the first case, \(E_2\) must be the direct sum of copies of \({\mathcal {O}}_X[1]\) and clearly (60) does not hold. In case (b), we get hom\(({\mathcal {O}}_X, M_L) \ne 0\) which is not possible by the definition of \(M_L\) (6), thus there is no such destabilising sequence and the claim follows.
If \(k = \frac{L.H}{H^2} =1\), Lemma 3.5 implies that there is no wall for \(M_L[1]\) crossing the vertical line \(b = 0\). Thus \(\nu _{b_0, w^+}\)-stability of \(M_L[1]\) implies that it is \(\nu _{b =0, w}\)-stable for \(w \gg 0\). Hence \(M_L\) is \(\mu \)-stable [7, Proposition 14.2].
If \(k>1\), we claim there is no wall for \(M_{L}[1]\) in the region V (57) and it is \(\nu _{b,w}\)-stable for any \((b,w) \in V\). Suppose there is a wall \(\ell '\) in V with a destabilising sequence \(E_1 \hookrightarrow M_L[1] \twoheadrightarrow E_2\). We know this wall ends at \(\Pi (M_L)\). For any \((b,w) \in \ell ' \cap V\), we have \(Z_{b,w}(E_i) \ne 0\) and
which implies \(\left|Z_{b,w}(E_i)\right| < \left|Z_{b,w}(M_L)\right|\). If we move (b, w) along the wall \(\ell '\) towards \(\Pi (M_L)\), then \( \left|Z_{b,w}(M_L[1])\right| \rightarrow 0\), thus
Therefore \({\text {ch}}_0(E_i) \ne 0\) and \(\Pi (E_i) = \Pi (M_{L})\), so the \(E_i\) have the same \(\nu _{b,w}\)-slope as \(M_L[1]\) for any \((b,w) \in V\) and cannot make a wall. Thus, in particular, \(M_L[1]\) is \(\nu _{b, w}\)-stable for any \((b,w) \in V\) with \(b= \mu (M_L)\), so it is \(\mu \)-semistable [5, Lemma 2.7]. If \(M_L\) is strictly \(\mu \)-semistable, there is an exact sequence \(F_1 \hookrightarrow M_L \twoheadrightarrow F_2\) of \(\mu \)-semistable coherent sheaves of the same slope. Thus \(\nu _{b=\mu (M_L), w}\)-slope of \(F_i[1]\) and \(M_L[1]\) are equal to \(+\infty \) and they are in the heart \({\text {Coh}}^{\mu (M_L)}(X)\). Hence \(M_L[1]\) is strictly \(\nu _{b=\mu (M_L), w}\)-semistable which is not possible by the above argument. \(\square \)
Notes
D can be singular.
To have a weak stability function whose imaginary part is non-negative and the real part is linear, we replace \(\overline{Z}_{\alpha , B = b H}\) in [5, Proposition 12.2] by
$$\begin{aligned} i\, \overline{Z}_{\alpha , bH} - b\, \text {Im}[i\, \overline{Z}_{\alpha , b H}] = -{\text {ch}}_2.H^{n-2} + {\text {ch}}_0H^n \left( \frac{\alpha ^2}{2} + \frac{b^2}{2} \right) + i({\text {ch}}_1.H^{n-1} -b{\text {ch}}_0H^n) \end{aligned}$$and substitute \(\frac{\alpha ^2}{2} + \frac{b^2}{2}\) with w.
References
Aprodu, M., Farkas, G., Ortega, A.: Restricted Lazarsfeld–Mukai bundles and canonical curves. In: Development of Moduli Theory—Kyoto 2013, Volume 69 of Advanced Studies in Pure Mathematics, pp. 303–322. Mathematical Society Japan [Tokyo] (2016)
Aprodu, M.: Lazarsfeld-Mukai bundles and applications. In: Commutative Algebra, pp. 1–23. Springer, New York (2013)
Bayer, A.: Wall-crossing implies Brill–Noether: applications of stability conditions on surfaces. In: Algebraic Geometry: Salt Lake City 2015, Volume 97 of Proceedings of Symposium in Pure Mathematics, pp. 3–27. American Mathematical Society, Providence, RI (2018)
Bakker, B., Farkas, G.: The Mercat conjecture for stable rank 2 vector bundles on generic curves. Am. J. Math. 140(5), 1277–1295 (2018)
Bayer, A., Macrì, E., Stellari, P.: The space of stability conditions on abelian threefolds, and on some Calabi–Yau threefolds. Invent. Math. 206(3), 869–933 (2016)
Bayer, A., Macrì, E., Toda, Y.: Bridgeland stability conditions on threefolds I: Bogomolov–Gieseker type inequalities. J. Algebr. Geom. 23(1), 117–163 (2014)
Bridgeland, T.: Stability conditions on \(K3\) surfaces. Duke Math. J. 141(2), 241–291 (2008)
Camere, C.: About the stability of the tangent bundle of \(\mathbb{P}^n\) restricted to a surface. Math. Z. 271(1–2), 499–507 (2012)
Feyzbakhsh, S.: Stability of restrictions of Lazarsfeld–Mukai bundles via wall-crossing, and Mercat’s conjecture. arXiv:1608.07825 (2016)
Feyzbakhsh, S.: Mukai’s program (reconstructing a K3 surface from a curve) via wall-crossing. J. Reine Angew. Math. 765, 101–137 (2020)
Feyzbakhsh, S., Li, C.: Higher rank Clifford indices of curves on a K3 surface. Selecta Math. (N.S.) 27(3):Paper No. 48, 34 (2021)
Farkas, G., Ortega, A.: Higher rank Brill–Noether theory on sections of \(K3\) surfaces. Int. J. Math. 23(7), 1250075 (2012). (18)
Feyzbakhsh, S., Thomas, R.P.: An application of wall-crossing to Noether–Lefschetz loci. Q. J. Math. 72(1–2), 51–70 (2021). (with an appendix by C. Voisin)
Feyzbakhsh, S., Thomas, R.P.: Rank r DT theory from rank 0. arXiv:2103.02915 (2021)
Hartshorne, R.: Stable reflexive sheaves. Math. Ann. 254(2), 121–176 (1980)
Huybrechts, D., Lehn, M.: The Geometry of Moduli Spaces of Sheaves. Cambridge Mathematical Library, 2nd edn. Cambridge University Press, Cambridge (2010)
Kopper, J.: Stability conditions for restrictions of vector bundles on projective surfaces. Michigan Math. J. 69(4), 711–732 (2020)
Koseki, N.: Stability conditions on Calabi–Yau double/triple solids. arXiv:2007.00044 (2020)
Langer, A.: Semistable sheaves in positive characteristic. Ann. Math. (2) 159(1), 251–276 (2004)
Lazarsfeld, R.: Brill–Noether–Petri without degenerations. J. Differ. Geom. 23(3), 299–307 (1986)
Li, C.: On stability conditions for the quintic threefold. Invent. Math. 218(1), 301–340 (2019)
Lange, H., Newstead, P.E.: Clifford indices for vector bundles on curves. In: Affine Flag Manifolds and Principal Bundles, Trends Mathematics, pp. 165–202. Birkhäuser/Springer Basel AG, Basel (2010)
Li, C., Zhao, X.: Birational models of moduli spaces of coherent sheaves on the projective plane. Geom. Topol. 23(1), 347–426 (2019)
Mercat, V.: Clifford’s theorem and higher rank vector bundles. Int. J. Math. 13(7), 785–796 (2002)
Sun, H.: Tilt-stability, vanishing theorems and Bogomolov–Gieseker type inequalities. Adv. Math. 347, 677–707 (2019)
Voisin, C.: Green’s canonical syzygy conjecture for generic curves of odd genus. Compos. Math. 141(5), 1163–1190 (2005)
Acknowledgements
I would like to thank Arend Bayer for many useful discussions. I am grateful for comments by Gavril Farkas, Chunyi Li, Angela Ortega and Richard Thomas. In addition, I am very grateful to the referee for many detailed comments. The author was supported by the ERC starting grant (PI: Arend Bayer) WallXBirGeom 337039 and EPSRC postdoctoral fellowship EP/T018658/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feyzbakhsh, S. An effective restriction theorem via wall-crossing and Mercat’s conjecture. Math. Z. 301, 4175–4199 (2022). https://doi.org/10.1007/s00209-022-03036-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-022-03036-1