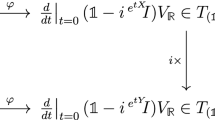Abstract
A family of irreducible holomorphic symplectic (ihs) manifolds over the complex projective line has unobstructed deformations if its period map is an embedding. This applies in particular to twistor spaces of ihs manifolds. Moreover, a family of ihs manifolds over a subspace of the period domain extends to a universal family over an open neighborhood in the period domain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Unobstructedness is one of the fundamental deformation-theoretic properties that a compact complex manifold X can enjoy. The term goes back to Kodaira and Spencer [19]. In modern terminology we say that X is unobstructed or has unobstructed deformations when X possesses a semi-universal, also known as “miniversal,” deformation over a smooth, pointed complex space germ \({{\,\mathrm{Def}\,}}(X)\), see (Sect. 2.9); in other words, X possesses a smooth local moduli space. The two most popular cases in which unobstructedness of X is well known are when \({\mathsf {H}}^{2}(X;\Theta _X)=0\) due to Kodaira–Spencer–Nirenberg [20] or when X is Kähler with trivial canonical bundle due to Tian–Todorov [29, 30].
In this note we investigate the local deformation theory of compact complex manifolds X that admit a holomorphic submersion \(f :X \rightarrow {\mathbb {P}}^{1}\) to the complex projective line such that every fiber is an irreducible holomorphic symplectic manifold. We call \((X,{\mathbb {P}}^{1},f)\) a family of ihs manifolds in this case.
Our main motivation for considering such X are the frequently studied twistor spaces. For every n-dimensional compact hyperkähler manifold M the space of complex structures on M is diffeomorphic to \(S^2\cong {\mathbb {P}}^{1}\). As a generalization of the Penrose twistor construction, Hitchin–Karlhede–Lindström–Roček constructed a complex structure on \(X=M\times {\mathbb {P}}^{1}\) such that the projection \(f:X\rightarrow {\mathbb {P}}^{1}\) is holomorphic and that the fibers are biholomorphic to M equipped with these different complex structures [13, p. 554–557]. By Yau’s solution of the Calabi conjecture this construction can be applied to any compact ihs manifold and gives rise to a family \((X, f,{\mathbb {P}}^{1})\) of ihs manifolds. We call X a twistor space and \((X, f,{\mathbb {P}}^{1})\) a twistor family. The main result of this article reduces the deformation theory of such an X to the study of the Douady space \({\mathsf {Dou}}\,{{\mathsf {D}}_{\Lambda }}\), see (Sect. 4.1), of the period domain \({\mathsf {D}}_{\Lambda }\) for a fixed ihs lattice \(\Lambda \).
Theorem 1.1
(Unobstructedness theorem) Let \((X,{\mathbb {P}}^{1},f)\) be a family of ihs manifolds whose period map \(h:{\mathbb {P}}^{1} \rightarrow {\mathsf {D}}_{\Lambda }\), with respect to a \(\Lambda \)-marking \(\mu \), is an embedding. Then X has unobstructed deformations. Furthermore, f induces a canonical isomorphism of complex space germs
that are smooth of dimension \((d+1)(r-2)-3\). Here the left side is a germ of a base space of a universal deformation of X and the right side a germ of the Douady space of the period domain, r is the second Betti number of a fiber of f and \(d:=-{\mathsf {deg }}(f_*\Omega ^2_{X/{\mathbb {P}}^{1}})\ge 2\).
When \((X,{\mathbb {P}}^{1},f)\) is a twistor family, we see that \(d=2\) (example 3.11), which implies that the condition on the period map in Theorem 1.1 is fulfilled (Proposition 3.12). Hence we obtain as a corollary that the deformations of such a twistor space X are unobstructed and build a family over a \((3r-9)\)-dimensional smooth open subspace of \({\mathsf {Dou}}\,{{\mathsf {D}}_{\Lambda }}\) corresponding to a family of quadratically embedded smooth rational curves in the period domain \({\mathsf {D}}_{\Lambda }\).
1.1 Idea of the proof
The two most popular unobstructedness criteria cannot be applied to prove Theorem 1.1 as the group \({\mathsf {H}}^{2}(X;\Theta _X)\) is typically nontrivial (Theorem 5.4) and X is neither Kählerian nor has trivial canonical bundle (Remark 5.3).
Our proof of Theorem 1.1 follows a hands-on approach. The first key ingredient is that, essentially by virtue of Kodaira’s theorem on the stability of fiber structures [18], every deformation of X induces a deformation of \(h({\mathbb {P}}^{1})\) in \({\mathsf {D}}_{\Lambda }\). As a second key ingredient we prove in Theorem 1.2 an extension theorem for \(\Lambda \)-marked families of ihs manifolds. This theorem implies that every deformation of \(h({\mathbb {P}}^{1})\) in \({\mathsf {D}}_{\Lambda }\) lifts to a deformation of X. To obtain a description of the local moduli space of X as a germ of the Douady space \({\mathsf {Dou}}\,{{\mathsf {D}}_{\Lambda }}\) of \({\mathsf {D}}_{\Lambda }\), we do cohomological computations to compare the dimensions (Corollary 4.2, Theorem 5.4) and show that the corresponding Kodaira–Spencer map is a bijection (Sect. 4.5).
1.2 The upshot and comparision of Theorem 1.1 to known results
Our methods enable us to think of Theorem 1.1 not merely as an abstract deformation-theoretic statement, but as the primary step towards a potential moduli theory for families of ihs manifolds over \({\mathbb {P}}^{1}\). We want to emphasize the advantage of our approach over, for instance, the techniques of Ran who has obtained similar unobstructedness results [27, p. 116–117]. Ran’s abstract functorial approach, however, can never yield a tangible description of the moduli space of interest.
Topiwala proved the unobstructedness of f for certain families of Kummer K3 surfaces over \({\mathbb {P}}^{1}\) with \(d=2\) by showing that \({\mathsf {H}}^{2}(X;\Theta _{X/{\mathbb {P}}^{1}})\) vanishes [31, p. 434]. For families of higher dimensional ihs manifolds \({\mathsf {H}}^{2}(X;\Theta _{X/{\mathbb {P}}^{1}})\) is, however, in general non-zero. This is the case for example when the third Betti number of the fibers is non-zero (Theorem 5.4). Concrete examples are provided by generalized Kummer varieties \(Kum _n(T)\) for \(n\ge 2\).
Theorem 1.2
(Extension theorem) Let \({\mathcal {F}}\) be a \(\Lambda \)-marked family of ihs manifolds over a complex space S such that the period map \(h :S \rightarrow {\mathsf {D}}_{\Lambda }\) of \({\mathcal {F}}\) is an embedding. Then there exists a \(\Lambda \)-marked family of ihs manifolds \({\widetilde{{\mathcal {F}}}}\) over an open subspace U of \({\mathsf {D}}_{\Lambda }\) such that
-
a)
h(S) is contained in U,
-
b)
there exists a morphism of \(\Lambda \)-marked families \(\phi :{\mathcal {F}}\rightarrow {\widetilde{{\mathcal {F}}}}\) over the induced map \(h :S \rightarrow U\), and
-
c)
the period map of \({\widetilde{{\mathcal {F}}}}\) is the canonical injection \(U \hookrightarrow {\mathsf {D}}_{\Lambda }\).
Item c) implies that the pair \(({\widetilde{{\mathcal {F}}}},\phi )\) is universal as an extension of \({\mathcal {F}}\) in the following sense, see Corollary 6.6: For every morphism of \(\Lambda \)-marked families \(\phi ' :{\mathcal {F}}\rightarrow {\mathcal {F}}'\) over an embedding of complex spaces \(h' :S \rightarrow U'\), up to shrinking \(U'\), there exists a unique morphism \(\theta :{\mathcal {F}}' \rightarrow {\widetilde{{\mathcal {F}}}}\) such that \(\phi = \theta \circ \phi '\).
Aside from its use in this paper, Theorem 1.2 can be applied to obtain universal families on large open subspaces of the moduli space of \(\Lambda \)-marked ihs manifolds, which is remarkable given that a universal family on the whole space does not exist [14, Remark 4.4].
1.3 Relation of Theorem 1.2 to a result of Markman
After finishing the first version of this article we were informed that Markman [23, Theorem 1.1] had already shown the existence of a “weakly universal” marked family \({\mathcal {X}}\) over the coarse moduli space \({\mathfrak {M}}_{\Lambda }\) of \(\Lambda \)-marked ihs manifolds. Explicitly, every \(\Lambda \)-marked family \({\mathcal {F}}\) with classifying map \(g :S \rightarrow {\mathfrak {M}}_\Lambda \) is S-isomorphic to the pullback \(g^*({\mathcal {X}})\) up to the twist by an \({{\mathscr {A}}\!\! ut }(g^*({\mathcal {X}}))\)-torsor. Here \({{\mathscr {A}}\!\! ut }(g^*({\mathcal {X}}))\) denotes the locally constant sheaf of V-automorphisms of the \(\Lambda \)-marked family \(\left. {g^*({\mathcal {X}})}\right| _{V}\), where \(V \subseteq S\) is open.
We briefly sketch how to deduce Theorem 1.2 from Markman’s result. First of all, there is an open neighbourhood U of h(S) in \({\mathsf {D}}_{\Lambda }\) together with a section \(s:U\rightarrow {\mathfrak {M}}_{\Lambda }\) in the étalé space \({\mathfrak {M}}_{\Lambda }\rightarrow {\mathsf {D}}_{\Lambda }\) such that \(s\circ h\) is the classifying map g of \({\mathcal {F}}\). This follows for instance from Lemma 6.4. By Markman’s result, \({\mathcal {F}}\) is S-isomorphic to the \(\Lambda \)-marked family \(g^*({\mathcal {X}})\) twisted by an \({{\mathscr {A}}\!\! ut }(g^*({\mathcal {X}}))\)-torsor T. Shrinking U we can assume h(S) to be a deformation retract of U. Then T will be the restriction of an \({{\mathscr {A}}\!\! ut }(s^*({\mathcal {X}}))\)-torsor \({\widetilde{T}}\). Taking \(\widetilde{{\mathcal {F}}}\) to be \(s^*({\mathcal {X}})\) twisted by \({\widetilde{T}}\) we find that \(\widetilde{{\mathcal {F}}}\) is an extension of \({\mathcal {F}}\) in the sense of Theorem 1.2.
In Sect. 7 below we give a proof of Theorem 1.2 that is completely independent of Markman’s work. While Markman uses an abstract categorical equivalence between two gerbes over \({\mathfrak {M}}_\Lambda \) to show the existence of \({\mathcal {X}}\), we proceed in a more constructive and more elementary way. Indeed, we construct the extension \({\widetilde{{\mathcal {F}}}}\) of \({\mathcal {F}}\) by gluing specific Kuranishi families along the subspace \(h(S) \subseteq {\mathsf {D}}_{\Lambda }\).
1.4 Outline of the paper
In Sect. 2 we compile, for easy reference, a list of terminology and notation that we employ throughout the paper. We begin a systematic investigation of families of ihs manifolds over smooth rational curves in Sect. 3. The main part of the proof of Theorem 1.1 is carried out in Sect. 4. Even though they enter into Sect. 4, we postpone on the one hand certain sheaf-cohomological computations to Sect. 5 and, on the other hand, the fairly technical aspects of gluing morphisms and families along subspaces to prove Theorem 1.2 to Sects. 6 and 7.
2 Conventions, terminology, notation
In our definitions of complex spaces, holomorphic maps, subspaces, etc. we follow Gerd Fischer [7, 9–10]. In particular we assume that the underlying topological space of a complex space is Hausdorff. Strictly speaking, second countability needs only be assumed in Theorem 6.3 and Sect. 6.3.4, but is fulfilled for all concrete complex spaces appearing in this article.
2.1 Families
A family of compact complex manifolds is a triple \({\mathcal {F}}=(X,S,f)\) where X and S are complex spaces and \(f :X\rightarrow S\) is a proper holomorphic submersion. We call S the base space of \({\mathcal {F}}\) and say that \({\mathcal {F}}\) is a family over S.
Given two families \({\mathcal {F}}= (X,S,f)\) and \({{\mathcal {F}}' = (X',S',f')}\) of compact complex manifolds, a morphism of families from \({\mathcal {F}}'\) to \({\mathcal {F}}\) is a pair \(\phi = (g,h)\) such that

is a Cartesian square of complex spaces and holomorphic maps. We write this as \(\phi :{\mathcal {F}}' \rightarrow {\mathcal {F}}\), and we say that \(\phi \) is a morphism over h. Note that \(\phi \) is an isomorphism of families if h is an isomorphism of complex spaces. We call a morphism of families over \(\mathsf {id}_{S}:S\rightarrow S\) an S-morphism, or S-isomorphism, of families.
2.2 Pullback of families
Let \(b :T \rightarrow S\) be a holomorphic map. Then for every family of compact complex manifolds \({\mathcal {F}}= (X,S,f)\) over S, the pullback of \({\mathcal {F}}\) by b is the triple
where \(X\times _ST\) denotes the fiber product of complex spaces over the holomorphic maps \(f:X\rightarrow S\) and \(b:T \rightarrow S\) and where \(p_i\), for \(i \in {\{}{\}}{1,2}\), denotes the ith projection map of this fiber product. Observe that \(b^*({\mathcal {F}})\) is a family of compact complex manifolds over T and that \(\eta :=(p_1,b) :b^*({\mathcal {F}}) \rightarrow {\mathcal {F}}\) is a morphism of families over b.
When \(\phi :{\mathcal {F}}' \rightarrow {\mathcal {F}}\) is an S-morphism of families, we denote by \(b^*(\phi )\) the unique T-morphism of families \(b^*({\mathcal {F}}')\rightarrow b^*({\mathcal {F}})\) such that \(\eta \circ b^*(\phi ) = \phi \circ \eta '\) where \(\eta '\) is the canonical morphism of families \(b^*({\mathcal {F}}') \rightarrow {\mathcal {F}}'\) over b.
2.3 Restriction of families
When the holomorphic map \(b :T\rightarrow S\) in Sect. 2.2 is the canonical injection of a complex subspace, we write \({\mathcal {F}}_T\) and \(\phi _T\) for \(b^*({\mathcal {F}})\) and \(b^*(\phi )\), respectively. Observe that in this case the fiber product \(X\times _ST\) appearing in equation 2.2.1 is nothing but the inverse image \(f^{-1}(T)\) of the complex subspace \(T \subseteq S\) under the holomorphic map \(f :X\rightarrow S\) [7, p. 23]. Moreover, the first and second projections of the fiber product correspond to the canonical injection of \(f^{-1}(T)\) and the restriction of f, respectively.
When \(f:X\rightarrow S\) is a holomorphic map and \(s \in S\) is a point, we use the standard notation \(X_s\) for the complex analytic fiber of f over s. When \({\mathcal {F}}= (X,S,f)\) is a family of compact complex manifolds, we write \({\mathcal {F}}(s)\) as a synonym for \(X_s\) and call this the fiber of \({\mathcal {F}}\) over s, too.
When \(\phi :{\mathcal {F}}' \rightarrow {\mathcal {F}}\) is a morphism of families over a holomorphic map \(h :S' \rightarrow S\), then for every point \(s \in S'\) we let \(\phi (s)\) denote the induced holomorphic map \({\mathcal {F}}'(s) \rightarrow {\mathcal {F}}(h(s))\), which is a biholomorphism.
2.4 Ihs manifolds and markings
An irreducible holomorphic symplectic manifold—for short, ihs manifold—is a simply connected, compact, Kählerian, holomorphic symplectic complex manifold X satisfying \({\mathsf {h}}^{0}(X;\Omega ^2_X) = 1\) [4, cf. p. 763–764].
The cohomology group \({\mathsf {H}}^{2}(X;{\mathbb {Z}})\) of an ihs manifold X is naturally, by virtue of a rescaling of the Beauville–Bogomolov form of X, a lattice—that is, a free abelian group of finite rank endowed with a symmetric integral bilinear form [4, Théorème 5]. Indeed there is a unique such rescaling by a minimal, strictly positive real number. When \(\Lambda \) is a lattice, a \(\Lambda \)-marking of X is a lattice isomorphism \(\mu :{\mathsf {H}}^{2}(X;{\mathbb {Z}})\rightarrow \Lambda \).
2.5 Families of ihs manifolds and markings
A family \({\mathcal {F}}= (X,S,f)\) is called a family of ihs manifolds when every fiber of f is an ihs manifold. When \(\Lambda \) is a lattice, a \(\Lambda \)-marking of \({\mathcal {F}}\) is an isomorphism of sheaves \(\mu :{\mathsf {R}}^{2}f_*{\underline{{\mathbb {Z}}}_{X}} \rightarrow \underline{\Lambda }_{S}\) such that, for every point \(s \in S\), the induced map \(\mu _s :{\mathsf {H}}^{2}(X_s;{\mathbb {Z}})\rightarrow \Lambda \) is a \(\Lambda \)-marking of the fiber \(X_s = {\mathcal {F}}(s)\) of \({\mathcal {F}}\). In this case, we call \(({\mathcal {F}},\mu )\) a \(\Lambda \)-marked family (of ihs manifolds) (over S).
A morphism of \(\Lambda \)-marked families of ihs manifolds from \(({\mathcal {F}},\mu ) = (X,S,f,\mu )\) to \(({\mathcal {F}}',\mu ') = (X',S',f',\mu ')\) is a morphism of families \(\phi = (g,h) :{\mathcal {F}}' \rightarrow {\mathcal {F}}\) such that the following diagram of sheaves of abelian groups on \(S'\) commutes:

In diagram 2.5.1, \(\alpha \) denotes the topological base change map associated to diagram 2.1.1 and the constant sheaves of abelian groups with value \({\mathbb {Z}}\). Analogously \(\beta \) denotes the canonical h-map between the constant sheaves of abelian groups with value \(\Lambda \).
Remark 2.1
Let \(\phi :{\mathcal {F}}' \rightarrow {\mathcal {F}}\) be a morphism of families of ihs manifolds, \(\Lambda \) be a lattice, and \(\mu \) be a \(\Lambda \)-marking of \({\mathcal {F}}\). Then there exists a unique \(\Lambda \)-marking \(\mu '\) of \({\mathcal {F}}'\) so that \(\phi :({\mathcal {F}}',\mu ') \rightarrow ({\mathcal {F}},\mu )\) is a morphism of \(\Lambda \)-marked families.
Proof
Write \({\mathcal {F}}= (X,S,f)\) and \({\mathcal {F}}' = (X',S',f')\). Then since \(f :X\rightarrow S\) is a proper holomorphic map and since diagram 2.1.1 is a Cartesian square of complex spaces, the topological base change map \(\alpha \) in diagram 2.5.1 is an isomorphism of sheaves of abelian groups on \(S'\). This proves the uniqueness. To see the existence define \(\mu '\) as the composition of \(\alpha ^{-1}\), \(h^{-1}(\mu )\), and \(\beta \). Then \(\mu '\) is an isomorphism of sheaves of abelian groups, for \(\alpha \), \(\beta \), and \(\mu \) are. Moreover, for every point \(s \in S'\), we see that \(\mu '_s \circ \phi (s)^* = \mu _{h(s)}\) where \(\mu _{h(s)} :{\mathsf {H}}^{2}(X_{h(s)};{\mathbb {Z}})\rightarrow \Lambda \) and \(\mu '_s :{\mathsf {H}}^{2}(X'_s;{\mathbb {Z}})\rightarrow \Lambda \) denote the maps induced by \(\mu \) and \(\mu '\), respectively, and where \(\phi (s)^*\) denotes the map that \(\phi (s) :X'_s \rightarrow X_{h(s)}\) induces on the second cohomology with values in \({\mathbb {Z}}\). Since \(\mu _{h(s)}\) and \(\phi (s)^*\) are isomorphisms of lattices, this proves that \(\mu '_s\) is a \(\Lambda \)-marking of \(X'_s\). \(\square \)
2.6 Pullbacks of marked families of ihs manifolds
By virtue of Remark 2.1 we are able to adapt the language and notation of Sects. 2.2 and 2.3 for marked families. Indeed when \(b :T\rightarrow S\) is a holomorphic map and \({\mathcal {F}}\) is a family of ihs manifolds over S, then \(b^*({\mathcal {F}})\) is a family of ihs manifolds over T. Moreover, when \(\Lambda \) is a lattice and \(\mu \) is a \(\Lambda \)-marking of \({\mathcal {F}}\), there exists a unique marking \(\nu \) of \(b^*({\mathcal {F}})\) so that the canonical morphism of families \(\eta :b^*({\mathcal {F}}) \rightarrow {\mathcal {F}}\) is a morphism of \(\Lambda \)-marked families from \((b^*({\mathcal {F}}),\nu )\) to \(({\mathcal {F}},\mu )\). Accordingly we define the pullback of the \(\Lambda \)-marked family \(({\mathcal {F}},\mu )\) by b as \(b^*({\mathcal {F}},\mu ) :=(b^*({\mathcal {F}}),\nu )\). Observe that when \(\phi :({\mathcal {F}}',\mu ') \rightarrow ({\mathcal {F}},\mu )\) is an S-morphism of \(\Lambda \)-marked families, then the T-morphism of families \(b^*(\phi ) :b^*({\mathcal {F}}') \rightarrow b^*({\mathcal {F}})\) defined in Sect. 2.2 is a morphism of \(\Lambda \)-marked families from \(b^*({\mathcal {F}}',\mu ')\) to \(b^*({\mathcal {F}},\mu )\).
2.7 Period domains
Given a lattice \(\Lambda \) of rank \(r\ge 3\) and signature \((3,r-3)\) we let \({\mathsf {D}}_{\Lambda }\) denote the period domain associated to \(\Lambda \); that is, \({\mathsf {D}}_{\Lambda }\) is the complex subspace of the projective space of lines \({\mathbb {P}}(\Lambda _{\mathbb {C}})\) induced on the locally closed analytic subset

where \(\Lambda _{\mathbb {C}}:={\mathbb {C}}\otimes _{\mathbb {Z}}\Lambda \). Note that the complex vector space \(\Lambda _{\mathbb {C}}\) is naturally endowed, for one, with a symmetric complex bilinear form written \((x,y) \mapsto xy\), which extends the bilinear form of \(\Lambda \), and, for another, with a real structure written \(x \mapsto \overline{x}\). Note furthermore that the equation \(xx = 0\) defines a nondegenerate (i.e., smooth) quadric Q in the projective space \({\mathbb {P}}(\Lambda _{\mathbb {C}})\). The period domain \({\mathsf {D}}_{\Lambda }\) can thus be viewed as an open complex submanifold of Q.
2.8 Period maps
Let \({\mathcal {F}}= (X,S,f)\) be a family of ihs manifolds. Then the sheaf of \({\mathscr {O}}_S\)-modules \(f_*\Omega ^2_{X/S}\) is locally free of rank 1. When the complex space S is reduced, this is a direct consequence of Grauert’s base change theorem [8, p. 64]. The statement remains true though for arbitrary S. One way to see this is to invoke the unobstructedness of ihs manifolds, see Remark 2.4, by which the family \({\mathcal {F}}\) is—at least locally at every point of S—isomorphic to the pullback of a family of ihs manifolds over a smooth complex space. For the family over the smooth space we then argue that the sheaf of relative 2-differentials is cohomologically flat in dimension 0; in particular the direct image sheaf will be compatible with the desired base change [2, p. 132–134]. Using the same reasoning, first assuming S smooth, we deduce that the relative Frölicher spectral sequence associated to \(f :X \rightarrow S\) degenerates at \(E_1\) [24, p. 251]. Specifically we obtain a canonical injection of sheaves of \({\mathscr {O}}_S\)-modules
whose cokernel is finite locally free.
Let \(\Lambda \) be a lattice of rank r and \(\mu \) be a \(\Lambda \)-marking of \({\mathcal {F}}\). Then \(f_*\Omega ^2_{X/S}\) becomes, by virtue of \(\mu \), a subsheaf of \({\mathscr {O}}_S\)-modules of \({\mathscr {O}}_S \otimes _{\underline{{\mathbb {Z}}}_{S}} \underline{\Lambda }_{S}\) whose cokernel is locally free of rank \(r-1\). Thus we obtain—for example, using Grothendieck’s theory of flag functors [10, §§2–3]—a unique holomorphic map \({{\widetilde{h}}} :S \rightarrow {\mathbb {P}}(\Lambda _{\mathbb {C}})\) such that the pullback by \({{\widetilde{h}}}\) of the tautological subsheaf of \({\mathscr {O}}_{{\mathbb {P}}(\Lambda _{\mathbb {C}})}\)-modules
yields precisely the image of \(f_*\Omega ^2_{X/S}\) inside \({\mathscr {O}}_S \otimes _{\underline{{\mathbb {Z}}}_{S}} \underline{\Lambda }_{S}\). We notice that for every point \(s \in S\),
where \({\mathsf {H}}^{2,0}(X_s)\) denotes the canonical image of \({\mathsf {H}}^{0}(X_s;\Omega ^2_{X_s})\) in \({\mathbb {C}}\otimes _{\mathbb {Z}}{\mathsf {H}}^{2}(X_s;{\mathbb {Z}})\) and
is the complexification of \(\mu _s\). Equation 2.12.2 implies that the holomorphic map \({{\widetilde{h}}}\) factorizes uniquely as \(j \circ h\) where \(j :{\mathsf {D}}_{\Lambda }\hookrightarrow {\mathbb {P}}(\Lambda _{\mathbb {C}})\) denotes the canonical injection and \(h :S \rightarrow {\mathsf {D}}_{\Lambda }\) is a holomorphic map. We call h the period map of \(({\mathcal {F}},\mu )\).
Remark 2.2
The literature typically gives equation 2.12.2 as the definition of the period map of a marked family. While this is sufficient for families over reduced complex spaces, it is certainly not sufficient as a definition for families over arbitrary complex spaces. Hence in Sect. 2.8 we work with the sheaf of \({\mathscr {O}}_S\)-modules \(f_*\Omega ^2_{X/S}\) rather than with the indexed family of complex vector spaces \({(}{)}{{\mathsf {H}}^{0}(X_s;\Omega ^2_{X_s})}_{s\in S}\).
Remark 2.3
Let \(\Lambda \) be a lattice, \(\phi = (g,h) :{\mathcal {F}}' \rightarrow {\mathcal {F}}\) be a morphism of \(\Lambda \)-marked families, and \(p' :S' \rightarrow {\mathsf {D}}_{\Lambda }\) and \(p :S \rightarrow {\mathsf {D}}_{\Lambda }\) be the period maps of \({\mathcal {F}}'\) and \({\mathcal {F}}\), respectively. Then, exploiting the commutativity of diagram 2.5.1 and noticing that the sheaf map of diagram 2.12.1 is compatible with the base change associated to the square in equation 2.1.1, we deduce that \(p' = p \circ h\). In other words, the period map is functorial.
2.9 Deformation theory
We denote by \(\mathsf {pt}\) the reduced complex space with underlying set \({\{}{\}}0\). Then every compact complex manifold X can be viewed as a family of compact complex manifolds over \(\mathsf {pt}\) by virtue of the constant map \(c :X \rightarrow \mathsf {pt}\). In this spirit a deformation of X is a pair \(({\mathcal {X}},\iota )\) where \({\mathcal {X}}\) is a family of compact complex manifolds and \(\iota :(X,\mathsf {pt},c) \rightarrow {\mathcal {X}}\) is a morphism of families.
A deformation \(({\mathcal {X}},\iota )\) of X is called complete when for every deformation \(({\mathcal {X}}',\iota ')\) of X, where \(\iota '\) is a morphism over \(j' :\mathsf {pt}\rightarrow D'\), there exists an open subspace \(U \subseteq D'\) with \(j'(0) \in U\) as well as a morphism of families \(\phi :{\mathcal {X}}'_U \rightarrow {\mathcal {X}}\) such that \(\iota = \phi \circ \iota '\). A deformation \(({\mathcal {X}},\iota )\) of X is called universal (resp. semi-universal) when it is complete and when for all deformations \(({\mathcal {X}}'',\iota '')\) of X, where \(\iota ''\) is a morphism over \(j'' :\mathsf {pt}\rightarrow D''\), and all morphisms of families \(\phi _1,\phi _2 :{\mathcal {X}}'' \rightarrow {\mathcal {X}}\) over \(h_1,h_2 :D'' \rightarrow D\) that satisfy
respectively, there exists an open neighborhood V of \(j''(0)\) in \(D''\) with \({\left. {h_1}\right| _{V} = \left. {h_2}\right| _{V}}\) (resp. the Jacobian maps of \(h_1\) and \(h_2\) at the point \(j''(0)\) coincide). The base space of a semi-universal deformation \(({\mathcal {X}},\iota )\) of X is often denoted as \({{\,\mathrm{Def}\,}}(X)\) and, as a complex space germ at \(\iota (0)\), it is by definition unique up to isomorphism. We say that X is unobstructed or has unobstructed deformations if \({{\,\mathrm{Def}\,}}(X)\) is smooth at \(\iota (0)\).
Remark 2.4
By virtue of its Kuranishi family every compact complex manifold X possesses a semi-universal deformation [21, Theorem 2]. Assume that X is an ihs manifold. Then according to Beauville and Bogomolov [4, p. 771–772] there exists a semi-universal deformation \(({\mathcal {X}},(i,j))\) of X such that \({\mathcal {X}}\) is a family of ihs manifolds over a simply connected complex manifold S. Moreover for every \(\Lambda \)-marking \(\mu \) of \({\mathcal {X}}\), the period map \(S \rightarrow {\mathsf {D}}_{\Lambda }\) of \(({\mathcal {X}},\mu )\) is a local biholomorphism at the point j(0). The latter fact is usually called the local Torelli theorem for ihs manifolds [15, 1.15].
Let \({\mathcal {F}}\) be a family of compact complex manifolds over S and \(s \in S\) be a point. Then the canonical injection of the fiber defines a morphism of families \(\iota :({\mathcal {F}}(s),\mathsf {pt},c) \rightarrow {\mathcal {F}}\) over the map \(\mathsf {pt}\rightarrow S\) sending 0 to s. In that regard we say that the family \({\mathcal {F}}\) is complete (resp. semi-universal, resp. universal) at s when \(({\mathcal {F}},\iota )\) is a complete (resp. semi-universal, resp. universal) deformation of \({\mathcal {F}}(s)\).
3 Families of ihs manifolds over smooth rational curves
3.1 Overview
In this section we focus our attention on families of ihs manifolds \({\mathcal {F}}\) over smooth rational curves. First of all, we note that any such family possesses a marking \(\mu \) as defined in Sect. 2.5 and admits an invariant, its degree, which turns out to be an integer \(d\ge 0\). In Proposition 3.3 we show that d can be characterized completely in terms of the period map of \(({\mathcal {F}},\mu )\).
Second of all, we discuss examples of families of low degree. In Proposition 3.6 we show that families of degree 0 are trivial. Due to a restriction related to the geometry of the period domain, explained in Lemma 3.7, families of degree 1 do not exist. In Proposition 3.12 we show that the period map of a marked family of degree 2 is an embedding. Thus families of ihs manifolds of degree 2—in particular, twistor families—are examples of families satisfying the assumptions of Theorem 1.1.
Last but not least, with Lemma 3.14 and Corollary 3.15 we study the behavior of our notions of degree under deformation. This becomes relevant in Sect. 4.
3.2 Degree of line bundles on smooth rational curves
A smooth rational curve is a complex space biholomorphic to \({\mathbb {P}}^{1}\). Given a smooth rational curve C and a locally free sheaf of \({\mathscr {O}}_C\)-modules \({\mathscr {L}}\) of rank 1, we let \({\mathsf {deg }}\!_C({\mathscr {L}})\) denote the degree of \({\mathscr {L}}\) on C. Note that the resulting map \({\mathsf {deg }}\!_C :{\mathsf {Pic}}~C \rightarrow {\mathbb {Z}}\) is a group isomorphism. When d is an integer, we write \({\mathscr {O}}_C(d)\) for an arbitrary locally free sheaf of \({\mathscr {O}}_C\)-modules of rank 1 whose degree is equal to d.
Definition 3.1
Let \({\mathcal {F}}= (X,C,f)\) be a family of ihs manifolds over a smooth rational curve C. We know—compare Sect. 2.8—that \(f_*\Omega ^2_{X/C}\) is a locally free sheaf of \({\mathscr {O}}_C\)-modules of rank 1. Thus it makes sense to define
We call \({\mathsf {deg }}\,{\mathcal {F}}\) the degree of \({\mathcal {F}}\), and we say that \({\mathcal {F}}\) is a family (of ihs manifolds) of degree d when \({\mathsf {deg }}\,{\mathcal {F}}= d\).
Definition 3.2
Let C be a smooth rational curve, V a finite-dimensional complex vector space, and \(g:C\rightarrow {\mathbb {P}}(V)\) a holomorphic map to the projective space of lines. Then the degree of g is
When U is a not necessarily open or closed complex subspace of \({\mathbb {P}}(V)\) and the reference to \({\mathbb {P}}(V)\) is understood, we can view a given holomorphic map \(h :C \rightarrow U\) as a holomorphic map \({{\widetilde{h}}} :C \rightarrow {\mathbb {P}}(V)\) by virtue of the canonical injection \(j :U \hookrightarrow {\mathbb {P}}(V)\). In that spirit the degree of h is \({\mathsf {deg }}h :={\mathsf {deg }}{{\widetilde{h}}}\). When, in addition, C is a subspace of U, we apply this definition to the canonical injection \(i :C \hookrightarrow U\) and speak of a smooth rational curve of degree \({\mathsf {deg }}i\) in U.
Proposition 3.3
Let \(({\mathcal {F}},\mu )\) be a \(\Lambda \)-marked family of ihs manifolds over a smooth rational curve, h be the associated period map. Then \({\mathsf {deg }}\,{\mathcal {F}}= {\mathsf {deg }}h\).
Proof
Writing \({\mathcal {F}}= (X,C,f)\) and letting \({{\widetilde{h}}}\) denote the composition of h and the canonical injection \({\mathsf {D}}_{\Lambda }\rightarrow {\mathbb {P}}(\Lambda _{\mathbb {C}})\), we know that \(f_*\Omega ^2_{X/C} \cong {{\widetilde{h}}}^*{(}{)}*{{\mathscr {O}}_{{\mathbb {P}}(\Lambda _{\mathbb {C}})}(-1)}\) by the definition of the period map in Sect. 2.8. Thus
\(\square \)
Remark 3.4
Let \({\mathcal {F}}= (X,S,f)\) be a family of ihs manifolds over a nonempty, simply connected space S. Then there exist a lattice \(\Lambda \) and a \(\Lambda \)-marking \(\mu \) of \({\mathcal {F}}\).
Indeed, pick a point \(t \in S\). Then there exist a lattice \(\Lambda \) and a lattice isomorphism \(\nu :{\mathsf {H}}^{2}(X_t;{\mathbb {Z}})\rightarrow \Lambda \); for example, take \(\Lambda \) equal to \({\mathsf {H}}^{2}(X_t;{\mathbb {Z}})\) and \(\nu = \mathsf {id}_{\Lambda }\). Since the holomorphic map \(f:X \rightarrow S\) is a proper submersion, we know that the sheaf of abelian groups \({\mathsf {R}}^{2}f_*{\underline{{\mathbb {Z}}}_{X}}\) is locally constant. Given that S is simply connected, we infer that the latter sheaf is constant. Therefore we obtain a unique isomorphism of sheaves of abelian groups
for which \(\mu _t = \nu \). Since the bilinear forms of the lattices \({\mathsf {H}}^{2}(X_s;{\mathbb {Z}})\) vary locally constantlyFootnote 1 with s in S, the map \(\mu _s :{\mathsf {H}}^{2}(X_s;{\mathbb {Z}})\rightarrow \Lambda \) is a \(\Lambda \)-marking of \(X_s\) for all points \(s \in S\). Hence \(\mu \) is a \(\Lambda \)-marking of \({\mathcal {F}}\).
Corollary 3.5
When \({\mathcal {F}}\) is a family of ihs manifolds over a smooth rational curve, then \({\mathsf {deg }}{\mathcal {F}}\ge 0\).
Proof
Use Remark 3.4, Proposition 3.3, and the fact that the degree of a holomorphic map in the sense of Definition 3.2 is always nonnegative. \(\square \)
Proposition 3.6
Let \({\mathcal {F}}= (X,C,f)\) be a family of ihs manifolds over a smooth rational curve. Then \({\mathsf {deg }}\,{\mathcal {F}}= 0\) if and only if the family \({\mathcal {F}}\) is trivial.
Proof
First of all, if \({\mathcal {F}}\) is trivial, then \(f_*\Omega ^2_{X/C} \cong {\mathscr {O}}_C\) and whence \({\mathcal {F}}\) is of degree 0. Conversely now, assume that \({\mathsf {deg }}\,{\mathcal {F}}=0\). By Proposition 3.3 we know that for every \(\Lambda \)-marking \(\mu \) of \({\mathcal {F}}\), the period map of \(({\mathcal {F}},\mu )\) is of degree 0, whence constant. By virtue of Remark 3.4 every \(\Lambda \)-marking of a particular fiber of \({\mathcal {F}}\) extends uniquely to a \(\Lambda \)-marking of \({\mathcal {F}}\). Thus for every open subspace \(U\subseteq C\) and every \(\Lambda \)-marking \(\nu \) of \({\mathcal {F}}_U\) we see that the period map of \(({\mathcal {F}}_U,\nu )\) is locally constant.
Fix a point \(s \in C\). According to Remark 2.4 there exist a semi-universal deformation \(({\mathcal {X}},\iota )\) of \(X_s\) as well as a \(\Lambda \)-marking \({\widetilde{\nu }}\) of the family of ihs manifolds \({\mathcal {X}}\) such that the period map of \(({\mathcal {X}},{\widetilde{\nu }})\) is an open embedding \(p :S \rightarrow {\mathsf {D}}_{\Lambda }\). Since the deformation \(({\mathcal {X}},\iota )\) is complete, there is a connected open neighborhood U of s in C and a morphism of families \(\phi :{\mathcal {F}}_U\rightarrow {\mathcal {X}}\) over a holomorphic map \(h:U\rightarrow S\). We let \(\nu \) denote the unique \(\Lambda \)-marking of \({\mathcal {F}}_U\) for which \(\phi \) becomes a morphism of \(\Lambda \)-marked families; see Remark 2.1. Then by Remark 2.3 the composition \(p \circ h\) is the period map of \(({\mathcal {F}}_U,\nu )\), which we know to be constant. We conclude that the holomorphic map h is constant, too, so that the family \({\mathcal {F}}_U\) is trivial by virtue of \(\phi \).
As \(s \in C\) was arbitrary, we have shown that the family \({\mathcal {F}}\) is locally trivial. Since the space C is connected, this implies that the family \({\mathcal {F}}\) is isotrivial in the sense that every two fibers of \({\mathcal {F}}\) are isomorphic. Therefore there exists an ihs manifold Y—for example, take an arbitrary fiber of \({\mathcal {F}}\)—together with an indexed open cover \({\mathfrak {U}} = (U_i)_{i\in I}\) of C and an indexed family \((\zeta _i)_{i\in I}\) of \(U_i\)-isomorphisms of families \(\zeta _i :{\mathcal {F}}_{U_i} \rightarrow {\mathcal {Y}}_{U_i}\) where \({\mathcal {Y}}\) denotes the trivial family of compact complex manifolds \((Y\times C,C,\mathsf {pr}_{2})\). For all \(i,j \in I\) define \(U_{ij} :=U_i\cap U_j\) and
Notice that the group \({\mathsf {H}}^{0}(Y;\Theta _Y)\) is trivial for Y is an ihs manifold. Thus the Lie group \(A :={\mathsf {Aut}}(Y)\) of holomorphic automorphisms of Y is discrete, and we may regard \(\psi _{ij}\) as a locally constant map \(U_{ij} \rightarrow A\). As such \((\psi _{ij})_{i,j \in I}\) is a Čech 1-cocycle of the constant sheaf of groups \(\underline{A}_{C}\) on \({\mathfrak {U}}\).
Since the space C is simply connected and locally pathwise connected, the first Čech cohomology of \(\underline{A}_{C}\) on \({\mathfrak {U}}\) is trivial [33, 7.5, 7.13, and 7.14]. Hence there exists an indexed family \((\omega _i)_{i\in I}\) of sections \(\omega _i\in \underline{A}_{C}(U_i)\) so that \(\omega _i\psi _{ij} = \omega _j\) on \(U_{ij}\) for all \(i,j \in I\). Interpreting \(\omega _k\) as a \(U_k\)-automorphism of the family \({\mathcal {Y}}_{U_k}\), we infer that
for all \(i,j \in I\). As a result there exists a C-isomorphism of families \({\mathcal {F}}\rightarrow {\mathcal {Y}}\). \(\square \)
Lemma 3.7
Let \(\Lambda \) be a lattice of rank \(r\ge 3\) and signature \((3,r-3)\). Then the period domain \({\mathsf {D}}_{\Lambda }\) contains no projective linear subspace of \({\mathbb {P}}(\Lambda _{{\mathbb {C}}})\) of positive dimension.
Proof
that \({\mathsf {D}}_{\Lambda }\) contains no projective line. We assume, to the contrary, that there exists a 2-dimensional complex linear subspace \(V \subseteq \Lambda _{{\mathbb {C}}}\) such that \({\mathbb {P}}(V)\subseteq {\mathsf {D}}_{\Lambda }\). By the definition of the period domain, \(x^2 = 0\) and \(x{\overline{x}} > 0\) for all \(x \in V \setminus {\{}{\}}0\). The second condition implies that there exists an orthogonal ordered basis (v, w) of V with respect to the Hermitian product \(H(x,y):=x\overline{y}\), which is defined on \(\Lambda _{{\mathbb {C}}}\). The first condition then implies that the quadruple \((v,w,\overline{v},\overline{w})\) is orthogonal with respect to H. Moreover, the entries of this quadruple are strictly positive for H, which, however, contradicts the fact that the positive index of inertia of H on \(\Lambda _{\mathbb {C}}\) is 3. \(\square \)
Remark 3.8
Gordon Heier [12] has obtained Lemma 3.7 for the K3 lattice \(\Lambda \) by means of a different argument.
Corollary 3.9
Let \({\mathcal {F}}\) be a family of ihs manifolds over a smooth rational curve, then \({\mathsf {deg }}\,{\mathcal {F}}\ne 1\).
Proof
By Remark 3.4 there exists a marking \(\mu \) of \({\mathcal {F}}\). Let h denote the associated period map. Then by Proposition 3.3, \({\mathsf {deg }}\,{\mathcal {F}}=1\) if and only if \({\mathsf {deg }}h=1\). The latter condition would imply that h(C) is a projective line in \({\mathbb {P}}(\Lambda _{\mathbb {C}})\), which is impossible by Lemma 3.7. \(\square \)
Proposition 3.10
Let \({\mathcal {F}}=(X,C,f)\) be a family of ihs manifolds over a smooth rational curve and \(d\in {\mathbb {Z}}\). Then \({\mathsf {deg }}\,{\mathcal {F}}=d\) if and only if there exists a global section \(\sigma \) in the sheaf
that defines a holomorphic symplectic structure on \(X_t\) for every \(t \in C\).
Proof
By Definition 3.1, Sect. 3.2, \({\mathsf {deg }}\,{\mathcal {F}}=d\) if and only if the sheaf of \({\mathscr {O}}_C\)-modules \(E :=f_*\Omega ^2_{X/C} \otimes _{{\mathscr {O}}_C} {\mathscr {O}}_{C}(d)\) is isomorphic to \({\mathscr {O}}_C\), which is the case if and only if there exists a global nowhere vanishing section in E.
By the projection formula the canonical morphism of sheaves of \({\mathscr {O}}_C\)-modules \(\pi :E \rightarrow f_*{(}{)}{\Omega ^2_{X/C}(d)}\) is an isomorphism. Let \(\tau \) be an arbitrary global section in E now, put \(\sigma :=\pi _C(\tau )\), and fix a point \(t \in C\). Then \(\sigma \) is a global section of \(\Omega ^2_{X/C}(d)\) which defines a global section \(\sigma _t\) of \(\Omega ^2_{X_t}\). By Grauert’s base change theorem we know that \(\sigma _t\ne 0\) in \({\mathsf {H}}^{0}(X_t;\Omega ^2_{X_t})\) if and only if \(\tau (t)\ne 0\) in E(t). Futhermore, since \(X_t\) is an ihs manifold, \(\sigma _t\ne 0\) if and only if \(\sigma _t\) is a holomorphic symplectic structure on \(X_t\). Hence the desired equivalence follows. \(\square \)
Example 3.11
(Twistor families) Let M be a compact ihs manifold. As mentioned in the introduction, its twistor space X is a complex manifold together with a differentiably trivial holomorphic submersion \(f :X\rightarrow {\mathbb {P}}^{1}\). It is known that there exists a global section \(\sigma \) of the sheaf \(\Omega ^2_{X/{\mathbb {P}}^{1}}(2)\) so that \(\sigma \) defines a holomorphic symplectic structure \(\sigma _t\) on the fiber \(X_t\) for every point \(t \in {\mathbb {P}}^{1}\), [13, (3.87)]. Therefore, according to Proposition 3.10, the triple \((X,{\mathbb {P}}^{1},f)\) is a family of ihs manifolds of degree 2, which we call a twistor family.
Proposition 3.12
Let \(({\mathcal {F}},\mu )\) be a \(\Lambda \)-marked family of ihs manifolds over a smooth rational curve C such that \({\mathsf {deg }}\,{\mathcal {F}}= 2\). Then the period map \(h:C\rightarrow {\mathsf {D}}_{\Lambda }\) of \(({\mathcal {F}},\mu )\) is a closed embedding.
Proof
We let \({{\widetilde{h}}}\) denote the composition of h and the canonical injection \({\mathsf {D}}_{\Lambda }\rightarrow {\mathbb {P}}(\Lambda _{{\mathbb {C}}})\). By Proposition 3.3, \({{\widetilde{h}}} :C \rightarrow {\mathbb {P}}(\Lambda _{\mathbb {C}})\) is a holomorphic map of degree 2. Thus \({{\widetilde{h}}}\) is given by a linear series |V| for a nonzero complex linear subspace \(V \subseteq {\mathsf {H}}^{0}(C;{\mathscr {O}}_C(2))\). The vector space V cannot be of dimension 1, for if it were, the map \({{\widetilde{h}}}\) would be constant and whence of degree 0. If V were of dimension 2, the set-theoretic image of \({{\widetilde{h}}}\) would be a 1-dimensional linear subspace of \({\mathbb {P}}(\Lambda _{\mathbb {C}})\), which is impossible by Lemma 3.7. Therefore \({{\widetilde{h}}}\) is given by the complete linear series \(|{{\mathscr {O}}_C(2)}|\), which implies that \({{\widetilde{h}}}\) and whence h are closed embeddings. \(\square \)
Remark 3.13
If \({\mathcal {F}}\) is a family of ihs manifolds of degree \(d'\) over \({\mathbb {P}}^{1}\) and \(g:{\mathbb {P}}^{1}\rightarrow {\mathbb {P}}^{1}\) is a branched covering of degree d, then \(g^*({\mathcal {F}})\) is a family of degree \(d'd\). Taking for \({\mathcal {F}}\) a twistor family as in example 3.11, this shows that there are families of ihs manifolds over \({\mathbb {P}}^{1}\) of every even degree \(2d>0\). We do not know whether families of odd degree occur.
Lemma 3.14
Let (W, S, p) be a family of smooth rational curves—that is, a family of compact complex manifolds every fiber of which is a smooth rational curve. Let \({\mathscr {L}}\) be a locally free sheaf of \({\mathscr {O}}_W\)-modules of rank 1 and write \(i_s :W_s \rightarrow W\) for the canonical injection when \(s \in S\). Then the function \(d:S\rightarrow {\mathbb {Z}}\) given by \(d(s) = {\mathsf {deg }}_{W_s}(i_s^*({\mathscr {L}}))\) is locally constant on S.
Proof
By the Riemann–Roch theorem we know that \(d(s) = \chi (W_s;i_s^*({\mathscr {L}})) - 1\) for all \(s \in S\). Thus our claim follows from the well-known invariance of the Euler–Poincaré characteristic [8, 28]. \(\square \)
Corollary 3.15
We proceed with the notation of Lemma 3.14.
-
(i)
When V is a finite dimensional complex vector space and \(g:W\rightarrow {\mathbb {P}}(V)\) is a holomorphic map, then the degree of the maps \(g \circ i_s\) is locally constant in \(s\in S\).
-
(ii)
Let \({\mathcal {F}}=(X,W,f)\) be a family of ihs manifolds. Then the degree of the induced families \({\mathcal {F}}_{W_s}\) is locally constant in \(s\in S\).
Proof
Item (i) follows from Lemma 3.14 when we apply it to \({\mathscr {L}}= g^*({\mathscr {O}}_{{\mathbb {P}}(V)}(1))\). As a matter of fact, for all \(s \in S\),
Concerning item (ii), let us write the family \({\mathcal {F}}_{W_s}\) and the canonical morphism of families \({\mathcal {F}}_{W_s} \rightarrow {\mathcal {F}}\) as \((X_s,W_s,f_s)\) and \((q,i_s)\), respectively. Then \({q^*(\Omega ^2_{X/W}) \cong \Omega ^2_{X_s/W_s}}\) since relative differentials are compatible with base change. Moreover, even though W might be nonreduced, we know by Sect. 2.8 that
Hence item (ii) follows when we apply Lemma 3.14 to \({\mathscr {L}}= f_*\Omega ^2_{X/W}\). \(\square \)
4 Proof of the unobstructedness theorem
4.1 Douady space
The proof of Theorem 1.1 makes use of the Douady space, a complex analytic analog of the algebraic Hilbert scheme, introduced by Douady [6]. When X is a complex space, the Douady space of X, denoted \({\mathsf {Dou}}(X)\), parametrizes the compact complex subspaces of X. If \(Y \subseteq X\) is a compact complex subspace, we let [Y] denote the corresponding point in \({\mathsf {Dou}}(X)\).
Recall that there is a closed complex subspace \(Z\subseteq {\mathsf {Dou}}(X)\times X\) universal with the property that the holomorphic map \(\left. {\mathsf {pr}_{1}}\right| _{Z} :Z \rightarrow {\mathsf {Dou}}(X)\) is flat and proper. In other words, for every complex space S and every closed complex subspace \(Y\subseteq S\times X\) that is flat and proper over S there exists a unique holomorphic map \(b:S\rightarrow {\mathsf {Dou}}(X)\) such that Y is the pullback of the complex subspace Z under \(b\times \mathsf {id}_{X}\).
4.2 Proof of Theorem 1.1
Let \({{\mathcal {F}}:=(X,C,f)}\) be a family of ihs manifolds with \(C\cong {\mathbb {P}}^{1}\) and \(\mu \) be a \(\Lambda \)-marking of \({\mathcal {F}}\) such that the period map \(h :C \rightarrow {\mathsf {D}}_{\Lambda }\) of \(({\mathcal {F}},\mu )\) is an embedding. Set \(d :=-{\mathsf {deg }}\!_C{(}{)}{f_*{\Omega ^2_{X/C}}}\) and \(r:={\mathsf {rk}}\,\Lambda \). Then by Proposition 3.3 the degree of the map h is equal to d and \(d\ge 2\) by corollaries 3.5 and 3.6 and Proposition 3.9. Moreover r is the second Betti number of every fiber of f. We divide the proof of Theorem 1.1 into the following four steps.
-
(i)
By Corollary 4.2 the space \(S_d({\mathsf {D}}_{\Lambda })\) of smooth rational curves of embedding degree d in \({\mathsf {D}}_{\Lambda }\) is a smooth open neighbourhood of dimension \({m:=(r-2)(d+1)-3}\) for the point [h(C)] in the Douady space \({\mathsf {Dou}}({\mathsf {D}}_{\Lambda })\).
-
(ii)
We construct a deformation \(({\mathcal {X}},(i,j))\) of X over an open subspace \(S\subseteq S_d({\mathsf {D}}_{\Lambda })\). This is done using the extension theorem, Theorem 1.2, which we prove in Sect. 7.
-
(iii)
We show that \(({\mathcal {X}},(i,j))\) is complete. For that matter we rely on the existence of universal morphisms to the extended family, as established in Sect. 6.
-
(iv)
We show that \(({\mathcal {X}},(i,j))\) is a universal deformation of X. Here we exploit that by Theorem 5.4 we have \({\mathsf {h}}^{1}(X;\Theta _X)=m\).
As \(({\mathcal {X}},(i,j))\) is a universal deformation of X over the smooth space S, the deformations of X are unobstructed and the complex space germ (S, [h(C)]) is commonly denoted by \({{\,\mathrm{Def}\,}}(X)\). By the construction in step (i), we also have \((S,[h(C)])=({\mathsf {Dou}}({\mathsf {D}}_{\Lambda }),[h(C)])\). This identification induces the canonical isomorphism in Theorem 1.1 and completes the proof. \(\square \)
4.3 Step (i) in the proof of Theorem 1.1
Theorem 4.1
Let \(r\ge 3\) and \(d\ge 2\) be integers, V be a complex vector space of dimension r, and \(Q\subseteq {\mathbb {P}}(V)\) be a smooth quadric hypersurface. Then the set of smooth rational curves of degree d in Q defines a smooth open subspace \(S_d(Q) \subseteq {\mathsf {Dou}}(Q)\) which is either empty or pure of dimension \((r-2)(d+1)-3\).
Proof
We divide the proof into the following two steps.
-
(i)
The set \(S_d(Q)\) is open in \({\mathsf {Dou}}(Q)\).
-
(ii)
For every smooth rational curve \(C\subseteq Q\) of degree d,
$$\begin{aligned} {\mathsf {h}}^{0}(C;{\mathscr {N}}_{C/Q}) = (r-2)(d+1)-3 \quad \text {and} \quad {\mathsf {h}}^{1}(C;{\mathscr {N}}_{C/ Q})=0.\end{aligned}$$
Theorem 4.1 then follows from Kodaira’s well-known criterion [18, Theorem 2]. Without loss of generality we may and do assume that \({\mathbb {P}}(V) = {\mathbb {P}}^{r-1}\).
Step (i).
Let \(s\in {\mathsf {Dou}}(Q)\) be a point corresponding to a smooth rational curve in Q. Let \(p :Z \rightarrow {\mathsf {Dou}}(Q)\) be the projection from the universal subspace \(Z\subseteq {\mathsf {Dou}}(Q)\times Q\). Then \(p^{-1}(s)\cong {\mathbb {P}}^{1}\) and thus, as \({\mathbb {P}}^{1}\) is rigid, there is an open neighborhood U of s in \({\mathsf {Dou}}(Q)\) with \(p^{-1}(t)\cong {\mathbb {P}}^{1}\) for all \(t\in U\). As s was arbitrary, the set of smooth rational curves in Q defines an open subspace \(S\subseteq {\mathsf {Dou}}(Q)\) and, moreover, the triple \((p^{-1}(S),S,\left. {p}\right| _{p^{-1}(S)})\) is a family of smooth rational curves.
Composing the canonical injections \(p^{-1}(S)\hookrightarrow S\times Q\hookrightarrow S\times {\mathbb {P}}^{r-1}\) with the projection onto \({\mathbb {P}}^{r-1}\), we obtain a holomorphic map \(g:p^{-1}(S)\rightarrow {\mathbb {P}}^{r-1}\). Applying item (i) of Corollary 3.15 we see that the degree of the image curves \(p^{-1}(t)\hookrightarrow {\mathbb {P}}^{r-1}\) is locally constant in \(t\in S\). Hence \(S_d(Q)\) is an open subset of \({\mathsf {Dou}}(Q)\).
Step (ii).
Let \(C \subseteq Q\) be a smooth rational curve of degree \(d\ge 2\). Define \(P \cong {\mathbb {P}}^{n}\) to be the projective linear subspace of \({\mathbb {P}}^{r-1}\) spanned by C. Then we have an exact sequence of sheaves of \({\mathscr {O}}_C\)-modules
We see that
and [11, Corollary 1.45] implies that
Therefore we deduce that \({\mathsf {h}}^{0}(C;{\mathscr {N}}_{C/{\mathbb {P}}^{r-1}})=r(d+1)-4\) and \({\mathsf {h}}^{1}(C;{\mathscr {N}}_{C/{\mathbb {P}}^{r-1}})=0\) from the long exact sequence in cohomology associated to sequence 4.2.1.
Now we use the exact sequence of sheaves
We see that
Note that \({\mathscr {N}}_{C/Q}\) is ample by [1, Theorem 1] as \(d\ge 2\). So \({\mathsf {h}}^{1}(C;{\mathscr {N}}_{C/Q})=0\). Hence the long exact sequence associated to sequence 4.2.2 yields the result. \(\square \)
Corollary 4.2
Let \(d\ge 2\) be an integer, \(\Lambda \) be a lattice of rank \(r\ge 3\) and signature \((3,r-3)\), and \(U \subseteq {\mathsf {D}}_{\Lambda }\) be an open subspace. Then the set of smooth rational curves of degree d in U defines a smooth open subspace \(S_d(U) \subseteq {\mathsf {Dou}}(U)\) which is either empty or pure of dimension \((r-2)(d+1)-3\).
Proof
Since the quadratic form of the lattice \(\Lambda \) is nondegenerate, we can apply Theorem 4.1 to the hypersurface \(Q\subseteq {\mathbb {P}}(\Lambda _{{\mathbb {C}}})\) defined by it. As \(U \subseteq Q\) is open, the canonical map \({\mathsf {Dou}}(U) \rightarrow {\mathsf {Dou}}(Q)\) is an open embedding. Regarding the embedding as an inclusion, \(S_d(U) = S_d(Q) \cap {\mathsf {Dou}}(U)\). Hence our claim follows. \(\square \)
4.4 Step (ii) in the proof of Theorem 1.1
As the period map \(h :C \rightarrow {\mathsf {D}}_{\Lambda }\) is an embedding, by Theorem 1.2 there exists a family of ihs manifolds \(\widetilde{{\mathcal {F}}} = ({\widetilde{X}},U,{\widetilde{f}})\) together with a \(\Lambda \)-marking \(\widetilde{\mu }\) and a holomorphic map \(g:X \rightarrow {\widetilde{X}}\) such that
-
a)
\(U \subseteq {\mathsf {D}}_{\Lambda }\) is an open subspace containing h(C),
-
b)
the period map of \((\widetilde{{\mathcal {F}}},\widetilde{\mu })\) is the canonical injection \(U \hookrightarrow {\mathsf {D}}_{\Lambda }\),
-
c)
\((g,h) :({\mathcal {F}},\mu ) \rightarrow (\widetilde{{\mathcal {F}}},\widetilde{\mu })\) is a morphism of \(\Lambda \)-marked families.
We let S be the set of points in \({\mathsf {Dou}}(U)\) corresponding to smooth rational curves in U of embedding degree d. By Corollary 4.2 we can consider S as a smooth open subspace of \({\mathsf {Dou}}(U)\), which is pure of dimension m for \(L_0 :=h(C) \subseteq U\) defines a point \([L_0]\in S\). Let \(Y\subseteq {\mathsf {Dou}}(U)\times U\) be the universal subspace, see Sect. 4.1, and define \(W:=Y\cap (S\times U)\) with projections \({\bar{p}}:W\rightarrow S\) and \(q:W\rightarrow U\). Since

we get a holomorphic map
Evidently, \({\bar{h}}\) embeds C into W as the fiber of \({{\bar{p}}}\) over \([L_0]\). By the defining properties of Y, the map \({\bar{p}}\) is a proper submersion so that \(({\mathcal {C}},({\bar{h}},j))\), with \({\mathcal {C}}:=(W,S,{\bar{p}})\), is a deformation of C where \(j(0):=[L_0]\).
We consider the pullback family \(q^*({\widetilde{{\mathcal {F}}}}) =: (Z,W,F)\) together with the canonical morphism of families \(({{\widetilde{q}}},q) :q^*({\widetilde{{\mathcal {F}}}}) \rightarrow {\widetilde{{\mathcal {F}}}}\). By the Cartesian property of the latter morphism, as \(q\circ {\bar{h}}=h\), there exists a unique holomorphic map \(i :X \rightarrow Z\) for which \((i,{\bar{h}}):{\mathcal {F}}\rightarrow q^*(\widetilde{{\mathcal {F}}})\) is a morphism of families and \(({{\widetilde{q}}},q) \circ (i,{{\bar{h}}}) = (g,h)\). We obtain the following commutative diagram:

Setting \(p :={{\bar{p}}}\circ F\) and \({\mathcal {X}}:=(Z,S,p)\), we obtain a deformation \(({\mathcal {X}},(i,j))\) of X.
For the third step in the proof of Theorem 1.1 we will need in Sect. 4.5 below that every deformation of X lifts to a deformation of the holomorphic map \(f:X \rightarrow C\) in the sense of Ran [25, Definition 1.1 and §3]. Hence we recall a theorem on the stability of fiber structures.
Theorem 4.3
Let (X, Y, f) be a family of compact complex manifolds over a compact complex manifold Y such that \(f_*{\mathscr {O}}_X \cong {\mathscr {O}}_Y\) and \({\mathsf {R}}^{1}f_*{{\mathscr {O}}_X}=0\). Let \(({\mathcal {X}},(i,j))\) be a deformation of X with \({\mathcal {X}}=(Z,S,p)\). Then, after possibly shrinking S around j(0), there are a deformation \(({\mathcal {Y}},({{\bar{i}}},j))\) of Y with \({\mathcal {Y}}=(W,S,{\bar{p}})\) and a holomorphic map \(F:Z\rightarrow W\) such that \((i,{{\bar{i}}}) :(X,Y,f) \rightarrow (Z,W,F)\) is a morphism of families of compact complex manifolds and \({{\bar{p}}} \circ F = p\).
Proof
When S is smooth, this is due to Kodaira [18, p. 87]. For arbitrary S the methods of Ran [26, Theorem 2.1] imply the existence of \({\mathcal {Y}}\), \({{\bar{i}}}\), and F subject to all stipulated properties except for F being a submersion. Since however \(f :X\rightarrow Y\) is a submersion, the following Lemma 4.4 implies that F is a submersion at all points of \(i(X) \subseteq Z\). Thus exploiting the properness of \(p :Z\rightarrow S\), we can shrink S further in order to make \(F:Z\rightarrow W\) a submersion entirely. \(\square \)
Lemma 4.4
Let \(F:Z\rightarrow W\) and \({\bar{p}}:W\rightarrow S\) be holomorphic maps of complex spaces such that \({\bar{p}}\) and \({\bar{p}}\circ F\) are submersions. Let \(z\in Z\) be a point and let \(Z_s\) and \(W_s\) denote the fibers of \({\bar{p}}\circ F\) and \({\bar{p}}\) over \(s :={\bar{p}}(F(z))\), respectively. Then the following are equivalent:
-
a)
F is a submersion at z.
-
b)
The induced map \(F_s:Z_s\rightarrow W_s\) is a submersion at z.
Proof
Item a) implies item b) because base changes preserve submersions. Assume item b) now. Moreover, first, assume that S is smooth. Then the spaces Z and W are smooth, too, and for item a) it suffices to check that the Jacobian map \({\mathsf {T}}_{z}F :{\mathsf {T}}_{z}Z \rightarrow {\mathsf {T}}_{F(z)}W\) is surjective. The latter follows from an elementary four-lemma type argument.
Let S be arbitrary now. Without loss of generality we assume that \(Z = S\times B'\) and \(W = S\times B\) with \(B'\) and B being open in \({\mathbb {C}}^{n'}\) and \({\mathbb {C}}^n\) and F and \({{\bar{p}}}\) being the first projection maps, respectively. Furthermore we may assume that S is a closed subspace of an open subspace \({{\widetilde{S}}} \subseteq {\mathbb {C}}^m\). By [7, 0.22, Corollary 2] we see that the holomorphic map \(F :S\times B' \rightarrow S\times B\) is—at least in a neighborhood of the point z—induced by a holomorphic map \({{\widetilde{F}}} :{{\widetilde{S}}}\times B' \rightarrow {{\widetilde{S}}}\times B\). The map \({{\widetilde{F}}}\) can be chosen so that it commutes with the projections to \({{\widetilde{S}}}\). The smooth case thus implies that \({{\widetilde{F}}}\) is a submersion at z. Hence we obtain item a). \(\square \)
4.5 Step (iii) in the proof of Theorem 1.1
To prove that the constructed deformation is complete, let there be given another deformation \(({\mathcal {X}}',(i',j'))\) of X with \({\mathcal {X}}'=(Z',S',p')\). Up to shrinking \(S'\) around \(j'(0)\), we have to construct a morphism of families \((a,b):{\mathcal {X}}'\rightarrow {\mathcal {X}}\) such that \((i,j) = (a,b) \circ (i',j')\). For the reader’s convenience, all spaces and morphisms appearing in this construction are pictured in Fig. 1.
As ihs manifolds are simply connected, \(f_*{\mathscr {O}}_{X}\cong {\mathscr {O}}_C\) and \({\mathsf {R}}^{1}f_*{{\mathscr {O}}_{X}}=0\) so that we can apply Theorem 4.3 to the family \({\mathcal {F}}=(X,C,f)\) and the deformation \(({\mathcal {X}}',(i',j'))\) of X. After possibly shrinking \(S'\) around \(j'(0)\), we obtain a deformation \(({\mathcal {C}}',({\bar{h}}',j'))\) of C with \({\mathcal {C}}'=(W',S',{\bar{p}}')\) as well as a family of compact complex manifolds \({\mathcal {F}}' :=(Z',W',F')\) such that \((i',{{\bar{h}}}') :{\mathcal {F}}\rightarrow {\mathcal {F}}'\) is a morphism of families and \(p' = {{\bar{p}}}' \circ F'\). By Remark 6.5, since the period map of \(({\widetilde{{\mathcal {F}}}},{\widetilde{\mu }})\) is the canonical injection \(U \hookrightarrow {\mathsf {D}}_{\Lambda }\), the family \({\widetilde{{\mathcal {F}}}}\) is semi-universal at all points of U. Hence we may apply item (i) of Theorem 6.3 and after another shrinking of \(S'\) around \(j'(0)\) there exists a morphism of families \((g',h') :{\mathcal {F}}' \rightarrow \widetilde{{\mathcal {F}}}\) such that \((g,h) = (g',h') \circ (i',{\bar{h}}')\).
As \(C\cong {\mathbb {P}}^{1}\) is rigid, we can shrink \(S'\) around \(j'(0)\) so that \({\mathcal {C}}'\) is a family of smooth rational curves. By item (i) of Corollary 3.15 we can assume that, for every point \(s \in S'\), the composition
is an embedding of degree d. In particular the holomorphic map
is an embedding. Therefore, by virtue of the universal property of the Douady space, see Sect. 4.1, there exists a unique morphism of families \((b',b):{\mathcal {C}}'\rightarrow {\mathcal {C}}\) such that \(b'\) commutes with the projections to U; that is, \(h' = q \circ b'\). Thus
Exploiting the uniqueness part of the universal property of the Douady space, we see that \(({{\bar{h}}},j) = (b',b) \circ ({{\bar{h}}}',j')\).
Just like in Sect. 4.4 above, using the Cartesian property of the canonical morphism of families \(({{\widetilde{q}}},q) :q^*({\widetilde{{\mathcal {F}}}}) \rightarrow {\widetilde{{\mathcal {F}}}}\), we deduce the existence of a unique holomorphic map \(a :Z' \rightarrow Z\) for which \((a,b'):{\mathcal {F}}' \rightarrow q^*({\widetilde{{\mathcal {F}}}})\) is a morphism of families such that \({(g',h') = ({{\widetilde{q}}},q) \circ (a,b')}\). As a consequence \((a,b):{\mathcal {X}}'\rightarrow {\mathcal {X}}\) is a morphism of families. We have seen that \(j = b \circ j'\). Using again the Cartesian property of \(({{\widetilde{q}}},q):q^*({\widetilde{{\mathcal {F}}}}) \rightarrow {\widetilde{{\mathcal {F}}}}\), we deduce that \(i=a\circ i'\) for
This proves that the deformation \(({\mathcal {X}},(i,j))\) of X is complete.
The complex spaces and holomorphic maps that occur in step (iii) of the proof of Theorem 1.1. The diagram is commutative. In addition, the evident squares are Cartesian
4.6 Step (iv) in the proof of Theorem 1.1
By Sect. 4.5 we know that the deformation \(({\mathcal {X}},(i,j))\) of X is complete. Hence, its associated Kodaira–Spencer map
is surjective [5, cf. Remark 5.2]. By Sect. 4.4, the complex space S is smooth and of dimension \(m=(r-2)(d+1)-3\) at j(0); in particular, \({\mathsf {T}}_{j(0)}S\) is of dimension m. Since by Theorem 5.4 the vector space \({\mathsf {H}}^{1}(X;\Theta _X)\) is of dimension m, too, we infer that \(\kappa \) is a bijection. This proves that \(({\mathcal {X}},(i,j))\) is a semi-universal deformation of X [5, loc. cit.]. As every holomorphic vector field on X is trivial, the family \(({\mathcal {X}},(i,j))\) is automatically a universal deformation of X [3, I.10.5–6].
5 Tangent cohomology of families of ihs manifolds
Throughout Sect. 5, employing Definition 3.1, we assume that \({\mathcal {F}}:=(X,{\mathbb {P}}^{1},f)\) is a family of ihs manifolds of degree d. By Corollary 3.5, \(d\ge 0\). Furthermore we know that for every integer k the sheaf of abelian groups \({\mathsf {R}}^{k}f_*{\underline{{\mathbb {Z}}}_{X}}\) is locally constant, whence constant, on \({\mathbb {P}}^{1}\). Let \(b_k\) denote the rank of \({\mathsf {R}}^{k}f_*{\underline{{\mathbb {Z}}}_{X}}\) which is likewise the kth Betti number of all fibers of \({\mathcal {F}}\).
Our goal is to prove Theorem 5.4. We use the relative Frölicher spectral sequence, the Leray spectral sequence, and the relative cotangent sequence associated to the holomorphic map \(f :X\rightarrow {\mathbb {P}}^{1}\) for that matter.
Proposition 5.1
-
(i)
Let \((p,q) \in {\mathbb {N}}^2\) and \(s \in {\mathbb {P}}^{1}\). Then \({\mathsf {R}}^{q}f_*{\Omega ^p_{X/{\mathbb {P}}^{1}}}\) is a locally free sheaf of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules of rank \({\mathsf {h}}^{p,q}(X_s) :={\mathsf {h}}^{q}(X_s;\Omega ^p_{X_s})\).
-
(ii)
The relative Frölicher spectral sequence of \({\mathcal {F}}\) degenerates at \(E_1\).
-
(iii)
\({\mathsf {R}}^{2}f_*{{\mathscr {O}}_X} \cong {\mathscr {O}}_{{\mathbb {P}}^{1}}(d)\) and \({\mathsf {R}}^{1}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}} \cong ({\mathsf {R}}^{1}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}})^\vee \) in the sense of sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules.
-
(iv)
$$\begin{aligned} {\mathsf {h}}^{i}({\mathbb {P}}^{1};{\mathsf {R}}^{1}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}}\otimes {\mathscr {O}}_{{\mathbb {P}}^{1}}(d))= {\left\{ \begin{array}{ll}(b_2-2)(d+1)&{}\text {when }i=0,\\ 0&{}\text {when }i=1.\end{array}\right. } \end{aligned}$$
-
(v)
There is a short exact sequence of sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules
$$\begin{aligned} 0 \rightarrow {\mathsf {R}}^{1}f_*{\Omega ^2_{X/{\mathbb {P}}^{1}}} \rightarrow {\mathscr {O}}^{\oplus b_3}_{{\mathbb {P}}^{1}} \rightarrow {\mathsf {R}}^{2}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}} \rightarrow 0 . \end{aligned}$$
Proof
Since every fiber of the family of compact complex manifolds \({\mathcal {F}}\) is Kählerian, the function \(h :{\mathbb {P}}^{1} \rightarrow {\mathbb {N}}\) given by \(h(t) = {\mathsf {h}}^{p,q}(X_t)\) is constant [32, Proposition 9.20]. Thus by Grauert’s base change theorem [8] the sheaf of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules \({\mathsf {R}}^{q}f_*{\Omega ^p_{X/{\mathbb {P}}^{1}}}\) is locally free and the evident base change map
is an isomorphism of complex vector spaces. This proves item (i). Furthermore, we obtain item (ii) as a consequence of these facts [24, p. 251].
Item (iii). The bilinear forms of the lattices \({\mathsf {H}}^{2}(X_t;{\mathbb {Z}})\), see Sect. 2.4, vary locally constantly with \(t \in {\mathbb {P}}^{1}\), thus yield a symmetric \({\mathbb {Z}}\)-bilinear sheaf map
which is stalkwise nondegenerate. Extending the scalars by virtue of the morphism of sheaves of rings \(\underline{{\mathbb {Z}}}_{{\mathbb {P}}^{1}} \rightarrow {\mathscr {O}}_{{\mathbb {P}}^{1}}\), we obtain a nondegenerate symmetric \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-bilinear sheaf map
Let us write \(({\mathscr {F}}^j)_{j \in {\mathbb {N}}}\) for the Hodge filtration on \({\mathscr {G}}\) [24, loc. cit.]. Then \({\mathscr {F}}^1\) is the perpendicular space of \({\mathscr {F}}^2\) with respect to the latter pairing, and vice versa, since the same holds for every Beauville–Bogomolov form [4, (1) on p. 773]. Consequently we dispose of isomorphisms of sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules
By item (ii) we know that
Hence the claim follows from our assumption that \({\mathsf {deg }}\,{\mathcal {F}}= d\) which entails that \(f_*\Omega ^2_{X/{\mathbb {P}}^{1}}\cong {\mathscr {O}}_{{\mathbb {P}}^{1}}(-d)\).
Step (iv). The results of items (ii) and (iii) give rise to the two short exact sequences of sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules
By the Birkhoff–Grothendieck theorem the locally free sheaf of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules \({\mathscr {F}}^1\) is isomorphic to a finite direct sum \(\bigoplus {\mathscr {O}}_{{\mathbb {P}}^{1}}(a_\nu )\) for some integers \(a_\nu \in {\mathbb {Z}}\). According to sequence 5.1, \({\mathscr {F}}^1\) is a subsheaf of a trivial sheaf of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules, so \(a_\nu \le 0\) for all \(\nu \). Moreover, sequence 5.1 shows that \({\mathsf {rk}}\,{\mathscr {F}}^1=b_2-1\) and that the sum of the \(a_\nu \) is \(-d\). Thus \(0\le a_\nu +d\le d\) for all \(\nu \), whence
Tensoring sequence 5.2 with \({\mathscr {O}}_{{\mathbb {P}}^{1}}(d)\) and passing to the associated long exact sequence in cohomology, we see that
which proves the result.
Step (v). Consider the Hodge filtration \(({\mathscr {F}}^j)_{j\in {\mathbb {N}}}\) on the sheaf of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules
now. Then by item (ii)
By item (i) the two sheaves on the left-hand side vanish, because the (0, 3) and (3, 0) Hodge numbers of every ihs manifold vanish [4, p. 762–764]. Hence we deduce the desired sequence from the short exact sequence
\(\square \)
Proposition 5.2
\(\Theta _{X/{\mathbb {P}}^{1}} \cong \Omega ^1_{X/{\mathbb {P}}^{1}} \otimes f^*{\mathscr {O}}_{{\mathbb {P}}^{1}}(d)\) as sheaves of \({\mathscr {O}}_X\)-modules.
Proof
From Proposition 3.10 we know that there exists a global section \(\sigma \) in the sheaf \(\Omega ^2_{X/{\mathbb {P}}^{1}} \otimes f^*{\mathscr {O}}_{{\mathbb {P}}^{1}}(d)\) such that for every \(t \in {\mathbb {P}}^{1}\) the pullback of \(\sigma \) defines a holomorphic symplectic structure on the fiber \(X_t\). Therefore the contraction with \(\sigma \), which is a morphism of sheaves of \({\mathscr {O}}_X\)-modules
is an isomorphism. \(\square \)
Remark 5.3
Assume that the fibers of \({\mathcal {F}}\) are of dimension 2n with \(n \in {\mathbb {N}}\). We calculate the relative canonical sheaf of X over \({\mathbb {P}}^{1}\) by taking the nth wedge power of the section \(\sigma \). A formula for the canonical sheaf of X then follows from the relative cotangent sequence:
Theorem 5.4
Assume that \(d={\mathsf {deg }}{\mathcal {F}}\ne 0\). Then
Moreover if \(b_3\ne 0\), the obstruction spaces \({\mathsf {H}}^{2}(X;\Theta _X)\) and \({\mathsf {H}}^{2}(X;\Theta _{X/{\mathbb {P}}^{1}})\) are both nontrivial. If \({\mathcal {F}}\) is a family of K3 surfaces, then
Proof
We consider the relative tangent sequence
which is short exact for \(f:X\rightarrow {\mathbb {P}}^{1}\) is a submersion. We prove in the following that the beginning of the associated long exact sequence with respect to the pushforward by f has the following form:

Indeed, for all \(i \in {\mathbb {Z}}\), we can calculate the sheaf \({\mathsf {R}}^{i}f_*(f^*\Theta _{{\mathbb {P}}^{1}})\) by means of the projection formula:
Since the (0, 0) and (0, 1) Hodge numbers of ihs manifolds are equal to 1 and 0, respectively, using items (i) and (iii) of Proposition 5.1, we obtain that
By Proposition 5.2 and the projection formula,
for all \(i \in {\mathbb {Z}}\); in particular \(f_*\Theta _{X/{\mathbb {P}}^{1}}=0\) because \({\mathsf {h}}^{1,0}(X_s)=0\) for \(s \in {\mathbb {P}}^{1}\) arbitrary.
To complete proving the claimed form of the long exact sequence sequence 5.5.1, it only remains to show \(f_*\Theta _X=0\). By Remark 3.4 there is a lattice \(\Lambda \) and a \(\Lambda \)-marking \(\mu \) of \({\mathcal {F}}\). Let h be the period map of \(({\mathcal {F}},\mu )\). By Proposition 3.3 we know that \({\mathsf {deg }}h = d\), which is not zero by assumption, so that \(h:{\mathbb {P}}^{1}\rightarrow {\mathsf {D}}_{\Lambda }\) is not constant. Hence h is a finite map, which is an immersion outside of its at most finitely many branching points. According to Griffiths’s interpretation [9, (1.20)], at every point \(s\in {\mathbb {P}}^{1}\) the Jacobian map of h factorizes over the Kodaira–Spencer map \(\kappa \) as follows:

When s is not a branching point of h, then \({\mathsf {T}}_{s}h\) and whence \(\kappa \) are injective. Thus the connecting homomorphism
in our long exact sequence is an injective sheaf map—first outside of the branching points of h, but therefore everywhere as \(\Theta _{{\mathbb {P}}^{1}}\) is locally free. With \(f_*\Theta _{X/{\mathbb {P}}^{1}}=0\) we conclude that \(f_*\Theta _X=0\).
The upshot of sequence 5.5.1 is that it gives rise to a short exact sequence of sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules
Passing to the long exact sequence in cohomology and applying step (iv) of Proposition 5.1, we deduce that
Next we consider the Leray spectral sequence
for the holomorphic map \(f :X\rightarrow {\mathbb {P}}^{1}\) and the sheaf of \({\mathscr {O}}_X\)-modules \(\Theta _X\). The entries \(E_2^{pq}\) are zero for \(p>1\), because \({\mathbb {P}}^{1}\) has dimension 1 and the sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules \({\mathsf {R}}^{q}f_*{\Theta }_X\) are coherent. Hence the spectral sequence degenerates on \(E_2\) and we get the following formulae:
Assume that \(b_3\ne 0\) now. Notice that \(b_3\) is an even number and that in the short exact sequence of step (v) of Proposition 5.1 the ranks of the locally free sheaves of \({\mathscr {O}}_{{\mathbb {P}}^{1}}\)-modules \({\mathsf {R}}^{1}f_*{\Omega ^2_{X/{\mathbb {P}}^{1}}}\) and \({\mathsf {R}}^{2}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}}\) are both equal to \(b_3/2\), which is a number strictly less than \(b_3\). In particular there exists a global section in the sheaf \({\mathscr {O}}_{{\mathbb {P}}^{1}}^{\oplus b_3}\) that does not vanish in the quotient \({\mathsf {R}}^{2}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}}\). Thus \({\mathsf {R}}^{2}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}}\otimes {\mathscr {O}}_{{\mathbb {P}}^{1}}(d)\) has a nontrivial global section, too. We conclude by invoking sequence 5.5.1 that
and similarly by the Leray spectral sequence, propositions 5.1 and 5.2 that
Last but not least, drop the assumption that \(b_3\ne 0\) and assume that \({\mathcal {F}}\) is a family of K3 surfaces instead. Then \({\mathsf {R}}^{i}f_*{\Omega ^1_{X/{\mathbb {P}}^{1}}}=0\) for \(i \in {\{}{\}}{2,3}\) and \({\mathsf {R}}^{3}f_*{{\mathscr {O}}_X} = 0\) given that the corresponding Hodge numbers of K3 surfaces vanish. Hence writing out the next line in the long exact sequence 5.5.1, we see that \({\mathsf {R}}^{2}f_*{\Theta _X} \cong {\mathscr {O}}_{{\mathbb {P}}^{1}}(d+2)\) and \({\mathsf {R}}^{3}f_*{\Theta _X} = 0\). Therefore
\(\square \)
6 Universal morphisms along subspaces
6.1 Introduction
Consider a compact complex manifold X for which every global holomorphic vector field on X is trivial. Then every semi-universal deformation of X is likewise universal [3, I.10.5–6]. Yet, more is true.
Consider, for \(k \in {\{}{\}}{1,2}\), a deformation \(({\mathcal {X}}_k,\iota _k)\) of X such that \({\mathcal {X}}_k\) is a family over \(D_k\) and \(\iota _k\) is a morphism of families over the holomorphic map \(b_k :\mathsf {pt}\rightarrow D_k\). Assume that \(({\mathcal {X}}_1,\iota _1)\) is semi-universal, whence universal. Moreover let U and \(U'\) be open subspaces of \(D_2\) containing the point \(b_2(0)\) and let
be morphisms of families satisfying \(\iota _1 = \phi \circ \iota _2\) and \(\iota _1 = \phi ' \circ \iota _2\), respectively. Then not only does there exist an open subspace \(V \subseteq U\cap U'\) so that \(b_2(0) \in V\) and \(\left. {h}\right| _{V} = \left. {h'}\right| _{V}\), but there exists an open subspace \(W \subseteq U\cap U'\) so that \(b_2(0) \in W\) and \(\left. {\phi }\right| _{W} = \left. {\phi '}\right| _{W}\) as morphisms of families \(({\mathcal {X}}_2)_W \rightarrow {\mathcal {X}}_1\) [3, cf. Remark after I.10.6].
For later reference we briefly elaborate on the argument.
Theorem 6.1
Let \({\mathcal {F}}\) be a family of compact complex manifolds over S and let \({\psi :{\mathcal {F}}\rightarrow {\mathcal {F}}}\) be an S-morphism of families so that \(\psi (t) = \mathsf {id}_{{\mathcal {F}}(t)}\) for a point \(t \in S\). Assume that \({\mathsf {H}}^{0}({\mathcal {F}}(t);\Theta _{{\mathcal {F}}(t)}) = {\{}{\}}0\). Then there exists an open subspace \(W \subseteq S\) such that \(t \in W\) and \(\psi _W = \mathsf {id}_{{\mathcal {F}}_W} :{\mathcal {F}}_W \rightarrow {\mathcal {F}}_W\).
Proof
See Looijenga and Peters [22, p. 170]. \(\square \)
Corollary 6.2
Let \({\mathcal {F}}_1\) and \({\mathcal {F}}_2\) be two families of compact complex manifolds and \(\phi ,\phi ' :{\mathcal {F}}_2 \rightarrow {\mathcal {F}}_1\) be two morphisms of families over the same base map \(h :D_2 \rightarrow D_1\). Assume that \({\mathsf {H}}^{0}({\mathcal {F}}_2(s);\Theta _{{\mathcal {F}}_2(s)}) = {\{}{\}}0\) for all \(s \in D_2\). Then the set

is open in \(D_2\). Moreover, the morphisms \(\phi \) and \(\phi '\) restrict to the same morphism of families \(({\mathcal {F}}_2)_W \rightarrow {\mathcal {F}}_1\).
Proof
We know that a pullback \(\eta :h^*({\mathcal {F}}_1) \rightarrow {\mathcal {F}}_1\) of the family of compact complex manifolds \({\mathcal {F}}_1\) by h exists; see Sect. 2.2. Thus \(\phi \) and \(\phi '\) factorize uniquely as \(\phi = \eta \circ {\bar{\phi }}\) and \(\phi ' = \eta \circ {\bar{\phi }}'\), respectively, where \({\bar{\phi }}\) and \({\bar{\phi }}'\) are \(D_2\)-isomorphisms. Define \(\psi :={\bar{\phi }}^{-1} \circ {\bar{\phi }}'\). Then \(\psi \) is a \(D_2\)-automorphism of \({\mathcal {F}}_2\) and W is precisely the set of points \(s \in D_2\) for which \(\psi \) induces the identity on the fiber over s. Applying Theorem 6.1, we see that W is an open subset of \(D_2\) and \(\psi _W :({\mathcal {F}}_2)_W \rightarrow ({\mathcal {F}}_2)_W\) is the identity. The latter implies that \({\bar{\phi }}_W = {{\bar{\phi }}'}_W\), which subsequently implies that \(\phi \) and \(\phi '\) restrict to the same morphism \(({\mathcal {F}}_2)_W \rightarrow {\mathcal {F}}_1\). \(\square \)
The goal of Sect. 6 is to generalize Sect. 6.1 to situations where not a single compact complex manifold X is given but a family of compact complex manifolds \({\mathcal {F}}\) over an arbitrary base space S. Precisely we prove the following; when \(S = \mathsf {pt}\), we recover the well-known facts of Sect. 6.1.
Theorem 6.3
Let \({\mathcal {F}}\), \({\mathcal {F}}_1\), and \({\mathcal {F}}_2\) be families of compact complex manifolds over S, \(D_1\), and \(D_2\), respectively, and \(\iota _k :{\mathcal {F}}\rightarrow {\mathcal {F}}_k\) be a morphism of families over \(b_k\) for \(k \in {\{}{\}}{1,2}\). Assume that \({\mathsf {H}}^{0}({\mathcal {F}}(s);\Theta _{{\mathcal {F}}(s)})={\{}{\}}0\) and that \({\mathcal {F}}_1\) is semi-universal at \(b_1(s)\) for all \(s \in S\). Moreover assume that \(b_2 :S\rightarrow D_2\) is an embedding into a second-countable space \(D_2\). Then:
-
(i)
There exists an open subspace W of \(D_2\) together with a morphism of families \(\phi :({\mathcal {F}}_2)_W \rightarrow {\mathcal {F}}_1\) such that \(b_2(S) \subseteq W\) and \(\iota _1 = \phi \circ \iota _2\).
-
(ii)
When \(W'\) is another open subspace of \(D_2\) and \(\phi ' :({\mathcal {F}}_2)_{W'} \rightarrow {\mathcal {F}}_1\) is a morphism of families such that \(b_2(S) \subseteq W'\) and \(\iota _1 = \phi '\circ \iota _2\), then \(\phi \) and \(\phi '\) agree on an open subspace \(W''\) of \(W\cap W'\) with \(b_2(S) \subseteq W''\).
6.2 Strategy of the proof
The idea of the proof of Theorem 6.3 is straightforward. Pick a point \(s \in S\). Then we dispose of biholomorphisms \(\iota _k(s) :{\mathcal {F}}(s) \rightarrow {\mathcal {F}}_k(b_k(s))\) for \(k \in {\{}{\}}{1,2}\) and hence of a biholomorphism
Exploiting the completeness of the family \({\mathcal {F}}_1\) at \(b_1(s)\), we obtain a morphism of families \(\psi :({\mathcal {F}}_2)_U \rightarrow {\mathcal {F}}_1\) defined on an open neighborhood U of \(b_2(s)\) in \(D_2\) which induces the isomorphism of equation 6.2.1. Furthermore, exploiting the universality of the family \({\mathcal {F}}_1\) at \(b_1(s)\) in conjunction with Corollary 6.2, we see that \(\iota _1 = \psi \circ \iota _2\) holds on an open neighborhood of s in \(b_2^{-1}(U) \subseteq S\). Thus locally at the point \(b_2(s)\) we have achieved what we wanted. If we are able to glue the pairs \((U,\psi )\) over an open neighborhood W of \(b_2(S)\) in \(D_2\), we are done.
Unfortunately though there is a catch in the gluing: Given two pairs \((U,\psi )\) and \((U',\psi ')\) as in the previous paragraph, the morphisms \(\psi \) and \(\psi '\) need not agree on the overlap \(U\cap U'\). As a matter of fact, the universality of the family \({\mathcal {F}}_1\) and Corollary 6.2 imply only that \(\psi \) and \(\psi '\) agree on an open subset V of \(U\cap U'\) containing all points \(b_2(s)\) with \(s \in b_2^{-1}(U\cap U')\). If \(V \ne U\cap U'\), then \(\psi \) and \(\psi '\) will simply not glue to a morphism \(({\mathcal {F}}_2)_{U\cup U'} \rightarrow {\mathcal {F}}_1\).
The following lemma shows a way out of this predicament. The trick is to first pass from the open cover \({\{}{\}}{U,U'}\) of \(U\cup U'\) to a suitably refined open cover—namely, to a so-called shrinking of \({\{}{\}}{U,U'}\). The restrictions of \(\psi \) and \(\psi '\) to the refined open cover will then glue over an open set that contains all points of \(b_2(S) \cap (U\cup U')\), which suffices for our purposes. Lemma 6.4 is inspired by an argument of Kashiwara’s and Schapira’s [17, p. 102–103].
Lemma 6.4
Let X be a topological space, \((U_i)_{i\in I}\) and \((V_i)_{i\in I}\) be indexed open covers of X, \({\mathscr {F}}\) be a sheaf of sets on X, and \((s_i)_{i \in I}\) be an indexed family of sections \(s_i \in {\mathscr {F}}(U_i)\). Assume that the family of closed subsets \((\overline{V_i})_{i\in I}\) of X is locally finite and satisfies \(\overline{V_i} \subseteq U_{i}\) for all \(i \in I\). Define

where \([\,\cdot \,]_x\) refers to taking the germ at x in the sheaf \({\mathscr {F}}\). Then there exists an open subset W of X together with a section \(t \in {\mathscr {F}}(W)\) such that \(A\subseteq W\) and
for all \(i \in I\).
Proof
For every point \(x \in X\) define  . Further define
. Further define

We contend that W is an open subset of X with \(A \subseteq W\). Indeed, take \(x \in A\). Then \(x \in X\). For all \(i,j \in I(x)\) we have that \(x \in \overline{V_i} \cap \overline{V_j}\), whence \(x \in U_{i}\cap U_{j}\) so that \([s_{i}]_x = [s_{j}]_x\) by the definition of A. This implies that \(x \in W\).
Now fix a point \(x \in W\). Since \((\overline{V_i})_{i\in I}\) is a locally finite indexed family of subsets of X, there exists an open subset \(N\subseteq X\) containing x such that the set  is finite. Note that \(I(y) \subseteq J\) for all \(y \in N\); in particular I(x) is finite. Therefore—use induction on the cardinality of I(x)—there exists an open neighborhood \(U' \subseteq \bigcap _{i \in I(x)}U_{i}\) of x such that \(\left. {s_{i}}\right| _{U'} = \left. {s_{j}}\right| _{U'}\) for all \(i,j \in I(x)\). Defining \(M :=N \setminus \bigcup _{j \in J\setminus I(x)}\overline{V_j}\), we observe that M is an open subset of X with \(x \in M\). Moreover for every \(y \in M\) we have that \(I(y) \subseteq I(x)\). Thus, \(M \cap U'\) is an open neighborhood of x in X such that \([s_{i}]_y = [s_{j}]_y\) for all \(y \in M\cap U'\) and all \(i,j \in I(y)\). In consequence \(M\cap U' \subseteq W\), and since \(x \in W\) was arbitrary, we see that W is an open subset of X as claimed.
is finite. Note that \(I(y) \subseteq J\) for all \(y \in N\); in particular I(x) is finite. Therefore—use induction on the cardinality of I(x)—there exists an open neighborhood \(U' \subseteq \bigcap _{i \in I(x)}U_{i}\) of x such that \(\left. {s_{i}}\right| _{U'} = \left. {s_{j}}\right| _{U'}\) for all \(i,j \in I(x)\). Defining \(M :=N \setminus \bigcup _{j \in J\setminus I(x)}\overline{V_j}\), we observe that M is an open subset of X with \(x \in M\). Moreover for every \(y \in M\) we have that \(I(y) \subseteq I(x)\). Thus, \(M \cap U'\) is an open neighborhood of x in X such that \([s_{i}]_y = [s_{j}]_y\) for all \(y \in M\cap U'\) and all \(i,j \in I(y)\). In consequence \(M\cap U' \subseteq W\), and since \(x \in W\) was arbitrary, we see that W is an open subset of X as claimed.
Since \((V_i)_{i \in I}\) is an open cover of X, it is clear that \((W_i)_{i\in I}\) with \(W_i = W\cap V_i\) is an open cover of W. Define the indexed family \((t_i)_{i\in I}\) by \(t_i = \left. {s_{i}}\right| _{W_i}\). Let \(i,j \in I\) be arbitrary indices and let \(y \in W_i\cap W_j\) be a point. Then \(y \in \overline{V_i}\) and \(y \in \overline{V_j}\) so that \(i,j \in I(y)\). Moreover, \(y\in W\) so that \([s_{i}]_y = [s_{j}]_y\) by the definition of W. Since \([t_i]_y = [s_{i}]_y\), and likewise for j, we obtain that \([t_i]_y = [t_j]_y\). Given that \({\mathscr {F}}\) is a sheaf of sets on X, it satisfies the locality sheaf axiom and we deduce that \(\left. {t_i}\right| _{W_i\cap W_j} = \left. {t_j}\right| _{W_i\cap W_j}\). Employing the gluing sheaf axiom for \({\mathscr {F}}\), this implies the existence of a section \(t \in {\mathscr {F}}(W)\) such that \(\left. {t}\right| _{W_i} = t_i=\left. {s_i}\right| _{W_i}\) for all \(i \in I\). \(\square \)
6.3 Proof of Theorem 6.3
We proceed in steps, following the strategy mapped out in Sect. 6.2.
6.3.1 Preparations
We define a presheaf of sets \({\mathscr {H}}\) on \(D_2\) by means of the following rules: \({\mathscr {H}}(U)\) is, for every open subset U of \(D_2\), the set of morphisms of families from \(({\mathcal {F}}_2)_U\) to \({\mathcal {F}}_1\)—that is,

For every two open subsets U and V of \(D_2\) with \(V\subseteq U\) the restriction map \(\rho ^U_V:{\mathscr {H}}(U) \rightarrow {\mathscr {H}}(V)\) of \({\mathscr {H}}\) satisfies \(\rho ^{U}_{V}(\phi ) = \left. {\phi }\right| _{V} = \phi \circ \eta \) where \(\eta :({\mathcal {F}}_2)_{V} \rightarrow ({\mathcal {F}}_2)_U\) denotes the canonical injection of families. Observe that \({\mathscr {H}}\) is not only a presheaf of sets on \(D_2\) but a sheaf of sets on \(D_2\).
We define I to be the set of all pairs \((U,\psi )\) where U is an open subset of \(D_2\) and \(\psi \in {\mathscr {H}}(U)\) is an element such that \(\iota _{1,U} = \psi \circ \iota _{2,U}\) where
denote the morphisms of families induced by \(\iota _1\) and \(\iota _2\), respectively. The notation \(\iota _{1,U}\) must not be confused with the notation \((\iota _1)_U\) of Sect. 2.3.
By the semicontinuity theorem [28], since the family of compact complex manifolds \({\mathcal {F}}_2\) is given by a proper holomorphic submersion, the function
is upper semicontinuous. Thus according to the assumptions in Theorem 6.3 there exists an open neighborhood N of \(b_2(S)\) in \(D_2\) such that \(d_0(y) = 0\) for all \(y \in N\). Without loss of generality we assume that \(N = D_2\).
6.3.2 Proof of the uniqueness
Let \((U,\psi )\) and \((U',\psi ')\) be two elements of I. Then \(\iota _{1,U} = \psi \circ \iota _{2,U}\) and likewise \(\iota _{1,U'} = \psi ' \circ \iota _{2,U'}\). Let \(s \in b_2^{-1}(U\cap U')\) be an arbitrary point. Then
Moreover, by Sect. 6.1 and the assumptions of Theorem 6.3, the family \({\mathcal {F}}_1\) is universal at the point \(b_1(s)\). Therefore, when \(\psi \) and \(\psi '\) are morphisms of families over h and \(h'\), respectively, we see that h and \(h'\) agree on an open neighborhood of \(b_2(s)\) in \(U\cap U'\). Since s was arbitrary, we deduce the existence of an open subset \(V \subseteq U\cap U'\) such that \(\left. {h}\right| _{V} = \left. {h'}\right| _{V}\) and \(b_2(b_2^{-1}(U\cap U')) \subseteq V\). Now applying Corollary 6.2 to the restrictions \(\left. {\psi }\right| _{V}\) and \(\left. {\psi '}\right| _{V}\), we deduce the existence of an open subset W of V such that \(b_2(b_2^{-1}(U\cap U')) \subseteq W\) and \(\left. {\psi }\right| _{W} = \left. {\psi '}\right| _{W}\).
When \(b_2(S) \subseteq U\) and \(b_2(S) \subseteq U'\), then \(b_2^{-1}(U\cap U') = S\) so that \(b_2(S) \subseteq W\). Thus the preceding argument proves item (ii) of Theorem 6.3.
6.3.3 Existence at points
Let \(s \in S\) be an arbitrary point. We contend the existence of a pair \((V,\phi ) \in I\) such that \(b_2(s) \in V\).
Indeed, since the family \({\mathcal {F}}_1\) is complete at \(b_1(s)\), there exists an open subset U of \(D_2\) containing \(b_2(s)\) as well as a morphism of families \(\psi :({\mathcal {F}}_2)_U \rightarrow {\mathcal {F}}_1\) so that
Applying Corollary 6.2 in conjunction with the fact that \({\mathcal {F}}_1\) is universal at \(b_1(s)\), we see there exists an open subset \(T \subseteq b_2^{-1}(U)\) such that \(s \in T\) and
As the holomorphic map \(b_2 :S\rightarrow D_2\) is an embedding by assumption, \(b_2\) induces a homeomorphism between S and the subspace \(b_2(S)\) of \(D_2\). This implies that \(T = b_2^{-1}(V)\) for an open subset V of U. Hence \(\iota _{1,V} = \phi \circ \iota _{2,V}\) where \(\phi :=\left. {\psi }\right| _{V}\), which proves our claim.
6.3.4 Gluing and global existence
Define \((U_i)_{i\in I}\) and \((\psi _i)_{i\in I}\) to be the indexed families given by the assignments \((U,\psi ) \mapsto U\) and \((U,\psi ) \mapsto \psi \), respectively, and define the open subspace \(Y:=\bigcup _{i\in I} U_i\subseteq D_2\). Then \((U_i)_{i\in I}\) is an indexed open cover of Y. Being a second-countable complex space, Y is regular and Lindelöf, whence paracompact [16, Theorem 41.5]. Thus there exists a locally finite indexed open cover \((V_i)_{i\in I}\) of Y such that \(\overline{V_i} \subseteq U_i\) for all \(i \in I\), where the closure is taken in Y [16, Lemma 41.6].
By Sect. 6.3.3 we know that \(b_2(S) \subseteq Y\). Let \(s \in S\) be an arbitrary point and \(i,j \in I\) be elements such that \(b_2(s) \in U_i\cap U_j\). Then according to Sect. 6.3.2 there exists an open subset \(U' \subseteq U_i\cap U_j\) such that \(b_2(s) \in U'\) and \(\left. {\psi _i}\right| _{U'} = \left. {\psi _j}\right| _{U'}\). In other words, the germs of \((U_i,\psi _i)\) and \((U_j,\psi _j)\) at \(b_2(s)\) in the sheaf \({\mathscr {H}}\), equivalently in the sheaf \(\left. {{\mathscr {H}}}\right| _{Y}\), agree. Therefore Lemma 6.4 implies the existence of an open subset \(W \subseteq Y\) and an element \(\phi \in {\mathscr {H}}(W)\) such that \(b_2(S) \subseteq W\) and
for all \(i \in I\).
6.3.5 Conclusion
We contend that \(\iota _1 = \phi \circ \iota _{2,W}\), which proves item (i) of Theorem 6.3 and is actually equivalent to saying that \((W,\phi ) \in I\). We note that \({\iota _{1,U_i} = \psi _i \circ \iota _{2,U_i}}\) for all \(i \in I\). Thus
for all \(i\in I\). In addition, since \(b_2(S) \subseteq W\), since \((V_i)_{i\in I}\) is an indexed open cover of Y, and since \(W\subseteq Y\), we see that
and our claim follows. \(\square \)
Remark 6.5
Let \(({\mathcal {F}}',\mu ')\) be a \(\Lambda \)-marked family of ihs manifolds over \(S'\) and \(s\in S'\) a point. Then \({\mathcal {F}}'\) is semi-universal at s if and only if the period map \(p' :S' \rightarrow {\mathsf {D}}_{\Lambda }\) of \(({\mathcal {F}}',\mu ')\) is a local biholomorphism at s.
Proof
By Remark 2.4 there exists a semi-universal deformation \(({\mathcal {X}},(i,j))\) of the fiber \({\mathcal {F}}'(s)\) where \({\mathcal {X}}\) is a family of ihs manifolds over a simply connected complex manifold S. Thus there is an open subspace \(U \subseteq S'\) and a morphism of families \((g,h) :{\mathcal {F}}'_U \rightarrow {\mathcal {X}}\) such that \(s \in U\) and \(h(s) = j(0)\). The marking \(\mu '_s\) of \({\mathcal {F}}'(s)\) induces via g a \(\Lambda \)-marking on \({\mathcal {X}}(h(s))\), which extends to a \(\Lambda \)-marking \(\mu \) of \({\mathcal {X}}\) by Remark 3.4. Then, by Remark 2.1, there exists a unique \(\Lambda \)-marking \(\nu \) of \({\mathcal {F}}'_U\) making \((g,h):({\mathcal {F}}'_U,\nu )\rightarrow ({\mathcal {X}},\mu )\) a morphism of \(\Lambda \)-marked families. As \(\nu _s=\mu '_s\) by construction, \(\nu \) and \(\mu '\) have to coincide at least in an open neighborhood of s. Hence, by shrinking U around s, we can assume that \((g,h) :({\mathcal {F}}',\mu ')_U \rightarrow ({\mathcal {X}},\mu )\) is a morphism of \(\Lambda \)-marked families. As a consequence, if \(p :S \rightarrow {\mathsf {D}}_{\Lambda }\) denotes the period map of \(({\mathcal {X}},\mu )\), we know that \(\left. {p'}\right| _{U} = p \circ h\) by Remark 2.3.
By Remark 2.4 we see that p is a local biholomorphism at j(0). Therefore \(p'\) is a local biholomorphism at s if and only if \(h :U \rightarrow S\) is a local biholomorphism at s. The latter is clearly equivalent to \({\mathcal {F}}'\) being semi-universal at s. \(\square \)
Remark 6.5 allows for a marked family version of Theorem 6.3 which we need in Sect. 7. We formulate only the existence part—that is, item (i)—as the uniqueness part would only be weaker than that of Theorem 6.3.
Corollary 6.6
Let \(\Lambda \) be a lattice, \({\mathcal {F}}\), \({\mathcal {F}}_1\), and \({\mathcal {F}}_2\) be \(\Lambda \)-marked families of ihs manifolds over S, \(D_1\), and \(D_2\), respectively, and \(\iota _k :{\mathcal {F}}\rightarrow {\mathcal {F}}_k\) be morphisms of \(\Lambda \)-marked families over \(b_k\) for \(k \in {\{}{\}}{1,2}\). Assume that the period map of \({\mathcal {F}}_1\) is a local biholomorphism \(D_1 \rightarrow {\mathsf {D}}_{\Lambda }\) and that \(b_2 :S\rightarrow D_2\) is an embedding into a second-countable space \(D_2\). Then there exists an open subset \(W \subseteq D_2\) as well as a morphism of \(\Lambda \)-marked families \(\phi :({\mathcal {F}}_2)_W \rightarrow {\mathcal {F}}_1\) such that \(b_2(S) \subseteq W\) and \(\iota _1 = \phi \circ \iota _2\).
Proof
Denote by \({\mathcal {F}}'\), \({\mathcal {F}}_1'\), and \({\mathcal {F}}_2'\) the families underlying the marked families \({\mathcal {F}}\), \({\mathcal {F}}_1\), and \({\mathcal {F}}_2\), respectively. Since the period map of \({\mathcal {F}}_1\) is a local biholomorphism, the family of compact complex manifolds \({\mathcal {F}}_1'\) is semi-universal at every point \(y \in D_1\) by Remark 6.5. Thus Theorem 6.3 implies the existence of an open subset \({\widetilde{W}} \subseteq D_2\) and a morphism of families \({\widetilde{\phi }} :({\mathcal {F}}_2')_{{{\widetilde{W}}}} \rightarrow {\mathcal {F}}_1'\) such that \(\iota _1 = {\widetilde{\phi }} \circ \iota _2\).
By Remark 2.1 we know there exists a unique marking \(\nu \) of the family of ihs manifolds \(({\mathcal {F}}_2')_{{{\widetilde{W}}}}\) for which \(\widetilde{\phi }\) becomes a morphism of marked families between \((({\mathcal {F}}_2')_{{{\widetilde{W}}}},\nu )\) and \({\mathcal {F}}_1\). Since \(\iota _1 = {\widetilde{\phi }} \circ \iota _2\) and since \(\iota _k :{\mathcal {F}}\rightarrow {\mathcal {F}}_k\) are morphisms of marked families for \(k \in {\{}{\}}{1,2}\), we see that \(\nu \) and the marking of \({\mathcal {F}}_2\) induce the same marking on the fiber \({\mathcal {F}}_2'(b_2(s))\) for all \(s \in S\). Define W to be the union of all connected components C of \({{\widetilde{W}}}\) for which there exists a point in \(b_2(S) \cap C\). Then W is open in \(D_2\), we know that \(b_2(S) \subseteq W\), and by Remark 6.7 the restriction \(\phi :=\left. {\widetilde{\phi }}\right| _{W} :({\mathcal {F}}_2)_W \rightarrow {\mathcal {F}}_1\) is a morphism of marked families with \(\iota _1 = \phi \circ \iota _2\). \(\square \)
Remark 6.7
Let \(\Lambda \) be a lattice, \({\mathcal {F}}\) be a family of ihs manifolds over a connected space S, and \(\mu \) and \(\nu \) be two \(\Lambda \)-markings of \({\mathcal {F}}\). Let \(s \in S\) be a point and assume that \(\mu \) and \(\nu \) induce the same marking
on the fiber \({\mathcal {F}}(s)\) in the sense of Sect. 2.5. Then \(\mu = \nu \).
Indeed, writing \({\mathcal {F}}= (X,S,f)\), the sheaf of abelian groups \({\mathsf {R}}^{2}f_*{\underline{{\mathbb {Z}}}_{X}}\) is constant, for it is isomorphic to \(\underline{\Lambda }_{S}\) by virtue of \(\mu \) (or \(\nu \)). Thus, as the space S is connected, the canonical map
from global sections to the stalk at s is bijective. In consequence the global section components of the morphisms of sheaves \(\mu \) and \(\nu \) coincide. Employing the same argument again, we conclude that \(\mu _t = \nu _t\) for all \(t \in S\), which implies our claim.
7 Proof of the extension theorem
7.1 Setup and structure of the proof
In what follows we prove Theorem 1.2. We assume throughout Sect. 7 that a lattice \(\Lambda \) and a \(\Lambda \)-marked family of ihs manifolds \({\mathcal {F}}\) over a complex space S are given such that the period map \(h :S\rightarrow {\mathsf {D}}_{\Lambda }\) of \({\mathcal {F}}\) is an embedding. In order to simplify the notation, we assume, without loss of generality, that \(S \subseteq {\mathsf {D}}_{\Lambda }\) is a complex subspace and h is the corresponding canonical injection. That way we need not distinguish between the points s and h(s) for \(s \in S\).
The construction of the extension \({\widetilde{{\mathcal {F}}}}\) of the marked family \({\mathcal {F}}\) somewhat parallels the proof of Theorem 6.3, compare Sect. 6.2: first we produce suitable extensions locally at every point of S, then we explain how to glue the local extensions to a global one. The local considerations are dealt with in propositions 7.2 to 7.4. Lemma 7.5 provides a general gluing device for \(\Lambda \)-marked families of ihs manifolds. The final conclusions are drawn in Sect. 7.2.
Definition 7.1
We say that \(({\mathcal {K}},\iota )\) is an admissible extension over U when \(U \subseteq {\mathsf {D}}_{\Lambda }\) is an open subspace, \({\mathcal {K}}\) is \(\Lambda \)-marked family of ihs manifolds whose period map is the canonical injection \(U \hookrightarrow {\mathsf {D}}_{\Lambda }\), and \(\iota :{\mathcal {F}}_{S\cap U} \rightarrow {\mathcal {K}}\) is a morphism of \(\Lambda \)-marked families over the canonical injection \(S\cap U \hookrightarrow U\).
Proposition 7.2
Let \(s \in S\) be a point. Then there exists an admissible extension \(({\mathcal {K}},\iota )\) over U such that \(s \in U\).
Proof
We can write \({\mathcal {F}}= ({\mathcal {Y}},\nu )\). By Remark 2.4 there exists a semi-universal deformation \(({\mathcal {X}},(i,j))\) of the fiber \({\mathcal {Y}}(s)\) such that \({\mathcal {X}}\) is a family of ihs manifolds over a simply connected complex manifold U. Due to the universality we obtain a morphism of families \((a,b) :{\mathcal {Y}}_V \rightarrow {\mathcal {X}}\) such that \(V \subseteq S\) is an open subspace with \(s \in V\) and \(b(s) = j(0)\). Just like in the proof of Remark 6.5 we can assume that \((a,b) :{\mathcal {F}}_V \rightarrow ({\mathcal {X}},\mu )\) is a morphism of \(\Lambda \)-marked families for a \(\Lambda \)-marking \(\mu \) of \({\mathcal {X}}\). Since the period map \(g :U \rightarrow {\mathsf {D}}_{\Lambda }\) of \(({\mathcal {X}},\mu )\) is a local biholomorphism at j(0), we can further assume that \(U \subseteq {\mathsf {D}}_{\Lambda }\) is an open subspace and g is the associated canonical injection. Now Remark 2.3 tells us that \(\left. {h}\right| _{V} = g \circ b\). Recalling from above that \(h :S \hookrightarrow {\mathsf {D}}_{\Lambda }\) is the canonical injection of a complex subspace, we conclude that \(b :V \hookrightarrow U\) is the canonical injection of a complex subspace, too. Finally we can replace U by a smaller open subspace of \({\mathsf {D}}_{\Lambda }\) so that \(V = S \cap U\). Hence \((({\mathcal {X}},\mu ),(a,b))\) is an admissible extension over U. \(\square \)
When \((U_i)_{i \in I}\) is an indexed family of open subsets of a given topological space and \(i,j,k \in I\) are indices, we emloy the standard notation \(U_{ij} :=U_i\cap U_j\) and \(U_{ijk} :=U_i\cap U_j\cap U_k\) for a double and a triple intersection, respectively.
Proposition 7.3
Let \(({\mathcal {K}}_1,\iota _1)\) and \(({\mathcal {K}}_2,\iota _2)\) be admissible extensions over \(U_1\) and \(U_2\), respectively. Then there exists an open subspace \(W \subseteq V :=U_{12}\) together with a W-morphism of \(\Lambda \)-marked families
such that \(S \cap V \subseteq W\) and \(\phi \circ {\bar{\iota }}_2 = {\bar{\iota }}_1\), where \({\bar{\iota }}_k :{\mathcal {F}}_{S\cap V} \rightarrow ({\mathcal {K}}_k)_W\) denotes the morphism induced by \(\iota _k\).
Proof
We apply Corollary 6.6 to the \(\Lambda \)-marked families \({\mathcal {F}}_{S\cap V}\), \(({\mathcal {K}}_1)_{V}\), and \(({\mathcal {K}}_2)_{V}\) and the morphisms of \(\Lambda \)-marked families \({\bar{\iota }}_k :{\mathcal {F}}_{S\cap V} \rightarrow ({\mathcal {K}}_k)_{V}\) induced by \(\iota _k\) for \(k \in {\{}{\}}{1,2}\). The assumptions of Corollary 6.6 are clearly fulfilled, so we obtain an open subspace \(W\subseteq V\) and a morphism of \(\Lambda \)-marked families \(\phi ' :({\mathcal {K}}_2)_W \rightarrow ({\mathcal {K}}_1)_{V}\) with \(S\cap V\subseteq W\) and \({\bar{\iota }}_1 = \phi ' \circ {\bar{\iota }}_2\). As the period maps of \(({\mathcal {K}}_1)_W\) and \(({\mathcal {K}}_2)_{V}\) are the canonical injections \(W \hookrightarrow {\mathsf {D}}_{\Lambda }\) and \(V \hookrightarrow {\mathsf {D}}_{\Lambda }\), respectively, Remark 2.3 implies that \(\phi '\) is a morphism over the canonical injection \(W \hookrightarrow V\). Thus \(\phi '\) induces the desired morphism of marked families \(\phi \). \(\square \)
Proposition 7.4
For \(k \in {\{}{\}}{1,2,3}\) let \(({\mathcal {K}}_k,\iota _k)\) be an admissible extension over \(U_k\). Moreover, for \(i,j \in {\{}{\}}{1,2,3}\) with \(i<j\), let \(W_{ij} \subseteq U_{ij}\) be an open subspace and
be a \(W_{ij}\)-morphism of \(\Lambda \)-marked families such that \(S \cap U_{ij} \subseteq W_{ij}\) and \({{\bar{\iota }}_i = \phi _{ij} \circ {\bar{\iota }}_j}\) for the induced morphisms. Then \({W:=W_{12} \cap W_{13} \cap W_{23}}\) contains an open subspace Z such that
and \(S \cap U_{123} \subseteq Z\).
Proof
For \(k \in {\{}{\}}{1,2,3}\) let \({\bar{\iota }}_k :{\mathcal {F}}_{S\cap W} \rightarrow ({\mathcal {K}}_k)_W\) denote the morphism of \(\Lambda \)-marked families that is induced by \(\iota _k\). Then by assumption
Thus the claim follows immediately from item (ii) of Theorem 6.3 if we notice that \(S\cap U_{123} \subseteq S\cap W\); in fact, the latter two sets are equal. \(\square \)
Lemma 7.5
Let D be a complex space and \(({\mathcal {F}}_i)_{i\in I}\) be an indexed family such that \({\mathcal {F}}_i\) is a \(\Lambda \)-marked family of ihs manifolds over an open subspace \(U_i \subseteq D\) for every \(i \in I\). Moreover let \((\phi _{ij})_{i,j \in I}\) be an indexed family such that, for all \(i,j,k \in I\), firstly,
is a \(U_{ij}\)-morphism of \(\Lambda \)-marked families and, secondly,
Then there exists a \(\Lambda \)-marked family of ihs manifolds \({\widetilde{{\mathcal {F}}}}\) over the open subspace \({{\widetilde{U}}} :=\bigcup _{i \in I}U_i\) of D together with an indexed family \((\eta _i)_{i \in I}\) such that, for all \(i,j \in I\),
is a \(U_i\)-morphism of \(\Lambda \)-marked families and
Proof
Let us write \({\mathcal {F}}_i\) as \((X_i,U_i,f_i,\mu _i)\) and \(\phi _{ij}\) as \((g_{ij},\mathsf {id}_{U_{ij}})\) for all \(i,j \in I\). Then the quadruple
is Hausdorff gluing data for a complex space in the sense of Fischer [7, 0.24]. Thus we obtain a complex space \({{\widetilde{X}}}\) together with an indexed family \((a_i)_{i \in I}\) such that \(a_i :X_i \rightarrow {{\widetilde{X}}}\) is an open embedding and
for all \(i,j \in I\). Since for all \(i,j \in I\)
there exists a unique holomorphic map \({{\widetilde{f}}} :{{\widetilde{X}}} \rightarrow {{\widetilde{U}}}\) such that \({{\widetilde{f}}} \circ a_i = b_i \circ f_i\) for all \(i \in I\) where \(b_i :U_i \rightarrow {{\widetilde{U}}}\) denotes the canonical injection. Therefore the triple \(({{\widetilde{X}}},{{\widetilde{U}}},{{\widetilde{f}}})\) is a family of ihs manifolds and, for all \(i \in I\), the pair \((a_i,b_i)\) is a morphism of families between \((X_i,U_i,f_i)\) and \(({{\widetilde{X}}},{{\widetilde{U}}},{{\widetilde{f}}})\).
Defining \(({{\widetilde{X}}}_i,U_i,{{\widetilde{f}}}_i) :=({{\widetilde{X}}},{{\widetilde{U}}},{{\widetilde{f}}})_{U_i}\) for \(i \in I\), there exists a unique morphism of sheaves of abelian groups
such that \((a_i,b_i)\) induces a \(U_i\)-morphism of \(\Lambda \)-marked families of ihs manifolds
We regard \({\widetilde{\mu }}_i\) as a morphism of sheaves of abelian groups
and notice that \(\left. {{\widetilde{\mu }}_i}\right| _{U_{ij}} = \left. {{\widetilde{\mu }}_j}\right| _{U_{ij}}\) for all \(i,j \in I\) since \(\phi _{ij}\) is a morphism of \(\Lambda \)-marked families. Hence there exists a unique morphism of sheaves of abelian groups
such that \(\left. {{\widetilde{\mu }}}\right| _{U_i} = {\widetilde{\mu }}_i\) for all \(i \in I\). As a consequence \({\widetilde{{\mathcal {F}}}} :=({{\widetilde{X}}},{{\widetilde{U}}},{{\widetilde{f}}},{\widetilde{\mu }})\) is a \(\Lambda \)-marked family of ihs manifolds with the property that \(\eta _i :{\mathcal {F}}_i \rightarrow {\widetilde{{\mathcal {F}}}}_{U_i}\) is a \(U_i\)-morphism of \(\Lambda \)-marked families for every \(i \in I\). \(\square \)
7.2 Proof of Theorem 1.2
We proceed in three steps.
7.2.1 Local extensions
From Proposition 7.2 we deduce the existence of indexed families \((U_i)_{i\in I}\) and \({(}{)}*{({\mathcal {K}}_i,\iota _i)}_{i\in I}\) such that, firstly, \(({\mathcal {K}}_i,\iota _i)\) is an admissible extension over \(U_i\) for all \(i \in I\) and, secondly, S is contained in the open subspace \(D :=\bigcup _{i\in I}U_i\) of \({\mathsf {D}}_{\Lambda }\). In fact we can take I equal to the set of points of S and stipulate that \(s \in U_s\) for all \(s \in S\). Employing Proposition 7.3 we deduce the existence of an indexed family \(((W_{ij},\phi _{ij}))_{i,j \in I}\) such that \(W_{ij} \subseteq U_{ij}\) is an open subspace with \(S\cap U_{ij} \subseteq W_{ij}\) and
is a \(W_{ij}\)-morphism of \(\Lambda \)-marked families satisfying \({\bar{\iota }}_i = \phi _{ij} \circ {\bar{\iota }}_j\) for all \(i,j \in I\). Employing Proposition 7.4 we deduce the existence of an indexed family \((Z_{ijk})_{i,j,k \in I}\) such that \(Z_{ijk} \subseteq W_{ij}\cap W_{ik}\cap W_{jk}\) is an open subspace with
and \(S \cap U_{ijk} \subseteq Z_{ijk}\).
7.2.2 Shrinking
Like in Sect. 6.3.4 there exists an indexed open cover \((V_i)_{i\in I}\) of D such that the family \((\overline{V_i})_{i\in I}\) of closed subsets of D is locally finite and satisfies \(\overline{V_i} \subseteq U_i\) for all \(i \in I\). For every \(x\in D\) define  and consider the set
and consider the set

Then in analogy to the proof of Lemma 6.4 we verify that
-
a)
W is open in D,
-
b)
\(S \subseteq W\),
-
c)
\((V_i\cap W)\cap (V_j\cap W) \subseteq W_{ij}\) for all \(i,j \in I\), and
-
d)
\((V_i\cap W)\cap (V_j\cap W)\cap (V_k\cap W) \subseteq Z_{ijk}\) for all \(i,j,k \in I\).
As \((\overline{V_i})_{i\in I}\) is locally finite, the set W is locally the intersection of finitely many of the open subspaces \(W_{ij}\) and \(Z_{ijk}\), which implies item a). Let \(s\in S\) be a point and \(i,j\in I(s)\). Then \(s\in \overline{V_i}\cap \overline{V_j}\subseteq U_{ij}\) and \(s\in S\cap U_{ij}\subseteq W_{ij}\). If moreover \(k\in I(s)\), then \(s\in U_{ijk}\) and \(s\in S\cap U_{ijk}\subseteq Z_{ijk}\). Thus \(s\in W\), which proves item b). If \(x\in V_{ij}\cap W\), then \(i,j\in I(x)\); and if \(x\in V_{ijk}\cap W\), then \(i,j,k\in I(x)\). So item c) and item d) follow immediately from the definition of W.
7.2.3 Gluing
Let the indexed families \((V'_i)_{i\in I}\), \(({\mathcal {F}}_i)_{i\in I}\), and \((\phi '_{ij})_{i,j\in I}\) be given by
respectively. Then applying Lemma 7.5, we obtain a \(\Lambda \)-marked family of ihs manifolds \({\widetilde{{\mathcal {F}}}}\) over the open subspace \(W = \bigcup _{i\in I}V'_i\) of D as well as an indexed family \((\eta _i)_{i\in I}\) of \(V'_i\)-morphisms of \(\Lambda \)-marked families \(\eta _i :{\mathcal {F}}_i \rightarrow {\widetilde{{\mathcal {F}}}}_{V'_i}\) such that
for all \(i,j \in I\).
Writing \({\bar{\iota }}_k :{\mathcal {F}}_{S\cap V'_k} \rightarrow {\mathcal {F}}_k\) for the morphism that is induced by \(\iota _k\), we conclude that the compositions \(\eta _i \circ {\bar{\iota }}_i\) and \(\eta _j \circ {\bar{\iota }}_j\) agree on the intersection \(V'_{ij}\) for all \(i,j \in I\). Hence, as S is contained in the union \(\bigcup _{i\in I}V'_i\), there exists a unique morphism of \(\Lambda \)-marked families \(\eta :{\mathcal {F}}\rightarrow {\widetilde{{\mathcal {F}}}}\) over \(h :S\hookrightarrow W \subseteq {\mathsf {D}}_{\Lambda }\) such that \(\eta \) induces \(\eta _i \circ {\bar{\iota }}_i\) on \(V'_i\) for all \(i \in I\). Last but not least, the period map of \({\widetilde{{\mathcal {F}}}}\) is the canonical injection \(W\hookrightarrow {\mathsf {D}}_{\Lambda }\) simply because, for all \(i \in I\), the period map of \({\mathcal {F}}_i\) is the canonical injection \(V'_i \hookrightarrow {\mathsf {D}}_{\Lambda }\). \(\square \)
Notes
At this point it is important that in Sect. 2.4 we have fixed a suitable convention on how to rescale the Beauville–Bogomolov form.
References
Ballico, E.: Normal bundle to curves in quadrics. Bull. Soc. Math. France 109(2), 227–235 (1981)
Bănică, C., Stănăşilă, O.: Algebraic methods in the global theory of complex spaces. Editura Academiei, Bucharest; John Wiley & Sons, London-New York-Sydney, 1976. Translated from the Romanian
Barth, W., Peters, C., Van de Ven, A.: Compact complex surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 4. Springer-Verlag, Berlin (1984)
Beauville, A.: Variétés Kähleriennes dont la première classe de Chern est nulle. J. Differ. Geom. 18(4), 755–782 (1984). (1983)
Catanese, F.: Moduli of algebraic surfaces. In Theory of moduli (Montecatini Terme, 1985), volume 1337 of Lecture Notes in Math., pages 1–83. Springer, Berlin, (1988)
Douady, A.: Le problème des modules pour les sous-espaces analytiques compacts d’un espace analytique donné. Ann. Inst. Fourier (Grenoble) 16(fasc. 1), 1–95 (1966)
Fischer, G.: Complex analytic geometry. Lecture Notes in Mathematics, vol. 538. Springer-Verlag, Berlin-New York (1976)
Grauert, H.: Ein Theorem der analytischen Garbentheorie und die Modulräume komplexer Strukturen. Inst. Hautes Études Sci. Publ. Math. (5), 64 (1960)
Griffiths, P.A.: Periods of integrals on algebraic manifolds. II. Local study of the period mapping. Am. J. Math. 90, 805–865 (1968)
Grothendieck, A.: Techniques de construction en géométrie analytique. v. fibrés vectoriels, fibrés projectifs, fibrés en drapeaux. In: Séminaire Henri Cartan, Volume 13 (1960–1961) no. 1, volume 13 of Séminaire Henri Cartan, pp. 1–15. Soc. Math. France, Paris (1961)
Harris, J., Morrison, I.: Moduli of curves. Graduate Texts in Mathematics, vol. 187. Springer-Verlag, New York (1998)
Heier, G.: The complex geometry of the period domain of K\(3\) surfaces. Unpublished thesis, (1999)
Hitchin, N.J., Karlhede, A., Lindström, U., Roček, M.: Hyper-Kähler metrics and supersymmetry. Commun. Math. Phys. 108(4), 535–589 (1987)
Huybrechts, D.: A global Torelli theorem for hyperkähler manifolds [after M. Verbitsky]. Astérisque, (348):Exp. No. 1040, x, 375–403, (2012). Séminaire Bourbaki: Vol. 2010/2011. Exposés 1027–1042
Huybrechts, D.: Compact hyper-Kähler manifolds: basic results. Invent. Math. 135(1), 63–113 (1999)
James, R.: Munkres. Topology. Prentice Hall Inc, Upper Saddle River, NJ (2000)
Kashiwara, M., Schapira, P.: Sheaves on manifolds, volume 292 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, Berlin, (1994). With a chapter in French by Christian Houzel, Corrected reprint of the 1990 original
Kodaira, K.: On stability of compact submanifolds of complex manifolds. Am. J. Math. 85, 79–94 (1963)
Kodaira, K., Spencer, D.C.: On deformations of complex analytic structures. I, II. Ann. Math. 2(67), 328–466 (1958)
Kodaira, K., Nirenberg, L., Spencer, D.C.: On the existence of deformations of complex analytic structures. Ann. Math. 2(68), 450–459 (1958)
Kuranishi, M.: On the locally complete families of complex analytic structures. Ann. Math. 2(75), 536–577 (1962)
Looijenga, E., Peters, C.: Torelli theorems for Kähler \(K3\) surfaces. Compositio Math., 42(2):145–186, (1980/81)
Markman, E.: On the existence of universal families of marked irreducible holomorphic symplectic manifolds. Kyoto J. Math. 61(1), 207–223 (2021)
Peters, C.A.M., Steenbrink, J.H.M.: Mixed Hodge structures, volume 52 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. In: A Series of Modern Surveys in Mathematics. Springer-Verlag, Berlin (2008)
Ran, Z.: Deformations of maps. In Algebraic curves and projective geometry (Trento, 1988), volume 1389 of Lecture Notes in Math., pages 246–253. Springer, Berlin, (1989)
Ran, Z.: Stability of certain holomorphic maps. J. Differ. Geom. 34(1), 37–47 (1991)
Ran, Z.: Lifting of cohomology and unobstructedness of certain holomorphic maps. Bull. Am. Math. Soc. (N.S.) 26(1), 113–117 (1992)
Riemenschneider, O.: über die Anwendung algebraischer Methoden in der Deformationstheorie komplexer Räume. Math. Ann. 187, 40–55 (1970)
Tian, G.: Smoothness of the universal deformation space of compact Calabi-Yau manifolds and its Petersson-Weil metric. In Mathematical aspects of string theory (San Diego, Calif., 1986), volume 1 of Adv. Ser. Math. Phys., pages 629–646. World Sci. Publishing, Singapore, (1987)
Todorov, A.N.: The Weil–Petersson geometry of the moduli space of \(\text{ SU }(n\ge 3)\) (Calabi-Yau) manifolds. I. Commun. Math. Phys. 126(2), 325–346 (1989)
Topiwala, P.: A new proof of the existence of Kähler-Einstein metrics on \(K3\). I, II. Invent. Math. 89(2):425–448, 449–454 (1987)
Voisin, C.: Théorie de Hodge et géométrie algébrique complexe, volume 10 of Cours Spécialisés [Specialized Courses]. Société Mathématique de France, Paris, (2002)
Wedhorn, T.: Manifolds, sheaves, and cohomology. Springer Studium Mathematik - Master. Springer Spektrum, Wiesbaden (2016)
Acknowledgements
Daniel Greb deserves considerable thanks for he has been fostering our collaboration since day one. We thank Daniel Huybrechts for answering several of our questions in the early stages of the project. Ana-Maria Brecan extends her gratitude to Alan Huckleberry and Hans Franzen for their unceasing support. Tim Kirschner thanks Jun-Muk Hwang for the opportunity to work on this paper at the Korea Institute for Advanced Study. We all thank the anonymous referee for pointing out how Theorem 1.2 is related to Markman’s work.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Tim Kirschner and Martin Schwald are supported by SFB/Transregio 45 of the DFG.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brecan, AM., Kirschner, T. & Schwald, M. Unobstructedness of hyperkähler twistor spaces. Math. Z. 300, 2485–2517 (2022). https://doi.org/10.1007/s00209-021-02841-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02841-4