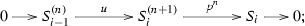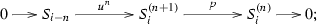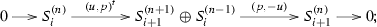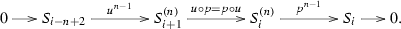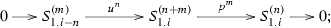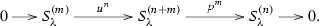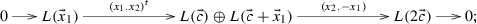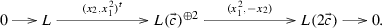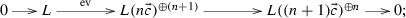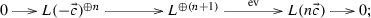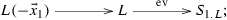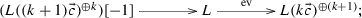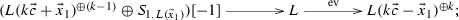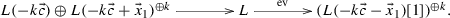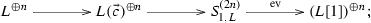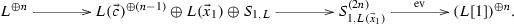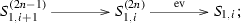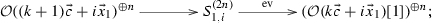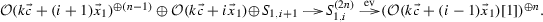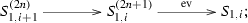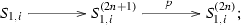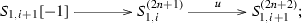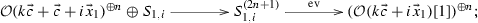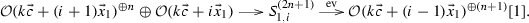t-Stabilities for a weighted projective line

Abstract

The present paper focuses on the study of t-stabilities on a triangulated category in the sense of Gorodentsev, Kuleshov and Rudakov. We give an equivalent description for the finest t-stabilities on certain triangulated category and, describe the semistable subcategories and last HN-triangles for coherent sheaves in $D^b(\mathrm{coh\,}{{\mathbb {X}}})$, which is the bounded derived category of coherent sheaves on the weighted projective line ${{\mathbb {X}}}$ of weight type (2). Furthermore, we show the existence of a t-exceptional triple for $D^b(\mathrm{coh\,}{{\mathbb {X}}})$. As an application, we obtain a result of Dimitrov–Katzarkov which states that each stability condition $\sigma$ in the sense of Bridgeland admits a $\sigma$-exceptional triple for the acyclic triangular quiver Q. This result plays an important role in the proof of Dimitrov–Katzarkov that the space of stability conditions associated to Q is connected and contractible.

Appendices

Appendix A. Exact sequences and last HN-triangles for coherent sheaves

In this appendix we collect some important exact sequences in the category of coherent sheaves over the weighted projective line of weight type (2), and apply them to describe the last HN-triangles for indecomposable coherent sheaves for any finest t-stability. We need to use the knowledge of pullback and pushout frequently, so let us briefly recall their definitions and properties, for more details we refer to [8].

A pullback of the morphisms f and g in an abelian category consists of an object P and two morphisms $p_1 : P \rightarrow X$ and $p_2 : P \rightarrow Y$ for which the following diagram commutes

Moreover, the pullback $(P, p_1, p_2)$ must be universal with respect to this diagram. That is, for any other such triple $(Q, q_1, q_2)$ with $f \circ q_{1}=g \circ q_{2}$, there must exist a unique $u : Q \rightarrow P$ such that $p_{1}\circ u=q_{1}$ and $p_{2}\circ u=q_{2}:$

In an abelian category all pullbacks exist, and they preserve kernels in the sense that $\ker (p_1)\cong \ker (g)$ and $\ker (p_2)\cong \ker (f)$. Moreover, there exists an exact sequence

Dually, we can define pushout. In particular, the following diagram commutes if and only if the middle square is a pushout and a pullback,

or equivalently, there is an exact sequence:

1.1 A.1 Exact sequences in a tube

In this subsection, we collect some exact sequences in a stable tube, for further discussion on tubes we refer to [20, Sect. 4.6] and [22, Chap. X].

Recall that a stable tube ${{\mathcal {T}}}_r$ of rank $r\ge 1$ is a uniserial category with simples $S_1, S_2,\cdots , S_r$, equipped with an Auslander-Reiten translation $\tau$ satisfying $\tau (S_{i})=S_{i-1}$, where the index is considered module r. A stable tube is called homogeneous if it has rank one and it is called non-homogeneous otherwise. For any simple object $S_i$ in a stable tube ${{\mathcal {T}}}_r$ and any $n\ge 1$, there is a unique object $S_i^{(n)}$ of length n and ${\mathrm{top}\,}(S_i^{(n)})=S_i$, and any indecomposable object in ${{\mathcal {T}}}_r$ has this form. The tube ${{\mathcal {T}}}_r$ is a uniserial category in the sense that all subobjects of $S_i^{(n)}$ form a chain with respect to the inclusion:

$$\begin{aligned} 0:=S_{i-n}^{(0)}\subseteq S_{i-n+1}^{(1)}\subseteq S_{i-n+2}^{(2)}\subseteq \cdots \subseteq S_{i-1}^{(n-1)}\subseteq S_{i}^{(n)}. \end{aligned}$$

(A.1)

Consequently, the socle of $S_{i}^{(n)}$ is given by ${\mathrm{soc}\,}(S_{i}^{(n)})=S_{i-n+1}$. We denote by $u_{i,n}: S_{i-1}^{(n-1)}\rightarrow S_{i}^{(n)}$ and $p_{i,n}: S_{i}^{(n)}\rightarrow S_{i}^{(n-1)}$ the irreducible injection map and surjection map respectively. For convenience, in the following we will simply denote them by u and p respectively if no confusions appear. For example, the composition

will be just denoted by $p^{n-1}:S_{i}^{(n)}\rightarrow S_{i}$. With this simplified notations, we have $u\circ p=p\circ u$ whenever it makes sense. We have the following fundamental exact sequences in the tube ${{\mathcal {T}}}_r$, see for example [22, Thm. 2.2].

Lemma A.1

The following are exact sequences in ${{\mathcal {T}}}_r$ for any $i\in {{\mathbb {Z}}}/r{{\mathbb {Z}}}$ and $n\ge 1$:

• (1)
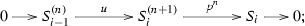
• (2)
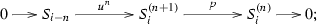
• (3)
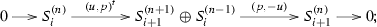
• (4)

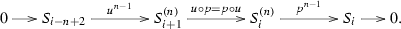
Now we focus on the weighted projective line ${{\mathbb {X}}}$ of weight type (2). The subcategory $\mathrm{coh}_0{{\mathbb {X}}}$ contains a non-homogeneous tube $\langle S_{1,0},S_{1,1}\rangle$ of rank two generated by exceptional simples $S_{1,0}$ and $S_{1,1}$, and a family of homogeneous tubes $\langle S_{\lambda }\rangle$’s generated by ordinary simple sheaves $S_{\lambda }$’s, where $\lambda$ runs through the closed points in ${\mathbb {H}}_ \mathbf {k}:={\mathbb {P}}^{1}_ \mathbf {k} \backslash \{\infty \}\cong \mathbf {k}$.

Lemma A.2

The following are exact sequences for any $0\le i\le 1$, $m,n\ge 1$, and $\lambda \in {\mathbb {H}}_{\mathbf {k}}$:

• (1)
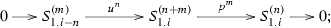
• (2)

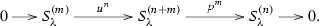
Proof

(1) By induction on n, we obtain the following pushout-pullback commutative diagram, where the first collum, the second and the third rows are all exact.

It follows that the second collum is also exact. Then we are done. The proof of (2) is similar. $\square$

Since the category $\mathrm{coh\,}{{\mathbb {X}}}$ is hereditary, for any $X,Y\in \mathrm{coh\,}{{\mathbb {X}}}$, we have ${\mathrm{Hom}\,}^{k}(X,Y)=0$ when $k\ne 0,1$. In the following we consider the non-zero morphisms in the subcategory $\langle S_{1,0}, S_{1,1}\rangle \subseteq \mathrm{coh\,}{{\mathbb {X}}}$.

Lemma A.3

Assume $0\le i,j\le 1$ and $n\ge 1$, then

• (1) ${\mathrm{Hom}\,}(S_{1,j}^{(n)}, S_{1,i})\ne 0 \;\;$ iff $\;\; {\mathrm{Ext}\,}^1(S_{1,i+1}, S_{1,j}^{(n)})\ne 0 \;\;$ iff $\;\; j=i$;

• (2) ${\mathrm{Hom}\,}(S_{1,i}, S_{1,j}^{(n)})\ne 0 \;\;$ iff $\;\; {\mathrm{Ext}\,}^1(S_{1,j}^{(n)}, S_{1,i+1})\ne 0 \;\;$ iff $\;\; j-n+1\equiv i\;({\mathrm{mod}\,}2)$.

Moreover, all the non-zero spaces have dimension one.

Proof

Observe that $S_{1,0}, S_{1,1}$ are the unique two simple objects in the subcategory $\langle S_{1,0}, S_{1,1}\rangle$. Thus, ${\mathrm{Hom}\,}(S_{1,j}^{(n)}, S_{1,i})\ne 0$ iff $S_{1,i}={\mathrm{top}\,}(S_{1,j}^{(n)})=S_{1,j}$, i.e. $j=i$; and ${\mathrm{Hom}\,}(S_{1,i}, S_{1,j}^{(n)})\ne 0$ iff $S_{1,i}={\mathrm{soc}\,}(S_{1,j}^{(n)})=S_{1,j-n+1}$, i.e. $j-n+1\equiv i\;({\mathrm{mod}\,}2)$. By Serre duality, we have ${\mathrm{Ext}\,}^1(X, Y)\cong \mathrm{D}{\mathrm{Hom}\,}(Y, \tau X)$ for any $X, Y\in \mathrm{coh\,}{{\mathbb {X}}}$, where $\tau (S_{1,i})=S_{1,i+1}$. Then we prove (1) and (2). Moreover, all the non-zero spaces have dimension one since $S_{1,0}, S_{1,1}$ are exceptional simple sheaves. $\square$

Lemma A.4

Assume $0\le i,j\le 1$ and $m,n\ge 2$, then

$$\begin{aligned} {\mathrm{Hom}\,}(S_{1,i}^{(m)}, S_{1,j}^{(n)})\ne 0 \text { and }{\mathrm{Ext}\,}^1(S_{1,i}^{(m)}, S_{1,j}^{(n)})\ne 0. \end{aligned}$$

Proof

Observe that the top of $S_{1,i}^{(m)}$ is $S_{1,i}$. If the socle of $S_{1,j}^{(n)}$ is $S_{1,i}$, then the composition $u^{n-1}p^{m-1}$ of the surjective map $p^{m-1}: S_{1,i}^{(m)}\twoheadrightarrow S_{1,i}$ and the injective map $u^{n-1}: S_{1,i}\rightarrowtail S_{1,j}^{(n)}$ is non-zero. If the socle of $S_{1,j}^{(n)}$ is not $S_{1,i}$, then it must be $S_{1,i+1}$. By the uniserial sequence (A.1) we know that $S_{1,i}^{(2)}$ is a subsheaf of $S_{1,j}^{(n)}$. Then the composition $u^{n-2}p^{m-2}$ of the surjective map $p^{m-2}: S_{1,i}^{(m)}\twoheadrightarrow S_{1,i}^{(2)}$ and the injective map $u^{n-2}: S_{1,i}^{(2)}\rightarrowtail S_{1,j}^{(n)}$ is non-zero. This proves ${\mathrm{Hom}\,}(S_{1,i}^{(m)}, S_{1,j}^{(n)})\ne 0$. Moreover, by Serre duality, we have ${\mathrm{Ext}\,}^1(S_{1,i}^{(m)}, S_{1,j}^{(n)})\cong \mathrm{D}{\mathrm{Hom}\,}(S_{1,j}^{(n)},S_{1,i+1}^{(m)})\ne 0$. We are done. $\square$

Lemma A.5

Assume $0\le i\le 1$ and $n\ge 2$, then the following sequence is exact in $\mathrm{coh\,}_0{{\mathbb {X}}}$:

Consequently,

$$\begin{aligned} \langle S_{1,i}^{(2n)}\rangle =\langle S_{1,i}^{(2)}\rangle =\mathrm{{add}}\{S_{1,i}^{(2m)}, m\ge 1\} \;\text {and}\;\langle S_{1,i}^{(2n-1)}\rangle =\langle S_{1,i}^{(3)}\rangle =\mathrm{{add}}\{S_{1,i}^{(2m-1)}, m\ge 1\}. \end{aligned}$$

In particular, for any non-zero objects $X, Y\in \langle S_{1,i}^{(n)}\rangle$, ${\mathrm{Hom}\,}(X,Y)\ne 0\ne {\mathrm{Hom}\,}(Y,X)$.

Proof

The exact sequence follows from the following pushout commutative diagram, where the exactness of rows follow from Lemma A.2:

Recall that $\langle S_{1,i}^{(n)}\rangle$ is the subcategory of coherent sheaves generated by $S_{1,i}^{(n)}$ under extensions and direct summands. Hence $S_{1,i}^{(n\pm 2)}\in \langle S_{1,i}^{(n)}\rangle$. It follows that $\langle S_{1,i}^{(n)}\rangle =\langle S_{1,i}^{(n+2)}\rangle$ for $n\ge 2$. In particular, $\langle S_{1,i}^{(2n-1)}\rangle =\langle S_{1,i}^{(3)}\rangle$ and $\langle S_{1,i}^{(2n)}\rangle =\langle S_{1,i}^{(2)}\rangle$. Hence $\mathrm{{add}}\{S_{1,i}^{(2m)}, m\ge 1\}\subseteq \langle S_{1,i}^{(2n)}\rangle$ and $\mathrm{{add}}\{S_{1,i}^{(2m-1)}, m\ge 1\}\subseteq \langle S_{1,i}^{(3)}\rangle$.

Denote by

$$\begin{aligned} S_{1,i}^{\perp _0}=\{X\in \langle S_{1,0}, S_{1,1}\rangle \;|\; {\mathrm{Hom}\,}(S_{1,i}, X)=0 \} \end{aligned}$$

and

$$\begin{aligned} {}^{\perp _0}S_{1,i}=\{X\in \langle S_{1,0}, S_{1,1}\rangle \;|\; {\mathrm{Hom}\,}(X, S_{1,i})=0\}. \end{aligned}$$

By Lemma A.3, ${\mathrm{Hom}\,}(S_{1,i}, X)= 0$ if and only if $\mathrm{soc}(X)=S_{1,i+1}$, while ${\mathrm{Hom}\,}(X, S_{1,i})= 0$ if and only if $\mathrm{top}(X)=S_{1,i+1}$. Then any indecomposable object $X\in S_{1,i+1}^{\perp _0}\bigcap {}^{\perp _0}S_{1,i+1}$ satisfies $\mathrm{soc}(X)=S_{1,i}=\mathrm{top}(X)$, that is, X has the form $S_{1,i}^{(2m-1)}$ for some $m\ge 1$, i.e. $S_{1,i+1}^{\perp _0}\bigcap {}^{\perp _0}S_{1,i+1}=\mathrm{{add}}\{S_{1,i}^{(2m-1)}, m\ge 1\}.$ Observe that both of $S_{1,i+1}^{\perp _0}$ and ${}^{\perp _0}S_{1,i+1}$ are closed under extensions and direct summands. Then $S_{1,i}^{(3)}\in S_{1,i+1}^{\perp _0}\bigcap {}^{\perp _0}S_{1,i+1}$ implies $\langle S_{1,i}^{(3)}\rangle \subseteq S_{1,i+1}^{\perp _0}\bigcap {}^{\perp _0}S_{1,i+1}$. This proves $\langle S_{1,i}^{(3)}\rangle =\mathrm{{add}}\{S_{1,i}^{(2m-1)}, m\ge 1\}$. Similarly, we can prove $\langle S_{1,i}^{(2n)}\rangle =\mathrm{{add}}\{S_{1,i}^{(2m)}, m\ge 1\}$. Then the non-zero homomorphisms between two non-zero objects in $\langle S_{1,i}^{(n)}\rangle$ follow from Lemma A.3 and Lemma A.4. $\square$

Lemma A.6

Each proper full subcategory of $\langle S_{1,0}, S_{1,1}\rangle$ closed under extensions and direct summands has one of the following forms for $i=0$ or 1:

• (1) $\langle S_{1,i}^{(j)}\rangle$ for $1\le j\le 3$;

• (2) $\langle S_{1,i}, S_{1,i}^{(2)}\rangle$;

• (3) $\langle S_{1,i}, S_{1,i+1}^{(2)}\rangle$.

Proof

Let ${\mathcal {U}}$ be a proper full subcategory of $\langle S_{1,0}, S_{1,1}\rangle$ closed under extensions and direct summands. By Lemma A.5, ${\mathcal {U}}$ is generated by a subset of $\{S_{1,i}^{(j)},0\le i\le 1 \;\text { and}\; 1\le j\le 3\}$. By assumption ${\mathcal {U}}\ne \langle S_{1,0}, S_{1,1}\rangle$, hence ${\mathcal {U}}$ contains at most one of $S_{1,0}$ or $S_{1,1}$. Now by Lemma A.1 (3) and Lemma A.5, at most one of $S_{1,0}^{(j)}$ and $S_{1,1}^{(j)}$ belongs to ${\mathcal {U}}$ for any $1\le j\le 3$. If neither $S_{1,0}$ nor $S_{1,1}$ belongs to ${\mathcal {U}}$, then so as $S_{1,0}^{(3)}$ and $S_{1,1}^{(3)}$. Hence ${\mathcal {U}}=\langle S_{1,i}^{(2)}\rangle$ for $i=0$ or 1. Now we assume that $S_{1,i}\in {\mathcal {U}}$ for some $i=0$ or 1, then $S_{1,i+1}\notin {\mathcal {U}}$ and so as $S_{1,i+1}^{(3)}$. By Lemma A.1 we have the following exact sequences:

Then $S_{1,i}^{(2)}\in {\mathcal {U}}$ or $S_{1,i+1}^{(2)}\in {\mathcal {U}}$ both implies $S_{1,i}^{(3)}\in {\mathcal {U}}$. Moveover, from Lemma A.5 we see that $S_{1,i}\in \langle S_{1,i}^{(3)}\rangle$. Hence ${\mathcal {U}}$ has one of the following forms:

$$\begin{aligned} \langle S_{1,i}\rangle ,\;\; \langle S_{1,i}^{(3)}\rangle , \;\;\langle S_{1,i}, S_{1,i}^{(2)}\rangle , \;\;\langle S_{1,i}, S_{1,i+1}^{(2)}\rangle . \end{aligned}$$

We are done. $\square$

1.2 A.2 Exact sequences in $\mathrm{coh\,}{{\mathbb {X}}}$

In this subsection we deal with exact sequences in the category $\mathrm{coh\,}{{\mathbb {X}}}$ which relates to line bundles. Recall that for any line bundle L, $S_{1,L}$ is the unique exceptional simple sheaf satisfying that ${\mathrm{Hom}\,}(L,S_{1,L})\ne 0$, and there are two kinds of fundamental exact sequences as follows (where $\lambda \in {\mathbb {H}}_{\mathbf {k}}$):

$$\begin{aligned} 0\longrightarrow L{\mathop {\longrightarrow }\limits ^{x_1}} L({\vec {x}}_1)\longrightarrow S_{1,L({\vec {x}}_1)}\longrightarrow 0 \end{aligned}$$

(A.2)

and

$$\begin{aligned} 0\longrightarrow L\xrightarrow {x_2-\lambda x_1^2}L({\vec {c}})\longrightarrow S_{\lambda }\longrightarrow 0.\end{aligned}$$

(A.3)

Lemma A.7

The following are exact sequences in $\mathrm{coh\,}{{\mathbb {X}}}$ for any $0\le i\le 1$ and $m,n\ge 1$:

In particular, we have the following two exact sequences:

• (1)
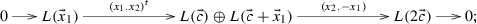
• (2)

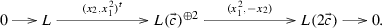
Proof

Let $\lambda$ be the point in ${{\mathbb {P}}}^1$ corresponding to the prime ideal $(x_2)$. Then we have an exact sequence for any line bundle L. Observe that $S_{1,L}^{(2n-i)}$ and $S_{\lambda }^{(m)}$ are orthogonal. By applying ${\mathrm{Hom}\,}(-, S_{\lambda }^{(m)})$ to the exact sequence

we obtain an isomorphism ${\mathrm{Hom}\,}(L(ix_1+m{\vec {c}}), S_{\lambda }^{(m)})\cong {\mathrm{Hom}\,}(L((m+n){\vec {c}}), S_{\lambda }^{(m)})$ induced by $x_1^{2n-i}$. Hence we have the following pushout commutative diagram, which yields the result:

$\square$

Let E and F be two indecomposable objects in ${{\mathcal {D}}}$. Recall that we have the evaluation maps and

Lemma A.8

The following are exact sequences in $\mathrm{coh\,}{{\mathbb {X}}}$ for any $n\ge 1$:

• (1)
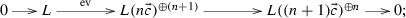
• (2)
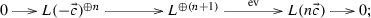
• (3)

Proof

Recall that there is a natural embedding $\mathrm{coh\,}{{\mathbb {P}}}^1\cong S_{1,L}^{\perp }\hookrightarrow \mathrm{coh\,}{{\mathbb {X}}}$. Then the first two exact sequences follow from [10, Sect. 6]. In the following we only prove (3). For $n\ge 1$, by applying ${\mathrm{Hom}\,}(-,L(n{\vec {c}}+{\vec {x}}_1))$ to the exact sequence

we get an isomorphism

$$\begin{aligned} {\mathrm{Hom}\,}(L,L(n{\vec {c}}+{\vec {x}}_1))\cong {\mathrm{Hom}\,}(L({\vec {x}}_1),L(n{\vec {c}}+{\vec {x}}_1)). \end{aligned}$$

Let $\mathrm{ev}'\triangleq (f_0, f_1, \cdots , f_n):L({\vec {x}}_1)\rightarrow L(n{\vec {c}}+{\vec {x}}_1)$, where $\{f_0, f_1, \cdots , f_n\}$ is a basis of the space ${\mathrm{Hom}\,}(L({\vec {x}}_1),L(n{\vec {c}}+{\vec {x}}_1))$, then $\{f_0\circ x_1, f_1\circ x_1, \cdots , f_n\circ x_1\}$ forms a basis of ${\mathrm{Hom}\,}(L, L(n{\vec {c}}+{\vec {x}}_1))$. Hence, the evaluation map $\mathrm{ev}: L\rightarrow L(n{\vec {c}}+{\vec {x}}_1))$ can be taken as $\mathrm{ev}=\mathrm{ev}'\circ x_1$. Consider the following pushout diagram, where the exactness of the second row follows from Lemma A.8:

We obtain an exact sequence

Observe that ${\mathrm{Ext}\,}^1(L((n+1){\vec {c}}+{\vec {x}}_1), S_{1,L({\vec {x}}_1)})=0$, hence $X=L((n+1){\vec {c}}+{\vec {x}}_1)^{\oplus n}\oplus S_{1,L({\vec {x}}_1)}$. We are done. $\square$

1.3 A.3 Last HN-triangles of indecomposable sheaves

In this subsection we describe the last HN-triangle for any finest t-stability and for any indecomposable coherent sheaf.

For any ordinary point $\lambda \in {{\mathbb {H}}}_{\mathbf {k}}$, the indecomposable torsion sheaf concentrated on $\lambda$ has the form $S_{\lambda }^{(k)}$ for some $k\ge 1$. It is easy to see (cf. [10, (6.5)]) that $\mathrm{{HN}}_-(S_{\lambda }^{(k)})$ has the following form for some semistable line bundle L:

For exceptional simple sheaves $S_{1,0}$ and $S_{1,1}$, the last HN-triangles have been given in Proposition 3.21 and Proposition 3.22 respectively. In the following we only consider $\mathrm{{HN}}_{-}(X)$ when X is a line bundle or $X=S_{1,i}^{(j)}$ for $0\le i\le 1$ and $j\ge 2$.

Proposition A.9

Let L be a line bundle. Then $\mathrm{{HN}}_{-}(L)$ has one of the following forms for some $k\ge 1$:

• (1)
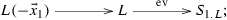
• (2)
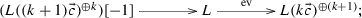
• (3)
• (4)
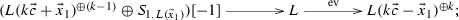
• (5)

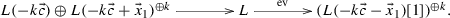
Proof

According to Lemma 3.14 and Lemma 3.15, the last HN-factors for L can only be some power of $S_{1,L}$, $L({\vec {x}})$ or $L(-{\vec {c}}-{\vec {x}})[1]$ for some ${\vec {x}}>0$. Now it remains to show that the (co)cone of the evaluation maps have the desired forms. The statement (1) follows from (A.2), and (2), (3) and (4) follow from Lemma A.8. We remain to prove (5).

By applying ${\mathrm{Hom}\,}(-,L(-k{\vec {c}}-{\vec {x}}_1))$ to the exact sequence $0\rightarrow L\xrightarrow {x_1} L({\vec {x}}_1) \rightarrow S_{1,L({\vec {x}}_1)}\rightarrow 0$, we get an isomorphism

$$\begin{aligned} {\mathrm{Hom}\,}(L,L(-k{\vec {c}}-{\vec {x}}_1)[1])\cong {\mathrm{Hom}\,}(L({\vec {x}}_1),L(-k{\vec {c}}-{\vec {x}}_1)[1]). \end{aligned}$$

Using Octahedron axiom in a triangulated category, we obtain the following commutative diagram with exact rows and columns (similar as in the proof of Lemma A.8, we can assume $\mathrm{ev}=\mathrm{ev}'\circ x_1$):

Observe that $\mathrm{dim}\,_\mathbf {k}{\mathrm{Hom}\,}(L(-k{\vec {c}}+{\vec {x}}_1), S_{1,L({\vec {x}}_1)})=1$. Up to an automorphism on $L(-k{\vec {c}}+{\vec {x}}_1)^{\oplus (k+1)}$, we can assume $g=(0,\cdots , 0, \pi )$, where $\pi$ fits into the exact sequence $0\rightarrow L(-k{\vec {c}})\rightarrow L(-k{\vec {c}}+{\vec {x}}_1)\xrightarrow {\pi } S_{1,L({\vec {x}}_1)}\rightarrow 0$. Hence $X=L(-k{\vec {c}})\oplus L(-k{\vec {c}}+{\vec {x}}_1)^{k}$. We are done. $\square$

Before giving a description of the last HN-triangle of torsion sheaf $S_{1,i}^{(n)}$ for $0\le i\le 1$ and $n\ge 2$, we first introduce some triangles involving them.

Lemma A.10

For any line bundle L and any $n\ge 1$, we have the following triangles:

• (1)
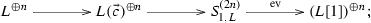
• (2)
• (3)
• (4)

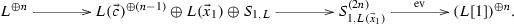
Proof

(1) Recall that there is a natural equivalence $S_{1,L}^{\bot }\cong \mathrm{coh\,}{{\mathbb {P}}}^1$, where $S_{1,L}^{(2)}$ corresponds to a simple sheaf in $\mathrm{coh\,}{{\mathbb {P}}}^1$. Then the triangle follows from [10] (6.5).

(2) By applying ${\mathrm{Hom}\,}(-,L)$ to the exact sequence $0\rightarrow S_{1,L}\rightarrow S_{1,L}^{(2n+1)} \xrightarrow {p} S_{1,L}^{(2n)}\rightarrow 0$, the surjection map p yields an isomorphism

$$\begin{aligned} {\mathrm{Hom}\,}(S_{1,L}^{(2n+1)} ,L[1])\cong {\mathrm{Hom}\,}(S_{1,L}^{(2n)}, L[1]). \end{aligned}$$

Hence we have the following commutative diagram with exact rows and columns by Octahedron axiom:

Now ${\mathrm{Ext}\,}^1(L({\vec {c}}), S_{1,L})=0$ implies $X=L({\vec {c}})^{\oplus n}\oplus S_{1,L}$. Then the exactness of the second row yields the result.

(3) By applying ${\mathrm{Hom}\,}(-,L[1])$ to the exact sequence $0\rightarrow S_{1,L({\vec {x}}_1)}^{(2n+1)} \xrightarrow {u} S_{1,L}^{(2n+2)} \rightarrow S_{1,L}\rightarrow 0$, the injection map u yields an isomorphism

$$\begin{aligned} {\mathrm{Hom}\,}(S_{1,L({\vec {x}}_1)}^{(2n+1)} ,L[1])\cong {\mathrm{Hom}\,}(S_{1,L}^{(2n+2)}, L[1]). \end{aligned}$$

Hence we have the following commutative diagram with exact rows and columns by Octahedron axiom:

Observe that $\mathrm{dim}\,{\mathrm{Hom}\,}(L({\vec {c}}), S_{1,L})=1$. Up to an automorphism of $L({\vec {c}})^{\oplus (n+1)}$, we can assume $g=(0,\cdots , 0, \pi )$, where $\pi$ fits into the exact sequence $0\rightarrow L({\vec {x}}_1)\rightarrow L({\vec {c}})\xrightarrow {\pi } S_{1,L}\rightarrow 0$. Hence $X=L({\vec {c}})^{\oplus n}\oplus L({\vec {x}}_1)$. Then the exactness of the first row yields the result.

(4) By Lemma A.1 (4) we know that there is a triangle in ${\mathcal {D}}$:

By applying the functor ${\mathrm{Hom}\,}(-, L[1])$ to this triangle, the map $p\circ u$ yields an isomorphism

$$\begin{aligned} {\mathrm{Hom}\,}(S_{1,L({\vec {x}}_1)}^{(2n)}, L[1])\cong {\mathrm{Hom}\,}(S_{1,L}^{(2n)}, L[1]). \end{aligned}$$

Hence we have the following commutative diagram by Octahedron axiom:

Note that ${\mathrm{Ext}\,}^1(L({\vec {c}}), S_{1,L})=0$ and ${\mathrm{Ext}\,}^1(L({\vec {c}}), S_{1,L}[-1])=\mathbf {k}$, which is given by a non-split triangle $S_{1,L}[-1]\rightarrow L({\vec {x}}_1)\rightarrow L({\vec {c}})\rightarrow S_{1,L}$. Obviously, X does not contain $S_{1,L}[-1]$ as a direct summand. It follows that $X=L({\vec {c}})^{\oplus (n-1)}\oplus L({\vec {x}}_1)\oplus S_{1,L}$. Then the exactness of the second row yields the result. $\square$

Proposition A.11

$\mathrm{{HN}}_-(S_{1,i}^{(2n)})$ has one of the following forms for some $k\in {{\mathbb {Z}}}$:

• (1)
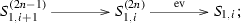
• (2)
• (3)
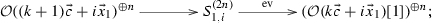
• (4)

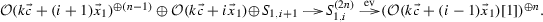
Proof

By Theorem 3.16, the last HN-factor of $S_{1,i}^{(2n)}$ can only be one of the following forms:

$$\begin{aligned} (1)\, S_{1,i}, \;(2)\, S_{1,i+1}^{(2m)}, \;(3)\, {{\mathcal {O}}}(k{\vec {c}}+i{\vec {x}}_1)^{\oplus n}[1], \;(4) \, {{\mathcal {O}}}(k{\vec {c}}+(i-1){\vec {x}}_1)^{\oplus n}[1] \end{aligned}$$

for some $m\ge 1$ and $k\in {{\mathbb {Z}}}$. Now it remains to show that the (co)cone of the evaluation maps have the desired forms. The first triangle follows from Lemma A.2, while the last two follow from Lemma . In the following we prove (2).

Assume the last HN-factor of $S_{1,i}^{(2n)}$ belongs to the subcategory $S_{1,i+1}^{(2)}$. By Lemma A.1 there is an Auslander-Reiten sequence as follows:

(A.4)

Moreover, for any $m\ge 1$, by applying ${\mathrm{Hom}\,}(-, S_{1,i+1}^{(2m)})$ to the exact sequence

we obtain that

any non-zero homomorphism in ${\mathrm{Hom}\,}(S_{1,i+1}^{(2n+1)}, S_{1,i+1}^{(2m)})$ factors through $p: S_{1,i+1}^{(2n+1)}\rightarrow S_{1,i+1}^{(2n)}$. Similarly, we can prove any homomorphism in ${\mathrm{Hom}\,}(S_{1,i+1}^{(2n-1)}, S_{1,i+1}^{(2m)})$ factors through $u: S_{1,i}^{(2n-1)}\rightarrow S_{1,i+1}^{(2n)}$. It follows from (A.4) that any non-zero homomorphism in ${\mathrm{Hom}\,}(S_{1,i}^{(2n)}, S_{1,i+1}^{(2m)})$ has a factor $p\circ u$, hence $p\circ u: S_{1,i}^{(2n)}\rightarrow S_{1,i+1}^{(2n)}$ is the minimal left $\langle S_{1,i+1}^{(2)}\rangle$-approximation of $S_{1,i}^{(2n)}$. Observe that $\mathrm{coker\,}(p\circ u)=\mathrm{coker\,}(u)\cong S_{1,i+1}$ and $\ker (p\circ u)=\ker (p)\cong S_{1,i+1}$, hence we have the following exact sequence:

Then the triangle (2) follows from Lemma 3.13. $\square$

Similarly, we have the following result for $S_{1,i}^{(2n+1)}$.

Proposition A.12

$\mathrm{{HN}}_-(S_{1,i}^{(2n+1)})$ has one of the following forms for some $k\in {{\mathbb {Z}}}$:

• (1)
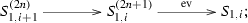
• (2)
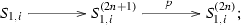
• (3)
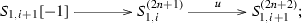
• (4)
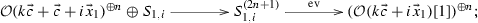
• (5)

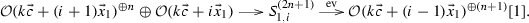
Appendix B. Finest t-stability for a kind of triangulated category

In this section we will give an equivalent description of finest t-stabilities for a triangulated category ${\mathcal {T}}$ which is piecewise hereditary and has coproducts and products. Two typical examples are given by

• bounded derived category $D^b({\mathrm{Mod}\,}A)$ of all modules for a hereditary algebra A;

• bounded derived category $D^b(\mathrm{Qcoh\,}X)$ of quasi-coherent sheaves for a (weighted) smooth projective curve X.

Here a triangulated category is called piecewise hereditary if it is triangle equivalent to $D^b({\mathcal {H}})$ for a hereditary abelian category ${\mathcal {H}}$.

Lemma B.1

Let $(\Phi ,\{\Pi _{\varphi }\}_{\varphi \in \Phi })$ be a finest t-stability on ${\mathcal {T}}$. Then $\tau _{\Phi }$ is strictly increasing.

Proof

Suppose there exists $\psi \in \Phi$ such that $\tau _{\Phi }(\psi )=\psi$. It follows that $\tau ^i _{\Phi }(\psi )=\psi$ for any $i\in {{\mathbb {Z}}}$. Let $X\ne 0$ be an indecomposable object in $\Pi _{\psi }$. Then $X[i]\in \Pi _{\tau ^i _{\Phi }(\psi )}=\Pi _{\psi }$. Hence $\Pi _{\psi _i}:=\Pi _\psi \cap ({\mathcal {H}}[i])$ is non-trivial for any $i\in {\mathbb {Z}}$, and $\Pi _{\psi }=\oplus _{i\in {\mathbb {Z}}}\Pi _{\psi _i}$. Set

$$\begin{aligned} \Psi :=\big (\Phi \setminus \{\psi \}\big )\bigcup \{\psi _{i}\mid i\in {{\mathbb {Z}}}\}. \end{aligned}$$

Define an automorphism $\tau _{\Psi }$ on $\Psi$ by setting

$$\begin{aligned} \tau _{\Psi }(\psi _{i})=\psi _{i+1},\,i\in {{\mathbb {Z}}}\; \;{\text { and }}\;\tau _{\Psi }(\varphi )=\tau _{\Phi }(\varphi ),\,\varphi \in \Phi \setminus \{\psi \}. \end{aligned}$$

A linear order is defined on $\Psi$ by keeping the order relations in $\Phi \setminus \{\psi \}$ and adding new relations

$$\begin{aligned} \varphi _1<\psi _i<\psi _{i+1}<\varphi _2\;\;(\forall \,i\in {{\mathbb {Z}}}) \end{aligned}$$

whenever $\varphi _1<\psi <\varphi _2$ with $\varphi _1,\varphi _2\in \Phi \setminus \{\psi \}$. Then $(\Psi ,\{\Pi _{\varphi }\}_{\varphi \in \Psi })$ is a t-stability which is strictly finer than $(\Phi ,\{\Pi _{\Phi }\}_{\varphi \in \Phi })$, a contradiction. $\square$

The following result gives an equivalent description of the finest t-stabilities on ${\mathcal {T}}$.

Theorem B.2

A t-stability $(\Phi ,\{\Pi _{\varphi }\}_{\varphi \in \Phi })$ on ${\mathcal {T}}$ is finest if and only if for any $\varphi \in \Phi$ and any non-zero objects $X,Y\in \Pi _{\varphi }$, ${\mathrm{Hom}\,}(X,Y)\ne 0\ne {\mathrm{Hom}\,}(Y,X)$.

Proof

The “if” part follows from [10, Prop. 5.5], hence we only need to prove the “only if” part in the following. For this we assume there exists some $\psi \in \Phi$ and non-zero objects $X,Y\in \Pi _{\psi }$ such that ${\mathrm{Hom}\,}(X,Y)=0$, and aim to show that $(\Phi ,\{\Pi _{\varphi }\}_{\varphi \in \Phi })$ is not finest.

By Lemma B.1, we know that $\tau _{\Phi }$ is strictly increasing. Denote by ${\mathcal {A}}:= \Pi _{(\tau _{\Phi }^{-1}(\psi ),\psi ]}$. By Proposition 3.3, ${\mathcal {A}}$ is abelian. By our assumption, ${\mathcal {C}}$ admits coproducts and products, hence ${\mathcal {A}}$ is cocomplete and complete according to [17, Prop. 3.2]. In particular, ${\mathcal {A}}$ is subcomplete in the sense of [4]. Let

$$\begin{aligned} {\mathcal {F}}=\{Z\in {\mathcal {A}}\mid {\mathrm{Hom}\,}(X,Z)=0\};\quad {\mathcal {T}}=\{W\in {\mathcal {A}}\mid {\mathrm{Hom}\,}(W,Z)=0, \forall Z\in {\mathcal {F}}\}. \end{aligned}$$

Then $({\mathcal {T}},{\mathcal {F}})$ forms a torsion pair in ${\mathcal {A}}$ according to [4, Prop. 3.3]. By definition, $Y\in {\mathcal {F}}$ and $X\in {\mathcal {T}}$. Moreover, we have $\Pi _{(\tau _{\Phi }^{-1}(\psi ),\psi )}\subseteq {\mathcal {F}}$, which implies that ${\mathcal {T}}\subseteq \Pi _{\psi }$. Set

$$\begin{aligned} \Psi :=\big (\Phi \setminus \{\tau _{\Phi }^{n}(\psi )\mid n\in {{\mathbb {Z}}}\}\big )\bigcup \{\psi _{1,n},\psi _{2,n}\mid n\in {{\mathbb {Z}}}\}. \end{aligned}$$

Define an automorphism $\tau _{\Psi }$ on $\Psi$ by setting

$$\begin{aligned} \tau _{\Psi }(\psi _{i,n})=\psi _{i,n+1},\;i=1,2\;\;{\text {and}}\;\; \tau _{\Psi }(\varphi )=\tau _{\Phi }(\varphi ),\;\forall \varphi \in \Phi \setminus \{\tau _{\Phi }^{n}(\psi )\!\mid \! n\in {{\mathbb {Z}}}\}. \end{aligned}$$

We define a linear order on $\Psi$ by keeping the order relations in $\Phi \setminus \{\tau _{\Phi }^{n}(\psi )\!\mid \! n\in {{\mathbb {Z}}}\}$ and adding new relations

$$\begin{aligned} \psi _{1,n}<\psi _{2,n}<\psi _{1,n+1}\;\;(\forall \,n\in {{\mathbb {Z}}}) \end{aligned}$$

and

$$\begin{aligned} \tau _{\Psi }^n(\varphi _1)<\psi _{1,n}<\psi _{2,n}<\tau _{\Psi }^n(\varphi _2) \end{aligned}$$

whenever $\varphi _1<\psi <\varphi _2$ with $\varphi _1,\varphi _2\in \Phi \setminus \{\tau _{\Phi }^{n}(\psi )\!\mid n\in {{\mathbb {Z}}}\}$.

Define $\Pi _{\psi _{1,0}}=\Pi _{\psi }\cap {\mathcal {F}}$, $\Pi _{\psi _{2,0}}=\Pi _{\psi }\cap {\mathcal {T}}={\mathcal {T}}$, and set $\Pi _{\psi _{i,n}}=\Pi _{\psi _{i,0}}[n]$ for $n\in {{\mathbb {Z}}}$, $i=1,2$. We claim that $\Pi _{\psi _{1,0}}, \Pi _{\psi _{2,0}}$ satisfy the following conditions:

• (i) ${\mathrm{Hom}\,}(\Pi _{\psi _{2,0}}, \Pi _{\psi _{1,0}})=0$;

• (ii) for each element $Z\in \Pi _{\psi }$, there exists a unique exact sequence $0\rightarrow Z_2\rightarrow Z\rightarrow Z_1\rightarrow 0$, where $Z_i\in \Pi _{\psi _{i,0}}$ for $i=1,2$.

In fact, since $({\mathcal {T}},{\mathcal {F}})$ is a torsion pair, the statement (i) follows immediately from the fact ${\mathrm{Hom}\,}({\mathcal {T}},{\mathcal {F}})=0$. For the second statement, note that Z has a unique decomposition $0\rightarrow Z_2\rightarrow Z\rightarrow Z_1\rightarrow 0$ with $Z_2\in {\mathcal {T}}$ and $Z_1\in {\mathcal {F}}$. Thus, it suffices to show that $Z_1\in \Pi _{\psi }$. This follows from the fact that ${\mathrm{Hom}\,}(Z,\Pi _{\varphi })=0$ for any $\varphi \in (\tau _{\Phi }^{-1}(\psi ),\psi )$. Thus, $(\Psi , \{\Pi _{\varphi }\}_{\varphi \in \Psi })$ is a t-stability on ${\mathcal {C}}$, which is strictly finer than $(\Phi ,\{\Pi _{\varphi }\}_{\varphi \in \Phi })$. We are done. $\square$