Topological stable rank of $\mathcal {E}'(\mathbb {R})$

Abstract

The set $\mathcal {E}'(\mathbb {R})$ of all compactly supported distributions, with the operations of addition, convolution, multiplication by complex scalars, and with the strong dual topology is a topological algebra. In this article, it is shown that the topological stable rank of $\mathcal {E}'(\mathbb {R})$ is 2.

1 Introduction

The aim of this article is to show that the topological stable rank (a notion from topological K-theory, recalled below) of $\mathcal {E}'(\mathbb {R})$ is 2, where $\mathcal {E}'(\mathbb {R})$ is the classical topological algebra of compactly supported distributions, with the strong dual topology $\beta (\mathcal {E}',\mathcal {E})$, pointwise vector space operations, and convolution taken as multiplication.

We recall some key notation and facts about $\mathcal {E}'(\mathbb {R})$ in Sect. 2 below, including its strong dual topology $\beta (\mathcal {E}',\mathcal {E})$, and in Sect. 3, we will recall the notion of topological stable rank of a topological algebra.

We will prove our main result, stated below, in Sects.  4 and 5.

Theorem 1.1

Let $\mathcal {E}'(\mathbb {R})$ be the algebra of all compactly supported distributions on $\mathbb {R}$, with

• pointwise addition, and pointwise multiplication by complex scalars,

• convolution taken as the multiplication in the algebra, and

• the strong dual topology $\beta (\mathcal {E}',\mathcal {E})$.

Then the topological stable rank of $\mathcal {E}'(\mathbb {R})$ is equal to 2.

2 The topological algebra $\mathcal {E}'(\mathbb {R})$

For background on topological vector spaces and distributions, we refer to [2, 6, 7, 11,12,13, 16].

Let $\mathcal {E}(\mathbb {R})=C^\infty (\mathbb {R})$ be the space of functions $\varphi :\mathbb {R}\rightarrow \mathbb {C}$ that are infinitely many times differentiable. We equip $\mathcal {E}(\mathbb {R})$ with the topology of uniform convergence on compact sets for the function and its derivatives. This is defined by the following family of seminorms: for a compact subset K of $\mathbb {R}$, and $M\in \{0,1,2,3\cdots \}=\mathbb {Z}_{ \tiny \small \scriptscriptstyle {\ge 0}}$, we define

$$\begin{aligned} p_{\scriptscriptstyle {K,M}}(\varphi )=\sup _{0\le m\le M}\sup _{x\in K}|\varphi ^{(m)}(x)|\;\;\text { for }\varphi \in \mathcal {E}(\mathbb {R}). \end{aligned}$$

The space $\mathcal {E}(\mathbb {R})$ is

• metrizable,

• a Fréchet space, and

• a Montel space;

see e.g. [7, Example 3, p.239].

By a topological algebra, we mean the following:

Definition 2.1

(Topological algebra) A complex algebra $\mathcal {A}$ is called a topological algebra if it is equipped with a topology $\mathcal {T}$ making the following maps continuous, with the product topologies on the domains:

• $\mathcal {A}\times \mathcal {A}\ni \;(a,b)\mapsto a+b\;\in \mathcal {A}$

• $\mathbb {C}\times \mathcal {A}\ni \;(\lambda , a)\mapsto \lambda \cdot a \;\;\in \mathcal {A}$

• $\mathcal {A}\times \mathcal {A}\ni \; (a,b)\mapsto ab\;\!\;\;\;\;\;\in \mathcal {A}$

We equip the dual space $\mathcal {E}'(\mathbb {R})$ of $\mathcal {E}(\mathbb {R})$ with the strong dual topology $\beta (\mathcal {E}',\mathcal {E})$, defined by the seminorms

$$\begin{aligned} p_{\scriptscriptstyle {B}}(T)=\sup _{\varphi \in B} |\langle T, \varphi \rangle |, \end{aligned}$$

for bounded subsets B of $\mathcal {E}(\mathbb {R})$. Then $\mathcal {E}'(\mathbb {R})$, being the strong dual of the Montel space $\mathcal {E}(\mathbb {R})$, is a Montel space too [12, 5.9, p. 147]. This has the consequence that a sequence in $\mathcal {E}'(\mathbb {R})$ is convergent in the $\beta (\mathcal {E}',\mathcal {E})$ topology if and only if it is convergent in the weak dual/weak-$*$ topology $\sigma (\mathcal {E}',\mathcal {E})$ of pointwise convergence on $\mathcal {E}(\mathbb {R})$; see e.g. [16, Corollary 1, p. 358].

As usual, let $\mathcal {D}(\mathbb {R})$ denote the space of all compactly supported functions from $C^\infty (\mathbb {R})$, and $\mathcal {D}'(\mathbb {R})$ denote the space of all distributions. The vector space $\mathcal {E}'(\mathbb {R})$ can be identified with the subspace of $\mathcal {D}'(\mathbb {R})$ consisting of all distributions having compact support. If $\mathcal {D}'(\mathbb {R})$ is also equipped with its strong dual topology, then one has a continuous injection $\mathcal {E}'(\mathbb {R})\hookrightarrow \mathcal {D}'(\mathbb {R}).$ For $T,S\in \mathcal {E}'(\mathbb {R})$, we define their convolution $T*S\in \mathcal {E}'(\mathbb {R})$ by

The map $*:\mathcal {E}'(\mathbb {R})\times \mathcal {E}'(\mathbb {R})\rightarrow \mathcal {E}'(\mathbb {R})$ is (jointly) continuous; see for instance [13, Chapter VI, §3, Theorem IV, p. 157].

Thus $\mathcal {E}'(\mathbb {R})$, endowed with the strong dual topology, forms a topological algebra with pointwise vector space operations, and with convolution taken as multiplication. The multiplicative identity element is $\delta _{\scriptscriptstyle {0}}$, the Dirac delta distribution supported at 0. In general, we will denote by $\delta _a$ the Dirac delta distribution supported at $a\in \mathbb {R}$.

We also recall that the Fourier–Laplace transform of a compactly supported distribution $T\in \mathcal {E}'(\mathbb {R})$ is an entire function, given by

$$\begin{aligned} {\widehat{T}}(z)=\Big \langle T, \;\big (x\mapsto e^{-2\pi i x z}\big )\;\Big \rangle \quad (z\in \mathbb {C}), \end{aligned}$$

see e.g. [16, Proposition 29.1, p. 307].

3 Topological stable rank

An analogue of the Bass stable rank (useful in algebraic K-theory) for topological rings, called the topological stable rank, was introduced in the seminal article [10].

Definition 3.1

(Unimodular tuple, Topological stable rank)

Let $\mathcal {A}$ be a commutative unital topological algebra with multiplicative identity element denoted by 1, endowed with a topology ${\mathcal {T}}$.

We define $\mathcal {A}^n:=\mathcal {A}\times \cdots \times \mathcal {A}$ (n times), endowed with the product topology.

• (Unimodular n-tuple)   Let $n\in \mathbb {N}:=\{1,2,3,\ldots \}$. We call an n-tuple $(a_1,\ldots ,a_n)\in \mathcal {A}^n$unimodular if there exists an n-tuple $(b_1,\ldots ,b_n)\in \mathcal {A}^n$ such that the Aryabhatta-Bézout equation $a_1 b_1+\cdots +a_nb_n=1$ is satisfied. The set of all unimodular n-tuples is denoted by $U_n(\mathcal {A})$. Note that $U_1(\mathcal {A})$ is the group of invertible elements of $\mathcal {A}$. An element from $U_2(\mathcal {A})$ is referred to as a coprime pair. It can be seen that if $U_n(\mathcal {A})$ is dense in $\mathcal {A}^n$, then $U_{n+1}(\mathcal {A})$ is dense in $\mathcal {A}^{n+1}$.

• (Topological stable rank)  If there exists a least natural number $n\in \mathbb {N}$ for which $U_n(\mathcal {A})$ is dense in $\mathcal {A}^n$, then that n is called the topological stable rank of $\mathcal {A}$, denoted by $\mathrm{tsr}\;\! \mathcal {A}$. If no such n exists, then ${\text {tsr}}\mathcal {A}$ is said to be infinite.

While the notion of topological stable rank was introduced in the context of Banach algebras, the above extends this notion in a natural manner to topological algebras. The topological stable rank of many concrete Banach algebras has been determined previously in several works (e.g. [5, 14, 15]). In this article, we determine the topological stable rank of the classical topological algebra $\mathcal {E}'(\mathbb {R})$ from Schwartz’s distribution theory.

4 $\mathrm {tsr}(\mathcal {E}'(\mathbb {R}))\ge 2$

The idea is that if tsr$(\mathcal {E}'(\mathbb {R}))$ were 1, then we could approximate any T from $\mathcal {E}'(\mathbb {R})$ by compactly supported distributions whose Fourier transform would be zero-free, and by an application of Hurwitz Theorem, ${\widehat{T}}$ would need to be zero-free too, which gives a contradiction, since we can easily choose T at the outset to not allow this.

Proposition 4.1

$\text {tsr}(\mathcal {E}'(\mathbb {R}))\ge 2$.

Proof

Suppose on the contrary that ${\text {tsr}}(\mathcal {E}'(\mathbb {R}))=1$. Let

$$\begin{aligned} T=\frac{\delta _{\scriptscriptstyle {-1}}-\delta _{\scriptscriptstyle {1}}}{2i}\in \mathcal {E}'(\mathbb {R}). \end{aligned}$$

By our assumption, $U_1(\mathcal {E}'(\mathbb {R}))$ is dense in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$. But then the set $U_1(\mathcal {E}'(\mathbb {R}))$ is also sequentially dense: This is a consequence of the fact that a subset F of $\mathcal {E}'(\mathbb {R})$ is closed in $\beta (\mathcal {E}',\mathcal {E})$ if and only if it is sequentially closed. (See [9, Satz 3.5, p. 231], which says that $E'$, with the $\beta (E',E)$-topology, is sequential whenever E is Fréchet–Montel. A locally convex space F is sequential if any subset of F is closed if and only if it is sequentially closed. If F has this property, then the closure of any subset equals its sequential closure, and therefore being dense is the same as being sequentially dense. In our case, $E=\mathcal {E}(\mathbb {R})$ is Fréchet–Montel, and so $\mathcal {E}'(\mathbb {R})$ is sequential. In fact, in the remark following [9, Satz 3.5], the case of $\mathcal {E}'(\mathbb {R})$ is mentioned as a corollary.)

Thus there exists a sequence $(T_n)_{n\in \mathbb {N}}$ in $U_1(\mathcal {E}'(\mathbb {R}))$ such that $T_n{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} T$ in $\mathcal {E}'(\mathbb {R})$. But since each $T_n$ is invertible in $\mathcal {E}'(\mathbb {R})$, there exists a sequence $(S_n)_{n\in \mathbb {N}}$ in $\mathcal {E}'(\mathbb {R})$ such that

$$\begin{aligned} T_n*S_n=\delta _{\scriptscriptstyle {0}}\;\; \text { for all } n\in \mathbb {N}. \end{aligned}$$

Taking the Fourier–Laplace transform, we obtain

$$\begin{aligned} \widehat{T_n}(z) \cdot \widehat{S_n}(z)=1 \;\;\text { for all }z\in \mathbb {C}\text { and all } n\in \mathbb {N}. \end{aligned}$$

In particular, the entire functions $\widehat{T_n}$ are all zero-free.

But as $T_n{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} T$ in $\mathcal {E}'(\mathbb {R})$, we now show that $(\widehat{T_n})_{n\in \mathbb {N}}$ converges to ${\widehat{T}}$ uniformly on compact subsets of $\mathbb {C}$ as $n\rightarrow \infty$. The pointwise convergence of $(\widehat{T_n})_{n\in \mathbb {N}}$ to ${\widehat{T}}$ is clear by taking the test function $x\mapsto e^{-2\pi i x z}$:

Now for any $\varphi \in \mathcal {E}(\mathbb {R})$, we know that the sequence $(\langle T_n,\varphi \rangle )_{n\in \mathbb {N}}$ converges to $\langle T,\varphi \rangle$, and in particular, the set

$$\begin{aligned} \Gamma (\varphi ):=\{\langle T_n,\varphi \rangle :n\in \mathbb {N}\} \end{aligned}$$

is bounded, for every $\varphi \in \mathcal {E}(\mathbb {R})$. By the Banach–Steinhaus Theorem for Fréchet spaces (see for example [11, Theorem 2.6, p. 45]), applied in our case to the Fréchet space $\mathcal {E}(\mathbb {R})$, we conclude that

$$\begin{aligned} \Gamma =\{T_n:n\in \mathbb {N}\} \end{aligned}$$

is equicontinuous. Thus for every $\epsilon >0$, there exists a neighbourhood V of 0 in $\mathcal {E}(\mathbb {R})$ such that $T_n(V)\subset B(0,\epsilon ):=\{z\in \mathbb {C}:|z|<\epsilon \}$ for all $n\in \mathbb {N}$. From here it follows that there exist $M\in \mathbb {Z}_{\scriptscriptstyle {\ge 0}}$, $R>0$ and $C>0$ such that

$$\begin{aligned} |\langle T_n,\varphi \rangle |\le C\Big (1+\sup _{0\le m\le M} \sup _{|x|\le R} |\varphi ^{(m)}(x)|\Big ) . \end{aligned}$$

By taking $\varphi =(x\mapsto e^{-2\pi i x z})$ in the above, we obtain

$$\begin{aligned} |\widehat{T_n}(z)|\le C'(1+|z|)^{M'} e^{R' |z|},\quad z\in \mathbb {C}, \;n\in \mathbb {N}. \end{aligned}$$

Also, by the Payley–Wiener–Schwartz Theorem [2, Theorem 4.12, p. 139] for $T\in \mathcal {E}'(\mathbb {R})$, we have

$$\begin{aligned} |{\widehat{T}}(z)|\le C''(1+|z|)^{M''} e^{R'' |z|},\quad z\in \mathbb {C}, \;n\in \mathbb {N}. \end{aligned}$$

It now follows that for some constants $C_*,M_*,R_*$ that

$$\begin{aligned} |\widehat{T_n}(z)-{\widehat{T}}(z)|\le C_*(1+|z|)^{M_*} e^{R_* |z|},\quad z\in \mathbb {C}, \;n\in \mathbb {N}. \end{aligned}$$

But this means that the pointwise convergent sequence $(\widehat{T_n})_{n\in \mathbb {N}}$ of entire functions is uniformly bounded on compact subsets of $\mathbb {C}$ (that is, the sequence constitutes a normal family). Then it follows from Montel’s Theorem (see e.g. [17, Exercise 9.4, p. 157]) that $(\widehat{T_n})_{n\in \mathbb {N}}$ converges to ${\widehat{T}}$ uniformly on compact subsets of $\mathbb {C}$ as $n\rightarrow \infty$.

But now by Hurwitz Theorem (see e.g. [17, Exercise 5.6, p.85]), and considering, say, the compact set $K=\{z\in \mathbb {C}:|z|\le 1\}$, we conclude that ${\widehat{T}}$ must be either be identically zero on K or that it must be zero-free in K. But ${\widehat{T}}$ is neither:

$$\begin{aligned} {\widehat{T}}(z)=\frac{e^{2\pi i z}-e^{-2\pi i z}}{2i}=\sin (2\pi z), \end{aligned}$$

a contradiction. Hence ${\text {tsr}}(\mathcal {E}'(\mathbb {R}))\ge 2$. $\square$

An alternative Proof of Proposition 4.1, suggested by Peter Wagner, is as follows. The theorem of supports ([6, Theorem 4.3.3]) implies that $U_1(\mathcal {E}'(\mathbb {R}))$ equals the set of nonzero multiples of $\delta _a$ for arbitrary $a\in \mathbb {R}$, and this set is not dense in $\mathcal {E}'(\mathbb {R})$. We give the details below. First, one can show the following structure result for $U_1(\mathcal {E}'(\mathbb {R}))$.

Proposition 4.2

$U_1(\mathcal {E}'(\mathbb {R}))=\{c\delta _a: a\in \mathbb {R}, \;0\ne c\in \mathbb {C}\}$.

Proof

It is clear that $\{c\delta _a:a\in \mathbb {R},\;0\ne c\in \mathbb {C}\}\subset U_1(\mathcal {E}'(\mathbb {R}))$ since

$$\begin{aligned} (c\delta _a)*(c^{-1} \delta _{-a})=\delta _0. \end{aligned}$$

Now suppose that $T\in U_1(\mathcal {E}'(\mathbb {R}))$. Then there exists an $S\in \mathcal {E}'(\mathbb {R})$ such that $T*S=\delta _0$. By the Theorem on Supports [6, Theorem 4.3.3, p. 107], we have

$$\begin{aligned} \text {c.h.supp}(T*S)=\text {c.h.supp}(T)+\text {c.h.supp}(S), \end{aligned}$$

where, for a distribution $E\in \mathcal {E}'(\mathbb {R})$, the notation $\text {c.h.supp}(E)$ is used for the closed convex hull of $\text {supp}(E)$, that is, the intersection of all closed convex sets containing $\text {supp}(E)$. So we obtain

$$\begin{aligned} \{0\}=\text {c.h.supp}(\delta _0)= \text {c.h.supp}(T*S)=\text {c.h.supp}(T)+\text {c.h.supp}(S), \end{aligned}$$

from which it follows that $\text {c.h.supp}(T)=\{a\}$ and $\text {c.h.supp}(S)=\{-a\}$ for some $a\in \mathbb {R}$. But then also $\text {supp}(T)=\{a\}$ and $\text {supp}(S)=\{-a\}$. As distributions with support in a point p are linear combinations of the Dirac delta distribution $\delta _p$ and its derivatives $\delta _p^{(n)}$ [16, Theorem 24.6, p. 266], we conclude that S and T have the form

$$\begin{aligned} T= & {} \sum _{n=0}^N t_n \delta _a^{(n)},\\ S= & {} \sum _{m=0}^M s_m \delta _{-a}^{(m)}, \end{aligned}$$

for some integers $N,M\ge 0$ and some complex numbers $t_n,s_m$ ($0\le n\le N$, $0\le m\le M$). Now $T*S=\delta _0$ implies that $N=M=0$ and $t_0s_0=1$, thanks to the linear independence of the set

$$\begin{aligned} \{\delta _{-a},\delta _{-a}',\delta _{-a}'',\ldots \}\cup \{\delta _{0},\delta _{0}',\delta _{0}'',\ldots \}\cup \{\delta _{a},\delta _{a}',\delta _{a}'',\ldots \} \end{aligned}$$

in the complex vector space $\mathcal {E}'(\mathbb {R})$. In particular $t_0\ne 0$. Thus

$$\begin{aligned} T= t_0 \delta _a\in \{c\delta _p: p\in \mathbb {R}, \;0\ne c\in \mathbb {C}\}. \end{aligned}$$

Consequently, $U_1(\mathcal {E}'(\mathbb {R}))=\{c\delta _a: a\in \mathbb {R}, \;0\ne c\in \mathbb {C}\}$. $\square$

Based on the above, we can now give the following alternative proof of Proposition 4.1.

Proof

We show $U_1(\mathcal {E}'(\mathbb {R}))$ is not dense in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$. If it were, then it would be sequentially dense too, and so for each element T of $\mathcal {E}'(\mathbb {R})$, there would exist a sequence in $U_1(\mathcal {E}'(\mathbb {R}))$ that converges to T in the $\beta (\mathcal {E}',\mathcal {E})$ topology, and hence also in the $\sigma (\mathcal {E}',\mathcal {E})$ topology. But we now show that $\delta _0'\in \mathcal {E}'(\mathbb {R})$ cannot be approximated in the $\sigma (\mathcal {E}',\mathcal {E})$ topology by elements from $U_1(\mathcal {E}'(\mathbb {R}))=\{c\delta _a: a\in \mathbb {R}, \;0\ne c\in \mathbb {C}\}$. Suppose, on the contrary, that $(c_n\delta _{a_n})_{n\in \mathbb {N}}$ converges to $\delta _0'$ in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$.

We first note that $(a_n)_{n\in \mathbb {N}}$ is bounded. For if not, then there exists a subsequence $(a_{n_k})_{k\in \mathbb {N}}$ of $(a_n)_{n\in \mathbb {N}}$ such that $|a_{n_k}|>2$ for all $k\in \mathbb {N}$. Now choose a $\varphi \in \mathcal {D}(\mathbb {R})$ such that $\varphi '(0)=1$ and $\varphi \equiv 0$ on $\mathbb {R}\setminus (-1,1)$. Then we arrive at the contradiction that

$$\begin{aligned} 0=c_{n_k}\cdot 0= c_{n_k}\cdot \varphi (a_{n_k})= \langle c_{n_k}\delta _{a_{n_k}},\varphi \rangle {\mathop {\longrightarrow }\limits ^{k\rightarrow \infty }} \langle \delta _0',\varphi \rangle = -\varphi '(0)=-1. \end{aligned}$$

So $(a_n)_{n\in \mathbb {N}}$ is bounded.

Next we show that $(c_n)_{n\in \mathbb {N}}$ converges to 0. Let $R>0$ be such that $|a_n|<R$ for all $n\in \mathbb {N}$. Let $\psi \in \mathcal {D}(\mathbb {R})$ be such that $\psi \equiv 1$ on $[-R,R]$. Then we have

$$\begin{aligned} c_n=c_n\cdot 1= c_n\cdot \psi (a_n)=\langle c_n \delta _{a_n},\psi \rangle {\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} \langle \delta '_0,\psi \rangle =-\psi '(0)=0. \end{aligned}$$

Finally, we show that $(c_n\delta _{a_n})_{n\in \mathbb {N}}$ converges to 0 in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$. For any $\chi \in \mathcal {D}(\mathbb {R})$, we have

$$\begin{aligned} |\langle c_n\delta _{a_n},\chi \rangle |=|c_n|\cdot |\chi (a_n)|\le |c_n|\cdot \Vert \chi \Vert _\infty {\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} 0\cdot \Vert \chi \Vert _\infty =0. \end{aligned}$$

So $(c_n\delta _{a_n})_{n\in \mathbb {N}}$ converges to 0 in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$. But this is a contradiction, since $0\ne \delta '_0$ in $\mathcal {E}'(\mathbb {R})$. Consequently, $U_1(\mathcal {E}'(\mathbb {R}))$ is not dense in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$, and so ${\text {tsr}}(\mathcal {E}'(\mathbb {R}))\ge 2$. $\square$

5 $\mathrm {tsr}(\mathcal {E}'(\mathbb {R}))\le 2$

The idea is to reduce the determination of tsr$(\mathcal {E}'(\mathbb {R}))$ to tsr($\mathbb {C}[z]$) of the polynomial ring $\mathbb {C}[z]$ as follows. Given a pair from $\mathcal {E}'(\mathbb {R})$, we use mollification to make a pair in $\mathcal {D}(\mathbb {R})$, and then approximate the resulting smooth functions by a linear combination of Dirac distributions with uniform spacing. The uniform spacing affords the identification of the linear combination of Dirac deltas with the ring of polynomials.

For $n\in \mathbb {N}$, we define the collection ${{\mathbf {D}}}_{n}$ of all ‘finitely supported Dirac delta combs’ with spacing 1 / n by

$$\begin{aligned} {{\mathbf {D}}}_{n}:=\text {span}\;\! \{ \delta _{\scriptscriptstyle {k/n}}:k\in \mathbb {Z}\}, \end{aligned}$$

where ‘span’ means the set of all (finite) linear combinations.

Lemma 5.1

(Approximating a pair of Dirac combs by a unimodular pair) Let $n\in \mathbb {N}$and $T,S\in {{\mathbf {D}}}_{n}$. Then there exist sequences $(T_k)_{k\in \mathbb {N}}$and $(S_k)_{k\in \mathbb {N}}$in ${{\mathbf {D}}}_n$, which converge to T, S, respectively, in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$, and hence¹also in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$, and are such that for each k, $(T_k,S_k)\in U_2(\mathcal {E}'(\mathbb {R}))$.

Proof

Write $T=\sum _{\ell =-L}^{L}t_{\scriptscriptstyle {\ell }} \delta _{\scriptscriptstyle {\ell /n}}$, and $S=\sum _{\ell =-L}^{L}s_{\scriptscriptstyle {\ell }} \delta _{\scriptscriptstyle {\ell /n}},$ for some $L\in \mathbb {N}$, $t_{\scriptscriptstyle {\ell }},s_{\scriptscriptstyle {\ell }} \in \mathbb {C}$.

Define

$$\begin{aligned} p_{\scriptscriptstyle {T}}:= & {} t_{\scriptscriptstyle {-L}}+t_{\scriptscriptstyle {-L+1}} z+\cdots +t_{\scriptscriptstyle {L}} z^{2L},\\ p_{\scriptscriptstyle {S}}:= & {} s_{\scriptscriptstyle {-L}}+s_{\scriptscriptstyle {-L+1}} z+\cdots +s_{\scriptscriptstyle {L}} z^{2L}. \end{aligned}$$

For a given $k\in \mathbb {N}$, let $\epsilon =1/(2^k \cdot 2L)>0$. Then we can perturb the coefficients of the polynomials $p_{\scriptscriptstyle {T}}, p_{\scriptscriptstyle {S}}$ within a distance of $\epsilon$ to make them have no common zeros, that is after perturbation of coefficients they are coprime in the ring $\mathbb {C}[z]$. Indeed any polynomial $p_{\scriptscriptstyle {T}}, p_{\scriptscriptstyle {S}}$ can be factorized as

$$\begin{aligned} p_{\scriptscriptstyle {T}}=C \prod (z-\alpha _{\scriptscriptstyle {\ell }}), \quad p_{\scriptscriptstyle {S}}=C'\prod (z-\beta _{\scriptscriptstyle {\ell }}), \end{aligned}$$

and if there is some common zero $\alpha _{\scriptscriptstyle {\ell }}=\beta _{\scriptscriptstyle {\ell '}}$, we simply replace $\beta _{\scriptscriptstyle {\ell '}}$ by $\beta _{\scriptscriptstyle {\ell '}}+\epsilon '$ with an $\epsilon '$ small enough so that the final coefficients (of this new perturbed polynomial obtained from $p_{\scriptscriptstyle {S}}$), which are polynomial functions of the zeros, lie within the desired $\epsilon$ distance of the coefficients of $p_{\scriptscriptstyle {S}}$. So we can choose ${\widetilde{t}}_{\scriptscriptstyle {-L,k}},\ldots ,{\widetilde{t}}_{\scriptscriptstyle {L,k}}$ and ${\widetilde{s}}_{\scriptscriptstyle {-L,k}},\ldots ,{\widetilde{s}}_{\scriptscriptstyle {L,k}}$ such that for all $\ell =-L,\ldots , L$, we have

$$\begin{aligned} |t_{\scriptscriptstyle {\ell }}-{\widetilde{t}}_{\scriptscriptstyle {\ell ,k}}|< \frac{1}{2^k}\cdot \frac{1}{2L} \quad \text { and } \quad |s_{\scriptscriptstyle {\ell }}-{\widetilde{s}}_{\scriptscriptstyle {\ell ,k}}| < \frac{1}{2^k}\cdot \frac{1}{2L} , \end{aligned}$$

and so that

$$\begin{aligned} {\widetilde{p}}_{\scriptscriptstyle {T,k}}:= & {} {\widetilde{t}}_{\scriptscriptstyle {-L,k}}+{\widetilde{t}}_{\scriptscriptstyle {-L+1,k}} z+ \cdots +{\widetilde{t}}_{\scriptscriptstyle {L,k}} z^{2L},\\ {\widetilde{p}}_{\scriptscriptstyle {S,k}}:= & {} {\widetilde{s}}_{\scriptscriptstyle {-L,k}}+{\widetilde{s}}_{\scriptscriptstyle {-L+1,k}} z+ \cdots +{\widetilde{s}}_{\scriptscriptstyle {L,k}} z^{2L} \end{aligned}$$

have no common zeros. Thus ${\widetilde{p}}_{\scriptscriptstyle {T,k}},{\widetilde{p}}_{\scriptscriptstyle {S,k}}$ are coprime in $\mathbb {C}[z]$, and hence there exist polynomials $q_{\scriptscriptstyle {T,k}},q_{\scriptscriptstyle {S,k}}\in \mathbb {C}[z]$ ([1, Corollary 8.5, p. 374]) such that

$$\begin{aligned} {\widetilde{p}}_{\scriptscriptstyle {T,k}}\cdot q_{\scriptscriptstyle {T,k}} +{\widetilde{p}}_{\scriptscriptstyle {S,k}} \cdot q_{\scriptscriptstyle {S,k}}=1. \end{aligned}$$

Set $Q_{\scriptscriptstyle {T,k}}:=z^L q_{\scriptscriptstyle {T,k}}$ and $Q_{\scriptscriptstyle {S,k}}:=z^L q_{\scriptscriptstyle {S,k}}$, and

$$\begin{aligned} P_{\scriptscriptstyle {T,k}}:= & {} {\widetilde{t}}_{\scriptscriptstyle {-L,k}}z^{-L}+{\widetilde{t}}_{\scriptscriptstyle {-L+1,k}} z^{-L+1} +\cdots +{\widetilde{t}}_{\scriptscriptstyle {L,k}} z^{L},\\ P_{\scriptscriptstyle {S,k}}:= & {} {\widetilde{s}}_{\scriptscriptstyle {-L,k}}z^{-L}+{\widetilde{s}}_{\scriptscriptstyle {-L+1,k}} z^{-L+1} +\cdots +{\widetilde{s}}_{\scriptscriptstyle {L,k}} z^{L}. \end{aligned}$$

Then in the ring $\mathbb {C}[z,z^{-1}]$ of linear combinations of monomials $z^n$, where $n\in \mathbb {Z}$ (i.e. the Laurent polynomial ring $\mathbb {C}[z,z^{-1}] =\mathbb {C}[z,w]/\langle zw-1 \rangle$; see for example [1, p. 367]), we have

$$\begin{aligned} P_{\scriptscriptstyle {T,k}}\cdot Q_{\scriptscriptstyle {T,k}}+ P_{\scriptscriptstyle {S,k}}\cdot Q_{\scriptscriptstyle {S,k}}=1. \end{aligned}$$

(1)

Suppose that $Q_{\scriptscriptstyle {T,k}}$ and $Q_{\scriptscriptstyle {S,k}}$ have the expansions

$$\begin{aligned} Q_{\scriptscriptstyle {T,k}}= & {} \tau _{\scriptscriptstyle {L',k}}z^{L+L'}+\tau _{\scriptscriptstyle {L'-1,k}} z^{L+L'-1}+\cdots +\tau _{\scriptscriptstyle {0,k}} z^{L},\\ Q_{\scriptscriptstyle {S,k}}= & {} \sigma _{\scriptscriptstyle {L',k}}z^{L+L'}+\sigma _{\scriptscriptstyle {L'-1,k}} z^{L+L'-1}+\cdots +\sigma _{\scriptscriptstyle {0,k}} z^{L}. \end{aligned}$$

Finally, set

$$\begin{aligned} T_k:=\sum _{\ell =-L}^{L}{\widetilde{t}}_{\scriptscriptstyle {\ell ,k}} \delta _{\scriptscriptstyle {\ell /n}}, \quad S_k:=\sum _{\ell =-L}^{L}{\widetilde{s}}_{\scriptscriptstyle {\ell ,k}} \delta _{\scriptscriptstyle {\ell /n}}, \end{aligned}$$

and

$$\begin{aligned} U_{k}:= & {} \tau _{\scriptscriptstyle {L',k}}\delta _{\scriptscriptstyle {(L+L')/n}}+\tau _{\scriptscriptstyle {L'-1,k}} \delta _{\scriptscriptstyle {(L+L'-1)/n}}+\cdots +\tau _{\scriptscriptstyle {0,k}} \delta _{\scriptscriptstyle {L/n}},\\ V_{k}:= & {} \sigma _{\scriptscriptstyle {L',k}}\delta _{\scriptscriptstyle {(L+L')/n}}+\sigma _{\scriptscriptstyle {L'-1,k}} \delta _{\scriptscriptstyle {(L+L'-1)/n}}+\cdots +\sigma _{\scriptscriptstyle {0,k}} \delta _{\scriptscriptstyle {L/n}}. \end{aligned}$$

Then it follows from (1) that

$$\begin{aligned} T_k*U_k +S_k *V_k=\delta _{\scriptscriptstyle {0}}. \end{aligned}$$

(2)

To see this, we note that $\Phi :\mathbb {C}[z,z^{-1}]\rightarrow {\mathbf {D}}_n$ given by

$$\begin{aligned} \Phi (z)=\delta _{\scriptscriptstyle 1/n}&\text { and }&\Phi (1)=\delta _{\scriptscriptstyle 0} \end{aligned}$$

defines a ring homomorphism, and then (2) above follows by applying $\Phi$ on both sides of (1). Hence $(T_k,U_k)\in U_2(\mathcal {E}'(\mathbb {R}))$. Also, for any $\varphi \in \mathcal {E}(\mathbb {R})$, we have

$$\begin{aligned} \Big |\big \langle (T-T_k),\varphi \big \rangle \Big |= & {} \left| \sum _{\ell =-L}^{L}(t_{\scriptscriptstyle {\ell }}-{\widetilde{t}}_{\scriptscriptstyle {\ell ,k}}) \langle \delta _{\scriptscriptstyle {\ell /n}},\varphi \rangle \right| \\= & {} \frac{1}{2^k} \cdot \frac{1}{2L}\cdot 2L\cdot \sup _{x\in [- \frac{L}{n},\frac{L}{n}]}|\varphi (x)|\\= & {} \frac{1}{2^k} \cdot \sup _{x\in [- \frac{L}{n},\frac{L}{n}]}|\varphi (x)| {\mathop {\longrightarrow }\limits ^{k\rightarrow \infty }}0. \end{aligned}$$

Hence $T_k{\mathop {\longrightarrow }\limits ^{k\rightarrow \infty }}T$ in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$ as $k\rightarrow \infty$. But then this convergence is also valid in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$, by [16, Corollary 1, p. 358], since $\mathcal {E}'(\mathbb {R})$ is a Montel space. Similarly, $S_k{\mathop {\longrightarrow }\limits ^{k\rightarrow \infty }}S$ in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$ as $k\rightarrow \infty$, and again, the convergence holds in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$. This completes the proof. $\square$

Lemma 5.2

(Approximation in $\mathcal {E}'(\mathbb {R})$ by Dirac combs)  

Let $T\in \mathcal {E}'(\mathbb {R})$. Then there exists a sequence $(T_n)_{n\in \mathbb {N}}$such that

• for all $n\in \mathbb {N}$, $T_n\in {{\mathbf {D}}}_n$, and

• $T_n{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} T$in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$, and hence also in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$.

Proof

Let $k\in \mathbb {N}$ be such that the support of T is contained in $(-k,k)$. We first produce a mollified approximating sequence for T. Let $\varphi :\mathbb {R}\rightarrow [0,\infty )$ be any test function in $\mathcal {D}(\mathbb {R})$ with support in $[-a,a]$ for some $a>0$, and such that

$$\begin{aligned} \int _\mathbb {R}\varphi (x) dx =1. \end{aligned}$$

Then we know that if we define $\varphi _m(x):=m\cdot \varphi (mx)$ ($m\in \mathbb {N}$), then for each m,

$$\begin{aligned} f_m:=T*\varphi _m \end{aligned}$$

is a smooth function having a compact support, and moreover,

$$\begin{aligned} T*\varphi _m{\mathop {\longrightarrow }\limits ^{m\rightarrow \infty }} T \end{aligned}$$

in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$; see for example [2, Theorem 3.3, p.97]. So the convergence is also valid in $(\mathcal {E}'(\mathbb {R}), \sigma (\mathcal {E}',\mathcal {E}))$. Moreover, as the support of $f_m= T*\varphi _m$ is contained in the sum of the supports of $\varphi _m$ and of T, for all m large enough, say $m\ge M$, we have

$$\begin{aligned} \text {supp}(T*\varphi _m)\subset & {} \text {supp}(T)+\text {supp}(\varphi _m)\\\subset & {} \text {supp}(T)+[-a/m,a/m]\\\subset & {} [-k,k]. \end{aligned}$$

From now on, we will assume that $m\ge M$, so that $\text {supp}(f_m)\subset [-k,k]$. Now we will approximate $f_m$ by Dirac comb elements. To this end, we define

$$\begin{aligned} T_{m, n}:= \sum _{\ell =0}^{n-1} \frac{2k}{n} \cdot f_m\Big (-k+\frac{2k}{n} \ell \Big ) \cdot \delta _{\scriptscriptstyle {-k+\frac{2k}{n}\ell }}\;\; \in {{\mathbf {D}}}_n. \end{aligned}$$

We will show that $T_{m,n}{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} f_m$ in $(\mathcal {E}'(\mathbb {R}), \sigma (\mathcal {E}',\mathcal {E}))$. Let $\psi \in \mathcal {E}(\mathbb {R})$. Then

$$\begin{aligned} \langle T_{m,n},\psi \rangle= & {} \left\langle \sum _{\ell =0}^{n-1} \frac{2k}{n} \cdot f_m\Big (-k+\frac{2k}{n} \ell \Big ) \cdot \delta _{\scriptscriptstyle {-k+\frac{2k}{n}\ell }},\; \psi \right\rangle \\= & {} \sum _{\ell =0}^{n-1} \frac{2k}{n}\cdot f_m\Big (-k+\frac{2k}{n} \ell \Big ) \left\langle \delta _{\scriptscriptstyle {-k+\frac{2k}{n}\ell }},\;\psi \right\rangle \\= & {} \sum _{\ell =0}^{n-1} \frac{2k}{n} \cdot f_m\Big (-k+\frac{2k}{n} \ell \Big )\cdot \psi \Big ( -k+\frac{2k}{n}\ell \Big ). \end{aligned}$$

Thus $\langle T_{m,n},\psi \rangle$ gives a Riemann sum for the integral of the continuous function $f_m\psi$ with compact support contained in $[-k,k]$, giving

$$\begin{aligned}&\big |\langle T_{m,n},\psi \rangle -\langle f_{m},\psi \rangle \big | \\&\quad = \, \left| \sum _{\ell =0}^{n-1} \frac{2k}{n} \!\cdot \!f_m\Big (\!-\!k\!+\!\frac{2k}{n} \ell \Big )\!\cdot \! \psi \Big ( \!-\!k\!+\!\frac{2k}{n}\ell \Big ) \!-\! \int _{-k}^k \!f_m(x) \psi (x) dx\right| {\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} 0. \end{aligned}$$

Hence $T_{m,n}{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} f_m$ in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$. As $\mathcal {E}'(\mathbb {R})$ is a Montel space, this convergence is also valid in $(\mathcal {E}'(\mathbb {R}),\beta (\mathcal {E}',\mathcal {E}))$, and the proof is completed. $\square$

Proposition 5.3

$\text {tsr}(\mathcal {E}'(\mathbb {R}))\le 2$.

Proof

Let $T,S\in \mathcal {E}'(\mathbb {R})$. Throughout this proof, $\mathcal {E}'(\mathbb {R})$ is endowed with the strong dual topology $\beta (\mathcal {E}',\mathcal {E})$, and then $(\mathcal {E}'(\mathbb {R}))^2=\mathcal {E}'(\mathbb {R})\times \mathcal {E}'(\mathbb {R})$ is equipped the product topology. Let V be a neighbourhood of (T, S) in $(\mathcal {E}'(\mathbb {R}))^2$. By Lemma 5.2, it follows that $\bigcup \limits _{n\in \mathbb {N}} ({{\mathbf {D}}}_n\times {{\mathbf {D}}}_n)$ is sequentially dense, and hence dense, in $(\mathcal {E}'(\mathbb {R}))^2$.

Thus there exists a pair $(T_*,S_*)\in V\cap ({{\mathbf {D}}}_n\times {{\mathbf {D}}}_n)$ for some $n\in \mathbb {N}$. By Lemma 5.1, there exists a sequence $(T_k,S_k)_{k\in \mathbb {N}}$ in $({{\mathbf {D}}}_n\times {{\mathbf {D}}}_n)\cap U_2(\mathcal {E}'(\mathbb {R}))$ that converges to $(T_*,S_*)$ in $(\mathcal {E}'(\mathbb {R}))^2$. Since V is also a neighbourhood of $(T_*,S_*)$ in $(\mathcal {E}'(\mathbb {R}))^2$, there exists an index K large enough so that for all $k>K$, $(T_k,S_k)\in V$.

Consequently, $U_2(\mathcal {E}'(\mathbb {R}))$ is dense in $(\mathcal {E}'(\mathbb {R}))^2$. $\square$

Proof of Theorem 1.1

It follows from Propositions 4.1 and 5.3 that the topological stable rank of $(\mathcal {E}'(\mathbb {R}), +,\cdot ,*, \beta (\mathcal {E}',\mathcal {E}))$ is equal to 2. $\square$

Remarks 5.4

• 1. From the proofs, it is clear that we have shown that $U_1(\mathcal {E}'(\mathbb {R}))$ is not dense in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$, while $U_2(\mathcal {E}'(\mathbb {R}))$ is sequentially dense, and hence dense, in $(\mathcal {E}'(\mathbb {R}))^2$ endowed with the product topology with $\mathcal {E}'(\mathbb {R})$ bearing the $\sigma (\mathcal {E}',\mathcal {E})$ topology. However, we note that $*:\mathcal {E}'(\mathbb {R})\times \mathcal {E}'(\mathbb {R})\rightarrow \mathcal {E}'(\mathbb {R})$ is not continuous if we use the $\sigma (\mathcal {E}',\mathcal {E})$ topology on $\mathcal {E}'(\mathbb {R})$: For example, in $(\mathcal {E}'(\mathbb {R}),\sigma (\mathcal {E}',\mathcal {E}))$, we have that $\delta _{\pm n}{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} 0,$ so that in the product topology on $(\mathcal {E}'(\mathbb {R}))^2$, we have $(\delta _n,\delta _{-n}){\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} (0,0)$. But on the other hand, we have $\delta _n*\delta _{-n}=\delta _{n-n}= \delta _0{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} \delta _0\ne 0=0*0$. So $(\mathcal {E}'(\mathbb {R}), +,\cdot ,*,\sigma (\mathcal {E}',\mathcal {E}))$ is not a topological algebra in the sense of our Definition 2.1.

• 2. We remark that in higher dimensions, with a similar analysis, it can be shown that ${\text {tsr}}(\mathcal {E}'(\mathbb {R}^d))\le d+1$.

• 3. The Bass stable rank (a notion from algebraic K-theory, recalled below) of $\mathcal {E}'(\mathbb {R})$ is not known. If $\mathcal {A}$ is a commutative unital ring, then $(a_1,\dots ,a_n,b)\in U_{n+1}(\mathcal {A})$ is called reducible if there exists an n-tuple $(\alpha _1,\ldots ,\alpha _n)\in \mathcal {A}^n$ such that $(a_1+\alpha _1 b,\ldots , a_n+\alpha _n b)\in U_n(\mathcal {A}).$ It can be seen that if every element of $U_{n+1}(\mathcal {A})$ is reducible, then every element of $U_{n+2}(\mathcal {A})$ is reducible too. The Bass stable rank of $\mathcal {A}$, denoted by $\text {bsr} \;\!\mathcal {A}$, is the smallest $n\in \mathbb {N}$ such that every element in $U_{n+1}(\mathcal {A})$ is reducible, and if no such n exists, then $\text {bsr} \;\!\mathcal {A}:=\infty$. It is known that for commutative unital Banach algebras $\mathcal {A}$, $\text {bsr}\;\! \mathcal {A}\le {\text {tsr}}\;\!\mathcal {A}$ [4, Theorem 3]. But the validity of such an inequality in the context of topological algebras does not seem to be known. We conjecture that $\text {bsr}(\mathcal {E}'(\mathbb {R}))=2$.

• 4. There are also several other natural convolution algebras of distributions on $\mathbb {R}$, for example

  

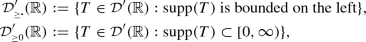
  and we leave the determination of the stable ranks of these algebras as open questions.

• 5. [8, Corollary 3.1] gives a ‘corona-type’ pointwise condition for coprimeness in $\mathcal {E}'(\mathbb {R})$, reminiscent of the famous Carleson corona condition² of coprimeness in the Banach algebra $H^\infty (\mathbb {D})$: $T_1, T_2\in U_2(\mathcal {E}'(\mathbb {R}))$ if and only if there exist positive C, N, M such that for all numbers $z\in \mathbb {C},\;\; |\widehat{T_1}(z)|+|\widehat{T_2}(z)|\ge C(1+|z|^2)^{-N} e^{-M|\text {Im}(z)|}.$