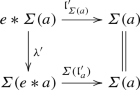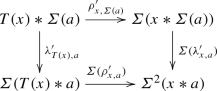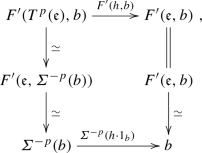Support varieties—an axiomatic approach

Abstract

We provide an axiomatic approach for studying support varieties of objects in a triangulated category via the action of a tensor triangulated category, where the tensor product is not necessarily symmetric. This is illustrated by examples, taken in particular from the representation theory of finite dimensional algebras.

1 Introduction

The main purpose of this paper is to present a common framework where most of the existing occurrences of support varieties fit in. Examples of such are support varieties for finite dimensional algebras, finite groups, restricted finite dimensional Lie algebras, smooth algebraic groups, finite group schemes, stable homotopy categories and complete intersections. This paper is an early thought of, but late arriving, companion of [14]. Some of the results were presented in [34, 35].

An inspiration for this work have been the notes on axiomatic stable homotopy theory by Hovey et al. [24], where tensor triangulated categories play a central role. There is also the more recent approach of Balmer towards a support theory for tensor triangulated categories [5, 6] and closely related a theory of support via central ring actions [8]. The purpose of this paper is to point out (1) that then one often misses a vital underlying structure, namely a tensor triangulated category acting on the category where the theory of support is constructed and (2) that one obtains a central ring action from the graded endomorphism ring of the tensor identity of the acting tensor triangulated category. This point of view has been taken successfully by Stevenson in [36, 37], but there the tensor triangulated category acting has a symmetric tensor product. This is not necessarily true in our setting as our prime example is to consider the category of bimodules over a finite dimensional algebra $\varLambda$, which are projective both as a left and as a right $\varLambda$-module.

The pivotal results for conceiving a theory of support varieties in a noncommutative setting were shown in [20, 21, 40] around 1960, where the group cohomology ring of a finite group is shown to be Noetherian, and further structural results of the cohomology ring were obtained in [32] in 1971. Then in 1981 Carlson defined a theory of support varieties for finitely generated modules over a group algebra of a finite group (see [17, 18]). These papers define the genesis of a theory of support varieties considered in noncommutative settings, as they have served as a motivation providing the means to associate geometric data to algebraic structures. We also have to adopt similar finiteness conditions to obtain a proper theory of support varieties in our setting, following ideas in [19, 33].

An interesting source of examples are the stable module categories of finite dimensional Hopf algebras. The Hopf structure gives rise to a tensor product which is not necessarily symmetric. In some cases, results from the theory of cocommutative Hopf algebras carry over to the noncommutative setting [30, 31], while other examples exhibit some new phenomena [10].

The rough outline of this paper is as follows: Sects. 1 and 2 are devoted to the foundations of triangulated categories with a tensor action. In Sects. 3–6 the basic properties of support varieties are discussed. The final Sects. 7–9 present various classes of examples.

2 Tensor categories and actions

A category with a tensor product is called a monoidal or a tensor category in the literature. This section is devoted to recalling the definition of a tensor category and an action of a tensor category on another category (see [26, 27]). The examples we have in mind are mostly triangulated categories, in particular those equipped with a suspension. Even though some of our results only depend on having suspended categories, in the main results we are assuming the presence of a triangulated structure. Therefore we focus throughout this paper on triangulated tensor categories and actions of such on triangulated categories. We end the section by reviewing our arsenal of examples of triangulated tensor categories and actions of these.

Recall that an additive category ${{\mathcal {C}}}$ is a tensor category if ${{\mathcal {C}}}$ carries an additional structure $({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}})$, where $-\otimes -:{{\mathcal {C}}}\times {{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$ is an additive bifunctor, ${\mathfrak {e}}$ is an object in ${{\mathcal {C}}}$, and ${\mathfrak {a}}:(-\otimes -)\otimes -\rightarrow -\otimes (-\otimes -)$ is an isomorphism of functors ${{\mathcal {C}}}\times {{\mathcal {C}}}\times {{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$. Furthermore, ${\mathfrak {l}}:{\mathfrak {e}}\otimes -\rightarrow -$ and ${\mathfrak {r}}:-\otimes {\mathfrak {e}}\rightarrow -$ are isomorphisms of functors ${{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$ making the following diagrams commute for all objects x, y, z and w in ${{\mathcal {C}}}$: (Pentagon Axiom)

and (Triangle Axiom)

Recall that

$$\begin{aligned} {\mathfrak {l}}_{{\mathfrak {e}}\otimes x}&= 1_{\mathfrak {e}}\otimes {\mathfrak {l}}_x,\\ {\mathfrak {r}}_{x\otimes {\mathfrak {e}}}&= {\mathfrak {r}}_x\otimes 1_{\mathfrak {e}},\\ {\mathfrak {l}}_{\mathfrak {e}}&={\mathfrak {r}}_{\mathfrak {e}}:{\mathfrak {e}}\otimes {\mathfrak {e}}\rightarrow {\mathfrak {e}}\end{aligned}$$

from ([27, Lemma XI.2.3]). A suspended category is a category ${{\mathcal {D}}}$ equipped with an autoequivalence $T:{{\mathcal {D}}}\rightarrow {{\mathcal {D}}}$.

Now we recall the definition of a triangulated tensor category. A triangulated tensor category [38] is a tensor category $({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}})$ and at the same time a triangulated category with a suspension $T:{{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$, where there exist isomorphisms of functors $\lambda :-\otimes T(-)\rightarrow T(-\otimes -)$ and $\rho :T(-)\otimes -\rightarrow T(-\otimes -)$ from ${{\mathcal {C}}}\times {{\mathcal {C}}}\rightarrow {{\mathcal {C}}}$ making the following diagrams commutative

and the following diagram anti-commutative

for all objects x and y in ${{\mathcal {C}}}$.

By an action of a tensor category on a category we mean the following. Let $({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}})$ be a tensor category, and let ${{\mathcal {A}}}$ be a category. An action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ is defined by the following data (see [26]):

• (i) an additive bifunctor $-*-:{{\mathcal {C}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$,

• (ii) a natural isomorphism $\alpha _{x,y,a}:(x\otimes y)*a \rightarrow x*(y*a)$ for all x and y in ${{\mathcal {C}}}$ and a in ${{\mathcal {A}}}$,

• (iii) a natural isomorphism ${\mathfrak {l}}'_a:{\mathfrak {e}}* a\rightarrow a$ for all a in ${{\mathcal {A}}}$,

where these satisfy the following commutative diagrams:

and

for all x, y and z in ${{\mathcal {C}}}$ and a in ${{\mathcal {A}}}$. Using that ${\mathfrak {l}}_{\mathfrak {e}}= {\mathfrak {r}}_{\mathfrak {e}}$ one obtains immediately from the above axioms that ${\mathfrak {l}}'_{{\mathfrak {e}}*a}=1_{\mathfrak {e}}*{\mathfrak {l}}'_a:{\mathfrak {e}}*({\mathfrak {e}}*a)\rightarrow {\mathfrak {e}}*a$ for all objects a in ${{\mathcal {A}}}$.

Finally we recall the definition of an action of a triangulated tensor category on a triangulated category. Let $({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}},T,\lambda ,\rho )$ be a triangulated tensor category, and let ${{\mathcal {A}}}=({{\mathcal {A}}},\varSigma )$ be a triangulated category. Then we define an action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ to be

• (i) a functor $-*-:{{\mathcal {C}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$, a natural isomorphism $\alpha _{x,y,a}$ and a natural isomorphism ${\mathfrak {l}}'_a$ for all x and y in ${{\mathcal {C}}}$ and a in ${{\mathcal {A}}}$ as above, such that

• (ii) there exist isomorphisms $\lambda '$ and $\rho '$ between the functors

  $$\begin{aligned}\lambda ':-*\varSigma (-) \rightarrow \varSigma (-*-)\end{aligned}$$

  and

  $$\begin{aligned}\rho ':T(-)*- \rightarrow \varSigma (-*-)\end{aligned}$$

  when viewed as bifunctors from ${{\mathcal {C}}}\times {{\mathcal {A}}}$ to ${{\mathcal {A}}}$, and such that

• (iii) the diagram

  

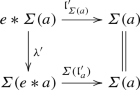
  commutes for all a in ${{\mathcal {A}}}$, and such that

• (iv) there is an anti-commutative diagram

  

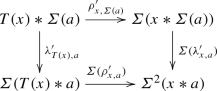
  for all x in ${{\mathcal {C}}}$ and a in ${{\mathcal {A}}}$.

Remark 1.1

Let ${{\mathcal {C}}}=({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}},T,\lambda ,\rho )$ be a triangulated tensor category. Then it follows directly from the definition, that there is an action of ${{\mathcal {C}}}$ on ${{\mathcal {C}}}$ by letting $-*-=-\otimes -$, $\alpha ={\mathfrak {a}}$, ${\mathfrak {l}}'={\mathfrak {l}}$, $\lambda '=\lambda$ and $\rho '=\rho$. Also note that we do not assume any exactness properties of the tensor product $-\otimes -$ in either of the variables. It is only the graded structure through the shift in the triangulated categories that is crucial for Sect. 2.

We end this section by giving some examples of triangulated tensor categories with actions on triangulated categories. To do this it is convenient to point out some elementary general facts about categories of complexes.

Let R be a ring. Denote by ${{\mathbf {C}}}(R)$ and ${{\mathbf {C}}}({\text {mod}}R)$ the category of complexes of all left R-modules and all finitely presented left R-modules, respectively. The tensor product gives rise to a functor ${{\mathbf {C}}}(R^{{\text {op}}})\times {{\mathbf {C}}}(R)\rightarrow {{\mathbf {C}}}({{\mathbb {Z}}})$ via the total complex. Our conventions for the signs are the following. The shift of a complex X is given by $X[p]^n=X^{n-p}$ and $d_{X[p]}=(-1)^p d_{X}$ for any integer p in ${{\mathbb {Z}}}$. For a morphism $f:X\rightarrow Y$ of complexes $f[p]^n=f^{n-p}$. Given a complex X in ${{\mathbf {C}}}(R^{{\text {op}}})$ and a complex Y in ${{\mathbf {C}}}(R)$, the total complex ${\text {Tot}}(X,Y)=X\otimes _R Y$ has $(X\otimes _R Y)^n =\amalg _{i\in {{\mathbb {Z}}}} X^i\otimes _R Y^{n-i}$ with differential $d^n:(X\otimes _R Y)^n\rightarrow (X\otimes _R Y)^{n+1}$ given by $x^i\otimes y^{n-i}\mapsto d_X(x^i)\otimes y^{n-i} + (-1)^ix^i\otimes d_Y(y^{n-i})$.

By abuse of notation let R also denote the stalk complex with R concentrated in degree zero. The multiplication maps $R\otimes _R M\rightarrow M$ and $N\otimes _R R\rightarrow N$ for an R-module M and an $R^{{\text {op}}}$-module N induce natural isomorphisms ${\mathfrak {r}}:X\otimes _R R\rightarrow X$ and ${\mathfrak {l}}:R\otimes _R Y\rightarrow Y$ for all complexes X in ${{\mathbf {C}}}(R^{{\text {op}}})$ and all complexes Y in ${{\mathbf {C}}}(R)$. Hence R is the tensor identity in ${{\mathbf {C}}}(R)$.

Define $\lambda :X\otimes _R Y[-1]\rightarrow (X\otimes _R Y)[-1]$ by letting

$$\begin{aligned}\lambda ^n=\amalg _{i\in {{\mathbb {Z}}}} (-1)^i {{\text {id}}}_{X^i}\otimes {{\text {id}}}_{Y^{n-i+1}}:(X\otimes _R Y[-1])^n\rightarrow (X\otimes _R Y)[-1]^n. \end{aligned}$$

Let $\rho :X[-1]\otimes _R Y\rightarrow (X\otimes _R Y)[-1]$ be given by

$$\begin{aligned}\rho ^n=\amalg _{i\in {{\mathbb {Z}}}}{{\text {id}}}_{X^{i+1}}\otimes {{\text {id}}}_{Y^{n-i}}:(X[-1]\otimes _R Y)^n\rightarrow (X\otimes _R Y)[-1]^n. \end{aligned}$$

Both of these maps are isomorphisms, which are natural in each variable. We leave it to the reader to check that the diagrams

are commutative and that the following diagram

is anti-commutative.

If we are in a setting where $(X\otimes _R Y)\otimes _S Z$ and $X\otimes _R(Y\otimes _S Z)$ are defined, then there is an associativity isomorphism between them induced by the associativity isomorphism for tensor products of modules. In addition the tensor product ${{\mathbf {C}}}(S^{{\text {op}}})\times {{\mathbf {C}}}(S)\rightarrow {{\mathbf {C}}}({{\mathbb {Z}}})$ given by the total tensor product over S sends null homotopic maps to null homotopic maps, such that the tensor product induces a functor ${{\mathbf {K}}}(S^{{\text {op}}})\times {{\mathbf {K}}}(S)\rightarrow {{\mathbf {K}}}({{\mathbb {Z}}})$. Here ${{\mathbf {K}}}(S)$ and ${{\mathbf {K}}}({\text {mod}}S)$ denote the homotopy category of complexes of all left S-modules and all finitely presented left S-modules over the ring S, respectively. Having this in mind it is easy to check that the other requirements for a triangulated tensor category are satisfied in the following examples.

Example 1.2

Let R be a commutative ring. Then ${{\mathbf {K}}}(R)$ is a triangulated tensor category with the tensor product induced by the total tensor product over R, and with ${\mathfrak {e}}=R$, ${\mathfrak {a}}$, ${\mathfrak {l}}$, ${\mathfrak {r}}$, T, and $\lambda$ and $\rho$ given as above. This gives rise to an action of ${{\mathbf {K}}}(R)$ on ${{\mathbf {K}}}(R)$.

Example 1.3

Let G be a finite group, and let k be a field. Then ${{\mathbf {K}}}(kG)$ is a triangulated tensor category with the tensor product induced by the total tensor product over k, and with ${\mathfrak {e}}=k$, ${\mathfrak {a}}$, ${\mathfrak {l}}$, ${\mathfrak {r}}$, T, and $\lambda$ and $\rho$ given as above. Consequently there is an action of ${{\mathbf {K}}}(kG)$ on ${{\mathbf {K}}}(kG)$.

Example 1.4

An easy generalization of the above example is to consider a finite dimensional Hopf algebra H over a field k. Then ${{\mathbf {K}}}(H)$ is a triangulated tensor category with the same choice of structures as for the group ring case. Hence there is an action of ${{\mathbf {K}}}(H)$ on ${{\mathbf {K}}}(H)$.

Example 1.5

Let $\varLambda$ be an algebra over a commutative ring k. Let $\varLambda ^e=\varLambda \otimes _k \varLambda ^{{\text {op}}}$ be the enveloping algebra of $\varLambda$. Then ${{\mathbf {K}}}(\varLambda ^e)$ is a triangulated tensor category with the tensor product induced by the total tensor product over $\varLambda$, and with ${\mathfrak {e}}=\varLambda$, ${\mathfrak {a}}$, ${\mathfrak {l}}={\mathfrak {r}}$, T, and $\lambda$ and $\rho$ given as above. As above this gives rise to an action of ${{\mathbf {K}}}(\varLambda ^e)$ on ${{\mathbf {K}}}(\varLambda ^e)$. Furthermore, we obtain an action of ${{\mathbf {K}}}(\varLambda ^e)$ on ${{\mathbf {K}}}(\varLambda )$ in a natural way.

In the examples ${{\mathbf {K}}}(kG)$ and ${{\mathbf {K}}}(H)$ the tensor product $\otimes _k$ in ${\text {Mod}}kG$ and ${\text {Mod}}H$ is exact, so that the tensor product of a complex with an acyclic complex is always an acyclic complex again, or equivalently tensoring with a fixed complex preserves quasi-isomorphisms. It follows from this that the tensor product in the homotopy categories induces a tensor product on the derived categories ${{\mathbf {D}}}(kG)$ and ${{\mathbf {D}}}(H)$. In addition, this induces a triangulated tensor structure on ${{\mathbf {D}}}(kG)$ and ${{\mathbf {D}}}(H)$.

The situation is different for ${{\mathbf {K}}}(\varLambda ^e)$. Here, we restrict to the full subcategory ${{\mathcal {B}}}$ in ${\text {Mod}}\varLambda ^e$ (or ${\text {mod}}\varLambda ^e$) consisting of those $\varLambda ^e$-modules which are projective over $\varLambda$ and $\varLambda ^{{\text {op}}}$. Then the tensor product $-\otimes _\varLambda -$ is exact on ${{\mathcal {B}}}$. Let ${{\mathcal {C}}}={{\mathbf {D}}}^{b}({{\mathcal {B}}})$ be the full subcategory of ${{\mathbf {D}}}(\varLambda ^e)$ generated by all complexes of modules in ${{\mathcal {B}}}$ with bounded homology. Similarly as above, the tensor product $-\otimes _\varLambda -$ induces a tensor product on ${{\mathcal {C}}}$ making it a triangulated tensor category with the tensor structure induced from ${{\mathbf {K}}}(\varLambda ^e)$. This also gives rise to an action of ${{\mathcal {C}}}$ on ${{\mathbf {D}}}(\varLambda )$, ${{\mathbf {D}}}^-({\text {mod}}\varLambda )$ and ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

The derived tensor product $-\otimes _\varLambda ^{\mathbb {L}} -$ on ${{\mathbf {D}}}(\varLambda ^e)$ given by $X\otimes _\varLambda p(Y)$ where $p(Y)\rightarrow Y$ is a quasi-isomorphism and p(Y) is a complex of projective modules, makes ${{\mathbf {D}}}(\varLambda ^e)$ into a triangulated tensor category. Similarly, if Y is in ${{\mathbf {D}}}(\varLambda )$, the derived tensor product $X\otimes _\varLambda ^{\mathbb {L}} Y$ yields an action of ${{\mathbf {D}}}(\varLambda ^e)$ on ${{\mathbf {D}}}(\varLambda )$.

As above, for a commutative Noetherian ring R the derived tensor product $-\otimes _R^{\mathbb {L}}-$ on ${{\mathbf {D}}}(R)$ makes ${{\mathbf {D}}}(R)$ into a triangulated tensor category. Consider the full subcategory ${{\mathbf {D}}}^{{\text {perf}}}(R)$ of perfect complexes and ${{\mathbf {D}}}^b({\text {mod}}R)$ under this action. It is easy to see that the above action restricts to an action of ${{\mathbf {D}}}^{{\text {perf}}}(R)$ on ${{\mathbf {D}}}^b({\text {mod}}R)$, where the tensor product is given by taking the total tensor product over R.

Example 1.6

For a selfinjective algebra $\varLambda$ let ${\underline{{\text {Mod}}}}\varLambda$ denote the category ${\text {Mod}}\varLambda$ modulo the morphisms factoring through projective modules. This is a triangulated category with suspension given by the first negative syzygy, $\varOmega ^{-1}_\varLambda$. In the stable categories ${\underline{{\text {Mod}}}}kG$ or ${\underline{{\text {Mod}}}}H$ there is an induced tensor product by the Hopf structure and since $P\otimes _k M$ and $M\otimes _k P$ are projective modules whenever P is a projective module and M is any module. In addition this tensor product induces exact functors (triangle functors) for a fixed object in each of the variables of the tensor product. Hence we obtain that the stable categories ${\underline{{\text {Mod}}}}kG$ and ${\underline{{\text {Mod}}}}H$ are triangulated tensor categories.

Example 1.7

Let $\varLambda$ be a finite dimensional selfinjective algebra over a field k. Again let ${{\mathcal {B}}}$ denote the full subcategory of ${\text {Mod}}\varLambda ^e$ consisting of the bimodules projective as modules on either side. Since $P\otimes _\varLambda B$ and $B\otimes _\varLambda P$ are projective $\varLambda ^e$-modules whenever P is a projective $\varLambda ^e$-module and B is in ${{\mathcal {B}}}$, the tensor product $-\otimes _\varLambda -$ also induces a tensor product on the stable category ${\underline{{{\mathcal {B}}}}}$ as a full subcategory of ${\underline{{\text {Mod}}}}\varLambda ^e$. As above the category ${\underline{{{\mathcal {B}}}}}$ becomes a triangulated tensor category.

Example 1.8

Let ${\mathfrak {S}}_d$ be the symmetric group permuting d elements and let k be a field. Let $n\ge d$ and set $V=k^n$. Then the Schur algebra $S_k(n,d)$ is by definition the endomorphism algebra ${\text {End}}_{k{\mathfrak {S}}_d}(V^{\otimes d})$ and there exists an idempotent e in $S_k(n,d)$ such that $e S_k(n,d)e\cong k\mathfrak S_d$. Multiplying with e yields the Schur functor${\text {mod}}S_k(n,d)\rightarrow {\text {mod}}k{\mathfrak {S}}_d$ (see [22]).

The category ${\text {mod}}S_k(n,d)$ carries a (not necessarily exact) symmetric tensor product [28]. On the other hand, ${\text {mod}}k{\mathfrak {S}}_d$ is a tensor category via $-\otimes _k -$ with the diagonal group action. The Schur functor preserves the tensor product [1] and this yields an exact functor ${{\mathbf {D}}}^b({\text {mod}}S_k(n,d))\rightarrow {{\mathbf {D}}}^b({\text {mod}}k{\mathfrak {S}}_d)$ between triangulated tensor categories. In fact, it is a triangulated quotient functor [25, Lemma 1.15]. Thus the known classification of thick tensor ideals of ${{\mathbf {D}}}^b({\text {mod}}k{\mathfrak {S}}_d)$ via homogeneous prime ideals of the cohomology ring $H^*({\mathfrak {S}}_d,k)$ (see [7]) embeds into the presently unknown classification for ${{\mathbf {D}}}^b({\text {mod}}S_k(n,d))$.

3 The endomorphism ring of the tensor identity

The endomorphism ring of the tensor identity in a suspended tensor category was considered in [38] and shown to be graded-commutative. Any homomorphism of graded rings from a positively graded and graded-commutative ring R to the graded centre of a triangulated category is shown to give rise to a theory of support varieties (see [4, 8, 9, 12]). This is called a central ring action of the graded ring R on the triangulated category ${{\mathcal {A}}}$.

This section is devoted to showing that there is a homomorphism of graded rings from the graded endomorphism ring of the tensor identity ${\mathfrak {e}}$ in a triangulated tensor category ${{\mathcal {C}}}$ to the graded centre of a triangulated category ${{\mathcal {A}}}$ on which ${{\mathcal {C}}}$ is acting. Hence it gives rise to a central ring action on ${{\mathcal {A}}}$.

Let ${{\mathcal {C}}}=({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}},T,\lambda ,\rho )$ be a triangulated tensor category acting on a triangulated category ${{\mathcal {A}}}=({{\mathcal {A}}},\varSigma )$. Consider the graded endomorphism ring ${\text {End}}^*_{{\mathcal {C}}}({\mathfrak {e}})=\amalg _{p\in {{\mathbb {Z}}}}{\text {Hom}}_{{\mathcal {C}}}({\mathfrak {e}}, T^p({\mathfrak {e}}))$ of the tensor identity in ${{\mathcal {C}}}$, which clearly is a naturally ${{\mathbb {Z}}}$-graded ring with multiplication given as follows: If $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ and $h':{\mathfrak {e}}\rightarrow T^q({\mathfrak {e}})$, then

$$\begin{aligned} h\cdot h'=T^q(h){\circ }h':{\mathfrak {e}}\rightarrow T^{p+q}({\mathfrak {e}}). \end{aligned}$$

Recall that the graded centre$Z^*({{\mathcal {A}}})$ of ${{\mathcal {A}}}$ is defined as the graded ring which in degree p in ${{\mathbb {Z}}}$ consists of all natural transformations $z:{{\text {id}}}_{{\mathcal {A}}}\rightarrow \varSigma ^p$ such that $\varSigma z=(-1)^p z\varSigma$ (see [16]). We want to define a homomorphism of graded rings from ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$ to $Z^*({{\mathcal {A}}})$. To this end we need to study the induced isomorphisms $x*\varSigma ^p(a)\rightarrow \varSigma ^p(x*a)$ and $T^p(x)*a\rightarrow \varSigma ^p(x*a)$ for all integers p. Let $\lambda '_0$ and $\rho '_0$ be the identity transformation of the functor $-*-:{{\mathcal {C}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$. For $p>0$ let

$$\begin{aligned} \lambda '_p=\varSigma ^{p-1}(\lambda '){\circ }\varSigma ^{p-2}(\lambda '){\circ }\cdots {\circ }\varSigma (\lambda '){\circ }\lambda ':-*\varSigma ^p(-)\rightarrow \varSigma ^p(-*-) \end{aligned}$$

and

$$\begin{aligned} \rho '_p=\varSigma ^{p-1}(\rho '){\circ }\varSigma ^{p-2}(\rho '){\circ }\cdots {\circ }\varSigma (\rho '){\circ }\rho ':T^p(-)*-\rightarrow \varSigma ^p(-*-). \end{aligned}$$

In particular,

$$\begin{aligned} (\lambda '_p)^{-1}:\varSigma ^p(-*\varSigma ^{-p}(-))\rightarrow -*\varSigma ^p\varSigma ^{-p}(-) \simeq -*- \end{aligned}$$

when $(\lambda '_p)^{-1}$ is starting in $\varSigma ^p(-*\varSigma ^{-p}(-))$, and therefore

$$\begin{aligned} \varSigma ^{-p}((\lambda '_p)^{-1}):-*\varSigma ^{-p}(-)\rightarrow \varSigma ^{-p}(-*-) \end{aligned}$$

for $p>0$. Let $\lambda '_{-p}=\varSigma ^{-p}((\lambda '_p)^{-1})$ for $p>0$. Similarly let

$$\begin{aligned} \rho '_{-p}=\varSigma ^{-p}((\rho '_p)^{-1}):T^{-p}(-)*-\rightarrow \varSigma ^{-p}(-*-) \end{aligned}$$

for $p>0$. With these definitions it is easy to check that

$$\begin{aligned} \varSigma ^p({\mathfrak {l}}'){\circ }\lambda '_p ={\mathfrak {l}}':e*\varSigma ^p(-)\rightarrow \varSigma ^p(-) \end{aligned}$$

(1)

and

$$\begin{aligned} \varSigma ^q(\lambda '_p){\circ }\rho '_q = (-1)^{pq} \varSigma ^p(\rho _q'){\circ }\lambda '_p :T^q(-)*\varSigma ^p(-)\rightarrow \varSigma ^{p+q}(-*-) \end{aligned}$$

(2)

for all integers p and q. This last relation corresponds to the diagram

being commutative up to the sign $(-1)^{pq}$.

Let $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ be a degree p element in ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$. Then consider the following composition of natural transformations of functors

$$\begin{aligned} {{\text {id}}}_{{\mathcal {A}}}\xrightarrow {{\mathfrak {l}}'^{-1}} {\mathfrak {e}}*-\xrightarrow {h*1} T^p({\mathfrak {e}})*- \xrightarrow {\rho _p'} \varSigma ^p({\mathfrak {e}}*-)\xrightarrow {\varSigma ^p({\mathfrak {l}}')} \varSigma ^p(-), \end{aligned}$$

which we denote by $\varphi _{{\mathcal {A}}}(h)$. We show that $\varphi _{{\mathcal {A}}}$ gives rise to a homomorphism of graded rings $\varphi _{{\mathcal {A}}}:{\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})\rightarrow Z^*({{\mathcal {A}}})$.

Proposition 2.1

The map $\varphi _{{\mathcal {A}}}:{\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})\rightarrow Z^*({{\mathcal {A}}})$ is a homomorphism of graded rings.

Proof

We need to show that $\varSigma \varphi _{{\mathcal {A}}}(h) = (-1)^p\varphi _{{\mathcal {A}}}(h)\varSigma$ for $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$. Consider the following diagram

The leftmost and the rightmost squares commute due to (1). The second square commutes since $\lambda '$ is a morphism of functors. The third square commutes up to the sign $(-1)^p$ by (2). Hence it follows that $\varphi _{{\mathcal {A}}}(h)$ is in $Z^*({{\mathcal {A}}})$. It is straightforward to check that $\varphi _{{\mathcal {A}}}$ is a homomorphism of graded rings. $\square$

Let

$$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}^*(a,b)=\amalg _{p\in {{\mathbb {Z}}}}{\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^p(b)) \end{aligned}$$

for any objects a and b in ${{\mathcal {A}}}$, and let ${\text {End}}_{{\mathcal {A}}}^*(a)={\text {Hom}}_{{\mathcal {A}}}^*(a,a)$. The homomorphism set ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is endowed with a left and a right module structure from ${\text {End}}_{{\mathcal {A}}}^*(b)$ and ${\text {End}}_{{\mathcal {A}}}^*(a)$, respectively. For each object a in ${{\mathcal {A}}}$ the evaluation at a induces a homomorphism of graded rings $\gamma _a:Z^*({{\mathcal {A}}})\rightarrow {\text {End}}_{{\mathcal {A}}}^*(a)$ given by $\gamma _a(\eta )=\eta _a:a\rightarrow \varSigma ^p(a)$ for $\eta :{{\text {id}}}_{{\mathcal {A}}}\rightarrow \varSigma ^p$ in $Z^*({{\mathcal {A}}})$. Then ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ has a left and a right $Z^*({{\mathcal {A}}})$-module structure via the ring homomorphisms $\gamma _b$ and $\gamma _a$ respectively. For completeness we recall the following.

Proposition 2.2

The action of $Z^*({{\mathcal {A}}})$ on the right and on the left of ${\text {Hom}}^*_{{\mathcal {A}}}(a,b)$ for a and b in ${{\mathcal {A}}}$ satisfies, for $\eta :{{\text {id}}}_{{\mathcal {A}}}\rightarrow \varSigma ^p$ in $Z^*({{\mathcal {A}}})$ and $f:a\rightarrow \varSigma ^q b$ in ${\text {Hom}}^*_{{\mathcal {A}}}(a,b)$, the following equality

$$\begin{aligned} \eta \cdot f = (-1)^{pq}f\cdot \eta . \end{aligned}$$

Proof

Let $\eta :{{\text {id}}}_{{\mathcal {A}}}\rightarrow \varSigma ^p$ be in $Z^*({{\mathcal {A}}})$ and $f:a\rightarrow \varSigma ^q(b)$ in ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$. Since $\eta$ is a natural transformation of functors, the following diagram commutes

As $\eta _{\varSigma ^q(b)}=(-1)^{pq}\varSigma ^q(\eta _b)$, the claim follows. $\square$

Using that a tensor triangulated category ${{\mathcal {C}}}$ acts on itself, we obtain the following immediate corollary.

Corollary 2.3

• (a) The composition

  $$\begin{aligned} {\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})\xrightarrow {\varphi _{{\mathcal {C}}}} Z^*({{\mathcal {C}}})\xrightarrow {\gamma _{\mathfrak {e}}} {\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}}) \end{aligned}$$

  of homomorphisms of graded rings is the identity.

• (b) The graded endomorphism ring ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$ is graded-commutative.

Proof

The proof of (a) is a direct computation. The claim in (b) is then an immediate consequence of Proposition 2.2. $\square$

Remark 2.4

(1) The triangulated tensor category ${{\mathcal {C}}}$ with an action on ${{\mathcal {A}}}$ can be viewed as a categorification of a central ring action, namely, a homomorphism of graded rings from a graded-commutative ring R to $Z^*({{\mathcal {A}}})$.

(2) The above gives rise to a homomorphism of graded rings $\varphi _a:{\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})\rightarrow {\text {End}}_{{\mathcal {A}}}^*(a)$ for any object a in ${{\mathcal {A}}}$ by letting $\varphi _a=\gamma _a\varphi _{{\mathcal {A}}}$. For $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$, the morphism $\varphi _a(h)$ is given as

$$\begin{aligned} a\xrightarrow {{\mathfrak {l}}'^{-1}} {\mathfrak {e}}*a\xrightarrow {h*1} T^p({\mathfrak {e}})*a\xrightarrow {\rho _p'} \varSigma ^p({\mathfrak {e}}*a)\xrightarrow {\varSigma ^p({\mathfrak {l}}')} \varSigma ^p(a). \end{aligned}$$

(3) Suppose that idempotents split in ${{\mathcal {C}}}$ and in ${{\mathcal {A}}}$. Then, if ${\text {End}}_{{\mathcal {C}}}^0({\mathfrak {e}})$ decomposes as a ring, then the categories ${{\mathcal {C}}}$ and ${{\mathcal {A}}}$ also decompose as categories. Hence we can always assume that ${{\mathcal {C}}}$ and ${{\mathcal {A}}}$ are indecomposable as categories and therefore that ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$ is indecomposable as a ring.

(4) The statement in (b) was first shown in [38, Theorem 1.7]. As pointed out in that paper, we obtain the graded-commutativity of the following graded rings (using the notation of Sect. 1 and Examples 1.2–1.7):

• (i) Let G be a finite group, and let k be a field. Then

  $$\begin{aligned} {\text {End}}^*_{{{\mathbf {D}}}(kG)}(k)=\amalg _{p\in {{\mathbb {Z}}}}{\text {Hom}}_{{{\mathbf {D}}}(kG)}(k,k[p]) \simeq \amalg _{p\geqslant 0} {\text {Ext}}^p_{kG}(k,k), \end{aligned}$$

  is the group cohomology ring of G. Also

  $$\begin{aligned} {\text {End}}^*_{{\underline{{\text {Mod}}}}kG}(k)=\amalg _{p\in {{\mathbb {Z}}}}{\underline{{\text {Hom}}}}_{kG}(k,\varOmega _{kG}^{-p}(k)) \simeq {\widehat{{\text {Ext}}}}^*_{kG}(k,k), \end{aligned}$$

  is the Tate cohomology ring of G.

• (ii) Let H be a Hopf algebra over a field k. Then

  $$\begin{aligned} {\text {End}}^*_{{{\mathbf {D}}}(H)}(k)=\amalg _{p\in {{\mathbb {Z}}}}{\text {Hom}}_{{{\mathbf {D}}}(H)}(k,k[p]) \simeq \amalg _{p\geqslant 0} {\text {Ext}}^p_H(k,k), \end{aligned}$$

  is the cohomology ring of k over H. Also

  $$\begin{aligned} {\text {End}}^*_{{\underline{{\text {Mod}}}}H}(k)=\amalg _{p\in {{\mathbb {Z}}}}{\underline{{\text {Hom}}}}_H(k,\varOmega _H^{-p}(k)) \simeq {\widehat{{\text {Ext}}}}^*_H(k,k), \end{aligned}$$

  is the Tate cohomology ring of k over H.

• (iii) Let $\varLambda$ be an algebra over a field k. Then

  $$\begin{aligned} {\text {End}}^*_{{{\mathbf {D}}}(\varLambda ^e)}(\varLambda )=\amalg _{p\in {{\mathbb {Z}}}}{\text {Hom}}_{{{\mathbf {D}}}(\varLambda ^e)}(\varLambda ,\varLambda [p]) \simeq \amalg _{p\geqslant 0} {\text {Ext}}^p_{\varLambda ^e}(\varLambda ,\varLambda ), \end{aligned}$$

  is the Hochschild cohomology ring of $\varLambda$ over k. Also, if $\varLambda$ is selfinjective,

  $$\begin{aligned} {\text {End}}^*_{{\underline{{{\mathcal {B}}}}}}(\varLambda )=\amalg _{p\in {{\mathbb {Z}}}}{\underline{{\text {Hom}}}}_{\varLambda ^e}(\varLambda , \varOmega _{\varLambda ^e}^{-p}(\varLambda )) \simeq {\widehat{{\text {Ext}}}}^*_{\varLambda ^e}(\varLambda ,\varLambda ), \end{aligned}$$

  is the Tate cohomology ring of $\varLambda$ over $\varLambda ^e$.

4 Support varieties

Throughout this section ${{\mathcal {C}}}=({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}},T,\lambda ,\rho )$ is a triangulated tensor category acting on a small triangulated category ${{\mathcal {A}}}=({{\mathcal {A}}},\varSigma )$. Let H be a positively graded and graded-commutative ring with a homomorphism of graded rings $H\rightarrow {\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$. As mentioned earlier this gives rise to a theory of support varieties in ${\text {Spec}}H$, where ${\text {Spec}}H$ is the set of all homogeneous prime ideals in H. We begin this section by pointing out the standard properties of these support varieties. We then give realizability results for closed homogeneous subvarieties of varieties of given objects and possible generators for ${{\mathcal {A}}}$.

In order to obtain our results, further assumptions are needed. So the following are our standing assumptions.

Assumption 3.1

For ${{\mathcal {C}}}$, ${{\mathcal {A}}}$ and H the following holds:

• (1) ${{\mathcal {C}}}=({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}},T,\lambda ,\rho )$ is a triangulated tensor category acting on a small triangulated category ${{\mathcal {A}}}=({{\mathcal {A}}},\varSigma )$.

• (2) H is a positively graded-commutative Noetherian ring with a homomorphism of graded rings $H\rightarrow {\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$.

• (3) The left H-module ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is finitely generated for all objects a, b in ${{\mathcal {A}}}$.

If the graded ring H has a non-trivial idempotent f in degree zero, and for some object a in ${{\mathcal {A}}}$ we have both $f*1_a$ and $(1_H - f)*1_a$ non-zero, then assuming that idempotents split in ${{\mathcal {A}}}$, one can show that the category ${{\mathcal {A}}}$ decomposes. Hence, in this case, we can assume that the graded ring H has only trivial idempotents in degree zero. We sometimes assume a stronger condition, namely that $H^0$ is a local ring.

In general the graded endomorphism ring ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$ need not be a positively graded ring making ${\text {Spec}}{\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$ a more difficult object to handle than ${\text {Spec}}H$. One could use the positive part ${\text {End}}_{{\mathcal {C}}}^{\geqslant 0}({\mathfrak {e}})$ of ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$ instead of some graded-commutative ring H. However, there are situations where assuming finite generation over H or over ${\text {End}}_{{\mathcal {C}}}^{\geqslant 0}({\mathfrak {e}})$, are equivalent, which we now demonstrate.

Having ${{\mathcal {C}}}$ acting on ${{\mathcal {A}}}$ gives rise to a functor from ${{\mathcal {C}}}$ to the endofunctors of ${{\mathcal {A}}}$. A necessary condition related for this functor to have a right adjoint, is as pointed out in [26], that each functor $-*a:{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ has a right adjoint, that is, there is a functor ${{\mathcal {A}}}\rightarrow {{\mathcal {C}}}$ for each object a in ${{\mathcal {A}}}$, denoted $F''(a,-)$ and an isomorphism

$$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}(x*a,b)\rightarrow {\text {Hom}}_{{\mathcal {C}}}(x,F''(a,b)), \end{aligned}$$

natural in all three variables. Having such a right adjoint induces an isomorphism ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)\simeq {\text {Hom}}_{{\mathcal {C}}}^*({\mathfrak {e}},F''(a,b))$ of ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$-modules. In some situations there are objects a and b in ${{\mathcal {A}}}$ such that ${\mathfrak {e}}$ is in the thick triangulated subcategory generated by $F''(a,b)$ in ${{\mathcal {C}}}$. Therefore, if ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is finitely generated for some positively graded commutative Noetherian ring H, then ${\text {End}}_{{\mathcal {C}}}^{\geqslant 0}({\mathfrak {e}})$ (also ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$) is Noetherian too. A further discussion on such functors $F''$, called function objects, can be found in Sect. 5. A classical isomorphism, which gives rise to such a function object, is the adjunction isomorphism

$$\begin{aligned} {\text {Hom}}_\varLambda (B\otimes _\varLambda M,N)\simeq {\text {Hom}}_{\varLambda ^e}(B,{\text {Hom}}_k(M,N)) \end{aligned}$$

for a k-algebra $\varLambda$, where B is a $\varLambda ^e$-module, and M and N are $\varLambda$-modules.

Now we give the definition of the support variety of a pair of objects (a, b) in ${{\mathcal {A}}}$.

Definition 3.2

For a pair of objects a and b in ${{\mathcal {A}}}$, the support variety V(a, b) of (a, b) with respect to H is given by

$$\begin{aligned} V(a,b)=\{{\mathfrak {p}}\in {\text {Spec}}H\mid {\text {Hom}}_{{\mathcal {A}}}^*(a,b)_{\mathfrak {p}}\ne (0)\} = {\text {Supp}}({\text {Hom}}_{{\mathcal {A}}}^*(a,b)). \end{aligned}$$

Proposition 2.2 implies that the annihilator ${\text {Ann}}_H{\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ of ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ as an H-module for any objects a and b in ${{\mathcal {A}}}$, is independent of viewing ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ as a left or as a right H-module. We denote this annihilator by A(a, b). For a graded ideal I in H we denote by $V(I)={\text {Supp}}(H/I)$.

The following properties of the support variety are standard and straightforward to verify, and we leave the proofs to the reader.

Proposition 3.3

The support variety $V(-,-)$ has the following properties:

• (a) Let $a_1\rightarrow a_2\rightarrow a_3\rightarrow \varSigma (a_1)$ be a triangle in ${{\mathcal {A}}}$. Let a be an object in ${{\mathcal {A}}}$.

  • (i) $V(a,a_r) \subseteq V(a,a_s)\cup V(a,a_t)$ whenever $\{r,s,t\}=\{1,2,3\}$.

  • (ii) $V(a_r,a) \subseteq V(a_s,a)\cup V(a_t,a)$ whenever $\{r,s,t\}=\{1,2,3\}$.

• (b) $V(a,b)=V(\varSigma ^i(a),\varSigma ^j(b))$ for any pair of objects (a, b) in ${{\mathcal {A}}}$ and integers i and j in ${{\mathbb {Z}}}$.

• (c) Let $\{a_i\}_{i=1}^r$ and $\{b_j\}_{j=1}^s$ be two finite sets of objects in ${{\mathcal {A}}}$. Then

  $$\begin{aligned} V(\amalg _{i=1}^r a_i,\amalg _{j=1}^s b_j)=\cup _{i,j=1}^{r,s} V(a_i,b_j). \end{aligned}$$

  $\square$

Since the action of H on ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ factors through the action of H on both ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$ and ${\text {Hom}}_{{\mathcal {A}}}^*(b,b)$ for any pair of objects a and b in ${{\mathcal {A}}}$, the following result is immediate.

Proposition 3.4

Let a and b be objects in ${{\mathcal {A}}}$.

• (a) $V(a,b) \subseteq V(a,a)\cap V(b,b)$.

• (b) $V(a,a) = \cup _{x\in {{\mathcal {A}}}}V(a,x) = \cup _{x\in {{\mathcal {A}}}} V(x,a)$. $\square$

Having these properties at hand we define the support variety of an object a in ${{\mathcal {A}}}$ to be $V(a)=V(a,a)$. The properties above give the following behaviour.

Proposition 3.5

The support variety $V(-)$ has the following properties:

• (a) If $a_1\rightarrow a_2\rightarrow a_3\rightarrow \varSigma (a_1)$ is an exact triangle in ${{\mathcal {A}}}$, then $V(a_r)\subseteq V(a_s)\cup V(a_t)$ whenever $\{r,s,t\}=\{1,2,3\}$.

• (b) $V(a)=V(\varSigma ^i(a))$ for all objects a in ${{\mathcal {A}}}$ and i in ${{\mathbb {Z}}}$.

• (c) $V(\amalg _{i=1}^n a_i)=\cup _{i=1}^n V(a_i)$.$\square$

Our next aim is to show that any closed homogeneous subvariety of the variety of an object a in ${{\mathcal {A}}}$ occurs as a variety of an object in ${{\mathcal {A}}}$. In doing so the construction of Koszul objects is crucial (see [24, §6]). Any morphism $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ induces for any object a in ${{\mathcal {A}}}$ a morphism

$$\begin{aligned} h* 1_a:{\mathfrak {e}}*a \rightarrow T^p({\mathfrak {e}})*a \end{aligned}$$

which we can identify with

$$\begin{aligned} h\cdot 1_a:a\simeq {\mathfrak {e}}*a\xrightarrow {h*1_a} T^p({\mathfrak {e}})*a\simeq \varSigma ^p({\mathfrak {e}}*a)\simeq \varSigma ^p(a). \end{aligned}$$

Complete this morphism to a triangle

$$\begin{aligned} a \xrightarrow {h\cdot 1_a} \varSigma ^p(a)\rightarrow a/\!\!/h\rightarrow \varSigma (a) \end{aligned}$$

in ${{\mathcal {A}}}$. An immediate consequence of the above construction is that the Koszul object $a/\!\!/h$ is in the thick subcategory generated by a in ${{\mathcal {A}}}$ for all homogeneous elements h in H. Moreover, as we also note below, $V(a/\!\!/h)\subseteq V(a)$.

Using the triangle $a\xrightarrow {h\cdot 1_a} \varSigma ^p(a) \rightarrow a/\!\!/h \rightarrow \varSigma (a)$ we have the following.

Proposition 3.6

Let $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ be in ${{\mathcal {C}}}$. Then the following assertions hold.

• (a) If h is in A(a, a), then $\varSigma (a)\amalg \varSigma ^p(a)\simeq a/\!\!/h$.

• (b) If $\{ h_1,h_2,\ldots ,h_t\}$ is in A(a, a), then $\varSigma ^t(a)$ is a direct summand of

  $$\begin{aligned}(\cdots ((a/\!\!/h_1)/\!\!/h_2)\cdots )/\!\!/h_t.\end{aligned}$$

• (c) $V(a/\!\!/h) \subseteq V(a)$.

• (d) The element $h^2$ is in $A(a/\!\!/h,a/\!\!/h)$. In particular,

  $$\begin{aligned}V(a/\!\!/h)\subseteq V(\langle h\rangle )\cap V(a).\end{aligned}$$

Proof

(a) This follows immediately from the triangle we constructed above.

(b) Repeated use of (a) shows this.

(c) We have the triangle $\varSigma ^p(a)\rightarrow a/\!\!/h\rightarrow \varSigma (a)\rightarrow \varSigma ^{p+1}(a)$ in ${{\mathcal {A}}}$. By Proposition 3.5 we infer that $V(a/\!\!/h)\subseteq V(\varSigma ^p(a))\cup V(\varSigma (a))=V(a)$.

(d) From the triangle $a\xrightarrow {h\cdot 1_a} \varSigma ^p(a)\rightarrow a/\!\!/h\rightarrow \varSigma (a)$ in ${{\mathcal {A}}}$ we get the exact sequence

$$\begin{aligned}&{\text {Hom}}_{{\mathcal {A}}}^*(b,a) \xrightarrow {{\text {Hom}}_{{\mathcal {A}}}(b,(h\cdot 1_a))} {\text {Hom}}_{{\mathcal {A}}}^*(b,\varSigma ^p(a))\\&\quad \rightarrow {\text {Hom}}_{{\mathcal {A}}}^*(b,a/\!\!/h)\rightarrow {\text {Hom}}_{{\mathcal {A}}}^*(b,\varSigma (a)) \end{aligned}$$

for all objects b in ${{\mathcal {A}}}$. A straightforward calculation shows that the map

$$\begin{aligned}{\text {Hom}}_{{\mathcal {A}}}(b,(h\cdot 1_a)):{\text {Hom}}_{{\mathcal {A}}}^*(b,a)\rightarrow {\text {Hom}}_{{\mathcal {A}}}^*(b,\varSigma ^p(a)) \end{aligned}$$

is given by multiplication by h from the left (up to sign). Since ${\text {Hom}}_{{\mathcal {A}}}^*(b,\varSigma ^p(a))={\text {Hom}}_{{\mathcal {A}}}^*(b,a)$, we obtain the exact sequence

$$\begin{aligned}0\rightarrow {\text {Hom}}_{{\mathcal {A}}}^*(b,a)/h\cdot {\text {Hom}}_{{\mathcal {A}}}^*(b,a) \rightarrow {\text {Hom}}_{{\mathcal {A}}}^*(b,a/\!\!/h)\rightarrow {\text {Ker}}(h\cdot -|_{{\text {Hom}}_{{\mathcal {A}}}^*(b,a)})\rightarrow 0,\end{aligned}$$

so that $h^2\cdot {\text {Hom}}_{{\mathcal {A}}}^*(b,a/\!\!/h)=(0)$ for all objects b in ${{\mathcal {A}}}$. It follows that $V(a/\!\!/h)\subseteq V(\langle h\rangle )\cap V(a)$.

If we impose the following extra condition on the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$,

• (4) The functor $-*a:{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ is an exact functor for all objects a in ${{\mathcal {A}}}$. In this case the action is said to be compatible with the triangulation in ${{\mathcal {C}}}$,

then we get an additional way of viewing $a/\!\!/h$. Given the morphism $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ in ${{\mathcal {C}}}$, complete it to a triangle

$$\begin{aligned} {\mathfrak {e}}\xrightarrow {h} T^p({\mathfrak {e}}) \rightarrow {\mathfrak {e}}/\!\!/h\rightarrow T({\mathfrak {e}}) \end{aligned}$$

in ${{\mathcal {C}}}$. Here ${\mathfrak {e}}/\!\!/h$ is unique up to a non-unique isomorphism. For any object a in ${{\mathcal {A}}}$ we get a commutative diagram in ${{\mathcal {A}}}$, where the upper and the lower rows are triangles in ${{\mathcal {A}}}$.

Since the two first vertical maps are isomorphisms, it follows that $({\mathfrak {e}}/\!\!/h)*a\simeq a/\!\!/h$.

Computing the support variety of $a/\!\!/h$ is the key to our main result in this section. The proof is similar to the analogous result in [19, Proposition 4.3]. Next we show that the inclusion in (d) above actually is an equality.

Proposition 3.7

Let $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ be in H. Then for any object a in ${{\mathcal {A}}}$

$$\begin{aligned} V(a/\!\!/h)=V(\langle h\rangle )\cap V(a). \end{aligned}$$

Proof

Choose a prime ideal ${\mathfrak {p}}$ in ${\text {Spec}}H$ lying over $\langle h,A(a,a)\rangle$. Suppose that $\cap _{b\in {{\mathcal {A}}}}A(b,a/\!\!/h)$ is not contained in ${\mathfrak {p}}$. Then $({\text {Hom}}_{{\mathcal {A}}}^*(b,a/\!\!/h))_{{\mathfrak {p}}}=(0)$ for all objects b in ${{\mathcal {A}}}$. From the short exact sequence in the proof of the previous result, we infer that

$$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}^*(b,a)_{{\mathfrak {p}}}=h\cdot {\text {Hom}}_{{\mathcal {A}}}^*(b,a)_{{\mathfrak {p}}}. \end{aligned}$$

Since ${\text {Hom}}_{{\mathcal {A}}}^*(b,a)_{{\mathfrak {p}}}$ is a finitely generated $H_{{\mathfrak {p}}}$-module and h is in ${\mathfrak {p}}H_{{\mathfrak {p}}}$, the Nakayama Lemma implies that ${\text {Hom}}_{{\mathcal {A}}}^*(b,a)_{{\mathfrak {p}}}=(0)$. As ${\text {Hom}}_{{\mathcal {A}}}^*(b,a)$ is a finitely generated H-module, the ideal A(b, a) is not contained in ${\mathfrak {p}}$ for all objects b in ${{\mathcal {A}}}$. In particular, A(a, a) is not contained in ${\mathfrak {p}}$. This is a contradiction by the choice of ${\mathfrak {p}}$, hence $\cap _{b\in {{\mathcal {A}}}}A(b,a/\!\!/h)=A(a/\!\!/h, a/\!\!/h)$ is contained in ${\mathfrak {p}}$. It follows that $V(\langle h\rangle )\cap V(a)\subseteq V(a/\!\!/h)$. This completes the proof using the previous result. $\square$

Our main result of this section now follows directly from the above.

Theorem 3.8

• (a) Let a be an object in ${{\mathcal {A}}}$. Then any closed homogeneous subvariety of V(a) occurs as the variety of some object in ${{\mathcal {A}}}$.

• (b) Suppose that ${{\mathcal {A}}}$ has a generator ${\mathfrak {g}}$ in the sense that ${{\mathcal {A}}}={\text {Thick}}({\mathfrak {g}})$. Then any closed homogeneous subvariety of $V({\mathfrak {g}})$ occurs as the variety of some object in ${{\mathcal {A}}}$. $\square$

5 Complexity and perfect and periodic objects

Throughout this section we keep the setup from the previous section. Thus we fix a triangulated tensor category ${{\mathcal {C}}}$ acting on a triangulated category ${{\mathcal {A}}}$ and a ring H satisfying Assumption 3.1.

In this context we define the class of perfect objects as the objects with support variety contained in $V(H^+)$ with $H^+=\langle \sqrt{0_{H^0}}, H^{\geqslant 1}\rangle$, where $\sqrt{0_{H^0}}$ is the nilradical of $H^0$. We introduce a notion of complexity of objects in ${{\mathcal {A}}}$, and we characterize the perfect objects as those being of complexity 0. We also define and characterize periodic objects in terms of complexity when $H^0$ is a local ring.

First we discuss the concept of complexity of objects in ${{\mathcal {A}}}$. Condition (2) is equivalent to $R=H^0$ being a (commutative) Noetherian ring and H being a finitely generated (graded-commutative) graded algebra over R (as for commutative graded rings). It follows from this that each graded part $H^i$ of H is a finitely generated R-module. Condition (3) says that any ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is a finitely generated H-module for all objects a and b in ${{\mathcal {A}}}$, hence ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(b))$ is a finitely generated R-module for all objects a and b in ${{\mathcal {A}}}$ and all i in ${{\mathbb {Z}}}$. For a finitely generated S-module M, denote by ${{\text {mingen}}}_S(M)$ the minimal number of generators as an S-module. Then we define the complexity of an object in ${{\mathcal {A}}}$ as follows.

Definition 4.1

The complexity${{\text {cx}}}(a)$ of an object a in ${{\mathcal {A}}}$ is given by

$$\begin{aligned}&\min \{ s\in \mathbb {N}_0\mid \forall \, b\in {{\mathcal {A}}}, \exists \, r_b\in \mathbb {R};\\&\quad {{\text {mingen}}}_R \left( {\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^n(b))\right) \leqslant r_b|n|^{s-1}, \forall \, |n|\gg 0\}, \end{aligned}$$

if such $r_b$ and s exist for all objects b in ${{\mathcal {A}}}$. Otherwise we set ${{\text {cx}}}(a)=\infty$.

Note that since (3) ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is a finitely generated H-module for all objects a and b in ${{\mathcal {A}}}$ and (2) H is graded-commutative and Noetherian, we have that the complexity is bounded by the polynomial growth of the graded parts of H as R-modules, which is finite. In addition, since ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is a finitely generated ${\text {End}}_{{\mathcal {A}}}^*(a)$-module, the complexity of a is bounded, and therefore equal to

$$\begin{aligned} \min \{ s\in \mathbb {N}_0\mid \exists \, r\in \mathbb {R}; {{\text {mingen}}}_R \left( {\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^n(a))\right) \leqslant r|n|^{s-1}, \forall \, |n|\gg 0\}. \end{aligned}$$

We collect some elementary properties of the complexity of objects next, where we leave the proofs to the reader.

Proposition 4.2

• (a) ${{\text {cx}}}(a)={{\text {cx}}}(\varSigma ^i(a))$ for all objects a in ${{\mathcal {A}}}$ and all integers i.

• (b) ${{\text {cx}}}(a\amalg b)=\max \{{{\text {cx}}}(a),{{\text {cx}}}(b)\}$ for all objects a and b in ${{\mathcal {A}}}$.

• (c) If $a_1\rightarrow a_2\rightarrow a_3\rightarrow \varSigma (a_1)$ is a triangle in ${{\mathcal {A}}}$, then

  $$\begin{aligned}{{\text {cx}}}(a_2)\leqslant \max \{{{\text {cx}}}(a_1),{{\text {cx}}}(a_3)\}.\end{aligned}$$

  $\square$

One of the focal points in this section is the following notion of a perfect object.

Definition 4.3

An object a in ${{\mathcal {A}}}$ is a perfect object if $V(a)\subseteq V(H^+)$.

Now we characterize the perfect objects as those of complexity zero.

Proposition 4.4

Let a be in ${{\mathcal {A}}}$. Then the following are equivalent.

• (a) a is perfect object in ${{\mathcal {A}}}$.

• (b) ${{\text {cx}}}(a)=0$.

• (c) $\forall \, b\in {{\mathcal {A}}}, \exists \, n_b\in \mathbb {N}$ such that ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(b))=(0)$ for $|i|\geqslant n_b$.

• (d) $\forall \, b\in {{\mathcal {A}}}, \exists \, m_b\in \mathbb {N}$ such that ${\text {Hom}}_{{\mathcal {A}}}(b,\varSigma ^i(a))=(0)$ for $|i|\geqslant m_b$.

Proof

(b) implies (c): assume that ${{\text {cx}}}(a)=0$. This means that for all b in ${{\mathcal {A}}}$ there exists $r_b$ in $\mathbb {R}$ such that ${{\text {mingen}}}_R\left( {\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^n(b))\right) \leqslant r_b|n|^{-1}$ for all n with $|n|\gg 0$. This implies in turn that for all b in ${{\mathcal {A}}}$ there exists $n_b$ in $\mathbb {N}$ such that ${{\text {mingen}}}_R{\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^n(b))=(0)$ for all n such that $|n|\geqslant n_b$, which is the statement of (c).

(c) implies (b): it follows immediately from the definition that ${{\text {cx}}}(a)=0$.

(c) implies (d): suppose that (c) holds. In particular, ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(a))=(0)$ for all i such that $|i|\geqslant n_a$ for some integer $n_a$. Fix an object b in ${{\mathcal {A}}}$. Since ${\text {Hom}}_{{\mathcal {A}}}^*(b,a)$ is a finitely generated module over ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$, say generated in degrees $r_1<r_2<\cdots <r_t$ as a module over ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$, then we have that ${\text {Hom}}_{{\mathcal {A}}}(b,\varSigma ^i(a))=(0)$ for $i< r_1-n_a$ and for $i> r_t+n_a$. The number $m_b=\max \{|r_1-n_a|, |r_t+n_1|\}+1$ depends only on b (when a is fixed), and this number makes (d) hold true.

(d) implies (a): suppose that for all b in ${{\mathcal {A}}}$ there exists $m_b$ in $\mathbb {N}$ such that ${\text {Hom}}_{{\mathcal {A}}}(b,\varSigma ^i(a))=(0)$ for all i with $|i|\geqslant m_b$. In particular, ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(a))=(0)$ for all i with $|i|\geqslant m_a$. Then $H^{\geqslant m_a}$ is in A(a, a). Since $\sqrt{H^{\geqslant m_a}}=H^+$, it follows that $V(a)\subseteq V(H^+)$ and a is a perfect object.

(a) implies (c): suppose that a is a perfect object in ${{\mathcal {A}}}$. Then $H^+\subseteq \sqrt{A(a,a)}$. Since H is a finitely generated algebra over R, we infer that $H^{\geqslant N}\subseteq A(a,a)$ for some integer N and ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$ is a finitely generated $H/H^{\geqslant N}$-module. Hence ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(a))=(0)$ for all i with $|i|\geqslant n_a$ for some integer $n_a$. Since ${\text {Hom}}_{{\mathcal {A}}}^*(a,b)$ is a finitely generated module over ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$ for all objects b in ${{\mathcal {A}}}$, it follows that there exists for all b in ${{\mathcal {A}}}$ an integer $n_b$ such that ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(b))=(0)$ for all i with $|i|\geqslant n_b$. Hence we have proved (c). This completes the proof of the proposition. $\square$

Remark 4.5

If the triangulated category ${{\mathcal {A}}}$ has a generator ${\mathfrak {g}}$ in the sense that ${{\mathcal {A}}}={\text {Thick}}({\mathfrak {g}})$, all of the above can be reformulated in terms of ${\mathfrak {g}}$ instead of for all objects b in ${{\mathcal {A}}}$.

We denote the full subcategory of ${{\mathcal {A}}}$ consisting of the perfect objects by ${{\mathcal {A}}}^{{\text {perf}}}$. The subcategory ${{\mathcal {A}}}^{{\text {perf}}}$ is a thick subcategory of ${{\mathcal {A}}}$, so we can form the Verdier quotient ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$. Using this quotient we can define periodic objects as follows.

Definition 4.6

An object a in ${{\mathcal {A}}}$ is periodic of periodn if a is not perfect and $a\simeq \varSigma ^n(a)$ in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$ for some positive integer n, where n is smallest possible.

We have the following characterization of periodic objects.

Proposition 4.7

Assume that $R=H^0$ is a local ring. Let a be an object in ${{\mathcal {A}}}$. Then a is a periodic object if and only if ${{\text {cx}}}(a)=1$.

Proof

Suppose that a is a periodic object in ${{\mathcal {A}}}$, say $a\simeq \varSigma ^n(a)$ in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$ for some non-zero integer n. This means that there exist exact triangles in ${{\mathcal {A}}}$ of the form $a'\rightarrow a\rightarrow p\rightarrow \varSigma (a')$ and $a'\rightarrow \varSigma ^n(a)\rightarrow p'\rightarrow \varSigma (a')$ for some perfect objects p and $p'$. It follows that for $|i|\gg 0$ we have that ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(a))\simeq {\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^{i+n}(a))$ and hence that ${{\text {cx}}}(a)\leqslant 1$. Since a is not perfect, that is, ${{\text {cx}}}(a)\geqslant 1$, we infer that ${{\text {cx}}}(a)=1$.

Conversely, suppose that ${{\text {cx}}}(a)=1$ and let $R=H^0$ be a local ring with maximal ideal ${\mathfrak {m}}$. Let ${\overline{H}}=H\otimes _R R/{\mathfrak {m}}$, which is a homomorphic image of H and hence Noetherian. Let $X={\text {Hom}}^*_{{\mathcal {A}}}(a,a)\otimes _R R/{\mathfrak {m}}$, which is a finitely generated ${\overline{H}}$-module and consequently Noetherian, since ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$ is a finitely generated H-module. Denote the inclusion map $H^{+}\hookrightarrow H$ by $\nu$, and $\overline{H^+}={\text {Im}}(\nu \otimes _R 1_{R/{\mathfrak {m}}})={\overline{H}}^{\geqslant 1}\subset {\overline{H}}$. Consider the ${\overline{H}}$-submodule

$$\begin{aligned} (0:_X \overline{H^+})= \{ x\in X\mid \overline{H^+}x=(0)\} \end{aligned}$$

of X, which is a finitely generated ${\overline{H}}$-module. Since $\overline{H^+}\cdot (0:_X \overline{H^+})=(0)$, the module $(0:_X \overline{H^+})$ is a finitely generated $R/{\mathfrak {m}}$-module as ${\overline{H}}/\overline{H^+}\simeq R/{\mathfrak {m}}$. This implies that $(0:_X \overline{H^+})$ only lives in a finite number of degrees. Hence there exists an integer w such that $(0:_X \overline{H^+})_i=(0)$ for $i\geqslant w$. Since H is positively graded and ${\text {Hom}}_{{\mathcal {A}}}^*(a,a)$ is a finitely generated H-module, ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(a))=(0)$ for $i \ll 0$. Therefore, since ${{\text {cx}}}(a)=1$, we infer that ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(a))\ne (0)$ for infinitely many $i\gg 0$. This implies that $X_{\geqslant w}\ne (0)$, and the set of associated primes ${\text {Ass}}_{{\overline{H}}} X_{\geqslant w}$ is a finite set consisting of graded prime ideals. The union of these primes is the set of homogeneous zero-divisors on $X_{\geqslant w}$. If $\overline{H^+}\subseteq {\mathfrak {p}}$ for some graded prime in ${\text {Ass}}_{{\overline{H}}} X_{\geqslant w}$, it follows that $\overline{H^+}$ annihilates some non-zero element of $X_{\geqslant w}$, which is a contradiction by the choice of w. We conclude that $\overline{H^+}$ is not contained in any of the prime ideals in ${\text {Ass}}_{{\overline{H}}} X_{\geqslant w}$. The Prime Avoidance Lemma implies that there exists a homogeneous $X_{\geqslant w}$-regular element $h'$ in $\overline{H^+}$, that is, $X_i\xrightarrow {h'} X_{i+|h'|}$ is an $(R/{\mathfrak {m}})$-monomorphism for $i\geqslant w$. This gives rise to the following commutative diagram

where h is an inverse image of $h'$ in H. Since ${{\text {cx}}}(a)=1$, there is a positive integer $r_a$ and epimorphisms of R-modules $R^{r_a}\rightarrow {\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^n(a))$ for n with $|n|\gg 0$. This shows that the dimension of the $R/{\mathfrak {m}}$-vectorspaces ${\text {Hom}}_{{\mathcal {A}}}^i(a,a)\otimes _R R/{\mathfrak {m}}$ are bounded by $r_a$ for $|i|\gg 0$. Hence the induced maps

$$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}^i(a,a)\otimes _R R/{\mathfrak {m}}\xrightarrow {h'} {\text {Hom}}_{{\mathcal {A}}}^{i+|h'|}(a,a)\otimes _R R/{\mathfrak {m}}\end{aligned}$$

are isomorphisms for $|i|\gg 0$. Since each graded piece ${\text {Hom}}_{{\mathcal {A}}}^i(a,a)$ is a finitely generated R-module, it follows from the commutative diagram above that the map ${\text {Hom}}_{{\mathcal {A}}}^i(a,a)\xrightarrow {h} {\text {Hom}}_{{\mathcal {A}}}^{i+|h|}(a,a)$ is an epimorphism for all $|i|\gg 0$. Let $M_t= {\text {Hom}}_{{\mathcal {A}}}^{\geqslant N+(t-1)|h|}(a,a)$ for integers t and N. Consider the map $M_t\xrightarrow {h\cdot -} M_{t+1}$. We have the commutative diagram

for some $N\gg 0$. Since $M_t$ is a finitely generated H-module for all t and H is Noetherian, there exists an integer L such that $M_t\xrightarrow {h\cdot -} M_{t+1}$ is an isomorphism for all $t\geqslant L$. Using the triangle $a\xrightarrow {h\cdot -} \varSigma ^{|h|}(a)\rightarrow a/\!\!/h\rightarrow \varSigma (a)$ and the long exact sequence induced from it, it follows that ${\text {Hom}}_{{\mathcal {A}}}^i(a,a/\!\!/h)=(0)$ for $|i|\gg 0$. Since $a/\!\!/h$ is in the thick subcategory generated by a, we infer that ${\text {Hom}}_{{\mathcal {A}}}^i(a/\!\!/h,a/\!\!/h)=(0)$ for $|i|\gg 0$ and ${{\text {cx}}}(a/\!\!/h)=0$. It then follows that $a/\!\!/h$ is a perfect object and that a is a periodic object in ${{\mathcal {A}}}$. $\square$

6 Function objects

Let us begin with explaining one example of a function object. Let ${{\mathcal {C}}}$ be the triangulated tensor category $({{\mathbf {D}}}^-(\varLambda ^e),-\otimes ^{\mathbb {L}}_\varLambda -,\varLambda )$ for a finite dimensional k-algebra $\varLambda$ where k is a field, and let ${{\mathcal {A}}}={{\mathbf {D}}}^-({\text {mod}}\varLambda )$. Then ${{\mathcal {C}}}$ acts on ${{\mathcal {A}}}$, and we have that

$$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}(B\otimes _\varLambda ^{\mathbb {L}}A,C) \simeq {\text {Hom}}_{{\mathcal {A}}}(A,\mathbb {R}{\text {Hom}}_\varLambda (B,C)) \end{aligned}$$

for all objects A and C in ${{\mathcal {A}}}$ and B in ${{\mathcal {C}}}$. Then $\mathbb {R}{\text {Hom}}_\varLambda (-,-):{{\mathcal {C}}}^{{\text {op}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ is called a left function object for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$. This section is devoted to recalling the definition of and giving some elementary properties of such function objects. In the next section we discuss the theory of support when the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ has a left function object.

Throughout this section let ${{\mathcal {C}}}=({{\mathcal {C}}},\otimes ,{\mathfrak {e}},{\mathfrak {a}},{\mathfrak {l}},{\mathfrak {r}},T,\lambda ,\rho )$ be a triangulated tensor category acting on a small triangulated category ${{\mathcal {A}}}=({{\mathcal {A}}},\varSigma )$. First we give the definition of a left function object for an action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$.

Definition 5.1

• (a) A left function object$F'$ for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ is a functor $F':{{\mathcal {C}}}^{{\text {op}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ such that

  • (i) $F'(x,-):{{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ is a covariant functor for each object x in ${{\mathcal {C}}}$.

  • (ii) $F'(-,a):{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ is a contravariant functor for each object a in ${{\mathcal {A}}}$.

  • (iii) there is an isomorphism

    $$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}(x*a,b)\rightarrow {\text {Hom}}_{{\mathcal {A}}}(a,F'(x,b)) \end{aligned}$$

    natural in all three variables.

• (b) A left function object $F':{{\mathcal {C}}}^{{\text {op}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ is compatible

  • (i) with the triangulation of${{\mathcal {C}}}$ if for each triangle $x\xrightarrow {u} y\xrightarrow {v} z\xrightarrow {w} T(x)$ in ${{\mathcal {C}}}$ and each object a in ${{\mathcal {A}}}$, then

    $$\begin{aligned} F'(T(x),a)\xrightarrow {-F'(w,1)} F'(z,a)\xrightarrow {F'(v,1)} F'(y,a)\xrightarrow {F'(u,1)} F'(x,a) \end{aligned}$$

    is a triangle in ${{\mathcal {A}}}$.

  • (ii) with the triangulation of${{\mathcal {A}}}$ if for each triangle $a\xrightarrow {u} b\xrightarrow {v} c\xrightarrow {w} \varSigma (a)$ in ${{\mathcal {A}}}$ and each object x in ${{\mathcal {C}}}$, then

    $$\begin{aligned} F'(x,a)\xrightarrow {F'(1,u)} F'(x,b)\xrightarrow {F'(1,v)} F'(x,c)\xrightarrow {F'(1,w)} F'(x,\varSigma (a)) \end{aligned}$$

    is a triangle in ${{\mathcal {A}}}$.

In Sect. 3 we briefly discussed one occurrence of a right function object in connection with the assumptions of the setup for support varieties via the action of the graded endomorphism ring ${\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})$. Next we give the precise definition of these function objects.

Definition 5.2

• (a) A right function object$F''$ for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ is a functor $F'':{{\mathcal {A}}}^{{\text {op}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {C}}}$ such that

  • (i) $F''(a,-):{{\mathcal {A}}}\rightarrow {{\mathcal {C}}}$ is a covariant functor for each object a in ${{\mathcal {A}}}$.

  • (ii) $F''(-,a):{{\mathcal {A}}}^{{\text {op}}}\rightarrow {{\mathcal {C}}}$ is a contravariant functor for each object a in ${{\mathcal {A}}}$.

  • (iii) there is an isomorphism

    $$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}(x*a,b)\rightarrow {\text {Hom}}_{{\mathcal {C}}}(x,F''(a,b)) \end{aligned}$$

    natural in all three variables.

• (b) A right function object $F'':{{\mathcal {A}}}^{{\text {op}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {C}}}$ is compatible with the triangulation of${{\mathcal {A}}}$

  • (i) if for each triangle $x\xrightarrow {u} y\xrightarrow {v} z\xrightarrow {w} \varSigma (x)$ in ${{\mathcal {A}}}$ and each object a in ${{\mathcal {A}}}$, then

    $$\begin{aligned} F''(T(x),a)\xrightarrow {-F''(w,1)} F''(z,a)\xrightarrow {F''(v,1)} F''(y,a)\xrightarrow {F''(u,1)} F''(x,a) \end{aligned}$$

    is a triangle in ${{\mathcal {C}}}$.

  • (ii) and if for each triangle $a\xrightarrow {u} b\xrightarrow {v} c\xrightarrow {w} \varSigma (a)$ in ${{\mathcal {A}}}$ and each object x in ${{\mathcal {A}}}$, then

    $$\begin{aligned} F''(x,a)\xrightarrow {F''(1,u)} F''(x,b)\xrightarrow {F''(1,v)} F''(x,c)\xrightarrow {F''(1,w)} F''(x,\varSigma (a)) \end{aligned}$$

    is a triangle in ${{\mathcal {C}}}$.

If the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ has a left or a right function object, then each of them is unique up to isomorphism as stated next.

Proposition 5.3

• (a) If the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ has a left function object, then it is unique up to isomorphism.

• (b) If the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ has a right function object, then it is unique up to isomorphism.$\square$

The tensor category ${{\mathcal {C}}}$ acting on itself, may have both a left and a right function object. They need not be isomorphic. However, the occasions when they are isomorphic can be characterized as follows. Recall that the tensor product $-\otimes -$ in ${{\mathcal {C}}}$ is symmetric if $x\otimes y\simeq y\otimes x$ via a natural isomorphism in both x and y.

Proposition 5.4

Suppose that ${{\mathcal {C}}}$ acting on itself has a left and a right function object. Then the tensor product in ${{\mathcal {C}}}$ is symmetric if and only if the left and the right function objects for ${{\mathcal {C}}}$ are isomorphic.$\square$

Next we point out how a left function object respects the triangulated and the tensor structure in ${{\mathcal {C}}}$. The following proposition only deals with left function objects, so we leave it to the reader to formulate the corresponding results for right function objects.

Proposition 5.5

Let $F'$ be a left function object for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$.

• (a) There is a natural isomorphism $F'(x,\varSigma (a))\simeq \varSigma (F'(x,a))$ for all objects x in ${{\mathcal {C}}}$ and a in ${{\mathcal {A}}}$.

• (b) There is a natural isomorphism $F'(T(x),a)\simeq F'(x,\varSigma ^{-1}(a))$ for all objects x in ${{\mathcal {C}}}$ and a in ${{\mathcal {A}}}$.

• (c) There is a natural isomorphism $F'(y\otimes x,a)\simeq F'(x,F'(y,a))$ for all objects x and y in ${{\mathcal {C}}}$, and a in ${{\mathcal {A}}}$.

• (d) There is a natural isomorphism $a\simeq F'({\mathfrak {e}},a)$ for all objects a in ${{\mathcal {A}}}$. $\square$

7 Support varieties for actions with a function object

This section is devoted to studying support varieties in a small triangulated category ${{\mathcal {A}}}$ having a triangulated tensor category ${{\mathcal {C}}}$ acting on ${{\mathcal {A}}}$ with a left function object. We indicate how this restricts what we can expect to classify, and how we obtain some control on the homomorphisms between one object and shifts of another object in ${{\mathcal {A}}}$.

Throughout we keep the Assumption 3.1 and add for this section the following.

Assumption 6.1

For ${{\mathcal {C}}}$ and ${{\mathcal {A}}}$ the following holds:

• (4) There exists a left function object $F':{{\mathcal {C}}}^{{\text {op}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$.

• (5) The functor $-*a:{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ is an exact functor for all objects a in ${{\mathcal {A}}}$.

In the presence of a left function object $F'$ for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ we denote the corresponding natural adjunction isomorphism by

$$\begin{aligned} \varphi =\varphi _{x,a,b}:{\text {Hom}}_{{\mathcal {A}}}(x*a,b)\rightarrow {\text {Hom}}_{{\mathcal {A}}}(a,F'(x,b)) \end{aligned}$$

for all objects a and b in ${{\mathcal {A}}}$ and all x in ${{\mathcal {C}}}$.

Remark 6.2

(1) It is tempting to believe that having this adjunction implies that

$$\begin{aligned} V(x * a, b) \subseteq V(a) \cap V(b). \end{aligned}$$

However this is in general not true as pointed out in [13]. But for $x = e/\!\!/h$ we do have $V(e/\!\!/h * a, b) \subseteq V(a) \cap V(b)$.

(2) When ${{\mathcal {A}}}$ is endowed with a theory of support varieties, the thick subcategories ${{\mathcal {X}}}$ of ${{\mathcal {A}}}$ are sometimes given as ${{\mathcal {X}}}_V=\{X\in {{\mathcal {A}}}\mid V(X)\subseteq V\}$ for some homogeneous subvariety V of ${\text {Spec}}H$. By the above remark one cannot expect that the subcategories ${{\mathcal {X}}}_V$ are tensor subcategories of ${{\mathcal {C}}}$. This is the case for thick subcategories of the stable category of a p-group.

Next we show that support varieties give us some control of the homomorphisms between objects in ${{\mathcal {A}}}$. To this end we first need to describe how a function object for the action acts on objects in ${{\mathcal {A}}}$.

Lemma 6.3

Let $F'$ be a left function object for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$, which is compatible with the triangulation in ${{\mathcal {C}}}$. Let $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$. Then $F'({\mathfrak {e}}/\!\!/h,a)$ is in ${\text {Thick}}(a)$ for all a in ${{\mathcal {A}}}$.

Proof

Let $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$, and let a be in ${{\mathcal {A}}}$. Then $F'(-,a)$ applied to the triangle ${\mathfrak {e}}\xrightarrow {h} T^p({\mathfrak {e}})\rightarrow {\mathfrak {e}}/\!\!/h\rightarrow T({\mathfrak {e}})$ in ${{\mathcal {C}}}$ gives rise to the triangle

$$\begin{aligned} F'(T({\mathfrak {e}}),a)\rightarrow F'({\mathfrak {e}}/\!\!/h,a)\rightarrow F'(T^p({\mathfrak {e}}),a)\rightarrow F'({\mathfrak {e}},a) \end{aligned}$$

in ${{\mathcal {A}}}$. Since $F'({\mathfrak {e}},a)\simeq a$ and $F'(T^p({\mathfrak {e}}),a)\simeq \varSigma ^{-p}(a)$ from Proposition 5.5, it follows directly that $F'({\mathfrak {e}}/\!\!/h,a)$ is in ${\text {Thick}}(a)$. $\square$

The following lemma is the last preliminary result we need before proving the main results of this section.

Lemma 6.4

Let $F'$ be a left function object for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$. Fix an object c in ${{\mathcal {C}}}$, and let a and b be two objects in ${{\mathcal {A}}}$. Let ${{\mathcal {X}}}$ be a thick subcategory of ${{\mathcal {A}}}$ such that $c*{{\mathcal {X}}}\subseteq {{\mathcal {X}}}$ and $F'(c,{{\mathcal {X}}})\subseteq {{\mathcal {X}}}$. Then a morphism $f:c*a\rightarrow b$ factors through an object in ${{\mathcal {X}}}$ if and only if $\varphi (f):a\rightarrow F'(c,b)$ factors through an object in ${{\mathcal {X}}}$.

Proof

This follows directly from the fact that $\varphi$ is natural in all three variables and from the assumptions. $\square$

Our first main result proves that any morphism $f:a\rightarrow \varSigma ^i(b)$ in ${{\mathcal {A}}}$ factors through an object c with variety contained in $V(a)\cap V(b)$ for any integer i.

Proposition 6.5

Assume that the functor $-*x:{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ is an exact functor for all objects x in ${{\mathcal {A}}}$. Let $F'$ be a left function object for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$, and assume that it is compatible with the triangulation in ${{\mathcal {C}}}$. For all $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ assume that the following diagram commutes for all b in ${{\mathcal {A}}}$

where the vertical isomorphisms are given in Proposition 5.5. In particular,

$$\begin{aligned} F'(e/\!\!/h,b)\simeq \varSigma ^{-p-1}(b/\!\!/h). \end{aligned}$$

Let a and b be two objects in ${{\mathcal {A}}}$. Then any morphism $a\rightarrow \varSigma ^i(b)$ factors through an object with support variety contained in $V(a)\cap V(b)$, for any integer i.

Proof

Suppose that $A(a,a)=\langle h_1,h_2,\ldots ,h_t\rangle$ for some homogeneous elements $h_1,h_2,\ldots ,h_t$ in H. Then by Proposition 3.6 (b) the object $\varSigma ^t(a)$ is a direct summand of $({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes {\mathfrak {e}}/\!\!/h_t)*a$, recalling that ${\mathfrak {e}}/\!\!/h*a' \simeq a'/\!\!/h$ for all homogeneous elements h in H and objects $a'$ in ${{\mathcal {A}}}$. If a shift of a morphism $f:a\rightarrow \varSigma ^i(b)$ factors through an object with variety in $V(a)\cap V(b)$, then also f has the same property. Therefore we can assume without loss of generality that $\varSigma ^t(a)$ is a. Consequently ${\text {Hom}}_{{\mathcal {A}}}(a,\varSigma ^i(b))$ is a direct summand of ${\text {Hom}}_{{\mathcal {A}}}(({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes {\mathfrak {e}}/\!\!/h_t)*a, \varSigma ^i(b))$ for all integers i. Furthermore, note that

$$\begin{aligned} {\text {Hom}}_{{\mathcal {A}}}(({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes {\mathfrak {e}}/\!\!/h_t)*a, \varSigma ^i(b)) \simeq {\text {Hom}}_{{\mathcal {A}}}(a, F'({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes {\mathfrak {e}}/\!\!/h_t, \varSigma ^i(b))). \end{aligned}$$

Hence by Lemma 6.4, we shall see that it is sufficient to show that

$$\begin{aligned} V(F'({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes {\mathfrak {e}}/\!\!/h_t,\varSigma ^i(b))) \subseteq V(a)\cap V(b). \end{aligned}$$

Applying the last assumption multiple times we obtain that

$$\begin{aligned} F'({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes e/\!\!/h_t, b) \simeq \varSigma ^{-p_t-1}(\cdots (\varSigma ^{-p_1-1}(b/\!\!/h_1)/\!\!/h_2)\cdots )/\!\!/h_t. \end{aligned}$$

Then we infer that

$$\begin{aligned} V(F'({\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes e/\!\!/h_t, b)) = V(\langle h_1,\ldots ,h_t\rangle ) \cap V(b) = V(a)\cap V(b). \end{aligned}$$

Let ${{\mathcal {X}}}=\{x\in {{\mathcal {A}}}\mid V(x)\subseteq V(a)\cap V(b)\}$. Then with $c = {\mathfrak {e}}/\!\!/h_1\otimes \cdots \otimes {\mathfrak {e}}/\!\!/h_t$, the assumptions of Lemma 6.4 are satisfied. Hence we conclude that any morphism $f:a \rightarrow \varSigma ^i(b)$ factors through an object in ${{\mathcal {X}}}$. This completes the proof. $\square$

For the last result of this section we show that the support variety of an indecomposable object in ${{\mathcal {A}}}$ is connected under additional assumptions. The proof is similar to the one of [11, Theorem 3.1].

Proposition 6.6

We assume the following conditions:

• (i) The functor $-*a:{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ is an exact functor for all objects a in ${{\mathcal {A}}}$.

• (ii) There exists a left function object $F'$ for the action of ${{\mathcal {C}}}$ on ${{\mathcal {A}}}$ compatible with the triangulation in ${{\mathcal {C}}}$.

• (iii) ${{\mathcal {A}}}$ is a Krull-Schmidt category and the idempotents split in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$.

• (iv) The degree zero part $H^0$ of H is a local artinian ring.

• (v) For all $h:{\mathfrak {e}}\rightarrow T^p({\mathfrak {e}})$ the following diagram commutes for all b in ${{\mathcal {A}}}$

  

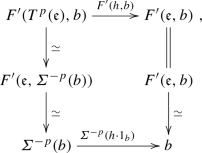
  where the vertical isomorphisms are given in Proposition 5.5.

Let a be a non-perfect object in ${{\mathcal {A}}}$, such that $V(a)=V_1\cup V_2$ for some homogeneous varieties $V_1$ and $V_2$ with $V_1\cap V_2\subseteq V(H^+)$. Then, in the Verdier quotient ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$ the object a decomposes as $a_1\amalg a_2$ where $V(a_i)=V_i$ for $i=1,2$.

Proof

When $H^0$ is a local artinian ring, all perfect objects have the same variety given by the ideal ${\mathfrak {m}}_{{\text {gr}}}=\langle {\text {rad}}H^0, H^{\geqslant 1}\rangle$, which is contained in the variety of any object in ${{\mathcal {A}}}$.

Assume that $V(a)=V_1\cup V_2$ for some homogeneous varieties $V_1=V({\mathfrak {a}}_1)$ and $V_2=V({\mathfrak {a}}_2)$ with $V_1\cap V_2\subseteq V(H^+)$ and ${\mathfrak {a}}_i$ homogeneous ideals in H for $i=1,2$. Denote by $\gamma (U)$ the polynomial growth of the minimal number of generators of the graded pieces of a positively graded H-module U as a $H^0$-module. The proof goes by induction on $\gamma (H/{\mathfrak {a}}_1) + \gamma (H/{\mathfrak {a}}_2)$. Note that we have ${{\text {cx}}}(b)=\gamma (H/A(b,b))$ for any object b in ${{\mathcal {A}}}$. Furthermore, we have $\gamma (U/{\text {rad}}(H^0) U) = \gamma (U)$, when $U/{\text {rad}}(H^0)U$ is considered as a graded module over $H/{\text {rad}}(H^0) H$. Hence we can think of H as a graded algebra over the field $H^0/{\text {rad}}(H^0)$.

Assume first that one of $\gamma (H/{\mathfrak {a}}_i)$ is zero, say for $i=1$. Since a is a non-perfect object, observe that $V(a) \ne \emptyset$. Then by Theorem 3.8 there exists a nonzero perfect object $p\in {{\mathcal {A}}}$. Then $p\amalg a \simeq a$ in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$. As $V_1$ is the variety of a perfect object, we have $V(p) = V_1$. Since $V(a) = V_1\cup V_2 = V_2$, we have that $V(a) = V_2$. Hence we can choose $a_1=p$ and $a_2=a$.

Assume that $\gamma (H/{\mathfrak {a}}_i) > 0$ for $i=1,2$. Since $V_1\cap V_2\subseteq V(H^+)$, we infer that $\gamma (H/\langle {\mathfrak {a}}_1, {\mathfrak {a}}_2\rangle ) = 0$. Then we can choose homogeneous elements $\eta _1\in {\mathfrak {a}}_1$ and $\eta _2\in {\mathfrak {a}}_2$ of degrees m and n, respectively, such that

$$\begin{aligned} \gamma (H/\langle {\mathfrak {a}}_2,\eta _1\rangle )=\gamma (H/{\mathfrak {a}}_2) - 1 \end{aligned}$$

and

$$\begin{aligned} \gamma (H/\langle {\mathfrak {a}}_1,\eta _2\rangle )=\gamma (H/{\mathfrak {a}}_1) - 1. \end{aligned}$$

We have that $V_i\subseteq V(\langle \eta _i\rangle )$ for $i=1,2$ and $V(\langle \eta _1\eta _2\rangle )= V(\langle \eta _1\rangle )\cup V(\langle \eta _2\rangle )$, which contains $V_1\cup V_2=V(a)$. This implies that $\eta _1\eta _2$ is in $\sqrt{{\text {Ann}}_H({\text {Hom}}_{{\mathcal {A}}}^*(a,a))}$. Choosing high enough powers of $\eta _1$ and $\eta _2$, we can without loss of generality assume that $\eta _1\eta _2$ is in ${\text {Ann}}_H({\text {Hom}}_{{\mathcal {A}}}^*(a,a))$. By Proposition 3.6 (a) we have that ${\mathfrak {e}}/\!\!/\eta _1\eta _2*a\simeq \varSigma (a)\amalg \varSigma ^{m+n}(a)$.

By the octahedral axiom there is a triangle $\theta$

$$\begin{aligned} {\mathfrak {e}}/\!\!/\eta _2 \rightarrow {\mathfrak {e}}/\!\!/\eta _1\eta _2\rightarrow T^n({\mathfrak {e}}/\!\!/\eta _1)\rightarrow T({\mathfrak {e}}/\!\!/\eta _2) \end{aligned}$$

in ${{\mathcal {C}}}$. Then

$$\begin{aligned} V({\mathfrak {e}}/\!\!/\eta _2*a)&= V(\langle \eta _2\rangle )\cap V(a)\\&= (V_1\cap V(\langle \eta _2\rangle ))\cup V_2. \end{aligned}$$

By induction ${\mathfrak {e}}/\!\!/\eta _2*a\simeq a_1\amalg a_2$ where $V(a_1)=V_1\cap V(\langle \eta _2\rangle )$ and $V(a_2)=V_2$. Similarly we have $V(T^n({\mathfrak {e}}/\!\!/\eta _1)*a)=V_1\cup (V_2\cap V(\langle \eta _1\rangle ))$, so that $T^n({\mathfrak {e}}/\!\!/\eta _1)*a\simeq a_1'\amalg a_2'$ with $V(a_1')=V_1$ and $V(a_2')=V_2\cap V(\langle \eta _2\rangle )$. Note that both $V(a_1)\cap V(a_2')$ and $V(a_2)\cap V(a_1')$ are contained in $V(H^+)$. Then the triangle $\theta *a$ in ${{\mathcal {A}}}$ has the form

$$\begin{aligned} a_1\amalg a_2 \rightarrow \varSigma (a)\amalg \varSigma ^{m+n}(a) \rightarrow a_1'\amalg a_2' \xrightarrow {\psi } \varSigma (a_1)\amalg \varSigma (a_2). \end{aligned}$$

By the above observations and Proposition 6.5 we have that $\psi =\left( {\begin{matrix} u_1 &{} 0\\ 0 &{} u_2\end{matrix}}\right)$ in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$. The image of this triangle in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$ is again a triangle. By the uniqueness of the cone, it follows that we have two triangles in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$

$$\begin{aligned} a_i \rightarrow b_i \rightarrow a_i'\rightarrow \varSigma (a_i) \end{aligned}$$

for $i=1,2$. Hence we have an isomorphism $\varphi :\varSigma (a)\amalg \varSigma ^{m+n}(a)\rightarrow b_1\amalg b_2$ in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$. Using that these triangles can be lifted back to ${{\mathcal {A}}}$, it is easy to see that $V(b_i) \subseteq V_i$ for $i=1,2$. Since $V(a) = V_1\cup V_2 = V(b_1\amalg b_2) = V(b_1)\cup V(b_2)$, we infer that $V(b_i)=V_i$ for $i=1,2$.

Consider the natural compositions $f_1$ given by

$$\begin{aligned}&\varSigma (a)\rightarrow \varSigma (a)\amalg \varSigma ^{m+n}(a) \xrightarrow {\varphi } b_1\amalg b_2 \xrightarrow {\left( {\begin{matrix} 1 &{} 0\\ 0 &{} 0\end{matrix}}\right) } b_1\amalg b_2\\&\quad \xrightarrow {\varphi ^{-1}} \varSigma (a)\amalg \varSigma ^{m+n}(a) \rightarrow \varSigma (a) \end{aligned}$$

and $f_2$ given by

$$\begin{aligned}&\varSigma (a)\rightarrow \varSigma (a)\amalg \varSigma ^{m+n}(a) \xrightarrow {\varphi } b_1\amalg b_2 \xrightarrow {\left( {\begin{matrix} 0 &{} 0\\ 0 &{} 1\end{matrix}}\right) } b_1\amalg b_2\\&\quad \xrightarrow {\varphi ^{-1}} \varSigma (a)\amalg \varSigma ^{m+n}(a) \rightarrow \varSigma (a). \end{aligned}$$

Using Proposition 6.5 we infer that $f_2f_1=f_1f_2=0$ in ${{\mathcal {A}}}/{{\mathcal {A}}}^{{\text {perf}}}$, so that $f_1$ and $f_2$ are orthogonal idempotents and their sum is the identity on $\varSigma (a)$. The claim follows from this. $\square$

8 Complete intersections

This section is devoted to reviewing our theory in the setting of complete intersections.

Let $A = k\llbracket x_1,x_2,\ldots ,x_n\rrbracket$ be the ring of formal power series in n indeterminants $\{x_1,x_2,\ldots , x_n\}$ over a field k. Let $(R,{\mathfrak {m}})$ be a complete intersection, where $R = A/(a_1,\ldots ,a_t)$ for a regular sequence $\{a_1,\ldots ,a_t\}$ in the square of the maximal ideal of A. In [2, 3] support varieties of finitely generated modules over R (and more general complete intersections) were defined in terms of ${\text {Spec}}R/{\mathfrak {m}}[\chi _1,\ldots ,\chi _t]$, where $\{\chi _1,\ldots ,\chi _t\}$ is a set of cohomological operators on ${\text {Ext}}^*_R(M,M)$ of degree two for any finitely generated R-module M. In our situation, the ring $R[\chi _1,\ldots ,\chi _t]$ can be viewed as a graded subring of the Hochschild cohomology ring ${\text {HH}}^*(R)$ (see [33]).

The derived category ${{\mathcal {C}}}'={{\mathbf {D}}}^{b}({\text {mod}}R\otimes _k R)$ is a triangulated tensor category via the derived tensor product $-\otimes _R^{\mathbb {L}}-:{{\mathcal {C}}}'\times {{\mathcal {C}}}'\rightarrow {{\mathcal {C}}}'$, and it acts on the derived category ${{\mathcal {A}}}=D^{b}({\text {mod}}R)$ via the derived tensor product $-\otimes _R^{\mathbb {L}}-:{{\mathcal {C}}}'\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$. The stalk complex R, with R concentrated in degree zero, is the tensor identity. Then one can show that we have the following commutative diagram

where ${{\mathcal {C}}}={\text {Thick}}(R)$ inside ${{\mathcal {C}}}'$ and $-\otimes _R-$ represents the total tensor product. Then ${{\mathcal {C}}}$ is a triangulated tensor category with an action on ${{\mathcal {A}}}$.

Consider $S={\text {End}}_{{\mathcal {C}}}^*(R)={\text {HH}}^*(R)$, which by our general theory is a graded-commutative ring, where we note that $S^0=R$. The ring $H=R[\chi _1,\ldots ,\chi _t]$ can be viewed as a graded subring of S, and the action on ${\text {Ext}}^*_R(M,N)$ for two finitely generated R-modules M and N factor through the inclusion into S. Since ${\text {Ext}}^*_R(M,N)$ is a finitely generated module over H for all finitely generated R-modules M and N (see [23]), our Assumptions 3.1 and 6.1 are satisfied with left function object $F'=\mathbb {R}{\text {Hom}}_R(-,-)$. Hence we can apply all the results obtained in the previous sections. In addition we point out the following.

Theorem 7.1

Let $(R,{\mathfrak {m}})$ be a complete intersection, where

$$\begin{aligned} R=k\llbracket x_1,x_2,\ldots ,x_n\rrbracket /(a_1,a_2,\ldots ,a_t) \end{aligned}$$

for a field k and for a regular sequence $\{a_1,a_2,\ldots ,a_t\}$ in the square of the maximal ideal of the ring of formal power series $k\llbracket x_1,x_2,\ldots ,x_n\rrbracket$ in n indeterminants $\{x_1,x_2,\ldots , x_n\}$.

• (a) The perfect objects in ${{\mathbf {D}}}^{b}({\text {mod}}R)$ are the perfect complexes.

• (b) Let ${\mathfrak {b}}=(y_1,y_2,\ldots ,y_t)$ be an ideal in R generated by elements in ${\mathfrak {m}}$. Let $K(y_1,y_2,\ldots ,y_t)$ be the Koszul complex on the set of the generators $\{y_1,y_2,\ldots ,y_t\}$ of ${\mathfrak {b}}$.

  Then $K(y_1,y_2,\ldots ,y_t)$ is a perfect complex and

  $$\begin{aligned} V(K(y_1,y_2,\ldots ,y_t)) = V(\langle {\mathfrak {b}},H^{\geqslant 1} \rangle ). \end{aligned}$$

• (c) Let X be a perfect complex, then

  $$\begin{aligned} \quad \quad \quad V(X)=\{\langle {\mathfrak {p}},H^+\rangle \in {\text {Spec}}H\mid {\mathfrak {p}}\in {\text {Spec}}R \text { with } X_{\mathfrak {p}}\ne 0\text { in }{{\mathbf {D}}}^{b}({\text {mod}}R_{\mathfrak {p}})\}. \end{aligned}$$

• (d) View M in ${\text {mod}}R$ as a stalk complex concentrated in degree 0, then

  $$\begin{aligned} V^*(M)=V(M)\cap V({\mathfrak {m}}H), \end{aligned}$$

  where $V^*(M)$ is the variety of M defined in [3].

• (e) For any X in ${{\mathbf {D}}}^{b}({\text {mod}}R)$ we have that

  $$\begin{aligned} V(X) \subseteq \cup _{{\mathfrak {p}}\in {\text {Spec}}R} V(R/{\mathfrak {p}}). \end{aligned}$$

Proof

(a) The support variety of the stalk complex of R is $V(H^+)$, so that all perfect complexes over R are perfect objects in ${{\mathbf {D}}}^{b}({\text {mod}}R)$.

Conversely, let X be a perfect object in ${{\mathbf {D}}}^{b}({\text {mod}}R)$. There exists a complex of projective R-modules p(X) and a quasi-isomorphism $p(X)\rightarrow X$ such that $p(X)^i=(0)$ for $i\gg 0$. Also, there is an integer n such that p(X) is exact to the left of $p(X)^{n-1}$. By assumption

$$\begin{aligned} (0)={\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,R/{\mathfrak {m}}[i])\simeq {\text {Hom}}_{{{\mathbf {K}}}^{-,b}({\text {mod}}R)}(p(X),R/{\mathfrak {m}}[i]) \end{aligned}$$

for $|i|\geqslant m$. Let $N=\max \{m,n\}$. Then ${\text {Hom}}_{{{\mathbf {K}}}(R)}(p(X),R/{\mathfrak {m}}[N+2])$ equals ${\text {Ext}}^1_R({\text {Im}}f^{N+1},R/{\mathfrak {m}})$. Hence ${\text {Im}}f^{N+1}$ is projective, and by soft truncation p(X) is a perfect complex.

(b) Let ${\mathfrak {b}}=(y_1,y_2,\ldots ,y_t)$ be an ideal in R generated by elements in ${\mathfrak {m}}$. Consider the triangles $R\xrightarrow {y_i\cdot -} R\rightarrow K_{y_i}\rightarrow R[1]$ for $i=1,2,\ldots ,t$, where all $\{K_{y_i}\}$ are perfect complexes. Then the Koszul complex $K(y_1,y_2,\ldots ,y_t)$ is given by $K_{y_1}\otimes _R \cdots \otimes _R K_{y_t}\otimes _R R$, which clearly is a perfect complex. By Proposition 3.7 we infer that $V(K(y_1,\ldots ,y_t))=V(\langle y_1,y_2,\ldots ,y_t\rangle )\cap V(R)= V(\langle {\mathfrak {b}}, H^{\geqslant 1}\rangle )$.

(c) Let X be a perfect complex. Then $\sqrt{{\text {Ann}}_H({\text {Hom}}^*_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X))}$ contains $H^{\geqslant 1}$. Hence we only need to find the variety of the ideal

$$\begin{aligned} {\mathfrak {a}}= \sqrt{{\text {Ann}}_R({\text {Hom}}^*_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X))}=\sqrt{\cap _{i\in \mathbb {Z}}{\text {Ann}}_R({\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X[i]))} \end{aligned}$$

in ${\text {Spec}}R$. Since ${\text {Ann}}_R({\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X)) \subseteq {\text {Ann}}_R({\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X[i]))$ for all integers i, we infer that

$$\begin{aligned} {\mathfrak {a}}= \sqrt{{\text {Ann}}_R({\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X))}. \end{aligned}$$

Then ${\mathfrak {a}}\subseteq {\mathfrak {p}}$ with ${\mathfrak {p}}$ in ${\text {Spec}}R$ if and only if

$$\begin{aligned} (0)\ne {\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}(X,X)_{{\mathfrak {p}}}\simeq {\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R_{{\mathfrak {p}}})}(X_{{\mathfrak {p}}},X_{{\mathfrak {p}}}). \end{aligned}$$

This is equivalent to that $X_{{\mathfrak {p}}}\ne (0)$ in ${{\mathbf {D}}}^{b}({\text {mod}}R_{{\mathfrak {p}}})$. Hence the claim follows.

(d) Let M be in ${\text {mod}}R$. Recall that

$$\begin{aligned} V^*(M)={\text {Supp}}_{H/{\mathfrak {m}}H}({\text {Ext}}^*_R(M,M)\otimes _R R/{\mathfrak {m}}). \end{aligned}$$

Let ${\mathfrak {p}}$ be in $V^*(M)$ and ${\mathfrak {q}}=\varphi ^*({\mathfrak {p}})$. Then ${\mathfrak {p}}$ is in $V^*(M)$ if and only if

$$\begin{aligned} (0)&\ne ({\text {Ext}}^*_R(M,M)/{\mathfrak {m}}{\text {Ext}}^*_R(M,M))_{{\mathfrak {p}}} \\&\simeq {\text {Ext}}^*_R(M,M)_{{\mathfrak {q}}}/{\mathfrak {m}}{\text {Ext}}^*_R(M,M)_{{\mathfrak {q}}}. \end{aligned}$$

Hence, ${\mathfrak {p}}$ is in $V^*(M)$ if and only if $(0)\ne {\text {Ext}}^*_R(M,M)_{{\mathfrak {q}}}\simeq {\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}R)}^*(M,M)_{{\mathfrak {q}}}$ or equivalently ${\mathfrak {q}}$ is in V(M). Since ${\mathfrak {m}}H\subseteq \varphi ^*({\mathfrak {p}})$ for all ${\mathfrak {p}}$ in ${\text {Spec}}(H/{\mathfrak {m}}H)$, the claim follows.

(e) Let X be in ${{\mathbf {D}}}^{b}({\text {mod}}R)$. Then X can be filtered in a finite set of finitely generated R-modules $\{M_i\}_{i=1}^m$, and each such R-module $M_i$ can be filtered in a finite set of $\{ R/{\mathfrak {p}}_{i_j}\}_{j=1}^{m_i}$ with ${\mathfrak {p}}_{i_j}$ in ${\text {Spec}}R$. The claim follows from this and Proposition 3.5. $\square$

We can reformulate (c) and (d) of the previous result as follows.

Proposition 7.2

Let $(R,{\mathfrak {m}})$ be a complete intersection, where

$$\begin{aligned} R=k\llbracket x_1,x_2,\ldots ,x_n\rrbracket /(a_1,a_2,\ldots ,a_t) \end{aligned}$$

for a field k and for a regular sequence $\{a_1,a_2,\ldots ,a_t\}$ in the square of the maximal ideal of the ring of formal power series $k\llbracket x_1,x_2,\ldots ,x_n\rrbracket$ in n indeterminants $\{x_1,x_2,\ldots , x_n\}$.

Let $\varphi :H\rightarrow H/{\mathfrak {m}}H$ and $\psi :H\rightarrow R$ be the natural ring homomorphisms, and consider the maps $\varphi ^*:{\text {Spec}}(H/{\mathfrak {m}})\rightarrow {\text {Spec}}H$ and $\psi ^*:{\text {Spec}}R\rightarrow {\text {Spec}}H$.

• (a) If X is a perfect complex in ${{\mathbf {D}}}^{b}({\text {mod}}R)$, then

  $$\begin{aligned} V(X)=\psi ^*(V_T(X)), \end{aligned}$$

  where $V_T(X)$ denotes the support of the perfect complex X in the sense of [29, 39].

• (b) If M in ${\text {mod}}R$ is viewed as a stalk complex concentrated in degree 0, then

  $$\begin{aligned} \varphi ^*(V(M)\cap V({\mathfrak {m}}H)) = V^*(M), \end{aligned}$$

  where $V^*(M)$ is the variety of M defined in [3].

9 Group rings over commutative Noetherian local rings

Here we apply our results to group rings of finite groups over commutative Noetherian local rings.

For a finite group G and a commutative Noetherian local ring R we can form the group ring RG. For a finitely generated RG-module M it is known that $H^*(G,M)={\text {Ext}}^*_{RG}(R,M)$ is Noetherian as a module over $H=H^*(G,R)={\text {Ext}}^*_{RG}(R,R)$ [20, 21, 40]. Let ${{\mathcal {C}}}=({{\mathbf {D}}}^{b}({\text {Proj}}RG), -\otimes _R-,{\mathfrak {e}}= R)$ act on ${{\mathcal {A}}}={{\mathbf {D}}}^{b}({\text {mod}}RG)$. Then our Assumptions 3.1 and 6.1 are satisfied, as $-\otimes _R M:{{\mathcal {C}}}\rightarrow {{\mathcal {A}}}$ is an exact functor for all modules/stalk complexes in ${{\mathcal {A}}}$ and $F'={\text {Hom}}_R(-,-):{{\mathcal {C}}}\times {{\mathcal {A}}}\rightarrow {{\mathcal {A}}}$ is a left function object for the action which is compatible with the triangulation in ${{\mathcal {C}}}$. Hence we can apply all of our results from the previous sections. In addition we point out the following.

Theorem 8.1

Let G be a finite group and let R be a commutative Noetherian local ring.

• (a) The perfect objects in ${{\mathbf {D}}}^{b}({\text {mod}}RG)$ are the perfect complexes.

• (b) Let X be a perfect complex in ${{\mathbf {D}}}^{b}({\text {mod}}RG)$, then

  $$\begin{aligned} \quad \quad \quad V(X)=\{\langle {\mathfrak {p}},H^{\geqslant 1}\rangle \in {\text {Spec}}H\mid {\mathfrak {p}}\in {\text {Spec}}R \text { with }X_{\mathfrak {p}}\ne 0\text { in } {{\mathbf {D}}}^{b}({\text {mod}}R_{\mathfrak {p}}G)\}. \end{aligned}$$

• (c) If $R=k$ is an algebraically closed field and M in ${\text {mod}}RG$ is viewed as a stalk complex concentrated in degree 0, then

  $$\begin{aligned} V^*(M)=V(M) \end{aligned}$$

  where $V^*(M)$ is the variety of M defined in [17].

Proof

(a) As before we have that all perfect complexes in ${{\mathbf {D}}}^{b}({\text {mod}}RG)$ are perfect objects in ${{\mathbf {D}}}^{b}({\text {mod}}RG)$.

Conversely, let X be a perfect object in ${{\mathbf {D}}}^{b}({\text {mod}}RG)$. There exists a complex of projective R-modules p(X) and a quasi-isomorphism $p(X)\rightarrow X$ such that $p(X)^i=(0)$ for $i\gg 0$. Also, there is an integer n such that p(X) is exact to the left of $p(X)^{n-1}$. We want to show that p(X) can be softly truncated to a perfect complex.

To this end we use the following observations. Given any finitely generated RG-module M, there exists an R-epimorphism $f:M\rightarrow R/{\mathfrak {p}}$ for some ${\mathfrak {p}}$ in ${\text {Spec}}R$. Then the map ${\widetilde{f}}:M\rightarrow R/{\mathfrak {p}}G$ given by ${\widetilde{f}}(m) = \sum _{g\in G} f(gm)g^{-1}$ is an RG-homomorphism, with non-zero image not contained in ${\mathfrak {m}}(R/{\mathfrak {p}}G)$. Furthermore, if M occurs as a kernel $0\rightarrow M\rightarrow P\rightarrow C\rightarrow 0$, where $P\rightarrow C$ is a projective cover, then there exists an RG-homomorphism $\varphi :M\rightarrow R/{\mathfrak {p}}G$ which induces a non-zero element in ${\text {Ext}}^1_{RG}(C,R/{\mathfrak {p}}G)$.

Using these observations the proof can be completed in a similar fashion as the proof of Theorem 7.1 (a).

(b) The proof is similar to the proof of Theorem 7.1 (c).

(c) This is immediate as ${\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}RG)}^*(M,M)$ and ${\text {Ext}}^*_{RG}(M,M)$ are isomorphic as H-modules. $\square$

10 Finite dimensional algebras

Throughout this section let $\varLambda$ be an indecomposable finite dimensional algebra over an algebraically closed field k with Jacobson radical ${\mathfrak {j}}$. We consider the action of the triangulated tensor category ${{\mathcal {C}}}={{\mathbf {D}}}^{b}({{\mathcal {B}}})$ on ${{\mathcal {A}}}={{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$, where ${{\mathcal {B}}}$ is the full subcategory of $\varLambda$-$\varLambda$-bimodules which are projective as a left and as a right module. The section is devoted to studying support varieties of objects in ${{\mathcal {A}}}$.

A theory of support varieties for ${\text {mod}}\varLambda$ was introduced in [33] and further developed in [19] using the Hochschild cohomology ring of $\varLambda$. To ensure the existence of a good theory of support, two finiteness conditions Fg1 and Fg2 were introduced in [19], which in [34, Proposition 5.7] are shown to be equivalent to the Fg condition:

• (i) ${\text {HH}}^*(\varLambda )$ is a Noetherian algebra,

• (ii) ${\text {Ext}}^*_\varLambda (\varLambda /{\mathfrak {j}}, \varLambda /{\mathfrak {j}})$ is a finitely generated ${\text {HH}}^*(\varLambda )$-module.

We show that our Assumption 3.1 is equivalent to the condition Fg. Furthermore, a perfect object in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is characterized as a perfect complex, and the support variety of X in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is shown to be contained in the union of the support varieties of homology modules of X and in the union of the support varieties of stalk complexes of which X is built up. Also, the support variety of a module, as defined in [33], coincides with the support variety when viewed as a complex concentrated in one degree.

Our usual Assumptions 3.1 and 6.1 translate into the following facts and requirements for the setting of this section:

(1):

${{\mathcal {C}}}=({{\mathbf {D}}}^{b}({{\mathcal {B}}}),-\otimes _\varLambda -,{\mathfrak {e}}=\varLambda )$ is a triangulated tensor category acting on the triangulated category ${{\mathcal {A}}}={{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

(2):

H is a positively graded-commutative Noetherian ring with a homomorphism of graded rings $H\rightarrow {\text {End}}_{{\mathcal {C}}}^*({\mathfrak {e}})={\text {HH}}^*(\varLambda )$.

(3):

The left H-module ${\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}\varLambda )}^*(a,b)$ is finitely generated for all objects a and b in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

(4):

The functor $-*a:{{\mathbf {D}}}^{b}({{\mathcal {B}}})\rightarrow {{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is an exact functor for all objects a in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

(5):

There exists a left function object

$$\begin{aligned} F'=\mathbb {R}{\text {Hom}}_\varLambda (-,-):{{\mathbf {D}}}^{b}({{\mathcal {B}}})\times {{\mathbf {D}}}^{b}({\text {mod}}\varLambda )\rightarrow {{\mathbf {D}}}^{b}({\text {mod}}\varLambda ) \end{aligned}$$

for the action of ${{\mathbf {D}}}^{b}({{\mathcal {B}}})$ on ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

We start by discussing the relationship between the condition (3) and Fg.

Proposition 9.1

Suppose $\varLambda$ and H satisfy condition (2). Then the following are equivalent.

• (i) ${\text {Ext}}^*_\varLambda (\varLambda /{\mathfrak {j}},\varLambda /{\mathfrak {j}})$ is a finitely generated H-module.

• (ii) ${\text {Ext}}^*_\varLambda (M,N)$ is a finitely generated H-module for all M and N in ${\text {mod}}\varLambda$.

• (iii) ${\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}\varLambda )}^*(X,Y)$ is a finitely generated H-module for all X and Y in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

Proof

The fact that (i) and (ii) are equivalent is proven in [19, Proposition 1.4].

Since ${\text {Ext}}_\varLambda ^*(M,N)\simeq {\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}\varLambda )}^*(M,N)$ as H-modules, we infer that (iii) implies (ii). Now assume that (ii) is satisfied. Since any object in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is isomorphic to a bounded complex and H is a Noetherian ring, it follows by induction on the length of the finite complexes that (iii) holds. $\square$

Hence, it follows that Fg is equivalent to the Assumption 3.1. From now on we assume that these conditions are satisfied for $\varLambda$ and H and in addition that $H^0$ is a (commutative) local artinian algebra.

As we noted in the above proof, ${\text {Ext}}_\varLambda ^*(M,N)$ and ${\text {Hom}}_{{{\mathbf {D}}}^{b}({\text {mod}}\varLambda )}^*(M,N)$ are isomorphic as H-modules for all finitely generated $\varLambda$-modules M and N. Hence we have the following.

Proposition 9.2

Any module M in ${\text {mod}}\varLambda$ viewed as a stalk complex concentrated in degree 0 (any single degree) satisfies

$$\begin{aligned} V_H(M) = V(M), \end{aligned}$$

where $V_H(M)$ denotes the support variety of M defined in [19, 33].

Since any object X in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is quasi-isomorphic to a bounded complex, X is in ${\text {Thick}}(\varLambda /{\mathfrak {j}})$. Using this, the following is an easy consequence of the general theory and [33, Proposition 4.4].

Proposition 9.3

For any complex X in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ we have the following:

• (a) $V(X)=V(X,\varLambda /{\mathfrak {j}})=V(X,X)=V(\varLambda /{\mathfrak {j}},X)$.

• (b) $V(X) \subseteq V(\varLambda /{\mathfrak {j}})={\text {Spec}}H$.$\square$

Next we show that the variety of an object in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is contained in the union of the varieties of its homology modules and in the union of the support varieties of the stalk complexes from which it is built. Furthermore the dimension of the support variety and the complexity of an object are shown to be equal, and periodic stalk complexes are characterized as eventually $\varOmega$-periodic $\varLambda$-modules.

Proposition 9.4

Let X be in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$. Then the following assertions hold.

• (a) $V(X)\subseteq \cup _{i\in \mathbb {Z}}V(H^i(X))$.

• (b) $V(X)\subseteq \cup _{i\in \mathbb {Z}} V(X^i)$.

• (c) $\dim V(X) = {{\text {cx}}}(X)$.

• (d) A module M in ${\text {mod}}\varLambda$ is a periodic object in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ if and only if M is an eventually $\varOmega$-periodic $\varLambda$-module.

Proof

(a) Here again, we use that any object in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is isomorphic to a bounded complex. If X is a stalk complex, the claim clearly holds. Suppose that the claim has been shown for all complexes of length $n-1$. Let $X:\cdots 0\rightarrow X^1\xrightarrow {d^1} X^2\xrightarrow {d^2} \cdots \xrightarrow {d^{n-1}} X^n\rightarrow 0\cdots$ be a complex of length n. Consider the triangle

By Proposition 3.3$V(X)\subseteq V(H^1(X))\cup V(Y)$. It is easy to see that Y is isomorphic to $Z:\cdots 0\rightarrow X^2/{\text {Im}}d^1\xrightarrow {\overline{d^2}} X^3\xrightarrow {d^3} \cdots \xrightarrow {d^{n-1}} X^n\rightarrow 0\cdots$, so that $V(Y)=V(Z)$ and by induction

$$\begin{aligned} V(X)&\subseteq V(H^1(X)) \cup (\cup _{i=2}^n V(H^i(Z))) \\&= \cup _{i=1}^n V(H^i(X)) \end{aligned}$$

since $H^i(Z)=H^i(X)$ for $i=2,3,\ldots ,n$.

(b) Use similar arguments as in the proof of (a).

(c) By assumption $H^0$ is a local ring. Let ${\mathfrak {r}}$ be the unique maximal ideal in $H^0$. Since ${\mathfrak {r}}$ and ${\mathfrak {r}}H$ are nilpotent ideals and therefore contained in any prime ideal, the dimensions

$$\begin{aligned} \dim V(X) =&\dim H/{\text {Ann}}_H{\text {Hom}}_{{{\mathbf {D}}}^b({\text {mod}}\varLambda )}^*(X,X)\\ =&\dim \left( (H/{\mathfrak {r}}H)/{\text {Ann}}_{H/{\mathfrak {r}}H} ({\text {Hom}}_{{{\mathbf {D}}}^b({\text {mod}}\varLambda )}^*(X,X)\otimes _{H^0} H/{\mathfrak {r}}H)\right) \end{aligned}$$

coincide. For this we observe that if ${\overline{\eta }}$ is in

$$\begin{aligned} {\text {Ann}}_{H/{\mathfrak {r}}H} {\text {Hom}}_{{{\mathbf {D}}}^b({\text {mod}}\varLambda )}^*(X,X)\otimes _{H^0} H^0/{\mathfrak {r}}, \end{aligned}$$

the element $\eta$ is in

$$\begin{aligned} \sqrt{{\text {Ann}}_H{\text {Hom}}_{{{\mathbf {D}}}^b({\text {mod}}\varLambda )}^*(X,X)}, \end{aligned}$$

and if $\eta$ is in

$$\begin{aligned} {\text {Ann}}_H{\text {Hom}}_{{{\mathbf {D}}}^b({\text {mod}}\varLambda )}^*(X,X) \end{aligned}$$

then ${\overline{\eta }}$ is in

$$\begin{aligned} {\text {Ann}}_{H/{\mathfrak {r}}H} {\text {Hom}}_{{{\mathbf {D}}}^b({\text {mod}}\varLambda )}^*(X,X)\otimes _{H^0} H. \end{aligned}$$

Now the claim follows from the fact that the Krull dimension of a finitely generated graded algebra over a field equals the polynomial growth of that graded ring.

(d) By the assumptions on $\varLambda$, it must be a Gorenstein algebra [33]. Then ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )/{{\mathbf {D}}}^{{\text {perf}}}({\text {mod}}\varLambda )$ is equivalent to ${\underline{{\text {CM}}}}(\varLambda )$, where ${\text {CM}}(\varLambda )$ is the full subcategory of the ${\text {mod}}\varLambda$ consisting of the maximal Cohen-Macaulay modules and ${\underline{{\text {CM}}}}(\varLambda )$ is ${\text {CM}}(\varLambda )$ modulo the ideal generated by the projective modules [15]. An equivalence

$$\begin{aligned} F:{{\mathbf {D}}}^{b}({\text {mod}}\varLambda )/{{\mathbf {D}}}^{{\text {perf}}}({\text {mod}}\varLambda )\rightarrow {\underline{{\text {CM}}}}(\varLambda ) \end{aligned}$$

is given as follows. Given an object X in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$, construct a projective resolution $p(X)\rightarrow X$ of X. Then $p(X)^{\geqslant t}$ is quasi-isomorphic to a maximal Cohen-Macaulay module $M'$ for some t. Take a coresolution of $M'$ in projective $\varLambda$-modules and splice it with $p(X)^{\geqslant t}$ to get an acyclic complex $X'$. Define F(X) to be the image of the differential starting in degree 0 of $X'$. How F acts on morphisms follows naturally. Moreover, for any module M we have that $\varOmega _\varLambda ^s(F(M))$ is isomorphic to $\varOmega _\varLambda ^t(M)$ for some positive integers s and t.

Assume that $M\simeq M[n]$ in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )/{{\mathbf {D}}}^{{\text {perf}}}({\text {mod}}\varLambda )$ for some positive integer n. Then since F is a triangle equivalence, $F(M)\simeq F(M[n])\simeq \varOmega _\varLambda ^{-n}(F(M))$, and consequently $\varOmega _\varLambda ^n(F(M))\simeq F(M)$. Then by the above remarks it follows that $\varOmega _\varLambda ^{n+p}(M)\simeq \varOmega _\varLambda ^p(M)$ for some positive integer p and M is eventually $\varOmega$-periodic.

Assume that M is eventually $\varOmega$-periodic. For any $\varLambda$-module N, it is easy to see that $N\simeq \varOmega ^t(N)[t]$ in ${{\mathbf {D}}}^b({\text {mod}}\varLambda )/{{\mathbf {D}}}^{{{\text {perf}}}}({\text {mod}}\varLambda )$ for all positive integers t. Since by assumption $\varOmega ^{p+q}_\varLambda (M)\simeq \varOmega ^q_\varLambda (M)$ for some positive integers p and q, we infer that $M\simeq M[n]$ in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )/{{\mathbf {D}}}^{{\text {perf}}}({\text {mod}}\varLambda )$ for some positive integer n, that is, M is periodic in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$. $\square$

Remark 9.5

The inclusion in (a) is not an equality in general, as there exist perfect complexes with homology whose support varieties are not contained in $V(H^+)$.

Now we show that the perfect objects in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ are exactly the perfect complexes in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$.

Proposition 9.6

Let X be in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$. Then an object X is perfect if and only if X is isomorphic to a perfect complex.

Proof

Suppose that X is isomorphic to a perfect complex P. Since $V(\varLambda )\subseteq V(H^+)$, it follows directly from Proposition 9.4 (b) that X is a perfect object.

Suppose that X in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ is perfect. Then ${\text {Hom}}_{{{\mathbf {D}}}^{b}(\varLambda )}(X,\varLambda /{\mathfrak {j}}[i])=(0)$ for all i such that $|i|\geqslant N$ for some N. There exists a complex of projective modules pX and a quasi-isomorphism $pX\rightarrow X$ such that $(pX)^i=(0)$ for $i\gg 0$. By assumption

$$\begin{aligned} (0)={\text {Hom}}_{{{\mathbf {D}}}^{b}(\varLambda )}(pX,\varLambda /{\mathfrak {j}}[i])\simeq {\text {Hom}}_{{{\mathbf {K}}}^{^-,b}(\varLambda )}(pX,\varLambda /{\mathfrak {j}}[i]) \end{aligned}$$

for $|i|\geqslant N$. In particular, ${\text {Hom}}_{{{\mathbf {K}}}^{-,b}(\varLambda )}(pX,D(\varLambda ^{{\text {op}}})[i])=(0)$ when $|i|\geqslant N$, so that pX is exact beyond N from degree zero. Then having ${\text {Hom}}_{{{\mathbf {K}}}^{-,b}(\varLambda )}(pX,\varLambda /{\mathfrak {j}}[i])=(0)$ when $|i|\geqslant N$ implies that pX is split exact beyond degree N. Hence we can choose pX such that $(pX)^i=(0)$ for $|i| > N$. This proves that X is isomorphic to the perfect complex pX. $\square$

To discuss properties of complexes with complexity $d>0$ we need the following characterization of the Koszul objects $\varLambda /\!\!/h$ for $h:\varLambda \rightarrow \varLambda [n]$ in the setting of this section when $n\geqslant 1$.

Lemma 9.7

Let $h:\varLambda \rightarrow \varLambda [n]$ be in ${\text {Hom}}_{{{\mathbf {D}}}^{b}({{\mathcal {B}}})}(\varLambda ,\varLambda [n])$ for $n\geqslant 1$. Then there exists a $\varLambda ^e$-module $M_h$ such that $\varLambda /\!\!/h$ is quasi-isomorphic to a shift of the complex

$$\begin{aligned} \cdots 0\rightarrow M_h\rightarrow P^{-n+2}\rightarrow \cdots \rightarrow P^{-1}\rightarrow P^0\rightarrow 0\cdots \end{aligned}$$

with homology isomorphic to $\varLambda$ in degrees 0 and n.

Proof

Fix a minimal projective resolution $\mathbb {P}:\cdots \rightarrow P^{-n}\rightarrow P^{-n+1}\rightarrow \cdots \rightarrow P^{-1}\rightarrow P^0\rightarrow \varLambda \rightarrow 0$ of $\varLambda$ over $\varLambda ^e$.

As an object in ${{\mathbf {D}}}^{b}({{\mathcal {B}}})$ the stalk complex $\varLambda$ is quasi-isomorphic to the truncated complex $\mathbb {P}_t:\cdots \rightarrow P^{-n}\rightarrow P^{-n+1}\rightarrow \cdots \rightarrow P^{-1}\rightarrow P^0\rightarrow 0\cdots$. Then h is a map from $\mathbb {P}_t$ to $\varLambda$ in degree n, and $\varLambda /\!\!/h$ is given by

$$\begin{aligned} \cdots \rightarrow P^{-n-1}\rightarrow P^{-n} \xrightarrow {\left( {\begin{matrix} h\\ d^{-n}\end{matrix}}\right) } \varLambda \amalg P^{-n+1}\xrightarrow {(0~d^{-n+1})} P^{-n+2}\cdots \rightarrow P^{-1}\rightarrow P^0\rightarrow 0\cdots . \end{aligned}$$

We have the following commutative diagram

where the maps are coming from the pushout diagram

Since the upper sequence is acyclic, $\varLambda /\!\!/h$ is quasi-isomorphic to the complex in the lower row. It is clear from the above pushout diagram that the homology in degrees 0 and n are isomorphic to $\varLambda$. $\square$

Using this we show that $\varLambda /\!\!/h\otimes _\varLambda X$ and $M_h\otimes _\varLambda X$ have the same varieties.

Lemma 9.8

Let X be in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$, and let $h:\varLambda \rightarrow \varLambda [n]$ be in ${\text {Hom}}_{{{\mathbf {D}}}^{b}({{\mathcal {B}}})}(\varLambda ,\varLambda [n])$ for $n\geqslant 1$. Then

$$\begin{aligned} V(\varLambda /\!\!/h\otimes _\varLambda X)=V(M_h\otimes _\varLambda X). \end{aligned}$$

Proof

Let $X:\cdots 0 \rightarrow X^0\xrightarrow {d^0} X^1\rightarrow \cdots \rightarrow X^t\rightarrow 0\cdots$ be in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$, and let $h:\varLambda \rightarrow \varLambda [n]$ be in ${\text {Hom}}_{{{\mathbf {D}}}^{b}({{\mathcal {B}}})}(\varLambda ,\varLambda [n])$.

Recall that $\varLambda /\!\!/h:\cdots 0\rightarrow M_h\xrightarrow {\beta _h} P^{-n+2}\rightarrow \cdots \rightarrow P^{-1}\rightarrow P^0\rightarrow 0\cdots$. Let $P:\cdots 0 \rightarrow P^{-n+1}\rightarrow \cdots \rightarrow P^0\rightarrow 0$.

Then

$$\begin{aligned} M_h\otimes _\varLambda X\xrightarrow {\beta _h\otimes {{\text {id}}}_{X}} P\otimes _\varLambda X \rightarrow \varLambda /\!\!/h\otimes _\varLambda X\rightarrow \end{aligned}$$

is a triangle with ${{\text {cone}}}(\beta _h\otimes {{\text {id}}}_{X})\simeq \varLambda /\!\!/h\otimes _\varLambda X$. Since $P\otimes _\varLambda X$ is a perfect complex, it follows that $V(M_h\otimes _\varLambda X)=V(\varLambda /\!\!/h\otimes _\varLambda X)$. $\square$

We end by showing how any object in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$ can be reduced to a perfect complex by tensoring with the special bimodules $M_h$ introduced above.

Proposition 9.9

Let X be in ${{\mathbf {D}}}^{b}({\text {mod}}\varLambda )$. Suppose that ${{\text {cx}}}(X)=d$.

• (a) There exist d homogeneous elements $h_1$, $h_2$,..., $h_d$ in H such that $M_{h_1}\otimes _\varLambda \cdots \otimes _\varLambda M_{h_d}\otimes _\varLambda X$ is isomorphic to a perfect complex.

• (b) If $\varLambda$ is selfinjective, then as an object in ${{\mathbf {K}}}^{-,b}({\text {mod}}\varLambda )$ the complex $M_{h_1}\otimes _\varLambda \cdots \otimes _\varLambda M_{h_d}\otimes _\varLambda X$ is isomorphic to a direct sum of a perfect complex and an acyclic complex.

Proof

Suppose that ${{\text {cx}}}(X)=d$. Then there exist d homogeneous elements $h_1$, $h_2,\ldots , h_d$ in $H^{\geqslant 1}$ such that $\dim H/\langle h_1,h_2,\ldots ,h_d,A(X,X)\rangle =0$. By Proposition 3.7 the variety $V(\varLambda /\!\!/h_1\otimes _\varLambda \cdots \otimes _\varLambda \varLambda /\!\!/h_d\otimes _\varLambda X)$ is equal to the variety of the ideal $\langle h_1,h_2,\ldots ,h_d,A(X,X)\rangle$, hence contained in $V(H^+)$. Using Lemma 9.8 the complex $M_{h_1}\otimes _\varLambda \cdots \otimes _\varLambda M_{h_d}\otimes _\varLambda X$ is perfect. The claims in (a) and (b) follow from this. $\square$