Exponential decay estimates for fundamental matrices of generalized Schrödinger systems

Abstract

In this article, we investigate systems of generalized Schrödinger operators and their fundamental matrices. More specifically, we establish the existence of such fundamental matrices and then prove sharp upper and lower exponential decay estimates for them. The Schrödinger operators that we consider have leading coefficients that are bounded and uniformly elliptic, while the zeroth-order terms are assumed to be nondegenerate and belong to a reverse Hölder class of matrices. In particular, our operators need not be self-adjoint. The exponential bounds are governed by the so-called upper and lower Agmon distances associated to the reverse Hölder matrix that serves as the potential function. Furthermore, we thoroughly discuss the relationship between this new reverse Hölder class of matrices, the more classical matrix ${\mathcal {A}_{p,\infty }}$ class, and the matrix ${\mathcal {A}_\infty }$ class introduced by Dall’Ara (J Funct Anal 268(12):3649–3679, 2015).

Appendices

The quantitative cancellability condition

In this section, we are trying to further motivate the ${\mathcal{Q}\mathcal{C}}$ condition that was introduced in Sect. 2. To do this, we show that the set of matrix weights $\left( {\mathcal {B}_p}\cap \mathcal{N}\mathcal{D} \right) {\setminus } {\mathcal{Q}\mathcal{C}}$ is nonempty and that there is a matrix function in this space that fails to satisfy the Fefferman–Phong inequality described by Lemma 15. As such, we hope to convince our reader that the additional assumption $V \in {\mathcal{Q}\mathcal{C}}$ is justified for our purposes.

We explore the properties of the matrix function that was introduced in Example 3. With $x = \left( x_1, \ldots , x_n \right) \in \mathbb {R}^n$, and $\left| x\right| = \sqrt{x_1^2 + \cdots + x_n^2} \ge 0$, recall that $V: \mathbb {R}^n \rightarrow \mathbb {R}^{2 \times 2}$ is defined as

$$\begin{aligned} V(x) = \begin{bmatrix}1 &{}\quad \left| x\right| ^2 \\ \left| x\right| ^2 &{}\quad \left| x\right| ^4 \end{bmatrix} = \begin{bmatrix}1 &{}\quad x_1^2 + \cdots x_n^2 \\ x_1^2 + \ldots x_n^2 &{}\quad \left( x_1^2 + \cdots x_n^2 \right) ^2 \end{bmatrix}. \end{aligned}$$

(89)

We begin with a result regarding polynomial matrices.

Proposition 13

Let $V:\mathbb {R}^n \rightarrow \mathbb {R}^{d \times d}$ be any $d \times d$ matrix with polynomial entries. Then $V^*V \in {\mathcal {B}_p}$ for every $p > 1$.

Proof

First, if $P: \mathbb {R}^n \rightarrow \mathbb {\mathbb {R}}_{\ge 0}$ is any nonnegative polynomial, then as shown in [7], for any $p > 1$, P is a scalar ${\text {B}_p}$ function with a ${\text {B}_p}$ constant that depends only on n and the degree of P.

Let $k = \max \left\{ \deg \left( V_{ij} \right) \right\} _{i, j=1}^d$ and observe that for any $\vec {e} \in \mathbb {R}^d$, $P(x; \vec {e}) = \left\langle V^* (x) V(x) \vec {e}, \vec {e} \right\rangle$ is a nonnegative polynomial of degree at most 2k. By the conclusion of the previous paragraph, for any $p > 1$, $P(x; \vec {e})$ belongs to ${\text {B}_p}$ with a constant depending only on n and the degree of $P(x; \vec {e})$. In particular, for any $p > 1$ and any $\vec {e} \in \mathbb {R}^d$, $P(x; \vec {e})$ belongs to ${\text {B}_p}$ with a constant that is independent of $\vec {e}$. Since $V^*V$ is symmetric and positive semidefinite, then we conclude that $V^* V$ belongs to ${\mathcal {B}_p}$. $\square$

We immediately have the following.

Corollary 5

Let $V:\mathbb {R}^n \rightarrow \mathbb {R}^{d \times d}$ be any $d \times d$, symmetric positive semidefinite matrix with polynomial entries. Then $V \in {\mathcal {B}_p}$ for every $p > 1$.

It follows that for V as defined in (89), $V \in {\mathcal {B}_p}$. Since V also satisfies (9), then $V \in \mathcal{N}\mathcal{D}$. Now we show that V is an example of positive definite polynomial matrix that doesn’t satisfy our quantitative cancellability condition.

Lemma 25

$({\mathcal{Q}\mathcal{C}}$ is a proper subset of ${\mathcal {B}_p}\cap \mathcal{N}\mathcal{D})$ For V as defined in (89), $V \notin {\mathcal{Q}\mathcal{C}}$.

Proof

We need to show that the condition (10) doesn’t hold. For any $x \in \mathbb {R}^n$,

$$\begin{aligned} \Psi \left( x, r; V \right)&= \frac{1}{r^{n-2}} \int _{Q(x, r)} V(y) dy = \frac{1}{r^{n-2}} \int _{Q(x, r)} \left[ \begin{array}{cc} 1 &{} \left| y\right| ^2 \\ \left| y\right| ^2 &{} \left| y\right| ^4 \end{array}\right] dy. \end{aligned}$$

Computing, we have

$$\begin{aligned} \int _{Q(x, r)} \left( y_1^2 + \cdots + y_n^2 \right) dy&= \sum _{j=1}^n \int _{x_n - r}^{x_n+r} \ldots \int _{x_1 - r}^{x_1+r} y_j^2 \, dy_1 \ldots dy_n\\&= \sum _{j=1}^n \left( 2r \right) ^{n-1} \int _{x_j - r}^{x_j+r} y_j^2 \, dy_j = 2^n r^{n} \left( \left| x\right| ^2 + \frac{n}{3} r^2 \right) \end{aligned}$$

and a similar computation shows that

$$\begin{aligned} \int _{Q(x, r)} \left( y_1^2 + \cdots + y_n^2 \right) ^2 dy&= \sum _{j=1}^n \int _{x_n - r}^{x_n+r} \cdots \int _{x_1 - r}^{x_1+r} y_j^2 \left( y_1^2 + \cdots + y_n^2 \right) dy_1 \ldots dy_n \\&= 2^n r^n f(x; r) , \end{aligned}$$

where $f(x; r) = \left| x\right| ^4 + 2 \frac{n+ 2}{3} \left| x\right| ^2 r^{2} + \frac{\left( 5n+4 \right) n}{45}r^{4}$. Therefore,

$$\begin{aligned} \Psi \left( x, r; V \right)&= 2^n r^2 \left[ \begin{array}{cc} 1 &{} \left| x\right| ^2 + \frac{n}{3} r^2 \\ \left| x\right| ^2 + \frac{n}{3} r^2 &{} f(x; r) \end{array}\right] . \end{aligned}$$

We choose $\underline{r}= \underline{r}(x)$ optimally so that $\Psi \left( x, \underline{r}; V \right) \ge I$. That is, we want both eigenvalues of $\Psi \left( x, \underline{r}; V \right)$ to exceed 1, so we solve

$$\begin{aligned} 1&= 2^{n-1} \underline{r}^2 \left( 1 + f(x; \underline{r}) \right) \left[ 1 - \sqrt{1 - 4\frac{\frac{4}{3} \left| x\right| ^2 \underline{r}^{2} + \frac{4n}{45}\underline{r}^{4}}{\left( 1 + f(x; \underline{r}) \right) ^2} }\right] \end{aligned}$$

or

$$\begin{aligned} \underline{r}^{8} + \left( \frac{15\left| x\right| ^2}{n} - \frac{{5n+4}}{2^{n+2}} \right) \underline{r}^{6} - \frac{15\left( n+ 2 \right) }{2^{n+1} n} \left| x\right| ^2 \underline{r}^{4} - 45\frac{{1 + \left| x\right| ^4 }}{2^{n+2} n}\underline{r}^2 + \frac{45}{2^{2n+2} n} = 0. \end{aligned}$$

(90)

If $\left| x\right| \gg 1$, say $\left| x\right| \ge \left( \frac{20}{27 n+ 60} \right) ^{\frac{1}{4}}$, then $\underline{r}\ge c_n {\left| x\right| }^{\frac{1}{2}}$, where $c_n = \left( \frac{3}{2^{n+2}} \right) ^{\frac{1}{4}}$. In particular, $\underline{r}\rightarrow \infty$ when $\left| x\right| \rightarrow \infty$. Therefore, we may construct an increasing sequence $\left\{ R_m\right\} _{m=1}^\infty$ such that whenever $\left| x_m\right| = R_m$, $\underline{r}(x_m)^2 = m$. That is, we solve (90) with $\left| x\right| = R_m$ and $\underline{r}= \sqrt{m}$ to get

$$\begin{aligned} R_m^2&= \frac{2^{n+1}m^2\left( 1 - \frac{{n+ 2}}{2^{n+1}m} \right) }{3} \left[ 1 + \sqrt{1 + \frac{ n\left( 1 -\frac{{5n+4}}{2^{n+2}m} - \frac{45}{2^{n+2}n m^3} + \frac{45}{2^{2n+2} n m^4} \right) }{ 5 m 2^{n}\left( 1 - \frac{n+ 2}{2^{n+1}m} \right) ^2}}\right] . \end{aligned}$$

Therefore, $\left| x_m\right| = c_m m$, for some sequence, $\left\{ c_m\right\} _{m=1}^\infty$, of bounded constants. With $r_m = \underline{r}(x_m)$, we have $r_m = \sqrt{m}$.

Now we set $Q_m = Q(x_m, r_m)$ and calculate

$$\begin{aligned} V(Q_m)&= \int _{Q_m} V(y) dy = \left( 2 r_m \right) ^n \left[ \begin{array}{cc} 1 &{}\quad \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \\ \left| x_m\right| ^2 + \frac{n}{3} r_m^2 &{}\quad f(\left| x_m\right| ; r_m) \end{array}\right] \end{aligned}$$

so that

$$\begin{aligned} V(Q_m)^{-1}&= \frac{3 r_m^{-n-2}}{2^{n+2}\left( \left| x_m\right| ^2 + \frac{n}{15} r_m^2 \right) } \left[ \begin{array}{cc} f(\left| x_m\right| ; r_m) &{}\quad -\left( \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \right) \\ -\left( \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \right) &{}\quad 1 \end{array}\right] . \end{aligned}$$

Since $\sqrt{1 + \left| y\right| ^4} \, V^{\frac{1}{2}}(y) = V(y)$, then

$$\begin{aligned}&\frac{2^{n+2}}{3} r_m^{n+2} \left( \left| x_m\right| ^2 + \frac{n}{15} r_m^2 \right) \left( 1 + \left| y\right| ^4 \right) V(y)^{\frac{1}{2}} V(Q_m)^{-1} V(y)^{\frac{1}{2}} \\&\quad = \left[ \begin{array}{ll} 1 &{}\quad \left| y\right| ^2 \\ \left| y\right| ^2 &{}\quad \left| y\right| ^4 \end{array}\right] \left[ \begin{array}{cc} f(\left| x_m\right| ; r_m) &{}\quad -\left( \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \right) \\ -\left( \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \right) &{}\quad 1 \end{array}\right] \left[ \begin{array}{ll} 1 &{}\quad \left| y\right| ^2 \\ \left| y\right| ^2 &{}\quad \left| y\right| ^4 \end{array}\right] \\&\quad = \left( f(\left| x_m\right| ; r_m)- 2 \left( \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \right) \left| y\right| ^2 + \left| y\right| ^4 \right) \left[ \begin{array}{ll} 1 &{}\quad \left| y\right| ^2 \\ \left| y\right| ^2 &{}\quad \left| y\right| ^4 \end{array}\right] \end{aligned}$$

and we see that

$$\begin{aligned} \frac{\left\langle V(y)^{\frac{1}{2}} V(Q_m)^{-1} V(y)^{\frac{1}{2}} \vec {e}_1, \vec {e}_1 \right\rangle }{3}&= \frac{ f(\left| x_m\right| ; r_m) - 2 \left( \left| x_m\right| ^2 + \frac{n}{3} r_m^2 \right) \left| y\right| ^2 + \left| y\right| ^4}{ 4r_m^{2} \left( \left| x_m\right| ^2 + \frac{n}{15} r_m^2 \right) \left| Q_m\right| \left( 1 + \left| y\right| ^4 \right) }. \end{aligned}$$

Therefore,

Recalling that $\left| x_m\right| = c_m m$ and $r_m = \sqrt{m}$, it follows that

$$\begin{aligned}&\lim _{m \rightarrow \infty }\int _{Q_m} \left\langle V(y)^{\frac{1}{2}} V(Q_m)^{-1} V(y)^{\frac{1}{2}} \vec {e}_1, \vec {e}_1 \right\rangle dy \\&\quad \le \lim _{m \rightarrow \infty } \frac{3\left( \left| x_m\right| ^4 + 2 \frac{n+ 2}{3} \left| x_m\right| ^2 r_m^{2} + \frac{\left( 5n+4 \right) n}{45}r_m^{4}+ \left( \left| x_m\right| - r_m \right) ^4 \right) }{4 r_m^{2}\left( \left| x_m\right| ^2 + \frac{n}{15} r_m^2 \right) \left[ 1 + \left( \left| x_m\right| - r_m \right) ^4\right] } \\&\quad = \lim _{m \rightarrow \infty } \frac{3 m^4 \left( c_m^4 + 2 c_m^2 \frac{n+ 2}{3m} + \frac{\left( 5n+4 \right) n}{45 m^2} + \left( c_m - \frac{1}{\sqrt{m}} \right) ^4 \right) }{4 m^7 \left( c_m^2 + \frac{n}{15m} \right) \left[ m^{-4} + \left( c_m - \frac{1}{\sqrt{m}} \right) ^4\right] } = 0. \end{aligned}$$

In particular, there is no constant $c > 0$ so that for all cubes $Q = Q(x, \frac{1}{\underline{m}(x, V)})$ and all $\vec {e} \in \mathbb {R}^d$,

$$\begin{aligned} \int _{Q} \left\langle V(y)^{\frac{1}{2}} V(Q)^{-1} V(y)^{\frac{1}{2}} \vec {e}, \vec {e} \right\rangle dy \ge c \left| \vec {e}\right| , \end{aligned}$$

showing that this choice of $V \in {\mathcal {B}_p}$ does not belong to $\mathcal{N}\mathcal{C}$. $\square$

Next, we show that this choice of V violates the Fefferman–Phong inequality described by Lemma 15.

Lemma 26

(Failure of the Fefferman–Phong inequality) For V as defined in (89), there is no choice of constant C so that for every $\vec {u} \in C^1_0\left( \mathbb {R}^n \right)$, it holds that

$$\begin{aligned} \int _{\mathbb {R}^n} \underline{m}\left( x, V \right) ^2 \left| \vec {u}\right| ^2 \le C \left( \int _{\mathbb {R}^n} \left| D\vec {u}\right| ^2 + \int _{\mathbb {R}^n} \left\langle V \vec {u}, \vec {u} \right\rangle \right) . \end{aligned}$$

(91)

Proof

We will construct a sequence $\left\{ \vec {u}_R\right\} \subseteq C^1_0\left( \mathbb {R}^n \right)$ that violates this inequality as $R \rightarrow \infty$. With $\vec {u} = \left[ - \left| x\right| ^2, 1\right] ^T$, we see that $V \vec {u} = \vec {0}$. For any $R \gg 1$, define $\xi _R \in C^\infty _0\left( \mathbb {R}^n \right)$ so that $\xi _R \equiv 1$ when $x \in B_{2R} {\setminus } B_R$ and ${{\,\textrm{supp}\,}}\xi _R \subseteq B_{3R} {\setminus } B_{R/2}$. In particular, ${{\,\textrm{supp}\,}}\nabla \xi _R \subseteq \left( B_{3R} {\setminus } B_{2R} \right) \cup \left( B_R {\setminus } B_{R/2} \right)$ with $\left| \nabla \xi _R\right| \lesssim \frac{1}{R}$. Then if we define $\vec {u}_R = \vec {u} \xi _R$, we see that $\vec {u}_R \in C^1_0\left( \mathbb {R}^n \right)$ and for any choice of $R > 0$, $V \vec {u}_R = \vec {0}$. In particular,

$$\begin{aligned} \int _{\mathbb {R}^n} \left\langle V \vec {u}_R, \vec {u}_R \right\rangle = 0. \end{aligned}$$

Now

$$\begin{aligned} D\vec {u}_R = \left[ \begin{array}{c} - 2 \vec {x} \xi _R \\ 0\end{array}\right] + \left[ \begin{array}{c} - \left| x\right| ^2 \nabla \xi _R \\ \nabla \xi _R \end{array}\right] \end{aligned}$$

so that

$$\begin{aligned} \int _{\mathbb {R}^n} \left| D\vec {u}_R\right| ^2&\le \int _{B_{3R} \setminus B_{R/2}} 4 \left| x\right| ^2 + \int _{\left( B_{3R} \setminus B_{2R} \right) \cup \left( B_R \setminus B_{R/2} \right) } \left( \left| x\right| ^4 +1 \right) \left| \nabla \xi _R\right| ^2\\&\lesssim \left| B_{3R}\right| R^2 \simeq R^{n+2} \end{aligned}$$

and then

$$\begin{aligned} \int _{\mathbb {R}^n} \left| D\vec {u}\right| ^2 + \int _{\mathbb {R}^n} \left\langle V \vec {u}, \vec {u} \right\rangle \lesssim _{(d, n)} R^{n+2}. \end{aligned}$$

(92)

Recall from the proof of Lemma 25 that there is a bounded sequence $\left\{ c_m\right\} _{m=1}^\infty \subseteq \mathbb {R}$ so that if $\left| x_m\right| = c_m m$ for all $m \in \mathbb {N}$, then $\underline{r}(x_m) = \sqrt{m}$. In other words, $\underline{r}(x_m) = \sqrt{\frac{\left| x_m\right| }{c_m}}$. Since $\underline{r}(x) = \frac{1}{\underline{m}(x)}$, then we conclude that $\underline{m}(x) \simeq \sqrt{ \frac{1}{\left| x\right| }}$ whenever $\left| x\right| \gg 1$. Thus, we see that

$$\begin{aligned} \int _{\mathbb {R}^n} \underline{m}\left( x, V \right) ^2 \left| \vec {u}_R\right| ^2&\ge \int _{B_{2R} \setminus B_R} \underline{m}\left( x, V \right) ^2 \left| \vec {u}_R\right| ^2 \gtrsim \int _{B_{2R} \setminus B_R} \underline{m}\left( R, V \right) ^2 R^4 \simeq R^{n+3}. \end{aligned}$$

If (91) were to hold, then there is a $C > 0$ so that $R^{n+3} \le C R^{n+2}$ for all $R \gg 1$. As this is impossible, the proof is complete. $\square$

The ${\mathcal {A}_{2,\infty }}$, ${\mathcal {A}_\infty }$, $\mathcal {R}_{\text {BM}},$ and ${\mathcal {B}_p}$ classes of matrices

The goal of this appendix is to provide precise and concrete connections between the classes of matrix weights that were introduced in Sect. 2: ${\mathcal {A}_{2,\infty }}$ (and more generally ${\mathcal {A}_{p,\infty }}$, which will be defined momentarily), $\mathcal {R}_{\text {BM}}$, ${\mathcal {A}_\infty },$ and ${\mathcal {B}_p}$. For the reader who is unfamiliar with the theory of ${\mathcal {A}_{p,\infty }}$ matrix weights, see [31] for proofs of well known results that are stated but not proved in this appendix.

Throughout this section, unless otherwise stated, we assume that $1< p < \infty$. Let V be a complex-valued matrix weight defined on $\mathbb {R}^n$; that is, V is a Hermitian positive semidefinite $d \times d$ matrix function with $\left| V\right| \in L_{\text {loc}}^1 (\mathbb {R}^n)$. Note that in the body of this paper, we assume that V is real-valued and symmetric. As pointed out in the introduction, for our purposes, there is no loss of generality in replacing “complex Hermitian” with “real symmetric”. However, here within the appendix, we follow the standard convention in matrix weight theory and work with complex Hermitian matrix weights. It should be noted that a matrix weight V is (unless otherwise stated) not necessarily positive definite a.e. on $\mathbb {R}^n$.

We use the notation $a_Q V$ to denote the average of the matrix function V over the cube $Q \subseteq \mathbb {R}^n$. That is, .

We begin by stating some useful and well known results regarding matrix weights. First we have what is known as the “matrix Jensen’s inequality”, which says that for any matrix weight V and any measurable $Q \subseteq \mathbb {R}^n$ with $\left| Q\right| > 0$ we have

$$\begin{aligned} \det (a_Q V) \ge \exp \left( a _Q (\ln \det V) \right) \end{aligned}$$

(93)

We refer the reader to [17, p. 48] for a proof.

The next inequality is sometimes called the “Hadamard determinant inequality”. See [38, p. 389] for a proof.

Lemma 27

(Determinant lemma) If A is a positive semidefinite Hermitian matrix and $\{\vec {e}_j\}_{j=1}^d$ is any orthonormal basis of $\mathbb {C}^d$, then $\det A \le \prod _{j = 1}^d \left\langle A \vec {e}_j, \vec {e}_j \right\rangle \le \prod _{j = 1}^d \left| A \vec {e}_j\right|$.

Definition 12

(p-nondegenerate) We say that a matrix weight V is p -nondegenerate if for every $\vec {e} \in \mathbb {C}^d$, it holds that

$$\begin{aligned} \left| V^\frac{1}{p} (x) \vec {e}\right| > 0 \quad \text {a.e. on} \;\; \mathbb {R}^n. \end{aligned}$$

In the setting where V is p-nondegenerate, for any cube Q, the map defines a norm on $\mathbb {C}^d$. Thus, the John ellipsoid theorem implies the existence of a “reducing matrix”, defined as follows.

Definition 13

(Reducing matrix) If V is a p-nondegenerate matrix weight, then for every cube $Q \subseteq \mathbb {R}^n$, there exists a positive definite, Hermitian $d \times d$ matrix $R_Q ^p (V)$, called a reducing matrix. This matrix $R_Q ^p (V)$ has the property that for any $\vec e \in \mathbb {C}^d$,

(94)

See [17, p. 79] for a proof with the same lower bound and a slightly worse upper bound of d. The reducing matrix need not be unique, but the choice of $R_Q ^p (V)$ is insignificant.

Note that if $p = 2$, then

That is, if $p = 2$, then $\left( a_Q V \right) ^\frac{1}{2}$ is a reducing matrix for V.

Also, observe that

(95)

showing that $R_Q^{2p} (V^p)$ is a reducing matrix for the norm .

We now introduce the ${\mathcal {A}_{p,\infty }}$ class from [17, 18]. In contrast to the scalar setting where there is a single class of ${\text {A}_\infty }$ weights, in the matrix setting, there is such a class for each p.

Definition 14

(${\mathcal {A}_{p,\infty }}$) We say that $V \in {\mathcal {A}_{p,\infty }}$  if V is a p-nondegenerate matrix weight and there exists a constant $A_{V} = A_{V,p} > 0$ so that for every cube $Q \subseteq \mathbb {R}^n$, it holds that

(96)

For example, when $p = 2$, it follows from the observation above that $V \in {\mathcal {A}_{2,\infty }}$ if there exists a constant $A_V > 0$ so that for every cube $Q \subseteq \mathbb {R}^n$, we have

$$\begin{aligned} \det (a_Q V) \le A_V \exp \left( a_Q (\ln \det V) \right) . \end{aligned}$$

(97)

Note that if $V \in {\mathcal {A}_{p,\infty }}\cap \mathcal{N}\mathcal{D}$ then V is positive definite a.e. For if there were a bounded $A \subseteq \mathbb {R}^n$ with $|A| > 0$ and $\det V = 0$ on A, then picking any cube $Q \supseteq A$ forces the right hand side of (96) to be zero while the left hand side is positive.

Now we give another useful characterization of the ${\mathcal {A}_{p,\infty }}$ class of matrices from [18, p. 451].

Lemma 28

$({\mathcal {A}_{p,\infty }}$ characterization) Let V be a p-nondegenerate matrix weight. Then $V \in {\mathcal {A}_{p,\infty }}$ iff V is positive definite and there exists a constant $C > 0$ so that for every $Q \subseteq \mathbb {R}^n$ and every $\vec {e} \in \mathbb {C}^d$, it holds that

(98)

While we will not need it, it should be noted that the reverse inequality in (98) is also true for all matrix weights with $C = 1$. See [18, p. 451] for a proof of that direction.

We also need the following elementary Lemma from [17, p. 49].

Lemma 29

(Determinant to norm lemma) Let A be a $d \times d$ matrix for which $\left| \det A\right| \le C < \infty$ and $\left| A\vec {e} \right| \ge \left| \vec {e}\right|$ for any $\vec {e} \in \mathbb {C}^d$. Then $\Vert A\Vert \le C$.

If $V \in \mathcal{N}\mathcal{D}$, where $\mathcal{N}\mathcal{D}$ is the “nondegenerate” class of matrix weights introduced and discussed in Sect. 2, then for any measurable set E with $\left| E\right| > 0$, it holds that $\int _E V > 0$. That is, for any $\vec {e} \in \mathbb {C}^d$, we have

$$\begin{aligned} 0 < \left\langle \left( \int _E V(x) \, dx \right) \vec {e}, \vec {e} \right\rangle = \int _E \left\langle V(x) \vec {e}, \vec {e} \right\rangle \, dx = \int _E \left| V^\frac{1}{2} (x) \vec {e}\right| ^2 \, dx. \end{aligned}$$

It follows that $V^p$ is 2p-nondegenerate. In particular, for each cube $Q \subseteq \mathbb {R}^n$, there exists a reducing matrix $R_Q ^{2p} (V^p)$. We now state and prove a determinant characterization of the matrix class ${\mathcal {B}_p}$.

Lemma 30

$({\mathcal {B}_p}$ determinant characterization) If $V \in \mathcal{N}\mathcal{D}$, then the following are equivalent:

• (i) There exists a constant $C > 0$ so that for every cube $Q \subseteq \mathbb {R}^n$,

  $$\begin{aligned} \det \left[ R_Q^{2p} (V^p)\right] \le C \det \left( a_Q V \right) ^\frac{1}{2}. \end{aligned}$$

  (99)

• (ii) There exists a constant $C > 0$ so that for every cube $Q \subseteq \mathbb {R}^n$ and every $\vec e \in \mathbb {C}^d$,

  

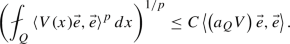  (100)

Remark 18

Notice that the condition described by (100) is our classical definition of $V \in {\mathcal {B}_p}$ as presented in Sect. 2. Therefore, this proposition gives an alternative definition in terms of determinants and reducing matrices.

Proof

We first prove that (99) implies (100). Observe that for any $\vec {e} \in \mathbb {C}^d$, we have by Hölder’s inequality and the property of the reducing matrix in (94) that

Thus, for any $\vec {e} \in \mathbb {C}^d$, $\left| \left[ R_Q^{2p} (V^p)\right] \left( a_Q V \right) ^{-\frac{1}{2}} \vec {e} \right| \ge \left| \vec {e}\right|$, while the assumption of (99) implies that

$$\begin{aligned} \det \left\{ \left[ R_Q^{2p} (V^p)\right] \left( a_Q V \right) ^{-\frac{1}{2}}\right\} \le C. \end{aligned}$$

An application of Lemma 29 shows that

$$\begin{aligned} \left\| \left[ R_Q^{2p} (V^p)\right] \left( a_Q V \right) ^{-\frac{1}{2}} \right\| \le C. \end{aligned}$$

Therefore, it follows from (95) that

showing that (100) holds.

For the converse, assume that (100) holds. As demonstrated above, this assumption is equivalent to

$$\begin{aligned}&\left| R_Q ^{2p} (V^p) \vec {e}\right| ^2 \le C \left| \left( a_Q V \right) ^\frac{1}{2} \vec {e}\right| ^2 \qquad \forall \vec {e} \in \mathbb {C}^d\\&\quad \Leftrightarrow \left| R_Q ^{2p} (V^p) \left( a_Q V \right) ^{-\frac{1}{2}} \vec {e}\right| ^2 \le C \left| \vec {e}\right| ^2 \qquad \forall \vec {e} \in \mathbb {C}^d\\&\quad \Leftrightarrow \left\| \left( a_Q V \right) ^{-\frac{1}{2}} \left[ R_Q^{2p} (V^p)\right] ^2 \left( a_Q V \right) ^{-\frac{1}{2}} \right\| = \left\| R_Q ^{2p} (V^p) \left( a_Q V \right) ^{-\frac{1}{2}}\right\| ^2 \le C^2. \end{aligned}$$

It follows that

$$\begin{aligned} \det \left[ \left( a_Q V \right) ^{-\frac{1}{2}} \left[ R_Q^{2p} (V^p)\right] ^2 \left( a_Q V \right) ^{-\frac{1}{2}}\right] \le C^{2d} \end{aligned}$$

which implies (99), as required. $\square$

Recall the classical assertion that for $p > 1$, a scalar weight $v \in {\text {B}_p}$ iff $v^p \in {\text {A}_\infty }$. The following proposition connects the classes ${\mathcal {B}_p}$ with ${\mathcal {A}_{p,\infty }}$ and provides a matrix analogue to the aforementioned scalar result. See also [28, Corollary 3.8] for a related result.

Proposition 14

If $V \in \mathcal{N}\mathcal{D}$, then $V^p \in \mathcal {A}_{2p, \infty }$ iff $V \in {\mathcal {A}_{2,\infty }}\cap {\mathcal {B}_p}$.

Proof

Assume that $V \in \mathcal{N}\mathcal{D}\cap {\mathcal {A}_{2,\infty }}\cap {\mathcal {B}_p}$. Since $V \in \mathcal{N}\mathcal{D}\cap {\mathcal {B}_p}$, then the conclusions from Lemma 30 hold. As $\left( a_Q V \right) ^\frac{1}{2}$ is a $p = 2$ reducing matrix, then (96) holds with $R_Q^2(V) = \left( a_Q V \right) ^\frac{1}{2}$ since $V \in {\mathcal {A}_{2,\infty }}$. Combining (99) and (96) shows that for any cube $Q \subseteq \mathbb {R}^n$, we have

Comparing with (96), this shows that $V^p \in \mathcal {A}_{2p, \infty }$.

Conversely, assume that $V^p \in \mathcal {A}_{2p, \infty }$ and $V \in \mathcal{N}\mathcal{D}$. By the definition of $\mathcal {A}_{2p, \infty }$ as in (96), then by an application (93), we see that for any cube $Q \subseteq \mathbb {R}^n$,

Since $V \in \mathcal{N}\mathcal{D}$, Lemma 30 implies that $V \in {\mathcal {B}_p}$.

For any $\vec {e} \in \mathbb {C}^d$, we have by Hölder’s inequality and (94) that

so that

$$\begin{aligned}&\left| \left( R_Q ^{2p} (V^p) \right) ^{-1} \left( a_Q V \right) \left( R_Q ^{2p} (V^p) \right) ^{-1}\right| = \left| \left( R_Q ^{2p} (V^p) \right) ^{-1} \left( a_Q V \right) ^\frac{1}{2}\right| ^2 \\&\quad = \left| \left( a_Q V \right) ^\frac{1}{2} \left( R_Q ^{2p} (V^p) \right) ^{-1} \right| ^2 \le 1. \end{aligned}$$

Therefore, for any cube $Q \subseteq \mathbb {R}^n$,

where the second inequality uses (96) since $V^p \in \mathcal {A}_{2p, \infty }$. In particular, since $\left( a_Q V \right) ^\frac{1}{2}$ is a reducing matrix for $p = 2$, it follows from (96) that $V \in {\mathcal {A}_{2,\infty }}$. $\square$

Now that we have discussed the ${\mathcal {A}_{p,\infty }}$ classes of matrices, we seek the connections between the classes ${\mathcal {A}_{p,\infty }}$ and ${\mathcal {A}_\infty }$. We first recall the definition of ${\mathcal {A}_\infty }$ from [1].

Definition 15

(${\mathcal {A}_\infty }$) We say that $V \in {\mathcal {A}_\infty }$ if for any $\varepsilon > 0$, there exists $\delta > 0$ so that for any cube $Q \subseteq \mathbb {R}^n$, it holds that

(101)

Note that when A and B are Hermitian, positive definite matrices, $A \ge B$ iff $\left\| B^{\frac{1}{2}} A^{-\frac{1}{2}}\right\| \le 1$. As observed in [1], we have that for V positive definite a.e., $V \in {\mathcal {A}_\infty }$ iff for any $\varepsilon > 0$ there exists $\gamma > 0$ such that for any cube $Q \subseteq \mathbb {R}^n$, it holds that

(102)

Our next pair of results examine the relationship between ${\mathcal {A}_{2,\infty }}$, $\mathcal {R}_{\text {BM}}$, and ${\mathcal {A}_\infty }$. We first prove the following more general result which implies the first inclusion.

Proposition 15

If $p \ge 1$ and $V^p \in \mathcal {A}_{2p, \infty }$, then $V \in {\mathcal {A}_\infty }$. In particular, ${\mathcal {A}_{2,\infty }}\subseteq {\mathcal {A}_\infty }$.

Proof

Let $Q \subseteq \mathbb {R}^n$ and let $\left\{ \vec {e}_i\right\} _{i = 1}^d$ be the standard orthonormal basis of $\mathbb {C}^d$. For any $\lambda > 0$ and $C > 0$, let $\mathcal {J}_i (Q)$ denote the collection of maximal dyadic subcubes J of Q satisfying

$$\begin{aligned} \left| \left[ R_J ^{2p} (V^p)\right] ^{-1} \left[ R_Q ^{2p} (V^p)\right] \vec {e}_i\right| > e^{C\lambda }. \end{aligned}$$

It was proved in [18, Lemma 3.1] that if $C> 0$ is sufficiently large (independent of Q and J), then

$$\begin{aligned} \sum _{i = 1}^d \sum _{J \in \mathcal {J}_i (Q)} \left| J\right| < \frac{1}{\lambda } \left| Q\right| . \end{aligned}$$

(103)

We now complete the proof using (103). If $x \in Q \backslash \left( \bigcup _{i = 1}^d \bigcup _{J \in \mathcal {J}_i (Q)} J \right)$, then for any dyadic subcube L of Q containing x, we must have that

$$\begin{aligned} \left\| R_Q ^{2p} (V^p)\left[ R_L ^{2p} (V^p)\right] ^{-1} \right\| = \left\| \left[ R_L ^{2p} (V^p)\right] ^{-1} R_Q ^{2p} (V^p)\right\| \le e^{C \lambda }. \end{aligned}$$

It follows that for any $\vec {e} \in \mathbb {C}^d$,

(104)

where we have applied (95) in the last inequality. Applications of Hölder’s inequality, (95), then (104) combined with the Lebesgue differentiation theorem show that for any $\vec {e} \in \mathbb {C}^d$,

However, this implies that, modulo a set of measure zero,

$$\begin{aligned} Q \backslash \left( \bigcup _{i = 1}^d \bigcup _{J \in \mathcal {J}_i (Q)} J \right) \subseteq \left\{ x \in Q : \left\| \left( a_Q V \right) ^\frac{1}{2} V^{-\frac{1}{2}} (x)\right\| \le \sqrt{d} e^{C\lambda }\right\} . \end{aligned}$$

In particular, an application of (103) shows that

$$\begin{aligned} \left| \left\{ x \in Q : \left\| \left( a_Q V \right) ^\frac{1}{2} V^{-\frac{1}{2}} (x)\right\| > \sqrt{d} e^{C\lambda }\right\} \right| \le \sum _{i = 1}^d \sum _{J \in \mathcal {J}_i (Q)} \left| J\right| < \frac{1}{\lambda } \left| Q\right| . \end{aligned}$$

The proof is complete since (102) holds with $\lambda = \frac{1}{\epsilon }$ and $\gamma = \sqrt{d} e^{C \lambda }$. $\square$

Next we show that the inclusion may be reversed. In fact, for the final result of this appendix, we prove three equivalent conditions for nondegenerate matrices. But first, we recall the following definition of the reverse Brunn–Minkowski class of matrices.

Definition 16

($\mathcal {R}_{\text {BM}}$) We say that a matrix weight V belongs to the reverse Brunn–Minkowski class, $V \in \mathcal {R}_{\text {BM}}$, if there exists a constant $B_V > 0$ so that for any cube $Q \subseteq \mathbb {R}^n$, it holds that

Proposition 16

If $V \in \mathcal{N}\mathcal{D}$, then the following are equivalent:

• (a) $V \in {\mathcal {A}_{2,\infty }}$,

• (b) $V \in {\mathcal {A}_\infty }$,

• (c) $V \in \mathcal {R}_{\text {BM}}$ and $(\det V)^\frac{1}{d} \in \text {A}_\infty$.

Proof

That $a) \Rightarrow b)$ was proved in Proposition 15.

We now prove $b) \Rightarrow c)$. Let $V \in \mathcal{N}\mathcal{D}\cap {\mathcal {A}_\infty }$. For any $\varepsilon > 0$, let $\delta = \delta (\varepsilon )$ be as given in the definition of ${\mathcal {A}_\infty }$. Let $\left\{ \vec {e}_k(x)\right\} _{k = 1}^d$ be an orthonormal basis of eigenvectors for V(x) and let $S\subseteq Q$ be the set on the lefthand side of (101) so that $\left| S\right| \ge (1 - \varepsilon ) \left| Q\right|$. Then for any $x \in S$, we have that

(105)

where here we have used both Lemma 27 and (14). In other words,

which shows that $\left( \det V \right) ^\frac{1}{d} \in \text {A}_\infty$.

Next, to show that $V \in \mathcal {R}_{\text {BM}},$ we use the first line of (105) with $\varepsilon = \frac{1}{2}$ and $\delta = \delta \left( \frac{1}{2} \right)$ to get

as required.

Finally we prove that $c) \Rightarrow a)$. If $(\det V) ^\frac{1}{d} \in \text {A}_\infty$, then by the classical reverse Jensen characterization of scalar ${\text {A}_\infty }$ weights (again see [30, Theorem 7.3.3]), there exists $C > 0$ so that for any $Q \subseteq \mathbb {R}^n$, we have

However, combining this bound with $V \in \mathcal {R}_{\text {BM}}$ gives us

which by (97) shows that $V \in {\mathcal {A}_{2,\infty }}$ and completes the proof. $\square$

Technical proofs

This final appendix provides the technical proofs that were skipped in the body of the paper. First we prove Proposition 2, which we recall states that a matrix weight of the form $A = \left( a_{ij} \left| x\right| ^{\gamma _{ij}} \right) _{i, j = 1}^d$ belongs to ${\mathcal {A}_{2,\infty }}\cap {\mathcal {B}_p}$ if $A = \left( a_{ij} \right) _{i, j = 1}^d$ is a Hermitian, positive definite matrix and $\gamma _{ij} = \frac{1}{2} \left( \gamma _i + \gamma _j \right)$ for some $\vec {\gamma } \in \mathbb {R}^d$ with $\gamma _{i} > - \frac{n}{p}$.

Proof of Proposition 2

First observe that since V is positive definite, then $V \in \mathcal{N}\mathcal{D}$. By Proposition 14, $V \in {\mathcal {A}_{2,\infty }}\cap {\mathcal {B}_p}$ iff $V^p \in \mathcal {A}_{2p, \infty }$. Therefore, we will show that $V^p \in \mathcal {A}_{2p, \infty }$. By Lemma 28, $V^p \in \mathcal {A}_{2p, \infty }$ iff there exists a constant $C > 0$ so that for every $\vec {e} \in \mathbb {C}^d$ and every cube $Q \subseteq \mathbb {R}^n$, it holds that

where $R_Q^{2p}$ is a reducing matrix of $V^p$; see (94). This condition is equivalent to the existence of $C > 0$ so that for every unit vector $\vec {e} \in \mathbb {C}^d$ and every cube $Q \subseteq \mathbb {R}^n$, it holds that

(106)

Therefore, to prove this proposition, we will show that there exists a constant $C > 0$ so that (106) holds for every unit vector $\vec {e} \in \mathbb {C}^d$ and every cube $Q \subseteq \mathbb {R}^n$.

First, using the facts that $\ln x \le \left| \ln x\right| = \left| \ln ^+ x - \ln ^+ x^{-1}\right| \le \ln ^+ x + \ln ^+ x^{-1}$ and $\left| A\vec {e}\right| ^{-1} \le \left| A^{-1} \vec {e}\right|$ for any invertible Hermitian matrix A and any unit vector $\vec {e}$, we get

(107)

We estimate $E_2$. If $\{e_j\}_{j = 1}^d$ is any orthonormal basis of $\mathbb {C}^d$, then since $\ln ^+x \le x$ for $x > 0$, we get

(108)

where we have applied Hölder’s inequality followed by the reducing matrix property from (94).

Next, we estimate $E_1$. We start with some preliminary estimates. For any unit vector $\vec {e} \in \mathbb {C}^d$ and any $x \in Q$, observe that by another application of (94),

(109)

where in the final line we have used the fact that whenever B and C are Hermitian, positive semidefinite matrices, it holds that $\left| B^\frac{1}{2} C^\frac{1}{2}\right| ^2 = \left| B ^\frac{1}{2} C B^\frac{1}{2}\right| \simeq _{(d)} {{\,\textrm{tr}\,}}\left( B^\frac{1}{2} C B^\frac{1}{2} \right) = {{\,\textrm{tr}\,}}\left( BC \right)$. Using the explicit presentation of V and $V^{-1}$ from (12) and (13), respectively, we see that

(110)

where we have introduced the notation $f_{ij}(y) = \left| y\right| ^{\gamma _{ij}}$. Since $p \gamma _{ij} = \frac{p}{2} (\gamma _{i} + \gamma _{j}) > - n$, then $f_{ij}^{p} \in \text {A}_{\infty } = \bigcup _{q \ge 1} \text {A}_q$ (see [30, p. 506],) which implies that $f_{ij} \in \text {B}_p$. In particular, it holds that

Thus, combining this final observation with (109) and (110) shows that there exists $C = C(d, n, p, A, \vec {\gamma })$ so that

(111)

To estimate $E_1$, we use that for any $C, x_1, x_2, \ldots , x_d > 0$, it holds that $\ln ^+\left( \sum _{i =1}^d x_i \right) \le d + \sum _{i = 1}^d \ln ^+x_i$ and $\ln ^+(C x) \le \ln ^+ C + \ln ^+ x$. (The proofs of these results follow from induction and case analysis.) Therefore, from (111) we see that

where in the last line we used that $\ln ^+ x = \ln x + \ln ^+ x^{-1}$. Since $\ln ^+ x \le x$, then

On the other hand, since $\gamma _{ij} = \frac{1}{2} \left( \gamma _i + \gamma _j \right) > -\frac{n}{p} \ge -n$, then $f_{ij} \in \text {A}_\infty$. An application of the reverse Jensen inequality (see [30, p. 525]) shows that there exists $C(n, p, \gamma _{ij}) > 0$ so that for any $Q \subseteq \mathbb {R}^n$, it holds that

It follows that $E_1 \lesssim _{(d, n, p, A, \vec {\gamma })} 1$, which, when combined with (107) and (108) shows that (106) holds, as required. $\square$

Next we prove Proposition 3, which states that if $V \in \mathcal{N}\mathcal{D}$ and there exists a constant $B_V > 0$ so that for every cube $Q \subseteq \mathbb {R}^n$, then $V \in {\mathcal{Q}\mathcal{C}}$.

Proof of Proposition 3

Observe that if $\{e_j\}_{j=1}^d$ is any orthonormal basis of $\mathbb {C}^d$, then

$$\begin{aligned}&\left| V^\frac{1}{2} (x) \left( a_Q V \right) ^{-1} V^\frac{1}{2} (x)\right| = \left| V^\frac{1}{2} (x) \left( a_Q V \right) ^{-\frac{1}{2} } \left[ V^\frac{1}{2} (x) \left( a_Q V \right) ^{-\frac{1}{2} }\right] ^*\right| \\&\quad = \left| \left[ V^\frac{1}{2} (x) \left( a_Q V \right) ^{-\frac{1}{2} }\right] ^* V^\frac{1}{2} (x) \left( a_Q V \right) ^{-\frac{1}{2} }\right| = \left| \left( a_Q V \right) ^{-\frac{1}{2} } V(x) \left( a_Q V \right) ^{-\frac{1}{2} }\right| \\&\quad \le \sum _{j = 1}^d \left\langle V(x) \left( a_Q V \right) ^{-\frac{1}{2} } \vec {e}_j, \left( a_Q V \right) ^{-\frac{1}{2} } \vec {e}_j \right\rangle . \end{aligned}$$

Thus, we have

which implies that the largest eigenvalue of is bounded above by d for every cube $Q \subseteq \mathbb {R}^n$.

Assume that $V \notin {\mathcal{Q}\mathcal{C}}$. Looking at (10), this means that there exists a sequence of cubes $\left\{ Q_k\right\} _{k=1}^\infty \subseteq \mathbb {R}^n$ so that if we define , then each $V_k$ has a smallest eigenvalue $\lambda _{k,1}:= \lambda _1(V_k)$ with the property that $\lambda _{k,1} \rightarrow 0$ as $k \rightarrow \infty$. For $j = 1, \ldots , d$, let $\lambda _{k,j}:= \lambda _j(V_k)$, the $j^{\text {th}}$ eigenvalue of $V_k$, and note that $\lambda _{k, j} \le d$ for $j = 2, \ldots , d$. Then

(112)

However, for any $Q \subseteq \mathbb {R}^n$, an application of (14) applied to $V^\frac{1}{2} \left( a_Q V \right) ^{-1} V^\frac{1}{2}$ shows that

where we have applied the assumption in the last inequality. This contradicts (112), and therefore gives the desired conclusion. $\square$