On extra-special Enriques surfaces

Abstract

We refine Cossec and Dolgachev’s classification of extra-special Enriques surfaces, providing a complete and concise proof.

1 Introduction

Throughout the paper, $X$ will denote an Enriques surface defined over an algebraically closed field of arbitrary characteristic $p$.

A half-fiber on $X$ is a divisor $F$ such that $2F$ is a fiber of a genus one fibration. A $c$-sequence on $X$ is a sequence of half-fibers $(F_1,\ldots ,F_c)$ such that $F_i.F_j = 1 - \delta _{ij}$. As observed by Enriques himself for classical Enriques surfaces, and later extended to non-classical Enriques surfaces by Bombieri and Mumford [1, Theorem 3], every Enriques surface admits a $1$-sequence. The maximal length of a $c$-sequence is $10$.

It is a natural question to ask whether every $c$-sequence can be extended to a $c'$-sequence with $c' > c$. In this context, extra-special Enriques surfaces play a fundamental role.

Definition 1.1

An Enriques surface $X$ is called

• extra-special of type $\tilde{E}_8$ if the dual graph of all $(-2)$-curves on $X$ is

  

  (A)

• extra-special of type $\tilde{D}_8$ if the dual graph of all $(-2)$-curves on $X$ is

  

  (B)

• extra-special of type $\tilde{E}_7$ if the dual graph of all $(-2)$-curves on $X$ is

  

  (C)

An Enriques surface is called extra-special if it is extra-special of type $\tilde{E}_8$, $\tilde{D}_8$, or $\tilde{E}_7$.

Extra-special Enriques surfaces do exist. Salomonsson [13] gave equations for all extra-special surfaces of type $\tilde{E}_8$ and $\tilde{E}_7$. An alternative construction of these surfaces as well as examples of extra-special surfaces of type $\tilde{D}_8$ were given by Katsura, Kondō and Martin [9, §§10, 11, 12]. A description of all genus one fibrations on these surfaces can be found in [7, Proposition 6.2.7].

The classification of Enriques surfaces on which every $1$-sequence can be extended to a $2$-sequence is well-known and is contained in the following theorem due to Cossec and Dolgachev.

Theorem 1.2

([3, Theorem 3.4.1] or [4, Theorem 6.1.10]) An Enriques surface $X$ is not extra-special of type $\tilde{E}_8$ if and only if every $1$-sequence on $X$ extends to a $2$-sequence.

More precisely, on extra-special surfaces of type $\tilde{E}_8$ there exists only one genus one fibration, so the only $1$-sequence is non-extendable.

The main result of this paper is the following theorem, whose proof is obtained by combining Theorem 3.4 and Corollary 4.3.

Theorem 1.3

An Enriques surface $X$ is not extra-special if and only if every $c$-sequence with $c \le 2$ on $X$ extends to a $3$-sequence.

More precisely, on extra-special surfaces of type $\tilde{D}_8$ there are exactly three genus one fibrations, giving rise to two distinct $2$-sequences, both non-extendable. On extra-special surfaces of type $\tilde{E}_7$ there are exactly two genus one fibrations, giving rise to a non-extendable $2$-sequence.

Remark 1.4

In their first book about Enriques surfaces, Cossec and Dolgachev proved that $X$ admits a $3$-sequence if $X$ is not extra-special [3, Theorem 3.5.1]. In a similar vein, Cossec proved that if $p \ne 2$, then every $1$-sequence on $X$ extends to a $3$-sequence [2, Theorem 3.5]. Note that our result is strictly stronger than both of these results, since it asserts the extendability of any given $2$-sequence in all characteristics. Big parts of the proof of the result of Cossec are left to the ‘patient reader’. Moreover, the proof of the result of Cossec–Dolgachev occupies 32 pages and is described as ‘lengthy’ in the new book on Enriques surfaces, with ‘no guarantee that it is correct’ (see [7, Remark 6.1.14 and Theorem 6.2.6]). The main ingredient that allows us to give a substantially shorter proof of a stronger result is the observation that in a non-extendable $2$-sequence one of the genus one fibrations is special with a fiber of type $\mathrm {II}^*$ (Theorem 3.4), and that Enriques surfaces with such a fibration can be easily classified in all characteristics (Theorem 4.2).

Remark 1.5

Every extra-special surface admits a genus one fibration with a half-fiber of additive type, and an extra-special surface of type $\tilde{E}_7$ even admits a quasi-elliptic fibration with two half-fibers [7, Proposition 6.2.7]. Consequently (cf. Lemma 2.2), extra-special Enriques surfaces can exist only in characteristic $2$ and they are either classical or supersingular. Additionally, extra-special surfaces of type $\tilde{E}_7$ can only be classical.

We infer an immediate corollary from Remark 1.5.

Corollary 1.6

If one of the following conditions holds:

• 1. $p \ne 2$,

• 2. $p = 2$ and $X$ is ordinary,

• 3. $p = 2$ and $X$ is not extra-special,

then every $c$-sequence on $X$ with $c \le 2$ extends to a $3$-sequence.

Let us describe one of the geometric consequences of the extendability of $1$- and $2$-sequences to $3$-sequences. By applying [4, Theorem 3.5.1 and the following discussion] and [5, Section 7.8.1] to a $3$-sequence that extends a given $2$-sequence $(F_1,F_2)$, we obtain the following strong version of the Enriques–Artin Theorem for non-extra-special, classical Enriques surfaces.

Corollary 1.7

If $X$ is a classical Enriques surface which is not extra-special, then $X$ is the minimal resolution of a sextic $S \subseteq \mathbb {P}^3$ given by an equation of the form

$$\begin{aligned} x_1x_2x_3 L Q + x_1^2x_2^2 L^2 + x_1^2x_3^2 L^2 + x_2^2x_3^2 L^2 + x_1^2x_2^2x_3^2, \end{aligned}$$

where $L$ is linear and $Q$ is a quadratic form. Moreover, for each half-fiber $F_1$ (resp. $2$-sequence $(F_1,F_2)$) on $X$, there is a sextic model as above such that $F_1$ (resp. $(F_1,F_2)$) maps to a line (resp. a pair of lines) in the non-normal locus of $S$.

Extending $3$-sequences to $4$-sequences is a much more difficult problem, even in characteristic $p \ne 2$. The classification of non-extendable $3$-sequences is the subject of our follow-up article [11].

2 Preliminaries

Recall that an Enriques surface is a smooth and proper surface $X$ of Kodaira dimension $0$ with $b_2(X) = 10$ over an algebraically closed field of arbitrary characteristic $p$. An Enriques surface $X$ is called classical if its canonical divisor is not linearly equivalent to $0$. A non-classical Enriques surface $X$ (which can only exist if $p = 2$) is called ordinary (or singular or a ${\mu }_2$-surface) if the absolute Frobenius morphism is bijective on $H^1(X,\mathcal O_X)$, and supersingular (or an ${\alpha }_2$-surface) otherwise.

A genus one fibration on $X$ is a fibration $f :X \rightarrow \mathbb {P}^1$ such that the generic fiber $X_\eta$ is a regular genus one curve. A genus one fibration is called elliptic if $X_\eta$ is smooth and quasi-elliptic otherwise. We will use Kodaira’s notation for singular fibers. Singular fibers of type $\mathrm {I}_n$ are called of multiplicative type, while all others are called of additive type. Any genus one fibration on $X$ admits at least one half-fiber, that is a curve $F$ of arithmetic genus one such that $2F$ is a fiber of the fibration. In particular, the degree of a multisection of a genus one fibration $f$ on $X$ is divisible by $2$ and if $f$ admits a $(-2)$-curve as a bisection, both $f$ and the bisection are called special. A non-multiple fiber of a genus one fibration is called simple.

By a component of a divisor $D$ on $X$, we always mean an irreducible component and we call a component simple, if it is reduced, that is, if it has multiplicity $1$ in $D$. We call $D$ primitive if its class in ${{\,\mathrm{Num}\,}}(X)$ spans a primitive sublattice.

Lemma 2.1

([4, Corollary 2.2.9]) An effective divisor $D$ on $X$ is a half-fiber of a genus one fibration on $X$ if and only if $D$ is nef, primitive, and $D^2 = 0$.

We recall here the behaviour of genus one fibrations on Enriques surfaces.

Lemma 2.2

([4, Theorem 4.10.3]) Let $f:X \rightarrow \mathbb {P}^1$ be a genus one fibration on $X$.

• If $p \ne 2$, then $f$ is an elliptic fibration with two half-fibers, and each of them is either non-singular or singular of multiplicative type.

• If $p = 2$ and $X$ is classical, then $f$ is an elliptic or quasi-elliptic fibration with two half-fibers, and each of them is either an ordinary elliptic curve or a singular curve of additive type.

• If $p = 2$ and $X$ is ordinary, then $f$ is an elliptic fibration with one half-fiber, which is either a non-singular ordinary elliptic curve or a singular curve of multiplicative type.

• If $p = 2$ and $X$ is supersingular, then $f$ is an elliptic or quasi-elliptic fibration with one half-fiber, which is either a supersingular elliptic curve or a singular curve of additive type.

The symbol $\sim$ denotes linear equivalence, and $W_X^{{\mathrm {nod}}}$ denotes the Weyl group generated by reflections in classes of $(-2)$-curves on $X$.

Lemma 2.3

([3, Theorem 3.2.1] or [4, Theorem 2.3.3]) If $D$ is an effective divisor on $X$ with $D^2 \ge 0$, then there exist non-negative integers $a_i$ and $(-2)$-curves $R_i$ such that

$$\begin{aligned} D \sim D' + \sum _i a_i R_i, \end{aligned}$$

where $D'$ is the unique nef divisor in the $W_X^{{\mathrm {nod}}}$-orbit of $D$. In particular, $D^2 = D'^2$.

The following bound is an immediate consequence of the Shioda–Tate formula.

Lemma 2.4

The number of irreducible curves contained in $s$ fibers of any genus one fibration on $X$ is at most $8+s$.

A $c$-degenerate (canonical isotropic) $n$-sequence on $X$ is an $n$-tuple of the form

$$\begin{aligned} \big (F_1,F_1 + R_{1,1},\ldots ,F_1 + \sum _{j=1}^{m_1} R_{1,j},F_2,F_2 + R_{2,1},\ldots ,F_{c} + \sum _{j=1}^{m_c} R_{c,j}\big ), \end{aligned}$$

where the $F_i$ are half-fibers of genus one fibrations on $X$ and the $R_{i,j}$ are $(-2)$-curves satisfying the conditions

• 1. $F_i.F_j = 1 - \delta _{ij}$.

• 2. $R_{i,j}.R_{i,j+1} = 1$.

• 3. $R_{i,j}.R_{k,l} = 0$ unless $(k,l) = (i,j)$ or $(k,l)=(i,j\pm 1)$.

• 4. $F_i.R_{i,1} = 1$ and $F_i.R_{k,l} = 0$ if $(k,l) \ne (i,1)$.

If $c = n$, we simply call the above sequence a $c$-sequence.

We say that a $c$-degenerate $n$-sequence extends to a $c'$-degenerate $n'$-sequence if the former is contained in the latter, disregarding the ordering. The following fundamental theorem is due to Cossec and holds also in positive characteristic (cf. [7, Proposition 6.1.7]).

Theorem 2.5

([2, Lemma 1.6.1, Theorem 3.3]) If $n \ne 9$, then every $c$-degenerate $n$-sequence on $X$ can be extended to a $c'$-degenerate $10$-sequence for some $c' \ge c$.

A generic Enriques surface does not contain any $(-2)$-curve. Thus, by Theorem 2.5 every $c$-sequence with $c \ne 9$ can be extended to a $10$-sequence.

Lemma 2.6

([4, Lemma 2.6.3] or [8, Lemma 3.5]) If $(F_1,F_2)$ is a $2$-sequence, then $F_1$ and $F_2$ do not have common irreducible components.

3 Non-extendable $2$-sequences

In this section, we investigate the extendability of $2$-sequences and the properties of non-extendable $2$-sequences.

Proposition 3.1

Let $(F_1,F_2)$ be a $2$-sequence on an Enriques surface $X$. If there are two simple fibers $G_1 \in |2F_1|$ and $G_2 \in |2F_2|$ with a common irreducible component, then there is a half-fiber $F_3$ extending $(F_1,F_2)$ to a $3$-sequence.

Proof

By [4, Proposition 2.6.1], the linear system $|F_1 + F_2|$ is a pencil of curves without fixed components. Let $R$ be a common component of $G_1$ and $G_2$. Then, $R$ is a $(-2)$-curve with $R.(F_1 + F_2) = 0$. Hence, there exists a curve $C \in |F_1 + F_2|$ containing $R$. Set $C' {:=}C - R$. Then, $C'.F_i = (F_1+F_2-R).F_i = 1$ and $C'^2 = (C - R)^2 = (F_1 + F_2)^2 - 2(F_1 + F_2).R + R^2 = 0$. Using Lemma 2.3, we write $C' = C'' + \sum _i a_iR_i$ with $a_i \ge 0$, $C''$ nef and $C''^2 = C'^2=0$. Then, $C''.F_i = C'.F_i - \sum a_jR_j.F_i \le 1$.

Since $C''$ is nef, $C''.F_i=0$ for at most one $i$ and then $C''.F_j=1$ for $j\ne i$. This implies that $C''$ is primitive, and therefore $C''$ is a half-fiber of some genus one fibration on $X$ by Lemma 2.1. Hence, if $C''.F_1 = C''.F_2 = 1$, then $(F_1,F_2,C'')$ is a $3$-sequence.

Thus, let us exclude the possibility that $C''.F_1 = 0$ (the case $C''.F_2 = 0$ is analogous). In this case, $C''$ is a half-fiber of $|2F_1|$. If $C'' = F_1$, then

$$\begin{aligned} F_2 \sim \left( F_1 + F_2 - C'' \right) \sim (F_1 + F_2 - C) + \left( R + \sum a_iR_i \right) \sim \left( R + \sum a_iR_i \right) . \end{aligned}$$

Since $|F_2|$ is $0$-dimensional, this shows that $R$ is a component of $F_2$. But this is impossible, since we assumed that $R$ is a component of a simple fiber $G_2 \in |2F_2|$. If $C'' \ne F_1$, then the above argument applied to $|F_2 + K_X|$ shows that $R$ is a component of the other half-fiber of $|2F_2|$, again contradicting the fact that $R$ is contained in the simple fiber $G_2 \in |2F_2|$. $\square$

Remark 3.2

Let us explain what happens geometrically in the situation of Proposition 3.1. We will restrict ourselves to characteristic $p \ne 2$ and leave it to the motivated reader to formulate the analogous picture in characteristic $p = 2$. We will use the notation of Proposition 3.1 and refer to [4, Section 3.3] for details on bielliptic models of Enriques surfaces.

The linear system $|2F_1 + 2F_2|$ induces morphisms $X \xrightarrow {\varphi _1} X' \xrightarrow {\varphi _2} \mathsf {D}$, where $\varphi _1$ is birational, and $\varphi _2$ is $2$-to-$1$ onto a $4$-nodal quartic symmetroid del Pezzo surface $\mathsf {D}$. The surface $\mathsf {D}$ contains a quadrangle of lines whose vertices are the nodes, and each of the four half-fibers maps to one of the lines. Since $R$ is not contained in a half-fiber and $R.(2F_1 + 2F_2) = 0$, the curve $R$ is contracted by $\varphi _1$ and maps to a singular point $P$ of the branch curve of $\varphi _2$ outside the quadrangle of lines. There are four pencils of conics on $\mathsf {D}$ and their preimages on $X$ are the pencils $|2F_1|,|2F_2|,|F_1 + F_2|,$ and $|F_1 + F_2 + K_X|$. The proof of Proposition 3.1 shows that the preimage $|F_1 + F_2|$ of one of the pencils of conics that contains two lines, which is a pencil of curves of genus $2$ on $X$, has a reducible member that contains the half-fiber $F_3$.

Another way of seeing this more geometrically was suggested by the referee: the linear system $|2F_1 + 2F_2 - R|$ induces morphisms $X \xrightarrow {\psi _1} X' \xrightarrow {\psi _2} \mathsf {C}$, where $\psi _1$ is birational, $\psi _2$ is $2$-to-$1$, and $\mathsf {C}$ is the blow-up of $\mathsf {D}$ in $P$. Since $P$ does not lie on a line, $\mathsf {C}$ is isomorphic to a cubic surface with four nodes, hence it is the Cayley cubic surface. The surface $\mathsf {C}$ contains exactly nine lines, and we can describe them explicitly in terms of $\mathsf {D}$: four of them are the strict transforms of the four lines on $\mathsf {D}$, four of them are the strict transforms of the four conics on $\mathsf {D}$ that pass through $P$, and one of them is the exceptional curve $E$ over $P$. Six of the nine lines form a tetrahedron, and the other three lie on a plane that intersects the tetrahedron away from the vertices. The three pencils of residual conics that we obtain from the latter three lines give rise to the genus one fibrations $|2F_1|$, $|2F_2|$, and $|2F_3|$, and the preimages of the former six lines are the six half-fibers. We refer the reader to our follow-up article [11] for a closer study of the so-called special $3$-sequences that give rise to this geometric situation.

Corollary 3.3

If $(F_1,F_2)$ is a $2$-sequence on $X$ that does not extend to a $3$-sequence, then one of the half-fibers of $|2F_1|$ or $|2F_2|$ is reducible and has at least $4$ irreducible components.

Proof

By Theorem 2.5, after possibly interchanging $F_1$ and $F_2$, we may assume that there exist $(-2)$-curves $R_{1,1},\ldots ,R_{1,m},R_{2,1},\ldots ,R_{2,n}$ with $m+n = 8$, $m \ge 4$, and such that $(F_1,F_1 + R_{1,1},\ldots ,F_2,F_2 + R_{2,1},\ldots )$ is a $2$-degenerate $10$-sequence. Since $R_{1,2}.F_1 = R_{1,2}.F_2 = 0$, $R_{1,2}$ is a component of two fibers $G_1 \in |2F_1|$ and $G_2 \in |2F_2|$. By Proposition 3.1, $G_1$ and $G_2$ cannot both be simple. Therefore, $R_{1,2}$ is a component of a reducible half-fiber, which also contains all the other $R_{1,j}$ with $j \ne 1$. Hence, one of the reducible half-fibers has at least $4$ components. $\square$

The bound of Corollary 3.3 on the number of irreducible components is not sharp, but it is enough to prove the following theorem, which is the key result of this paper.

Theorem 3.4

If $(F_1,F_2)$ is a $2$-sequence on $X$ that does not extend to a $3$-sequence, then either $|2F_1|$ or $|2F_2|$ is a special genus one fibration with a fiber of type $\mathrm {II}^*$.

Proof

By Corollary 3.3 we can suppose that $F_1$ is reducible and has at least $4$ components. Let $R_{2,1}$ be the component of $F_1$ meeting $F_2$. Since $R_{2,1}$ is a simple component of $F_1$, we can find two more components $R_{2,2}$, $R_{2,3}$ of $F_1$ forming a chain with $R_{2,1}$.

Applying Theorem 2.5, we extend the $2$-degenerate $5$-sequence $(F_1,F_2,\ldots ,F_2+R_{2,1}+R_{2,2}+R_{2,3})$ to a $2$-degenerate $10$-sequence $(F_1,\ldots , F_1 + \sum _{i=1}^m R_{1,i},F_2,\!\ldots ,F_2 + \sum _{i=1}^n R_{2,i})$ with $n \ge 3$. Clearly, all the $R_{2,i}$ are contained in $F_1$.

Note that $R_{2,1}$ is a special bisection of $|2F_2|$. Since $F_2.F_1 = F_2.R_{2,1} = 1$ and $F_1 - R_{2,1}$ is connected ($R_{2,1}$ being a simple component), all components of $F_1$ except $R_{2,1}$ are contained in a fiber $G_2 \in |2F_2|$. We want to prove that $G_2$ is of type $\mathrm {II}^*$.

The fiber $G_2$ is necessarily simple because of Lemma 2.6. Let $\Lambda$ be the sublattice of ${{\,\mathrm{Num}\,}}(X)$ generated by the components of $G_2$ and $R_{2,1}$ and let $\Lambda '=\Lambda [F_2]$ be the sublattice of ${{\,\mathrm{Num}\,}}(X)$ obtained from $\Lambda$ by adjoining $F_2=\frac{1}{2}G_2\in \frac{1}{2}\Lambda$.

If $m \ge 1$, then $R_{1,1}$ meets a component of $F_1$ distinct from $R_{2,1}$, hence $R_{1,1}$ meets a component of $G_2$. But $R_{1,1}.G_2 = 2R_{1,1}.F_2 = 0$, so $R_{1,1}$ is contained in $G_2$ and then so are all the $R_{1,j}$. This shows that $\Lambda$ has rank $10$, because it contains all $R_{i,j}$, the class of $F_1$ and the class of $G_2 \equiv 2F_2$. Since $\Lambda '$ contains all the $10$ divisors of the $10$-sequence and since these divisors generate a lattice of rank $10$ and discriminant $9$, $\Lambda '$ has index $1$ or $3$ in ${{\,\mathrm{Num}\,}}(X)$.

By [2, Lemma 1.6.2], there exists a vector $e \in {{\,\mathrm{Num}\,}}(X)$ with $e^2 = 0, e.F_1 = e.F_2 = 1$, $e.R_{i,j} = 0$ for all $(i,j)$ except for $e.R_{2,n-1} = 1$, and such that $e$ and the components of the $10$-sequence generate ${{\,\mathrm{Num}\,}}(X)$. (In the notation of [2, Lemma 1.6.2], we can choose $e = e_{9,10} = d - f_9 - f_{10}$, since $n \ge 3$.)

Note that it suffices to show that $e$ is contained in the sublattice $\Lambda '$. Indeed, if this holds, then $\Lambda '={{\,\mathrm{Num}\,}}(X)$ and therefore $\Lambda$ has index at most $2$ in ${{\,\mathrm{Num}\,}}(X)$. Then, consider the basis of $\Lambda$ given by $G_2, R_{2,1}$ and all the components of $G_2$ except a simple one. The intersection matrix of $\Lambda$ with respect to this basis is

$$\begin{aligned} \left( \begin{array}{c c |c} 0 &{}2 &{}0\\ 2 &{} -2 &{}*\\ \hline 0 &{}* &{}L \end{array}\right) , \end{aligned}$$

where $L$ is a root lattice of rank $8$ depending on the type of $G_2$. More precisely, $L$ is the root lattice associated to the Dynkin diagram obtained by removing a simple component from $G_2$. By reducing along the first row and first column, we obtain that $\det (\Lambda )=-4\det (L)$. Since $\Lambda$ has index at most $2$ in the unimodular lattice ${{\,\mathrm{Num}\,}}(X)$, we have $|{\det (\Lambda )}|\le 4$, and hence $\det (L)=1$. This forces $L$ to be isometric to the lattice $E_8$, and in turn $G_2$ to be of type $\mathrm {II}^*$.

It remains to show that $e \in \Lambda '$. Let $D$ be an effective lift of $e$ to ${{\,\mathrm{Pic}\,}}(X)$. Write $D \sim D' + \sum _i a_iR_i$ as in Lemma 2.3. Since $D'^2 = D^2 = 0$ and $D'.F_i \le 1$ with equality for at least one $i$, $D'$ is nef and primitive, hence equal to a half-fiber by Lemma 2.1. If $D'$ is not a half-fiber of $|2F_1|$ or $|2F_2|$, then $(F_1,F_2,D')$ is a $3$-sequence, contradicting our assumption that $(F_1,F_2)$ does not extend to a $3$-sequence. Therefore, we can suppose that $D'$ is a half-fiber of $|2F_k|$ for some $k \in \{1,2\}$.

Take $j \in \{1,2\}$ with $j \ne k$. Then, $D'.F_j = 1$ and $D'.F_k = 0$, while $D.F_j = D.F_k = 1$, so $(\sum _i a_iR_i)^2 = (D - D')^2 = (D - F_k)^2 = -2$ and $(\sum _i a_iR_i).F_j = (D - D').F_j = 0$. Thus, $\sum _i a_iR_i$ is a connected configuration of $(-2)$-curves contained in a single fiber of $|2F_j|$. But $(\sum _i a_iR_i).R_{2,n-1} = (D - D').R_{2,n-1} = D.R_{2,n-1} = 1$, since $R_{2,n-1}.F_1 = R_{2,n-1}.F_2 = 0$, hence $\sum _i a_iR_i$ is contained in the fiber of $|2F_j|$ containing $R_{2,n-1}$. If $j = 1$, this fiber is $F_1$, whereas if $j = 2$ this fiber is $G_2$. In both cases, we obtain that $e \in \Lambda '$. $\square$

4 Special genus one fibrations with a fiber of type $\mathrm {II}^*$

By Theorem 3.4, one of the two fibrations in a non-extendable $2$-sequence is special with a fiber of type $\mathrm {II}^*$. It turns out that admitting such a fibration is such a restrictive property that all Enriques surfaces satisfying this property can be classified. We will carry out this classification in this section, thereby proving Theorem 1.3 (see Corollary 4.3).

Definition 4.1

An Enriques surface $X$ is called

• of type $\mathrm {I}$ if the dual graph of all $(-2)$-curves on $X$ is

  

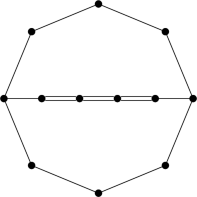  (D)

• of type $\tilde{E}_7^{(2)}$ if the dual graph of all $(-2)$-curves on $X$ is

  

  (E)

Theorem 4.2

If an Enriques surface $X$ admits a special genus one fibration with a fiber of type $\mathrm {II}^*$, then one of the following holds:

• 1. $X$ is of type $\mathrm {I}$,

• 2. $X$ is of type $\tilde{E}_7^{(2)}$,

• 3. $X$ is extra-special.

Proof

First, note that it suffices to show that $X$ contains a configuration of $(-2)$-curves whose dual graph is one of the Graphs (A), (B), (C), (D), or (E). Indeed, by [14, Theorem 2.3] and [9, Remark 2.15], the group generated by reflections in the $(-2)$-curves in the dual graph of one of these surfaces has finite index in the orthogonal group of ${{\,\mathrm{Num}\,}}(X)$. By [12, Proposition 6.9], this implies that the $(-2)$-curves in the graph are in fact all the $(-2)$-curves on a surface containing such a configuration.

Assume first that the fiber of type $\mathrm {II}^*$ is a half-fiber. Its special bisection must meet the only component of the half-fiber of multiplicity $1$, giving rise to Graph (A).

Assume instead that the fiber of type $\mathrm {II}^*$ is simple. Since this fiber has only one simple component, the special bisection $R$ intersects transversely one of the two components of multiplicity $2$ or it intersects doubly the component of multiplicity $1$. If $R$ intersects the component of multiplicity $2$ next to the simple component, then we obtain Graph (B). If $R$ intersects the other component of multiplicity $2$, then we obtain a new half-fiber of type $\mathrm {III}^*$:

The component $C$ is orthogonal to the fiber of type $\mathrm {III}^*$, hence it belongs to another reducible fiber $G$ of this new fibration. By Lemma 2.4, $G$ must be of type $\mathrm {I}_2$ or $\mathrm {III}$. If $G$ is a half-fiber, then we obtain Graph (C). If instead it is a simple fiber, we obtain Graph (E). Finally, if $R$ intersects doubly the simple component of the fiber of type $\mathrm {II}^*$, then we obtain a new half-fiber $G$ of type $\mathrm {I}_2$ or $\mathrm {III}$. The seven components orthogonal to $G$ are contained in a fiber of type $\mathrm {III}^*$ by Lemma 2.4, which can be a half-fiber or a simple fiber. In the former case, we obtain Graph (C). In the latter, the bisection of the $\mathrm {III}^*$ fiber also intersects the other simple component:

There is a half-fiber of type $\mathrm {I}_8$, hence, by Lemma 2.2, either $p \ne 2$ or $X$ is ordinary. Thus, it follows from [10, Theorem 3.1] that $X$ is of type $\mathrm {I}$. $\square$

Corollary 4.3

If $X$ is an Enriques surface with a special genus one fibration with a fiber of type $\mathrm {II}^*$, then $X$ satisfies the following properties:

• 1. $X$ contains finitely many $(-2)$-curves,

• 2. $X$ has finite automorphism group,

• 3. if $p \ne 2$ or $X$ is ordinary, then $X$ is of type $\mathrm {I}$,

• 4. $X$ is not extra-special if and only if every $c$-sequence with $c \le 2$ extends to a $3$-sequence.

Proof

Claim (1) follows from the classification in Theorem 4.2, since all the surfaces listed there contain only finitely many $(-2)$-curves.

By the first paragraph of the proof of Theorem 4.2, the Weyl group $W_X^{{\mathrm {nod}}}$ has finite index in the orthogonal group of ${{\,\mathrm{Num}\,}}(X)$. Since ${{\,\mathrm{Aut}\,}}(X)$ acts with finite kernel on ${{\,\mathrm{Num}\,}}(X)/W_X^{{\mathrm {nod}}}$ by [8, Theorem], this implies Claim  (2) (see also [6, Corollary 3.4]).

For Claim  (3), by Lemma 2.2 it suffices to observe that if $X$ is not of type $\mathrm {I}$, then there exists an additive half-fiber on $X$.

Finally, for Claim (4), one can simply list all genus one fibrations on $X$. For the surfaces of type $\mathrm {I}$, we refer to [7, Proposition 8.9.6]. For the extra-special surfaces and for the surfaces of type $\tilde{E}_7^{(2)}$, we refer to [7, Proposition 6.2.5]. $\square$

Remark 4.4

Enriques surfaces of type $\mathrm {I}$ and of type $\tilde{E}_7^{(2)}$ also display a special behaviour with respect to $c$-sequences: on both types of surfaces, there exist $3$-sequences that cannot be extended to $4$-sequences. In fact, there are no $4$-sequences at all on type $\tilde{E}_7^{(2)}$ [7, Proposition 6.2.5].