The extra-nice dimensions

Abstract

We define the extra-nice dimensions and prove that the subset of locally stable 1-parameter families in $C^{\infty }(N\times [0,1],P)$ is dense if and only if the pair of dimensions $(\dim N, \dim P)$ is in the extra-nice dimensions. This result is parallel to Mather’s characterization of the nice dimensions as the pairs (n, p) for which stable maps are dense. The extra-nice dimensions are characterized by the property that discriminants of stable germs in one dimension higher have ${\mathscr {A}}_e$-codimension 1 hyperplane sections. They are also related to the simplicity of ${\mathscr {A}}_e$-codimension 2 germs. We give a sufficient condition for any ${\mathscr {A}}_e$-codimension 2 germ to be simple and give an example of a corank 2 codimension 2 germ in the nice dimensions which is not simple. Then we establish the boundary of the extra-nice dimensions. Finally we answer a question posed by Wall about the codimension of non-simple maps.

1 Introduction

Around the middle of last century Whitney formulated the concept of stability of smooth maps and characterized stable singularities in dimensions (n, p) with $p \ge 2n$, $(n,2n-1)$, (2, 2) showing that in these cases stable maps are dense in the space of $C^{\infty }$ maps. He then conjectured that this holds in any pair (n, p). Thom showed that this is not the case (see [35]) by giving an example in (9, 9) of a singularity which appears generically in a 1-parameter family of maps. This singularity has ${\mathscr {A}}_e$-codimension 1 and is not simple. A germ is simple if there are only a finite number of orbits nearby, therefore, in the pair of dimensions (9, 9) not all maps can be approximated by stable maps and so the stable maps are not dense. He then conjectured that topologically stable maps are always dense and this was proved by Mather [20].

In his well known series of papers about stability of $C^{\infty }$ maps Mather showed that the set of stable maps $f: N^n \rightarrow P^p$ is dense in $C_{pr}^{\infty }(N,P)$ (proper $C^{\infty }$ maps) with the Whitney strong topology if and only if the pair of dimensions (n, p) is in the nice dimensions [18], which he determined completely in [19]. Mather gave a stratification of the set $J^k(n,p)$ of k-jets of smooth maps by ${\mathscr {K}}$-orbits and characterized stability in terms of transversality of the jet extension of the map to this stratification. More precisely, he defined the nice dimensions as the pairs (n, p) such that there exists a Zariski closed ${\mathscr {K}}$-invariant set $\Pi (n,p)$ in $J^k(n,p),$ for sufficiently high k,  of codimension bigger than n such that its complement in $J^k(n,p)$ is the union of finitely many ${\mathscr {K}}$-orbits.

When the pair (n, p) is in the nice dimensions and the source manifold N is compact, an important problem in the applications of singularity theory to differential topology is the characterization of the simplest existing paths between two stable maps, also known as pseudo-isotopies. A 1-parameter family $F: N\times [0,1] \rightarrow P$ connecting two non-equivalent stable maps always intersects the set of non stable maps for a finite number of values of the parameter, the bifurcation points. The classification of singularities of bifurcation points in generic families of maps is a fundamental step in results on elimination of singularities, which is still an active field of research [1, 15], and on various results about the topology of the space of smooth maps such as work by Cerf [3] or Igusa [14] or even Vassiliev’s theory of topological invariants [36].

We say that a family $F: N\times [0,1] \rightarrow P$ is a locally stable family if $F_t: N \rightarrow P$ is a stable map for all $t \in \mathbb [0,1]$ except possibly for a finite number of values $\{t_1,\ldots , t_k\}$ and the non-stable singularities of $F_{t_i}$ are a finite number of points $x_j \in N,$ and the map $(F, t): N\times [0,1] \rightarrow P\times [0,1]$ is a locally ${\mathcal {A}}_e$-versal unfolding of $F_{t_i}$ for all non-stable points $x_j.$ This definition implies that the non-stable singularities of $F_{t_i}$ are ${\mathcal {A}}$-finitely determined and their ${\mathcal {A}}_e$-codimension is equal to 1.

In this paper we obtain a parallel result to Mather’s characterization of the nice dimensions. First we define the extra-nice dimensions as the pairs (n, p) where there exists a smallest Zariski closed ${\mathscr {A}}$-invariant set $\Lambda (n,p)$ in $J^k(n,p),$ for sufficiently high k,  of codimension greater than $n+1$ whose complement is a finite number of ${\mathscr {A}}$-orbits. Then we prove that the subset of stable 1-parameter families in $C^{\infty }(N\times [0,1],P)$ is dense if and only if the pair (n, p) is in the extra-nice dimensions.

In the nice dimensions all the ${\mathscr {A}}_e$-codimension 1 singularities are simple (see Proposition 3.5). Goryunov [9], Cooper et al. [4] and Houston [12] studied the classification of germs and multigerms of ${\mathscr {A}}_e$-codimension 1, corank 1. A recent work by Oset Sinha et al. [27] defined operations that allow the classification of ${\mathscr {A}}_e$-codimension 2 multigerms in the nice dimensions and a natural question arises: are all of these simple? In Sect. 3 we prove that all corank 1 ${\mathscr {A}}_e$-codimension 2 monogerms in (n, p) are simple when $(n+1,p+1)$ is in the nice dimensions. We give a sufficient condition for any ${\mathscr {A}}_e$-codimension 2 germ to be simple. This condition is related to stable germs in one dimension higher having ${\mathscr {A}}_e$-codimension 1 hyperplane sections. We also give an example of a corank 2 codimension 2 germ in the nice dimensions which is not simple.

In Sect. 4 we define the extra-nice dimensions, we relate them to the simplicity of ${\mathscr {A}}_e$-codimension 2 germs and we characterize them by stable germs in one dimension higher having ${\mathscr {A}}_e$-codimension 1 hyperplane sections (the sufficient condition in Sect. 3). In Sect. 5 we determine the boundary of the extra-nice dimensions completely. Figure 1 shows this boundary and compares it to the boundary of the nice dimensions. In Sect. 6 we characterize the extra-nice dimensions by the density of locally stable 1-parameter families.

Section 2 establishes the necessary notation and basic results. Finally, in Sect. 7, we answer a question posed by Wall about the codimension of non-simple maps. We define further refinements of the nice dimensions and give an example in the equidimensional case of a stratification in terms of increasing codimension of the subset of non-simple maps.

2 Notation

We consider map-germs $f:({\mathbb {K}}^n,S)\rightarrow ({\mathbb {K}}^p,0)$, where ${\mathbb {K}}={\mathbb {R}}$ or ${\mathbb {K}}={\mathbb {C}}$, and $S\subset {\mathbb {K}}^n$ a finite subset. For simplicity, we will say that f is smooth if it is smooth (i.e. $C^\infty$) when ${\mathbb {K}}={\mathbb {R}}$ or holomorphic when ${\mathbb {K}}={\mathbb {C}}$. We denote by ${\mathcal {O}}_n={\mathcal {O}}_{{\mathbb {K}}^n,S}$ and ${\mathcal {O}}_p={\mathcal {O}}_{{\mathbb {K}}^p,0}$ the rings of smooth function germs in the source and target respectively, by ${\mathscr {M}}_n$ and ${\mathscr {M}}_p$ the maximal ideals of ${\mathcal {O}}_n$ and ${\mathcal {O}}_p$ respectively and by $\theta _n=\theta _{{\mathbb {K}}^n,S}$ and $\theta _p=\theta _{{\mathbb {K}}^p,0}$ the corresponding modules of vector field germs. The module of vector fields along f will be denoted by $\theta (f)$. Associated with $\theta (f)$ we have two morphisms $tf:\theta _n\rightarrow \theta (f)$, given by $tf(\chi )=df\circ \chi$, and $wf:\theta _p\rightarrow \theta (f)$, given by $wf(\eta )=\eta \circ f$. Let $f^*:{\mathcal {O}}_p\rightarrow {\mathcal {O}}_n$ be the induced map of f given by composition with f on the right. Let ${\mathscr {G}}={\mathscr {A}}_e,{\mathscr {A}},{\mathscr {K}}_e,{\mathscr {K}}$. The ${\mathscr {G}}$-tangent space and the ${\mathscr {G}}$-codimension of f are defined respectively as

$$\begin{aligned} T{\mathscr {A}}_e f= & {} tf(\theta _n)+wf(\theta _p),\quad {{\mathscr {A}}_{e}\hbox {-cod}}(f)=\dim _{\mathbb {K}}\frac{\theta (f)}{T{\mathscr {A}}_e f}, \\ T{\mathscr {A}}f= & {} tf({\mathscr {M}}_n\theta _n)+wf({\mathscr {M}}_p\theta _p),\quad {{\mathscr {A}}\hbox {-cod}}(f)=\dim _{\mathbb {K}}\frac{{\mathscr {M}}_n\theta (f)}{T{\mathscr {A}}f}, \\ T{\mathscr {K}}_e f= & {} tf(\theta _n)+f^*{\mathscr {M}}_p\theta (f),\quad {\mathscr {K}_{e}\hbox {-cod}}(f)=\dim _{\mathbb {K}}\frac{\theta (f)}{T{\mathscr {K}}_e f}, \\ T{\mathscr {K}} f= & {} tf({\mathscr {M}}_n\theta _n)+f^*{\mathscr {M}}_p\theta (f),\quad {\mathscr {K}\hbox {-cod}}(f)=\dim _{\mathbb {K}}\frac{{\mathscr {M}}_n\theta (f)}{T{\mathscr {K}} f}. \end{aligned}$$

It follows from Mather’s infinitesimal stability criterion [16] that a germ is stable if and only if its ${\mathscr {A}}_e$-codimension is 0. The ${\mathscr {A}}$-codimension and the ${\mathscr {K}}$-codimension correspond to the codimension of the ${\mathscr {A}}$-orbit and ${\mathscr {K}}$-orbit in the jet space, respectively. We refer to Wall’s survey paper [37] and Nuño-Ballesteros and Mond book [23] for general background on the theory of singularities of mappings.

There are some relations between the different codimensions. One between the ${\mathscr {A}}$-codimension and the ${\mathscr {A}}_e$-codimension due to Wilson [39] (a proof can be found in [30]):

$$\begin{aligned} {{\mathscr {A}}_{e}\hbox {-cod}}(f)={{\mathscr {A}}\hbox {-cod}}(f)+r(p-n)-p, \end{aligned}$$

if f has finite ${\mathscr {A}}_e$-codimension and is not stable, where $r=|S|$ is the number of branches. And another one between the ${\mathscr {K}}$-codimension and the ${\mathscr {K}}_e$-codimension, which can be found in [37]:

$$\begin{aligned} {\mathscr {K}_{e}\hbox {-cod}}(f)={\mathscr {K}\hbox {-cod}}(f)+r(p-n). \end{aligned}$$

We say that $f:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^p,0)$ has corank r if df(0) has rank $\min {n,p}-r$.

We say that f has finite singularity type or it is ${\mathscr {K}}$-finite if ${\mathscr {K}_{e}\hbox {-cod}}(f)<\infty$. Another remarkable result of Mather is that f has finite singularity type if and only if it admits an s-parameter stable unfolding (see [37]). We recall that an s-parameter unfolding of f is another map-germ

$$\begin{aligned} F:({\mathbb {K}}^n\times {\mathbb {K}}^s,S\times \{0\})\rightarrow ({\mathbb {K}}^p\times {\mathbb {K}}^s,0) \end{aligned}$$

of the form $F(x,\lambda )=(f_\lambda (x),\lambda )$ and such that $f_0=f$.

Along the paper, we use the notation of small letters $x_1,\dots ,x_n,\lambda _1,\dots ,\lambda _r$ for the coordinates in ${\mathbb {K}}^n\times {\mathbb {K}}^r$ and capital letters $X_1,\dots ,X_p,\Lambda _1,\dots ,\Lambda _r$ for the coordinates in ${\mathbb {K}}^p\times {\mathbb {K}}^r$.

A multigerm $f=\{f_1,\ldots ,f_r\}:({\mathbb {K}}^n,S)\rightarrow ({\mathbb {K}}^p,0)$ with $S=\{x_1,\ldots ,x_r\}$ is simple if there exists a finite number of ${\mathscr {A}}$-classes such that for every unfolding $F:({\mathbb {K}}^n\times {\mathbb {K}}^s,S\times \{0\})\rightarrow ({\mathbb {K}}^p\times {\mathbb {K}}^s,0)$ with $F(x,\lambda )=(f_{\lambda }(x),\lambda )$ and $f_0=f$ there exists a sufficiently small neighbourhood U of $S\times \{0\}$ such that for every $(y_1,\lambda ),\ldots ,(y_r,\lambda )\in U$ where $F(y_1,\lambda )=\ldots =F(y_r,\lambda )$ the multigerm $f_{\lambda }:({\mathbb {K}}^n,\{y_1,\ldots ,y_r\})\rightarrow ({\mathbb {K}}^p,f_{\lambda }(y_i))$ lies in one of those finite classes.

Definition 2.1

Let $f:({\mathbb {K}}^n,S)\rightarrow ({\mathbb {K}}^p,0)$ be a smooth map-germ. A vector field germ $\eta \in \theta _p$ is called liftable over f, if there exists $\xi \in \theta _n$ such that $df\circ \xi =\eta \circ f$ (i.e., $tf(\xi )=wf(\eta )$). The set of vector field germs liftable over f is denoted by ${\text {Lift}}(f)$ and is an ${\mathcal {O}}_p$-submodule of $\theta _p$.

When ${\mathbb {K}}={\mathbb {C}}$ and f has finite singularity type, we always have the inclusion ${\text {Lift}}(f)\subseteq {\text {Derlog}}(\Delta (f))$, where $\Delta (f)$ is the discriminant of f (i.e., the image of non submersive points of f) and ${\text {Derlog}}(\Delta (f))$ is the submodule of $\theta _p$ of vector fields which are tangent to $\Delta (f)$. Moreover, we have the equality ${\text {Lift}}(f)={\text {Derlog}}(\Delta (f))$ when either f is stable, $n\le p$ or $n>p>2$ (see [5, 23]).

Definition 2.2

Let $h:({\mathbb {K}}^n,S)\rightarrow ({\mathbb {K}}^p,0)$ be a map-germ with a 1-parameter stable unfolding $H(x,\lambda )=(h_{\lambda }(x),\lambda )$. Let $g:({\mathbb {K}}^q,0)\rightarrow ({\mathbb {K}},0)$ be a function-germ. Then, the augmentation of h by H and g is the map $A_{H,g}(h)$ given by $(x,z)\mapsto (h_{g(z)}(x),z)$. Any map ${\mathscr {A}}$-equivalent to an augmentation is called an augmentation too. A map which is not an augmentation is called primitive.

By construction, any augmentation has a 1-parameter stable unfolding given by $(x,z,u)\mapsto (h_{g(z)+u}(x),z)$ which is ${\mathscr {A}}$-equivalent to $H\times Id_{{\mathbb {K}}^q}$. In Theorem 4.4 in [11] it is proved that

$$\begin{aligned} {{\mathscr {A}}_{e}\hbox {-cod}}(A_{H,g}(h))\ge {{\mathscr {A}}_{e}\hbox {-cod}}(h)\tau (g) \end{aligned}$$

(1)

where $\tau$ is the Tjurina number of the function g. Equality is reached if g is quasihomogeneous or H is a substantial unfolding (see [11]). In this paper we will only use augmentations where g is quasi-homogeneous and so ${{\mathscr {A}}_{e}\hbox {-cod}}{({A}_{{H,g}}(h))}={{\mathscr {A}}_{e}\hbox {-cod}}{(h)\tau (g)}$. In particular, if ${{\mathscr {A}}_{e}\hbox {-cod}}(h)=1$ and it is augmented by a Morse function, then ${{\mathscr {A}}_{e}\hbox {-cod}}{({A}_{{H,g}}(h))}=1$.

Following Mather [17] if $f:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^p,0)$ has finite singularity type then there is a stable germ $F:({\mathbb {K}}^{n+s},0)\rightarrow ({\mathbb {K}}^{p+s},0)$ and a germ of an immersion $i:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^{p+s},0),$ $i\pitchfork F,$ such that f is the pull-back of F by i in the diagram:

Any germ f is a pull-back of a stable s-parameter unfolding F by the natural inclusion i. Damon ([5], for ${\mathbb {K}}={\mathbb {C}}$) and Houston ([11], for ${\mathbb {K}}={\mathbb {R}}$) proved that ${{\mathscr {A}}_{e}\hbox {-cod}}(f)={\mathscr {K}}_{\Delta {(F)},e}$-cod(i), where

$$\begin{aligned} {\mathscr {K}}_{\Delta (F),e}\text{-cod }(i)=\dim _{{\mathbb {K}}} N{\mathscr {K}}_{\Delta (F),e}(i)=\dim _{{\mathbb {K}}}\frac{\theta (i)}{ti(\theta _p)+i^*{\text {Lift}}(F)}. \end{aligned}$$

Furthermore, if $L:({\mathbb {K}}^{p+s},0)\longrightarrow ({\mathbb {K}}^s,0)$ is such that $L\circ i=0$, then ${{\mathscr {A}}_{e}\hbox {-cod}}(f)= _{\Delta (F)}{\mathscr {K}}_e$-${\text {cod}}(L)$, where

$$\begin{aligned} _{\Delta (F)}{\mathscr {K}}_e\text{-cod }(L)=\dim _{{\mathbb {K}}} N_{\Delta (F)}{\mathscr {K}}_e(L)=\dim _{{\mathbb {K}}}\frac{\theta (L)}{tL({\text {Lift}}(F))+L^*{\mathscr {M}}_s\theta (L)}. \end{aligned}$$

When $s=1$ we say that L defines the hyperplane section f of F. Besides, to obtain a hyperplane section of ${\mathscr {A}}_e$-codimension 1 it is sufficient to consider the 1-jet of L (see for example [24]). Also notice that if F is minimal, $_{\Delta (F)}{\mathscr {K}}_e$-${\text {cod}}(L)=1$ if and only if ${\mathscr {M}}_{p+1}\theta (L)\subset tL({\text {Lift}}(F))+L^*{\mathscr {M}}_s\theta (L)$.

3 On simplicity of codimension 2 germs in the nice dimensions

The following definition is crucial throughout the paper.

Definition 3.1

A germ f has the ${\mathscr {A}}$-orbit open in the ${\mathscr {K}}$-orbit if $T{\mathscr {A}}f=T{\mathscr {K}} f$.

The ${\mathscr {A}}$-orbit is open in the ${\mathscr {K}}$-orbit if and only if ${{\mathscr {A}}\hbox {-cod}}(f)={\mathscr {K}\hbox {-cod}}(f)$. By the formulas relating the ${\mathscr {G}}$-codimension to the $\mathscr {G}_e$-codimension in the previous section, this is equivalent to ${{\mathscr {A}}_{e}\hbox {-cod}}(f)={\mathscr {K}_{e}\hbox {-cod}}(f)-p$. In other words, a non stable germ has the ${\mathscr {A}}$-orbit open in the ${\mathscr {K}}$-orbit if and only if the minimal number of parameters needed to obtain a stable unfolding is equal to the number of parameters of an ${\mathscr {A}}_e$-miniversal unfolding (i.e. there is no stable unfolding before the ${\mathscr {A}}_e$-miniversal unfolding). Also, if f is stable, the ${\mathscr {A}}$-orbit is open in the ${\mathscr {K}}$-orbit.

Some characterisations and results regarding the openness of an ${\mathscr {A}}$-orbit in the ${\mathscr {K}}$-orbit can be found in [33, 34]. In particular, we will use Theorem 5.7 in [34]. We add a sketch of the proof for the sake of completeness.

Theorem 3.2

[34] Let $f:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^p,0)$ be a smooth germ.

• (i) If ${\mathbb {K}}={\mathbb {C}}$, then there is at most one open ${\mathscr {A}}$-orbit in the ${\mathscr {K}}$-orbit of f.

• (ii) If ${\mathbb {K}}={\mathbb {R}}$, then there are at most a finite number of open ${\mathscr {A}}$-orbits in the ${\mathscr {K}}$-orbit of f.

In case there exist open ${\mathscr {A}}$-orbits in the ${\mathscr {K}}$-orbit, the complement of the open ${\mathscr {A}}$-orbits has codimension greater than the codimension of the ${\mathscr {K}}$-orbit.

Proof

(Sketch) Suppose ${\mathscr {K}\hbox {-cod}}(f)=r$. For s big enough, let $V^s$ denote the union of all ${\mathscr {A}}$-orbits of codimension greater than or equal to r in $J^s(n,p)$. Denote by $U^s$ the subset of $V^s$ of all ${\mathscr {A}}$-orbits of codimension r. $V^s$ is an algebraic variety and $U^s$ is a Zariski open subset. Denote by $\overline{{\mathscr {K}}^s(f)}$ the closure of the ${\mathscr {K}}$-orbit of f in $J^s(n,p)$. Then $V^s\cap \overline{{\mathscr {K}}^s(f)}=\overline{{\mathscr {K}}^s(f)}$ is an algebraic variety and $U^s\cap \overline{{\mathscr {K}}^s(f)}$ is a Zariski open subset. Therefore, the complement of $U^s\cap \overline{{\mathscr {K}}^s(f)}$ is an algebraic set and, given $U^s\cap \overline{{\mathscr {K}}^s(f)}\ne \emptyset$, this complement is a proper algebraic subvariety of $\overline{{\mathscr {K}}^s(f)}$.

If f is holomorphic, ${\mathscr {K}}^s(f)$ is connected (because ${\mathscr {K}}^s$ is connected). Since the complement of any proper complex analytic subvariety is open and connected, it follows that $U^s\cap \overline{{\mathscr {K}}^s(f)}$ is connected. Any ${\mathscr {A}}$-orbit in this set is open and its complement is a union of open sets, thus, it is closed too. Therefore, there is a unique open ${\mathscr {A}}$-orbit.

In the real case, since the set $U^s \cap \overline{{\mathscr {K}}^s(f)}$ is semialgebraic, if it is nonempty, it has at most a finite number of connected components and so a finite number of open ${\mathscr {A}}$-orbits. $\square$

Example 3.3

The germ $(x^5+yx,y)$ has ${\mathscr {A}}_e$-codimension 3 but admits a 2-parameter stable unfolding, so its ${\mathscr {A}}$-orbit is not open in the ${\mathscr {K}}$-orbit. However, $(x^5+yx\pm x^7,y)$ have ${\mathscr {A}}_e$-codimension 2 and their ${\mathscr {A}}$-orbit is open in the ${\mathscr {K}}$-orbit (see [29]). In the complex case these two germs are ${\mathscr {A}}$-equivalent, and so there is a unique open ${\mathscr {A}}$-orbit, but in the real case, there are two open ${\mathscr {A}}$-orbits in the ${\mathscr {K}}$-orbit.

In Sect. 3.10 we will see an example of a ${\mathscr {K}}$-orbit which does not admit an open ${\mathscr {A}}$-orbit.

The germs of ${\mathscr {A}}_e$-codimension 1 and corank 1 in the nice dimensions are well known and are hyperplane linear sections of stable germs. We review them here for the sake of completeness. The case of hyperplane sections of stable corank 2 germs in $(n,n+1)$ has been studied in [8].

Proposition 3.4

Let $F:({\mathbb {K}}^{n+1},0)\longrightarrow ({\mathbb {K}}^{p+1},0)$ be a stable corank 1 germ, (n, p) nice dimensions. Then there exists $f:({\mathbb {K}}^n,0)\longrightarrow (\mathbb K^p,0)$ obtained by a hyperplane section of F such that $\mathscr {A}_e$-${\text {cod}}(f)=1$.

Proof

Suppose first that F is minimal.

• 1. Case $n\ge p$. Let $g_0:({\mathbb {K}}^m,0)\rightarrow ({\mathbb {K}},0)$ be a simple function singularity of type $A_k$, $D_k$, $E_6$, $E_7$ or $E_8$ and let $\varphi _1=1,\varphi _2,\ldots ,\varphi _{\mu }$ be a homogeneous basis for $\frac{{\mathcal {O}}_n}{Jg_0}$ where $\varphi _{\mu }$ is the unique highest weight term. Following Mather’s method of constructing stable germs in [17], the map germs $G:({\mathbb {K}}^m\times {\mathbb {K}}^{\mu -1},0)\rightarrow ({\mathbb {K}}\times {\mathbb {K}}^{\mu -1},0)$ given by

  $$\begin{aligned} G(x,u_2,\ldots ,u_{\mu })=(g_0(x)+\sum _{i=2}^{\mu }u_i\varphi _i,u_2,\ldots ,u_{\mu }) \end{aligned}$$

  are stable minimal corank 1 germs. Moreover, in the nice dimensions, any stable minimal corank 1 germ is ${\mathscr {A}}$-equivalent to $A_k$ for $1\le k\le 6$, $D_k$ for $k=4,5,6$ or $E_6$ (see page 236 in [23]). The section $u_{\mu }=0$ defines an ${\mathscr {A}}_e$-codimension 1 section, it is the case $q=0$ in Theorem 1.4 in [22] (see also [9]).

• 2. Case $n<p$. By [17], any stable minimal corank 1 germ is ${\mathscr {A}}$-equivalent to $G:({\mathbb {K}}^n\times {\mathbb {K}},0)\rightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$ given by

  

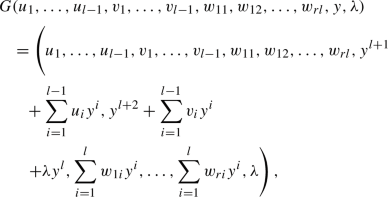
  where $r=p-n-1$ and l is such that $l+1$ is the multiplicity of the germ and $n=l(r+2)-1$. In particular, when $p+1=n+2$, then $r=0$ and so $n+1=2l$ is even, which means that there is no stable minimal germ $G:({\mathbb {K}}^n\times {\mathbb {K}},0)\rightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$ when $n+1$ is odd (this is also pointed out in [4]). The section $\lambda =0$ defines an ${\mathscr {A}}_e$-codimension 1 section, see Theorem 3.1 in [12]. This proof also holds outside the nice dimensions.

Now let F be ${\mathscr {A}}$-equivalent to G. Then there exist germs of diffeomorphisms $\phi :({\mathbb {K}}^n\times {\mathbb {K}},0)\longrightarrow ({\mathbb {K}}^n\times {\mathbb {K}},0)$ and $\psi :({\mathbb {K}}^p\times \mathbb K,0)\longrightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$ such that $\psi \circ F= G\circ \phi .$ By Lemma 6.1 in [26] $d\psi ({\text {Lift}}(F))=\psi ^*({\text {Lift}}(G)).$ Suppose L defines a hyperplane section of G of ${\mathscr {A}}_e$-codimension 1. We have

$$\begin{aligned}&t(L\circ \psi )({\text {Lift}}(F))+\langle L\circ \psi \rangle \theta (L\circ \psi )= tL(\psi ^*({\text {Lift}}(G)))+\langle L\circ \psi \rangle \theta (L\circ \psi ) \\&\quad = \psi ^*(tL({\text {Lift}}(G))+\langle L\rangle \theta (L))=\psi ^*({\mathscr {M}}_{p+1}\theta (L))=\mathscr {M}_{p+1}\theta (L\circ \psi ) \end{aligned}$$

by linearity of L. Therefore $L\circ \psi$ defines a hyperplane section of F of ${\mathscr {A}}_e$-codimension 1.

If F is not minimal, then F is ${\mathscr {A}}$-equivalent to $Id_{\mathbb K^r}\times F'$ where $F':({\mathbb {K}}^{n-r},0)\longrightarrow (\mathbb K^{p-r},0)$ is minimal. So there exists an ${\mathscr {A}}_e$-codimension 1 hyperplane section $f':({\mathbb {K}}^{n-r-1},0)\longrightarrow ({\mathbb {K}}^{p-r-1},0)$ of $F'$. If we augment $f'$ by the function $\phi (x_1,\ldots ,x_{r+1})=x_1^2+\cdots +x_{r+1}^2$ we obtain a germ $f:({\mathbb {K}}^n,0)\longrightarrow ({\mathbb {K}}^p,0)$ of ${\mathscr {A}}_e$-codimension 1. $\square$

From the normal forms showed above all corank 1 $\mathscr {A}_e$-codimension 1 germs in the nice dimensions are simple. We give here a proof of this fact for any corank.

Proposition 3.5

If a pair (n, p) is in the nice dimensions then all ${\mathscr {A}}_e$-codimension 1 germs in that pair are simple.

Proof

Let $f:({\mathbb {K}}^n,0)\longrightarrow (\mathbb K^p,0)$ be an ${\mathscr {A}}_e$-codimension 1 germ.

Recall from [4, 11] that f is either primitive or a quadratic augmentation, that is, an augmentation of a primitive ${\mathscr {A}}_e$-codimension 1 germ $h:({\mathbb {K}}^{n-l},0)\longrightarrow (\mathbb K^{p-l},0)$ by a Morse function g.

For germs of ${\mathscr {A}}_e$-codimension 1, the ${\mathscr {A}}$-orbit is open in its ${\mathscr {K}}$-orbit if and only if the germ is primitive (see [13] or [34]). In fact, if f is primitive then, by Theorem 4.6 in [11], its miniversal unfolding F is minimal. In general, the minimal number of parameters in order to have a stable unfolding, i.e. ${\mathscr {K}_{e}\hbox {-cod}}(f)-p$, is less than or equal to ${{\mathscr {A}}_{e}\hbox {-cod}}(f)$, so ${\mathscr {K}_{e}\hbox {-cod}}(f)-p\le 1$. Since the 1-parameter unfolding F is minimal, ${\mathscr {K}_{e}\hbox {-cod}}(f)-p\ne 0$, so ${\mathscr {K}_{e}\hbox {-cod}}(f)-p=1={{\mathscr {A}}_{e}\hbox {-cod}}(f)$, or, equivalently, ${\mathscr {K}\hbox {-cod}}(f)={{\mathscr {A}}\hbox {-cod}}(f)$, i.e. the ${\mathscr {A}}$-orbit of f is open in the ${\mathscr {K}}$-orbit of f.

Suppose f is non simple, then there must be a modal stratum Y with ${\text {cod}}_{J^k(n,p)} (Y)\le {{\mathscr {A}}\hbox {-cod}}(f)-1={{\mathscr {A}}_{e}\hbox {-cod}}(f)+n-1=n$. So we cannot find a subset of $J^k(n,p)$ with codimension greater than n whose complement is a finite union of ${\mathscr {K}}$-orbits and this contradicts the fact that we are in the nice dimensions.

When f is an augmentation then f is ${\mathscr {A}}$-equivalent to $A_{H,g(z)}(h)$ where $H(x,\lambda )=(h_{\lambda }(x),\lambda )$ is the versal unfolding of the primitive germ h and g is a Morse function. Therefore $(x,z,u)\mapsto (h_{g(z)+u}(x),z,u)$ is a versal unfolding of f and f can be deformed only in a finite number of ${\mathscr {A}}$-classes. $\square$

Proposition 3.6

Let $F:({\mathbb {K}}^n\times \mathbb K,0)\longrightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$ be a stable minimal germ, the following are equivalent:

• (i) There exists $f:({\mathbb {K}}^n,0)\longrightarrow ({\mathbb {K}}^p,0)$ such that F is a versal unfolding of f and its ${\mathscr {A}}$-orbit is open in its ${\mathscr {K}}$-orbit.

• (ii) There exists f (unfolded by F) which is a primitive ${\mathscr {A}}_e$-codimension 1 germ.

• (iii) There exists an immersion $i:({\mathbb {K}}^p,0)\rightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$ such that $i^*(F)$ is an ${\mathscr {A}}_e$-codimension 1 germ.

• (iv) There exists a linear map $L:{\mathbb {K}}^p\times {\mathbb {K}}\longrightarrow {\mathbb {K}}$ such that ${\mathscr {M}}_{p+1}$ is contained in $L({\text {Lift}}(F))+\langle L\rangle .$

Proof

(i) if and only if (ii) can be found in [34] or [13]. Notice that since F is minimal, the ${\mathscr {K}}$-codimension of F (and of f) must be $n+1$. If the ${\mathscr {A}}$-orbit of f is open in its ${\mathscr {K}}$-orbit, then f has ${\mathscr {A}}$-codimension $n+1$ and thus ${\mathscr {A}}_e$-codimension 1. (ii) if and only if (iii) is trivial by Damon’s Theorem on transverse fibre squares and the fact that F is minimal. (iii) if and only if (iv) follows directly from Damon’s result ${{\mathscr {A}}_{e}\hbox {-cod}}(f)= _{\Delta (F)}{\mathscr {K}}_e$-${\text {cod}}(L)$ and the fact that $i({\mathbb {K}}^p)=L^{-1}(0)$. $\square$

Theorem 3.7

Let $(n+1,p+1)$ be nice dimensions. All corank 1 ${\mathscr {A}}_e$-codimension 2 germs in (n, p) are simple.

Proof

We will prove first by contradiction that corank 1 ${\mathscr {A}}_e$-codimension 2 primitive germs are simple. Suppose we have a primitive corank 1 germ $f:({\mathbb {K}}^n,0)\longrightarrow (\mathbb K^p,0)$ with ${\mathscr {A}}_e$-codimension 2 which is not simple. Let X denote the ${\mathscr {A}}$-orbit of f. Then ${\text {cod}}_{J^k(n,p)} (X)={{\mathscr {A}}\hbox {-cod}}(f)=n+2$ and the codimension of the modal stratum Y is ${\text {cod}}_{J^k(n,p)} (Y)\le {{\mathscr {A}}\hbox {-cod}}(f)-1=n+1$.

Suppose f does not admit a 1-parameter stable unfolding. As in the proof of 3.5, we have that $1\ne {\mathscr {K}_{e}\hbox {-cod}}(f)-p\le {{\mathscr {A}}_{e}\hbox {-cod}}(f)=2$. This implies that ${\mathscr {K}_{e}\hbox {-cod}}(f)-p=2={{\mathscr {A}}_{e}\hbox {-cod}}(f)$ and so the ${\mathscr {A}}$-orbit is open in the ${\mathscr {K}}$-orbit. Therefore the codimension of the $\mathscr {K}$-orbit is equal to $n+2$. Since the codimension of the modal stratum is $n+1$ we have a 1-parameter family of $\mathscr {K}$-orbits of codimension $n+2$. So in $(n+1,p+1)$ we have modality of $\mathscr {K}$-orbits of codimension $n+2$, which contradicts that $(n+1,p+1)$ are nice dimensions.

Now suppose f admits a 1-parameter stable unfolding $F:(\mathbb K^n\times {\mathbb {K}},0)\longrightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$. By Proposition 3.4, there exists $f'$ in the same ${\mathscr {K}}$-orbit such that ${{\mathscr {A}}_{e}\hbox {-cod}}(f')=1$. So ${\text {cod}}_{J^k(n,p)}(X')=n+1$, where $X'$ denotes the ${\mathscr {A}}$-orbit of $f'$. By Theorem 4.6 in [11] $f'$ is primitive too, so, by Proposition 3.6, $X'$ is open in the ${\mathscr {K}}$-orbit. Then, by Theorem 3.2, the complement of $X'$ (or the complement of the union of open ${\mathscr {A}}$-orbits in the real case) in the ${\mathcal {K}}$-orbit is a Zariski closed subset of codimension greater than or equal to $n+2$ which contains the modal stratum Y, and this is a contradiction by the codimension of Y.

Now we will prove that corank 1 ${\mathscr {A}}_e$-codimension 2 augmentations are simple. Suppose f is a corank 1 ${\mathscr {A}}_e$-codimension 2 augmentation. Then it admits a 1-parameter stable unfolding $F:(\mathbb K^n\times {\mathbb {K}},0)\longrightarrow ({\mathbb {K}}^p\times {\mathbb {K}},0)$. Since F has corank 1, by Proposition 3.4, there exists $f'$ in the same ${\mathscr {K}}$-orbit such that ${{\mathscr {A}}_{e}\hbox {-cod}}(f')=1$. By Theorem 4.6 in [11] $f'$ is an augmentation too, therefore it is an augmentation of a primitive germ $h':({\mathbb {K}}^{n-r},0)\longrightarrow ({\mathbb {K}}^{p-r},0)$ with ${{\mathscr {A}}_{e}\hbox {-cod}}(h')=1$. By Proposition 3.5$h'$ is simple. Now, since ${{\mathscr {A}}_{e}\hbox {-cod}}(f)=2$, by Equation (1) it is either an augmentation of $h'$ by a simple function $g_1:{\mathbb {K}}^r\longrightarrow {\mathbb {K}}$ of type $A_2$ or it is an augmentation of an ${\mathscr {A}}_e$-codimension 2 primitive germ $h:({\mathbb {K}}^{n-r},0)\longrightarrow ({\mathbb {K}}^{p-r},0)$ by a simple function $g_2:{\mathbb {K}}^r\longrightarrow {\mathbb {K}}$ of type $A_1$. Since h is primitive, by the first part of the proof it is also simple. In the first case, the versal unfolding of f is given by $(h'_{g_1(z)+u_1z_1+u_2}(x),z_1,...,z_r,u_1,u_2)$ where $u_1$ corresponds to the parameter which versally unfolds $g_1$ and $u_2$ corresponds to the parameter which versally unfolds $h'$ (see [4]), and so f can be deformed only in a finite number of ${\mathscr {A}}$-classes. In the second case, the versal unfolding of f is given by $(h_{g_2(z)+u,\lambda }(x),z_1,...,z_2,u,\lambda )$ where u and $\lambda$ correspond to the two parameters which versally unfold h (see [4]). Again f can be deformed only in a finite number of ${\mathscr {A}}$-classes and is therefore simple. $\square$

Notice that in the above proof the hypothesis of corank 1 is only used to ensure the existence of ${\mathscr {A}}_e$-codimension 1 hyperplane sections so the above result can be rephrased as

Proposition 3.8

Let $(n+1,p+1)$ be nice dimensions. If all stable germs $F:(\mathbb K^{n+1},0)\longrightarrow ({\mathbb {K}}^{p+1},0)$ admit a codimension 1 hyperplane section, then all codimension 2 germs $f:(\mathbb K^{n},0)\longrightarrow ({\mathbb {K}}^{p},0)$ are simple.

We believe that the results in this section hold also for multigerms, but in this paper we are concerned only with monogerms.

3.1 An example of a corank 2 codimension 2 germ which is not simple

From Theorem 3.7 in order to find ${\mathscr {A}}_e$-codimension 2 non simple germs we have two possibilities, either it has corank greater than 1, or it is has corank 1 and is just below the boundary of the nice dimensions. In the latter case it must come from a section of an ${\mathscr {A}}_e$-codimension 1 non simple germ in the boundary of the nice dimensions and must have ${\mathscr {A}}$-orbits open in the ${\mathscr {K}}$-orbits.

From Proposition 3.6 it follows that a stable germ $F:(\mathbb K^{n+1},S)\longrightarrow ({\mathbb {K}}^{p+1},0)$ admits an ${\mathscr {A}}_e$-codimension 1 hyperplane section if and only if there exists a linear map L such that ${\mathscr {M}}_{p+1}\subset L({\text {Lift}}(F))+\langle L \rangle$.

Consider the stable germ $F_{3,3}:({\mathbb {K}}^6,0)\rightarrow ({\mathbb {K}}^6,0)$ given by

$$\begin{aligned}&F_{3,3}(x,y,u_1,u_2,u_3,u_4)=(x^3+y^3+u_1x+u_2y+u_3x^2+u_4y^2,xy,u_1, \\&u_2,u_3,u_4) = (X,Y,U_1,...,U_4). \end{aligned}$$

Lemma 3.9

${\text {Lift}}(F_{3,3})$ is generated by

$$\begin{aligned}&\eta _{1,2,3}=\left( \begin{array}{c} 3X\\ 2Y\\ 2U_1\\ 2U_2\\ U_3\\ U_4\end{array}\right) , \left( \begin{array}{c} 2U_1U_2+6Y^2+4U_3U_4Y\\ X\\ -3U_2U_3-5U_4Y\\ -3U_1U_4-5U_3Y\\ -4U_2\\ -4U_1\end{array}\right) , \left( \begin{array}{c} \frac{4}{3}U_2Y\\ -\frac{1}{9} U_3Y\\ X+\frac{1}{9}U_1U_3\\ -\frac{5}{3} U_4Y\\ -\frac{2}{3} U_1+\frac{2}{9} U_3^2\\ -2Y\end{array}\right) \\&\eta _{4,5,6}=\left( \begin{array}{c} \frac{4}{3}U_1Y\\ -\frac{1}{9} U_4Y\\ -\frac{5}{3} U_3Y\\ X+\frac{1}{9}U_2U_4\\ -2Y\\ -\frac{2}{3} U_2+\frac{2}{9} U_4^2\\ \end{array}\right) , \left( \begin{array}{c} \frac{5}{3}U_4Y^2+\frac{1}{9}U_2U_3Y\\ (-\frac{2}{9}U_1+\frac{2}{27}U_3^2)Y\\ -\frac{4}{3}U_2Y+\frac{2}{9}U_1^2-\frac{2}{27}U_1U_3^2\\ -2Y^2-\frac{2}{9}U_3U_4Y\\ X+\frac{5}{9}U_1U_3-\frac{4}{27}U_3^3\\ -\frac{1}{3}U_3Y \end{array}\right) ,\\&\left( \begin{array}{c} \frac{5}{3}U_3Y^2+\frac{1}{9}U_1U_4Y\\ -\frac{2}{9}U_2Y+\frac{2}{27}U_4^2Y\\ -2Y^2-\frac{2}{9}U_3U_4Y\\ -\frac{4}{3}U_1Y+\frac{2}{9}U_2^2-\frac{2}{27}U_4^2U_2\\ -\frac{1}{3}U_4Y\\ X+\frac{5}{9}U_2U_4-\frac{4}{27}U_4^3\end{array}\right) . \end{aligned}$$

Proof

$F_{3,3}$ is a free divisor so ${\text {Lift}}(F_{3,3})$ is generated by 6 vector fields. The Euler vector field is clearly liftable and the other five are all linearly independent and liftable by the following lowerable vector fields:

$$\begin{aligned}&\xi _2=\left( \begin{array}{c} u_2+y^2+u_4y\\ u_1+x^2+u_3x\\ -3u_2u_3-5u_4xy\\ -3u_1u_4-5u_3xy\\ -4u_2\\ -4u_1\end{array}\right) ,\\&\xi _3=\left( \begin{array}{c} -\frac{1}{3}x^2-\frac{1}{9}u_3x\\ \frac{1}{3}xy\\ x^3+y^3+u_1x+u_2y+u_3x^2+u_4y^2+\frac{1}{9}u_1u_3\\ -\frac{5}{3}u_4xy\\ -\frac{2}{3}u_1+\frac{2}{9}u_3^2\\ -2xy\end{array}\right) \\&\xi _{4}=\left( \begin{array}{c} \frac{1}{3}xy\\ -\frac{1}{3}y^2-\frac{1}{9}u_4y\\ -\frac{5}{3}u_3xy\\ x^3+y^3+u_1x+u_2y+u_3x^2+u_4y^2+\frac{1}{9}u_2u_4\\ -2xy\\ -\frac{2}{3}u_2+\frac{2}{9}u_4^2\end{array}\right) , \\&\xi _{5}=\left( \begin{array}{c} -\frac{1}{3}x^3-\frac{1}{9}u_3x^2+(-\frac{2}{9}u_1+\frac{2}{27}u_3^2)x\\ \frac{1}{3}x^2y+\frac{1}{9}u_3xy\\ -\frac{4}{3}u_2xy+\frac{2}{9}u_1^2-\frac{2}{27}u_1u_3^2\\ -2x^2y^2-\frac{2}{9}u_3u_4xy\\ x^3\!+\!y^3\!+\!u_1x\!+\!u_2y\!+\!u_3x^2\!+\!u_4y^2+\frac{5}{9}u_1u_3-\frac{4}{27}u_3^3\\ -\frac{1}{3}u_3xy\end{array}\right) \\&\xi _6=\left( \begin{array}{c} \frac{1}{3}xy^2+\frac{1}{9}u_4xy\\ -\frac{1}{3}y^3-\frac{2}{9}u_2y-\frac{1}{9}u_4y^2+\frac{2}{27}u_4^2y\\ -2x^2y^2-\frac{2}{9}u_3u_4xy\\ -\frac{4}{3}u_1xy+\frac{2}{9}u_2^2-\frac{2}{27}u_4^2u_2\\ -\frac{1}{3}u_4xy\\ x^3\!+\!y^3\!+\!u_1x\!+\!u_2y\!+\!u_3x^2\!+\!u_4y^2+\frac{5}{9}u_2u_4-\frac{4}{27}u_4^3\end{array}\right) \end{aligned}$$

$\square$

Therefore, there does not exist L such that ${\mathscr {M}}_{6}\subset L({\text {Lift}}(F_{3,3}))+\langle L \rangle$ and so $F_{3,3}$ does not admit a codimension 1 hyperplane section.

Theorem 3.10

The corank 2 germ $f:({\mathbb {R}}^5,0)\rightarrow ({\mathbb {R}}^5,0)$ given by

$$\begin{aligned}&f(x,y,u_1,u_2,u_4)=\\&\quad (x^3+y^3+u_1x+u_2y+(-\lambda u_4-u_4^2)x^2+u_4y^2,xy,u_1,u_2,u_4), \end{aligned}$$

with $\lambda \ne 0,-1$, has ${\mathscr {A}}_e$-codimension 2 and is not simple.

Proof

The idea is to use Damon’s Theorem relating ${\mathscr {A}}_e$-codimension and $_V{{\mathscr {K}}}_e$-codimension where V is the discriminant of $F_{3,3}.$ By integrating the linear parts of the vector fields in ${\text {Lift}}(F_{3,3})$ we obtain the linear parts of diffeomorphisms in $_V{\mathscr {K}}$, which are:

$$\begin{aligned}&\eta _1=(e^{3\alpha }X,e^{2\alpha }Y,e^{2\alpha }U_1,e^{2\alpha }U_2,e^{\alpha }U_3,e^{\alpha }U_4), \\&\eta _2=(X,Y+\alpha X,U_1,U_2,U_3-4\alpha U_2,U_4-4\alpha U_1), \\&\eta _3=(X,Y,U_1+\alpha X,U_2,U_3,U_4-2\alpha Y), \\&\eta _4=(X,Y,U_1;U_2+\alpha X,U_3-2\alpha Y,U_4-2/3\alpha U_2),\\&\eta _5=(X,Y,U_1,U_2,U_3+\alpha X,U_4),\\&\eta _6=(X,Y,U_1,U_2,U_3,U_4+\alpha X). \end{aligned}$$

Let $L:({\mathbb {R}}^6,0)\rightarrow {\mathbb {R}}$ and suppose $j^1L(X,Y,U_1,U_2,U_3,U_4)=aX+bY+cU_1+dU_2+eU_3+fU_4.$ If $f\ne 0$, by using $\eta _2,\ldots ,\eta _6$ we can fix $a=b=c=d=0$, and by using $\eta _1$ we get $j^1L=U_3+\lambda U_4$ where $\lambda$ is a modulus. A complete 2-transversal is given by $U_4^2$ when $\lambda \ne -1$ since ${\mathscr {M}}_6^2\subset T_V{\mathscr {K}}_1 L+sp\{U_4^2\}+{\mathscr {M}}_6^3$ where $T_V{\mathscr {K}}_1L=tL({\text {Lift}}_1(F_{3,3}))+L^*{\mathscr {M}}_1{\mathscr {O}}_6$ and ${\text {Lift}}_1(F_{3,3})$ is the space of vector fields in ${\text {Lift}}(F_{3,3})$ with zero 1-jet (see [2]). Rescaling we set $L=U_3+\lambda U_4+U_4^2$. If $\lambda \ne 0$, this germ has $_V{{\mathscr {K}}}_e$-codimension 2 and is not simple, so the ${\mathscr {A}}_e$-codimension of f is 2 and it is not simple. $\square$

By Proposition 3.6, this is an example of a ${\mathscr {K}}$-orbit which does not admit an open ${\mathscr {A}}$-orbit.

4 The extra-nice dimensions

Mather gave a stratification of the set $J^k(n,p)$ of k-jets of smooth mappings by ${\mathscr {K}}$-orbits and a bad set. This induces a partition of $J^k(N,P)$ by ${\mathscr {K}}$-orbit bundles. Mather characterized stability in terms of transversality of the k-jet extension $j^kf:N\rightarrow J^k(N,P)$ to this stratification. He showed that there exists a smallest Zariski closed ${\mathscr {K}}^k$-invariant set $\Pi ^k(n,p)$ in $J^k(n,p)$ such that its complement in $J^k(n,p)$ is the union of finitely many ${\mathscr {K}}^k$-orbits. The codimension of $\Pi ^k(n,p)$ decreases as k increases. Moreover, there exists a big enough k for which the codimension of $\Pi ^k(n,p)$ attains its minimum. For this k the codimension of the bad set $\Pi (n,p)$ is denoted by $\sigma (n,p.)$ When $\sigma (n,p) > n,$ then the k-jet of a generic map does not meet the set $\Pi (n,p)$ and therefore it is transversal to Mather’s stratification in $J^k(N,P)$ and hence it is stable. He defined the nice dimensions as the pairs (n, p) such that $\sigma (n,p)>n.$ See [6] for the notion of semi-nice dimensions, where 2-modality of ${\mathscr {K}}$-orbits appears.

As a consequence of Proposition 3.5, the fact that Mather’s bad set has codimension greater than n means that one can detect lack of simplicity at the ${\mathscr {A}}_e$-codimension 1 level. Take also into account that ${\mathscr {K}}$-orbits of codimension less than or equal to n have stable representatives of ${\mathscr {A}}$-codimension less than or equal to n (i.e. there is an open ${\mathscr {A}}$-orbit in the ${\mathscr {K}}$-orbit). If we want to refine this definition to detect lack of simplicity in the ${\mathscr {A}}_e$-codimension 2 level we must consider bad sets of codimension greater than $n+1$. Furthermore, since ${\mathscr {A}}$-orbits of non stable germs may or may not be open in their ${\mathscr {K}}$-orbit, we must consider stratification by ${\mathscr {A}}$-orbits instead of ${\mathscr {K}}$-orbits. This leads to the following

Definition 4.1

The pair (n, p) is said to be in the extra-nice dimensions if, for large enough l, there is a Zariski closed ${\mathscr {A}}$-invariant subset $\Lambda$ of $J^l(n,p)$, of codimension greater than $n+1$, whose complement is a finite union of ${\mathscr {A}}$-orbits.

It follows from the definition that

Proposition 4.2

If (n, p) is in the extra-nice dimensions then all ${\mathscr {A}}_e$-codimension 2 germs are simple.

Proof

Suppose we have an ${\mathscr {A}}_e$-codimension 2 non simple germ. Then there is a 1-parameter family of ${\mathscr {A}}$-orbits of codimension $n+2$, so we cannot find and ${\mathscr {A}}$-invariant subset $\Lambda$ of $J^l(n,p)$, of codimension greater than $n+1$, whose complement is a finite union of ${\mathscr {A}}$-orbits. $\square$

The converse of Proposition 4.2 is not true as we shall see in a further example (Proposition 5.8).

The subset $\Lambda$ in the definition can be constructed containing all non-simple ${\mathscr {A}}$-orbits and all ${\mathscr {A}}$-orbits of codimension greater than or equal to $n+2$. In order to be in the extra-nice dimensions, the codimension of this set must be greater than or equal to $n+2$ (see Sect. 6, Proposition 6.2). It is not contained and it does not contain Mather’s bad set, because in a ${\mathscr {K}}$-orbit of codimension less than or equal to n there can be an infinite number of simple ${\mathscr {A}}$-orbits (for example, augmentations), and in order to have finite ${\mathscr {A}}$-orbits in the complement of our bad set $\Lambda$ we must include in $\Lambda$ some of these $\mathscr {A}$-orbits (i.e. we include the ones of codimension greater than or equal to $n+2$). In Remark 5.3 we compare Mather’s bad set and ours for some examples.

The previous definition is well defined because there is an estimate (depending on n and p) for the degree of determinacy of ${\mathscr {A}}_e$-codimension 1 germs. Namely, results by Mather and Gaffney which can be found in [23, 37] state that if ${\mathscr {A}}$-cod$(f)=d$ then ${\mathscr {M}}_n^{(rp+d)^2}\theta (f)\subset T{\mathscr {A}} f$, where r is the number of branches, and if ${\mathscr {M}}_n^{k+1}\theta (f)\subset T{\mathscr {A}} f$ then f is $(2k+1)$-${\mathscr {A}}$-determined. Combining this we have that f is $(2((rp+d)^2-1)+1)$-${\mathscr {A}}$-determined. So for monogerms we obtain that if ${\mathscr {A}}_e$-cod$(f)=i$, then f is $(2(p+n+i) ^2-1)$-${\mathscr {A}}$-determined, in particular any ${\mathscr {A}}_e$-codimension 1 (and therefore ${\mathscr {A}}$-codimension $n+1$) germ $f:({\mathbb {R}}^n,0)\rightarrow ({\mathbb {R}}^p,0)$ is $(2(p+n+1)^2-1)$-${\mathscr {A}}$-determined.

Proposition 4.3

If the pair (n, p) is in the extra-nice dimensions, then $(n+1,p+1)$ is in the nice dimensions (in particular, (n, p) is nice dimensions too).

Proof

By definition there exists an ${\mathscr {A}}$-invariant subset $\Lambda$ of $J^l(n,p)$, of codimension greater than $n+1$, whose complement is a finite union of ${\mathscr {A}}$-orbits. For each one of those $\mathscr {A}$-orbits, consider the ${\mathscr {K}}$-orbit which contains it. We therefore have a finite number of ${\mathscr {K}}$-orbits of codimension less than or equal to $n+1$ which may include some ${\mathscr {A}}$-orbits which were originally in $\Lambda$. The complement of this finite number of ${\mathscr {K}}$-orbits is included in $\Lambda$, and therefore the codimension of this complement is greater than $n+1$. This complement contains all the ${\mathscr {K}}$-orbits of codimension greater than or equal to $n+2$ and is Zariski closed. In conclusion, there exists a ${\mathscr {K}}$-invariant subset $\Lambda '$ of codimension greater than $n+1$ such that its complement is a finite number of ${\mathscr {K}}$-orbits. The codimensions of these strata are the same in $(n+1,p+1)$ and so $(n+1,p+1)$ is in the nice dimensions. $\square$

This means that if $(n+1,p+1)$ is not in the nice dimensions, then (n, p) is not in the extra-nice dimensions.

It is obvious from the definition of nice dimensions that if a pair $(n+1,p+1)$ is in the nice dimensions, then (n, p) is in the nice dimensions, since the codimension of ${\mathscr {K}}$-orbits is invariant under unfoldings. However, this is not so obvious for the extra-nice dimensions:

Proposition 4.4

If the pair $(n+1,p+1)$ is in the extra-nice dimensions, then (n, p) is in the extra-nice dimensions.

Proof

Suppose that (n, p) is not in the extra-nice dimensions. Then, for any Zariski closed ${\mathscr {A}}$-invariant subset $\Gamma$ of $J^l(n,p)$ of codimension greater than $n+1$, its complement is an infinite number of ${\mathscr {A}}$-orbits.

Let $\Gamma$ be the union of all the ${\mathscr {A}}$-orbits of codimension greater than or equal to $n+2$. If the codimension of $\Gamma$ is greater than or equal to $n+2$, since it is an $\mathscr {A}$-invariant set, its complement is an infinite number of $\mathscr {A}$-orbits. On the other hand, the complement of $\Gamma$ is the union of all ${\mathscr {A}}$-orbits of codimension less than or equal to $n+1$. In the nice dimensions there are a finite number of stable and ${\mathscr {A}}_e$-codimension 1 orbits (see [4]), therefore we have a contradiction. Hence, the codimension of $\Gamma$ must be less than or equal to $n+1$. This means that there is a Zariski open set in $\Gamma$ foliated by an infinite number of ${\mathscr {A}}$-orbits of the same codimension (greater than $n+1$, i.e. ${\mathscr {A}}_e$-codimension greater than 1).

If these infinite ${\mathscr {A}}$-orbits are contained in a single ${\mathscr {K}}$-orbit X then ${\text {cod}}_{J^k(n,p)}X\le {\text {cod}}_{J^k(n,p)} \Gamma \le n+1$. Therefore the ${\mathscr {K}}$-orbit has a stable germ $F:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ which is a 1-parameter stable unfolding of the germs of the ${\mathscr {A}}$-orbits. By augmenting these germs by F and a Morse function we obtain a stratum of codimension equal to the codimension of $\Gamma$ (less than or equal to $n+1$) of germs of ${\mathscr {A}}_e$-codimension equal to the ${\mathscr {A}}_e$-codimension of the germs before augmenting (greater than 1) in $(n+1,p+1)$, and so $(n+1,p+1)$ is not in the extra-nice dimensions.

If no single ${\mathscr {K}}$-orbit contains the infinite ${\mathscr {A}}$-orbits, there is a stratum of codimension equal to the codimension of $\Gamma$ with modality of ${\mathscr {K}}$-orbits. This implies that $(n+1,p+1)$ cannot be nice dimensions. Therefore, by Proposition 4.3, $(n+1,p+1)$ is not in the extra-nice dimensions. $\square$

Remark 4.5

The above proof implies that if a pair (n, p) is in the nice dimensions but not in the extra-nice dimensions, then there exists a ${\mathscr {K}}$-orbit which contains a stratum of codimension less than or equal to $n+1$ of non-simple germs. In fact, the codimension is equal to $n+1$ (see Sect. 7).

Theorem 4.6

The pair (n, p) is in the extra-nice dimensions if and only if $(n+1,p+1)$ is in the nice dimensions and every stable germ $F:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ admits a hyperplane ${\mathscr {A}}_e$-codimension 1 section $f:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^p,0).$

Proof

1. By Proposition 4.3 if (n, p) is in the extra-nice dimensions then $(n+1,p+1)$ is in the nice dimensions. We start by proving that if (n, p) is in the extra-nice dimensions then every stable germ $F:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ of ${\mathscr {K}}$-codimension $n+1$ admits a hyperplane section of ${\mathscr {A}}_e$-codimension 1.

Suppose that there exists a stable germ $F:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ of ${\mathscr {K}}$-codimension $n+1$ which does not admit an ${\mathscr {A}}_e$-codimension 1 hyperplane section. Then there exists a $k>1$ and a section $f':({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^p,0)$ of ${\mathscr {A}}_e$-codimension k such that all sections of F have ${\mathscr {A}}_e$-codimension greater than or equal to k (i.e. ${\mathscr {A}}$-codimension greater than or equal to $n+k$). Therefore there is no ${\mathscr {A}}$-orbit open in the ${\mathscr {K}}$-orbit. This means that the ${\mathscr {K}}$-orbit is a codimension $n+1$ subset of $J^l(n,p)$ which is a union of infinite ${\mathscr {A}}$-orbits, none of which has codimension $n+1$. Any subset of codimension greater than $n+1$ will contain in its complement infinite ${\mathscr {A}}$-orbits of the ${\mathscr {K}}$-orbit, which contradicts the fact that (n, p) is in the extra-nice dimensions.

Lets consider now $F:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ a stable germ of ${\mathscr {K}}$-codimension $n-r$, $r\ge 0$. Then F is a trivial unfolding of a minimal stable germ ${\tilde{F}}:({\mathbb {K}}^{n-r},0)\rightarrow ({\mathbb {K}}^{p-r},0).$ As (n, p) is in the extra-nice dimensions hence, by Proposition 4.4, $(n-r-1,p-r-1)$ also is and we can apply the above argument to find an ${\mathscr {A}}_e$-codimension 1 hyperplane section ${\tilde{f}}$ of ${\tilde{F}}.$ Then the augmentation of ${\tilde{f}}$ is an ${\mathscr {A}}_e$-codimension 1 hyperplane section of F (see [4]).

2.  Suppose that $(n+1,p+1)$ is in the nice dimensions. Then there exists a ${\mathscr {K}}$-invariant Zariski closed bad set $\Pi '\subset J^k(n+1,p+1)$ of codimension greater than $n+1$, such that its complement is a finite union of ${\mathscr {K}}$-orbits, $K_1',\ldots ,K_n'$, of codimension less than or equal to $n+1$. Denote by $\Pi$ and $K_1,\ldots ,K_n$ the corresponding sets in $J^k(n,p)$, which have the same codimension since the ${\mathscr {K}}$-codimension is invariant under unfoldings. Since the ${\mathscr {K}}$-orbits $K_1,\ldots ,K_n$ have codimension less than or equal to $n+1$, for each orbit there is a stable germ $F_i:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ which is a 1-parameter stable unfolding of all the augmentations in the corresponding ${\mathscr {K}}$-orbit. By hypothesis, all these stable germs admit a hyperplane section $f_i$ of ${\mathscr {A}}_e$-codimension 1. By Theorem 4.6 in [11] $f_i$ is primitive if $F_i$ is minimal and it is an augmentation otherwise.

We want to construct an ${\mathscr {A}}$-invariant Zariski closed subset of $J^k(n,p)$ of codimension greater than $n+1$ such that its complement is a finite union of ${\mathscr {A}}$-orbits. We will do this by extracting “bad sets" from each ${\mathscr {K}}$-orbit and considering their union with $\Pi$.

Suppose first the codimension of $K_i$ is exactly $n+1$, i.e. the ${\mathscr {K}}$-codimension of $F_i$ is $n+1$ and so it is minimal. Since $f_i$ is primitive, the ${\mathscr {A}}$-orbit $A_i$ of $f_i$ is open in its ${\mathscr {K}}$-orbit $K_i$. By Theorem 3.2, the complement of the (finite union of open) ${\mathscr {A}}$-orbit(s) in the ${\mathscr {K}}$-orbit, which we denote by $A_i^{c}$, has codimension greater than $n+1$.

Suppose the codimension of $K_j$ is less than $n+1$. Now $f_j$ is an augmentation (and all the other non stable finitely determined germs with 1-parameter stable unfolding in $K_j$ too). In $K_j$ there are ${\mathscr {A}}$-orbits of stable germs, so the ${\mathscr {A}}$-orbit of $f_j$ is not open in $K_j$. Denote by $B_j^c$ the complement in $K_j$ of the union of the ${\mathscr {A}}$-orbits of stable germs and of germs of ${\mathscr {A}}_e$-codimension 1. If $r=n+1-{\mathscr {K}\hbox {-cod}}(F_j)$, then $f_j$ is an augmentation of an ${\mathscr {A}}_e$-codimension 1 primitive germ $h_j:({\mathbb {K}}^{n-r},0)\rightarrow ({\mathbb {K}}^{p-r},0)$ by a 1-parameter stable minimal unfolding of it, denoted by $H_j$, and a Morse function in r variables. All the finitely determined augmentations in the ${\mathscr {A}}$-orbits of $K_j$ are also augmentations of primitive germs in $(n-r,p-r)$ by $H_j$ and a function in r variables. Repeating the above argument, the ${\mathscr {A}}$-orbit of $h_j$ is open in its ${\mathscr {K}}$-orbit. By Theorem 3.2, the complement of the (finite union of open) ${\mathscr {A}}$-orbit(s) in the ${\mathscr {K}}$-orbit of $h_j$, which we denote by $M_j^c$, has codimension greater than $n-r+1$. Consider the germs in $B_j^c$ which are augmentations of the germs in $M_j^c$. The ${\mathscr {A}}_e$-codimension of these augmentations is greater than or equal to the ${\mathscr {A}}_e$-codimension of the germs in $M_j^c$ (see Equation (1)), so the ${\mathscr {A}}$-codimension of the augmentations is greater than or equal to r plus the ${\mathscr {A}}$-codimension of the germs in $M_j^c$. In conclusion, ${\text {cod}}_{J^k(n,p)} B_j^c\ge {\text {cod}}_{J^k(n,p)} M_j^c+r> n-r+1+r=n+1$. Notice that for primitive germs in $B_j^c$ we apply Proposition 3.8.

Finally, $\Lambda =\Pi \cup (\bigcup A_i^c)\cup (\bigcup B_j^c)$ is an ${\mathscr {A}}$-invariant subset of $J^k(n,p)$ which is a finite union of sets of codimension greater than $n+1$, and so its codimension is greater than $n+1$. Considering the closure of $\Lambda$ it can be seen that it is Zariski closed. Moreover, the complement of $\Lambda$ in $J^k(n,p)$ is a finite union of ${\mathscr {A}}$-orbits (the ones in the $A_i$’s and the ones in the $B_j$’s). Therefore, (n, p) is in the extra-nice dimensions. $\square$

In order to determine when a pair (n, p) is in the extra-nice dimensions, by Theorem 4.6, we need to know the stable germs $({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$, so we describe Mather’s procedure to obtain the normal forms for all stable germs. Start with a germ $f_0:({\mathbb {K}}^s,0)\rightarrow ({\mathbb {K}}^t,0)$ of rank 0 and find a basis $\{\phi _1,\ldots ,\phi _d\}$ of $\frac{{\mathscr {M}}_n\theta (f_0)}{T{\mathscr {K}}_e f_0}$. Then, $F:({\mathbb {K}}^{s+d},0)\rightarrow ({\mathbb {K}}^{t+d},0)$ given by

$$\begin{aligned} F(x,u_1,\ldots ,u_d)=(f_0(x)+\sum _{i=1}^d u_i\phi _i(x),u_1,\ldots ,u_d) \end{aligned}$$

is stable. Furthermore, any stable germ can be obtained by this procedure.

By Proposition 3.4, all stable corank 1 germs admit an ${\mathscr {A}}_e$-codimension 1 hyperplane section, so we need to study simple germs $f_0$ of corank at least 2. The rank 0 germs $f_0$ have been classified by several authors such as Mather, Arnol’d, Giusti, Wirthmüller, Damon, du Plessis, Wall and Gibson. A good account can be found in the book by du Plessis and Wall [7].

In the following discussion of simple algebras of corank greater than 1, there are two of corank 2 which play a special role:

$$\begin{aligned} B_{p,q}=(x^p+y^q,xy),\,\,\, B_{p,q}'=(x^p,y^q,xy). \end{aligned}$$

Notice that $B_{p,q}'$ is obtained from $B_{p,q}$ by adding its jacobian.

4.1 Algebras

We describe the algebras by the number of variables and generators. We only list the least degenerate ones (which will be enough for our purpose as we will see in the next section).

Case $n\ge p$:

• 1. With 1 generator and any number of variables: $A_k$, $D_k$, $E_6$, $E_7$ and $E_8$, which are of corank 1.

• 2. With 2 generators and 2 variables: $B_{p,q}$. The stable germs in these algebras are in $(p+q,p+q)$.

• 3. With 2 generators and 3 variables: $P_{p,q}=B_{p,q}+(z^2,0)$. The stable germs in these algebras are in $(p+q+2,p+q+1)$.

• 4. With 2 generators and more than 3 variables there are no simple algebras. For example, the simplest algebra of corank 2 with 4 variables is $(x^2+y^2+z^2,y^2+z^2+\lambda w^2)$ (non-simple because there are 4 quadratics), whose stable germ is in (9, 7) and (8, 6) is the boundary of the nice dimensions.

• 5. With more than 2 generators: there are no simple algebras.

Case $n<p$:

• 1. With 2 variables: $(B'_{p,q},0,\ldots ,0)$ whose stable germs are in $(2p+2q-2+k(p+q-2),2p+2q-1+k(p+q-1))$ and $(B_{p,q},0,\ldots ,0)$ whose stable germs are in $(p+q+k(p+q-1),p+q+k(p+q))$, where k is the number of zeros.

• 2. With 3 variables.

  • (a) With 4 generators: $f(x,y,z)=(x^2-y^2,y^2+z^2,xz,yz)$. The stable germ is in (12, 13). If we add k zeros the stable germ is in $(12+9k,13+10k).$

  • (b) With 5 generators: $f(x,y,z)=(x^2-y^2,y^2+z^2,xy,xz,yz)$ which is obtained from $P_{2,2}$ by adding its jacobian. The stable germ is in (15, 17). If we add k zeros the stable germ is in $(15+12k,17+13k).$

  • (c) With 6 generators: $f(x,y,z)=(x^2,y^2,z^2,xy,xz,yz).$ The stable germ is in (18, 21).If we add k zeros the stable germ is in $(18+15k,21+16k).$

  • (d) With more than 6 generators they are obtained from the above ones by adding zeros.

• 3. With 4 variables the stable germs are in the boundary of the nice dimensions.

5 The boundary of the extra-nice dimensions

Many of the calculations which did not make it to the final version of this article were either done or double-checked using an algorithm implemented in the computer package Singular developed by Hernandes et al. [10]. The calculations which appear in this section have been done by hand unless otherwise stated.

5.1 The case $n=p$

In Theorem 3.10 we obtain a non-simple ${\mathscr {A}}_e$-codimension 2 germs in (5, 5) of type $B_{3,3}$. By Proposition 3.8 this means that there exists a stable germ in (6, 6) which does not admit a hyperplane section of ${\mathscr {A}}_e$-codimension 1. Therefore, by Theorem 4.6, (5, 5) is not in the extra-nice dimensions. Since (5, 5) is in the nice dimensions we have the converse of Theorem 4.6, so to establish the boundary of the extra-nice dimensions we must verify if all stable germs in (5, 5) admit hyperplane sections of ${\mathscr {A}}_e$-codimension 1. Taking into account the adjacencies of discrete algebra types we only have to investigate the stable germ in $B_{3,2}$:

$$\begin{aligned} F_{3,2}(x,y,u_1,u_2,u_3)= & {} (x^3+y^2+u_1x+u_2y+u_3x^2,xy,u_1,u_2,u_3)\\ \quad= & {} (X,Y,U_1,U_2,U_3). \end{aligned}$$

Lemma 5.1

${\text {Lift}}(F_{3,2})$ is generated by

$$\begin{aligned}&\eta _1=\left( \begin{array}{c}6X\\ 5Y\\ 4U_1\\ 3U_2\\ 2U_3\end{array}\right) ,\quad \eta _2=\left( \begin{array}{c} 4U_3Y+2U_1U_2\\ X\\ -5Y-3U_2U_3\\ -3U_1\\ -4U_2\end{array}\right) ,\quad \eta _3=\left( \begin{array}{c} \frac{4}{3}U_2Y\\ -\frac{1}{9} U_3Y\\ X+\frac{1}{9}U_1U_3\\ -\frac{5}{3} Y\\ -\frac{2}{3} U_1+\frac{2}{9} U_3^2\end{array}\right) \\&\eta _4=\left( \begin{array}{c} \frac{3}{2}U_1Y\\ -\frac{1}{4} U_2Y\\ -2U_3Y\\ X+\frac{1}{4}U_2^2\\ -\frac{5}{2}Y\end{array}\right) ,\quad \eta _5=\left( \begin{array}{c} \frac{5}{3}Y^2+\frac{1}{9}U_2U_3Y\\ (-\frac{2}{9}U_1+\frac{2}{27}U_3^2)Y\\ -\frac{4}{3}U_2Y+\frac{2}{9}U_1^2-\frac{2}{27}U_1U_3^2\\ -\frac{2}{9}U_3Y\\ X+\frac{5}{9}U_1U_3-\frac{4}{27}U_3^3\end{array}\right) \end{aligned}$$

Proof

$F_{3,2}$ is a free divisor so ${\text {Lift}}(F_{3,2})$ is generated by 5 vector fields. The Euler vector field is clearly liftable and the other 4 are all linearly independent and liftable by the following lowerable vector fields:

$$\begin{aligned}&\xi _2=\left( \begin{array}{c} y+u_2\\ x^2+u_1+u_3x\\ -5xy-3u_2u_3\\ -3u_1\\ -4u_2\end{array}\right) ,\quad \xi _3=\left( \begin{array}{c} -\frac{1}{3}x^2-\frac{1}{9}u_3x\\ \frac{1}{3}xy\\ x^3+y^2+u_1x+u_2y+u_3x^2+\frac{1}{9}u_1u_3\\ -\frac{5}{3}xy\\ -\frac{2}{3}u_1+\frac{2}{9}u_3^2\end{array}\right) \\&\xi _4=\left( \begin{array}{c} \frac{1}{2}xy\\ -\frac{1}{2}y^2-\frac{1}{4}u_2y\\ -2u_3xy\\ x^3+y^2+u_1x+u_2y+u_3x^2+\frac{1}{4}u_2^2\\ -\frac{5}{2}xy\end{array}\right) ,\\&\quad \xi _5\left( \begin{array}{c} -\frac{1}{3}x^3-\frac{1}{9}u_3x^2+(-\frac{2}{9}u_1+\frac{2}{27}u_3^2)x\\ \frac{1}{3}x^2y+\frac{1}{9}u_3xy\\ -\frac{4}{3}u_2xy+\frac{2}{9}u_1^2-\frac{2}{27}u_1u_3^2\\ -\frac{2}{9}u_3xy\\ x^3\!+\!y^2\!+\!u_1x\!+\!u_2y\!+\!u_3x^2\!+\frac{5}{9}u_1u_3-\frac{4}{27}u_3^3 \end{array}\right) \end{aligned}$$

$\square$

Proposition 5.2

When $n=p$, (5, 5) is the boundary of the extra-nice dimensions.

Proof

It remains to prove the existence of a hyperplane section of ${\mathscr {A}}_e$-codimension 1 of $F_{3,2}.$ Let $L:{\mathbb {K}}^5\rightarrow {\mathbb {K}}$ be given by $L(X,Y,U_1,U_2,U_3)=U_3$. Then ${\mathscr {M}}_5\subset L({\text {Lift}}(F_{3,2}))$ and by Proposition 3.6(iv), $F_{3,2}$ admits a hyperplane section of ${\mathscr {A}}_e$-codimension 1, so (4, 4) is in the extra-nice dimensions. $\square$

Remark 5.3

The pair (5, 5) is in the nice dimensions but not in the extra-nice dimensions. In $J^l(5,5)$ for a sufficiently high l Mather’s bad set $\Pi (5,5)$ is a codimension 6 ${\mathscr {K}}$-invariant set given by $\Pi (5,5)=\overline{A_6\cup B_{3,3}}.$ Its complement is composed by the ${\mathscr {K}}$-orbits $A_i$, $i=1,\ldots ,5$, $B_{2,2}$ and $B_{3,2}$, all of which have a stable representative in (5, 5). In the ${\mathscr {K}}$-orbit of $B_{3,3}$ there is a 1-parameter family of ${\mathscr {A}}$-orbits of ${\mathscr {A}}_e$-codimension 2 (i.e. ${\mathscr {A}}$-codimension 7) which is dense in the ${\mathscr {K}}$-orbit (Theorem 3.10). Therefore we cannot find an ${\mathscr {A}}$-invariant set of codimension greater than or equal to 7 such that the complement is a finite number of ${\mathscr {A}}$-orbits, and hence (5, 5) is not in the extra-nice dimensions.

On the other hand, in (4, 4) the set $\Pi (4,4)$ is a codimension 5 ${\mathscr {K}}$-invariant set in $J^l(4,4)$ given by $\Pi (4,4)=\overline{A_5\cup B_{3,2}}.$ Its complement is composed by the ${\mathscr {K}}$-orbits $A_i$, $i=1,\ldots ,4$ and $B_{2,2}$. Both ${\mathscr {K}}$-orbits $A_5$ and $B_{3,2}$ have an open ${\mathscr {A}}$-orbit. Let $\Lambda$ be the union of the closure of the complement of these open orbits in $A_5$ and $B_{3,2}$ and of all the ${\mathscr {A}}$-orbits of codimension greater than or equal to 6 in all the $\mathscr {K}$-orbits. This is a codimension 6 ${\mathscr {A}}$-invariant subset such that the complement of it is a finite number of $\mathscr {A}$-orbits and hence (4, 4) is in the extra-nice dimensions.

5.2 How to go from (n, p) ($n\le p$) to $(n,p+1)$ by adding a 0 component

Let $f_0:({\mathbb {K}}^n,0)\longrightarrow ({\mathbb {K}}^p,0)$, $n\le p$, be a ${\mathscr {K}}$-finitely determined map-germ. Suppose $\displaystyle \frac{{\mathcal {O}}_n}{\langle f_0\rangle }\cong {\mathbb {K}}\{\sigma _0,\ldots ,\sigma _r\}$, where $\sigma _0=1$. When $n=p$ we shall consider $\sigma _r=J(f_0)$.

Let $f:({\mathbb {K}}^n,0)\longrightarrow ({\mathbb {K}}^{p+1},0)$ be given by $f=(f_0,0)$.

Let $F_0:({\mathbb {K}}^{n+k},0)\longrightarrow ({\mathbb {K}}^{p+k},0)$ be a minimal stable unfolding of $f_0$, $F_0(x,u_1,\ldots ,u_k)=({\tilde{F}}(x,u),u).$

Let $F:({\mathbb {K}}^{n+k+r},0)\longrightarrow ({\mathbb {K}}^{p+k+r+1},0)$ be a minimal stable unfolding of f given by $F(x,u,w)=({\tilde{F}}(x,u),u, Z(x,w),w)$ where $Z(x,w)=\sum _{i=1}^r\sigma _i(x)w_i.$ We denote the coordinates in target by (X, U, Z, W).

We have that

$$\begin{aligned} dF=\left( \begin{array}{ccccccccc} \frac{\partial {\tilde{F}}_1}{\partial x_1} &{} \cdots &{} \frac{\partial {\tilde{F}}_1}{\partial x_n} &{} \frac{\partial {\tilde{F}}_1}{\partial u_1} &{} \cdots &{} \frac{\partial {\tilde{F}}_1}{\partial u_k} &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} &{} &{} &{} \\ \frac{\partial {\tilde{F}}_p}{\partial x_1} &{} \cdots &{} \frac{\partial {\tilde{F}}_p}{\partial x_n} &{} \frac{\partial {\tilde{F}}_p}{\partial u_1} &{} \cdots &{} \frac{\partial {\tilde{F}}_p}{\partial u_k} &{} 0 &{} \cdots &{} 0\\ 0 &{} &{} 0 &{} 1 &{} \cdots &{} 0 &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} &{} &{} &{} \\ 0 &{} &{} 0 &{} 0 &{} \cdots &{} 1 &{} 0 &{} \cdots &{} 0\\ \frac{\partial Z}{\partial x_1} &{} \cdots &{} \frac{\partial Z}{\partial x_n} &{} 0 &{} &{} 0 &{} \sigma _1 &{} \cdots &{} \sigma _r\\ 0 &{} &{} 0 &{} 0 &{} \cdots &{} 0 &{} 1 &{} \cdots &{} 0\\ \vdots &{} &{} &{} &{} &{} &{} &{} &{} \\ 0 &{} &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} \cdots &{} 1\end{array}\right) \end{aligned}$$

Proposition 5.4

Let $\pi _1:({\mathbb {K}}^{p+k+r+1},0)\longrightarrow ({\mathbb {K}}^{p+k},0)$ be the natural projection. Then ${\text {Lift}}(F_0)=\pi _1({\text {Lift}}(F)|_{Z=W=0}).$

Proof

It is immediate that ${\text {Lift}}(F_0)\supset \pi _1({\text {Lift}}(F)|_{Z=W=0}).$ Only write $dF(\xi )=\eta \circ F$, take $Z=W=0$ and project $\xi$ into the first $n+k$ coordinates and $\eta$ into the first $p+k$ coordinates.

Now let $\xi _0=(\xi _0^1(x,u),\ldots ,\xi _0^{n+k}(x,u))\in \theta _{n+k}$ and $\eta _0=(\eta _0^1(X,U),$$\ldots ,\eta _0^{p+k}(X,U))\in \theta _{p+k}$ such that $dF_0(\xi _0)=\eta _0\circ F_0$.

We have that

$$\begin{aligned} dF(\xi _0,0,\ldots ,0)=(\eta _0^1\circ F_0,\ldots ,\eta _0^{p+k}\circ F_0,\lambda (x,u,w),0,\ldots ,0) \end{aligned}$$

where $\lambda (x,u,w)=\sum _{i=1}^n\xi _0^i\frac{\partial Z}{\partial x_i}.$

Since $\displaystyle \frac{{\mathcal {O}}_{\{(x,u,w)\}}}{\langle F_0,w\rangle }\cong {\mathbb {K}}\{\sigma _0,\ldots ,\sigma _r\}$, it follows from the Preparation Theorem that there exist functions $a_i=a_i(x,u,w)$ such that

$$\begin{aligned} \lambda (x,u,w)=\sum _{i=0}^r a_i(F_0,w)\sigma _i(x). \end{aligned}$$

Now let $\zeta =(\xi _0^1,\ldots ,\xi _0^{n+k},-a_1(F_0,w),\ldots ,-a_r(F_0,w))\in \theta _{n+k+r}$ and $\eta =(\eta _0^1,\ldots ,\eta _0^{p+k},a_0(X,U,W),-a_1(X,U,W),\ldots ,-a_r(X,U,W))$. Then, $dF(\zeta )=\eta \circ F$, that is, $\eta \in {\text {Lift}}(F)$, and $\pi _1(\eta |_{Z=W=0})=\eta _0.$ $\square$

Lemma 5.5

The vectors $\eta _{ZW_j}=Z\sigma _j\frac{\partial }{\partial Z}+Z\frac{\partial }{\partial W_j}\in \theta _{p+k+r+1}$, $j=1,\ldots ,r$, and $\eta _{W_iW_j}=W_i\sigma _j\frac{\partial }{\partial Z}+W_i\frac{\partial }{\partial W_j}\in \theta _{p+k+r+1}$, $i,j=1,\ldots ,r$, belong to ${\text {Lift}}(F).$

Proof

Write $\xi _{Zw_j}=Z\frac{\partial }{\partial w_j}\in \theta _{n+k+r}$ and $\xi _{w_iw_j}=w_i\frac{\partial }{\partial w_j}\in \theta _{n+k+r}$, $i,j=1,\ldots ,r.$ Then $wF(\eta _{ZW_j})=tF(\xi _{Zw_i})$ and $wF(\eta _{W_iW_j})=tF(\xi _{w_iw_j}).$ $\square$

Theorem 5.6

If $F_0$ admits a hyperplane ${\mathscr {A}}_e$-codimension 1 section then F also does. The converse is true if the image of the set of linear part of vector fields in ${\text {Lift}}(F)$ by $\pi _2$ is a subset of ${\mathscr {M}}_{Z,W}\theta (\pi _2),$ where $\pi _2:({\mathbb {K}}^{p+k+r+1},0)\longrightarrow ({\mathbb {K}}^{r+1},0)$ is the projection $\pi _2(X,U,Z,W)=(Z,W)$.

Proof

Let $h_0:({\mathbb {K}}^{p+k},0)\rightarrow ({\mathbb {K}},0)$ be a linear function such that $h_0=0$ defines the ${\mathscr {A}}_e$-codimension 1 hyperplane section of the discriminant $V_0\subset ({\mathbb {K}}^{p+k},0)$ of $F_0,$ that is, $h_0$ has $_{V_0}{\mathscr {K}}_e$-codimension 1. Then $th_0({\text {Lift}}(F_0))+\langle h_0\rangle \supset {\mathscr {M}}_{p+k}.$

Let $h:({\mathbb {K}}^{p+k+r+1},0)\rightarrow ({\mathbb {K}},0)$ be given by $h(X,U,Z,W)=h_0(X,U)+W_r.$ We are going to prove that $h=0$ defines an ${\mathscr {A}}_e$-codimension 1 hyperplane section of the discriminant $V\subset ({\mathbb {K}}^{p+k+r+1},0)$ of F, that is, h has $_{V}{\mathscr {K}}_e$-codimension 1.

As $F_0$ and F are both minimal stable unfoldings, all liftable vector fields in both cases vanish at zero.

Using notation from the previous lemma, it follows that $\langle th(\eta _{ZW_r}),th(\eta _{W_iW_r})\rangle \supseteq \langle Z,W\rangle _{{\mathcal {O}}_{{p+k+r+1}}}.$ So $th({\text {Lift}}(F))\supseteq \langle Z,W\rangle _{{\mathcal {O}}_{{p+k+r+1}}}.$

It remains to prove that $X_i,U_j\in th({\text {Lift}}(F))+\langle h\rangle$, $i=1,\ldots ,n$; $j=1,\ldots ,k.$

From hypothesis $X_i,U_j\in th_0({\text {Lift}}(F_0))+\langle h_0\rangle$. So, there exists $\eta _i^0(X,U)\in {\text {Lift}}(F_0)$ such that $X_i=th_0(\eta _i^0)+\alpha h_0,$ $i=1,\ldots ,n.$ It follows from Proposition 5.4 that there exists $\eta _i\in {\text {Lift}}(F)$, such that $\pi (\eta _i(X,U,0,0))=\eta _i^0(X,U).$ Now, from the definitions of h and $h_0$, $th(\eta _i)+ \langle Z,W\rangle _{{\mathcal {O}}_{p+k+r+1}}=th_0(\eta _i^0)+ \langle Z,W\rangle _{{\mathcal {O}}_{p+k+r+1}}.$ Then, $X_i\in th({\text {Lift}}(F))+\langle h\rangle$, $i=1,\ldots ,n.$ Similar arguments hold for $U_j$, $j=1,\ldots ,k.$ Therefore h has $_{V}{\mathscr {K}}_e$-codimension 1.

Conversely, let $h:({\mathbb {K}}^{p+k+r+1},0)\rightarrow ({\mathbb {K}},0)$ be a linear function such that $h=0$ defines an ${\mathscr {A}}_e$-codimension 1 hyperplane section of the discriminant $V\subset ({\mathbb {K}}^{p+k+r+1},0)$ of F. Then $th({\text {Lift}}(F))+\langle h\rangle \supset {\mathscr {M}}_{p+k+r+1}.$

Since h is linear we can write $h(X,U,Z,W)=h_0(X,U)+h_1(Z,W).$ It follows from the derivative of F above that $\pi _2({\text {Lift}}(F))\cap {\mathscr {M}}_{X,U}\theta (\pi _2)=\emptyset .$ Therefore $h_0\ne 0$ and $X_i,U_j\in h_0({\text {Lift}}(F))+\langle h_0\rangle ,$ for all $i=1,\ldots ,n$, $j=1,\ldots ,k.$ Now from Proposition 5.4 and as $\pi _2({\text {Lift}}(F))\subset {\mathscr {M}}_{Z,W}\theta (\pi _2),$ we actually have $X_i,U_j\in h_0({\text {Lift}}(F_0))+\langle h_0\rangle ,$ for all $i=1,\ldots ,n$, $j=1,\ldots ,k,$ that is, $h_0$ has $_{V_0}{\mathscr {K}}_e$-codimension 1. $\square$

5.3 The case $n=p-1$

First we consider $B'_{3,3}$ whose stable germ is $F'_{3,3}:({\mathbb {K}}^{10},0)\rightarrow ({\mathbb {K}}^{11},0)$ given by $F'_{3,3}(x,y,u_1,u_2,u_3,v_1,v_2,v_3,w_1,w_2)=(x^3+u_1x+u_2y+u_3y^2,y^3+v_1x+v_2y+v_3x^2,xy+w_1x+w_2y,u,v,w).$ In her PhD thesis at Warwick University under the supervision of David Mond, Mirna Gómez-Morales studied the existence of hyperplane sections of ${\mathscr {A}}_e$-codimension 1 for all stable germs in the algebra $B'_{p,q}$ [8]. She showed that the stable germ $F'_{3,2}$ of type $B'_{3,2}$ has an ${\mathscr {A}}_e$-codimension 1 hyperplane section but $B'_{3,3}$ does not, therefore (9, 10) is not in the extra-nice dimensions. Their method is the following. Consider $L:({\mathbb {K}}^{11},0)\rightarrow ({\mathbb {K}},0)$ be a linear polynomial given by $L(X_1,\ldots ,X_{11})=a_1X_1+\ldots +a_{11}X_{11}$. Given an immersion $i:({\mathbb {K}}^{10},0)\rightarrow ({\mathbb {K}}^{11},0)$, such that $L\circ i=0$, by Damon’s Theorem we have that ${\mathscr {A}}_e$-${\text {cod}}(i^*(F'_{3,3}))=\mathscr {K}_{V_e}$-${\text {cod}}(i)= _V{\mathscr {K}}_e$-${\text {cod}}(L)$, where V is the discriminant of $F'_{3,3}$. Let $M_{F'_{3,3}}(X_1,\ldots ,X_{11})$ be the matrix whose entries correspond to the linear parts in $X_1,\ldots ,X_{11}$ of the generators of $tL({\text {Derlog}}(\Delta (F'_{3,3})))+\langle L\rangle \theta (L)$. Then

$$\begin{aligned} M_{F'_{3,3}}(X_1,\ldots ,X_{11})=(X_1,\ldots ,X_{11})\cdot N_{F'_{3,3}}(a_1,\ldots ,a_{11}). \end{aligned}$$

Therefore, ${\mathscr {A}}_e$-${\text {cod}}(i^*(F'_{3,3}))=1$ if and only if the rank of $N_{F'_{3,3}}$ is 11. In fact, the same argument proves that ${\mathscr {A}}_e$-${\text {cod}}(i^*(F'_{3,3}))=k$ if and only if the rank of $N_{F'_{3,3}}$ is $12-k$ for $k\ge 1$.

Lemma 5.7

The linear parts of the generators of ${\text {Lift}}(F'_{3,3})$ are

$$\begin{aligned} \begin{array}{lll} \eta _1&{}=&{}3X\frac{\partial }{\partial X}+3Y\frac{\partial }{\partial Y}+2Z\frac{\partial }{\partial Z}+2U_1\frac{\partial }{\partial U_1}+2U_2\frac{\partial }{\partial U_2}+U_3\frac{\partial }{\partial U_3}+2V_1\frac{\partial }{\partial V_1}\\ &{}&{}+2V_2\frac{\partial }{\partial V_2}+V_3\frac{\partial }{\partial V_3}+W_1\frac{\partial }{\partial W_1}+W_2\frac{\partial }{\partial W_2},\\ \eta _2&{}=&{}3X\frac{\partial }{\partial Z}-3V_2\frac{\partial }{\partial V_3}+3U_1\frac{\partial }{\partial W_1}+4U_2\frac{\partial }{\partial W_2},\\ \eta _3&{}=&{}3Y\frac{\partial }{\partial Z}-3U_1\frac{\partial }{\partial U_3}+4V_1\frac{\partial }{\partial W_1}+3V_2\frac{\partial }{\partial W_2},\\ \eta _4&{}=&{}9X\frac{\partial }{\partial U_1}+3V_1\frac{\partial }{\partial V_3}+3Z\frac{\partial }{\partial W_1}+2U_1\frac{\partial }{\partial W_2},\\ \eta _5&{}=&{}3Y\frac{\partial }{\partial U_1}-3Z\frac{\partial }{\partial U_3}+V_1\frac{\partial }{\partial W_2},\\ \eta _6&{}=&{}3X\frac{\partial }{\partial U_2}-3U_2\frac{\partial }{\partial U_3}+Z\frac{\partial }{\partial W_2},\\ \eta _7&{}=&{}X\frac{\partial }{\partial U_3},\\ \eta _8&{}=&{}3U_2\frac{\partial }{\partial U_3}+9Y\frac{\partial }{\partial V_2}+2V_2\frac{\partial }{\partial W_1}+3Z\frac{\partial }{\partial W_2},\\ \eta _9&{}=&{}3Y\frac{\partial }{\partial V_1}-3V_1\frac{\partial }{\partial V_3}+Z\frac{\partial }{\partial W_1},\\ \eta _{10}&{}=&{}3X\frac{\partial }{\partial V_2}-3Z\frac{\partial }{\partial V_3}+U_2\frac{\partial }{\partial W_1},\\ \eta _{11}&{}=&{}3Y\frac{\partial }{\partial V_3}+X\frac{\partial }{\partial W_2},\\ \eta _{12}&{}=&{}X\frac{\partial }{\partial W_1}, \eta _{13}=Y\frac{\partial }{\partial W_1}, \eta _{14}=Y\frac{\partial }{\partial W_2}, \end{array} \end{aligned}$$

where $(X,Y,Z,U_1,U_2,U_3,V_1,V_2,V_3,W_1,W_2)$ are the coordinates of the target.

Proof

$\eta _1$ is the Euler vector field and lowerable vector fields for the remaining ones are

$$\begin{aligned} \xi _2= & {} -u_2\frac{\partial }{\partial x}+x^2\frac{\partial }{\partial y}-3v_2\frac{\partial }{\partial v_3}+3u_1\frac{\partial }{\partial w_1}+4u_2\frac{\partial }{\partial w_2},\\ \xi _3= & {} 3y^2\frac{\partial }{\partial x}-v_1\frac{\partial }{\partial y}-3u_1\frac{\partial }{\partial u_3}+4v_1\frac{\partial }{\partial w_1}+3v_2\frac{\partial }{\partial w_2},\\ \xi _4= & {} (-3x^2-2u_1)\frac{\partial }{\partial x}+X\frac{\partial }{\partial u_1}+3v_1\frac{\partial }{\partial v_3}+3Z\frac{\partial }{\partial w_1}+2u_1\frac{\partial }{\partial w_2},\\ \xi _5= & {} -v_1\frac{\partial }{\partial x}+3Y\frac{\partial }{\partial u_1}-3Z\frac{\partial }{\partial u_3}+v_1\frac{\partial }{\partial w_1},\\ \xi _6= & {} -xy\frac{\partial }{\partial x}+3X\frac{\partial }{\partial u_2}-3u_2\frac{\partial }{\partial u_3}+z\frac{\partial }{\partial w_2},\\ \xi _7= & {} X\frac{\partial }{\partial u_3},\\ \xi _8= & {} (-3y^2-2v_2)\frac{\partial }{\partial y}+3u_2\frac{\partial }{\partial u_3}+9Y\frac{\partial }{\partial v_2}+2v_2\frac{\partial }{\partial w_1}+3Z\frac{\partial }{\partial w_2},\\ \xi _9= & {} (-v_1x-xy)\frac{\partial }{\partial y}+3Y\frac{\partial }{\partial v_1}-3v_1\frac{\partial }{\partial v_3}+Z\frac{\partial }{\partial w_1},\\ \xi _{10}= & {} -u_2\frac{\partial }{\partial y}+3X\frac{\partial }{\partial v_2}-3Z\frac{\partial }{\partial v_3}+u_2\frac{\partial }{\partial w_1},\\ \xi _{11}= & {} -x^2y\frac{\partial }{\partial y}+3Y\frac{\partial }{\partial v_3}+X\frac{\partial }{\partial w_2},\\ \xi _{12}= & {} X\frac{\partial }{\partial w_1}, \xi _{13}=Y\frac{\partial }{\partial w_1}, \xi _{14}=Y\frac{\partial }{\partial w_2},\\ \end{aligned}$$

where $X=x^3+u_1x+u_2y+u_3y^2$, $Y=y^3+v_1x+v_2y+v_3x^2$ and $Z=xy+w_1x+w_2y.$ $\square$

The next result shows a counterexample of the converse of Proposition 4.2.

Proposition 5.8

Any hyperplane section of $F'_{3,3}$ has ${\mathscr {A}}_e$-codimension greater than 2.

Proof

Analyzing the linear parts of ${\text {Lift}}(F'_{3,3})$ we can see that the rank of $N_{F'_{3,3}}$ is 8 so the best possible hyperplane section has ${\mathscr {A}}_e$-codimension 4. $\square$

This means that in (9, 10) all ${\mathscr {A}}_e$-codimension 2 germs are simple, but (9, 10) is not in the extra-nice dimensions.

Proposition 5.9

When $n=p-1$, (9, 10) is the boundary of the extra-nice dimensions.

Proof

We must analyze corank 2 stable germs in (9, 10). These are given by the algebra type $(B_{3,2},0)$. By Lemma 5.1, $F_{3,2}$ admits an ${\mathscr {A}}_e$-codimension 1 hyperplane section, and by Theorem 5.6 the stable germ for $(B_{3,2},0)$ admits a section too. Since (9, 10) is in the nice dimensions, by the converse of Theorem 4.6, (8, 9) is in the extra-nice dimensions. $\square$

5.4 The case $n<p-1$

Up to now we have at the boundary of the extra-nice dimensions (5,5) and (9,10). These two pairs of dimensions lie in the line of equation $5n-4p-5=0$ in the (n, p)-plane. In fact, we can generalise this to include the case $n<p-1$:

Proposition 5.10

If $n\le p$ the boundary of the extra-nice dimensions is given by $5n-4p-5=0$, $p\ge 5$.

Proof

Let $F_0:({\mathbb {K}}^{10},0)\rightarrow ({\mathbb {K}}^{11},0)$ be the minimal stable germ in $B'_{3,3}$ algebra and $F:({\mathbb {K}}^{10+4k},0)\rightarrow ({\mathbb {K}}^{11+5k},0)$ be the minimal stable germ in $(B'_{3,3},0,\ldots ,0)$ where k is the number of zeros. Following notation of Sect. 5.2 we have $\sigma _1=x,$ $\sigma _2=y,$ $\sigma _3=x^2,$ $\sigma _4=y^2$ and $Z(x,y,w_1,w_2,w_3,w_4)=w_1x+w_2y+w_3x^2+w_4y^2$. Therefore, $\partial Z/\partial x=w_1+2w_3x$ and $\partial Z/\partial y=w_2+2w_4y$. So one can see that F satisfies the conditions of Theorem 5.6. As $F_0$ does not admit a hyperplane section of ${\mathscr {A}}_e$-codimension 1 then by Theorem 5.6F does not. If $F_0:({\mathbb {K}}^6,0)\rightarrow ({\mathbb {K}}^6,0)$ is the minimal stable germ in $B_{3,3}$ algebra and $F:({\mathbb {K}}^{6+5k},0)\rightarrow ({\mathbb {K}}^{6+6k},0)$ is the minimal stable germ in $(B_{3,3},0,\ldots ,0)$ where k is the number of zeros, then similarly F does not admit a hyperplane section of ${\mathscr {A}}_e$-codimension 1 since $\sigma _1=x,$ $\sigma _2=y,$ $\sigma _3=x^2,$ $\sigma _4=y^2.$

Let now $F_0:({\mathbb {K}}^8,0)\rightarrow ({\mathbb {K}}^9,0)$ be the minimal stable germ in $B'_{3,2}$ algebra and $F:({\mathbb {K}}^{8+3k},0)\rightarrow ({\mathbb {K}}^{9+4k},0)$ be the minimal stable germ in $(B'_{3,2},0,\ldots ,0)$ where k is the number of zeros. We have $Z(x,y,w_1,w_2,w_3)=w_1x+w_2y+w_3x^2$. Therefore, $\partial Z/\partial x=w_1+2w_3x$ and $\partial Z/\partial y=w_2$. So one can see that F satisfies the conditions of Theorem 5.6. As $F_0$ admits a hyperplane section of ${\mathscr {A}}_e$-codimension 1 then by Theorem 5.6F does. Similarly if $F_0:({\mathbb {K}}^5,0)\rightarrow ({\mathbb {K}}^5,0)$ is the minimal stable germ in $B_{3,2}$ algebra and $F:({\mathbb {K}}^{5+4k},0)\rightarrow ({\mathbb {K}}^{5+5k},0)$ is the minimal stable germ in $(B_{3,2},0,\ldots ,0)$ where k is the number of zeros, then similarly F admits a hyperplane section of ${\mathscr {A}}_e$-codimension 1.

Suppose $p=n+\ell$. We have:

Algebra	k	Stable germ	Hyperplane section
$(B_{3,3},0,\ldots ,0)$	$k=\ell$	$(6+5\ell ,6+6\ell )$	$(5+5\ell ,5+6\ell )$
$(B'_{3,3},0,\ldots ,0)$	$k=\ell -1$	$(6+4\ell ,6+5\ell )$	$(5+4\ell ,5+5\ell )$
$(B_{3,2},0,\ldots ,0)$	$k=\ell$	$(5+4\ell ,5+5\ell )$	$(4+4\ell ,4+5\ell )$
$(B'_{3,2},0,\ldots ,0)$	$k=\ell -1$	$(5+3\ell ,5+4\ell )$	$(4+3\ell ,4+4\ell )$

In conclusion, all the pairs of dimensions of sections of stable germs corresponding to algebras $B_{p,q}$ or $B_{p,q}'$ (or these two with zeros added) with $p+q\le 5$ lie in the extra-nice dimensions. The ones corresponding to $B_{p,q}$ or $B_{p,q}'$ (or these two with zeros added) with $p+q\ge 6$ are not in the extra-nice dimensions.

Therefore $(5+4\ell ,5+5\ell )$ is in the boundary of the extra-nice dimensions and belongs to the line $5n-4p-5=0.$ The sections of stable germs corresponding to algebras with 3 or more variables lie to the right of this line and are not in the extra-nice dimensions. $\square$

5.5 The case $n=p+1$

Consider the simplest corank 2 algebra in this setting and its stable unfolding $P_{2,2}:({\mathbb {K}}^6,0)\rightarrow ({\mathbb {K}}^5,0)$ given by

$$\begin{aligned} P_{2,2}(x,y,z,u_1,u_2,u_3)=(x^2+y^2+z^2+u_1x+u_2y,xy+u_3z,u_1,u_2,u_3). \end{aligned}$$

Lemma 5.11

The generators of ${\text {Lift}}(P_{2,2})$ are

$$\begin{aligned} \eta _1= & {} \left( \begin{array}{c}2X\\ 2Y\\ U_1\\ U_2\\ U_3\end{array}\right) , \eta _2=\left( \begin{array}{c} 6YU_1-2U_2U_3^2\\ -YU_2+2U_1U_3^2\\ -8Y\\ 4X+U_2^2+4U_3^2\\ -U_2U_3\end{array}\right) , \eta _3=\left( \begin{array}{c} 4YU_3+3U_1U_2U_3\\ 2XU_3+2U_3^2\\ -4U_2U_3\\ -4U_1U_3\\ 2Y\end{array}\right) \\ \eta _{4,5}= & {} \left( \begin{array}{c} 6YU_2-2U_1U_3^2\\ -YU_1+2U_2U_3^2\\ 4X+U_1^2+4U_3^2\\ -8Y\\ -U_1U_3\end{array}\right) ,\\&\left( \begin{array}{c} 4(X^2-12Y^2-6YU_1U_2+U_3^2(5X+3U_1^2+3U_2^2))\\ -8XY-16YU_3^2-9U_1U_2U_3^2\\ 2XU_1+36YU_2-14U_1U_3^2\\ 36YU_1+2XU_2-14U_1U_3^2\\ -10XU_3-2U_3^3\end{array}\right) \end{aligned}$$

Proof

The discriminant (image of critical points set) V of $P_{2,2}$ is a free divisor so ${\text {Derlog}}(V)$ is generated by 5 vector fields. In order to obtain them we calculate the order 5 minors of the differential and eliminate the variables x, y, z from the ideal generated by $2x^2-2y^2+u_1x-u_2y, u_1u_3+2U_3x-2yz, u_2u_3-2u_3y-2xz, X-(x^2+y^2+z^2+u_1x+u_2y), Y-(xy+u_3z)$ (the first three are the minors). Using the computer package Singular we obtain the defining equation of V. Again using Singular we can compute with syzygies the generators of ${\text {Derlog}}(V)$. It can be seen that all of them are linearly independent and liftable. $\square$

Notice that there are only 4 vector fields with non zero linear parts.

Proposition 5.12

When $n=p+1$, (5, 4) is the boundary of the extra-nice dimensions.

Proof

Analyzing the vector fields in Lemma 5.11 and by Proposition 3.6(iv), $P_{2,2}$ does not admit a hyperplane section of ${\mathscr {A}}_e$-codimension 1, so (5, 4) is not in the extra-nice dimensions. In fact, it does not admit an ${\mathscr {A}}_e$-codimension 2 section either. Since $P_{2,2}$ is the simplest corank 2 algebra in $(n+1,n)$ and (5, 4) is in the nice dimensions, by the converse of Theorem 4.6, (4, 3) is in the extra-nice dimensions and so (5, 4) is the boundary of the extra-nice dimensions. $\square$

5.6 The case $n>p+1$

From the discussion of the algebras, we know that there are no rank 0 simple algebras in this case. Here the boundary of the nice dimensions is given by the non simple ${\mathscr {A}}_e$-codimension 1 section of the stable unfolding of the simplest rank 0 germ for each case $(n+k,n)$, $k>2$.

In the case $(n+2,n)$ this algebra is $(x^2+y^2+z^2,y^2+\lambda z^2+w^2)$, whose stable unfolding is in (9, 7) and the boundary of the nice dimensions is (8, 6). By Proposition 4.3 (7, 5) is not in the extra-nice dimensions. Since there are no stable corank 2 germs in (7, 5) (or below) the boundary of the extra-nice dimensions is (7, 5).

On the other hand, for $(n+k,n)$ with $k>2$, the boundary of the nice dimensions is given by the non simple ${\mathscr {A}}_e$-codimension 1 section of the stable unfolding of $x^3+y^3+z^3+\lambda xyz+\Sigma _{i=1}^k w_i^2$, whose stable unfolding is in $(10+k,8)$, and so this boundary is $(9+k,7)$. By Proposition 4.3$(8+k,6)$ is not in the extra-nice dimensions. Since there are no stable corank 2 germs in $(8+k,6)$ (or below) the boundary of the extra-nice dimensions is $(8+k,6)$. We remark that in $(8+k,6)$ there may be a non simple ${\mathscr {A}}_e$-codimension 2 corank 1 germ obtained as a section (by a codimension 2 plane) of the stable unfolding of the germ $x^3+y^3+z^3+\lambda xyz+\Sigma _{i=1}^k w_i^2$.

5.7 Diagram of the boundary

From all the above discussions we can draw the boundary of the extra-nice dimensions and compare it to the boundary of the nice dimensions. In Fig. 1 the dotted line represents the boundary of the nice dimensions and the continuous line is the boundary of the extra-nice dimensions.

Fig. 1

The border of the nice (dashed line) and extra-nice dimensions

6 Locally stable 1-parameter families are dense in the extra-nice dimensions

In analogy to Mather’s characterization of the nice dimensions as those where stable maps are dense, we characterize the extra-nice dimensions as those where stable 1-parameter families are dense. Let N be a compact manifold.

Definition 6.1

Let $F: N\times [0,1] \rightarrow P$ be a family of maps. Then F is a locally stable 1-parameter family if $F_t: N \rightarrow P$ is a stable map for all $t \in [0,1]$ except for possibly a finite number of values $\{t_1,\ldots , t_k\}$ and the non-stable singularities of $F_{t_i}$ are a finite number of points $x_j \in N,$ such that the map $(F, t): N\times [0,1] \rightarrow P\times [0,1]$ is a locally ${\mathcal {A}}_e$-versal unfolding of $F_{t_i}$ for all non-stable points $x_j.$

From this definition it follows that $F_{t_i}:(N,x_j)\rightarrow (P,F_{t_i}(x_j))$ has ${\mathscr {A}}_e$-codimension 1. Locally stable 1-parameter families are a type of local pseudo-isotopies as appear in [3] or [14].

Suppose that (n, p) is in the nice dimensions. We define a stratification of $J^k(n,p)$ by ${\mathscr {A}}$-orbits and a bad set. Let $\Lambda (n,p)=\{\sigma \in J^k(n,p)/$ ${\mathscr {A}}^k$-codimension of $\sigma \ge n+2\}.$ $\Lambda (n,p)$ is a semi-algebraic set, hence it admits an ${\mathscr {A}}^k$-invariant stratification. The set $J^k(n,p)\backslash \Lambda (n,p)$ has a finite stratification by ${\mathscr {A}}$-orbits of codimension less than or equal to $n+1$ (i.e. orbits of germs of ${\mathscr {A}}_e$-codimension less than or equal to 1). Since this stratification is ${\mathscr {A}}$-invariant it induces an stratification S(N, P) of $J^k(N,P)$.

Lemma 6.2

Let (n, p) be in the nice dimensions. (n, p) is in the extra-nice dimensions if and only if the set $\Lambda (n,p)$ has codimension bigger than or equal to $n+2.$

Proof

If the codimension of $\Lambda (n,p)$ is less than or equal to $n+1$, then it is foliated by infinite ${\mathscr {A}}$-orbits and you cannot find a subset of codimension greater than $n+1$ such that its complement is a finite number of ${\mathscr {A}}$-orbits. The “if" part is trivial by definition since in the nice dimensions there are a finite number of ${\mathscr {A}}$-orbits of codimension less than or equal to $n+1$. $\square$

Consider a 1-parameter family $F: N\times [0,1] \rightarrow P$ and consider the partial jet extension

$$\begin{aligned} j_1^kF:N\times [0,1]\rightarrow J^k(N,P) \end{aligned}$$

given by $j_1^kF(x,t)=j^kF_t(x)$.

Lemma 6.3

If $F:N\times [0,1] \rightarrow P$ is a locally stable 1-parameter family then $j_1^kF$ is transverse to the stratification S(N, P). The converse holds if (n, p) is in the extra-nice dimensions.

Proof

First of all, the Versality Theorem 3.3 in [37] (or 4.1.4 in [23]) says that an unfolding (F, t) of f is locally ${\mathscr {A}}_e$-versal if and only if $T{\mathscr {A}}_e(f)+Sp\{\frac{\partial F}{\partial t}\}=\theta (f)$. Based on this it can be seen (Theorem 4.1.11 in [23] or Proposition 2.2 in [38] for ${\mathscr {K}}$-equivalence) that (F, t) is locally ${\mathscr {A}}_e$-versal if and only if $j_1^kF$ is transversal to the ${\mathscr {A}}$-orbit of f.

If F is a locally stable 1-parameter family, by definition (F, t) is an ${\mathscr {A}}_e$-versal unfolding of $F_{t_i}$ at the points where it has non stable singularities (and these are of ${\mathscr {A}}_e$-codimension 1 only). By the above result this means that $j_1^kF$ is transversal to all ${\mathscr {A}}$-orbits of codimension less than or equal to $n+1$. Since F does not have singularities of ${\mathscr {A}}_e$-codimension greater than 1 for any t, $j_1^kF$ is also transversal to $\Lambda (N,P)$. Therefore, $j_1^kF$ is transversal to the stratification S(N, P).

Conversely, if (n, p) is in the extra-nice dimensions, $\Lambda (N,P)$ has codimension greater than or equal to $n+2$, so transversality to the stratification S(N, P) means that $j_1^kF$ is transversal to all ${\mathscr {A}}$-orbits of codimension less than or equal to $n+1$ and avoids $\Lambda (N,P)$. Therefore, (F, t) unfolds versally all the $F_{t_i}$ which have non stable singularities of ${\mathscr {A}}_e$-codimension 1. Since N is compact the points $x_j$ where $F_{t_i}$ is non stable are finite, so F is a locally stable 1-parameter family. $\square$

Theorem 6.4

Let N and P be manifolds of dimension n and p, with $(n+1,p+1)$ nice dimensions. The subset of locally stable 1-parameter families in $C^{\infty }(N\times [0,1],P)$ is dense if and only if (n, p) is in the extra-nice dimensions.

Proof

The pair (n, p) is in the extra-nice dimensions if, by definition, there exists a bad set $\Lambda (n,p)\subset J^k(n,p)$ of codimension greater than $n+1$ such that its complement is a finite number of ${\mathscr {A}}$-orbits. This set induces a bad set $\Lambda (N,P)$ in $J^k(N,P)$ of codimension greater than $n+1$. Thus, for a generic family $F\in C^{\infty }(N\times [0,1],P)$, $j_1^kF(N\times [0,1])\cap \Lambda (N,P)=\emptyset$. By Thom’s transversality theorem, the set of families F such that $j^k_1F$ is transversal to any ${\mathscr {A}}$-orbit of codimension less than or equal to $n+1$ is also a residual set. Since there are finite ${\mathscr {A}}$-orbits of codimension less than or equal to $n+1$, the set of families F such that their partial jet extension is transverse to S(N, P) is a finite intersection of residual sets and so is residual. Equivalently, by Lemma 6.3, the set of locally stable 1-parameter families in $C^{\infty }(N\times [0,1],P)$ is dense.

Now suppose (n, p) is not in the extra-nice dimensions. Then the codimension of $\Lambda (N,P)$ is less than or equal to $n+1$. In Sect. 5, for any (n, p) in the boundary of the extra-nice dimensions such that $(n+1,p+1)$ is nice dimensions, we construct a stable germ ${\widetilde{F}}$ in $(n+1,p+1)$ such that any section of it $f_0$ is not simple and such that ${\widetilde{F}}=(F,t)$ is a 1-parameter stable unfolding of $f_0$. By taking a trivial unfolding of these stable germs we obtain stable germs with this property in any pair of dimensions outside the extra-nice dimensions. Considering one of the sections of these stable germs in (n, p) and its deformation F, F is clearly not a locally stable 1-parameter family but $j_1^kF(N\times [0,1])\cap \Lambda (N,P)\ne \emptyset$ and $j_1^kF$ is transversal to S(N, P). There is a sufficiently small neighbourhood of F in $C^{\infty }(N\times [0,1],P)$ such that any G in that neighbourhood satisfies that $j_1^kG$ is transversal to S(N, P) and $j_1^kG(N\times [0,1])\cap \Lambda (N,P)\ne \emptyset$. Therefore, there is an open set of non locally stable 1-parameter families and so the set of locally stable 1-parameter families is not dense. $\square$

A summary of our main results in Theorems 4.6 and 6.4 we have the following

Corollary 6.5

Let $(n+1,p+1)$ be in the nice dimensions. The following are equivalent

• (i) (n, p) is in the extra-nice dimensions,

• (ii) $cod_{J^k(n,p)}\Lambda (n,p)\ge n+2$,

• (iii) the subset of locally stable 1-parameter families in $C^{\infty }(N\times [0,1],P)$ is dense,

• (iv) every stable germ $F:({\mathbb {K}}^{n+1},0)\rightarrow ({\mathbb {K}}^{p+1},0)$ admits a hyperplane ${\mathscr {A}}_e$-codimension 1 section $f:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^p,0).$

7 Codimension of non-simple germs

In this section we answer partially a question posed by Wall to the first author during his talk at the workshop on “Singularities in Generic Geometry and Applications III" held in Edinburgh in 2013: what is the codimension of the non-simple germs?

Let NS denote the ${\mathscr {A}}$-invariant subset of $J^l(n,p)$ composed of all non ${\mathscr {A}}$-simple orbits. If (n, p) is in the nice dimensions, by Proposition 3.5, all $\mathscr {A}_e$-codimension 1 germs are simple, so if a germ is not simple its ${\mathscr {A}}_e$-codimension is at least 2 (${\mathscr {A}}$-codimension $n+2$). Therefore ${\text {cod}}_{J^l(n,p)}(NS)\ge n+1$. Similarly, from the definition of the extra-nice dimensions, if (n, p) is in the extra nice dimensions, then ${\text {cod}}_{J^l(n,p)}(NS)\ge n+2$. In fact, if (n, p) is in the nice dimensions but not in the extra-nice dimensions, Remark 4.5 shows that ${\text {cod}}_{J^l(n,p)}(NS)\le n+1$, so ${\text {cod}}_{J^l(n,p)}(NS)=n+1$.

This naturally leads to the following definition

Definition 7.1

The pair (n, p) is said to be in the $\Delta _m$-nice dimensions if, for large enough k, there is an ${\mathscr {A}}$-invariant subset $\Lambda$ of $J^l(n,p)$, of codimension greater than $n+m$, whose complement is a finite union of ${\mathscr {A}}$-orbits.

$\Delta _1$-nice dimensions are the extra-nice dimensions and $\Delta _0$-nice dimensions are the nice dimensions. With this definition, if (n, p) is in the $\Delta _m$-nice dimensions but not in the $\Delta _{m+1}$-nice dimensions, then ${\text {cod}}_{J^l(n,p)}(NS)=n+m+1$.

Example 7.2

In the case $n=p$, the Thom–Levine example in the introduction is an example in the boundary of the $\Delta _0$-nice dimensions of an ${\mathscr {A}}_e$-codimension 1 germ which is not simple. It has corank 3. Inside the $\Delta _0$-nice dimensions all ${\mathscr {A}}_e$-codimension 1 germs are simple.

From Theorem 3.10 we have an example in the boundary of the $\Delta _1$-nice dimensions of an ${\mathscr {A}}_e$-codimension 2 germ which is not simple. It has corank 2. Inside the $\Delta _1$-nice dimensions all ${\mathscr {A}}_e$-codimension 2 germs are simple.

From [25, 33] we know that if $n\ge 3$, then a germ $f:({\mathbb {K}}^n,0)\rightarrow ({\mathbb {K}}^n,0)$ with $m_0(f)\ge n+3$ is not simple. In fact, in (3, 3) we find the germ $(x,y,z^6+yz^2+xz)$ which has ${\mathscr {A}}_e$-codimension 3 and is not simple with 1 modal parameter. It has corank 1. From [29, 31] we know that all ${\mathscr {A}}_e$-codimension 3 germs in (2, 2) are simple. This means that (3, 3) is the boundary of the $\Delta _2$-nice dimensions. Inside the $\Delta _2$-nice dimensions all ${\mathscr {A}}_e$-codimension 3 germs are simple.

Finally, in (2, 2) there is an ${\mathscr {A}}_e$-codimension 4 germ which is not simple. It can be found in [29], $(x,xy+y^6\pm y^9+\alpha y^9)$. Since in (1, 1) all germs are simple, this means that (2, 2) is the boundary of the $\Delta _3$-nice dimensions. In fact, (2, 2) is the boundary of the $\Delta _m$-nice dimensions for $m\ge 3$!

So we get a stratification of the $n=p$ dimensions by $(9,9)\supset (5,5)\supset (3,3)\supset (2,2)$.