Finiteness and infiniteness results for Torelli groups of (hyper-)Kähler manifolds

Abstract

The Torelli group $\mathcal T(X)$ of a closed smooth manifold X is the subgroup of the mapping class group $\pi _0(\mathrm {Diff}^+(X))$ consisting of elements which act trivially on the integral cohomology of X. In this note we give counterexamples to Theorem 3.4 by Verbitsky (Duke Math J 162(15):2929–2986, 2013) which states that the Torelli group of simply connected Kähler manifolds of complex dimension $\ge 3$ is finite. This is done by constructing under some mild conditions homomorphisms $J: \mathcal T(X) \rightarrow H^3(X;\mathbb Q)$ and showing that for certain Kähler manifolds this map is non-trivial. We also give a counterexample to Theorem 3.5 (iv) in (Verbitsky in Duke Math J 162(15):2929–2986, 2013) where Verbitsky claims that the Torelli group of hyperkähler manifolds are finite. These examples are detected by the action of diffeomorphsims on $\pi _4(X)$. Finally we confirm the finiteness result for the special case of the hyperkähler manifold $K^{[2]}$.

1 Introduction

Let X be a closed connected oriented manifold. The mapping class group $\mathcal M (X)$ is the group of connected components of the orientation preserving self diffeomorphisms of X. The subgroup consisting of diffeomorphisms which act trivially on the integral cohomology ring is called the Torelli group of X, denote by $\mathcal T (X)$. In this note we consider two classes of manifolds, the first is characterized by the following assumptions:

Assumption (*) The manifold X has trivial first rational homology and the first Pontrjagin class (considered in rational cohomology) $p_1(X)\in H^4(X; \mathbb Q)$ is a linear combination of products of 2-dimensional classes, i.e. there exist classes $z_i \in H^2(X;\mathbb Q)$ and rational numbers $a_{ij}$ such that $p_1(X) = \sum a_{ij}z_i \cup z_j$. We denote the set consisting of the classes $z_i$ and of the rational numbers $a_{ij}$ by D, like definition data.

We construct a homomorphism

$$\begin{aligned} J_D : \mathcal T (X) \rightarrow H^3(X;\mathbb Q) \end{aligned}$$

which we consider as a sort of Johnson homomorphism since it is landing in an abelian group and constructed via the mapping torus. The construction is as follows. Consider the mapping torus $X_f$ of f. Since f acts trivially on the cohomology groups the Wang sequence looks like:

$$\begin{aligned} 0 \rightarrow H^{k-1}(X; \mathbb Q) {\mathop {\rightarrow }\limits ^{\delta }} H^{k}(X_f; \mathbb Q) {\mathop {\rightarrow }\limits ^{i^{*}}} H^k(X;\mathbb Q) \rightarrow 0 \end{aligned}$$

Since $H^1(X;\mathbb Q) = 0$ this implies that the inclusion induces an isomomorphism $H^2(X_f;\mathbb Q) \rightarrow H^2(X;\mathbb Q)$ and so for each class $z \in H^2(X;\mathbb Q)$ there is a unique class $\bar{z} \in H^2(X_f;\mathbb Q)$ restricting to z. Next we look at $p_1(X_f) - \sum a_{ij} \bar{z}_i \cup \bar{z}_j \in H^4(X_f; \mathbb Q)$. By construction its restriction to $H^4(X;\mathbb Q)$ is zero. Thus there exists a unique class denoted by $J_D(f) \in H^3(X;\mathbb Q)$ mapping to this class in the Wang sequence.

Proposition 1.1

Let X fulfill the Assumptions (*), then the map

$$\begin{aligned} J_D: \mathcal T(X) \rightarrow H^3(X;\mathbb Q) \end{aligned}$$

is a homomorphism.

Next we are looking for Kähler manifolds where this invariant is non-trivial. For this we prove a purely topological result.

Theorem 1.2

Let X be a simply connected 6-manifold with $H_2(X;\mathbb Z) \cong \mathbb Z$ and nontrivial cohomology product $H^{2}(X;\mathbb Z) \times H^{2}(X;\mathbb Z) \rightarrow H^{4}(X;\mathbb Z)$. Then the Assumptions (*) are fulfilled and the invariant is independent of any choices and is denoted by J. The image of J is a lattice in $H^3(X; \mathbb Q)$, i.e. a finitely generated abelian group of same rank as the dimension of $H^3(X;\mathbb Q)$.

Considering hypersurfaces X(d) of degree $d>1$ in $\mathbb CP^4$ we obtain complex three-dimensional Kähler manifolds with infinite Torelli group, since $d>1$ implies that $H^3(X(d);\mathbb Q) \ne 0$. Taking the product with copies of $\mathbb C \mathrm P^1$ one obtains examples in all complex dimensions $\ge 3$. Namely if $f \in \mathcal T(X(d))$ then by definition of $J_D$ we have for $f \times \mathrm {id}: X(d) \times (\mathbb C \mathrm P^1)^r \rightarrow X(d) \times (\mathbb C \mathrm P^1)^r$ and the obvious choice of D

$$\begin{aligned} J_D(f \times \mathrm {id}) = J(f) \end{aligned}$$

where we identify $H^3(X(d); \mathbb Q)$ with $H^{3}(X(d)\times (\mathbb C \mathrm P^1)^r; \mathbb Q)$ under the projection map.

Thus we obtain the Corollary contradicting Verbitsky’s theorem:

Corollary 1.3

For all $n\ge 3$ there are Kähler manifolds of complex dimension n with infinite Torelli group, actually containing elements of infinite order. In particular taking for example the quintic in $\mathbb CP^4$ we obtain Calabi–Yau manifolds with infinite Torelli group.

Remark 1.4

For simply connected 6-manifolds X with $H_2(X; \mathbb Z) \cong \mathbb Z$ we compute in [7] the full mapping class group as well as the Torelli group and give generators of these groups. In particular we prove that an element f in the Torelli group has finite order if and only if $J(f) = 0$.

Remark 1.5

In general the invariant $J_D$ depends on the choice of the data. So, in general there are many homomorphisms depending on the choice of the data. The simplest example is $X = S^2 \times S^4 \sharp S^3 \times S^3$, where for $z=0$ and z the generator of $H^2(X;\mathbb Z)$ the difference of the J-invariants with these data is non-trivial, as shown in [7].

Now we come to the second class of manifolds which is characterized by the following assumptions:

Assumption (**) The manifolds X are simply connected and eight-dimensional, whose Betti numbers satisfy one of the following conditions

• (1) $b_2 > 2$, $b_3 \ge 1$, $b_4 > b_2(b_2+1)/2$;

• (2) $b_2=2$, $b_3 > 1$, $b_4 > b_2(b_2+1)/2$;

• (3) $b_2=2$, $b_3 =1$, $b_4 > b_2(b_2+1)/2$ and $p_1(X) = 0 \in H^4(X;\mathbb Q)$).

Theorem 1.6

If X satisfies the assumptions (**), then the Torelli group $\mathcal T(X)$ is infinite.

We apply this result to find a counterexample to Theorem 3.5 (iv) in [13]. For this we consider the complex four-dimensional hyperkähler manifold $K^2(T)$. For the construction and the following information we refer to [11] (where it is called $K_2$). The manifold is simply connected and the Betti numbers are: $b_2(K ^2(T)) = 7$, $b_3(K^2(T)) = 8$ and $b_4(K^2(T)) = 108$. Thus our theorem implies:

Corollary 1.7

The Torelli group of the hyperkähler manifold $K^2(T)$ is not finite.

This contradicts Verbitsky’s Theorem 3.5, iv ([13]).

There is another complex four-dimensional hyperkähler manifold denoted by $K^{[2]}$, where K is a $K_3$-surface (for the construction see again for example [11]). In this case we show that the Torelli group is finite. This follows from:

Theorem 1.8

Let X be a simply-connected closed 8-manifold satisfying the following conditions

• (1) the cup product induces an isomorphism $\cup :\mathrm {Sym}^{2}(H^{2}(X;\mathbb Q)) \rightarrow H^{4}(X;\mathbb Q)$.

• (2) $H^{3}(X;\mathbb Q)=0$,

• (3) $p_1(X) \ne 0 \in H^4(X;\mathbb Q)$.

Then $\mathcal T(X)$ is finite.

Corollary 1.9

The Torelli group of $K^{[2]}$, where K is a $K_3$-surface, is finite.

Proof

By [11] the Betti numbers are $b_2 = 23$, $b_3 =0$ and $b_4 = 276$, which is the same as the dimension of the second symmetric product of $\mathbb Q^{23}$. Since the second symmetric power of the second cohomology of a hyperkähler manifold always injects into the 4-th cohomology [2], this implies (1). That $p_1(K^{[2]})$ is non-zero follows from [1].

Remark 1.10

This implies that Verbitsky’s Theorem 3.5 is true for $K^{[2]}$ and so his argument for his main result about the moduli space of hyperkähler manifolds holds for $K^{[2]}$. In the general case the finiteness statement is used at several places in the paper so that the corresponding statements are either wrong or open. This is summarized in an erratum [14].

Looijenga [9] has defined a different moduli space, called the separated moduli space, and gives a complete proof of the global Torelli Theorem for this space. He further proves that this moduli space is equal to the one considered by Verbitsky (giving a different proof that the relation defining the moduli space is transitive). Thus the global Torelli Theorem by Verbitsky holds, but with a different proof.

We would like to thank Daniel Huybrechts for bringing Verbitsky’s paper [13] to our attention when we told him about our paper [7] where we give a complete computation of the mapping class group of certain 6-manifolds. Since counterexamples to Verbitsky’s theorem might be of separate interest we wrote this note. We have sent this note to several people and received a paper by Richard Hain [4] confirming our result that Theorem 3.4 in [13] is incorrect by showing that the Torelli group of certain complex three-dimensional Kähler manifolds M have an abelian quotient of infinite order. These examples are different from our examples, they are detected by the induced map $\pi _3(M)\otimes \mathbb Q \rightarrow \pi _3(M)\otimes \mathbb Q$, whereas for complex three-dimensional complete intersections $\pi _3(X)\otimes \mathbb Q\cong H_3(X; \mathbb Q)$, and so the Torelli groups acts trivial on $\pi _3(X)\otimes \mathbb Q$. We would like to thank the referee for his suggestions to improve the paper.

2 Proofs

Proof of Proposition 1.1

To prove that $J_D$ is a homomorphism we first note that if X is a fibre in $X_f$ then we have an exact sequence with rational coefficients

$$\begin{aligned} 0 \rightarrow H^4(X_f,X) \rightarrow H^4(X_f) \rightarrow H^4(X) \rightarrow 0 \end{aligned}$$

and the term on the left is by suspension isomorphism isomorphic to $H^3(X)$ and under this isomorphism $J_D(f)$ corresponds to the class in $H^4(X_f,X)$ which restricts to $p_1(X_f) - \sum a_{ij} \bar{z}_i \cup \bar{z}_j$.

Now we construct $X_{fg}$ from $X_f$ by cutting $I \times X$ along $1/2 \times X$ and reglueing it via g from the left to the right. Then we consider the two fibres over 1/4 and 3/4 and denote them by $X_1$ and $X_2$. We consider the restriction map (with rational coefficients)

$$\begin{aligned} H^4(X_{fg}, X_1 \cup X_2) \rightarrow H^4(X_{fg}, X_1) \end{aligned}$$

We have an isomorphism

$$\begin{aligned} H^4(X_f, X) \oplus H^4(X_g, X) {\mathop {\rightarrow }\limits ^{\cong }} H^4(X_{fg}, X_1 \cup X_2) \end{aligned}$$

If we identify $H^4(X_{fg},X_1)$ with $H^3(X)$, the homomorphism

$$\begin{aligned} H^4(X_f, X) \oplus H^4(X_g, X) {\mathop {\rightarrow }\limits ^{\cong }} H^4(X_{fg}, X_1 \cup X_2) \rightarrow H^4(X_{fg}, X_1) \end{aligned}$$

corresponds to the homomorphism $H^3(X) \oplus H^3(X) \rightarrow H^3(X)$ given by the sum, and the element (to distinguish the $\bar{z}_{i}$’s corresponding to $X_{f}$, $X_{g}$ and $X_{fg}$ we name them as $i_{f}^{-1}(z_{i})$, $i_{g}^{-1}(z_{i})$ and $i_{fg}^{-1}(z_{i})$ respectively)

$$\begin{aligned} (p_1(X_f)-\sum a_{ij}i_{f}^{-1} (z_i) \cup i_{f}^{-1} (z_j), p_1(X_g)-\sum a_{ij} i_{g}^{-1} (z_i )\cup i_{g}^{-1} (z_j)) \end{aligned}$$

is mapped to $p_1(X_{fg})-\sum a_{ij}i_{fg}^{-1} (z_i) \cup i_{fg}^{-1} (z_j)$. This implies that $J_D(fg) = J_D(f) + J_D(g)$.

Next we consider the 6-manifolds in Theorem 1.2. Let $z \in H^{2}(X)$ be a generator, by Poincaré duality $H^{4}(X) \cong \mathbb Z$ and thus $z^{2}$ equals to d times a generator of $H^{4}(X)$. The condition that the cohomology product $H^2(X) \times H^2(X) \rightarrow H^4(X)$ is non-trivial is equivalent to saying that d is nonzero. It’s shown in [5, 15] that for every $d \ne 0$ there exist such X. Furthermore there is a connected sum decomposition $X = N \sharp g(S^{3} \times S^{3})$, where N has the same homology as $\mathbb C \mathrm P^{3}$.

We introduce a construction of diffeomorphisms, which is a generalization of Dehn twists. Let $S^{3} \times D^{3} \subset X$, $\alpha \in \pi _{3}(SO(4))$, choose a smooth map $\varphi :(D^{3},\partial ) \rightarrow (SO(4),I)$ representing $\alpha$, such that a neighborhood of $\partial D^3$ is mapped to the identity. Define $f :X \rightarrow X$ by

$$\begin{aligned} f(u)= \left\{ \begin{array}{cl} (\varphi (y) \cdot x, y) &{} \text {if} \, u=(x,y) \in S^{3} \times D^{3} \\ u &{} \text {otherwise} \end{array} \right. \end{aligned}$$

We call f a Dehn twist in $S^{3} \times D^{3}$ with parameter $\alpha$.

Proof of Theorem 1.2

The main ingredients of Theorem 1.2 already appeared in [6]. The proof of a slightly different situation will be given in [7]. For convenience of the reader we repeat the proof.

By the assumptions the rational Pontrjagin class $p_{1}(X) \in H^{4}(X;\mathbb Q)$ is a multiple of $z^{2}$, say, $p_{1}(X)=l\cdot z^{2}$, $l \in \mathbb Q$. Therefore our invariant J(f) is the pre-image of $p_{1}(X_{f})-l \cdot \bar{z}^{2}$ in $H^{3}(X)$.

In the decomposition $X = N \sharp g(S^{3} \times S^{3})$ we number the standard embedded spheres

$$\begin{aligned} (S^{3} \times \{pt\})_{1}=S^{3}_{1}, \ (\{pt\} \times S^{3})_{1}=S^{3}_{2}, \ldots , (S^{3} \times \{pt\})_{g}=S^{3}_{2g-1}, \ (\{pt\} \times S^{3})_{g}=S^{3}_{2g}. \end{aligned}$$

They represent a symplectic basis $\{e_{1}, \ldots , e_{2g} \}$ of $H_{3}(X)$.

Let $\alpha \in \pi _{3}(SO(3)) \cong \mathbb Z$ be a generator, $\xi$ be the three-dimensional vector bundle over $S^{4}$ corresponding to $\alpha$, $i_{*} (\alpha ) \in \pi _{3}(SO(4))$ be the image induced by the inclusion $i :SO(3) \rightarrow SO(4)$. Then it’s known that $p_{1}(\xi )$ equals 4 times a generator of $H^{4}(S^{4})$ (see [10, Lemma 20.10]), and the four-dimensional vector bundle over $S^{4}$ corresponding to $i_{*}(\alpha )$ has trivial Euler class.

Now let $f_{i} :X \rightarrow X$ be the Dehn twist in $S^{3}_{i} \times D^{3}$ with parameter $i_{*} (\alpha )$. By the geometric construction, the action of $f_{i}$ on homology is seen as follows: $f_{i}$ acts trivially on all basis elements of the homology groups but one, namely the one $e_{j}$ dual to $e_{i}$ in the symplectic basis of $H_{3}(X)$, and $f_{i*}(e_{j})=e_{j}+\chi (i_{*}(\alpha )) \cdot e_{i}$, where $\chi (i_{*}(\alpha )$ is the Euler characteristic of $i_{*}(\alpha )$. Since the Euler class of $i_{*} (\alpha )$ is trivial, $f_{i}$ acts trivially on homology and hence is in $\mathcal T(X)$. We claim that $J(f_{i})$ equals 4 times the Poincaré dual of $e_{i}$ in $H^{3}(X)$. Notice that for the manifolds X under consideration, the homomorphism J can be defined using integral cohomology and is indeed a homomorphism from $\mathcal T(X)$ to $H^{3}(X)$. This implies that the image of J is a subgroup of $H^{3}(X)$ of the same rank, hence it is a lattice in $H^{3}(X;\mathbb Q)$.

It is enough to show the claim for $i=1$. By the adjunction formula this is equivalent to

$$\begin{aligned} \langle J(f_{1}), e_i \rangle = 0 \ \ \text {for} \quad i \ne 2 \quad \hbox {and } \ \langle J(f_{1}), e_2 \rangle = 4. \end{aligned}$$

Since $f_{1}|_{S^{3}_{i}}$ is the identity, we have embeddings $S^{3}_{i} \times S^{1} \subset X_{f_{1}}$. Let $\bar{e}_{i}=[S^{3}_{i} \times S^{1}] \in H_{4}(X_{f_{1}})$, then $\bar{e}_{i}$ is a pre-iamge of $e_{i}$ in the short exact sequence

$$\begin{aligned} 0 \rightarrow H_{4}(X) \rightarrow H_{4}(X_{f_{1}}) {\mathop {\rightarrow }\limits ^{\partial }} H_{3}(X) \rightarrow 0 \end{aligned}$$

There is a decomposition $X_{f_{1}} = (N \times S^{1}) \sharp _{S^{1}} (\sharp _{g}(S^{3} \times S^{3})_{f_{1}})$, where $\sharp _{S^{1}}$ denotes the fiber connected sum along $S^{1}$. Then $H^{4}(X_{f_{1}}) = H^{4}(N) \oplus H^{4}(\sharp _{g}(S^{3} \times S^{3})_{f_{1}})$ and $\bar{z}^{2}=(z^{2}, 0)$. This implies $\langle \bar{z}^{2}, \bar{e}_{i} \rangle =0$. Therefore we have

$$\begin{aligned} \langle J(f_{1}), e_{i}\rangle = \langle J(f_{1}), \partial \bar{e}_{i} \rangle = \langle \delta J(f_{1}), \bar{e}_{i} \rangle = \langle p_{1}(X_{f_{1}}) - l \cdot \bar{z}^{2}, \bar{e}_{i} \rangle = \langle p_{1}(X_{f_{1}}), [S^{3}_{i} \times S^{1}] \rangle \end{aligned}$$

Now notice that $f_{1}$ is the identity on a tubular neighborhood of $S^{3}_{i}$’s for $i \ne 2$, therefore the normal bundle of $S^{3}_{i} \times S^{1}$ in $X_{f_{1}}$ is trivial, and we have

$$\begin{aligned} \langle p_{1}(X_{f_{1}}), [S^{3}_{i} \times S^{1}] \rangle =0 \end{aligned}$$

for $i \ne 2$. Let

$$\begin{aligned} c :S^{3} \times S^{1} \rightarrow S^{3} \times S^{1}/S^{3}\times \{pt\} = S^{4}\vee S^{1} \rightarrow S^{4} \end{aligned}$$

be the quotient map, from the geometric construction it’s easy to see that the normal bundle of $S^{3}_{2} \times S^{1}$ in $X_{f_{1}}$ equals $c^{*}\xi$. Therefore

$$\begin{aligned} \langle p_{1}(X_{f_{1}}), [S^{3}_{2} \times S^{1}]\rangle =\langle c^{*}p_{1}(\xi ), [S^{3}_{2} \times S^{1}]\rangle = \langle p_{1}(\xi ), [S^{4}] \rangle = 4. \end{aligned}$$

The proofs of Theorems 1.6 and 1.8 are based on modified surgery theory [8]. We recall some basic definitions here. The normal k-type of a smooth oriented manifold X is a fibration $p:B \rightarrow BSO$, which is characterized by the assumptions that there is a lift of the normal Gauss map $\nu : X \rightarrow BO$ by a $(k+1)$-equivalence $\bar{\nu }: X \rightarrow B$ and that the homotopy groups of the homotopy fibre F of p are trivial in degree $\ge k+1$ (for details see [8]).

To show Theorem 1.6 we will construct infinitely many mapping classes in $\mathcal T(X)$, whose actions on $\pi _{4}(X)$ are pairwise distinct. Let $p :B \rightarrow BSO$ be the normal 4-type of X, denote the homotopy fiber of p by F, and the kernel of the Hurewicz homomorphism $\pi _4(F) \rightarrow H_4(F)$ by $K\pi _{4}(F)$.

Lemma 2.1

Under the assumptions (**) we have

• (1) the image of the Hurewicz map $\pi _{4}(B) \rightarrow H_{4}(B)$ has rank $>0$;

• (2) the abelian group $K\pi _{4}(F)$ has rank $>0$.

Proof

We use Sullivan’s rational homotopy theory [12] to show the assumptions (**) imply the conclusions in this lemma. For this we construct the minimal model from information of the cohomology ring.

Let $x_{1}, \ldots , x_{b_{2}}$ be free generators of the minimal model in degree 2 with differential 0. Let $y_{1}, \ldots , y_{b_{3}}$ be a part of the free generators in degree 3, which generate $H^{3}(X;\mathbb Q)$. They have trivial differentials. The elements $x_{i}y_{j}$ generate a space of dimension $b_{2}b_{3}$, on which the differential is trivial. Since by Poincaré duality the 5-th Betti number is $b_{3}$, there must be at least $k=(b_{2}-1)b_{3}$ linearly independent indecomposable elements $z_{1}, \ldots , z_{k}$ in degree 4, which by the differential are mapped injectively to a subspace of the vector space generated by the $x_{i}y_{j}$. In degree 4 the dimension of the subspace generated by $x_{i}x_{j}$ ($i \le j$) is $b_{2}(b_{2}+1)/2$, whereas the 4-th Betti number is $b_{4}$, there are additional (to the $z_{i}$) free generators $u_{1}, \ldots , u_{l}$ (where $l \ge b_{4}-b_{2}(b_{1}+1)/2 \ge 1$) with trivial differential. There might be more generators in degree 4 depending on the product $H^2(X ;\mathbb Q) \otimes H^3(X; \mathbb Q) \rightarrow H^5(X ;\mathbb Q)$. But alone from this information the two conclusions in the lemma follow. Namely $\mathrm {Hom}(\pi _4(X), \mathbb Q)$ is isomorphic to the degree 4 subspace modulo the decomposable elements and so contains the subspace with basis $u_1,...., u_{l}$, $z_1,..., z_{k}$. The dual of the rational Hurewicz homomorphism maps $u_i$ injectively. Dualizing we see that the dual of the $u_i$ are mapped injectively showing (1) and the dual of the $z_i$ are mapped to 0 in rational homology, so the rank of $K\pi _{4}(B)=\mathrm {Ker}(\pi _{4}(B) \rightarrow H_{4}(B))$ is at least $k=(b_{2}-1)b_{3}$.

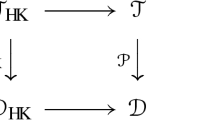
To analyze the rank of $K\pi _{4}(F)$, first note that $\pi _{4}(F)\otimes \mathbb Q \rightarrow \pi _{4}(B) \otimes \mathbb Q$ is an isomorphism if $p_{1}(X) =0 \in H^{4}(X;\mathbb Q)$ and is injective with a codimension 1 image if $p_{1}(X) \ne 0 \in H^{4}(X;\mathbb Q)$. This follows from the long exact sequence of homotopy groups of the fibration $F \rightarrow B \rightarrow BSO$ and the facts that $\pi _{5}(BSO)=0$, $\pi _{4}(BSO)\otimes \mathbb Q \cong \mathbb Q$ by the universal Pontrjagin class $p_{1}$. The Leray–Serre spectral sequence of the fibration shows that $H_{4}(F;\mathbb Q) \rightarrow H_{4}(B;\mathbb Q)$ is injective. Now a little diagram chasing in the following commutative diagram

shows that

$$\begin{aligned} K\pi _{4}(B) \otimes \mathbb Q \cap \mathrm {Im} (\pi _{4}(F) \otimes \mathbb Q \rightarrow \pi _{4}(B) \otimes \mathbb Q) = K\pi _{4}(F)\otimes \mathbb Q. \end{aligned}$$

This shows that under the assumptions (**) we have $\dim _{\mathbb Q}K\pi _{4}(F)\otimes \mathbb Q \ge 1$.

Let $Z^{4}(B; K\pi _{4}(F))$ be the group of 4-cocycles with coefficients in $K\pi _{4}(F)$, $\mathrm {Aut}(B)$ be the group of fiber homotopy classes of fiber homotopy equivalences of $p :B \rightarrow BSO$. We will first define a map

$$\begin{aligned} \Phi :Z^{4}(B;K\pi _{4}(F)) \rightarrow \mathrm {Aut}(B)\end{aligned}$$

as follows. (Here we remark that $\Phi$ is only a map between sets, and depends on various choices.)

Let $B^{(4)}$ be the 4-skeleton of B, $e_{1}^{4}, \ldots ,e_{m}^{4}$ be the 4-cells, then the 4 dimensional cellular chain group $C_{4}(B)$ is a free abelian group generated by $e_{i}^{4}$ ($i=1, \ldots , m$). Let $q :B^{(4)} \rightarrow B^{(4)} \vee \vee _{i=1}^{m}S^{4}_{i}$ be the pinch map, where we pinch each 4-cell $e^{4}_{i}$ to $e^{4}_{i} \vee S^{4}_{i}$. Let $\alpha :C_{4}(B) \rightarrow K\pi _{4}(F)$ be a cocycle. For each $\alpha (e_{i}^{4}) \in K\pi _{4}(F)$, by abuse of notation, we view it as a map $S_{i}^{4} \rightarrow B$. Let $i :B^{(4)} \rightarrow B$ be the inclusion, define $h :B^{(4)} \rightarrow B$ to be the composition

$$\begin{aligned} h=(i \vee \vee _{i=1}^{m} \alpha (e_{i}^{4})) \circ q :B^{(4)} \rightarrow B^{(4)} \vee \vee _{i=1}^{m}S^{4}_{i} \rightarrow B. \end{aligned}$$

By the construction h is compatible with the fiber projection p, i. e. the following diagram commutes up to homotopy

Now we show that we can extend h to a map on the 5-skeleton of B compatible with p. Let $e^{5}$ be a 5-cell, with attaching map $f :S^{4} \rightarrow B^{(4)}$. By Blakers-Massey theorem we have an isomorphism

$$\begin{aligned} \pi _{4}(B^{(4)} \vee \vee _{i=1}^{m}S^{4}_{i}) \cong \pi _{4}(B^{(4)}) \oplus \oplus _{i=1}^{m}\pi _{4}(S^{4}_{i}), \end{aligned}$$

under this isomorphism the image of $[q \circ f]$ is clearly $([f], \partial e^{5})$. Since $\alpha$ is a cocyle, $\langle \alpha , \partial e^{5} \rangle =\langle \delta \alpha , e^{5}\rangle =0$, therefore h extends to a map $h :B^{(5)} \rightarrow B$, compatible with the fiber projection p. (The extension may not be unique, we choose one extension.) Since $\pi _{n}(F)=0$ for $n \ge 5$, we can extend h further to a fiber map $h :B \rightarrow B$.

Lemma 2.2

h is a fiber homotopy equivalence. $h_{*}$ is the identity on $H_{i}(B)$ for $i \le 4$. $h^{*}$ is the identity on $H^{i}(B)$ for $i \le 3$. $h_{*}$ is the identity on $H_{8}(B;\mathbb Q)$.

Proof

It’s clear from the construction that $h_{*}$ is the identity on $H_{i}(B)$ for $i \le 3$ and $h^{*}$ is the identity on $H^{i}(B)$ for $i \le 3$. On the chain level $h_{*}$ is

$$\begin{aligned} h_{*} :C_{4}(B) \rightarrow C_{4}(B), \ \ e_{i}^{4} \mapsto e_{i}^{4}+ \alpha (e_{i}^{4}) \end{aligned}$$

where $\alpha (e_{i}^{4})$ is a boundary by definition. Therefore $h_{*}$ is the identity on $H_{4}(B)$. By the Hurewicz theorem we see that $h_{*} :\pi _{i}(B) \rightarrow \pi _{i}(B)$ is an isomorphism for $i \le 3$ and is a surjection for $i=4$. Notice that $\pi _{4}(B)$ is a finitely generated abelian group, a surjective endomorphism of a finitely generated abelian group must also be injective, therefore $h_{*}$ is an isomorphism on $\pi _{4}(B)$. Since $p :B \rightarrow B\mathrm {SO}$ is 4-coconnected, h induces isomorphisms on $\pi _{i}(B)$ for all i. Therefore h is a fiber homotopy equivalence.

Since $\pi _{n}(F)=0$ for $n \ge 5$, by rational homotopy theory, there are no indecomposable cohomology classes in $H^{n}(F;\mathbb Q)$ for $n \ge 5$. Therefore elements in $H^{8}(F; \mathbb Q)$ are linear combinations of products of cohomology classes of degree $\le 4$. Since $h_{*}$ is the identity on $H_{i}(F)$ for $i \le 4$, $h^{*}$ is the identity on $H^{i}(F;\mathbb Q)$ for $i \le 4$ and hence also the identity on $H^{8}(F;\mathbb Q)$. Thus $h_{*}$ is the identity on $H_{8}(F;\mathbb Q)$. By the Leray–Serre spectral sequence of the fibration $F \rightarrow B \rightarrow B\mathrm {SO}$, $h_{*}$ is the identity on $H_{8}(B;\mathbb Q)$.

Proof of Theorem 1.6

By Lemma 2.1 the image of $\pi _{4}(B) \rightarrow H_{4}(B)$ has rank $k>0$. Let $x_{1}, \ldots , x_{k}$ be homology classes in the image which generate a free abelian subgroup of rank k in $H_{4}(B)$, $y_{i} \in \pi _{4}(B)$ be a pre-image of $x_{i}$, represented by a map $S^{4} \rightarrow B$. Then we may take $B^{(4)}$ of the form

$$\begin{aligned} B^{(4)}=X \vee \vee _{i=1}^{k}S^{4}_{i} \end{aligned}$$

where X is a 4-complex, and $[S^4_i]=y_i$ for $i=1,\ldots , k$.

Let $\varphi \in \mathrm {Hom}(H_{4}(B), K\pi _{4}(F))$ be a homomorphism, since there are surjective homomorphisms

$$\begin{aligned} Z^{4}(B, K\pi _{4}(F)) \rightarrow H^{4}(B, K\pi _{4}(F)) \rightarrow \mathrm {Hom}(H_{4}(B), K\pi _{4}(F))\end{aligned}$$

we may pick a pre-image of $\varphi$, say $\alpha \in Z^{4}(B, K\pi _{4}(F))$. Let $h :B \rightarrow B$ be the image of $\alpha$ under $\Phi$. Consider the action of h on $\pi _{4}(B)$, especially the image of $y_{i}$ under $h_{*}$: let $\iota :S^{4} \rightarrow B$ be the inclusion of $S^{4}_{i}$, clearly the homotopy class of the composition

$$\begin{aligned} h \circ \iota :S^{4} \rightarrow B^{(4)} \rightarrow B^{(4)} \vee \vee _{i=1}^{m}S^{4}_{i} \rightarrow B \end{aligned}$$

equals $y_{i}+\varphi (x_{i}) \in \pi _{4}(B)$.

By Lemma 2.1 there are infinitely many $\varphi \in \mathrm {Hom}(H_{4}(B), K\pi _{4}(F))$ such that $\{ \varphi (x_{i}) | \ i=1, \ldots , k \}$ are pairwise distinct. Therefore we have constructed infinitely many $h \in \mathrm {Aut}(B)$ with properties in Lemma 2.2.

Let $\Omega _{8}(B,p)$ be the 8 dimensional B-bordism group. It’s isomorphic to the eight-dimensional stable homotopy group of the corresponding Thom spectrum. By the Atiyah–Hirzebruch spectral sequence there is an isomorphism

$$\begin{aligned} \Omega _{8}(B,p) \otimes \mathbb Q \rightarrow H_{8}(B;\mathbb Q)\end{aligned}$$

where the image of a bordism class $[N,f] \in \Omega _8(B,p)$ is the image of the fundamental class $f_{*}[N] \in H_8(B;\mathbb Q)$.

Now we fix a normal 4-smoothing $\bar{\nu }:X \rightarrow B$. Consider the normal 4-smoothing $\bar{\nu }\circ h$, where $h \in \mathrm {Aut}(B)$ is constructed as above. Since $h_{*}$ is the identity on $H_{8}(B;\mathbb Q)$, we have

$$\begin{aligned}{}[X, \bar{\nu }]=[X, h \circ \bar{\nu }] \in \Omega _{8}(B,p) \otimes \mathbb Q \end{aligned}$$

Therefore there are infinitely many h (indexed by $i \in \mathbb N$) such that

$$\begin{aligned}{}[X, h_{i} \circ \bar{\nu }]=[X, h_{j} \circ \bar{\nu }] \in \Omega _{8}(B,p). \end{aligned}$$

Let $W_{i}$ be a B-bordism between $[X, h_{0} \circ \bar{\nu }]$ and $[X, h_{i} \circ \bar{\nu }]$, by the theory of modified surgery, the obstruction to changing W by surgery to an h-cobordism is in $L_{9}(\mathbb Z)=0$. Therefore there is a diffeomorphism $f_{i} :X \rightarrow X$ such that $h_{i} \circ \bar{\nu }\circ f_i \simeq h_{0} \circ \bar{\nu }$. Since $\bar{\nu }$ is a 5-equivalence, we see that $f_{i*}$ is the identity on $H_{i}(X)$ for $i \le 4$, and $f_{i}^{*}$ is the identity on $H^{i}(X)$ for $i \le 3$. Therefore by Poincaré duality, $f_{i*}$ is the identity on $H_{*}(X)$ and hence $f \in \mathcal T(X)$. But $f_{i*}$ on $\pi _{4}(X)$ are pairwise distinct. Therefore we have constructed infinitely many elements in $\mathcal T(X)$.

Proof of Theorem 1.8

Let $p :B \rightarrow BSO$ be the normal 4-type of X, F be the homotopy fiber of p. Fix a normal 4-smoothing $\bar{\nu }:X \rightarrow B$.

We claim that $\pi _3(X)$ and $\pi _4(X)$ are finite. For this we consider the minimal model of X. It has generators $x_1,..., x_r$ in degree 2, where r is the second Betti number. By assumption $x_i \cup x_j$ for $i \le j$ is a basis of $H^4(X;\mathbb Q)$. This and the fact that $H^3(X;\mathbb Q) = 0$ implies that there are no generators in degree 3 and hence $\pi _3(X)$ is finite. This implies that there are no decomposable elements in degree 5. Thus the differential on elements of degree 4 is zero. But then there are no indecomposable elements in degree 4, since they would produce indecomposable cohomology classes. Thus $\pi _4(X)$ is finite. Finally we conclude that also $\pi _3(F)$ and $\pi _4(F)$ are finite. This follows from the homotopy sequence of the fibration $F \rightarrow B \rightarrow BSO$ since $\pi _i(X) \cong \pi _i(B)$ for $i\le 4$ and $p_1(X) \ne 0$ implying that $\pi _4(B) \rightarrow \pi _4(BSO)$ is non-trivial.

Let $f \in \mathcal T(X)$ be a self-diffeomorphism, then $\bar{\nu }\circ f$ is also a normal 4-smoothing. Let $\mathcal T_0(X)$ be the subset of $\mathcal T(X)$ consisting of self-diffeomorphisms f such that $\bar{\nu }\circ f$ and $\bar{\nu }$ are homotopic as liftings of $\nu$.

Lemma 2.3

Under our conditions $\mathcal T_0(X)$ is a finite index subgroup of $\mathcal T(X)$.

Proof

It suffices to show that there are finitely many homotopy classes of $\bar{\nu }\circ f$ over p, which in turn follows if there are finitely many lifts of the Gauss map $\nu$ over p. This follows by induction over the skeletons and the Puppe sequence and the fact that f induces the identity on $\pi _2(X) = H_2(X)$ from the fact that the homotopy groups $\pi _3(F)$ and $\pi _4(F)$ are finite and $\pi _i(F) =0$ for $i \ge 5$.

We finish the proof of the theorem by showing that $\mathcal T_0(X)$ is finite. Given $f \in \mathcal T_0(X)$, choosing a homotopy $h :X \times [0,1] \rightarrow B$ between $\bar{\nu }$ and $\bar{\nu }\circ f$ we obtain a normal B-structure $\varphi :X_{f} \rightarrow B$, where $X_{f}$ is the mapping torus. This represents an element $[X_{f} ,\varphi ]$ in $\Omega _{9}(B,p)$. Again by the Atiyah–Hirzebruch spectral sequence we have $\Omega _{9}(B,p) \otimes \mathbb Q \cong H_{9}(B;\mathbb Q)$.

Lemma 2.4

$H_9(B;\mathbb Q)=0$.

Proof

By the Leray–Serre spectral sequence of the fibration $F \rightarrow B \rightarrow BSO$, it suffices to show that $H^5(F;\mathbb Q)=0=H^9(F;\mathbb Q)$. But since there are no indecomposable classes in $H^n(F;\mathbb Q)$ for $n \ge 5$, it is enough to show that $H^3(F;\mathbb Q)=0$. Again by the Leray–Serre spectral sequence there is an exact sequence

$$\begin{aligned} H_4(BSO;\mathbb Q) {\mathop {\rightarrow }\limits ^{d}} H_3(F;\mathbb Q) \rightarrow H_3(B;\mathbb Q)=0 \end{aligned}$$

where d can be identified with the composition

$$\begin{aligned} H_4(BSO;\mathbb Q) = \pi _4(BSO) \otimes \mathbb Q {\mathop {\rightarrow }\limits ^{\partial }} \pi _3(F) \otimes \mathbb Q \rightarrow H_3(F;\mathbb Q). \end{aligned}$$

If $p_1(X) \ne 0 \in H^4(X;\mathbb Q)$, then $p_* :\pi _4(B) \otimes \mathbb Q \rightarrow \pi _4(BSO) \otimes \mathbb Q$ is surjective. This implies $H_3(F;\mathbb Q)=0$.

Therefore the finitely generated abelian group $\Omega _9(B,p)$ is finite. There are finitely many $f_1, \ldots , f_r \in \mathcal T_0(X)$, together with homotopies $h_1, \ldots , h_r$ such that for any $f \in \mathcal T_0(X)$ and homotopy h, $[X_f, \varphi ] = [X_{f_i}, \varphi _i]$ for some $1 \le i \le r$. This implies that there is a B-bordism W between $X \times [0,1]$ and $X \times [0,1]$, where the two boundary components are identified by f and $f_i$ respectively. The modified surgery obstruction to changing W to a relative h-cobordism is $\theta (W) \in L_{10}(\mathbb Z) \cong \mathbb Z/2$. If $\theta (W)=0$, there is a relative h-cobordism between $X \times [0,1]$ and $X \times [0,1]$. Such an h-cobordism gives rise to a diffeomorphism $F :X \times [0,1] \rightarrow X \times [0,1]$ which is a pseudo-isotopy between f and $f_i$. Therefore by Cerf’s pseudo-isotopy theorem [3] f is isotopic to $f_i$. If $\theta (W) \ne 0$, then for any $f'$ with this property, we may glue W and $W'$ and get a B-bordism V between $X \times [0,1]$ and $X \times [0,1]$ where the two boundary components are identified by f and $f'$ respectively. Now the surgery obstruction $\theta (V)=0$, therefore f and $f'$ are isotopic. This shows that there are at most 2r elements in $\mathcal T_0(X)$.