Abstract
Motivated by the relation between (twisted) K3 surfaces and special cubic fourfolds, we construct moduli spaces of polarized twisted K3 surfaces of any fixed degree and order. We do this by mimicking the construction of the moduli space of untwisted polarized K3 surfaces as a quotient of a bounded symmetric domain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A twisted K3 surface is a pair \((S,\alpha )\) consisting of a K3 surface S and a Brauer class \(\alpha \) on S. Using the isomorphism \({{\,\mathrm{Br}\,}}(S)\cong {{\,\mathrm{H}\,}}^2(S,{\mathscr {O}}_S^*)_{{{\,\mathrm{tors}\,}}}\), twisted K3 surfaces can be seen as a degree two version of polarized K3 surfaces. We may also view them from the perspective of Hitchin’s generalized K3 surfaces [11], using \(\alpha \) to change the volume form on S. This gives us a generalized Calabi–Yau structure, to which we associate a Hodge structure \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\) of K3 type on the full cohomology of S [17]. In this way, we can view \((S,\alpha )\) as a geometric realization of a point in the extended period domain for K3 surfaces.
This paper is concerned with polarized twisted K3 surfaces, that is, K3 surfaces together with a Brauer class and a primitive ample class in \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})\). Our first goal is to construct a moduli space of these objects, fixing the degree of the polarization and the order of the Brauer class. This can be done up to the following concession: when \(\rho (S)>1\), one parametrizes lifts of Brauer classes to \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Q}})\), which gives a strictly bigger group than \({{\,\mathrm{Br}\,}}(S)\).
Theorem 1
(Def. 2.1, Prop. 2.4) There exists a scheme \({{\,\mathrm{M}\,}}_d[r]\) which is a coarse moduli space for triples \((S,L,\alpha )\) where S is a K3 surface, \(L\in {{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})\) is a polarization of degree \((L)^2=d\) and \(\alpha \) is an element of \({{\,\mathrm{Hom}\,}}({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}},{\mathbb {Z}}/r{\mathbb {Z}})\). This group has a surjection to \({{\,\mathrm{Br}\,}}(S)[r]\), which is an isomorphism if and only if \(\rho (S)=1\).
We prove this by mimicking the construction of the moduli space of (untwisted) polarized K3 surfaces via the period domain. In particular, \({{\,\mathrm{M}\,}}_d[r]\) is a quasi-projective variety with at most finite quotient singularities, whose number of connected components can be bounded in terms of d and r (Proposition 2.5).
In the second part of the paper, we will concentrate on a Hodge-theoretic relation between twisted K3 surfaces and special cubic fourfolds. For untwisted K3 surfaces, this relation was first studied by Hassett [10]. He also constructed, for d satisfying a numerical condition \((**)\), rational maps
from the moduli space of polarized K3 surfaces of degree d to the moduli space of special cubic fourfolds of discriminant d, sending a K3 surface to the cubic it is associated to.
Associated twisted K3 surfaces were studied by Huybrechts in [16], extending results of [1]. The numerical condition on the discriminant given by Huybrechts can be formulated as follows:
We give a full generalization of Hassett’s results to the setting of twisted K3 surfaces.
Theorem 2
(Cor. 4.2) A cubic fourfold X is in \({\mathscr {C}}_{d'}\) for some \(d'\) satisfying \((**')\) if and only if for every decomposition \(d'=dr^2\) with d satisfying \((**)\), X has an associated polarized twisted K3 surface of degree d and order r.
We also give the analogous construction of Hassett’s rational maps to \({\mathscr {C}}_d\). Just like for untwisted K3 surfaces, these maps are either birational or of degree two. We end with a discussion of the covering involution in the degree two case, relating this paper to [6].
1.1 Notation
For basics on lattices, see e.g. [15, Chapter 14].
-
U is the rank two lattice with intersection matrix \(\bigl ({\begin{matrix}0 &{} 1 \\ 1 &{} 0\end{matrix}}\bigr )\).
-
\(E_8\) is the unique positive definite even unimodular lattice of rank eight.
-
\(\varLambda {:}{=}E_8(-1)^{\oplus 2}\oplus U^{\oplus 3}\) is the lattice isomorphic to the second cohomology \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})\) of a K3 surface S.
-
\({\widetilde{{{\,\mathrm{H}\,}}}}(S,{\mathbb {Z}})\) is the full cohomology of S with the Mukai pairing, viewed as an ungraded ring.
-
\({\widetilde{\varLambda }}{:}{=}\varLambda \oplus U\) is the lattice isomorphic to \({\widetilde{{{\,\mathrm{H}\,}}}}(S,{\mathbb {Z}})\).
-
\(\varLambda _d\subset \varLambda \) is the orthogonal complement of a primitive element \(\ell _d\in \varLambda \) of square d, which is unique up to \({{\,\mathrm{O}\,}}(\varLambda )\).
-
. -
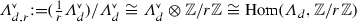\({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d){:}{=}{{\,\mathrm{Ker}\,}}({{\,\mathrm{O}\,}}(\varLambda _d)\rightarrow {{\,\mathrm{O}\,}}({{\,\mathrm{Disc}\,}}\varLambda _d))\). This group acts naturally on
. -
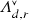For an isomorphism \(\varphi :L\rightarrow L'\) of lattices, \(\varphi _r\) is the induced map
. -
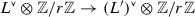For a lattice L of signature \((n_+,n_-)\) with \(n_+\ge 2\), \({\mathscr {D}}(L)\) is the period domain \(\{x\in {\mathbb {P}}(L\otimes {\mathbb {C}})\mid (x)^2=0,\, (x,{\bar{x}})>0\}\).
-
G[r] is the r-torsion subgroup of an abelian group G.
-
Cohomology with coefficients in \({\mathbb {G}}_m\) means étale cohomology. Otherwise we always use the analytic topology.
-
\({\mathscr {M}}_d\) is the moduli functor for polarized K3 surfaces of degree d, and \(\varPhi :{\mathscr {M}}_d\rightarrow {{\,\mathrm{M}\,}}_d\) is the associated coarse moduli space.
.
.
.Remark 0.1
By a moduli functor \({\mathscr {M}}\), we will mean a functor on the category of schemes of finite type over \({{\,\mathrm{Spec}\,}}{\mathbb {C}}\). A coarse moduli space for \({\mathscr {M}}\) is a scheme \({{\,\mathrm{M}\,}}\) with a morphism \(\xi :{\mathscr {M}}\rightarrow {{\,\mathrm{M}\,}}\) such that \(\xi ({\mathbb {C}})\) is a bijection, and we have factorization over \({{\,\mathrm{M}\,}}\) of morphisms \({\mathscr {M}}\rightarrow T\) for T any \({\mathbb {C}}\)-scheme of finite type.
2 Twisted K3 surfaces
2.1 Definitions
For references, see [14, 13]]. Recall that the Brauer group\({{\,\mathrm{Br}\,}}(X)\) of a scheme X is the group of sheaves of Azumaya algebras modulo Morita equivalence, with multiplication given by the tensor product. If X is quasi-compact and separated and has an ample line bundle, then \({{\,\mathrm{Br}\,}}(X)\) is isomorphic to the cohomological Brauer group
which equals \({{\,\mathrm{H}\,}}^2(X,{\mathbb {G}}_m)\) when X is regular and integral. If X is a complex K3 surface, one can moreover show that
A twisted K3 surface is a pair \((S,\alpha )\) where S is a K3 surface and \(\alpha \in {{\,\mathrm{Br}\,}}(S)\). Two twisted K3 surfaces \((S,\alpha )\) and \((S',\alpha ')\) are isomorphic if there exists an isomorphism \(f:S\rightarrow S'\) such that \(f^*\alpha '=\alpha \).
The exponential sequence on S induces the following exact sequence:
It follows that any Brauer class \(\alpha \in {{\,\mathrm{H}\,}}^2(S,{\mathscr {O}}_S^*)_{{{\,\mathrm{tors}\,}}}\) is of the form \(\exp (B^{0,2})\) for some \({B\in {{\,\mathrm{H}\,}}^2(S,{\mathbb {Q}})}\), unique up to \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})\) and \({{\,\mathrm{NS}\,}}(S)\otimes {\mathbb {Q}}\). Thus, denoting by T(S) the transcendental lattice of S, intersecting with B gives a linear map \(f_{\alpha }=(B,-):T(S)\rightarrow {\mathbb {Q}}/{\mathbb {Z}}\) which only depends on \(\alpha \). One can show that \(\alpha \mapsto f_{\alpha }\) yields an isomorphism \({{\,\mathrm{Br}\,}}(S)\cong {{\,\mathrm{Hom}\,}}(T(S),{\mathbb {Q}}/{\mathbb {Z}})\).
Given a lift \(B\in {{\,\mathrm{H}\,}}^2(S,{\mathbb {Q}})\) of \(\alpha \), we define a weight two Hodge structure of K3 type \({\widetilde{{{\,\mathrm{H}\,}}}}(S,B,{\mathbb {Z}})\) on the full cohomology of S by
where \(\sigma \) is a nowhere degenerate holomorphic 2-form on S and \(\exp (B)\sigma {:}{=} \sigma +B\wedge \sigma \). This Hodge structure does not depend on our choice of B (up to non-canonical isomorphism [17, Section 2]), so we can define
for any \(B\in {{\,\mathrm{H}\,}}^2(X,{\mathbb {Q}})\) with \(\exp (B^{0,2})=\alpha \). When \(\alpha \) is trivial, this gives back the usual Hodge structure on \({{\,\mathrm{H}\,}}^*(S,{\mathbb {Z}})\).
The Picard group of \((S,\alpha )\) is defined as \({\widetilde{{{\,\mathrm{H}\,}}}}{}^{1,1}(S,\alpha )\cap {\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\), so
for \(B\in {{\,\mathrm{H}\,}}^2(S,{\mathbb {Q}})\) lifting \(\alpha \). If \(\alpha \) is trivial, then \({{{\,\mathrm{Pic}\,}}(S,\alpha )={{\,\mathrm{H}\,}}^0(S,{\mathbb {Z}})\oplus {{\,\mathrm{Pic}\,}}(S)\oplus }\)\({{{\,\mathrm{H}\,}}^4(S,{\mathbb {Z}})}\). The transcendental lattice\(T(S,\alpha )\) is defined as the orthogonal complement of \({{\,\mathrm{Pic}\,}}(S,\alpha )\) in \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\). If \(\alpha \) is trivial, then \(T(S,\alpha )\) is the transcendental lattice T(S) of S. One can show that \(T(S,\alpha )\) is isometric, as an abstract lattice, to
Definition 1.1
A polarized twisted K3 surface is a triple \((S,L,\alpha )\), where S is a K3 surface, \(L\in {{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})\) is a primitive ample class and \(\alpha \in {{\,\mathrm{Br}\,}}(S)\). Two twisted polarized K3 surfaces \((S,L,\alpha )\) and \((S',L',\alpha ')\) are isomorphic if there exists an isomorphism \(f:S\rightarrow S'\) such that \(f^*L'=L\) and \(f^*\alpha '=\alpha \).
We define two invariants of \((S,L,\alpha )\): its degree\(d=(L)^2\) and its order\(r={{\,\mathrm{ord}\,}}(\alpha )\) (also known as its period).
2.2 A non-existence result for moduli spaces
Ideally, one would like to find a (coarse) moduli space \({{\,\mathrm{N}\,}}_d[r]\) for the following functor:
Here, \((f:S\rightarrow T,L\in {{\,\mathrm{H}\,}}^0(T,R^1f_*{\mathbb {G}}_m))\in \mathscr {M}_d(T)\) is a smooth proper family of polarized K3 surfaces of degree d and \(\alpha \in {{\,\mathrm{H}\,}}^0(T,R^2f_*{\mathbb {G}}_m)\) such that for any closed point \(x\in T\), base change gives a Brauer class \(\alpha _x\in {{\,\mathrm{H}\,}}^2(S_x,{\mathbb {G}}_m)[r]\).
It is, however, not difficult to show that \({{\,\mathrm{N}\,}}_d[r]\) does not exist as a locally Noetherian scheme. Namely, suppose \({\mathscr {N}}_d[r]\rightarrow {{\,\mathrm{N}\,}}_d[r]\) exists. Consider the natural transformation \(\xi :{\mathscr {N}}_d[r]\rightarrow {\mathscr {M}}_d\) which at a scheme T is defined by \({(S\rightarrow T,L,\alpha )\mapsto (S\rightarrow T,L)}\). By the properties of a coarse moduli space, there exists a unique morphism \({\pi :{{\,\mathrm{N}\,}}_d[r]\rightarrow {{\,\mathrm{M}\,}}_d}\) which makes the following diagram commute:
For a closed point \(y\in {{\,\mathrm{N}\,}}_d[r]\) corresponding to a tuple \((S,L,\alpha )\), the image \(\pi (y)\) should be the point x of \({{\,\mathrm{M}\,}}_d\) corresponding to (S, L). So the fibre of \(\pi \) over x is
For \(d>2\), let \(U\subset {{\,\mathrm{M}\,}}_d\) be the open subset where \({{\,\mathrm{Aut}\,}}(S,L)\) is trivial. Over U, we have \(({{\,\mathrm{N}\,}}_d[r])_x\cong {{\,\mathrm{Br}\,}}(S)[r]\cong ({\mathbb {Z}}/r{\mathbb {Z}})^{22-\rho (S)}\). In particular, \(\pi |_{{{\,\mathrm{N}\,}}_d[r]\times _{{{\,\mathrm{M}\,}}_d} U}\) is ramified exactly over the locus where \(\rho (S)>1\). Now this set is dense in U, thus not Zariski closed, giving a contradiction.
For \(d=2\), let \(U\subset {{\,\mathrm{M}\,}}_2\) be the open subset where \({{\,\mathrm{Aut}\,}}(S,L)\cong {\mathbb {Z}}/2{\mathbb {Z}}\). Then over U, we have \(2^{21-\rho (S)}\le |({{\,\mathrm{N}\,}}_2[r])_x|\le 2^{22-\rho (S)}\). So \(\pi |_{{{\,\mathrm{N}\,}}_2^r\times _{{{\,\mathrm{M}\,}}_2} U}\) is ramified (at least) over the locus where \(\rho (S)>2\), again a dense set in U, which leads to a contradiction.
When requiring that \(\alpha \) has order r (on each connected component of T), non-existence is proven similarly. One obtains a morphism \(\pi \) to \({{\,\mathrm{M}\,}}_d\) such that over an open subset \(U\subset {{\,\mathrm{M}\,}}_d\), the cardinality of the fibre of \(\pi \) over \((S,L)\in U\) is the number of elements of order r in \(({\mathbb {Z}}/r{\mathbb {Z}})^{22-\rho (S)}\) (or half this number when \(d=2\)). Again, \(\pi |_{\pi ^{-1}(U)}\) is ramified exactly over the locus where \(\rho (S)>1\) (at least over the locus where \(\rho (S)>2\) when \(d=2\)), a contradiction.
3 Moduli spaces of polarized twisted K3 surfaces
We will construct a slightly different moduli space \({{\,\mathrm{M}\,}}_d[r]\) mapping to \({{\,\mathrm{M}\,}}_d\), whose fibre over \((S,L)\in {{\,\mathrm{M}\,}}_d\) parametrizes triples \((S,L,\alpha )\) with \(\alpha \in {{\,\mathrm{Hom}\,}}({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}},{\mathbb {Z}}/r{\mathbb {Z}})\). There is a surjective homomorphism from this group to \({{\,\mathrm{Br}\,}}(S)[r]\), which is an isomorphism if and only if \(\rho (S)=1\).
3.1 Definition of the moduli functor
The Kummer sequence \(0\rightarrow \mu _r\rightarrow {\mathbb {G}}_m{\mathop {\rightarrow }\limits ^{(\cdot )^r}}{\mathbb {G}}_m\rightarrow 0\) induces a short exact sequence
If \(L\in {{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})\) is a polarization, we have injections
Hence, we get a surjective map
which is an isomorphism if and only if \(\rho (S)=1\).
We define a relative version of 
as follows. For a smooth proper family \((f:S\rightarrow T,L)\) of polarized K3 surfaces, set
where \(c_1(L)\) is the image of L under \({{\,\mathrm{H}\,}}^0(T,R^1f_*{\mathbb {G}}_m)\rightarrow {{\,\mathrm{H}\,}}^0(T,R^2f_*{\mathbb {Z}})\). Let \({\mathscr {F}}[r]\) be the following local system:
where \(\mathscr {H}om_{{{\,\mathrm{Ab}\,}}}\) means morphisms of sheaves of abelian groups.
Definition 2.1
The moduli functor \({\mathscr {M}}_d[r]\) is defined as
where \(\big (f:S\rightarrow T,L\in {{\,\mathrm{H}\,}}^0(T,R^1f_*{\mathbb {G}}_m)\big )\) is a smooth proper family of polarized K3 surfaces of degree d and \(\alpha \in {{\,\mathrm{H}\,}}^0(T,{\mathscr {F}}[r])\). We define
to be the subfunctor sending a scheme T to the set of those tuples \((f,L,\alpha )\) for which \(\alpha \) has order r on each connected component of T.
We will construct coarse moduli spaces for \({\mathscr {M}}_d[r]\) and \({\mathscr {M}}_d^r\).
3.2 Construction of the moduli space
We recall the construction of \({{\,\mathrm{M}\,}}_d\) as a subvariety of a quotient of a bounded symmetric domain (see e.g. [15]). The primitive cohomology \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\) of a degree-d polarized K3 surface only depends, as a lattice, on d, and is isomorphic to \(\varLambda _d\). The moduli functor \({\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}\) of marked polarized K3 surfaces of degree d is given by
where \((f:S\rightarrow T,L)\in \mathscr {M}_d(T)\). It has an analytic fine moduli space \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\), which can be constructed as an open submanifold of the period domain \({\mathscr {D}}(\varLambda _d)\) of \(\varLambda _d\). In particular, there exists a universal family
We denote the morphism \({\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}\rightarrow {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\) by \(\varPhi ^{{{\,\mathrm{mar}\,}}}\). The moduli space \({{\,\mathrm{M}\,}}_d\) is obtained from \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\) by taking the quotient under the action of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\).
Note that \(\varphi ^{{{\,\mathrm{mar}\,}}}\) induces an isomorphism 
. Thus, \({\mathscr {F}}[r]\) is the sheaf of sections of the trivial finite cover
where \(\mathscr {H}om_{{{\,\mathrm{Sets}\,}}}\) means morphisms of sheaves of sets. The space \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\) is a coarse moduli space for the functor
where \((f:S\rightarrow T,L,\varphi )\in {\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}(T)\) and \(\alpha \in {{\,\mathrm{H}\,}}^0(T,{\mathscr {F}}[r])\). Namely, let
be the morphism defined over a connected scheme T by
so we have a commutative diagram
Then \(\varPhi _d^{{{\,\mathrm{mar}\,}}}[r]\) is a bijection over \({{\,\mathrm{Spec}\,}}{\mathbb {C}}\). Moreover, suppose we have a map G from \({\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}[r]\) to a \({\mathbb {C}}\)-scheme X. For any 
, there is a map \(G_{\alpha }:{\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}\rightarrow X\) defined over a connected scheme T by \((S\rightarrow T, L, \varphi )\mapsto G(S\rightarrow T,L,\varphi ,\varphi _r^{-1}(\alpha ))\). The \(G_{\alpha }\) induce maps \(g_{\alpha }:{{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\rightarrow X\), which combine to a morphism \(g:{{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\rightarrow X\) satisfying \(g\circ \varPhi ^{{{\,\mathrm{mar}\,}}}[r] = G\).
The action of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) on \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\) lifts to \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\) via
Under 
, this is the restriction of the natural action of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) on 
. This action is properly discontinuous: it is on \({\mathscr {D}}(\varLambda _d)\) (see [15, Remark 6.1.10]), so also on the product with the finite group 
. It follows that the quotient
exists as a complex space. Similarly, let \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}},r}\subset {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\) be the union of those components \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\times \{v\}\) for elements 
of order r. Then the quotient
exists as a complex space.
We claim that \({{\,\mathrm{M}\,}}_d[r]\) and \({{\,\mathrm{M}\,}}_d^r\) are quasi-projective varieties. Consider the following commutative diagram:
Giving the sets on the right side the discrete topology, all these maps are continuous. So under \(\bar{\pi }\), each connected component of \({{\,\mathrm{M}\,}}_d[r]\) is mapped to a point. Vice versa, given 
, the inverse image of 
under \(\bar{\pi }\) is
where \({{\,\mathrm{Stab}\,}}\,[w]\subset {\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) is the stabilizer of [w] under the acion of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) on 
. Now \({{\,\mathrm{Stab}\,}}\,[w]\) contains the reflection \(s_{\delta }\) for an element \(\delta \in \varLambda _d\) of square \(-2\) orthogonal to w and \(\ell _d'\), which interchanges the two connected components of \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\). Hence, \({{\,\mathrm{M}\,}}_w\) is connected; even irreducible. This shows that the connected components of \({{\,\mathrm{M}\,}}_d[r]\) are in one-to-one correspondence with 
. Each component \({{\,\mathrm{M}\,}}_w\) parametrizes triples \((S,L,\alpha )\) that admit a marking \(\varphi \) with \(\varphi _r(\alpha )=[w]\). The components belonging to \({{\,\mathrm{M}\,}}_d^r\) are those \({{\,\mathrm{M}\,}}_w\) for which [w] has order r.
Remark 2.2
Recall (see e.g. [15, Section 6.4.2]) that for \(\ell \) large enough, there exists a fine moduli space \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{lev}\,}}}\) of polarized K3 surfaces (S, L) of degree d with a \(\varLambda /\ell \varLambda \)-level structure, i.e. an isometry \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\otimes {\mathbb {Z}}/\ell {\mathbb {Z}}\cong \varLambda _d\otimes {\mathbb {Z}}/\ell {\mathbb {Z}}\). The space \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{lev}\,}}}\) is a smooth quasi-projective variety which is a finite cover of \({{\,\mathrm{M}\,}}_d\). We could have constructed \({{\,\mathrm{M}\,}}_d[r]\) as a quotient of 
instead, choosing \(\ell \) to be a large enough multiple of r.
Corollary 2.3
Every connected component of \({{\,\mathrm{M}\,}}_d[r]\) (and therefore of \({{\,\mathrm{M}\,}}_d^r\)) is an irreducible, quasi-projective variety with at most finite quotient singularities.
Proof
The finite index subgroup \({{\,\mathrm{Stab}\,}}\,[w]\subset {\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) being arithmetic, the quotient \({\mathscr {D}}(\varLambda _d)/{{\,\mathrm{Stab}\,}}\,[w]\) is a quasi-projective variety with finite quotient singularities, by [2] and [24, Lemma IV.7.2]. We will show that \({{\,\mathrm{M}\,}}_w=\big ({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\times \{[w]\}\big )/{{\,\mathrm{Stab}\,}}\,[w]\) is a Zariski open subset of it, using the same argument as for the algebraicity of the moduli space of untwisted polarized K3 surfaces (see e.g. [15, Section 6.4.1]).
Let \(\ell \) be a large enough multiple of r such that there exists a fine moduli space \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{lev}\,}}}\) of polarized K3 surfaces with a \(\varLambda /\ell \varLambda \)-level structure, see Remark 2.2. For the universal family \(\pi :S^{{{\,\mathrm{lev}\,}}}\rightarrow {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{lev}\,}}}\), there exists a marking \(R^2_{{{\,\mathrm{pr}\,}}}\pi _*{\mathbb {Z}}\otimes \underline{{\mathbb {Z}}/\ell {\mathbb {Z}}}\cong \underline{\varLambda _d\otimes {\mathbb {Z}}/\ell {\mathbb {Z}}}\). This induces a holomorphic map \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{lev}\,}}}\rightarrow {\mathscr {D}}(\varLambda _d)/\varGamma _{\ell }\), where
The image of this map is \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}/\varGamma _{\ell }\). Dividing out further by \({{\,\mathrm{Stab}\,}}\,[w]\) yields a holomorphic map
By a theorem of Borel [4] (and also [24, Lemma IV.7.2]), this map is algebraic, and therefore the image \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}/{{\,\mathrm{Stab}\,}}\,[w]\) is constructible. As it is also analytically open in \({\mathscr {D}}(\varLambda _d)/{{\,\mathrm{Stab}\,}}\,[w]\), it is Zariski open [9, Corollary XII.2.3]. \(\square \)
One constructs a morphism \(\varPsi :{\mathscr {M}}_d[r]\rightarrow {{\,\mathrm{M}\,}}_d[r]\) in the following way. Consider a point \((f:S\rightarrow T,L,\alpha )\) in \({\mathscr {M}}_d[r](T)\). Proceeding as for untwisted polarized K3 surfaces, we pass to the (infinite) étale covering
which has a natural \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\)-action, satisfying \({\widetilde{T}}/{\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\cong T\). Write \({\widetilde{f}}:{\widetilde{S}}\rightarrow {\widetilde{T}}\) for the pullback family. The local system \(R^2_{{{\,\mathrm{pr}\,}}}{\widetilde{f}}_*{\mathbb {Z}}\) is trivial: there exists a canonical isomorphism \({\varphi :R^2_{{{\,\mathrm{pr}\,}}}{\widetilde{f}}_*{\mathbb {Z}}\cong \underline{\varLambda _d}}\). Now \(\varPhi ^{{{\,\mathrm{mar}\,}}}[r]\big ({\widetilde{S}},\eta ^*L,\varphi ,\eta ^*\alpha \big )\) is an element of \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]({\widetilde{T}})\), i.e. a holomorphic map \({\widetilde{T}}\rightarrow {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\). This map is \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\)-equivariant, hence descends to a map \(T\rightarrow {{\,\mathrm{M}\,}}_d[r]\). This map is algebraic by [4], thus defines a point in \({{\,\mathrm{M}\,}}_d[r](T)\). We let \(\varPsi (S\rightarrow T,L,\alpha )\) be this point.
Proposition 2.4
The space \({{\,\mathrm{M}\,}}_d[r]\) is a coarse moduli space for the functor \({\mathscr {M}}_d[r]\).
Proof
By definition, there is a commutative diagram
where the map F forgets the marking and q is the quotient map. We need to show that \(\varPsi ({\mathbb {C}}):{\mathscr {M}}_d[r]({\mathbb {C}})\rightarrow {{\,\mathrm{M}\,}}_d[r]({\mathbb {C}})\) is a bijection. For \(x\in {{\,\mathrm{M}\,}}_d[r]({\mathbb {C}})\), let \(y\in {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]({\mathbb {C}})\) such that \(q(y)=x\). Set \(\varPsi ({\mathbb {C}})^{-1}(x){:}{=} F(\varPhi ^{{{\,\mathrm{mar}\,}}}[r]({\mathbb {C}})^{-1}(y))\); note that this does not depend on the choice of y. One checks that \(\varPsi ({\mathbb {C}})^{-1}\) defines a set-theoretic inverse to \(\varPsi ({\mathbb {C}})\).
For the universal property of \(\varPsi \), let \(s:{\mathscr {M}}_d[r]\rightarrow T\) be a morphism to a finite type \({\mathbb {C}}\)-scheme T. Then \(s\circ F\) is a map from \({\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}[r]\) to T; since \({\mathscr {M}}_d^{{{\,\mathrm{mar}\,}}}[r]\rightarrow {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\) is a coarse moduli space, this induces a unique holomorphic map \(t:{{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\rightarrow T\) such that \(t\circ \varPhi ^{{{\,\mathrm{mar}\,}}}[r]=s\circ F\). It follows from the uniqueness that t is equivariant, thus factors over a holomorphic map \({{\,\mathrm{M}\,}}_d[r]\rightarrow T\). We will show that this map is algebraic.
Like before, let \(\ell \) be a large enough multiple of r such that there exists a fine moduli space \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{lev}\,}}}\) of K3 surfaces with a \(\varLambda /\ell \varLambda \)-level structure. The map \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}[r]\rightarrow T\) factors as
(see Remark 2.2). The map 
is algebraic and equivariant under the algebraic action of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\). The induced algebraic morphism 
is the given map \({{\,\mathrm{M}\,}}_d[r]\rightarrow T\). \(\square \)
The proof that \({{\,\mathrm{M}\,}}_d^r\) is a coarse moduli space for \({\mathscr {M}}_d^r\) is analogous.
Proposition 2.5
The space \({{\,\mathrm{M}\,}}_d^r\) has at most \(r\cdot \gcd (r,d)\) many connected components.
This follows directly from the following lemma. Denote \({\varLambda =E_8(-1)^{\oplus 2}\oplus U_1\oplus U_2}\)\({\oplus U_3}\). Let \(\{e_i,f_i\}\) be the standard basis for the i-th copy of U. Fix \(\ell _d{:}{=}e_3+\tfrac{d}{2}f_3\) and \(\ell _d'{:}{=} e_3-\tfrac{d}{2}f_3\), so 
. For integers n, k, we let
Lemma 2.6
Every element of order r in 
is equivalent under the action of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) to \([w_{n,k}]\) for some \(n,k\in {\mathbb {Z}}\). Moreover, if \(n\equiv n'\, mod \,r\) and \(k\equiv k'\, mod \,\gcd (r,d)\), then \([w_{n,k}]\) and \([w_{n',k'}]\) are equivalent.
Proof
Elements in 
of order r are of the form \(m[\tfrac{1}{r} x]\) where \(\gcd (m,r)=1\) and 
is primitive, so \(x=sy+\tfrac{t}{d}\ell _d'\) for some primitive \(y\in E_8(-1)^{\oplus 2}\oplus U_1\oplus U_2\) and integers s, t with \(\gcd (s,t)=1\). Write \(d=d_0\cdot \gcd (d,t)\) and \(t=t_0\cdot \gcd (d,t)\). Then \(d_0x=d_0sy+t_0\ell _d'\in \varLambda _d\) is primitive and
By Eichler’s criterion [8, Proposition 3.3], \(d_0x\) is equivalent under \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) to \(d_0(e_1+nf_1)+t_0\ell _d'\) for some n. So \(\tfrac{1}{r} x\) is equivalent to \(\tfrac{1}{r}(e_1+nf_1+\tfrac{t}{d}\ell _d')=w_{n,t}\).
Now \(\tfrac{m}{r}x\equiv mw_{n,t}\) is equivalent modulo 
to \(\tfrac{1}{r}(me_1+(mn+r)f_1+\tfrac{mt}{d}\ell _d')\). As \(\gcd (r,m)=1\), the element 
is primitive, so by the above, \(\tfrac{1}{r} y\) is equivalent under \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\) to some \(w_{n',t'}\). It follows that 
is equivalent to \([w_{n',t'}]\).
Next, note that if \(t'\equiv t\, mod \,d\), then \(w_{n,t}\) is equivalent to \(w_{n',t'}\) for some \(n'\) (by Eichler’s criterion). In particular, writing \(\gcd (r,d)=pr+qd\), the class
in 
is equivalent to \([\tfrac{1}{r}(e_1+n'f_1+\tfrac{t}{d}\ell _d')]=[w_{n',t}]\) for some \(n'\). This shows that every \([w_{n,k}]\) is equivalent to some \([w_{n',k'}]\) with \(0\le n'< r\) and \(0\le k'<\gcd (r,d)\). \(\square \)
4 Period maps
We show how to construct period maps on the connected components of \({{\,\mathrm{M}\,}}_d^r\), which will be an important ingredient in relating twisted K3 surfaces to cubic fourfolds in Sect. 4.
4.1 Construction
We have seen that the connected components of \({{\,\mathrm{M}\,}}_d^r\) are of the form
for 
of order r. We will construct a period map from \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\times \{[w]\}\) to the period domain \({\mathscr {D}}(T_w)\) of the lattice
Let \((S,L,\varphi ,[w])\in {{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\times \{[w]\}\). The corresponding twisted Hodge structure \({\widetilde{{{\,\mathrm{H}\,}}}}(S,[w],{\mathbb {Z}})\) on S is given as follows. Let
Then \({\widetilde{{{\,\mathrm{H}\,}}}}{}^{2,0}(S,[w])\) is \({\mathbb {C}}[\sigma + w'\wedge \sigma ]\), where \(\sigma \) is a non-degenerate holomorphic 2-form on S. Let \({\widetilde{\varLambda }}=\varLambda \oplus U_4\) be the extended K3 lattice. We can extend \(\varphi \) to an isomorphism \({\widetilde{\varphi }}:{\widetilde{{{\,\mathrm{H}\,}}}}(S,{\mathbb {Z}})\rightarrow {\widetilde{\varLambda }}\) by sending \(1\in {{\,\mathrm{H}\,}}^0(S,{\mathbb {Z}})\) to \(e_4\in U_4\) and \(1\in {{\,\mathrm{H}\,}}^4(S,{\mathbb {Z}})\) to \(f_4\in U_4\). Then
Recall that for an even lattice N and \(B\in N\), the B-field shift\({\exp (B)\in {{\,\mathrm{O}\,}}(N\oplus U)}\) is defined by
for \(z\in N\), where \(\{e,f\}\) is the standard basis of the hyperbolic plane U. For \(B\in N_{{\mathbb {Q}}}\), we define \(\exp (B)\in {{\,\mathrm{O}\,}}((N\oplus U)_{{\mathbb {Q}}})\) by linear extension. The discussion above shows that \({\widetilde{\varphi }}(\sigma + w'\wedge \sigma )= \exp (w)\varphi (\sigma )\) (note: \(U\cong U(-1)=\langle e,-f\rangle \)). We thus obtain a map
sending \((S,L,\varphi ,[w])\) to \([{\widetilde{\varphi }}({\widetilde{{{\,\mathrm{H}\,}}}}{}^{2,0}(S,[w]))]\).
The above depends on the choice of a representative 
of 
. We can get rid of this choice in the following way. First, the lattice \(T_w\) is a finite index sublattice of \(\varLambda _d\), so we have \({\mathscr {D}}(T_w)={\mathscr {D}}(\varLambda _d)\). Second, note that the map \(\exp (w)\) gives an isomorphism \(T_w\cong (\exp (w)\varLambda _d)\cap {\widetilde{\varLambda }}\). We see that \({\mathscr {Q}}_w\) factors over the usual period map \({\mathscr {P}}\) for \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\): the diagram
commutes. Denote by \({\mathscr {P}}_w\) the composition from \({{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\times \{[w]\}\) to \({\mathscr {D}}(T_w)\). It follows from the above diagram that \({\mathscr {P}}_w\) is holomorphic and injective.
Just like \({{\,\mathrm{M}\,}}_w\), the quotient \({\mathscr {D}}(T_w)/{{\,\mathrm{Stab}\,}}\,[w]\) is a quasi-projective variety by [2]. There is a commutative diagram
where \(\overline{{\mathscr {P}}}_w\) is algebraic by the same argument as in Corollary 2.3 (note that when \(\ell \) is a multiple of \(r^2d\), the group \(\varGamma _{\ell }=\{g\in {\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\mid g\equiv {{\,\mathrm{id}\,}}\, mod \,\ell \}\) is contained in \({{\,\mathrm{Stab}\,}}\,[w]\)).
Recall (see e.g. [15, Remark 6.4.5]) that \({\mathscr {D}}(T_w)\backslash {{\,\mathrm{im}\,}}{\mathscr {P}}_w={\mathscr {D}}(\varLambda _d)\backslash {{\,\mathrm{im}\,}}{\mathscr {P}}\) is a union of hyperplanes \(\bigcup _{\delta \in \varDelta (\varLambda _d)}\delta ^{\perp }\), where \(\varDelta (\varLambda _d)\) is the set of \((-2)\)-classes in \(\varLambda _d\). It follows that \({\mathscr {D}}(T_w)\) parametrizes periods of twisted quasi-polarized K3 surfaces, i.e. twisted K3 surfaces with a line bundle that is nef and big (however, the corresponding moduli stack is not separated). Hence, the quotient \({\mathscr {D}}(T_w)/{{\,\mathrm{Stab}\,}}\,[w]\) can be viewed as a moduli space of quasi-polarized twisted K3 surfaces.
4.2 The discriminant group of \(T_w\)
We collect some results about the lattice \(T_w\), in preparation of Sect. 4. Let 
such that 
has order r. We will describe the group \({{\,\mathrm{Disc}\,}}T_w\) and the quadratic form on it. Note that if \(g\in {\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\), then g induces an isomorphism \(T_w\cong T_{g(w)}\). So by Lemma 2.6, we can assume that
for some n, k. Then \(T_w=E_8(-1)^{\oplus 2}\oplus U_2\oplus T_0\), where
Since \(E_8(-1)^{\oplus 2}\oplus U_2\) is unimodular, \({{\,\mathrm{Disc}\,}}T_w\) is isomorphic to \({{\,\mathrm{Disc}\,}}T_0\). The intersection matrix of \(T_0\) is (compare [23, Lemma 2.12])
As the map 
is given by the matrix \(M^t=M\), we have
where the invariant factors \(g_i\) can be computed using the \(i\times i\)-minors of M [5, Satz 2.9.6]:
We will be interested in the following two cases:
Proposition 3.1
Let 
.
-
(i)
The group \({{\,\mathrm{Disc}\,}}T_w\) is cyclic if and only if \(\gcd (r,2nd-k^2)=1\).
-
(ii)
We have
$$\begin{aligned} {{\,\mathrm{Disc}\,}}T_w\cong {\mathbb {Z}}/(r^2d/3){\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\end{aligned}$$if and only if \(\gcd (r,2nd-k^2)=3\), and if 3|d then \(9\not \mid nd\).
In order to determine the quadratic form on \({{\,\mathrm{Disc}\,}}T_w\), we write down explicit generators. Consider the following elements of \({{\,\mathrm{Disc}\,}}T_0\):
The order of [x] is the smallest natural number a such that \(ax\in T_w\), that is, \((ax,w)\in {\mathbb {Z}}\). For the elements above, this gives
The class of 
in \({{\,\mathrm{Disc}\,}}T_w\) is
This shows that \({{\,\mathrm{Disc}\,}}T_w\) is generated by \([f_1]\), \([\ell _d'/d]\) and [w].
Lemma 3.2
If \(\gcd (d,k,r)=s\), then there is an integer p such that \(\gcd (d,k+pr)=s\).
Proof
Let \(d=d_0\gcd (r,d)\), so \(\gcd (r,sd_0)=s\). Write \(xsd_0+yr=s\). Then
\(\square \)
First assume \({{\,\mathrm{Disc}\,}}T_w\) is cyclic, so \(\gcd (r,2nd-k^2)=1\). In particular, we have \({\gcd (r,d,k)=1}\). By Lemma 3.2 there exists a p such that \(\gcd (d,k+pr)=1\). Since \(T_{w_{n,k}}\cong T_{w_{n,k+pr}}\), we can replace k by \(k+pr\). Then we have \({\gcd (r^2d,2nd-k^2)=1}\); hence, [w] generates \({{\,\mathrm{Disc}\,}}T_w\). So the quadratic form \(q_{T_w}\) on \({{\,\mathrm{Disc}\,}}T_w\) is determined by
Next, assume \({{\,\mathrm{Disc}\,}}T_w\cong {\mathbb {Z}}/(r^2d/3){\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\). If 3|d, then \(\gcd (r,2nd-k^2)=3\), and \(9\not \mid nd\) implies \(9\not \mid 2nd-k^2\). It follows that \(\gcd (r^2,2nd-k^2)=3\), so [w] generates \({\mathbb {Z}}/(dr^2/3){\mathbb {Z}}\). As a generator of the factor \({\mathbb {Z}}/3{\mathbb {Z}}\), we take the element
which satisfies \(q_{T_w}(u)=-\tfrac{d}{9}\, mod \,2{\mathbb {Z}}\). If u were a multiple m[w] of [w], we would have \(q_{T_w}(u)\equiv m^2\tfrac{2nd-k^2}{3}\, mod \,2\); multiplying by \(\tfrac{r^2d}{3}\) gives \(-\left( \tfrac{d}{3}\right) ^2\tfrac{r^2}{3}\equiv m^2\tfrac{2nd-k^2}{3}\, mod \,\tfrac{2r^2d}{3}.\) This implies that \(m=rm_0\) for some \(m_0\); hence \(-\left( \tfrac{d}{3}\right) ^2\equiv 3m_0^2\tfrac{2nd-k^2}{3}\, mod \,2d\). This is not possible as 3 does not divide the left hand side.
If \(3\not \mid d\), we may have \(9|2nd-k^2\), but this implies \(9\not \mid r\). Using that \({T_{w_{n,k}}\cong T_{w_{n+r,k}}}\), we may replace n by \(n+r\) and obtain \(9\not \mid 2nd-k^2\). This gives \(\gcd (r^2,2nd-k^2)=3\), so [w] generates \({\mathbb {Z}}/(dr^2/3){\mathbb {Z}}\). As a generator of the factor \({\mathbb {Z}}/3{\mathbb {Z}}\), we take
We have \(q_{T_w}(u')=-\tfrac{d}{9}(2nd-k^2)\, mod \,2{\mathbb {Z}}\). Like before, if \(u'\) were a multiple m[w] of [w], we would find \(-d^2\left( \tfrac{r}{3}\right) ^2\tfrac{2nd-k^2}{3}\equiv m^2\tfrac{2nd-k^2}{3}\, mod \,\tfrac{2r^2d}{3}\). It follows that \(m = m_0r/3\) for some \(m_0\), and hence \(\tfrac{2nd-k^2}{3}(m_0^2+d^2)\equiv 0\, mod \,6d\). But this is not possible, since the left hand side is not divisible by 3.
Corollary 3.3
Let 
.
-
(i)
If \({{\,\mathrm{Disc}\,}}T_w\) is cyclic, there exists a generator t such that
$$\begin{aligned} q_{T_w}(t)=\tfrac{1}{r^2d}(2nd-k^2)\, mod \,2{\mathbb {Z}}. \end{aligned}$$ -
(ii)
If \({{\,\mathrm{Disc}\,}}T_w\cong {\mathbb {Z}}/(r^2d/3){\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\) and \(3\not \mid d\), there exist generators (1, 0) and (0, 1) such that
$$\begin{aligned} q_{T_w}(1,0)=\tfrac{1}{r^2d}(2nd-k^2)\, mod \,2{\mathbb {Z}}\end{aligned}$$and
$$\begin{aligned} q_{T_w}(0,1)=-\tfrac{d}{9}(2nd-k^2)\, mod \,2{\mathbb {Z}}. \end{aligned}$$ -
(iii)
If \({{\,\mathrm{Disc}\,}}T_w\cong {\mathbb {Z}}/(r^2d/3){\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\) and 3|d, there exist generators (1, 0) and (0, 1) such that
$$\begin{aligned} q_{T_w}(1,0)=\tfrac{1}{r^2d}(2nd-k^2)\, mod \,2{\mathbb {Z}}\end{aligned}$$and
$$\begin{aligned} q_{T_w}(0,1)=-\tfrac{d}{9}\, mod \,2{\mathbb {Z}}. \end{aligned}$$
5 Twisted K3 surfaces and cubic fourfolds
A smooth cubic fourfold X is special if the lattice \({{\,\mathrm{H}\,}}^{2,2}(X)\cap {{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})\) has rank at least two. Hassett [10] showed that special cubic fourfolds form a countably infinite union of irreducible divisors \({\mathscr {C}}_d\) in the moduli space of cubic fourfolds. Here \({\mathscr {C}}_d\ne \emptyset \) if and only if \(d>6\) and \(d\equiv 0,2\, mod \,6\). Hassett proved that X is in \({\mathscr {C}}_d\) with d satisfying
if and only if there exists a polarized K3 surface (S, L) of degree d whose primitive cohomology \({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\) can be embedded Hodge-isometrically into \({{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\), up to a sign and a Tate twist.
In this section, we will generalize this result to twisted K3 surfaces.
5.1 Associated twisted K3 surfaces
We denote by \({{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})(1)\) the middle cohomology of a cubic fourfold X with the intersection product changed by a sign and the weight of the Hodge structure shifted by two. There is a lattice isometry
The isometry can be chosen such that the square of the hyperplane class on X is mapped to \(h{:}{=}(1,1,1)\in {\mathbb {Z}}(-1)^{\oplus 3}\). We denote the orthogonal complement to h by \(\varGamma \), so \(\varGamma \) is isomorphic to \({{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}(1)\).
The cubic X lies in the divisor \({\mathscr {C}}_d\) if and only if there exists a primitive sublattice
of rank two and discriminant d containing the square of the hyperplane class. The orthogonal complement \(K^{\perp }\subset {{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})(1)\) has an induced Hodge structure which determines X when \(X\in {\mathscr {C}}_d\) is very general. As abstract lattices, K and \(K^{\perp }\) only depend on d.
Under the isometry (1), the lattice K corresponds to a primitive sublattice of \(E_8(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus {\mathbb {Z}}(-1)^{\oplus 3}\) of rank two and discriminant d containing h. Such a sublattice is unique up to the action of the stable orthogonal group \({\widetilde{{{\,\mathrm{O}\,}}}}(\varGamma )={{\,\mathrm{Ker}\,}}({{\,\mathrm{O}\,}}(\varGamma )\rightarrow {{\,\mathrm{O}\,}}({{\,\mathrm{Disc}\,}}\varGamma ))\). We fix one such sublattice for each discriminant d and denote it by \(K_d\). Its orthogonal complement \(K_d^{\perp }\) is contained in \(\varGamma \).
Hassett proved that d satisfies \((**)\) if and only if there is an isometry \(K_d^{\perp }\cong \varLambda _d\). In generalizing this to the situation of twisted K3 surfaces, we replace \(\varLambda _d\) by \(T_w\) and \((**)\) by the condition \((**')\) introduced in [16]:
Theorem 4.1
The number \(d'\) satisfies \((**')\) if and only if for every decomposition \(d'=dr^2\) with d satisfying \((**)\), there exists an element 
of order r such that \(K_{d'}^{\perp }\) is isomorphic to \({{\,\mathrm{Ker}\,}}((w,-):\varLambda _d\rightarrow {\mathbb {Q}}/{\mathbb {Z}})\).
For a cubic fourfold \(X\in {\mathscr {C}}_{d'}\), the inclusion \(K_{d'}^{\perp }\subset {{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})(1)\) gives an induced Hodge structure of K3 type on \(K_{d'}^{\perp }\) and thus on \(T_w={{\,\mathrm{Ker}\,}}\, (w,-)\), yielding a point x in the period domain \({\mathscr {D}}(T_w)\). In [25], it was shown that for a smooth cubic fourfold X, there are no classes in \({{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\cap {{\,\mathrm{H}\,}}^{2,2}(X)\) of square 2. It follows that the class of x in \({\mathscr {D}}(T_w)/{{\,\mathrm{Stab}\,}}\,[w]\) lies in the image of the period map \({\mathscr {P}}_w\). As a consequence, we obtain
Corollary 4.2
A cubic fourfold X is in \({\mathscr {C}}_{d'}\) for some \(d'\) satisfying \((**')\) if and only if for every decomposition \(d'=dr^2\) with d satisfying \((**)\), there exists a polarized K3 surface (S, L) of degree d and an element \(\alpha \in {{\,\mathrm{Hom}\,}}({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}},{\mathbb {Q}}/{\mathbb {Z}})\) of order r such that \(K_{d'}^{\perp }\) is Hodge isometric to \({{\,\mathrm{Ker}\,}}\alpha \).
We say that the twisted K3 surface in Corollary 4.2 is associated to X.
Remark 4.3
This notion of associated twisted K3 surfaces almost coincides with the one given by Huybrechts [16]. He relates the full cohomology \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\) to the Hodge structure \({\widetilde{{{\,\mathrm{H}\,}}}}({\mathscr {A}}_X,{\mathbb {Z}})\) of K3 type associated to the K3 category \({\mathscr {A}}_X\subset {{\,\mathrm{D^b}\,}}(X)\), which was introduced in [1].
To be precise, Huybrechts shows that a cubic X is in \({\mathscr {C}}_{d'}\) for some \(d'\) satisfying \((**')\) if and only if there is a twisted K3 surface \((S,\alpha )\) such that \({\widetilde{{{\,\mathrm{H}\,}}}}({\mathscr {A}}_X,{\mathbb {Z}})\) is Hodge isometric to \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\). One can show that a Hodge isometry \({K_{d'}^{\perp }\cong {{\,\mathrm{Ker}\,}}(\alpha :{{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\rightarrow {\mathbb {Q}}/{\mathbb {Z}})}\) always extends to \({{\widetilde{{{\,\mathrm{H}\,}}}}({\mathscr {A}}_X,{\mathbb {Z}})\cong {\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})}\), see Proposition 5.6.
Vice versa, assume \({{\widetilde{{{\,\mathrm{H}\,}}}}({\mathscr {A}}_X,{\mathbb {Z}})\cong {\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})}\). When S has Picard number one, it follows that \({K_d^{\perp }\subset {{\,\mathrm{H}\,}}^4(X,{\mathbb {Z}})(1)}\) is Hodge isometric to \({{\,\mathrm{Ker}\,}}(\alpha :{{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}}\rightarrow {\mathbb {Q}}/{\mathbb {Z}})\) (these are the transcendental parts of \({\widetilde{{{\,\mathrm{H}\,}}}}({\mathscr {A}}_X,{\mathbb {Z}})\) and \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\)). When \(\rho (S)>1\), there exists a Hodge isometry \({K_{d'}^{\perp }\cong {{\,\mathrm{Ker}\,}}(\alpha ')}\) for a possibly different K3 surface \(S'\) and \(\alpha '\in {{\,\mathrm{Hom}\,}}({{\,\mathrm{H}\,}}^2(S',{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}},{\mathbb {Q}}/{\mathbb {Z}})\) that satisfies \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\cong {\widetilde{{{\,\mathrm{H}\,}}}}(S',\alpha ',{\mathbb {Z}})\).
The above is completely analogous to the untwisted situation. Note that Corollary 4.2 implies a strengthening of Huybrechts’ result, replacing “there is a twisted K3 surface” by “for any decomposition \(d'=dr^2\) with d satisfying \((**)\), there is a twisted K3 surface of degree d and order r”.
Finally, we should mention that these Hodge-theoretical notions (both twisted and untwisted) have a categorical counterpart due to [1, 16, 3]]: There exists a Hodge isometry \({\widetilde{{{\,\mathrm{H}\,}}}}({\mathscr {A}}_X,{\mathbb {Z}})\cong {\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\) if and only if the category \({\mathscr {A}}_X\) is equivalent to the bounded derived category \({{\,\mathrm{D^b}\,}}(S,\alpha )\) of \(\alpha \)-twisted sheaves on S.
5.2 Proof of Theorem 4.1
We have seen that the discriminant group of \(T_w\) can always be generated by three elements. As \(T_w\) has signature (2, 19), it follows that \(T_w\) is determined by its discriminant group and the quadratic form on it [22, Corollary 1.13.3]. To prove Theorem 4.1, it thus suffices to determine when
Write \(d'=dr^2\). We will use the following result by Hassett (using our sign convention):
Proposition 4.4
[10, Proposition 3.2.5] When \(d'\equiv 0\, mod \,6\), then \({{\,\mathrm{Disc}\,}}(K_{d'}^{\perp })\) is isomorphic to \({\mathbb {Z}}/\tfrac{d'}{3}{\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\), which is cyclic unless 9 divides \(d'\). One can choose generators (1, 0) and (0, 1) such that the quadratic form \(q_{K_{d'}^{\perp }}\) satisfies \(q_{K_{d'}^{\perp }}(1,0)=3/d'\, mod \,2{\mathbb {Z}}\) and \({q_{K_{d'}^{\perp }}(0,1)=-2/3\, mod \,2{\mathbb {Z}}}\). When \(d'\equiv 2\, mod \,6\), then \({{\,\mathrm{Disc}\,}}(K_{d'}^{\perp })\) is \({\mathbb {Z}}/d'{\mathbb {Z}}\). One can choose a generator u such that \(q_{K_{d'}^{\perp }}(u) = (1-2d')/3d'\, mod \,2{\mathbb {Z}}\).
We prove Theorem 4.1 by comparing the quadratic forms on \({{\,\mathrm{Disc}\,}}K_{d'}^{\perp }\) and \({{\,\mathrm{Disc}\,}}T_w\). We distinguish the cases when the groups are cyclic and non-cyclic. We will use the following statements, which follow from quadratic reciprocity [10, proof of Proposition 5.1.4].
Lemma 4.5
When \(d\equiv 2\, mod \,6\), then d satisfies \((**)\) if and only if \(-3\) is a square modulo 2d. When \(d\equiv 0\, mod \,6\), write \(d=6t\). Then d satisfies \((**)\) if and only if \(-3\) is a square modulo 4t and 4t is a square modulo 3.
5.2.1 Cyclic case
Assuming that \({{\,\mathrm{Disc}\,}}K_{d'}^{\perp }\) is cyclic, we will show that \(d'=dr^2\) with d satisfying \((**')\) if and only if there exists a 
of order r such that \(K_{d'}^{\perp }\cong T_w\). The proof consists of Propositions 4.6 and 4.7.
Proposition 4.6
Assume that \({{\,\mathrm{Disc}\,}}K_{d'}^{\perp }\) is cyclic. If there is a 
of order r such that \(K_{d'}^{\perp }\cong T_w\) (so in particular, \(d'=dr^2\)), then d satisfies \((**)\).
Proof
First assume that 3 does not divide d. By Proposition 4.4 and Corollary 3.3, we have \(K_{d'}^{\perp }\cong T_{w_{n,k}}\) if and only if there is an x such that
Multiplying by \(3dr^2\) gives
which is equivalent to
It follows that \(-3\) is a square modulo 2d, so by Lemma 4.5, d satisfies \((**)\).
Next we assume 3|d. By Proposition 4.4 and Corollary 3.3, we have \(K_{d'}^{\perp }\cong T_{w_{n,k}}\) if and only if there is an x such that
Writing \(d=6t\) and multiplying by \(dr^2\) gives
In particular, \(-3\) is a square modulo 4t, and we have \(4tr^2\equiv x^2k^2\, mod \,3\). Since 3 does not divide r, this implies that 4t is a square modulo 3. It follows from Lemma 4.5 that d satisfies \((**)\). \(\square \)
Write \(r = 2^sqr_0\) where q consists of all prime factors of r which are 1 modulo 3, and \(r_0\) consists of all odd prime factors of r which are 2 modulo 3. In particular, \(dq^2\) still satisfies \((**)\), and we have \(\gcd (r_0,dq^2)=1\).
Proposition 4.7
There exists an n such that for 
, we have \(K_{d'}^{\perp }\cong T_w\).
Proof
We first assume \(3\not \mid d\). By (2) we have to show that for some x and some n,
where \(m=2dr^2\).
Since \(dq^2\) satisfies \((**)\), the number \(-3\) is a square modulo \(2dq^2\). As \(3r_0\) is invertible in \({\mathbb {Z}}/2dq^2{\mathbb {Z}}\), we get \(-3\equiv (3r_0x)^2\, mod \,2dq^2\) for some \(x\in {\mathbb {Z}}\). This gives \({3x^2r_0^2+1\equiv 0\, mod \,2dq^2}\), which shows that (4) has a solution modulo \(m=2dq^2\), for any n. In particular, it has solutions modulo \(dq^2/2\) and modulo 4.
It follows that \((f_n/2)(x)\equiv 0\) has a solution modulo 2. Also, \({(f_n/2)'(x)=3x(r_0^2-}\)\({2ndq^2)}\) is always odd. By Hensel’s lemma, \((f_n/2)(x)=0\) has a solution modulo \(2^l\) for any \(l\ge 1\). It follows that (4) has a solution modulo \(2^l\) for any \(l\ge 2\).
By the Chinese remainder theorem, there exists a solution x for (4) modulo \({m=2d(2^sq)^2}\). We can assume \(\gcd (x,r_0)=1\): otherwise, write \(ar_0+b\cdot 2d(2^sq)^2=1\) and replace x by \({x+b\cdot 2d(2^sq)^2(1-x) = 1+ar_0(x-1)}\).
Now we have \(\gcd (r_0^2,6x^2dq^2)=1\), so there exist a and b such that \({ar_0^2+b\cdot 6x^2dq^2}\)\({=1}\). In particular, \(r_0^2\) divides \(3x^2\cdot -2bdq^2+1\). We see that for \(n=b\), there is a solution to (4) modulo \(m=r_0^2\). By the Chinese remainder theorem, there exists a solution modulo \(2dr^2\).
Next, assume 3|d. Write \(d=6t\). By (3) we have to show that for some x and n,
where \(m=12tr^2\).
Since \(dq^2\) satisfies \((**)\), first, \(4tq^2\) is a square modulo 3, so also \(4tr^2=4t(2^sqr_0)^2\) is a square modulo 3. Second, \(-3\) is a square modulo \(4tq^2\). Since 3 does not divide \(4tq^2\), it follows that \(4tr^2-3\) is a square modulo \(12tq^2\).
Now \(r_0\) is invertible in \({\mathbb {Z}}/12tq^2{\mathbb {Z}}\), which implies that \(4tr^2-3\equiv (xr_0)^2\, mod \,12tq^2\) for some x. So \(x^2r_0^2-4tr^2+3\) is divisible by \(12tq^2\), which shows that (5) has a solution modulo \(m=12tq^2\), for any n. In particular, there exist solutions modulo \(3tq^2\) and modulo 4.
Like before, it follows from Hensel’s lemma that (5) has a solution modulo \(2^l\) for any \(l\ge 2\).
By the Chinese remainder theorem, there exists a solution x for (5) modulo \(12t(2^sq)^2\). Like before, if \(\gcd (x,r_0)\ne 1\), take a and b such that \(ar_0+b\cdot 12t(2^sq)^2 = 1\) and replace x by \(x+b\cdot 12t(2^sq)^2\cdot (1-x) = 1+ar_0(x-1)\).
Now we have \(\gcd (r_0^2,4tx^2q^2)=1\), so we can write \(3ar_0^2 + bx^2\cdot 12tx^2q^2=3\) for some a and b. So for \(n=b\), we find that \(r_0^2\) divides \(x^2\cdot -12ntq^2+3\), hence (5) has a solution modulo \(m=r_0^2\). By the Chinese remainder theorem, it has a solution modulo \(2dr^2\). \(\square \)
5.2.2 Non-cyclic case
We now assume \({{\,\mathrm{Disc}\,}}(K_{d'}^{\perp })\cong {\mathbb {Z}}/3{\mathbb {Z}}\times {\mathbb {Z}}/\tfrac{d'}{3}{\mathbb {Z}}\), and we again show that \(d'=dr^2\) with d satisfying \((**')\) if and only if there exists a 
of order r such that \(K_{d'}^{\perp }\cong T_w\). The proof consists of Propositions 4.8, 4.9 and 4.10.
Proposition 4.8
Assume that \({{\,\mathrm{Disc}\,}}K_{d'}^{\perp }\cong {\mathbb {Z}}/(d'/3){\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\). If there is a 
of order r such that \(K_{d'}^{\perp }\cong T_w\) (so in particular, \(d'=dr^2\)), then d satisfies \((**)\).
Proof
Consider the factor \({\mathbb {Z}}/(d'/3){\mathbb {Z}}={\mathbb {Z}}/(dr^2/3){\mathbb {Z}}\). By Proposition 4.4 and Corollary 3.3, there exists an x such that \(x^2\tfrac{2nd-k^2}{r^2d}\) is congruent to \(\tfrac{3}{dr^2}\) modulo 2. Multiplying both expressions with \(-dr^2\) gives
We see that \(-3\) is a square modulo 2d, which implies that d satisfies \((**)\). \(\square \)
Write \(r = 2^sqr_0\), where q consists of all prime factors of r which are congruent to 1 modulo 3, and \(r_0\) consists of all other odd prime factors of r. In particular, \(dq^2\) still satisfies \((**)\) and \(\gcd (r_0,dq^2)\) is 1 or 3. Note that 3 divides \(r_0\).
Proposition 4.9
Suppose that 3 does not divide d. There exists an integer n such that for 
, we have \(K_{d'}^{\perp }\cong T_w\).
Proof
By (6), we need n and x such that
where \(m=2dr^2\).
Since \(dq^2\) satisfies \((**)\), \(-3\) is a square modulo \(2dq^2\), and as \(r_0\) is divisible in \({\mathbb {Z}}/2dq^2{\mathbb {Z}}\), we have \(-3\equiv (r_0x)^2\, mod \,2dq^2\) for some x. This shows that (7) has a solution modulo \(2dq^2\) for any n. In particular, there exist solutions modulo \(dq^2/2\) and modulo 4.
Using Hensel’s lemma again, one shows that there exist solutions modulo \(2^{\ell }\) for any \(\ell \ge 2\), and by the Chinese remainder theorem, there exists a solution x modulo \(m=2d(2^sq)^2\). We may assume that \(\gcd (x,r_0)=1\) by writing \(ar_0+b\cdot 2d(2^sq)^2=1\) and replacing x by \({x+b\cdot 2d(2^sq)^2(1-x) = 1+ar_0(x-1)}\).
Now \(\gcd (r_0^2/3,2x^2dq^2)=1\); take a and b such that \(ar_0^2/3+b\cdot 2x^2dq^2=1\). Then \(r_0^2\) divides \(-6bx^2dq^2+3\), so for \(n=b\), there exists a solution to (7) modulo \(r_0^2\). By the Chinese remainder theorem, there is a solution modulo \(m=2dr^2\).
We still need to check that for the generator u of \({\mathbb {Z}}/3{\mathbb {Z}}\subset {{\,\mathrm{Disc}\,}}T_w\), there exists \(y\in {\mathbb {Z}}\) such that \(y^2(u)^2=y^2\cdot \tfrac{d}{9}(r_0^2-6nq^2d)\) is congruent to \(-2/3\) modulo 2. Multiplying both expressions by 3/2 gives
Now note that \(d/2\equiv 1\, mod \,3\), so taking y such that 3 does not divide y, we have
The element on the right hand side is
where b was defined by the equation \(ar_0^2/3+b\cdot 2x^2dq^2=1\). Reducing this modulo 3, we indeed find \(b\equiv 1\, mod \,3\). \(\square \)
We are left with the case 3|d.
Proposition 4.10
Suppose 3 divides d. There is an n such that for 
, we have \(K_{d'}^{\perp }\cong T_w\).
Proof
By (6), we need n and x such that
Write \(d=6t\), then this is equivalent to
where \(m=4tr^2\).
As \(dq^2\) satisfies \((**)\), Lemma 4.5 tells us that \(-3\) is a square modulo \(4tq^2\). Since \({\gcd (3r_0,4tq^2)=1}\), it follows that \(-3\equiv (3r_0x)^2\, mod \,4tq^2\) for some x. So we have \({3x^2r_0^2+1\equiv 0\, mod \,4tq^2}\), which shows that (8) has a solution modulo \(m=4tq^2\).
By Hensel’s lemma once more, (8) also has a solution modulo \(2^{\ell }\) for all \(\ell \ge 2\), and by the Chinese remainder theorem it then has a solution x modulo \(4t(2^sq)^2\). Like before, we may assume \(\gcd (x,r_0)=1\) by writing \(ar_0+b\cdot 2d(2^sq)^2=1\) and replacing x by \({x+b\cdot 2d(2^sq)^2(1-x) = 1+ar_0(x-1)}\).
Now note that \(\gcd (r_0^2,4tx^2q^2)=1\) and take a, b such that \(ar_0^2+b\cdot 4tx^2q^2=1\). Then \(r_0^2\) divides \(-b\cdot 4tx^2q^2+1\), showing that for \(n=b\), (8) has a solution modulo \(m=r_0^2\). By the Chinese remainder theorem, there exists a solution modulo \(4tr^2\).
Finally, we need to check that for the generator \(u'\) of \({\mathbb {Z}}/3{\mathbb {Z}}\subset {{\,\mathrm{Disc}\,}}T_w\), there exists a y such that \(y^2(u')^2=-y^2d/9\) is congruent to \(-2/3\) modulo 2. Multiplying by \(-3/2\), we get
which is true whenever 3 does not divide y. \(\square \)
6 Rational maps to \({\mathscr {C}}_{d'}\)
For untwisted K3 surfaces, an isomorphism \(\varLambda _d\cong K_d^{\perp }\) can be used to construct a rational map \({{\,\mathrm{M}\,}}_d\dashrightarrow {\mathscr {C}}_d\). We will generalize these maps to the situation of twisted K3 surfaces.
Throughout this section, we will assume \(d'\) satisfies \((**')\) and fix a decomposition \(d'=dr^2\) with d satisfying \((**)\). Moreover, we fix 
as in Theorem 4.1 and choose an isomorphism \(K_{d'}^{\perp }\cong T_w={{\,\mathrm{Ker}\,}}\, (w,-)\).
6.1 Construction
Note that the group \({\widetilde{{{\,\mathrm{O}\,}}}}(K_{d'}^{\perp })\) can be viewed as a subgroup of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varGamma )\): any element \(f\in {\widetilde{{{\,\mathrm{O}\,}}}}(K_{d'}^{\perp })\) can be extended to an orthogonal transformation \({\widetilde{f}}\) of the unimodular lattice \({E_8(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus {\mathbb {Z}}(-1)^{\oplus 3}}\) such that \({\widetilde{f}}|_{K_{d'}}\) is the identity. Then restrict to \(\varGamma \) to get an element of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varGamma )\).
On the level of the period domain, we have a commutative diagram
where \(\overline{{\mathscr {C}}}_{d'}\) is the image of \({\mathscr {D}}(K_{d'}^{\perp })\) under \({\mathscr {D}}(\varGamma )\rightarrow {\mathscr {D}}(\varGamma )/{\widetilde{{{\,\mathrm{O}\,}}}}(\varGamma )\). Embedding the moduli space \({\mathscr {C}}\) of smooth cubic fourfolds into \({\mathscr {D}}(\varGamma )/{\widetilde{{{\,\mathrm{O}\,}}}}(\varGamma )\) via the period map, one shows that \(\overline{{\mathscr {C}}}_{d'}\) is the closure of \({\mathscr {C}}_{d'}\subset {\mathscr {C}}\) in \({\mathscr {D}}(\varGamma )/{\widetilde{{{\,\mathrm{O}\,}}}}(\varGamma )\).
Lemma 5.1
The group \({\widetilde{{{\,\mathrm{O}\,}}}}(T_w)\) is a subgroup of \({{\,\mathrm{Stab}\,}}\,[w]\subset {\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\).
Proof
Let \(g\in {\widetilde{{{\,\mathrm{O}\,}}}}(T_w)\). By assumption, 
sends any 
to \(x+y\) for some \({y\in T_w\subset \varLambda _d}\). In particular, this holds for 
, which shows that 
preserves \(\varLambda _d\). Moreover, 
induces the identity on \({{\,\mathrm{Disc}\,}}\varLambda _d\), so 
is an element of \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\).
Now 
lies in 
, so we also have 
for some 
. This implies that when acting on 
, the map 
stabilizes [w]. \(\square \)
The period map \({\mathscr {P}}_w:{{\,\mathrm{M}\,}}_d^{{{\,\mathrm{mar}\,}}}\times \{[w]\}\rightarrow {\mathscr {D}}(T_w)\) induces an embedding of
into \({\mathscr {D}}(T_w)/{\widetilde{{{\,\mathrm{O}\,}}}}(T_w)\). This map is algebraic, which is shown similarly as for the embedding \({{\,\mathrm{M}\,}}_w\hookrightarrow {\mathscr {D}}(T_w)/{{\,\mathrm{Stab}\,}}\,[w]\). The space \({\widetilde{{{\,\mathrm{M}\,}}}}_w\) parametrizes tuples \((S,L,\alpha ,f)\) where \((S,L,\alpha )\) is in \({{\,\mathrm{M}\,}}_w\) and f is an isomorphism from \({{\,\mathrm{Disc}\,}}({{\,\mathrm{Ker}\,}}\alpha )\) to \({{\,\mathrm{Disc}\,}}T_w\). The composition
induces a rational map \({\widetilde{{{\,\mathrm{M}\,}}}}_w\dashrightarrow {\mathscr {C}}_{d'}\), which is regular on an open subset that maps surjectively (by Corollary 4.2) to \({\mathscr {C}}_{d'}\). Hassett showed that \({\mathscr {D}}(K_{d'}^{\perp })/{\widetilde{{{\,\mathrm{O}\,}}}}(K_{d'}^{\perp }) \rightarrow \overline{{\mathscr {C}}}_{d'}\) generically has degree one when \(d'\equiv 2\, mod \,6\), and degree two when \(d'\equiv 0\, mod \,6\). Hence, \({\widetilde{{{\,\mathrm{M}\,}}}}_w\dashrightarrow {\mathscr {C}}_{d'}\) is birational in the first case and has degree two in the second case; see also Sect. 5.3.
The map \(\gamma :{\widetilde{{{\,\mathrm{M}\,}}}}_w\dashrightarrow {\mathscr {C}}_{d'}\) is in general not unique: it depends on the choice of an isomorphism \(T_w\cong K_{d'}^{\perp }\). To be precise, let \(\iota :{{\,\mathrm{O}\,}}(T_w)\rightarrow {{\,\mathrm{Aut}\,}}({\mathscr {D}}(T_w))\) send an isometry of \(T_w\) to the induced action on the period domain. Then \(\gamma \) is unique up to \(\iota ({{\,\mathrm{O}\,}}(T_w))/\iota ({\widetilde{{{\,\mathrm{O}\,}}}}(T_w))\). We can compute this group as in [12, Lemma 3.1]: there is a short exact sequence
Using \(\iota ({\widetilde{{{\,\mathrm{O}\,}}}}(T_w))\cong {\widetilde{{{\,\mathrm{O}\,}}}}(T_w)\) and \(\iota ({{\,\mathrm{O}\,}}(T_w))\cong {{\,\mathrm{O}\,}}(T_w)/\pm {{\,\mathrm{id}\,}}\), we find that
Corollary 5.2
The map \({\widetilde{{{\,\mathrm{M}\,}}}}_w\dashrightarrow {\mathscr {C}}_{d'}\) is unique up to elements of \({{\,\mathrm{O}\,}}({{\,\mathrm{Disc}\,}}T_w)/\pm {{\,\mathrm{id}\,}}\).
When \({{\,\mathrm{Disc}\,}}T_w\cong {\mathbb {Z}}/d'{\mathbb {Z}}\), this group is isomorphic to \(({\mathbb {Z}}/2{\mathbb {Z}})^{\oplus \tau (d'/2)-1}\), where \(\tau (d'/2)\) is the number of prime factors of \(d'/2\).
We have seen that there is a difference to the untwisted situation: the rational map to \({\mathscr {C}}_{d'}\) can only be defined after taking a finite covering \(\pi :{\widetilde{{{\,\mathrm{M}\,}}}}_w\rightarrow {{\,\mathrm{M}\,}}_w\). We give an upper bound for the degree of this covering.
Corollary 5.3
The degree of the quotient map \(\pi :{\widetilde{{{\,\mathrm{M}\,}}}}_w\rightarrow {{\,\mathrm{M}\,}}_w\) is at most
If \({{\,\mathrm{Disc}\,}}T_w\) is cyclic, then \(I=2^{\tau (d'/2)-1}\).
Proof
The degree of \(\pi \) is the index of \(\iota ({\widetilde{{{\,\mathrm{O}\,}}}}(T_w))\cong {\widetilde{{{\,\mathrm{O}\,}}}}(T_w)\) in \(\iota ({{\,\mathrm{Stab}\,}}\,[w])\). This is at most the index I of \({\widetilde{{{\,\mathrm{O}\,}}}}(T_w)\) in \(\iota ({{\,\mathrm{O}\,}}(T_w))\). \(\square \)
6.2 Example
We consider the case \(d=r=2\), so \(d'=8\). The cubic fourfolds in \({\mathscr {C}}_8\) are those containing a plane. For a generic such cubic X, it was shown already in [19] that X has an associated twisted K3 surface \((S,\alpha )\) in the categorical sense (see Remark 4.3). In this special case, there is a geometric construction for \((S,\alpha )\), which was used before by Voisin in her proof of the Torelli theorem for cubic fourfolds [25]. As explained in Remark 4.3, \((S,\alpha )\) is also Hodge-theoretically associated to X.
By Lemma 2.6, the moduli space \({{\,\mathrm{M}\,}}_2^2\) has at most four connected components, corresponding to the vectors \(w_{n,k}=\tfrac{1}{2}(e_1+nf_1+\tfrac{k}{2}\ell _2')\) with \(n,k\in \{0,1\}\). Now by Eichler’s criterion, \(e_1\) is equivalent to \(e_1+f_1+\ell _2'\) under \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _2)\), and this is equivalent to \(e_1+f_1\) modulo 
. Thus, the components \({{\,\mathrm{M}\,}}_{w_{0,0}}\) and \({{\,\mathrm{M}\,}}_{w_{1,0}}\) are the same.
The discriminant group of \(K_8^{\perp }\) is cyclic, and one can choose a generator u such that \(q_{K_8^{\perp }}(u)=-\tfrac{5}{8}\, mod \,2{\mathbb {Z}}\). By Proposition 3.1, the discriminant group of \(T_{w_{n,k}}\) is cyclic if and only if \(k=1\). By Corollary 3.3, \(T_{w_{n,1}}\) is isomorphic to \(K_8^{\perp }\) if and only if there exists an \(x\in {\mathbb {Z}}\) such that \(\tfrac{x^2(4n-1)}{2}\equiv -\tfrac{5}{8}\, mod \,2\). For \(n=0\), we have
which is never equivalent to \(-\tfrac{5}{8}\) modulo 2. For \(n=1\), we have
which is equivalent to \(-\tfrac{5}{8}\) modulo 2 when \(x=3\).
We see that for \(w=w_{1,1}\), there exists a rational map \({\widetilde{{{\,\mathrm{M}\,}}}}_w\dashrightarrow {\mathscr {C}}_{d'}\) as above. Since \(d'/2=4\) has only one prime factor, Corollary 5.2 tells us that there is a unique choice for the rational map \({\widetilde{{{\,\mathrm{M}\,}}}}_{w_{1,1}}\dashrightarrow {\mathscr {C}}_8\). Moreover, it follows from Corollary 5.3 that \(\pi :{\widetilde{{{\,\mathrm{M}\,}}}}_{w_{1,1}}\rightarrow {{\,\mathrm{M}\,}}_{w_{1,1}}\) is an isomorphism. Hence, we obtain a rational map
which gives an inverse to the geometric construction of associated twisted K3 surfaces over the locus where \(\rho (S)=1\).
Remark 5.4
The three types of Brauer classes occurring in this example have been studied before by Van Geemen [7] (see also [20, Section 2]). He relates the twisted K3 surfaces in the components \({{\,\mathrm{M}\,}}_{w_{0,0}}\) and \({{\,\mathrm{M}\,}}_{w_{0,1}}\) to certain double covers of \({\mathbb {P}}^2\times {\mathbb {P}}^2\) and to complete intersections of three quartics in \({\mathbb {P}}^4\), respectively.
Remark 5.5
In general, the component \({{\,\mathrm{M}\,}}_w\subset {{\,\mathrm{M}\,}}_d^r\) for which a rational map \({\widetilde{{{\,\mathrm{M}\,}}}}_w\dashrightarrow {\mathscr {C}}_{d'}\) exists is not unique, because the class 
satisfying \(T_w\cong K_{d'}^{\perp }\) is not unique modulo \({\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _d)\). We work out an example.
Let \(d=14\) and \(r=7\), so \({{\,\mathrm{Disc}\,}}K_{d'}^{\perp }\) is cyclic. Since r divides d, [20, Theorem 9] tells us that for 
of order r, there is only one isomorphism class of lattices \(T_w\) with cyclic discriminant group. By Theorem 4.1, these \(T_w\) are isomorphic to \(K_{d'}^{\perp }\).
Consider \(w_{0,1}=\tfrac{1}{7}(e_1+\ell _{14}'/14)\) and \(w_{1,3}=\tfrac{1}{7}(e_1+f_1+3\ell _{14}'/14)\). By Proposition 3.1, \({{\,\mathrm{Disc}\,}}T_{w_{0,1}}\) and \({{\,\mathrm{Disc}\,}}T_{w_{1,3}}\) are both cyclic. By the above, we have \(T_{w_{0,1}}\cong T_{w_{1,3}}\cong K_{14\cdot 7^2}^{\perp }\). We show that \([w_{0,1}]\not \equiv [w_{1,3}]\) in 
.
Namely, suppose \([w_{1,3}]\) lies in the orbit 
. Then there exists 
such that \(f_7(w_{0,1})=w_{1,3}+z\) for some \(f\in {\widetilde{{{\,\mathrm{O}\,}}}}(\varLambda _{14})\), that is, \(f(14\cdot 7w_{0,1}) = 14\cdot 7( w_{1,3}+z)\). Write \(z=z_0+\tfrac{t}{14}\ell _{14}'\) for some \(z_0\in E_8(-1)^{\oplus 2}\oplus U_1\oplus U_2\) and \(t\in {\mathbb {Z}}\), so
The square of the right hand side should be equal to \((14\cdot 7w_{0,1})^2=-14\). This gives
which simplifies to
Reducing modulo 7, one sees that this is not possible.
6.3 Pairs of associated twisted K3 surfaces
In [6], we studied the covering involution of Hassett’s rational map \({{\,\mathrm{M}\,}}_d\dashrightarrow {\mathscr {C}}_d\) in the case this has degree two. We showed that if \((S,L)\in {{\,\mathrm{M}\,}}_d\) is mapped to \((S^{\tau },L^{\tau })\) under this involution, then \(S^{\tau }\) is isomorphic to a moduli space of stable sheaves on S with Mukai vector (3, L, d/6). In this section, we discuss the analogous twisted situation.
We denote the bounded derived category of \(\alpha \)-twisted coherent sheaves on S by \({{\,\mathrm{D^b}\,}}(S,\alpha )\). When \(\alpha \in {{\,\mathrm{Hom}\,}}({{\,\mathrm{H}\,}}^2(S,{\mathbb {Z}})_{{{\,\mathrm{pr}\,}}},{\mathbb {Z}}/r{\mathbb {Z}})\), then by \(\alpha \)-twisted sheaves we mean \(\overline{\alpha }\)-twisted sheaves, where \(\overline{\alpha }\) is the image of \(\alpha \) in \({{\,\mathrm{Hom}\,}}(T(S),{\mathbb {Z}}/r{\mathbb {Z}})={{\,\mathrm{Br}\,}}(S)[r]\). Similarly, \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\) means \({\widetilde{{{\,\mathrm{H}\,}}}}(S,\overline{\alpha },{\mathbb {Z}})\).
Assume that 3 divides \(d'=dr^2\). Hassett showed (see also [6]) that the map \({{\mathscr {D}}(K_{d'}^{\perp })/{\widetilde{{{\,\mathrm{O}\,}}}}(K_{d'}^{\perp })\rightarrow \overline{{\mathscr {C}}}_{d^\prime }}\) is a composition \(\nu \circ f\), where \(\nu \) is the normalization of \(\overline{{\mathscr {C}}}_{d^\prime }\) and f is generically of degree two, induced by an element in \({{\,\mathrm{O}\,}}(K_{d'}^{\perp })\) of order two. The corresponding element \({g\in {{\,\mathrm{O}\,}}(T_w)}\) induces a covering involution
that preserves \({\widetilde{{{\,\mathrm{M}\,}}}}_w\). We claim that g extends to an orthogonal transformation of \({\widetilde{\varLambda }}\). This follows from [22, Corollary 1.5.2] and the following statement. We embed \(T_w\subset \varLambda _d\) primitively into \({\widetilde{\varLambda }}\) using the map \(\exp (w)\), as in Sect. 3.1.
Proposition 5.6
Let \(S_w{:}{=}T_w^{\perp }\subset {\widetilde{\varLambda }}\). The map \({{\,\mathrm{O}\,}}(S_w)\rightarrow {{\,\mathrm{O}\,}}({{\,\mathrm{Disc}\,}}S_w)\) is surjective.
Proof
The lattice \(S_w\) has rank three. When \({{\,\mathrm{Disc}\,}}T_w\cong {{\,\mathrm{Disc}\,}}S_w\) is cyclic, the statement follows from [22, Theorem 1.14.2]. When \({{\,\mathrm{Disc}\,}}T_w\) is \({\mathbb {Z}}/(d'/3){\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}\), it follows from Corollary VIII.7.3 in [21]. \(\square \)
This implies that when \(\tau \) maps \((S,L,\alpha ,f)\in {\widetilde{{{\,\mathrm{M}\,}}}}_w\) to \((S',L',\alpha ',f')\), then there is a Hodge isometry
This map might not preserve the orientation of the four positive directions. However, by [16, Lemma 2.3], there exists an orientation reversing Hodge isometry in \({{\,\mathrm{O}\,}}({\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}}))\). By composing with it, we see that there exists a Hodge isometry \(g:{\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\rightarrow {\widetilde{{{\,\mathrm{H}\,}}}}(S',\alpha ',{\mathbb {Z}})\) which is orientation preserving. By [18], g is induced by a Fourier–Mukai equivalence
for some \({\mathscr {E}}\in {{\,\mathrm{D^b}\,}}(S\times S',\alpha ^{-1}\boxtimes \alpha ')\), that is, the associated cohomological Fourier–Mukai transform \(\varPhi _{{\mathscr {E}}}^H:{\widetilde{{{\,\mathrm{H}\,}}}}(S,\alpha ,{\mathbb {Z}})\rightarrow {\widetilde{{{\,\mathrm{H}\,}}}}(S',\alpha ',{\mathbb {Z}})\) equals g. Now \(S'\) is a moduli space of stable complexes of \(\alpha \)-twisted sheaves on S with Mukai vector
where x is any closed point in \(S'\). It is a coarse moduli space: the universal family on \(S\times S'\) exists as an \(\alpha ^{-1}\boxtimes \alpha '\)-twisted sheaf, which is an untwisted sheaf if and only if \(\alpha '\) is trivial.
In fact, one can show that \(S'\) is isomorphic to a moduli space of stable \(\alpha \)-twisted sheaves on S. Namely, by [26] (see also [18]), there exists a (coarse) moduli space M(v) of stable \(\alpha \)-twisted sheaves on S with Mukai vector v. By precomposing \(\varPhi _{{\mathscr {E}}}\) with autoequivalences of \({{\,\mathrm{D^b}\,}}(S,\alpha )\), we may assume M(v) is non-empty [18, Section 2]. Hence, as \((v)^2=0\), the space M(v) is a K3 surface.
For some B-field \(\beta \in {{\,\mathrm{H}\,}}^2(M(v),{\mathbb {Q}})\), there exists a universal family \({\mathscr {E}}_v\) on \(S\times M(v)\) which is an \(\alpha ^{-1}\boxtimes \beta \)-twisted sheaf. It induces an equivalence of categories \({\varPhi _{{\mathscr {E}}_v}:{{\,\mathrm{D^b}\,}}(S,\alpha )\rightarrow {{\,\mathrm{D^b}\,}}(M(v),\beta )}\) whose associated cohomological Fourier–Mukai transform \(\varPhi _{{\mathscr {E}}_v}^H\) sends v to \({(0,0,1)\in {\widetilde{{{\,\mathrm{H}\,}}}}(M(v),\beta ,{\mathbb {Z}})}\). The composition
is a Hodge isometry that sends (0, 0, 1) to (0, 0, 1) and is orientation preserving, since both \(\varPhi _{{\mathscr {E}}_v}^H\) and \(\varPhi _{{\mathscr {E}}}^H\) are (for \(\varPhi _{{\mathscr {E}}_v}^H\), see [17]). It follows from [18, Section 2] that \(S'\) is isomorphic to M(v).
References
Addington, N., Thomas, R.: Hodge theory and derived categories of cubic fourfolds. Duke Math. J. 163, 1885–1927 (2014)
Baily, W.L., Borel, A.: Compactification of arithmetic quotients of bounded symmetric domains. Ann. Math. 84, 442–528 (1966)
Bayer, A., Lahoz, M., Macrì, M., Nuer, H., Perry, A., Stellari, P.: Stability conditions in families (2019). Preprint, arXiv:1902.08184
Borel, A.: Some metric properties of arithmetic quotients of symmetric spaces and an extension theorem. J. Differ. Geom. 6, 543–560 (1972)
Bosch, S.: Algebra, 7th edn. Springer-Lehrbuch. Springer-Verlag, Berlin Heidelberg (2009)
Brakkee, E.: Two polarized K3 surfaces associated to the same cubic fourfold. Math. Proc. Cambridge Philos. Soc., to appear (2018)
van Geemen, B.: Some remarks on Brauer groups of K3 surfaces. Adv. Math. 197, 222–247 (2005)
Gritsenko, V., Hulek, K., Sankaran, G.: Abelianisation of orthogonal groups and the fundamental group of modular varieties. J. Algebra 322, 463–478 (2009)
Grothendieck, A.: Revêtements étale et groupe fondamental. Lecture notes in mathematics, vol. 224. Springer-Verlag, Berlin Heidelberg (1971)
Hassett, B.: Special cubic fourfolds. Compos. Math. 120, 1–23 (2000)
Hitchin, N.: Generalized Calabi-Yau manifolds. Q. J. Math. 54, 281–308 (2003)
Hosono, S., Lian, B., Oguiso, K., Yau, S.: Fourier–Mukai partners of a K3 surface of Picard number one. In: Vector bundles and representation theory, Contemp. Math., vol. 322, pp. 43–55. Am. Math. Soc., Providence, RI (2003)
Huybrechts, D.: Generalized Calabi-Yau structures, K3 surfaces, and B-fields. Int. J. Math. 16, 13–36 (2005)
Huybrechts, D.: The global Torelli theorem: classical, derived, twisted. In: Algebraic geometry–Seattle 2005. Part 1, Proc. Sympos. Pure Math., vol. 80, Part 1, pp. 235–258. Am. Math. Soc., Providence, RI (2009)
Huybrechts, D.: Lectures on K3 surfaces, Cambridge Studies in Advanced Mathematics, vol. 158. Cambridge University Press, Cambridge (2016)
Huybrechts, D.: The K3 category of a cubic fourfold. Compos. Math. 153, 586–620 (2017)
Huybrechts, D., Stellari, P.: Equivalences of twisted K3 surfaces. Math. Ann. 332, 901–936 (2005)
Huybrechts, D., Stellari, P.: Proof of Cldraru’s conjecture. Appendix to “Moduli spaces of twisted sheaves on a projective variety” by K. Yoshioka. In: Moduli spaces and arithmetic geometry, Adv. Stud. Pure Math., vol. 45, pp. 31–42. Math. Soc. Japan, Tokyo (2006)
Kuznetsov, A.: Derived categories of cubic fourfolds. In: Cohomological and geometric approaches to rationality problems, Progr. Math., vol. 282, pp. 219–243. Birkhäuser Boston, Inc., Boston, MA (2010)
McKinnie, K., Sawon, J., Tanimoto, S., Várilly-Alvarado, A.: Brauer groups on K3 surfaces and arithmetic applications. In: Brauer groups and obstruction problems, Progr. Math., vol. 320, pp. 177–218. Birkhäuser/Springer, Cham (2017)
Miranda, R., Morrison, D.: Embeddings of integral quadratic forms (2009). https://web.math.ucsb.edu/~drm/manuscripts/eiqf.pdf
Nikulin, V.V.: Integer symmetric bilinear forms and some of their applications. Math. USSR Izvestija 14, 103–167 (1980)
Reinecke, E.: Autoequivalences of twisted K3 surfaces. Compos. Math. 155, 912–937 (2019)
Satake, I.: Algebraic structures of symmetric domains. Princeton University Press, Princeton (1980)
Voisin, C.: Théorème de Torelli pour les cubiques de \(\mathbb{P}^5\). Invent. Math. 86, 577–601 (1986)
Yoshioka, K.: Moduli spaces of twisted sheaves on a projective variety. In: Moduli spaces and arithmetic geometry, Adv. Stud. Pure Math., vol. 45, pp. 1–30. Math. Soc. Japan, Tokyo (2006)
Acknowledgements
This work was part of my research as a PhD candidate. I want to thank my advisor Daniel Huybrechts for suggesting the topic and for many helpful discussions. I am also grateful to Thorsten Beckmann, Matthew Dawes and Emmanuel Reinecke for their help, and to Georg Oberdieck for comments on an earlier version. Finally, I would like to thank Tony Várilly-Alvarado for his enthusiasm and insights.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Vasudevan Srinivas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the Bonn International Graduate School of Mathematics and the SFB/TR 45 ‘Periods, Moduli Spaces and Arithmetic of Algebraic Varieties’ of the DFG (German Research Foundation).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brakkee, E. Moduli spaces of twisted K3 surfaces and cubic fourfolds. Math. Ann. 377, 1453–1479 (2020). https://doi.org/10.1007/s00208-020-01990-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-020-01990-x
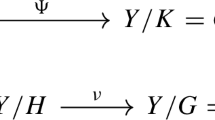
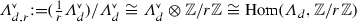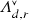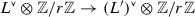