Abstract
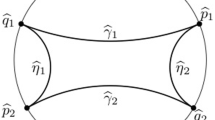
In this paper we study the moduli space of properly Alexandrov-embedded, minimal annuli in \(\mathbb {H}^2 \times \mathbb {R}\) with horizontal ends. We say that the ends are horizontal when they are graphs of \({\mathcal {C}}^{2, \alpha }\) functions over \(\partial _\infty \mathbb {H}^2\). Contrary to expectation, we show that one can not fully prescribe the two boundary curves at infinity, but rather, one can prescribe one of the boundary curves, but the other one only up to a translation and a tilt, along with the position of the neck and the vertical flux of the annulus. We also prove general existence theorems for minimal annuli with discrete groups of symmetries.










Similar content being viewed by others
Notes
The Gauss map is well defined in any Cartan-Hadamard manifold since there is a natural identification of the unit sphere bundle at a point with the sphere at infinity. In the present setting the horizontal equator is also well-defined since it corresponds to the unit normals which have no \({\mathbb {R}}\) component.
A noncompact surface is called area minimizing if any compact domain minimizes the area among all the surfaces with the same boundary.
References
Collin, P., Hauswirth, L., Rosenberg, H.: Properly immersed minimal surface in a slab of \({\mathbb{H}} \times {\mathbb{R}}\), \({\mathbb{H}}\) the hyperbolic plane. Arch. Math. 104, 471–484 (2015)
Coskunuzer, B.: Minimal surfaces with arbitrary topology in \(\mathbb{H}^2 \times \mathbb{R}\). Preprint arXiv:1404.0214
Coskunuzer, B.: Asymptotic Plateau problem in \(\mathbb{H}^2\times \mathbb{R}\). Select. Math. (to appear.)
Daniel, B.: Isometric immersions into \({\mathbb{S}}^n\times {\mathbb{R}}\) and applications to minimal. Trans. AMS 361, 6255–6282 (2009)
Hauswirth, L.: Minimal surfaces of Riemann type in three-dimensional product manifolds. Pac. J. Math. 224, 91–117 (2006)
Hauswirth, L., Menezes, A., Rodríguez, M.: On thecharacterization of minimal surfaces with finite total curvature in \(\mathbb{H}^2\times \mathbb{R}\) and \({\widetilde{PSL}}_2(\mathbb{R},\tau )\). Preprint arXiv:1604.07083
Kloeckner, B., Mazzeo, R.: On the asymptotic behavior of minimal surfaces in \({\mathbb{H}}^2\times {\mathbb{R}}\). Indiana Math J. 66(2), 631–658 (2017)
Martín, F., Mazzeo, R., Rodrí guez, M.: Minimal surfaces with positive genus and finite total curvature in \(\mathbb{H}^2 \times \mathbb{R}\). Geometr. Topol. 18, 141–177 (2014)
Mazet, L., Rodríguez, M., Rosenberg, H.: Periodic constant mean curvature surfaces in \({\mathbb{H}}^2 \times {\mathbb{R}}\). Asian J. Math. 18(5), 829–858 (2014)
Mazzeo, R.: Elliptic theory of differential edge operators. I. Commun. Part. Differ. Eq. 16, 1616–1664 (1991)
Mazzeo, R., Pacard, F.: Constant mean curvature surfaces with Delaunay ends. Commun. Anal. Geom. 9(1), 169–237 (2001)
Morabito, F.: A Costa-Hoffman-Meeks type surface in \({\mathbb{H}}^2\times {\mathbb{R}}\). Trans. Am. Math. Soc. 363(1), 1–36 (2011)
Nelli, B., Rosenberg, H.: Minimal surfaces in \(\mathbb{H}^2\times \mathbb{R}\). Bull. Br. Math. Soc. (N.S.) 33(2), 263–292 (2002). Errata: Bull. Br. Math. Soc. (N.S.) 38(4), 661–664 (2007)
Nelli, B., Sa Earp, R., Toubiana, E.: Maximum principle and symmetry for minimal hypersurfaces in \(\mathbb{H}^n \times \mathbb{R}\). Ann. Sci. Norm. Super. Pisa Cl. Sci. (5) XIV, 387–400 (2015)
Sa Earp, R., Toubiana, E.: Screw motion surfaces in \({\mathbb{S}}^2 \times {\mathbb{R}}\) and \({\mathbb{H}}^2 \times {\mathbb{R}}\). Illinois J. Math. 49(4), 1323–1362 (2005)
Sa Earp, R., Toubiana, E.: An asymptotic theorem for minimal surfaces and existence results for minimal graphs in \({\mathbb{H}}^2 \times {\mathbb{R}}\). Math. Ann. 342(2), 309–331 (2008)
Mo, X., Osserman, R.: On the Gauss map and total curvature of complete minimal surfaces and an extension of Fujimoto’s theorem. J. Differ. Geom. 31(2), 343–355 (1990)
White, B.: The space of \(m\)-dimensional surfaces that are stationary for a parametric elliptic functional. Indiana Univ. Math. J. 36(3), 567–602 (1987)
White, B.: Controlling area blow-up in minimal or bounded mean curvature varieties. J. Differ. Geom. 102(3), 501–535 (2016)
White, B.: On the compactness theorem for embedded minimal surfaces in 3-manifolds with locally bounded area and genus. Commun. Anal. Geom. 26(3), 659–678 (2018)
Acknowledgements
We thank B. White, J. Pérez and A. Ros for valuable conversations and suggestions. L. Ferrer and F. Martín are very grateful to the Mathematics Department of Stanford University for its hospitality during part of the time the research and preparation of this article were conducted. R. Mazzeo is also very grateful to the Institute of Mathematics at the University of Granada for sponsoring a visit where this work started. Finally, we would like to thank the anonymous referee for many helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by F. C. Marques.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
L. Ferrer, F. Martín and M. M. Rodríguez are partially supported by the MINECO/FEDER Grant MTM2014-52368-P and MTM2017-89677-P; R. Mazzeo supported by the NSF Grant DMS-1105050 and DMS-1608223; F. Martin is also partially supported by the Leverhulme Trust Grant IN-2016-019.
Appendix A: Two tall rectangles are not area-minimizing
Appendix A: Two tall rectangles are not area-minimizing
The purpose of this appendix is to prove that a couple of tall rectangles in \(\mathbb {H}^2 \times \mathbb {R}\) of the same height with the vertical segments in common are not an area-minimizing surface. Recall that for a complete surface area-minimizing means that any compact piece minimizes the area among all the surfaces with the same boundary. To prove this, we are going to see that, in general, a couple of horizontal disks connected by vertical totally geodesic planes near infinity (see Fig. 11) are better competitors for the area functional.
The simplest analytic representation of these surfaces is obtained using the upper half-space model for \(\mathbb {H}^2\). Thus we use standard coordinates \((x,y) \in \mathbb {H}^2\) with \(y > 0\), and hence coordinates (x, y, t) on \(\mathbb {H}^2 \times {\mathbb {R}}\). We shall place the vertical segments of the tall rectangles over the points (0, 0) and infinity. For a given \(r >0\) we denote \(\Gamma _r\) the geodesic in \(\mathbb {H}^2\) with end points (r, 0) and \((-r,0)\). Let \(P_r:=\Gamma _r \times \mathbb {R}\) be the corresponding totally geodesic plane. For simplicity we will write \(\Gamma =\Gamma _1\) and \(P=P_1\). Finally, we denote \(\Lambda \) as the geodesic given by \(\{x=0, y>0\}\). The point in the intersection \(\Gamma \cap \Lambda \) is denoted by \(o=(0,1)\).
On the geodesic \(\Gamma \) we consider \(\rho \) the signed distance to the point o. Then the induced metric in P is given by \(d \rho ^2 +dt^2.\) We write a curve in P in coordinates \((\rho ,t)\) of the form
If we impose that the surface generated by horizontal translations along the geodesic \(\Lambda \) of the above curve is minimal, then we get (see [16, page 316]) that the function \(\lambda (\rho )\) satisfies the equation
If \(d>1\) we have
We parametrize \(\Gamma \) as \(\theta \mapsto \mathrm{e}^{\mathrm{i}\theta },\)\(\theta \in (0,\pi ).\) Then it is straightforward to check that
Combining the above expression and (A.1) then we obtain:
and
So the upper half part of the tall rectangle is given by the parametrization
The lower half part is parametrized by \((r,\theta ) \mapsto (r \cos (\theta ), r \sin (\theta ),- \lambda (\theta )).\) Let \(R_1\) be the complete tall rectangle described above.
The height of the tall rectangle \(R_1\) is given by \(2 \lambda (0) >\pi \). Moreover, notice that the intersection of the tall rectangle with the slice \(t=\lambda (\theta )\) consists of the straight line \(\{ r \mathrm{e}^{\mathrm{i} \theta } \; : \; r>0\}.\)
Let \(R_2\) be the tall rectangle obtained from \(R_1\) applying the symmetry \((x,y,t) \mapsto (-x,y,t).\)
Fix \(r \in (0,1)\) and \(\theta \in (0,\theta _0)\). We consider the two horizontal slices, \(S_{\lambda (\theta )}\) and \(S_{-\lambda (\theta )}\), at height \(\lambda (\theta )\) and \(- \lambda (\theta )\), respectively, and the two vertical planes \(P_r\) and \(P_{1/r}.\) We cut the tall rectangles \(R_1 \cup R_2\) with the union
The resulting curve is a compact curve in \(R_1 \cup R_2\) with two connected components: \(\beta _i \subset R_i\), \(i=1,2.\) These two curves are symmetric with respect to the plane \(x=0\). Let \(\Sigma _i\) the disk in \(R_i\) spanned by \(\beta _i\), \(i=1,2\). Observe that \(\Sigma _i\) is a symmetric bi-graph over the annular sector \(\Delta _i\) (see Fig. 12). Moreover we will denote:
-
\(D_1=\{ (u \cdot \mathrm{e}^{\mathrm{i} v}, \lambda (\theta )) \; : \; (u,v) \in (r,1/r) \times (\theta ,\pi -\theta )\}.\)
-
\(D_2=\{ (u \cdot \mathrm{e}^{\mathrm{i} v} , - \lambda (\theta )) \; : \; (u,v) \in (r,1/r) \times (\theta ,\pi -\theta )\}.\)
-
\(B_1\) the region of \(P_r\) bounded by \(\beta _1 \cup \beta _2\) and the curves \(D_1 \cap P_r\) and \(D_2 \cap P_r\).
-
\(B_2\) the region of \(P_{1/r}\) bounded by \(\beta _1 \cup \beta _2\) and the curves \(D_1 \cap P_{1/r}\) and \(D_2 \cap P_{1/r}\).
We want to prove that
Lemma A.1
The area of the region \(D_1 \cup D_2 \cup B_1 \cup B_2\) is smaller than the area of \(\Sigma _1 \cup \Sigma _2\). In particular, \(R_1 \cup R_2\) is not area-minimizing.
Proof
By the symmety of the surface it is enough to prove that for some \(\theta \) and r
From (A.4) it is not difficult to see that
where E and F are the classical elliptic functions given by
Similarly, we have
Finally, observe that \(Area(B_1)\) is less than the area of the region in \(P_r\) given by
So,
Now we take \(r(\theta )=\tan ^n \left( \frac{\theta }{2}\right) \), where \(n \in \mathbb {N}\) will be taken big enough in terms of d. Notice that for this choice of r we have
It is straitforward that
As \(F\left( \theta _0\left| \csc ^2(\theta _0)\right. \right) -E\left( \theta _0\left| \csc ^2(\theta _0)\right. \right) >0\), then
for n big enough. So, we have that for \(\theta \) small enough \(f(\theta )>1\), which proves our lemma. \(\square \)
Rights and permissions
About this article
Cite this article
Ferrer, L., Martín, F., Mazzeo, R. et al. Properly embedded minimal annuli in \(\mathbb {H}^2 \times \mathbb {R}\). Math. Ann. 375, 541–594 (2019). https://doi.org/10.1007/s00208-019-01840-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-019-01840-5