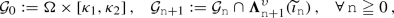Abstract
We prove the first bifurcation result of time quasi-periodic traveling wave solutions for space periodic water waves with vorticity. In particular, we prove the existence of small amplitude time quasi-periodic solutions of the gravity-capillary water waves equations with constant vorticity, for a bidimensional fluid over a flat bottom delimited by a space-periodic free interface. These quasi-periodic solutions exist for all the values of depth, gravity and vorticity, and restrict the surface tension to a Borel set of asymptotically full Lebesgue measure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Result
The search for traveling surface waves in inviscid fluids is a very important problem in fluid mechanics, widely studied since the pioneering work of Stokes [38] in 1847. The existence of steady traveling waves, namely solutions which look stationary in a moving frame, either periodic or localized in space, is nowadays well understood in many different situations, mainly for bidimensional fluids.
On the other hand, the natural question regarding the existence of time quasi-periodic traveling waves – which cannot be reduced to steady solutions in a moving frame – has been not answered so far. This is the goal of the present paper. We consider space periodic waves. Major difficulties in this project concern the presence of “small divisors” and the quasi-linear nature of the equations. Related difficulties appear in the search of time periodic standing waves which have been constructed in the last few years in a series of papers by Iooss, Plotnikov, Toland [22, 23, 25, 34] for pure gravity waves, by Alazard-Baldi [1] in presence of surface tension and subsequently extended to time quasi-periodic standing waves solutions by Berti-Montalto [6] and Baldi-Berti-Haus-Montalto [2]. Standing waves are not traveling as they are even in the space variable. We also mention that all these recent results concern irrotational fluids.
In this paper we prove the first existence result of time quasi-periodic traveling wave solutions for the gravity-capillary water waves equations with constant vorticity for bidimensional fluids. The small amplitude solutions that we construct exist for any value of the vorticity (so also for irrotational fluids), any value of the gravity and depth of the fluid, and provided the surface tension is restricted to a Borel set of asymptotically full measure, see Theorem 1.5. For irrotational fluids the traveling wave solutions that we construct do not clearly reduce to the standing wave solutions in [6]. We remark that, in case of non zero vorticity, one cannot expect the bifurcation of standing waves since they are not allowed by the linear theory.
Before presenting in detail our main result, we introduce the water waves equations.
The water waves equations. We consider the Euler equations of hydrodynamics for a 2-dimensional perfect, incompressible, inviscid fluid with constant vorticity \(\gamma \), under the action of gravity and capillary forces at the free surface. The fluid fills an ocean with depth \(\mathtt{h}> 0 \) (eventually infinite) and with space periodic boundary conditions, namely it occupies the region
The unknowns of the problem are the divergence free velocity field \(\begin{pmatrix} u(t,x,y) \\ v(t,x,y) \end{pmatrix} \), which solves the Euler equation and the free surface \( y = \eta (t, x)\) of the time dependent domain \(\mathcal {D}_{\eta ,\mathtt{h}} \). In case of a fluid with constant vorticity
the velocity field is the sum of the Couette flow \(\begin{pmatrix} - \gamma y \\ 0 \end{pmatrix}\), which carries all the vorticity \( \gamma \) of the fluid, and an irrotational field, expressed as the gradient of a harmonic function \(\Phi \), called the generalized velocity potential.
Denoting by \(\psi (t,x)\) the evaluation of the generalized velocity potential at the free interface \( \psi (t,x) := \Phi (t,x, \eta (t,x)) \), one recovers \( \Phi \) by solving the elliptic problem
The third condition in (1.2) means the impermeability property of the bottom
Imposing that the fluid particles at the free surface remain on it along the evolution (kinematic boundary condition), and that the pressure of the fluid plus the capillary forces at the free surface is equal to the constant atmospheric pressure (dynamic boundary condition), the time evolution of the fluid is determined by the following system of equations (see [8, 42]):
Here g is the gravity, \( \kappa \) is the surface tension coefficient, which we assume to belong to an interval \( [\kappa _1, \kappa _2] \) with \( \kappa _1 > 0 \), and \(G(\eta )\) is the Dirichlet-Neumann operator
The water waves equations (1.3) are a Hamiltonian system that we describe in Section 2.1, and enjoy two important symmetries. First, they are time reversible: we say that a solution of (1.3) is reversible if
Second, since the bottom of the fluid domain is flat, the equations (1.3) are invariant by space translations. We refer to Section 2.1 for more details.
Let us comment shortly about the phase space of (1.3). As \( G(\eta )\psi \) is a function with zero average, the quantity \(\int _\mathbb {T}\eta (x) \, {\mathrm{d}}x\) is a prime integral of (1.3). Thus, with no loss of generality, we restrict to interfaces with zero spatial average \( \int _\mathbb {T}\eta (x) \, {\mathrm{d}}x = 0 \). Moreover, since \( G(\eta ) [1] = 0 \), the vector field on the right hand side of (1.4) depends only on \( \eta \) and \( \psi - \frac{1}{2 \pi }\int _\mathbb {T}\psi \, {\mathrm{d}}x \). As a consequence, the variables \( (\eta , \psi ) \) of system (1.3) belong to some Sobolev space \( H^s_0(\mathbb {T}) \times \dot{H}^s (\mathbb {T}) \) for some s large. Here \(H^s_0(\mathbb {T})\), \(s \in \mathbb {R}\), denotes the Sobolev space of functions with zero average
and \(\dot{H}^s(\mathbb {T})\), \(s \in \mathbb {R}\), the corresponding homogeneous Sobolev space, namely the quotient space obtained by identifying all the \(H^s(\mathbb {T})\) functions which differ only by a constant. For simplicity of notation we shall denote the equivalent class \( [\psi ] = \{ \psi + c, c \in \mathbb {R}\} \), just by \( \psi \).
Linear water waves. When looking to small amplitude solutions of (1.3), a fundamental role is played by the system obtained linearizing (1.3) at the equilibrium \((\eta , \psi ) = (0,0)\), namely
The Dirichlet-Neumann operator at the flat surface \(\eta = 0\) is the Fourier multiplier
with the symbol
As we will show in Section 2.2, all reversible solutions (see (1.5)) of (1.6) are
where \(\rho _n\geqq 0\) are arbitrary amplitudes and \(M_n\) and \(P_{\pm n}\) are the real coefficients
Note that the map \( j \mapsto M_j\) is even. The frequencies \(\Omega _{\pm n}(\kappa )\) in (1.9) are
Note that the map \( j \mapsto \Omega _j (\kappa )\) is not even due to the vorticity term \( \gamma G_j (0) / j \), which is odd in j. Note that \(\Omega _j(\kappa ) \) actually depends also on the depth \( \mathtt{h}\), the gravity g and the vorticity \( \gamma \), but we highlight in (1.11) only its dependence with respect to the surface tension coefficient \( \kappa \), since in this paper we shall move just \( \kappa \) as a parameter to impose suitable non-resonance conditions; see Theorem 1.5. Other choices are possible.
All the linear solutions (1.9), depending on the irrationality properties of the frequencies \( \Omega _{\pm n} (\kappa ) \) and the number of non zero amplitudes \(\rho _{\pm n} > 0 \), are either time periodic, quasi-periodic or almost-periodic. Note that the functions (1.9) are the linear superposition of plane waves traveling either to the right or to the left.
Remark 1.1
Actually, (1.9) contains also standing waves, for example when the vorticity \(\gamma = 0\) (which implies \( \Omega _{-n}(\kappa ) = \Omega _n(\kappa ) \), \( P_{-n} = - P_n\)) and \( \rho _{-n} = \rho _n \), giving solutions even in x. This is the well known superposition effect of waves with the same amplitude, frequency and wavelength traveling in opposite directions.
Main result. We first provide the notion of quasi-periodic traveling wave.
Definition 1.2
(Quasi-periodic traveling wave) We say that \( (\eta (t,x), \psi (t,x)) \) is a time quasi-periodic traveling wave with irrational frequency vector \( \omega = ( \omega _1, \ldots , \omega _\nu ) \in \mathbb {R}^\nu \), \( \nu \in \mathbb {N}\), that is \( \omega \cdot \ell \ne 0 \), \( \forall \ell \in \mathbb {Z}^\nu {\setminus } \{0 \} \), and “wave vectors” \( ( j_1, \ldots , j_\nu ) \in \mathbb {Z}^\nu \), if there exist functions \( ( \breve{\eta }, \breve{\psi }) : \mathbb {T}^\nu \rightarrow \mathbb {R}^2 \) such that
Remark 1.3
If \( \nu = 1 \), such functions are time periodic and indeed stationary in a moving frame with speed \( \omega _1 / j_1 \). On the other hand, if the number of frequencies \( \nu \) is \( \geqq 2 \), the waves (1.12) cannot be reduced to steady waves by any appropriate choice of the moving frame.
In this paper we shall construct traveling quasi-periodic solutions of (1.3) with a diophantine frequency vector \( \omega \) belonging to an open bounded subset  in \( \mathbb {R}^\nu \), namely, for some \( \upsilon \in (0,1) \), \( \tau > \nu - 1 \), with
in \( \mathbb {R}^\nu \), namely, for some \( \upsilon \in (0,1) \), \( \tau > \nu - 1 \), with  ,
,

Regarding regularity, we will prove the existence of quasi-periodic traveling waves \( (\breve{\eta }, \breve{\psi }) \) belonging to some Sobolev space
Fixed finitely many arbitrary distinct natural numbers
and signs
consider the reversible quasi-periodic traveling wave solutions of the linear system (1.6) given by
where \( \xi _{\pm \overline{n}_a} > 0 \), \( a = 1, \ldots , \nu \). The frequency vector of (1.17) is
Remark 1.4
If \(\sigma _a = +1\), we select in (1.17) a right traveling wave, whereas, if \(\sigma _a = -1\), a left traveling one. By (1.15), the linear solutions (1.17) are genuinely traveling waves: superposition of identical waves traveling in opposite direction, generating standing waves, does not happen.
The main result of this paper proves that the linear solutions (1.17) can be continued to quasi-periodic traveling wave solutions of the nonlinear water waves equations (1.3), for most values of the surface tension \( \kappa \in [\kappa _1, \kappa _2 ]\), with a frequency vector \( \widetilde{\Omega } := ( \widetilde{\Omega }_{\sigma _a \overline{n}_a})_{a=1, \ldots , \nu } \), close to \( \vec {\Omega } (\kappa ) := (\Omega _{\sigma _a \overline{n}_a} (\kappa ))_{a =1, \ldots , \nu } \). Here is the precise statement:
Theorem 1.5
(KAM for traveling gravity-capillary water waves with constant vorticity) Consider finitely many tangential sites \( \mathbb {S}^+ \subset \mathbb {N}\) as in (1.15) and signs \( \Sigma \) as in (1.16). Then there exist \( \overline{s} > 0 \), \( \varepsilon _0 \in (0,1) \) such that, for every \( |\xi | \leqq \varepsilon _0^2 \), \( \xi := (\xi _{ \sigma _a {\overline{n}}_a} )_{a = 1, \ldots , \nu } \in \mathbb {R}_+^\nu \), the following hold:
-
1.
there exists a Cantor-like set \( \mathcal{G}_\xi \subset [\kappa _1, \kappa _2] \) with asymptotically full measure as \( \xi \rightarrow 0 \), that is \( \lim _{\xi \rightarrow 0} | \mathcal{G}_\xi | = {\kappa }_2- {\kappa }_1 \);
-
2.
for any \( \kappa \in \mathcal{G}_\xi \), the gravity-capillary water waves equations (1.3) have a reversible quasi-periodic traveling wave solution (according to Definition 1.2) of the form
$$\begin{aligned} \begin{aligned}&\begin{pmatrix} \eta ( t ,x) \\ \psi ( t ,x) \end{pmatrix} = \sum _{a \in \{1, \ldots , \nu \} :\sigma _a = + 1} \begin{pmatrix} M_{\overline{n}_a} \sqrt{\xi _{\overline{n}_a}} \cos ( \overline{n}_a x - \widetilde{\Omega }_{ \overline{n}_a} t) \\ P_{\overline{n}_a} \sqrt{\xi _{\overline{n}_a}} \sin ( \overline{n}_a x - \widetilde{\Omega }_{\overline{n}_a} t) \end{pmatrix} \\&\ \ \ \ + \sum _{a \in \{1, \ldots , \nu \} :\sigma _a = - 1} \begin{pmatrix} M_{\overline{n}_a} \sqrt{\xi _{- \overline{n}_a}} \cos ( \overline{n}_a x + \widetilde{\Omega }_{-\overline{n}_a} t) \\ P_{-\overline{n}_a} \sqrt{\xi _{- \overline{n}_a}} \sin ( \overline{n}_a x + \widetilde{\Omega }_{-\overline{n}_a} t) \end{pmatrix} + r ( t, x ) \end{aligned} \end{aligned}$$(1.19)where, for some \( \breve{r} \in H^{\overline{s}} ( \mathbb {T}^\nu , \mathbb {R}^2)\),
$$\begin{aligned} r ( t, x ) = \breve{r}({\widetilde{\Omega }}_{\sigma _1 \overline{n}_1}t-\sigma _1\overline{n}_1 x,\ldots , {\widetilde{\Omega }}_{\sigma _\nu \overline{n}_\nu }t-\sigma _\nu \overline{n}_\nu x) , \quad \lim _{\xi \rightarrow 0} \frac{\Vert \breve{r} \Vert _{\overline{s}}}{\sqrt{|\xi |}} = 0 \, , \end{aligned}$$with a Diophantine frequency vector \( \widetilde{\Omega } := ( \widetilde{\Omega }_{\sigma _a \overline{n}_a})_{a=1, \ldots , \nu } \in \mathbb {R}^\nu \), depending on \(\kappa , \xi \), and satisfying \( \lim _{\xi \rightarrow 0}{\widetilde{\Omega }} = \vec {\Omega } (\kappa ) \). In addition these quasi-periodic solutions are linearly stable.
Let us make some comments.
-
1)
Theorem 1.5 holds for any value of the vorticity \(\gamma \), so in particular it guarantees existence of quasi-periodic traveling waves also for irrotational fluids, that is \(\gamma =0\). In this case the solutions (1.19) do not reduce to those in [6], which are standing, that is even in x. If the vorticity \( \gamma \ne 0 \), one does not expect the existence of standing wave solutions since the water waves vector field (1.3) does not leave invariant the subspace of functions even in x.
-
2)
Theorem 1.5 produces time quasi-periodic solutions of the Euler equation with a velocity field which is a small perturbation of the Couette flow \(\begin{pmatrix} -\gamma y \\ 0 \end{pmatrix}\). Indeed, from the solution \( (\eta (t, x), \psi (t, x))\) in (1.19), one recovers the generalized velocity potential \(\Phi (t, x,y)\) by solving the elliptic problem (1.2) and finally constructs the velocity field \( \begin{pmatrix} u(t,x,y) \\ v(t,x,y) \end{pmatrix} = \begin{pmatrix} -\gamma y\\ 0 \end{pmatrix} + \nabla \Phi (t,x,y)\). The time quasi-periodic potential \(\Phi (t, x,y)\) has size \(O(\sqrt{|\xi |})\), as \(\eta (t,x)\) and \(\psi (t,x)\).
-
3)
In the case \( \nu = 1 \) the solutions constructed in Theorem 1.5 reduce to steady periodic traveling waves, which can be obtained by an application of the Crandall-Rabinowitz theorem, see for example [30, 41, 43].
-
4)
Theorem 1.5 selects initial data giving raise to global in time solutions (1.19) of the water waves equations (1.3). So far, no results about global existence for (1.3) with periodic boundary conditions are known. The available results concern local well posedness with a general vorticity, see for example [10], and a \( \varepsilon ^{-2} \) existence for initial data of size \( \varepsilon \) in the case of constant vorticity [21].
-
5)
With the choice (1.15)–(1.16) the unperturbed frequency vector \( \vec {\Omega } (\kappa ) = (\Omega _{\sigma _a \overline{n}_a} (\kappa ) )_{a = 1, \ldots , \nu } \) is diophantine for most values of the surface tension \( \kappa \) and for all values of vorticity, gravity and depth. It follows by the more general results of Sections 4 and 5.2. This may not be true for an arbitrary choice of the linear frequencies \( \Omega _{j}(\kappa ) \), \( {j \in \mathbb {Z}{\setminus }\{0\}}\). For example, in the case \( \mathtt{h}= + \infty \), the vector
$$\begin{aligned} \vec {\Omega }(\kappa ) = \big ( \Omega _{-n_3}(\kappa ), \Omega _{-n_2}(\kappa ), \Omega _{-n_1}(\kappa ), \Omega _{n_1}(\kappa ), \Omega _{n_2}(\kappa ), \Omega _{n_3}(\kappa ) \big ) \end{aligned}$$is resonant, for all the values of \( \kappa \), also taking into account the restrictions on the indexes for the search of traveling waves, see Section 3.4. Indeed, recalling (1.11) and that, for \( \mathtt{h}= + \infty \), \( G_j (0, \mathtt{h}) = |j| \), we have, for \( \ell = \big ( - \ell _{n_3}, - \ell _{n_2}, - \ell _{n_1}, \ell _{n_1}, \ell _{n_2}, \ell _{n_3} \big ) \) that the system
$$\begin{aligned} \vec {\Omega }(\kappa ) \cdot \vec {\ell } = \gamma ( \ell _{n_1} + \ell _{n_2} + \ell _{n_3} ) = 0 \, , \quad n_1 \ell _{n_1} + n_2 \ell _{n_2} + n_3 \ell _{n_3} = 0 \, , \end{aligned}$$has integer solutions. In this case the possible existence of quasi-periodic solutions of the water waves system (1.3) depends on the frequency modulation induced by the nonlinear terms.
-
6)
Comparison with [6]. There are significant differences with respect to [6], which proves the existence of quasi-periodic standing waves for irrotational fluids, not only in the result – the solutions of Theorem 1.5 are traveling waves of fluids with constant vorticity – but also in the techniques.
-
(1)
The first difference –which is a novelty of this paper– is a new formulation of degenerate KAM theory exploiting the “momentum conservation”, namely the space invariance of the Hamilton equations. The degenerate KAM theory approach for PDEs has been developed in [3], and then [2, 6], in order to prove the non-trivial dependence of the linear frequencies with respect to a parameter –in our case the surface tension \( \kappa \)–, see the “Transversality” Proposition 4.5. A key assumption used in [2, 3, 6] is that the linear frequencies are simple (because of Dirichlet boundary conditions in [3] and Neumann boundary conditions in [2, 6]). This is not true for traveling waves (for example in case of zero vorticity one has \(\Omega _j(\kappa ) = \Omega _{-j}(\kappa )\) identically in \(\kappa \)). In order to deal with these resonances we strongly exploit the invariance of the equations (1.3) under space translations, which ultimately imply the restrictions to the indexes (4.8)–(4.10). In this way, assuming that the moduli of the tangential sites are all different as in (1.15), cfr. with item 5), we can remove some otherwise possibly degenerate case. This requires us to keep track along all of the proof of the “momentum conservation property” that we characterize in different ways in Section 3.4. The momentum conservation law has been used in several KAM results for semilinear PDEs since the works [16, 17, 28, 35]; see also [15, 20, 31] and references therein. The present paper gives a new application in the context of degenerate KAM theory (with additional difficulties arising by the quasi-linear nature of the water waves equations).
-
(2)
Other significant differences with respect to [6] arise in the reduction in orders (Section 7) of the quasi-periodic linear operators obtained along the Nash–Moser iteration. In particular, we mention that we have to preserve the Hamiltonian nature of these operators (at least until Section 7.4). Otherwise it would appear a time dependent operator at the order \( |D|^{1/2} \), of the form \( {\mathrm{i}}a({\varphi }) \mathcal{H} |D|^{\frac{1}{2}} \), with \( a({\varphi }) \in \mathbb {R}\) independent of x, compatible with the reversible structure, which can not be eliminated. Note that the operator \( {\mathrm{i}}a({\varphi }) \mathcal{H} |D|^{\frac{1}{2}} \) is not Hamiltonian (unless \( a({\varphi }) = 0 \)). Note also that the above difficulty was not present in [6] dealing with standing waves, because an operator of the form \( {\mathrm{i}}a({\varphi }) \mathcal{H} |D|^{\frac{1}{2}} \) does not map even functions into even functions. In order to overcome this difficulty we have to perform always symplectic changes of variables (at least until Section 7.4), and not just reversible ones as in [2, 6]. We finally mention that we perform as a first step in Section 7.1 a quasi-periodic time reparametrization to avoid otherwise a technical difficulty in the conjugation of the remainders obtained by the Egorov theorem in Section 7.3. This difficulty was not present in [6], since it arises conjugating the additional pseudodifferential term due to vorticity, see Remark 7.5.
-
7)
Another novelty of our result is to exploit the momentum conservation also to prove that the obtained quasi-periodic solutions are indeed quasi-periodic traveling waves, according to Definition 1.2. This requires checking that the approximate solutions constructed along the Nash–Moser iteration of Section 9 (and Section 6) are indeed traveling waves. Actually this approach shows that the preservation of the momentum condition along the Nash–Moser-KAM iteration is equivalent to the construction of embedded invariant tori which support quasi-periodic traveling waves, namely of the form \( u({\varphi },x) = U({\varphi }-\vec {\jmath }x) \) (see Definition 3.1), or equivalently, in action-angle-normal variables, which satisfy (3.52). We expect that this method can be used to obtain quasi-periodic traveling waves for other PDE’s which are translation invariant.
Literature. We now shortly describe the literature regarding the existence of time periodic or quasi-periodic solutions of the water waves equations, focusing on the results more related to Theorem 1.5. We describes only results concerning space periodic waves, that we divide in three distinct groups:
-
(i) steady traveling solutions,
-
(ii) time periodic standing waves,
-
(iii) time quasi-periodic standing waves.
This distinction takes into account not only the different shapes of the waves, but also the techniques for their construction.
(i) Time and space periodic traveling waves which are steady in a moving frame. The literature concerning steady traveling wave solutions is huge, and we refer to [7] for an extended presentation. Here we only mention that, after the pioneering work of Stokes [38], the first rigorous construction of small amplitude space periodic steady traveling waves goes back to the 1920s with the papers of Nekrasov [33], Levi-Civita [27] and Struik [39], in case of irrotational bidimensional flows under the action of pure gravity. Later Zeidler [47] considered the effect of capillarity. In the presence of vorticity, the first result is due to Gerstner [18] in 1802, who gave an explicit example of periodic traveling wave, in infinite depth, and with a particular non-zero vorticity. One has to await the work of Dubreil-Jacotin [14] in 1934 for the first existence results of small amplitude, periodic traveling waves with general (Hölder continuous, small) vorticity, and, later, the works of Goyon [19] and Zeidler [48] in the case of large vorticity. More recently we point out the works of Wahlén [41] for capillary-gravity waves and non-constant vorticity, and of Martin [30] and Walhén [42] for constant vorticity. All these results deal with 2d water waves and can ultimately be deduced by the Crandall-Rabinowitz bifurcation theorem from a simple eigenvalue.
We also mention that these local bifurcation results can be extended to global branches of steady traveling waves by applying the methods of global bifurcation theory. We refer to Keady-Norbury [29], Toland [40], McLeod [32] for irrotational flows and Constantin-Strauss [9] for fluids with non-constant vorticity.
In the case of three dimensional irrotational fluids, bifurcation of small amplitude traveling waves periodic in space has been proved in Reeder-Shinbrot [36], Craig-Nicholls [11, 12] for both gravity-capillary waves (by variational bifurcation arguments a la Weinstein-Moser) and by Iooss-Plotnikov [23, 24] for gravity waves (this is a small divisor problem). These solutions, in a moving frame, look steady bi-periodic waves.
(ii) Time periodic standing waves. Bifurcation of time periodic standing water waves were obtained in a series of pioneering papers by Iooss, Plotnikov and Toland [22, 23, 25, 34] for pure gravity waves, and by Alazard-Baldi [1] for gravity-capillary fluids. Standing waves are even in the space variable and so they do not travel in space. There is a huge difference with the results of the first group: the construction of time periodic standing waves involves small divisors. Thus the proof is based on Nash–Moser implicit function techniques and not only on the classical implicit function theorem.
(iii) Time quasi-periodic standing waves. The first results in this direction were obtained very recently by Berti-Montalto [6] for the gravity-capillary system and by Baldi-Berti-Haus-Montalto [2] for the gravity water waves. Both papers deal with irrotational fluids.
We finally mention the very recent numerical works of Wilkening-Zhao [44, 45] about spatially quasi-periodic gravity-capillary 1d-water waves. In particular, the analysis in [45] is complementary to Theorem 1.5; the solutions (1.19) are time-quasi-periodic traveling waves on a spatially periodic domain, whereas [45] concerns pure traveling waves with multiple spatial periods.
2 Hamiltonian Structure and Linearization at the Origin
In this section we describe the Hamiltonian structure of the water waves equations (1.3), their symmetries and the solutions of the linearized system (1.6) at the equilibrium.
2.1 Hamiltonian Structure
The Hamiltonian formulation of the water waves equations (1.3) with non-zero constant vorticity was obtained by Constantin-Ivanov-Prodanov [8] and Wahlén [42] in the case of finite depth. For irrotational flows it reduces to the classical Craig-Sulem-Zakharov formulation in [13, 46].
On the phase space \(H^1_0(\mathbb {T}) \times \dot{H}^1(\mathbb {T})\), endowed with the non canonical Poisson tensor
we consider the Hamiltonian
Such Hamiltonian is well defined on \( H^1_0(\mathbb {T}) \times \dot{H}^1(\mathbb {T}) \) since \( G(\eta ) [1] = 0 \) and \( \int _{\mathbb {T}} G(\eta ) \psi \, {\mathrm{d}}x = 0 \).
It turns out [8, 42] that equations (1.3) are the Hamiltonian system generated by \(H(\eta , \psi )\) with respect to the Poisson tensor \(J_M(\gamma )\), namely
where \( (\nabla _\eta H, \nabla _\psi H) \in \dot{L}^2(\mathbb {T}) \times L^2_0(\mathbb {T}) \) denote the \( L^2 \)-gradients.
Remark 2.1
The non canonical Poisson tensor \(J_M(\gamma )\) in (2.1) has to be regarded as an operator from (subspaces of) \((L_0^2\times \dot{L}^2)^* = \dot{L}^2\times L_0^2\) to \(L_0^2\times \dot{L}^2\), that is
The operator \( \partial _x^{-1} \) maps a dense subspace of \( L^2_0 \) in \( \dot{L}^2 \). For sake of simplicity, throughout the paper we may omit this detail. Above the dual space \((L_0^2\times \dot{L}^2)^* \) with respect to the scalar product in \(L^2\) is identified with \( \dot{L}^2\times L_0^2 \).
The Hamiltonian (2.2) enjoys several symmetries which we now describe.
Reversible structure. Defining on the phase space \(H_0^1(\mathbb {T}) \times \dot{H}^1(\mathbb {T})\) the involution
the Hamiltonian (2.2) is invariant under \(\mathcal {S}\); that is
or, equivalently, the water waves vector field X defined in the right hand side on (1.3) satisfies
This property follows, noting that the Dirichlet-Neumann operator satisfies
Translation invariance. Since the bottom of the fluid domain (1.1) is flat (or in case of infinite depth there is no bottom), the water waves equations (1.3) are invariant under space translations. Specifically, defining the translation operator
the Hamiltonian (2.2) satisfies \( H \circ \tau _\varsigma = H \) for any \(\varsigma \in \mathbb {R}\), or, equivalently, the water waves vector field X defined in the right hand side on (1.3) satisfies
In order to verify this property, note that the Dirichlet-Neumann operator satisfies
Wahlén coordinates. The variables \((\eta , \psi )\) are not Darboux coordinates, in the sense that the Poisson tensor (2.1) is not the canonical one for values of the vorticity \(\gamma \ne 0\). Wahlén [42] noted that in the variables \((\eta , \zeta )\), where \(\zeta \) is defined by
the symplectic form induced by \(J_M(\gamma )\) becomes the canonical one. Indeed, under the linear transformation of the phase space \(H^1_0 \times \dot{H}^1 \) into itself defined by
the Poisson tensor \( J_M(\gamma )\) is transformed into the canonical one,
Here \( W^* \) and \( (W^{-1})^*\) are the adjoints maps from (a dense subspace of) \( \dot{L}^2 \times L^2_0 \) into itself, and the Poisson tensor J acts from (subspaces of) \( \dot{L}^2\times L_0^2\) to \(L_0^2\times \dot{L}^2\). Then the Hamiltonian (2.2) becomes
and the Hamiltonian equations (2.3) (that is (1.3)) are transformed into
By (2.12), the symplectic form of (2.14) is the standard one,
where \( J^{-1} \) is the symplectic operator
regarded as a map from \(L_0^2\times \dot{L}^2\) into \( \dot{L}^2\times L_0^2 \). Note that \( J J^{-1} = {\mathrm{Id}}_{L_0^2\times \dot{L}^2}\) and \( J^{-1}J = {\mathrm{Id}}_{\dot{L}^2\times L_0^2}\). The Hamiltonian vector field \( X_\mathcal{H} (\eta , \zeta ) \) in (2.14) is characterized by the identity
The transformation W defined in (2.11) is reversibility preserving, namely it commutes with the involution \( \mathcal{S} \) in (2.4) (see Definition 3.17 below), and thus also the Hamiltonian \(\mathcal {H}\) in (2.13) is invariant under the involution \(\mathcal {S}\), as well as H in (2.2). For this reason we look for solutions \((\eta (t,x),\zeta (t,x))\) of (2.14) which are reversible, that is see (1.5),
The corresponding solutions \((\eta (t,x), \psi (t,x))\) of (1.3) induced by (2.11) are reversible as well.
We finally note that the transformation W defined in (2.11) commutes with the translation operator \( \tau _\varsigma \), therefore the Hamiltonian \(\mathcal {H}\) in (2.13) is invariant under \( \tau _\varsigma \), as well as H in (2.2). By Noether theorem, the horizontal momentum \( \int _\mathbb {T}\zeta \eta _x \,{\mathrm{d}}{x} \) is a prime integral of (2.14).
2.2 Linearization at the Equilibrium
In this section we study the linear system (1.6) and prove that its reversible solutions have the form (1.9).
In view of the Hamiltonian (2.2) of the water waves equations (1.3), also the linear system (1.6) is Hamiltonian and it is generated by the quadratic Hamiltonian
Thus, recalling (2.3), the linear system (1.6) is
The linear operator \( {\varvec{\Omega }}_L \) acts from (a dense subspace) of \( L^2_0 \times \dot{L}^2 \) to \( \dot{L}^2 \times L^2_0 \). In the Wahlén coordinates (2.11), the linear Hamiltonian system (1.6), that is (2.18), transforms into the linear Hamiltonian system

generated by the quadratic Hamiltonian
The linear operator \( {\varvec{\Omega }}_W \) acts from (a dense subspace) of \( L^2_0 \times \dot{L}^2 \) to \( \dot{L}^2 \times L^2_0 \). The linear system (2.19) is the Hamiltonian system obtained by linearizing (2.14) at the equilibrium \( (\eta , \zeta ) = (0, 0) \). We want to transform (2.19) in diagonal form by using a symmetrizer and then introducing complex coordinates. We first conjugate (2.19) under the symplectic transformation (with respect to the standard symplectic form \( \mathcal{W} \) in (2.15)) of the phase space
where \( \mathcal {M}\) is the diagonal matrix of self-adjoint Fourier multipliers

with the real valued symbol \( M_j \) defined in (1.10). The map \( \mathcal {M} \) is reversibility preserving.
Remark 2.2
In (2.21) the Fourier multiplier M(D) acts in \( H^1_0 \). On the other hand, with a slight abuse of notation, \(M(D)^{-1} \) denotes the Fourier multiplier operator in \( \dot{H}^1 \) defined as
where \([\zeta ] \) is the element in \( \dot{H}^1 \) with representant \( \zeta (x) \).
By a direct computation, the Hamiltonian system (2.19) assumes the symmetric form

where
Remark 2.3
To be precise, the Fourier multiplier operator \( \omega (\kappa , D) \) in the top left position in (2.22) maps \( H^1_0 \) into \( \dot{H}^1 \) and the one in the bottom right position maps \( \dot{H}^1 \) into \( H^1_0 \). The operator \(\partial _x^{-1}G(0) \) acts on \( \dot{H}^1 \) and \( G(0) \partial _x^{-1} \) on \( H^1_0 \).
Now we introduce complex coordinates by the transformation

In these variables, the Hamiltonian system (2.22) becomes the diagonal system
where
is the Fourier multiplier with symbol \( \Omega _j(\kappa ) \) defined in (1.11) and \(\overline{\Omega }(\kappa , D)\) is defined by
Note that \(\overline{\Omega }(\kappa , D)\) is the Fourier multiplier with symbol \(\{\Omega _{-j}(\kappa )\}_{j \in \mathbb {Z}{\setminus }\{0\}}\).
Remark 2.4
We regard the system (2.25) in \( \dot{H}^1 \times \dot{H}^1 \).
The diagonal system (2.25) amounts to the scalar equation
and, writing (2.27) in the exponential Fourier basis, to the infinitely many decoupled harmonic oscillators
Note that, in these complex coordinates, the involution \(\mathcal {S}\) defined in (2.4) reads as the map
which we may read just as the scalar map \(z(x)\mapsto \overline{z(-x)}\). Moreover, in the Fourier coordinates introduced in (2.27), it amounts to
In view of (2.28) and (2.30) every reversible solution (which is characterized as in (2.17)) of (2.27) has the form

Let us see the form of these solutions back in the original variables \( (\eta , \psi )\). First, by (2.21), (2.24),

and the solutions (2.31) assume the form

Back to the variables \((\eta , \psi )\) with the change of coordinates (2.11) one obtains formula (1.9).
Decomposition of the phase space in Lagrangian subspaces invariant under (2.19). We express the Fourier coefficients \( z_j \in \mathbb {C}\) in (2.27) as
In the new coordinates \( (\alpha _j, \beta _j)_{ j \in \mathbb {Z}{\setminus }\{0\}} \), we write (2.32) as (recall that \( M_j = M_{-j} \))
with
The symplectic form (2.15) then becomes
Each 2-dimensional subspace in the sum (2.33), spanned by \( (\alpha _j, \beta _j ) \in \mathbb {R}^2 \) is therefore a symplectic subspace. The quadratic Hamiltonian \( \mathcal {H}_L \) in (2.20) reads as
In view of (2.33), the involution \( \mathcal {S}\) defined in (2.4) reads as
and the translation operator \( \tau _\varsigma \) defined in (2.7) as
We may also enumerate the independent variables \( (\alpha _j, \beta _j )_{j \in \mathbb {Z}{\setminus }\{0\}} \) as \( \big ( \alpha _{-n}, \beta _{-n}, \alpha _{n}, \beta _{n} \big ) \), \( n \in \mathbb {N}\). Thus the phase space \(\mathfrak {H}:= L^2_0 \times \dot{L}^2 \) of (2.14) decomposes as the direct sum
of 2-dimensional Lagrangian symplectic subspaces
which are invariant for the linear Hamiltonian system (2.19), namely \( J {\varvec{\Omega }}_W : V_{n,\sigma } \mapsto V_{n,\sigma } \) (for a proof see for example remark 2.10). The symplectic projectors \( \Pi _{V_{n,\sigma }}\), \( \sigma \in \{ \pm \} \), on the symplectic subspaces \( V_{n, \sigma } \) are explicitly provided by (2.33) and (2.34) with \( j = n \sigma \).
Note that the involution \( \mathcal {S}\) defined in (2.4) and the translation operator \( \tau _\varsigma \) in (2.7) leave the subspaces \( V_{n,\sigma } \), \( \sigma \in \{ \pm \} \), invariant.
2.3 Tangential and Normal Subspaces of the Phase Space
We decompose the phase space \( \mathfrak {H}\) of (2.14) into a direct sum of tangential and normal Lagrangian subspaces \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \). Note that the main part of the solutions (1.19) that we shall obtain in Theorem 1.5 is the component in the tangential subspace \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \), whereas the component in the normal subspace \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) is much smaller.
Recalling the definition of the sets \(\mathbb {S}^+\) and \(\Sigma \) defined in (1.15) respectively (1.16), we split
where \(\mathfrak {H}^{\intercal }_{\mathbb {S}^+, \Sigma } \) is the finite dimensional tangential subspace
and \(\mathfrak {H}^{\angle }_{\mathbb {S}^+, \Sigma } \) is the normal subspace defined as its symplectic orthogonal
Both the subspaces \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) are Lagrangian. We denote by \( \Pi _{\mathbb {S}^+,\Sigma }^\intercal \) and \( \Pi _{\mathbb {S}^+,\Sigma }^\angle \) the symplectic projections on the subspaces \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \), respectively. Since \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) are symplectic orthogonal, the symplectic form \( \mathcal{W} \) in (2.15) decomposes, for any \(v_1, v_2 \in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \(w_1, w_2 \in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \), as
The symplectic projections \( \Pi _{\mathbb {S}^+,\Sigma }^\intercal \) and \( \Pi _{\mathbb {S}^+,\Sigma }^\angle \) satisfy
Lemma 2.5
We have that
Proof
Since the subspaces \(\mathfrak {H}^\intercal := \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \(\mathfrak {H}^\angle := \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) are symplectic orthogonal, we have, recalling (2.15), that
Thus, using the projectors \( \Pi ^\intercal := \Pi ^\intercal _{\mathbb {S}^+, \Sigma } \), \(\Pi ^\angle := \Pi ^\angle _{\mathbb {S}^+, \Sigma } \), we have that
and, taking adjoints, \( ( (\Pi ^\angle )^* J^{-1} \Pi ^\intercal v , w )_{L^2} = ( (\Pi ^\intercal )^* J^{-1} \Pi ^\angle w , v )_{L^2} = 0 \) for any \( v, w \in \mathfrak {H}\), so that
Now inserting the identity \(\Pi ^\angle = {\mathrm{Id}} - \Pi ^\intercal \) in (2.45), we get
proving the second identity of (2.43). The first identity of (2.43) follows applying J to the left and to the right of the second identity. The identity (2.44) follows in the same way. \(\square \)
Note that the restricted symplectic form \(\mathcal {W}\vert _{\mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle } \) is represented by the symplectic structure
where \( \Pi ^{L^2}_\angle \) is the \( L^2 \)-projector on the subspace \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \). Indeed
We also denote the associated (restricted) Poisson tensor
In the next lemma we prove that \(J^{-1}_\angle \) and \(J_\angle \) are each other inverses.
Lemma 2.6
\(J^{-1}_\angle \, J_\angle = J_\angle \, J^{-1}_\angle = {\mathrm{Id}}_{ \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle } \).
Proof
Let \(v \in \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle \). By (2.46) and (2.47), for any \(h \in \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle \) one has
The proof that \( J_\angle J^{-1}_\angle \, = {\mathrm{Id}}_{ \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle }\) is similar. \(\square \)
Lemma 2.7
\( \Pi ^\angle _{\mathbb {S}^+, \Sigma } J \Pi ^{L^2}_\angle = \Pi ^\angle _{\mathbb {S}^+, \Sigma } J \).
Proof
For any \( u, h \in \mathfrak {H}\) we have, using Lemma 2.5,
implying the lemma. \(\quad \square \)
Action-angle coordinates. Finally we introduce action-angle coordinates on the tangential subspace \( \mathfrak {H}^{ \intercal }_{\mathbb {S}^+, \Sigma }\) defined in (2.41). Given the sets \(\mathbb {S}^+\) and \(\Sigma \) defined respectively in (1.15) and (1.16), we define the set
and the action-angle coordinates \( (\theta _j, I_j)_{j \in {\mathbb {S}}} \), by the relations, for any \(j\in \mathbb {S}\),
In view of (2.40)–(2.42), we represent any function of the phase space \( \mathfrak {H}\) as
where \( \theta := (\theta _j)_{j \in \mathbb {S}} \in \mathbb {T}^\nu \), \( I := (I_j)_{j \in \mathbb {S}} \in \mathbb {R}^\nu \) and \( w \in \mathfrak {H}^{ \angle }_{\mathbb {S}^+, \Sigma } \).
Remark 2.8
In these coordinates the solutions (1.17) of the linear system (1.6) simply read as \( W v^\intercal (\vec {\Omega }(\kappa )t, 0) \), where \( \vec {\Omega }(\kappa ) := (\Omega _j(\kappa ))_{j \in \mathbb {S}} \) is given in (1.18).
In view of (2.50), the involution \(\mathcal {S}\) in (2.4) reads as
the translation operator \(\tau _\varsigma \) in (2.7) reads as
where
and the symplectic 2-form (2.15) becomes
We also note that \(\mathcal{W} \) is exact, namely
is the associated Liouville 1-form (the operator \(J_\angle ^{-1} \) is defined in (2.46)).
Finally, given a Hamiltonian \( K :\mathbb {T}^\nu \times \mathbb {R}^\nu \times \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle \rightarrow \mathbb {R}\), the associated Hamiltonian vector field (with respect to the symplectic form (2.54)) is
where \(\nabla _w K \) denotes the \(L^2\) gradient of K with respect to \( w \in \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle \). Indeed, the only nontrivial component of the vector field \(X_K\) is the last one, which we denote by \([X_K]_w \in \mathfrak {H}_{\mathbb {S}^+, \Sigma }^\angle \). It fulfills
and (2.56) follows by Lemma 2.6. We remark that along the paper we only consider Hamiltonians such that the \( L^2\)-gradient \( \nabla _w K \) defined by (2.57), as well as the Hamiltonian vector field \( \Pi _{\mathbb {S}^+,\Sigma }^\angle J \nabla _{w} K \), maps spaces of Sobolev functions into Sobolev functions (not just distributions), with possible loss of derivatives.
Tangential and normal subspaces in complex variables. Each 2-dimensional symplectic subspace \( V_{n,\sigma } \), \( n \in \mathbb {N}\), \( \sigma = \pm 1 \), defined in (2.382.39)–(2.382.39) is isomorphic, through the linear map \( \mathcal{M } \mathcal{C} \) defined in (2.32), to the complex subspace
Denoting by \( \Pi _j \) the \( L^2 \)-projection on \( \mathbf{H}_j \), we have that \(\Pi _{V_{n, \sigma }} = \mathcal{M } \mathcal{C} \, \Pi _j \, (\mathcal{M } \mathcal{C})^{-1} \). Thus \( \mathcal{M } \mathcal{C} \) is an isomorphism between the tangential subspace \( \mathfrak {H}^{\intercal }_{\mathbb {S}^+, \Sigma } \) defined in (2.41) and
and between the normal subspace \( \mathfrak {H}^{\angle }_{\mathbb {S}^+, \Sigma } \) defined in (2.42) and
Denoting by \( \Pi _{\mathbb {S}}^\intercal \), \(\Pi _{\mathbb {S}_0}^\perp \), the \( L^2 \)-orthogonal projections on the subspaces \( \mathbf{H}_\mathbb {S}\) and \( \mathbf{H}_{\mathbb {S}_0}^\perp \), we have that
The following lemma, used in Section 5, is an easy corollary of the previous analysis.
Lemma 2.9
We have that \(\left( v^\intercal , {\varvec{\Omega }}_W w \right) _{L^2} = 0\), for any \( v^\intercal \in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \( w \in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \).
Proof
Write \( v^\intercal = \mathcal {M}\mathcal {C}z^\intercal \) and \( \mathcal {M}\mathcal {C}z^\perp \) with \(z^\intercal \in \mathbf{H}_\mathbb {S}\) and \(z^\perp \in \mathbf{H}_{\mathbb {S}_0}^\perp \). Then, by (2.22) and (2.25),
since \({\varvec{\Omega }}_D\) preserves the subspace \(\mathbf{H}_{\mathbb {S}_0}^\perp \). \(\square \)
Remark 2.10
The same proof of Lemma 2.9 actually shows that \( (v_{n,-\sigma }, {\varvec{\Omega }}_W v_{n,{\sigma }} )_{L^2} = 0 \) for any \( v_{n,\pm \sigma } \in V_{n, \pm \sigma }\), for any \( n \in \mathbb {N}\), \( \sigma = \pm 1 \). Thus \( \mathcal{W}( v_{n,-\sigma } , J {\varvec{\Omega }}_W v_{n,{\sigma }} ) = ( v_{n,-\sigma } , J^{-1} J {\varvec{\Omega }}_W v_{n,{\sigma }} )_{L^2} = 0 \) which shows that \( J {\varvec{\Omega }}_W \) maps \( V_{n,\sigma } \) in itself.
Notation. The notation \( a \lesssim _s b \) means that \( a \leqq C(s) b \) for some positive constant C(s) . We denote \( \mathbb {N}:= \{1, 2, \ldots \} \) and \( \mathbb {N}_0 := \{0\} \cup \mathbb {N}\).
3 Functional Setting
Along the paper we consider functions \(u({\varphi },x)\in L^2\left( \mathbb {T}^{\nu +1},\mathbb {C}\right) \) depending on the space variable \(x\in \mathbb {T}=\mathbb {T}_x\) and the angles \({\varphi }\in \mathbb {T}^\nu =\mathbb {T}_{\varphi }^\nu \) (so that \(\mathbb {T}^{\nu +1}= \mathbb {T}_{\varphi }^\nu \times \mathbb {T}_x\)) which we expand in Fourier series as
We also consider real valued functions \(u({\varphi },x)\in \mathbb {R}\), as well as vector valued functions \(u({\varphi },x)\in \mathbb {C}^2\) (or \(u({\varphi },x)\in \mathbb {R}^2\)). When no confusion appears, we denote simply by \(L^2\), \(L^2(\mathbb {T}^{\nu +1})\), \(L_x^2:=L^2(\mathbb {T}_x)\), \(L_{\varphi }^2:= L^2(\mathbb {T}^\nu )\) either the spaces of real/complex valued, scalar/vector valued, \(L^2\)-functions.
In this paper a crucial role is played by the following subspace of functions of \( ({\varphi },x) \).
Definition 3.1
(Quasi-periodic traveling waves) Let \( \vec {\jmath } := (\overline{\jmath }_1, \ldots ,\overline{\jmath }_\nu ) \in \mathbb {Z}^\nu \) be the vector defined in (2.53). A function \( u ({\varphi }, x) \) is called a quasi-periodic traveling wave if it has the form \( u({\varphi },x) = U({\varphi }-\vec {\jmath }x) \) where \( U : \mathbb {T}^\nu \rightarrow \mathbb {C}^K \), \( K \in \mathbb {N}\), is a \( (2 \pi )^\nu \)-periodic function.
Comparing with Definition 1.2, we find convenient to call quasi-periodic traveling wave both the function \( u({\varphi },x) = U({\varphi }-\vec {\jmath }x) \) and the function of time \( u(\omega t,x) = U(\omega t-\vec {\jmath }x) \).
Quasi-periodic traveling waves are characterized by the relation
where \(\tau _\varsigma \) is the translation operator in (2.7). Product and composition of quasi-periodic traveling waves is a quasi-periodic traveling wave. Expanded in Fourier series as in (3.1), a quasi-periodic traveling wave has the form
namely, comparing with Definition 3.1,
The traveling waves \( u ({\varphi }, x) = U ({\varphi }- \vec {\jmath } x ) \) where \( U (\cdot ) \) belongs to the Sobolev space \( H^s (\mathbb {T}^\nu , \mathbb {C}^K ) \) in (1.14) (with values in \( \mathbb {C}^K \), \( K \in \mathbb {N}\)), form a subspace of the Sobolev space
where \(\langle \ell ,j \rangle := \max \{ 1, |\ell |, |j| \} \). Note the equivalence of the norms (use (3.4))
For \( s \geqq s_0 := \big [ \frac{\nu +1}{2} \big ] +1 \in \mathbb {N}\) one has \( H^s ( \mathbb {T}^{\nu +1}) \subset C ( \mathbb {T}^{\nu +1})\), and \(H^s(\mathbb {T}^{\nu +1})\) is an algebra. Along the paper we denote by \( \Vert \ \Vert _s \) both the Sobolev norms in (1.14) and (3.5).
For \(K\geqq 1\) we define the smoothing operator \(\Pi _{K}\) on the traveling waves
and \( \Pi _K^\perp := {\mathrm{Id}}-\Pi _K \). Note that, writing a traveling wave as in (3.4), the projector \( \Pi _K \) in (3.6) is equal to
Whitney-Sobolev functions. Along the paper we consider families of Sobolev functions \(\lambda \mapsto u(\lambda )\in H^s (\mathbb {T}^{\nu +1}) \) and \(\lambda \mapsto U(\lambda )\in H^s (\mathbb {T}^{\nu }) \) which are \(k_0\)-times differentiable in the sense of Whitney with respect to the parameter \( \lambda :=(\omega ,\kappa ) \in F \subset \mathbb {R}^\nu \times [\kappa _1,\kappa _2] \) where \(F\subset \mathbb {R}^{\nu +1}\) is a closed set. The case that we encounter is when \( \omega \) belongs to the closed set of Diophantine vectors \( \mathtt{D}\mathtt{C}(\upsilon , \tau ) \) defined in (1.13). We refer to Definition 2.1 in [2], for the definition of a Whitney-Sobolev function \( u : F \rightarrow H^s \) where \( H^s \) may be either the Hilbert space \( H^s (\mathbb {T}^\nu \times \mathbb {T}) \) or \( H^s (\mathbb {T}^\nu ) \). Here we mention that, given \( \upsilon \in (0,1) \), we can identify a Whitney-Sobolev function \( u : F \rightarrow H^s \) with \( k_0 \) derivatives with the equivalence class of functions \( f \in W^{k_0,\infty ,\upsilon }(\mathbb {R}^{\nu +1},H^s)/\sim \) with respect to the equivalence relation \(f\sim g\) when \(\partial _\lambda ^j f(\lambda ) = \partial _\lambda ^j g(\lambda )\) for all \(\lambda \in F\), \(\left| j \right| \leqq k_0-1\), with equivalence of the norms
The key result is the Whitney extension theorem, which associates to a Whitney-Sobolev function \(u : F \rightarrow H^s \) with \( k_0 \)-derivatives a function \({\widetilde{u}}: \mathbb {R}^{\nu +1} \rightarrow H^s \), \({\widetilde{u}}\) in \( W^{k_0,\infty }(\mathbb {R}^{\nu +1},H^s) \) (independently of the target Sobolev space \(H^s\)) with an equivalent norm. For sake of simplicity in the notation we often denote \( \Vert \ \Vert _{s,F}^{k_0,\upsilon } = \Vert \ \Vert _{s}^{k_0,\upsilon } \).
Thanks to this equivalence, all the tame estimates which hold for Sobolev spaces carry over for Whitney-Sobolev functions. For example the following classical tame estimate for the product holds: (see for example Lemma 2.4 in [2]): for all \(s\geqq s_0 > (\nu +1)/2\),
Moreover the following estimates hold for the smoothing operators defined in (3.6): for any traveling wave u
We also state a standard Moser tame estimate for the nonlinear composition operator, see for example Lemma 2.6 in [2],
Since the variables \(({\varphi },x)=:y\) have the same role, we state it for a generic Sobolev space \(H^s(\mathbb {T}^d)\).
Lemma 3.2
(Composition operator) Let \(f\in \mathcal {C}^\infty (\mathbb {T}^d\times \mathbb {R},\mathbb {R})\). If \(u(\lambda )\in H^s(\mathbb {T}^d)\) is a family of Sobolev functions satisfying \(\Vert u \Vert _{s_0}^{k_0,\upsilon }\leqq 1\), then, for all \(s\geqq s_0:=(d+1)/2\),
If \( f(\varphi , x, 0) = 0 \) then \( \Vert \mathtt{f}(u) \Vert _{s}^{k_0,\upsilon }\leqq C(s,k_0,f) \Vert u \Vert _{s}^{k_0,\upsilon } \).
Diophantine equation. If \(\omega \) is a Diophantine vector in \( \mathtt{D}\mathtt{C}(\upsilon ,\tau )\), see (1.13), then the equation \(\omega \cdot \partial _{\varphi }v = u\), where \(u({\varphi },x)\) has zero average with respect to \({\varphi }\), has the periodic solution
For all \(\omega \in \mathbb {R}^\nu \), we define its extension
where \(\chi \in \mathcal {C}^\infty (\mathbb {R},\mathbb {R})\) is an even positive \(\mathcal {C}^\infty \) cut-off function such that
Note that \((\omega \cdot \partial _{\varphi })_{\mathrm{ext}}^{-1} u = (\omega \cdot \partial _{\varphi })^{-1}u\) for all \(\omega \in \mathtt{D}\mathtt{C}(\upsilon ,\tau )\). Moreover, if \( u ({\varphi }, x) \) is a quasi-periodic traveling wave with zero average with respect to \( {\varphi }\), then, by (3.3), we see that \( (\omega \cdot \partial _{\varphi })_{\mathrm{ext}}^{-1} u({\varphi },x) \) is a quasi-periodic traveling wave. It holds that
and, for \(F\subseteq \mathtt{D}\mathtt{C}(\upsilon ,\tau )\times \mathbb {R}_+\), one has \(\Vert (\omega \cdot \partial _{\varphi })^{-1}u \Vert _{s,F}^{k_0,\upsilon } \leqq C(k_0)\upsilon ^{-1}\Vert u \Vert _{s+\mu ,F}^{k_0,\upsilon } \).
Linear operators. Along the paper we consider \({\varphi }\)-dependent families of linear operators \(A:\mathbb {T}^\nu \mapsto \mathcal {L}(L^2(\mathbb {T}_x))\), \({\varphi }\mapsto A({\varphi })\), acting on subspaces of \(L^2(\mathbb {T}_x)\), either real or complex valued. We also regard A as an operator (which for simplicity we denote by A as well) that acts on functions \(u({\varphi },x)\) of space and time; that is
The action of an operator A as in (3.12) on a scalar function \(u({\varphi },x)\in L^2\) expanded as in (3.1) is
We identify an operator A with its matrix \( \big ( A_j^{j'}(\ell -\ell ') \big )_{j,j'\in \mathbb {Z},\ell ,\ell '\in \mathbb {Z}^\nu }\), which is Töplitz with respect to the index \(\ell \). In this paper we always consider Töplitz operators as in (3.12), (3.13).
Real operators. A linear operator A is real if \( A = \overline{A} \), where \( \overline{A} \) is defined by \( \overline{A}(u):= \overline{A(\overline{u})} \). Equivalently A is real if it maps real valued functions into real valued functions. We represent a real operator acting on \((\eta ,\zeta ) \) belonging to (a subspace of) \( L^2(\mathbb {T}_x,\mathbb {R}^2) \) by a matrix
where A, B, C, D are real operators acting on the scalar valued components \(\eta ,\zeta \in L^2(\mathbb {T}_x,\mathbb {R}) \).
The change of coordinates (2.24) transforms the real operator \(\mathcal {R}\) into a complex one acting on the variables \((z,\overline{z}) \), given by the matrix
A matrix operator acting on the complex variables \((z,\overline{z})\) of the form (3.15), we call it real. We shall also consider real operators \(\mathbf{R}\) of the form (3.15) acting on subspaces of \( L^2 \).
Lie expansion. Let \(X({\varphi })\) be a linear operator with associated flow \(\Phi ^\tau ( {\varphi })\) defined by
Let \( \Phi ({\varphi }) := \Phi ^\tau ({\varphi })_{|\tau = 1} \) denote the time-1 flow. Given a linear operator \( A ( {\varphi }) \), the conjugated operator
admits the Lie expansion; that is for any \( M \in \mathbb {N}_0 \),
where \({\mathrm{ad}}_{X({\varphi })}(A({\varphi })) := [X({\varphi }), A({\varphi })] = X({\varphi }) A({\varphi }) - A({\varphi }) X({\varphi }) \) and \({\mathrm{ad}}_{X({\varphi })}^0 := {\mathrm{Id}} \).
In particular, for \(A=\omega \cdot \partial _{\varphi }\), since \([X({\varphi }), \omega \cdot \partial _{\varphi }] = - ( \omega \cdot \partial _{\varphi }X)({\varphi }) \), we obtain
For matrices of operators \(\mathbf{X}({\varphi })\) and \(\mathbf{A}({\varphi })\) as in (3.15), the same formula (3.16) holds.
3.1 Pseudodifferential Calculus
In this section we report fundamental notions of pseudodifferential calculus, following [6].
Definition 3.3
(\(\Psi \)DO) A pseudodifferential symbol a(x, j) of order m is the restriction to \( \mathbb {R}\times \mathbb {Z}\) of a function \( a (x, \xi ) \) which is \( \mathcal {C}^\infty \)-smooth on \( \mathbb {R}\times \mathbb {R}\), \( 2 \pi \)-periodic in x, and satisfies
We denote by \( S^m \) the class of symbols of order m and \( S^{-\infty } := \cap _{m \geqq 0} S^m \). To a symbol \( a(x, \xi ) \) in \(S^m\) we associate its quantization acting on a \( 2 \pi \)-periodic function \( u(x) = \sum _{j \in \mathbb {Z}} u_j \, e^{{\mathrm{i}}j x} \) as
We denote by \( {\mathrm{OP}}S^m \) the set of pseudodifferential operators of order m and \( {\mathrm{OP}}S^{-\infty } := \bigcap _{m \in \mathbb {R}} {\mathrm{OP}}S^{m} \). For a matrix of pseudodifferential operators
we say that \(\mathbf{A}\in {\mathrm{OP}}S^m\).
When the symbol a(x) is independent of \( \xi \), the operator \( {\mathrm{Op}}(a) \) is the multiplication operator by the function a(x), that is \( {\mathrm{Op}}(a) : u (x) \mapsto a ( x) u(x )\). In such a case we also denote \( {\mathrm{Op}}(a) = a (x) \).
We shall use the following notation, used also in [1, 2, 6]. For any \(m \in \mathbb {R}{\setminus } \{ 0\}\), we set
where \(\chi \) is an even, positive \(\mathcal {C}^\infty \) cut-off satisfying (3.10). We also identify the Hilbert transform \(\mathcal {H}\), acting on the \(2 \pi \)-periodic functions, defined by
with the Fourier multiplier \({\mathrm{Op}}(- {\mathrm{i}}\, {\mathrm{sign}}\,(\xi ) \chi (\xi ) )\). Similarly we regard the operator
as the Fourier multiplier \(\partial _x^{-1} = {\mathrm{Op}}\left( - {\mathrm{i}}\,\chi (\xi ) \xi ^{-1} \right) \) and the projector \(\pi _0 \), defined on the \( 2 \pi \)-periodic functions as
with the Fourier multiplier \( {\mathrm{Op}}\big ( 1 - \chi (\xi ) \big )\). Finally we define, for any \(m \in \mathbb {R}{\setminus } \{ 0 \}\),
Along the paper we consider families of pseudodifferential operators with a symbol \( a(\lambda ;{\varphi },x,\xi ) \) which is \(k_0\)-times differentiable with respect to a parameter \( \lambda :=(\omega ,\kappa ) \) in an open subset \( \Lambda _0 \subset \mathbb {R}^\nu \times [\kappa _1,\kappa _2] \). Note that \(\partial _\lambda ^k A = {\mathrm{Op}}\left( \partial _\lambda ^k a \right) \) for any \(k\in \mathbb {N}_0^{\nu +1}\).
We recall the pseudodifferential norm introduced in Definition 2.11 in [6].
Definition 3.4
(Weighted \(\Psi DO\) norm) Let \( A(\lambda ) := a(\lambda ; {\varphi }, x, D) \in {\mathrm{OP}}S^m \) be a family of pseudodifferential operators with symbol \( a(\lambda ; {\varphi }, x, \xi ) \in S^m \), \( m \in \mathbb {R}\), which are \(k_0\)-times differentiable with respect to \( \lambda \in \Lambda _0 \subset \mathbb {R}^{\nu + 1} \). For \( \upsilon \in (0,1) \), \( \alpha \in \mathbb {N}_0 \), \( s \geqq 0 \), we define
where \( \left\| A(\lambda ) \right\| _{m, s, \alpha } := \max _{0 \leqq \beta \leqq \alpha } \, \sup _{\xi \in \mathbb {R}} \Vert \partial _\xi ^\beta a(\lambda , \cdot , \cdot , \xi ) \Vert _{s} \ \langle \xi \rangle ^{-m + \beta } \). For a matrix of pseudodifferential operators \(\mathbf{A}\in {\mathrm{OP}}S^m\) as in (3.18), we define \( \left\| \mathbf{A} \right\| _{m, s, \alpha }^{k_0, \upsilon } := \max _{i = 1, \ldots , 4} \left\| A_i \right\| _{m, s, \alpha }^{k_0, \upsilon }\,. \)
Given a function \(a(\lambda ; {\varphi }, x) \in \mathcal {C}^\infty \) which is \(k_0\)-times differentiable with respect to \(\lambda \), the weighted norm of the corresponding multiplication operator is
Composition of pseudodifferential operators. If \( {\mathrm{Op}}(a) \), \({\mathrm{Op}}(b) \) are pseudodifferential operators with symbols \(a\in S^m\), \(b\in S^{m'}\), \(m,m'\in \mathbb {R}\), then the composition operator \( {\mathrm{Op}}(a) {\mathrm{Op}}(b) \) is a pseudodifferential operator \( {\mathrm{Op}}(a\# b) \) with symbol \(a\# b\in S^{m+m'}\). It admits the asymptotic expansion: for any \(N\geqq 1\)
where \( r_N(a,b) \in S^{m+m'-N} \). The following result is proved in Lemma 2.13 in [6]:
Lemma 3.5
(Composition) Let \( A = a(\lambda ; {\varphi }, x, D) \), \( B = b(\lambda ; {\varphi }, x, D) \) be pseudodifferential operators with symbols \( a (\lambda ;{\varphi }, x, \xi ) \in S^m \), \( b (\lambda ; {\varphi }, x, \xi ) \in S^{m'} \), \( m , m' \in \mathbb {R}\). Then \( A \circ B \in {\mathrm{OP}}S^{m + m'} \) satisfies, for any \( \alpha \in \mathbb {N}_0 \), \( s \geqq s_0 \),
Moreover, for any integer \( N \geqq 1 \), the remainder \( R_N := {\mathrm{Op}}(r_N) \) in (3.23) satisfies
Both (3.24)–(3.25) hold with the constant \( C(s_0) \) interchanged with C(s) .
Analogous estimates hold if \(\mathbf{A}\) and \(\mathbf{B}\) are matrix operators of the form (3.18).
The commutator between two pseudodifferential operators \( {\mathrm{Op}}(a)\in {\mathrm{OP}}S^m\) and \({\mathrm{Op}}(b)\in {\mathrm{OP}}S^{m'}\) is a pseudodifferential operator in \( {\mathrm{OP}}S^{m+m'-1}\) with symbol \(a\star b\in S^{m+m'-1}\), namely \( \left[ {\mathrm{Op}}(a), {\mathrm{Op}}(b)\right] = {\mathrm{Op}}\left( a\star b \right) \), that admits, by (3.23), the expansion
is the Poisson bracket between \(a(x,\xi )\) and \(b(x,\xi )\). As a corollary of Lemma 3.5 we have
Lemma 3.6
(Commutator) Let \(A = {\mathrm{Op}}(a) \) and \(B = {\mathrm{Op}} (b) \) be pseudodifferential operators with symbols \(a(\lambda ;{\varphi },x,\xi )\in S^{m}\), \(b(\lambda ;{\varphi },x,\xi )\in S^{m'}\), \(m,m'\in \mathbb {R}\). Then the commutator \([A,B]:=AB-BA\in {\mathrm{OP}}S^{m+m'-1}\) satisfies
Finally we consider the exponential of a pseudodifferential operator of order 0. The following lemma follows as in Lemma 2.12 of [5] (or Lemma 2.17 in [6]).
Lemma 3.7
(Exponential map) If \( A := {\mathrm{Op}}(a(\lambda ; {\varphi }, x, \xi ))\) is in \( \mathrm{OP}S^{0} \), then \(e^A\) is in \( \mathrm{OP}S^{0} \) and for any \(s \geqq s_0\), \(\alpha \in \mathbb {N}_0 \), there is a constant \(C(s, \alpha ) > 0\) so that
The same holds for a matrix \(\mathbf{A}\) of the form (3.18) in \({\mathrm{OP}}S^0\).
Egorov Theorem. Consider the family of \( \varphi \)-dependent diffeomorphisms of \( \mathbb {T}_x \) defined by
where \(\beta ({\varphi }, x)\) is a small smooth function, and the induced operators
Lemma 3.8
(Composition) Let \(\Vert \beta \Vert _{2s_0+k_0+2}^{k_0,\upsilon }\leqq \delta (s_0,k_0)\) small enough. Then the composition operator \( \mathcal {B}\) satisfies the tame estimates, for any \(s\geqq s_0\),
and the function \(\breve{\beta }\) defined in (3.28) by the inverse diffeomorphism satisfies \( \Vert \breve{\beta } \Vert _{s}^{k_0,\upsilon } \lesssim _{s,k_0} \Vert \beta \Vert _{s+k_0}^{k_0,\upsilon } \).
The following result is a small variation of Proposition 2.28 of [5]:
Proposition 3.9
(Egorov) Let \(N \in \mathbb {N}\), \(\mathtt{q}_0 \in \mathbb {N}_0 \), \(S > s_0\) and assume that \(\partial _\lambda ^k \beta (\lambda ; \cdot , \cdot )\) are \( \mathcal {C}^\infty \) for all \(|k| \leqq k_0\). There exist constants \(\sigma _N, \sigma _N(\mathtt{q}_0) >0\), \(\delta = \delta (S, N, \mathtt{q}_0, k_0) \in (0,1)\) such that, if \( \Vert \beta \Vert _{s_0 + \sigma _N(\mathtt{q}_0)}^{k_0,\upsilon } \leqq \delta \), then the conjugated operator \( \mathcal {B}^{-1} \circ \partial _x^{m}\circ \mathcal {B}\), \( m \in \mathbb {Z}\), is a pseudodifferential operator of order m with an expansion of the form
with the following properties:
-
1.
The principal symbol of \(p_{m}\) is
$$\begin{aligned} p_{m}(\lambda ; {\varphi }, y) = \Big ( [1+\beta _x(\lambda ;{\varphi },x)]^{m} \Big )\vert _{x=y+ \breve{\beta }(\lambda ;{\varphi },y)} \end{aligned}$$where \(\breve{\beta }(\lambda ;{\varphi },y)\) has been introduced in (3.28). For any \(s \geqq s_0\) and \(i=1, \ldots , N\),
$$\begin{aligned} \Vert p_m - 1 \Vert _{s}^{k_0,\upsilon } \, , \ \Vert p_{m-i} \Vert _{s}^{k_0,\upsilon } \lesssim _{s, N} \Vert \beta \Vert _{s+\sigma _N}^{k_0,\upsilon }. \end{aligned}$$(3.30) -
2.
For any \( \mathtt{q}\in \mathbb {N}^\nu _0 \) with \( |\mathtt{q}| \leqq \mathtt{q}_0\), \(n_1, n_2 \in \mathbb {N}_0 \) with \( n_1 + n_2 + \mathtt{q}_0 \leqq N + 1 - k_0 - m \), the operator \(\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathcal{R}_N(\varphi ) \langle D \rangle ^{n_2}\) is \(\mathcal {D}^{k_0} \)-tame with a tame constant satisfying, for any \(s_0 \leqq s \leqq S \),
$$\begin{aligned} {\mathfrak {M}}_{\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathcal{R}_N(\varphi ) \langle D \rangle ^{n_2}}(s) \lesssim _{S, N, \mathtt{q}_0} \Vert \beta \Vert _{s + \sigma _N(\mathtt{q}_0)}^{k_0,\upsilon }. \end{aligned}$$(3.31) -
3.
Let \(s_0 < s_1 \) and assume that \(\Vert \beta _j \Vert _{s_1 + \sigma _N(\mathtt{q}_0)} \leqq \delta ,\) \(j = 1,2\). Then \( \Vert \Delta _{12} p_{m - i} \Vert _{s_1} \lesssim _{s_1, N} \Vert \Delta _{12} \beta \Vert _{s_1 + \sigma _N} \), \( i = 0, \ldots , N \), and, for any \( |\mathtt{q}| \leqq \mathtt{q}_0\), \(n_1, n_2 \in \mathbb {N}_0 \) with \(n_1 + n_2 + \mathtt{q}_0 \leqq N - m\),
$$\begin{aligned} \Vert \langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\Delta _{12} \mathcal{R}_N(\varphi ) \langle D \rangle ^{n_2} \Vert _{\mathcal{B}(H^{s_1})} \lesssim _{s_1, N, n_1, n_2} \Vert \Delta _{12} \beta \Vert _{s_1 + \sigma _N(\mathtt{q}_0)}. \end{aligned}$$Finally, if \( \beta ({\varphi }, x ) \) is a quasi-periodic traveling wave, then \( \mathcal {B}\) is momentum preserving (we refer to Definition 3.24 and Lemma 3.30), as well as the conjugated operator \( \mathcal {B}^{-1} \circ \partial _x^m \circ \mathcal {B}\), and each function \( p_{m-i} \), \( i = 0, \ldots , N \), is a quasi-periodic traveling wave.
Dirichlet-Neumann operator. We finally remind the following decomposition of the Dirichlet-Neumann operator proved in [6], in the case of infinite depth, and in [2], for finite depth.
Lemma 3.10
(Dirichlet-Neumann) Assume that \(\partial _\lambda ^k \eta (\lambda , \cdot , \cdot ) \) is \(\mathcal {C}^\infty (\mathbb {T}^\nu \times \mathbb {T}_x)\) for all \(|k| \leqq k_0\). There exists \( \delta (s_0, k_0) >0\) such that, if \( \Vert \eta \Vert _{2s_0 +2k_0 +1}^{k_0,\upsilon } \leqq \delta (s_0, k_0) \), then the Dirichlet-Neumann operator \( G(\eta ) = G(\eta , \mathtt{h})\) may be written as
where \( \mathcal {R}_G(\eta ) := \mathcal {R}_G(\eta , \mathtt{h}) \in {\mathrm{OP}}S^{-\infty }\) satisfies, for all \(m, s, \alpha \in \mathbb {N}_0\), the estimate
3.2 \(\mathcal {D}^{k_0}\)-Tame and Modulo-Tame Operators
We present the notion of tame and modulo tame operators introduced in [6]. Let \( A := A(\lambda ) \) be a linear operator as in (3.12), \( k_0 \)-times differentiable with respect to the parameter \( \lambda \) in the open set \( \Lambda _0 \subset \mathbb {R}^{\nu +1}\).
Definition 3.11
(\(\mathcal {D}^{k_0}\)-\(\sigma \)-tame) Let \(\sigma \geqq 0\). A linear operator \(A:=A(\lambda )\) is \(\mathcal {D}^{k_0}\)-\(\sigma \)-tame if there exists a non-decreasing function \([s_0,S]\rightarrow [0,+\infty )\), \(s\mapsto {\mathfrak {M}}_A(s)\), with possibly \(S=+\infty \), such that, for all \(s_0\leqq s\leqq S\) and \(u\in H^{s+\sigma } \),
We say that \({\mathfrak {M}}_A(s)\) is a tame constant of the operator A. The constant \({\mathfrak {M}}_A(s)={\mathfrak {M}}_A(k_0,\sigma ,s)\) may also depend on \(k_0,\sigma \) but we shall often omit to write them. When the "loss of derivatives" \(\sigma \) is zero, we simply write \(\mathcal {D}^{k_0}\)-tame instead of \(\mathcal {D}^{k_0}\)-0-tame. For a matrix operator as in (3.15), we denote the tame constant \({\mathfrak {M}}_{\mathbf{R}}(s):=\max \left\{ {\mathfrak {M}}_{\mathcal {R}_1}(s),{\mathfrak {M}}_{\mathcal {R}_2}(s) \right\} \).
Note that the tame constants \({\mathfrak {M}}_A(s)\) are not uniquely determined. An immediate consequence of (3.34) is that \(\left\| A \right\| _{\mathcal {L}\left( H^{s_0+\sigma },H^{s_0}\right) }\leqq 2 {\mathfrak {M}}_{A}(s_0)\). Also note that, representing the operator A by its matrix elements \( (A_j^{j'}(\ell -\ell ') )_{\ell ,\ell '\in \mathbb {Z}^\nu ,j,j'\in \mathbb {Z}}\) as in (3.13), we have for all \(\left| k \right| \leqq k_0\), \(j'\in \mathbb {Z}\), \(\ell '\in \mathbb {Z}^\nu \),
The class of \(\mathcal {D}^{k_0}\)-\(\sigma \)-tame operators is closed under composition.
Lemma 3.12
(Composition, Lemma 2.20 in [6]) Let A, B be respectively \(\mathcal {D}^{k_0}\)-\(\sigma _A\)-tame and \(\mathcal {D}^{k_0}\)-\(\sigma _B\)-tame operators with tame constants respectively \({\mathfrak {M}}_A(s)\) and \({\mathfrak {M}}_B(s)\). Then the composed operator \(A\circ B\) is \(\mathcal {D}^{k_0}\)-\((\sigma _A+\sigma _B)\)-tame with tame constant
It is proved in Lemma 2.22 in [6] that the action of a \(\mathcal {D}^{k_0}\)-\(\sigma \)-tame operator \(A(\lambda )\) on a Sobolev function \( u = u(\lambda )\in H^{s+\sigma }\) is bounded by
Pseudodifferential operators are tame operators. We use, in particular, the following lemma:
Lemma 3.13
(Lemma 2.21 in [6]) Let \(A=a(\lambda ;{\varphi },x,D)\in {\mathrm{OP}}S^0\) be a family of pseudodifferential operators satisfying \(\Vert A \Vert _{0,s,0}^{k_0,\upsilon }<\infty \) for \(s\geqq s_0\). Then A is \(\mathcal {D}^{k_0}\)-tame with a tame constant \( {\mathfrak {M}}_A(s) \) satisfying, for any \(s\geqq s_0\),
The same statement holds for a matrix operator \(\mathbf{R}\) as in (3.15).
In view of the KAM reducibility scheme of Section 8 we also consider the stronger notion of \(\mathcal {D}^{k_0}\)-modulo-tame operator, that we need only for operators with loss of derivative \(\sigma =0\). We first recall the notion of majorant operator: given a linear operator A acting as in (3.13), we define the majorant operator |A| by its matrix elements \( (|A_j^{j'}(\ell -\ell ') |)_{\ell ,\ell '\in \mathbb {Z}^\nu , j,j'\in \mathbb {Z}} \).
Definition 3.14
(\(\mathcal {D}^{k_0}\)-modulo-tame) A linear operator \(A=A(\lambda )\) is \(\mathcal {D}^{k_0}\)-modulo-tame if there exists a non-decreasing function \([s_0,S]\rightarrow [0,+\infty ]\), \(s\mapsto {\mathfrak {M}}_A^\sharp (s)\), such that for all \(k\in \mathbb {N}_0^{\nu +1}\), \(\left| k \right| \leqq k_0\), the majorant operator \(\left| \partial _\lambda ^k A \right| \) satisfies, for all \(s_0\leqq s\leqq S\) and \(u\in H^s\),
The constant \({\mathfrak {M}}_A^\sharp (s)\) is called a modulo-tame constant for the operator A. For a matrix of operators as in (3.15), we denote the modulo-tame constant \({\mathfrak {M}}_{\mathbf{R}}^\sharp (s):= \max \{ {\mathfrak {M}}_{\mathcal {R}_1}^\sharp (s),{\mathfrak {M}}_{\mathcal {R}_2}^\sharp (s) \}\).
If A, B are \(\mathcal {D}^{k_0}\)-modulo-tame operators with \( | A_j^{j'}(\ell ) | \leqq | B_j^{j'}(\ell ) | \), then \({\mathfrak {M}}_A^\sharp (s)\leqq {\mathfrak {M}}_B^\sharp (s)\). A \(\mathcal {D}^{k_0}\)-modulo-tame operator is also \(\mathcal {D}^{k_0}\)-tame and \({\mathfrak {M}}_A(s)\leqq {\mathfrak {M}}_A^\sharp (s)\).
In view of the next lemma, given a linear operator A acting as in (3.13), we define the operator \(\langle \partial _{{\varphi }}\rangle ^\mathtt{b}A\), \( \mathtt{b}\in \mathbb {R}\), whose matrix elements are \(\langle \ell -\ell '\rangle ^\mathtt{b}A_j^{j'}(\ell -\ell ')\).
Lemma 3.15
(Sum and composition, Lemma 2.25 in [6]) Let A, B, \(\langle \partial _{{\varphi }}\rangle ^\mathtt{b}A\), \(\langle \partial _{{\varphi }}\rangle ^\mathtt{b}B\) be \(\mathcal {D}^{k_0}\)-modulo-tame operators. Then \(A+B\), \(A\circ B\) and \(\langle \partial _{{\varphi }}\rangle ^\mathtt{b}(AB)\) are \(\mathcal {D}^{k_0}\)-modulo-tame with
The same statement holds for matrix operators \(\mathbf{A}\), \(\mathbf{B}\) as in (3.15).
By Lemma 3.15 we deduce the following result, cfr. Lemma 2.20 in [5].
Lemma 3.16
(Exponential) Let A and \(\langle \partial _{\varphi }\rangle ^\mathtt{b}A\) be \(\mathcal {D}^{k_0}\)-modulo-tame and assume that \({\mathfrak {M}}_A^\sharp (s_0) \leqq 1 \). Then the operators \(e^{\pm A}-{\mathrm{Id}}\) and \(\langle \partial _{\varphi }\rangle ^\mathtt{b}e^{\pm A}- {\mathrm{Id}}\) are \(\mathcal {D}^{k_0}\)-modulo-tame with modulo-tame constants satisfying
Given a linear operator A acting as in (3.13), we define the smoothed operator \(\Pi _N A\), \(N\in \mathbb {N}\) whose matrix elements are
We also denote \(\Pi _N^\perp := {\mathrm{Id}}-\Pi _N\). It is proved in Lemma 2.27 in [6] that
The same estimate holds with a matrix operator \(\mathbf{R}\) as in (3.15).
3.3 Hamiltonian and Reversible Operators
In this paper we shall exploit both the Hamiltonian and reversible structure along the reduction of the linearized operators, that we now present.
Hamiltonian operators. A matrix operator \(\mathcal {R}\) as in (3.14) is Hamiltonian if the matrix
is self-adjoint, namely \( B^* = B \), \( C^*=C \), \( A^* = - D \) and A, B, C, D are real.
Correspondingly, a matrix operator as in (3.15) is Hamiltonian if
Symplectic operators. A \(\varphi \)-dependent family of linear operators \( \mathcal {R}(\varphi ) \), \( \varphi \in \mathbb {T}^\nu \), as in (3.14) is symplectic if
where the symplectic 2-form \( \mathcal{W} \) is defined in (2.15).
Reversible and reversibility preserving operators. Let \(\mathcal {S}\) be an involution as in (2.4) acting on the real variables \( (\eta , \zeta ) \in \mathbb {R}^2 \), or as in (2.51) acting on the action-angle-normal variables \( (\theta , I, w ) \), or as in (2.29) acting in the \( (z, \overline{z} )\) complex variables introduced in (2.24).
Definition 3.17
(Reversibility) A \( {\varphi }\)-dependent family of operators \(\mathcal {R}({\varphi }) \), \( {\varphi }\in \mathbb {T}^\nu \), is
-
reversible if \(\mathcal {R}(-{\varphi }) \circ \mathcal {S}= -\mathcal {S}\circ \mathcal {R}({\varphi })\) for all \({\varphi }\in \mathbb {T}^\nu \);
-
reversibility preserving if \(\mathcal {R}(-{\varphi })\circ \mathcal {S}= \mathcal {S}\circ \mathcal {R}({\varphi })\) for all \({\varphi }\in \mathbb {T}^\nu \).
Since in the complex coordinates \((z,\overline{z}) \) the involution \(\mathcal {S}\) defined in (2.4) reads as in (2.29), an operator \(\mathbf{R}({\varphi })\) as in (3.15) is reversible, respectively anti-reversible, if, for any \(i=1,2\),
where, with a small abuse of notation, we still denote \( (\mathcal {S}u)(x) = \overline{u(-x)}\). Moreover, recalling that in the Fourier coordinates such involution reads as in (2.30), we obtain the following lemma.
Lemma 3.18
A \( {\varphi }\)-dependent family of operators \(\mathbf{R}({\varphi })\), \( {\varphi }\in \mathbb {T}^\nu \), as in (3.15) is
-
reversible if, for any \( i = 1, 2 \),
$$\begin{aligned} \left( \mathcal {R}_{i} \right) _j^{j'}(-{\varphi }) = - \overline{ \left( \mathcal {R}_{i} \right) _{j}^{j'}({\varphi }) } \quad \forall \,{\varphi }\in \mathbb {T}^\nu \, , \ \ that\, is \ \left( \mathcal {R}_{i} \right) _j^{j'}(\ell ) = - \overline{ \left( \mathcal {R}_{i} \right) _{j}^{j'}(\ell ) } \quad \forall \,\ell \in \mathbb {Z}^\nu \,; \end{aligned}$$(3.44) -
reversibility preserving if, for any \( i = 1, 2 \),
$$\begin{aligned} \left( \mathcal {R}_{i} \right) _j^{j'}(-{\varphi }) = \overline{ \left( \mathcal {R}_{i} \right) _{j}^{j'}({\varphi }) } \ \ \forall \,{\varphi }\in \mathbb {T}^\nu , \ \ {{that\, is}} \ \left( \mathcal {R}_{i} \right) _j^{j'}(\ell ) = \overline{ \left( \mathcal {R}_{i} \right) _{j}^{j'}(\ell ) } \, \ \ \forall \,\ell \in \mathbb {Z}^\nu . \end{aligned}$$(3.45)
Note that the composition of a reversible operator with a reversibility preserving operator is reversible. The flow generated by a reversibility preserving operator is reversibility preserving. If \( \mathcal {R}({\varphi }) \) is reversibility preserving, then \( (\omega \cdot \partial _{\varphi }\mathcal {R}) ({\varphi }) \) is reversible.
We shall say that a linear operator of the form \( \omega \cdot \partial _{\varphi }+ A({\varphi })\) is reversible if \(A({\varphi })\) is reversible. Conjugating the linear operator \( \omega \cdot \partial _{\varphi }+A({\varphi })\) by a family of invertible linear maps \(\Phi ({\varphi })\), we get the transformed operator
The conjugation of a reversible operator with a reversibility preserving operator is reversible.
Lemma 3.19
A pseudodifferential operator \( {\mathrm{Op}}(a({\varphi }, x, \xi ))\) is reversible, respectively reversibility preserving, if and only if its symbol satisfies
Proof
If the symbols a satisfies (3.47), then, recalling the complex form of the involution \( \mathcal {S}\) in (2.29)–(2.30), we deduce that \( {\mathrm{Op}}(a({\varphi }, x, \xi )) \) is reversible, respectively anti-reversible. The vice versa follows using that \( a({\varphi }, x, j) = e^{- {\mathrm{i}}j x } {\mathrm{Op}}(a({\varphi }, x, \xi )) [ e^{ {\mathrm{i}}j x } ]\). \(\square \)
Remark 3.20
Let \( A({\varphi }) = R({\varphi }) + T({\varphi })\) be a reversible operator. Then \( A({\varphi }) = R_+({\varphi }) + T_+({\varphi }) \) where both operators
are reversible. If \( R(\varphi ) = {\mathrm{Op}}(r ({\varphi },x, \xi ))\) is pseudodifferential, then
and the pseudodifferential norms of \( {\mathrm{Op}}(r)\) and \( {\mathrm{Op}}(r_+) \) are equivalent. If \( T({\varphi })\) is a tame operator with a tame constant \( {\mathfrak {M}}_T (s) \), then \( T_+ ({\varphi }) \) is a tame operator as well with an equivalent tame constant.
Definition 3.21
(Reversible and anti-reversible function) A function \( u ({\varphi }, \cdot ) \) is called reversible if \(\mathcal {S}u ({\varphi }, \cdot ) = u(-{\varphi }, \cdot )\) (cfr. (2.17)), or is called anti-reversible if \(-\mathcal {S}u ({\varphi }, \cdot ) = u(-{\varphi }, \cdot )\). The same definition holds in the action-angle-normal variables \( (\theta , I, w ) \) with the involution \( \vec {\mathcal {S}} \) defined in (2.51) and in the \( (z, \overline{z} )\) complex variables with the involution in (2.29).
A reversibility preserving operator maps reversible, respectively anti-reversible, functions into reversible, respectively anti-reversible, functions.
Lemma 3.22
Let X be a reversible vector field, according to (2.5), and \( u({\varphi }, x) \) be a reversible quasi-periodic function. Then the linearized operator \( {\mathrm{d}}_u X( u({\varphi }, \cdot ) ) \) is reversible, according to Definition 3.17.
Proof
Differentiating (2.5) we get \( ({\mathrm{d}}_u X)( \mathcal {S}u) \circ \mathcal {S}= - \mathcal {S}({\mathrm{d}}_u X)(u) \) and use \( \mathcal {S}u ( {\varphi }, \cdot ) = u (- {\varphi }, \cdot ) \). \(\square \)
Finally we note the following lemma:
Lemma 3.23
The projections \(\Pi ^\intercal _{\mathbb {S}^+, \Sigma }\), \(\Pi ^\angle _{\mathbb {S}^+, \Sigma }\) defined in Section 2.3 commute with the involution \( \mathcal {S}\) defined in (2.4), that is are reversibility preserving. The orthogonal projectors \(\Pi _{\mathbb {S}}\) and \(\Pi _{\mathbb {S}_0}^{\bot } \) commute with the involution in (2.29), that is are reversibility preserving.
Proof
The involution \( \mathcal {S}\) defined in (2.4) maps \( V_{n,\pm }\) into itself, acting as in (2.36). Then, by the decomposition (2.33), each projector \( \Pi _{V_{n,\sigma }} \) commutes with \( \mathcal {S}\). \(\square \)
3.4 Momentum Preserving Operators
The following definition is crucial in the construction of traveling waves.
Definition 3.24
(Momentum preserving) A \( {\varphi }\)-dependent family of linear operators \(A({\varphi }) \), \( {\varphi }\in \mathbb {T}^\nu \), is momentum preserving if
where the translation operator \(\tau _\varsigma \) is defined in (2.7). A linear matrix operator \(\mathbf{A}({\varphi }) \) of the form (3.14) or (3.15) is momentum preserving if each of its components is momentum preserving.
Momentum preserving operators are closed under several operations.
Lemma 3.25
Let \(A({\varphi }), B({\varphi })\) be momentum preserving operators. Then
-
(i)
(Composition): \(A ({\varphi }) \circ B ({\varphi }) \) is a momentum preserving operator.
-
(ii)
(Adjoint): the adjoint \( (A({\varphi }))^*\) is momentum preserving.
-
(iii)
(Inversion): If \(A({\varphi })\) is invertible then \(A({\varphi })^{-1}\) is momentum preserving.
-
(iv)
(Flow): Assume that
$$\begin{aligned} \partial _{t} \Phi ^t ({\varphi }) = A ({\varphi }) \Phi ^t ({\varphi }) , \quad \Phi ^0 ({\varphi }) = {\mathrm{Id}}, \end{aligned}$$(3.49)has a unique propagator \(\Phi ^t ({\varphi }) \) for any \( t\in [0,1] \). Then \(\Phi ^t ( {\varphi }) \) is momentum preserving.
Proof
Item (i) follows directly by (3.48). Item (ii), respectively (iii), follows by taking the adjoint, respectively the inverse, of (3.48) and using that \( \tau _\varsigma ^* = \tau _{-\varsigma } = \tau _\varsigma ^{-1} \). Finally, item (iv) holds because \( \tau _\varsigma ^{-1} \Phi ^t ( {\varphi }- \vec {\jmath } \varsigma ) \tau _\varsigma \) solves the same Cauchy problem in (3.49). \(\square \)
We shall say that a linear operator of the form \( \omega \cdot \partial _{\varphi }+ A({\varphi })\) is momentum preserving if \(A({\varphi })\) is momentum preserving. In particular, conjugating a momentum preserving operator \( \omega \cdot \partial _{\varphi }+A({\varphi }) \) by a family of invertible linear momentum preserving maps \(\Phi ({\varphi })\), we obtain the transformed operator \( \omega \cdot \partial _{\varphi }+ A_+({\varphi }) \) in (3.46) which is momentum preserving.
Lemma 3.26
Let \(A({\varphi })\) be a momentum preserving linear operator and u a quasi-periodic traveling wave, according to Definition 3.1. Then \(A({\varphi }) u \) is a quasi-periodic traveling wave.
Proof
It follows by Definition 3.24 and by the characterization of traveling waves in (3.2). \(\square \)
Lemma 3.27
Let X be a vector field translation invariant, according to (2.8). Let u be a quasi-periodic traveling wave. Then the linearized operator \( {\mathrm{d}}_u X( u({\varphi }, \cdot ) ) \) is momentum preserving.
Proof
Differentiating (2.8) we get \( ({\mathrm{d}}_u X)(\tau _\varsigma u) \circ \tau _\varsigma = \tau _\varsigma ({\mathrm{d}}_u X)(u) \), \( \varsigma \in \mathbb {R}\). Then, apply (3.2). \(\square \)
We now provide a characterization of the momentum preserving property in Fourier space.
Lemma 3.28
Let \( {\varphi }\)-dependent family of operators \( A({\varphi }) \), \( {\varphi }\in \mathbb {T}^\nu \), is momentum preserving if and only if the matrix elements of \(A({\varphi })\), defined by (3.13), fulfill
Proof
By (3.13) we have, for any function u(x),
and
Therefore (3.48) is equivalent to (3.50). \(\square \)
We characterize the symbol of a pseudodifferential operator which is momentum preserving.
Lemma 3.29
A pseudodifferential operator \(A({\varphi }, x,D)= {\mathrm{Op}}(a({\varphi }, x, \xi ))\) is momentum preserving if and only if its symbol satisfies
Proof
If the symbol a satisfies (3.51), then, for all \( \varsigma \in \mathbb {R}\),
proving that \( \tau _\varsigma \circ A({\varphi }, x,D) = A({\varphi }- \vec {\jmath }\varsigma , x,D) \circ \tau _\varsigma \). The vice versa follows using that \( a({\varphi }, x, \xi ) = e^{- {\mathrm{i}}\xi x } A({\varphi }, x,D) [ e^{ {\mathrm{i}}\xi x } ]\). \(\square \)
Note that, if a symbol \( a({\varphi }, x, \xi ) \) satisfies (3.51), then \( (\omega \cdot \partial _{\varphi }a)({\varphi }, x, \xi ) \) satisfies (3.51) as well.
Lemma 3.30
If \( \beta ({\varphi }, x ) \) is a quasi-periodic traveling wave, then the operator \( \mathcal {B}({\varphi }) \) defined in (3.29) is momentum preserving.
Proof
We have \( \mathcal {B}({\varphi }- \vec {\jmath } \varsigma ) [\tau _\varsigma u] = u(x+ \beta ({\varphi }- \vec {\jmath } \varsigma ,x) + \varsigma ) = u(x+ \varsigma + \beta ({\varphi },x+ \varsigma )) = \tau _\varsigma \big ( \mathcal {B}({\varphi }) u\big )\). \(\square \)
We also note the following lemma:
Lemma 3.31
The symplectic projections \( \Pi ^\intercal _{\mathbb {S}^+, \Sigma }\), \( \Pi ^\angle _{\mathbb {S}^+, \Sigma }\), the \( L^2 \)-projections \( \Pi ^{L^2}_\angle \) and \(\Pi _{\mathbb {S}}\), \(\Pi _{\mathbb {S}_0}^{\bot } \) defined in Section 2.3 commute with the translation operators \( \tau _\varsigma \) defined in (2.7), that is are momentum preserving.
Proof
Recall that the translation \( \tau _\varsigma \) maps \( V_{n,\pm }\) into itself, acting as in (2.37). Consider the \( L^2 \)-orthogonal decomposition \( \mathfrak {H}= \mathfrak {H}_\angle \oplus \mathfrak {H}_\angle ^{\bot } \), setting \( \mathfrak {H}_\angle := \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) for brevity, to get
Applying \(\tau _\varsigma \) we get \( \tau _\varsigma u = \tau _\varsigma \Pi _{\mathfrak {H}_\angle }^{L^2} u + \tau _\varsigma \Pi _{\mathfrak {H}_\angle ^{\bot }}^{L^2} u \). As shown above, \( \tau _\varsigma \) maps \( \mathfrak {H}_\angle \) into itself for all \( \varsigma \). Thus also the \( L^2 \)-orthogonal subspace \( \mathfrak {H}_\angle ^{\bot } \) is invariant under the action of \( \tau _\varsigma \) and we conclude, by the uniqueness of the orthogonal decomposition, that \( \tau _\varsigma \Pi _{\mathfrak {H}_\angle }^{L^2} u = \Pi _{\mathfrak {H}_\angle }^{L^2} \tau _\varsigma u \), \( \tau _\varsigma \Pi _{\mathfrak {H}_\angle ^{\bot }}^{L^2} u = \Pi _{\mathfrak {H}_\angle ^{\bot }}^{L^2} \tau _\varsigma u \). \(\square \)
The next lemma concerns the Dirichlet-Neumann operator.
Lemma 3.32
The Dirichlet-Neumann operator \(G(\overline{\eta },\mathtt{h})\), evaluated at a quasi-periodic traveling wave \(\overline{\eta } ({\varphi }, x) \), is momentum preserving.
Proof
It follows by (2.9) and the characterization in (3.2) of the quasi-periodic traveling wave \(\overline{\eta }({\varphi },x) \). \(\square \)
Quasi-periodic traveling waves in action-angle-normal coordinates. We now discuss how the momentum preserving condition reads in the coordinates \((\theta , I, w)\) introduced in (2.50). Recalling (2.52), if \(u({\varphi },x)\) is a quasi-periodic traveling wave with action-angle-normal components \((\theta ({\varphi }), I({\varphi }), w({\varphi }, x))\), the condition \(\tau _\varsigma u = u({\varphi }- \vec {\jmath } \varsigma , \cdot )\) becomes
As we look for \(\theta ({\varphi })\) of the form \(\theta ({\varphi }) = {\varphi }+ \Theta ({\varphi })\), with a \( (2 \pi )^\nu \)-periodic function \( \Theta : \mathbb {R}^\nu \mapsto \mathbb {R}^\nu \), \( {\varphi }\mapsto \Theta ({\varphi }) \), the traveling wave condition becomes
Definition 3.33
(Traveling wave variation) We call a traveling wave variation \( g({\varphi }) = (g_1({\varphi }), g_2({\varphi }), g_3({\varphi }, \cdot )) \in \mathbb {R}^\nu \times \mathbb {R}^\nu \times \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) a function satisfying (3.53), that is
or, equivalently, \(D \vec {\tau }_\varsigma g({\varphi }) = g({\varphi }- \vec {\jmath }\varsigma ) \) for any \(\varsigma \in \mathbb {R}\), where \(D \vec {\tau }_\varsigma \) is the differential of \( \vec {\tau }_\varsigma \), namely
According to Definition 3.24, a linear operator acting in \( \mathbb {R}^\nu \times \mathbb {R}^\nu \times \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) is momentum preserving if
In a fashion similar to Lemma 3.26, one proves the following result:
Lemma 3.34
Let \(A({\varphi })\) be a momentum preserving linear operator acting on \(\mathbb {R}^\nu \times \mathbb {R}^\nu \times \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) and \(g \in \mathbb {R}^\nu \times \mathbb {R}^\nu \times \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) be a traveling wave variation. Then \( A({\varphi }) g({\varphi })\) is a traveling wave variation.
4 Transversality of Linear Frequencies
In this section we extend the KAM theory approach of [3, 6] in order to deal with the linear frequencies \( \Omega _j(\kappa ) \) defined in (1.11). The main novelty is the use of the momentum condition in the proof of Proposition 4.5. We shall also exploit that the tangential sites \( \mathbb {S}:=\{ \overline{\jmath }_1, \ldots ,\overline{\jmath }_\nu \} \subset \mathbb {Z}{\setminus }\{0\}\) defined in (2.48), have all distinct modulus \( | \overline{\jmath }_a | = \overline{n}_a \), see assumption (1.15).
We first introduce the following definition:
Definition 4.1
A function \(f=(f_1,\dots ,f_N):[\kappa _1,\kappa _2]\rightarrow \mathbb {R}^N\) is non-degenerate if, for any \(c\in \mathbb {R}^N{\setminus }\{0\}\), the scalar function \(f\cdot c\) is not identically zero on the whole interval \([\kappa _1,\kappa _2]\).
From a geometric point of view, if f is non-degenerate it means that the image of the curve \( f([\kappa _1,\kappa _2]) \subset \mathbb {R}^N \) is not contained in any hyperplane of \( \mathbb {R}^N \).
We shall use in the sequel that the maps \( \kappa \mapsto \Omega _j (\kappa ) \) are analytic in \( [\kappa _1, \kappa _2] \). We decompose
Note that the dependence on \( \kappa \) of \( \Omega _j (\kappa ) \) enters only through \( \omega _j(\kappa ) \), because \( \frac{G_j(0)}{j}\) is independent of \( \kappa \). Note also that \( j \mapsto \omega _j (\kappa ) \) is even in j, whereas the component due to the vorticity \( j \mapsto \gamma \frac{G_j(0)}{j} \) is odd. Moreover this term is, in view of (1.8), uniformly bounded in j.
Lemma 4.2
(Non-degeneracy-I) The following frequency vectors are non-degenerate:
-
1.
\(\vec {\Omega }(\kappa ) := ( \Omega _j (\kappa ) )_{j \in \mathbb {S}} \in \mathbb {R}^\nu \);
-
2.
\(\big ( \vec {\Omega }(\kappa ),\sqrt{\kappa }\big )\in \mathbb {R}^{\nu +1}\);
-
3.
\(\big ( \vec {\Omega }(\kappa ),\Omega _j(\kappa ) \big ) \in \mathbb {R}^{\nu +1}\), for any \(j\in \mathbb {Z}{\setminus }\left( \{ 0 \}\cup \mathbb {S}\cup (-\mathbb {S})\right) \);
-
4.
\(\big ( \vec {\Omega }(\kappa ),\Omega _j(\kappa ) ,\Omega _{j'}(\kappa ) \big )\in \mathbb {R}^{\nu +2}\), for any \(j, j'\in \mathbb {Z}{\setminus }\left( \{0\}\cup \mathbb {S}\cup (-\mathbb {S}) \right) \) and \(|j| \ne |j'|\).
Proof
Let
Recalling (4.1), we have that, for any \( j \in \mathbb {Z}\),
Moreover \(\partial _\kappa \lambda _j(\kappa )= -2 \lambda _j(\kappa )^2 \), for any \(j\in \mathbb {Z}\), and therefore, for any \(n\in \mathbb {N}\),
We now prove items 2 and 3, that is the non-degeneracy of the vector \(\big ( \vec {\Omega }(\kappa ),{\widetilde{\Omega }}_j(\kappa ) \big ) \in \mathbb {R}^{\nu +1}\) for any \(j \in \mathbb {Z}{\setminus } ( \mathbb {S}\cup (-\mathbb {S})) \), where \({\widetilde{\Omega }}_j(\kappa ) \) is defined in (4.2). Items 1 and 4 follow similarly. For this purpose, by analyticity, it is sufficient to find one value of \(\kappa \in [\kappa _1, \kappa _2]\) so that the determinant of the \((\nu +1)\times (\nu +1)\) matrix
is not zero. We actually show that \(\det \mathcal {A}(\kappa ) \ne 0\) for any \(\kappa \in [\kappa _1, \kappa _2]\). By (4.2)–(4.4) and the multilinearity of the determinant function, we get
where
Since \(\mathcal {B}(\kappa )\) is a Vandermorde matrix, we conclude that
Now, the fact that \(\det \mathcal {A}(\kappa )\ne 0\) for any \(\kappa \in [\kappa _1,\kappa _2]\) is a consequence from the following
Claim: For any \(p,p'\in \{\overline{\jmath }_1,\ldots ,\overline{\jmath }_\nu ,j\}\), \(p \ne p'\), one has \(\lambda _p(\kappa )\ne \lambda _{p'}(\kappa )\) for any \(\kappa \in [\kappa _1,\kappa _2]\).
Proof of the Claim: If \(p' = 0\) and \(p \ne 0\), the claim follows because, by (4.3),
Consider now the case \(p, p' \ne 0 \). We now prove that the map \( p \mapsto \lambda _p(\kappa ) \) is strictly monotone on \((0, + \infty )\). In case of finite depth, \(G_p(0) =p\tanh (\mathtt{h}p) \), and
The function \(f(y):= 3 \tanh (y)-(1-\tanh ^2(y))y \) is positive for any \(y>0\). Indeed \(f(y)\rightarrow 0\) as \(y\rightarrow 0\), and it is strictly monotone increasing for \( y > 0 \), since \( f'(y) = 2(1-\tanh ^2(y)) ( 1+ y \tanh (y) ) > 0 \). We deduce that \(\partial _p\lambda _p(\kappa ) > 0 \), also if the depth \( \mathtt{h}= + \infty \). Since the function \( p \mapsto \lambda _p(\kappa )\) is even we have proved that that it is strictly monotone decreasing on \((-\infty ,0)\) and increasing in \((0, +\infty )\). Thus, if \(\lambda _p(\kappa ) = \lambda _{p'}(\kappa )\) then \(p = -p'\). But this case is excluded by the assumption (1.15) and the condition \( j \not \in \mathbb {S}\cup (-\mathbb {S}) \), which together imply \(|p| \ne |p'|\). \(\square \)
Note that in items 3 and 4 of Lemma 4.2 we require that j and \( j' \) do not belong to \( \{0\} \cup {\mathbb {S}} \cup (-{\mathbb {S}}) \). In order to deal in Proposition 4.5 when j and \( j' \) are in \( {\mathbb {S}} \cup (-{\mathbb {S}}) \), we need also the following lemma. It is actually a direct consequence of the proof of Lemma 4.2, noting that \(\Omega _j (\kappa ) - \omega _j (\kappa )\) is independent of \( \kappa \).
Lemma 4.3
(Non-degeneracy-II) Let \(\vec {\omega }(\kappa ):= \left( \omega _{\overline{\jmath }_1}(\kappa ),\ldots ,\omega _{\overline{\jmath }_\nu }(\kappa ) \right) \). The following vectors are non-degenerate:
-
1.
\((\vec {\omega }(\kappa ),1)\in \mathbb {R}^{\nu +1}\);
-
2.
\(\left( \vec {\omega }(\kappa ),\omega _j(\kappa ),1 \right) \in \mathbb {R}^{\nu +2}\), for any \(j\in \mathbb {Z}{\setminus }\left( \{ 0 \}\cup \mathbb {S}\cup (-\mathbb {S})\right) \).
For later use, we provide the following asymptotic estimate of the linear frequencies:
Lemma 4.4
(Asymptotics) For any \(j\in \mathbb {Z}{\setminus }\{0\}\), we have
where, for any \( n \in \mathbb {N}_0 \), there exists a constant \(C_{n,\mathtt{h}} >0\) such that
Proof
Then (4.6) follows exploiting that (both for finite and infinite depth) the quantities \(|j| (G_j(0) - |j|)\) and \(G_j(0)/|j|\) are uniformly bounded in j, see (1.8). \(\square \)
The next proposition is the key of the argument. We remind that \(\vec {\jmath } = ( \overline{\jmath }_1, \ldots ,\overline{\jmath }_\nu ) \) denotes the vector in \( \mathbb {Z}^\nu \) of tangential sites introduced in (2.53).
Proposition 4.5
(Transversality) There exist \(m_0\in \mathbb {N}\) and \(\rho _0>0\) such that, for any \(\kappa \in [\kappa _1,\kappa _2]\), the following hold:
We call \(\rho _0\) the amount of non-degeneracy and \(m_0\) the index of non-degeneracy.
Proof
We prove separately (4.7)–(4.10). In this proof we set for brevity \( \mathfrak {K}:= [ \kappa _1, \kappa _2]\).
Proof of (4.7). By contradiction, assume that for any \(m\in \mathbb {N}\) there exist \(\kappa _m\in \mathfrak {K}\) and \(\ell _m\in \mathbb {Z}^\nu {\setminus }\{0\}\) such that
The sequences \((\kappa _m)_{m\in \mathbb {N}}\subset \mathfrak {K}\) and \((\ell _m/\langle \ell _m\rangle )_{m\in \mathbb {N}}\subset \mathbb {R}^\nu {\setminus }\{0\}\) are both bounded. By compactness, up to subsequences \(\kappa _m\rightarrow \overline{\kappa }\in \mathfrak {K}\) and \(\ell _m/\langle \ell _m\rangle \rightarrow \overline{c}\ne 0\). Therefore, in the limit for \(m\rightarrow + \infty \), by (4.11) we get \(\partial _\kappa ^n \vec {\Omega }(\overline{\kappa })\cdot \overline{c} = 0\) for any \(n\in \mathbb {N}_0\). By the analyticity of \( \vec {\Omega }(\kappa )\), we deduce that the function \( \kappa \mapsto \vec {\Omega }(\kappa )\cdot \overline{c}\) is identically zero on \(\mathfrak {K}\), which contradicts Lemma 4.2-1.
Proof of (4.8). We divide the proof in 4 steps.
Step 1. Recalling (4.1) and Lemma 4.4, we have that, for any \(\kappa \in \mathfrak {K}\),
whenever \(\left| j \right| ^\frac{3}{2} \geqq C_0 \langle \ell \rangle \), for some \(C_0>0\). In this cases (4.8) is already fulfilled with \(n=0\). Hence we restrict in the sequel to indexes \(\ell \in \mathbb {Z}^{\nu }\) and \(j \in \mathbb {S}_0^c\) satisfying
Step 2. By contradiction, we assume that, for any \(m\in \mathbb {N}\), there exist \(\kappa _m\in \mathfrak {K}\), \(\ell _m\in \mathbb {Z}^\nu \) and \(j_m\in \mathbb {S}_0^c\), with \(\left| j_m \right| ^\frac{3}{2}<C_0 \langle \ell _m \rangle \), such that, for any \(n\in \mathbb {N}_0\) with \(n\leqq m\),
Up to subsequences \(\kappa _m\rightarrow \overline{\kappa }\in \mathfrak {K}\) and \(\ell _m/\langle \ell _m\rangle \rightarrow \overline{c}\in \mathbb {R}^\nu \).
Step 3. We consider first the case when the sequence \((\ell _m)_{m\in \mathbb {N}}\subset \mathbb {Z}^\nu \) is bounded. Up to subsequences, we have definitively that \(\ell _m=\overline{\ell }\in \mathbb {Z}^\nu \). Moreover, since \(j_m\) and \(\ell _m\) satisfy (4.12), also the sequence \((j_m)_{m\in \mathbb {N}}\) is bounded and, up to subsequences, definitively \( j_m = \overline{\jmath } \in \mathbb {S}_0^c \). Therefore, in the limit \(m\rightarrow \infty \), from (4.13) we obtain
By analyticity, this implies
We distinguish two cases:
-
Let \(\overline{\jmath } \notin -\mathbb {S}\). By (4.14) the vector \(\big ( \vec {\Omega }(\kappa ),\Omega _{\overline{\jmath }}(\kappa ) \big ) \) is degenerate according to Definition 4.1 with \(c:=(\overline{\ell }, 1)\ne 0\). This contradicts Lemma 4.2-3.
-
Let \(\overline{\jmath } \in -\mathbb {S}\). With no loss of generality suppose \(\overline{\jmath } = - \overline{\jmath }_1\). Then, denoting \(\overline{\ell } = (\overline{\ell _1}, \ldots ,\overline{\ell _\nu })\), system (4.14) reads, for any \( \kappa \in \mathfrak {K}\),
$$\begin{aligned} {\left\{ \begin{array}{ll} (\overline{\ell _1}+1)\omega _{\overline{\jmath }_1}(\kappa ) + \sum _{a=2}^{\nu }\overline{\ell _a}\omega _{\overline{\jmath }_a}(\kappa ) + \frac{\gamma }{2}\left( (\overline{\ell _1}-1)\frac{G_{\overline{\jmath }_1}(0)}{\overline{\jmath }_1} + \sum _{a=2}^\nu \overline{\ell _a} \frac{G_{\overline{\jmath }_a}(0)}{\overline{\jmath }_a} \right) = 0 \\ (\overline{\ell _1}-1)\overline{\jmath }_1 + \sum _{a=2}^\nu \overline{\ell _a}\, \overline{\jmath }_a = 0. \end{array}\right. } \end{aligned}$$(4.15)By Lemma 4.3-1 the vector \((\vec {\omega }(\kappa ),1) \) is non-degenerate, which is a contradiction for \(\gamma \ne 0 \). If \( \gamma = 0 \) we only deduce \(\overline{\ell _1}= - 1\) and \(\overline{\ell _2}=\ldots =\overline{\ell _\nu }=0\). Inserting these values in the momentum condition in (4.15), we get \(2\overline{\jmath }_1=0\). This is a contradiction with \( \overline{\jmath }_1 \ne 0\).
Step 4. We consider now the case when the sequence \((\ell _m)_{m\in \mathbb {N}}\) is unbounded. Up to subsequences \(\left| \ell _m \right| \rightarrow \infty \) as \(m\rightarrow \infty \) and \( \lim _{m\rightarrow \infty }\ell _m/\langle \ell _m\rangle =: \overline{c} \ne 0 \). By (4.1) and (4.5), for any \( n \in \mathbb {N}_0 \),
with \(\overline{d}:= \lim _{m\rightarrow \infty }\left| j_m \right| ^\frac{3}{2}/\langle \ell _m\rangle \in \mathbb {R}\). Note that \( \overline{d} \) is finite because \(j_m\) and \(\ell _m\) satisfy (4.12). Therefore (4.13) becomes, in the limit \(m\rightarrow \infty \),
By analyticity, this implies that \(\vec {\Omega }(\kappa )\cdot \overline{c} + \overline{d}\sqrt{\kappa } = 0 \) for any \(\kappa \in \mathfrak {K}\). This contradicts the non-degeneracy of the vector \((\vec {\Omega }(\kappa ), \sqrt{\kappa })\) in Lemma 4.2-2, since \((\overline{c}, \overline{d}) \ne 0\).
Proof of (4.9). We split again the proof into 4 steps.
Step 1. By Lemma 4.4, for any \(\kappa \in \mathfrak {K}\),
whenever \( | \left| j \right| ^\frac{3}{2} - |j'|^\frac{3}{2} | \geqq C_1 \langle \ell \rangle \) for some \(C_1>0\). In this case (4.10) is already fulfilled with \( n = 0 \). Thus we restrict to indexes \(\ell \in \mathbb {Z}^\nu \) and \(j,j'\in \mathbb {S}_0^c\), such that
Furthermore we may assume \( j_m \ne j_m' \) because the case \( j_m = j_m' \) is included in (4.7).
Step 2. By contradiction, we assume that, for any \(m\in \mathbb {N}\), there exist \(\kappa _m\in \mathfrak {K}\), \(\ell _m\in \mathbb {Z}^\nu \) and \(j_m,j_m'\in \mathbb {S}_0^c\), satisfying (4.16), such that, for any \(0\leqq n\leqq m\),
Up to subsequences \(\kappa _m\rightarrow \overline{\kappa }\in \mathfrak {K}\) and \(\ell _m/\langle \ell _m\rangle \rightarrow \overline{c}\in \mathbb {R}^\nu \).
Step 3. We start with the case when \((\ell _m)_{m\in \mathbb {N}}\subset \mathbb {Z}^\nu \) is bounded. Up to subsequences, we have definitively that \(\ell _m = \overline{\ell }\in \mathbb {Z}^\nu \). Moreover, if \( |j_m| \ne |j_m'| \), there is \( c > 0 \) such that
If \( j_m = - j_m' \) we deduce by the momentum relation that \( |j_m| = |j_m'| \leqq C \langle \ell _m \rangle \leqq C \), and we conclude that in any case the sequences \((j_m)_{m\in \mathbb {N}}\) and \((j_m')_{m\in \mathbb {N}}\) are bounded. Up to subsequences, we have definitively that \(j_m= \overline{\jmath }\) and \( j_m'=\overline{\jmath }' \), with \(\overline{\jmath }, \overline{\jmath }'\in \mathbb {S}_0^c\) and such that
Therefore (4.17) becomes, in the limit \(m\rightarrow \infty \),
By analyticity, we obtain that
We distinguish several cases:
-
Let \(\overline{\jmath },\overline{\jmath }' \notin -\mathbb {S}\) and \(|\overline{\jmath }|\ne |\overline{\jmath }'|\). By (4.19) the vector \((\vec {\Omega }(\kappa ),\Omega _{\overline{\jmath }}(\kappa ),\Omega _{\overline{\jmath }'}(\kappa ))\) is degenerate with \(c:= (\overline{\ell },1,-1)\ne 0\), contradicting Lemma 4.2-4.
-
Let \(\overline{\jmath },\overline{\jmath }' \notin -\mathbb {S}\) and \(\overline{\jmath }'=- \overline{\jmath }\). In view of (4.1), system (4.19) becomes
$$\begin{aligned} {\left\{ \begin{array}{ll} \vec {\omega }(\kappa )\cdot \overline{\ell } + \frac{\gamma }{2} \left( \sum _{a=1}^{\nu }\overline{\ell _a}\frac{G_{\overline{\jmath }_a }(0)}{\overline{\jmath }_a} +2 \frac{G_{\overline{\jmath }}(0)}{\overline{\jmath }} \right) = 0, \qquad \forall \kappa \in \mathfrak {K}\, , \\ \vec {\jmath }\cdot \overline{\ell } +2 \overline{\jmath } = 0. \end{array}\right. } \end{aligned}$$(4.20)By Lemma 4.3-1, the vector \((\vec {\omega }(\kappa ),1)\) is non-degenerate, which is a contradiction for \( \gamma \ne 0 \). If \( \gamma = 0 \) the first equation in (4.20) implies \(\overline{\ell } = 0\). Then the momentum condition implies \( 2 \overline{\jmath } =0\), which is a contradiction with \(\overline{\jmath } \ne 0\).
-
Let \(\overline{\jmath }'\notin -\mathbb {S}\) and \(\overline{\jmath }\in -\mathbb {S}\). With no loss of generality suppose \(\overline{\jmath }= -\overline{\jmath }_1 \). In view of (4.1), the first equation in (4.19) implies that, for any \(\kappa \in \mathfrak {K}\),
$$\begin{aligned}&(\overline{\ell _1}+1)\omega _{\overline{\jmath }_1}(\kappa ) + \sum _{a=2}^{\nu }\overline{\ell _a}\omega _{\overline{\jmath }_a}(\kappa )-\omega _{\overline{\jmath }'}(\kappa ) \\&\quad + \frac{\gamma }{2}\Big ( (\overline{\ell _1}-1)\frac{G_{\overline{\jmath }_1}(0)}{\overline{\jmath }_1} + \sum _{a=2}^\nu \overline{\ell _a} \frac{G_{\overline{\jmath }_a}(0)}{\overline{\jmath }_a} -\frac{G_{\overline{\jmath }'}(0)}{\overline{\jmath }'} \Big ) = 0. \end{aligned}$$By Lemma 4.3-2, the vector \(\big ( \vec {\omega }(\kappa ),\omega _{\overline{\jmath }'}(\kappa ),1 \big )\) is non-degenerate, which is a contradiction.
-
Last, let \(\overline{\jmath },\overline{\jmath }'\in -\mathbb {S}\) and \(\overline{\jmath }\ne \overline{\jmath }'\), by (4.18). With no loss of generality suppose \(\overline{\jmath } =- \overline{\jmath }_1\) and \(\overline{\jmath }' = -\overline{\jmath }_2\). Then (4.19) reads, for any \(\kappa \in \mathfrak {K}\),
$$\begin{aligned} {\left\{ \begin{array}{ll} (\overline{\ell _1}+1)\omega _{\overline{\jmath }_1}(\kappa ) + \left( \overline{\ell _2} - 1 \right) \omega _{\overline{\jmath }_2} +\sum _{a=3}^{\nu }\overline{\ell _a}\omega _{\overline{\jmath }_a}(\kappa )\\ + \frac{\gamma }{2}\left( (\overline{\ell _1}-1)\frac{G_{\overline{\jmath }_1}(0)}{\overline{\jmath }_1}+ (\overline{\ell _2}+1 )\frac{G_{\overline{\jmath }_2}(0)}{\overline{\jmath }_2} + \sum _{a=3}^\nu \overline{\ell _a} \frac{G_{\overline{\jmath }_a}(0)}{\overline{\jmath }_a} ) \right) = 0, \\ (\overline{\ell _1}-1)\overline{\jmath }_1+ (\overline{\ell _2}+1)\overline{\jmath }_2 +\sum _{a=3}^\nu \overline{\ell _a}\, \overline{\jmath }_a = 0. \end{array}\right. } \end{aligned}$$(4.21)By Lemma 4.3-1, the vector \( (\vec {\omega }(\kappa ),1) \) is non-degenerate, therefore the first equation in (4.21) can hold only if \(\overline{\ell _1}=-1\), \(\overline{\ell _2} = 1\), \(\overline{\ell _3}=\ldots =\overline{\ell _\nu }=0\). Inserting these values in the momentum condition we obtain \(-2\overline{\jmath }_1+ 2 \overline{\jmath }_2 = 0\). This contradicts \(\overline{\jmath }\ne \overline{\jmath }'\).
Step 4. We finally consider the case when \((\ell _m)_{m\in \mathbb {N}}\) is unbounded. Up to subsequences \(\left| \ell _m \right| \rightarrow \infty \) as \(m\rightarrow \infty \) and \( \lim _{m\rightarrow \infty }\ell _m/\langle \ell _m\rangle =: \overline{c} \ne 0 \). In addition, by (4.16), up to subsequences
By (4.1) and (4.5) we have, for any n,
using (4.22) and \(\left\langle \ell _m \right\rangle \rightarrow \infty \). Therefore (4.17) becomes, in the limit \(m\rightarrow \infty \),
By analyticity this implies \(\vec {\Omega }(\kappa )\cdot \overline{c} + \overline{d}_1 \sqrt{\kappa }= 0\), for all \( \kappa \in \mathfrak {K}\). Thus \((\vec {\Omega }(\kappa ), \sqrt{\kappa })\) is degenerate with \(c = (\overline{c}, \overline{d}_1) \ne 0\), contradicting Lemma 4.2-2.
Proof of (4.10). The proof is similar to that for (4.9) and we omit it. \(\square \)
5 Nash–Moser Theorem and Measure Estimates
Under the rescaling \( (\eta ,\zeta )\mapsto (\varepsilon \eta , \varepsilon \zeta ) \), the Hamiltonian system (2.14) transforms into the Hamiltonian system generated by
where \( \mathcal {H}\) is the water waves Hamiltonian (2.13) expressed in the Wahlén coordinates (2.11), \(\mathcal {H}_L \) is defined in (2.20) and
We now study the Hamiltonian system generated by the Hamiltonian \(\mathcal {H}_\varepsilon (\eta ,\zeta ) \), in the action-angle and normal coordinates \( (\theta , I, w) \) defined in Section 2.3. Thus we consider the Hamiltonian \(H_\varepsilon (\theta , I, w )\) defined by
where A is the map defined in (2.50). The associated symplectic form is given in (2.54).
By Lemma 2.9 (see also (2.35), (2.49)), in the variables \( (\theta , I, w) \) the quadratic Hamiltonian \(\mathcal {H}_L \) defined in (2.20) simply reads, up to a constant, as
where \(\vec {\Omega }(\kappa ) \in \mathbb {R}^\nu \) is defined in (1.18) and \({\varvec{\Omega }}_W\) in (2.19). Thus the Hamiltonian \(H_\varepsilon \) in (5.2) is
We look for an embedded invariant torus
of the Hamiltonian vector field \( X_{H_\varepsilon } := ( \partial _I H_\varepsilon , -\partial _\theta H_\varepsilon , \Pi _{\mathbb {S}^+,\Sigma }^\angle J \nabla _{w} H_\varepsilon ) \) filled by quasi-periodic solutions with Diophantine frequency vector \(\omega \in \mathbb {R}^\nu \) (which satisfies also first and second order Melnikov non-resonance conditions, see (5.14)–(5.165.17)).
5.1 Nash–Moser Theorem of Hypothetical Conjugation
For \(\alpha \in \mathbb {R}^\nu \), we consider the family of modified Hamiltonians
and the nonlinear operator
If \(\mathcal {F}(i,\alpha )=0\), then the embedding \({\varphi }\mapsto i({\varphi })\) is an invariant torus for the Hamiltonian vector field \(X_{H_\alpha }\), filled with quasi-periodic solutions with frequency \(\omega \).
Each Hamiltonian \(H_\alpha \) in (5.4) is invariant under the involution \(\vec {\mathcal {S}}\) and the translations \(\vec {\tau }_\varsigma \), \(\varsigma \in \mathbb {R}\), defined in (2.51) and (2.52), respectively, as
We look for a reversible traveling torus embedding \( \varphi \mapsto i (\varphi ) = \) \( ( \theta ({\varphi }), I({\varphi }), w({\varphi })) \); namely one satisfying
Lemma 5.1
The operator \( \mathcal {F}( \cdot , \alpha ) \) maps a reversible, respectively traveling, wave into an anti-reversible, respectively traveling, wave variation, according to Definition 3.33.
Proof
It follows directly by (5.5) and (5.6). \(\square \)
The norm of the periodic components of the embedded torus
is \( \left\| {\mathfrak {I}} \right\| _s^{k_0,\upsilon } := \left\| \Theta \right\| _{H_{\varphi }^s}^{k_0,\upsilon } + \left\| I \right\| _{H_{\varphi }^s}^{k_0,\upsilon } + \left\| w \right\| _s^{k_0,\upsilon } \), where
and \(m_0 \in \mathbb {N}\) is the index of non-degeneracy provided by Proposition 4.5, which only depends on the linear unperturbed frequencies. Thus, \(k_0\) is considered as an absolute constant and we will often omit to write the dependence of the various constants with respect to \(k_0\). We look for quasi-periodic solutions of frequency \(\omega \) belonging to a \(\delta \)-neighbourhood (independent of \(\varepsilon \))

of the curve \(\vec {\Omega }[\kappa _1,\kappa _2]\) defined by (1.18).
Theorem 5.2
(Nash–Moser) There exist positive constants \({\mathrm{a_0}},\varepsilon _0, C\) depending on \(\mathbb {S}\), \(k_0 \) and \(\tau \geqq 1\) such that, for all \(\upsilon = \varepsilon ^{\mathrm{a}}\), \({\mathrm{a}}\in (0,{\mathrm{a}}_0)\) and for all \(\varepsilon \in (0,\varepsilon _0)\), there exist
-
1.
a \(k_0\)-times differentiable function
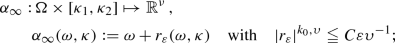 (5.10)
(5.10) -
2.
a family of embedded reversible traveling tori \(i_\infty ({\varphi }) \) (cfr. (5.7)), defined for all
 , satisfying $$\begin{aligned} \Vert i_\infty ({\varphi }) -({\varphi },0,0) \Vert _{s_0}^{k_0,\upsilon } \leqq C \varepsilon \upsilon ^{-1} \, ; \end{aligned}$$(5.11)
, satisfying $$\begin{aligned} \Vert i_\infty ({\varphi }) -({\varphi },0,0) \Vert _{s_0}^{k_0,\upsilon } \leqq C \varepsilon \upsilon ^{-1} \, ; \end{aligned}$$(5.11) -
3.
a sequence of \(k_0\)-times differentiable functions \(\mu _j^\infty : \mathbb {R}^\nu \times [\kappa _1,\kappa _2] \rightarrow \mathbb {R}\), \(j\in \mathbb {S}_0^c = \mathbb {Z}\,{\setminus }\,(\mathbb {S}\cup \{0\})\), of the form
$$\begin{aligned} \mu _j^\infty (\omega ,\kappa ) = \mathtt{m}_{\frac{3}{2}}^\infty (\omega ,\kappa ) \Omega _j(\kappa ) + \mathtt{m}_1^\infty (\omega ,\kappa )j + \mathtt{m}_{\frac{1}{2}}^\infty (\omega ,\kappa )\left| j \right| ^\frac{1}{2} + {\mathfrak {r}}_j^\infty (\omega ,\kappa )\,, \end{aligned}$$(5.12)with \(\Omega _j(\kappa ) \) defined in (1.11), satisfying
$$\begin{aligned} | \mathtt{m}_{\frac{3}{2}}^\infty -1 |^{k_0,\upsilon } ,\, |\mathtt{m}_1^\infty |^{k_0,\upsilon }, \, |\mathtt{m}_{\frac{1}{2}}^\infty |^{k_0,\upsilon } \leqq C\varepsilon , \quad \sup _{j\in \mathbb {S}_0^c} | {\mathfrak {r}}_j^\infty |^{k_0,\upsilon } \leqq C \varepsilon \upsilon ^{-1}, \end{aligned}$$(5.13)
such that, for all \((\omega ,\kappa )\) in the Cantor-like set




the function \(i_\infty ({\varphi }):= i_\infty (\omega ,\kappa ,\varepsilon ;{\varphi })\) is a solution of \(\mathcal {F}(\omega ,\kappa ,\varepsilon ; i_\infty ,\alpha _\infty (\omega ,\kappa ))=0\). As a consequence, the embedded torus \({\varphi }\mapsto i_\infty ({\varphi })\) is invariant for the Hamiltonian vector field \(X_{H_{\alpha _\infty (\omega ,\kappa )}}\) as it is filled by quasi-periodic reversible traveling wave solutions with frequency \(\omega \).
We remind that the conditions on the indexes in (5.15)–(5.165.17) (where \( \vec {\jmath } \in \mathbb {Z}^\nu \) is the vector in (2.53)) are due to the fact that we look for traveling wave solutions. These restrictions are essential to prove the measure estimates of the next section.
5.2 Measure Estimates
By (5.10), the function \(\alpha _\infty (\,\cdot \,,\kappa )\) from  into its image
into its image  is invertible and
is invertible and
Then, for any \(\beta \in \alpha _\infty (\mathcal {C}_\infty ^\upsilon )\), Theorem 5.2 proves the existence of an embedded invariant torus filled by quasi-periodic solutions with Diophantine frequency \(\omega =\alpha _\infty ^{-1}(\beta ,\kappa )\) for the Hamiltonian
Consider the curve of the unperturbed tangential frequency vector \( \vec {\Omega }(\kappa ) \) in (1.18). In Theorem 5.3 below we prove that for “most” values of \(\kappa \in [\kappa _1,\kappa _2]\) the vector \((\alpha _\infty ^{-1}(\vec {\Omega }(\kappa ),\kappa ) ,\kappa )\) is in \(\mathcal {C}_\infty ^\upsilon \), obtaining an embedded torus for the Hamiltonian \(H_\varepsilon \) in (5.2), filled by quasi-periodic solutions with Diophantine frequency vector \(\omega = \alpha _\infty ^{-1}(\vec {\Omega }(\kappa ),\kappa ) \), denoted \( {\widetilde{\Omega }}\) in Theorem 1.5. Thus \(\varepsilon A(i_\infty ({\widetilde{\Omega }}t))\), where A is defined in (2.50), is a quasi-periodic traveling wave solution of the water waves equations (2.14) written in the Wahlén variables. Finally, going back to the original Zakharov variables via (2.10) we obtain solutions of (1.3). This proves Theorem 1.5 together with the following measure estimate.
Theorem 5.3
(Measure estimates) Let
where \(m_0\) is the index of non-degeneracy given in Proposition 4.5 and \(k_0:= m_0+2\). Then, for \( \varepsilon \in (0, \varepsilon _0) \) small enough, the measure of the set
satisfies \( | \mathcal {G}_\varepsilon | \rightarrow \kappa _2-\kappa _1\) as \(\varepsilon \rightarrow 0\).
The rest of this section is devoted to prove Theorem 5.3. By (5.18) we have
where \(\vec {r}_\varepsilon (\kappa ) := \breve{r}_\varepsilon (\vec {\Omega }(\kappa ),\kappa ) \) satisfies
We also denote, with a small abuse of notation, for all \(j\in \mathbb {S}_0^c\),
where \(\mathtt{m}_{\frac{3}{2}}^\infty (\kappa ) :=\mathtt{m}_{\frac{3}{2}}^\infty (\vec {\Omega }_\varepsilon (\kappa ),\kappa ) \), \(\mathtt{m}_1^\infty (\kappa ) :=\mathtt{m}_1^\infty (\vec {\Omega }_\varepsilon (\kappa ),\kappa ) \), \(\mathtt{m}_{\frac{1}{2}}^\infty (\kappa ) :=\mathtt{m}_{\frac{1}{2}}^\infty (\vec {\Omega }_\varepsilon (\kappa ),\kappa ) \) and \({\mathfrak {r}}_j^\infty (\kappa ) :={\mathfrak {r}}_j^\infty (\vec {\Omega }_\varepsilon (\kappa ),\kappa ) \).
Recalling (5.14)–(5.165.17), the Cantor set in (5.20) becomes
We estimate the measure of the complementary set
where the “nearly-resonant sets”
Note that in the third union in (5.26) we may require \( j \ne j' \) because \(R_{\ell ,j,j}^{(II)} \subset R_\ell ^{(0)}\). In the sequel we shall always suppose the momentum conditions on the indexes \( \ell , j, j' \) written in (5.26). Some of the above sets are empty.
Lemma 5.4
Consider the sets in (5.26)–(5.30). For \(\varepsilon \in (0,\varepsilon _0)\) small enough, we have that
-
1.
If \(R_{\ell ,j}^{(I)}\ne \emptyset \) then \( |j|^\frac{3}{2} \leqq C \langle \ell \rangle \);
-
2.
If \(R_{\ell ,j,j'}^{(II)}\ne \emptyset \) then \(\big | | j|^\frac{3}{2} -|j'|^\frac{3}{2} \big |\leqq C \langle \ell \rangle \);
-
3.
If \(Q_{\ell ,j,j'}^{(II)}\ne \emptyset \) then \( |j|^\frac{3}{2} + |j'|^\frac{3}{2}\leqq C \langle \ell \rangle \).
Proof
We provide the proof for \(R_{\ell ,j,j'}^{(II)}\). If \(R_{\ell ,j,j'}^{(II)}\ne \emptyset \) then there exists \(\kappa \in [\kappa _1,\kappa _2]\) such that
By (5.23) we have
Then, by (5.24)–(5.25) with \( k = 0 \), (4.5)–(4.6), the momentum condition \(j-j'=-\vec {\jmath }\cdot \ell \), and the elementary inequality \( | |j|^\frac{3}{2} - |j'|^\frac{3}{2} | \geqq | |j|^\frac{1}{2} - |j'|^\frac{1}{2} | \), we deduce the lower bound
Combining (5.31) and (5.32), we deduce \( | |j|^{\frac{3}{2}}-|j'|^\frac{3}{2} | \leqq C\langle \ell \rangle \), for \( \varepsilon \) small enough.
\(\square \)
In order to estimate the measure of the sets (5.27)–(5.30) that are nonempty, the key point is to prove that the perturbed frequencies satisfy estimates similar to (4.7)–(4.10).
Lemma 5.5
(Perturbed transversality) For \(\varepsilon \in (0,\varepsilon _0)\) small enough and for all \(\kappa \in [\kappa _1,\kappa _2]\),
We recall that \(\rho _0\) is the amount of non-degeneracy that has been defined in Proposition 4.5.
Proof
We prove (5.355.36). The proofs of (5.33), (5.34) and (5.355.36) are similar. By (5.23) we have
By Lemma 4.4 we get that, for any \(n\in \{ 0,\ldots ,m_0 \} \),
because, by Lemma 5.4-2, we can restrict to indexes \(\ell , j,j' \) such that \( | |j|^\frac{3}{2} - |j'|^\frac{3}{2} | \leqq C \langle \ell \rangle \). Furthermore
Therefore, by (5.37), (5.24), (5.25), (5.22), (5.38), (5.39), and the momentum condition \(j-j'= -\vec {\jmath }\cdot \ell \), we have that, for any \(n\in \{ 0,\ldots ,m_0 \} \),
Since \(\vec {\Omega }(\kappa )\cdot \ell +\Omega _j(\kappa )-\Omega _{j'}(\kappa )\) satisfies (4.10), we deduce that
for \(\varepsilon >0\) small enough. \(\square \)
As an application of Rüssmann Theorem 17.1 in [37], we deduce the following result:
Lemma 5.6
(Estimates of the resonant sets) The measure of the sets (5.26)- (5.30) satisfy
and, recalling Lemma 5.4,
Proof
We estimate \(R_{\ell ,j,j'}^{(II)}\) defined in (5.29). The other cases follow similarly. Defining \( f_{\ell ,j,j'}(\kappa ):= ( \vec {\Omega }_\varepsilon (\kappa )\cdot \ell + \mu _j^\infty (\kappa )-\mu _{j'}^\infty (\kappa ) )\langle \ell \rangle ^{-1} \), we write
By Lemma 5.4-2 we restrict to indexes satisfying \( \big | | j|^\frac{3}{2} -|j'|^\frac{3}{2} \big |\leqq C \langle \ell \rangle \). By (5.355.36),
In addition, by (5.21)–(5.25), Lemma 4.4, the momentum condition \( |j-j'| = | \vec {\jmath } \cdot \ell |\), and (5.39), we deduce that \(\max _{0\leqq n \leqq k_0}\left| \partial _\kappa ^n f_{\ell ,j,j'}(\kappa ) \right| \leqq C\) for all \(\kappa \in [\kappa _1,\kappa _2]\), provided \(\varepsilon \upsilon ^{-(1+k_0)}\) is small enough, namely, by (5.19) and \(\varepsilon \) small enough. In particular, \(f_{\ell ,j,j'}\) is of class \(\mathcal {C}^{k_0-1}=\mathcal {C}^{m_0+1}\). Thus Theorem 17.1 in [37] applies. \(\square \)
Proof of Theorem 5.3 completed
We estimate the measure of all the sets in (5.26). By Lemma 5.4 and Lemma 5.6 we have that
We are left with estimating the measure of
By the momentum condition \(\vec {\jmath }\cdot \ell + 2j =0\) we get \(|j| \leqq C \left\langle \ell \right\rangle \), and, by Lemma 5.6,
Finally we estimate the measure of the second union in (5.43). By Lemma 5.4-2 we can restrict to indexes satisfying \( | |j|^{3/2} - |j'|^{3/2} | \leqq C \left\langle \ell \right\rangle . \) Now, for any \(|j| \ne |j'|\), we have
implying the upper bounds \(|j|, |j'| \leqq C \left\langle \ell \right\rangle ^2\). Hence
As \(\frac{\tau }{m_0}- 4> \nu \) by (5.19), all the series in (5.40), (5.41), (5.42), (5.44), (5.45) are convergent, and we deduce
For \(\upsilon = \varepsilon ^\mathtt{a}\) as in (5.19), we get \(| \mathcal {G}_\varepsilon | \geqq \kappa _2-\kappa _1 - C \varepsilon ^{\mathtt{a}/m_0} \). The proof of Theorem 5.3 is concluded. \(\square \)
6 Approximate Inverse
In order to implement a convergent Nash–Moser scheme that leads to a solution of \(\mathcal {F}(i,\alpha )=0\), where \( \mathcal {F}(i, \alpha ) \) is the nonlinear operator defined in (5.5), we construct an almost approximate right inverse of the linearized operator
Note that \({\mathrm{d}}_{i,\alpha }\mathcal {F}(i_0,\alpha _0)={\mathrm{d}}_{i,\alpha }\mathcal {F}(i_0)\) is independent of \(\alpha _0\). We assume that the torus \( i_0 ({\varphi }) = ( \theta _0 ({\varphi }), I_0 ({\varphi }), w_0 ({\varphi })) \) is reversible and traveling, according to (5.7).
In the sequel we shall assume the smallness condition, for some \(\mathtt{k}:= \mathtt{k}(\tau ,\nu )>0\),
We closely follow the strategy presented in [4] and implemented for the water waves equations in [2, 6]. The main novelty is to check that this construction preserves the momentum preserving properties needed for the search of traveling waves. Therefore, along this section we shall focus on this verification. The estimates are very similar to those in [2, 6].
First of all, we state tame estimates for the composition operator induced by the Hamiltonian vector field \(X_{P}= ( \partial _I P , - \partial _\theta P, \Pi _{\mathbb {S}^+,\Sigma }^\angle J \nabla _{w} P )\) in (5.5).
Lemma 6.1
(Estimates of the perturbation P) Let \({\mathfrak {I}}({\varphi })\) in (5.8) satisfy \(\left\| {\mathfrak {I}} \right\| _{3 s_0 + 2 k_0 + 5}^{k_0,\upsilon }\leqq 1\). Then, for any \( s \geqq s_0 \), \( \left\| X_{P}(i) \right\| _{s}^{k_0,\upsilon } \lesssim _s 1 + \left\| {\mathfrak {I}} \right\| _{s+2 s_0 + 2 k_0 + 3}^{k_0,\upsilon } \), and, for all \(\widehat{\imath }:= ({\widehat{\theta }},\widehat{I},\widehat{w})\),
Proof
The proof goes as in Lemma 5.1 of [6], using also the estimates of the Dirichlet-Neumann operator in Lemma 3.10. \(\square \)
Throughout this section, we assume the following hypothesis, which is verified by the approximate solutions obtained at each step of the Nash–Moser Theorem 9.2:
-
ANSATZ. The map \((\omega ,\kappa )\mapsto {\mathfrak {I}}_0(\omega ,\kappa ) = i_0({\varphi };\omega ,\kappa )- ({\varphi },0,0)\) is \(k_0\)-times differentiable with respect to the parameters \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\) and, for some \(\mu :=\mu (\tau ,\nu )>0\), \(\upsilon \in (0,1)\),
$$\begin{aligned} \left\| {\mathfrak {I}}_0 \right\| _{s_0+\mu }^{k_0,\upsilon } + \left| \alpha _0-\omega \right| ^{k_0,\upsilon } \leqq C \varepsilon \upsilon ^{-1}. \end{aligned}$$(6.1)
As in [2, 4, 6], we first modify the approximate torus \(i_0 ({\varphi }) \) to obtain a nearby isotropic torus \(i_\delta ({\varphi }) \), namely such that the pull-back 1-form \(i_\delta ^*\Lambda \) is closed, where \(\Lambda \) is the Liouville 1-form defined in (2.55). We first consider the pull-back 1-form
and its exterior differential
By the formula given in Lemma 5 in [4], we deduce, if \(\omega \) belongs to \(\mathtt{DC}(\upsilon ,\tau ) \), the estimate
where \(Z({\varphi }) \) is the “error function”
Note that if \( Z ({\varphi }) = 0 \), the torus \( i_0 ({\varphi }) \) is invariant for \( X_{H_{\alpha _0}} \) and the 1-form \( i_0^* \Lambda \) is closed, namely the torus \( i_0 ({\varphi }) \) is isotropic. We denote below the Laplacian \(\Delta _{\varphi }:= \sum _{k=1}^{\nu }\partial _{{\varphi }_k}^2\).
Lemma 6.2
(Isotropic torus) The torus \(i_\delta ({\varphi }):= ( \theta _0({\varphi }),I_\delta ({\varphi }),w_0({\varphi }) )\), defined by
is isotropic. Moreover, there is \(\sigma := \sigma (\nu ,\tau )\) such that, for all \( s \geqq s_0 \),
for \( s_1 \leqq s_0 + \mu \) (cfr. (6.1)). Furthermore \(i_\delta ({\varphi })\) is a reversible and traveling torus, cfr. (5.7).
Proof
Since \(i_0({\varphi })\) is a traveling torus (see (3.52)), in order to prove that \(i_\delta ({\varphi })\) is a traveling torus it is sufficient to prove that \( I_\delta ({\varphi }- \vec {\jmath } \varsigma ) = I_\delta ({\varphi }) \), for any \(\varsigma \in \mathbb {R}\). In view of (6.3), this follows by checking that \( \partial _{\varphi }\theta _0({\varphi }- \vec {\jmath }\varsigma ) = \partial _{\varphi }\theta _0({\varphi })\) and \(\rho ({\varphi }- \vec {\jmath }\varsigma ) = \rho ({\varphi }) \) for any \(\varsigma \in \mathbb {R}\). The first identity is a trivial consequence of the fact that \( \theta _0({\varphi }- \vec {\jmath }\varsigma ) = \theta _0 ({\varphi }) - \vec {\jmath } \varsigma \) for any \( \varsigma \in \mathbb {R}\), whereas the second one follows once we prove that the functions \( a_k ({\varphi })\) defined in (6.2) satisfy
Using that \(i_0({\varphi })\) is a traveling torus, we get, for any \(\varsigma \in \mathbb {R}\),
and, recalling (6.2), we deduce (6.8). Moreover, since \( i_0 ({\varphi }) \) is reversible, in order to prove that \( i_\delta ({\varphi }) \) is reversible as well, it is sufficient to show that \( I_\delta ({\varphi }) \) is even. This follows by (6.2), Lemma 3.23 and \( \mathcal {S}J^{-1} = - J^{-1} \mathcal {S}\). Finally, the estimates (6.4)–(6.7) follow for example as in Lemma 5.3 in [2]. \(\square \)
In the sequel we denote by \(\sigma = \sigma (\nu ,\tau ) \) constants, which may increase from lemma to lemma, which represent “loss of derivatives”.
In order to find an approximate inverse of the linearized operator \({\mathrm{d}}_{i,\alpha }\mathcal {F}(i_\delta )\), we introduce the symplectic diffeomorphism \(G_\delta :(\phi ,y,\mathtt{w}) \rightarrow (\theta ,I,w)\) of the phase space \( \mathbb {T}^\nu \times \mathbb {R}^\nu \times \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \),
where \({\widetilde{w}}_0(\theta ):= w_0(\theta _0^{-1}(\theta ))\). It is proved in Lemma 2 of [4] that \(G_\delta \) is symplectic, because the torus \(i_\delta \) is isotropic (Lemma 6.2). In the new coordinates, \(i_\delta \) is the trivial embedded torus \((\phi ,y,\mathtt{w})=(\phi ,0,0)\).
Lemma 6.3
The diffeomorphism \(G_\delta \) in (6.9) is reversibility and momentum preserving, in the sense that
where \(\vec {\mathcal {S}} \) and \( \vec {\tau }_\varsigma \) are defined respectively in (2.51), (2.52).
Proof
We prove the second identity in (6.10), which, in view of (6.9), (2.52) amounts to
Identities (6.11) and (6.13) follow because \(i_\delta ({\varphi })\) is a traveling torus (Lemma 6.2). For the same reason \(I_\delta (\phi ) = I_\delta (\phi - \vec {\jmath }\varsigma ) \) and \( \partial _\phi \theta _0(\phi ) = \partial _\phi \theta _0(\phi - \vec {\jmath }\varsigma )\) for any \(\varsigma \in \mathbb {R}\). Hence, for verifying (6.12) it is sufficient to check that \( [(\partial _\theta {\widetilde{w}}_0)(\theta _0(\phi )) ]^\top = [(\partial _\theta {\widetilde{w}}_0)(\theta _0(\phi - \vec {\jmath }\varsigma )) ]^\top \tau _\varsigma \) (we have used that \(J_\angle ^{-1}\) and \(\tau _\varsigma \) commute by Lemma 3.31), which in turn follows by
by taking the transpose and using that \(\tau _\varsigma ^\top = \tau _{-\varsigma } = \tau _\varsigma ^{-1} \). We claim that (6.14) is implied by \({\widetilde{w}}_0\) being a traveling wave, that is
Indeed, taking the differential of (6.15) with respect to \(\theta \), evaluating at \(\theta = \theta _0({\varphi }) \), and using that \(\theta _0({\varphi }) - \vec {\jmath }\varsigma = \theta _0({\varphi }- \vec {\jmath }\varsigma )\) one deduces (6.14). It remains to prove (6.15). By the definition of \({\widetilde{w}}_0\), and since \(w_0\) is a traveling wave, we have
using also that \( \theta _0^{-1}(\theta - \vec {\jmath }\varsigma ) = \theta _0^{-1}(\theta ) - \vec {\jmath }\varsigma \), which follows by inverting (6.11). The proof of the first identity in (6.10) follows by (6.9), (2.51), the fact that \( i_\delta \) is reversible, Lemma 3.23 and since \( J^{-1} \) and \( \mathcal {S}\) anti-commute. \(\square \)
Under the symplectic diffeomorphism \(G_\delta \), the Hamiltonian vector field \(X_{H_\alpha }\) changes into
By (6.10) and (5.6) we deduce that \( K_\alpha \) is reversible and momentum preserving, in the sense that
The Taylor expansion of \(K_\alpha \) at the trivial torus \((\phi ,0,0)\) is
where \(K_{\geqq 3}\) collects all terms at least cubic in the variables \((y,\mathtt{w})\). By (5.4) and (6.9), the only Taylor coefficients that depend on \(\alpha \) are \(K_{00}\in \mathbb {R}\), \(K_{10}\in \mathbb {R}^\nu \) and \(K_{01}\in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \), whereas the \( \nu \times \nu \) symmetric matrix \(K_{20} \), \(K_{11}\in \mathcal {L}( \mathbb {R}^\nu ,\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle )\) and the linear self-adjoint operator \( K_{02} \), acting on \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \), are independent of it.
Differentiating the identities in (6.17) at \((\phi ,0,0)\), we have (recalling (2.51))
and, recalling (2.52) and using that \(\tau _\varsigma ^\top = \tau _{-\varsigma } = \tau _\varsigma ^{-1} \), for any \(\varsigma \in \mathbb {R}\),
The Hamilton equations associated to (6.18) are
where \(\partial _\phi K_{10}^\top \) is the \(\nu \times \nu \) transposed matrix and \(\partial _\phi K_{01}^\top , K_{11}^\top : \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \rightarrow \mathbb {R}^\nu \) are defined by the duality relation \( (\partial _\phi K_{01}[{\widehat{\phi }}],\mathtt{w})_{L^2}={\widehat{\phi }}\cdot [\partial _\phi K_{01} ]^\top \mathtt{w}\) for any \({\widehat{\phi }}\in \mathbb {R}^\nu \), \(\mathtt{w}\in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \). The transpose \( K_{11}^\top (\phi ) \) is defined similarly.
On an exact solution (that is \(Z=0\)), the terms \(K_{00}, K_{01}\) in the Taylor expansion (6.18) vanish and \(K_{10}= \omega \). More precisely, arguing as in Lemma 5.4 in [2], we have
Lemma 6.4
There is \( \sigma := \sigma (\nu , \tau ) > 0 \), such that, for all \( s \geqq s_0 \),
Under the linear change of variables
the linearized operator \({\mathrm{d}}_{i,\alpha }\mathcal {F}(i_\delta )\) is approximately transformed into the one obtained when one linearizes the Hamiltonian system (6.21) at \((\phi ,y,\mathtt{w}) = ({\varphi },0,0)\), differentiating also in \(\alpha \) at \(\alpha _0\) and changing \(\partial _t \rightsquigarrow \omega \cdot \partial _{\varphi }\), namely

In order to construct an “almost approximate” inverse of (6.22), we need that
is “almost invertible” (on traveling waves) up to remainders of size \(O(N_{n-1}^{-{\mathtt{a}}})\), where, for \(n\in \mathbb {N}_0\)
The \( (K_n)_{n \geqq 0} \) is the scale used in the nonlinear Nash–Moser iteration of Section 9 and \( (N_n)_{n \geqq 0} \) is the one in the reducibility scheme of Section 8. Let \(H_\angle ^s(\mathbb {T}^{\nu +1}):= H^s(\mathbb {T}^{\nu +1})\cap \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \).
-
(AI)
Almost invertibility of \(\mathcal {L}_\omega \): There exist positive real numbers \( \sigma \), \( \mu (\mathtt{b}) \), \( \mathtt{a}\), p, \( K_0 \) and a subset
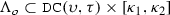 such that, for all
such that, for all  , the operator \(\mathcal {L}_\omega \) may be decomposed as$$\begin{aligned} \mathcal {L}_\omega = \mathcal {L}_\omega ^{<} + \mathcal {R}_\omega + \mathcal {R}_\omega ^\perp \,, \end{aligned}$$(6.25)
, the operator \(\mathcal {L}_\omega \) may be decomposed as$$\begin{aligned} \mathcal {L}_\omega = \mathcal {L}_\omega ^{<} + \mathcal {R}_\omega + \mathcal {R}_\omega ^\perp \,, \end{aligned}$$(6.25)where, for every traveling wave function \( g\in H_\angle ^{s+\sigma }(\mathbb {T}^{\nu +1},\mathbb {R}^2)\) and for every
 , there is a traveling wave solution \( h \in H_\angle ^{s}(\mathbb {T}^{\nu +1},\mathbb {R}^2) \) of \( \mathcal {L}_\omega ^{<} h = g\) satisfying, for all \(s_0\leqq s\leqq S\), $$\begin{aligned} \left\| (\mathcal {L}_\omega ^{<})^{-1}g \right\| _s^{k_0,\upsilon } \lesssim _S \upsilon ^{-1} \big ( \left\| g \right\| _{s+\sigma }^{k_0,\upsilon }+ \left\| g \right\| _{s_0+\sigma }^{k_0,\upsilon }\left\| {\mathfrak {I}}_0 \right\| _{s+\mu ({\mathtt{b}})+\sigma }^{k_0,\upsilon } \big ). \end{aligned}$$(6.26)
, there is a traveling wave solution \( h \in H_\angle ^{s}(\mathbb {T}^{\nu +1},\mathbb {R}^2) \) of \( \mathcal {L}_\omega ^{<} h = g\) satisfying, for all \(s_0\leqq s\leqq S\), $$\begin{aligned} \left\| (\mathcal {L}_\omega ^{<})^{-1}g \right\| _s^{k_0,\upsilon } \lesssim _S \upsilon ^{-1} \big ( \left\| g \right\| _{s+\sigma }^{k_0,\upsilon }+ \left\| g \right\| _{s_0+\sigma }^{k_0,\upsilon }\left\| {\mathfrak {I}}_0 \right\| _{s+\mu ({\mathtt{b}})+\sigma }^{k_0,\upsilon } \big ). \end{aligned}$$(6.26)In addition, if g is anti-reversible, then h is reversible. Moreover, for any \(s_0\leqq s \leqq S\), for any traveling wave \( h \in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \), the operators \(\mathcal {R}_\omega , \mathcal {R}_\omega ^\perp \) satisfy the estimates
$$\begin{aligned} \left\| \mathcal {R}_\omega h \right\| _s^{k_0,\upsilon }&\lesssim _S \varepsilon \upsilon ^{-1}N_{n-1}^{- \mathtt{a}} \big ( \left\| h \right\| _{s+\sigma }^{k_0,\upsilon }+ \left\| h \right\| _{s_0+\sigma }^{k_0,\upsilon } \left\| {\mathfrak {I}}_0 \right\| _{s+\mu (\mathtt{b})+\sigma }^{k_0,\upsilon } \big ) \,, \\ \left\| \mathcal {R}_\omega ^\perp h \right\| _{s_0}^{k_0,\upsilon }&\lesssim _S K_n^{-b} \big ( \left\| h \right\| _{s_0+b+\sigma }^{k_0,\upsilon } + \left\| h \right\| _{s_0+\sigma }^{k_0,\upsilon }\left\| {\mathfrak {I}}_0 \right\| _{s_0+\mu (\mathtt{b})+\sigma +b} \big ) \,, \ \forall \, b>0 \,, \\ \left\| \mathcal {R}_\omega ^\perp h \right\| _s^{k_0,\upsilon }&\lesssim _S \left\| h \right\| _{s+\sigma }^{k_0,\upsilon }+ \left\| h \right\| _{s_0+\sigma }^{k_0,\upsilon }\left\| {\mathfrak {I}}_0 \right\| _{s+\mu (\mathtt{b})+\sigma }^{k_0,\upsilon } \,. \end{aligned}$$
This assumption shall be verified by Theorem 8.10 at each n-th step of the Nash–Moser nonlinear iteration.
In order to find an almost approximate inverse of the linear operator in (6.22) (and so of \({\mathrm{d}}_{i,\alpha }\mathcal {F}(i_\delta )\)), it is sufficient to invert the operator
obtained neglecting in (6.22) the terms \(\partial _\phi K_{10}\), \(\partial _{\phi \phi }K_{00}\), \(\partial _\phi K_{00}\), \(\partial _\phi K_{01}\) (they vanish at an exact solution by Lemma 6.4) and the small remainders \(\mathcal {R}_\omega \), \(\mathcal {R}_\omega ^\perp \) appearing in (6.25). We look for an inverse of \(\mathbb {D}\) by solving the system
where \( (g_1, g_2, g_3) \) is an anti-reversible traveling wave variation (cfr. Definition 3.33), that is
We first consider the second equation in (6.27)–(6.28), that is \(\omega \cdot \partial _{\varphi }\widehat{y}= g_2-\partial _\alpha \partial _\phi K_{00}({\varphi })[{\widehat{\alpha }}]\). By (6.29) and (6.19), the right hand side of this equation is odd in \( {\varphi }\). In particular, this has zero average, and so
Since \( g_2({\varphi }) = g_2({\varphi }-\vec {\jmath }\varsigma ) \) for any \( \varsigma \in \mathbb {R}\) by (6.30) and \( \partial _\alpha \partial _\phi K_{00}({\varphi })[{\widehat{\alpha }}]\) satisfies the same property by (6.20), we also deduce that
Next we consider the third equation \(\mathcal {L}_\omega ^{<} {\widehat{\mathtt{w}}}= g_3 + J_\angle ( \partial _\alpha K_{01}({\varphi })[{\widehat{\alpha }}]+ K_{11}({\varphi })\widehat{y})\). The right hand side of this equation is a traveling wave by (6.30), (6.20), (6.32) and since \( J_\angle = \Pi ^\angle _{\mathbb {S}^+, \Sigma } \, J_{| \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle } \) commutes with \( \tau _\varsigma \) (by Lemma 3.31). Thus, by assumption (AI), there is a traveling wave solution
Finally, we solve the first equation in (6.28), which, inserting (6.31) and (6.33), becomes
where
In order to solve (6.34), we choose \({\widehat{\alpha }}\) such that the average in \({\varphi }\) of the right hand side is zero. By Lemma 6.4 and (6.1), the \( {\varphi }\)-average of the matrix \( M_1 \) satisfies \(\langle M_1\rangle _{\varphi }= {\mathrm{Id}} + O(\varepsilon \upsilon ^{-1})\). Then, for \(\varepsilon \upsilon ^{-1}\) small enough, \(\langle M_1\rangle _{\varphi }\) is invertible and \(\langle M_1\rangle _{\varphi }^{-1} = {\mathrm{Id}} + O(\varepsilon \upsilon ^{-1})\). Thus we define
and the solution of equation (6.34)
Finally the property \( {\widehat{\phi }}({\varphi }- \vec {\jmath }\varsigma ) = {\widehat{\phi }}({\varphi })\) for any \( \varsigma \in \mathbb {R}\) follows by (6.20), (6.32) and the fact that \({\widehat{\mathtt{w}}}\) in (6.33) is a traveling wave. This proves that \(({\widehat{\phi }}, \widehat{y}, {\widehat{\mathtt{w}}})\) is a traveling wave variation, that is (6.30) holds. Moreover, using (6.29), (6.19), Lemma 3.23, the fact that J and \( \mathcal {S}\) anti-commutes and (AI), one checks that \( ({\widehat{\phi }}, \widehat{y}, {\widehat{\mathtt{w}}})\) is reversible, that is
In conclusion, we have obtained a solution \( ( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}},{\widehat{\alpha }})\) of the linear system (6.28), and, denoting the norm \( \Vert (\phi ,y,\mathtt{w},\alpha ) \Vert _{s}^{k_0,\upsilon }:= \max \big \{ \Vert (\phi ,y,\mathtt{w}) \Vert _{s}^{k_0,\upsilon },\left| \alpha \right| ^{k_0,\upsilon } \big \} \), we have
Proposition 6.5
Assume (6.1) (with \(\mu =\mu ({\mathtt{b}})+\sigma \)) and (AI). Then, for all  , for any anti-reversible traveling wave variation \( g =(g_1,g_2,g_3)\) (that is satisfying (6.29)–(6.30)), system (6.28) has a solution \(\mathbb {D}^{-1}g:= ( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}},{\widehat{\alpha }})\), with \( ( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}},{\widehat{\alpha }})\) defined in (6.36),(6.31),(6.33),(6.35), where \(( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}})\) is a reversible traveling wave variation, satisfying, for any \(s_0\leqq s\leqq S\)
, for any anti-reversible traveling wave variation \( g =(g_1,g_2,g_3)\) (that is satisfying (6.29)–(6.30)), system (6.28) has a solution \(\mathbb {D}^{-1}g:= ( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}},{\widehat{\alpha }})\), with \( ( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}},{\widehat{\alpha }})\) defined in (6.36),(6.31),(6.33),(6.35), where \(( {\widehat{\phi }},\widehat{y},{\widehat{\mathtt{w}}})\) is a reversible traveling wave variation, satisfying, for any \(s_0\leqq s\leqq S\)
Proof
The estimate (6.38) follows by the explicit expression of the solution in (6.31), (6.33), (6.35), (6.36), and Lemma 6.4, (6.26), (6.1). \(\square \)
Finally we prove that the operator
is an almost approximate right inverse for \({\mathrm{d}}_{i,\alpha }\mathcal {F}(i_0)\), where \( {\widetilde{G}}_\delta (\phi ,y,\mathtt{w},\alpha ) := \left( G_\delta (\phi ,y,\mathtt{w}),\alpha \right) \) is the identity on the \(\alpha \)-component.
Theorem 6.6
(Almost approximate inverse) Assume (AI). Then there is \(\overline{\sigma } :=\overline{\sigma }(\tau ,\nu ,k_0)>0\) such that, if (6.1) holds with \(\mu =\mu (\mathtt{b})+\overline{\sigma }\), then, for all  and for any anti-reversible traveling wave variation \(g:=(g_1,g_2,g_3)\) (that is satisfying (6.29)–(6.30)), the operator \(\mathbf{T}_0\) defined in (6.39) satisfies, for all \(s_0 \leqq s \leqq S\),
and for any anti-reversible traveling wave variation \(g:=(g_1,g_2,g_3)\) (that is satisfying (6.29)–(6.30)), the operator \(\mathbf{T}_0\) defined in (6.39) satisfies, for all \(s_0 \leqq s \leqq S\),
Moreover, the first three components of \(\mathbf{T}_0 g \) form a reversible traveling wave variation (that is satisfy (6.37) and (6.30)). Finally, \(\mathbf{T}_0\) is an almost approximate right inverse of \({\mathrm{d}}_{i,\alpha }\mathcal {F}(i_0)\), namely
where, for any traveling wave variation g, for all \(s_0 \leqq s \leqq S\),
Proof
We claim that the first three components of \(\mathbf{T}_0 g \) form a reversible traveling wave variation. Indeed, differentiating (6.10) it follows that \( DG_\delta ({\varphi },0,0)\), thus \( (DG_\delta ({\varphi },0,0))^{-1} \), is reversibility and momentum preserving (cfr. (3.54)). In particular these operators map an (anti)-reversible, respectively traveling, waves variation into a (anti)-reversible traveling waves variation (cfr. Lemma 3.34). Moreover, by Proposition 6.5, the operator \( \mathbb {D}^{-1}\) maps an anti-reversible traveling wave into a vector whose first three components form a reversible traveling wave. This proves the claim.
We now prove that the operators \(\mathcal{P}, \mathcal{P}_\omega \) and \(\mathcal{P}_\omega ^{\bot }\) are defined on traveling waves. They are computed for example in Theorem 5.6 of [2]. To define them, introduce first the linear operators
and
Next, we denote by \( \Pi \) the projection \( (\widehat{\imath }, \widehat{\alpha } ) \mapsto \widehat{\imath } \), by \(\mathtt{u}_\delta ({\varphi }) = ({\varphi }, 0, 0)\) the trivial torus, and by \(\mathcal {E}\), \(\mathcal {E}_\omega \), \(\mathcal {E}_\omega ^\perp \) the linear operators
It is then proved in Theorem 5.6 of [2] that \( \mathcal{P} := \mathcal{E} \circ \mathbf{T}_0 \), \( \mathcal{P}_\omega := \mathcal{E}_\omega \circ \mathbf{T}_0 \), \( \mathcal{P}_\omega ^{\bot } := \mathcal{E}_\omega ^{\bot } \circ \mathbf{T}_0 \). A direct inspection of these formulas shows that \(\mathcal {P}, \mathcal {P}_\omega \) and \(\mathcal {P}_\omega ^{\bot }\) are defined on traveling wave variations. In particular, note that the operators \( {\mathbb {R}}_\omega \), \({\mathbb {R}}_\omega ^{\bot } \) in (6.45) are defined only if \( {\widehat{\mathtt{w}}}\) is a traveling wave, because the operators \(\mathcal{R}_\omega , \mathcal{R}_\omega ^{\bot } \) defined in (AI) act only on a traveling wave. However, note that, if g is a traveling wave variation, the third component of \( D {\widetilde{G}}_\delta (\mathtt{u}_\delta )^{-1} \mathbf{T}_0 g \) is a traveling wave and therefore the operators \( \mathcal{E}_\omega , \mathcal{E}_\omega ^{\bot } \) in (6.46) are well defined.
The estimates (6.41)–(6.44) are proved as in Theorem 5.6 of [2], using Lemma 6.5. \(\square \)
7 The Linearized Operator in the Normal Subspace
We now write an explicit expression of the linear operator \(\mathcal {L}_\omega \) defined in (6.23).
Lemma 7.1
The Hamiltonian operator \(\mathcal {L}_\omega \) defined in (6.23), acting on the normal subspace \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \), has the form
where :
-
1.
\( \mathcal {L}\) is the Hamiltonian operator
$$\begin{aligned} \mathcal {L}:= \omega \cdot \partial _{\varphi }- J \partial _u\nabla _u \mathcal {H}(T_\delta (\varphi )) \, , \end{aligned}$$(7.2)where \(\mathcal {H}\) is the water waves Hamiltonian in the Wahlén variables defined in (2.13), evaluated at
$$\begin{aligned} \begin{aligned} T_\delta (\phi )&:= \varepsilon A ( i_\delta (\phi ) ) = \varepsilon A\left( \theta _0(\phi ),I_\delta (\phi ),w_0(\phi ) \right) \\&= \varepsilon v^\intercal \left( \theta _0(\phi ),I_\delta (\phi ) \right) + \varepsilon w_0(\phi )\,, \end{aligned} \end{aligned}$$(7.3)the torus \(i_\delta ({\varphi }):= ( \theta _0({\varphi }),I_\delta ({\varphi }),w_0({\varphi }) )\) is defined in Lemma 6.2 and \(A(\theta ,I,w) \), \( v^\intercal (\theta ,I)\) in (2.50);
-
2.
\( R (\phi ) \) has the finite rank form
$$\begin{aligned} R(\phi )[h] = \sum _{j=1}^\nu \left( h,g_j \right) _{L^2} \chi _j \,, \quad \forall \, h\in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \,, \end{aligned}$$(7.4)for functions \(g_j,\chi _j \in \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) which satisfy, for some \(\sigma := \sigma (\tau ,\nu , k_0) > 0 \), for all \( j = 1, \ldots , \nu \), for all \(s\geqq s_0\),
$$\begin{aligned} \begin{aligned} \left\| g_j \right\| _s^{k_0,\upsilon } + \left\| \chi _j \right\| _s^{k_0,\upsilon }&\lesssim _s 1 + \left\| {\mathfrak {I}}_\delta \right\| _{s+\sigma }^{k_0,\upsilon } \,, \\ \left\| {\mathrm{d}}_i g_j [\widehat{\imath }] \right\| _s + \left\| {\mathrm{d}}_i \chi _j [\widehat{\imath }] \right\| _s&\lesssim _s \left\| \widehat{\imath } \right\| _{s+\sigma } + \left\| \widehat{\imath } \right\| _{s_0+\sigma } \left\| {\mathfrak {I}}_\delta \right\| _{s+\sigma }. \end{aligned} \end{aligned}$$(7.5)
The operator \( \mathcal {L}_\omega \) is reversible and momentum preserving.
Proof
In view of (6.18), (6.16) and (5.4) we have
where \({\varvec{\Omega }}_W\) is defined in (2.19) and \(G_\delta \) in (6.9). Differentiating with respect to \(\mathtt{w}\) the Hamiltonian
where \(L_1(\phi ):= [\partial _\phi \theta _0(\phi ) ]^{-\top }\) and \(L_2(\phi ):= [\partial _\phi {\widetilde{w}}_0(\theta _0(\phi ))]^\top J_\angle ^{-1} \) (see (6.9)), we get
where \( R(\phi ) := R_1(\phi )+ R_2(\phi ) + R_3(\phi ) \) and
Each operator \(R_1,R_2,R_3\) has the finite rank form (7.4) because it is the composition of at least one operator with finite rank \(\mathbb {R}^\nu \) in the space variable (for more details see for example Lemma 6.1 in [6]) and the estimates (7.5) follow by Lemma 6.1. By (7.6), (7.7), (5.3), (5.2), (5.1), we obtain
In conclusion, by (7.8), Lemma 2.7, and since \(T_\delta (\phi ) = \varepsilon A(i_\delta (\phi )) \), we deduce that the operator \( \mathcal {L}_\omega \) in (6.23) has the form (7.1)–(7.2). Finally the operator \( \Pi _{\mathbb {S}^+,\Sigma }^\angle J K_{02} ({\varphi }) \) is reversible and momentum preserving, by (6.19), (6.20), Lemmata 3.23, 3.31, and the fact that J commutes with \( \tau _\varsigma \) and anti-commutes with \( \mathcal {S}\). \(\square \)
We remark that \(\mathcal {L}\) in (7.2) is obtained by linearizing the water waves Hamiltonian system (2.13), (2.14) in the Wahlén variables defined in (2.11) at the torus \(u=(\eta ,\zeta )=T_\delta ({\varphi })\) defined in (7.3) and changing \(\partial _t \rightsquigarrow \omega \cdot \partial _{\varphi }\). This is equal to
where X is the water waves vector field on the right hand side of (1.3). The operator \( \mathcal {L}\) acts on (a dense subspace) of the phase space \( L^2_0 \times \dot{L}^2 \).
In order to compute dX we use the "shape derivative" formula, see for example [26],
where
It turns out that \( (V,B) = ( \Phi _x, \Phi _y ) \) is the gradient of the generalized velocity potential defined in (1.2), evaluated at the free surface \( y = \eta (x) \).
Using (7.9), (1.3), (7.10), (7.11), the operator \( \mathcal {L}\) is
where
and the functions \( B := B(\eta ,\psi ) \), \( V := V(\eta ,\psi )\), \( c := c(\eta ) \) in (7.12) are evaluated at the reversible traveling wave \( (\eta ,\psi ) := W T_\delta ({\varphi }) \) where \( T_\delta ({\varphi }) \) is defined in (7.3).
Remark 7.2
From now on we consider the operator \( \mathcal {L}\) in (7.12) acting on (a dense subspace of) the whole \( L^2 (\mathbb {T}) \times L^2 (\mathbb {T}) \). In particular we extend the operator \( \partial _x^{-1} \) to act on the whole \( L^2 (\mathbb {T}) \) as in (3.20). In Sections 7.1-7.6 we are going to make several transformations, whose aim is to conjugate \( \mathcal{L} \) to a constant coefficients Fourier multiplier, up to a pseudodifferential operator of order zero plus a remainder that satisfies tame estimates, both small in size, see \( \mathcal{L}_9 \) in (7.168). Finally, in Section 7.7 we shall conjugate the restricted operator \( \mathcal{L}_\omega \) in (7.1).
Notation. In (7.12) and hereafter any function a is identified with the corresponding multiplication operators \(h \mapsto a h\), and, where there is no parenthesis, composition of operators is understood. For example, \(\partial _x c \partial _x\) means: \(h \mapsto \partial _x (c \partial _x h)\).
Lemma 7.3
The functions \( (\eta , \zeta ) = T_\delta ({\varphi }) \) and \(B, {\widetilde{V}}, c \) defined in (7.11), (7.13) are quasi-periodic traveling waves. The functions \((\eta ,\zeta )= T_\delta ({\varphi })\) are \( ({\mathrm{even}}({\varphi },x),{\mathrm{odd}}({\varphi },x))\), B is \({\mathrm{odd}}({\varphi },x)\), \({\widetilde{V}}\) is \({\mathrm{even}}({\varphi },x)\) and c is \({\mathrm{even}}({\varphi },x) \). The Hamiltonian operator \( \mathcal {L}\) is reversible and momentum preserving.
Proof
The function \( (\eta , \zeta ) = T_\delta ({\varphi }) \) is a quasi-periodic traveling wave and, using also Lemmata 3.32 and 3.26, we deduce that \(B, {\widetilde{V}}, c \) are quasi-periodic traveling waves. Since \((\eta ,\zeta )= T_\delta ({\varphi })\) is reversible, we have that \((\eta ,\zeta ) \) is \( ( {\mathrm{even}}({\varphi },x), {\mathrm{odd}}({\varphi },x) ) \). Therefore, using also (2.6), we deduce that B is \({\mathrm{odd}}({\varphi },x)\), \({\widetilde{V}}\) is \({\mathrm{even}}({\varphi },x)\) and c is \({\mathrm{even}}({\varphi },x)\). By Lemmata 3.22 and 3.27, the operator \(\mathcal {L}\) in (7.9) evaluated at the reversible quasi-periodic traveling wave \( W T_\delta ({\varphi }) \) is reversible and momentum preserving. \(\square \)
For the sequel we will always assume the following ansatz (satisfied by the approximate solutions obtained along the nonlinear Nash–Moser iteration of Section 9): for some constants \(\mu _0 :=\mu _0(\tau ,\nu )>0\), \(\upsilon \in (0,1)\), (cfr. Lemma 6.2)
In order to estimate the variation of the eigenvalues with respect to the approximate invariant torus, we need also to estimate the variation with respect to the torus \(i({\varphi })\) in another low norm \(\left\| \ \right\| _{s_1}\) for all Sobolev indexes \(s_1\) such that
Thus, by (7.14), we have
The constants \(\mu _0\) and \(\sigma _0\) represent the loss of derivatives accumulated along the reduction procedure of the next sections. What is important is that they are independent of the Sobolev index s. In the following sections we shall denote by \(\sigma :=\sigma (\tau ,\nu ,k_0)>0 \), \( \sigma _N(\mathtt{q}_0) := \sigma _N(\mathtt{q}_0,\tau ,\nu ,k_0) \), \( \sigma _M:= \sigma _M(k_0,\tau ,\nu )>0 \), \( \aleph _M (\alpha ) \) constants (which possibly increase from lemma to lemma) representing losses of derivatives along the finitely many steps of the reduction procedure.
Remark 7.4
In the next sections \( \mu _0 :=\mu _0(\tau ,\nu , M, \alpha ) > 0 \) will depend also on indexes \( M, \alpha \), whose maximal values will be fixed depending only on \( \tau \) and \( \nu \) (and \( k_0 \) which is however considered an absolute constant along the paper). In particular M is fixed in (8.5), whereas the maximal value of \( \alpha \) depends on M, as explained in Remark 7.14.
As a consequence of Moser composition Lemma 3.2 and (6.4), the Sobolev norm of the function \(u=T_\delta ({\varphi })\) defined in (7.3) satisfies for all \(s\geqq s_0\)
(the map A defined in (2.50) is smooth). Similarly, using (6.7),
We finally recall that \({\mathfrak {I}}_0 = {\mathfrak {I}}_0(\omega ,\kappa )\) is defined for all \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\) and that the functions \(B,{\widetilde{V}}\) and c appearing in \(\mathcal {L}\) in (7.12) are \(\mathcal {C}^\infty \) in \(({\varphi },x)\), as \(u=(\eta ,\zeta )=T_\delta ({\varphi })\) is.
7.1 Quasi-periodic Reparametrization of Time
We conjugate the operator \( \mathcal{L} \) in (7.12) by the change of variables induced by the quasi-periodic reparametrization of time
where \(p({\varphi })\) is the real \(\mathbb {T}^\nu \)-periodic function defined in (7.87). Since \( \eta ({\varphi },x) \) is a quasi-periodic traveling wave, even in \( ({\varphi }, x) \) (cfr. Lemma 7.3), it results that
Moreover, by (7.87), (3.11), Lemma 3.2, (7.16) and (7.14) and Lemma 2.30 in [6], both p and \( \breve{p} \) satisfy, for some \(\sigma :=\sigma (\tau ,\nu ,k_0) > 0 \), the tame estimates, for \(s\geqq s_0\),
Remark 7.5
We perform as a first step the time reparametrization (7.17) of \( \mathcal {L}\), with a function \( p ( {\varphi }) \) which will be fixed only later in Step 4 of Section 7.3, to avoid otherwise a technical difficulty in the conjugation of the remainders obtained by the Egorov theorem in Step 1 of Section 7.3. We need indeed to apply the Egorov Proposition 3.9 for conjugating the additional pseudodifferential term in (7.12) due to vorticity.
Denoting by
the induced diffeomorphism of functions \( h (\varphi , x ) \in \mathbb {C}^2 \), we have
Therefore, for any \( \omega \in \mathtt{D}\mathtt{C}(\upsilon , \tau ) \), we get
where \( {\widetilde{V}}, B, c, V \) and \(G(\eta )\) are evaluated at \( (\eta _p, \psi _p) := \mathcal {P}^{-1} (\eta , \psi ) \). For simplicity in the notation we do not report in (7.21) the explicit dependence on p, writing for example (cfr. (7.13))
Lemma 7.6
The maps \(\mathcal {P}\), \(\mathcal {P}^{-1}\) are \(\mathcal {D}^{k_0}\)-\((k_0+1)\)-tame, the maps \(\mathcal {P}-{\mathrm{Id}}\) and \(\mathcal {P}^{-1}-{\mathrm{Id}}\) are \(\mathcal {D}^{k_0}\)-\((k_0+2)\)-tame, with tame constants satisfying, for some \(\sigma :=\sigma (\tau ,\nu ,k_0)>0\) and for any \( s_0\leqq s\leqq S \),
The function \( \rho \) defined in (7.20) satisfies
The operator \( \mathcal{L}_{0} \) is Hamiltonian, reversible and momentum preserving.
Proof
Estimates (7.23) follow by (7.19) and Lemma 2.30 in [6], writing \( ( \mathcal {P}-{\mathrm{Id}} ) h = p \int _0^1 \mathcal {P}_\tau ( \omega \cdot \partial _{\varphi }h ) \,{\mathrm{d}}{\tau }\), where \( (\mathcal {P}_\tau h)({\varphi },x):= h({\varphi }+\tau \omega p({\varphi }), x) \). We deduce (7.24) by (7.18) and (7.20). Denoting \( \mathcal {L}= \omega \cdot \partial _{\varphi }+ A ( {\varphi }) \) the operator \( \mathcal {L}\) in (7.12), then the operator \( \mathcal {L}_0 \) in (7.21) is \( \mathcal {L}_0 = \omega \cdot \partial _\vartheta + A_+ ( \vartheta ) \) with \( A_+ ( \vartheta ) = \rho ^{-1} (\vartheta ) A( \vartheta + \breve{p} (\vartheta ) \omega ) \). It follows that \( A_+({\varphi }) \) is Hamiltonian, reversible and momentum preserving as \( A({\varphi }) \) (Lemma 7.3). \(\square \)
Remark 7.7
The map \( \mathcal {P}\) is not reversibility and momentum preserving according to Definitions 3.17 and, respectively, 3.24, but maps (anti)-reversible, respectively traveling, waves, into (anti)-reversible, respectively traveling, waves. Note that the multiplication operator for the function \( \rho (\vartheta )\), which satisfies (7.24), is reversibility and momentum preserving according to Definitions 3.17 and 3.24.
7.2 Linearized Good Unknown of Alinhac
We conjugate the linear operator \( \mathcal {L}_0 \) in (7.21), where we rename \( \vartheta \) with \( {\varphi }\), by the multiplication matrix operator
obtaining (in view of (3.46))
where a is the function
The matrix \(\mathcal {Z}\) amounts to introduce, as in [26] and [2, 6], a linearized version of the “good unknown of Alinhac”.
Lemma 7.8
The maps \(\mathcal {Z}^{\pm 1}-{\mathrm{Id}}\) are \(\mathcal {D}^{k_0}\)-tame with tame constants satisfying, for some \(\sigma :=\sigma (\tau ,\nu ,k_0)> 0 \), for all \( s \geqq s_0 \),
The function a is a quasi-periodic traveling wave \({\mathrm{even}}({\varphi },x)\). There is \(\sigma := \sigma (\tau ,\nu ,k_0)>0\) such that, for all \( s \geqq s_0 \),
Moreover, for any \(s_1\) as in (7.15),
The operator \(\mathcal {L}_1\) is Hamiltonian, reversible and momentum preserving.
Proof
The estimates (7.28) follow by the expressions of \(a, {\widetilde{V}}, B, c\) in (7.26), (7.11), (7.13), (reparametrized by \( \mathcal {P}^{-1} \) as in (7.22)), Lemma 3.2 and (7.23), (3.7), (3.33), (3.37) and (3.36). The estimate (7.27) follows by (3.37), (3.22), (7.28) and since the adjoint \(\mathcal {Z}^* = \begin{pmatrix} {\mathrm{Id}} &{} B\\ 0 &{} {\mathrm{Id}} \end{pmatrix}\). The estimates (7.29)–(7.31) follow similarly. Since B is a \( {\mathrm{odd}}({\varphi },x)\) quasi-periodic traveling wave, then the operators \(\mathcal {Z}^{\pm }\) are reversibility and momentum preserving. \(\square \)
7.3 Symmetrization and Reduction of the Highest Order
The aim of this long section is to conjugate the Hamiltonian operator \( \mathcal {L}_1 \) in (7.25) to the Hamiltonian operator \( \mathcal {L}_5 \) in (7.89) whose coefficient \( \mathtt{m}_{\frac{3}{2}} \) of the highest order is constant. This is achieved in several steps. All the transformations of this section are symplectic.
Recalling the expansion (3.32) of the Dirichlet-Neumann operator, we first write
where
is a small remainder in \( {\mathrm{OP}}S^{-\infty }\).
Step 1: We first conjugate \(\mathcal {L}_1 \) with the symplectic change of variable (cfr. (3.42))
induced by a family of \({\varphi }\)-dependent diffeomorphisms of the torus \( y = x+ \beta ({\varphi }, x) \), where \(\beta ({\varphi }, x)\) is a small function to be determined, see (7.68). We denote the inverse diffeomorphism by \( x = y + \breve{\beta }({\varphi }, y) \). By direct computation we have that
Then we write the Dirichlet-Neumann operator G(0) in (1.7) as
where \( \mathcal {H}\) is the Hilbert transform in (3.19) and
We have the conjugation formula (see formula (7.42) in [2])
where
The operator \(\mathcal {R}_1 \) is in \( {\mathrm{OP}}S^{-\infty } \) because both \( \mathcal {B}^{-1} {\mathrm{Op}}(r_\mathtt{h}) \mathcal {B}- {\mathrm{Op}}(r_\mathtt{h}) \) and \(\mathcal {B}^{-1}\mathcal {H}\mathcal {B}- \mathcal {H}\) are in \( {\mathrm{OP}}S^{-\infty } \) and there is \( {\sigma }> 0 \) such that, for any \(m \in \mathbb {N}\), \(s \geqq s_0 \), and \(\alpha \in \mathbb {N}_0\),
The first estimate is given in Lemmata 2.36 and 2.32 in [6], whereas the second one follows by that fact that \(r_\mathtt{h}\in S^{-\infty }\) (see (7.41)), Lemma 2.18 in [2] and Lemmata 2.34 and 2.32 in [6]. Therefore by (7.42) we obtain
where
Next we transform \(G(0)\partial _x^{-1}\). By (7.40) and using the identities \( \mathcal {H}\partial _x \partial _x^{-1} = \mathcal {H}\) and \( \mathcal {H}T(\mathtt{h}) = G(0) \partial _y^{-1} \) on the periodic functions, we have that
where
The operator \( \mathcal {R}_2 \) is in \( {\mathrm{OP}}S^{-\infty } \) by (7.44), (7.41) and because the commutator of \(\mathcal {H}\) with any smooth function a is in \({\mathrm{OP}}S^{-\infty }\), in particular (see Lemma 2.35 of [6]) there is \( {\sigma }> 0 \) such that, for any \(m \in \mathbb {N}\), \(s \geqq s_0 \), and \(\alpha \in \mathbb {N}_0\),
Finally we conjugate \(\partial _x^{-1} G(0)\partial _x^{-1}\). By the Egorov Proposition 3.9, we have that, for any \( N \in \mathbb {N}\),
where \( P^{(1)}_{-2,N} (\varphi , x, D) \in {\mathrm{OP}}S^{-2}\) is
with functions \( p_{-1-j}(\lambda ; \varphi , y)\), \( j = 0, \ldots , N \), satisfying (3.30) and \(\mathtt{R}_N\) is a regularizing operator satisfying the estimate (3.31). So, using (7.50) and (7.47), we obtain
where
and \(\mathtt{R}_{2,N} \) is the regularizing operator
The smoothing order \(N\in \mathbb {N}\) will be chosen in Section 8 during the KAM iteration (see also Remark 7.11).
In conclusion, by (7.35)–(7.39), (7.45), (7.47) and (7.51) we obtain
where
the operator \(P_{-1, N}^{(2)} \in {\mathrm{OP}}S^{-1} \) is defined in (7.52) and
with \({\widetilde{\mathcal {R}}}_1 \), \(\mathcal {R}_2 \), \( \mathtt{R}_{2,N} \) defined in (7.46), (7.48), (7.53) and \(\mathbf{R}_1\) in (7.33).
Step 2: We now conjugate the operator \(\mathcal {L}_2 \) in (7.54) with the multiplication matrix operator
where \( q({\varphi }, y) \) is a real function, close to 1, to be determined. The maps \( \mathcal {Q}\) and \( \mathcal {Q}^{-1} \) are symplectic (cfr. (3.42)). We have that
where
We choose the function q so that the coefficients of the highest order terms of the off-diagonal operators B and C satisfy
with \( m_{\frac{3}{2}}({\varphi }) \) independent of x. This is achieved by choosing
and, recalling (7.56), the function \(\beta \), so that
with \( m ({\varphi }) \) independent of x (the function c is defined in (7.22)). The solution of (7.67) is
In such a way, by (7.56), we obtain (7.65) with \( m_{\frac{3}{2}} ({\varphi }) := \sqrt{m (\varphi ) } \). By (7.68) and (7.22) we have
Note that, since by (7.65) the function \( q^{-1} a_2 \) is independent of x, we have
Moreover we have the expansion
In conclusion, the operator \(\mathcal {L}_3 \) in (7.60) is, in view of (7.61)–(7.64) and (7.70), (7.71),
where
with \(P^{(3)}_{-1, N} \in {\mathrm{OP}}S^{-1}\) and where \( \mathbf{R}_{3}^\Psi \in {\mathrm{OP}}S^{-\infty }, \mathbf{T}_{3,N}\) are the smoothing remainders
Step 3: We now conjugate \(\mathcal {L}_3 \) in (7.72), where we rename the space variable y by x, by the symplectic transformation (cfr. (3.42))
where \(\Lambda \in {\mathrm{OP}}S^{- \frac{1}{4}} \) is the Fourier multiplier
with \(\pi _0 \) defined in (3.21) and M(D) in (2.21). We have the identity
where \(\omega (\kappa , D)\) is defined in (2.23). In (7.79) and (7.80) we mean that the symbols of \( M(D), M(D)^{-1} \) and \( \omega (\kappa , D) \) are extended to 0 at \( j = 0 \), multiplying them by the cut-off function \( \chi \) defined in (3.10). Thus we obtain
where
and \( \mathbf{R}_{4}^\Psi , \mathbf{T}_{4,N}\) are the smoothing remainders
Step 4: We finally move in complex coordinates, conjugating the operator \(\mathcal {L}_4 \) in (7.81) via the transformation \(\mathcal {C}\) defined in (2.24). We use the transformation formula (3.15). We choose the function \( p(\varphi ) \) in (7.17) in order to obtain a constant coefficient at the highest order. More precisely we choose the periodic function \( p(\varphi )\) such that
is a real constant independent of \( \varphi \). Thus, recalling (3.9), we define the periodic function
and the real constant
Note that (7.86) holds for \( \omega \in \mathtt{D}\mathtt{C}(\upsilon , \tau ) \). Moreover, by Lemmata 3.2, 7.3 and (7.16), p satisfies (7.19) and it is odd in \({\varphi }\). Let
Lemma 7.9
Let \(N \in \mathbb {N}\), \( \mathtt{q}_0 \in \mathbb {N}_0 \). For all \( \omega \in \mathtt{D}\mathtt{C}(\upsilon , \tau ) \), we have that
where:
-
1.
The operators \(\mathcal {E}^{\pm 1}\) are \(\mathcal {D}^{k_0}\)-\((k_0+1)\)-tame, the operators \(\mathcal {E}^{\pm 1}-{\mathrm{Id}}\), \((\mathcal {E}^{\pm 1}-{\mathrm{Id}})^*\) are \(\mathcal {D}^{k_0}\)-\((k_0+2)\)-tame and the operators \(\mathcal {Q}^{\pm 1}\), \(\mathcal {Q}^{\pm 1}-{\mathrm{Id}}\), \((\mathcal {Q}^{\pm 1}-{\mathrm{Id}})^*\) are \(\mathcal {D}^{k_0}\)-tame with tame constants satisfying, for some \(\sigma :=\sigma (\tau ,\nu ,k_0)>0\) and for all \(s_0\leqq s\leqq S\),
$$\begin{aligned}&{\mathfrak {M}}_{\mathcal {E}^{\pm 1}}(s) \lesssim _{S} 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma }^{k_0,\upsilon }\,, \quad {\mathfrak {M}}_{\mathcal {Q}^{\pm 1}}(s) \lesssim _{S} 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma }^{k_0,\upsilon } \,, \end{aligned}$$(7.90)$$\begin{aligned}&{\mathfrak {M}}_{\mathcal {E}^{\pm 1}-{\mathrm{Id}}}(s) + {\mathfrak {M}}_{\left( \mathcal {E}^{\pm 1}-{\mathrm{Id}}\right) ^*}(s) \lesssim _{S}\varepsilon ^2 ( 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma }^{k_0,\upsilon })\,, \end{aligned}$$(7.91)$$\begin{aligned}&{\mathfrak {M}}_{\mathcal {Q}^{\pm 1}-{\mathrm{Id}}}(s) + {\mathfrak {M}}_{\left( \mathcal {Q}^{\pm 1}-{\mathrm{Id}}\right) ^*}(s) \lesssim _{S}\varepsilon ^2 ( 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma }^{k_0,\upsilon }) \,; \end{aligned}$$(7.92) -
2.
the constant \(\mathtt{m}_{\frac{3}{2}} \in \mathbb {R}\) defined in (7.88) satisfies \( | \mathtt{m}_{\frac{3}{2}} - 1 |^{k_0, \upsilon } \lesssim \varepsilon ^2 \);
-
3.
\({\varvec{\Omega }}(\kappa , D)\) is the Fourier multiplier (see (2.25), (2.26))
$$\begin{aligned} \begin{aligned} {\varvec{\Omega }}(\kappa , D)= \begin{pmatrix} \Omega (\kappa , D) &{} 0\\ 0 &{} - \overline{\Omega (\kappa , D)} \end{pmatrix}, \quad \Omega (\kappa , D) = \omega (\kappa , D) + {\mathrm{i}}\,\frac{\gamma }{2}\partial _x^{-1} G(0) \, ; \end{aligned} \end{aligned}$$(7.93) -
4.
the matrix of functions \(\mathbf{A}_1 \) is
$$\begin{aligned} \mathbf{A}_1 := \begin{pmatrix} a_1^{(d)} &{} 0\\ 0&{} a_1^{(d)} \end{pmatrix}, \end{aligned}$$(7.94)for a real function \(a_1^{(d)}({\varphi }, x) \) which is a quasi-periodic traveling wave, \( {\mathrm{even}}({\varphi },x) \), satisfying, for some \(\sigma := \sigma (k_0,\tau , \nu )>0\) and for all \(s\geqq s_0\),
$$\begin{aligned} \begin{aligned} \Vert a_1^{(d)} \Vert _{s}^{k_0,\upsilon } \lesssim _{s} \varepsilon ( 1 + \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma }^{k_0,\upsilon } ) \,; \end{aligned} \end{aligned}$$(7.95) -
5.
\(\mathbf{R}_5^{(0,d)}\) and \(\mathbf{R}_5^{(0,o)}\) are pseudodifferential operators in \({\mathrm{OP}}S^{0}\) of the form
$$\begin{aligned} \begin{aligned}&\mathbf{R}_5^{(0,d)} := \begin{pmatrix} r_5^{(d)}({\varphi }, x, D) &{} 0 \\ 0 &{} \overline{r_5^{(d)}({\varphi },x, D)} \end{pmatrix} \in {\mathrm{OP}}S^0\,, \\&\mathbf{R}_5^{(0,o)} := \begin{pmatrix} 0 &{} r_5^{(o)}({\varphi },x, D) \\ \overline{r_5^{(d)}({\varphi },x, D)} &{} 0 \end{pmatrix}\in {\mathrm{OP}}S^0 \, , \end{aligned} \end{aligned}$$(7.96)reversibility and momentum preserving, satisfying, for some \(\sigma _N := \sigma (\tau , \nu , N)>0\), for all \(s\geqq s_0 \), \(\alpha \in \mathbb {N}_0\),
$$\begin{aligned} \Vert \mathbf{R}_5^{(0,d)} \Vert _{0,s,\alpha }^{k_0,\upsilon } + \Vert \mathbf{R}_5^{(0,o)} \Vert _{0,s,\alpha }^{k_0,\upsilon } \lesssim _{ s,N, \alpha } \varepsilon ( 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma _N +2\alpha }^{k_0,\upsilon } )\,; \end{aligned}$$(7.97) -
6.
For any \( \mathtt{q}\in \mathbb {N}^\nu _0 \) with \( |\mathtt{q}| \leqq \mathtt{q}_0\), \(n_1, n_2 \in \mathbb {N}_0 \) with \( n_1 + n_2 \leqq N -(k_0 + \mathtt{q}_0) + \frac{5}{2} \), the operator \(\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{5, N}(\varphi ) \langle D \rangle ^{n_2}\) is \(\mathcal {D}^{k_0} \)-tame with a tame constant satisfying, for some \(\sigma _N(\mathtt{q}_0) := \sigma _N(\mathtt{q}_0,k_0,\tau ,\nu )>0\) and for any \(s_0 \leqq s \leqq S \),
$$\begin{aligned} {\mathfrak {M}}_{\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{5, N}(\varphi ) \langle D \rangle ^{n_2}}(s) \lesssim _{S, N, \mathtt{q}_0} \varepsilon \big ( 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma _N(\mathtt{q}_0)}^{k_0,\upsilon } \big )\,; \end{aligned}$$(7.98) -
7.
Moreover, for any \(s_1\) as in (7.15), \(\alpha \in \mathbb {N}_0\), \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\), and \(n_1,n_2 \in \mathbb {N}_0\), with \(n_1+n_2\leqq N- \mathtt{q}_0 + \frac{3}{2} \),
$$\begin{aligned}&\Vert \Delta _{12} (\mathcal {A}) h \Vert _{s_1} \lesssim _{s_1} \varepsilon \left\| i_1-i_2 \right\| _{s_1+\sigma }\left\| h \right\| _{s_1+\sigma } \,, \ \ \mathcal {A}\in \{ \mathcal {E}^{\pm 1} , (\mathcal {E}^{\pm 1})^*, \mathcal {Q}^{\pm 1} = (\mathcal {Q}^{\pm 1})^* \}\,, \end{aligned}$$(7.99)$$\begin{aligned}&\Vert \Delta _{12}a_1^{(d)} \Vert _{s_1} \lesssim _{s_1} \varepsilon \left\| i_1-i_2 \right\| _{s_1+\sigma } \,, \ | \Delta _{12} \mathtt{m}_{\frac{3}{2}} | \lesssim \varepsilon ^2 \left\| i_1-i_2 \right\| _{s_1+\sigma }, \end{aligned}$$(7.100)$$\begin{aligned}&\Vert \Delta _{12} \mathbf{R}_5^{(d)} \Vert _{0,s_1,\alpha } + \Vert \Delta _{12} \mathbf{R}_5^{(o)}\Vert _{0,s_1,\alpha } \lesssim _{s_1,N,\alpha } \varepsilon \left\| i_1-i_2 \right\| _{s_1+\sigma _N+2\alpha }\,,\end{aligned}$$(7.101)$$\begin{aligned}&\left\| \langle D\rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{5,N}({\varphi })\langle D\rangle ^{n_2} \right\| _{\mathcal {L}(H^{s_1})} \lesssim _{s_1, N, \mathtt{q}_0} \varepsilon \left\| i_1-i_2 \right\| _{s_1+\sigma _N(\mathtt{q}_0)}. \end{aligned}$$(7.102)
The real operator \(\mathcal {L}_5\) is Hamiltonian, reversible and momentum preserving.
Proof
By the expression of \( \mathcal {L}_4 \) in (7.81), using (3.15), and (7.86), we obtain that \( \mathcal{L}_5 \) has the form (7.89). The functions \(\beta \) and q, defined respectively in (7.68) and (7.66) with \( a_3 \) defined in (7.56), satisfy, by Lemmata 3.8, 3.2 and (7.28), for some \(\sigma :=\sigma (k_0,\tau ,\nu ) > 0 \) and for all \(s\geqq s_0\),
The estimates (7.90)–(7.92) follow by Lemmata 3.12, 3.13, 3.8, (7.103) and writing
\( \mathcal {B}^*h({\varphi },y) = ( 1+\breve{\beta }({\varphi },y )) h({\varphi },y+\breve{\beta }({\varphi },y)) \), and similar expressions for \(\mathcal {B}^{-1}-{\mathrm{Id}}\), \((\mathcal {B}^{-1})^*\). The estimate for \(\mathtt{m}_{\frac{3}{2}}\) follows by (7.88), Lemma 3.2 and (7.16). The real function \(a_1^{(d)}\) in (7.94) is
where \(\rho \) and \(a_1\) are defined respectively in (7.20) and (7.55). Recalling Lemmata 7.3 and 7.6, the function \( a_1^{(d)} \) is a quasi-periodic traveling wave, even in \( ({\varphi },x) \). Moreover, (7.95) follows by Lemma 3.2 and (7.16), (7.19), (7.28), (7.103). By direct computations, we have
where \(P_0^{(41)}\), \(P_{-\frac{1}{2},N}^{(43)}\), \(P_0^{(44)}\) are defined in (7.82), (7.83), (7.84) and \( \rho \,\mathtt{m}_\frac{3}{2} = m_\frac{3}{2} ({\varphi }) \) with \( m_\frac{3}{2} ({\varphi }) \) defined in (7.69) (cfr. (7.86)). Therefore, the estimate (7.97) follows by (7.73), (7.71), (7.55), (7.56), (7.57), (7.58), (7.75), (7.52), (7.79), (2.21), applying Lemmata 3.5, 3.6, 3.8, 3.2, Proposition 3.9 and estimates (7.16), (7.19), (7.28), (7.103). The estimate (7.98), where
follows by (7.85), (7.77), (7.76), (7.59), (7.53), (7.50), (7.48), (7.46), (7.43), Lemmata 3.12, 3.13, estimates (7.44), (7.49), Proposition 3.9 and (7.90), (7.103), Lemma 3.10 and Lemmata 2.34, 2.32 in [6]. The estimates (7.99), (7.100), (7.101), (7.102) are proved in the same fashion. Since the transformations \(\mathcal {E}\), \(\mathcal {Q}\), \({\widetilde{\mathcal {M}}}\) are symplectic, the operator \( \mathcal{L}_4\) is Hamiltonian. Hence the operator \(\mathcal {L}_{5}\) obtained conjugating with \( \mathcal {C}\) is Hamiltonian according to (3.41). By Lemma 7.3, the functions \(\beta ({\varphi },x)\) and \(q({\varphi },x)\), defined in (7.68), (7.66) (with \( a_3 \) defined in (7.56)), are both quasi-periodic traveling waves, respectively \({\mathrm{odd}}({\varphi },x)\) and \({\mathrm{even}}({\varphi },x)\). Therefore, the transformations \(\mathcal {E}\) and \(\mathcal {Q}\) are momentum and reversibility preserving. Moreover, also \({\widetilde{\mathcal {M}}}\) and \(\mathcal {C}\) are momentum and reversibility preserving (writing the involution in complex variables as in (2.29)). Hence, since \( \mathcal {L}_1 \) is momentum preserving and reversible (Lemma 7.8), the operator \(\mathcal {L}_{5}\) is momentum preserving and reversible as well, in particular the operators \( \mathbf{R}_5^{(0,d)} \) and \( \mathbf{R}_5^{(0,o)} \) in (7.96) (for example check the definition in (7.105), see also Remark 3.20). \(\square \)
7.4 Symmetrization up to Smoothing Remainders
The goal of this section is to transform the operator \(\mathcal {L}_5\) in (7.89) into the operator \(\mathcal {L}_{6}\) in (7.108) which is block diagonal up to a regularizing remainder. From this step we do not preserve any further the Hamiltonian structure, but only the reversible and momentum preserving one (it is now sufficient for proving Theorem 5.2).
Lemma 7.10
Fix \(M, N \in \mathbb {N}\), \( \mathtt{q}_0 \in \mathbb {N}_0\). There exist real, reversibility and momentum preserving operator matrices \(\{ \mathbf{X}_m \}_{m=1}^M\) of the form
such that, conjugating the operator \( \mathcal {L}_5 \) in (7.89) via the map
we obtain the real, reversible and momentum preserving operator
with a block-diagonal operator
and a smoothing off diagonal remainder
both reversibility and momentum preserving, which satisfy for all \(\alpha \in \mathbb {N}_0 \), for some \( \sigma _N := \sigma _N(k_0,\tau , \nu , N)>0 \), \(\aleph _{M}(\alpha ) > 0 \), for all \( s\geqq s_0 \),
For any \( \mathtt{q}\in \mathbb {N}^\nu _0 \) with \( |\mathtt{q}| \leqq \mathtt{q}_0\), \(n_1, n_2 \in \mathbb {N}_0 \) with \( n_1 + n_2 \leqq N -(k_0+\mathtt{q}_0) + \frac{5}{2} \), the operator \(\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{6, N}(\varphi ) \langle D \rangle ^{n_2}\) is \(\mathcal {D}^{k_0} \)-tame with a tame constant satisfying, for some \(\sigma _N(\mathtt{q}_0) := \sigma _N(k_0,\tau , \nu , \mathtt{q}_0) \), for any \(s_0 \leqq s \leqq S \),
The conjugation map \( {\varvec{\Phi }}_M \) in (7.107) satisfies, for all \(s\geqq s_0\),
Furthermore, for any \(s_1\) as in (7.15), \(\alpha \in \mathbb {N}_0\), \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\), and \(n_1,n_2\in \mathbb {N}_0\), with \(n_1+n_2\leqq N- \mathtt{q}_0 + \frac{3}{2}\), we have
Proof
The proof is inductive on the index M. The operator \(\mathcal {L}_6^{(0)}:= \mathcal {L}_5 \) satisfy (7.110)–(7.111) with \( \aleph _0(\alpha ) := 2\alpha \), by Lemma 7.9. Suppose we have done already M steps obtaining an operator \( \mathcal {L}_6^{(M)} \) as in (7.108) with a remainder \( \mathbf{\Phi }_{M}^{-1} \mathbf{T}_{5,N} {\varvec{\Phi }}_{M}\), instead of \( \mathbf{T}_{6,N} \). We now show how to perform the \((M+1)\)-th step. Define the symbol
where \( \chi \) is the cut-off function defined in (3.10) and \(\omega (\kappa , \xi ) \) is the symbol (cfr. (2.23))
Note that \(\chi _{M+1} \) in (7.116) is well defined because \( \omega (\kappa , \xi ) \) is positive on the support of \( \chi (\xi ) \). We conjugate the operator \(\mathcal {L}_6^{(M)} \) in (7.108) by the flow generated by \(\mathbf{X}_{M+1}\) of the form (7.106) with \( \chi _{M+1} (\varphi , x, \xi ) \) defined in (7.116). By (7.110) and Lemma 7.9-2, for any \(s\geqq s_0\) and \(\alpha \in \mathbb {N}_0\),
Therefore, by Lemmata 3.7, 3.5 and the induction assumption (7.112) for \({\varvec{\Phi }}_{M}\), the conjugation map \({\varvec{\Phi }}_{M+1}:= {\varvec{\Phi }}_{M}e^{\mathbf{X}_{M+1}}\) is well defined and satisfies estimate (7.112) with \(M+1\). By the Lie expansion (3.16) we have
In view of (7.106), (7.93) and (7.109), we have that
where, denoting for brevity \( \chi _{M+1} := \chi _{M+1}({\varphi },x,\xi ) \), it results
By (3.23), Lemma 3.5 and since \( \chi _{M+1}({\varphi },x,\xi ) \in S^{-\frac{3}{2} -M } \) by (7.116), we have that
where \(\mathtt{r}_{M+1} \) is in \( {\mathrm{OP}}S^{-M-1} \). By (7.116) and (7.122)
The remaining pseudodifferential operators in (7.119)–(7.121) have order \( {\mathrm{OP}}S^{-M-\frac{3}{2}} \). Therefore the operator \( \mathcal {L}_6^{(M+1)} \) in (7.118) has the form (7.108) at \( M+ 1 \) with
and a remainder \( {\varvec{\Phi }}_{M+1}^{-1} \mathbf{T}_{5,N} {\varvec{\Phi }}_{M+1}\). By Lemmata 3.5, 3.6, the induction assumption (7.110), (7.117), (7.95), we conclude that \(\mathbf{R}_{6,M+1}^{(0,d)}\) and \(\mathbf{R}_{6,M+1}^{(-(M+1),o)}\) satisfy (7.110) at order \(M+1\) for suitable constants \( \aleph _{M+1} (\alpha ) > \aleph _{M} (\alpha ) \). Moreover the operator \({\varvec{\Phi }}_{M+1}^{-1} \mathbf{T}_{5, N} {\varvec{\Phi }}_{M+1} \) satisfies (7.112) (with \(M+1\)) by Lemmata 3.12, 3.13 and estimates (7.98), (7.112). Estimates (7.113), (7.114), (7.115) follow similarly. By (7.116), (3.43), Lemmata 3.19, 3.29, and the induction assumption that \(\mathbf{R}_{6,M}^{(-M,o)}\) is reversible and momentum preserving, we conclude that \(\mathbf{X}_{M+1}\) is reversibility and momentum preserving, and so are \(e^{\pm \mathbf{X}_{M+1}}\). By the induction assumption \(\mathcal {L}_{6}^{(M)}\) is reversible and momentum preserving, and so \(\mathcal {L}_{6}^{(M+1)}\) is reversible and momentum preserving as well, in particular the terms \( \mathbf{R}_{6,M+1}^{(0,d)}+\mathbf{R}_{6,M+1}^{(-(M+1),o)} \) in (7.123). \(\square \)
Remark 7.11
The number of regularizing iterations \(M\in \mathbb {N}\) will be fixed by the KAM reduction scheme in Section 8, see (8.5). Note that it is independent of the Sobolev index s.
So far the operator \( \mathcal {L}_6 \) of Lemma 7.10 depends on two indexes M, N which provide respectively the order of the regularizing off-diagonal remainder \( \mathbf{R}_{6}^{(- \frac{M}{2}, o)} \) and of the smoothing tame operator \( \mathbf{T}_{6,N} \). From now on we fix
7.5 Reduction of the Order 1
The goal of this section is to transform the operator \(\mathcal {L}_6\) in (7.108), with \(N=M\) (cfr. (7.124)), into the operator \(\mathcal {L}_8 \) in (7.146) whose coefficient in front of \( \partial _x \) is a constant. We first eliminate the x-dependence and then the \( {\varphi }\)-dependence.
Space reduction. First we rewrite the operator \(\mathcal {L}_{6}\) in (7.108), with \(N=M\), as
having denoted
We conjugate \(\mathcal {L}_{6}\) through the real operator
where \(\Phi ({\varphi }):=\Phi ^\tau ({\varphi })|_{\tau =1} \) is the time 1-flow of the PDE
and \(b({\varphi },x) \) is a real, smooth, odd \(({\varphi },x)\), periodic function chosen later, see (7.133), (7.135), (7.141). Usual energy estimates imply that the flow \( \Phi ^\tau ({\varphi }) \) of (7.127) is a bounded operator in \(H_x^s \). The operator \(\partial _\lambda ^k\partial _{\varphi }^\beta \Phi \) loses \(\left| D \right| ^{\frac{\left| \beta \right| +\left| k \right| }{2}}\) derivatives, which are compensated by \(\langle D\rangle ^{-m_1}\) on the left hand side and \(\langle D\rangle ^{-m_2}\) on the right hand side, with \(m_1,m_2\in \mathbb {R}\) satisfying \(m_1+m_2= \tfrac{1}{2}\left( \left| \beta \right| +\left| k \right| \right) \), according to the tame estimates in the Sobolev spaces \(H_{{\varphi },x}^s\) of Proposition 2.37 in [2]. Moreover, since \( b({\varphi },x)\) is \({\mathrm{odd}}({\varphi },x)\), then \( b({\varphi }, x) |D|^{\frac{1}{2}}\) is reversibility preserving as well as \( {\varvec{\Phi }} ({\varphi }) \). Finally, note that \(\Phi \pi _0 = \pi _0 = \Phi ^{-1}\pi _0\), which implies that
By the Lie expansion (3.16), we have
and, by (3.17),
Note that \( {\mathrm{ad}}_{A({\varphi })}^{2M+3}(P_6) \) and \( {\mathrm{ad}}_{A({\varphi })}^{2M+1}(\omega \cdot \partial _{\varphi }A({\varphi })) \) are in \( {\mathrm{OP}}S^{-M} \). The number M will be fixed in (8.5). Note also that in the expansions (7.129), (7.130) the operators have decreasing order and size. The terms of order 1 come from (7.129), in particular from \(P_6 - {\mathrm{i}}[A, P_6] \). Recalling (7.125), that \( A({\varphi }) := b({\varphi }, x) |D|^{\frac{1}{2}} \), (3.26) and that (cfr. (4.1), (4.5))
(the cut-off function \( \chi \) is defined in (3.10)) we deduce that
where \( r_{b,0} \in S^0 \) is small with b. As a consequence, the first order term of \(P_6 - {\mathrm{i}}[A, P_6] \) is \((a_1^{(d)}+ \tfrac{3}{2}\, \sqrt{\kappa }\, \mathtt{m}_{\frac{3}{2}}\, b_x )\partial _x \) and we choose \( b ({\varphi },x) \) so that it is independent of x: we look for a solution
of the equation
Therefore
We now determine \( b_2 ({\varphi }) \) by imposing a condition at the order 1/2. We deduce by (7.129), (7.130), (7.125), (7.132)–(7.134), that
where \(a_2^{(d)}({\varphi },x)\) is the real function
and
where \( r_{b,-\frac{1}{2}} \in S^{-\frac{1}{2}} \) is small in b. In view of Section 7.6 we now determine the function \( b_2 (\varphi ) \) so that the space average of the function \( a_2^{(d)} \) in (7.137) is independent of \( \varphi \), that is
Noting that the space average \( \big \langle \big ( \tfrac{1}{2} (a_1^{(d)})_x + \frac{3}{8} \mathtt{m}_{\frac{3}{2}} \sqrt{\kappa } (b_1)_{xx} \big ) b_2 ({\varphi }) \big \rangle _x = 0 \) and that \( \big \langle \omega \cdot \partial _{\varphi }b_1 \big \rangle _{{\varphi },x} = 0 \), we get
Note that (7.139) holds for any \( \omega \in \mathtt{D}\mathtt{C}(\upsilon , \tau ) \).
Time reduction. In order to remove the \({\varphi }\)-dependence of the coefficient \(\langle a_1^{(d)}\rangle _x({\varphi }) \) of the first order term of the operator \( L_7 \) in (7.136), we conjugate \( L_7 \) with the map
where \(\varrho ({\varphi })\) is a real periodic function to be chosen, see (7.145). Note that \( \mathcal {V}\) is a particular case of the transformation \( \mathcal {E}\) in (7.34) for a function \( \beta ({\varphi }, x) = \varrho ({\varphi }) \), independent of x. We have that
whereas the Fourier multipliers are left unchanged and a pseudodifferential operator of symbol \( a({\varphi }, x, \xi ) \) transforms as
We choose \( \varrho ({\varphi })\) such that
(where \(a_1^{(d)}\) is fixed in Lemma 7.9), namely we define
Note that (7.144) holds for any \(\omega \in \mathtt{D}\mathtt{C}(\upsilon ,\tau )\).
We sum up these two transformations into the following lemma.
Lemma 7.12
Let \( M \in \mathbb {N}\), \( \mathtt{q}_0 \in \mathbb {N}_0 \). Let \(b({\varphi },x)= b_1({\varphi },x) + b_2({\varphi })\) and \(\varrho ({\varphi }) \) be the functions defined respectively in (7.135), (7.141), (7.145). Then, conjugating \( \mathcal {L}_6 \) in (7.108) via the invertible, real, reversibility preserving and momentum preserving maps \( {\varvec{\Phi }} \), \( \mathcal {V}\) defined in (7.126)–(7.127) and (7.142), we obtain, for any \( \omega \in \mathtt{D}\mathtt{C}(\upsilon , \tau ) \), the real, reversible and momentum preserving operator
where:
-
1.
the real constant \( \mathtt{m}_1\) defined in (7.144) satisfies \( | \mathtt{m}_1 |^{k_0, \upsilon } \lesssim \varepsilon \);
-
2.
\(\mathbf{A}_3^{(d)} \) is a diagonal matrix of multiplication
$$\begin{aligned} \mathbf{A}_3^{(d)} := \begin{pmatrix} a_3^{(d)} &{} 0\\ 0&{} a_3^{(d)} \end{pmatrix} , \end{aligned}$$for a real function \( a_3^{(d)} \) which is a quasi-periodic traveling wave, \({\mathrm{even}}({\varphi },x)\), satisfying
$$\begin{aligned} \langle a_3^{(d)}\rangle _{x}({\varphi }) = \mathtt{m}_{\frac{1}{2}} \in \mathbb {R}, \quad \forall \, {\varphi }\in \mathbb {T}^{\nu }\, , \end{aligned}$$(7.147)where \(\mathtt{m}_{\frac{1}{2}} \in \mathbb {R}\) is the constant in (7.140), and for some \(\sigma = \sigma (\tau ,\nu ,k_0)>0\), for all \(s\geqq s_0\),
$$\begin{aligned} \Vert a_3^{(d)} \Vert _{s}^{k_0,\upsilon }\lesssim _{s} \varepsilon \upsilon ^{-1} ( 1 + \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma }^{k_0,\upsilon } )\,; \end{aligned}$$(7.148) -
3.
\( \mathbf{R}_{8}^{(0,d)} \) is a block-diagonal operator
$$\begin{aligned} \mathbf{R}_{8}^{(0,d)}&= \begin{pmatrix} r_{8}^{(d)}({\varphi },x,D) &{} 0 \\ 0 &{}\overline{r_{8}^{(d)}({\varphi },x,D)} \end{pmatrix} \in {\mathrm{OP}}S^{0} \,, \end{aligned}$$that satisfies for all \(\alpha \in \mathbb {N}_0 \), for some \(\sigma _M (\alpha ):= \sigma _M(k_0,\tau , \nu , \alpha )>0\) and for all \(s\geqq s_0\),
$$\begin{aligned} \Vert \mathbf{R}_{8}^{(0,d)} \Vert _{0,s,\alpha }^{k_0,\upsilon } \lesssim _{s, M, \alpha } \varepsilon \upsilon ^{-1}( 1+\Vert {\mathfrak {I}}_0 \Vert _{s+\sigma _M( \alpha )}^{k_0,\upsilon } ) \, \,; \end{aligned}$$(7.149) -
4.
For any \( \mathtt{q}\in \mathbb {N}^\nu _0 \) with \( |\mathtt{q}| \leqq \mathtt{q}_0\), \( n_1, n_2 \in \mathbb {N}_0 \) with \( n_1 + n_2 \leqq M - 2(k_0+\mathtt{q}_0) + \frac{5}{2} \), the operator \(\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{8,M}(\varphi ) \langle D \rangle ^{n_2}\) is \(\mathcal {D}^{k_0} \)-tame with a tame constant satisfying, for some \( \sigma _M(\mathtt{q}_0) := \sigma _M(k_0,\tau , \nu , \mathtt{q}_0) \), for any \(s_0 \leqq s \leqq S \),
$$\begin{aligned} {\mathfrak {M}}_{\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{8,M}(\varphi ) \langle D \rangle ^{n_2}}(s) \lesssim _{S, M, \mathtt{q}_0} \varepsilon \upsilon ^{-1}( 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma _M(\mathtt{q}_0)}^{k_0,\upsilon } )\,; \end{aligned}$$(7.150) -
5.
The operators \( {\varvec{\Phi }}^{\pm 1} -{\mathrm{Id}}\), \(({\varvec{\Phi }}^{\pm 1}-{\mathrm{Id}})^*\) are \(\mathcal {D}^{k_0}\)-\(\frac{1}{2}(k_0+1)\)-tame and the operators \(\mathcal {V}^{\pm 1}- {\mathrm{Id}}\), \((\mathcal {V}^{\pm 1}-{\mathrm{Id}})^*\) are \(\mathcal {D}^{k_0}\)-\((k_0+2)\)-tame, with tame constants satisfying, for some \(\sigma >0\) and for all \(s_0\leqq s \leqq S\),
$$\begin{aligned}&{\mathfrak {M}}_{{\varvec{\Phi }}^{\pm 1} -{\mathrm{Id}}}(s) + {\mathfrak {M}}_{({\varvec{\Phi }}^{\pm 1}-{\mathrm{Id}})^*}(s) \lesssim _{S} \varepsilon \upsilon ^{-1}( 1 + \Vert {\mathfrak {I}}_0 \Vert _{s+ \sigma }^{k_0,\upsilon })\,, \end{aligned}$$(7.151)$$\begin{aligned}&{\mathfrak {M}}_{\mathcal {V}^{\pm 1} -{\mathrm{Id}}}(s) + {\mathfrak {M}}_{(\mathcal {V}^{\pm 1}-{\mathrm{Id}})^*}(s) \lesssim _{S} \varepsilon \upsilon ^{-1}( 1 + \Vert {\mathfrak {I}}_0 \Vert _{s+ \sigma }^{k_0,\upsilon })\,. \end{aligned}$$(7.152)
Furthermore, for any \(s_1\) as in (7.15), \(\alpha \in \mathbb {N}_0\), \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\), and \(n_1,n_2\in \mathbb {N}_0\), with \(n_1+n_2\leqq M-2 \mathtt{q}_0 + \frac{1}{2}\), we have
Proof
The function \(b({\varphi },x)= b_1({\varphi },x) + b_2({\varphi })\), with \(b_1\) and \(b_2\), defined in (7.135) and (7.141) and the function \(\varrho ({\varphi })\) in (7.145), satisfy, by Lemma 3.8 and (7.95),
for some \(\sigma >0\) and for all \(s\geqq s_0\). The estimate \( | \mathtt{m}_1 |^{k_0, \upsilon } \lesssim \varepsilon \) follows by (7.144) and (7.95). The function
where \(a_2^{(d)}\) is defined in (7.137), satisfies (7.147) by (7.139). Moreover, the estimate (7.148) follows by Lemma 3.8 and (7.95), (7.157). The estimate (7.149) for (cfr. (7.143))
with \(r_7^{(d)}\) defined in (7.138), follows by Lemmata 3.5, 3.6, 3.8 and (7.157), (7.110). The smoothing term \( \mathbf{T}_{8, M} \) in (7.146) is, using also (7.128),
with \(T_M\) and \(T_M'\) defined in (7.129), (7.130). The estimate (7.150) follows by (7.125), Lemmata 3.12, 3.13, the tame estimates of \( {\varvec{\Phi }} \) in Proposition 2.37 in [2], and estimates (7.95), (7.157), (7.151), (7.111), noting that operators of the form \( \partial _\lambda ^k \partial _{\varphi }^\mathtt{q}\mathcal {V}^{\pm 1}\) lose \(\left| k \right| + \left| \mathtt{q} \right| \) derivatives. The estimate (7.151) follows by Lemma 2.38 in [2] and (7.157), whereas (7.152) follows by the equivalent representation for \(\mathcal {V}\) as in (7.104), Lemmata 3.12, 3.8 and (7.157). The estimates (7.153), (7.154), (7.155), (7.156) are proved in the same fashion. By Lemma 7.9-3, the function \(a_1^{(d)}\) is an \({\mathrm{even}}({\varphi },x)\) quasi-periodic traveling wave, hence the function \(b_1\) in (7.135) is an \({\mathrm{odd}}({\varphi },x)\) quasi-periodic traveling wave, the function \(b_2\) in (7.141) is odd in \({\varphi }\) and satisfies \(b_2({\varphi }- \vec {\jmath }\varsigma ) = b_2({\varphi })\) for all \(\varsigma \in \mathbb {R}\), whereas the function \(\varrho \) in (7.145) is odd in \({\varphi }\) and satisfies \(\varrho ({\varphi }- \vec {\jmath }\varsigma ) = \varrho ({\varphi })\) for all \(\varsigma \in \mathbb {R}\). By Lemmata 3.19, 3.29, and 3.25, the transformations \({\varvec{\Phi }}\) and \(\mathcal {V}\) are reversibility and momentum preserving. Then the operator \(\mathcal {L}_{8}\) is reversible and momentum preserving. The function \( a_3^{(d) }\) is an \({\mathrm{even}}({\varphi },x)\) quasi-periodic traveling wave. \(\square \)
7.6 Reduction of the Order 1/2
The goal of this section is to transform the operator \(\mathcal {L}_8\) in (7.146) into the operator \(\mathcal {L}_9\) in (7.168) whose coefficient in front of \(|D|^{1/2}\) is a constant. We eliminate the x-dependence and, in view of the property (7.147), we obtain that this transformation removes also the \({\varphi }\)-dependence.
We first write the operator \(\mathcal {L}_{8}\) in (7.146) as
where
We conjugate \(\mathcal {L}_{8}\) through the real operator
where \(\Psi ({\varphi }):= \Psi ^\tau ({\varphi })|_{\tau =1}\) is the time-1 flow of
the function \(b_ 3 ({\varphi }, x)\) is a smooth, real, periodic function to be chosen later (see (7.165)) and \(\mathcal {H}\) is the Hilbert transform defined in (3.19). Note that \(\Psi \pi _0 = \pi _0 = \Psi ^{-1}\pi _0\), so that
By the Lie expansion in (3.16) we have
and, by (3.17),
The number M will be fixed in (8.5). The contributions at order 1/2 come from (7.162), in particular from \( P_8 - [B, P_8] \) (recall (7.158)). Since \( B = b_3 \mathcal {H}\) (see (7.160)), by (3.26) and (7.131) we have
where \( {\mathrm{Op}}(r_{b_3, - \frac{1}{2}}) \in {\mathrm{OP}}S^{- \frac{1}{2}} \) is small with \(b_3\). Recalling that, by (7.147), the space average \( \langle a_3^{(d)}\rangle _x({\varphi }) = \mathtt{m}_{\frac{1}{2}} \) for all \( {\varphi }\in \mathbb {T}^\nu \), we choose the function \(b_3({\varphi },x)\) such that \( a_3^{(d)} - \tfrac{3}{2} \mathtt{m}_{\frac{3}{2}} \sqrt{\kappa }(b_3)_x = \mathtt{m}_{\frac{1}{2}} \), namely
We deduce by (7.162)–(7.163) and (7.164), (7.165) that
where
Define the matrix \({\varvec{\Sigma }}:= \begin{pmatrix} 1 &{} 0 \\ 0 &{} -1 \end{pmatrix}\). Summing up, we have obtained the following lemma.
Lemma 7.13
Let \( M \in \mathbb {N}\), \( \mathtt{q}_0 \in \mathbb {N}_0 \). Let \(b_3\) be the function defined in (7.165). Then, conjugating the operator \( \mathcal {L}_8 \) in (7.146) via the invertible, real, reversibility and momentum preserving map \( {\varvec{\Psi }} \) defined in (7.159), (7.160), we obtain, for any \( \omega \in \mathtt{D}\mathtt{C}(\upsilon , \tau ) \), the real, reversible and momentum preserving operator
where
-
1.
the constant \( \mathtt{m}_{\frac{1}{2}}\) defined in (7.140) satisfies \(| \mathtt{m}_{\frac{1}{2}} |^{k_0, \upsilon } \lesssim \varepsilon ^2 \);
-
2.
\( \mathbf{R}_{9}^{(0,d)} \) is a block-diagonal operator
$$\begin{aligned} \mathbf{R}_{9}^{(0,d)}&= \begin{pmatrix} r_{9}^{(d)}({\varphi },x,D) &{} 0 \\ 0 &{}\overline{r_{9}^{(d)}({\varphi },x,D)} \end{pmatrix} \in {\mathrm{OP}}S^{0}, \end{aligned}$$that satisfies, for some \(\sigma _M:= \sigma _M(k_0,\tau ,\nu )>0\), and for all \( s\geqq s_0\),
$$\begin{aligned} \Vert \mathbf{R}_{9}^{(0,d)} \Vert _{0,s,1}^{k_0,\upsilon } \lesssim _{s,M} \varepsilon \upsilon ^{-1} ( 1+\Vert {\mathfrak {I}}_0 \Vert _{s+\sigma _M}^{k_0,\upsilon } ) \,; \end{aligned}$$(7.169) -
3.
For any \( \mathtt{q}\in \mathbb {N}^\nu _0 \) with \( |\mathtt{q}| \leqq \mathtt{q}_0\), \(n_1, n_2 \in \mathbb {N}_0 \) with \( n_1 + n_2 \leqq M - 2 (k_0+\mathtt{q}_0) + \frac{5}{2} \), the operator \(\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{9, M}(\varphi ) \langle D \rangle ^{n_2}\) is \(\mathcal {D}^{k_0} \)-tame with a tame constant satisfying, for some \(\sigma _M(\mathtt{q}_0) := \sigma _M(k_0, \tau , \nu , \mathtt{q}_0) \), for any \(s_0 \leqq s \leqq S \),
$$\begin{aligned} {\mathfrak {M}}_{\langle D \rangle ^{n_1}\partial _{\varphi }^\mathtt{q}\mathbf{T}_{9,M}(\varphi ) \langle D \rangle ^{n_2}}(s) \lesssim _{S, M, \mathtt{q}_0} \varepsilon \upsilon ^{-1}( 1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\sigma _M(\mathtt{q}_0)}^{k_0,\upsilon } )\,; \end{aligned}$$(7.170) -
4.
The operators \( {\varvec{\Psi }}^{\pm 1} -{\mathrm{Id}}\), \(({\varvec{\Psi }}^{\pm 1}-{\mathrm{Id}})^*\) are \(\mathcal {D}^{k_0}\)-tame, with tame constants satisfying, for some \(\sigma := \sigma (k_0, \tau , \nu ) > 0 \) and for all \(s \geqq s_0\),
$$\begin{aligned} {\mathfrak {M}}_{{\varvec{\Psi }}^{\pm 1} -{\mathrm{Id}}}(s) + {\mathfrak {M}}_{({\varvec{\Psi }}^{\pm 1}-{\mathrm{Id}})^*}(s) \lesssim _{s} \varepsilon \upsilon ^{-1}( 1 + \Vert {\mathfrak {I}}_0 \Vert _{s+ \sigma }^{k_0,\upsilon })\,. \end{aligned}$$(7.171)
Furthermore, for any \(s_1\) as in (7.15), \(\alpha \in \mathbb {N}_0\), \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\), and \(n_1,n_2\in \mathbb {N}_0\), with \(n_1+n_2\leqq M-2 \mathtt{q}_0 + \frac{1}{2}\), we have
Proof
The function \(b_3({\varphi },x)\) defined in (7.165), satisfies, by (7.148) and the estimate of \( \mathtt{m}_{\frac{3}{2}}\) given in Lemma 7.9-2, for some \(\sigma >0\) and for all \(s\geqq s_0\),
The estimate for \(\mathtt{m}_{\frac{1}{2}}\) follows by (7.140), (3.7) and (7.95), (7.157). The estimate (7.169) follows by (7.167), (7.158), Lemmata 3.5, 3.6, and (7.148), (7.149), (7.175). By (7.146), (7.158), (7.166), and (7.161), the smoothing term \( \mathbf{T}_{9,M} \) in (7.168) is
with \(L_M\) and \(L_M'\) introduced in (7.162), (7.163). The estimate (7.170) follows by Lemmata 3.12, 3.13, 3.7, (7.158), (7.148), (7.150), (7.175), (7.171). The estimate (7.171) follows by Lemma 3.13 and (7.175). The estimates (7.172), (7.173), (7.174) are proved in the same fashion. By Lemma 7.12, the function \(a_3^{(d)}\) is a \({\mathrm{even}}({\varphi },x)\) quasi-periodic traveling wave. Hence the function \(b_3\) in (7.165) is a \({\mathrm{odd}}({\varphi },x)\) quasi-periodic traveling wave. By Lemmata 3.19, 3.29, and 3.25, the transformation \({\varvec{\Psi }}\) is reversibility and momentum preserving, therefore the operator \(\mathcal {L}_{9}\) is reversible and momentum preserving. \(\square \)
Remark 7.14
In Proposition 7.18 we shall estimate \( \Vert [\partial _x, \mathbf{R}_9^{(0,d)} ]\Vert _{0,s,0}^{k_0,\upsilon }\) using (7.169) and (3.27). In order to control \( \Vert \mathbf{R}_9^{(0,d)} \Vert _{0,s,1}^{k_0, \upsilon } \) we used the estimates (7.97) for finitely many \( \alpha \in \mathbb {N}_0 \), \( \alpha \leqq \alpha (M) \), depending on M. Furthermore in Proposition 7.18 we shall use (7.172)–(7.173) only for \( s_1 = s_0 \).
7.7 Conclusion: Partial Reduction of \(\mathcal {L}_\omega \)
By Sections 7.1-7.6, the linear operator \(\mathcal {L}\) in (7.12) is semi-conjugated, for all \( \omega \in \mathtt{DC}(\upsilon ,\tau ) \), to the real, reversible and momentum preserving operator \(\mathcal {L}_{9}\) defined in (7.168), namely
where
Moreover \(\mathcal {L}_{9} \) is defined for all \( \omega \in \mathbb {R}^\nu \).
Now we deduce a similar conjugation result for the projected operator \( \mathcal {L}_\omega \) in (6.23), that is (7.1), which acts in the normal subspace \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \). We first introduce some notation.
We denote by \( \Pi _{\mathbb {S}^+,\Sigma }^\intercal \) and \( \Pi _{\mathbb {S}^+,\Sigma }^\angle \) the projections on the subspaces \(\mathfrak {H}_{\mathbb {S}^+,\Sigma }^\intercal \) and \( \mathfrak {H}_{\mathbb {S}^+,\Sigma }^\angle \) defined in Section 2.3. In view of Remark 7.2, we denote, with a small abuse of notation, \( \Pi _{\mathbb {S}_0^+, \Sigma }^\intercal := \Pi _{\mathbb {S}^+, \Sigma }^\intercal + \pi _0 \), so that \( \Pi _{\mathbb {S}_0^+, \Sigma }^\intercal + \Pi _{\mathbb {S}^+,\Sigma }^\angle = {\mathrm{Id}}\) on the whole \( L^2 \times L^2 \). We remind that \( \mathbb {S}_0 = \mathbb {S}\cup \{0\} \), where \( \mathbb {S}\) is the set defined in (2.48). We denote by \( \Pi _{{\mathbb {S}}_0} := \Pi _\mathbb {S}^\intercal + \pi _0 \), where \( \Pi _\mathbb {S}^\intercal \) is defined below (2.58) together with the definition of \( \Pi _{{\mathbb {S}}_0}^\perp \), so that we have \( \Pi _{{\mathbb {S}}_0} + \Pi _{{\mathbb {S}}_0}^\perp = {\mathrm{Id}} \).
Lemma 7.15
Let \( M > 0 \). There is \( \sigma _M > 0 \) (depending also on \( k_0, \tau , \nu \)) such that, assuming (7.14) with \( \mu _0 \geqq \sigma _M \), the following holds: the maps \(\mathcal {W}_1\), \(\mathcal {W}_2\) defined in (7.177) have the form
where, for any \( i = 1, 2 \), for all \(s_0 \leqq s \leqq S\),
Moreover, for \(\varepsilon \upsilon ^{-1} \leqq \delta (S) \) small enough, the operators
are invertible and, for all \(s_0 \leqq s \leqq S\), \(i=1,2\),
The operators \( \mathcal {W}_1^\perp \), \( \mathcal {W}_2^\perp \) map (anti)-reversible, respectively traveling, waves, into (anti)-reversible, respectively traveling, waves.
Proof
The formulae (7.178) and the estimates (7.179) follow by (7.177), Lemmata 3.12, 3.13, and (3.36), (7.23), (7.27), (7.91), (7.92), (7.112), (7.151), (7.152), (7.171). The invertibility of each \( \mathcal {W}_i^\perp \) and the estimates (7.181) follow as in [2] and noting that \(\Pi _{\mathbb {S}^+,\Sigma }^\angle \, {\widetilde{\mathcal {M}}}\mathcal {C}\, \Pi _{{\mathbb {S}}_0}^\perp =\Pi _{\mathbb {S}^+,\Sigma }^\angle \, \mathcal {M}\mathcal {C}\, \Pi _{{\mathbb {S}}_0}^\perp \) are invertible on their ranges, with inverses \( (\Pi _{\mathbb {S}^+,\Sigma }^\angle \, \mathcal {M}\mathcal {C}\,\Pi _{{\mathbb {S}}_0}^\perp )^{-1} = \Pi _{{\mathbb {S}}_0}^\perp (\mathcal {M}\mathcal {C})^{-1} \Pi _{\mathbb {S}^+,\Sigma }^\angle \). Since \( \mathcal {Z}, \mathcal {E}, \mathcal {Q}, {\widetilde{\mathcal {M}}}, {\varvec{\Phi }}_{M}, {\varvec{\Phi }}, \mathcal {V}, {\varvec{\Psi }} \) are reversibility and momentum preserving and using Remark 7.7 and Lemmata 3.23, 3.31, we deduce that \( \mathcal {W}_1^\perp \), \( \mathcal {W}_2^\perp \) map (anti)-reversible, respectively traveling, waves, into (anti)-reversible, respectively traveling, waves. \(\square \)
Remark 7.16
The time reparametrization \( \mathcal {P}\) and the multiplication for the function \( \rho \) (which is independent of the space variable), commute with the projections \( \Pi _{\mathbb {S}^+,\Sigma }^\angle \) and \( \Pi _{{\mathbb {S}}_0}^\perp \).
The operator \(\mathcal {L}_\omega \) in (6.23) (that is (7.1)) is semi-conjugated to
where \(\mathcal {R}^f\) is, by (7.180), (7.176), (7.178) (recall that \( {\widetilde{\mathcal {M}}}\) is defined in (7.78)–(7.79)), and (2.59),
Lemma 7.17
The operator \(\mathcal {R}^f\) in (7.184) has the finite rank form (7.4), (7.5). Moreover, let \(\mathtt{q}_0\in \mathbb {N}_0\) and \(M \geqq 2(k_0+\mathtt{q}_0) - \frac{3}{2}\). There exists \(\aleph (M,\mathtt{q}_0)>0\) (depending also on \(k_0\), \(\tau \), \(\nu \)) such that, for any \(n_1, n_2\in \mathbb {N}_0\), with \(n_1+n_2 \leqq M - 2(k_0+\mathtt{q}_0)+\frac{5}{2}\), and any \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\), the operator \(\langle D\rangle ^{n_1} \partial _{\varphi }^\mathtt{q}\mathcal {R}^f \langle D\rangle ^{n_2} \) is \(\mathcal {D}^{k_0}\)-tame, with a tame constant satisfying
for any \(s_1\) as in (7.15).
Proof
The first two terms in (7.184) have the finite rank form (7.4) because of the presence of the finite dimensional projector \( \Pi _{\mathbb {S}_0} \), respectively \( \Pi _{\mathbb {S}_0^+,\Sigma }^\intercal \). In the last term, the operator R has the finite rank form (7.4). The estimate (7.185) follows by (7.184), (7.177), (7.180), (7.168), (7.4), (3.7) and (7.179), (7.181), (7.169), (7.170), (7.5). The estimate (7.186) follows similarly. \(\square \)
Proposition 7.18
(Reduction of \( \mathcal{L}_\omega \) up to smoothing operators) For all \((\omega ,\kappa )\in \mathtt{D}\mathtt{C}(\upsilon ,\tau )\times [\kappa _1,\kappa _2]\), the operator \(\mathcal {L}_\omega \) in (6.23) (that is (7.1)) is semi-conjugated via (7.180) to the real, reversible and momentum preserving operator \(\mathcal {L}_{\perp } \) in (7.183). For all \( (\omega , \kappa ) \in \mathbb {R}^\nu \times [\kappa _1, \kappa _2] \), the extended operator defined by the right hand side in (7.183) has the form

where  denotes the identity map of \( \mathbf{H}_{{\mathbb {S}}_0}^{\bot } \) (cfr. (2.58)) and
denotes the identity map of \( \mathbf{H}_{{\mathbb {S}}_0}^{\bot } \) (cfr. (2.58)) and
-
1.
\(\mathbf{D}_{\perp }\) is the diagonal operator
$$\begin{aligned} \mathbf{D}_{\perp } := \begin{pmatrix} \mathcal {D}_{\perp } &{} 0 \\ 0 &{} -\overline{\mathcal {D}_{\perp }} \end{pmatrix} \,, \quad \mathcal {D}_{\perp }:= {{\,\mathrm{diag}\,}}_{j\in \mathbb {S}_0^c} \mu _j \,, \quad \mathbb {S}_0^c:= \mathbb {Z}{\setminus } (\mathbb {S}\cup \{0\}), \end{aligned}$$with eigenvalues \( \mu _j :=\mathtt{m}_{\frac{3}{2}}\Omega _j(\kappa ) + \mathtt{m}_1 j + \mathtt{m}_{\frac{1}{2}}\left| j \right| ^\frac{1}{2} \in \mathbb {R}\,, \) where the real constants \(\mathtt{m}_{\frac{3}{2}}, \mathtt{m}_1, \mathtt{m}_{\frac{1}{2}} \), defined respectively in (7.88), (7.144), (7.140), satisfy
$$\begin{aligned} \begin{aligned}&| \mathtt{m}_{\frac{3}{2}} - 1 |^{k_0,\upsilon } + | \mathtt{m}_1|^{k_0,\upsilon } + |\mathtt{m}_{\frac{1}{2}} |^{k_0,\upsilon } \lesssim \varepsilon \,; \end{aligned} \end{aligned}$$(7.188)in addition, for some \( \sigma > 0 \),
$$\begin{aligned} | \Delta _{12} \mathtt{m}_{\frac{3}{2}} | + | \Delta _{12} \mathtt{m}_1| + |\Delta _{12} \mathtt{m}_{\frac{1}{2}} | \lesssim \varepsilon \left\| i_1-i_2 \right\| _{s_0+\sigma }. \end{aligned}$$(7.189) -
2.
The operator \(\mathbf{R}_{\perp } \) is real, reversible and momentum preserving. Moreover, for any \(\mathtt{q}_0\in \mathbb {N}_0\), \(M > 2(k_0+\mathtt{q}_0) - \frac{3}{2}\), there is a constant \(\aleph (M,\mathtt{q}_0)>0\) (depending also on \(k_0\), \(\tau \), \(\nu \)) such that, assuming (7.14) with \(\mu _0 \geqq \aleph (M,\mathtt{q}_0)\), for any \(s_0\leqq s \leqq S\), \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\), the operators \( \partial _{\varphi }^\mathtt{q}\mathbf{R}_{\perp } \), \( [\partial _{\varphi }^\mathtt{q}\mathbf{R}_{\perp }, \partial _x] \) are \(\mathcal {D}^{k_0}\)-tame with tame constants satisfying
$$\begin{aligned} {\mathfrak {M}}_{\partial _{\varphi }^\mathtt{q}\mathbf{R}_{\perp } } (s), \ {\mathfrak {M}}_{[\partial _{\varphi }^\mathtt{q}\mathbf{R}_{\perp }, \partial _x]} (s) \lesssim _{ S, M, \mathtt{q}_0} \varepsilon \upsilon ^{-1} (1+ \Vert {\mathfrak {I}}_0 \Vert _{s+\aleph (M,\mathtt{q}_0)}^{k_0,\upsilon })\,. \end{aligned}$$(7.190)Moreover, for any \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq \mathtt{q}_0\),
$$\begin{aligned} \Vert \partial _{\varphi }^\mathtt{q}\Delta _{12}\mathbf{R}_{\perp } \Vert _{\mathcal {L}(H^{s_0})} + \Vert \partial _{\varphi }^\mathtt{q}\Delta _{12}[\mathbf{R}_{\perp }, \partial _x] \Vert _{\mathcal {L}(H^{s_0})} \lesssim _{M} \varepsilon \upsilon ^{-1} \left\| i_1-i_2 \right\| _{s_0+\aleph (M,\mathtt{q}_0)}. \end{aligned}$$(7.191)
Proof
By (7.183) and (7.168) we deduce (7.187) with
The estimates (7.188)–(7.189) follow by Lemmata 7.9, 7.12, 7.13. The estimate (7.190) follows by Lemmata 3.6, 3.13, (7.169) and (7.170), (7.185), choosing \((n_1,n_2)=(1,0),(0,1)\). The estimate (7.191) follows similarly. The operator \( \mathcal {L}_\omega \) in (6.23) is reversible and momentum preserving (Lemma 7.1). By Sections 7.2-7.6, the maps \( \mathcal {Z}, \mathcal {E}, \mathcal {Q}, {\widetilde{\mathcal {M}}}, {\varvec{\Phi }}_{M}, {\varvec{\Phi }}, \mathcal {V}, {\varvec{\Psi }} \) are reversibility and momentum preserving. Therefore, using also (7.18), (7.24) and Lemmata 3.23 and 3.31, we deduce that the operator \( \mathcal {L}_\bot \) in (7.183) is reversible and momentum preserving. Since \( {\mathrm{i}}\,\mathbf{D}_{\perp } \) is reversible and momentum preserving, we deduce that \(\mathbf{R}_{\perp } \) is reversible and momentum preserving. \(\square \)
8 Almost-Diagonalization and Invertibility of \(\mathcal {L}_\omega \)
In Proposition 7.18 we obtained the operator \( \mathcal {L}_{\perp } \) in (7.187) which is diagonal and constant coefficient up to the bounded operator \(\mathbf{R}_{\perp } (\varphi ) \). In this section we complete the diagonalization of \( \mathcal {L}_{\perp } \) implementing a KAM iterative scheme. As starting point, we consider the real, reversible and momentum preserving operator, acting in \( \mathbf{H}_{{\mathbb {S}}_0}^{\bot } \),

defined for all \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\), with diagonal part (with respect to the exponential basis)
where \( \mathbb {S}_0^c = \mathbb {Z}{\setminus } \mathbb {S}_0 \), \( \mathbb {S}_0 = \mathbb {S}\cup \{0\} \), the real constants \(\mathtt{m}_{\frac{3}{2}} \), \( \mathtt{m}_1 \), \( \mathtt{m}_{\frac{1}{2}} \) satisfy (7.188)–(7.189) and
which is a real, reversible, momentum preserving operator satisfying (7.190), (7.191). We denote \( H_{\pm \mathbb {S}_0}^{\bot } = \{ h(x) = \sum _{j \not \in \pm \mathbb {S}_0} h_j e^{ \pm {\mathrm{i}}j x} \in L^2 \} \). Note that
Proposition 7.18 implies that the operator \( \mathbf{R}_{\perp }^{(0)} \) satisfies the tame estimates of Lemma 8.1 below by fixing the constant M large enough (which means performing sufficiently many regularizing steps in Section 7.4), namely
where
These conditions imply the convergence of the iterative scheme (8.46)–(8.47), see Lemma 8.8. We also set
where the constant \(\aleph (M,\mathtt{q}_0)\) is given in Proposition 7.18.
Lemma 8.1
(Smallness of \( \mathbf{R}_{\perp }^{(0)})\) Assume (7.14) with \(\mu _0 \geqq \mu (\mathtt{b})\). Then the operators \( \mathbf{R}_{\perp }^{(0)} \), \( [\mathbf{R}_{\perp }^{(0)} , \partial _x] \), and \( \partial _{{\varphi }_m}^{s_0} \mathbf{R}_{\perp }^{(0)} \), \( [\partial _{{\varphi }_m}^{s_0} \mathbf{R}_{\perp }^{(0)}, \partial _x] \), \( \partial _{{\varphi }_m}^{s_0+\mathtt{b}} \mathbf{R}^{(0)}_{\perp } \), \( [\partial _{{\varphi }_m}^{s_0+\mathtt{b}} \mathbf{R}^{(0)}_{\perp }, \partial _x] \), \( m = 1, \ldots , \nu \), are \(\mathcal {D}^{k_0}\)-tame and, defining
we have, for all \( s_0 \leqq s \leqq S\),
Moreover, for all \(\mathtt{q}\in \mathbb {N}_0^\nu \), with \(\left| \mathtt{q} \right| \leqq s_0+\mathtt{b}\),
Proof
Recalling (8.8), (8.9), the bounds (8.10)–(8.11) follow by (7.190), (8.5), (8.7), (7.191). \(\square \)
We perform the almost-reducibility of \(\mathbf{L}_0\) along the scale
Theorem 8.2
(Almost-diagonalization of \(\mathbf{L}_0\): KAM iteration) There exists \(\tau _2(\tau ,\nu )> \tau _1(\tau ,\nu ) + \mathtt{a}\) (with \( \tau _1 , \mathtt{a}\) defined in (8.6)) such that, for all \(S >s_0\), there is \(N_0:=N_0(S,\mathtt{b})\in \mathbb {N}\) such that, if
then, for all \(\overline{\mathtt{n}}\in \mathbb {N}_0\), \(\mathtt{n}=0,1,\ldots ,\overline{\mathtt{n}}\):
\((\mathbf{S1})_\mathtt{n}\) There exists a real, reversible and momentum preserving operator

defined for all \((\omega ,\kappa )\) in \(\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\), where \(\mu _{j}^{(\mathtt{n})}\) are \(k_0\)-times differentiable real functions
satisfying \( {\mathfrak {r}}_j^{(0)} = 0 \) and, for \( \mathtt{n}\geqq 1 \),
The remainder
is \(\mathcal {D}^{k_0}\)-modulo-tame: more precisely, the operators \(R_{\perp }^{(\mathtt{n},d)} \), \(R_{\perp }^{(\mathtt{n},o)} \), \(\langle \partial _{\varphi }\rangle ^\mathtt{b}R_{\perp }^{(\mathtt{n},d)} \), \(\langle \partial _{\varphi }\rangle ^\mathtt{b}R_{\perp }^{(\mathtt{n},o)} \), are \(\mathcal {D}^{k_0}\)-modulo-tame with modulo-tame constants
which satisfy, for some constant \(C_*(s_0,\mathtt{b}) > 0 \), for all \(s_0\leqq s \leqq S\),
Define the sets  by
by  and, for \( \mathtt{n}\geqq 1 \),
and, for \( \mathtt{n}\geqq 1 \),

For \(\mathtt{n}\geqq 1\) there exists a real, reversibility and momentum preserving map, defined for all \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\), of the form
such that, for all  , the following conjugation formula holds:
, the following conjugation formula holds:
The operators \(\mathbf{X}_{\mathtt{n}-1}\), \(\langle \partial _{\varphi }\rangle ^\mathtt{b}\mathbf{X}_{\mathtt{n}-1}\), are \(\mathcal {D}^{k_0}\)-modulo-tame with modulo tame constants satisfying, for all \(s_0\leqq s \leqq S\),
\((\mathbf{S2})_\mathtt{n}\) Let \(i_1(\omega ,\kappa )\), \(i_2(\omega ,\kappa )\) such that \(\mathbf{R}_{\perp }^{(\mathtt{n})}(i_1)\), \(\mathbf{R}_{\perp }^{(\mathtt{n})}(i_2)\) satisfy (8.10), (8.11). Then, for all  with \(\upsilon _1,\upsilon _2 \in [\upsilon /2,2\upsilon ]\),
with \(\upsilon _1,\upsilon _2 \in [\upsilon /2,2\upsilon ]\),
Furthermore, for \( \mathtt{n}\geqq 1 \), for all \(j\in \mathbb {S}_0^c\),
\((\mathbf{S3})_\mathtt{n}\) Let \(i_1, i_2\) be like in \((\mathbf{S2})_\mathtt{n}\) and \(0< \rho < \upsilon /2\). Then

Theorem 8.2 implies also that the invertible operator
has almost diagonalized \(\mathbf{L}_0\). We have indeed the following corollary.
Theorem 8.3
(Almost-diagonalization of \(\mathbf{L}_0)\) Assume (7.14) with \(\mu _0 \geqq \mu (\mathtt{b})\). For all \(S>s_0\), there exist \(N_0=N_0(S,\mathtt{b})>0\) and \(\delta _0=\delta _0(S)>0\) such that, if the smallness condition
holds, where \(\tau _2=\tau _2(\tau ,\nu )\) is defined in Theorem 8.2, then, for all \(\overline{\mathtt{n}}\in \mathbb {N}\) and for all \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\) the operator \(\mathbf{U}_{\overline{\mathtt{n}}}\) in (8.28) is well-defined, the operators  are \(\mathcal {D}^{k_0}\)-modulo-tame with modulo-tame constants satisfying, for all \(s_0\leqq s \leqq S\),
are \(\mathcal {D}^{k_0}\)-modulo-tame with modulo-tame constants satisfying, for all \(s_0\leqq s \leqq S\),

where \(\tau _1\) is given by (8.6). Moreover \(\mathbf{U}_{\overline{\mathtt{n}}}\), \(\mathbf{U}_{\overline{\mathtt{n}}}^{-1}\) are real, reversibility and momentum preserving. The operator  , defined in (8.14) with \(\mathtt{n}=\overline{\mathtt{n}}\) is real, reversible and momentum preserving. The operator \( \mathbf{R}_{\perp }^{(\overline{\mathtt{n}})} \) is \(\mathcal {D}^{k_0}\)-modulo-tame with a modulo-tame constant satisfying, for all \( s_0 \leqq s \leqq S \),
, defined in (8.14) with \(\mathtt{n}=\overline{\mathtt{n}}\) is real, reversible and momentum preserving. The operator \( \mathbf{R}_{\perp }^{(\overline{\mathtt{n}})} \) is \(\mathcal {D}^{k_0}\)-modulo-tame with a modulo-tame constant satisfying, for all \( s_0 \leqq s \leqq S \),
Moreover, for all \((\omega ,\kappa )\) in  , where the sets
, where the sets  are defined in (8.20), the conjugation formula \( \mathbf{L}_{\overline{\mathtt{n}}} := \mathbf{U}_{\overline{\mathtt{n}}}^{-1} \mathbf{L}_0 \mathbf{U}_{\overline{\mathtt{n}}} \) holds.
are defined in (8.20), the conjugation formula \( \mathbf{L}_{\overline{\mathtt{n}}} := \mathbf{U}_{\overline{\mathtt{n}}}^{-1} \mathbf{L}_0 \mathbf{U}_{\overline{\mathtt{n}}} \) holds.
8.1 Proof of Theorem 8.2
The proof of Theorem 8.2 is inductive. We first show that \((\mathbf{S1})_\mathtt{n}\)-\((\mathbf{S3})_\mathtt{n}\) hold when \(\mathtt{n}=0\).
The step \(\mathtt{n}=0\). Proof of \((\mathbf{S1})_0\). Properties (8.14)–(8.15), (8.17) for \(\mathtt{n}=0\) hold by (8.1), (8.2), (8.3) with \({\mathfrak {r}}_j^{(0)} =0\). We now prove that also (8.19) for \(\mathtt{n}=0\) holds.
Lemma 8.4
We have \({\mathfrak {M}}_0^\sharp (s), {\mathfrak {M}}_0^\sharp (s,\mathtt{b}) \lesssim _{s_0,\mathtt{b}} {\mathfrak {M}}_0(s,\mathtt{b})\).
Proof
Let \(R \in \{ R_{\perp }^{(0,d)}, R_{\perp }^{(0,o)} \} \). We prove that \(\langle \partial _{\varphi }\rangle ^\mathtt{b}R\) is \(\mathcal {D}^{k_0}\)-modulo-tame. Using the inequality
it follows, recalling (3.35), (8.10), (the matrix elements of the commutator \([\partial _x,A]\) are \({\mathrm{i}}(j-j')A_j^{j'}(\ell -\ell ')\)), that, for any \(j'\in \mathbb {S}_0^c\), \(\ell '\in \mathbb {Z}^\nu \),
Let \(s_0\leqq s \leqq S\). Then, for any \(\left| k \right| \leqq k_0\), by Cauchy-Schwartz inequality, we have
Therefore, we obtain \({\mathfrak {M}}_{\langle \partial _{\varphi }\rangle ^\mathtt{b}R}^\sharp (s) \lesssim _{s_0,\mathtt{b}} {\mathfrak {M}}_0(s,\mathtt{b})\) and then \( {\mathfrak {M}}_0^\sharp (s,\mathtt{b}) \lesssim _{s_0,\mathtt{b}} {\mathfrak {M}}_0(s,\mathtt{b}) \). The inequality \({\mathfrak {M}}_0^\sharp (s) \lesssim _{s_0} {\mathfrak {M}}_0(s,\mathtt{b}) \) follows similarly. \(\square \)
Proof of \((\mathbf{S2})_0\). The proof of estimates (8.23), (8.24) at \( \mathtt{n}= 0 \) follows by (8.11), arguing similarly to Lemma 8.4.
Proof of \((\mathbf{S3})_0\). It is trivial since, by definition,  .
.
The reducibility step. We now describe the generic inductive step, showing how to transform \(\mathbf{L}_\mathtt{n}\) into \(\mathbf{L}_{\mathtt{n}+1}\) by the conjugation with \({\varvec{\Phi }}_{\mathtt{n}}\). For sake of simplicity in the notation, we drop the index \(\mathtt{n}\) and we write \(+\) instead of \(\mathtt{n}+1\), so that we write \(\mathbf{L}:=\mathbf{L}_\mathtt{n}\), \(\mathbf{L}_+:=\mathbf{L}_{\mathtt{n}+1}\), \(\mathbf{R}_{\perp }:= \mathbf{R}_{\perp }^{(\mathtt{n})}\), \(\mathbf{R}_{\perp }^{(+)}:= \mathbf{R}_{\perp }^{(\mathtt{n}+1)}\), \(N:= N_\mathtt{n}\), etc. We conjugate \(\mathbf{L}\) in (8.14) by a transformation of the form
where \(\mathbf{X}\) is a bounded linear operator, chosen below in (8.37), (8.38). By the Lie expansions (3.16)–(3.17) we have

where \(\Pi _N\) is defined in (3.39) and \(\Pi _N^\perp := {\mathrm{Id}}- \Pi _N\). We want to solve the homological equation
where
By (8.14), (8.17) and (8.32), the homological equation (8.34) is equivalent to the two scalar homological equations
Recalling (8.14) and since \( \overline{\mathcal {D}} = {\mathrm{diag}}_{j \in - \mathbb {S}_0^c}( \mu _{-j}) \), acting in \( H_{- \mathbb {S}_0}^{\bot } \) (see (8.4)) the solutions of (8.36) are, for all  (see (8.20) with \( \mathtt{n}\rightsquigarrow \mathtt{n}+ 1 \))
(see (8.20) with \( \mathtt{n}\rightsquigarrow \mathtt{n}+ 1 \))
Note that, since \( - j' \in \mathbb {S}_0^c \), we can apply the bounds (8.20) for  .
.
Lemma 8.5
(Homological equations) The real operator \(\mathbf{X}\) defined in (8.32), (8.37), (8.38), (which for all  solves the homological equation (8.20))) admits an extension to the whole parameter space \( \mathbb {R}^\nu \times [\kappa _1, \kappa _2] \). Such extended operator is \(\mathcal {D}^{k_0}\)-modulo-tame with a modulo-tame constant satisfying, for all \(s_0\leqq s \leqq S\),
solves the homological equation (8.20))) admits an extension to the whole parameter space \( \mathbb {R}^\nu \times [\kappa _1, \kappa _2] \). Such extended operator is \(\mathcal {D}^{k_0}\)-modulo-tame with a modulo-tame constant satisfying, for all \(s_0\leqq s \leqq S\),
where \(\tau _1:=\tau (k_0+1)+k_0\). If \(\upsilon /2 \leqq \upsilon _1,\upsilon _2 \leqq 2\upsilon \), then, for all  ,
,
The operator \(\mathbf{X}\) is reversibility and momentum preserving.
Proof
We prove that (8.39) holds for \(X^{(d)}\). The proof for \(X^{(o)}\) holds analogously. First, we extend the solution in (8.37) to all \(\lambda \) in \(\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\) by setting (without any further relabeling) \( (X^{(d)})_j^{j'}(\ell ) = {\mathrm{i}}\,g_{\ell ,j,j'}(\lambda ) (R_{\perp }^{(d)})_j^{j'}(\ell ) \), where
and \(\chi \) is the cut-off function (3.10). By (8.15), (8.16), (7.188), (8.20), Lemma 4.4, (5.39), together with (3.10), we deduce that, for any \( k_1 \in \mathbb {N}_0^\nu \), \(\left| k_1 \right| \leqq k_0\),
and we deduce, for all \(0\leqq \left| k \right| \leqq k_0\),
By (8.37) we have that \( (X^{(d)})_j^{j'}(\ell )= 0 \) for all \( \langle \ell \rangle > N \). Therefore, for all \( |k| \leqq k_0 \), we have
and, by Definition 3.14, we conclude that \( {\mathfrak {M}}_{\langle \partial _{\varphi }\rangle ^\mathtt{b}X^{(d)}}^\sharp (s) \lesssim _{k_0} N^{\tau _1} \upsilon ^{-1} {\mathfrak {M}}^\sharp (s,\mathtt{b}) \). The analogous estimates for \(\langle \partial _{\varphi }\rangle ^\mathtt{b}X^{(o)}\), \(X^{(d)}\), \(X^{(o)}\) and (8.40), (8.41) follow similarly. By induction, the operator \(\mathbf{R}_{\perp }\) is reversible and momentum preserving. Therefore, by (8.32), (8.37), (8.38) and Lemmata 3.18, 3.28, it follows that \(\mathbf{X}\) is reversibility and momentum preserving. \(\square \)
By (8.33), (8.34), for all  , we have
, we have

where
The right hand side of (8.43)–(8.44) define an extension of \(\mathbf{L}_+\) to the whole parameter space \( \mathbb {R}^\nu \times [\kappa _1, \kappa _2] \), since \( \mathbf{R}_{\perp } \) and \( \mathbf{X}\) are defined on \( \mathbb {R}^\nu \times [\kappa _1, \kappa _2] \).
The new operator \(\mathbf{L}_+\) in (8.43) has the same form of \(\mathbf{L}\) in (8.14) with the non-diagonal remainder \(\mathbf{R}_{\perp }^{(+)}\) which is the sum of a term \( \Pi _N^\perp \mathbf{R}_{\perp } \) supported on high frequencies and a quadratic function of \(\mathbf{X}\) and \(\mathbf{R}_{\perp } \). The new normal form \(\mathbf{D}_+\) is diagonal:
Lemma 8.6
(New diagonal part) For all \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\), the new normal form is
where each \( \mathtt{r}_j \) satisfies, on \(\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\),
Moreover, given tori \(i_1(\omega ,\kappa ), i_2(\omega ,\kappa )\), we have \( | \mathtt{r}_j (i_1)- \mathtt{r}_j(i_2) | \lesssim \Vert | \Delta _{12} \mathbf{R}_{\perp } | \Vert _{\mathcal {L}(H^{s_0})} \).
Proof
Recalling (8.35), we have that \( \mathtt{r}_j:= - {\mathrm{i}}(R_{\perp }^{(d)})_j^j(0)\), for all \( j \in \mathbb {S}_0^c \). By the reversibility of \(R_{\perp }^{(d)} \) and (3.44) we deduce that \(\mathtt{r}_j\in \mathbb {R}\). Recalling the definition of \({\mathfrak {M}}^\sharp (s_0)\) in (8.18) (with \(s=s_0\)) and Definition 3.14, we have, for all \(0\leqq \left| k \right| \leqq k_0\), \(\Vert | \partial _\lambda ^k R_{\perp }^{(d)} | h \Vert _{s_0} \leqq 2 \upsilon ^{-\left| k \right| } {\mathfrak {M}}^\sharp (s_0) \left\| h \right\| _{s_0} \), and therefore \( | \partial _\lambda ^k (R_{\perp }^{(d)})_j^j(0) | \lesssim \upsilon ^{-\left| k \right| } {\mathfrak {M}}^\sharp (s_0) \,. \) Hence (8.45) follows. The last bound for \( | \mathtt{r}_j (i_1)- \mathtt{r}_j(i_2) |\) follows analogously. \(\square \)
The iterative step. Let \(\mathtt{n}\in \mathbb {N}_0\) and assume that the statements \((\mathbf{S1})_{\mathtt{n}}\)-\((\mathbf{S3})_{\mathtt{n}}\) are true. We now prove \((\mathbf{S1})_{\mathtt{n}+1}\)-\((\mathbf{S3})_{\mathtt{n}+1}\). For sake of simplicity in the notation (as in other parts of the paper) we omit to write the dependence on \( k_0 \), which is considered as a fixed constant.
Proof of \((\mathbf{S1})_{\mathtt{n}+1}\). The real operator \(\mathbf{X}_{\mathtt{n}}\) defined in Lemma 8.5 is defined for all \((\omega ,\kappa )\in \mathbb {R}^\nu \times [\kappa _1,\kappa _2]\) and, by (8.39), (8.19), satisfies the estimates (8.22) at the step \(\mathtt{n}+1\). The flow maps \({\varvec{\Phi }}_{\mathtt{n}}^{\pm 1} = e^{\pm \mathbf{X}_{\mathtt{n}}} \) are well defined by Lemma 3.16. By (8.43), for all  , the conjugation formula (8.21) holds at the step \(\mathtt{n}+1\). The operator \(\mathbf{X}_{\mathtt{n}}\) is reversibility and momentum preserving, and so are the operators \({\varvec{\Phi }}_{\mathtt{n}}^{\pm 1} = e^{\pm \mathbf{X}_{\mathtt{n}}} \). By Lemma 8.6, the operator \(\mathbf{D}_{\mathtt{n}+1}\) is diagonal with eigenvalues \( \mu _{j}^{(\mathtt{n}+1)}:\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\rightarrow \mathbb {R}\), \( \mu _{j}^{(\mathtt{n}+1)} = \mu _{j}^{(0)} + {\mathfrak {r}}_j^{(\mathtt{n}+1)} \) with \( {\mathfrak {r}}_j^{(\mathtt{n}+1)} := {\mathfrak {r}}_j^{(\mathtt{n})} + \mathtt{r}_j^{(\mathtt{n})}\) satisfying, using also (8.19), (8.16) at the step \(\mathtt{n}+1\). The next lemma provides the estimates of the remainder \( \mathbf{R}_{\perp }^{(\mathtt{n}+1)} = \mathbf{R}_{\perp }^{(+)} \) defined in (8.44).
, the conjugation formula (8.21) holds at the step \(\mathtt{n}+1\). The operator \(\mathbf{X}_{\mathtt{n}}\) is reversibility and momentum preserving, and so are the operators \({\varvec{\Phi }}_{\mathtt{n}}^{\pm 1} = e^{\pm \mathbf{X}_{\mathtt{n}}} \). By Lemma 8.6, the operator \(\mathbf{D}_{\mathtt{n}+1}\) is diagonal with eigenvalues \( \mu _{j}^{(\mathtt{n}+1)}:\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\rightarrow \mathbb {R}\), \( \mu _{j}^{(\mathtt{n}+1)} = \mu _{j}^{(0)} + {\mathfrak {r}}_j^{(\mathtt{n}+1)} \) with \( {\mathfrak {r}}_j^{(\mathtt{n}+1)} := {\mathfrak {r}}_j^{(\mathtt{n})} + \mathtt{r}_j^{(\mathtt{n})}\) satisfying, using also (8.19), (8.16) at the step \(\mathtt{n}+1\). The next lemma provides the estimates of the remainder \( \mathbf{R}_{\perp }^{(\mathtt{n}+1)} = \mathbf{R}_{\perp }^{(+)} \) defined in (8.44).
Lemma 8.7
The operators \(\mathbf{R}_{\perp }^{(\mathtt{n}+1)}\) and \(\langle \partial _{\varphi }\rangle ^\mathtt{b}\mathbf{R}_{\perp }^{(\mathtt{n}+1)}\) are \(\mathcal {D}^{k_0}\)-modulo-tame with modulo-tame constants satisfying
Proof
The estimates (8.46), (8.47) follow by (8.44), Lemmata 3.15, 3.16, the bounds (3.40) and (8.39), (8.19), (8.6), (8.12), (8.13). \(\square \)
Lemma 8.8
Estimates (8.19) holds at the step \(\mathtt{n}+1\).
Proof
It follows by (8.46), (8.47), (8.19) at the step \(\mathtt{n}\), (8.6), the smallness condition (8.13) with \(N_0=N_0(s_0,\mathtt{b}) >0\) large enough and taking \( \tau _2 > \tau _1 + \mathtt{a}\).
\(\square \)
Finally \(\mathbf{R}_{\perp }^{(\mathtt{n}+1)}\) is real, reversible and momentum preserving as \(\mathbf{R}_{\perp }^{(\mathtt{n})}\), since \(\mathbf{X}_\mathtt{n}\) is real, reversibility and momentum preserving. This concludes the proof of \((\mathbf{S1})_{\mathtt{n}+1}\).
Proof of \((\mathbf{S2})_{\mathtt{n}+1}\). It follows by similar arguments and we omit it.
Proof of \((\mathbf{S3})_{\mathtt{n}+1}\). The proof follows as for \((\mathbf{S4})_{\nu +1}\) of Theorem 7.3 in [6], using \((\mathbf{S2})_{\mathtt{n}}\) and the fact that the momentum condition in (8.20) implies \( | j - j' | \lesssim N_{\mathtt{n}} \).
8.2 Almost invertibility of \(\mathcal {L}_\omega \)
By (7.183) and Theorem 8.3 (where \(\mathbf{L}_0= \mathcal {L}_{\perp }\)) we obtain
where the operator \(\mathbf{L}_{\overline{\mathtt{n}}}\) is defined in (8.14) with \(\mathtt{n}=\overline{\mathtt{n}} \). By (7.181) and (8.30), we have, for some \(\sigma :=\sigma (\tau ,\nu ,k_0) > 0 \), for any \( s_0 \leqq s \leqq S \),
In order to verify the almost invertibility assumption (AI) of \( \mathcal {L}_\omega \) in Section 6, we decompose the operator \(\mathbf{L}_{\overline{\mathtt{n}}}\) in (8.14) (with \(\overline{\mathtt{n}}\) instead of \(\mathtt{n}\)) as
where

and the smoothing operator \(\Pi _{K}\) on the traveling waves is defined in (3.6), and \( \Pi _K^\perp := {\mathrm{Id}}-\Pi _K \). The constants \( K_{\overline{\mathtt{n}}} \) in (8.51) are \( K_{\overline{\mathtt{n}}} := K_0^{\chi ^{\overline{\mathtt{n}}}} \), \( \chi = 3/2 \) (cfr. (6.24)), and \( K_0 \) will be fixed in (9.5).
Lemma 8.9
(First order Melnikov non-resonance conditions) For all \(\lambda =(\omega ,\kappa )\) in
on the subspace of the traveling waves \( \tau _\varsigma g({\varphi }) = g({\varphi }- \vec {\jmath }\varsigma ) \), \( \varsigma \in \mathbb {R}\), such that \( g({\varphi }, \cdot ) \in \mathbf{H}_{{\mathbb {S}}_0}^{\bot } \), the operator \(\mathbf{D}_{\overline{\mathtt{n}}}^{<}\) in (8.51) is invertible and there exists an extension of the inverse operator (that we denote in the same way) to the whole \(\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\) satisfying the estimate
Moreover \( (\mathbf{D}_{\overline{\mathtt{n}}}^{<})^{-1} g \) is a traveling wave.
Proof
The estimate (8.53) follows arguing as in Lemma 8.5. \(\square \)
Standard smoothing properties imply that the operator \(\mathbf{Q}_{\perp }^{(\overline{\mathtt{n}})}\) in (8.51) satisfies, for any traveling wave \( h \in \mathbf{H}_{{\mathbb {S}}_0}^{\bot } \), for all \( b>0\),
By the decompositions (8.48), (8.50), Theorem 8.3 (note that (6.1) and Lemma 6.2 imply (7.14)), Proposition 7.18, the fact that \( \mathbf{W}_{1,\overline{\mathtt{n}}} \), \( \mathbf{W}_{2,\overline{\mathtt{n}}} \) map (anti)-reversible, respectively traveling, waves, into (anti)-reversible, respectively traveling, waves (Lemma 7.15) and estimates (8.49), (8.53), (8.54), (3.8) we deduce the following theorem.
Theorem 8.10
(Almost invertibility of \( \mathcal {L}_\omega )\) Assume (6.1). Let \( \mathtt{a}, \mathtt{b}\) as in (8.6) and M as in (8.5). Let \(S>s_0\) and assume the smallness condition (8.29). Then the almost invertibility assumption (AI) in Section 6 holds with  replaced by
replaced by

(see (8.20), (8.52)) and, with \(\mu (\mathtt{b})\) defined in (8.7),
9 Proof of Theorem 5.2
Theorem 5.2 is a consequence of Theorem 9.2 below. We consider the finite dimensional subspaces of traveling wave variations
where \(\Pi _\mathtt{n}w := \Pi _{K_\mathtt{n}} w \) are defined as in (3.6) with \( K_n \) in (6.24), and we denote with the same symbol \(\Pi _\mathtt{n}g({\varphi }) := \sum _{\left| \ell \right| \leqq K_\mathtt{n}} g_\ell e^{{\mathrm{i}}\ell \cdot {\varphi }}\). Note that the projector \(\Pi _{\mathtt{n}}\) maps (anti)-reversible traveling variations into (anti)-reversible traveling variations.
In view of the Nash–Moser Theorem 9.2 we introduce the constants
where \(\overline{\sigma }=\overline{\sigma }(\tau ,\nu ,k_0)>0\) is defined by Theorem 6.6, \( 2 s_0+2k_0+5\) is the largest loss of regularity in the estimates of the Hamiltonian vector field \(X_P\) in Lemma 6.1, \(\mu (\mathtt{b})\) is defined in (8.7), and \(\mathtt{b}=[\mathtt{a}]+2 \) is defined in (8.6). The exponent p in (6.24) is required to satisfy
By (8.6), and the definition of \(\mathtt{a}_1\) in (9.1), there exists \(p=p(\tau ,\nu ,k_0)\) such that (9.4) holds, for example we fix
Remark 9.1
The constant \(\mathtt{a}_1\) is the exponent in (9.9). The constant \(\mathtt{a}_2\) is the exponent in the second bound in (9.7). The constant \(\mu _1\) is the exponent in \((\mathcal {P}3)_\mathtt{n}\). The conditions on the constants \( \mu _1, \mathtt{b}_1, \mathtt{a}_1 \) to allow the convergence of the Nash–Moser scheme in Theorem 9.2 are
as well as \(\mu _1 > 3(\mu (\mathtt{b})+2\sigma _1) \). In addition, we require \( \mathtt{a}_1 \geqq \chi (p(\tau +1) + \mu (\mathtt{b})+2\sigma _1) + 1 \) so that \(\mathtt{a}_2\geqq p(\tau +1) +\chi ^{-1} \), which is used in the proof of Lemma 9.3.
Given a function \( W = ({\mathfrak {I}},\beta ) \) where \( {\mathfrak {I}}\) is the periodic component of a torus as in (5.8) and \( \beta \in \mathbb {R}^\nu \), we denote \( \Vert W \Vert _{s}^{k_0,\upsilon } := \Vert {\mathfrak {I}} \Vert _{s}^{k_0,\upsilon }+\left| \beta \right| ^{k_0,\upsilon } \).
Theorem 9.2
(Nash–Moser) There exist \(\delta _0, C_*>0\) such that, if
where \(\tau _2=\tau _2(\tau ,\nu )\) is given by Theorem 8.2, then, for all \(\mathtt{n}\geqq 0\):
-
\((\mathcal {P}1)_\mathtt{n}\) There exists a \(k_0\)-times differentiable function \({\widetilde{W}}_\mathtt{n}:\mathbb {R}^\nu \times [\kappa _1,\kappa _2]\rightarrow E_{\mathtt{n}-1}\times \mathbb {R}^\nu \), \(\lambda =(\omega ,\kappa )\mapsto {\widetilde{W}}_\mathtt{n}(\lambda ):= ({\widetilde{{\mathfrak {I}}}}_\mathtt{n}, {\widetilde{\alpha }}_\mathtt{n}-\omega )\), for \(\mathtt{n}\geqq 1 \), and \({\widetilde{W}}_0:=0\), satisfying
$$\begin{aligned} \Vert {\widetilde{W}}_\mathtt{n} \Vert _{s_0+\mu (\mathtt{b})+\sigma _1}^{k_0,\upsilon } \leqq C_*\varepsilon \upsilon ^{-1}. \end{aligned}$$(9.6)Let \({\widetilde{U}}_\mathtt{n}:= U_0+{\widetilde{W}}_\mathtt{n}\), where \(U_0:= ({\varphi },0,0,\omega )\). The difference \({\widetilde{H}}_\mathtt{n}:= {\widetilde{U}}_\mathtt{n}-{\widetilde{U}}_{\mathtt{n}-1}\), for \(\mathtt{n}\geqq 1 \), satisfies
$$\begin{aligned} \begin{aligned}&\Vert {\widetilde{H}}_1 \Vert _{s_0+\mu (\mathtt{b})+\sigma _1}^{k_0,\upsilon }\leqq C_* \varepsilon \upsilon ^{-1}\,, \ \Vert {\widetilde{H}}_\mathtt{n} \Vert _{s_0+\mu (\mathtt{b})+\sigma _1}^{k_0,\upsilon } \leqq C_* \varepsilon \upsilon ^{-1} K_{\mathtt{n}-1}^{-\mathtt{a}_2}\,, \ \forall \, \mathtt{n}\geqq 2 \,. \end{aligned} \end{aligned}$$(9.7)The torus embedding \( \widetilde{\imath }_\mathtt{n}:= ({\varphi },0,0) + {\widetilde{{\mathfrak {I}}}}_\mathtt{n}\) is reversible and traveling, that is (5.7) holds.
-
\((\mathcal {P}2)_\mathtt{n}\) We define
 (9.8)
(9.8)where \({\varvec{\Lambda }}_{\mathtt{n}+1}^\upsilon (\widetilde{\imath }_\mathtt{n})\) is defined in (8.55). Then, for all \(\lambda \in \mathcal {G}_{\mathtt{n}}\) , setting \(K_{-1}:=1\), we have
$$\begin{aligned} \Vert \mathcal {F}({\widetilde{U}}_\mathtt{n}) \Vert _{s_0}^{k_0,\upsilon } \leqq C_* \varepsilon K_{\mathtt{n}-1}^{-\mathtt{a}_1} \,. \end{aligned}$$(9.9) -
\((\mathcal {P}3)_\mathtt{n}\) (High norms) For all \(\lambda \in \mathcal {G}_{\mathtt{n}}\), we have \( \Vert {\widetilde{W}}_\mathtt{n} \Vert _{s_0+\mathtt{b}_1}^{k_0,\upsilon } \leqq C_* \varepsilon \upsilon ^{-1} K_{\mathtt{n}-1}^{\mu _1} \).
Proof
The inductive proof follows exactly as in [2, 6]. Note that the almost invertibility property proved in Theorem 8.10, as well as in Theorem 6.6, is formulated exactly as in [2, 6]. The only novelty is to check that each approximate torus \( \widetilde{\imath }_\mathtt{n}\) is reversible and traveling. Clearly \(i_0:=({\varphi },0,0) \) satisfies (5.7). Supposing inductively that \( \widetilde{\imath }_{\mathtt{n}} \) is reversible and traveling, we now prove that the successive approximation \(\widetilde{\imath }_{\mathtt{n}+1}\) defined by the modified Nash–Moser scheme in [2, 6] is a reversible and traveling wave as well. By (9.5), the smallness condition (8.29) holds for \(\varepsilon \) small enough. Moreover (6.1) holds by (9.6). Therefore Theorem 8.10 holds and the almost invertibility assumption (AI) of Section 6 holds for all \(\lambda \in {\varvec{\Lambda }}_{\mathtt{n}+1}^{\upsilon }\), see (8.55). Then Theorem 6.6 implies the existence of an almost approximate inverse \(\mathbf{T}_\mathtt{n}:= \mathbf{T}_\mathtt{n}(\lambda ,\widetilde{\imath }_\mathtt{n})\) of the linearized operator \( {\mathrm{d}}_{i,\alpha } \mathcal {F}( \widetilde{\imath }_{\mathtt{n}} ) \), which satisfies, for any anti-reversible traveling wave variation g, the tame estimate (6.40). Moreover. the first three components of \(\mathbf{T}_\mathtt{n}g \) form a reversible traveling wave variation. For all \(\lambda \in \mathcal {G}_{\mathtt{n}+1} = \mathcal {G}_{\mathtt{n}} \cap \Lambda _{\mathtt{n}+1}^\upsilon (\widetilde{\imath }_\mathtt{n}) \) (cfr. (9.8)) we define the successive approximation
where \({\varvec{\Pi }}_\mathtt{n}\) is defined for any \(({\mathfrak {I}},\alpha )\), with \( {\mathfrak {I}}\) a traveling wave variation, by \( {\varvec{\Pi }}_\mathtt{n}({\mathfrak {I}},\alpha ) := ( \Pi _\mathtt{n}{\mathfrak {I}},\alpha ) \). By Lemma 5.1 and since \( \widetilde{\imath }_{\mathtt{n}} \) is a reversible traveling wave, we have that \( \mathcal {F}({\widetilde{U}}_\mathtt{n}) = \mathcal {F}(\widetilde{\imath }_\mathtt{n}, \widetilde{\alpha }_n) \) is an anti-reversible traveling wave variation, i.e (6.29)–(6.30) hold. Thus the first three components of \(\mathbf{T}_\mathtt{n}\Pi _\mathtt{n}\mathcal {F}({\widetilde{U}}_\mathtt{n}) \) form a reversible traveling wave variation, as well as \( {\varvec{\Pi }}_\mathtt{n}\mathbf{T}_\mathtt{n}\Pi _\mathtt{n}\mathcal {F}({\widetilde{U}}_\mathtt{n}) \). Finally one extends \( H_{\mathtt{n}+1} \), defined for \( \lambda \in \mathcal {G}_{\mathtt{n}+1} \), to \( {\widetilde{H}}_{\mathtt{n}+1} \) defined for all \( \lambda \in \mathbb {R}^\nu \times [\kappa _1, \kappa _2] \), with an equivalent \(\Vert \ \Vert _s^{k_0,\upsilon }\)-norm. Set \( {\widetilde{U}}_{\mathtt{n}+1} := {\widetilde{U}}_{\mathtt{n}} + {\widetilde{H}}_{\mathtt{n}+1} \).
The estimates (9.6)–(9.9) and \((\mathcal {P}3)_{\mathtt{n}+1}\) follow exactly as in [2, 6]. \(\square \)
Proof of Theorem 5.2
Let \(\upsilon = \varepsilon ^{\mathrm{a}}\), with \(0<{\mathrm{a}}<{\mathrm{a_0}}:= 1/(2+\tau _3)\). Then, the smallness condition in (9.5) holds for \(0<\varepsilon <\varepsilon _0\) small enough and Theorem 9.2 holds. By (9.7), the sequence of functions \( {\widetilde{W}}_\mathtt{n}= {\widetilde{U}}_\mathtt{n}- ({\varphi },0,0,\omega ) = ({\widetilde{{\mathfrak {I}}}}_\mathtt{n},{\widetilde{\alpha }}_\mathtt{n}-\omega ) \) converges to a function \( W_\infty : \mathbb {R}^\nu \times [\kappa _1,\kappa _2] \rightarrow H_{\varphi }^{s_0} \times H_{\varphi }^{s_0} \times H^{s_0} \times \mathbb {R}^\nu \), and we define
The torus \( i_\infty \) is reversible and traveling, that is (5.7) holds. By (9.6), (9.7), we also deduce
In particular (5.10)–(5.11) hold.
By Theorem 9.2-\((\mathcal {P}2)_\mathtt{n}\), we deduce that \(\mathcal {F}(\lambda ;U_\infty (\lambda ))=0\) for any

where  . To conclude the proof of Theorem 5.2 it remains only to define the \( \mu _j^\infty \) in (5.12) and prove that the set \(\mathcal {C}_\infty ^\upsilon \) in (5.14)–(5.165.17) is contained in \(\cap _{\mathtt{n}\geqq 0}\mathcal {G}_{\mathtt{n}} \). We first define
. To conclude the proof of Theorem 5.2 it remains only to define the \( \mu _j^\infty \) in (5.12) and prove that the set \(\mathcal {C}_\infty ^\upsilon \) in (5.14)–(5.165.17) is contained in \(\cap _{\mathtt{n}\geqq 0}\mathcal {G}_{\mathtt{n}} \). We first define

Lemma 9.3
\(\mathcal {G}_\infty \subseteq \cap _{\mathtt{n}\geqq 0}\mathcal {G}_{\mathtt{n}}\), where \(\mathcal {G}_{\mathtt{n}}\) are defined in (9.8).
Proof
We shall use the inclusion property (8.27), with S fixed in (9.3). By (9.10) we have
and \(\forall \mathtt{n}\geqq 2\,,\)
since \( \tau _3 > p (\tau +1) \) (by (9.5) and \( \tau _2 > \tau _1 = \tau (k_0 +1) + k_0\)) and \(\mathtt{a}_2 > p (\tau +1) \) (see Remark 9.1). Therefore (8.27) implies  , \( \forall \,\mathtt{n}\geqq 1 \). By similar arguments we deduce that
, \( \forall \,\mathtt{n}\geqq 1 \). By similar arguments we deduce that  . \(\square \)
. \(\square \)
Then we define the \( \mu _{j}^\infty \) in (5.12), where \( \mathtt{m}_{\frac{3}{2}}^\infty := \mathtt{m}_{\frac{3}{2}}(i_\infty ) \), \( \mathtt{m}_1^\infty =\mathtt{m}_1(i_\infty )\), \( \mathtt{m}_{\frac{1}{2}}^\infty = \mathtt{m}_{\frac{1}{2}}(i_\infty )\), with \(\mathtt{m}_{\frac{3}{2}}, \mathtt{m}_1, \mathtt{m}_{\frac{1}{2}}\) provided in Proposition 7.18. By (8.16), the sequence \(({\mathfrak {r}}_j^{(\mathtt{n})}(i_\infty ))_{\mathtt{n}\in \mathbb {N}}\), with \({\mathfrak {r}}_j^{(\mathtt{n})}\) given by Theorem 8.2-\((\mathbf{S1})_\mathtt{n}\) (evaluated at \( i = i_\infty \)), is a Cauchy sequence in \(|\,\cdot \, |^{k_0,\upsilon }\). Then we define \( {\mathfrak {r}}_j^\infty := \lim _{\mathtt{n}\rightarrow \infty } {\mathfrak {r}}_j^{(\mathtt{n})} (i_\infty ) \), for any \( j\in \mathbb {S}_0^c \), which satisfies \( | {\mathfrak {r}}_j^\infty - {\mathfrak {r}}_j^{(\mathtt{n})}(i_\infty )|^{k_0,\upsilon } \leqq C \varepsilon \upsilon ^{-1} N_{\mathtt{n}-1}^{-\mathtt{a}} \) for any \( \mathtt{n}\geqq 0 \). Then, recalling \({\mathfrak {r}}_j^{(0)}(i_\infty ) = 0 \) and (7.188), the estimates (5.13) hold (here \(C= C(S)\) with S fixed in (9.3)). Finally one checks (see for example Lemma 8.7 in [6]) that the Cantor set \(\mathcal {C}_\infty ^\upsilon \) in (5.14)–(5.165.17) satisfies \(\mathcal {C}_\infty ^\upsilon \subseteq \mathcal {G}_\infty \), with \(\mathcal {G}_\infty \) defined in (9.11), and Lemma 9.3 implies that \(\mathcal {C}_\infty ^\upsilon \subseteq \cap _{\mathtt{n}\geqq 0} \mathcal {G}_{\mathtt{n}}\). This concludes the proof of Theorem 5.2.
References
Alazard, T., Baldi, P.: Gravity capillary standing water waves. Arch. Ration. Mech. Anal. 217(3), 741–830, 2015
Baldi, P., Berti, M., Haus, E., Montalto, R.: Time quasi-periodic gravity water waves in finite depth. Invent. Math. 214(2), 739–911, 2018
Bambusi, D., Berti, M., Magistrelli, E.: Degenerate KAM theory for partial differential equations. J. Differ. Equ. 250(8), 3379–3397, 2011
Berti, M., Bolle, P.: A Nash–Moser approach to KAM theory. Fields Institute Communications, special volume “Hamiltonian PDEs and Applications”, pp. 255–284, 2015
Berti, M., Kappeler, T., Montalto, R.: Large KAM tori for quasi-linear perturbations of KdV. Arch Rational Mech Anal 239, 1395–1500 (2021). https://doi.org/10.1007/s00205-020-01596-2
Berti, M., Montalto, R.: Quasi-periodic standing wave solutions of gravity-capillary water waves, MEMO, Volume 263, 1273, Memoires AMS, ISSN 0065-9266, 2020
Constantin, A.: Nonlinear Water Waves with Applications to Wave-Current Interaction and Tsunamis, CBMS-NSF Regional Conf, Series in Applied Math., 81, SIAM, 2011
Constantin, A., Ivanov, R.I., Prodanov, E.M.: Nearly-Hamiltonian structure for water waves with constant vorticity. J. Math. Fluid Mech. 10, 224–237, 2008
Constantin, A., Strauss, W.: Exact steady periodic water waves with vorticity. Commun. Pure Appl. Math. 57(4), 481–527, 2004
Coutand, D., Shkoller, S.: Wellposedness of the free-surface incompressible Euler equations with or without surface tension. J. Am. Math. Soc. 20(3), 829–930, 2007
Craig, W., Nicholls, D.: Travelling two and three dimensional capillary gravity water waves. SIAM J. Math. Anal. 32(2), 323–359, 2000. (electronic)
Craig, W., Nicholls, D.: Traveling gravity water waves in two and three dimensions. Eur. J. Mech. B Fluids 21(6), 615–641, 2002
Craig, W., Sulem, C.: Numerical simulation of gravity waves. J. Comput. Phys. 108(1), 73–83, 1993
Dubreil-Jacotin, M.-L.: Sur la détermination rigoureuse des ondes permanentes périodiques d’ampleur finie. J. Math. Pures Appl. 13, 217–291, 1934
Feola, R., Giuliani, F., Procesi, M.: Reducible KAM tori for Degasperis-Procesi equation. Commun. Math. Phys. 377, 1681–1759, 2020
Geng, J., You, J.: A KAM theorem for one dimensional Schrödinger equation with periodic boundary conditions. J. Differ. Equ. 209(1), 1–56, 2005
Geng, J., You, J.: A KAM theorem for Hamiltonian partial differential equations in higher dimensional spaces. Commun. Math. Phys. 262, 343–372, 2006
Gerstner, F.: Theorie der Wellen, Abh. Königl. Böhm. Ges. Wiss, 1802
Goyon, R.: Contribution á la théorie des houles. Ann. Sci. Univ. Toulouse 22, 1–55, 1958
Grébert, B., Vilaça Da Rocha, V.: Stable and unstable time quasi periodic solutions for a system of coupled NLS equations. Nonlinearity 31(10), 4776–4811, 2018
Ifrim, M., Tataru, D.: Two dimensional gravity water waves with constant vorticity: I. Cubic lifespan. Anal. PDE 12(4), 903–967, 2019
Iooss, G., Plotnikov, P.: Multimodal standing gravity waves: a completely resonant system. J. Math. Fluid Mech. 7(suppl. 1), S110–S126, 2005
Iooss, G., Plotnikov, P.: Small divisor problem in the theory of three-dimensional water gravity waves. Mem. Am. Math. Soc. 200(940), viii+128, 2009
Iooss, G., Plotnikov, P.: Asymmetrical tridimensional traveling gravity waves. Arch. Rat. Mech. Anal. 200(3), 789–880, 2011
Iooss, G., Plotnikov, P., Toland, J.: Standing waves on an infinitely deep perfect fluid under gravity. Arch. Ration. Mech. Anal. 177(3), 367–478, 2005
Lannes, D.: Well-posedness of the water-waves equations. J. Am. Math. Soc. 3, 605–654, 2005
Levi-Civita, T.: Détermination rigoureuse des ondes permanentes d’ ampleur finie. Math. Ann. 93, 264–314, 1925
Kappeler, T., Liang, Z.: A KAM theorem for the defocusing NLS equation. J. Differ. Equ. 252, 4068–4113, 2012
Keady, G., Norbury, J.: On the existence theory for irrotational water waves. Math. Proc. Camb. Philos. Soc. 83(1), 137–157, 1978
Martin, C.: Local bifurcation and regularity for steady periodic capillary-gravity water waves with constant vorticity. Nonlinear Anal. Real World Appl. 14(1), 131–149, 2013
Maspero, A., Procesi, M.: Long time stability of small finite gap solutions of the cubic Nonlinear Schrödinger equation on \(\mathbb{T}^2\). J. Differ. Equ. 265(7), 3212–3309, 2018
McLeod, J.B.: The Stokes and Krasovskii conjectures for the wave of greatest height. Stud. Appl. Math. 98(4), 311–333, 1997
Nekrasov, A.I.: On steady waves. Izv. Ivanovo-Voznesenk. Politekhn. 3, 1921
Plotnikov, P., Toland, J.: Nash-Moser theory for standing water waves. Arch. Ration. Mech. Anal. 159(1), 1–83, 2001
Procesi, C., Procesi, M.: A KAM algorithm for the completely resonant nonlinear Schrödinger equation. Adv. Math. 272, 399–470, 2015
Reeder, J., Shinbrot, M.: Three-dimensional, nonlinear wave interaction in water of constant depth. Nonlinear Anal. T.M.A. 5(3), 303–323, 1981
Rüssmann, H.: Invariant tori in non-degenerate nearly integrable Hamiltonian systems. Regul. Chaotic Dyn. 6(2), 199–204, 2001
Stokes, G.: On the theory of oscillatory waves. Trans. Camb. Philos. Soc. 8, 441–455, 1847
Struik, D.: Détermination rigoureuse des ondes irrotationelles périodiques dans un canal á profondeur finie. Math. Ann. 95, 595–634, 1926
Toland, J.F.: On the existence of a wave of greatest height and Stokes conjecture. Proc. R. Soc. Lond. Ser. A 363(1715), 469–485, 1978
Wahlén, E.: Steady periodic capillary-gravity waves with vorticity. SIAM J. Math. Anal. 38, 921–943, 2006
Wahlén, E.: A Hamiltonian formulation of water waves with constant vorticity. Lett. Math. Phys. 79, 303–315, 2007
Wahlén, E.: Steady water waves with a critical layer. J. Differ. Equ. 246, 2468–2483, 2009
Wilkening, J., Zhao X.: Spatially quasi-periodic water waves of infinite depth, arXiv:2001.10745, 2020
Wilkening, J., Zhao X.: Quasi-periodic traveling gravity-capillary waves, arXiv:2002.09487, 2020
Zakharov, V.E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. Zhurnal Prikladnoi Mekhaniki i Teckhnicheskoi Fiziki 9(2), 86–94, 1969
Zeidler, E.: Existenzbeweis für cnoidal waves unter Berücksichtigung der Oberflächen spannung. Arch. Ration. Mech. Anal 41, 81–107, 1971
Zeidler, E.: Existenzbeweis fúr permanente Kapillar-Schwerewellen mit allgemeinen Wirbelverteilungen. Arch. Ration. Mech. Anal. 50, 34–72, 1973
Funding
Open Access funding provided by Scuola Internazionale Superiore di Studi Avanzati – SISSA
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Rabinowitz
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Berti, M., Franzoi, L. & Maspero, A. Traveling Quasi-periodic Water Waves with Constant Vorticity. Arch Rational Mech Anal 240, 99–202 (2021). https://doi.org/10.1007/s00205-021-01607-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-021-01607-w



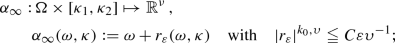
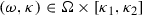 , satisfying
, satisfying 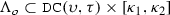 such that, for all
such that, for all 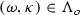 , the operator
, the operator 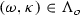 , there is a traveling wave solution
, there is a traveling wave solution