Zero-voltage and frequency pattern selection for DC-link loss minimization in PWM-VSI drives

Abstract

The modulation of a voltage source inverter output causes losses and harmonic distortions on the load side and the DC-link capacitor due to the discrete switching of the semiconductors. High-frequent voltage pulses are digitally programmed to control the inverter output and determine the harmonic distortions. This paper presents an optimization in terms of pulse- and frequency-pattern selection for reducing load distortions while keeping DC-link losses minimal. In detail, the fact that pulse and frequency patterns are independent from each other is utilized and a modified three-zone hybrid space vector pulse-width modulation is proposed where optimal frequency patterns are selected for every carrier cycle. Simulations and experimental results validate the optimizations.

1 Introduction

In the area of electric drives and inverters, the three-phase voltage source inverter (VSI) with two switching states per phase is still amongst the most commonly utilized systems when it comes to DC $\leftrightarrow$ AC energy conversion [1]. Since the 1970s, several pulse-programming methods have been developed, while only the carrier-based pulse-width modulation (PWM) [2] and the space vector pulse-width modulation (SVPWM) [3] reached significant importance in practical applications. Both techniques offer implementation simplicity and low run-time effort leading to a wide spread application for electric drives. In the literature, they reached significant interest due to their predictable performance criteria, i.e. total harmonic current distortion (THD) on the load side, DC-link distortions, as well as semiconductor losses and EMC behaviour [1, 4].

In detail, the modulator performance is determined by the switching sequence and the injected voltage in the neutral point. This voltage injection does not affect the phase voltage and leads to the degree of freedom for any pulse-modulation method, extending the volt-second linearity and improving the waveform quality, respectively [4]. Therefore, especially the influence of the modulation technique on the THD of the line current as well as on the inverter switching losses has been studied extensively in [5,6,7] for load distortions and in [7, 8] for semiconductor losses, respectively. In detail, both continuous PWM (CPWM) and discontinuous PWM (DPWM) methods have been investigated and optimal continuous PWM (OCPWM) and optimal discontinuous PWM (ODPWM) methods have been proposed, e.g. for maximum DC-link voltage utilization in [9] or minimum torque ripples in [6, 7, 10]. Specifically for discontinuous methods the modulator performance strongly depends on the chosen zero vector, thus continual clamp PWM (CCPWM) and split clamp PWM (SCPWM) modulation techniques have been proposed to minimize load distortions and semiconductor losses [11,12,13]. Furthermore, advanced methods with active vector splitting have been investigated showing significant influence on load distortions and switching losses [7, 12]. Moreover, latest research focused on hybrid PWM methods for further minimizing losses over the complete modulation range of the inverter [7, 8, 12]. Additionally, analysis of multi-converter topologies [14, 15] was carried out.

Conversely, DC-link distortions have not received as much attention in the literature as most articles focus on the load distortions and the semiconductors losses [16,17,18]. However, with rising electrification of the automotive area, where two-level three-phase inverter topologies are the most common solution due to their inexpensive structure [18], keeping DC-link distortions minimal is crucial as in battery powered systems the DC-link distortions directly influence the size of the DC-link capacitor and the battery filter [19]. Especially as DC-link capacitor and battery filter are the largest components in terms of size and the second largest in terms of cost, they significantly influence the inverter size and cost, as well as the power density [18]. Therefore, this paper introduces an optimized selection of inverter switching sequences, through utilizing a modified three-zone hybrid PWM similar as in [6,7,8], as well as optimal frequency patterns for each carrier cycle by minimizing a cost function. The goal is to reduce the load distortions to state-of-the-art values of multi-zone hybrid PWM techniques, while keeping the DC-link distortions minimal. The proposed technique is evaluated through simulations and experiments, respectively.

The rest of the paper is structured as follows: The state-of-the-art SVPWM modulation is reviewed in Sect. 2, the load and DC-link distortions are reviewed in Sect. 3, the proposed modulation technique is introduced in Sect. 4 and the experimental results are presented in Sects. 5. The paper is discussed and concluded in Sects. 6 and 7, respectively.

2 Background

The topology considered in this article consists of a three-phase load and a common three-phase VSI (Sect. 2.1) controlled by digital SVPWM (Sect. 2.2) under restriction of certain switching sequences (Sect. 2.3).

2.1 Topology

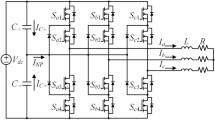
The typical structure of the three-phase two-level VSI with semiconductors (IGBTs) as switches, ideal DC-current supply, DC-link capacitor and active, symmetrical R-L-load is illustrated in Fig. 1. In detail, the control of the three-phase output, hence the generation of the desired low-frequency sinusoidal fundamental voltage waveform, is achieved by programming high-frequent voltage pulses on the inverter causing additional losses on the respective components [4].

Fig. 1

Circuit diagram of the three-phase PWM-VSI with ideal DC-current supply ($I_\textrm{dc,avg}$), the DC-link capacitor ($C_\textrm{dc}$), the B6-bridge inverter with semiconductors (IGBTs) as switches ($S_{u,v,w}^{+/-}$) and the symmetrical, neutral point isolated, active R-L-load

The modelling of the PWM-VSI drive in Fig. 1 underlies the following four assumptions:

• 1. The DC-link capacitor ($C_\textrm{dc}$) is large, so that the current on the load side ($i_\textrm{dc}$) can be assumed time-invariant for the switching duration.

• 2. The switching behaviour of the IGBTs is ideal, hence no dead-time or nonlinearities appear.

• 3. The switching frequency $f_s$ is much higher than the fundamental frequency ($f_{s} \gg f_{el}$), thus $\omega _{el}L \gg R$.

• 4. The load elements (R,L) are ideal and symmetrical, thus without temperature, current or modulator dependencies.

2.2 Space vector modulation

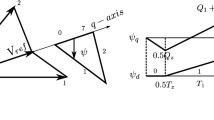
The space vector approach is based on the representation of the three-phase voltages ($v_{u,v,w}$) on a two-dimensional orthogonal reference frame. Therefore, the resulting voltage can be expressed as a rotating space vector $V^*$ with angular speed $\omega _{el}$ and displacement angle $\theta$ as shown in Eq. 1 and Fig. 2.

$$\begin{aligned} V^* = \frac{2}{3}\left( v_u + av_v + a^2v_w\right) = V_{1m}^* e^{j \omega _{el} t} \end{aligned}$$

(1)

where $a=e^{j(2\pi /3)}$ is a complex rotational factor describing the displacement between the three phases u, v, w.

Fig. 2

The inverter hexagon displays the eight inverter switching states ($V_{1-7}$) on the $\alpha$-$\beta$-plane defining six sectors $R=1$ to $R=6$. The high-side switches ($S_{uvw}^+$) are shown in brackets, while ‘1’ corresponds to ‘on’ and ‘0’ to ‘off’, respectively

The space vector $V^*$ can be described by two principal components ($\alpha ,\beta$), which are independent of each other. In detail, the sixfold symmetry of the inverter hexagon leads to the volt-second balance equation for the active inverter states $T_R$ and $T_{R+1}$. The cyclic boundary implies the update rules for the adjacent inverter sector: $R \rightarrow R+1$ ($R=6 \rightarrow R+1=1$) as described in Eq. 2.

$$\begin{aligned} V_R T_R + V_{R+1} T_{R+1} = V^* T_s. \end{aligned}$$

(2)

Solving for the active inverter state times $T_1$ and $T_{2}$ ($R=1$) results in the following $M_i$ and $\theta$ dependent functions.

$$\begin{aligned} \begin{bmatrix} T_1 \\ T_2 \end{bmatrix}&= \frac{\sqrt{3}M_i}{\pi } \begin{bmatrix} -1 &{} \sqrt{3} \\ 2 &{} 0 \end{bmatrix} \begin{bmatrix} \hbox {sin}(\theta )\\ \hbox {cos}(\theta ) \end{bmatrix} T_s \end{aligned}$$

(3)

$$\begin{aligned} T_Z&= T_s - T_1 - T_{2} \end{aligned}$$

(4)

where $T_Z$ is total inverter zero time and $M_i$ the modulation index. The modulation index is defined as the line-to-neutral inverter output voltage $V_{1m}$ divided by the fundamental component magnitude of the six-step operation $V_{1m,six}$ [4]:

$$\begin{aligned} M_i = \frac{V_{1m}}{V_{1m,\textrm{six}}}. \end{aligned}$$

(5)

To assure comparability of PWM methods and switching frequencies, Eqs. 3–4 are normalized with the length of the carrier cycle $T_s$. With normalized inverter times the rotating space vector $V^*$ and the inverter states are given as in Eq. 6.

$$\begin{aligned} V^* e^{j \theta } = d_1 e^{j0} + d_2 e^{j \frac{\pi }{3}} \end{aligned}$$

(6)

where $d_R = \frac{T_R}{T_s}$ is the normalized inverter time for the $R^{th}$ space vector.

2.3 Possible switching sequences

There are numerous possible ways to create valid switching sequences to program the reference voltage vector $V^*$. In this article, valid switching sequences are symmetric for the carrier cycle and have a number of switching instances less than or equal to three during one PWM half-cycle [8]. In detail, sequences can be created including two active vectors with one or two zero vectors [4], two active vectors and one zero vector with active vector splitting [7, 8], or even four active vectors where two additional active vectors are programmed in such a way that they cancel each other out [20]. These sequences, excluding sequences without zero vectors, are 0127, 012, 721, 0121, 7212, 1012 and 2721 for the first sector of the inverter hexagon ($R=1$). As different switching sequences have different numbers of switching per-carrier cycle the average switching frequency ($f_{s,avg}$) depends on the switching sequence [8]. Especially for DPWM methods the switching frequency of a phase varies over the fundamental cycle, as one phase is clamped for $\frac{2}{3}\pi$ of the fundamental cycle. To compare different switching sequences the frequency coefficient $k_f$ is introduced, giving the ratio of the average switching frequencies of two switching sequences, e.g. $k_f=\frac{f_{CPWM}}{f_{DPWM}}=\frac{3}{2}$ as for the comparison of continuous and discontinuous switching sequences.

3 Modulation losses

The modulator performance is determined through the choice of the switching sequence and the degree of freedom of separating the total inverter zero time $T_Z$ towards the upper and lower zero-state of the inverter ($V_0$ and $V_7$) [21].

3.1 Machine losses

Instead of investigating the harmonic current trajectories as loss measure, in this article the harmonic flux $(\lambda _h = L i$) is chosen to simplify the loss calculation as described in [4]. Utilizing the previous assumption of a pure inductive load ($f_s \gg f_{el}$), the harmonic losses for the carrier cycle are calculated as:

$$\begin{aligned} \lambda _h = \int _{0}^{T_s} (V_k - V^*) \, dt \end{aligned}$$

(7)

where $V_k$ is the inverter output voltage of the $k^{th}$ state and $k \in \{0,1,2,7\}$.

Solving the integral in Eq. 7 for each switching sequences results in a piecewise solution for every switching transition [22]. The approach, intermediate steps and normalization procedure can be found in [4], while the analytical solutions for all sequences are given in [8]. Since mostly not the distortions for the per-carrier cycle ($\lambda _{1,\textrm{rms}}^2$) are of interest, but the distortions for the fundamental cycle ($\lambda _{1,\textrm{frms}}^2$), Eq. 7 is integrated for the first sector of the inverter hexagon.

$$\begin{aligned} \lambda _{1,\textrm{frms}}^2 = \frac{3}{\pi } \int _{0}^{\frac{\pi }{3}} \int _{0}^{1} \lambda _{h}^2 \; dd \; d\theta . \end{aligned}$$

(8)

After normalizing $\lambda _{1,\textrm{frms}}^2$ with the distortion value in the six-step-mode ($\lambda _{1,\textrm{six}}^2 = \frac{\pi }{288}$ [4]) the machine independent harmonic distortion functions (HDF) for the seven switching sequences from Sect. 2.3 are shown in Fig. 3.

Fig. 3

Simulated HDF values for seven standard switching sequences (dotted) and the proposed optimal zero pattern (OZP) sequence (solid) with and without variable frequencies (see Sect. 4.1)

As illustrated in Fig. 3, the switching sequence has major influence on the modulator performance reducing the distortions up to a factor of 2.2 when using switching sequence 0127 as reference. Conversely, sequence 1012 (2721) shows increased distortions for the complete modulation range, thus it is not further considered in this article.

3.2 DC-link losses

To determine the harmonic distortions of the DC-link capacitor two metrics can be evaluated, namely the harmonic capacitor current ($I_{c,\textrm{frms}}^2$) and the harmonic capacitor voltage ($V_{dc,\textrm{frms}}^2$), respectively. The relationship between the two metrics is determined by the fundamental capacitor equation as given in Eq. 9.

$$\begin{aligned} v_\textrm{dc} = \frac{1}{C_\textrm{dc}} \int i_c \, dt. \end{aligned}$$

(9)

In this work, $C_\textrm{dc}$ is assumed to be normalized to unity and voltage and current are related through an unscaled integration. Furthermore, all derivations are explicitly given for current distortions only and can be found for voltages in [17, 23]. Moreover, it will be assumed that the inverter controls the phase currents to be purely sinusoidal, with a specific load angle $\phi$ and RMS current $I_\textrm{rms}$ [20, 24], which is valid since $f_s \gg f_{el}$ [4]. Furthermore, considering a symmetrical three-phase system the currents are given as follows:

$$\begin{aligned} i_{u,v,w} = \sqrt{2} I_\textrm{frms} \hbox {cos}\left( \omega _{el}t-\phi -\frac{2\pi }{3}x \right) \end{aligned}$$

(10)

where $x \in \{0,1,2\}$ indicates the phases shift for u, v, w. From Eq. 10, the instantaneous inverter current $i_\textrm{dc}$ can be written as:

$$\begin{aligned} i_\textrm{dc} = \sum _{x=1}^3 S_{x}^{+} i_{x} \end{aligned}$$

(11)

where $x \in \{u,v,w\}$. From Eq. 11, the average inverter input current $i_\textrm{dc,avg}$ for one half of the carrier cycle can be derived as follows:

$$\begin{aligned} i_\textrm{dc,avg} = \frac{2}{T_s} \int _0^{\frac{T_s}{2}} i_\textrm{dc} \, dt = d_{1}i_u - d_{2}i_w. \end{aligned}$$

(12)

For the fundamental cycle, the average inverter input current $I_\textrm{dc,avg}$ for a three-phase inverter is given as follows:

$$\begin{aligned} I_\textrm{dc,avg} = \frac{3\sqrt{2}}{\pi } M_i I_\textrm{rms} \hbox {cos}(\phi ). \end{aligned}$$

(13)

The DC-link capacitor current $i_c$ can be determined by Kirchhoff’s law as:

$$\begin{aligned} i_c = i_\textrm{dc} - I_\textrm{dc,avg}. \end{aligned}$$

(14)

Assuming $I_\textrm{dc,avg}$ to be constant [20], the RMS value of the capacitor current $I_{c,\textrm{frms}}^2$ can be written as:

$$\begin{aligned} I_{c,\textrm{frms}}^2 = I_{dc,\textrm{frms}}^2 - I_\textrm{dc,avg}^2. \end{aligned}$$

(15)

As shown in Eq. 12, $i_\textrm{dc,avg} \ne f(d_{0},d_{7})$, hence there is no modulator dependence of the total harmonic content of the capacitor current for a common three-phase, two-level VSI. This is due to the fact that during the inverter zero states the DC-Link is decoupled from the AC load and a selection of different zero states does not influence the total harmonic capacitor current [4]. However, since the harmonic capacitor voltage is the integration of the harmonic capacitor current, strong modulator dependencies appear for voltage distortions. Fig. 4 illustrates the strong modulator and $cos(\phi )$ dependencies for DC-link distortions.

Fig. 4

Simulated harmonic DC-link losses ($V_{dc,\textrm{frms}}^2$) for different switching sequences and values of $cos(\phi )$: a) 0127 b) 012 (721) c) 0121 (7212) d) OZP e) OZP ($T_s(\theta )=T_{s,opt}$)

Since the size of the DC-link capacitor depends on the maximum voltage distortion each switching sequence is normalized with the maximum distortion when using continuous modulation (0127). The results are illustrated in Fig. 5.

Fig. 5

Normalized maximum DC-link distortion for different switching sequences: a) 0127 b) 012 (721) c) 0121 (7212) d) OZP e) OZP ($T_{s,opt}$)

In detail, Fig. 5 shows that switching sequence 012 is optimal for $cos(\phi ) = \{0.75,0.5\}$ while sequence 0127 is optimal for $cos(\phi ) = 1$. Contrary switching sequences with active state splitting (e.g. 0121) show significantly increased distortion values for all $cos(\phi )$.

3.3 Switching losses

For the semiconductor losses, a simplified linear and analytical commutation model introduced in [25] and investigated in [4] is applied to the possible switching sequences in Sect. 2.3. The assumption for the device modelling is ideal linear commutation and lossless behaviour during conduction or blocking. Assuming the ideal linear commutation the time dependencies of the turn-on and turn-off characteristics can be modelled for the fundamental component. The local semiconductor stress is derived through the current flow in the carrier cycle and the corresponding switching states. The per-carrier switching losses $P_{s}$ can be written similar as in [4, 8]:

$$\begin{aligned} P_{s} = \frac{\sum _{x=1}^3 n_{x} \mid i_{x,1} \mid }{I_{max}} \frac{f_s}{2f_{s,avg}} \end{aligned}$$

(16)

where $n_{x}$ are the number of switching instances of the respective phase $x \in \{u,v,w\}$ within a carrier cycle, $i_{x,1}$ are the fundamental components of the phase current and $I_{max}$ is the peak current. Integrated for the fundamental cycle a switching loss function (SLF) can be defined as in [4].

$$\begin{aligned} SLF = \frac{1}{2} \int _{0}^{\frac{\pi }{3}} P_{s} \, d\theta \end{aligned}$$

(17)

where the local semiconductor losses per-carrier cycle $P_{s}$ are integrated for one sector of the inverter hexagon. In detail, for CPWM methods $n_{u,v,w}$=1, as every phases switches once per cycle. However, in the discontinuous case $n_{u,v,w}$=0 for one-third of the cycle, and the current becomes zero for those parts where the signal is unmodulated resulting in different SLF for DPWM methods. The results for the seven switching sequences for different load angles $\phi$ are shown in Fig. 6.

Fig. 6

Normalized semiconductor losses for the seven possible switching sequences and different values of $cos(\phi )$ (OZP at $M_i=\frac{\sqrt{3}\pi }{6}$)

4 Proposed modulation strategy

As shown in Sect. 3, the modulator performance, thus the load distortions, DC-link distortions and semiconductor losses, depend on the selection of the appropriate inverter switching sequence [26, 27] and the switching frequency distribution in the per-carrier cycle [28, 29]. In detail, the fact that pulse and frequency patterns are independent from each other [30] is utilized to reduce the load distortions to state-of-the-art values while keeping DC-link distortions minimal. Therefore, a hybrid PWM method called optimal zero patterns (OZPs) will be introduced in Sect. 4.1, while according frequency patterns are derived in Sect. 4.2.

4.1 Optimal zero pattern selection

Finding the minimum of any optimization problem can be achieved by formalizing the cost of the considered variables under certain constraints [31]. The idea is to find the global minimum by defining boundaries and searching through the multidimensional cost-space. In this case the considered variables are the losses influenced by the modulator, thus load distortions (HDF), DC-link distortions (DCD) and semiconductor losses (SLF) as shown in Eq. 18.

$$\begin{aligned} g(M_i,\phi ) = HDF(M_i) + DCD(M_i,\phi ) + SLF(\phi ) \end{aligned}$$

(18)

where for convenience the DC-link distortions are presented in normalized form, i.e. $DCD=\frac{V_{dc,\textrm{frms}}^2(M_i,\phi )}{V_{dc,\textrm{frms}}^2(M_i,\phi )(0127)}$. As can be seen in Eq. 18 the cost function $g(\cdot )$ depends on $M_i$ and $\phi$. Whereas in previous publications the focus was mainly on minimizing load distortions under consideration of semiconductor losses, thus the one-dimensional cost criteria ${\text {HDF}}(M_i)$ and ${\text {SLF}}(\phi )$ have been evaluated, in the proposed approach the variables to be minimized are the load distortions under consideration of the DC-link distortions. Therefore, a one-dimensional cost criteria $HDF(M_i$) is optimized under consideration of the two-dimensional cost criteria of DC-link distortions ${\text {DCD}}(M_i,\phi )$.

$$\begin{aligned}&g(M_i,\phi ) \rightarrow \text {min} \nonumber \\&s.t. \; {\text {HDF}}(M_i) \rightarrow \text {min} \\&s.t. \; {\text {DCD}}(M_i,\phi ) \le 1 \nonumber \end{aligned}$$

(19)

As shown in Eq. 19, the cost function $g(\cdot )$ is minimized under the constraints of minimal load distortions and DC-link distortions smaller than those of CPWM for previously evaluated switching sequences. Solving Eq. 19 leads to Eq. 20:

$$\begin{aligned} \theta _s = 18.2 M_i^4 - 59.6 M_i^3 + 73.8 M_i^2 -41.5 M_i + 9.1 \end{aligned}$$

(20)

where $\theta _s$ defines the switching angle for updating the modulation sequence as a function of the modulation index $M_i$ for $R=1$, $0 \le \theta \le \frac{\pi }{6}$, $0.54 \le M_i < \frac{\sqrt{3} \pi }{6}$ at $cos(\phi )=1$. The graphical representation of Eq. 20 is illustrated in Fig. 7.

Fig. 7

Proposed three-zone hybrid PWM (solid) utilizing switching sequences 0127, 012 and 721 and original three-zone hybrid PWM (dashed) [12]. In detail, the optimized areas (x,y,z) are shown for the $V_{dc,\textrm{rms}}^2$ values ($M_i=0.77$)

As illustrated in Fig. 7, the proposed method is a three-zone hybrid PWM similar to [6, 8, 12] utilizing a combination of CPWM and DPWM methods within one fundamental cycle. In detail, the solution includes a maximum of two active inverter states without active state splitting, as sequences 0121 and 7212 drastically increase DC-link distortion as previously illustrated in Fig. 5. Specifically the proposed modulation method uses switching sequence 0127 for small modulation indices ($M_i \le 0.54$), while for higher modulation indices a combination of sequences 0127 and 012/721 depending on the angle $\theta$ is utilized as illustrated in Fig. 7a and Eq. 20. Specifically the switching sequences along the angle $\theta$ is chosen such as the restriction of the DC-link distortions are met and $DCD(M_i,\phi ) \le 1$ holds for all values of $M_i$ and $cos(\phi )$.

The resulting $\lambda _{1,\textrm{frms}}^2$ and $V_{dc,\textrm{frms}}^2$ trajectories can be found in Figs. 3 and  4d and are labelled as OZP. In detail, the load distortions in Fig. 3 converge to switching sequence 0127 ($M_i \rightarrow 0$) or 012 ($M_i \rightarrow \frac{\sqrt{3} \pi }{6}$), respectively, offering a maximum optimization potential in the region of $\frac{1}{2} \le M_i < \frac{\sqrt{3} \pi }{6}$ with a maximum value of $11.2\%$. For the DC-link it can be seen that the constraint of Eq. 19 ($DCD(M_i,\phi ) \le 1$) forces the distortions to stay below the distortions of the CPWM modulation at $cos(\phi )$=1 (Fig. 4d). Considering switching losses the OZP has a constant $SLF=1$ for areas of CPWM modulation and switching losses of $SLF_{OZP}=(SLF_{012}+SLF_{721})/2$ in areas of DPWM modulation. Since the SLF of switching sequences 012 and 721 are inverse the OZP has relatively low influence on semiconductor losses for different load angles with $0.93 \le SLF_{OZP} \le 1.2$ as illustrated in Fig. 6.

4.2 Optimal frequency pattern selection

Not only the selection of appropriate switching sequences influences the modulator performance, but also a frequency variation along the fundamental angle $\theta$ [28]. As can be seen in Fig. 7b/c load and DC-link distortions for the per-carrier cycle are functions of the angle $\theta$. Especially the distortion functions for $\lambda _{1,\textrm{rms}}^2$ and $V_{dc,\textrm{rms}}^2$ for the selected sequence 012/721 are similar in shape, thus having similar curvature as illustrated in Fig. 7bc (markings x,y,z). Therefore, since the growth law of the distortions is proportional to $\frac{1}{f_{s}^2}$ the $\lambda _{1,\textrm{frms}}^2$ and $V_{dc,\textrm{frms}}^2$ values can be both reduced by varying the frequency as a function of the angle $\theta$ while keeping the average number of semiconductor switching instances constant [30]. Let $X(M_i,\phi ,\theta )$ be a variable depending on the angle $\theta$ within the region $\theta \in [0,...,\frac{\pi }{3}]$, i.e. $\lambda _{1,\textrm{rms}}^2$ or $V_{dc,\textrm{rms}}^2$. It follows, that the switching time distribution $T_s^2(\theta )$ minimizing X can be written as in Eq. 21 for each modulation index $M_i$ and load angle $\phi$.

$$\begin{aligned}&X_{min} = \int _{0}^{\frac{\pi }{3}} X \cdot T_{s}^2 \, d\theta \\&s.t. \; \int _{0}^{\frac{\pi }{3}} \frac{T_{s}}{T_{s,avg}} \, d\theta = 1.\nonumber \end{aligned}$$

(21)

To minimize X, the function $T_{s}(M_{i},\phi ,\theta )$ has to be chosen such as it minimizes X for all values of $\theta$ separately for each $M_i$ and $\phi$. Using Lagrange multipliers, X and $T_s$ can be separated as shown in Eq. 22.

$$\begin{aligned} \Lambda \left( M_{i},\theta ,\phi ,\lambda \right) = X_{min} + \lambda \cdot \left( \int _{0}^{\frac{\pi }{3}} \frac{T_{s}}{T_{s,avg}} \, d\theta - 1\right) . \end{aligned}$$

(22)

Solving Eq. 21 using Eq. 22, it can be shown that the function $T_{s}(M_{i},\phi ,\theta )$ can be written in closed form as in Eq. 23.

$$\begin{aligned} T_{s,opt}(M_{i},\phi ,\theta ) = \frac{\frac{3}{\pi }\int _{0}^{\frac{\pi }{3}} \sqrt{X(M_{i},\theta ,\phi )}}{\sqrt{X(M_{i},\theta ,\phi )}}. \end{aligned}$$

(23)

The results for the optimized frequency patterns ($f_{s,opt}=\frac{1}{T_{s,opt}}$) for $cos(\phi )=1$ can be found in Fig. 8. Applying the optimal frequency patterns to the load side can further reduce the load distortions compared to the standard OZP showing improvements up to $31.8\%$, and thus reaching state-of-the-art distortions of the five- and seven-zone hybrid PWM techniques as in [7, 12]. Furthermore, similar results can be observed for the DC-link where distortions reduce for $cos(\phi )=\{0.75,0.50\}$ as illustrated in Fig. 5, but cannot be further reduced for $cos(\phi )=1$.

Fig. 8

Optimal frequency patterns $f_{s,opt}(M_i,\theta )$ normalized with the average inverter frequency $f_{s,avg}$ for optimizing $\lambda _{1,\textrm{frms}}^2$ (upper subfigure) and $V_{dc,\textrm{frms}}^2$ (lower subfigure) for OZP at $\cos (\phi )=1.0$

To further compare the proposed method two different hybrid PWM methods, namely [6] and [8], are chosen for comparison. In detail, two different steady-state operational points are compared, namely $M_i=\frac{\sqrt{3}\pi }{6}$ at $cos(\phi )=\{0.5,1.0\}$. The results are tabulated in Table 1.

Table 1 Distortion comparison with [6] and [8]

As can be seen in Table 1 each of the three approaches has its own optimization goal. In detail, [6] aims to reduce load distortions with a moderate increase in DC-link distortions and constantly reduced semiconductor losses for different $cos(\phi )$. The approach in [8] reduces the load distortions and semiconductor losses to a minimum, while accepting a strong increase in DC-link distortions. Conversely, the proposed approach reduces load distortions almost to the state of the art of [8] while keeping DC-link distortions minimal and semiconductor losses close to CPWM modulation techniques with only a small influence on $cos(\phi )$ as illustrated in Fig. 6.

5 Experimental results

The experimental results were carried out using a common three-phase two-level inverter fed by a highly stabilized power supply, powering a three-phase stator in static configuration approximating a pure inductive load, while a set of resistors is used to change the value of $cos(\phi )$. A powerful dSPACE 1007 rapid prototyping system with 2 GHz processor is used to implement the modulation strategy via the Xilinx library in Simulink on a dSPACE DS5202 FPGA card. The parameters of the test set-up are tabulated in Table 2.

Table 2 Parameters of the test set-up

To vary the modulation index the DC-Link voltage is changed while the switching frequency is kept constant assuring the pulse-number $p=\frac{f_s}{f_{el}} \ge 20$. To calculate the HDF, the harmonic spectrum of the phase currents is measured. Since the fundamental amplitude of the phase current is a function of the modulation index $M_{i}$ the HDF function is normalized to its corresponding fundamental current, while the overall curve is normalized to the six-step value. Fig. 9 is correspondent to Fig. 4 and displays the measured HDF curves (measurements start at $M_i=0.2$ through normalization errors for $M_i < 0.2$).

Fig. 9

Measured HDF curves for reference sequences 0127, 012 and 0121 ($k_f=\frac{2}{3}$ for 012) and for the proposed OZP methods

As can be seen in Fig. 9, the measured results are in good correlation with the simulations. Waveform and points of intersection between switching sequences 0127 and 012 show good correlations. The HDF values for sequence 012 show a slight offset from the simulation. Investigating the measurements corresponding to the OZP curvature shape and points of intersection are according to the simulation. In detail, within the area of $0.55< M_i < 0.8$ the OZP leads to a decrease in distortions as determined in the simulation. The improvement for the measured values is approximately $6.5\%$ for the best operating point, while the simulation showed a maximum possible improvement up to $11.2\%$. When applying the optimal frequency patterns distortions decrease further up to $20.9\%$ with $31.8\%$ being calculated in the simulation.

For inspecting the DC-link voltage distortions, it is essential to change the value of $cos(\phi )$. Accordingly, the load of the test set-up is extended with a passive R-L-load with a fixed set of pure resistors R as tabulated in Table 2. The voltage waveforms are directly measured on DC-link capacitor and normalized with the DC-link voltage $V_\textrm{dc}$. Fig. 10 displays the measured harmonic voltage $V_{dc,\textrm{frms}}^2$ for the reference sequences (0127/012/0121) in Fig. 10abc, for the OZP method in Fig. 10d and for the OZP method including frequency variation in Fig. 10e for different values of $cos(\phi )$.

Fig. 10

Measured harmonic DC-link losses $V_{dc,\textrm{rms}}^2$ for different values of $cos(\phi )$: a) 0127 b) 012 c) 0121 d) OZP e) OZP ($T_s(\theta )=T_{s,opt}$)

Comparing the simulations from Fig. 5 to the measurements in Fig. 10, excellent correlation in terms of absolute distortion values appears. Considering the location of the distortion maximum it can be seen that it is located at $M_i \approx 0.6$ while $M_i \approx 0.48$ has been simulated. As this effect is constant across all measurements it could be due to the larger resistive component violating $w_{el}L \gg R$ or any parasitic component in R itself. However, since the design on the DC-link capacitor depends mainly on the maximum voltage distortion within the complete operation area, low errors in absolute distortion are more crucial than the location of the maximum.

To further evaluate the performance of the proposed modulation technique, the harmonic spectra of the line current and the DC-link voltage are evaluated in steady-state operation. To compare the distortions of the different switching sequences the THD is used:

$$\begin{aligned} \text {THD} = \frac{\sqrt{X_{\textrm{rms}}-X_1}}{X_1} \; \; \; \text {with} \; \; \; X=\{I,V\} \end{aligned}$$

(24)

where $X_1$ is the fundamental component of the current or the dc component of the voltage and $X_\textrm{rms}$ are the root mean square values of the Fourier spectra, respectively. The measured spectra of the line current and DC-link voltage are illustrated in Fig. 11.

Fig. 11

Steady-State harmonic spectra of line current ($i_u$) and DC-link voltage ($v_\textrm{dc}$) for $V_\textrm{dc}=50$, $f_s=10 kHz$, $f_{el}=100Hz$, $M_i=0.9$ and $cos(\phi )=1.0$. In detail, the fundamental component is illustrated and its magnitude is given for each switching sequence and a detailed view of the sub-fundamental distortions is given as well: a) 0127 b) 012 c) 0121 d) OZP e) OZP ($T_s(\theta )=T_{s,opt}$)

As can be seen in Fig. 11, the steady-state distortions of the load current reduced from 1.57% when utilizing switching sequence 0127, to 1.05% or 1.03% when utilizing switching sequence 0121 or OZP ($T_s(\theta )=T_{s,opt}$). Therefore, the proposed method is able to reduce load distortions to values equal to sequences with active vector splitting. When comparing steady-state DC-link distortions the voltage distortions increase from 0.31% to 0.37% when changing from switching sequence 0127 to 0121 and reduce to 0.27% when utilizing OZP ($T_s(\theta )=T_{s,opt}$). Therefore, it was shown that the proposed method is able to reduce load distortion to state-of-the-art values, while keeping DC-link distortions minimal.

6 Discussion

In the previous sections, two different optimization approaches, namely the selection of switching sequences and frequency patterns, have been introduced. Each of these methods has its own influence on load distortions and DC-link distortions and optimal solutions can be found depending on the objective function being optimized. In detail, it was shown that an appropriate selection of switching sequences and frequency patterns can significantly reduce load distortions while keeping DC-link distortions minimal. However, when taking into account all modulation losses, thus load and DC-link distortions as well as semiconductor losses finding an optimal operation strategy is not trivial any more. Therefore, to find an optimal solution the cost function $g(M_i,\phi )$ as formulated in Eq. 18, should be extended with empirical determined weighting coefficients $k_{1,2}$ for DC-link and semiconductor losses in order to find optimal solutions.

$$\begin{aligned} g(M_i,\phi ) = HDF + k_1 \cdot DCD + k_2 \cdot SLF. \end{aligned}$$

(25)

Finding the optimal solution for Eq. 25 is now dependent on the application, hence the coefficients $k_{1,2}$. However, finding these coefficients is not straightforward, since cost evaluation for the DC-link capacitor and the IGBTs as function of the losses and operating strategy is necessary.

7 Conclusion

In this paper, significant influences from both selected switching sequences and frequency patterns on the modulator performance have been reported. It was shown, that switching sequences and frequency patterns are two independent optimization criteria under the assumption of high pulse numbers. The influence on load and DC-link distortions was shown. Furthermore, the coupling between load distortions, DC-link distortions and semiconductor losses was demonstrated and shows the need for cost function evaluation as discussed in Sect. 6. In detail, it was shown, that a properly selected switching sequence in combination with optimized frequency patterns can reduce load distortions to state-of-the-art hybrid PWM techniques without affecting DC-link losses. The experiments on the test bench have proven the validity of the proposed modulation techniques and the results are in good correlation with the simulation. Further research should focus on finding optimal solutions for a more generic cost function as described in Sect. 6, thus optimizing load distortions, DC-link distortions and semiconductor losses application dependent. Apart from that, the evaluation of modulator performance in the over-modulation region would be of interest.