1 Introduction

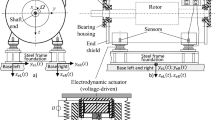
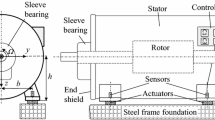
Nowadays, the requirements regarding low vibrations in rotating machinery are increasing and therefore also the challenge of vibration analysis [1,2,3,4,5], also for electrical motors. Additionally, induction motors are driven by converters very often these days, in order to use a wide speed range for efficient operation. Therefore, induction motors have to be designed for that speed range, avoiding critical speeds concerning vibrations. Referring to motor standards—e.g. IEC 60034-14 [6]—induction motors with power ratings larger than 1 MW are mostly designed for operation on massive foundations. However, in praxis, the load machine and the induction motor are often mounted together on flexible steel frame foundations and have to fulfill vibration standards in situ, e.g. ISO 10816-3 [7]. Due to the flexibility of the foundation, critical speeds may occur now in the operational speed range and off-speed ranges have to be accepted. The idea is now to use active vibration control, which is nowadays more and more implemented in many different technical applications [8,9,10,11,12,13,14,15,16,17,18]. The main goal of this concept here is to prevent off-speed ranges, by active vibration control. Therefore, actuators are placed between the motor feet and the steel frame foundation. The vertical acceleration of each motor foot is measured by a sensor and lead back to a separate controller (Fig. 1). The idea using actuators as motor foot mounts is not new. It has been investigated in different researches. For example, Ushijima and Kumakawa described in [14] the behavior of piezo actuators, used as active engine mounts for vibration control. Ulbrich described and compared in [15] different actuators for rotating machines. Also, Sun et al. investigated in [16] electrohydraulic actuators, used for active suspensions of cars. Sohn et al. described in [17] their experimental research regarding an electromagnetic actuator, for active vibration control. Zhang et al. showed in [18] the current status and development of electromagnetic active engine mounts. The goal of this paper now is to point out the use of active motor foot mounts for large induction motors (power rating > 1 MW). This concept was basically described and investigated in [19] to reduce bearing housing vibrations, caused by radial excitations like e.g. mechanical unbalance [1,2,3,4,5] and electromagnetic forces [20,21,22,23,24], which occur as period excitations. However, not only radial excitations but also dynamic air gap torques [24,25,26,27,28] occur in induction motors. These dynamic air gap torques act on the rotor and in phase opposition on the stator (Fig. 2). Usually, the air gap torques acting on the rotor, do not lead to lateral vibrations or foundation forces if there is no transmission e.g. by a gearbox. However, the air gap torques acting at the stator, lead to lateral vibrations and foundation forces.

Fig. 1
figure 1

Converter driven induction motor with load machine mounted on a combined steel frame foundation

Full size image
Fig. 2
figure 2

Vibration model for active vibration control

Full size image

The intention of the paper is to show, that this concept also may help to reduce foundation force caused by dynamic air gap torques, which occur as periodic excitations (pulsating air gap torques) but also as transient excitations (transient air gap torques) in induction motors. Therefore, the main novelty of this paper, compared to [19], is now that:

  • Dynamic air gap torques are considered instead of radial excitations

  • Not only periodic excitations but also transient excitations are considered

  • Dynamic foundations forces are analyzed instead of bearing housing vibrations

  • Motor feet accelerations are controlled instead of motor feet displacements

2 Vibration model

The vibration model (Fig. 2) presents a simplified plane model of an induction motor with roller bearings, mounted on active motor foot mounts (actuators), which are placed between motor feet and foundation, referring to [19]. The load machine is not considered here, assuming that the influence of the connections—e.g. by a very elastic coupling for both shafts and by very soft actuators—is here so low, that the load machine can be neglected in this theoretical investigation. However, in praxis, there may be influence by the load machine.

The main masses are the rotor mass \(m_{{\text{w}}}\) and the stator mass \(m_{{\text{s}}}\) with the mass moment of inertia \(\theta_{{{\text{sx}}}}\) at the x-axis. The shaft journal masses \(m_{{\text{v}}}\), the bearing housing masses \(m_{{\text{b}}}\), the masses of the actuators—\(m_{{{\text{as}}}}\) for the stator and \(m_{{{\text{aa}}}}\) for the armature at each motor side—as well as the foundation masses \(m_{{{\text{fL}}}}\) and \(m_{{{\text{fR}}}}\) for each motor side (L: left; R: right) are considered as additional masses. The rotor rotates with the rotary angular frequency Ω and has the stiffness c. Internal (rotating) damping is not considered here, as well as the gyroscopic effect. The shaft journals of the rotor are connected to the bearing housings by the roller bearing stiffness matrices \({\mathbf{C}}_{{\text{r}}}\), with the vertical and horizontal bearing stiffness \(c_{{{\text{rz}}}}\) and \(c_{{{\text{ry}}}}\) (z: vertical; y: horizontal). The bearing housings are connected to the stator by the stiffness matrices \({\mathbf{C}}_{{\text{b}}}\) with the vertical and horizontal stiffness \(c_{{{\text{bz}}}}\) and \(c_{{{\text{by}}}}\). Damping is not considered here for these connections. The electromagnetism of the induction motor is simplified considered by the electromagnetic spring matrices \({\mathbf{C}}_{{\text{m}}}\), with the electromagnetic spring coefficient \(c_{{\text{m}}}\) [20,21,22,23]. Electromagnetic field damping is not considered here. The stator structure is supposed to be rigid. The actuator stiffness matrix \({\mathbf{C}}_{{\text{a}}}\) include the vertical and horizontal stiffness values \(c_{{{\text{az}}}}\) and \(c_{{{\text{ay}}}}\) and the actuator damping matrix \({\mathbf{D}}_{{\text{a}}}\) the corresponding damping coefficients \(d_{{{\text{az}}}}\) and \(d_{{{\text{ay}}}}\). The actuator forces are described by \(f_{{{\text{azL}}}}\) and \(f_{{{\text{azR}}}}\). All values of the actuators are defined for each motor side. The foundation stiffness matrices \({\mathbf{C}}_{{{\text{fL}}}}\) and \({\mathbf{C}}_{{{\text{fR}}}}\) for left and right side and the corresponding damping matrices \({\mathbf{D}}_{{{\text{fL}}}}\) and \({\mathbf{D}}_{{{\text{fR}}}}\) include the stiffness coefficients \(c_{{{\text{fzL}}}}\), \(c_{{{\text{fzR}}}}\), \(c_{{{\text{fyL}}}}\), \(c_{{{\text{fyR}}}}\) and the damping coefficients \(d_{{{\text{fzL}}}}\), \(d_{{{\text{fzR}}}}\), \(d_{{{\text{fyL}}}}\), \(d_{{{\text{fyR}}}}\).

The coordinates \(y_{{\text{w}}}\) and \(z_{{\text{w}}}\) describe the translational displacements of the shaft centre point \(W\), \(y_{{\text{v}}}\) and \(z_{{\text{v}}}\) the translational displacements of the shaft journal points \(V\), \(y_{{\text{b}}}\) and \(z_{{\text{b}}}\) the translational displacements of the bearing housing center points \(B\). The coordinates \(y_{{\text{s}}}\) and \(z_{{\text{s}}}\) describe the translational displacements and \(\varphi_{{\text{s}}}\) the angular displacement of centre of the stator \(S\). The coordinates \(y_{{{\text{aL}}}}\) and \(z_{{{\text{aL}}}}\) represent the translational displacements of the motor feet points \(A_{{\text{L}}}\) on the left side, \(y_{{{\text{aR}}}}\) and \(z_{{{\text{aR}}}}\) the translational displacements of the motor feet points \(A_{{\text{R}}}\) on the right side. Whereas \(y_{{{\text{fL}}}}\) and \(z_{{{\text{fL}}}}\) represent the translational displacements of the foundation connecting points \(F_{{\text{L}}}\) on the left side \(y_{{{\text{fR}}}}\) and \(z_{{{\text{fR}}}}\) the translational displacements of the foundation connecting points \(F_{{\text{R}}}\) on the right side. The distance \(h\) describes the height of the stator centre point \(S\) to the motor feet. \(\psi\) describes the angle between \(h\) and \(\overline{{SA_{{\text{L}}} }}\) and \(\overline{{SA_{R} }}\). The parameter \(b\) describes the half distance between the motor feet. The dynamic air gap torque is described by \(m_{{\text{e}}} (t)\), acting on the rotor and in phase opposition on the stator. Because of the plane model, only one acceleration sensor is placed on each motor side, measuring the vertical motor feet accelerations \(a_{{{\text{aL}}}}\) (\(= \ddot{z}_{{{\text{aL}}}}\)) and \(a_{{{\text{aR}}}}\) (\(= \ddot{z}_{{{\text{aR}}}}\)) and transmitting the signals to the controllers, contrarily to [19], where a lead back of the motor feet displacements has been investigated. The chosen controllers have arbitrary controller structures, described in the Laplace domain—with the Laplace variable \(s\)—by the transfer functions \(G_{{{\text{cL}}}} (s)\) and \(G_{{{\text{cR}}}} (s)\):

$$ G_{{{\text{cL}}}} (s) = \frac{{\sum\nolimits_{{\upmu {\text{L}} = 0}}^{{{\text{mL}}}} {b_{{\upmu {\text{L}}}} \cdot s^{{\upmu {\text{L}}}} } }}{{\sum\nolimits_{{\upnu {\text{L}} = 0}}^{{{\text{nL}}}} {a_{{\upnu {\text{L}}}} \cdot s^{{\upnu {\text{L}}}} } }};\quad G_{{{\text{cR}}}} (s) = \frac{{\sum\nolimits_{{\upmu {\text{R}} = 0}}^{{{\text{mR}}}} {b_{{\upmu {\text{R}}}} \cdot s^{{\upmu {\text{R}}}} } }}{{\sum\nolimits_{{\upnu {\text{R}} = 0}}^{{{\text{nR}}}} {a_{{\upnu {\text{R}}}} \cdot s^{{\upnu {\text{R}}}} } }}. $$
(1)

where \(b_{{\upmu {\text{L}}}}\), \(b_{{\upmu {\text{R}}}}\), \(a_{{\upnu {\text{L}}}}\), \(a_{{\upnu {\text{R}}}}\) are the constants of the polynomial functions. The excitation, which is here considered, is the electromagnetic torque \(m_{e} (t)\) in the air gap of the induction motor, which acts at the rotor and opposite direction at the stator (Fig. 2). The relevant air gap torques are on the one hand pulsating air gap torques (torque ripples), caused by converter operation, leading to harmonics and interharmonics/subharmonics [27, 28], and on the other hand transient air gap torques, caused by 2-phase and 3-phase terminal short circuits [24,25,26] (Fig. 3). The dynamic air gap torques \(m_{e} (t)\) can be simplified described by following formula:

$$ m_{{\text{e}}} (t) = \mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot e^{{ - \alpha_{{{\text{e}},{\text{k}}}} \cdot t}} \cdot \sin \left( {\omega_{{{\text{e}},{\text{k}}}} \cdot t + \varphi_{{{\text{e}},{\text{k}}}} } \right), $$
(2)

with the amplitude \(\hat{m}_{{{\text{e}},{\text{k}}}}\), the angular frequency \(\omega_{{{\text{e}},{\text{k}}}} = 2\pi \cdot f_{{{\text{e}},{\text{k}}}}\), the phase angle \(\varphi_{{{\text{e}},{\text{k}}}}\) and with the decaying coefficient \(\alpha_{{{\text{e}},{\text{k}}}}\), for each component. For pulsating air gap torques, the decaying coefficients are zero. This analytical description of the air gap torques for the short circuits can be used under the condition that the rotor speed will not change during the short circuit.

Fig. 3
figure 3

Schematic diagram of a converter (voltage source DC-link) with induction motor and different kinds of dynamic air gap torques

Full size image

3 Mathematical description

3.1 Formulation in the time domain

Based on [19], the differential equation system can be described by

$$ {\mathbf{M}} \cdot {\ddot{\mathbf{q}}} + {\mathbf{D}} \cdot {\dot{\mathbf{q}}} + {\mathbf{C}} \cdot {\mathbf{q}} = {\mathbf{m}}_{{\text{e}}} + {\mathbf{f}}_{{\text{a}}} , $$
(3)

including the linearization of the motor feet displacements, because of small displacements:

$$\begin{aligned}& z_{{{\text{aL}}}} = z_{{\text{s}}} - \varphi_{{\text{s}}} \cdot b;\\ & z_{{{\text{aR}}}} = z_{{\text{s}}} + \varphi_{{\text{s}}} \cdot b;\;y_{{{\text{aL}}}} = y_{{{\text{aR}}}} = y_{{\text{s}}} - \varphi_{{\text{s}}} \cdot h.\end{aligned} $$
(4)

The vector \({\mathbf{q}}(t)\) contains the coordinates for the displacements of important points and the rotation \(\varphi_{s}\) of the stator mass:

$$ {\mathbf{q}}(t) = \left[ {z_{{\text{s}}} ;z_{{\text{w}}} ;y_{{\text{s}}} ;y_{{\text{w}}} ;\varphi_{{\text{s}}} ;z_{{\text{v}}} ;z_{{\text{b}}} ;z_{{{\text{fL}}}} ;z_{{{\text{fR}}}} ;y_{{\text{v}}} ;y_{{\text{b}}} ;y_{{{\text{fL}}}} ;y_{{{\text{fR}}}} } \right]^{T} . $$
(5)

The mass matrix \({\mathbf{M}}\), the damping matrix \({\mathbf{D}}\) and the stiffness matrix \({\mathbf{C}}\) are shown in the "Appendix", referring to [19]. The excitation vector \({\mathbf{m}}_{{\text{e}}} (t)\) for the dynamic air gap torque is described by:

$$ {\mathbf{m}}_{{\text{e}}} (t) = \underbrace {{[0;0;0;0;1;0;0;0;0;0;0;0;0]^{T} }}_{{{\mathbf{P}}_{{\text{e}}} }} \cdot \underbrace {{\mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot e^{{ - \alpha_{{{\text{e}},{\text{k}}}} \cdot t}} \cdot \sin \left( {\omega_{{{\text{e}},{\text{k}}}} \cdot t + \varphi_{{{\text{e}},{\text{k}}}} } \right)}}_{{m_{{\text{e}}} (t)}}. $$
(6)

The actuator force vector can be split into the actuator force vector on the left side \({\mathbf{f}}_{{{\text{azL}}}} (t)\) and on the right side \({\mathbf{f}}_{{{\text{azR}}}} (t)\) of the motor, referring to [19]:

$$ {\mathbf{f}}_{{\text{a}}} (t) = {\mathbf{f}}_{{{\text{azL}}}} (t) + {\mathbf{f}}_{{{\text{azR}}}} (t)\;{\text{with:}} $$
(7)
$$ {\mathbf{f}}_{{{\text{azL}}}} (t) = \underbrace {{[1;0;0;0; - b;0;0; - 1;0;0;0;0;0]^{T} }}_{{{\mathbf{P}}_{{{\text{azL}}}} }} \cdot f_{{{\text{azL}}}} (t); $$
(8)
$$ {\mathbf{f}}_{{{\text{azR}}}} (t) = \underbrace {{[1;0;0;0;b;0;0;0; - 1;0;0;0;0]^{T} }}_{{{\mathbf{P}}_{{{\text{azR}}}} }} \cdot f_{{{\text{azR}}}} (t). $$
(9)

The actuator forces \(f_{{{\text{azL}}}} (t)\) and \(f_{{{\text{azR}}}} (t)\) depend on the controller transfer functions and the vertical motor feet accelerations. When solving the differential Eq. (3) the coordinate vector \({\mathbf{q}}(t)\) can be derived, and therefore the dynamic foundation forces at each side in vertical and horizontal direction can be calculated by:

$$\begin{aligned} & f_{{{\text{fqn}}}} (t) = c_{{{\text{fqn}}}} \cdot q_{{{\text{fn}}}} (t) + d_{{{\text{fqn}}}} \cdot \dot{q}_{{{\text{fn}}}} (t)\\ &\quad {\text{with:}}\; n = L,R;\;q = y,z.\end{aligned} $$
(10)

3.2 Formulation in the Laplace domain

To analyze the dynamic foundation forces due to the transient air gap torques, it is useful to describe the system in the Laplace domain and to use a state-space formulation, based on [29,30,31]. The index “st” is used in the matrices of the state space to avoid mix up with the stiffness matrix \({\mathbf{C}}\) and damping matrix \({\mathbf{D}}\). The differential equation system (3) is transferred into the Laplace domain and then described in the state-space model (Fig. 4).

Fig. 4
figure 4

State-space model for vibration control with negative feedback of the output vector in the Laplace domain, for excitation by transient air gap torques, considering initial conditions

Full size image

\({\mathbf{M}}_{{\text{e}}} (s)\) is the Laplace transferred excitation vector (16) and \({\mathbf{F}}_{{\text{a}}} (s)\) the Laplace transferred actuator force vector (19). \( {\mathbf{X}}(s)\) is the Laplace transferred state-space vector (11) and \({\mathbf{x}}\left( { - 0} \right)\) is the vector for the initial conditions (12). The vector \({\mathbf{Y}}(s)\) is the Laplace transferred output vector (22). \({\mathbf{A}}_{{{\text{st}}}}\) presents the system matrix, \({\mathbf{B}}_{{{\text{st}}}}\) the input matrix, \({\mathbf{C}}_{{{\text{st}}}}\) the output matrix, and \({\mathbf{D}}_{{{\text{st}}}}\) the straight-way matrix, which are all described in (15).\( {\mathbf{T}}_{{{\text{st}}}}\) presents the controller matrix, described in (20).

Following mathematical descriptions can be used, where \({\mathbf{x}}(t)\) is the state space vector, described by the coordinate vector q and the velocity vector \({\dot{\mathbf{q}}}\), transferred in the Laplace domain:

$$ {\mathbf{X}}(s) = {\mathcal{L}}\left\{ {{\mathbf{x}}(t)} \right\} = {\mathcal{L}}\left\{ {\left[ {\begin{array}{*{20}c} {{\mathbf{q}}(t)} \\ {{\dot{\mathbf{q}}}(t)} \\ \end{array} } \right]} \right\}. $$
(11)

The vector of the initial conditions is described by:

$$ {\mathbf{x}}( - 0) = {\mathbf{x}}(t = - 0). $$
(12)

The vector \({\mathbf{x}}( - 0)\) is necessary to describe the system behavior for the terminal short circuit, where the air gap torque changes, starting from the stationary torque \(m_{{{\text{stat}}}}\):

$$ m_{e} ( - 0) = m_{{{\text{stat}}}} . $$
(13)

The vector \({\mathbf{y}}(t)\) is the output vector, described by the coordinate vector q, the velocity vector \({\dot{\mathbf{q}}}\), and the acceleration vector \({\ddot{\mathbf{q}}}\), transferred in the Laplace domain:

$$ {\mathbf{Y}}(s) = {\mathcal{L}}\left\{ {{\mathbf{y}}(t)} \right\} = {\mathcal{L}}\left\{ {\left[ {\begin{array}{*{20}c} {{\mathbf{q}}(t)} \\ {{\dot{\mathbf{q}}}(t)} \\ {{\ddot{\mathbf{q}}}(t)} \\ \end{array} } \right]} \right\}. $$
(14)

The system matrix \({\mathbf{A}}_{{{\text{st}}}}\), the input matrix \({\mathbf{B}}_{{{\text{st}}}}\), the output matrix \({\mathbf{C}}_{{{\text{st}}}}\), and the straight-way matrix \({\mathbf{D}}_{{{\text{st}}}}\) are:

$$ \begin{gathered} {\mathbf{A}}_{{{\text{st}}}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}_{13} } & {{\mathbf{I}}_{13} } \\ { - {\mathbf{M}}^{ - 1} \cdot {\mathbf{C}}} & { - {\mathbf{M}}^{ - 1} \cdot {\mathbf{D}}} \\ \end{array} } \right];\;\;{\mathbf{B}}_{{{\text{st}}}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}_{13} } \\ {{\mathbf{M}}^{ - 1} } \\ \end{array} } \right]; \hfill \\ {\mathbf{C}}_{{{\text{st}}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{13} } & {\mathbf{0}_{13} } \\ {\mathbf{0}_{13} } & {{\mathbf{I}}_{13} } \\ { - {\mathbf{M}}^{ - 1} \cdot {\mathbf{C}}} & { - {\mathbf{M}}^{ - 1} \cdot {\mathbf{D}}} \\ \end{array} } \right];\;\;{\mathbf{D}}_{{{\text{st}}}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}_{13} } \\ {\mathbf{0}_{13} } \\ {{\mathbf{M}}^{ - 1} } \\ \end{array} } \right], \hfill \\ \end{gathered} $$
(15)

with the zero-matrix \({\mathbf{0}}_{13} \in {\mathbb{R}}^{13 \times 13}\) and the unit-matrix \({\mathbf{I}}_{13} \in {\mathbb{R}}^{13 \times 13}\). The transient excitation vector \({\mathbf{m}}_{{\text{e}}}\) is also transferred into the Laplace domain, considering that the signal \({\mathbf{m}}_{{\text{e}}} (t)\) is described as right-hand signal, using the Heaviside function \(\sigma (t)\):

$$ \begin{aligned} {\mathbf{M}}_{{\text{e}}} (s) & = {\mathcal{L}}\left\{ {{\mathbf{m}}_{{\text{e}}} (t)} \right\} = {\mathbf{P}}_{{\text{e}}} \cdot {\mathcal{L}}\left\{ {\mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot e^{{ - \alpha_{{{\text{e}},{\text{k}}}} \cdot t}} \cdot \sin \left( {\omega_{{{\text{e}},{\text{k}}}} \cdot t + \varphi_{{{\text{e}},{\text{k}}}} } \right) \cdot \sigma (t)} \right\} \\ & = {\mathbf{P}}_{{\text{e}}} \cdot \mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot \frac{{\cos \varphi_{{{\text{e}},{\text{k}}}} \cdot \omega_{{{\text{e}},{\text{k}}}} + \sin \varphi_{{{\text{e}},{\text{k}}}} \cdot \left( {s + \alpha_{{{\text{e}},{\text{k}}}} } \right)}}{{\left( {s + \alpha_{{{\text{e}},{\text{k}}}} } \right)^{2} + \omega_{{{\text{e}},{\text{k}}}}^{2} }} = {\mathbf{P}}_{{\text{e}}} \cdot M_{{\text{e}}} (s). \\ \end{aligned} $$
(16)

According to the state-space model (Fig. 4), the state space formulation can be written as:

$$ {\text{s}} \cdot {\mathbf{X}}(s) = {\mathbf{A}}_{{{\text{st}}}} \cdot {\mathbf{X}}(s) + {\mathbf{B}}_{{{\text{st}}}} \cdot [{\mathbf{M}}_{{\text{e}}} (s) + {\mathbf{F}}_{{\text{a}}} (s)] + {\mathbf{x}}( - 0) $$
(17)
$$ {\mathbf{Y}}(s) = {\mathbf{C}}_{{{\text{st}}}} \cdot {\mathbf{X}}(s) + {\mathbf{D}}_{{{\text{st}}}} \cdot [{\mathbf{M}}_{{\text{e}}} (s) + {\mathbf{F}}_{{\text{a}}} (s)], $$
(18)

with the Laplace transformed actuator force vector \({\mathbf{F}}_{{\text{a}}} (s)\), which can be described by the kinematic constrains (4), the Laplace-transformed vertical acceleration \(A_{{{\text{z}},{\text{s}}}} (s)\) and angular acceleration \(A_{{{\varphi },{\text{s}}}} (s)\) of the machine centre point \(S\), the controller transfer functions \(G_{{{\text{cL}}}} (s)\) and \(G_{{{\text{cR}}}} (s)\) in (1) and the force transmission vectors \({\mathbf{P}}_{{{\text{azL}}}}\) and \({\mathbf{P}}_{{{\text{azR}}}}\) in (8) and (9), or alternatively by the output vector \({\mathbf{Y}}(s)\) and a controller matrix \({\text{T}}_{{{\text{st}}}}\), referring to Fig. 4.

$$ {\mathbf{F}}_{{\text{a}}} (s) = - \left( {A_{{{\text{z}},{\text{s}}}} (s) - A_{{{{\varphi }},{\text{s}}}} (s) \cdot b} \right) \cdot G_{{{\text{cL}}}} (s) \cdot {\mathbf{P}}_{{{\text{azL}}}} - \left( {A_{{{\text{z}},{\text{s}}}} (s) + A_{{{\varphi },{\text{s}}}} (s) \cdot b} \right) \cdot G_{{{\text{cR}}}} (s) \cdot {\mathbf{P}}_{{{\text{azR}}}} = - {\mathbf{T}}_{{{\text{st}}}} \cdot {\mathbf{Y}}(s). $$
(19)

With Eq. (19), the controller matrix \({\mathbf{T}}_{{{\text{st}}}}\) can now by described by:

$$ {\mathbf{T}}_{{{\text{st}}}} = {\mathbf{T}}_{{{\text{st}}}} (s) = [\mathbf{0}_{13} ;\mathbf{0}_{13} ;{\mathbf{T}}_{{\text{a}}} (s)]\quad {\text{with:}} $$
(20)
$$ {\mathbf{T}}_{{\text{a}}} (s) = \left[ {\begin{array}{*{20}c} {G_{{{\text{cL}}}} (s) + G_{{{\text{cR}}}} (s)} & 0 & 0 & 0 & {b[G_{{{\text{cR}}}} (s) - G_{{{\text{cL}}}} (s)]} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {b[G_{{{\text{cR}}}} (s) - G_{{{\text{cL}}}} (s)]} & 0 & 0 & 0 & {b^{2} [G_{{{\text{cL}}}} (s) + G_{{{\text{cR}}}} (s)]} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ { - G_{{{\text{cL}}}} (s)} & 0 & 0 & 0 & {b \cdot G_{{{\text{cL}}}} (s)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ { - G_{{{\text{cR}}}} (s)} & 0 & 0 & 0 & { - b \cdot G_{{{\text{cR}}}} (s)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

With inserting Eq. (19) in (17) follows:

$$ {\mathbf{X}}(s) = \left( {s \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot \left\{ {{\mathbf{B}}_{{{\text{st}}}} \cdot \left[ {{\mathbf{M}}_{{\text{e}}} (s) - {\mathbf{T}}_{{{\text{st}}}} (s) \cdot {\mathbf{Y}}(s)} \right] + {\mathbf{x}}\left( { - 0} \right)} \right\}. $$
(21)

Now the Laplace transformed output vector \({\mathbf{Y}}(s)\) can be derived by inserting Eqs. (19) and (21) into (18), with the unit-matrices \({\mathbf{I}}_{39} \in {\mathbb{R}}^{39 \times 39}\) and \({\mathbf{I}}_{26} \in {\mathbb{R}}^{26 \times 26}\):

$$ \begin{aligned} {\mathbf{Y}}(s) & = \left[ {{\mathbf{I}}_{39} + {\mathbf{C}}_{{{\text{st}}}} \cdot \left( {s \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s) + {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s)} \right]^{ - 1} \\ & \quad \cdot \left[ {{\mathbf{C}}_{{{\text{st}}}} \cdot \left( {{\text{s}} \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot \left\{ {{\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{M}}_{{\text{e}}} (s) + {\mathbf{x}}\left( { - 0} \right)} \right\} + {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{M}}_{{\text{e}}} (s)} \right]. \\ \end{aligned} $$
(22)

To solve Eq. (22) the vector of the initial conditions \({\mathbf{x}}\left( { - 0} \right)\) has to be derived.

$$ {\mathbf{x}}\left( { - 0} \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}\left( { - 0} \right)} \\ {{\dot{\mathbf{q}}}\left( { - 0} \right)} \\ \end{array} } \right]. $$
(23)

For the 2-phase terminal shot circuit and the 3-phase terminal shot circuit, a stationary condition has to be considered, where the static torque (\(m_{{\text{e}}} = m_{{{\text{stat}}}} = {\text{cons}}.\)) is acting. The initial translational and rotational displacements can now be calculated by using Eq. (3), with the static conditions \({\dot{\mathbf{q}}} = {\ddot{\mathbf{q}}} = \mathbf{0}\) and \({\mathbf{f}}_{{\text{a}}} = \mathbf{0}\):

$$ {\mathbf{q}}\left( { - 0} \right) = {\mathbf{C}}^{ - 1} \cdot {\mathbf{m}}_{{{\text{stat}}}} = {\mathbf{C}}^{ - 1} \cdot {\mathbf{P}}_{{\text{e}}} \cdot m_{{{\text{stat}}}} . $$
(24)

Therefore, the vector of the initial conditions \({\mathbf{x}}\left( { - 0} \right)\) can be described by:

$$ {\mathbf{x}}\left( { - 0} \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}^{ - 1} \cdot {\mathbf{P}}_{{\text{e}}} \cdot m_{{{\text{stat}}}} } \\ \mathbf{0} \\ \end{array} } \right]. $$
(25)

Now, the Laplace transformed output vector \(Y(s) \) can be calculated and hereby the Laplace transformed dynamic foundation forces:

$$ {\text{Left side}},{\text{ vertical:}}\;F_{{{\text{fzL}}}} (s) = c_{{{\text{fzL}}}} \cdot Y_{8} (s) + d_{{{\text{fzL}}}} \cdot Y_{21} (s). $$
(26)
$$ {\text{Right side}},{\text{ vertical:}}\;F_{{{\text{fzR}}}} (s) = c_{{{\text{fzR}}}} \cdot Y_{9} (s) + d_{{{\text{fzR}}}} \cdot Y_{22} (s). $$
(27)
$$ {\text{Left side}},{\text{ horizontal:}}\;F_{{{\text{fyL}}}} (s) = c_{{{\text{fyL}}}} \cdot Y_{12} (s) + d_{{{\text{fyL}}}} \cdot Y_{25} (s). $$
(28)
$$ {\text{Right side}},{\text{ horizontal:}}\;F_{{{\text{fyR}}}} (s) = c_{{{\text{fyR}}}} \cdot Y_{13} (s) + d_{{{\text{fyR}}}} \cdot Y_{26} (s). $$
(29)

and the Laplace transformed actuator forces for each motor side by:

$$ {\text{Left side:}}\;F_{{{\text{azL}}}} (s) = - G_{{{\text{cL}}}} (s) \cdot \left[ {Y_{27} (s) - Y_{31} (s) \cdot b} \right]. $$
(30)
$$ {\text{Right side:}}\;F_{{{\text{azR}}}} (s) = - G_{{{\text{cR}}}} (s) \cdot \left[ {Y_{27} (s) + Y_{31} (s) \cdot b} \right]. $$
(31)

The element \(Y_{n} (s)\) is the nth element of the Laplace transformed output vector \({\mathbf{Y}}(s)\). When transforming the output vector \({\mathbf{Y}}(s)\) back into the time domain—\({\mathbf{y}}(t) = {\mathcal{L} }^{ - 1} \left\{ {{\mathbf{Y}}(s)} \right\}\)—the foundation and actuator forces in the time domain can be derived.

To derive the transfer matrix \({\mathbf{G}}(s)\), the vector for the initial conditions has to be the zero vector \({\mathbf{x}}\left( { - 0} \right) = \mathbf{0}\). Therefore, follows for the output vector \({\mathbf{Y}}(s)\):

$$ {\mathbf{Y}}(s) = {\mathbf{G}}(s) \cdot {\mathbf{M}}_{{\text{e}}} (s). $$
(32)

with the transfer matrix \({\mathbf{G}}(s)\):

$$ {\mathbf{G}}(s) = \left[ {{\mathbf{I}}_{39} + {\mathbf{C}}_{{{\text{st}}}} \cdot \left( {s \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s) + {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s)} \right]^{ - 1} \cdot \left[ {{\mathbf{C}}_{{{\text{st}}}} \cdot \left( {s \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\text{st}}}} + {\mathbf{D}}_{{{\text{st}}}} } \right]. $$
(33)

Considering Eq. (16), follows:

$$ {\mathbf{Y}}(s) = {\mathbf{G}}(s) \cdot \underbrace {{{\mathbf{P}}_{{\text{e}}} \cdot M_{{\text{e}}} (s)}}_{{{\mathbf{M}}_{{\text{e}}} (s)}}, $$
(34)

and the transfer vector \({\mathbf{G}}_{{\text{v}}} (s)\) can be written by:

$$ {\mathbf{G}}_{{\text{v}}} (s) = \frac{{{\mathbf{Y}}(s)}}{{M_{{\text{e}}} (s)}} = {\mathbf{G}}(s) \cdot {\mathbf{P}}_{{\text{e}}} . $$
(35)

For deriving the poles of the system, the vector \({\mathbf{M}}_{{\text{e}}} (s)\) has to be set to the zero vector \({\mathbf{M}}_{{\text{e}}} (s) = \mathbf{0}\), as well as the vector of the initial conditions \({\mathbf{x}}\left( { - 0} \right) = \mathbf{0}\). Therefore follows:

$$ s \cdot {\mathbf{X}}(s) = {\mathbf{A}}_{{{\text{st}}}} \cdot {\mathbf{X}}(s) - {\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} \cdot {\mathbf{Y}}(s) $$
(36)
$$ {\mathbf{Y}}(s) = {\mathbf{C}}_{{{\text{st}}}} \cdot {\mathbf{X}}(s) - {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} \cdot {\mathbf{Y}}(s). $$
(37)

These two equations, lead to

$$ \begin{aligned} & \left[ {{\mathbf{I}}_{26} \cdot s - {\mathbf{A}}_{{{\text{st}}}} + {\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s) \cdot \left( {{\mathbf{I}}_{39} + {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s)} \right)^{ - 1} \cdot {\mathbf{C}}_{{{\text{st}}}} } \right]\\ &\quad \cdot {\mathbf{X}}(s) = \mathbf{0}, \end{aligned} $$
(38)

and the poles can be directly calculated by solving the following equation:

$$ {\text{det}}\left[ {{\mathbf{I}}_{26} \cdot s - {\mathbf{A}}_{{{\text{st}}}} + {\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s) \cdot \left( {{\mathbf{I}}_{39} + {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} (s)} \right)^{ - 1} \cdot {\mathbf{C}}_{{{\text{st}}}} } \right] = 0. $$
(39)

3.3 Description in Fourier domain

For analysis of the system behavior regarding pulsating air gap torques, caused by the converter, following Fourier transformation can be done:

$$ \begin{aligned} {\mathbf{M}}_{{\text{e}}} \left( {j\omega } \right) & = {\mathcal{F}}\left\{ {{\mathbf{m}}_{{\text{e}}} (t)} \right\} = {\mathcal{F}}\left\{ {{\mathbf{P}}_{{\text{e}}} \cdot m_{{\text{e}}} (t)} \right\} = {\mathbf{P}}_{{\text{e}}} \cdot {\mathcal{F}}\left\{ {\underbrace {{\mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot \sin \left( {\omega_{{{\text{e}},{\text{k}}}} \cdot t + \varphi_{{{\text{e}},{\text{k}}}} } \right)}}_{{m_{{\text{e}}} (t)}}} \right\} \\ & = {\mathbf{P}}_{{\text{e}}} \cdot \frac{\pi }{j} \cdot \mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot \left[ {e^{{j\varphi_{{{\text{e}},{\text{k}}}} }} \cdot \delta \left( {\omega - \omega_{{{\text{e}},{\text{k}}}} } \right) - e^{{ - j\varphi_{{{\text{e}},{\text{k}}}} }} \cdot \delta \left( {\omega + \omega_{{{\text{e}},{\text{k}}}} } \right)} \right]. \\ \end{aligned} $$
(40)

With transferring the transfer matrix (33) into the Fourier-domain: \({\mathbf{G}}(s) \xrightarrow{s = j\omega } {\mathbf{G}}\left( {j\omega } \right)\) follows:

$$ \begin{aligned} {\mathbf{G}}\left( {j\omega } \right) & = \left[ {{\mathbf{I}}_{39} + {\mathbf{C}}_{{{\text{st}}}} \cdot \left( {j\omega \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} \left( {j\omega } \right) + {\mathbf{D}}_{{{\text{st}}}} \cdot {\mathbf{T}}_{{{\text{st}}}} \left( {j\omega } \right)} \right]^{ - 1} \\ & \quad \cdot \left[ {{\mathbf{C}}_{{{\text{st}}}} \cdot \left( {j\omega \cdot {\mathbf{I}}_{26} - {\mathbf{A}}_{{{\text{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\text{st}}}} + {\mathbf{D}}_{{{\text{st}}}} } \right]. \\ \end{aligned} $$
(41)

Therefore, the output vector in the Fourier domain gets:

$$ \begin{aligned} {\mathbf{Y}}\left( {j\omega } \right) & = {\mathbf{G}}\left( {j\omega } \right) \cdot {\mathbf{M}}_{{\text{e}}} \left( {j\omega } \right) \\ & = \underbrace {{{\mathbf{G}}(j\omega ) \cdot {\mathbf{P}}_{{\text{e}}} }}_{{{\mathbf{G}}_{{\text{v}}} (j\omega )}} \cdot \underbrace {{\frac{\pi }{j} \cdot \mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot [e^{{j\varphi_{{{\text{e}},{\text{k}}}} }} \cdot \delta (\omega - \omega_{{{\text{e}},{\text{k}}}} ) - e^{{ - j\varphi_{{{\text{e}},{\text{k}}}} }} \cdot \delta (\omega + \omega_{{{\text{e}},{\text{k}}}} )]}}_{{M_{e} (j\omega )}} \\ \end{aligned} $$
(42)

With the shifting property of the Dirca delta functions \(\delta \left( {\omega - \omega_{{{\text{e}},{\text{k}}}} } \right)\) and \(\delta \left( {\omega + \omega_{{{\text{e}},{\text{k}}}} } \right)\) follows:

$$ {\mathbf{Y}}\left( {j\omega } \right) = \frac{\pi }{j} \cdot \mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \left[ {{\mathbf{G}}_{{\text{v}}} \left( {j\omega_{{{\text{e}},{\text{k}}}} } \right) \cdot e^{{j\varphi_{{{\text{e}},{\text{k}}}} }} \cdot \delta \left( {\omega - \omega_{{{\text{e}},{\text{k}}}} } \right) - {\mathbf{G}}_{{\text{v}}} \left( { - j\omega_{{{\text{e}},{\text{k}}}} } \right) \cdot e^{{ - j\varphi_{{{\text{e}},{\text{k}}}} }} \cdot \delta \left( {\omega + \omega_{{{\text{e}},{\text{k}}}} } \right)} \right]. $$
(43)

By transferring (43) back into the time domain, follows the output vector in the time domain:

$$ \begin{aligned} {\mathbf{y}}(t) & = {\mathcal{F}}^{ - 1} \left\{ {{\mathbf{Y}}\left( {j\omega } \right)} \right\} \\ & = \mathop \sum \limits_{k} \hat{m}_{{{\text{e}},{\text{k}}}} \cdot \left[ {\begin{array}{*{20}c} {\left| {G_{{{\text{v}},1}} \left( {j\omega_{{{\text{e}},{\text{k}}}} } \right)} \right| \cdot \sin \left( {\omega_{{{\text{e}},{\text{k}}}} \cdot t + \varphi_{{{\text{e}},{\text{k}}}} + \arg G_{{{\text{v}},1}} \left( {j\omega_{{{\text{e}},{\text{k}}}} } \right)} \right)} \\ \vdots \\ {\left| {G_{{{\text{v}},39}} \left( {j\omega_{{{\text{e}},{\text{k}}}} } \right)} \right| \cdot \sin \left( {\omega_{{{\text{e}},{\text{k}}}} \cdot t + \varphi_{{{\text{e}},{\text{k}}}} + \arg G_{{{\text{v}},39}} \left( {j\omega_{{{\text{e}},{\text{k}}}} } \right)} \right)} \\ \end{array} } \right]. \\ \end{aligned} $$
(44)

For a single pulsating excitation torque, the transfer vector can be written by:

$$ {\mathbf{G}}_{{\text{v}}} \left( {j\omega } \right) = \frac{{{\mathbf{Y}}\left( {j\omega } \right)}}{{M_{e} \left( {j\omega } \right)}} = {\mathbf{G}}\left( {j\omega } \right) \cdot {\mathbf{P}}_{{\text{e}}} , $$
(45)

and the frequency response functions regarding the dynamic foundation forces follow with:

$$ {\text{Left side}},{\text{ vertical:}}\;G_{{{\text{FfzL}}}} \left( {j\omega } \right) = c_{{{\text{fzL}}}} \cdot G_{{{\text{v}},8}} \left( {j\omega } \right) + d_{{{\text{fzL}}}} \cdot G_{{{\text{v}},21}} \left( {j\omega } \right). $$
(46)
$$ {\text{Right side}},{\text{ vertical:}}\;G_{{{\text{FfzR}}}} \left( {j\omega } \right) = c_{{{\text{fzR}}}} \cdot G_{{{\text{v}},9}} \left( {j\omega } \right) + d_{{{\text{fzR}}}} \cdot G_{{{\text{v}},22}} \left( {j\omega } \right). $$
(47)
$$ {\text{Left side}},{\text{ horizontal:}}\;G_{{{\text{FfyL}}}} \left( {j\omega } \right) = c_{{{\text{fyL}}}} \cdot G_{{{\text{v}},12}} \left( {j\omega } \right) + d_{{{\text{fyL}}}} \cdot G_{{{\text{v}},25}} \left( {j\omega } \right). $$
(48)
$$ {\text{Right side}},{\text{ horizontal:}}\;G_{{{\text{FfyR}}}} \left( {j\omega } \right) = c_{{{\text{fyR}}}} \cdot G_{{{\text{v}},13}} \left( {j\omega } \right) + d_{{{\text{fyR}}}} \cdot G_{{{\text{v}},26}} \left( {j\omega } \right). $$
(49)

as well as the frequency response functions regarding the actuator forces for each motor side:

$$ {\text{Left side:}}\;G_{{{\text{FazL}}}} \left( {j\omega } \right) = - G_{{{\text{cL}}}} \left( {j\omega } \right) \cdot \left[ {G_{{{\text{v}},27}} \left( {j\omega } \right) - G_{{{\text{v}},31}} \left( {j\omega } \right) \cdot b} \right]. $$
(50)
$$ {\text{Right side:}}\;G_{{{\text{FazR}}}} \left( {j\omega } \right) = - G_{{{\text{cR}}}} \left( {j\omega } \right) \cdot \left[ {G_{{{\text{v}},27}} \left( {j\omega } \right) + G_{{{\text{v}},31}} \left( {j\omega } \right) \cdot b} \right]. $$
(51)

The element \(G_{{{\text{v}},{\text{n}}}} \left( {j\omega } \right)\) is the nth element of the transfer vector \({\mathbf{G}}_{{\text{v}}} \left( {j\omega } \right)\).

4 Simulation model

After the mathematical coherences of the system are described the simulation tool SIMULINK is used for numerical solution. The basic block diagram is shown in Fig. 5.

Fig. 5
figure 5

Simulation model in SIMULINK (block diagram)

Full size image

The excitation by a dynamic air gap torque “\(\mathrm{me}\)” is implemented in the model by the orange-colored block. By multiplying the signal \("\mathrm{me}"\) with the vector “\(\mathrm{Pe}\)” from (6) the dynamic air gap torque becomes a vector and can be used as input signal for the state space block. In the state space block the matrices \({\mathbf{A}}_{\mathrm{st}}\), \({\mathbf{B}}_{\mathrm{st}}\), \({\mathbf{C}}_{\mathrm{st}}\) and \({\mathbf{D}}_{\mathrm{st}}\) from (15) are used, as well as the vector for the initial conditions \(\mathbf{x}\left(-0\right)\) from (25). The actuator forces “fazL” and “fazR” are created by the negative feedback loops of the vertical motor feet accelerations “a_zaL” and “a_zaR” considering (4) and the controller transfer functions “GcL(s)” and “GcR(s)” (marked yellow) from (1). By multiplying the scalar quantities “fazL” and “fazR” with the vectors “PazL” and “PazR” from (8) and (9) the actuator force vectors are created, which are also used as input signals for the state space block. If the feedback loops are closed, the control system is operating. If the switches are open, the control system is switched off and the actuator forces are zero. In this case, the actuators are only acting passively. In a subsystem—marked blue—, the dynamic foundation forces “fzL”, “fzR”, “fyL” and “fyR” are calculated, according to (26), (27), (28) and (29).

5 Numerical example

In this section, a numerical example is presented, where dynamic foundation forces, as well as actuator forces due to dynamic air gap torques of a 2-pole induction motor, are analyzed. Additionally, a natural vibration analysis is deduced.

5.1 Boundary conditions

The motor is a 2-pole induction motor with roller bearings, converter driven with constant magnetization and with constant load—which corresponds here to the rated load—in the speed range from 300 to 3600 rpm. Three different cases are analyzed:

  • Case 1: Motor directly mounted on a steel frame foundation.

  • Case 2: Actuators between motor feet and steel frame foundation, passive operation.

  • Case 3: Actuators between motor feet and steel frame foundation, active operation.

The most important data are shown in Table 1.

Table 1 Main data of the induction motor, bearings, foundation and actuators
Full size table
Table 2 Poles \(s_{\infty ,i}\), natural frequencies \(f_{{\text{i}}}\), and modal damping values \(D_{{\text{i}}}\) of the first five natural vibrations modes for the different cases
Full size table

The used actuators are here electrodynamic actuators (voice coil actuators), acting in vertical direction (z-direction). The motor weight is completely carried by separate springs, which are positioned near each actuator. Therefore, the generated actuator forces only have to compensate dynamic loads, no static loads.

The damping coefficients of the foundation and of the actuators at each motor side for the arrangement according to Fig. 2 are calculated simplified—referring to [5]—by:

$$ \begin{aligned} d_{{{\text{fqn}}}} & = 2D_{{\text{f}}} \cdot \sqrt {\left( {m_{{{\text{fn}}}} + m_{{{\text{as}}}} } \right) \cdot c_{{{\text{fqn}}}} } ;\\ d_{{{\text{aq}}}} &= 2D_{a} \cdot \sqrt {\left( {\frac{{m_{{\text{s}}} }}{2} + m_{{{\text{aa}}}} } \right) \cdot c_{{{\text{aq}}}} } \\ & \quad \quad {\text{with:}}\; n = L,R;\; q = y,z. \\ \end{aligned} $$
(52)

For this pure theoretical analysis—without considering parasitic dynamics, measuring noise, etc.—simply I-controllers are used for the control system, with following controller transfer functions for both sides:

$$ G_{{{\text{cL}}}} (s) = G_{{{\text{cR}}}} (s) = \frac{{b_{0} }}{s} \quad {\text{with:}}\;b_{0} = 2.0 \times 10^{5} \frac{{{\text{kg}}}}{{\text{s}}}. $$
(53)

In praxis, more practical controllers are useful, e.g. low-pass controllers or lag controllers for stabilization of the acceleration feedbacks [8]. The coefficient \(b_{0}\) is here only roughly chosen because it is not the aim of the paper to find the optimal justification of the controllers for this example but to show the fundamental influence of the control system.

5.2 Natural vibration analysis

The interesting poles for the three different cases are shown in Fig. 6.

Fig. 6
figure 6

Pole diagram for the different cases

Full size image

Only the first five natural vibrations are here of interest. Higher modes are not useful here and the vibration model is also not detailed enough for calculating higher modes. Figure 6 shows, that no poles are lying on the right side of the pole diagram, therefore the system is stable for all three cases. It can be shown in Fig. 6, that four of five conjugate complex poles for case 2 can be clearly shifted to the left—increasing the modal damping—, when the control system is switched on (case 3). The conjugate complex poles \(s_{\infty ,i}\), the natural frequencies \(f_{{\text{i}}}\), and the modal damping values \(D_{{\text{i}}}\) of the first five natural vibrations modes for the different cases are shown in Table 2. It has to be pointed out, that the modes in Table 2 are ascending numbered according to their natural frequency. Therefore, mode 5 in case 3 corresponds to mode 4 in case 2 in terms of shape. The modes for case 1 and case 2 are pictured in Fig. 7.

Fig. 7
figure 7

First five natural modes for case 1 and case 2

Full size image

It can be shown that for case 1 (motor directly mounted on the steel frame foundation) the natural frequencies of the first five modes are lying in a range between 16.8 and 69.7 Hz. When placing actuators between motor feet and steel frame foundation—without using the control system—(case 2), the first three natural frequencies decrease strongly. In both cases, the modal damping values of all modes are very low. When using the control system (case 3), the natural frequencies are changing only marginal compared to case 2, which can be seen in Table 2. However, the modal damping of the first four modes can be increased significantly. Only mode 4 for case 2 in Fig. 7 can hardly be influenced by the control system, because nearly no vertical motor feet vibrations occur for this mode shape (Fig. 7). For this mode, the control system is not effective. Additionally Fig. 7 shows that for case 1 the motor feet points \(A_{{\text{L}}}\) and \(A_{{\text{R}}}\) are identical with the foundation points \(F_{{\text{L}}}\) and \(F_{{\text{R}}}\), because the motor is directly mounted on the foundation. For case 2 the movements of the motor feet points are much higher for all mode shapes, compared to the movement of the foundation points. The reason is here that the stiffness of the actuators is much lower than the stiffness of the foundation.

5.3 Frequency response analysis

Now, the amplitudes of the frequency response functions between foundation and actuator forces (outputs) and a single pulsating air gap torque (input) are calculated. The amplitudes of the frequency response functions are calculated in \(\left[ {{\text{dB}}} \right]\) with the reference gauge in SI-Unit, in a frequency range from 1 to 100 Hz. Amplitudes of the frequency response functions regarding the dynamic foundation forces (54) and the actuator forces (55):

$$ \left| {G_{{{\text{Ffqn}},{\text{case m }}}} \left( {j\omega } \right)} \right|_{{{\text{dB}}}} = 20 \cdot \log \left( {\frac{{\left| {G_{{{\text{Ffqn}},{\text{case m }}}} \left( {j\omega } \right)} \right|}}{{G_{{{\text{ref}}}} }}} \right); $$
(54)
$$ \begin{aligned} \left| {G_{{{\text{Fazn}}}} \left( {j\omega } \right)} \right|_{{{\text{dB}}}} & = 20 \cdot {\text{log}}\left( {\frac{{\left| {G_{{{\text{Fazn}}}} \left( {j\omega } \right)} \right|}}{{G_{{{\text{ref}}}} }}} \right); \\ & \quad \quad {\text{with:}}\;n = L,R;\; q = y,z;\\ & m = 1,2,3;\;\;G_{{{\text{ref}}}} = 1\;\frac{{\text{N}}}{{{\text{Nm}}}}. \\ \end{aligned} $$
(55)

Additionally, the phase response functions for the actuator forces are calculated. The amplitude response functions regarding the dynamic vertical and horizontal foundation forces are shown in Fig. 8 for the different cases. They are identical for the left and right sides of the motor.

Fig. 8
figure 8

Amplitude response functions regarding a vertical dynamic foundation forces and b horizontal dynamic foundation forces, for the different cases

Full size image

For case 1, three significant resonances occur regarding the dynamic vertical and horizontal foundation forces, which correspond to the natural frequencies of modes 1, 3 and 4 in Fig. 7. For cases 1 and 2, modes 2 and 5 in Fig. 7 will not be excited by a dynamic air gap torque and therefore no resonances occur at these frequencies in Fig. 8. For case 2, the resonances are shifted to lower frequencies—compared to case 1—and only two resonance frequencies occur regarding vertical dynamic foundation forces. Regarding horizontal dynamic foundation forces still, three resonances exist, but the third resonance has only a very small amplitude. The reason is that mode 4 (for case 2) is hardly excited by a torque (Fig. 7). Figure 8 shows, that the important resonances can be damped clearly by active vibration control (case 3). Only the third resonance regarding the horizontal dynamic foundation forces can hardly be influenced. However, this resonance seems uncritical, because of its low amplitude. In Fig. 9 the amplitude response functions regarding the actuator forces (case 3) on the left side and on the right side of the motor are presented. It can be demonstrated, that the amplitudes are identical on the right side and on the left side, and that a phase shift of 180° to each other exists and that the maximum amplitudes in Fig. 9 occur at nearly the same resonance frequencies as for the vertical dynamic foundation forces (case 2 in Fig. 8).

Fig. 9
figure 9

Response functions (amplitude and phase) regarding the actuator forces (case 3) on the left side (red line) and on the right side (blue line) of the motor

Full size image

5.4 Simulation of a 3-phase terminal short circuit

Now, the dynamic foundation forces due to a 3-phase terminal short circuit are analyzed for all three cases, first at rated conditions (see Table 1). The dynamic air gap torque \(m_{{\text{e}}} (t)\) of the 3-phase terminal short at rated conditions is shown in Fig. 10.

Fig. 10
figure 10

Dynamic air gap torque due to 3-phase terminal short circuit at rated conditions

Full size image

The vertical and horizontal dynamic foundation forces on the left side of the motor due to a 3-phase terminal short circuit at rated conditions for different cases are show in Fig. 11. The horizontal foundation forces are identical on the right and on the left side of the motor. However, the vertical foundation forces on the right side are only mirrored at the time axis in Fig. 11a. Figure 11 shows, that the highest dynamic foundation forces occur for case 1, where the motor is directly mounted on the steel frame foundation. The horizontal dynamic foundation forces start at zero, whereas the vertical dynamic foundation forces start at 6026 N, which is caused by the rated torque, corresponding to initial conditions in Eq. (25). Using active vibration control (case 3) reduces the maximum peak of the dynamic foundation forces compared to case 2 at about 4% for vertical direction and at about 28% for horizontal direction. Additionally, the dynamic foundation forces decay much faster for case 3.

Fig. 11
figure 11

Vertical a and horizontal b dynamic foundation forces on the left side of the motor due to a 3-phase terminal short circuit at rated conditions for different cases

Full size image

The actuator forces on the left side and on the right side of the motor are pictured in Fig. 12. It can be seen, that they are opposite to each other and decaying fast.

Fig. 12
figure 12

Actuator forces (left and right side) of the motor due to a 3-phase terminal short circuit at rated conditions

Full size image

Now, an analysis of 3-phase terminal short circuits at different electrical supply frequencies is presented. The maximum peak of the vertical and horizontal dynamic foundation forces per motor side for different electrical supply frequencies is shown in Fig. 13.

Fig. 13
figure 13

Maximum peak of a vertical and b horizontal dynamic foundation forces per motor side due to a 3-phase terminal short circuit at different electrical supply frequencies and for different cases

Full size image

The electrical supply frequency is increased from 5 to 60 Hz in 5 Hz steps. Two additionally supply frequencies—6.7 Hz and 17.2 Hz—are added, so that now all critical states can be simulated, where the frequency of the oscillating air gap torque is close a critical natural frequency of modes 1 and 3 (Table 3).

Table 3 Electrical supply frequencies, where the frequency of the oscillating air gap torque is close a critical natural frequency
Full size table

Figure 13 shows that for case 1 and case 2 the maximum peaks of the dynamic foundation forces occur when the frequency of the oscillating air gap torque is close a critical natural frequency. This means at an electrical supply of 17.2 Hz and 50 Hz for case 1 and at an electrical supply of 6.7 Hz and 20 Hz for case 2. Figure 13 shows clearly that with active vibration control (case 3) the maximum peak of the vertical dynamic foundation force can be reduced from \(5.60 \times 10^{4} \;{\text{N}}\)—occurring at 50 Hz operation for case 1—to \(3.44 \times 10^{4} \;{\text{N}}\)—occurring at 5 Hz operation for case 3, which presents a reduction of about 38.6%. The maximum peak of the horizontal dynamic foundation force can be reduced from \(5.11 \times 10^{4} \;{\text{N}}\)—occurring at 50 Hz operation for case 1—to \(2.63 \times 10^{4} \;{\text{N}}\)—occurring at 15 Hz operation for case 3, which presents a reduction of about 48.5%. The maximum peak of the actuator force per motor side occurs at electrical supply frequency of 25 Hz with an amplitude of \(1.58 \times 10^{4} \;{\text{N}}\) actuator force for each motor side (Fig. 14).

Fig. 14
figure 14

Maximum peak of the actuator force per motor side due to a 3-phase terminal short circuit at different electrical supply frequencies

Full size image

6 Conclusion

In the paper, a theoretical analysis regarding foundation forces caused by dynamic air gap torques of converter-driven induction motors, influenced by active vibration control, was shown. Based on a plane model, where actuators are placed between the motor feet and steel frame foundation and where the vertical motor feet accelerations are controlled, a mathematical description in the time domain, in the Laplace domain and in the Fourier domain was presented, as well as a block diagram for numerical simulation. The mathematical model was verified with numerical simulations in SIMULINK, and also a finite element analysis was used for verification. A numerical example was presented, where a 2-pole induction motor (2 MW) was analyzed. Three different cases—motor directly mounted on a steel frame foundation (case 1), actuators between motor feet and foundation, operating passively (case 2) and actively (case 3)—have been investigated. It could be shown, that with the chosen active vibration control system the most important natural vibrations can be clearly damped (Sect. 5.2). A harmonic analysis regarding excitation by a single pulsating air gap torque (Sect. 5.3) showed, that the resonance amplitudes of the foundation forces can be reduced strongly by active vibration control. Therefore, this concept seems to be very effective for reducing foundation forces caused by pulsating air gap torques of converter-driven induction motors, not least because the maximum amplitudes of such pulsating air gap torques are usually very low (only a few percentage of the rated torque for such applications). Section 5.4 showed, that also the possibility seems to be given to reduce foundation forces, caused by transient air gap torques (e.g. 3-phase terminal short circuit). However, this belongs on different boundary conditions, e.g. limit of actuator force, transfer function of the actuators, dead time and clock frequency in a digital control system, etc. Therefore, a more detailed control system analysis has to be done, to make a definitely statement for active vibration control regarding transient air gap torques. Finally, this theoretical analysis shows that with the presented control system a possibility seams to be given to reduce foundation forces caused by pulsating and transient air gap torques of converter-driven induction motors.