1 Introduction

The inverter supply of electrical motors can lead to EDM bearing currents, which can result in matted raceway and rolling element surfaces, periodic raceway corrugation structures and chemical lubricant changes [1]. EDM currents occur in the area of liquid friction/full lubrication when the critical field strength of the lubricating film in the rolling bearing is exceeded and resulted from the discharge of the bearing capacitance [2]. The bearing voltage \( U_{\text{l}} \) is the image of the common mode voltage \( U_{\text{cm}} \) and can be calculated by means of the capacitive voltage divider [3] as

$$ U_{\text{l}} = \frac{{C_{\text{wr}} }}{{C_{\text{wr}} + C_{\text{sr}} + C_{l1} + C_{l2} }} \cdot U_{\text{cm}} . $$
(1)

The capacitive voltage divider is composed of the winding-to-rotor capacitance \( C_{\text{wr}} \), the stator-to-rotor capacitance \( C_{\text{sr}} \) and the capacitances of the two bearings \( C_{{{\text{l}}1}} \) and \( C_{{{\text{l}}2}} \). The winding-to-rotor capacitance, which is composed of the motor’s slot and end-winding portion, is decisive for the amount of bearing voltage applied [4, 5]. The end-winding portion of the winding-to-rotor capacitance can be estimated analytically or numerically. In [6], a complex 3D FEM simulation is performed to determine the capacitance. The current analytical determination of the end-winding portion of the winding-to-rotor capacitance is based on the calculation of a cylindrical capacitor [7,8,9]. The basic problem when applying the calculation rule for a cylindrical capacitor is the one-dimensional potential problem used for derivation. When using a cylindrical capacitor, the influenced charge on the front surface of the rotor is not taken into account due to the purely radially assumed E-field.

In order to consider the influence of the charge influenced on the lateral surface of the rotor properly in the calculation of the end-winding portion of the winding-to-rotor capacitance, a limited, two-dimensional field problem can be solved.

2 Modelling the end-winding of an electrical machine

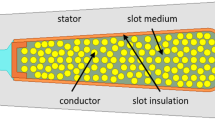
Figure 1 illustrates a simplified, rotationally symmetrical geometry of an electric machine. An electric machine consists of an active part, which extends over the length of the stator core, and the end-windings. The stator winding is galvanically separated from the stator core by insulation.

Fig. 1
figure 1

Simplified longitudinal section of an electric machine

Full size image

For the determination of the end-winding portion of the winding-to-rotor capacitance, only the end-winding geometry is considered.

A simplified, rotationally symmetrical end-winding geometry of an electric machine is shown in Fig. 2. The entire area, which consists of the insulation protruding into the end-winding region, the potting compound, if applicable, and the air region, is axially limited by the stator core and the end shield. In radial direction, the area is limited by the rotor and the stator housing.

Fig. 2
figure 2

Simplified longitudinal section of the end-winding of an electric machine

Full size image

It is assumed that the majority of the capacitive coupling between the stator end-winding and the rotor takes place in the field area of interest marked with dashes in Fig. 2.

On the area’s left-hand side, the stator core is located between the insulation and the air gap. On the right-hand boundary in longitudinal direction, the E-field should only have a tangential component. Assuming Neumann boundary conditions, no E-field escapes from the area (Fig. 3).

Fig. 3
figure 3

Model of the considered geometry with boundary conditions

Full size image

Overall, the calculation model is based on the following simplifications:

  • The capacitive coupling between the stator end-winding and the rotor takes place in the area between the end-winding and the rotor.

  • The stator core, the stator winding and the rotor are ideally electrically conductive.

  • There are no space charges within the considered area.

  • The media within the considered geometry consist of materials with constant permittivity.

3 Determination of the end-winding portion of the winding-to-rotor capacitance

The field area of the area of interest drawn in Fig. 2 is enlarged. The spatial area is described in cylindrical coordinates and is rotationally symmetrical around the longitudinal coordinate. It is limited in radial direction by the horizontal stator end-winding with the potential \( \varphi_{\text{w}} \) and the stepped contour of the rotor with the potential \( \varphi_{\text{r}} \). The stator has the potential \( \varphi_{\text{s}} \). The total length in the axial direction of the area of interest corresponds to the winding overhang.

The area of interest consists of three materials with different permittivities. The first medium with the permittivity \( \varepsilon_{1} \) is used to consider an insulation with the axial length \( l_{\text{iso}} \) protruding into the end-winding region. A possibly casting component of the end-winding is covered by the second material with the permittivity \( \varepsilon_{2} \). The third medium considers the medium adjacent to the rotor with the permittivity \( \varepsilon_{3} \), i.e. air. With the exception of the Dirichlet boundary condition on the radial axis used to consider the stator lamination, the axial limitation of the area is done by specifying Neumann boundary conditions. The Dirichlet boundary conditions specify the values of the solution along the boundaries, and the Neumann boundary conditions specify the derivate of the solution along the boundaries.

The determination of the end-winding portion of the winding-to-rotor capacitance is carried out with the aid of Maxwell’s capacitance coefficients, with which the concept of capacitance can be transferred to systems consisting of several electrodes insulated from each other [10]. In the present problem, the electrodes are considered to be the stator end-winding with the charge \( Q_{\text{w}} \) and the potential \( \varphi_{\text{w}} \), the stator with the charge \( Q_{s} \) and the potential \( \varphi_{\text{s}} \) and the rotor with the charge \( Q_{\text{r}} \) and the potential \( \varphi_{\text{r}} \). The corresponding capacitance coefficient matrix is

$$ \left( {\begin{array}{*{20}c} {Q_{\text{w}} } \\ {Q_{\text{s}} } \\ {Q_{\text{r}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {c_{\text{ww}} } & {c_{\text{ws}} } & {c_{\text{wr}} } \\ {c_{\text{sw}} } & {c_{\text{ss}} } & {c_{\text{sr}} } \\ {c_{\text{rw}} } & {c_{\text{rs}} } & {c_{\text{rr}} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\varphi_{\text{w}} } \\ {\varphi_{\text{s}} } \\ {\varphi_{\text{r}} } \\ \end{array} } \right). $$
(2)

The capacitance coefficients \( c_{\mu v} \) correspond to the capacitances \( C_{\mu v} \) for counter capacitances \( \mu \ne v \), establishing a connection between the charges and the potential differences. By selecting a stator and a rotor potential of zero volts each, the end-winding portion of the winding-to-rotor capacitance \( C_{\text{wr}} \) is calculated according to (2) as

$$ C_{\text{wr}} = c_{\text{rw}} = \frac{{Q_{\text{r}} }}{{\varphi_{\text{w}} }}. $$
(3)

The charge influenced on the rotor \( Q_{r} \) is composed of the partial surface charges on the lateral surface and the front surface of the rotor.

To calculate the charge stored on the rotor, the field area is divided into the sections as shown in Fig. 4. The determination of the partial charges \( Q_{r3,1} \), \( Q_{r3,2} \), \( Q_{r3,3} \), \( Q_{r4,1} \) on the lateral surface and \( Q_{z4,1} \) on the front surface is carried out independently of each other. The areas are separated when the materials or the rotor radius changes (see dashed lines in Fig. 4).

Fig. 4
figure 4

Representation of the partial charges on the rotor

Full size image

The total rotor charge corresponds to the sum of the charges present in the single sections. The end-winding portion of the winding-to-rotor capacitance is calculated according to (3) to

$$ C_{\text{wr}} = \frac{{Q_{\text{r}} }}{{\varphi_{\text{w}} }} = \frac{{Q_{r3,1} + Q_{r3,2} + Q_{z4,1} + Q_{r4,1} + Q_{r3,3} }}{{\varphi_{\text{w}} }}. $$
(4)

Due to the complex consideration of the alternating boundary conditions present on the radial axis, the stator lamination is initially ignored and the corresponding Dirichlet boundary condition is replaced by a Neumann boundary condition. Afterwards, the influence of the stator core on the end-winding portion of the winding-to-rotor capacitance is analysed and considered in the calculation.

4 Calculation of the influenced rotor charge without considering the stator lamination

Figure 5 shows exemplarily FEM-determined equipotential lines of the modified model presented in Fig. 3. Neumann boundary conditions serve as axial boundaries on both sides. With the exception of the dashed area shown in Figs. 3 and 5, the equipotential lines represent approximately concentric circles. The E-field has a dominant radial component. The determination of the partial rotor charges \( Q_{r3,1} \), \( Q_{r3,2} \), \( Q_{r3,3} \) on the lateral surface is based on the assumption of a purely radial E-field.

Fig. 5
figure 5

FEM-determined equipotential lines of the considered geometry

Full size image

Within the marked square step area, there is a radial and axial dependence of the potential. The pitch of the rotor contour corresponds to the side length of the marked area. The determination of the surface charges \( Q_{r4,1} \) and \( Q_{z4,1} \) is done separately from the other partial charges.

4.1 Partial determination of the rotor charge outside the step range

In electrostatics, it is necessary to solve the Poisson equation with the charge density \( \rho \) and the permittivity \( \varepsilon \) for the determination of the scalar potential field \( \varphi \) in a considered space area with linear, isotropic and homogeneous materials [11]:

$$ \Delta \varphi = - \frac{\rho }{\varepsilon }. $$
(5)

If there are no space charges in the region, (5) is simplified to Laplace’s equation:

$$ \Delta \varphi = 0. $$
(6)

For the sectional calculation of the rotor charge outside the step area depicted in Fig. 3 as dashed lines, the area shown in Fig. 6 is modelled. It consists of three materials with different permittivities. The end-winding of the stator winding and the outer rotor radius limit the field in radial direction.

Fig. 6
figure 6

Representation of the cylindrical field area, i.e. the area outside the dashed lines in Fig. 4

Full size image

Using the Laplace operator in the cylindrical coordinate system yields

$$ \Delta \varphi \left( {r,\gamma ,z} \right) = \frac{1}{r} \cdot \frac{\partial }{\partial r}\left( {r \cdot \frac{{\partial \varphi \left( {r,\gamma ,z} \right)}}{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} \varphi \left( {r,\gamma ,z} \right)}}{{\partial \gamma^{2} }} + \frac{{\partial^{2} \varphi \left( {r,\gamma ,z} \right)}}{{\partial z^{2} }} = 0. $$
(7)

The scalar potential field is independent of the angular coordinate \( \gamma \) due to the rotationally symmetrical spatial region, and by assuming a purely radial E-field, the dependence on the longitudinal coordinate \( z \) is eliminated.

The Laplace operator is simplified to the ordinary differential equation:

$$ \Delta \varphi \left( r \right) = \frac{1}{r} \cdot \frac{\partial }{\partial r}\left( {r \cdot \frac{\partial \varphi \left( r \right)}{\partial r}} \right) = 0. $$
(8)

The solution of the differential equation dependent on the radius yields the general solution of the Laplace equation for the three space regions considered:

$$ \varphi_{1} \left( r \right) = A_{1} + B_{1} \cdot { \ln }\left( r \right), $$
(9)
$$ \varphi_{2} \left( r \right) = A_{2} + B_{2} \cdot { \ln }\left( r \right), $$
(10)
$$ \varphi_{3} \left( r \right) = A_{3} + B_{3} \cdot { \ln }\left( r \right). $$
(11)

The coefficients are determined by means of the two boundary conditions:

$$ \varphi_{1} \left( {r = r_{w} } \right) = \varphi_{\text{w}} , $$
(12)
$$ \varphi_{3} \left( {r = r_{r} } \right) = 0 $$
(13)

and by considering the continuity conditions of the potential and the normal component of the D-field at the material boundaries:

$$ \varphi_{1} \left( {r = r_{g1} } \right) = \varphi_{2} \left( {r = r_{g1} } \right), $$
(14)
$$ \varphi_{2} \left( {r = r_{g2} } \right) = \varphi_{3} \left( {r = r_{g2} } \right), $$
(15)
$$ - \varepsilon_{1} \cdot \frac{{\partial \varphi_{1} \left( {r = r_{g1} } \right)}}{\partial r} = - \varepsilon_{2} \cdot \frac{{\partial \varphi_{2} \left( {r = r_{g1} } \right)}}{\partial r}, $$
(16)
$$ - \varepsilon_{2} \cdot \frac{{\partial \varphi_{2} \left( {r = r_{g2} } \right)}}{\partial r} = - \varepsilon_{3} \cdot \frac{{\partial \varphi_{3} \left( {r = r_{g2} } \right)}}{\partial r}. $$
(17)

The boundary conditions (12) and (13) lead to the equations

$$ A_{1} + B_{1} \cdot { \ln }\left( {r_{\text{w}} } \right) = \varphi_{\text{w}} , $$
(18)
$$ A_{3} = - B_{3} \cdot \ln \left( {r_{\text{r}} } \right). $$
(19)

The continuity conditions of the potential (14) and (15) result in

$$ A_{1} + B_{1} \cdot \ln \left( {r_{g1} } \right) = A_{2} + B_{2} \cdot { \ln }\left( {r_{g1} } \right), $$
(20)
$$ A_{2} + B_{2} \cdot { \ln }\left( {r_{g2} } \right) = A_{3} + B_{3} \cdot { \ln }\left( {r_{g2} } \right), $$
(21)

and the differentiability conditions (16) and (17) lead to

$$ - \varepsilon_{1} \cdot \frac{{B_{1} }}{{r_{g1} }} = - \varepsilon_{2} \cdot \frac{{B_{2} }}{{r_{g1} }}, $$
(22)
$$ - \varepsilon_{2} \cdot \frac{{B_{2} }}{{r_{g2} }} = - \varepsilon_{3} \cdot \frac{{B_{3} }}{{r_{g2} }}. $$
(23)

The unknown constants \( A_{1} \), \( B_{1} \), \( A_{2} \), \( B_{2} \), \( A_{3} \) and \( B_{3} \) of the potential fields of the three regions (9)–(11) can be determined using Eqs. (18)–(23). To determine the charge on the rotor, the surface charge density \( \sigma_{r3} \) is initially calculated with the aid of the electric field \( \vec{E}_{3} \)

$$ \vec{E}_{3} = E_{3r} \vec{e}_{r} = - {\text{grad}}\left( {\varphi_{3} } \right) = - \frac{{B_{3} }}{r}\vec{e}_{r} $$
(24)

and the surface normal vector \( \vec{n} \) of the rotor to

$$ \sigma_{r3} = \vec{n} \cdot \vec{D}_{3} \left( {r = r_{r} } \right) = \vec{e}_{r} \cdot \varepsilon_{3} E_{3r} \left( {r = r_{r} } \right)\vec{e}_{r} = - \varepsilon_{3} \cdot \frac{{B_{3} }}{{r_{r} }}. $$
(25)

The charge on the lateral surface of the rotor section \( Q_{r3} \) is calculated using the surface integral of the surface charge density over the length \( l_{r} \) in the longitudinal direction of the rotor section as

$$ Q_{r3} = \mathop \smallint \limits_{0}^{{l_{r} }} \mathop \smallint \limits_{0}^{2 \cdot \pi } \sigma_{r3} \cdot r \cdot {\text{d}}\gamma \cdot {\text{d}}z = - 2 \cdot \pi \cdot \varepsilon_{3} \cdot l_{r} \cdot B_{3} . $$
(26)

Equation (26) is applied depending on the number of layers and on the rotor radius to determine the partial rotor charges \( Q_{r3,1} \), \( Q_{r3,2} \), \( Q_{r3,3} \) on the lateral surface.

4.2 Partial determination of the rotor charge within the step region

For the calculation of the rotor charge within the step region, the area shown in Fig. 7 is modelled. The field is filled with the material adjacent to the rotor. In radial direction, the space area is limited by the two radii of the step area of the rotor. The front face of the rotor is on the left side of the considered field area. At the two edges adjacent to the rotor, the potential of the rotor is present. For reasons of simplification, the spatial area is infinitely extended in the longitudinal direction.

Fig. 7
figure 7

Field area in the step region of the rotor

Full size image

Figure 5 shows that, dependent on the longitudinal coordinate, a potential is present at the upper side of the area. To determine the potential function \( \varphi_{\text{s}} \), the potential curve of the spatial area is analysed by means of FEM software. Figure 8 shows the potential dependence on the longitudinal direction of the upper side of the step area (potential curve along the upper horizontal dashed line in the positive z-direction shown in Fig. 5) of the first model geometry of Table 1. As already shown in the scalar potential field in Fig. 5, this is a nonlinear potential curve.

Fig. 8
figure 8

Representation of the potential curves \( \varphi_{\text{s}} \left( z \right) \) of the first model geometry of Table 1

Full size image
Table 1 Geometric and material properties of the investigated models
Full size table

The potential curve can be modelled using the exponential function:

$$ \varphi_{ \exp } \left( z \right) = \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{{ - \frac{z}{\tau }}} } \right) $$
(27)

with the steady-state end value

$$ \tilde{\varphi }_{3} \left( {r_{r1} } \right) = \tilde{A}_{3} + \tilde{B}_{3} \cdot { \ln }\left( {r_{r1} } \right) $$
(28)

and the constant

$$ \tau = \frac{{r_{r1} - r_{r2} }}{5}. $$
(29)

The stationary final value \( \tilde{\varphi }_{3} \left( {r_{r1} } \right) \) corresponds to the potential at the upper right edge of the square step range. This can be calculated using the third potential field (11) in order to determine the partial rotor charge \( Q_{r3,3} \). The stationary final value corresponds to the potential which would be present at the position with a purely radial E-field. The constant \( \tau \) describes the rise of the potential. It is assumed that the stationary final value is approximately reached in the axial direction at the position of the step height. This distance corresponds approximately to five times the constant \( \tau \).

A significant simplification of the solution of the Laplace equation for the field area shown in Fig. 7, however, results from the assumption of a linear potential function. Consequently, there is a linearly increasing potential curve

$$ \varphi_{s} \left( z \right) = m \cdot z + b $$
(30)

with the slope \( m \) on the upper side of the area in the axial direction. The ordinate section \( b \) is set to zero volts due to the selected rotor potential. The linear approximation function contained in Fig. 8 intersects the exponential function in the longitudinal direction at the location of the constant \( \tau \). The slope of the function results in

$$ m = \frac{{\Delta \varphi_{\text{s}} }}{\Delta z} = \frac{{\varphi_{\text{s}} \left( \tau \right)}}{\tau } = \frac{{5 \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{r_{r1} - r_{r2} }}. $$
(31)

The linear function reaches the stationary final value after the distance

$$ z_{c} = \frac{{\tilde{\varphi }_{3} \left( {r_{r1} } \right)}}{m} = \frac{{r_{r1} - r_{r2} }}{{5 \cdot \left( {1 - e^{ - 1} } \right)}}. $$
(32)

From this position, as shown in Fig. 8, the constant potential of the stationary final value is assumed for the approximation of the potential curve, independent of the longitudinal direction. The determination of the rotor charge in the step range is carried out with this model in the axial direction at the maximum over the distance \( z_{\text{c}} \). Axially, the potential field, which only depends on the radius, is connected to determine \( Q_{r3,3} \).

One of the most important methods for the analytical treatment of partial differential equations is the so-called separation method [9]. In this method, the partial differential equation is transformed into ordinary differential equations in the selected coordinate system by means of a product approach. Finally, the solution is adapted to the given boundary conditions.

Due to the rotationally symmetrical spatial region, the scalar potential field is independent of the angular coordinate \( \gamma \), which simplifies the Laplace operator (7) to

$$ \Delta \varphi \left( {r,z} \right) = \frac{1}{r} \cdot \frac{\partial }{\partial r}\left( {r \cdot \frac{{\partial \varphi \left( {r,z} \right)}}{\partial r}} \right) + \frac{{\partial^{2} \varphi \left( {r,z} \right)}}{{\partial z^{2} }} = 0. $$
(33)

By inserting the selected product approach

$$ \varphi \left( {r,z} \right) = R\left( r \right) \cdot Z\left( z \right) $$
(34)

into the Laplace Eq. (33)

$$ \frac{Z\left( z \right)}{r} \cdot \frac{\partial }{\partial r}\left( {r \cdot \frac{\partial R\left( r \right)}{\partial r}} \right) + R\left( r \right) \cdot \frac{{\partial^{2} Z\left( z \right)}}{{\partial z^{2} }} = 0 $$
(35)

and then dividing it by the product approach (34), the relation

$$ \frac{1}{r \cdot R\left( r \right)} \cdot \frac{\partial }{\partial r}\left( {r \cdot \frac{\partial R\left( r \right)}{\partial r}} \right) + \frac{1}{Z\left( z \right)} \cdot \frac{{\partial^{2} Z\left( z \right)}}{{\partial z^{2} }} = 0 $$
(36)

is obtained. The summands of Eq. (36) are constant functions, and by means of the definitions

$$ k_{r}^{2} = \frac{1}{r \cdot R\left( r \right)} \cdot \frac{\partial }{\partial r}\left( {r \cdot \frac{\partial R\left( r \right)}{\partial r}} \right), $$
(37)
$$ k_{z}^{2} = \frac{1}{Z\left( z \right)} \cdot \frac{{\partial^{2} Z\left( z \right)}}{{\partial z^{2} }}, $$
(38)

the partial differential Eq. (33) breaks down into the two decoupled ordinary differential Eqs. (37) and (38), taking into account the constraint

$$ k_{r}^{2} + k_{z}^{2} = 0. $$
(39)

For the realization of a linear potential curve in the longitudinal direction, the constant \( k_{z} \) is set to zero, so that, according to the separation condition (39), the constant \( k_{r} \) must also be zero. The solutions of the homogeneous differential Eqs. (37) and (38) result in the general solution of the Laplace equation for the area under consideration:

$$ \varphi_{4} \left( {r,z} \right) = \left[ {A_{4} + B_{4} \cdot \ln \left( r \right)} \right] \cdot \left( {C_{4} \cdot z + D_{4} } \right). $$
(40)

The coefficients are determined by means of the boundary conditions:

$$ \varphi_{4} \left( {r, z = 0} \right) = 0, $$
(41)
$$ \varphi_{4} \left( {r = r_{r2} ,z} \right) = 0, $$
(42)
$$ \varphi_{4} \left( {r = r_{r1} ,z} \right) = \varphi_{s} \left( z \right). $$
(43)

The coefficient \( D_{4} \) must be zero according to boundary condition (41). The boundary condition on the lateral surface of the rotor (42) leads to

$$ A_{4} = - B_{4} \cdot \ln \left( {r_{r2} } \right). $$
(44)

The remaining boundary condition (43) gives

$$ \tilde{B}_{4} \cdot \left[ {\ln \left( {r_{r1} } \right) - \ln \left( {r_{r2} } \right)} \right] \cdot z = \frac{{5 \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{r_{r1} - r_{r2} }} \cdot z, $$
(45)
$$ \tilde{B}_{4} = \frac{{5 \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - { \ln }\left( {r_{r2} } \right)} \right]}} $$
(46)

with

$$ \tilde{B}_{4} = B_{4} \cdot C_{4} . $$
(47)

The scalar potential function adapted to the given boundary conditions is

$$ \varphi_{4} \left( {r,z} \right) = \tilde{B}_{4} \cdot \left[ {\ln \left( r \right) - \ln \left( {r_{r2} } \right)} \right] \cdot z. $$
(48)

To determine the charge present on the front and on the lateral surface of the step area, the D-field \( \vec{D}_{4} \) in the spatial area is determined as

$$ \vec{D}_{4} = \left( {\begin{array}{*{20}c} {D_{4r} } \\ {D_{4z} } \\ \end{array} } \right) = \varepsilon_{3} \cdot \left( {\begin{array}{*{20}c} {E_{4r} } \\ {E_{4z} } \\ \end{array} } \right) = - \varepsilon_{3} \cdot {\text{grad}}\left( {\varphi_{4} } \right) $$
(49)

with

$$ D_{4r} = - \frac{{5 \cdot \varepsilon_{3} \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - { \ln }\left( {r_{r2} } \right)} \right]}} \cdot \frac{z}{r} $$
(50)

and

$$ D_{4z} = - \frac{{5 \cdot \varepsilon_{3} \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - \ln \left( {r_{r2} } \right)} \right]}} \cdot \left[ {\ln \left( r \right) - \ln \left( {r_{r2} } \right)} \right]. $$
(51)

The surface charge density \( \sigma_{r4} \) on the lateral surface of the step area is calculated with the surface normal vector \( \vec{n} \) to

$$ \sigma_{r4} = \vec{n} \cdot \vec{D}_{4} \left( {r = r_{r2} } \right) = \vec{e}_{r} \cdot \vec{D}_{4} \left( {r = r_{r2} } \right) = - \frac{{5 \cdot \varepsilon_{3} \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - { \ln }\left( {r_{r2} } \right)} \right]}} \cdot \frac{z}{{r_{r2} }}. $$
(52)

The charge on the lateral surface of the step area \( Q_{r4} \) is calculated using the surface integral of the surface charge density over the length \( l_{r4} \) in the axial direction of the rotor section as

$$ Q_{r4} = \mathop \smallint \limits_{0}^{{l_{r4} }} \mathop \smallint \limits_{0}^{2 \cdot \pi } \sigma_{r4} \cdot r \cdot d\gamma \cdot dz = - \frac{{5 \cdot \pi \cdot \varepsilon_{3} \cdot l_{r4}^{2} \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right)}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - \ln \left( {r_{r2} } \right)} \right]}}. $$
(53)

The length \( l_{r4} \) of the rotor section corresponds to the distance \( z_{\text{c}} \), provided that the length \( l_{r2} \) in the longitudinal direction, as shown in Fig. 3, is greater than or equal to the distance \( z_{\text{c}} \). Otherwise, the length \( l_{r4} \) is equal to the length \( l_{r2} \). To determine the charge on the front face of the step area of the rotor, the surface charge density \( \sigma_{z4} \) is first determined as

$$ \sigma_{z4} = \vec{n} \cdot \vec{D}_{4} \left( {r,z = 0} \right) = \vec{e}_{z} \cdot \vec{D}_{4} \left( {r,z = 0} \right) = - \frac{{5 \cdot \varepsilon_{3} \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right) \cdot \left[ {\ln \left( r \right) - \ln \left( {r_{r2} } \right)} \right]}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - \ln \left( {r_{r2} } \right)} \right]}}. $$
(54)

The charge on the front surface of the step area \( Q_{z4} \) is calculated using the surface integral of the surface charge density over the height of the step in the radial direction to

$$ Q_{z4} = \mathop \smallint \limits_{{r_{r2} }}^{{r_{r1} }} \mathop \smallint \limits_{0}^{2 \cdot \pi } \sigma_{z4} \cdot r \cdot {\text{d}}\gamma \cdot {\text{d}}r, $$
(55)
$$ Q_{z4} = - \frac{{5 \cdot \pi \cdot \varepsilon_{3} \cdot \tilde{\varphi }_{3} \left( {r_{r1} } \right) \cdot \left( {1 - e^{ - 1} } \right) \cdot \left[ {r_{r1}^{2} \cdot \ln \left( {r_{r1} } \right) - r_{r1}^{2} \cdot \ln \left( {r_{r2} } \right) - \frac{{r_{r1}^{2} }}{2} + \frac{{r_{r2}^{2} }}{2}} \right]}}{{\left( {r_{r1} - r_{r2} } \right) \cdot \left[ {\ln \left( {r_{r1} } \right) - \ln \left( {r_{r2} } \right)} \right]}}. $$
(56)

The total charge present at the step area on the rotor surface is the sum of the partial charges on the lateral surface and the front surface of the step area. It should be noted that this model only determines the charge on the lateral surface up to the axial position \( z_{\text{c}} \) in the step area. The charge on the lateral surface from \( z_{\text{c}} \) to the axial position of the pitch of the rotor step is calculated separately using (26).

5 Calculation of the influenced rotor charge within consideration of the stator lamination

Figure 9 shows an example of FEM-determined equipotential lines of the model presented in Fig. 3. Compared to the equipotential lines in Fig. 5, a significant distortion of the potential field can be seen due to the consideration of the sheet metal stator core with a specified potential of zero volts. The height of the stator core part corresponds to the difference between the radius of the insulation \( r_{g1} \) and the radius of the air gap \( r_{g2} . \)

Fig. 9
figure 9

FEM-determined equipotential lines considering the stator core

Full size image

FEM simulations of the axial course of the D-field on the rotor radius \( r_{r1} \) show that there is a minimum of the radial component at \( z = 0 \) due to the grounded stator lamination. The radial component of the D-field increases in the longitudinal direction to the stationary value derived in Sect. 4.1. In the presented model, the increase in the radial component of the D-field in the axial direction can be approximated by a linear function. To determine the course of the D-field, it is assumed that the radial component of the D-field at \( z = 0 \) is \( 0 \frac{\text{C}}{{{\text{m}}^{2} }} \) and reaches the stationary final value at the z position of the stator core part height (\( r_{g1} - r_{g2} \)). When determining the partial rotor charge \( Q^{*}_{r3,1} \) presented in Sect. 4.1, however, a constant radial component of the D-field over the length of the slot insulation \( l_{\text{iso}} \) on the rotor radius \( r_{r1} \) is assumed. The line charge density of \( Q^{*}_{r3,1} \) is

$$ Q^{*'}_{r3,1} = \frac{{Q^{*}_{r3,1} }}{{l_{\text{iso}} }}. $$
(57)

Taking into account the linear approximation of the D-field, the rotor charge \( Q^{*}_{r3,1} \) is overestimated by the charge

$$ Q_{r3,1,s} = \frac{{Q^{*'}_{r3,1} \cdot \left( {r_{g1} - r_{g2} } \right)}}{2} = \frac{{Q^{*}_{r3,1} \cdot \left( {r_{g1} - r_{g2} } \right)}}{{2 \cdot l_{iso} }}. $$
(58)

By the distance of the stator lamination, the charge \( Q_{r3,1,s} \) corresponds to the half of the rotor charge originally assumed over the axial length of the stator core part height. Under the assumptions made, the consideration of the stator lamination leads to the modified equation for the partial rotor charge \( Q_{r3,1} \) in the section of the insulation shown in Fig. 4:

$$ Q_{r3,1} = Q^{*}_{r3,1} - Q_{r3,1,s} = Q^{*}_{r3,1} \cdot \left( {1 - \frac{{r_{g1} - r_{g2} }}{{2 \cdot l_{\text{iso}} }}} \right). $$
(59)

6 Validation of the model

The model is validated using FEM software. The six investigated geometry variants, which are based on different actually built motors with different material properties, are given in Table 1.

Table 2 shows the analytically calculated and the numerically determined end space portions of the winding rotor capacities without consideration of the stator lamination. The deviations are in the single-digit percentage range. The errors can be explained by the non-analytically closed solution of the considered range. Deviations are also caused by the linearization of the potential function at the upper side of the step range and by neglecting the superelevation of the E-field at the edge of the rotor.

Table 2 Comparison of the analytically calculated end-winding portions of the winding-to-rotor capacitances with the FEM results
Full size table

The differences between the analytically and the numerically determined capacitances of the fifth and the sixth variant are due to the given Neumann boundary condition at \( z = l_{r1} + l_{r2} \) and the smaller value of \( l_{r2} \). In the analysis, it is assumed that the stationary final value of the potential is present on the upper side of the square step area in the axial direction. This point lies outside the considered geometries. Due to the Neumann boundary condition, the stationary final value of the potential is reached at the edge, so that the result is a steeper increase in potential compared to the analytical solution. The gradient is proportional to the rotor charge on the lateral surface and end face of the step area, and consequently, the analytically determined rotor charge is lower compared to the numerically determined rotor charge. Table 3 contains the analytically calculated rotor charges of the sections shown in Fig. 5. The simulated potential of the stator end-winding is 1 volt.

Table 3 Comparison of the analytically calculated partial rotor charges
Full size table

From Table 3, it can be seen that the charge on the face of the rotor \( Q_{z4.1} \) has an effect on the capacitance of the end-winding portion of the winding-to-rotor capacitance due to its value. Moreover, it becomes apparent that most of the rotor charge is present on sections with a small distance between the head of the stator winding and the rotor. The highest line charge density is present on the sections with the smallest distance.

Table 4 contains the analytically calculated and the numerically determined end-winding portions of the winding-to-rotor capacitances of the models presented in Table 1, taking into account the stator lamination.

Table 4 Comparison of the analytically calculated end-winding portions of the winding-to-rotor capacitances with the FEM results in consideration of the earthed stator lamination
Full size table

It can be seen that the capacitances shown in Table 4 are smaller than those collated in Table 2. The stator lamination leads to a reduction in the capacitive coupling between the stator end-winding and the rotor. It can also be seen from Table 4 that the simple calculation and consideration of the differential charge \( Q_{r3,1,s} \) lead to an acceptable deviation between the analytically calculated and the numerically determined capacitances. The errors are resulted from the non-closed solution of the field problem and the linearization of the course of the radial component of the D-field on the rotor surface.

In contrast to the 3D FEM simulation described in [6], the application of the analytical method presented here is less complex due to the simple equations. In a three-dimensional model, on the other hand, the position and the shape of the coils can be taken into account. In comparison with the 3D FEM simulation, the assumption of a rotationally symmetrical end-winding described here leads to an overestimation of the capacitive coupling due to the lack of stator winding in the teeth area of the stator core. Nevertheless, that assumption is fair, as the E-field exiting the coils spreads radially within the teeth area towards the rotor.

7 Conclusion

This paper presents a simple, two-dimensional analytical calculation of the end-winding portion of the winding-to-rotor capacitance. The considered capacitive coupling between the stator end-winding and the rotor extends in the axial direction over the winding overhang. A closed solution of the field problem is not determined. Instead, the solution for the step-shaped rotor contour is carried out separately for the step area and the remaining lateral surface of the rotor. The determination of the capacitance is based on the separation method for solving the Laplace equation of a one- and a two-dimensional area. The modelled end-winding consists of three media with different permittivities. An extension to a higher number of media is easily possible due to the repeating boundary conditions. Further steps on the rotor contour can also be taken into account by calculating the additional rotor charge influenced on the rotor surface.

The stator lamination between the air gap and the deck slide contained in the extended field area leads to a reduction in the capacitive coupling. The decrease can be taken into account by the presented reduction in the rotor charge.

With the help of the presented model, the effect of different geometries and materials on the end-winding portion of the winding-to-rotor capacitance can be determined fast and reliable with only small deviations.