Abstract
We introduce the concept of a horizon-K farsighted set to study the influence of the degree of farsightedness on network stability. The concept generalizes existing concepts where all players are either fully myopic or fully farsighted. A set of networks \(G_{K}\) is a horizon-K farsighted set if three conditions are satisfied. First, external deviations should be horizon-K deterred. Second, from any network outside of \(G_{K}\) there is a sequence of farsighted improving paths of length smaller than or equal to K leading to some network in \(G_{K}\). Third, there is no proper subset of \(G_{K}\) satisfying the first two conditions. We show that a horizon-K farsighted set always exists and that the horizon-1 farsighted set \(G_{1}\) is always unique. For generic allocation rules, the set \(G_{1}\) always contains a horizon-K farsighted set for any K. We provide easy to verify conditions for a set of networks to be a horizon-K farsighted set, and we consider the efficiency of networks in horizon-K farsighted sets. We discuss the effects of players with different horizons in an example of criminal networks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Networks of relationships help determine the careers that people choose, the jobs they obtain, the products they buy and how they vote. The many aspects of our lives that are governed by social networks make it critical to understand how they impact behavior and which network structures are likely to emerge in a society. A simple way to analyze the networks that one might expect to emerge in the long run is to examine the requirement that individuals do not benefit from altering the structure of the network.
A prominent example of such a condition is the pairwise stability notion defined by Jackson and Wolinsky (1996).Footnote 1 A network is pairwise stable if no individual benefits from deleting a link and no two individuals benefit from adding a link between them, with at least one benefitting strictly. While pairwise stability is natural, easy to work with and a very important tool in network analysis,Footnote 2 it assumes that individuals are myopic, and not farsighted, in the sense that they do not forecast how others might react to their actions. Indeed, the addition or deletion of one link might lead to subsequent additions or deletions of other links. For instance, individuals might not add a link that appears valuable to them given the current network, as this might induce the formation of other links, ultimately leading to lower payoffs for them.
Herings et al. (2009) introduce the notion of a pairwise farsightedly stable set. A set of networks is a pairwise farsightedly stable set if (i) all possible pairwise deviations from any network within the set to a network outside the set are deterred by the threat of ending worse off or equally well off, (ii) there exists a farsighted improving path from any network outside the set leading to some network in the set, and (iii) there is no proper subset satisfying conditions (i) and (ii).Footnote 3 The concept of a pairwise farsightedly stable set makes sense if players have perfect anticipation of how others might react to changes in the network. But in general, especially when the set of players becomes large, it requires too much foresight on behalf of the players.Footnote 4
Herings et al. (2009) also introduce the notion of a pairwise myopically stable set. Our aim is to provide a concept that encompasses both the pairwise farsightedly stable set and the pairwise myopically stable set and that can be used to study the influence of an arbitrary degree of farsightedness on network stability. A set of networks \( G_{K}\) is a horizon-K farsighted set if three conditions are satisfied. First, external deviations should be horizon-K deterred. That is, adding a link ij to a network \(g\in G_{K}\) that leads to a network outside of \( G_{K}\) is deterred by the threat of ending in \(g^{\prime }\). Here \(g^{\prime }\) is such that either there is a farsighted improving path of length smaller than or equal to \(K-2\) from \(g+ij\) to \(g^{\prime }\) and \(g^{\prime }\) belongs to \(G_{K}\) or there is a farsighted improving path of length equal to \(K-1\) from \(g+ij\) to \(g^{\prime }\) and there is no farsighted improving path from \(g+ij\) to \(g^{\prime }\) of smaller length. A similar requirement is imposed for the case where a link is severed. Second, horizon-K external stability is required. That is, from any network outside of \(G_{K}\) there is a sequence of farsighted improving paths of length smaller than or equal to K leading to some network in \(G_{K}\). Third, a minimality condition is required. That is, there is no proper subset of \(G_{K}\) satisfying the first two conditions.
We show that a horizon-K farsighted set always exists and we provide a sufficient condition for its uniqueness. We find that there always is a unique horizon-1 farsighted set \(G_{1}\). It is given by the set consisting of all networks that belong to closed cycles, so it includes all pairwise stable networks. A horizon-K farsighted set leads to a refinement of \( G_{1} \) in case of generic allocation rules: for any \(K\ge 1\), the horizon-1 farsighted set \(G_{1}\) contains a horizon-K farsighted set \( G_{K} \). Thus, an analysis based on myopic behavior may not rule out some networks that are not stable when players are sufficiently farsighted. At the same time, a myopic analysis is compatible with farsightedness, and for any value of K there is always a horizon-K farsighted set that consists exclusively of networks that belong to closed cycles. But, some networks that are not part of any closed cycle may constitute a horizon-K farsighted set when K strictly exceeds one. In this case, there are multiple horizon-K farsighted sets.
We provide easy to verify conditions for a set of networks to be a horizon-K farsighted set. We also consider the efficiency of networks in a horizon-K farsighted set. We show that if there is a network that Pareto dominates all other networks, then that network constitutes the unique horizon-K farsighted set if K is greater than the number of links in the complete network. In addition, we introduce a property on the allocation rule under which the complete network constitutes the unique horizon-K farsighted set. Finally, we discuss the effects of players with different horizons in an example of criminal networks.
Morbitzer et al. (2014) develop a model of network formation where players look a finite number of steps ahead when anticipating the reaction of other players to their change. The decision to initiate a change to the network is based on rules that weigh improving paths that might follow their change, but which are not necessarily improving paths for the players who made the initial change. Using computer simulations they show that, in the co-author model of Jackson and Wolinsky (1996), limited farsighted players can overcome the tension between stability and efficiency only if the number of players is small. Their concept is a refinement of the set of pairwise stable networks.
The paper is organized as follows. In Sect. 2, we introduce some notations and basic properties and definitions for networks. In Sect. 3, we define the notions of improving paths and horizon-K pairwise stability and we show that horizon-K pairwise stable networks may fail to exist. In Sect. 4, we define the notion of a horizon-K farsighted set and show such a set to exist. In Sect. 5, we study its relationship to other solution concepts. In Sect. 6, we provide easy to verify sufficient conditions for a set of networks to be a horizon-K farsighted set. We look at the efficiency of networks in a horizon-K farsighted set in Sect. 7. In that section, we also show that under increasing returns to link creation, the complete network constitutes the unique horizon-K farsighted set. In Sect. 8, we discuss the effects of players with different horizons using an example of criminal networks. Finally, in Sect. 9 we conclude.
2 Networks
Let \(N=\{1,\ldots ,n\}\) be the finite set of players who are involved in some network relationship. The network relationships are reciprocal, and the network is thus modeled as a non-directed graph. Individuals are the nodes in the graph, and links indicate bilateral relationships between individuals. Thus, a network g is simply a list of which pairs of individuals are linked to each other. We write \(ij\in g\) to indicate that i and j are linked under the network g. The complete network on the set of players \( S\subseteq N\) is denoted \(g^{S}\) and is equal to the set of all subsets of S of size 2.Footnote 5 It follows in particular that the empty network is denoted by \(g^{\emptyset }\). The set of all possible networks or graphs on N is denoted by \(\mathbb {G}\) and consists of all subsets of \(g^{N}\). The cardinality of \(\mathbb {G}\) is denoted by \(n^{\prime }=2^{n(n-1)/2}\).
The network obtained by adding link ij to an existing network g is denoted by \(g+ij\) and the network that results from deleting link ij from an existing network g by \(g-ij\). Let
Thus, \(g_{\mid S}\) is the network found by deleting all links from g except those that are between players in S. For any network g, let \(N(g)=\{i\in N\mid \exists j\in N\) such that \(ij\in g\}\) be the set of players who have at least one link in the network g.
A path in a network \(g\in \mathbb {G}\) between players i and j of length \( K\ge 1\) is a finite sequence of players \(i_{0},\ldots ,i_{K}\) with \(i_{0}=i\) and \(i_{K}=j\) such that for any \(k\in \{0,\ldots ,K-1\}\), \(i_{k}i_{k+1}\in g\), and such that each player in the sequence \(i_{0},\ldots ,i_{K}\) is distinct. A network g is connected if for each pair of players i and j in N such that \(i\ne j\) there exists a path between i and j in g. A non-empty network \(h\subseteq g\) is a component of g if for all \(i\in N(h)\) and \(j\in N(h){\setminus } \{i\}\), there exists a path in h connecting i and j, and for any \(i\in N(h)\) and \(j\in N(g)\), \(ij\in g\) implies \( ij\in h\). The set of components of g is denoted by C(g). Using the components of a network, we can partition the players into maximal groups within which players are connected. Let P(g) denote the partition of N induced by the network g. That is, the set S of players belongs to P(g) if and only if either there exists a network h in C(g) such that \(S=N(h)\) or there exists \(i\notin N(g)\) such that \(S=\{i\}\).
An allocation rule is a function \(Y:\mathbb {G}\rightarrow \mathbb {R}^{N}\) which gives for every player i and network g a payoff \(Y_{i}(g)\).
3 Improving paths
A farsighted improving path of length \(K\ge 0\) from a network g to a network \(g^{\prime } \) is a finite sequence of networks \(g_{0},\ldots ,g_{K}\) with \(g_{0}=g\) and \(g_{K}=g^{\prime }\) such that for any \(k\in \{0,\ldots ,K-1\}\) either (i) \(g_{k+1}=g_{k}-ij\) for some ij such that \( Y_{i}(g_{K})>Y_{i}(g_{k})\) or \(Y_{j}(g_{K})>Y_{j}(g_{k})\), or (ii) \( g_{k+1}=g_{k}+ij\) for some ij such that \(Y_{i}(g_{K})>Y_{i}(g_{k})\) and \( Y_{j}(g_{K})\ge Y_{j}(g_{k})\). Since the set \(\{0,\ldots ,K-1\}\) is empty for \(K=0\), this definition implies that there is a farsighted improving path of length 0 from each network g to itself, but clearly there are no farsighted improving paths of length 0 from g to any other network. If \( K \ge 1, \) then the definition of a farsighted improving path implies that \( g^{\prime } \ne g. \) If there exists a farsighted improving path of length K from g to \( g^{\prime }\), then we write \(g\rightarrow _{K}g^{\prime }\).Footnote 6
Our notion of farsighted improving path assumes that the technology to change the network involves the deletion or the addition of one link at a time, which is very much in the tradition of the concept of pairwise stability as introduced by Jackson and Wolinsky (1996). Dutta and Mutuswami (1997) and Jackson and van den Nouweland (2005) introduce the notion of strong stability, where stability of the network against deviations by arbitrary coalitions is required. In the same spirit, our theory of farsighted improving paths can easily be modified to study coalitional moves rather than pairwise moves. Even more abstractly, we could simply take the networks that can be reached from a given network g in K steps as a primitive of the model. We leave a further investigation of these issues to future research.
For a given network g and some \(K^{\prime }\ge 0\), let \(f_{K^{\prime }}(g) \) be the set of networks that can be reached from g by a farsighted improving path of length \(K\le K^{\prime }\). That is,
This defines \(f_{K^{\prime }}\) as a correspondence on the set \(\mathbb {G}\). The set of networks that can be reached from g by some farsighted improving path is denoted by \(f_{\infty }(g)\), so
The following lemma follows almost immediately and is presented without proof.
Lemma 1
For \(K\ge 0\), for every \(g\in \mathbb {G}\), it holds that \( f_{K}(g)\subseteq f_{K+1}(g)\). For \(K\ge n^{\prime }-1\), for every \(g\in \mathbb {G}\), it holds that \(f_{K}(g)=f_{K+1}(g)=f_{\infty }(g)\).
For \(K\ge 0\), we define the relation \(\tilde{f}_{K}\) on \(\mathbb {G}\) as
so the network g is dropped from \(f_{K}(g)\) and the set \(\tilde{f}_{K}(g)\) corresponds to the networks different from g that can be reached from g by a farsighted improving path of length at most K. Similarly, we define the relation \(\tilde{f}_{\infty }\) on \( \mathbb {G} \) by \(\tilde{f}_{\infty }(g)=f_{\infty }(g){\setminus } \{g\} \) for every \(g\in \mathbb {G}\).
An important concept in the analysis of networks is the one of pairwise stability as introduced in Jackson and Wolinsky (1996). A network \(g\in \mathbb {G}\) is pairwise stable if (i) for every \( ij\in g\), \(Y_{i}(g)\ge Y_{i}(g-ij)\) and \(Y_{j}(g)\ge Y_{j}(g-ij)\) and (ii) for every \(ij\notin g\), if \(Y_{i}(g)<Y_{i}(g+ij)\), then \( Y_{j}(g)>Y_{j}(g+ij)\). We say that a network \(g^{\prime }\) is adjacent to g if \(g^{\prime }=g+ij\) or \(g^{\prime }=g-ij\) for some ij. A network \(g^{\prime }\)defeatsg if either \( g^{\prime }=g-ij\) and \(Y_{i}(g^{\prime })>Y_{i}(g)\) or \(Y_{j}(g^{\prime })>Y_{j}(g)\), or if \(g^{\prime }=g+ij\) with \((Y_{i}(g^{\prime }),Y_{j}(g^{\prime }))>(Y_{i}(g),Y_{j}(g))\).Footnote 7 A network is pairwise stable if and only if it is not defeated by another network. It is also easy to see that \(g^{\prime }\in \tilde{f}_{1}(g)\) if and only if \( g^{\prime }\) defeats g. We can therefore characterize the pairwise stable networks as those \(g\in \mathbb {G}\) for which \(\tilde{f}_{1}(g)=\emptyset \), or, alternatively, \(f_{1}(g)=\{g\}\).
Pairwise stability requires that networks are immune to immediate deviations. On top of this requirement, one may look for networks that are also immune to deviations of length up to K. These considerations lead to the following definition of a horizon-K pairwise stable network.
Definition 1
For \(K\ge 1\), a network \(g\in \mathbb {G}\) is horizon-K pairwise stable if \(f_{K}(g)=\{g\}\).
The set of horizon-K pairwise stable networks is denoted by \(P_{K}\). Jackson (2008) defines the set of farsightedly pairwise stable networks as those that are immune to deviations of arbitrary length, which corresponds to \(P_{\infty }. \) The set \(P_{K} \) is useful in deriving some of the results in Sects. 5 and 6. As a solution concept in its own right, it is subject to the same criticism as already expressed in Jackson (2008) with respect to \(P_{\infty }. \) Horizon-K pairwise stability suffers from the drawback that the networks to which players plan to deviate may not be horizon-K pairwise stable themselves. Also, similar to the case of myopic players, there is no guarantee that the set \(P_{K} \) is non-empty. It follows from Lemma 1 that \(P_{K}\supseteq P_{K+1}\), so emptiness is more likely to become a problem for higher values of K.
The set \(f_{K}^{2}(g)=f_{K}(f_{K}(g))=\{g^{\prime \prime }\in \mathbb {G}\mid \exists g^{\prime }\in f_{K}(g)\) such that \(g^{\prime \prime }\in f_{K}(g^{\prime })\}\) consists of those networks that can be reached by a composition of two farsighted improving paths of length at most K from g . We extend this definition, and for \(m\in \mathbb {N}\), we define \( f_{K}^{m}(g)\) as those networks that can be reached from g by means of m compositions of farsighted improving paths of length at most K. Since there are \(n^{\prime }\) networks in \(\mathbb {G}\), it follows that \(f_{K}^{m}\) is the same for all values of m greater than or equal to \(n^{\prime }-1\). The resulting correspondence for such values of m is called the transitive closure of \(f_{K}\) and is denoted by \(f_{K}^{\infty }\). In an analogous way, we define \( \tilde{f}^{m}_{K} \) and \( \tilde{f}^{\infty }_{K}.\)Footnote 8
Lemma 1 extends to compositions of \(f_{K}\) and in particular to the transitive closure \(f_{K}^{\infty }\) of \(f_{K}\) as is shown in the following lemma, which is presented without proof.
Lemma 2
For \(K\ge 0\), for every \(g\in \mathbb {G}\), it holds that \( f_{K}^{\infty }(g)\subseteq f_{K+1}^{\infty }(g)\). For \(K\ge n^{\prime }-1\) , for every \(g\in \mathbb {G}\), it holds that \(f_{K}^{\infty }(g)=f_{K+1}^{\infty }(g)=f_{\infty }^{\infty }(g)\).
Jackson and Watts (2002) have defined the notion of a closed cycle. A set of networks C is a cycle if for any \(g^{\prime }\in C\) and \(g\in C{\setminus } \{g^{\prime }\}\), there exists a sequence of improving paths of length 1 connecting g to \(g^{\prime }\), i.e., \(g^{\prime }\in f_{1}^{\infty }(g)\). A cycle C is a maximal cycle if it is not a proper subset of a cycle. A cycle C is a closed cycle if \(f_{1}^{\infty }(C)=C\), so there is no sequence of improving paths of length 1 starting at some network in C and leading to a network that is not in C. A closed cycle is necessarily a maximal cycle. For every network \(g\in P_{1}\), the set \(\{g\}\) is a closed cycle. The set of networks belonging to a closed cycle is non-empty.Footnote 9
4 The horizon-K farsighted set
To analyze the influence of the degree of farsightedness on the stability of networks, we define the notion of a horizon-K farsighted set. It is based on two main requirements: horizon-K deterrence of external deviations and horizon-K external stability.
The move from a network g to an adjacent network is called a deviation. A set of networks G satisfies horizon-K deterrence of external deviations if all possible deviations from any network \(g \in G \) to a network outside G are deterred by the threat of ending worse off or equally well off. In the formal definition below, we use the notational convention that \(f_{-1}(g)=\emptyset \) for every \(g\in \mathbb {G}\).
Definition 2
For \(K\ge 1\), a set of networks \(G\subseteq \mathbb {G}\) satisfies horizon-K deterrence of external deviations if for every \(g\in G,\)
- (a):
-
\(\forall \)\(ij\notin g\) such that \(g+ij\notin G\),\(\exists g^{\prime }\in [f_{K-2}(g+ij)\cap G]\cup [f_{K-1}(g+ij){\setminus } f_{K-2}(g+ij)]\) such that\((Y_{i}(g^{\prime }),Y_{j}(g^{\prime }))=(Y_{i}(g),Y_{j}(g))\) or \( Y_{i}(g^{\prime })<Y_{i}(g)\) or \(Y_{j}(g^{\prime })<Y_{j}(g)\),
- (b):
-
\(\forall \)\(ij\in g\) such that \(g-ij\notin G\),\(\exists g^{\prime },g^{\prime \prime }\in [f_{K-2}(g-ij)\cap G]\cup [f_{K-1}(g-ij){\setminus } f_{K-2}(g-ij)]\) such that\(Y_{i}(g^{\prime })\le Y_{i}(g)\) and \(Y_{j}(g^{\prime \prime })\le Y_{j}(g) \).
Condition (a) in Definition 2 captures that adding a link ij to a network \(g\in G \) that leads to a network \(g+ij \) outside of G, is deterred by the threat of ending in \(g^{\prime }\). Here \(g^{\prime }\) is such that either there is a farsighted improving path of length smaller than or equal to \(K-2\) from \(g+ij\) to \(g^{\prime }\) and \(g^{\prime }\) belongs to G or there is a farsighted improving path of length equal to \(K-1\) from \( g+ij\) to \(g^{\prime }\) and there is no farsighted improving path from \(g+ij\) to \(g^{\prime }\) of smaller length. Condition (b) is a similar requirement, but then for the case where a link is severed.Footnote 10
If the degree of farsightedness of players is equal to K, we have to distinguish farsighted improving paths of length less than or equal to \(K-2\) after a deviation from g to \(g+ij\) and farsighted improving paths of length equal to \(K-1\). In the former case, the reasoning capacity of the players is not yet reached, and the threat of ending in \(g^{\prime }\) is only credible if it belongs to the set G. In the latter case, to reach \( g^{\prime }\) from g requires at least K steps of reasoning, one step in the deviation to \(g+ij\) and at least \(K-1\) additional steps in any farsighted improving path from \(g+ij\) to \(g^{\prime }\). Since this exhausts the reasoning capacity of the players, the threat of ending in \(g^{\prime }\) is credible, irrespective of whether it belongs to G or not.
A set of networks G satisfies horizon-K external stability if from any network outside of G there is a sequence of farsighted improving paths of length smaller than or equal to K leading to some network in G.
Definition 3
For \(K\ge 1\), a set of networks \(G\subseteq \mathbb {G}\) satisfies horizon-K external stability if for every \( g^{\prime }\in \mathbb {G}{\setminus } G\), \(f_{K}^{\infty }(g^{\prime })\cap G\ne \emptyset \).
There is a conceptual difference between Definition 2, which applies to networks in G, and Definition 3, which applies to networks not in G. Horizon-K deterrence of external deviations guarantees that a network g inside the set G is stable for players whose reasoning horizon is of length K. The players are therefore not actually deviating from g, and deterring networks belong to \(f_{K-1}(g+ij) \) or \(f_{K-1}(g-ij). \) The networks \(g \notin G \) are not stable, and the players are therefore deviating from such networks. When players make linking decisions at a network outside G, they move according to some horizon-K farsighted improving path without being able to anticipate that other linking decisions might be taken afterward. After the first step of such a deviation has taken place, say to a network \(g^{\prime }, \) the players can again use a reasoning horizon of K, and this may cause their anticipations to change since they may now be able to envision networks that they could not see before. Hence, \(f_{K}^{\infty }\) rather than \( f_{K} \) is used to capture what could happen at a network outside G in the requirement of horizon-K external stability. This requirement implies that if we allow players with a degree of farsightedness equal to K to successively create or delete links, they will ultimately reach the set G irrespective of the initial network.
Definition 4
For \(K\ge 1\), a set of networks \(G_{K}\subseteq \mathbb { G}\) is a horizon-K farsighted set if it is a minimal set satisfying horizon-K deterrence of external deviations and horizon-K external stability.
Chwe (1994) gives the definition of a stable set as in von Neumann and Morgenstern (1944) based on farsighted improving paths of any length. According to this notion a set of networks is stable if it satisfies internal stability and externality stability with respect to \(\tilde{f} _{\infty }. \) For the framework of transferable utility games, Ray and Vohra (2015) propose to call this set the Harsanyi set in case the rules for coalitions to move from one imputation to another are in accordance with the specification in Harsanyi (1974). They also propose a more compelling set of rules for coalitions to change imputations and use the name farsighted stable set for the resulting stable set of networks. To avoid confusion with the notions of farsightedly pairwise stable networks of Jackson (2008) and of the pairwise farsightedly stable set as introduced in Herings et al. (2009), we will use the term Harsanyi set for the von Neumann and Morgenstern stable set as based on \( \tilde{f}_{\infty }. \) Page and Wooders (2009) extends this notion by requiring both external and internal stability with respect to \(\tilde{f}_{\infty }^{m}\) for given \(m\in \mathbb {N}\) and refers to the resulting concept as the stable set with respect to path dominance.
Horizon-K external stability immediately implies that a horizon-K farsighted set of networks contains at least one network, so satisfies non-emptiness. The next result claims existence.
Theorem 1
A horizon-K farsighted set of networks exists.
Proof
Notice that \(\mathbb {G}\) trivially satisfies horizon-K deterrence of external deviations and horizon-K external stability. Suppose that \( G^{0}_{K} = \mathbb {G} \) is not a horizon-K farsighted set. Then \( G^{0}_{K} \) does not satisfy minimality, and we can find a proper subset \( G_{K}^{1}\) that satisfies horizon-K deterrence of external deviations and horizon-K external stability. Iterating this reasoning, we can construct a sequence \(\{G_{K}^{k}\}_{k\ge 0}\) of subsets of \(\mathbb {G}\) satisfying horizon-K deterrence of external deviations and horizon-K external stability with the property that \(G_{K}^{k}\subsetneq G_{K}^{k-1}.\) Since \( \mathbb {G}\) has finite cardinality \(n^{\prime },\) this process has to stop after a finite number of steps with a minimal set of networks satisfying horizon-K deterrence of external deviations and horizon-K external stability, that is a horizon-K farsighted set. \(\square \)
For the special case where K is equal to 1, we can use the fact that \( f_{-1}(g)=\emptyset \) and \(f_{0}(g)=\{g\}\) to simplify the definition of horizon-K deterrence of external deviations. Also for \(K=2\), Definition 2 simplifies somewhat, since if a network \(g+ij\) belongs to \(\mathbb {G}{\setminus } G\) for some set G, it holds that \(f_{0}(g+ij)\cap G=\{g+ij\}\cap G=\emptyset \). The proof of the following result follows easily from these observations and is therefore omitted.
Theorem 2
A set of networks \(G \subseteq \mathbb {G} \) satisfies horizon-1 deterrence of external deviations if and only if for every \(g \in G,\)
- (a):
-
\(\forall \)\(ij\notin g\) such that \(g^{\prime }=g+ij\notin G\) it holds that \((Y_{i}(g^{\prime }),Y_{j}(g^{\prime }))=(Y_{i}(g),Y_{j}(g))\) or \( Y_{i}(g^{\prime })<Y_{i}(g)\) or \(Y_{j}(g^{\prime })<Y_{j}(g)\),
- (b):
-
\(\forall \)\(ij\in g\) such that \(g^{\prime }=g-ij\notin G\) it holds that \(Y_{i}(g^{\prime })\le Y_{i}(g)\) and \(Y_{j}(g^{\prime })\le Y_{j}(g)\).
A set of networks \(G \subseteq \mathbb {G} \) satisfies horizon-2 deterrence of external deviations if and only if for every \(g \in G,\)
- (a):
-
\(\forall \)\(ij\notin g\) such that \(g+ij\notin G\), \(\exists g^{\prime }\in \tilde{f}_{1}(g+ij)\) such that \((Y_{i}(g^{\prime }),Y_{j}(g^{\prime }))=(Y_{i}(g),Y_{j}(g))\) or \(Y_{i}(g^{\prime })<Y_{i}(g)\) or \(Y_{j}(g^{\prime })<Y_{j}(g)\),
- (b):
-
\(\forall \)\(ij\in g\) such that \(g-ij\notin G\), \(\exists g^{\prime },g^{\prime \prime }\in \tilde{f}_{1}(g-ij)\) such that \(Y_{i}(g^{\prime })\le Y_{i}(g)\) and \(Y_{j}(g^{\prime \prime })\le Y_{j}(g)\).
Theorem 2 is useful when computing horizon-1 and horizon-2 farsighted sets in examples. It also shows that a horizon-1 farsighted set is identical to a pairwise myopically stable set as defined in Herings et al. (2009). Herings et al. (2009) have shown that there is a unique pairwise myopically stable set. It is equal to the set of networks consisting of all networks that belong to a closed cycle. Theorem 3 below follows.
Theorem 3
There is a unique horizon-1 farsighted set. It is given by the set consisting of all networks that belong to a closed cycle.
Since a horizon-K farsighted set cannot be empty, it follows from Theorem 3 that there is at least one closed cycle. Horizon-1 farsighted sets are unique. This result does not carry over to higher values of K.
When K is greater than or equal to \(n^{\prime }+1,\) it follows from Lemma 1 that \(f_{K-2}(g)=f_{K-1}(g) = f_{\infty }(g) \) for every \(g\in \mathbb {G}. \) It follows immediately from this fact that the collection of horizon-K farsighted sets is independent of K when \(K\ge n^{\prime }+1\). Herings et al. (2009) define a pairwise farsightedly stable set as a set \(G_{\infty }\) of networks satisfying horizon-\(\infty \) deterrence of external deviations and minimality, but with horizon-\(\infty \) external stability replaced by the requirement that
so the correspondence \(f_{\infty }^{\infty }\) is replaced by \(f_{\infty }. \) In many applications, the correspondence \(f_{\infty }\) is transitive, in which case it coincides with \(f_{\infty }^{\infty }\), and pairwise farsightedly stable sets are identical to horizon-\((n^{\prime }+1)\) farsighted sets, but in general it only holds that \(f_{\infty }(g) \subseteq f_{\infty }^{\infty }(g)\) for \(g\in \mathbb {G}\). We can therefore conclude that for every pairwise farsightedly stable set \(G_{\infty }\) there is a set \(G^{\prime }\subseteq G_{\infty }\) such that \(G^{\prime }\) is a horizon-\( (n^{\prime }+1)\) farsighted set.
5 The relation to other solution concepts
In this section, we discuss how horizon-K farsighted sets \( G_{K} \) are related to notions based on pairwise stability such as the set of pairwise stable networks \(P_{1}\), the set of closed cycles \(G_{1}\) and the set of horizon-K pairwise stable networks \(P_{K}\). We also introduce the von Neumann–Morgenstern stable set \( V_{K} \) and examine its relation to \( G_{K}. \)
Theorem 3 implies that any pairwise stable network belongs to \( G_{1}\). The following theorem shows that this result carries over to higher values of K.
Theorem 4
For \(K\ge 1\), the set \(P_{K}\) of horizon-K pairwise stable networks is a subset of any horizon-K farsighted set \(G_{K}\).
Proof
Suppose \(G_{K}\) is a horizon-K farsighted set, but does not contain some \( g\in P_{K}.\) By Definition 1, we have \(f_{K}(g)=\{g\}.\) We find that \(f_{K}^{\infty }(g)=\{g\},\) so \(f_{K}^{\infty }(g)\cap G_{K}=\emptyset .\) By horizon-K external stability, it holds that \( f_{K}^{\infty }(g)\cap G_{K}\ne \emptyset ,\) a contradiction.
\(\square \)
Theorem 4 shows that any network g from which there are no farsighted improving paths of length smaller than or equal to K to networks different from g belongs to \(G_{K}\). Horizon-K pairwise stability is quite demanding for higher horizons of K. Since \( f_{K}(g)\subseteq f_{K+1}(g)\), we have that \(P_{K}\supseteq P_{K+1}\).
Theorem 4 yields an easy sufficient condition for the uniqueness of a horizon-K farsighted set as a corollary, where we make use of the minimality requirement.
Corollary 1
For \(K\ge 1\), if \(P_{K}\) is a horizon-K farsighted set, then it is uniquely so.
An allocation rule is said to be generic if for every \(g,g^{\prime }\in \mathbb {G}\) such that g and \(g^{\prime }\) are adjacent it holds that either \(g\in f_{1}(g^{\prime })\) or \(g^{\prime }\in f_{1}(g)\). If an allocation rule is not generic, then some arbitrarily small perturbation of it will be, and genericity can therefore be thought of as a weak requirement on allocation rules. The next result shows that for generic allocation rules, the set \(G_{1} \) contains a horizon-K farsighted set.
Theorem 5
Let the allocation rule be generic. For every \(K\ge 1\), the horizon-1 farsighted set \(G_{1}\) contains a horizon-K farsighted set \(G_{K}\).
Proof
The statement is trivial for \(K=1\), so we consider \(K\ge 2\).
We show first that the set \(G_{1}\) satisfies horizon-K deterrence of external deviations. Consider some \(g\in G_{1}\) and a deviation to \( g^{\prime }\in \mathbb {G}{\setminus } G_{1}\).
Suppose that \(g^{\prime }\in f_{1}(g)\). Since \(g \in G_{1} \) and \(G_{1}\) contains all networks in a closed cycle by Theorem 3, it follows that \(g^{\prime }\in G_{1}\), a contradiction to \(g^{\prime }\in \mathbb {G}{\setminus } G_{1}\). Consequently, it holds that \(g^{\prime }\notin f_{1}(g)\).
Since the allocation rule is generic, we find that \(g\in f_{1}(g^{\prime }).\) We have that \( g \in \tilde{f}_{1}(g^{\prime }) {\setminus } \{g^{\prime }\}\), so for \( K=2\) the deviation from g to \(g^{\prime }\) is deterred by g. For \(K\ge 3 \), we have by Lemma 1 that \(g\in f_{1}(g^{\prime })\cap G_{1}\subseteq f_{K-2}(g^{\prime })\cap G_{1}\), so again the deviation from g to \(g^{\prime }\) is deterred by g.
We show next that the set \(G_{1}\) satisfies horizon-K external stability. Since \(G_{1}\) is a horizon-1 farsighted set, it holds for every \(g^{\prime }\in \mathbb {G}{\setminus } G_{1}\) that \(f_{1}^{\infty }(g^{\prime })\cap G_{1}\ne \emptyset \). By Lemma 2 it holds that \(f_{1}^{\infty }(g^{\prime })\subseteq f_{K}^{\infty }(g^{\prime })\), so \(f_{K}^{\infty }(g^{\prime })\cap G_{1}\ne \emptyset \), and it follows that \(G_{1}\) satisfies horizon-K external stability.
Either the set \(G_{1}\) itself is a minimal set satisfying horizon-K deterrence of external deviations and horizon-K external stability and is therefore a horizon-K farsighted set, or it has a proper subset \(G_{K}\) which is a minimal set satisfying these two properties, so \(G_{K}\) is a horizon-K farsighted set. In both cases, the statement of the theorem holds. \(\square \)
Theorem 3 asserts that there is a unique horizon-1 farsighted set \(G_{1}\), given by the union of all closed cycles. Theorem 5 shows that higher horizons of farsightedness lead to a refinement of the networks that belong to closed cycles. For any value of K, there is always a subset of \(G_{1}\) that is a horizon-K farsighted set. Theorem shows that an analysis based on myopic behavior may not rule out some networks that are not stable when players are sufficiently farsighted. At the same time, a myopic analysis is compatible with farsightedness, and for any value of K there is always a horizon-K farsighted set that consists exclusively of networks that belong to closed cycles.
Theorem 5 does not claim that horizon-K farsighted sets are always subsets of networks in \(G_{1}\). The following example shows that networks that are not part of any closed cycle may be part of a horizon-K farsighted set for values of K greater than or equal to 2.
Networks outside closed cycles can belong to horizon-K farsighted sets in Example 1
Example 1
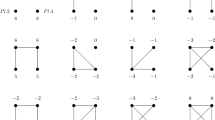
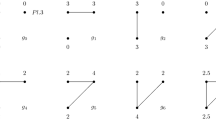
Consider the situation where three players can form and sever links and where the payoffs are given as in Fig. 1. The farsighted improving paths of various lengths are presented in Table 1.
In this example there is a unique pairwise stable network, \(g^{3}\). By inspecting \(\tilde{f}_{1}\) as presented in Table 1, it is easily verified that there are no other closed cycles in this example, so \(G_{1}=\{g^{3}\}\). By Theorem 5, and the fact that each horizon-K farsighted set contains at least one element, it holds that \(\{g^{3}\}\) is a horizon-K farsighted set for any value of K. At the same time, the payoffs resulting from the network \(g^{3}\) are Pareto dominated by those of \(g^{1}\). The problem with network \(g^{1}\) is that Player 1 has myopic incentives to cut his link with Player 2 to obtain a payoff of 5 from the network \(g^{0}\) instead of 4 from the network \(g^{1}\). Once at \(g^{0}\), Players 2 and 3 have myopic incentives to form a link and form the pairwise stable network \(g^{3}\) . The question is whether the Pareto efficient network \(g^{1}\) is stable when the players are less myopic.
We first show that \(\{g^{1}\}\) is a horizon-2 farsighted set by verifying that \(\{g^{1}\}\) satisfies horizon-2 deterrence of external deviations as characterized in Theorem 2, horizon-2 external stability and minimality. There are three possible deviations from \(g^{1}\). Players 1 and 2 can cut their link and move to \(g^{0}\), Players 1 and 3 can form a link to arrive at \(g^{4}\), and Players 2 and 3 can form a link to go to \(g^{5}\). From Table 1 it follows immediately that \(g^{3}\in \tilde{f}_{1}(g^{0})\), \( g^{1}\in \tilde{f}_{1}(g^{4})\) and \(g^{1}\in \tilde{f}_{1}(g^{5})\). Since Players 1 and 2 both have lower payoffs at \(g^{3}\) than at \(g^{1}\), the first deviation is deterred. The other two deviations are deterred by the possible return to \(g^{1}\). We conclude that horizon-2 deterrence of external deviations holds.
One degree of farsightedness is needed to move from \(g^{4}\) or \(g^{5}\) to \( g^{1}\), and two such degrees are needed to move from \(g^{2}\), \(g^{3}\) or \( g^{7}\) to \(g^{1}\). Since \(g^{0}\rightarrow _{1}g^{3}\rightarrow _{2}g^{1}\) and \(g^{6}\rightarrow _{1}g^{3}\rightarrow _{2}g^{1}\), we have shown that for every \(g^{\prime }\in \mathbb {G}{\setminus } \{g^{1}\}\), \(g^{1}\in f_{2}^{\infty }(g^{\prime })\), so horizon-2 external stability holds. Minimality is trivially satisfied by \(\{g^{1}\}\). \(\square \)
We conclude this section by observing that horizon-K farsighted sets may depend in a non-monotonic way on the degree of farsightedness. In the network of Example 1, the set \(\{g^{1}\} \) is a horizon-2 farsighted set. In Example 2, it is shown not to be a horizon-3 farsighted set. For \(K \ge n^{\prime }+1, \) the set \(\{g^{1}\} \) reappears as a horizon-K farsighted set.
Example 2
Consider the same network situation as in Example , so \(\{g^{1}\}\) is a horizon-2 farsighted set. We argue by contradiction that it is not a horizon-3 farsighted set.
Suppose that \(\{g^{1}\}\) is a horizon-3 farsighted set. Consider a deviation by Player 1, who cuts the link with Player 2 to arrive at the network \(g^{0}\) . When Player 1 has only two degrees of farsightedness, he might fear a further move to \(g^{3}\), which would deter the deviation. With three degrees of farsightedness, Player 1 realizes that the threat of ending in \(g^{3}\) is not credible, since \(g^{3}\) does not belong to the horizon-3 farsighted set \( \{g^{1}\}\). Since the set \(f_{2}(g^{0}){\setminus } f_{1}(g^{0})=\emptyset \), the deviation by Player 1 to \(g^{0}\) is not deterred according to Definition 2.
However, when players are sufficiently farsighted, \(\{g^{1}\}\) reemerges as a horizon-K farsighted set. We consider some \(K\ge n^{\prime }+1\) and verify that \(\{g^{1}\}\) satisfies horizon-K deterrence of external deviations, horizon-K external stability and minimality. As before, the only deviations from \(g^{1}\) are to \(g^{0}\), \(g^{4}\) and \(g^{5}\). Since \( f_{n^{\prime }-1}(g^{0})\), \(f_{n^{\prime }-1}(g^{4})\) and \(f_{n^{\prime }-1}(g^{5})\) all contain \(g^{1}\), such deviations are deterred, and horizon-K deterrence of external deviations is satisfied. Since \(g^{1}\in f_{n^{\prime }-1}(g^{\prime })\subseteq f_{n^{\prime }-1}^{\infty }(g^{\prime })\) for all \(g^{\prime }\in \mathbb {G}{\setminus } \{g^{1}\}\), we know that horizon-K external stability is satisfied by \(\{g^{1}\}\). Minimality is trivially satisfied. It follows that \(\{g^{1}\}\) is a horizon-K farsighted set for every \(K\ge n^{\prime }+1\). \(\square \)
The non-monotonic behavior of horizon-K farsighted sets in the horizon K does not come as a surprise. By Lemma 1, the correspondence \( f_{K} \) is monotonic in K in the sense that \(f_{K}(g)\subseteq f_{K+1}(g)\) for every \(g\in \mathbb {G}.\) For higher values of K, it is therefore easier to satisfy the requirement of horizon-K external stability. On the other hand, if K increases, it may become more difficult to satisfy horizon-K deterrence of external deviations, since the networks that can be reached after a deviation may not be monotonic in K as \( f_{K-1}(g+ij){\setminus } f_{K-2}(g+ij)\) may not be monotonic in K. Intuitively, more farsighted players might be less deterred to deviate since there are less networks at the end of their reasoning horizon.
The horizon-K farsighted set requires horizon-K deterrence of external deviations, horizon-K external stability and minimality. The von Neumann–Morgenstern pairwise farsightedly stable set (Herings et al. 2009) imposes internal and external stability based on the correspondence \(f_{\infty }\).Footnote 11 Incorporating the notion of farsighted improving path of length K into the original definition of the von Neumann–Morgenstern stable set, we obtain the horizon-K von Neumann–Morgenstern stable set.
Definition 5
The set \(V_{K}\) is a horizon-K von Neumann–Morgenstern stable set if (i) for every \(g\in V_{K}\), \(f_{K}(g)\cap V_{K}=\emptyset \) and (ii) for every \(g\in \mathbb {G}{\setminus } V_{K}\), \( f_{K}(g)\cap V_{K}\ne \emptyset \).
Like Harsanyi sets, horizon-K von Neumann–Morgenstern stable sets do not always exist. Moreover, when the horizon-K von Neumann–Morgenstern stable set exists, there is no a priori relationship with the horizon-K farsighted set \(G_{K}. \) The next example illustrates these observations.
Example 3
We derive the horizon-K von Neumann–Morgenstern stable sets \( V_{K} \) in Example 1.
For \(K=1\), we have \( \tilde{f}_{1}(g^{3})= \emptyset , \) so \(g^{3}\in V_{1}\). Internal stability implies that \(g^{0}\), \(g^{5}\) and \(g^{6}\) do not belong to \(V_{1}\). Since \( \tilde{f}_{1}(g^{1})=\left\{ g^{0}\right\} \) and \(g^{0}\notin V_{1}\), we have that \( g^{1}\in V_{1}\) to satisfy external stability. Internal stability now implies that \(g^{4}\) does not belong to \(V_{1}\). Then, also \(g^{2}\) and \(g^{7}\) must belong to \( V_{1}\) (since \( \tilde{f}_{1}(g^{2})=\left\{ g^{0},g^{4},g^{6}\right\} \) and \(\tilde{f}_{1}(g^{7})=\left\{ g^{4},g^{5},g^{6}\right\} ).\) We find that \(V_{1}=\left\{ g^{1},g^{2},g^{3},g^{7}\right\} \), while \(G_{1}=\left\{ g^{3}\right\} \) by Example 1.
We next consider the case \( K=2. \) Suppose \(g^{1}\in V_{2}\). Then, internal stability implies that \(g^{2}\), \(g^{3}\), \(g^{4}\), \(g^{5}\) and \(g^{7}\) do not belong to \(V_{2}\). Since \(\tilde{f}_{2}(g^{6})=\left\{ g^{3},g^{4}\right\} \), by external stability we have that \(g^{6}\) must belong to \(V_{2}\). Finally, since \( \tilde{f}_{2}(g^{0})=\left\{ g^{3}\right\} \), by external stability we have that \(g^{0}\) must belong to \( V_{2}\). But then internal stability is violated because \( \tilde{f}_{2}(g^{1})=\left\{ g^{0}\right\} \). We conclude that \(g^{1}\notin V_{2}\). By external stability, it follows that \(g^{3}\in V_{2}\). Then, internal stability implies that \( g^{0}\), \(g^{2}\), \(g^{5}\), \(g^{6}\) and \(g^{7}\) do not belong to \(V_{2}\). Since \(\tilde{f}_{2}(g^{1})=\left\{ g^{0}\right\} \), and \(g^{0}\notin V_{2}\), \(g^{1}\) must belong to \(V_{2}\) by external stability. Since we already concluded \( g^{1} \notin V_{2}, \) we have obtained a contradiction. We have shown that there is no horizon-2 von Neumann–Morgenstern stable set. On the other hand, \( \left\{ g^{1}\right\} \) and \( \left\{ g^{3}\right\} \) are horizon-2 farsighted sets as shown in Example 1.
For \(K\ge 3\), we have that \( V_{K}=\left\{ g^{1}\right\} . \) On the other hand, we have shown in Example 2 that \( \{g^{1}\} \) is not a horizon 3 farsighted set. By Theorem 6 it holds that \( \left\{ g^{3}\right\} \) is a horizon-K farsighted set whenever \( K \ge 3. \)\(\square \)
Provided it exists, a horizon-K von Neumann–Morgenstern stable set \(V_{K}\) is related to the horizon-K pairwise stable networks \(P_{K}\). In particular, it can easily be shown that Theorem 4 also holds if we replace \(G_{K}\) by \(V_{K}\). This implies that any network g from which there are no farsighted improving paths of length smaller or equal to K to networks different from g belongs to \(V_{K}.\)
6 Sufficient conditions
In this section, we present two sets of sufficient conditions for a set to be a horizon-K farsighted set. In many examples, these conditions are easy to verify.
A refinement of pairwise stability is obtained when we require the network g to defeat every other adjacent network, so \(g\in f_{1}(g^{\prime })\) for every network \(g^{\prime }\) adjacent to g. We call such a network gpairwise dominant. The following definition generalizes this idea and allows for farsighted improving paths of any length K.
Definition 6
For \(K\ge 1\), a network \(g\in \mathbb {G}\) is horizon-K pairwise dominant if for every \(g^{\prime }\) adjacent to g it holds that \(g\in f_{K}(g^{\prime })\). The set of horizon-K pairwise dominant networks is denoted by \(D_{K}\).
It follows immediately from the definition that \(D_{1}\subseteq P_{1}\). For generic allocation rules, the concepts of pairwise stability and pairwise dominance coincide, \(D_{1}=P_{1}\). This coincidence does not hold for values of K greater than or equal to 2. By Lemma 1 it follows that \( D_{K}\subseteq D_{K+1}\), whereas \(P_{K}\supseteq P_{K+1}\).
The first set of sufficient conditions applies to the case where \(K=1\).
Theorem 6
If \(g\in P_{1}\) and for every \(g^{\prime }\in \mathbb {G} {\setminus } \{g\}\) it holds that \(g\in f_{1}^{\infty }(g^{\prime })\), then \( \{g\}\) is the unique horizon-1 farsighted set.
Proof
We show that \(\{g\}\) is a horizon-1 farsighted set by applying Theorem . The uniqueness then follows from Theorem 3. Since \( g\in P_{1},\) it holds that \(f_{1}(g)=\{g\},\) so for a deviation from g to \( g^{\prime }=g+ij\) it holds that \((Y_{i}(g^{\prime }),Y_{j}(g^{\prime }))=(Y_{i}(g),Y_{j}(g))\) or \(Y_{i}(g^{\prime })<Y_{i}(g)\) or \( Y_{j}(g^{\prime })<Y_{j}(g)\) and for a deviation from g to \(g^{\prime }=g-ij\) it holds that \(Y_{i}(g^{\prime })\le Y_{i}(g)\) and \(Y_{j}(g^{\prime })\le Y_{j}(g),\) so horizon-1 deterrence of external deviations as characterized in Theorem 2 is satisfied. Horizon-1 external stability and minimality are trivially satisfied. \(\square \)
The next result applies when \(K\ge 2\).
Theorem 7
Consider some \(K\ge 2\). If \(g\in D_{J}\) for some \(J<K\) and for every \(g^{\prime }\in \mathbb {G}{\setminus } \{g\}\) it holds that \(g\in f_{K}^{\infty }(g^{\prime })\), then \(\{g\}\) is a horizon-K farsighted set. If, moreover, \(g\in P_{K}\), then \(\{g\}\) is the unique horizon-K farsighted set.
Proof
We start by showing that \(\{g\}\) is a horizon-K farsighted set.
We first consider \(K = 2 \) and apply Theorem 2. If \(K = 2, \) then the only possibility is that \(J = 1, \) so \(g \in D_{1}, \) or equivalently \(g \in \tilde{f}_{1}(\bar{g}) \) for every \(\bar{g} \) adjacent to g. Horizon-2 deterrence of external deviations as characterized in Theorem 2 is satisfied since a deviation from g to \(\bar{g} \) is deterred by the return to \(g \in \tilde{f}_{1}(\bar{g}). \) Horizon-2 external stability and minimality are trivially satisfied.
We next consider \(K \ge 3 \) and apply Definition 2. Since \( g \in D_{J} \) for some \(J < K, \) it holds that \(g \in f_{J}(\bar{g}) \subseteq f_{K-1}(\bar{g}) \) for every \(\bar{g} \) adjacent to g, where the inclusion uses Lemma 1. It holds that either \(g \in f_{K-2}( \bar{g}), \) so \(g \in f_{K-2}(\bar{g}) \cap \{g\}, \) or \(g \notin f_{K-2}( \bar{g}), \) so \(g \in f_{K-1}(\bar{g}) {\setminus } f_{K-2}(\bar{g}). \) Horizon-K deterrence of external deviations is satisfied since a deviation from g to \(\bar{g} \) is deterred by the return to \(g \in [f_{K-2}(\bar{g}) \cap \{g\}] \cup [f_{K-1}(\bar{g}) {\setminus } f_{K-2}(\bar{g})]. \) Horizon-K external stability and minimality are trivially satisfied.
We complete the proof by showing that \(\{g\}\) is the unique horizon-K farsighted set if in addition \(g\in P_{K}.\) Since \(g\in f_{K}^{\infty }(g^{\prime })\) for every \(g^{\prime }\in \mathbb {G}{\setminus } \{g\}\) and \( g\in P_{K},\) we have that \(P_{K}=\{g\},\) and therefore \(P_{K}\) is a horizon-K farsighted set. Corollary 1 yields the desired result. \(\square \)
The conditions of Theorems 6 and 7 are usually easy to verify. To show that \(g\in P_{1}\) requires that \(f_{1}(g)\) does not contain networks different from g. To show that \(g\in f_{1}^{\infty }(g^{\prime })\) for all \(g^{\prime }\ne g\), we have to find a sequence of farsighted improving paths of length one that connect \(g^{\prime }\) to g. In Theorem 7, the requirement of Theorem 6 that g belongs to \(P_{1}\) is replaced by the requirement that \(g\in D_{J}\) for some \(J<K\), so we have to show that \(g\in f_{J}(g^{\prime })\) for all \(g^{\prime } \) adjacent to g. The higher the J, the weaker this requirement, so we could replace the requirement \(g\in D_{J}\) for some \(J<K\) by \(g\in D_{K-1}\). To show that \(g\in f_{K}^{\infty }(g^{\prime })\) for all \(g^{\prime }\ne g\), we have to find a sequence of farsighted improving paths of length at most K that connect \(g^{\prime }\) to g. Very often the analysis of farsighted improving paths of small lengths is already sufficient. The higher the K, the easier it is to satisfy the conditions of Theorem 7 and to find a singleton horizon-K farsighted set. Finally, to show that \(g\in P_{K}\) requires that \(f_{K}(g)\) does not contain networks different from g. This requirement is more difficult to satisfy for increasing values of K.
We show next how Theorems 6 and 7 can be used to analyze the stability of \(g^{3}\) in Example 1. In Example it holds that \(g^{3}\in P_{1}\) and for every \(g\in ~\mathbb {G} {\setminus } \{g^{3}\}\), \(g^{3}\in f_{1}^{\infty }(g)\). We can then apply Theorem 6 to conclude that \(\{g^{3}\}\) is the unique horizon-1 farsighted set.
In Example 1 it also holds that \(g^{3}\in D_{1}\). Since for every \(g\in \mathbb {G}{\setminus } \{g^{3}\}\), \(g^{3}\in f_{1}^{\infty }(g)\), we have by Lemma 2 that \(g^{3}\in f_{K}^{\infty }(g)\) for every \( K\ge 2\). We can then apply Theorem 7 to conclude that \( \{g^{3}\}\) is a horizon-K farsighted set for any value of \(K\ge 2\).
We have illustrated in Example 1 that there are other horizon-K farsighted sets for higher values of K; in particular, \(\{g^{1}\}\) can be sustained as a horizon-K farsighted set for higher values of K. Indeed, for \(K\ge 2\), \(f_{K}(g^{3})\) contains networks different from \( g^{3} \), so the condition \(g^{3}\in P_{K}\) in Theorem 7, which is sufficient for uniqueness of \(\{g^{3}\}\) as a horizon-K farsighted set, does not hold.
In Example 1, \(\{g^{1}\}\) has been shown to be a horizon-2 farsighted set. In Example 2 we have argued that \(g^{1}\) is not a horizon-3 farsighted set. We show next that Theorem 7 can be used to show that \(\{g^{1}\}\) is a horizon-K farsighted set for any \( K\ge 4\). The adjacent networks of \(g^{1}\) are \(g^{0}\), \(g^{4}\) and \(g^{5}\) . It follows from Table 1 that \(f_{3}(g^{0})\), \(f_{3}(g^{4})\) and \( f_{3}(g^{5})\) all contain \(g^{1}\), so \(g^{1}\in D_{3}\). We have already argued in Example 1 that for every \(g^{\prime }\in \mathbb {G} {\setminus } \{g^{1}\}\) it holds that \(g^{1}\in f_{2}^{\infty }(g^{\prime })\) so, by Lemma 2, we have that \(g^{1}\in f_{K}^{\infty }(g^{\prime })\) for all \(K\ge 2\). Combining the conclusions in the previous two sentences and applying Theorem 7 proves that \(\{g^{1}\}\) is a horizon-K farsighted set for any \(K\ge 4\).
7 Efficiency and stability
We now turn to the question of how horizon-K farsighted sets are related to the efficiency of networks. A network g is strongly efficient if \( \sum _{i\in N}Y_{i}(g)>\sum _{i\in N}Y_{i}(g^{\prime })\) for all \(g^{\prime }\ne g\). Assume that there is a network \(\tilde{g}\) that strictly Pareto dominates all other networks. That is, \(Y_{i}(\tilde{g})>Y_{i}(g)\) for all \(i\in N\) and for all \(g\in \mathbb {G}{\setminus } \left\{ \tilde{g} \right\} \). Hence, \(\tilde{g}\) is both Pareto efficient and strongly efficient.
Theorem 8
Assume that the network \(\tilde{g}\) strictly Pareto dominates all networks \(g\in \mathbb {G}{\setminus } \left\{ \tilde{g} \right\} \). Then, \(\left\{ \tilde{g}\right\} \) is the unique horizon-K farsighted set for all \(K\ge n(n-1)/2\).
Proof
First, we show that \(\tilde{g}\in D_{1}\). For all \(g\in \mathbb {G} {\setminus } \left\{ \tilde{g}\right\} ,\) it holds that \(Y_{i}(\tilde{g} )>Y_{i}(g)\) for all \(i\in N,\) so we have that \(\tilde{g}\in f_{1}(g)\) for any network g adjacent to \(\tilde{g}\), so \(\tilde{g}\in D_{1}\) . Moreover, for every \(g\in \mathbb {G}{\setminus } \left\{ \tilde{g} \right\} \), we have that \(\tilde{g}\in f_{K}(g)\) when \(K\ge n(n-1)/2\). Indeed, all players like to move from g to \(\tilde{g}\) given that \( Y_{i}(\tilde{g})>Y_{i}(g)\) for all \(i\in N\), and the maximum number of links that one needs to cut or form from g in order to reach \(\tilde{g} \) is equal to the number of links in the complete network, \(n(n-1)/2\). It follows that \(\tilde{g}\in f_{K}^{\infty }(g)\) for all \(g\in \mathbb {G} {\setminus } \left\{ \tilde{g}\right\} \). Finally, since \(\tilde{g}\) strictly Pareto dominates all other networks, we have that \(f_{K}(\tilde{ g})=\left\{ \tilde{g}\right\} \) for all \(K\ge 1\). Thus, \(\tilde{g} \in P_{K}\) for all \(K\ge 1\), and by Theorem 7 we have that \( \left\{ \tilde{g}\right\} \) is the unique horizon-K farsighted set for all \(K\ge n(n-1)/2\). \(\square \)
There are many situations where a Pareto dominating network does not exist. We therefore turn our attention to allocation rules satisfying increasing returns to link creation. An allocation rule Y displays no externalities across components (NEC) if for every \(g\in \mathbb {G}\), for every \(h\in C(g)\), we have \(Y_{i}(g)=Y_{i}(h)\) for all \(i\in N(h)\) and \( Y_{i}(g)=0\) for all \(i\in N {\setminus } N(g)\). In particular, it holds that \( Y_{i}(g^{\emptyset })=0\) for all \(i\in N\). If an allocation rule satisfies NEC, then it is sufficient to specify the allocation rule for connected networks. The set of connected networks is denoted by \(\mathbb {C}\).
Consider some allocation rule Y and let
be the set of connected networks with nonnegative aggregate payoffs. The allocation rule Y satisfies increasing returns to link creation (IRL)Footnote 12 if:
-
(i)
Y satisfies NEC.
-
(ii)
If \(h\in C^{+}(Y)\) and \(h\subseteq h^{\prime }\in \mathbb {C}\), then \(h^{\prime }\in C^{+}(Y)\).
-
(iii)
If \(h\in C^{+}(Y)\) and \(ij\in h\), then \(Y_{i}(h-ij)\le Y_{i}(h) \) and \(Y_{j}(h-ij)\le Y_{j}(h)\) with at least one inequality holding strictly.
-
(iv)
There exists \(h^{\prime }\in C^{+}(Y)\) such that for all \(h\in \mathbb {C\cup }\left\{ g^{\emptyset }\right\} \) with \(h\varsubsetneq h^{\prime }\), for all \(i\in N(h^{\prime })\), we have \(Y_{i}(h)<Y_{i}(h^{ \prime })\).
If an allocation rule satisfies increasing returns to link creation, then by Condition (iv) of IRL there is a connected network \(h^{\prime }\) for which the payoff of all players having at least one link is greater than the payoffs they could obtain in any network \(h\varsubsetneq h^{\prime }\). If we take \(h=g^{\emptyset },\) then it follows that \(Y_{i}(h^{\prime })>0\) for all \(i\in N(h^{\prime }).\) By Condition (ii) of IRL, the aggregate payoffs in any connected network containing \(h^{\prime }\) are nonnegative, and it follows in particular that \(\sum _{i\in N}Y_{i}(g^{N})\ge 0\).Footnote 13 Notice that in connected networks containing \(h^{\prime }\), some players may have negative payoffs, but that their payoffs increase when making additional links by Condition (iii) of IRL. A model that satisfies IRL is the symmetric connections model of Jackson and Wolinsky (1996) when the cost for maintaining a link is small, \(c<\delta (1-\delta )\).
We now show that if the allocation rule satisfies IRL, then there exists a value of \(K^{\prime }\) such that, for all \(K\ge K^{\prime }\), \(\{g^{N}\}\) is a horizon-K farsighted set. A minimal network \(h^{\prime }\) as in Condition (iv) of IRL is called critical. Let \(\tilde{K}=\min \{\#h^{\prime }\mid h^{\prime }\) is a critical network\(\}\) be the number of links in the critical network with the lowest number of links, and let \(\bar{K}\) be the highest number of links in a connected network that does not contain any critical network. Then \(K^{\prime }\) can be taken equal to \(\max \{\tilde{K}, \bar{K}\}\).
Theorem 9
Let the allocation rule Y satisfy IRL. Then \(\left\{ g^{N}\right\} \) is a horizon-K farsighted set for all \(K\ge \max \{\tilde{K},\bar{K} \} \).
Proof
First, we show that \(g^{N}\in D_{1}\). We argued before that IRL implies \( g^{N}\in C^{+}(Y)\). By Condition (iii) of IRL, we have that \( Y_{i}(g^{N})\ge Y_{i}(g^{N}-ij)\) and \(Y_{j}(g^{N})\ge Y_{j}(g^{N}-ij)\) with at least one inequality holding strictly. It follows that \(g^{N}\in f_{1}(g)\) for any network g adjacent to \(g^{N}\), so \(g^{N}\in D_{1}\).
To apply Theorem 7, or Theorem 6 when \(K=1\), we need to show that \(g^{N}\in f_{K}^{\infty }(g)\) for every \(g\ne g^{N}\).
(a) First, consider any network \(g^{\prime }\in G\) having a component \( h^{\prime }\in C(g^{\prime })\) such that \(\sum _{i\in N}Y_{i}(h^{\prime })<0\) . By Condition (ii) of IRL it follows for any non-empty and connected \( h\subseteq h^{\prime }\) that \(\sum _{i\in N}Y_{i}(h)<0\), so \(h^{\prime }\) does not contain a critical network. Moreover, for any non-empty \(h\subseteq h^{\prime }\) there is a player \(i\in N(h)\) who has a payoff \(Y_{i}(h)<0\), and so i has incentives to cut a link, say link ij, foreseeing the empty network where \(Y_{i}(g^{\emptyset })=0\). We have that \(g^{\emptyset }\in f_{ \bar{K}}(h^{\prime })\), and therefore that \(g^{\prime }{\setminus } h^{\prime }\in f_{\bar{K}}(g^{\prime })\).
If \(g^{\prime }{\setminus } h^{\prime }\) has a component \(h^{\prime \prime }\in C(g^{\prime }{\setminus } h^{\prime })\) such that \(\sum _{i\in N}Y_{i}(h^{\prime \prime })<0\), then we can use the argument of the previous paragraph to obtain that \(g^{\prime }{\setminus } (h^{\prime }\cup h^{\prime \prime })\in f_{ \bar{K}}(g^{\prime }{\setminus } h^{\prime })\), and therefore that \( g^{\prime }{\setminus } (h^{\prime }\cup h^{\prime \prime })\in f_{\bar{K} }^{2}(g^{\prime })\). Repeating this argument a finite number of times, we arrive at a network g that is either equal to \(g^{\emptyset }\) or has only components belonging to \(C^{+}(Y)\).
(b) Second, consider the empty network \(g^{\emptyset }\). From Condition (iv) of IRL, there is a network \(h^{\prime }\in C^{+}(Y)\) such that for all \(h\in \mathbb {C}\) with \(h\subsetneq h^{\prime }\) it holds that \(Y_{i}(h^{\prime })>Y_{i}(h)\) for all \(i\in N(h^{\prime })\). In particular, we have that \( Y_{i}(h^{\prime })>Y_{i}(g^{\emptyset })\) for all \(i\in N(h^{\prime })\). Let \(h^{\prime }\) be such a network with \(\tilde{K}\) links. The players in \( N(h^{\prime })\) have incentives to form sequentially the missing links in \( g^{\emptyset }\) foreseeing \(h^{\prime }\), so \(h^{\prime }\in f_{\tilde{K} }(g^{\emptyset })\).
(c) Third, consider any non-empty network \(g^{\prime }\ne g^{N}\) having only components in \(C^{+}(Y)\) and let i be a player in \(N(g^{\prime })\) with degree \(d_{i}(g^{\prime })<n-1\). Let \(j\in N\) be such that \(ij\notin g^{\prime }\). It follows from Conditions (i) and (ii) of IRL that all components of \(g^{\prime }+ij\) belong to \(C^{+}(Y)\). We find by Conditions (i) and (iii) of IRL that \(Y_{i}(g^{\prime }+ij)\ge Y_{i}(g^{\prime })\) and \(Y_{j}(g^{\prime }+ij)\ge Y_{j}(g^{\prime })\) with at least one inequality strict, so \(g^{\prime }+ij\in f_{1}(g^{\prime })\). Repeating this argument m times, where m is the number of links in \(g^{N}{\setminus } g^{\prime }\), we find that \(g^{N}\in f_{1}^{m}(g^{\prime })\).
Theorem 7 now implies that \(\left\{ g^{N}\right\} \) is a horizon-K farsighted set for all \(K\ge \max \{\tilde{K},\bar{K} \} \). \(\square \)
In the symmetric connections model, there is a sequence of improving paths of length 1 from any \(g\ne g^{N}\) to \(g^{N}\) when \(c<\delta (1-\delta )\) . Hence, if \(c<\delta (1-\delta )\), then \(g^{N}\in f_{1}^{\infty }(g)\) for any \(g\ne g^{N},\) and \(\{g^{N}\}\) is the unique horizon-K farsighted set for all \(K\ge 1\). In this model, the complete network is strongly efficient.
8 Heterogeneous horizons
The methodology of this paper can be extended to the case where players have different horizons. Although a full study of the heterogeneous case deserves a careful analysis in its own right and is beyond the scope of this paper, we illustrate the effect of heterogeneity in an example of criminal networks.
Example 4
Calvo-Armengol and Zenou (2004) provide a network analysis of criminal behavior. Here, we present a simplified version of their model. Given some criminal network g, the elements of P(g) are called criminal groups. Each criminal group S has a probability \(p_{S}(g)=\#S/n\) of winning the loot \(B>0\). The network architecture determines how the loot is shared among the criminals in the group. Consider some player \(i\in N\) and let \(S\in P(g)\) be the criminal group i belongs to. We define \( c_{i}(g)=\max _{j\in S}d_{j}(g)\) as the maximum degree in this criminal group. A criminal i who is part of a group \(S\in P(g)\) expects a share \( \alpha _{i}(g)\) of the loot given by
That is, within each criminal group, the criminal that has the highest number of links gets the loot. If two or more criminals have the highest number of links, then they share the loot equally among them.
Criminal i has a probability \(q_{i}(g)\) of being caught, in which case his rewards are punished at a rate \(\phi >0\). It is assumed that the higher the number of links a criminal has, the lower his individual probability of being caught. We assume that the probability of being caught is given by
The total payoffs of criminal i belonging to criminal group \(S\in P(g)\) are therefore equal to
We require \(\phi <n/(n-1)\) to guarantee that payoffs are nonnegative and positive for a player with the highest degree in his group.
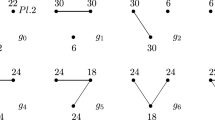
Figure 2 presents the payoffs for 3-player criminal networks with \(B=9\) and \( \phi =1\).
Table 2 shows the farsighted improving paths for the different possible values of K. It can be verified that the farsighted improving paths for the 3-player case do not depend on the specific choices for B and \(\phi \).
For the three-player case, we compute the closed cycles and use Theorem 3 to conclude that \(G_{1}=P_{1}=\{g^{1},g^{2},g^{3},g^{7}\}\) is the horizon-1 farsighted set, so \(G_{1}\) consists of all pairwise stable networks. There are many networks that are stable when players are myopic.
For \(K\ge 2\), we apply Theorem 7 to show that \(G_{K}=\{g^{7}\}\) is the unique horizon-K farsighted set. It holds that \(g^{7}\in D_{1}\) and \(g^{7}\in f_{2}^{\infty }(g)\) for every \(g\ne g^{7}\), so \(\{g^{7}\}\) is a horizon-K farsighted set. Since \(g^{7}\in P_{K}\), it follows from Theorem 7 that \(\{g^{7}\}\) is the unique horizon-K farsighted set. If criminals behave myopically, they may not go beyond forming a single link in the three-player case. But with a common horizon of at least 2, the complete criminal network emerges as the unique prediction.
We show that it is not sufficient that two of the players, without loss of generality Players 1 and 2, have a horizon equal to 2 in order to reach the conclusion that only \(g_{7},\) the complete network, is stable. Player 3 is assumed to have a horizon equal to 1. The crucial step is to show that it is not possible to leave \(g^{1}\) in this case, so \(\{g_{7}\}\) fails external stability.
It is evident that \(g^{0}\) cannot be reached from \(g^{1}\) since no player prefers \(g^{0}\) to \(g^{1}.\) The horizon-2 players do not prefer \(g^{2}\) and \( g^{3}\) to \(g^{1},\) whereas the horizon-1 Player 3 gets payoff 0 after forming a link, strictly lower than his payoff at \(g^{1}.\) It is therefore impossible to reach \(g^{2}\) or \(g^{3}\) from \(g^{1}.\) It takes 3 steps to reach \(g^{6}\) from \(g^{1},\) which is not possible since the maximum horizon of the players is equal to 2. After the deletion of the link 12 from \(g^{1},\) it takes two additional steps to reach \(g^{4}\) or \(g^{5}.\) Since the maximum horizon of the players is equal to 2, it follows that the only way to reach \( g^{4}\) or \(g^{5}\) from \(g^{1}\) is by forming the link directly. Since Player 3 has horizon 1 and gets strictly lower payoff, this is not possible. Finally, we consider whether it is possible to reach \(g^{7}.\) The only possibility to do so is via \(g^{4}\) or \(g^{5},\) which requires the horizon-1 Player 3 to get strictly lower payoff. We conclude that it is not possible to leave \(g^{1}.\)
On the other hand, only Player 2 needs to have horizon 2 to reach \(g^{7}\) from \(g^{2}.\) Player 2 is willing to form a link with Player 1 and move to \( g^{4}\) even though this means getting temporarily a payoff equal to 0, since Player 2 realizes that in the next step the horizon-1 Player 3 is willing to form a link to complete the network. Player 1 is willing to form the link with Player 1 and move to \(g^{4}\) since this entitles Player 1 to a payoff of 9. From \(g^{3},\) one only needs Player 1 to have horizon 2 in order to reach \(g^{7}.\)
We denote the correspondence that indicates which networks can be reached if Player 1 has horizon 2 and the other players horizon 1 by \(f_{211}.\) Similarly, \(f_{221}\) corresponds to the case where Players 1 and 2 have horizon 2 and Player 3 has horizon 1. Table 3 presents both correspondences.
Since \(\tilde{f}_{211}(g^{1})=\tilde{f}_{211}(g^{2})=\tilde{f} _{211}(g^{7})=\left\{ \emptyset \right\} \), we have that \(g^{1}\), \(g^{2}\) and \(g^{7}\) must all belong to \(G_{211}\). Then, external stability is also satisfied. It follows that \(G_{211}=\{g^{1},g^{2},g^{7}\}\). Since \(\tilde{f} _{221}(g^{1})=\tilde{f}_{221}(g^{7})=\left\{ \emptyset \right\} \), we have that \(g^{1}\) and \(g^{7}\) must both belong to \(G_{221}\). In that case, external stability is also satisfied. It follows that \(G_{221}=\{g^{1},g^{7} \} \). We therefore find a connection between the reasoning horizon and the ability to achieve better payoffs.
Herings et al. (2017b) analyze the von Neumann–Morgenstern stable set of the case where some players have horizon 1 and some players have horizon \(\infty \) in the context of the marriage model of Gale and Shapley (1962). The predictions of the heterogeneous case can be quite different from the two extremes where either all players have horizon 1 or all players have horizon \(\infty .\) In the homogeneous case, the prediction is always a subset of the core, whereas in the heterogeneous case it is also sometimes possible to sustain non-core elements. In case one side of the market is more farsighted, it is also found that the more farsighted side is able to reach their preferred stable matching.
In general, we do not expect a relation between the stable configurations in the heterogeneous case and those obtained at the minimum and the maximum horizon of the players. Also, we do not expect one can derive general implications about the horizon of a player and his degree or centrality in the network. But in particular applications it is often possible to say more.
9 Conclusion
We study the stability of social and economic networks when players are limited farsighted. Pairwise stability is a very important tool in network analysis. One shortcoming of pairwise stability is the lack of farsightedness. Players do not anticipate that other players may react to their changes. However, unlimited farsightedness often requires too much foresight on behalf of the players. Hence, we propose an intermediate concept, the horizon-K farsighted set, that can be used to study the influence of the degree of farsightedness on network stability.
In the present paper, we assume that all players have a reasoning horizon of length K, where K can be any natural number. By doing so, we cover myopic and full farsighted behavior as extreme cases, and we are able to provide a tractable concept to study the influence of the degree of farsightedness on the predictions of network formation models. Recently, Kirchsteiger et al. (2016) show experimental evidence that suggests that subjects are consistent with intermediate horizons of farsightedness.
We think that our concept of a horizon-K farsighted set could be useful in the study of the reasoning horizon needed in order to sustain certain networks as stable outcomes. Consider for instance the formation of a network of bilateral free trade agreements. Goyal and Joshi (2006) show that global free trade, represented by the complete network, is pairwise stable, implying that global free trade, if reached, will prevail. However, the complete network is not the unique pairwise stable network and Goyal and Joshi’s analysis leaves out the issue whether global free trade can be obtained from the empty network or any preexisting free trade network when countries are myopic.
Recently, Zhang et al. (2013) complements the analysis of Goyal and Joshi (2006) by examining whether global free trade can result from a sequence of bilateral free trade agreements when countries are farsighted. They show that the complete network constitutes a pairwise farsightedly stable set, though is not uniquely so. In particular, they show that there is a farsighted improving path from the empty network to the complete network which involves link additions only, while farsighted improving paths from preexisting free trade networks may involve both link deletion and addition. However, in order to obtain this result, Zhang et al. (2013) assumes that countries have perfect foresight. Could global free trade result from a sequence of bilateral free trade agreements when countries are neither myopic nor completely farsighted but have some limited degree of farsightedness? Which is the reasoning horizon needed in order to reach the global free trade network from any preexisting free trade network? Structural properties of free trade networks must be taken into account to better understand whether free trade areas are conducive or detrimental to globalization. Hence, it is important to acquire knowledge about the horizon of farsightedness of countries to determine which free trade networks are likely to emerge in the long run and the kind of intervention that supranational authorities should undertake in order to promote global free trade.
One-to-one matching problems are another simple example of network formation. Agents are either male or female, and want to be matched to a partner of the opposite sex or remain single. For one-to-one matching problems, Ehlers (1997) characterizes the von Neumann–Morgenstern stable set using a direct dominance relation and shows that this set can be larger than the core. Requiring coalitional sovereignty (C) and using the path dominance relation (P) to define internal and external stability, Herings et al. (2017a) have shown that there is a unique CP vNM set that coincides with the core. Thus, contrary to the stable sets, CP VNM sets cannot include matchings that are not in the core. Mauleon et al. (2011) provides the characterization of Harsanyi sets (that are also pairwise farsightedly stable sets of Herings et al. 2009): a set of matchings is a Harsanyi set if and only if it is a singleton subset of the core. However, to obtain this result, Mauleon et al. (2011) assumes that agents are completely farsighted. When this is the case, each core element can be reached by means of a farsighted improving path from any other matching. How robust are these results to the introduction of limited farsightedness? Which is the reasoning horizon that guarantees that only core elements are stable in the long run?
Empirical work suggests that R&D collaboration between firms is common. Typically, collaboration ties are bilateral and are embedded within a broader network of similar ties with other firms. Several recent contributions have examined the incentives of firms to collaborate with each other in order to reduce its marginal cost of production (see, for instance, Goyal and Moraga-Gonzalez (2001) and Goyal and Joshi (2003)). All these contributions differ in the way they model the reduction in marginal cost due to the R&D collaborative agreement as well as the spillovers on competitors, but they all assume that firms are myopic. Recently, Mauleon et al. (2014) studies the R&D networks that would arise in the long run, analyzing both the case with myopic firms and the one with farsighted firms. The reduction of the marginal cost of production for one firm is assumed to be proportional to the number of firms it is connected to. They show that firms form networks consisting of two components, with firms in the largest component obtaining a competitive advantage upon the other group. The difference in the number of firms between the two components is at most three if firms are myopic. However, if firms are farsighted, the largest component comprises roughly three-quarters of the firms; hence, the larger group of firms can derive a much greater competitive advantage from R&D collaborations relative to the other group. In order to give the correct incentives for firms to form collaborative agreements, it is necessary to know the structural properties of the R&D networks that will emerge in the long run. For this reason, and given the different predictions about the stable R&D networks when firms are either myopic or farsighted, it is crucial to know which R&D network firms with intermediate degrees of farsightedness would form. Which is the reasoning horizon needed to obtain the predictions for completely farsighted firms? How do the predictions about stable R&D networks relate to the degree of farsightedness? We argue here that our concept could be used as a first step in trying to answer all these questions.
Notes
An alternative way to model network stability is to explicitly model a game by which links form and then to solve that game using the concept of Nash equilibrium or one of its refinements. See Aumann and Myerson (1988), Myerson (1991) and Dutta and Mutuswami (1997) among others. Also dynamic approaches have been explored, see Jackson and Watts (2002) and Song and van der Schaar (2015).
Krishnan and Sciubba (2009) find that pairwise stability leads to testable predictions for the network architectures generated by labor-sharing groups in village economies of rural Ethiopia. In addition, their empirical results confirm strongly that the architecture of a social network and not just the number of links, has an important role to play in understanding network formation and the role of social networks on economic performance.
Kirchsteiger et al. (2016) design a simple network formation experiment to test between pairwise stability and farsighted stability, but find evidence against both of them. Their experimental evidence suggests that subjects are consistent with an intermediate rule of behavior, which can be interpreted as a form of limited farsightedness. Similar experimental evidence for limited farsightedness is found in van van Dolder and Buskens (2014).
Throughout the paper we use the notation \(\subseteq \) for weak inclusion and \(\varsubsetneq \) for strict inclusion. Finally, \(\#\) will refer to the notion of cardinality.
The notion of farsighted improving path, without restrictions on the length, has been suggested in “Section 11. Postscript” of Harsanyi (1974).
We use the notation \( (Y_{i}(g^{\prime }), Y_{j}(g^{\prime })) \gg (Y_{i}(g), Y_{j}(g)) \) for \( Y_{i}(g^{\prime }) > Y_{i}(g) \) and \( Y_{j}(g^{\prime }) > Y_{j}(g), \)\( (Y_{i}(g^{\prime }), Y_{j}(g^{\prime })) > (Y_{i}(g),Y_{j}(g)) \) for \( Y_{i}(g^{\prime }) \ge Y_{i}(g) \) and \( Y_{j}(g^{\prime }) \ge Y_{j}(g) \) with at least one inequality holding strictly, and \( (Y_{i}(g^{\prime }), Y_{j}(g^{\prime })) \ge (Y_{i}(g),Y_{j}(g)) \) for \( Y_{i}(g^{\prime }) \ge Y_{i}(g) \) and \( Y_{j}(g^{\prime }) \ge Y_{j}(g). \)
Page and Wooders (2009) use the path dominance relation to define the notion of path dominance core. For some given \(m \in \mathbb {N}, \) a network g path dominates \(g^{\prime }\) if \(g\in \tilde{f}_{\infty }^{m}(g^{\prime })\). The path dominance core contains all networks that are not path dominated, but it often fails to be non-empty.
Page and Wooders (2009) define the notion of a basin of attraction. A basin of attraction corresponds to a closed cycle for an arbitrary dominance relation. A special case is to use the dominance relation \(f_{1}. \)
Chwe (1994) defines the notion of largest consistent set. A set G is a consistent set if both external and internal deviations with respect to \( \tilde{f}_{\infty }\) are deterred. The largest consistent is the set that contains all consistent sets.
The set G is a von Neumann–Morgenstern pairwise farsightedly stable set if (i) for every \(g\in G\), \( \tilde{f}_{\infty }(g)\cap G=\emptyset \) and (ii) for every \(g\in \mathbb {G}{\setminus } G\), \( \tilde{f}_{\infty }(g)\cap G\ne \emptyset \). See Herings et al. (2009).
Dutta et al. (2005) defines the property of increasing returns to link creation for a value function. A value function satisfies this property if there is a threshold network for which the value is nonnegative, and each time a new link is added to this threshold network, both aggregate payoffs and payoffs of players who are adding a link to the network increase. Here, we translate the main idea behind this property to an allocation rule.
Dutta et al. (2005) defines the property of increasing returns to link creation for a value function by imposing the value of each network \( h\supsetneq h^{\prime }\) to be greater than the value of \(h^{\prime }\) and, in particular, that the complete network generates the highest possible value, i.e., the complete network is the strongly efficient network.
References
Aumann, R., Myerson, R.: Endogenous formation of links between players and coalitions: An application of the Shapley value. In: Roth, A. (ed.) The Shapley Value, pp. 175–191. Cambridge University Press, Cambridge (1988)
Calvo-Armengol, A., Zenou, Y.: Social networks and crime decisions: the role of social structure in facilitating delinquent behavior. Int. Econ. Rev. 45, 939–958 (2004)
Chwe, M.S.: Farsighted coalitional stability. J. Econ. Theory 63, 299–325 (1994)
Dutta, B., Ghosal, S., Ray, D.: Farsighted network formation. J. Econ. Theory 122, 143–164 (2005)
Dutta, B., Mutuswami, S.: Stable networks. J. Econ. Theory 76, 322–344 (1997)
Ehlers, L.: Von Neumann–Morgenstern stable sets in matching problems. J. Econ. Theory 134, 537–547 (2007)
Gale, D., Shapley, L.S.: College admissions and the stability of marriage. Am. Math. Mon. 69, 9–15 (1962)
Goyal, S., Moraga-Gonzalez, J.L.: R&D networks. RAND J. Econ. 32, 686–707 (2001)
Goyal, S., Joshi, S.: Networks of collaboration in oligopoly. Games Econ. Behav. 43, 57–85 (2003)
Goyal, S., Joshi, S.: Bilateralism and free trade. Int. Econ. Rev. 47, 749–778 (2006)
Harsanyi, J.C.: An equilibrium-point interpretation of stable sets and a proposed alternative definition. Manag. Sci. 20, 1472–1495 (1974)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Rationalizability for social environments. Games Econ. Behav. 49, 135–156 (2004)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Farsightedly stable networks. Games Econ. Behav. 67, 526–541 (2009)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Stable sets in matching problems with coalitional sovereignty and path dominance. J. Math. Econ. 71, 14–19 (2017a)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Matching with Myopic and Farsighted Players. GSBE Research Memorandum 17/11, Maastricht University, Maastricht, pp. 1–36 (2017b)
Jackson, M.O.: Social and Economic Networks. Princeton University Press, Princeton (2008)
Jackson, M.O., van den Nouweland, A.: Strongly stable networks. Games Econ. Behav. 51, 420–444 (2005)
Jackson, M.O., Watts, A.: The evolution of social and economic networks. J. Econ. Theory 106, 265–295 (2002)
Jackson, M.O., Wolinsky, A.: A strategic model of social and economic networks. J. Econ. Theory 71, 44–74 (1996)
Kirchsteiger, G., Mantovani, M., Mauleon, A., Vannetelbosch, V.: Limited farsightedness in network formation. J. Econ. Behav. Organ. 128, 97–120 (2016)
Krishnan, P., Sciubba, E.: Links and architecture in village networks. Econ. J. 119, 917–949 (2009)
Mauleon, A., Sempere-Monerris, J.J., Vannetelbosch, V.: Farsighted R&D networks. Econ. Lett. 125, 340–342 (2014)
Mauleon, A., Vannetelbosch, V.: Farsightedness and cautiousness in coalition formation games with positive spillovers. Theor. Decis. 56, 291–324 (2004)
Mauleon, A., Vannetelbosch, V., Vergote, W.: von Neumann Morgenstern farsightedly stable sets in two-sided matching. Theor. Econ. 6, 499–521 (2011)
Morbitzer, D., Buskens, V., Rosenkranz, S., Raub, W.: How farsightedness affects network formation. Anal. Kritik 36, 103–133 (2014)
Myerson, R.: Game Theory: Analysis of Conflict. Harvard University Press, Cambridge (1991)
Page Jr., F.H., Wooders, M., Kamat, S.: Networks and farsighted stability. J. Econ. Theory 120, 257–269 (2005)
Page Jr., F.H., Wooders, M.: Strategic basins of attraction, the path dominance core, and network formation games. Games Econ. Behav. 66, 462–487 (2009)
Ray, D., Vohra, R.: The farsighted stable set. Econometrica 83, 977–1011 (2015)
Song, Y., van der Schaar, M.: Dynamic network formation with incomplete information. Econ. Theor. 59, 301–331 (2015)
van Dolder, D., Buskens, V.: Individual choices in dynamic networks: an experiment on social preferences. PLoS ONE 9, 1–16 (2014)
von Neumann, J., Morgenstern, O.: Theory of Games and Economic Behavior. Princeton University Press, Princeton (1944)
Xue, L.: Coalitional stability under perfect foresight. Econ. Theor. 11, 603–627 (1998)
Zhang, J., Xue, L., Zu, L.: Farsighted free trade networks. Int. J. Game Theory 42, 375–398 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
We thank the editor and two anonymous referees for their valuable comments and suggestions to improve the paper. Vincent Vannetelbosch and Ana Mauleon are Senior Research Associates of the National Fund for Scientific Research (FNRS). Financial support from the Spanish Ministry of Economy and Competition-FEDER-European Union under the project ECO2015-64467-R (MINECO/FEDER, EU), from the MSCA ITN Expectations and Social Influence Dynamics in Economics (ExSIDE), Grant No 721846 (1/9/2017-31/8/2020), and from the Belgian French-speaking community ARC project \(\hbox {n}{{}^\circ } \)15/20-072 of Saint-Louis University, Brussels, is gratefully acknowledged.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Herings, P.JJ., Mauleon, A. & Vannetelbosch, V. Stability of networks under horizon-K farsightedness. Econ Theory 68, 177–201 (2019). https://doi.org/10.1007/s00199-018-1119-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-018-1119-7