1 Introduction

The addition of reactive particles in solid propellants, pyrotechnics, and energetic materials is a well-known technique used to enhance the performance [1,2,3]. In propellants, the aluminium particles will add energy to the reaction and increase the burn rate, whereas in high explosives the addition of aluminium will enhance the blast effect, as the total energy output is increased. According to Tanguay et al. [4], the addition of aluminium or magnesium particles in a high explosive will lead to an increase in energy release of 5–6 times more than the bare high explosive. The results are observed in the far field [5] as an increase in the blast peak overpressure. This is due to the fact that aluminium has a high density and a high heat of combustion.

Table 1 Pressure sensor positions in the shock tube measured relative to driver section end wall
Full size table

Ignition is defined as a process in which sufficient energy is provided to initiate a combustion process. Frank-Kamenetskii [6] describes ignition as a thermal run-away process in the transition between the kinetic and diffusive regime. In the current work, the term “ignition” is used to describe the reaction taking place when the aluminium cloud has been sufficiently heated to initiate a reaction onset in the aluminium particle cloud. The reaction is easily observed as small intense sources of light in an otherwise dark film.

A large fraction of published work on the ignition and burning of aluminium particles focuses on single or small amounts of particles and studies the ignition and burning of the particles under different pressures and temperatures, preferably at rest [7,8,9]. The defined combustion regimes depend on the particle size. For particles in the micrometer regime, sized \(d > 10\,\upmu \hbox {m}\), a diffusion-limited combustion is assumed, whereas in the nanometer range, the combustion is assumed to be governed by surface reaction kinetics [10,11,12].

The properties of the aluminium particle surface are important for the understanding of the ignition and burning of particles. When aluminium particles are left in contact with air, a 5–10-nm-thick layer forms immediately on the particle surface [13]. The burning of the aluminium particles depends on the disruption of the oxide layer. The melting temperature of aluminium oxide is approximately 2300 K, whereas the pure aluminium melting temperature is 933 K. Due to the difference in thermal expansion of the aluminium and the oxide, the heating of the particle surface leads to cracks formed on the oxide layer. The self-heating reaction occurs when the temperature reaches the melting point of the aluminium oxide [13]. At this point, the oxide shell is cracked, and the reaction proceeds via the vapour phase. The self-ignition theory does not explain low-temperature ignition. The effect of the heating rate is therefore considered, defining low-speed heating at 8–10 degrees per second, and high-speed heating at 20 degrees per second or more [13]. If the particle heating is sufficiently slow, the cracks are repaired by pure aluminium passing through, sealing the cracks and avoiding substantial self-heating. In the case of high-speed heating, however, the shell cracking is more prominent, and self-heating more efficient. Consequently, a reduction in the ignition temperature is observed.

Table 2 Definitions
Full size table

When studying aluminium particle clouds, the risk of particle agglomeration also has to be considered. According to Ho and Sommerfeld [14], particle agglomeration is most frequently observed for small particles with diameter 1–10 \(\upmu \hbox {m}\). Conditions favourable for agglomeration are high particle concentration, good sticking properties due to van der Waals forces, and large size ratio between particle diameters, whereas conditions unfavourable for particle agglomeration are high particle density, large particle stiffness, and high turbulent kinetic energy. The result of particle agglomeration is an effectively smaller particle surface area and thus a reduction in heat loss. Additionally, the interior surface allows oxidation at lower temperatures than for the individual particles. Agglomeration may therefore lead to a reduced ignition temperature. The effect of agglomeration is difficult to measure and therefore frequently neglected in previous work [15].

Spontaneous ignition of reactive particles was studied experimentally by Roberts et al. [16]. They presented results from shock tube experiments with particles in an oxygen atmosphere for pressures up to 34 MPa. Particle heating due to heterogenous reactions on the particle surface was found to be significant for the lower temperatures, whereas for higher temperatures, the heat transfer from gas to particles becomes more important. For temperatures exceeding 3000 K, the heterogenous heating was found to be negligible. They also found that the burning time for aluminium particles was not strongly dependent on pressure although an increase in pressure leads to a decrease in burning time.

Boiko et al. [17] presented experimental results for spontaneous ignition of aluminium particles in the “low- temperature” regime, from 1000 to 1800 K. Their experiments were performed with particles in three different size ranges (3–5, 10–14, 14–20 \(\upmu \hbox {m}\)), with particle mass varied from 0.2 to 20 mg. The smallest particles were observed to ignite first. Their published shock tube results do not agree with the experimental data for single particle ignition under static conditions, for which higher ignition temperatures are observed [18].

In the present work, we wish to study spontaneous ignition of aluminium particle clouds in closer detail. The work is the first step in a study of the effect of including reactive additives in various high explosives. Prior to that, however, we wish to isolate the effect of the shock interaction with the aluminium particle cloud to establish an experimental database that can be used for developing numerical models for cloud ignition and burning.

The experiments are conducted in a high-pressure shock tube, with a pile of reactive aluminium particles placed on a splitter plate at the shock tube end wall. Avoiding the additional complexity of introducing high explosives, our goal is a more fundamental study of the acceleration, heating and ignition of the aluminium particle cloud due to interactions with the initial and reflected shock.

Fig. 1
figure 1

Sketch of the shock tube with the test section mounted at the right end. The distances are given in millimeters

Full size image
Fig. 2
figure 2

Left-hand side: Picture of an aluminium membrane prior to test. Right-hand side: Aluminium membrane photographed after test

Full size image

2 Experimental setup

The present experimental work was conducted in a high-pressure shock tube, with a driver section specifically constructed to withstand pressure up to 200 MPa. The shock tube has a total length of 5.780 m and a driver section of 1.380 m. A sketch of the shock tube is presented in Fig. 1. The inner dimensions of the tube are \(83\times 83\) mm. The membranes used to separate the driver section from the driven tube are made from aluminium plates of thickness 3–6 mm. Prior to each test, a cross is scared into the membrane to aid the rupture pattern, as illustrated in the left-hand side of Fig. 2. This technique is chosen to improve the repeatability of the resulting shock Mach numbers. The depth of the scaring is measured, and variations in depth allow for fine tuning of the obtained shock wave strength. The right photograph in Fig. 2 shows the membrane after use, illustrating how the pre-scaring leads to a clean membrane opening, avoiding loose parts from being thrown into the driven section. There are adapter positions in the shock tube ceiling. The exact sensor positions are given in Table 1, measured relative to the driver section left end wall. Kulite pressure sensors, HKS-375, are used, with a sampling frequency of 500 kHz. An air-cooled compressor was used to pressurise the driver section, with specifications given in [19].

A test section with vertical windows on both sides is added at the end of the driven section. Inside the test section, a vertical end block is used to close the tube, as illustrated in the left sketch of Fig. 3. A splitter plate of 90 mm in length is mounted horizontally onto the end block. The splitter plate has an angle of 12 degrees on the lower side and is constructed to allow material to be deposited, while avoiding disturbances in the shock as much as possible. The concept of a splitter plate is frequently used in aerodynamical research [20] as well as for pressure sensor mounting in free field [21]. Although the geometry of the splitter plate varies, these previous studies emphasise the importance of ensuring that the splitter plate is mounted perpendicular to the incident shock wave direction.

The mid-photograph of Fig. 3 shows a typical experimental setup. For symmetry reasons, the aluminium powder ridge is deposited on the centre line in the axial direction of the shock tube. A 3D-printed form of dimensions \(80.0\times 3.0\times 1.5\) mm was used to shape the aluminium ridge. In all of the present experiments, the amount of aluminium was 340 mg, distributed as 4.25 mg/mm. The aluminium particles used in the experiments are produced by Carlfors Bruk, with designation A 100. The average particle diameter is 40 \(\upmu \hbox {m}\). Except for the oxide layer, the powder is uncoated. Screen analysis performed by the manufacture estimates a size distribution where 86% of the particles have a diameter less than 42 \(\upmu \hbox {m}\), and only 1% is estimated to be larger than 75 \(\upmu \hbox {m}\). The active aluminium content is estimated to be 99.6%. All experiments were performed with air as driver and driven gas. Atmospheric pressure and room temperature are measured to be approximately \(P_1=101\) kPa and \(T_1= 296.4\) K.

Fig. 3
figure 3

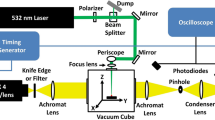
Left panel: Prospective sketch of wedge for deposition of solid particles and the accompanying end block. Mid-panel: Wedge with aluminium powder ridge deposited. Right panel: Illustration of the optical setup showing the lens with the light source in front, beamsplitter in the middle and high-speed video cameras mounted to the right at a 90-degree angle

Full size image

The optical instrumentation is mounted on a separate table, carefully positioned to avoid direct physical contact with the tube. This is important in order to eliminate vibrations due to the generation of the shock, which will otherwise degrade the optical results drastically for the Mach numbers of interest. High-speed video cameras and light sources are mounted on opposite sides of the window section. The optical arrangement is tested before mounting, as illustrated in Fig. 3. Two Phantom v2012 high-speed video cameras are used together with a 45-degrees CMBS080 beamsplitter from Opto Engineering. The schlieren setup is compact, based on the use of telecentric lenses from Opto Engineering and a laser light source from Cavilux HF. Preliminary results showed that the schlieren setup was not capable of visualising the density discontinuities due to the burning particles. A thick smoke was, however, observed, indicating that ignition did in fact take place. The nature of the micron-sized particles igniting and burning is therefore captured on a completely dark film which is time interlaced with the light source of the schlieren setup. The second camera is mounted at the other end of the beamsplitter without the telecentric lenses. Since the dark film does not allow a clear representation of the shock wave propagation and reflection phenomena, the optimal setup was found to be a combination of the schlieren setup and a separate dark-film camera.

The experimental design is a result of a comprehensive work on developing the shock tube setup and mounting, to reduce the effect of vibrations and horizontal movements caused by the shock generation. Based on experience from preliminary tests, a new shock tube cradle and a damper mounted behind the driver was constructed. The instrumentation table was also modified to avoid direct contact with the shock tube.

Table 3 Experimental setup
Full size table

3 Results

The present work is based on 30 experiments with a selection of different membrane thicknesses and membrane scaring depths. The test conditions and estimated Mach numbers are summarised in Table 3.

Fig. 4
figure 4

Pressure–time history for positions as given in Table 1. Time is given relative to \(t_\textrm{zero}\). The first sensor, S1, is mounted in the ceiling of the driver section. The signals are processed with a boxcar running filter of 40. The shock time of arrival at the sensor is marked, \(t_\textrm{toa}\). For the endplate sensor shock refection, \(t_\textrm{refl}\), is illustrated with a red colour. Ignition time, \(t_\textrm{ign}\), is illustrated with a blue colour

Full size image

3.1 Results from pressure gauges

Pressure sensors are mounted in the ceiling of the driver, driven, and window sections, with their distances given relative to the left-hand driver wall (Table 1). Figure 4 shows the results from the pressure sensor recordings. The figure is based on experiment number 30 (Table 3). The first sensor, Fig. 4a, shows the pressure–time history in the driver section. The short time period before membrane rupture is observed as a high-pressure plateau. When the membrane ruptures, a shock is formed, propagating along the shock tube. The figure shows the increasing delay in the shock arrival times with distance. The last sensor, Fig. 4h, is mounted to the end wall. This sensor illustrates the shock reflection effect, as the initial pressure increase appears to be significantly higher than that observed for the other pressure sensors. The instrumentation setup does not give a “time zero” (\(t_\textrm{zero}\)) to define the exact shock initiation time. Therefore, the shock time of arrival (\(t_\textrm{toa}\)) data is used together with their sensor positions to extrapolate the data back to time zero at the membrane. The timing of the sensor data is then adjusted accordingly. A list of the different time definitions is given in Table 2. The remaining results are presented using a timescale with \(t_\textrm{refl}=0\).

The Mach number is a dimensionless parameter, defined as the ratio between the shock velocity and the speed of sound. The average Mach number is estimated using pairs of sensors, their shock TOA, and their internal distance. The results are presented in Table 3 for all experiments. The average Mach number for the example in Fig. 4 was found to be \(M_\textrm{S} = 2.36\).

An x–t diagram is presented in Fig. 5. The plot shows the propagation and reflection of the first shock (dashed black line). When the shock arrives at the window section end wall, it is reflected and starts propagating in the opposite direction. This point in time is defined as \(t_\textrm{refl}\). The ignition delay time \(t_\textrm{ign}\) is measured relative to the reflection time. The contact surface (red line) is a second density discontinuity observed behind the leading shock. The contact surface line is only plotted until it collides with the reflected shock. At this point, the shock is affected by the contact surface, giving a kink to the reflected shock curve. The reflected shock then propagates until it reaches the driver wall and is reflected a second time.

The different regions of the shock tube, relative to the shock wave, are usually given different numbers. Initially, the driver section is region 4, and the undisturbed region ahead of the shock is region 1. When the shock is formed, the region between the shock and the contact surface is called region 2, and the region behind the contact discontinuity is called region 3. In case of a closed-end shock tube, the region behind the reflected shock is called region 5.

The pressure behind the reflected shock, \(P_5\), is computed from basic shock tube relations [22, 23]:

$$\begin{aligned} \frac{P_5}{P_1}=\frac{P_5}{P_2} \frac{P_2}{P_1} =\frac{[2\gamma M_\textrm{R}^2-(\gamma -1)]}{\gamma +1}\frac{[2\gamma M_\textrm{S}^2-(\gamma -1)]}{\gamma +1}, \end{aligned}$$
(1)

where the reflected Mach number \(M_\textrm{R}\) is determined from,

$$\begin{aligned} \frac{M_\textrm{R}}{M_\textrm{R}^2-1} =\frac{M_\textrm{S}}{M_\textrm{S}^2-1}\sqrt{1+\frac{2(\gamma -1)}{(\gamma +1)^2}(M_\textrm{S}^2-1)\Big (\gamma +\frac{1}{M_\textrm{S}^2}\Big )}.\nonumber \\ \end{aligned}$$
(2)

Here, \({M}_\textrm{R}\) is solved as a quadratic equation using the positive solution. In Fig. 6a, we have plotted the pressure ratio \(P_5/P_1\) as a function of Mach number, \(M_\textrm{S}\). The red diamond symbols show the results from (1). The pressure plateau behind the reflected shock has been identified in all experiments, and the results are illustrated with black star symbols. As Fig. 6a illustrates, the results show good agreement with the experimental results, even if the equations do not take the aluminium particle cloud into account. The temperature in region 5 is found from the following equation [24, 25]:

$$\begin{aligned} \frac{T_5}{T_1} =\frac{[(2(\gamma -1)M_\text {S}^2+(3-\gamma )] [(3\gamma -1)M_\textrm{S}^2-2(\gamma -1)]}{(\gamma +1)^2M_\textrm{S}^2}, \end{aligned}$$
(3)

again ignoring the presence of the aluminium particle cloud. The results are plotted as a function of the experimentally obtained Mach number as shown in Fig. 6b. The green colour is used to identify the experiments where ignition did not occur. As the figure illustrates, ignition of the aluminium particle cloud in the reflected region does not take place unless the gas temperature is above approximately 635 K.

Fig. 5
figure 5

Sketch of a x–t diagram for the shock and contact surface. The shock is initiated at \(t_\textrm{zero}\), and reflected at \(t_\textrm{refl}\). The membrane is positioned at \(x=1.38\), and the vertical line at \(x = 5.780\) m marks the window section end wall

Full size image
Fig. 6
figure 6

a Pressure sensor readings for the ratio \(P_5/P_1\) (red diamonds). The black symbols show the computed ratio. b Temperature, \(T_5\), computed based on measured Mach number. The experiments with no particle ignitions present, are plotted in green

Full size image
Fig. 7
figure 7

Schlieren images for experiment 30 for a \(t=-0.08\) ms and b \(t=-0.04\) ms. Time is measured relative to the shock reflection at the end wall, \(t_\textrm{refl}\)

Full size image

3.2 Schlieren images from the high-speed video camera

For all 30 experiments, approximately 1000 images are generated from each of the two high-speed video cameras. This leaves an extensive amount of data to be further processed. A frame rate of 45,998 frames per second is used for both cameras. The compact schlieren setup has an exposure time of 1 \(\upmu \hbox {s}\).

The schlieren technique is an imaging method used to visualise density discontinuities due to changes in the refractive index. In this way, the shock and density discontinuities are visualised as dark streaks against the lighter background [26]. When such a technique is used in a shock tube, the light source is positioned on the opposite side of the window section. The images we observe are therefore a result of the integrated light path across the width of the tube. Since the shock interacts with the reactive particles, the local shock velocity here is slightly reduced. A consequence of this local shock deceleration is that the shock appears slightly thicker on the high-speed images in this region.

The schlieren images are used to estimate the timing of the shock wave phenomena. We identify the first frame for which the incident shock is observable. Next, the frame where the shock is reflected at the end wall is identified. Since the exact reflection time may occur sometime in between two images, the image before and after are used to confirm the frame identification. The uncertainty in the timing is linked to the frame rate, giving a timing uncertainty less than 21.7 \(\upmu \hbox {s}\). The last image before the shock leaves the window section is also identified.

In Fig. 7, two schlieren images are presented. The time interval between the images is \(\Delta t=0.05\) ms. Figure 7a shows the shock propagating along the splitter plate. The shock has just passed the front of the aluminium particle ridge, observed as a small dark elevation. Since the aluminium particles are much heavier than the gas molecules, their shock acceleration process is slow. At this point in time, the aluminium particles therefore appear not to have moved. Since the splitter plate has an angle of 12 degrees, a shock reflection phenomenon is observed on the downside of the splitter plate, formed as a wedge. The shock reflection develops from a regular reflection with the reflection point on the wedge, into a Mach reflection. A Mach reflection is easily recognised from the triple point observed below the lower wedge surface. A triple point connects the incident shock wave, the reflected shock, and the Mach stem which is observed behind the incident shock pointing in the direction towards the wedge. In Fig. 7b, the shock has propagated further down towards the end wall. At this point, the left corner of the aluminium particle ridge has started to move and is observed as a dark region. Also the distance of the triple point from the lower wedge surface increases as the shock propagates along the wedge. In this image (Fig. 7b), the triple point has almost reached the bottom of the tube.

The schlieren images are further used to investigate possible effects due to the introduction of the splitter plate. Using edge detection routines to identify the shock position, the part of the shock observed above the aluminium ridge is observed to remain perpendicular to the wedge surface. The average Mach numbers computed from the high-speed film agree well with the Mach numbers computed from the pressure sensors.

Prior to every experiment, the massive steel block with the splitter plate mounted has to be ejected from the tube. Such an operation is only possible if there is enough space for the construction to be moved relative to the tube wall. Circulation of gas and aluminium particles from above to below the splitter plate is therefore possible, as observed in the results on the dark film. Between each experiment, the shock tube is cleared for soot by running a shock through the tube without the end plate mounted.

3.3 Studying the images from the dark-film high-speed video

Fig. 8
figure 8

Dark-film images for experiment 30, for a \(t=2.30\) and b \(t=2.53\) ms. Time is measured relative to the time of shock reflection at the end wall, \(t_\textrm{refl}\)

Full size image

The second high-speed video camera is used as a dark-film camera to capture the particle ignition and burning. The dark-film setup uses an exposure time of 20 \(\upmu \hbox {s}\). The relatively long exposure time gives the opportunity to observe not only the ignition of the aluminium particles, but also the light traces showing the motion pattern of the individual burning particles. In Fig. 8, we have presented the result for two time frames with a time difference of \(\Delta t=0.23\) ms. Although the images are dark, large areas of burning particles are observed. Since the shock is not observable with this dark-film setup, the time of shock reflection is found in the time interlaced schlieren series.

In the present work, we define the ignition delay as the time it takes from when the shock has reflected off the end wall until ignition is observed. Although this definition is used in the literature, it is not a very precise definition, as it depends on the initial particle positions relative to the end wall. In the present case, the aluminium particle ridge is lined up on the centre line of the shock tube, and extends all the way to the end wall. The same amount of aluminium is used in all the experiments, keeping the aluminium ridge position constant for all experiments.

Given the large number of images from every test, an image processing routine was used to run through all the images. In order to identify the burning aluminium particles in the otherwise dark picture, the images were processed with a histogram equal function [27]. Additionally, one image for each series was identified as a “zero image,” chosen as an empty image, prior to shock arrival. The image processing routine defines that particle ignition and burning only occurs if there is more than a 25% increase in the pixel intensity relative to the “zero image.” A selection of curves generated with this image processing routine is shown in Fig. 9. Each colour represents the results from a specific experiment, with details given in Table 3. The typical pixel intensity curve has an instantaneous intensity increase, whereas the particle burning process reduction is more gradual. In some more atypical situations, two distinct intensity peaks are observed. The figure illustrates how the strongest shocks show the highest pixel intensities, here illustrated by test number 30. The strongest shocks also appear to have a more efficient particle heating, which lead to shorter ignition delay of the aluminium particles.

Fig. 9
figure 9

Pixel intensity for a selection of experiments. Time is given relative to the time of shock reflection at the end wall, \(t_\textrm{refl}\)

Full size image
Fig. 10
figure 10

a Star symbols show ignition delay measured relative to the shock reflection at end wall. The red line shows a curve fit to our data. Blue diamond symbols represent experimental data from [17], and blue triangle symbol represents data from [28]. b The black star symbols show the particle burning time. The red line is a curve fit to the experimental data. The green line represents Beckstead equation [18], whereas the solid black line shows the result from Huang et al. [29]. The blue symbols represent results from nano-particle burning [10]

Full size image

Our definition of particle ignition delay time \(\tau _\textrm{ign}\) is based on Roberts et al. [16]. For each experiment, they determine the maximum pixel intensity value and define ignition to occur when the intensity exceeds half the maximum intensity. Similarly, the particle burning is defined to end when the intensity has decreased to half the maximum value. In the few cases where two distinct intensity peaks are observed, the secondary peak was used to determine the end of the particle burning.

Figure 10a shows the ignition delay time as a function of the estimated temperature in region 5. The ignition delay is largest for the lowest reflected shock gas temperatures, and decays as the reflected temperature increases. The red line is an exponential curve fit to the experimental data given as

$$\begin{aligned} \tau _\textrm{ign}=c_{1}\exp {\left( \frac{E_\textrm{a1}}{R_\textrm{g}T_5}\right) }, \end{aligned}$$
(4)

where \(c_1=0.31\) and \(E_\textrm{a1}=15.67\) kJ/mol. The universal gas constant is \(R_\textrm{g}=8.3145\) J/(K\(\cdot \)mol), and \(\tau _\textrm{ign}\) is given in milliseconds. The curve fit is good for the experimental data, and scatter is only seen close to the lower ignition limit. The blue diamond-shaped symbols show the results from the work of Boiko et al. [17].

The particle burning time is plotted in Fig. 10b. The burning time has significant scatter in the results, and a few outliers have been discarded (see Table 3 for details). These are data points close to the lower ignition temperature limit, where the burning process is observed either as a few single peaks of particles burning or with very low intensity. Still the results indicate a trend, that for the highest gas temperatures \(T_5\) the shortest burning times are observed. The curve plotted in red is an exponential fit to the Arrhenius curve, given as

$$\begin{aligned} \tau _\textrm{b}=c_2\exp {\left( \frac{E_\textrm{a2}}{R_\textrm{g}T_5}\right) }, \end{aligned}$$
(5)

with \(E_\textrm{a2}=30.85\) kJ/mol and \(c_2 = 0.0139\).

The blue symbols illustrate results from Bazyn et al. [10] for two different gas pressures. The green line represents the results obtained using the Beckstead equation [18] for single particle burning of diameter \(d > 20\,\upmu \)m [30],

$$\begin{aligned} \tau _\textrm{b}=\frac{c_{3}d^{n}}{p_5^{0.1}T_5^{0.2}X_\textrm{eff}}, \end{aligned}$$
(6)

where \(n=1.8\), \(c_{3}=0.735\times 10^6\), and \(X_\textrm{eff}=0.21\) in air.

The solid black line in Fig. 10b represents the results from Huangs’ kinetically controlled combustion equation [29],

$$\begin{aligned} \tau _\textrm{b}=\frac{d^{0.3} \exp {\left( \frac{E_\textrm{a4}}{R_\textrm{g}T_5}\right) }}{c_4X_\textrm{eff}}, \end{aligned}$$
(7)

with the activation energy \(E_\textrm{a4}=73.6\) kJ/mol, and \(c_4=5.5 \times {10^4}\). Clearly, the curve gives a poor representation of the experimental data.

4 Discussion and recommendation for further work

The experimental test setup in the present study, was designed to vary as few parameters as possible, and fairly good repeatability was observed. The same amount of aluminium powder was used in all the experiments and formed in the same 3D-printed form. Measures were taken to reduce the probability of agglomeration as much as possible, using micron-sized particles with a fairly homogenous particle size distribution.

A new photographic setup was also developed, as it was discovered that the compact schlieren setup did not capture the ignition of the aluminium particles. A thick smoke did, however, indicate that ignition did in fact take place. The beamsplitter was therefore introduced to allow both shock wave phenomena and aluminium ignition to be observed simultaneously. Although we do not have temperature sensors suitable for measuring the reflected shock gas temperature or aluminium cloud ignition temperature, the results indicate a relatively low gas temperature in the reflected shock area where the aluminium cloud react.

As discussed in Sect. 1, aluminium particle behaviour changes significantly when exposed to shock waves. Although the initial particle velocity is low compared to the shock velocity, the relative velocity between the shocked gas and the aluminium particles is high. The particles collide with the shock tube end wall and are then reflected back into the window section. The effect of the shock acceleration and the end wall collisions are not studied separately. The gas temperature behind the reflected shock is estimated and indicates that ignition of the aluminium particle cloud is possible for gas temperatures above \(T_5=635\) K. The relative temperature between the shocked gas and the individual particles is also high initially. The ignition delay is observed to decrease with increasing shock strength. Although the observed particle burning time results have significant scatter, it is clear that the increase in shock strength leads to more efficient burning and therefore also shorter burning time. This finding agrees with the trend observed by [16].

Comparisons with published shock ignition data are challenging, as there are often a number of parameters not specified that may influence the results, including particle diameter, total aluminium pile weight, initial particle volume fraction, and initial gas contents. The results show that aluminium particle clouds ignited by shock waves are observed at lower temperatures than published studies of stationary single particles. As illustrated in Fig. 10b, the Beckstead equation for aluminium burning time did not give the best representation of the experimental data. The equation is developed for single particles ignited at low velocity. The heating rate, in this case due to shock acceleration of the individual aluminium particles, alters the cloud ignition temperature significantly. The present result agrees with the heat rate classification suggested by Pokhil [13]. Since the aluminium particle diameter is kept constant in the current study, the burning time dependency on particle diameter is less relevant for the present work. This is illustrated by the additional curves presented in Fig. 10b. The solid black curve represents nanoparticle burning in the the kinetic regime, whereas the red line represents a typical diffusive burning time curve. Although the scattering is prominent, the diffusive burning curve gives the better representation. It is therefore likely that the combustion process present in our experiments is diffusively limited.

The current work is part of a project, dedicated to understanding the more fundamental behaviour of aluminium particle clouds, both numerically and experimentally. The present study has demonstrated a significantly reduced ignition temperature for aluminium particle clouds, a shock strength-dependent ignition delay time, and gas temperature-dependent combustion burning time.

Combustion models implemented in numerical methods are based on empirical data. The use of such data numerically may therefore have limited validity outside the range of the original test parameters when it comes to shock Mach number, reflected shock gas temperatures, particle size, particle mass, or particle velocity. The main goal has therefore been to establish an experimental database for shock-ignited clouds that can be used to further study the present problem numerically. The applications of interest mainly involve larger quantities of aluminium particles; consequently, the models and studies of single particles will not be relevant for our work. A numerical study of the experiments presented here is expected to result in modifications to the combustion model presently used for simulations of shock ignited aluminium particle clouds of the current size.