Fully conservative overset mesh to overcome the blunt body metric singularity in finite difference methods

Abstract

A fully conservative overset mesh method is proposed and applied to overcome the metric singularity at the symmetry line for blunt bodies, e.g., capsules and blunted cones, in general curvilinear coordinates. The overset mesh is placed automatically at the symmetry line by avoiding the collapse of the grid lines using a hexahedral structure in contrast to the prismatic structure of a body-orientated mesh. In addition, the grid points of the overset mesh coincide with those of the body-orientated mesh to avoid interpolation techniques to interchange the flow variables between the two meshes. This coincidence ensures the conservation of the flow variables and avoids uncertainties at the shock as the method is naturally conservative. The thin-layer Navier–Stokes equations for high Reynolds number flows are solved using an AUSM+ or an AUSMPW+ flux vector splitting in combination with a mesh adaption to capture the shock accurately. For verification purposes of the proposed method, a supersonic 2D-axisymmetric hemisphere cylinder is chosen and the results along the wall are verified. Furthermore, the conservative properties of the applied overset mesh method are shown and the results on the stagnation line are presented. In addition, a supersonic 3D calculation is investigated to show the applicability of the presented method for simulations with an angle of attack.

1 Introduction

Solving the Navier–Stokes equations in general curvilinear coordinates in a finite difference manner for blunt bodies, e.g., capsules and blunted cones, has the drawback that a metric singularity occurs at the symmetry line. This singularity is not of physical type but of numerical since it arises from the transformation of the coordinate system. For blunt bodies, all grid lines collapse into a single line at the symmetry line. Due to the collapse, the metric derivatives, which describe the transformation between the Cartesian and the general curvilinear coordinates, become zero in the circumferential direction. This issue arises because the Cartesian coordinates are equal on the singular line in this direction. In consequence, the determinant of the metric Jacobian J is infinite, which makes a calculation of the governing equations impossible. However, calculations in general curvilinear coordinates have the advantage that curved and stretched meshes can be treated with uniform finite difference stencils on an equidistant grid [1]. Additionally, applying boundary conditions is more convenient, e.g., at the wall because the wall normal velocity for the no-penetration condition in computing the Euler equations is known from the transformation of a surface-orientated grid or in using a shock fitting method in which the shock normal direction has to be determined [2]. Although the metric singularity can be naturally avoided in finite volume methods, e.g., [3, 4], because no coordinate transformation is necessary, for finite difference methods the transformation is mandatory for curved grids and a solution for the metric singularity needs to be applied. An advantage in using finite differences for the discretization is that a grid point lies directly on the wall. In contrast, in finite volume methods the flow variables are stored in the cell center and therefore no direct flowfield information at the wall can be estimated. Different approaches have been developed over the last decades by many researchers to treat this issue. Some examples are outlined in the following to give an overview of the developed methods and to emphasize the research activity in this article.

The first approaches to calculate the flow variables at the singularity were to use modified governing equations . One of these developments was done by Palmer and Venkatapathy [5]. They redefined the metric Jacobian as a combination of the radial distance from the symmetry line and the metric Jacobian written in cylindrical coordinates. Using this approach, source terms occur in the modified Navier–Stokes equations that become zero at the symmetry line instead of being singular. This method gave good results in the 2D-axisymmetric case but did not perform as well in 3D cases. Another example of modified equations was given by Kim and Morris [6]. In their method, redefining the grid metrics, the calculation of the fluxes at the singular line is possible but the Euler equations itself remain indeterminate at the singular line.

Widely used approaches are averaging or extrapolation techniques, excluding the symmetry line from the calculation of the governing equations. Kutler et al. [7] calculated the flow variables at the symmetry line by local averaging of the flowfield. A combination of a local arithmetic average and a one-sided two-point extrapolation was developed by Riedelbauch and Müller [8] and high-order polynomial curve fits were used by Prakash et al. [9]. Techniques like these allow the calculation of the governing equations downstream of the symmetry line. But, by excluding the symmetry line from the discretization of the governing equations, the estimation of the flow variables at the symmetry line is not conservative.

Overset meshes are another approach found in the literature to deal with metric singularities in general. In this method, a second mesh is overlapped to the original mesh. The structure of the overset mesh is chosen such that the collapse of the grid lines is avoided. Using an overset mesh, the meshes have to interchange their flow variables after each iteration step, which serve as the boundary conditions for the respective other mesh in the next iteration step. Typically, this interchange is performed via interpolation techniques. Bin et al. [10] and Uzun and Hussaini [11] for example used the overset mesh method in combination with an interpolation to avoid the singularity at the centerline in the simulation of jets. Using interpolation techniques to interchange the flow variables has the drawback that the conservation of the flow variables cannot be ensured. Therefore, Wang [12] and Wang et al. [13] developed an overset mesh method that avoids interpolation techniques. In their development, new patched boundaries are created between the overlapping finite volume cells which enable the calculation without any interpolation. Their applied fully conservative method showed good results compared to the non-conservative method using an interpolation but is only applicable to finite volume discretizations.

In this article, we propose a new approach on how the general method of an overset mesh can be applied in a fully conservative way to avoid the before-mentioned blunt body metric singularity in finite differences. The overset mesh will be placed at the symmetry line by avoiding the collapse of the grid lines. Additionally, a coincidence between the grid points of the two meshes will be required. As stated by Hessenius [14], who used a point-discontinues patched grid to simplify the meshing around 3D geometries, a point-continuous patched grid approach enables a naturally conservative calculation. This is the case because the grid points of the meshes coincide at the boundaries and thus no interpolation techniques are necessary for the interchange of the flow variables. Patched grids, in contrast to overset meshes, share a common boundary but do not overlap. We will adopt this requirement of the coincidence of the grid points to the overset mesh in this article to, in contrast to the before-mentioned methods for finite difference methods, enable the fully conservative calculation of the singular line without any simplifications.

The article is organized in the following way. Firstly, an overview of the governing equations will be given, including the thin-layer Navier–Stokes equations, the thermodynamic model, and the metric calculation for general curvilinear coordinates. Secondly, the numerical method of the newly developed code is presented. This section contains the implementation of the mesh adaption, the spatial and temporal discretization, and the boundary conditions. In the next section, the implementation of the fully conservative overset mesh method is explained. This section is followed by the ”Results and discussion” section. In this section, first the results along the wall for a supersonic 2D-axisymmetric hemisphere cylinder are compared to the results of Esfahanian et al. [15] to verify the newly developed code containing the fully conservative overset mesh method and to compare the results to the method of [8]. Furthermore, the conservation properties and accuracy of the singular line treatment will be investigated. To demonstrate the applicability of the presented method for simulations with an angle of attack, lastly the results of a supersonic 3D calculation are shown and discussed with regard to the conservation of the flow variables and the accuracy of the predicted flowfield.

2 Governing equations

For verification purposes of the proposed method, test cases at high Reynolds numbers are presented. For high Reynolds number flows, the diffusion terms in the body tangential and circumferential direction can be neglected as they are of order $1/{\mathrm{Re}}_{\infty }^{1/2}$ or smaller [16]. The resulting set of equations are the thin-layer Navier–Stokes equations. The dimensionless compressible thin-layer Navier–Stokes equations in general curvilinear coordinates read

$$\begin{aligned} \frac{\partial \varvec{{{\mathrm{Q}}}}}{\partial t}+\frac{\partial \varvec{\mathrm{E}}}{\partial \xi }+\frac{\partial \varvec{\mathrm{F}}}{\partial \eta }+\frac{\partial \varvec{\mathrm{G}}}{\partial \zeta }=\frac{1}{{\mathrm{Re}}_{\infty }}\frac{\partial \varvec{{\mathrm{G}}}_{{\mathrm{v}}}}{\partial \zeta }, \end{aligned}$$

(1)

where

$$\begin{aligned} \varvec{{{\mathrm{Q}}}}= & {} J^{-1} \left[ \rho , \rho v_1, \rho v_2, \rho v_3, e\right] ^{{\mathrm{T}}}, \end{aligned}$$

(2)

$$\begin{aligned} \varvec{{{\mathrm{E}}}}= & {} J^{-1} \left[ \begin{array}{c} \rho v_{\xi } \\ \rho v_1v_{\xi }+\xi _{x_1}p \\ \rho v_2v_{\xi }+\xi _{x_2}p\\ \rho v_3v_{\xi }+\xi _{x_3}p \\ \rho v_{\xi }H\\ \end{array} \right] ,~ \varvec{{{{\mathrm{F}}}}} =J^{-1} \left[ \begin{array}{c} \rho v_{\eta } \\ \rho v_1v_{\eta }+\eta _{x_1}p \\ \rho v_2v_{\eta }+\eta _{x_2}p\\ \rho v_3v_{\eta }+\eta _{x_3}p \\ \rho v_{\eta }H\\ \end{array} \right] ,\nonumber \\ \varvec{{{\mathrm{G}}}}= & {} J^{-1} \left[ \begin{array}{c} \rho v_{\zeta } \\ \rho v_1v_{\zeta }+\zeta _{x_1}p \\ \rho v_2v_{\zeta }+\zeta _{x_2}p\\ \rho v_3v_{\zeta }+\zeta _{x_3}p \\ \rho v_{\zeta }H\\ \end{array} \right] \end{aligned}$$

(3)

and

$$\begin{aligned} \begin{aligned} \varvec{{{\mathrm{G}}}}_{{\mathrm{v}}} =J^{-1} \left[ \begin{array}{c} 0 \\ \mu a\frac{\partial v_1}{\partial \zeta }+\frac{\mu }{3}b \zeta _{x_1} \\ \mu a\frac{\partial v_2}{\partial \zeta }+\frac{\mu }{3}b \zeta _{x_2} \\ \mu a\frac{\partial v_3}{\partial \zeta }+\frac{\mu }{3}b\zeta _{x_3} \\ a\left( \frac{\mu }{2}\frac{\partial (v_1^2+v_2^2+v_3^2)}{\partial \zeta }+\frac{c_{p_\infty }^*T_\infty ^*}{{\mathrm{Pr}}_\infty ^* V_{\infty }^{*^2}} \kappa \frac{\partial T}{\partial \zeta }\right) \\ +\frac{\mu }{3}(\zeta _{x_1}v_1+\zeta _{x_2}v_2+\zeta _{x_3}v_3)b \\ \end{array} \right] ,\\ \end{aligned} \end{aligned}$$

(4)

with

$$\begin{aligned} \begin{aligned} a&=\zeta _{x_1}^2+\zeta _{x_2}^2+\zeta _{x_3}^2\\ b&=\zeta _{x_1}\frac{\partial v_1}{\partial \zeta }+\zeta _{x_2}\frac{\partial v_2}{\partial \zeta }+\zeta _{x_3}\frac{\partial v_3}{\partial \zeta }. \end{aligned} \end{aligned}$$

(5)

The total energy per unit volume is given by

$$\begin{aligned} e=\frac{p}{\gamma -1}+\frac{1}{2}\rho (v_1^2+v_2^2+v_3^2) \end{aligned}$$

(6)

and the total enthalpy by

$$\begin{aligned} H=\frac{\gamma }{\gamma -1}\frac{p}{\rho }+\frac{1}{2}(v_1^2+v_2^2+v_3^2). \end{aligned}$$

(7)

The Reynolds number is

$$\begin{aligned} {\mathrm{Re}}_{\infty }=\frac{\rho _{\infty }^* V_{\infty }^* R_{{\mathrm{N}}}^* }{\mu _{\infty }^*}. \end{aligned}$$

(8)

In (1)–(7), the flow variables are made non-dimensional by their respective free-stream parameters $\rho _{\infty }^*$, $V_{\infty }^*$, $T_{\infty }^*$, $\mu _{\infty }^*$, and $\kappa _{\infty }^*$, except the pressure which is made non-dimensional by $\rho _{\infty }^* V_{\infty }^{*2}$.

In our investigations, the thermodynamic model is assumed as a perfect gas. The dimensionless temperature is then calculated by

$$\begin{aligned} T=\gamma M_{\infty }^2\frac{p}{\rho }, \end{aligned}$$

(9)

with the free-stream Mach number

$$\begin{aligned} M_{\infty }=\frac{V_{\infty }}{c_{\infty }}. \end{aligned}$$

(10)

As the Prandtl number is constant in the simulations, the dimensionless thermal conductivity $\kappa$ equals the dimensionless dynamic viscosity $\mu$. The dynamic viscosity $\mu ^*$ is calculated by Sutherland’s law:

$$\begin{aligned} \mu ^*=\mu _0\left( \frac{T^*}{T_0}\right) ^{\frac{3}{2}}\left( \frac{T_0+ T_{{\mathrm{s}}}}{T^*+T_{{\mathrm{s}}}}\right) , \end{aligned}$$

(11)

with

$$\begin{aligned} \begin{aligned} \mu _0&=0.17894\times 10^{-4}~\frac{{\mathrm{kg}}}{{\mathrm{m}}\cdot {\mathrm{s}}},\\ T_0&=288~{\mathrm{K}},\\ T_{{\mathrm{s}}}&=110.33~{\mathrm{K}}. \end{aligned} \end{aligned}$$

(12)

Fig. 1

Cartesian ($x_1$, $x_2$, and $x_3$) and curvilinear ($\xi$, $\eta$, and $\zeta$) coordinate systems around the hemisphere cylinder

The metric derivatives, describing the derivation of the Cartesian physical coordinates to the equidistant curvilinear computational coordinates (see Fig. 1), are calculated via finite differences of second order. The inverse transformation is

$$\begin{aligned} \xi _{x_1}&= J(x_{2_\zeta }x_{3_\eta }-x_{2_\eta }x_{3_\zeta }), ~ \eta _{x_1}=J(x_{2_\xi }x_{3_\zeta }-x_{2_\zeta }x_{3_\xi }),\nonumber \\ \xi _{x_2}&= J(x_{3_\zeta }x_{1_\eta }-x_{3_\eta }x_{1_\zeta }), ~ \eta _{x_2}=J(x_{3_\xi }x_{1_\zeta }-x_{3_\zeta }x_{1_\xi }), \nonumber \\ \xi _{x_3}&= J(x_{1_\zeta }x_{2_\eta }-x_{1_\eta }x_{2_\zeta }), ~ \eta _{x_3}=J(x_{1_\xi }x_{2_\zeta }-x_{1_\zeta }x_{2_\xi }), \nonumber \\ \zeta _{x_1}&= J(x_{2_\eta }x_{3_\xi }-x_{2_\xi }x_{3_\eta }), \nonumber \\ \zeta _{x_2}&= J(x_{3_\eta }x_{1_\xi }-x_{3_\xi }x_{1_\eta }), \\ \zeta _{x_3}&= J(x_{1_\eta }x_{2_\xi }-x_{1_\xi }x_{2_\eta }), \nonumber \\ J^{-1}&= (x_{2_\zeta }x_{3_\eta }-x_{2_\eta }x_{3_\zeta })x_{1_\xi }+(x_{3_\zeta }x_{1_\eta }-x_{3_\eta }x_{1_\zeta })x_{2_\xi }\nonumber \\&\quad +(x_{1_\zeta }x_{2_\eta }-x_{1_\eta }x_{2_\zeta })x_{3_\xi }. \nonumber \end{aligned}$$

(13)

Knowing these metric derivatives, the contravariant velocities can be derived from the Cartesian velocities by

$$\begin{aligned} v_k=k_{x_1}v_1+k_{x_2}v_2+k_{x_3}v_3, \quad (k=\xi ,\eta ,\zeta ). \end{aligned}$$

(14)

3 Numerical method

3.1 Mesh adaption

Our newly developed code, CONSST3D (Compressible Navier–Stokes Steady 3D), uses a finite difference approach in combination with a mesh adaption to capture the shock accurately. The mesh adaption detects the shock at each body tangential location $\xi$ after a specified number of iteration steps via the shock normal Mach number:

$$\begin{aligned} \left. \begin{array}{ll} \displaystyle M_n\ge 1 \quad \text{ for } \text{ low-pressure } \text{ side }\\ \displaystyle M_n<1 \quad \text{ for } \text{ high-pressure } \text{ side } \end{array}\right\} , \end{aligned}$$

(15)

where

$$\begin{aligned} M_n=\frac{(v_1\zeta ^{{\mathrm{s}}}_{x_1}+v_2\zeta ^{{\mathrm{s}}}_{x_2}+v_3\zeta ^{{\mathrm{s}}}_{x_3})/\sqrt{\zeta _{x_1}^{{\mathrm{s}}^2}+\zeta _{x_2}^{{\mathrm{s}}^2}+\zeta _{x_3}^{{\mathrm{s}}^2}}}{c}. \end{aligned}$$

(16)

Because the grid is aligned to the body and the shock shape differs from the body shape, the grid lines are not perpendicular to each other at the shock ($\varGamma \ne 90^{\circ }$ in Fig. 2). In consequence, the shock normal metric derivatives ($\zeta ^{{\mathrm{s}}}_{x_1}$, $\zeta ^{{\mathrm{s}}}_{x_2}$, and $\zeta ^{{\mathrm{s}}}_{x_3}$) also differ from those in (13). By transforming the tangential metric derivatives of (13), as explained in [2], the required shock normal metric derivatives can be obtained. In a second step, a linear interpolation is performed in the wall normal direction $\zeta$ between the two previously detected points to get the exact position that satisfies $M_n=1$ ($\times$ in Fig. 2). Finally, the resulting shock shape is smoothed and the mesh is adapted in the wall normal direction. In the mesh adaption step, the flow variables are linearly interpolated onto the new mesh. This mesh adaption process is applied at only a few time steps of the overall computation, e.g., two times, at a time step where the solution is converged. After each mesh adaption step, the calculation of the governing equations is again performed until the solution converges.

Fig. 2

Illustration of the mesh adaption algorithm to align the mesh with the shock shape

3.2 Spatial and temporal discretization

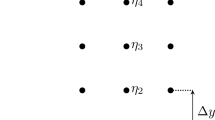
The spatial discretization is done by an AUSM+ [17] or an AUSMPW+ [18] flux vector splitting. Two different flux vector splittings are implemented in the code to use their individual advantages. Starting from the initial solution, AUSM+ has shown to be the more stable method. Once the mesh adaption is performed and the grid is aligned with the shock, AUSMPW+ is used as it gives more accurate results. In contrast to AUSM+, it avoids overshoots of the flow variables at the shock and suppresses oscillations in the boundary layer [18]. The primitive flow variables are interpolated by a fully upwind MUSCL reconstruction of second-order [19]. To accomplish a TVD-character, the van Albada limiter [20] is used for the simulations. The metric derivatives at $i\pm 1/2$, to obtain the fluxes $\varvec{\mathrm{F}}_{i\pm 1/2}$, are calculated by the local average of the metric derivatives of the two neighboring grid points (see Fig. 3). For the temporal discretization, a four-stage low-storage Runge–Kutta method of second order is used [21]. To accelerate the convergence to the steady state, a local time-stepping is implemented into the code. At each body tangential location, the time step is calculated via the maximum eigenvalue of the Jacobian matrices of the inviscid fluxes [22].

Fig. 3

Local averaging at $i \pm 1/2$ of the metric derivatives for the flux reconstruction of $\varvec{\mathrm{F}}_{i \pm 1/2}$

3.3 Boundary conditions

At the wall, the Navier–Stokes characteristic boundary condition (NSCBC) for a no-slip wall is applied [23]. In addition, the heat flux at the wall is set to zero for an adiabatic wall. In curvilinear coordinates, this boundary condition is [8]

$$\begin{aligned} \begin{aligned} 0=\frac{\partial T}{\partial n}&=\frac{1}{\sqrt{\zeta ^2_{x_1} +\zeta ^2_{x_2}+\zeta ^2_{x_3}}}\\&\quad \bigg [(\xi _{x_1}\zeta _{x_1}+\xi _{x_2}\zeta _{x_2} +\xi _{x_3}\zeta _{x_3})\frac{\partial T}{\partial \xi }\\&\quad +(\eta _{x_1}\zeta _{x_1}+\eta _{x_2}\zeta _{x_2} +\eta _{x_3}\zeta _{x_3})\frac{\partial T}{\partial \eta }\\&\quad +(\zeta _{x_1}\zeta _{x_1}+\zeta _{x_2}\zeta _{x_2} +\zeta _{x_3}\zeta _{x_3})\frac{\partial T}{\partial \zeta }\bigg ]. \end{aligned} \end{aligned}$$

(17)

Fig. 4

Sketch of the mesh discontinuity at the symmetry line

To sustain second-order accuracy at the boundaries, ghost points are used. The ghost points are extrapolated from the interior region into the wall, the free-stream and the outflow by a second-order extrapolation. In addition, for 2D-axisymmetric calculations, the ghost cells are mirrored at the symmetry line from the interior region. Therefore, care must be taken calculating the metric derivatives at the symmetry line. Because the grid points are mirrored on this axis, a mesh discontinuity occurs for stretched meshes (see Fig. 4). Employing a stretching factor, the arclength s, respectively, the Cartesian $x_j$-coordinates ($j=1,2,\,\mathrm{and}\,3$) of the grid points vary along the geometry by a factor of $\varDelta$. This is the case for all points except at the symmetry line where $\varDelta s_{-1}=\varDelta s_{1}$ due to the mirroring of the points. In consequence, the metric derivatives of some of the Cartesian coordinates with respect to the curvilinear coordinates, e.g., $x_{2_\xi }$, exhibit a discontinuity at the symmetry line by employing a central finite difference for their calculation. To guarantee a smooth metric, a one-sided finite difference of second order is used at the symmetry line on the body-orientated mesh and the overset mesh in all directions that show this discontinuity. A central finite difference is only employed for the metric derivatives that have to become zero around the singular line, e.g., $x_{1_{\xi }}$, because the coordinates are equal on both sides of the singular line. The one-sided finite difference is also performed for the 3D calculations at the symmetry line as the same discontinuity occurs.

Fig. 5

Schematic sketch of the grid in the circumferential direction at $\times$ in Fig. 1 for 2D-axisymmetric (a) and 3D (b) blunt body calculations including the ghost points (dashed lines)

To apply the boundary conditions at the ghost points, the flow variables are extrapolated into the wall and the outflow with a second-order extrapolation. The extrapolation of the flow variables into the wall only serves to sustain the second-order accuracy as the wall boundary condition is applied using the NSCBC and the thermal boundary condition of (17). In the free-stream, the free-stream flow conditions are specified and for 2D-axisymmetric calculations a no-penetration boundary condition is applied at the ghost points at the symmetry line. In this article, two kinds of simulations are performed, 2D-axisymmetric, and 3D calculations. For 2D-axisymmetric calculations, the governing equations can be discretized either with the 2D-axisymmetric governing equations [24] or performing a 3D calculation on only one plane with the 3D governing equations of (1). The latter approach is used in this article. In this case, the governing equations are discretized on the median plane (solid line in Fig. 5a). Two additional planes are placed in the circumferential direction on each side (dashed lines in Fig. 5a) by rotating the median plane around the $x_1$-axis. These planes are necessary to apply the boundary conditions because the flux reconstruction also needs to be performed in the circumferential direction. Due to the use of a MUSCL-reconstruction of second order (see Sect. 3.2), two planes are added. An axisymmetric flow is characterized by a symmetric flow around the $x_1$-axis. Therefore, the density, pressure, and the velocity $v_1$ at the ghost points are set equal to values on the median plane, and the velocities $v_2$ and $v_3$ are rotated around the $x_1$-axis in order to keep the spanwise velocity $v_{\eta }$ to zero. For the 3D calculations, one half of the geometry is calculated (see Fig. 5b). As for the 2D-axisymmetric calculations, two additional planes are placed for the boundary conditions in the circumferential direction on each side. In this case, the grid points and the flow variables are mirrored around the $x_1/x_2$-plane to set the boundary conditions at the ghost points.

Fig. 6

Metric singularity (red line) at the nose of a blunt body configuration on the body-orientated mesh

4 Fully conservative overset mesh method

The metric singularity, mentioned in the introduction, is shown in Fig. 6 (red line) for a 2D-axisymmetric calculation. In this figure, the median plane is shown and the ghost points on each side as described in Sect. 3.3. Because the mesh is rotated around the $x_1$-axis, all grid lines collapse in a single line, at this location only, because the symmetry line is the rotation axis for the mesh. Therefore, the metric derivatives in the $\eta$-direction vanish ($x_{1_\eta }$, $x_{2_\eta }$, and $x_{3_\eta } =0$) since the $x_{1}$-, $x_{2}$-, and $x_{3}$-coordinates are equal in the $\eta$-direction for all grid lines at the symmetry line ($i=0$), e.g.,

$$\begin{aligned} x_{1_\eta }=\frac{-x_{1_{i-1}}+x_{1_{i+1}}}{2}=0, \quad \text{ with }~x_{1_{i-1}}=x_{1_{i+1}}. \end{aligned}$$

(18)

Consequently, the determinant of the metric Jacobian J is infinite due to $J^{-1}=0$ (see (13)) and $J=1/J^{-1}$. Due to the indeterminate metric, a calculation of the governing equations at the symmetry line is impossible in this coordinate system since the state vector $\varvec{{{\mathrm{Q}}}}$ and the fluxes $\varvec{\mathrm{E}}$, $\varvec{\mathrm{F}}$, $\varvec{\mathrm{G}}$, and $\varvec{\mathrm{G}}_{{\mathrm{v}}}$ become zero. This behavior is nonphysical since the state vector in Cartesian coordinates ($\varvec{{{\mathrm{Q}}}}_{{\mathrm{cart}}}=[\rho , \rho v_1, \rho v_2, \rho v_3, e]^{{\mathrm{T}}}$) is not restricted to become zero and the transformation relation between the coordinate systems must be satisfied. To overcome this issue, an overset mesh, originally developed by Benek et al. [25] and Steger et al. [26], is placed at the symmetry line in the newly developed code. In the overset mesh method, different meshes are overlapped and calculated separately. After each iteration step, the meshes interchange their flow variables at the boundaries, to receive the flowfield information of the other mesh for the discretization of the governing equations. The interchange of the flow variables can be performed in different ways, having their individual advantages and disadvantages. If the meshes do not coincide, interpolation techniques are convenient ways to interchange the flow variables but have the disadvantage that the conservation of the flow variables is not given and numerical difficulties and uncertainties occur at shocks [13]. Therefore, conservative methods were developed for finite volume codes to avoid these difficulties and to ensure the conservation of the flow variables, e.g., [12, 13]. These methods create new patched boundaries between the finite volume cells to ensure an interchange of the flow variables without interpolation techniques. This method however is not applicable to finite differences. Therefore, another approach is applied in this article, explained in the following, which requires a coincidence of the meshes. By the coincidence, the interchange of the flow variables can be performed without any interpolation which is conservative in a natural way [14]. The method will be named fully conservative overset mesh method in this article because the conservative governing equations are used for the discretization and in addition, caused by the coincidence of the two meshes, the interchange of the flow variables is also conservative due to the avoidance of interpolation techniques. If interpolation techniques would be used only the governing equations remain conservative but the overall method would not sustain the conservation of the flow variables.

Fig. 7

Overset mesh at the symmetry line for 2D-axisymmetric calculations: Body-orientated mesh (red lines), Overset mesh (black lines)

In Fig. 7a, the detailed view of Fig. 6 is shown containing two grid planes of the body-orientated mesh (red lines) parallel to the surface of the geometry to explain the applied method. In addition, the overset mesh is presented (black lines). The latter has a hexahedral structure in contrast to the prismatic one of the body-orientated mesh. This hexahedral structure avoids the collapse of the grid lines, by which the metric becomes determinate, and enables a calculation of the governing equations. The overset mesh is generated containing two grid points in the $x_2$- and $x_3$-direction to perform the calculation on the symmetry line ((0, 0) in Fig. 7b) with a second-order accuracy. The points marked with a $\circ$ (calculation points) are used as the boundary values for the discretization of the governing equations on the singular line (0, 0) and the points marked with $\times$ (metric points) are necessary to calculate the metric derivatives for each $\circ$. Two different routines are developed to calculate the grid points of the overset mesh, depending on whether a 2D-axisymmetric case or a 3D case is investigated. For both cases, the calculation points ($\circ$) are calculated with the restriction of the coincidence between the meshes, respectively, that the coordinates of the calculation points are equal on both meshes, which enable the before-mentioned interchange of the flow variables without interpolation techniques.

Fig. 8

Overset mesh (red lines) at the symmetry line for 3D calculations

In the 2D-axisymmetric case, the calculation points ($\circ$) can be placed directly at $\varTheta = 0^{\circ }$ knowing the coordinates of the body-orientated mesh and at $\varTheta = 90^{\circ }, 180^{\circ }, \mathrm{and}\,\, 270^{\circ }$, by rotating the body-orientated mesh. The angle $\varTheta$ is the rotation angle around the symmetry line (singularity) shown in Fig. 7b. The metric points ($\times$) are estimated as follows. As shown in Fig. 7b, due to the rectangular shape in the $x_2/x_3$-plane, the $x_2$- and $x_3$-coordinates equal the corresponding coordinates of the calculation points ($\circ$). As an example, the $x_2$-coordinate of point 3 equals the $x_2$-coordinate of point 1 and the $x_3$-coordinate equals the $x_3$-coordinate of point 2. In consequence, the $x_1$-coordinate is the remaining variable to be determined. For 2D-axisymmetric calculations, the shock, respectively, the mesh, is axisymmetric around the $x_1$-axis. Therefore, the $x_1$-coordinate of the metric points can be estimated from the coordinate information on the median plane of the body-orientated mesh. With the previous assumption, the distance from the singular line $R_1$ on the median plane is equal to the distance of the metric point $R_2$,

$$\begin{aligned} R_1=R_2, \quad \text{ with } \quad R_2=\sqrt{x_2^2+x_3^2}. \end{aligned}$$

(19)

With the estimated distance $R_1$, the $x_1$-coordinate is determined by a linear interpolation between the two respective grid points on the body-orientated mesh (green $\circ$ in Fig. 7b) by

$$\begin{aligned} x_1=\frac{R_1-x_{2_i}}{x_{2_{i+1}}-x_{2_{i}}}(x_{1_{i+1}}-x_{1_{i}})+x_{1_{i}}. \end{aligned}$$

(20)

Due to the axisymmetric assumption, this $x_1$-coordinate matches the respective coordinate at the metric point.

Fig. 9

Sketches of the overset mesh generation for 3D calculations

For 3D calculations, the overset mesh is generated by a surface fitting method developed by Harder and Desmarais [27]. The method differs from the applied procedure for 2D-axisymmetric cases because for an angle of attack in combination with the mesh adaption the assumption of (19) is not valid anymore. This is the case because the shock contour and, respectively, the mesh after the mesh adaption is not symmetric around the $x_1$-axis. Thus, the assumptions made in the 2D-axisymmetric case to generate the overset mesh are not valid and a 3D approach has to be used. In Fig. 8, the mesh part around the singularity of half of the 3D geometry (see Fig. 5b) is shown, similar to Fig. 6, containing the body-orientated mesh (black lines) and the overset mesh (red lines). To apply the surface fitting method, first the body-orientated mesh of half of the geometry is mirrored around the $x_1$/$x_2$-plane (blue lines in Fig. 9a). This step is not necessary if the whole geometry ($360^\circ$) is calculated. In a next step, the coefficients for the surface fitting method (21) are calculated for each grid surface in the $\zeta$-direction, as shown in Fig. 9a, separately by using an appropriate number of grid points. A number of $m_{{\mathrm{max}}}=10$ points on each circumferential grid line l on the current grid surface on the body-aligned mesh is used in our code for this estimation. Thereafter, the resulting spline functions are used to determine the $x_1$-coordinates of the overset mesh. In order to calculate this coordinate, first the $x_2$- and $x_3$-coordinates need to be estimated. A sketch presenting the process for this estimation to generate the overset mesh for one grid line in the circumferential $\eta$-direction (see Fig. 8a) is given in Fig. 9b. In this sketch, the red solid lines represent the grid lines on the body-orientated mesh. Firstly, these lines are transformed into the $x_2/x_3$-plane by the rotation angle $\varTheta$ (red dashed lines). In this plane, the $x_2$- and $x_3$-coordinates of the calculation points (green $\circ$) and the metric points can be estimated as explained for the 2D-axisymmetric case (see Fig. 7b). The determined coordinates are transformed back (red solid lines) and the $x_1$-coordinates of all calculation and metric points are calculated for the actual grid line by the spline functions of the surface fitting method as

$$\begin{aligned} x_1=a_0+a_1x_2+a_2x_3+\sum _{l=0}^{l_{{\mathrm{max}}}-1} \sum _{m=0}^{m_{{\mathrm{max}}}-1} a_{l,m}r_{l,m}^2{\mathrm{ln}}r_{l,m}^2,\nonumber \\ \end{aligned}$$

(21)

with $r_{l,m}^2=(x_2-x_{2_{l,m}})^2+(x_3-x_{3_{l,m}})^2$ and $a_{l,m}$, $a_0$, $a_1$, and $a_2$ are the coefficients calculated before [27]. This method is applied for each grid line in the circumferential $\eta$-direction as shown in Fig. 8a to calculate the metric derivatives at the singularity which will be explained later in this section. Only the mesh displayed in Fig. 8b is used for the discretization of the governing equations. Using the mentioned surface spline method, including 10 points on each circumferential grid line for the calculation, a maximum deviation between the dimensionless coordinates of the two meshes on the calculation points ($\circ$) was estimated to be $2\times 10^{-12}$ for the test case investigated in this article. This very good agreement allows the interchange of the flow variables without any interpolation, respectively, fully conservative.

The interchange of the flow variables between the meshes is performed in the following way. In 2D-axisymmetric cases, the flow variables for the calculation points $\circ$ on the overset mesh at $\varTheta = 0^{\circ }$ are known from the discretization of the governing equations on the body-orientated mesh. At $\varTheta = 90^{\circ }, 180^{\circ },\,\, \mathrm{and}\,\, 270^{\circ }$, the flow variables are determined by the boundary condition in the circumferential direction and the no-penetration condition at the symmetry line, explained in Sect. 3.3. For 3D cases, the flow variables can be interchanged directly between the meshes shown in Fig. 8b. The only restriction is that grid lines of the body-orientated mesh have to be placed at $\varTheta = 0^{\circ }, 90^{\circ }, \mathrm{and}\,\, 180^{\circ }$. At $\varTheta = 270^{\circ }$, the flow variables are given by the mirror condition (see Sect. 3.3) for simulations of half of the geometry. Vice versa, the body-orientated mesh receives the flow variables at the singular line from the overset mesh to calculate the fluxes at $i+1$ for both cases.

The governing equations are discretized on the overset mesh only on the symmetry line with the same spatial and temporal accuracy (second order) as on the body-orientated mesh (see Sect. 3.2). The surrounding grid points ($\circ$) serve as the boundary conditions. In general curvilinear coordinates, the metric transformation can be performed with (13) as for the body-orientated mesh. Therefore, the same code is applied for both meshes switching between the two different metrics. The generation of the overset mesh and the interchange of the flow variables between the two meshes are implemented fully automatically in the code. In the initialization step and after each mesh adaption, an algorithm places the grid points of the overset mesh based on the grid points of the body-orientated mesh. The flow variables are interchanged between the two meshes after each time step. Although a second-order accuracy is chosen for the discretization, the proposed method is applicable to higher-order methods by including more discretization points.

Another issue of the indeterminate metric at the symmetry line ($i=0$) is that the flux reconstruction for the first grid point downstream of the symmetry line ($i=1$) on the body-orientated mesh is not possible. Since the metric terms are calculated by a local averaging between the two neighboring points and the metric at $i=0$ is indeterminate, also the metric at $i=1/2$ is indeterminate. Nevertheless, the metric can be calculated at $i=1/2$ due to the coincidence of the overset mesh (OM) and the body-orientated mesh (BM). The tangential and normal metric derivatives equal at the symmetry line on the two meshes, which results in the metric derivatives for the body-orientated mesh at the symmetry line as

$$\begin{aligned} \begin{aligned}&\xi _{x_1}^{{\mathrm{BM}}}=\xi _{x_1}^{{\mathrm{OM}}},\quad \eta _{x_1}^{{\mathrm{BM}}}=0,\quad \zeta _{x_1}^{{\mathrm{BM}}}=\zeta _{x_1}^{{\mathrm{OM}}},\\&\xi _{x_2}^{{\mathrm{BM}}}=\xi _{x_2}^{{\mathrm{OM}}},\quad \eta _{x_2}^{{\mathrm{BM}}}=0,\quad \zeta _{x_2}^{{\mathrm{BM}}}=\zeta _{x_2}^{{\mathrm{OM}}},\\&\xi _{x_3}^{{\mathrm{BM}}}=\xi _{x_3}^{{\mathrm{OM}}},\quad \eta _{x_3}^{{\mathrm{BM}}}=0,\quad \zeta _{x_3}^{{\mathrm{BM}}}=\zeta _{x_3}^{{\mathrm{OM}}},\\&J^{-1 {\mathrm{BM}}}=0. \end{aligned} \end{aligned}$$

(22)

Knowing these metric derivatives, the local averaging can be performed and the flux reconstruction at $i=1/2$ is possible. For the 3D calculations, this method to calculate the metric derivatives has to be performed for each grid line in the circumferential direction (see Fig. 8a) because the metric derivatives differ at the singular line for each. For example, $x_{2_{\eta }}=0$ for the grid lines at $\varTheta =0^\circ$ and $\varTheta =180^\circ$ but $x_{2_{\eta }} \ne 0$ for the other grid lines.

Another approach to calculate the metric derivatives at the singular line for the flux reconstruction on the body-orientated mesh for the first point downstream is as follows. The metric derivatives describing the transformation relation between the Cartesian and the curvilinear coordinates, $x_{j_{k}}$ with $j=1,2,\,\mathrm{and}\,\, 3$ and $k=\xi ,~\zeta , \mathrm{and}~\eta$, can be computed at the singular line also on the body-orientated mesh. The issue arises in the inversion to estimate the back transformation. As the metric derivatives for the flux reconstruction only need to be estimated at $i=1{/}2$ to calculate the flux at $i=1$, the following process can be applied. Firstly, the metric derivatives $x_{j_{k}}$ are averaged between $i=0$ and $i=1$ as explained in Sect. 3.2. In a second step, the inversion of the metric derivatives is applied for these averaged metric derivatives and the flux reconstruction can be performed. In this case, the inversion is possible because the metric becomes determinate half a grid point distance away from the singularity.

In this article, the first method presented in this chapter is used for the following test cases. To apply the method to more complex geometries, e.g., ellipsoids and hyperboloids, the second method should be preferred. In addition to saving computational time because only one overset mesh needs to be build, this method is more general without the assumption of an equal metric on the two meshes at the singular line.

The whole process outlined in this section is performed for each grid point in the wall normal direction on the singular line.

5 Results and discussion

5.1 Supersonic 2D-axisymmetric hemisphere cylinder

We chose a 2D-axisymmetric hemisphere cylinder [15] as the test case to verify the presented method to overcome the metric singularity and to compare the results of the new proposed method in this article with the extrapolation technique of Riedelbauch and Müller [8]. The free-stream conditions are given in Table 1. With respect to (8) and a randomly chosen density, the nose radius of the geometry can be estimated. The mesh consisted of $100\times 180$ grid points in the tangential and normal direction, respectively. Twenty of those 180 points in the wall normal direction are used for the free-stream to enable a constant inflow upstream of the shock and to guarantee that the shock lies inside the simulation domain. Therefore, the mesh adaption is performed by placing the 160th grid point at the detected shock location. A number of 20 points for the free-stream was chosen because Kufner et al. [28] used seven points in similar simulations. To guarantee that the shock lies inside the simulation domain, a slightly higher number of grid points was chosen for the following test cases. To resolve the boundary layer and the shock accurately, the mesh was refined in these regions. Therefore, the one-dimensional stretching function of Vinokur [29] was used. This function enables a clustering of the grid points near the wall and the shock, but remains smooth over the whole wall normal direction. At the shock, the grid spacing was mirrored for the grid points in the free-stream. The gas was assumed as a perfect gas with ${\mathrm{Pr}}=0.723$ and a specific heat ratio of $\gamma =1.4$. The investigations were performed for a laminar flow, and the wall was assumed to be adiabatic. The initial shock shape was calculated via Billig’s correlation [30]. On the low-pressure side, upstream of the shock, the initial flow variables were set as the free-stream values and on the high-pressure side, downstream of the shock, the flow variables were initialized using the Rankine–Hugoniot relations. Starting from the initial solution, the AUSM+ flux vector splitting was used. After the mesh adaption was performed, the flux vector splitting was changed to AUSMPW+. The calculations were performed on the median plane (see Fig. 5a) using the full 3D Navier–Stokes equations.

Table 1 Free-stream conditions for the hemisphere cylinder [15]

Fig. 10

Computational domain before and after the mesh adaption (black line)

Fig. 11

Mesh independence study comparing the stagnation point temperature of different grid distributions in the wall normal direction

Fig. 12

Wall distributions along the dimensionless arclength for the 2D-axisymmetric calculation

The mesh adaption of Sect. 3.1 is shown in Fig. 10. The initial shock shape, calculated via Billig’s correlation, is represented by the outer boundary of the domain. After the mesh adaption, the computational domain reduces to the surrounding black line and the mesh is aligned with the shock. The black line lies aside of the shock due to the 20 points in the free-stream mentioned before.

Fig. 13

Contour plots at the hemisphere part of the 2D-axisymmetric calculation

Firstly, a grid independence study was performed with different number of grid points in the wall normal direction ranging from 80 to 240 points. Because this article focus on the treatment of the singularity, the stagnation point temperature was chosen for the grid independence study. In Fig. 11, the dimensionless stagnation point temperature is plotted over the different grid distributions. Comparing the results, a slightly lower temperature can be recognized on the grid containing 80 points in the wall normal direction. With higher number of grid points, the value for the temperature remains nearly constant with a small deviation around a mean value of 2.7288 (dashed line in Fig. 11), calculated from the temperatures between 100 and 240 grid points. With respect to these results, 180 points in the wall normal direction were chosen for the further investigations because this value enables a good balance between accuracy and time efficiency.

The current results are compared to those of Esfahanian et al. [15] to verify the capability of the code to accurately predict the flow variables at the wall and to Riedelbauch and Müller [8] to compare their one-sided two-point extrapolation technique with the proposed method of this article. In Fig. 12a, b, the dimensionless pressure and temperature are plotted along the wall over the dimensionless arc length $s^*/R^*_{{\mathrm{N}}}$. Comparing the pressure distribution with [15] in Fig. 12a, a very good agreement is observed between the two results along the entire wall. The more sensitive flow variable is the temperature in Fig. 12b. A good agreement is found here as well with the results of [15], except at the junction between the hemisphere and the cylinder, where a slight undershoot occurs although a grid point is located directly at the junction point. This undershoot is also reported by other researchers, e.g., [31, 32], and is caused by the curvature discontinuity at this point. In addition, the thin-layer Navier–Stokes equations may have an effect on the undershoot because the body tangential diffusive terms are neglected [15]. Investigations were performed with our code varying the number of grid points in the wall normal direction but no significant influence on the undershoot was observed. Although an undershoot occurs at the junction point, the effect on the temperature further downstream is small. The oscillations in the temperature distribution damp out after a few grid points and the results are again comparable to those in [15]. Comparing the temperature with the results of the extrapolation technique of [8], a good agreement is found at the stagnation point as well. Further downstream, the results of [8] overpredict the temperature compared to the results of [15] and the results using our proposed overset mesh method. The reason for the overprediction can be the relatively small grid point number of 31 points in the wall normal direction in their calculation. In their study, this test case was chosen to calibrate the weighting factors of the one-sided two-point extrapolation technique with the stagnation point temperature of an axisymmetric code. In comparison with their method, no calibration of the proposed method in this article is necessary to accurately predict the stagnation point temperature.

To show the applicability of the fully conservative overset mesh method, contour plots of the dimensionless density $\rho$, dimensionless pressure p, dimensionless temperature T, and the Mach number M are shown in Fig. 13a–d at the hemisphere part of the computed geometry. Notice that the pressure is made non-dimensional with the free-stream static pressure $p_{\infty }$ for this figure. The results in these figures show the properties observed by Kim et al. [18], using their developed AUSMPW+ flux vector splitting on the overset mesh and the body-orientated mesh. A detailed view of these properties is shown in Fig. 14 for the dimensionless temperature at a surface location of $s^*/R_{{\mathrm{N}}}^*=0.3778$. Firstly, no oscillations of the temperature occur in the boundary layer. Secondly, only a small overshoot can be recognized at the shock. As no overshoot occurs at the stagnation line (see Fig. 17), where a normal shock appears, the small overshoots downstream can be caused by a small misalignment of the mesh with the shock. In the AUSMPW+ flux vector splitting, the normal total enthalpy is used to calculate the speed of sound. Therefore, a small misalignment results in an inaccurate calculation of the normal total enthalpy and in inaccuracies at the shock, respectively. Although this slight overshoot occurs, the shock is captured adequately using the implemented flux vector splitting in combination with the mesh adaption of Sect. 3.1. In addition to these results, the contour plots show a smooth transition of the contour lines from the overset mesh to the body-orientated mesh. No non-physical behavior is observed, namely oscillations of the flow variables or the shock.

Fig. 14

Detailed view of the wall normal temperature distribution at $s^*/R_{{\mathrm{N}}}^*=0.3778$

To verify the conservation properties of the current overset mesh method, the stagnation point temperature and the total enthalpy of the flowfield are investigated. The computed stagnation point temperature is compared to the analytical expression for an inviscid flow to show the conservation of the total temperature along the stagnation line on the overset mesh. The analytical stagnation point temperature is calculated with the free-stream Mach number $M_{\infty }$ to:

$$\begin{aligned} T_{\text {Stag,Analytical}}=1+\frac{\gamma -1}{2} M_{\infty }^2=2.72872. \end{aligned}$$

(23)

In the simulations, the stagnation point temperature is predicted with $T_{\text {Stag,Simulation}}=2.72878$. The deviation to the analytical result is $2.199\times 10^{-3}\%$. The computed total temperature at the stagnation point is slightly higher than the analytical expression. The rise is caused by the viscous dissipation in the boundary layer. Nevertheless, the two values are compared because the boundary layer is very small at the stagnation point and therefore also the viscous effects are small.

Fig. 15

Contour plot of the normalized total enthalpy at the hemisphere part of the 2D-axisymmetric calculation

Fig. 16

Contour plot of the residual at the hemisphere part of the 2D-axisymmetric calculation

To show the conservation of the flow variables between the two meshes, a contour plot of the normalized total enthalpy at the hemisphere part is presented in Fig. 15. The total enthalpy H is normalized with the free-stream value $H_{\infty }$. The flowfield is separated into an inviscid region and a viscous region near the wall. Near the wall, the total enthalpy shows the typical behavior for an adiabatic wall condition. In the boundary layer, the total enthalpy decreases with a slight overshoot at the boundary layer edge, see e.g., [33]. In the inviscid region of the flowfield, a conservation of the total enthalpy is expected. Therefore, the investigation of the conservation of the total enthalpy is focused on the inviscid region. Here a maximum deviation of the normalized total enthalpy of 0.03% is observed. The slight deviation is caused by different reasons, e.g., non-conservative calculation of the metric derivatives, see [34], or small inaccuracies at the shock. Overall, the deviation of the total enthalpy is the same on both, the overset mesh and the body-orientated mesh. Therefore, the conservation of the total enthalpy between the two meshes is given.

To present the convergence properties of the proposed method, the residual of (1)

$$\begin{aligned} {\mathrm{Res}}=\left| -\frac{\partial \varvec{\mathrm{E}}}{\partial \xi }-\frac{\partial \varvec{\mathrm{F}}}{\partial \eta }-\frac{\partial \varvec{\mathrm{G}}}{\partial \zeta }+\frac{1}{{\mathrm{Re}}_{\infty }}\frac{\partial \varvec{\mathrm{G}}_{{\mathrm{v}}}}{\partial \zeta }\right| \end{aligned}$$

(24)

is shown in Fig. 16. The residual decreases to maximum values around $5\times 10^{-7}$, where the highest residual is found near the shock. Due to the mesh adaption, a small misalignment can be the reason for the slightly higher residual at this location. At the stagnation line (overset mesh), the residual decreases to even lower values at the order of $1\times 10^{-10}$. Overall, a good convergence employing the proposed overset mesh method is observed.

Fig. 17

Stagnation line results on the overset mesh of the 2D-axisymmetric calculation

Fig. 18

Contour plots at the hemisphere part of the 3D calculation

As the investigations in this article focus on the applicability and accuracy of the fully conservative implementation of the overset mesh method, finally the stagnation line results are presented. In Fig. 17, the stagnation line results are plotted over the dimensionless wall normal distance $X_n^*/R_{{\mathrm{N}}}^*$. The smooth profiles described for the contour plots in Fig. 13a–d can be seen in detail in this plot. Accurate results are computed at the stagnation line without any oscillations of the flow variables even at the shock.

5.2 Supersonic 3D hemisphere cylinder

In this section, results are presented for a 3D simulation of the hemisphere cylinder of Sect. 5.1 with an angle of attack of $\alpha =-5^{\circ }$. The calculations were performed on a 3D mesh containing half of the geometry as shown in Fig. 5b consisting of $100\times 180\times 37$ grid points in the tangential, normal and circumferential direction, respectively. The free-stream conditions were kept the same such as in the investigations of the 2D-axisymmetric case.

Fig. 19

Wall distributions along the dimensionless arclength for the 3D calculation

Fig. 20

Contour plot of the normalized total enthalpy at the hemisphere part of the 3D calculation

First of all, the contour plots of the dimensionless density $\rho$, dimensionless pressure p, dimensionless temperature T, and the Mach number M are shown in Fig. 18a–d. Notice again that the pressure is made non-dimensional with the free-stream static pressure $p_{\infty }$ for this figure. The results are presented on the $x_1/x_2$ median plane of the flowfield. It can be recognized that also for an angle of attack no oscillations of the shock occur. In contrast to the results without an angle of attack, minimal oscillations of the pressure, temperature, and density occur at the symmetry line. In contrast, the Mach number does not show any of these oscillations and remains smooth. Discussion on these oscillations will be made in the following.

In Fig. 19a, b the dimensionless pressure and the dimensionless temperature at the wall are shown along the dimensionless arc length $s^*/R^*_{{\mathrm{N}}}$ for the 3D case. The distributions are plotted for the windward side of the geometry and the leeward side where the symmetry line, respectively, the metric singularity, is located at $s^*/R_{{\mathrm{N}}}^*=0$. The stagnation point can be recognized on the windward side slightly downstream of the symmetry line. In these figures, no significant oscillations can be recognized for both the pressure and the temperature. The transition of the flow variables is smooth between the overset mesh and the body-orientated mesh. This implies that the small oscillations seen in Fig. 18a–c have no influence on the flow variables at the wall and can be caused by several reasons which will be outlined in the following paragraph with respect to the total enthalpy.

In Fig. 20, the normalized total enthalpy is shown for the 3D test case at the hemisphere part of the computed geometry. Compared to the 2D-axisymmetric case in Sect. 5.1, the deviation is slightly higher. In the 3D simulation, a maximum deviation of 0.09% is observed compared to 0.03% in the 2D-axisymmetric case. This slightly higher deviation can be caused by 3D effects which makes the simulation more sensitive and can cause the minimal oscillations of the flow variables explained before especially because the oscillations occur in the region with the highest deviation. The 3D effects occur because the simulation domain contains of 37 grid planes in the circumferential direction compared to 1 grid plane in the 2D-axisymmetric case. Therefore, the mesh adaption has to be performed on each of these grid lines. Slight inaccuracies in the flowfield during the mesh adaption can cause small misalignments of the mesh after the mesh adaption, although the mesh is smoothed thereafter. These misalignments can cause the difference in the conservation of the total enthalpy between the 2D-axisymmetric and 3D case.

Fig. 21

Oscillations in the dimensionless temperature T around the singular line for the 3D calculations

To further investigate the before-mentioned oscillations of the flow variables around the singularity, plots of the dimensionless temperature T over the arclength around the nose part of the geometry are shown in Fig. 21a, b. An additional computation with $\alpha =-10^{\circ }$ was performed to examine the influence of the angle of attack. The plots show the temperature distribution on different grid lines parallel to the surface of the geometry starting from the wall up to the 140th grid line. At $\alpha =-5^{\circ }$, the small oscillations occur at the 100th and 120th grid line. At the other grid locations, a smooth profile can be recognized. Increasing the angle of attack to $\alpha =-10^{\circ }$, the oscillations vanish and smooth profiles occur for every grid line. A reason for the difference between the two computations can be the before-mentioned inaccuracies in the mesh adaption, which in this case seem to have a higher influence at an angle of attack of $\alpha =-5^{\circ }$.

Nevertheless, with regard to the small inaccuracies presented before, the results show that the fully conservative overset mesh method is also applicable to 3D simulations with only minimal oscillations in the flow variables which have no significant influences on the shock or the flowfield.

6 Conclusion

In this article, we presented a fully conservative overset mesh method to overcome the metric singularity at the symmetry line for blunt bodies in general curvilinear coordinates. The results for the presented 2D-axisymmetric calculations showed that the method accurately predicts the flowfield without oscillations. Further, the conservation of the total enthalpy is ensured with only a minimal deviation of 0.03%. In contrast to the other methods for finite differences presented in the introduction, the proposed method avoids simplifications concerning the governing equations and calibration processes to accurately predict the flowfield at the stagnation line. The 3D calculations with an angle of attack showed similar properties applying the fully conservative overset mesh method. Minimal oscillations of the flow variables occurred for an angle of attack of $\alpha =-5^{\circ }$ but no oscillations could be recognized for $\alpha =-10^{\circ }$. A conservation of the total enthalpy was ensured also in this case with a deviation of 0.09%. Overall we showed that the proposed method can be applied in 2D-axisymmetric and 3D cases to overcome the blunt body metric singularity in finite differences in a conservative way.

To perform calculations for different thermodynamic models, e.g., equilibrium or non-equilibrium flows, the presented method can be applied in a straightforward way. For equilibrium flows, the method remains the same as for the perfect gas because only the thermodynamic equations are modified. For calculations in thermochemical non-equilibrium, additional equations are added to the governing equations and additional flow variables have to be interchanged between the meshes in the same way as for the perfect gas case in this article. Similar changes have to be applied for calculations including turbulence models.

The proposed method is currently applicable to steady flowfield simulations of blunted axisymmetric bodies. In Sect. 4, a possible modification of the metric calculation is given to apply the presented method to geometries with an ellipsoid or hyperboloid as the nose part. An application to more complex nose parts can cause issues due to the surface fitting method to generate the overset mesh. Precisely, generating the overset mesh with our proposed method for abruptly varying geometries can result in inaccuracies not satisfying the required coincidence of the grid points. Nevertheless, most blunt re-entry configurations contain a spherical cap, ellipsoid, or hyperboloid as the nose part, and thus, the calculation of the flowfield in these cases can be significantly improved with the proposed method in this article. Further, in case of moving body problems, the method is also limited to smooth grid changes. Additionally, in this case the overset mesh generation and the applied mesh adaption have to be performed in each iteration step of the calculation. As the interpolation in the mesh adaption in this article is non-conservative and would violate the overall conservation of the proposed method, conservative approaches have to be applied for the mesh adaption, e.g., [35].