Flame propagation and acceleration in narrow channels: sensitivity to facility specific parameters

Abstract

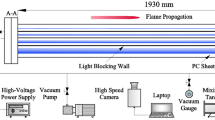
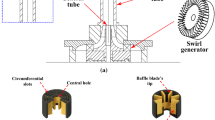
Flame propagation experiments in stoichiometric H$_2$–air are conducted in a smooth 482-mm-long, 10-mm $\times$ 10-mm square-cross-section channel, closed at the ignition end and open at the opposite end. Direct observation is used to track the flame acceleration dynamics. The effect of facility specific parameters (i.e., ignition energy, boundary conditions near the ignition end, window material, and settling time between filling and ignition) on flame propagation and acceleration is assessed. The absolute mean deviation is used as a metric to determine the effect of the aforementioned parameters on the collected front position data, and response surface methods for experimental design are applied to examine inter-parameter interactions. Results show that the boundary conditions near the ignition end (i.e., large/small ignition offset) have the largest influence on the recorded front position with the remaining parameters playing a less important role. The early stages of flame propagation are compared against theoretical predictions to understand the discrepancies observed in the data; a simple acoustic model was found sufficient to explain the increased acceleration rates observed for the large ignition offset cases. Finally, a link between the observed front oscillations during flame acceleration and the flow rate dynamics at the channel’s open end is highlighted.

Appendices

Appendix 1: Response surface methods—mathematical framework

A response surface model including potential interactions among n parameters reads:

$$\begin{aligned} \underset{(2^n,1)}{\varvec{y}} = \underset{(2^n,2^n)}{\varvec{X}} \underset{(2^{n},1)}{\varvec{a}} \end{aligned}$$

(6)

which defines a $2^n \times 2^n$ system of linear equations, where $\varvec{y}$ is the vector of responses (i.e., experimental output), $\varvec{X}$ is a Hadamard matrix¹ defining the test conditions from a full experimental matrix, and $\varvec{a}$ is the vector of coefficients sought for. More specifically, the magnitude of the elements of vector $\varvec{a}$ allows to evaluate the influence of a particular parameter, $a_{1}$ for parameter 1, or the interactions between different parameters, $a_{12}$ for the interaction of parameter 1 with parameter 2, and so on, on the response, $\varvec{y}$. Accounting for $n=4$ parameters results in 16 coefficients that need to be determined, see (6), which entails performing 16 tests at different conditions, $\varvec{X}$, to obtain an equal number of responses, $\varvec{y}$. Instead of directly computing these coefficients to construct a response surface, the model can be simplified by neglecting high-order interactions, among three or more parameters, for example (which are less likely), and by using aliases, $\varvec{l}$, in which the different experimental factors are confounded based on the experimental matrix reduction methodology described in [14].

Doing so, the following reduced model is obtained:

(7)

where the elements of $\varvec{l}$ are determined by combining the elements of $\varvec{a}$ as follows:

$$\begin{aligned}&l_{0} \approx a_{0}; \quad l_{1} \approx a_{1} + a_{24}; \quad l_{2} \approx a_{2} + a_{14}; \quad l_{3} \approx a_{3}; \\&l_{4} \approx a_{4} + a_{12};\quad l_{23} \approx a_{23}; \quad l_{13} \approx a_{13}; \quad l_{34} \approx a_{34} \end{aligned}$$

where subscripts 1, 2, 3, and 4 correspond to the settling time, ignition offset, material, and ignition energy, respectively; the remaining subscripts are interactions among parameters. As per (7), only eight tests are needed to determine the aliases vector, $\varvec{l}$. The conditions at which the tests need being carried out are given in Table 3, constructed from the Hadamard matrix, $\varvec{X}_\mathrm{s}$, by arbitrarily assigning values of $+1$ or $-1$ to the limits of each parameter, i.e., $-1$ for small ignition offset, glass, $E_{\text {min}}$ and $t_{\text {min}}$ and $+1$ for large ignition offset, plastic, $E_{\text {max}}$ and $t_{\text {max}}$. The remaining four columns (5, 6, 7, and 8) that would complete Table 3 are the product of ignition offset and material; settling time and material; ignition energy and material; and settling time, ignition offset, and ignition energy. Finally, using the mean front position, $\bar{x}$, as our response, $\varvec{y}$, we can solve for $\varvec{l}$ and plot their temporal evolution. The results are shown in Fig. 8 of Sect. 3.3.

Table 3 Experimental conditions determined following [14] to compute the alias vector $\varvec{l}$; all tests were performed using Igniter 1 as an ignition source

Appendix 2: Additional parameters tested

1.1 A2.1 Settling time between end of filling and ignition

Figure 16 shows front position results comparing two settling times, $t_{\text {min}} = 15 \, \text {s}$ and $t_{\text {max}} = 60 \, \text {s}$, for glass (top) and polycarbonate (bottom).

With glass, $d_{t_{\text {min}}}$ and $d_{t_{\text {max}}}$ are less than 5 mm and subsequently increase to $\sim$ 30 mm for $t \ge$ 5 ms; furthermore, all three deviations ($d_{t_{\text {min}}}$, $d_{t_{\text {max}}}$, and $d_{\text {g}}$) follow the same evolution, with differences of less than 5 mm. With plastic, both deviations are similar ($\sim$ 10 mm) for $t \le 5$ ms and gradually increase to $\sim$ 20 mm. For 5 ms $< t < 11$ ms, the maximum difference $|d_\mathrm {g} - d_{t_{\text {max}}}|_{\text {max}}$ reaches 15 mm; the flame positions follow different paths before rejoining near the end. Although $d_\mathrm {g}$ is greater than both $d_{t_{\text {max}}}$ and $d_{t_{\text {max}}}$ in this time interval, the difference is small compared to the usual scattering of the results. Besides, all three deviations ($d_{t_{\text {min}}}$, $d_{t_{\text {max}}}$, and $d_{\text {g}}$) are equal close to the end ($\sim$ 20 mm); $d_{g}$ is larger for $t < 11$ ms which could imply an interaction between two parameters, namely the settling time and material, as this is observed with this material only. However, since $|d_{\text {g}}-d_{t_{\text {max}}}|_{\text {max}} \le 5$ mm with glass, this suggests that the settling time is not responsible for the discrepancies shown. Finally, the coefficient $l_{\text {13}}$ of the response model, shown in Sect. 3.3, rules out the potential interaction between these parameters, as its value is low compared to $l_{\text {2}}$. Due to size of the channel used, settling times of at least 15 s are sufficient to avoid potential effects on FA.

Fig. 16

Influence of settling time before ignition of mixture on mean flame position, $\bar{x}$ (dashed line). Absolute maximum deviation from mean value $|x-\bar{x}|_{\text {max}}$. Top: glass (sample size includes 6 tests), bottom: plastic (sample size includes 6 tests). Configuration: small ignition offset and Igniter 1; conditions: stoichiometric H$_{2}$–air at $p_0 =$ 100 kPa and $T_0 =$ 290 K; settling times: $t_{\mathrm {max}}$ = 60 s, $t_{\mathrm {min}}$ = 15 s

1.2 A2.2 Material utilized for optical access

In Fig. 17, we compare the front position data changing the material used for optical access for small ignition offset (top) and large ignition offset (bottom).

Fig. 17

Influence of window material on mean flame position, $\bar{x}$ (dashed line). Absolute maximum deviation from mean value $|x-\bar{x}|_{\text {max}}$. Top: small ignition offset (sample size includes 12 tests), bottom: large ignition offset (sample size includes 10 tests). Configuration: Igniter 1 for both figures; conditions: stoichiometric H$_{2}$–air at $p_0 =$ 100 kPa and $T_0 =$ 290 K

For small ignition offset, deviations are small up to $t \sim 5$ ms for both materials. Thereafter, $d_{\text {plastic}}$ increases to 20 mm, whereas $d_{\text {glass}}$ stays below 30 mm. The global deviation, $d_{\text {g}}$, follows that of plastic closely, once again showing that the materials are not responsible for the observed scatter. Tests performed with large ignition offset confirm this trend. For large ignition offset, $d_{\text {plastic}} < 10$ mm throughout the propagation period; $d_{\text {glass}} < 10$ mm for $t \le 5$ ms increasing up to a maximum of 25 mm. Note that since both materials have similar roughness [16], this was somewhat expected; however, the main purpose of evaluating this parameter was to assess its effect on the chemiluminescence signal; the same luminous intensity was observed, suggesting that plastic does not burn during flame propagation and acceleration. Continuous testing, on the other hand, does leave visible marks on the plastic, but, based on our data, these do not seem to perturb the recorded flame propagation. The global deviation remains above their intrinsic counterpart until $t \sim 8$ ms slightly decreasing before the open end of the channel. The time of arrival of the flame with glass being smaller than with plastic, a bifurcation is visible. This discrepancy was not seen with large ignition offset, where in contrast, glass presents a larger deviation. This result may again imply an interaction between two parameters, namely ignition offset and materials, an outcome similar to that described in Fig. 16. It is not straightforward to conclusively determine why this is the case; however, a lead would be the different stiffness of plastic and the aluminum frame holding the glass, resulting in different acoustic impedances in a section prone to acoustic effects (the open end of the channel). In summary, using glass or plastic did not show significant deviations until the open end was approached.

Appendix 3: Effect of ignition offset for less diluted mixtures

As the nitrogen dilution is reduced, the sensitivity to detonation onset increases; 20 additional experiments were conducted to determine whether the behaviors observed for H$_2$–air at small/large ignition offsets also apply to stoichiometric H$_2$–O$_2$ mixtures. To choose appropriate framing rates to capture detonations, the steady Chapman–Jouguet velocity is used (2840 m/s); 360,000 fps, the maximum allowed by the camera with the spatial resolution specified in Sect. 2.2, is thus sufficient. A significantly shorter exposure time (159 ns) is necessary to avoid saturation during DDT and detonation propagation. Note, however, that this choice decreases the accuracy of the luminous front detection during the flame acceleration stage. Figure 18 shows the $x{-}t$ diagram. DDT was not systematically captured as in most cases (18 out of 20 tests) detonation onset occurred outside of the viewing window (i.e., $x \ge 400 \, \text {mm}$).

Fig. 18

Influence of ignition offset on mean flame position $\bar{x}$ (dashed line). Blue: large ignition offset (sample size includes 7 tests), red: small ignition offset (sample size includes 13 tests). Configuration: Igniter 2 and plastic; condition: stoichiometric H$_{2}$–O$_{2}$ at $p_0 =$ 100 kPa and $T_0 =$ 290 K

For the remaining two cases: one with a small ignition offset and one with a large ignition offset, DDT occurred at $x=365$ mm and $x=377$ mm, respectively, showing that the ignition offset does not seem to influence significantly the run-up distances prior to DDT compared to the detonation onset time, $t=2.43$ ms for small ignition offset and $t=1.23$ ms for large ignition offset. Note that the backward motion shown in our data could in principle come from the reflection of precursor shocks as expansions from the open end of the channel and their subsequent interaction with the reactive front as previously discussed in [38]; however, this may not be the case here. The camera settings required to capture the detonation phase accurately (159 ns exposure time) do not perform well during the FA phase, resulting in incorrect estimates of the front position; this represents one of the main limitations of direct observation to study DDT in hydrogen mixtures compared to hydrocarbons [22]. The steep acceleration phase shown in the figure is nonetheless correctly detected, but does not correspond to actual transition to detonation as computed velocities are in the range of $u_\mathrm {f} = 800-1800\,\text {m/s}$. Only for the aforementioned two cases where DDT occurred within the viewing window, velocities reached 2800 m/s. Abrupt acceleration leading to quasi-steady propagation velocities has been identified previously to have complex structures that include planar shocks trailed by funnel-shaped flames [39,40,41]; unfortunately, with direct observation we cannot verify whether this is the case for our data. Finally, it is worth mentioning that pollution due to the presence of sodium in air does not seem to contribute to enhanced light emissions in the combustion products as we observed the same intensity levels in the raw images captured with H$_2$–O$_2$ (not shown).