Abstract
Curved shock theory is introduced and applied to calculate the flow behind concave shock waves. For sonic conditions, three characterizing types of flow are identified, based on the orientation of the sonic line, and it is shown that, depending on the ratio of shock curvatures, a continuously curving shock can exist with Type III flow, where the sonic line intercepts the reflected characteristics from the shock, thus preventing the formation of a reflected shock. The necessary shock curvature ratio for a Type III sonic point does not exist for a hyperbolic shock so that it will revert to Mach reflection for all Mach numbers. A demonstration is provided, by CFD calculations, at Mach 1.2 and 3.













Similar content being viewed by others
Notes
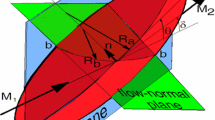
The flow-plane is the plane surface that contains the smallest angle between the down-shock flow vector and the shock surface; it also contains both the pre-shock and post-shock flow vectors [4]. The flow-normal plane is normal to both the shock and the flow-plane.
It is possible to study the flow behind a convex hyperbolic shock by taking the positive values of x as generated in step 2y above.
For planar flow, these quantities are not functions of shock curvature and for axial flow they are functions not of the individual curvatures but of their ratio.
The calculation of a body surface required to produce a given shock shape is not always a mathematically well-posed problem for it may yield an unrealistic surface and streamlines with folds and cusps.
References
Anderson, J.D.: Hypersonic and High Temperature Gas Dynamics. AIAA Education Series. American Institute of Aeronautics and Astronautics, Reston, VA (2006)
Mölder, S., Romeskie J.M.: Modular hypersonic inlets with conical flow. In: AGARD Conference Proceedings No. 30 (1968)
Mölder, S.: Curved shock theory. Shock Waves 26, 337–353 (2016)
Kaneshige, M.J., Hornung, H.G.: Gradients at a curved shock in reacting flow. Shock Waves 9, 219–232 (1999)
Liepmann, H.W., Roshko, A.: Elements of Gasdynamics. Wiley, New York (1957)
Lin, C.C., Rubinov, S.I.: On the flow behind curved shocks. J. Math. Phys. 27(1–4), 105–129 (1948)
Gerber, N., Bartos, J.M.: Tables for determining flow variable gradients behind curved shock waves. U.S.A. Ballistics Research Laboratories Rep. 1086 (1960)
Thomas, T.Y.: On curved shock waves. J. Math. Phys. 26, 62–68 (1947)
Thomas, T.Y.: The consistency relations for shock waves. J. Math. Phys. 28(2), 62–90 (1949)
Truesdell, C.: On curved shocks in steady plane flow of an ideal fluid. J. Aeronaut. Sci. 19, 826–828 (1952)
Mölder, S.: Reflection of curved shock waves. Shock Waves (2017). doi:10.1007/s00193-017-0710-3
Hayes, W.D., Probstein, R.F.: Hypersonic Flow Theory. Academic Press, London (1966)
Pant, J.C.: Some aspects of unsteady curved shock waves. Int. J. Eng. Sci. 7, 235–245 (1969)
Henderson, L.F.: Regions and boundaries for diffracting shock wave systems. Zeitschrift für Angewandte Mathematik und Mechanik 67(2), 73–86 (1987)
Masterix. Software Package. Ver. 3.40.0.3018, RBT Consultants, Toronto, ON (2004–2015)
Saito, T., Voinovich, P., Timofeev, E., Takayama, K.: Development and application of high-resolution adaptive numerical techniques in Shock Wave Research Center. In: Toro, E.F. (ed.) Godunov Methods: Theory and Applications, pp. 763–784. Kluwer Academic/Plenum Publishers, New York (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Brouillette and E. Timofeev.
Appendix: Coefficients for the curved shock equations
Appendix: Coefficients for the curved shock equations
The curved shock equations are, Mölder [3],
where the coefficients A, B, E, C, G and their primed and subscripted variants (14 in all) are given by,
where
The matrices [XY] are,
The vorticity equation is, Mölder [3],
The vorticity equation coefficients are,
Rights and permissions
About this article
Cite this article
Mölder, S. Flow behind concave shock waves. Shock Waves 27, 721–730 (2017). https://doi.org/10.1007/s00193-017-0713-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-017-0713-0