Abstract
The Firm Ecosystem Model is a dynamical model based on the empirical finding that firm characteristics, such as the tendency to innovate and competitive advantages, vary according to firm size. Firm dynamics leading to various population distributions are considered as a competition-colonization scenario in a spatially defined market, where firms of differing sizes are treated as separate species with different competition and colonization characteristics. Smaller firms, given adequate investment funds to innovate, are able to colonize available space more quickly than larger firms, and larger firms are assumed to have stronger competition characteristics and are able to outcompete smaller firms for occupied space. With startup and mortality parameters determined empirically, firm populations reach equilibria dependent on the values of the capital investment parameters. The model predictions provide a good qualitative fit to empirical data from the Business Dynamics Statistics database. Finally, we explore how alternative mortality or investment conditions affect the firm size distributions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Firms are the medium through which individuals participate in the productive aspect of an economy, and in aggregate compose the domain of business that is one of the three pillars of macroeconomic theory. Despite the central role in a myriad of economic questions, an individual firm is classically modeled as a black box that essentially serves as a vehicle for a production function. This formulation is unsatisfying to anyone interested in understanding the macroeconomic implications of firm dynamics where heterogeneity in firm characteristics is important, firms interact with each other and dynamics are endogenous.
Firm dynamics determine the relative proportions of different size firm populations, and these proportions are linked to macroeconomic questions, such as what types of firms provide the most employment (Birch 1981; Haltiwanger et al. 2013), which types innovate (Acs and Audretsch 1987; Hathaway and Litan 2014) and whether a large variety of firm types promotes social well-being (Hannan and Freeman 1993). Understanding the drivers of firm dynamics is therefore of importance not only to academics but also to management professionals and policy makers.
Early models exploring firm dynamics focused on empirical firm size distributions and the equations that described them. In 1931, Robert Gibrat examined firm plant sizes across France and derived a logarithmic relationship between firm population and size where firm growth was in proportion to its size. This became popularly known as Gibrat’s Law of Proportional Effect. Later work built on this law and produced variants that modified birth, growth and mortality parameters (Kalecki 1945; Simon and Bonini 1958; Mansfield 1962). The Gibrat distribution and its variants fit the larger end of the firm size spectrum well but failed to adequately predict the distribution of small firm sizes, as demonstrated in Fig. 1 where the Gibrat distribution is mapped against empirical firm size data from the Business Dynamics Statistics (BDS) database. The BDS dataset is an aggregated longitudinal dataset with complete representation across all firm size categories.Footnote 1 Firm sizes are organized into 12 categories based on numbers of employees: 1 to 4, 5 to 9, 10 to 19, 20 to 49, 50 to 99, 100 to 249, 250 to 499, 500 to 999, 1000 to 2499, 2500 to 4999, 5000 to 9999 and 10000+. Econometric work attempting to clarify these breakdowns in the Gibrat assumption (Hall 1986; Dunne et al. 1988) found statistical regularities in the empirical data, namely that survival increases with size and growth decreases with size. Smaller firms fail more often and grow faster than larger firms. These results appear to hold regardless of how size is defined, whether by output, plant size or employees (Sutton 1997; deWit 2005).
BDS Statistics for Average Size. The Business Dynamics Database (BDS) firm size distribution averaged over all industries and all years from 1977 to 2014 is shown as solid blue line with a dashed line describing the classic Gibrat distribution, and a dotted line the Zipf distribution. Note the ‘hump’ toward the left hand side of the empirical distribution
More recent size distribution work proposes alternative distributions such as the Zipf (Axtell 2001; Bottazzi et al. 2015), Rank (Podobnik et al. 2010), log-log OLS (Di Giovanni et al. 2011) and Hill (Gabaix 2009). These distributions are considered valid only above a minimum firm size and don’t attempt to explain the distributions at the smaller end of the size spectrum, in part due to data collection methods that focus on larger firms. Our use of the BDS dataset with representation across all firm sizes should mitigate this issue, as well as the fact that we are not seeking a statistical fit to the empirical data. Of particular interest is the ‘hump’ between the second and sixth size category presented by the empirical data, which is unexplained by the Gibrat or related distributions.
A more descriptive exploration of firm dynamics arises out of the management literature, where populations of firms are considered in the context of industries and firm dynamics considered as industry life cycles. This industry life cycle work identified regularities in behavior within populations of various sized firms such as shakeouts, where a large number of entrants falls to a small number of persistent firms, explained as the process of winnowing excess capacity and settling on a minimum efficient scale, as well as a positive correlation between firm entry and exit rates within an industry, known as turbulenceFootnote 2Klepper and Miller (1995), Klepper (1996), Klepper (1997), and Haltiwanger et al. (2013). This industrial dynamics theory considers competition as monopolistic, an imperfect form of competition as understood classically, whereby firm offerings are differentiated and surviving firms’ products and services address the needs of a particular niche. But there also exists a heterogeneous institutionalFootnote 3 competitive advantage enjoyed by established firms by way of supply chain relationships, established brands and legal protections, which is not explicitly addressed in these studies. These institutional advantages create barriers to entry for new firms (Bain 1954; Stigler 1964; Caves and Porter 1977; Demsetz 1982).
Meanwhile, organizational ecologists viewed firm dynamics as determined by processes of competition (Sleuwaegen and Goedhuys 1998). Hannan and Freeman (1977), in particular, considered questions of firm dynamics to be “fundamentally ecological in nature”. Organizational ecologists paid considerable attention to the institutional setting in which firms complete (Nugent and Nabli 1992; Hannan and Carroll 1992; Hannan and Freeman 1993). Firm growth and survival depend on the competitive characteristics of other firms as well as the institutional settings that determine such factors as access to capital and the nature of competitive advantage. Generally speaking, “If processes generating variation and retention are present in a system and that system is subject to selection processes, evolution will occur” (Aldrich 1999). In this view, firms are adaptive entities that respond, according to their unique characteristics, to the environments in which they operate (Nelson and Winter 1982; Beinhocker 2006; Ebeling and Feistel 2011). Firms that don’t adapt will fail due to institutional and competitive selection pressures.Footnote 4 Hannan and Freeman theorized that firms don’t necessarily adapt to changing conditions due to the difficulties for large established organizations to change quickly, a quality described as structural inertia (Hannan and Freeman 1984).
Larger firms may enjoy institutional competitive advantage, but smaller firms are more agile when it comes to adapting to new market opportunities because they are less inertial. Small firms also tend to have less available capital than larger firms to pursue innovations, but they also enjoy more attention from external investors, and the degree to which small firms can take advantage of their agility depends on the availability of this external investment. Venture capital typically funds startup firms for five years, at which point investment falls off dramatically as investors turn their attention toward exit strategies and realizing returns (Hall and Lerner 2010; Feld and Mendelson 2013; Gompers and Lerner 2001).Footnote 5 Venture capital chases startups because they have potential for higher growth through innovation and market capture than incumbent firms.Footnote 6
Putting this ecological picture together with the observed size-specific characteristics previously described, we could consider firms of various sizes as unique species with size-specific behaviors and characteristics, all competing within an institutional context. The outcome of these competitive dynamics produces a particular firm population distribution. Specifically, larger firms have a stronger competitive advantage, both through economies of scale and institutional barriers to entry, but are less able to adapt to changing environments due to structural inertia. They have lower mortality and growth rates than smaller firms. Smaller firms are better at adapting to change because they are less inertial, but the degree to which they can innovate is dependent on external investment. In summary, a brief inventory of the empirical regularities described gives us a list of seven stylized facts:
-
1.
Firm survival increases with size (Dunne et al. 1988)
-
2.
Firm growth decreases with size (Hall 1986)
-
3.
A new market will initially generate a large numbers of small firms that fail (shakeout) (Klepper and Miller 1995)
-
4.
When mortality increases, more firms enter the market (turbulence) (Klepper 1997)
-
5.
Larger firms enjoy a competitive advantage over smaller firms (Demsetz 1982)
-
6.
Smaller firms attract more outside investment than larger firms (Feld and Mendelson 2013)
-
7.
Smaller firms are more agile than larger firms because they have less structural inertia (Hannan and Freeman 1984).
The last two items are of particular interest, because taken together they suggest multiple flavors of competition at play in firm dynamics: institutional competitive advantage in established markets and agility in capturing new markets. Our premise of established firms operating under comparative advantages and newer firms innovating is reflective of the early Schumpeterian or entrepreneurial technology regime described by Winter (1984) and demonstrated econometrically by Breschi et al. (2000).
We postulate that smaller firms are particularly susceptible to institutional effects, such as barriers to entry and investment incentives, and a model that directly addresses these realities will provide useful insights into firm dynamics, better explain how those dynamics affect the distribution of firms at the small end of the spectrum, and serve as an experimental sandbox to explore how modifications to the institutional context that modulate the selection pressures and innovation opportunities may affect firm size distributions. Given the emphasis on competition in the standard narratives of firm dynamics, combined with the growing understanding that firm size distributions are not fully explained by of market selection forces, minimum efficient scales, relative efficiencies or profitability (Dosi 2005; Dosi and Nelson 2010), we believe ecological modeling of firm dynamics is underutilized. Is there an ecological analogy that would apply to the multilevel competition description of firm population dynamics described above?
We believe we have found such an analogy in David Tilman’s spatially structured competition-colonization dynamics (Hastings 1980; Tilman 1994). Tilman describes a Wisconsin prairie populated by different species of grass. One particular species has superior nitrogen-fixing ability, so tends to overrun areas populated by species with lesser ability. But all grass organisms have a mortality rate so regions of empty patches are continuously emerging, which can be populated by lesser-fixating grass species. The population dynamics on the prairie therefore consist of empty patches colonized by lesser fixating species that were eventually overrun by superior fixating species, while new space regularly becomes available for colonization through the deaths of individual plants.
In the context of firm dynamics, a market could be analogous to a prairie, and larger firms with superior competitive advantage will take over the marketshare populated by smaller firms. Meanwhile, smaller firms will populate new marketshare (empty prairie in our analogy) before larger species because they are more agile. The degree to which they can populate empty space is governed by investment. Large firms excel at competition, while small firms excel at colonization, and we make use of the distinction between the types of competitive dynamics identified previously.
The remainder of this paper will further develop the competition-colonization firm dynamics model with appropriate modifications. We will then propose a parameterization scheme based on empirical US firm size data and demonstrate that our model fit is superior in the small firm region than other distribution fits. We will then use the model to conduct experiments by altering a subset of the institutional parameters and observing the effects on firm size distributions.
2 The model
In building the model, we assume that firms of differing sizes have different competition, mortality and investment profiles. Firms of various sizes compete over marketshare, conceived as a spatial entity and henceforth referred to as marketspace, and are considered analogous to different species competing over any bounded resource, such as prairie grasses competing for space in a field (Tilman 1994).Footnote 7 Competition describes firms vying for space in populated marketspace, and differences in competitive ability are decided by disparities in economies of scale and barriers to entry. Colonization, on the other hand, describes firms vying for empty marketspace by innovating to develop new offerings. Each size category of firms is considered a species with different effective competition and colonization characteristics, where size is defined by number of employees. However, firms are not completely analogous to species of grass because a firm of a given size can either grow or contract into a firm of another size. We account for this additional dynamic by allowing for a given size-species to mutate into an adjacent size-species. The model further assumes that all firms will grow to the greatest extent possible and are not intended to remain small concerns or limited by economies of scale.
Firm populations for each size-species i are specified by μi. Larger firms will outperform smaller firms in acquiring occupied marketspace because of efficiencies of scale and institutional competitive advantage. Smaller firms will outperform larger firms in populating empty marketspace because they are more agile since they have less structural inertia; however, the degree to which a small firm can take advantage of this agility is mitigated by its available capital. All firms face a mortality rate, which decreases with size, so at every time step a portion of firms will fail and their marketspace will become empty and available for colonization.
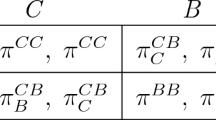
The rate of change of marketspace that firms occupy in each size-species is the sum of the marketspace change acquired through colonization and that acquired through competition, minus the proportion of firms that fail due to mortality processes (Fig. 2).
Empty marketspace is all the space not currently filled by firms, modeled as \(1 - {{\sum }_{1}^{n}}\mu _{j}\) where j indexes all the size species categories. Species colonize this empty space at a rate proportional to their current population, μi, and an investment parameter νi, and the colonized marketspace is represented as
Larger firms win populated marketspace from smaller firms due to economies of scale and institutional competitive advantages, so species will win marketspace from smaller species and lose marketspace to larger species. This process is modeled as
The change in marketspace, si, for a given size-species i is therefore
We can compare this competition-colonization firm dynamics model with the original Tilman model, which wasFootnote 8
Aside from notational differences (pi in the Tilman model is the population of species i and ci is that species competitive value) we see that Equations 3 and 4 are structurally similar, both consisting of a colonization term, a competition term and a mortality term. The mortality terms are identical, and differences in the remaining terms are due to the specifics of modeling firm dynamics where competition and colonization are governed by different parameters and firms grow or shrink into neighboring size-species.
In our model, mortality is modeled linearly and described by
where a is the slope and b is the intercept. Investment, as a proxy for innovation, is modeled as a logistic function with three parameters, K, p and q, which respectively control the height, position and steepness of the curve. This innovation investment curve describes the tendency of smaller firms to innovate more than larger firms due to structural inertia, and the parameterization of the curve describes the availability and conditions on external investment which makes small firm innovation activity possible.
A detailed discussion of the parameterizations for m and ν can be found in Appendices B and B.
Growth and decline are considered to be instantaneous so any change in quantity of marketspace for a size species will result in that quantity moving to an adjacent species category, either a smaller or larger category depending on the sign of the change. Thus any net change in the marketspace of a given size-species will come from firms of the smaller category growing and firms from the larger category declining. In other words, since firms of a given size-species can grow or decline into another size-species according to changes in marketspace, if the marketspace for a size-species increases or decreases, that marketspace should be attributed to either the larger or smaller size-species.
According to our definition of size, as a firm grows it obtains more employees. Ultimately, the model will need to describe a population distribution of size-species in order to compare with empirical distributions, so we need to transform marketshare into a number of firms. For example, consider x dollars of marketspace populated by small firms. If that same x dollars were populated by larger firms, the number of larger firms would necessarily be less than the number of smaller firms populating that marketspace. To resolve this logical inconsistency, we assume a fixed proportional relationship between an employee and marketshare, and then scale the marketshare transferred from growing or declining size-species such that marketshare effectively contracts as it moves up to larger firms and expands as it moves down to smaller firms by a growth scaling factor, γ. This growth scaling allows us to speak of marketspace and number of firms synonymously.
The growth scaling factor gamma is modeled as
where N is the number of size-species categories. A discussion of the derivation and parameterization of γ can be found in Appendix B, and is essentially describing a power law between the number of employees and marketshare.
The total change in size-species population over time will involve competition-colonization dynamics along with growth and decline dynamics. Therefore
where si is given by Eq. 3 and 𝜃 is the step function defined by
The boundary conditions for the largest and smallest firms size-species, i = [1,n], are handled as exceptions. For i = 1, new firms occupy empty marketspace at a startup rate σ and this smallest species population also grows through declines in i = 2 species.
The largest size category retains the species that otherwise would have grown into larger species, as well as through growth in the n − 1 size species.
This model complements many historical and recent models attempting to explain firms size distributions. Instead of explicitly specifying entry, exit or growth, we model dynamics between various populations of firms with each population of a given size having distinct behaviors. Since firms are economic entities, microeconomics are implied in these dynamics. The prairie grasses in our analogy have innate production functions which cause them to exist and to grow or die, likewise firms have production functions which cause them to maintain, acquire, or lose marketspace. While prairie grasses don’t have preferences, our marketspace represents aggregate demand which shifts according to changing household preferences, and this shifting causes firms to fail and opens up space for new firms. Investment activity in the model changes according to free marketspace and the number of investing firms. The size-specific firm characteristics represent a complex interaction of production decisions, costs, and efficiencies of scale as well as non-market driven institutional effects. Previous work has explored neoclassical formulations of these size-specific characteristics, such as modeling the competitive advantage versus innovation tradeoff (Winter 1984) or shakeouts (Dietrich and Krafft 2012). Based on this work we use derived firm characteristics to model the ecological processes that evolve a national industry structure. This approach is also based on previous work. For example competitiveness of entrants has been modeled as available opportunities (free marketspace), entry barriers and average competitiveness of incumbents (Dosi et al. 1995), and growth rates have been modeled as a function of entry conditions, financial availability (investment), adjustment gaps (free marketspace) and intensity of competition (Saviotti and Pyka 2004).
3 Results
The model in its full representation is analytically intractable,Footnote 9 yet analysis is straightforward computationally using an Euler method. The model dynamics produce distributions of either one, two or three peaks of varying sizes in the equilibrium population distribution, depending on parameter value combinations for K, p, q, a, b, g, and σ. Of particular importance is the ratio between maximum investment K and startup rate σ. Both ν, investment, and σ, startup rate, produce gains related to empty space. Too high a value of σ leaves too little space for other firms to obtain investment gains. Too low a value of σ with respect to ν produces too few startups to allow for sustained growth, and the equilibrium state has all firms in the smallest size category and zero populations in larger categories.
The single peak occurs at either the first size category or in the size category just above the inflection point of the investment curve, specified by p. Two peaks will occur at the smallest size and the inflection size (p + 1) for certain ratios of K and σ, and the dynamics are sensitive to small changes in this ratio. In these scenarios, startup dynamics continually populate the smallest size and investment encourages growth up to the inflection category p. The growth dynamics slow down for larger firm sizes so the larger categories have small but non-zero populations. Three peaks, in the first, last and inflection categories, manifest in cases where the growth scaling factor γ is greater than 1. This three-peak scenario occurs when a significant number of firms to grow through to the largest size category, but is not consistent with the firms and marketspace paradigm described in Section 2.
We began our exploration with the model by recreating the observed distribution of US firms. We modeled mortality, mi, as a negatively sloped line, with values parameterized from the Business Dynamics Statistics (BDS) database. We also modeled investment, νi, as a logistic function with inflection point, p, and gradient, q, set to represent a steep drop at the second size-species to mimic observed innovation investment behavior, where small firms are funded for short time periods. These parameterizations account for observations 1, 6 and 7 of our stylized facts inventory, namely that survival increases with size and that the will to innovate is higher for smaller firms because they are more agile and attract more innovation investment. The growth scaling factor, γ, is also parameterized from the BDS data.Footnote 10
The BDS data gives a mean entry rate over the last thirty years as 10% of the existing population each year. This metric is not directly applicable to the model since σ multiplies the empty space in order to determine the entry into the first size category. Therefore using a σ value of .1 would significantly underestimate the startup rate.
Because the model is sensitive to K and σ values, for which we don’t have a clear empirical parameterization, we have conducted a detailed analyses over a large portion of the K-σ parameter space. The model produces distributions as output so we needed to identify a single-valued measure to describe these distributions for comparison purposes. We therefore developed a stylized version of the Kolmogorov-Smirnov D-statistic to obtain a measure of similarity between the model distributions and the empirical BDS distribution. The D-statistic can be understood as the maximum distance between corresponding points of two cumulative distributions, thus a smaller value suggests a better match between the distributions (the null hypothesis is that the distributions are identical with a D-statistic of 0).
The BDS data represented in Fig. 1 demonstrates two features, one we’ll call the ‘peak’ in the smallest firm size, and the other a ‘hump’ between the second and fifth size categories, and similar D-statistic values can be obtained either by the model distribution replicating the peak or the hump. To generate the stylized D-statistic, we first found the maximum distance between corresponding population values at each size category in a model distribution (scaled up to a total population of one) and the BDS distribution for both the full distribution and then for all sizes greater than 1. We then multiplied these two values to obtain a measure of fit that attempts to balance the peak fit with the hump fit as well as corrects for the distance between distributions due to the model producing an equilibrium result that leaves empty market space. Values of this statistic are plotted as a heat map over the two-dimensional K-σ parameter space in Fig. 3.
For our base model parameterization, we chose a σ value of .4 to represent 40% of empty space each year being populated by startups, and a corresponding value of K = 2.5 to represent the maximum investment over all small firms to be 2.5 times the empty marketshare. This combination of parameters falls within the dark blue diagonal band in Fig. 3 describing the σ/K ratios that give the best fits to the BDS data according to our stylized D-statistic. Higher values of σ produce more pronounced peaks in the first size category.
Figure 4 shows the resulting population distribution as a histogram for investment parameterized by K = 2.5, p = 2 and q = .1, mortality parameterized by a = − 1.8 and b = − 1.8, and with growth scaling factor γ = .5 and the startup rate σ = .4. Competitive advantage due to economies of scale and other institutional size advantages is built into the model dynamics as described by Eq. 2, accounting for observation 5 that larger firms enjoy a competitive advantage over smaller firms.
Regardless of parameterization, the model’s equilibrium values are independent of starting conditions so the same equilibrium distribution emerges regardless of the initial conditions. Figure 5 demonstrates this by comparing the results of a simulation starting from empty marketspace with a simulation starting with equal populations across all size-species. We also see in the left hand plot Fig. 5 the differences in growth rates between firm sizes, with smaller firms having steeper slopes than larger firms, thus accounting for observation 2 in our inventory that smaller firms having faster growth rates than larger firms. We also see in the right hand plot the expected shakeout in small firm populations where initially the population grows then falls, thus accounting for observation 3, shakeout, but without any reference to minimum efficient scale.
Evolution of Equilibrium State from Different Initial Conditions. The figure on the left shows the model results starting with all populations equal to zero, and the figure on the right shows the results starting with equal populations. Investment is parameterized by K = 2.5, p = 2 and q = .1. Mortality is parameterized by a = − 1.8 and b = − 1.8. The growth scaling factor γ = .5 and the startup rate σ = .4
Also of note is that the model populations do not add to one, suggesting that there is always empty marketspace and unrealized opportunity for expansion and growth within the economic ecosystem.
In Fig. 6 we show the model results plotted against empirical data from the BDS dataset. We also include the classic Gibrat and Zipf distributions for comparison. We see that the model prediction qualitatively follows the shape of the empirical curve for smaller firm sizes compared to the Gibrat or Zipf curves. Table 1 shows the results for Kolmogorov-Smirnov tests comparing each theoretical distribution with the empirical distribution, and though the Zipf distribution is a better fit than the Gibrat distribution, we see our model fit is superior to that of the Zipf. Therefore, as postulated, competition and investment dynamics could indeed be important drivers of firm size distributions at the lower end of the spectrum.
BDS Statistics for Average Size with Model Results. Business Dynamics Database (BDS) statistics for average size distribution averaged over all industries and all years from 1977 to 2014 is described by the blue line. The model-predicted size distribution for the described parameter set is shown by the red line. The dashed line describes the classic Gibrat distribution and the dotted line the Zipf distribution. Note the model’s approximation of the ‘hump’ in the empirical data
Despite the greatly improved fit in small firm sizes, the model predicts significantly lower populations of the smallest size category than indicated by the data. A possible explanation could be that there is a distinction between small business owners and entrepreneurs, where small businesses are structures to provide professional services while entrepreneurial firms are innovators. Hurst and Pugsley (2011) demonstrate that a significant portion of firms in the first size categories are small businesses that do not intend to grow or innovate. Since these firms aren’t founded with the intent to grow, they do not fully participate in the described dynamics. The model results show that the predicted population of smallest size firms is smaller than actually found in data, though the strength of this finding is somewhat dependent on the choice of σ.
Next we conduct some experiments with the model whereby we modify the selection pressures by changing the mortality and investment parameters, singly and in combination in order to explore how modifications in the institutional conditions controlling competitive advantage and innovation investment affect the distributions of smaller firms. We first modified the mortality parameter to represent a reduction in the institutional competitive advantage enjoyed by larger firms, meaning that more larger firms will fail. We then modified the external investment parameter such that investment is available to firms in small to medium size categories, which represents a lengthening in the timelines for innovation investment. Next we combined both these modifications, and finally we combined both modifications with a smoothing of the investment curve, which represents larger firms innovating more. Table 2 summarizes the four experiments described above with their parameter configurations. To see how the dynamics change with an increase in mortality for larger firms, corresponding to a lessening of competitive advantage, we increased the mortality rate across larger size-species by flattening the slope of the mortality line, setting a = −.01, and produced the distribution described in Fig. 7. This figure demonstrates that, compared to the BDS parameterized fit, an increase in mortality rates does indeed result in an increase in the population of the smallest size category, thus accounting for observation 4, that turbulence increases firm entry. (Thus we have now accounted for all seven of the size-specific firm observations in our inventory; see Table 3 for a summary.) There is also a slight increase in the second size category and decreases in the populations for the remaining size categories.
If we increase the length of time an innovation investment is made, then investment would be available to intermediate firms sizes. If we effect this change by moving the inflection point of our investment logistic to p = 4 we obtain the equilibrium shown in Fig. 8. Notice the emergence of a second peak in the fifth size category. Compared to the BDS parameterized fit, the populations decrease for the first four size categories and increase for the remaining categories.
Modifying both mortality and investment results by a = −.01 and p = 4, we arrive at the equilibrium shown in Fig. 9. Now there is less of a decrease in the first four size categories than with just an investment change.
In Fig. 9 we moved the inflection point of the investment curve, but left the investment curve steep, which means larger firms spend little investment funds on innovation. We can smooth the investment curve so that the drop off is more gradual, which represents larger firms being more willing and able to innovate. Combining all three modification, mortality slope and investment inflection and steepness changes, we obtain the equilibrium given in Fig. 10. With the smoothed curve, the middle peak is not as prominent and size categories two, three, and eight through ten see slight population increases.
Model Results for the Long-Run Equilibrium Size Distribution with Increased Mortality and Longer-Term Investment with a Smooth Investment Curve. Investment is parameterized by K = 2.5, p = 4 and q = .5. Mortality is parameterized by a = −.01 and b = − 1.8. The growth scaling factor γ = .5 and the startup rate σ = .4
In summary, Fig. 11 shows all five model configurations together: the BDS parameterization with investment only in small firms with a sharp investment drop off, an increased mortality rate for larger firms, increased investment for middle-size firms, both increased mortality for larger firms and increased investment for smaller firms, and increased mortality and smoothed increase in investment. Note that the smoothest increase in middle-sized firms emerges from the combination of parameter modifications for m, p and q. This suggests that increasing available marketspace by decreasing the competitive advantage is not enough on its own, and innovation investment by both small and large firms is also required for a vibrant middle-size firm population.
Comparison of Distributions for Selected Model Configurations. Model predictions of firm-size population distributions for five different parameter scenarios: BDS parameterization with small firm investment and sharp drop off, same investment with increased mortality, same mortality with increased investment, with both increased mortality and investment, and both increased investment and mortality with smoothed investment curve
A regression-based response surface analysis exploring the parameter space defined by K, σ, p, q and a, using the distribution entropy as a response, is presented in Appendix B (Table 4).
4 Discussion
Several model assumptions warrant specific consideration. We have modeled all startup firms as populating the smallest size category, which is mostly accurate but not always true, notably in the case of spin-offs, and we have neglected merger and acquisition dynamics. Also, real firms grow or contract in a sticky manner. Thus the instantaneous growth assumption would not necessarily hold in the short term but are reasonable over the long term. Finally, we have been using interchangeably size-specific and age-specific characteristics, which are correlated but don’t always hold in specific instances (Haltiwanger et al. 2013). For example, we have used investment cutoffs according to size, when actually the investment cutoff is determined by time, therefore a function of age rather than size. Further model exploration could examine if and where these size/age equivalency assumptions break down.
This model is both dynamic and explanatory, so while it isn’t detailed enough to advocate and test the expected outcomes of specific policies, it can serve as a sandbox for consideration of different institutional arrangements on firm-size distributions. For example, there is a noted decline in the scale-up of young American firms (Hathaway and Litan 2014). Yet the intermediate-aged firms are also the biggest contributors to net employment growth, and it is suggested that firms under ten years of age may require institutional support in order to persist into the middle age ranges (Haltiwanger et al. 2013). Given that this middle phase of a firm life-cycle is vital to employment, policy intervention could be justified. How could this support be implemented?
This model proposes three possible levers: longer-term innovation investment, reducing the effects of institutional competitive advantage, and encouraging larger firms to innovate. Investment exits could be curtailed such that investments extend over longer periods of time than the typical five to ten year window. This doesn’t directly mitigate structural inertia for older, larger firms, but it does supply investment for R&D and innovation to a broader swath of more agile firms. This continued investment allows intermediate size firms to participate more aggressively in colonization activity.
Creative destruction theoretically should ensure a failure rate for older, larger firms, but there is evidence that mortality for larger firms is mitigated through institutional mechanisms such as non-competitive consolidation and legislated industry protections, all of which encourage the persistence of larger firms and construct barriers to entry for smaller firms. If larger firms were to fail more often, more marketspace would become available for smaller and even intermediate firms to populate.
Increasing turbulence could also incentivize larger firms to participate in colonization activity. If the reward for seeking institutional competitive advantage were to diminish, and firms were required to actively compete in order to survive, larger firms may be willing to overcome structural inertia issues and innovate (Baumol 1996).
The experimental results illustrated in Fig. 11 suggest a balanced combination of all three of these effects, increased competition, focus on innovation investment for middle-sized firms and encouraging larger firms to innovate, could be effective. Increasing competition alone increases the population of small firms but not middle-sized firms. Raising the cutoff size for innovation investment commitments produces a second peak at the cutoff point, suggesting that the investment money props up growth to that point since the growth doesn’t continue. Extending innovation investment throughout the spectrum of firm sizes as well as increasing competition produces a smooth curve with increased middle size populations. (This last experiment produces conditions similar to the intermediate technology regime described by Dosi et al. (1995).) These experimental results are indications of effects of policy outcomes, and don’t make distinctions between the sources of entry barriers, reduced competition, or mechanisms for innovation and growth which actual policies would explicitly address.
As mentioned in the Section 3, the total population of firms is less than one, suggesting that marketspace is left unfilled. We have not increased the total amount of investment, K, in our experiments, which should increase that colonization activity that fills empty marketspace. It would be interesting to explore what the model can tell us about when firm activity fills a marketspace and when it does not. We are reminded here again of the market adjustment gap modeled by Saviotti and Pyka (2004).
We’ve also neglected sector heterogeneity and haven’t made a distinction between firm-level technological learning made by innovation versus imitation. As demonstrated in Appendix A, the hump in the population distributions in small firm sizes persists across sectors, and even revolutionary advances such as information and communication technologies (ICT) do not generate industries with significantly different structures (Dosi et al. 2008). These ICT industries may include yet another dynamic, whereby a firm ecosystem develops as series of symbiotic relationships (Adner 2017; Adner and Kapoor 2016; Jacobides et al. 2018). It would be interesting to add this cooperative dynamic to our model, where symbiotic firms are established around a keystone species, perhaps building on Polya urn geographical or opportunity preference models (Bottazzi and Secchi 2006; Bottazzi et al. 2007).
In conclusion, we have shown that modeling competition and colonization as an endogenous driver of firm dynamics not only offers a viable theoretical explanation for those dynamics, but also provides the current best fit to empirical observations for US firm data. The model also is demonstrably useful as an experimental tool to explore modifications to innovation investment and competition conditions, suggesting that working the levers of competition and investment could indeed alter distributions of firm sizes, but that they need to work in conjunction with each other.
Notes
This turbulence was previously described by Joseph Schumpeter in 1942 as creative destruction.
Here we employ Douglass North’s (North 1991) definition of an institution as any form of constraint that shapes interactions, which include formal institutions such as laws and policies as well as informal institutions such as cultural norms.
A unique twist to modeling economic considerations through population ecology is that we have a great deal of agency in determining the evolutionary selection pressures and responses in an economic ecosystem (Jones and Breslin 2012).
By investment we refer to money a firm attracts from outside sources for the development of new products and services, and not exchanges of existing shares or money used as leverage to obtain operating efficiencies.
Alternatively, venture capitalists can obtain a much larger ownership stake in startups than incumbent firms for relatively little investment.
There are myriad reasons for firms to fail, and in this analogy we consider failures as resulting from changing market conditions, therefore colonization implies innovation to address these new conditions.
Equation 6 (Tilman 1994).
With a grossly simplified two-dimensional version of the model, neglecting growth dynamics, fixing four out of six parameters and using only two firm sizes (the smaller being x, the larger y), we could demonstrate 1) a stable node at (0, 0) when mortality rate exceeded investment rate for both sizes, 2) a stable x-axis with mx < νx and my > νy, 3) a stable y-axis if mx > νxand my < νy and 4) nonzero populations for x and y which under some parameter conditions was a stable spiral, under others a linear center.
Details about this database and our use of it for the parameterization of m,ν and γ are explained in Appendix B.
References
Acs ZJ, Audretsch DB (1987) Innovation, market structure, and firm size. Rev Econ Stat 69(4):567–574
Adner R (2017) Ecosystem as structure: an actionable construct for strategy. J Manage 43(1):39–58
Adner R, Kapoor R (2016) Innovation ecosystems and the pace of substitution: Re-examining technology s-curves. Strategic Management Journal 37 (4):625–648
Aldrich H (1999) Organizations Evolving. Sage
Axtell RL (2001) Zipf distribution of us firm sizes. Science 293 (5536):1818–1820
Bain JS (1954) Conditions of entry and the emergence of monopoly. In: Monopoly and Competition and their Regulation, Springer, pp 215–241
Baumol WJ (1996) Entrepreneurship: Productive, unproductive, and destructive. J Bus Ventur 11(1):3–22
Beinhocker ED (2006) The Origin of wealth: Evolution, Complexity, and the Radical Remaking of Economics. Harvard Business Press
Birch DL (1981) Who creates jobs? The Public Interest 65:3
Bottazzi G, Secchi A (2006) Explaining the distribution of firm growth rates. The RAND Journal of Economics 37(2):235–256
Bottazzi G, Dosi G, Fagiolo G, Secchi A (2007) Modeling industrial evolution in geographical space. J Econ Geogr 7(5):651–672
Bottazzi G, Pirino D, Tamagni F (2015) Zipf law and the firm size distribution: a critical discussion of popular estimators. J Evol Econ 25 (3):585–610
Breschi S, Malerba F, Orsenigo L (2000) Technological regimes and schumpeterian patterns of innovation. The Economic Journal 110 (463):388–410
Caves RE, Porter ME (1977) From entry barriers to mobility barriers: Conjectural decisions and contrived deterrence to new competition. The Quarterly Journal of Economics, pp 241–261
Demsetz H (1982) Barriers to entry. The American Economic Review 72(1):47–57
deWit G (2005) Firm size distributions: an overview of steady-state distributions resulting from firm dynamics models. Int J Ind Organ 23(5):423–450
Di Giovanni J, Levchenko AA, Ranciere R (2011) Power laws in firm size and openness to rrade: Measurement and implications. J Int Econ 85 (1):42–52
Dietrich M, Krafft J (2012) The economics and theory of the firm. In: Handbook on the economics and theory of the firm, Edward Elgar Publishing
Dosi G (2005) Statistical regularities in the evolution of industries: a guide through some evidence and challenges for the theory. Tech. rep., LEM working paper series
Dosi G, Nelson RR (2010) Technical change and industrial dynamics as evolutionary processes. In: Handbook of the Economics of Innovation, vol 1, Elsevier, pp 51–127
Dosi G, Marsili O, Orsenigo L, Salvatore R (1995) Learning, market selection and the evolution of industrial structures. Small Bus Econ 7 (6):411–436
Dosi G, Gambardella A, Grazzi M, Orsenigo L (2008) Technological revolutions and the evolution of industrial structures: assessing the impact of new technologies upon the size and boundaries of firms. Capitalism and Society, 3(1)
Dunne T, Roberts MJ, Samuelson L (1988) Patterns of firm entry and exit in us manufacturing industries. The RAND Journal of Economics, pp 495–515
Ebeling W, Feistel R (2011) Physics of Self-organization and Evolution. John Wiley & Sons
Feld B, Mendelson J (2013) Venture deals. Be Smarter than Your Lawyer and Venture Capitalist
Gabaix X (2009) Power laws in economics and finance. Annual Review of Economics 1(1):255–294
Gibrat R (1931) Les Inégalités Économiques. Librairie du Recueil Sirey
Gompers P, Lerner J (2001) The venture capital revolution. J Econ Perspect 15(2):145–168
Hall BH (1986) The relationship between firm size and firm growth in the us manufacturing sector
Hall BH, Lerner J (2010) The financing of r&d and innovation. In: Handbook of the Economics of Innovation, vol 1, Elsevier, pp 609–639
Haltiwanger J, Jarmin RS, Miranda J (2013) Who creates jobs? small versus large versus young. Review of Economics and Statistics 95(2):347–361
Hannan MT, Carroll GR (1992) Dynamics of Organizational Populations: Density, Legitimation, and Competition. Oxford University Press
Hannan MT, Freeman J (1977) The population ecology of organizations. Am J Sociol, pp 929–964
Hannan MT, Freeman J (1984) Structural inertia and organizational change. Am Sociol Rev, pp 149–164
Hannan MT, Freeman J (1993) Organizational Ecology. Harvard University Press
Hastings A (1980) Disturbance, coexistence, history and competition for space. Theor Popul Biol 18(3):363–373
Hathaway I, Litan RE (2014) The other aging of america: the increasing dominance of older firms. Tech. rep., Brookings Institution
Hurst E, Pugsley BW (2011) What do small businesses do? Tech. rep., National Bureau of Economic Research
Jacobides MG, Cennamo C, Gawer A (2018) Towards a theory of ecosystems. Strat Manag J 39(8):2255–2276
Jones C, Breslin D (2012) Innovative uses of evolutionary/ecological approaches in the study and understanding of organizations. Int J Organ Anal, 20(3)
Kalecki M (1945) On the gibrat distribution. Econometrica: Journal of the Econometric Society, pp 161–170
Klepper S (1996) Entry, exit, growth and innovation over the product life cycle. The American Economic Review, pp 562–583
Klepper S (1997) Industry life cycles. Ind Corp Chang 6(1):145–182
Klepper S, Miller JH (1995) Entry, exit, and shakeouts in the United States in new manufactured products. Int J Ind Organ 13(4):567–591
Mansfield E (1962) Entry, gibrat’s law, innovation, and the growth of firms. The American Economic Review 52(5):1023–1051
Nelson RR, Winter SG (1982) An Evolutionary Theory of Economic Change. Harvard University Press
North DC (1991) Institutions. Journal of Economic Perspectives 5(1):97–112
Nugent JB, Nabli MK (1992) Development of financial markets and the size distribution of manufacturing establishments: International comparisons. World Dev 20(10):1489–1499
Podobnik B, Horvatic D, Petersen AM, Njavro M, Stanley HE (2010) Common scaling behavior in finance and macroeconomics. The European Physical Journal B 76(4):487–490
Saviotti PP, Pyka A (2004) Economic development by the creation of new sectors. Journal of Evolutionary Economics 14(1):1–35
Schumpeter JA (1942) Capitalism, Socialism and Democracy. Routledge
Simon HA, Bonini CP (1958) The size distribution of business firms. The American Economic Review 48(4):607–617
Sleuwaegen L, Goedhuys M (1998) Barriers to growth of firms in developing countries: Evidence from burundi. Washington, DC: The World Bank, Manuscript
Stigler GJ (1964) A theory of oligopoly. J Polit Econ 72(1):44–61
Sutton J (1997) Gibrat’s legacy. J Econ Lit 35(1):40–59
Tilman D (1994) Competition and biodiversity in spatially structured habitats. Ecol 75(1):2–16
Winter SG (1984) Schumpeterian competition in alternative technological regimes. Journal of Economic Behavior & Organization 5(3-4):287–320
Acknowledgments
The first author would like to thank Marco Janssen for institutional support, and Armin Haas, Carlo Jaeger and Josephine Mauskopf for profitable discussions throughout the review process.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Supplementary materials
1.1 A.1 The BDS database
We use the Business Dynamics Statistics (BDS) database produced by the US Census Bureau to explore firm size distribution empirically. The BDS is public database of anonymized and aggregated data from the Longitudinal Business Database (LBD), a research database developed by the Center for Economic Studies, which contains data from 1975 to present.
The LBD contains information on all U.S. business establishments that have paid employees and who are listed in the Census Bureaus business register. Data for the LBD is collected through the Standard Statistical Establishment List (SSEL) and is completed on a voluntary basis by firms. The SSEL collects information such as establishment size, payroll, age, industry, location, ownership, and legal form of organization as well as characteristics of the firms they belong to including firm age and firm size.
Despite numerous shortcomings and challenges arising from its aggregated nature, the BDS database is the most comprehensive and complete longitudinal picture of US firm dynamics publicly available.
This model uses BDS firm size data from the bds_f_szsic_release.csv dataset available at https://www.census.govcesdataproductsbdsdata_firm.html. Firm sizes are organized into 12 categories based on numbers of employees: 1 to 4, 5 to 9, 10 to 19, 20 to 49, 50 to 99, 100 to 249, 250 to 499, 500 to 999, 1000 to 2499, 2500 to 4999, 5000 to 9999 and 10000+. Firm size distributions described by this dataset are shown for all industries in Fig. 12 and for representative years in Fig. 13.
Appendix B:: Model parameterization
1.1 B.1 Parameterization of mortality
The parameterization of mortality was obtained by fitting a straight line with slope a and intercept b to the logarithmic plot for average exit rates per year for each firm size over industries and years from the BDS data, shown in the left hand plot in Fig. 14. The right hand plot uses the same a and b parameters to predict the fit of the actual BDS exit data values with xaeb.
1.2 B.2 Parameterization of ν
Investment is modeling as a logistic curve with maximum investment K, inflection point p and steepness q. The model results are based on the three investment curves shown in Fig. 15.
Investment Curves Used in the Model. The plot on the left shows ν values with p = 2, q = .1 and K = 2.5, and is intended to mimic current investment behavior. The figure in the middle modifies this behavior by changing the inflection point parameter p = 4, thus extending the length of an investment. The right hand plot is a smoothed version of the middle plot, with p = 4 and q = .5
1.3 B.3 Parameterization of γ
We assume a constant relationship p between marketshare si and a single employee such that s1p ∝ x1 and s2p ∝ x2. We then need to find γ such that x1 = γx2 and less than 1 in order for marketspace to shrink as it moves to larger firms. Substituting for x1 and x2 we have
Since the ratios of consecutive sizes are constant, we infer \(s_{n} = A{a_{N}^{n}}\) where aN is a function of N and
The exponent needs to be normalized for any value of N so that the model will behave as intended for any number of size divisions. Therefore
and
Figure 16 shows a plot of the integer size categories against the geometric mean of each size category, and the fit of \(s_{n} = A{a_{N}^{n}}\) where aN ≈ 2 therefore g ≈ 4096 and γ ≈ .5. The largest size category was omitted since the geometric mean of the size category 10,000+ is unknown.
1.4 B.4 Response surface analysis
To gain a better understanding of the model behavior, we conducted a response surface analysis using the distribution entropy as the response variable, which we have chosen to maximize. A single, sharp peak will produce a low entropy value while a distribution with equal populations in each size category will produce the maximum entropy value of \(\ln (12) \approx 2.5\). This analysis gives us some indication of how the distribution shape responds to the model parameters K,σ,p,q and a. Since simulation experiments in this case were inexpensive, we ran a 35 full factorial design experiment and then explored different linear regression fits. The best fit is described in Table 5, with only the significant terms retained. We note that with respect to predicting the evenness of the distribution, only the investment parameters, K, σ and p, along with their interactions and a quadratic term in p, have significance. The predicted stationary point indicating the highest value of entropy (see Table 6), or the flattest distribution, is out of bounds of the model with a negative σ, which would mean negative market space is occupied by startups. Regardless, we can still see that the most even predicted distribution occurs with high investment running through the fifth size category, low mortality for large firms and no startups. As the eigenvalues are of mixed sign, this stationary point is not a strict maximum, but a saddle point.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Applegate, J.M., Lampert, A. Firm size populations modeled through competition-colonization dynamics. J Evol Econ 31, 91–116 (2021). https://doi.org/10.1007/s00191-020-00703-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00191-020-00703-6