Labor market intermediaries make the world smaller

Abstract

This paper uses network analysis to study how employment intermediaries have influenced inter-firm worker mobility in a region of Italy, in response to a 1997 reform that introduced temporary employment agencies. Worker reallocations from a matched employer-employee dataset are mapped onto a directed graph where the vertices are firms and the links denote transfers of workers between firms. Temporary employment agencies significantly improve network integration and practicability, while rapidly increasing the control over mobility channels. The trade off inherent in intermediation activity is captured and discussed. The potential of network analysis as a tool for monitoring regional labor markets is highlighted.

Introduction

This paper provides an empirical contribution on how to capture the effects of employment intermediation by exploiting complex network analysis applied to worker mobility data. Network models are operationalized in the attempt to provide a novel understanding of two central issues of labor intermediation: (1) how and to what extent the arrival of labor intermediaries following enactment of a reform affects market integration and accessibility of different employers by people who reallocate within the market, and (2) whether and how the power of intermediaries in controlling and directing worker flows grows over time, and the fundamental dynamics of this process.

These questions are derived directly from the fundamental trade-off characterizing brokerage activity, according to which, on the one side, intermediation increases matching opportunities by reducing both parties’ information costs, and on the other side, it produces monopolistic rents for the intermediary, due to the information asymmetries inherent in information brokerage which also favor concentration of the market in the hands of a few intermediaries.

To explore these issues, we apply for the first time a complex network approach to employer-employee matched data covering the universe of private employment in Veneto, a highly industrialized region in the North–East of Italy. A network representation is used to organize individual mobility events over a ten-year period, and network models are used to capture the effects of labor intermediaries on the structure of inter-firm reallocations.

We focus on a special category of intermediaries, temporary employment agencies (TEAs), that was introduced in Italy by the 1997 “Treu” reform of the labor market as a response to the persistently high level of unemployment especially in the southern regions of the country and among young people. Prior to the Treu reform, employment services were a public monopoly operated through a network of provincial agencies, which generally were inefficient and of little help to unemployed people (Barbieri et al. 2001). TEAs are, thus, the very first example of a private employment intermediary in contemporary Italy (detailed information about the novelties introduced by the Treu reform are provided in Appendix I).

The main object of the analysis is a directed graph where the vertices indicate employers, private firms or TEAs, and the links denote transfers of workers between employers. The data track all worker reallocations involving TEAs as either origin or destination, which captures all labor mobility involving intermediaries.

The first analytical focus is on the degree to which the network of labor mobility works as an integrated and easily practicable system for workers reallocating from one job to another, measured by the small-world characteristics of the network. The impact of TEAs on the network architecture is assessed by interpreting the tendency of the “world” of worker mobility to become smaller as a sign that the labor market is more accessible and more pervious to reallocation flows, and vice versa.

The second main focus is on the position of TEAs in the reallocation market or, more specifically, on their power in controlling hiring channels, as revealed by the number of incoming links pointing to intermediaries in the labor mobility network. To this purpose, the evolution of the statistical distribution of connections over vertices is tracked, highlighting the way in which global labor flows adjust to the presence of labor market intermediaries (LMIs). This is followed by a discussion of the predictions of several models of network formation describing evolution of the link distribution in the presence of information costs.

Exploratory in its nature, the approach developed in this work allows for quantitative analysis of the effects of employment intermediation on the labor market system as a whole, while also identifying the possible mechanisms governing the evolution of intermediaries’ market power. Ultimately, the paper provides a novel set of tools for monitoring labor market functioning and supporting policy actions aimed, for instance, at improving the efficiency of job matching through intermediation or formulating better regulations for intermediated markets.

The paper is organized as follows. Section 2 discusses the theoretical foundations of economic intermediation, with a special focus on the labor market; Section 3 introduces the network framework and the empirical strategy; Section 4 describes the data. Sections 5 and 6 present the results; Section 7 discusses the empirical evidence on the evolution of TEAs market power in the light of network formation models; Section 8 concludes.

Theoretical background

The conceptual foundations of labor intermediation are rooted in the existence of market imperfections that hamper an efficient matching of demand and supply. A major feature of real, imperfect labor markets is the difficulty encountered by both individuals and firms to locate matches/partners and/or to negotiate successfully the terms of matching agreements. Third parties –intermediaries – may exploit these circumstances and attempt to realize profits by selling information or ad hoc matching services to workers and firms.

The economic literature has long recognized that information in real markets is costly and asymmetrically distributed between prospective parties in a transaction. It has been demonstrated that the existence of private information can have substantial implications in terms of market functioning and deviation from perfect competition benchmark.

Akerlof (1970) highlighted in a seminal paper the potential magnitude of market failure under asymmetric information. When the quality of a good is uncertain or difficult to determine for prospective buyers, there is an incentive for sellers to offer goods of poor quality. Buyers who are aware of such behavior may refrain from buying, generating a reduction in the size of the market, up to the emergence of no-transaction equilibria, that is, the disappearance of the market while demand and supply remain unsatisfied and resources unemployed. In these cases, public or private institutions may come into play to solve information asymmetries to everyone’s advantage and, in the case of private organizations, make a profit out of such activity. Interestingly, Akerlof warned of the possible concentration of power in the hands of intermediary institutions that control information.

Transaction cost economics, rooted in the work of Coase (1937) and Williamson (1975), describe how incomplete and costly information result in transaction costs that are at the foundation of decisions between markets and hierarchies. Spulber (1996) extended the same argument to the organization of market institutions, identifying four main activities of intermediary organizations: setting prices, providing liquidity to markets, coordinating transactions between buyers and sellers, and generating market information about the quality of goods. Dixit (2003) explored a model of private intermediation as a mode of governance that helps enforcing contracts by means of collecting and conveying costly information about individual behaviors. In all these cases, the role of intermediaries is to facilitate transactions, putting their skills at the service of market clearing.

The central problem of information being asymmetrically distributed and costly to obtain has been assumed in macroeconomic models of search and matching in the labor market. Decentralized search for information has been demonstrated to generate non-market-clearing equilibria characterized by frictional unemployment. This is because jobs and workers are heterogeneous and thus a degree of mismatch is possible between the parties on different sides of the market. While people may be willing to accept some of the risk associated with imperfect matching, they can reduce the risk by engaging in costly search for potential matching opportunities. The important element here is the trade off individuals face between the option value of keeping on searching and the increasing cost of delaying matching. In equilibrium, frictional unemployment would be a direct consequence of search activity and represent a departure from the market-clearing hypothesis.

Search and matching theory integrates these elements in a consistent framework that describes the formation of new relationships between parties as a function of workers’ search decisions and firms’ decisions about disclosures of job vacancies. Mortensen and Pissarides (1994) provided a comprehensive formalization of search and matching in the labor market, building on previous individual work. Diamond (1982) probably presented the first model of a search economy where traders’ expectations about the level of aggregate activity determine the actual level of activity, resulting in multiple, non-market-clearing equilibria. Again, this framework opens up the potential for intermediaries to come into play offering market-clearing support services.

One of the most harmful consequences of asymmetric information prior to a contractual agreement is adverse selection of prospective matching counterparts. To mitigate the effects of adverse selection in the labor market, workers and firms can typically engage in screening (Stiglitz 1975) and signalling (Spence 1973) activities. Screening is the activity of collecting and processing information about the qualities or characteristics of individuals, firms and jobs. Signalling is the activity of reporting own characteristics to prospective counterparts in a credible way. Both such activities are costly and require specialized skills, thus offering the possibility for third parties to specialize in these activities and perform them on behalf of clients. This is precisely one of the roles of intermediaries in the labor market, or LMIs.

Workers bear the direct costs of exploring the employers’ side of the market, applying for jobs and attending interviews, as well as the indirect costs of lost working or leisure time. Employers bear the direct costs of advertising vacancies and screening applicants, and the indirect costs of reduced output until a vacancy is filled. LMIs reduce search costs for both parties by collecting information on players on one side of the market and then selling it to the players on the other side, at a price that is lower than the cost to the buyers of searching on their own.

Workers may hide or distort some of the information provided in their CVs or credentials, in order to make them more attractive to potential employers. Similarly, firms might exploit asymmetric information to the detriment of workers, for instance, by under-promoting deserving workers in order to save on wages (Garcia-Pérez and Muñoz-Bullón 2005), or by misrepresenting job conditions in order to attract workers (Lee 2009). LMIs can mitigate the problem of adverse selection due to asymmetric information by performing accurate screening of both job seekers and employers, and assuming direct responsibility for selection through special contractual provisions.

The literature highlights an additional aspect of information asymmetry that is specific to intermediation activity, namely, the asymmetry between the LMI and its clients. LMIs, which are in the business of selling information, are inherently better informed about the information they sell than are their customers. The informational advantage of LMIs over participants in a labor market transaction represents a potentially strong incentive for the intermediary to use its information to extract rents from its service. The analyses in Lee (2009) and Kleiner and Todd (2009) provide examples of how intermediaries can use their advantage to the detriment of customers.

The potentially harmful consequences of this sort of informational asymmetry anticipated by Akerlof (1970) highlight the compelling trade off in any information brokerage/concentration process, between the benefits of increased accessibility to information, in our case, represented by the availability of huge chunks of information at low prices, and the costs in the form of the monopolistic and/or monopsonistic position of the mass information provider. In our cases, these costs are translated into the non-competitive mark ups charged by LMIs for their intermediation services, or the promotion of high mark-up matches, rather than matches that would be optimal for the parties.

In markets with imperfect information, the amount of information available to the parties through a broker depends positively on the broker’s access to information through its clientele, hence on its actual market share. A self-reinforcing incentive mechanism is therefore at play, according to which the bigger the broker the larger the number of people who will be tempted to use its services, which further increases the broker’s influence in the market. The informational advantage of the intermediary over its clients and the resulting monopolistic/monopsonistic behavior also increase with market share, up to the point where they may neutralize the benefits of information brokerage and produce net damages and the market reaches a level of major concentration.

According to standard arguments related to the effects of competition, rivalry between private LMIs, and/or between private LMIs and public employment agencies, can favor workers and firms by keeping the price of intermediation services low (competitive) and preventing the emergence of dominant positions, while guaranteeing quality matching. In this respect, the role of policy makers in market design and regulation is of fundamental importance in order to have intermediated labor markets that encourage innovation and performance through mechanisms of labor reallocation (Kılıçaslan and Taymaz 2008); in turn, economic research should feed policy decisions with new evidence and thorough explanation of the evolutionary dynamics of labor markets.

The present paper focuses on a particular category of LMIs, namely temporary employment agencies. People apply to TEAs to access short-term employment opportunities through negligible investment in job search, and as an entry stage to more long-term positions (Autor 2001; Autor and Houseman 2002). Firms rely on TEAs in order to reduce the fixed costs of searching for temporary workers, and they also often outsource to TEAs the recruitment of critical worker categories or even whole workforces. In the latter case, workers seeking employment in these firms are forced to work through TEAs (Houseman 2001; Ichino et al. 2005).

Garcia-Perez and Muñoz-Bullón (2005: 1) advance a strong argument that TEAs ‘in fact offer a unique screening device that matches the individual with the most appropriate skill-level to the job in question’. Using TEAs in order to screen their workers and offering permanent positions to the most suitable ones is becoming a common strategy for firms. Autor (2001) shows that, in several sectors of the US economy, TEA services represent the most important channel for recruiting permanent workers.

In Italy, in the period analyzed in this study, TEAs were the only intermediaries in the market; therefore, using TEAs is a unique means available to firms and workers to access search and screening services. This context extends the scope of TEAs to the whole range of typical LMI functions and provides an ideal setting within which to appreciate the effect of intermediaries on labor market flows.

Network setup and empirical strategy

Analysis of labor mobility at the individual level using network concepts dates back to the seminal work of Granovetter (1973), which illustrates the importance of different types of social connections for successful job search. Since then, joint research on labor mobility and network analysis has attracted attention from scholars in economics and economic geography on aspects related to innovation mechanisms, knowledge spillovers and the spatial diffusion of economic activities.¹

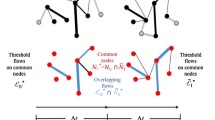
The properties and structure of the global architecture of firm to firm labor flows, their evolution and determinants remain today largely unexplored and unknown.² At the firm level, worker reallocation appears to be a gradual process that can be likened to percolation through a porous material, the microscopic architecture of which ultimately determines the direction and timing of flows usually observed at some higher level of aggregation. This study assumes a network representation of inter-firm worker mobility – where the vertices are firms and the links are worker flows occurring in the space of one year – which is used to support an original investigation of the role of labor intermediaries in shaping the web of inter-firm worker flows. The precise graph-theoretic definitions used in the paper are provided in Appendix II.

The extent to which one type of vertex with the function of intermediary (TEA) affects the degree of integration and practicability of the web of inter-firm flows is the first focus. The goal is to see whether and how TEAs contribute to linking different parts of the labor market in a robust and reliable way, while shortening the network distance between firms and making the reallocation market potentially more accessible for mobile workers.

Network theory relates the notion of integration and practicability directly to a specific network model known as the “small world” (Watts and Strogatz 1998; Newman 2000; Goyal et al. 2006), the functional significance of which is precisely that vertices are easily reachable from one to another via a minimum assembly of links. The small-world model has been shown to be highly efficient for enabling reliable communication and flows between vertices (Latora and Marchiori 2001).

We use measurable small-world properties of the inter-firm network as indicators of the effects of TEA on labor market integration and permeability to reallocation flows: the closer the network to a small world model, the more integrated and permeable the system will be to reallocation flows.

A network is said to be a small world if the following four conditions simultaneously apply:

• (i) A large number of vertices are reachable from/can reach many other vertices in the network, that is, there are uninterrupted sequences of links connecting a relevant fraction of possible pairs of vertices.

• (i) Vertices are reachable with little effort, that is, interconnected vertices on average are just a few steps/links apart (going along a link is assumed to be costly).

• (iii) The system is parsimonious overall, that is, the actual number of links is much smaller than the maximum possible if there is a link between every possible pair of vertices (and providing additional links is assumed to be costly).

• (iv) Vertices form cohesive groups, that is, vertex neighbors or vertices directly connected to the given one tend also to be interconnected with each other, resulting in alternative ways of reaching a former neighbor vertex should the direct connection be lost.

Reframing these conditions in economic terms, we can consider a network to be a small world when, whichever vertex is considered, the number of vertices potentially reachable is high (condition 1), the cost of actually reaching these vertices, on average, is low (conditions 2 and 3), and the system is robust to local disconnections (condition 4). In real world situations, there is often a positive relationship between the actual number and variety of alternatives for moves or choices, and the average cost of exploiting these opportunities for achieving targets. The small world has been shown to be an extremely effective configuration in the context of problematic relationships of this kind because it guarantees maximum reachability while minimizing the costs to both the system designer (i.e. the cost of providing links) and the system user (i.e. the cost of moving through sequences of links in order to reach a given target).³

For workers reallocating between firms, the cost of linking is given by several components, for instance, the cost of performing direct job search or the price paid to an intermediary in order to screen the market and identify suitable vacancies, the loss of salary during possible periods of inactivity between subsequent job spells, the cost of adapting to a new job environment or the effort of learning new tasks and procedures, or the short-term cost of lower wages in the new job, because information about the real value of the match, and hence of the worker, is not completely disclosed to the employer at the very beginning of the employment relationship.

The costly move of a worker from one firm to another is not neutral with respect to other workers employed in the origin or destination firms. The reallocation of an individual from firm A to firm B links the social network of employees of company A to the social network of employees of company B. As demonstrated in Granovetter (1974) and more recently in Cingano and Rosolia (2012), this is likely to produce positive externalities for other employees in A, because personal relationships act as preferential channels for transmitting information about employment opportunities in B and mitigate the asymmetric information problem associated with job changes, possibly leading to other employees from firm A to later follow the same reallocation path, should firm B be recognized as a good employer. A small-world network is therefore parsimonious with respect to reallocation costs, for so long as workers move along established paths they bear lower costs.

A small-world network appears to be an integrated system dominated by local clustering, with a relatively small number of long-range links acting as shortcuts between different clusters of vertices that otherwise would be much farther from one another. A giant strongly connected component guarantees the existence of connecting paths between all possible vertices within its boundaries, while short distance indicates that vertices can be reached with little effort. Clustering or redundancy of local level links promotes robustness to disconnection and reliable connectivity based on multiple independent pathways (White and Houseman 2002).

The four defining properties of the small-world model can be formulated, for a directed network, in exact graph-theoretical terms, to obtain the four propositions presented in Table 1, column 2; the evaluation rules in Table 1, column 3, identify a range of network parameter values within which a network exhibits small-world characteristics (Watts 1999; Newman 2003). Based on these rules, Section 5 describes how far the empirical labor mobility network resembles a small world, and how TEAs push the network architecture farther from or closer to a small world.

Table 1 The four defining properties of a small-world network

The second research question is how TEAs affect the distribution of labor flows, namely, whether and how reallocation flows crowd into TEAs resulting in appreciable concentration of the market in the hands of intermediaries. In the labor mobility network, this can be addressed by considering the degree centrality, i.e. the number of incident links, of TEA vertices and comparing this indicator across firms and time.

In networked systems, the presence of pivotal actors with high degree centrality, called hubs, is signalled by a right-skewed degree distribution, with a long or fat tail that contains vertices with many more connections than average and which appear more frequently than in a standard Gaussian distribution. The literature on complex networks shows that the tail of the degree distribution of a network with hubs can often be approximated by a Pareto distribution or a negative power law (Barabási and Albert 1999; Albert and Barabási 2002; Newman 2003).

Building on this ground, in the present study we verify whether TEAs form a hub tail, searching for Paretian behaviors in the in-degree distribution of labor flows and using the power law as a benchmark for evaluation. This is accomplished in two steps. First, we calculate the total-degree distribution of the network, i.e. the distribution of both incoming and outgoing links, and we determine the TEAs ranking within the distribution. Second, we focus on hiring channels, as given by the in-degree of the network vertices, or the number of incoming labor flows, representing the capacity of firms to attract applicant workers from other source firms in the network. The in-degree provides a measure of firm shares of new hires, and therefore the evolution of TEAs market power can be appreciated by determining the TEAs position within the in-degree distribution while assessing how the distribution overall evolves over time before and after TEAs arrival.

Data

The empirical investigation is based upon the Veneto Worker History panel (VWH), a matched employer-employee dataset derived from the Italian Social Security Institute (Inps) administrative records and covering the entire population of workers and employers in Veneto in the period 1991–2001.⁴

Veneto is a dynamic regional economy centered on manufacturing. The industrial system is represented by a large population of small and medium sized firms, often organized in industrial districts, the specializations of which are garment manufacture, textiles, leather and shoes, goldsmithing, mechanical products, furniture, and plastics. The average firm size in 2001 was three employees for the whole economy and nine for manufacturing, according to census data from Istat.

In the late 1980s and the second half of the 1990s, the Veneto labor market was characterized by a positive rate of job creation in almost every economic sector and decreasing unemployment to almost frictional levels.⁵ The employment stock in the private sector was 968,149 in 1991 and 1,120,278 in 2001, according to census data. The manufacturing sector represented 55.7 % and 50.7 % of total private sector employment in 1991 and 2001, respectively.

The VWH data cover all individual workers employed in the private sector, and every establishment with at least one employee. The available information allows to build a monthly history of the working lives of all employees hired for at least one day during the period of observation by firms based in Veneto, including TEAs. VWH covers only employment spells, while no direct observations are available for transitions to/from unemployment status. Individual inactivity between job spells cannot be distinguished between unemployment and exit from the labor force on the basis of the registered information.

The labor mobility network is obtained by counting the individual hires occurring within a 12-month window that give rise to reallocations, where a reallocation is defined as a pair of events constituted by a separation (i.e. conclusion of a job relationship with a given employer) and a subsequent engagement of the same individual in a job relationship with another employer. Reallocations are mapped onto a binary directed graph the vertices of which are firms and TEAs, and the links between them the flows of workers between firms or between TEAs and firms.

The structure of provisional contracts is triangular; TEAs are formal employers of temporary workers. We do not know which client firms the temporary employees work for when contracted through a TEA, but we can track all reallocations the origins or destinations of which are a TEA. Most important, it is possible to track the network of mobility episodes related to people – especially young people – who enter the labor market via a TEA, and subsequently become direct employees of a private firm.

Eleven networks are constructed for the period 1991–2001; the analytical focus is restricted to reallocations of workers, of either sex, aged between 15 and 65 years, whose engagement occurred between 1st January and 31st December each year, and where the time between the separation and subsequent engagement did not exceed six months.⁶ Reallocations are tracked cutting across the administrative boundaries of Veneto, meaning that firms located outside the region can enter the network sample if they transfer/receive workers to/from firms located in Veneto. No restrictions are made for job spell duration or type of occupation; reallocations to the same firm are excluded.

Table 2 reports the total number of individual reallocations occurred in the period 1997–2001 originating from TEA and non-TEA firms, by worker and firm characteristics. In the five-years period, an average of 171,000 individual reallocations per year are reported. TEAs constitute the destination of 34,215 reallocations and the origin of 40,088 reallocations; 7.1 % of total reallocations registered in the Veneto labor market in the 1997–2001 period has TEAs either as origin or destination, increasing from just 1 % in 1998 to more than 14 % in 2001.

Table 2 Reallocations originating from TEA and non-TEA firms, by worker and firm characteristics

TEA and non-TEA flows are substantially aligned in terms of gender composition, with only a slightly higher percentage of men in TEAs. Intermediated employment flows are on average younger than non-TEA ones, with the age group 25–34 overrepresented by 6.5 percentage points, and the age group 35–49 underrepresented by 4.3 points. TEA reallocations are directed towards larger firms, especially those sized 50 and above that represent one of the more dynamic components of the Italian manufacturing system (Caprio 2002). Finally, TEA flows target manufacturing and professional services comparatively more than non-TEA flows, and less than the construction and hotel trades.

Results I: Network integration and practicability

For each year network, the following indicators are calculated: number of vertices and links, density, size of the WCC and SCC, APL, and ACC. The structural properties of the actual networks for the 1997–2001 period are compared to the corresponding properties of two series of randomized networks taken as null models:

• Null model (1): all TEA vertices and incident links are removed from the actual network to obtain a new network with the same architecture, but no TEA vertices and no reallocation flows involving TEAs.

• Null model (2): for each TEA vertex j in the actual network, the non-TEA vertex i is removed which satisfies k _i =min(k) subject to the condition k≥k _j , where k is the total-degree; in this way a network is obtained that excludes the non-TEA firms most equivalent to TEAs in terms of number of connections.

The difference between the actual networks and null model (1) provides an estimate of the impact of the TEAs conditional on TEA mobility (i.e. labor mobility involving TEAs as the origin or destination) having no substitute in the labor market; this yields an upper bound to the real TEA effect. The difference between the actual network and null model (2) provides an estimate of the mobility effect of those firms that are most similar to TEAs in terms of the number of labor flows involved. On the assumption that this effect can proxy for the substitution of TEA mobility by other non-TEA firms, the difference between null model (1) and null model (2) provides a more reliable approximation of the TEA effect. In practice, if TEAs play a substantial role in shaping the network architecture, null model (1) will exhibit different structural properties from the actual network, and null model (2) will be more similar to the actual network.

Figure 1 depicts the evolution of network size. The system exhibits a minimum extension in 1993, with 67,578 vertices and 86,602 links, and a maximum extension in 2001, with 104,439 vertices and 207,504 links. Link density is always very low at around 2.0e-05, with a minimum of 1.84e-05 in 1992, and a maximum of 2.23e-05 in 1995. Over the whole period considered, the network is extremely sparse, which complies with the small-world model.

Fig. 1

Vertices and links

Time series of labor mobility networks of the type considered in the present analyses are affected by the business cycle, since worker turnover tends to be markedly pro-cyclical, and job-to-job mobility constitutes the most dynamic component of this trend.⁷ The business cycle thus affects the size and the density of the reallocation network; when the level of economic activity is low – as was the case in Italy during the 1992-93 recession – the network appears comparatively much sparser and less interconnected than in high performing business cycle periods (as occurred in 1994-95 in Veneto).

In Fig. 1, the number of links exhibit a clear pro-cyclical pattern during the period 1991-1997. There is a pronounced downward spike corresponding to the 1992-93 recession (−25 % links), followed by rapid growth in 1994-95 (+ 47 % links), as the economy recovered due to a Lira devaluation that boosted export competitiveness which, in turn, especially favored the largely export-oriented economy of Veneto. After 1997, the impact of the business cycle is less clear: across the whole period 1997-2001, in the presence of moderate economic growth, the network exhibits an intense, sustained increase in the number of vertices and links (respectively + 29 % and + 49 %), with a slight slowdown in 2001 corresponding to the downturn induced by the burst of the new-economy bubble and increasing uncertainty about the international geopolitical scenario.

Comparing the actual trend with null model (1), it can be seen that TEA links contribute significantly to explaining the observed growth in connections, increasing the null model base by 1 % in 1998, 5 % in 1999, 10 % in 2000, and 14 % in 2001. Notably, null model (1) exhibits a reduction in the number of links in 2001 compared to 2000 so that, in the last year of observation, the activity of labor market intermediaries appears to be the sole driver of the increase in the actual number of reallocation channels between firms. Null model (2) has 8 % more links in 2001 than null model (1); this figure represents our prudent estimate of the impact of TEA at the end of the period of observation, which reveals that the 1997 reform, through the establishment of private intermediaries, was able effectively to unlock new mobility opportunities.

Figure 2 shows the extent of the largest strongly/weakly connected components in terms of the percentage of vertices covered, allowing a first inspection of network interconnection or integration. A pro-cyclical pattern is clearly identifiable. The SCC shows a minimum in 1993 at 13 % and a maximum in 2000 at 30 %; for the WCC the figures are 77 % and 90 %, respectively. Starting in 1995, the SCC remains above 25 %, and the WCC remains above 85 %; in the same period, the second largest strongly connected component never covers more than six vertices, while the second largest weakly connected component has just 14 vertices. So, from 1995, the system exhibits the inter-connectivity structure distinctive of a small world.

Fig. 2

SCC (left axis) and WCC (right axis), % coverage of the entire network

In 1997, the giant components embark on a steady growth path leading to a cumulative increase of 13 % for the SCC, and 4 % for the WCC for the period 1997–2001. In 2001, the SCC of null model (2) essentially superimposes the actual SCC, and both are 6 % larger than the null model (1) SCC, revealing that mutual connectivity appears to be positively affected by TEAs, but insensitive to the exclusion of non-TEA firms. TEAs seem to favor integration of the system.

Figure 3 shows the APL and ACC; the first (left axis) is expressed by the number of links between vertices, the second (right axis) is an index number that varies between 0 (no clustering) and 1 (complete clustering). Across the whole period, the ACC of the actual network is at least one order of magnitude higher than the ACC of a comparable network with the same joint distribution of in-degree and out-degree, but with links positioned randomly. This clustering pattern is typical of a small world network. Up to 1998, the ACC fluctuates between 0.007 and 0.010, with a very slight tendency to increase over time; from 1999 to 2001, it shows a phase of intense growth to reach 0.015 by the end of the period, 57 % higher than the 1997 level.

Fig. 3

APL and ACC

The ACC of null model (1) remains substantially flat, at the pre-reform level; the ACC of null model (2) closely follows the actual path. In 2001, the actual ACC is 63 % higher than the null model (1) ACC, while the ACC of null model (2) is 46 % above null model (1), pointing to a strong, positive effect of TEAs on clustering.

The APL reaches a maximum in 1993 of 8.5, and a minimum in 2001 of 5, and across the whole period it is strictly lower than the APL of a random network of equivalent size, which fits the requirements for a small world network. After the 1997 reform, mutually interconnected vertices are much closer to each other: between 1997 and 2001, the average distance reduces by 24 %.

The APL of null model (1) exhibits an almost flat behavior, while the APL of null model (2) is just one percentage point above the actual APL. In 2001, the actual APL is 20 % less than the null model (1) APL which indicates that TEAs provide effective shortcuts within the network by substantially reducing the distances between firms.

Comparing the null model (1) in Figs. 1 and 3, it can be seen that the number of links increases over time, but this expansion is not accompanied by an appreciable change in the link arrangement, as revealed by the ACC and the APL. On the contrary, the increase in network size due to labor intermediation modifies the network structure in the direction of higher cohesion and lower distances.

The results of the analysis suggest that TEAs act to make the small-world network of labor mobility significantly smaller and, therefore, more integrated and more permeable to reallocation flows, through the establishment of shortcut paths that span the economy, interweaving distant vertices into more cohesive communities, and reducing average distances.

Results II: Distribution of labor flows

The total-degree distributions for each year network are derived and some descriptive statistics are presented in Table 3, including: average degree (k _G), median degree (k ₅₀), degree of the 99 ^th percentile (k ₉₉), and maximum degree (k _max).

Table 3 Total-degree distributions: main descriptive statistics

The total-degree sequences exhibit a broad range of values that tends to increase over time. Despite the relatively high maxima (315 in 1992, increasing to 6,524 in 2001), the average degree is always very low, ranging from 2.6 in 1993 to 4 in 2000 and 2001. This is due to the extreme concentration of the distribution around the minimum degree, revealed by the median values which are 1 up to 1994, and 2 thereafter. Two features are striking: the degree value of the largest fraction of vertices is smaller than the average, with the majority of vertices having just the minimum degree; a small fraction of vertices has a degree value that is many times larger than the average, e.g. the scores for the 99 ^th percentile are six to nine times larger than average.

Across the whole period, the total-degree distribution exhibits a markedly right-skewed pattern, with a heavy or fat tail. This applies also if we consider in-degree and out-degree distributions separately. Therefore, network architecture of labor mobility appears to be dominated by a few vertices, referred to as hubs, which have many more connections than average. Moreover, the maximum degrees increase steeply just after 1997, with average annual growth of around 100 %, suggesting that the 1997 reform favored the formation of large hubs.

Table 4 reports the overall ranking based on total degree, of the ten biggest TEAs, labelled a to k. In 1997, only two TEAs were operating with very limited activity, as revealed by their low ranking. By 1998, one TEA was at the extreme tail of the connectivity distribution, and ranked 4 ^th overall; four TEAs were positioned within the first hundred positions, and all the first ten ranked TEAs were within the 99 ^th percentile of the distribution. In 1999, TEAs dominated the degree distribution, with four intermediaries in the first four positions. Soon after their appearance in the system, TEAs showed high levels of attractiveness and a strong capacity to redirect labor flows, and quickly became the most important hubs in the mobility network.

Table 4 Ranking of the ten biggest TEA according to total-degree

Following the 1997 labor market reform, the system became progressively more dependent on TEAs, and on a few in particular. This situation is critical because collapse or malfunction of even a small number of TEA hubs could compromise connectivity (Albert et al. 2000); policy makers might be concerned about growing monopolistic/monopsonistic power of a few TEAs in the labor reallocation market.

The distribution of hiring channels, the in-degree distribution, is of particular relevance for capturing the evolution of TEA market power. Figure 4 shows the complementary cumulative in-degree distributions (CCDD), plotted on a double logarithmic scale, together with the corresponding power-law fits. Power law-like degree distributions have been extensively investigated in network analysis and are widely acknowledged to represent a benchmark model for many real-world phenomena (Barabási and Albert 1999; Newman 2005). Most relevant for the present study, power-law models support the existence of hubs.

Fig. 4

In-degree distributions and power-law fits

Each year plot in Fig. 4 follows a negative and almost linear trend; at the extreme tail of the distribution, a downward departure from the power-law fit is evident for the years 1991, 1992, 1995, 1996, 1997, and 1998, but is less pronounced for 1993 and 1994. In 1999, the empirical data almost exactly overlap the power-law fit, while in 2000 and 2001, the distribution tail drifts progressively upwards, concentrating greater weight than predicted by a pure power law.

Visual inspection of the plots suggests several things. First, a necessary condition for data to be power-law distributed is that they align along a straight line, on a double logarithmic plot; the empirical distributions would seem to match this condition. Second, the rapid decay of the tail or the truncation observed up to the year 1998 means that extreme, massive events are less likely in reality than predicted by pure power law. Third, after 1998 and coincident with the materialization of TEA effects on the connectivity structure, the in-degree distribution shows a transition from an upper truncated to a much more unequal pattern with a much heavier tail.

In 1999, 2000, and 2001 the four biggest hubs are TEAs, and several other TEAs occupy the extreme percentiles of the degree distribution, concentrating shares of hiring channels which increase constantly over time, and being ultimately responsible for the transitions observed in the distribution tail. Intermediaries produce a sharp polarization of the degree distribution which consistently deviates from both a pure and a truncated power law distribution.

This evidence is explored more deeply by statistically comparing the empirical distributions with pure power-law models, and with power law with exponential cut off that allows for tail decay. The general form of a power-law distribution for the quantity k is p(k)=c k ^−α for k>k _min, c being a constant of proportionality; the general form of a power-law distribution with exponential cut off is p(k)=c k ^−α e ^βk. Following the procedure developed in Clauset et al. (2009):

• We fit the complementary cumulative in-degree distribution using maximum likelihood, simultaneously estimating the scaling parameter, α, and the minimum threshold above which power law behavior holds, k _min.

• We evaluate the goodness of the power-law fit by calculating an appropriate p-value.

• We conduct a likelihood-ratio test to contrast the pure power law with a power law with exponential cut off.⁸

Table 5 presents the key parameters of the fitted power laws and the p-values of the related goodness-of-fit tests; the likelihood-ratio tests comparing the pure power law and a power law with exponential cut off, and the related p-values, are reported in the last two columns.⁹ With the exception of 1992 and 1995, in all years the power-law model provides good fits, with excellent performance in 1991, 1994, and in the period 1998-2001; in 1993, 1996 and 1997 there is only moderate evidence in support of the model, but, overall, the power law performs quite well, which means it is a reasonable theoretical benchmark for the data.

Table 5 Distribution fit

For 1991, 1996, 1997 and 1998 the power law with exponential cut off is strictly preferred to a pure power law, but for 1999, 2000, and especially 2001, the models are not statistically different based on the likelihood-ratio test. However, the plots in Fig. 4 show that, in the last three years of observation, the pure power law is unquestionably favored over the cut-off version.

Overall, the analyses reveal the following: up to 1998, the data are well fitted to a power law with upper truncation; in 1999, as TEAs reach the tail of the distribution, pure power-law sets in; in 2000–2001 the tail of the distribution, led by the biggest TEAs, drifts upward away from power law prediction and pushes the system towards an increasingly polarized configuration in which a few of the biggest TEA hubs control major hiring channel shares.

Discussion on the evolution of TEA market power

Consideration of the functional shape of the degree distribution, rather than just the number of links incident to the TEAs, helps us to understand how the system adjusts to the presence of TEAs and allows us to relate observed behaviors to the vast literature on models of network formation, which should increase understanding of the dynamics of intermediation activity.

Several network formation models have been proposed, which can produce degree distributions with similar functional forms to those observed in the labor mobility network, and account for transition paths comparable to the one triggered by the arrival of intermediaries. There are two classes of models that build on an information cost argument and provide insights for understanding the possible dynamics of intermediation in the labor reallocation market.

In the literature on complex networks, right-skewed degree distributions with heavy tails are usually associated with link formation mechanisms based on preferential attachment rules, where the probability that one vertex connects to another is assumed proportional to the degree of the recipient vertex (Barabási and Albert 1999). Based on this simple framework, scholars have built models that account for upper truncation to power-law behavior, by introducing constraints on the attachment mechanism that limit the addition of new vertex links. Varying the intensity or bindingness of constraints provides a range of distributions with more or less pronounced cut offs, where the pure power law is a special case, and extremely concentrated distributions are obtained when attachment constraints are sufficiently weak.

In Mossa et al. (2000), the constraint on link formation is modelled explicitly as an information cost. Agents/vertices are assumed to bear some costs for gathering and analyzing information about the other vertices. This assumption is especially realistic if the system is large, because it is unlikely that agents know in advance the state of the entire network. The decision about which vertex to connect to is most likely taken based only on the information about a subset – a fraction or a fixed number – of possible vertices; within such a subset, some form of preferential attachment then comes into play. The link distribution resulting from these rules is a power law with an upper exponential cut off the strength of which depends on the incidence of information costs.

Other studies propose a network formation paradigm in which preferential attachment is not assumed, but arises naturally from the simultaneous optimization of multiple competing objectives. This approach is of particular interest from an economic perspective because it explicitly models the trade off between the typical costs and benefits for agents making decisions in a context of scarce resources, which is characteristic of job search problems.

The fundamentals of this sort of model are described and discussed in Fabrikant et al. (2002) and developed further in D’Souza et al. (2007). Agents/vertices are randomly arranged in a given space; they are assumed to benefit from linking with vertices that are centrally located in the system, that is, high degree vertices, but carry attachment costs that are proportional to the Euclidean distance between the current and target location. Linking decisions will then involve targets that are both close to the actual position in the space and centrally located in the network.

In other words, networking activity tries to optimize on a trade off between the search and attachment costs represented by distance, and the benefits or option values represented by network centrality. As search costs fall relative to centrality benefits, the resulting degree distribution will shift from a power law with cut off to a pure power law and even beyond, ultimately resulting in a winner-take-all distribution, corresponding to a star configuration network in which one vertex receives all incoming connections.

The behavior of these trade-off models can be likened to the introduction of intermediation in a system in which link formation is subject to information costs. Also, the empirical evidence provided in Section 6 would seem to match the theoretical predictions (taking account of the models’ abstractness). In the real world, intermediaries exactly concentrate information and provide low-cost shortcuts to employment opportunities. Their value as gateways to future employment makes them attractive for workers.

In the Veneto mobility network, a few years after their entry, a small group of TEAs overtakes the power law distribution of labor flows, triggering an evident polarization of the system, which likely will deepen over time. This tendency, identified and evidenced through the network approach in this study, is extremely relevant for policy. The theory hints that the polarization process is self sustaining and eventually will produce strong concentration of the market in a few TEAs. The presence of intermediaries will likely increase the systemic risks inherent in the labor reallocation system and result in eventual monopolistic/monopsonistic power.

Conclusions

This paper investigated the role of labor market intermediaries in shaping the inter-firm network of worker mobility in a highly industrialized regional economy. The proposed methodology attempts to assess and quantify in an original way the effects that constitute the major trade-off in intermediation activity. We show that TEAs significantly enhance integration and perviousness of the reallocation market, while leading to a process of market concentration which is identifiable at an early stage and the determinants of which are embedded in the activity of intermediation.

In relation to the dynamics involved, on the one side, TEAs are very effective at fostering labor market inter-connection; on the other side, the largest TEA firms threat to corner the labor market, exacerbating the effects of information asymmetries which have a negative impact on their clients.

In future research, it would be desirable to produce causal evidence of the effects of TEAs on the probability to transit from unemployment to employment. However, to assess how much of the unemployment reduction observed in Veneto in 1997-2001 is due to the introduction of TEAs goes beyond the scope of the present paper. This work is a first and exploratory attempt of showing how network analysis can be used as tool for monitoring intermediated labor markets and the activities of single intermediaries.

An efficient reallocation of labor is essential in order for the economy to be productive, to allocate the available resources effectively, and to absorb local and transitory shocks that affect sectors and industries selectively. An easy and smooth reallocation process is fundamental for guaranteeing more rapid and less costly job market transitions for workers, with immediate and long-lasting benefits for individual incomes. A decrease in the dimensions of the small world of labor mobility favors the good functioning of a reallocation market.

When intermediation is allowed, policy interventions might be needed to ensure that the sector remains competitive. Certain regulatory mechanisms should be devised to prevent the market from becoming concentrated in a few intermediaries.

The trend we observed in the empirical distribution of hiring channels indicate that TEA market shares might increase over time, leaving the market for hiring services controlled by a few large intermediaries. Their dominant positions could be used to exploit their informational advantage, to the detriment of their customers. This would be harmful because of the high rents that the dominant TEAs could extract from their activity, and because of the poor matching services firms and workers would likely receive in a non-competitive intermediation market.

Theoretical insights from network formation provide compelling evidence for the need for well-timed policy interventions. Once self-sustaining linkage mechanisms, for example, preferential attachments, are set in motion, it is more difficult to intervene in order to modify the underlying individual-level incentive structure. It is better to rectify budding adverse market trends rather than to wait until they are fully developed and widespread. Good market monitoring is essential to enable this.

Network-based methodologies for mapping labor markets, of the type we proposed in this paper, could help policy makers in detecting early signs of market concentration, and therefore could provide useful evidence-based input about whether and how to control the activities of intermediaries through appropriate regulatory measures or to foster competition through the setting up of efficient public intermediaries.

As for the Italian case, currently debated, influential proposals of labor market reform suggest a profound revision of employment protection mechanisms that would imply a wider and more critical role for private intermediaries.¹⁰ In this light, policy makers can, and perhaps should, be interested in having a better knowledge of the way in which intermediated labor markets actually work and how to effectively monitor their functioning.

The set of methodologies presented in this paper nonetheless requires further development. In particular, the trade off between the economic efficiency gained from centralized brokerage, and the opportunity for monopolistic behavior of the top TEAs deserves a separate and more sophisticated analysis that yields finer indications about market evolution.

For instance, the time span after TEAs establishment should be expanded and labor network evolution tracked beyond 2001, in order to demonstrate the existence/persistency/evolution of the observed trends. Moreover, complementary information about the quality of matching through TEAs (e.g. duration of the new job, wage progression, changes of occupation between old and new jobs, etc.) and the mark ups charged by labor market intermediaries, in particular the biggest ones, should be collected and analyzed in order to give further evidence of the monopolistic/monopsonistic behavior of intermediaries.

Unfortunately, the VWH dataset alone does not provide the necessary information to carry out such analyses and hence the answer should be based on other sources or on merging several sources into one dataset. The present limitations would be valuable topics for an exciting, future research on possible applications of network methodologies to labor mobility, based on matched employer-employee data.

Appendices

Appendix I - The first phase of TEAs in Italy (1997–2001)

Private TEAs are a relatively new phenomenon in Italy. They were allowed to operate by Legge (Law) no. 196 of 1997, the so called Treu reform of the labor market, and the first TEAs were established between 1997 and 1998.¹¹ The reform signalled the end of the public monopoly on employment services and introduced a new type of employment agreement, the “interinale”, a provisional contract allowing agencies to hire people in order to place them in client firms for a fixed period. Up to 2003, the only type of contract available to Italian intermediaries was the interinale.¹²

The essential articulation of the Treu reform was conceived already in 1995 with the declared aim of providing a solution to the high level of unemployment registered especially in the southern regions of the country and among young people and that had been steadily growing during the early and mid-1990s following the economic downturn of 1992.¹³ The bulk of interventions aimed at facilitating labor market entry through the introduction of a more flexible and less costly fixed-term contract, the interinale, and liberalizing labor intermediation. Before 1997, Italian legislation prohibited the intermediation of subordinate labor, even when the service was freely given, and inflicted heavy penalties for failure to comply with the law.¹⁴

Fixed-term contracts signed by both parties without the intervention of an intermediary were allowed in post-war Italy, and their use massively increased during the 1990s; in Veneto they represented 42 % of total engagements in the private sector in 2001 (the last year relevant for our analysis), corresponding to 6.2 % of employment in terms of days worked (Veneto Lavoro 2008a, b). Nevertheless, in 2001, the share of days worked based on open-ended contracts was 84 %, revealing a labor market still dominated largely by arrangements characterized by high firing costs and tight regulatory restrictions.¹⁵

Provisional contracts became much common immediately after their introduction, generating 58,500 engagements in Veneto in 2001, corresponding to 11 % of total engagements in the private sector, and 0.8 % of employment in terms of days worked. Even in the northern regions of Italy, characterized by much lower unemployment than southern regions, the interinale contract thus emerges as a practice widely used by companies.¹⁶ TEAs operating in Veneto were only two in 1997, rising to 29 in 1998, 36 in 1999, 41 in 2000, and 51 in 2001.

The Italian Department of Labor (Ministero del Lavoro e delle Politiche Sociali 2001) pointed out that the use of provisional contracts in practice responded to a variety of conditions that go far beyond what is needed for temporary working. Italian employers often use provisional agreements to select candidates to fill posts, pending a permanent appointment. In contrast to other forms of fixed-term contracts this allows the firms to access the search and screening services provided by TEAs, in order to identify the professional and individual profiles most appropriate for the vacancies they want to fill.

In the first years of TEA activity, the importance of the screening motivation is well illustrated by the high rate of transformation of provisional into permanent positions. A survey conducted by the Italian Department of Labor shows that in 2000 and 2001 roughly a quarter of provisional contracts developed into permanent appointments (Ministero del Lavoro e delle Politiche Sociali 2001). Based on head counts the percentage is higher, since the same individual might take up several separate temporary positions with the same employer.

The role of TEAs in searching and screening is also revealed by the fact that firms frequently request agencies to provide skilled workers with very specific profiles, as reported by Iacus and Porro (2002). In the years immediately following the Treu reform, only 50 % of provisional jobs in Veneto involved low-skilled workers, and this percentage has decreased over time (Lavoro 2008b). More generally, the literature has acknowledged how Italian TEAs have demonstrated their capacity to supply a variety of worker profiles. They do not specialize solely in contracting the archetypical young, male, low-skilled worker; they have on their books more mature manual workers with particular skills, and young men and women with medium-high educational qualifications, who usually seek employment in the service sector (Porro et al. 2004).

The literature on the effects of the Treu reform has focused almost exclusively on individual labor market outcomes that could be immediately related to the introduction of the interinale contract, and in particular on the stability of job relationships of people who started working with interinale contracts. Conclusions are rather contrasting. While some authors argue that interinale jobs turn out to lead to prolonged instability (Barbieri and Scherer 2009; Sciulli 2006), others claim that these contracts constitutes effective springboards for more fluid careers (Ichino et al. 2005).

From a macroeconomic point of view, the Treu reform of the labor market is descriptively associated with a significant reduction of unemployment rate both at the national and regional level. According to Istat data, in the period 1997–2001 in Veneto, unemployment decreased by one third, from 6.4 % to 4.5 %, to reach the minimum of the decade in 2007 at 3.3 %.

Appendix II - Graph-theoretic definitions

This appendix provides the formal definitions of the graph-theoretic concepts used in this study (Boccaletti et al. 2006). Let V={i:1,2,...,n} be a finite set of firms representing network vertices. For each ordered pair of firms (i,j), with i,j∈V and i≠j, let l _{i j} ∈{0,1} be a link pointing from i to j, with l _{i j} =1 if a flow of workers has passed from firm i to firm j (active link), and l _{i j} = 0 otherwise (inactive link); let then L={l _{i j} } be the collection of such links. The set of firms and the set of links form the binary directed labor mobility network G(V, L). The total number of vertices in a graph is n, the number of active links is $m=\underset {i\in V}{\sum } \underset {j\in V}{\sum }l_{ij}$; the number of active links divided by the maximum possible number of active links gives the network density, denoted by δ(G)=m/n(n−1). In the text, links refers to active links only.

The number of links pointing towards i is defined as the in-degree of vertex i, and is denoted by $k_{i}^{in}$; similarly, the number of links originating from iis defined as the out-degree of vertex i, and it is denoted by $k_{i}^{out}$. The total-degree of vertex i, indicated by $k_{i}^{tot}$, is the sum of in-degree and out-degree. In formal terms,

$$ k_{i}^{in}=\underset{j\in V}{\sum}l_{ji}, $$

(1a)

$$ k_{i}^{out}=\underset{j\in V}{\sum}l_{ij}, $$

(1b)

$$ k_{j}^{tot}=k_{i}^{in}+k_{i}^{out}. $$

(1c)

For the sake of simplicity, in the text degree refers to total-degree. The average degree of a network is equal to the average degree of its vertices, denoted by k(G). The highest degree vertices are referred to as hubs. If we think of the degree of a vertex as the realization of a random variable K, the degree distribution is the probability distribution of K, that is the probability that the degree of a vertex is equal to k, and is indicated by p(k)=Pr(K=k). In directed networks there are three different degree distributions for in-degree, out-degree, and total-degree. The complementary cumulative degree distribution (CCDD) is denoted by P(k), and is defined as P(k)=Pr(K≥k)

A path from vertex i to vertex j is said to exist if l _{i j} =1 or if there is a set of distinct intermediate vertices j ₁,j ₂,...,j _n such that $l_{ij_{1}}=l_{j{1}j_{2}}=\ldots =l_{j_{n}j}=1$. A network component is a set of vertices all of which are either mutually reachable through paths, obtaining a strongly connected component, or one-way reachable only, obtaining a weakly connected component. A network can consist of several components, which can be ordered according to size, that is, the number of their vertices. A network is said to have a giant component if the largest weakly connected component covers at least 50 % of the vertices (n _wcc≥n/2), the largest strongly connected component covers at least 25 % of vertices (n _scc≥n/4), and the other components are small (typically of order ln (n)). Giant weakly/strongly connected components are referred to as WCC and SCC, respectively.

The length of the path from i to j is equal to the number of links between iand j. The shortest path between i and j is the geodesic, and its length is denoted by d _{i j} . The average path length (APL) of a network is defined as the average of the geodesics between all possible pairs of vertices in the SCC, and is denoted by d(G), yielding

$$ d(G)=\frac{\underset{i\in SCC}{\sum} \underset{j\in SCC}{\sum}d_{ij}}{n_{SCC-1}}. $$

(2)

The set of vertices with which vertex i is directly connected, on both entry and exit, is called the (nearest) neighborhood of i, and is defined as N _i ={j∈V:l _{i j} =1∨l _{j i} =1}; the number of neighbor vertices of i is thus η _i =|N _i |. This notion leads to the definition of the metric clustering coefficient. The clustering coefficient of vertex i, denoted by C _i , measures the extent to which the neighbor vertices of i are linked to form a densely connected group. Following Watts and Strogatz (1998), the clustering coefficient of vertex i is defined as the ratio of the actual number of links between the neighbors of i and the maximum possible number of these links. Denoting by u and v two generic neighbors of i, the following expression is obtained

$$ C_{i}\frac{\underset{u\in N_{i}}{\sum}\underset{v\in N_{i}}{\sum}l_{uv}}{\eta_{i}(\eta_{i}-1)}, $$

(3)

which takes values in the interval [0,1]. Vertices with η _i = 1 are assigned C _i = 0. The average clustering coefficient of a network is indicated by C(G), and is referred to with the acronym ACC.