A network theory of inter-firm labor flows

Abstract

Using detailed administrative microdata for two countries, we build a modeling framework that yields new explanations for the origin of firm sizes, the firm contributions to unemployment, and the job-to-job mobility of workers between firms. Firms are organized as nodes in networks where connections represent low mobility barriers for workers. These labor flow networks are determined empirically, and serve as the substrate in which workers transition between jobs. We show that highly skewed firm size distributions are predicted from the connectivity of firms. Further, our model permits the reconceptualization of unemployment as a local network phenomenon related to both a notion of firm-specific unemployment and the network vicinity of each firm. We find that firm-specific unemployment has a highly skewed distribution. In coupling the study of job mobility and firm dynamics the model provides a new analytical tool for industrial organization and makes it possible to synthesize more targeted policies managing job mobility.

1 Introduction

The explanation of macro-phenomena on the basis of microscopic rules is a classic problem in social, economic and natural sciences [1]. Theoretical frameworks such as analytical sociology [2], economic microfoundations [3], and agent-based-modelling [4, 5] have emerged to address the need to connect the known rules of behavior at the individual level, along with interactions between those individuals, and the characteristics of the macro-behavior these rules generate. A distinctive element of micro to macro studies is their ability to address system heterogeneity [6, 7] where agent-based modelling (computational or otherwise) is especially useful due to its flexibility.

In the context of employment, the micro to macro problem is also present. However, its study has mostly been done through fundamentally macro-level approaches [8, 9] at the exclusion of much underlying micro-behavior. These approaches have utilized aggregation as one of their pillars, eliminating the numerous non-trivial and potentially dominant effects played by the ecology of heterogeneous employers, the firms [10, 11]. Most of the approaches that do incorporate some of the heterogeneity in the system [12, 13] do so by sectorizing the economy and coarsening the firm-level view (recent notable exceptions are [14–16] that incorporate firms).

Recently, through the use of microdata, the study of inter-firm networks of job-to-job mobility [14, 17, 18] (the phenomenon of an individual separating from one firm, potentially spending some unemployment time, and eventually reaching another firm) suggests that there is a rich set of phenomena taking place at the micro-level of the system that couples employers (firms) and their workers. Neither work on firm dynamics, nor work on employment had been able to identify or characterize such phenomena. Development of a new disaggregate model of the behavior of the firm-employee joint system, disciplined by microdata, is our main goal here.

Guided by micro-level empirical observations of the behavior of workers (which we also call agents) and the firms in which they work, we develop a model of job-to-job mobility that successfully establishes the micro-to-macro connection, empirically grounded at both levels. Our model is designed to understand the dynamics of agents in the firm landscape of large socioeconomic systems, and accurately predict large scale system behavior. We base our work on high resolution, extensive firm-employee matched records in two separate countries (Finland and Mexico), with data spanning large numbers of workers, firms, and multiple decades. The model we introduce is consistent with known key micro and macro-level regularities of the problem.

One of the main features of our model is that agents move between jobs inside an empirically constructed network of firms [14, 19]. This inter-firm network, acts as the substrate for workforce mobility. With this framework, we achieve some important results. First, we find that firm-size distributions are synthesized in the combination of the connectivity of firms in the firm network and the steady state movements of agents in the network. Furthermore, we propose a new notion of firm-specific unemployment, an intermediate state of agents between employment spells that offers a disaggregate picture of job-to-job mobility at the level of individual firms, and how each firm may contribute to unemployment. The use of a high resolution model to deal with job-to-job mobility is in itself an advance because it moves away from aggregate approaches to deal with the problem; aggregation destroys information about local effects like the specific dynamics of agent movements between close-neighbor firms in the network. Finally, our approach leads to the possibility to connect two areas of study that have traditionally been separate: job-to-job mobility and distribution of firm sizes.

We believe our framework has the great virtue of being applicable to a wide spectrum of situations, from calibrated models of true behavior, to idealized situations of academic or exploratory value. The reason for this flexibility is that the model captures and isolates the main ingredients of movement dynamics of workers and employers. These ingredients are: 1) the firm environment, where individuals travel as they change jobs, and 2) the rules of movement and behavior that individuals and firms satisfy. In this article, we choose those ingredients with enough realism to allow us to show proof of principle, i.e., to reproduce some important known facts about firms and worker dynamics at the best resolutions yet studied. However, the framework can be deployed with different environments and behavior to address many useful scenarios such as the potential consequences of policy interventions or the construction of baseline statistical models, to name a few.

It is important to emphasize that the dynamics that emerge from the coupled firm-employee system are of great practical interest. These dynamics have received attention in labour studies [8, 9], firm dynamics [20–23], and employment mobility [24, 25]. Usually, this research is parcelled into two separate problems: employment [8, 26] and firms [23, 27, 28]. Such division reflects the absence of a theoretical framework capable of coupling them together. This division is mainly rooted on modelling choices. On one hand, employment models are often fully aggregate or very course-grained, eliminating the role of firm heterogeneity and the structure of job-to-job mobility. On the other, models of firm dynamics do not consider the reallocation of workers, discarding employment trajectories (e.g., Gibrat’s law [29–31] focuses on the firm abstracted from its workers). Our model connects the labor mobility and firm dynamics literature, providing an integrated framework. Since our model is disaggregate and constructed to match data, it can serve as the starting point for more detailed work on dynamical aspects of employment and firms. Such work may be particularly useful to inform policy (specific measures with specific targets), provide better analysis of economic scenarios, and develop better forecasting frameworks.

2 Labor flow network

Evidence suggests that a worker’s transition from a firm (i) to another firm (j) increases the probability of observing one or more subsequent worker transitions between the same firms i and j [18]. Such firm-to-firm transitions are the result of a confluence of factors (geography, social ties, skills, industry types, etc.) that affect choices made by individuals when navigating the employment landscape, and of firms when deciding to hire workers. Considerable research has been directed at the social ties factor [32–34] which has shown to be relevant but still constitutes just one out of numerous factors that play a large, if not larger roles.

A more data-driven and simultaneously disaggregate approach has been taken by Guerrero and Axtell [14] who proposed to represent firm-to-firm transitions with the use of a so-called labor flow network (LFN), where firms (nodes) are connected to one another if a job-to-job transition has been observed between them. Using administrative records from Finland and Mexico (see Sect. A.1), the authors constructed empirical networks, studied their structural properties, and found a highly heterogeneous firm environment with interesting regularities in the flow of workers such as virtually balanced flows in and out of individual firms. The advantage of the approach in Ref. [14] is that it takes into account all transitions regardless of their driving mechanism.

Our approach is to directly tackle the problem of modeling job-to-job transitions on the basis of empirically justified mechanisms, using as a starting point the evidence that previous job-to-job transitions may be predictive of new ones in the future, and that this justifies the use of inter-firm networks as part of the modeling framework for this problem. We model an agents-and-firms system by establishing: i) the LFN in which agents move on the basis of data, ii) a set of basic rules of how agents choose to navigate this network, and iii) how firms deal with the inflow and outflow of agents. In this section we focus on i), while ii) and iii) are developed in the next section.

Given available data for firms and agents, one would like to determine those persistent firm-to-firm transitions that, collected together as a set of edges interconnecting firms, constitute the substrate for a considerable fraction of the steady flow of the workforce. Intuitively, there is reason to believe in such a network (e.g., medical professionals move between hospitals, auto-technicians between car repair shops, the unemployed are more likely to search for a job where they live rather than far away, etc.), notions also captured in work such as [13, 35]. Note that persistent transitions justify the use of labor flow networks. If transitions were a consequence of simple random events with no repeated transitions other than by chance, then there would be no need for a network: a transition from one node would simply be a random jump to any other node (this is a view consistently presented in current literature on aggregate studies in labor economics [8]). Transitions for which one cannot build evidence that they will occur again in the future are labelled random.

To understand persistent transitions and their consequences better, we proceed as follows.

2.1 Testing flow persistence between firms

The work by Collet and Hedström [18] focused on virtually comprehensive data for Stockholm found that the probability that two firms i and j experience new worker transitions between them after having had at least one prior transition is approximately 1027 times larger than transitions between any two random firms in the same system. The implication of this is that observing one transition between firms is a strong indicator of future transitions and thus, a strong suggestion that worker movements can be reliably modelled by introducing links between firms that exhibit certain flow amounts between them. In this article, we perform three¹ related tests (the last one is mainly contained in Sect. A.3.3) to confirm that employee transitions between firms have the same temporal predictability reported in Ref. [18]. Two of our tests are designed to adjust for firm sizes (an improvement over the methods in [18]); our results support the notion that past transitions are predictive of future ones.

We focus on the Finnish data. Consider worker flows in a window of time of $2\Delta t$ years centered around a given year t. Loosely speaking, we want to test for every pair of firms with flows in the first Δt years, from $t-\Delta t+1$ to t, if they also tend to have flows in the second Δt years from $t+1$ to $t+\Delta t$, above what would be expected from chance. We label the two time periods of size Δt before and after t as $\mathcal{T}_{<}=[t-\Delta t+1,t]$ and $\mathcal{T}_{>}=[t+1,t+\Delta t]$. To be specific, we define $f_{ij}(t)$ as the number of individuals changing jobs from firm i to firm j in year t, $F_{ij}(t)=f_{ij}(t)+f_{ji}(t)$ the total undirected flow between i and j in t, $\mathcal{F}_{ij}(t,\Delta t)=\sum_{t'=t-\Delta t+1}^{t}F_{ij}(t')$ the total flow between a pair ij during $\mathcal{T}_{<}$, and $\bar{\mathcal{F}}_{ij}(t,\Delta t)=\sum_{t'=t+1}^{t+\Delta t}F_{ij}(t')$ the flow between ij during $\mathcal{T}_{>}$. Let us introduce an arbitrary threshold $\mathcal{W}$ for $\mathcal{F}_{ij}$ such that, if the pair of nodes i and j satisfy it ($\mathcal{F}_{ij}\geq \mathcal{W}$), we check if the pair ij has flow $\bar{\mathcal{F}}_{ij}>0$. In other words, we require a minimum flow amount $\mathcal{W}$ to track a pair of nodes from $\mathcal{T}_{<}$ during $\mathcal{T}_{>}$. We then test how informative the value of $\mathcal{W}$ is when trying to forecast which node pairs have flow in $\mathcal{T}_{>}$. If $\mathcal{W}$ successfully helps forecast active node pairs in the future, then we can treat $\mathcal{W}$ as an acceptance criterion for adding a link between i and j, thus generating a labor flow network.

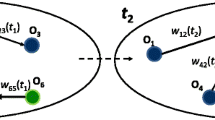
To determine if the criterion is useful, we define several quantities. First, we capture the set of flows $\mathcal{E}(t,\Delta t,\mathcal{W})=\{(ij)|\mathcal{F}_{ij}(t, \Delta t)\geq \mathcal{W}\}$, i.e. the pairs of nodes during $\mathcal{T}_{<}$ that achieve threshold $\mathcal{W}$. Together with these node pairs, we collect the unique nodes $\mathcal{N}(t,\Delta t, \mathcal{W})=\{q|(q=i\lor q=j)\land (i,j) \in \mathcal{E}(t,\Delta t,\mathcal{W})\}$, that is, all the nodes that take part in any of the node pairs in $\mathcal{E}(t,\Delta t,\mathcal{W})$. We also define a set $\bar{\mathcal{E}}(t,\Delta t,1)=\{(ij)|\bar{\mathcal{F}}_{ij}(t, \Delta t)\geq 1\}$, the node pairs that have at least one flow event during $\mathcal{T}_{>}$. Associated with this, we define $\bar{\mathcal{N}}(t,\Delta t,\mathcal{W}=1)=\{q|(q=i\lor q=j)\land (i,j) \in \bar{\mathcal{E}}(t,\Delta t,1)\}$, the nodes that take part in $\bar{\mathcal{E}}(t,\Delta t,1)$. Since the nodes in $\mathcal{N}(t,\Delta t,\mathcal{W})$ or in $\bar{\mathcal{N}}(t,\Delta t,1)$ may not all be present through the entirety of the time period between $t-\Delta t+1$ and $t+\Delta t$, we also define the intersection $\mathcal{N}^{*}(t,\Delta t,\mathcal{W})=\mathcal{N}(t,\Delta t, \mathcal{W})\cap \bar{\mathcal{N}}(t,\Delta t,1)$, composed of nodes that are present in both $\mathcal{E}(t,\Delta t,\mathcal{W})$ and $\bar{\mathcal{E}}(t,\Delta t,1)$, and also the sets $\mathcal{E}^{*}(t,\Delta t,\mathcal{W})$ and $\bar{\mathcal{E}}^{*}(t,\Delta t,1)$ which are, respectively, the subsets of $\mathcal{E}(t,\Delta t,\mathcal{W})$ and $\bar{\mathcal{E}}(t,\Delta t,1)$ that only include node pairs where both nodes are in $\mathcal{N}^{*}(t,\Delta t,\mathcal{W})$. This guarantees that comparisons between flows before and after year t are well defined. To avoid cumbersome notation, from here we use the shortened notation $\mathcal{E}^{*}_{\mathcal{W}}\equiv \mathcal{E}^{*}(t,\Delta t, \mathcal{W})$, $\bar{\mathcal{E}}^{*}_{1}\equiv \bar{\mathcal{E}}^{*}(t,\Delta t,1)$, and $\mathcal{N}^{*}_{\mathcal{W}}\equiv \mathcal{N}^{*}(t,\Delta t, \mathcal{W})$ (an illustrative diagram of the process can be found in Fig. 1).

Figure 1

Illustration of the various sets defined to determine flow persistence and the usefulness of the threshold $\mathcal{W}$. From the data for flows in the time period $\mathcal{T}_{<}=[t-\Delta t+1,t]$, we identify those node pairs with a flow equal or exceeding $\mathcal{W}$ (width of lines represents flow amounts) and construct a set $\mathcal{E}_{\mathcal{W}}$ whose elements are those pairs. Similarly, in the time period $\mathcal{T}_{>}=[t+1,t+\Delta t]$ we identify node pairs with flow and build the set of pairs $\bar{\mathcal{E}}_{1}$. The set of nodes present in the pairs $\mathcal{E}_{\mathcal{W}}$ is $\mathcal{N}_{\mathcal{W}}$, and the set of those present in $\bar{\mathcal{E}}_{1}$ is $\bar{\mathcal{N}}_{1}$. The common nodes (in red) are $\mathcal{N}_{\mathcal{W}}^{*}=\mathcal{N}_{\mathcal{W}}\cap \bar{\mathcal{N}}_{1}$. The node pairs of $\mathcal{E}_{\mathcal{W}}$ and $\bar{\mathcal{E}}_{1}$ that involve exclusively the nodes $\mathcal{N}_{\mathcal{W}}^{*}$ are, respectively, $\mathcal{E}^{*}_{\mathcal{W}}$ and $\bar{\mathcal{E}}^{*}_{1}$. The intersection (in blue) $\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}$ is the set of node pairs both in $\mathcal{E}^{*}_{\mathcal{W}}$ and $\bar{\mathcal{E}}^{*}_{1}$. Our statistical model tests whether the observed $|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}|$ is larger than expected from chance

If the information of which pairs “are connected” in $\mathcal{E}^{*}_{\mathcal{W}}$ allows us to predict to some extend the flows in $\bar{\mathcal{E}}^{*}_{1}$, then it means that the criterion used to create $\mathcal{E}^{*}_{\mathcal{W}}$ is informative. To test if there is a relationship between $\mathcal{E}^{*}_{\mathcal{W}}$ and $\bar{\mathcal{E}}^{*}_{1}$, we determine the number of firm-pair flows in the period $\mathcal{T}_{>}$ that were also firm-pair flows ($\geq \mathcal{W}$) in the years $\mathcal{T}_{<}$; to obtain a fraction, we divide the number by $|\mathcal{E}^{*}_{\mathcal{W}}|$. This produces the density $\wp _{\mathcal{W}}(t)$, defined as

$$ \wp _{\mathcal{W}}(t,\Delta t)= \frac{ \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert }{ \vert \mathcal{E}^{*}_{\mathcal{W}} \vert }. $$

(1)

The denominator counts the opportunities for a node pair that satisfies the flow threshold during $\mathcal{T}_{<}$ to also have flow subsequently; the numerator counts how many times the opportunities are actually realized. Note that if the fraction took the value of 1 it would mean that all pairs that had flows of magnitude $\geq \mathcal{W}$ up to year t also had flows after year t; if the value were 0, it would mean that none of the pairs with flows $\geq \mathcal{W}$ up to year t had flows after that year. Crucially (establishing a null model, developed in detail in Sect. A.3.1), if the flows captured in $\mathcal{E}^{*}_{\mathcal{W}}$ provided no relevant information about the flows captured in $\bar{\mathcal{E}}^{*}(t,\Delta t,1)$, one would expect $\wp _{\mathcal{W}}(t,\Delta t)$ to be the same as

$$ \wp (t,\Delta t)= \frac{ \vert \bar{\mathcal{E}}^{*}_{1} \vert }{\binom{ \vert \mathcal{N}^{*}_{\mathcal{W}} \vert }{2}}, $$

(2)

the density of node pairs with a flow of at least 1 during $\mathcal{T}_{>}$. The numerator in Eq. (2) counts the number of node pairs with flow and the denominator the total number of possible node pairs (this equation is the usual link density equation of a network). An intuitive way to understand why ℘ and $\wp _{\mathcal{W}}$ should be the same when the flows before and after t are not related is to note that by pure chance the expectation $\langle |\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}| \rangle$ of the number of times a node pair in $\mathcal{E}^{*}_{\mathcal{W}}$ is also in $\bar{\mathcal{E}}^{*}_{1}$ is given by $\wp |\mathcal{E}^{*}_{\mathcal{W}}|$, i.e. the number of trials $|\mathcal{E}^{*}_{\mathcal{W}}|$ of finding a connection times the success rate ℘; if we insert this expectation into the numerator of Eq. (1), we confirm our claim. In fact, the null model is described by a hypergeometric distribution for which ℘ is the expected value for $\wp _{\mathcal{W}}$ (in Sect. A.3.1 we explain this and estimate the p-value which confirms the significance of our threshold test). If the flows $\mathcal{E}^{*}_{\mathcal{W}}$ are indicative of the flows $\bar{\mathcal{E}}^{*}_{1}$, we expect $\wp _{\mathcal{W}}>\wp$. To test this, we calculate the excess probability $x_{\mathcal{W}}$, given by the ratio

$$ x_{\mathcal{W}}(t,\Delta t)= \frac{\wp _{\mathcal{W}}(t,\Delta t)}{\wp (t,\Delta t)} $$

(3)

that highlights any potential increase of $\wp _{\mathcal{W}}$ over ℘.

We compute $\wp (t,\Delta t),\wp _{\mathcal{W}}(t,\Delta t)$, and $x_{\mathcal{W}}(t,\Delta t)$ for a combination of years t and time windows Δt to get a comprehensive picture of the situation (see Sect. A.1 for details on data). Note that the size of the time window Δt impacts the range of years used: since the earliest dataset is for 1988 and the latest for 2007, then a window of time Δt means the years of analysis are $1987+\Delta t\leq t\leq 2007-\Delta t$. In Fig. 2 we present results for thresholds $\mathcal{W}=1,2,3$, and for time windows $\Delta t=2,3,4,5$ (additional analysis and robustness checks are shown in Sect. A.7). Clearly, $\wp _{\mathcal{W}}\gg \wp$ by orders of magnitude across all combinations of $\mathcal{W},\Delta t$. This is because the observed values of $|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}|$ are indeed also orders of magnitude larger than their expectations $\langle |\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}| \rangle =\wp |\mathcal{E}^{*}_{\mathcal{W}}|$ (see Table 3). The size of the time window Δt does not have a pronounced effect on any of the probabilities, although ℘ seems slightly more sensitive to it than $\wp _{\mathcal{W}}$. On the other hand, $\mathcal{W}$ increases all the probabilities in the plot. More importantly, specifically for $\wp _{\mathcal{W}}$ we can see that as $\mathcal{W}$ increases from 1 to 3, the likelihoods of any of the flows in $\mathcal{E}^{*}_{\mathcal{W}}$ to also appear in $\bar{\mathcal{E}}^{*}_{1}$ increase from over ($\wp _{\mathcal{W}} \approx$) 10% to around ($\wp _{\mathcal{W}}\approx$) 50–60% and in some years even more.²

Figure 2

The densities $\wp (t,\Delta t)$ and $\wp _{\mathcal{W}}(t,\Delta t)$ with the following color and symbol code: black without symbols represents $\Delta t=2$, red with + represents $\Delta t=3$, green with ∗ represents $\Delta t=4$, blue with × represents $\Delta t=5$; (—) lines represent $\mathcal{W}=1$, $(-\cdot \cdot -)$ lines represent $\mathcal{W}=2$, $(-\phantom{.}-\phantom{.}-)$ lines represent $\mathcal{W}=3$; thin lines represent $\wp (t,\Delta t)$, and thick lines represent $\wp _{\mathcal{W}}(t,\Delta t)$. The brackets signal the location of $\wp (t,\Delta t)$ and $\wp _{\mathcal{W}}(t,\Delta t)$ in the plot

The excess probabilities for some of the previous curves are presented next, restricted only to $\Delta t=2$ given the minor impact of Δt on the results, but including the thresholds $\mathcal{W}=1,2,3$ (see Fig. 3). For $\mathcal{W}=1$, the excess probability is largest, which means that the first flow event generates the greatest fractional increase between ℘ and $\wp _{\mathcal{W}}$ (an increase of more than 10³, the same order of magnitude as in [18]). The threshold $\mathcal{W}=2$ has an excess probability in the 400 to 500 range. Threshold $\mathcal{W}=3$ has excess probabilities in the range of 150 to 350. The decrease of the, still considerably large, excess probabilities $x_{\mathcal{W}}$ with $\mathcal{W}$ is a consequence of the saturation effect that $\wp _{\mathcal{W}}$ undergoes (as it approaches 1 with increasing $\mathcal{W}$) in comparison to the unsaturated evolution of ℘ with $\mathcal{W}$.

Figure 3

Excess probability $x_{\mathcal{W}}$ for $\mathcal{W}=1$ (—), $\mathcal{W}=2$ $(-\cdot \cdot -)$, and $\mathcal{W}=3$ $(- \phantom{.} - \phantom{.} -)$

To improve on the previous test, we present a modification that addresses the heterogeneity of firm sizes. Concretely, note that if flow occurs between two large firms within the time interval $\mathcal{T}_{<}$, then just by random chance the likelihood that another flow event occurs between these firms in the interval $\mathcal{T}_{>}$ should be larger than when the same situation occurs between two small firms. Thus, one could wonder if $\wp _{\mathcal{W}}\gg \wp$ might break down due to the firm-size heterogeneity.

The modification we introduce concerns a change to the null model. In the previous test, the null model predicts that $\wp _{\mathcal{W}}$ should approach the value of ℘, but is instead found to be orders of magnitude larger. That test rests on the assumption that any of the flows in $\bar{\mathcal{E}}^{*}_{1}$ are equally likely to occur among any pair of nodes in $\mathcal{N}^{*}_{\mathcal{W}}$, despite the differences in those nodes.

The new null model is constructed via Monte Carlo by randomizing the flows contained in $\bar{\mathcal{E}}^{*}_{1}$ among the nodes $i\in \mathcal{N}^{*}_{\mathcal{W}}$ with each node i preserving its observed in- and out-flows. For each random rewiring of $\bar{\mathcal{E}}^{*}_{1}$ we obtain a set of simulated flows $\bar{\mathcal{S}}^{*}_{1}$, and determine the size $|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|$ of their overlap with the flows for the period $\mathcal{T}_{<}$. For M realizations, we can calculate an expectation value $\langle |\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}| \rangle _{(\mathrm{HF})}$ where HF stands for heterogeneous firms. In a similar way to the previous test, we compare $\wp _{\mathcal{W}}$ against the average density

$$ \wp ^{(\mathrm{HF})}=\bigl\langle \wp (t,\Delta t)\bigr\rangle _{\mathrm{HF}}= \frac{\langle \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1} \vert \rangle _{(\mathrm{HF})}}{ \vert \mathcal{E}^{*}_{\mathcal{W}} \vert }, $$

(4)

as well as the excess probability $x^{(\mathrm{HF})}=\wp _{\mathcal{W}}/\wp ^{(\mathrm{HF})}$. The results are shown in Fig. 4. In a similar way to the previous test, we find that $\wp _{\mathcal{W}}\gg \wp ^{(\mathrm{HF})}$. The excess probability $x^{(\mathrm{HF})}_{\mathcal{W}}$ has values that roughly correspond to a factor of 10, not as large as $x_{\mathcal{W}}$ but still significant; the fact that $x^{(\mathrm{HF})}_{\mathcal{W}}< x_{\mathcal{W}}$ provides an a posteriori justification for the need for this new test. Additional considerations, including a discussion of p-values can be found in Sect. A.3.2.

Figure 4

The densities $\wp ^{(\mathrm{HF})}(t,\Delta t)$, $\wp _{\mathcal{W}}(t,\Delta t)$ and the excess probability $x^{(\mathrm{HF})}_{\mathcal{W}}(t,\Delta t)$, where $\Delta t=2$ with the following symbol code: (—) lines represent $\mathcal{W}=1$, $(-\cdot \cdot -)$ lines represent $\mathcal{W}=2$, $(- \phantom{.} - \phantom{.} -)$ lines represent $\mathcal{W}=3$; thin lines represent $\wp ^{(\mathrm{HF})}(t,\Delta t)$, thick lines represent $\wp _{\mathcal{W}}(t,\Delta t)$, and thick lines with ∘ represent $x^{(\mathrm{HF})}_{\mathcal{W}}(t,\Delta t)$. The brackets signal the location of $\wp (t,\Delta t)$, $\wp _{\mathcal{W}}(t,\Delta t)$, and $x^{(\mathrm{HF})}_{\mathcal{W}}(t,\Delta t)$ in the plot. The plot has been constructed with $M=10^{4}$ simulations

As a final check, we present in Sect. A.3.3 an additional test that focuses on the amount of flow predicted by our threshold method in comparison with the heterogeneous firm null model. We find that the node pairs identified by the threshold method carry anywhere from about 30% to as much as 70% of the overall flow in the network depending on the specific t. The flows carried by the node pairs emerging from the null model consistently carry about a tenth of this flow.

Summarizing the results of the previous three tests, it is clear that the use of a threshold $\mathcal{W}$ identifies flows that persist into the future, and carry a very large fraction of the overall flow of the system. Furthermore, the likelihood that these flows are seen again increases monotonically with $\mathcal{W}$. For $\mathcal{W}=2$, we already find that the likelihood of a pair of nodes having repeated flows is around ($\wp _{ \mathcal{W}=2}\approx$) 40%. As we argue in Sect. A.7, the qualitative results of our analyses do not change by increasing this parameter, and therefore, in the main article we present results with $\mathcal{W}=2$ which balances size of the sample with a significant certainty that flows are persistent.

2.2 Assembling the labor flow network

We construct the LFN G for a given dataset (Finland or Mexico) by assembling all N firms together with the edges that are found to be persistent according to the criterion above. The network is unweighted and undirected, characterized by the symmetric adjacency matrix A of dimension $N\times N$, with $\mathbf{A}_{ij}=\mathbf{A}_{ji}=1$ if i and j are connected and zero otherwise. In order to make better use of the data, we construct a network on the basis of the entire time frame for each dataset (20 years for Finland, and just over 29 years for Mexico). This is supported by results in Sect. A.8, specially those associated with Fig. 24. The LFNs built by this procedure ($\mathcal{W}=2$) are found to carry a large portion of the job-to-job transitions: in Finland $\approx 60.33\%$ out of the total of $1\text{,}808\text{,}412$ transitions observed, and in Mexico, $\approx 33.7\%$ out of the total of $624\text{,}880$ transitions. Extending the criterion to include edges where transitions occur 3 times or more ($\mathcal{W}=3$), the number of transitions captured is still high, with $\approx 51.17\%$ for Finland, and $\approx 24.8\%$ for Mexico.

The network that results from this procedure is characterized by a skew distributions of degree $k_{i}$ (number of neighbors of i), total transitions through each node $\tau _{i}$ (typically called node strength in the networks literature), and link weights $F_{ij}$. Beyond the non-trivial nature of the distributions, it is worth mentioning that each of the quantities is necessary for a full description of the network: for instance, it is not enough to know the strength of a node τ (or even its directed versions $\tau ^{(in)},\tau ^{(out)}$) in order to know k. This is important to realize as it indicates that the network structure or the results we describe later do not emerge directly from a single mechanism such as labor supply (which would imply that τ statistically describes k). The distributions, along with a lengthy discussion of their interpretation, are shown in the Appendix, Sect. A.4.

As a final point in this section, let us discuss the unweighted undirected nature of G. Qualitatively, LFNs are defined to reflect the presence (or absence when there is no edge) of employment “affinity” between two firms, necessary for firm-to-firm transitions. This approach captures the notion of a categorical relationship between firms [36]. Considering the limited microscopic data available, this is the most unbiased choice we can make when modelling observed persistent transitions between firms. If the choice is sound, the model should be able to accurately reproduce observations, as we confirm in this article. The choice of considering an edge as a categorical relationship also leads to the undirected assumption, as there is no a priori reason to discard transitions in either direction, and since the weights are all equal, there is no need to have directed edges.

3 Modelling firms and individuals

Having established that LFNs capture a large number of job-to-job transitions, we proceed to model agents navigating these networks.

Given that the specific choices made by agents travelling in the LFN are likely to be partially driven by chance, we introduce a discrete time stochastic model that encodes the behavior of agents and firms in the network.³ The rules of the model are given by the following:

• 1. Agents: These can have two states, employed or unemployed. At the start of the time step, an employed agent remains in its firm, say i, with probability $1-\lambda _{i}$, and leaves (or separates) with probability $\lambda _{i}$. An unemployed agent at the start of the time step first determines whether neighbors of firm i are accepting applications and, if any of them are, chooses one of them to apply to with uniform probability.

• 2. Firms: At the start of the time step, firms make a choice to receive applications with probability $v_{i}$ or not receive them with probability $1-v_{i}$. If firms choose to receive applicants, then each is accepted with a probability $h_{i}$.

The set of neighbors of i is denoted by $\Gamma _{i}$, and has size $k_{i}=|\Gamma _{i}|$, the degree of i. A specific subset of neighbors of node i receiving applicants in a given time step is denoted by $\gamma _{i}$, and this can change from step to step. In this time step, the number of open neighbors is $|\gamma _{i}|$. Our calculation contains terms for configurations for which we condition $\gamma _{i}$ to have neighbor j open, and in those cases the configuration is denoted by $\gamma _{i}^{(j)}$. The occurrence of configuration $\gamma _{i}$ is a random event with probability $\operatorname{Pr}(\gamma _{i})=\prod_{j\in \gamma _{i}}v_{j}\prod_{\ell \in \Gamma _{i}\backslash \{\gamma _{i}\}}(1-v_{\ell })$. We also find it useful to define the average hiring rate $\langle h\rangle _{\gamma _{i}}=\sum_{j\in \gamma _{i}}h_{j}/| \gamma _{i}|$ of neighbors of i given $\gamma _{i}$.

To track the state of the system, we define the probabilities $r(i,t)$ and $s(i,t)$ that an agent is, respectively, employed or unemployed at node i at time t. These two probabilities, explained in detail below, satisfy the equations

$$ r(i,t)=(1-\lambda _{i})r(i,t-1) +h_{i}\sum _{j\in \Gamma _{i}}s(j,t-1) \sum_{\{\gamma ^{(i)}_{j}\}} \frac{1}{ \vert \gamma ^{(i)}_{j} \vert }\operatorname{Pr}\bigl( \gamma ^{(i)}_{j}\bigr) $$

(5)

and

$$\begin{aligned} s(i,t)={}&\lambda _{i} r(i,t-1) \\ &{}+s(i,t-1) \biggl[\sum_{\{\gamma _{i}\neq \emptyset \}}\operatorname{Pr}( \gamma _{i})\frac{1}{ \vert \gamma _{i} \vert }\sum_{j\in \gamma _{i}}(1-h_{j}) +\operatorname{Pr}(\gamma _{i}=\emptyset ) \biggr]. \end{aligned}$$

(6)

The first equation states that the probability for an agent to be employed at node i at time t is given by the probability to be employed at node i at time $t-1$ and to not separate, plus the probability that the agent is unemployed at one of the neighbors of i, that i is accepting applications, that the agent chooses to apply to i, and that the application by the agent leads to being hired. The second equation states that the probability to be unemployed at i at time t is given by the probability to be employed at i at time $t-1$ and be separated, or to have been unemployed at time $t-1$ at i but not find a job among the neighbors of i, either because none of them are receiving applications, or because the agent chooses to apply to one of the neighbors and is not hired. Note that the brackets in Eq. (6) simplify to $1-\sum_{\{\gamma _{i}\neq \emptyset \}} \langle h\rangle _{\gamma _{i}}\operatorname{Pr}(\gamma _{i})$.

The rules and equations above (Eqs. (5) and (6)) give rise to a Markov chain, where workers act independently of one another, and the model parameters are static in time. We assume that the parameters $h_{i}$ and $v_{i}$ are independent of $k_{i}$, and that $0< h_{i},v_{i}\leq 1$. With these assumptions, and by calibrating from data the remaining model parameters, namely $k_{i}$ and $\lambda _{i}$, we show below that the model reproduces key empirical observations. To explore the model, we now present an analysis of its steady state for the cases of heterogeneous $v_{i}$ (each firm has its on value of v) and homogeneous $v_{i}=v$ (constant v).

In the steady state, the conditions $r(i,t)-r(i,t-1)=0$ and $s(i,t)-s(i,t-1)=0$ are satisfied. Using the notation $r(i,t)\to r_{\infty }(i)$ and $s(i,t)\to s_{\infty }(i)$ we find

$$\begin{aligned} &0=-\lambda _{i} r_{\infty }(i) +h_{i}\sum _{j\in \Gamma _{i}}s_{\infty }(j)\sum_{\{\gamma ^{(i)}_{j}\}} \frac{1}{ \vert \gamma ^{(i)}_{j} \vert }\operatorname{Pr}\bigl(\gamma ^{(i)}_{j}\bigr), \end{aligned}$$

(7)

$$\begin{aligned} &0=\lambda _{i} r_{\infty }(i)-s_{\infty }(i)\sum _{\{\gamma _{i}\neq \emptyset \}}\langle h\rangle _{\gamma _{i}}\operatorname{Pr}(\gamma _{i}), \end{aligned}$$

(8)

which, when solved for $r_{\infty }(i)$, lead to the matrix equation

$$ \boldsymbol{\Lambda }\mathbf{X}=\mathbf{0}, $$

(9)

where Λ is an $N\times N$ matrix given by

$$ \boldsymbol{\Lambda }_{ij}:=\mathbf{A}_{ji} \frac{h_{i}\sum_{\{\gamma _{j}^{(i)}\}}\operatorname{Pr}(\gamma _{j}^{(i)})/ \vert \gamma _{j}^{(i)} \vert }{\sum_{\{\gamma _{j}\neq \emptyset \}}\langle h\rangle _{\gamma _{j}}\operatorname{Pr}(\gamma _{j})}- \delta [i,j], $$

(10)

and X and 0 are column matrices of size $N\times 1$ with $\mathbf{X}_{i}=\lambda _{i} r_{\infty }(i)$ and $\mathbf{0}_{i}=0$, and $\delta [i,j]$ is the Kronecker delta. To determine $s_{\infty }(i)$ one can either construct a similar expression to Eq. (9) or solve for X and then apply Eq. (8).

A unique solution⁴ to Eq. (9) can be obtained upon introduction of the normalization condition $1=\sum_{i}[r(i,t)+s(i,t)]=\sum_{i}[r_{\infty }(i)+s_{\infty }(i)]$ (details in Sect. A.6). For the general case where for each i the parameters $v_{i},\lambda _{i}$ and $h_{i}$ have different values, there is no simple closed form solution. However, for the simpler case $v_{i}=v$, the probability $\operatorname{Pr}(\gamma _{i})$ simplifies to $v^{|\gamma _{i}|}(1-v)^{k_{i}-|\gamma _{i}|}$, making the matrix elements $\boldsymbol{\Lambda }_{ij}$ take the form $\mathbf{A}_{ij}h_{i}/(k_{j}\langle h\rangle _{\Gamma _{i}})-\delta [i,j]$, leading to

$$\begin{aligned} &r_{\infty }^{(v)}(i)=\frac{\chi h_{i}\langle h\rangle _{\Gamma _{i}}k_{i}}{\lambda _{i}}, \end{aligned}$$

(11)

$$\begin{aligned} &s_{\infty }^{(v)}(i)=\frac{\chi h_{i}k_{i}}{1-(1-v)^{k_{i}}} , \end{aligned}$$

(12)

$$\begin{aligned} &\chi =\frac{1}{\sum_{i\in G} h_{i}\langle h\rangle _{\Gamma _{i}}k_{i} [\frac{1}{\lambda _{i}} +\frac{1}{\langle h\rangle _{\Gamma _{i}}[1-(1-v)^{k_{i}}]} ]}. \end{aligned}$$

(13)

The expression for $s_{\infty }^{(v)}(i)$ can be rewritten by noting that the agent unemployed at i has the same probability $\xi _{i}$ for any time step to find a job among its neighbors, given by $\xi_{i}=\langle h\rangle _{\Gamma _{i}}[1-(1-v)^{k_{i}}]$. This is because the likelihood that at least one of the $\Gamma _{i}$ neighbors is open is $1-(1-v)^{k_{i}}$ for all time steps, and over configurations, the effective probability to be hired at any of them is $\langle h\rangle _{\Gamma _{i}}$. With this result

$$ s_{\infty }^{(v)}(i)= \frac{\chi h_{i}\langle h\rangle _{\Gamma _{i}}k_{i}}{\xi _{i}}. $$

(14)

The rates $\lambda _{i}$ and $\xi _{i}$ play similar roles for employment and unemployment, respectively. An agent has a probability $\lambda _{i}(1-\lambda _{i})^{t-1}$ to be employed at i for t time steps, and similarly a probability $\xi _{i}(1-\xi _{i})^{t-1}$ to be unemployed t time steps at i. These are geometric distributions, for which the average times of employment (job tenure) and unemployment (spells) are, respectively, $1/\lambda _{i}$ and $1/\xi _{i}$. Fortunately, in data sets where the span of time spent unemployed is available (such as for the Mexican data we utilize here), $\xi _{i}$ can be empirically estimated (together with $k_{i}$ and $\lambda _{i}$), adding important practical value to this new parameter. As we explain below, $\xi _{i}$ plays an important role when studying the unemployment consequences of our approach.

If the system has H agents, the steady state probabilities for the numbers of employed ($L_{i}$) and unemployed ($U_{i}$) agents at firm i can then be computed via

$$ \operatorname{Pr}(L_{i})=\binom{H}{L_{i}}\bigl[r_{\infty }(i) \bigr]^{L_{i}}\bigl[1-r_{\infty }(i)\bigr]^{H-L_{i}} $$

(15)

and

$$ \operatorname{Pr}(U_{i})=\binom{H}{U_{i}}\bigl[s_{\infty }(i) \bigr]^{U_{i}}\bigl[1-s_{\infty }(i)\bigr]^{H-U_{i}}. $$

(16)

These expressions are broadly useful because they are always valid in the steady state. Thus, even if $r_{\infty }(i)$ and $s_{\infty }(i)$ cannot be determined analytically but, say, numerically, their values can be used directly to determine $\operatorname{Pr}(L_{i})$ and $\operatorname{Pr}(U_{i})$.

One other important concept arises from this derivation: the quantity $U_{i}$ can be interpreted as a firm-specific unemployment, which corresponds to the number of individuals that had i as their last employer but that are yet to find new employment. This notion is a powerful one, as it captures the essential nature of the network effect on mobility: if firm neighbors are not receiving new agents (probability $1-v$), there is no place for the unemployed from i to go.

To illustrate some possible circumstances in which $U_{i}$ can be useful we now discuss three scenarios. These represent examples of how the network introduces local effects to job markets, which cannot be captured in aggregate models, and can only be understood through firm-specific notions like those defined here. First, consider that there are regions of the LFN in which links are present because the connected firms hire similar individuals, and thus agents in one firm can more easily change jobs by going to the other firms in the same region of the network. This is a common situation and in numerous cases the regions of the network are rather cohesive (composed, say, of firms in the same or adjacent industrial sectors). This means that nodes in that region of the network are likely to react in similar ways to economic shocks. Therefore, if the firms in this region begin to lay off workers, they will quickly flood the local network neighborhood with job-seekers, most of which would have a hard time finding work. In addition to this, there would be nodes adjacent to the affected network region that would soon feel the effects of the employment shock by being flooded with new job seekers. In contrast, nodes in distant regions of the economy would feel a much more attenuated effect in a considerably longer time frame. In this shock scenario, the specific initial nodes affected, their unemployment values $U_{i}$, and the structure of the local network play significant roles.

There are other scenarios that can take place where $U_{i}$ is informative. For example, in some cases links may be present due to differences in nodes rather than similarities (in two firms that react in opposite ways to an economic shock, for instance, one firm can become an alternative destinations for the workforce of the other firm). Knowing firm-specific unemployment for the neighboring nodes could be used to measure how anticorrelated their reactions are to economic shocks.

One more example is related to the steady state behavior of $U_{i}$ for any given firm. Note that firms that have simultaneously large $\lambda _{i}$ and $h_{i}$ have a tendency to contribute large $U_{i}$ to the network, and thus influence their neighboring nodes with a correspondingly large number of unemployed individuals seeking jobs, rapidly flooding their hiring capacities and then creating local unemployment in the network.

It is important to note that many individuals perform job searches while still employed. Therefore, to assume as we do that an agent must first separate from a job before looking for another job is an idiosyncratic choice. However, performing a job search while still employed is not fundamentally different from our approach since the individual still has to seek jobs with similar rules among firm neighbors, and thus the results of the Markov process are not qualitatively different, with the caveat that additional parameters are required to model the more nuanced case. Fortunately, as we see in our empirical analysis below, our current model assumptions seem to be effective in practice.

Note the versatility of our approach: since the equations are fully disaggregate, it is always possible to construct coarse-grained versions of the problem that can range from partially to fully aggregate. For instance, one known improvement over fully aggregate labor models are sectoral specialization models [12], which segment the labor market into submarkets each with its own set of shared employment mechanisms and parameters (also called matching technologies). In this context, one can picture the economy as constituted by an aggregation of several sectors (say, healthcare, technology, etc.) which have internal and external employment dynamics. In our model, this partial aggregation can be efficiently tackled by fully connecting all firms in a given sector and also adding links from each of these firms to all other firms in all other sectors of the economy. On the basis of the equations above, all firms of a given sector behave identically, effectively becoming a single representative firm. Representative firms connect to all other representative firms in the economy with appropriate weights (possibly adjusted on the basis of survey data such as the Job Openings and Labor Turnover Survey from the US Bureau of Labor Statistics). The result of applying our methods directly to the disaggregate description while introducing sectorized information or, alternatively, creating from scratch a reduced economy made of only representative firms are equivalent, and it is a matter of choice which approach to take, or even how to decide what firms are assigned to what sectors.

4 Empirical tests and results of the model

Armed with tools to determine the labor flow network as well as rules to model the behavior of agents, we now proceed to test the quality of our model. First, we focus on determining whether the system can be reliably modeled in the steady state. After that, we contrast the predictions emerging from the model with data from Finland and Mexico .⁵ As we see below, the data and the model are consistent.

4.1 Testing the steady state assumption

In the previous section, we have constructed solutions for the steady state. In order to determine if such solutions are representative of typical economic situations, we check whether the number of individuals entering and exiting a node approximately match one another. In Fig. 5 we present the distribution of net flow at a node.

Figure 5

Distribution of the difference between flow of workers into and out of a firm. In this plot, there are over 49,000 firms for Mexico and close to 300,000 firms for Finland

It is clear from our results that indeed firms typically operate around a steady state where the number of workers entering and leaving a firm approximately balance out. This provides empirical validity at the micro-level. For further support, in the Appendix we present several other tests that highlight the steady state nature of the system (see Sect. A.8).

4.2 Firm sizes

Data available to explore the dynamics of the firm-employee system do not contain information about $\{v_{i}\}_{i=1,\dots,N}$ or $\{h_{i}\}_{i=1,\dots,N}$. However, data is available to estimate the values of $\lambda _{i}$. For Finland, this is done by calculating the ratio of agents leaving a firm with respect to the size of the firm. A value of $\lambda _{i}$ is created for every year of the sample, and then all the values for a given firm are averaged over those yearly samples.

To deal with the absence of information for $h_{i},v_{i}$, we concentrate on comparing the data with the homogeneous $v_{i}=v$ version of our model in the hope that, if some of the main qualitative features of the system have been properly captured, we could find a reasonable level of agreement between data and prediction.

We now proceed to test the homogeneous model with $v_{i}=v$ (a constant) for all i. However, we retain the freedom for each firm i to have its own independent acceptance rate $h_{i}$ in order to conform with experience (there are more selective and less selective firms in terms of hiring). Focusing first on the sizes of firms, we make use of Eqs. (11) and (15) to find that the most probable (or mode) firm size $L^{*}_{i}$ is

$$ L^{*}_{i}=\bigl\lfloor (H+1)r^{(v)}_{\infty }(i) \bigr\rfloor \sim \frac{H\chi h_{i}\langle h\rangle _{\Gamma _{i}}k_{i}}{\lambda _{i}}. $$

(17)

This is a model prediction. One possible check for our model against the available data is to determine whether the measured $L^{*}_{i}$ and $k_{i}/\lambda _{i}$ relate as predicted by Eq. (17), assuming independence among the variables $h_{i}$, $k_{i}$, and $\lambda _{i}$. Furthermore, we can also study the distribution $\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})$ to develop a broader picture.

To simultaneously learn about $\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})$ and $L_{i}^{*}$, we use the Finnish data to generate Fig. 6, a 3-dimensional plot of $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L_{i}^{*}|k_{i}/ \lambda _{i}) ]$ as a function of $\log _{10}L_{i}$ and $\log _{10}(k_{i}/\lambda _{i})$, where each $L_{i}$ is the size of a Finnish firm, $k_{i}$ its degree based on repeated observed transitions, and $\lambda _{i}$ its separation rate estimated over the years of data as explained above. Here, $\operatorname{Pr}(L_{i}^{*}|k_{i}/\lambda _{i})$ is the probability associated with the conditional mode $L_{i}^{*}$. For a given $k_{i}/\lambda _{i}$, the logarithm of the ratio $\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L_{i}^{*}|k_{i}/\lambda _{i})$ becomes 0 when $L_{i}=L_{i}^{*}$, and is <0 for other values of $L_{i}$. To interpret the plot, we introduce a plane $\mathcal{P}$ parametrized as indicated in Fig. 6, normal to the base plane $\log _{10}L_{i},\log _{10}(k_{i}/\lambda _{i})$ and running parallel to its diagonal (which means it is a proportionality plane between $L_{i}$ and $k_{i}/\lambda _{i}$). This normal plane also cuts the ratio $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L_{i}^{*}|k_{i}/ \lambda _{i}) ]$ at or very close to 0, i.e., when $L_{i}=L_{i}^{*}$. Therefore, it means that $L_{i}^{*}$ from the data is proportional to $k_{i}/\lambda _{i}$, supporting the prediction from Eq. (17). The correspondence we observe between the data and prediction also supports the assumption that, on average, the parameters $h_{i}$ and $\langle h\rangle _{\Gamma _{i}}$ do not depend strongly on $k_{i}$ or $\lambda _{i}$ [15] (see Table 1 for a summary of the relation between parameters and results).

Figure 6

Behavior of $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L^{*}_{i}|k_{i}/ \lambda _{i}) ]$ (surface $\mathcal{S}$) with respect to $\log _{10} L_{i}$ and $\log _{10} k_{i}/\lambda _{i}$ for Finland. The data is logarithmically binned as follows: $L_{i}$ belongs to bin b (a non-negative integer) if $L_{\mathrm{min}}\zeta ^{b}< L_{i}\leq L_{\mathrm{min}}\zeta ^{b+1}$ with $\zeta >1$ (for this plot $\zeta =2$) and $L_{\mathrm{min}}=\min [\{L_{i}\}]$ (smallest firm size in the data); $k_{i}/\lambda _{i}$ is binned in the same way with ζ and $(k/\lambda )_{\mathrm{min}}=\min [\{(k_{i}/\lambda _{i})\}]$. Blue points represent the local maximum of $\mathcal{S}$ at each bin. The vertical plane $\mathcal{P}$ is parametrized as $(k_{i}/\lambda _{i}, C_{L} k_{i}/\lambda _{i},z)$ where z is a free parameter. $C_{L}$ is chosen to minimize $\sum_{b} (L^{*}_{b}-C_{L}(k/\lambda )_{b} )^{2}$ with the first three bins excluded because the smallest firm size is 1. The large range within which the intersection of $\mathcal{P}$ and $\mathcal{S}$ runs parallel to the maxima of $\mathcal{S}$ strongly supports Eq. (17)

Table 1 Parameters that are either used directly as inputs in our model, Eqs. (5) and (6), or used to determine or postulate those input parameters. The firm-size distribution (FSD) emerges for the conditions stated in the table, particularly that there are no interdependencies among the parameters for a node (one particularly problematic one would be that $h_{i}$ and/or $k_{i}$ were correlated, but our results do not support this)

If indeed $k_{i}/\lambda _{i}$ is strongly correlated to $L_{i}$ as indicated by the results above, we can assume the relation

$$ L_{i}\approx C_{L}\frac{k_{i}}{\lambda _{i}}, $$

(18)

where $C_{L}$ is independent of $k_{i}$ and $\lambda _{i}$ (but still depends on the remaining model parameters $v,\{h_{i}\},\chi$). Under this assumption, the distributions of both $L_{i}$ and $k_{i}/\lambda _{i}$ should be related by the change of variables theorem, which (written in the continuous limit) yields

$$ \operatorname{Pr}(L_{i})dL_{i}=\operatorname{Pr}(k_{i}/ \lambda _{i})d(k_{i}/\lambda _{i}). $$

(19)

In Fig. 7, we show the probability distributions of both $L_{i}$ and $k_{i}/\lambda _{i}$ which are close to parallel, and display a heavy tail, indeed supporting our assumption. It has been known for a long time that $\operatorname{Pr}(L_{i})$ satisfies Zipf’s law [20–23], which supports the notion that the probabilities in Fig. 7 follow a power law. Employing this functional form in Eq. (19) with decay exponent z, i.e., $\operatorname{Pr}(k_{i}/\lambda _{i})\sim (k_{i}/\lambda _{i})^{-z}$, we find

$$ \operatorname{Pr}(L_{i})\sim L_{i}^{-z}. $$

(20)

The value of z estimated from a least squares fit of the slope of $\log \operatorname{Pr}(k_{i}/\lambda _{i})$ with respect to $k_{i}/\lambda _{i}$ turns out to be $\approx 1.97\pm 0.02$, consistent with the exponent of the decay of $\operatorname{Pr}(L_{i})$ that we measure against our data (see Table 2). Note also that this exponent is consistent with the decay exponent close to −1 of the cumulative distributions of $L_{i}$ observed for numerous countries [23].

Figure 7

Probability distributions of $L_{i}$ (red) and $k_{i}/\lambda _{i}$ (blue) for Finland binned logarithmically with 30 bins for the range of values of both sets. For most of the range of $L_{i}$ and $k_{i}/\lambda _{i}$, the two distributions are almost parallel, supporting the validity of Eq. (19) to explain $\operatorname{Pr}(L_{i})$

Table 2 Quantities predicted by the model against measured counterparts

This result offers a new interpretation for the origin of the power law distribution of firm sizes [20–22]. In our picture, the collection of employment affinities, and hence connectivity distribution, plays a dominant role (together with the separation rates) in the observed distribution of firm sizes. We should emphasize that this does not equate to a statement of causality (ultimate causes of employment affinity are structural variables such as geography, employee skills, etc.), but rather the realization that employment affinities are highly useful quantities with which to model because they possess a great power of synthesis about the system behavior.

4.3 Firm-specific unemployment

The homogeneous model with $v_{i}=v$ also provides an estimate for our new concept of firm-specific unemployment. This quantity can be calculated in a similar way as $L_{i}^{*}$, and it is given by

$$ U_{i}^{*}\sim \frac{H\chi h_{i}\langle h\rangle _{\Gamma _{i}}k_{i}}{\xi _{i}}. $$

(21)

Although we do not have enough information in the Finnish dataset to determine the set $\{\xi _{i}\}$, we do for the Mexican dataset. From the latter, we determine the $\{\xi _{i}\}$ through maximum likelihood (see Sect. A.5). We test Eq. (21) in a similar way as Eq. (17), through a 3-dimensional plot of $\log _{10} [\operatorname{Pr}(U_{i}|k_{i}/\xi _{i})/\operatorname{Pr}(U_{i}^{*}|k_{i}/ \xi _{i}) ]$ as a function of $\log _{10}U_{i}$ and $\log _{10}(k_{i}/\xi _{i})$, where $U_{i}, k_{i}$, and $\xi _{i}$ are all determined empirically for Mexico. The results are shown in Fig. 8, and support the conclusion that $U^{*}\sim k_{i}/\xi _{i}$. For Mexico, we average $U_{i}$ over the whole observation window of $D=10\text{,}612$ days to obtain stable values for firm-specific unemployment.

Figure 8

Behavior of $\log _{10} [\operatorname{Pr}(U_{i}|k_{i}/\xi _{i})/\operatorname{Pr}(U^{*}_{i}|k_{i}/ \xi _{i}) ]$ (surface $\mathcal{S}$) with respect to $\log _{10} U_{i}$ and $\log _{10} k_{i}/\xi _{i}$ for Mexico. The data is logarithmically binned as in the same way as in Fig. 6 ($\zeta =2$) with $U_{\mathrm{min}}=\min [\{U_{i}\}_{\{i\}}]$ (smallest firm-specific unemployment size in the data) and $(k/\xi )_{\mathrm{min}}=\min [\{(k_{i}/\xi _{i})\}_{\{i\}}]$. Blue points represent the local maximum of $\mathcal{S}$ at each bin. The vertical plane $\mathcal{P}$ is parametrized as $(k_{i}/\xi _{i}, C_{U} k_{i}/\xi _{i},z)$ where z is a free parameter. $C_{U}$ is chosen to minimize $\sum_{b} (U^{*}_{b}-C_{U}(k/\xi )_{b} )^{2}$ with the last five bins excluded at the point where the linear relationship breaks down. The large range within which the intersection of $\mathcal{P}$ and $\mathcal{S}$ runs parallel to the maxima of $\mathcal{S}$ strongly supports Eq. (21)

To better understand firm-specific unemployment, we present in Fig. 9 its probability distribution. This is the first time this quantity is reported. Its importance revolves around the fact that firms which have a large contribution to unemployment may constitute a major problem for economies as a whole. In the same plot, we also display the probability distribution of $k_{i}/\xi _{i}$. The parallel between the two distributions mirrors the situation with $L_{i}$ and $k_{i}/\lambda _{i}$: Eq. (21), which connects $U_{i}$ to $k_{i}/\xi _{i}$, allows explaining $\operatorname{Pr}(U_{i})dU_{i}$ through a change of variables so that $\operatorname{Pr}(U_{i})dU_{i}=\operatorname{Pr}(k_{i}/\xi _{i})d(k_{i}/\xi _{i})$. This plot also indicates the presence of a heavy-tail distribution for $\operatorname{Pr}(U_{i})$. Some care must be taken in interpreting Fig. 9 due to the way in which the Mexican data was collected, focusing on uniformly sampling individuals rather than firms. This may play a role in the cross-over in slopes observed in the distributions of both $U_{i}$ and $k_{i}/\xi _{i}$.

Figure 9

Probability distributions of $U_{i}$ (red) and $k_{i}/\xi _{i}$ (blue) for Mexico binned logarithmically with 30 bins for the range of values of both sets. For most of the range of $U_{i}$ and $k_{i}/\xi _{i}$, the two distributions are almost parallel

4.4 Ratio of firm separation to waiting rates

An additional test can be performed on the basis of the symmetry between Eqs. (17) and (21). The ratio between these leads to

$$ \frac{\langle L_{i}\rangle }{\langle U_{i}\rangle } = \frac{L^{*}_{i}}{U^{*}_{i}}=\alpha \biggl( \frac{\xi _{i}}{\lambda _{i}} \biggr)^{\beta } $$

(22)

with α and β equal to 1. To determine if the prediction is matched by the data, we applied the re-sample consensus algorithm (RANSAC) [37] (see Sect. A.10) with 10⁶ estimations for the Mexican data. The results can be seen in Fig. 10. The average β is $1.00000\pm 2\times 10^{-5}$, while the most frequent is 1.0065. The average estimator α of the intercept is $1.13637 \pm 5\times 10^{-5}$. These results are quite close to the theoretical prediction of (22).⁶

Figure 10

Distribution of β̂ obtained form 1,000,000 estimations of the RANSAC algorithm, using OLS as the underlying model

5 Discussion and conclusions

Detailed microdata, such as the one analyzed in this article, provides an opportunity to construct new, highly resolved models of macro level phenomena from micro level empirically justified mechanisms. In our particular case, our approach offers a picture of firms and employment that links them together in a precise way, opening the opportunity for an integrated theory of these two areas of research.

Our network picture of firms and employment offers the novel idea that the sizes of firms become encoded in the number of independent connections firms have with other firms. These connections, which reflect an economic affinity (low mobility barriers) relevant to employment transitions, synthesize the numerous possible structural variables (skills, geography, social contacts, etc.) that an agent is affected by when searching for employment, but because the connections are determined from the data (empirically calibrated), even those variables that may not be traditionally tracked are taken into account.

The ability of this data-driven approach to incorporate both known and unknown mechanisms in the firm-employee system makes our method less prone to idiosyncrasies associated with methods of modelling that require choosing a set of starting assumptions and then trying to model from that point on. For instance, if one had assumed that labor supply was the main mechanism, the result would be that the model would not fit the data, and thus additional assumptions would have been needed to explain observation. This strategy would create a model that has to be adjusted ad hoc, is not parsimonious (due to the need for additional variables to control the adjustments), and is thus less tractable conceptually. Even if additional well-known mechanisms are incorporated into the modelling to try to achieve the adjustments, there is no guarantee that one can capture all relevant effects, producing the same incomplete and non-parsimonious modelling situation.

A new concept of firm-specific unemployment is also introduced here. From the standpoint of the theory of processes on graphs, it is a useful tool to account for a ‘search’ state of the agent, as one would see in queuing processes such as data routing on computer networks. In our particular case of employment and firm sizes, beyond its technical value, firm-specific unemployment introduces new economic notions about employment, relating to the relevance that specific firms along with their surroundings contribute to the overall unemployment rate.

The time scales that our model addresses (and their relation to real time scales), depend on whether the economy is steady enough that its behaviour between samples is not changing a great deal (see the discussion on the steady state in Sect. A.8) or if, in contrast, it is very dynamic. In the steady (or even in the slow dynamic) state, the model time scale and the real-world time scales basically match as the solutions to the model quickly adjust to the model parameters for that sampling period. When the dynamics are very rapid due to a fast economic shock, the time scales of the model need to be considered within the sampling period, a problematic situation since we would be unable to compare model results with data. In this regime, the time scale of the dynamics would be dictated by the first eigenvalue of the stochastic matrix of the Markov chain.

In the future, as our models improve and further data is gathered and analyzed, it may become possible to develop even more detailed models that could tackle more complex problems such as the formation of new firms and the construction of realistic shock scenarios, which are necessary to design real-time high resolution forecasting of employment flow. This task, which has not yet been possible, may be within our reach for the first time, with considerable potential for social policy design that is well grounded empirically and for which its effect can be forecast in great detail.

Appendix A

1.1 A.1 Data

We use two different datasets of employer-employee matched records. The first is the Finnish Longitudinal Employer-Employee Data (FLEED), which consists of an annual panel of employer-employee matched records of the universe of firms and employees in Finland. The panel was constructed by Statistics Finland from social security registries by recording the association between each worker and each firm (enterprise codes, not establishments), at the end of each calendar year. If a worker is not employed, it is not part of the corresponding cross-section. The result is a panel of 20 years (1988 to 2007) that tracks every firm and every employed individual at the end of each year (approximately $3\times 10^{5}$ firms and $2\times 10^{6}$ workers). From two consecutive years of this data, one can determine if an employee in one firm has moved to another, hence generating data for inter-firm job-to-job transitions. We have direct access to this data on transition, but not the entirety of FLEED.

Unemployment periods cannot be determined from FLEED. For this we use a dataset from Mexico consisting of employer-employee matched records with daily resolution. The data was obtained by sampling raw social security records from the Mexican Social Security Institute. Approximately $4\times 10^{5}$ individuals who were active between 1989 and 2008 were randomly selected and their entire employment history was extracted (hence, covering dates prior to 1989). This procedure generates a dataset with nearly $2\times 10^{5}$ firms. The records contain information about the exact date in which a person became hired/separated by/from a firm. Therefore, it is possible to identify unemployment spells, duration of each spell, and associations between job seekers and their last employer.

As a supplementary dataset, useful for determining sizes of firms and separation rates, we use Statistics Finland’s Business Register, constructed from administrative data from the Tax Administration, and from direct inquiries from Statistics Finland to business with more than 20 employees. This data provides firm sizes and profits from different sources.

1.2 A.2 Summary of empirical and model parameters. Model predictions

To facilitate the presentation as well as provide a summary of the role of the parameters of the model, we present in this section Table 1 with all the parameters that bear relevance to the inputs of the model. We also indicate the conditions under which these parameters are consistent with the empirical observations we attempt to reproduce in this work, namely the firm-size distribution (FSD).

In Table 2, we provide a summary of the quantities predicted by the model and those that are measured empirically and matched against the model.

1.3 A.3 Testing persistence in the Finnish dataset

In this section we explain further details, particularly regarding the null models, about the effectiveness of the threshold criterion in determining which node pairs should be connected using a link on the basis of the flow of individuals between the firms.

1.3.1 A.3.1 Null model and p-values for threshold criterion

To address the construction of a p-value for the analysis of persistence carried out in Sect. 2.1, we can define the null model mathematically. For this purpose, suppose that among the nodes $\mathcal{N}^{*}(t,\Delta t,\mathcal{W})$, the null model is defined by the fact that the flows captured in $\mathcal{E}^{*}(t,\Delta t,\mathcal{W})$ and those captured in $\bar{\mathcal{E}}^{*}(t,\Delta t, 1)$ overlap only as a consequence of random chance. Concretely, every flow in $\mathcal{E}^{*}(t,\Delta t,\mathcal{W})$ that also belongs to $\bar{\mathcal{E}}^{*}(t,\Delta t, 1)$ is considered a successful random trial, which takes away a success state (sampling without replacement). The success states are the flows in $\bar{\mathcal{E}}^{*}(t,\Delta t, 1)$. The overall population, i.e., places where the flows $\bar{\mathcal{E}}^{*}(t,\Delta t, 1)$ can be placed, consists of all the unique pairs of nodes among $\mathcal{N}^{*}(t,\Delta t,\mathcal{W})$. Therefore, the likelihood that there are $|\mathcal{E}^{*}(t,\Delta t,\mathcal{W})\cap \bar{\mathcal{E}}^{*}(t, \Delta t,1)|$ successful trials is given by the hypergeometric distribution

$$ \operatorname{Pr}\bigl( \bigl\vert \mathcal{E}^{*}\cap \bar{ \mathcal{E}}^{*} \bigr\vert \bigr)= \frac{\binom{ \vert \mathcal{E}^{*} \vert }{ \vert \mathcal{E}^{*}\cap \bar{\mathcal{E}}^{*} \vert }\binom{\binom{ \vert \mathcal{N}^{*} \vert }{2}- \vert \mathcal{E}^{*} \vert }{ \vert \bar{\mathcal{E}}^{*} \vert - \vert \mathcal{E}^{*}\cap \bar{\mathcal{E}}^{*} \vert }}{\binom{\binom{ \vert \mathcal{N}^{*} \vert }{2}}{ \vert \bar{\mathcal{E}}^{*} \vert }}, $$

(23)

where, for brevity, we use the shortened notation $\mathcal{E}^{*}_{\mathcal{W}},\bar{\mathcal{E}}^{*}_{1}$, and $\mathcal{N}^{*}_{\mathcal{W}}$. Therefore, the expectation value $\langle |\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}| \rangle$ for $|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}|$ is given by

$$ \bigl\langle \bigl\vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{ \mathcal{E}}^{*}_{1} \bigr\vert \bigr\rangle = \frac{ \vert \bar{\mathcal{E}}^{*}_{1} \vert \vert \mathcal{E}^{*}_{\mathcal{W}} \vert }{\binom{ \vert \mathcal{N}^{*}_{\mathcal{W}} \vert }{2}}, $$

(24)

where $|\mathcal{E}^{*}_{\mathcal{W}}|/\binom{|\mathcal{N}^{*}_{\mathcal{W}}| }{2}$ is the probability of picking a pair of nodes among $\mathcal{N}^{*}_{\mathcal{W}}$ between which there is flow that belongs to $\mathcal{E}^{*}_{\mathcal{W}}$; if $\operatorname{Pr}(|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}|)$ were given by a binomial instead, the expectation value would be the same (this is relevant below). Rewriting the last expression somewhat, we find

$$ \frac{\langle \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert \rangle }{ \vert \mathcal{E}^{*}_{\mathcal{W}} \vert }= \frac{ \vert \bar{\mathcal{E}}^{*}_{1} \vert }{\binom{ \vert \mathcal{N}^{*}_{\mathcal{W}} \vert }{2}}= \wp, $$

(25)

where the second equality comes from the definition of ℘ in Eq. (2) above. Note also that the left hand side is the expectation value for $\wp _{\mathcal{W}}$ in the null model. In other words, Eq. (25) is a proof of our statement that, in the random model, the expected value for $\wp _{\mathcal{W}}$ should correspond to ℘. However, the observed $\wp _{\mathcal{W}}$ are much larger than ℘, supporting the use of $\mathcal{W}$ as a selection criterion for links. To estimate a p-value using the hypergeometric distribution is difficult because the values of $\mathcal{E}^{*}_{\mathcal{W}},\bar{\mathcal{E}}^{*}_{1}$, and $\mathcal{N}^{*}_{\mathcal{W}}$ are quite large (see the table below). Therefore, we estimate the p-values using a normal distribution which can, in turn, be explained from a binomial distribution approximation to the hypergeomatric distribution, well justified in our case given that $\binom{|\mathcal{N}^{*}_{\mathcal{W}}|}{2}\gg |\mathcal{E}^{*}_{ \mathcal{W}}|,|\bar{\mathcal{E}}^{*}_{1}|$. In the binomial approximation, in order to maintain the same expectation value, the success probability $\rho _{s}$ is given by

$$ \rho _{s}= \frac{ \vert \mathcal{E}^{*}_{\mathcal{W}} \vert }{\binom{ \vert \mathcal{N}^{*}_{\mathcal{W}} \vert }{2}}, $$

(26)

which says that to pick a node pair where there was flow during $\mathcal{T}_{<}$, the chances are proportional to the number of node pairs $|\mathcal{E}^{*}_{\mathcal{W}}|$ in that time period. In the normal approximation to this binomial distribution, the mean and standard deviation are given by

$$ \mu = \bigl\vert \bar{\mathcal{E}}^{*}_{1} \bigr\vert \rho _{s}, \mathcal{Q}=\sqrt{ \bigl\vert \bar{ \mathcal{E}}^{*}_{1} \bigr\vert \rho _{s}(1-\rho _{s})} $$

(27)

since $|\bar{\mathcal{E}}^{*}_{1}|$ is the number of trials. For this approximation, the p-value is then given by the integral

$$ p\text{-value of } \bigl\vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \bigr\vert \approx \frac{1}{\sqrt{2\pi \mathcal{Q}^{2}}} \int _{ \vert \mathcal{E}^{*}_{ \mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert }^{\infty }e^{- \frac{(\phi -\mu )^{2}}{2\mathcal{Q}^{2}}}\,d\phi. $$

(28)

On the basis of the values in the table below, the magnitude of ϕ is very large in comparison to μ and therefore, one can approximate the integral via an asymptotic expansion of first order derived by integration by parts, giving estimates for the p-value of

$$ p\text{-value of } \bigl\vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \bigr\vert \approx \frac{1}{\sqrt{2\pi }} \frac{ \mathcal{Q}}{ \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu }e^{- \frac{( \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu )^{2}}{2\mathcal{Q}^{2}}}. $$

(29)

Subsequent terms in the expansion are also dominated by the exponential term and therefore, it is reasonable to truncate the expansion at first order. The values of the exponent are large enough that it is better to express these results under a logarithm, producing

$$\begin{aligned} &\ln \bigl[p\text{-value of } \bigl\vert \mathcal{E}^{*}_{\mathcal{W}} \cap \bar{\mathcal{E}}^{*}_{1} \bigr\vert \bigr] \\ &\quad\approx - \frac{( \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu )^{2}}{2\mathcal{Q}^{2}}+ \ln \biggl[\frac{1}{\sqrt{2\pi }} \frac{ \mathcal{Q}}{ \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu } \biggr] \\ &\quad\approx - \frac{( \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu )^{2}}{2\mathcal{Q}^{2}}- \ln \biggl[ \frac{ \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu }{\sqrt{2}\mathcal{Q}} \biggr]-\ln (2 \sqrt{\pi }) \\ &\quad\approx - \frac{( \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\mu )^{2}}{2\mathcal{Q}^{2}}=- \frac{( \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert -\langle \vert \mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1} \vert \rangle )^{2}}{2\mathcal{Q}^{2}}, \end{aligned}$$

(30)

where the last equality uses the fact that $\mu =|\bar{\mathcal{E}}^{*}_{1}||\mathcal{E}^{*}_{\mathcal{W}}|/\binom{| \mathcal{N}^{*}_{\mathcal{W}}|}{2}=\langle |\mathcal{E}^{*}_{1} \cap \bar{\mathcal{E}}^{*}_{1}|\rangle$, and drops the logarithmic term and the constant since they are much smaller in magnitude than the quadratic term.

The p-value estimates are contained in Table 3. The order of magnitude of these results is overwhelmingly below the usual significance threshold of 10⁻³. To illustrate this with one of the combinations of values below ($t=1989, \Delta t=2,\mathcal{W}=1$), note that $\rho _{s}=2.2\times 10^{-4}$, $\mu =|\bar{\mathcal{E}}^{*}_{1}|\rho _{s}=8.78$, and $\mathcal{Q}=\sqrt{|\bar{\mathcal{E}}^{*}_{1}|\rho _{s}(1-\rho _{s})}=2.96$. Therefore, our estimate produces $\ln [p\text{-value}]\approx -4.64\times 10^{6}\ll \ln 10^{-3}$. For reference, $\ln 10^{-3}\approx -6.91$ where 10⁻³ comes from a $p\text{-value}=10^{-3}$. All other results in the table show similar behavior, orders of magnitude removed from the 10⁻³ significance threshold. This provides convincing evidence for the validity of our method. The results of our tests for several combinations of years, time windows Δt, and values of $\mathcal{W}$ is shown in Table 3.

Table 3 Table for test of threshold method for the cases that ignore or take into account the firm heterogeneity (HF). The table only includes $\Delta t=2$, as other values of Δt have only a minor effect on the probability densities $\wp,\wp ^{(\mathrm{HF})}$, and $\wp _{\mathcal{W}}$. We show a selection of years for each of the three values of $\mathcal{W}=1,2,3$. Note that the p-values are exceedingly small for both tests

1.3.2 A.3.2 Null model and p-values for threshold criterion for heterogeneous firms

The p-values for the null model addressing the heterogeneity are calculated from the Monte Carlo simulations. As explained in the main text, we generate random realizations $\bar{\mathcal{S}}^{*}_{1}$ of the flows $\bar{\mathcal{E}}^{*}_{1}$ (for $\mathcal{T}_{>}$) that respect the total in- and out-flows of each of the nodes in $\mathcal{N}^{*}_{\mathcal{W}}$. We then determine for each $\bar{\mathcal{S}}^{*}_{1}$ its overlap $\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}$ with the flows in the period $\mathcal{T}_{<}$. The equivalent quantity to ℘ of the previous test is $\wp ^{(\mathrm{HF})}= \frac{\langle |\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|\rangle _{(\mathrm{HF})}}{|\mathcal{E}^{*}_{\mathcal{W}}|}$ (defined in Eq. (4)) or, alternatively we can calculate the distribution $\operatorname{Pr}( \frac{|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|}{|\mathcal{E}^{*}_{\mathcal{W}}|})$ from the values of $|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|/| \mathcal{E}^{*}_{\mathcal{W}}|$ of each realization. Both $\wp ^{(\mathrm{HF})}$ or the distribution over realizations can be compared against $\wp _{\mathcal{W}}$, but we require the distribution to determine a p-value. Our results indicate that a Gaussian fits well the distribution $\operatorname{Pr}(\wp ^{(\mathrm{HF})})$.

Since both ℘ and $\wp ^{(\mathrm{HF})}$ are defined with the $|\mathcal{E}^{*}_{\mathcal{W}}|$ in the denominator, we can determine p-values equally well by comparing $\operatorname{Pr}(|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|)$ and $|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1}|$. This can be seen in a general way using $\phi =\tilde{\phi }/\alpha$ and $\mu =\tilde{\mu }/\alpha$, which lead to the identity

$$ \frac{1}{\sqrt{2\pi }\sigma } \int _{\phi _{o}}^{\infty }e^{- \frac{(\phi -\mu )^{2}}{2\sigma ^{2}}}\,d\phi = \frac{1}{\sqrt{2\pi }\tilde{\sigma }} \int _{\phi _{o}/\alpha }^{\infty }e^{- \frac{(\tilde{\phi }-\tilde{\mu })^{2}}{2\tilde{\sigma }^{2}}}\,d \tilde{\phi }, $$

(31)

where σ is the standard deviation for x, and its transformed version $\sigma \alpha =\tilde{\sigma }$ provides the standard deviation for ϕ̃. This transformation also highlights that, in terms of functional form, if $\operatorname{Pr}(\wp ^{(\mathrm{HF})})$ is Gaussian, then so is $\operatorname{Pr}(|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|)$.

In Fig. 11(a) we present histograms $h(|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|)$ for $t=1992$ and in Fig. 11(b) histograms for $t=2000$, both for $\mathcal{W}=1,2,3$, as well as their regressions (described next). Since we do not have a theoretical way to specify $\langle |\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}| \rangle _{(\mathrm{HF})}$ or its distribution $\operatorname{Pr}(|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|)$, we resort to regression to determine the parameters of the histogram and subsequently estimate p-values using Eq. (30) (results in Table 3). With $\phi =|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|$, we use

$$ h(\phi )=h_{o} e^{-\frac{(\phi -\mu _{\mathrm{HF}})^{2}}{2\sigma _{\mathrm{HF}}^{2}}}, $$

(32)

where $\mu _{\mathrm{HF}}$ and $\sigma _{\mathrm{HF}}$ emerge from the regression. These are the two parameters we care about, as the normalization constant of the Gaussian is determined by $\sigma _{\mathrm{HF}}$. The quality of the fit is clear from Fig. 11.

Figure 11

Histograms $h(|\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}|)$ from simulations (symbols) and their least square fits (lines) with $\mathcal{W}=1$ (black ∘), 2 (red □), 3 (green ◊) for years $t=1992$ (top) and $t=2000$ (bottom). All histograms have been constructed from $M=10^{4}$ Monte Carlo realizations

1.3.3 A.3.3 Overall flows captured by threshold criterion

The final test we carry out concerns how the threshold criterion performs with regards to accounting for the overall flow in the network.

Specifically, we define the total flow

$$ \bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}\bigl(t,\Delta t| \bar{ \mathcal{E}}^{*}(t,\Delta t,1)\bigr)=\sum_{(i,j)\in \bar{\mathcal{E}}^{*}(t,\Delta t,1)} \bar{\mathcal{F}}^{*}_{i,j}(t, \Delta t), $$

(33)

that is, the total number of individuals changing firms over the pairs of nodes in $\bar{\mathcal{E}}^{*}(t,\Delta t,1)$. As above, we use the simplified notation $\bar{\mathcal{F}}^{*}_{\cdot }(\bar{\mathcal{E}}^{*}_{1})$ to mean $\bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(t,\Delta t| \bar{\mathcal{E}}^{*}(t,\Delta t,1))$ as typically there is no confusion about the time t and time window Δt we are concentrating on. Note that $\bar{\mathcal{F}}^{*}_{\cdot }(\bar{\mathcal{E}}^{*}_{1})$ counts all the repeated transitions between node pairs, i.e., all the flows happening during $\mathcal{T}_{>}$.

Our test consists of comparing $\bar{\mathcal{F}}^{*}_{\cdot }(\bar{\mathcal{E}}^{*}_{1})$ to the average of the quantity

$$ \bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}\bigl(t,\Delta t| \mathcal{E}^{*}(t, \Delta t,\mathcal{W})\cap \bar{\mathcal{ E}}^{*}(t,\Delta t,1)\bigr)=\sum_{(i,j) \in \mathcal{E}^{*}(t,\Delta t,\mathcal{W})\cap \bar{\mathcal{E}}^{*}(t, \Delta t,1)} \bar{\mathcal{F}}^{*}_{i,j}(t,\Delta t), $$

(34)

which is the number of individuals that change jobs in the time period $\mathcal{T}_{>}$ exclusively on those node pairs that also had flows $\geq \mathcal{W}$ in the time period $\mathcal{T}_{<}$. We denote this flow as $\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1})$. The main purpose of this test is to show that a considerable percentage of future flow is captured using the threshold criterion, much more than the flow predicted by the null model for heterogeneous firm sizes presented above in Sects. 2.1 and A.3.2.

The overall flow during $\mathcal{T}_{>}$ associated with a given Monte Carlo realization of the null model for heterogeneous firm sizes is denoted by $\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1})$ where $\bar{\mathcal{S}}^{*}_{1}$ is the set of flows that emerges from one random rewiring that preserves in- and out-flows for each and every firm. As we discussed in Sect. A.3.2, flows $\mathcal{T}_{>}$ are reliably predicted by flows in the interval $\mathcal{T}_{<}$. Thus, we expect that typically $\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1})$ is greater or even much greater than any typical $\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1})$. To confirm this is the case, we generate the histogram $h(\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}))$ of the overall flows predicted by the null model in order to compute $\operatorname{Pr}(\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}} \cap \bar{\mathcal{S}}^{*}_{1}))$, its average $\langle \bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\mathcal{E}^{*}_{ \mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1})\rangle _{\mathrm{HF}}$, and the p-value for the actual measured flow $\bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\mathcal{E}^{*}_{ \mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1})$. In addition, following the same conceptual framework as for the previous two tests, we define the fractions

$$ \theta _{\mathcal{W}}(t,\Delta t)= \frac{\bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{E}}^{*}_{1})}{\bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\bar{\mathcal{E}}^{*}_{1})} $$

(35)

and

$$ \theta ^{(\mathrm{HF})}(t,\Delta t)=\bigl\langle \theta (t,\Delta t)\bigr\rangle _{\mathrm{HF}}= \frac{\langle \bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1})\rangle _{\mathrm{HF}}}{\bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\bar{\mathcal{E}}^{*}_{1})}, $$

(36)

and the excess probability

$$ y_{\mathcal{W}}= \frac{\theta _{\mathcal{W}}(t,\Delta t)}{\theta ^{(\mathrm{HF})}(t,\Delta t)}. $$

(37)

Figure 12 corresponds to $\theta _{\mathcal{W}}, \theta ^{(\mathrm{HF})}$, and $y_{\mathcal{W}}$. In consistent fashion with the results for $\wp ^{(\mathrm{HF})},\wp _{\mathcal{W}}$, and $x_{\mathcal{W}}$, the values of $\theta _{\mathcal{W}}$ are roughly an order of magnitude larger than those for $\theta ^{(\mathrm{HF})}$, measured by $y_{\mathcal{W}}$. The values for $\theta _{\mathcal{W}}$ in particular are largely in a range that spans between 30% and 50% and reaches as high as just over 70%.

Figure 12

The fractions $\theta (t,\Delta t)$ and $\theta _{\mathcal{W}}(t,\Delta t)$ and the excess probability $y^{(\mathrm{HF})}_{\mathcal{W}}(t,\Delta t)$, where $\Delta t=2$ with the following symbol code: (—) lines represent $\mathcal{W}=1$, $(-\cdot \cdot -)$ lines represent $\mathcal{W}=2$, $(- \phantom{.} - \phantom{.} -)$ lines represent $\mathcal{W}=3$; thin lines represent $\theta ^{(\mathrm{HF})}(t,\Delta t)$, thick lines represent $\theta _{\mathcal{W}}(t,\Delta t)$, and thick lines with ∘ represent $y^{(\mathrm{HF})}_{\mathcal{W}}(t,\Delta t)$. The brackets signal the location of $\theta (t,\Delta t)$, $\theta _{\mathcal{W}}(t,\Delta t)$, and $y^{(\mathrm{HF})}_{\mathcal{W}}(t,\Delta t)$ in the plot

The calculation of p-values follows the same approach as the two previous tests. Figure 13 shows the histograms $h(\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}))$ for $\mathcal{W}=1,2,3$ and the years (a) $t=1992$ and (b) $t=2000$, along with their least square fit (solid lines). The histograms were create with $M=10^{4}$ rewirings of each individual yearly network. From the fits we estimate $\operatorname{Pr}(\bar{\mathcal{F}}^{*}_{\cdot }(\mathcal{E}^{*}_{\mathcal{W}} \cap \bar{\mathcal{S}}^{*}_{1}))$, its average $\langle \bar{\mathcal{F}}^{*}_{\boldsymbol{\cdot }}(\mathcal{E}^{*}_{ \mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1})\rangle _{\mathrm{HF}}$ and standard deviation, which we then use in estimating the p-value of each set of years and thresholds. The results of this analysis are shown in Table 4.

Figure 13

Histograms $h(\bar{\mathcal{F}}^{*}_{\cdots }(\mathcal{E}^{*}_{\mathcal{W}}\cap \bar{\mathcal{S}}^{*}_{1}))$ from simulations (symbols) and their least square fits (lines) with $\mathcal{W}=1$ (black ∘), 2 (red □), 3 (green ◊) for years $t=1992$ (top) and $t=2000$ (bottom). All histograms have been constructed from $M=10^{4}$ Monte Carlo realizations

Table 4 Table for test of overall flow carried by node pairs predicted by threshold test. The table only includes $\Delta t=2$, as other values of Δt have only a minor effect on the probability densities $\theta ^{(\mathrm{HF})}$ and $\theta _{\mathcal{W}}$. We show a selection of years for each of the three values of $\mathcal{W}=1,2,3$. Note that the p-values are exceedingly small

1.4 A.4 Topological properties of labor flow network

The use of the criteria developed in Sects. 2.1 and A.3 leads to a labor flow network with certain topological properties that are captured in the distributions of degree, node strength, and link weights. These distributions are found in Figs. 14, 15, and 16 for a range of values of $\mathcal{W}$. A satisfactory feature of these distributions is that their functional forms remain stable even as $\mathcal{W}$ increases.

Figure 14

Distributions of degree $\operatorname{Pr}(k_{i})$ of the networks created by applying the threshold criterion $\mathcal{W}=2$ (black ∘), $\mathcal{W}=3$ (red □), $\mathcal{W}=4$ (green ◊), and $\mathcal{W}=5$ (blue △)

Figure 15

Distributions of total flow $\operatorname{Pr}(\tau _{i})$ through nodes of the networks created by applying the threshold criterion $\mathcal{W}=2$ (black ∘), $\mathcal{W}=3$ (red □), $\mathcal{W}=4$ (green ◊), and $\mathcal{W}=5$ (blue △)

Figure 16

Distributions of flow weights $\operatorname{Pr}(F_{i,j})$ through node pairs of the networks created by applying the threshold criterion $\mathcal{W}=2$ (black ∘), $\mathcal{W}=3$ (red □), $\mathcal{W}=4$ (green ◊), and $\mathcal{W}=5$ (blue △)

An important observation that it worth highlighting is that, while $k_{i}$ and $\tau _{i}$ are clearly related, one is not predictive of the other. In other words, as has been found in prior research on real weighted networks compared to weighted network models, a full description of such networks typically requires knowledge of all the variables describing a node i, including $k_{i},\tau _{i}$ and the distribution of the link weights $F_{ij}$ [38]. The relevance of this point stems from the fact that it confirms that the labor flow network is not simply a direct effect of the sizes of firms present in the economy: the observed $k_{i}$ is not trivially predicted as the result of the $\tau _{i}$ transitions firm i exhibits. If this were true, the system could be explained by so called labor supply assumptions, i.e., that the sizes of firms (numbers of employees or numbers of individuals moving through the firms) determine other properties of the firms such as their degree; for the labor supply assumption to be sufficient to explain the system, transitions between firms would need to be considered random so that additional assumptions can be avoided. Thus, a configuration model reconstruction of the labor network only fixing $\tau _{i}$ per node would confirm (or reject) the labor supply assumption.

The counter-side to the labor supply assumption is that meaningful links between firms do exist which cannot be simply a consequence of the random jumps of individuals between firms. We have already provided evidence that indeed links are meaningful in our persistence tests above. Here we provide further evidence of the need for a labor flow network with specific links by showing that the configuration network model where only the observed $\tau _{i}$ are fixed does not match observation.

In Figs. 17, 18, and 19 we show, respectively, comparisons of the observed distributions of $k_{i},\tau _{i},F_{ij}$ with respect to their Monte Carlo simulated versions $k_{i}^{(s)},\tau _{i}^{(s)},F_{ij}^{(s)}$. The Monte Carlo distributions have been generated with $M=10^{3}$ realizations. Distributions $\operatorname{Pr}(\tau _{i})$ and $\operatorname{Pr}(\tau _{i}^{(s)})$ are virtually identical given the condition of the Monte Carlo to fix $\tau _{i}$ per node to satisfy the labor supply assumption.⁷ The other distributions, however, differ between their observed and random versions. The fixed flow condition has a tendency to spread flows evenly over nodes which leads simultaneously to nodes that tend to have larger degree in simulation than in reality and links that tend to have more homogenized flows than in the real system. The effect on weights is strong enough that it is patently easy to see in the distributions. However, it is slightly harder to see the effect on $k_{i}$, but an eloquent illustration of the effect can be found in the scatter plot Fig. 20. In this plot, we see that virtually none of the degrees generated as a result of the labor flow assumption is smaller than $k_{i}$. The results systematically generated larger degree. If labor supply was properly descriptive of the real network, the cloud of generated degrees should lie evenly along the diagonal. It is of note that only approximately 0.12% of the nodes have a degree in the simulated networks that is less than the actual degree of the node; most simulated degrees are equal or larger than observed degrees. This makes clear the disparity between the networks that emerge from the labor supply assumption versus the observed network.

Figure 17

Distributions $\operatorname{Pr}(k_{i})$ (black ‘∘’) and $\operatorname{Pr}(k_{i}^{(s)})$ (red ‘□’) for $M=10^{3}$ Monte Carlo realizations. The distributions are similar but $\operatorname{Pr}(k_{i}^{(s)})$ systematically deviates to become more skewed as $k_{i},k_{i}^{(s)}$ increase, signaling that fixing the overall flow through a node and allowing the degree to emerge as a consequence of this leads to larger degree than in observation

Figure 18

Distributions $\operatorname{Pr}(\tau _{i})$ (black ‘∘’) and $\operatorname{Pr}(\tau _{i}^{(s)})$ (red ‘□’) for $M=10^{3}$ Monte Carlo realizations. The distributions are virtually identical as the Monte Carlo has been set up to preserve each node’s overall flow $\tau _{i}$

Figure 19

Distributions $\operatorname{Pr}(F_{ij})$ (black ‘◯’) and $\operatorname{Pr}(F_{ij}^{(s)})$ (red ‘□’) for $M=10^{3}$ Monte Carlo realizations. The distributions differ widely, with $\operatorname{Pr}(F_{ij}^{(s)})$ considerably steeper than $\operatorname{Pr}(F_{ij})$, illustrating the way that the condition to fix $\tau _{i}$ for each node has the effect of spreading flows evenly over the network, thereby eliminating large flow between node pairs

Figure 20

Scatter plot of observed $k_{i}$ versus $k^{(s)}_{i}$. It is clear from this plot that the model with only a constraint of $\tau _{i}^{(in)}$, $\tau _{i}^{(out)}$ predicts the wrong degree for the nodes

1.5 A.5 Determining $\xi _{i}$ from the data via MLE

We determine the values of $\xi _{i}$ by using the fact they are the rates of success of the geometric distributions of the waiting times to be hired. Consider $S_{i}$ agents that have experienced an unemployment spell from i, each with duration $t_{m}, m=1,\dots,S_{i}$. The log-likelihood to observe those unemployment spells is given by

$$ \log \Biggl[\prod_{\ell =1}^{S_{i}}\xi _{i}(1-\xi _{i})^{t_{\ell }-1} \Biggr]=S_{i} \bigl[\log \xi _{i}+ \bigl(\langle t\rangle _{S_{i}}-1 \bigr) \log (1-\xi _{i}) \bigr], $$

(38)

where $\langle t\rangle _{S_{i}}=\sum_{\ell =1}^{S_{i}}t_{\ell }/S_{i}$. The maximum likelihood estimator for $\xi _{i}$ corresponds to

$$ \xi _{i}=1/\langle t\rangle _{S_{i}}. $$

(39)

Thus, to determine $\xi _{i}$, we calculate the average length of time agents that last worked at i spend waiting to get their next job.

1.6 A.6 Unique solutions of the model

Equations (7) and (8) of the main text constitute a homogeneous system of linear equations for the steady state probabilities of being employed at firm i. Repeating the equations here, we have

$$ \boldsymbol{\Lambda }\mathbf{X}=\mathbf{0} $$

(40)

with

$$ \boldsymbol{\Lambda }_{ij}=\mathbf{A}_{ji} \frac{h_{i}\sum_{\{\gamma ^{(i)}_{j}\}}\operatorname{Pr}(\gamma ^{(i)}_{j})/ \vert \gamma ^{(i)}_{j} \vert }{\sum_{\{\gamma _{j}\neq \emptyset \}}\langle h\rangle _{\gamma _{j}}\operatorname{Pr}(\gamma _{j})}- \delta [i,j] $$

(41)

and

$$ \mathbf{X}_{i}=\lambda _{i} r_{\infty }(i), $$

(42)

where A is the adjacency matrix of the LFN. A homogeneous system such as the one above always has, at least, the trivial solution $\mathbf{X}=\mathbf{0}$. For there to be interesting, non-trivial solutions, it is necessary for the matrix Λ to be singular, i.e., to have determinant equal to zero [39].

In this section we show that Λ is indeed singular and, furthermore, that for a connected network with adjacency matrix A, the singularity stems from matrix Λ having a reduced rank of $N-1$, where N is the number of network nodes (matrix Λ is $N\times N$). This means that there is a 1-dimensional space of solutions for X which satisfies $\boldsymbol{\Lambda }\mathbf{X}=\mathbf{0}$. To obtain a unique solution, one simply needs to make use of the normalization condition

$$ \sum_{i=1}^{N}\bigl(r_{\infty }(i)+s_{\infty }(i) \bigr)=1 $$

(43)

together with [4] of the main text,⁸ which makes Eq. (43) take on the form

$$ \sum_{i=1}^{N} \biggl[\frac{1}{\lambda _{i}}+ \frac{1}{\sum_{\{\gamma _{i}\neq \emptyset \}}\langle h\rangle _{\gamma _{i}}\operatorname{Pr}(\gamma _{i})} \biggr]\lambda _{i} r_{\infty }(i)=1. $$

(44)

Before we embark on showing the proofs, we should note the intuitive reason why Λ is not of full rank, but instead has a rank reduced by one unit: since the probability flow is conserved, it is not necessary to know the probabilities at all nodes. Clearly, due to conservation, if we know the probabilities in $N-1$ nodes, then the probability for the Nth node can be determined from Eqs. (43) or (44). Matrix Λ encodes the way the probabilities flow across the system without normalizing them.

To show first that Λ is singular, it is sufficient to show that all of its columns add to zero, which is equivalent to saying that at least one of its rows is linearly dependent on other rows. This can be seen if we first sum $\boldsymbol{\Lambda }_{ij}$ over i

$$ \sum_{i=1}^{N}\boldsymbol{\Lambda }_{ij}=-1+\sum_{i=1}^{N} \mathbf{A}_{ji} \frac{h_{i}\sum_{\{\gamma _{j}^{(i)}\}}\operatorname{Pr}(\gamma _{j}^{(i)})/ \vert \gamma _{j}^{(i)} \vert }{\sum_{\{\gamma _{j}\neq \emptyset \}} \langle h\rangle _{\gamma _{j}}\operatorname{Pr}(\gamma _{j})}, $$

(45)

where −1 comes from $-\sum_{i}\delta [i,j]$. We can now show that the numerator and denominator of the second term are indeed equal. To see this in detail, we organize the elements of $\{\gamma _{j}^{(i)}\}$ by cardinality $|\gamma _{j}^{(i)}|$, and rewrite the numerator as

$$ \sum_{i=1}^{N}\mathbf{A}_{ji}h_{i} \sum_{\{\gamma _{j}^{(i)}\}}\operatorname{Pr}\bigl( \gamma _{j}^{(i)}\bigr)/ \bigl\vert \gamma _{j}^{(i)} \bigr\vert =\sum_{c=1}^{ \vert \Gamma _{j} \vert } \frac{1}{c}\sum_{i} \mathbf{A}_{ji}h_{i} \sum_{\{ \vert \gamma _{j}^{(i)} \vert =c \}}\operatorname{Pr}\bigl(\gamma _{j}^{(i)}\bigr), $$

(46)

where the last sum is over all elements of $\{\gamma _{j}^{(i)}\}$ with equal size c. Now, the sum over i guarantees that each neighbor of j belonging to a particular $\gamma _{j}^{(i)}$ is summed, along with the corresponding $h_{r}$, where $r\in \gamma _{j}^{(i)}$. Therefore, the sum over i can be rewritten as

$$ \sum_{i} \mathbf{A}_{ji}h_{i} \sum_{\{|\gamma _{j}^{(i)}|=c\}}\operatorname{Pr}\bigl( \gamma _{j}^{(i)}\bigr) =\sum_{\{|\gamma _{j}|=c\}} \biggl(\sum_{r\in \gamma _{j}} h_{r} \biggr)\operatorname{Pr}(\gamma _{j}) $$

(47)

and inserting this into the sum over c leads to

$$ \sum_{c=1}^{ \vert \Gamma _{j} \vert }\frac{1}{c}\sum _{\{ \vert \gamma _{j} \vert =c\}} \biggl(\sum_{r\in \gamma _{j}} h_{r} \biggr)\operatorname{Pr}(\gamma _{j}) = \sum _{\{\gamma _{j}\neq \emptyset \}} \frac{\sum_{r\in \gamma _{j}}h_{r}}{ \vert \gamma _{j} \vert }\operatorname{Pr}(\gamma _{j}) =\sum_{\{\gamma _{j}\neq \emptyset \}}\langle h\rangle _{\gamma _{j}}\operatorname{Pr}(\gamma _{j}) $$

(48)

Therefore,

$$ \sum_{i=1}^{N}\mathbf{A}_{ij}h_{i} \sum_{\{\gamma _{j}^{(i)}\}}\operatorname{Pr}\bigl( \gamma _{j}^{(i)}\bigr)/ \bigl\vert \gamma _{j}^{(i)} \bigr\vert =\sum_{\{\gamma _{j}\neq \emptyset \}}\langle h\rangle _{\gamma _{j}}\operatorname{Pr}(\gamma _{j}), $$

(49)

which means that for all j, (45) is identically zero.

In order to determine the rank of matrix Λ, we first highlight the following relations to the flow probabilities of the random walker. First, note that

$$ h_{i}s(j,t)\sum_{\{\gamma _{j}^{(i)}\}}\operatorname{Pr}\bigl( \gamma _{j}^{(i)}\bigr)/ \bigl\vert \gamma _{j}^{(i)} \bigr\vert =\eta _{ji}, $$

(50)

is the probability current for the transition $s(j,t)\to r(i,t+1)$ from unemployment at node j to employment at node i. Also,

$$ s(j,t)\sum_{\gamma _{j}\neq \emptyset }\operatorname{Pr}(\gamma _{j})\langle h \rangle _{\gamma _{j}}=\eta _{j.}, $$

(51)

is the entire probability flow out of j, which is to say $s(j,t)\to r(\Gamma _{j},t+1)$ (i.e., the probability of being employed at any of the neighbors of j). Due to conservation of probability, it is clear that

$$ \eta _{j.}=\sum_{i\in \Gamma _{j}}\eta _{ji}, $$

(52)

which we use below.

The proof that Λ has incomplete rank can also be written by making use of Eq. (52). Hence

$$ \sum_{i=1}^{N}\boldsymbol{A}_{ji}h_{i} \sum_{\{\gamma _{j}^{(i)}\}}\operatorname{Pr}\bigl(\gamma _{j}^{(i)}\bigr)/ \bigl\vert \gamma _{j}^{(i)} \bigr\vert = \frac{\sum_{i\in \Gamma _{j}}\eta _{ji}}{s(j,t)}= \frac{\eta _{j.}}{s(j,t)}=\sum _{\gamma _{j}\neq \emptyset }\operatorname{Pr}( \gamma _{j})\langle h\rangle _{\gamma _{j}}. $$

(53)

In addition to this simplification, one can also make use of this reformulation to test for the rank of a reduced matrix $\boldsymbol{\Lambda '}$ which is equivalent to Λ but missing a row and a column. In this case, we choose to eliminate the Nth row/column, which is a fully general choice given the arbitrary nature of the labeling of nodes.

We want to show that, for a connected graph, the rows of $\boldsymbol{\Lambda '}$ form a linearly independent set of vectors. Thus, defining

$$ \vec{\Lambda }_{i}=(\Lambda _{i,1},\dots,\Lambda _{i,N-1}),\quad [i=1, \dots, N-1], $$

(54)

where each $\Lambda _{ij}$, when rewritten by using Eqs. (50) and (51), is

$$ \Lambda _{ij}=\boldsymbol{A}_{ji}\frac{\eta _{ji}}{\eta _{j.}}- \delta [i,j], $$

(55)

we can form an equation on the coefficients $\{\mu _{i}\}$

$$ \vec{0}=\sum_{i=1}^{N-1}\mu _{i} \vec{\Lambda }_{i} $$

(56)

and show that it can only be satisfied if all $\mu _{i}$ are zero, which would prove that the set of vectors $\vec{\Lambda }_{1},\dots,\vec{\Lambda }_{N-1}$ are linearly independent. Expanding the right hand side of this last expression, we obtain

$$\begin{aligned} \sum_{i=1}^{N-1}\mu _{i}\vec{ \Lambda }_{i}&= \Biggl(\sum_{i=1}^{N-1} \mu _{i}\Lambda _{i1},\sum_{i=1}^{N-1} \mu _{i}\Lambda _{i2},\dots, \sum _{i=1}^{N-1}\mu _{i}\Lambda _{i,N-1} \Biggr) \\ &= \biggl( \frac{\sum_{i=1}^{N-1}\mu _{i}\boldsymbol{A}_{1i}\eta _{1i}}{\eta _{1.}}- \mu _{1},\dots, \frac{\sum_{i=1}^{N-1}\mu _{i}\boldsymbol{A}_{N-1,i}\eta _{N-1,i}}{\eta _{N-1.}}- \mu _{N-1} \biggr). \end{aligned}$$

(57)

Equating this to $\vec{0}$, we obtain the set of equations

$$ \frac{\sum_{i\in \Gamma ^{\prime }_{j}}\mu _{i}\eta _{ji}}{\eta _{j.}}- \mu _{j}=0\quad [\forall j=1,\dots,N-1], $$

(58)

where $\Gamma ^{\prime }_{j}$ represents the graph neighbors of j excluding node N. With the aid of Eq. (52), this set of equations can be rewritten as

$$ \sum_{i\in \Gamma ^{\prime }_{j}}\mu _{i}\eta _{ji}- \mu _{j}\sum_{i\in \Gamma _{j}}\eta _{ji}=0 \quad[ \forall j=1,\dots,N-1], $$

(59)

where one should note that for $\eta _{j.}$, the set of neighbors used includes N. Explicitly separating the (possible) flow between j and N, this becomes

$$\begin{aligned} &\sum_{i\in \Gamma ^{\prime }_{j}}\mu _{i}\eta _{ji}- \mu _{j}\sum_{i\in \Gamma ^{\prime }_{j}}\eta _{ji}=\mu _{j}\boldsymbol{A}_{j,N}\eta _{j,N} \\ &\quad \Rightarrow\quad \sum_{i\in \Gamma ^{\prime }_{j}}(\mu _{i}-\mu _{j})\eta _{ji}= \mu _{j}\boldsymbol{A}_{j,N} \eta _{j,N}\quad [\forall j=1,\dots,N-1]. \end{aligned}$$

(60)

The last expression highlights the relationships that need to hold among the otherwise independent link flows to satisfy Eq. (56). From a physical standpoint, these relations tell us that the vectors in Eq. (54) are indeed linearly independent in contrast to the case when all the nodes are present (i.e., the full matrix Λ as opposed to the reduced matrix $\boldsymbol{\Lambda }'$). In matrix Λ, there is redundant information because knowing all the flows for $N-1$ nodes provides the information needed to determine the flows to the remaining node. But for the row vectors of $\boldsymbol{\Lambda }'$, that is Eq. (54), the absence of the variables accounting for the flows going into and out of one of the nodes (in our case N) breaks the linear dependence. We see this in more detail next.

In order to find the $\{\mu _{i}\}$ that solve Eq. (56), or equivalently Eq. (60), we proceed as follows. Out of the $N-1$ members of Eq. (60), consider the ones where j is not a neighbor of N. This means that $\mathbf{A}_{j,N}=0$, making the right hand sides equal to 0. It also means that, for this case, $\Gamma ^{\prime }_{j}=\Gamma _{j}$ because there are no connections to N. Then, the only admissible solutions require that $\mu _{i}=\mu _{j}$ (which we label μ for simplicity) for all $i\in \Gamma _{j}$, since the flows $\eta _{ji}\neq 0$. In other words

$$ \sum_{i\in \Gamma _{j}}(\mu _{i}-\mu _{j}) \eta _{ji}=\sum_{i\in \Gamma _{j}}(\mu -\mu )\eta _{ji}=0\quad [j\notin \Gamma _{N}]. $$

(61)

Furthermore, we note that the μ chosen for one j “propagates” to other nodes since the network is connected (has a single cluster). To understand this, let us consider two situations for i: 1) i is itself not a neighbor of N, in which case it also needs to satisfy Eq. (61), but because this i is connected to j, also satisfying Eq. (61), then they must share the same μ value for consistency, or 2) i is a neighbor of N (which we consider next). Before we tackle 2), note that 1) implies all the neighbors of N ($\Gamma _{N}$) also have $\mu _{j}=\mu$ because the nodes that are at distance 2 from N all propagate μ to the nodes in $\Gamma _{N}$.

When a node j is a neighbor of N, $\mathbf{A}_{j,N}=1$, and it is clearer to write Eq. (60) in the form (59), and use Eq. (52) to obtain

$$ \sum_{i\in \Gamma ^{\prime }_{j}}\mu _{i}\eta _{ji}- \mu _{j}\eta _{j.}=0\quad [j\in \Gamma _{N}]. $$

(62)

But because all the $\mu _{i}$ above have been shown to be equal to μ, we have

$$ \mu \sum_{i\in \Gamma ^{\prime }_{j}}\eta _{ji}-\mu \eta _{j.}=\mu (\eta _{j.}- \eta _{j,N})-\mu \eta _{j.}=-\mu \eta _{j,N}=0 \quad[j\in \Gamma _{N}], $$

(63)

which cannot be generally satisfied unless $\mu =0$, showing that indeed the only solution for Eq. (56) is $\mu _{i}=0, \forall i=1,\dots, N$.

If all nodes are neighbors of N, Eq. (60) for all nodes is given by

$$ \sum_{j\in \Gamma ^{\prime }_{j}}(\mu _{i}-\mu _{j}) \eta _{ji}=\mu _{j} \eta _{j,N} $$

(64)

but because the $\eta _{ji}$ are independent, the only way to satisfy the equation is if $\mu _{i}=0$ for all i.

1.7 A.7 Robustness of results to changes in the $\mathcal{W}$ threshold

In the main text and in Sect. A.3, we discuss how we construct the network encoded in A. We indicate that the edges are considered significant if multiple transitions take place between the two firms connected by the edge, and we set the minimum number of transitions to $\mathcal{W}=2$. This choice ensures maximum amount of data to increase statistical significance of the results.

However, for this threshold to be acceptable, we have to check whether our results are robust to increasing $\mathcal{W}$. This is the purpose of this section and, as we indicated in the main text, the results below support our choice to use $\mathcal{W}=2$ for our main analysis. To undertake the robustness test, we construct plots of the quantity $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L^{*}_{i}|k_{i}/ \lambda _{i}) ]$ which are equivalent to Fig. 2 of the main text, but here we use the minimum number of job-to-job transitions to be $\mathcal{W}=3,4,5$ (Fig. 21). If the key characteristics of the surface $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L^{*}_{i}|k_{i}/ \lambda _{i}) ]$ remain as $\mathcal{W}$ increases, it means that the results for $\mathcal{W}=2$ are not an artifact of such a choice. The key characteristic we care about is the typical functional relation between $L_{i}^{*}$ and $k_{i}/\lambda _{i}$. Just as for the plot discussed in the main text, we can see that the level sets of maximum probability are parallel to the linear “best fit” planes. Note that in all the plots, for values of $L_{i} \sim 10^{2}$ and above together with $k_{i}/\lambda _{i}\sim 10^{2}$ and above, the level sets of highest probability run parallel to the linear planes of “best fit”. Furthermore, we can observe that as $\mathcal{W}$ increases, the range of the level sets that deviates from the “best fit” planes is located at the small values of $L_{i}^{*}$ and $k_{i}/\lambda _{i}$, which should not be surprising since an increase in $\mathcal{W}$ means that firms with very few numbers of employees cannot be well represented.

Figure 21

Behavior of $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L^{*}_{i}|k_{i}/ \lambda _{i}) ]$ (surface $\mathcal{S}$) with respect to $\log _{10} L_{i}$ and $\log _{10} k_{i}/\lambda _{i}$ for Finland when A is created with links where the traffic has a minimum of 3,4,5 transitions (top, middle, bottom plots). The data is logarithmically binned as follows: $L_{i}$ belongs to bin b (a non-negative integer) if $L_{\mathrm{min}}\zeta ^{b}< L_{i}\leq L_{\mathrm{min}}\zeta ^{b+1}$ with $\zeta >1$ (for this plot $\zeta =2$) and $L_{\mathrm{min}}=\min [\{L_{i}\}]$ (smallest firm size in the data); $k_{i}/\lambda _{i}$ is binned in the same way with ζ and $(k/\lambda )_{\mathrm{min}}=\min [\{(k_{i}/\lambda _{i})\}]$. Blue points represent the local maximum of $\mathcal{S}$ at each bin. The vertical plane $\mathcal{P}$ (linear “best fit”) is parametrized as $(k_{i}/\lambda _{i}, C_{L} k_{i}/\lambda _{i},z)$ where z is a free parameter. $C_{L}$ is chosen to minimize $\sum_{b} (L^{*}_{b}-C_{L}(k/\lambda )_{b} )^{2}$ with the first three bins excluded because the smallest firm size is 1. The large range within which the intersection of $\mathcal{P}$ and $\mathcal{S}$ runs parallel to the maxima of $\mathcal{S}$ strongly supports Eq. (18) of the main text

Therefore, the overall conclusion is that the match between the homogeneous model, represented by Eqs. (15) and (16) with $r_{\infty }(i)=r_{\infty }^{(v)}(i)$ and $s_{\infty }(i)=s_{\infty }^{(v)}(i)$ from Eqs. (11) and (12), respectively, are supported by our analysis of the Finnish data even as the criterion for including a link in A is made more stringent.

1.8 A.8 Further evidence of steady-state behavior

While the balanced-flows plot presented in the main text provide evidence of steady-state behavior in the data, the reader might be concerned about other types of fluctuations that are not addressed by such test. For example, it might be the case that, even with balanced flows and a constant population, the firm size cumulative distribution might change its shape through time. Figure 22 shows the firm size cumulative distribution obtained for yearly measurements from the Finnish data. It is clear that the distribution is robust across time, and that the only changes are upward shifts due to the population growth through several years. This way of showing evidence of steady-state behavior is more standard in the study of firm dynamics.

Figure 22

Annual firm size cumulative distributions for Finland between 1988 and 2008

In addition to the previous test, we also check that the effects that may be proportional to firm size do not hide systematic behavior that we cannot see in the simple study of raw flows. In Fig. 23, we plot the histogram of the net fractional flow for Finland. Here too, we see a very large concentration of the histogram around a zero fractional flow. Note the vertical logarithmic scale.

Figure 23

Histogram of fractional net flows with respect to firm size for the Finnish dataset. The results are concentrated around 0, supporting the steady state assumption

As a final test, we look at the changes in the network structure from year to year using the time dimension of our data. Consider $V(t)$ the set of network links that are accepted to the overall labor flow network when the data is analyzed starting from the year t and going to the end of the data in year $t_{f}$ (the data spans from $t_{o}=1988$ to $t_{f}=2007$). In other words, the links in $V(t)$ are between node pairs that had flow at or above the threshold $\mathcal{W}=2$ between years t and $t_{f}$. Now, we calculate $V(t)$ for all possible t (i.e. systematically varying the starting year) which creates the series $V(t_{o}),V(t_{o}+1),\dots,V(t_{f}-1)$. From these results, we define the Jaccard index $J(t)$ of the links as the quotient

$$ J(t)=\frac{ \vert V(t)\cap V(t+1) \vert }{ \vert V(t)\cup V(t+1) \vert }, $$

(65)

where the numerator counts how many links that are accepted into $V(t)$ from analyzing the data from year t to $t_{f}$ are also accepted into $V(t+1)$ using years $t+1$ to $t_{f}$ of the data, and the denominator counts the number of unique links that belong to either $V(t)$ or $V(t+1)$ including links belonging to both. In other words, $J(t)$ measures how similar $V(t)$ and $V(t+1)$ are to one another; at its limit values, $J(t)$ is equal to 1 when $V(t)=V(t+1)$ and 0 when $V(t)\cap V(t+1)=\emptyset$, i.e., $V(t)$ and $V(t+1)$ do not have any common links. Figure 24 shows the results of this analysis. For the vast majority of years, the Jaccard index is close to 1 and decays slightly towards the later years due to the short time range available to test links against the acceptance criterion. The meaning of these results is that despite the dynamics of the network, the labor flow network determined from persistent links changes by 10% or less in any typical year. Thus our method should be stable to yearly changes in the network over time to a level that generally exceeds 90%.

Figure 24

Jaccard index for the link sets $V(t)$ of the data, defined as $J(t)=|V(t)\cap V(t+1)|/|V(t)\cup V(t+1)|$. The solid line corresponds to the points $(t_{o},J(t_{o})),(t_{o}+1,J(t_{o}+1)),\dots,(t_{f}-1,J(t_{f}-1))$

1.9 A.9 Firm sizes for Mexican data

In the main text, we present the analysis of firm sizes for Finland and the firm-specific unemployment for Mexico but, because there is no data available to deal with Finnish firm-specific unemployment, we do not present results for this case. However, there is data for firm sizes for Mexico which, in the interest of space, we do not show in the main text. Here, we present this analysis as a supplement to our main analysis. Because of the method of collection of the data for Mexico, it is not possible to have results as clean as those for Finland since the sampling has not been done uniformly on firms but rather on individuals. However, the results for the Mexican data are not inconsistent with the Finnish results.

As in the main text, we use the data to draw a comparison with the homogeneous model that assumes $v_{i}=v$. This model predicts that $L_{i}\sim k_{i}/\lambda _{i}$, as seen from Eq. (18) of the main article. Therefore, in Fig. 25, we present the 3-dimensional plot of $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/ \operatorname{Pr}(L_{i}^{*}|k_{i}/ \lambda _{i}) ]$ as a function of $\log _{10}L_{i}$ and $\log _{10}(k_{i}/\lambda _{i})$. Once again, $\operatorname{Pr}(L_{i}^{*}|k_{i}/\lambda _{i})$ corresponds to the probability associated with the conditional mode $L_{i}^{*}$. The normal plane is parametrized as indicated in the caption. The relation between $L_{i}$ and $k_{i}/\lambda _{i}$ is again supported by this plot, although more fluctuations appear towards firms of larger size and/or of large degree $k_{i}$. These firms are less likely to be properly sampled because, even though they have more employees, there are fewer of them (the same complication emerges for the plots of firm-specific unemployment, by the way).

Figure 25

Behavior of $\log _{10} [\operatorname{Pr}(L_{i}|k_{i}/\lambda _{i})/\operatorname{Pr}(L^{*}_{i}|k_{i}/ \lambda _{i}) ]$ (surface $\mathcal{S}$) with respect to $\log _{10} L_{i}$ and $\log _{10} k_{i}/\lambda _{i}$ for Mexico. The data is logarithmically binned as follows: $L_{i}$ belongs to bin b (a non-negative integer) if $L_{\mathrm{min}}\zeta ^{b}< L_{i}\leq L_{\mathrm{min}}\zeta ^{b+1}$ with $\zeta >1$ (for this plot $\zeta =2$) and $L_{\mathrm{min}}=\min [\{L_{i}\}]$ (smallest firm size in the data); $k_{i}/\lambda _{i}$ is binned in the same way with ζ and $(k/\lambda )_{\mathrm{min}}=\min [\{(k_{i}/\lambda _{i})\}]$. Blue points represent the local maximum of $\mathcal{S}$ at each bin. The vertical plane $\mathcal{P}$ is parametrized as $(k_{i}/\lambda _{i}, C_{L} k_{i}/\lambda _{i},z)$ where z is a free parameter. $C_{L}$ is chosen to minimize $\sum_{b} (L^{*}_{b}-C_{L}(k/\lambda )_{b} )^{2}$ with the first three bins excluded because the smallest firm size is 1. The large range within which the intersection of $\mathcal{P}$ and $\mathcal{S}$ runs parallel to the maxima of $\mathcal{S}$ strongly supports Eq. (18) of the main text

1.10 A.10 RANSAC

The RANSAC algorithm [37] is a popular method to estimate parametric models when data has large amounts of outliers, which is our case. The algorithm performs an OLS estimation by randomly sampling the minimum number of data points needed to fit the model. Then, it identifies those data points from the entire dataset that fall within a given distance from the estimated model. These two steps are repeated until a model with a maximum number of inlier data points is found. Since RANSAC is non-deterministic, it yields slightly different estimations every time it is performed. For this reason, we performed 1 million RANSAC estimations and analyzed the distribution of their estimates. We employed the default parameters of 2 minimum observations, the median absolute deviation as a threshold to distinguish between inliers and outliers, and the maximum number of trials of 100 which are standard values in the literature.

To be specific, each RANSAC run consists of two steps. First, a data subset is sampled and the model is estimated. The sample size has to be of the minimum necessary to estimate the model. Second, the data that was not sampled is compared against the predictions of the estimated model. Given an error threshold, those data points that are not predicted by the model are considered outliers. The points that are correctly predicted form the consensus set. If the consensus set contains too few data points, the estimated model is dropped and the algorithm goes back to step one. Otherwise, the model is re-estimated with the consensus set and the error is computed. These steps are repeated until the error term reaches a threshold. Parameter calibration used default values from the implementation in the SciKit Learn package.