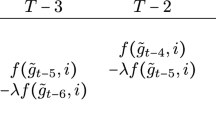Abstract
The network theory developed by physicists has several critical drawbacks in characterizing the structure of social networks. First, they largely neglect considering the link cost and the link benefit that agents usually take into account in forming their links. Second, they view a social network as a consequence of unilateral decisions of agents, not of bilateral decisions of linking parties, although a link of an agent can be formed only after he obtains the consent of the other side. Third, there is no logical justification for the assumption of preferential attachment upon which their analysis heavily relies. In this paper, we provide several models that overcome the three drawbacks. By analyzing the models, we can explain preferential attachment as rational equilibrium behavior. The main idea is that people are not certain of the value that they can obtain from forming a link with someone. Based on this assumption, we will argue that a person has an incentive to form a link with another who has many links because the number of his links can convey some information about his value.





Similar content being viewed by others
Notes
The power law says that the distribution of nodes with a certain number of links follows a power function.
For example, Liljeros et al. (2001) showed the distribution of the number of sexual partners decays as a scale-free power law. Ahn (2005) recently studied the network structure of the closest friends (that can be linked with each other after mutual agreement) in the CyWorld, which is one of the most popular online communities, and found that the degree distribution in the network follows a pattern close to the power law.
A scale-free network is a network in which the distribution of connectivity is extremely uneven in the sense that some nodes act as very connected hubs using a power-law distribution.
Evidences for preferential attachment have been documented in literature. See, for example, Jeong et al. (2003) identified the evidence of preferential attachment in the science citation network, the actor collaboration network, the science coauthorship network.
Economists use the word “signal” to mean an observable variable containing some information about an unobservable characteristic. This concept has been widely used in economics since Spence (1973).
Economists classify goods roughly into two categories, search goods and experience goods. The former refers to goods the quality of which can be ascertained by consumers before purchase, and the latter refers to goods the quality of which is learned only after purchase. This taxonomy follows from Nelson (1970).
If agents can get some benefit from indirect connections as well, they may have an incentive to behave strategically, since their utility would also depend on the decisions of other agents. This would complicate the analysis significantly.
If agents are not myopic, their decisions to sever a link can be affected. We will consider this possibility in Section 7.
If v 1 =L, agent 2 gains nothing by postponing severing his link (regardless of v 2 =H or L), because subsequent entrants will keep forming links with agent 1 anyway.
In a pooling equilibrium, players choose the same action (postponing severing their links) regardless of their private information (neighbor’s types), while a different type of player chooses a different action in a separating equilibrium.
This notion follows the spirit of “trembling hand perfectness” by Selten (1975), allowing some mistakes of players.
All that is needed in making a decision to sever a link with an agent is to know whether he is L or H, while a linking decision requires much more information (probabilities that each senior is of H type).
A behavioral strategy, which involves randomization over pure actions at an information set, is distinguished from a mixed strategy involving randomization over pure strategies. For a relation between the behavioral strategy and the mixed strategy, see Kuhn (1953).
References
Ahn Y-Y (2005) CyWorld (in Korean). http://janice.kaist.ac.kr/~gomeisa/wiki/wiki.php/CyWorld/Summary?action=print
Aumann R, Myerson R (1988) Endogenous formation of links between players and coalition: an application of the shapley value. In: Roth A (ed) The shapley value. Cambridge University Press, Cambridge
Bala V, Goyal S (2000) A noncooperative model of network formation. Econometrica 68:1181–1229
Barabási A-L, Albert R (1999) Emergence of scaling in random networks. Science 286:509–512
Bianconi G, Barabási A-L (2001) Bose-Einstein condensation in complex networks. Phys Rev Lett 86:5632–5635
Dutta B, Mutuswami S (1997) Stable networks. J Econ Theory 76:322–344
Jackson M (2005) The economics of social networks. Based on a lecture in the 9th World Congress of the Econometric Society. http://www.hss.caltech.edu/~jacksonm/netect.pdf
Jackson M, van den Nouweland A (2005) Strongly stable networks. Games Econom Behav 51:420–444
Jackson M, Watts A (2002) The evolution of social and economic networks. J Econ Theory 106:265–295
Jackson M, Wolinsky A (1996) A strategic model of social and economic networks. J Econ Theory 71:44–74
Jeong H, Neda Z, Barabási A-L (2003) Measuring preferential attachment in evolving networks. Europhys Lett 61:567–572
Kuhn HW (1953) Extensive games and the problem of information. Ann Math Stud 28:193–216
Liljeros F, Edling C, Amaral LA, Stanley HE, Åberg Y (2001) The web of human sexual contacts. Nature 411:907–908
Myerson R (1978) Refinements of the Nash equilibrium concepts. Int J Game Theory 7:73–80
Nelson P (1970) Information and consumer behavior. J Polit Econ 78:311–329
Page F, Wooders M, Kamat S (2005) Networks and farsighted stability. J Econ Theory 120:257–269
Price D (1965) Networks of scientific papers. Science 149:510–515
Price D (1976) A general bibliometric and other cumulative advantage processes. J Am Soc Inf Sci 27:292–306
Selten R (1975) Reexamination of the perfectness concept for equilibrium points in extensive games. Int J Game Theory 4:25–55
Spence M (1973) Job market signaling. Q J Econ 87:355–374
Watts A (2001) A dynamic model of network formation. Games Econom Behav 34:331–341
Watts A (2002) Non-myopic formation of circle networks. Econ Lett 74:277–282
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by Kyung Hee University Research Fund 2007 (KHU-20071591).
Appendix
Appendix
Proof of Lemma 2
(i) Since player i has been once linked with some j, either v i = L or v j = L if d(i; g t − 1, 2) = 0. Thus, \(\alpha_t (i)=\frac{\alpha}{1+\alpha}<\alpha_t (t-1)=\alpha\). (ii) If (i, j) ∈ g t − 1, 2 for some j < t − 1, α t (i) = 1 > α t (t − 1) = α by Lemma 1. (iii) Let (i, j) ∈ g i, 1. Clearly, j < i. If (i, t − 1) ∈ g t − 1, 2 and d(i; g t − 1, 2) = 1, this implies that (i,j) has been deleted. This implies that either v i = L or v j = L. Thus, \(\alpha_t (i{\kern1.5pt})=\frac{\alpha}{1+\alpha}<\alpha_t (t-1)=\alpha\). □
Proof of Lemma 4
It is clear that g 2, 1 = g 2, 2 satisfies [UNC], since it is connected. Suppose g t − 1, 2 satisfies [UNC]. From Lemma 2(i), it is clear that g t, 1 also satisfies [UNC]. It only remains to show that g t, 2 satisfies [UNC]. Two possible cases are that either (i) (i, t) ∈ g t, 1 for i ≠ t − 1 or (ii) (t − 1, t) ∈ g t, 1. In the case (i), supposing (t − 1, k) ∈ g t, 1 for some k ∈ N t − 2 and deleting (t − 1, k) decomposes g t, 1 − (t − 1, k) into more than one nonempty component. This means that d(t − 1; g t, 1) ≥ 2, which is not possible. Consider the other case (ii). Since g t − 1, 2 satisfies [UNC], d(t − 1; g t − 1, 2) = 1. Let the neighbor of player t − 1 be k ∈ N t − 1, i.e., (t − 1, k) ∈ g t − 1, 2. If d(k; g t − 1, 2) = 1, g t, 2 − (t − 1, k) still satisfies [UNC]. If d(k; g t − 1, 2) ≥ 2, it is a contradiction to (t, t − 1) ∈ g t, 1 due to Lemma 2(ii). □
Proof Proposition 1
For any t, define
Then, \(N_{t-1}=\{t-1\}\cup N_{t-1}^{0}\cup N_{t-1}^{1}\cup N_{t-1}^{2}\). Also, define
From Lemma 2, it is clear that (i) t − 1 ≻ t i for \(i\in N_{t-1}^{0}\cup N_{t-1}^{1, 0}\) and (ii) i ≻ t t − 1 for \(i\in N_{t-1}^{2}\cup N_{t-1}^{1, 2} \equiv \bar{N}_{t-1}\). If \(\bar{N}_{t-1}\neq \emptyset\), it is optimal for player t to choose to link with player \(i\in \bar{N}_{t-1}\). If \(\bar{N}_{t-1}=\emptyset\), it is optimal for him to choose to link with player t − 1. Thus, the decision of agent t to choose to link with a player \(i\in N_{t-1}^{2}\) if \(\bar{N}_{t-1}\neq \emptyset\) and to link with a player t − 1 otherwise satisfies preferential attachment. □
Proof of Lemma 5
Suppose v i = L. If i = t − 1, d(i; g t − 1, 2) = 1( < 2), so it must be that i < t − 1. Then, the links of player i except the link with t − 1 would have been deleted at latest by period t − 1. Thus, d(i; g t − 1, 2) could be at most one. Contradiction. □
Proof of Lemma 6
(i) It is clear, because α t (i) = α t (j) = 1 by Lemma 5. (ii) This is also clear because α t (i) = 1 > α t (j). (iii) We have \(\alpha_t (j{\kern1.5pt})=\frac{\alpha}{1+\alpha}\) for j such that d(j; g t − 1, 2) = 0. On the other hand, consider player i such that d(i; g t − 1, 2) = 0. Either i = t − 1 or i ≠ t − 1. If i = t − 1, \(\mbox{Prob}(v_i =H)=\alpha\). If i ≠ t − 1, \(\mbox{Prob}(v_i =H \mid i\neq t-1)=\frac{\alpha}{1+\alpha}\). Thus, \(\alpha_t (i)=\theta \alpha+(1-\theta)\frac{\alpha}{1+\alpha}\) for some θ ∈ (0, 1). Since \(\alpha >\frac{\alpha}{1+\alpha}\), \(\alpha_t (i{\kern1.5pt})>\frac{\alpha}{1+\alpha}=\alpha_t (j{\kern1.5pt})\). □
Proof of Proposition 3
(i) \((\Longrightarrow )\) Under (A2), the myopic equilibrium is not viable, as argued in the text, so this is clear. \((\Longleftarrow)\) Note that \(\frac{\delta}{2}(M-c)\) is the maximum gain attainable by postponing severing a link for one or more than one period, while c − L is the minimum loss from postponing severing a link. (Postponing severance for more than one period incurs c − L + δ(c − L) + ⋯.) Thus, if \(c-L>\frac{\delta}{2}(M-c)\), no other deviation will be profitable, implying that the myopic equilibrium is sustainable. (ii) The proof is similar. □
Proof of Proposition 4
Let x(t) be the number of H types in N t , that is, \(x(t)=\sum_{i=1}^{t} x_i\) where x i = 1 if v i = H and x i = 0 if v i = L. Since E(x i ) = α and \(\mbox{Var}(x_i )=\alpha (1-\alpha)\), we have μ ≡ E(x(t)) = αt and \(\sigma^2 \equiv \mbox{Var}(x(t))=\alpha (1-\alpha) t\).
Suppose that for some t * x(t * ) = n for some large n such that \(L-c+\delta \frac{M-c}{n}<0\), or equivalently, \(n>\delta \frac{M-c}{c-L}\). Then, for i, j ≤ t * − 1, link (i, j) with v i = L or v j = L will not survive the second stage of period t *. Knowing this, it is optimal for agent i (i ≥ t * + 1) to choose the equilibrium strategy of a myopic agent.
It remains to show that with probability one, there exists t * such that x(t * ) = n, in other words, that x(t) < n for all t with probability zero. By Chebyshev’s inequality, we have
Let 1/k 2 = ε, i.e., \(k=1/\sqrt{\epsilon}\). Then, inequality (2) can be written as
Note that inequality (2) holds for any t. Thus, we have \(P\big(x(t)<\mu-\sigma/\sqrt{\epsilon}\big)<\epsilon\). Since μ = αt and σ 2 = α(1 − α)t, we have
where \(\bar{x}(t)=\alpha t -\sqrt{\frac{\alpha (1-\alpha)t}{\epsilon}}\). Note that \(d\bar{x}(t)/dt>0\) if t ≥ t 1 for some large t 1 and that \(\lim_{t\rightarrow \infty} \bar{x}(t)=\infty\). Since \(\lim_{t\rightarrow \infty} \bar{x}(t)=\infty\), we can take t 2 such that \(\bar{x}(t_2 )\equiv \alpha t_2 -\sqrt{\frac{\alpha (1-\alpha)t_2}{\epsilon}}>n\). Take \(\bar{t}=\max\{t_1, t_2\}\). Then, \(P(x(t)<n)<P\big(x(t)<\alpha t -\sqrt{\frac{\alpha (1-\alpha)t}{\epsilon}}\big)<\epsilon\) for all \(t\geq \bar{t}\). This implies that there exists t * such that x (t * ) = n with probability one. □
Rights and permissions
About this article
Cite this article
Kim, JY., Jo, HH. A signalling explanation for preferential attachment in the evolution of social networks. J Evol Econ 20, 375–393 (2010). https://doi.org/10.1007/s00191-009-0155-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00191-009-0155-7