Bias-constrained integer least squares estimation: distributional properties and applications in GNSS ambiguity resolution

Abstract

To accommodate the presence of bounded biases in mixed-integer models, Khodabandeh (2022) extended integer estimation theory by introducing a new admissible integer estimator. The estimator follows the principle of integer least squares estimation and is computed via the integer search method of BEAT. In this contribution, we present the probability distributions of a class of estimators to which the proposed bias-constrained integer least squares estimation belongs. Some important interferometric measuring systems, whose estimation problems can be covered by BEAT, are identified. To show the proposed estimator at work, we apply BEAT to the problem of GLONASS single-differenced (SD) ambiguity resolution. Numerical results of several short-baseline datasets are presented to illustrate why one can achieve more accurate positioning solutions when considering between-receiver SD ambiguity resolution for the cases where carrier phase data are captured on frequency-varying signals with bounded SD receiver phase delays.

1 Introduction

Integer ambiguity resolution (IAR) is the process of finding the ambiguous cycles of carrier phase measurements as integers. It has found a widespread usage in GNSS (Teunissen 1993; de Jonge and Tiberius 1996; Han 1997; Hassibi and Boyd 1998) and has been applied to several other high-precision interferometric measurement systems (Hanssen 2001; Maróti et al. 2005; Viegas and Cunha 2007; Hobiger et al. 2009; Wang et al. 2015; Zaminpardaz 2016). Provided that IAR is successfully conducted, the ambiguity-resolved phase measurements can deliver ultra precise parameter solutions and, in the case of GNSS, offer instantaneous precise positioning, navigation, and Earth atmospheric-sensing services, see  (Gunther and Henkel 2012; Li et al. 2014; Banville 2016; Khodabandeh and Teunissen 2016; Brack et al. 2021).

Successful IAR often relies on the provision of ‘auxiliary’ data such as GNSS code measurements and/or external pseudo-observations so as to ensure ‘unbiased’ estimation of the integer ambiguities, bypassing their linear dependency with the remaining parameters that are involved in the phase observation equations. When such extra sources are absent or when the quality description of the data is not properly specified, the phase ambiguities experience non-integer biases, seriously deteriorating the underlying parameter estimation process (Teunissen 2001). To accommodate the presence of such unaccounted ambiguity biases, Khodabandeh (2022) developed a new integer estimator that incorporates the prior knowledge of a bounded set, in which the bias resides, into the estimation process. The estimator follows the principle of integer least squares estimation and its search method is coined as the method of ‘Bias-bounded Estimation of AmbiguiTy’ (BEAT). The goal of this contribution is to present the probability distributions of a class of estimators to which the proposed bias-constrained integer least squares estimation belongs, and illustrate its BEAT at work. We present a formal proof stating that the estimator delivers a bias solution that has, on average, the smallest inconsistency with its underlying model as compared to other members of the class of admissible integer estimators.

This contribution is organized as follows. In Sect. 2 we first, by means of examples, provide an overview of some important interferometric measuring systems whose estimation problems can be addressed by the BEAT method. Despite being employed for different applications, the observation equations of these systems are thereby shown to be cast in the form of a bias-bounded mixed-integer model. In Sect. 3, we therefore address how the unknown parameters, involved in such model, can be estimated via integer estimation theory, characterizing their associated class of estimators. The distributional behaviour of these estimators is studied through their respective probability density functions (PDFs), where the input observables are assumed to be normally distributed. To show the underlying search method, i.e. BEAT, at work, the analytical results are supported by the problem of GLONASS single-differenced (SD) ambiguity resolution in Sect. 4. Provided that the bound on the corresponding SD receiver phase delays is correctly specified, SD IAR of several globally distributed short-baselines is shown to deliver more accurate fixed positioning solutions than its existing partial IAR counterpart. Finally, a summary with conclusions is provided in Sect. 5.

We make use of the following notation: The expectation operator is symbolized by $\textsf{E}(\cdot )$, while the symbol $\textrm{P}(\cdot )$ stands for the probability of a random event. The notation ‘|’ is used to indicate the ‘conditional’ nature of a random event. Thus X|Y refers to random event X, given that event Y has occurred. The m-dimensional spaces of real and integer numbers are denoted by $\mathbb {R}^m$ and $\mathbb {Z}^m$, respectively. The transpose of a matrix is indicated by the superscript T, i.e. $(\cdot )^\textrm{T}$. The identity matrix of order n is denoted as $I_n$. The capital Q is reserved for variance (covariance) matrices. Thus $Q_{xy}$ denotes the $m\times n$ covariance matrix of random vectors $y\in \mathbb {R}^m$ and $x\in \mathbb {R}^n$, while the $m\times m$ variance matrix of y is given by $Q_{yy}$. The PDF of random vector $y\in \mathbb {R}^m$ is denoted by $f_y(\alpha )$, with $\alpha \in \mathbb {R}^m$ being its argument. The notation $y \sim \mathcal {N}_{m}(\mu , Q_{yy})$ means that the random vector $y\in \mathbb {R}^m$ follows an m-dimensional normal (Gaussian) distribution, with mean $\mu$ and variance matrix $Q_{yy}$. The notation $||\cdot ||_{Q}$ is a weighted norm whose weight matrix is given by the inverse of the positive definite matrix Q. Thus $||x||_{Q}^2 = x^\textrm{T}Q^{-1}x$, where $x\in \mathbb {R}^n$. When $Q=I_n$, the weighted norm reduces to the standard Euclidean norm $||\cdot ||$. The notation $\textrm{det}(\cdot )$ indicates the determinant of a square matrix.

2 Bias-bounded mixed-integer models

As our point of departure, consider the following mixed-integer model

$$\begin{aligned} \textsf{E}(y) = A\, a+ C\, c \end{aligned}$$

(1)

where the observable random vector $y\in \mathbb {R}^m$ is linked to the unknown parameter vectors $a\in \mathbb {Z}^n$ and $c\in \mathbb {R}^k$ via the known full-column rank design matrix [A, C]. Thus, $m\ge n+k$. A leading example of model (1) is the system of GNSS network observation equations where the role of y is taken by pseudo-range (code) and carrier phase measurements. The integer-estimable phase ambiguities form the integer vector a, while vector c is formed by the remaining estimable parameters like network position coordinates, satellite and receiver clock offsets, instrumental biases, and atmospheric delays (Teunissen and Montenbruck 2017).

The mixed-integer model (1) is versatile and has been employed, next to GNSS, in several other interferometric techniques such as Very Long Baseline Interferometry (VLBI) (Hobiger et al. 2009), Interferometric Synthetic Aperture Radar (InSAR) (Kampes and Hanssen 2004), and underwater acoustic carrier phase positioning (Viegas and Cunha 2007). As the examples below will show, however, there are cases for which the model (1) becomes restrictive in the sense that it fails to account for the presence of biases in the ambiguity vector a. In such cases, the ambiguity vector a may contain non-integer entries, i.e. $a\notin \mathbb {Z}^n$. The deviation of a from an integer target vector $z\in \mathbb {Z}^n$ is thus characterized by an unknown non-integer term. Let such term be parameterized as $B\,b$, where $b\in \mathbb {R}^q$ denotes the bias vector accompanied by the known full-column rank matrix $B\in \mathbb {R}^{n\times q}$ ($n\ge q$). Accordingly, the revised version of (1) reads

$$\begin{aligned} \textsf{E}(y) = A\,(\underbrace{z+B\,b}_a)+ C\, c \end{aligned}$$

(2)

The above model follows from (1) by replacing the vector a with its bias-affected version $a=z+Bb$. Due to the inherent rank-deficiency between z and b in $a=z+Bb$, one cannot obtain a unique integer solution for the target vector $z\in \mathbb {Z}^n$ without imposing an extra constraint on the bias vector b. Thanks to the robustness of integer ambiguity resolution (IAR) against ‘not-too-large’ biases (Teunissen 2001; Li et al. 2014), one may augment the mixed-integer model (2) with a known bounded subset $\mathcal {B}\subset \mathbb {R}^q$ in which the bias vector b resides. The nonempty set $\mathcal {B}$ is said to be ‘bounded’ if for all $\nu \in \mathcal {B}$, there exist $\nu _o\in \mathcal {B}$ and scalar $h\ge 0$ such that $||\nu -\nu _o|| \le h$. The augmentation of model (2) with the bias constraint $b\in \mathcal {B}$ is referred to as the ‘bias-bounded mixed-integer model’ (Khodabandeh 2022).

Before addressing how the three parameter vectors $z\in \mathbb {Z}^n$, $b\in \mathcal {B}\subset \mathbb {R}^{q}$ and $c\in \mathbb {R}^k$ are estimated, let us first briefly review, by means of examples, some interferometric measuring systems whose estimation problems can be covered by the bias-bounded mixed-integer model (2).

Example 1

(Stacked radar interferometry) InSAR has found a widespread usage in Earth deformation monitoring and subsidence analysis, see e.g., (Hanssen 2001; Wu et al. 2023). As electromagnetic phase sensory data form the basis of InSAR measuring techniques, their parameter estimation relies on the successful execution of ambiguity resolution. Let the observation vector y contain $y_{lj}^{i}$ as the observed phase differences (expressed in cycles) between two pixels l and j that are captured by m interferograms over epochs i ($i=1,\ldots ,m$) relative to a reference epoch $i=0$. The corresponding observation equation reads (Hanssen et al. 2001)

$$\begin{aligned} \textsf{E}(y) = z-\frac{2\tau }{\lambda }[1,2,\ldots ,m]^\textrm{T}\,b \end{aligned}$$

(3)

where $\tau$ is the time-interval between two successive interferograms, with the effective radar wavelength $\lambda$. Here, the unknown deformation rate plays the role of the bias vector $b\in \mathbb {R}^{q}$, i.e. $q=1$. The system of observation equations (3) follows as a special case of (2) by recognizing that $A=I_m$ (identity matrix), and $B=-\frac{2\tau }{\lambda }[1,2,\ldots ,m]^\textrm{T}$, while matrix C is absent. The goal is to estimate the deformation rate b. This would, however, not be realized with the sole use of (3). This is because the model is not solvable for both $z\in \mathbb {Z}^m$ and b. As a consequence, an extra pseudo-observation of the deformation rate b is often considered to remove the rank-deficiency between z and b. In the event that a proper quality description of such pseudo-observation is not specified, the information content in the phase observations y cannot be fully exploited. Instead of introducing a pseudo-observation, one may incorporate lower and upper bounds of the values, that the deformation rate b can take on, into the model (Teunissen 2006). For this case, the subset $\mathcal {B}$ is characterized as

$$\begin{aligned} \mathcal {B}=\left\{ \nu \in \mathbb {R}|~\nu _{_L}\le \nu \le \nu _{_U}\right\} \end{aligned}$$

(4)

with $\nu _{_L}$ and $\nu _{_U}$ being the stated lower and upper bounds, respectively. This subset is bounded because $|\nu -\nu _o|\le h$ with $h=\textrm{max}(|\nu _{_L}-\nu _o|,|\nu _{_U}-\nu _o|)$ for all $\nu \in \mathcal {B}$. $\boxtimes$

Example 2

(Ionospheric gradient monitoring) The Earth ionospheric disturbance is regarded as one of the main potential threats to aerospace navigation (Giorgi and Henkel 2015; Zaminpardaz et al. 2015; Yoshihara et al. 2019). Ground-Based Augmentation Systems (GBAS) are therefore established within the premises of airports to detect and monitor ionospheric spatial gradients, thereby supporting GNSS guidance during the landing phases of an aircraft. To avoid code multipath and phase cycle-slips, single-epoch carrier phase data of the GBAS antennas may be utilized. The observation equations of such phase-only setup are given as (Khanafseh et al. 2012)

$$\begin{aligned} \textsf{E}(y) = \lambda \, z + B\,b,~\text {with}~ B = \left[ \begin{array}{cccc} e_{1} &{} e_{2} &{}\ldots &{} e_{m}\\ n_{1} &{} n_{2} &{}\ldots &{} n_{m}\end{array}\right] ^\textrm{T} \end{aligned}$$

(5)

where $e_{r}$ and $n_{r}$ are, respectively, the local east and north coordinates of the GBAS antenna r ($r=1,\ldots ,m$) relative to the coordinates of a reference antenna $r=0$. Here, the GNSS double-differenced (DD) carrier phase data $y\in \mathbb {R}^m$ are expressed in units of range, with the L-band wavelength $\lambda$. The goal is to estimate the ionospheric spatial gradient $b\in \mathbb {R}^2$ ($q=2$) on a local east-north horizontal plane, and raise alarms in case the magnitude of b exceeds certain thresholds. As with (3), model (5) is rank-defect and follows as a special case of (2) with $A=\lambda \, I_m$, while matrix C is absent. To deliver unique solutions for both z and b, bounds on the magnitude of b need to be imposed. Although the magnitude of ionospheric spatial gradients occasionally exceeds 300 mm/km, one may consider an ellipsoidal region of conservative size in which the vector b lies (Giorgi and Henkel 2015). Accordingly, the subset $\mathcal {B}$ is characterized as

$$\begin{aligned} \mathcal {B}=\left\{ \nu \in \mathbb {R}^2|~||\nu ||_Q^2\le \chi ^2\right\} \end{aligned}$$

(6)

in which Q is a given positive definite matrix, with a known positive scalar $\chi$ governing the size of the ellipse. The boundedness of subset $\mathcal {B}$ follows from $||\nu ||\le h$ with $h=\sqrt{\gamma _\textrm{max}}\,\chi$ for all $\nu \in \mathcal {B}$, where $\gamma _\textrm{max}$ denotes the largest eigenvalue of matrix Q. $\boxtimes$

Example 3

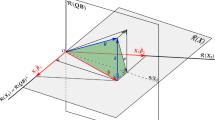
(Interferometric wireless networks) While GNSS users enjoy the support of code data with time-constant phase ambiguities, the users of wireless sensor localization techniques, like Radio Interferometric Positioning Systems, are often left with phase data whose ambiguities are not constant over time, see e.g., Maróti et al. (2005) and Khodabandeh (2022). Broadcasting radio phase signals on several ‘distinct’ frequencies, a network of wireless sensors are aimed to deliver high-precision positioning solutions. Their system of observation equations reads (Maróti et al. 2005)

$$\begin{aligned} \textsf{E}(y) = z + B \,b, ~\text {with}~ B = \left[ I_{q},\frac{\lambda _1}{\lambda _2}I_{q},\ldots ,\frac{\lambda _1}{\lambda _f}I_{q}\right] ^\textrm{T} \end{aligned}$$

(7)

where $\lambda _j$ is the wavelength on frequency j ($j=1,\ldots ,f$). The observation vector $y\in \mathbb {R}^m$ contains DD phase data (expressed in cycles) that are collected by a pair of pivot and rover receivers tracking $q+1$ transmitters. Thus $m=fq$ (f: number of frequencies). The role of bias vector $b\in \mathbb {R}^q$ is taken by the unknown DD ranges of the receivers and transmitters. The position of the rover receiver $x_r\in \mathbb {R}^3$ can be determined once the DD ranges are estimated. It is assumed that the position vectors of the pivot receiver $x_p\in \mathbb {R}^3$ and the transmitters $x^s\in \mathbb {R}^3$ ($s=1,\ldots ,q+1$) are known. If the distance between the rover receiver and a certain location $x_o\in \mathbb {R}^3$ is known to be not longer than a positive scalar $\chi$, i.e. $||x_r-x_o||\le \chi$, the subset ${\mathcal {B}}$ can then be identified as (Khodabandeh 2022)

$$\begin{aligned} {\mathcal {B} {=} \left\{ \nu \in \mathbb {R}^q |~ \nu {=} \frac{1}{\lambda _1}D_{q{+}1}^\textrm{T}\,\rho (x_r),~||x_r{-}x_o||\le \chi , x_r\in \mathbb {R}^3\right\} }\nonumber \\ \end{aligned}$$

(8)

where the $(q+1)\times q$ between-transmitter differencing matrix is indicated by $D_{q+1}$. The entries of the $(q+1)$-vector $\rho (x_r)$ are $||x_r-x^s||\!-\!||x_p-x^s||$ ($s=1,\ldots ,q+1$). The set $\mathcal {B}$ is bounded because $||\nu \!-\!\nu _o|| < h$ for all $\nu \in \mathcal {B}$ with $h=(q\!+\!1)(\chi /\lambda _1)$, where $\nu _o\!=\!(1/\lambda _1)D_{q+1}^\textrm{T}\,\rho (x_o)$. $\boxtimes$

Example 4

(Bounded SD receiver phase delays) In the previous examples, the focus was confined to phase-only measurement setups in which the parameter vector c of model (2) is absent. We now consider the case where not only do the unknowns c exist, but also code data support their phase counterparts. Consider a short baseline of two receivers tracking n satellites where each satellite ‘s’ may broadcast signals on a different frequency $f_s$ ($s=1,\ldots ,n$). The term ‘short’ indicates that both the receivers experience almost the same atmospheric delays in their measurements. The system of between-receiver single-differenced (SD) observation equations, in its linearized form, is given as (Khodabandeh and Teunissen 2023)

$$\begin{aligned} \textsf{E}(\underbrace{\left[ \begin{array}{c}\phi \\ p\end{array}\right] }_y)=\underbrace{\left[ \!\begin{array}{c}\lambda _o\,R^{-1} \\ 0 \end{array}\!\right] }_A(\underbrace{z+B\,b}_a) +\underbrace{\left[ \begin{array}{cc}G, &{} e_n \\ G, &{} e_n\end{array}\right] }_C\underbrace{\left[ \begin{array}{c}x_{1r} \\ dt_{1r}\end{array}\right] }_c \end{aligned}$$

(9)

where $\phi \in \mathbb {R}^n$ and $p\in \mathbb {R}^n$ denote the observed-minus-computed SD phase and code measurements ($m=2n$). It is assumed that the n frequencies $f_s$ are multiples of a common base frequency $f_o$, that is $f_s = r_s f_o$, with known integer ratios $r_s$ ($s=1,\ldots ,n$) forming the $n\times n$ diagonal matrix $R=\textrm{diag}(r_1,\ldots ,r_n)$. Thus, matrix R reduces to the identity matrix $I_n$ for the CDMA case having identical frequencies $f_s=f_o$ ($s=1,\ldots ,n$). The $n\times 3$ matrix G contains the n receiver-to-satellite line-of-sight unit vectors on its rows, with $e_n$ being the n-vector of ones. Here, the parameter vector $c\in \mathbb {R}^k$ contains the $3\times 1$ baseline vector $x_{1r}$, and the estimable SD receiver clock offset $dt_{1r}$ that has absorbed code biases. Thus $k=4$. The SD receiver phase delay $\delta _{1r}$, that is scaled by the base wavelength $\lambda _o$, plays the role of the bias vector $b\in \mathbb {R}^q$, i.e. $b = \delta _{1r}/\lambda _o$ ($q=1$). The corresponding B-matrix is given by $B = R\, e_n$. Note, in (9), that only the integer ambiguity vector $z\in \mathbb {Z}^n$ and the bias b are expressed in cycles. The remaining quantities are expressed in units of range.

As with the previous examples, there is a rank-deficiency between z and b. In contrast to the previous examples where the bias vector b is the parameter of interest, here the bias b is deemed to be a nuisance parameter. One can therefore remove the stated rank-deficiency at the expense of lumping a combination of the SD ambiguity vector z into the bias b. To see this, we apply the integer-sweeping algorithm (Teunissen 2019; Teunissen and Khodabandeh 2022) to the integer matrix (n-vector) $B=Re_n$. It is assumed that the greatest common divisor of the integer ratios $r_s$ ($s=1,\ldots ,n$) is one. Otherwise, these ratios are down-scaled by being divided by their greatest common divisor. Under this condition, the integer-sweeping algorithm returns an integer matrix, say $Z_1\in \mathbb {Z}^{n\times (n-1)}$, which together with B, forms an ‘admissible integer transformation’ $[Z_1,B]$. An admissible integer transformation is a square integer matrix whose inverse is also integer. Let $[\tilde{Z}_1,\tilde{Z}_2]$ be the inverse-transpose of $[Z_1,B]$. Pre-multiplying the ambiguity vector z by the both sides of the matrix identity $I_n = [Z_1,B][\tilde{Z}_1,\tilde{Z}_2]^\textrm{T}$ gives $z = Z_1\,\tilde{z}_1+ B\,\tilde{z}_2$, where $\tilde{z}_1=\tilde{Z}_1^\textrm{T}z$ and $\tilde{z}_2=\tilde{Z}_2^\textrm{T}z$. Since the integer combination $\tilde{z}_2\in \mathbb {Z}$ have the same coefficient matrix B as that of b, it is absorbed by bias b, forming the estimable bias $\tilde{b} = b + \tilde{z}_2$. What is left from z is the integer-estimable vector $\tilde{z}_1\in \mathbb {Z}^{n-1}$. Substitution of $z+Bb = Z_1\,\tilde{z}_1+ B\,\tilde{b}$ into (9) gives the full-rank model

$$\begin{aligned} \textsf{E}(y) = AZ_1\,\tilde{z}_1 + AB\,\tilde{b} + C\,c \end{aligned}$$

(10)

The above full-rank model enables one to unbiasedly estimate all the three parameter vectors $\tilde{z}_1$, $\tilde{b}$ and c. The price to pay is, of course, to sacrifice the integer ambiguity $\tilde{z}_2\in \mathbb {Z}$. In the CDMA case, this corresponds to letting the ambiguity of the pivot satellite be absorbed by the SD phase bias b so that the DD ambiguities $\tilde{z}_1$ show up as integer-estimable. Instead of using the full-rank model (10), in Sect. 4 we will address whether the positioning user is better off considering integer-resolution of the whole SD ambiguities z via the rank-deficient model (9) in which the bias constraint $b\in \mathcal {B}$ with subset $\mathcal {B}=\{\nu \in \mathbb {R}^q|~||\nu ||\le h\}$ is leveraged. $\boxtimes$

3 Estimators and their distributional properties

In this section, we discuss how the three parameter vectors $z\in \mathbb {Z}^n$, $b\in \mathcal {B}$ and $c\in \mathbb {R}^k$ can be estimated via integer estimation theory. We will then study the distributional properties of their estimators through their restrictive PDFs.

3.1 A class of estimators

The estimators of the parameter vectors $a=z+Bb$ and c can be obtained by an application of least squares adjustment. Let the positive definite matrix $Q_{yy}$ denote the variance matrix of the observations y in (2). In the standard least squares estimation, the squared-norm $||y-Aa-Cc||_{Q_{yy}}^2$ is minimized over the ‘unconstrained’ Euclidean spaces $a\in \mathbb {R}^n$ and $c\in \mathbb {R}^k$. This would result in the so-called float estimators $\hat{a}$ and $\hat{c}$, together with their joint variance matrix

$$\begin{aligned} \left[ \begin{array}{c}\hat{a}\\ \hat{c}\end{array}\right] ~,~\left[ \begin{array}{cc}Q_{\hat{a}\hat{a}}~ &{}\quad Q_{\hat{a}\hat{c}}\\ Q_{\hat{c}\hat{a}}~ &{}\quad Q_{\hat{c}\hat{c}}\end{array}\right] \end{aligned}$$

(11)

However, both the integer constraint $z\in \mathbb {Z}^n$ and the bias constraint $b\in \mathcal {B}$ imply that the ambiguity vector a has to lie in a ‘proper’ subset of $\mathbb {R}^n$, say $\Omega =\{x\in \mathbb {R}^n|x = u+B\nu ,u\in \mathbb {Z}^n, \nu \in \mathcal {B}\}$. Such restriction placed on a leads to least squares estimators that are different from their float versions (11). To see this, consider the corresponding mixed-integer least squares problem (Teunissen 1993)

$$\begin{aligned} {\begin{array}{l} \min \limits _{a\in \Omega ,c\in \mathbb {R}^k}||y-Aa-Cc||_{Q_{yy}}^2=\\ ||\hat{e}||_{Q_{yy}}^2+\min \limits _{a\in \Omega }\left\{ ||\hat{a}-a||_{Q_{\hat{a}\hat{a}}}^2+\min \limits _{c\in \mathbb {R}^k}||\hat{c}(a)-c||_{Q_{\hat{c}(a)\hat{c}(a)}}^2\right\} \end{array}} \end{aligned}$$

(12)

with the least squares residual vector $\hat{e} = y-A\hat{a}-C\hat{c}$, and

$$\begin{aligned} \begin{array}{lcl} \hat{c}(a) &{}=&{} \hat{c} - Q_{\hat{c}\hat{a}}Q_{\hat{a}\hat{a}}^{-1}(\hat{a}-a)\\ Q_{\hat{c}(a)\hat{c}(a)} &{}=&{} Q_{\hat{c}\hat{c}} - Q_{\hat{c}\hat{a}}Q_{\hat{a}\hat{a}}^{-1}Q_{\hat{c}\hat{a}} \end{array} \end{aligned}$$

(13)

As no restriction is placed on $c\in \mathbb {R}^k$, the last term in (12) can be made zero for any $a\in \Omega$. Therefore, the minimization problem (12) boils down to finding the minimizer $\check{a}\in \Omega$ as

$$\begin{aligned} \check{a} = \arg \min \limits _{a\in \Omega }||\hat{a}-a||_{Q_{\hat{a}\hat{a}}}^2,~\text {with}~\check{c} = \hat{c}(\check{a}) \end{aligned}$$

(14)

Thus, $\check{a}$ is the closest member of $\Omega$, with metric $Q_{\hat{a}\hat{a}}^{-1}$, to the float ambiguity vector $\hat{a}$. The extent to which the estimator $\check{a}$ is different from its float counterpart $\hat{a}$ is dictated by the subset $\Omega$. For instance, when $B=I_n$ and the bias vector b is unbounded, i.e. $\mathcal {B}=\mathbb {R}^n$, the set $\Omega$ spans the whole Euclidean space $\mathbb {R}^n$. For this case, the minimizer $\check{a}$ coincides with $\hat{a}$. When the bias vector b is known to be zero, i.e. $\mathcal {B}=\{0\}$, the set $\Omega$ reduces to the integer space $\mathbb {Z}^n$. For this case, the minimizer $\check{a}$ is the well-known Integer Least Squares (ILS) estimator of z (Teunissen 1999). For the general case, the minimizer $\check{a}$ can be viewed as a trade-off between the float estimator $\hat{a}$ and the ILS estimator.

Instead of using the least squares principle (14), one may take recourse to a different estimation strategy and prefer another member of $\Omega$ as estimate of $a=z+Bb$. Such member should take the form of $\check{a}=\check{z}+B\check{b}$, where $\check{z}\in \mathbb {Z}^n$ and $\check{b}\in \mathcal {B}$. To obtain the integer vector $\check{z}$, there exists a class of admissible integer estimators $\mathcal {I}: \mathbb {R}^n\mapsto \mathbb {Z}^n$ that map the float ambiguity vector $\hat{a}$ to an integer vector $\check{z}$, i.e. $\check{z}=\mathcal {I}(\hat{a})$. These estimators possess the following three properties (Teunissen 1998)

$$\begin{aligned} {\begin{array}{ccl} {\mathrm{(I)}}&{} &{} \text {for every}~x\in \mathbb {R}^n,~\text {there exits}~u\in \mathbb {Z}^n:\mathcal {I}(x)=u\\ {\mathrm{(II)}}&{} &{} \mathcal {I}(x)\in \mathbb {Z}^n~\text {is unique for every}~x\in \mathbb {R}^n\\ {\mathrm{(III)}}&{} &{} \mathcal {I}(x+u)=\mathcal {I}(x)+u~\text {for every}~x\in \mathbb {R}^n,\,u\in \mathbb {Z}^n \end{array}} \end{aligned}$$

(15)

The bias estimator $\check{b}\in \mathcal {B}$ may be taken as a function of the float ambiguity $\hat{a}$, say $\tilde{\mathcal {J}}(\hat{a})$. The last property of (15) implies, if $\hat{a}$ is shifted by an integer amount u, the integer estimator $\check{z}=\mathcal {I}(\hat{a})$ is shifted by the same amount. Therefore, it is plausible to ask of the functions $\tilde{\mathcal {J}}$ to remain invariant for any integer shift in their argument, i.e. $\tilde{\mathcal {J}}(x+u)=\tilde{\mathcal {J}}(x)$ for all $u\in \mathbb {Z}^n$. Otherwise, the estimator $\check{a}=\check{z}+B\check{b}$ would not possess the integer equivariant property (III) in (15) as the integer estimator $\check{z}$ does. Such function can be equivalently expressed as $\tilde{\mathcal {J}}(x) = \mathcal {J}(x-\mathcal {I}(x))$, with $\mathcal {J}:\mathbb {R}^n\mapsto \mathcal {B}$ being an arbitrary function. This can be understood as follows. Clearly, this expression ensures $\tilde{\mathcal {J}}(x+u)=\tilde{\mathcal {J}}(x)$ for all $u\in \mathbb {Z}^n$ as $\mathcal {I}(x+u)=\mathcal {I}(x)+u$. Conversely, the identity $\tilde{\mathcal {J}}(x+u)=\tilde{\mathcal {J}}(x)$ ($u\in \mathbb {Z}^n$) shall also hold for $u=-\mathcal {I}(x)$. Thus $\tilde{\mathcal {J}}(x) = \tilde{\mathcal {J}}(x-\mathcal {I}(x))$ which is a function of $x-\mathcal {I}(x)$. We therefore arrive at the following class of estimators for the ‘bias-affected’ ambiguity vector $a=z+Bb$,

$$\begin{aligned} \check{a} = \check{z}+B\check{b},\quad \text {with}\quad \left\{ \begin{array}{l}\check{z}=\mathcal {I}(\hat{a})\\ \check{b}=\mathcal {J}(\hat{a}-\check{z})\end{array}\right. \end{aligned}$$

(16)

The integer mapping $\mathcal {I}: \mathbb {R}^n\mapsto \mathbb {Z}^n$ satisfies the three admissibility conditions (15), while $\mathcal {J}:\mathbb {R}^n\mapsto \mathcal {B}$ is an arbitrary function of the ambiguity residual $\check{\epsilon }:=\hat{a}-\check{z}$. By definition, the term ‘function’ for $\mathcal {J}$ implies that every $x\in \mathbb {R}^n$ cannot have multiple images $\mathcal {J}(x)$. Only one unique image $\mathcal {J}(x)$ must therefore be assigned to x. The results of the following sections rely on such assumption.

3.2 PDFs of the estimators

The arbitrariness of the two functions $\mathcal {I}(\hat{a})$ and $\mathcal {J}(\check{\epsilon })$, in (16), allows one to devise many estimators for the bias-affected ambiguity vector $a=z+Bb$. The distributional properties of such estimators are captured by the corresponding PDFs.

Theorem 1

(Joint PDF of the estimators) Let $\hat{a} \sim \mathcal {N}_{n}(a=z+Bb, Q_{\hat{a}\hat{a}})$, $\hat{c} \sim \mathcal {N}_{k}(c, Q_{\hat{c}\hat{c}})$, and $\hat{c}(a)=\hat{c}-Q_{\hat{c}\hat{a}}Q_{\hat{a}\hat{a}}^{-1}(\hat{a}-a)$. Then the joint PDF of the three estimators $\check{z}=\mathcal {I}(\hat{a})$, $\check{b}=\mathcal {J}(\hat{a}-\check{z})$ and $\check{c}=\hat{c}(\check{z}+B\check{b})$ can be expressed as

$$\begin{aligned} {f_{\check{z},\check{b},\check{c}}(u,\nu ,w)=\textrm{P}(\hat{a}\in S_u)f_{\hat{c}(u)}(w-L\nu )f_{\check{b}_u}(\nu ) } \end{aligned}$$

(17)

where $L=Q_{\hat{c}\hat{a}}Q_{\hat{a}\hat{a}}^{-1}B$, $u \in \mathbb {Z}^{n}$, $w\in \mathbb {R}^k$, $\nu \in \mathcal {B}$, and pull-in region $S_{u}=\{x\in \mathbb {R}^n|~\mathcal {I}(x)=u\}$. It is assumed that $\mathcal {B}$ is such that the PDF of $\check{b}_{u} = \check{b}_{|\hat{a} \in S_{u}}$ exists. $\square$

Proof

From conditioning $\check{c}=\hat{c}-Q_{\hat{c}\hat{a}}Q_{\hat{a}\hat{a}}^{-1}(\hat{a}-\check{z}-B\check{b})$ on $\hat{a} \in S_{u}$, we obtain, since $\check{z}=\mathcal {I}(\hat{a})$, $\hat{c}(u)=\hat{c}-Q_{\hat{c}\hat{a}}Q_{\hat{a}\hat{a}}^{-1}(\hat{a}-u)$, and $\hat{c}(u)$ is independent of $\hat{a}$,

$$\begin{aligned} \check{c}_{|\hat{a} \in S_{u}}=\hat{c}(u)+L\,\check{b}_{|\hat{a} \in S_{u}} \end{aligned}$$

Recognizing that $\hat{c}(u)$ and $\check{b}_{|\hat{a} \in S_{u}}$ are independent, an application of the PDF-transformation rule to

$$\begin{aligned} \left[ \begin{array}{c} \check{c}_{|\hat{a} \in S_{u}}\\ \check{b}_{|\hat{a} \in S_{u}} \end{array}\right] = \left[ \begin{array}{cc} I_k &{} L\\ 0 &{} I_q \end{array} \right] \left[ \begin{array}{c} \hat{c}(u)\\ \check{b}_{|\hat{a} \in S_{u}} \end{array} \right] \end{aligned}$$

gives

$$\begin{aligned} f_{(\check{c}, \check{b})_{|\hat{a} \in S_{u}}}(w, \nu )= f_{\hat{c}(u)}(w-L\nu )f_{\check{b}_{|\hat{a} \in S_{u}}}(\nu ) \end{aligned}$$

Therefore

$$\begin{aligned} f_{\check{z}, \check{c}, \check{b}}(u,\nu ,w)= & {} \textrm{P}(\hat{a} \in S_{u})f_{(\check{c}, \check{b})_{|\hat{a} \in S_{u}}}(w, \nu )\\= & {} \textrm{P}(\hat{a} \in S_{u})f_{\hat{c}(u)}(w-L\nu )f_{\check{b}_{|\hat{a} \in S_{u}}}(\nu )\\= & {} \textrm{P}(\hat{a} \in S_{u}|\check{b}=\nu ) f_{\hat{c}(u)}(w-L\nu )f_{\check{b}}(\nu ) \end{aligned}$$

$\square$

From the joint PDF (17), one can infer the complete probabilistic properties of the estimators $\check{z}$, $\check{b}$ and $\check{c}$. The marginal PDF of each estimator follows by summing or integrating this joint PDF over the arguments of the other two estimators. For instance, the PDF of the estimator $\check{c}$ follows as

$$\begin{aligned} {f_{\check{c}}(w) =\sum \limits _{u\in \mathbb {Z}^n}\textrm{P}(\hat{a}\in S_u)\int _{\mathcal {B}}f_{\hat{c}(u)}(w-L\nu )f_{\check{b}_u}(\nu )d\nu } \end{aligned}$$

(18)

To better appreciate the above PDF, consider two extreme cases. In the first case, the bias b is assumed to be zero, i.e. $\mathcal {B}=\{0\}$. For this case, the function $\mathcal {J}(x)$ maps every $x\in \mathbb {R}^n$ to 0. Thus $\check{b}_u=0$ with probability one, having the Dirac delta (impulse) function $\delta (\nu )$ as its PDF, i.e. $f_{\check{b}_u}(\nu ) = \delta (\nu )$, where $\int _{\mathcal {B}}\delta (\nu )d\nu =1$ and $\delta (\nu )=0$ for $\nu \ne 0$. Therefore, the PDF (18) reduces to

$$\begin{aligned} f_{\check{c}}(w) =\sum \limits _{u\in \mathbb {Z}^n}\textrm{P}(\hat{a}\in S_u)f_{\hat{c}(u)}(w) \end{aligned}$$

(19)

This is the PDF of the fixed estimator $\check{c}$ corresponding to the ‘bias-free’ model (1), see (Teunissen 2002).

The second extreme case is when $B=I_n$ and the bounded set $\mathcal {B}$ is large enough to encompass the pull-in region $S_0$. Then $\check{b}_{|\hat{a} \in S_{u}}=\mathcal {J}(\hat{a}-\mathcal {I}(\hat{a}))_{|\hat{a}\in S_{u}}=\mathcal {J}(\hat{a}-u)_{|(\hat{a}-u)\in S_{0}}=(\hat{a}-u)_{|\hat{a} \in S_{u}}$, and the PDF of $\check{b}_{u}=\check{b}_{|\hat{a} \in S_{u}}$ becomes $f_{\check{b}_u}(\nu ) = f_{\hat{a}}(\nu +u)/\textrm{P}(\hat{a}\in S_u)$ when $\nu \in S_0$, vanishing for $\nu \notin S_0$. Substitution into (18) gives

$$\begin{aligned} \begin{array}{lcl} f_{\check{c}}(w) &{}=&{}\sum \limits _{u\in \mathbb {Z}^n}\int _{S_0}f_{\hat{c}(u)}(w-L\nu )f_{\hat{a}}(\nu +u)d\nu \\ &{}=&{}\int \limits _{\cup _{u\in \mathbb {Z}^n} S_u}f_{\hat{c}(u)}(w-L(x-u))f_{\hat{a}}(x)dx\\ &{}=&{}\int \limits _{\mathbb {R}^{n}}f_{\hat{c}(x)}(w)f_{\hat{a}}(x)dx\\ &{}=&{}f_{\hat{c}}(w)\int _{\mathbb {R}^n}f_{\hat{a}|\hat{c}}(x|w)dx=f_{\hat{c}}(w) \end{array} \end{aligned}$$

(20)

The second equality follows by applying the change of variable $x = \nu +u$ with $x\in S_u\Leftrightarrow \nu \in S_0$, the third equality by using $f_{\hat{c}(x)}(w)=f_{\hat{c}(u)}(w-L(x-u))$ and $\cup _{u\in \mathbb {Z}^n} S_u=\mathbb {R}^n$, while the last equality follows from $f_{\hat{c}(x)}(w)=f_{\hat{c}|\hat{a}}(w|x)$ and the PDF identity $f_{\hat{c}|\hat{a}}(w|x)f_{\hat{a}}(x)=f_{\hat{c}}(w)f_{\hat{a}|\hat{c}}(x|w)$, thereby recognizing that $\int _{\mathbb {R}^n}f_{\hat{a}|\hat{c}}(x|w)dx=1$. Therefore, the PDF (18) reduces to that of the float estimator $\hat{c}$ which is a normal distribution.

Fig. 1

Examples of the marginal PDF $f_{\check{c}}(w)$ in (18) when $b=0$ (top) and when $b\ne 0$ (bottom). The green curves correspond to the special case $\mathcal {B}=\{0\}$ given in (19). The grey curves indicate a class of such PDFs for different subsets $\mathcal {B}$. The cyan curves highlight a member of such class. When the subset $\mathcal {B}$ is large enough to contain $S_0$, the PDF reduces to the normal distribution (20), i.e. the white curves, cf. model (21)

Figure 1 visualizes examples of the PDF $f_{\check{c}}(w)$ (18) as cyan curves when $b=0$ (top) and when $b\ne 0$ (bottom), together with the two special cases (19) and (20) using the green and white curves, respectively. The model considered is specified as

$$\begin{aligned} \textsf{E}\left( \left[ \begin{array}{c}y_1\\ y_2\end{array}\right] \right) =\left[ \begin{array}{c}1\\ 1\end{array}\right] \,c+\left[ \begin{array}{c}0\\ \lambda \end{array}\right] \,(z+b),~|b|\le h \end{aligned}$$

(21)

in which the two normally distributed observables $y_1$ and $y_2$ are assumed independent with standard deviations $\sigma _{y_1}=15.0$ [cm] and $\sigma _{y_2}=2.3$ [cm], respectively. The wavelength is set to $\lambda = 11$ [cm], while the bias bound h may range from zero to half a cycle, i.e. $0\le h\le 0.5$. When the bias b is absent, the PDFs are symmetric around the expected value c. However, except for the white curves, the nonzero bias b skews all the other PDFs. The white curves indicate the normal distribution of the float estimator $\hat{c}$ that remains unbiased irrespective of the size of the ambiguity-bias Bb. The figure also shows a class of such PDFs for different subsets $\mathcal {B}$ in grey. When the bound h is close to zero, these PDFs resemble that of the fixed estimator (19). The larger the bound h becomes, the more the curves are pushed towards the normal distribution of the float estimator (20).

Let us now consider the PDF of the bias estimator $\check{b}$. The PDF follows by summing and integrating the joint PDF (17) over $u\in \mathbb {Z}^n$ and $w\in \mathbb {R}^k$, respectively. This gives

$$\begin{aligned} f_{\check{b}}(\nu ) =\sum \limits _{u\in \mathbb {Z}^n}\textrm{P}(\hat{a}\in S_u)f_{\check{b}_u}(\nu ) \end{aligned}$$

(22)

since $\int _{\mathbb {R}^n}f_{\hat{c}(u)}(w)dw=1$. Next to the probability values $\textrm{P}(\hat{a}\in S_u)$ ($u\in \mathbb {Z}^n$), the above PDF is driven by the distributional behaviour of the random vector $\check{b}_{u} = \check{b}_{|\hat{a} \in S_{u}}$.

Example 5

(Hybrid structure of the PDF $f_{\check{b}}(\nu )$) To get a better understanding of the distributional behaviour of $\check{b}$, consider a two-dimensional example ($n=2$) in which the ambiguity variance matrix $Q_{\hat{a}\hat{a}}$ is specified as

$$\begin{aligned} Q_{\hat{a}\hat{a}} = \left[ \begin{array}{cc}+0.1056~ &{}\quad -0.0808\\ -0.0808~ &{}\quad +0.0648\end{array}\right] ~{\textrm{cycle}}^2 \end{aligned}$$

(23)

The bias-affected float ambiguity vector $\hat{a}$ has the expected value $\textsf{E}(\hat{a})=z+Bb$, with $z=[0,0]^\textrm{T}$, $B=[0,1]^\textrm{T}$. The corresponding bounded set is given by $\mathcal {B} = \{\nu \in \mathbb {R}|~ |\nu |\le h\}$ ($h=0.2$), where b is set to 0.15 cycles. Function $\mathcal {J}(x)$ is chosen as

$$\begin{aligned} \mathcal {J}(x) = \arg \min _{|\nu |\le h} ||x-B\nu ||_{Q_{\hat{a}\hat{a}}}^2 \end{aligned}$$

(24)

This choice of function $\mathcal {J}$ picks the member of subset $\mathcal {B}$ whose ambiguity bias $B\nu$ is closest to the ambiguity residual $\check{\epsilon }$ with respect to metric $Q_{\hat{a}\hat{a}}^{-1}$. With this choice, the outcomes of the conditional random variable $\check{b}_{u} = \check{b}_{|\hat{a} \in S_{u}}$ are simply characterized by

$$\begin{aligned} \check{b}_{u}=\left\{ \begin{array}{cl} -h &{} {\textrm{if}}~\hat{b}_{u} \le -h\\ \hat{b}_{u} &{} {\textrm{if}}~-h<\hat{b}_{u} < +h \\ +h &{} {\textrm{if}}~\hat{b}_{u} \ge +h\end{array}\right. \end{aligned}$$

(25)

where $\hat{b}_u = B^+(\hat{a}-u)_{|\hat{a} \in S_{u}}$, with the least squares inverse matrix $B^+ = (B^\textrm{T}Q_{\hat{a}\hat{a}}^{-1}B)^{-1}B^\textrm{T}Q_{\hat{a}\hat{a}}^{-1}$. Therefore, the PDF of $\check{b}_u$ reads

$$\begin{aligned} \begin{array}{l} f_{\check{b}_u}(\nu ) = f_{\hat{b}_u}(\nu )\textbf{1}_{|\nu |< h}(\nu )+\\ \qquad \delta (\nu +h){\textrm{P}}(\hat{b}_u \le -h)+\delta (\nu -h)\textrm{P}(\hat{b}_u \ge +h) \end{array} \end{aligned}$$

(26)

Fig. 2

Marginal PDF $f_{\check{b}}(\nu )$ in (22) when $b=0.15$ cycles, where function $\mathcal {J}(x)$ is set to be (24) with $\mathcal {B}=\mathbb {R}$ (green) and $\mathcal {B}=\{\nu \in \mathbb {R}|~|\nu |\le 0.2\}$ (cyan), cf. Example 5. Two zoom-in windows are also given to highlight the peaks around the values of $-2.3$ and 0.15 cycles

where $f_{\hat{b}_u}(\nu )$ denotes the PDF of $\hat{b}_{u}$, with the indicator function $\textbf{1}_{|\nu |< h}(\nu )$ being 1 if $|\nu |< h$ and zero otherwise. According to (22), the PDF $f_{\check{b}}(\nu )$ is a weighted average of the PDFs $f_{\check{b}_u}(\nu )$ in (26), where the probabilities $\textrm{P}(\hat{a}\in S_u)$ ($u\in \mathbb {Z}^n$) serve as weights. The expression (26) shows the hybrid nature of $f_{\check{b}_u}(\nu )$, and therefore, of the PDF $f_{\check{b}}(\nu )$. While the first term on right-hand side of (26) represents a probability ‘density’ function of a continuous random variable $\hat{b}_{u}$, the second and third terms represents a probability ‘mass’ function of discrete random variables with outcomes $\pm h$. Figure 2 visualizes the PDF (22) for the model specified in (23). The green curve in the figure corresponds to the unconstrained case $\mathcal {B}=\mathbb {R}$ (i.e. $h\rightarrow \infty$), whereas the cyan curve corresponds to the bound $h=0.2$. As a result, the probability mass of the cyan curve only lies inside the interval $[-0.2, +0.2]$ cycles. On the contrary, the green curve represents, next to the true value $b=0.15$ cycles, also a considerable probability mass around $-2.3$ cycles. Such behaviour follows when the success-rate $\textrm{P}(\hat{a}\in S_z)$ is not large enough compared to probability values $\textrm{P}(\hat{a}\in S_u)$ ($u\ne z$). Consequently, the corresponding variables $\check{b}_u$ also contribute to the distributional behaviour of the bias estimator $\check{b}$, leading to probability masses that can be around values way farther from the true value $b=0.15$ cycles. By imposing the bias constraint $|b|\le 0.2$ cycles, such unwanted probability masses can be curbed. This may result in probability masses that are condensed into the endpoints $\pm h$ cycles, see the terms with the impulse functions $\delta (\nu \pm h)$ in (26). $\boxtimes$

3.3 Bias-constrained ILS estimator

Up to now, the role of the bias constraint $b\in \mathcal {B}$ in ensuring the quality of the bias estimator $\check{b}=\mathcal {J}(\check{\epsilon })$, given in (16), has been pointed out, i.e. avoiding probability masses that can be around values outside the subset $\mathcal {B}$, the values that are deemed to be far from the target value b (cf. Fig. 2). However, we have not yet addressed the stated role in the integer estimator $\check{z} = \mathcal {I}(\hat{a})$. When the bias b, in $a=z+Bb$, is absent, the ILS estimator

$$\begin{aligned} \mathcal {I}(\hat{a}) = \arg \min \limits _{z\in \mathbb {Z}^n}||\hat{a}-z||_{Q_{\hat{a}\hat{a}}}^2 \end{aligned}$$

(27)

is optimal as it delivers the largest success rate, i.e. the maximum probability $\textrm{P}(\hat{a}\in S_z)$, among all admissible ambiguity estimators (Teunissen 1999). However, the presence of nonzero bias vectors b can significantly lower the ILS success-rate.

Fig. 3

Two-dimensional examples of BEAT pull-in regions for two bounded sets of $\mathcal {B}=\{\nu \in \mathbb {R}|~|\nu |\le h\}$, one with $h=0$ (left) and the other with $h=0.2$ cycles (right), cf. Example 6. Two sets of 100,000 normally distributed samples of $\hat{a}$ are simulated (coloured dots), one with the expectation $\textsf{E}(\hat{a})=[0,0]^\textrm{T}$ (top) and the other with the expectation $\textsf{E}(\hat{a})=[0,0.15]^\textrm{T}$ cycles (bottom). The samples residing in the pull-in regions $S_0$ are depicted in green and cyan, while the remaining samples in red are mapped to incorrect integers

To account for the bias b in the rank-defect model (2), Teunissen (2006) showed the feasibility of finding a unique ILS solution by imposing the bounds (4) on b. For non-empty bounded sets $\mathcal {B}$, Khodabandeh (2022) developed the bias-constrained ILS estimator and its BEAT integer search method, identifying the conditions under which the estimator obeys the admissibility rules (15). The results are summarized below.

Theorem 2

(Admissibility of BEAT) As a member of the class of estimators (16), the joint integer mapping $\mathcal {I}_{_\textrm{B}}: \mathbb {R}^n\mapsto \mathbb {Z}^n$ and bias estimator $\mathcal {J}_{_\textrm{B}}: \mathbb {R}^n\mapsto \mathcal {B}$

$$\begin{aligned} \left\{ \begin{array}{lcl} \mathcal {I}_{_\textrm{B}}(x) &{}=&{} \arg \min \limits _{u\in \mathbb {Z}^n} F_{x}(u)\\ \mathcal {J}_{_\textrm{B}}(x) &{}=&{} \arg \min \limits _{\nu \in \mathcal {B}}||x-B\nu ||_{Q_{\hat{a}\hat{a}}}^2 \end{array}\right. \end{aligned}$$

(28)

are referred to as the bias-constrained ILS estimator and its integer search to the method of BEAT, where $F_{x}(u) = \min _{\nu \in \mathcal {B}}||x-u-B\nu ||_{Q_{\hat{a}\hat{a}}}^2$. The integer mapping $\mathcal {I}_{_\textrm{B}}$ is admissible if and only if

$$\begin{aligned} B(\mathcal {J}_{_\textrm{B}}(x)-\!\mathcal {J}_{_\textrm{B}}(x\!-\!u))\ne u,\;\forall u\in \mathbb {Z}^n\backslash \{0\},~\forall x\in S_{0,\mathrm B} \end{aligned}$$

(29)

where the BEAT pull-in region $S_{0,\mathrm B}=\{x\in \mathbb {R}^n|~\mathcal {I}_{_\textrm{B}}(x)=0\}$ is distinguished from $S_0$ of an arbitrary estimator (16) via the subscript ‘$\textrm{B}$’. $\square$

Proof

The proof is given in (Khodabandeh 2022). $\square$

In (28) and the following, we use the discriminatory subscript ‘$\textrm{B}$’ for the BEAT functions $\mathcal {I}_{_\textrm{B}}$ and $\mathcal {J}_{_\textrm{B}}$ to distinguish them from their counterparts $\mathcal {I}$ and $\mathcal {J}$ of an arbitrary estimator (16). The comparison of the BEAT integer mapping (28) with that of ILS (27) shows that BEAT needs an ‘additional’ input, i.e. the bounded set $\mathcal {B}$, next to the float ambiguity vector $\hat{a}$ and its variance matrix $Q_{\hat{a}\hat{a}}$ so as to deliver the output $\check{z}=\mathcal {I}_{_\textrm{B}}(\hat{a})$. Also note that the proposed estimator becomes ILS when the set $\mathcal {B}$ takes the special form of $\mathcal {B}=\{0\}$, i.e. when bias b is known to be zero. Similar to the ILS estimator, the estimator $\check{z}$ has to be obtained through an integer search. A fast search strategy for the computation of $\check{z}$ is developed in (Khodabandeh 2022). As shown in (ibid), the condition (29) restricts the choice of an arbitrary bounded set $\mathcal {B}$. For instance when B takes the form of the identity matrix $I_n$, the sets whose members have Euclidean norms larger than half a cycle do not ensure the admissibility of BEAT. When condition (29) holds, BEAT produces a unique integer estimator $\check{z}=\mathcal {I}_{_\textrm{B}}(\hat{a})$ for the rank-defect model (2). Note, however, that the bias estimator $\check{b}=\mathcal {J}_{_\textrm{B}}(\check{\epsilon })$ may not be unique for some non-convex sets $\mathcal {B}$ (Boyd and Vandenberghe 2004). In the following, we therefore assume that the bounded set $\mathcal {B}$ ensures that the mapping $\mathcal {J}_{_\textrm{B}}: \mathbb {R}^n\mapsto \mathcal {B}$ in (28) is a ‘function’, i.e. the image $\mathcal {J}_{_\textrm{B}}(x)$ is uniquely assigned to every $x\in \mathbb {R}^n$.

Example 6

(BEAT pull-in regions) To get some insight into the performance of BEAT compared to ILS, again consider the two-dimensional example in (23), with $z=[0,0]^\textrm{T}$, $B=[0,1]^\textrm{T}$. Two sets of 100,000 normally-distributed samples of $\hat{a}$ are simulated, one with $b=0$ and the other with $b=0.15$ cycles. To estimate $\check{z}$, we consider two bounded sets of $\mathcal {B}=\{\nu \in \mathbb {R}|~|\nu |\le h\}$, one with $h=0$ and the other with $h=0.2$ cycles. With the first set, the presence of bias b is ignored as $\mathcal {B}=\{0\}$. With the second set, the unknown bias b is constrained to lie inside the interval $[-0.2,~0.2]$ cycles. The corresponding results are shown in Fig. 3. On the left-panel of the figure, the BEAT pull-in regions (in black and grey) are depicted as ‘hexagons’ for the choice $\mathcal {B}=\{0\}$. This is because the integer mapping $\mathcal {I}_{_\textrm{B}}$ in (28) reduces to the ILS estimator (27) for the special case $\mathcal {B}=\{0\}$. Apart from this case however, the BEAT pull-in regions, and thus its performance, are different from those of ILS as indicated for the case $\mathcal {B}=\{\nu \in \mathbb {R}|~|\nu |\le 0.2\}$ on the right-panel of the figure. As shown, not all the samples lie inside the pull-in region $S_0$ due to the randomness of $\hat{a}$ (red dots). As expected, for the bias-free case, ILS pull-in region $S_0$ captures the largest possible number of samples with successful mapping $\mathcal {I}(\hat{a})=0$, i.e. 99.2% of the samples (green dots). However, the stated success-rate drops to 66.3% for bias $b=0.15$ cycles present in the second entry of $\hat{a}$. Upon imposing the constraint $|b|\le 0.2$ cycles, BEAT ensures success-rates above 90% for both the bias-free case (90.6%) and bias-affected case (93.3%), see the cyan dots. Figure 4 shows the stated ambiguity success-rate as a function of bias b for both the ILS and bias-constrained ILS estimators. As shown, ILS exhibits higher success-rates for the biases whose magnitude is smaller than 0.08 cycles. The ILS success-rate does, however, rapidly decrease the larger the bias magnitude |b| becomes, reaching the minimum value of 40% for $b=\pm 0.2$ cycles. On the contrary, BEAT does not deliver largest success-rates. Instead, its associated success-rates remain relatively unchanged over the interval $|b|\le 0.2$ cycles. $\boxtimes$

Note, as the bias-constrained ILS estimator (cf. 28) minimizes the inconsistency measure $i(x)=||x-\mathcal {I}(x)-B\mathcal {J}(x-\mathcal {I}(x))||_{Q_{\hat{a}\hat{a}}}^{2}$ within the estimator class (16), that we have $i_\textrm{B}(x) \le i(x),\; \forall x \in \mathbb {R}^{n}$, and therefore

$$\begin{aligned} \int _{S_{0,\mathrm B}} i_{\textrm{B}}(x)dx \le \int _{S_{0, \mathrm B}} i(x)dx = \int _{S_{0}} i(x)dx \end{aligned}$$

(30)

where the last equality follows from the property $i(x+u)=i(x)$, $\forall u \in \mathbb {Z}^{n}$ (Teunissen 1999). Since $\mathcal {I}_\textrm{B}(x)=0$ for $x \in S_{0, \mathrm B}$ and $\mathcal {I}(x)=0$ for $x \in S_{0}$, inequality (30) can be written as

$$\begin{aligned} \int _{S_{0,\mathrm B}}\!||x-B\mathcal {J}_\textrm{B}(x)||_{Q_{\hat{a}\hat{a}}}^{2}dx \le \int _{S_{0}} \! ||x-B\mathcal {J}(x)||_{Q_{\hat{a}\hat{a}}}^{2}dx \end{aligned}$$

(31)

thus showing, since the pull-in regions $S_{0, \mathrm B}$ and $S_{0}$ have volume 1, that the average inconsistency of the bias-constrained ILS estimator $\check{b}$ over its own pull-in region is never larger than that of any other bias solution from the estimator class (16). Hence, application of the bias-constrained ILS principle also implies that its bias solution has, on average, the smallest inconsistency with its underlying model.

Fig. 4

Evaluation of the success-rate $\textrm{P}(\check{z}=z)$ as function of bias b. The green curves correspond to the ILS estimator, while the cyan curves correspond to the bias-constrained ILS estimator with $\mathcal {B}=\{\nu \in \mathbb {R}|~|\nu |\le 0.2\}$, cf. Example 6

4 Application in SD ambiguity resolution

In this section we apply the BEAT method to the GLONASS short-baseline models (9) and (10). In the ambiguity domain $a=z+B\,b$, the stated models can be, respectively, characterized as (Example 4)

$$\begin{aligned} {\begin{array}{ll} \text {Bias-bounded:} &{} \textsf{E}(\hat{a}) = \overbrace{Z_1\,\tilde{z}_1 + B\,\tilde{z}_2}^z + B\,b,\; ||b||\le \sqrt{2}h\\ \text {Bias-estimable:} &{} \textsf{E}(\hat{a}) = Z_1\,\tilde{z}_1 + B\,\tilde{b},\; \tilde{b}\in \mathbb {R}^2 \end{array}} \end{aligned}$$

(32)

where m is the number of tracked satellites. The role of $\hat{a}\in \mathbb {R}^{2m}$ is taken by the baseline SD float ambiguity vector on the two GLONASS frequency bands L1 and L2. In the ‘bias-bounded’ model above, there are 2 times m equations versus $2m+2$ unknowns, i.e. 2 times $(m-1)$ integer-estimable ambiguities $\tilde{z}_1\in \mathbb {Z}^{2(m-1)}$, two frequency band-specific biases $b_1$ and $b_2$ in $b=[b_1,b_2]^\textrm{T}$, and the two extra integer ambiguities $\tilde{z}_2\in \mathbb {Z}^2$. Therefore, this model is underdetermined and cannot be solved for all the unknowns without using the bias constraint $||b||\le \sqrt{2}h$. The term $\sqrt{2}$ is given to highlight the dimension of the bias vector $b\in \mathbb {R}^2$. The fixed bias bound $\sqrt{2}h$ should not exceed half a cycle so as to ensure the BEAT admissibility condition (29), see (Khodabandeh 2022). On the other hand, the ‘bias-estimable’ model contains two unknowns less than the ‘bias-bounded’ model, that is, the extra unknown vector $\tilde{z}_2\in \mathbb {Z}^2$ has been absorbed by the estimable bias vector $\tilde{b}=b+\tilde{z}_2$. Therefore, the ‘bias-estimable’ model is full-rank and can deliver unbiased solutions for $\tilde{z}_1$ and $\tilde{b}$.

4.1 Motivation: FDMA vs CDMA

While the full-rank ‘bias-estimable’ model in (32) forms the basis of FDMA ambiguity resolution (Teunissen 2019), several studies have reported that GLONASS ‘full’ ambiguity resolution cannot be successfully performed even for the case where the positions of the receivers are perfectly known, restricting one to choose the option of partial ambiguity resolution, see e.g., (Teunissen and Khodabandeh 2019; Brack et al. 2021; Zaminpardaz et al. 2021; Zhang et al. 2021). To see why such restriction holds for the FDMA case and not for the CDMA case, consider the following ‘determinant identity’ (Odijk and Teunissen 2008)

$$\begin{aligned} {\textrm{det}}(Q_{\hat{\tilde{z}}_1\hat{\tilde{z}}_1})=\dfrac{{\textrm{det}}(Q_{\hat{a}\hat{a}})}{{\textrm{det}}(Q_{\hat{\tilde{b}}\hat{\tilde{b}}|\tilde{z}_1})} \end{aligned}$$

(33)

The above equation states that the precision of the integer-estimable float ambiguities $\hat{\tilde{z}}_1$, i.e. $\textrm{det}(Q_{\hat{\tilde{z}}_1\hat{\tilde{z}}_1})$, is proportional to that of the SD float $\hat{a}$, i.e. $\textrm{det}(Q_{\hat{a}\hat{a}})$. Thus, the more precise SD float ambiguities, the more precise $\hat{\tilde{z}}_1$ becomes. As the GLONASS L1 and L2 frequency bands are, respectively, close to their GPS L1 and L2 counterparts, the determinant $\textrm{det}(Q_{\hat{a}\hat{a}})$ remains almost unchanged by switching from the GLONASS FDMA case to the GPS CDMA case for a similar satellite configuration with observables of the same precision. Therefore, it is the denominator in (33) that plays a decisive role in making the precision of the FDMA float ambiguities $\hat{\tilde{z}}_1$ different from their GPS versions. The determinant $\textrm{det}(Q_{\hat{\tilde{z}}_1\hat{\tilde{z}}_1})$ is inversely proportional to $\textrm{det}(Q_{\hat{\tilde{b}}\hat{\tilde{b}}|\tilde{z}_1})$, where

$$\begin{aligned} Q_{\hat{\tilde{b}}\hat{\tilde{b}}|\tilde{z}_1} = (B^\textrm{T}Q_{\hat{a}\hat{a}}^{-1}B)^{-1} \end{aligned}$$

(34)

denotes the variance matrix of the float bias solution $\hat{\tilde{b}}|\tilde{z}_1$ when $\tilde{z}_1$ is perfectly known. Thus, the more precise the bias solution $\hat{\tilde{b}}|\tilde{z}_1$, the larger the determinant $\textrm{det}(Q_{\hat{\tilde{z}}_1\hat{\tilde{z}}_1})$, thereby the lower the ambiguity success-rate becomes. As shown in (34), the precision of $\hat{\tilde{b}}|\tilde{z}_1$ is governed by the coefficient vector $B = R\, e_n$. For the CDMA case, this vector reduces to the vector of ones $e_n$ as $R=I_n$. For the GLONASS FDMA case however, this vector is formed by the large frequency ratios $r_s = 2848+\kappa _s$ in which the integer channel number $\kappa _s$ varies within the interval $[-7,6]$. The much larger coefficients of the FDMA vector $B = R\, e_n$ than its CDMA version $B=e_n$ imply that the bias solution $\hat{\tilde{b}}|\tilde{z}_1$ is three orders of magnitude more precise for the GLONASS FDMA case, making the corresponding determinant $\textrm{det}(Q_{\hat{\tilde{z}}_1\hat{\tilde{z}}_1})$ three orders of magnitude larger than its GPS CDMA version.

Fig. 5

Examples of the conditional standard deviations of the augmented vector $[\hat{\tilde{z}}_1^\textrm{T},\hat{\tilde{b}}^\textrm{T}]^\textrm{T}$ (black dots) compared to those of the SD float ambiguities $\hat{a}$ (white dots) after decorrelation applied to $\hat{\tilde{z}}_1$ and $\hat{\tilde{b}}$ by the LAMBDA method. The light blue areas correspond to those of the bias solution $\hat{\tilde{b}}$. The CDMA case corresponds to a GPS L1/L2 constellation, while the FDMA case corresponds to a GLONASS L1/L2 constellation of 7 satellites. Zoom-in windows are given to highlight the variation in the standard deviations

Table 1 Receiver and antenna types of the IGS (zero$^{*}$) short-baselines used in the GLONASS FDMA experiment

To show how the presence of such high-precision bias solution reflects in the GLONASS IAR performance, Fig. 5 compares the conditional standard deviations of the SD float ambiguities $\hat{a}$ with those of the augmented vector $[\hat{\tilde{z}}_1^\textrm{T},\hat{\tilde{b}}^\textrm{T}]^\textrm{T}$ after decorrelation performed by the LAMBDA method (Teunissen et al. 1997). The conditional standard deviation of the jth entry of a random vector $y=[y_1,y_2,\ldots ,y_m]^\textrm{T}$ is defined as the square root of the conditional variance $\sigma _{j}^2 = \sigma _{y_j}^2-Q_{y_jy_{J}}Q_{y_{J}y_{J}}^{-1}Q_{y_{J}y_j}$ $(j=2,\ldots ,m)$, where $y_{J}=[y_1,y_2,\ldots ,y_{j-1}]^\textrm{T}$ with $\sigma _{1}^2 =\sigma _{y_1}^2$. For the CDMA case, the conditional standard deviations corresponding to the DD ambiguities $\hat{\tilde{z}}_1$ are around 0.08 cycles, while those of the bias solution $\hat{\tilde{b}}$ reach 0.12 cycles. Such flat spectra are, however, not observed for their FDMA versions. Two of the standard deviations of $\hat{\tilde{z}}_1$ (one per frequency band) exceed 8 cycles. On the other hand, the conditional standard deviations corresponding to the FDMA bias solution $\hat{\tilde{b}}$ are shown to be 3 orders of magnitude smaller than their CDMA versions (light blue areas). The large discrepancy between the standard deviations of $\hat{\tilde{b}}$ and the last two standard deviations of the GLONASS ambiguities $\hat{\tilde{z}}_1$ would have disappeared if the estimable bias $\tilde{b}=b+\tilde{z}_2$ were integer-estimable, i.e. if $b=0$. In the absence of bias b, the SD ambiguities a are integer-estimable. To get an indication of the corresponding ambiguity resolution performance, one may evaluate the geometric average of these conditional standard deviations, known as the Ambiguity Dilution Of Precision (ADOP) (Teunissen 1997). As shown in the figure, the corresponding spectra are flat and around 0.1 cycles, leading to small ADOP of $\textrm{ADOP}_\textrm{SD}=0.12$ cycles (Teunissen 1997). However, the ADOP of $\hat{\tilde{z}}_1$ is shown to be large $\textrm{ADOP}_\textrm{DD}=0.45$ cycles, hindering successful full ambiguity resolution. As stated previously, the bias constraint $||b||\le \sqrt{2}h$ can provide a trade-off between the ideal case $a\in \mathbb {Z}^{2m}$ (when $h=0$) and the case $[\tilde{z}_1\in \mathbb {Z}^{2(m-1)}, \tilde{b}\in \mathbb {R}^2]$ (when $\sqrt{2}h=0.5$ cycles). But this can only be realized if the magnitude of the bias vector b would be a bounded value.

4.2 GLONASS SD bounded phase biases

To verify whether GLONASS SD phase biases $b = \delta _{1r}/\lambda _o$ are bounded, we process the GLONASS L1/L2 daily datasets of seven globally distributed IGS zero-/short-baselines. The receiver and antenna types of the baselines are listed in Table 1. Use is made of the ‘bias-estimable’ model in (32) where the coordinates of the antennas, and therefore the baseline vector $x_{1r}$ (cf. 9), are known. Such strong model can deliver precise solutions for the estimable bias $\tilde{b}=b+\tilde{z}_2$. Nevertheless, we only consider the ‘single-epoch’ bias solutions $\hat{\tilde{b}}$ whose formal standard deviations are smaller than 0.003 cycles so that their rounded values to the nearest integer represent $\tilde{z}_2$ with a high probability. Thus $\lfloor \hat{\tilde{b}}\rceil = \tilde{z}_2$, where $\lfloor \cdot \rceil$ denotes the entry-wise integer rounding operator. In this way, the fractional parts $\hat{\tilde{b}}-\lfloor \hat{\tilde{b}}\rceil$ should represent solutions of the unknown bias $b = \delta _{1r}/\lambda _o$

Figure 6 presents time-series of the stated fractional parts $\hat{\tilde{b}}-\lfloor \hat{\tilde{b}}\rceil$ for each of the seven baselines. To check whether the biases are repeatable and if they be can be calibrated, we have computed their solutions on two different days with one month apart, i.e. 31st of March 2023 (left) and 30th of April 2023 (right). As shown, the biases are indeed bounded. Despite being of similar magnitudes, the biases corresponding to each baseline exhibit different patterns over time for the two days. Also note that the bias magnitude is baseline-specific. For the zero-baseline ZIM2–ZIM3 having the receivers of the same type, the stated magnitude is smaller than 0.001 cycles. For the short-baseline YARR–YAR3 which also has the receivers of the same type, but with different antennas, the bias magnitude is below 0.01 cycles. Apart from the baseline WTZR–WTZS whose bias magnitude exceeds 0.1 cycles, the remaining baselines represent bias magnitude bounded by 0.05 cycles.

Fig. 6

Time-series of the fractional parts $\hat{\tilde{b}}-\lfloor \hat{\tilde{b}}\rceil$ (cycles) of GLONASS L1 (black) and L2 (grey) SD phase biases corresponding to the seven baselines listed in Table 1. Their 10-sample moving averages are shown in white colour. Single-epoch bias solutions $\hat{\tilde{b}}$ whose formal standard deviations are smaller than 0.003 cycles are considered to have $\lfloor \hat{\tilde{b}}\rceil = \tilde{z}_2$ with a high probability

Fig. 7

Single-epoch east-north positioning scatters of the baseline WTZR–WTZS, together with time-series of the up component and the number of tracked GLONASS satellites corresponding to the five scenarios (i) to (v) in Sect. 4.3. The float solutions are shown in grey, whereas the fixed solutions with error-magnitude larger (smaller) than 10 cm are shown in red (cyan)

4.3 GLONASS-only positioning solutions

The GLONASS bounded SD phase biases, shown in Fig. 6, suggest that one can indeed incorporate the bias constraint $||b||\le \sqrt{2}h$ into the rank-defect baseline model (9), applying the BEAT method to the bias-affected float ambiguities $\hat{a}$, thus computing ambiguity-resolved baseline solutions for $x_{1r}$. Considering that small (in magnitude) biases are observed for most of the baselines, one may also consider the case in which the presence of bias b is completely ignored, i.e. $h=0$. To obtain the baseline solutions, we therefore consider the following five scenarios:

• (i) The presence of bias b is ignored, fixing the whole SD float ambiguities $\hat{a}$ as integers.

• (ii) The bias-estimable model (10) is employed, partially fixing the integer-estimable part $\hat{\tilde{z}}_1$ via ILS. By ‘partially’, we mean that the least precise ambiguity solution (per frequency band) remains float and is not mapped to its integer, see Fig. 5, the FDMA case.

• (iii) The bias-bounded model (9) is employed, with the bias bound $h=0.15$ cycles.

• (iv) Estimated mean values of the bias of the previous month are applied to the phase data as corrections, ignoring the presence of any leftover biases.

• (v) Estimated mean values of the bias of the previous month are applied to the phase data as corrections, with the bias bound $h=0.02$ cycles applied to (9).

Therefore, no external solutions of the unknown bias vector b are applied to the phase data for the first three scenarios. For the last two scenarios however, the estimated bias solutions, that are obtained on 31st of March 2023, are applied to the phase data of 30th of April 2023. The corresponding positioning results of the baseline WTZR–WTZS are shown in Fig. 7. To highlight if ambiguity-fixing is beneficial to the solutions’ accuracy improvement, we distinguish fixed positioning solutions with error-magnitude smaller than 10 cm in cyan colour from the remaining fixed solutions (red dots). For the first scenario (i), none of the fixed solutions have error-magnitude smaller than 10 cm. This is attributed to the corresponding rather large SD phase biases b in Fig. 6 which have been ignored. For Scenario (ii), 68.1% of the fixed solutions have error-magnitudes smaller than 10 cm. The increase in the positioning accuracy is because Scenario (ii) accounts for the unknown bias b by computing its estimable version $\tilde{b}=b+\tilde{z}_2$. However, this comes at the cost of lumping the integer ambiguity $\tilde{z}_2$ with b. This can be avoided if the constraint $||b||\le \sqrt{2}\times 0.15$ cycles is imposed on the rank-defect model (9). Accordingly, the percentage of such accurate fixed solutions increases to 77.8% for Scenario (iii). Although, the external bias solutions are applied up to 3 decimal places, the percentage of such accurate fixed solutions decreases to 23.9% for Scenario (iv). This is because leftover ambiguity biases, although small, are magnified by the large entries of the matrix B in $\textsf{E}(\hat{a})=z+B\,b$. Scenario (v) accounts for such leftover biases by imposing the constraint $||b||\le \sqrt{2}\times 0.02$ cycles, increasing the stated percentage to 94.8%.

Table 2 Percentages of the GLONASS-only L1/L2 fixed positioning solutions having error-magnitude smaller than 10 cm of the baselines listed in Table 1, corresponding to the five scenarios (i) to (v) in Sect. 4.3

Fig. 8

Single-epoch east-north positioning scatters of the baseline TLSG–TLSE ($\sim$1.2 km), together with time-series of the up component and the number of tracked GLONASS satellites, corresponding to the bias constraint $||b||\le \sqrt{2}\,h$, $h=0.01$ (left), $h=0.05$ (middle) and $h=0.25$ (right) cycles. The float solutions are shown in grey, whereas the fixed solutions with error-magnitude larger (smaller) than 10 cm are shown in red (cyan)

Fig. 9

Two-dimensional histograms (percentages) of the estimated biases of $b=[b_1,b_2]^\textrm{T}$ corresponding to baseline TLSG–TLSE. The bias vector b is constrained to lie inside or on the blue circles $\mathcal {B}=\{\nu \in \mathbb {R}^2|~||\nu ||\le \sqrt{2}\,h\}$, $h=0.01$ (left) cycles, $h=0.05$ (middle) and $h=0.25$ (right) cycles

Fig. 10

Percentage of the GLONASS-only L1/L2 fixed positioning solutions having error-magnitude smaller than 10 cm as function of the bias bound $\sqrt{2}\,h$. The results correspond to the short baseline TLSG–TLSE

A closer look at the time-series of the up component in Fig. 7 reveals that stated error-magnitude is largely driven by the number of tracked satellites. To make this relation more explicit, we compute the positioning results of all the seven baselines and summarize the percentages of their accurate fixed solutions in Table 2. As shown in the table, all the solutions have error-magnitudes smaller than 10 cm for the zero-baseline ZIM2–ZIM3 when at least 7 satellites are tracked. This holds for all the five scenarios (i) to (v). This can be understood from the statistically insignificant bias solutions shown in Fig. 6 for the zero-baseline ZIM2–ZIM3. Table 2 also shows that Scenario (iv) outperforms Scenario (v) for some of the baselines when the number of tracked satellites is less than seven. This indicates that ignoring leftover (but small) ambiguity biases may lead to accurate fixed solutions, instead of weakening the model by considering an unknown ambiguity bias varying within the interval $[-0.02, +0.02]$ cycles. However, Scenario (v) ‘on average’ outperforms all the other scenarios in terms of delivering more accurate fixed positioning results.

What we can also learn from Table 2 is that Scenario (iii) ‘on average’ delivers a relatively high percentage of accurate fixed solutions (i.e. 98.7%) when at least 7 satellites are tracked. This important result implies that one can switch from the ‘bias-estimable’ model (10) to the ‘bias-bounded’ model (9) to improve the baseline positioning performance even when no external solutions of the SD phase biases are provided as corrections. Observing bounded GLONASS SD biases (Fig. 6), one may therefore only incorporate the bias constraint $||b||\le \sqrt{2}h$ into (9) to obtain SD ambiguity-fixed positioning without relying on an external source. The results presented so far have been confined to baselines shorter than 100 ms. To verify the applicability of Scenario (iii) to longer baselines, we also process a GLONASS L1/L2 dataset of the short baseline TLSG–TLSE whose length is around 1.2 km. Its receiver-types are ‘Septentrio PolaRx5–Trimble Alloy’. In contrast to the earlier baselines whose SD phase biases are a-priori evaluated, we directly apply Scenario (iii) to this baseline using the bias constraint $||b||\le \sqrt{2}h$ with different bias bounds $0\le \sqrt{2}h \le 0.5$. The corresponding positioning results are shown in Fig. 8. When looking from left to right, it can be observed that the percentages of accurate fixed solutions are around 35.9% for the tight bound $h=0.01$ cycles, 97.0% for the bound $h=0.05$ cycles, and 86.3% for the bound $h=0.25$ cycles. The low percentage corresponding to $h=0.01$ cycles indicates that $||b||\le \sqrt{2}\times 0.01$ does not hold and, therefore, the bias constraint is misspecified. This can be also understood from the distribution of the corresponding bias estimates $\check{b}$. Recall from (22) that the PDF $f_{\check{b}}(\nu )$ is a weighted average of the PDFs $f_{\check{b}_u}(\nu )$ ($u\in \mathbb {Z}^n$). Due to the hybrid structure of $f_{\check{b}_u}(\nu )$, probability masses can be condensed on the boundary of set $\mathcal {B}$ (see Example 5). Figure 9 presents histograms of the estimated biases. As shown, the tight constraint $h= 0.01$ cycles pushes the majority of the estimates to lie on the boundary of $\mathcal {B}$ (the blue circle on the left-panel), discarding any possibility of having bias-vector solutions whose norms are larger than $\sqrt{2}\,h$. By loosening the constraint, the probability masses are mainly concentrated around the unknown bias b that lies inside the circles. On the other hand, an unnecessary increase in the bounds from $h=0.05$ to $h=0.25$ cycles weakens the model, delivering few percentages of accurate positioning solutions.

This notion has been made precise in Fig. 10, showing the percentage of accurate fixed positioning solutions as function of the bias bound $\sqrt{2}\,h$. For small h, only less than 20% of the solutions have error-magnitude smaller than 10 cm. The percentage gets larger as the bound increases, reaching its maximum value of 97.1% for $\sqrt{2}h=0.04$ cycles. However, the percentage starts decreasing as the bound exceeds 0.04 cycles, tending to its asymptote of 80% at $\sqrt{2}h=0.5$ cycles. This is the percentage that one would obtain using the ‘bias-estimable’ model (10).

We conclude this section by making a remark about the choice of bias bound $\sqrt{2}h$. According to Fig. 10, the bias constraint $||b||\le \sqrt{2}h$ does not really pay off when h exceeds a certain threshold. To find a sharp bound, one may be inclined to first estimate the bias solutions via the bias-estimable model (10) where the c-parameters are unknown. The maximum magnitude of such solutions may then be chosen as $\sqrt{2}h$. Such choice does, however, not lead to the accuracy-improvement of $\hat{c}$, see the right-panel of Fig. 9. The reason which enables us to find sharp bounds for the above GLONASS positioning examples is the use of a stronger model in which part of the c-parameters (i.e. the baseline vector $x_{1r}$) is known. Therefore, a strategy to find a sharp bound for the problem of SD GLONASS IAR is to employ the geometry-known model of zero- to very short-baseline setups, thereby a-priori quantifying bias magnitudes for different pairs of receiver-types, see Fig. 6.

5 Summary and conclusions

The joint integer and bias estimators, $\check{z}=\mathcal {I}_{_\textrm{B}}(\hat{a})$ and $\check{b}=\mathcal {J}_{_\textrm{B}}(\hat{a}-\check{z})$, are the minimizers of the following mixed-integer least squares problem

$$\begin{aligned} \min \limits _{z\in \mathbb {Z}^n}\min \limits _{b\in \mathcal {B}}||\hat{a}-z-Bb||_{Q_{\hat{a}\hat{a}}}^2~. \end{aligned}$$

(35)

They are meant to estimate the integer- and bias-parts of the bias-affected float ambiguity vector $\textsf{E}(\hat{a})= z+Bb$, i.e. $z\in \mathbb {Z}^n$ and $b\in \mathcal {B}$, respectively. The model to which these joint estimators are applicable is referred to as the bias-bounded mixed-integer model (2). Despite being rank-defect, the model leverages the bias constraint $b\in \mathcal {B}$ so as to realize the unique mappings $\mathcal {I}_{_\textrm{B}}:\mathbb {R}^n\mapsto \mathbb {Z}^n$ and $\mathcal {J}_{_\textrm{B}}:\mathbb {R}^n\mapsto \mathcal {B}$.

In this contribution, we proved that BEAT offers ‘best’ estimation of $z\in \mathbb {Z}^n$ and $b\in \mathcal {B}$ in the sense of delivering a bias solution that has, on average, the smallest inconsistency with its underlying model (cf. 31). We first reviewed some important interferometric measuring systems whose estimation problems can be covered by BEAT (cf. Examples 1 to 4). A class of admissible estimators were then characterized, serving to determine the integer- and bias-parts of the carrier phase ambiguities (cf. 16). We studied the PDFs of the involved estimators, highlighting that the presence of the nonempty bounded subset $\mathcal {B}\subset \mathbb {R}^q$ ‘curbs’ probability masses around values that are deemed to be far from the target value b (cf. Fig. 2).

To show the BEAT at work, we studied the problem of GLONASS SD ambiguity resolution. It was highlighted, for current GLONASS frequency channel numbers, that the FDMA bias solutions—when the corresponding integer-estimable ambiguities are constrained to be known—are three orders of magnitude more precise than their CDMA versions. While the bias constraint $||b||\le \sqrt{2}h$ significantly benefits FDMA SD ambiguity resolution, it does not considerably improve the performance of the CDMA case. By evaluating the ambiguity-fixed positioning solutions of several short-baselines, it was demonstrated that GLONASS bias-bounded SD ambiguity resolution can produce considerably more accurate fixed positioning solutions than its existing bias-estimable counterpart in which an extra integer ambiguity (per frequency band) is sacrificed (cf. 32 and Fig. 5). However, such superiority in performance holds if the involved SD receiver phase delays are bounded (cf. Fig. 6) and the constraint $b\in \mathcal {B}$ is correctly specified (cf. Fig. 10).

Although in this contribution we restricted our attention to single baseline models, the proposed methodology can of course be also employed for GNSS network models. As with between-receiver SD ambiguity resolution, the applicability of the bias-constrained ILS estimation can potentially be extended to between-satellite SD ambiguity resolution. While such extension can be attractive for single-receiver GNSS applications like precise point positioning (PPP), one should bear in mind that constraining phase biases improves the accuracy of model parameter solutions only when (1) the constraints are not misspecified and (2) the constraints are considerably tight in such a way that they can penalize wrong ambiguity-fixing.