Abstract
For the purposes of routinely providing reliable and low-latency Global Ionosphere Maps (GIMs), a method of estimating hourly updated near real-time GIM with a time latency of about 1–2 h based on a 24-h data sliding window of Global Navigation Satellite System (GNSS) near real-time observations and real-time data streams was presented. On the basis of the implementation of near real-time GIM estimation, an hourly updated GIM nowcasting method was further proposed to improve the accurate of short-term total electron content (TEC) prediction. We estimated the Shanghai Astronomical Observatory near real-time GIM (SHUG) and nowcasting GIM (SHPG) in the solar relatively active year (2014) and quiet year (2021), and employed GIMs provided by the International GNSS Service, the Global Positioning System (GPS) differential slant TECs (dSTECs) extracted from global independent GNSS stations, and the vertical TECs (VTECs) inverted from satellite altimetry as the references to validate the estimated results. The GPS dSTECs evaluation results show that SHUG behaves fairly consistent with the rapid GIMs, with a discrepancy of less than 1 TEC unit (TECu) overall. The standard deviations (STDs) of SHUG with respect to Jason-2/-3 VTECs are no more than 10% over the majority of rapid GIMs due to the instability of observations. The performance of 1-h nowcasting SHPG is significantlybetter than the Center for Orbit Determination in Europe (CODE) 1-day predicted GIM (C1PG). GPS dSTEC validation results indicate that 1-h nowcasting SHPG is 1 to 2 TECu more reliable than C1PG in eventful ionospheric electron activity regions, and it outperforms the C1PG by 10% overall versus Jason-2/-3 VTECs. The hourly updated SHUG and SHPG have relatively high reliability and low time latency, and thus can provide excellent service for (near) real-time users and offer more accurate TEC background information than daily predicted GIM for real-time GIM estimation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The terrestrial ionosphere is defined as the upper atmosphere extending from about 60 km to 1500 km above the earth’s surface and contains a large collection of free electrons and ions (Bilitza et al. 2011; Schaer 1999). As an important part of solar-terrestrial space environment, the ionosphere induces the phase advance and the group delay of electromagnetic signals such as navigation and telecommunication passing through this layer. Moreover, strong ionospheric disturbances threaten the safety of low earth orbit satellites, space vehicles and human space activities, and even cause damage to terrestrial infrastructure such as the electric power grid and communication network. Therefore, the development of high-precision and low-latency global ionospheric models are of great significance for radio signal error correction and space environment monitoring (Buonsanto 1999; Hernandez-Pajares et al. 2009; Klobuchar 1987; Li et al. 2020; Mannucci et al. 1993).
With the advantages of providing massive high-precision and real-time observations at a global scale, Global Navigation Satellite System (GNSS) has become a vital technology for real-time and near real-time global ionospheric modeling (Erdogan et al. 2021, 2017; Liu et al. 2021). In 1998, the International GNSS Service (IGS) set up the ionosphere working group (IWG) with the goal of organizing and coordinating the Ionosphere Associate Analysis Centers (IAACs) to routinely provide Global Ionosphere Maps (GIMs) and calculate combined GIMs (Feltens and Schaer 1998; Hernandez-Pajares et al. 2009). Currently, IGS IAACs consist of Jet Propulsion Laboratory (JPL), Center for Orbit Determination in Europe (CODE), Universitat Politècnica de Catalunya (UPC), European Space Agency/European Space Operations Center (ESA/ESOC), Chinese Academy of Sciences (CAS), Wuhan University (WHU), Natural Resources Canada (NRCan) and Operational Tool for Ionosphere Mapping and Prediction (OPTIMAP), and the eight institutions submit multiple GIMs with different latency and reliability to IGS, including final, rapid, daily predicted and real-time GIMs (https://igs.org/wg/ionosphere/). The final and rapid GIM estimation is commonly performed in a post-processing mode, allowing the extraction of high-precision Total Electron Contents (TECs) and the generation of post-processed GIMs with sufficient observations and processing time, so that the rapid and final GIMs maintain high reliability but have relatively long latency of about 1–2 days and 1–2 weeks, respectively. The daily predicted GIM is commonly based on the rapid and final global ionospheric models and has no time latency, and thus the reliability of daily predicted GIM is essentially lower than post-processing GIMs. As the ionosphere is affected by multiple factors such as solar and geomagnetic activities and coupled with magnetosphere and thermosphere, it presents complex nonlinear changes. Therefore, it is difficult to accurately predict the variation in ionospheric TECs for a long period of time, especially during the periods of intense irregular TEC perturbations (García-Rigo et al. 2011; Lu et al. 1995).
The rapid and final GIMs have high reliability, but the long latency makes them not suitable for (near) real-time applications. The 1-day and 2-day predicted GIMs provided by IGS, which are generated by 1-day and 2-day model coefficient extrapolation based on the post-processing global ionospheric models, respectively, can meet the requirements of real-time users. However, the accuracy of prediction principally degrades with the increase in extrapolation time and it is not sensitive to short-term ionospheric irregularities, scintillations and sudden ionospheric disturbances. In order to meet the demand for high accuracy real-time GNSS applications, IGS set up the Real-Time Working Group (RTWG) and has provided the Real-Time Service (RTS) (https://igs.org/wg/real-time/), including the provision of precise real-time corrections for orbits, clock, biases and atmospheric delays, and providing high quality real-time data streams (Caissy et al. 2012). The IGS IWG has been working to provide reliable real-time ionospheric products to serve real-time users (Li et al. 2020; Liu et al. 2021). The real-time GIM estimation commonly employs the global GNSS real-time data stream provided by IGS RTS and background information such as the daily predicted ionospheric models, and thus there is almost no latency in real-time GIM estimation. However, in real-time global ionospheric modeling, due to the constraints such as the short arcs of satellite observation, sparsely distributed real-time GNSS stations, limited processing time and relatively low quality of background information, the accuracy and stability of real-time GIMs is typically worse than the post-processing GIMs (Li et al. 2020; Liu et al. 2021; Ren et al. 2019).
The near real-time and nowcasting GIMs can provide accurate and stable TECs in near real-time and real-time, respectively, and thus are of great value in (near) real-time application areas (Chen et al. 2022; Erdogan et al. 2021, 2017). For example, the current real-time GIM commonly relies on the daily predicted GIM, yet the nowcasting GIM provides more accurate TECs than daily predicted GIM, so the nowcasting GIM can contribute to enhance the quality of real-time GIM. In the field of applications, high-precision near real-time and nowcasting GIMs provide precise priori ionospheric delay constrained for near real-time and real-time single-frequency and multi-frequency precise point positioning (PPP) and precise point position and real-time kinematic (PPP-RTK) positioning applications, which can reduce the convergence time for ambiguity-fixing and improve the robustness of the solution (Li et al. 2013; Zhang et al. 2013, 2022). Validation results show that the 1-h nowcasting GIM has an accuracy improvement of about 1–2 TECu over the daily predicted GIM. As 1–2 TECu corresponds to a pseudorange delay of about 16.2–32.4 cm in the GPS L1 frequency band, the accuracy improvement of nowcasting GIM is of great importance for high-precision navigation and positioning applications, such as decimeter- and centimeter-level PPP and PPP-RTK services. The nowcasting GIM is useful for space measurement techniques using electromagnetic wave such as GNSS, VLBI and space vehicle navigation, and the near real-time GIMs can supply the spatial and temporal variation in TEC in near real-time and thus play a good role in space weather monitoring (Klobuchar 1987; Orus Perez 2016; Sekido et al. 2003; Sezen et al. 2013).
Moreover, natural disasters such as earthquakes, tsunamis and volcanic eruptions generate acoustic and gravity waves that propagate upward from the Earth's surface, the waves cause intense irregular spatial and temporal TEC perturbations when they reach the ionosphere, and the TEC perturbations could be detected by near real-time ionospheric models with high spatial and temporal resolution (Astafyeva 2019; Blanc 1985). The TEC perturbations caused by acoustic and gravity waves are helpful to find the epicenter location and main shock time, invert the process of volcanic eruption and estimate the energy released and the extent of damage triggered (Astafyeva et al. 2022; Jin et al. 2015). In addition, studies have shown that precursors induced by earthquakes, tsunamis, and volcanic eruptions can result in the anomalies of electron density in the E and F layers of the ionosphere, and these anomalies are observed between several days to a few hours priori these events (Liu et al. 2004; Pulinets et al. 2003). Therefore, we can monitor the change of TEC from continuous hourly updated near real-time GIM with high spatial and temporal resolution for early warnings, monitoring and evaluation of natural disasters (Falck et al. 2010; Savastano et al. 2017; Tariq et al. 2019).
Through the above analysis, it can be inferred that the development of high-precision near real-time GIM and the realization of short-term GIM nowcasting are of great significance for supplementing the types of GIM products to better meet the demand of applications with different time latency, accuracy and stability of TEC, further improving the quality of real-time GIM, and warning, monitoring and assessing natural disasters. Therefore, we proposed a method of integrating multi-GNSS near real-time hourly observations and real-time data stream provided by IGS RTS into a 24-h data sliding window and generating the Shanghai Astronomical Observatory (SHAO) hourly updated near real-time GIM (SHUG). SHUG is characterized by its time latency of 1–2 h only, which is significantly better than the post-processed GIMs, while its reliability is basically comparable to that of the post-processed GIMs. On the basis of the implementation of SHUG estimation, we further came up with a high-precision ionospheric nowcasting strategy that combine the hourly updated near real-time and rapid ionospheric models into time series and generate the hourly updated nowcasting GIM (SHPG) with autoregressive and moving average (ARMA) model. Because the extrapolation time of hourly nowcasting GIM is generally shorter than daily predicted GIM, the hourly nowcasting GIM provides more reliable predicted vertical TECs (VTECs) than daily predicted GIM in a short period of time.
The accuracy of TECs or electron density (Ne) principally determine the quality of GIM. A variety of strategies of extracting TECs from GNSS observations have been proposed, such as the carrier phase to code leveling (CCL) method (Lanyi and Roth 1988; Mannucci et al. 1993, 1998), the carrier phase combination and ambiguity estimation method (Hernández-Pajares et al. 1999), the undifferenced and uncombined PPP method (Zhang et al. 2012) and the undifferenced ambiguity fixed method (Ren et al. 2021). Compared with other methods, the CCL method uses carrier phase to smooth pseudorange, which reduces the noise of pseudorange effectively, and eliminates the ambiguity of carrier phase, making it simple to implement and suitable for real-time and near real-time modeling (Li et al. 2020). Therefore, we employed the CCL method to extract TEC information from GNSS observations from GPS, GLONASS, Galileo and BEIDOU. Since the CCL method contains relatively large error, the effect of smoothing is affected by the arc length, and the differential code biases (DCBs) of satellites and receivers are considered as constants throughout a single day in post-processing mode (Ciraolo et al. 2006; Schaer 1999; Wang et al. 2015), in this study, we set up a sliding window of GNSS observations with a length of 24 h for hourly near real-time GIM estimation.
Selecting and configuring a reasonable mathematical model to express the extracted TECs is also a major factor in determining the quality of GIM. IGS IAACs adopt a variety of models, including the spherical harmonic expansion (Schaer 1999), the spherical triangles with splines (Mannucci et al. 1998), tomographic with splines and kriging (Hernández-Pajares et al. 1999; Orus et al. 2005) and B-spline expansion (Schmidt et al. 2013). As the spherical harmonic expansion has a excellent mathematical structure and is well suited to express the spatiotemporal distribution and variation in the ionosphere TECs on a global scale, it has been adopted by many IGS IAACs (Feltens 2007; Ghoddousi-Fard 2014; Li et al. 2014; Zhang and Zhao 2018). Therefore, we employ the spherical harmonic expansion to fit the extracted TECs in near real-time.
This paper is organized as follows. Section 2 mainly introduces the algorithm of extracting GNSS slant TEC (STEC) using CCL method, the method and process of hourly near real-time modeling with spherical harmonic expansion, and the principle and process of hourly nowcasting GIM generation with ARMA model. Sections 3, 4 and 5 present the validation results of estimated hourly near real-time and nowcasting GIMs in 2014 and 2021 with rapid and predicted GIMs, the GPS differential slant TECs (dSTECs) observed in independent global evaluation stations, and the VTECs extracted form satellite altimetry data, respectively. Section 6 draws conclusions and put forward prospects.
2 Strategies of hourly near real-time modeling and nowcasting
The strategies of estimating hourly near real-time and nowcasting GIMs are introduced in this section. We derive the process of extracting TECs from dual-frequency GNSS observations and presented the distribution of IGS network that provides real-time, near real-time and daily GNSS observations, respectively. The strategies of hourly near real-time global ionospheric modeling were introduced. The algorithm of hourly GIM nowcasting based on ARMA model and validation results was presented in detail.
2.1 Deriving TECs from GNSS observations
The STEC can be inverted by dual-frequency GNSS observations as the ionosphere has a dispersive nature. Ignoring the effects of multipath error, observation noise and carrier phase delay of satellite and receiver, the dual-frequency geometry-free linear combinations of pseudorange \(P4\) and carrier phase \(L4\) are expressed as follows (Lanyi and Roth 1988):
where \(s\), \(r\) and \(i\) represent the satellite, receiver and epoch, respectively; \(L_{A}\) and \(L_{B}\) correspond to two frequency points of GNSS; \(\alpha = \frac{{e^{2} }}{{8\pi^{2} m\varepsilon_{0} }} \approx 40.308\) in S.I. units, being \(e\) and \(m\) are the electron charge and mass; \(\varepsilon_{0}\) is the permittivity of the free space; \(f\) is the frequency of carrier phase; \( c\) is the speed of light in vacuum, \({\text{DCB}}^{s}\) and \({\text{DCB}}_{r}\) are differential code biases (DCBs) of satellites and receivers, respectively; \(N\) and \(\lambda\) denotes the ambiguity and the wavelength of carrier phase, respectively.
Since \(P4\) are affected by relatively large observation noise and multipath error, the CCL method is introduced to reduce the effects of noises and errors (Mannucci et al. 1993, 1998):
where \(\Delta L4_{r}^{s}\) is the average of a continuous arc which contains DCB and ambiguity information; \(n\) represent the epochs of a continuous arc; \(\widehat{L4}_{r,i}^{s}\) is the smoothed geometry-free linear combined value at epoch \(i\).
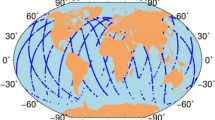
Figure 1 depicts the distribution of IGS stations providing available daily, hourly (near real-time) and real-time available observations on April 10, 2022. The stations providing daily observations have the largest number and most homogeneous distribution, which offer good condition for global ionospheric modeling, and thus the GIMs based on daily observations have relatively high reliability. Although the number of stations providing hourly observations is comparatively small, the stations are well distributed to meet the basic demands of global near real-time ionospheric modeling. IGS real-time stations currently are the least in number and are unevenly distributed, and are mostly distributed in North and South America, Europe and Oceania, which are not well suited for global real-time modeling. Therefore, background information such as predicted TECs is commonly introduced in real-time ionospheric modeling, which also leads to the reliability of real-time GIMs is restricted by the quality of background information (Liu et al. 2021; Ren et al. 2019).
2.2 Methods of near real-time global ionospheric modeling
As the spherical harmonic expansion has a excellent mathematical structure and is well suited to express the spatiotemporal distribution and variation in the ionosphere TECs on a global scale (Li et al. 2014; Zhang and Zhao 2019), we adopt spherical harmonic expansion and the mapping function of modified single-layer model (MSLM) to convert and fit the extracted TECs (Schaer 1999). The two-dimensional spherical harmonic expansion and MSLM can be expressed as follows:
where \(\beta\) and \(\gamma\) represent the geomagnetic latitude and sun-fixed longitude of ionospheric pierce point (IPP), respectively; \(n\) and \(m\) are the degree and order of spherical harmonic expansion and the maximum values are both set to 15; \(\tilde{P}_{nm}\) denotes the normalized associated Legendre function; \(\tilde{C}_{nm}\) and \(\tilde{S}_{nm}\) are the ionospheric model coefficients to be estimated; \({\text{MF }}\) indicates the mapping function; \(z^{\prime}\) and \(z\) are the corrected and uncorrected satellite zeniths, respectively; \(R\) and \(H\) represent the mean radius of the Earth and the height of single-layer spherical shell, and are set to 6378 km and 450 km, respectively.
As the ionospheric information derived from GNSS contains the DCBs of satellite and receiver, in this study, the DCBs are simultaneously estimated with the ionospheric model coefficients. The zero mean of satellite DCBs constraint condition (Schaer 1999; Wang et al. 2015) is imposed to each GNSS constellation to separate the DCBs of satellites and receivers:
where the \(N\) denotes the number of satellites for the specific GNSS constellation, and \(S\) stands for the GNSS constellation. Considering the significant diurnal variation in ionospheric electron activity and the fact that DCB is commonly assumed to be a constant for 1 day (24 h) in post-processing of ionospheric modeling, we designed a 24-h data sliding window of observations and estimated the hourly updated near real-time GIM to ensure the reliability of near real-time GIM and DCB.
The inhomogeneous global distribution of ground-based GNSS stations leads to inaccurate VTECs in GIMs over areas with large GNSS data gaps. Several virtual observation stations (VOSs) are established based on the VTECs provided by the International Reference Ionosphere 2016 model (IRI-2016) to compensate for the large gaps between GNSS stations, and VOS biases (VBs) are attached to each VOS to absorb the VTEC biases (VBs) between GNSS and IRI-2016 (Bilitza et al. 2017; Jin et al. 2022):
where \(n\) denotes the number of VOS and \({\text{VTEC}}_{{{\text{VOS}}}}\) represents the VTEC of VOS.
The flow diagram of hourly updated near real-time SHUG and nowcasting SHPG estimation is shown in Fig. 2 (with the example of the SHUG and SHPG solving process at 21:00 on the day of year (DOY) 356 of 2021). The IGS real-time and hourly observations and hourly broadcast ephemeris are combined into 24-h observation and broadcast ephemeris windows. Meanwhile, establish VOSs and generate 24-h virtual observations for each VOS by calculating the VTECs from IRI-2016. The TurboEdit method (Blewitt 1990) is used for quality control of GNSS observations and the ionospheric information is obtained using CCL method according to Eq. (2). Then establish and stack the normal equations for each GNSS and VOS station according to Eq. (3) and Eq. (4), and the least square method is adopted to solve the parameters to be estimated:
where the parameter vector \(\hat{X} = \left[ {{\text{ION}},{\text{DCB}}^{s} ,{\text{DCB}}_{r} ,{\text{VB}} } \right]^{T}\); \({\text{ION}}\) consists of the model coefficients \(\tilde{C}_{nm}\) and \(\tilde{S}_{nm}\), and is estimated as a set every 1 h; \({\text{DCB}}^{s}\), \({\text{DCB}}_{r}\), are the DCBs of satellites and receivers, respectively, and are estimated every 24 h; \({\text{VB}}\) represents the VOS bias parameters with an estimated interval of 1 h; \(n\) indicates the total number of GNSS and VOS stations; \(B\) stands for the design matrix of station; \(P\) denotes the weight matrix of observations; \(L\) represents the observation vector. After solving the vector \(\hat{X}\) and calculating the covariance information, the hourly updated near real-time GIM (SHUG) in the IONosphere map EXchange (IONEX) format (Schaer et al. 1998) is generated with the spatiotemporal resolution of 1-h × 2.5° × 5.0° in time, latitude and longitude, respectively. As the IGS hourly data has a time delay of over 1 h, while the near real-time modeling typically takes less than 15 min, the time latency of SHUG is about 1–2 h.
2.3 Method of GIM nowcasting
In this study, ARMA model was employed to build a probabilistic statistical model for the time series of ionospheric model coefficients with near real-time and rapid ionospheric products and predict the model coefficients (Li et al. 2007). The \({\text{ARMA}}\left( {p,q} \right)\) model can be expressed as follows:
where \(z_{t}\) represents the zero mean and stationary random time series of ionosphere model coefficients, \(p\) and \(q\) denote the orders of autoregressive and moving average, respectively; \(\varphi_{i}\) and \(\theta_{j}\) are the autoregressive coefficients and moving average coefficients, respectively; \(a_{t}\) stands for the white noise time series. The auto-covariance function \(\hat{R}_{k}\) can be calculated using Eq. (8), respectively.
where \(N\) represents the length of \(z_{t}\). We establish Yule–Walker function to solve the autoregressive coefficients \(\hat{\varphi }_{i}\) of \({\text{AR}}\left( p \right)\) model:
where \(\hat{R}_{q}\), \(\hat{R}_{q + 1}\), \(\cdots\), \(\hat{R}_{q + p}\) represent the auto-covariance function of \(z_{t}\) and can be calculated with Eq. (8). Then build \(AR\left( p \right)\) model with \(\hat{\varphi }_{i}\) to fit \(z_{t}\) and calculate the residual error time series \(\hat{v}_{t}\):
The \({\text{MA}}\left( q \right)\) coefficients \(\hat{\theta }_{j}\) can be solved using least squares method for the residual error time series \(\hat{v}_{t}\) using the least squares method. After obtaining \(\hat{\varphi }_{i}\) and \(\hat{\theta }_{j}\), the ARMA model is built, and then we can extrapolate the ionosphere model coefficients and generate the predicted GIM.
In the practical prediction, the values of \(p\) and \(q\) for ARMA model are unknown in advance, so we need to determine the order of \(p\) and \(q\) before we can make a prediction. In this study, the Akaike information criterion \(\left( {{\text{AIC}}} \right)\) (Akaike 1974) is adopted to determine \(p\) and \(q\), and can be expressed as follows:
The maximum orders of \(p\) and \(q\) are given firstly (usually taken as \(\sqrt N\), \(N/10\) or \(\ln N\)), and denote them as \(p^{*}\) and \(q^{*}\), respectively. Calculate each of \(\hat{\varphi }_{i}\), \(\hat{\theta }_{j}\) and \({\text{AIC}}\left( {p,q} \right)\) in the range of \(0 \le p \le p^{*}\) and \(0 \le q \le q^{*}\) using the above strategies. The \(p\) and \(q\) corresponding to the minimal value of \({\text{AIC}}\left( {p,q} \right)\) are taken as the orders of the ARMA model, and then the ARMA model coefficients \(\hat{\varphi }_{i}\), \(\hat{\theta }_{j}\) are determined.
In the ionospheric coefficient prediction, we compose the prediction time series of spherical harmonic expansion coefficients of the same degree and order:
where \(\tilde{C}\) and \(\tilde{S}\) correspond the spherical harmonic coefficients in Eq. (3); \(n\) and \(m\) denote the degree and order of spherical harmonic expansion; \(N\) represents the length of prediction series. For example, in order to predict 15 degree × 15 order spherical harmonic coefficients with a length 100 days and an interval of 1 h, we need to compose 256 groups of prediction series with a length of 2400 h, establish ARMA model for each group of prediction series, and predict the coefficient \(z_{t + 1} , \ldots , z_{t + n}\), where \(n\) is the prediction length. After obtaining the predicted coefficients, the predicted GIM can be generated.
In order to verify the effect of using ARMA model for ionospheric prediction and find a reasonable length of prediction sequence, we estimated 1-day predicted GIM (S1PG) in the solar relatively active year (2014) and quiet year (2021) based on 3-day, 7-day, 30-day, 60-day and 100-day prediction sequences, named S1PG-3d, S1PG-7d, S1PG-30d, S1PG-60d, S1PG-100d, respectively, and compared the S1PG with CODE 1-day predicted GIM (C1PG) and IGS final GIM (IGSG). In this study, the bias, mean bias, standard deviation (STD) and root mean square error (RMSE) of VTEC are calculated as follows:
where the \({\text{VTEC}}_{{{\text{bias}}}}\), \({\text{VTEC}}_{{{\text{mean}}\_{\text{bias}}}}\), \({\text{VTEC}}_{{{\text{STD}}}}\) and \({\text{VTEC}}_{{{\text{RMSE}}}}\) represent the bias, the mean bias, the STD and the RMSE of VTEC with respect to the reference VTEC (\({\text{VTEC}}_{{{\text{ref}}}}\)), respectively, and \(n\) denotes the number of VTEC. Since the GIM VTEC maps at different times vary considerably throughout a day, in order to verify the reliability of the GIM in detail, we calculate the hourly mean bias, hourly STD and hourly RMSE of validated VTECs in each hour of VTEC map in GIM with respect to the referenced VTECs, that is, where \(n\) in Eq. (14) equals to the number of grid points of in a map of VTECs.
The VTEC RMSEs of S1PG with different length of prediction sequence and C1PG with respect to IGSG in 2014 and 2021 are listed in Table 1, and the hourly RMSEs of S1PG-100d and C1PG with respect to IGSG in 2014 and 2021 are shown in Fig. 3. It can be seen that the prediction accuracy of S1PG is improved as the length increase in prediction sequence, but the magnitude of the accuracy improvement gradually decreases. Meanwhile, S1PG-100d shows an insignificant reduction in RMSE with respect to S1PG-60d (less than 0.1 TECu) and its reliability has been essentially comparable to that of C1PG. Based on the above analysis, we can infer that the AMRA model is feasible for ionospheric model prediction, and a high-precision ionospheric prediction can be achieved by using 100 days of prediction sequence. Therefore, we also adopt 100-day prediction sequence for hourly sliding ionospheric model prediction.
As shown in Fig. 2, we use a sliding mode with a sliding step of 1 h for hourly ionospheric nowcasting. After solving the hourly near real-time ionospheric model, we discretize the daily rapid ionospheric model into hourly rapid ionospheric model, and combine the latest estimated 24-h near real-time models and hourly rapid models into a prediction sequence with a total length of 2400 h (100 days) for ionospheric nowcasting. The ARMA model is adopted to predict several hours of ionospheric models and then the SHPG can be generated.
3 Consistency analysis of GIMs
We estimated the near real-time SHUG and 1-h to 4-h predicted SHPG in the solar relatively active year (2014) and quiet year (2021), respectively. In order to validate the reliability of estimated results, the consistency of SHUG and rapid GIMs with respect to IGSG, and the agreement of SHPG and C1PG with respect to CODE final GIM (CODG) are analyzed in this section.
3.1 Consistency analysis of SHUG with IGS GIMs
As IGSG is a combination of IGS final GIMs and provides accurate and reliable VTECs (Hernandez-Pajares et al. 2009), IGSG was adopted as a reference to compare the consistency of SHUG with rapid GIMs of JPL (JPRG), UPC (UQRG), CODE (CORG) and SHAO (SHRG). The hourly mean VTEC biases of JPRG, UQRG, CORG, SHRG and SHUG with respect to IGSG in 2014 and 2021 are depicted in Fig. 4. It can be seen that SHUG is in good agreement with SHRG and CORG but has relatively large discrepancy with JPLG and UQRG. This is mainly because SHUG, SHAG and CODG are based on spherical harmonic expansion, and JPLG and UQRG are based on spherical triangles with splines and tomographic with kriging, respectively (Mannucci et al. 1998; Orus et al. 2005; Schaer 1999). The hourly VTEC biases of SHUG with respect to IGSG are about − 2.7 to 1.5 TECu in 2014 and about − 1.6 to 0.4 TECu in 2021, which are almost the same with those of CORG and SHRG.
3.2 Consistency analysis of SHPG with CODE GIMs
As C1PG is the prediction of CODE ionospheric harmonic coefficients with least square collocation and has good consistency with CODG, we compared the 1-h, 2-h, 3-h and 4-h predicted SHPG (named SHPG (1 h), SHPG (2 h), SHPG (3 h) and SHPG (4 h)) and C1PG in 2014 and 2021, using CODG as a reference. Figure 5 shows the VTEC difference distributions of SHPG (1 h) and C1PG with respect to CODG at UTC 0:00, 6:00, 12:00 and 18:00 on the days of spring equinox, summer solstice, autumnal equinox and winter solstice in 2021. It can be seen that SHPG is generally in better consistency with CODG than C1PG. Meanwhile, the VTEC biases of SHPG with respect to CODG at different moments of a day are significantly smaller than those of the C1PG except for the summer solstice, especially in the Equatorial Ionization Anomaly (EIA) region on the daytime of spring and autumn equinoxes and in the Weddell Sea Anomaly (WSA) region on the night of winter solstice.
The VTEC bias distribution maps for on the days of spring equinox (DOY 079), summer solstice (DOY 172), autumnal equinox (DOY 266) and winter solstice (DOY 355) in 2021 at UTC 00:00, 06:00, 12:00, 18:00 for SHPG (1 h) with respect to CODG (a) and C1PG with respect to CODG (b) (unit: TECu). The solid black line in each center of the figures represents the geomagnetic equator. The region between the two dashed lines (± 20° of the geomagnetic equator) is represented as the EIA region
The hourly VTEC biases of SHPG (1 h), SHPG (2 h), SHPG (3 h), SHPG (4 h) and C1PG with respect to CODG in 2014 and 2021 are shown in Fig. 6. The VTEC biases of SHPG (1 h), SHPG (2 h) are mainly ranged from − 3.0 to 2.0 TECu in 2014 and from − 1.0 to 1.0 TECu in 2021, and those of C1PG are about − 4.0 to 4.0 TECu and − 2.0 to 2.0 TECu in 2014 and 2021, respectively. From the above analysis we can see that the consistency of SHPG (1 h) and SHPG (2 h) with respect to CODG is obviously better than that of C1PG.
4 GPS dSTECs validation
The GPS dSTEC extracted from the difference of dual-frequency geometry-free combination of GNSS carrier phase observations, provides an excellent high-precision ionospheric reference with an accuracy better than 0.1 TECu, and has been widely adopted for GIM validation (Feltens et al. 2011; Hernandez-Pajares et al. 2017; Roma-Dollase et al. 2018). The dSTEC is defined as the difference of \(L_{4}\) at epoch \(t\) with respect to the \(L_{4}\) at the epoch with highest elevation alone the line-of-sight (\(t_{{E_{\max } }}\)) in a phase-continuous observation arc without cycle-slip and can be expressed as follows:
Since the dSTEC is the difference between the STECs at two IPPs, we need to calculate the VTEC values at the corresponding positions of dSTEC, convert the VTECs to STECs with a mapping function, and then calculate the difference between this two converted STECs. The RMSE of dSTEC (\({\text{RMSE}}_{{{\text{dSTEC}}}}\)) is computed as follows:
where the \({\text{dSTEC}}_{{{\text{ref}}}}\) is the dSTEC extracted from GNSS observations, \({\text{dSTEC}}_{{{\text{GIM}}}}\) denotes the dSTEC calculated by GIMs at the corresponding position of \({\text{dSTEC}}_{{{\text{GIM}}}}\), \(n\) represents the total number of dSTEC for one validation station.
Twenty-two global independent GNSS stations not involved in modeling providing by University Navstar Consortium (UNAVCO) and Système d’observation du Niveau des aux Littorales (SONEL) networks are selected as the evaluation stations to validate SHUG and SHPG. As shown in Fig. 7, the GPS dSTECs evaluation stations are homogeneously distributed around the world and the validation dates are set to the two equinox and two solstice days in 2014 (DOY 080, 172, 266 and 356) and 2021 (DOY 079, 172, 266 and 355) to comprehensively evaluate the performance of SHUG and SHPG in different latitudes and during different solar activities.
4.1 SHUG validation with GPS dSTECs
Figure 8 presents the RMSEs of JPRG, UQRG, CORG, SHRG and SHUG with respect to GPS dSTECs of 22 evaluation stations on spring equinox, summer solstice, autumnal equinox and winter solstice days in 2014 and 2021, respectively. We can see that the RMSEs of near real-time and rapid GIMs are quite consistent for different evaluation stations and periods, and the accuracy of SHUG in solar active year is significantly lower than that in solar quiet year, which is consistent with the annual variation in TECs. It can be observed that for some stations and evaluations days, the RMSEs of some GIMs are obviously higher than other GIMs. For example, UQRG performs very well overall, but the RMSEs of UQRG versus APNT on DOY 266 and 356 in 2014 (corresponding to Fig. 8e, g) are significantly higher than other GIMs. We found that UQRG did not use modeling stations in a larger area near the ANPT station on those two days, which resulted in a significant degradation of model accuracy in that area. This explains to some extent that for ionospheric modeling, the number and distribution of stations is an important factor affecting the reliability of GIM. As we adopt all available GNSS stations (typically more than 300 stations) in SHUG and SHRG estimation, the RMSEs of SHUG and SHRG is relatively more stable.
The RMSEs of JPRG, UQRG, CORG, SHRG and SHUG with respect to GPS dSTECs of evaluation stations on spring equinox, summer solstice, autumnal equinox and winter solstice days in 2014: 080 (a), 172 (c), 266 (e) and 356 (g), and in 2021: 079 (b), 172 (d), 266 (f) and 355 (h). Results are listed in order of the station geographical latitudes from − 90° to 90° (unit: TECu)
Since the ionospheric TEC significantly varies at different latitudes, in order to better analyze the performance of GIMs in different latitudinal bands, we divide the globe from 90° S to 90° N into six latitude bands, with an interval of 30°. The RMSEs of GIMs with respect to GPS dSTEC at each latitude band and global scale are listed in Table 2. We can see that the performance of near real-time SHUG and rapid GIMs with respect to GPS dSTEC are quite consistent in different latitude bands and at global scales, the RMSEs of GIMs in the low latitude bands are significantly higher than those in middle and high latitude bands, and the discrepancy between the GIMs is less than 1 TECu overall. Moreover, SHUG performs slightly better than other GIMs in the southern hemisphere middle and low latitude bands.
4.2 SHPG validation with GPS dSTECs
The RMSEs of C1PG, SHPG (1 h), SHPG (2 h), SHPG (3 h), and SHPG (4 h) with respect to GPS dSTECs of 22 evaluation stations on spring equinox, summer solstice, autumnal equinox and winter solstice days in 2014 and 2021 are shown in Fig. 9, and the corresponding RMSEs at different latitude bands and global scales are listed in Table 2. From Fig. 9 we can observe that for different solar active years, the RMSEs of each evaluation station and GIM are quite different on the same equinox and solstice days, specifically, the RMSEs on the same days in the solar active periods are all higher than those in the solar quiet periods, and this is the same as the results of SHUG and rapid GIMs. Moreover, the GPS dSTECs RMSEs of SHPG with respect to evaluation stations located in the southern hemisphere (e.g., AUTF, KEPA, GISB and HARB) on the winter solstice in 2014 (see Fig. 9g) and 2021 (see Fig. 9h) is better than those of C1PG, and this is mostly dominated by the sparse and inhomogeneous distribution of GNSS stations in the southern hemisphere.
The RMSEs of C1PG, SHPG (1 h), SHPG (2 h), SHPG (3 h), and SHPG (4 h) with respect to GPS dSTECs of evaluation stations on spring equinox, summer solstice, autumnal equinox and winter solstice days in 2014: DOY 080 (a), 172 (c), 266 (e) and 356 (g), and in 2021: DOY 079 (b), 172 (d), 266 (f) and 355 (h). Results are listed in order of the station geographical latitudes from − 90° to 90° (unit: TECu)
On a global scale, the RMSEs of nowcasting SHPG are about 3.8–4.5 TECu, and that of C1PG is 4.4 TECu. The 1-h nowcasting SHPG is about 0.6 TECu better than the C1PG, and yet the longer nowcasting GIM is not significantly different from the C1PG. In the high latitude bands, there are no obvious difference in the performance of the nowcasting and daily predicted GIMs. However, in the middle and low latitude bands, the 1-h and 2-h nowcasting GIMs perform better than the daily predicted GIMs, especially in the low latitude bands, which mainly correspond to the ionospheric EIA regions, and the RMSE of 1-h nowcasting SHPG and 1-day predicted C1PG are about 3.6–6.1 TECu and 4.8–7.1 TECu, respectively, which means that 1-h nowcasting SHPG is approximately 1 to 2 TECu more accurate than C1PG. This is mainly because of the eventful ionospheric activities in the corresponding regions, which makes long-term accurate TEC prediction relatively difficult. Since 1–2 TECu corresponds to 16.2–32.4 cm pseudorange delay in GPS L1 frequency band, this accuracy improvement of is significant for navigation and positioning applications, especially for PPP and PPP-RTK services with decimeter- and centimeter-level positioning.
5 Satellite altimetry VTEC validation
Satellite altimetry is capable of providing high-precision VTECs from the Earth’s surface to the orbit altitude of satellites but differs in principle from GNSS. The VTECs derived from dual-frequency (Ku-/C- band) altimeter observations of satellite altimetry satellites such as TOPEX and Jason series have become a typical reference for GIM validation, especially for validating the reliability of GIMs in the ocean regions (Hernández-Pajares et al. 1999; Hernandez-Pajares et al. 2017; Imel 1994; Mannucci et al. 1998; Roma-Dollase et al. 2018). The altimeter ionospheric corrections in Ku-band (\(I_{{{\text{ku}}}}\)) in Level-2 high-precision reduced 1 Hz geophysical data record (GDR) version ‘D’ products (GDR_D) of Jason-2 in 2014 and version ‘F’ products (GDR_F) of Jason-3 in 2021 are adopted to extract the VTECs of satellite altimetry (\({\text{VTEC}}_{{{\text{SA}}}}\)) and validate the GIMs during different periods of solar activity (Azpilicueta and Nava 2021). The \({\text{VTEC}}_{{{\text{SA}}}}\) can be inverted by using this following equation:
where the \(f_{{{\text{ku}}}}\) represents the frequency of 13.575 GHz in Ku-band. As the ionospheric correction of satellite altimetry is affected by relatively large measurement noise and some points are of poor quality, the corrections such as the points reflections on the ice and the isolated and jump points are rejected, and the corrections are smoothed with a sliding window of 16 consecutive samples (see more details in Roma-Dollase et al. 2018). The processed distribution of subastral points and VTEC values of Jason-2 in the 210th cycle (from March 15, 2014 to March 25, 2014) is shown in Fig. 10. As GNSS and satellite altimetry satellites operate at different orbital altitudes, there exists a systematic bias of several TECu between the VTECs of GNSS and satellite altimetry inversions mainly due to the plasmaspheric electron content (Jee et al. 2010). Therefore, the STD, which minimizes the differences between the VTECs of GIM and satellite altimetry and reflects the degree of dispersion of differences, has been commonly adopted as the main indicator to evaluate the performance of GIM (Hernandez-Pajares et al. 2017; Roma-Dollase et al. 2018; Zhang and Zhao 2019). The RMSE and bias are used to assess the consistency between GIMs.
5.1 SHUG validation with satellite altimetry VTECs
The hourly VTEC biases and STDs of JPRG, UQRG, CORG, SHRG and SHUG with respect to Jason-2 VTECs in 2014 and Jason-3 VTECs in 2021 are shown in Figs. 11 and 12, respectively. The corresponding STDs, RMSEs and biases of GIMs with respect to Jason-2 and Jason-3 VTECs in 2014 and 2021 are listed in Tables 3 and 4, respectively. It can be seen that the hourly VTEC biases of GNSS versus satellite altimetry are positive, and this biases mainly correspond to the TECs in the plasmasphere. Moreover, the hourly VTEC biases and STDs in spring and autumn are generally larger than those in other seasons, which is consistent with the seasonal variation in TECs. SHUG is in good agreement with the rapid GIMs, with the corresponding STDs of 6.0 TECu in 2014 and 3.0 TECu in 2021, and the STDs of rapid GIMs are 4.2–6.2 TECu and 2.6–3.0 TECu in 2014 and 2021, respectively. It can be concluded that the STD of SHUG with respect to Jason-2 and Jason-3 VTECs is no more than 10% over the majority of the rapid GIMs, and this is mainly caused by the instability of real-time and hourly observations.
5.2 SHPG validation with satellite altimetry VTECs
The hourly VTEC biases and STDs of C1PG, SHPG (1 h), SHPG (2 h), SHPG (3 h) and SHPG (4 h) with respect to Jason-2 VTECs in 2014 and Jason-3 VTECs in 2021 are demonstrated in Figs. 13 and 14, respectively. We can see that the predicted GIMs have good consistency, and the hourly VTEC biases are mostly concentrated between −5.0–15.0 TECu in 2014 and 0.0–10.0 TECu in 2021. Tables 3 and 4 present the STDs, RMSEs and biases of predicted GIMs with respect to Jason-2 and Jason-3 VTECs in 2014 and 2021, respectively. The STDs of SHPG are about 6.2–6.6 TECu in 2014 and 3.1–3.3 TECu in 2021, and those of C1PG are 7.1 and 3.4 TECu, respectively. The performance of SHPG is generally better than C1PG, and the STDs of SHPG (1 h) are 12.0% and 10.2% lower than C1PG in 2014 and 2021, respectively. In 2014, the STD of SHPG is about 1 TECu lower than that of C1PG, which means that the reliability of SHPG is 1 TECu better than C1PG overall, and this improvement is significant for centimeter- and decimeter-level high-precision and real-time navigation and positioning. Moreover, from the STD and RMSE results we can clearly see that the reliability SHPG has been improved with the shortening of prediction time.
6 Conclusion
In order to reduce the time latency of post-processing GIMs and enhance the reliability predicted GIMs, we propose a method of estimating hourly updated near real-time SHUG and nowcasting SHPG. SHUG is an hourly estimation based on a 24-h real-time and hourly GNSS data sliding window and fitted with spherical harmonic expansion. SHPG is an hourly nowcasting with ARMA model based on near real-time and rapid ionospheric models. In order to verify the reliability of SHUG and SHPG, we estimated SHUG and SHPG in the solar active year (2014) and solar quiet year (2021) and validated them with rapid GIMs, GPS dSTECs extracted from 22 global independent GNSS stations and Jason-2/-3 VTECs.
Compared with the rapid GIMs, the hourly VTEC biases of SHUG with respect to IGSG are about − 2.7 to 1.5 TECu in 2014 and about − 1.6 to 0.4 TECu in 2021, and SHUG is in good agreement with CODG and SHAG. As for SHPG, consistency analysis results show that SHPG is in better agreement with CODG than C1PG. The VTEC biases of SHPG (1 h) with respect to CODG at different moments of spring and autumnal equinox and winter solstice are significantly smaller than those of the C1PG, especially in the EIA region on the daytime of spring and autumn equinoxes and in the WSA region on the night of winter solstice.
GPS dSTEC validation results show that the RMSEs of SHUG with respect to GPS dSTECs range from 1.4 to 5.3 TECu at different latitude bands and is 3.2 TECu at a global scale. SHUG behaves fairly consistent with the rapid GIMs, and the discrepancy between the SHUG and rapid GIMs is less than 1 TECu overall. Moreover, SHUG performs slightly better than some of rapid GIMs in the southern hemisphere middle and low latitude bands. For the GPS dSTEC validation result of SHPG, the RMSEs of 1-h to 4-h nowcasting SHPG are about 3.8–4.5 TECu on a global scale, and that of C1PG is 4.4 TECu. The 1-h nowcasting SHPG is about 0.6 TECu better than the C1PG overall. In the middle and low latitude bands, the 1-h and 2-h nowcasting GIMs perform better than the daily predicted GIMs, especially in the low latitude bands, which mainly correspond to the ionospheric EIA regions, and the RMSEs of 1-h nowcasting SHPG and 1-day predicted C1PG are about 3.6–6.1 TECu and 4.8–7.1 TECu, respectively, which indicates that the accuracy of 1-h nowcasting SHPG is approximately 1 to 2 TECu better than C1PG. This is mainly due to the active ionospheric electron density activity in the corresponding regions, which makes daily accurate prediction relatively difficult.
Satellite altimetry VTEC validation results show that the STDs of SHUG are 6.0 TECu and 3.0 TECu in 2014 with respect to Jason-2 VTECs and 2021 with respect to Jason-3 VTECs, respectively, and those of rapid GIMs are 4.2–6.2 TECu and 2.6–3.0 TECu in 2014 and 2021, respectively, which indicates that SHUG is in good agreement with the rapid GIMs. The STD of SHUG with respect to Jason-2 and Jason-3 VTECs is no more than 10% over the majority of the rapid GIMs, and this is mainly due to the instability of real-time and near real-time observations. The hourly nowcasting SHPG performs better than daily predicted C1PG in a short period of time. The STDs of 1-h to 4-h nowcasting SHPG versus Jason-2/-3 VTECs are 6.2–6.6 TECu in 2014 and 3.1–3.3 TECu in 2021, and those of C1PG are 7.1 and 3.4 TECu, respectively. The performance of 1-h nowcasting SHPG is 12.0% and 10.2% better than that of C1PG in 2014 and 2021, respectively.
From above analysis, we can conclude that the reliability of near real-time SHUG is basically equivalent to rapid GIMs, and the time latency of SHUG is shortened from at least 1 day to 1–2 h. The nowcasting SHPG performs better than daily predicted GIM, especially during periods when the ionospheric electron density rapidly changes and in EIA and WSA regions, so it can provide more accurate short-term predicted TEC information. Therefore, the development of near real-time and nowcasting can contribute to accurate estimation of TEC and offer more accurate TEC background information than daily predicted GIM for real-time GIM estimation. Furthermore, the realization of near real-time and nowcasting GIM can complement the type of GIM products to better serve the users with different requirements for TEC time delay, accuracy and stability, such as the multi-frequency and single-frequency PPP, PPP-RTK users, VLBI and space vehicle navigation signal ionospheric delay real-time correction, space weather monitoring, and early warning, monitoring and damage evaluation of natural disasters.
It should be pointed out that 1-h predicted SHPG have a fairly high accuracy, indicating that the hourly nowcast strategy is effective. However, since the hourly ionospheric nowcasting is the initial implementation based on the method of daily prediction, the quality of nowcasting GIM decreases obviously with the increase in extrapolation time. Therefore, the next steps are to study and develop a high-precision ionospheric nowcasting model based on near real-time models to further improve the accuracy of nowcasting models, and apply the near real-time and nowcasting models to real-time ionospheric modeling.
Data availability
The IGS real-time GNSS data stream at https://igs-ip.net/home/ can be obtained through BNC software. The IGS hourly GNSS data can be accessed at https://cddis.nasa.gov/archive/gps/data/hourly/. The hourly updated GPS, GLONASS, Galileo and BEIDOU broadcast ephemeris provided by iGMAS analysis center of SHAO, CAS is available at https://gnss.shao.ac.cn/home/. The C1PG, CODG, IGSG, JPLG and UQRG can be obtained at https://cddis.nasa.gov/archive/gnss/products/ionex/. The GNSS data provided by UNAVCO is available at ftp://data-out.unavco.org/pub/rinex/obs/. The GNSS data provided by SONEL can be found at ftp://ftp.sonel.org/gps/data/. The Jason-2 and Jason-3 altimetry datasets used for this study are available at ftp://ftp-oceans.ncei.noaa.gov/pub/data.nodc/. The datasets supporting the findings of this study are available from the corresponding authors upon reasonable request.
References
Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom Control 19:716–723. https://doi.org/10.1109/TAC.1974.1100705
Astafyeva E (2019) Ionospheric detection of natural hazards. Rev Geophys 57:1265–1288. https://doi.org/10.1029/2019rg000668
Astafyeva E, Maletckii B, Mikesell TD, Munaibari E, Ravanelli M, Coisson P, Manta F, Rolland L (2022) The 15 January 2022 Hunga Tonga eruption history as inferred from ionospheric observations. Geophys Res Lett. https://doi.org/10.1029/2022gl098827
Azpilicueta F, Nava B (2021) On the TEC bias of altimeter satellites. J Geod. https://doi.org/10.1007/s00190-021-01564-y
Bilitza D, Altadill D, Truhlik V, Shubin V, Galkin I, Reinisch B, Huang X (2017) International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather Int J Res Appl 15:418–429. https://doi.org/10.1002/2016sw001593
Bilitza D, McKinnell L-A, Reinisch B, Fuller-Rowell T (2011) The international reference ionosphere today and in the future. J Geod 85:909–920. https://doi.org/10.1007/s00190-010-0427-x
Blanc E (1985) Observations in the upper atmosphere of infrasonic waves from natural or artificial sources: a summary. Ann Geophys 3:673–687
Blewitt G (1990) An automatic editing algorithm for GPS data. Geophys Res Lett 17:199–202. https://doi.org/10.1029/GL017i003p00199
Buonsanto MJ (1999) Ionospheric storms—a review. Space Sci Rev 88:563–601
Caissy M, Agrotis L, Weber G, Hernandezpajares M, Hugentobler U (2012) Coming soon: the international GNSS real-time service. GPS World
Chen P, Liu H, Schmidt M, Yao Y, Yao W (2022) Near real-time global ionospheric modeling based on an adaptive Kalman filter state error covariance matrix determination method. IEEE Trans Geosci Remote Sens 60:1–12. https://doi.org/10.1109/tgrs.2021.3091705
Ciraolo L, Azpilicueta F, Brunini C, Meza A, Radicella SM (2006) Calibration errors on experimental slant total electron content (TEC) determined with GPS. J Geod 81:111–120. https://doi.org/10.1007/s00190-006-0093-1
Erdogan E, Schmidt M, Goss A, Görres B, Seitz F (2021) Real-time monitoring of ionosphere VTEC using multi-GNSS carrier-phase observations and B-splines. Space Weather. https://doi.org/10.1029/2021sw002858
Erdogan E, Schmidt M, Seitz F, Durmaz M (2017) Near real-time estimation of ionosphere vertical total electron content from GNSS satellites using B-splines in a Kalman filter. Ann Geophys 35:263–277. https://doi.org/10.5194/angeo-35-263-2017
Falck C, Ramatschi M, Subarya C, Bartsch M, Merx A, Hoeberechts J, Schmidt G (2010) Near real-time GPS applications for tsunami early warning systems. Nat Hazards Earth Syst Sci 10:181–189. https://doi.org/10.5194/nhess-10-181-2010
Feltens J (2007) Development of a new three-dimensional mathematical ionosphere model at European space Agency/European space operations centre. Space Weather Int J Res Appl. https://doi.org/10.1029/2006sw000294
Feltens J, Angling M, Jackson-Booth N, Jakowski N, Hoque M, Hernandez-Pajares M, Aragon-Angel A, Orus R, Zandbergen R (2011) Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci. https://doi.org/10.1029/2010rs004584
Feltens J, Schaer S (1998) IGS Products for the Ionosphere. In: Proceedings of the IGS analysis centers workshop. Darmstadt, Germany, pp 225–232
García-Rigo A, Monte E, Hernández-Pajares M, Juan JM, Sanz J, Aragón-Angel A, Salazar D (2011) Global prediction of the vertical total electron content of the ionosphere based on GPS data. Radio Sci. https://doi.org/10.1029/2010rs004643
Ghoddousi-Fard R (2014) GPS ionospheric mapping at Natural Resources Canada. In: IGS workshop, Pasadena
Hernández-Pajares M, Juan J, Sanz J (1999) New approaches in global ionospheric determination using ground GPS data. J Atmos Sol Terr Phys J Atmos Sol-Terr Phys 61:1237–1247
Hernandez-Pajares M, Juan J, Sanz J, Orus R, Garcia-Rigo A, Feltens J, Komjathy A, Schaer S, Krankowski A (2009) The IGS VTEC maps: a reliable source of ionospheric information since 1998. J Geod 83:263–275. https://doi.org/10.1007/s00190-008-0266-1
Hernandez-Pajares M, Roma-Dollase D, Krankowski A, Garcia-Rigo A, Orus-Perez R (2017) Methodology and consistency of slant and vertical assessments for ionospheric electron content models. J Geod 91:1405–1414. https://doi.org/10.1007/s00190-017-1032-z
Imel D (1994) Evaluation of the TOPEX/POSEIDON dual-frequency ionosphere correction. J Geophys Res Oceans 99:24895–24906. https://doi.org/10.1029/94jc01869
Jee G, Lee H, Kim Y, Chung J, Cho J (2010) Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: ionospheric perspective. J Geophys Res Space Phys. https://doi.org/10.1029/2010ja015432
Jin S, Occhipinti G, Jin R (2015) GNSS ionospheric seismology: recent observation evidences and characteristics. Earth Sci Rev 147:54–64. https://doi.org/10.1016/j.earscirev.2015.05.003
Jin X, Song S, Zhou W, Cheng N (2022) Multi-GNSS global ionosphere modeling enhanced by virtual observation stations based on IRI-2016 model. J Geod. https://doi.org/10.1007/s00190-022-01667-0
Klobuchar JA (1987) Ionospheric time-delay algorithms for single-frequency GPS users. IEEE Trans Aerosp Electron Syst AES 23:325–331
Lanyi G, Roth T (1988) A comparison of mapped and measured total ionospheric electron-content using global positioning system and beacon satellite-observations. Radio Sci 23:483–492. https://doi.org/10.1029/RS023i004p00483
Li X, Ge M, Zhang H, Wickert J (2013) A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J Geod 87:405–416. https://doi.org/10.1007/s00190-013-0611-x
Li Z, Wang N, Hernandez-Pajares M, Yuan Y, Krankowski A, Liu A, Zha J, Garcia-Rigo A, Roma-Dollase D, Yang H, Laurichesse D, Blot A (2020) IGS real-time service for global ionospheric total electron content modeling. J Geod. https://doi.org/10.1007/s00190-020-01360-0
Li Z, Yuan Y, Wang N, Hernandez-Pajares M, Huo X (2014) SHPTS: towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J Geod 89:331–345. https://doi.org/10.1007/s00190-014-0778-9
Li ZG, Cheng ZY, Feng CG, Li WC, Li HR (2007) A study of prediction models for ionosphere. Chin J Geophys Chin Ed 50:327–337
Liu JY, Chuo YJ, Shan SJ, Tsai YB, Chen YI, Pulinets SA, Yu SB (2004) Pre-earthquake ionospheric anomalies registered by continuous GPS TEC measurements. Ann Geophys 22:1585–1593. https://doi.org/10.5194/angeo-22-1585-2004
Liu Q, Hernández-Pajares M, Yang H, Monte-Moreno E, Roma-Dollase D, García-Rigo A, Li Z, Wang N, Laurichesse D, Blot A, Zhao Q, Zhang Q, Hauschild A, Agrotis L, Schmitz M, Wübbena G, Stürze A, Krankowski A, Schaer S, Feltens J, Komjathy A, Ghoddousi-Fard R (2021) The cooperative IGS RT-GIMs: a reliable estimation of the global ionospheric electron content distribution in real time. Earth Syst Sci Data 13:4567–4582. https://doi.org/10.5194/essd-13-4567-2021
Lu G, Richmond AD, Emery BA, Roble RG (1995) Magnetosphere-ionosphere-thermosphere coupling: effect of neutral winds on energy transfer and field-aligned current. J Geophys Res Space Phys 100:19643–19659
Mannucci A, Wilson B, Edwards C (1993) A new method for monitoring the Earth ionosphere total electron content using the GPS global network. In: Proceedings of the 6th international technical meeting of the satellite division of the institute of navigation (ION GPS 1993), Salt Lake City, UT, September 1993, pp 1323–1332
Mannucci A, Wilson B, Yuan D, Ho C, Lindqwister U, Runge T (1998) A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci 33:565–582. https://doi.org/10.1029/97rs02707
Orus Perez R (2016) Ionospheric error contribution to GNSS single-frequency navigation at the 2014 solar maximum. J Geod 91:397–407. https://doi.org/10.1007/s00190-016-0971-0
Orus R, Hernandez-Pajares M, Juan J, Sanz J (2005) Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J Atmos Solar Terr Phys 67:1598–1609. https://doi.org/10.1016/j.jastp.2005.07.017
Pulinets SA, Legen’ka AD, Gaivoronskaya TV, Depuev VK (2003) Main phenomenological features of ionospheric precursors of strong earthquakes. J Atmos Solar Terr Phys 65:1337–1347. https://doi.org/10.1016/j.jastp.2003.07.011
Ren X, Chen J, Li X, Zhang X, Freeshah M (2019) Performance evaluation of real-time global ionospheric maps provided by different IGS analysis centers. GPS Solut. https://doi.org/10.1007/s10291-019-0904-5
Ren XD, Chen J, Li XX, Zhang XH (2021) Ionospheric total electron content estimation using GNSS carrier phase observations based on zero-difference integer ambiguity: methodology and assessment. IEEE Trans Geosci Remote Sens 59:817–830. https://doi.org/10.1109/Tgrs.2020.2989131
Roma-Dollase D, Hernandez-Pajares M, Krankowski A, Kotulak K, Ghoddousi-Fard R, Yuan Y, Li Z, Zhang H, Shi C, Wang C, Feltens J, Vergados P, Komjathy A, Schaer S, Garcia-Rigo A, Gomez-Cama J (2018) Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J Geod 92:691–706. https://doi.org/10.1007/s00190-017-1088-9
Savastano G, Komjathy A, Verkhoglyadova O, Mazzoni A, Crespi M, Wei Y, Mannucci AJ (2017) Real-time detection of tsunami ionospheric disturbances with a stand-alone GNSS receiver: a preliminary feasibility demonstration. Sci Rep 7:46607. https://doi.org/10.1038/srep46607
Schaer S (1999) Mapping and predicting the Earth’s ionosphere using the global positioning system. Geod Geophys Arb Schweiz 59
Schaer S, Gurtner W, Feltens J (1998) IONEX: the ionosphere map exchange format version 1. In: Proceedings of the IGS analysis center workshop, Darmstadt, pp 233–247
Schmidt M, Dettmering D, Seitz F (2013) Using B-spline expansions for ionosphere modeling. In: Handbook of geomathematics
Sekido M, Kondo T, Kawai E, Imae M (2003) Evaluation of GPS-based ionospheric TEC map by comparing with VLBI data. Radio Sci. https://doi.org/10.1029/2000rs002620
Sezen U, Arikan F, Arikan O, Ugurlu O, Sadeghimorad A (2013) Online, automatic, near-real time estimation of GPS-TEC: IONOLAB-TEC. Space Weather 11:297–305. https://doi.org/10.1002/swe.20054
Tariq MA, Shah M, Hernández-Pajares M, Iqbal T (2019) Pre-earthquake ionospheric anomalies before three major earthquakes by GPS-TEC and GIM-TEC data during 2015–2017. Adv Space Res 63:2088–2099. https://doi.org/10.1016/j.asr.2018.12.028
Wang N, Yuan Y, Li Z, Montenbruck O, Tan B (2015) Determination of differential code biases with multi-GNSS observations. J Geod 90:209–228. https://doi.org/10.1007/s00190-015-0867-4
Zhang B, Ou J, Yuan Y, Li Z (2012) Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning. Sci China Earth Sci 55:1919–1928. https://doi.org/10.1007/s11430-012-4454-8
Zhang H, Gao Z, Ge M, Niu X, Huang L, Tu R, Li X (2013) On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors (basel) 13:15708–15725. https://doi.org/10.3390/s131115708
Zhang Q, Zhao QL (2018) Global ionosphere mapping and differential code bias estimation during low and high solar activity periods with GIMAS software. Remote Sens. https://doi.org/10.3390/rs10050705
Zhang Q, Zhao QL (2019) Evaluation and analysis of the global ionosphere maps from Wuhan University IGS Ionosphere Associate Analysis Center. Chin J Geophys 62(12):4493–4505. https://doi.org/10.6038/cjg2019N0021. (in Chinese)
Zhang X, Ren X, Chen J, Zuo X, Mei D, Liu W (2022) Investigating GNSS PPP–RTK with external ionospheric constraints. Satell Navig. https://doi.org/10.1186/s43020-022-00067-1
Acknowledgements
This study is supported by the National Natural Science Foundation of China (12073063, 41730109) and the National Key Research and Development Program of China (2016YFB0501503-3). The authors are grateful to the IGS, Crustal Dynamics Data Information System (CDDIS) data center, International GNSS Monitoring and Assessment System (iGMAS), UNAVCO, SONEL, German Federal Agency for Cartography and Geodesy (BKG), CODE, JPL and UPC for providing daily, hourly and real-time GNSS observation data, broadcast ephemeris, BKG Ntrip Client (BNC) software and GIM products. The authors would like to acknowledge the National Aeronautics and Space Administration (NASA), Centre National d'Etudes Spatiales (CNES) and National Oceanic and Atmospheric Administration (NOAA) for providing Jason-2 satellite altimetry products.
Author information
Authors and Affiliations
Contributions
XJ and SS designed this research; XJ performed this research, solved the datasets and analyzed the datasets; XJ and SS wrote and revised this manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jin, X., Song, S. Near real-time global ionospheric total electron content modeling and nowcasting based on GNSS observations. J Geod 97, 27 (2023). https://doi.org/10.1007/s00190-023-01715-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-023-01715-3