1 Introduction

Accurate time and frequency transfer are essential for relativistic geodesy, high-resolution radio astronomy, and precision measurement (He et al. 2018; Lisdat et al. 2016; Lopez et al. 2013; Milner et al. 2019; Roberts et al. 2017). In addition, time and frequency transfer is essential for many critical infrastructures such as financial services, space missions, transport, and defense applications (Davis et al. 2011). Compared with optical fiber, the global navigation satellite system (GNSS) is currently used as a more classical means of time and frequency transfer thanks to its simplicity and low cost (Defraigne and Baire 2011; Guyennon et al. 2009). Two major approaches, namely common view (CV) and precise point positioning (PPP) are widely used for time and frequency transfer in time laboratories.

The CV approach is based on the inter-station single-differenced (SD) model, requiring that the two stations track signals from identical satellites (Lewandowski et al. 1993; Luna et al. 2017). The advantage of the CV approach is that only the broadcast ephemeris is needed, and the errors on satellite clocks and orbits are significantly mitigated during the SD process (Lee et al. 2008; Ray and Senior 2005). However, since the CV approach depends on the number of satellites in common-view, it is unsuitable for long-baseline time and frequency transfer (Ge et al. 2019).

With precise satellite orbits and clocks, PPP can provide the local time concerning the reference time scale of the satellite clock products (Defraigne et al. 2015; Zhang et al. 2020). Then, time and frequency transfer between the two stations can be accomplished by a simple difference between the two PPP local receiver time solutions. At this stage, the PPP approach is independent of the distance between the stations, which enables nanosecond time comparisons for intercontinental baselines. Traditional PPP is based on an ionosphere-free (IF) combination and is usually applied to dual-frequency observations (Ge et al. 2020; Khodabandeh and Teunissen 2016). However, in a multi-frequency scenario, although different IF combinations can be formed, this is not the optimal choice (Tu et al. 2019; Zhang et al. 2021). IF PPP does not take full advantage of all the observations because only one independent parameter, the ionospheric delay, gets eliminated, but more than one of the observables for both code and phase observations is sacrificed (Teunissen 2020). Instead of forming linear combinations of observables, some studies have implemented PPP based on the undifferenced and uncombined (UDUC) GNSS observations, namely UC PPP (Liu et al. 2017; Su and Jin 2019). The UC PPP contributes to strengthening the model to the best extent possible as it can flexibly impose dynamic constraints on all parameters (Zhang et al. 2019). In this case, ionospheric delays are no longer eliminated but estimated, making the model flexible in multi-frequency scenarios. In addition, the simplest observational variance matrix is used in the UC PPP (Odijk et al. 2016).

The ambiguity in the float form that exists in traditional PPP, limits the performance of the time and frequency transfer. Through theoretical deduction, Khodabandeh and Teunissen (2018) preliminarily demonstrates how integer ambiguity resolution benefits time and frequency transfer. Petit et al. (2015) have proposed the integer PPP (IPPP) method, which can recover the integer characteristic of ambiguities by considering the fractional-cycle biases (FCB) (Geng et al. 2012; Petit 2021). However, IPPP is still based on the IF combinations and is thus only suitable for dual-frequency scenarios. In addition, the IPPP solution is highly dependent on external FCB products, which may have a discrepancy in their timestamp that may affect the process of time transfer, and therefore requires consistent processing strategies at the user- and the network-end (Geng et al. 2020).

In this contribution, we propose a time and frequency transfer model that can achieve integer ambiguity resolution without external FCB products. The model is based on UDUC GNSS observations, which could benefit from several advantages (Odijk et al. 2016; Zhang et al. 2019). In this process, we present the method to eliminate the rank deficiencies from UDUC observations and then construct the full-rank time and frequency model with the ambiguities estimated in the double-differenced (DD) form.

The remainder of this paper proceeds as follows. Section 2 first develops a general UDUC model, namely the ionosphere-float model, without any ionospheric constraints. On this basis, the ionosphere-weighted and -fixed models suitable for medium and short baselines are derived. Then, how to implement time and frequency transfer using the UDUC models is given in Sect. 3. Section 4 presents the experimental results, including time and frequency transfer over short, medium, and long baselines. Finally, we summarize our findings and give our conclusions in Sect. 5.

2 UDUC models with different ionospheric constraints

This section first gives the ionosphere-float UDUC model without ionospheric constraints, which is compatible with time and frequency transfer from short to long baselines. Next, we propose two particular UDUC models, namely the ionosphere-fixed and -weighted models, over short and medium baselines, respectively, with a between-receiver SD ionospheric constraint.

2.1 Ionosphere-float UDUC model

The UDUC code and phase observation equations of two stations (A and B), in one GNSS constellation serving as a starting point of the proposed algorithm, are expressed as follows,

$$ \begin{aligned} & p_{A,j}^{s} = \rho_{A}^{s} + \tau_{A}^{s} + dt_{A} - dt^{s} + \mu_{j} I_{A}^{s} + d_{A,j} - d_{,j}^{s} + \varepsilon_{p,j}^{s} \\ & \phi_{A,j}^{s} = \rho_{A}^{s} + \tau_{A}^{s} + dt_{A} - dt^{s} - \mu_{j} I_{A}^{s} + \lambda_{j} N_{A,j}^{s} + \delta_{A,j} - \delta_{,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ & p_{B,j}^{s} = \rho_{B}^{s} + \tau_{B}^{s} + dt_{B} - dt^{s} + \mu_{j} I_{B}^{s} + d_{B,j} - d_{,j}^{s} + \varepsilon_{p,j}^{s} \\ & \phi_{B,j}^{s} = \rho_{B}^{s} + \tau_{B}^{s} + dt_{B} - dt^{s} - \mu_{j} I_{B}^{s} + \lambda_{j} N_{B,j}^{s} + \delta_{B,j} - \delta_{,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ \end{aligned} $$
(1)

where the description of the notations used is given in Table 1. However, Eq. (1) represents a rank deficient system, which indicates that not all unknowns can be estimated separately, but only their linear combinations. In this case, the S-system theory is used to identify the rank deficiencies, find the S-basis parameters, and construct a full-rank model (Odijk et al. 2017; Odolinski and Teunissen 2017).

Table 1 Symbol definitions used in Eq. (1) (The symbol r denotes stations A or B)
Full size table

For high-precision time and frequency transfer, the procedure is conducted at stations where the ground-truth positions of the receivers are available. In addition, the precise satellite orbits that can be accessed by an external provider such as the International GNSS Service (IGS) allow the satellite-receiver ranges \(\rho_{r}^{s}\) to be computed accurately (Dow et al. 2009). The IF satellite clock offset (\(d\tilde{t}^{s} = dt^{s} + d_{,IF}^{s}\)) can also be provided by the IGS (Johnston et al. 2017), where \(d_{,IF}^{s} = \tfrac{{\mu_{2} }}{{\mu_{2} - \mu_{1} }}d_{,1}^{s} - \tfrac{{\mu_{1} }}{{\mu_{2} - \mu_{1} }}d_{,2}^{s}\). In addition, the tropospheric delay \(\tau_{r}^{s}\) is usually expressed as the sum of the dry and wet delays, \(\tau_{r}^{s} = (\tau_{d} )_{r}^{s} + m_{r}^{s} \tau_{r}\), in which \((\tau_{d} )_{r}^{s}\) is the slant dry delay, which can be corrected a priori using empirical models. The wet delay is modeled as the product of the known elevation-dependent mapping function \(m_{r}^{s}\) and the unknown tropospheric wet zenith delay (ZWD)\(\tau_{r}\).

Assuming that \(m\) satellites are tracked, all are transmitting signals on \(f\) frequencies. For stations A and B, the model contains several types of rank deficiencies for each receiver as follows (Odijk et al. 2016):

  1. 1.

    Between the receiver and satellite code biases with the rank deficiency of size \(f\);

  2. 2.

    Between the receiver and satellite phase biases with the rank deficiency of size \(f\);

  3. 3.

    Between the receiver clock, code biases, and phase biases with the rank deficiency of size 1;

  4. 4.

    Between the receiver phase biases and ambiguities with the rank deficiency of size \(f\);

  5. 5.

    Between the satellite phase biases and ambiguities with the rank deficiency of size \(f \times m\);

  6. 6.

    Between the ionospheric delays and receiver code/phase biases with the rank deficiency of size 1;

  7. 7.

    Between the ionospheric delays and satellite code/phase biases with the rank deficiency of size \(m\).

As mentioned before, to deal with these rank deficiencies, one can apply the S-system theory, which constrains the S-basis parameters and lumps the parameters from their original forms to estimable forms (Mi et al. 2020; Odolindski et al. 2015). Table 2 shows the S-basis constraints for the ionosphere-float UDUC model and their associated removed rank deficiencies.

Table 2 The S-basis constraints for the ionosphere-float UDUC model, together with the types of rank deficiencies they eliminate, where \(d_{r,GF} = \tfrac{1}{{\mu_{2} - \mu_{1} }}(d_{r,2} - d_{r,1} )\), \(d_{{_{,GF} }}^{s} = \tfrac{1}{{\mu_{2} - \mu_{1} }}(d_{{_{,2} }}^{s} - d_{{_{,1} }}^{s} )\) and \(d_{r,IF} = \tfrac{{\mu_{2} }}{{\mu_{2} - \mu_{1} }}d_{r,1} - \tfrac{{\mu_{1} }}{{\mu_{2} - \mu_{1} }}d_{r,2}\)
Full size table

Applying the S-basis constraints in Table 2, with the coordinates of points A and B known, the full-rank model can be expressed as follows,

$$ \begin{aligned} & \tilde{p}_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} + \mu_{j} \tilde{I}_{A}^{s} - \tilde{d}_{A,j}^{s} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} - \mu_{j} \tilde{I}_{A}^{s} - \tilde{\delta }_{A,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ & \tilde{p}_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} + \mu_{j} \tilde{I}_{B}^{s} - \tilde{d}_{B,j}^{s} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} - \mu_{j} \tilde{I}_{B}^{s} - \tilde{\delta }_{B,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ \end{aligned} $$
(2)

where \(\tilde{p}_{r,j}^{s} = p_{r,j}^{s} + d\tilde{t}^{s} - (\tau_{d} )_{r}^{s}\) and \(\tilde{\phi }_{r,j}^{s} = \phi_{r,j}^{s} + d\tilde{t}^{s} - (\tau_{d} )_{r}^{s}\). The estimable parameters and their interpretations are given in Table 3. Equation (2) is the UC PPP model, which is more flexible in multi-frequency scenarios than the classical IF PPP.

Table 3 Estimable parameters and their interpretation in the UDUC model using S-basis in Table 2 for stations A and B
Full size table

There are satellites in common view for most of the baseline lengths used in the time and frequency transfer scenarios. Hence, it is expected to use the common-view satellites to resolve the integer ambiguities and obtain high precision in the time and frequency transfer. Note that the satellite code and phase biases (\(d_{,j}^{s} - d_{,IF}^{s} - \mu_{j} d_{,GF}^{s}\) and \(\delta_{,j}^{s} - d_{,IF}^{s} + \mu_{j} d_{,GF}^{s}\)) are the same for different receivers tracking these satellites. Taking those of receiver A as the reference, the between-receiver code and phase biases are estimated instead of estimating those of receiver B. More importantly, the ambiguities of the common-view satellite are reformed into the DD form so that the integer property can be recovered. In this case, the ionosphere-float UDUC model can be formulated as follows:

$$ \begin{aligned} & \tilde{p}_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} + \mu_{j} \tilde{I}_{A}^{s} - \tilde{d}_{A,j}^{s} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} - \mu_{j} \tilde{I}_{A}^{s} - \tilde{\delta }_{A,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ & \tilde{p}_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} + \mu_{j} \tilde{I}_{B}^{s} - \tilde{d}_{A,j}^{s} + \tilde{d}_{AB,j} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} - \mu_{j} \tilde{I}_{B}^{s} - \tilde{\delta }_{A,j}^{s} \\ &\quad + \tilde{\delta }_{AB,j} + \lambda_{j} N_{AB,j}^{1s} + \varepsilon_{\phi ,j}^{s} \\ \end{aligned} $$
(3)

where \(\tilde{d}_{AB,j}\) and \(\tilde{\delta }_{AB,j}\) are the between-receiver code and phase biases,\(N_{AB,j}^{1s}\) is the DD ambiguity (see Table 3).

The ionosphere-float UDUC model can be regarded as combining the advantages of the PPP and the real-time kinematic (RTK). On the one hand, the model utilizes the RTK principle, which integrates ambiguity into the DD form through the S-basis. The DD ambiguities can be fixed using integer ambiguity resolution theories, including integer rounding, integer bootstrapping and integer least-squares (Teunissen 1999), which improves the time and frequency transfer performance. On the other hand, when the baseline is long, there are no common-view satellites, the ionosphere-float UDUC model would be equivalent to the UC PPP one.

2.2 Ionosphere-weighted UDUC model

It is acceptable to use the model in Eq. (3) for time and frequency transfer over baselines of tens to hundreds of kilometers. However, the spatial correlation of the regional ionospheric delays from the same satellite is ignored in this process, which is assumed to be approximately equal for the different receivers at this distance (Mi et al. 2019a; Teunissen 1998). Therefore, the ionospheric delays are introduced as a third group of observables, aside from the code and phase observables. Their observation equation reads \(\overline{I}_{AB}^{s} = I_{AB}^{s}\), where \(I_{AB}^{s}\) is the between-receiver SD ionospheric delays, and \(\overline{I}_{AB}^{s}\) is the between-station SD ionospheric pseudo-observables (Interpolate by reference network or assume zero). Adding those observables and configuring the corresponding stochastic model makes it possible to provide a-priori reasonable information on the ionospheric delay (Mi et al. 2019b; Odijk and Teunissen 2008). The UDUC model becomes flexible for a wide range of baseline lengths, enabling fast integer ambiguity resolution. This ionosphere-weighted UDUC model can be written as

$$ \begin{aligned} & \tilde{p}_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} + \mu_{j} \tilde{I}_{A}^{s} - \tilde{d}_{A,j}^{s} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} - \mu_{j} \tilde{I}_{A}^{s} - \tilde{\delta }_{A,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ & \tilde{p}_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} + \mu_{j} \tilde{I}_{A}^{s} + \mu_{j} I_{AB}^{s}\\ & + \mu_{j} \tilde{d}_{AB} - \tilde{d}_{A,j}^{s} + \tilde{d}_{AB,j} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} - \mu_{j} \tilde{I}_{A}^{s} - \mu_{j} I_{AB}^{s} \\ & + \mu_{j} \tilde{d}_{AB} - \tilde{\delta }_{A,j}^{s} + \tilde{\delta }_{AB,j} + \lambda_{j} N_{AB,j}^{1s} + \varepsilon_{\phi ,j}^{s} \\ & \overline{I}_{AB}^{s} = I_{AB}^{s} + \varepsilon_{AB}^{s} \\ \end{aligned} $$
(4)

where \(\varepsilon_{AB}^{s}\) is random observation noise of between-receiver SD ionospheric delay. \(\tilde{d}_{AB} = \frac{1}{{\mu_{2} - 1}}((d_{B,2} - d_{B,1} ) - (d_{A,2} - d_{A,1} ))\) is the between-receiver differential code biases (DCB), which makes the separated ionospheric delay completely independent of receiver B and thus improves the model strength.

2.3 Ionosphere-fixed UDUC model

Provided that the distance between the two receivers involved is less than a few kilometers, one can assume that the ionospheric delays are the same for both receivers (Mi et al. 2021). With this knowledge, the ionosphere-fixed UDUC model can be constructed as,

$$ \begin{aligned} & \tilde{p}_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} + \mu_{j} \tilde{I}_{A}^{s} - \tilde{d}_{A,j}^{s} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{A,j}^{s} = \rho_{A}^{s} + m_{A}^{s} \tau_{A} + d\tilde{t}_{A} - \mu_{j} \tilde{I}_{A}^{s} - \tilde{\delta }_{A,j}^{s} + \varepsilon_{\phi ,j}^{s} \\ & \tilde{p}_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} + \mu_{j} \tilde{I}_{A}^{s}\\ & \quad + \mu_{j} \tilde{d}_{AB} - \tilde{d}_{A,j}^{s} + \tilde{d}_{AB,j} + \varepsilon_{p,j}^{s} \\ & \tilde{\phi }_{B,j}^{s} = \rho_{B}^{s} + m_{B}^{s} \tau_{B} + d\tilde{t}_{B} \\ &\quad - \mu_{j} \tilde{I}_{A}^{s} + \mu_{j} \tilde{d}_{AB} - \tilde{\delta }_{A,j}^{s} + \tilde{\delta }_{AB,j} + \lambda_{j} N_{AB,j}^{1s} + \varepsilon_{\phi ,j}^{s} \\ \end{aligned} $$
(5)

where the forms of the estimable parameters are identical to those in the ionosphere-weighted model. The ionosphere-fixed UDUC model is a particular form of the ionosphere-weighted model: the weight of between-receiver SD ionospheric pseudo-observables (\(\overline{I}_{AB}^{s} = 0\)) is large enough and thus can be ignored in the model.

3 Implementation of time and frequency transfer with the UDUC models

This section details the implementation of time and frequency transfer with short-, medium- and long-baseline.

3.1 Time and frequency transfer over short-baseline

The ionospheric-fixed UDUC model is advantageous for time and frequency transfer over a short baseline as the zero between-receiver SD ionospheric delays at this distance are considered. Assuming a short baseline here, receiver A with a time and frequency standard and receiver B obtains the time difference with receiver A to adjust the local clock. From Eq. (5), the critical information \(d\tilde{t}_{A} = dt_{A} + d_{A,IF}\) and \(d\tilde{t}_{B} = dt_{B} + d_{B,IF}\) are estimated using the ionosphere-fixed UDUC model. Two concepts need to be clarified. First, the IF receiver code bias (\(d_{r,IF}\)) is contained in the receiver clock (\(d\tilde{t}_{r}\)); therefore \(d\tilde{t}_{r}\) is the biased receiver clock. This bias is challenging to calibrate by true GNSS signals, and it is usually regularly corrected by absolute calibration means using simulated GNSS signals in the time laboratories (Defraigne 2017). Fortunately, previous studies have shown that this bias is stable for months under certain conditions in the time laboratories (Kanj et al. 2014). Second, for all timing applications using GNSS,\(dt_{r}\) is the synchronization error between the receiver and the reference of the precise satellite clock products (denoted as ref), where \(dt_{r} = d\overline{t}_{r} - dt_{ref}\).\(d\overline{t}_{r}\) is the true time of the receiver and \(dt_{ref}\) is the reference time of the satellite products. Then, we can get \(d\tilde{t}_{AB}\) by a simple difference and eliminate the influence of the reference time, which can be expressed as \((d\overline{t}_{B} - dt_{ref} + d_{B,IF} ) - (d\overline{t}_{A} - dt_{ref} + d_{A,IF} ) = d\overline{t}_{AB} + d_{AB,IF}\). As we mentioned earlier,\(d_{AB,IF}\) can be corrected by calibration means so that the time transfer from A to B can be achieved.

Furthermore, the short-baseline time transfer can also assist the receiver biases calibration. Assuming that A and B are receivers with the same frequency standard in the same time laboratory, A is the primary receiver used to maintain time. While bias calibration can also be done with code observations only, it is difficult to achieve high accuracy. However, this can be achieved using the ionosphere-fixed UDUC model with the common frequency standard. Thanks to the integer ambiguity resolution, this calibration is also guaranteed with high precision. This can be done as follows. First, since receiver A is pre-calibrated, using the ionosphere-fixed UDUC model, we can get \(d\tilde{t}_{A} = d\overline{t}_{A} - dt_{ref}\) and \(d\tilde{t}_{B} = d\overline{t}_{B} - dt_{ref} + d_{B,IF}\). Second, since the same frequency standard is connected,\(d\overline{t}_{A} = d\overline{t}_{B}\). Then, the IF receiver code bias of receiver B can be obtained by the difference \((d\overline{t}_{B} - dt_{ref} + d_{B,IF} ) - (d\overline{t}_{A} - dt_{ref} ) = d_{B,IF}\). Compared with other calibration methods, this method has higher accuracy and is suitable for real-time calibration.

3.2 Time and frequency transfer over medium-baseline

The time transfer of medium baselines (tens to hundreds of kilometers) is of practical significance, especially the time synchronization within countries. In those cases, the ionosphere-weighted model is particularly significant by fully considering the characteristics of the between-receiver SD ionospheric delays. We assume receivers A and B form a medium baseline and apply time transfer between them, where A has the desired time and frequency standard. The synchronization error between the receiver and the reference time scale obtained by the ionosphere-weighted model (see Eq. (4) and Table 2) are identical to that by the ionosphere-fixed model, where \(d\tilde{t}_{A} = dt_{A} + d_{A,IF}\) and \(d\tilde{t}_{B} = dt_{B} + d_{B,IF}\). Then, time transfer can be realized through their difference (\(d\tilde{t}_{AB}\)), and here calibration of \(d_{AB,IF}\) is required.

3.3 Time and frequency transfer over long-baseline

Theoretically, it is acceptable to realize long-baseline time and frequency transfer using the ionosphere-float UDUC model after reaching stable carrier-phase ambiguities. However, the limited number of common-view satellites makes it challenging to observe the improvement of the model relative to UC PPP. In addition, it is also challenging to achieve integer ambiguity resolution with the ionosphere-float model.

We consider the ionosphere-fixed and -weighted UDUC models to make the integer ambiguity resolution available. See Eqs. (4) and (5), the synchronization error between the receiver and the satellite products of two receivers can be obtained, just like PPP, respectively. Suppose a long-baseline time transfer between A and B needs to be implemented. Then, we choose one reference station C and D, near A and B, respectively. The distances requirement between A and C and between B and D are loose, which can be several to hundreds of kilometers. In the baseline formed between A and C, \(d\tilde{t}_{A} = dt_{A} + d_{A,IF}\) can be obtained using the ionosphere-fixed or -weighted UDUC model. Similarly, \(d\tilde{t}_{B} = dt_{B} + d_{B,IF}\) can be available in the baseline between B and D. In this case, \(d\tilde{t}_{A}\) and \(d\tilde{t}_{B}\) are the same as with the PPP approach, but the integer ambiguity resolution can be achieved. Finally, by computing the simple difference (\(d\tilde{t}_{AB} = d\tilde{t}_{B} - d\tilde{t}_{A}\)), the time transfer with integer ambiguity resolution between A and B can be achieved. It can be said that this is similar to IPPP, which is to achieve integer ambiguity resolution at both sides and then estimate the difference. Note that it does not concern whether the reference stations C and D have external time and frequency standards. Their role is to better estimate the satellite phase biases and constrain the ionospheric delays, thus enabling the integer ambiguity resolution and delivering a high precision for the estimable receiver clock offsets.

4 Results

This section provides the experimental results of applying time and frequency transfer based on the models developed earlier. First, the collected data and our processing strategies are introduced. Next, short-, medium- and long-baseline time and frequency transfer performances are assessed. In addition, the time and frequency transfer performance of the PPP with the same configuration is also given.

4.1 Experimental setup

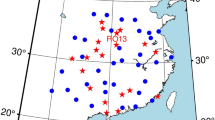
To validate the feasibility and effectiveness of the proposed models, we select GPS data sets from several time laboratories, including USNO (USA), NIST (USA), ROB (Belgium), ROA (Spain), OP (France) and PTB (Germany). Our analysis uses observations of GPS dual-frequency (L1 and L2) to verify the model, which facilitates comparison with the traditional PPP. The relevant characteristics of the experimental data sets considered for this study are shown in Table 4. The H-maser clocks are high-performance atomic clocks whose intra-day stability (\(1 \times 10^{ - 15}\)) is beyond what can be achieved with GNSS (Weinbach and Schön 2013). Therefore, we can evaluate the improvement of the UDUC model relative to the PPP from the analysis of the time difference noise and the corresponding frequency stability. The main processing strategies for the PPP and the UDUC model are summarized in Table 5.

Table 4 An overview of GNSS data sets used in our analysis, including station name, institute, type of reference clock, receiver and antenna type, and observation period
Full size table
Table 5 Data processing strategies in this study for both the PPP and the UDUC models
Full size table

4.2 Short-baseline time and frequency transfer

The first time and frequency transfer experiments were carried out at two time laboratories: (1) USN7 and USN8, operated with a common H-Maser clock at the USNO; and (2) ROAG and SFER, operated with an H-maser clock and a Cesium clock at the ROA, respectively. The time link of USN7-USN8 is a zero-baseline connected to a common antenna, while the time link of ROAG-SFER is a short baseline of 124 m. As mentioned earlier, the ionospheric delays can be sufficiently eliminated at short baselines, so the ionosphere-fixed UDUC model was adopted in this case. With the ionospheric constraints, the instantaneous integer ambiguity resolution can be realized by the ionosphere-fixed UDUC model.

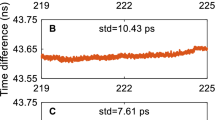
Figure 1 shows the time differences of the USN7-USN8 time link using the ionospheric-fixed UDUC model and the PPP. Since USN7 and USN8 are operated with the same H-maser clock, their time link directly reflects the noise and stability of the hardware delays with the same type of receivers. The gain of the ionosphere-fixed UDUC model with integer ambiguity resolution is that the noise of the time difference is effectively reduced compared with using the PPP. Results show that the standard deviation of the link values of time difference for the ionosphere-fixed UDUC model is 12.1 ps, 72.2% lower than the 43.5 ps for the PPP model. Figure 2 illustrates the modified Allan deviation (MDEV) of the USN7-USN8 time link over the week of the UDUC model and the PPP. It can be observed that the short-term and long-term frequency stability of the ionosphere-fixed UDUC model has improved compared to that of the PPP model. For example, the ionosphere-fixed UDUC model has frequency stability of \(1.3 \times 10^{ - 14}\) at 120 s average time, while the PPP it amounts to \(2.8 \times 10^{ - 14}\), showing a 53.6% improvement. In addition, the frequency stability for an averaging time of 1 day of the ionosphere-fixed UDUC model is 64.9% higher than that of the PPP model, which is about \(3.3 \times 10^{ - 17}\) and \(9.4 \times 10^{ - 17}\), respectively. Different from the conclusion of Petit et al. (2015), the UDUC model improves long-term stability and improves short-term one for the following reasons. First, the ionospheric constraints are considered; thus, the fast integer ambiguity resolution can be realized by the ionosphere-fixed UDUC model. Second, the satellite phase biases are estimated in the UDUC model, while the FCB in the IPPP is generated from a global network. Therefore, satellite phase biases are more consistent with the model, although also a product of auxiliary integer ambiguity resolution. Third, the UDUC model avoids the amplification of observation noise in the error propagation when differencing or using a measurement combination.

Fig. 1
figure 1

A common-clock zero-baseline time link of the UNS7-UNS8 at the USNO computed with the ionosphere-fixed UDUC model (top) and the PPP (bottom) from 21 to 27 November 2021

Full size image
Fig. 2
figure 2

Comparison of the MDEV between the ionosphere-fixed UDUC model and the PPP for the USN7-USN8 time-link

Full size image

Another 124 m short baseline time link experiment is performed between ROAG and SFER at the ROA, equipped with H-maser and Cesium clocks. Like the USN7-USN8, we can also see the noise reduction of the time difference in Fig. 3. Since the time difference of the non-common-clock time link will be affected by atomic clocks themselves and is no longer constant, so the epoch difference is introduced. Epoch difference is a critical evaluation index in time and frequency transfer, reflecting the change of atomic clock per unit time and further the time transfer accuracy. The standard deviations in the following time difference results (Figs. 3, 5,  7, 9, 11) are the standard deviations of the epoch difference of the time difference. The epoch difference standard deviation of the ROAG-SFER link is 31.7% lower for the ionosphere-fixed UDUC model than that for the PPP over the test week, which is 5.65 ps and 8.27 ps, respectively. Figure 4 shows the MDEV of the ROAG-SFER time link over the week of the two models, from which the gain from the ionosphere-fixed UDUC model is visible. Taking the results at 3840 s average time as an example, the MDEV of the PPP and the ionosphere-fixed UDUC model is \(6.9 \times 10^{ - 15}\) and \(3.7 \times 10^{ - 15}\), respectively, with an improvement of 46.4%. In addition, for an averaging time of 1 day for this time link, the improvement of the UDUC model over the PPP is 25.0% with \(3.6 \times 10^{ - 16}\) and \(4.8 \times 10^{ - 16}\), respectively.

Fig. 3
figure 3

A short-baseline time link of the ROAG-SFER at the ROA computed with the ionosphere-fixed UDUC model (top) and the PPP (bottom) from 21 to 27 November 2021

Full size image
Fig. 4
figure 4

Comparison of the MDEV between the ionosphere-fixed UDUC model and the PPP for the ROAG-SFER time-link

Full size image

4.3 Medium-baseline time and frequency transfer

The next series of experiments have been carried out in four time laboratories, forming two medium baseline time links. One is the time link between NIST and AMC4, with a 146.8 km baseline length. The other, 262.3 km, is the time link between BRUX and OPMT. Based on the ionosphere-weighted UDUC model, 94.2% and 84.5% integer ambiguity resolutions are realized for the two time links, guaranteeing high-precision time and frequency transfer.

Figure 5 depicts the time difference of the NIST-AMC4 time link, from which the gain achieved from the ionosphere-weighted UDUC model compared to the PPP can be seen. The standard deviation of the epoch difference over the week of the link values concerning the mean is also 16.4% lower for the ionosphere-weighted UDUC model (5.61 ps) than for PPP (6.71 ps). Concerning the frequency stability in Fig. 6, we can see the improvement with the UDUC model for both the short- and long-term. For averaging times at a few 1000 s and below, the frequency stability of the ionosphere-weighted UDUC model is 15% to 30% better than that of the PPP. In addition, the frequency stability for an averaging time of 1 day of the UDUC model is 9.0% higher than that of the PPP model, which is not significant but demonstrates the improvement in long-term stability.

Fig. 5
figure 5

A medium-baseline time link of the NIST-AMC4 at the NIST and the USNO computed with the ionosphere-weighted UDUC model (top) and the PPP (bottom) from 21 to 27 November 2021

Full size image
Fig. 6
figure 6

Comparison of the MDEV between the ionosphere-weighted UDUC model and the PPP for the NIST-AMC4 time-link

Full size image

Similar to Figs. 5 and 6, 7 and 8 show the time and frequency transfer results but for the BRUX-OPMT time link. It can be observed from Fig. 7 that the ionosphere-weighted UDUC model reduces the noise of time difference. The standard deviation over the test week of the epoch difference for the ionosphere-weighted UDUC model and the PPP is 4.37 ps and 5.94 ps, respectively. Figure 8 reflects the improvement of the ionosphere-weighted UDUC model in frequency stability compared with PPP, from which two phenomena are worth mentioning. First, the ionosphere-weighted UDUC model has 10–25% higher frequency stability than the PPP for averaging times at a few 1000 s and below. Second, at a few thousand to tens of thousands of seconds average time of frequency stability, the improvement of the ionosphere-weighted UDUC model became less noticeable (10–15%). This can be attributed to the weak ionospheric constraint due to the length of the BRUX-OPMT (262.3 km). Therefore, the contribution of this constraint becomes invalid in the later stage of filtering. Hence, the difference in long-term frequency stability between the ionosphere-weighted UDUC model and the PPP is smaller.

Fig. 7
figure 7

A medium-baseline time link of the BRUX-OPMT at the ROB and the OP computed with the ionosphere-weighted UDUC model (top) and the PPP (bottom) from 21 to 27 November 2021

Full size image
Fig. 8
figure 8

Comparison of the MDEV between the ionosphere-weighted UDUC model and the PPP for the BRUX-OPMT time-link

Full size image

4.4 Long-baseline time and frequency transfer

In this scenario, the first time link is the PTBB-ROAG, a baseline length of 2182.3 km. In this situation, the number of common-view satellites is small, so it isn't easy to benefit from the ionosphere-float UDUC model. Therefore, two short baselines are used to calculate the time of PTBB and ROAG stations, respectively. Then a simple difference is performed to realize the long baseline time transfer between them. Both PTB and ROA time laboratories have multiple GNSS receivers available. Therefore, the clocks of PTBB and ROAG with ambiguity-fixed can be obtained by calculating PTBB-PT11 and ROAG-SFER, respectively, using the ionosphere-fixed UDUC model. Figure 9 shows the time differences of the time link, the variation of the time difference sequence of the UDUC model is smaller than that of PPP. The standard deviation of the epoch difference for the UDUC model is 4.72 ps, 9.40% lower than the 5.21 ps obtained using PPP. Figure 10 illustrates the frequency stability of the UDUC model and the PPP. The UDUC model improves frequency stability for averaging times at a few 1000 s and below. For averaging times within 4000 to 30,000 s, the performance of the UDUC model becomes close to that of the PPP. It can be seen that the frequency stability of the UDUC model performs better than the PPP at and over 1 day average time. The reasons can be explained as follows. First, the UDUC model can achieve fast integer ambiguity resolution with ionospheric constraints, thus improving the short-term stability. Second, at a few hours of averaging, the accuracy of the UDUC model is similar to that of the convergent PPP and IPPP, and the satellite clock products play the main influencing factor. Third, for the long-term frequency stability, the integer ambiguity resolution can maintain parameter estimation accuracy and perform better than PPP, which has also been verified in IPPP.

Fig. 9
figure 9

A long-baseline time link of the PTBB-ROAG at the PTB and the ROA computed with the UDUC model (top) and the PPP (bottom) from 21 to 27 November 2021

Full size image
Fig. 10
figure 10

Comparison of the MDEV between the UDUC model and the PPP for the PTBB-ROAG time-link

Full size image

Another long-baseline test is for the time link between USN7 and ROAG, with a length of 5863.3 km. Similarly, the clocks of USN7 and ROAG are obtained by calculating USN7-USN8 and ROAG-SFER using the ionosphere-fixed UDUC model so that the time and frequency transfer between USN7 and ROAG is realized. As we can see, this is exactly the time link involved in the two experiments of the short-baseline time and frequency transfer. As shown in Fig. 11, the standard deviation of the epoch difference for the PPP and the UDUC model is 6.06 ps and 6.91 ps, showing a 12.3% improvement. The frequency stability is depicted in Fig. 12, from which we can get a similar conclusion as in the PTBB-ROAG time link. Indeed, the UDUC model performed better at levels where the average time is below a few hours and over 1 day. Taking the result at 120 s, 3840 s and 1-day average time as an example, the frequency stability of the PPP model is \(5.5 \times 10^{ - 14}\), \(1.1 \times 10^{ - 14}\) and \(2.1 \times 10^{ - 15}\), and of the UDUC model is \(4.7 \times 10^{ - 14}\), \(1.1 \times 10^{ - 14}\) and \(1.8 \times 10^{ - 15}\), with 14.5%, 0% and 14.3% improvement, respectively (Fig. 12).

Fig. 11
figure 11

A long-baseline time link of USN7-ROAG at the USNO and the ROA computed with the UDUC model (top) and the PPP (bottom) from 21 to 27 November 2021

Full size image
Fig. 12
figure 12

Comparison of MDEV between the UDUC model and the PPP on USN7-ROAG time-link

Full size image

5 Conclusions

In this contribution, we presented a time and frequency transfer model with integer ambiguity resolution based on the UDUC observations. This model has the following characteristics, making it well suited for the time and frequency transfer in multi-constellation and multi-frequency scenarios. First, the UDUC model has flexibility that can easily be extended to any number of frequencies and constellations. Second, the UDUC model forms the DD ambiguities, enabling the integer ambiguity resolution, and thus recovers the high-precision of carrier phase observations. Third, there is a chance to apply ionospheric constraints for short and medium baselines, thus, further strengthening the observations model.

In short- and medium-baseline time and frequency transfer, with the ionosphere-fixed and ionosphere-weighted UDUC models applied and the integer ambiguities resolved, the time differences obtained by the ionosphere-fixed and ionosphere-weighted UDUC model have shown smaller noise than that by using PPP. Consequently, in terms of frequency stability, the improvement of the ionosphere-fixed (25–60%) and ionosphere-weighted (9–30%) models over the PPP for averaging time from several tens of seconds to 1 day can be observed. These experiments fully illustrate the advantages of the UDUC model with ionospheric constraints and integer ambiguity resolution in improving time and frequency transfer performance over short and medium baselines.

In long-baseline time and frequency transfer, the number of common-view satellites is small, and the realization of integer ambiguity resolution is difficult. Hence, the ionospheric-float UDUC model is similar to the PPP. In this case, we introduced a reference station at each end of the time comparison to utilize the advantages of the ionospheric constraints and obtain integer ambiguity resolution. The results show that the frequency stability of the UDUC model performs better than the PPP for averaging time below a few thousands second and over 1 day, which fully demonstrates the advantages of the proposed models.

This study provides experience in the implementation of time and frequency transfer at the UDUC level. It facilitates our understanding of the advantages of integer ambiguity resolution in time and frequency transfer. The performance of the UDUC model in time and frequency transfer within the framework of multi-frequency multi-constellation will be the focus of our future work.