Modeling gravimetric signatures of third-degree ocean tides and their detection in superconducting gravimeter records

Abstract

We employ the barotropic, data-unconstrained ocean tide model TiME to derive an atlas for degree-3 tidal constituents including monthly to terdiurnal tidal species. The model is optimized with respect to the tide gauge data set TICON-td that is extended to include the respective tidal constituents of diurnal and higher frequencies. The tide gauge validation shows a root-mean-square (RMS) deviation of 0.9–1.3 mm for the individual species. We further model the load tide-induced gravimetric signals by two means (1) a global load Love number approach and (2) evaluating Greens-integrals at 16 selected locations of superconducting gravimeters. The RMS deviation between the amplitudes derived using both methods is below $0.5 \$nGal ($1 \$nGal $= 0.01 \frac{\text {nm}}{\text {s}^2}$) when excluding near-coastal gravimeters. Utilizing ETERNA-x, a recently upgraded and reworked tidal analysis software, we additionally derive degree-3 gravimetric tidal constituents for these stations, based on a hypothesis-free wave grouping approach. We demonstrate that this analysis is feasible, yielding amplitude predictions of only a few 10 nGal, and that it agrees with the modeled constituents on a level of 63–80% of the mean signal amplitude. Larger deviations are only found for lowest amplitude signals, near-coastal stations, or shorter and noisier data sets.

Introduction

When recapitulating the theory of tides, one finds that the gravitational potential of a celestial body is not symmetric but radially asymmetric at any given distance, d, from its center of mass as it decreases proportionally to $\frac{1}{d}$, thus changing its rate of abatement continuously. However, given the vastness of the distances of these objects relative to the Earth radius, a, the lunisolar tide generating potential (TGP) can be approximated to first order by a set of symmetrical degree-2 spherical harmonic functions. The asymmetrical part of the TGP is encoded in harmonic contributions of higher degree ($l \ge 3$), while their magnitudes are reduced by the factor $\left( \frac{a}{d} \right) ^{l-2}$ with respect to degree-2 tides. For solar degree-3 tides this factor is as small as $\frac{1}{23000}$, while for the Moon it is close to $\frac{1}{60}$ (e.g.,  Agnew 2007). Furthermore, there are planet-moon constellations in the solar system, for which this ratio is even more elevated, e.g., $\frac{3}{10}$ for the Mars–Phobos dyad (Rosenblatt 2011) augmenting the relative weight of the respective $l>2$ tides so far that they contribute a significant fraction to tidal dissipation by body tides (Bills et al. 2005).

Although the third-degree TGP can be seen as a small correction to the degree-2 approximation for terrestrial tides, the effect of the respective tide-generating forces on the Earth system is strong enough to be detected with geodetic techniques. This detection is easiest for the terdiurnal $^3\hbox {M}_3$ wave as it does not neighbor degree-2 excitations, appearing in a practically isolated position in the frequency domain (Melchior and Venedikov 1968). The detection of degree-3 tides with semidiurnal or even longer periods is more complicated due to significantly stronger degree-2 excitations at nearby frequencies, being only separated by one complete cycle during the precession period of the Lunar perigee of $8.85\,$yr. In addition, some degree-3 partial tides are significantly modulated with the regression period of the lunar nodes of $18.6\,$yr (Ray 2020). This dense overlap of closely neighboring partial tides together with their small signal-to-noise ratio implies the need for long-term time-series to identify lunar degree-3 tidal constituents (Munk and Hasselmann 1964). Relying on such long-term records, degree-3 signatures were detected in pioneering studies based on tide gauge (Cartwright 1975; Ray 2001) and gravimetric records (Dittfeld 1991; Melchior et al. 1996; Ducarme 2012) . In particular, records from superconducting gravimeters (Prothero and Goodkind 1968; Goodkind 1999; Hinderer et al. 2015) are of very low noise and high resolution, rendering them well suited for the detection of low amplitude signals (Van Camp et al. 2017).

The derived degree-3 gravimetric factors can be compared to predictions by theoretical Earth models, which were progressively refined (e.g., Wahr 1981; Dehant et al. 1999; Mathews 2001). However, body tide gravimetric signatures are superimposed by load tide signals arising from mass redistribution due to ocean tides (e.g.,  Baker et al. 1996; Jentzsch 1997; Bos et al. 2000), also for degree-3 tides (Ducarme 2012; Meurers et al. 2016). The gravitational ocean loading effect comprises both gravity perturbations stemming from the yielding of the solid Earth under the ocean masses, and direct Newtonian attraction from the redistributed sea water. This loading effect can be predicted and thus removed by combining ocean tide models with information about the structure of the solid Earth. Possible techniques include global Green’s function convolution integrals or spectral approaches constrained by load Love numbers (e.g., Longman 1963; Farrell 1972; Boy et al. 2003).

As the induced load tides provoke a significant back-action on ocean tidal dynamics in terms of the induced Self-Attraction and Loading (SAL) potential (e.g.,  Henderschott 1972; Ray 1998), its precise representation is a vital issue for purely hydrodynamic tidal modeling (e.g., Zahel 1991; Schindelegger et al. 2018). On the other hand, altimetry-constrained tidal models have reached impressive levels of accuracy (e.g., Egbert and Erofeeva 2002, updated; Ray 1999, updated; Lyard et al. 2021; Hart-Davis et al. 2021a) and can provide precise estimates of load tide-induced gravimetric fluctuations. As those modern models rely on the quality of available altimetry data, their relative accuracy decreases with the amplitude of the respective tidal constituents and towards the polar regions, where altimetry data coverage is sparse due to the inclination of those satellites and the presence of sea-ice. Subsequently, the accuracy of data constrained ocean tide models is lowest for small amplitude tides (minor tides) and can only be increased by prolonging altimetric time series length. As the first tide-dedicated satellite altimetry mission was launched only in 1992, the data basis was not sufficient to extract estimates for degree-3 ocean tides for many years. However, with the continued accumulation of satellite altimetry data, this situation has changed, as the late-breaking study by Ray (2020) shows.

For purely hydrodynamic tide models, the limitations of available empirical data are irrelevant as they are not incorporated into the modeling process. While there were a number of articles that provided data-unconstrained solutions for individual degree-3 tides (Platzman 1984; Woodworth 2019), a full catalog comprising purely hydrodynamical degree-3 tides of all possible orders (0, 1, 2 and 3) has to our knowledge not been published, yet. Clearly, the lack of satisfactory means for identifying tidal loading vectors in degree-3 gravimetric constituents calls for accurate and complete degree-3 ocean tide models (Ducarme 2012). In turn, such models will enable the correction of gravimetric time series to better assess solid Earth models.

Further, the process of de-aliasing satellite gravimetric data begins to pose the need for degree-3 tidal solutions. In fact, the expected signal strength of minor tides amounts to a relevant fraction of the currently unresolved aliased tidal oscillation. This signal is among the three most prominent sources of uncertainty in Gravity Recovery And Climate Experiment data (GRACE and the successor GRACE-FO)  (Tapley et al. 2019; Flechtner et al. 2016).

Here, we complement novel, empirical degree-3 solutions (Ray 2020) by presenting an integrated, data-unconstrained atlas of degree-3 partial tides. These hydrodynamic solutions benefit from several recent advances made with the barotropic model TiME (Sulzbach et al. 2021a). In contrast to the aforementioned empirical solutions, which are confined to latitudes $|\phi | < 66^\circ$, our global results allow for the determination of global load tide solutions. The comparison of those degree-3 solutions to empirical results allows for the validation of the state-of-the-art barotropic modeling approaches. The obtained tidal solutions are subsequently used to derive gravimetric load tide constituents that are compared to the empirically estimated load tide vector at 16 superconducting gravimeter (SG) stations distributed over all continents. The highly sensitive SG instruments offer both, an independent way to validate the expected small-amplitude degree-3 tidal solutions, and the possibility to verify the consistency of solid Earth models.

Sections 2 and 3 describe the employed tidal model and the specification of the tide-raising potential of third degree. Section 4 explains the optimization of modeling parameters and discusses the performance of the tidal model before we present and discuss the obtained tidal solutions in Sect. 5. The derivation and extraction of gravimetric tidal parameters is outlined in Sect. 6, along with a detailed comparison to the obtained modeling results. We summarize our results and draw conclusions in the final Sect. 7.

Hydrodynamical tidal modeling

To model barotropic tidal dynamics, we employ the purely hydrodynamic (unconstrained by data) computer model TiME that was introduced by Weis et al. (2008) and upgraded by Sulzbach et al. (2021a). TiME integrates the shallow water equations (e.g., Pekeris 1974)

$$\begin{aligned} \partial _t {\mathbf {v}} + {\mathbf {f}} \times {\mathbf {v}} + \left( {\mathbf {v}} \cdot {\nabla } \right) {\mathbf {v}}= & {} - g {\nabla } \left( \zeta - \zeta _{SAL} (\zeta ) - \zeta _{eq} \right) - {\mathbb {D}} , \nonumber \\ \partial _t \zeta= & {} - {\nabla } \left( (H+\zeta ) \ {\mathbf {v}} \right) , \end{aligned}$$

(1)

in time, employing the semi-implicit algorithm developed by Backhaus (1982, 1985). The model is run with partial tide forcing $\zeta _{eq} = V_{tid}({\mathbf {x}}, t)/g$, where $V_{tid}$ is proportional to the fully normalized, real-valued spherical harmonic function of degree l and order m, denoted $Y_{lm}$ (see Sect. 3). Further, ${\mathbf {f}} = 2 \varOmega \sin \phi \ {\mathbf {e}}_{vert}$ is the vertical Coriolis vector at latitude $\phi$, $\varOmega =\frac{2 \pi }{1d}$ is the Earth rotation angular frequency, and $g=9.80665 \frac{m}{s^2}$ (World Meteorological Organisation 2008) is a conventional, constant value of surface gravity acceleration. The effect of the SAL-potential, $V_{SAL} = g \ \zeta _{SAL}(\zeta )$ (Henderschott 1972; Ray 1998), describes dynamic, gravitational forces that are induced self-consistently by the redistribution of water mass and the yielding of the Earth. It is calculated by employing a spectral approach, reintroduced by Schindelegger et al. (2018) that is constrained by load Love Numbers (LLNs taken from Wang et al. (2012); PREM), where the spectral decomposition is truncated at maximum degree and order $l_{max}=1024$. Further a local, scalar approximation of the effect, $\zeta _{SAL}=\epsilon \zeta$, can be employed (Accad and Pekeris 1978). $H({\mathbf {x}})$ is the bathymetric function that is constructed from the rtopo2 data set (Schaffer et al. 2016) and includes the watercolumn below the lower Antarctic ice shelf boundary. Dissipative forces are comprised in the operator ${\mathbb {D}}$ that includes dissipation by quadratic bottom friction, parameterized eddy-viscosity ($\sim A_h$: horizontal eddy-viscosity coefficient) and topographic wave drag dissipation ($\sim \kappa _w$: wave drag coefficient) (Nycander 2005). It is important to note that wave drag is a frequency-dependent effect (Green and Nycander 2013). While drag is quasi-absent for long-period tides, the individual wave drag tensor differs for diurnal, semidiurnal and terdiurnal species.

Simulations are performed on a rotated, spherical lat/lon- grid with poles located on dry grid cells at ($114.5^\circ$E, $28.5^\circ$N) in East Asia and the Antipodic point in South America at a resolution of $\frac{1}{12} ^\circ$. The zonal resolution is halved at two latitude circles ($60^\circ$ and $75^\circ$) toward the poles. This allows for simulations to be performed with time step lengths of $\frac{1}{14400}$/$\frac{1}{480}$/$\frac{1}{240}$/$\frac{1}{160}$ of the respective tidal period for monthly/diurnal/semidiurnal/terdiurnal tides yielding numerical values close to 180 seconds.

The initially transient solution is $\varvec{\zeta }(\varvec{x}, t) = \left( {\mathbf {v}}, \zeta \right) (\varvec{x}, t)$, where ${\mathbf {v}}$ is the tidal flow velocity and $\zeta$ the sea surface elevation. It converges to the harmonic time series, reading

$$\begin{aligned} {\zeta }({\mathbf {x}}, \omega t) = {\zeta }^\omega _{cos} \cos \omega t + {\zeta }^\omega _{sin} \sin \omega t + \left( {\mathrm{N}} \right) , \end{aligned}$$

(2)

for the sea surface elevation. In the following, nonlinear contributions N are neglected as they are generally much smaller than the linear component.

From Eq. (2) the tidal amplitude $|\zeta ^\omega | = \sqrt{(\zeta ^\omega _{cos})^2+(\zeta ^\omega _{sin})^2}$ and Greenwich-phase-lag $\psi _{G}$ can be derived and will be used to present the obtained tidal solutions. We want to stress that $\psi _G=0$ usually refers to the TGP having its maximum value at the equator on Greenwich-longitude $\lambda =0$ (or slightly North of the equator if it is zero at $\phi =0$). This situation is not reflected at $t=0$ for all spherical harmonic functions constituting the TGP as later defined in Eq. (3). For certain combinations of (l, m), including (2, 0), (3, 0) and (3, 1), an additional phase-shift of $180^\circ$ has to be introduced to obtain the correct phase-convention for $\psi _G=0$ at $t=0$.

Fig. 1

Diurnal tide gauge data (TICON-td, see Sect. 4.1) for 2 example stations in the Atlantic (left, green $\bullet$) and southern Pacific Ocean (right, red $\bullet$). The real (in-phase) part of the admittance function $\mathbf{Re} (Z)$ (blue, dot) and the imaginary (quadrature) counterpart $\mathbf{Im} (Z)$ (blue, x) are approximated by a linear admittance approach sustained by $^2\hbox {Q}_1$, $^2\hbox {O}_1$, $^2\hbox {K}_1$ (black line). Inleted the TiME-native chi- and the std-grid are shown with the respective TG-positions

We recall that the tidal simulations are run in partial tide forcing mode. This means that only tide raising forces of a certain frequency are considered which disables the nonlinear generation of compound tides by interaction of different partial tides. The nonlinear interactions of certain minor tides can in principle generate oscillations at the considered degree-3 frequencies, e.g., N ($^2$ $\hbox {M}_2$, $^3$ $\hbox {M}_1$) $\rightarrow$ $\hbox {M}_3$, and would contribute to the modeled tidal solutions. On the other hand, these contributions are expected to be negligible as they can only be produced by interaction of at least one of the presented minor amplitude, degree-3 tides with another partial tide. Therefore, these compound tides are smaller by a factor of 60 compared to compound and overtides tides of degree-2 origin. Here, $\hbox {M}_4$ (see, e.g., FES14-model: Lyard et al. 2021) is the most prominent example with sub-cm amplitudes in the open ocean. Nonetheless, we acknowledge that those contributions could produce minor modifications of the results.

Tide-raising potential of second and third degree

The TGP allows describing the tidal forces generated by celestial bodies. The astronomical gravity potential exerted by these objects can be decomposed into temporal harmonic functions (Wenzel 1997b) that excite partial tides in the atmosphere, solid Earth and ocean. We use the expansion of Hartmann and Wenzel (1994, 1995b) (HW95). The resulting ocean tide-raising potential for a partial tide with frequency $\omega$, degree l and order m can be expressed as

$$\begin{aligned}&V_{tid}({\mathbf {x}}, \omega t)\nonumber \\&\quad = A_\omega \cdot \alpha _l \left( Y_{lm}(\phi , \lambda ) \cos \omega t - Y_{l-m}(\phi , \lambda ) \sin \omega t\right) , \end{aligned}$$

(3)

where $\hbox {A}_\omega = | \hbox {A}_\omega |$ is the excitation amplitude for a partial tide of frequency $\omega$, $\alpha _l = 1 + k_l - h_l$ is a combination of body-tide Love numbers that evaluates to $\alpha _{3}=0.801$ (Spiridonov (2018): model 9) and $Y_{l,m\ge 0} \equiv {\overline{P}}_{lm}(\sin \phi ) \cos (m \lambda )$, $Y_{l,m<0} \equiv {\overline{P}}_{lm}(\sin \phi )\sin (|m| \lambda )$ are real-valued spherical harmonic functions, where the normalized, associated Legendre functions ${\overline{P}}_{lm}$ are defined as in  Heiskanen and Moritz (1967) or the Appendix of Hartmann and Wenzel (1995a). Within this article, we use the term “Tide-Raising Potential” (TRP) that is the generator of ocean tides and includes the back-action of solid Earth body tides upon water masses included in $\alpha _3$ to demarcate its difference to the concept of the TGP solely including gravitational forces originating from celestial bodies. Our definition of the TRP does not comprise the SAL-forces that are induced by the ocean tides themselves, but only the forcing potentials that are not influenced by ocean tidal dynamics.

Forces exerted by $V_{tid}({\mathbf {x}}, \omega t)$ induce tidal surface oscillations that can be described by the complex-valued solution vector ${\zeta }^{\omega } = {\zeta }^\omega _{cos} + i {\zeta }^\omega _{sin}$. This quantity will be employed for model validation (compare Eq. 2). Normalization by the equilibrium tide length scale, $\frac{A_\omega \alpha _l}{g}$, yields the admittance function that we define as

$$\begin{aligned} Z_{lm}(\phi , \lambda , \omega ) = \frac{\zeta ^{\omega ,lm}}{A_\omega \alpha _l} g. \end{aligned}$$

(4)

Here we restored l, m to the superscript of $\zeta ^{\omega ,lm}$ to recall degree and order of the respective partial TRP, the generator of $\zeta ^{\omega ,lm}$. As $\partial _\omega Z_{lm}$ varies only weakly with $\omega$ for modern-day tides, the admittance function $Z_{lm}(\omega )$ is often interpolated (and extrapolated) by assuming linear admittance (Munk and Cartwright 1966; Gérard and Luzum 2010; Rieser et al. 2012) (compare Figs. 1 and 10). As those assumptions are feasible for most tides, this approach is employed to improve tidal predictions substantially, as direct estimation of tides by satellite-data-constrained tidal models shows reduced precision for small tidal amplitudes (Hart-Davis et al. 2021b). On the other hand, this technique can only be employed for tides with identical degrees and orders. For degree-3 tides, the admittance assumptions sustained by degree-2 tides are generally invalid, as is easily verified with tide gauge data derived admittance functions. From Fig. 1, it becomes clear that the degree-3 tide $^3\hbox {M}_1$ as well as the primarily radiationally excited tide $^{*}$ $\hbox {S}_1$ cannot be estimated by linear admittance assumptions and must be estimated, or simulated, explicitly. Here, $^*$ signifies the atmospherically influenced excitation pattern that differs from pure degree-2 excitation.

Table 1 Third-degree tides and neighboring second-degree tides in the same tidal group as appearing in HW95-TGP of  Hartmann and Wenzel (1995b) after the nomenclature of Ray (2020). The table shows the Doodson-Coefficients, the tidal frequency f, the excitation amplitude $A_{\omega }$ as well as degree l and order m of the generating spherical harmonic functions $Y_{lm}$. Additionally, naming conventions employed in recent publications are listed

As degree-3 partial tides are reduced by the factor of approximately $\frac{1}{60}$, they are difficult to detect in observational records. Thus, we only consider the most prominent excitations for the possible tidal bands ($m=0,1,2,3$) of third-degree origin even though additional excitations can be detected in gravimetric measurements (Ducarme 2012) and in several tide gauge records (Ray 2001). Since the nomenclature for those tides has never been unified (Ray 2020) and differs in geodetic (Ducarme 2012) and oceanographic literature (Woodworth 2019), they are listed in Table 1 with respect to their mentioning in recent publications along with neighboring tides of second-degree origin. Within this paper, we will utilize the naming convention introduced by Ray (2020), presented in bold font. It considers historical developments in the oceanographic nomenclature, incorporates a direct reference to the degree of the exciting potential and excludes confusion with oceanographic compound and overtides. Further, the utilized leading superscript has been extended to all second-degree partial tides (e.g., $^2$ $\hbox {M}_2$, $^2$ $\hbox {O}_1$) mentioned in this paper for means of continuity.

Model setup and validation

Since TiME is data-unconstrained, simulation errors cannot be rectified by assimilating satellite altimetry data. Therefore, the influence of the model parameters on the simulation results is critical. To optimize the accuracy of the obtained tidal solutions, an ensemble of simulations is prepared where the relative weights of the implemented dissipation mechanisms are tuned. The results are then validated with a reference tide gauge data set.

Tide gauge data set

TICON is a global tide gauge (TG) data set that provides tidal constants of 40 tidal constituents (Piccioni et al. 2019). These constants are estimated by least-squares harmonic analysis on individual tide gauge time series obtained from the Global Extreme Sea Level Analysis (GESLA: Woodworth et al. 2017) project. In this study, the number of tidal constituents is increased to include the $^3\hbox {M}_1$, $^3\hbox {M}_3$, $^3\hbox {N}_2$ and $^3\hbox {L}_2$ tides and the data set is henceforth called TICON-td. As stated by Ray (2020), these degree-3 tides have frequencies similar to those of larger degree-2 tides and are significantly modulated during the $18.61\,$yr cycle of the Lunar node regression and, therefore, require a long time series of observations to properly separate these tides. The required time series length is hereby related to the noise apparent in the tidal record (Munk and Hasselmann 1964). The extension of TICON-td was designed to only include tide gauges that exceed 10 years of continuous sampling and include the nodal corrections as presented by Ray (2020). Furthermore, we only include stations that are placed in an open ocean environment (mean surrounding depth $> 500 \$m in a $2^\circ$ radius) ending up with an ensemble of $N_T=134$ stations. We further remove closely neighboring stations by only allowing one station in a $0.2^{\circ }$ radius.

Formal uncertainties of these tidal estimations are also provided in order to evaluate the comparisons between the model and these data. For these four tidal constituents, the average standard deviation of the individual tide gauge estimations was $<0.01\,$mm and, therefore, should not influence the comparisons with the model estimations.

Further, we employ $N_R = 130$ selected deep ocean tide gauge stations that were analyzed by Ray (2013). This data set provides constituents for a large number of partial tides including $^3$ $\hbox {M}_3$, which allows the comparison to TICON-td for this specific partial tide. The spatial distribution of the tide gauge data sets is non-uniform, where a concentration of stations around Japan for TICON-td is the most striking feature.

Table 2 Tuning experiments for dynamical degree-3 tides. RMS$(^3\text {M}_3)$ comprises the evaluation for both tide gauge data sets (TICON-td/ (Ray 2013)). All RMS values are given in mm

The employed metric is the root-mean-square (RMS) deviation with respect to the tide gauge station data

$$\begin{aligned} RMS(\zeta ^\omega ) = \sqrt{\frac{1}{2N} \sum _{i=1}^N|\zeta ^\omega (\varvec{x}_i)-\zeta ^\omega _{TG}(\varvec{x}_i)|^2}~, \end{aligned}$$

(5)

where the summation is performed for all $N=N_R,N_T$ tide gauge stations. This deviation can be compared to the respective mean signal ${s \equiv RMS(\zeta ^\omega =0)}$, representing the captured signal fraction

$$\begin{aligned} c = 1 - \frac{RMS}{s}~, \end{aligned}$$

(6)

that we will employ as an effective score metric.

Model tuning

Employing the previously introduced tide gauge metric, an ensemble of tidal simulations was prepared to find an optimum interplay between the implemented dissipation mechanisms (wave drag, bottom friction, eddy-viscosity). The results are displayed in Table 2. For all partial tides, we obtain the highest accuracy with setting RE, which was initially derived as an optimized setting for the main lunar tide $^2\hbox {M}_2$ (Sulzbach et al. 2021a).

The parameterized eddy-viscosity of $A_h= 2 \cdot 10^4 \frac{m^2}{s}$ implies a large lateral momentum transfer which we find hard to justify hydrodynamically (Egbert et al. 2004). Therefore, we further conducted experiments with $A_h$ minimized (W0), which confirmed the results of Sulzbach et al. (2021a), where RE is favorable for enhanced accuracy. Similar to this finding, reduced accuracy is observed when employing setting W1, where wave drag dissipation is completely suppressed. This confirms that terdiurnal and semidiurnal tides are strongly controlled by wave drag dissipation and thus require a precise representation of this effect for accurate modeling results. The influence on $^3\hbox {M}_1$, on the other hand, is smaller, while $^3$Mm is simulated with setting W1 as it is not expected to dissipate energy by wave drag mechanisms (compare Table 2). In comparison with neighboring degree-2 tides tabulated in Table 1, the wavedrag dissipation fraction is almost identical ($^2\hbox {N}_2$: $34 \ \%$; $^2\hbox {L}_2$: $38 \ \%$; $^2\hbox {M}_1$: $16 \ \%$) in spite of gravely altered admittance patterns. The overall dissipation is well below $1 \$GW with the most prominent contribution of $240 \$MW coming from the $^3\hbox {M}_3$ tide.

In agreement with results obtained for major tides (Sulzbach et al. 2021a), we find that the full consideration of the effect of SAL is crucial to obtain high precision results. The locally approximated SAL-effect utilized for experiment S1 showed a substantial RMS-increase, especially for the small-scale oscillation systems of $^3\hbox {M}_3$, where the increase was close to $1 \,$mm. A possible explanation is the smoothing effect of the SAL-convolution integral that is highly important for short-scale oscillation systems as those of $^3\hbox {M}_3$. The captured signal fraction c (compare Eq. 6) exhibits values between $55 \%$ and $65 \%$, where the agreement for $^3\hbox {M}_1$ is particularly low ($33 \%$). We find that the amount of captured signal for $^3\hbox {M}_3$ by both tide gauge data sets is similar.

Fig. 2

$^3\hbox {M}_1$-tide; a Greenwich-phase lag $\psi _G$ of the modeled ocean tide (degree) with cotidal lines in increments of 60$^\circ$ (Thick: $0^\circ$) ; b ocean tide amplitude (right, mm) and ocean loading induced gravity amplitude (left, nGal). The plots are overlaid with Greenwich-phases and amplitudes measured at TICON-td tide gauge stations (triangles) and phases modeled with SPOTL (inner circle) and analyzed (outer circle) for the SG-stations. The displayed gravity signal partially exceeds the presented scale by far in near-coastal regions, but is cropped at $28 \$nGal for better depiction of smaller signals

Fig. 3

$^3\hbox {N}_2/^3\hbox {L}_2$-tide; (a/c) Greenwich-phase lag $\psi _G$ of the modeled ocean tide (degree) with cotidal lines in increments of 60$^\circ$ (Thick: $0^\circ$) ; (b/d) ocean tide amplitude (right, mm) and ocean loading-induced gravity amplitude (left, nGal). The plots are overlaid with Greenwich-phases and amplitudes measured at TICON-td tide gauge stations (triangles) and phases modeled with SPOTL (inner circle) and analyzed (outer circle) for the SG-stations

Fig. 4

$^3\hbox {M}_3$-tide; a Greenwich-phase lag $\psi _G$ of the modeled ocean tide (degree) with cotidal lines in increments of 60$^\circ$ (Thick: $0^\circ$) ; b ocean tide amplitude (right, mm) and ocean loading induced gravity amplitude (left, nGal). The plots are overlaid with Greenwich-phases and amplitudes measured at TICON-td tide gauge stations (triangles) and tide gauge stations compiled by Ray (2013) (polygons) and phases modeled with SPOTL (inner circle) and analyzed (outer circle) for the SG-stations

Global solutions for ocean tides and loading-induced gravity signals

Ocean tidal loading induces terrestrial gravity variations that can be measured with gravimeters on solid ground even far away from the coast. In analogy to Eq. (2), the ocean loading-induced gravity signal can be described by

$$\begin{aligned} g({\mathbf {x}}, \omega t) = g^\omega _{cos} \cos \omega t + g^\omega _{sin} \sin \omega t + \left( {\mathrm{N}} \right) . \end{aligned}$$

(7)

Global solutions $g^\omega = g^\omega _{cos} + i g^\omega _{sin}$ for the induced gravity at sea level height can be derived by a spectral approach, constrained by load Love numbers, that translates ${\zeta ^\omega _{cos} \rightarrow g^\omega _{cos}}$ and analogously for the sine-coefficients (Agnew 1997; Merriam 1980). Therefore, we evaluate

$$\begin{aligned} g_{cos}^\omega ({\mathbf {x}})= & {} - g \frac{3 \rho _{sw}}{2 a \rho _{se}} \sum _{l,|m|\le l}^{l_{max}} \frac{4 h_l - 2 k_l (l+1) -1}{2l+1}\nonumber \\&\times \zeta ^\omega _{lm, cos} Y_{lm}(\phi , \lambda ) ~. \end{aligned}$$

(8)

Here $\zeta _{cos}^\omega = \sum _{l,|m| <= l} \zeta _{lm, cos}^\omega Y_{lm}(\phi , \lambda )$, $k_l$ and $h_{l}$ are LLNs describe the effect of the yielding of the solid Earth on gravity, $\rho _{sw} = 1024 \frac{kg}{m^3}$ and $\rho _{se} = 5510 \frac{kg}{m^3}$ are the mean density of sea water and the solid Earth, respectively. This sum converges uniformly as $k_l l \rightarrow (k_l \cdot l)_{\infty }$ and $h_l \rightarrow h_{\infty }$. We take $l_{max} = 2599$, where the ocean load input is interpolated conservatively to a resolution of $\frac{1}{30}^\circ$, with coastlines derived from the rtopo2-bathymetry (Schaffer et al. 2016). In line with the definition of the tide-raising forces in Eq. (1), the gravity acceleration in Eq. (8) acts towards potential maxima: Positive vectors point to the Earth’ core. This evaluation is strictly valid only at sea level height ($H=0$), because otherwise the spectral decomposition does not converge sufficiently fast with increasing $l_{max}$ (Merriam 1980).

This formula solely encompasses the far-field or large-scale effect of the induced gravity variations. In this approximation, mass variations are treated as a layer of depth zero on the ocean surface. Newtonian attraction of close-by wet grid cells is thus ignored, as they are assumed to be at the same height as the evaluation point (at sea level). Therefore, this approximation is only valid at locations with a distance from the ocean $r_0$ and height H forming a ratio $\tan (\beta ) = \frac{H}{r_0} \rightarrow 0$. While this is true for most SG stations treated in this paper, deviations are to be expected for near-coastal stations, that we will define within this paper as stations with $\beta ^{max} > 1^\circ$ comprising the OS ($r_0^{min} \approx 250\,\text {m}$ $\rightarrow$ $\beta ^{max} \approx 1.6^{\circ }$) and NY station (SG Kongepunktet: $r_0^{min} \approx 120\,\text {m} \rightarrow \beta ^{max}$ $\approx$ $20.0^{\circ }$, Breili et al. 2017). Other gravimeters in coastal regions (e.g., TC, LP) are situated at distances $r_0>10\,$km from the ocean and violate the defined criterion for near coastal stations. However, the restriction to sea level height is only relevant for the introduced spectral approach. The here neglected local attraction effect can be easily incorporated with a Greens-function approach (e.g., Olsson et al. 2009).

In the following subsections, the modeled results for ocean and induced gravity signatures appearing in Table 1 are discussed and refer to Figs. 2, 3, 4, 5.

Diurnal species

In close agreement with the results of (Ray 2020) and (Woodworth 2019), the displayed $^3\hbox {M}_1$-oscillation patterns have a typically diurnal character with tidal amplitudes that are elevated at coastlines (see Fig. 2). Yet the observed cotidal chart completely contradicts the well-known degree-2 patterns (compare also Appendix B and Fig. 10). Tidal amplitudes are enhanced in the North Atlantic (in accordance with Cartwright 1975) and even more pronounced in the Indian Ocean. On the other hand, $^3\hbox {M}_1$-oscillation in the Pacific is strongly suppressed. As TiME is data-unconstrained and includes polar latitudes, we further report large-scale elevations of up to $5\,$mm in the Southern Ocean around Antarctica as well as high amplitudes in Baffin Bay (max: $14\,$mm) and the Barents Sea (max: $19\,$mm East of the Kanin Peninsula), while Arctic $^3\hbox {M}_1$-amplitudes are small but reach up to $3\,$mm in some places. We further report a number of local maxima, including the Sea of Okhotsk (max: $33\,$mm); the Patagonian Shelf (max: $12\,$mm) and South of New Guinea (max: $42\,$mm).

While the comparison to TICON-td shows a convincing agreement in tidal phases, the amplitudes are depicted less precisely, resulting in an RMS of $1\,$mm while capturing $c=33 \%$ of the signal (Table 2). Besides possible shortcomings of the tidal model for the $^3\hbox {M}_1$ (e.g., underestimated bottom friction, shallow water processes) a possible reason for this low agreement might be the generally small $^3\hbox {M}_1$-signal with especially high concentrations of TG-stations in low amplitude regions (e.g., Pacific Ocean). In spite of the small $^3\hbox {M}_1$ ocean tide signal the modeled ocean loading induced gravity signal features high amplitudes in coastal proximity, partially exceeding $100 \$nGal (e.g., Horn of Africa) that only slowly decay towards the continental interior. Reasonably high signals are to be expected for gravimeters situated in Europe, South America and Australia.

Fig. 5

Amplitude of the long-period $^3$Mm-tide (a) and complex deviation $|\zeta _\omega - \zeta _{seqt}(^3\text {Mm})|$ to self-consistent equilibrium tide (b). Elevations are given in mm

Semidiurnal species

Being members of the same admittance band described by $Z_{32}$, the $^3\hbox {N}_2$ and $^3\hbox {L}_2$ tides exhibit quite similar oscillation patterns. In agreement with the findings of Ray (2020), TiME predicts the semidiurnal degree-3 response to be strongest in the Pacific Ocean with smaller amplitudes in the southern Atlantic Ocean (see Fig. 3). In contrast to the diurnal results, amplitude maxima of up to $10\,$mm height appear in the open ocean. The strong semidiurnal response in the Southern Ocean, especially the Weddell Sea, is fully depicted on TiME’s global domain with large-scale amplitudes reaching over $10\,$mm. On the other hand, semidiurnal responses in the Arctic region are found to be negligible. As discussed by Ray (2020), the $^3\hbox {L}_2$-response is observed to be considerably stronger, despite its smaller equilibrium tidal height ($- 8 \%$ to $^3\hbox {N}_2$), which can be related to a more resonant coupling to oceanic normal modes (compare Müller 2007).

We report a number of local maxima that reach highest values North-East of Australia ($94\,$mm), Bristol Bay (Alaska, $77\,$mm), western Australia ($41\,$mm) and the Weddell Sea ($38\,$mm) for $^3\hbox {L}_2$.

The validation with TICON-td shows a good agreement in tidal phases and amplitudes that is substantially higher than the results obtained for $^3\hbox {M}_1$ ($55 \% /64 \%$) and comparable to the results obtained by Ray (2020). Relevant gravimetric amplitudes are predicted close to large-scale oceanic signals, with dominant amplitudes in North/South America, South Africa and Australia. As, due to their shorter tidal period, the semidiurnal amphidromic systems have a shorter spatial length scale compared to $^3\hbox {M}_1$, their respective gravimetric amplitudes decay faster towards the continental centers. For a comparison with degree-2 tidal solutions please consider Appendix B and Fig. 11.

Terdiurnal species

$^3\hbox {M}_3$ displays the most fine-structured response patterns due to its higher terdiurnal frequency. More than for the semidiurnal species, open ocean amplitude maxima appear in each major basin with amplitudes reaching $>5\,$mm and even higher in the northeast of Brazil (see Fig. 4). The most prominent large-scale amplitudes are yet again confined to shelf areas and marginal seas (Ray 2020). The largest signals are obtained in the Mozambique Channel and Western Europe. Amplitudes up to $5\,$mm are predicted at Antarctic coasts, while Pan-Arctic $^3\hbox {M}_3$ amplitudes are close to zero.

In contrast, small-scale $^3\hbox {M}_3$ shelf resonances can reach considerable heights. Here we only mention the largest predicted amplitudes near Beira (Mozambique Channel: $151\,$mm), the Suriname river mouth ($131\,$mm), southern Australia ($88\,$mm) and Bristol Channel (UK: $69\,$mm).

As for the semidiurnal tidal species, the comparison to TG-data shows a good agreement with both data sets at levels of around $c=60 \%$. Combining both data sets, a dense coverage of TG-data is achieved. Providing an interesting result for satellite gravimetry, the predicted open ocean amplitude maxima are recorded and confirmed by the TG stations for both terdiurnal and semidiurnal tidal species. As $^3\hbox {M}_3$ oscillation systems are of small scale and often confined to coasts, the resulting ocean loading-induced gravity signal reaches high amplitudes in coastal environments while quickly decaying with increasing distance from the coast. The loading-induced gravity signature on the South American continent represents an interesting case: As the coastal terdiurnal ocean tides mainly exhibit phase lags between $240^\circ$ and $360 ^\circ$, the continent is pushed down in a synchronized way yielding high gravimetric amplitudes that depict relevant magnitudes over the larger part of the continent. As the gravimetric amplitude rapidly changes in coastal margins, the detectability of $^3\hbox {M}_3$ in, e.g., European and Japanese stations primarily depends on the exact position of the gravimeter station.

Fig. 6

Locations of the discussed SG-Stations over the globe with Station-ID, Site and Country-ID

Long-period species

As the $^3$Mm oscillation period is close to 1 month, dynamic forces are strongly suppressed resulting in an ocean tide amplitude generally below $3\,$mm. The results can directly be compared to the self-consistent equilibrium tide $\zeta _{seqt}$ resulting from Eq. (1) with dynamic forces eliminated,

$$\begin{aligned} \zeta _{seqt} - \zeta _{eq} - \zeta _{SAL}(\zeta _{seqt}) = const, \end{aligned}$$

(9)

that depends on the degree and order of the selected partial tide forcing expressed by $\zeta _{eq}$. The constant value has to be chosen to ensure mass conservation. The deviation between $^3$Mm and $\zeta _{seqt}$($^3$Mm) that is displayed in Fig. 5b confirms the non-dynamic character of $^3$Mm. Aberrations from the equilibrium solution only reach relevant magnitudes in the Pan-Arctic region, especially on the Siberian Shelf where deviation amplitudes over $2\,$mm are obtained. Some marginal seas (Baltic Sea, Mediterranean Sea) also exhibit small deviations from equilibrium.

As the $^3$Mm-constituent is not contained in TICON-td, the results displayed in Fig. 5a cannot be validated directly in this study. Further, the $^3$Mm-amplitudes are small compared to effects of local water storage changes which appear in the same temporal range (weeks to months). Therefore, it turned out to be difficult to find evidence in the gravimetric time series, but the results may contribute to isolate those hydrological signals.

Gravimetric data and modeling

Long records from superconducting gravimeters (SG) (Goodkind 1999; Hinderer et al. 2015) provide temporal gravity variations with highest sensitivity and long-term stability. The excellent signal-to-noise ratio of these instruments together with recent advances in tidal analysis enables for a separate parameter estimation of degree-3 tidal constituents.

Gravity time series

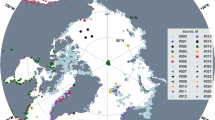
Records from 16 SG stations worldwide (Fig. 6) contributing to the International Geodynamics and Earth Tide Service (IGETS, Boy et al. 2020) were analyzed. The time series covering periods from 5 to 23 years were selected based on a global simulation of the tidal constituents (Table 2, Figs. 2, 3, 4 and 5). Stations having a signal of at least $10 \$nGal for one component were included. This covers in particular the Atlantic coast of Europe, the West coast of North America, southern Australia and Japan and includes stations in South Africa and South America.

The data were provided either by the station operators or obtained from the IGETS database (Voigt et al. 2016). Raw data sets (IGETS Level-1) were pre-processed in a remove-restore procedure by applying preliminary tidal models and atmospheric corrections only to remove spikes and disturbances and correct instrumental steps. Also IGETS Level-2 data sets were partially post-processed in this way. In data sets provided by the operators and IGETS Level-3, the instrumental drift was already reduced. In some cases, a second degree polynomial function was applied, while for station OS a more complex nonlinear drift function was necessary (Scherneck and Rajner 2019). Only minor revisions of specific sections were found to be necessary. All applied gravity reductions were restored before analysis.

Tidal analysis

Within the tidal analysis, the complex transfer function of the measured Earth’s response to tidal forcing (Wang 1997) relative to an Earth model is determined from observations. Because it is impossible to resolve the large number of individual frequencies of the TGP (Wenzel (1997b), Sect. 3) even with the longest records, wave groups are introduced. Besides a Bayesian approach (Tamura et al. 1991), parameters for each wave group are usually determined by a least square adjustment (Wenzel 1997a), including a trend and regression channels, mostly used to determine an air pressure admittance to correct for atmosphere pressure effects. Following Schüller (2015), the basic observation equations (without regression channels) are for a number of wave groups q

$$\begin{aligned} y_{ET}(t) = \sum _{i=1}^q \delta ^\star _i \sum _{j=a_i}^{b_i} A^{EM}_{ij} \cos (\omega _{ij} t + \varphi _{ij} + \kappa _i), \end{aligned}$$

(10)

where $A^{EM}_{ij} = \delta ^{EM}_{ij}\times A_{ij}$ are the amplitudes, scaled by the admittance factor $\delta ^{EM}$ of the Earth model EM, while $\varphi _{ij}$ are phases, both for the respective frequency $\omega _{ij}$ and harmonic degree and order within the index range $[a_i, b_i]$ of the tidal potential catalogue. This model is fit to the observations by the relative amplitude factor $\delta ^\star$ and the phase shift $\kappa$. Equation (10) is transformed into the linear problem

$$\begin{aligned} y_{ET}(t) = \sum _{i=1}^q x_{c_i} e_i(t) - x_{s_i} f_i(t), \end{aligned}$$

(11)

with the unknown parameters $x_{c_i} = \delta ^\star _i \cos (\kappa _i)$, $x_{s_i} = \delta ^\star _i \sin (\kappa _i)$ for each tidal wave group i, relative to the contribution of the partial waves

$$\begin{aligned}&e_i(t) = \sum _{j=a_i}^{b_i} A^{EM}_{ij} \cos (\omega _{ij} t + \varphi _{ij}),\\&f_i(t) = \sum _{j=a_i}^{b_i} A^{EM}_{ij} \sin (\omega _{ij} t + \varphi _{ij})~. \end{aligned}$$

In order to separate the contributions of different degrees of the harmonic potential development within each wave group, Eq.(10) can be reordered depending on degree l and order m of the harmonic potential $Y_{lm}$ (Schüller 2020), reading

$$\begin{aligned} y_{ET}(t)= & {} \sum _{l=1}^{l_{max}} \sum _{m=0}^{l} \sum _{i=1}^{q_{lm}} \delta ^\star _{lmi} \sum _{j=a_i}^{b_i}\nonumber \\&\times A^{EM}_{lmij} \cos (\omega _{lmij} + \varphi _{lmij} + \kappa _{lmi})~. \end{aligned}$$

(12)

This allows a hypothesis-free wave grouping because a pre-scaling of the response of the Earth to tidal forcing of different harmonic degrees is not required anymore. However, the resolution of this approach is limited by the length and signal-to-noise ratio of the observed time series. Actually, ETERNA-x allows for three different grouping schemes: a) separate groups for selected reference wave groups and a specific degree, b) grouping of selected constituents of a specific degree and order into one group, and c) collecting all selected waves of a specific degree into one group. Here, we include the degree-3 waves under test as separate groups by scheme a), the so-called satellite wave groups. The schemes R04 and R18 from Ducarme and Schüller (2019) were modified, resulting in 76 to 125 wave groups. High correlations between tidal parameters of different degrees need to be avoided. We followed the correlation analysis as proposed by Ducarme and Schüller (2019) and used the ratio between error estimates propagated from the full covariance matrix and the uncorrelated case (Correlation RMSE Amplifier, CRA). A ratio of 1 stands for no correlation, while large values indicate a high dependency between parameters. In this way, it was decided if the more detailed scheme R18 or the more robust scheme R04 is applied. The majority of parameters showed a CRA close to 1; only for stations BO, AP, LP and TC this indicator was around 2 for $^3$ $\hbox {M}_1$ and $^3$ $\hbox {L}_2$, most likely related to a higher noise level in these registrations. The parameters relative to those of an ellipsoidal Earth model with an inelastic mantle and a non-hydrostatic initial state (DDW-NHi, Dehant et al. 1999) and the TGP from Hartmann and Wenzel (1995b) were estimated with software ETERNA-x.¹ Shorter time series or records with strong non-tidal effects in the long-period tidal range were high-pass filtered. Whether a filter was applied is documented in the last column of Table 3. Otherwise, only an overall linear trend was reduced. Table 3 provides an overview of the time span, number of continuous blocks, the applied wave grouping scheme and filtering, while further properties of the gravity residuals are discussed in Appendix A.

Table 3 Statistical properties of the SG times series used in this study. The instrument names include an abbreviation indicating the generation: T–tidal, C–compact, O–observatory, R–first remote controlled and sensor coils in series, DS–dual sphere. The last column indicates whether the times series was high-pass filtered to suppress signal with periods longer than diurnal tides

The effects of Earth rotation (polar motion, length-of-day variations) were reduced by a predefined amplitude factor of 1.16 (Wahr 1985). Atmospheric effects were corrected by a simple regression factor for local air pressure variations. More advanced atmospheric corrections based on numerical weather models from the service Atmacs (Klügel and Wziontek 2009) or applied in IGETS Level-3 were tested but gave not the same level of agreement—a surprising result which needs further investigation.

Comparison with simulated loading signals

The tidal loading signal from TiME was predicted for the 16 SG stations by two approaches: (1) employing the program NLOADF (Agnew 1997) from the package SPOTL (Agnew 2012) that was run with the respective partial tide solutions, and (2) the global solution as described in Sect. 5 based on load Love numbers (LLN). To discuss the agreement between simulated and analyzed data set, we employ the metrices introduced in Eqs. 5 and 6, where we replace $\zeta ^{\omega } \rightarrow g^{\omega }$ and evaluate at the 16 SG stations. We additionally calculate the captured signal fraction for individual stations, defined as $c_{s}= 1-\sqrt{|g^{\omega }({x_{SG}})-g^{\omega }_{SG}|^2/|g^{\omega }_{SG}|^2}$, with $g^\omega (\varvec{x}_{SG})$ and $g_{SG}^\omega$ being the result obtained with SPOTL and ETERNA-x at the SG-location $\varvec{x}_{SG}$, respectively.

Fig. 7

Measured amplitudes (black $\bullet$), modeled amplitudes (SPOTL: red $\blacktriangleleft$; LLN-approach; blue $\blacktriangleright$), phase-difference between SGs and model $|\varDelta \varPhi | = |\varPhi _{SG} - \varPhi _m|$ (red x), and captured signal fraction $c_s$ (cyan columns) evaluated at the considered ensemble of 16 SG stations for $^3\hbox {M}_1$, $^3\hbox {M}_3$, $^3\hbox {N}_2$ and $^3\hbox {L}_2$ (top to bottom). The error bars represent the formal uncertainties $\varDelta$amp and $\varDelta \varPhi _{SG}$ stemming from tidal analysis. The vertical dashed lines divide the SG stations into global domains (Europe, Africa, North America, South America, Asia, Oceania)

Amplitudes and phases of the obtained loading vectors are displayed together with the results of the tidal analysis in Fig. 7. Both simulations, SPOTL and LLN, agree remarkably well, except for stations OS and NY which are located close to the coast at finite height above sea level. As described in Sect. 5, these stations exhibit a nonzero angle $\beta$ and Newtonian attraction of local ocean mass will affect the gravimeter. This effect is not included in the LLN-approach and only to a certain resolution in SPOTL. When excluding the near coastal stations NY and OS the RMS of the modeled gravity amplitudes between both approaches amounts to $0.28/0.4/0.41/0.45 \$nGal for $^3\hbox {N}_2/^3\hbox {M}_3/^3\hbox {L}_2/^3\hbox {M}_1$. In the case of $^3\hbox {M}_1$ at OS, the agreement of SPOTL with the observed parameters is much better, as the distance between SG and coast is larger (approx. $250 \,m$) which means that a coarser representation of the coastline for OS will be sufficient. On the other hand, the effect at NY will require a much finer resolved coastline (distance to coast approx. $120 \,m$; Breili et al. 2017).

For most of the stations and waves, the agreement between simulated and analyzed loading effects is high, where the mean captured signal, Eq. (6), for all stations ranges between 65% und 79% (Table 4).

For $^3\hbox {M}_1$, an excellent agreement is found for stations MB, MC, YS, SU and CB, as indicated by cyan bars, while for stations CA and BO the modeled signal is close to zero confirming the result of the analysis. In these cases, large phase deviations may appear because the phase is not well resolved for non-significant amplitudes. Nonetheless, a correctly predicted zero signal is a confirmation of a high agreement between model and tidal analysis. Therefore, in cases of non-significant amplitudes the formally low agreement $c_s$ should not be regarded as poorly modeled stations.

The agreement for station TC and LP in South America is good as well, although with higher uncertainties. The latter is close to the Río de La Plata estuary and affected by shallow water tides and storm surge effects (Oreiro et al. 2018). A correction for storm surge effects has not yet been applied because they include small tidal constituents (mainly related to $^2\hbox {M}_2$) and were not available for the whole analysis period. However, the impact of the estuary should be studied in more detail at a later stage.

In the case of $^3\hbox {N}_2$, large signals are confirmed for the Japanese SG stations ES and KA, CB in Australia and for AP, CA and BO in North America. The results for BO agree well, but exhibit large uncertainties, eventually related to the quality of the data set. A zero signal was confirmed by all European stations; the small amplitudes in the range of a few nGal are even significant with 95% confidence, but show large phase deviations, for the same reasons as explained above.

The results for $^3\hbox {L}_2$ show the best agreement for almost all stations. The zero signal is confirmed for NY and OS, documenting the high quality of both records and that deviations for the other waves are most certainly not observational artifacts but should be subject of further interpretation. Even the small signal at several European stations is well confirmed and in-phase. The only larger deviation is found at AP and TC, located close to the Pacific coast in South America, where the amplitude is significantly underestimated by TiME compared to the tidal analysis result.

Table 4 Degree-3 ocean tide induced gravity validation metrics at 16 SG stations

Fig. 8

Relationship between signal amplitude and captured signal fraction for $^3\hbox {M}_1$ (blue circles), $^3\hbox {N}_2$ (green triangle), $^3\hbox {L}_2$ (red triangle) and $^3\hbox {M}_3$ (black triangle). Negative agreement $c<0$ is displayed as $0 \%$

The $^3\hbox {M}_3$ wave’s large amplitudes in Japan are well matched by TiME. Also for YS and SU larger signals close to $20 \$nGal are predicted, showing more than 50 % agreement with the TiME solutions. Also here, the zero signal was well confirmed by most European and North American stations.

Altogether, there is an agreement of more than 50 % for all the stations having an amplitude of at least $20 \$nGal, see Fig. 8. This shows not only that TiME is able to predict degree-3 gravimetric signals at a mean level of 63 % to 80 % depending on the respective tidal constituent but also the high resolution of SG records from IGETS in the range of a few nGal and the capabilities of ETERNA-x to resolve independent estimates for constituents of higher degree.

Conclusions

In this study, we presented the first data-unconstrained, global atlas for degree-3 ocean tides encompassing at least one partial tide of each tidal band. The validation with a set of tide gauge stations gave an RMS-deviation of $1 \$mm for each partial tide solution and confirmed a good agreement with our solutions. We also made a first assessment of the respective degree-3 signal in a globally distributed set of superconducting gravimeters. The extraction of the respective tidal constituents with nGal-amplitudes proved to be feasible and yielded a tight agreement with the modeled gravimetric signals. The modeled signal was obtained with two different approaches that showed to be equally reliable at altitudes close to mean sea level and far away from coasts. For near-coastal gravimeters at finite height, we found a significantly reduced agreement, presumably due to rather strong gravitational attraction effects by local mass variations.

The presented comparison of ocean tide solution with its associated gravimetric signals bears mutual benefits for geodesy and oceanography. On the one hand, the comparison of modeled vs. observed loading vectors represents an independent approach to validate ocean tides models as, e.g., pursued by Llubes and Mazzega (1996, 1997); Boy et al. (2003). Potential is also seen in inverting observed loading vectors to obtain information about ocean tidal dynamics (Jourdin et al. 1991). This consideration could be valuable for tidal constituents that cannot yet be resolved by satellite altimetry (e.g., due to small ocean tide amplitudes), as for additional diurnal degree-3 constituents like $^3$ $\hbox {J}_1$, $^3$ $\hbox {O}_1$, $^3$ $\hbox {Q}_1$ and $^3$2$\hbox {Q}_1$ that were detected in a number of tide gauge records which were longer than 35 years (Ray 2001). Complementary to the routinely applied validation with tide gauge data that represents a discrete set of local measurements of tidal heights, each SG constituent contains information about the global ocean mass distribution (via the integrative characteristics of gravity measurements) and is thus sensitive to changes in the tidal solution at much larger spatial scales. In particular, this could be handy for assessing the expected de-aliasing performance for satellite gravimetric solutions as those are sensitive to long-wavelength characteristics of the terrestrial mass distribution. The complementary characteristics of using TG and SG data sets for validating ocean tide models also reflect on their mean signals: While for $^3\hbox {M}_1$ the TG signal was the smallest in the ensemble ($1.5\,$mm vs. $2.9\,$mm for $^3\hbox {M}_3$), the induced mean SG signal was the most prominent ($21.7\,$nGal vs. $14.1\,$nGal for $^3\hbox {M}_3$). While this partially reflects on the dense SG concentration in Europe, a second reason is the long spatial wavelength of diurnal tides that leads to higher gravimetric amplitudes in interior of the continents. As this is also the case for $^3$Mm, SG data could be a valuable metric for validating small amplitude tides with long periods. Therefore, SG results as presented here should serve as additional benchmarks for ocean tide model development that will (in case of TiME) focus in the near future on the representation of nonlinear effects that are particularly important in shallow marginal seas.

Table 5 Properties of gravity residuals after tidal analysis. In the cases of filtered data, the unfiltered residual has been restored. See Fig. 9 for detailed explanation of the equally scaled tiny power spectra in column PSP. The ratio $\log (P)/\log (f)$ was obtained from the average amplitude in dB per octave. The goodness of this fit is provided by the chi-squared test. Values $\chi ^2/n>> 1$ indicate larger fluctuations in the spectrum, also visible in the deviations of the mean (blue) and maximum (amber) magnitude of the PSP. The RMS is given in $\text {nm}/\text {s}^2$, and the last column flags whether the time series was filtered before tidal analysis

Moreover, the high level of agreement between the predictions from the numerical ocean model and the tidal analysis results confirms the advanced methods introduced in ETERNA-x. Potentially, such comparisons may contribute to identify deficiencies in reductions of non-tidal loading or local mass attraction effects. In principle, the separation of body and load tide component in the gravimetric degree 3 signals is now possible by employing the modeled SG signals enabling further tests of the routinely applied solid Earth models. As discussed by Ray (2020), $^3$ $\hbox {M}_3$ ocean tide signatures correlate with GRACE/GRACE-FO acceleration residuals. Therefore, GRACE-reprocessing is likely to benefit from the inclusion of degree-3 tides, as imperfect tidal background modeling represents a prominent de-aliasing error (Flechtner et al. 2016). Motivated by this finding, unconstrained TiME solutions might be of interest to satellite gravimetry and other geodetic techniques such as GNSS surface loading (Penna et al. 2015) particularly for partial tides that are not readily available from data-constrained atlases.

Appendices

Appendix A: Properties of the gravity residuals

Fig. 9

Average power spectrum of gravity residuals explaining the tiny images in column PSP of Table 5. The abscissa is logarithmic in frequency; the corresponding periods are given at the top. Resolution has been devised such that bar number 5 contains the diurnal, semidiurnal and terdiurnal periods. All bars are equally wide in log(f). The amber colored part shows the maximum power in each band, and the blue part the arithmetic average of the dB values of power within the bin

The interpretation of the standard deviation derived by error propagation as confidence interval depends on the spectral characteristics of the gravity residuals, which are required to be normally distributed. With the quantities given in Table 5, the properties are summarized for each station: the RMS, a power spectrum and the power vs. frequency ratio, providing the noise color. The effect of high-pass filtering in ETERNA-x in the underlying data series has been restored, when applied (last column of Table 5).

Fig. 10

Dimensionless, diurnal admittance functions $Z_{l1}$ (right color bar) and $Z_{l1}^*$ (left color bar) evaluated for diurnal excitations (top: $l=3$ for $^3\hbox {M}_1$; bottom: $l=2$ for $^2\hbox {M}_1$). Lines indicate the tidal phase $\psi _G$ in increments of $60^\circ$, where the continuous, fat line marks $0^\circ$ and the dashed, fat line represents $60^\circ$ phase lag

Fig. 11

Dimensionless, semidiurnal admittance functions $Z_{l2}$ (right color bar) and $Z_{l2}^*$ (left color bar) evaluated for semidiurnal excitations (top to bottom: $l=3$ for $^3\hbox {L}_2$ and $^3\hbox {N}_2$; $l=2$ for $^2\hbox {L}_2$ and $^2\hbox {N}_2$). Lines indicate the tidal phase $\psi _G$ in increments of $60^\circ$, where the continuous, fat line marks $0^\circ$ and the dashed, fat line represents $60^\circ$ phase lag

Together with the RMS value of each site’s residual, the spectra indicate the presence of signal, be it from instrumental or environmental sources, that has escaped reduction in the tidal analysis because it was neither included in the functional model nor as prior data correction. The noise color as given by the ratio $\log (P)/\log (f)$ in Table 5 is mostly close to red (or Brownian), with larger deviations for some sites, as indicated by the Chi-squared test for the linear fit of this parameter from the power spectrum.

The average power within spectral bands defined equally wide in $\log (f)$ is shown in blue in the small figures of Table 2. Diurnal and semidiurnal tidal frequencies are covered by bar 5, while the other bars are assumed to be dominated by non-tidal sources, i.e., periods longer than one day, and are typically dominated by the effects of water storage changes. Strong but narrow spectral lines occur at specific periods and are represented by an amber surplus above the average. Such deviations indicate that attention is required, specifically if appearing in band 5. For most conspicuous stations such as BO, SU or YS, non-stationary behavior of solar tides $^*$ $\hbox {S}_n$ is the most likely cause, suggesting an advanced atmospheric correction.

Appendix B: Global admittance functions

Here we present global admittance functions of selected tides appearing in Table 1 to highlight differences in the underlying response patterns. The depiction of $Z_{lm}$ that was introduced in Eq. (4) facilitates a direct comparison between partial tides that possess excitation amplitudes encroaching several scales as ocean responses are normalized by their excitation amplitudes. We extend this concept to the gravimetric response $g^\omega$ induced by ocean tide $\zeta ^\omega$ (compare Eq. 7). For this purpose, $g^\omega = g^\omega _{cos} + i g^{\omega }_{sin}$ is normalized with the Newtonian gravitational shift induced by a localized, uniform layer of sea water of height $\frac{A_{\omega } \alpha _l}{g}$, which is the measure we employed for the equilibrium tidal height. This corresponds to the limit of a locally flat Earth, covered with said layer and amounts to half the gravity of the a uniformly water-covered sphere

$$\begin{aligned} g_{eq} =2 \pi G \rho _{sw} \frac{A_\omega \alpha _l}{g} = \frac{3 \rho _{sw}}{2 \rho _{se}} \frac{A_\omega \alpha _l}{a}~. \end{aligned}$$

(13)

The resulting ocean loading-induced gravity admittance function is then obtained by

$$\begin{aligned} Z^*_{lm}(\phi , \lambda , \omega ) = \frac{g^\omega }{A_{\omega } \alpha _l } \frac{2 \rho _{se}}{3 \rho _{sw}} a = g \frac{\sum _{l'm'}\beta _{l'} \zeta ^{\omega ,lm}_{l'm'} Y_{l'm'}}{A_\omega \alpha _l}, \end{aligned}$$

(14)

where $\beta _l$ is the LLN-composed prefactor in Eq. (8). Results for $Z_{lm}$ and $Z_{lm}^*$ are presented in a combined plot in Figs. 10 and 11. $^3\hbox {M}_3$-results are not presented as they cannot be compared to a neighboring degree-2 tide. The following features can be identified

• Degree-2 and degree-3 admittance functions take unrelated, independent shapes both in terms of amplitude and phase.

• At coastal margins, the phase lag of ocean tide and the respective induced gravity signal is not a steady function but can exhibit visible phase shifts due to the non-local character of ocean tidal loading (e.g., $^3\hbox {M}_1$-tide at West African coast).

• The strongly enhanced $^3\hbox {L}_2$-admittance can be easily identified and clearly exceeds $^3\hbox {N}_2$ (Ray 2020).

• Inverted behavior can be asserted in the case of semidiurnal degree-2 tides where $^2\hbox {N}_2$ admittance exceeds the $^2\hbox {L}_2$ response in Atlantic and Pacific Ocean. This result seems to be counter-intuitive. On the other hand, this behavior is not unexpected as the different excitation patterns of degree-3 and 2 tides will profoundly change the underlying normal mode decomposition of the respective partial tide, hence changing the relative importance of modes with specific resonance frequencies (Müller 2007).