1 Introduction

Seismic ground motion is fundamental for determination of earth structure and inversion of rupture processes of earthquakes (Aki and Richards 1980; Lay and Wallace 1995) and for both design and construction of seismic resistant man-made structures in earthquake engineering and seismic hazard analysis (see, e.g., Chopra 2012; Ivanov 2015). However, a complete precise prediction of seismic ground motion at a particular location for any potential earthquake may never be possible to obtain, because there are too many uncertain and even unknown factors to prevent us from obtaining a precise nonlinear seismic wave motion. Critical uncertain and/or unknown factors that affect the precision of predicting seismic ground motion include locations and magnitudes of earthquakes, rupture processes of earthquakes, highly heterogeneous properties of media, local site amplifications, discontinuity of boundaries and topographies (see, e.g., Aki and Richards 1980; Douglas 2003). As a result, earthquake engineering and seismic hazard analysis have to be practically simplified by focusing on a few important parameters such as magnitudes of earthquakes, seismic intensity, peak ground acceleration (PGA), peak ground velocity (PGV) and natural frequencies of structures.

As an important parameter in earthquake engineering and seismic hazard analysis, PGA, defined as the maximum ground acceleration at a location during an earthquake (Douglas 2003), is closely related to damage to buildings and infrastructures (see, e.g., Chopra 2012; IAEA 2011). PGA has been computed either directly from strong motion records with accelerographs or empirically from using some approximate regression functions (see, e.g., Murphy and O’Brien 1977; Campbell 1997; Douglas 2003; Boore and Bommer 2005; Bindi et al. 2011; Douglas and Edwards 2016). However, to our knowledge, there are apparently no reports on physically meaningful check and/or confirmation of PGA, independent of strong motion instruments of accelerometers. There are also some major problems with strong motion seismometers, including instrumental drift, saturation and clipping due to instrumental tilts and rotations (see, e.g., Emore et al. 2007; Graizer 2009, 2010). An even more serious problem with seismic waveforms is that strong motion records in the hypocenter area of a large earthquake can be simply unusable, because all conventional seismometers do not measure attitudes (Graizer 2010) and strong motion records at different time instants can be in different reference systems in this case (Xu et al. 2013, 2019a). There is no way to turn all the strong motion records at different time instants under different reference systems into a unified reference system without attitude measurements. As a consequence, the integrated velocities and the double-integrated displacements with accelerograms in the hypocenter area during a large and/or mega-earthquake are actually in different reference systems at different time epochs, and are practically unusable and not comparable due to the lack of attitude information. Any idea to combine global navigation satellite systems (GNSS) with seismic data is highly undesirable and should be avoided in hypocenter areas, in particular, in the case of large earthquakes, as may be seen in Xu et al. (2019b). Nevertheless, if a simple uniform velocity model to describe the kinematic motion of an accelerograph is valid for Kalman filtering, such a combination could be possible and successful (see, e.g., Bock et al. 2011). We may note that attitude information does not affect the peak ground acceleration under the assumption of correct scaling factors, but the horizontal and vertical components of PGA and PGV can become unreliable without attitude information, as is exactly the case of strong motion seismometers. Scaling and other unknown factors could affect the reliability of PGA values as well. For more problems of strong motions with accelerographs, the reader is referred to Boore and Bommer (2005).

To measure PGA correctly and precisely, there can be two methods. The first method is to use more expensive accelerographs of inertial measurement unit (IMU) type, which measure both three components of acceleration and three rotation angles of attitude, as can be seen in Graizer (2009, 2010), for example. However, updating all seismographs to precise but expensive IMU type in a large network of strong motions could be economically unrealistic. The second method is to indirectly compute PGA and PGV with precise positions in a unified reference system. In this latter case, GNSS has been repeatedly demonstrated to be a great success in precise positioning at any point on the surface of the earth in the earth-fixed reference frame. Actually, GNSS precise positions have been always used to compute the velocity of an object in motion since its inception, though often only at the sampling rate of 1 Hz.

Computing PGA and PGV from precise GNSS positions for applications in earthquake engineering, seismic hazard analysis and earthquake early warning is mathematically equivalent to numerical differentiations with discrete random data. Numerical differentiation with discrete random data is ill-posed and significantly amplifies measurement noise (see, e.g., Anderssen and Bloomeld 1974; Ramm and Smirnova 2001). In the seismological community, a common practice could be to transform GNSS-based displacement waveforms into frequency domain, readily obtain the velocity and acceleration convolution results in frequency domain by the rule of derivatives and then deconvolute them for the velocity and acceleration waveforms in time domain. This practice can be easily proved to be mathematically infeasible for two reasons: (i) since the power spectral density of white noise is constant, velocity and acceleration waveforms in time domain cannot be correctly reconstructed mathematically by deconvoluting their corresponding functions in frequency domain contaminated with white noise; and (ii) an inverse ill-posed problem can never be turned into a well-posed one through transformation. Thus, we will focus on reconstructing velocity and acceleration waveforms, PGA and PGV in time domain from GNSS-derived precise position waveforms in this paper.

There are mainly three classes of methods for numerical differentiations with random data. The simplest class of methods is to directly apply the difference operator to compute the derivatives with random discrete data (see, e.g., Anderssen and de Hoog 1984). The second class of methods is to first fit discrete random data with some functions and then use the fitted function to compute the derivatives (see, e.g., Savitzky and Golay 1964; Rivlin 1975). To suppress the noise of computed derivatives, the third class of methods is to incorporate regularization into the process of numerical differentiation (see, e.g., Cullum 1971; Anderssen and Bloomeld 1974; Ramm and Smirnova 2001).

In satellite positioning and navigation, it is a common practice to use the first two classes of methods to compute the velocity and acceleration of a vehicle from precise GNSS carrier phases and Doppler shifts (see, e.g., Kleusberg et al. 1990; Jekeli and Garcia 1997; Bruton et al. 1999; Bruton and Schwarz 2002; Kennedy 2003; Serrano et al. 2004). GNSS Doppler measurements are known to be still too noisy to be useful for precise velocity determination (Zhang and Guo 2013; Crespi 2018, private email communication on 2018 March 6). GNSS measurement of speed has also found many applications in sports (see, e.g., Waldron et al. 2011; Buchheit et al. 2014; Beato et al. 2016; Muñoz-López et al. 2017; Hoppe et al. 2018). Gatti (2018) also applied the time difference method to process 1 Hz global positioning system (GPS) data and compute the peak vibrations for three earthquakes of magnitudes Mw6.0, Mw5.9 and Mw6.5 in Italy. GNSS determination of velocity and acceleration is mainly based on precise relative GNSS positioning with a low sampling rate in geodesy and navigation (see, e.g., Kleusberg et al. 1990; Jekeli and Garcia 1997; Bruton et al. 1999; Bruton and Schwarz 2002; Kennedy 2003; Serrano et al. 2004). Other methods such as the variometric approach with a stand-alone receiver (see, e.g., Colosimo et al. 2011; Fratarcangeli et al. 2018) are becoming more and more important to determine velocity and acceleration in seismic applications.

Because GNSS receivers directly measure carrier phases precisely, GNSS can routinely measure positions precisely at a high sampling rate, up to mm-level of precision within a few minutes of time or cm-level in the long term of hours and days. However, high sampling rates can become a serious problem in GNSS determination of velocity and acceleration. If a moving vehicle is assumed to be only a few km away from a reference station, the baseline can be determined at a few mm level of accuracy with GNSS. Actually, GNSS precise point positioning (PPP), as first invented by Zumberge et al. (1997), can also achieve a few mm level of accuracy over a short period of time (say up to a few minutes), as first shown and explained in Xu et al. (2013) and Shu et al. (2017). As a result, if the sampling rate is supposed to be 1 Hz and if one directly applies the time difference method to compute the velocity and acceleration of the vehicle, then the accuracy of both the average velocities and accelerations of the vehicle would roughly be equal to a few mm per second and slightly better than 1 Gal (or equivalently 1 cm/\(\text {s}^2\)), respectively. A direct consequence is that aliasing effects on velocity and acceleration within this second remain unknown and it is not feasible to obtain instantaneous velocities and accelerations. With the increase in sampling rates (say above 10 Hz), although the resolution of acceleration has been increased, acceleration results have been found to be useless in sports experiments (see, e.g., Waldron et al. 2011; Buchheit et al. 2014; Hoppe et al. 2018). Waldron et al. (2011) reported a random error of 2.25g in GPS acceleration measurement with a sampling rate of only 5 Hz. Buchheit et al. (2014) obtained an even much larger error of GNSS accelerations with a sampling rate of 15 Hz (also personal email communication on 2018 Sept 9). They also found that GNSS accelerations with the same GNSS models of receivers can be different by a factor of two to six times.

In the case of earthquake engineering and seismic hazard analysis, since frequencies of seismic waves during a large (say Mw6) or mega-earthquake would be up to 20 Hz or even higher (see, e.g., Smalley 2009; Ivanov 2015), we will need a sampling rate of above 40 Hz to fully reconstruct a seismic wave. A direct time difference computation of acceleration from precise relative GNSS positions will result in a noise level of 1600 Gal or roughly 1.6g, which is far too large to be acceptable for earthquake engineering and hazard analysis applications. In other words, no useful PGA information would be expected physically from very high-rate GNSS positioning with difference methods, if the sampling rate is sufficiently high. To clarify the terminology of “high-rate”, we note that researchers classify sampling rates differently, depending on their scientific applications. Seismologists generally use “high-rate” to describe a sampling rate of 1–10 Hz (see, e.g., Larson 2009). However, for more instantaneous applications of GNSS, as in the case of sports (see, e.g., Waldron et al. 2011; Buchheit et al. 2014; Hoppe et al. 2018) and our PGA/PGV applications of earthquake engineering, 1 Hz is still too low a rate, since important instantaneous physical parameters cannot be obtained. Therefore for our applications, we adopt the term “high-rate” to refer to any sampling rate from 1 to 10 Hz, and “very high-rate” to refer to all sampling rates above 10 Hz.

As the first purpose of this research, we will reformulate the reconstruction of acceleration waveforms and PGA from precise GNSS positions as an inverse problem with a high sampling rate and propose a regularization method to solve the inverse problem. According to Wald et al. (1999), a high level of damage during a large earthquake is more associated with ground velocity than acceleration. Because no GNSS stations in the hypocenter area can be assumed to not move during a large or mega-earthquake, as the second purpose of this research, we will also investigate the reconstruction of velocity waveforms and peak ground velocity (PGV) from very high-rate GNSS PPP displacement or position waveforms.

The paper is organized in the following manner. Section 2 will formulate and solve the reconstruction of velocity and acceleration waveforms, PGA and PGV from very high-rate GNSS PPP position waveforms as inverse ill-posed problems. Regularization will be proposed in this section on the basis of mean squared errors (MSE) of solutions. We will then apply the regularization method developed in this paper to the 2013 Lushan Mw6.6 earthquake in Sect. 3. Since difference methods have been almost always used to compute velocity and acceleration from GNSS positioning, we will also compare the performances of reconstructing velocity and acceleration waveforms, PGV and PGA by regularization and the difference methods with the (very high-rate) 50 Hz PPP position waveforms from the Lushan earthquake. Some comparisons with the results of strong motion accelerograms on the Lushan earthquake will be made as well.

2 Methods for reconstructing velocity and acceleration from very high-rate precise GNSS positions

For many problems in engineering and science, one often has to compute the first and second derivatives mathematically from a number of discrete data contaminated with random errors, which are physically equivalent to computing the velocity and acceleration from discrete position measurements. In earth sciences, for example, one may first compute the accelerations of a low orbiting satellite from its orbital positions obtained from GNSS and then use them to further reconstruct the gravitational field of the earth (see, e.g., Reubelt et al. 2003; Ditmar and van der Sluijs 2004). GNSS precise positioning has been well applied to compute velocities and accelerations with a low sampling rate for many years (see, e.g., Kleusberg et al. 1990; Jekeli and Garcia 1997; Bruton and Schwarz 2002; Serrano et al. 2004; Gatti 2018); however, recent experiments in sports have demonstrated that GNSS accelerations can be in error that can be as large as a few g (see, e.g., Waldron et al. 2011; Buchheit et al. 2014). The time difference method, though most widely used in earth sciences, sports and beyond, is not practically applicable with the increase in sampling rates, since the errors of results are proportional to the sampling rate in the case of velocity and the square of the sampling rate in the case of acceleration. Thus, in this paper, we will reformulate the determination of velocity and acceleration from GNSS precise positioning as a standard inverse ill-posed problem and apply regularization to reconstruct PGA and PGV from GNSS measurements for earthquake engineering and seismic hazard analysis applications.

2.1 The starting differential and integral equations to invert for velocity and acceleration from position measurements

To start with, let us assume a function of precise position of a GNSS station, say r(t). We can then compute its first derivative, which is denoted by the velocity function v(t), as follows:

$$\begin{aligned} \frac{\hbox {d}r(t)}{\mathrm{{d}}t} = v(t). \end{aligned}$$
(1)

The solution to the differential equation (1) is given by the following Volterra’s integral equation of the first kind:

$$\begin{aligned} r(t) = \int _{t_0}^t v(\tau ) \hbox {d}\tau + r(t_0), \end{aligned}$$
(2)

where \(t_0\) is the starting time and \(r(t_0)\) is the value of function r(t) at the time instant \(t_0\). In practice, given a number of measurements on r(t) at discrete time instants \((t_0, t_1, t_2, ..., t_n)\), the first main purpose of this paper is to reconstruct the function of first derivative or velocity v(t) and thus to identify PGV at the GNSS station due to an earthquake.

In the similar manner, again assuming a function r(t) of precise position of a GNSS station, we can now compute its second derivative or equivalently the acceleration function, which is denoted by the acceleration function a(t), as follows:

$$\begin{aligned} \frac{\mathrm{{d}}^2r(t)}{\hbox {d}t^2} = a(t). \end{aligned}$$
(3)

The solution to the second-order differential equation (3) can be readily derived by using the method of variation of constants, which turns the non-homogeneous differential equation (3) into the following Volterra’s integral equation of the first kind:

$$\begin{aligned} r(t) = \int _{t_0}^t (t - \tau ) a(\tau ) \hbox {d}\tau + (t-t_0) v(t_0) + r(t_0), \end{aligned}$$
(4)

(see, e.g., Lonseth 1977; Lubansky et al. 2006), where \(t_0\) and \(r(t_0)\) have been defined in (2), \(v(t_0)\) is the velocity at the time instant \(t_0\). Actually, even if the acceleration function on the right hand side of (3) is a function of both r(t) and t, namely a(t, r(t)), the solution form (4) is still valid (Lonseth 1977), namely

$$\begin{aligned} r(t) = \int _{t_0}^t (t - \tau ) a(\tau , r(\tau )) \hbox {d}\tau + (t-t_0) v(t_0) + r(t_0). \end{aligned}$$
(5)

Alternatively, given two boundary points \(r(t_0)\) and \(r(t_1)\), the solution to the differential equation (3) can be written as a Fredholm’s integral equation of the first kind and given as follows:

$$\begin{aligned} r(t)&= - T^2 \int _{0}^1 G(\tau , \tau ') a(\tau ') \hbox {d}\tau ' \nonumber \\&\quad + \frac{(t-t_0)}{T} \{r(t_1)-r(t_0)\} + r(t_0), \end{aligned}$$
(6)

(see, e.g., Courant and Hilbert 1953; Stakgold 1967; Schneider 1968), where

$$\begin{aligned} T= & {} t_1 - t_0, \\ \tau= & {} \frac{(t-t_0)}{T}, \end{aligned}$$

and the symmetric kernel or Green function \(G(\tau , \tau ')\) is given by

$$\begin{aligned} G(\tau , \tau ') = \left\{ \begin{array}{ll} \tau ( 1 - \tau ' ), &{} \quad \text {if} \,\, 0 \le \tau \le \tau ' \le 1, \\ \tau ' ( 1 - \tau ), &{} \quad \text {if} \,\, 0 \le \tau ' \le \tau \le 1. \end{array} \right. \end{aligned}$$

The kernel function \(G(\tau , \tau ')\) is continuous at \(\tau =\tau '\) but its derivative with respect to \(\tau '\) or \(\tau \) is obviously discontinuous. Formula (6) also holds for the acceleration function a(t, r(t)) that is changing with time and position, as in the case of (5).

Although (4) and (5) can be used to reconstruct the acceleration function from the position function r(t), (4) will be more suitable for fixed monitoring objects such as permanent GNSS stations and (5) for GNSS navigation applications with objects in motion such as vehicles and satellites. In this paper, since our interest is in reconstructing the acceleration waveforms as the functions of time from precise position measurements r(t) of permanent GNSS stations, (4) will serve our purpose better. Given a number of measurements on r(t) at discrete time instants \((t_0, t_1, t_2, ..., t_n)\) at a GNSS station, the second main purpose of this paper now is to reconstruct the function of second derivative or acceleration a(t) and thus to obtain PGA at stations from precise GNSS measurements for an earthquake. In geodesy, Jekeli and Habana (2018) recently used the Volterra’s integral equation (5) and applied the measurement-based perturbation theory of Xu (2008, 2018) for the reconstruction of the Earth’s gravity field from almost continuous satellite tracking measurements. The Fredholm’s integral equation (6) of the first kind has been systematically investigated by Schneider (1968, 1984) and becomes popular for gravitational recovery from short-arc orbital measurements of satellite tracking (see, e.g., Schneider 1968, 1984; Ilk et al. 2005).

2.2 Discretization and regularization

The Volterra’s integral equations of the first kind (2) and (4) assume a continuous function of measurements r(t). In practice, one often has only a finite number of discrete measurements of r(t) at discrete time instants \((t_0, t_1, t_2, ..., t_n)\). Accordingly, we can only reconstruct the velocity and acceleration functions at a number of discrete time instants. As a result, we have to first discretize the integral equations (2) and (4). To start with, we divide the time interval \((t_0, t_n)\) into m equal sub-intervals, which is equivalent to reconstructing \((m+1)\) equally timed velocities and accelerations. In general, since we only have \((n+1)\) position measurements \([r(t_0), r(t_1), r(t_2), ..., r(t_n)]\), it is not reasonable to recover more points of velocities and/or accelerations than \((n+1)\). In other words, in what follows, we always assume \(m<n\). Although any rule of numerical integration can be applied to compute the integrals (2) and (4) numerically, we use the Trapezoidal rule to discretize both (2) and (4). Given the discrete measurements \({\mathbf {y}}=[r(t_0), r(t_1), r(t_2), ..., r(t_n)]^\mathrm{{T}}\), the discretized version of either (2) or (4) can then be used to link to \({\mathbf {y}}\), which results symbolically in the following linearized system of observational equations:

$$\begin{aligned} {\mathbf {y}} = {\mathbf {A}} \varvec{\beta } + \varvec{\epsilon }, \end{aligned}$$
(7)

where \(\varvec{\beta }\) stands for the discrete values of either velocity v(t) in the case of (2) or acceleration a(t) in the case of (4), \({\mathbf {A}}\) is the deterministic coefficient matrix and depends on what quadrature rules are used to discretize (2) and (4), and \(\varvec{\epsilon }\) is the random error vector of the measurements \({\mathbf {y}}\). In general, \(\varvec{\epsilon }\) is assumed to be of mean zero and variance–covariance matrix \({\mathbf {W}}^{-1}\sigma ^2\), with \({\mathbf {W}}\) being the positive definite weight matrix and \(\sigma ^2\) a positive (given or unknown) scalar of the variance of unit weight.

Since Volterra’s integral equations of the first kind (2) and (4) have been well known to be typically ill-posed, their corresponding discretized linear version (7) is ill-conditioned, the extent of which depends on the required resolution or equivalently, the number of points to be resolved from the precise positions \({\mathbf {y}}\). Since ill-posedness will significantly amplify the noises of measurements r(t), regularization has to be applied in order to attain the best possible balance among the three more or less conflicting criteria of stability, bias and precision. Regularization can generally be implemented by either determining regularization parameters or discarding the smallest eigenvalues according to a certain sense of optimality (see, e.g., Tikhonov and Arsenin 1977; Xu 1998).

Given a positive regularization parameter \(\kappa \), a regularized solution to (7) has been formally constructed by minimizing the following augmented weighted least squares (LS) cost function,

$$\begin{aligned} \text {min:} \quad F(\varvec{\beta }) = ({\mathbf {y}}-{\mathbf {A}}\varvec{\beta })^\mathrm{{T}}{\mathbf {W}}({\mathbf {y}}-{\mathbf {A}}\varvec{\beta }) + \kappa \varvec{\beta }^\mathrm{{T}} {\mathbf {S}}_r\varvec{\beta }. \end{aligned}$$
(8)

The given regularization parameter \(\kappa \) is also better known as a ridge parameter in statistics (see, e.g., Hoerl and Kennard 1970), and \({\mathbf {S}}_r\) is positive and/or semi-positive definite matrix. The matrix \({\mathbf {S}}_r\) generally represents a certain requirement of smoothness on the source function to be inverted or reconstructed, which can often be derived, for example, by imposing the smoothness condition of the first and/or second derivatives of the source function v(t) or a(t). In this work, we follow Phillips (1962) (see also Twomey 1963; Wahba 1992) and require the smoothness of the second derivatives of the function to be reconstructed. More specifically, the corresponding matrix, denoted by \({\mathbf {S}}\), can be written as follows:

$$\begin{aligned} {\mathbf {S}} = \left[ \begin{array}{rrrrrrrr} 1 &{} -2 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots \\ -2 &{} 5 &{} -4 &{} 1 &{} 0 &{} 0 &{} 0 &{} \cdots \\ 1 &{} -4 &{} 6 &{} -4 &{} 1 &{} 0 &{} 0 &{} \cdots \\ 0 &{} 1 &{} -4 &{} 6 &{} -4 &{} 1 &{} 0 &{} \cdots \\ \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdots \\ \end{array} \right] . \end{aligned}$$
(9)

Since \({\mathbf {S}}\) is singular, we prefer to add an identity matrix \({\mathbf {I}}\) of dimension m to \({\mathbf {S}}\) and construct a final smoother matrix as follows:

$$\begin{aligned} {\mathbf {S}}_r = {\mathbf {S}} + {\mathbf {I}}. \end{aligned}$$
(10)

The optimal solution to the minimization problem (8) can be formally written as follows:

$$\begin{aligned} \hat{\varvec{\beta }}= & {} ({\mathbf {A}}^\mathrm{{T}}{\mathbf {W}}{\mathbf {A}} +\kappa {\mathbf {S}}_r )^{-1} {\mathbf {A}}^\mathrm{{T}}{\mathbf {W}} {\mathbf {y}} \nonumber \\= & {} {\mathbf {N}}_{\kappa }^{-1}{\mathbf {A}}^\mathrm{{T}}{\mathbf {W}} {\mathbf {y}}, \end{aligned}$$
(11)

where \(\hat{\varvec{\beta }}\) is a regularized solution to the inverse ill-posed problem (7), and

$$\begin{aligned} {\mathbf {N}}_{\kappa } = {\mathbf {A}}^\mathrm{{T}}{\mathbf {W}}{\mathbf {A}} +\kappa {\mathbf {S}}_r. \end{aligned}$$

The statistical quality of the solution \(\hat{\varvec{\beta }}\) strongly depends on a proper choice of the regularization parameter \(\kappa \). If \(\kappa \) is set to zero, the solution \(\hat{\varvec{\beta }}\) of (11) becomes the weighted LS solution, which is numerically unstable and statistically too noisy to be physically meaningful for an inverse ill-posed problem. However, a large parameter \(\kappa \) tends to reduce the importance of the measurements \({\mathbf {y}}\) and result in too smoothed a solution towards any pre-determined values. In particular, if \(\kappa \) tends to infinity, the solution \(\hat{\varvec{\beta }}\) becomes null and irrelevant to \({\mathbf {y}}\).

The regularized solution (11) has been interpreted along two completely different lines of ideologies, namely Bayesian and frequentist (see, e.g., Xu 1992; Xu et al. 2006a). If (11) is interpreted as a Bayesian estimator, this is equivalent to assuming some prior information on the unknown parameters \(\varvec{\beta }\). In other words, the prior mean and variance–covariance matrix of \(\varvec{\beta }\) are assumed to be equal to zero and \({\mathbf {S}}^{-1}_r\sigma ^2/\kappa \). In general, no one expects that the true values of \(\varvec{\beta }\) can be zero; otherwise, there is no reason to collect measurements to reconstruct \(\varvec{\beta }\), as argued by Xu (1992), Xu and Rummel (1994) and Xu et al. (2006a). Thus, in this paper, we will make no prior assumption on \(\varvec{\beta }\) and follow the frequentist point of view to choose the optimal regularization parameter \(\kappa \). As a result, the bias and variance–covariance matrix of \(\hat{\varvec{\beta }}\) in (11) are given as follows:

$$\begin{aligned} \text {bias}(\hat{\varvec{\beta }}) = E(\hat{\varvec{\beta }})- \varvec{\beta } = - \kappa {\mathbf {N}}_{\kappa }^{-1}{\mathbf {S}}_r \varvec{\beta }, \end{aligned}$$
(12)

and

$$\begin{aligned} D(\hat{\varvec{\beta }}) = {\mathbf {N}}_{\kappa }^{-1}{\mathbf {A}}^\mathrm{{T}}{\mathbf {W}}{\mathbf {A}}{\mathbf {N}}_{\kappa }^{-1}\sigma ^2 \end{aligned}$$
(13)

(see, e.g., Hoerl and Kennard 1970; Xu 1992; Xu et al. 2006a), where \(\text {bias}(\hat{\varvec{\beta }})\) and \(D(\hat{\varvec{\beta }})\) stand for the bias and variance–covariance matrix of \(\hat{\varvec{\beta }}\), respectively. Thus, the mean squared error matrix of \(\hat{\varvec{\beta }}\) in (11) is given by

$$\begin{aligned} \text {MSE}(\hat{\varvec{\beta }})= & {} D(\hat{\varvec{\beta }}) + \text {bias}(\hat{\varvec{\beta }})[\text {bias}(\hat{\varvec{\beta }})]^\mathrm{{T}} \nonumber \\= & {} {\mathbf {N}}_{\kappa }^{-1} [ {\mathbf {A}}^\mathrm{{T}}{\mathbf {W}}{\mathbf {A}} \sigma ^2 + \kappa ^2{\mathbf {S}}_r\varvec{\beta }\varvec{\beta }^\mathrm{{T}} {\mathbf {S}}_r]{\mathbf {N}}_{\kappa }^{-1}, \end{aligned}$$
(14)

where \(\text {MSE}(\hat{\varvec{\beta }})\) is the mean squared error matrix of \(\hat{\varvec{\beta }}\).

The bias \(\text {bias}(\hat{\varvec{\beta }})\) of (12) represents the systematic derivation of the regularized solution (11) from the true vector \(\varvec{\beta }\). The larger \(\text {bias}(\hat{\varvec{\beta }})\), the worse \(\hat{\varvec{\beta }}\). On the other hand, \(D(\hat{\varvec{\beta }})\) of (13) stands for the random dispersion of the regularized solution \(\hat{\varvec{\beta }}\). If \(\kappa =0\), \(\text {bias}(\hat{\varvec{\beta }})={\mathbf {0}}\); but \(D(\hat{\varvec{\beta }})\) is too large for \(\hat{\varvec{\beta }}\) to be physically useful. Thus, from the frequentist point of view, the optimal regularization parameter \(\kappa \) should be chosen to simultaneously minimize both \(\text {bias}(\hat{\varvec{\beta }})\) and \(D(\hat{\varvec{\beta }})\) in a certain sense of optimality. More precisely, we find the optimal \(\kappa \) to minimize the trace of \(\text {MSE}(\hat{\varvec{\beta }})\), namely

$$\begin{aligned} \text {min:} \quad f(\kappa )= & {} \text {tr}\{ \text {MSE}(\hat{\varvec{\beta }}) \} \nonumber \\= & {} \sigma ^2 \text {tr}\{ {\mathbf {A}}^\mathrm{{T}}{\mathbf {W}}{\mathbf {A}}{\mathbf {N}}_{\kappa }^{-2} \} + \kappa ^2\varvec{\beta }^\mathrm{{T}}{\mathbf {S}}_r{\mathbf {N}}_{\kappa }^{-2}{\mathbf {S}}_r\varvec{\beta }, \end{aligned}$$
(15)

where \(\text {tr}(\cdot )\) stands for the trace of a square matrix.

Given \(\sigma ^2\) and \(\varvec{\beta }\), we could then use optimization methods to solve for the optimal solution to (15). Alternatively, we can compute the derivative of \(f(\kappa )\) with respect to \(\kappa \), let it be equal to zero and obtain the nonlinear normal equation as follows:

$$\begin{aligned} \frac{\mathrm{{d}}f(\kappa )}{\hbox {d}\kappa }= & {} - \sigma ^2 \text {tr}\{ {\mathbf {A}}^\mathrm{{T}}{\mathbf {W}}{\mathbf {A}}{\mathbf {N}}_{\kappa }^{-1} [ {\mathbf {N}}_{\kappa }^{-1}{\mathbf {S}}_r+{\mathbf {S}}_r {\mathbf {N}}_{\kappa }^{-1}]{\mathbf {N}}_{\kappa }^{-1}\} \nonumber \\&+ 2 \kappa \varvec{\beta }^\mathrm{{T}}{\mathbf {S}}_r{\mathbf {N}}_{\kappa }^{-2}{\mathbf {S}}_r\varvec{\beta } \nonumber \\&- \kappa ^2\varvec{\beta }^\mathrm{{T}}{\mathbf {S}}_r{\mathbf {N}}_{\kappa }^{-1} [ {\mathbf {N}}_{\kappa }^{-1}{\mathbf {S}}_r+{\mathbf {S}}_r {\mathbf {N}}_{\kappa }^{-1}]{\mathbf {N}}_{\kappa }^{-1} {\mathbf {S}}_r\varvec{\beta } \nonumber \\= & {} 0. \end{aligned}$$
(16)

Since both \(\sigma ^2\) and \(\varvec{\beta }\) are unknown, we cannot directly solve the minimization problem (15) or the nonlinear equation (16). If the linear observational equations (7) are theoretically over-determined, we can replace the unknown \(\sigma ^2\) with its almost unbiased estimators proposed by Xu et al. (2006b) and Xu (2009). However, we can never have more observations to reconstruct a continuous function from a finite number of discrete measurements. Thus, in this paper, we prefer to use empirical stochastic parameters which may be reliably obtained for GNSS measurements. On the other hand, the minimization problem (15) also requires the true values of \(\varvec{\beta }\), which are certainly not available in practice. Instead, we may start with the weighted LS estimate of \(\varvec{\beta }\) and iteratively solve for the optimal regularization parameter \(\kappa \). If the weighted LS estimate of \(\varvec{\beta }\) is too poor or inaccurate to use, we can use a number of small regularization parameters, compute the corresponding regularized solutions and use their mean to replace \(\varvec{\beta }\).

3 Applications to the 2013 Lushan Mw6.6 earthquake

An earthquake Mw6.6 hit Lushan county, Sichuan Province, People’s Republic of China, around 8:02:47 (local time) in the early morning of April 20, 2013, which occurred on the southern segment of the Longmenshan fault system (see, e.g., Du et al. 2013; Han et al. 2014). The earthquake was well recorded by the dense strong motion network and two GNSS networks, namely the Crustal Movement Observation Network of China (CMONOC) and the Sichuan Continuous Operational Reference System (SCCORS). Both GNSS networks are equipped with Trimble NetR8 receivers and collect GNSS data at three different sampling rates, namely 30 s, 1 Hz and 50 Hz.

The GNSS measurements of CMONOC and SCCORS on the 2013 Lushan Mw6.6 earthquake have been well studied and used to determine the coseismic displacements and invert for the slip distribution. Huang et al. (2013) used the software system GAMIT to estimate daily loose solutions of GNSS stations and then determined the coseismic displacements from the averages of the 7-day positions (or daily solutions) of the GNSS stations before and after the earthquake. They found that the three stations close to the epicenter of the earthquake, namely QLAI, SCTQ and YAAN, were of the largest coseismic displacements of 10.5 mm, 20.9 mm and 9.2 mm, respectively. The coseismic displacements were very small at all the other GNSS stations, as may be seen from Fig. 2 of Huang et al. (2013). Liu et al. (2013) processed the 1 Hz GPS data and used the first and second difference methods to compute PGV and PGA. As in the case of Huang et al. (2013), Liu et al. (2013) found that station SCTQ was subject to the largest PGV and PGA values of 3.1 cm/s and 5.3 cm/\(\text {s}^2\) in the horizontal components, respectively. Li et al. (2014) also used the software system GAMIT to process the 50 Hz GNSS data, then reduced the position series of 50 Hz to 10 Hz (private communications with Prof. Dingfa Huang on 6 August 2019) for the computation of velocities and accelerations and further the PGV and PGA values for the GNSS stations and estimated the epicenter, the origin time and magnitude of the earthquake.

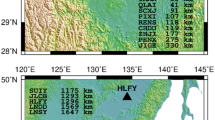
Since the difference methods will result in significant noise amplification, one has to confine oneself to a low sampling rate (e.g., 1 Hz GNSS data) in order to compute GNSS-based PGV and PGA, even though high-rate GNSS data are available at a sampling rate of 50 Hz in the case of the 2013 Lushan Mw6.6 earthquake. Avoiding the use of higher-rate GNSS data up to 50 Hz will substantially reduce the resolution of velocity and acceleration waveforms, PGV and PGA on one hand and will increase their aliasing effects on the other hand. In what follows, we will apply the regularized numerical differentiation method developed in this paper to reconstruct velocity and acceleration waveforms from very high-rate GNSS and thus to further compute the PGV and PGA values for the Lushan earthquake. Based on the work by Huang et al. (2013), Liu et al. (2013) and Li et al. (2014), we will focus on the three GNSS stations, namely QLAI, SCTQ and YAAN, which are of the largest coseismic deformations, the highest sampling rate of 50 Hz and the closest to the epicenter of the Lushan earthquake by about 33 km, 32 km and 36 km away, respectively, as computed with the relocation results of Han et al. (2014). The three GNSS stations (QLAI, SCTQ and YAAN) are shown in Fig. 1, together with the epicenter of the 2013 Lushan Mw6.6 earthquake, the locations of some strong motion stations and some major fault systems in this area. The fault systems are based on Deng et al. (2003).

Fig. 1
figure 1

GNSS stations QLAI, SCTQ and YAAN in the red squares and the hypocenter of the 2013 Lushan Mw6.6 earthquake in the red star. The strong motion stations are also plotted in the solid triangles for the comparative purpose

Full size image

3.1 PPP position waveforms from 50 Hz GPS data

Although a reference station, which is sufficiently far away from the epicenter and usually supposed to not move due to an earthquake, has been used to process the GNSS data for the Lushan earthquake (see, e.g., Huang et al. 2013; Liu et al. 2013; Li et al. 2014), a distant reference station could introduce a larger uncertainty of un-modeled or un-corrected (residual) systematic errors, and as a result, would degrade the GNSS positioning accuracy. In this work, we prefer to use the GNSS PPP mode to process the GPS data of stations QLAI, SCTQ and YAAN. The reasons are twofold: (i) GNSS PPP does not require any reference station. Relative positioning (with a reference station) strongly depends on a sufficiently short baseline to warrant precise relative positioning, since all systematic errors can be readily cancelled. However, if a reference station is too close to the epicenter of an earthquake, it will move by itself due to the earthquake, which will, in turn, distort the computed displacement field. Thus, GNSS PPP would be more suitable for earthquake applications; and (ii) GNSS PPP has been shown to enable to obtain waveforms for all the three components at the mm level of precision within a short period of time of up to a few minutes (Xu et al. 2013, 2019b; Shu et al. 2017), since most GNSS errors behave systematically, remain almost unchanged within such a short time and can be cancelled out by time difference. This high precision is advantageous and most suitable to derive precise PPP displacement and/or position waveforms.

More precisely, we use the PPP mode of the software system PANDA developed by Wuhan University GNSS Research Center to compute the GNSS position waveforms of QLAI, SCTQ and YAAN. The PPP processing procedures of PANDA have been well described in Liu and Ge (2003) and Xu et al. (2013, 2019a, 2019b) and will not be repeated here. The PPP position waveforms of QLAI, SCTQ and YAAN for the Lushan Mw6.6 earthquake, as computed with the PPP-determined coordinates minus the approximate coordinates of the stations, are shown in Fig. 2 under the local coordinate system of East, North and Up (ENU). By averaging 1 min of PPP positions before and after the earthquake, we can obtain the coseismic displacements for QLAI, SCTQ and YAAN, respectively, which are listed in Table 1. Among the three GNSS stations under investigation, the maximum ENU coseismic displacements of \(-\) 11.5 mm, \(-\) 17.6 mm and 23.4 mm took place at SCTQ, moving along the southwestern direction and upwards. The patterns of the coseismic displacements at these GNSS stations can well be explained by the focal mechanism of the earthquake, which was found to be of a pure thrust type (see, e.g., Du et al. 2013). These coseismic displacements are basically consistent with those reported by Huang et al. (2013) for these three stations and Liu et al. (2013) in the case of SCTQ. The horizontal EN peaks at the three stations are 58.1 mm and 56.8 mm for QLAI, 28.2 mm and 58.4 mm for SCTQ, and 49.8 mm and 49.0 mm for YAAN, respectively, which are consistent with those in Li et al. (2014). The maximum ENU amplitudes between the highest and lowest peaks are 94.2 mm, 82.3 mm and 68.9 mm for QLAI, 45.0 mm, 68.0 mm and 92.1 mm for SCTQ, and 65.1 mm, 74.7 mm and 66.6 mm for YAAN, respectively. Although SCTQ is subject to the largest permanent coseismic displacements, as can be seen from Table 1, the most violent movement due to the earthquake occurred at station QLAI in terms of the maximum ENU amplitudes of motion. We may like to note that the vertical kinematic GNSS waveforms were not included in Huang et al. (2013) nor in Li et al. (2014) due to the reported poor accuracy in the vertical component.

Fig. 2
figure 2

The 50 Hz PPP position waveforms of QLAI, SCTQ and YAAN associated with the 2013 Lushan Mw6.6 earthquake, which refer to the upper-left panel, the upper-right panel and the lower-left panel, each with three components in the East, North and Up directions, respectively. The thick black vertical lines mark the origin time of the earthquake. The parts of the position waveforms inside the dotted lines will be used to reconstruct the velocity and acceleration waveforms, PGV and PGA for the earthquake

Full size image
Table 1 The coseismic displacements, PGV and PGA of QLAI, SCTQ and YAAN stations
Full size table

To give the reader a comparative idea of waveforms between PPP and strong motion recordings, we select the YAD strong motion station shown in Fig. 1, which is about 266 m away from the YAAN GNSS station, and show its three-component accelerograms in Fig. 3. One could distinguish the slightly different arrivals of P and S waves of the earthquake in the accelerograms of Fig. 3. However, we could only see the S waves at this station but hardly identify the P wave arrivals in the YAAN position waveforms in Fig. 2. This is mainly because the PPP position waveforms are only of mm-level of precision and could not be sensitive to small P wave displacements. Even worse, P wave may generally show up more in the vertical component, but GNSS is well known to be of the worst precision exactly in this component.

Fig. 3
figure 3

The accelerograms of the YAD strong motion station. The origin time of the earthquake and the trigger time at the YAD strong motion station are shown with red and black arrows, respectively

Full size image

3.2 Reconstructing the velocity waveforms and PGV from 50 Hz GPS data

Although the single difference method is popular to compute velocity from precise GNSS positioning, the uncertainty of velocity has been well known to increase proportionally with the increase in sampling rates. As a result, most practical applications in geodesy and navigation have been limited to a low sampling rate. A high sampling rate of up to 10 Hz was recently tested in earth sciences (Li et al. 2014) by down-sampling 50 Hz displacement waveforms to 10 Hz. A recent work by Hohensinn and Geiger (2018) proposed first down-sampling any GNSS measurements with a higher sampling rate to 2 Hz before they applied high-rate GNSS velocity to hypocenter location for earthquake early warning, even though the sampling rate for most GNSS measurements was up to 20 Hz in their work. The experiments in sports with a sampling rate of up to 18 Hz were reported to end up with a very poor accuracy and physically useless results of velocity and acceleration, where a GNSS unit was attached to a sled and towed by a football player (Buchheit et al. 2014) or was worn by a sprinter (Hoppe et al. 2018).

In order to reconstruct velocity and PGV with a very high sampling rate, we apply the regularized numerical differentiation method developed in Sect. 2 to the 2013 Lushan Mw6.6 earthquake. To practically implement the MSE-based regularization method, we need to address \(\sigma ^2\) and \(\varvec{\beta }\) in the minimization problem (15). Theoretically, we can never have enough (discrete) measurements to reconstruct a continuous function such as the velocity and acceleration functions in the Volterra’s integral equations (2) and (4) of the first kind. Practically, although \(\sigma ^2\) can be estimated with static PPP data, kinematic PPP has been well known to be much noisier than static PPP. Since the static horizontal PPP precisions with the GNSS results of QLAI, SCTQ and YAAN from the Lushan earthquake are roughly consistent with the static results of Xu et al. (2013) and Shu et al. (2017), we decide to use the mean standard deviation of 3.45 mm in the horizontal components from the dynamic experiments reported in Xu et al. (2013). In geodetic practice, it is also well known that the accuracy in the vertical component is generally two or a few more times larger than that in the horizontal components. Because the PPP accuracy of QLAI, SCTQ and YAAN in the vertical component is about two times worse than 3.45 mm, we can reasonably use this factor for the error estimate in the vertical component.

In the case of \(\varvec{\beta }\), one usually starts with the LS estimate and iteratively solves for the optimal regularized solution. Unfortunately, this strategy does not work, since the iteration process ends up divergently. Thus, as an alternative scheme, we use a number of regularization parameters between 0.005 and 0.4, which are not only sufficiently large to avoid highly unstable solutions but also sufficiently small to control over-smoothed solutions, compute the mean of the regularized solutions and then substitute it for \(\varvec{\beta }\) in the MSE objective function (15) such that the optimal regularization parameter \(\kappa \) can be found. We may note that finding an approximate vector of \(\varvec{\beta }\) is mainly dependent on the condition number of the ill-posed problem (7) and the distribution of its eigenvalues. The magnitude of an earthquake is irrelevant, since it has no role to play in the constraint of the \({\mathbf {A}}\) matrix in (7). Because our interest is in the reconstruction of velocity, acceleration waveforms, PGV and PGA for the 2013 Lushan Mw6.6 earthquake, we will need to only focus on the related parts of the PPP position waveforms marked inside the dotted lines in Fig. 2.

Since the sampling rates of GPS PPP position waveforms at the three stations QLAI, SCTQ and YAAN are all 50 Hz, we will use these 50 Hz PPP positioning time series to reconstruct the velocity waveforms of 25 Hz and the corresponding PGV values. The optimal regularized velocity waveforms of 25 Hz from the 50 Hz PPP position measurements at QLAI, SCTQ and YAAN are shown in the right panel of Fig. 5. For the comparative purpose, we apply the LS method to the discretized version of the observational or integral equation (2) and compute the LS velocity waveforms of 25 Hz, which are shown in Fig. 4. The median standard deviations of the LS velocity waveforms and the median MSE roots of the regularized velocity waveforms are listed in Table 2. In addition, we also directly use the difference method to compute the difference velocity waveforms of 25 Hz for QLAI, SCTQ and YAAN, which are plotted in the left panel of Fig. 5, respectively. Bearing in mind that 1 Hz GNSS data was a standard product to compute velocity, we have also computed the 1 Hz velocity waveforms for these three stations and shown them in Fig. 6.

Fig. 4
figure 4

The 25 Hz LS velocity waveforms for QLAI, SCTQ and YAAN derived from the 50 Hz PPP position waveforms. QLAI—the upper-left panel; SCTQ—the upper-right panel; YAAN—the lower-left panel

Full size image
Fig. 5
figure 5

The difference and optimal regularized 25 Hz velocity waveforms for QLAI, SCTQ and YAAN derived from the 50 Hz PPP position waveforms, which are shown in the left and right panels for QLAI, SCTQ and YAAN, respectively

Full size image
Fig. 6
figure 6

The 1 Hz velocity waveforms computed with the 1 Hz PPP position waveforms for QLAI, SCTQ and YAAN derived, down-sampled from the 50 Hz PPP position waveforms. QLAI—the upper-left panel; SCTQ—the upper-right panel; YAAN—the lower-left panel

Full size image

It is obvious from Fig. 4 that the LS velocity waveforms for QLAI, SCTQ and YAAN are too noisy to be physically useful. Although we can clearly identify the earthquake signals in the PPP position waveforms in Fig. 2, nothing can be said about the earthquake in the LS-reconstructed velocity waveforms at any of the three GNSS stations, since the earthquake signals have become completely obscured or immersed into the large uncertainty of the LS solutions (compare the second column of Table 2). Actually, the median formal standard deviation of the LS velocity waveforms is about 88.4 mm/s in the horizontal components and ranges from 104.8 to 152.6 mm/s in the vertical component for QLAI, SCTQ and YAAN.

In the case of the 25 Hz velocity waveforms with the difference method (compare the left panel of Fig. 5), we generally cannot identify any clear earthquake signals either at any of the three GNSS stations, as in the case of the LS velocity waveforms. Actually, if we compare the corresponding velocity waveforms for each component of stations QLAI, SCTQ and YAAN in Figs. 4 and 5, we can see that they are more or less similar to each other. The reason is that the difference method may be thought of as a simplified version of the LS method. The results of velocity waveforms have indicated that the difference method cannot reconstruct a physically meaningful velocity waveform from a very high sampling rate of GNSS measurements either. Thus, no meaningful PGV can be derived either with the difference method in this case. This may well explain why Li et al. (2014) had to first reduce the 50 Hz GNSS position waveforms to 10 Hz before using the difference method to compute the velocity waveforms.

The optimal regularized velocity waveforms in the right panel of Fig. 5 have successfully shown the earthquake signals, which are very well in agreement with the motion patterns of the PPP position waveforms in Fig. 2. More precisely, we can clearly identify the major velocity signals in the time interval [3790, 3810] for QLAI, SCTQ and YAAN from the plots on the right side of Fig. 5, which correspond very well to almost the same time intervals in the PPP position waveforms in Fig. 2. The reconstructed velocities seem to be not significant in the first few seconds, which might indicate that the displacements at these stations only increase slowly at the beginning. The reconstructed PGV values from the 50 Hz PPP solutions for QLAI, SCTQ and YAAN are listed in Table 1. The median MSE roots of the reconstructed velocity waveforms are listed in Table 2, with the maximum values equal to 3.4 mm/s, 3.6 mm/s and 3.5 mm/s for QLAI, SCTQ and YAAN, respectively. When comparing the optimal regularized velocity waveforms in Fig. 5 with the 1 Hz difference velocity waveforms in Fig. 6, we can see that the latter is of rather poor resolution and hardly provides useful information on the earthquake, though both waveforms seem to be very roughly consistent in showing some motion features. But meaningful details in the optimal regularized velocity waveforms are all missing in the 1 Hz velocity waveforms. In addition, the 1 Hz velocity waveforms clearly result in much smaller PGV values, sometimes, by about two times in some components at all these three GNSS stations.

When compared with the PGV values reported by Li et al. (2014), our maximum PGV of 96.0 mm/s consistently occurs in the East component of QLAI but is larger than that of Li et al. (2014) by 23.6 mm/s. Our maximum PGV values at SCTQ are larger than those reported in Li et al. (2014) by about 10 mm/s. We should note that with the increase in sampling rate to 25 Hz, the difference method can result in a maximum horizontal PGV of 325.8 mm/s at QLAI, 334.8 mm/s at SCTQ and 380.4 mm/s at YAAN, and a maximum vertical PGV of 339.2 mm/s at QLAI, 395.1 mm/s at SCTQ and 416.4 mm/s at YAAN, respectively. These results further explain that the errors of the difference method will significantly increase with the increase in sampling rate and the velocity results will become physically unreliable. If we compare the difference-based PGV values with the PPP position waveforms in Fig. 2, we may conclude that these PGV values are geophysically not reasonable. We like to note that we have successfully used the regularization method to reconstruct the 25 Hz velocity waveforms and PGV in the vertical component; but Li et al. (2014) reported a very poor accuracy of about 4–5 cm for the vertical displacement waveforms and, as a result, gave up making any attempt to recover vertical velocity waveforms and PGV. Since the resolution of our regularized velocity waveforms is much higher than that of Li et al. (2014), our results will be able to reflect quick changes in velocity more correctly. Our PGV values are larger than the limited results of SCTQ computed only at 1 Hz sampling rate by Liu et al. (2013) by about 30 mm/s in the North component. However, when compared our regularized PGV values with those in Mooney and Wang (2014) from seismometers, our PGV values are much smaller. More precisely, Mooney and Wang (2014) reported the PGV values of 14.3 cm/s and 13.6 cm/s in the east-west component at the two strong motion stations close to QLAI and YAAN, respectively, while our corresponding precise GNSS-reconstructed PGV values are only 9.60 cm/s and 4.66 cm/s for QLAI and YAAN. Since our velocity waveforms fit the PPP position waveforms well, the inconsistency between seismometers and GNSS should be further investigated in the future.

Table 2 The median formal standard deviations of the 25 Hz LS-reconstructed velocity waveforms and the median MSE roots of the regularized velocity waveforms at QLAI, SCTQ and YAAN stations
Full size table
Table 3 The median standard deviations of the 25 Hz LS-reconstructed acceleration waveforms and the median MSE roots of the regularized acceleration waveforms at QLAI, SCTQ and YAAN stations
Full size table
Fig. 7
figure 7

The 25 Hz LS acceleration waveforms for QLAI, SCTQ and YAAN derived from the 50 Hz PPP position waveforms. QLAI—the upper-left panel; SCTQ—the upper-right panel; YAAN—the lower-left panel

Full size image
Fig. 8
figure 8

The difference and optimal regularized 25 Hz acceleration waveforms for QLAI, SCTQ and YAAN derived from the 50 Hz PPP position waveforms, which are shown in the left and right panels for QLAI, SCTQ and YAAN, respectively

Full size image
Fig. 9
figure 9

The 1 Hz acceleration waveforms computed with the 1 Hz PPP position waveforms for QLAI, SCTQ and YAAN derived, down-sampled from the 50 Hz PPP position waveforms. QLAI—the upper-left panel; SCTQ—the upper-right panel; YAAN—the lower-left panel

Full size image

3.3 Reconstructing the acceleration waveforms and PGA from 50 Hz GPS data

In a similar manner to velocity reconstruction in Sect. 3.2, we use the observational integral equation (4), apply the regularized numerical differentiation method to the 50 Hz PPP position waveforms of QLAI, SCTQ and YAAN and reconstruct the 25 Hz acceleration waveforms and PGA at these stations. Since there are no motions at QLAI, SCTQ and YAAN right before the Lushan Mw6.6 earthquake, we can assume zero initial velocity at the time epoch \(t_0\), namely \(v(t_0)=0\) for earthquake applications.

For the comparative purpose, we also apply the LS method to the discretized version of (4) and the double-difference method directly to the 50 Hz PPP position waveforms, and compute 25 Hz acceleration waveforms and PGA for QLAI, SCTQ and YAAN, respectively. The LS-estimated 25 Hz acceleration waveforms are shown in Fig. 7, while the double-difference and optimal regularized 25 Hz acceleration waveforms are plotted in the left and right panels of Fig. 8, respectively. We compute the formal standard deviations of the LS-estimated waveforms of acceleration and list their median values in Table 3 for the GNSS stations. It is clear from Table 3 that the LS solutions of acceleration are too noisy to identify any signals of the earthquake, as can be further confirmed in Fig. 7, even though the LS formal standard deviations might look a bit too large due to numerical instability. By comparing the LS-based acceleration waveforms in Fig. 7 with the LS-based velocity waveforms in Fig. 4, we can see that the reconstructed waveforms of acceleration are much noisier than those of velocity.

The 25 Hz acceleration waveforms of QLAI, SCTQ and YAAN are computed by applying the double-difference method to the 50 Hz PPP position waveforms and shown in the left panels of Fig. 8. They are also too noisy to identify any earthquake signals, as in the case of the LS-estimated acceleration waveforms. This is understandable, since the difference method is actually a simplified version of the LS method. The uncertainty in the vertical component is larger than that in the horizontal components, which is consistent with the well-known fact that GNSS better determines the horizontal components of a station than its vertical component. As a result, no physical meaningful PGA values can be recovered from the 50 Hz PPP position waveforms with the double-difference method. More precisely, the maximum difference-based PGA values for QLAI, SCTQ and YAAN are 9018.1 mm/\(\text {s}^2\), 8218.7 mm/\(\text {s}^2\) and 13201.9 mm/\(\text {s}^2\) in the horizontal components, and 9836.2 mm/\(\text {s}^2\), 11688.1 mm/\(\text {s}^2\) and 12659.4 mm/\(\text {s}^2\) in the vertical component, respectively. These PGA values are probably too large to be acceptable physically, when compared to the PPP position waveforms in Fig. 2. The uncertainty of the double-difference acceleration waveforms is also much larger than that of the difference velocity ones, as can be clearly seen by comparing Fig. 5 with the left panels of Fig. 8, because the uncertainty of double-difference numerical differentiation is expected to be larger than that of (first-order) difference differentiation by a factor of the sampling rate of a reconstructed waveform (or more precisely, in this work, 25).

The regularized acceleration waveforms are plotted in the right panels of Fig. 8. They are clearly successful to reveal the earthquake signals at all the three GNSS stations, when compared with the corresponding PPP position waveforms in Fig. 2. We compute the MSE roots for the regularized acceleration waveforms and summarize their maximum median MSE roots in the right column of Table 3, which are equal to 1.6 mm/\(\text {s}^2\), 0.6 mm/\(\text {s}^2\) and 0.8 mm/\(\text {s}^2\) for QLAI, SCTQ and YAAN, respectively. It is interesting to see that the regularized acceleration curves are much smoother than the regularized velocity waveforms (compare Fig. 8 with Fig. 5). The PGA values obtained from the 50 Hz PPP position waveforms are listed in Table 1. QLAI is subject to the largest PGA values in all the three components. Although SCTQ is known to be of the largest permanent coseismic displacements, it is of the least PGA values among these three GNSS stations.

Since a low sampling rate of GNSS data has been often used to compute the acceleration of a moving object (see, e.g., Kleusberg et al. 1990; Jekeli and Garcia 1997; Bruton and Schwarz 2002; Serrano et al. 2004; Gatti 2018), we apply the standard difference method to 1 Hz PPP position data down-sampled from our 50 Hz position waveforms, compute one set of the 1 Hz acceleration waveforms for the three GNSS stations and plot them in Fig. 9. Comparing the 1 Hz acceleration waveforms with those regularized ones in the right panels of Fig. 8, we can see that: (i) the 1 Hz acceleration waveforms are of rough resolution. Physically meaningful accelerations in the regularized solutions are missing in the 1 Hz acceleration waveforms; (ii) although both acceleration waveforms at QLAI seem to be roughly consistent in shape, they are very different at the other two stations SCTQ and YAAN; and (iii) the 1 Hz acceleration waveforms tend to produce a much larger PGA value in all the components at these three stations, with a maximum factor of more than 10 times in the East component of SCTQ.

Comparing the regularized PGA values in Table 1 with those by Li et al. (2014), we can see that our PGA results are a few times smaller for all the three stations. Basically, the PGA results by Li et al. (2014) are consistent with our own 1 Hz results. Our maximum regularized PGA is 24.3 mm/\(\text {s}^2\) in the north component of QLAI, while Li et al. (2014) obtained the value of 105.9 mm/\(\text {s}^2\) in the east component of the same station. One reason is that when a low sampling rate is applied, the motion pattern may have changed between two consecutive time intervals of motion. Let us take the vertical component as an example by assuming that an object is moving upwards during the first interval of time and then downwards during the second interval of time. As a result, we expect a larger value of acceleration, because the difference computation of acceleration is involved with three consecutive samples of position. Theoretically speaking, with the increase in sampling rates, the phenomenon of seemingly sudden change of movement directions between two consecutive intervals of time would become less significant, though the noise will be substantially amplified and should be handled through regularization. Another reason is likely attributed to a higher uncertainty in the double-difference acceleration waveforms of Li et al. (2014), as might also be well inferred from the left panels of Fig. 8. Actually, Li et al. (2014) reported the positioning accuracy of at least 2 cm in the horizontal components in their GNSS positioning results. If this would be true, and bearing in mind that they down-sampled the 50 Hz GNSS position waveforms to 10 Hz to compute the accelerations, then by a simple calculation, their accelerations could be roughly in errors with a standard deviation of 200 cm/\(\text {s}^2\) (or 2000 mm/\(\text {s}^2\)) in the horizontal components. Our regularized acceleration waveforms also allow us to well identify the PGA values in the vertical component for QLAI, SCTQ and YAAN. Nevertheless, since the vertical positioning is quite poor, no PGA in this component was ever attempted by Li et al. (2014). With the 1 Hz GNSS positioning results, Liu et al. (2013) reported the PGA values of 5.3 cm/\(\text {s}^2\) and 4.5 cm/\(\text {s}^2\) in the horizontal and vertical components for SCTQ, respectively, which are a few times larger than our PGA results. Since their sampling rate is 1 Hz, the resolution is much lower with a larger aliasing effect and not able to reflect the changes in acceleration within tens of milliseconds.

Mooney and Wang (2014) reported that the seven strong motion seismometers all recorded the PGA values exceeding 380 cm/\(\text {s}^2\) in the epicenter of the Lushan earthquake, with a maximum PGA value of 1005.35 cm/\(\text {s}^2\) in the east-west component at a strong motion station near Baoxing (see also Wen and Ren 2014). For the purpose of illustratively comparing the strong motion and GPS results, we only choose the YAD strong motion station and show its accelerograms in Fig. 3, because it is close to the YAAN GNSS station by only about 266 m. As can be seen from Fig. 9(a) of Mooney and Wang (2014) and Fig. 3 in this paper, the seismic PGA values in the east-west component at the two strong motion stations near QLAI and YAAN are equal to 270.461 cm/\(\text {s}^2\) and 524.501 cm/\(\text {s}^2\), respectively. Nevertheless, our very high-rate GPS-based PGA values are equal to 2.36 cm/\(\text {s}^2\) and 0.63 cm/\(\text {s}^2\) for the same component at QLAI and YAAN, respectively. The seismometer-based PGA values are obviously much larger than ours by a factor of some hundreds. Since the GPS PPP position waveforms in Fig. 2, with a maximum peak-to-peak displacement magnitude of 9.42 cm, are free of any potential problems such as instrumental drift, saturation, clipping, scaling and uncertainty due to instrumental tilts, rotations and likely other unknown factors inherent in seismometers, the PPP-reconstructed PGA values should probably be more reliable. As in the case of PGV, further investigations are needed to find out causes of the differences in PGV and PGA between seismometers and precise GNSS, since they can be of important implications, in particular, in earthquake engineering, disaster assessment and relief, and beyond.

4 Conclusions

Difference methods have been almost always used to determine velocity and acceleration from GNSS precise positioning, for example, in geodesy and navigation (see, e.g., Kleusberg et al. 1990; Jekeli and Garcia 1997; Bruton et al. 1999; Bruton and Schwarz 2002; Serrano et al. 2004), earthquake engineering and earthquake early warning (see, e.g., Huang et al. 2013; Li et al. 2014; Hohensinn and Geiger 2018) and sports science (see, e.g., Waldron et al. 2011; Buchheit et al. 2014; Beato et al. 2016; Muñoz-López et al. 2017; Hoppe et al. 2018). The difference methods almost always assume a low sampling rate (say 1 Hz) of GNSS measurements, because the random errors of GNSS-based velocity and acceleration are either proportional to the sampling rate in the case of velocity or square-proportional to the sampling rate in the case of acceleration. With the increase in a sampling rate, measurement errors will be significantly amplified such that computed velocity and acceleration could be completely immersed into the noise and of no physical significance, as can be seen in the sports experiments with GNSS (see, e.g., Waldron et al. 2011; Buchheit et al. 2014; Hoppe et al. 2018) and the difference-based waveforms of velocity and acceleration in this paper. As a result, GNSS precise positioning with a sampling rate higher than a few Hz has to be first down-sampled to, say 1 or 2 Hz (see, e.g., Hohensinn and Geiger 2018). However, down-sampling very high-rate GNSS precise positioning measurements will directly result in a lower resolution of velocity and acceleration, a larger aliasing effect and signal distortion. A low sampling rate also implies impossibility to provide more or less instantaneous velocity and acceleration.

We have reformulated the reconstruction of velocity and acceleration waveforms from very high-rate GNSS PPP position measurements into two Volterra’s integral equations of the first kind, which are well known to be typical inverse ill-posed problems. The ill-posed nature of the problems has theoretically implied that difference methods will fail to produce physically meaningful velocity and acceleration waveforms from very high-rate GNSS, because the single or double difference methods are a simplified version of the LS method applied to the corresponding discretized versions of Volterra’s integral equations of the first kind, as shown in this paper. We have proposed to regularize velocity and acceleration solutions by minimizing the MSE of solutions. The MSE-based regularized method has been applied to reconstruct the 25 Hz velocity and acceleration waveforms, the peak ground velocity (PGV) and the peak ground acceleration (PGA) from 50 Hz GPS precise point positioning (PPP) position waveforms for the 2013 Lushan Mw6.6 earthquake. The reconstructed very high-rate velocity and acceleration waveforms have been shown to correspond very well to the very high-rate PPP position waveforms and correctly recover the earthquake signal. Among the three GNSS stations closest to the hypocenter, the maximum PGV and PGA values occurred at QLAI station, with the PGV of 96.0 mm/s in the east component and the PGA of 24.3 mm/\(\text {s}^2\) in the north component, respectively, though the maximum coseismic displacements were detected at SCTQ station.

For the comparative purpose, we have also used the difference methods and the LS method to compute the 25 Hz velocity and acceleration waveforms, which are shown to be too noisy to be useful physically and fail to show any signals of the 2013 Lushan Mw6.6 earthquake. The reconstructed 1 Hz velocity and acceleration waveforms with the difference methods have been shown to be poor in resolution and not able to provide instantaneous physical parameters of velocity and acceleration. The 1 Hz acceleration waveforms at two of the GNSS stations fail to reveal any information on the earthquake either and result in too large PGA values at all the three GNSS stations.

Finally, we should like to note that our very high-rate PPP-reconstructed PGV and PGA values are much smaller than those from strong motion seismometers reported in Mooney and Wang (2014) (also see the YAD strong motion recordings, namely Fig. 3 in this paper), by a factor of some hundreds in the case of PGA. Reasons for such large differences are not clear yet. This should be a very important issue to be investigated in the future because of important implications in earthquake engineering, disaster assessment and beyond.