Abstract
The precise orbit determination (POD) of Global Navigation Satellite System (GNSS) satellites and low Earth orbiters (LEOs) are usually performed independently. It is a potential way to improve the GNSS orbits by integrating LEOs onboard observations into the processing, especially for the developing GNSS, e.g., Galileo with a sparse sensor station network and Beidou with a regional distributed operating network. In recent years, few studies combined the processing of ground- and space-based GNSS observations. The integrated POD of GPS satellites and seven LEOs, including GRACE-A/B, OSTM/Jason-2, Jason-3 and, Swarm-A/B/C, is discussed in this study. GPS code and phase observations obtained by onboard GPS receivers of LEOs and ground-based receivers of the International GNSS Service (IGS) tracking network are used together in one least-squares adjustment. The POD solutions of the integrated processing with different subsets of LEOs and ground stations are analyzed in detail. The derived GPS satellite orbits are validated by comparing with the official IGS products and internal comparison based on the differences of overlapping orbits and satellite positions at the day-boundary epoch. The differences between the GPS satellite orbits derived based on a 26-station network and the official IGS products decrease from 37.5 to 23.9 mm (\(34\%\) improvement) in 1D-mean RMS when adding seven LEOs. Both the number of the space-based observations and the LEO orbit geometry affect the GPS satellite orbits derived in the integrated processing. In this study, the latter one is proved to be more critical. By including three LEOs in three different orbital planes, the GPS satellite orbits improve more than from adding seven well-selected additional stations to the network. Experiments with a ten-station and regional network show an improvement of the GPS satellite orbits from about 25 cm to less than five centimeters in 1D-mean RMS after integrating the seven LEOs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The precise orbit determination (POD) of Global Navigation Satellite System (GNSS) satellites is mainly performed with ground-based observations by a dynamic approach (e.g., Montenbruck and Gill 2000; Hackel et al. 2015; Zhao et al. 2018). The weighted RMS of individual GPS orbit products provided by the International GNSS Service (IGS, Johnston et al. 2018) Analysis Centers with respect to the combined solution is 6.3 mm to 11 mm (Choi 2014). Orbits of low Earth orbiters (LEOs) are usually determined by introducing GPS orbit and clock products to process the onboard GNSS observations. With a reduced dynamic strategy (Wu et al. 1991), the orbits of different LEOs are determined to an accuracy level of one to three centimeters (e.g., Haines et al. 2004; Jäggi et al. 2007; Montenbruck et al. 2018).
There are also some studies on the integrated processing of ground- and space-based observations, mainly focusing on the estimation of Earth parameters, including gravity field parameters (König et al. 2005), the geocenter (Kuang et al. 2015; Männel and Rothacher 2017), and the terrestrial reference frame (König 2018). The integrated POD of GPS satellites and LEOs was also performed by several studies. Zhu et al. (2004) and König et al. (2005) compared two POD approaches for GPS, the Gravity Recovery and Climate Experiment (GRACE), and the Challenging Minisatellite Payload (CHAMP) satellites. In the first approach named ‘one-step’, the orbits of the above-mentioned satellites are estimated simultaneously. In the other approach, the orbits of the GPS satellites and the LEOs are determined sequentially. The authors concluded that the orbits determined by the ‘one-step’ approach are more accurate. Geng et al. (2008) shown that the GPS satellite orbits derived by supplementing a 21-station network with GRACE and CHAMP satellites are more accurate than the solution based on a 43-station network. Otten et al. (2012) combined various GNSS satellites and LEOs at the observation level including GNSS, Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), and Satellite Laser Ranging (SLR). Zoulida et al. (2016) and Zhao et al. (2017) performed an integrated POD for OSTM/Jason-2 and FengYun-3C with GPS and Beidou, respectively. These studies reported the benefits of integrating LEOs into the POD in different aspects. However, only one or two LEO missions that have GNSS data were considered in the above-mentioned studies.
In this study, we considered seven LEOs, including GRACE-A, GRACE-B, OSTM/Jason-2, Jason-3, Swarm-A, Swarm-B, and Swarm-C. For the selection of ground stations, the characteristics of the ground segments of Galileo and Beidou are taken into consideration. The Galileo Sensor Station (GSS) network includes 16 sites (Sakic et al. 2018) and Beidou has a regionally distributed ground segment (Yang 2018). It is a potential way to supplement the limited ground segment by integrating LEOs in joint POD processing. Based on the integrated processing of different subsets of ground stations and LEOs, the impact of integrating LEOs on the GPS satellite orbits is discussed.
In Sect. 2, the integrated processing is introduced briefly. The characteristics of the LEOs and their data selection are presented. The processing days are selected based on the data status of the LEOs. Two main sparse subsets of the available IGS stations are selected based on the motivation of our study. The strategy of our processing and analysis and all the designed scenarios are explained in detail. All the results and analysis are given in Sect. 3. It includes four parts. Firstly, the impact of the number of LEOs and their orbital planes on GPS satellite orbits is discussed. Secondly, internal comparisons of the orbit quality based on the differences of overlapping orbits and satellite positions at day-boundary epochs are performed. Thirdly, the effects of supplementing a sparse and non-homogeneously distributed station network by seven carefully selected additional stations or three LEOs in different orbital planes are compared. Fourthly, we present an additional experiment to show the GPS satellite orbit improvement by adding seven LEOs to a regional ground network. The conclusions are given based on the above-mentioned results and analysis in Sect. 4.
2 Integrated POD of GPS satellites and LEOs
2.1 The method of integrated POD
The method of the integrated POD applied in this study is known as the one-step method (Montenbruck and Gill 2000). The approximate initial epoch status of GPS satellites and LEOs are computed from broadcast ephemerides and by single point positioning, respectively. Based on the equations of motion of GPS satellites and LEOs, the initial orbits of GPS and LEOs are delivered by numerical integration. The state equation reads
where \(x_{i}\) is the state vector of the satellite at epoch \(t_i\), \(x_{0}\) is the initial epoch state vector, f contains the force model parameters, and \(T(t_{i},t_{0})\) and \(S(t_{i},t_{0})\) are transition matrices and sensitivity matrices, respectively. In the one-step estimation, the ground- and space-based observation equations at epoch \(t_{i}\) read
where \(L_{sta}\) and \(L_{leo} \) are ground- and space-based measurements, \(x_{gps}\) and \(x_{leo}\) are the positions of GPS satellites and LEOs at the current epoch, \(x_{sta}\) is the static position of the ground station, c denotes the receiver clock offset, C denotes the GPS satellite clock offset, T is the troposphere delay, I is the ionosphere delay, \(A^{gps}_{sta}\) and \(A^{gps}_{leo}\) are carrier phase ambiguities of stations and LEOs, and \(v^{gps}_{sta}\) and \(v^{gps}_{leo}\) contain unmodeled effects and measurement errors. The estimation is performed by inserting Eq. 1 to linearized Eq. 2. The accurate initial epoch states and force model parameters of GPS satellites and LEOs are estimated in a least-squares adjustment by using ground-based and LEOs onboard observations simultaneously. It has to be mentioned that we formed ionosphere-free linear combinations of the measurements.
Figure 1 presents the flowchart of the whole processing. Before the one-step estimation, all the observations are cleaned based on the TurboEdit algorithm (Blewitt 1990). Several iterations of estimation are performed to improve the solution. After each estimation, the orbits of GPS satellites and LEOs are updated by orbit integration based on the new solution of initial epoch states and force model parameters. Meanwhile, the data are cleaned based on the residuals of observations. After completing the data cleaning, the ambiguities of the ground station observations are fixed to improve the solution. After one more iteration of estimation and orbit updating, the final orbits of GPS satellites and LEOs are determined.
2.2 LEO data and processing period selection
The seven LEOs in this study are part of four different missions. GRACE is a geodetic mission with the overall objective to obtain long-term data for global (high-resolution) models of the mean and the time-variable components of the Earth’s gravity field (Tapley et al. 2004). OSTM/Jason-2 (Lambin et al. 2010) is a follow-on satellite to the joint NASA/CNES oceanography mission Jason-1 (Ménard et al. 2003), and Jason-3 (Vaze et al. 2010) is a follow-on satellite of OSTM/Jason-2. Swarm is a mini-satellite constellation mission to survey the geomagnetic field (Friis-Christensen et al. 2008).
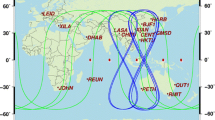
Our processing period starts shortly after the launch of Jason-3, which is operated in the same orbital plane (\(66^{\circ }\) inclination and 1336 km altitude) as OSTM/Jason-2. By mission definition, GRACE satellites are operating in the same orbital plane (GRACE-B leading GRACE-A in \(89^{\circ }\) inclination and 485 km altitude). The three satellites of the Swarm mission are operating in two different orbital configurations. Swarm-A and Swarm-C are flying at a mean altitude of 480 km in orbital planes with \(87.4^{\circ }\) inclination, while the Swarm-B orbit has a higher inclination (\(87.8^{\circ }\)) and a larger mean altitude of 530 km. According to the operation status mentioned above, the seven LEOs are in four different orbital planes as summarized in Table 1. The colored symbols indicate the orbital planes. It has to be mentioned that Swarm-A and Swarm-C satellites remain side by side with separations about 50 to 200 km. However, due to the identical orbital characteristics of Swarm-A/C, we assume that they are in the same orbital plane. The daily ground tracks of GPS satellites and the seven LEOs are plotted with corresponding colors in Fig. 2.
Since the processing includes seven LEOs from four missions, the availability of the LEOs’ data is a major limitation when defining the processing period. After checking the data availability of the seven LEOs, we choose day of year (DOY) 115 to 260 in 2016 as our processing period. In this period, all seven LEOs were in operation. GRACE satellites were at the end of their operating life, but the quaternion data of Jason-3 started to be available from DOY 115 in 2016. To check the LEOs’ data quality, a daily POD of each LEO is processed with a 300-second data sampling rate. The IGS final orbit and clock products are introduced as a priori information. We noticed missing data (onboard GPS observation or attitude) for some days. Some additional days were excluded for maneuvering or low data quality caused by spacecraft problems. Please note that we excluded these days completely also in the following integrated processing. In the integrated processing, we also excluded maneuvering GPS satellites based on the information provided in the GPS NANU Messages. Finally, 112 days are selected for the integrated processing and are indicated by green dots in Fig. 3. The LEOs’ daily orbits are compared with the official orbit products (Case et al. 2002; Dumont et al. 2009, 2016; Olsen 2019). The RMS of the orbit differences is computed over the epochs and three orbital directions in a daily solution. The average of the daily RMS values over the 112 days are presented in Table 2. We abbreviate the LEOs as G-A/B (GRACE-A/B), J-2/3 (OSTM/Jason-2 and Jason3), and S-A/B/C (Swarm-A/B/C). The larger RMS of Jason-3 compared to that of OSTM/Jason-2 is related to orbit modeling issues, as we applied the model of OSTM/Jason-2 to Jason-3, since some detailed information of Jason-3, for instance, the receiver antenna phase center location, are not yet available. Compared with previous studies and considering the 300-second data sampling rate, a comparable accuracy level of the LEO orbits is achieved.
2.3 Ground networks selection
There are 319 IGS stations available during the selected 112 processing days. The distribution of the 319 stations is presented in Fig. 4. The operation of all GNSS is mainly based on their own ground segments and tracking stations. For example, as mentioned in Sect. 1, there are only 16 sites with GSS operating for Galileo. Considering this situation, we selected a sparse and homogeneously distributed subset from the 319 available IGS stations to study the sparse-network-based POD. This network contains 33 stations which are plotted as blue triangles in Fig. 5. The color of the bins in Figs. 5 and 6 presents the number of stations in sight of a potential GPS satellite position with an altitude of 20, 200 km and an inclination of \(57^{\circ }\) (i.e., Depth of Coverage, DoC). In general, more than five stations are visible, and this is also what we expected based on the selection criteria.
A subset of the available IGS stations including 33 homogeneously and sparsely distributed stations (blue triangles). The number of stations in sight of a potential GPS satellite position (Depth of Coverage) is presented as a colored bin (\(2^{\circ }\times 2^{\circ }\) resolution, 20,200 km altitude)
A subset of the available IGS stations including 26 non-homogeneously and sparsely distributed stations (blue triangles). The red triangles are the seven excluded stations. The number of stations in sight of a potential GPS satellite position (Depth of Coverage) is presented as a colored bin (\(2^{\circ }\times 2^{\circ }\) resolution, 20,200 km altitude)
Despite the large and dense IGS tracking network in certain circumstances, depending on constellations and frequencies, one might be confronted with large regions without tracking stations, especially over the oceans and Africa. Seen from Fig. 4, although 319 stations are globally available, there are regions with only a few tracking stations. Moreover, IGS stations could be unavailable for various reasons, and it might happen to Galileo Sensor Stations as well, for instance, caused by the withdrawal of the United Kingdom from the European Union (Gutierrez 2018). To investigate how the LEOs could contribute to the GPS POD, we selected a sparser station network (see Fig. 6) by excluding seven (red triangles) of the 33 stations mentioned above. Consequently, gaps in some regions of the Pacific Ocean, the Indian Ocean, and Africa are visible. There are large areas where a fictitious GPS satellite could be tracked by only two to four (yellow bins) stations. Although two simultaneous observations can support the estimation of satellite clock corrections and orbit parameters in a dynamic solution, the fewer observations still lead to a reduced contribution.
The GPS satellite orbits derived from the two sparse networks mentioned above are our benchmark which will be compared with different integrated solutions. All selected stations are used to define the datum. Since we applied a Helmert transformation when comparing our orbits with the IGS final products, there will be little systematic effect when we analyze the RMS of the orbit differences compared to these two benchmark results.
To investigate the performance of the integrated POD with regional networks, another network including stations mainly located in China will be introduced in Sect. 3.4.
2.4 Processing and analysis strategy
We use the software PANDA (Liu and Ge 2003) to do all the processing. PANDA is capable of GNSS satellite and LEO orbit modeling. Separated and integrated POD of GNSS satellites and LEOs can be performed. For this study, the implementation of OSTM/Jason-2, Jason-3, and Swarm-A/B/C data formats (observation, attitude, and precise orbit) was necessary. Table 3 shows the dynamic models used for the orbit integration of GPS satellites and LEOs. Table 4 introduces the processing configuration and the estimated parameters.
To investigate the impact of the number of integrated LEOs and their orbital planes on the determined GPS satellite orbits, we applied a total of 26 different scenarios for the POD processing. All the scenarios are summarized in Table 5. The first two are the GPS-only POD by applying the two sparse station networks which are described in Sect. 2.3. The other 24 scenarios are the integrated POD of GPS satellites and LEOs, and all of them supplement the sparser network with 26 stations by including different subsets of the seven LEOs. We compared the estimated GPS satellite orbits of all scenarios to the IGS final products to show the orbit quality and the differences between the scenarios. Due to the large number of satellites and scenarios, we computed statistical measures of the orbit comparisons to quantify the result of each scenario. The statistical computation is shown in Fig. 7. For each daily orbit comparison, we computed the RMS of orbit differences in three orbital directions (along-track, cross-track, and radial) and the 1D-mean RMS. The RMS in three orbital directions is computed over epochs and satellites. The 1D-mean RMS is computed over epochs, satellites, and the three orbital directions. Based on the 112-day solutions, we computed the mean and the empirical standard deviation of the time series of the above-mentioned RMS values. The statistical measures mentioned above are highlighted in green in Fig. 7, and the analysis in Sect. 3.1 is mainly based on these measures.
Besides the external orbit comparison, internal comparisons are performed in two different ways. The first one is the comparison of the orbit overlaps. We expand the POD arc length of scenarios 1, 2, and 26 from 24 hours to 30 hours (three hours to both the previous and the next day). Consequently, a pair of 6-hour overlapping orbit arcs derived by real data processing is generated between two adjacent days. The 1D-mean RMS of the orbit differences of the 6-hour overlap is computed. Another comparison is about the satellite position differences at the day-boundary epoch of two adjacent 24-hour orbits at midnight. We extrapolate one more epoch from a 24-hour orbit by orbit integration, then the GPS satellite positions at the extrapolated epoch are compared with the estimated satellite positions in the first epoch of the next 24-hour orbit. The RMS of the satellite position differences is computed over the satellites and the three orbital directions at the day-boundary epochs. The detailed discussion will be given in Sect. 3.2.
Based on a geolocated comparison of epoch-wise satellite orbit differences (yellow box in Fig. 7) between scenarios 1, 2, and 19, we will discuss the different effects of supplementing a sparse station network with additional stations and LEOs in Sect. 3.3. An additional experiment is designed to show the GPS satellite orbit improvement by adding the seven LEOs to a small and mainly regionally distributed station network. The 1D-mean RMS of the GPS satellite orbit differences compared to IGS final products will be used for the analysis in Sect. 3.4.
Although the focus of this study is on improving the GPS satellite orbits derived from limited ground networks, we also presented the quality of the GPS satellite orbits derived from a 62-station globally distributed network as a reference for interested readers. The network distribution and the GPS satellite orbit comparison with scenario 26 are given in the Appendix.
3 Results and discussions
3.1 Orbit comparison with IGS final products
Statistical results of the GPS satellite orbit differences compared to the IGS final products of scenarios 1, 2, 7, 14, 19, and 26. The RMS of orbit differences in the along-track, the cross-track, and the radial directions are computed over epochs and satellites in each day. The 1D-mean RMS is computed over epochs, satellites, and the three orbital directions
Based on the statistical results shown in Table 5, we will discuss the impact of the number of integrated LEOs and their orbital planes on the GPS satellite orbits. Except for the first two ground-based only solutions, different subsets of the seven LEOs are integrated with the 26-station network. Besides the mean and the standard deviation values of the orbit RMS time series listed in Table 5, the time series of scenarios 1, 2, 7, 14, 19, and 26 are shown in Fig. 8. Correspondingly, the time series of the 1D-mean orbit improvements of scenarios 2, 7, 14, 19, and 26 compared to scenario 1 is shown in Fig. 9.
Generally, we observe improved GPS satellite orbits and reduced variations of the time series when increasing the number of ground stations or the integrated LEOs. The GPS satellite orbit accuracy improves most when all the seven LEOs are integrated into the POD. In all scenarios, the orbit accuracy of the three directions is ranked as along-track < cross-track < radial, while the orbit improvements in the three directions are ranked in the reverse order (along-track > cross-track > radial). With only three LEOs integrated, the determined GPS satellite orbits of scenario 19 (\(28\%\) improvement) are slightly better than those of scenario 2 (\(27\%\) improvement) which includes seven well-selected additional ground stations, with a stronger improvement mainly in the along-track direction. There are two peaks in all the plots. One is on DOY 196, and the other one is on DOY 209 and 210. These three days are presented as orange dots in Fig. 3. After checking the residuals, we realized that the large RMS is caused by large errors in code measurements of a ground station (GODN). Since our data editing strategy is based on the residuals of the phase measurements, the station GODN with large residuals in its code measurements was not excluded. The GPS orbit improvements for these three days are more significant (about \(50\%\) to \(82\%\) in different scenarios) than for the other days (about \(10\%\) to \(35\%\)), and with only one LEO included, the improvement is close to the scenario including seven additional stations.
With only one LEO integrated (scenarios 3 to 9), the solutions are similar, for example, the 1D-mean RMS values vary slightly from 30.6 mm to 31.7 mm. Thus, compared to the 26-station only solution, the orbit improvements vary from \(14\%\) to \(17\%\). However, the standard deviations of the RMS of these one-LEO scenarios have larger differences (up to 4 mm in 1D-mean). Seen from Fig. 10, there is no systematic difference between these one-LEO scenarios. The impact of different LEOs on the derived GPS satellite orbits is not visible.
Comparing the values given in Table 5 by considering the different LEO subsets, we find some phenomenons. In scenarios 10 to 15, two LEOs are included in the estimation. If the additional LEO is in the same orbital plane as the first one, the GPS orbit accuracy improves only by about 1 mm compared to the one-LEO scenarios (see scenarios 3 and 4 versus 10; 5 and 6 versus 11; 7 and 8 versus 12). Thus, the GPS orbit improvements compared to scenario 1 remain below \(20\%\) (\(16\%\) to \(19\%\)). However, if the LEOs are flying in two different orbital planes, the orbit improvements compared to scenario 1 increase up to \(24\%\), and the 1D-mean RMS values of the GPS orbits decrease to around 28 mm. By increasing the number of the integrated LEOs, the impact of the space-based observations and the LEO orbital planes on the derived GPS satellite orbits is getting more obvious. Figure 11 shows the orbit improvements sorted with respect to the numbers of LEOs (upper) and the numbers of orbital planes (lower). The number of integrated LEOs is marked with yellow dots, and the number of different orbital planes is represented by colored bars. Seen from the upper plot, GPS satellite orbits improve generally by integrating more LEOs. However, the improvement does not correspond strictly to the increasing number of LEOs. For example, scenario 20 (with four LEOs in two orbital planes) includes one more LEO than scenario 19 (with three LEOs in three orbital planes), but the GPS orbit improvement of it is smaller (\(25\%\) against \(31\%\)). This phenomenon happens also to the comparison between scenario 22 (with four LEOs in four orbital planes) and scenario 23 (with four LEOs in three orbital planes). When we sort the results by the number of LEO orbital planes, a clear trend is visible. One can see the increasing GPS orbit improvement related to the increasing number of LEO orbital planes from the lower plot of Fig. 11. In summary, the LEO orbital geometry is more critical for the improvement of the GPS satellite orbits than the number of space-based observations.
The positive effect of different LEO orbit geometries to the geocenter estimation is also given by some other studies, for example, the simulation study of the LEOs+GPS combined processing for geocenter estimation by Kuang et al. (2015) and the real data study on the geocenter variations derived from combined processing of the ground- and space-based GPS observations by Männel and Rothacher (2017).
3.2 Internal comparison of the orbits
In this section, we will discuss the overlaps and the day-boundary epochs of the GPS satellite orbits derived from scenarios 1, 2, and 26. Due to the excluded days described in Sect. 2.1 and the overlapping processing strategy introduced in Sect. 2.4, only 65 pairs of overlapping orbits with a 6-hour arc length are available for the comparison. Figure 12 shows the 1D-mean RMS of the differences between the overlapping orbits. Seen from the time series of the three scenarios, the differences of the overlapping orbits are ranked as scenarios \(1>2>26\), and the mean values and the standard deviations of the overlapping orbit differences computed over 65 days are 57/27 mm, 44/19 mm and 38/10 mm.
There are 92 day-boundary epochs between the processed 112 days. The GPS satellite position differences in these day-boundary epochs are plotted in Fig. 13. The mean values and the standard deviations of the results computed over the 92 epochs are 76/25 mm, 55/12 mm, and 50/8 mm in scenarios 1, 2, and 26, respectively. This plot agrees with the comparison of the overlapping orbits in Fig. 12 and the external orbit comparison in Fig. 8. The outliers in Figs. 12 and 13 are caused by the observation errors of station GODN which have been mentioned in the last section.
3.3 Geolocated visualization of orbit comparison
In Sect. 2.3, we explained that the seven additional stations in scenario 2 were selected in the regions with few stations in scenario 1. For the analysis regarding station distributions, the GPS satellite orbit improvements of scenarios 2 and 19 compared to scenario 1 are projected to the surface of the Earth. Based on the epoch-wise orbit difference of each GPS satellite compared to the IGS final products, we computed the improvements of the GPS satellite orbits of scenarios 2 and 19 compared to scenario 1 with a 900-second sampling rate for all GPS satellites in 112 days (approximate 344,064 epoch-wise solutions). The results are presented in Figs. 14 and 15. In these two figures, the potential GPS satellite position area is divided into geographical \(2^{\circ }\times 2^{\circ }\) bins (10,260 in total). We computed the average of all the epoch-wise solutions located in the same bin. These geolocated statistical results are presented as the color of the corresponding bins. Green means the satellite orbits are closer to the IGS final products (improvement), and red means getting further (degradation). Additionally, the ground tracks of GPS satellites are also visible in the plots.
In general, with seven well-selected additional stations (scenario 2) or three LEOs (scenario 19), the GPS satellite orbits improve globally (as indicated by the green bins). The improvements are more clearly presented in Fig. 16. The density distributions of all the epoch-wise solutions from both comparisons are mainly positive. However, there are still regions without significant improvement (as indicated by the yellow bins), and there are only a few bins in red with degradation caused by the additional observations. Comparing Figs. 14 and 15, there are more dark-green bins and fewer red bins in the plot of scenario 19. Correspondingly, the density distribution of the epoch-wise solutions of scenario 19 is located on the right of that of scenario 2 in Fig. 16. Therefore, compared to scenario 1, the GPS satellite orbits derived in scenario 19 improve more than those of scenario 2. Particularly in some regions of the Pacific Ocean, the Indian Ocean, and Africa, seen from the color of the bins, the improvement of scenario 19 is more significant than that of scenario 2. In summary, to a sparsely and non-homogeneously distributed network of ground stations, the derived GPS satellite orbits are improved more by supplementing the network with three LEOs in different orbital planes than with seven well located additional stations, especially for the orbit arcs above the regions lacking stations.
3.4 Results about regional station network
To show the potential benefits of supplementing a regionally distributed ground network by integrating LEOs, we selected an additional subset of the available IGS stations. Figure 17 represents the network with five stations in China and another five stations in other regions. The figure shows that about two-thirds of potential GPS satellite positions (\(2^{\circ }\times 2^{\circ }\) resolution, 20,200 km altitude) can be observed by only two or even fewer stations. The GPS-only and seven-LEO-integrated POD were performed with this network. The 1D-mean RMS of the GPS satellite orbit differences compared to the IGS final products are presented in Fig. 18. Enhanced by seven LEOs, the 1D-mean RMS decreases significantly from about 25 cm to 4 cm. Also, the variations of the time series are reduced significantly from about 4.3 cm to 0.7 cm. The GPS orbit improvement by integrating LEOs to a regional ground network was also demonstrated by Wang et al. (2016) with seven stations within China and three LEOs (GRACE-A/B and FengYun-3C). We also performed a test of just using five stations in China. To get an acceptable result, the number of observations should be increased by expending the arc length to three days and increasing the sampling rate to 30 seconds. The derived GPS satellite orbits differ from the IGS final products by about 20 cm in 1D-mean RMS, but the LEO orbits degrade significantly. Further studies should be done to improve the solution in this situation.
4 Conclusions
It is a potential way to improve the GPS satellite orbits by including LEOs in the POD processing due to the additional observations and geometries offered by the LEOs, especially when there is no additional station available. The benefit of integrating LEOs into the POD is convincing for a sparse or regional network. The GPS satellite orbits are improved more by supplementing a sparse ground network with LEOs than with comparable numbers of additional stations. By integrating three LEOs in three different orbital planes into the POD, the determined GPS satellite orbits (25.1 mm 1D-mean RMS compared to the IGS final products) are more accurate than those of the scenario with seven carefully selected additional ground stations (26.7 mm 1D-mean RMS). The benefits of adding LEOs do not correspond strictly to the number of the integrated LEOs but the diversity of their orbit planes. With the LEOs in different orbital planes, the GPS satellite orbits are improved. Ground stations might bring some undetectable outliers in the observations, especially in sparse networks with less redundancy. In general, the effect of these bad observations can be reduced with more ground stations or LEOs. The mitigation with LEOs introduced is more significant than with more ground stations added. By integrating seven LEOs, the GPS satellite orbits derived from a 10-station and regional ground network are improved impressively with decreased 1D-mean RMS compared to IGS final products from about 25 cm to 4 cm. The impact of LEO orbit modeling quality on derived GPS satellite orbits is not discussed in this study. The impact of different characteristics of the LEO orbits on the integrated POD is a topic for further studies.
Change history
30 August 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00190-021-01557-x
References
Berger C, Biancale R, Barlier F, Ill M (1998) Improvement of the empirical thermospheric model DTM: DTM94: a comparative review of various temporal variations and prospects in space geodesy applications. J Geod 72(3):161–178. https://doi.org/10.1007/s001900050158
Blewitt G (1990) An automatic editing algorithm for GPS data. Geophys Res Lett 17(3):199–202. https://doi.org/10.1029/GL017I003P00199
Case K, Kruizinga G, Wu S (2002) Grace level 1b data product user handbook. Technical report, JPL
Choi KK (2014) Status of core products of the international gnss service. AGU Fall Meeting Abstr 2014:G21A–0426
Dumont J, Rosmorduc V, Picot N, Desai S, Bonekamp H, Figa J, Lillibridge J, Scharroo R (2009) Ostm/jason-2 products handbook. Technical representative, CNES and EUMETSAT and JPL and NOAA/NESDIS
Dumont J, Rosmorduc V, Carrere L, Picot N, Bronner E, Couhert A, Guillot A, Desai S, Bonekamp H, Figa J et al (2016) Jason-3 products handbook. Technical representative, CNES and EUMETSAT and JPL and NOAA/NESDIS
Friis-Christensen E, Lühr H, Knudsen D, Haagmans R (2008) Swarm: an earth observation mission investigating geospace. Adv Space Res 41(1):210–216. https://doi.org/10.1016/J.ASR.2006.10.008
Geng JH, Shi C, Zhao QL, Ge MR, Liu JN (2008) Integrated adjustment of LEO and GPS in precision orbit determination. Int Assoc Geod Symp 132:133–137. https://doi.org/10.1007/978-3-540-74584-6_20
Gutierrez P (2018) Brexit and Galileo - Plenty of rumblings, but Where’s the Beef? https://insidegnss.com/brexit-and-galileo-plenty-of-rumblings-but-wheres-the-beef/, online article of insidegnss.com
Hackel S, Steigenberger P, Hugentobler U, Uhlemann M, Montenbruck O (2015) Galileo orbit determination using combined GNSS and SLR observations. GPS Solut 19(1):15–25. https://doi.org/10.1007/s10291-013-0361-5
Haines B, Bar-Sever Y, Bertiger W, Desai S, Willis P (2004) One-centimeter orbit determination for Jason-1: new GPS-based strategies. Mar Geod. https://doi.org/10.1080/01490410490465300
Jäggi A, Hugentobler U, Bock H, Beutler G (2007) Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data. Adv Space Res 39(10):1612–1619. https://doi.org/10.1016/j.asr.2007.03.012
Johnston G, Neilan R, Craddock A, Dach R, Meertens C, Rizos C (2018) The international GNSS service 2018 update. In: EGU General Assembly Conference Abstracts, vol 20, p 19675
König D (2018) A terrestrial reference frame realised on the observation level using a GPS-LEO satellite constellation. J Geod. https://doi.org/10.1007/s00190-018-1121-7
König R, Reigber C, Zhu S (2005) Dynamic model orbits and Earth system parameters from combined GPS and LEO data. Adv Space Res 36(3):431–437. https://doi.org/10.1016/J.ASR.2005.03.064
Kuang D, Bar-Sever Y, Haines B (2015) Analysis of orbital configurations for geocenter determination with GPS and low-Earth orbiters. J Geod 89(5):471–481. https://doi.org/10.1007/s00190-015-0792-6
Lambin J, Morrow R, Fu LL, Willis JK, Bonekamp H, Lillibridge J, Perbos J, Zaouche G, Vaze P, Bannoura W, Parisot F, Thouvenot E, Coutin-Faye S, Lindstrom E, Mignogno M (2010) The OSTM/Jason-2 mission. Mar Geod 10(1080/01490419):491030
Liu J, Ge M (2003) PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ J Nat Sci 8(2):603–609. https://doi.org/10.1007/BF02899825
Männel B, Rothacher M (2017) Geocenter variations derived from a combined processing of LEO- and ground-based GPS observations. J Geod 91(8):933–944. https://doi.org/10.1007/s00190-017-0997-y
Marshall JA, Antreasian PG, Rosborough GW, Putney BH (1992) Modeling radiation forces acting on satellites for precision orbit determination. Adv Astron Sci 76(pt 1):73–96. https://doi.org/10.2514/3.26408
Ménard Y, Fu LL, Escudier P, Parisot F, Perbos J, Vincent P, Desai S, Haines B, Kunstmann G (2003) The jason-1 mission special issue: Jason-1 calibration/validation. Mar Geod 26(3–4):131–146. https://doi.org/10.1080/714044514
Montenbruck O, Gill E (2000) Satellite orbits: models, methods, and applications, 1st edn. Springer, Berlin. https://doi.org/10.1007/978-3-642-58351-3
Montenbruck O, Hackel S, van den Ijssel J, Arnold D (2018) Reduced dynamic and kinematic precise orbit determination for the Swarm mission from 4 years of GPS tracking. GPS Solut 22(3):79. https://doi.org/10.1007/s10291-018-0746-6
Nischan T (2016) GFZRNX-RINEX GNSS data conversion and manipulation toolbox (Version 1.05). GFZ Data Services. https://doi.org/10.5880/GFZ.1.1.2016.002
Olsen PEH (2019) Swarm l1b product definition. National Space Institute Technical University of Denmark, Technical report
Otten M, Flohrer C, Springer T, Enderle W (2012) Multi-technique combination at observation level with napeos: combining GPS, GLONASS and leo satellites. In: EGU general assembly conference abstracts, vol 14, p 7925
Petit G, Luzum B (2010) IERS conventions (2010). Technical report, Bureau international des poids et mesures sevres (France)
Rebischung P, Griffiths J, Ray J, Schmid R, Collilieux X, Garayt B (2012) IGS08: the IGS realization of ITRF2008. GPS Solut 16(4):483–494. https://doi.org/10.1007/s10291-011-0248-2
Reigber C, Schmidt R, Flechtner F, König R, Meyer U, Neumayer KH, Schwintzer P, Zhu SY (2005) An earth gravity field model complete to degree and order 150 from grace: Eigen-grace02s. J Geodyn 39(1):1–10. https://doi.org/10.1016/j.jog.2004.07.001
Sakic P, Männel B, Nischan T (2018) Operational geodetic products determination and combination for Galileo. In: EGU general assembly conference abstracts, vol 20, p 17515
Schmid R, Dach R, Collilieux X, Jäggi A, Schmitz M, Dilssner F (2016) Absolute IGS antenna phase center model igs08.atx: status and potential improvements. J Geod 90(4):343–364
Springer T, Beutler G, Rothacher M (1999) A new solar radiation pressure model for GPS satellites. GPS Solut 2(3):50–62. https://doi.org/10.1007/PL00012757
Standish EM (1998) JPL planetary and lunar ephemerides, DE405/LE405. Jpl Iom 312F-98-048
Tapley BD, Bettadpur S, Ries JC, Thompson PF, Watkins MM (2004) GRACE measurements of mass variability in the Earth system. Science. https://doi.org/10.1126/science.1099192
Vaze P, Neeck S, Bannoura W, Green J, Wade A, Mignogno M, Zaouche G, Couderc V, Thouvenot E, Parisot F (2010) The Jason-3 mission: completing the transition of ocean altimetry from research to operations. In: Sensors, systems, and next-generation satellites XIV, International Society for Optics and Photonics, vol 7826, p 78260Y
Wang L, Zhang Q, Huang G, Yan X, Qin Z (2016) Combining regional monitoring stations with space-based data to determine the MEO satellite orbit. Acta Geod Cartograph Sin 45(S2):101
Wu SC, Yunck TP, Thornton CL (1991) Reduced-dynamic technique for precise orbit determination of low earth satellites. J Guid Control Dyn 14(1):24–30. https://doi.org/10.2514/3.20600
Yang Y (2018) Introduction to BeiDou-3 navigation satellite system. Presented in IGS workshop October 2018, Wuhan, China
Zhao Q, Wang C, Guo J, Yang G, Liao M, Ma H, Liu J (2017) Enhanced orbit determination for BeiDou satellites with FengYun-3C onboard GNSS data. GPS Solut 21(3):1179–1190. https://doi.org/10.1007/s10291-017-0604-y
Zhao Q, Wang C, Guo J, Wang B, Liu J (2018) Precise orbit and clock determination for BeiDou-3 experimental satellites with yaw attitude analysis. GPS Solut 22(1):4. https://doi.org/10.1007/s10291-017-0673-y
Zhu S, Reigber C, König R (2004) Integrated adjustment of CHAMP, GRACE, and GPS data. J Geod 78(1–2):103–108. https://doi.org/10.1007/s00190-004-0379-0
Zoulida M, Pollet A, Coulot D, Perosanz F, Loyer S, Biancale R, Rebischung P (2016) Multi-technique combination of space geodesy observations: impact of the Jason-2 satellite on the GPS satellite orbits estimation. Adv Space Res 58(7):1376–1389. https://doi.org/10.1016/j.asr.2016.06.019
Acknowledgements
Author Wen Huang was financially supported by Chinese Scholarship Council. The merged data for overlapping comparison is processed by GFZRNX software (Nischan 2016). The data of GRACE, Jason and Swarm satellites are provided by ISDC (ftp://isdcftp.gfz-potsdam.de), AVISO (https://www.aviso.altimetry.fr) and ESA (ftp://swarm-diss.eo.esa.int), respectively. GPS ground observations and related products are provided by IGS (http://www.igs.org/products). The GPS NANU message is offered by the U.S. Coast Guard Navigation Center. Author contributions: Wen Huang designed the research and wrote the paper; Benjamin Männel contributed to the experiment design and the results analysis; Pierre Sakic contributed to the station network selection and the results analysis; Maorong Ge contributed to the software programming and the theoretical considerations; All the authors joined the research discussion and data analysis, and gave comments for the paper writing.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
Statistical results of the GPS satellite orbit differences w.r.t. the IGS final products of 62-station scenario and 26-station+7-LEO scenario. The RMS of orbit differences in the along-track, the cross-track, and the radial directions are computed over epochs and satellites in each day. The 1D-mean RMS is computed over epochs, satellites, and the three orbital directions
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, W., Männel, B., Sakic, P. et al. Integrated processing of ground- and space-based GPS observations: improving GPS satellite orbits observed with sparse ground networks. J Geod 94, 96 (2020). https://doi.org/10.1007/s00190-020-01424-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-020-01424-1