Measuring phase scintillation at different frequencies with conventional GNSS receivers operating at 1 Hz

Abstract

Ionospheric scintillation causes rapid fluctuations of measurements from Global Navigation Satellite Systems (GNSSs), thus threatening space-based communication and geolocation services. The phenomenon is most intense in equatorial regions, around the equinoxes and in maximum solar cycle conditions. Currently, ionospheric scintillation monitoring receivers (ISMRs) measure scintillation with high-pass filter algorithms involving high sampling rates, e.g. 50 Hz, and highly stable clocks, e.g. an ultra-low-noise Oven-Controlled Crystal Oscillator. The present paper evolves phase scintillation indices implemented in conventional geodetic receivers with sampling rates of 1 Hz and rapidly fluctuating clocks. The method is capable to mitigate ISMR artefacts that contaminate the readings of the state-of-the-art phase scintillation index. Our results agree in more than 99.9% within ± 0.05 rad (2 mm) of the ISMRs, with a data set of 8 days which include periods of moderate and strong scintillation. The discrepancies are clearly identified, being associated with data gaps and to cycle-slips in the carrier-phase tracking of ISMR that occur simultaneously with ionospheric scintillation. The technique opens the door to use huge databases available from the International GNSS Service and other centres for scintillation studies. This involves GNSS measurements from hundreds of worldwide-distributed geodetic receivers over more than one Solar Cycle. This overcomes the current limitations of scintillation studies using ISMRs, as only a few tens of ISMRs are available and their data are provided just for short periods of time.

1 Introduction

The Earth ionosphere is defined as the upper part of the atmosphere (at an altitude comprised between 60 and 2000 km), where ions and free electrons are present in quantities sufficient to affect the propagation of radio waves (Institute of Electrical and Electronics Engineers Standard 211 1997). Ionospheric scintillation occurs when Global Navigation Satellite System (GNSS) signals experience fast fluctuations, when they are refracted or diffracted by irregularities of the electron distribution along their propagation paths (Kintner et al. 2007). These irregularities are present at equatorial and high latitudes, predominantly in the F layer at altitudes comprised from 250 to 400 km, but also in the E layer at high latitudes (Prikryl et al. 2016) with altitudes ranging from 90 to 120 km (Aarons 1982). Ionospheric perturbations affecting GNSS are associated with space weather events (such as geomagnetic storms) at high latitudes, and associated with plasma bubbles after the sunset at low latitudes (Juan et al. 2018a).

This phenomenon endangers GNSS navigation by giving rise to significant fluctuations in the amplitude and/or the carrier-phase of GNSS measurements, or causing losses of lock in the tracking loop of the GNSS receiver (Humphreys et al. 2005). Large-scale variations of the electron density (experienced mainly in high-latitude regions) cause signal refraction with remarkable carrier-phase fluctuations but moderate signal amplitude fluctuations (Skone et al. 2008). The carrier-phase measurement L_f can be decomposed as (Sanz Subirana et al. 2013):

$$ L_{f} = \rho + \delta_{\text{ant}} + \delta_{\text{tide}} + \delta t_{\text{rec}} - \delta t^{\text{sat}} + Tr + I_{f} + (B_{f} + \lambda_{f} N_{f}) + w_{f} + \epsilon_{f} $$

(1)

where the frequency-independent terms are: the geometric range $\rho$ between the satellite antenna phase centre (APC) at emission time and the receiver APC at reception time, the effect $\delta_{\text{ant}}$ caused by phase centre variations of the satellite and the receiver, the solid tides effect $\delta_{\text{tide}}$, the receiver and satellite clock offsets $\delta t_{\text{rec}}$ and $\delta t^{\text{sat}}$, and the tropospheric delay ${\text{Tr}}$.

Frequency-dependent terms at frequency $f$ are: the phase ambiguity including a real-valued offset $B_{f}$ and an integer number $N_{f}$ of cycles bias with wavelength $\lambda_{f}$, the phase wind-up effect $w_{f}$, $\epsilon_{f}$ is the effect of noise and multipath error in carrier-phase measurements. The ionospheric effect $I_{f}$ can be decomposed into two different terms: $I_{f} = I_{f}^{r} + I_{f}^{d}$, where:

• $I_{f}^{r}$ is the refractive ionospheric effect at frequency $f$, which can be eliminated up to 99.9% with the dual-frequency ionosphere-free (IF) combination, which is commonly used in the precise point positioning (PPP) method (Zumberge et al. 1997).

• $I_{f}^{d}$ is the diffractive ionospheric effect at frequency $f$. In low-latitude regions, ionospheric irregularities with a size close to the Fresnel length for GNSS frequencies, which is 400 m, can scatter the signal into multiple paths producing signal diffraction (Kintner and Humphreys 2009). The diffractive effects can be observed as rapid fluctuations in both carrier-phase and signal amplitude, losses of lock, and frequent cycle-slips (Carrano et al. 2013). Unlike the ionospheric refraction, the diffraction is not proportional to the inverse squared frequency. Thus, diffractive effects cannot be eliminated with the IF combination and degrade the accuracy of highly accurate GNSS positioning under severe scintillation conditions (Béniguel et al. 2009).

In order to measure the scintillation of GNSS signals, it is common to use a special type of equipment termed ionospheric scintillation monitoring receiver (ISMR). Thanks to the high sampling rate (SR), typically 50 Hz, ISMRs are able to track signals experiencing rapid phase variations due to scintillation. Moreover, ISMRs are equipped with ultra-low-noise Oven-Controlled Crystal Oscillators that are more precise and stable than the internal clocks equipped in conventional geodetic receivers, such as those used in the International GNSS Service (IGS) network (Beutler et al. 2009).

ISMRs provide two types of scintillation indices. The first one is the amplitude scintillation index, denoted as $S_{4}$, defined as the standard deviation of the signal intensity normalized by its mean (Briggs and Parkin 1963). In the current work, we focus on the second one, which is the phase scintillation index, denoted as $\sigma_{{\varphi_{f} }}$.

In order to compute $\sigma_{{\varphi_{f} }}$, the first step consists in detrending $L_{f}$ into $\varphi_{f}$. That is, to apply a high-pass filter (HPF) to $L_{f}$, typically a sixth-order Butterworth (Van Dierendonck and Arbesser-Ratsburg 2004), with a cut-off frequency of $f_{\text{c}} = 0.1\,{\text{Hz}}$. The HPF cancels out all low-frequency components caused by the variation of receiver–satellite geometry $\rho$ and the tropospheric delay ${\text{Tr}}$ or even variations in the hardware delays associated with temperature (Zhang et al. 2017). Therefore, the HPF isolates high-frequency effects such as carrier-phase fluctuations associated with ionospheric scintillation in $I_{f}$.

The second step consists in computing the standard deviation of the detrended carrier-phase $\varphi_{f}$ at frequency $f$ (Yeh and Chao-Han 1982):

$$ \sigma_{{\varphi_{f} }} = \sqrt {\left\langle {\varphi_{f}^{2} } \right\rangle - \left\langle {\varphi_{f}^{2} } \right\rangle } $$

(2)

where $\langle \rangle$ is the time-windowed expectation over time windows of 1 s, 30 s and 60 s, hence termed Phi01, Phi30 and Phi60, respectively. In what remains of the paper, we refer to Phi60.

Two effects contribute to erroneous readings of $\sigma_{{\varphi_{f} }}$. First, the receiver-clock oscillator $\delta t_{\text{rec}}$, which has an unknown value, can vary with unpredictable rapid fluctuations. In ISMRs, the effect is limited by using an ultra-low-noise clock, and thus, ionospheric scintillation is the only significant high-frequency component in the detrended carrier-phase $\varphi_{f}$. On the contrary, carrier-phase measurements of conventional geodetic receivers contain high-frequency effects from its own clock. Those fluctuations remain after detrending of $L_{f}$ into $\hat{\emptyset }_{f}$, despite using the same conventional sixth-order Butterworth HPF as in the ISMR. The accent “^” remarks the presence of the receiver clock in $\hat{\emptyset }_{f}$, whose fluctuations contaminate the phase scintillation index computed as a standard deviation as in (1) but using carrier-phase measurements from a conventional receiver:

$$ \sigma_{{\hat{\emptyset }_{f} }} = \sqrt {\langle\hat{\emptyset }_{f}^{2} \rangle- \langle\hat{\emptyset }_{f}^{2}\rangle } $$

(3)

This contamination is continuous in time, and it is the reason why, up to now, conventional receivers are not used to compute the phase scintillation index $\sigma_{{\hat{\emptyset }_{f} }}$.

The second source of contamination of $\sigma_{\varphi f}$ and $\sigma_{{\hat{\emptyset }_{f} }}$ in ISMR and conventional receivers occurs during scintillation. The carrier-phase tracked by the receiver may experience variations on the ambiguity $N_{f}$ present in the carrier-phase measurements, named cycle-slips (Takasu and Yasuda 2008; Liu et al. 2018; Juan et al. 2018b). These changes are not necessarily discontinuities, see, for instance, Fig. 6 in Juan et al. (2018b). Indeed, transition between integer cycles can last several seconds, so they are difficult to detect. If cycle-slips are not detected, the HPF of the ISMR cannot filter out high-frequency parts caused by cycle-slips. As a result, erroneous values of $\sigma_{{\varphi_{f} }}$ can be calculated. Unlike the clock fluctuations, the effect of cycle-slips remains as a challenge for ISMRs and conventional receivers.

In conventional receivers, because of the difficulty in filtering out high-frequency effects of the receiver clock, another indicator of scintillation known as Rate Of Total electron content Index (ROTI) (Pi et al. 1997) is commonly used in ionospheric studies (Cherniak et al. 2014). ROTI is based on the time variation of the geometry-free (GF) combination of carrier measurements in (1):

$$ L_{\text{GF}} = L_{1} - L_{2} $$

(4)

where $L_{1}$ and $L_{2}$ denote the carrier-phase measurement $L_{f}$ at the frequencies $f_{1} = 1575.42\,{\text{MHz}}$ and $f_{2} = 1227.6\,{\text{MHz}}$ of GPS. These differences of carrier-phase measurements cancel out the effect of high-frequency fluctuations of the receiver clock, which are typical on conventional receivers.

The time derivative of the GF combination is computed from its values at two epochs $k$ and $k - 1$ by:

$$ \dot{L}_{\text{GF}} \left( k \right) = \frac{{L_{\text{GF}} \left( k \right) - L_{\text{GF}} \left( {k - 1} \right)}}{{t\left( k \right) - t\left( {k - 1} \right)}} $$

(5)

Thus, ROTI is calculated as the standard deviation of $\dot{L}_{\text{GF}}$, i.e. ${\text{ROTI}} = \sigma_{\tau } \left( {\dot{L}_{\text{GF}} } \right)$, for a moving window of $\tau$ samples. A typical value of $\tau$ is 300 s when the SR is 30 s.

Notice that all frequency-independent terms are eliminated in (4), including the tropospheric effect, the receiver clock $\delta t_{\text{rec}}$ and satellite clock $\delta t^{\text{sat}}$. In this way, one can have a straightforward sampling of scintillation without requiring a stable receiver clock. However, ROTI presents some drawbacks with respect to $\sigma_{{\varphi_{f} }}$.

First, unlike $\sigma_{{\varphi_{f} }}$, ROTI measures the scintillation effect in the GF combination of $L_{1}$ and $L_{2}$. But, as it is shown in (Bhattacharyya et al. 2000) and (Juan et al. 2017), when diffractive scintillation is present the scintillation effects on $L_{1}$ and $L_{2}$ frequencies are not proportional. Then, with ROTI, one cannot extract the scintillation on each individual frequency.

Second, miss-detected cycle-slips may cause a high value of ROTI not associated with any ionospheric fluctuation but to receiver artefacts (Juan et al. 2017). These cycle-slips are more frequent at $L_{2}$, so large values of ROTI in low latitude can be associated with miss-detected cycle-slips. On the contrary, if cycle-slips are detected, the transitions can last several seconds and this period should be excluded from the ROTI computation, thus reducing the availability of ROTI values under scintillation conditions. This reduction would not occur, if one could isolate the ionospheric effect in $L_{1}$, which is less affected by cycle-slips, as it is the case of $\sigma_{{\varphi_{1} }}$.

A new scintillation index termed $\sigma_{\text{IF}}$ was introduced in (Juan et al. 2017), computed as the standard deviation of the residuals in the IF combination of carrier-phase measurements. Because the refractive effect of scintillation is cancelled in the IF combination, $\sigma_{\text{IF}}$ measures the diffractive effect, which is relevant to the accuracy of PPP. One of the key innovations was the estimation of the receiver clock to remove the influence of its fluctuation on the $\sigma_{\text{IF}}$ indicator.

The current paper proposes an evolution of the technique described in Juan et al. (2017). The main advantage of the method presented in this contribution is that the scintillation effect can be studied on each frequency individually. This is a clear benefit with respect to indicators using the GF combination (e.g. ROTI) and the IF combination (e.g. $\sigma_{\text{IF}}$). The proposed evolution also takes benefit of the receiver-clock removal introduced in (Juan et al. 2017), which is explained with a great level of detail in this paper. Hence, the method can exploit data from conventional geodetic receivers operating at 1 Hz without the requirement of a high stable clock.

The second contribution of this study addresses the cycle-slip problem. Not only the cycle-slips are detected as in (Juan et al. 2017), but also the carrier-phases are corrected in real time, obtaining continuous measurements. Thus, the phase scintillation index can be computed despite the cycle-slip occurrence. The third contribution is the extension to multiple frequencies of the comparisons regarding the phase scintillation index values obtained with conventional receivers with respect to those readings of co-located ISMRs introduced in Juan et al. (2018b).

The paper is organized as follows. Section 2 describes the methodology. Then, we detail the data set of 8 days and the experiment design in Sect. 3. The results of the phase scintillation index using our method are compared to those of the traditional ISMR in Sect. 4. Section 5 discusses the effects of cycle-slips and satellite clock fluctuation on the computation. The summary and conclusions of the work are presented in the last section.

2 Methodology

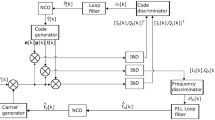
In this section, the proposed method to sample phase scintillation through conventional geodetic receivers is described in detail. The diagram of Fig. 1 presents the different modules explained hereafter. The first processing step is to model the carrier-phase measurements $L_{f}$ to obtain the carrier-phase residuals $\hat{r}_{{L_{f} }}$. Then, the receiver-clock fluctuation is estimated $\widehat{\delta t}_{\text{rec}}$ and removed, obtaining a clock-free carrier-phase residual $r_{{L_{f} }}^{ *}$. The stability of the clock-corrected carrier-phases allows the identification and correction of the cycle-slips, producing a continuous residual $r_{{L_{f} }}$ in real time. Finally, the strategy uses a HPF to obtain the high-frequency component $\emptyset_{f}$ of the carrier-phase residual that allows computing the phase scintillations index $\sigma_{{\emptyset_{f} }}$ by means of a standard deviation over a moving window of 60 s, as $\sigma_{{\varphi_{f} }}$ in (2) and $\sigma_{{\hat{\emptyset }_{f} }}$ in (3).

Fig. 1

Methodology, experimental design and computed indices: $\left. {\sigma_{{\varphi_{f} }} } \right|_{{50{\text{Hz}}}}$, $\left. {\sigma_{{\emptyset_{f} }} } \right|_{{1{\text{Hz}}}}$, and $\left. {\sigma_{{\hat{\emptyset }_{f} }} } \right|_{{1{\text{Hz}}}}$

2.1 Geodetic detrending

As in Juan et al. (2017), the first step is to apply the geodetic detrending that consists in subtracting from the carrier-phase $L_{f}$ in (1) all the terms that can be estimated with well-known geodetic models such as $\delta_{\text{tide}}$, $w_{f}$ and ${\text{Tr}}$, and using IGS products (IGS 2017) such as $\delta_{\text{ant}}$ and $\delta t^{\text{sat}}$. The geometric range $\rho$ can be computed with few centimetres of accuracy with the precisely known coordinates of the APC of the station and the satellite thanks to the antenna exchange format (ANTEX) file provided by IGS. Hence, we obtain the residual $\hat{r}_{{L_{f} }}$ to each frequency measurement:

$$ \hat{r}_{{L_{f}}} = \delta t_{\text{rec}} + \left({B_{f} + \lambda_{f} N_{f}} \right) + I_{f}^{r} + I_{f}^{d} + \epsilon_{f} $$

(6)

In this regard, the detrending with geodetic models at centimetre level of accuracy eliminates most of the effects except the receiver-clock offset $\delta t_{\text{rec}}$, phase ambiguity $\left( {B_{f} + \lambda_{f} N_{f} } \right)$, ionospheric effects $I_{f}$ and measurement noise $\epsilon_{f}$. The first two terms are addressed in Sects. 2.2 and 2.3.

2.2 Receiver-clock estimation

The second step of the method consists in the determination of the fluctuation of the receiver clock $\delta t_{\text{rec}}$. In order to eliminate 99.9% of the refractive ionospheric effect (Sanz Subirana et al. 2013) from $\hat{r}_{{L_{1} }}$ and $\hat{r}_{{L_{2} }}$ in (6), the IF combination of these residuals at frequencies $f_{1}$ and $f_{2}$ is built as follows:

$$ \begin{aligned} \hat{r}_{{L_{\text{IF}} }} & = \frac{{f_{1}^{2} \hat{r}_{{L_{1} }} - f_{2}^{2} \hat{r}_{{L_{2} }} }}{{f_{1}^{2} - f_{2}^{2} }} \\ & = \delta t_{\text{rec}} + B_{\text{IF}} + \lambda_{1}^{\text{IF}} N_{1} + \lambda_{2}^{\text{IF}} N_{2} + I_{\text{IF}}^{d} + \varepsilon_{\text{IF}} \\ \end{aligned} $$

(7)

where $\delta t_{\text{rec}}$ is the receiver-clock offset; $I_{\text{IF}}^{d}$ is the remaining diffractive ionospheric effect; $\epsilon_{\rm IF}$ is the unmodelled noise of around 1 cm in the IF combination. The combined ambiguity $\left( {B_{\text{IF}} + \lambda_{1}^{\text{IF}} N_{1} + \lambda_{2}^{\text{IF}} N_{2} } \right)$ contains a real-valued constant offset $B_{\text{IF}}$ and the integer ambiguities $(N_{1} ,N_{2} )$ in $L_{1}$ and $L_{2}$, respectively. As the result of the IF combination in (7), one cycle-slip in $L_{1}$ causes an increase in $\hat{r}_{{L_{\text{IF}} }}$ of $\lambda_{1}^{\text{IF}} = \frac{{f_{1}^{2} \lambda_{1} }}{{f_{1}^{2} - f_{2}^{2} }} = 48.4\,{\text{cm}}$, and one cycle-slip in $L_{2}$ causes an increase of $\lambda_{2}^{\text{IF}} = \frac{{f_{2}^{2} \lambda_{2} }}{{f_{1}^{2} - f_{2}^{2} }} = 37.7 {\text{cm}}$.

From the mathematical point of view, and neglecting the noise term, the time derivative of $\hat{r}_{{L_{\text{IF}} }}$ of each satellite at epoch $k$ can be computed, as follows:

$$ \begin{aligned} \hat{\dot{r}}_{{L_{\text{IF}} }} \left( k \right) = & \frac{{\hat{r}_{{L_{\text{IF}} }} \left( k \right) - \hat{r}_{{L_{\text{IF}} }} \left( {k - 1} \right)}}{{t\left( k \right) - t\left( {k - 1} \right)}} \\ = &\, \dot{\delta }t_{\text{rec}} \left( k \right) + \lambda_{1}^{\text{IF}} \Delta N_{1} \left( k \right) + \lambda_{2}^{\text{IF}} \Delta N_{2} \left( k \right) + \dot{I}_{\text{IF}}^{d} (k) \\ \end{aligned} $$

(8)

where $\Delta N_{1} \left( k \right)$ and $\Delta N_{2} \left( k \right)$ are, respectively, the numbers of cycles increasing in $L_{1}$ and $L_{2}$ when a cycle-slip occurs, the constant offset $B_{\text{IF}}$ is cancelled out by the derivation, and the variation of diffractive ionospheric effect $\dot{I}_{\text{IF}}^{d} \left( k \right)$ is significant only during periods of diffractive scintillation. Therefore, $\hat{r}_{{L_{\text{IF}} }}$ with neither scintillation (i.e. $\dot{I}_{\text{IF}}^{d} = 0$) nor cycle-slips (i.e. $\Delta N_{1} = \Delta N_{2} = 0$) for all satellites will exhibit a common variation corresponding to the variation of the receiver clock $\dot{\delta }t_{\text{rec}}$.

Thus, one can estimate $\dot{\delta }t_{\text{rec}}$ by taking the mean value of $\hat{\dot{r}}_{{L_{IF} }}$ over all the satellites in view. In order to improve the estimation of $\dot{\delta }t_{\text{rec}}$, we down-weight those $\hat{\dot{r}}_{{L_{\text{IF}} }}$ values from satellites contaminated by cycle-slips and/or scintillation. In particular, the down-weight is similar to ROTI, termed ROTIM, because it exhibits high values (i.e. low weights) when scintillation and/or a cycle-slip occurs:

$$ {\text{ROTIM}} = \sigma_{\tau } \left( {\frac{{\dot{L}_{\text{GF}} }}{M\left( \alpha \right)}} \right) $$

(9)

where $\sigma_{\tau } \left( {} \right)$ denotes the standard deviation computed with a moving window of length $\tau = 10\,{\text{s}}$ using our SR of 1 Hz. The only difference of ROTIM with respect to ROTI is that, in order to mitigate large ROTI values at low elevations, we apply to all $\dot{L}_{\text{GF}}$ observations a mapping function $M\left( \alpha \right)$, similar to (Ghoddousi-Fard et al. 2013), that depends on the satellite elevation $\alpha$:

$$ M\left( \alpha \right) = \sqrt {1 - \left( {\frac{{R_{E} }}{{R_{E} + h}}\cos \left( \alpha \right)} \right)^{2} } $$

(10)

where $R_{E}$ is the radius of the Earth and $h$ is the height of the ionospheric layer (assumed at 350 km). Besides the use of $M\left( \alpha \right)$, we apply an elevation mask of 5º to further mitigate the noise of the carrier-phase measurements and mismodelling occurring at low elevation. The low value of the elevation mask allows low-elevation satellites to take part in the receiver-clock determination. In contrast, when comparing our results with those of the phase scintillation index $\sigma_{\varphi }^{f}$ output by the ISMRs, we use a higher mask of 25º to filter low-elevation values.

Therefore, ROTIM-weighted average of $\hat{\dot{r}}_{{L_{\text{IF}} }}$ from all satellites in view is used to estimate the time derivative of the receiver-clock offset, $\dot{\delta }t_{\text{rec}}$, according to the following expression:

$$ \widehat{{\dot{\delta }t}}_{\text{rec}} = \frac{{\mathop \sum \nolimits_{s = 1}^{n} \frac{{\hat{\dot{r}}_{{L_{{{\text{IF}}_{s} }} }} }}{{{\text{ROTIM}}_{s}^{2} }}}}{{\mathop \sum \nolimits_{s = 1}^{n} \frac{1}{{{\text{ROTIM}}_{s}^{2} }}}} $$

(11)

where $n$ is the number of satellites in view, $s$ is the index of each satellite, and $\hat{\dot{r}}_{{L_{{{\text{IF}}_{s} }} }}$ is the time derivative in 8) for satellite $s$. Hence, the fluctuation of the receiver-clock offset $\delta t_{\text{rec}}$ is estimated as the numerical integral of $\widehat{{\dot{\delta }t}}_{\text{rec}}$:

$$ \widehat{\delta t}_{\text{rec}} \left( k \right) = \mathop \int \limits_{0}^{k} \widehat{{\dot{\delta }t}}_{\text{rec}} \left( n \right){\text{d}}n $$

(12)

where $k$ is the epoch of interest in which the receiver-clock offset $\widehat{\delta t}_{\text{rec}}$ is to be evaluated, $n$ indicates the integration variable between 0 and $k$, and ${\text{d}}n$ is the integration step.

After removing the estimated receiver-clock fluctuation $\widehat{\delta t}_{\text{rec}}$ from $\hat{r}_{{L_{\text{IF}} }}$ in (7), the residual $r_{{L_{\text{IF}} }}^{*}$ is obtained as:

$$ r_{{L_{\text{IF}} }}^{ *} = \hat{r}_{{L_{\text{IF}} }} - \widehat{\delta t}_{\text{rec}} \left( k \right) = I_{\text{IF}}^{d} + B_{\text{IF}} + \lambda_{1}^{\text{IF}} N_{1} + \lambda_{2}^{\text{IF}} N_{2} $$

(13)

This receiver-clock-free residual $r_{{L_{\text{IF}} }}^{*}$ contains only the diffractive scintillation $I_{\text{IF}}^{d}$, the integer ambiguities ($N_{1} , N_{2}$) and the constant ambiguity $B_{\text{IF}}$. As commented in Introduction section, Juan et al. (2017) defined the scintillation index $\sigma_{\text{IF}}$ as the standard deviation of the IF combination in (13). In contrast, we propose to generalize such a concept by removing the estimated clock fluctuation $\widehat{\delta t}_{\text{rec}}$ to the $\hat{r}_{{L_{f} }}$ of each individual frequency $f$ in (6) to obtain a receiver-clock-free residual, $r_{{L_{f} }}^{ *}$:

$$ r_{{L_{f} }}^{ *} = \hat{r}_{{L_{f} }} - \widehat{\delta t}_{\text{rec}} = I_{f}^{r} + I_{f}^{d} + \left( {B_{f} + \lambda_{f} N_{f} } \right) $$

(14)

Therefore, the evolved approach can sample refractive $I_{f}^{r}$ and diffractive $I_{f}^{d}$ scintillation in the uncombined carrier-phase measurements.

2.3 Cycle-slips detector–corrector

The third step of the proposed method is to detect and correct cycle-slips occurring in the GNSS carrier-phase measurements. Cycle-slips are variations of integers, $\Delta N_{f}$, that cause unalignment in $r_{{L_{f} }}^{ *}$ (and hence in $r_{{L_{\text{IF}} }}^{*}$) in the form of jumps. Those discontinuities are proportional to the wavelength $\lambda_{\text{f}}^{\text{IF}}$ or $\lambda_{f}$ (recall that $\lambda_{1}^{IF} = 48.4$ cm and $\lambda_{1} = 19.03$ cm), several times greater than the fluctuation attributable to the diffractive scintillation. Indeed, $I_{\text{IF}}^{d}$ is typically less than 20 cm and during conditions of strong phase scintillation to 1 rad, which corresponds to $I_{1}^{d}$ of 3 cm. Thus, cycle-slips can be isolated from scintillation. Conversely, undetected cycle-slips would contaminate the scintillation measurements. The cycle-slip detection–correction approach is described hereafter.

2.3.1 Cycle-slip detection

The cycle-slip occurrence is detected in the IF combination, exploiting the fact that the detrended $r_{{L_{\text{IF}} }}^{*}$ should be flat. A predicted value of $r_{{L_{\text{IF}} }}^{*}$ at epoch $k$, denoted as $\tilde{r}_{{L_{\text{IF}} }} \left( k \right)$, is computed averaging the previous $r_{{L_{\text{IF}} }}^{*}$ during an interval of 6 s. When the difference between the actual value and the prediction, defined as $\xi_{\text{IF}} = r_{{L_{\text{IF}} }}^{*} \left( k \right) - \tilde{r}_{{L_{\text{IF}} }} \left( k \right)$, is greater than a threshold $\theta_{\text{IF}} = 20\,{\text{cm}}$, a cycle-slip is declared.

2.3.2 Cycle-slip identification

Following the detection of one cycle-slip, we target to identify on which frequency (or frequencies) the variation of cycles $\Delta N_{1}$ and/or $\Delta N_{2}$ occurred. If the computation is conclusive, the cycle-slip can be corrected and the uncombined signal $r_{{L_{f} }}^{ *}$ repaired. Otherwise, a new computation arc starts.

An initial estimation of the variation of the number of cycles from epoch $t\left( {k - 1} \right)$ to epoch t($k)$ is denoted as $\Delta N_{f}^{0}$ and can be computed subtracting the uncombined signal $r_{{L_{f} }}^{ *}$ between adjacent epochs:

$$ \Delta N_{f}^{0} \left( k \right) = \frac{{r_{{L_{f} }}^{ *} \left( k \right) - r_{{L_{f} }}^{ *} \left( {k - 1} \right)}}{{\lambda_{f} }} $$

(15)

where it is assumed that ionospheric effects $\left( {I_{f}^{r} + I_{f}^{d} } \right)$ and constant ambiguity $B_{f}$ do not vary in one second, thanks to the high SR used by conventional geodetic receivers.

A search space is built within ± 4 cycles from the rough initial estimation $\Delta N_{f}^{0}$. That is, we look for nine possible integer values, denoted as $\widehat{\Delta N}_{f}^{i}$, for each frequency:

$$ \Delta N_{f}^{0} - 4 \le \widehat{\Delta N}_{f}^{i} \le \Delta N_{f}^{0} + 4 $$

(16)

where index “i” denotes the “ith” integer candidate per frequency and ranges from $\widehat{\Delta N}_{f}^{1} \,{\text{to}}\,\widehat{\Delta N}_{f}^{9}$. As we have two frequencies, the complete search space accounts for a total of 81 possible pairs of $\widehat{\Delta N}_{1}^{i}$ and $\widehat{\Delta N}_{2}^{j}$ being “i” and “j” the indices for candidates at frequencies $f_{1}$ and $f_{2}$, respectively.

For every “i, j” pair, we compute the residual at epoch $k$ subtracting the candidate integer values $\widehat{\Delta N}_{1}^{i} \left( k \right)$ and $\widehat{\Delta N}_{2}^{j} \left( k \right)$ to the combined $r_{{L_{IF} }}^{*}$:

$$ \begin{aligned} r_{{L_{\text{IF}} }}^{{{\text{i}},{\text{j}}}} \left( k \right) = &\,r_{{L_{\text{IF}} }}^{ *} \left( k \right) - \lambda_{1}^{\text{IF}} \widehat{\Delta N}_{1}^{i} \left( k \right) - \lambda_{2}^{\text{IF}} \widehat{\Delta N}_{2}^{j} \left( k \right) \\ = &\, I_{\text{IF}}^{d} \left( k \right) + B_{\text{IF}} \\ \end{aligned} $$

(17)

obtaining 81 candidate carrier-phase residuals, $r_{{L_{\text{IF}} }}^{i,j} ,$ free of receiver clock and cycle-slips. We select the “i, j” pair that provides the minimum jump with respect to the previous six $r_{{L_{\text{IF}} }}^{*}$ samples, i.e. before the cycle-slip was detected. For this purpose, we use the predicted $\tilde{r}_{{L_{\text{IF}} }} \left( k \right)$ in the “i, j” integer search with the following criteria:

• $\left| {r_{{L_{\text{IF}} }}^{i,j} \left( k \right) - \tilde{r}_{{L_{\text{IF}} }} \left( k \right)} \right|$ is minimized;

• $\left| {r_{{L_{\text{IF}} }}^{i,j} \left( k \right) - \tilde{r}_{{L_{\text{IF}} }} \left( k \right)} \right| \le \theta_{\text{IF}}$.

The last condition guarantees that the selected pair ($\widehat{\Delta N}_{1}^{{\min} } ,\widehat{\Delta N}_{2}^{{\min} } )$ aligns with the previous samples within the cycle-slip tolerance previously defined. This protection is necessary, as we only evaluate ± 4 cycles from the rough initial estimation $\Delta N_{f}^{0}$, whereas the number of integers $\Delta N_{f}$, occurred by the cycle-slip, might fall out of the search space.

In case that a cycle-slip is detected, but no candidate pair fulfils simultaneously the previous two conditions, the identification is inconclusive. Then, a new computing arc is started with the new value of $N_{f}$.

2.3.3 Cycle-slip correction

In case $\Delta N_{1}$ and $\Delta N_{2}$ are identified, the carrier-phase measurements of $L_{1}$ and $L_{2}$ are corrected by adding $\widehat{\Delta N}_{f}^{{\min} }$ to the corresponding $r_{{L_{\text{IF}} }}^{*} , r_{{L_{f} }}^{*}$ and the computation of the arc is continued:

$$ r_{{L_{\text{IF}} }} = r_{{L_{\text{IF}} }}^{*} - \lambda_{1}^{IF} \widehat{\Delta N}_{1}^{{\min} } - \lambda_{2}^{IF} \widehat{\Delta N}_{2}^{{\min} } = I_{\text{IF}}^{d} + B_{\text{IF}} $$

(18)

and

$$ r_{{L_{f} }} = r_{{L_{f} }}^{*} - \lambda_{f} \widehat{\Delta N}_{f}^{{\min} } = I_{f}^{r} + I_{f}^{d} + B_{f} $$

(19)

where $r_{{L_{f} }}$ contains the fluctuation of the carrier-phase attributable to refractive and diffractive ionospheric scintillation, whereas $r_{{L_{\text{IF}} }}$ contains only the diffractive one. The offsets $B_{\text{IF}}$ and $B_{f}$ are constant per arc and given in length units.

2.4 Phase scintillation index

The fourth and final step is to calculate the phase scintillation index. For this purpose, we apply the aforementioned sixth-order Butterworth HPF with a cut-off frequency of 0.1 Hz to $r_{{L_{f} }}$, obtaining its high-frequency component, $\emptyset_{f}$. Then, the phase scintillation index is computed as the standard deviation of $\emptyset_{f}$, hence $\sigma_{{\emptyset_{f} }}$, using a moving window of 60 s as in (2) and (3):

$$ \sigma_{{\emptyset_{f} }} = \sqrt {\langle\emptyset_{f}^{2}\rangle - \langle\emptyset_{f}^{2}\rangle } $$

(20)

where in order to compare with usual units in phase scintillation indices, $\sigma_{{\emptyset_{f} }}$ is scaled from length units to radians.

3 Data and experimental design

The experimental data used in this study have been collected by ISMRs at a SR of 50 Hz and geodetic receivers at a SR of 1 Hz, specified in Table 1. FAA1 (geodetic-grade) and FAAS (ISMR-type) are set up in Tahiti with a short baseline of 9 m. Both receivers are manufactured by Septentrio. JNAV (geodetic) and TQBS (ISMR) are set up on the top of the same building (Ta Quang Buu library, Hanoi, Vietnam) with a baseline of 3 m. In addition, the conventional IGS station GLPS (Galápagos Islands, Ecuador) is used as an example of noisy receiver clock with frequent jumps.

Table 1 Details of the experimental campaign: selected stations, location, dates and IGS product availability

Although the geodetic detrending proposed in Sect. 2 can sample any kind of scintillation in the carrier-phase measurements, we have focused on low-latitude receivers because the equatorial scintillation affects differently each GNSS frequency, see, for instance, Jiao and Morton (2015) or Juan et al. (2017). Thus, studying this particular type of scintillation requires isolating the ionospheric effects on different frequencies as the proposed geodetic detrending does. In contrast, the effect of scintillation at high-latitude is usually proportional at different frequencies, and therefore, it can be isolated by building the GF combination of carrier-phase measurements as in (4), which is a more straightforward manner for detrending the carrier-phase measurements than the geodetic detrending proposed in Sect. 2.

The geodetic detrending has been performed using the GNSS-Lab Tool (gLAB) (Ibáñez et al. 2018). The precise satellite orbits and clocks were obtained from the final products of IGS every 900 s and 30 s, respectively. In order to crosscheck results, we have used also satellite clocks every 5 s computed by the Center for Orbit Determination in Europe (CODE), obtaining similar results.

It is assumed that close stations have common tropospheric and ionospheric effects. Tropospheric Zenith Path Delay (ZPD) data from the IGS are available for FAA1 and GLPS. ZPD data of FAA1 are also used for FAAS. The tropospheric delays of JNAV and TQBS are modelled with a centimetre-level accuracy using the nominal tropospheric delay prediction from Black and Eisner (1984) and the mapping of Niell (1996). Equivalently, the ionospheric scintillation indices $\sigma_{{\varphi_{f} }}$ from ISMRs of FAAS and TQBS are representative of the collocated IGS receivers FAA1 and JNAV, respectively.

Table 1 lists the dates with high values of $\sigma_{{\varphi_{f} }}$ selected in the experiment, which include moderate and strong scintillation. The high $\sigma_{{\varphi_{f} }}$ associated with scintillation have been found in JNAV/TQBS on days 251, 260 and 263 of 2017 and in FAA1/FAAS on days from day 081 to 084 and 086 of 2014. In order to facilitate the correspondence from local time (LT) to universal time (UT), Table 1 indicates the UT at which sunset occurs, assuming 18 h LT.

The experimental design together with all indices computed in the present study is described in the diagram of Fig. 1. In this manner, we can compare the phase scintillation index $\sigma_{{\varphi_{f} }}$ computed by the ISMR at a SR of 50 Hz against the indices $\sigma_{{\hat{\emptyset }_{f} }}$ and $\sigma_{{\emptyset_{f} }}$ computed at 1 Hz. Therefore, the measurements of phase scintillation analysed in Sects. 4 and 5 correspond to the following indices:

• $\left. {\sigma_{{\varphi_{f} }} } \right|_{{50{\text{Hz}}}}$: Output of ISMRs, calculated as in (2) from data with SR of 50 Hz. This can be considered as the reference value;

• $\left. {\sigma_{{\hat{\emptyset }_{f} }} } \right|_{{1{\text{Hz}}}}$: Index calculated by the conventional HPF method as in (3), from RINEX data with SR of 1 Hz;

• $\left. {\sigma_{{\emptyset_{f} }} } \right|_{{1{\text{Hz}}}}$: Index by the proposed methodology described in Sect. 2 as in (20), calculated from RINEX data with SR of 1 Hz.

4 Results

This section presents the results of applying the procedure described in Methodology section. In order to illustrate how the process works as clearly as possible, each step of the calculus is applied to a selected subset of the data presented in Table 1. Then, we compare the capability of the final $\left. {\sigma_{{\emptyset_{f} }} } \right|_{{1{\text{Hz}}}}$ to measure phase scintillation with respect to the state-of-the-art HPF method as $\left. {\sigma_{{\hat{\emptyset }_{f} }} } \right|_{{1{\text{Hz}}}}$ calculated from 1 Hz RINEX data and with respect to $\left. {\sigma_{{\varphi_{f} }} } \right|_{{50{\text{Hz}}}}$ provided directly by the ISMRs at 50 Hz.

4.1 Estimation of receiver-clock fluctuation

The first step is to apply the geodetic detrending described in Sect. 2.1. The top panel of Fig. 2 depicts the result of geodetic detrending applied to the data of receiver JNAV and for all GPS satellites in view during 5 h of day 251 of 2017. As one can see, most of the $\hat{r}_{{L_{\text{IF}} }}$ residuals after applying (7) share the same pattern, which corresponds to the variation of the receiver-clock offset $\delta t_{\text{rec}}$. Therefore, we can use these residuals for estimating the variation of the receiver-clock offset $\widehat{{\delta \dot{t}}}_{\text{rec}}$ by means of the ROTIM-weighted average calculation of (11) in Sect. 2.2. Note that observations affected by scintillation present noisy residuals or even cycle-slips. In such situations, those $\hat{r}_{{L_{\text{IF}} }}$ values are down-weighted by high ROTIM values. The more uncontaminated satellites that take part in the average calculation in (11), the more precise $\widehat{{\delta \dot{t}}}_{\text{rec}}$ is obtained. The result of the numerical integration in (12) yields $\widehat{\delta t}_{\text{rec}}$, which is depicted in the bottom subplot of Fig. 2.

Fig. 2

For IGS receiver JNAV on day 251 of 2017: $\hat{r}_{{L_{\text{IF}} }}$ of ten GPS satellites (top) and estimated receiver clock $\widehat{\delta t}_{\text{rec}}$ (bottom)

4.2 Correction of cycle-slips

Once the receiver-clock fluctuation $\widehat{\delta t}_{\text{rec}}$ is estimated, we can apply (13) in Sect. 2.2 to obtain a receiver-clock-free residual in the IF combination, $r_{{L_{\text{IF}} }}^{ *}$. After this operation, two effects remain: carrier-phase ambiguities and diffractive ionospheric effect. If the geodetic detrending is accurate enough, cycle-slips can be identified as jumps larger than the noise of the remaining diffractive effect (Juan et al. 2017).

Figure 3 depicts two examples of cycle-slip correction, corresponding to the collocated receivers FAA1 and FAAS for the satellite GPS15 on day 81 of day 2014. In order to identify easily the cycle-slips in $L_{1}$ and $L_{2}$, the y-tics of the figure correspond to jumps in the $r_{{L_{\text{IF}} }}^{*}$ associated with the one wavelength in the IF combination for $L_{1}$ ($\lambda_{1}^{\text{IF}} = 48.4\,{\text{cm}}$) and for $L_{2}$$\left( {\lambda_{1}^{\text{IF}} = 37.7\,{\text{cm}}} \right)$, as it is defined in (7). As it can be seen in the figure, the cycle-slips do not occur simultaneously in the two stations (i.e. they affect independently the tracking loops of the receivers). Furthermore, cycle-slips can be easily identified and corrected with great confidence since the noise of $r_{{L_{\text{IF}} }}^{ *}$ is 2.62 cm. In this way, $r_{{L_{\text{IF}} }}^{*}$ is completely detrended into $r_{{L_{\text{IF}} }}$, only remaining $I_{\text{IF}}^{d} \,{\text{and}}\,B_{\text{IF}}$ as in (15).

Fig. 3

Cycle-slips occur in the $r_{{L_{\text{IF}} }}^{*}$ (red pluses) for satellite GPS15 tracked by FAA1 (top) and FAAS (bottom) on day 81 of 2014. The $r_{{L_{\text{IF}} }}$ (blue crosses) remains flat after cycle-slip correction. The Y-axis is scaled to the corresponding integer number of cycles in $L_{1}$ and $L_{2}$ in the IF combination

The issue of cycle-slips affects also to carrier-phase measurements of modern signals at other frequencies. Figure 4 depicts other two examples of cycle-slip correction in the IF combination of $L_{1}$ and $L_{5}$ carrier-phase measurements. Using the same collocated receivers and date of Fig. 3, it can be observed how multiple cycle-slips occur in the $r_{{L_{\text{IF}} }}^{*}$ residuals of $L_{5}$ from satellite GPS24 that belong to the Block II-F. In this case, the y-tics of the figure are of size $\lambda_{5}^{\text{IF}} = \frac{{f_{5}^{2} \lambda_{5} }}{{f_{1}^{2} - f_{5}^{2} }} = 32.1\,{\text{cm}}$. As in the previous case depicted in Fig. 3, the noise of $r_{{L_{\text{IF}} }}^{ *}$ is 2.19 cm. Hence, cycle-slips can be detected, identified and corrected.

Fig. 4

Satellite GPS24 tracked by the collocated receivers FAA1 (top) and FAAS (bottom) on day 081 of 2014 with the $r_{{L_{IF} }}^{ *}$ (red pluses) before cycle-slips correction and the $r_{{L_{\text{IF}} }}$ (blue crosses) after cycle-slips correction. The Y-axis is scaled to the corresponding integer number of cycles in $L_{1}$ and $L_{5}$ in the IF combination

4.3 Calculation of phase scintillation index

Once the carrier-phase measurements are clean from receiver-clock and cycle-slips effects, we can obtain the ionospheric delays $r_{{L_{f} }}$ at any frequency, as it is proposed in (19) in Sect. 2.3.3. The bottom panels of Fig. 5 depict an example of the ionospheric delays on $L_{1}$ (left column) and $L_{2}$ (right column) for the IGS receiver GLPS on day 83 of 2014 for the satellite GPS17, jointly with the receiver-clock estimate $\widehat{\delta t}_{\text{rec}}$. Because the ionospheric delay is isolated, we are able to compute the phase scintillation index at any frequency using expression (20) in Sect. 2.4. The top panels of Fig. 5 show the corresponding phase scintillation indices for L1 (left column) and L2 (right column). The results computed with the proposed method: $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\emptyset_{2} }} } \right|_{{1{\text{Hz}}}}$ are compared with $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\hat{\emptyset }_{2} }} } \right|_{{1{\text{Hz}}}}$ applying directly (3) to carrier-phases $\hat{\emptyset }_{1}$ and $\hat{\emptyset }_{2}$ detrended by the HPF without correcting the receiver clock, nor detecting cycle-slips, neither applying the geodetic detrending, i.e. as ISMRs do.

Fig. 5

Calculation of phase scintillation indices at frequency $L_{1}$ (left) and $L_{2}$ (right) for satellite GPS17 in station GLPS on day 83 of 2014 with a SR of 1 Hz. Top: $\left. {\sigma_{{\hat{\emptyset }_{f} }} } \right|_{{1{\text{Hz}}}}$ by the state of the art (red line) and $\left. {\sigma_{{\emptyset_{\text{f}} }} } \right|_{{1{\text{Hz}}}}$ by the proposed method (green line). Bottom: receiver-clock fluctuation $\widehat{\delta t}_{\text{rec}}$ (black line) and Ionospheric fluctuations $r_{{L_{1} }}$ and $r_{{L_{2} }}$ (green line) estimated by the proposed method

It can be observed that the fluctuations and jumps in the receiver-clock offset, labelled as $\widehat{\delta t}_{\text{rec}}$ in the estimation depicted in the bottom subplots of Fig. 5 cause high values and spikes in the $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\hat{\emptyset }_{2} }} } \right|_{{1{\text{Hz}}}}$, as shown in the top panels. In such cases, the ionospheric phase scintillation $r_{{L_{1} }}$ and $r_{{L_{2} }}$ of GPS17 cannot be properly sampled, due to the contamination of the high-noise receiver clock. On the contrary, our proposed method based on the geodetic detrending, the receiver-clock estimation, and the cycle-slip correction is capable of sampling the scintillation, as confirmed in the values of $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\emptyset_{2} }} } \right|_{{1{\text{Hz}}}}$ observed in the top panels of Fig. 5. In this manner, the proposed approach opens the door to perform climatological studies in the long term (e.g. an entire Solar Cycle) with hundreds of receivers that will contribute to a better understanding of scintillation phenomena.

4.4 The capability of the proposed method in comparison with the state of the art

This subsection compares the phase scintillation indices computed with the proposed method and those output by ISMRs. Figure 6 depicts two examples corresponding to four receivers of Table 1. The top row depicts the results for the receivers situated at Tahiti, whereas the bottom row depicts the results at Hanoi. In each of these locations, the results of an ISMR are depicted in the left column, next to the results of its collocated conventional geodetic receiver in the right column.

Fig. 6

Four panels with phase scintillation indices computed in four stations: FAAS/FAA1 (top) and TQBS/JNAV (bottom). Top subplot of each panel: phase scintillation measured with the proposed $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ (blue line) and the state-of-the-art $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$ (red line) from 1 Hz data compared with $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of ISMR output (black dots) at 50 Hz. Bottom subplot of each panel: ionospheric fluctuation $r_{{L_{1} }}$ (red line) at $L_{1}$ estimated by the proposed method and receiver-clock estimates $\widehat{\delta t}_{\text{rec}}$ (black line). Note: the linear trends of the estimated receiver-clock fluctuation $\widehat{\delta t}_{\text{rec}}$ of the ISMRs in (a) and (c) have been subtracted

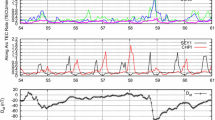
In every panel, the black dots depict the $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ readings output by the ISMR. Those values are considered as the reference values. In Tahiti (top row), phase scintillation values up to 0.385 rad are recorded in epoch 27,420 s in day 81 of 2014, whereas in Hanoi scintillation up to 0.382 rad can be seen in epoch 45,480 s in day 251 of 2017.

We start examining the capability to sample scintillation of the phase scintillation index $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$. That is, to apply directly (3) to carrier-phase $\hat{\emptyset }_{1}$ detrended by the HPF without correcting the receiver clock, nor detecting cycle-slips, neither applying the geodetic detrending. In both ISMRs, Fig. 6a (FAAS) and Fig. 6c (TQBS) depict equivalent results obtained, $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$. This occurs thanks to the stable clock oscillator embedded in the ISMRs, confirmed in the bottom subplots depicting $\widehat{\delta t}_{\text{rec}} .$ In contrast, the results of $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$ obtained from data of conventional geodetic receivers clearly fail to detect scintillation. Figure 6b (FAA1) and Fig. 6d (JNAV) depict continuous $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{1{\text{Hz}}}}$ values of 1.3 rad in FAA1 and 0.3 rad in JNAV. As in the previous case of GLPS depicted in Fig. 5, fluctuations of the receiver clocks, $\widehat{\delta t}_{\text{rec}}$, mask the ionospheric scintillation.

The results obtained in the geodetic receivers by the proposed method based on the receiver-clock removal are examined hereafter. It can be observed how $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ produces significantly different values in scintillation and non-scintillation periods in the geodetic receivers Fig. 6b (FAA1) and Fig. 6d (JNAV). Thus, $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ can correctly identify the scintillation, even using a geodetic receiver with an unstable clock. In Tahiti, Fig. 6b shows an excellent agreement of $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ in FAA1 with the $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of its collocated ISMR FAAS. In Hanoi, Fig. 6d shows that in non-scintillation periods, the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ of the proposed method in JNAV is approximately 0.03 rad (1 mm) larger than the $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of its collocated ISMR of TQBS. Other few non-negligible differences between $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ of the proposed method and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ from ISMRs have also been identified. We discuss these differences of the two methods with a statistical analysis next Sect. 4.5.

Figure 7 illustrates how the method works at different frequencies. For that purpose, the right panel Fig. 7 depicts the residuals $r_{{L_{f} }}$ obtained for $L_{1}$, $L_{2}$ and $L_{5}$ from the satellite GPS10, which belongs to the Block II-F. It can be seen how the scintillation affects differently each frequency and, in particular, how the effect in $r_{{L_{2} }}$ is more similar to $r_{{L_{5} }}$ than to $r_{{L_{1} }}$, because $L_{2}$ and $L_{5}$ are closer in frequency. The left panel depicts the $\left. {\sigma_{{\emptyset_{f} }} } \right|_{{1{\text{Hz}}}}$ at each frequency, computed with our method following (20) from 1 Hz data of the conventional receiver JNAV. For each frequency, we include the results of the $\left. {\sigma_{{\varphi_{f} }} } \right|_{{50{\text{Hz}}}}$ obtained with (2) from the co-located ISMR TQBS working at 50 Hz. It can be seen that the values of the phase scintillation indices for the $L_{2}$ and $L_{5}$ are greater than for $L_{1}$. Thus, our method is able to characterize the scintillation effect on each individual frequency.

Fig. 7

Left: ionospheric fluctuation $r_{{L_{\text{f}} }}$ at the corresponding frequencies estimated by the proposed method. The results correspond to satellite GPS10 on day 251 of 2017. Right: calculation of phase scintillation indices $\sigma_{{\emptyset_{f} }}$ at frequencies $L_{1}$, $L_{2}$ and $L_{5}$ in IGS station JNAV with a SR of 1 Hz compared to the values $\sigma_{{\varphi_{f} }}$ of the co-located ISMR TQBS with a SR of 50 Hz

4.5 Statistics of the difference between $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$

This subsection analyses the differences between the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ computed from 1 Hz RINEX data and the $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ output from ISMRs at 50 Hz. Figure 8 depicts four scatter plots for all aggregate dates in Table 1, with the following organization. The left column shows the agreement of the two methods at the same ISMR. Conversely, the right column shows the results of the IGS receiver versus the collocated ISMR receiver. Every panel contains a dashed line indicating differences greater than ± 0.05 rad which correspond to ± 2 mm in the GPS L1 frequency. Points beyond these lines can be termed as outliers.

Fig. 8

Scatter plots of the relation of $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$. Left column: relation at the same ISMR: FAAS (top left) and TQBS (bottom left). Right column: relation at a conventional geodetic receiver and its collocated ISMR: FAA1/FAAS (top right) and JNAV/TBQS (bottom right). Dashed lines indicate $\sigma_{{\emptyset_{1} }}$ outliers greater than ± 0.05 rad of $\sigma_{{\varphi_{1} }}$. Satellites GPS28 on day 260 (red triangles) and GPS20 on day 263 (green squares) of 2017 are affected by satellite clock fluctuations contaminating other satellites (black pentagons)

Table 2 quantifies numerically the discrepancies of each panel by using the percentiles of the absolute difference. In this regard, this arrangement allows us to infer the accuracy of the geodetic detrending and its impact on the phase scintillation index $\sigma_{{\emptyset_{1} }}$. This is done by means of the 68th and the 95th percentiles in the fourth and fifth columns, respectively. Finally, the sixth column depicts the number of outliers.

Table 2 Differences between the phase scintillation indices $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$: percentiles, epochs computed and outliers found

We start the comparison at the same ISMR: Fig. 8a for FAAS and in Fig. 8c for TQBS, which corresponds to the second and fourth columns in Table 2. Over 99% of the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ values computed by the proposed method agree within 0.03 rad (1 mm) of the reference $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ values. A total of 11 outliers (less than 0.1%) have been found. The reason of this observed disagreement is full- or half-cycle-slips occurring in the 50 Hz data that appear as data gaps in the 1 Hz RINEX file of the ISMR. These cases are discussed in Sect. 5.1 with more details.

We continue the comparison by looking at the values of the conventional geodetic receivers and their co-located ISMR. Figure 8b depicts an excellent agreement between $\left. {\sigma_{{\emptyset_{1} }} } \right|_{1Hz}$ values of FAA1 and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of FAAS for scintillation and non-scintillation conditions. The fourth row of Table 2 confirms this finding, with a difference smaller than 0.015 rad (0.45 mm) at the 95th percentile.

At the other geodetic/ISMR pair, Table 2 reads that the 95th percentile of the difference between the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ of JNAV and the $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of TQBS is 0.04 rad (1.20 mm). This larger discrepancy is attributable to the difference between the measurement noise of the receiver of JNAV and that of TQBS. Indeed, according to Table 1, JNAV and TBQS are equipped with a Trimble and a Septentrio receiver, respectively. In contrast, FAAS and FAA1 are equipped with Septentrio receivers.

The analysis finishes with observing the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ values higher than 0.3 rad in Fig. 8c, d that correspond to satellites GPS28 of day 260 (red triangles) and GPS20 of day 263 (green squares). Both indices $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of these particular days are influenced by fast satellite clock fluctuations rather than by ionospheric scintillation. The black pentagons indicate $\sigma_{{\emptyset_{1} }}$ values from other satellites in view that are contaminated by these rapidly fluctuating satellites. For instance, Fig. 8d shows that the difference of $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ of JNAV and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of TQBS increases up to 0.1 rad for $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ values smaller than 0.2 rad, that is, in the absence of scintillation conditions. The effect of unmodelled satellite clock is discussed in detail in Sect. 5.3.

From the previous analysis, one can conclude that $\sigma_{{\emptyset_{1} }}$, computed with the new method, and $\sigma_{{\varphi_{1} }}$, provided by the ISMR, are nearly equivalent, being the 95th percentile of the differences below 0.04 rad and the largest differences are due to outliers which represent less than 0.02% of the comparisons. We will analyse these outliers in the next section.

5 Discussion

This section analyses the discrepancies previously observed in the results of the phase scintillation indices. In particular, it assesses the effect of cycle-slips observed in the ISMR readings, which are considered as the reference values. Second, it analyses the effect of different SR in the calculation of the indices. The section ends with a discussion of the contamination of phase scintillation indices in the presence of satellite clock fluctuations that affect ISMRs and geodetic receivers using the proposed approach.

5.1 Effect of uncorrected cycle-slips in the index $\sigma_{{\varphi_{1} }}$ of ISMR

This subsection discusses the first origin of the outliers found in Fig. 8. That is, how undetected cycle-slips contaminate the phase index $\sigma_{\varphi }$ output by ISMR that we consider as a reference value. In order to ease the explanation of the phenomenon, we use the previous case depicted in Fig. 4, where several cycle-slips are detected in $L_{5}$ for satellite GPS24 in the ISMR FAAS on day 81 of 2014.

Figure 9 depicts the computation of phase scintillation in $L_{5}$ with the original data and with the cycle-slip-corrected data. As it can be seen, $\left. {\sigma_{{\varphi_{5} }} } \right|_{{50{\text{Hz}}}}$ of ISMR is affected by cycle-slips in $L_{5}$. When these cycle-slips occur and are not corrected, the ionospheric fluctuation $r_{{L_{5} }}^{*}$ is incorrectly increased or decreased, as shown in the bottom subplot of Fig. 9. The top subplot shows the contamination of the $\left. {\sigma_{{\hat{\emptyset }_{5} }} } \right|_{{1{\text{Hz}}}}$ values which reach − 0.14 rad (i.e. − 25.79%) with respect to the values of the proposed method $\left. {\sigma_{{\emptyset_{5} }} } \right|_{{1{\text{Hz}}}}$ that are not contaminated by cycle-slips. Therefore, an accurate cycle-slips correction must be taken into account to achieve a correct measurement of phase scintillation.

Fig. 9

Effect of uncorrected cycle-slips in the output of ISMR of satellite GPS24 in FAAS on day 081 of 2014. Top: $\left. {\sigma_{{\emptyset_{5} }} } \right|_{{1{\text{Hz}}}}$ of $L_{5}$ by the proposed method (blue line) and $\left. {\sigma_{{\hat{\emptyset }_{5} }} } \right|_{{1{\text{Hz}}}}$ without cycle-slips correction (red line) in comparison with $\left. {\sigma_{{\varphi_{5} }} } \right|_{{50{\text{Hz}}}}$ of ISMR (black dots). Bottom: ionospheric fluctuations in the carrier-phase residuals before ($r_{{L_{5} }}^{*}$) and after ($r_{{L_{5} }}$) the cycle-slips correction

5.2 Effect of half-cycle-slips in the 50 Hz data

The second origin of outliers previously identified in Fig. 8 is related with the difference of the two input data sources for computing $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$. Indeed, the lower subplot of Fig. 10 depicts the estimated ionospheric fluctuations at $L_{1}$ of the 1 Hz RINEX data $\left. {r_{{L_{1} }} } \right|_{{1{\text{Hz}}}}$ and the 50 Hz data $\left. {r_{{L_{1} }} } \right|_{{50{\text{Hz}}}}$. In the 50 Hz data, one half-cycle increase can be observed at epoch 21,053.42 s and a corresponding half-cycle decrease is observed at epoch 21,055.24 s. In contrast, these observations are not recorded in the 1 Hz RINEX file despite being generated by the same receiver, thus creating a data gap of 2 s from epoch 21,054 to 21,056 s.

Fig. 10

Effect of a half-cycle phase on the computed phase scintillation indices of satellite GPS26 in FAAS on day 082 of 2014. Bottom: ionospheric fluctuation $\left. {r_{{L_{1} }} } \right|_{{1{\text{Hz}}}}$ (blue line) obtained from 1 Hz RINEX data presents a data hole of 2 s from epoch 21,054 to 21,056 s, whereas $\left. {r_{{L_{1} }} } \right|_{{50{\text{Hz}}}}$ (red line) presents one half-cycle increase at epoch 21,053.42 s and one half-cycle decrease at epoch 21,055.24 s. Top: phase scintillation indices of the state-of-the-art method using 50 Hz data ($\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{50{\text{Hz}}}}$, red line) and the reference value of $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ of ISMR (black dots) present higher readings than the proposed method using 1 Hz data ($\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$, blue line), because they include two half-cycle jumps

The uncorrected half-cycle jump affects the value of $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ at epochs 21,060 s and 21,120 s. Note that although the jump occurred at epoch 21,055 s, the effect lasts until epoch 21,120 s due to the HPF. In order to confirm this finding, the index $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{50{\text{Hz}}}}$ of the conventional HPF method as in (3) has been computed with the 50 Hz data that contains two half-cycle jumps. The results show that both the computed $\left. {\sigma_{{\hat{\emptyset }_{1} }} } \right|_{{50{\text{Hz}}}}$ and the ISMR reference $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ with the half-cycle-slips present values up to 0.4 rad higher than those of $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ computed as in (20) from 1 Hz data.

5.3 Effect of satellite clock fluctuation

Actual high-frequency fluctuations of satellite clocks have been observed on days 260 and 263 of 2017, as previously mentioned in the analysis of Fig. 8. The results have been cross-checked with the final clock products at a SR of 5 and 30 s from CODE and IGS, respectively, obtaining identical results. The case depicted in Fig. 11 corresponds to station JNAV on day 260 of 2017 with satellite clock data from CODE. In this example, the clock of the satellite GPS28 fluctuates at high frequency during 11 min, from epoch 9986 to 10,670 s. This mismodelled fluctuation cannot be cancelled out by the HPF of the ISMR and thus distorts the provided $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$, as illustrated in the top left panel of Fig. 11. These fluctuations are also observed in the estimated ionospheric fluctuation $r_{{L_{1} }}$, as in (19), which in turn contaminate the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ of the geodetic receiver JNAV. Therefore, the high values observed in phase scintillation indices $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ and $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ of satellite GPS28 are not linked to any scintillation effect as in Benton and Mitchell (2014), but to satellite clock fluctuations at a higher frequency than the SR of the precise clock files used in (6).

Fig. 11

Top: phase scintillation indices $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ and $\left. {\sigma_{{\varphi_{1} }} } \right|_{{50{\text{Hz}}}}$ compared with ROTIM, scaled to the corresponding radian values at frequency $f_{1}$, of satellites GPS28 (left) and GPS19 (right) in JNAV on day 260 of 2017. Bottom: estimated ionospheric fluctuation $r_{{L_{1} }}$ (red) at $L_{1}$ and the interpolated precise satellite clock $\delta t^{\text{sat}}$ provided by CODE (black)

This phenomenon also contaminates the estimation of the receiver clock in (12). The reason is that ROTIM calculus in (9) cancels the satellite clock, thus the measurements with mismodelled satellite clock are not down-weighted in (11). Consequently, this erroneous receiver-clock estimate is propagated and contaminates the estimated ionospheric fluctuation $r_{{L_{1} }}$ of all other satellites in view and their scintillation measurements. An example of this contamination is depicted in right panel of Fig. 11, where the $\left. {\sigma_{{\emptyset_{1} }} } \right|_{{1{\text{Hz}}}}$ for satellite GPS19 is artificially increased by the fluctuations of GPS28 during the aforementioned 11 min.

A possible protection against erroneous readings of the phase scintillation index due to high-frequency effects on other satellites is to use a geometry-and-clock-free index, e.g. ROTIM, as an extra indicator. This is the reason to include the ROTIM values in the two upper panels in Fig. 11. In both cases, low ROTIM values can be used to identify false scintillation due to mismodelled fluctuation of non-dispersive effects such as the satellite clock. In this way, when a particular satellite presents high values of $\sigma_{{\emptyset_{f} }}$ simultaneously with low values of ROTIM, the satellite should be thus discarded to avoid the contamination of the estimation of the receiver-clock fluctuation and subsequently $\sigma_{\emptyset }$ of all satellites in view.

6 Conclusions

This paper contributes to a recently introduced approach to sense the ionospheric phase scintillation with GNSS signals collected by conventional multi-frequency geodetic receivers, operating at 1 Hz. The technique is based on an accurate geodetic modelling of carrier measurements, at the centimetre level. The method can be applied in geodetic receivers, without the requirement of high SR nor the stability of receiver clock as in ISMRs. Thanks to the GNSS growth, hundreds of geodetic receivers are available worldwide and capable of adopting the proposed approach. This fact constitutes an unprecedented frame to improve radio-navigation and ionospheric-sounding techniques, especially in Southeast Asia, the only region where all global and regional constellations of navigation satellite can be tracked.

Up to now, scintillation studies could be performed using combinations of carrier-phase measurements such as the GF in ROTI or the IF in $\sigma_{\text{IF}}$. The proposed evolution overcomes some of the problems associated with those indicators. First, it is capable to estimate ionospheric fluctuations on each individual frequency rather than in a combination of signals. This turns very adequate when studying diffractive scintillation at low latitude, in which effects are not proportional between frequencies. Second, the accurate modelling of the carrier-phase measurements allows identifying and correcting cycle-slips which are due to receiver artefacts. Miss-detected cycle-slips contaminate the readings $\sigma_{{\varphi_{f} }}$ provided by ISMRs or ROTIs provided by geodetic receivers.

The results of the phase scintillation index $\sigma_{{\emptyset_{f} }}$, obtained with our evolved method, agree with the $\sigma_{{\varphi_{f} }}$ provided by ISMRs at different frequencies. We have found some cases where mismodelled satellite clock fluctuations contaminate the phase scintillation indices measured by ISMRs and by geodetic receivers. However, using a GF index such as ROTIM, it is possible to detect and counteract mismodelled satellite clock fluctuations at a higher frequency than the cadence of precise satellite clock determinations used within the geodetic detrending.