An approach for estimating time-variable rates from geodetic time series

Abstract

There has been considerable research in the literature focused on computing and forecasting sea-level changes in terms of constant trends or rates. The Antarctic ice sheet is one of the main contributors to sea-level change with highly uncertain rates of glacial thinning and accumulation. Geodetic observing systems such as the Gravity Recovery and Climate Experiment (GRACE) and the Global Positioning System (GPS) are routinely used to estimate these trends. In an effort to improve the accuracy and reliability of these trends, this study investigates a technique that allows the estimated rates, along with co-estimated seasonal components, to vary in time. For this, state space models are defined and then solved by a Kalman filter (KF). The reliable estimation of noise parameters is one of the main problems encountered when using a KF approach, which is solved by numerically optimizing likelihood. Since the optimization problem is non-convex, it is challenging to find an optimal solution. To address this issue, we limited the parameter search space using classical least-squares adjustment (LSA). In this context, we also tested the usage of inequality constraints by directly verifying whether they are supported by the data. The suggested technique for time-series analysis is expanded to classify and handle time-correlated observational noise within the state space framework. The performance of the method is demonstrated using GRACE and GPS data at the CAS1 station located in East Antarctica and compared to commonly used LSA. The results suggest that the outlined technique allows for more reliable trend estimates, as well as for more physically valuable interpretations, while validating independent observing systems.

Introduction

Antarctica is one of the largest contributors to global sea-level rise (IPCC 2014), making the knowledge of its ice-mass change of considerable societal and ecological importance. The GRACE satellite gravimetry mission has provided an extremely useful tool for observing the global integral effects of mass changes. Nevertheless, Antarctic ice-mass change estimates derived from GRACE remain challenging due to, among others, the effect of glacial isostatic adjustment (GIA, Velicogna and Wahr 2006). GPS vertical site displacements are gaining importance in constraining GIA-induced rates in Antarctica (Whitehouse et al. 2012; Ivins et al. 2013; Sasgen et al. 2013; van der Wal et al. 2015).

Normally, all the above-mentioned processes related to sea-level involving ice mass and GIA rates are estimated as constant trends along with deterministically modeled seasonal components (e.g., Velicogna et al. 2014; Gunter et al. 2014; Shepherd et al. 2012) without allowing for inter-annual and seasonal variability, which might not have captured the true trend estimates (Davis et al. 2012). Accurately modeling known sources of temporal variation is crucial for interpreting geodetic data properly, especially because of large inter-annual variations in the Antarctic climate (Ligtenberg et al. 2012). Moreover, very few geophysical processes are exactly periodic; instead there are signal constituents which fluctuate around a reference value, e.g., around a 1-year period with slightly varying amplitudes. Therefore, modeling seasonal processes using traditional deterministic fitting methods may not provide very accurate results. In this study, we model them stochastically within a KF framework allowing for physically natural variations of signal constituents in time. This idea was brought to the geodetic community by Davis et al. (2012) while being a well-established technique in econometrics since the 1980s (Harvey 1989). However, Davis et al. (2012) assumed the statistical noise parameters to be known. Moreover, the econometric literature lacks methods for a robust estimation of the noise parameters as the optimization problem to be solved for those parameters turns out to be non-convex (i.e., there can be multiple local minima).

Therefore, the goal of this study is to provide a robust tool for estimating time-variable trends from geodetic time series. For this purpose, detailed descriptions are provided on how different components, such as trend and known periodicities, can be modeled stochastically and put into KF form (Sect. 2). Special attention is paid towards carefully estimating the noise parameters, which is an essential step in the KF. The presented statistical framework is appropriate to any time series, but is demonstrated in this study on GRACE and GPS time series that have been widely used in the context of trend estimation (Sect. 3). A spectral analysis of the results shows that the developed tool yields more reliable estimates compared to those derived from commonly used LSA. Moreover, the technique presented allows different geodetic time series to be analyzed for validation purposes.

Methodology

The theory described below is largely based on Durbin and Koopman (2012) and Harvey (1989).

As we demonstrate the methodology on GRACE and GPS data, Sects. 2.1–2.4 are relevant for both types of datasets, whereas Sect. 2.5 is devoted to the analysis of features typical of GPS time series. Section 2.6 summarizes the major steps of the time-series analysis by the suggested method.

Trend modeling

The following function is commonly fit to time series data to obtain a trend:

$$\begin{aligned} y_t = \mu _t + \sum _{i=1}^2 (c_i \cos (\omega _i t) + s_i \sin (\omega _i t)) + \varepsilon _t, \quad t =1,\ldots ,n, \end{aligned}$$

(1)

where $y_t$ denotes an observation at time $t, \mu _t= \alpha + \beta {t}$ is a linear trend with an intercept $\alpha$ and a slope $\beta$, and $(c_i \cos (w_i t)\,+\, s_i \sin (w_i t))$ are harmonic variations with angular frequency $\omega _i = \frac{2\pi }{T_i}$, where $T_1 = 1$ for an annual signal, and $T_2 = 0.5$ for a semi-annual signal. The irregular term $\varepsilon _t$ includes unmodeled signal and measurement noise in the series and is often assumed to be an independent and identically distributed (iid) random variable with zero mean and variance $\sigma ^2_{\varepsilon }$ [i.e., $\varepsilon _t \sim N(0,\sigma ^2_{\varepsilon })$].

The deterministic linear trend $\mu _t= \alpha + \beta t$ can be made stochastic by letting $\alpha$ and $\beta$ follow random walks. This leads to a discontinuous pattern for $\mu _t$. A better model is obtained when working directly with the current $\mu _t$ rather than with the intercept $\alpha$. Since $\mu _t$ can be obtained recursively from

$$\begin{aligned} \mu _{t+1} = \mu _t + \beta , \quad \text {with} \;\; \mu _0 = \alpha , \end{aligned}$$

(2)

stochastic terms are now introduced as

$$\begin{aligned} \begin{array}{lll} \mu _{t+1} &{} = \mu _t +\beta _t + \xi _t, &{}\quad \xi _t \sim N(0,\sigma ^2_{\xi }), \\ \beta _{t+1} &{} = \beta _t + \zeta _t, &{}\quad \zeta _t \sim N(0,\sigma ^2_{\zeta }). \end{array} \end{aligned}$$

(3)

Equation (3) with $\sigma ^2_{\xi } > 0$ allows the intercept of the trend to move up and down, while $\sigma ^2_{\zeta } > 0$ allows the slope to vary over time. A deterministic trend is obtained if $\sigma ^2_{\xi } = \sigma ^2_{\zeta }= 0$. Because there is no physical reason for the intercept to change over time, we model it deterministically by setting $\sigma ^2_{\xi } = 0$; this leads to a stochastic trend model called an integrated random walk. The larger the variance $\sigma ^2_{\zeta }$, the greater the stochastic movements in the trend. In other words, $\sigma ^2_{\zeta }$ defines how much the slope $\beta$ in Eq. (3) is allowed to change from one time step to another.

A deterministic harmonic term of angular frequency $\omega$ is

$$\begin{aligned} c_t = c \cos (\omega t) +s \sin (\omega t), \end{aligned}$$

(4)

where $\sqrt{c^2 + s^2}$ is the amplitude and $\tan ^{-1}(s/c)$ is the phase. Equivalent to the linear trend, the harmonic term can be built up recursively, leading to the stochastic model

$$\begin{aligned} \begin{aligned} \begin{array}{ll} c_t &{}{} = c_{t-1} \cos \omega +s_{t-1} \sin \omega +\varsigma _t,\\ s_t &{}{} = -c_{t-1} \sin \omega +s_{t-1} \cos \omega + \varsigma _t^*, \end{array} \end{aligned} \end{aligned}$$

(5)

where $\varsigma _t$ and $\varsigma _t^*$ are white-noise disturbances that are assumed to have the same variance and to be uncorrelated [i.e., $\varsigma _t \sim N(0,\sigma ^2_{\varsigma })$]. These stochastic components allow the parameters c and s and hence the corresponding amplitude and phase to evolve over time. Note that $c_t$ in Eq. (5) is the current value of the harmonic signal and $s_{t-1}$ appears by construction to form $c_t$.

Introducing the stochastic trend and stochastic harmonic models into Eq. (1) yields

$$\begin{aligned} y_t = \mu _t+ c_{1,t} + c_{2,t} + \varepsilon _t, \quad \varepsilon _t \sim N(0,\sigma ^2_{\varepsilon }) \end{aligned}$$

(6)

with $c_{1,t}$ and $c_{2,t}$ being annual and semi-annual terms, respectively. It is straightforward to extend Eq. (6) by additional harmonic terms using the stochastic model of Eq. (5) with the corresponding angular frequencies.

State space model

The state space form of the equations defined in Sect. 2.1 is

$$\begin{aligned} \begin{array}{lll} y_t = Z_t \alpha _t + \varepsilon _t, &{} \varepsilon _t \sim N(0,H), &{}\\ \alpha _{t+1} = T_t \alpha _t + R_t \eta _t, &{} \eta _t \sim N(0,Q), &{} \quad t = 1,\ldots ,n,\\ &{}\alpha _1 \sim N(a_1,P_1),&{} \end{array} \end{aligned}$$

(7)

where $y_t$ is still an observation vector, $\alpha _t$ is an unknown state vector, and $\varepsilon _t$ is the irregular term with $H = I\sigma ^2_{\varepsilon }$. The first equation of (7), where the design matrix Z links $y_t$ to $\alpha _t$, is called the observation equation and the second is called the state equation. Any model that includes an observation process and a state process is called a state space model. The observation equation has the structure of a linear regression model where the vector $\alpha _t$ varies over time. The second equation represents a first-order vector autoregressive model. The transition matrix T describes how the state changes from t to $t+1$, and $\eta _t$ is the process noise with $Q=I\sigma ^2_{\eta }$. The initial state $\alpha _1$ is $N(a_1,P_1)$ where $a_1$ and $P_1$ are assumed to be known.

We define the state vector as

$$\begin{aligned} \alpha _t = \begin{bmatrix} \mu _t&\beta _t&c_{1,t}&s_{1,t}&c_{2,t}&s_{2,t} \end{bmatrix} ^\mathrm{T}. \end{aligned}$$

(8)

The observation equations read

$$\begin{aligned} y_t = \begin{bmatrix} 1&0&1&0&1&0 \end{bmatrix} \alpha _t + \varepsilon _t \end{aligned}$$

(9)

and the state space matrices are

$$\begin{aligned} T = \begin{bmatrix} 1&\quad 1&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 1&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad \cos \omega _1&\quad \sin \omega _1&\quad 0&\quad 0\\ 0&\quad 0&\quad -\sin \omega _1&\quad \cos \omega _1&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad \cos \omega _2&\quad \sin \omega _2\\ 0&\quad 0&\quad 0&\quad 0&\quad -\sin \omega _2&\quad \cos \omega _2\\ \end{bmatrix}, \end{aligned}$$

(10)

$$\begin{aligned} R= & {} \begin{bmatrix} 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 1&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 1&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 1&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 1&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 1 \end{bmatrix},\\ Q = I\sigma ^2_{\eta }= & {} \begin{bmatrix} \sigma ^2_{\zeta }&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad \sigma ^2_{\varsigma _1}&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad \sigma ^2_{\varsigma _1}&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad \sigma ^2_{\varsigma _2}&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad \sigma ^2_{\varsigma _2} \end{bmatrix}. \end{aligned}$$

For the defined state space model, the system matrices Z, T, R, H, and Q are independent of time. Therefore, the corresponding index t is dropped out hereinafter. Another reason for not including any time reference is that we use equally spaced data. It is worth pointing out that a state space model can also be defined for time series containing data gaps or for unevenly spaced time series. While dealing with missing observations is particularly simple as shown in Durbin and Koopman (2012, chap. 4.10), some modifications might be required for unevenly spaced time series depending on the complexity of the desired state space model (Harvey 1989, chap. 9).

Kalman filter and smoother

To solve the linear state space model of Sect. 2.2 the Kalman filter approach described by Durbin and Koopman (2012, chap. 4.3) is used. The KF recursion for $t=1,\ldots ,n$ processes the data sequentially and comprises the equations:

$$\begin{aligned} \begin{array}{ll} v_t = y_t -Za_t, &{} \quad F_t = ZP_tZ^{T}+ H,\\ a_{t|t} = a_t + P_tZ^{T}F_t^{-1}v_t, &{}\quad P_{t|t} = P_t - P_tZ^{T}F_t^{-1}ZP_t,\\ a_{t+1} = Ta_t + K_tv_t, &{}\quad P_{t+1} = TP_t(T-K_tZ)^{T} + RQR^{T}, \end{array} \end{aligned}$$

(11)

where $K_t = TP_tZ^{T}F^{-1}_t$ is referred to as the Kalman gain and $v_t$ is the innovation with variance $F_t$. Once $a_{t|t}$ and $P_{t|t}$ are computed, the following relation can be used to predict the state vector $\alpha _{t+1}$ and its variance matrix at time t

$$\begin{aligned} \begin{array}{llll} a_{t+1}&= Ta_{t|t},&P_{t+1}&= TP_{t|t}T^{T} + RQR^{T}. \end{array} \end{aligned}$$

(12)

While filtering aims at obtaining the expected value for the state vector using the information available so far, the aim of Kalman smoothing is to use the information made available for the entire time series. Because the smoothed estimator is based on more information than the filtered estimator, smoothing yields, in general, a smaller mean squared error than filtering. According to Durbin and Koopman (2012, chap. 4.4), a smoothed state $\hat{\alpha }_t$ and its error variance $V_t$ can be obtained by evaluating

$$\begin{aligned} \begin{array}{ll} r_{t-1} = Z^{T}F^{-1}_tv_t + L^{T}_t r_t, &{}\quad N_{t-1} = Z^{T}F^{-1}_t Z + L^{T}_t N_t L_t,\\ \hat{\alpha }_t = a_t + P_t r_{t-1}, &{}\quad V_t = P_t - P_t N_{t-1}P_t \end{array} \end{aligned}$$

(13)

in a backward loop for $t=n,\ldots ,1$ initialized with $r_n=0$ and $N_n=0$, where $L_t = T -K_tZ$.

Estimation of hyperparameters

Until now, we have assumed that the parameters $\sigma ^2_{\varepsilon }$ and $\sigma ^2_{\eta }$, which determine the stochastic movements of the state variables and therefore have a significant influence on the results, are known. In practical applications, they are usually unknown except for the measurement noise error where we often have some level of a priori information. The estimation of these so-called hyperparameters is itself based on the Kalman filter and is performed by maximizing the likelihood. If a process is governed by hyperparameters $\psi$, which generate observations $y_t$, the likelihood of producing the given data for known hyperparameters is according to Harvey (1989)

$$\begin{aligned} L(Y_n| \psi ) = p(y_1,\ldots ,y_n) = p(y_1)\prod _{t=2}^{n} p(y_t|Y_{t-1}), \end{aligned}$$

(14)

where $p(y_t|Y_{t-1})$ represents the distribution of $y_t$ conditional on the information set at time $t-1$, that is $Y_{t-1} = \{y_{t-1},y_{t-2},\ldots ,y_1\}$. The hyperparameters $\psi$ are chosen in such a way that the likelihood function is maximized. Equivalently, we may maximize the loglikelihood $\log L$

$$\begin{aligned} \log L(Y_n| \psi ) = \sum _{t=1}^{n} p(y_t|Y_{t-1}). \end{aligned}$$

(15)

The distribution of $y_t$, conditional on $Y_{t-1}$, is assumed to be normal (or gaussian). Therefore, substituting $N(Z_ta_t,F_t)$ for $p(y_t|Y_{t-1})$ in Eq. (15) yields

$$\begin{aligned} \log L(Y_n| \psi ) = -\frac{n}{2}\log (2\pi ) -\frac{1}{2}\sum _{t=1}^{n}\left( \log | F_t | + v^{T}_t F^{-1}_t v_t\right) ,\nonumber \\ \end{aligned}$$

(16)

which is computed from the Kalman filter output (Eq. 11) according to Durbin and Koopman (2012, chap. 7).

The hyperparameters are defined as

$$\begin{aligned} \psi = 0.5 \log \begin{bmatrix} \sigma ^2_{\varepsilon }&\sigma ^2_{\eta } \end{bmatrix}^\mathrm{T} = 0.5 \log \begin{bmatrix} \sigma ^2_{\varepsilon }&\sigma ^2_{\zeta }&\sigma ^2_{\varsigma _1}&\sigma ^2_{\varsigma _2} \end{bmatrix}^\mathrm{T}, \end{aligned}$$

(17)

which ensures that they are non-negative, since here they represent standard deviations.

Fig. 1

The importance of an initial guess in the context of non-convex optimization problem illustrated using a fictitious one parameter model. Depending on the starting point (initial guess), globally suboptimal (e.g., starting from points a or b) or globally optimal solution (e.g., starting from point c) can be found

Optimization

Maximizing $\log L$ is equivalent to minimizing $-\log L$. We search numerically for a set of optimal parameters that provides the minimum value for negative $\log L$, given the process and the observed data. This optimization problem is carried out by using an interior-point (IP) algorithm as described in Byrd et al. (1999). The function $-\log L(Y_n| \psi )$ to be minimized is called the objective function. Since the IP algorithm of Byrd et al. (1999) is a gradient-based local solver, the gradient for the objective function is computed analytically according to Durbin and Koopman (2012, chap. 7):

$$\begin{aligned} \frac{\partial \log L(Y_n|\psi )}{\partial \psi }= & {} \frac{1}{2}\sum _{t=1}^{n} {{\mathrm{tr}}}\left\{ \begin{matrix} \left( u_t u_t^{T} -D_t\right) \frac{\partial H_t}{\partial \psi } \end{matrix}\right\} \nonumber \\&+\,\frac{1}{2}\sum _{t=2}^{n} {{\mathrm{tr}}}\left\{ \begin{matrix} \left( r_{t-1} r_{t-1}^{T} -N_{t-1}\right) \frac{\partial R_t Q_t R_t^{T}}{\partial \psi } \end{matrix}\right\} \nonumber \\ \end{aligned}$$

(18)

using quantities calculated in Sect. 2.3 with $u_t = F^{-1}_t v_t - K^{T}_t r_t$ and $D_t = F^{-1}_t + K^{T}_t N_t K_t$.

Fig. 2

Amplitude spectrums of the estimated slope (top), annual (middle) and semi-annual (bottom) components in mm. The estimation of the signal components is based on differently estimated hyperparameters (noise parameters): a by limiting the parameter search space for finding an optimal minimum and b without limiting the parameter search space

The IP algorithm is used because it accounts for a potential non-convexity, and the problem we are dealing with is non-convex. If an optimization problem is non-convex, there can be multiple local minimum points with objective function values different from the global minimum (Horst et al. 2000). Finding a globally optimal solution of a multivariate objective function that has many local minima is very challenging. One of the main difficulties is the choice of the initial guess for the starting point ${\psi _{0}}$ (initial solution) that is required for the optimization. If the initial guess is sufficiently close to a local minimum, the optimization algorithm terminates at this local minimum (Fig. 1). Visualizing the objective function is helpful to choose a suitable initial guess, but the problem we are describing is at least four-dimensional. Dimensionality may further increase, for instance, if other periodic constituents are considered (e.g., the S2 tidal alias in GRACE data analysis); another example of a higher dimension is discussed in Sect. 2.5.3. Therefore, our approach is to compute the objective function for a number of starting points and use the solution in further computations that provides the smallest objective function value and thus is more likely to be a global minimum (Anderssen and Bloomfield 1975). The question, however, is how to define suitable starting points that allow all or as many as possible local minima to be identified, which in turn will increase the probability of finding the global minimum. For this, a set of uniformly distributed starting points is randomly generated within a finite search space. As a result, the same optimal solution is obtained after each run despite the fact that the method is heuristic, ensuring the existence of an optimal solution within the predefined bounds.

Limiting the parameter space

In the following, we limit the parameter search space in the context of a non-convex optimization problem to improve the chance of finding a global optimum. First, all lower bounds are set equal to zero. The upper bounds are chosen from LSAs to the given data as follows. We fit the model described by Eq. (1) to the data, and use the variance of the postfit residuals as an upper bound for $\sigma ^2_{\varepsilon }$ in Eq. (9). This choice is justified, since LSA-residuals contain the unmodeled signal, measurement noise and possible fluctuations in the modeled terms (in our case in trend, annual and semi-annual components), whereas $\sigma ^2_{\varepsilon }$ in Eq. (9) does not include possible fluctuations in the modeled terms, because we model them stochastically as described in Sect. 2.1. Similarly, the upper bounds for annual and semi-annual terms are found. After subtracting a deterministic trend from the time series, annual and semi-annual signals are simultaneously estimated using LSA within a sliding window that has a minimum timespan of 2 years. The maximum size of the sliding window corresponds to the length of the time series used. Done this way, a sufficient amount of annual and semi-annual amplitudes are estimated and the corresponding variances are used as upper bounds for $\sigma ^2_{\varsigma _1}$ and $\sigma ^2_{\varsigma _2}$, respectively. The choice of the upper bounds is justified by the fact that the standard deviation of the signal computed for different time intervals is never smaller than the process noise of this signal, since here standard deviations indicate possible signal variations within the considered time span, whereas process noise represents the signal variations from one time step to the next only. Moreover, these upper bounds still include possible variations within the trend component supporting the idea of being the upper limits for the process noise associated with estimated harmonics. Regarding the process noise associated with the trend component $\sigma ^2_{\zeta }$, no upper bound is set.

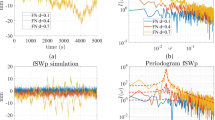
By bounding the search space for $\psi$ in the manner described above and by setting the amount of start points to 200 (chosen by trial and error), we obtain after each run numerically the same optimal solution. To substantiate the reliability of the estimated hyperparameters, we additionally analyze the amplitude distribution of the estimated signal constituents (Eq. 8) as a function of frequency. Investigating whether the amplitude spectrum shows a peak around the expected frequency allows us to draw conclusions on the reasonableness of the estimated noise parameters, since they determine the estimation of the signal constituents.

To illustrate the idea of the analysis in the spectral domain, an example based on GPS time series, which will be described later, is presented in Fig. 2. To produce this figure, we first estimated noise parameters stored in $\psi$ (Eq. 17) with and without limiting the parameter space for $\sigma ^2_{\varepsilon }, \sigma ^2_{\varsigma _1}$ and $\sigma ^2_{\varsigma _2}$. For these two cases, we then estimated the state vector $\alpha _t$ and computed the amplitude spectrum for the rate $\beta _t$, annual $c_{1,t}$ and semi-annual $c_{2,t}$ estimates. Figure 2a provides an indication of reasonably estimated hyperparameters, since the amplitude spectrums of the corresponding signal estimates show significant peaks over the expected frequencies and there are no significant peaks elsewhere. For comparison, Fig. 2b provides an example generated without limiting the parameter space, where the hyperparameter associated with the annual signal is overestimated including variations of the rate/slope component while the amplitude of the slope has an unrealistically small magnitude of zero mm. This example also emphasizes the importance of limiting the parameter search space within a non-convex optimization problem.

The solution we obtain for the hyperparameters $\psi$ is referred to as an unconstrained solution hereinafter, since only the search space for the global solver has been limited, but no restrictions are applied yet to the parameters themselves.

Constrained optimization

Introducing constraints on some of the noise parameters may improve the chance of finding a global minimum within a non-convex optimization. Sometimes, we have prior knowledge about some noise parameters, e.g., we know that $\sigma ^2_{\varepsilon }$ must be larger than some threshold. This inequality constraint can be easily applied within the numerical optimization (Nocedal and Wright 2006). However, if the introduced constraints are not supported by the data, applying them may significantly change the estimated noise parameters and, in turn, the estimate of the state vector $\alpha _t$, yielding erroneous geophysical interpretations. As we are dealing with a non-convex problem, the testing procedure proposed in Roese-Koerner et al. (2012) cannot be applied. Therefore, we outline a method to verify whether the data support the applied constraints, paying particular attention to non-convexity.

Firstly, we perform a so-called basic test to check the plausibility of the applied constraints. For this, we compute the absolute difference between the constrained and unconstrained case which should be smaller than the estimated standard deviations of the unconstrained hyperparameters:

$$\begin{aligned} | \psi _{\mathrm{con}} - \psi _{\mathrm{uncon}} | < \sigma _{ \psi _{\mathrm{uncon}}}, \end{aligned}$$

(19)

where $\sigma _{ \psi _{\mathrm{uncon}}}$ is derived using the corresponding Hessian. This is a quick test for serious mistakes meaning that constraints are absolutely not supported by the data if the left-hand side of the equation is larger than the right-hand side. If the basic test does not reject introduced constraints (meaning the test is positive), the second, computationally more comprehensive likelihood ratio test (LR-test) is performed.

The basic idea of the LR-test is the following: if the constraint is valid, imposing it should not lead to a large reduction in the loglikelihood function (Greene 1993). Therefore, the test statistic is

$$\begin{aligned} \mathrm{LR} = 2(\log L(Y_n|\psi _{\mathrm{uncon}}) - \log L(Y_n|\psi _{\mathrm{con}})). \end{aligned}$$

(20)

LR is asymptotically $\chi ^2$ distributed with degrees of freedom equal to the number of constraints imposed (Wilks 1938). The null hypothesis is rejected (the test is negative) if this value exceeds the appropriate critical value from the $\chi ^2$ tables, meaning that the data do not support the constraints applied.

According to Greene (1993) the parameter spaces, and hence the likelihood functions of the two cases must be related. Moreover, the degrees of freedom of the $\chi ^2$ statistic for the LR-test (Eq. 20) equals the reduction in the number of dimensions in the parameter space that results from imposing the constraints. Hence, the degree of freedom equals the amount of active constraints. A constraint is called active (or binding) if it is exactly satisfied, and therefore, holds as an equality constraint (Boyd and Vandenberghe 2004, p. 128). In short, the LR-test is usually applied in the equality constrained case. However, if one constraint is active it reduces the number of dimensions in the parameter space by one, since it defines one parameter on which this constraint is applied. If a constraint is active it simultaneously means that this constraint strongly influences the solution. Since we are dealing with a non-convex optimization problem having multiple local minima, it may be the case that a constraint can still strongly affect the solution without becoming active, e.g., by simply shifting the solution to the next minima. Therefore, to estimate the degree of freedom for the LR-test performed in the context of a non-convex optimization problem with inequality constraints, we have to estimate how many restrictions do indeed influence the solution. This will be achieved by using a brute force method summarized in Algorithm 1. The idea of the method is to successively apply the constraints until all restrictions are satisfied and thereby, to control the number of degrees of freedom for the LR-test. As it might be the case that applying a constraint to one parameter will already satisfy the constraints to the other parameters, we check whether newly added restrictions make previously added ones superfluous.

It is important to note that the degrees of freedom of the $\chi ^2$ statistic may differ already because of the used state space form; for details, the reader is referred to Harvey (1989, chap. 5). If both tests, i.e., the basic test and the LR-test, indicate that the data do not support the constraints, the constraints are relaxed towards unconstrained values until both tests are positive (see Algorithm 2). In this context, it is worth mentioning again that the basic test is performed for the purpose of reducing the computational complexity: if the constraints do not pass the basic test, there is no need to perform the LR test.

By doing so, we avoid using constraints that are too strong and not supported by the data, but still try to find a compromise between a statistically based and a physically meaningful estimate.

GPS

The analysis of GPS time series often differs substantially from that of GRACE data. GRACE time series have a sampling period of typically one month, data gaps are sparse, and noise correlations between the monthly data (if there are any) are negligible. GPS data are known to contain colored (temporally correlated) observational noise that cannot be neglected (Williams 2003a). Moreover, GPS time series are frequently unevenly spaced in time and may contain large data gaps as well as outliers. In the following sections, we describe how we handle these different features present in the GPS data.

Pre-processing

A KF can easily deal with unevenly distributed observations. However, equally spaced data will be beneficial when we later define the state space model for temporally correlated noise. Therefore, we generate equally spaced data by filling short gaps with interpolated values and long gaps with NaN values. We define a gap to be long if more than seven consecutive measurements are missing, i.e., more than 1 week of daily GPS data.

Since the KF is not robust to outliers, they should be removed beforehand. Outliers are detected here by a Hampel filter according to Pearson (2011). The measurements are removed from the time series where horizontal or vertical site displacements of a GPS station were identified as outliers.

Colored noise

The white noise assumption in Sect. 2.2 is too strong for the observational noise when dealing with GPS measurements. A classical approach to consider the colored noise within the framework of KF is to extend the state vector $\alpha _t$ in Eq. (7) with the noise (so-called “shaping filter”) (Bryson and Johansen 1965). To do so, we first need to assess the type of noise. For this reason, we estimate the state vector from Eq. (8) using filtering and smoothing recursions described in Sect. 2.3, but now the components of the state vector are made deterministic by setting the process noise variance $\sigma ^2_{\eta }$ to zero and $\sigma ^2_{\varepsilon }$ to one. This is equivalent to the classical LSA. Dealing with missing observations in the derivation of the KF and smoother is particularly simple as shown in Durbin and Koopman (2012, chap. 4.10). Using KF here instead of LSA permits us to compute smoothed residuals at each time step $t = n,\ldots ,1$

$$\begin{aligned} \hat{\varepsilon }_t = H\left( F_t^{-1}v_t - K_t^\mathrm{T}r_t\right) \end{aligned}$$

(21)

by using quantities computed in Sect. 2.3. In this way computed residuals are now equally distributed in time. They represent an approximation of the noise, which we model as an autoregressive moving average (ARMA) process of order (p, q). The ARMA process is defined as

$$\begin{aligned} {\varepsilon }_t = \sum _{j=1}^{l}\phi _j{\varepsilon }_{t-j} + \varkappa _t + \sum _{j=1}^{l-1}\theta _j\varkappa _{t-j}, \quad t = 1,\ldots ,n, \end{aligned}$$

(22)

where $\phi _1,\ldots , \phi _p$ are the autoregressive parameters, $\theta _1,\ldots ,\theta _q$ are the moving average parameters and $\varkappa _t$ is a serially independent series of $N(0,\sigma _\varkappa ^2)$ disturbances and $l=\max (p,q+1)$ with $p,\,q \in \{0, \ldots , 5\}$. Some parameters of an ARMA model can be zero, which yields two special cases: if $q = 0$, the process is autoregressive (AR) of order p; if $p = 0$, the process is a moving-average (MA) process of order q.

The postfit residuals obtained after fitting a deterministic model to the data represent colored noise. It is important to understand that it is only an approximation of the observational noise, since the residuals contain a potentially unmodeled time-dependent portion of the signal. To parameterize this approximate colored noise using an ARMA(p, q) model, we need to determine how p and q should be chosen. For this, we follow the idea of Klees et al. (2003) and use the ARMA(p, q) model that best fits the noise power spectral density (PSD) function. Thus, using the PSD function of the approximate colored noise we estimate the pure recursive part of the filter (MA) and non-recursive part of the filter (AR) by applying the standard Levinson–Durbin algorithm (Farhang-Boroujeny 1998). The parameters of the MA and AR models are computed using a defined p and q, which are then used to compute the PSD function of the combined ARMA(p, q) solution. To control the dimension of the state vector $\alpha _t$ we limit the maximum order of the ARMA process to 5, which means we compute the PSD for ARMA(p, q) generated for $p,\,q \in \{0, \ldots , 5\}$ (including two special cases AR(p) and MA(q)). Then, we use GIC (Generalized Information Criterion) order selection criterion to select the PSD of the ARMA model that best fits the PSD of the approximate colored noise. The p and q of this ARMA model define the number of $\phi$ and $\theta$ coefficients used to parameterize colored noise $\varepsilon _t$. More details about the use of ARMA models in the context of GPS time series can be found in accompanying Supplement.

State space model

GPS data are often contaminated by offsets (Gazeaux et al. 2013). If undetected, they might produce an error in trend estimates (Williams 2003b). For Antarctica, the offsets are usually related to hardware changes and thus are step-like. To incorporate an offset into state space form we define a variable $w_t$ as:

$$\begin{aligned} w_t = {\left\{ \begin{array}{ll} 0, &{} t < \tau ,\\ 1, &{} t \ge \tau . \end{array}\right. } \end{aligned}$$

(23)

Adding this to the observation Eq. (6) gives

$$\begin{aligned} y_t = \mu _t+ c_{1,t} + c_{2,t} + \delta \, w_t + \varepsilon _t, \quad t = 1,\ldots ,n, \end{aligned}$$

(24)

where $\delta$ measures the change in the offset at a known epoch $\tau$. For k offsets, the state vector can be written as

$$\begin{aligned} \alpha _t^{[\delta ]} = [\delta _1 \cdots \delta _k]^\mathrm{T}. \end{aligned}$$

(25)

Colored noise ${\varepsilon }_t$ can be included into the state space model as:

$$\begin{aligned} \alpha _t^{[\varepsilon ]} = \begin{bmatrix} \varepsilon _t \\ \phi _2\varepsilon _{t-1}+\cdots + \phi _l\varepsilon _{t-l+1}+ \theta _1\varkappa _t+ \cdots + \theta _{l-1}\varkappa _{t-l+2} \\ \phi _3\varepsilon _{t-1}+\cdots + \phi _l\varepsilon _{t-l+2}+ \theta _2\varkappa _t+ \cdots + \theta _{l-1}\varkappa _{t-l+3} \\ \vdots \\ \phi _l\varepsilon _{t-1} + \theta _{l-1}\varkappa _t \end{bmatrix}\nonumber \\ \end{aligned}$$

(26)

with $\eta ^{[\varepsilon ]}= \varkappa _{t+1}$; then, the corresponding system matrices are given by

$$\begin{aligned} \begin{array}{lllll} &{} T^{[\varepsilon ]}= \begin{bmatrix} &{} \phi _1 &{} 1 &{} \quad &{} 0 \\ &{} \vdots &{} \quad &{} \ddots \\ &{} \phi _{l-1} &{} 0 &{} \quad &{} 1\\ &{} \phi _l &{} 0 &{} \cdots &{} 0 \end{bmatrix}, \quad R^{[\varepsilon ]}= \begin{bmatrix} 1&{} \theta _1 &{} \cdots &{} \theta _{l-1} \end{bmatrix} ^\mathrm{T}, \\ &{} Z^{[\varepsilon ]}= \begin{bmatrix} 1 &{} 0 &{} 0 \cdots 0\end{bmatrix}. \end{array} \end{aligned}$$

(27)

It is worth noting that for irregularly spaced observations, it is less straightforward to put an ARMA(p, q) process for models of order $p > 2$ into state space form. Therefore, the data were pre-processed as outlined in Sect. 2.5.1.

Combining the parameterization of k offsets (Eq. 25) and of the “shaping filter” (Eq. 26) with the basic model defined in Eq. (8) (hereafter $\alpha _t$ used with the index b for basic), we take the state vector as

$$\begin{aligned} \alpha _t = \left( \alpha _t^{[\varepsilon ]}, \alpha _t^{[b]},\alpha _t^{[\delta ]}\right) , \end{aligned}$$

(28)

and the system matrices as

$$\begin{aligned} \begin{array}{ll} &{} Z_t = \left( Z ^{[\varepsilon ]}, Z,I_k\right) , \quad T = \mathrm{diag}\left( T^{[\varepsilon ]}, T, {I}_k\right) ,\\ &{} R = \mathrm{diag}\left( R^{[\varepsilon ]}, R, {0}_k\right) , \\ &{} Q = I\sigma ^2_{\eta } = \mathrm{diag}\left( \begin{bmatrix} \sigma ^2_{\varkappa _{t+1}} &{} \sigma ^2_{\zeta } &{} \sigma ^2_{\varsigma _1} &{} \sigma ^2_{\varsigma _1} &{}\sigma ^2_{\varsigma _2} &{}\sigma ^2_{\varsigma _2} \end{bmatrix}\right) \end{array} \end{aligned}$$

(29)

with Z, T and R being defined in Eqs. (9)–(10).

After defining this modified state space model, GPS time series can be processed in the same way as the GRACE time series. In particular, the search space for the global solver associated with the ARMA parameters does not experience any bounds.

Fig. 3

Flow diagram to summarize the major steps of the described approach for time-series analysis

Summary of the developed framework

The flow diagram in Fig. 3 outlines the major steps of the time-series analysis by the suggested method. The method can be applied to any equally spaced data; it can cope with missing observations and different stochastic properties of the data. Once the components of interest are defined in the state vector, the corresponding state space model with all required matrices can be formulated. If present, time-correlated observational noise can be modeled using a general ARMA model that subsumes two special cases (AR and MA) as described in Sect. 2.5.3 or in more detail in the accompanying Supplement. Another representation of the colored observational noise within the state space formalism can be found in, e.g., Dmitrieva et al. (2015), in which a linear combination of independent first-order Gauss–Markov (FOGM) processes is used to approximate the noise.

Once in the state space form, the parameters governing the stochastic movements of the state components are estimated by numerically optimizing likelihood. The likelihood function is computed using the by-products of the Kalman filter (Eq. 16). Finding an optimal solution as demonstrated in Sect. 2.4 is the key of the proposed methodology, since it ensures optimal estimates for the hyperparameters, which in turn determine the estimates of the signal constituents. Limiting the parameter search space (Sect. 2.4.2), as well as imposing constraints (Sect. 2.4.3) that are supported by the data, both increase the likelihood of getting the optimal solution. Once the hyperparameters are estimated, the Kalman filter and smoother can be used (Sect. 2.3) for obtaining the best estimate of the state at any point within the analyzed time span. This can be important for investigating the way in which a component such as trend has evolved in the past.

Application to real data

In this section, we demonstrate the performance of the proposed methodology compared with the commonly used LSA technique on two different types of geodetic time series. As an example, we use GRACE and GPS time series, although the methodology can be applied to any other time series. After a brief description of the data sets, the results of computational experiments are presented and discussed.

Fig. 4

Vertical site displacements in mm derived based on GRACE data (black), the fit of a trend function (blue), and the fit of a trend function together with annual, semi-annual and tidal S2 periodic terms (red) using a LSA and b KF framework. Error bars are $1\sigma$

Data

We use daily GPS vertical site velocities at the CAS1 station, which is located in Wilkes Land, East Antarctica. There are three reasons for selecting this GPS station: first, it is a GPS site with continuous long-term observations; second, the time series data contain all the features described in Sect. 2.5; and third, because of its geolocation. A significant accumulation anomaly event was concentrated along the Wilkes Land coast in 2009 (Luthcke et al. 2013). Due to a high signal-to-noise ratio, we expect this event to be detected by both observing systems, GPS and GRACE. Consequently, we can use this prior knowledge about geophysical processes to verify the plausibility of the proposed methodology.

Fig. 5

Vertical site displacements in mm observed by GPS (grey), the fit of a trend function (blue), and the fit of a trend function together with annual and semi-annual terms and two offsets (red) using a LSA and b KF framework. Error bars are $1\sigma$. Starting from Oct. 2004, there are inflated uncertainty estimates in b, because of the co-estimation of two step-like offsets. In a, the over-optimistic formal LSA errors are barely perceptible

The GPS data at CAS1 are processed similar to Thomas et al. (2011). The GPS time series contains two step-like offsets (in Oct. 2004 and Dec. 2008) within the chosen estimation period, which is Feb. 2003 to Dec. 2010. For the same period, GRACE monthly time series are computed at Delft University of Technology (Farahani 2013) complete to spherical harmonic degree/order 120 and optimally filtered using a Wiener filter (Klees et al. 2008). Stokes coefficients representing the monthly gravity fields were converted into vertical deformations following Kusche and Schrama (2005) making GRACE data comparable with GPS observations. This conversion is done for potential validation which, as will be shown later, leaves room for physical interpretations if the proposed methodology is applied.

Results

Results derived by modeling signal constituents stochastically within the KF framework are called hereinafter KF results for brevity. We show plots in the time and frequency domain for GPS and GRACE time series at the same geolocation. Both time series represent vertical deformations due to GIA and the elastic response of the solid Earth to the surface load. Before discussing the results it is worth noting that what is called trend (in mm) thereafter is the integrated random walk part of the signal ($\mu _{t}$ in Eq. 8) with deterministically modeled intercept and time-varying slope (or rate) in mm/year introduced as $\beta _{t}$ in Eq. (8).

For GRACE time series, we estimate the slope, and annual, semi-annual and tidal S2 periodic terms deterministically using LSA and stochastically using the KF framework. In both cases, the intercept is co-estimated deterministically. Figure 4 shows vertical deformation derived based on GRACE data, the LSA fit and the KF fit, as well as estimated trends using different techniques. Error bars represent one-sigma uncertainties. Figure 4a, b serves as a visual inspection and indicate that the model which allows signal components to vary in time represents the data considerably better than the model that assumes a linear trend and exactly periodic processes with constant amplitudes.

Figure 5 demonstrates similar results as Fig. 4, but for GPS vertical site displacements. LSA results shown in Fig. 5a were generated by fitting intercept, slope, annual and semi-annual terms and two offsets to the time series without modeling colored noise. Time-correlated noise model is usually used to estimate more realistic parameter uncertainties than those resulting from white noise assumption (Thomas et al. 2011). However, to generate the KF results, we co-estimated time-correlated noise parameters as well. Following the procedure described in Sect. 2.5.2, we computed the noise PSD function of the LSA residuals, which is shown in black in Fig. 6. An AR(3) model (red in Fig. 6) was found to provide the best fit to the PSD of the approximate colored noise. Colored noise in the GPS time series was then parameterized with three autoregressive coefficients and co-estimated along with signal components. The results in Fig. 5 suggest that the KF method (Fig. 5b) outperforms the LSA method (Fig. 5a).

Fig. 6

The PSD (power spectral density) of AR(3) model (red) that best fits the PSD of the postfit residuals (black), whereby LSA was used to fit a multi-parameter model to the GPS time series at the CAS1 site

Fig. 7

Slope estimates in mm/year: KF time-varying slope (black), mean slope derived from KF time-varying slope (red), and LSA estimated slope (blue). a GRACE time series and b GPS time series. Error bars are $1\sigma$. The legend shows the values for the mean slope derived from KF time-varying slope (red) and for the LSA estimated slope (blue). Note, that different scales are used

Because estimating rates/slopes as accurately as possible is the primary motivation of this study, Fig. 7 outlines the corresponding results. A constant slope as a result of a deterministic fitting along with the stochastically modeled time-varying slope are shown for GRACE (Fig. 7a) and GPS time series (Fig. 7b). To allow for a direct comparison between LSA and KF results, we compute a mean slope from the time-varying slope. If there were no changes in the rates of vertical deformation, the two constant values should be the same. In fact they differ significantly, as the proposed methodology suggests the presence of low-frequency variability in the slope component (black curves in Fig. 7) that cannot be explained by any other modeled component. For GRACE, the constant slope estimated using LSA is $0.20 \pm 0.07$ mm, whereas the mean slope determined from the time-varying estimates is $0.36\pm 0.12$ mm. Although these are small numbers in absolute terms, their relative difference is larger than 50 $\%$. For GPS, the slope derived based on KF is almost 2.5 times smaller than the LSA based slope estimate being $0.77 \pm 0.46$ and $1.89 \pm 0.11$ for KF and LSA, respectively.

Fig. 8

Amplitude spectra for observations (black), postfit residuals using the proposed KF technique (red) and the LSA technique (blue). a GRACE time series and b GPS time series. Root mean square (RMS) misfits are indicated for both KF and LSA. Note, that different scales are used

To explain the different uncertainty estimates shown in Fig. 7, it is worth mentioning here that we propagated the correlations between errors of subsequent KF slope estimates into the mean slope. To compute the covariance matrix for the smoothed state vector $\hat{\alpha }_t$, that is, $\mathrm{Cov}(\alpha _t-\hat{\alpha }_t, \alpha _j-\hat{\alpha }_j)$ for $t = 1, \ldots , n$ and $j = t+1,\ldots ,n$, the quantities defined in Sect. 2.3 were used according to Durbin and Koopman (2012, chap. 4.7):

$$\begin{aligned} \mathrm{Cov}(\alpha _t-\hat{\alpha }_t, \alpha _j-\hat{\alpha }_j) = P_t L_t^\mathrm{T} L_{t+1}^\mathrm{T} \cdots L_{j-1}^\mathrm{T}(I- N_{j-1}P_j). \end{aligned}$$

(30)

For the case $j = t+1, L_{t+1}^\mathrm{T} \cdots L_t^\mathrm{T}$ is replaced by the identity matrix I, which has a dimension of the estimated state vector. To compute the uncertainty estimates from LSA, formal errors were rescaled by the a posteriori variance. This is a commonly used approach (e.g., Baur 2012) which yields over-optimistic uncertainties (e.g., Williams 2003a).

In the context of slope estimation, we find it worth noting that, especially for Antarctic GPS site velocities that are used to constrain GIA rates, each erroneously estimated millimeter of vertical deformation corresponds to significantly erroneous ice-mass change estimates (Gunter et al. 2014) highlighting the need to estimate these rates as accurately as possible.

To prove the presence of low-frequency variability in the slope component estimated with the KF technique, we compute the amplitude spectrum of the GRACE and GPS time series (cf. Fig. 8a, b, respectively). The results confirm the presence of long-term variations that deviate from a linear trend in both time series. While these inter-annual variations are absorbed in the residuals when using LSA (blue graphs in Fig. 8), they are captured by the KF (red graphs in Fig. 8) and map into the time-varying slope component (Fig. 7). Considering root mean square (RMS) misfits for quantitative comparison, there is an approximate 41 % and 13 % reduction in RMS misfits for GRACE and GPS time series, respectively, as a result of using the proposed KF instead of the LSA technique. As can be seen from Fig. 8, the dominant reduction of the RMS misfit is due to the time-varying slope with a smaller part being explained by the time-varying annual signal (the amplitude of the KF residuals around the 1 cycle-per-year frequency is smaller than the amplitude of the LSA residuals). The signals in the high-frequency domain are considered as noise.

Fig. 9

Time-varying slope for GRACE and GPS time series at the geolocation of the CAS1 site when using the proposed KF technique. Time-varying error bars are $1\sigma$

Fig. 10

Estimated time-varying slope (top) and annual signal (bottom, dashed line) along with the time-varying annual amplitude (bottom, solid line) for GPS vertical site displacements using the proposed KF framework. a When limiting the parameter search space for finding an optimal minimum and b without limiting the parameter search space. Note, that different scales are used

To validate the results based on the proposed methodology from the geophysical point of view, we plot the estimated time-varying rates derived from GPS and GRACE time series, respectively, in Fig. 9. The known accumulation anomaly event from 2009 is clearly evident. In this year, GPS and GRACE observe maximum subsidence of the solid Earth as an immediate response to the high levels of accumulation within the analyzed time period. Although the two observing systems do not agree perfectly, they do observe similar processes starting from 2005. In fact, there are a number of different factors to be considered when comparing GPS and GRACE time series, such as the spatial resolutions of the data sets (GPS-derived deformations are discrete point measurements, while GRACE results represent a spatial average), the effects of geocenter motion should be considered when converting GRACE coefficients into vertical deformation, etc. Though the validation of different geodetic observing techniques is beyond the scope of this study, we feel the proposed methodology provides better interpretation opportunities (Fig. 9) than the traditional LSA approach. It should also be noted that once GRACE and GPS time series are corrected such that they represent the same signal, it is straightforward to combine them within the described approach. However, the GRACE and GPS time series are used in this study only to validate the proposed methodology, and their data combination is also beyond the scope of this paper. It is also worth mentioning here that we have chosen this GPS station because of the existing prior knowledge about the geophysical process (accumulation anomaly) that took place there in 2009. Two different observing systems, GPS and GRACE, detected this geophysical process because of its high magnitude. While estimating time-variable rates, the time series from these two different observing systems were treated in two different ways with respect to the observational noise model used: white noise for GRACE and colored noise for GPS time series. Nonetheless, the time-varying trends derived from the GRACE and GPS time series show the same behavior. We therefore interpret this behavior as a signal and not as potentially mismodeled observational noise.

The target of this study is to provide a robust tool for reliable trend estimation. The robustness of the proposed methodology is determined by finding an optimal minimum that is necessary for estimating the noise parameters (Sect. 2.4) which, in turn, are the key for reliable rate estimates. To demonstrate the role of the noise parameters on the estimated signal components, we use the example shown in Fig. 2. Based on the GPS time series, we estimate the noise parameters by limiting the parameter search space for finding an optimal solution (as it is done through this section) and without limiting the parameter search space. Using these differently estimated noise parameters, we estimate modeled signal constituents. In Fig. 10, we illustrate the results for the slope and the annual component in the time domain (there is no evident difference in the semi-annual component, as can be seen in Fig. 2). By limiting the parameter search space, the process noise for the slope and annual component is estimated to be 0.37 mm/year and 0.06 mm, respectively. The corresponding estimates are shown in Fig. 10a suggesting a correlation between both the changes in the rates of vertical deformation and their annual variability. This is physically reasonable, as both are responses to the changing climate.

If the parameter search space is not limited, the process noise for slope and annual signal is $5.75\times 10^{-8}$ mm/year and 0.34 mm, respectively. Figure 10b shows the corresponding plots. Because the slope is not allowed to vary much, it is comparable with the LSA estimate shown in Fig. 7b. However, the variance of the annual component is much higher than the one used in Fig. 10a, which is why the corresponding annual amplitude in Fig. 10b shows an erratic behavior.

We could also assume the noise parameters to be known, e.g., by modeling the slope deterministically and using a fixed standard deviation for the annual signal. The higher we set this standard deviation the more we force the annual signal to absorb long-term variations and possible variations originating from other sources, yielding wrong interpretations. Therefore, we recommend to limit the parameter search space as described in Sect. 2.4.2 and to verify potentially existing prior knowledge about noise parameters according to Sect. 2.4.3 to ensure the reliability of the estimated signal constituents. Moreover, we suggest modeling all signal components stochastically to ensure a reliable noise parameter estimation, unless there are good reasons not to do so.

Conclusions

We developed a robust method for estimating time-variable trends from geodetic time series. This method is more sophisticated compared to commonly used LSA, as it allows the rate and seasonal signals to change in time. The advantages are twofold: more reliable trend estimation, because (i) there is no contamination by seasonal variability and (ii) it accounts for any long-term evolution in the time series, which would appear as noise when modeled as a time-invariant slope.

The right choice of the noise parameters is at the heart of the proposed methodology. We suggested a method which allows a robust estimation of the noise parameters. We verified the reliability of the estimates using spectral analysis. The plausibility of the estimated time-varying rates was additionally confirmed by existing geophysical knowledge. Furthermore, the results estimated using the KF framework were visually compared with those derived using LSA in the time and frequency domains. Visual inspections and RMS misfits suggested that the KF outperforms LSA. The proposed methodology is not limited to GPS and GRACE time series, but can be used for any other time series.

Our results suggest that potential changes in rates may yield significantly different trends when post-processed compared to the deterministic linear trend. Indeed, the longer the time series, the more deviations can be expected from the deterministic linear trend assumption as well as from the constant seasonal amplitudes and phases. Moreover, any change in the trend term reflects an acceleration, making the stochastic approach much more flexible than the deterministic one. It can therefore be reasonable to consider signal as a stochastic process in particular when analyzing climatological data.