Abstract
The time variable Earth’s gravity field contains information about the mass transport within the system Earth, i.e., the relationship between mass variations in the atmosphere, oceans, land hydrology, and ice sheets. For many years, satellite laser ranging (SLR) observations to geodetic satellites have provided valuable information of the low-degree coefficients of the Earth’s gravity field. Today, the Gravity Recovery and Climate Experiment (GRACE) mission is the major source of information for the time variable field of a high spatial resolution. We recover the low-degree coefficients of the time variable Earth’s gravity field using SLR observations up to nine geodetic satellites: LAGEOS-1, LAGEOS-2, Starlette, Stella, AJISAI, LARES, Larets, BLITS, and Beacon-C. We estimate monthly gravity field coefficients up to degree and order 10/10 for the time span 2003–2013 and we compare the results with the GRACE-derived gravity field coefficients. We show that not only degree-2 gravity field coefficients can be well determined from SLR, but also other coefficients up to degree 10 using the combination of short 1-day arcs for low orbiting satellites and 10-day arcs for LAGEOS-1/2. In this way, LAGEOS-1/2 allow recovering zonal terms, which are associated with long-term satellite orbit perturbations, whereas the tesseral and sectorial terms benefit most from low orbiting satellites, whose orbit modeling deficiencies are minimized due to short 1-day arcs. The amplitudes of the annual signal in the low-degree gravity field coefficients derived from SLR agree with GRACE K-band results at a level of 77 %. This implies that SLR has a great potential to fill the gap between the current GRACE and the future GRACE Follow-On mission for recovering of the seasonal variations and secular trends of the longest wavelengths in gravity field, which are associated with the large-scale mass transport in the system Earth.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Before the advent of the satellite missions dedicated to gravity field recovery, i.e., CHAllenging Minisatellite Payload (CHAMP), Gravity Recovery and Climate Experiment (GRACE), and Gravity field and steady-state Ocean Circulation Explorer (GOCE), the geodetic satellite laser ranging (SLR) satellites contributed most to the determination of Earth’s gravity field models (Cheng et al. 1997; Bianco et al. 1998). The high-degree coefficients of the SLR-derived gravity field were, however, of poor quality due to an inhomogeneous and sparse SLR network and due to correlations between coefficients of similar parity and same order. Using several SLR satellites, the coefficients could be decorrelated to some extent (Bianco et al. 1998) or the correlations could be addressed by deriving lumped geopotential harmonics (Cheng et al. 1997).
The CHAMP (Reigber et al. 1998) mission, launched in 2000, was the first satellite dedicated to the recovery of the Earth’s gravity field. The high quality of the CHAMP-derived static gravity models was obtained from continuous GPS observations (e.g., Reigber et al. 1998; Prange 2011).
The knowledge of mass transport within the system Earth was substantially improved after the launch of the GRACE (Tapley et al. 2004) mission in 2002. The tandem GRACE-A/B satellites allowed defining the relationship between mass variations in the atmosphere, oceans, land hydrology, and ice sheets with high temporal and spatial resolutions. The lowest-degree coefficients of the gravity field are, however, still better defined through the geodetic SLR satellites, because the K-band GRACE observations are nearly insensitive to the coefficients of degree 1 (geocenter), due to being a differenced measurement type, whereas the coefficient \(C_{20}\) is degraded due to long-period signals, because some signals in \(C_{20}\) have the same period as the \(S_2\) and \(S_1\) tidal aliases with GRACE orbits (Seo et al. 2008; Chen et al. 2009). Therefore, the SLR satellites have still a non-negligible potential to determine the low-degree parameters of Earth’s gravity field (Maier et al. 2012; Ries and Cheng 2014).
The GRACE mission was originally designed for 5 years, but even today, after 13 years of the mission, the GRACE satellites still provide accurate data. There is, however, a serious risk that the mission may be terminated at any time. The GRACE Follow-On mission (the successor of the GRACE mission) is planned to be launched in 2017 (Watkins et al. 2014), implying that most likely there will be a gap between the missions. This paper addresses the contribution of SLR in a view of filling this gap in recovering the time variable low-degree coefficients of the Earth’s gravity field from non-dedicated satellite missions, namely the SLR satellites.
In the framework of gravity field recovery, the geodetic SLR satellites were typically used for defining the low degree Earth’s static gravity field (Maier et al. 2012) or for defining the variations of the zonal spherical harmonics (Bianco et al. 1998; Cheng et al. 1997). The analysis of SLR-derived time variable tesseral and sectorial harmonics was typically limited to the coefficients of degree 2, which are well recoverable from SLR data (e.g., Chen and Wilson 2003, 2008; Chen et al. 2009; Bloßfeld et al. 2015). Lemoine et al. (2006) and Matsuo et al. (2013) show that the temporal changes in gravity field parameters up to degree/order (d/o) 4/4 can also be recovered from SLR data. Here we study the possibility of recovering the time variable geopotential coefficients from SLR and we compare the results with the GRACE solutions. We focus, in particular, on the comparison of seasonal variations of the coefficients derived from SLR and GRACE solutions.
Ries and Cheng (2014) recommend that the SLR gravity field solutions should be estimated with the expansion up to at least d/o 7/7 in order to capture continental scale signals and to discriminate of finer scale features with full amplitudes. The authors also find that the truncation of the SLR solution to an insufficient d/o causes, e.g., a change in the estimated trend in \(C_{21}\) due to a strong correlation with \(C_{61}\). Only the expansion of the gravity field solution to a higher d/o allows resolving the \(C_{21}\) trend that is comparable with the GRACE results.
In Sect. 2, we describe the methods and models applied in the SLR gravity field solutions, including in particular the orbit parameterization of spherical satellites’ orbits. We characterize and compare the observation principles, advantages and disadvantages of SLR and GRACE solutions. Section 3 is devoted to the sensitivity of SLR satellites and sensitivity of SLR solutions to the Earth’s gravity field. Our work was motivated by the wish to extract from SLR the maximum possible spatial resolution for time variable gravity fields based on 1 month of data. We decided to use the expansion of SLR solutions to d/o 10/10. However, due to strong correlations between the gravity field parameters, not all coefficients can be freely recovered by SLR. This issue is addressed in Sects. 2 and 3. Section 4 compares and analyzes the seasonal gravity field variations and secular geoid deformations obtained from SLR and GRACE solutions, addresses the limitations of both techniques, and presents the advantage of the combined SLR-GRACE solution. The final discussion and the summary are included in Sect. 5.
The monthly SLR gravity field solutions are available at the AIUB aftp.Footnote 1
2 Method of analysis
We generate the Earth’s gravity field coefficients derived from SLR observations to two high orbiting LAGEOS satellites, and up to seven low orbiting geodetic satellites: Starlette, Stella, AJISAI, LARES, Larets, BLITS, and Beacon-C (see Table 1). However, the results depend primarily on five satellites: LAGEOS-1/2, Starlette, Stella, AJISAI, because LARES contributes since February 2012, whereas Larets and BLITS provide little additional information that was not already being provided better by Stella, and the contribution of Beacon-C is strongly downweighted. The SLR gravity field solutions are computed using a development version of the Bernese GNSS Software (Dach et al. 2007; Thaller et al. 2011). The gravity field is expanded up to d/o 10/10 with a monthly temporal resolution for 2003.0–2014.0 with a simultaneous estimation of satellite orbits, Earth rotation parameters (ERP), and station coordinates from a combined SLR solutions incorporating many geodetic satellites.
The temporal variations of the Earth’s gravity field, namely the AIUB-RL02 GRACE series, are computed from GRACE K-Band observations and satellite positions (Meyer et al. 2012) with the so-called celestial mechanics approach (Beutler et al. 2010). These GRACE results serve here as a reference for our SLR solutions.
2.1 SLR solutions
In our SLR gravity field solutions, 10-day orbital arcs are generated for both LAGEOS satellites and 1-day arcs for low orbiting geodetic satellites (see Table 2). Pseudo-stochastic pulses in the along-track direction (S) are set up once-per-revolution for low orbiting satellites, because they improve, e.g., the quality of simultaneously estimated ERP by 34 % (Sośnica et al. 2014). The once-per-revolution empirical orbit parameters in the out-of-plane direction (W) are estimated only for low orbiting satellites, because they absorb the modeling deficiencies, e.g., in a priori ocean tide models (Sośnica 2015). They are, however, not estimated for LAGEOS, because of the direct correlation between \(C_{20}\) and the sine term \(W_{\mathrm{S}}\) (e.g., Jäggi et al. 2012; Sośnica et al. 2012). The once-per-revolution empirical orbit parameters in along-track are estimated for all satellites in order to absorb mismodeled albedo and solar radiation pressure, or the not explicitly modeled Yarkovsky and Yarkovsky–Schach effects (Sośnica 2015).
The static part of AIUB-GRACE03 up to d/o 30/30 for LAGEOS and up to d/o 90/90 for low orbiting geodetic satellites is used as the a priori Earth’s gravity field model for both, the SLR and the AIUB-RL02 GRACE series (Meyer and Jäggi 2014; Jäggi et al. 2011). The a priori gravity field coefficients for two terms, i.e., \(C_{21}\) and \(S_{21}\) are not taken from this model, but replaced as proposed by the IERS Conventions 2010 (Petit and Luzum 2011). The IERS model for \(C_{21}\)/\(S_{21}\) is restored in the final processing stage, thus, the SLR and the GRACE solutions are consistent and fully comparable. EOT11a (Savcenko and Bosch 2010) was used as the a priori ocean tide model. The station displacement corrections due to atmospheric loading are applied in order to remove the impact of the Blue-Sky effect (Sośnica et al. 2013). The pole tide is considered for both, the SLR and GRACE solutions in the way described by IERS Conventions 2010, including the conventional mean pole definition, whereas for the ocean pole tide the model described by Desai (2002) is applied for GRACE and SLR.
Atmosphere and ocean de-aliasing product (AOD, Flechtner 2007) RL05 has been used for de-aliasing with the corrections applied at the observation level with both atmosphere and ocean-induced gravity variations.
SLRF2008,Footnote 2 i.e., the International Laser Ranging Service’s (ILRS) realization of the International Terrestrial Reference Frame 2008 (Altamimi et al. 2011), serves as a priori reference frame. The datum is defined for every solution by imposing the no-net-rotation and no-net-translation minimum conditions on a set of core stations as recommended by ILRS. The ILRS table of data correctionsFootnote 3 containing, e.g., range biases and data exclusions is used, as well.
The orbit perturbations due to the direct and indirect solar radiation pressure (albedo reflectivity and Earth’s infrared emissivity) are applied assuming the satellites as uniform spheres with fixed radiation coefficients. The specularity of the Earth’s surface is neglected (Rodriguez-Solano et al. 2012). For low orbiting satellites, we apply the NRLMSISE-00 (Picone et al. 2002) atmospheric drag model and we estimate daily scaling factors instead of a constant acceleration in along-track (\(S_0\), see Table 2) along with the once-per-revolution pseudo-stochastic pulses in along-track.
We use the piecewise-linear (PWL) ERP parameterization. In PWL the polar motion and UT1–UTC parameters are continuous at the day boundaries due to a polygonal representation, as opposed to the piecewise-constant parameterization. UT1–UTC is fixed to the a priori IERS-08-C04 series (Bizouard and Gambis 2012) at the boundary between the fourteenth and fifteenth day of the solution. The pole coordinates and length-of-day (LoD) parameters are loosely constrained (1 m sigma) to the IERS-08-C04 series.
Sośnica (2015) shows that the simultaneous estimation of gravity field coefficients along with ERPs and station coordinates is particularly beneficial for the determination of the LoD. The co-estimation of the gravity field parameters reduces the a posteriori error of estimated LoD values by a factor of thirteen, and reduces by a factor of twelve the offset of LoD estimates w.r.t. the IERS-08-C04 series, which is mostly due to absorption of the \(C_{20}\) variations by LoD estimates. As a result, Sośnica (2015) concludes that the SLR solutions with the simultaneous estimation of gravity field coefficients along with ERPs and station coordinates are superior as compared to the SLR solutions in which only a selected group of parameters is estimated. We estimate simultaneously SLR station coordinates along with the gravity field parameters. Zelensky et al. (2014) prove that the temporal changes in the Earth’s gravity field are crucial when the high-quality SLR station coordinates are to be obtained.
The gravity field parameters are obtained in a three-step procedure. In the first step, 1-day normal equations are generated individually for every low orbiting satellite and 10-day normal equations are generated for LAGEOS-1/2 using screened observation files. In the second step, 10-day solutions are generated by combining SLR observations to all satellites through stacking all common parameters except for the orbital parameters which are pre-eliminated before stacking, and thus, just implicitly contained in the resulting normal equation. At this stage, the continuity of ERPs is enforced at day boundaries, and the pseudo-stochastic pulses are constrained with sigma \(1.0\times 10 ^{-8}\) m/s before stacking. Finally, monthly solutions are generated by stacking all parameters from three 10-day normal equations and by imposing minimum constraints on the core stations in the network, on ERPs, and on gravity field parameters. We found that the gravity field parameters up to d/o 6/6 can be derived from SLR without any regularization. Solutions up to d/o 10/10, which are discussed in this paper, require imposing some constraints (in this case of \(2.5\times 10 ^{-10}\)) due to a limited sensitivity of SLR solutions to the coefficients between degrees 7 and 10 (see Sect. 3), especially for the period before the launch of LARES.Footnote 4 Different weights are introduced for normal points to different satellites; ranging from 8 mm for LAGEOS-1/2, 15 mm for LARES, 20 mm for Starlette and Stella, 25 mm for AJISAI, 30 mm for Larets and BLITS, and finally 50 mm for non-spherical Beacon-C (see Table 1).
2.2 Satellite parameters
Due to the lack of information about some satellite parameters, we estimated first the center of mass corrections (CoM) and area-to-mass ratios (A/m) for some low orbiting satellites. We found a significant difference of CoM for Larets (63.1 mm) with respect to the nominal value (56.2 mm). This result agrees well with the findings of the ILRS Analysis Working Group,Footnote 5 reporting that the nominal value of CoM for Larets should be about 65 mm. For Beacon-C (BE-C, also known as Explorer 27), which is hardly observable by SLR stations in the Southern hemisphere due to the stabilization w.r.t. the Earth’s magnetic field (Cheng et al. 1997), we found a significant difference between CoM corrections for stations in the Northern and Southern hemisphere, amounting to 285 and 220 mm, respectively. It is the only non-spherical satellite used in our analysis. Beacon-C was the second satellite with laser retro-reflector arrays in Earth’s orbit (launch on April 29, 1965). The satellite is pyramidal in shape and equipped with solar panels, which increase its area-to-mass ratio (see Table 1), but due to low orbital inclination (41\(^{\circ }\)) and high eccentricity, it is useful for the separation of the secular variations in the odd zonal harmonics (Cheng et al. 1997). However, Beacon-C is subject to large orbit perturbations due to the solar radiation pressure and atmospheric drag. Its contribution is therefore downweighted in the combined solutions (see Table 1). For BLITS and LARES we did not find any significant differences w.r.t. the nominal CoM values. For Starlette, Stella, and AJISAI we used the values as provided by Sośnica (2015).
The range biases for LAGEOS are estimated only for selected SLR stations, as recommended by the ILRS Analysis Working Group, whereas the range biases for low orbiting satellites are estimated for all stations and all satellites.
2.3 Spatial distribution of SLR observations
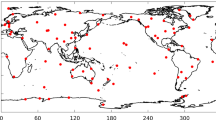
Figure 1 shows the groundtrack residuals of LAGEOS-1/2 and Starlette, Stella, AJISAI, respectively. The spatial gaps due to the inhomogeneous distribution of SLR sites and due to the orbital inclinations are larger for low orbiting SLR satellites. The observation distribution reveals that only few SLR data were collected when the satellites were passing over Greenland and hardly any data were collected over Antarctica. These regions are of special interest for the assessment of the ice mass loss in gravity field studies. A limited number of observations, especially to low orbiting satellites, suggests that the recovery of higher degree gravity field coefficients may be difficult over these regions, because the LAGEOS satellites alone are not sufficiently sensitive to high-degree gravity field variations.
2.4 Differences between SLR and GRACE solutions
The SLR solutions and the GRACE solutions, which serve as a reference in this paper, are based on entirely different measurement types (i.e., laser and microwave, respectively) and on different observation principles (direct ranges and differential inter-satellite observations, respectively), which lead to different limitations and superiorities of both techniques. Table 3 summarizes the differences, advantages, and disadvantages of the both, GRACE and SLR solutions.
3 Sensitivity of SLR solutions
Figure 2 shows the observability of the geopotential coefficients as the mean a posteriori formal errors of the SLR-derived coefficients. A combined LAGEOS-1/2 solution is very sensitive to \(C_{20}\). The LAGEOS sensitivity to coefficients of degree higher than 4 decreases rapidly. Coefficients of degrees 5 and 6 cannot be satisfactorily recovered from the LAGEOS-only solutions, whereas for degree 4 LAGEOS are highly sensitive to \(C_{40}\). Low LAGEOS sensitivity to \(C_{30}\) can be related to the estimated once-per-revolution orbit parameters in along-track, which are correlated with \(C_{30}\) as the odd zonal harmonics impose just short-term periodic variations and no secular drifts of satellite’s orbital elements. The once-per-revolution orbit parameters in along-track absorb, however, deficiencies in direct and indirect solar radiation pressure modeling and thermal effects. Thus, they should be estimated, because the modeling of thermal effects on LAGEOS is currently impossible due to little information about the satellites’ spin axis evolution.
Starlette, Stella, and AJISAI are most sensitive to tesseral and sectorial coefficients (Fig. 2). The low sensitivity to zonals can be explained by the short arcs (1-day) used for low orbiting satellites (as opposed to 10-day arcs for LAGEOS), because the even zonal coefficients can be derived particularly from secular variations in the orbital elements, i.e., a secular drift of the node and the argument of perigee. The estimation of empirical orbit parameters further reduces the sensitivity to zonal harmonics. Nevertheless, the correlations between empirical orbit parameters and gravity field coefficients can be substantially reduced in the solution using satellites with different inclinations and different altitudes. By additionally adding the LARES observations (third solution from top in Fig. 2) the formal errors of \(C_{30}\) and \(C_{50}\) are reduced by a factor of 8. The contributions of Beacon-C, Larets, and BLITS are much smaller, because the orbit quality of these satellites is poor, which is why their normal equation systems (NEQs) have to be downweighted. Moreover, Larets and BLITS have inclinations and altitudes similar as Stella. Therefore, they are also subject to resonances with diurnal and semi-diurnal tides and they do not contribute to a further decorrelation of gravity field parameters as long as the observations to Stella are used.
The formal errors of the solutions based on a single low orbiting satellite are quite high, because other parameters which are simultaneously estimated (e.g., station coordinates, ERPs) are not well established without the LAGEOS contribution (Sośnica et al. 2014). One should also bear in mind that a posteriori formal errors provide information on the observability of the parameters, but they say nothing about the effect of systematic errors, which supposed to be absorbed by empirical orbit parameters.
Nevertheless, when comparing the solution using three low orbiting satellites (fifth row from top in Fig. 2) and a combined solution of five satellites (sixth row from the top), the contribution of LAGEOS-1/2 is remarkable, even for coefficients of degree 6. This fact implies that the LAGEOS satellites substantially stabilize the combined solutions by providing a good observation geometry and the information related to other simultaneously estimated parameters, namely station coordinates and ERPs, even if the LAGEOS satellites do not contribute much to the estimation of high order coefficients directly. This means that a combined solution is preferable for the gravity field recovery.
The combined SLR solutions show a particularly high sensitivity to the sectorial gravity field coefficients (\(C_{22}\), \(S_{44}\), \(C_{66}\)), to the zonal terms, i.e., \(C_{20}\) and \(C_{40}\), and to the coefficients related to the Earth’s figure axis, i.e., \(C_{21}\) and \(S_{21}\). The formal error for none of the coefficients up to d/o 10/10 exceeds the value of \(3.5\times 10 ^{-11}\) in a combined solution, implying that all low-degree geopotential parameters are characterized by a good observability in the multi-satellite SLR solutions.
4 Results
Subsequently, we study the consistency between the SLR and GRACE gravity field solutions by comparing:
-
the amplitudes of seasonal signals,
-
the significance of seasonal signals,
-
the RMS of differences between the coefficients,
-
the correlation coefficients of gravity field parameters,
-
the spatial distribution of geoid deformations, and
-
the secular changes in the geoid height.
4.1 Seasonal signals
Before the actual analysis of the seasonal signals in gravity field coefficients, we checked first the significance of the SLR-derived amplitudes using a Fisher test. We assume that the significance of the estimated temporal variations may be calculated provided that their errors are normally distributed (their variances are \(\chi ^2\)-distributed). A detailed description of the F-test procedure for gravity field coefficients can be found in Davis et al. (2008) and Meyer et al. (2012).
Figure 3 shows the associated cumulative distribution function which is plotted to illustrate the significance of the estimated annual variations per coefficient displayed in triangular figures for SLR solutions (left) and GRACE solutions (right). In the GRACE solutions most of the gravity field coefficients up to d/o 10/10 are significant. Most of the annual signals recovered by SLR are significant up to d/o 6/6. For higher degree coefficients, the SLR solutions are contaminated by noise. On the other hand, SLR is able to recover the seasonal signals for degrees 7, 8, 9, and even 10, but only for selected coefficients. The majority of the SLR-derived signals are contained in coefficients up to d/o 6/6 and thus in the subsequent analyses we will concentrate in particular on these coefficients. Figure 3 also shows a lower sensitivity of SLR solutions to odd-degree coefficients (5, 7, and 9) as compared to even-degree coefficients. The \(S_{n1}\) coefficients, where \(n>3\), seem to be recovered by SLR to a lesser extent as compared to other coefficients. This is however not due to an insufficient sensitivity of SLR to these coefficients, but due to strong correlations between coefficients, e.g., between \(S_{41}\), \(-S_{61}\), \(S_{81}\), and \(-S_{10\, 1}\). Although the single coefficients typically indicate reduced seasonal variations, the total gravity signal is included in the lumped sum of all these harmonics.
The seasonal signals in SLR and GRACE solutions are derived through a fit to monthly solutions. Figure 4 shows the amplitudes of annual signals for low-degree coefficients in the SLR (left) and GRACE solutions (center) and the differences of the amplitudes in both solutions (right). The amplitudes in SLR solutions are typically smaller as compared to the GRACE results, with a median difference of 10 % when excluding zonal terms. The smaller amplitudes in the SLR solutions can be explained by the higher altitudes of SLR satellites as compared to GRACE, a truncation of SLR solutions up to different maximum degree than the GRACE solutions which may lead to an increase or to a decrease of the signal in some coefficients, or to correlations between harmonics resulting in the lumped coefficients. The level of agreement between SLR and GRACE results increases in time: it is lowest in 2003–2006 when the only one SLR station in South America, Arequipa, was subject to some technical issues, whereas newly established stations, San Juan and Concepción, were in the latest stage of the station deployment. The ILRS network achieved a good global distribution about 2008–2009, which also increased the observability of SLR-derived gravity field coefficients. The best level of the SLR-GRACE agreement is obtained after the launch of LARES in 2012. Nevertheless, the median difference of seasonal signals for low-degree coefficients up to d/o 6/6 between SLR-only and GRACE K-band for the whole period is \(7.5\times 10 ^{-12}\), i.e., 23 % of the median amplitude of the annual signal recovered by GRACE, which may be interpreted that the SLR-derived and GRACE-derived amplitudes agree at the level of 77 %.
Figure 4 (right) shows that the largest differences between the GRACE and SLR results are for the zonal harmonics. The coefficient \(C_{20}\) is affected by the \(S_2\) alias period in the GRACE solutions, whereas \(C_{30}\) and \(C_{50}\) are highly correlated in the SLR solutions (Devoti et al. 2001), therefore not possible to recover the whole seasonal variations. The maximum difference between the SLR and GRACE amplitudes in a relative sense is for \(C_{30}\), amounting to 128 %, and in the absolute sense for \(C_{50}\), amounting to \(4.6\times 10 ^{-11}\), whereas for non-zonal coefficients the maximum difference does not exceed \(1.9\times 10 ^{-11}\).
Figure 5 reveals, indeed, that the seasonal variations of \(C_{50}\) in the SLR solutions are noticeably smaller as compared to the GRACE results. The SLR-derived amplitude of the annual signal is 48 % smaller than the amplitude from GRACE solutions. However, including LARES into the SLR solutions, after its launch in February 2012, substantially improves the SLR solutions and, as a result, reduces the difference of the annual signal. This fact clearly shows that combining SLR observations to low and high orbiting geodetic satellites of different inclination angles is essential for deriving the geodetic parameters of the highest quality. The LARES contribution is essential thanks to the lowest A/m ratio of all artificial satellites, thanks to its low altitude, and its inclination of 69.5\(^{\circ }\) (see Table 1). Including LARES data reduces the formal errors of \(C_{50}\) from \(1.7\times 10 ^{-11}\) to \(0.6\times 10 ^{-11}\), i.e., almost by a factor of three.
\(C_{50}\) variations w.r.t. EGM2008 (Pavlis et al. 2012) derived from SLR and GRACE solutions (left) and the spectral analysis of the series (right). Green vertical line denotes the first epoch with the LARES’ contribution
Figure 6 shows examples of the time series of tesseral (\(S_{42}\) and \(C_{31}\)) and sectorial (\(S_{44}\) and \(C_{66}\)) coefficients. Coefficient \(C_{31}\) from the SLR solutions fails in the Fisher test for the significance of the annual signal (see Fig. 3), whereas GRACE-derived results show small seasonal variations. Nevertheless, the annual variations are not prominent in \(C_{31}\) even in the GRACE series. In the SLR series orbit modeling errors, which are larger than the seasonal amplitudes, dominate variations of this coefficient.
However, \(S_{42}\), \(S_{44}\), and \(C_{66}\) from Fig. 6 underline that not only the zonal and degree 2 coefficients can be established well from SLR solutions, but also some of the tesseral and sectorial terms with prominent seasonal variations. Although the non-zonal harmonics are associated with relatively small scale or regional mass transport, which results in smaller amplitude and higher frequency oscillations in the satellite orbit, they are detectable by SLR.
The spectral analysis of the GRACE time series in \(S_{44}\) (Fig. 6) shows a peak close to the \(S_2\) alias period of GRACE orbits (about 160 days) with an amplitude of \(20\times 10 ^{-12}\), whereas the SLR solutions are free of this peak. The \(S_2\) tidal alias is responsible for a low quality of the \(C_{20}\) variations derived from GRACE (Chen et al. 2009). However, not only \(C_{20}\), but also some other low-degree parameters are affected by the \(S_2\) tidal alias in the GRACE solutions. These peaks are possibly not due to actual tide model errors, but they should rather be associated with some twice-per-revolution thermal effects of the system GRACE. The SLR solutions are less sensitive to the \(S_2\) alias, because of the assimilation of the satellites with different \(S_2\) alias periods
On the other hand, the SLR solutions have their own orbit modeling issues mostly related to the modeling of radiation pressure or thermal effects, e.g., a period of 73 days corresponding to the draconitic year of Starlette (see Table 1), a period of 188 days which can be related to the draconitic year of Stella, BLITS or Larets, a peak related to the draconitic year of LAGEOS-2 (222 days), a peak related to Stella’s revolution period of the perigee (122 days) or a peak related to Starlette’s secular drift of the ascending node w.r.t. the sidereal year (\(365.25 \times \dot{\Omega }_{\mathrm{Starlette}}/(365.25-\dot{\Omega }_{\mathrm{Starlette}})=121\) days). Nevertheless, these peaks are small compared to the seasonal signals and their amplitudes do not exceed \(9\times 10 ^{-12}\), i.e., they are a factor of two smaller than the GRACE-\(S_2\) alias period seen in \(S_{44}\).
4.2 Correlations and RMS of differences
The RMS of differences provides a discrepancy between gravity field coefficients in an absolute sense. The RMS assumes large values in particular when the estimated coefficients are shifted by an offset or when they exhibit different seasonal variations. Correlation coefficients are meaningful as soon as the series is not only noise, thus, they shall reveal discrepancies of the ‘periodic’ (seasonal) signals, because the mean values (offsets) are removed. When a gravity field coefficient has no or only minor seasonal variations, the correlation coefficient between different series can be close to or equal zero, despite a very good agreement in terms of the RMS of differences. The comparison based on correlation coefficients is meaningful only for gravity field coefficients with explicit seasonal signals.
Figure 7, left shows the correlation coefficients between the SLR and GRACE series. The correlations are computed from the monthly time series of coefficients. The mean coefficient is 0.47 when taking all low-degree gravity field parameters and 0.51 when excluding zonal terms. The correlation coefficient is positive for all terms. However, it is close to zero for \(C_{40}\) and \(C_{43}\). Bettadpur et al. (2014) also found a low agreement between \(C_{40}\) variations derived from SLR and GRACE, resulting in the correlation coefficient close to zero.
However, despite a low correlation coefficient between SLR and GRACE solutions, the total RMS variations are close to the average for \(C_{40}\) and \(C_{43}\) (see Fig. 7 right) and the relative difference of RMS is at the level of 36 and 34 %, respectively. The seasonal variations in \(C_{40}\) and \(C_{43}\) are very small, implying that the correlation coefficients can also be low, but the overall RMS of differences does not show a remarkable offset or an incoherent signal between SLR and GRACE. All in all, the RMS of differences is at the comparable level of 30–40 % for all non-zonal gravity field coefficients. The differences are larger for \(C_{20}\) and \(C_{30}\) amounting to 80 and 53 %, respectively. This agrees with the findings of Bettadpur et al. (2014), who also disclose that the agreement between the zonal harmonics from GRACE and SLR is weaker than, e.g., that for the sectorial harmonics.
From a hypothesis test, the annual amplitudes of some zonal coefficient \(C_{20}\), \(C_{30}\), \(C_{60}\), and two tesseral \(C_{61}\) and \(S_{61}\) coefficients are statistically different between SLR and GRACE solutions at the confidence interval of \(2\sigma \). The other tesseral and sectorial coefficients are not different mostly due to high formal errors of these parameters in SLR solutions.
4.3 Spatial distribution of geoid deformations
Figure 8 compares gravity field models obtained by GRACE up to d/o 60/60 (top), GRACE up to d/o 10/10 (middle) and SLR up to d/o 10/10 (bottom) w.r.t. the reference field EGM2008 for March 2011. Figure 8 discloses that the most pronounced temporal geoid deformations, e.g., in Greenland, Amazonia, North America, Northern Australia agree well in GRACE and SLR solutions. On the other hand, the smaller geoid deformations can be recovered by SLR only to a limited extent, e.g., in Africa and Southeast Asia. SLR-derived deformations are smoothed as compared to the GRACE results and the amplitudes of geoid deformations are reduced. Nevertheless, the large-scale mass redistribution can be also recovered from an SLR analysis.
The largest temporal gravity variations are typically expected over the continents due to land hydrology. However, the SLR and GRACE solutions show also a comparable signal over the Indian Ocean, the Pacific, and the Northern part of the Atlantic. These variations can be associated with low-frequency and large-scale signals in ocean bottom pressure observations, which are not entirely modeled in the AOD corrections, because the AOD corrections are not able to model mass variations properly with time scales longer than roughly 1 month.
Interestingly, SLR is also able to recover the differences in the ice mass loss in the Antarctic region (see Fig. 8). None of the low orbiting SLR satellites were observed over this region (see Fig. 1). There is no SLR station in Antarctica, and moreover, in March 2011 there were only six active SLR stations in the Southern hemisphere, from which only three were used for the network constraints, i.e., the so-called SLR core stations. Fine and small-scale geoid variations can only be recovered from low orbiting satellites. The geoid recovery is however possible, despite large gaps in spatial coverage of SLR stations in the Southern hemisphere (see Fig. 1, right). As opposed to continuous satellite-to-satellite tracking in the GRACE solutions (low–low) or in the CHAMP, GRACE, or GOCE solutions (high–low), the SLR observations are noncontinuous, sparse and limited by the inhomogeneous distribution of SLR stations. The intrinsic analysis of orbit dynamics allows, however, the SLR solutions to determine the geoid deformation even of the areas over which none of the SLR satellite was observed, because the orbit dynamics implicitly carries valuable information about the Earth’s gravity potential as a whole.
The SLR solutions are, however, limited in their spatial resolution, implying that only the largest variations can be recovered by SLR. The spatial resolution can be increased by introducing mascons or by combining the SLR solutions with GRACE or with other satellite-to-satellite tracking data, e.g., CHAMP or SWARM (Weigelt et al. 2014, 2015). The latter approach allows for the recovery of gravity field variations between GRACE and GRACE Follow-On missions and even before the launch of GRACE.
Figure 9 shows the comparison between SLR and GRACE solutions not only for one example month, but for the entire period of the common solutions. The sine coefficients (top) agree substantially well in both solutions with almost identical locations of the largest geoid variations which, as expected, are mostly limited to the areas of continents. However, the amplitudes are smaller in the SLR solutions, which is indicated in different scales of the colorbars. The smaller amplitudes of annual signal in SLR solutions can be associated with a limited sensitivity of the SLR solution to coefficients of degree between 7 and 10, for which SLR is capable of recovering variations only for the selected coefficients (see Fig. 3). All in all, for the sine coefficient the patterns in GRACE and SLR match remarkably well. For the cosine term, for which the amplitudes are typically much smaller, the agreement is poorer. The bottom figures with the amplitudes of the annual signal show that all the largest geoid variations, which are determined by GRACE, can also be recovered by SLR. However, there is one exception in South Africa, where the SLR recovery fails. Although the SLR solutions are slightly noisier over the oceans, the largest variations are concentrated over the lands and agree with the GRACE solutions.
4.4 Secular changes in geoid height
Figure 10 compares the secular changes in the geoid height derived from GRACE and SLR for the same period. The comparison shows that the geoid changes in SLR solutions are ’spilled’ over oceans and they are not limited to the areas of continents, because of the truncation of the spherical harmonic expansion. Some of the smaller geoid changes, e.g., the post-glacial rebound in Scandinavia could not be properly resolved by SLR, due to opposite trends in neighboring areas. Not all trends in the SLR-derived coefficients between degrees 7 and 10 can be fully recovered due to insensitivity of SLR solutions to a few coefficients (Sect. 4.1; Fig. 3). On the other hand, not only the largest secular changes in Greenland and Antarctica agree well between SLR and GRACE, but also some of the smaller deformations in the Amazonian region and Africa show similar trends in the SLR and GRACE solutions. The signals related to, e.g., the Patagonian glaciers melting or to droughts in California can also be recovered by SLR, to some extent.
We can conclude that the agreement for secular geoid changes between SLR and GRACE solution is at a high level, especially for the regions crucial for geophysical gravity studies, e.g., Greenland and Antarctica, however, SLR-derived fields have a limited spatial resolution.
4.5 The GRACE-SLR combined solution
Combination of SLR and GRACE solution at the observation level is superior compared to a solution with replacing \(C_{20}\) values in the GRACE series by the SLR-derived values (Lemoine et al. 2010). This, however, raises a question: whether SLR solutions provide sufficient information to contribute to GRACE-derived gravity field coefficients other than \(C_{20}\)?
Figure 11 shows the formal errors of the SLR solutions (top), GRACE solutions (middle), and GRACE-SLR combined solutions (bottom) in log scales. The GRACE-SLR combination was done at the NEQ level with minimizing the sum of squares of the formal a posteriori errors in the combination. In the GRACE solutions, the largest formal errors result for the sectorial terms and for degree 2 coefficients. In the SLR solutions the formal errors are smallest for \(C_{20}\) and \(C_{40}\), whereas for other coefficients the values are comparable without a clear distinction between the sectorial, tesseral and zonal terms. However, in the SLR series the formal errors are noticeably smaller for even degrees (2, 4, 6) than for odd degrees (3, 5). All in all, the formal errors are on average a factor of 10–20 larger in the SLR solutions than in the GRACE solutions.
One has to bear in mind that the gravity field coefficients in SLR solutions are strongly correlated, which has also an impact on formal errors. For instance, the mean correlation coefficient \(\rho \) between gravity field parameters of similar parity and same order amount to: \(\rho ^{C_{20}}_{C_{40}}=-0.67\), \(\rho ^{C_{20}}_{C_{60}}=+0.42\), \(\rho ^{C_{21}}_{C_{41}}=-0.47\), \(\rho ^{C_{21}}_{C_{61}}=+0.78\). The largest value of the correlation for \(\rho ^{C_{30}}_{C_{50}}=-0.98\) is reduced to \(-0.86\) when including LARES data. In the GRACE solutions the correlations are typically smaller. However, the GRACE-derived coefficients of the same order show as well some correlations, e.g., \(\rho ^{C_{21}}_{C_{41}}=-0.11\), \(\rho ^{C_{41}}_{C_{61}}=-0.17\), \(\rho ^{C_{61}}_{C_{81}}=-0.24\), whereas the largest correlations are between sectorial coefficients and corresponding tesseral coefficients of the same order, e.g., \(\rho ^{C_{44}}_{C_{64}}=+0.67\), \(\rho ^{C_{66}}_{C_{86}}=+0.60\).
The combination of SLR and GRACE solutions (Fig. 11, bottom) substantially reduces the formal error of \(C_{20}\) (by a factor of 12 compared to GRACE-only) and slightly reduces the errors of \(C_{21}\) and \(S_{21}\) (by 11 %), which are related to the excitation of the pole. The formal errors of other coefficients remain at the same level in GRACE-only and GRACE-SLR solutions, illustrating a dominating character and the strength of GRACE K-band observations as compared to the sparse SLR data. The combination of SLR and GRACE solutions reduces the correlations between some parameters, e.g., \(\rho ^{C_{20}}_{C_{40}}=-0.134\) in the GRACE solutions is reduced to \(-0.002\) in the combined GRACE-SLR solution, and \(\rho ^{C_{60}}_{C_{80}}=-0.298\) is reduced to \(-0.004\). The correlations between sectorial coefficients and tesseral coefficients of the same order are only marginally reduced, e.g., from \(\rho ^{C_{66}}_{C_{86}}=+0.60\) to \(+0.58\) for GRACE-only and the combined solution, respectively.
5 Summary
We have shown that the low-degree gravity field coefficients can be well established from SLR observations to geodetic satellites. Low-degree coefficients carry information about large-scale mass transport in the system Earth. The largest seasonal variations in the geoid deformation, e.g., in Amazonia, Southeast Asia, Greenland and Africa can be derived from the solutions combining SLR observations to high orbiting LAGEOS and to low orbiting Starlette, Stella, AJISAI, LARES, Larets, BLITS, and Beacon-C satellites. However, the results depend primarily on five satellites: LAGEOS-1/2, Starlette, Stella, AJISAI, because LARES contributes since February 2012, whereas Larets and BLITS provide little additional information that was not already being provided better by Stella, and the contribution of Beacon-C is strongly downweigthed. The solutions benefit from the 10-day arc solutions for LAGEOS and 1-day arc solutions for low orbiting satellites, whose orbit modeling deficiencies are minimized due to short 1-day arcs. Our analysis showed that the SLR observations have the capability to retrieve the time variable gravity signal with a spatial resolution up to d/o 10/10 when applying the methods and constraints described in Sect. 2.1. However, only the coefficients up to d/o 6/6 can freely be recovered in the period before the launch of LARES due to a low sensitivity of SLR solutions to coefficients of degree between 7 and 10 (see Fig. 3) and due to high correlations between coefficients (see Sect. 4.5).
We discussed three factors limiting the quality of SLR solutions, which are related to:
-
deficiencies in the background models and in the orbit parameterization (in particular, the \(S_2\) tidal alias),
-
deficiencies in modeling non-gravitational orbit perturbations, which typically have periods of the draconitic year or its harmonics,
-
correlations between geopotential parameters (e.g., \(C_{30}\) and \(C_{50}\)) or correlations between geopotential parameters and satellite orbit parameters.
Fortunately, the problem related to the alias with the \(S_2\) tide is much smaller in the SLR solutions compared to the GRACE analyses. The deficiencies in modeling of non-gravitational orbit perturbations related to solar radiation pressure can be mitigated by estimating a small number of empirical orbit parameters, whereas the perturbation due to variations of atmosphere density can be addressed by estimating pseudo-stochastic pulses in the along-track direction. The simultaneous estimation of ERPs and station coordinates further reduces the insufficient quality of a priori models. The correlations between geopotential parameters can be reduced by including many geodetic satellites with different altitudes and inclinations. The contribution of LARES, starting from February 2014, is substantial for the quality of the estimated \(C_{50}\) series.
The largest disagreement between SLR and GRACE solutions was found for zonal terms. The mean correlation coefficient is 0.47 when taking all low-degree gravity field parameters and 0.51 when excluding zonal coefficients. The amplitudes of the annual signal in SLR solutions up to d/o 6/6 are typically smaller by about 10 % as compared to the GRACE results. The smaller amplitudes in the SLR solutions can be associated with a lower sensitivity of SLR satellites due to their higher altitudes as compared to GRACE satellites and empirical once-per-revolution orbit parameters which are estimated in the SLR solutions along with other parameters and may also absorb some geopotential signals. The truncation of SLR solutions up to different maximum degree than the GRACE solutions may also lead to a change in the estimated amplitudes of seasonal signals. However, the secular trends in geoid deformations agree between the SLR and GRACE results to a very high extent.
The median differences of seasonal signals for low-degree coefficients up to d/o 6/6 is \(7.5\times 10 ^{-12}\) between SLR-only and GRACE K-band solutions, i.e., only 23 % of the mean total annual signal recovered by GRACE. The Antarctic and Greenland regions are essential in the geophysical studies of the mass transport. We have shown that the SLR solutions are also able to recover the differences in the ice mass loss in the Antarctica and Greenland, including both the secular and seasonal variations, although none of the low orbiting SLR satellites were observed over Antarctica directly. The secular changes in geoid height related to the Patagonian glaciers melting or the droughts in California can also be recovered by SLR.
The SLR solutions are limited in their spatial resolution, implying that only the largest mass transport can be recovered. The spatial resolution can be increased, e.g., by combining the SLR solutions with GRACE or with other satellite-to-satellite tracking data. The latter approach allows for filling the gap in gravity field recovery between GRACE and GRACE Follow-On missions or allows even for a multi-decadal analysis of the mass transport in the system Earth prior to the launch of GRACE or CHAMP.
Notes
The unconstrained solutions up to d/o 6/6 and the constrained solutions up to 10/10 are available through the AIUB aftp.
References
Altamimi Z, Collilieux X, Métivier L (2011) ITRF2008: an improved solution of the international terrestrial reference frame. J Geod 85(8):457–473. doi:10.1007/s00190-011-0444-4
Beutler G, Jäggi A, Mervart L, Meyer U (2010) The celestial mechanics approach—theoretical foundations. J Geod 84(10):605624. doi:10.1007/s00190-010-0401-7
Bettadpur S, McCullough C, Ries J, Cheng M (2014) Use of GNSS and SLR tracking of LEO satellites for bridging between GRACE and GRACE-FO. In: Proceedings from the GRACE science team meeting, Potsdam
Bianco G, Devoti R, Fermi M, Luceri V, Rutigliano P, Sciarretta C (1998) Estimation of low degree geopotential coefficients using SLR data. Planet Space Sci 46(11–12): 1633–1638. ISSN 0032–0633. doi:10.1016/S0032-0633(97)00215-8
Bizouard C, Gambis D (2012) The combined solution C04 for Earth orientation parameters consistent with International Terrestrial Reference Frame 2008. Observatoire de Paris, Paris
Bloßfeld M, Müller H, Gerstl M, Stefka V, Bouman J, Göttl F, Horwath M (2015) Second-degree Stokes coefficients from multi-satellite SLR. J Geod. doi:10.1007/s00190-015-0819-z
Chen JL, Wilson CR (2003) Low degree gravitational changes from Earth rotation and geophysical models. Geophys Res Lett 30(24):2257. doi:10.1029/2003GL018688
Chen JL, Wilson CR (2008) Low degree gravity changes from GRACE, Earth rotation, geophysical models, and satellite laser ranging. J Geophys Res 113:B06402. doi:10.1029/2007JB005397
Chen JL, Wilson CR, Seo KW (2009) \(S_2\) tide aliasing in GRACE time-variable gravity solutions. J Geod 83:679687. doi:10.1007/s00190-008-0282-1
Cheng M, Shum C, Tapley B (1997) Determination of long-term changes in the Earth’s gravity field from satellite laser ranging observations. J Geophys Res 102(B10):22,377–22,390. doi:10.1029/97JB01740
Dach R, Hugentobler U, Fridez P, Meindl M (2007) Bernese GPS software version 5.0. Astronomical Institute, University of Bern, Switzerland
Davis LJ, Tamisiea ME, Elosegui P, Mitrovica J, Hil EM (2008) A statistical filtering approach for Gravity Recovery and Climate Experiment (GRACE) gravity data. J Geophys Res 113:B04410. doi:10.1029/2007JB005043
Desai SD (2002) Observing the pole tide with satellite altimetry. J Geophys Res 107(C11):3186. doi:10.1029/2001JC001224
Devoti R, Luceri V, Sciarretta C, Bianco G, Di Donato G, Vermeersen LLA, Sabadini R (2001) The SLR secular gravity variations and their impact on the inference of mantle rheology and lithospheric thickness. Geophys Res Lett 18(5):855–858. doi:10.1029/2000GL011566
Flechtner F (2007) AOD1B product description document for product releases 01 to 04. Report from GeoForschungszentrum Potsdam
Jäggi A, Meyer U, Beutler G, Prange L, Dach R, Mervart L (2011) AIUB-GRACE03S: a static gravity field model computed with simultaneously solved-for time variations from 6 years of GRACE data using the Celestial Mechanics Approach. http://icgem.gfz-potsdam.de/ICGEM/shms/aiub-grace03s.gfc
Jäggi A, Sośnica K, Thaller D, Beutler G (2012) Validation and estimation of low-degree gravity field coefficients using LAGEOS. In: Proceedings of 17th ILRS workshop, vol 48. Bundesamt für Kartographie und Geodäsie, Frankfurt
Lemoine F, Klosko S, Cox C, Johnson T (2006) Time-variable gravity from SLR and DORIS tracking. In: Proceedings of the 15th international workshop on laser ranging, Canberra
Lemoine JM, Bruinsma S, Loyer S, Biancale R, Marty JC, Perosanz F, Balmino G (2010) Temporal gravity field models inferred from GRACE data. Adv Sp Res 39(10):1620–1629. doi:10.1016/j.asr.2007.03.062
Maier A, Krauss S, Hausleitner W, Baur O (2012) Contribution of satellite laser ranging to combined gravity field models. Adv Sp Res 49(3):556–565. ISSN 0273–1177. doi:10.1016/j.asr.2011.10.026
Matsuo K, Chao BF, Otsubo T, Heki K (2013) Accelerated ice mass depletion revealed by low-degree gravity field from satellite laser ranging: Greenland, 1991–2011. Geophys Res Lett 40. doi:10.1002/grl.50900
Meyer U, Jäggi A (2014) AIUB-RL02 monthly gravity field solutions from GRACE kinematic orbits and range rate observations. GRACE Science Team Meeting 2014, GFZ Potsdam
Meyer U, Jäggi A, Beutler G (2012) Monthly gravity field solutions based on GRACE observations generated with the celestial mechanics approach. Earth Plan Sci Lett 345(72). doi:10.1016/j.epsl.2012.06.026
Pavlis NK, Holmes SA, Kenyon SC, Factor JK (2012) The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J Geophys Res 117:B04406. doi:10.1029/2011JB008916
Pearlman MR, Degnan JJ, Bosworth JM (2002) The International Laser Ranging Service. Adv Sp Res 30(2):135–143. doi:10.1016/S0273-1177(02)00277-6
Petit G, Luzum B (eds) (2011) IERS Conventions 2010. IERS Technical Note 36. Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main
Picone JM, Hedin AE, Drob DP, Aikin AC (2002) NRL-MSISE-00 empirical model of the atmosphere: statistical comparisons and scientific issues. J Geophys Res 107(1468):16. doi:10.1029/2002JA009430
Prange L (2011) Global gravity field determination using the GPS measurements made onboard the low Earth orbiting satellite CHAMP. In: Geodätisch-geophysikalische Arbeiten in der Schweiz, vol 81
Reigber C, Lühr H, Schwinzer P (1998) Status of the CHAMP mission. In: Rummel R, Drewes H, Bosch W, Hornik H (eds) Towards an integrated global geodetic observing system (IGGOS). AIG Symp., vol 120, pp 63–65. ISBN 3540670793
Ries J, Cheng M (2014) Satellite laser ranging applications for gravity field determination. In: Proceedings from the 19th international workshop on laser ranging, Annapolis
Rodriguez-Solano CJ, Hugentobler U, Steigenberger P, Lutz S (2012) Impact of Earth radiation pressure on GPS position estimates. J Geod 86(5):309–317. doi:10.1007/s00190-011-0517-4
Savcenko R, Bosch W (2010) EOT11a—empirical ocean tide model from multi-mission satellite altimetry. Deutsches Geodätisches Forschungsinstitut, Munich. Report 89. doi:10.1594/PANGAEA.834232
Seo KW, Wilson C, Chen J, Waliser D (2008) GRACE’s spatial aliasing error. Geophys J Int 172(1):41–48. doi:10.1111/j.1365-246X.2007.03611.x
Sośnica K (2015) Determination of precise satellite orbits and geodetic parameters using satellite laser ranging. Swiss Geodetic Commission, Geodätisch-geophysikalische Arbeiten in der Schweiz, vol 93. Zurich. ISBN: 978-3-908440-38-3
Sośnica K, Thaller D, Jäggi A, Dach R, Beutler G (2012) Sensitivity of Lageos orbits to global gravity field models. Art Sat 47(2):35–79. doi:10.2478/v10018-012-0013-y
Sośnica K, Thaller D, Dach R, Jäggi A, Beutler G (2013) Impact of atmospheric pressure loading on SLR-derived parameters and on the consistency between GNSS and SLR results. J Geod 87(8):751–769. doi:10.1007/s00190-013-0644-1
Sośnica K, Jäggi A, Thaller D, Beutler G, Dach R (2014) Contribution of Starlette, Stella, and AJISAI to the SLR-derived global refernce frame. J Geod 88(8):789–804. doi:10.1007/s00190-014-0722-z
Tapley B, Bettadpur S, Watkins M, et al., (2004) The gravity recovery and climate experiment: mission overview and early results. Geophys Res Lett 31(9):L09607. doi:10.1029/2004GL019920
Thaller D, Sośnica K, Dach R, Jäggi A, Beutler G (2011) LAGEOS-ETALON solutions using the Bernese Software. Mitteilungen des Bundesamtes fuer Kartographie und Geodaesie. In: Proceedings of the 17th international workshop on laser ranging, extending the range, vol 48. Bad Kötzting, Frankfurt, pp 333–336
Watkins M, Flechtner F, Morton P, Webb F, Massmann F, Grunwaldt L (2014) Status of the GRACE Follow-On mission. In: Proceedings from the GRACE science team meeting, Potsdam
Weigelt M, van Dam T, Baur O, Tourian MJ, Steffen H, Sośnica K, Jäggi A, Zehentner N, Mayer-Gürr T, Sneeuw N (2014) How well can the combination hlSST and SLR replace GRACE? A discussion from the point of view of applications. GRACE Science Team Meeting 2014, GFZ Potsdam
Weigelt M, van Dam T, Baur O, Steffen H, Tourian MJ, Sośnica K, Jäggi A, Zehentner N, Mayer-Gürr T, Sneeuw N (2015) How well can the combination hlSST and SLR replace GRACE? J Geod. (to be submitted)
Zelensky N, Lemoine F, Chinn D, Melachroinos S, Beckley B, Beall J, Bordyugov O (2014) Estimated SLR station position and network frame sensitivity to time-varying gravity. J Geod 88(6):517–537. doi:10.1007/s00190-014-0701-4
Acknowledgments
The authors would like to express their gratitude to the ILRS Analysis Working Group for providing the improved corrections and biases for SLR observations as well as the satellite and station-dependent CoM corrections for LAGEOS satellites. The ILRS (Pearlman et al. 2002) is acknowledged for providing SLR data. The SLR stations, including particularly the Zimmerwald Observatory, are acknowledged for a continuous tracking of the geodetic satellites and for providing high-quality SLR observations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sośnica, K., Jäggi, A., Meyer, U. et al. Time variable Earth’s gravity field from SLR satellites. J Geod 89, 945–960 (2015). https://doi.org/10.1007/s00190-015-0825-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00190-015-0825-1