A test instance generator for multiobjective mixed-integer optimization

Abstract

Application problems can often not be solved adequately by numerical algorithms as several difficulties might arise at the same time. When developing and improving algorithms which hopefully allow to handle those difficulties in the future, good test instances are required. These can then be used to detect the strengths and weaknesses of different algorithmic approaches. In this paper we present a generator for test instances to evaluate solvers for multiobjective mixed-integer linear and nonlinear optimization problems. Based on test instances for purely continuous and purely integer problems with known efficient solutions and known nondominated points, suitable multiobjective mixed-integer test instances can be generated. The special structure allows to construct instances scalable in the number of variables and objective functions. Moreover, it allows to control the resulting efficient and nondominated sets as well as the number of efficient integer assignments.

1 Introduction

Optimization problems that arise within practical applications often turn out to be very challenging for solution algorithms from a numerical point of view. Thereby, the challenges can be caused, for instance, by a high number of variables or objective functions as well as certain properties of the objective and constraint functions including nonlinearity or nonconvexity. Hence, there is a need to evaluate the strengths and weaknesses of different solution algorithms. This is important to decide which of them might perform best for a specific type of optimization problems or how the algorithm can be improved to do so in the future. This is typically done by evaluating the performance of an algorithm on a set of certain test instances that cover the above mentioned challenges. In this paper we present a generator for such test instances that yields multiobjective mixed-integer optimization problems. This means that multiple objective functions have to be optimized at the same time and that some of the variables are continuous while others are only allowed to take integer values.

When it comes to multiobjective mixed-integer optimization, most of the literature focuses on multiobjective mixed-integer linear optimization problems. This includes, for instance, the Triangle Splitting Method from Boland et al. (2015) and the Boxed Line Method from Perini et al. (2019) for the biobjective setting, as well as the GoNDEF algorithm from Rasmi and Türkay (2019) for an arbitrary number of objective functions. For a comprehensive overview of algorithmic approaches to solve multiobjective mixed-integer linear optimization problems we refer to Halffmann et al. (2022). To the best of our knowledge, the first deterministic solution method for multiobjective mixed-integer convex optimization problems is given in De Santis et al. (2020). Only recently, also a solution approach for multiobjective mixed-integer nonconvex optimization problems has been presented in Eichfelder et al. (2022). Further solution methods can be found for multiobjective mixed-integer convex optimization problems in Eichfelder and Warnow (2021a, 2023), for biobjective mixed-integer convex optimization problems in Cabrera-Guerrero et al. (2022), Diessel (2022), for biobjective mixed-integer quadratic optimization problems in Jayasekara Merenchige and Wiecek (2022), and for multiobjective mixed-integer nonconvex optimization problems in Link and Volkwein (2022), respectively.

While a relatively large number of (even scalable) test instances exists for multiobjective continuous optimization (e.g. Brockhoff et al. 2022; Cheng et al. 2017; Deb et al. 2005; Fonseca and Fleming 1995; Fonseca et al. 2020; Huband et al. 2006; Schaffer 1985), so far only a limited number of test instances for multiobjective mixed-integer optimization problems was introduced and used for numerical testing. Such instances can be found for the convex case in De Santis et al. (2020), Eichfelder and Warnow (2021a, 2021b, 2023), Jayasekara Merenchige and Wiecek (2022), Papalexandri and Dimkou (1998) and for the nonconvex case in Cabrera-Guerrero et al. (2022), Eichfelder et al. (2022); Eichfelder and Warnow (2023), Link and Volkwein (2022), Mela et al. (2007), respectively. Note that these test instances consist of 16 biobjective and four triobjective mixed-integer problems. Only one test problem is scalable in the number of objective functions (by using the identity for the continuous variables). We refer to Eichfelder et al. (2023) for a more in-depth discussion and classification of these existing test instances.

However, for a systematic evaluation of the strengths and weaknesses of solution algorithms for multiobjective mixed-integer optimization problems more test instances are needed. For instance, there is a demand for test instances that allow to investigate the influence of the number of continuous and integer variables on the performance of the solver, i.e., test instances scalable in the number of variables. This property is especially useful to evaluate the performance of decision space based solution approaches and to compare them with criterion space based solution approaches. Typically, one would expect that decision space based approaches are more influenced by the size of the decision space than criterion space based approaches. In this regard it should be noted that only six of the above mentioned test instances from the literature are scalable in the number of integer variables, and only four of them are additionally scalable in the number of continuous variables. Further important properties of test instances to evaluate the performance of different solution algorithms are for instance the number of so called feasible integer assignments and of efficient integer assignments. These are fixings of the integer variables in such a way that there also exists a fixing of the continuous variables which together yield a feasible or efficient solution of the optimization problem. Especially for algorithms that decompose the mixed-integer optimization problem into a family of purely continuous optimization problems obtained for certain fixings of the integer variables (see also the forthcoming Remark 2.1) these are of high importance.

Taking all of this into account, the new generator for test instances allows to vary the numbers of variables as well as the number of objective functions depending on its input. The proposed method generates test instances that possess a separable structure. This is also the case for several of the known test instances for multiobjective mixed-integer optimization problems from the literature. Thereby, separable means that these test instances can be decomposed into a multiobjective continuous subproblem and into a multiobjective integer subproblem. We will show that under certain assumptions this provides us with full control over the resulting efficient and nondominated sets of the test instances, as well as their number of efficient integer assignments. This allows to verify the correctness of the results from a solution algorithm for multiobjective mixed-integer optimization problems and to evaluate the quality of its output. Especially for the evaluation of nondeterministic or heuristic approaches this is an important feature.

The remaining paper is structured as follows. In Sect. 2 we briefly present the notations and definitions that are used within this paper. We then analyze separable multiobjective mixed-integer optimization problems in Sect. 3. Based on this, in Sect. 4, we provide the test instance generator for multiobjective mixed-integer optimization problems. Some (scalable) multiobjective continuous and integer optimization problems as possible inputs for the generator are listed and discussed in Sect.  4.1 and Sect.  4.2, respectively. Finally, we provide an outlook for future research in Sect. 5.

2 Notations and definitions

For a positive integer $p \in {\mathbb {N}}$ and real numbers $a,b \in {\mathbb {R}}$ with $a \le b$ we use the notations $[p]:= \{1,\ldots ,p\}$, $[a,b]:=\{x \in {\mathbb {R}}\mid a \le x \le b\}$, and $]a,b]:=\{x \in {\mathbb {R}}\mid a < x \le b\}$. Moreover, the inequalities $\le$ and < between vectors are understood componentwise, i.e., for $x,x' \in {\mathbb {R}}^p$ it holds $x \le x'$ or $x < x'$ if and only if $x_i \le x'_i$ or $x_i < x'_i$ is fulfilled for all $i \in [p]$, respectively. Based on this we denote for $l,u \in {\mathbb {R}}^{p}$ with $l \le u$ by $[l,u]:=\{y \in {\mathbb {R}}^{p}\mid l \le y \le u\}$ the box with lower bound l and upper bound u. Throughout the paper the addition of functions is defined pointwise, i.e., for two functions $g,h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^p$ we define $g+h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^p$ by $(g+h)(x):=g(x)+h(x)$ for all $x\in {\mathbb {R}}^n$, and the addition of two sets is defined in the Minkowski-sense. For two sets A, B the Cartesian product is defined as $A\times B:=\{(a,b)\mid a\in A,\ b\in B\}$. For two vectors $x,x' \in {\mathbb {R}}^p$ their Hadamard product is defined by $x \circ x':=(x_1x_1',\ldots ,x_px_p')$. Finally, for a nonempty set $\Omega \subseteq {\mathbb {R}}^p$ we denote its cardinality by $|\Omega |$ and its convex hull by ${{\,\textrm{conv}\,}}(\Omega )$.

In the following, we consider multiobjective mixed-integer optimization problems, i.e., multiobjective optimization problems defined by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad f(x)&\\ \text{ s.t. }&\quad g(x) \le 0_q, \\&\quad x \in X := X_C \times X_I. \end{aligned} \end{aligned}$$

(MOMIP)

Thereby, let $n,m \in {\mathbb {N}}_0$ with $n \ge 1$ or $m \ge 1$ and let $f_i :{\mathbb {R}}^{n+m} \rightarrow {\mathbb {R}}$, $i \in [p]$, $p\ge 2$, $g_j :{\mathbb {R}}^{n+m} \rightarrow {\mathbb {R}}$, $j \in [q]$ be continuous functions, where $f = (f_1,\ldots ,f_p) :{\mathbb {R}}^{n+m} \rightarrow {\mathbb {R}}^{p}$, $g = (g_1,\ldots ,g_q) :{\mathbb {R}}^{n+m} \rightarrow {\mathbb {R}}^{q}$, and $0_q:= 0_{{\mathbb {R}}^q}$. Moreover, let $X_C:= [l_C,u_C] \subseteq {\mathbb {R}}^n$ be a box with $l_C,u_C \in {\mathbb {R}}^n$, let $X_I:= [l_I,u_I] \cap {\mathbb {Z}}^m$ be a finite subset of ${\mathbb {Z}}^m$ with $l_I,u_I \in {\mathbb {Z}}^m$ and let the feasible set $S:=\{x \in {\mathbb {R}}^{n+m} \mid g(x) \le 0_q,\; x \in X\}$ of (MOMIP) be nonempty.

For the variables $x\in X$ of (MOMIP), we will write in the following $x = (x_C,x_I)$ with $x_C \in X_C$ and $x_I \in X_I$ to distinguish between the continuous and the integer variables. We call (MOMIP) a multiobjective mixed-integer convex optimization problem if all involved functions $f_i, i \in [p]$ and $g_j, j \in [q]$ are convex. Otherwise, we call it a multiobjective mixed-integer nonconvex optimization problem.

Obviously, for $m=0$ and for $n=0$ the special cases of a multiobjective continuous optimization problem (MOP) given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad f(x)&\\ \text{ s.t. }&\quad g(x) \le 0_q, \\&\quad x \in X_C \end{aligned} \end{aligned}$$

(MOP)

and of a multiobjective integer optimization problem (MOIP) given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad f(x)&\\ \text{ s.t. }&\quad g(x) \le 0_q, \\&\quad x \in X_I \end{aligned} \end{aligned}$$

(MOIP)

are included in (MOMIP).

Recall that a feasible point ${\bar{x}} \in S$ is called an efficient solution of (MOMIP) if there exists no $x \in S$ with $f(x)\le f({\bar{x}})$ and $f(x)\ne f({\bar{x}})$. Moreover, a point ${\bar{y}} = f({\bar{x}})$ with ${\bar{x}} \in S$ is called a nondominated point of (MOMIP) if ${\bar{x}}$ is an efficient solution. The set ${\mathcal {E}}\subseteq S$ denotes the set of all efficient solutions (also called the efficient set) and the set ${\mathcal {N}}\subseteq f(S)$ denotes the set of all nondominated points (also called the nondominated set) of (MOMIP). If for all $x \in S$ there exists an ${\bar{x}} \in {\mathcal {E}}$ such that $f({\bar{x}}) \le f(x)$, then the multiobjective optimization problem is said to satisfy the so called domination property. Note that by the continuity of the objective and constraint functions and the box constraints (MOMIP), and thus also the special cases (MOP) and (MOIP), fulfill the domination property and it holds ${\mathcal {E}}\ne \emptyset$ and ${\mathcal {N}}\ne \emptyset$.

For the multiobjective mixed-integer optimization problem (MOMIP) we call $x_I \in X_I$ a feasible integer assignment if there exists $x_C \in X_C$ such that $(x_C,x_I)$ is feasible for (MOMIP). Analogously, we call $x_I \in X_I$ an efficient integer assignment if there exists $x_C \in X_C$ such that $(x_C,x_I) \in {\mathcal {E}}$, i.e., $(x_C,x_I)$ is an efficient solution of (MOMIP). We denote by $S_I$ the set of all feasible integer assignments and by ${\mathcal {E}}_I$ the set of all efficient integer assignments of (MOMIP).

Remark 2.1

The absolute number (and the percentage) of efficient integer assignments within the set of feasible integer assignments is an important characteristic of a multiobjective mixed-integer optimization problem. It might also influence the performance of numerical algorithms depending on how they are constructed. Note that this is a significant difference to the singleobjective setting: in singleobjective mixed-integer optimization the optimal value is unique and hence it is enough to find one optimal integer assignment. For $p\ge 2$ there are in general infinitely many nondominated points. As a consequence, there can be instances with a large number of efficient integer assignments which lead to different nondominated points. Even all feasible integer assignments can be efficient. Hence, algorithms that decompose (MOMIP) into a family of purely continuous problems may be forced to a full enumeration in that case.

3 Separable multiobjective mixed-integer optimization problems

Many of the known test instances for multiobjective mixed-integer (nonlinear) optimization have a common structure, which we will formalize and study in this section. The results form the basis for our approach regarding the test instance generator.

A multiobjective mixed-integer optimization problem (MOMIP) which can be formulated by a decomposition

$$\begin{aligned} \begin{aligned} \min \limits _{x = (x_C,x_I)}&\quad f_C(x_C)+f_I(x_I)&\\ \text{ s.t. }&\quad g_C(x_C) \le 0_{q_{C}}, \\&\quad g_I(x_I) \le 0_{q_{I}}, \\&\quad x \in X = X_C \times X_I \end{aligned} \end{aligned}$$

(sMOMIP)

with continuous objective functions $f_C :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{p},f_I :{\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{p}$ with $n,m\in {\mathbb {N}}$, and continuous constraint functions $g_C :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{q_C},g_I :{\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{q_I}$ is called separable. To the separable multiobjective mixed-integer optimization problem (sMOMIP) we formulate the following two subproblems: the multiobjective continuous subproblem

and the multiobjective integer subproblem

The efficient solutions and the nondominated points of the subproblems and of the original separable problem are related to what we discuss next. We denote by $S_C^{\textrm{s}}$/${\mathcal {E}}_C^{\textrm{s}}$/${\mathcal {N}}_C^{\textrm{s}}$ and by $S_I^{\textrm{s}}$/${\mathcal {E}}_I^{\textrm{s}}$/${\mathcal {N}}_I^{\textrm{s}}$ the feasible set/the set of all efficient solutions/the set of all nondominated points of ($\hbox {sMOMIP}_C$) and of ($\hbox {sMOMIP}_I$), respectively. It is easy to see that for a separable multiobjective mixed-integer optimization problem (sMOMIP) and the corresponding subproblems ($\hbox {sMOMIP}_C$) and ($\hbox {sMOMIP}_I$) it holds $S=S_C^{\textrm{s}} \times S_I^{\textrm{s}}$ and $S_I=S_I^{\textrm{s}}$. Here, S denotes the feasible set and $S_I$ denotes the set of all feasible integer assignments of (sMOMIP). Note that under our assumptions it holds $S_C^{\textrm{s}}\ne \emptyset$ and $S_I^{\textrm{s}}\ne \emptyset$, and both subproblems fulfill the domination property. Hence, it holds ${\mathcal {E}}_C^{\textrm{s}}\ne \emptyset$, ${\mathcal {E}}_I^{\textrm{s}}\ne \emptyset$, ${\mathcal {N}}_C^{\textrm{s}}\ne \emptyset$, and ${\mathcal {N}}_I^{\textrm{s}}\ne \emptyset$. We illustrate such a decomposable mixed-integer optimization problem with the following example.

Example 3.1

The separable biobjective mixed-integer nonconvex optimization problem given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i-\frac{1}{\sqrt{{n}}}\right) ^2\right) +x_{n+1}+x_{n+2}\\ 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i+\frac{1}{\sqrt{{n}}}\right) ^2\right) -x_{n+1}-x_{n+2} \end{pmatrix}\\ \text{ s.t. }&\quad x \in X=[-4,4]^{n} \times ([-1,1]^2 \cap {\mathbb {Z}}^{2}). \end{aligned} \end{aligned}$$

(3.1)

can be decomposed into the (well known) biobjective continuous subproblem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i-\frac{1}{\sqrt{{n}}}\right) ^2\right) \\ 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i+\frac{1}{\sqrt{{n}}}\right) ^2\right) \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_C=[-4,4]^{n} \end{aligned} \end{aligned}$$

(3.2)

introduced in Fonseca and Fleming (1995) and into the biobjective integer linear subproblem given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} x_1+x_2 \\ -x_1-x_2 \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_I=\{-1,0,1\}^{2}. \end{aligned} \end{aligned}$$

(3.3)

The efficient and nondominated sets of the subproblems are given by

$$\begin{aligned} \begin{aligned} {{\mathcal {E}}_C^{\textrm{s}}}&={\left\{ x\in X_C \mid x_1=x_2=\ldots =x_n \in \left[ -\frac{1}{\sqrt{{n}}},\frac{1}{\sqrt{{n}}}\right] \right\} ,}\\ {{\mathcal {N}}_C^{\textrm{s}}}&={\left\{ \left( 1-\exp (-4(t-1)^2),1-\exp (-4t^2)\right) \mid t \in [0,1]\right\} ,}\\ {\mathcal {E}}_I^{\textrm{s}}&=X_I=\{-1,0,1\}^{2},\\ {\mathcal {N}}_I^{\textrm{s}}&= \{(\delta ,-\delta )\mid \delta \in \{-2,-1,0,1,2\}\} = \{ (-2,2),(-1,1),(0,0),(1,-1),(2,-2) \}. \end{aligned} \end{aligned}$$

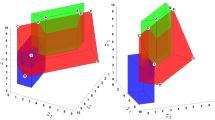
For further explanations regarding the corresponding sets ${\mathcal {E}}$, ${\mathcal {N}}$, and ${\mathcal {E}}_I$ we refer to Example 4.8 (i). For an illustration of the nondominated sets ${\mathcal {N}}_I^{\textrm{s}}$ and ${\mathcal {N}}$ see Fig. 1.

Fig. 1

Nondominated set ${\mathcal {N}}$ of the separable optimization problem (3.1) and nondominated set ${\mathcal {N}}_I^\textrm{s}$ of the integer subproblem (3.3) from Example 3.1

With the following lemma we start the examination of the relations between the efficient solutions and the nondominated points regarding the subproblems and the original separable problem.

Lemma 3.2

Let ${\mathcal {E}}$ denote the set of all efficient solutions, ${\mathcal {N}}$ the set of all nondominated points, and ${\mathcal {E}}_I$ the set of all efficient integer assignments of (sMOMIP). Then for the corresponding subproblems ($\hbox {sMOMIP}_C$) and ($\hbox {sMOMIP}_I$) it holds:

• (i) ${\mathcal {E}}\subseteq {\mathcal {E}}_C^{\textrm{s}}\times {\mathcal {E}}_I^{\textrm{s}}$.

• (ii) ${\mathcal {N}}\subseteq {\mathcal {N}}_C^{\textrm{s}}+ {\mathcal {N}}_I^{\textrm{s}}$.

• (iii) ${\mathcal {E}}_I \subseteq {\mathcal {E}}_I^{\textrm{s}}$.

Proof

The relations (ii) and (iii) follow immediately by (i). For the proof of (i) let ${\bar{x}} =({\bar{x}}_{C},{\bar{x}}_{I}) \in {\mathcal {E}}\subseteq S=S_C^{\textrm{s}} \times S_I^{\textrm{s}}$ and assume that ${\bar{x}}_{C} \notin {\mathcal {E}}_C^{\textrm{s}}$. Then there exists ${\hat{x}}_C \in S_C^{\textrm{s}}$ such that $f_C({\hat{x}}_C) \le f_C({\bar{x}}_{C})$ and $f_C({\hat{x}}_C) \ne f_C({\bar{x}}_{C})$. Thus we obtain for $x=({\hat{x}}_C,{\bar{x}}_{I})\in S_C^{\textrm{s}} \times S_I^{\textrm{s}}=S$ that

$$\begin{aligned} f(x) =f_C({\hat{x}}_C)+f_I({\bar{x}}_{I}) \le f_C({\bar{x}}_{C})+f_I({\bar{x}}_{I}) =f({\bar{x}}) \text{ and } f(x) \ne f({\bar{x}}), \end{aligned}$$

which contradicts ${\bar{x}} \in {\mathcal {E}}$. The proof for ${\bar{x}}_{I} \in {\mathcal {E}}_I^{\textrm{s}}$ is analogous. $\square$

Note that equality for (i), (ii) and (iii) from Lemma 3.2 is trivially fulfilled in the scalar-valued setting $p=1$. In the vector-valued case $p\ge 2$ these equalities do, in general, not hold as the following example shows.

Example 3.3

We consider the separable biobjective mixed-integer optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} x_1+x_2\ +0.75x_{3}\\ -x_1-x_2\ -0.25x_{3} \end{pmatrix}\\ \text{ s.t. }&\quad x \in X=[0,1] \times ([-1,1]\times [0,1]) \cap {\mathbb {Z}}^{2}. \end{aligned} \end{aligned}$$

(3.4)

It can be decomposed into the biobjective continuous subproblem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} x\\ -x \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_C=[0,1] \end{aligned} \end{aligned}$$

(3.5)

and the biobjective integer subproblem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} x_1\ +0.75x_{2}\\ -x_1\ -0.25x_{2} \end{pmatrix}\\ \text{ s.t. }&\quad x\in X_I =\{-1,0,1\}\times \{0,1\}. \end{aligned} \end{aligned}$$

(3.6)

The efficient and nondominated sets of (3.4), (3.5) and (3.6) are given by

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_C^{\textrm{s}}&= X_C,\\ {\mathcal {E}}_I^{\textrm{s}}&= X_I,\\ {\mathcal {E}}&= \bigl ([0,1] \times \{(-1,0),(0,0),(1,0)\}\bigr )\cup \bigl ( ]\frac{3}{4},1] \times (1,1)\bigr ),\\ {\mathcal {N}}_C^{\textrm{s}}&= {{\,\textrm{conv}\,}}\{(0,0),(1,-1)\},\\ {\mathcal {N}}_I^{\textrm{s}}&= \left\{ (-1,1),(0,0),(1,-1),\left( -\frac{1}{4},\frac{3}{4}\right) , \left( \frac{3}{4},-\frac{1}{4}\right) ,\left( \frac{7}{4},-\frac{5}{4}\right) \right\} , \text{ and }\\ {\mathcal {N}}&= \bigl ({{\,\textrm{conv}\,}}\{(0,0),(1,-1)\}+\{(-1,1),(0,0),(1,-1)\}\bigr )\\&\quad \cup \left( \left( {{\,\textrm{conv}\,}}\left\{ \left( \frac{3}{4},-\frac{3}{4}\right) ,(1,-1)\right\} \setminus \left\{ \left( \frac{3}{4},-\frac{3}{4}\right) \right\} \right) +\left\{ \left( \frac{7}{4},-\frac{5}{4}\right) \right\} \right) . \end{aligned} \end{aligned}$$

Hence, we obtain ${\mathcal {E}}_I =\{(-1,0),(0,0),(1,0),(1,1)\} \subsetneq {\mathcal {E}}_I^{\textrm{s}}$ and ${\mathcal {N}}\subsetneq {\mathcal {N}}_C^{\textrm{s}}+ {\mathcal {N}}_I^{\textrm{s}}$. In Fig. 2 we provide an illustration of the nondominated sets ${\mathcal {N}}$ and ${\mathcal {N}}_I^{\textrm{s}}$.

Fig. 2

Nondominated set ${\mathcal {N}}$ of the separable optimization problem (3.4) and nondominated set ${\mathcal {N}}_I^{\textrm{s}}$ of the integer subproblem (3.6) from Example 3.3

For the test instance generator in the forthcoming Sect. 4 we intend to have (as much as possible) control over the efficient sets and over the nondominated sets of the resulting test instances. Hence, we are interested in additional assumptions to ensure equality for the statements of Lemma 3.2. The following theorem provides a sufficient condition for that.

Theorem 3.4

Let (sMOMIP) be given and let $\Delta _C \in {\mathbb {R}}^p, \Delta _I \in ({\mathbb {R}}\cup \{\infty \})^p$ be the vectors defined by

$$\begin{aligned} \Delta _{C,i}&:= \sup \{y_i-{\hat{y}}_i \mid y,{\hat{y}} \in {\mathcal {N}}_C^{\textrm{s}}\},\\ \Delta _{I,i}&:= \inf \{|y_i-{\hat{y}}_i |\mid y,{\hat{y}} \in {\mathcal {N}}_I^{\textrm{s}},\ y_i \ne {\hat{y}}_i\} \end{aligned}$$

for all $i \in [p]$. If $\Delta _C < \Delta _I$, then it holds:

• (i) ${\mathcal {E}}= {\mathcal {E}}_C^{\textrm{s}}\times {\mathcal {E}}_I^{\textrm{s}}$.

• (ii) ${\mathcal {N}}= {\mathcal {N}}_C^{\textrm{s}}+ {\mathcal {N}}_I^{\textrm{s}}$.

• (iii) ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}}$.

Proof

The equalities (ii) and (iii) follow immediately by (i). Moreover, for the proof of (i), by Lemma 3.2 (i), it only remains to show that ${\mathcal {E}}_C^{\textrm{s}} \times {\mathcal {E}}_I^{\textrm{s}} \subseteq {\mathcal {E}}$. Hence, let $\Delta _{C} < \Delta _{I}$ and assume that there exist ${\hat{x}}_C \in {\mathcal {E}}_C^{\textrm{s}}$ and ${\hat{x}}_I \in {\mathcal {E}}_I^{\textrm{s}}$ such that ${\hat{x}}=({\hat{x}}_C,{\hat{x}}_I) \notin {\mathcal {E}}$. Then it holds $f_C({\hat{x}}_C) \in {\mathcal {N}}_C^{\textrm{s}}$, $f_I({\hat{x}}_I) \in {\mathcal {N}}_I^{\textrm{s}}$ and ${\hat{x}} \in S{\setminus } {\mathcal {E}}$. Thus, by the domination property and Lemma 3.2 (i), there exists ${\bar{x}}=({\bar{x}}_C,{\bar{x}}_I)\in {\mathcal {E}}\subseteq {\mathcal {E}}_C^{\textrm{s}}\times {\mathcal {E}}_I^{\textrm{s}}$ such that $f_C({\bar{x}}_C) \in {\mathcal {N}}_C^{\textrm{s}}$, $f_I({\bar{x}}_I) \in {\mathcal {N}}_I^{\textrm{s}}$ and

$$\begin{aligned} f_C({\bar{x}}_C) + f_I({\bar{x}}_I) = f({\bar{x}}) \le f({\hat{x}}) = f_C({\hat{x}}_C) + f_I({\hat{x}}_I) \text{ and } f({\bar{x}}) \ne f({\hat{x}}). \end{aligned}$$

(3.7)

Hence, we obtain by the definition of $\Delta _C \in {\mathbb {R}}^p$ that

$$\begin{aligned} f_{I,i}({\bar{x}}_I)-f_{I,i}({\hat{x}}_I) \le f_{C,i}({\hat{x}}_C) - f_{C,i}({\bar{x}}_C) \le \Delta _{C,i} < \Delta _{I,i} \end{aligned}$$

(3.8)

for all $i \in [p]$. Assume now that there exists $i \in [p]$ such that $f_{I,i}({\bar{x}}_I) > f_{I,i}({\hat{x}}_I)$ (and thus $f_I({\bar{x}}_I)\not =f_I({\hat{x}}_I)$ and $\Delta _{I,i} \in {\mathbb {R}}$). Then it follows by (3.8) and by the definition of $\Delta _{I,i}$ that

$$\begin{aligned} 0< f_{I,i}({\bar{x}}_I)-f_{I,i}({\hat{x}}_I) < \Delta _{I,i} \le |f_{I,i}({\bar{x}}_I)-f_{I,i}({\hat{x}}_I) |= f_{I,i}({\bar{x}}_I)-f_{I,i}({\hat{x}}_I), \end{aligned}$$

which is obviously a contradiction. Hence, we obtain $f_{I}({\bar{x}}_I) \le f_{I}({\hat{x}}_I)$ and by ${\hat{x}}_I \in {\mathcal {E}}_I^{\textrm{s}}$ this implies $f_{I}({\bar{x}}_I) = f_{I}({\hat{x}}_I)$. Thus, by (3.7) it follows $f_{C}({\bar{x}}_C) \le f_{C}({\hat{x}}_C)$ and by ${\hat{x}}_C \in {\mathcal {E}}_C^{\textrm{s}}$ we conclude $f_{C}({\bar{x}}_C) = f_{C}({\hat{x}}_C)$. As a result, we get $f({\bar{x}}) = f({\hat{x}})$, which contradicts (3.7), and (i) is proven. $\square$

In Example 3.3 the sufficient condition to ensure equality by Theorem 3.4 is not fulfilled since $\Delta _{C,1}=\Delta _{C,2}=1$ and $\Delta _{I,1}=\Delta _{I,2}=0.25$.

Remark 3.5

We remark that the infimum (instead of the minimum) in the definition of the components of $\Delta _I$ in Theorem 3.4 is only necessary since it could be the case that for some index $i \in [p]$ all nondominated points of ($\hbox {sMOMIP}_I$) share the same value. In that case the set $\{|y_i-{\hat{y}}_i |\mid y,{\hat{y}} \in {\mathcal {N}}_I^{\textrm{s}},\ y_i \ne {\hat{y}}_i\}$ is empty. We then follow the standard convention that $\inf (\emptyset ):= +\infty$. However, as long as there exist $y,{\hat{y}} \in {\mathcal {N}}_I^{\textrm{s}}$ such that $y_i \ne {\hat{y}}_i$ the finiteness of the feasible set $S_I^{\textrm{s}} \subseteq {\mathbb {Z}}^m$, in particular due to the box constraints $x_I \in X_I$, immediately implies that the infimum is actually a minimum and $\Delta _{I,i} = \min \{|y_i-{\hat{y}}_i |\mid y,{\hat{y}} \in {\mathcal {N}}_I^{\textrm{s}}, y_i \ne {\hat{y}}_i\} \in {\mathbb {R}}$.

For the third equality from Theorem 3.4, i.e. ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}}$, it is actually sufficient that $\Delta _{C,i} < \Delta _{I,i}$ holds for $p-1$ indices $i \in [p]$ only. In particular, this means that for biobjective optimization problems (sMOMIP) the inequality $\Delta _{C,i} < \Delta _{I,i}$ needs to hold for only one index $i \in \{1,2\}$. This is particularly useful for such algorithms as the one from Cabrera-Guerrero et al. (2022) that assume prior knowledge of the set $S_I$ of feasible integer assignments and hence would highly benefit if even the set ${\mathcal {E}}_I$ of efficient integer assignments would be known.

Lemma 3.6

Let (sMOMIP) be given, let the vectors $\Delta _C, \Delta _I$ be defined as in Theorem 3.4, and let $j \in [p]$ be an arbitrary index. If $\Delta _{C,i} < \Delta _{I,i}$ is fulfilled for all $i \in [p] \setminus \{j\}$, then it holds ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}}$.

Proof

By Lemma 3.2 (iii) it only remains to prove that ${\mathcal {E}}_I^{\textrm{s}} \subseteq {\mathcal {E}}_I$. Hence, let $\Delta _{C,i} < \Delta _{I,i}$ for all $i \in [p] \setminus \{j\}$ and assume that there exists ${\hat{x}}_I \in {\mathcal {E}}_I^{\textrm{s}} \setminus {\mathcal {E}}_I$. Moreover, let

$$\begin{aligned} {\hat{x}}_C \in {{\,\textrm{argmin}\,}}\{f_{C,j}(x_C) \mid x_C \in S_C^{\textrm{s}}\} \cap {\mathcal {E}}_C^{\textrm{s}}. \end{aligned}$$

(3.9)

Such a point ${\hat{x}}_C \in S_C^{\textrm{s}}$ always exists since $f_{C,j}$ is continuous, $S_C^{\textrm{s}}$ is compact, and the domination property holds for ($\hbox {sMOMIP}_C$). Since ${\hat{x}} = ({\hat{x}}_C,{\hat{x}}_I) \in S \setminus {\mathcal {E}}$ and the domination property holds for (sMOMIP), there exists ${\bar{x}}=({\bar{x}}_C,{\bar{x}}_I) \in {\mathcal {E}}$ such that (3.7) holds. Further, by Lemma 3.2 (i) we have that $({\bar{x}}_C, {\bar{x}}_I) \in {\mathcal {E}}_C^{\textrm{s}} \times {\mathcal {E}}_I^{\textrm{s}}$ and with the same reasoning as in the proof of Theorem 3.4 it holds (3.8) and $f_{I,i}({\bar{x}}_I) \le f_{I,i}({\hat{x}}_I)$ but only for all $i \in [p]{\setminus } \{j\}$. Assume now that also for j-th component it holds $f_{I,j}({\bar{x}}_I) \le f_{I,j}({\hat{x}}_I)$. Then we obtain $f_{I}({\bar{x}}_I) \le f_{I}({\hat{x}}_I)$ and since ${\hat{x}}_I \in {\mathcal {E}}_I^{\textrm{s}}$ this implies $f_{I}({\bar{x}}_I) = f_{I}({\hat{x}}_I)$. Again, with the same reasoning as in the proof of Theorem 3.4, we get $f_{C}({\bar{x}}_C) = f_{C}({\hat{x}}_C)$ and thus $f({\bar{x}}) = f({\hat{x}})$ which contradicts (3.7). Hence, it holds that $f_{I,j}({\bar{x}}_I) > f_{I,j}({\hat{x}}_I)$ and by (3.7) it follows

$$\begin{aligned} 0 < f_{I,j}({\bar{x}}_I) - f_{I,j}({\hat{x}}_I) \le f_{C,j}({\hat{x}}_C) - f_{C,j}({\bar{x}}_C). \end{aligned}$$

This leads to $f_{C,j}({\bar{x}}_C) < f_{C,j}({\hat{x}}_C)$ which contradicts the choice of ${\hat{x}}_C$ by (3.9). $\square$

The biobjective optimization problem in the following Example 3.7 is a slight modification of the optimization problem (3.4) from Example 3.3 with $\Delta _{C,2} < \Delta _{I,2}$ but $\Delta _{C,1} \not < \Delta _{I,1}$. While the equality ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}}$ holds in that case due to Lemma 3.6, the example also shows that none of the other equalities ${\mathcal {E}}= {\mathcal {E}}_C^{\textrm{s}}\times {\mathcal {E}}_I^{\textrm{s}}$ and ${\mathcal {N}}= {\mathcal {N}}_C^{\textrm{s}}+ {\mathcal {N}}_I^{\textrm{s}}$ from Theorem 3.4 holds in that scenario. Hence, for those equalities only the stronger assumption $\Delta _{C,i} < \Delta _{I,i}$ for all $i \in [p]$ (without any exception for an index $j \in [p]$) is sufficient.

Example 3.7

We consider the following slight modification of the separable biobjective mixed-integer optimization problem from Example 3.3 given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} x_1+x_2\ +0.75x_{3}\\ -0.2x_1-x_2\ -0.25x_{3} \end{pmatrix}\\ \text{ s.t. }&\quad x \in X=[0,1] \times ([-1,1]\times [0,1]) \cap {\mathbb {Z}}^{2}. \end{aligned} \end{aligned}$$

(3.10)

While the biobjective integer subproblem remains unchanged and is again given by (3.6), we use here the biobjective continuous subproblem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} x\\ -0.2x \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_C=[0,1] \end{aligned} \end{aligned}$$

with ${\mathcal {E}}_C^{\textrm{s}}=X_C$ and ${\mathcal {N}}_C^{\textrm{s}}={{\,\textrm{conv}\,}}\{(0,0),(1,-0.2)\}$. Then it holds $\Delta _{C,1}=1 > 0.25 = \Delta _{I,1}$ and $\Delta _{C,2}=0.2 < 0.25 = \Delta _{I,2}$. Thus the sufficient condition to ensure ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}}$ in Lemma 3.6 is fulfilled. For the efficient and for the nondominated set of (3.10) it holds that

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&=\bigl ([0,\frac{3}{4}[ \times \{(-1,0),(0,0),(1,0)\}\bigr ) \cup \bigl ( [0,\frac{1}{4}[ \times \{(-1,1),(0,1)\}\bigr ) \cup \bigl ( [0,1] \times \{(1,1)\}\bigr ),\\ {\mathcal {N}}&= \left( \left( {{\,\textrm{conv}\,}}\left\{ (0,0),\left( \frac{3}{4},-\frac{3}{20}\right) \right\} \setminus \left\{ \left( \frac{3}{4},-\frac{3}{20}\right) \right\} \right) +\{(-1,1),(0,0),(1,-1)\}\right) \\&\quad \cup \left( \left( {{\,\textrm{conv}\,}}\left\{ (0,0),\left( \frac{1}{4},-\frac{1}{20}\right) \right\} \setminus \left\{ \left( \frac{1}{4},-\frac{1}{20}\right) \right\} \right) +\left\{ \left( -\frac{1}{4},\frac{3}{4}\right) , \left( \frac{3}{4},-\frac{1}{4}\right) \right\} \right) \\&\quad \cup \left( {{\,\textrm{conv}\,}}\left\{ (0,0),\left( 1,-\frac{1}{5}\right) \right\} +\left\{ \left( \frac{7}{4},-\frac{5}{4}\right) \right\} \right) . \end{aligned} \end{aligned}$$

We obtain ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}} = X_I = \{-1,0,1\}\times \{0,1\}$, but also ${\mathcal {E}}\subsetneq {\mathcal {E}}_C^{\textrm{s}}\times {\mathcal {E}}_I^{\textrm{s}}$ and ${\mathcal {N}}\subsetneq {\mathcal {N}}_C^{\textrm{s}}+ {\mathcal {N}}_I^{\textrm{s}}$. We provide an illustration of the nondominated sets ${\mathcal {N}}$ and ${\mathcal {N}}_I^{\textrm{s}}$ in Fig. 3.

Fig. 3

Nondominated set ${\mathcal {N}}$ of the separable optimization problem (3.10) and nondominated set ${\mathcal {N}}_I^{\textrm{s}}$ of the integer subproblem (3.6) from Example 3.7

4 A test instance generator for multiobjective mixed-integer optimization problems

Based on the results of the previous section we are now able to formulate the test instance generator for multiobjective mixed-integer optimization problems. As Input it requires two optimization problems:

$\blacktriangleright$:

A multiobjective continuous optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x_C}&\quad f_C(x_C)&\\ \text{ s.t. }&\quad g_C(x_C) \le 0_{q_{C}}, \\&\quad x_C \in X_C, \end{aligned} \end{aligned}$$

(4.1)

with a continuous objective function $f_C :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{p}$, a continuous constraint function $g_C :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{q_C}$, bounds on the variables defined by a box $X_C:= [l_C,u_C] \subseteq {\mathbb {R}}^n$, known efficient set ${\mathcal {E}}_C^\textrm{s}$ and known nondominated set ${\mathcal {N}}_C^{\textrm{s}}\ne \emptyset$, and a vector $\blacktriangle _{C} \in {\mathbb {R}}^p$ for which it holds $\Delta _{C} \le \blacktriangle _{C}$ (i.e., an upper bound is sufficient). Here $\Delta _{C}$ is defined as in Theorem 3.4, i.e., it holds

$$\begin{aligned} \blacktriangle _{C,i}\ge \Delta _{C,i} = \sup \{y_i-{\hat{y}}_i \mid y,{\hat{y}} \in {\mathcal {N}}_C^{\textrm{s}}\} \end{aligned}$$

for all $i \in [p]$.

$\blacktriangleright$:

A multiobjective integer optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x_I}&\quad f_I(x_I)&\\ \text{ s.t. }&\quad g_I(x_I) \le 0_{q_{I}}, \\&\quad x_I \in X_I, \end{aligned} \end{aligned}$$

(4.2)

with a continuous objective function $f_I :{\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{p}$, a continuous constraint function $g_I :{\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{q_I}$, bounds on the variables defined by a box $X_I:= [l_I,u_I] \cap {\mathbb {Z}}^m$, known efficient set ${\mathcal {E}}_I^\textrm{s}$ and known nondominated set ${\mathcal {N}}_I^{\textrm{s}}$, and a vector $\blacktriangle _{I} \in ({\mathbb {R}}\cup \{\infty \})^p$ for which it holds $0_p < \blacktriangle _{I} \le \Delta _{I}$ (i.e., a positive lower bound is sufficient). Here $\Delta _{I}$ is defined as in Theorem 3.4, i.e., it holds

$$\begin{aligned} 0< \blacktriangle _{I,i} \le \Delta _{I,i} = \inf \{|y_i-{\hat{y}}_i |\mid y,{\hat{y}} \in {\mathcal {N}}_I^{\textrm{s}}, y_i \ne {\hat{y}}_i\} \end{aligned}$$

for all $i \in [p]$.

Further, one needs to provide scaling factors $\alpha _i>0$ for all $i\in [p]$, such that for the vector $\alpha \in {\mathbb {R}}^p$ it holds

$$\begin{aligned} \alpha \circ \blacktriangle _{C} < \blacktriangle _{I}. \end{aligned}$$

Finally, the Output of the generator is the separable multiobjective mixed-integer optimization problem defined by

$$\begin{aligned} \begin{aligned} \min \limits _{x = (x_C,x_I)}&\quad \alpha \circ f_C(x_C)+ f_I(x_I)&\\ \text{ s.t. }&\quad g_C(x_C) \le 0_{q_{C}}, \\&\quad g_I(x_I) \le 0_{q_{I}}, \\&\quad x \in X = X_C \times X_I, \end{aligned} \end{aligned}$$

such that the assumptions of Theorem 3.4 are fulfilled. As a consequence, it holds ${\mathcal {E}}= {\mathcal {E}}_C^{\textrm{s}}\times {\mathcal {E}}_I^{\textrm{s}}$, ${\mathcal {N}}= \{\alpha \circ y \mid \; y \in {\mathcal {N}}_C^{\textrm{s}}\}+ {\mathcal {N}}_I^{\textrm{s}}$ and ${\mathcal {E}}_I = {\mathcal {E}}_I^{\textrm{s}}$.

We continue with a first example for the application of the generator using the subproblems given in Example 3.3.

Example 4.1

We choose as input for the proposed test instance generator for the multiobjective continuous optimization problem and for the multiobjective integer optimization problem the biobjective subproblems (3.5) and (3.6) of Example 3.3. Then, as already mentioned above Remark 3.5, it holds $\Delta _{C,1}=\Delta _{C,2}=1$ and $\Delta _{I,1}=\Delta _{I,2}=0.25$. Further, we choose $\blacktriangle _{C}:=\Delta _{C}$ and $\blacktriangle _{I}:=\Delta _{I}$. To ensure $\alpha \circ \blacktriangle _{C} < \blacktriangle _{I}$, we set $\alpha :=\left( 0.2,0.2\right)$. Then we obtain as output the separable biobjective mixed-integer optimization problem given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} 0.2x_1+x_2\ +0.75x_{3}\\ -0.2x_1-x_2\ -0.25x_{3} \end{pmatrix}\\ \text{ s.t. }&\quad x \in X=[0,1] \times ([-1,1]\times [0,1]) \cap {\mathbb {Z}}^{2}. \end{aligned} \end{aligned}$$

(4.3)

We derive

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&= [0,1] \times \{(-1,0),(0,0),(1,0),(-1,1),(0,1),(1,1)\},\\ {\mathcal {N}}&= {{\,\textrm{conv}\,}}\left\{ (0,0),\left( \frac{1}{5},-\frac{1}{5}\right) \right\} \\&+\left\{ (-1,1),(0,0),(1,-1),\left( -\frac{1}{4},\frac{3}{4}\right) , \left( \frac{3}{4},-\frac{1}{4}\right) ,\left( \frac{7}{4},-\frac{5}{4}\right) \right\} ,\\ {\mathcal {E}}_I&= \{(-1,0),(0,0),(1,0),(-1,1),(0,1),(1,1)\}. \end{aligned} \end{aligned}$$

We provide an illustration of the nondominated sets ${\mathcal {N}}$ and ${\mathcal {N}}_I^{\textrm{s}}$ in Fig. 4.

Fig. 4

Nondominated set ${\mathcal {N}}$ of the separable optimization problem (4.3) and nondominated set ${\mathcal {N}}_I^{\textrm{s}}$ of the integer subproblem (3.6) from Example 4.1

If for the chosen input problems (4.1) and (4.2) the exact values of $\Delta _{C} \in {\mathbb {R}}^p$ and of $\Delta _{I} \in ({\mathbb {R}}\cup \{\infty \})^p$ are not known, then the determination of some vectors $\blacktriangle _{C} \in {\mathbb {R}}^p$ and $\blacktriangle _{I} \in ({\mathbb {R}}\cup \{\infty \})^p$ with $\Delta _{C} \le \blacktriangle _{C}$ and $0_p < \blacktriangle _{I} \le \Delta _{I}$ is of great importance in terms of applicability of the formulated test instance generator. If, for instance, a set $M \supseteq {\mathcal {E}}_C^{\textrm{s}}$ with known ideal point ${{\,\textrm{ideal}\,}}_{C}$ of $f_C$ over M defined by

$$\begin{aligned} {{\,\textrm{ideal}\,}}_{C,i}:=\inf _{x_C \in M} f_{C,i}(x_C) = \inf _{y \in f_C(M)} y_i \; \text{ for } \text{ all } i \in [p] \end{aligned}$$

and known anti-ideal point ${{\,\mathrm{a-ideal}\,}}_{C}$ of $f_C$ over M defined by

$$\begin{aligned} {{\,\mathrm{a-ideal}\,}}_{C,i}:=\sup _{x_C \in M} f_{C,i}(x_C) = \sup _{y \in f_C(M)} y_i \; \text{ for } \text{ all } i \in [p], \end{aligned}$$

is given, then every $\blacktriangle _{C}$ with $\blacktriangle _{C} \ge {{\,\mathrm{a-ideal}\,}}_C-{{\,\textrm{ideal}\,}}_C$ is an upper bound of $\Delta _C$.

Example 4.2

If we choose in the test instance generator for the multiobjective continuous optimization problem (4.1) the optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} (1+x_3)(x_1^3x_2^2-10x_1-4x_2)\\ (1+x_3)(x_1^3x_2^2-10x_1+4x_2)\\ 3(1+x_3)x_1^2 \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_C=[1,3.5]\times [-2,2]\times [0,1] \end{aligned} \end{aligned}$$

as introduced in Deb et al. (2005), then it holds

$$\begin{aligned} {\mathcal {E}}_C^{\textrm{s}}\subseteq \left\{ x \in {\mathbb {R}}^3 \mid \ 1 \le x_1 \le 3.5,\;-2 \le x_1^3x_2 \le 2,\; -2 \le x_2 \le 2,\;x_3=0\right\} =:M. \end{aligned}$$

By simple calculations we obtain $(-47,-47,3) \le {{\,\textrm{ideal}\,}}_C$ and ${{\,\mathrm{a-ideal}\,}}_{C} \le (2,2,37)$. Thus every $\blacktriangle _{C} \in {\mathbb {R}}^3$ with $\blacktriangle _{C} \ge (49,49,34) \ge {{\,\mathrm{a-ideal}\,}}_C-{{\,\textrm{ideal}\,}}_C$ is an upper bound of $\Delta _C$.

A possibility for the determination of a lower bound $\blacktriangle _{I}$ of $\Delta _{I}$ is to use the finite cardinality of the set $X_I = [l_I,u_I] \cap {\mathbb {Z}}^m$. Moreover, to ensure that $\Delta _{I}>0_p$ and thus $\blacktriangle _{I}\le \Delta _{I}$ can be chosen such that $\blacktriangle _{I}>0_p$ we can use the following property introduced and examined in De Santis et al. (2022, 2020).

Definition 4.3

(De Santis et al. 2022, Definition 2.3) Let ${\mathcal {X}} \subseteq {\mathbb {R}}^m$ and $\gamma >0$. A function $g:{\mathcal {X}} \rightarrow {\mathbb {R}}$ is called a positive $\gamma$-function over ${\mathcal {X}}\cap {\mathbb {Z}}^m$ if it holds $|g(x)-g(x')|\ge \gamma$ for all $x,x' \in {\mathcal {X}}\cap {\mathbb {Z}}^m$ with $g(x) \ne g(x')$.

For instance, every quadratic function $g:{\mathcal {X}} \rightarrow {\mathbb {R}}$ with $g(x):= x^\top Q x + c^\top x$ for all $x \in {\mathcal {X}}$ with $Q \in {\mathbb {Z}}^{m\times m}, c \in {\mathbb {Z}}^m$ is a positive $\gamma$-function over ${\mathcal {X}}\cap {\mathbb {Z}}^m$ with $\gamma =1$. For more classes of positive $\gamma$-functions and the corresponding values of $\gamma$ we refer to (De Santis et al. 2020, Section 4.3).

If now $f_{I,i}$, $i\in [p]$ is a positive $\gamma _i$-function over $X_I = [l_I,u_I] \cap {\mathbb {Z}}^m$, then we obtain

$$\begin{aligned} \begin{aligned} \Delta _{I,i}&=\inf \{|y_i-{\hat{y}}_i |\mid y,{\hat{y}} \in {\mathcal {N}}_I^{\textrm{s}}, y_i \ne {\hat{y}}_i\}\\&=\inf \{|f_{I,i}(x)-f_{I,i}(x') |\mid x,x' \in {\mathcal {E}}_I^{\textrm{s}}, f_{I,i}(x)\ne f_{I,i}(x')\}\\&\ge \inf \{|f_{I,i}(x)- f_{I,i}(x') |\mid x,x' \in X_I, f_{I,i}(x)\ne f_{I,i}(x')\}\\&\ge \gamma _i >0. \end{aligned} \end{aligned}$$

Hence, if there exists some $\gamma \in {\mathbb {R}}^p$ such that $\gamma _i>0$ and $f_{I,i}$ is a positive $\gamma _i$-function over $X_I$ for all $i \in [p]$, then every $\blacktriangle _{I}$ with $0_p < \blacktriangle _{I} \le \gamma$ is a lower bound of $\Delta _I$.

In the following we provide some multiobjective continuous optimization problems and some multiobjective integer optimization problems that can be used as input for the formulated test instance generator. What is more, all of these optimization problems are scalable in the number of decision variables.

4.1 Scalable multiobjective continuous problems

The major advantage of Theorem 3.4 is that we can generate test instances for which the efficient set, the nondominated set, and the set of efficient integer assignments are known as long as the nondominated and the efficient sets of the input problems (4.1) and (4.2) are known. Regarding a listing of suitable inputs for the test instance generator we start with two biobjective continuous optimization problems scalable in the number of variables. This scalability is a useful property in order to evaluate and compare the performance of (especially decision space based) solution algorithms.

The following simple convex optimization problem is based on a well known univariate biobjective test instance introduced in Schaffer (1985):

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} \frac{1}{{n}} \sum \limits _{i=1}^{n} x_i^2\\ \frac{1}{{n}} \sum \limits _{i=1}^{n} (x_i-2)^2 \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_C=[0,2]^{n}. \end{aligned} \end{aligned}$$

(4.4)

Besides the efficient and nondominated sets also the vector $\Delta _C \in {\mathbb {R}}^2$ is known for this optimization problems. More precisely, we have that

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&= \left\{ x\in X_C \left| \ x_1=x_2=\ldots =x_n \right. \right\} ,\\ {\mathcal {N}}&=\left\{ \left. \left( t^2,(t-2)^2\right) \right| t \in [0,2] \right\} , \text{ and }\\ \Delta _{C,i}&=4 \; \text{ for } \text{ all } i \in [2]. \end{aligned} \end{aligned}$$

(4.5)

Another possible choice for (4.1) is the biobjective continuous nonconvex optimization problem introduced in Fonseca and Fleming (1995):

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i-\frac{1}{\sqrt{{n}}}\right) ^2\right) \\ 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i+\frac{1}{\sqrt{{n}}}\right) ^2\right) \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_C=[-4,4]^{n}. \end{aligned} \end{aligned}$$

(4.6)

For the efficient set, the nondominated set, and $\Delta _C \in {\mathbb {R}}^2$ we obtain

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&= \left\{ x\in X_C \left| \ x_1=x_2=\ldots =x_n \in \left[ -\frac{1}{\sqrt{{n}}},\frac{1}{\sqrt{{n}}}\right] \right. \right\} ,\\ {\mathcal {N}}&= \left\{ \left. \left( 1-\exp (-4(t-1)^2),1-\exp (-4t^2)\right) \right| t \in [0,1] \right\} , \text{ and } \\ \Delta _{C,i}&= 1-\exp (-4) \; \text{ for } \text{ all } i \in [2]. \end{aligned} \end{aligned}$$

(4.7)

One well-known method to generate other input problems where ${\mathcal {E}}$, ${\mathcal {N}}$ and also an overestimator $\blacktriangle _C$ of $\Delta _C$ are known is presented in (Deb et al. 2005, Section 6.4). The main idea of this approach is to start with a parametric description of the nondominated set (for instance a part of the unit sphere in the forthcoming optimization problem (4.9)) and then to extend this in order to obtain an optimization problem. What is more, all of the multiobjective continuous optimization problems that are generated with that technique are scalable in the number of variables. Besides that, one can also generate problems that are scalable in the number of objective functions. Again, this is a useful property when generating a collection of test instances to evaluate and compare the performance of different (especially criterion space based) solution algorithms.

In the following, we present two examples of continuous optimization problems from Deb et al. (2005) that are scalable in both the number $n \in {\mathbb {N}}$ of (continuous) variables and $p \in {\mathbb {N}}$ of objective functions. The first one is test problem DTLZ1 given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad f(x)\\ \text{ s.t. }&\quad g(x) \le 0, \\&\quad x \in X_C=[0,1]^n \end{aligned} \end{aligned}$$

(4.8)

where $n>p$. The objective functions $f_{i} :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, i \in [p]$ are defined as

$$\begin{aligned} f_{1}(x)&:= 0.5 (1-g(x)) x_1 x_2 \cdots x_{p-1}, \\ f_{i}(x)&:= 0.5 (1-g(x)) x_1 x_2 \cdots x_{p-i} (1-x_{p-i+1}) \text{ for } \text{ all } i \in ([p] \setminus \{1,p\}), \\ f_{p}(x)&:= 0.5 (1-g(x)) (1-x_1) \end{aligned}$$

and $g :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}$ only depends on the last $n-p$ variables, i.e., there exists $h :{\mathbb {R}}^{n-p} \rightarrow {\mathbb {R}}$ such that $g(x) = h(x_{p+1},\ldots ,x_n)$ for all $x \in [0,1]^n$. Further, we assume that there exists some $x^\prime \in [0,1]^n$ such that $g(x^\prime ) = 0$. It then holds for (4.8) that

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&=\{x \in [0,1]^n \mid g(x) = 0\},\\ {\mathcal {N}}&=\{y \in [0,1]^p \mid \left\Vert y \right\Vert _1 = 0.5\}, \text{ and } \\ \Delta _{C,i}&= 0.5 \; \text{ for } \text{ all } i \in [p]. \end{aligned} \end{aligned}$$

The next optimization problem can be found as (6.7) in Deb et al. (2005) and is given by

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad f(x)\\ \text{ s.t. }&\quad g(x) \le 0, \\&\quad x \in X_C=[0,\pi /2]^n \end{aligned} \end{aligned}$$

(4.9)

where $n>p$, the objective functions $f_{i} :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, i \in [p]$ are defined as

$$\begin{aligned} f_{1}(x)&:= (1-g(x)) \cos (x_1) \cos (x_2) \cdots \cos (x_{p-1}), \\ f_{i}(x)&:= (1-g(x)) \cos (x_1) \cos (x_2) \cdots \cos (x_{p-i}) \sin (x_{p-i+1}) \text{ for } \text{ all } i \in ([p] \setminus \{1,p\}), \\ f_{p}(x)&:= (1-g(x)) \sin (x_1) \end{aligned}$$

and $g :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}$ only depends on the last $n-p$ variables. Again, we assume that there exists some $x^\prime \in [0,\pi /2]^n$ such that $g(x^\prime ) = 0$. Then it holds for (4.9) that

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&=\{x \in [0,\pi /2]^n \mid g(x) = 0\},\\ {\mathcal {N}}&= \{y \in [0,1]^p \mid \left\Vert y \right\Vert _2 = 1\}, \text{ and } \\ \Delta _{C,i}&= 1 \; \text{ for } \text{ all } i \in [p]. \end{aligned} \end{aligned}$$

We remark that for the specific choice of $g(x):= \sum _{i=p+1}^n (x_i-\pi /4)^2,\ x \in [0,\pi /2]^n$ this leads to the test problem DTLZ2 from Deb et al. (2005).

4.2 Scalable multiobjective integer problems

Besides the continuous subproblems we also need suitable integer subproblems. In the following we present two such problems that are not only scalable in the number of variables, but for which we are also able to control the number of efficient solutions and nondominated points.

Lemma 4.4

Let $J \subsetneq [m]$. Then for the scalable biobjective integer linear optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} \sum \limits _{i\in J }x_i+\sum \limits _{i\in [m]\setminus J }x_i\\ \sum \limits _{i\in J }x_i-\sum \limits _{i\in [m]\setminus J }x_i \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_I=[-1,1]^{m} \cap {\mathbb {Z}}^{m} \end{aligned} \end{aligned}$$

(4.10)

it holds:

• (i) ${\mathcal {E}}=\left\{ x \in X_I \left| \ x_i=-1 \text{ for } \text{ all } i \in J \right. \right\}$.

• (ii) $|{\mathcal {E}}|=3^{m-|J|}$.

• (iii) ${\mathcal {N}}=\{(-m +\delta ,m-2|J |-\delta ) \in {\mathbb {Z}}^2\mid \ \delta \in \{0\}\cup [2(m- |J|)]\}$.

• (iv) $|{\mathcal {N}}|=2 (m-|J |)+1$.

• (v) $\Delta _{I,i}=1$ for all $i \in [2]$.

Proof

Statement (ii) follows by (i), and the statements (iv) and (v) follow by (iii). We start with the proof of (i). Here, for every ${\bar{x}}\in {\mathcal {E}}\subseteq X_I$ it obviously holds that ${\bar{x}}_i=-1$ for all $i \in J$ and we obtain ${\mathcal {E}}\subseteq \left\{ x \in X_I \left| \ x_i=-1 \text{ for } \text{ all } i \in J \right. \right\}$. Let now ${\bar{x}} \in \left\{ x \in X_I \left| \ x_i=-1 \text{ for } \text{ all } i \in J \right. \right\}$ and assume that ${\bar{x}} \notin {\mathcal {E}}$. Then by the domination property there exists $x \in {\mathcal {E}}$ with

$$\begin{aligned} \begin{pmatrix} \sum \limits _{i\in J }x_i+\sum \limits _{i\in [m]\setminus J}x_i\\ \sum \limits _{i\in J }x_i-\sum \limits _{i\in [m]\setminus J }x_i \end{pmatrix} \le \begin{pmatrix} \sum \limits _{i\in J }{\bar{x}}_i+\sum \limits _{i\in [m]\setminus J }{\bar{x}}_i\\ \sum \limits _{i\in J }{\bar{x}}_i-\sum \limits _{i\in [m]\setminus J }{\bar{x}}_i \end{pmatrix} \end{aligned}$$

and with strict inequality in one component. By componentwise addition of the inequalities it follows

$$\begin{aligned} 2\sum \limits _{i\in J }x_i < 2\sum \limits _{i\in J }{\bar{x}}_i. \end{aligned}$$

In case $J \ne \emptyset$ this contradicts $x \in {\mathcal {E}}\subseteq X_I$ and ${\bar{x}}_i=-1$ for all $i \in J$. In case $J = \emptyset$ we obtain $0 < 0$. Hence, it holds ${\bar{x}} \in {\mathcal {E}}$ and thus also $\left\{ x \in X_I \left| \ x_i=-1 \text{ for } \text{ all } i \in J \right. \right\} \subseteq {\mathcal {E}}$.

For the proof of (iii) let at first ${{\bar{y}}} \in {\mathcal {N}}$. Then by definition there exists ${{\bar{x}}} \in {\mathcal {E}}$ such that $f({{\bar{x}}})={{\bar{y}}}$, and by (i) it holds ${{\bar{x}}}_i=-1$ for all $i \in J$. Moreover, let ${\bar{J}}^{-1}:=\{i\in [m]\setminus J\mid {{\bar{x}}}_i=-1\},$ ${\bar{J}}^{0}:=\{i\in [m]\setminus J\mid {{\bar{x}}}_i=0\}$ and ${\bar{J}}^{1}:=\{i\in [m]\setminus J\mid {{\bar{x}}}_i=1\}$. Then we obtain that

$$\begin{aligned} \begin{aligned} {\bar{y}}_1=f_1({{\bar{x}}})&=\sum \limits _{i\in J }x_i +\sum \limits _{i\in {\bar{J}}^{-1}}x_i +\sum \limits _{i\in {\bar{J}}^{1}}x_i\\&=-|J| -|{\bar{J}}^{-1}| +|{\bar{J}}^{1}|\\&=-|J| -|{\bar{J}}^{-1}| -|{\bar{J}}^{0}| -|{\bar{J}}^{1}| +|{\bar{J}}^{0}|+2|{\bar{J}}^{1}|\\&=-|J| -(m-|J|) +|{\bar{J}}^{0}| +2|{\bar{J}}^{1}|\\&=-m +|{\bar{J}}^{0}| +2|{\bar{J}}^{1}| \end{aligned} \end{aligned}$$

and similarly ${\bar{y}}_2=m-2|J| -\left( |{\bar{J}}^{0}| +2|{\bar{J}}^{1}|\right)$. Thus, we derive for $\delta :=|{\bar{J}}^{0}|+2|{\bar{J}}^{1}|\ge 0$ that

$$\begin{aligned} \begin{aligned} \delta&=|{\bar{J}}^{0}|+2|{\bar{J}}^{1}|\\&=|{\bar{J}}^{-1}|+|{\bar{J}}^{0}|+|{\bar{J}}^{1}| -|{\bar{J}}^{-1}|+|{\bar{J}}^{1}|\\&= m-|J|-|{\bar{J}}^{-1}|+|{\bar{J}}^{1}|\\&\le m-|J|+|{\bar{J}}^{1}|\\&\le 2(m-|J|), \end{aligned} \end{aligned}$$

and consequently ${\mathcal {N}}\subseteq \{(-m +\delta ,m-2|J |-\delta ) \in {\mathbb {Z}}^2\mid \ \delta \in \{0\}\cup [2(m- |J|)]\}$.

Let now $\delta \in {\mathbb {N}}_0$ with $0 \le \delta \le 2(m-|J|)$ and let ${{\bar{y}}} \in {\mathbb {R}}^2$ with ${{\bar{y}}}_1:=-m+\delta$ and ${{\bar{y}}}_2:=m-2|J |-\delta$. Further, let ${{\bar{J}}}^{-1},{{\bar{J}}}^{1} \subseteq [m]\setminus J$ with

$$\begin{aligned} \left|{{\bar{J}}}^{-1} \right|=\max \{m-\left|J \right|-\delta ,0\} \ \text{ and } \ \left|{{\bar{J}}}^{1} \right|=\max \{\delta -(m-\left|J \right|),0\}. \end{aligned}$$

Then at least one of the sets ${{\bar{J}}}^{-1}$ or ${{\bar{J}}}^{1}$ is empty (as at least $m-\left|J \right|-\delta \le 0$ or $\delta -(m-\left|J \right|)\le 0$). Moreover, $\left|J\cup {{\bar{J}}}^{-1}\cup {{\bar{J}}}^{1} \right|\le m$. Define ${{\bar{x}}} \in X_I$ by ${\bar{x}}_i=-1$ for all $i \in J \cup {\bar{J}}^{-1}$, ${\bar{x}}_i=1$ for all $i \in {\bar{J}}^{1}$, and ${\bar{x}}_i=0$ for all $i \in m\setminus (J\cup {\bar{J}}^{-1} \cup {\bar{J}}^1)$. Then we obtain ${{\bar{x}}} \in {\mathcal {E}}$ by (i). Moreover, one can verify that $f_1({{\bar{x}}}) =-m+\delta ={{\bar{y}}}_1$, $f_2({{\bar{x}}}) =m-2|J|-\delta ={{\bar{y}}}_2$, and thus $\{(-m +\delta ,m-2|J |-\delta ) \in {\mathbb {Z}}^2\mid \ \delta \in \{0\}\cup [2(m- |J|)]\} \subseteq {\mathcal {N}}$, which concludes the proof. $\square$

The structure of the nondominated set of (4.10) is quite simple, since all nondominated points are located on a line. In particular, all of the nondominated points are so-called supported nondominated points. This means that they can be found by solving a weighted sum scalarization of (4.10). For this reason, we also present a slight modification of this problem, see (4.11), for which only nearly half of the nondominated set consists of supported nondominated points. The proof of Lemma 4.5 is similar to the proof of Lemma 4.4 and thus omitted.

Lemma 4.5

Let $J \subsetneq [m-1]$. Then for the scalable biobjective integer linear optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} \sum \limits _{i\in J}x_i+\sum \limits _{i\in [m-1]\setminus J}x_i\ +0.75x_{m}\\ \sum \limits _{i\in J}x_i-\sum \limits _{i\in [m-1]\setminus J}x_i\ -0.25x_{m} \end{pmatrix}\\ \text{ s.t. }&\quad x \in X_I=([-1,1]^{m-1}\times [0,1]) \cap {\mathbb {Z}}^{m} \end{aligned} \end{aligned}$$

(4.11)

it holds:

• (i) ${\mathcal {E}}=\left\{ x \in X_I \left| \ x_i=-1 \text{ for } \text{ all } i \in J \right. \right\}$.

• (ii) $|{\mathcal {E}}|=2\cdot 3^{m-1-|J|}$.

• (iii) ${\mathcal {N}}={\mathcal {N}}_1 \cup {\mathcal {N}}_2$ with

  $$\begin{aligned} {\mathcal {N}}_1&:=\{(-(m-1)+\delta ,m-1-2|J|-\delta ) \in {\mathbb {Z}}^2\mid \ \delta \in \Xi \},\\ {\mathcal {N}}_2&:=\left\{ \left. \left( -(m-1)+0.75+\delta , m-1-2|J|-0.25-\delta \right) \in {\mathbb {Z}}^2 \right| \ \delta \in \Xi \right\} ,\\ \Xi&:= \{0\}\cup [2(m-1- |J|)]. \end{aligned}$$

• (iv) $|{\mathcal {N}}|= 4(m-1-|J|)+2$.

• (v) $\Delta _{I,i}=0.25$ for all $i \in [2]$.

Remark 4.6

Note that for the optimization problems (4.10) in Lemma 4.4 and (4.11) in Lemma 4.5 not only the absolute number of efficient solutions but also their share in relation to the feasible set $X_I$ can be controlled by the choice of the set J. We obtain in both cases $\frac{|{\mathcal {E}}|}{|X_I|}=3^{-|J|}$. This equals the percentage of efficient integer assignments within the set of feasible integer assignments if one of these problems is chosen as input for the test instance generator.

Further examples for an integer optimization problem ($\hbox {sMOMIP}_I$) can be obtained from (4.10) and (4.11) and basically any other multiobjective integer optimization problem by replacing the decision variables $x \in X_I$ by functions ${\tilde{x}} :{\mathbb {R}}^{k} \rightarrow {\mathbb {R}}^{m}, k \in {\mathbb {N}}$ such that for some box ${\tilde{X}} \subseteq {\mathbb {R}}^k$ it holds that ${\tilde{x}}({\tilde{X}} \cap {\mathbb {Z}}^k) = X_I$. The following lemma presents one possible realization of such a replacement of the decision variables $x \in X_I$ for (4.10) and (4.11).

Lemma 4.7

Let $u_1,u_2,u_3,u_4\in {\mathbb {N}}_0$ with $u:=u_1+u_2+u_3+u_4\ge 1$, u odd, and let $x \in \{-1,0,1\}$. Then it holds

$$\begin{aligned} x= \Bigl [x^{u_1}\Bigr ] \cdot \Bigl [\sin ^{u_2}\bigl (x \cdot \frac{\pi }{2}\bigr )\Bigr ] \cdot \Bigl [ \cos ^{u_3}\bigl ((x-1) \cdot \frac{\pi }{2}\bigr ) \Bigr ]\cdot \Bigl [\tan ^{u_4} \bigl (x \cdot \frac{\pi }{4}\bigr )\Bigr ]. \end{aligned}$$

The idea of replacing decision variables by functions is also mentioned in Deb et al. (2005) as one possibility to obtain new optimization problems out of an existing one for which the nondominated set is already known.

Moreover, while in Deb et al. (2005) the authors focus on purely continuous optimization problems, their approach to generate (scalable) test problems works in the purely integer case as well. Hence, we can use the exact same approach to also obtain multiobjective integer optimization problems (4.2). In fact, we can even reuse the presented test problem. More precisely, we can modify (4.8) and reduce it to the multiobjective binary optimization problem

$$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad f(x)\\ \text{ s.t. }&\quad g(x) \le 0, \\&\quad x \in X_I=\{0,1\}^n \end{aligned} \end{aligned}$$

(4.12)

with the same assumptions, objective functions $f_{i} :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, i \in [p]$ and constraint function $g :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}$. Then it holds for (4.12) that

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&=\{x \in \{0,1\}^n \mid g(x) = 0\},\\ {\mathcal {N}}&=\{y \in \{0,0.5\}^p \mid \left\Vert y \right\Vert _1 = 0.5\}, \text{ and } \\ \Delta _{I,i}&= 0.5 \; \text{ for } \text{ all } i \in [p]. \end{aligned} \end{aligned}$$

However, one should keep in mind that for the construction of a test instance with the methods from Deb et al. (2005) a parametric description of the nondominated set is needed as a starting point. While this is often possible in continuous optimization, for the discrete nondominated set of multiobjective integer optimization problems this is usually much harder or leads to nondominated sets of a very simple structure as in the example above. For the same reason the approach from Deb et al. (2005) is not well suited in order to directly obtain test instances for multiobjective mixed-integer optimization problems. However, if there was some (nontrivial) nondominated set that has a parametric description consisting of both continuous and integer parameters then such a construction of test instances would be possible.

To conclude this section, we present some examples for multiobjective mixed-integer optimization problems that are obtained by the proposed test instance generator when using the continuous and integer subproblems from the previous subsections as input.

Example 4.8

• (i) We choose as input for the multiobjective continuous optimization problem the biobjective subproblem (4.6) and for the multiobjective integer optimization problem the biobjective subproblem (4.10) with $J=\emptyset$ and $m=2$. Then we obtain by (4.7) and Lemma 4.4 (v) that $\Delta _{C,i}=1-\exp (-4) < 1 =\Delta _{I,i}$ for all $i \in [2]$. Thus, we can set $\blacktriangle _{C}:=\Delta _{C}$, $\blacktriangle _{I}:=\Delta _{I}$, and $\alpha :=(1,1)$. The output of the test instance generator then is the separable biobjective mixed-integer nonconvex optimization problem (3.1) of Example 3.1 with

  $$\begin{aligned} {\mathcal {E}}= & {} \left\{ x\in [-4,4]^{n} \left| \ x_1=x_2=\ldots =x_n \in \left[ -\frac{1}{\sqrt{{n}}},\frac{1}{\sqrt{{n}}}\right] \right. \right\} \\{} & {} \quad \times \{-1,0,1\}^2,\\ {\mathcal {N}}= & {} \left\{ \left. \left( 1-\exp (-4(t-1)^2),1-\exp (-4t^2)\right) \right| t \in [0,1]\right\} \\{} & {} \quad +\{(\delta ,-\delta )\mid \delta \in \{-2,-1,0,1,2\}\}, \text{ and }\\ {\mathcal {E}}_I= & {} \{-1,0,1\}^2. \end{aligned}$$

• (ii) Let (4.4) be the input for the multiobjective continuous subproblem and (4.10) the input for the multiobjective integer subproblem. Then by (4.5) and Lemma 4.4 (v) it holds $\Delta _{C,i} =4>1=\Delta _{I,i}$ for all $i \in [2]$. Thus, we can use $\blacktriangle _{C}:=\Delta _{C}$, $\blacktriangle _{I}:=\Delta _{I}$, and $0< \alpha _i < 0.25$ for all $i\in [2]$. The resulting test instance is the scalable separable biobjective mixed-integer convex optimization problem given by

  $$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} \frac{\alpha _1}{{n}} \sum \limits _{i=1}^{n} x_i^2 + \sum \limits _{i\in J }x_i+\sum \limits _{i\in \{n+1,\ldots ,n+m\}\setminus J }x_i\\ \frac{\alpha _2}{{n}} \sum \limits _{i=1}^{n} (x_i-2)^2 + \sum \limits _{i\in J }x_i-\sum \limits _{i\in \{n+1,\ldots ,n+m\}\setminus J }x_i \end{pmatrix}\\ \text{ s.t. }&\quad x\in X=[0,2]^{n}\times \left( [-1,1]^{m} \cap {\mathbb {Z}}^{m}\right) \end{aligned} \end{aligned}$$

  (4.13)

  with $J \subsetneq \{n+1,\ldots ,n+m\}$. For the efficient set, the nondominated set, and the set of efficient integer assignments we derive

  $$\begin{aligned} \begin{aligned} {\mathcal {E}}&= \left\{ x\in [0,2]^{n} \left| \ x_1=x_2=\ldots =x_n \right. \right\} \\&\quad \times \left\{ x \in [-1,1]^{m} \cap {\mathbb {Z}}^{m} \left| \ x_i=-1 \text{ for } \text{ all } i+n \in J \right. \right\} ,\\ {\mathcal {N}}&=\left\{ \left. \left( \alpha _1t^2,\alpha _2(t-2)^2\right) \right| t \in [0,2]\right\} \\&\quad +\{(-m +\delta ,m-2|J |-\delta ) \in {\mathbb {Z}}^2\mid \ \delta \in \{0\}\cup [2(m- |J|)]\}, \text{ and }\\ {\mathcal {E}}_I&= \left\{ x \in [-1,1]^{m} \cap {\mathbb {Z}}^{m} \left| \ x_i=-1 \text{ for } \text{ all } i+n \in J \right. \right\} . \end{aligned} \end{aligned}$$

  For an illustration of the nondominated set ${\mathcal {N}}$ see Fig. 5.

• (iii) If (4.6) and (4.11) are chosen as input, then it holds $\Delta _{C,i} =1-\exp (-4) > 0.25 =\Delta _{I,i}$ for all $i \in [2]$ by (4.7) and Lemma 4.5 (v). Thus, we can again choose $\blacktriangle _{C}:=\Delta _{C}$ and $\blacktriangle _{I}:=\Delta _{I}$. For any choice $0< \alpha _i < \frac{1}{4\cdot \left( 1-\exp (-4)\right) }$ for all $i\in [2]$ we then obtain the scalable separable biobjective mixed-integer nonconvex optimization problem

  $$\begin{aligned} \begin{aligned} \min \limits _{x}&\quad \begin{pmatrix} \alpha _1\left( 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i-\frac{1}{\sqrt{{n}}}\right) ^2\right) \right) \\ +\sum \limits _{i\in J}x_i+\sum \limits _{i\in \{n+1,\ldots ,n+m-1\}\setminus J}x_i\ +0.75x_{m+n}\\ \quad \alpha _2\left( 1-\exp \left( -\sum \limits _{i=1}^{n} \left( x_i+\frac{1}{\sqrt{{n}}}\right) ^2\right) \right) \\ +\sum \limits _{i\in J}x_i-\sum \limits _{i\in \{n+1,\ldots ,n+m-1\}\setminus J}x_i\ -0.25x_{m+n} \end{pmatrix}\\ \text{ s.t. }&\quad x \in X=[-4,4]^{n} \times \left( ([-1,1]^{m-1}\times [0,1]) \cap {\mathbb {Z}}^{m}\right) \end{aligned} \end{aligned}$$

  (4.14)

  with $J \subsetneq \{n+1,\ldots ,n+m-1\}$. This leads to the efficient set, nondominated set, and set of efficient integer assignments given by

  $$\begin{aligned} \begin{aligned} {\mathcal {E}}&=\left\{ x\in [-4,4]^{n} \left| \ x_1=x_2=\ldots =x_n \in \left[ -\frac{1}{\sqrt{{n}}},\frac{1}{\sqrt{{n}}}\right] \right. \right\} \\&\quad \times \left\{ x \in ([-1,1]^{m-1}\times [0,1]) \cap {\mathbb {Z}}^{m} \left| \ x_i=-1 \text{ for } \text{ all } i+n \in J\right. \right\} ,\\ {\mathcal {N}}&=\left\{ \left. \left( \alpha _1(1-\exp (-4(t-1)^2)),\alpha _2(1-\exp (-4t^2))\right) \right| t \in [0,1] \right\} +\left( {\mathcal {N}}_1 \cup {\mathcal {N}}_2\right) ,\\&\quad {\mathcal {N}}_1 =\{(-(m-1)+\delta ,m-1-2|J|-\delta ) \in {\mathbb {Z}}^2\mid \ \delta \in \Xi \},\\&\quad {\mathcal {N}}_2 =\left\{ \left. \left( -(m-1)+0.75+\delta , m-1-2|J|-0.25-\delta \right) \in {\mathbb {Z}}^2 \right| \ \delta \in \Xi \right\} ,\\&\quad \Xi = \{0\}\cup [2(m-1- |J|)], \text{ and }\\ {\mathcal {E}}_I&=\left\{ x \in ([-1,1]^{m-1}\times [0,1]) \cap {\mathbb {Z}}^{m} \left| \ x_i=-1 \text{ for } \text{ all } i+n \in J \right. \right\} . \end{aligned} \end{aligned}$$

  For an illustration of the nondominated set ${\mathcal {N}}$ see Fig. 6.

Fig. 5

Nondominated set ${\mathcal {N}}$ of the separable optimization problem (4.13) and nondominated set ${\mathcal {N}}_I^{\textrm{s}}$ of the corresponding integer subproblem (4.10) from Example 4.8 (ii) for $J=\{n+1\}$, $m=3$, and $\alpha {{_1=\alpha _2}}=0.2$

Fig. 6

Nondominated set ${\mathcal {N}}$ of the separable optimization problem (4.14) and nondominated set ${\mathcal {N}}_I^{\textrm{s}}$ of the corresponding integer subproblem (4.11) from Example 4.8 (iii) for $J=\{n+1\}$, $m=4$, and $\alpha {{_1=\alpha _2}}=0.2$

5 Outlook

In this paper, we presented a test instance generator for multiobjective mixed-integer optimization problems based on test instances for purely continuous and purely integer subproblems. By using the special separable structure, we were able to control the resulting efficient and nondominated sets as well as the number of efficient integer assignments. In this final section, we provide a brief outlook for three topics for further research.

A first direction to follow is the collection and development of continuous and integer subproblems for the test instance generator. In particular, there is a need for subproblems with more than two or even a scalable number of objective functions. With regard to the purely integer subproblems ($\hbox {sMOMIP}_I$), it would also be interesting to find examples that allow even more control over the efficient and nondominated set than (4.11). For instance, one could think of subproblems where the portion of supported nondominated points, i.e, nondominated points which can be found by solving a weighted sum of the objectives, can be controlled in a more direct way.

Another aspect for future work would be a generalization of the test instance generator for non-separable test instances. A possible approach in this regard could be the use of a finite family of continuous subproblems instead of only a single subproblem (4.1). This would allow for a slightly stronger coupling of the integer and the continuous variables.

Finally, recall that the main motivation for the development of the test instance generator was to obtain a set of benchmark problems that allows to compare and evaluate the strengths and weaknesses of solution algorithms for multiobjective mixed-integer optimization problems. Since such a set of benchmark problems can now be generated, corresponding numerical experiments would be the logical next step and a highly valuable contribution for the community.