Portfolio optimization: not necessarily concave utility and constraints on wealth and allocation

Abstract

We consider a portfolio optimization problem for a utility maximizing investor who is simultaneously restricted by convex constraints on portfolio allocation and upper and lower bounds on terminal wealth. After introducing a capped version of the Legendre–Fenchel-transformation, we use it to suitably extend the well-known auxiliary market framework for convex allocation constraints to derive equivalent optimality conditions for our setting with additional bounds on terminal wealth. The considered utility does not have to be strictly concave or smooth, as long as it can be concavified.

1 Introduction

We consider a finite-horizon portfolio optimization problem for an expected utility maximizing investor whose portfolio choice is simultaneously restricted by convex allocation constraints (such as no-shortselling constraints, non-traded asset constraints or borrowing constraints) as well as a lower and upper bound on terminal wealth. The asset universe considered consists of a generalized Black–Scholes (B.S.) market with one risk-free asset and d risky assets with possibly random but bounded coefficients. All of the uncertainty enters the market through a d dimensional Brownian motion which drives the diffusion component of the risky assets.

The basis for this portfolio optimization problem goes back to Merton (1969), Merton (1971), who considered an unconstrained portfolio optimization problem in a multi-asset B.S. market with constant market coefficients and a smooth concave utility. This set-up has been extended to general complete market models through the works of Pliska (1986), Karatzas et al. (1987) and Cox and Huang (1989). Further extensions were achieved trough the addition of transaction costs in Davis and Norman (1990), Shreve and Soner (1994), Cuoco and Liu (2000) and Kallsen and Muhle-Karbe (2010), illiquid assets in Desmettre and Seifried (2016), Choi (2020) as well as stochastic volatility in Liu and Pan (2003), Kraft (2005) and Branger et al. (2008). Moreover, general optimality results for incomplete markets were derived in Karatzas et al. (1991), Kramkov and Schachermayer (1999) and Larsen and Žitkoviç (2013). Despite these extensions on the model dynamics, the existence of most closed-form solutions to the portfolio optimization problem remained closely linked to the smoothness and concavity of the underlying utility function. Using concavification techniques, Carpenter (2000) expanded the existing literature in regards to non-concave and non-smooth utility functions. In light of the growing reception towards Kahnemann and Tversky’s presentation of CPT in Tversky and Kahneman (1992), continuous-time portfolio optimization under non-concave, non-smooth preferences has been extensively studied since, for example in Berkelaar et al. (2004), Cuoco and Kaniel (2011), Jin and Yu Zhou (2008), Reichlin (2013), Rásonyi and Rodrigues (2013) and Rásonyi and Rodríguez-Villarreal (2016). Due to the thorough treatment in the literature, the classical unconstrained portfolio optimization problem can be considered well-studied and well-understood.

Once the investor faces constraints that restrict his investment decisions, for example imposed by a regulator, the problem complexity quickly increases. One natural example for this is a lower bound on terminal wealth, which forces the investor to ensure that his wealth must not fall below a predetermined level at the end of his investment horizon. Such a bound is very natural as it directly limits the investor’s downside risk. A portfolio optimization problem, which includes a (possibly stochastic) lower bound was solved by Tepla (2001) and Korn (2005). Shortly thereafter, more complex wealth constraints were considered in the context of portfolio optimization. Notable examples include constraints on Value-at-Risk, expected shortfall or more general risk measures in Basak and Shapiro (2001), Kraft and Steffensen (2013), Pirvu (2007), Moreno-Bromberg et al. (2013), Chen et al. (2013) and Chen et al. (2020), which do not impose a strict lower bound on terminal wealth while still limiting the investor’s downside. Further, a more uncommon constraint, an additional upper bound on terminal wealth, was considered in Donnelly et al. (2015). This additional restriction reduces the probability of large losses at the cost of limiting the upside. However, solutions to portfolio problems including the preceding constraints were mostly obtained for smooth and concave utility functions and are heavily dependent on the underlying market being complete.

Once the investor’s portfolio allocation is restricted, this is not the case anymore. For an investor facing convex portfolio allocation constraints, but no direct constraints on terminal wealth, Cvitanic and Karatzas (1992) embedded this allocation constrained portfolio optimization problem into a family of unconstrained portfolio optimization problems formulated for an auxiliary market with changed market coefficients. Given that the right market coefficients are found, one can can derive an optimal portfolio for the original allocation constrained portfolio optimization problem. Notably, the approach presented in Cvitanic and Karatzas (1992) generalizes the methods for incomplete markets presented in Karatzas et al. (1991). While Cvitanic and Karatzas (1992) considered constraints on the fraction of wealth invested in the individual assets, Zariphopoulou (1994) and Cuoco (1997) considered a portfolio optimization problem with constraints on the absolute amount of wealth invested in the individual assets. Further advancements in the area of allocation constrained portfolio optimization have since been made by Zariphopoulou (1994), Bouchard et al. (2004), Bian et al. (2011), Larsen and Žitkoviç (2013) and Li and Zheng (2018). All of these advances required that no additional constraints on terminal wealth are present.

So far, the literature on portfolio optimization under simultaneous terminal wealth and allocation constraints has been scarce and, if existent, did not aim to create a holistic approach to treating these types of problems. Notable examples include Bardhan (1994), Dong and Zheng (2019), Escobar et al. (2019) and Dong and Zheng (2020). We aim to fill this gap in the literature by:

• Introducing the intuitive concept of a capped Legendre–Fenchel transformation, which allows us to solve a portfolio optimization problem under simultaneous lower and upper bounds on terminal wealth.

• Extending the auxiliary market framework to include lower and upper bounds on terminal wealth as well as a large class of non-smooth, non-concave utility functions.

• Deriving explicit solutions to portfolio optimization problems with non-concave, non-smooth utility functions, with lower and upper bounds on terminal wealth and simultaneous convex cone constraints on allocation via the extended auxiliary market framework.

The paper is structured as follows: Section 2 introduces the market model and the portfolio optimization problem with simultaneous constraints on wealth and allocation. Before we solve this fully constrained problem, we first review the solution technique to a fully unconstrained portfolio optimization problem and a wealth-constrained portfolio optimization problem, which we proceed to solve by introducing the capped Legendre–Fenchel transformation in Sect. 3. Afterwards we extend the auxiliary market from Cvitanic and Karatzas (1992) framework to include constraints on the allocation and treat the fully constrained portfolio optimization problem in Sect. 4. Section 5 introduces and solves a related dual optimization problem, which can be used to explicitly solve the fully constrained portfolio optimization problem for concave utility functions as well as for not necessarily concave utility functions. Section 6 concludes the paper.

2 The portfolio optimization problem with constraints on wealth and allocation

We consider a finite time horizon $T>0$ and a complete, filtered probability space $(\varOmega , {\mathcal {F}}_T,\mathbbm {F} = ({\mathcal {F}}_t)_{t \in [0,T]}, Q)$, where the filtration $\mathbbm {F}$ is generated by a d-dimensional Wiener process $W = (W(t))_{t \in [0,T]}$. We employ this setting to define a market model $\mathbf {{\mathcal {M}}}$ with d risky assets (e.g. stocks) $P = (P_1,..., P_d)'$ and a risk-free asset (e.g. a bank account) $P_0$, which evolve according to the following dynamics:

$$\begin{aligned} \begin{aligned} dP(t)&= P(t) \big ( \mu (t)dt + \sigma (t)dW(t)\big ) \\ dP_0(t)&= P_0(t) r(t) dt\\ P_i(0)&= 1 \quad \text {for } i=0,...,d. \end{aligned} \end{aligned}$$

The market coefficients $\mu , \sigma ,$ and r are assumed to be progressively measurable processes w.r.t. $\mathbbm {F}$ and uniformly bounded in $(t,\omega )\in [0,T] \times \varOmega$. Moreover, we assume that the volatility matrix ${\mathcal {L}}[0,T]\otimes Q-a.s.$ satisfies the strong nondegeneracy condition

$$\begin{aligned} \Vert \sigma (t)'x \Vert ^2 \ge \xi \Vert x \Vert ^2, \quad \forall x \in \mathbbm {R}^d \end{aligned}$$

(2.1)

for some constant $\xi > 0$. This condition ensures that the inverse $\sigma (t)^{-1}$ exists for every $t \in [0,T]$ and is uniformly bounded in $(t,\omega )$, too. These conditions imply that the considered market is complete (e.g. see Cvitanic and Karatzas (1992), Proposition 7.3). Note that market completeness is not a prerequisite for the theory developed in this paper, but instead an instrument to facilitate the exposition. Just as in Karatzas et al. (1991), in the case of an incomplete market, one can add additional fictitious assets to complete the market and use the theory developed in Sect. 4 to rule out investments into these assets through an allocation constraint.

Under these conditions we are allowed to define the market price of risk $\gamma$, the corresponding Doléans-Dade-exponential Z and pricing Kernel ${\tilde{Z}}$ as

$$\begin{aligned} \begin{aligned} \gamma (t)&:= \sigma ^{-1}(t)\big (\mu (t) - r(t) \mathbbm {1} \big ) \\ Z(t)&:= \exp \Big \{-\frac{1}{2}\int _0^t \Vert \gamma (s) \Vert ^2ds - \int _0^t \gamma (s)'dW(s) \Big \} \\ {\tilde{Z}}(t)&:= \frac{Z(t)}{P_0(t)} = \exp \Big \{-\int _0^t r(s) + \frac{1}{2}\Vert \gamma (s) \Vert ^2ds - \int _0^t \gamma (s)'dW(s) \Big \} \end{aligned} \end{aligned}$$

for $t \in [0,T]$. Note that Z and ${\tilde{Z}}$ satisfy the SDEs

$$\begin{aligned} \begin{aligned} dZ(t)&= -Z(t) \gamma (t)'dW(t) \\ d{\tilde{Z}}(t)&= -{\tilde{Z}}(t)\big (r(t)dt + \gamma (t)'dW(t)\big ). \end{aligned} \end{aligned}$$

In particular, due to the uniform boundedness of the market coefficients (and thus $\gamma$), Z satisfies Novikov’s condition and is a martingale.

We consider a single investor who trades in ${\mathcal {M}}$. Provided he has initial wealth $v_0>0$ at time $t=0$, his wealth process in ${\mathcal {M}}$ satisfies the SDE

$$\begin{aligned} dV^{v_0, \pi }(t) = V^{v_0, \pi }(t) \Big ( [r(t) + (\mu (t) - r(t)\mathbbm {1})'\pi (t)]dt + \pi (t)'\sigma (t)dW(t)\Big ) \quad \ \forall t \in [0,T]\nonumber \\ \end{aligned}$$

(2.2)

with $V^{v_0, \pi }(0)=v_0$. The d-dimensional portfolio process $\pi$ is chosen by the investor and determines the fraction of wealth $\pi _i(t)$ that is allocated to the risky asset $P_i(t)$ at time t, while the remaining fraction $1-\sum _{i=1}^d \pi _i(t)$ is allocated to the risk-free asset. Note that $1-\sum _{i=1}^d \pi _i(t)$ may be negative, in which case the investor goes short the risk-free asset, or more intuitively, borrows from the bank account. To ensure that the investor allocates his wealth solely based on past price developments and to ensure that (2.2) is well-defined, we restrict the admissible portfolio processes $\pi$ to the following set:

$$\begin{aligned} \varLambda = \Big \{&\pi = \big ((\pi _1(t),...,\pi _d(t))'\big )_{t \in [0,T]} \ \text {progr. measurable} \ \Big | \nonumber \\&\quad \ \int _0^T \big (V^{v_0, \pi }(t) \Vert \pi (t) \Vert \big )^2 dt < \infty \ Q-a.s.\Big \} \end{aligned}$$

(2.3)

Note that despite $v_0$ appearing in the integrability condition in (2.3), $\varLambda$ is independent of the specific value of $v_0$ because the initial wealth is just a constant multiplier to any wealth process $V^{v_0, \pi }(t)$ and hence does not affect the integrability condition in (2.3).

Apart from these mathematical restrictions, investors in the real-world often face additional constraints when allocating their wealth. We incorporate two general classes of such constraints into our model: allocation constraints and bounds on terminal wealth. Both types of constraints have been discussed extensively in the existing literature, (see e.g. Cvitanic and Karatzas (1992) for allocation constraints and Donnelly et al. (2015) for upper and lower bounds on terminal wealth), but to the best of our knowledge a general mathematical theory that handles both types of constraints simultaneously in the context of portfolio optimization is still absent from the literature.

From now on, let $K \subset \mathbbm {R}^d$ be a closed convex set, which we call allocation constraints. Further, let $0 \le B_1 < B_2 \le \infty$ be two constants, which we call bounds on terminal wealth (note that $B_2$ may be infinite). The set of admissible portfolio processes under allocation constraints K and bounds on terminal wealth $B_1, B_2$ is given as

$$\begin{aligned} \varLambda (v_0,K,B_1,B_2) = \Big \{ \pi \in \varLambda \ \Big | \ \pi \in K, \ B_1 \le V^{v_0, \pi }(T) \le B_2 \Big \}, \end{aligned}$$

where both the statement about $\pi$ and $V^{v_0, \pi }(T)$ are interpreted in an a.e. sense, i.e. $\pi (t) \in K$ ${\mathcal {L}}[0,T]\otimes Q$-a.e. and $B_1 \le V^{v_0, \pi }(T) \le B_2$ Q-a.s.. Note that due to the additional bounds on terminal wealth, $\varLambda (v_0,K,B_1,B_2)$ is in general not independent of $v_0$.

The investor’s risk preferences are incorporated through the choice of an appropriate utility function, which derives utility from terminal wealth.

For this purpose we define the class of utility functions ${\mathcal {U}}(B_1,B_2)$, which contains all functions $U:(0,\infty )\rightarrow \mathbbm {R}$, which satisfy:

$$\begin{aligned} (i)&\quad U \ \text {is upper semi-continuous} \nonumber \\ (ii)&\quad U \ \text {is non-decreasing and non-constant} \nonumber \\ (iii)&\quad \lim _{x\rightarrow \infty } \frac{U(x)}{x}= 0 \nonumber \\ (iv)&\quad U(B_2)> U(x) \ \text {and} \ U(x)>-\infty \ \text {for all} \ x\in (B_1,B_2). \nonumber \\ \end{aligned}$$

(2.4)

If U is finite on $(B_1,B_2)$, differentiable and strictly increasing (as in Cvitanic and Karatzas (1992)), then (iv) holds automatically and (iii) is equivalent to the condition $\lim _{x\rightarrow \infty }U'(x) = 0$. We set $U(0) = \lim _{x\downarrow 0}U(x)$ and $U(\infty ) = \lim _{x\rightarrow \infty }U(x)$. For Sects. 3 and 4 we will restrict ourselves to concave utility functions $U\in {\mathcal {U}}^{\text {conc}}(B_1,B_2):= \{ u\in {\mathcal {U}}(B_1,B_2) \ |\ u \ \text {is concave}\}$.

Note that we do not put any restrictions regarding continuity on $(B_1,\infty )$ or differentiability on the functions in ${\mathcal {U}}(B_1, B_2)$. However, any $U \in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$ is continuous, where it is finite (as it is concave) and is even twice differentiable Lebesgue a.e. (due to Alexandrov’s Theorem, e.g. Theorem 14.25 in Villani (2009)). Keeping this in mind, we may refer to the first or second derivative of a $U\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$ in an Lebesgue a.e.-sense.

We are now able to formulate the portfolio optimization problem (P) for the utility-maximizing investor with a given utility $U:(0,\infty )\rightarrow \mathbbm {R}$:

$$\begin{aligned} \mathbf {(P)} {\left\{ \begin{array}{ll} \varPhi (v_0) = \underset{\pi \in \varLambda (v_0, K, B_1, B_2)}{\sup } \mathbbm {E}\big [U(V^{v_0, \pi }(T)) \big ] \end{array}\right. } \end{aligned}$$

Clearly, we can rewrite (P) directly as a maximization over all attainable terminal wealths:

$$\begin{aligned} \mathbf {(P)} {\left\{ \begin{array}{ll} \varPhi (v_0) &{}= \underset{D \in C(v_0, K, B_1, B_2)}{\sup } \mathbbm {E}\big [U(D) \big ] \\ C(v_0, K, B_1, B_2) &{}= \big \{V^{v_0, \pi }(T) \ \big | \ \pi \in \varLambda (v_0, K, B_1, B_2) \big \} \end{array}\right. } \end{aligned}$$

This may seem trivial at first, but since $C(v_0,K,B_1,B_2)$ can often be simplified substantially (depending on the choice of $K, \ B_1$ and $B_2$), it is more convenient to write (P) this way.

Note that there are many instances for which $\varLambda (v_0, K, B_1, B_2)$ is an empty set (for example for $B_1 := v_0\cdot P_0(T) + 1$)¹ or for which any $\pi \in \varLambda (v_0, K, B_1, B_2)$ is optimal for $\mathbf {(P)}$ (i.e. if U is constant on $[B_1, B_2]$). Hence, we need to make suitable assumptions on $K, B_1,B_2$ and U to rule out these instances.

Assumption 2.1

• (i) K is a closed convex set, which contains the origin $0\in \mathbbm {R}^d$.

• (ii) $B_1< v_0 P_0(T) < B_2$ $Q-a.s.$

• (iii) $U \in {\mathcal {U}}(B_1,B_2)$.

Unless otherwise stated, Assumption 2.1 is always assumed throughout this paper. It guarantees that the risk-neutral strategy $\pi \equiv 0$ is admissible, but not an immediate solution to $\mathbf {(P)}$, as the investor’s utility is maximized at the upper bound $B_2$. Further, it guarantees that the utility U does not impose an artificial constraint on the investor’s terminal wealth beside the bounds $B_1, B_2$.

(P) is the most general portfolio optimization problem solved in this paper. In the following section, we start off by solving the well-known unconstrained portfolio optimization problem (with $K = \mathbbm {R}^d$, $B_1 = 0$, $B_2 = \infty$) for concave utility functions U and gradually increase the problem complexity, by adding constraints on terminal wealth and portfolio allocation step-by-step.

3 The capped Legendre–Fenchel-transformation

For the entirety of this section we assume that no allocation constraints are present, i.e. $K = \mathbbm {R}^d$ and the considered utility U is concave.

3.1 Fully unconstrained portfolio optimization

Let us first consider the by now well-understood unconstrained portfolio optimization problem, i.e. $K = \mathbbm {R}^d, \ B_1 = 0$ and $B_2 = \infty$ (see. e.g. Pliska 1986 or Karatzas et al. 1987). Then, (P) simplifies to

$$\begin{aligned} \mathbf {(P^{unc})} {\left\{ \begin{array}{ll} \varPhi (v_0) &{}= \underset{D \in C(v_0)}{\sup } \mathbbm {E}\big [U(D) \big ] \\ C(v_0) &{}= C(v_0,\mathbbm {R}^d,0,\infty ) = \big \{V^{v_0, \pi }(T) \ \big | \ \pi \in \varLambda \big \} \end{array}\right. } \end{aligned}$$

It is a well-known fact (see e.g. Cvitanic and Karatzas 1992, Proposition 7.3) that under the present assumptions on market coefficients and admissible portfolio processes $\pi$, the considered market is complete and $C(v_0)$ simplifies to

$$\begin{aligned} C(v_0) = \big \{ D \ge 0 \ {\mathcal {F}}_T-\text {measurable} \ \big | \ \mathbbm {E}[D{\tilde{Z}}(T)] = v_0 \big \}. \end{aligned}$$

(3.1)

The requirement $\mathbbm {E}[D{\tilde{Z}}(T)] = v_0$ for any admissible terminal wealth D is also referred to as budget condition.

The classic approach to solving $\mathbf {(P^{unc})}$ now introduces the Legendre–Fenchel transformation (LFT) $U^{*}:(0,\infty ) \rightarrow \mathbbm {R}$ of the investor’s utility U as

$$\begin{aligned} U^{*}(y) := \underset{x \ge 0}{\text {sup}}\Big ( U(x)-yx \Big ) = U({\mathcal {I}}(y)) - y{\mathcal {I}}(y) \end{aligned}$$

with

$$\begin{aligned} {\mathcal {I}}(y) := \inf \big \{ x \ge 0 \ \big | \ U^{*}(y) = U(x) - yx \big \}. \end{aligned}$$

We further introduce the help function $H:(0,\infty ) \rightarrow \mathbbm {R}$ as

$$\begin{aligned} H(y):= \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}(T)) {\tilde{Z}}(T)]. \end{aligned}$$

Lemma 3.1

Assume that $H(y) < \infty \ \forall y > 0$. Then, H is strictly decreasing, continuous and satisfies

$$\begin{aligned} \lim _{y \downarrow 0} \ H(y)&= \lim _{y \downarrow 0} \ \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}(T)) {\tilde{Z}}(T)] = \infty \\ \text { and } \quad \lim _{y \rightarrow \infty } \ H(y)&= \lim _{y \rightarrow \infty } \ \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}(T)) {\tilde{Z}}(T)] = 0. \end{aligned}$$

In particular, there exists a continuous and strictly decreasing bijection

$$\begin{aligned} Y:(0,\infty ) \rightarrow (0,\infty ) \end{aligned}$$

such that

$$\begin{aligned} H(Y(v)) = v \quad \forall v\in (0,\infty ). \end{aligned}$$

Proof

A more general version of this lemma, Lemma 4.4, is proved in the appendix. $\square$

This convenient construction of $U^{*}, {\mathcal {I}},$ and H enables us to solve $\mathbf {(P^{unc})}$ fairly easily:

Theorem 3.2

(Optimal Terminal Wealth of the Fully Unconstrained Portfolio Optimization Problem) Let U be concave, $K = \mathbbm {R}^d$, $B_1 = 0$, $B_2 = \infty$ and assume that $H(y) < \infty \ \forall y>0$. Then,

$$\begin{aligned} D^{*} := {\mathcal {I}}(y{\tilde{Z}}(T)), \end{aligned}$$

with $y = Y(v_0)$, is the optimal terminal wealth for $\mathbf {(P^{unc})}$.

Proof

By definition of ${\mathcal {I}}$ and y, $D^{*}$ is non-negative and $\mathbbm {E}[D^{*}{\tilde{Z}}(T)] =v_0$. Thus, $D^{*} \in C(v_0)$ is admissible for $\mathbf {(P^{unc})}$. Further, let ${\hat{D}} \in C(v_0)$ be any other admissible terminal wealth for $\mathbf {(P^{unc})}$. Then,

$$\begin{aligned} \begin{aligned} \mathbbm {E}[U({\hat{D}})]&= \mathbbm {E}[U({\hat{D}}) - y{\tilde{Z}}(T){\hat{D}}] + yv_0\le \underset{D \in C(v_0)}{\sup }\big (\mathbbm {E}[U(D) - y{\tilde{Z}}(T)D] \big )+ yv_0\\&\le \mathbbm {E}[\underset{x \ge 0}{\text {sup}}\big (U(x) - y{\tilde{Z}}(T)x\big )]+ yv_0\\&= \mathbbm {E}[U(\underbrace{{\mathcal {I}}(y{\tilde{Z}}(T))}_{= D^{*}})]-y\underbrace{\mathbbm {E}[{\tilde{Z}}(T){\mathcal {I}}(y{\tilde{Z}}(T))]}_{=v_0}+yv_0 = \mathbbm {E}[U(D^{*})]. \end{aligned} \end{aligned}$$

$\square$

Remark 3.3

Theorem 3.2 is a well-known result in the mathematical finance literature. To name a few sources, the theorem can be found with varying degrees of generality as Theorem 4 in Pliska (1986), Theorem 5.2 in Karatzas et al. (1987) and Proposition B.1 in Reichlin (2013).

Now that we have solved the fully unconstrained portfolio optimization problem $\mathbf {(P^{unc})}$, we turn to upper and lower bounds on terminal wealth.

3.2 Wealth-constrained portfolio optimization

We now consider the wealth-constrained portfolio optimization problem, i.e. $K = \mathbbm {R}^d$ and $B_1, \ B_2$ are constants satisfying Assumption 2.1. A similar problem was considered in Donnelly et al. (2015) for $d=1$ with constant market coefficients. In our setting, (P) reduces to the form

$$\begin{aligned} \mathbf {(P^{Vcons})} {\left\{ \begin{array}{ll} \quad \varPhi (v_0) &{}= \underset{D \in C(v_0,B_1,B_2)}{\sup } \mathbbm {E}\big [U(D) \big ] \\ C(v_0,B_1,B_2) &{}= C(v_0,\mathbbm {R}^d,B_1,B_2) \\ {} &{}= \big \{V^{v_0, \pi }(T) \ \big | \ \pi \in \varLambda , \ B_1 \le V^{v_0, \pi }(T) \le B_2 \big \} \end{array}\right. } \end{aligned}$$

Since $C(v_0, B_1, B_2) \subset C(v_0)$ and all $D \in C(v_0)$ with $B_1 \le D \le B_2$ are necessarily in $C(v_0, B_1, B_2)$, we obtain the following simplified characterization of $C(v_0, B_1, B_2)$:

$$\begin{aligned} C(v_0, B_1, B_2)&= \big \{D \in C(v_0) \ | \ B_1 \le D \le B_2 \} \\&\overset{ (3.1)}{=} \big \{ D \ge 0 \ {\mathcal {F}}_T-\text {measurable} \ \big | \ \mathbbm {E}[D{\tilde{Z}}(T)] = v_0, \ B_1 \le D \le B_2 \big \} \end{aligned}$$

Let us now recall the proof of optimality in the fully unconstrained setting, from Theorem 3.2. Two points were critical in this argument:

• (i) The change from maximizing over $C(v_0)$ to a pointwise maximization over $(0, \infty )$ within the expectation.

• (ii) The convenient construction of the LFT $U^{*}$ and the help function H.

The first point was possible because the non-negativity “constraint” on terminal wealth works pointwise. The construction of $U^{*}$ and H was specifically chosen to exploit this as well as the concavity of U.

Since the bounds $B_1$, $B_2$ on terminal wealth are pointwise constraints, too, (i) is still valid as long as we restrict the maximization to the interval $[B_1, B_2]$. The construction of $U^{*}$ and H has to be adjusted accordingly. This leads to a natural extension of the LFT:

We define the capped Legendre–Fenchel transformation (capped LFT)

$U^{*}(\cdot , B_1, B_2): (0,\infty )\rightarrow \mathbbm {R}$ of the investor’s utility U as

$$\begin{aligned} U^{*}(y,B_1, B_2) := \underset{B_1 \le x \le B_2}{\text {sup}}\Big ( U(x)-yx \Big ) = U({\mathcal {I}}(y,B_1,B_2)) - y{\mathcal {I}}(y,B_1,B_2) \end{aligned}$$

with

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2):= & {} \inf \big \{ B_1 \le x \le B_2 \ \big | \ U^{*}(y,B_1,B_2) = U(x) - yx \big \} \\&\overset{ U \text { concave}}{=}&B_1 + ({\mathcal {I}}(y)-B_1)^{+} - ({\mathcal {I}}(y)-B_2)^{+}. \end{aligned}$$

The defined capped LFT $U^{*}(\cdot ,B_1,B_2)$ is convex and strictly decreasing (Fig. 1). Moreover, one can show that the maximizer ${\mathcal {I}}(\cdot ,B_1,B_2)$ is non-increasing, has at most countably infinite points of discontinuity and its limits satisfy $\lim _{y\downarrow 0}{\mathcal {I}}(y,B_1,B_2) = B_2$ and $\lim _{y\rightarrow \infty }{\mathcal {I}}(y,B_1,B_2) = B_1$.²

Fig. 1

In the “capped” areas, the capped LFT $U^{*}(y,B_1, B_2)$ is an affine, decreasing function while the maximizer ${\mathcal {I}}(y,B_1,B_2)$ is constant

Analogous to the previous section, we introduce the capped help function $H(\cdot , B_1, B_2):(0,\infty ) \rightarrow \mathbbm {R}$ as

$$\begin{aligned} H(y,B_1, B_2):= \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}(T) ,B_1, B_2){\tilde{Z}}(T)]. \end{aligned}$$

Lemma 3.4

Assume that $H(y,B_1,B_2)<\infty$ $\forall y>0$. Then, $H(\cdot , B_1, B_2)$ is strictly decreasing, continuous and satisfies

$$\begin{aligned} \lim _{y \downarrow 0} \ H(y,B_1,B_2) = \lim _{y \downarrow 0} \ \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}(T),B_1, B_2) {\tilde{Z}}(T)] = \mathbbm {E}[B_2 {\tilde{Z}}(T)]=: v(B_2) \end{aligned}$$

and

$$\begin{aligned} \lim _{y \rightarrow \infty } \ H(y,B_1, B_2)= & {} \lim _{y \rightarrow \infty } \ \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}(T),B_1,B_2) {\tilde{Z}}(T)] \\= & {} \mathbbm {E}[B_1 {\tilde{Z}}(T)]=: v(B_1) \end{aligned}$$

In particular, there exists a continuous and strictly decreasing bijection

$$\begin{aligned} Y(v,B_1, B_2):(v(B_1),v(B_2)) \rightarrow (0,\infty ) \end{aligned}$$

such that

$$\begin{aligned} H(Y(v,B_1, B_2),B_1,B_2) = v \quad \forall v\in (v(B_1),v(B_2)). \end{aligned}$$

Proof

A more general version of this lemma, Lemma 4.4, is proved in the appendix. $\square$

By virtue of the properties of the capped LFT and capped help function, we are now in a position to solve $\mathbf {(P^{Vcons})}$.

Theorem 3.5

(Optimal Terminal Wealth of the Wealth-Constrained Portfolio Optimization Problem)

Let U be concave and assume that $H(y,B_1,B_2)<\infty$ $\forall y>0$. Let $K = \mathbbm {R}^d$, and $0 \le B_1 < B_2 \le \infty$ be constants. Then,

$$\begin{aligned} D^{*} := {\mathcal {I}}(y{\tilde{Z}}(T),B_1, B_2) = B_1 + ({\mathcal {I}}(y{\tilde{Z}}(T))-B_1)^{+} - ({\mathcal {I}}(y{\tilde{Z}}(T))-B_2)^{+}, \end{aligned}$$

with $y = Y(v_0,B_1,B_2)$, is the optimal terminal wealth for $\mathbf {(P^{Vcons})}$.

Proof

By definition of ${\mathcal {I}}(\cdot , B_1, B_2)$, $B_1 \le D^{*} \le B_2$ and y, we have $\mathbbm {E}[D^{*}{\tilde{Z}}(T)] = v_0$. Thus, $D^{*} \in C(v_0,B_1, B_2)$ is admissible for $\mathbf {(P^{Vcons})}$. Further, let ${\hat{D}} \in C(v_0,B_1, B_2)$ be any other admissible terminal wealth for $\mathbf {(P^{Vcons})}$. Then,

$$\begin{aligned} \begin{aligned} \mathbbm {E}[U({\hat{D}})]&= \mathbbm {E}[U({\hat{D}}) - y{\tilde{Z}}(T){\hat{D}}] + yv_0 \le \underset{D \in C(v_0,B_1, B_2)}{\sup }\big (\mathbbm {E}[U(D) - y{\tilde{Z}}(T)D] \big )+ yv_0 \\ {}&\le \mathbbm {E}[\underset{B_1 \le x \le B_2}{\text {sup}}\big (U(x) - y{\tilde{Z}}(T)x\big )]+ yv_0\\&= \mathbbm {E}[U(\underbrace{{\mathcal {I}}(y{\tilde{Z}}(T),B_1,B_2)}_{= D^{*}})]-y\underbrace{\mathbbm {E}[{\tilde{Z}}(T){\mathcal {I}}(y{\tilde{Z}}(T),B_1,B_2)]}_{=v_0}+yv_0 = \mathbbm {E}[U(D^{*})]. \end{aligned} \end{aligned}$$

$\square$

4 Auxiliary markets with bounds on terminal wealth

In this section we finally consider the original fully constrained portfolio optimization problem with general allocation constraints $K\subset \mathbbm {R}^d$, simultaneous lower and upper bounds on terminal wealth $B_1, B_2$ and concave utility function U. The aim of this section is the generalization of the well-known auxiliary market framework from Cvitanic and Karatzas (1992) to include terminal wealth constraints $B_1$ and $B_2$.

4.1 Formulation of the auxiliary markets

For setting up the auxiliary markets we need to introduce the support function $\delta$ and barrier cone $X_K$ of K as

$$\begin{aligned} \delta :\mathbbm {R}^d \rightarrow \mathbbm {R}, \quad \delta (x)= - \underset{y \in K}{\text {inf}}(x'y), \quad X_{K}:= \big \{ x \in \mathbbm {R}^d \ \big | \ \delta (x) < \infty \big \}. \end{aligned}$$

Note that due to Assumption 2.1, $0\in K$ and thus $\delta (x) \ge 0$ for all $x\in \mathbbm {R}^d$. Moreover, the support-function $\delta$ is positive homogenous of order 1, sub-additive and is zero for all $x\in X_K$ if and only if K is a convex cone.³ Further, we may use the notions of $\delta$ and $X_K$ to characterize K (see e.g. Rockafellar 1970, Theorem 13.1), as for any $x\in \mathbbm {R}^d$

$$\begin{aligned} x \in K \quad \Leftrightarrow \quad \delta (\uplambda ) + \uplambda 'x \ge 0 \quad \forall \uplambda \in X_K. \end{aligned}$$

(4.1)

Remark 4.1

By scaling any non-zero $\uplambda \in X_K$, to have norm $\Vert \uplambda \Vert \le 1$, one can see

$$\begin{aligned} x \in K \quad \Leftrightarrow \quad \delta (\uplambda ) + \uplambda 'x \ge 0 \quad \forall \uplambda \in X_K, \ \Vert \uplambda \Vert \le 1. \end{aligned}$$

Further, we introduce the set of $\mathbbm {R}^d$-valued dual processes ${\mathcal {D}}$, which will parametrize the auxiliary markets.

$$\begin{aligned} {\mathcal {D}}:= \Big \{&\uplambda =\big ((\uplambda _1(t),...,\uplambda _d(t))'\big )_{t \in [0,T]} \ \text {prog. measurable} \ \Big | \\&\quad \mathbbm {E}\Big [\int _0^T \Vert \uplambda (t) \Vert ^2dt\Big ]< \infty , \ \mathbbm {E}\Big [\int _0^T \delta (\uplambda (t))dt\Big ]<\infty \Big \} \end{aligned}$$

For any $\uplambda \in {\mathcal {D}}$, the latter integrability condition guarantees $\uplambda (t) \in X_K$ ${\mathcal {L}}[0,T]\otimes Q$-a.e..

Finally, for a given $\uplambda \in {\mathcal {D}}$ we define the auxiliary market ${\mathcal {M}}_{\uplambda }$ as the asset universe with d risky assets $P^{\uplambda }= (P^{\uplambda }_1, ...,P^{\uplambda }_d)$ and one risk-free asset $P^{\uplambda }_0$, which evolve according to the following dynamics:

$$\begin{aligned} \begin{aligned} dP^{\uplambda }(t)&= P^{\uplambda }(t) \big ( \underbrace{\mu (t)+\uplambda (t)+\delta (\uplambda (t))\mathbbm {1}}_{=: \ \mu _{\uplambda }(t)}dt + \sigma (t)dW(t)\big ) = P^{\uplambda }(t) \big ( \mu _{\uplambda }(t)dt +\sigma (t)dW(t)\big ) \\ dP^{\uplambda }_0(t)&= P^{\uplambda }_0(t) \big ( \underbrace{r(t)+\delta (\uplambda (t))}_{=: \ r_{\uplambda }(t)} \big ) dt = P^{\uplambda }_0(t) r_{\uplambda }(t) dt\\ P^{\uplambda }_i(0)&= 1 \quad \text {for } i=0,...,d. \end{aligned} \end{aligned}$$

The risk-free asset $P^{\uplambda }_0$ still represents the same bank account, whereas the assets $P^{\uplambda }_i$ represent the same risky assets from our original setting but with changed drift coefficients.

Moreover, in ${\mathcal {M}}_{\uplambda }$, the market price of risk $\gamma _{\uplambda }$, the corresponding Doléans-Dade-exponential $Z_{\uplambda }$ and pricing kernel ${\tilde{Z}}_{\uplambda }$ are given as

$$\begin{aligned} \begin{aligned} \gamma _{\uplambda }(t)&:= \sigma ^{-1}(t)\big (\mu _{\uplambda }(t) - r_{\uplambda }(t) \mathbbm {1} \big ) = \sigma ^{-1}(t)(\mu (t)-r(t)\mathbbm {1}+\uplambda (t)) \\ Z_{\uplambda }(t)&:= \exp \Big \{-\frac{1}{2}\int _0^t \Vert \gamma _{\uplambda }(s) \Vert ^2ds - \int _0^t \gamma _{\uplambda }(s)'dW(s) \Big \} \\ {\tilde{Z}}_{\uplambda }(t)&:= \frac{Z_{\uplambda }(t)}{P^{\uplambda }_0(t)} = \exp \Big \{-\int _0^t r_{\uplambda }(s) + \frac{1}{2}\Vert \gamma _{\uplambda }(s) \Vert ^2ds - \int _0^t \gamma _{\uplambda }(s)'dW(s) \Big \} \end{aligned} \end{aligned}$$

for $t\in [0,T]$. Again, $Z_{\uplambda }$ and ${\tilde{Z}}_{\uplambda }$ satisfy the SDEs

$$\begin{aligned} \begin{aligned} dZ_{\uplambda }(t)&= -Z_{\uplambda }(t) \gamma _{\uplambda }(t)'dW(t)\\ d{\tilde{Z}}_{\uplambda }(t)&=-{\tilde{Z}}_{\uplambda }(t)\big (r_{\uplambda }(t)dt + \gamma _{\uplambda }(t)'dW(t)\big ). \end{aligned} \end{aligned}$$

Since $\uplambda \in {\mathcal {D}}$ need not be uniformly bounded, the market coefficients in ${\mathcal {M}}_{\uplambda }$ need not be uniformly bounded either. Hence, it is not clear if the local martingale $Z_{\uplambda }$ is indeed a true martingale. However, since $Z_{\uplambda }$ is non-negative, it is a supermartingale.

In the auxiliary market, we accordingly adjust the definition of $V_{\uplambda }^{v_0,\pi }$, the wealth process of an investor trading according to $\pi \in \varLambda$ in the market ${\mathcal {M}}_{\uplambda }$ to

$$\begin{aligned} \begin{aligned} dV_{\uplambda }^{v_0, \pi }(t)&= V_{\uplambda }^{v_0, \pi }(t) \big ( [r_{\uplambda }(t) + (\mu _{\uplambda }(t) - r_{\uplambda }(t)\mathbbm {1})'\pi (t)]dt + \pi (t)'\sigma (t)dW(t)\big )\\&= V_{\uplambda }^{v_0, \pi }(t) \big ( [r(t) + (\mu (t) - r(t)\mathbbm {1})'\pi (t)] + \pi (t)'\sigma (t)dW(t)\big ) \\&\qquad + \underbrace{V_{\uplambda }^{v_0, \pi }(t)[\delta (\uplambda (t)) + \uplambda (t)'\pi (t)]}_{(*)}dt \end{aligned} \end{aligned}$$

(4.2)

$\forall t \in [0,T]$. This is the same SDE as in the original market ${\mathcal {M}}$, apart from the additional drift term $(*)$. Due to (4.1), $(*)$ is non-negative as long $\pi (t)\in K$. Hence, for an investor who abides by the allocation constraints, the wealth process in ${\mathcal {M}}_{\uplambda }$, will be larger or equal than the wealth process in ${\mathcal {M}}$, i.e. $V_{\uplambda }^{v_0, \pi }(t) \ge V^{v_0, \pi }(t)$.

In particular, we need to restrict an investor’s portfolio choice in ${\mathcal {M}}_{\uplambda }$ to the set

$$\begin{aligned} \varLambda _{\uplambda }= \Big \{&\pi = \big ((\pi _1(t),...,\pi _d(t))'\big )_{t \in [0,T]} \ \text {progr. measurable} \ \Big | \\&\quad \int _0^T \big (V_{\uplambda }^{v_0, \pi }(t) \Vert \pi (t) \Vert \big )^2 dt < \infty \ Q-a.s. \Big \} \end{aligned}$$

The allocation-unconstrained, wealth-constrained portfolio optimization problem $\mathbf {(P_{\uplambda }^{Vcons})}$ in ${\mathcal {M}}_{\uplambda }$ is defined as

$$\begin{aligned} \mathbf {(P_{\uplambda }^{Vcons})} {\left\{ \begin{array}{ll} \quad \ \varPhi _{\uplambda }(v_0) &{}= \underset{\pi \in \varLambda _{\uplambda }(v_0,B_1, B_2)}{\sup } \mathbbm {E}\big [U(V_{\uplambda }^{v_0, \pi }(T)) \big ] \\ \varLambda _{\uplambda }(v_0, B_1, B_2) &{}= \big \{\pi \in \varLambda _{\uplambda } \ \big | \ B_1 \le V_{\uplambda }^{v_0, \pi }(T) \le B_2 \big \} \end{array}\right. } \end{aligned}$$

Note that $\mathbf {(P_{\uplambda }^{Vcons})}$ is a similar optimization problem as $\mathbf {(P^{Vcons})}$, but formulated in a different market ${\mathcal {M}}_{\uplambda }$, rather than ${\mathcal {M}}$. Our program is now to derive a similar slackness condition to Condition (B) from Cvitanic and Karatzas (1992). Since $B_1$ and $B_2$ not only constrain the downside of the portfolio value, but also its upside, such a condition is not straightforward. An increase of the terminal wealth in an auxiliary market ${\mathcal {M}}_{\uplambda }$ (due to the added positive drift in (4.2)) may now lead to a violation of the terminal wealth constraints and may even lead to $\mathbf {(P_{\uplambda }^{Vcons})}$ being infeasible. Therefore, we need to do a small work-around first.

For every $\uplambda \in {\mathcal {D}}$, we bypass the upper bound $B_2$, by formulating an auxiliary problem $({\tilde{\mathbf {P}}_{\uplambda }})$ with capped utility function ${\tilde{U}}(x):= U(x-(x-B_2)^{+})$

$$\begin{aligned} ({\tilde{\mathbf {P}}_{\uplambda }}) {\left\{ \begin{array}{ll} \quad \ {\tilde{\varPhi }}_{\uplambda }(v_0) &{}= \underset{\pi \in \varLambda _{\uplambda }(v_0,B_1)}{\sup } \mathbbm {E}\big [{\tilde{U}}(V_{\uplambda }^{v_0, \pi }(T)) \big ] \\ \varLambda _{\uplambda }(v_0, B_1) &{}= \big \{\pi \in \varLambda _{\uplambda } \ \big | \ B_1 \le V_{\uplambda }^{v_0, \pi }(T) \big \} \end{array}\right. } \end{aligned}$$

We use ${\tilde{U}} \in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$ to remove the “hard” upper bound $B_2$, but cap the utility gain at $B_2$ to ensure that we don’t gain any additional utility from having more terminal wealth than $B_2$. The optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda }})$ should not take on any unrewarded risk and thus should automatically abide by the upper bound $B_2$. Similarly, one could have removed the lower bound $B_1$, by setting ${\tilde{U}}(x)=-\infty$ for $x<B_1$. We arrive at the following optimality Condition $({\tilde{B}})$:

Lemma 4.2

(Condition (${\tilde{B}}$)) Let $\uplambda ^{*}\in {\mathcal {D}}$, $\pi _{\uplambda ^{*}}$ be the optimal portfolio process for $({\tilde{\mathbf {P}}_{\uplambda ^{*}}})$ and $D_{\uplambda ^{*}}=V^{v_0, \pi _{\uplambda ^{*}}}(T).$ If further

$$\begin{aligned} \pi _{\uplambda ^{*}} \in \varLambda (v_0,K,B_1,B_2) \ \ \text {and} \ \ \delta (\uplambda ^{*}(t))+\pi _{\uplambda ^{*}}(t)'\uplambda ^{*}(t) = 0 \quad {\mathcal {L}}[0,T)\otimes Q-a.s.,\nonumber \\ \end{aligned}$$

(4.3)

then $\pi _{\uplambda ^{*}}$ is admissible and optimal for the primal problem $\mathbf {(P)}$ and ${\tilde{\varPhi }}_{\uplambda ^{*}}(v_0) = \varPhi (v_0)$.

Proof

The argument goes along the lines of Cvitanic and Karatzas (1992), Proposition 8.3. Any $\pi \in \varLambda (v_0,K,B_1, B_2)$ satisfies $\pi (t) \in K \ \ {\mathcal {L}}[0,T)\otimes Q-a.e.$ and the terminal wealth in ${\mathcal {M}}$ satisfies $B_1 \le V^{v_0, \pi }(T) \le B_2$ $Q-a.s.$. Further, for any $\uplambda \in {\mathcal {D}}$ the terminal wealth process of the same portfolio process $\pi$ in ${\mathcal {M}}_{\uplambda }$ satisfies

$$\begin{aligned} B_1 \le V^{v_0, \pi }(T) \le V_{\uplambda }^{v_0, \pi }(T), \end{aligned}$$

due to (4.2). Hence, $\varLambda (v_0,K,B_1,B_2) \subset \varLambda _{\uplambda }(v_0,B_1)$ and $\varPhi (v_0) \le {\tilde{\varPhi }}_{\uplambda }(v_0)$.

For the choice of $\uplambda = \uplambda ^{*}$, we know that $\pi _{\uplambda ^{*}}$ is optimal for $({\tilde{\mathbf {P}}_{\uplambda ^{*}}})$, $\pi _{\uplambda ^{*}}\in \varLambda (v_0,K,B_1,B_2)$ and $V^{v_0, \pi _{\uplambda ^{*}}}(T) = V_{\uplambda ^{*}}^{v_0, \pi _{\uplambda ^{*}}}(T)$, due to (4.3). Hence,

$$\begin{aligned} {\tilde{\varPhi }}_{\uplambda ^{*}}(v_0) = \mathbbm {E}[{\tilde{U}}(V_{\uplambda ^{*}}^{v_0, \pi _{\uplambda ^{*}}}(T))] = \mathbbm {E}[{\tilde{U}}(V^{v_0, \pi _{\uplambda ^{*}}}(T))] \le \mathbbm {E}[U(V^{v_0, \pi _{\uplambda ^{*}}}(T))] \le \varPhi (v_0). \end{aligned}$$

Therefore, ${\tilde{\varPhi }}_{\uplambda ^{*}}(v_0) = \varPhi (v_0)$ and $\pi _{\uplambda ^{*}}$ is optimal for (P). $\square$

Condition $({\tilde{B}})$ allows us to relate the solutions of the allocation unconstrained auxiliary problem $({\tilde{\mathbf {P}}_{\uplambda }})$ and the original problem (P). We now know, provided we have chosen the right auxiliary market ${\mathcal {M}}_{\uplambda ^{*}}$, the solutions to both problems coincide. Correspondingly, it makes sense to first study the simpler problem $({\tilde{\mathbf {P}}_{\uplambda })}$ for all $\uplambda \in {\mathcal {D}}$ and try to find $\uplambda ^{*}$ afterwards.

Similar to the previous sections, we can alternatively express $({\tilde{\mathbf {P}}_{\uplambda }})$ as an optimization over admissible terminal wealths. Again, due to the market completeness of ${\mathcal {M}}_{\uplambda }$, this optimization simplifies to

$$\begin{aligned} ({\tilde{\mathbf {P}}_{\uplambda })} {\left\{ \begin{array}{ll} \quad \ {\tilde{\varPhi }}_{\uplambda }(v_0) &{}= \underset{D \in C_{\uplambda }(v_0,B_1)}{\sup } \mathbbm {E}\big [{\tilde{U}}(D) \big ] \\ C_{\uplambda }(v_0,B_1) &{}= \big \{D \ge 0 \ {\mathcal {F}}_T-\text {measurable} \ \big | \ \mathbbm {E}[D {\tilde{Z}}_{\uplambda }(T)]= v_0, \ B_1 \le D \ \big \} \end{array}\right. } \end{aligned}$$

As we have seen in the previous section, the form of the solution to a wealth-constrained problem depends on the market’s pricing kernel and the maximizing argument of the capped LFT. The key observation for obtaining the solution to $({\tilde{\mathbf {P}}_{\uplambda })}$ is that even though U and ${\tilde{U}}$ are different utility functions, their capped LFT, as well as the corresponding maximizing arguments, can be related nicely.

Lemma 4.3

$$\begin{aligned} {\tilde{U}}^{*}(y,B_1,\infty ) = U^{*}(y,B_1,B_2) \end{aligned}$$

In particular, the corresponding maximizing arguments coincide:

$$\begin{aligned} {\tilde{{\mathcal {I}}}}(y,B_1,B_2)&= \inf \big \{ B_1 \le x \le B_2 \ \big | \ {\tilde{U}}^{*}(y,B_1,B_2) = {\tilde{U}}(x) - yx \big \} \\&= \inf \big \{ B_1 \le x \le B_2 \ \big | \ U^{*}(y,B_1,B_2) = U(x) - yx \big \}= {\mathcal {I}}(y,B_1,B_2) \end{aligned}$$

Proof

For any $y>0$, $x\ge B_2$

$$\begin{aligned} {\tilde{U}}(x)-yx = U(B_2) - yx \le U(B_2) - yB_2 \end{aligned}$$

and since ${\tilde{U}} \equiv U$ on $[0,B_2]$

$$\begin{aligned} {\tilde{U}}^{*}(y,B_1,\infty ) = \underset{B_1 \le x}{\sup }\Big ( {\tilde{U}}(x)-yx \Big ) = \underset{B_1 \le x \le B_2}{\sup }\Big ( \underbrace{{\tilde{U}}(x)}_{=U(x)}-yx \Big )=U^{*}(y,B_1,B_2) \end{aligned}$$

$\square$

Due to Lemma 4.3, it is sensible to define the capped help function in ${\mathcal {M}}_{\uplambda }$ as $H_{\uplambda }(\cdot , B_1, B_2):(0,\infty ) \rightarrow \mathbbm {R}$

$$\begin{aligned} H_{\uplambda }(y,B_1, B_2):= \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1, B_2){\tilde{Z}}_{\uplambda }(T)] \end{aligned}$$

The capped help function in ${\mathcal {M}}_{\uplambda }$ inherits similar properties as in the original market ${\mathcal {M}}$.

Lemma 4.4

Let $U\in {\mathcal {U}}(B_1,B_2)$, $\uplambda \in {\mathcal {D}}$ and assume that $H_{\uplambda }(y,B_1,B_2) < \infty \ \forall y > 0$. Then, $H_{\uplambda }(\cdot ,B_1,B_2)$ is strictly decreasing, continuous and satisfies

$$\begin{aligned} \lim _{y \downarrow 0} \ H_{\uplambda }(y,B_1,B_2) = \lim _{y \downarrow 0} \ \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2) {\tilde{Z}}_{\uplambda }(T)] = \mathbbm {E}[B_2 {\tilde{Z}}_{\uplambda }(T)] =: v_{\uplambda }(B_2) \end{aligned}$$

and

$$\begin{aligned} \lim _{y \rightarrow \infty } \ H_{\uplambda }(y,B_1,B_2)= & {} \lim _{y \rightarrow \infty } \ \mathbbm {E}[{\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2) {\tilde{Z}}_{\uplambda }(T)] \\= & {} \mathbbm {E}[B_1 {\tilde{Z}}_{\uplambda }(T)] =: v_{\uplambda }(B_1) \end{aligned}$$

In particular, there exists a continuous and strictly decreasing bijection

$$\begin{aligned} Y_{\uplambda }(\cdot , B_1,B_2):\quad (v_{\uplambda }(B_1),v_{\uplambda }(B_2)) \rightarrow (0,\infty ) \end{aligned}$$

such that

$$\begin{aligned} H_{\uplambda }(Y_{\uplambda }(v, B_1,B_2),B_1,B_2) = v \quad \forall v\in (v_{\uplambda }(B_1),v_{\uplambda }(B_2)) \end{aligned}$$

Proof

The proof of this lemma can be found in the appendix. $\square$

This naturally leads to the following assumption:

Assumption 4.5

$$\begin{aligned} v_0 < \mathbbm {E}[B_2 {\tilde{Z}}_{\uplambda }(T)] = v_{\uplambda }(B_2). \end{aligned}$$

Theorem 4.6

(Optimal Terminal Wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$)

Let U be concave, let $\uplambda \in {\mathcal {D}}$ and $H_{\uplambda }(y,B_1,B_2) < \infty \ \forall y >0$. If $\uplambda \in {\mathcal {D}}$ satisfies Assumption 4.5, then

$$\begin{aligned} D_{\uplambda }^{*} := {\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1, B_2) = B_1 + ({\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T))-B_1)^{+} - ({\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T))-B_2)^{+} \end{aligned}$$

with $y = Y_{\uplambda }(v_0,B_1,B_2)$, is the optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$. If $\uplambda \in {\mathcal {D}}$ does not satisfy Assumption 4.5, then

$$\begin{aligned} D_{\uplambda }^{*}= B_2 + \frac{v_0-v_{\uplambda }(B_2)}{\mathbbm {E}[{\tilde{Z}}_{\uplambda }(T)]} \end{aligned}$$

is an optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$ and $\uplambda$ does not satisfy Condition $({\tilde{B}})$.

Proof

$\underline{\hbox {Case}: \uplambda \in {\mathcal {D}} \hbox {satisfies Assumption} 4.5.}$ By Assumption 4.5 and

$$\begin{aligned} v_{\uplambda }(B_1) = \mathbbm {E}[B_1{\tilde{Z}}_{\uplambda }(T)] \overset{\text {Asm.} 2.1}{<} v_0 \mathbbm {E}[P_0(T){\tilde{Z}}_{\uplambda }(T)] \overset{\delta \ge 0}{\le }v_0 \underbrace{\mathbbm {E}[Z_{\uplambda }(T)]}_{\le \ 1} \le v_0, \end{aligned}$$

we know that $Y_{\uplambda }(v_0,B_1,B_2)$ is well-defined. Further, by definition of ${\mathcal {I}}(\cdot , B_1, B_2)$ and y, we have $B_1 \le D_{\uplambda }^{*}$ and $\mathbbm {E}[D_{\uplambda }^{*}{\tilde{Z}}_{\uplambda }(T)] =v_0$. Thus, $D_{\uplambda }^{*} \in C_{\uplambda }(v_0,B_1)$ is admissible for $({\tilde{\mathbf {P}}_{\uplambda })}$. Further, let ${\hat{D}} \in C_{\uplambda }(v_0,B_1)$ be any other admissible terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$. Then,

$$\begin{aligned} \begin{aligned} \mathbbm {E}[{\tilde{U}}({\hat{D}})] =&\mathbbm {E}[{\tilde{U}}({\hat{D}}) - y{\tilde{Z}}(T){\hat{D}}] + yv_0 \le \underset{D \in C_{\uplambda }(v_0,B_1)}{\sup }\big (\mathbbm {E}[{\tilde{U}}(D) - y{\tilde{Z}}_{\uplambda }(T)D] \big )+ yv_0\\ \le&\mathbbm {E}[\underset{B_1 \le x}{\text {sup}}\big ({\tilde{U}}(x) - y{\tilde{Z}}_{\uplambda }(T)x\big )]+ yv_0 \le \mathbbm {E}[\underset{B_1 \le x\le B_2}{\text {sup}}\big (U(x) - y{\tilde{Z}}_{\uplambda }(T)x\big )]+ yv_0 \\ =&\mathbbm {E}[U(\underbrace{{\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2)}_{= D_{\uplambda }^{*}})]-y\underbrace{\mathbbm {E}[{\tilde{Z}}_{\uplambda }(T){\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2)]}_{=v_0}+yv_0 \\ =&\mathbbm {E}[U(D_{\uplambda }^{*})] \overset{D_{\uplambda }^{*}\le B_2}{=}\mathbbm {E}[{\tilde{U}} (D_{\uplambda }^{*})]. \end{aligned} \end{aligned}$$

$\underline{\hbox {Case}: \uplambda \in {\mathcal {D}} \hbox {does not satisfy Assumption} 4.5.}$ Clearly, $D_{\uplambda }^{*}\ge B_2 > B_1$ and

$\mathbbm {E}[D_{\uplambda }^{*}{\tilde{Z}}_{\uplambda }(T)] = v_0$ and therefore $D_{\uplambda }^{*}$ is admissible for $({\tilde{\mathbf {P}}_{\uplambda })}$. Further,

$$\begin{aligned} \mathbbm {E}[{\tilde{U}}(D_{\uplambda }^{*})]\ge \mathbbm {E}[{\tilde{U}}(B_2)] = U(B_2) \ge \underset{D\in C_{\uplambda }(v_0,B_1)}{\sup } \mathbbm {E}[{\tilde{U}}(D)] = {\tilde{\varPhi }}_{\uplambda }(v_0), \end{aligned}$$

as ${\tilde{U}}(x)\le U(B_2)$ for all $x\ge 0$. Hence, $D_{\uplambda }^{*}$ must be an optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$. Assume now that $\uplambda$ satisfies Condition $({\tilde{B}})$. Then, by (4.3), there exists a $\pi _{\uplambda } \in \varLambda (v_0,K,B_1,B_2)$, which is optimal for $({\tilde{\mathbf {P}}_{\uplambda })}$ and satisfies $\delta (\uplambda (t))+\pi _{\uplambda }(t)'\uplambda (t) = 0$ ${\mathcal {L}}[0,T]\otimes Q-$a.s.. In particular, this implies

$$\begin{aligned}&D:= V_{\uplambda }^{v_0,\pi _{\uplambda }}(T) = V^{v_0,\pi _{\uplambda }}(T) \overset{\pi _{\uplambda } \in \varLambda (v_0,K,B_1,B_2)}{\le }B_2 \quad Q-a.s. \\ \text {and} \qquad&\mathbbm {E}[D{\tilde{Z}}_{\uplambda }(T)] \overset{D \in C_{\uplambda }(v_0,B_1)}{=} v_0 \overset{D\in C(v_0,B_1,B_2)}{=} \mathbbm {E}[D{\tilde{Z}}(T)]. \end{aligned}$$

Moreover, we have

$$\begin{aligned} v_0 \ge v_{\uplambda }(B_2) = \mathbbm {E}[\underbrace{B_2}_{\ge D} {\tilde{Z}}_{\uplambda }(T)] \ge \mathbbm {E}[D{\tilde{Z}}_{\uplambda }(T)] = v_0, \end{aligned}$$

i.e. $v_0 = v_{\uplambda }(B_2)$. This implies

$$\begin{aligned} 0 = v_{\uplambda }(B_2) - v_0 = \mathbbm {E}[\underbrace{(B_2 - D)}_{\ge 0}\underbrace{{\tilde{Z}}_{\uplambda }(T)}_{>0}] \Rightarrow D = B_2 \ Q-a.s.. \end{aligned}$$

However, using Assumption 2.1 we get

$$\begin{aligned} v_0 = \mathbbm {E}[D {\tilde{Z}}(T)]= \mathbbm {E}[B_2{\tilde{Z}}(T)] \overset{\text {Asm.} 2.1}{>} v_0 \underbrace{\mathbbm {E}[Z(T)]}_{=1} = v_0, \end{aligned}$$

which is a contradiction. Hence, $\uplambda$ cannot satisfy Condition $({\tilde{B}})$. $\square$

The underlying observation is simple: as long as the capital necessary to perfectly hedge $B_2$ in ${\mathcal {M}}_{\uplambda }$ $v_{\uplambda }(B_2)$ is larger than $v_0$, the optimal wealth corresponding to $({\tilde{\mathbf {P}}_{\uplambda })}$ will be smaller or equal than $B_2$. This is in line with our previous intuition.

We restrict the definition of ${\mathcal {D}}'$ to additionally enforce that for every $\uplambda \in {\mathcal {D}}'$ we can solve $({\tilde{\mathbf {P}}_{\uplambda })}$ and Assumption 4.5 is satisfied

$$\begin{aligned} \mathcal {D'} := \big \{ \uplambda \in {\mathcal {D}} \ \big | \ v_0<v_{\uplambda }(B_2), \ H_{\uplambda }(y, B_1, B_2) < \infty \ \forall y >0 \big \} \end{aligned}$$

and summarize our findings in a corollary:

Corollary 4.7

Let U be concave and $\uplambda ^{*}\in {\mathcal {D}}'$, let $\pi _{\uplambda ^{*}}$ be the optimal portfolio process for $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$. If $\uplambda ^{*}$ and $\pi _{\uplambda ^{*}}$ satisfy

$$\begin{aligned} \ \delta (\uplambda ^{*}(t))+\pi _{\uplambda ^{*}}(t)'\uplambda ^{*}(t) = 0 \ \text {and } \ \pi _{\uplambda ^{*}}(t) \in K \quad {\mathcal {L}}[0,T)\otimes Q-a.e., \end{aligned}$$

then $\pi _{\uplambda ^{*}}$ is admissible and optimal for $\mathbf {(P)}$.

We are now in a position to formulate the analog to the equivalent optimality conditions from Cvitanic and Karatzas (1992).

Remark 4.8

If K is a convex cone, then $\delta (x)=0$ on $X_K$ and any uniformly bounded $\uplambda \in {\mathcal {D}}$ satisfies Assumption 4.5. In particular, this is true for short-selling constraints ($K=[0,\infty )^d$), non-traded asset constraints ($K= \{0\}^m\times \mathbbm {R}^{d-m}$, for $0<m<d$) and any combination thereof. If $B_2$ is finite, then $H_{\uplambda }(\cdot , B_1, B_2) \le B_2$ and thus $H_{\uplambda }(y, B_1, B_2) < \infty$, $\forall y>0$ holds for all $\uplambda \in {\mathcal {D}}$.

Hence, if K is a convex cone and $B_2$ is finite, any uniformly bounded $\uplambda \in {\mathcal {D}}$ is in ${\mathcal {D}}'$. This slightly technical observation will be useful when verifying $\uplambda ^{*}\in {\mathcal {D}}'$ for a given candidate $\uplambda ^{*}$ in Sect. 5.

4.2 Equivalent optimality conditions

Fix some initial wealth $v_0 > 0$, let $\pi ^{*}\in \varLambda (v_0,K,B_1,B_2)$, let $\uplambda ^{*}\in {\mathcal {D}}'$ and $y = Y_{\uplambda ^{*}}(v_0, B_1, B_2)$. Define conditions:

$({\tilde{A}})$:

$\forall \pi \in \varLambda (v_0,K,B_1,B_2)$ we have

$$\begin{aligned} \mathbbm {E}[U(V^{v_0,\pi }(T))] \le \mathbbm {E}[U(V^{v_0,\pi ^{*}}(T))] \end{aligned}$$

$({\tilde{B}})$:

The optimal portfolio process $\pi _{\uplambda ^{*}} \in \varLambda _{\uplambda ^{*}}(v_0,B_1)$ for ${({\tilde{\mathbf {P}}}_{\uplambda ^{*}})}$ in ${\mathcal {M}}_{\uplambda ^{*}}$ satisfies:

$$\begin{aligned} \pi _{\uplambda ^{*}} \in K \quad \text {and} \quad [\delta (\uplambda ^{*})+ \pi _{\uplambda ^{*}}(t)' \uplambda ^{*}(t)]=0 \quad {\mathcal {L}}[0,T]\otimes Q-a.s. \end{aligned}$$

$({\tilde{C}})$:

$\forall \uplambda \in {\mathcal {D}}$ we have

$$\begin{aligned} {\tilde{\varPhi }}_{\uplambda }(v_0) \ge {\tilde{\varPhi }}_{\uplambda ^{*}}(v_0) \end{aligned}$$

$({\tilde{D}})$:

$\forall \uplambda \in {\mathcal {D}}$ we have

$$\begin{aligned} \mathbbm {E}\big [U^{*}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2)\big ] \ge \mathbbm {E}\big [U^{*}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2)\big ] \end{aligned}$$

$({\tilde{E}})$:

$\forall \uplambda \in {\mathcal {D}}$ we have

$$\begin{aligned} \mathbbm {E}\big [{\mathcal {I}}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2) \cdot {\tilde{Z}}_\uplambda (T)\big ] \le v_0 \end{aligned}$$

Theorem 4.9

Let U be concave and let $\uplambda ^{*}\in {\mathcal {D}}'$. The Conditions $({\tilde{B}})$, $({\tilde{C}})$, $({\tilde{D}})$ and $({\tilde{E}})$ are equivalent for $\uplambda ^{*}$ and imply $({\tilde{A}})$ with $\pi ^{*}:= \pi _{\uplambda ^{*}}$.

Proof

The proof of this theorem can be found in the appendix. $\square$

Remark 4.10

Due to Remark 4.1, it is sufficient in the proof of $({\tilde{D}}) \Rightarrow ({\tilde{B}})$ to consider only $\rho \in {\mathcal {D}}$ with $\Vert \rho (t) \Vert \le 1 \ {\mathcal {L}}[0,T]\otimes Q-a.s.$ and $\rho (t) = -\uplambda ^{*}(t) / \max (1, \Vert \uplambda ^{*}(t)\Vert )$. Even though, this does not affect the proof of Theorem 4.9 in any meaningful way, it has the satisfying consequence that any local minimizer $\uplambda ^{*}$ of Conditions $({\tilde{C}})$ or $({\tilde{D}})$ is indeed a global minimizer over the whole space ${\mathcal {D}}$ and satisfies Condition $({\tilde{B}})$. This will be useful in a verification theorem in the upcoming section.

The optimality conditions $({\tilde{B}})-({\tilde{E}})$ offer alternative ways to find and verify the optimality of a portfolio process $\pi ^{*}$ for the fully constrained portfolio optimization problem $(\mathbf{P })$ in ${\mathcal {M}}$. The central underlying assumption is that we can find a different market with adjusted market coefficients ${\mathcal {M}}_{\uplambda ^{*}}$, where the optimal portfolio $\pi _{\uplambda ^{*}}$ for the wealth-constrained problem $({\tilde{\mathbf {P}}_{\uplambda ^{*}}})$ coincides with $\pi ^{*}$.

According to Condition $({\tilde{B}})$, $\pi ^{*}$ and $\pi _{\uplambda ^{*}}$ coincide if the wealth processes $V^{v_0,\pi _{\uplambda ^{*}}}$ in ${\mathcal {M}}$ and $V_{\uplambda ^{*}}^{v_0,\pi _{\uplambda ^{*}}}$ in ${\mathcal {M}}_{\uplambda ^{*}}$ are equal. Hence, the change in market coefficients from the original ${\mathcal {M}}$ to ${\mathcal {M}}_{\uplambda ^{*}}$ must not have any impact on the portfolio performance of $\pi ^{*}$. Following Condition $({\tilde{C}})$, we additionally know that ${\mathcal {M}}_{\uplambda ^{*}}$ yields the least expected utility under all ${\mathcal {M}}_{\uplambda },$ $\uplambda \in {\mathcal {D}}$, if the investor follows an optimal strategy. In this sense, ${\mathcal {M}}_{\uplambda ^{*}}$ has the least favorable market coefficients from the investor’s perspective. Condition $({\tilde{D}})$ is in fact just a dual reformulation of Condition $({\tilde{C}})$, where the duality is now induced not by the allocation constraints K, but by the bounds on terminal wealth $B_1, \ B_2$ and the budget condition. As we will see in Sect. 5, Condition $({\tilde{D}})$ proves to be particularly useful in explicitly determining $\uplambda ^{*}$ and $\pi ^{*}$. Lastly, Condition $({\tilde{E}})$ states that there exists no market ${\mathcal {M}}_{\uplambda }$, where hedging the optimal terminal wealth $D^{*}_{\uplambda ^{*}}:= V^{v_0, \pi _{\uplambda ^{*}}}_{\uplambda ^{*}}(T)={\mathcal {I}}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2)$ for $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$ is more expensive than in ${\mathcal {M}}_{\uplambda ^{*}}$. Again, the market coefficients of ${\mathcal {M}}_{\uplambda ^{*}}$ can be regarded as least favorable for the investor. This is a special case of more general results about hedging contingent claims under allocation constraints, which is discussed in great detail in Cvitanic and Karatzas (1993).

5 Solving the fully constrained portfolio optimization problem

In this section we illustrate how one can make use of the equivalent optimality conditions derived in the previous section to solve the fully constrained portfolio optimization problem $\mathbf {(P)}$. This will be achieved by introducing a dual optimization problem (D) in Sect. 5.1, which arises from condition $({\tilde{D}})$ from the previous section. In Sect. 5.2, we then proceed to solve (D) explicitly for convex cone constraints K and concave utility functions, for which the capped LFT satisfies a polynomial growth condition. For logarithmic utility and power utility we determine the optimal terminal wealth for $\mathbf {(P)}$ explicitly. Furthermore, in Sect. 5.3 we are able to show that the equivalent optimality conditions from the previous section hold true for not necessarily concave utility functions, as long as Assumption 2.1 holds, i.e. $U\in {\mathcal {U}}(B_1,B_2)$. We illustrate this result by determining the optimal terminal wealth for $\mathbf {(P)}$ with S-shaped utility functions explicitly.

Throughout the whole of Sect. 5 we make the following additional assumptions about the market coefficients and bounds on terminal wealth:

Assumption 5.1

The market coefficients $r, \ \mu$ and $\sigma$ as well as the bounds on terminal wealth $0<B_1< v_0 e^{rT}< B_2<\infty$ are constants and $\delta$ is continuous on $X_K$.

Note however that a generalization to deterministic and continuous $r(t), \ \mu (t)$ and $\sigma (t)$ is straightforward. To include the case $B_1 =0$ or $B_2 = \infty$ one has to make additional growth assumptions on ${\mathcal {I}}$. Assumption 5.1 allows the use of the ensuing dynamic programming techniques, which lead to closed-form solutions to the primal, fully constrained portfolio optimization problem $\mathbf {(P)}$ for convex cone allocation constraints K. In contrast, the extension of the theoretical results from Sect. 4 to non-concave utility functions in Sect. 5.3 holds irrespective of 5.1. In particular, Lemma 5.13, Theorem 5.14 and Theorem 5.15 do not require Assumption 5.1.

5.1 Dual optimization problem

For any $t \in [0,T]$, we define the dual optimization problem $({\mathbf {D}})$ as

$$\begin{aligned} ({\mathbf {D}}) {\left\{ \begin{array}{ll} \varPsi (t,y)&= \underset{\uplambda \in {\mathcal {D}}}{\inf } \mathbbm {E}\big [U^{*}(y{\tilde{Z}}_{\uplambda }(t,T),B_1, B_2)\ \big | \ {\mathcal {F}}_t\big ], \end{array}\right. } \end{aligned}$$

with

$$\begin{aligned} {\tilde{Z}}_{\uplambda }(t,T) = \exp \Big \{ -\int _t^T r+\delta (\uplambda (s)) + \frac{1}{2} \Vert \gamma _{\uplambda }(s) \Vert ^2 ds - \int _t^T \gamma _{\uplambda }(s)'dW(s)\Big \} \quad \text {for any} \ \uplambda \in {\mathcal {D}}. \end{aligned}$$

Note that besides the fact that $({\mathbf {D}})$ is dynamic in time, there is a subtle difference between the optimization Problem $({\mathbf {D}})$ and the statement of Condition $({\tilde{D}})$.

Condition $({\tilde{D}})$ is formulated for $t=0$ and a specific $y = Y_{\uplambda ^{*}}(v_0,B_1, B_2)$, which already depends on the optimal $\uplambda ^{*}= \uplambda ^{*}(v_0) \in {\mathcal {D}}'$, satisfying condition (B) for a given initial wealth $v_0$. Hence, we cannot directly use Condition $({\tilde{D}})$ to compute $\uplambda ^{*}$ as the minimizer of an optimization problem.

However, given $t=0$ and $y>0$, if we manage to compute an optimal $\uplambda ^{*}= \uplambda ^{*}(0,y) \in {\mathcal {D}}$ for the dual problem $({\mathbf {D}})$ and this optimal $\uplambda ^{*}$ is an element of ${\mathcal {D}}'$, then this $\uplambda ^{*}$ satisfies Condition $({\tilde{B}})$ for the initial wealth $v_y = H_{\uplambda ^{*}(y)}(y,B_1,B_2)$. Hence, we can reconnect the solution to the dual problem $\mathbf (D)$ with the primal problem $\mathbf (P)$, if we can find a $y>0$ such that

$$\begin{aligned} v_0 = v_y = H_{\uplambda ^{*}(y)}(y,B_1,B_2). \end{aligned}$$

Our goal will be now to compute the minimizer $\uplambda ^{*}(y)$ for arbitrary $y>0$.

Remark 5.2

In particular, the existence of such a y can be guaranteed by virtue of Lemma 4.4, if $\uplambda ^{*}(y)\in {\mathcal {D}}'$ is independent of $y>0$. Conveniently, this will be the case for the combination of a large class of utility functions U and convex cone constraints K.

The HJB equation associated with $\mathbf (D)$ and the value function $\varPsi$ is

$$\begin{aligned} \begin{aligned} 0&= G_t(t,y) - ryG_y(t,y) \\&\quad + \underset{x \in X_K}{\inf }\Big ( - \delta (x)yG_y(t,y) + \frac{1}{2}\Vert \gamma +\sigma ^{-1}x \Vert ^2y^2 G_{yy}(t,y)\Big ) \\ G(T,y)&= U^{*}(y, B_1, B_2). \end{aligned} \end{aligned}$$

(5.1)

For the remainder of this section, we focus on the pointwise HJB equation (5.1) and will show that its solution, provided it satisfies some regularity conditions, induces a solution to the dual optimization problem (D).

Assuming that G solves (5.1) and is strictly decreasing and convex in y, there exists a minimizer $\uplambda ^{*}(t,y)$, which attains the infimium in (5.1). By slightly rewriting the PDE, one can see that $\uplambda ^{*}(t,y)$ actually minimizes

$$\begin{aligned} \uplambda ^{*}(t,y)&= \underset{x\in X_K}{\text {argmin}}\Big ( \frac{y^2}{2}\Vert \gamma + \sigma ^{-1}x\Vert ^2G_{yy}(t,y)-\delta (x)yG_y(t,y) \Big ) \nonumber \\&= \underset{x\in X_K}{\text {argmin}}\Big ( \underbrace{-\frac{1}{2}\frac{yG_{yy}(t,y)}{G_y(t,y)}}_{\ge 0} \Vert \gamma + \sigma ^{-1}x\Vert ^2+\delta (x) \Big ). \end{aligned}$$

(5.2)

This means that the (non-negative) relative risk aversion $\text {RRA}(t,y) = -\frac{yG_{yy}(t,y)}{G_y(t,y)}$ of G serves as a weighting factor in the minimization between the non-negative components $\Vert \gamma + \sigma ^{-1}x\Vert ^2$ and $\delta (x)$.

Lemma 5.3

Let $G\in C^{(1,2)}((0,T]\times (0,\infty ))$ be a convex and strictly decreasing solution to the HJB equation (5.1). Then there exists a corresponding minimizing argument $\uplambda ^{*}(t,y)$ (as in (5.2)), which is uniformly bounded in (t, y).

Proof

Due to G being convex and strictly decreasing, $\text {RRA}(t,y)\ge 0$. Furthermore, since $\sigma ^{-1}$ is non-singular, there exists a constant $c_{-} > 0$ such that $\Vert \sigma ^{-1}x\Vert \ge c_{-}\Vert x\Vert$ for all $x \in \mathbbm {R}^d$.

For a given minimizer $\uplambda ^{*}(t,y)\in X_K$, define

$$\begin{aligned} \nu (t,y) := \uplambda ^{*}(t,y)\cdot \mathbbm {1}_{\{ \Vert \uplambda ^{*}(t,y)\Vert \le \frac{2}{c_{-}}\Vert \gamma \Vert \}} \end{aligned}$$

Then, $\nu \in X_K$ and $\nu$ coincides with $\uplambda ^{*}$ whenever $\Vert \uplambda ^{*}(t,y)\Vert \le \frac{2}{c_{-}}\Vert \gamma \Vert$. Otherwise let $\Vert \uplambda ^{*}(t,y) \Vert > \frac{2}{c_{-}}\Vert \gamma \Vert$. Then, $\nu (t,y)= 0$ and

$$\begin{aligned}&\frac{1}{2}\text {RRA}(t,y) \Vert \gamma + \sigma ^{-1}\uplambda ^{*}(t,y)\Vert ^2+\delta (\uplambda ^{*}(t,y)) \\&\quad \ge \frac{1}{2}\text {RRA}(t,y) \big ( \Vert \gamma \Vert ^2 - 2 \Vert \gamma \Vert \Vert \sigma ^{-1}\uplambda ^{*}(t,y)\Vert + \Vert \sigma ^{-1}\uplambda ^{*}(t,y)\Vert ^2 \big ) + \delta (\uplambda ^{*}(t,y)) \\&\quad =\frac{1}{2}\text {RRA}(t,y) \big ( \Vert \gamma \Vert ^2 + \Vert \sigma ^{-1}\uplambda ^{*}(t,y)\Vert (- 2 \Vert \gamma \Vert + \underbrace{\Vert \sigma ^{-1}\uplambda ^{*}(t,y)\Vert )}_{\ge c_{-}\Vert \uplambda ^{*}(t,y)\Vert \ge 2 \Vert \gamma \Vert } \big ) + \underbrace{\delta (\uplambda ^{*}(t,y))}_{\ge 0}\\&\quad \ge \frac{1}{2}\text {RRA}(t,y) \Vert \gamma \Vert ^2 \overset{\nu (t,y)= 0}{=} \frac{1}{2}\text {RRA}(t,y) \Vert \gamma +\sigma ^{-1}\nu (t,y) \Vert ^2 + \delta (\nu (t,y)). \end{aligned}$$

Hence, $\nu (t,y)$ is also a minimizer of (5.2) and $\Vert \nu (t,y) \Vert \le \frac{2}{c_{-}}\Vert \gamma \Vert$, for all $(t,y)\in [0,T]\times (0,\infty )$, which concludes the proof. $\square$

Using this observation and assuming polynomial growth, convexity and monotonicity conditions (which are plausible given the properties of the terminal condition), we are able to locally prove a verification theorem for the HJB equation (5.1). Having the minimization property locally is sufficient for our purposes as noted in Remark 4.1. Note that this verification theorem is only applicable if G is a smooth solution to (5.1) and not a viscosity solution. In general, this requirement cannot be guaranteed (see e.g. Fleming and Soner 2006 for a thorough discussion of the topic). However, we will be able to derive an explicit, smooth solution to (5.1) in Subsection 5.2, if K is a convex cone.

Theorem 5.4

rm (Verification Theorem) Let Assumption 5.1 hold and let $G \in C^{(1,2)}([0,T)\times (0,\infty ))$ be a solution to the HJB equation (5.1), be convex, strictly decreasing and satisfy the polynomial growth condition

$$\begin{aligned} G(t,y) \le C \big ( y^{-\alpha } + y^{\alpha }), \qquad \text {for some }\alpha>0,\ C>0. \end{aligned}$$

Further, let

$$\begin{aligned} \uplambda ^{*}(t,y) := \underset{x\in X_K}{\text {argmin}}\Big ( \frac{y^2}{2}\Vert \gamma + \sigma ^{-1}x\Vert ^2G_{yy}(t,y)-\delta (x)yG_y(t,y) \Big ), \end{aligned}$$

be uniformly bounded in $(t,y)\in [0,T]\times (0,\infty )$. Then, $\forall \uplambda \in {\mathcal {D}}$ with $\Vert \uplambda (s)-\uplambda ^{*}(s)\Vert \le 1$

$$\begin{aligned} G(t,y) \le \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda }(t,T),B_1,B_2) | {\mathcal {F}}_t] \end{aligned}$$

and

$$\begin{aligned} G(t,y) = \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda ^{*}}(t,T),B_1, B_2) | {\mathcal {F}}_t], \end{aligned}$$

for all $(t,y)\in [0,T]\times (0,\infty )$, with $\uplambda ^{*}(s) = \uplambda ^{*}(s,\omega ) := \uplambda ^{*}(s,y{\tilde{Z}}_{\uplambda ^{*}}(t,s))\in {\mathcal {D}}$ defined in feedback-form.

Proof

The proof of this theorem can be found in the appendix. $\square$

Remark 5.5

Note that Theorem 5.4 does not provide verification for the fully constrained portfolio optimization problem (P), but only for the dual optimization problem (D). We still need to show that the obtained $\uplambda ^{*}$ is indeed an element of ${\mathcal {D}}'$. For convex cone constraints, this will be shown in Sect. 5.2.

5.2 Concave utility functions

In this section we solve the HJB equation (5.1) associated with the dual optimization problem (D) for general convex cone constraints, given a concave utility function $U\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$, whose capped LFT satisfies a polynomial growth condition. Provided that $0< B_1< B_2 < \infty$, this growth condition is always satisfied. We then use the Verification Theorem from the previous section to link the solution to optimality Condition $({\tilde{D}})$ and finally solve the fully constrained portfolio optimization problem (P).

The allocation constraints K form a convex cone if and only if $\delta (x)=0$ for all $x\in X_K$. In this special case the HJB equation (5.1) simplifies to

$$\begin{aligned} 0&= G_t(t,y) - ryG_y(t,y) + \frac{y^2}{2}\underset{x \in X_K}{\inf }\Big ( \Vert \gamma + \sigma ^{-1}x \Vert ^2G_{yy}(t,y)\Big ) \nonumber \\ G(T,y)&= U^{*}(y, B_1, B_2). \end{aligned}$$

(5.3)

The infimum here can in general only be attained if G is convex, as $X_K$ is typically unbounded and so is $\Vert \gamma + \sigma ^{-1}x\Vert ^2$. If G is convex however, the infimum is attained by the pointwise minimizer

$$\begin{aligned} \uplambda ^{*}= \uplambda ^{*}(y) := \underset{x\in X_K}{\text {argmin}}\Vert \gamma + \sigma ^{-1}x\Vert ^2. \end{aligned}$$

The resulting PDE reduces to a linear PDE, which can be solved through a transformation to the well-studied heat equation (see e.g. Bian et al. 2011). For this purpose, recall the following result about the heat equation:

Lemma 5.6

Consider a real function $f:\mathbbm {R}\rightarrow \mathbbm {R}$ for which exist constants $C_0$, $\alpha _0$ such that

$$\begin{aligned} |f(z)| \le C_0e^{\alpha _0 z^2} \quad \forall z\in \mathbbm {R}. \end{aligned}$$

(5.4)

Then, for all $0<T<\frac{1}{4\alpha _0}$ the function $F:(0,T]\times \mathbbm {R}\rightarrow \mathbbm {R}$ defined by

$$\begin{aligned} F(\tau ,z) = \frac{1}{\sqrt{4\pi \tau }}\int _{\mathbbm {R}}e^{-\frac{(z-x)^2}{4\tau }}f(x)dx =\frac{1}{\sqrt{4\pi \tau }}\int _{\mathbbm {R}}e^{-\frac{x^2}{4\tau }}f(z-x)dx, \end{aligned}$$

is in $C^{(1,2)}((0,T]\times \mathbbm {R})$ and is a solution to the heat equation

$$\begin{aligned} \begin{array}{llll} &{}F_{\tau }(\tau ,z) &{}= F_{zz}(\tau ,z) \quad &{}\forall (\tau ,z)\in (0,T]\times \mathbbm {R}\\ F(0,z):= \lim _{\tau \downarrow 0} \ &{}F(\tau ,z) &{}= f(z) \quad &{} \text {for almost all} \ z\in \mathbbm {R}. \end{array} \end{aligned}$$

(5.5)

Proof

Follows immediately from Chapter 5, Theorem 6.1 in DiBenedetto (2009). $\square$

Lemma 5.7

Let $U\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$ and let $U^{*}(\cdot ,B_1,B_2)$ satisfy the polynomial growth condition

$$\begin{aligned} |U^{*}(y,B_1,B_2)| \le C\big (y^{-\alpha } + y^{\alpha }\big ), \quad \forall y\in (0,\infty ) \end{aligned}$$

(5.6)

for some constants $C, \ \alpha >0$. Further, let the allocation constraints K be a convex cone. Then,

$$\begin{aligned} G(t,y):= \frac{1}{\sqrt{4\pi (T-t)}}\int _{\mathbbm {R}}e^{-\frac{x^2}{4(T-t)}}U^{*}\Big (ye^{-(r+\frac{1}{2}\Vert \gamma _{\uplambda ^{*}}\Vert ^2)(T-t)-\frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}}x},B_1,B_2\Big )dx \end{aligned}$$

is in $C^{(1,2)}([0,T)\times (0,\infty ))$, is convex, strictly decreasing and satisfies the HJB equation (5.1) with

$$\begin{aligned} \uplambda ^{*}(t,y):= \uplambda ^{*}:= \underset{x\in X_K}{\text {argmin}}\Vert \gamma + \sigma ^{-1}x\Vert ^2 \quad \text {and} \quad \gamma _{\uplambda ^{*}}:= \gamma + \sigma ^{-1}\uplambda ^{*}. \end{aligned}$$

Further, G satisfies the polynomial growth condition

$$\begin{aligned} |G(t,y)| \le {\tilde{C}} \big (y^{-\alpha } + y^{\alpha }\big ) \quad \forall y\in (0,\infty ) \end{aligned}$$

(5.7)

and for some constant ${\tilde{C}}>0$.

Proof

The proof of this lemma can be found in the appendix. $\square$

Remark 5.8

It is important to emphasize that the previous techniques heavily relied on K being a convex cone (hence $\delta (\uplambda ^{*})=0$) as this simplifies the HJB equation (5.1) to a linear PDE. For more general allocation constraints with $\delta (\uplambda ^{*})\ne 0$, the PDE may become non-linear and extremely difficult to solve. We leave this type of problem as an area for future research.

Remark 5.9

Note that under Assumption 5.1 the growth condition (5.6) is satisfied for any $U \in {\mathcal {U}}(B_1,B_2)$, with $\alpha := 1$ and $C:= |U(B_2)| + B_1 + B_2$, because for all $y>0$

$$\begin{aligned} U^{*}(y,B_1,B_2)&= \underset{B_1\le x \le B_2}{\sup }\big ( U(x)-yx \big ) \ge U(B_2)-yB_2\\ \text {and} \quad U^{*}(y,B_1,B_2)&\!=\!\!\underset{B_1\le x \le B_2}{\sup }\!\big ( \underbrace{\!U(x)}_{\le U(B_2)}\!-yx \big ) \le U(B_2)\!+\underset{B_1\le x \le B_2}{\inf }(yx)\! =\! U(B_2)\!-\!yB_1 \\ \Rightarrow |U^{*}(y,B_1,B_2)|&\le |U(B_2)|\! + y(B_1 + B_2) \le |U(B_2)|\frac{1}{y} \!+ \big (| U(B_2)|+B_1\!+\!B_2\big )y \\&\le C\cdot \big (y^{\alpha }+y^{-\alpha }\big ) . \end{aligned}$$

Corollary 5.10

Let U be concave, let K be a convex cone, and let Assumption 5.1 hold. Then $\uplambda ^{*}\in {\mathcal {D}}'$ defined by,

$$\begin{aligned} \uplambda ^{*}:= \underset{x\in X_K}{\text {argmin}} \ \Vert \gamma + \sigma ^{-1}x\Vert ^2 \end{aligned}$$

satisfies condition $({\tilde{D}})$ and the optimal portfolio for the wealth-constrained portfolio optimization problem $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$ is optimal for the fully constrained portfolio optimization problem $(\mathbf{P })$.

Proof

First of all, K is a convex cone, $\uplambda ^{*}$ and $B_2$ are constant and finite, and therefore $\uplambda ^{*}\in {\mathcal {D}}'$ according to Remark 5.2. Further, since all prerequisites of Lemma 5.7 are satisfied, G (as defined in Lemma 5.7) satisfies the HJB equation (5.1), is convex, strictly decreasing in y and satisfies a polynomial growth condition. According to Theorem 5.4, since the minimizing $\uplambda ^{*}(t,y) = \uplambda ^{*}$ is independent of $y>0$, this implies for all $y>0$:

$$\begin{aligned} G(0,y)&= \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2)] \\&\le \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2)], \quad \forall \uplambda \in {\mathcal {D}} \ \text {with} \ \Vert \uplambda ^{*}- \uplambda (t) \Vert ^2 \ {\mathcal {L}}[0,T]\otimes Q\text {-a.s.}. \end{aligned}$$

As realized in Remark 4.10, this implies for all $y>0$

$$\begin{aligned} G(0,y) = \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2)] \le \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2)], \quad \forall \uplambda \in {\mathcal {D}}. \end{aligned}$$

In particular, this holds for the choice of $y=Y_{\uplambda ^{*}}(v_0,B_1,B_2)$, which is guaranteed to exist due to Lemma 4.4 and thus $\uplambda ^{*}$ satisfies Condition $({\tilde{D}})$. The statement of the Corollary now follows due to the equivalence of Condition $({\tilde{B}})$ and Condition $({\tilde{D}})$ by virtue of Theorem 4.9. $\square$

Example 5.11

(Optimal Terminal Wealth for Logarithmic Utility) Consider a logarithmic utility function U with

$$\begin{aligned} U(x):= \log (x) \end{aligned}$$

Let K be a convex cone, let Assumption 5.1 hold and define $\uplambda ^{*}\in {\mathcal {D}}'$ as

$$\begin{aligned} \uplambda ^{*}:= \underset{x\in X_K}{\text {argmin}} \ \Vert \gamma + \sigma ^{-1}x\Vert ^2. \end{aligned}$$

Then, the optimal terminal wealth for (P) is given as

$$\begin{aligned} D^{*} = B_1 + \Big ( \frac{1}{y{\tilde{Z}}_{\uplambda ^{*}}(T)}- B_1\Big )^{+} - \Big ( \frac{1}{y{\tilde{Z}}_{\uplambda ^{*}}(T)}- B_2\Big )^{+}, \end{aligned}$$

for $y:= Y_{\uplambda ^{*}}(v_0,B_1,B_2)$.

Proof

As $U\in {\mathcal {U}}^{conc}(B_1,B_2)$ and

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2) = B_1 + \Big ( \frac{1}{y}- B_1\Big )^{+} - \Big ( \frac{1}{y}- B_2\Big )^{+}, \end{aligned}$$

the remaining statements follow immediately from Corollary 5.10 and Theorem 4.6. $\square$

Example 5.12

(Optimal Terminal Wealth for Power Utility) Consider a power utility function U with

$$\begin{aligned} U(x):= \frac{1}{b}x^b, \quad b\in (-\infty , 1) \backslash \{0\}. \end{aligned}$$

Let K be a convex cone, let Assumption 5.1 hold and define $\uplambda ^{*}\in {\mathcal {D}}'$ as

$$\begin{aligned} \uplambda ^{*}(t,\omega ) := \underset{x\in X_K}{\text {argmin}}\ \Vert \gamma + \sigma ^{-1}x\Vert ^2. \end{aligned}$$

Then, the optimal terminal wealth for (P) is given as

$$\begin{aligned} D^{*}= B_1 + \Big ( \big (y{\tilde{Z}}_{\uplambda ^{*}}(T)\big )^{\frac{1}{b-1}} - B_1\Big )^{+} - \Big ( \big (y{\tilde{Z}}_{\uplambda ^{*}}(T)\big )^{\frac{1}{b-1}} - B_2\Big )^{+}, \end{aligned}$$

for $y:= Y_{\uplambda ^{*}}(v_0,B_1,B_2)$.

Proof

As $U\in {\mathcal {U}}^{conc}(B_1,B_2)$ and

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2) = B_1 + \Big ( y^{\frac{1}{b-1}}- B_1\Big )^{+} - \Big ( y^{\frac{1}{b-1}}- B_2\Big )^{+}, \end{aligned}$$

the remaining statements follow immediately from Corollary 5.10 and Theorem 4.6. $\square$

5.3 Not necessarily concave utility functions

So far we have only considered concave utility functions U in our portfolio optimization problems. However, there exists extensive theory on portfolio optimization for non-concave utility functions in the literature. Specifically, one approach, presented in Reichlin (2013) uses concavification arguments, which allow to transform the optimization problem for a non-concave utility function U into an equivalent optimization problem for a concave utility function ${\hat{U}}$, which is the smallest concave function larger or equal than U (i.e. the concavification of U). The equivalence of the optimization problems is meant in the sense that the optimal portfolio process, optimal terminal wealth and optimal expected utility coincide for both U and ${\hat{U}}$.

In this section we will slightly adjust the theory presented in Reichlin (2013) to fit our needs, prove that the equivalence between Conditions $({\tilde{B}})-({\tilde{E}})$ holds for general, not necessarily concave $U \in {\mathcal {U}}(B_1,B_2)$ and illustrate this finding on the example of an S-shaped utility.

Even though we have so far only introduced the (capped) LFT $U^{*}(\cdot , B_1,B_2)$ for concave utility functions, the definition of the capped LFT and its properties carry over to general $U\in {\mathcal {U}}(B_1,B_2)$ as well.

For $U\in {\mathcal {U}}(B_1,B_2)$, we define its concavification on $[B_1,B_2]$ as the smallest function ${\hat{U}}$, with

• ${\hat{U}}$ is concave on $[B_1,B_2]$.

• ${\hat{U}}(x) \ge U(x) \quad \forall x\in [B_1,B_2]$

• ${\hat{U}}(x) = U(B_1) + h_{-}(x-B_1) \ \forall x\in [0,B_1)$, with $h_{-}:= \lim _{x\downarrow B_1}{\hat{U}}'(x)$

• ${\hat{U}}(x) = U(B_2) \ \forall x\in (B_2,\infty )$

We derive some important properties of this new construction.

Lemma 5.13

Let $U\in {\mathcal {U}}(B_1,B_2)$ and ${\hat{U}}$ be its concavification on $[B_1, B_2]$. Then, ${\hat{U}}\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$ and for all $y>0$,

$$\begin{aligned} U^{*}(y,B_1,B_2)&= U({\mathcal {I}}(y,B_1,B_2))-y{\mathcal {I}}(y,B_1,B_2) \\&= {\hat{U}}({\mathcal {I}}(y,B_1,B_2))-y{\mathcal {I}}(y,B_1,B_2)={\hat{U}}^{*}(y,B_1,B_2), \end{aligned}$$

and

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2) :=&\inf \{ x \in [B_1,B_2] \ | \ U^{*}(y,B_1,B_2) = U(x)-yx\} \nonumber \\ =&\inf \{ x \in [B_1,B_2] \ | \ {\hat{U}}^{*}(y,B_1,B_2)= {\hat{U}}(x)-yx\}=:\hat{{\mathcal {I}}}(y,B_1,B_2), \end{aligned}$$

(5.8)

which is decreasing, has at most countably infinite points of discontinuity and satisfies

$$\begin{aligned} U({\mathcal {I}}(y,B_1,B_2)) = {\hat{U}}({\mathcal {I}}(y,B_1,B_2)), \quad \forall y>0. \end{aligned}$$

(5.9)

Proof

The proof of this lemma can be found in the appendix. $\square$

In our setting, since any admissible terminal wealth can only take values within $[B_1,B_2]$, the values of the utility function U (and for ${\hat{U}}$) outside of $[B_1,B_2]$ do not affect the optimization. We chose the values of ${\hat{U}}$ outside of $[B_1,B_2]$ in such a way that ${\hat{U}}$ is concave on $(0,\infty )$ and therefore ${\hat{U}}\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$ by Lemma 2.1 and Lemma 5.13.

Recall that the optimal terminal wealth corresponding to the wealth-constrained portfolio optimization problem $({\tilde{\mathbf {P}}_{\uplambda })}$, for any $\uplambda \in {\mathcal {D}}$, only depends on the underlying utility U through the maximizer of the capped LFT ${\mathcal {I}}(y,B_1,B_2)$. Using the previous Lemma, we are able to solve $({\tilde{\mathbf {P}}_{\uplambda })}$ for non-concave utility functions U.

Theorem 5.14

(Optimal Terminal Wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$ for non-concave U) Let $\uplambda \in {\mathcal {D}}$ and let Assumption 4.5 hold. Then,

$$\begin{aligned} D_{\uplambda }^{*} := {\mathcal {I}}(y{\tilde{Z}}_{\uplambda }(T),B_1, B_2) \text { with }y = Y_{\uplambda }(v_0,B_1,B_2) \end{aligned}$$

is the optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$ and $Q\big (U(D_{\uplambda }^{*}) = {\hat{U}}(D_{\uplambda }^{*})\big ) = 1$.

Proof

From Assumption 2.1, $U\in {\mathcal {U}}(B_1,B_2)$. Therefore, we may define ${\hat{U}}\in {\mathcal {U}}^{conc}(B_1,B_2)$ as the concavification of U on $[B_1,B_2]$ and $\hat{{\mathcal {I}}}(y,B_1,B_2)$ be the maximizing arguments of its capped LFT. Due to Lemma 5.13, $\hat{{\mathcal {I}}}(y,B_1,B_2)={\mathcal {I}}(y,B_1,B_2)$ and $U({\mathcal {I}}(y,B_1,B_2)) = {\hat{U}}({\mathcal {I}}(y,B_1,B_2))$ for all $y>0$. Thus,

$$\begin{aligned} Q\big (U(D_{\uplambda }^{*}) = {\hat{U}}(D_{\uplambda }^{*})\big ) = 1. \end{aligned}$$

Further, by virtue of Theorem 4.6

$$\begin{aligned} D_{\uplambda }^{*}= {\mathcal {I}}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2) =\hat{{\mathcal {I}}}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2) \end{aligned}$$

is the optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$ with utility ${\hat{U}}\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$. However, since ${\hat{U}}(x)\ge U(x)$ for all $x \in [B_1,B_2]$, $U(D_{\uplambda }^{*})={\hat{U}}(D_{\uplambda }^{*})$ Q-a.s. and the set of admissible terminal wealths $C_{\uplambda }(v_0, B_1)$ is independent of the choice of utility, $D_{\uplambda }^{*}$ must be the optimal terminal wealth for $({\tilde{\mathbf {P}}_{\uplambda })}$ with utility U. $\square$

Using the statements of Lemma 5.13 and Theorem 5.14, we realize that any of the Conditions $({\tilde{B}})-({\tilde{E}})$ holds for a utility $U\in {\mathcal {U}}(B_1,B_2)$ if and only if they hold for its concavification on $[B_1,B_2]$ ${\hat{U}}\in {\mathcal {U}}^{\text {conc}}(B_1,B_2).$ This leads to a generalization of Theorem 4.9.

Theorem 5.15

Let $\uplambda ^{*}\in {\mathcal {D}}'$. Then, Conditions $({\tilde{B}})$, $({\tilde{C}})$, $({\tilde{D}})$ and $({\tilde{E}})$ are equivalent for $\uplambda ^{*}$ and imply $({\tilde{A}})$ with $\pi ^{*}:= \pi _{\uplambda ^{*}}$.

Proof

$\underline{\hbox {Implication} ({\tilde{B}})\Rightarrow ({\tilde{A}})}$: The argument is analogous the proof of Corollary 4.2, as non-decreasingness is the only necessary property of U for this proof.

$\underline{\hbox {Condition} ({\tilde{B}})}$: $\pi _{\uplambda ^{*}}$ is optimal for $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$ with utility U if and only if it is optimal for $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$ with utility ${\hat{U}}$, due to Theorem 5.14. Therefore, $\pi _{\uplambda ^{*}}$ satisfies Condition $({\tilde{B}})$ for U if and only if it satisfies Condition $({\tilde{B}})$ for ${\hat{U}}$.

$\underline{\hbox {Condition} ({\tilde{C}})}$: For any $\uplambda \in {\mathcal {D}}$, $Q(U(D^{*}_{\uplambda }) ={\hat{U}}(D^{*}_{\uplambda }))=1$, as per Theorem 5.14. Hence, for any $\uplambda \in {\mathcal {D}}$ the value functions of $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$ coincide for U and ${\hat{U}}$. Therefore, $\pi _{\uplambda ^{*}}$ satisfies Condition $({\tilde{C}})$ for U if and only if it satisfies Condition $({\tilde{C}})$ for ${\hat{U}}$.

$\underline{\hbox {Condition} ({\tilde{D}})}$: From Lemma 5.13 we know that $U^{*}(y,B_1,B_2) = {\hat{U}}^{*}(y,B_1,B_2)$ for all $y>0$. Therefore, $\pi _{\uplambda ^{*}}$ satisfies Condition $({\tilde{D}})$ for U if and only if it satisfies Condition $({\tilde{D}})$ for ${\hat{U}}$.

$\underline{\hbox {Condition} ({\tilde{E}})}$: From Lemma 5.13 we know that ${\mathcal {I}}(y,B_1,B_2) = \hat{{\mathcal {I}}}(y,B_1,B_2)$ for all $y>0$ Therefore, $\pi _{\uplambda ^{*}}$ satisfies Condition $({\tilde{E}})$ for U if and only if it satisfies Condition $({\tilde{E}})$ for ${\hat{U}}$.

Since Conditions $({\tilde{B}})-({\tilde{E}})$ are equivalent for the concave utility function ${\hat{U}}\in {\mathcal {U}}^{conc}(B_1,B_2)$, this concludes the proof of the Theorem. $\square$

The Verification Theorem 5.4 and Lemma 5.7 from the previous sections did not rely on the underlying utility U being concave, but only needed its capped LFT $U^{*}$ to satisfy a polynomial growth condition. Hence, Corollary 5.10 can be generalized for non-concave utility U.

Corollary 5.16

Let K be a convex cone and let Assumption 5.1 hold.

Then, $\uplambda ^{*}\in {\mathcal {D}}'$ defined by

$$\begin{aligned} \uplambda ^{*}(t,\omega ) := \underset{x\in X_K}{\text {argmin}} \ \Vert \gamma + \sigma ^{-1}x\Vert ^2 \end{aligned}$$

satisfies condition $({\tilde{D}})$ and the optimal portfolio for the wealth-constrained portfolio optimization problem $({\tilde{\mathbf {P}}_{\uplambda ^{*}})}$ is optimal for the fully constrained portfolio optimization problem $\mathbf {(P)}$.

Proof

The proof is analogous to the proof of Corollary 5.10. The only difference is that we reference Theorem 5.15 instead of Theorem 4.9 in the last step of the proof. $\square$

Example 5.17

(Optimal Terminal Wealth for S-Shaped Utility) Let the utility $U\in {\mathcal {U}}(B_1,B_2)$ be an S-shaped utility function, i.e. $U:(0,\infty )\rightarrow \mathbbm {R}$,

$$\begin{aligned} U(x) = {\left\{ \begin{array}{ll} -U_1(\theta -x), \quad &{} \ x\le \theta \\ U_2(x-\theta ), \quad &{} \ x>\theta , \end{array}\right. } \end{aligned}$$

for some reflection point $\theta \ge 0$, strictly increasing $U_1, \ U_2 \in {\mathcal {U}}^{conc}(0,\infty )$ with $U_1(0) = U_2(0)$ and ${\mathcal {I}}_2$ denoting the (capped) minimizer of the (capped) LFT of $U_2$.

Let K be a convex cone, let Assumption 5.1 hold and define $\uplambda ^{*}\in {\mathcal {D}}'$ as

$$\begin{aligned} \uplambda ^{*}(t,\omega ) := \underset{x\in X_K}{\text {argmin}}\Vert \gamma + \sigma ^{-1}x\Vert ^2. \end{aligned}$$

Consider the fully constrained portfolio optimization problem $\mathbf {(P)}$ with utility U. Then, $\uplambda ^{*}$ satisfies condition $({\tilde{D}})$ for $\mathbf {(P)}$. We make a distinction between the possible orderings of $B_1, \ B_2$ and $\theta$ (Fig. 2):

• (i) If $B_1 < B_2 \le \theta$, then the optimal terminal wealth for $\mathbf {(P)}$ is given as

  $$\begin{aligned} D^{*}= {\left\{ \begin{array}{ll}B_1, \ &{}\text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}\le y{\tilde{Z}}_{\uplambda ^{*}}(T) \\ B_2, \ &{}\text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}>y{\tilde{Z}}_{\uplambda ^{*}}(T). \end{array}\right. } \end{aligned}$$

• (ii) If $\theta \le B_1 < B_2$, then the optimal terminal wealth for $\mathbf {(P)}$ is given as

  $$\begin{aligned} D^{*}= {\mathcal {I}}_2(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1 - \theta , B_2-\theta )+\theta . \end{aligned}$$

• (iii) If $B_1< \theta < B_2$, define

  $$\begin{aligned} h = \sup \{ x\ge \theta \ | \ \forall z \in [B_1, x]: U(z) \le U(B_1) + \frac{U(x)-U(B_1)}{x-B_1}(z-B_1)\}. \end{aligned}$$

  • (iii).a If $h\ge B_2$, then the optimal terminal wealth for $\mathbf {(P)}$ is given as

    $$\begin{aligned} D^{*}= {\left\{ \begin{array}{ll}B_1, \ &{}\text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}\le y{\tilde{Z}}_{\uplambda ^{*}}(T) \\ B_2, \ &{}\text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}> y{\tilde{Z}}_{\uplambda ^{*}}(T). \end{array}\right. } \end{aligned}$$

  • (iii).b If $h < B_2$, then the optimal terminal wealth for $\mathbf {(P)}$ is given as

    $$\begin{aligned} D^{*}= {\left\{ \begin{array}{ll}B_1, \quad &{}\text {if } \ \frac{U(h)-U(B_1)}{h-B_1}\le y{\tilde{Z}}_{\uplambda ^{*}}(T) \\ {\mathcal {I}}_2(y{\tilde{Z}}_{\uplambda ^{*}}(T),h-\theta , B_2 - \theta )+\theta , \quad &{}\text {if } \ \frac{U(h)-U(B_1)}{h-B_1}> y{\tilde{Z}}_{\uplambda ^{*}}(T), \end{array}\right. } \end{aligned}$$

where $y>0$ is chosen such that $\mathbbm {E}[D^{*}{\tilde{Z}}_{\uplambda ^{*}}(T)]=v_0$ (i.e. $y=Y_{\uplambda ^{*}}(v_0,B_1,B_2)$) in each of the above cases.

Fig. 2

Illustration of the concavification of an S-shaped utility function on $[B_1,B_2]$, depending on the ordering of $B_1, \ B_2$ and $\theta$

Proof

The proof of this example can be found in the appendix. $\square$

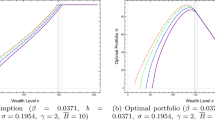
Figures 3 and 4 illustrate the effect of different values for $B_1$,$B_2$ on the optimal portfolio allocation $\pi ^{*}$ for an investor who follows an S-shaped utility function from Example 5.17 and does not face any allocation constraints. We created the figures using a similar setting as in Berkelaar et al. (2004), with a market consisting of one stock and one bond (i.e. $d=1$), constant market coefficients $r= 0.05$, $\mu = 0.13$, $\sigma = 0.2$, which result in a constant market price of risk $\gamma = 0.4$. Moreover, we chose $U_1(x)=2.25x^{0.12}$ and $U_2(x) = x^{0.12}$, i.e. both $U_1$ and $U_2$ are power utility functions (see Example 5.12) with $b = 0.12$. In this market, we estimate the optimal portfolio for an investor, who allocates from time $t=0$ until time $T=0.5$, with initial wealth $v_0 = 1$ and observe how the investor’s allocation changes with respect to different reflection points $\theta$ and different constraints $B_1, \ B_2.$

Fig. 3

Varying levels of $B_1$ and $B_2 = \infty$

Fig. 4

$B_1 = 0$ and varying levels of $B_2$

We approximated these portfolios numerically, by simulating $10^6$ optimal terminal wealths $D^{*}$ as determined in Example 5.17, estimating the corresponding value function $\varPhi$ and its first and second derivatives $\varPhi _V$, $\varPhi _{VV}$ to determine the corresponding optimal portfolio process as the minimizer of the primal HJB equation (see e.g. Karatzas and Shreve 1998, Chapter 3, equation (8.38)). Due to estimation errors from the underlying Monte-Carlo simulations, the estimated optimal portfolios did not appear to be a completely smooth functions of $B_1, B_2$. However, we did observe that the smoothness increased with an increasing number of simulations. For this reason, we additionally used smoothing splines on the estimated portfolios that are displayed in Figs. 3 and 4.

Overall, both an increase of the lower bound $B_1$ and a decrease of the upper bound $B_2$ tends to lead to a reduction of the optimal allocation to the risky asset. This reduction and its monotonicity are not surprising, as now the investor’s constrained optimal terminal wealth is bounded by deterministic constants, which enforce an allocation to the risk-free asset if the investor’s wealth becomes too large or too small.

In particular, the optimal allocation approaches the optimal unconstrained allocation for small lower bounds $B_1$ and large upper bounds $B_2$. Vice-versa, the optimal allocation approaches 0, as $B_1$ approaches the maximal feasible lower bound and $B_2$ approaches the minimal feasible upper bound $v_0\exp (rT) \approx 1.0253$. The reduction in allocation to the risky asset from the presence of lower bounds $B_1$ on terminal wealth appears to be strongest, when the investor’s initial wealth is in the gambling area, i.e. when $\theta \ge v_0 = 1$. The reduction is less extreme when considering upper bounds on terminal wealth $B_2$.

Only for upper bounds $B_2$ close to the corresponding concavification point h (i.e. when the investor’s initial wealth transitions to the gambling area) do we not observe a general reduction of the allocation to the risky asset: A small increase in allocation to the risky-asset can be clearly seen for $\theta = 1$ (with $h=1.0276$) and is still slightly visible for $\theta = 1.2$ (with $h=1.2332$). For $\theta \in \{0,0.5,0.8\}$, the concavification point h is not visible in the plot and for $\theta = 1.5$, the effect is too small to be visible.

6 Conclusion

In this paper we have seen how the capped Legendre–Fenchel transformation can be used to naturally extend the auxiliary market framework from Cvitanic and Karatzas (1992) for portfolio optimization under allocation constraints to include lower and upper bounds on terminal wealth and non-concave, non-smooth utility functions. In our setting, the solution to the fully constrained portfolio optimization problem $\mathbf {(P)}$ can be found by solving the corresponding dual optimization problem $\mathbf {(D)}$. In the case of convex-cone allocation constraints a solution to $\mathbf {(D)}$ can be found explicitly by solving an associated HJB equation. For more general cases, we were able to prove a verification theorem which guarantees that the solution to the HJB equation indeed induces a solution to $\mathbf {(D)}$, hence $\mathbf {(P)}$.

Appendix A

Proof of Lemma 4.4

Since I is non-constant, non-increasing and ${\tilde{Z}}_{\uplambda }$ has a continuous distribution, which takes arbitrarily small and large real values with positive probability, the capped help function is strictly decreasing in y. Moreover, since ${\mathcal {I}}(\cdot , B_1,B_2)$ is continuous Lebesque-a.e., we can conclude the limiting behavior of $H_{\uplambda }(\cdot ,B_1,B_2)$ for $y\rightarrow \infty$ and $y\downarrow 0$ from the monotone convergence theorem and $\lim _{y\downarrow 0}{\mathcal {I}}(y,B_1,B_2) = B_2$ and $\lim _{y\rightarrow \infty }{\mathcal {I}}(y,B_1,B_2) = B_1$. Finally, as $H_{\uplambda }(y,B_1,B_2)<\infty$ $\forall y >0$, Lebesgue’s dominated convergence theorem can be utilized to follow the continuity of $H_{\uplambda }(\cdot , B_1,B_2)$ from the Lebesgue-a.e. continuity of $I(\cdot , B_1,B_2).$⁴$\square$

Proof of Theorem 4.9

The implication (${\tilde{B}}$) $\Rightarrow$ (${\tilde{A}}$) is the statement of Corollary 4.7. The implications (${\tilde{B}}$) $\Rightarrow$ (${\tilde{C}}$), (${\tilde{B}}$) $\Rightarrow$ (${\tilde{E}}$), (${\tilde{E}}$) $\Rightarrow$ (${\tilde{B}}$) and (${\tilde{C}}$) $\Rightarrow$ (${\tilde{D}}$) can be shown by following the arguments in the proof of Theorem 10.1 in Cvitanic and Karatzas (1992), disregarding consumption and replacing the LFT and its maximizer by the capped LFT and its capped maximizer.

It remains to consider the implication (${\tilde{D}}$) $\Rightarrow$ (${\tilde{B}}$). By replacing the LFT with the capped LFT and its maximizer with the capped maximizer, we can carefully follow the steps of the proof of Theorem 9.1 and Theorem 10.1 in Cvitanic and Karatzas (1992)⁵ to show that

$$\begin{aligned} \mathbbm {E}\big [ U^{*}(y{\tilde{Z}}_{\uplambda }(T),B_1,B_2)\big ] \le \mathbbm {E}\big [ U^{*}(y{\tilde{Z}}_{\uplambda +\rho }(T),B_1,B_2)\big ] \ \forall \rho \in {\mathcal {D}}, \quad (*) \end{aligned}$$

implies

$$\begin{aligned} 0 \le \pi (t)'\rho (t) + \delta (\rho (t)) \qquad \qquad \quad Q\otimes {\mathcal {L}}[0,T]-a.e. \ \forall \rho \in {\mathcal {D}}, \quad (**) \end{aligned}$$

as well as

$$\begin{aligned} 0 \ge \pi (t)'\uplambda ^{*}(t) + \delta (\uplambda ^{*}(t)) \qquad \qquad \qquad \quad Q\otimes {\mathcal {L}}[0,T]-a.e.. \quad (***) \end{aligned}$$

Hence, we have

$$\begin{aligned}&\pi (t) \in K \quad {\mathcal {L}}[0,T]\otimes Q-a.e. \\ \text {and}\quad&[\pi (t)'\uplambda ^{*}(t) + \delta (\uplambda ^{*}(t))] = 0 \quad {\mathcal {L}}[0,T]\otimes Q-a.e., \end{aligned}$$

i.e. Condition $({\tilde{B}})$ is satisfied. Analogously, if $(*)$ holds for all $\rho \in {\mathcal {D}}$ with $\Vert \rho (t) \Vert \le 1$ ${\mathcal {L}}[0,T]\otimes Q-a.e.$, then we obtain $(**)$ restricted to all such $\rho$ as well as $(***)$, if we choose $\rho (t) = -\uplambda ^{*}(t) / \max (1, \Vert \uplambda ^{*}(t)\Vert )$. $\square$

Proof of Theorem 5.4

First, note that the uniform boundedness of $\uplambda ^{*}(t,y)\in X_K$ and the continuity of $\delta$ guarantee that the corresponding stochastic process $\uplambda ^{*}(s,\omega )$ satisfies the integrability conditions from the definition of ${\mathcal {D}}$. Due to measurable selection theorems (for example Corollary 3.48 in Rockafellar and Wets (1984)) we may w.l.o.g. assume the mapping $(t,y)\rightarrow \uplambda ^{*}(t,y)$ to be Borel-measurable. Hence, the corresponding stochastic process $\uplambda ^{*}(s,\omega )$ is progressively measurable and thus an element of ${\mathcal {D}}$.

For convenience, we define the characteristic operator ${\mathcal {H}}^{\uplambda }$ of G with respect to $\uplambda \in {\mathcal {D}}$ as

$$\begin{aligned} {\mathcal {H}}^{\uplambda }(t,y) = G_t(t,y) - \big (r+\delta (\uplambda (t))\big )yG(t,y) + \frac{1}{2}\Vert \gamma + \sigma ^{-1}\uplambda (t)\Vert ^2 y^2 G_{yy}(t,y). \end{aligned}$$

Note that ${\mathcal {H}}^{\uplambda }(t,y)\ge 0$ for any $\uplambda \in {\mathcal {D}}$ and ${\mathcal {H}}^{\uplambda }(t,y)= 0$ if $\uplambda (t) = \uplambda ^{*}(t,y)$.

Let now $\uplambda \in {\mathcal {D}}$ with $\Vert \uplambda (t) - \uplambda ^{*}(t)\Vert \le 1 \ {\mathcal {L}}[0,T]\otimes \mathbbm {Q}$-a.s., be arbitrary but fixed. Due to Lemma 5.3, we can assume that $C>0$ from the polynomial growth condition was chosen large enough such that

$$\begin{aligned} \max \big (\Vert \gamma _{\uplambda }(t)\Vert ^2, \delta (\uplambda ^{*}(t)),\delta (\uplambda (t))\big ) \le C \quad {\mathcal {L}}[0,T]\otimes \mathbbm {Q}\text {-a.s..} \end{aligned}$$

Finally, for any $p >0$, we define the stopping times

$$\begin{aligned} {\bar{\tau }}_p&= \inf \big \{ S \in [t,T] \ \big | \int _t^S \big (G_y(s,y{\tilde{Z}}_{\uplambda }(t,s))y{\tilde{Z}}_{\uplambda }(t,s)\Vert \gamma _{\uplambda }(s)\Vert \big )^2ds \ge p \big \} \\ \tau _p&= \min \big ({\bar{\tau }}_p, T\big ) \end{aligned}$$

This choice of $\tau _p$ ensures that

$$\begin{aligned} \mathbbm {E}\big [\int _t^{\tau _p}G_y(s,y{\tilde{Z}}_{\uplambda }(t,s))y{\tilde{Z}}_{\uplambda }(t,s)\gamma _{\uplambda }(s)'dW(s)|{\mathcal {F}}_t\big ] = 0. \end{aligned}$$

Therefore,

$$\begin{aligned}&\mathbbm {E}[G(\tau _p,y{\tilde{Z}}_{\uplambda }(t,\tau _p))|{\mathcal {F}}_t] \nonumber \\&\quad \overset{\text {It}\hat{\text {o}}}{=} \ G(t,y) + \mathbbm {E}\big [ \int _t^{\tau _p}\underbrace{{\mathcal {H}}^{\uplambda }(s,y{\tilde{Z}}_{\uplambda }(t,s))}_{\ge 0}ds|{\mathcal {F}}_t\big ] \nonumber \\&\quad + \underbrace{\mathbbm {E}\big [\int _t^{\tau _p}G_y(s,y{\tilde{Z}}_{\uplambda }(t,s))y{\tilde{Z}}_{\uplambda }(t,s)\gamma _{\uplambda }(s)'dW(s)|{\mathcal {F}}_t\big ]}_{=0} \nonumber \\&\quad \ge G(t,y) \end{aligned}$$

(7.1)

Clearly, $\tau _p \rightarrow T$, for $p\rightarrow \infty$ and hence $G(\tau _p,y{\tilde{Z}}_{\uplambda }(t,\tau _p)) \rightarrow G(T,y{\tilde{Z}}_{\uplambda }(t,T)) = U^{*}(y{\tilde{Z}}_{\uplambda }(t,T),B_1,B_2)$ for $p \rightarrow \infty$.

Inequality (7.1) holds with equality for $\uplambda = \uplambda ^{*}$. Further, the polynomial growth condition for G gives us a dominating random variable for $G(\tau _p, y{\tilde{Z}}_{\uplambda }(t,\tau _p))$:

$$\begin{aligned} |G(\tau _p, y{\tilde{Z}}_{\uplambda }(t,\tau _p)|&\le C | (y{\tilde{Z}}_{\uplambda }(t,\tau _p))^{-\alpha } + (y{\tilde{Z}}_{\uplambda }(t,\tau _p))^{\alpha }| \\&\le C \Big ( \underbrace{\underset{t\le s \le T}{\sup }\big ((y{\tilde{Z}}_{\uplambda }(t,s))^{-\alpha }}_{=: X^{-}}\big ) +\underbrace{\underset{t\le s \le T}{\sup }\big ((y{\tilde{Z}}_{\uplambda }(t,s))^{\alpha }\big )}_{=: X^{+}}\Big ). \end{aligned}$$

As $\uplambda$ and the remaining market coefficients are bounded, we can use Novikov’s condition and Doob’s martingale inequality to show that $X^{-}$ and $X^{+}$ have finite expectation. This allows us to apply the dominated convergence Theorem to conclude the proof:

$$\begin{aligned} G(t,y)&= \mathbbm {E}[G(t,y)|{\mathcal {F}}_t]\overset{ (7.1)}{\le } \lim _{p\rightarrow \infty } \mathbbm {E}[G(\tau _p,y{\tilde{Z}}_{\uplambda }(t,\tau _p))|{\mathcal {F}}_t] \\&{\mathop {\underset{\text {convergence}}{=}}\limits ^{\text {dominated}}} \mathbbm {E}[\lim _{p \rightarrow \infty }\big (G(\tau _p,y{\tilde{Z}}_{\uplambda }(t,\tau _p))\big )|{\mathcal {F}}_t] = \mathbbm {E}[G(T,y{\tilde{Z}}_{\uplambda }(t,T))|{\mathcal {F}}_t] \\&= \mathbbm {E}[U^{*}(y{\tilde{Z}}_{\uplambda }(t,T),B_1,B_2)|{\mathcal {F}}_t], \end{aligned}$$

with equality if $\uplambda = \uplambda ^{*}$. $\square$

Proof of Lemma 5.7

Note that for any given constant $\beta >0$, we have

$$\begin{aligned} \beta z^2 + \frac{1}{\beta } \ge |z| \quad \forall z \in \mathbbm {R}. \end{aligned}$$

(7.2)

For $z\in \mathbbm {R}$, define $f(z):= U^{*}\big (\exp \big (\frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}}z\big ),B_1,B_2\big )$. Then f satisfies the prerequisites of Lemma 5.6, since for any $z\in \mathbbm {R}$ and any $\beta >0$

$$\begin{aligned} |f(z)|&= |U^{*}\big (\exp \big (\frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}}z\big ),B_1,B_2\big )|\overset{ (5.6)}{\le } C(e^{-\alpha \frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}} z}+e^{\alpha \frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}} z})\\&\le 2C e^{\alpha \frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}}|z|} \overset{ (7.2)}{\le }2C e^{\alpha \frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}}(\beta z^2 + \frac{1}{\beta })}. \end{aligned}$$

Choosing $\beta$ small enough such that $\alpha \frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}} \beta < \frac{1}{4T}$ guarantees that F, as in (5.5), defines a $C^{(1,2)}((0,T]\times \mathbbm {R})$-function, which satisfies the heat equation $F_{\tau }(\tau ,z) = F_{zz}(\tau ,z)$ for all $(\tau ,z)\in (0,\infty )\times \mathbbm {R}$ with initial condition $F(0,z) = f(z)$. We substitute

$$\begin{aligned} t:=T-\tau \quad \text {and} \quad z:= \frac{\sqrt{2}}{\Vert \gamma _{\uplambda ^{*}}\Vert }\big ( \log (y)-(r+\frac{1}{2}\Vert \gamma _{\uplambda ^{*}}\Vert ^2)(T-t)\big ) \end{aligned}$$

and define $G\in C^{(1,2)}([0,T)\times (0,\infty ))$ as

$$\begin{aligned} G(t, y):=&F(\tau ,z) = F\Big (T-t, \frac{\sqrt{2}}{\Vert \gamma _{\uplambda ^{*}}\Vert }\big ( \log (y)-(r+\frac{1}{2}\Vert \gamma _{\uplambda ^{*}}\Vert ^2)(T-t)\big )\Big ) \\ =&\frac{1}{\sqrt{4\pi (T-t)}}\int _{\mathbbm {R}}e^{-\frac{x^2}{4(T-t)}}U^{*}\big (ye^{-(r+\frac{1}{2}\Vert \gamma _{\uplambda ^{*}}\Vert ^2)(T-t)-\frac{\Vert \gamma _{\uplambda ^{*}}\Vert }{\sqrt{2}}x},B_1,B_2\big )dx. \\ \end{aligned}$$

As $U^{*}(y,B_1,B_2)$ is convex and strictly decreasing on $(0,\infty )$, G is convex and strictly decreasing in y. Further, by expressing the derivatives of G in terms of derivatives of Q, one can easily show that G satisfies the HJB PDE (5.3). Moreover, by using the fact that G is defined as an integral of $U^{*}(\cdot ,B_1,B_2)$ weighted by a Gaussian density over $\mathbbm {R}$ and $U^{*}(\cdot ,B_1,B_2)$ satisfies (5.6), one can easily show that G satisfies the polynomial growth condition (5.7) with ${\tilde{C}}:=C e^{\alpha |r+\frac{1}{2}\Vert \gamma _{\uplambda ^{*}}\Vert ^2|T + \frac{1}{2}\alpha ^2 \Vert \gamma _{\uplambda ^{*}} \Vert ^2T}$. $\square$

Proof of Lemma 5.13

${\hat{U}}$ is defined as the smallest concave function larger than

$$\begin{aligned} f(x) := \big ( U(B_1) + h_{-}(x-B_1) \big )\mathbbm {1}_{[0,B_1)}(x) + U(x)\mathbbm {1}_{[B_1,B_2]}(x) + U(B_2)\mathbbm {1}_{(B_2,\infty )}(x). \end{aligned}$$

This corresponds to ${\hat{U}}$ being the concave envelope (as in Reichlin (2013)) of f. Then, as $f\in {\mathcal {U}}(B_1,B_2)$ and f(x) is constant for $x\ge B_2$ , Lemma 2.8 from Reichlin (2013) implies:

• (i) ${\hat{U}}\in {\mathcal {U}}^{\text {conc}}(B_1,B_2)$

• (ii) $\{x>0 \ | \ f(x) < {\hat{U}}(x)\}= \bigcup _{n\in \mathbbm {N}}I_n$, for a collection of bounded, disjoint and open intervals $\big (I_n\big )_{n\in \mathbbm {N}}.$

• (iii) ${\hat{U}}$ is locally affine on $I_n$ for each $n\in \mathbbm {N}$.

Due to (ii) and (iii), the supremum in the definition of ${\hat{U}}^{*}(y,B_1,B_2)$ can only be attained by $x^{*}\in I_n$ if $x^{*}\in \{B_1,B_2\}$ or ${\hat{U}}(x)-yx$ is constant for all $x\in I_n$. However, in the latter case, as $\hat{{\mathcal {I}}}(y,B_1,B_2)$, is defined as an infimum, $I_n$ is open and as ${\hat{U}}\in {\mathcal {U}}^{conc}(B_1,B_2)$ (hence ${\hat{U}}$ is continuous), $\hat{{\mathcal {I}}}(y,B_1,B_2)$ will not take values in $I_n$. Thus, in both cases

$$\begin{aligned}&\hat{{\mathcal {I}}}(y,B_1,B_2) \notin \{x>0 \ | \ f(x) < {\hat{U}}(x)\} \quad \forall y>0 \\ \Rightarrow \quad&{\hat{U}}(\hat{{\mathcal {I}}}(y,B_1,B_2)) = f(\hat{{\mathcal {I}}}(y,B_1,B_2)) \quad \forall y>0. \end{aligned}$$

However, as ${\hat{U}}(x)\ge f(x) = U(x)$ for $x\in [B_1,B_2]$, (5.8) and (5.9) follow. Since ${\hat{U}}\in {\mathcal {U}}^{conc}(B_1,B_2)$, the maximizer $\hat{{\mathcal {I}}}(y,B_1,B_2)$ is decreasing and has at most countably infinite points of discontinuity. By (5.8) the maximizer ${\mathcal {I}}(y,B_1,B_2)$ has the same properties. $\square$

Proof of Example 5.17

$U\in {\mathcal {U}}(B_1,B_2)$, as $U_1,U_2 \in {\mathcal {U}}^{\text {conc}}(0,\infty )$ are strictly increasing. Hence, by virtue of Corollary 5.16 and Theorem 4.6, the optimal terminal wealth for $\mathbf {(P)}$ is given by $D^{*}= {\mathcal {I}}(y{\tilde{Z}}_{\uplambda ^{*}}(T),B_1,B_2)$. Our task is now to compute ${\mathcal {I}}(\cdot , B_1, B_2)$ in the cases (i)-(iii).

Case (i): $B_1 < B_2 \le \theta$: In this case $U(x) = -U_1(\theta -x)$ is convex and increasing on $[B_1,B_2]$. Therefore, its concavification on $[B_1,B_2]$ is given by

$$\begin{aligned} {\hat{U}}(x) = U(B_1) + \frac{U(B_2)-U(B_1)}{B_2-B_1}(x-B_1), \quad \text {for }x\in [B_1,B_2]. \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2) = \hat{{\mathcal {I}}}(y,B_1,B_2)= {\left\{ \begin{array}{ll} B_1, \quad &{} \text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}\le y\\ B_2, \quad &{} \text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}> y \end{array}\right. }. \end{aligned}$$

Case (ii): $\theta \le B_1 < B_2$: In this case $U(x) = U_2(x-\theta )$ is concave and increasing on $[B_1,B_2]$. Therefore, U(x) is equal to its concavification ${\hat{U}}(x)$ on $[B_1,B_2]$, for $x\in [B_1,B_2]$. Hence, for any given $y>0$ its capped LFT can be expressed as

$$\begin{aligned} U^{*}(y,B_1, B_2)&= \underset{B_1\le x \le B_2}{\sup } \big ( U(x) -yx \big )= \underset{B_1\le x \le B_2}{\sup } \big ( U_2(x-\theta ) -yx \big ) \\&\overset{z= x-\theta }{=}\underset{B_1-\theta \le z \le B_2 - \theta }{\sup } \big ( U_2(z) -yz \big )-y\theta \\&=U_2({\mathcal {I}}_2(y,B_1 -\theta , B_2 - \theta )) -y ({\mathcal {I}}_2(y,B_1 -\theta , B_2 - \theta ) + \theta ) \\&= U({\mathcal {I}}_2(y,B_1 -\theta , B_2 - \theta ) + \theta )-y({\mathcal {I}}_2(y,B_1 -\theta , B_2 - \theta )+\theta ) \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2) = {\mathcal {I}}_2(y,B_1 -\theta , B_2 - \theta ) + \theta \end{aligned}$$

Case (iii): $B_1< \theta < B_2$: Define the set M as

$$\begin{aligned} M = \big \{ x \ge \theta | \ \forall z \in [B_1, x]: U(z) \le U(B_1) + \frac{U(x)-U(B_1)}{x-B_1}(z-B_1)\big \}. \end{aligned}$$

Then $\theta \in M$, since U is convex on $[B_1,B_2]$ and $h = \sup M< \infty$, as $\lim _{x\rightarrow \infty }\frac{U(x)}{x}=0$. Due to the concavity of U on $[\theta , \infty )$ one can alternatively write M as $M = [\theta , h]$.

(iii).a: $B_2 \le h$: In this case, the concavification of U on $[B_1,B_2]$ is given by

$$\begin{aligned} {\hat{U}}(x) = U(B_1) + \frac{U(B_2)-U(B_1)}{B_2-B_1}(x-B_1), \quad \text {for }x\in [B_1,B_2]. \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2) = \hat{{\mathcal {I}}}(y,B_1,B_2)= {\left\{ \begin{array}{ll} B_1, \quad &{} \text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}\le y\\ B_2, \quad &{} \text {if } \ \frac{U(B_2)-U(B_1)}{B_2-B_1}> y \end{array}\right. }. \end{aligned}$$

(iii).b: $B_2 > h$: In this case, the concavification of U on $[B_1,B_2]$ is given by

$$\begin{aligned} {\hat{U}}(x) = {\left\{ \begin{array}{ll} U(B_1) + \frac{U(h)-U(B_1)}{h-B_1}(x-B_1), \quad &{}\text {if} \ B_1 \le x \le h \\ U(x), \quad &{}\text {if} \ h \le x \le B_2 \end{array}\right. }. \end{aligned}$$

Therefore,

$$\begin{aligned} {\mathcal {I}}(y,B_1,B_2)=\hat{{\mathcal {I}}}(y,B_1,B_2) = {\left\{ \begin{array}{ll} B_1, \quad &{}\text {if }\frac{U(h)-U(B_1)}{h-B_1}\le y\\ {\mathcal {I}}_2(y,h -\theta , B_2 - \theta ) + \theta &{}\text {if }\frac{U(h)-U(B_1)}{h-B_1}> y\\ \end{array}\right. }. \end{aligned}$$

$\square$