Abstract
We discuss the estimation of a change-point \(t_0\) at which the parameter of a (non-stationary) AR(1)-process possibly changes in a gradual way. Making use of the observations \(X_1,\ldots ,X_n\), we shall study the least squares estimator \(\widehat{t}_0\) for \(t_0\), which is obtained by minimizing the sum of squares of residuals with respect to the given parameters. As a first result it can be shown that, under certain regularity and moment assumptions, \(\widehat{t}_0/n\) is a consistent estimator for \(\tau _0\), where \(t_0 =\lfloor n\tau _0\rfloor \), with \(0<\tau _0<1\), i.e., \(\widehat{t}_0/n \,{\mathop {\rightarrow }\limits ^{P}}\,\tau _0\) \((n\rightarrow \infty )\). Based on the rates obtained in the proof of the consistency result, a first, but rough, convergence rate statement can immediately be given. Under somewhat stronger assumptions, a precise rate can be derived via the asymptotic normality of our estimator. Some results from a small simulation study are included to give an idea of the finite sample behaviour of the proposed estimator.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and statistical framework
In this work we study the estimation of a change-point at which the parameter of a (non-stationary) AR(1)-process possibly changes in a gradual way. More precisely, we observe a time series \(X_1,\ldots ,X_n\) possessing the structure
where \(\{e_t\}_{t=0,1,\ldots }\) is a sequence of independent, identically distributed (i.i.d.) random variables with \(Ee_0=0\), \(0<Ee_0^2=\sigma ^2\), \(Ee_0^4<\infty \), \(\beta _0\), \(\beta _1\) are unknown parameters satisfying
and \(g(\cdot ,t_0)=g_n(\cdot ,t_0)\) is a (known) real function such that
(see more detailed assumptions below). That is, we assume that the parameter \(\beta _0\) of the (stationary) AR(1)-process changes gradually at an unknown time-point \(t_0=t_{0,n} =\lfloor n\tau _0\rfloor \), with \(0<\tau _0<1\), \(\lfloor \,\cdot \,\rfloor \) denoting the integer part, and our aim is to provide an estimator for \(t_0\) making use of the observations \(X_1,\ldots ,X_n\) and under certain assumptions on the function \(g_n(\cdot ,t_0)\) to be specified below.
Remark 1
-
(a)
As in earlier works, we only study the case of a gradual change under “local alternatives” here, i.e., under \(\beta _{1,n}\rightarrow 0\), but \(\beta _{1,n}\sqrt{n}\rightarrow \infty \) as \(n\rightarrow \infty \) (cf., e.g., Dümbgen (1991), Jarušková (1998a), Hušková (1998a), Hušková (2001), or Hušková and Steinebach (2002)).
-
(b)
In case of the gradual change function \(g_n\) being unknown, it would be sufficient to have an estimating function \(\widehat{g}_n\) (say), which approximates \(g_n\) at a certain rate. For a more detailed discussion we refer to Remarks 5 and 7 below.
Note that, if \(g(\cdot ,t_0)\) is a bounded function, then
for sufficiently large n and, by a repeated application of (1.1),
Before we turn to formulating our main results, we give a brief account of related works, particularly concerning the detection of gradual changes in various dependent data sets. Most of the earlier papers on the change analysis in autoregressive processes deal with abrupt changes, either in the mean or in the autoregressive parameters, respectively in the variance of the error process. Picard (1985) proposed a procedure for testing changes in the covariance structure of an AR(p)-process based on a likelihood ratio approach and obtained the asymptotic distribution of the likelihood estimators of the change parameters. Gaussian-type likelihood ratio procedures for testing abrupt changes in autoregressive models were studied in Davis et al. (1995), where also the limit distribution of the test statistic was established. Gombay (2008) used efficient score vectors to develop statistics that are able to test changes in any of the parameters of a Gaussian AR(p)-model separately, or in any collection of them, and she also studied large sample properties of the change-point estimator.
Other results were based on partial sums of residual processes, see, e.g., Horváth (1993) for testing or Bai (1994) for proving consistency of the change-point estimator. Hušková et al. (2007) used an approach based on partial sums of weighted residuals and obtained asymptotic distributions for various max-type test statistics together with proving the consistency of the change-point estimator in an AR(p)-model. Moreover, bootstrap versions of the proposed tests were studied in Hušková et al. (2008).
A quasi-maximum likelihood method was used in Bai (2000) to analyze vector autoregressive models (VAR) possessing multiple structural changes. The approach developed in Davis et al. (1995) has been extended to VAR models by Dvořák (2015), who dealt with asymptotic tests for an abrupt change in the autoregressive parameters and the variance structure under various assumptions on the correlations of the errors. Kirch et al. (2015) extended the class of max-type change-point statistics considered in Hušková et al. (2007) to the VAR case and epidemic change alternatives and developed a new approach taking possible misspecification of the model into account.
Slama and Saggou (2017) considered a Bayesian analysis of a possible change in the parameters of an AR(p)-model and developed a test, which can detect a change in any of the parameters separately. Moreover, the posterior density of the change-point is given by using a Gibbs sampler. Many references on the change-point analysis in time series can also be found in a survey paper by Aue and Horváth (2013).
Concerning gradual changes in autoregression, Salazar (1982) studied a model similar to (1.1) from a Bayesian point of view. Under the assumption of normality of the error process and with some joint prior distribution of the change-point \(t_0\) and other parameters under consideration, he obtained a joint posterior distribution from which the marginal distribution of the change-point could be obtained via numerical integration. A similar, though not identical problem was solved by Venkatesan and Arumugam (2007), who considered an AR(p)-model with a gradual switch in the parameters over a finite interval. Here again, computation of the posterior distribution of the change-point requires the use of numerical integration.
He et al. (2008) derived a parameter constancy test in a stationary vector autoregressive model against the hypothesis that the parameters of the model change smoothly over time. Though model (1.1) could be considered a special case of the model studied in He et al. (2008), the authors treat other type of smooth functions and do not consider any estimator of the breaking point.
Our approach below is motivated by the previous work by Hušková, see, e.g., Hušková (1998a, 1998b, 1999, 2001), Jarušková (1998a, 1998b, 1999, 2001, 2002, 2003), or by Hušková and Steinebach (2000), Hušková and Steinebach (2002), respectively by Albin and Jarušková (2003). In the above cited papers a gradual-type change in the mean of a location model is considered and asymptotic tests for detecting the change together with limit properties of the estimator of the change-point are developed for various types of smoothly changing parameters. More specifically, the mentioned model can be written in the form
where \(\mu , \delta _n, t_0\) are unknown parameters, \(\epsilon _1,\ldots , \epsilon _n\) are i.i.d. errors, with zero mean and finite moments of order \(2+\Delta \), \(\Delta > 0\), and the function g satisfies the assumption
together with other assumptions specified for the formulated problems.
Döring and Jensen (2015), and also Döring (2015a, 2015b), extended the methodology proposed by Hušková (1999) to regression models with independently distributed random regressors. Wang (2007) studied the same location model as Hušková (1999) with errors that exhibit long memory dependence, and Slabý (2001) considered a test based on ranks. Hlávka and Hušková (2017), motivated by gender differences observed in a real data set, proposed a two-sample gradual change test that leads to more precise results than the application of a procedure based on the standard two-sample t-test. Račkauskas and Tamulis (2013) studied epidemic changes in a location model, in which the transition between regimes is gradual.
Several authors studied smooth changes in other contexts. For example, Aue and Steinebach (2002) discuss an extension of Hušková’s (1999) approach to certain statistical models, which cover more general classes of stochastic processes satisfying an invariance principle (see also Kirch and Steinebach (2006), Steinebach (2000), Steinebach and Timmermann (2011) or Timmermann (2014), Timmermann (2015)).
Vogt and Dette (2015) developed a nonparametric method to estimate a smooth change-point in a locally stationary framework and established the rate of convergence of the change-point estimator. Their procedure allows to deal with a wide variety of stochastic characteristics including the mean, covariances and higher moments.
Hoffmann et al. (2018) and Hoffmann and Dette (2019) discuss statistical inference for the detection and the localization of gradual changes in the jump characteristic of a discretely observed Itô semimartingale.
Quessy (2019) proposed a general class of consistent test statistics for the detection of gradual changes in copulas and developed their large-sample properties.
Now, let us turn to our problem. We shall study the least squares estimator \({\widehat{t}}_0\) for \(t_0\), which is obtained by minimizing
with respect to (w.r.t.) \(b_0,b_1\in \mathbb {R}\), \(t_*=0,1,\ldots ,\lfloor n(1-\delta )\rfloor \), \(\delta >0\) arbitrarily small, i.e.,
Remark 2
The technical condition \(t_*\le \lfloor n(1-\delta )\rfloor \), with \(\delta >0\) fixed, could be weakened to allow for \(\delta =\delta _n\rightarrow 0\) \((n\rightarrow \infty )\) at a certain rate, which, however, would depend on the parameter \(\beta _1 =\beta _{1,n}\) from (1.2) and the function \(g=g_n\) from (1.3) as well. Since \(\beta _{1,n}\) is unknown, one should choose \(\delta >0\) fixed, but small, for practical use.
Via partial derivatives, it is not difficult to show that, for fixed \(t_*\),
On plugging this into (1.7), we obtain
Since the first term in (1.10) does not depend on \(t_*\), a combination of (1.7)–(1.10) eventually results in
Remark 3
Note that
can be used as a test statistic for testing “no change” versus “there is a change”, even if the true function g is unknown, just some integral has to be nonzero (see, e.g., Hušková and Steinebach (2002)). In practice, before starting to estimate \(t_0=\lfloor n\tau _0\rfloor \), one should first carry out such a test for the existence of a change-point \(\tau _0\), with \(0<\tau _0<1\).
For our theoretical studies of \({\widehat{t}}_0\) below, it will be convenient to make use of the model equation (1.1) and rewrite (1.11), after a multiplication with 1/n, as
For later asymptotics it may also be convenient to express \(\widehat{t}_0\) as
where
The paper is organized as follows. Based on the required assumptions, which are collected first, Sect. 2 presents the main results of our work. As a first statement it can be shown in Theorem 1 that \(\widehat{t}_0/n\) is a consistent estimator for \(\tau _0\), where \(t_0 =\lfloor n\tau _0\rfloor \), with \(0<\tau _0<1\), i.e., \(\widehat{t}_0/n \,{\mathop {\rightarrow }\limits ^{P}}\,\tau _0\) \((n\rightarrow \infty )\). Based on the rates obtained in the proof of Theorem 1, a rough convergence rate estimate can immediately be given (see Theorem 2). Under somewhat stronger assumptions, a precise rate can then be derived in Theorem 3 by showing that our estimator has an asymptotically normal limit distribution. In Sect. 3, some results from a small simulation study are included to give an idea of the finite sample behaviour of the proposed estimator. Section 4 collects some auxiliary results which are used in the proofs of the main theorems. The latter are finally given in Sect. 5.
2 Assumptions and main results
For our asymptotic results we assume the gradual change function \(g(\cdot ,t_*)\) to satisfy the following assumptions:
-
(A.1)
For every \(t_*=0,1,\ldots ,n-1\), the function \(g(\cdot ,t_*)\) is of the form
$$\begin{aligned} g(t,t_*)= g_0\Big (\frac{t-t_*}{n}\Big ),\qquad t=0,1,\ldots ,n, \end{aligned}$$where \(g_0:(-\infty ,1]\rightarrow \mathbb {R}\) is a real function satisfying:
-
(A.2)
It holds that
$$\begin{aligned} g_0(x)= 0\qquad (x\le 0)\qquad \text {and}\qquad g_0(x)> 0\qquad (0<x\le 1). \end{aligned}$$ -
(A.3)
The function \(g_0:(-\infty ,1]\rightarrow \mathbb {R}\) is bounded and Lipschitz continuous, i.e.
$$\begin{aligned} |g_0(x)|\le D_1\qquad \text {and}\qquad |g_0(x)-g_0(y)|\le D_2|x-y|,\qquad x,y\le 1, \end{aligned}$$with some positive constants \(D_1\) and \(D_2\).
-
(A.4)
It holds that
$$\begin{aligned}&|g_0(x)-g_0(y)-(x-y) g_0'(y)| \le D_3|x-y|^{1+\Delta },\quad 0<x,y<1,\\&|g_0(x)-x g'_{0+}(0)| \le D_3|x|^{1+\Delta },\quad 0\le x<1 ,\\&\Big (\int _0^{1}{\widetilde{g}}_0(x-\tau _0) \,{\widetilde{g}}_0'(x-\tau _0) dx\Big )^2 < \int _0^{1}{\widetilde{g}}_0^2(x-\tau _0) dx \int _0^{1}{\widetilde{g}}_0^{\prime 2}(x-\tau _0) dx,\\&\text {with}\quad {\widetilde{g}}_0 (x) = g_0 (x)- \int _0^{1}g_0(y-\tau _0)dy, \end{aligned}$$where \(g'_{0+}(0) \) denotes the right derivative at 0, \( g_0'(\cdot )\) denotes the derivative, assumed to be bounded and Riemann integrable, \(1/2<\Delta \le 1\), and \(D_3\) is a positive constant.
Remark 4
-
(a)
The case of a negative change, i.e., \(g_0(x)<0\) for \(0<x\le 1\), can be reduced to the positive one by just reparametrizing \({\bar{\beta }}_1:=-\beta _1\) and \({\bar{g}}_0(\cdot )=-g_0(\cdot )\).
-
(b)
The function \(g_0\), for example, could be such that \(g_0(x)=\pm \,x_+^\kappa \) \((x\le 1)\), where \(x_+\) denotes the positive part of x and \(\kappa \ge 1\) is a fixed exponent.
In our first result it will be shown that \({\widehat{t}}_0/n\) is a consistent estimator for \(\tau _0\), where \(t_0=\lfloor n\tau _0\rfloor \), with \(0<\tau _0<1\), i.e., \({\widehat{t}}_0/n\,{\mathop {\rightarrow }\limits ^{P}}\,\tau _0\) \((n\rightarrow \infty )\).
Theorem 1
Let Assumptions (A.1)–(A.3) be satisfied. Then, under the model (1.1) and the corresponding conditions formulated above, the estimator \({\widehat{t}}_0\) from (1.11) is consistent, i.e.,
Remark 5
In case of an unknown change function g, it will be obvious from the proof of Theorem 1 that (2.1) still holds, if g in (1.11) is replaced by an estimator \(\widehat{g}_n\) at a rate \(o_P(\beta _1)\), more precisely, if there is an estimating function \(\widehat{g}_0=\widehat{g}_{0,n}\) such that, as \(n\rightarrow \infty \),
In this case, \(\widehat{g}_n(t,t_*)=\widehat{g}_0((t-t_*)/n)\) can be used in (1.11) resp. (1.13) instead of \(g(t,t_*)=g_0((t-t_*)/n)\) and, in view of the rate \(o_P(\beta _1)\), the convergence in (2.1) will be retained.
If, for example, \(g_0(x)=x_+^\kappa \), with some \(\kappa \ge 1\), it would be sufficient to have an estimator \(\widehat{\kappa }_n\) such that \(|\widehat{\kappa }_n-\kappa |=o_P(\beta _1)\), e.g., \(|\widehat{\kappa }_n-\kappa |=O_P(1/\sqrt{n})\) as \(n\rightarrow \infty \). Such estimates have been obtained in other settings (cf., e.g., Döring and Jensen (2015) for a regression model). In our time series setting, it is an open question and has to be left for future research.
Another possible model to deal with would be the case \(\beta _1 g_0(x)=\beta _1 x_+ +\beta _2 x_+^2\), with unknown parameters \(\beta _1,\beta _2\). Here, least squares estimation means to minimize
w.r.t. \(b_0,b_1,b_2\in \mathbb {R}\), \(t_*=0,1,\ldots ,\lfloor n(1-\delta )\rfloor \), \(\delta >0\), and then to modify the corresponding steps in the proofs. For the sake of conciseness, this may also be left for further investigations.
The proofs of Theorem 1 and Remark 5 are postponed to Sect. 5.
Remark 6
It would also be quite straightforward to get a consistent estimator of \(\beta _1\), i.e., \({\widehat{b}}_1({\widehat{t}}_0)\), together with some limiting properties. For the sake of conciseness, we want to omit details here.
Also, if the function \(g(\cdot )\) is only known up to a multiplicative constant, then the resulting estimator is still consistent, but the limit distribution below, however, would depend on this multiplicative constant, which is unknown.
On checking the proof of Theorem 1 more carefully, a rough rate of consistency for our estimator \(\widehat{t}_0\) can be obtained as follows.
Theorem 2
Under the conditions of Theorem 1, assume that the limit function \(f(\tau _*)\) in (5.4) is twice continuously differentiable in a small neighbourhood of \(\tau _0\), with \(f''(\tau _*) >D\) for some \(D>0\). Then, with \(\widehat{t}_0=\lfloor n\widehat{\tau }_0\rfloor \), for every sequence \(\{\varepsilon _n\}\) with \(\varepsilon _n \rightarrow 0\),
Remark 7
If (2.2) in Remark 5 is replaced by
the approximation rate \(O_P\big (|\beta _1|^{1/2}\big )+o_P\big (1/(|\beta _1|^{1/2}\,\varepsilon _n\,n^{1/4})\big )\) in Theorem 2 can be retained.
The proofs of Theorem 2 and Remark 7 are also postponed to Sect. 5.
Remark 8
If, for example, \(\beta _1=n^{-\alpha }\), with \(0<\alpha < 1/2\), then \(\varepsilon _n\) could be chosen as \((\log n)^{-p}\), with \(p>0\), so that one would have the polynomial consistency rate
Next it will be shown that the estimator \({\widehat{t}}_0\) of \(t_0\) (or equivalently \({\widehat{\tau }}_0\) of \(\tau _0\)) has an asymptotically normal limit distribution.
Theorem 3
Let Assumptions (A.1)–(A.4) be satisfied. Then, as \(n\rightarrow \infty \),
or, in a standardized form,
equivalently
where
Remark 9
Note that the limit distribution in Theorem 3 does not depend on \(\sigma ^2.\)
3 Some simulations
In this section, before we turn to the proofs of Theorems 1–3, we first present some results from a small simulation study. We simulated observations of the time series (1.1) with the function \(g_0(x) = x_+\), \(x\le 1\), for various combinations of \(\beta _0\) and \(\beta _1\) and for various change-points \(t_0\). The errors \(e_t\) were considered to be i.i.d. with a standard normal distribution. The first 50 simulated values were deleted to start computations with stationary observations \(X_t\) for \(t=1, \ldots , t_0.\) We simulated either \(n=500\), 1000 or 5000 observations of (1.1). For each realization of \(\{X_t, t=1,\ldots , n\}\), we estimated the change-point \({\widehat{t}}_0 \) according to (1.11) with the given function \(g_0\) and for \(t_*\) running from 0 to \(\lfloor n(1-\delta )\rfloor \), where \(\delta > 0\) denotes the proportion of observations, which were excluded. For each combination we used 10 000 simulation runs.
The change-point was chosen to be either \(t_0 =n/4\), n/2 or 3/4n, \(\tau _0 = t_0/n\), and \(\delta = 0.05\). The parameters \(\beta _0\) and \(\beta _1\) should satisfy the asymptotic relation (1.2), i.e., \(|\beta _0| <1, \beta _1 \rightarrow 0\), and \(|\beta _1|\sqrt{n} \rightarrow \infty \) as \(n\rightarrow \infty \). For \(\beta _1\) we used small multiples of \(1/\sqrt{\log \log n}\) such that the asymptotic condition (1.2) and also the condition \(|\beta _0 + \beta _1 g_0((t-t_0)/n)| <1\) for \(t=1,\ldots , \lfloor n(1-\delta )\rfloor \) were satisfied. Though in fact \(\beta _1 \) depends on n, we used the same value always for all considered sample sizes n, to make the presentation of the results more transparent.
In Tables 1, 2, 3, 4, the estimator \({\widehat{\tau }}_0\) computed as \({\widehat{\tau }}_0 = {\widehat{t}}_0/n\), the 90% confidence interval for \(\tau _0\) computed from the Monte Carlo percentiles of \(\sqrt{n}({\widehat{\tau }}_0 -\tau _0)\), and estimators of \(\beta _0, \beta _1\) computed from (1.8) and (1.9) with \(t_{*} = {\widehat{t}}_0\) are presented. The empirical standard deviations of the corresponding point estimators are given in parentheses.
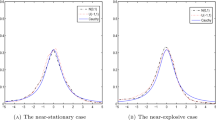
It can be seen that the point estimators of \(\tau _0\) (or \(t_0\), respectively) and of \(\beta _0\) are systematically slightly underestimated, but otherwise behave quite well for all considered variants. The estimators of \(\beta _1\) are more volatile, but they converge to the true value with growing number of observations. To study the behaviour of the estimator of the change-point in finite samples, we also displayed histograms and Q-Q plots of the standardized statistic in (2.8). Some results are presented in Figs. 1, 2, 3, 4, 5, 6. The simulations show that the behaviour of the estimator \({\widehat{t}}_0\) depends both on the size of the sample and on the parameters \(\beta _0\) and \(\beta _1.\) The assumption \(|\beta _0 + \beta _1 g_0((t-t_0)/n)| <1\) guarantees the stability of the time series (1.1) even after the local change, expressed by the time varying part of the autoregressive coefficient. Due to the local character of the change the convergence to the normal distribution is slow and it can only be expected for sufficiently large samples. In Figs. 1, 2, 3, 4, 5, 6 convergence to normality is demonstrated for respective sample sizes \(n=500\) (left panels) and \(n=5000\) (right panels). The role of the parameter \(\beta _1\), which represents the rate of the change of the autoregressive coefficient, can be seen on comparing Figs. 3 and 4. In Fig. 3, the value of \(\beta _0 + \beta _1 g_0((t-t_0)/n)\) changes from 0 to 0.9, while in Fig. 4 it varies from 0.5 to 0.9 for the same values of \(t=t_0 + 1,\ldots , n\). The gradual change in the first case is much faster than in the second one, where the change is slow and the increments to the autoregressive coefficient are very small. In this case, the graph of the function on the right-hand side of () can be very flat and its global maximum can be incorrectly detected or it is detected either very soon or very late. This explains the large values of the side column in the histogram and the large skewness of the test statistic, especially in the left part of Fig. 4. Also the position of \(t_0\), and thus the length of the stationary part of the time series under consideration, plays a role. In general, we observe better results, when the change occurs in the middle of the observed time intervals. For smaller sample sizes the kurtosis of the standardized statistics is larger and the finite sample distribution has heavier tails than the normal distribution, but it improves with growing sample size.
4 Some auxiliary results
In this section, we collect a series of auxiliary results, which are used in the proofs of our Theorems 1–3. In the sequel, C denotes a generic positive constant, independent of \(t,t_*\) and n, which may vary from case to case.
Lemma 1
Under the assumptions of Theorem 1, as \(n\rightarrow \infty \),
Proof
-
(a)
In view of (1.5) and the independence and moment assumptions on \(\{e_t\}\),
$$\begin{aligned} EX_{t-1}^2=\sigma ^2 \sum _{j=0}^{t-1} c_j^2\quad \text {with}\quad c_0=1,~ c_j=\prod _{i=0}^{j-1}\big (\beta _0+\beta _1g(t-1-i,t_0)\big ),~j=1,\ldots ,t-1. \end{aligned}$$Now, according to (1.2), for sufficiently large n,
$$\begin{aligned}&\big (\beta _0+\beta _1g(t-1-i,t_0)\big )^2\\&\quad =\beta _0^2+\beta _1\big (2\beta _0 g(t-1-i,t_0)+\beta _1 g^2(t-1-i,t_0)\big ) \le \beta _0^2+|\beta _1|\,C=: q_1, \end{aligned}$$where \(0\le q_1<1\). So, \(c_j^2\le q_1^j\) and
$$\begin{aligned} EX_{t-1}^2\le \sigma ^2 \frac{1-q_1^{t}}{1-q_1}\le \sigma ^2 \frac{1}{1-q_1}=O(1). \end{aligned}$$Again due to the moment and independence assumptions on \(\{e_t\}\), a similar estimation yields
$$\begin{aligned} EX_{t-1}^4 =E e_0^4\, \sum _{j=0}^{t-1} c_j^4+3\sigma ^4\,\sum _{j\ne k} c_j^2 c_k^2 \le E e_0^4\, \sum _{j=0}^{t-1} c_j^4+3\sigma ^4\,\Big (\sum _{j=0}^{t-1} c_j^2\Big )^2=O(1), \end{aligned}$$which proves (4.1).
-
(b)
Moreover, since \(\beta _1\rightarrow 0\) as \(n\rightarrow \infty \),
$$\begin{aligned}&EX_{t-1}^2-\frac{\sigma ^2}{1-\beta _0^2}\le \sigma ^2\Big (\frac{1}{1-\beta _0^2-|\beta _1|\,C}-\frac{1}{1-\beta _0^2}\Big )\\&\quad =\sigma ^2\frac{|\beta _1|\,C}{(1-\beta _0^2-|\beta _1|\,C)(1-\beta _0^2)}\le C|\beta _1|. \end{aligned}$$Analogously,
$$\begin{aligned} EX_{t-1}^2\ge \sigma ^2 \frac{1-q_2^{t}}{1-q_2}, \end{aligned}$$with \(0\le q_2:=\beta _0^2-|\beta _1|\,C<1\), and, as \(n\rightarrow \infty \),
$$\begin{aligned} EX_{t-1}^2-\frac{\sigma ^2}{1-\beta _0^2}\ge \sigma ^2\Big (\frac{1}{1-\beta _0^2+|\beta _1|\,C}-\frac{1}{1-\beta _0^2}\Big ) -\sigma ^2\frac{q_2^{t}}{1-q_2}\ge -C\big (|\beta _1|+q_2^{t}\big ). \end{aligned}$$Hence,
$$\begin{aligned} \Big |EX_{t-1}^2- \frac{\sigma ^2}{1-\beta _0^2}\Big |\le C\big (|\beta _1|+q_2^{t}\big ), \end{aligned}$$(4.4)which suffices to prove (4.2), since \(\sum _{t=1}^nq_2^{t}\le C\) and \(\beta _1\gg 1/n\) as \(n\rightarrow \infty \).
-
(c)
In view of (4.4) and the assumptions on \(\beta _1\) and g, as \(n\rightarrow \infty \),
$$\begin{aligned}&\Big |\frac{1}{n} \sum _{t=1}^ng(t,t_0)EX_{t-1}^2- \frac{\sigma ^2}{1-\beta _0^2}\int _0^1 g_0(x-\tau _0)dx\Big |\\&\le ~ \frac{1}{n} \sum _{t=1}^n\Big |g(t,t_0)\Big | \Big |EX_{t-1}^2- \frac{\sigma ^2}{1-\beta _0^2}\Big | +\frac{\sigma ^2}{1-\beta _0^2}\Big |\frac{1}{n} \sum _{t=1}^ng(t,t_0)- \int _0^1 g_0(x-\tau _0)dx\Big |\\&\le ~ C\Big (|\beta _1| +\frac{1}{n}\sum _{t=1}^nq_2^t +\sum _{t=1}^n\int _{\frac{t-1}{n}}^{\frac{t}{n}}\Big |g_0\Big (\frac{t-t_0}{n}\Big ) -g_0(x-\tau _0)\Big |dx\Big )\\&\le ~ C\Big (|\beta _1| +\frac{1}{n} +\sum _{t=1}^n\int _{\frac{t-1}{n}}^{\frac{t}{n}}\Big |\frac{t}{n} -x-\frac{t_0}{n}+\tau _0\Big |dx\Big ) \le C\Big (|\beta _1| +\frac{1}{n}\Big )=O\big (|\beta _1|\big ), \end{aligned}$$which completes the proof. \(\square \)
Lemma 2
Under the assumptions of Theorem 1, as \(n\rightarrow \infty \), with \(t_*=\lfloor n\tau _*\rfloor \),
and
Proof
The proof of (4.5) – (4.7) is similar to that of (4.3), so that details can be omitted. Note that the functions \(g_0(\cdot -\tau _0)g_0(\cdot -\tau _*)\), \(g_0(\cdot -\tau _*)\) and \(g_0^2(\cdot -\tau _*)\) are also bounded and Lipschitz continuous, uniformly in \(0\le \tau _*\le 1\).\(\square \)
Remark 10
It is obvious from the proofs of Lemmas 1 and 2 that, if the function \(g_0\) is just continuous (instead of Lipschitz continuous), assertions (4.3)–(4.7) still hold true with \(t_*=\lfloor n\tau _*\rfloor \), \(\tau _*\in [0,1]\) fixed (instead of \(\max _{t_*}\)), but with \(O\big (|\beta _1|\big )\) being replaced by o(1).
Lemma 3
Under the assumptions of Theorem 1, as \(n\rightarrow \infty \), with \(t_*=\lfloor n\tau _*\rfloor \),
and
Proof
-
(a)
Let \({{\mathcal {F}}}_{j-1}\) denote the \(\sigma \)-field generated by \(e_0,\ldots ,e_{j-1}\). Then, in view of our assumptions on \(\{e_t\}\) and (4.2), as \(n\rightarrow \infty \),
$$\begin{aligned}&E\Bigg (\sum _{j=1}^ne_j X_{j-1}\Bigg )^2 = \sum _{j=1}^nE\big (e_j^2 X_{j-1}^2\big ) +2\sum _{i<j} E\big (e_i X_{i-1} e_j X_{j-1}\big )\\&\qquad = \sum _{j=1}^nE\big (E\big [e_j^2 X_{j-1}^2\big |{{\mathcal {F}}}_{j-1}\big ]\big ) +2\sum _{i<j} E\big (E\big [e_i X_{i-1} e_j X_{j-1}|{{\mathcal {F}}}_{j-1}\big ]\big ) = \sigma ^2\sum _{j=1}^nEX_{j-1}^2 =O(n), \end{aligned}$$which suffices to prove (4.8).
-
(b)
Via similar arguments, along the lines of proof of (4.3), as \(n\rightarrow \infty \),
$$\begin{aligned} E\Big (\sum _{t=1}^ne_t X_{t-1}g(t,t_*)\Big )^2=\sigma ^2 \sum _{t=1}^ng^2(t,t_*)EX_{t-1}^2=O(n), \end{aligned}$$which proves (4.9).
-
(c)
Consider, with \(t_*=\lfloor n\tau _*\rfloor \), the sequence of stochastic processes \(\{X_n(\cdot )\}_{n=1,2,\ldots }\) in D[0, 1], where
$$\begin{aligned} X_n(\tau _*)=\frac{\varepsilon _n}{\sqrt{n}}~\sum _{t=1}^ne_t X_{t-1}g(t,t_*),\quad 0\le \tau _*\le 1. \end{aligned}$$In view of (4.9), the finite-dimensional distributions of \(X_n\) tend to 0. Moreover, for \(0\le \tau _1\le \tau _*\le \tau _2\le 1\),
$$\begin{aligned} E|X_n(\tau _*)-X_n(\tau _1)||X_n(\tau _2)-X_n(\tau _*)| \le \big (E|X_n(\tau _*)-X_n(\tau _1)|^2\big )^{1/2} \big (E|X_n(\tau _2)-X_n(\tau _*)|^2\big )^{1/2}, \end{aligned}$$and, according to our assumptions on g, with \(t_1=\lfloor n\tau _1\rfloor \),
$$\begin{aligned} E|X_n(\tau _*)-X_n(\tau _1)|^2&= \,\sigma ^2\,\frac{\varepsilon _n^2}{n}\,\sum _{t=1}^n|g(t,t_*)-g(t,t_1)|^2 EX_{t-1}^2\\&\le \,C\,\varepsilon _n^2\,\Big |\frac{t_*-t_1}{n}\Big |^2\le \,C\,\varepsilon _n^2\,|\tau _2-\tau _1|^2. \end{aligned}$$Analogously, with \(t_2=\lfloor n\tau _2\rfloor \),
$$\begin{aligned} E|X_n(\tau _2)-X_n(\tau _*)|^2 \le \,C\,\varepsilon _n^2\,\Big |\frac{t_2-t_*}{n}\Big |^2\le \,C\,\varepsilon _n^2\,|\tau _2-\tau _1|^2, \end{aligned}$$so that
$$\begin{aligned} E|X_n(\tau _*)-X_n(\tau _1)||X_n(\tau _2)-X_n(\tau _*)| \le \,C\,\varepsilon _n^2\,|\tau _2-\tau _1|^2. \end{aligned}$$In view of Billingsley (1968), Theorem 15.6, this proves that
$$\begin{aligned} X_n \,{\mathop {\longrightarrow }\limits ^{\mathcal {D}[0,1]}}\,0\qquad \text {as}\qquad n\rightarrow \infty , \end{aligned}$$which suffices for the proof of (4.10).
\(\square \)
Lemma 4
Under the assumptions of Theorem 1, as \(n\rightarrow \infty \), with \(t_*=\lfloor n\tau _*\rfloor \),
and, for every sequence \(\{\varepsilon _n\}_{n=1,2,\ldots }\) with \(\varepsilon _n\rightarrow 0\),
Proof
We only give a proof of (4.13) and (4.16) here. The other assertions can be shown in a similar manner.
-
(a)
In view of (1.5),
$$\begin{aligned}&\sum _{t=1}^ng(t,t_*)X_{t-1}^2= \sum _{t=1}^ng(t,t_*)\Big (e_{t-1} +\sum _{j=1}^{t-1}e_{t-1-j}\prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )\Big )^2 \nonumber \\&\quad = \sum _{t=1}^ng(t,t_*)e_{t-1}^2 +\sum _{t=1}^ng(t,t_*)\sum _{j=1}^{t-1}e_{t-1-j}^2\prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )^2 \nonumber \\&\qquad + 2 \sum _{t=1}^ng(t,t_*)e_{t-1} \sum _{j=1}^{t-1}e_{t-1-j}\prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big ) \nonumber \\&\qquad + 2 \sum _{t=1}^ng(t,t_*)\sum _{j_1<j_2}e_{t-1-j_1}e_{t-1-j_2}\prod _{i_1=1}^{j_1-1}\big (\beta _0+\beta _1 g(t-1-i_1,t_0)\big )\nonumber \\&\qquad \times \prod _{i_2=1}^{j_2-1}\big (\beta _0+\beta _1 g(t-1-i_2,t_0)\big ) \nonumber \\&\quad =: S_1 +S_2 +2S_3 +2 S_4. \end{aligned}$$(4.18)Since g is bounded and \(\{e_t\}\) is an i.i.d. sequence,
$$\begin{aligned} E(S_1-ES_1)^2 =\sum _{t=1}^ng^2(t,t_*)E\big (e_t^2-Ee_t^2\big )^2 \le C\,n. \end{aligned}$$(4.19)Next, with \(v^2:=Var(e_0^2)\) and b as in (1.4), due to the independence of \(e_{t_1-1-j}^2\) and \(e_{t_2-1-k}^2\), if \(t_1-1-j\ne t_2-1-k\), i.e., if \(k\ne j+t_2-t_1\), for sufficiently large n,
$$\begin{aligned}&E(S_2-ES_2)^2 =E\Big (\sum _{t=1}^ng(t,t_*)\sum _{j=1}^{t-1}\big (e_{t-1-j}^2-Ee_{t-1-j}^2\big ) \prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )^2\Big )^2 \nonumber \\&= v^2 \sum _{t=1}^ng^2(t,t_*)\sum _{j=1}^{t-1}\prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )^4 \nonumber \\&\quad +2 v^2 \sum _{t_1<t_2}g(t_1,t_*)g(t_2,t_*)\sum _{j=1}^{t_1-1} \prod _{i_1=1}^{j-1} \big (\beta _0+\beta _1 g(t_1-1-i_1,t_0)\big )^2 \prod _{i_2=1}^{j-1+t_2-t_1}\big (\beta _0+\beta _1 g(t_2-1-i_2,t_0)\big )^2 \nonumber \\&\le C\,\Big (\sum _{t=1}^ng^2(t,t_*)\sum _{j=1}^{t-1}b^{4(j-1)}+ \sum _{t_2=2}^n g(t_2,t_*) \sum _{t_1=1}^{t_2-1} g(t_1,t_*) \sum _{j=1}^{t_1-1} b^{4(j-1)+2(t_2-t_1)}\Big )\le C\,n. \end{aligned}$$(4.20)Similarly, since \(ES_3=0\),
$$\begin{aligned}&E(S_3-ES_3)^2 =E\Big (\sum _{t=1}^ng(t,t_*)e_{t-1} \sum _{j=1}^{t-1}e_{t-1-j} \prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )^2\Big )^2 \nonumber \\ \qquad&= \sigma ^2 \sum _{t=1}^ng^2(t,t_*)E\Big (\sum _{j=1}^{t-1}e_{t-1-j} \prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )^2\Big )^2 \nonumber \\ \qquad&= \sigma ^4 \sum _{t=1}^ng^2(t,t_*)\sum _{j=1}^{t-1}\prod _{i=1}^{j-1}\big (\beta _0+\beta _1 g(t-1-i,t_0)\big )^4 \,\le C\,\sum _{t=1}^ng^2(t,t_*)\sum _{j=1}^{t-1}b^{4(j-1)} \le C\,n. \end{aligned}$$(4.21)Finally, via a corresponding estimation,
$$\begin{aligned}&E(S_4-ES_4)^2 \nonumber \\&=\sum _{t=1}^ng^2(t,t_*)E\Big (\sum _{j_1<j_2}e_{t-1-j_1}e_{t-1-j_2}\prod _{i_1=1}^{j_1-1}\big (\beta _0+\beta _1 g(t-1-i_1,t_0)\big ) \prod _{i_2=1}^{j_2-1}\big (\beta _0+\beta _1 g(t-1-i_2,t_0)\big )\Big )^2 \nonumber \\&\le C\sum _{t=1}^ng^2(t,t_*)\le C\,n. \end{aligned}$$(4.22)On combining (4.18)–(4.22), we see that
$$\begin{aligned} E\Bigg (\sum _{t=1}^ng(t,t_*)\big (X_{t-1}^2-EX_{t-1}^2\big )\Bigg )^2 \le C\,n, \end{aligned}$$which suffices to prove (4.13).
-
b)
The proof of (4.16) can be given analogously to that of (4.10) in Lemma 3. Consider, with \(t_*=\lfloor n\tau _*\rfloor \), the sequence of stochastic processes \(\{\widetilde{X}_n(\cdot )\}_{n=1,2,\ldots }\) in D[0, 1], where
$$\begin{aligned} \widetilde{X}_n(\tau _*)=\frac{\varepsilon _n}{\sqrt{n}}~\sum _{t=1}^ng(t,t_*)\big (X_{t-1}^2-EX_{t-1}^2\big ),\quad 0\le \tau _*\le 1. \end{aligned}$$In view of (4.13), the finite-dimensional distributions of \(\widetilde{X}_n\) tend to 0. Moreover, for \(0\le \tau _1\le \tau _*\le \tau _1\le 1\), by just replacing \(g(t,t_*)\) in the estimations (4.18)-(4.22) by \(g(t,t_*)-g(t,t_1)\) and taking the Lipschitz continuity of \(g_0\) into account,
$$\begin{aligned} E\big (\widetilde{X}_n(\tau _*)-\widetilde{X}_n(\tau _1)\big )^2 \le \,C\,\frac{\varepsilon _n^2}{n}\,\sum _{t=1}^n|g(t,t_*)-g(t,t_1)|^2 \le \,C\,\varepsilon _n^2\,|\tau _2-\tau _1|^2. \end{aligned}$$Analogously,
$$\begin{aligned} E\big (\widetilde{X}_n(\tau _2)-\widetilde{X}_n(\tau _*)\big )^2 \le \,C\,\varepsilon _n^2\,|\tau _2-\tau _1|^2, \end{aligned}$$and, via the Cauchy-Schwarz inequality,
$$\begin{aligned} E\big |\widetilde{X}_n(\tau _*)-\widetilde{X}_n(\tau _1)\big |\big |\widetilde{X}_n(\tau _2)-\widetilde{X}_n(\tau _*)\big | \le \,C\,\varepsilon _n^2\,|\tau _2-\tau _1|^2. \end{aligned}$$In view of Billingsley (1968), Theorem 15.6, this proves that
$$\begin{aligned} \widetilde{X}_n \,{\mathop {\longrightarrow }\limits ^{\mathcal {D}[0,1]}}\,0\qquad \text {as}\qquad n\rightarrow \infty , \end{aligned}$$which suffices for the proof of (4.16).
\(\square \)
The following two lemmas from real analysis will also be used in the proof of Theorem 1.
Lemma 5
Let \(\{b_n\}_{n=1,2,\ldots }\) be a real sequence such that \(b_n\rightarrow \infty \) as \(n\rightarrow \infty \). Then there is a sequence \(\{\varepsilon _n\}_{n=1,2,\ldots }\) of positive reals, with \(\varepsilon _n\rightarrow 0\), such that still \(\varepsilon _n b_n\rightarrow \infty \) as \(n\rightarrow \infty \).
Proof
For n sufficiently large, there exists an integer \(k_n\) such that \(2^{k_n}\le b_n <2^{k_n+1}\). Obviously, \(k_n\rightarrow \infty \) as \(n\rightarrow \infty \), so that a choice of \(\varepsilon _n =1/k_n\) completes the proof.
\(\square \)
Lemma 6
Let f be a continuous real function on a compact set K and \(x_0\) be a unique maximizer of f, i.e., \(x_0 = \mathrm{arg\,max}_x f(x)\). Furthermore assume that \(\lim _{n\rightarrow \infty }\max _{x\in K} |f_n(x)-f(x)|=0\) and let \(\widehat{x}_n =\mathrm{arg\,max}_x f_n(x)\) be a maximizer of \(f_n\) (not necessarily unique). Then,
Proof
Suppose \(\widehat{x}_n \nrightarrow x_0\) as \(n\rightarrow \infty \). Since K is compact, there exists a subsequence \(\{\widehat{x}_{k_n}\}\) and an \(x_1\ne x_0\) such that \(\widehat{x}_{k_n}\rightarrow x_1\), hence
because of the continuity of f. Since \(x_0\) is the unique maximizer of f, it holds \(f(x_1) < f(x_0)\) implying that
This, however, contradicts our assumptions, since
so that the proof is complete.\(\square \)
Next, we need some extensions of Lemmas 1–4. Particularly, we study properties of the following quantities for \(|t_0-t_*|\le b_n\), with \(b_n\rightarrow \infty ,~b_n/n \rightarrow 0\):
We start with an extension of Lemma 3.
Lemma 7
Let the assumptions of Theorem 3 be satisfied and let \(t_*\) be such that \(|t_*-t_0|\le r_n\,\sqrt{n} \,|\beta _1|^{-1}\), with
Then, for \(j=0,1,2\), \(L_j(t_0,t_*)\) has an asymptotically normal limit distribution, with zero mean and variance \( \sigma _j^2\), where
Moreover, as \(n\rightarrow \infty \),
for some \(c_n\rightarrow 0\) and any \(t_{*} \) such that \(|t_0-t_{*}|\le b_n,\, b_n\rightarrow \infty ,\, b_n/n\rightarrow 0\).
Proof
We focus on \(L_0(t_0,t_*)\). The desired results for \(L_1(t_0, t_*)\) and \(L_2(t_0, t_*)\) can be derived in the same way, the obtained expressions are just somewhat more complex, but can be omitted.
Note that, for fixed \(t_*\) and \(t_0\), \(L_j (t_0, t_*),\, j=0,1,2\), are sums of martingale difference arrays. Hence to obtain their limit properties, we can apply Theorem 24.3 in Davidson (1994), p. 383, which means for \(L_0(t_0,t_*)\) to verify validity of the conditions
We make repeated use of assumption (A.4), particularly
Consider first the denominator in (4.25). Direct calculations give
By Assumption (A.4) and using the same arguments as in the proofs of Lemmas 2 and 4 , we get
as \(n\rightarrow \infty \), and combining all these results we have
For the numerator in (4.25) we have
The first term on the r.h.s. is the sum of martingale difference arrays, with zero mean and variance
which follows from the finiteness of \(E e_t^4,\) Assumption (A.3) and the uniform boundedness of \(EX_{t-1}^4\) (cf. (4.1)). Thus,
Next, proceeding in the same way as in the proofs of Lemmas 1 and 4, we get
and combining (4.28), (4.29) and (4.27) we obtain (4.25).
To verify (4.26) note that, due to (4.27), it suffices to prove
For this we have, using similar arguments as above,
and we can conclude that the asymptotic normality of \(L_0 (t_0, t_*)\) holds for fixed \(t_*\).
Next we show (4.24) for \(j=0\). We proceed as in the proof of Lemma 3, part c). Toward this we study for \(t_0<t_*<t_{**}\) and \(|t_0-t_*|+ |t_*-t_{**}|\le b_n\), satisfying \(b_n\rightarrow \infty ,\, b_n/n\rightarrow 0\), the quantity
for some \(C>0\). By Assumption (A.4)
which gives
since \(|t_0-t_*|\vee |t_*-t_{**}|\le |t_0-t_{**}|\) and \(\Delta \le 1\).
In view of \(2\Delta >1\) by Assumption (A.4), assertion (4.24) can now be finished by again making use of Billingsley (1968), Theorem 15.6, as in the proof of Lemma 3, part c). \(\square \)
The next lemma is an extension of Lemma 4.
Lemma 8
Under the assumptions of Theorem 3 we have
Moreover, as \(n\rightarrow \infty \),
for some \(c_n\rightarrow 0\) and any \(|t_{*}-t_0| \le b_n \), with \(b_n\rightarrow \infty ,~b_n/n\rightarrow 0\).
Proof
Note that
We have
The latter sum on the r.h.s has only \(|t_0-t_*|\le 2 b_n\) summands, with \(b_n\rightarrow \infty ,~b_n/n\rightarrow 0\), and the terms \( \big (g(j,t_0)-g(j,t_*)\big )\big / \big ((t_*-t_0)/n\big )\) are bounded in j, thus the respective terms are not influential. By (A.4),
where the last relation follows from (4.1) and (4.11). Proceeding as in the proofs of Lemmas 1 and 2, we get
and hence
The result for \( L_{42}(t_*,t_0)\) is obtained in the same way and thus the assertion on \(L_{4}(t_*,t_0)\) follows.
The proof for \( L_{3}(t_*,t_0)\) follows the same lines and can therefore be omitted.
To prove (4.32) we proceed as in the proof of (4.24). To avoid too many technicalities we study only
where
Now
As in the proof of Lemma 4 and utilizing Assumption (A.4),
where we also used arguments from the proof of Lemma 7. Finally,
On combining all these estimates, we can conclude that (4.32) holds true.\(\square \)
By Theorem 1 and since \( Q(t_0)\) (defined below) does not depend on \(t_*\), the estimator \({\widehat{t}}_0\) has the same limit distribution as
for some \( b_n\rightarrow \infty ,~b_n/n\rightarrow 0\), and
We need to study the properties of \(Q_j(t_*)- Q_j(t_0),~j=1,2,3\), separately. This is formulated in the next three Propositions.
Proposition 1
Under the Assumptions (A.1)– (A.4) we get
Proof
Direct but long calculations give
Using the assertions in Lemma 1, 2, 4 and the calculations in Lemma 8, we get after some steps, uniformly in \(|t_*-t_0)|\le b_n\),
which suffices for the proof.\(\square \)
Proposition 2
Under Assumptions (A.1)–(A.4) we get
where \(r_n\) satisfies (4.23) and
Moreover, the limit distribution of \(\frac{1}{\sqrt{n}}\sum _{t=1}^ne_t X_{t-1} {\widetilde{h}}_n(t,t_*,t_0)\) is normal \(\mathcal N\big (0,\frac{\sigma ^4}{1-\beta _0^2} {\widetilde{H}}\big )\) for each \(|t_*-t_0|\le r_n|\beta _1|^{-1} \sqrt{n}\), which follows from Lemma 7.
Proof
Direct calculations give
On applying Lemmas 1–3 and 7 to the above sums, we get that the first term on the r.h.s. is influential, while the latter one is negligible. So, both assertions follow from here. \(\square \)
Proposition 3
Under Assumptions (A.1)–(A.4) we get
where \( r_n\) satisfies (4.23).
Proof
Direct calculations give
uniformly for \(|t_*-t_0|\le b_n\), where the last relation is implied by a combination of Lemmas 7 and 8. Then both assertions follow immediately.\(\square \)
5 Proofs of the main theorems
Now we are ready to turn to the proofs of Theorems 1–3. We first prove the consistency of our least squares estimator \(\widehat{t}_0\).
Proof of Theorem 1
In view of (1.13), we consider, for \(t_*=0,1,\ldots ,\lfloor n(1-\delta )\rfloor \),
where
In view of Lemma 5 and the assumptions on \(\beta _1\), there exists a sequence \(\{\varepsilon _n\}\) of positive reals such that \(\varepsilon _n\rightarrow 0\), but \(|\beta _1|\,\varepsilon _n\sqrt{n}\rightarrow \infty \) as \(n\rightarrow \infty \). Then, on combining Lemmas 1–4, as \(n\rightarrow \infty \),
and, with \(t_*=\lfloor n\tau _*\rfloor \), for every fixed \(\tau _*\in [0,1-\delta ]\),
as a consequence of (5.1)–(5.3) in combination with the approximations obtained in Lemmas 1–4.
Note that the denominator in f is bounded away from 0 on \([0,1-\delta ]\), with \(0<\delta <1\), since, via Jensen’s inequality, first for \(\tau _* \in [\tilde{\delta },1-\delta ]\), with \(0<\tilde{\delta }<1-\delta \),
Secondly, since \(\int _0^1 g_0^2(x)dx-\big (\int _0^1 g_0(x)dx\big )^2 >0\) and the denominator in f is continuous in \(\tau _*\), also
for \(\tau _* \in [0,\tilde{\delta })\), with some \(\tilde{\delta }>0\).
So, (5.5) and (5.6) prove the positivity on \([0,1-\delta ]\) and, in view of Lemmas 1–4, the latter positivity also implies that the convergence in (5.4) is uniform on \([0,1-\delta ]\), i.e.
We finally show that the limit function f has a unique maximum at \(\tau _*=\tau _0\). First, via the Cauchy-Schwarz inequality,
Hence
and the bound is attained for \(\tau _* =\tau _0\).
It remains to prove that \(\tau _0\) is the unique maximizer of f. To do so, we show that strict inequality holds in (5.8), if \(\tau _*\ne \tau _0\). Assume equality. Then, there is a \(\lambda \ne 0\) such that, for almost every \(x\in [0,1]\),
This, however, is impossible, since, e.g., for \(\tau _* >\tau _0\),
Similarly, for \(\tau _*<\tau _0\),
which proves that \(\tau _0\) is the unique maximizer of f.
Via the subsequence principle for convergence in probability, the proof of Theorem 1 can now be completed from (5.7) by applying Lemma 6. \(\square \)
Proof of Remark 5
In case of an unknown change function g, it is obvious from the proof of Theorem 1 that, under (2.2), \(g(t,t_*)=g_0((t-t_*)/n)\) in (1.11) resp. (1.13) can be replaced by \(\widehat{g}_n(t,t_*)=\widehat{g}_0((t-t_*)/n)\). The reason is that, in view of (5.1)–(5.3) and the rate \(o_P(\beta _1)\), the convergence in (5.4) still holds with estimated \(g(t,t_*)\)’s, so that the proof can be completed as before.
If \(g_0(x)=x_+^\kappa \), with some \(\kappa \ge 1\), and \(|\widehat{\kappa }_n-\kappa |=o_P(\beta _1)\) as \(n\rightarrow \infty \) for an estimator \(\widehat{\kappa }_n\), note that on \(\{\widehat{\kappa }_n>\kappa _1\}\), with \(0<\kappa _1<\kappa \), by the mean-value theorem, for some \({\bar{\kappa }}_n\) between \(\widehat{\kappa }_n\) and \(\kappa \),
In view of \(|\log x||x^{\kappa _1}|\rightarrow 0\) as \(x\downarrow 0\), \(|\log x||x^{\kappa _1}|\) is bounded on (0, 1], which suffices to prove that
since the \(\max \) is attained for \(x>0\) and \(P(\widehat{\kappa }_n>\kappa _1)\rightarrow 1\) as \(n\rightarrow \infty \). \(\square \)
Proof of Theorem 2
In view of the consistency obtained in Theorem 1, it suffices to concentrate on a small neighbourhood \([\tau _1,\tau _2]\) of \(\tau _0\). With the notations in (5.4), we have
where \(\tau _n\) is between \(\widehat{\tau }_0\) and \(\tau _0\).
Since \(f'(\tau _0)=0\) and \(|f''(\tau _n)|\ge C\), for some \(C>0\), this results in the estimate
Now, on checking the steps in the proof of Theorem 1 more carefully, one can show that
Note that, in view of Lemmas 2–4, the uniform rate of approximation for the denominator of \(f_n\) in (5.4) by that of f is \(O_P(|\beta _1|)+o_P(1/(\varepsilon _n\sqrt{n}))\), whereas the one for the numerator is \(O_P(|\beta _1|)+o_P(1/(|\beta _1|\,\varepsilon _n\sqrt{n}))\). This, together with the positivity of the denominator of f on \([\tau _1,\tau _2]\), results in (5.9) after some elementary calculation, which completes the proof. \(\square \)
Proof of Remark 7
Under (2.4), the approximation rate \(O_P\big (|\beta _1|\big )+o_P\big (1/(|\beta _1|\,\varepsilon _n\sqrt{n})\big )\) in (5.9) still holds, since only an additional rate \(O_P\big (1/\sqrt{n}\big )\) would have to be added in the denominator of \(f_n\) and \(O_P\big (1/(|\beta _1|\sqrt{n})\big )\) in the numerator, which are negligible compared to the other terms. \(\square \)
Proof of Theorem 3
The proof follows the usual lines of proofs of the limit behavior of estimators under a gradual change (see, e.g., Hušková (1998b) or Jarušková (1998a)). Therefore we will focus on the main steps only. \(\square \)
Gathering the assertions in Propositions 1 –3 and Theorem 1, we can conclude that \({\widehat{t}}_0\) has the same asymptotic distribution as
By Lemma 7, particularly by (4.24), its limit behavior does not change if \({\widetilde{h}}_n(t,t_*,t_0)\) is replaced by \({\widetilde{h}}_n(t,t_{**},t_0)\), with any fixed \(t_{**}\) such that \(|t_{**}-t_0|\le r_n\sqrt{n} \,|\beta _1|^{-1}\). Also, by Lemma 7,
has an asymptotic normal distribution with zero mean and variance
Thus it suffices to study the estimator
The boundary can only be a attained with probability tending to 0, since \(Z_n=O_P(1)\), and, on plugging the upper bound into the above expression, one gets
Using the assumption on \(r_n\) (see (4.23)) together with \(Z_n=O_P(1)\), it is now straightforward to check that this estimator satisfies
From here and the asymptotic normality of \(Z_n\) it can be concluded that the assertion of Theorem 3 holds true. \(\square \)
References
Albin JMP, Jarušková D (2003) On a test statistic for linear trend. Extremes 6:247–258
Aue A, Horváth L (2013) Structural breaks in time series. J Time Ser Anal 34:1–16
Aue A, Steinebach J (2002) A note on estimating the change-point of a gradually changing stochastic process. Stat Probab Lett 56:177–191
Bai J (1994) Least squares estimation of a shift in linear processes. J Time Ser Anal 15:453–472
Bai J (2000) Vector autoregressive models with structural changes in regression coefficients and in variance-covariance matrices. Ann Econom Finance 1:303–339
Billingsley P (1968) Convergence of probability measures. Wiley, New York
Davidson D (1994) Stochastic limit theory. Oxford University Press, Oxford
Davis RA, Huang D, Yao YC (1995) Testing for a change in the parameter value and order of an autoregressive model. Ann Stat 23:282–304
Döring M (2015a) Asymmetric cusp estimation in regression models. Statistics 49:1279–1297
Döring M (2015b) Rate of convergence of a change point estimator in a misspecified regression model. In: A. Steland, E. Rafajłowicz, K. Szajowski (eds.) Stochastic Models, Statistics and Their Applications (Wrocław, 2015), Springer Proc. Math. Statist., vol. 122, pp. 49–55. Springer, Cham
Döring M, Jensen U (2015) Smooth change point estimation in regression models with random design. Ann Inst Stat Math 67:595–619
Dümbgen L (1991) The asymptotic behavior of some nonparametric change-point estimators. Ann Stat 19:1471–1495
Dvořák M (2015) Stability in Autoregressive Time Series Models. Ph.D. thesis, Charles University, Prague
Gombay E (2008) Change detection in autoregressive time series. J Multiv Anal 99:451–464
He C, Teräsvirta T, González A (2008) Testing parameter constancy in stationary vector autoregressive models against continuous change. Econom Rev 28:225–245
Hlávka Z, Hušková M (2017) Two-sample gradual change analysis. Revstat 15:355–372
Hoffmann M, Dette H (2019) On detecting changes in the jumps of arbitrary size of a time-continuous stochastic process. Electr J Stat 13:3654–3709
Hoffmann M, Vetter M, Dette H (2018) Nonparametric inference of gradual changes in the jump behaviour of time-continuous processes. Stoch Process Appl 128:3679–3723
Horváth L (1993) Change in autoregressive processes. Stoch Process Appl 44:221–242
Hušková M (1998a) Estimators in the location model with gradual changes. Comment Math Univ Carolin 39:147–157
Hušková M (1998b) Remarks on test procedures for gradual changes. In: Szyszkowicz B (ed) Asymptotic methods in probability and statistics (Ottawa, 1997). North-Holland, Amsterdam, pp. 577–583
Hušková M (1999) Gradual changes versus abrupt changes. J Statist Plann Infer 76:109–125
Hušková M (2001) A note on estimators of gradual changes. In: M. de Gunst, C. Klaassen, A. van der Vaart (eds.) State of the Art in Probability and Statistics (Leiden, 1999), IMS Lecture Notes Monogr. Ser., vol. 36, pp. 345–358. Institute of Mathematical Statistics, Beachwood, OH
Hušková M, Kirch C, Prášková Z, Steinebach J (2008) On the detection of changes in autoregressive time series. II. Resampling procedures. J Stat Plann Infer 138:1697–1721
Hušková M, Prášková Z, Steinebach J (2007) On the detection of changes in autoregressive time series. I. Asymptotics. J Stat Plann Infer 137:1243–1259
Hušková M, Steinebach J (2000) Limit theorems for a class of tests of gradual changes. J Stat Plann Infer 89:57–77
Hušková M, Steinebach J (2002) Asymptotic tests for gradual changes. Stat Decis 20:137–151
Jarušková D (1998a) Change-point estimator in gradually changing sequences. Comment Math Univ Carolin 39:551–561
Jarušková D (1998b) Testing appearance of linear trend. J Stat Plann Infer 70:263–276
Jarušková D (1999) Testing appearance of polynomial trend. Extremes 2:25–37
Jarušková D (2001) Change-point estimator in continuous quadratic regression. Comment Math Univ Carolin 42:741–752
Jarušková D (2002) Change in polynomial regression and related processes. Theory Stoch Process 8:162–168
Jarušková D (2003) Asymptotic distribution of a statistic testing a change in simple linear regression with equidistant design. Stat Probab Lett 64:89–95
Kirch C, Muhsal B, Ombao H (2015) Detection of changes in multivariate time series with application to EEG data. J Am Stat Assoc 110:1197–1216
Kirch C, Steinebach J (2006) Permutation principles for the change analysis of stochastic processes under strong invariance. J Comput Appl Math 186:64–88
Picard D (1985) Testing and estimating change-points in time series. Adv Appl Probab 17:841–867
Quessy JF (2019) Consistent nonparametric tests for detecting gradual changes in the marginals and the copula of multivariate time series. Stat Papers 60:717–746
Račkauskas A, Tamulis A (2013) Modeling of gradual epidemic changes. Liet Mat Rink, Proc Lith Math Soc, Ser A 54:55–60
Salazar D (1982) Structural changes in time series models. J Econom 19:147–163
Slabý A (2001) Limit theorems for rank statistics detecting gradual changes. Comment Math Univ Carolin 42:591–600
Slama A, Saggou H (2017) A Bayesian analysis of a change in the parameters of autoregressive time series. Comm Stat Simul Comput 46:7008–7021
Steinebach J (2000) Some remarks on the testing of smooth changes in the linear drift of a stochastic process. Theory Probab Math Stat 61:173–185
Steinebach J, Timmermann H (2011) Sequential testing of gradual changes in the drift of a stochastic process. J Stat Plann Infer 141:2682–2699
Timmermann H (2014) Monitoring Procedures for Detecting Gradual Changes. Ph.D. thesis, University of Cologne
Timmermann H (2015) Sequential detection of gradual changes in the location of a general stochastic process. Stat Probab Lett 99:85–93
Venkatesan D, Arumugam P (2007) Bayesian analysis of structural changes in autoregressive models. Am J Math Manag Sci 27:153–162
Vogt M, Dette H (2015) Detecting gradual changes in locally stationary processes. Ann Stat 43:713–740
Wang L (2007) Gradual changes in long memory processes with applications. Statistics 41:221–240
Acknowledgements
The authors thank two anonymous referees for their constructive suggestions, which led to improve the presentation of their results. They also gratefully acknowledge support by the grants GAČR 18-08888S (M. Hušková) and GX19-28231X (Z. Prášková) of the Czech Science Foundation and by the partnership program of Charles University in Prague with the University of Cologne.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hušková, M., Prášková, Z. & Steinebach, J.G. Estimating a gradual parameter change in an AR(1)-process. Metrika 85, 771–808 (2022). https://doi.org/10.1007/s00184-021-00844-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00184-021-00844-z