Axiomatic characterizations of the core without consistency

Abstract

A TU game is totally positive if it is a linear combination of unanimity games with nonnegative coefficients. We show that the core on each cone of convex games that contains the set of totally positive games is characterized by the traditional properties Pareto efficiency, additivity (ADD), individual rationality, and the null-player property together with one new property, called unanimity requiring that the solution, when applied to a unanimity game on an arbitrary coalition, allows to distribute the entire available amount of money to each player of this coalition. We also show that the foregoing characterization can be generalized to the domain of balanced games by replacing ADD by “ADD on the set of totally positive games plus super-additivity (SUPA) in general”. Adding converse SUPA allows to characterize the core on arbitrary domains of TU games that contain the set of all totally positive games. Converse SUPA requires a vector to be a member of the solution to a game whenever, when adding a totally positive game such that the sum becomes totally additive, the sum of the vector and each solution element of the totally positive game belongs to the solution of the aggregate game. Unlike in traditional characterizations of the core, our results do not use consistency properties.

1 Introduction

The core is one of the most prominent solution concepts in cooperative game theory. It assigns to a transferable utility game (for short, a TU game, or a game) all Pareto-efficient payoff vectors such that each coalition of players obtains at least the amount that is available in the coalition. We offer an axiomatic characterization of the core on domains of games with a fixed player set. Axiomatic characterizations of the core on several classes of TU and nontransferable utility games, typically with varying sets of players, have been provided by Peleg (1986), Tadenuma (1992), Winter and Wooders (1994), Voorneveld and van den Nouweland (1998), Hwang and Sudhölter (2001), and Llerena and Rafels (2007). We should like to mention in particular the characterizations on totally balanced games by Peleg (1989) and Sudhölter and Peleg (2002) and on convex games by Hokari et al. (2020) and Dietzenbacher and Sudhölter (2022), among others. All these characterizations invoke a consistency axiom.¹ A solution is consistent if the restriction to the remaining players of each vector selected by this solution is also selected in each reduced game on the set of remaining players, in which only the subset of remaining players considers its reduced game. We refer to Funaki and Yamato (2001) for some forms of reduced games used in some of the characterizations of the core. Merits of several variants of consistency and its converse for characterizing the core and several extensions were recently discussed by Bejan et al. (2022).

We provide characterizations of the core on several classes of TU games with a fixed player set which do not invoke any consistency axiom. One of the crucial properties in these characterizations is the additivity axiom requiring that the solution of the sum of two games is the sum of the solutions in these two games. Bloch and de Clippel (2010) show that the set of all balanced games, i.e., the set of games with a nonempty core, can be partitioned into subsets in which the core is an additive solution. One of these subsets is the set of convex games as proved already by Tijs and Branzei (2002), which contains the set of totally positive games. These two subsets of games are of particular interest in view of the rapidly increasing number of applications of the theory of cooperative games in various fields. For example, O’Neill (1982) and Aumann and Maschler (1985) analyzed bankruptcy games, Maniquet (2003) considered queuing games, and, more recently, Lucchetti et al. (2010), Ginsburgh and Zang (2012), Dehez and Ferey (2013), and Karpov (2014) used cooperative games to model problems in the fields of medicine, voting theory, law, and scientometrics, respectively. In all these applications the arising cooperative TU games are convex and/or totally positive. According to Sudhölter and Zarzuelo (2017, Theorem 5.1), a game is totally positive if and only if it is the cost game of a generalized highway problem in which each customer selects an arbitrary, not necessarily connected, part of the highway.

For replacing consistency, we introduce two new axioms. A solution satisfies unanimity (UNA) if, when applied to the unanimity game on a coalition, it contains, for each player of this coalition, the vectors that assign the whole amount (i.e., one utility unit) to this player. UNA, hence, requires that the solution to a unanimity game contains the vertices of the imputation set of this game. This property is similar to Peleg’s condition of “unanimity for 2-person games” (UTPG) in a characterization of the core on totally balanced games (Peleg 1989; Sudhölter and Peleg 2002). On the one hand, UTPG is stronger than UNA as it requires coincidence with the imputation set for all unanimity games (even for all games that are strategically equivalent to unanimity games). On the other hand, UNA is a generalization of UTPG because it is a condition for games that may have more than two players.

The other new property employed in some of our characterizations is called converse super-additivity (CSUPA). The traditional axiom super-additivity (SUPA) requires that the sum of solution elements of two games is a vector of the solution of the sum of these two games. CSUPA may be regarded as a converse super-additivity property because it requires that a payoff vector belongs to the solution of a game v if, for each totally positive game $w \ne 0$ such that $v+w$ is also totally positive, the sum of this vector and an arbitrary element of the solution of w belongs to the solution of $v+w$.

In addition to the aforementioned new properties, we invoke classical axioms such as Pareto efficiency, the null-player property, individual rationality, and non-emptiness. We also introduce variants of the well-known reasonableness properties. A solution is coalition-wise reasonable from above (REAB) or below (REBE), respectively, if each coalition receives at most its maximal or at least its minimal, respectively, contribution.

Our axiomatic characterizations of the core are valid for various domains. The first and main result is that, on each cone of convex games which contains the set of totally positive games, the core is the unique solution which satisfies UNA, additivity, Pareto efficiency, the null-player property, and individual rationality (Theorem 3.2). This result can be extended to the larger set of balanced games (Corollary 4.1). To do so, as in the previous result, we employ UNA, Pareto efficiency, the null-player property, and individual rationality on balanced games. Furthermore, we require non-emptiness and super-additivity on the set of balanced games, and additivity on the set of totally positive games. Replacing non-emptiness by CSUPA yields a characterization of the core on each set of games which contains the set of totally positive games (Corollary 4.4). Moreover, we show that REBE (alternatively, Pareto efficiency and REAB) may be used to replace “additivity on totally positive games”.

The article is organized as follows. Section 2 provides definitions and notation. Section 3 introduces and motivates UNA and states the first main result, the characterization of the core on several domains of convex games. Section 4 states the characterization results of the core on the domain of balanced games and on more general domains. It also introduces converse super-additivity and the new reasonableness properties and presents the second main result, the characterization of the core on arbitrary sets of games with a fixed player set that contain the set of totally positive games (Theorem 4.6). Section 5 concludes.

2 Preliminaries

Let N be a finite set of at least two elements, which is called the set of players. Throughout, let $n=|N|$. A coalitional game with transferable utility (for short, a game) on N is a pair (N, v) where v is a function that associates a real number v(S) with each subset S of N. We always assume that $v(\emptyset )=0$. As N is fixed in this article, we identify a game (N, v) with its coalition function v. A coalition is a nonempty subset of N. Player $i\in N$ is a null-player in game v if $v(S\cup \{i\})=v(S)$ for all $S\subseteq N\setminus \{i\}$. Two players $i,j\in N$ are substitutes of the game v if $v(S\cup \{i\})=v(S\cup \{j\})$ for all $S\subseteq N\setminus \{i,j\}$.

For each nonempty coalition T we denote by $u^T$ the unanimity game on T, i.e., for each $S\subseteq N$,

$$\begin{aligned} u^T(S)=\left\{ \begin{array}{l}1\text{, } \text{ if } S\supseteq T,\\ 0\text{, } \text{ otherwise. } \end{array} \right. \end{aligned}$$

According to Shapley (1953), the unanimity games form a basis of the set of all games. Therefore, for each game v there exists a unique collection $(\alpha ^T(v))_{T\in 2^N\setminus \{\emptyset \}}$ of real coefficients such that

$$\begin{aligned} v=\sum _{T\in 2^N\setminus \{\emptyset \}}\alpha ^T(v)u^T. \end{aligned}$$

(2.1)

A game v is totally positive (Vasil’ev 1975) if $\alpha ^T(v) \ge 0$ for all $T\in 2^N\setminus \{\emptyset \}$.

For each $S\subseteq N$ and each vector $x=(x_i)_{i\in N}\in \mathbb {R}^N$, let $x(S)=\sum _{i\in S}x_ i$ ($x(\emptyset )=0$). We also denote the indicator function of S by $\mathbbm {1}^S\in \mathbb {R}^N$, i.e.,

$$\begin{aligned} \mathbbm {1}^S_i=\left\{ \begin{array}{l}1\text{, } \text{ if } i\in S,\\ 0\text{, } \text{ if } i\in N\setminus S.\end{array}\right. \end{aligned}$$

Let $X^*(v)$ and X(v) be the sets of feasible and Pareto efficient feasible vectors, respectively, i.e.,

$$\begin{aligned} { X^*(v)=\{x\in \mathbb {R}^N\mid x(N)\le v(N)\} \text{ and } }X(v)=\{x\in \mathbb {R}^N\mid x(N)=v(N)\}. \end{aligned}$$

The core of a game v is the set of vectors

$$\begin{aligned} C(v)=\{x\in X(v)\mid x(S)\ge v(S)\forall S\subseteq N\}. \end{aligned}$$

Remark 2.1

For each game v there exist totally positive games u, w such that $v+u=w$. Indeed, with $\mathcal{A}=\{T\in 2^N\setminus \{\emptyset \}\mid \alpha ^T(v)\le 0\}$ and $\mathcal{B}=\{T\in 2^N\setminus \{\emptyset \}\mid \alpha ^T(v)\ge 0\}$ put $u=\sum _{T\in {{\mathcal {A}}}}(-\alpha ^T(v))u^T$ and $w=\sum _{T\in \mathcal{B}}\alpha ^T(v)u^T.$ Then u and w are totally positive and $v+u=w$.

A game v is convex (Shapley 1971) if $v(S)+v(T)\le v(S\cap T)+v(S\cup T)$ for all $S,T\subseteq N$. A game v is balanced (Bondareva 1963; Shapley 1967) if and only if $C(v)\ne \emptyset$. Let $\Gamma ^{pos}$, $\Gamma ^{vex}$ and $\Gamma ^{bal}$ denote the sets of totally positive, convex and balanced games, respectively. As unanimity games are convex and the set of convex games is closed under summation and under multiplication by a non-negative scalar, each totally positive game is convex. Furthermore, each convex game is balanced (Shapley 1971).

An ordering of N is a bijective mapping $\pi :N\rightarrow \{1,\ldots ,n\}$. Denote by $\Pi ^N$ the set of orderings of N. For each $\pi \in \Pi ^N$ and $i\in N$, denote by $P^\pi _i$ the coalition of predecessors of i, i.e., $P^\pi _i=\{j\in N\mid \pi (j)\le \pi (i)\}$. Moreover, for each game v, denote by $a^\pi (v)$ the contribution vector of $\pi$, i.e., the vector defined by

$$\begin{aligned} a_i^\pi (v)= v(P^\pi _i)-v(P^\pi _i\setminus \{i\}) \forall i\in N. \end{aligned}$$

(2.2)

Note that $a^\pi (v)=x\in {\mathbb {R}}^N$ is uniquely determined by the n equations $x(P^\pi _i)=v(P^\pi _i)$ for all $i\in N$.

Remark 2.2

According to Shapley (1971) the core of a convex game v is the convex hull of all of its contribution vectors:

$$\begin{aligned} C(v)=\left\{ \sum _{\pi \in \Pi ^N}\lambda _\pi a^\pi (v)\bigg |\lambda _\pi \ge 0\forall \pi \in \Pi ^N,\sum _{\pi \in \Pi ^N}\lambda _\pi =1\right\} . \end{aligned}$$

(2.3)

As a consequence, for each $c \ge 0$ and each coalition S,

$$\begin{aligned} C(cu^S)=\bigg \{x\in \mathbb {R}_+^N\bigg | x(S)=c,x_j=0\forall j\in N\setminus S\bigg \}. \end{aligned}$$

(2.4)

A (set-valued) solution $\sigma$ on a set $\Gamma$ of games assigns to each game $v\in \Gamma$ a set of vectors $\sigma (v)\subseteq { X^*(v)}$. Let $\sigma$ be a solution on a set $\Gamma$ of games on N. Then $\sigma$ satisfies

• Non-emptiness (NE) if $\sigma (v)\ne \emptyset$ for all $v\in \Gamma$,

• The null-player property (NP) if, for all $v\in \Gamma$ and all null-players $i\in N$, $x_i=0$ for all $x\in \sigma (v)$,

• Additivity (ADD) if, for all $v,u,w\in \Gamma$ with $w=u+v$, $\sigma (u)+\sigma (v)=\sigma (w)$,

• Super-additivity (SUPA) if, for all $v,u,w\in \Gamma$ with $w=u+v$, $\sigma (u)+\sigma (v)\subseteq \sigma (w)$,

• Individual rationality (IR) if, for all $v\in \Gamma$ and all $x\in \sigma (v)$, $x_i \ge v(\{i\})$ for all $i\in N$,

• Pareto efficiency (EFF) if $\sigma (v)\subseteq X(N,v)$ for all $v\in \Gamma$,

• Scale covariance (SCOV) if, for all $v\in \Gamma$ and all $\alpha >0$ with $\alpha v\in \Gamma$, $\sigma (\alpha v)=\alpha \sigma (v)$.

The core satisfies NP, SUPA, IR, EFF, and SCOV on each set of games. It satisfies NE on each subset of balanced games. The core satisfies ADD on certain sets of games as shown by Bloch and de Clippel (2010), e.g., on each subset of $\Gamma ^{vex}$. Note also that a solution satisfying ADD also satisfies SUPA, while the converse implication may not hold.

We conclude this section by proving the following useful lemma.

Lemma 2.3

Let $\Gamma$ be a set of games such that $\Gamma ^{pos}\subseteq \Gamma$. Then the core on $\Gamma$ satisfies ADD if and only if $\Gamma \subseteq \Gamma ^{vex}$.

Proof

Let $\Gamma$ be as hypothesized. The if part is well-known as mentioned. To show the only if part, assume that the core on $\Gamma$ satisfies ADD on $\Gamma$ . Let $v\in \Gamma$ and let $S,T\subseteq N$. It remains to show that $v(S)+v(T)\le v(S\cap T)+v(S\cup T)$. We may assume that $S\not \subseteq T$ and $T\not \subseteq S$ because otherwise the inequality is obviously satisfied. Hence, there exists $\pi \in \Pi ^N$ such that $S\cap T=\{i\in N\mid \pi (i)\le |S\cap T|\}$ and $S\cup T=\{i\in N\mid \pi (i)\le |S\cup T|\}$. By Remark 2.1 there exist $u,w\in \Gamma ^{pos}$ such that $v+u=w$. By Remark 2.2, $z:=a^\pi (w)\in C(w)$. As $\Gamma ^{pos} \subseteq \Gamma$ and as the core is assumed to satisfy ADD, there exist $x\in C(u)$ and $y\in C(v)$ such that $x+y=z$. As $z(S\cap T)=w(S\cap T)$ and $z(S\cup T)=w(S\cup T)$, we conclude that $x(S\cap T)=u(S\cap T), x(S\cup T)=u(S\cup T), y(S\cap T)=v(S\cap T)$, and $y(S\cup T)=v(S\cup T)$. However, $v(S\cap T)+v(S\cup T)= y(S\cap T)+y(S\cup T)= y(S)+y(T)\ge v(S)+v(T)$. $\square$

3 Axiomatization of the core on domains of convex games

In this section we provide a characterization of the core on an arbitrary cone of convex games that contains all totally positive games. Here, we say that a set of games is a cone if it is closed under multiplication with positive scalars (a set $\Gamma$ of games is closed under multiplication with positive scalars if $cv\in \Gamma$ for all $v\in \Gamma$ and $c>0$).

For this purpose we introduce one further property. This axiom may be regarded as a weakening of a natural generalization to n-person games of a well-known property for 2-person games used by Peleg (1989) in an axiomatization of the core based on some consistency properties. As our characterization results do not rely on consistency properties, such a generalization to n-person games seems reasonable. Recall that, according to Peleg (1989), a solution satisfies unanimity for 2-person games (UTPG) if the solution assigns the set of all imputations, i.e., $X^{ir}(v)=\{x\in X(v)\mid x_i\ge v(\{i\}) \text{ for } \text{ all } i\in N\}$, to each 2-person game v under consideration. Now, a 2-person game for which $X^{ir}$ is nonempty is, up to strategic equivalence, a unanimity game. Hence, UTPG mainly requires that the solution selects the set of imputations for each 2-person unanimity game. Hence, a natural generalization of UTPG to n-person games would be to require that the solution assigns to each unanimity game its set of imputations, i.e., its core. Our new axiom is weaker. It only requires that the vertices of the imputation set are contained in the solution of every unanimity game. The formal definition is as follows. Let $\Gamma$ be a set of games and let $\sigma$ be a solution on $\Gamma$. Then $\sigma$ satisfies

• Unanimity (UNA) if, for all $T\in 2^N\setminus \{\emptyset \}$ such that $u^T\in \Gamma$, $\mathbbm {1}^{\{i\}}\in \sigma (u^T)$ for each $i\in T$.

The interpretation of UNA is simple: A solution that satisfies UNA is liberal in the sense that it allows to assign the entire amount of money available in a unanimity game to each player in the determining coalition. Hence, the convex hull of these vectors is the entire set of imputations, i.e., the entire core. Clearly, the core satisfies UNA on any domain of games.

The following lemma is useful.

Lemma 3.1

Let $\Gamma \supseteq \Gamma ^{pos}$ and $\sigma$ be a solution on $\Gamma$ that satisfies SUPA such that $a^\pi (v)\in \sigma (v)\subseteq C(v)$ for all $\pi \in \Pi ^N$ and $v\in \Gamma ^{pos}$. Then $\sigma (w)\subseteq C(w)$ for all $w\in \Gamma$.

Proof

Let $v\in \Gamma$. By Remark 2.1, there exist $u,w\in \Gamma ^{pos}$ such that $v+u=w$. Let $y\in \sigma (v)$. Let $S\in 2^N\setminus \{\emptyset \}.$ It remains to show that $y(S)\ge v(S)$. To this end let $\pi \in \Pi ^N$ such that $S=\{j\in N\mid \pi (j)\le |S|\}$. By (2.2), $\sum _{j\in S}a_j^\pi (u)=u(S)$. Hence, by SUPA, $a^\pi ({ u})+y\in \sigma (w)\subseteq C(w)$, which implies that $y(S) \ge v(S)$.$\square$

Theorem 3.2

Let $\Gamma$ be a cone of games such that $\Gamma ^{pos}\subseteq \Gamma \subseteq \Gamma ^{vex}$. Then the core is the unique solution on $\Gamma$ that satisfies EFF, ADD, IR, NP, and UNA.

Proof

The core satisfies the axioms (see the two preceding sections). It remains to show uniqueness. To this end let $\sigma$ be a solution on $\Gamma$ that satisfies the desired six axioms. Step 1: We first show that the prerequisites of Lemma 3.1 are satisfied. Let $v\in \Gamma ^{pos}.$ If $v= cu^S$ for some $c\ge 0,$ $S\in 2^N\setminus \{\emptyset \}$ and $x\in \sigma (v)$, then, by EFF, $x(N)=v(N)=c$, and, by NP, $x_i=0$ for all $i\in N\setminus S$. Hence, $x(S)=v(N)$. By IR, $x_j\ge 0$ for all $j\in S$. Hence, $x\in C(v)$ by (2.4). For $\pi \in \Pi ^N$, $a^\pi (v)=ca^\pi (u^S)$. Hence, for $c\in {\mathbb {N}}$, ${ a}^\pi (v)\in \sigma (v)$ by UNA and ADD. If $c=0$, then $a^\pi (v)=(0,\dots ,0)\in {\mathbb {R}}^N$ is the unique core element by (2.4). By ADD, $\sigma (v)+\sigma (u^N)=\sigma (u^N)$ so that, by UNA, $\sigma (v)\ne \emptyset$, hence $\sigma (v)=\{(0,\dots ,0)\}$. If $c>0$ such that $c\in {\mathbb {R}}\setminus {\mathbb {N}}$, then, for $c'\in {\mathbb {N}}$ with $c'>c$, $a^\pi (c'u^S)\in \sigma (c'u^S)$ as shown before. By ADD, $\sigma (cu^S)+\sigma ((c'-c)u^S)\ni c'a^\pi (u^S)$. As $\sigma (cu^S)\subseteq cC(u^S)=C(cu^S)$ and $\sigma ((c'-c)u^S)\subseteq (c'-c)C(u^S)=C((c'-c)u^S)$, ADD guarantees that there are $y\in C(cu^S)$ and $z\in C((c'-c)u^S)$ such that $y+z=a^\pi (c'u^S):=x'$. By (2.2), $x'(P^\pi _i)=c'u^S(P^\pi _i)$ for all $i\in N$. Hence, $y(P^\pi _i)=cu^S(P^\pi _i)$ and $z(P^\pi _i)=(c'-c)u^S(P^\pi _i)$ for all $i\in N$ so that $y=a^\pi (cu^S)$ and $z=a^\pi ((c'-c)u^S).$ If $v\in \Gamma ^{pos}$ is arbitrary, then $a^\pi (v)\in \sigma (v)\subseteq C(v)$ by ADD.

Step 2: We now show that, for each $v\in \Gamma$ and $\pi \in \Pi ^N$, $a^\pi (v)\in \sigma (v)\subseteq C(v)$. Indeed, by Lemma 3.1, $\sigma (v)\subseteq C(v)$. By Remark 2.1, there exist $u,w\in \Gamma ^{pos}$ such that $v+u=w$. As $w\in \Gamma ^{pos}$, $z:=a^\pi (w)\in \sigma (w)$. By ADD, there exist $x\in \sigma (u)\subseteq C(u)$ and $y\in \sigma (v)$ such that $x+y=z$. For each $r\in \{1,\ldots ,n\}$ put $S^r=\{i\in N\mid \pi (i)\le r\}$ and note that $z(S^r)=w(S^r)$. As $\sigma (v)\subseteq C(v)$, we conclude that $x(S^r)=u(S^r)$ and $y(S^r)=v(S^r)$ so that $y=a^\pi (v)$.

Step 3: We now finish the proof. If y is an arbitrary element of C(v), then, by (2.3), $y=\sum _{\pi \in \Pi ^N}\lambda _\pi a^\pi (v)$ for some $\lambda _\pi \ge 0$, $\pi \in \Pi ^N$, such that $\sum _{\pi \in \Pi ^N}\lambda _\pi =1$. As $v=\sum _{\pi \in \Pi ^N}\lambda _\pi v$, and as $c a^\pi (v)=a^\pi (cv)$ and $cv\in \Gamma$ for all $c\ge 0$, we get $y\in \sigma (v)$ because $\sigma$ satisfies ADD. $\square$

Let $\Gamma$ be a cone of games such that $\Gamma ^{pos}\subseteq \Gamma \subseteq \Gamma ^{vex}$. The following examples show that each of the axioms employed in Theorem 3.2 is logically independent of the remaining axioms:

• The solution $\sigma ^1$ on $\Gamma$, defined by

  $$\begin{aligned} \sigma ^1(v)=(C(v)-\mathbb {R}^N_+)\cap \{x\in {\mathbb {R}}^N\mid x_i\ge v(\{i\}) \text{ for } \text{ all } i\in N\} \end{aligned}$$

  for each $v\in \Gamma$, satisfies all axioms except EFF.

• The solution $\sigma ^2$ on $\Gamma$, defined by $\sigma ^2(v)=C(v)$ if $v\in \Gamma$ contains at least one null player and $\sigma ^2(v)=C(v)\cup \{ESD(v)\}$ if $v\in \Gamma$ does not contain a null player, where ESD is the equal surplus division value given by $ESD_i(v)=v(\{i\})+(v(N)-\sum _{j\in N}v(\{j\}))/n$ for each $v\in \Gamma$ and each $i\in N$, satisfies all axioms except ADD.

• The solution $\sigma ^3$ on $\Gamma$, defined by $\sigma ^3(u^T)=\{x\in X(u^T)\mid x_j=0 \text{ for } \text{ all } j\in N\setminus T\}$ for all $T\in 2^N\setminus \{\emptyset \}$ and, for each $v\in \Gamma$, by $\sigma ^3(v)=\sum _{T\in 2^N\setminus \{\emptyset \}}\alpha ^T(v)\sigma ^3(u^T)$, satisfies all axioms except IR.

• The solution $\sigma ^4$ on $\Gamma$, defined by $\sigma ^4(v)=\{x\in X(v)\mid x_i\ge v(\{i\}) \text{ for } \text{ all } i\in N\}$ for all $v\in \Gamma$, satisfies all axioms except NP provided that $n\ge 3$. For $n=2$, NP follows from IR and EFF.

• The solution $\sigma ^5$ on $\Gamma$, defined by $\sigma ^5(v)=\{\phi (v)\}$ for each $v\in \Gamma$, where $\phi (v)$ is the Shapley value $\left({\rm recall\,that}\; \phi (v)=\sum _{\pi \in \Pi ^N}\frac{a^\pi (v)}{n!}\right),$ satisfies all axioms except UNA.

The following example, which can easily be generalized to the case $n>3$, shows that it is crucial to assume in Theorem 3.2 that the set $\Gamma$ is a cone. For $n=2$, all convex games are totally positive.

Example 3.3

Let $n=3$, say $N=\{1,2,3\}$, let $v_0=u^{\{2\}}+2u^{\{3\}}+u^{\{1,2\}}+u^{\{1,3\}}+u^{\{2,3\}}-u^N$, and let $\Gamma =\Gamma ^{pos}\cup \{v_0\}$. Note that $v_0\in \Gamma ^{vex}$. We define the solution $\sigma$ on $\Gamma$ by $\sigma (v_0)=\{\lambda a^\pi (v_0)+(1-\lambda )a^{\pi '}(v_0)\mid 0\le \lambda \le 1,\pi ,\pi '\in \Pi ^N\}$ and $\sigma (v)=C(v)$ for all $v\in \Gamma ^{pos}$. As $\{a^\pi (v_0)\mid \pi \in \Pi ^N\}=\{(0,2,3),(1,1,3),(1,2,2)\}$, we obtain

$$\begin{aligned} \sigma (v_0)=\{(\lambda ,2-\lambda ,3)\mid 0\le \lambda \le 1\}\cup \{(\lambda ,2,3-\lambda )\mid 0\le \lambda \le 1\}\cup \{(1,2-\lambda ,2+\lambda )\mid 0\le \lambda \le 1\}, \end{aligned}$$

i.e.,

$$\begin{aligned} X\!\!:=\!\sigma (v_0)-(0,1,2)\,=\,\{(\lambda ,1-\lambda ,1)\mid 0\le \lambda \le 1\} \cup \{(\lambda ,1,1-\lambda )\mid 0\le \lambda \le 1\}\cup \{(1,1-\lambda ,\lambda )\mid 0\le \lambda \le 1\}. \end{aligned}$$

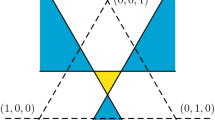
Except ADD, the remaining axioms in Theorem 3.2 are punctual/“local” properties, i.e., properties that do not require to compare games. All properties are satisfied for all games in $\Gamma ^{pos}$ because restricted to this domain our solution is the core. EFF, IR, and NP are also satisfied for $v_0$ because $\sigma (v_0)\subseteq C(v_0)$. As $v_0$ is not a unanimity game, UNA is also trivially valid. Hence, it remains to show that ADD is satisfied. For this purpose, let $u,v,w\in \Gamma$ such that $u+v=w$. By SUPA of the core it remains to show that $\sigma (w)\subseteq \sigma (u)+\sigma (v)$. If $u,v\in \Gamma ^{pos}$, then $w\in \Gamma ^{pos}$ and the proof is finished by ADD of the core. The case that $u=v=v_0$ does not appear because $2v_0\notin \Gamma$. Hence, we may assume that $u=v_0, v\in \Gamma ^{pos},$ and $w\in \Gamma ^{pos}$. Hence, $v=u^N+v'$ for some $v'\in \Gamma ^{pos}$. By ADD of the core, $\sigma (w)=C(w)=C(v_0+v)=C(v_0+u^N)+C(v')=\sigma (v_0+u^N)+\sigma (v').$ Hence, it suffices to consider the case $v=u^N$. Let $v_1=v_0-u^{\{2\}}-2u^{\{3\}}$, i.e., $v_1$ is the 0-normalization of $v_0$. As the core is covariant under strategic equivalence, it remains to show that $C(v_1+u^N)\subseteq X+C(u^N)$. Let $z\in \sigma (v_1+u^N)=C(v_1+u^N)$. By symmetry of $v_1$, hence of $v_1+u^N$, we may assume that $z_3\ge 1$ because $z(N)=3$. Let $x=\left( \frac{z_1}{z_1+z_2},\frac{z_2}{z_1+z_2},1\right)$ and $y=z-x$. Then (see Fig. 1) $x\in X$ and $y\in C(u^N)$ so that the proof is finished.

Fig. 1

Sketch to Example 3.3

4 Axiomatization of the core on general domains of games

We use the results of the former section to establish characterizations of the core on broader domains of games. An immediate consequence of Theorem 3.2 is the following corollary.

Corollary 4.1

The core is the unique solution on $\Gamma ^{bal}$ that satisfies EFF, IR, NP, NE, UNA and SUPA and, on $\Gamma ^{pos}$, ADD.

Proof

The core satisfies the desired properties. In order to show uniqueness, let $\sigma$ be solution that satisfies EFF, IR, NP, NE, UNA, and SUPA on $\Gamma ^{bal}$ and ADD on $\Gamma ^{pos}$. Let $v\in \Gamma ^{bal}$. It remains to show that $\sigma (v)=C(v)$. For $w\in \Gamma ^{pos}$, $\sigma (w)=C(w)$ by Theorem 3.2. Hence, by Lemma 3.1, $\sigma (v)\subseteq C(v)$ for all $v\in \Gamma ^{bal}$. In order to prove the converse inclusion, let $x\in C(v)$. If $n=2$, then v is convex so that $\alpha ^N(v)\ge 0$ and $\sigma (\alpha ^N(v)u^N)=C(\alpha ^N(v)u^N)$. Moreover, $C(\alpha ^{\{i\}}(v)u^{\{i\}})=\{\alpha ^{\{i\}}\mathbbm {1}^{\{i\}}\}$ for all $i\in N$ so that, by NE, $C(\alpha ^{\{i\}}(v)u^{\{i\}})=\sigma (\alpha ^{\{i\}}(v)u^{\{i\}})$. By ADD of the core on $\Gamma ^{vex}$, $x\in \sum _{i\in N}C(\alpha ^{\{i\}}(v)u^{\{i\}})+C(\alpha ^N(v)u(N))$ so that, by SUPA, $x\in \sigma (v)$.

For $n\ge 3$ we proceed as Peleg (1986) by considering the game w given by $w(\{i\})=v(\{i\})$ for all $i\in N$ and $w(S)=x(S)$ otherwise. Note that $C(w)=\{x\}$. By Lemma 3.1 and NE, $\sigma (w)=C(w)=\{x\}$. Furthermore, set $u=v-w$ and note that $C(u)=\{(0,\dots ,0)\}$. As before we conclude that $\sigma (u)=\{0\}$. SUPA finishes the proof.$\square$

Note that NE is not only crucial in the foregoing proof, but also necessary for the statement of Corollary 4.1. Indeed, the solution that assigns the core to each totally positive game and the empty set to each other balanced game satisfies EFF, IR, NP, UNA, SUPA, and, on $\Gamma ^{pos}$, ADD, and it violates NE.

In order to provide a characterization of the core on an arbitrary set of games that contains the set of totally positive games, we note that, by Lemma 3.1, the core on such a set of games is the maximum solution that coincides with the core on $\Gamma ^{pos}$ and satisfies SUPA. Here, “maximum” is meant in the sense that each solution $\sigma$ that satisfies the mentioned properties is a subsolution of the core (i.e., $\sigma (v)\subseteq C(v)$ for all $v\in \Gamma$) and that the core satisfies the mentioned properties. In order to replace “maximum”, we reconsider the axiom SUPA. Recall that a solution $\sigma$ on a set $\Gamma$ of games satisfies SUPA if for each $v\in \Gamma$ and all $x\in {\mathbb {R}}^N$:

$$\begin{aligned} x\in \sigma (v)\Rightarrow \{x\}+\sigma (w)\subseteq \sigma (v+w) \text{ for } \text{ all } w\in \Gamma \text{ such } \text{ that } v+w\in \Gamma. \end{aligned}$$

This formulation of SUPA motivates to define the following “converse” version of SUPA, which requires that, for each $v\in \Gamma$ and all $x\in {\mathbb {R}}^N$:

$$\begin{aligned} x\in \sigma (v)\Leftarrow \{x\}+\sigma (w)\subseteq \sigma (v+w) \text{ for } \text{ all } w\in \Gamma \text{ such } \text{ that } v+w\in \Gamma. \end{aligned}$$

(4.1)

Assume that $\Gamma$ contains $\Gamma ^{pos}$, the set of totally positive games. Then (4.1) is satisfied for a solution $\sigma$ if and only if $0\in {\mathbb {R}}^N$ is a member of $\sigma (0)$. But even if the condition $w\ne 0$ is added in (4.1), the arising property remains very weak. For instance, the solution that assigns the core to each totally positive game and the empty set to each other game is still satisfying the aforementioned slightly stronger property provided $\Gamma$ contains, for each $v\in \Gamma$, also $v+w$ for each $w\in \Gamma ^{pos}\setminus \{0\}$. We now show that the core on $\Gamma$ satisfies the following property that is even stronger than this modification of (4.1). A solution $\sigma$ on a set $\Gamma$ of games satisfies

• Converse super-additivity (CSUPA) if, for all $v\in \Gamma$ and all $x\in {\mathbb {R}}^N$ the following condition is satisfied: If $x+y\in \sigma (v+w)$ for all $y\in \sigma (w)$ and all $w\in \Gamma \cap \Gamma ^{pos}$ such that $w\ne 0$ and $v+w\in \Gamma \cap \Gamma ^{pos}$, then $x\in \sigma (v)$.

Lemma 4.2

Let $\Gamma$ be a set of games that contains $\Gamma ^{pos}$. Then the core on $\Gamma$ satisfies CSUPA.

Proof

Let $v\in \Gamma$ and $x\in {\mathbb {R}}^N$ such that $\{x\}+C(w)\subseteq C(v+w)$ for each $w\in \Gamma ^{pos}\setminus \{0\}$ such that $v+w\in \Gamma ^{pos}$. It remains to show that $x\in C(v)$. By Remark 2.1, there exists $w\in \Gamma ^{pos}$ such that $v+w\in \Gamma ^{pos}$. We may assume that $w\ne 0$ because in the case that $v\in \Gamma ^{pos}$ we may select an arbitrary $w\in \Gamma ^{pos}\setminus \{0\}$. Assume, on the contrary, $x\in \mathbb {R}^N\setminus C(v)$, then either $x(N)>v(N)$ or there exists $S\subseteq N$ such that $x(S)<v(S)$. In the former case $(x+z)(N)>(v+w)(N)$ for all $z\in C(w)$ so that $x+z\notin C(v+w)$. In the latter case, there exists $z\in C(w)$ such that $z(S)=w(S)$. Hence, $(x+z)(S)<(v+w)(S),$ i.e., $x+z\notin C(v+w)$ as well, and the desired contradiction has been obtained.$\square$

Thus, we may now show the following result.

Proposition 4.3

Let $\Gamma ^\textrm{pos}\subseteq \Gamma$. A solution on $\Gamma$ that coincides with the core on $\Gamma ^\textrm{pos}$ satisfies SUPA and CSUPA if and only if it coincides with the core on the entire set $\Gamma$.

Proof

The core satisfies SUPA so that the if part is due to Lemma 4.2. For the only if part, assume that $\sigma$ satisfies SUPA and CSUPA on $\Gamma \supseteq \Gamma ^\textrm{pos}$ and coincides with the core on $\Gamma ^{pos}$. Let $v \in \Gamma$. By Lemma 3.1, $\sigma (v)\subseteq C(v)$. In order to show the other inclusion, let $x \in C(v)$. By SUPA of the core, $\{x\}+C(w)\subseteq C(v+w)$ for all $w\in \Gamma$ such that $v+w\in \Gamma$, hence $x\in \sigma (v)$ by CSUPA.$\square$

Therefore, Proposition 4.3 and Theorem 3.2 lead to the following corollary.

Corollary 4.4

Let $\Gamma$ be a set of games that contains $\Gamma ^{pos}$. Then the core is the unique solution on $\Gamma$ that satisfies EFF, SUPA, CSUPA, IR, NP, and UNA and, when restricted to $\Gamma ^{pos}$, ADD.

Further axiomatizations of the core that avoid “ADD on $\Gamma ^{pos}$” may be obtained by replacing IR and NP by one of the following versions of reasonableness.

For a game v and $i\in N$ denote the maximal and minimal contribution of i by $b_i^{\max }(v)$ and $b_i^{\min }(v)$, i.e.,

$$\begin{aligned} \begin{array}{ll}b_i^{\max }(v)&{}=\max _{S\subseteq N\setminus \{i\}}(v(S\cup \{i\})-v(S)) \text{ and } \\ b_i^{\min }(v)&{}=\min _{S\subseteq N\setminus \{i\}}(v(S\cup \{i\})-v(S)).\end{array} \end{aligned}$$

Recall that $x\in {\mathbb {R}}^N$ is called reasonable from above (Milnor 1952) if $x_i\le b_i^{\max }(v)$ for all $i\in N$. Similarly, we say that x is reasonable from below if $x_i \ge b_i^{\min }(v)$ for all $i\in N$. Arguments supporting these kinds of reasonableness are as follows. It seems, indeed, unreasonable to pay to any player more than her maximal contribution to any coalition and, vice versa, a player may refuse to join any coalition if she does not receive at least her minimal contribution. Note that individual rationality implies reasonableness from below.

We now define coalition-wise reasonableness as follows. The maximal and minimal contribution of a coalition $T\in 2^N\setminus \{\emptyset \}$, respectively, is

$$\begin{aligned} \begin{array}{ll}b_T^{\max }(v)&{}=\max _{S\subseteq N\setminus T}(v(S\cup T)-v(S)) \text{ and } \\ b_T^{\min }(v)&{}=\min _{S\subseteq N\setminus T}(v(S\cup T)-v(S)).\end{array} \end{aligned}$$

Let $\Gamma$ be a set of games and $\sigma$ be a solution on $\Gamma$. Say that $\sigma$ satisfies

• Coalition-wise reasonableness from above (REAB) if, for all $v\in \Gamma \text{, } x\in \sigma (v)$ and $T\in 2^N\setminus \{\emptyset \}$, $x(T) \le b_T^{\max }(v)$;

• Coalition-wise reasonableness from below (REBE) if, for all $v\in \Gamma \text{, } x\in \sigma (v)$ and $T\in 2^N\setminus \{\emptyset \}$, $x(T) \ge b_T^{\min }(v)$.

Note that the core satisfies REBE by definition. If $x\in X^*(v)$ does not satisfy REAB, then there exists a coalition T such that $x(T)>v(S\cup T)-v(S)$ for all $S\subseteq N\setminus T$, hence, $x(T)>v(N)-v(N\setminus T)$ which implies $T\ne N$ and, as $x(N) \le v(N)$, $x(N\setminus T)<v(N\setminus T)$. Hence, the core also satisfies REAB.

Now, if $v\in \Gamma ^{vex}$, $T\in 2^N\setminus \{\emptyset \}$, and $S\subseteq N\setminus T$, then

$$\begin{aligned} v(S)+v(T)\le v(S\cup T) \text{ and } v(S\cup T)+v(N\setminus T)\le v(N)+v(S) \end{aligned}$$

so that $b^{\min }_T(v)=v(T)$ and $b^{\max }_T(v)=v(N)-v(N\setminus T)$.

Remark 4.5

Let $v\in \Gamma ^{vex}$.

• (1) The core of v coincides with the set of all feasible vectors that are coalition-wise reasonable from below because $b^{\min }_T(v)=v(T)$ for all $T\in 2^N\setminus \{\emptyset \}$.

• (2) Similarly it can be shown that the core of v is the set of Pareto efficient feasible vectors that are coalition-wise reasonable from above.

We conclude with the following result.

Theorem 4.6

Let $\Gamma ^{pos}\subseteq \Gamma$. The core on $\Gamma$ is the unique solution that satisfies REBE, UNA, SUPA, SCOV, and CSUPA. Moreover, in this characterization REBE can be replaced by EFF and REAB.

Proof

It remains to show the uniqueness part. Let $\sigma$ be a solution that satisfies REBE (or EFF and REAB, respectively), UNA, SUPA, SCOV, and CSUPA. In view of Proposition 4.3 it suffices to show that $\sigma$ coincides with the core on $\Gamma ^{pos}$. In view of Remark 4.5, $\sigma$ is a subsolution of the core on $\Gamma ^{pos}$. Now, we proceed similarly as in the proof of Theorem 3.2. Let $v\in \Gamma ^{pos}$. Let $T\in 2^N\setminus \{\emptyset \},$ $c>0$, and $\pi \in \Pi ^N$. By UNA and SCOV, $a^\pi (cu^T)\in \sigma (cu^T)$. Hence, if $v\ne 0$, then ${ a}^\pi (v)\in \sigma (v)$ by SUPA. If $v=0$, then $0+{ a}^\pi (w)\in \sigma (0+w)$ for each $w\in \Gamma ^{pos}\setminus \{0\}$ so $0=a^\pi (0)\in \sigma (0)$ is guaranteed by CSUPA. The proof can now be completed by literally copying Step 3 of the proof of Theorem 3.2 by using SUPA instead of ADD.$\square$

It should be noted that each property in Theorem 4.6 is logically independent of the remaining properties. Indeed, the solution that assigns X(v), the set of feasible Pareto efficient vectors, to each $v\in \Gamma$ exclusively violates REBE or REAB, respectively. The solution $\sigma$ defined by $\sigma (v)=\{x\in X^*(V)\mid x(T)\ge v(T)\forall T\in 2^N\setminus \{N\}\}$ for all $v\in \Gamma$ exclusively violates EFF and REBE. The solution that assigns the empty set to each additive game and the core to each other game in $\Gamma$ exclusively violates UNA. The solution $\sigma$ defined by $\sigma (v)=\{a^\pi (v)\mid \pi \in \Pi ^N\}$ for all $v\in \Gamma ^{pos}$ and $\sigma (w)=C(w)$ for all $w\in \Gamma \setminus \Gamma ^{pos}$ exclusively violates SUPA. The solution that assigns the core to each game $v\in \Gamma$ satisfying $v(S)\in {\mathbb {N}}\cup \{0\}$ for all $S\subseteq N$ and the empty set to all other games in $\Gamma$ satisfies all axioms except SCOV. The solution $\sigma ^*$ defined by $\sigma ^*(v)=C(v)$ for all $v\in \Gamma ^{pos}$ and $\sigma ^*(w)=\emptyset$ for all $w\in \Gamma \setminus \Gamma ^{pos}$ exclusively violates CSUPA provided that $\Gamma ^{pos}\subsetneqq \Gamma$. On $\Gamma ^{pos}$ the core is characterized by the remaining properties.

5 Concluding remarks

Some final remarks are of interest.

• For ${{\mathcal {T}}}\subseteq 2^N\setminus \{\emptyset \}$, put $\Gamma ^{vex}_{{\mathcal {T}}}=\{v\in \Gamma ^{vex}\mid \alpha ^T(v)\ne 0\Rightarrow T\in {{\mathcal {T}}}\}$ , where $\alpha ^T$ is defined by (2.1). That is, $\Gamma ^{vex}_{{\mathcal {T}}}$ is the set of convex games that are linear combinations of unanimity games on coalitions in ${{\mathcal {T}}}$. Moreover, let $\Gamma ^{pos}_{{\mathcal {T}}}$ be the set of all totally positive games that are linear combinations of such unanimity games, i.e., $\Gamma ^{pos}_{{\mathcal {T}}}=\Gamma ^{vex}_{{\mathcal {T}}}\cap \Gamma ^{pos}$. Then the statement of Theorem 3.2 is valid for each cone $\Gamma$ satisfying $\Gamma ^{pos}_{{\mathcal {T}}}\subseteq \Gamma \subseteq \Gamma ^{vex}_\mathcal{T}$.

• A game v is called almost positive if $\alpha ^T(v)\ge 0$ for all $T\subseteq N$ with $|T|\ge 2$. Hence, almost positive games arise by adding inessential (additive) games to totally positive games. It should be noted that despite of Example 3.3 the statement of Theorem 3.2 holds for an arbitrary set of almost positive games (not necessarily a cone) that contains all totally positive games because the core of an inessential game is a singleton.

• Note that CSUPA is the only axiom invoked in Corollary 4.4 that has to be requested for all games in $\Gamma$, whereas it is sufficient to apply all other axioms to totally positive games.

Fig. 2 illustrates the domains for which our results are formulated. The union of the green cones reminds us that Theorem 3.2 works on each set of games contained in the set of convex games (the purple cone) that contains all totally positive games (the blue cone) and is a cone. Corollary 4.4 and Theorem 4.6 are valid on each set of games that contains all totally positive games (the blue cone). Such a set of games can include non-balanced games and not all convex games. Fig. 2 illustrates that Theorem 3.2 can be applied to sets of games that are not necessarily convex. This is also true for the sets of games for which Corollary 4.4 and Theorem 4.6 work. Finally, Corollary 4.1 applies to the set of balanced games (the orange cone).

Fig. 2

Domains of Games