Abstract
We contrast and compare three ways of predicting efficiency in a forced contribution threshold public good game. The three alternatives are based on ordinal potential, quantal response and impulse balance theory. We report an experiment designed to test the respective predictions and find that impulse balance gives the best predictions. A simple expression detailing when enforced contributions result in high or low efficiency is provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A threshold public good is provided if and only if total contributions towards its provision are sufficiently high. The classic example would be a capital project such as a new community school (Andreoni 1998). The notion of threshold public good is, however, far more general than this classic example. Consider, for example, a charity that requires sufficient funds to cover large fixed costs. Or, consider a political party deciding whether to adopt a policy which is socially efficient but, for some reason, unpopular with voters; the policy will be enacted if and only if enough party members are willing to back the policy (Goeree and Holt 2005).
In a threshold public good game the provision of the public good is consistent with Nash equilibrium. There are, however, typically multiple equilibria (Palfrey and Rosenthal 1984; Alberti and Cartwright 2016). This leads to a coordination problem that creates a natural uncertainty about total contributions. The literature has decomposed this uncertainty into a fear and greed motive for non contribution (Dawes et al. 1986; Rapoport 1987, see also Coombs 1973). The fear motive recognizes that a person may decide not to contribute because he is pessimistic that sufficiently many others will contribute.Footnote 1 The greed motive recognizes that a person may decide not to contribute in the hope that others will fund the public good.
Dawes et al. (1986) noted that the fear motive can be alleviated by providing a refund (or money back guarantee) if contributions are short of the threshold (see also Isaac et al. 1989). Similarly, the greed motive can be alleviated by forcing everyone to contribute if sufficiently many people volunteer to contribute. In three independent experimental studies Dawes et al. (1986) observed significantly higher efficiency in a forced contribution game. On this basis they concluded that inefficiency was primarily caused by the greed motive. Rapoport and Eshed-Levy (1989) challenged this conclusion by showing that the fear motive can cause inefficiency (see also Rapoport 1987). They still, however, observed highest efficiency in a forced contribution game.Footnote 2
These experimental results suggest that enforcing contributions is an effective way to obtain high efficiency. This is a potentially important finding in designing mechanisms for the provision of public goods. Existing evidence, however, is limited to the two papers mentioned above. Our objective in this paper is to explore in detail, both theoretically and experimentally, the conditions under which forced contributions leads to high efficiency in binary threshold public good games.Footnote 3
Our theoretical contribution consists of applying three, alternative approaches to modelling behavior that are, respectively, based on ordinal potential (Monderer and Shapley 1996), quantal response (McKelvey and Palfrey 1995), and impulse balance (Selten 2004). We demonstrate that the three approaches give very different predictions on the efficiency of enforcing contributions. We complement the theory with an experimental study where the number of players and return to the public good are systematically varied in order to test the respective predictions of the three theoretical models. We find that impulse balance provides the best fit with the experimental data. This allows us to derive a simple expression with which to predict when enforced contributions result in high or low efficiency. Our predictions are consistent with the uniformly high efficiency observed in previous studies. We also find, however, that enforced contributions are not a guarantee of high efficiency. The interpretation of this finding will be discussed more in the conclusion.
Our analysis shows that a forced contribution game is of theoretical interest; for instance, it’s tractability allows a direct test on the predictive power of three commonly used theoretical models. A point we also want to emphasize, however, is that the forced contribution game is of applied interest as well. To motivate this latter point it is important to explain why forced contribution is not inconsistent with the notion of voluntary provision of a public good. A forced contribution game encapsulates the following basic properties: (1a) If enough people voluntarily contribute to the public good then the public good is provided and (b) everybody gets the same payoff, irrespective of whether they contributed or not.Footnote 4 (2a) If not enough people voluntarily contribute then the public good is not provided and (b) those who contributed are worse off than those who did not contribute. Property (2a) means that it is endogenously determined whether the public good is provided; hence, public good provision is voluntary at the level of the group. Property (2b) means that the fear motive for not contributing is present and so it is far from trivial whether the efficient outcome will be obtained.
To illustrate further, we provide three examples of a forced contribution game.Footnote 5 First, consider an organization or department being run by an incompetent manager. To get rid of the manager will require a sufficiently large number of colleagues to complain. Hence to complain can be interpreted as contributing towards the public good. Suppose that if the manager is removed then everyone benefits and no one (including those who complained) will receive any recrimination. Further, suppose that if the manager is not removed then things carry on as before except that those who complained will receive recriminations. One can readily check that this situation satisfies all the properties required of a forced contribution game (as we more formally show in footnote 10). In particular, those who contribute only earn a lower payoff than those who did not contribute if the manager is not removed.
As a second example, consider a firm attempting a takeover of a competitor. Various rules on the conditions for takeover are possible (e.g. Kale and Noe 1997). Of interest to us is the case where the takeover will proceed if and only if the proportion of shareholders willing to sell reaches some threshold. Moreover, it must be the case that no shares are sold if the threshold is not met while all shares are compulsorily purchased if the threshold is met. This is an all-or-nothing, restricted-conditional offer (Holmström and Nalebuff 1992).Footnote 6 Again, properties (1a) and (2a) are trivially satisfied and so the focus is on property (2b). For a forced contribution game we require that there are some legal, anticipatory, or other costs that mean a person would prefer not to offer to sell if the takeover will not take place.
As a final example, consider a political party deciding whether to endorse a particular policy. Suppose the policy is unpopular with voters but ultimately beneficial for the party. Also suppose that party will adopt the policy if and only if sufficiently many members back it. If the policy is not adopted then one could reasonably expect that only those members of the party who were seen to promote the policy will incur a cost with voters. If, however, the policy is adopted and becomes party policy then it is likely that all members of the party will incur a cost. This makes it a forced contribution game.
The preceding examples illustrate that the forced contribution game is of practical relevance, even though we would not want to argue it is the most commonly observed type of threshold public good game. The examples also illustrate that enforcing contributions is a practical possibility in numerous situations. Our analysis will provide insight on when this possibility is worth pursuing. In particular, enforcing contributions is likely to be costly to implement and so it is crucial to know whether enforcement will lead to high efficiency.Footnote 7
As a final preliminary we highlight that an important contribution of the current paper is to apply impulse balance theory in a novel context. Impulse balance theory, which builds on learning direction theory, says that players will tend to change their behavior in a way that is consistent with ex-post rationality (Selten and Stoeker 1986; Selten 1998, 2004; Ockenfels and Selten 2005; Selten and Chmura 2008, see also Cason and Friedman 1997, 1999). In Alberti et al. (2013) we apply impulse balance to look at continuous threshold public good games. Here we focus on the binary forced contribution game. As already previewed, we find that impulse balance successfully predicts observed efficiency. This is clearly a positive finding in evaluating the merit of impulse balance theory.Footnote 8 It should be noted, however, that the predictive power of impulse balance is dependent on its one degree of freedom, an issue we discuss more below.
We proceed as follows: in Sect. 2 we describe the forced contribution game. In Sect. 3 we provide some theoretical preliminaries, in Sect. 4 we describe three models to predict efficiency and in Sect. 5 we compare the three models predictions. In Sect. 6 we report our experimental results and in Sect. 7 we conclude.
2 Forced contribution game
In this section we describe the forced contribution threshold public good game. There is a set of players \(N=\left\{ 1,\ldots ,n\right\} \). Each player is endowed with E units of private good. Simultaneously, and independently of each other, every player \(i\in N\) chooses whether to contribute 0 or to contribute E towards the provision of a public good. Note that this is a binary, all or nothing, decision. For any \(i\in N\), let \(a_{i}\in \left\{ 0,1\right\} \) denote the action of player i, where \(a_{i}=0\) indicates his choice to contribute 0 and \(a_{i}=1\) indicates his choice to contribute E . Action profile \(a=\left( a_{1},\ldots ,a_{n}\right) \) details the action of each player. Let A denote the set of action profiles. Given action profile \(a\in A\), let
denote the number of players who contribute E.
There is an exogenously given threshold level \(1<t<n\).Footnote 9 The payoff of player i given action profile a is
where \(V>E\) is the value of the public good. So, if t or more players contribute E then the public good is provided and every player gets a return of V. In interpretation, every player is forced to contribute E irrespective of whether they chose to contribute 0 or E. If less than t players contribute E then the public good is not provided and there is no refund for a player who chose to contribute E.Footnote 10
For any player \(i\in N\) the strategy of player i is given by \(\sigma _{i}\in [0,1]\) where \(\sigma _{i}\) is the probability with which he chooses to contribute E (and \(1-\sigma _{i}\) is the probability with which he chooses to contribute 0). Let \(\sigma =\left( \sigma _{1},\ldots ,\sigma _{n}\right) \) be a strategy profile. With a slight abuse of notation we use \( u_{i}\left( \sigma _{i},\sigma _{-i}\right) \) to denote the expected payoff of player i given strategy profile \(\sigma \), where \(\sigma _{-i}\) lists the strategies of every player except i.
3 Theoretical preliminaries
We say that a strategy profile \(\sigma =\left( \sigma _{1},\ldots ,\sigma _{n}\right) \) is symmetric if \(\sigma _{i}=\sigma _{j}\) for all \(i,j\in N\). Given that choices are made simultaneously and independently it is natural to impose a homogeneity assumption on beliefs (Rapoport 1987; Rapoport and Eshed-Levy 1989).Footnote 11 This justifies a focus on symmetric strategy profiles. Symmetric strategy profiles \(\sigma ^{0}=\left( 0,\ldots ,0\right) \) and \(\sigma ^{1}=\left( 1,\ldots ,1\right) \) will prove particularly important in the following. We shall refer to \(\sigma ^{0}\) as the zero contribution strategy profile and \( \sigma ^{1}\) as the full contribution strategy profile.
Any symmetric strategy profile \(\sigma =\left( \sigma _{1},\ldots ,\sigma _{n}\right) \) can be summarized by real number \(p\left( \sigma \right) \in [0,1]\) where \(p\left( \sigma \right) =\sigma _{1}=\cdots =\sigma _{n}\). In interpretation, \(p(\sigma )\) is the probability that each player independently chooses to contribute E. Where it shall cause no confusion we simplify notation by writing p instead of \(p\left( \sigma \right) \). Given symmetric strategy profile \(\sigma \), the expected payoff of player i if he chooses, ceteris paribus, to contribute E is
If he chooses to contribute 0 his expected payoff is
Note that player i’s expected payoff from strategy profile \(\sigma \) is
The following function will prove useful in the subsequent analysis,
To illustrate, Fig. 1 plots \(\Delta (p)\) for \(p\in [0,1]\) when \( n=5,t=3,E=6\) and \(V=13\). If \(\Delta \left( p\right) <0\) then player i’s expected payoff is highest if he chooses to contribute 0. If \(\Delta \left( p\right) =0\) then player i is indifferent between choosing to contribute 0 and E. Finally, if \(\Delta \left( p\right) >0\) then player i’s expected payoff is highest if he chooses to contribute E.
3.1 Nash equilibrium
Previous theoretical analysis of binary threshold public good games has largely focussed on Nash equilibria (see, in particular, Palfrey and Rosenthal 1984). The set of Nash equilibria for the forced contribution game has not, however, been explicitly studied and so we begin the analysis by considering this. Strategy profile \(\sigma ^{*}=\left( \sigma _{1}^{*},\ldots ,\sigma _{n}^{*}\right) \) is a Nash equilibrium if and only if \( u_{i}\left( \sigma _{i}^{*},\sigma _{-i}^{*}\right) \ge u_{i}\left( s,\sigma _{-i}^{*}\right) \) for any \(s\in [0,1]\) and all \(i\in N\) . In the following we focus on symmetric Nash equilibria.Footnote 12
The set of symmetric Nash equilibria is easily discernible from the function \(\Delta (p)\). To illustrate, consider again Fig. 1. In this example there are three Nash equilibria. The zero contribution strategy profile \(\sigma ^{0}\) is a Nash equilibrium because \(\Delta (0)<0\). The ‘mixed’ strategy profile \(\sigma ^{m}\) where \(p\left( \sigma ^{m}\right) =0.43\), and the full contribution strategy profile \(\sigma ^{1}\) are also Nash equilibria because \(\Delta (0.43)=\Delta (1)=0\).
Our first result shows that Fig. 1 is representative of the general case (see also Rapoport 1987).
Proposition 1
For any value of \(V>E\) and \(n>t>1\) there are three symmetric Nash equilibria: (i) the zero contribution strategy profile \(\sigma ^{0}\), (ii) a mixed strategy profile \(\sigma ^{m}\) where \(p\left( \sigma _{i}^{m}\right) \in (0,1)\), (iii) the full contribution strategy profile \(\sigma ^{1}\).
Proof
For \(p=0\) it is simple to show that \( \Delta \left( p\right) =-E\). This proves part (i) of the proposition. For \( p=1\) it is simple to show that \(\Delta \left( p\right) =0\). This proves part (iii) of the proposition. In order to prove part (ii) consider separately the two terms in \(\Delta (p)\) by writing \(\Delta (p)=V\alpha (p)-E\beta (p)\) . Term \(\alpha (p)\) is the probability that exactly \(t-1\) out of \(n-1\) players contribute E and so it takes a bell shape. Formally, \(\alpha (0)=0,\alpha (1)=0\) and
implying \(\frac{d}{dp}\alpha \left( p\right) \gtrless 0\) for \(p\lessgtr \frac{t-1}{n-1}\). Term \(\beta (p)\) is the probability \(t-1\) or less of \(n-1\) players contribute E and so is a decreasing function of p. Formally, \( \beta (0)=1,\beta (1)=0\) and
For \(p<1\) it is clear that \(\alpha \left( p\right) <\beta \left( p\right) \). As \(p\rightarrow 1\) we know \(\beta \left( p\right) -\alpha \left( p\right) \rightarrow 0\). Given that \(V>E\) this means there exists some \({\overline{p}} \in (0,1)\) such that \(\Delta \left( {\overline{p}}\right) >0\). This proves part (ii) of the theorem. Note that we have also done enough to show that there exists a unique value \(p^{*}\in (0,1)\) where \(\Delta \left( p^{*}\right) =0\). \(\square \)
Proposition 1 shows that there are multiple symmetric Nash equilibria. In the following section we shall consider and contrast three possible approaches to predict which, if any, of these equilibria are most likely to occur. Before doing that let us briefly comment on the experimental evidence concerning \(\Delta \left( p\right) \). Rapoport (1987) and Rapoport and Eshed-Levy (1989) proposed the relatively weak hypothesis (their monotonicity hypothesis) that a player is more likely to contribute the higher is \(\Delta \left( p\right) \). Rapoport and Eshed-Levy (1989) experimentally elicit subjects beliefs in order to test this hypothesis and find only weak support for it. Offerman et al. (2001) obtain similar results. The challenge, therefore, is to develop a model that can not only predict outcomes but also capture the forces behind individual choice.
4 Main theoretical analysis
In this section we describe three alternative approaches to ‘predict’ behavior in a forced contribution game. The three alternatives are based on ordinal potential, logit equilibrium and impulse balance theory.
4.1 Ordinal potential
A potential game is one in which a single function, called the ordinal potential of the game, can capture the change in payoff that any player obtains from a unilateral change in action (Monderer and Shapley 1996). Examples of potential games include the minimum effort game, Cournot quantity competition and congestion games (e.g. Rosenthal 1973). If a game is a potential game then the set of Nash equilibria can be refined by finding the Nash equilibria that maximize potential (Monderer and Shapley 1996). We now demonstrate that this idea can be applied to the forced contribution game.
Using the definition of Monderer and Shapley (1996), see their equation (2.1), function \(W:A\rightarrow {\mathbb {R}} \) is an ordinal potential of the forced contribution game if for every \(i\in N\) and \(a\in A\)
Our next result shows that the forced contribution game admits an ordinal potential and is, therefore, a potential game. Moreover, the full contribution strategy profile maximizes potential. In this sense the full contribution Nash equilibrium is ‘selected’.
Proposition 2
The forced contribution game is a potential game and the ordinal potential is maximized at the full contribution strategy profile \(\sigma ^{1}\).
Proof
The aggregate payoff, given action profile \(a=\left( a_{1},\ldots ,a_{n}\right) \), is
If W is an ordinal potential then the potential is maximized for \(c(a)\ge t\). In order to verify that W is an ordinal potential there are five cases to consider:
-
(i)
If \(c\left( a\right) >t\) or \(c(a)=t\) and \(a_{i}=0\) then \(c\left( 1-a_{i},a_{-i}\right) \ge t\) implying \(u_{i}\left( a_{i},a_{-i}\right) =u_{i}\left( 1-a_{i},a_{-i}\right) =V\) and \(W(a_{i},a_{-i})=W\left( 1-a_{i},a_{-i}\right) =nV\).
-
(ii)
If \(c\left( a\right) =t\) and \(a_{i}=1\) then \(c\left( 1-a_{i},a_{-i}\right) =t-1\) implying \(u_{i}\left( a_{i},a_{-i}\right) =V>u_{i}\left( 1-a_{i},a_{-i}\right) =E\) and \(W(a_{i},a_{-i})=nV>W\left( 1-a_{i},a_{-i}\right) =E\left( n-t+1\right) \).
-
(iii)
If \(c\left( a\right) =t-1\) and \(a_{i}=0\) then \(c\left( 1-a_{i},a_{i}\right) =t\) implying \(u_{i}\left( a_{i},a_{-i}\right) =E<u_{i}\left( 1-a_{i},a_{-i}\right) =V\) and \(W(a_{i},a_{-i})=E\left( n-t+1\right) <W\left( 1-a_{i},a_{-i}\right) =nV\).
-
(iv)
If \(c\left( a\right) \le t-1\) and \(a_{i}=1\) then \(u_{i}\left( a_{i},a_{-i}\right) =0<u_{i}\left( 1-a_{i},a_{-i}\right) =E\) and \( W(a_{i},a_{-i})=E\left( n-c(a)\right) <W\left( 1-a_{i},a_{-i}\right) =E\left( n-c\left( a\right) +1\right) \).
-
(v)
If \(c\left( a\right) <t-1\) and \(a_{i}=0\) then \(u_{i}\left( a_{i},a_{-i}\right) =E>u_{i}\left( 1-a_{i},a_{-i}\right) =0\) and \( W(a_{i},a_{-i})=E\left( n-c(a)\right) >W\left( 1-a_{i},a_{-i}\right) =E\left( n-c\left( a\right) -1\right) \). \(\square \)
With a slight abuse of terminology we shall interpret Proposition 2 as saying ordinal potential predicts perfect efficiency in the forced contribution game. Interestingly, this prediction is consistent with the prior experimental evidence (Dawes et al. 1986; Rapoport and Eshed-Levy 1989). However, while Monderer and Shapley (1996) show that ordinal potential can be used to refine the set of Nash equilibria they also openly admit that they have no explanation for why ordinal potential would be maximized. So, to paraphrase Monderer and Shapley (p. 136), ‘it may be just a coincidence’ that ordinal potential is consistent with the prior evidence. The conjecture that ordinal potential can predict behavior in the forced contribution game needs a more rigorous empirical test.
4.2 Logit equilibrium
Quantal response provides a way to model behavior that allows for ‘noisy’ decision making (McKelvey and Palfrey 1995). In particular, quantal response equilibrium (QRE) is a generalization of Nash equilibrium that allows for mistakes or random perturbations to payoffs, while maintaining an assumption of rational expectations. QRE has proved successful in explaining deviations from Nash equilibrium in a number of settings including auctions and coordination games (Goeree et al. 2008). Offerman et al. (1998) apply a quantal response model to a no refund threshold public good game (see also Goeree and Holt 2005).Footnote 13 Here we apply the approach to a forced contribution game. Specifically, we consider the logit equilibrium (McKelvey and Palfrey 1995).
Symmetric contribution profile \(\sigma \) is a logit equilibrium if
for any player \(i\in N\) where \(\gamma \ge 0\) is a parameter. In interpretation, \(\gamma \) is inversely related to the level of error, where error can be thought of as resulting from random mistakes in calculating expected payoff.Footnote 14 Figure 2 plots the logit equilibria for the example \(n=5,t=3,E=6\) and \(V=13\) . We see that there is a unique equilibrium for small \(\gamma \) (i.e. a high level of error) and three equilibria for large \(\gamma \). If there is no error (\(\gamma \rightarrow \infty \)) the set of logit equilibria coincides with the set of Nash equilibria (Tumennasan 2013). The higher the level of error (the smaller is \(\gamma \)) the more the set of logit equilibria diverges from the set of Nash equilibria.
One criticism of quantal response is that it can rationalize any behavior (Haile et al. 2008, see also Goeree et al. 2005). This criticism does not always apply to logit equilibrium but it is a concern in our case. In Fig. 2, for instance, we see that just about any value of p is consistent with logit equilibrium. To obtain a testable prediction we, therefore, need to either fix \(\gamma \) or restrict attention to a particular set of logit equilibria. We shall focus on the latter option here (although in the data analysis we also explore the former option). McKelvey and Palfrey (1995) demonstrate that a graph of the logit equilibrium can be used to select a Nash equilibrium. Specifically, the graph of logit equilibria contains a unique branch starting at 0.5 and converging to a Nash equilibrium as \(\gamma \rightarrow \infty \).Footnote 15 The resultant Nash equilibrium is called the limiting logit equilibrium. If players are initially inexperienced (\(\gamma \) is near 0) and become more experienced over time (\(\gamma \) increases) then one can argue play should move along this branch of equilibria towards the limiting logit equilibria (McKelvey and Palfrey 1995). Offerman et al. (1998) found that their experimental data did lay on the branch starting at 0.5, although there was little evidence of learning with experience.
In the example of Fig. 2 the limiting logit equilibrium is the full contribution Nash equilibrium \(\sigma ^{1}\). For different parameter values the limiting logit equilibrium can be the zero contribution Nash equilibrium \(\sigma ^{0}\). To illustrate, Fig. 3 plots the logit equilibria when \( n=7,t=5,E=6\) and \(V=13\). The proceeding examples demonstrate that the limiting logit equilibrium can be \(\sigma ^{0}\) or \(\sigma ^{1}\) depending on the parameters of the game. We shall pick up on this point further in Sect. 5. For now we note that (for fixed values of n, t and E) there exists a critical value \({\widetilde{V}}\) such that \(\sigma ^{0}\) is the limiting logit equilibrium for \(V<{\widetilde{V}}\) and \(\sigma ^{1}\) is the limiting logit equilibrium for \(V>{\widetilde{V}}\). We highlight that this critical value is also relevant for interpreting the branch of logit equilibria starting at 0.5. More specifically, if we restrict attention to this branch of equilibria then, for any \(\gamma \), the logit equilibrium value of p is less than 0.5 if \(V<{\widetilde{V}}\) and greater than 0.5 if \(V>{\widetilde{V}}\).
4.3 Impulse balance theory
A key contribution of the current paper is to apply impulse balance theory. Impulse balance theory provides a quantitative prediction on outcomes based on ex-post rationality (Ockenfels and Selten 2005; Selten and Chmura 2008; Chmura et al. 2012). It posits that a player who could have gained by playing a different action will have an impulse to change his action the next time he plays the game. The size of impulse is proportional to the difference between the payoff he could have received and the one he did. The player is said to have an upward or downward impulse depending on whether a ‘higher’ or ‘lower’ action is ex-post rational. At a (weighted) impulse balance equilibrium the expected upward and (weighted) downward impulse are equalized. Impulse balance theory has been applied in many contexts including first price auctions, the newsvendor game and minimum effort game (Ockenfels and Selten 2005, 2014, 2015; Goerg et al. 2016).
To apply impulse balance theory to a forced contribution game we need to determine the direction and strength of impulse of each player for any action profile (Selten 1998). In order to do this we distinguish the four experience conditions defined below. Take as given an action profile \( (a_{1},\ldots ,a_{n})\) and a player \(i\in N\). Let \({\overline{u}}_{i}=u_{i}\left( a_{i},a_{-i}\right) \) denote the realized payoff of player i and let \( {\overline{gu}}_{i}=u_{i}\left( 1-a_{i},a_{-i}\right) \) denote the payoff player i would have got from choosing the alternative action.
Zero no: Player i faces the zero no experience condition if \(c(a)<t-1\) and \(a_{i}=0\). In this case \({\overline{u}}_{i}=E\) and \({\overline{gu}}_{i}=0\). Given that \({\overline{gu}}_{i}<{\overline{u}}_{i}\) we say that player i has no impulse. Equivalently, the strength of impulse is 0.
Wasted contribution: Player i faces the wasted contribution experience condition if \(c(a)\le t-1\) and \(a_{i}=1\). In this case \({\overline{u}}_{i}=0\) while \({\overline{gu}}_{i}=E>0\). We say that player i has a downward impulse of strength \({\overline{gu}}_{i}-{\overline{u}}_{i}=E\).
Lost opportunity: Player i faces the lost opportunity experience condition if \(c(a)=t-1\) and \(a_{i}=0\). In this case \( {\overline{u}}_{i}=E\) while \({\overline{gu}}_{i}=V>E\). We say that player i has an upward impulse of strength \({\overline{gu}}_{i}-{\overline{u}}_{i}=V-E\).
Spot on: Player i faces the spot on experience condition if \(c(a)\ge t\). In this case \({\overline{u}}_{i}=V\) and \({\overline{gu}}_{i}\le V\) so we say player i has no impulse.
The direction and size of impulse for each of the experience conditions are summarized in Table 1.
We can now define expected upward and downward impulse. In doing this we retain a focus on symmetric strategy profiles. The upward impulse of player \(i\in N\) comes from the lost opportunity experience condition. So, given a symmetric strategy profile \(\sigma \) the expected upward impulse of player i is
We note at this point that
implying that
Thus, the upward impulse is an inverse U shaped function of p (on interval [0, 1]). To illustrate, Fig. 4 plots \(I^{+}(p)\) (and \(I^{-}(p)\) to be defined shortly) for the example \(n=5,t=3,E=6\) and \(V=13\).
The expected downward impulse of player i comes from the wasted contribution experience condition. It is given by
Note that
and so the downward impulse is also an inverse U shaped function of p. Moreover,
implying that the maximum downward impulse occurs for a lower value of p than the maximum upward impulse. This is readily apparent in Fig. 4.
Symmetric strategy profile \(\sigma ^{*}\) is a weighted impulse balance equilibrium if \(I^{+}(p\left( \sigma ^{*}\right) )=\lambda I^{-}(p\left( \sigma ^{*}\right) )\), where \(\lambda \) is an exogenously given weight on the downward impulse. Note that a value of \(\lambda <1\) indicates that, in equilibrium, the downward impulse must be larger than the upward impulse. In interpretation this would suggest that players are less responsive in the wasted contribution condition than the lost opportunity condition. This could reflect a desire to contribute or to provide the public good which is not captured in monetary payoffs (Rapoport 1987). Under this interpretation \( \lambda \) is a ‘psychological’ parameter to be estimated empirically from individual behavior (Ockenfels and Selten 2005).
We shall say that an impulse balance equilibrium \(\sigma ^{*}\) is stable if \(I^{+}(p)>\lambda I^{-}\left( p\right) \) for \(p\in (p\left( \sigma ^{*}\right) -\varepsilon ,p\left( \sigma ^{*}\right) )\) and \( I^{+}(p)<\lambda I^{-}\left( p\right) \) for \(p\in (p\left( \sigma ^{*}\right) ,p\left( \sigma ^{*}\right) +\varepsilon )\) for some \( \varepsilon >0\).Footnote 16 Otherwise we say the equilibrium is unstable. Intuitively, an equilibrium is stable if a small deviation from the equilibrium does not result in impulses that drive strategies further away from the equilibrium. In Fig. 4, where \( \lambda =1\), there are two stable impulse balance equilibria: (i) the zero strategy profile \(\sigma ^{0}\), and (ii) full contribution strategy profile \( \sigma ^{1}\). There is also (iii) an unstable mixed strategy equilibrium \( \sigma ^{m}\) where \(p\left( \sigma ^{m}\right) =0.25\). Note that this mixed strategy impulse balance equilibrium takes a different value of p to the mixed strategy Nash equilibrium.
We are now in a position to state our main theoretical result.
Proposition 3
-
(a)
If \(V\le \overline{ V}\left( \lambda \right) \) where
$$\begin{aligned} {\overline{V}}\left( \lambda \right) =\frac{E\left( n-\left( t-1\right) \left( 1-\lambda \right) \right) }{n-t+1} \end{aligned}$$then there are two impulse balance equilibria: the zero strategy profile \( \sigma ^{0}\) is a stable equilibrium, and the full contribution strategy profile \(\sigma ^{1}\) is an unstable equilibrium.
-
(b)
If \(V>{\overline{V}}\left( \lambda \right) \) and \(t\ge 3\) there are three impulse balance equilibria: the zero strategy profile \(\sigma ^{0}\) is a stable equilibrium, the full contribution strategy profile \(\sigma ^{1}\) is a stable equilibrium, and there is an unstable mixed strategy equilibrium \(\sigma ^{m}\) where \(p\left( \sigma ^{m}\right) \in \left( 0,1\right) \).
-
(c)
If \(V>{\overline{V}}\left( \lambda \right) \) and \(t=2\) there are two impulse balance equilibria: the zero strategy profile \(\sigma ^{0}\) is an unstable equilibrium, and the full contribution strategy profile \(\sigma ^{1}\) is a stable equilibrium.
Proof
Let \(C_{k}^{\nu }=\left( {\begin{array}{c}\nu \\ k\end{array}}\right) \) and let
denote the difference between upward and downward impulse. We have
Symmetric strategy profile \(\sigma \) is an impulse balance equilibrium if and only if \(DI\left( p\left( \sigma \right) \right) =0\). If \(p=0\) then \( DI\left( p\right) =0\) implying the zero strategy profile is an impulse balance equilibrium. If \(p=1\) then \(DI\left( p\right) =0\) implying the full contribution strategy profile is also an impulse balance equilibrium.
Suppose for now that \(t\ge 3\). Then
If \(V\le {\overline{V}}\) then \(DI\left( p\right) <0\) for all \(p\in (0,1)\). This implies that there is no mixed strategy impulse balance equilibrium. It also implies that the zero strategy profile is stable and the full contribution strategy profile is unstable.
If \(V>{\overline{V}}\) we need look in more detail at
It is simple to see that \(G(0)<0\) and \(G(1)>0\). Continuity of G(p) implies at least one value \(p^{*}\in \left( 0,1\right) \) such that \(G\left( p^{*}\right) =0\). At \(p^{*}\) we obtain an impulse balance equilibrium. Moreover, we obtain stable equilibria corresponding to \(p=0\) and \(p=1\).
It remains to consider the case \(t=2\). Now
As before, if \(V\le {\overline{V}}\) then \(DI\left( p\right) <0\) for all \(p\in (0,1)\). In this case there are two equilibria, the zero strategy profile is stable and the full contribution strategy profile is unstable. If \(V> {\overline{V}}\) then \(DI\left( p\right) >0\) for all \(p\in (0,1)\). In this case there are still only two equilibria but the zero strategy profile is unstable and the full contribution strategy profile is stable. \(\square \)
Proposition 3 shows that if \(V\le {\overline{V}}\left( \lambda \right) \) then impulse balance theory gives a sharp prediction—the zero strategy profile is the unique stable impulse balance equilibrium. If \(V> {\overline{V}}\left( \lambda \right) \) then, with the exception of the extreme case \(t=2\), we obtain a less sharp prediction - both the zero and full contribution equilibria are stable. In this case we shall hypothesize that play converges to the Pareto optimal, full contribution, impulse balance equilibrium. Given this hypothesis, we shall informally say that impulse balance theory predicts perfect efficiency if \(V>{\overline{V}}\left( \lambda \right) \) and zero contributions if \(V\le {\overline{V}}\left( \lambda \right) .\)
In justifying our hypothesis that play will converge on the Pareto optimal impulse balance equilibrium we first emphasize that this hypothesis differs from saying play will converge on the Pareto optimal Nash equilibrium. To appreciate this point note that the full contribution strategy profile is the Pareto optimal Nash equilibrium for any \(V>E\). So, the Pareto optimal stable impulse balance equilibrium is the same as the Pareto optimal Nash equilibrium if and only if \(V>{\overline{V}}\left( \lambda \right) \). If \(V\le {\overline{V}}\left( \lambda \right) \) the Pareto optimal stable impulse balance equilibrium is the zero strategy profile while the Pareto optimal Nash equilibrium is the full contribution strategy profile. Our approach, therefore, makes a testable prediction. Moreover, our approach is not inconsistent with the evidence that play in many games, such as the minimum effort game, does not converge to the Pareto optimal Nash equilibrium. It remains an open question whether play converges on Pareto optimal, stable impulse balance equilibria. For further insight on this issue we quote from Harsanyi and Selten (1988, p. 356), ‘[O]ur theory in general gives precedence to payoff dominance. ... [P]ayoff dominance is based on collective rationality: it is based on the assumption that in the absence of special reasons to the contrary, rational players will choose an equilibrium point yielding all of them higher payoffs, rather than one yielding them lower payoffs’. Essentially, we are suggesting that instability of the full contribution equilibrium counts as ‘special reasons to the contrary’.
5 Comparing model predictions
Having introduced three alternative approaches of modelling behavior in the forced contribution game we will now demonstrate that they can give very different predictions. To do so we begin by analyzing the four games detailed in Table 2. This analysis will serve to illustrate the stark differences between model predictions. Our focus is on games with \(n=5\) or 7 players where we vary V keeping \(E=6\) and \(n-t=2\) fixed. When comparing models we shall focus on predicted efficiency measured by the probability of the public good being provided.Footnote 17
Ordinal potential (see Proposition 2) predicts perfect efficiency for all four games. Consider next quantal response. For \(n=5\) and \(t=3\) one can show numerically that the full contribution strategy profile is the limiting logit equilibrium if and only if \(V>{\widetilde{V}}\) where \( {\widetilde{V}}\approx 11\). Otherwise, the zero strategy profile is the limiting logit equilibrium. For \(n=7\) and \(t=5\) the analogous cut-off point is \({\widetilde{V}}\approx 22.8\). Only in the few-large game, therefore, efficiency is predicted to be high. This prediction does not change significantly if we consider (non-limiting) logit equilibria (on the branch of equilibria starting at 0.5). To illustrate, Table 3 details predicted efficiency for a range of values of \(\gamma \). There is clearly a stark contrast between the predictions obtained using ordinal potential and quantal response. Note that Offerman et al. (1998) obtained fitted estimates of \(\gamma \) between 0.001 and 0.34 in threshold public good games (while McKelvey and Palfrey (1995) obtain estimates of \(\gamma \) consistently above 0.2 and as a high as 3).
Consider next impulse balance and the case \(n=5\) and \(t=3\). From Proposition 3 we know that the full contribution strategy profile \(\sigma ^{1}\) is a stable impulse balance equilibrium if and only if
So, if \(V=7\) (recalling \(E=6\)) the equilibrium \(\sigma ^{1}\) is stable if and only if \(\lambda <0.25\). If \(V=13\) the equilibrium \(\sigma ^{1}\) is stable if and only if \(\lambda <\frac{7}{4}\). When \(n=7\) and \(t=5\) we obtain analogous condition
So, if \(V=7\) the equilibrium \(\sigma ^{1}\) is stable if and only if \(\lambda <\frac{1}{8}\) and if \(V=13\) it is stable if and only if \(\lambda <\frac{7}{8} \).
Prior estimates of \(\lambda \) are in the range of 0.3 to 1 (Ockenfels and Selten 2005, Alberti et al. 2013). Recall, that we predict play will converge to the full contribution equilibrium if and only if it is stable. Table 4 summarizes predicted efficiency for five different values of \(\lambda \). Efficiency is predicted to be high in the few-large game and low in the many-small game. In the few-small and many-large game predictions depend on \(\lambda \). Comparing Tables 3 and 4 we see that predicted efficiency with impulse balance lies somewhere in-between the extremes obtained with ordinal potential and quantal response.
Having looked at the four games above as illustrative examples let us now turn to the general setting. We have already shown (Proposition 2) that ordinal potential gives the ‘optimistic’ prediction of perfect efficiency. We have also shown (Proposition 3) that impulse balance gives a less optimistic prediction of zero efficiency if \(V<{\overline{V}}\left( \lambda \right) \). While a general prediction for quantal response is not possible, one can show numerically that it gives the least optimistic prediction. In particular, the critical value above which \(\sigma ^{1}\) is the limiting logit equilibrium is greater than the critical value above which \(\sigma ^{1} \) is a stable impulse balance equilibrium, \({\widetilde{V}}>{\overline{V}} \left( \lambda \right) \) for \(\lambda \le 1\). This is clear in the examples, and illustrated more generally in Fig. 5.
Figure 5 plots the critical values \({\overline{V}}\left( \lambda \right) /E\) and \({\widetilde{V}}/E\) above which the full contribution equilibrium \(\sigma ^{1}\) is a stable impulse balance equilibrium (for \(\lambda =0.2\) and 1) and a limiting logit equilibrium. We consider 6 possible values of n and all relevant values of t. As one would expect, the higher is the threshold t the higher has to be the return on the public good V in order to predict full efficiency. The main thing we wish to highlight is that \( {\widetilde{V}}>{\overline{V}}\left( 1\right) \) across the entire range of n and t. In other words, there are always values of V where the full contribution strategy profile is a stable impulse balance equilibrium but not the limiting logit equilibrium. This gap between \({\widetilde{V}}\) and \( {\overline{V}}\left( 1\right) \) widens the higher is t.
Recall, see the introduction, that forced contributions have been suggested as a means to promote efficiency in public good games. This conjecture is consistent with the predictions of ordinal potential but not of impulse balance or quantal response. It is natural, therefore, to want to test which model is more powerful at predicting observed efficiency, and to explore whether efficiency can be low despite forced contributions. That motivates the experiments that we shall discuss shortly. Before doing that we briefly comment on experimental results from the previous literature.
Table 5 summarizes the forced contribution experiments reported by Dawes et al. (1986) and Rapoport and Eshed-Levy (1989).Footnote 18 For the game in experiment 1 of Dawes et al. (1986) and that of Rapoport and Eshed-Levy (1989) all three approaches we have considered predict high efficiency and this is what was observed. Experiment 2 of Dawes et al. (1986) is more interesting in that the zero contribution profile is the limiting logit equilibrium while the full contribution profile is a stable impulse balance equilibrium for low values of \(\lambda \) (but not for values of \(\lambda \) near 1). The observed high efficiency appears inconsistent with the former prediction. It is difficult, however, to infer much from this one experiment. We shall now introduce our experiments, which provide a more detailed test of the three models.
6 Experiment design and results
Our experiment was designed to test the predictive power of the three theoretical approaches discussed above. In order to do this we used a between subject design in which the four games introduced in Table 2 were compared. This gives four treatments corresponding to the four games.
Subjects were randomly assigned to a group and interacted anonymously via computer. We used z-Tree (Fischbacher 2007). The instructions given to subjects were game specific, in detailing n, t and V, and so subjects could not have known that these differed across groups. In order to observe dynamic effects subjects played the game for 30 periods in fixed groups. The instructions given to subjects are available in the appendix. As detailed in Table 6, we observed a total of 27 groups and 155 subjects. A typical session lasted 30–40 min and the average payoff was £9.
6.1 Observed efficiency
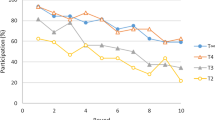
Table 7 summarizes average efficiency (measured by the proportion of periods out of 30 the public good was provided) in the four treatments. In interpreting these numbers we highlight that in the last 10 periods, every group provided the public good either (i) 8, 9 or 10 times or (ii) 0 or 1 time. We observed, therefore, a very clear distinction between groups that, we shall say, converged on efficiency and those that converged on inefficiency. (Group specific data is provided in Table 10 in the appendix). This means that observed efficiency in periods 21–30 is essentially measuring the proportion of groups that converged on efficiency.
In the few-large treatment efficiency was very high, with 7 of the 8 groups converging on efficiency. This result is consistent with the predictions derived from all three theoretical approaches. In the many-small treatment efficiency was very low, with all of the 5 groups converging on inefficiency. Efficiency was significantly lower than in all other treatments (\(p\le 0.02\), proportions test).Footnote 19 This matches the predictions derived from impulse balance and quantal response but not that of ordinal potential. Let us remark at this point that the very low efficiency we observed in the many-small treatment is clear evidence that enforcing contributions does not guarantee high efficiency.
In the few-small and many-large treatments efficiency was not as high as that in the few-large treatment but the differences are statistically insignificant (\(p>0.15\), proportions test). A total of 7 out of 9 and 3 out of 5 groups, respectively, converged on efficiency. The success rate in the many-large treatment did decline over the 30 periods (\(p=0.02\), LR test). Even if we focus on periods 11 to 30, however, the differences between the many-large, few-small and few-large treatments are insignificant (\(p>0.1\), proportions test). The relatively high level of efficiency in the few-small and many-large treatments matches our predictions derived from ordinal potential and impulse balance (provided the weight on the downward impulse is within the bound, \(0.125<\lambda <0.25\)) but not that from quantal response.
The proceeding discussion suggests that the approach most consistent with observed efficiency across all four games is impulse balance. Ordinal potential does not capture the low efficiency in the many-small treatment and quantal response does not capture the high efficiency in the few-small and many-small treatments. This interpretation, however, is focussed primarily on limiting logit equilibria. Moreover, the predictive power of impulse balance is dependent on \(\lambda \) being relatively small. We shall now look at each of these issues in turn in the following two sections.
6.2 Goodness of fit
Both impulse balance and quantal response have one degree of freedom, the weight on downward impulse \(\lambda \) and the inverse error rate \(\gamma \), respectively. Our claim that impulse balance is the only approach (of the three we consider) that is consistent with observed efficiency was based on \( 0.125<\lambda <0.25\) and \(\gamma =\infty \). In this section we consider alternative values of \(\gamma \) in order to give a fair comparison across models. Before we get to the analysis let us make one remark.
Recall that every group converged to either efficiency or inefficiency in terms of aggregate success at providing the public good. This is not the same as saying groups converged on the full contribution or zero contribution strategy profile. In some groups that were highly efficient (providing the public good 10 times in the last 10 periods) we see an average probability of contributing around 70–80%. Similarly, in some groups that were highly inefficient (never providing the public good in the last 10 periods) we see an average probability of contributing around 20–30%. (See Table 10 in the appendix for the full data.) The only stable impulse balance equilibria are the zero contribution and full contribution strategy profiles and so impulse balance suggests convergence on one of these equilibria. This, as we have said, was not the case in all groups. Quantal response, by contrast, is a story of noisy decision making and so can more easily accommodate non-convergence to the zero or full contribution strategy profiles.
Estimates of \(\gamma \) can be obtained for each treatment by finding the value of \(\gamma \) that fits the observed probability with which subjects contributed to the public good (Offerman et al. 1998). In estimating \(\gamma \) we do not restrict attention to the branch of equilibria starting at 0.5.Footnote 20 Table 8 provides the estimates of the \(\gamma \)s we obtain and the corresponding log likelihood. In the few-small treatment logit equilibria performs no better than a random model (in which each subject chooses to contribute E with probability 0.5). In the other three treatments logit equilibria does outperform a random model (\(p<0.001\), LR test). Clearly, however, the estimates of \(\gamma \) differ across treatments. While one can make the argument that \(\gamma \) (and \(\lambda \)) may vary across different experimental studies because of framing or subject effects it is harder to make this argument within a particular study. We, therefore, also solve for the value of \(\gamma \) that maximizes the likelihood of observed contributions across all four treatments. This is given by the aggregate estimate in Table 8. Interestingly, we do see evidence of \(\gamma \) increasing through the 30 periods (\(p<0.001\), LR test).
We now compare the predictive power of the three theoretical approaches. Following the method of Erev et al. (2010) we derive the mean squared deviation of observed from predicted values. We focus on predictions of group efficiency (proportion of times the public good is provided) and individual contributions (proportion of times a player chooses to contribute E). Table 9 presents the results (and Table 11 in an appendix provides the relevant observations and predictions). In terms of predicting group efficiency we see that impulse balance performs best, followed by the random model and then logit equilibrium. This is consistent with the analysis of the preceding section (Sect. 6.1). In terms of predicting individual contributions we see that logit equilibrium is best, followed by the random model and impulse balance. This is consistent with the preceding discussion on quantal responses ability to capture noisy decision making. In terms of overall performance we see that impulse balance is best, followed by the random model and logit equilibrium. Impulse balance does well because it can predict both efficiency and contributions relatively well.
6.3 Impulse and behavior
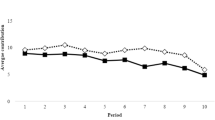
It remains to question why the weight on the downward impulse appears to be relatively low, \(\lambda <0.25\). To get some insight on this issue we shall look at how subjects changed contribution from one period to the next. Recall that impulse balance theory assumes players will change contribution based on ex-post rationality. We want to check whether subjects behaved consistent with this assumption. A relatively low weight on the downward impulse would imply that subjects are less responsive to a downward impulse than an upward impulse. Figure 6 details the proportion of players who changed contribution aggregating across all four treatments. We distinguish three cases. Recall that c(a) denotes the number of players who contributed E.
-
(i)
If \(c(a)<t-1\) then any player who contributed E has a downward impulse (because they face the wasted contribution experience condition) and any player who contributed 0 has no impulse (zero no). Consistent with this we see, in Fig. 6, a strong tendency for those who contributed E to reduce their contribution and a weak tendency for those who contributed 0 to increase their contribution.
-
(ii)
If \(c(a)=t-1\) then any player who contributed E has a downward impulse (wasted contribution) and any player who contributed 0 has an upward impulse (lost opportunity). Consistent with this we see a strong tendency for both those who contributed E and those who contributed 0 to change their contribution. Importantly, those who contributed 0 are more likely to increase contribution than those who contributed E are to decrease contribution. This is consistent with a low weight on the downward impulse and pushes the group towards successful provision of the public good in the next period.
-
(iii)
If \(c(a)\ge t\) then no player has an impulse (spot on). What we observe is a relatively strong tendency for those who contributed 0 to increase their contribution, particularly when \(c(a)=t\). This could be interpreted as a reaction to the ‘near-miss’ of the lost opportunity experience condition (Kahneman and Miller 1986; De Cremer and van Dijk 2011). The effect is to push the group towards sustained provision of the public good.
The proportion of subjects who changed contribution from one period to the next distinguishing by initial contribution and the number of players who contributed E. The number of observations is given in square brackets. Also, ZN denotes zero no, LO lost opportunity, SO spot on and WC wasted contribution
In all the three cases discussed above we observe that subjects change contribution consistent with ex-post rationality. Of particular note is that for \(c(a)\ge t-1\) we see a stronger tendency to increase than decrease contributions. This explains why we find that the weight on the downward impulse is relatively low. Not only, therefore, does impulse balance theory predict aggregate success rates it is also consistent with individual behavior.
7 Conclusion
In this paper we contrast three approaches to predicting efficiency in a forced contribution threshold public good game. The three approaches are based on ordinal potential, quantal response and impulse balance theory. We also report an experiment to test the respective predictions. We found that impulse balance theory provides the best overall predictions. The predictive power of impulse balance is, however, highly dependent on its one degree of freedom, the weight on the downward impulse, \(\lambda \). Our estimate of \( 0.125<\lambda <0.25\) is lower than those (\(\lambda =0.32\) and 0.37) obtained by Ockenfels and Selten (2005) or those (\(\lambda =0.5\) and 1) obtained by Alberti et al. (2013). We take the view that \( \lambda \) can differ depending on the game, and the framing of the game, and so different estimates of \(\lambda \) are not unexpected. Application of impulse balance theory is, though, almost entirely reliant on knowing the appropriate value of \(\lambda \) and so it should be a priority for future work to build a better understanding of the determinants of \(\lambda \).
To put our results in context we highlight that impulse balance theory allows us to derive a simple expression with which we can predict when forced contributions result in high or low efficiency. This prediction depends on the number of players n, threshold t, relative return to the public good V / E and weight on the downward impulse \(\lambda \). If we set \( \lambda =0.25\) then we get a prediction of high or low efficiency as
Thus, a ceteris paribus increase in the number of players lowers the critical value of the return to the public good. In other words, an increase in the number of players is predicted to enhance efficiency. Conversely, a ceteris paribus increase in the threshold is predicted to lower efficiency.
Consider next what happens if we fix the ratio between t and n at \( t=\alpha n\). Figure 7 plots the critical value of the return to the public good as a function of \(\alpha \). One can also derive that high efficiency is predicted if
High efficiency is predicted, therefore, provided t is not ‘too large’ a proportion of n. For example, if the relative return to the public good is 2 then we need \(\alpha \le 0.8\). This prediction is consistent with the high efficiency observed in previous forced contribution experiments (Dawes et al. 1986; Rapoport and Eshed-Levy 1989). It also shows, however, that enforcing contributions does not always lead to high efficiency. This is clearly demonstrated in our many-small treatment where \(\alpha =5/7\approx 0.71\), \(V/E=7/6\approx 1.17\) and efficiency is near zero.
Notes
Our focus in this paper will be on binary threshold public good games where people decide either to contribute or not towards the public good. The alternative, continuous threshold public good game, is that people can choose how much to contribute on a continuum (e.g. Suleiman and Rapoport 1992).
Property (1b) captures the notion of ‘forced’ contribution in that there is no gain from not volunteering to contribute to a public good that is provided. In specific situations, see for instance the example in the next paragraph, the term ‘forced’ need not be taken literally.
A further example, looking at a firm trying to acquire an apartment block for redevelopment, is considered by Dawes et al. (1986).
To provide some background: Consider a simple, any-and-all takeover bid where a raider offers to buy any shares sold but only takes over the company if sufficiently many shares (e.g. 50%) are sold. This structure does not give rise to a threshold public good game, let alone a forced contribution game. There are two basic reasons why a raider may not prefer an any-and-all bid. First, it can give incentives for shareholders to not sell in the hope the takeover will increase the value of the firm (Grossman and Hart 1980). A freezout rule is one way to overcome this problem (Amihud et al. 2004) and essentially involves forcing those who hold out to sell in the event of a takeover. A second issue is that the raider may end up buying shares and yet fall short of the threshold for ownership. One way to potentially overcome this problem is for the firm to only buy shares conditional on the takeover going ahead (e.g. Cadsby and Maynes 1998). An all-or-nothing bid involves both a freezout rule and conditional buying of shares (Bagnoli and Lipman 1988, see also Holmström and Nalebuff 1992).
Voting may be a simple solution to obtaining efficiency if forced contributions are possible. (We thank a referee for pointing this out.) Voting, however, may not be practicable. For instance, in the takeover example there may be no way to implement a binding vote. Moreover, as our first and third examples illustrate, if there is an asymmetry whereby voting ‘yes for the public good’ is more costly than voting no we still have a forced contribution game. This asymmetry may arise if abstention is treated as a no vote.
If \(t=n\) then we have the weak link game. If \(t=1\) then we have a form of best shot game. For simplicity we exclude these ‘special cases’ from the analysis.
To see how this description of the game relates to our earlier examples consider our first example of an incompetent manager. To get rid of the manager will require t or more colleagues to complain. Hence to complain can be interpreted as contributing towards the public good. If the manager is removed then everyone benefits and no one (including those who complained) will receive any recrimination. Let X denote payoffs in this case. If the manager is not removed then things carry on as before except that those who complained will receive recriminations. Let Y denote current payoffs and R the cost of recrimination. So,
$$\begin{aligned} u_{i}\left( a\right) =\left\{ \begin{array}{ll} X &{} \text { if }c(a)\ge t \\ Y-a_{i}R &{} \text { otherwise} \end{array} \right. . \end{aligned}$$To fit this into our framework, we can set \(E=R\) and \(V=X-Y+R\). This gives,
$$\begin{aligned} u_{i}\left( a\right) =\left\{ \begin{array}{ll} V+Y-R &{}\text { if }c(a)\ge t \\ E(1-a_{i})+Y-R &{}\text { otherwise} \end{array} \right. . \end{aligned}$$The linearity of payoffs means we can subtract the fixed term \(Y-R\).
See Offerman et al. (1996) for an alternative perspective.
There are many asymmetric Nash equilibria. For example, it is a Nash equilibrium for t players to contribute E (with probability 1) and \(n-t \) players to contribute 0 (with probability 1). If players have some form of pre-play communication such equilibria have been seen to arise in related games (Van de Kragt et al. 1983). If, however, players choose simultaneously and independently it is difficult to see how players could coordinate on such equilibria.
They also consider a naive Bayesian quantal response model.
Conventionally \(\lambda \) is used rather than \(\gamma \). We use \(\gamma \) to avoid confusion with a \(\lambda \) term used in impulse balance theory.
More formally, they state that it holds for ‘almost all games’. The games that we consider in this paper do have this property.
If \(p^{*}=0\) or \(p^{*}=1\) the definition is amended as appropriate.
The logit equilibrium and impulse balance equilibrium give a value for p, the probability of a player choosing to contribute E. From this one can obtain the probability of the public good being provided.
Dawes et al. (1986) report the results of 3 experiments. We have combined their experiments 2 and 3 because they are identical for our purposes.
All of the statistical tests in this section treat the group as the unit of observation. We, thus, have 27 observations in total (see Table 6).
For the few-large and many-small the best fit does lie on the branch of equilibria starting at 0.5. For the many-large it does not. In the few small treatment the best fit is the random model, \(p=0.5\).
References
Alberti F, Cartwright EJ (2016) Full agreement and the provision of threshold public goods. Public Choice 166(1–2):205–233
Alberti F, Cartwright E, Stepanova A (2013) Explaining success rates at providing threshold public goods: an approach based on impulse balance theory. SSRN working paper no. 2309361
Amihud Y, Kahan M, Sundaram RK (2004) The foundations of freezeout laws in takeovers. J Finance 59(3):1325–1344
Andreoni J (1998) Toward a theory of charitable fundraising. J Polit Econ 106:1186–1213
Bagnoli M, Lipman BL (1988) Successful takeovers without exclusion. Rev Financ Stud 1(1):89–110
Bchir MA, Willinger M (2013) Does a membership fee foster successful public good provision? An experimental investigation of the provision of a step-level collective good. Public Choice 157(1–2):25–39
Berninghaus SK, Neumann T, Vogt B (2014) Learning in networks: an experimental study using stationary concepts. Games 5(3):140–159
Cadsby CB, Croson R, Marks M, Maynes E (2008) Step return versus net reward in the voluntary provision of a threshold public good: an adversarial collaboration. Public Choice 135:277–289
Cadsby CB, Maynes E (1998) Corporate takeovers in the laboratory when shareholders own more than one share. J Bus 71(4):537–572
Cartwright E, Stepanova A (2015) The consequences of a refund in threshold public good games. Econ Lett 134:29–33
Cason TN, Friedman D (1997) Price formation in single call markets. Econometrica 65:311–345
Cason TN, Friedman D (1999) Learning in a laboratory market with random supply and demand. Exp Econ 2:77–98
Chmura T, Georg SJ, Selten R (2012) Learning in experimental 2x2 games. Games Econ Behav 76:44–73
Coombs CH (1973) A reparameterization of the prisoner’s dilemma game. Behav Sci 18(6):424–428
Croson R, Marks M (2000) Step returns in threshold public goods: a meta- and experimental analysis. Exp Econ 2:239–259
Dawes RM, Orbell JM, Simmons RT, Van De Kragt AJ (1986) Organizing groups for collective action. Am Polit Sci Rev 1171–1185
De Cremer D, van Dijk E (2011) On the near miss in public good dilemmas: how upward counterfactuals influence group stability when the group fails. J Exp Soc Psychol 47:139–146
Erev I, Ert E, Roth AE, Haruvy E, Herzog SM, Hau R, Hertwig R, Stewart T, West R, Lebiere C (2010) A choice prediction competition: choices from experience and from description. J Behav Decis Mak 23(1):15–47
Fischbacher U (2007) z-Tree: zurich toolbox for ready-made economic experiments. Exp Econ 10(2):171–178
Goeree JK, Holt CA, Palfrey TR (2005) Regular quantal response equilibrium. Exp Econ 8(4):347–367
Goeree JK, Holt CA, Palfrey TR (2008) Quantal response equilibrium. The New Palgrave Dictionary of Economics, Palgrave Macmillan, Basingstoke
Goeree JK, Holt CA (2005) An explanation of anomalous behavior in models of political participation. Am Polit Sci Rev 99(02):201–213
Goerg SJ, Neugebauer T, Sadrieh A (2016) Impulse response dynamics in weakest link games. German Econ Rev (online)
Grossman SJ, Hart OD (1980) Takeover bids, the free-rider problem, and the theory of the corporation. Bell J Econ 42–64
Haile PA, Hortaçsu A, Kosenok G (2008) On the empirical content of quantal response equilibrium. Am Econ Rev 98(1):180–200
Harsanyi JC, Selten R (1988) A general theory of equilibrium selection in games. MIT Press, Cambridge, p 378. doi:10.1002/bs.3830340206
Holmström B, Nalebuff B (1992) To The raider goes the surplus? A reexaminationof the free-rider problem. J Econ Manag Strategy 1(1):37–62
Isaac RM, Schmidtz D, Walker JM (1989) The assurance problem in a laboratory market. Public Choice 62(3):217–236
Kahneman D, Miller DT (1986) Norm theory: comparing reality to its alternatives. Psychol Rev 93:136–153
Kale JR, Noe TH (1997) Unconditional and conditional takeover offers: experimental evidence. Rev Financ Stud 10(3):735–766
McKelvey RD, Palfrey TR (1995) Quantal response equilibria for normal form games. Games Econ Behav 10(1):6–38
Monderer D, Shapley LS (1996) Potential games. Games Econ Behav 14(1):124–143
Ockenfels A, Selten R (2005) Impulse balance equilibrium and feedback in first price auctions. Games Econ Behav 51:155–170
Ockenfels A, Selten R (2014) Impulse balance in the newsvendor game. Games Econ Behav 86:237–247
Ockenfels A, Selten R (2015) Impulse balance and multiple-period feedback in the newsvendor game. Product Oper Manag 24(12):1901–1906
Offerman T, Sonnemans J, Schram A (1996) Value orientations, expectations and voluntary contributions in public goods. Econ J 106:817–845
Offerman T, Schram A, Sonnemans J (1998) Quantal response models in step-level public good games. Eur J Polit Econ 14(1):89–100
Offerman T, Sonnemans J, Schram A (2001) Expectation formation in step-level public good games. Econ Inq 39:250–269
Palfrey T, Rosenthal H (1984) Participation and the provision of discrete public goods: a strategic analysis. J Public Econ 24:171–193
Rapoport A (1987) Research paradigms and expected utility models for the provision of step-level public goods. Psychol Rev 94:74–83
Rapoport A, Eshed-Levy D (1989) Provision of step-level public goods: effects of greed and fear of being gypped. Organ Behav Hum Decis Process 44(3):325–344
Rosenthal RW (1973) A class of games possessing pure-strategy Nash equilibria. Int J Game Theory 2(1):65–67
Schram A, Offerman T, Sonnemans J (2008) Explaining the comparative statics in step-level public good games. Handb Exp Econ Results 1:817–824
Selten R (1998) Features of experimentally observed bounded rationality. Eur Econ Rev 42:413–436
Selten R (2004) Learning direction theory and impulse balance equilibrium. In: Friedman D, Cassar A (eds) Economics lab—an intensive course in experimental economics. Routledge, London
Selten R, Chmura T (2008) Stationary concepts for experimental 2x2 games. Am Econ Rev 98:938–966
Selten R, Stoeker R (1986) End behavior in sequences of finite prisoner’s dilemma supergames. J Econ Behav Organ 7:47–70
Suleiman R, Rapoport A (1992) Provision of step-level public goods with continuous contribution. J Behav Decis Making 5(2):133–153
Tumennasan N (2013) To err is human: implementation in quantal response equilibria. Games Econ Behav 77(1):138–152
Van de Kragt AJ, Orbell JM, Dawes RM (1983) The minimal contributing set as a solution to public goods problems. Am Polit Sci Rev 112–122
Author information
Authors and Affiliations
Corresponding author
Additional information
The research in this paper was supported by a University of Kent, Social Sciences Faculty Grant for project ‘Impulse balance theory and binary threshold public good games’. We would like to thank two anonymous referees for their very helpful and constructive comments on an earlier version.
Appendix
Appendix
1.1 Instructions for subjects
In this experiment you will be asked to make a series of decisions. Depending on the choices that you make you will accumulate ‘tokens’ that will subsequently be converted into money. Each token will be converted into £0.02. You will be individually paid in cash at the end of the experiment.
At the start of the experiment you will be randomly assigned to a group of 5 people. You will remain with the same group throughout the experiment.
The experiment will last 30 rounds.
At the beginning of each round you will be allocated 6 tokens. You must decide whether to contribute these six tokens towards a group project. This is a yes or no decision, i.e. you either contribute all 6 tokens towards the group project or contribute none.
Everybody in the group faces the same choice as you do. And all group members will be asked to make their choice at the same time. Everybody, therefore, makes their choice without knowing what others in the group have chosen to do.
Your payoff will be determined by your choice whether or not to contribute towards the group project and the choices of others in the group as explained on the next page.
If the group project goes ahead successfully
If three or more group members contribute towards the group project then it goes ahead successfully. As a consequence, everyone in the group who initially opted (earlier in the round) not to contribute towards the project will now be required to contribute. And, everyone in the group will receive a return from the group project worth 7 tokens. Thus, everyone in the group will get a payoff of 7 tokens irrespective of whether they initially opted to contribute or not.
If three of more contribute towards the group project:
Your payoff = 7 tokens
If the group project does not go ahead successfully
If less than three group members contribute towards the group project then it does not go ahead successfully. Those who opted to contribute towards the project will get a payoff of 0 tokens. Those who opted not to contribute towards the project will get a payoff of 6 tokens.
If less than three contribute towards the group project:
“Your payoff” \(=\left\{ \begin{array}{ll} 0 &{} \text { tokens if you chose to contribute }E \\ 6 &{} \text { tokens if you chose not to contribute} \end{array} \right. \).
At the end of the round you will be told the number of people that initially opted to contribute towards the group project, whether or not the project went ahead successfully, and your payoff for the round.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cartwright, E., Stepanova, A. Efficiency in a forced contribution threshold public good game. Int J Game Theory 46, 1163–1191 (2017). https://doi.org/10.1007/s00182-017-0570-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-017-0570-1