Abstract
This paper applies the framework of endogenous timing in games to mixed quantity duopoly, wherein a private—domestic or foreign—firm competes with a public, welfare-maximizing firm. A central goal of the paper is to present a unified and general treatment of the basic question of what constitutes the appropriate solution concept—Cournot or Stackelberg—in such duopolies. We show that simultaneous play never emerges as a subgame-perfect equilibrium of the extended game, in sharp contrast to private duopoly games. We demonstrate that this result is due to the objective function of the public firm being increasing in the rival’s output (instead of decreasing for a private firm). We provide sufficient conditions for the emergence of public and/or private leadership equilibrium. In all cases, private profits and social welfare are higher than under the corresponding Cournot equilibrium. We make extensive use of the basic results from the theory of supermodular games in order to avoid common extraneous assumptions such as concavity, existence and uniqueness of the different equilibria, whenever possible. Some policy implications are drawn, in particular those relating to the merits of privatization.



Similar content being viewed by others
Notes
Even more tenuous is the claim that the public follower can unilaterally implement the Stackelberg equilibrium because of its dominant position, as in Beato and Mas-Colell (1984).
Throughout the paper, “increasing” (“decreasing”) will mean “weakly increasing” (“weakly decreasing”).
This is the reason why we require \(lim_{x\rightarrow \infty }P\left( x\right) =0\). \(P\left( x\right) \) can of course be equal to zero also for some \( 0<x<\infty \).
What the literature on endogenous timing refers to as “basic game” actually consists of three distinct games, depending on whether play is simultaneous or sequential, and in the latter case on whether player 0 or 1 is the first-mover. With this point clarified, we continue to abuse terminology by referring to these three games collectively as the “basic game”.
This fact is always true when the reaction correspondences are continuous functions, but as the present setting allows for discontinuities, the same result requires proof.
Note that IDP is a cardinal property of the function \(F\), while SCP is an ordinal property.
It is worth noting that sufficient conditions for these properties are given in Lemmas 1(a) and 2(a).
Reversing the natural order of the public firm’s action set, the game becomes supermodular (Vives 1990), with effective strategy set \(\left[ 0,k_{0}\right] \times \left[ 0,k_{1}\right] \). By Tarski’s fixed point theorem the set \(N\) is non-empty.
Note that the effective action spaces are compact and the payoff functions are jointly continuous, so that the follower’s best response correspondence has a closed graph. Then, as proved by Hellwig and Leininger (1987), Stackelberg equilibria exist.
Any function \(F(x)\) that is log-concave for \(x\in [0,a]\) and equal to 0 for \(x\ge a\) is globally log-concave.
An alternative (not used here) would be to revert to the standard approach for establishing existence of pure-strategy Cournot equilibrium, which uses the strict quasi-concavity of each firm’s objective function in own output to ensure single-valuedness and continuity of the firms’ reaction functions. To this end, it can be shown that the private firm’s profit function is strictly quasi-concave in own output if \(1/P(\cdot )\) is a strictly convex function, i.e. if
$$\begin{aligned} P(\cdot )P^{\prime \prime }(\cdot )-2(P^{\prime })^{2}(\cdot )<0 \end{aligned}$$and that the public firm’s objective function is strictly concave in own output if
$$\begin{aligned} P^{\prime }\left( q_{0}+q_{1}\right) -C_{0}^{\prime \prime }\left( q_{0}\right) <0,\quad \forall q_{0},q_{1}\ge 0. \end{aligned}$$It is worth noting that sufficient conditions for these properties are given in Lemmas 1(a) and 2(b).
On the other hand, a well known class of demand functions that satisfies both conditions is the iso-elastic class, given by \(P\left( x\right) =1/x^{\alpha }\) with \(\alpha >1\).
It is worth noting that sufficient conditions for these properties are given in Lemmas 1(b) and 2(a).
A sufficient condition for this property is given in Lemma 2(a).
Lemma 2(b) provides a sufficient condition for this property.
See Milgrom and Roberts (1990, Theorem 5).
The four Dini derivates are the \(\lim \sup \) and \(\lim \inf \) of the one-sided (left and right) directional slopes starting at any point and always exist in the extended reals.
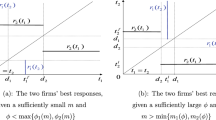
\(GR\) stands for the graph of the best-reply function \(r_{i}\left( \cdot \right) \).
Since both \(\left( r_{0}\left( q_{1}^{f}\right) \!,q_{1}^{f}\right) \) and \( \left( \underline{q_{0}},\overline{q_{1}}\right) \) lay on \(GR\,r_{0}\left( \cdot \right) \) and given the contradiction hypothesis that \(q_{1}^{f}<\overline{ q_{1}}\), it follows that \(r_{0}\left( q_{1}^{f}\right) >\underline{q_{0}}\) because any selection of \(r_{0}\left( \cdot \right) \) is strictly decreasing.
References
Amir R (1995) Endogenous timing in two-player games: a counterexample. Games Econ Behav 9(2): 234–237
Amir R (1996a) Cournot oligopoly and the theory of supermodular games. Games Econ Behav 15(2): 132–148
Amir R (1996b) Sensitivity analysis of multisector optimal economic dynamics. J Math Econ 25(1):123–141
Amir R, Grilo I (1999) Stackelberg versus cournot equilibrium. Games Econ Behav 26(1):1–21
Beato P, Mas-Colell A (1984) The marginal cost pricing rule as a regulation mechanism in mixed markets. In: Marchand M, Pestieu P, Tulkens H (eds) The performance of public enterprises. Studies in mathematical and managerial economics, vol 33. Elsevier Science B.V, Amsterdam, pp 81–100
Bös D (1986) Public enterprise economics: theory and applications. In: Advanced textbooks in economics, vol 23, 2nd edn. North Holland, Amsterdam
Cornes RC, Sepahvand M (2003) Cournot vs stackelberg equilibria with a public enterprise and international competition. Economics discussion paper 12, University of Nottingham, Nottingham
Cremer H, Marchand M, Thisse JF (1989) The public firm as an instrument for regulating an oligopolistic market. Oxf Econ Pap 41(2):283–301
de Fraja G, Delbono F (1989) Alternative strategies of a public enterprise in oligopoly. Oxf Econ Pap 41(2):302–311
de Fraja G, Delbono F (1990) Game theoretic models of mixed oligopoly. J Econ Surv 4(1):1–17
Edlin AS, Shannon C (1998) Strict monotonicity in comparative statics. J Econ Theory 81(1):201–219
Fjell K, Heywood JS (2002) Public stackelberg leadership in a mixed oligopoly with foreign firms. Aust Econ Pap 41(3):267–281. doi:10.1111/1467-8454.00164
Fjell K, Pal D (1996) A mixed oligopoly in the presence of foreign private firms. Canad J Econ 29(3): 737–743
Hamilton JH, Slutsky SM (1990) Endogenous timing in duopoly games: Stackelberg or cournot equilibria. Games Econ Behav 2(1):29–46
Hellwig M, Leininger W (1987) On the existence of subgame-perfect equilibrium in infinite-action games of perfect information. J Econ Theory 43(1):55–75
Lipsey RG, Lancaster K (1956–1957) The general theory of second best. Rev Econ Stud 24(1):11–32
Matsumura T (2003) Stackelberg mixed duopoly with a foreign competitor. Bull Econ Res 55(3):275–287. doi:10.1111/1467-8586.00175
Milgrom P, Roberts J (1990) Rationalizability, learning, and equilibrium in games with strategic complementarities. Econometrica 58(6):1255–1277
Milgrom P, Shannon C (1994) Monotone comparative statics. Econometrica 62(1):157–180
Nett L (1993) Mixed oligopoly with homogeneous goods. Ann Public Cooperative Econ 64(3):367–393
Novshek W (1985) On the existence of cournot equilibrium. Rev Econ Stud 52(168):85–98
Pal D (1998) Endogenous timing in a mixed oligopoly. Econ Lett 61(2):181–185
Pal D, White MD (1998) Mixed oligopoly, privatization, and strategic trade policy. South Econ J 65(2): 264–281
Rees R (1984) Public enterprise economics, 2nd edn. Palgrave Macmillan, London
Sepahvand M (2004) Public enterprise strategies in a market open to domestic and international competition. Annales d’Économie et de Statistique 75–76:135–153
von Stengel B (2010) Follower payoffs in symmetric duopoly games. Games Econ Behav 69(2):512–516
von Stengel B, Zamir S (2010) Leadership games with convex strategy sets. Games Econ Behav 69(2):446–457
Topkis DM (1978) Minimizing a submodular function on a lattice. Oper Res 26(2):305–321
Topkis DM (1979) Equilibrium points in nonzero-sum \(n\)-person submodular games. SIAM J Control Optim 17(6):773–787. doi: 10.1137/0317054
Topkis DM (1998) Supermodularity and complementarity. Princeton University Press, Princeton
Vives X (1990) Nash equilibrium with strategic complementarities. J Math Econ 19(3):305–321
Acknowledgments
We wish to thank Vijay Krishna, the Associate Editor and two anonymous referees for very helpful suggestions, as well as audiences at CORE, University of Strathclyde, Università degli studi di Pavia, 2007 EARIE Conference in Valencia, 2008 ESEM Conference in Milano, and 2009 PET conference in Galway. The second author gratefully acknowledges financial support from Fondazione Alma Mater Ticinensis - Pavia, project ‘The governance of markets and firms after the global crisis’. The scientific responsibility is assumed by the authors.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The Appendix includes most of the proofs of the paper but also some intermediate results that are needed for the proof of the main theorems of the paper.
Proof of Lemma 1
A sufficient condition for \(W^{f}\left( q_{0},q_{1}\right) \) to have the strict IDP (strict DDP) is \(\frac{\partial ^{2}W^{f}\left( q_{0},q_{1}\right) }{\partial q_{0}\partial q_{1}}>(<)0\). By the strengthening of Topkis’s Theorem given in Amir (1996b) or Edlin and Shannon (1998), a sufficient condition for every selection of \( r_{0}\left( .\right) \) to be strictly increasing (strictly decreasing) whenever interior is for \(\frac{\partial W^{f}\left( q_{0},q_{1}\right) }{ \partial q_{0}}\) to be strictly increasing (decreasing) in \(q_{1}\). The latter condition is in turn implied by \(P^{\prime \prime }\left( q_{0}+q_{1}\right) <(>)0\) since
\(\square \)
Proof of Lemma 2
-
(a)
A sufficient condition for the private firm’s objective to have the strict DDP is (see Novshek 1985)
$$\begin{aligned} \frac{\partial ^{2}\varPi _{1}\left( q_{0},q_{1}\right) }{\partial q_{0}\partial q_{1}}=P^{\prime }\left( q_{0}+q_{1}\right) +q_{1}P^{\prime \prime }\left( q_{0}+q_{1}\right) <0,\quad \forall q_{0},q_{1}\ge 0 \end{aligned}$$which is equivalent to
$$\begin{aligned} P^{\prime }\left( x\right) +xP^{\prime \prime }\left( x\right) <0,\quad \forall x\ge 0 \end{aligned}$$A sufficient condition for the strict dual SSCP is
$$\begin{aligned} P\left( x\right) P^{\prime \prime }\left( x\right) -P^{\prime 2}\left( x\right) <0,\quad \forall x\ge 0 \end{aligned}$$as defined in Amir (1996a). If one of these conditions holds, then any selection of the private firm’s best-response correspondence is strictly decreasing (Amir 1996b).
-
(b)
Since the production costs of the private firm are zero, its objective is \(q_{1}P\left( q_{0}+q_{1}\right) \). Given that \(\log P\left( \cdot \right) \) is convex by assumption, it follows that the objective is strictly log-supermodular, i.e.
$$\begin{aligned} \frac{\partial ^{2}\log q_{1}P\left( q_{0}+q_{1}\right) }{\partial q_{0}\partial q_{1}}=\frac{P\left( q_{0}+q_{1}\right) P^{\prime \prime }\left( q_{0}+q_{1}\right) -P^{\prime 2}\left( q_{0}+q_{1}\right) }{ P^{2}\left( q_{0}+q_{1}\right) }>0. \end{aligned}$$
So, every selection of the private firm best-response correspondence is strictly increasing (Amir 1996b). \(\square \)
Before starting the proof of Theorem 1 we need to establish some intermediate results in the following Lemmas 4, 5, and 6.
Lemma 4
Consider the case of a foreign private firm. Assume the game if of strict strategic substitutes. Then the set N includes a point \(\left( \underline{q_{0}},\overline{q_{1}}\right) \), with \(\underline{q_{0}}\) being the public firm’s smallest output and \(\overline{ q_{1}}\) the private firm’s largest output in the set N, which is the Pareto dominant mixed-duopoly Cournot equilibrium.
Proof
Reversing the natural order on the public firm’s action set, the set \(N\) has a largest Cournot equilibrium in the new order, which is clearly \(\left( { \underline{q_{0}},\overline{q_{1}}}\right) \).Footnote 21 We show that this is the most preferred Cournot equilibrium by both private and public firms. Consider any \(\left( \widehat{q}_{0},\widehat{q}_{1}\right) \in N\). By the extremal nature of \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) it follows that \(\widehat{q}_{1}\le \overline{q_{1}}\) and \(\widehat{q}_{0}\ge \underline{q_{0}}\).
-
(i)
For the private firm the following relation holds:
$$\begin{aligned} \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge \varPi _{1}\left( {\underline{q_{0}},\widehat{q}_{1}}\right) \ge \varPi _{1}\left( \widehat{q} _{0},\widehat{q}_{1}\right) \end{aligned}$$(7)where the first inequality derives from \(\overline{q_{1}}\) being best response to \(\underline{q_{0}}\), and the second inequality is due to private firm’s objective being strictly decreasing in \(q_{0}\).
-
(ii)
For the public firm, we have
$$\begin{aligned} W^{f}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge W^{f}\left( \widehat{q}_{0},\overline{q_{1}}\right) \ge W^{f}\left( \widehat{q}_{0}, \widehat{q}_{1}\right) \end{aligned}$$(8)where the first inequality is due to the fact that \(\underline{q_{0}}\) is a best response to \(\overline{q_{1}}\) and the second derives from \(W^{f}\) being strictly increasing in \(q_{1}\).
This completes the proof. \(\square \)
Lemma 5
Consider the case of a foreign private firm. Assume the game is of strict strategic substitutes. Then the output of the private firm (public firm) in a Stackelberg game under either order of moves is larger (smaller) than in the Pareto-dominant mixed-duopoly Cournot equilibrium.
Proof
We have to distinguish the two cases of (i) private leadership, and (ii) public leadership.
-
(i)
Suppose, towards contradiction, that there exists a point \(\left( q_{0}^{f},q_{1}^{l}\right) \in S_{1}\) such that \(q_{1}^{l}<\overline{q_{1}}\). Since both \(\left( q_{0}^{f},q_{1}^{l}\right) \) and \(\left( \underline{ q_{0}},\overline{q_{1}}\right) \) lay on \(GR\,r_{0}(.)\), which has only strictly decreasing selections, it follows that \(q_{0}^{f}>\underline{q_{0}}\). Then
$$\begin{aligned} \varPi _{1}\left( {\underline{q_{0}},\overline{q_{1}}}\right) \ge \varPi _{1}\left( {\underline{q_{0}},q_{1}^{l}}\right) >\varPi _{1}\left( q_{0}^{f},q_{1}^{l}\right) \end{aligned}$$(9)where the first inequality is due to \(\overline{q_{1}}\) being a best response to \(\underline{q_{0}}\) and the second by the fact that \(\varPi _{1}\) is strictly decreasing in \(q_{0}\). Inequality (9) contradicts the nature of Stackelberg equilibrium. Hence it is always the case that \(q_{1}^{l}\ge \overline{q_{1}}\) and \(q_{0}^{f}\le \underline{ q_{0}}\).
-
(ii)
Suppose, towards contradiction, that there exists a point \( \left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) such that \(q_{0}^{l}>\underline{ q_{0}}\), and so \(q_{1}^{f}<\overline{q_{1}}\) since \(r_{1}\) is strictly decreasing. Then, the following inequalities hold:
$$\begin{aligned} W^{f}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge W^{f}\left( {q} _{0}^{l},\overline{q_{1}}\right) >W^{f}\left( q_{0}^{l},q_{1}^{f}\right) \end{aligned}$$(10)where the first inequality is due to \(\underline{q_{0}}\) being a best response to \(\overline{q_{1}}\) and the second to the fact that \(W^{f}\left( \cdot \right) \) is strictly increasing in \(q_{1}\). Inequality (10) contradicts the nature of Stackelberg equilibria and so it is always the case that \(q_{0}^{l}\le \underline{q_{0}}\) and \( q_{1}^{f}\ge \overline{q_{1}}\).
This completes the proof. \(\square \)
Lemma 6
Assume the game is of strict strategic substitutes. Then the payoff of the leader in any Stackelberg equilibrium is strictly larger than in any Cournot equilibrium as long as the Pareto dominant Cournot equilibrium is interior.
Proof
If \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) is interior, the following first-order conditions for private and public firms must hold:
We analyze the two possible Stackelberg games separately again.
-
(i)
By Remark 1 in Sect. 3.2, with private leadership, the private firm’s objective can be shown to be \( \varPi _{1}\left( \underline{r_{0}}(q_{1}),q_{1}\right) \) where \(\underline{ r_{0}}(\cdot )\) is the minimal selection from the public firm’s optimal reaction correspondence (see Amir and Grilo 1999 for a proof). By the Maximum Theorem, the correspondence \(r_{0}\) has a closed graph. Hence, \(\underline{r_{0}}\) is lower semi-continuous and right-continuous (for a proof, see Amir 1996b). Since \(\varPi _{1}\) is decreasing in its first argument and \(\underline{r_{0}}\) is decreasing and right-continuous, \(\varPi _{1}\left( \underline{r_{0}}\left( q_{1}^{l}\right) ,q_{1}^{l}\right) \) can have only upward jumps in \(q_{1}\) (and no downward jumps) and is right-continuous in \(q_{1}\). Hence, if \(\left( q_{0}^{f},q_{1}^{l}\right) \in S_{1}\) is also interior, then the following first-order condition for the private leader must hold
$$\begin{aligned} \frac{\partial \varPi _{1}\left( q_{0}^{f},q_{1}^{l}\right) }{\partial q_{1}}+ \frac{\partial \varPi _{1}\left( q_{0}^{f},q_{1}^{l}\right) }{\partial q_{0}}{ \underline{r_{0}}^{\prime }}\left( q_{1}^{l}\right) \le 0 \end{aligned}$$(11)where \(r_{0}^{\prime }\left( q_{1}^{l}\right) \) is a right Dini derivate.Footnote 22 Since \(\frac{\partial \varPi _{1}\left( { \underline{q_{0}}\overline{q_{1}}}\right) }{\partial q_{0}}<0\) by Eq. (5), and \(\underline{r_{0}}^{\prime }\left( q_{1}^{l}\right) =-\frac{\partial ^{2}W^{i}\left( {q}_{0},\overline{q_{1}}\right) /\partial q_{0}\partial q_{1}}{\partial ^{2}W^{i}\left( {q}_{0},\overline{q_{1}} \right) / \partial q_{0}^{2}}<0\) whenever \(\underline{r_{0}}\) is interior by point (a) of Lemma 1, it follows from (11) that \(\frac{\partial \varPi _{1}\left( q_{0}^{f},q_{1}^{l}\right) }{\partial q_{1}}<0\) at any interior point. Hence, \(\left( \underline{q_{0}},\overline{ q_{1}}\right) \not \in S_{1}\), andhence \(q_{1}^{l} > \overline{q_{1}}\) and \(q_{0}^{f} < \underline{ q_{0}}\). If \(\left( q_{0}^{f},q_{1}^{l}\right) \) is not interior, then the conclusion follows from the interiority of \(\left( \underline{q_{0}},\overline{q_{1}} \right) \).
-
(ii)
With public leadership, the public firm’s objective can be shown to be \(W^{i}\left( q_{0},\overline{r_{1}}(q_{0})\right) \) where \(\overline{ r_{1}}(\cdot )\) is the maximal selection from the public firm’s optimal reaction correspondence (see Amir and Grilo 1999 for a proof). Since the point \(\left( q_{0}^{l},q_{1}^{f}\right) \) lies on \(\overline{r_{1}}\left( \cdot \right) \), the following first-order condition of the private firm holds:
$$\begin{aligned} P\left( q_{0}+\overline{r_{1}}\left( q_{0}\right) \right) +\overline{r_{1}} \left( q_{0}\right) P^{\prime }\left( q_{0}+\overline{r_{1}}\left( q_{0}\right) \right) -C_{1}^{\prime }\left( \overline{r_{1}}\left( q_{0}\right) \right) =0 \end{aligned}$$Then, at \(\left( q_{0}^{l},q_{1}^{f}\right) \), price is strictly above the private firm’s marginal cost and it follows that \(\frac{\partial W^{i}\left( q_{0}^{l},q_{1}^{f}\right) }{\partial q_{1}}>0\). Using also the fact that \( \overline{r_{1}}\) is decreasing and left-continuous (as in Part (i)), we know that \(W^{i}\left( q_{0},\overline{r_{1}}(q_{0})\right) \) can have only downward jumps in \(q_{0}\) (and no upward jumps) and is left-continuous in \( q_{0}\). Hence, if \(\left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) is interior, the following first-order condition for the public leader must hold (here, \( r_{1}^{\prime }\left( q_{0}^{l}\right) \) is a left Dini derivate)
$$\begin{aligned} \frac{\partial W^{i}\left( q_{0}^{l},q_{1}^{f}\right) }{\partial q_{0}}+ \frac{\partial W^{i}\left( q_{0}^{l},q_{1}^{f}\right) }{\partial q_{1}} r_{1}^{\prime }\left( q_{0}^{l}\right) \ge 0,\quad i=f,d. \end{aligned}$$(12)Since \(\left( q_{0}^{l},q_{1}^{f}\right) \) is interior, we have \( r_{1}^{\prime }(q_{0}^{l})<0\) via an argument similar to the analogous step in part (i). Then (12) implies that \(\frac{\partial W^{i}\left( q_{0}^{l},q_{1}^{f}\right) }{\partial q_{0}}>0\). This implies that \(\left( { \underline{q_{0}},\overline{q_{1}}}\right) \not \in S_{0}\). Therefore \(q_{0}^{l}<\underline{q_{0}}\) and \(q_{1}^{f}>\overline{q_{1}}\) . If \(\left( q_{0}^{l},q_{1}^{f}\right) \) is not interior, then the conclusion follows from the interiority of \(\left( \underline{q_{0}},\overline{q_{1}} \right) \).
This completes the proof. \(\square \)
Proof of Theorem 1
In Lemma 4 we have shown that the point \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) is the most preferred simultaneous-move equilibrium by both firms. Moreover, by Lemmas 5–6, any \(\left( q_{0}^{f},q_{1}^{l}\right) \in S_{1}\) is such that \(q_{1}^{l}>\overline{q_{1} }\) and \(q_{0}^{f}<\underline{q_{0}}\), and any \(\left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) is such that \(q_{1}^{f}>\overline{q_{1} }\) and \(q_{0}^{l}<\underline{q_{0}}\). Now we show that each firm strictly prefers being a follower in a sequential-move game to the Pareto dominant Cournot equilibrium.
For the private firm, the following relation holds
where the first inequality comes from the fact that \(q_{1}^{f}\) is a best response to \(q_{0}^{l}\) and the second is due to the private firm’s objective being strictly decreasing in \(q_{0}\).
For the public firm the following relation holds:
where the first inequality is due to \(q_{0}^{f}\) being a best response to \( q_{1}^{l}\), and the second derives from the fact that W is strictly increasing in \(q_{1}\).
Then, the conditions of point (ii) of Proposition 1 hold and both Stackelberg equilibria are SPEs of the endogenous timing game. \(\square \)
Proof of Theorem 2
Since the reaction correspondences of the two firms are strictly monotonic in opposite directions when interior, the postulated mixed duopoly Cournot equilibrium must be unique. Call it \(\left( \underline{q_{0}}, \overline{q_{1}}\right) \). We now prove that: (i) the public firm is better off in the private leadership than in the mixed-duopoly Cournot equilibrium; while (ii) the private firm’s payoff is strictly larger in the Cournot than in the public leadership equilibrium.
-
(i)
For the private leadership equilibrium, since \(r_{0}\) is strictly decreasing in the interior, we can apply the same analysis as in point \((i)\) of the proofs of Lemmas 5–6 to show that \(q_{1}^{l}>\overline{q_{1}}\) and \(q_{0}^{f}<\underline{q_{0}}\). It follows that
$$\begin{aligned} W^{f}\left( q_{0}^{f},q_{1}^{l}\right) \ge W^{f}\left( \underline{q_{0}}, q_{1}^{l}\right) >W^{f}\left( \underline{q_{0}},\overline{q_{1}}\right) \end{aligned}$$where the first inequality is due to \(q_{0}^{f}\) being best response to \( q_{1}^{l}\), and the second derives from the fact that \(W_{f}\) is strictly increasing in \(q_{1}\).
-
(ii)
We now analyze the public firm’s leadership equilibrium. First we show that the Stackelberg equilibrium \(\left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) is such that \(q_{0}^{l}\!>\!\underline{q_{0}}\) and \(q_{1}^{f}\!>\! \overline{q_{1}}\). Suppose by contradiction that \(q_{0}^{l}<\underline{q_{0}} \). Since \(r_{1}\) is strictly increasing when interior, it follows that \( q_{1}^{f}<\overline{q_{1}}\). Then,
$$\begin{aligned} W^{f}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge W^{f}\left( q_{0}^{l},\overline{q_{1}}\right) >W^{f}\left( q_{0}^{l},q_{1}^{f}\right) \end{aligned}$$where the first inequality comes from \(\underline{q_{0}}\) being a best response to \(\overline{q_{1}}\) and the second is due to \(W^{f}\left( q_{0},q_{1}\right) \) being strictly increasing in \(q_{1}\). Therefore \( q_{0}^{l}\ge \underline{q_{0}}\). Moreover, by an argument analogous to the one used in point \((i)\) of the proof of Lemma 6, \( \left( \underline{q_{0}},\overline{q_{1}}\right) \not \in S_{0}\) and therefore \(q_{0}^{l}>\underline{q_{0}}\). Since \(r_{1}\) is strictly increasing in the interior, it follows that \(q_{1}^{f}>\overline{q_{1}}\). As a consequence, we can rank the private firm’s payoffs in the following way:
$$\begin{aligned} \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge \varPi _{1}( \underline{q_{0}},q_{1}^{f})>\varPi _{1}(q_{0}^{l},q_{1}^{f}) \end{aligned}$$where the first inequality follows from the property of Cournot equilibria and the second from the fact that \(\varPi _{1}\) is strictly decreasing in \( q_{0} \). Hence, the private firm strictly prefers Cournot to public leadership equilibria.
The conditions of point (iii) of Proposition 1 hold and the private leadership equilibrium is the unique SPE of the endogenous timing game. \(\square \)
Proof of Theorem 3
As in the previous Theorem, the postulated mixed duopoly Cournot equilibrium must be unique (since \(r_{0}\left( q_{1}\right) \) is strictly increasing and \(r_{1}\left( q_{0}\right) \) is strictly decreasing in the interior). Call it \(\left( \underline{q_{0}},\overline{q_{1}}\right) \). We now prove that: (i) the public firm’s payoff is strictly larger in the Cournot equilibrium that in the private leadership equilibrium; while (ii) the private firm is better off in the public leadership equilibrium than in the Cournot equilibrium.
-
(i)
First we show that the private leadership equilibrium is such that \(q_{1}^{l}<\overline{q_{1}}\) and \(q_{0}^{f}<\underline{q_{0}}\). Suppose by contradiction that \(q_{1}^{l}>\overline{q_{1}}\); since \(r_{0}\) is strictly increasing in the interior \(q_{0}^{f}>\underline{q_{0}}\). It follows that
$$\begin{aligned} \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge \varPi _{1}\left( \underline{q_{0}},q_{1}^{l}\right) >\varPi _{1}\left( q_{0}^{f},q_{1}^{l}\right) \end{aligned}$$where the first inequality is due to \(\overline{q_{1}}\) being a best response to \(\underline{q_{0}}\), and the second derives from the fact that \( \varPi _{1}\left( q_{0},q_{1}\right) \) is strictly decreasing in \(q_{0}\). Therefore \(q_{1}^{l}\le \overline{q_{1}}\) and \(q_{0}^{f}\le \underline{q_{0} }\). By an argument analogous to the one in point \((i)\) of the proof of Lemma 6, \(\left( \underline{q_{0}},\overline{q_{1}}\right) \not \in S_{1}\) and therefore \(q_{1}^{l}<\overline{q_{1}}\) and \(q_{0}^{f}< \underline{q_{0}}\). Furthermore, we have
$$\begin{aligned} W^{f}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge W^{f}\left( q_{0}^{f},\overline{q_{1}}\right) >W^{f}\left( q_{0}^{f},q_{1}^{l}\right) \end{aligned}$$where the first inequality is due to \(\underline{q_{0}}\) being a best response to \(\overline{q_{1}}\) and the second to \(W^{f}\left( q_{0},q_{1}\right) \) being strictly increasing in \(q_{1}\).
-
(ii)
From the interiority of \(\left( \underline{q_{0}},\overline{q_{1} }\right) \) and since \(r_{1}\) is strictly decreasing in the interior, we can apply the same analysis as point \((ii)\) in the proof of Lemma 5 to show that \(q_{0}^{l}\le \underline{q_{0}}\) and \( q_{1}^{f}\ge \overline{q_{1}}\). Moreover, by point \((ii)\) in the proof of Lemma 6, \(\left( \underline{q_{0}},\overline{q_{1}} \right) \not \in S_{0}\) and therefore \(q_{0}^{l}<\underline{q_{0}}\) and \( q_{1}^{f}>\overline{q_{1}}\). It follows that
$$\begin{aligned} \varPi _{1}\left( q_{0}^{l},q_{1}^{f}\right) \ge \varPi _{1}\left( q_{0}^{l}, \overline{q_{1}}\right) >\varPi _{1}\left( \underline{q_{0}},\overline{q_{1}} \right) \end{aligned}$$where the first inequality follows from the fact that \(q_{1}^{f}\) is a best response to \(q_{0}^{l}\) and the second from the fact that \(\varPi _{1}\left( q_{0},q_{1}\right) \) is strictly decreasing in \(q_{0}\). Then, the private firm strictly prefers public leadership to the best Cournot equilibrium.
The conditions of point (iii) of Proposition 1 hold and public leadership is the unique SPE of the endogenous timing game. \(\square \)
Proof of Lemma 3
Since the public firm maximizes total welfare as defined in Eq. (1), its objective has DDP since
So, under the standard assumptions, any selection of the best-response correspondence of the public firm is strictly decreasing. \(\square \)
In order to prove Theorem 4, we need to establish some intermediate results in the following Lemmas 7 and 8.
Lemma 7
Consider the case of a domestic private firm. A sufficient condition for the extremal equilibrium \(\left( \underline{q_{0}}, \overline{q_{1}}\right) \) to be the Pareto dominant mixed-duopoly Cournot equilibrium is that the public firm’s cost function is convex in the relevant range.
Proof
As in Lemma 4, since both reaction correspondences are strictly decreasing in the interior, \(\left( \underline{ q_{0}},\overline{q_{1}}\right) \) is the extremal point in \(N\) and any other \( \left( \widehat{q}_{0},\widehat{q}_{1}\right) \in N\) distinct from \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) is such that \(\widehat{q}_{1}< \overline{q_{1}}\) and \(\widehat{q}_{0}>\underline{q_{0}}\).
-
(i)
For the private firm, we have that \(\varPi _{1}\left( \underline{q_{0} },\overline{q_{1}}\right) >\varPi _{1}\left( \widehat{q}_{0},\widehat{q} _{1}\right) \), as shown in Lemma 4 by the inequality chain (7);
-
(ii)
For the public firm, we first show that the slopes of \( r_{0}\left( q_{1}\right) \) are all in \([-1,0)\). To this end, consider the change of variable \(x=q_{0}+q_{1}\) and view \(x\) as the new decision variable for the public firm in the modified objective
$$\begin{aligned} \max _{x\ge 0}\int \limits _{0}^{x}P\left( t\right) dt-C_{0}\left( x-q_{1}\right) -C_{1}\left( q_{1}\right) \end{aligned}$$Since the cross-partial of this objective w.r.t. \(x\) and \(q_{1}\) is equal to \(C_{0}^{\prime \prime }\left( x-q_{1}\right) \ge 0\), by the convexity assumption, we conclude that the argmax \(x^{*}(q_{1})\) is increasing in \( q_{1}\ (\)note here that \(x^{*}(q_{1})\) is single-valued since \(W^{d}\) is strictly concave in \(q_{0}\)). Since \(x^{*}(q_{1})=r_{0}(q_{1})+q_{1}\), we conclude that the slopes of \(r_{0}(q_{1})\) are all \(\ge -1\). A standard application of the smooth Implicit Function Theorem shows that \( r_{0}^{\prime }(q_{1})\ge -1\). Given that both \(\left( \widehat{q}_{0},\widehat{q}_{1}\right) \) and \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) lie on \(GR\,r_{0}\left( q_{1}\right) \), it follows thatFootnote 23
$$\begin{aligned} W^{d}\left( \underline{q_{0}},\overline{q_{1}}\right) -W^{d}\left( \widehat{q }_{0},\widehat{q}_{1}\right)&= \int \limits _{\widehat{q}_{1}}^{\overline{q_{1}}}\frac{ dW^{d}\left( r_{0}\left( q_{1}\right) , q_{1}\right) }{dq_{1}}dq_{1} \nonumber \\&= \int \limits _{ \widehat{q}_{1}}^{\overline{q_{1}}}\frac{\partial W^{d}\left( r_{0}\left( q_{1}\right) , q_{1}\right) }{\partial q_{1}}dq_{1} \end{aligned}$$(13)where the latter equality derives from an application of the Envelope Theorem. Hence,
$$\begin{aligned} \frac{\partial W^{d}\left( r_{0}\left( q_{1}\right) , q_{1}\right) }{\partial q_{1}}&= P\left( r_{0}\left( q_{1}\right) +q_{1}\right) -C_{1}^{\prime }\left( q_{1}\right) \\&\ge P\left( r_{0}\left( q_{1}\right) +q_{1}\right) -C_{1}^{\prime }\left( q_{1}\right) \\&+\left[ 1+r_{0}^{\prime }\left( q_{1}\right) \right] q_{1}P^{\prime }\left( r_{0}\left( q_{1}\right) +q_{1}\right) \\&= \frac{d\varPi _{1}\left( r_{0}\left( q_{1}\right) , q_{1}\right) }{dq_{1}} \end{aligned}$$where the inequality follows from the fact that \(-1\le r_{0}^{\prime }\left( q_{1}\right) \le 0,\forall q_{1}\ge 0\). Then:
$$\begin{aligned} \int \limits _{\widehat{q}_{1}}^{\overline{q_{1}}}\frac{dW^{d}\left( r_{0}\left( q_{1}\right) ,q_{1}\right) }{dq_{1}}dq_{1}&\ge \int \limits _{\widehat{q}_{1}}^{ \overline{q_{1}}}\frac{d\varPi _{1}\left( r_{0}\left( q_{1}\right) ,q_{1}\right) }{dq_{1}}dq_{1} \\&= \varPi _{1}\left( \underline{q_{0}},\overline{q_{1} }\right) -\varPi _{1}\left( \widehat{q}_{0},\widehat{q}_{1}\right) >0 \end{aligned}$$where the latter inequality comes from the result in point (i).
This completes the proof. \(\square \)
Lemma 8
Consider the case of a domestic private firm. Assume that the game is of strict strategic substitutes, and that the public firm’s cost function is convex. Then, the output of the private firm (public firm) in any Stackelberg game with both orders of moves is strictly larger (strictly smaller) than in the Pareto-dominant mixed duopoly Cournot equilibrium.
Proof
We distinguish the two cases of (i) private leadership, and (ii) public leadership.
-
(i)
The case of private leadership has been already discussed in Lemmas 5-6 where it is shown that \(q_{1}^{l}>\overline{q_{1}}\) and \(q_{0}^{f}<\underline{q_{0}}\) always, and \(\left( \underline{q_{0}},\overline{q_{1}}\right) \not \in S_{1}\).
-
(ii)
The case of public leadership is instead different since \(W^{d}\) is not always increasing in \(q_{1}\). We need therefore a different proof. Suppose by contradiction that \(q_{1}^{l}<\overline{q_{1}}\). First observe that, since \(r_{0}\left( q_{1}^{f}\right) \) is a best response,
$$\begin{aligned} W^{d}\left( q_{0}^{l},q_{1}^{f}\right) \le W^{d}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) . \end{aligned}$$(14)Moreover, given that both \(\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \) and \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) lie on \(GR\,r_{0}\left( \cdot \right) \), we can apply the envelope theorem as in Eq. (13) and obtain the following relation between welfare and profits
$$\begin{aligned} W^{d}\left( \underline{q_{0}},\overline{q_{1}}\right) -W^{d}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \ge \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) -\varPi _{1}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) >0 \nonumber \\ \end{aligned}$$(15)(15) comes from the fact that
$$\begin{aligned} \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge \varPi _{1}\left( \underline{q_{0}},q_{1}^{f}\right) >\varPi _{1}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \end{aligned}$$where the first inequality comes from \(\overline{q_{1}}\) being a best response to \(\underline{q_{0}}\), and the second is due to the fact that \(\varPi _{1}\left( \cdot \right) \) is strictly decreasing in \(q_{0}\) and \(r_{0}\left( q_{1}^{f}\right) >\underline{q_{0}}\).Footnote 24 So, combining inequalities (14) and (15), whenever \(q_{1}^{f}<\overline{q_{1}}\), the following relation holds
$$\begin{aligned} W^{d}\left( q_{0}^{l},q_{1}^{f}\right) \le W^{d}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) <W^{d}\left( \underline{q_{0}},\overline{ q_{1}}\right) , \end{aligned}$$which contradicts the nature of Stackelberg equilibrium. Therefore, it must be that \(q_{1}^{f}\ge \overline{q_{1}}\) and \(q_{0}^{l}\le \underline{ q_{0}}\). Moreover, we can apply the result in point \((ii)\) of the proof of Lemma 6 to show that \(\left( \underline{q_{0}},\overline{q_{1}} \right) \not \in S_{0}\) and to conclude that the inequalities are strict, i.e., \(q_{1}^{f}>\overline{q_{1}}\) and \(q_{0}^{l}<\underline{q_{0}}\).
This completes the proof. \(\square \)
Proof of Theorem 4
To prove this result we need to show that both firms prefer the follower outcome to any simultaneous play solution whenever the Pareto dominant Cournot equilibrium \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) is interior.
-
(i)
By point (i) of Lemma 8 we know that any \( \left( q_{0}^{f},q_{1}^{l}\right) \in S_{1}\) is such that \(q_{0}^{f}< \underline{q_{0}}\) and \(q_{1}^{l}>\overline{q_{1}}\). Moreover, from the definitions of Cournot and Stackelberg equilibria, both \(\left( q_{0}^{f},q_{1}^{l}\right) \) and \(\left( \underline{q_{0}},\overline{q_{1}} \right) \) lay on \(GR\,r_{0}\left( q_{1}\right) \). Then, as in proof of Lemma 7, we can apply the Envelope Theorem and obtain the following relation between welfare and profits:
$$\begin{aligned} W^{d}\left( q_{0}^{f},q_{1}^{l}\right) -W^{d}\left( \underline{q_{0}}, \overline{q_{1}}\right) \ge \varPi _{1}\left( q_{0}^{f},q_{1}^{l}\right) -\varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) >0 \end{aligned}$$(16)where the latter inequality comes from the property of Stackelberg equilibria, and it is strict by the result in point \((i)\) of the proof of Lemma 6.
-
(ii)
By point (ii) of Lemma 8, we know that any \(\left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) is such that \(q_{0}^{l}< \underline{q_{0}}\) and \(q_{1}^{f}>\overline{q_{1}}\). Then it follows that
$$\begin{aligned} \varPi _{1}\left( q_{0}^{l},q_{1}^{f}\right) \ge \varPi _{1}\left( q_{0}^{l}, \overline{q_{1}}\right) >\varPi _{1}\left( \underline{q_{0}},\overline{q_{1}} \right) \end{aligned}$$(17)where the first inequality comes from the fact that \(q_{1}^{f}\) is best response to \(q_{0}^{l}\) and the second is due to the private firm’s objective being strictly decreasing in \(q_{0}\).
The conditions of point (ii) of Proposition 1 hold and both Stackelberg equilibria are SPE of the endogenous timing game. \(\square \)
Proof of Theorem 5
Here \(r_{1}\left( q_{0}\right) \) is strictly increasing and \(r_{0}\left( q_{1}\right) \) is strictly decreasing, when interior. Hence, the mixed duopoly Cournot equilibrium is unique (call it \(\left( \underline{q_{0}}, \overline{q_{1}}\right) \)). As in the proof of Theorem 3, we now prove that: (i) the public firm is better off in the private leadership than in the mixed-duopoly Cournot equilibrium; while (ii) the private firm’s payoff is strictly larger in the Cournot than in the public leadership equilibrium.
-
(i)
For the private leadership equilibrium, since \(r_{0}\) is strictly decreasing in the interior, we can apply the same analysis as in point \((i)\) in Theorem 4 to show that from inequality (16) it follows that
$$\begin{aligned} W^{d}\left( q_{0}^{f},q_{1}^{l}\right) >W^{d}\left( \underline{q_{0}}, \overline{q_{1}}\right) \end{aligned}$$ -
(ii)
We now analyze the public firm’s leadership equilibrium. We first show the public leadership equilibrium \(\left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) is such that \(q_{0}^{l}>\underline{q_{0} }\) and \(q_{1}^{f}>\overline{q_{1}}\). Suppose by contradiction that \( q_{0}^{l}<\underline{q_{0}}\). First observe that
$$\begin{aligned} W^{d}\left( q_{0}^{l},q_{1}^{f}\right) \le W^{d}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \end{aligned}$$(18)because \(r_{0}\left( q_{1}^{f}\right) \) is a best response. Moreover, given that both \(\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \) and \(\left( \underline{q_{0}},\overline{q_{1}}\right) \) lay on \(GR\,r_{0}\left( .\right) \) with \(q_{1}^{F}<\overline{q_{1}}\), we can apply the envelope theorem as in Eq. (13) to show that
$$\begin{aligned} W^{d}\left( \underline{q_{0}},\overline{q_{1}}\right) -W^{d}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \ge \varPi _{1}\left( \underline{ q_{0}},\overline{q_{1}}\right) -\varPi _{1}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) >0 \nonumber \\ \end{aligned}$$(19)The latter inequality comes from the fact that
$$\begin{aligned} \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge \varPi _{1}\left( \underline{q_{0}},q_{1}^{f}\right) >\varPi _{1}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) \end{aligned}$$where the first inequality comes from \(\overline{q_{1}}\) being a best response to \(\underline{q_{0}}\), and the second is due to the fact that \(\varPi _{1}\left( \cdot \right) \) is strictly decreasing in \(q_{0}\) and \(r_{0}\left( q_{1}^{f}\right) >\underline{q_{0}}\). Considering the two inequalities (18) and (19), it follows that
$$\begin{aligned} W^{d}\left( q_{0}^{l},q_{1}^{f}\right) \le W^{d}\left( r_{0}\left( q_{1}^{f}\right) ,q_{1}^{f}\right) <W^{d}\left( \underline{q_{0}},\overline{ q_{1}}\right) \end{aligned}$$which contradicts the nature of Stackelberg equilibrium. Therefore it must be that \(q_{0}^{l}\ge \underline{q_{0}}\) and \(q_{1}^{f}\ge \overline{q_{1}}\). Moreover, we can apply the result in point \((ii)\) of the proof of Lemma 6 to show that \(\left( \underline{q_{0}},\overline{q_{1} }\right) \not \in S_{0}\) and to conclude that the inequalities are strict. So, since the Stackelberg equilibrium \(\left( q_{0}^{l},q_{1}^{f}\right) \in S_{0}\) is such that \(q_{0}^{l}>\underline{q_{0}}\) and \(q_{1}^{f}>\overline{ q_{1}}\), then
$$\begin{aligned} \varPi _{1}\left( \underline{q_{0}},\overline{q_{1}}\right) \ge \varPi _{1}\left( \underline{q_{0}},q_{1}^{f}\right) >\varPi _{1}\left( q_{0}^{l},q_{1}^{f}\right) \end{aligned}$$where the first inequality follows from the property of Cournot equilibria and the second from the fact that \(\varPi _{1}\) is strictly decreasing in \( q_{0} \). Then, the private firm strictly prefers Cournot to public leadership equilibria. Therefore the conditions of point (iii) of Proposition 1 hold and the private leadership equilibrium is the unique SPE of the endogenous timing game. \(\square \)
Rights and permissions
About this article
Cite this article
Amir, R., De Feo, G. Endogenous timing in a mixed duopoly. Int J Game Theory 43, 629–658 (2014). https://doi.org/10.1007/s00182-013-0401-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-013-0401-y