Constraints in models of production and cost via slack-based measures

Abstract

In this paper, we propose the use of stochastic frontier models to impose theoretical regularity constraints (like monotonicity and concavity) on flexible functional forms. These constraints take the form of inequalities involving the data and the parameters of the model. We address a major concern when statistically endogenous variables are present in these inequalities. We present results with and without endogeneity in the inequality constraints. In the system case (e.g., cost-share equations) or more generally, in production function-first-order conditions case, we detect an econometric problem which we solve successfully. We provide an empirical application to US electric power generation plants during 1986–1997, previously used by several authors.

1 Introduction

In many areas of applied economics operations research and applied economics, equations or systems of equations are often estimated that must satisfy certain theoretical constraints either globally or locally (that is at a specific point of approximation). Other times the equations must satisfy certain monotonicity or other constraints at each observation. Although globally flexible functional forms that satisfy the constraints (globally), often practitioners use flexible forms that cannot satisfy these restrictions using only parametric restrictions. Instead, the constraints also involve the data. Suppose, for example, we have a translog production function of the form:

$$\begin{aligned} y=\beta _{1}+\beta _{2}x_{1}+\beta _{3}x_{2}+\tfrac{1}{2}\beta _{4}x_{1}^{2}+\tfrac{1}{2}\beta _{5}x_{2}^{2}+\beta _{6}x_{1}x_{2}, \end{aligned}$$

(1)

where $y,x_{1},x_{2}$ denote the logs of output, capital and labor. The input elasticities must be positive, so we have the constraints:

$$\begin{aligned} \begin{array}{c} \beta _{2}+\beta _{4}x_{1}+\beta _{6}x_{2}\geqslant 0,\\ \beta _{3}+\beta _{6}x_{1}+\beta _{5}x_{2}\geqslant 0. \end{array} \end{aligned}$$

(2)

For problems related to the use of the translog see, for example, O’Donnell (2018, p. 286, footnote 11). We expand on this point below.

Imposing constraints has given rise to a significant literature including O’Donnell et al. (2001) and O’Donnell and Coelli (2005). McCausland (2008) uses orthogonal polynomials, while other authors proposed the use of neural networks (Vouldis et al. 2010). Diewert and Wales (1987) spell out the conditions that must be satisfied, while Gallant and Golub (1984), and Lau (1978) represent earlier attempts. Ivaldi et al. (1996) compare different functional forms in a concise way.

The dominant approach seems to be the one adopted by O’Donnell et al. (2001) and O’Donnell and Coelli (2005) who impose the constraints by assuming a different technology for each firm. Terrell (1996) is more in line with Geweke (1986), while Wolff et al. (2010) present new “local” approaches. In this paper, we retain the original problem: Given an equation or a system of equations of the traditional form, is it possible to use standard Markov Chain Monte Carlo (MCMC) methods to perform Bayesian inference subject to many data- and parameter-specific inequality constraints? This problem is fundamentally different from Geweke (1991) since we have, more often than not, a number of constraints exceeding the number of equations, and the inequality constraints must be imposed exactly without regard for their posterior probability. Surely, the constraints must not be imposed at all data points when they depend on the data as, for example, a translog cost or production function would reduce to a Cobb–Douglas which is not second-order flexible.

It turns out that there are two approaches to solve the problem. In the first approach that we call “naive,” all inequality constraints are converted to equalities using a surplus formulation. The surpluses are modeled within the stochastic frontier approach. This is, essentially, the approach in Huang and Huang (2019) which has been proposed independently of this paper. In the second approach, we take up a major problem with this model; viz. the fact that endogenous variables may appear in the inequality constraints. To the best of our knowledge, the problem (and a potential solution) has not been realized before. As we mentioned, the first approach has been proposed independently by Huang and Huang (2019) where the surpluses are assumed to follow independent half-normal distributions. The problems with this approach are: First, the surpluses cannot be independent as violation of some constraints (say monotonicity) are known to have effects on other constraints (like curvature). Second, endogeneity is not taken into account although endogenous variables appear in the frontier equations that impose the constraints. In turn, specialized methods can be used. Third, it is well known that imposition of theoretical constraints (which is necessary in any functional form to account for the information provided by neoclassical production theory) affects estimates of technical inefficiency, so the surpluses should be correlated with the one-sided error term in the production or cost function.

Moreover, we apply the new techniques to the translog as it is used widely. If researchers want to use globally flexible functional forms that satisfy monotonicity and curvature via only parametric restrictions (e.g., Koop et al. 1997 and the Generalized McFadden functional form), they can certainly do it and the methods in this paper are not necessary. However, as the translog is quite popular, we use it here as our benchmark case. Another case of flexible functional forms where the constraints also depend on the data has been analyzed in Tsionas (2016).

2 Equations and constraints linear in the parameters

2.1 General

Let us consider the simplest case of an equation which is linear in the parameters:

$$\begin{aligned} y_{i}=g\left( {z_{i}}\right) ^{\prime }\beta +v_{i}-u_{i},\quad i=1,\ldots ,n, \end{aligned}$$

(3)

where $z_{i}$ is an $m\times 1$ vector of basic covariates, $\beta$ is a $k\times 1$ vector of parameters, $g:{\mathbb {R}}^{m}\rightarrow {\mathbb {R}}^{k}$ is a vector function, and $u_{i}$ is a nonnegative error component representing technical inefficiency. The translog or polynomials in certain variables $z_{i}$ are leading examples. Apparently, we can write:

$$\begin{aligned} y_{i}={x}'_{i}\beta +v_{i}-u_{i}, \end{aligned}$$

(4)

where $x_{i}=g(z_{i})$ is $k\times 1$. Suppose we require the function $g\left( z\right) ^{\prime }\beta$ to be monotonic, and without loss of generality assume that all first-order partial derivatives must be nonnegative, that is $Dg\left( z\right) \beta \ge {\mathbf {0}}_{\left( {m\times 1}\right) }$. Since no parameters are involved in g, it is clear that the (transposed) Jacobian $Dg\left( z\right) \equiv X_{0}$, which is $m\times k$, is a simple function of z and, therefore, a simple function of X.

Suppose that for the ith observation, we have $X_{i0}=\left[ \begin{array}{cccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad x_{i1} &{}\quad 0 &{}\quad x_{i2}\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad x_{i2} &{}\quad x_{i1} \end{array}\right]$, $(i=1,\ldots ,n)$.

Bayesian inference in the linear model subject to a few inequality constraints has been considered by Geweke using both importance sampling (Geweke 1986) and Gibbs sampling (Geweke 1996). Here, we follow a different approach, independently proposed by Huang and Huang (2019).

Suppose we write the constraints as follows:

$$\begin{aligned} {\mathbf {0}}_{\left( {m\times 1}\right) }=X'_{i0}\beta +v_{i0}-{\widetilde{u}}_{i0},i=1,\ldots ,n, \end{aligned}$$

(5)

where $v_{i0}$ is an $m\times 1$ two-sided error term and ${\widetilde{u}}_{i0}$ is an $m\times 1$ nonnegative error component. Here, $v_{i0}$ represents noise in the inequality constraints and inequality constraints themselves are represented by ${\widetilde{u}}_{i0}$. So, (5) imposes the constraints $X'_{i0}\beta \ge {\mathbf {0}}_{m\times 1}$ up to measurement errors ($v_{i0}$). Moreover, ${\widetilde{u}}_{i0}$ represents slacks in the constraints.

If we write the equations together, we have:

$$\begin{aligned} \begin{array}{c} y_{i}=x'_{i}\beta +v_{i}-u_{i},i=1,\ldots ,n,\\ {\mathbf {0}}_{\left( {m\times 1}\right) }=X_{i0}\beta +v_{i0}-{\widetilde{u}}_{i0},i=1,\ldots ,n. \end{array} \end{aligned}$$

(6)

We are now ready to specify our distributional assumptions on the error components:

$$\begin{aligned} {\mathbf {v}}_{i}=[v_{i},v'_{i0}]'\sim N_{m+1}({\mathbf {0}},\Sigma ),\,{\mathbf {u}}_{i}=[u_{i},{\widetilde{u}}_{i0}']'\sim N_{m+1}^{+}({\mathbf {0}},\varPhi ),\,i=1,\ldots ,n. \end{aligned}$$

(7)

In this specification, the two-sided and one-sided error components are correlated across equations. This specification, unlike the one in Huang and Huang (2019), has certain advantages. First, the error terms $v_{i}$ and $v_{i0}$ are allowed to be correlated, as the imposition of theoretical constraints affects parameter estimates in the first equation of (6). Second, the one-sided error terms $u_{i}$ and ${\widetilde{u}}_{i0}$ are allowed to be correlated, since the extent of violation of certain constraints is very likely to affect the degree of violation of other constraints.

2.2 Simplified example

For ease of presentation and to establish the techniques, we assume $\Sigma =\left[ \begin{array}{cc} \sigma ^{2}\\ &{} \omega ^{2}I_{m} \end{array}\right]$, and $\varPhi =\left[ \begin{array}{cc} 0\\ &{} \phi ^{2}I_{m} \end{array}\right]$. In this case, we have no technical inefficiency (viz. $u_{i}=0$) and the scale parameter of surpluses, ${\widetilde{u}}_{i}$, have the same scale parameter ($\phi$). Clearly, the scales could have been different (Huang and Huang 2019), but most importantly $\varPhi$ should allow for correlations between the violations of different constraints. Here, we focus on the simplest possible case to provide the background of the new approach. For a fixed value of $\omega$, which controls the degree of satisfaction of the constraints, the posterior distribution of this model is given by:

$$\begin{aligned} \begin{array}{l} p\left( {\beta ,\sigma ,\phi ,u\vert y,X,\omega }\right) \propto \\ \sigma ^{-\left( {n+1}\right) }\phi ^{-\left( {n+1}\right) }\exp \left[ {-\frac{\left( {y-X\beta }\right) ^{\prime }\left( {y-X\beta }\right) }{2\sigma ^{2}}-\frac{\left( {u-X_{0}\beta }\right) ^{\prime }\left( {u-X_{0}\beta }\right) }{2\omega ^{2}}-\frac{{u}'u}{2\phi ^{2}}}\right] \cdot p\left( {\beta ,\sigma ,\phi }\right) , \end{array} \end{aligned}$$

(8)

where

$$\begin{aligned} X_{0\;(nm\times k)}=\left[ \begin{array}{c} X_{10}\\ X_{20}\\ \cdots \\ X_{n0} \end{array}\right] . \end{aligned}$$

(9)

For the prior, we have:

$$\begin{aligned} p\left( {\beta ,\sigma ,\phi }\right) \propto p(\beta |\sigma ,\phi )p(\sigma |\phi )p(\phi )\propto p(\beta )p(\sigma )p(\phi ). \end{aligned}$$

(10)

The only parameters of interest are the elements of $\beta$, and possibly $\sigma$, but not $\phi$, which like u, are artificial parameters introduced to facilitate Bayesian inference. Alternatively, u represents prior parameters with a prior given by (5) in which $\phi$ and $\omega$ are parameters. The user may have high relative prior precision with respect to the degree of satisfaction of the constraints (so parameter $\omega$ can be set in advance) but in other respects the user does not particularly care about how far in the acceptable region are the parameters. Of course, if this is not the case, it can always be controlled via choice of an informative prior of $\beta$.

Suppose for simplicity that $p\left( {\beta ,\sigma ,\phi }\right) \propto \sigma ^{-1}\phi ^{-1}$. Then, we can use the Gibbs sampler based on the following standard full posterior conditional distributions:

$$\begin{aligned} \beta \vert \sigma ,\phi ,u,y,X\sim N_{k}\left( {\bar{\beta },\bar{V}}\right) , \end{aligned}$$

(11)

where $\bar{\beta }=\left( {\omega ^{2}{X}'X+\sigma ^{2}{X}'_{0}X_{0}}\right) ^{-1}\left( {\omega ^{2}{X}'y+\sigma ^{2}{X}'_{0}u}\right)$, and

$\bar{V}=\sigma ^{2}\omega ^{2}\left( {\omega ^{2}{X}'X+\sigma ^{2}{X}'X}\right) ^{-1}$,

$$\begin{aligned}&\displaystyle \frac{\left( {y-X\beta }\right) ^{\prime }\left( {y-X\beta }\right) }{\sigma ^{2}}\vert \beta ,\phi ,u,y,X\sim \chi _{n}^{2}, \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \frac{{u}'u}{\phi ^{2}}\vert \sigma ,u,y,X\sim \chi _{n}^{2}, \end{aligned}$$

(13)

and finally:

$$\begin{aligned} u_{i}\vert \beta ,\sigma ,\phi ,y,X\sim N_{+}\left( \frac{\phi ^{2}}{\phi ^{2}+\omega ^{2}}X_{0}\beta ,{\, }\frac{\phi ^{2}\omega ^{2}}{\phi ^{2}+\omega ^{2}}1_{nm}\right) ,\,i=1,\ldots ,n, \end{aligned}$$

(14)

where $1_{nm}$ is a vector of ones whose dimensionality is $nm\times 1$. For details on the derivations, see Tsionas (2000). Generating random draws from these full posterior conditional distributions is straightforward. The last distribution is quite standard in Bayesian analysis of the normal–half normal stochastic model. So far, we have assumed that $\omega$ can be set in advance. This is, of course, a possibility. If the user does not feel comfortable about this choice, then one can use the following prior:

$$\begin{aligned} \frac{\overline{q}}{\omega ^{2}}\sim \chi _{\overline{n}}^{2}, \end{aligned}$$

(15)

where $\overline{n},\overline{q}\ge 0$ are prior parameters. In this case, the posterior conditional of $\omega$ is:

$$\begin{aligned} \frac{\overline{q}+\left( {u-X_{0}\beta }\right) ^{\prime }\left( {u-X_{0}\beta }\right) }{\omega ^{2}}|\beta ,\sigma ,\phi ,u,y,X\sim \chi _{n+\overline{n}}^{2}. \end{aligned}$$

(16)

The interpretation of (15) is that from a fictitious sample of size $\overline{n}$ the average $\omega ^{2}$ would be close to $\tfrac{\left( {u-X_{0}\beta }\right) ^{\prime }\left( {u-X_{0}\beta }\right) }{\overline{n}}$. There is nothing wrong with setting these parameters so that the prior is extremely informative if that is necessary; for example $\overline{n}=n$, and $\overline{q}=0.001$. The interpretation, in this case, is that we need the errors $v_{0}$ to be quite small, so that the constraints satisfy “exactly” the inequality constraints. Of course, this is related to Theil’s mixed estimator.

2.3 An artificial example

Following Parmeter et al. (2009), we have the following model:

$$\begin{aligned} y=10+3x+x^{2}-3x^{3}+x^{4}+v, \end{aligned}$$

where the x’s are generated as uniform in the interval [0, 2.5], and $v\sim N\left( {0,{\, }0.1^{2}}\right)$. We have $n=100$ observations, and the x’s are sorted. The constraint is that we need this function to be non-decreasing that is $3+2x-9x^{2}+4x^{3}\geqslant 0$ at all observed data points.

In this case, $x_{i}=\left[ {1,x,x^{2},x^{3},x^{4}}\right]$, and $x_{0i}=\left[ {0,1,2x,-9x^{2},4x^{3}}\right] ^{\prime }$. So the model is $y_{i}={x}'_{i}\beta +v_{i}$ subject to the constraints ${x}'_{0i}\beta \geqslant 0$. For this example, we set $\overline{n}=50$ and ${Q}=0.001$. Gibbs sampling is implemented using 15,000 passes the first 5000 of which are discarded to mitigate possible start up effects. The Least Squares (LS) fit has 22 violations of the constraints, while the Bayes fit has none. The Bayes fit is computed as follows. For each draw $\beta ^{\left( s\right) }$, we compute $f_{i}^{\left( s\right) }=X_{1}\beta ^{\left( s\right) }$. After the burn-in period, our estimate of the fit is $\hat{f}_{i}=S^{-1}\sum \nolimits _{s=1}^{S}{{x}'_{i1}\beta ^{\left( s\right) }}$ which is equivalent to $\hat{f}_{i}={x}'_{i}\hat{\beta }$ where $\hat{\beta }=E\left( {\beta \vert y,X}\right)$ is the posterior expectation of $\beta$ that can be approximated arbitrarily well (since it is simulation—consistent) by $\hat{\beta }=S^{-1}\sum \nolimits _{s=1}^{S}{\beta ^{\left( s\right) }}$. The same is true for the derivative. These computations involve only a standard Gibbs sampling scheme and the trivial computation of the posterior mean of $\beta$. In Fig. 1, we present the original data points, the LS fit, the Bayes fit and the constrained least squares (LS) fit as it is more appropriate to compare restricted LS with the Bayesian estimates.

Fig. 1

LS and Bayes fit in an artificial example

Even in this case, one may argue that the selection of parameters results in satisfaction of the constraints, but it does not guarantee the best fit. This criticism is not totally unfounded. For example, it would be possible to select these parameters so as to pass a line with positive slope through the points that would, apparently, satisfy all the constraints. Therefore, it may be necessary to device a mechanism by which $\omega$ is truly adjusted to the data so as to guarantee the best possible fit and also satisfying the constraints. Therefore, we search directly over the minimum value of $\omega$ that guarantees satisfaction of all constraints. It turns out that this value is 1.076 (when we use 15,000 Gibbs passes and the first 5000 are discarded). It turned out that this problem requires a fine grid of values (of the order 10$^{-4})$ in the relevant range which is determined empirically by trial-and-error.

Despite the effort it does not appear that the results are any better compared to standard Bayes analysis when $\omega$ is assigned a prior. The results are presented in panel (b) of Fig. 1. By “full Bayes fit,” we mean the fit when $\omega$ is drawn from its full conditional distribution. By “conditional Bayes fit,” we mean the fit when a detailed search is made over $\omega$ to determine the optimal value $\omega ^{*}=1.076$ that constitutes the value for which all constraints are satisfied along with fully Bayesian solutions for $\beta$, $\sigma$, $\phi$, and u.

3 The general formulation

3.1 Posterior

In the general case of technical inefficiency and correlated error components, we can write the posterior of the model in (6) as follows:

$$\begin{aligned} \begin{array}{c} p(\beta ,\Sigma ,\varPhi ,{\mathbf {u}}|y,X)\propto \\ |\Sigma |^{-n/2}|\varPhi |^{-n/2}\exp \left\{ -\tfrac{1}{2}\sum \limits _{i=1}^{n}\left( \psi _{i}-X_{i}\beta +{\mathbf {u}}_{i}\right) '\Sigma ^{-1}\left( \psi _{i}-X_{i}\beta +{\mathbf {u}}_{i}\right) -\tfrac{1}{2}\sum \limits _{i=1}^{n}{\mathbf {u}}'_{i}\varPhi ^{-1}{\mathbf {u}}_{i}\right\} \cdot \\ p(\beta ,\Sigma ,\varPhi ), \end{array} \end{aligned}$$

(17)

where $p(\beta ,\Sigma ,\varPhi )$ denotes the prior, $\psi _{i}=\left[ \begin{array}{c} y_{i}\\ {\mathbf {0}}_{(m\times 1)} \end{array}\right]$ , and $X_{i}=\left[ \begin{array}{c} x'_{i}\\ X'_{io} \end{array}\right]$. As we mentioned above, ${\mathbf {u}}_{i}=\left[ \begin{array}{c} u_{i}\\ {\widetilde{u}}_{i\qquad (m\times 1)} \end{array}\right]$, for all $i=1,\ldots ,n$. Our prior is a reference flat prior:¹

$$\begin{aligned} p(\beta ,\Sigma ,\varPhi )\propto |\Sigma |^{-(m+2)/2}|\varPhi |^{-(m+2)/2}. \end{aligned}$$

(18)

Therefore, the posterior becomes:

$$\begin{aligned} \begin{array}{l} p(\beta ,\Sigma ,\varPhi ,{\mathbf {u}}|y,X)\propto \\ \quad |\Sigma |^{-(n+m+2)/2}|\varPhi |^{-(n+m+2)/2}\\ \qquad \exp \left\{ -\tfrac{1}{2}\sum \limits _{i=1}^{n}\left( \psi _{i}-X_{i}\beta +{\mathbf {u}}_{i}\right) '\Sigma ^{-1}\left( \psi _{i}-X_{i}\beta +{\mathbf {u}}_{i}\right) -\tfrac{1}{2}\sum \limits _{i=1}^{n}{\mathbf {u}}'_{i}\varPhi ^{-1}{\mathbf {u}}_{i}\right\} . \end{array} \end{aligned}$$

(19)

In this formulation, $\varPhi$ is a general (positive-definite) covariance matrix which allows for the fact that violations of different constraints may be related in an unknown way. The posterior can be analyzed easily using MCMC as shown in part 5.1 of the “Technical Appendix.”

3.2 Economic applications

3.2.1 Systems of equations

Many important systems of equations like the translog can be written in the form:²

$$\begin{aligned} \begin{array}{c} y_{t1}={x}'_{t}\beta _{J(1)}+v_{t1},\\ y_{t2}={x}'_{t0}\beta _{J(2)}+v_{t2},\\ \vdots \\ y_{tM}={x}'_{t0}\beta _{J(M)}+v_{tM}, \end{array} \end{aligned}$$

(20)

where $\beta _{J(m)}$ represents a particular selection of elements of vector $\beta$ with the indices in $J\left( m\right)$, $m=1,\ldots ,M$. We agree that $\beta _{J(1)}=\beta$ so that $J\left( 1\right) =\left\{ {1,2,\ldots ,d}\right\}$. Suppose, for example, that we have a translog cost function with K inputs and N outputs³:

$$\begin{aligned} \ln C= & {} \alpha _{0}+\sum \limits _{k=1}^{K}{\alpha _{k}}\ln p_{k}+\sum \limits _{n=1}^{N}{\beta _{n}}\ln y_{n}+\tfrac{1}{2}\sum \limits _{k=1}^{K}{\sum \limits _{l=1}^{K}{\alpha _{kl}}}\ln p_{k}\ln p_{l}\nonumber \\ \qquad&+\tfrac{1}{2}\sum \limits _{n=1}^{N}{\sum \limits _{s=1}^{N}{\beta _{ns}}}\ln y_{n}\ln y_{s}+\sum \limits _{k=1}^{K}{\sum \limits _{n=1}^{N}{\gamma _{kn}\ln p_{k}}}\ln y_{n}, \end{aligned}$$

(21)

where C is cost. We assume linear homogeneity with respect to prices which can be imposed directly by dividing C and all prices by $p_{K}$. The share equations are:

$$\begin{aligned} S_{k}\equiv \tfrac{w_{k}\mathrm{e}^{x_{kit}}}{\sum _{k'=1}^{K}w_{k'}\mathrm{e}^{x_{k'it}}}=\alpha _{k}+\sum \limits _{l=1}^{K}{\alpha _{kl}\ln p_{l}}+\sum \limits _{n=1}^{N}{\gamma _{kn}\ln y_{n}},\quad k=1,\ldots ,K-1.\nonumber \\ \end{aligned}$$

(22)

Clearly, $x_{t}$ consists of the regressors in the cost function, whose dimensionality is $d=1+K+N+\frac{K\left( {K+1}\right) }{2}+\frac{N\left( {N+1}\right) }{2}+KN$.

Also $x_{t0}=\left[ {\begin{array}{l} {\, }1\\ \ln p_{t}\\ \ln y_{t} \end{array}}\right]$ whose dimensionality is $L=K+N+1$ . Moreover, $\beta _{J(m)}=A_{m}\beta$ where $A_{m}$ is an $L\times d$ selection matrix (consisting of ones and zeros), for all $m=2,\ldots ,M$, and $A_{1}=I_{\left( {d\times d}\right) }$. Defining ${x}'_{t0}A_{m}={x}'_{tm}$ for $m=1,\ldots ,M$, we can write the full system in the form:

$$\begin{aligned} \begin{array}{c} y_{t1}={x}'_{t1}\beta +v_{t1}\\ y_{t2}={x}'_{t2}\beta +v_{t2}\\ \vdots \\ y_{tM}={x}'_{tM}\beta +v_{tM}, \end{array} \end{aligned}$$

(23)

where $M=K+1$. The complete system is $Y_{t}=X_{t}\beta +v_{t}$ or

$$\begin{aligned} {\mathbf{Y}}={\mathbf{X}}\beta +{\mathbf{v}}, \end{aligned}$$

(24)

where ${\mathbf{Y}}=\left[ {\begin{array}{l} Y_{1}\\ \vdots \\ Y_{T} \end{array}}\right]$, $Y_{t}=\left[ {\begin{array}{l} y_{t1}\\ \vdots \\ y_{tM} \end{array}}\right]$, $X_{t}=\left[ {\begin{array}{l} {x}'_{t1}\\ \cdots \\ {x}'_{tM} \end{array}}\right]$, ${\mathbf{X}}=\left[ {\begin{array}{l} X_{1}\\ \cdots \\ X_{T} \end{array}}\right]$.

The output cost elasticities are:

$$\begin{aligned} \frac{\partial \ln C}{\partial \ln y_{n}}=\beta _{n}+\sum \limits _{k=1}^{K}{\gamma _{kn}\ln p_{k}}+\sum \limits _{s=1}^{N}{\beta _{ns}\ln y_{s}}={x}'_{t0}\beta _{I\left( n\right) }={x}'_{t0}D_{n}\beta , \end{aligned}$$

(25)

where $D_{n}$ is an $L\times d$ selection matrix, and $I\left( n\right)$ represents the proper set of indices. Therefore, we have:

$\frac{\partial \ln C}{\partial \ln y_{n}}={z}'_{tn}\beta ,$ where ${z}'_{tn}={x}'_{t0}D_{n}$, for $n=1,\ldots ,N$.

Monotonicity with respect to prices and outputs implies the following restrictions:

$$\begin{aligned}&{x}'_{tm}\beta \geqslant 0,\quad m=2,\ldots ,K, \end{aligned}$$

(26)

$$\begin{aligned}&{z}'_{tn}\beta \geqslant 0,\quad n=1,\ldots ,N, \end{aligned}$$

(27)

for all $t=1,\ldots ,T$. In total, we have $r=T\left( {K+N-1}\right)$ monotonicity restrictions that we can represent in the form:

$$\begin{aligned} {\mathbf{0}}_{r\times 1}={\mathbf {W}}\beta +{{\xi }}+{\mathbf{u}}, \end{aligned}$$

(28)

where ${\mathbf{W}}$ is $r\times d$ and ${W}'_{t}=\left[ {\left( {{x}'_{tm},m=2,\ldots ,K}\right) , \left( {{z}'_{tn},n=1,\ldots ,N}\right) }\right]$ is the tth row of ${\mathbf{W}}$. We assume ${\varvec{\xi }}\sim N_{r}\left( {{\mathbf{0}},\, \omega ^{2}{\mathbf{I}}}\right)$, and ${\mathbf{u}}\sim N_{r}^{+}\left( {{\mathbf{0}},{\, }\sigma _{u}^{2}{\mathbf{I}}}\right)$. Further, we assume: ${\mathbf{v}}\sim N\left( {{\mathbf{0}},{\, }{\varvec{\Sigma }}\otimes {\mathbf{I}}_{T}}\right)$. Therefore, the complete system along with monotonicity constraints is:

$$\begin{aligned} \left[ {\begin{array}{l} {\mathbf{Y}}\\ {\mathbf{0}}_{r\times 1} \end{array}}\right] =\left[ {\begin{array}{l} {\mathbf{X}}\\ {\mathbf{W}} \end{array}}\right] \beta +\left[ {\begin{array}{l} {\mathbf{v}}\\ {\varvec{\xi }} \end{array}}\right] +\left[ {\begin{array}{l} {\mathbf{0}}_{MT\times 1}\\ {\mathbf{u}} \end{array}}\right] . \end{aligned}$$

(29)

Moreover, we assume $\Sigma =\sigma ^{2}{\mathbf {I}}$.

The conditional posterior distributions required to implement Gibbs sampling are presented in part 5.2 of the “Technical Appendix.”

3.2.2 Concavity

Diewert and Wales (1987) showed that concavity of the translog cost function requiring negative semidefiniteness of $\nabla _{pp}C\left( {p,y}\right)$ amounts to negative semidefiniteness of ${\mathrm{M}}_{t}={\mathbf{A}}-\mathrm{diag}\left( {{\mathbf{S}}_{t}}\right) +{\mathbf{S}}_{t}{\mathbf{{S}'}}_{t}$, where ${\mathbf{S}}_{t}$ is the vector of shares, and ${\mathbf{A}}$ is the $K\times K$ matrix $\left[ {\alpha _{kl}}\right]$. This matrix (after recalling $M=K+1$) is

$$\begin{aligned} {\mathbf{M}}_{t}={\mathbf{A}}-\left[ {\begin{array}{llll} {x}'_{t2}\beta &{}&{}&{}\\ &{}{x}'_{t3}\beta &{}&{}\\ &{}&{}\ddots &{}\\ &{}&{}&{}{x}'_{tM}\beta \end{array}}\right] +\left[ {\begin{array}{l} {x}'_{t2}\beta {x}'_{t2}\beta {\, \, \, \, \, }{x}'_{t2}\beta {x}'_{t3}\beta {\, \, \, }\cdots {\, \, }{x}'_{t2}\beta {x}'_{tM}\beta \\ {x}'_{t2}\beta {x}'_{t3}\beta {\, \, \, \, \, }{x}'_{t3}\beta {x}'_{t3}\beta {\, \, \, \, }\cdots {\, \, }{x}'_{t3}\beta {x}'_{tM3}\beta \\ {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, }\cdots \cdots \cdots \\ {x}'_{t2}\beta {x}'_{tM}\beta {\, \, \, \, }{x}'_{t3}\beta {x}'_{tM}\beta {\, }\cdots {\, \, \, }{x}'_{tM}\beta {x}'_{tM}\beta \end{array}}\right] .\nonumber \\ \end{aligned}$$

(30)

Suppose the eigenvalues of ${\mathrm{M}}_{t}$ are ${\lambda }'_{t}\left( \beta \right) =\left[ {\lambda _{t1}\left( \beta \right) ,\lambda _{t2}\left( \beta \right) ,\ldots ,\lambda _{tK}\left( \beta \right) }\right]$. Suppose ${\varvec{\varLambda }}\left( \beta \right)$ is the $T\times K$ matrix whose rows are ${\lambda }'_{t}\left( \beta \right)$, $t=1,\ldots ,T$. The concavity restrictions can be expressed in the form:

$$\begin{aligned} -{\varvec{\varLambda }}\left( \beta \right) ={\varvec{\zeta }}+{\mathbf{w}},\quad {\varvec{\zeta }}\sim N_{TK}\left( {{\mathbf{0}},{\, }\varOmega ^{2}{\mathbf{I}}}\right) ,\,{\mathbf{w}}\sim N_{TK}^{+}\left( {{\mathbf{0}},{\, }\sigma _{w}^{2}{\mathbf{I}}}\right) , \end{aligned}$$

(31)

where $\varOmega ^{2}$ and $\sigma _{w}^{2}$ are parameters. If we set $\varOmega ^{2}$ to a small number, the meaning of this expression is that all eigenvalues of the ${{M}}_{t}$ matrix are nonnegative. In practice, we can treat $\varOmega$ as a parameter to examine systematically the extent of violation of the constraint(s). Moreover, it is straightforward to have different $\varOmega$ parameters for different constraints or treat $\varOmega$ as a general covariance matrix.

4 Endogeneity issues

In the case of the cost function where input prices and outputs are taken as predetermined or in the case of (4) where the covariates are weakly exogenous, the Bayesian techniques, we have described, can be applied easily. However, there are many instances in which the covariates or explanatory variables are endogenously determined. An extremely important case is when (4) represents a production function. Under the assumption of cost minimization, inputs are decision variables (and, therefore, endogenous), while output (the left-hand-side variable) is predetermined. Moreover, economic exogeneity and econometric exogeneity are different things. If econometric exogeneity is rejected, this does not mean that the economic assumptions are wrong. Measurement errors, for example, would be a typical example. Lai and Kumbhakar (2019) consider the case of a Cobb–Douglas production function along with the first-order conditions for cost minimization. To summarize the approach of Lai and Kumbhakar (2019), we have the following Cobb–Douglas production function:

$$\begin{aligned} y_{it}=\beta _{0}+\sum _{k=1}^{K}\beta _{k}x_{kit}+v_{it}-u_{it},i=1,\ldots ,n,t=1,\ldots ,T, \end{aligned}$$

(32)

where $y_{it}$ is log output for firm i and date t, $x_{kit}$ is the log of kth input for firm i and date t , $v_{it}$ is a two-sided error term, $u_{it}$ is a non-negative error component that represents technical inefficiency in production, and $\beta _{k}>0,k=1,\ldots ,K$. Suppose also input prices are $w_{kit}.$ From the first-order conditions of cost minimization (where inputs are endogenous choice variables and output is predetermined), we obtain:

$$\begin{aligned} \frac{\partial y_{it}/\partial x_{kit}}{\partial y_{it}/\partial x_{1it}}=\frac{w_{kit}x_{kit}}{w_{1it}x_{1it}}=\frac{\beta _{k}}{\beta _{1}}\mathrm{e}^{v_{kit}},2=1,\ldots ,K. \end{aligned}$$

(33)

These conditions can be expressed as follows:

$$\begin{aligned} x_{1it}-x_{kit}=\ln (w_{kit}/w_{1it})+(\ln \beta _{1}-\ln \beta _{j})+v_{kit},k=2,\ldots ,K. \end{aligned}$$

(34)

The constraints are only on the parameters $\beta _{k}$ ($k=1,\ldots ,K$), so this is not a very interesting example. However, if we generalize (32) to the translog case, we have:

$$\begin{aligned}&y_{it}=\beta _{0}+\sum _{k=1}^{K}\beta _{k}x_{kit}+\tfrac{1}{2}\nonumber \\&\sum _{k=1}^{K}\sum _{k'=1}^{K}\beta _{kk'}x_{kit}x_{k'it}+v_{it}-u_{it},i=1,\ldots ,n,t=1,\ldots ,T. \end{aligned}$$

(35)

Suppose all parameters are collected into the vector $\beta$ whose dimension is $d=1+K+\tfrac{K(K+1)}{2}$, after imposing symmetry, viz. $\beta _{kk'}=\beta _{k'k},\,k,k'=1,\ldots ,K$. The first-order conditions for cost minimization are as follows:

$$\begin{aligned} \frac{\partial y_{it}/\partial x_{kit}}{\partial y_{it}/\partial x_{1it}}=\frac{w_{kit}x_{kit}}{w_{1it}x_{1it}}=\frac{\beta _{k}+\sum _{k'=1}^{K}\beta _{kk'}\ln x_{k',it}}{\beta _{1}+\sum _{k'=1}^{K}\beta _{1k'}\ln x_{k',it}}\mathrm{e}^{v_{kit}},k=2,\ldots ,K. \end{aligned}$$

(36)

These equations can be rewritten as follows:

$$\begin{aligned}&x_{kit}-x_{1it}= \ln \left( \beta _{k}+\sum \limits _{k'=1}^{K}\beta _{kk'}x_{k',it}\right) \nonumber \\&\quad -\ln \left( \beta _{1}+\sum \limits _{k'=1}^{K}\beta _{1k'}x_{k',it}\right) -\ln (w_{kit}/w_{1it})+v_{kit},\,k=2,\ldots ,K. \end{aligned}$$

(37)

Moreover, it is convenient to rewrite (35) in the form:

$$\begin{aligned} y_{it}=\psi (x_{it})\beta +v_{it}-u_{it},\,i=1,\ldots ,n,t=1,\ldots ,T, \end{aligned}$$

(38)

where $\psi (x_{it})=[1,x_{1it},\ldots ,x_{Kit},\tfrac{1}{2}x_{1it}^{2},\ldots ,\tfrac{1}{2}x_{Kit}^{2},x_{1it}x_{2it},\ldots ,x_{(K-1)it}x_{Kit}]'$ are the nonlinear terms in the translog functional form.

From (35) and (37), we have a system of K equations in K endogenous variables.

The economic restrictions are as follows. First, we have monotonicity:

$$\begin{aligned} \beta _{k}+\sum _{k'=1}^{K}\beta _{kk'}x_{k',it}\ge 0,\,k=1,\ldots ,K. \end{aligned}$$

(39)

This imposes the following set of restrictions:

$$\begin{aligned} 0=\beta _{k}+\sum _{k'=1}^{K}\beta _{kk'}x_{k',it}+{\tilde{v}}_{k,it}+{\tilde{u}}_{k,it},\,k=1,\ldots ,K. \end{aligned}$$

(40)

Following Diewert and Wales (1987), given the monotonicity restrictions, we need the matrix $B=[\beta _{kk'},k,k'=1,\ldots ,K]$ to be negative semi-definite. Therefore, it is necessary and sufficient that the eigenvalues of B, say $\varLambda (\beta )=[\lambda _{1}(\beta ),\ldots ,\lambda _{K}(\beta )]'$, are all non-positive. This imposes the following set of nonlinear restrictions:

$$\begin{aligned} -\mathrm {vec}\varvec{\varLambda }(\beta )_{(TK\times 1)}=v_{(TK\times 1)}^{o}+u_{(TK\times 1)}^{o}. \end{aligned}$$

(41)

From (40) and (41), we have 2K additional equations so in total we have K endogenous variables but 3K stochastic equations. From the econometric point of view, this is, clearly, a major problem, as we lack 2K endogenous variables to complete the system in (35), (37), (40), and (41). Let us write the entire system as follows:

$$\begin{aligned} \left[ \begin{array}{c} -y_{it}\\ x_{2it}-x_{1it}\\ \vdots \\ x_{Kit}-x_{1it}\\ {\mathbf {0}}_{K}\\ {\mathbf {0}}_{K} \end{array}\right] =\left[ \begin{array}{c} -\psi (x{}_{it})\beta \\ g_{2}(x_{it};\beta )\\ \vdots \\ g_{K}(x_{it};\beta )\\ {\mathbf {m}}(x_{it};\beta )\\ {\mathbf {s}}(x_{it};\beta ) \end{array}\right] +\left[ \begin{array}{c} v_{it,1}\\ v_{it,2}\\ \vdots \\ v_{it,K}\\ {\tilde{v}}_{it,(K\times 1)}\\ v_{it,(K\times 1)}^{o} \end{array}\right] +\left[ \begin{array}{c} u_{it,1}\\ u_{it,2}\\ \vdots \\ u_{it,K}\\ {\tilde{u}}_{it,(K\times 1)}\\ {\check{u}}_{it,(K\times 1)} \end{array}\right] \end{aligned}$$

(42)

where $g_{k}(x_{it};\beta )=\ln \left( \beta _{k}+\sum _{k'=1}^{K}\beta _{kk'}\ln x_{k',it}\right) -\ln \left( \beta _{1}+\sum _{k'=1}^{K}\beta _{1k'}\ln x_{k',it}\right) -\ln (w_{kit}/w_{1it}),\,k=2,\ldots ,K$, ${\mathbf {m}}(x_{it};\beta )=[m_{1}(x_{it};\beta ),\ldots ,m_{K}(x_{it};\beta )]'$, $m_{k}(x_{it};\beta )=\beta _{k}+\sum _{k'=1}^{K}\beta _{kk'}\ln x_{k',it},\,k=1,\ldots ,K$, ${\mathbf {s}}(x_{it};\beta )=[s_{1}(x_{it};\beta ),\ldots ,s_{K}(x_{it};\beta )]'$, $s_{k}(x_{it};\beta )=\lambda _{k}(x_{it};\beta ),\,k=1,\ldots ,K$. Let us write the system in (42) compactly as follows:

$$\begin{aligned} {\mathbf {Y}}_{it}={\mathbf {f}}(x_{it};\beta )+{\mathbf {v}}_{it}+{\mathbf {u}}_{it}. \end{aligned}$$

(43)

Although we have 3K equations, there are only K endogenous variables. To provide 2K additional equations, it seems that the only possibility is to assume that ${\mathbf {U}}_{it}\equiv [{\tilde{u}}_{it}',{\check{u}}'_{it}]'$ are, in fact, endogenous variables. This provides, indeed, the missing 2K additional equations. To accomplish this, we depart from the assumption that ${\mathbf {U}}_{it}$ is a (vector) random variable, and, instead, we make use of the following device originally proposed by Paul and Shankar (2018) and further developed by Tsionas and Mamatzakis (2019):

$$\begin{aligned} {\mathbf {U}}_{it}=\left[ \begin{array}{c} U_{it,1}\\ \vdots \\ U_{it,2K} \end{array}\right] =\left[ \begin{array}{c} -\ln \varPhi (x'_{it}\gamma _{1})\\ \vdots \\ -\ln \varPhi (x'_{it}\gamma _{K}) \end{array}\right] \equiv {\mathbf {h}}(x_{it};\gamma ), \end{aligned}$$

(44)

where $\varPhi (\cdot )$ is any distribution function (for example, the standard normal), and $\gamma =[\gamma '_{1},\ldots ,\gamma _{K}']'\in {\mathbb {R}}^{2K}$ is a vector of parameters. The idea of Paul and Shankar (2018) is that efficiency, $r=\mathrm{e}^{-u}$ is in the interval (0, 1] and, therefore, r can be modeled using any distribution function. In turn, we have:

$$\begin{aligned} \left[ \begin{array}{c} -y_{it}\\ \Delta x_{it}\\ {\widetilde{u}}_{it} \end{array}\right] =\left[ \begin{array}{c} -\psi (x_{it})\beta \\ {\mathbf {g}}(x_{it};\beta )\\ {\mathbf {h}}(x_{it};\beta ,\gamma ) \end{array}\right] +\left[ \begin{array}{c} v_{it,1}\\ {\widetilde{v}}_{it}\\ \mathring{v}_{it,(2K\times 1)} \end{array}\right] +\left[ \begin{array}{c} u_{it,1}\\ {\widetilde{u}}_{it}\\ {\mathbf {0}}_{(2K\times 1)} \end{array}\right] , \end{aligned}$$

(45)

where $\mathring{v}_{it}=[{\tilde{v}}'_{it},{\check{v}}'_{it}]'$, ${\mathbf {V}}_{it}=[v_{it,1},\ldots ,v_{it,K},\mathring{v}_{it}']'$, ${\mathbf {U}}_{it}=[u_{it,1},\ldots ,u_{it,K}]'$, $\triangle x_{it}=[x_{2it}-x_{1it},\ldots ,x_{Kit}-x_{1it}]'$, ${\mathbf {g}}(x_{it};\beta )=[g_{2}(x_{it};\beta ),\ldots ,g_{K}(x_{it};\beta )]'$, ${\widetilde{v}}_{it}=[v_{it,2},\ldots ,v_{it,K}]'$, ${\widetilde{u}}_{it}=[u_{it,2},\ldots ,u_{it,K}]'$. MCMC for this model is detailed in the “Technical Appendix” (section 5.4).

5 Empirical application

We use the same data as in Lai and Kumbhakar (2019) which have been used before by Rungsuriyawiboon and Stefanou (2008). We have panel data on $n=82$ US electric power generation plants during 1986–1997 ($T=12$). The three inputs are labor and maintenance, fuel, and capital. We use a production frontier approach. Output is net steam electric power generation in megawatt-hours. Input prices are available, and a time trend is included in both the production function and the predetermined variables. MCMC is implemented using 150,000 draws discarding the first 50,000 to mitigate possible start up effects. Since we have 984 observations, we impose the constraints in (40) and (41) at randomly chosen points. The reason is that imposing the constraints in (40) and (41) at all points, compromises the flexibility of the translog and reduces it to the Cobb–Douglas production function, which is, clearly, very restrictive. We select the points by using the following methodology. Suppose we impose the constraints at the means of the data and P other points ($P=1,\ldots ,\overline{P}$) where $\overline{P}<nT$. The points are randomly chosen, and we set $\overline{P}=500$ which is, roughly, half the number of available observations. P itself is randomly chosen, uniformly distributed in $\left\{ 1,2,\ldots ,\overline{P}\right\}$. We repeat the process 10,000 times, and we compute the marginal likelihood of the model. The marginal likelihood is defined as:

$$\begin{aligned} {\mathcal {M}}({\mathscr {D}})=\int p(\beta ,\gamma ,\sigma _{u},{\mathbf {u}}_{1};{\mathscr {D}})\mathrm{d}\beta \,\mathrm{d}\gamma \,\mathrm{d}\sigma _{u}\,\mathrm{d}{\mathbf {u}}_{1}. \end{aligned}$$

(46)

The integral is not available analytically but can be computed numerically using the methodology of Perrakis et al. (2015). In turn, we select the value of P as well as the particular points at which the constraints are imposed, by maximizing the value of ${\mathcal {M}}({\mathscr {D}})$. For each P, we average across all datasets with this number of points, and we present the normalized log marginal likelihood in Fig. 6.

Marginal posterior densities of input elasticities are reported in Fig. 1. Without imposing the theoretical constraints, we have a number of violations in fuel and capital elasticities and even labor (where there is a distinct mode around zero). After imposing the constraints, the marginal posteriors are much more concentrated around their mean or median, showing that imposition of theoretical constraints improves the accuracy of statistical inference for these elasticities.

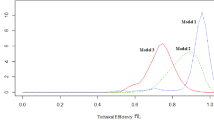
Marginal posterior densities of aspects of the model are reported in Fig. 2. Technical efficiency is defined as $r_{it}=\mathrm{e}^{-u_{it}}$ where $u_{it}\ge 0$ represents technical inefficiency. Technical change (TC) is defined as the derivative of the log production function with respect to time, viz. $\mathrm{TC}_{it}=\tfrac{\partial E(y_{it})}{\partial t}$. Efficiency change ($\mathrm{EC}_{it}$) is $\mathrm{EC}_{it}=\tfrac{u_{it}-u_{i,t-1}}{u_{i,t-1}}$. Productivity growth ($\mathrm{PG}_{it}$) is $\mathrm{PG}_{it}=\mathrm{TC}_{it}+\mathrm{EC}_{it}+\mathrm{SCE}_{it}$ , where $\mathrm{SCE}_{it}$ is the scale effect (Kumbhakar et al. 2015, equation 11.8). Under monotonicity and/or concavity, technical efficiency averages 85% and ranges from 78 to 93%. Without imposition of theoretical constraints technical efficiency is considerable lower, averaging 78% and ranging from 74 to 84%. Therefore, imposing the constraints is quite informative for efficiency and delivers results that are different compared to an unrestricted translog production function. Technical change averages 1% and ranges from − 3 to 5% per annum. Efficiency change is much more pronounced when monotonicity and/or concavity restrictions are imposed. Without the restrictions, it averages 1% and ranges from − 1 to 3.5%. With the restrictions in place, it averages 3.2% and ranges from − 1 to 6%. In turn, productivity growth (the sum of technical change, efficiency change and scale effect) averages 4.2% relative to only 2% in the translog model without the constraints.

In relation to (13), let us define $\varvec{\Sigma }=\left[ \begin{array}{cc} \sigma _{11} &{} \varvec{\sigma }_{1}'\\ \varvec{\sigma }_{1} &{} \varvec{\Sigma }^{*} \end{array}\right]$, where $\sigma _{11}$ is the variance of $v_{it,1}$, $\varvec{\sigma }_{1}$ represents the vector of covariances between $v_{it,1}$ and ${\widetilde{v}}_{it}$, and $\varvec{\Sigma }^{*}$ is the covariance matrix of ${\widetilde{v}}_{it}$. To examine whether the artificial error terms ${\widetilde{v}}_{it}$ are of quantitative importance, we can use the measure $|\varvec{\Sigma }^{*}|/\sigma _{11}$. This measure provides the (generalized) variability of ${\widetilde{v}}_{it}$ in terms of the variance of $v_{it,1}$, viz. the stochastic error in the production function.

Aspects of the posterior distribution of the model are reported in Figs. 2 and 3.

The marginal posterior densities of measure $|\varvec{\Sigma }^{*}|/\sigma _{11}$ are reported in the upper left panel of Fig. 3. The (generalized) variance of two-sided error terms in the constraints is only 3.5% relative to the variance of production function error term, implying that the one-sided error terms account for most of the variability of the equations corresponding to the restrictions. In the upper right panel of Fig. 4, we report the marginal posterior density of $\lambda =\tfrac{\sigma _{u}^{2}}{\sigma _{11}}$ which represents the signal-to-noise ratio in frontier models. This ratio averages 1.3 (ranging from 0.5 to 2.7) without the constraints and 2.5 (ranging from 1.5 to 3.7) when the constraints are imposed. This suggests that the imposition of theoretical constraints allows for more precise inferences in the stochastic frontier model. To allow for the presence of the constraints, it is more appropriate to define the signal-to-noise ratio as $\lambda ^{*}=\tfrac{\sigma _{u}^{2}}{|\varvec{\Sigma }|}$. The marginal posterior density of $\lambda ^{*}$ is reported in the bottom panel of Fig. 3. Evidently, the new measure is lower compared to $\lambda$, but it is still considerably larger than the ratio without imposition of the theoretical constraints.

Fig. 2

Marginal posterior densities of input elasticities. Notes: input elasticities are defined as $\tfrac{\partial E(y_{it})}{\partial x_{it}}$. in relation to (35)

Fig. 3

Marginal posterior densities of aspects of the model. Notes: Technical efficiency is defined as $r_{it}=\mathrm{e}^{-u_{it}}$ where $u_{it}\ge 0$ represents technical inefficiency. Technical change (TC) is defined as the derivative of the log production function with respect to time. Efficiency change (EC) is $\mathrm{EC}=\tfrac{u_{it}-u_{i,t-1}}{u_{i,t-1}}$. Productivity growth (PG) is $\mathrm{PG}=\mathrm{TC}+\mathrm{EC}$

Fig. 4

Marginal posterior densities of $\det (\varvec{\Sigma }^{*})/\sigma _{11}$ and $\lambda ^{*}$. Notes: In relation to (13), let us define $\varvec{\Sigma }=\left[ \begin{array}{cc} \sigma _{11} &{} \varvec{\sigma }_{1}'\\ \varvec{\sigma }_{1} &{} \varvec{\Sigma }^{*} \end{array}\right]$, where $\sigma _{11}$ is the variance of $v_{it,1}$, $\varvec{\sigma }_{1}$ represents the vector of covariances between $v_{it,1}$ and ${\widetilde{v}}_{it}$, and $\varvec{\Sigma }^{*}$ is the covariance matrix of ${\widetilde{v}}_{it}$ . To examine whether the artificial error terms ${\widetilde{v}}_{it}$ are of quantitative importance, we can use the measure $|\varvec{\Sigma }^{*}|/\sigma _{11}$. This measure provides the (generalized) variability of ${\widetilde{v}}_{it}$ in terms of the variance of $v_{it,1}$, viz. the stochastic error in the production function. To allow for the presence of the constraints, it is more appropriate to define the signal-to-noise ratio as $\lambda ^{*}=\tfrac{\sigma _{u}^{2}}{|\varvec{\Sigma }|}$

Posterior moments are presented in Table 1.

Table 1 Posterior moments and functions of interest

Another important issue is whether posterior predictive densities of efficiency estimates are more informative relative to unconstrained estimates. From Table in O’Donnell et al. (1999) who used Metropolis–Hastings to impose the constraints, unconstrained maximum likelihood estimates and Bayes estimates that impose concavity, sometimes yield higher efficiency estimates and sometimes they yield lower efficiency estimates. Standard errors without concavity and standard errors with concavity are, more often than not, lower in the second case, but there are some exceptions. On the other hand, the results of O’Donnell and Coelli (2005) suggest that imposing monotonicity and curvature yields more precise estimates (Table 3 and Figures 2–9).

In Fig. 4, we present posterior predictive densities of efficiency for nine randomly selected observations.

Fig. 5

Posterior predictive efficiency densities

In line with O’Donnell and Coelli (2005) or O’Donnell et al. (1999), we find that, more often than not, the posterior predictive efficiency densities are more concentrated around their modal values. The posterior predictive efficiency densities of other farms behave in the same way, and results are available on request. A related issue is whether imposition of monotonicity and curvature result in stochastic dominance over the model without these restrictions. From the evidence in Fig. 5, where we report normalized cumulative distribution functions (cdf), we have stochastic dominance of the model with monotonicity and curvature only for farms 6 and 9. Therefore, as a rule, imposition of the restrictions does not, necessarily, imply stochastic dominance mostly because the average posterior predictive efficiency estimates change as well.

6 Concluding remarks

An issue of great practical importance is the imposition of theoretical inequality constraints on cost or production functions. These constraints can be handled efficiently using a novel formulation that converts inequality constraints to equalities using surpluses which are treated in the context of stochastic frontier analysis. The idea has been developed independently by Huang and Huang (2019). However, the authors did not deal with the case of cost-share systems (in which more problems arise and need to be addressed) neither they allowed for correlation between violations of monotonicity and curvature which is quite likely in practice. There are two problems that are successfully resolved in this paper. First, the constraints are not independent as it is known, for example, that imposing monotonicity leads to fewer violations of concavity. Second, when explanatory variables are endogenous, special endogeneity problems arise which cannot be solved easily. In turn, proposed are special techniques to address this issue, and they are shown to perform well in an empirical application.

Technical Appendix

See Fig. 6.

Fig. 6

Posterior predictive cumulative distribution functions

1.1 5.1 MCMC associated with (19)

Conditional on all other parameters the posterior density of ${\mathbf {u}}_{i}$ is as follows:

$$\begin{aligned} {\mathbf {u}}_{i}|\beta ,\Sigma ,\varPhi ,y,X\sim N_{m+1}^{+}\left( \hat{{\mathbf {u}}}_{i},\,{\mathbf {V}}\right) ,\,i=1,\ldots ,n, \end{aligned}$$

(1)

where $\hat{{\mathbf {u}}}_{i}=-\left( \Sigma ^{-1}+\varPhi ^{-1}\right) ^{-1}\left( \psi _{i}-X_{i}\beta \right) ,\,i=1,\ldots ,n$, and ${\mathbf {V}}=\left( \Sigma ^{-1}+\varPhi ^{-1}\right) ^{-1}$.

We remind that in the main part we have assumed $\Sigma =\left[ \begin{array}{cc} \sigma ^{2}\\ &{} \omega ^{2}I_{m} \end{array}\right]$, and $\varPhi =\left[ \begin{array}{cc} 0\\ &{} \phi ^{2}I_{m} \end{array}\right]$. Here, we allow for general covariance matrices with the following prior:

$$\begin{aligned} p(\Sigma ,\varPhi )\propto |\Sigma |^{-(n+m+1)/2}|\varPhi |^{-(n+m+1)/2}. \end{aligned}$$

(2)

We adopt general covariance matrices because of the following reasons. It is always possible to fix $\Sigma$ in advance in the form $\Sigma =\left[ \begin{array}{cc} \sigma ^{2}\\ &{} \omega ^{2}I_{m} \end{array}\right]$, where $\sigma ^{2}$ remains an unknown parameter, but $\omega$ is fixed to a small value (say 0.001). In this case, the posterior conditional distribution of $\sigma ^{2}$ is:

$$\begin{aligned} \frac{(y+{\mathbf {u}}-X\beta )'(y+{\mathbf {u}}-X\beta )}{\sigma ^{2}}|\beta ,\omega ,{\mathbf {u}},y,X\sim \chi _{n}^{2}. \end{aligned}$$

(3)

We do not recommend this practice for three reasons. First, assuming independent two-sided errors is too restrictive as imposition of one constraint is not independent of imposing other constraints. Second, assuming independent one-sided errors is too restrictive as well. Third, a common value of $\phi$ is too restrictive as different constraints may require different surplus. However, with regard to the third point, it is not difficult to replace $\phi ^{2}I_{m}$ with an $m\times m$ diagonal matrix whose diagonal elements are $\phi _{1},\ldots ,\phi _{m}$. Moreover, it is possible to treat $\phi$ as a general covariance matrix (denoted $\varPhi$), as we do here.

The posterior conditional distributions are in the well-known inverted-Wishart family:

$$\begin{aligned} \begin{array}{c} p(\Sigma |\beta ,\varPhi ,{\mathbf {u}},y,X)\propto |\Sigma |^{-(n+m+1)/2}\exp \left( -\tfrac{1}{2}tr{\mathbf {A}}_{\Sigma }\Sigma ^{-1}\right) ,\\ p(\varPhi |\beta ,\Sigma ,{\mathbf {u}},y,X)\propto |\varPhi |^{-(n+m+1)/2}\exp \left( -\tfrac{1}{2}tr{\mathbf {A}}_{\varPhi }\varPhi ^{-1}\right) , \end{array} \end{aligned}$$

(4)

where ${\mathbf {A}}_{\Sigma }=\sum _{i=1}^{n}(\psi _{i}-X_{i}\beta +{\mathbf {u}}_{i})(\psi _{i}-X_{i}\beta +{\mathbf {u}}_{i})'$, and ${\mathbf {A}}_{\varOmega }=\sum _{i=1}^{n}{\mathbf {u}}_{i}{\mathbf {u}}'_{i}$. Finally, the posterior conditional distribution of $\beta$ is a multivariate normal:

$$\begin{aligned} \beta |\Sigma ,\varOmega ,{\mathbf {u}},y,X\sim N\left( {\hat{\beta }},\,{\mathbf {V}}_{\beta }\right) , \end{aligned}$$

(5)

where ${\hat{\beta }}=({\widetilde{X}}'\Sigma ^{-1}{\widetilde{X}})^{-1}{\widetilde{X}}'\Sigma ^{-1}(y+{\mathbf {u}})$, ${\mathbf {V}}_{\beta }=({\widetilde{X}}'\Sigma ^{-1}{\widetilde{X}})^{-1}$, and ${\widetilde{X}}=\left[ \begin{array}{c} X\\ X_{0} \end{array}\right]$.

All conditionals are in standard forms which facilitate random number generation for implementation of MCMC.

Fig. 7

Normalized log marginal likelihood. Notes: The log marginal likelihood is normalized in the interval [0, 1]. We select the value of P as well as the particular points at which the constraints are imposed, by maximizing the value of ${\mathcal {M}}({\mathscr {D}})$. For each P, we average across all data sets with this number of points. The constraints include monotonicity as well as concavity

1.2 5.2 MCMC associated with (29)

We remind that we assume $\Sigma =\left[ \begin{array}{cc} \sigma ^{2}\\ &{} \omega ^{2}I_{m} \end{array}\right]$, $\xi \sim N({\mathbf {0}},\omega ^{2}{\mathbf {I}})$, and ${\mathbf {u}}\sim N_{r}^{+}({\mathbf {0}},\sigma _{u}^{2}I)$. In this case, we have no technical inefficiency (viz. $u_{i}=0$) and the scale parameter of surpluses, ${\widetilde{u}}_{i}$, have the same scale parameter.

It is not difficult to show that

$$\begin{aligned} \beta \vert \cdot ,{\mathbf{Y}},{\mathbf{X}}\sim N_{d}\left( {\hat{\beta },{\, }{\mathbf{V}}}\right) , \end{aligned}$$

(6)

where $|\cdot ,{\mathbf{Y}},{\mathbf{X}}$ denotes conditioning on all other parameters, latent variables, and the data, and

$$\begin{aligned} \begin{array}{c} \hat{\beta }=\left[ {\omega ^{2}{\mathbf{{X}'}}\left( {{\varvec{\Sigma }}^{-1}\otimes {\mathbf{I}}_{T}}\right) {\mathbf{X}}+\sigma ^{2}{\mathbf{{W}'W}}}\right] ^{-1}\left[ {\omega ^{2}{\mathbf{{X}'}}\left( {{\varvec{\Sigma }}^{-1}\otimes {\mathbf{I}}_{T}}\right) {\mathbf{Y}}-{\mathbf{{W}'u}}}\right] ,\\ {\mathbf{V}}=\sigma ^{2}\omega ^{2}\left[ {\omega ^{2}{\mathbf{{X}'}}\left( {{\varvec{\Sigma }}^{-1}\otimes {\mathbf{I}}_{T}}\right) {\mathbf{X}}+\sigma ^{2}{\mathbf{{W}'W}}}\right] ^{-1}. \end{array} \end{aligned}$$

(7)

Also:

$$\begin{aligned} {\mathbf{u}}\vert \cdot ,{\mathbf{Y}},{\mathbf{X}}\sim N_{r}^{+}\left( {{\varvec{\hat{u}}},{\, }\sigma _{*}^{2}{\mathbf{I}}_{r}}\right) , \end{aligned}$$

(8)

where ${\varvec{\hat{u}}}=-\frac{\sigma _{u}^{2}}{\sigma _{u}^{2}+\omega ^{2}}{\mathbf{W}}\beta ,$ and $\sigma _{*}^{2}=\frac{\sigma _{u}^{2}\omega ^{2}}{\sigma _{u}^{2}+\omega ^{2}}$. Draws from the conditional distributions of $\sigma _{u}^{2}$ and $\omega ^{2}$ (given $\beta ,{\mathbf{u}},{\varvec{\Sigma }},{\mathbf{Y}},{\mathbf{X}})$ can be obtained as

$$\begin{aligned} \dfrac{{\mathbf {u}}'{\mathbf {u}}+{\bar{S}}_{u}}{\sigma _{u}^{2}}|\cdot ,{\mathbf{Y}},{\mathbf{X}}\sim \chi _{r+{\bar{r}}_{u}}^{2},\,\dfrac{\left( {{\mathbf{W}}\beta +{\mathbf{u}}}\right) ^{\prime }\left( {{\mathbf{W}}\beta +{\mathbf{u}}}\right) +\bar{S}_{\omega }}{\omega ^{2}}|\cdot \sim \chi ^{2}\left( {r+\bar{r}_{\omega }}\right) , \end{aligned}$$

(9)

where $\bar{S}_{\omega }$, $\bar{S}_{u}$, $\bar{r}_{\omega }$ and $\bar{r}_{u}$ represent prior parameters. The priors are such that

$\frac{\bar{S}_{\omega }}{\omega ^{2}}\sim \chi ^{2}\left( {\bar{r}_{\omega }}\right) ,$ and independently $\frac{\bar{S}_{u}}{\sigma _{u}^{2}}\sim \chi ^{2}\left( {\bar{r}_{u}}\right)$, $\dfrac{{\bar{S}}}{\sigma ^{2}}\sim \chi _{{\bar{r}}}^{2}$.

The values of the hyperparameters are ${\bar{r}}_{u}={\bar{r}}_{\omega }={\bar{r}}=1$, and ${\bar{S}}_{u}={\bar{S}}_{\omega }={\bar{S}}=10^{-6}$.

The conditional posterior distribution of $\sigma ^{2}$ is

$$\begin{aligned} \dfrac{{\bar{S}}+\sum \nolimits _{t=1}^{T}{\left( {Y_{t}-X_{t}\beta }\right) '\left( {Y_{t}-X_{t}\beta }\right) }}{\sigma ^{2}}|\cdot ,{\mathbf{Y}},{\mathbf{X}}\sim \chi _{nT+r}^{2}. \end{aligned}$$

(10)

.

Fig. 8

Autocorrelation functions (acf). Notes: OC (2005) is O’Donnell and Coelli (2005). For each set of parameters (in panels a, c, and d, we report the median acf across all parameters

Fig. 9

Relative Numerical Efficiency (RNE). Notes: OC (2005) is O’Donnell and Coelli (2005). For each set of parameters (in panels a, c, and d, we report the median acf across all parameters

Fig. 10

Percentage differences. Notes: OC (2005) is O’Donnell and Coelli (2005). For each set of parameters (in panels a, c, and d, we report the median acf across all parameters

Fig. 11

Geweke’s (1992) convergence diagnostic. Notes: OC (2005) is O’Donnell and Coelli (2005). For each set of parameters (in panels a, c, and d, we report the median acf across all parameters

1.3 5.3 MCMC associated with (45)

We write the system in (45) as follows:

$$\begin{aligned} {\mathbf {Y}}_{it}={\mathbf {F}}(x_{it};\beta ,\gamma )+{\mathbf {V}}_{it}+\left[ \begin{array}{c} {\mathbf {U}}_{it}\\ {\mathbf {0}}_{(2K\times 1)} \end{array}\right] , \end{aligned}$$

(11)

We need the Jacobian of transformation from ${\mathbf {V}}_{it}$ to the endogenous variables $[x_{it}',{\widetilde{u}}'_{it}]'$. The required Jacobian is:

$$\begin{aligned} J_{it}(\beta )=\sum _{k=1}^{K}\left( \beta _{k}+\sum _{k'=1}^{K}\beta _{kk'}x_{k',it}\right) =1, \end{aligned}$$

(12)

because $\sum _{k=1}^{K}\beta _{k}=1$ and $\sum _{k=1}^{K}\sum _{k'=1}^{K}\beta _{kk'}=0$ so that cost shares sum to unity. These constraints can be easily implemented in advance.

We are now able to make the following distributional assumptions:

$$\begin{aligned} {\mathbf {V}}_{it}\sim iid\,N_{K}({\mathbf {0}},\varvec{\Sigma }),\,u_{it,1}\sim iid\,N_{+}({\mathbf {0}},\sigma _{u}^{2}),\,i=1,\ldots ,n,\,t=1,\ldots ,T. \end{aligned}$$

(13)

Under these assumptions, the likelihood function of the model is as follows:

$$\begin{aligned} \begin{array}{c} {\mathcal {L}}(\beta ,\gamma ,\varvec{\Sigma },\varvec{\varOmega };{\mathscr {D}})\propto \intop _{{\mathbb {R}}_{+}^{nT}}|\varvec{\Sigma }|^{-nT/2}\sigma _{u}^{-nT/2}\cdot \exp \left( -\frac{\sum _{i=1}^{n}\sum _{t=1}^{T}u_{it,1}^{2}}{2\sigma _{u}^{2}}\right) \cdot \\ \exp \left\{ -\tfrac{1}{2}\left[ {\mathbf {Y}}_{it}-{\mathbf {F}}(x_{it};\beta ,\gamma )\right] \varvec{\Sigma }^{-1}\left[ {\mathbf {Y}}_{it}-{\mathbf {F}}(x_{it};\beta ,\gamma )\right] \right\} \text {d}{\mathbf {u}}_{1}. \end{array} \end{aligned}$$

(14)

where ${\mathscr {D}}$ denotes the data, ${\mathbf {u}}_{1}=[u_{it},i=1,\ldots ,n,t=1,\ldots ,T]$. Our prior for the parameters is given by:

$$\begin{aligned} p(\beta ,\gamma ,\varvec{\Sigma },\sigma _{u})\propto |\varvec{\Sigma }|^{-(d_{\Sigma }+1)/2}\cdot \sigma _{u}^{-1}, \end{aligned}$$

(15)

where $d_{\Sigma }=3K$ is the dimensionality of $\Sigma$.

By Bayes’ theorem, the posterior is $p(\beta ,\gamma ,\varvec{\Sigma },\sigma _{u}|{\mathscr {D}})\propto {\mathcal {L}}(\beta ,\gamma ,\varvec{\Sigma },\sigma _{u};{\mathscr {D}})\cdot p(\beta ,\gamma ,\varvec{\Sigma },\sigma _{u})$. To access the posterior, we consider the augmented (by ${\mathbf {u}}_{1}$) posterior which is:

$$\begin{aligned} \begin{array}{c} p(\beta ,\gamma ,\varvec{\Sigma },\sigma _{u},{\mathbf {u}}_{1};{\mathscr {D}})\propto |\varvec{\Sigma }|^{-(nT+3K+1)/2}\sigma _{u}^{-(nT+1)/2}\cdot \exp \left( -\frac{\sum _{i=1}^{n}\sum _{t=1}^{T}u_{it,1}^{2}}{2\sigma _{u}^{2}}\right) \cdot \\ \exp \left\{ -\tfrac{1}{2}\left[ {\mathbf {Y}}_{it}-{\mathbf {F}}(x_{it};\beta ,\gamma )\right] '\varvec{\Sigma }^{-1}\left[ {\mathbf {Y}}_{it}-{\mathbf {F}}(x_{it};\beta ,\gamma )\right] \right\} . \end{array} \end{aligned}$$

(16)

We use MCMC to obtain draws from $p(\beta ,\gamma ,\varvec{\Sigma },\sigma _{u},{\mathbf {u}}_{1};{\mathscr {D}})$. It is possible to integrate out $\varvec{\Sigma }$ analytically from (16) using properties of the inverted Wishart distribution (Zellner 1971, p. 229, formula (8.24) and p. 243, formula (8.86)) and we obtain:

$$\begin{aligned} \begin{array}{c} p(\beta ,\gamma ,\sigma _{u},{\mathbf {u}}_{1};{\mathscr {D}})\propto \sigma _{u}^{-(nT+1)/2}\cdot \exp \left( -\frac{\sum _{i=1}^{n}\sum _{t=1}^{T}u_{it,1}^{2}}{2\sigma _{u}^{2}}\right) \cdot \\ \left| \sum _{i=1}^{n}\sum _{t=1}^{T}\left[ {\mathbf {Y}}_{it}-{\mathbf {F}}(x_{it};\beta ,\gamma )\right] \left[ {\mathbf {Y}}_{it}-{\mathbf {F}}(x_{it};\beta ,\gamma )\right] '\right| ^{-nT/2}. \end{array} \end{aligned}$$

(17)

First, we draw $\sigma _{u}$ from its posterior conditional:

$$\begin{aligned} \frac{\sum _{i=1}^{n}\sum _{t=1}^{T}u_{it,1}^{2}}{\sigma _{u}^{2}}|\beta ,\gamma ,{\mathbf {u}}_{1},{\mathscr {D}}\sim \chi _{nT}^{2}. \end{aligned}$$

(18)

To update $\beta$ and $\gamma$, we use a Girolami and Calderhead (2011) algorithm which uses first- and second-order derivative information from the log of (17).

From Fig. 6, we see that the log marginal likelihood is largest when we use, approximately, 50 points to impose the monotonicity and curvature restrictions.

1.4 5.4 Comparison with other techniques to impose the restrictions

Other techniques to impose the constraints include (i) to use LS in the production function and examine points at which the restrictions do not hold. (ii) One can in turn use the accept-reject algorithm used by Terrell (1996) or the Metropolis–Hastings (M-H) algorithm used by O’Donnell and Coelli (2005), for example. Terrell (1996) used an accept–reject Gibbs sampling algorithm to impose monotonicity and concavity constraints on the parameters of a cost function (through parametric restrictions only). A problem is that it may be necessary to generate an extremely large number of candidate MCMC draws before finding one that is acceptable. O’Donnell and Coelli (2005) simulate from the constrained posterior using a random-walk Metropolis–Hastings algorithm. The same criticism that applies to Terrell’s (1996) approach possibly holds for the O’Donnell and Coelli (2005) approach as the acceptance rate could be too high or too low and it requires some tuning. Moreover, its performance can potentially be rather poor due to autocorrelation in MCMC.

Here, we consider both Terrell’s (1996) and ODonnell and Coelli’s (2005) approach. First, we consider autocorrelation functions (acf’s) for these techniques compared to ours in Fig. 7. Relative numerical efficiency (RNE, Geweke 1992) for the various techniques is reported in Fig. 8. If i.i.d sampling from the posterior were feasible, then RNE would be equal to one. As we use MCMC, we have, of course, to settle for lower values, provided they are not small in order to be sure that we are exploring the posterior in a thorough manner.

Autocorrelation functions drop to zero more rapidly compared to Terrell (1996) and O’Donnell and Coelli (2005). We use the same number of MCMC draws and the same length of burn-in.

In Fig. 9, we report the density of percentage differences between Terrell (1996) and O’Donnell (2005) for production function parameters (panel (a)), technical inefficiency (panel (b)), returns to scale (panel (c)), and productivity growth in panel (d). The rank correlations were from 0.30 to 0.60.

These differences between our method and Terrell (1996) or O’Donnell and Coelli (2005) can be explained by their higher acf’s which do not help convergence. As we see from Fig. 10, Geweke’s (1992) convergence diagnostic (GCD) (which is distributed as standard normal, asymptotically in the number of draws) fails to support convergence for Terrell’s (1996) or O’Donnell and Coelli’s (2005) approach (as it is greater than 2 in absolute value, more often than not). Results for technical inefficiency (panel (b)), and scale parameters (panel (c)) are similar. Reported in panel (c) is GCD for the latent variables in our constraints. From GCD, we can see that MCMC has converged (Fig. 11).