Stochastic frontier models using the Generalized Exponential distribution

Abstract

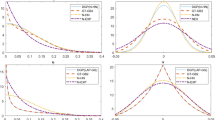
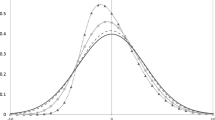
We present a new, single-parameter distributional specification for the one-sided error components in single-tier and two-tier stochastic frontier models. The distribution has its mode away from zero, and can represent cases where the most likely outcome is non-zero inefficiency. We present the necessary formulas for estimating production, cost and two-tier stochastic frontier models in logarithmic form. We pay particular attention to the use of the conditional mode as a predictor of individual inefficiency. We use simulations to assess the performance of existing models when the data include an inefficiency term with non-zero mode, and we also contrast the conditional mode to the conditional expectation as measures of individual (in)efficiency.

Appendix

1.1 The conditional expectation in the NGE production frontier

In the production SF model we want to compute

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right)=\displaystyle{\int\nolimits_{0}^{\infty }}{e}^{-u}{f}_{u| \varepsilon }(u| \varepsilon )du\\ \qquad\qquad\qquad\,\,\,=\frac{2}{{\sigma }_{v}{f}_{\varepsilon }(\varepsilon )}\displaystyle{\int\nolimits_{0}^{\infty }}{e}^{-u}\phi ((\varepsilon +u)/{\sigma }_{v}){h}_{E}(u;{\theta }_{u})du\\ \qquad\qquad\qquad\quad\,\,\,-\frac{1}{{\sigma }_{v}{f}_{\varepsilon }(\varepsilon )}\displaystyle{\int\nolimits_{0}^{\infty }}{e}^{-u}\phi ((\varepsilon +u)/{\sigma }_{v}){h}_{E}(u;{\theta }_{u}/2)du,\end{array}$$

where we have used the additive form of the GE density, eq. (2). Decomposing the integrands,

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right)=\frac{2\exp \{-{\varepsilon }^{2}/2{\sigma }_{v}^{2}\}}{{\theta }_{u}{\sigma }_{v}{f}_{\varepsilon }(\varepsilon )\sqrt{2\pi }}\times ({I}_{1}-{I}_{2}),\\ {I}_{1}=\displaystyle{\int\nolimits_{0}^{\infty }}\exp \left\{-{u}^{2}/2{\sigma }_{v}^{2}-\left(\varepsilon /{\sigma }_{v}^{2}+1+1/{\theta }_{u}\right)u\right\}du\\ {I}_{2}=\displaystyle{\int\nolimits_{0}^{\infty }}\exp \left\{-{u}^{2}/2{\sigma }_{v}^{2}-\left(\varepsilon /{\sigma }_{v}^{2}+1+2/{\theta }_{u}\right)u\right\}du.\end{array}$$

Combining formulas from Gradshteyn and Ryzhik (2007) and Erdelyi et al. (1954), we have (for a > 0),

$${\int\nolimits_{0}^{\infty }}\exp \{-a{z}^{2}-bz\}dz=\frac{\sqrt{\pi }}{\sqrt{a}}\exp \left\{\frac{{b}^{2}}{4a}\right\}\Phi \left(-\frac{b}{\sqrt{2a}}\right).$$

For both integrals, we have the common mapping

$$a=1/2{\sigma }_{v}^{2}\ \Rightarrow \ \frac{1}{\sqrt{a}}={\sigma }_{v}\sqrt{2},\ \frac{1}{\sqrt{2a}}={\sigma }_{v},\ \frac{1}{4a}={\sigma }_{v}^{2}/2.$$

Moreover we have, using indices 1 and 2 for the two integrands,

$${b}_{1}=\varepsilon /{\sigma }_{v}^{2}+1+1/{\theta }_{u},\ {b}_{2}={b}_{1}+1/{\theta }_{u}$$

$$\ \Rightarrow \ {b}_{2}^{2}={b}_{1}^{2}+2{b}_{1}/{\theta }_{u}+1/{\theta }_{u}^{2}.$$

Exploiting these results to make some initial simplifications we can write

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right) =\frac{2\exp \{-{\varepsilon }^{2}/2{\sigma }_{v}^{2}\}}{{\theta }_{u}{f}_{\varepsilon }(\varepsilon )}\exp \left\{\frac{{\sigma }_{v}^{2}{b}_{1}^{2}}{2}\right\}\times ({A}_{1}-{A}_{2}),\\ {A}_{1}=\Phi \left(-{\sigma }_{v}{b}_{1}\right),\\ {A}_{2}=\exp \left\{\frac{{\sigma }_{v}^{2}{b}_{1}}{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{2{\theta }_{u}^{2}}\right\}\Phi \left(-{\sigma }_{v}{b}_{1}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right).\end{array}$$

Now,

$${b}_{1}^{2}=\frac{{\varepsilon }^{2}}{{\sigma }_{v}^{4}}+2\frac{1+{\theta }_{u}}{{\theta }_{u}}\frac{\varepsilon }{{\sigma }_{v}^{2}}+{\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right)}^{2}$$

$$\ \Rightarrow \ \frac{{\sigma }_{v}^{2}{b}_{1}^{2}}{2}=\frac{{\varepsilon }^{2}}{2{\sigma }_{v}^{2}}+\frac{1+{\theta }_{u}}{{\theta }_{u}}\varepsilon +\frac{{\sigma }_{v}^{2}}{2}{\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right)}^{2}.$$

Also,

$${\sigma }_{v}{b}_{1}=\frac{\varepsilon }{{\sigma }_{v}}+{\sigma }_{v}\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right),\ \frac{{\sigma }_{v}^{2}}{{\theta }_{u}}{b}_{1}=\frac{\varepsilon }{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}.$$

Combining all, we arrive at

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right) =\frac{2}{{\theta }_{u}{f}_{\varepsilon }(\varepsilon )}\exp \left\{\frac{1\;+\;{\theta }_{u}}{{\theta }_{u}}\varepsilon +\frac{{\sigma }_{v}^{2}}{2}{\left(\frac{1\;+\;{\theta }_{u}}{{\theta }_{u}}\right)}^{2}\right\} \\ \qquad\qquad\qquad\qquad\!\times\left[\Phi \left(-\frac{\varepsilon }{{\sigma }_{v}}-{\sigma }_{v}\left(\frac{1\;+\;{\theta }_{u}}{{\theta }_{u}}\right)\right)\right.\\ \qquad\qquad\qquad\qquad\left.-\exp \left\{\frac{\varepsilon }{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\left({\theta }_{u}+\frac{3}{2}\right)\right\}\Phi \left(-\frac{\varepsilon }{{\sigma }_{v}}-{\sigma }_{v}\left(\frac{2\;+\;{\theta }_{u}}{{\theta }_{u}}\right)\right)\right].\end{array}$$

1.2 The conditional mode in the NGE production frontier

We want to maximize the conditional density in eq. (9) with respect to q. Ignoring the terms that do not include q, the derivative we want to set equal to zero is

$$\frac{\partial }{\partial q}\left[\phi \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right)\cdot \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\right]$$

$$\begin{array}{l}=\phi ^{\prime} \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right)\left(-1/q{\sigma }_{v}\right)\cdot \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\\ \quad+\,\frac{1}{q}\phi \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right) \times \left[\left(-1+\frac{1}{{\theta }_{u}}\right){q}^{-1+1/{\theta }_{u}}-\left(-1+\frac{2}{{\theta }_{u}}\right){q}^{-1+2/{\theta }_{u}}\right]\end{array}$$

Using the property of the standard Normal density $\phi ^{\prime} (z)=-z\phi (z)$ we obtain

$$\begin{array}{l}...=\frac{1}{q}\phi \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right) \times \left\{\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}^{2}}\cdot \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\right.\\ \qquad\,\,\left.+\,\left(-1+\frac{1}{{\theta }_{u}}\right){q}^{-1+1/{\theta }_{u}}-\left(-1+\frac{2}{{\theta }_{u}}\right){q}^{-1+2/{\theta }_{u}}\right\}.\end{array}$$

Setting this expression equal to zero is equivalent to setting the expression in curly brackets equal to zero since the term outside is always positive. Manipulating further,

$$\begin{array}{l}...\ \Rightarrow \ \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\cdot \left[\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}^{2}}-1+\frac{1}{{\theta }_{u}}\right]\\ \qquad\quad\,\,\,\,-\frac{1}{{\theta }_{u}}{q}^{-1+2/{\theta }_{u}}=0.\end{array}$$

Taking ${q}^{-1+2/{\theta }_{u}}$ out as common factor we arrive at the expression used in the main text.