A pivot-based simulated annealing algorithm to determine oblique splits for decision tree induction

Abstract

We describe a new simulated annealing algorithm to compute near-optimal oblique splits in the context of decision tree induction. The algorithm can be interpreted as a walk on the cells of a hyperplane arrangement defined by the observations in the training set. The cells of this hyperplane arrangement correspond to subsets of oblique splits that divide the feature space in the same manner and the vertices of this arrangement reveal multiple neighboring solutions. We use a pivoting strategy to iterate over the vertices and to explore this neighborhood. Embedding this neighborhood search in a simulated annealing framework allows to escape local minima and increases the probability of finding global optimal solutions. To overcome the problems related to degeneracy, we rely on a lexicographic pivoting scheme. Our experimental results indicate that our approach is well-suited for inducing small and accurate decision trees and capable of outperforming existing univariate and oblique decision tree induction algorithms. Furthermore, oblique decision trees obtained with this method are competitive with other popular prediction models.

1 Introduction

Decision trees play an important role in the field of data science and statistical learning for solving classification and regression tasks. Their major benefit is that they are easy to understand due to their comprehensible hierarchical structure. A drawback of the most widely employed univariate decision trees is that the restriction to a single attribute per split often fails to capture the problem’s underlying structure adequately which leads to extensively large trees and makes interpretation difficult. Moreover, they are often less accurate than other available prediction models. Oblique decision trees, on the other hand, rely on affine hyperplanes to divide the feature space more efficiently. As a consequence, they are usually much smaller and often more accurate. Although the individual splits are harder to interpret, the hyperplane coefficients, which can be interpreted as weights for the individual attributes, still allow to draw meaningful conclusions regarding the data under consideration.

Given d real-valued features $X_1,\ldots ,X_d$ and a response variable Y with domain ${{\,\textrm{dom}\,}}(Y)$, an oblique decision tree is a rooted tree structure for which every internal node is associated with an oblique split of the form

$$\begin{aligned} a_1X_1+\ldots +a_dX_d\le b \end{aligned}$$

for $a\in \mathbb {R}^d$ and $b\in \mathbb {R}$ and each leaf node is associated with a certain label in ${{\,\textrm{dom}\,}}(Y)$. The label of an unseen observation $x\in \mathbb {R}^d$ can be predicted by pursuing a unique path from the root node to one of the leaf nodes according to the specified rules. The label stored at the end of this path then serves as a predictor for the label of x.

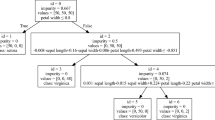
As an example, an oblique decision tree for the well-known Iris dataset (Fisher 1936) induced by our proposed method is illustrated in Fig. 1.

Fig. 1

Oblique decision tree for the Iris datset constructed with our simulated annealing algorithm

The most common way of learning decision trees, which is also pursued in this work, is to construct them in a top-down manner. For this, one makes use of a training set (X, y) that consists of a matrix $X\in \mathbb {R}^{n\times d}$, where each row $x_i$ corresponds to a specific observation and a vector $y\in {{\,\textrm{dom}\,}}(Y)^n$ which stores a label for each of those observations. Here, one distinguishes two kinds of data, that is regression data, where each label is a numerical value and classification data where each label stands for a certain category. This training set is then recursively divided by greedily introducing splits that minimize a certain splitting criterion. This process is carried out until no further splitting is possible or the labels of observations associated with each leaf node are sufficiently homogeneous.

It has been shown that the task of determining whether there exists an oblique split which misclassifies no more than a given number of observations is NP-complete (Heath 1993). Hence, unless $\text {P}=\text {NP}$, it is generally not possible to compute an optimal oblique split in polynomial time. Therefore, we present a new simulated annealing heuristic to determine near-optimal oblique splits. Our neighborhood operations are based on cells of auxiliary hyperplane arrangements and we employ a pivoting strategy to define random walks over neighboring cells. This idea yields an efficient algorithm for determining near-optimal oblique splits which is well-suited for the induction of oblique decision trees.

2 Related work and contribution

The top-down induction method is the most common approach for learning decision trees and various heuristics have been proposed in this context for finding oblique splits. Breiman et al. (1984) develop the first major algorithm, named CART-LC, to solve this problem. They propose a deterministic hill-climbing approach that cycles over the features and optimizes the corresponding coefficients of the oblique split individually until a local optimum is reached. Heath et al. (1993) develop a simulated annealing algorithm that allows it to escape local optima. Their algorithm repeatedly perturbs the coefficients of the oblique split one at a time by adding or subtracting a small value chosen uniformly at random from a predefined interval. In their oblique decision tree induction algorithm called OC1, Murthy et al. (1993, 1994) combine the hill-climbing approach with randomization techniques also with the goal of preventing premature convergence. When the hill-climbing is stuck at a local optimum, the split’s coefficients are either perturbed with a random vector or the optimization process is restarted at a new, randomly chosen hyperplane. Cantú-Paz and Kamath (2003) explore evolutionary algorithms to find near-optimal splits. They also present a simulated annealing algorithm that, in contrasts to Heath et al. (1993), in each iteration, perturbs all the coefficients of the oblique split by independently adding values chosen from a univariate normal distribution. In Bollwein and Westphal (2022) a cross-entropy optimization heuristic is developed that randomly samples new splits from the von Mises-Fisher distribution and iteratively updates the distribution’s parameters based on the best performing samples to converge towards a region of near-optimal splits. Other approaches for generating oblique splits include algorithms relying on logistic regression (Truong 2009), linear discriminants (López-Chau et al. 2013), angle bisectors (Manwani and Sastry 2011) or reflections of the feature space using householder transformations (Wickramarachchi et al. 2016, 2019).

In recent years, approaches that formulate the tree construction problem as a mathematical optimization program have become increasingly popular. Instead of constructing the trees in a top-down manner, integer linear programming (Bertsimas and Dunn 2017) or continuous optimization techniques (Blanquero et al. 2020, 2021) are used to induce trees of a predetermined fixed depth. Although this circumvents some shortcomings of the greedy top-down strategy, solving these models is very time-consuming and optimal solutions can only be computed for small to medium sized datasets and small depths. Due to the limitations of this approach, Dunn (2018) develops a local search heuristic which iteratively improves a decision tree by changing one randomly selected node at a time. For the induction of oblique decision trees, a perturbation approach similar to CART-LC and OC1 is employed for updating the splits.

In this work, we introduce a new simulated annealing heuristic for computing oblique splits that can naturally be integrated into the top-down strategy. It is based on the observation that subsets of equivalent splits correspond to cells of a suitably defined hyperplane arrangement. Compared to previous approaches, our algorithm is not restricted to random perturbations or updating the coefficients individually. Instead, we exploit the inherent structure of the problem and use a pivoting strategy to iterate over the vertices of the hyperplane arrangement which are the natural connecting points between neighboring cells. Similar ideas have been used for vertex enumeration in hyperplane arrangements (Avis and Fukuda 1992; Avis 2000) but our goal in this work is substantially different. Instead of enumerating all vertices, which would be computationally infeasible in many of the scenarios considered in this work, our simulated annealing algorithm visits only a subset of vertices with the goal of finding an optimal incident cell.

3 Preliminary definitions and preparations

3.1 Oblique splits and splitting criteria

Oblique splits can be interpreted as affine hyperplanes that divide the feature space into two halfspaces. Therefore, mathematically, an oblique split in $d\in \mathbb {N}$ dimensions can be defined as an indicator function that assigns the respective halfspace to every point $x\in \mathbb {R}^d$ in the feature space.

Definition 1

An oblique split is a function $\sigma _{a,b}:\mathbb {R}^d\rightarrow \lbrace -1,1\rbrace$ such that

$$\begin{aligned} \sigma _{a,b}(x)={\left\{ \begin{array}{ll} 1, &{}\quad \text {if } x^Ta\le b\\ -1, &{}\quad \text {if } x^Ta> b \end{array}\right. } \end{aligned}$$

for some $a\in \mathbb {R}^d$ and $b\in \mathbb {R}$. If $b=1$, we simplify the notation by writing $\sigma _a$ instead. For a matrix of observations $X\in \mathbb {R}^{n\times d}$ we further use the notation $\sigma _{a,b}(X)$ to refer to the vector $(\sigma _{a,b}(x_1),\ldots ,\sigma _{a,b}(x_n))^T$.

Based on this definition, a splitting criterion is very generally defined as follows.

Definition 2

A splitting criterion is a function $q:\lbrace -1,1 \rbrace ^n\times {{\,\textrm{dom}\,}}(Y)^n\rightarrow \mathbb {R}$ such that $q(\delta ,y)=q(-\delta ,y)$ for $\delta \in \lbrace -1,1 \rbrace ^n$.

The value of the splitting criterion for a dataset (X, y) and the split $\sigma _{a,b}$ is computed as $q(\sigma _{a,b}(X),y)$.

For classification tasks, these splitting criteria are typically based on so-called impurity measures such as classification error, entropy or Gini impurity. These measure the inhomogeneity of the labels of observations in the two subsets obtained by the split and the splitting criterion becomes the weighted sum of those impurities. Another well-known splitting criterion for classification is the twoing rule (Breiman et al. 1984). For regression tasks, one usually uses the weighted sum of mean squared errors or mean absolute errors from the mean or the median value of the labels of observations in the two respective halfspaces.

Although an oblique split is formally defined by $d+1$ parameters, the upcoming proposition shows that we can safely assume that $b=1$ to lower the dimension of the search space for the optimal parameters. Moreover, it states that for every oblique split there exists an alternative oblique split that is not satisfied with equality by any observation in the training data.

Proposition 1

For every oblique split $\sigma _{a,b}$ on the dataset (X, y) there exists $a'\in \mathbb {R}^d$ satisfying $x_i^Ta'\ne 1$ for $i=1,\ldots ,n$ such that $q(\sigma _{a,b}(X),y)=q(\sigma _{a'}(X),y)$.

Proof

Define

$$\begin{aligned} a':=\frac{a}{b+\epsilon } \end{aligned}$$

for a constant $\epsilon >0$ that satisfies $\epsilon \ne |b|$ and $\epsilon <x_i^Ta-b$ for all $i=1,\ldots ,n$ with $x_i^Ta>b$. Intuitively, the first condition ensures that $b+\epsilon \ne 0$ and the second condition guarantees that

$$\begin{aligned} x_i^Ta\le b \Leftrightarrow x_i^Ta<b+\epsilon \end{aligned}$$

and

$$\begin{aligned} x_i^Ta> b \Leftrightarrow x_i^Ta>b+\epsilon \end{aligned}$$

for all $i=1,\ldots ,n$. It therefore holds that

$$\begin{aligned} \sigma _{a,b}(X)={\left\{ \begin{array}{ll}\phantom{-} \sigma _{a'}(X), &{}\quad \text {if }b+\epsilon >0\\ -\sigma _{a'}(X), &{} \quad \text {if }b+\epsilon <0 \end{array}\right. } \end{aligned}$$

which ensures that $q(\sigma _{a,b}(X),y)=q(\sigma _{a'}(X),y)$.$\square$

Due to this observation, we focus on oblique splits with a right-hand side equal to one throughout the rest of this work and we further require that no observation satisfies the split with equality. Further, without loss of generality, we assume that the splitting criterion should be minimized. Hence, we can identify the solution space by $\mathcal {F}:=\lbrace a\in \mathbb {R}^d: x_i^Ta\ne 1 \ \forall i=1,\ldots ,n \rbrace$ and the optimization problem tackled in this work is to find

$$\begin{aligned} a^*\in \mathop {\mathrm {arg\,min}}\limits _{a\in \mathcal {F}} q(\sigma _{a}(X),y). \end{aligned}$$

3.2 Duplicate handling

It is not uncommon that the data matrix contains duplicated rows, i.e., it holds $x_i=x_{i'}$ for $i,i'\in \lbrace 1,\ldots ,n\rbrace$ and $i\ne i'$. Obviously, the corresponding observations $(x_i,y_i)$ and $(x_{i'},y_{i'})$ cannot be separated by an oblique split. For the upcoming definition of the neighborhood and the description of our simulated annealing algorithm, it is convenient to avoid this special case and to assume that the data matrix X does not contain duplicates. This problem can easily be circumvented by storing only a single representative row per group of duplicated observations. Instead of a single label per row one maintains a list that contains the labels of this group. The splitting criterion can then be evaluated in a straightforward manner using these lists. Without loss of generality, we can therefore assume that each $x_i$ for $i\in \lbrace 1,\ldots ,n\rbrace$ is unique in the data matrix X for the remainder of this work.

3.3 Redundancy due to perfect multicollinearity

Apart from duplicated rows in the data matrix, the dataset to be split can also involve redundant features. A common source for redundancy is perfect multicollinearity (Bollwein and Westphal 2022). Perfect multicollinearity occurs if there exist $a\in \mathbb {R}^d\setminus \lbrace \textbf{0} \rbrace$ and $b\in \mathbb {R}$ such that $x_i^Ta=b$ for all $i=1,\ldots ,n$. In the context of oblique decision tree induction such situations naturally occur as the decision tree grows and the number of observations associated with a node to be split becomes smaller than or equal to the number of features involved.

Perfect multicollinearity is equivalent to the existence of some column $X_{j^*}$ for $j^*\in \lbrace 1,\ldots ,d \rbrace$ of the data matrix X and values $\lambda _0,\lambda _j\in \mathbb {R}$ for $j\in \lbrace 1,\ldots ,d \rbrace \setminus \lbrace j^*\rbrace$ such that

$$\begin{aligned} X_{j^*}=\lambda _0\textbf{1}+\sum _{\substack{j=1:\\ j\ne j^* }}^d \lambda _j X_j. \end{aligned}$$

Therefore, for every oblique split $\sigma _{a,b}$ we can derive an equivalent oblique split $\sigma _{a',b'}$ that does not involve the feature $X_{j^*}$ by defining $b'=(b+a_{j^*}\lambda _0)$ and

$$\begin{aligned} a'_j={\left\{ \begin{array}{ll} (a_j+a_{j^*}\lambda _j),&{}\quad \text {if } j\ne j^*\\ 0,&{}\quad \text {else } \end{array}\right. } \end{aligned}$$

for $j=1,\ldots ,d$. It is easy to see that $\sigma _{a,b}(X)=\sigma _{a',b'}(X)$ and the two oblique splits are equivalent with respect to the splitting criterion. Subsequently, using the transformation described in the proof of Proposition 1, an equivalent split with a bias equal to one can be derived.

Removing such redundant features before computing an oblique split has several advantages. It increases the interpretability of the oblique splits and guarantees that the number of features involved in the split is lower than the number of observations in the subset of training data associated with a node. Moreover, it reduces the dimension of the solution space and therefore reduces the effort for finding (near-) optimal splits.

As perfect multicollinearity of a dataset (X, y) is equivalent to linear dependency of the vectors $\textbf{1},X_1,\ldots ,X_d$, in order to identify a maximum subset of features that is not perfectly multicollinear, one can carry out Gaussian elimination on the matrix $(\textbf{1}\ X)^T$. The pivot rows then correspond to the respective subset of non-redundant features.

We want to point out the fact that if the dataset is not perfectly multicollinear, the columns of X are linearly independent which is a useful property for the description of the upcoming algorithm. Therefore, for the remainder of this work we assume that the prior described preprocessing has been carried out beforehand to avoid perfect multicollinearity.

4 Geometric motivation

4.1 Induced hyperplane arrangement and neighborhood definition

While oblique splits are usually associated with hyperplanes and observations from a dataset with points in $\mathbb {R}^d$, we can also establish an alternative view which exchanges those roles. When viewing the vector of parameters $a\in \mathbb {R}^d$ of an oblique split $\sigma _{a}$ as a point in $\mathbb {R}^d$, each observation $x_i\in \mathbb {R}^{d}$ for $i=1,\ldots ,n$ defines an affine hyperplane $H_{x_i}:=\lbrace a\in \mathbb {R}^d: a^Tx_i= 1 \rbrace$ which divides $\mathbb {R}^d$ into the two open half-spaces $H^+_{x_i}:=\lbrace a\in \mathbb {R}^d: x_i^Ta< 1 \rbrace$ and $H^-_{x_i}:=\lbrace a\in \mathbb {R}^d: x_i^Ta> 1\rbrace$. If for some $i\in \lbrace 1,\ldots ,n\rbrace$ a point $a\in \mathbb {R}^d$ is included in the half-space $H^+_{x_i}$, it holds that $\sigma _{a}(x_i)=1$ and if $a\in H^-_{x_i}$ we have $\sigma _{a}(x_i)=-1$.

Following this view, the rows of the matrix X of the dataset (X, y) induce a hyperplane arrangement $\mathcal {A}_X=\lbrace H_{x_i}: i=1,\ldots ,n \rbrace$ in $\mathbb {R}^{d}$ and due to Proposition 1 the search space for an optimal oblique split $\mathcal {F}$ is equal to the complement $\mathcal {M}(\mathcal {A}_X):=\mathbb {R}^d{\setminus } \bigcup _{i=1}^n H_{x_i}$ of this arrangement. The cells $\mathcal {P}(\mathcal {A}_X)$ are the maximal connected subsets of $\mathcal {M}(\mathcal {A}_X)$. As each cell $P\in \mathcal {P}(\mathcal {A}_X)$ corresponds to an intersection of open half-spaces defined by the hyperplanes in $\mathcal {A}$ its closure $\overline{P}$ is a convex (possibly unbounded) polyhedron. Each cell $P\in \mathcal {P}(\mathcal {A})$ can be uniquely identified by the function ${{\,\textrm{sign}\,}}:\mathcal {P}(\mathcal {A}_X)\rightarrow \lbrace -1,1 \rbrace ^n$ such that

$$\begin{aligned} {{\,\textrm{sign}\,}}(P)_i={\left\{ \begin{array}{ll}\phantom{-} 1, &{}\quad \text {if } P\subseteq H^+_{x_i}\\ -1, &{}\quad \text {if } P\subseteq H^-_{x_i} \end{array}\right. } \end{aligned}$$

for $i=1,\ldots ,n$ that maps each cell to a sign vector $\delta \in \lbrace -1,+1 \rbrace ^n$. A sign vector $\delta$ is called feasible if and only if there exists some $P\in \mathcal {P}(\mathcal {A}_X)$ such that ${{\,\textrm{sign}\,}}(P)=\delta$. Figure 2 illustrates this idea for an exemplary training set consisting of three observations.

Clearly, for all $a\in P$ for some $P\in \mathcal {P}(\mathcal {A}_X)$ it holds that $\sigma _{a}(X)={{\,\textrm{sign}\,}}(P)$. Thus, points belonging to the same cell of the hyperplane arrangement yield the same objective value. Further, it is easy to see that a sign vector $\delta \in \lbrace -1,+1 \rbrace ^n$ is feasible if and only if there exists $a\in \mathbb {R}^d$ with $x_i^Ta\ne 1$ for all $i=1,\ldots ,n$ such that $\sigma _{a}(X)=\delta$.

Fig. 2

The hyperplane arrangement induced by a training set consisting of three observations. The sign vectors are depicted in the respective cells

The previous observation raises the idea that it is possible to obtain an optimal split by enumerating all the cells of the hyperplane arrangement $\mathcal {A}_X$. Yet, there is a well-known result that states that any hyperplane arrangement in $\mathbb {R}^d$ consisting of n hyperplanes divides the space into up to $\sum _{i=0}^{d} \left( {\begin{array}{c}n\\ i\end{array}}\right)$ distinct cells and this value is attained for hyperplane arrangements such that any d hyperplanes intersect in a unique vertex and any $d+1$ hyperplanes possess no common points (Edelsbrunner 2012). Unfortunately, this means that an exhaustive search over all possible cells is in general intractable. Nevertheless, this alternative geometric interpretation of the problem motivates a heuristic neighborhood search procedure on the cells of the hyperplane arrangement $\mathcal {A}_X$ that iteratively moves from one cell to another by crossing a facet of the closure of the cell. Formally, we can define this neighborhood on the arrangement $\mathcal {A}_X$ in terms of the sign vectors.

Definition 3

Let ${{\,\textrm{flip}\,}}:\lbrace -1,+1 \rbrace ^n\times \lbrace 1,\ldots ,n \rbrace \rightarrow \lbrace -1,+1 \rbrace ^n$ denote the operator defined by

$$\begin{aligned} {{\,\textrm{flip}\,}}(\delta ,i^*)_i={\left\{ \begin{array}{ll} \phantom{-}\delta _i,&{} \quad \text {if } x_i\ne x_{i^*}\\ -\delta _i,&{} \quad \text {if } x_i= x_{i^*} \end{array}\right. } \end{aligned}$$

for $i=1,\ldots ,n$. A flip is called feasible if and only if both $\delta$ and ${{\,\textrm{flip}\,}}(\delta ,i^*)$ are feasible sign vectors. Further, let $P\in \mathcal {P}(\mathcal {A}_X)$ denote a cell with ${{\,\textrm{sign}\,}}(P)=\delta$. $P'\in \mathcal {P}(\mathcal {A}_X)$ is a neighbor of P if and only if there exists some $i^*\in \lbrace 1,\ldots ,n \rbrace$ such that ${{\,\textrm{sign}\,}}(P')={{\,\textrm{flip}\,}}(\delta ,i^*)$.

Intuitively, this definition states that two cells are neighbors if they are separated by a single hyperplane which, in case some of the rows of X are duplicated, is potentially defined by multiple observations in the dataset. If we assume that X does not contain duplicated rows, which is justified due to Sect. 3.2, the definition simply states that two cells are neighbors if their sign vectors differ in exactly one position.

4.2 Algorithm outline

Our approach for exploring this neighborhood is a pivoting algorithm that iterates over the vertices of the hyperplane arrangement. As the vertices of $\mathcal {A}_X$ are incident to multiple cells, they reveal multiple suitable neighboring cells to move to. In general, it is not guaranteed that each cell is incident to a vertex. Yet, if we assume that the dataset is not perfectly multicollinear, it follows that ${{\,\textrm{rank}\,}}(X)=d$ which guarantees that each cell possesses at least one vertex (Grötschel et al. 2012). With these preparations, we are now ready to present the basic outline of our proposed algorithm.

Algorithm 1 summarizes our proposed simulated annealing method. As input the training set (X, y), an initial split $\sigma _{a}$, the splitting criterion q and an initial temperature $T_0$ is specified. A convenient choice for the initial split would be the best univariate split, yet any other oblique split, for example obtained with CART-LC, can be used.

After the initialization, $\delta \in \lbrace -1,+1 \rbrace ^n$ stores the sign vector $\sigma _a(X)$ and a vertex $v\in \mathbb {R}^d$ of the cell P with ${{\,\textrm{sign}\,}}(P)=\delta$ is determined. Variable $\delta ^*$ is used to store the best sign vector during the optimization process and it is initially set to $\delta$. Variable $t\in \mathbb {N}_0$ is used to keep track of the number of temperature updates.

Until a certain stopping criterion is met, the algorithm proceeds by choosing either to update the vertex of P or to move to a neighboring cell. In the latter case one chooses a hyperplane $H_{x_i}\in \mathcal {A}_X$ which contains v such that the sign vector $\delta '={{\,\textrm{flip}\,}}(\delta ,i)$ is feasible. The cell corresponding to sign vector $\delta '$ is denoted by $P'$. The new sign vector is accepted either if it improves the value of the splitting criterion or with a probability of $\exp \left( -\frac{q(\delta ',y)-q(\delta ,y)}{T}\right)$ which is the well-known Metropolis acceptance criterion (Metropolis et al. 1953). In this case, $\delta$ and P are set to $\delta '$ and $P'$, respectively. Then, if $\delta$ improves the value of the splitting criterion, $\delta ^*$ is updated accordingly. As the last step, the temperature $T_t$ is decreased such that the probability for accepting worsening sign vectors decreases and eventually, the optimization procedure reaches a stable state. For a discussion of various simulated annealing temperature schedules, the interested reader is referred to Gendreau and Potvin (2010).

Finally, $\delta ^*$ corresponds to a near-optimal sign vector and an oblique split $\sigma _{a^*,b^*}$ with $\sigma _{a^*,b^*}(X)=\delta ^*$ needs to be returned. Although for all $a\in \mathbb {R}^d$ and $b\in \mathbb {R}$ with $\sigma _{a,b}(X)=\delta ^*$ the value of the splitting criterion is identical, we empirically found that employing the hyperplane which maximizes the distance between the positively and the negatively labeled observations by the split usually achieves the best generalization performance. As a result, instead of choosing the final split arbitrarily, we therefore recommend solving the optimization problem

$$\begin{aligned} \begin{array}{rlll} \min &{} \Vert a \Vert _p^p &{}\\ s.t. &{}\delta ^*_i(x_i^Ta-b)\le -1, &{}\quad \forall i{}=1,\ldots ,n\\ &{} a\in \mathbb {R}^d,b\in \mathbb {R}\\ \end{array} \end{aligned}$$

(1)

for $1\le p<\infty$ to obtain the final split. Note, that this is the same problem that is solved for training generalized support vector machines (Bradley and Mangasarian 1998) in the linear separable case. It is usually preferable to use the 1-norm in the objective function as it has the advantage that the problem can be solved by linear programming. Moreover, it simplifies the oblique split by setting many of the coefficients $a_j$ for $j\in \lbrace 1,\ldots ,d\rbrace$ to zero which reduces the risk of overfitting the decision trees.

The upcoming sections are now dedicated to the implementation of Algorithm 1 based on basic solutions of auxiliary linear systems.

5 Algorithmic description

5.1 Basic solutions and dictionaries

Our approach to iterate over the neighborhood uses basic solutions of auxiliary system of linear inequalities. For each sign vector $\delta$ we define

$$\begin{aligned} \begin{array}{llr} x_i^Ta\le 1, &{}\quad \forall i=1,\ldots ,n: \delta _i=1\\ x_i^Ta\ge 1, &{}\quad \forall i=1,\ldots ,n: \delta _i=-1\\ \end{array} \end{aligned}$$

with decision variables $a_j\in \mathbb {R}$ for $j=1,\ldots ,d$. Clearly, $\delta$ is feasible if and only if this system has a solution $a\in \mathbb {R}^d$ such that $x_i^Ta\ne 1$ for $i=1,\ldots ,n$. If $P\in \mathcal {P}(\mathcal {A}_X)$ with ${{\,\textrm{sign}\,}}(P)=\delta$, this system of linear inequalities describes the closure $\overline{P}$. Let $\varDelta =\mathop {\textrm{diag}}\limits (\delta )$ denote the square diagonal matrix with the entries of $\delta$ on its main diagonal. By introducing non-negative slack variables $s_i$ for $i=1,\ldots ,n$ the inequality constraints can be transformed into equality constraints which results in the following linear system:

$$\begin{aligned} \begin{array}{llll} \mathop {\textrm{LS}}\limits (\delta ):&{} Xa+\varDelta s= \textbf{1}\\ &{} a_{j}\in \mathbb {R}, &{}\quad \forall j=1,\ldots ,d\\ &{} s_{i}\ge 0, &{}\quad \forall i=1,\ldots ,n\\ \end{array} \end{aligned}$$

For any matrix M and a subset of column indices J, let $M_J$ denote the submatrix of M limited to the columns specified in J. Similarly, for a vector v and a subset of indices, let $v_J$ denote the vector v restricted to the indices specified in J. A basis $B=(B_1,B_2)$ of $\mathop {\textrm{LS}}\limits (\delta )$ is a tuple of indices of decision variables $B_1\subseteq \lbrace 1,\ldots ,d \rbrace$ and slack variables $B_2\subseteq \lbrace 1,\ldots ,n \rbrace$ such that $|B_1|+|B_2|=n$ and $(X \ \varDelta )_B:=(X_{B_1}\ \varDelta _{B_2})$ is non-singular. For every basis B, the co-basis is defined by the tuple $N=(N_1,N_2)$ such that $N_1=\lbrace 1,\ldots ,d \rbrace {\setminus } B_1$ and $N_2=\lbrace 1,\ldots ,n \rbrace {\setminus } B_2$. The associated basic solution is the unique solution $(a,s)\in \mathbb {R}^d\times \mathbb {R}^n$ such that $\begin{pmatrix} a_{B_1}\\ s_{B_2} \end{pmatrix}=(X \ \varDelta )_B^{-1}\textbf{1}$ and $\begin{pmatrix} a_{N_1}\\ s_{N_2} \end{pmatrix}=\textbf{0}$. The basis B is feasible if $s_{i}\ge 0$ for $i=1,\ldots ,n$. If $s_{i}=0$ for some $i\in B_2$, the basis is called degenerate. Furthemore, a basis is called non-redundant if all decision variables are basic, i.e., $B_1=\lbrace 1,\ldots ,d \rbrace$. These feasible non-redundant bases correspond to the vertices of the closures of the cells of $\mathcal {A}_X$.

Proposition 2

Let $P\in \mathcal {P}(\mathcal {A}_X)$ with ${{\,\textrm{sign}\,}}(P)=\delta$ and B a non-redundant feasible basis of $\mathop {\textrm{LS}}\limits (\delta )$ with basic solution (a, s). Then, a is a vertex of $\overline{P}$. Conversely, if $v\in \mathbb {R}^d$ is a vertex of $\overline{P}$, there exists a non-redundant feasible basis of $\mathop {\textrm{LS}}\limits (\delta )$ such that its basic solution (a, s) satisfies $v=a$.

Proof

Let (a, s) denote the basic feasible solution of B. For each $i\in N_2$ we have $s_{i}=0$ and therefore, $a\in H_{x_i}$. As $|B_1|=d$ it holds that $|N_2|=d$. Hence, a is in the intersection of d hyperplanes in $\mathcal {A}_X$. Moreover, due to feasibility it holds that $a\in \overline{P}$. As $(X \ \varDelta )_B$ is non-singular, it is also the unique point in this intersection and thus, a vertex of $\overline{P}$.

Now, let v denote a vertex of $\overline{P}$. Then, there exists a subset of indices $N_2\subseteq \lbrace 1,\ldots ,n \rbrace$ with $|N|=d$ such that $x_i^Tv=1$ for all $i\in N_2$ and the vectors $x_i$ for $i\in N_2$ are linearly independent. Let $B_1=\lbrace 1,\ldots ,d \rbrace$, $B_2=\lbrace 1,\ldots ,n \rbrace {\setminus } N_2$ and $B=(B_1,B_2)$. As the rows of $(X \ \varDelta )_B$ are linearly independent, it follows that B is a basis. The corresponding basic solution (a, s) is feasible as it satisfies $a=v$, $s_{i}=0$ for $i\in N_2$ and thus also $s_{i}=\delta _i(1-x_i^Tv)\ge 0$ for all $i\in B_2$. As $\lbrace 1,\ldots ,d\rbrace =B_1$, it is also non-redundant.$\square$

The dictionary of $B=(B_1,B_2)$ is obtained by rearranging $\mathop {\textrm{LS}}\limits (\delta )$ into the following form:

$$\begin{aligned} \begin{pmatrix} a_{B_1}\\ s_{B_2} \end{pmatrix}&=(X \ \varDelta )_B^{-1}\textbf{1}-(X \ \varDelta )_B^{-1}\varDelta _{N_2}s_{N_2}-(X \ \varDelta )_B^{-1}X_{N_1}a_{N_1} \end{aligned}$$

For $i\in \lbrace 1,\ldots ,n\rbrace$ and $j\in N_1$ and we define

$$\begin{aligned} \begin{pmatrix} {(v_{ri})}_{r\in B_1}\\ {(w_{ki})}_{k\in B_2} \end{pmatrix}:=-(X\ \varDelta )_B^{-1}\varDelta _i \text { and } \begin{pmatrix} {(u_{rj})}_{r\in B_1}\\ {(z_{kj})}_{k\in B_2} \end{pmatrix}:=-(X \ \varDelta )_B^{-1}X_{j}. \end{aligned}$$

(2)

Note that for all $k\in B_2$ it holds that $v_{rk}=0$, $w_{kk}=-1$ and $w_{kk'}=0$ for all $k'\in B_2$ with $k'\ne k$. Further, it holds that $(X\ \varDelta )_B^{-1}\textbf{1}=(X\ \varDelta )_B^{-1}(\varDelta \delta )$. Thus, if we define

$$\begin{aligned} v_{r0}:=-\sum _{i\in N_2}\delta _i v_{ri} \text { and } w_{k0}:=\delta _{k}-\sum _{i\in N_2}\delta _i w_{ki} \end{aligned}$$

(3)

for $r\in B_1$ and $k\in B_2$, the dictionary can alternatively be expressed as follows:

$$\begin{aligned}a_{r}&{}=v_{r0}&&{}+\sum\limits_{i\in N_2}v_{ri}s_i&&{}+\sum\limits_{j\in N_1} u_{rj}a_j,&&{}\qquad \forall r\in B_1\\s_{k}&{}=w_{k0}&&{}+\sum\limits_{i\in N_2}w_{ki}s_i&&{}+\sum\limits_{j\in N_1} z_{kj}a_j,&&{}\qquad \forall k\in B_2\end{aligned}$$

5.2 The non-degenerate case

For the implementation of Algorithm 1 three major building blocks have to be discussed: pivoting operations to move between different bases, a method to derive a non-redundant feasible basis for the initial sign vector and a method to identify neighboring cells. For simplicity, we first consider the case in which no basis is degenerate for any sign vector. The more involved degenerate case is then discussed in Sect. 5.3.

Pivoting By performing pivot operations, we can move between different basic solutions of $\mathop {\textrm{LS}}\limits (\delta )$. A pivot operation exchanges a co-basic decision or slack variable with a basic slack variable to obtain a new basis $B'$. These pivot operations can be regarded as an increase or decrease of the value of a co-basic variable to a value where a non-negative basic variable restricted in sign would become zero. Basic decision variables are not leaving the basis due to the fact that they are not restricted in sign. A pivot operation is called feasible if both B and $B'$ are feasible. For a feasible pivot operation of a slack variable $s_i$ with $i\in N_2$ one determines the set:

$$\begin{aligned} L:=\mathop {\mathrm {arg\,min}}\limits _{k\in B_2}\left\{ -\frac{s_k}{w_{ki}}: {w_{ki}}< 0 \right\} . \end{aligned}$$

If $L=\emptyset$, i cannot be pivoted into the basis. Otherwise, we choose $k\in L$ as the leaving variable and the new basis becomes $B'=(B_1,B_2\setminus \lbrace k \rbrace \cup \lbrace i \rbrace )$. To pivot a decision variable $a_j$ with $j\in N_1$ into the basis, we determine

$$\begin{aligned} L_1:=\mathop {\mathrm {arg\,min}}\limits _{k\in B_2}\left\{ -\frac{s_k}{z_{kj}}: {z_{kj}}< 0 \right\} \end{aligned}$$

and

$$\begin{aligned} L_2:=\mathop {\mathrm {arg\,max}}\limits _{k\in B_2}\left\{ -\frac{s_k}{z_{kj}}: {z_{kj}}> 0 \right\} . \end{aligned}$$

The leaving variable $k\in B_2$ can then be chosen from $L_1\cup L_2$ and the new basis becomes $B'=(B_1\cup \lbrace j \rbrace ,B_2{\setminus }\lbrace k \rbrace )$. If $k\in L_1$, the value of $a_j$ is increased and otherwise, it is decreased. Under the assumption that X is not perfectly multicollinear, $L_1\cup L_2\ne \emptyset$ and therefore, a non-redundant basis can always be derived from a feasible basis by pivoting the co-basic decision variables into the basis.

Proposition 3

Let $P\in \mathcal {P}(\mathcal {A}_X)$ with sign vector ${{\,\textrm{sign}\,}}(P)=\delta$. For every feasible basis B of $\mathop {\textrm{LS}}\limits (\delta )$ there exists a sequence of feasible pivot operations such that the resulting basis is non-redundant.

Proof

Suppose B is redundant and there exists some $j^*\in N_1$ that cannot be pivoted into the basis because $L_1\cup L_2=\emptyset$. This implies that $z_{kj^*}=0$ for all $k\in B_2$. Thus, for any $t\in \mathbb {R}$ the solution defined by

$$\begin{aligned}& a(t)_{j^*}&&{}:=t\\& a(t)_{j}&&{}:=0, &&{}\qquad \forall j\in N_1\\& a(t)_{r}&&{}:=a_r+tu_{rj}, &&{}\qquad \forall r\in B_1\\& s(t)_{i}&&{}:=s_i, &&{}\qquad \forall i \in B_2\cup N_2 \\ \end{aligned}$$

is feasible. Hence, $\overline{P}$ contains a line which contradicts the fact that $\overline{P}$ has at least one vertex under the assumption that X is not perfectly multicollinear. The previous observation holds for any arbitrary redundant feasible basis and therefore, the co-basic decision variables can be iteratively pivoted into the basis in arbitrary order to obtain a non-redundant feasible basis. $\square$

Due to this observation, we can concentrate on non-redundant bases in our algorithm which represent the vertices of the closures of the cells in $\mathcal {P}(\mathcal {A}_X)$.

Initialization The algorithm is initialized at an arbitrary basic solution of a cell of $\mathcal {A}_X$. This can be achieved by choosing an initial split $\sigma _{a}$ arbitrarily. Then, we know that $\delta =\sigma _{a}(X)$ is a feasible sign vector and analogously to the Phase I of the simplex algorithm, we can solve the following auxiliary linear program:

$$\begin{aligned} \begin{array}{lrll} \mathop{\textrm{LP}}_I(\delta ):&{}\min &{} s_{0} &{}\\ &{}\mathop{\textrm{s.t.}} &{}\sum \limits _{j=1}^d x_{ij}a_{j}+\delta _i s_i-\delta _i s_{0}= 1, &{}\quad \forall i{}=1,\ldots ,n\\ &{}&{} a_{j}\in \mathbb {R}, &{}\quad \forall j{}=1,\ldots ,d\\ &{}&{} s_{i}\ge 0, &{}\quad \forall i{}=0,\ldots ,n\\ \end{array} \end{aligned}$$

The final basis that does not include $a_{0}$ is then a feasible basis of $\mathop {\textrm{LS}}\limits (\delta )$. Subsequently, in order to obtain a non-redundant basis, decision variables which are non-basic can be iteratively pivoted into the basis as described in the proof of Proposition 3.

Neighbor Selection As seen in the proof of Proposition 2, the intersection of the d hyperplanes associated with the co-basic slack variables of a feasible non-redundant basis of $\mathop {\textrm{LS}}\limits (\delta )$ define a vertex of $\overline{P}$ for $P\in \mathcal {P}(\mathcal {A}_X)$ with ${{\,\textrm{sign}\,}}(P)=\delta$. If the basis is non-degenerate, all of the entries in the sign vector corresponding to these co-basic slack variables can be flipped to obtain a new feasible sign vector. Hence, we can directly identify d different neighboring cells from the basic solution.

Theorem 1

Let $P\in \mathcal {P}(\mathcal {A}_X)$ with sign vector ${{\,\textrm{sign}\,}}(P)=\delta$. If $\mathop {\textrm{LS}}\limits (\delta )$ possesses a non-degenerate feasible basis B with co-basis N, then the sign vectors $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$ are feasible for all $i^*\in N_2$ and B is a feasible basis of $\mathop {\textrm{LS}}\limits (\delta ')$.

Proof

For $i^*\in N_2$ and $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$, it holds that $(X\ \varDelta )_B=(X\ \varDelta ')_B$ and therefore, the basic solution (a, s) of B for $\mathop {\textrm{LS}}\limits (\delta )$ corresponds to the basic solution of B for $\mathop {\textrm{LS}}\limits (\delta ')$. As $s_k> 0$ for all $k\in B_2$ and $s_i=0$ for all $i\in N_2$, B is also feasible and non-degenerate for $\mathop {\textrm{LS}}\limits (\delta ')$. Let $v'_{ri}$, $w'_{ki}$, $u'_{rj}$ and $z'_{kj}$ for $r\in B_1$, $k\in B_2$, $i\in N_2\cup \lbrace 0 \rbrace$ and $j\in N_1$ denote the respective values in the dictionary of B for $\mathop {\textrm{LS}}\limits (\delta ')$. We consider the following solution of $\mathop {\textrm{LS}}\limits (\delta ')$ for $t\ge 0$:

$$\begin{aligned}&{} s(t)_{i}&&{}:=t,&&{}\qquad \forall i\in N_2\\&{} s(t)_{k}&&{}:=w^{\prime}_{k0}+\sum _{i\in N_2}w^{\prime}_{ki}s(t)_i, &&{}\qquad \forall k\in B_2\\&{} a(t)_j&&{}:=0, &&{}\qquad \forall j\in N_1\\&{} a(t)_{r}&&{}:=v^{\prime}_{r0}+\sum _{i\in N_2}v^{\prime}_{ri}s(t)_i, &&{}\qquad \forall r\in B_1 \end{aligned}$$

For all $k\in B_2$ it holds that $s(t)_{k}>0$ if and only if

$$\begin{aligned} w'_{k0}>-\sum _{i\in N_2} w'_{ki}s(t)_{i} =-t\left( \sum _{i\in N_2} w'_{ki}\right) . \end{aligned}$$

As B is a non-degenerate feasible basis of $\mathop {\textrm{LS}}\limits (\delta ')$, we have $w'_{k0}>0$ for all $i\in B_2$. Thus, there exists a sufficiently small $\epsilon >0$ such that for $t=\epsilon$ the inequality is satisfied for all $k\in B_2$. Hence, the solution $(a(\epsilon ),s(\epsilon ))$ satisfies $s(\epsilon )_{i}>0$ for all $i\in \lbrace 1,\ldots ,n\rbrace$. We conclude that $x_i^Ta(\epsilon )\ne 1$ for all $i=1,\ldots ,n$ and $\sigma _{a(\epsilon )}(X)=\delta '$ and therefore, $\delta '$ is feasible.$\square$

5.3 The degenerate case

Degeneracy is one of the greatest challenges in the context of pivoting algorithms. One problem related to degeneracy is that the same basic solution of $\mathop {\textrm{LS}}\limits (\delta )$ can be expressed by multiple bases and thus, pivoting may not lead to different vertices which can cause the algorithm to stall for a large number of iterations. Another problem arising in our context is that it complicates the identification of neighboring cells as Theorem 1 is not applicable.

A common strategy for dealing with degeneracy is lexicographic perturbation. This technique was initially proposed for the simplex algorithm (Dantzig et al. 1955) and has also been successfully applied in other areas such as enumerating the vertices of a hyperplane arrangement (Avis 2000).

Lex-feasible bases Let P denote a cell in the hyperplane arrangement with sign vector ${{\,\textrm{sign}\,}}(P)=\delta$. The main idea behind perturbation is to resolve degeneracies by making small changes to the right-hand side of the equations. Hence, for $\epsilon _1,\ldots ,\epsilon _n>0$ we consider the following perturbed linear system:

$$\begin{aligned} \begin{array}{llll} \mathop {\textrm{LS}}^\epsilon (\delta ):&{} Xa+\varDelta s = \textbf{1}-\varDelta \epsilon \\ &{} a_{j}\in \mathbb {R}, &{}\quad \forall j{}=1,\ldots ,d\\ &{} s_{i}\ge 0, &{}\quad \forall i{}=1,\ldots ,n\\ \end{array} \end{aligned}$$

(4)

By this definition the feasible region is slightly narrowed down and every feasible solution of $\mathop {\textrm{LS}}^\epsilon (\delta )$ is also feasible for $\mathop {\textrm{LS}}\limits (\delta )$. As P is an open polyhedron of dimension d, we can choose $\epsilon _1,\ldots ,\epsilon _n$ small enough such that the perturbed cell $P^\epsilon :=\lbrace a\in \mathbb {R}^d: \delta _i(x_i^Ta)\le \delta _i-\epsilon _i\ \forall i=1,\ldots ,n \rbrace$ is non-empty.

Choosing explicit values for the perturbation constants has the major drawback that it is prone to numerical instabilities in computer implementations. Instead, in the lexicographic perturbation scheme $\epsilon _1,\ldots ,\epsilon _n$ are treated as symbolic values satisfying $1\gg \epsilon _{\pi ^{-1}(1)}\gg \cdots \gg \epsilon _{\pi ^{-1}(n)}> 0$ for some permutation $\pi$ of $\lbrace 1,\ldots ,n\rbrace$. This order defined by the permutation $\pi$ allows to compare expressions including $\epsilon _1,\ldots ,\epsilon _n$ without assigning explicit values. Formally, such a lexicographical order is defined as follows in this work.

Definition 4

Given a permutation $\pi$ of $\lbrace 1,\ldots ,n \rbrace$. A vector $w=(w_0,\ldots ,w_n)\in \mathbb {R}^{n+1}$ with $w\ne \textbf{0}$ is lexicographically positive (lex-positive) if the first non-zero entry in $(w_0,w_{\pi ^{-1}(1)},\ldots ,w_{\pi ^{-1}(n)})$ is positive. Analogously, it is lexicographically negative (lex-negative) if the first non-zero entry is negative. Vector $w_1\in \mathbb {R}^{n+1}$ is lexicographically greater than $w_2\in \mathbb {R}^{n+1}$ and we write $w_1>_\pi w_2$, if $w_1-w_2$ is lex-positive. We say that “$>_\pi$” is the lexicographic order induced by the permutation $\pi$. Moreover, we use the notation $w_1\ge _\pi w_2$ to express that either $w_1-w_2=\textbf{0}$ or $w_1>_\pi w_2$.

With the same definitions as in Eqs. (2) and (3), the dictionary of a basis $B=(B_1,B_2)$ of $\mathop {\textrm{LS}}^\epsilon (\delta )$ is given by

$$\begin{aligned}& a_{r}&&=v_{r0}&&+\sum \limits _{i\in N_2}v_{ri}\epsilon _i&&+\sum \limits _{i\in N_2}v_{ri}s_i&&+\sum \limits _{j\in N_1} u_{rj}a_j,&&\qquad \forall r\in B_1\\& s_{k}&&=w_{k0}-\epsilon_{k}&&+\sum \limits _{i\in N_2}w_{ki}\epsilon _i&&+\sum \limits _{i\in N_2}w_{ki}s_i&&+\sum \limits _{j\in N_1} z_{kj}a_j,&&\qquad \forall k\in B_2 \end{aligned}$$

and it follows that the basis is feasible for $\mathop {\textrm{LS}}^\epsilon (\delta )$ if for each $k\in B_2$ it holds that

$$\begin{aligned} w_{k0}-\epsilon _k+\sum _{i\in N_2} w_{ki}\epsilon _i\ge 0. \end{aligned}$$

Therefore, the basis is feasible in the lexicographical sense (lex-feasible) for the permutation $\pi$ if the vectors

$$\begin{aligned} w_{k}:=(w_{k0},w_{k1},\ldots ,w_{kn}) \end{aligned}$$

with $w_{kk}= -1$ and $w_{kk'}= 0$ for $k'\in B_2{\setminus }\lbrace k \rbrace$ are lex-positive for all $k\in B_2$. As each lex-feasible basis satisfies $w_{k0}\ge 0$ for all $k\in B_2$, it follows that the lex-feasible bases of $\mathop {\textrm{LS}}^\epsilon (\delta )$ are a subset of the feasible bases of $\mathop {\textrm{LS}}\limits (\delta )$.

An important property of lex-positive bases is that no two vectors $w_{k}$ and $w_{k'}$ for $k,k'\in B_2$ are equal or even multiples of each other. Moreover, every $w_{k}$ for $k\in B_2$ has at least one non-zero entry and therefore, no lex-feasible basis of the perturbed problem is degenerate. This is due to the fact that the vectors $(w_{k1},\ldots ,w_{kn})$ for $k\in B_2$ correspond to the first $|B_2|$ rows of $-(X \ \varDelta )_B^{-1}\varDelta$ which is a non-singular matrix due to the non-singularity of $(X \ \varDelta )_B^{-1}$.

Lexicographic Pivoting In order to maintain lex-feasibility, the pivoting scheme has to be slightly altered. To pivot a slack variable $s_i$ with $i\in N_2$ into the basis, one determines

$$\begin{aligned} L:=\mathop {{\mathop {\mathop {\mathrm {arg\,lexmin}}\limits }\nolimits _\pi }}\limits _{k\in B_2}\left\{ -\frac{w_{k}}{w_{ki}}: {w_{ki}}< 0\right\} . \end{aligned}$$

As no $w_{k}$ for $k\in B_2$ is a multiple of any other $w_{k'}$ for $k'\in B_2\setminus \lbrace k\rbrace$, it holds that $|L|\le 1$. If $L=\emptyset$, i cannot be pivoted into the basis. Otherwise, the unique element $k\in L$ is chosen as the leaving variable and the new basis becomes $B'=(B_1,B_2{\setminus }\lbrace k \rbrace \cup \lbrace i \rbrace )$. For a pivot operation of a decision variable $a_j$ with $j\in N_1$, we determine

$$\begin{aligned} L_1:=\mathop {{\mathop {\mathop {\mathrm {arg\,lexmin}}\limits }\nolimits _\pi }}\limits _{k\in B_2}\left\{ -\frac{w_{k}}{z_{kj}}: {z_{kj}}< 0\right\} \end{aligned}$$

and

$$\begin{aligned} L_2:=\mathop {{\mathop {\mathop {\mathrm {arg\,lexmax}}\limits }\nolimits _\pi }}\limits _{k\in B_2}\left\{ -\frac{w_{k}}{z_{kj}}: {z_{kj}}> 0 \right\} . \end{aligned}$$

With the same argument as before, we conclude that $|L_1|\le 1$ and $|L_2|\le 1$. Analogously to the proof of Proposition 3, it can be shown that $L_1\cup L_2\ne \emptyset$. The leaving variable $k\in B_2$ can then be chosen from $L_1\cup L_2$ and the new basis becomes $B'=(B_1\cup \lbrace j \rbrace ,B_2{\setminus }\lbrace k \rbrace )$.

Initialization In order to determine a lex-feasible starting solution, we consider the perturbed Phase I problem for some initial split $\sigma _{a}$ with $\sigma _{a}(X)=\delta$:

$$\begin{aligned} \begin{array}{lrlll} \mathop {\textrm{LP}}^\epsilon_I(\delta ):&{}\min &{} s_{0} &{}\\ &{}\textrm{s.t.}&{}\sum \limits _{j=1}^dx_{ij}a_{j}+\delta _i s_i-\delta _i s_{0}= 1-\delta _i\epsilon _i, &{}\quad \forall i{}=1,\ldots ,n\\ &{}&{} a_{j}\in \mathbb {R}, &{}\quad \forall j{}=1,\ldots ,d\\ &{}&{} s_{i}\ge 0, &{}\quad \forall i{}=0,\ldots ,n\\ \end{array} \end{aligned}$$

To solve this problem, we start at the initial basis $B=(B_1,B_2)=(\emptyset ,\lbrace 1,\ldots ,n \rbrace )$ consisting of all the slack variables. If $\delta _i=1$ for all $i=1,\ldots ,n$, this basis is lex-feasible for $\mathop {\textrm{LP}}^\epsilon _I(\delta )$. Otherwise, we can identify

$$\begin{aligned} k\in \mathop {{\mathop {\mathop {\mathrm {arg\,lexmin}}\limits }\nolimits _\pi }}\limits _{i=1,\ldots ,n} \lbrace (\delta _i\ -e_i^T)\rbrace \end{aligned}$$

where $e_i\in \mathbb {R}^n$ for $i=1,\ldots ,n$ denotes the standard unit vector with all entries equal to zero except the i-th which is equal to one and obtain a lex-feasible basis of $\mathop {\textrm{LP}}^\epsilon _I(\delta )$ by setting $B':=(B_1,B_2{\setminus }\lbrace k \rbrace \cup \lbrace 0 \rbrace )$. $\mathop {\textrm{LP}}^\epsilon_I(\delta )$ can then be solved with the simplex algorithm and the lexicographic pivoting scheme to obtain a lex-positive feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta )$. The final basis that does not include $s_{0}$ is then a feasible basis of $\mathop {\textrm{LS}}\limits (\delta )$. The correctness of this approach is shown by the proof of the following proposition.

Proposition 4

If $\delta$ is a feasible sign vector, there exists a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta )$ for every permutation $\pi$ of $\lbrace 1,\ldots ,n \rbrace$.

Proof

Let $\pi$ denote a permutation of $\lbrace 1,\ldots ,n \rbrace$. If $\mathop {\textrm{LP}}^\epsilon _I(\delta )$ is solved with the simplex algorithm as described above, $s_0$ strictly decreases lexicographically and one reaches an optimal lex-feasible basis after a finite number of iterations with reduced costs greater than or equal to zero. Note that the reduced costs are independent of the perturbation and therefore, this basis is optimal for any assignment of values to $\epsilon _1,\ldots ,\epsilon _n$ such that $1\gg \epsilon _{\pi ^{-1}(1)}\gg \cdots \gg \epsilon _{\pi ^{-1}(n)}> 0$. Suppose $s_0$ is part of the basis after the termination of the algorithm. Then, $s_0$ is lex-positive and thus, the objective value is positive for such an assignment. Therefore, $\mathop {\textrm{LS}}^\epsilon (\delta )$ is infeasible for any $\epsilon _1,\ldots ,\epsilon _n\in \mathbb {R}$ with $1\gg \epsilon _{\pi ^{-1}(1)}\gg \cdots \gg \epsilon _{\pi ^{-1}(n)}> 0$ which contradicts the feasibility of $\delta$.$\square$

Finally, analogously to the non-degenerate case, a non-redundant lex-feasible basis can be derived by sequentially pivoting the decision variables into the basis.

Neighbor Selection After the initialization, our algorithm is using non-redundant bases only. In this case, each non-basic variable is a slack variable and the dictionary of a basis B can be simplified as follows:

$$\begin{aligned}& a_{r}&&=v_{r0}&&+\sum \limits _{i\in N_2}v_{ri}\epsilon _i&&+\sum \limits _{i\in N_2}v_{ri}s_i,&&\qquad \forall r\in B_1\\ &s_{k}&&=w_{k0}-\epsilon_{k}&&+\sum \limits _{i\in N_2}w_{ki}\epsilon _i&&+\sum \limits _{i\in N_2}w_{ki}s_i,&&\qquad \forall k\in B_2 \end{aligned}$$

As $w_{kk}=-1$ and $w_{kk'}=0$ for all $k,k'\in B_2$ with $k\ne k'$, it is easy to see that in a lex-feasible basis for each $k\in B_2$ either $w_{k0}>0$ or there exists $i\in N_2$ with $\pi (i)<\pi (k)$ such that $w_{ki}>0$. Therefore, the indices corresponding to basic slack variables can be sorted back in the lexicographic order to derive a permutation $\pi '$ of $\lbrace 1,\ldots ,n \rbrace$ such that

• $\pi '(i_1)< \pi '(i_2)$ if $i_1,i_2\in N_2$ and $\pi (i_1)<\pi (i_2)$

• $\pi '(i)< \pi '(k)$ if $i\in N_2$ and $k\in B_2$

and the basis remains lex-feasible for $\pi '$. Using this permutation instead vastly simplifies the following theoretical analysis of our method to obtain neighboring solutions.

With these preparations, we can now present our method to determine neighboring cells. Hereafter, let P with ${{\,\textrm{sign}\,}}(P)=\delta$ denote the cell for which a neighbor should be determined and let $B=(B_1,B_2)$ and $N=(N_1,N_2)$ denote a non-redundant lex-feasible basis and the corresponding co-basis of $\mathop {\textrm{LS}}^\epsilon (\delta )$ with the lexicographic order induced by the permutation $\pi$ which satisfies $\pi (i)<\pi (k)$ if $i\in N_2$ and $k\in B_2$.

Our approach is motivated by the observation that, in order to move to a neighboring cell, it suffices to construct a lex-feasible basis for $\mathop {\textrm{LS}}^\epsilon (\delta ')$ where $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$ for some $i^*\in \lbrace 1,\ldots ,n \rbrace$. This is a consequence of the following lemma.

Lemma 1

If $\mathop {\textrm{LS}}^\epsilon (\delta )$ possesses a lex-feasible basis B for some permutation $\pi$ of $\lbrace 1,\ldots ,n \rbrace$, then there exists $P\in \mathcal {P}(\mathcal {A}_X)$ with ${{\,\textrm{sign}\,}}(P)=\delta$.

Proof

Suppose $\mathop {\textrm{LS}}^\epsilon (\delta )$ possesses a lex-feasible basis for some permutation $\pi$ of $\lbrace 1,\ldots ,n \rbrace$. Then, there exists an $\epsilon ^*>0$ such that for all $\epsilon _1,\ldots ,\epsilon _n$ satisfying $\epsilon ^*> \epsilon _{\pi ^{-1}(1)}\gg \cdots \gg \epsilon _{\pi ^{-1}(n)}> 0$ the solution $(a',s')\in \mathbb {R}^d\times \mathbb {R}^n$ defined by

$$\begin{aligned} & a'_j&&{}=0, &&{}\qquad \forall j\in N_1\\ &a'_r&&{}=v_{r0}+\sum _{i\in N_2}v_{ri}\epsilon _i, &&{}\qquad \forall r\in B_1\\& s'_i&&{}=\epsilon _i, &&{}\qquad \forall i\in N_2\\ &s'_k&&{}=w_{k0}-\epsilon _k+\sum _{i\in N_2}w_{ki}\epsilon _i, &&{}\qquad \forall k\in B_2 \end{aligned}$$

is feasible for $\mathop {\textrm{LS}}\limits (\delta )$. As $s'_i>0$, it holds that $x_i^Ta'\ne 1$ for all $i=1,\ldots ,n$ and $\sigma _{a'}(X)=\delta$. Therefore, there exists $P\in \mathcal {P}(\mathcal {A}_X)$ with ${{\,\textrm{sign}\,}}(P)=\delta$.$\square$

Our idea to obtain such a lex-feasible basis of a neighboring cell is similar to performing a pivot operation on one of the co-basic slack variables $i^*\in N_2$. Yet, instead of increasing its value, we deliberately try to decrease it to move across one of the facets of $\overline{P}$. We show that by using this strategy, we either find that $\delta '={{\,\textrm{flip}\,}}(\delta ,i^{*})$ is feasible or we get an unique candidate $l\in B_2$ such $\delta '={{\,\textrm{flip}\,}}(\delta ,l)$ is feasible. We further explain how to derive a new lex-feasible basis $B'$ for $\mathop {\textrm{LS}}^\epsilon (\delta ')$ and some possibly updated lexicographic ordering. The following lemma is helpful for the proofs of the upcoming theorems.

Lemma 2

For each $k\in B_2$ with $w_{k0}=0$, there exist at least two indices $i_1,i_2\in N_2$ such that $w_{ki_1}\ne 0$ and $w_{ki_2}\ne 0$ in the dictionary of B.

Proof

Suppose that for some $k\in B_2$ with $w_{k0}=0$ there exists only one $i^*\in N_2$ such that $w_{ki^*}\ne 0$. The existence of at least one such index follows from the lex-feasibility of the basis. Then, the row of variable $s_{k}$ in the dictionary can be transformed into:

$$\begin{aligned} s_k+\epsilon _k=w_{ki^*}(s_{i^*}+\epsilon _{i^*}) \end{aligned}$$

From the definition of $\mathop {\textrm{LS}}^\epsilon (\delta )$, we know that

$$\begin{aligned} s_i+\epsilon _i=\delta _i(1- x_i^Ta) \end{aligned}$$

for $i=1,\ldots ,n$. Hence, it follows that

$$\begin{aligned} \delta _k(1-x_k^Ta)=w_{ki^*} \delta _{i^*}(1-x_{i^*}^Ta). \end{aligned}$$

Due to $w_{k0}=\delta _k-\delta _{i^*}w_{ki^*}$ and $w_{k0}=0$, it holds that $\delta _k=\delta _{i^*}w_{ki^*}$. Therefore, we conclude

$$\begin{aligned} x_k^Ta=x_{i^*}^Ta\ \Leftrightarrow \ (x_k-x_i^*)^Ta=0. \end{aligned}$$

From the dictionary we get

$$\begin{aligned} a_j=v_{j0}+\sum _{i\in N_2} v_{ji}\epsilon _{i} \end{aligned}$$

for all $j\in B_1=\lbrace 1,\ldots ,d \rbrace$ and therefore, the following equation is satisfied:

$$\begin{aligned} \sum _{j=1}^d\left( v_{j0}+\sum _{i\in N_2}v_{ji}\epsilon _i\right) (x_{kj}-x_{i^*j})=0 \end{aligned}$$

This equation has to be satisfied for arbitrary $\epsilon _1,\ldots ,\epsilon _n>0$ which implies

$$\begin{aligned} \sum _{j=1}^dv_{ji}(x_{kj}-x_{i^*j})=0 \end{aligned}$$

for all $i\in N_2\cup \lbrace 0\rbrace$. By assumption, the matrix X does not have duplicated rows and therefore, there is at least one $j\in \lbrace 1,\ldots ,d\rbrace$ such that $x_{kj}-x_{i^*j}\ne 0$. Hence, the vectors $v_j:=(v_{j1},\ldots ,v_{jn})$ for $j=1,\ldots ,d$ with $v_{ji}=0$ if $i\in B_2$ are linearly dependent. This contradicts the fact that $(v_j)_{j=1,\ldots ,d}$ corresponds to the submatrix consisting of the first d rows of $-(X \ \varDelta )_B^{-1}\varDelta$ which is non-singular.$\square$

In the simplest case, the decrease of variable $s_{i^*}$ would only increase basic slack variables. Then, $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$ is a feasible sign vector and B is also a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta ')$ with the lexicographic order induced by $\pi$.

Theorem 2

Let $i^*\in N_2$. If $w_{ki^*}\le 0$ for all $k\in B$, the sign vector $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$ is feasible and B is a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta ')$ for the lexicographic order induced by $\pi$.

Proof

Let

$$\begin{aligned}& a_{r}&&=v'_{r0}&&+\sum \limits _{i\in N_2}v'_{ri}\epsilon _i&&+\sum \limits _{i\in N_2}v'_{ri}s_i,&&\qquad \forall r\in B_1\\ &s_{k}&&=w'_{k0}-\epsilon _{k}&&+\sum \limits _{i\in N_2}w'_{ki}\epsilon _i&&+\sum \limits _{i\in N_2}w'_{ki}s_i,&&\qquad \forall k\in B_2 \end{aligned}$$

denote the dictionary of B for $\mathop {\textrm{LS}}^\epsilon (\delta ')$. As $\delta$ differs from $\delta '$ only at an index corresponding to a co-basic slack variable, it holds that $(X\ \varDelta )_B=(X \ \varDelta ')_B$. Therefore,

$$\begin{aligned} \begin{pmatrix} {(v'_{ri})}_{r\in B_1}\\ {(w'_{ki})}_{k\in B_2} \end{pmatrix}=-(X \ \varDelta ')_B^{-1}\varDelta '_i=-(X \ \varDelta )_B^{-1}\varDelta _i=\begin{pmatrix} {(v_{ri})}_{r\in B_1}\\ {(w_{ki})}_{k\in B_2} \end{pmatrix} \end{aligned}$$

if $i\in N_2\setminus \lbrace i^* \rbrace$ and

$$\begin{aligned} \begin{pmatrix} {(v'_{ri^*})}_{r\in B_1}\\ {(w'_{ki^*})}_{k\in B_2} \end{pmatrix}=-(X \ \varDelta ')_B^{-1}\varDelta '_{i^*}= (X \ \varDelta )_B^{-1}\varDelta _{i^*}=-\begin{pmatrix} {(v_{ri^*})}_{r\in B_1}\\ {(w_{ki^*})}_{k\in B_2} \end{pmatrix}. \end{aligned}$$

Moreover, we have

$$\begin{aligned} (X\ \varDelta ')_B^{-1}\textbf{1}=(X \ \varDelta )_B^{-1}\textbf{1}. \end{aligned}$$

Thus, the vectors $w'_{k}$ for $k\in B$ and $i\in N_2$ are given by

$$\begin{aligned} w'_{k}=(w'_{k0},\ldots ,w'_{kn})=(w_{k0},\ldots ,w_{ki^*-1},-w_{ki^*},w_{ki^*+1},\ldots ,w_{kn}). \end{aligned}$$

As $w_{ki^*}\le 0$, this implies that $w'_{k}\ge _\pi w_{k}$ and therefore, as $w_{k}$ is lex-positive, $w'_{k}$ is lex-positive for every $k\in B$. We conclude that B is a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta ')$ and it follows from Lemma 1 that $\delta '$ is a feasible sign vector.$\square$

Similarly, if $s_{i^*}$ could be decreased to a value $s_{i^*}<-\epsilon _{i^*}$ such that all basic slack variables remain positive, the sign vector $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$ is feasible. In this case, B remains a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta ')$ if we update the permutation that induces the lexicographic order.

Theorem 3

Let $i^*\in N_2$ such that $w_{ki^*}>0$ for some $k\in B_2$ and let

$$\begin{aligned} \lambda :=\mathop {{\mathop {\mathop {\textrm{lexmax}}\limits }\nolimits _\pi }}\limits _{k\in B_2}\left\{ -\frac{w_{k}}{w_{ki^*}}: w_{ki^*}>0\right\} . \end{aligned}$$

The sign vector $\delta '={{\,\textrm{flip}\,}}(\delta ,i^*)$ is feasible if $\lambda \le _\pi -(0\ e_{i^*}^T)$. Moreover, B is a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta ')$ for the lexicographic order induced by $\pi '$ where

$$\begin{aligned} \pi '(i):={\left\{ \begin{array}{ll} \pi (i),&{}\quad \text {if } \pi (i)<\pi (i^*)\\ \pi (i)-1,&{}\quad \text {if } \pi (i)>\pi (i^*)\\ n-d,&{} \quad \text {if } i=i^*\\ \end{array}\right. } \end{aligned}$$

for $i\in N_2$ and $\pi '(k)=\pi (k)$ for $k\in B_2$.

Proof

As in the proof of Theorem 2, the vectors $w'_{k}$ for $k\in B_2$ in the dictionary of B for $\mathop {\textrm{LS}}^\epsilon (\delta ')$ are

$$\begin{aligned} w'_{k}=(w'_{k0},\ldots ,w'_{kn})=(w_{k0},\ldots ,w_{ki^*-1},-w_{ki^*},w_{ki^*+1},\ldots ,w_{kn}) \end{aligned}$$

and it holds that $w'_{kk'}=w_{kk'}\le 0$ for all $k'\in B_2$. Due to the lex-positivity of $w_{k}$ for all $k\in B$ with respect to $\pi$, a vector $w'_{k}$ for $k\in B$ can only be lex-negative with respect to $\pi '$ if $w_{k0}=0$ and $w_{ki}=0$ for all $i\in N_2$ with $\pi (i)<\pi (i^*)$. Then, $w'_{k}$ can only be lex-negative if $w_{ki'}<0$ for $i'\in \mathop {\mathrm {arg\,min}}\limits _{i\in N_2}\lbrace \pi (i): w_{ki}\ne 0 \ \wedge \ \pi (i)>\pi (i^*)\rbrace$. The existence of such an index $i'$ follows from Lemma 2. Due to $w_{ki^*}>0$, this implies $\frac{w_{k}}{w_{ki^*}}<_\pi (0\ e_{i^*}^T)$ or equivalently $-\frac{w_{k}}{w_{ki^*}}>_{\pi }- (0\ e_{i^*}^T)$ which contradicts $\lambda \le _\pi -(0\ e_{i^*}^T)$. Thus, B is a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon(\delta ')$ for the permutation $\pi '$ and the feasibility of $\delta '$ follows from Lemma 1. $\square$

For the remaining case in which $\lambda >_\pi -(0\ e_{i^*}^T)$, we can show that $\delta '={{\,\textrm{flip}\,}}(\delta ,l)$ for the unique index $l\in B_2$ with $w_{li^*}>0$ and $-\frac{w_l}{w_{li^*}}=\lambda$ is feasible.

Theorem 4

Let $i^*\in N_2$ such that $w_{ki^*}>0$ for some $k\in B_2$ and let

$$\begin{aligned} L:=\mathop {{\mathop {\mathop {\mathrm {arg\,lexmax}}\limits }\nolimits _\pi }}\limits _{k\in B_2}\left\{ -\frac{w_{k}}{w_{ki^*}}: w_{ki^*}>0\right\} . \end{aligned}$$

If $L\ne \emptyset$, then $|L|=1$. If l is the unique element in L and $-\frac{w_{l}}{w_{li^*}}>_\pi - (0\ e_{i^*}^T)$, the sign vector $\delta '={{\,\textrm{flip}\,}}(\delta ,l)$ is feasible and $B'=(B_1',B_2')=(B_1,B_2{\setminus }\lbrace l \rbrace \cup \lbrace i^* \rbrace )$ is a lex-feasible basis of $\mathop {\textrm{LS}}^\epsilon (\delta ')$ for the lexicographic order induced by $\pi '$ defined by

$$\begin{aligned} \pi '(i):={\left\{ \begin{array}{ll} \pi (i),&{}\quad \text {if } i\in N_2\ \wedge \ \pi (i)<\pi (i^*)\\ \pi (i)-1,&{}\quad \text {if } i\in N_2\ \wedge \ \pi (i)>\pi (i^*)\\ n-d,&{}\quad \text {if } i=l\\ \pi (l),&{}\quad \text {if } i=i^*\\ \pi (i),&{}\quad \text {if } i\in B_2\setminus \lbrace l \rbrace \\ \end{array}\right. } \end{aligned}$$

for $i\in \lbrace 1,\ldots ,n \rbrace$.

Proof

If $L\ne \emptyset$, then $|L|=1$ follows from the fact that no two $w_{k}$ and $w_{k'}$ for $k,k'\in B_2$ with $k\ne k'$ can be multiples of each other. The remainder of this proof is now laid out as follows. We first show that $B'$ is a lex-feasible basis of $\mathop {\textrm{LS}} ^{\epsilon }(\delta )$ with the lexicographic order induced by $\pi '$. Subsequently, we show that it is also lex-feasible for $\mathop {\textrm{LS}} ^{\epsilon }(\delta ')$ by applying Theorem 2 or 3.

After the infeasible pivot on $s_i^*$, the dictionary of $B'$ for $\mathop {\textrm{LS}} ^{\epsilon }(\delta )$ reads as follows:

$$\begin{aligned}& a_{r}&&=\left( v_{r0}-\frac{v_{ri^*}}{w_{li^*}} w_{l0}\right) &&+\sum \limits _{i\in N'_2}\left( v_{ri}-\frac{v_{ri^*}}{w_{li^*}} w_{li}\right) (\epsilon _i+s_i),&&\quad \forall r\in B'_1\\ &s_{k}&&=\left( w_{k0}-\frac{w_{ki^*}}{w_{li^*}} w_{l0}\right) -\epsilon _{k}&&+\sum \limits _{i\in N'_2}\left( w_{ki}-\frac{w_{ki^*}}{w_{li^*}} w_{li}\right) (\epsilon _i+s_i),&&\quad \forall k\in B'_2\setminus \lbrace i^* \rbrace \\& s_{i^*}&&=-\frac{w_{l0}}{w_{li^*}}-\epsilon _{i^*}&&-\sum _{i\in N'_2}\frac{w_{li}}{w_{li^*}}(\epsilon _i+s_i) \end{aligned}$$

We therefore have to show that the vectors $w'_{i^*}=-\frac{w_l}{w_{li^*}}$ and $w'_k=w_{k}-\frac{w_{ki^*}}{w_{li^*}}w_l$ for $k\in B'_2{\setminus }\lbrace i^* \rbrace$ are lex-positive with respect to the lexicographic order induced by $\pi '$. Due to $\frac{w_{l}}{w_{li^*}}<_\pi (0\ e_{i^*}^T)$ and $w_{li^*}>0$, it holds that $w_{l0}=0$ and $w_{li}=0$ for all $i\in N_2$ with $\pi (i)<\pi (i^*)$. Thus, it follows that $w'_{i^*0}=0$ and $w'_{i^*i}=0$ for all $i\in N_2$ with $\pi (i)<\pi (i^*)$. Due to Lemma 2 there exists $i'\in \mathop {\mathrm {arg\,min}}\nolimits _{i\in N_2}\lbrace \pi (i): w_{li}\ne 0 \ \wedge \ \pi (i)>\pi (i^*)\rbrace$ and because of $\frac{w_{l}}{w_{li^*}}<_\pi (0\ e_{i^*}^T)$, it holds that $w_{li'}<0$. Therefore, it holds that $w'_{i^*0}=0$, $w'_{i^*i}=0$ for all $i\in N_2\setminus \lbrace i^* \rbrace$ with $\pi (i)<\pi (i')$ and $w'_{i^*i'}=-\frac{w_{li'}}{w_{li^*}}> 0$. The permutation $\pi '$ maintains the order of all indices different from $i^*$ and l. Moreover, it satisfies $\pi '(i)<\pi '(l)<\pi '(i^*)$ for all $i\in N'_2\setminus \lbrace l \rbrace$ and we can conclude that $w'_{i^*}$ is lex-positive with respect to $\pi '$.

For each $k\in B'_2\setminus \lbrace i^* \rbrace$ it holds that $w'_k=w_k-\frac{w_{ki^*}}{w_{li^*}}w_l>_\pi \textbf{0}$ due to the choice of $l\in L$. Further, it holds that $w'_{kk'}\le 0$ for all $k'\in B'_2$ and in particular $w'_{ki^*}=0$. If $w'_{kl}\le 0$, $w'_k>_\pi \textbf{0}$ can therefore only be satisfied if there exists $i'\in \mathop {\mathrm {arg\,min}}\limits _{i\in N_2}\lbrace \pi (i): w'_{ki}\ne 0 \ \wedge \ i\ne i^*\rbrace$ such that $w'_{ki'}>0$. Then, $w'_k$ is also lex-positive with respect to $\pi '$ because of $\pi '(i')<\pi '(l)<\pi '(i^*)$. If $w'_{kl}>0$, $w'_k$ is also lex-positive with respect to $\pi '$ due to $\pi '(l)<\pi (l)$, $w'_{ki^*}=0$ and the fact that $\pi '$ maintains the order of all indices different from $i^*$ and l. Thus, we conclude that the vectors $w'_k$ for $k\in B'_2$ are lex-positive and therefore, $B'$ is lex-feasible with respect to $\pi '$.

Due to Lemma 2 and $\pi '(l)>\pi '(i)$ for all $i\in N'_2{\setminus }\lbrace l \rbrace$, there must exist $i'\in N'_2{\setminus }\lbrace l \rbrace$ such that $w'_{ki'}>0$ for every $k\in B'_2$. Hence, either the condition of Theorem 2 or Theorem 3 is satisfied for $l\in N'_2$. As $\pi '(i)<\pi '(l)$ for all $i\in N'_2{\setminus }\lbrace l \rbrace$, the permutation does not have to be updated if we apply Theorem 3 and we conclude that $B'$ is a lex-feasible basis of $\mathop {\textrm{LS}} ^\epsilon (\delta ')$ for the permutation $\pi '$. The feasibility of $\delta '$ again follows from Lemma 1. $\square$

6 Evaluation

6.1 Experimental setup

In this section, we provide an extensive evaluation of our proposed decision tree induction method which is henceforth denoted by SA-DT. We implemented it in C++ and all experiments were conducted on a computer equipped with an Intel Xeon E3-1231v3 @3.40GHz (4 Cores) and 32GB DDR3 RAM running Ubuntu 20.04.

We asses three different criteria which are out-of-sample accuracy, tree size measured in terms of the number of leaf nodes and the time necessary for inducing the trees. To evaluate these quality measures, we use 20 popular classification datasets from the UCI machine learning repository which are summarized in Table 1 and we compare our method to our own implementation of the univariate CART algorithm (Breiman et al. 1984) and to the popular oblique decision tree induction method OC1. All three methods use Gini impurity as the splitting criterion and the recursive partitioning is stopped either when all the labels of observations associated with a leaf node are equal or when the number of observations to be split is lower than four. The latter condition is the standard setting for OC1 and a reasonable choice to slightly prevent overfitting the decision trees. No post-pruning of the decision trees is carried out in order to evaluate solely the effects of the different methods to find the splits on the decision tree induction process. For out-of-sample accuracy, we further compare our method to the four other prediction models k-nearest neighbors (KNN), neural networks (NN), support vector machines (SVM) and random forests (RF). Here, we use the implementations provided in the Scikit-learn library (Pedregosa et al. 2011), version 0.23.2, with all parameters left at their default value.

Table 1 Dataset description

As the starting solution for our simulated annealing algorithm, we always use the best univariate split and in each iteration and we choose to perform a pivoting step or to move to a neighboring cell with a probability of 50%. For the initial temperature, we run our heuristic with a temperature of $T=\infty$ such that all neighbors are accepted and we record the observed differences in the value of the splitting criterion. This process is carried out until 100 differences are recorded. Subsequently, we compute $c_{97}\in \mathbb {R}$ as the minimal value such that 97% of these values are within $[-c_{97},c_{97}]$. Then, we set the initial temperature to

$$\begin{aligned} T_0=-\frac{c_{97}}{\ln (0.85)} \end{aligned}$$

such that initially a deterioration of the splitting criterion of $c_{97}$ is accepted with a probability of 85%. Subsequently, a geometric cooling schedule, defined by the update formula

$$\begin{aligned} T_{t+1}=\beta \cdot T_t \end{aligned}$$

with $\beta =0.85$ is used during the optimization process. The simulated annealing heuristic is stopped when the best solution could not be improved for $\max (d,100)$ consecutive neighborhood operations. Finally, the optimization program in Eq. (1) with $p=1$ for the best sign vector is solved using the Gurobi optimization solver (Gurobi 2022). Note that, as for the other prediction models, these parameters are not tuned for each dataset individually. Instead, they are chosen because they provided good and stable results in our preliminary experiments. Further refinement may improve the performance for a specific learning task under consideration.

For each dataset 10-fold cross-validation is carried out to obtain the scores for each prediction model. One-hot encoding is used beforehand to transform categorical features into numerical features and missing values are imputed with the median value of the respective column in the training set.

We follow Demšar (2006)’s proposal to analyze whether there is a significant difference in the performance of SA-DT compared to the other methods. First, we perform a Friedman test (Friedman 1937, 1940) to check whether there is a significant difference between at least two methods. Subsequently, if a significant difference is detected, a post-hoc Holm test (Holm 1979) is carried out to compare SA-DT with the other methods individually. For both statistical test, we require a significance level of $\alpha =0.05$.

The Friedman test is a non-parametric statistical test that ranks the performances of the models under consideration for each dataset. The lowest rank is assigned to the best and the highest rank is assigned to the worst performing model. Ties are broken by assigning the average rank. It tests the null-hypothesis that all models perform equally well at the given significance level $\alpha$. Under this hypothesis, the observed average ranks of the models should be approximately equal.

The post-hoc Holm test is used to compare the performance of a control method, in our case SA-DT, to two or more other methods. For each of these other methods the null-hypothesis is that it performs equally well as the control method. It controls the family-wise error by adjusting the individual p-values of the hypotheses sequentially. Let m denote the number of methods different from the control method and let $p_1,p_2,\ldots ,p_m$ such that $p_1\le p_2\le \ldots \le p_m$ denote the ordered p-values. The Holm adjusted p-values are then computed as $p'_1=\min \lbrace 1, mp_1 \rbrace$ and $p'_i=\max \lbrace p'_{i-1}, \min \lbrace 1,(m-i+1)p_i\rbrace \rbrace$ for $i=2,\ldots ,m$. Then, a hypothesis is rejected if and only if the respective adjusted p-value is lower than the specified significance level $\alpha$.

We present our findings in the upcoming three sections and a detailed discussion of the results is provided in Sect. 6.5.

6.2 Comparison of accuracy

We start off by comparing the out-of-sample accuracy of SA-DT, CART and OC1. The mean accuracies of the 10-fold cross-validation procedure together with the standard deviation for each dataset are reported in Table 2. Moreover, the table includes the average rank computed over all datasets for each method. SA-DT has an average rank of 1.4, CART’s average rank is 2.45 and the rank of OC1 is 2.45. With a p-value of $2.9\times 10^{-3}$ the Friedman test identifies a significant difference between at least two of the three methods. Furthermore, the post-hoc Holm test, which is summarized in Table 3, reports a significant difference between SA-DT and both CART and OC1. AS SA-DT has the lowest average rank, we can conclude that SA-DT is significantly more accurate in our evaluation than the other two decision tree induction methods.

Table 2 Comparison of accuracy between SA-DT, CART, OC1

Table 3 Holm post-hoc test for accuracy of SA-DT, CART, OC1

The results of the comparison of out-of-sample accuracy for SA-DT, KNN, NN SVM and RF are summarized in Table 4. RF has the lowest rank of 2.2, followed by SA-DT with a rank of 3.05. NN is in the third place with a rank of 3.1. SVM’s rank is 3.15 and KNN has the highest rank of 3.5. With a p-value of 0.12, the Friedman test does not provide sufficient evidence for a significant difference between the compared methods.

Table 4 Comparison of accuracy between SA-DT, KNN, NN, SVM and RF

6.3 Comparison of tree size

Next, we compare the tree size measured in terms of the number of leaf nodes of the three decision tree induction methods SA-DT CART and OC1. The results of our evaluation are summarized in Table 5. For all but two datasets SA-DT managed to induce the smallest decision trees and therefore, it has the lowest rank of 1.1. With a rank of 1.95 OC1 is in the second place and CART induced the largest tree for all but one dataset and consequently has the highest rank of 2.95. The Friedman test reports a significant difference between at least two methods with a p-value of $3.6\times 10^{-8}$ and the post-hoc Holm test, summarized in Table 6, confirms that SA-DT induces significantly smaller trees than the other two methods.

Table 5 Comparison of tree size between SA-DT, CART, OC1

Table 6 Holm post-hoc test for tree size of SA-DT, CART and OC1

6.4 Comparison of induction times

Lastly, we compare the induction times of SA-DT, CART and OC1. Table 7 summarizes the results of this evaluation. CART is the fastest algorithm for all of the datasets and therefore has a rank of 1.0. With a rank of 2.45 OC1 is in the second place followed by SA-DT with rank 2.55. With a p-value of $2.9\times 10^{-7}$ the Friedman test reports a significant difference between at least two methods. The results of the post-hoc Holm test are summarized in Table 8. It confirms the obvious difference between CART and SA-DT but it does not provide evidence for a significant difference between OC1 and SA-DT.

Table 7 Comparison of induction time between SA-DT, CART, OC1

Table 8 Holm post-hoc test for induction time of SA-DT, CART and OC1

6.5 Discussion of the results

All in all, our experimental results show that our simulated annealing algorithm is well-suited for the induction of oblique decision trees. SA-DT induces significantly more accurate decision trees than both CART and OC1 in our evaluation. On average SA-DT improves the accuracy by around 3% compared to the other two tree induction methods. Moreover, the decision trees induced by SA-DT are significantly smaller. The observation that they are smaller, on average by around 69%, than the ones induced by CART is not surprising and is due to the fact that oblique splits use affine hyperplanes instead of axis parallel hyperplanes to divide the feature space. The fact that they are smaller for all but two datasets than the ones induced by OC1 and that the average observed decrease is around 34% is, however, remarkable and shows the effectiveness of our simulated annealing method for dividing the underlying feature space.

The better performance of SA-DT in terms of accuracy and tree size comes at the cost of increased induction times compared to CART. This is simply due to the fact that determining the best univariate splits is far less complex than finding good oblique splits. Nonetheless, no significant difference is observed between SA-DT and OC1 and it seems that the two algorithms’ induction times are approximately in the same order of magnitude for most datasets. The fact that SA-DT induces the smallest trees certainly contributes to keeping the induction times low. Overall, we think that the increased induction time is acceptable for most applications, especially when considering the improvements with respect to accuracy and tree size. Still, there is room for further increasing the efficiency of the proposed simulated annealing algorithm, for example by using better starting solutions, alternative cooling schedules or advanced techniques for implementing the pivoting strategy.

The fact that no significant difference in accuracy is observed in the comparison with KNN, NN and SVM shows that SA-DT is also competitive with these other popular prediction models. It should, however, be noted that the Friedman test only considers the average ranks and not the individual differences. For specific datasets, the performances may actually be quite dissimilar. For the datasets Wine and Monks problems 1, for example, SA-DT is considerably more accurate than the other three methods. On the other hand, for the Semeion dataset, the other methods clearly outperform SA-DT. This observation is not surprising and can be attributed to the fact that different models are more suitable depending on the underlying task. The major advantage of SA-DT compared to the other models is that the decision trees are much more interpretable.

RF has the lowest average rank in the comparison and although the difference to SA-DT is not found significant, it is reasonable to assume that the combination of multiple decision trees in an ensemble will generally yield more accurate and robust predictors than a single decision tree. Still, the loss of interpretability might be a reason to use SA-DT instead. Furthermore, random forests are not necessarily restricted to univariate decision trees and our proposed simulated annealing method can easily be integrated in the construction of oblique random forests. Studying the capabilities of this approach is certainly an interesting topic for further research.

7 Conclusion

In this work we introduced a new simulated annealing algorithm for finding near-optimal oblique splits for decision tree induction. It is motivated geometrically by the observation that subsets of equivalent splits correspond to cells in a hyperplane arrangement defined by the observations in the training data. Using a pivoting strategy, the algorithm iterates over the vertices which reveal multiple neighboring cells to move to. To deal with degeneracy, we resort to a lexicographic pivoting scheme. Our experimental results show the benefits of this approach for the induction of small and accurate decision trees. As a future work it would be interesting to explore different methods for computing the starting solution, alternative cooling schedules and other techniques to increase the speed of the algorithm. Moreover, our simulated annealing algorithm should be evaluated for the construction of oblique random forests.