A branch & bound algorithm to determine optimal bivariate splits for oblique decision tree induction

Abstract

Univariate decision tree induction methods for multiclass classification problems such as CART, C4.5 and ID3 continue to be very popular in the context of machine learning due to their major benefit of being easy to interpret. However, as these trees only consider a single attribute per node, they often get quite large which lowers their explanatory value. Oblique decision tree building algorithms, which divide the feature space by multidimensional hyperplanes, often produce much smaller trees but the individual splits are hard to interpret. Moreover, the effort of finding optimal oblique splits is very high such that heuristics have to be applied to determine local optimal solutions. In this work, we introduce an effective branch and bound procedure to determine global optimal bivariate oblique splits for concave impurity measures. Decision trees based on these bivariate oblique splits remain fairly interpretable due to the restriction to two attributes per split. The resulting trees are significantly smaller and more accurate than their univariate counterparts due to their ability of adapting better to the underlying data and capturing interactions of attribute pairs. Moreover, our evaluation shows that our algorithm even outperforms algorithms based on heuristically obtained multivariate oblique splits despite the fact that we are focusing on two attributes only.

1 Introduction

In recent years, an increasing necessity for interpretable machine learning models has become apparent. Univariate decision trees are a popular tool in this context for solving classification tasks. Their major advantage is that they are easy to understand and interpret, giving insight into the underlying data’s structure. Drawbacks of the common univariate decision tree induction methods are that the resulting trees often become very large, even after pruning, and the prediction accuracy is often lower than that of other classification methods.

To tackle these drawbacks, oblique decision tree induction algorithms which employ hyperplanes splits have been developed to produce smaller and more accurate trees. Given m attributes X₁,…,X_m, these splits correspond to rules of the form

$$a_{1}X_{1}+\ldots+a_{m}X_{m}\leq b$$

for $a\in \mathbb {R}^{m}$ and $b\in \mathbb {R}$. Interpreting these splits, however, is far more difficult and finding global optimal hyperplanes has been proven to be NP-complete for some splitting criteria [1]. Thus, heuristics are necessary for finding local optimal solutions.

In this work, we propose a branch and bound algorithm to determine global optimal bivariate oblique splits for concave impurity measures. These splits correspond to oblique splits for which only two coefficients $a_{j_{1}}$ and $a_{j_{2}}$ for j₁,j₂ ∈{1,…,m} are non-zero. Thus, they have the form

$$a_{j_{1}}X_{j_{1}}+a_{j_{2}}X_{j_{2}}\leq b$$

or equivalently,

$$a^{\prime}X_{j_{1}}+b^{\prime}\leq X_{j_{2}}$$

for suitable parameters $a^{\prime }$ and $b^{\prime }$. Compared to univariate decision tree induction algorithms these splits result in smaller more accurate trees due to the inclusion of an additional attribute. On the other hand, by allowing only two attributes per split, the trees remain fairly interpretable and the risk of including irrelevant features in the splits during tree induction is reduced compared to general oblique splits.

To show the strength of bivariate splits, we want to look at simple data consisting of two attributes X₁ and X₂ which is labeled as positive if the ratio $\frac {X_{1}}{X_{2}}$ is greater than or equal to a certain value $a\in \mathbb {R}$ and negative, otherwise. Clearly, the rule $\frac {X_{1}}{X_{2}}\geq a$ is equivalent to X₁ ≥ aX₂ and can thus be expressed as a bivariate split. Univariate decision trees, on the other hand, require a stepwise approximation of this rule. This observation is illustrated in Fig. 1. Such dependencies are likely to appear in real-life applications. As an example from the medical domain there is the so-called waist-to-height ratio which is a measure for abdominal obesity and, according to a study from 2010 (see [2]), a superior measure to the well-known body mass index for the risk of heart attacks. This measure is defined as $WHtR=\frac {U}{H}$ where U denotes a person’s waist circumference and H its height. A WHtR greater than 0.5 indicates an increased risk of obesity-related cardiovascular diseases. As we have seen, this rule can only be approximated by univariate splits while a single bivariate oblique split suffices to express this rule.

This simple example shows various major benefits of bivariate splits: First, it is possible to express rules based on ratios of two attributes. Furthermore, if the rules are learned algorithmically from data, a human understandable interpretation is possible. The possibility of creating a two-dimensional visual representation of the splits also helps to get a deeper understanding of the data at hand.

Fig. 1

Comparison of a bivariate split and an approximation by univariate splits for the rule $\frac {X_{1}}{X_{2}}\leq 0.5$

Our algorithm is compatible with the very general class of concave impurity measures which includes the most commonly used splitting criteria such as entropy, gini impurity and classification error. This is a major advantage as it is not restricted to one specific criterion and we obviate the need to introduce a new criterion specifically designed for our purposes.

In our evaluation we show that the trees based on global optimal bivariate oblique splits outperform univariate decision trees as well as general oblique decision trees in terms of prediction accuracy and tree size. The biggest disadvantage of our tree building algorithm is the increased runtime compared to univariate decision tree induction algorithms due to the higher complexity of finding bivariate splits. Nevertheless, due to the efficient implementation of the branch and bound procedure, acceptable results are achieved such that our method is applicable in real-life scenarios. Overall, our proposed bivariate decision tree induction algorithm is a reasonable alternative when univariate decision trees fail to give accurate results, yet interpretation of the data at hand is desired.

2 Related work and contribution

Artificial intelligence is more and more affecting our lives in a variety of fields such as health care, finance, criminal justice and defense and researchers have become increasingly aware of the importance of interpretability of machine learning models. Extensive overviews discussing concepts, challenges, trends and existing approaches regarding this topic are, for example, presented in [3, 4]. While there is a significant amount of research that tries to derive interpretable surrogate models [5], including decision trees [6], from black-box models such as neural networks, support vector machines or random forests, some authors plead for relying on inherently interpretable and transparent prediction models instead [7].

Univariate decision tree algorithms such as CART [8] and C4.5 [9] which recursively divide the feature space in a top-down manner by introducing splits minimizing some splitting criterion induce such inherently interpretable models. The general aim of finding the smallest binary decision tree has been proven to be NP-complete [10], yet the greedy strategy made it possible to induce high-quality decision trees fast in practice. Nevertheless, the resulting trees are often not as accurate as other classification models. Moreover, the data can often not be split in a compact way by splits involving only a single attribute which makes interpretation and deriving understandable rules more complicated.

Oblique decision trees are often smaller and more accurate in practice, yet finding optimal oblique splits is NP-complete for some splitting criteria [1] including classification error. Therefore, efficient heuristics are necessary to induce the decision trees in a reasonable amount of time with the greedy recursive partitioning scheme. The first heuristic was introduced by [8]. They use a deterministic hill climbing approach to find local optimal oblique splits. Heath et al. [11] develop a simulated annealing heuristic which perturbs one hyperplane parameter at a time to escape local optima. Murthy et al. [12] combine these two approaches by introducing randomization techniques in the hill climbing approach. Other approaches for finding near optimal oblique splits include meta-heuristics such as simulated annealing, genetic algorithms and evolutionary strategies [13] or heuristics based on Householder transformation [14], linear discriminant analysis [15] and logistic regression [16]. Although these oblique decision tree induction approaches generally produce better classifiers, their main problem is that the oblique splits, involving all of the variables, are hard to understand and interpret. Thus, one loses one of the most advantageous properties of tree-based classification models.

Recently, also integer linear programming has been employed to determine global optimal univariate and oblique decision trees of a prior specified maximum size [17, 18]. Blanquero et al. [19] develop a continuous optimization formulation instead to determine optimal randomized oblique decision trees. Additionally, penalty terms are introduced in the objective function to limit the number of overall involved attributes and the number of attributes per split to improve interpretability. The major drawback of these approaches is that solving the proposed optimization problems is much more time consuming than using the top-down strategy and optimal solutions can only be obtained in a reasonable amount of time for shallow trees and for small to medium-sized datasets.

A common strategy to obtain interpretable machine learning models is to restrict the complexity of the model to be learned beforehand. Lubinsky et al. [20] follows this approach and investigates different kinds of bivariate splits as an interpretable alternative to univariate splits for decision tree induction. He focuses on two-class classification tasks and shows, by using a brute-force algorithm for determining the splits, that decision trees based on bivariate splits, including bivariate oblique splits, are in fact able to produce much smaller and more accurate decision trees compared to their univariate counterparts while remaining interpretable. He states that the brute-force algorithm is very time consuming and often intractable for large datasets. He further introduces additive splitting criteria which enable the development of efficient divide-and-conquer algorithms. Although these additive splitting criteria yield good results in terms of accuracy, they are not as effective as traditional impurity measures such as gini impurity in terms of tree size.

Bioch et al. [21] also argue that oblique decision trees based on many variables are hard to interpret and therefore propose using bivariate oblique splits. They suggest using the hill climbing approach of [8] for finding good splits as well as the simpler approach of considering only 45^∘ lines in addition to standard univariate splits. The evaluation of this approach shows that bivariate oblique decision trees are superior to univariate decision trees and competitive with multivariate decision trees in terms of tree size and accuracy.

In this work, we follow Lubinsky and Bioch et al.’s argumentation that bivariate oblique decision trees can be a true interpretable alternative to univariate as well as multivariate decision trees. However, we aim at finding the best possible split in each node to ensure that we capture the underlying structure of the data as well as possible to produce highly accurate and compact decision trees. This task is computationally intractable for general oblique splits. In contrast to Lubinsky, we also allow for an arbitrary amount of classes and we rely on traditional concave impurity measures including classification error, entropy and gini impurity. We develop an effective branch and bound procedure that exploits the concavity of these impurity measures to compute good lower bounds which is the key for our branch and bound algorithm. Furthermore, we evaluate our method to show that it is capable of producing interpretable, compact and highly accurate decision trees.

3 Preliminaries

3.1 Bivariate oblique decision tree induction

In this work, we study bivariate oblique decision trees for multiclass classification problems. Given m real-valued attributes (or features) X₁,…,X_m and a set of class labels L = {1,…,k}, a bivariate oblique decision tree is a binary rooted tree that classifies each point $x\in \mathbb {R}^{m}$ to a certain label y ∈ L. For that, each internal node is associated with a rule of the form $aX_{j_{1}}+b\leq X_{j_{2}}$ for some indices j₁,j₂ ∈{1,…,m} and values $a,b\in \mathbb {R}$ and each leaf node is associated with a certain class label. Throughout the remainder of this work, we abbreviate the set of all possible rules as $\varTheta := \lbrace aX_{j_{1}}+b\leq X_{j_{2}}: j_{1},j_{2}=1,\ldots ,m;\ a,b\in \mathbb {R} \rbrace$. Depending on the context, we will also sometimes refer to the rules as split or line, because the expression basically describes a line in the two dimensional space spanned by the attributes $X_{j_{1}}$ and $X_{j_{2}}$ which splits the feature space into two subspaces. In order to classify a point $x\in \mathbb {R}^{m}$, it pursues a path from the root to a leaf node according to the specified rules. If the rule is satisfied, x is sent to the left sibling and otherwise, x is sent to the right. Finally, the point is assigned the class label of the leaf node at the end of this path. An example of a simple bivariate oblique decision tree of depth two is illustrated in Fig. 2.

Fig. 2

Simple example of a bivariate oblique decision tree of depth two for a 3-class classification problem

To automatically learn such decision trees, we make use of a training set $\mathcal {X}:=\lbrace (x^{i},y^{i}) : i=1,\ldots ,n;\ x^{i}\in \mathbb {R}^{m};\ y^{i}\in L \rbrace$ that consists of a sequence of n data points $x^{i}\in \mathbb {R}^{m}$ with a corresponding label yⁱ ∈ L. We iteratively divide the training data into subsets by introducing bivariate oblique splits that minimize a certain impurity measure. This process is carried out until all subsets are pure or no further splitting is possible, i.e., all points in the subsets have the same attribute values. The resulting leaf node is then assigned the most frequent label among the subset of training samples. This algorithm is summarized in Algorithm 1.

The general idea of iteratively splitting the training set in a greedy fashion according to some impurity measure in a top-down manner forms the base of many univariate and multivariate decision tree algorithms. Our major contribution lies in the technique to effectively determine optimal bivariate oblique splits which we explain in detail in Section 4. Before that, we take a closer look at the properties of the underlying impurity measures.

3.2 Concave impurity measures

Similar to common univariate decision tree methods such as CART and C4.5 our decision tree induction algorithms iteratively determines splits that minimize a certain impurity measure. In this work, we focus on so-called concave impurity measures as introduced in [22]. These impurity measures are concave functions $i:\mathcal {P}_{k}\to \mathbb {R}_{\geq 0}$ defined on the probability space $\mathcal {P}_{k}:=\lbrace (p_{1},\ldots ,p_{k})\in [0,1]^{k}: {\sum }_{j=1}^{k} p_{j}=1 \rbrace$ that satisfy i(λp + (1 − λ)q) ≥ λi(p) + (1 − λ)i(q) for λ ∈ [0,1] and $p,q\in \mathcal {P}_{k}$. Moreover, for every $p\in \mathcal {P}_{k}$ with p_j = 1 for some j ∈{1,…,k} it holds that i(p) = 0. The most popular among those concave impurity measures are:

• Classification Error: $e(p)=1-\max \limits _{j=1,\ldots ,k} p_{j}$

• Entropy: $h(p)=-{\sum }_{j=1}^{k} p_{j}\log p_{j}$

• Gini Impurity: $g(p)=1-{\sum }_{j=1}^{k} {p_{j}^{2}}$

In our tree building algorithm we iteratively split a set of training samples into two subsets. To determine the quality of the split we compute the weighted sum of impurities of these subsets. This leads to the definition of frequency-weighted impurity measures: Let i denote a concave impurity measure, the corresponding frequency-weighted impurity measure is the function $I:\mathbb {R}^{k}\to \mathbb {R}_{\geq 0}$ defined by $I(n):= {\Vert n\Vert _{1}}\cdot i\left (\frac {n_{1}}{\Vert n\Vert _{1}},\ldots ,\frac {n_{k}}{\Vert n\Vert _{1}}\right )$. These frequency-weighted impurity measures satisfy the following properties (see [22]):

• Homogeneity: I(λn) = λI(n)

• Strict Concavity: I(m + n) ≥ I(m) + I(n) with equality if and only if m and n are proportional, i.e., $\left (\frac {n_{1}}{\Vert n\Vert _{1}},\ldots ,\frac {n_{k}}{\Vert n\Vert _{1}}\right )=\left (\frac {m_{1}}{\Vert m\Vert _{1}},\ldots ,\frac {m_{k}}{\Vert m\Vert _{1}}\right )$

Finally, this definition lets us define the impurity of a split $\theta := aX_{j_{1}}+b\leq X_{j_{2}}$ on a set of training samples $\mathcal {X}_{0}$. The split divides the training samples into two new subset $\mathcal {X}_{1}$ and $\mathcal {X}_{2}$ such that $ax^{i}_{j_{1}}+b\leq x^{i}_{j_{2}}$ for all $(x^{i},y^{i})\in \mathcal {X}_{1}$ and $ax^{i}_{j_{1}}+b> x^{i}_{j_{2}}$ for all $(x^{i},y^{i})\in \mathcal {X}_{2}$. Let n₁ = (n₁₁,…n_1k), n₂ = (n₂₁,…n_2k) denote the vector of absolute frequencies of class labels of the two subsets, respectively. Then, the impurity of the split is calculated as:

$$ \hat{I}(\theta,\mathcal{X}_{0}):= I(n_{1})+I(n_{2}) $$

4 A branch and bound algorithm for optimal bivariate oblique splits

4.1 General outline

Branch and bound algorithms are successfully used in the field of operations research to solve difficult optimization problems. In contrast to heuristic approaches, they determine global optimal solutions for problems for which a total enumeration of all feasible solutions is very time consuming or even impossible. The basic idea behind a branch and bound algorithm is to recursively divide the set of solutions of the optimization problem into two or more subsets and to compute upper and lower bounds for the value of the objective function of these subsets. This procedure can be seen as the branching of a rooted tree for which each node represents a certain subset of the search space. In case of a minimization problem, the upper bounds are typically arbitrary feasible solutions of the respective subsets. If the lower bound of any node exceeds the current best objective value we know that no solution of this node can improve the objective value and therefore, no further branching of it is necessary. This procedure is carried out until no more unexamined nodes are left. Although branch and bound procedures usually have exponential worst case-time complexity, they are widely used in practice when the bounding operations allow to reduce the domain of feasible solutions effectively.

Given a set of attributes X₁,…,X_m, a set of labels L = {1,…,k}, a training set $\mathcal {X}$ consisting of n labeled observations and an impurity measure i, the minimization problem we are trying to solve is finding features $j^{*}_{1},j^{*}_{2}=1,\ldots ,m$ and values $a^{*},b^{*},\in \mathbb {R}$ such that the bivariate oblique split $\theta ^{*}:= a^{*}X_{j^{*}_{1}}+b^{*}\leq X_{j^{*}_{2}}$ minimizes $\hat {I}(\theta ^{*},\mathcal {X})$.

As [12] observe, the number of distinct bivariate oblique splits for n data points and two attributes is at most $O(\binom {n}{2})$. The general idea behind this result is that any two data points define a line that has to be considered as a split. This line can be slightly rotated upwards and downwards. As every distinct combination of attributes j₁,j₂ = 1,…,m with j₁≠j₂ has to be examined, the overall number of splits that have to be considered is in the order of O(m²n²). Deciding which points satisfy a rule for evaluating the impurity of a split requires an additional factor of O(n). This results in an overall complexity of O(m²n³) to find the optimal bivariate oblique split if a brute-force algorithm is applied. Although the effort is polynomial, especially for large datasets the explicit enumeration and evaluation of all possible splits is very time consuming. It should also be kept in mind that for the top-down approach of Algorithm 1 the optimization problem has to be solved not only once, but for every non-leaf node of the resulting decision tree. Thus, an efficient algorithm to determine optimal bivariate oblique splits is crucial for the algorithm to run in a reasonable amount of time.

Up next, we describe our proposed branch and bound algorithm for determining optimal bivariate oblique splits for two attributes. This procedure is carried out for all combinations j₁,j₂ = 1,…,m with j₁≠j₂. We emphasize the fact that these executions are not completely separate as we can reuse the impurity of the best split found for different attributes as an initial bound for the branch and bound procedure.

Suppose, we want to find the best split $aX_{j_{1}}+b\leq X_{j_{2}}$ for the two attributes j₁ and j₂ on $\mathcal {X}$. The parameters that have to be determined are $a,b\in \mathbb {R}$. Therefore, the search space corresponds to the Euclidean plane $\mathbb {R}^{2}$. Note, that for any split $aX_{j_{1}}+b\leq X_{j_{2}}$ with |a| > 1 there is a split $a^{\prime }X_{j_{2}}+b^{\prime }\leq X_{j_{1}}$ with $|a^{\prime }|\leq 1$ with the same impurity. For a > 1 the equivalent rules in terms of impurity are $a^{\prime }=\frac {1}{a}$ and $b^{\prime }=-\frac {b}{a}+\epsilon$ for 𝜖 > 0 sufficiently small and for a < − 1, the parameters are $a^{\prime }=\frac {1}{a}$ and $b^{\prime }=-\frac {b}{a}$. Hence, by considering any combination of attributes j₁≠j₂ instead of just j₂ > j₁, we can restrict the search space to $[-1,1]\times \mathbb {R}$. As we only have to consider slopes in the range [− 1,1], we can further restrict the range of the axis intercept b. Let $\underline {B}:={\min \limits } \lbrace x^{i}_{j_{2}}\pm x^{i}_{j_{1}}:i=1,\ldots ,n \rbrace$ and $\overline {B}:={\max \limits } \lbrace x^{i}_{j_{2}}\pm x^{i}_{j_{1}}+\epsilon :i=1,\ldots ,n \rbrace$, then any rule $aX_{j_{1}}+b\leq X_{j_{2}}$ with a ∈ [− 1,1] and $b>\overline {B}$ will be satisfied and any rule with a ∈ [− 1,1] and $b<\underline {B}$ will not be satisfied by all the points in the training data. Hence, it suffices to consider $[-1,1]\times [\underline {B},\overline {B}]$ as the overall search space for the parameters a and b. This is also the root problem of our branch and bound procedure.

Subsequently, we branch on the variables a and b to divide the problem into smaller subproblems. Hence, all subproblems that are explored can be characterized by a region $C:= [\underline {a},\overline {a}]\times [\underline {b},\overline {b}]$ with $\underline {a},\overline {a}\in [-1,1]$ and $\underline {b},\overline {b}\in [\underline {B},\overline {B}]$. For any such region C, a feasible candidate solution can be obtained by choosing any $a\in [\underline {a},\overline {a}]$ and $b\in [\underline {b},\overline {b}]$ and computing $\hat {I}(aX_{j_{1}}+b\leq X_{j_{2}},\mathcal {X})$. If this solution is better than the current best solution, we store it as the new so-called incumbent solution. In Section 4.6, we explain how a lower bound for any rule within the bounds of C can be established. If this lower bound is greater than or equal to the current incumbent solution, the subproblem is pruned.

One peculiarity of our algorithm is that we also introduce so-called node exploration criteria for the subproblems C. We say that such an exploration criteria is met, if we can efficiently enumerate all relevant rules within the subproblem’s bounds. If such a criteria is met, we explore the node and prune it. On the one hand, these exploration criteria help reducing the number of nodes to explore, on the other hand, they are necessary to ensure that the branch and bound procedure terminates. We explore these exploration criteria in more detail in Section 4.3.

If a node is not pruned, we branch on it. This means that we choose $(a,b)\in (\underline {a},\overline {a})\times (\underline {b},\overline {b})$ and create four new subproblems $C_{1}:=[\underline {a},a]\times [\underline {b},b]$, $C_{2}:=[\underline {a},a]\times [b,\overline {b}]$, $C_{3}:=[a,\overline {a}]\times [\underline {b},b]$ and $C_{4}:=[a,\overline {a}]\times [b,\overline {b}]$.

Clearly, any univariate split on an attribute $X_{j_{2}}$ can be interpreted as a bivariate oblique split $0X_{j_{1}}+b\leq X_{j_{2}}$ for an arbitrary attribute $X_{j_{1}}$. As an optimal univariate split can be found at relatively low costs of $O(mn\log n)$ by sorting each attribute and evaluating each possible value of an attribute from left to right, it makes sense to start off the branch and bound procedure with such a split as an initial feasible solution.

Another technique we have found to be very effective is normalization. For each feature X_j, we compute the median Med(X_j) and the interquartile range IQR(X_j) of the training samples and replace ${x^{i}_{j}}$ by $\frac {{x^{i}_{j}}-Med(X_{j})}{IQR(X_{j})}$. An optimal rule $aX^{\prime }_{j_{1}}+b\leq X^{\prime }_{j_{2}}$ for the transformed features $X^{\prime }_{1},\ldots ,X^{\prime }_{m}$, can afterwards be transformed into an optimal split $a^{*}X_{j_{1}}+b^{*}\leq X_{j_{2}}$ for the original features by choosing the values $a^{*}:= a\frac {IQR(X_{j_{2}})}{IQR(X_{j_{1}})}$ and $b^{*}:=- a\frac {Med(X_{j_{1}})IQR(X_{j_{2}})}{IQR(X_{j_{1}})}+b\cdot IQR(X_{j_{2}})+Med(X_{j_{2}})$.

All in all our branch and bound procedure is summarized in Algorithm 2.

4.2 Preliminary definitions

Before we describe the branching strategy, the node exploration criteria and the computation of the lower and upper bounds in detail, we introduce some necessary definitions for the subproblems C of the branch and bound procedure. First, we define the set of valid rules of the subproblem as $\varTheta (C):=\lbrace aX_{j_{1}}+b\leq X_{j_{2}}: (a,b)\in C\rbrace$.

Every subproblem divides the feature space into the three disjoint regions $R_{U}(C):= \lbrace x\in \mathbb {R}^{m}: ax_{j_{1}}+b\leq x_{j_{2}}\ \forall (a,b)\in C \rbrace$, $R_{L}:= \lbrace x\in \mathbb {R}^{m}: ax_{j_{1}}+b> x_{j_{2}}\ \forall (a,b)\in C \rbrace$ and R_I(C) := X ∖ (R_U(C) ∪ R_L(C)). Accordingly, we define $\mathcal {X}_{U}(C):= \lbrace (x^{i},y^{i})\in \mathcal {X}: x^{i}\in R_{U}(C) \rbrace$, $\mathcal {X}_{L}(C):= \lbrace (x^{i},y^{i})\in \mathcal {X}: x^{i}\in R_{L}(C) \rbrace$ and $\mathcal {X}_{I}(C):= \lbrace (x^{i},y^{i})\in \mathcal {X}: x^{i}\in R_{I}(C) \rbrace$ as the set of training samples in the respective regions. Note, that for all training samples in $\mathcal {X}_{L}(C)$ any rule in Θ(C) is satisfied and for all $\mathcal {X}_{U}(C)$ no rule in Θ(C) can be satisfied. Hence, we also refer to these regions as lower and upper invariant, respectively. Uncertainty regarding the location of a point relative to an optimal rule within C only remains for points in R_I(C). This observation is illustrated in Fig. 3.

Fig. 3

Illustration of a subproblem $C=[\underline {a},\overline {a}]\times [\underline {b},\overline {b}]$ of the branch and bound procedure

4.3 Node exploration criteria

As already mentioned before, we introduce node exploration criteria in our branch and bound procedure to identify situations for which we can efficiently enumerate all relevant rules within a subproblem C.

Node Exploration Criterion 1

This criterion is met if $|\mathcal {X}_{I}(C)|=0$. In this case any rule in R(C) will be satisfied by the points in $\mathcal {X}_{L}(C)$ and violated by the points in $\mathcal {X}_{U}(C)$. Hence, any split within the subproblem’s bounds will yield the same impurity. This means that we can simply evaluate an arbitrary feasible split of the subproblem and no further exploration is necessary.

Node Exploration Criterion 2

The second criterion is met if the points in $|\mathcal {X}_{I}(C)|$ are not distinguishable, i.e., it holds that $x^{i}_{j_{1}}=x^{i^{\prime }}_{j_{1}}:= v$ and $x^{i}_{j_{2}}=x^{i^{\prime }}_{j_{2}}$ for all $(x^{i},y^{i}),(x^{i^{\prime }},y^{i^{\prime }})\in \mathcal {X}_{I}(C)$. If v ≥ 0, we know that $\overline {a}X_{j_{1}}+\overline {b}\leq X_{j_{2}}$ or $\underline {a}X_{j_{1}}+\underline {b}\leq X_{j_{2}}$ is an optimal rule within the bounds of C. Otherwise, either $\underline {a}X_{j_{1}}+\overline {b}\leq X_{j_{2}}$ or $\overline {a}X_{j_{1}}+\underline {b}\leq X_{j_{2}}$ is optimal. Thus, it is possible to test all relevant candidate solutions of the subproblem.

Node Exploration Criterion 3

The third criterion is based on an interesting behavior of concave impurity measures found by [23]. He shows that if a set of labeled data points could be arbitrarily partitioned into two subsets, there would exist an optimal partition which does not split any class. We will generalize this result by showing that if we want to distribute a set of points among two possibly non-empty subsets such that the weighted impurity of the two resulting sets is minimal, there exists an optimal distribution that does not split any class. Before proving this result, we introduce the notation u ∘ v = (u₁v₁,…,u_kv_k)^T to denote the component-wise product of two vectors $u,v\in \mathbb {R}^{k}$.

Theorem 1

Let $\mathcal {X}_{L}(C)$, $\mathcal {X}_{U}(C)$ and $\mathcal {X}_{I}(C)$ denote sets of labeled data points with vectors of absolute frequencies of class labels $n_{L},n_{U},n_{I}\in \mathbb {N}^{k}$. For any frequency-weighted impurity measure I there exist α_L,α_U ∈{0,1}^k with α_L + α_U = 1 such that

$$ I(n_{L}+\alpha_{L}\circ n_{I})+I(n_{U}+\alpha_{U}\circ n_{I})\leq I(n_{L}+\beta_{L}\circ n_{I})+ I(n_{U}+\beta_{U}\circ n_{I}) $$

for all β_L,β_U ∈ [0,1]^k with β_L + β_U = 1.

Proof

It is a well-known result that a concave function defined on a convex polytope attains a minimum at a vertex of the domain. Such a convex polytope is defined by $\mathcal {P}:= [0,1]^{k}$. Moreover, we know that the composition of a concave function with an affine transformation remains concave and that the sum of concave functions is again concave. Therefore, $\mathcal {I}:\mathcal {P}\mapsto \mathbb {R}_{\geq 0}$ defined by $\mathcal {I}(\beta ):= I(n_{L}+\beta \circ n_{I})+ I(n_{U}+(\mathbf {1}-\beta )\circ n_{I})$ is a concave function. Hence, $\mathcal {I}$ is minimized by some $\alpha \in \mathcal {P}\cap \lbrace 0,1 \rbrace ^{k}$. Clearly, this observation is equivalent to the statement of the theorem. □

Suppose all of the points in $\mathcal {X}_{I}(C)$ have the same class label. Theorem 1 tells us that if we could arbitrarily distribute those points among $\mathcal {X}_{L}(C)$ and $\mathcal {X}_{U}(C)$, it would be optimal to put all of the points into one of the sets. Therefore, if we find two rules $a_{L}X_{j_{1}}+b_{L}\leq X_{j_{2}}$ and $a_{U}X_{j_{1}}+b_{U}\leq X_{j_{2}}$ with (a_L,b_L),(a_U,a_U) ∈ C such that $a_{L}x^{i}_{j_{1}}+b_{L}\leq x^{i}_{j_{2}}$ and $a_{U}x^{i}_{j_{1}}+b_{U}> x^{i}_{j_{2}}$ for all $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$ we know that one of them has minimal impurity among all other rules within the bounds of C. Therefore, we can test those lines, choose the one with minimal impurity and test whether it becomes the new incumbent solution. No further analysis of the subproblem is needed.

Finding such rules or deciding that they don’t exist can be carried out with the following method: If there exists (a_L,b_L) ∈ C such that $a_{L}x^{i}_{j_{1}}+b_{L}\leq x^{i}_{j_{2}}$ for all $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$, then it also holds that $a_{L}x^{i}_{j_{1}}+\underline {b} \leq x^{i}_{j_{2}}$. Thus, we have to solve the following system of inequalities:

$$ \begin{array}{@{}rcl@{}} a_{L}x^{i}_{j_{1}}+\underline{b}&\leq& x^{i}_{j_{2}} \text{, for all } (x^{i},y^{i})\in \mathcal{X}_{I}(C),\ x^{i}_{j_{1}}\neq 0\\a_{L}&\geq& \underline{a}\\ a_{L}&\leq& \overline{a}. \end{array} $$

This is equivalent to

$$a_{L}\!\leq\! \min \left\lbrace \lbrace \overline{a} \rbrace \cup \left\lbrace \frac{x^{i}_{j_{2}}-\underline{b}}{x^{i}_{j_{1}}} : (x^{i},y^{i})\in \mathcal{X}_{I}(C),\ x^{i}_{j_{1}}> 0 \right\rbrace \right\rbrace$$

and

$$a_{L}\!\geq\! \max \left\lbrace \lbrace \underline{a} \rbrace \cup \left\lbrace \frac{x^{i}_{j_{2}}-\underline{b}}{x^{i}_{j_{1}}}: (x^{i},y^{i})\!\in\! \mathcal{X}_{I}(C),\ x^{i}_{j_{1}}\!< 0 \right\rbrace \right\rbrace.$$

The existence of such a value a_L is easily verified. Similar arguments lead to the conclusion that there exists $a_{U}x^{i}_{j_{1}}+b_{U}> x^{i}_{j_{1}}$ if and only if there exists a_U such that

$$a_{U}\!>\! \max \left\lbrace \lbrace \underline{a} \rbrace \cup \left\lbrace \frac{x^{i}_{j_{2}}-\overline{b}}{x^{i}_{j_{1}}} : (x^{i},y^{i})\in \mathcal{X}_{I}(C),\ x^{i}_{j_{1}}> 0 \right\rbrace \right\rbrace$$

and

$$a_{U}\!<\! \min \left\lbrace \lbrace \overline{a} \rbrace \cup \left\lbrace \frac{x^{i}_{j_{2}}-\overline{b}}{x^{i}_{j_{1}}} : (x^{i},y^{i})\!\in\! \mathcal{X}_{I}(C),\ x^{i}_{j_{1}}< 0 \right\rbrace \right\rbrace.$$

Node Exploration Criterion 4

The last node exploration criteria is met, if there exist $a^{*},b^{*}\in \mathbb {R}$ such that $a^{*}x^{i}_{j_{1}}+b^{*}=x^{i}_{j_{2}}$ for all $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$. In other words, the points in $\mathcal {X}_{I}(C)$ are colinear. This criterion is necessary to ensure termination of the branch and bound procedure. Suppose, for example $\underline {a}\leq a^{*}\leq \overline {a}$ and $\underline {b}\leq b^{*}\leq \overline {b}$ and we are branching on (a,b) which results in the subproblems $C_{1}:=[\underline {a},a]\times [\underline {b},b]$, $C_{2}:=[\underline {a},a]\times [b,\overline {b}]$, $C_{3}:=[a,\overline {a}]\times [\underline {b},b]$ and $C_{4}:=[a,\overline {a}]\times [b,\overline {b}]$. For one of the subproblems C_l with l ∈{1,…,4} it holds that (a^∗,b^∗) ∈ C_l and therefore $\mathcal {X}_{I}(C)=\mathcal {X}_{I}(C_{l})$. Hence, there will always remain a subproblem for which the uncertainty set does not change. Clearly, this means that the first two node exploration criteria are not sufficient to ensure termination of the branch and bound procedure. Luckily, in the situation where all points are colinear, all relevant rules can be efficiently evaluated. This result is summarized in the following theorem and the proof yields an efficient algorithm to determine these rules.

Theorem 2

Let $C=[\underline {a},\overline {a}]\times [\underline {b},\overline {b}]\subseteq \mathbb {R}^{2}$ with $\underline {a}<\overline {a}$ and $\underline {b}<\overline {b}$ and $\mathcal {X}_{I}(C)$ such that there exist $a^{*},b^{*}\in \mathbb {R}$ with $a^{*}x^{i}_{j_{1}}+b^{*}=x^{i}_{j_{2}}$ for all $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$. We can find (a,b) ∈ C such that $\theta := aX_{j_{1}}+b\leq X_{j_{2}}$ has minimal impurity among all other splits $\theta ^{prime}:= a^{\prime }X_{j_{1}}+b^{\prime }\leq X_{j_{2}}$ with $(a^{\prime },b^{\prime })\in C$ in $O(|\mathcal {X}_{I}(C)|)$ time if the samples $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$ are sorted by attribute $X_{j_{1}}$, i.e., it holds that $x^{i}_{j_{1}}\leq x^{i^{\prime }}_{j_{1}}$ if $i<i^{\prime }$. Otherwise, the time complexity is $O(|\mathcal {X}_{I}(C)|\log |\mathcal {X}_{I}(C)|)$.

Proof

Let $n_{C}=|\mathcal {X}_{I}(C)|$ and w.l.o.g. $\mathcal {X}_{I}(C)=\lbrace (x^{1},y^{1}),\ldots ,(x^{n_{C}},y^{n_{C}}) \rbrace$. Moreover, we assume that $\mathcal {X}_{I}(C)$ is sorted by attribute $X_{j_{1}}$. Otherwise, we employ any efficient sorting algorithm to sort the samples in $O(|\mathcal {X}_{I}(C)|\log |\mathcal {X}_{I}(C)|)$ time.

For all (a,b) ∈ C, we call $(\mathcal {X}^{+}_{(a,b)},\mathcal {X}^{-}_{(a,b)})$ with $\mathcal {X}^{+}_{(a,b)}:=\lbrace (x^{i},y^{i})\in \mathcal {X}_{I}(C): ax^{i}_{j_{1}}+b\leq x^{i}_{j_{2}} \rbrace$ and $\mathcal {X}^{-}_{(a,b)}:=\lbrace (x^{i},y^{i})\in \mathcal {X}_{I}(C): ax^{i}_{j_{1}}+b> x^{i}_{j_{2}} \rbrace$ a linear partition of $\mathcal {X}_{I}(C)$. Further, let $\mathcal {P}:= \lbrace (\mathcal {X}^{+}_{(a,b)},\mathcal {X}^{-}_{(a,b)}):(a,b)\in C\rbrace$ denote the set of all possible linear partitions of $\mathcal {X}_{I}(C)$. Clearly, lines that yield the same linear partition will have the same impurity. Therefore, to find the parameters (a,b) ∈ C which lead to a rule of minimal impurity we have to investigate each possible linear partition and find according parameters for the line.

Let us first assume that there is no limitation on the parameters of the line, i.e., $C=\mathbb {R}^{2}$. In this case $\mathcal {P}$ contains the partitions $(\mathcal {X}(C),\emptyset )$, $(\emptyset ,\mathcal {X}(C))$. These partitions can, for example, be realized by choosing the parameters a := a^∗ and b := b^∗ + 𝜖 or b := b^∗− 𝜖, respectively. Further, $\mathcal {P}$ contains the partitions $(\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }\leq i \rbrace ,\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }> i \rbrace )$ and $(\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }> i \rbrace ,\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }\leq i \rbrace )$ for i = 1,…,n_C − 1. The lines to create these partitions have to pass a point on the line segment $L_{i}:=\lbrace (x,a^{*}x+b^{*}): x^{i}_{j_{1}}\leq x< x^{i+1}_{j_{1}} \rbrace$ or $L^{\prime }_{i}:=\lbrace (x,a^{*}x+b^{*}): x^{i}_{j_{1}}< x\leq x^{i+1}_{j_{1}} \rbrace$ and need to have a greater or smaller slope than a^∗, respectively.

Clearly, if we limit the range of the subproblem to $C:= [\underline {a},\overline {a}]\times [\underline {b},\overline {b}]$ the number of possible linear partitions reduces. Therefore, we have to check which ones of these 2n_C partitions are still realizable.

We start off by introducing a method to find a line that goes above all points and creates the partition $(\emptyset ,\mathcal {X}(C))$ or tells us that such a line does not exist. Suppose, there exists a line (a,b) ∈ C that satisfies $ax^{i}_{j_{1}}+b>x^{i}_{j_{2}}$ for all (xⁱ,yⁱ) ∈ C. Clearly, also $ax^{i}_{j_{1}}+\overline {b}>x^{i}_{j_{2}}$ holds. In other words, we can restrict the search to lines with an axis intercept of $\overline {b}$. Due to the sorting, if $x^{1}_{j_{1}}\geq 0$ it holds that $x^{n_{C}}_{j_{1}}\geq 0$ and we choose $a:=\overline {a}$. Else, if $x^{n_{C}}_{j_{1}}\leq 0$, we know that also $x^{1}_{j_{1}}\leq 0$ holds and we choose $a:=\underline {a}$. In all other situations, a necessary and sufficient set of conditions for the parameter a is:

$$ \begin{array}{@{}rcl@{}} ax^{1}_{j_{1}}+\overline{b}&>&x^{1}_{j_{2}}\\ ax^{n_{C}}_{j_{1}}+\overline{b}&>&x^{n_{C}}_{j_{2}}\\ a&\geq& \underline{a}\\ a&\leq& \overline{a} \end{array} $$

Since $x^{1}_{j_{1}}< 0$ and $x^{n_{C}}_{j_{1}}>0$ we deduce the inequalities $a<\frac {x^{1}_{j_{2}}-\overline {b}}{x^{1}_{j_{1}}}$ and $a>\frac {x^{n_{C}}_{j_{2}}-\overline {b}}{x^{n_{C}}_{j_{1}}}$. Therefore, if $a_{1}:={\max \limits } \left \lbrace \frac {x^{n_{C}}_{j_{2}}-\overline {b}}{x^{n_{C}}_{j_{1}}}, \underline {a} \right \rbrace \geq {\min \limits } \left \lbrace \frac {x^{1}_{j_{2}}-\overline {b}}{x^{1}_{j_{1}}}, \overline {a}\right \rbrace := a_{2}$, no line above all of the points is possible. Otherwise, we choose $a:=\frac {a_{1}+a_{2}}{2}$.

Finding a line beneath all points to create the partition $(\mathcal {X}(C),\emptyset )$ is analogous to the case discussed above. If $x^{1}_{j_{1}}\geq 0$, we choose $a:=\underline {a}$ and $b:=\underline {b}$, if $x^{n_{C}}_{j_{1}}\leq 0$, we choose $a:=\overline {a}$ and $b:=\underline {b}$. Otherwise, we check whether $a_{1}:={\max \limits } \left \lbrace \frac {x^{1}_{j_{2}}-\underline {b}}{x^{1}_{j_{1}}}, \underline {a} \right \rbrace > {\min \limits } \left \lbrace \frac {x^{n_{C}}_{j_{2}}-\underline {b}}{x^{n_{C}}_{j_{1}}}, \overline {a}\right \rbrace := a_{2}$. If this evaluates to true, no line beneath all points exists. Otherwise, $a:=\frac {a_{1}+a_{2}}{2}$ and $b:= \underline {b}$ yields the desired partition.

Next, we want to find lines for the partitions $(\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }\leq i \rbrace ,\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }> i \rbrace )$ for i = 1,…,n_C − 1 or decide that such a line does not exist. This is equivalent to solving the following linear program for sufficiently small 𝜖 > 0:

$$\begin{array}{rll} (LP)\quad \max& \delta_{1}\\ \textrm{s.t.}& (\underline{a}+\delta_{a})x^{i}_{j_{1}} +(\underline{b}+\delta_{b}) +\delta_{1}= x^{i}_{j_{2}} \\ & (\underline{a}+\delta_{a})x^{i+1}_{j_{1}} +(\underline{b}+\delta_{b})-\delta_{2}-\epsilon= x^{i+1}_{j_{2}} \\ & \delta_{a}+\delta_{3}=\overline{a}-\underline{a}\\ & \delta_{b}+\delta_{4}=\overline{b}-\underline{b}\\ & \delta_{a},\delta_{b},\delta_{1},\delta_{2},\delta_{3},\delta_{4}\geq 0 \end{array}$$

There exists a line for the partition if and only if (LP) has an optimal solution with an objective value greater than zero. Such a line is then defined by $a:=\underline {a}+\delta ^{*}_{a}$ and $b:=\underline {b}+\delta ^{*}_{b}$ for any feasible solution $\delta ^{*}_{a},\delta ^{*}_{b},\delta ^{*}_{1},\delta ^{*}_{2},\delta ^{*}_{3},\delta ^{*}_{4}\geq 0$ with $\delta _{1}^{*}>0$. If (LP) has an optimal solution with δ₁ > 0 then it also has an optimal basic solution with δ₁ > 0. As $\underline {a}<\overline {a}$, we further know that in an optimal basic solution either δ_a or δ₃ must be part of the basis. Similarly, we know that δ_b or δ₄ must be part of the basis. Hence, there remain eight bases to be checked: {δ₁,δ_a,δ_b,δ₂}, {δ₁, δ_a, δ_b,δ₃}, {δ₁, δ_a, δ_b,δ₄}, {δ₁,δ₃,δ_b,δ₂}, {δ₁, δ₃, δ_b, δ₄},{δ₁, δ_a, δ₄, δ₂},{δ₁, δ_a, δ₄, δ₃},{δ₁,δ₃,δ₄,δ₂}.

Similarly, finding a line (a,b) ∈ C such $(\mathcal {X}^{+}_{(a,b)},\mathcal {X}^{-}_{(a,b)})=(\lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }> i \rbrace , \lbrace (x^{i^{\prime }},y^{i^{\prime }}):i^{\prime }\leq i \rbrace )$ for i = 1,…,n_C − 1 is equivalent to solving the linear program

$$\begin{array}{rll} (LP)\quad \max& \delta_{1}\\ \textrm{s.t.}& (\underline{a}+\delta_{a})x^{i+1}_{j_{1}} +(\underline{b}+\delta_{b})+\delta_{1}= x^{i+1}_{j_{2}} \\ & (\underline{a}+\delta_{a})x^{i}_{j_{1}} +(\underline{b}+\delta_{b}) -\delta_{2}-\epsilon= x^{i}_{j_{2}} \\ & \delta_{a}+\delta_{3}=\overline{a}-\underline{a}\\ & \delta_{b}+\delta_{4}=\overline{b}-\underline{b}\\ & \delta_{a},\delta_{b},\delta_{1},\delta_{2},\delta_{3},\delta_{4}\geq 0 \end{array}$$

for small 𝜖 > 0 and the same set of basic solutions has to be evaluated as in the previous case.

Altogether, we introduced a constant time method for all of the 2n_C partitions P which either yields parameters (a,b) such that $(\mathcal {X}^{+}_{(a,b)},\mathcal {X}^{-}_{(a,b)})=P$ or decides that the partition is not possible. □

The necessity of sorting the data points in each subproblem can be avoided easily. Before starting the tree building algorithm one creates m arrays of pointers to the actual training data. These arrays are then sorted according to the values of the respective attribute. From that point on one can work with these arrays of pointers instead of the actual values of the training data.

4.4 Branching strategy

In this section, we present the strategy for choosing the parameter a or b used for branching a subproblem $C:=[\underline {a},\overline {a}]\times [\underline {b},\overline {b}]$. We require the computation of the parameters to be simple, i.e., the time complexity should be $O(|\mathcal {X}_{I}(C)|)$, because we found that more elaborate branching strategies could not compensate the drawback of being able to process less subproblems in the same amount of time.

Branching strategy 1

The simplest, most obvious choice for the parameters is $a:= \frac {\underline {a}+\overline {a}}{2}$ and $b:= \frac {\underline {b}+\overline {b}}{2}$. A shortcoming of this strategy is that it does not take into account the position of the points in R_I(C). Hence, we develop a more elaborate strategy that is still fairly easy to compute.

Branching strategy 2

In the previous section, we introduced node exploration criteria for situations in which there are no points in $\mathcal {X}_{I}(C)$ or the points in this set are not distinguishable. Hence, it would be desirable if the number of uncertain datapoints of the resulting subproblems would be as small as possible. In the best case, we would evenly distribute the points in $\mathcal {X}_{I}(C)$ among the four subproblems. Obviously, this is not always possible. It is also very likely that certain points will have to be in the region of uncertainty of two or more subproblems, i.e., for $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$ and two subproblems $C^{\prime }$ and $C^{\prime \prime }$ of C it holds that $(x^{i},y^{i})\in \mathcal {X}_{I}(C^{\prime })$ and $(x^{i},y^{i})\in \mathcal {X}_{I}(C^{\prime \prime })$. Still, it does make sense to approximate the desired aim by choosing some sort of mean parameters for branching which we construct as follows: For each $(x^{i},y^{i})\in \mathcal {X}_{I}(C)$, we find $a^{i}\in [\underline {a},\overline {b}]$ and $b^{i}\in [\underline {b},\overline {b}]$ such that $a^{i}x^{i}_{j_{1}}+b^{i}=x^{i}_{j_{2}}$. As values for bⁱ, we choose the mean intercept of all possible lines that pass through the point $(x^{i}_{j_{1}},x^{i}_{j_{2}})$ that have a slope within the interval $[\underline {a},\overline {a}]$:

$$b^{i}:=\begin{cases} \frac{\max\lbrace \underline{b},x^{i}_{j_{2}}-\overline{a}x^{i}_{j_{1}}\rbrace+\min\lbrace \overline{b},x^{i}_{j_{2}}-\underline{a}x^{i}_{j_{1}} \rbrace}{2} \text{, if } x^{i}_{j_{1}}> 0\\ \frac{\max\lbrace \underline{b},x^{i}_{j_{2}}-\underline{a}x^{i}_{j_{1}}\rbrace+\min\lbrace \overline{b},x^{i}_{j_{2}}-\overline{a}x^{i}_{j_{1}} \rbrace}{2} \text{, if } x^{i}_{j_{1}}< 0\\ x^{i}_{j_{2}}\text{, if } x^{i}_{j_{1}}= 0 \end{cases}$$

It follows that $a^{i}=\frac {x^{i}_{j_{2}}-b^{i}}{x^{i}_{j_{1}}}$ if $x^{i}_{j_{1}}\neq 0$. If $x^{i}_{j_{1}}=0$ we set $a^{i}=\frac {\underline {a}+\overline {a}}{2}$. Subsequently, we choose the respective means

$$a:=\sum\limits_{(x^{i},y^{i})\in\mathcal{X}_{I}(C)}\frac{ a^{i}}{|\mathcal{X}_{I}(C)|} \text{ and } b:=\sum\limits_{(x^{i},y^{i})\in\mathcal{X}_{I}(C)}\frac{b^{i}}{|\mathcal{X}_{I}(C)|}$$

as the values for branching. The idea of this construction is illustrated in Fig. 4. In our experiments we found that this simple strategy outperforms the initial idea of choosing $a:= \frac {\underline {a}+\overline {a}}{2}$ and $b:= \frac {\underline {b}+\overline {b}}{2}$ and due to the linear complexity it does not significantly slow down the branch and bound procedure.

Fig. 4

The dashed lines illustrate the lines $a^{i}X_{j_{1}}+b^{i}=X_{j_{2}}$ and the solid line illustrates the line $aX_{j_{1}}+b=X_{j_{2}}$ from which the branching parameters are derived

4.5 Termination of the algorithm

An important issue to be addressed for a branch and bound algorithm over a continuous domain is the termination of the algorithm. The following theorem states that our algorithm does in fact terminate after a finite number of iterations for the first branching strategy.

Theorem 3

If for each subproblem $C=[\underline {a},\overline {a}]\times [\underline {b},\overline {b}]$ the point $(\frac {\underline {a}+\overline {a}}{2},\frac {\underline {b}+\overline {b}}{2})$ is chosen for branching, the algorithm terminates after a finite number of iterations.

Proof

To proof this theorem, we have to show that the branch and bound procedure terminates for each individual pair of attributes j₁,j₂ ∈{1,…,m} such that j₁≠j₂. More specifically, for each pair of attributes, the while loop at line 8 in Algorithm 2 must terminate after a finite number of iterations. Let’s assume that this is not the case. Then, there exist attributes j₁,j₂ with j₁≠j₂ and a sequence $(C_{k})_{k\in \mathbb {N}}=([\underline {a}_{k},\overline {a}_{k}]\times [\underline {b}_{k},\overline {b}_{k}])_{k\in \mathbb {N}}$ of consecutive subproblems for that particular pair of attributes such that C_k+ 1 ⊂ C_k and none of these subproblems satisfies one of the node exploration criteria. As the first three node exploration criteria are not satisfied the sets $\mathcal {X}_{I}(C_{k})$ contain at least two distinct points and these sets remain equal for k ≥ k_I for some specific $k_{I}\in \mathbb {N}$. W.l.o.g we can therefore assume that there exists $\tilde {\mathcal {X}}\subseteq \mathcal {X}$ such that $\mathcal {X}_{I}(C_{k})=\tilde {\mathcal {X}}$ for all $k\in \mathbb {N}$. Due to the branching strategy, the sequence converges towards a single point $(\tilde {a},\tilde {b})\in \mathbb {R}^{2}$ and for each 𝜖 > 0 there exists $k_{\epsilon }\in \mathbb {N}$ such that for each k ≥ k_𝜖 it holds that $C_{k}\subseteq [\tilde {a}-\epsilon ,\tilde {a}+\epsilon ]\times [\tilde {b}-\epsilon ,\tilde {b}+\epsilon ]$. As the fourth node exploration criterion is not satisfied, there exists at least one point $(x^{i},y^{i})\in \tilde {\mathcal {X}}$ such that $\tilde {a}x^{i}_{j_{1}}+\tilde {b}\neq x^{i}_{j_{2}}$. We define $d:= |\tilde {a}x^{i}_{j_{1}}+\tilde {b}-x^{i}_{j_{2}}|$. Clearly, it holds that d > 0 Then, for $\epsilon =\frac {d}{2(|x^{i}_{j_{1}}|+1)}$, and any $(a^{\prime },b^{\prime })\in [\tilde {a}-\epsilon ,\tilde {a}+\epsilon ]\times [\tilde {b}-\epsilon ,\tilde {b}+\epsilon ]$ we conclude:

• Case 1: $x^{i}_{j_{1}}\geq 0$ and $\tilde {a}x^{i}_{j_{1}}+\tilde {b}-x^{i}_{j_{2}}>0$

  $$ \begin{array}{@{}rcl@{}} a^{\prime}x^{i}_{j_{1}}+b^{\prime}-x^{i}_{j_{2}}&\!\geq\!& (\tilde{a}-\epsilon)x^{i}_{j_{1}}+(\tilde{b}-\epsilon)-x^{i}_{j_{2}}\\ &\!\geq\!&\tilde{a}x^{i}_{j_{1}}+\tilde{b}-x^{i}_{j_{2}}-\epsilon(x^{i}_{j_{1}}+1)=d-\frac{d}{2}=\frac{d}{2}>0 \end{array} $$

• Case 2: $x^{i}_{j_{1}}< 0$ and $\tilde {a}x^{i}_{j_{1}}+\tilde {b}-x^{i}_{j_{2}}>0$

  $$ \begin{array}{@{}rcl@{}} a^{\prime}x^{i}_{j_{1}}\!+b^{\prime} - x^{i}_{j_{2}}\!\geq\! \tilde{a}x^{i}_{j_{1}}+\tilde{b}-x^{i}_{j_{2}}-\epsilon(-x^{i}_{j_{1}}+1)=d-\frac{d}{2}=\frac{d}{2}>0 \end{array} $$

• Case 3: $x^{i}_{j_{1}}\geq 0$ and $\tilde {a}x^{i}_{j_{1}}+\tilde {b}-x^{i}_{j_{2}}<0$

  $$ \begin{array}{@{}rcl@{}} a^{\prime}x^{i}_{j_{1}} + b^{\prime} - x^{i}_{j_{2}}\!\leq\! \tilde{a}x^{i}_{j_{1}} + \tilde{b} - x^{i}_{j_{2}} + \epsilon(x^{i}_{j_{1}}+1)=-d+\frac{d}{2}=-\frac{d}{2}<0 \end{array} $$

• Case 4: $x^{i}_{j_{1}}< 0$ and $\tilde {a}x^{i}_{j_{1}}+\tilde {b}-x^{i}_{j_{2}}<0$

  $$ \begin{array}{@{}rcl@{}} a^{\prime}x^{i}_{j_{1}} + b^{\prime} - x^{i}_{j_{2}}\!\leq\! \tilde{a}x^{i}_{j_{1}} + \tilde{b}-x^{i}_{j_{2}}+\epsilon(-x^{i}_{j_{1}} + 1) = -d+\frac{d}{2} = -\frac{d}{2}<0 \end{array} $$

Thus, in all of the four cases there is no $(a^{\prime },b^{\prime })\in [\tilde {a}-\epsilon ,\tilde {a}+\epsilon ]\times [\tilde {b}-\epsilon ,\tilde {b}+\epsilon ]$ such that $a^{\prime }x^{i}_{j_{1}}+b^{\prime }=x^{i}_{j_{2}}$. Hence, $(x^{i},y^{i})\not \in \mathcal {X}_{I}(C_{k})$ for all k ≥ k_𝜖 which contradicts the assumption that $(x^{i},y^{i})\in \tilde {\mathcal {X}}$ which is equivalent to $(x^{i},y^{i})\in \mathcal {X}_{I}(C_{k})$ for all $k\in \mathbb {N}$. □

The second branching strategy presented in Section 4.4 should be regarded as a suggestion to improve the runtime of the algorithm in practice. The idea is purely heuristic and for that reason it is provided without theoretical justification. Nevertheless, we want to point out the fact that due to Theorem 3 we can ensure termination for any branching strategy by combining it appropriately with Branching Strategy 1.

4.6 Upper and lower bounds

Upper bounds

The computation of an upper bound for the currently observed subproblem can be carried out by choosing arbitrary parameters a and b such that (a,b) ∈ C and compute the impurity of the split $aX_{j_{1}}+b\leq X_{j_{2}}$. In our implementation we choose the values used for branching the subproblem.

Lower bounds

For the lower bound of a subproblem C we exploit the concavity of the impurity measures. In fact, it turns out that the weighted impurity of the two invariants is a lower bound for any rule $aX_{j_{1}}+b\leq X_{j_{2}}$ with (a,b) ∈ C.

Theorem 4

Let I denote a frequency-weighted impurity measure and let $\hat {I}$ denote the corresponding impurity measure for a bivariate oblique split on the training set $\mathcal {X}$. For a subproblem $C\subseteq \mathbb {R}^{2}$ let n_L and n_U denote the vector of absolute frequencies of class labels of the sets $\mathcal {X}_{L}(C)$ and $\mathcal {X}_{U}(C)$, respectively. Further, let $\theta := aX_{j_{1}}+b\leq X_{j_{2}}$ with (a,b) ∈ C denote a valid rule within the bounds of the subproblem Then, it holds that

$$ I(n_{L})+I(n_{U}) \leq\hat{I}(\theta,\mathcal{X})$$

Proof

The rule 𝜃 partitions $\mathcal {X}_{I}(C)$ into two subsets $\mathcal {X}^{-}_{I}(C),\mathcal {X}^{+}_{I}(C)$ with class frequencies m_L and m_U. It divides the overall set of training samples $\mathcal {X}$ into two subsets $\mathcal {X}_{L}$ and $\mathcal {X}_{U}$ such that $\mathcal {X}_{L}=\mathcal {X}^{-}_{I}(C)\overset {.}{\cup } \mathcal {X}_{L}(C)$ and $\mathcal {X}_{U}=\mathcal {X}^{+}_{I}(C)\overset {.}{\cup } \mathcal {X}_{U}(C)$. Hence, the impurity of the split is

$$\hat{I}(\theta,\mathcal{X})=I(n_{L}+m_{L})+I(n_{U}+m_{U}).$$

Using strict concavity of I, we have

$$ \begin{array}{@{}rcl@{}} I(n_{L} + m_{L}) + I(n_{U}+m_{U})&\geq& I(n_{L}) + I(m_{L}) + I(n_{U}) + I(m_{U}) \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} &\geq& I(n_{L})+I(n_{U}). \end{array} $$

(2)

□

4.7 Improved lower bounds for specific impurity measures

In this section we present two improved lower bounds for the popular impurity measures entropy and gini impurity. The improvements are based on the work of [23] who summarizes useful properties of concave impurity measures.

Theorem 4 states that the weighted impurity of the invariants is a lower bound for any rule of the examined subproblem C. In its proof, we ignored the sum I(m_L) + I(m_U) to get from (1) and (2). Thus, if we can lower bound this sum by some value greater than zero, we can improve the lower bound of the subproblem. Note, that this expression corresponds to the impurity of a feasible partition of the points in $\mathcal {X}_{I}(C)$ into two subsets. Recalling Theorem 1, we know that there exists an optimal partition of these points that does not split any class. Those optimal partitions, however, can be very different depending on the underlying impurity measure.

For the entropy, Breiman shows that an optimal partition would distribute the points evenly among the subsets. More precisely, a partition $(\mathcal {X}_{L},\mathcal {X}_{U})$ of $\mathcal {X}_{I}(C)$ such that $\mathcal {X}_{L}\dot {\cup }\mathcal {X}_{U}=\mathcal {X}_{I}(C)$ with respective vectors of absolute frequencies of the class labels m_L and m_U which does not split any class minimizes the weighted entropy E(m_L) + E(m_U) if it minimizes $\max \limits \lbrace |\mathcal {X}_{L}|,|\mathcal {X}_{U}| \rbrace$. If m denotes the vector of absolute frequencies of class labels of $\mathcal {X}_{I}(C)$ the result can be derived from the following equation:

$$ \begin{array}{@{}rcl@{}} E(m_{L}) + E(m_{U}) & = &-\sum\limits_{r\in\lbrace L,U \rbrace}|\mathcal{X}_{r}|\sum\limits_{{j=1,\ldots,k:\atop m_{r_{j}}=m_{j}}} \frac{m_{j}}{|\mathcal{X}_{r}|}\log \frac{m_{j}}{|\mathcal{X}_{r}|}\\ & = &-\sum\limits_{j=1}^{k} m_{j}\log m_{j}+\sum\limits_{r\in\lbrace L,U \rbrace} |\mathcal{X}_{r}|\log |\mathcal{X}_{r}| \end{array} $$

The first equation stems from the fact either m_Lj or m_Rj is equal to m_j as the we only consider partitions which do not split any class. Unfortunately, determining such an optimal partition is equivalent to solving the well-known NP-hard partition problem. Nevertheless, the second part of the equation is clearly bounded by the expression $|\mathcal {X}_{I}(C)|\log \frac {|\mathcal {X}_{I}(C)|}{2}$ which motivates the following theorem.

Theorem 5

Let E denote the frequency weighted entropy impurity measure and let $\hat {E}$ denote the corresponding impurity measure for a bivariate oblique split on the training set $\mathcal {X}$. For a subproblem $C\subseteq \mathbb {R}^{2}$ let n_L and n_U denote the vector of absolute frequencies of the class labels in the invariants. Further, let m denote the vector of absolute frequencies of $\mathcal {X}_{I}(C)$ and $M:=|\mathcal {X}_{I}(C)|$. For any rule $\theta := aX_{j_{1}}+b\leq X_{j_{2}}$ such that (a,b) ∈ C it holds that

$$ \max\left\lbrace \sum\limits_{r\in\lbrace L,U \rbrace}E(n_{r}), \sum\limits_{r\in\lbrace L,U \rbrace}E(n_{r})-\sum\limits_{j=1}^{k} m_{j}\log m_{j} + M\log \frac{M}{2} \right\rbrace\leq \hat{E}(\theta,\mathcal{X}). $$

For the gini impurity Breiman proves that an optimal partition separates the maximum class from the other classes. This observation leads to the following theorem.

Theorem 6

Let G denote the frequency weighted gini impurity measure and let $\hat {G}$ denote the corresponding impurity measure for a bivariate oblique split on the training set $\mathcal {X}$. Let C, n_L, n_U and m as in Theorem 5. Furthermore, let $j^{*}:= \arg \max \limits _{j=1,\ldots ,k} m_{j}$. For any rule $\theta := aX_{j_{1}}+b\leq X_{j_{2}}$ such that (a,b) ∈ C it holds that

$$ \sum\limits_{r\in\lbrace L,U \rbrace}G(n_{r})+G((m_{1},\ldots,m_{j^{*}-1},0,m_{j^{*}+1},\ldots,m_{k})) \leq \hat{G}(\theta,\mathcal{X}). $$

These improved lower bounds are especially useful in the early stage of the branch and bound procedure when the number of points in the invariants is still quite low. In this stage, the lower bound stated in Theorem 4 is quite small and the additionally added term will have a high proportion of the value of the improved bound. At a later stage, when the invariants contain many points the original term which corresponds to the lower bound stated in Theorem 4 becomes dominant as the invariants already yield a good picture of any feasible split of the subproblem.

5 Extensions for the tree building algorithm

5.1 Early stopping

As the outer loop of the decision tree induction algorithm (see Algorithm 1) is a greedy approach, global optimality of the splits might sometimes not be absolutely essential and one might want to speed up the algorithm instead. Nevertheless, even in these situations it is desirable to be close to the global optimum and to have a global quality guarantee. Heuristic approaches which yield local optima usually don’t provide such a guarantee and it is not clear whether the local optimal solution’s impurity is close to the best value possible. Branch and bound on the other hand, although belonging to the class of exact algorithms for solving optimization problems, can also be employed heuristically while providing a global quality guarantee. Instead of pruning subproblems only when the lower bound lb is smaller than or equal to the upper bound ub, one can prune whenever lb ≥ (1 − 𝜖)ub for 𝜖 ∈ [0,1]. For such nodes, no significant improvement is possible. Although this might lead to pruning the optimal solution, we still know that an optimal solution’s objective value can only improve the final solution by a factor of (1 − 𝜖). That way the decision tree induction can be sped up while ensuring that the bivariate splits’ are provably near optimal.

5.2 Parallelization

Another benefit of branch and bound algorithms is the fact that they are easily parallelizable to make the best use of modern multi-core hardware. Each core can process an individual subproblem while keeping the current incumbent solution as a shared resource. For our specific problem of finding the best bivariate oblique split, we propose parallelization at attribute level, i.e., the cores are assigned tuples of attributes and run a full branch and bound procedure for them (steps 4-27 of Algorithm 2).

5.3 Categorical data

Bivariate oblique splits are only applicable for numerical data. However, in many application the data to be analyzed contains categorical features with no specific ordering. For such situations we propose to use a so-called one-hot encoding. For each category, we add an additional feature which is equal to one if the data sample belongs to the respective category and zero, otherwise. The transformed dataset can then be processed by our presented algorithm.

5.4 Decision tree pruning

When decision trees are fully branched, they are usually overfitted. This means that they describe the training data perfectly but are incapable of predicting well on unseen data. A common technique to overcome this problem is to use pruning methods. An overview over different pruning methods is presented in [24]. These can be categorized into two classes, pre- and post-pruning methods. Pre-pruning methods stop the tree building procedure when certain criteria are met. For example, if the reduction of the impurity is below a certain threshold. Post-pruning methods, on the other hand, are applied after the tree has been fully grown. If nodes of the tree satisfy certain criteria, they are pruned. These techniques are independent of the type of split used for building the tree. Therefore, they are all applicable with our method and similar results as for other decision tree induction methods are expected in terms of prediction accuracy.

6 Evaluation

6.1 Experimental setup

In this section, we provide a comprehensive evaluation of our proposed method. We compare our method (BiDT) to our own implementation of the well-known greedy top-down univariate decision tree building method (DT) which is also implemented by CART and C4.5 and to the OC1 decision tree induction algorithm [12]. The latter is probably the most popular oblique decision tree induction method which uses a randomized hill climbing approach to determine local optimal multidimensional hyperplanes to divide the feature space. Using our own implementation for the univariate trees ensures maximal comparability to the bivariate oblique trees as we are basically just omitting the branch and bound procedure. We implemented our algorithm in C++ and we carried out all of the experiments on a computer equipped with an Intel Xeon E3-1231v3 @3.40GHz (4 Cores), 32GB DDR3 RAM running Ubuntu 18.04.

For our experiments we test the three methods on 20 popular datasets from the UCI Learning Repository [25]. The collection contains datasets of variable size ranging from 80 to 25010 data points, 6 to 256 attributes and 2 to 16 classes. An overview over the examined datasets is presented in Table 1. Note, that we report the number of attributes after the application of the one-hot encoding scheme for categorical features and we dropped samples with missing values beforehand.

Table 1 Dataset description

We compare the algorithms with and without an additional post-pruning step. The chosen pruning method is minimal cost-complexity pruning introduced by [8]. We perform 10-fold cross validation to retrieve the following three quality measures:

• Out-of-sample accuracy

• Tree size in terms of the number of leaf nodes

• Required time for building the trees

We report the runtime of our bivariate oblique decision tree induction algorithm if the branch and bound procedures are carried out by a single thread as well as when they are carried out in parallel by 4 threads simultaneously (see Section 5.2).

Following Demšar’s proposal [26] for comparing multiple classifiers we perform a Friedman test (see [27, 28]) to check whether there is a significant difference for at least two of the methods and subsequently, if a significant difference is detected, we execute the Holm test (see [29]) with BiDT as a control method for a post-hoc analysis.

The Friedman test is a non-parametric statistical test based on ranks to detect differences across measurements taken by three or more different methods. For each individual dataset the performances are ranked from best to worst, i.e., the best classifier has rank one, the second best has rank two and so forth. Ties are broken by assigning the average rank. The null-hypothesis being tested is that the classifiers perform equally well and the differences are due to random error. Thus, if the null-hypothesis is true the observed ranks should be equal. If the p-value computed by the Friedman test is below a certain significance level α we reject the null-hypothesis and conclude that at least two methods differ significantly.

If a significant difference is detected by the Friedman test, the Holm test let’s us decide whether the control method BiDT performs significantly better or worse than the other algorithms at a given significance level α. For each of the methods that BiDT should be compared to, the null-hypotheses is that the method’s performance is equal to BiDT’s. The p-values for these null-hypotheses are computed and ordered from lowest to highest. To control the family-wise error rate, the Holm test adjusts these p-values by multiplying it with (k + 1 − i) where k denotes the number of methods different from the control method and i denotes the position in the ordering. Thus, smaller p-values are increased more strongly than higher ones. Then, starting from the most significant null-hypothesis (based on the original p-values) the adjusted p-values are compared to the significance level until it is exceeded for the first time. All null-hypotheses before that are rejected and the others are not and we can conclude which methods in fact differ significantly from the control method.

In our experiments we require a significance level of α = 0.05 for both, the Friedman and the Holm test.

6.2 Comparison of accuracy

In this section, we compare the accuracy of the three methods. An overview of our results for the unpruned trees can be found in Table 2 and for the pruned trees in Table 4. We report the average accuracy together with the standard deviation resulting from the 10-fold cross validation. The best value for each dataset is highlighted in bold. The last line of the table reports the average rank computed over all the datasets.

Table 2 Comparison of accuracy between unpruned BiDT, OC1 and DT

For the unpruned decision trees BiDT is in first place with a rank of 1.4, OC1 is in second place with a rank of 2.1 and DT is in the third place with a rank of 2.5 (Table 2). The Friedman test confirms that there is a significant difference for at least two average ranks with a p-value of 2 × 10^− 3 < α. A summary of the subsequent Holm test with BiDT as control method is presented in Table 3 and we can see that both OC1’s and DT’s accuracy differs significantly from BiDT’s. Thus, we conclude that BiDT is the most accurate of the three methods for the datasets at hand.

Table 3 Holm post-hoc test for accuracy of unpruned trees

We see similar results for the pruned decision trees. BiDT has the lowest rank of 1.425, OC1 has rank 2.15 and DT has rank 2.425 (Table 4). The Friedman test returns a p-value of 4 × 10^− 3 and therefore, we reject the null-hypothesis that the methods perform equally. The Holm test, which is summarized in Table 5, confirms that both OC1 and DT are in fact less accurate than BiDT.

Table 4 Comparison of accuracy between pruned BiDT, OC1 and DT

Table 5 Holm post-hoc test for accuracy of pruned trees

6.3 Comparison of tree size

We now present our findings on the tree sizes obtained by the three algorithms. The results for the unpruned trees are presented in Tables 6 and 8 summarizes the results for the pruned trees. Again, the best value for each dataset is highlighted in bold and the average rank is stated in the last line of the respective table.

Table 6 Comparison of tree size between unpruned BiDT, OC1 and DT

For the unpruned trees we see that BiDT has the lowest rank of 1.2, OC1 has a rank of 1.85 and DT has the highest rank of 2.95 (Table 6) and this difference is confirmed to be significant by the Friedman test with a p-value of 2 × 10^− 7. The post-hoc analysis which is summarized in Table 7 rejects both null-hypotheses which allows the conclusion that BiDT produces smaller trees than OC1 and DT.

Table 7 Holm post-hoc test for size of unpruned trees

For the pruned trees we get a different result. BiDT has a slightly higher rank of 1.625 than OC1 which has a rank of 1.55. DT has the highest rank with a value 2.825 (Table 8). The Friedman test confirms that there is a significant difference between at least two methods with a p-value of 3 × 10^− 5. The post-hoc Holm test, summarized in Table 9, only confirms that the difference between BiDT and DT is significant while it does not provide evidence for a significant difference between BiDT and OC1.

Table 8 Comparison of tree size between pruned BiDT, OC1 and DT

Table 9 Holm post-hoc test for size of pruned trees

6.4 Comparison of induction times

Lastly, we compare the induction times of the methods. We include the multi-threaded variant of BiDT, which is abbreviated by BiDTMT, to check whether a noticable difference can be achieved through parallelization. As suggested in Section 5.2 parallelization is carried out at attribute level and we employ a total of 4 CPU cores. For the comparison of induction times, we don’t include a comparison of the pruned trees as the post-pruning method is equal for all three methods and its runtime is neglectable in comparison to the time necessary to grow the trees. Thus, our findings would be equivalent to the results for the unpruned trees. Table 10 summarizes the induction times of our experiments.

Table 10 Comparison of induction time between unpruned BiDT, BiDTMT, OC1 and DT

Looking at the results, we see that DT has rank 1, BiDTMT has rank 2.2, OC1 has rank 3.3 and BiDT has rank 3.5. This result obviously reveals a significant difference as DT is the fastest algorithm for all datasets. Therefore, the Friedman test yields a p-value of 2 × 10^− 10. The Holm test which is summarized in Table 11 confirms that DT is faster than BiDT. Moreover, the difference between BiDT and BiDTMT is found significant while there is no evidence for a significant difference between BiDT and OC1.

Table 11 Holm post-hoc test for build-up time for unpruned trees

6.5 Discussion

Overall these results show the benefits of our proposed method. The inclusion of an additional attribute allows bivariate trees to capture the structure of the data better than univariate trees which results in a higher prediction accuracy for the majority of the datasets. Moreover, due to the global optimality of the splits, our bivariate decision tree algorithm manages to be more accurate than OC1 although the latter is not restricted to two attibutes per split. Pruning had no noticable effect on this result.

Without pruning BiDT manages to induce trees with a fewer amount of leaf nodes than DT and OC1. While it is not suprising that bivariate splits lead to smaller trees than univariate splits, the fact that BiDT performs better than OC1 is quite remarkable. As bivariate splits are a special case of oblique splits, theoretically, oblique decision trees are always capable of dividing the feature space with an equal number or fewer splits. The only advantage of BiDT is that the bivariate splits are provably global optimal while OC1’s splits are only local optimal. From our experiments we therefore conclude that global optimal bivariate splits are often more efficient at dividing the feature space than local optimal oblique splits. This result further raises the assumption that global optimal splits are in fact desirable despite the greedy nature of the outer loop of the top-down induction algorithm.

For the pruned trees, the difference in tree size between BiDT and DT can again be explained by the fact that bivariate splits are more general than univariate splits and pruning the trees does not yield an advantage for DT. What is more interesting is the fact that no significant difference is observed between BiDT and OC1, although the difference was significant for the unpruned trees. We assume that this result can also be explained by the fact that BiDT’s splits are global optimal while OC1’s splits are only local optimal. The global optimal bivariate splits seem to be stronger and therefore less likely to be pruned while many local optimal oblique splits are less important to ensure the accuracy of the decision trees and are therefore pruned. Although after pruning our bivariate trees might not be smaller than OC1’s oblique decision trees, they still have the advantage of being more interpretable.

The difference in induction time between BiDT and DT can be explained by the fact determining optimal univariate splits is much less complex than finding optimal bivariate splits or oblique splits in general. No significant difference is observed between BiDT’s and OC1’s induction time and by looking at the results we suspect that they are in the same order of magnitude for many applications. Interestingly, there is a significant difference between BiDT’s and BiDTMT’s induction time. On average BiDTMT is 2.9 times faster than BiDT which allows the conclusion that our induction algorithm does in fact profit from parallelization. Parallelization seems to be especially benefitial for larger datasets such as “optical_recognition”, “pen_based_recognition” or “poker_hand”. For these datasets the induction time is reduced by a factor greater than 3.5 which is about the best we can expect, considering the fact that four CPU cores were employed in our experiments. The smallest speed-up is achieved for the “seeds” dataset, yet the induction time is still reduced by a factor of two.

7 Illustration of interpretability

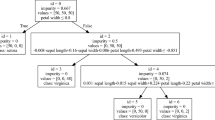
In this section, we provide an illustrative example to investigate the interpretability of bivariate decision trees. For this evaluation we test our induction algorithm on the “monks_problem_1” dataset [30]. It is an artifical dataset consisting of 124 samples and 6 attributes. Attributes X₁,X₂,X₄ take values in {1,2,3}, attributes X₃,X₆ in {1,2} and X₅ in {1,2,3,4}. The labels are assigned according to the logical rule (X₁ = X2) ∨ (X₅ = 1). A label of 1 means that the rule is satisfied and 0 means that it is not. The major advantage of using such a artificially crafted dataset for this exploration is that we can check whether the decision tree actually captures the underlying structure.

The bivariate decision tree obtained by our algorithm is shown in Fig. 5. As we can see, the root node’s rule is univariate and equivalent to X₅ ≥ 1.5. As all values are integer and greater than zero, the negation of this rule corresponds to X₅ = 1 and therefore, Node 2 comprises the positive samples that satisfy the second part of the disjunction to be learned. What is worth mentioning here is the observation that the split is in fact univariate which means that no bivariate split could reduce the impurity after the initial univariate bound is computed in Step 2 of Algorithm 2. This is actually desirable as the inclusion of another variable could cause misinterpretations or misclassifications. This shows that it is a reasonable choice to use the best univariate split as an initial solution.

Fig. 5

Bivariate tree for the “monks_problem_1” dataset

The subtree rooted at Node 1 is responsible for the condition X₁ = X2. We can rewrite the conditions at Node 1 and 3 to X1 ≥ 0.75X₂ and X₁ ≤ X₂ + 0.5 which are equivalent to X1 ≥ X₂ and X₁ ≤ X₂ for X₁,X₂ ∈{1,2,3}. Thus, both conditions are satisfied if and only if X₁ = X₂ and we can conclude that Node 5 comprises all positive samples with X₁ = X₂ and Node 4 and 6 hold all negative samples with X₁≠X₂. Therefore, Nodes 2 and 5, the ones with the positive labels, are reached if and only if the underlying rule is satisfied. Thus, this tree captures the logic of the dataset perfectly. Furthermore, it is also an oblique tree of minimal size as at least three splits are necessary to express the underlying rule.

Overall, this illustrative example shows how bivariate trees can capture the underlying structure of the data and how they can be interpreted with some basic algebraic reasoning.

8 Conclusion and future work

Interpretable machine learning becomes increasingly popular and decision trees play an import role in this context due to their easy to understand recursive nature. However, univariate decision trees are sometimes less accurate as other classification models. One reason for that is that they only use one feature per split such that complex interactions are not detected. This also often leads to huge trees which are also hard to interpret due to their size. Oblique decision trees can make up for this shortcoming at the cost of an increased induction time and the loss of interpretability when many features are involved in the splits. Moreover, the task of finding these oblique splits is far more complex and heuristics have to be applied to yield local optimal solutions with no global quality guarantee.

Bivariate decision trees based on our branch and bound algorithm overcome the issues of univariate decision trees while preserving the advantages of oblique trees. They are fairly interpretable due to the restriction to two attributes per split and due to the global optimality of the rules they are often more likely to capture the underlying structure of the data at hand. Their major disadvantage is the increased induction time compared to univariate trees. Our efficient branch and bound algorithm reduces this disadvantage effectively, especially due to the fact that it is easily parallizable and thus leverages the capabilities of modern hardware. For these reasons, they are a viable alternative to the commonly used univariate methods when extremely fast induction is less important and accurate yet interpretable trees are desired.

As a future work it would be interesting to test our proposed algorithm against different non-tree-based classification methods such as neural networks and support vector machines. Moreover, it would be interesting to investigate the advantages of bivariate decision trees in ensemble methods and to take advantage of their interpretability to analyze real world data.