Quantile regression with interval-censored data in questionnaire-based studies

Abstract

Interval-censored data can arise in questionnaire-based studies when the respondent gives an answer in the form of an interval without having pre-specified ranges. Such data are called self-selected interval data. In this case, the assumption of independent censoring is not fulfilled, and therefore the ordinary methods for interval-censored data are not suitable. This paper explores a quantile regression model for self-selected interval data and suggests an estimator based on estimating equations. The consistency of the estimator is shown. Bootstrap procedures for constructing confidence intervals are considered. A simulation study indicates satisfactory performance of the proposed methods. An application to data concerning price estimates is presented.

1 Introduction

Quantile regression is a flexible approach to analyzing relationships between a response variable and a set of covariates. While the classical least-squares regression methods capture the central tendency of the data, quantile regression methods allow estimating the full range of conditional quantile functions and thus can provide a more complete analysis. Other attractive properties of quantile regression are equivariance to monotone transformations, robustness to outlying observations, and flexibility to distributional assumptions (Koenker 2005).

In many studies, the response variable of interest is observed to lie within an interval instead of being observed exactly. Such observations are called interval-censored and they often arise when the variable of interest is the time to some event (Kalbfleisch and Prentice 2002; Sun 2006; Bogaerts et al. 2017). Interval-censored data may also occur in questionnaire-based studies when the respondent is requested to give an answer in the form of an interval without having a list of ranges to choose from. This type of data is referred to as self-selected interval data (Belyaev and Kriström 2010, 2012, 2015). Similar question formats have been explored by Press and Tanur (2004a, 2004b), Håkansson (2008), and Mahieu et al. (2017). Such formats are appropriate for asking questions which are hard to answer with an exact amount and for sensitive questions because they allow partial information to be elicited from respondents who are unable or unwilling to provide exact values.

Estimation procedures for quantile regression with interval-censored data have been suggested by Kim et al. (2010), Shen (2013), Zhou et al. (2017), Li et al. (2020), and Frumento (2022). These methods rely on the assumption of independent censoring, i.e., the observation process that generates the censoring is independent of the variable of interest, conditional on the covariates included in the model (Sun 2006). However, for self-selected interval data this is not a reasonable assumption because the respondent is the one who chooses the interval. Not accounting for the dependent censoring in self-selected interval data can lead to bias in the estimation (Angelov and Ekström 2017, 2019).

Building upon the ideas of McKeague et al. (2001), Shen (2013), and Angelov and Ekström (2017), we suggest an estimator for quantile regression where the response variable is of self-selected interval data type and the covariates are discrete. In questionnaire-based studies, most often the covariates are discrete, such as gender, level of education, employment status, and answers to Likert-scale questions, or ones that are discretized such as age, personal income, and monthly expenses. In Sect. 2, we outline the sampling scheme for self-selected interval data. Section 3 describes the model and the suggested estimation procedure. A simulation study is reported in Sect. 4. In Sect. 5, the methods are applied to data from a study where the respondents provided estimates of the prices of rice and two types of fish. In the Appendix are given proofs and auxiliary results.

2 Data collection scheme

We consider a two-stage scheme for collecting data. The motivation behind this scheme is that more information is needed than a single interval from each respondent in order to consistently estimate the underlying distribution function or related parameters. Therefore the respondent is asked to select a sub-interval of the interval that he/she stated. The problem of deciding where to split the stated interval into sub-intervals can be resolved using some previously collected data (in a pilot stage or an earlier survey) or based on other knowledge about the quantity of interest. Another possibility is to include a predetermined degree of rounding in the instruction for the respondents, e.g., to state intervals with endpoints rounded to a multiple of 10, and then the points of split will be chosen among the multiples of 10.

In the pilot stage, a random sample of individuals is selected and each individual is requested to give an answer in the form of an interval containing his/her value of the quantity of interest. It is assumed that the endpoints of the intervals are rounded (e.g., to the nearest multiple of 10) and that they are bounded from above by some large number. Let $\{ d_j^{\star } \}$ be the set of endpoints of all observed intervals. The pilot-stage data are used only for obtaining the set $\{ d_j^{\star } \}$.

In the main stage, a new random sample of n individuals is selected and each individual is asked to state an interval containing his/her value of the quantity of interest. We refer to this question as Qu1. Then, follow-up questions are asked according to one of the following designs.

Design A. The interval stated at Qu1 is split into two or three sub-intervals and the respondent is asked to select one of these sub-intervals. The points of split are chosen in some random fashion among the points $d_j^{\star }$ that are within the stated interval, e.g., equally likely. We refer to this question as Qu2.

Design B. The interval stated at Qu1 is split into two sub-intervals and the respondent is asked to select one of these sub-intervals. The point of split is the $d_j^{\star }$ that is the closest to the middle of the interval; if there are two points that are equally close to the middle, one of them is taken at random. We refer to this question as Qu2a. The interval selected at Qu2a is thereafter split similarly into two sub-intervals and the respondent is asked to select one of them. We refer to this question as Qu2b.

The respondent may refuse to answer Qu2 (Qu2a and Qu2b); we assume that the respondent chooses not to answer independently of his/her true value. If there are no points $d_j^{\star }$ within the interval stated at Qu1 or Qu2a, the respective follow-up question is not asked. We assume that if a respondent has answered Qu2 (Qu2a), he/she has chosen the interval containing his/her true value, independent of how the interval stated at Qu1 was split. An analogous assumption is made about the response to Qu2b.

In Design B, if we know the intervals stated at Qu1 and Qu2b, we can find out the answer to Qu2a. Thus, if Qu2b is answered, the data from Qu2a can be omitted. Let Qu2$\Delta$ denote the last follow-up question that was answered by the respondent. If the respondent did not answer Qu2a (Qu2 in Design A), we say that there is no answer at Qu2$\Delta$. Designs A and B are studied in Angelov and Ekström (2019), where they are referred to as schemes A and B.

Let $d_0< d_1< \ldots< d_{J-1} < d_J$ be the endpoints of all intervals observed at the main stage. The assumptions that the endpoints are rounded and bounded from above imply that J remains fixed for large sample sizes. Let us define a set of intervals ${\mathcal {V}} = \{ \mathbf {v}_j \}$, where $\mathbf {v}_j = (d_{j-1}, d_{j}], \, j=1, \ldots , J$, and let ${\mathcal {U}} = \{ \mathbf {u}_h \}$ be the set of all intervals that can be expressed as a union of intervals from ${\mathcal {V}}$, i.e., ${\mathcal {U}} = \{ (d_l, d_r] : \,\, d_l < d_r, \,\, l,r=0,\ldots ,J \}$. We denote ${\mathcal {J}}_{\scriptstyle h}$ to be the set of indices of intervals from ${\mathcal {V}}$ contained in $\mathbf {u}_h$, i.e., ${\mathcal {J}}_{\scriptstyle h} = \{ j: \,\, \mathbf {v}_j \subseteq \mathbf {u}_h \}$. For example, if ${\mathcal {V}} = \{ (0,2], \, (2,5], \, (5,10] \}$, then ${\mathcal {U}} = \{ (0,2], \, (2,5], \, (5,10], \, (0,5], \, (2,10],$ $\, (0,10] \}$. Also, $\mathbf {u}_4 = (0,5] = \mathbf {v}_1 \cup \mathbf {v}_2$, hence ${\mathcal {J}}_4 = \{1,2\}$.

3 Model and methods

Let us denote the observations $\mathbf {dat}_i = ( l_{1i}, r_{1i}, l_{2i}, r_{2i}, \mathbf {x}_i )$, $i=1,\ldots ,n$, where $(l_{1i}, r_{1i}]$ is the interval stated at Qu1, $(l_{2i}, r_{2i}]$ is the interval stated at Qu2$\Delta$, and $\mathbf {x}_i = ( 1, x_{1i}, \ldots , x_{di})$ is a covariate vector. Each data point $( l_{1i}, r_{1i}, l_{2i}, r_{2i}, \mathbf {x}_i )$ is an observed value of random vector $(L_{1i}, R_{1i}, L_{2i}, R_{2i}, \mathbf {X}_i)$, $i=1,\ldots ,n$, $\mathbf {X}_i = ( 1, X_{1i}, \ldots , X_{di})$. The unobservable values $y_1, \ldots , y_n$ of the quantity of interest are values of independent random variables $Y_{1}, \ldots , Y_{n}$ and $L_{1i} \le L_{2i} < Y_i \le R_{2i} \le R_{1i}$. The distribution of $Y_i$ depends on the value of $\mathbf {X}_i$. It is assumed that $\mathbf {X}_i$ takes finitely many values.

Let $Q_{\tau }(\mathbf {x}_i)$ be the $\tau$-th quantile of $Y_i$ conditional on $\mathbf {X}_i = \mathbf {x}_i$,

$$\begin{aligned} Q_{\tau }(\mathbf {x}_i) = \inf \{ y: \mathbb {P}\,( Y_i \le y \,|\, \mathbf {x}_i ) \ge \tau \} . \end{aligned}$$

We assume that

$$\begin{aligned} Q_{\tau }(\mathbf {x}_i) = \varvec{\beta }_{\tau }\mathbf {x}_i^{\intercal } = \beta _{0\tau } + \beta _{1\tau } x_{1i} + \ldots + \beta _{d\tau } x_{di}, \end{aligned}$$

where $\varvec{\beta }_{\tau } \in \varvec{\Theta }\subseteq \mathbb {R}^{d+1}$ is a parameter vector (a vector of regression coefficients).

For uncensored data, an estimate of $\varvec{\beta }_{\tau }$ can be obtained by solving the estimating equation

$$\begin{aligned} \sum _{i=1}^{n} \Bigl ( \mathbbm {1}\{y_i \ge \varvec{\beta }_{\tau }\mathbf {x}_i^{\intercal }\} - (1-\tau ) \Bigr ) \mathbf {x}_i = 0 . \end{aligned}$$

(1)

Following the ideas of McKeague et al. (2001) and Shen (2013), we replace the unobservable $\mathbbm {1}\{y_i \ge \varvec{\beta }_{\tau } \mathbf {x}_i^{\intercal }\}$ in (1) by an estimate of the conditional probability that $Y_i \ge \varvec{\beta }_{\tau } \mathbf {x}_i^{\intercal }$ given $\mathbf {dat}_i$. Thus we arrive at the following estimating equation:

$$\begin{aligned} \varvec{\Psi }_{\tau }(\varvec{\beta }_{\tau }) = \sum _{i=1}^{n} \left( \widetilde{G}_i( \varvec{\beta }_{\tau } \mathbf {x}_i^{\intercal } \,|\, \mathbf {dat}_i ) - (1-\tau ) \right) \mathbf {x}_i = 0 , \end{aligned}$$

(2)

where $\widetilde{G}_i( \varvec{\beta }_{\tau } \mathbf {x}_i^{\intercal } \,|\, \mathbf {dat}_i )$ is an estimate of the probability $G_i( \varvec{\beta }_{\tau } \mathbf {x}_i^{\intercal } \,|\, \mathbf {dat}_i ) = \mathbb {P}\,( Y_i \ge \varvec{\beta }_{\tau } \mathbf {x}_i^{\intercal } \,|\, \mathbf {dat}_i )$. We define $\widehat{\varvec{\beta }}_{\tau }$ to be the root of estimating equation (2).

Unless otherwise stated, hereafter we focus on the case $\tau =0.5$ which corresponds to a median regression model and we omit the subscript $\tau$ in $\varvec{\beta }_{\tau }$ and $\varvec{\Psi }_{\tau }$. However, the suggested estimation procedure is applicable to an arbitrary $\tau \in (0,1)$.

The set of combinations of possible values of $\mathbf {X}_i$ is denoted by $\{ \varvec{\xi }_k \}, \, k = 1,\ldots ,K$, i.e., there are K combinations in total. Let $c(h) = |{\mathcal {J}}_{\scriptstyle h}|$; thus we can write ${\mathcal {J}}_{\scriptstyle h} = \{ j_{1(h)}, \ldots , j_{c(h)} \}$, where $j_{1(h)}< j_{2(h)}< \ldots < j_{c(h)}$ and $d_{j_{1(h)}}< d_{j_{2(h)}}< \ldots < d_{j_{c(h)}}$.

Let us define

$$\begin{aligned} p_{j|h,k}&= \mathbb {P}\,( Y_i \in \mathbf {v}_j \,|\, (L_{1i}, R_{1i}] = \mathbf {u}_h, \, \mathbf {X}_i=\varvec{\xi }_k ) , \\ p_{j|h*s,k}&= \mathbb {P}\,( Y_i \in \mathbf {v}_j \,|\, (L_{1i}, R_{1i}] = \mathbf {u}_h, \, (L_{2i}, R_{2i}] = \mathbf {u}_s, \, \mathbf {X}_i=\varvec{\xi }_k ) , \end{aligned}$$

where $\mathbf {u}_s \subset \mathbf {u}_h$. The following relation between $p_{j|h,k}$ and $p_{j|h*s,k}$ is fulfilled:

$$\begin{aligned} p_{j|h*s,k} = \dfrac{ p_{j|h,k} }{ \sum _{j\in {\mathcal {J}}_{\scriptstyle s}} p_{j|h,k} } . \end{aligned}$$

(3)

We need to estimate $p_{j|h,k}$ and $p_{j|h*s,k}$ in order to find an estimate $\widetilde{G}_i$, which is needed in (2). The conditional probabilities $p_{j|h,k}$ reflect the relative position of $Y_i$ within the stated interval $(L_{1i}, R_{1i}]$. These probabilities are estimated using the data from Qu2$\Delta$, where the respondent selects a sub-interval of $(L_{1i}, R_{1i}]$. The estimate $\widetilde{p}_{j|h,k}$ is obtained by applying the procedure proposed in Angelov and Ekström (2017) to the subset of data corresponding to $\mathbf {X}_i=\varvec{\xi }_k$, namely, $\widetilde{p}_{j|h,k}, \,j \in {\mathcal {J}}_{\scriptstyle h}$, is the maximizer of the log-likelihood

$$\begin{aligned} \sum _{j} n_{hjk} \log p_{j|h,k} + \sum _{s} n_{h*s,k}\log \Biggl (\,\sum _{j\in {\mathcal {J}}_{\scriptstyle s}} p_{j|h,k} \Biggr ) , \end{aligned}$$

where $n_{hjk}$ is the number of respondents who stated $\mathbf {u}_h$ at Qu1, $\mathbf {v}_j$ at Qu2$\Delta$ ($\mathbf {v}_j \subseteq \mathbf {u}_h$) and have covariate value $\varvec{\xi }_k$, while $n_{h*s,k}$ is the number of respondents who stated $\mathbf {u}_h$ at Qu1, $\mathbf {u}_s$ at Qu2$\Delta$ ($\mathbf {u}_s$ is a union of at least two intervals from ${\mathcal {V}}$, $\mathbf {u}_s \subset \mathbf {u}_h$) and have covariate value $\varvec{\xi }_k$.

The estimate $\widetilde{p}_{j|h*s,k}$ is computed using the relation (3), i.e.,

$$\begin{aligned} \widetilde{p}_{j|h*s,k} = \dfrac{ \widetilde{p}_{j|h,k} }{ \sum _{j\in {\mathcal {J}}_{\scriptstyle s}} \widetilde{p}_{j|h,k} } . \end{aligned}$$

If independent censoring is assumed and the survival function of $Y_i$ is close to linear over $(L_{1i}, R_{1i}]$, then the distribution of the relative position of $Y_i$ within the interval $(L_{1i}, R_{1i}]$ will be close to uniform. This will not be realistic if the respondents exhibit some specific behavior when choosing the intervals, e.g., if they tend to choose an interval such that the true value is located in the right half of the interval. Therefore, assuming independent censoring in such cases may lead to bias in the estimation of $\varvec{\beta }$.

If $(L_{1i}, R_{1i}] = \mathbf {u}_h$,   $(L_{2i}, R_{2i}] = \text{NA (no answer)}$, and $\mathbf {X}_i=\varvec{\xi }_k$, then an estimate, ${\overline{G}}_i(y \,|\, \mathbf {dat}_i)$, of $G_i(y \,|\, \mathbf {dat}_i)$ can be derived as follows:

$$\begin{aligned} {\overline{G}}_i(y \,|\, \mathbf {dat}_i) = {\left\{ \begin{array}{ll} 1 &{} \text {if } y < d_{j_{1(h)}} ; \\ 1-\sum _{j=j_{1(h)}}^{j_{1(h)}} \widetilde{p}_{j|h,k} &{} \text {if } y \in [ d_{j_{1(h)}}, d_{j_{2(h)}} ) ; \\ 1-\sum _{j=j_{1(h)}}^{j_{2(h)}} \widetilde{p}_{j|h,k} &{} \text {if } y \in [ d_{j_{2(h)}}, d_{j_{3(h)}} ) ; \\ \ldots &{} \\ 1-\sum _{j=j_{1(h)}}^{j_{c(h)-1}} \widetilde{p}_{j|h,k} &{} \text {if } y \in [ d_{j_{c(h)-1}}, d_{j_{c(h)}} ) ; \\ 0 &{} \text {if } y \ge d_{j_{c(h)}} . \end{array}\right. } \end{aligned}$$

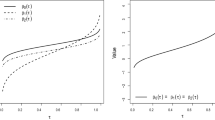
Thus, ${\overline{G}}_i$ is a step function with jumps at the points $d_{j_{1(h)}}, \ldots , d_{j_{c(h)}}$. However, it will be more convenient to use a smoothed version of ${\overline{G}}_i$ and we employ spline interpolation for that purpose. The procedure for obtaining the smooth version $\widetilde{G}_i$ is described below. Figure 1 visualizes the functions ${\overline{G}}_i$ and $\widetilde{G}_i$ in an artificial example. Let $\delta$ be a positive constant.

Case 1 Suppose that $(L_{1i}, R_{1i}] = \mathbf {u}_h$,   $(L_{2i}, R_{2i}] = \text{ NA }$, and $\mathbf {X}_i=\varvec{\xi }_k$. Then $\widetilde{G}_i$ is the monotone cubic spline (see Fritsch and Carlson 1980) through the points:

$$\begin{aligned} \begin{array}{ll} \text{ First } \text{ coordinate } &{} \text{ Second } \text{ coordinate } \\ d_{j_{1(h)}-1}-\delta &{} 1 \\ d_{j_{1(h)}-1} &{} 1 \\ d_{j_{1(h)}} &{} 1-\sum _{j=j_{1(h)}}^{j_{1(h)}} \widetilde{p}_{j|h,k} \\ \ldots &{} \ldots \\ d_{j_{c(h)-1}} &{} 1-\sum _{j=j_{1(h)}}^{j_{c(h)-1}} \widetilde{p}_{j|h,k} \\ d_{j_{c(h)}} &{} 0 \\ d_{j_{c(h)}}+\delta &{} 0 \end{array} \end{aligned}$$

By adding the points $(d_{j_{1(h)}-1}-\delta , 1)$ and $(d_{j_{c(h)}}+\delta , 0)$, we get a spline $\widetilde{G}_i(y \,|\, \mathbf {dat}_i)$ such that $\widetilde{G}_i(y \,|\, \mathbf {dat}_i) = 1$ if $y \le d_{j_{1(h)}-1}$ and $\widetilde{G}_i(y \,|\, \mathbf {dat}_i) = 0$ if $y \ge d_{j_{c(h)}}$. The constant $\delta$ can be chosen, e.g., as $\delta = \min _j |d_j-d_{j+1}|$; although any positive constant should work.

Case 2 Suppose that $(L_{1i}, R_{1i}] = \mathbf {u}_h$,   $(L_{2i}, R_{2i}] = \mathbf {u}_s$, and $\mathbf {X}_i=\varvec{\xi }_k$. Then $\widetilde{G}_i$ is the monotone cubic spline through the points:

$$\begin{aligned} \begin{array}{ll} \text{ First } \text{ coordinate } &{} \text{ Second } \text{ coordinate } \\ d_{j_{1(s)}-1}-\delta &{} 1 \\ d_{j_{1(s)}-1} &{} 1 \\ d_{j_{1(s)}} &{} 1-\sum _{j=j_{1(s)}}^{j_{1(s)}} \widetilde{p}_{j|h*s,k} \\ \ldots &{} \ldots \\ d_{j_{c(s)-1}} &{} 1-\sum _{j=j_{1(s)}}^{j_{c(s)-1}} \widetilde{p}_{j|h*s,k} \\ d_{j_{c(s)}} &{} 0 \\ d_{j_{c(s)}}+\delta &{} 0 \end{array} \end{aligned}$$

Case 3 Suppose that $(L_{2i}, R_{2i}] = \mathbf {v}_j$. Then $\widetilde{G}_i$ is the monotone cubic spline through the points:

$$\begin{aligned} \begin{array}{ll} \text{ First } \text{ coordinate } &{} \text{ Second } \text{ coordinate } \\ d_{j-1}-\delta &{} 1 \\ d_{j-1} &{} 1 \\ d_{j} &{} 0 \\ d_{j}+\delta &{} 0 \end{array} \end{aligned}$$

Let $\varvec{\Psi }^{\bullet }(\varvec{\beta })$ be an estimating function based on the true $G_i$ rather than on $\widetilde{G}_i$, i.e.,

$$\begin{aligned} \varvec{\Psi }^{\bullet }(\varvec{\beta }) = \sum _{i=1}^{n} \left( G_i( \varvec{\beta }\,\mathbf {x}_i^{\intercal } \,|\, \mathbf {dat}_i ) - \frac{1}{2} \right) \mathbf {x}_i . \end{aligned}$$

Let $D(\varvec{\beta }) = n^{-1} \frac{\partial }{\partial \varvec{\beta }} \varvec{\Psi }^{\bullet }(\varvec{\beta })$. Let $\varvec{\beta }^0$ be the true value of $\varvec{\beta }$, i.e., the median of $Y_i$ conditional on $\mathbf {X}_i = \mathbf {x}_i$ is given by $\varvec{\beta }^{0}\mathbf {x}_i^{\intercal }$.

Assumption 1

$D(\varvec{\beta }^0) \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }A$, where A is negative definite.

Assumption 2

If the probabilities $\mathbb {P}\,( Y_i \ge d_j \,|\, \mathbf {dat}_i )$ are known for all possibly observed points $d_j$, then the survival function $G_i( y \,|\, \mathbf {dat}_i ) = \mathbb {P}\,( Y_i \ge y \,|\, \mathbf {dat}_i )$ is the monotone cubic spline through the points $(d_j, \,\mathbb {P}\,( Y_i \ge d_j \,|\, \mathbf {dat}_i ))$.

Assumption 3

$\sum _{j} n_{hjk} / (\sum _{j} n_{hjk} + \sum _{s} n_{h*s,k}) \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }\gamma _{h,k} > 0$ as $n \longrightarrow \infty$.

We can regard Assumption 2 as a sensible approximation of the true underlying survival function. The very nature of a distributional model is a simplified and idealized representation of the underlying survival function, and thus there is no ’true’ model that perfectly describes the survival function and how it depends on the covariates.

Assumption 3 ensures the strong consistency of $\widetilde{p}_{j|h,k}$, see Angelov and Ekström (2017).

The almost sure convergence of $\widehat{\varvec{\beta }}$ is established in the following theorem.

Theorem 1

Suppose that Assumptions 1–3 are satisfied. Then $\widehat{\varvec{\beta }} \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }\varvec{\beta }^0$ as $n \longrightarrow \infty$.

For $b=1,\ldots ,B$, let $\mathbf {dat}_{1,b}^{*}, \ldots , \mathbf {dat}_{n,b}^{*}$ be a random sample with replacement from the data $\mathbf {dat}_1, \ldots , \mathbf {dat}_n$. We say that $\mathbf {dat}_{1,b}^{*}, \ldots , \mathbf {dat}_{n,b}^{*}$ is the b-th bootstrap sample. Let $\widehat{\varvec{\beta }}_{b}^{*} = (\widehat{\beta }_{0,b}^{*}, \ldots , \widehat{\beta }_{d,b}^{*})$ be the estimate of $\varvec{\beta }= (\beta _0, \ldots , \beta _d)$ from the bootstrap sample $\mathbf {dat}_{1,b}^{*}, \ldots , \mathbf {dat}_{n,b}^{*}$. Let $\widehat{\beta }_{r}^{\,\mathrm {boot}}(\alpha )$ be the sample $\alpha$ quantile of $\widehat{\beta }_{r,1}^{*}, \ldots , \widehat{\beta }_{r,B}^{*}$ and let $\widehat{s}_{r}^{\,\mathrm {boot}}$ be the sample standard deviation of $\widehat{\beta }_{r,1}^{*}, \ldots , \widehat{\beta }_{r,B}^{*}$, i.e.,

$$\begin{aligned} \widehat{s}_{r}^{\,\mathrm {boot}} = \sqrt{ \frac{1}{B-1} \sum _{b=1}^B \left( \widehat{\beta }_{r,b}^{*} - \frac{1}{B} \sum _{t=1}^B \widehat{\beta }_{r,t}^{*} \right) ^2 } . \end{aligned}$$

Let $z_{1-\alpha }$ denote the $(1-\alpha )$ quantile of the standard normal distribution, i.e., for $Z \sim {\mathcal {N}}(0,1)$,   $\mathbb {P}\,(Z<z_{1-\alpha }) = 1-\alpha$ .

We will explore the following confidence intervals for $\beta _r$ with nominal level $1-\alpha$:

• Bootstrap percentile confidence interval

  $$\begin{aligned} \left[ \widehat{\beta }_{r}^{\,\mathrm {boot}}(\alpha /2) , \quad \widehat{\beta }_{r}^{\,\mathrm {boot}}(1-\alpha /2) \right] , \end{aligned}$$

  (4)

• Wald-type confidence interval with bootstrap standard error

  $$\begin{aligned} \left[ \widehat{\beta _r} - z_{1-\alpha /2}\,\widehat{s}_{r}^{\,\mathrm {boot}} , \quad \widehat{\beta _r} + z_{1-\alpha /2}\,\widehat{s}_{r}^{\,\mathrm {boot}} \right] . \end{aligned}$$

  (5)

For monotone cubic spline interpolation, we use the R function splinefun with the option method="monoH.FC", which corresponds to the method of Fritsch and Carlson (1980). The estimate $\widehat{\varvec{\beta }}_{\tau }$ is obtained as a minimizer of $\Vert \varvec{\Psi }_{\tau } (\varvec{\beta }_{\tau })\Vert$, where $\Vert \cdot \Vert$ is the Euclidean norm. For this task, the Nelder–Mead (NM) algorithm is used (the R function optim with the option method="Nelder-Mead"). The Broyden–Fletcher–Goldfarb–Shanno (BFGS) method can also be used (the R function optim with method="BFGS"); however, our experiments suggested that it is much slower than the Nelder–Mead algorithm for this particular optimization problem. Table 1 displays the average computation time for the suggested estimation procedure (using the NM algorithm and the BFGS algorithm) under different settings on a laptop computer with Intel(R) Pentium(R) CPU 2117U 1.8 GHz, RAM 4.0 GB.

Fig. 1

An illustration of ${\overline{G}}_i$ and $\widetilde{G}_i$ for some i, where $(L_{1i}, R_{1i}] = \mathbf {u}_h$,   $(L_{2i}, R_{2i}] = \text{ NA }$,   $\mathbf {X}_i=\varvec{\xi }_k$, and $\mathbf {u}_h = \mathbf {v}_1 \cup \mathbf {v}_2 \cup \mathbf {v}_3 \cup \mathbf {v}_4 = (d_0, d_4]$

Table 1 Average computation time (in seconds)

4 Simulation study

4.1 Setup

Let $Y_{1}, \ldots , Y_{n}$ be independent random variables that have a Weibull distribution,

$$\begin{aligned} \mathbb {P}\,( Y_i > y \,|\, \mathbf {x}_i )= & {} \exp \left( - \left( \frac{y}{\lambda _i} \right) ^{\nu } \,\right) , \\ \lambda _i= & {} \frac{\varvec{\beta }\,\mathbf {x}_i^{\intercal }}{ \left( \log \frac{1}{1-\tau } \right) ^{1/\nu }}. \end{aligned}$$

Then, the $\tau$-th quantile of $Y_i$ is $\varvec{\beta }\,\mathbf {x}_i^{\intercal }$.

We generate $Y_{1}, \ldots , Y_{n}$ according to the above definition with $\nu =1.5$ and consider two cases for the covariates: (i) one covariate $x_{1i}$ taking values 1, 2, or 3; (ii) two covariates $x_{1i}$ and $x_{2i}$, where $x_{1i}$ takes values 2 or 3 and $x_{2i}$ takes values 0 or 1.

Let $U_{1}^{\mathrm {L}}, \ldots , U_{n}^{\mathrm {L}}$ and $U_{1}^{\mathrm {R}}, \ldots , U_{n}^{\mathrm {R}}$ be sequences of independent random variables:

$$\begin{aligned} \begin{aligned} U_{i}^{\mathrm {L}}&= M_i \,U_{i}^{(1)} + (1 - M_i) \,U_{i}^{(2)} , \\ U_{i}^{\mathrm {R}}&= M_i \,U_{i}^{(2)} + (1 - M_i) \,U_{i}^{(1)} , \end{aligned} \end{aligned}$$

(6)

where $M_i \sim \mathrm {Bernoulli}(p_{\mathrm {M}})$, $U_{i}^{(1)}$ and $U_{i}^{(2)}$ are random variables defined later. Let $( L_{1i}, R_{1i} ]$ be the interval stated by the i-th respondent at question Qu1. The left endpoints are generated as $L_{1i} = (Y_i - U_{i}^{\mathrm {L}}) \,\mathbbm {1}\{Y_i - U_{i}^{\mathrm {L}} > 0\}$ rounded downwards to the nearest multiple of 10. The right endpoints are generated as $R_{1i} = Y_i + U_{i}^{\mathrm {R}}$ rounded upwards to the nearest multiple of 10. We consider two settings for the random variables $U_{i}^{(1)}$ and $U_{i}^{(2)}$ in (6), see Table 2. In setting S11, the median length of the interval at Qu1 is 50, while in settings S21 and S22 the median length is 30. The data for the follow-up question are generated according to Design A; the interval $( L_{1i}, R_{1i} ]$ is split into two sub-intervals, the point of split is chosen equally likely from all the possible points $d_j^{\star }$ that are within the interval. The probability that a respondent gives no answer to Qu2$\Delta$ is $p_{\mathrm {NA}} = 1/4$. The parameter $p_{\mathrm {M}}$ of the Bernoulli random variables $M_i$ is considered to be a function of the covariates (see Table 2). For example, in setting S11, $p_{\mathrm {M}} = 0.2 x_{1i} - 0.1$, which leads to tree possible values, $p_{\mathrm {M}} = 0.1, 0.3, 0.5$. Figure 2 illustrates the relative position of $Y_i$ in the interval $( L_{1i}, R_{1i} ]$, i.e., $(Y_i-L_{1i})/(R_{1i}-L_{1i})$, for the different values of $p_{\mathrm {M}}$ under setting S11. Instead of simulating pilot-stage data, a pre-determined set of points $\{ d_j^{\star } \} = \{ 0, 10, 20, \ldots , 450 \}$ is used (cf. Angelov and Ekström 2019).

All computations were performed with R (see R Core Team 2019). The R code can be obtained from the corresponding author upon request.

Table 2 Simulation settings

4.2 Results

We conducted simulations for a range of sample sizes where we compare the proposed estimator with the estimator of Shen (2013), which assumes independent censoring. Our estimator can be seen as an extension of Shen’s estimator to the case of dependent censoring. With such comparison we can see the benefit of using an estimator that accounts for dependent censoring. Shen’s estimator is applied to the dataset where each data point includes only the last interval stated by the respondent. Relative bias is defined as the bias divided by the true value of the parameter. Tables 3, 4, and 5 display the results based on 10000 simulated datasets (replications). We see that in most cases the root mean square error is smaller for our estimator. The bias of our estimator is considerably lower than the bias of Shen’s estimator (with some exceptions for $n=100$ under setting S22). Moreover, the bias of our estimator gets closer to zero as the sample size increases, while the bias of the other estimator does not change noticeably when increasing the sample size. The bias of our estimator for smaller sample sizes might be explained by the not large number of observations for each combination of h and k which may lead to poor estimates of some of the probabilities $p_{j|h,k}$.

Simulations concerning the bootstrap confidence intervals (4) and (5) are reported in Table 6. The results are based on 1000 simulated samples of sizes $n = 100$ and $n = 1500$. One bootstrap confidence interval is calculated using 1000 bootstrap samples. For the bootstrap percentile confidence intervals, the coverage is fairly close to the nominal level of 0.95. The bootstrap percentile method has previously shown good performance in the context of quantile regression (see, e.g., Wang and Wang 2009; De Backer et al. 2019). The Wald-type confidence intervals with bootstrap standard error (Wald with BootSE) are on average longer and their coverage is in some cases too low. Therefore, the bootstrap percentile confidence intervals are recommended.

Fig. 2

Relative position of $Y_i$ in the interval $( L_{1i}, R_{1i} ]$, i.e., $(Y_i-L_{1i})/(R_{1i}-L_{1i})$ for three different values of $p_{\mathrm {M}}$ corresponding to $x_i = 1, 2, 3$. The histograms are based on a generated dataset of size $n=50000$ under setting S11

Table 3 Simulation results under setting S11. Mean, relative bias (RB), and root mean square error (RMSE) based on 10000 replications. Comparison of our estimator (New) and the estimator of Shen (2013). The true value of the parameter is $\varvec{\beta }^0 = (50,12)$,  $\tau = 0.5$

Table 4 Simulation results under setting S21. Mean, relative bias (RB), and root mean square error (RMSE) based on 10000 replications. Comparison of our estimator (New) and the estimator of Shen (2013)

Table 5 Simulation results under setting S22. Mean, relative bias (RB), and root mean square error (RMSE) based on 10000 replications. Comparison of our estimator (New) and the estimator of Shen (2013)

Table 6 Confidence intervals: coverage proportion (CP) and average length (AL) based on 1000 replications and 1000 bootstrap samples under setting S11. The nominal level is 0.95. The true value of the parameter is $\varvec{\beta }^0 = (50,12)$,  $\tau = 0.5$

5 Application

We apply the proposed methods to data concerning price estimates from a study conducted in Aklan, a province in the Philippines. The focus of the sampling process was the capital city, Kalibo. The administrative divisions, barangays, of Kalibo were classified into either coastal or inland communities. Two coastal barangays (Pook and Old Buswang) and two inland barangays (Tigayon and Estancia) were randomly selected. In each barangay, a number of households were randomly chosen. With their consent, a member of a sampled household (preferably, the head) was asked to participate in a survey. They were told to answer as honest as possible, and that their identity and personal data gathered will be kept confidential. The questionnaire was written in English, but trained enumerators explained questions in the local language Tagalog.

The participants were asked to provide estimates of the prices of rice and two types of fish (galunggong and bangus). They answered by means of self-selected intervals. As a follow-up question, the respondents were asked whether the price is more likely to be in the left or in the right half of the interval. Price estimates were given for two time periods: April 2019 (summer/fishing season) and September 2019 (typhoon/non-fishing season); thus the dataset contains six price estimates:

(RA):

Price of 1 kg of rice in April 2019;

(RS):

Price of 1 kg of rice in September 2019;

(GA):

Price of 1 kg of galunggong in April 2019;

(GS):

Price of 1 kg of galunggong in September 2019;

(BA):

Price of 1 kg of bangus in April 2019;

(BS):

Price of 1 kg of bangus in September 2019.

Data collection took place in August 2019, therefore the price estimate for April 2019 is a recall, while the price estimate for September 2019 is a forecast. The observed market prices for the given periods can be found in Table 7.

First, we investigated how the 0.25-quantile, the median, and the 0.75-quantile of the price depend on the level of education of the respondent. Consider the following models:

$$\begin{aligned} \texttt {Qnt025(Price)}&= \beta _0 + \beta _1\,\texttt {Education} , \end{aligned}$$

(7)

$$\begin{aligned} \texttt {Median(Price)}&= \beta _0 + \beta _1\,\texttt {Education} , \end{aligned}$$

(8)

$$\begin{aligned} \texttt {Qnt075(Price)}&= \beta _0 + \beta _1\,\texttt {Education} , \end{aligned}$$

(9)

where Education is a variable with values 1 $=$ ’Lower than college level’ and 2 $=$ ’College level or higher’. In the first model, the parameter $\beta _1$ shows how the 0.25-quantile of the price differs between respondents with college education compared to those with lower education. In the second model, the parameter $\beta _1$ shows how the median price differs between respondents with college education compared to those with lower education. In the third model, the interpretation is similar.

Point estimates and confidence intervals for the parameter $\beta _1$ based on the collected data ($n=178$) are presented in Fig. 3. The results indicate that people with college education tend to give higher price estimates. However, for each of the six prices, the confidence intervals are quite long and contain zero, which implies that the hypothesis that $\beta _1=0$ can not be rejected at the 5% significance level.

Point estimates for the 0.25-quantile, the median, and the 0.75-quantile of the prices together with confidence intervals are shown in Fig. 4. For rice and galunggong (cheaper fish), respondents tend to overestimate the prices (observed market price is below the lower bound of the confidence intervals for the medians). For bangus (luxury fish), respondents underestimated the price in April (observed market price is above the upper bound of the confidence intervals for the medians and the 0.75-quantiles). However, they gave more accurate estimates for the price of bangus in September (observed market price is within the confidence intervals for the medians).

Respondents expected prices to be higher in the typhoon season compared to the non-typhoon season, which in reality happened only with the price of galunggong, while the prices of rice and bangus remained stable.

We also considered models with two covariates:

$$\begin{aligned} \texttt {Qnt025(Price)}&= \beta _0 + \beta _1\,\texttt {Education} + \beta _2\,\texttt {HouseholdHead}, \end{aligned}$$

(10)

$$\begin{aligned} \texttt {Median(Price)}&= \beta _0 + \beta _1\,\texttt {Education} + \beta _2\,\texttt {HouseholdHead}, \end{aligned}$$

(11)

$$\begin{aligned} \texttt {Qnt075(Price)}&= \beta _0 + \beta _1\,\texttt {Education} + \beta _2\,\texttt {HouseholdHead}, \end{aligned}$$

(12)

where HouseholdHead is a variable which takes value 1, if the respondent is head of the household, and 0 otherwise.

Point estimates and confidence intervals for the parameters $\beta _1$ and $\beta _2$ are presented in Figs. 5 and 6. The results indicate that people with college education tend to give higher price estimates compared to those without college education. Heads of households tend to give higher price estimates for galunggong and bangus compared to people who are not heads of households. However, all the confidence intervals for the parameters $\beta _1$ and $\beta _2$ contain zero. Therefore, in each case the hypotheses $\beta _1=0$ and $\beta _2=0$ can not be rejected at the 5% significance level.

Table 7 Observed market prices per kilogram

Fig. 3

Estimates and bootstrap percentile confidence intervals for the parameter $\beta _1$ in the models with one covariate (7, 8 and 9). The confidence intervals are based on 50000 bootstrap samples. The confidence level is 0.95

Fig. 4

Estimates and bootstrap percentile confidence intervals for the 0.25-quantile, the median, and the 0.75-quantile of the prices using the models with one covariate (7, 8 and 9). The confidence intervals are based on 50000 bootstrap samples. The confidence level is 0.95. In each plot, the observed market price (see Table 7) is displayed with a horizontal dashed line

Fig. 5

Estimates and bootstrap percentile confidence intervals for the parameter $\beta _1$ in the models with two covariates (10, 11 and 12). The confidence intervals are based on 50000 bootstrap samples. The confidence level is 0.95

Fig. 6

Estimates and bootstrap percentile confidence intervals for the parameter $\beta _2$ in the models with two covariates (10, 11 and 12). The confidence intervals are based on 50000 bootstrap samples. The confidence level is 0.95

6 Concluding remarks

We suggested an estimator for quantile regression for self-selected interval data with discrete covariates. We proved the strong consistency of the estimator. Our simulation study indicated that the proposed estimator performs better than an existing estimator which assumes independent censoring. A simple bootstrap procedure for constructing confidence intervals (the bootstrap percentile) showed satisfactory performance in the simulations.

A Appendix

1.1 A.1 Continuity of splines

Here we show the continuity of monotone cubic splines (see Fritsch and Carlson 1980) with respect to the data points. The notation in this section is independent of that in the rest of the paper.

Suppose that we have data points $(x_i, y_i), \, i=1, \ldots , m$, where $x_1< x_2< \ldots < x_m$ and $y_1 \ge y_2 \ge \ldots \ge y_m$. Let g(x) be a monotone piecewise cubic function such that $g(x_i) = y_i, \, i=1, \ldots , m$. In each interval $[x_i, x_{i+1}]$, g(x) is a cubic polynomial:

$$\begin{aligned} g(x) = y_i H_1(x) + y_{i+1} H_2(x) + a_i H_3(x) + a_{i+1} H_4(x) , \end{aligned}$$

where

$$\begin{aligned} H_1(x)&= \varphi _1((x_{i+1}-x)/(x_{i+1}-x_i)) , \\ H_2(x)&= \varphi _1((x-x_i)/(x_{i+1}-x_i)) , \\ H_3(x)&= -(x_{i+1}-x_i)\, \varphi _2((x_{i+1}-x)/(x_{i+1}-x_i)) , \\ H_4(x)&= (x_{i+1}-x_i)\, \varphi _2((x-x_i)/(x_{i+1}-x_i)) , \\ \varphi _1(t)&= 3t^2 - 2t^3 , \\ \varphi _2(t)&= t^3-t^2 . \end{aligned}$$

We use the following procedure for calculating $a_i, \, i=1, \ldots , m$.

Step 1. If $y_{i+1} = y_i$, set $a_i^{[0]} = a_{i+1}^{[0]} = 0$. Else,

$$\begin{aligned} a_i^{[0]}&= \frac{1}{2} \left( \frac{y_{i}-y_{i-1}}{x_{i}-x_{i-1}} + \frac{y_{i+1}-y_{i}}{x_{i+1}-x_{i}} \right) , \quad i = 2, \ldots , m-1 ; \\ a_1^{[0]}&= a_m^{[0]} = 0 . \end{aligned}$$

Step 2. Let

$$\begin{aligned} \Delta _i&= (y_{i+1}-y_i)/(x_{i+1}-x_i) , \\ \lambda _i&= {\mathbb {I}}\{ \Delta _i \ne 0 \} \,a_i/\Delta _i , \\ \mu _i&= {\mathbb {I}}\{ \Delta _i \ne 0 \} \,a_{i+1}/\Delta _i , \\ \tau _i&= \sqrt{(\lambda _i^2+\mu _i^2)/9} . \end{aligned}$$

Then

$$\begin{aligned} a_i = \frac{a_i^{[0]}}{\max \{ 1, \tau _i \}}, \qquad a_{i+1} = \frac{a_{i+1}^{[0]}}{\max \{ 1, \tau _i \}} . \end{aligned}$$

Suppose that $\widehat{y}_{i}$ is an estimator of $y_{i}, \, i=1, \ldots , m$, and $\widehat{y}_{i} \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }y_{i}$ as $n \longrightarrow \infty$, where n is the size of the sample used for obtaining $\widehat{y}_{i}$. All quantities with a hat (e.g., $\widehat{a}_i$) imply that $y_{i}$ is substituted with $\widehat{y}_{i}$. Let

$$\begin{aligned} \widehat{g}(x) = \widehat{y}_i H_1(x) + \widehat{y}_{i+1} H_2(x) + \widehat{a}_i H_3(x) + \widehat{a}_{i+1} H_4(x) . \end{aligned}$$

Lemma 1

If $\widehat{y}_{i} \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }y_{i}$ as $n \longrightarrow \infty$, then $\sup _{x\in [x_1,\,x_m]} |\widehat{g}(x) - g(x)| \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }0$ as $n \longrightarrow \infty$.

Proof

Taking into account that each $\widehat{a}_i$ is a continuous function of $\widehat{y}_{1}, \ldots , \widehat{y}_{m}$, it follows that $\widehat{a}_{i} \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }a_{i}$ as $n \longrightarrow \infty$.

Note that there is a constant c such that $\max _{1 \le i\le m} |x_{i} - x_{i+1}| \le c$. Also, $\sup _{t\in [0,1]} |\varphi _1(t)| = 1$,   $\sup _{t\in [0,1]} |\varphi _2(t)| = 4/27$. Then

$$\begin{aligned} \sup _{x\in [x_1,\,x_m]} |\widehat{g}(x) - g(x)| \le 2 \max _{1 \le i\le m} |\widehat{y}_i - y_i| + \frac{8c}{27} \max _{1 \le i\le m} |\widehat{a}_i - a_i| \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }0 . \end{aligned}$$

$\square$

1.2 A.2 Consistency of the proposed estimator

Lemma 2

If Assumption 3 is satisfied, then

$$\begin{aligned} \sup _{y \in \mathbb {R}} \left| \widetilde{G}_i( y \,|\, \mathbf {dat}_i ) - G_i( y \,|\, \mathbf {dat}_i ) \right| \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }0 \,\,\text{ as }\,\, n \longrightarrow \infty . \end{aligned}$$

Proof

The functions $\widetilde{G}_i$ and $G_i$ are splines based on two different sets of data points. Assumption 3 guarantees that $\widetilde{p}_{j|h,k}$ is a strongly consistent estimator of $p_{j|h,k}$ (see Angelov and Ekström 2017). Therefore, the data points used for $\widetilde{G}_i$ converge almost surely to the data points used for $G_i$. Then, the claim follows from Lemma 1. $\square$

Proof of Theorem 1

Using Lemma 2, we get

$$\begin{aligned} \sup _{\varvec{\beta }\in \varvec{\Theta }} \Vert n^{-1}\varvec{\Psi }(\varvec{\beta }) - n^{-1}\varvec{\Psi }^{\bullet }(\varvec{\beta }) \Vert \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }0 \,\,\text{ as }\,\, n \longrightarrow \infty . \end{aligned}$$

By definition, $\varvec{\Psi }(\widehat{\varvec{\beta }}) = 0$. Then $n^{-1}\varvec{\Psi }^{\bullet }(\widehat{\varvec{\beta }}) \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }0$ as $n \longrightarrow \infty$. Also, we have $\varvec{\Psi }^{\bullet }(\varvec{\beta }^0) = 0$.

Applying Taylor’s expansion (see Feng et al. 2013), we obtain

$$\begin{aligned} n^{-1}\varvec{\Psi }^{\bullet }(\widehat{\varvec{\beta }}) - n^{-1}\varvec{\Psi }^{\bullet }(\varvec{\beta }^0) = D(\varvec{\beta }^0)( \widehat{\varvec{\beta }} - \varvec{\beta }^0) + o(\Vert \widehat{\varvec{\beta }} - \varvec{\beta }^0 \Vert ). \end{aligned}$$

By Assumption 1, $D(\varvec{\beta }^0)$ is negative definite for large n. Therefore $\widehat{\varvec{\beta }} \,\overset{\mathop {\mathrm {a.s.}}\limits }{\longrightarrow }\varvec{\beta }^0$ as $n \longrightarrow \infty$. $\square$